Chủđề1.KHẢOSÁTHÀMSỐ&ỨNGDỤNG
Câu1: SGDVĨNHPHÚCChohàmsố
3
5yx mx
, m làthamsố.Hỏihàmsốđãchocónhiều
nhấtbaonhiêuđiểmcựctrị
A.
3
. B.
1
. C.
2
. D.
4
.
Hướngdẫngiải
ChọnB.
Tacó:
6
5
y
xmx
Suyra:
3
5
5
33
3
3
x
mx
x
ym
xx
vàhàmsốkhôngcóđạohàmtại
0x
.
TH1:
0m
.Tacó:
5
3
5
0
x
y
x
vônghiệmvàhàmsốkhôngcóđạohàmtại
0x
.
x
0
y
y
Dođóhàmsốcóđúngmộtcựctrị.
TH2:
0m
.Tacó:
3
5
53
0
03
3
3
x
m
yxmx x
xmx
Bảng
biếnthiên
x
0
3
m
y
0
y
Dođóhàmsốcóđúngmộtcựctrị.
TH3:
0m
.Tacó:
3
5
53
0
03
3
3
x
m
yxmx x
xmx
BÀI TOÁN VẬN DỤNG (8 - 9 - 10)
_______________________________
x
3
m
0
y
0
y
Dođóhàmsốcóđúngmộtcựctrị.
Vậytrongmọitrườnghợphàmsốcóđúngmộtcựctrịvớimọithamsố
m
Ch
úý:Thayvìtrườnghợp
2 taxét
0m
,tacóthểchọn m làmộtsốdươngnhư
3m
đểlàm.Tươngtựởtrườnghợp
3
,tachọn
3m
đểlàmsẽcholờigiảinhanhhơn.
Câu2: SGDVĨNHPHÚCChohàmsố
22017
(1)
1
x
y
x
.Mệnhđềnàodướiđâylàđúng?
A. Đ
ồthịhàmsố1khôngcótiệmcậnngangvàcóđúngmộttiệmcậnđứnglàđường
thẳng
1.x
B. Đồthịhàmsố1cóhaitiệmcậnnganglàcácđườngthẳng
2, 2yy
vàkhôngcó
tiệmcậnđứng.
C.
Đ
ồthịhàmsố1cóđúngmộttiệmcậnnganglàđườngthẳng
2y
vàkhôngcótiệm
cậnđứng.
D. Đồthịhàmsố1khôngcótiệmcậnngangvàcóđúnghaitiệmcậnđứnglàcácđường
thẳng
1, 1.xx
Hướngd
ẫngiải
ChọnB
Hàmsố
22017
(1)
1
x
y
x
cótậpxácđịnhlà
,nênđồthịkhôngcótiệmcậnđứng
2 2017 2 2017
lim 2; lim 2
11
xx
xx
xx
,nênđồthịhàmsốcóhaitiệmcậnnganglàcác
đườngthẳng
2, 2yy
.
Câu3: SGDVĨNHPHÚCTìmtấtcả
m saochođiểmcựctiểucủađồthịhàmsố
32
1
y
xxmx
nằmbênphảitrụctung.
A. K
hôngtồntại
m
. B.
1
0
3
m
. C.
1
3
m
. D.
0m
.
Hướngd
ẫngiải
ChọnD.

Đểhàmsốcócựctiểu,tứchàmsốcóhaicựctrịthìphươngtrình
0y
cóhainghiệmphân
biệt
2
32 0(1)xxm cóhainghiệmphânbiệt
1
13 0
3
mm
.
Khiđó
(1) cóhainghiệmphânbiệt
C
Đ
x
,
CT
x
làhoànhđộhaiđiểmcựctrị.TheođịnhlíViet
tacó
2
0(2)
3
.(3)
3
CĐ
CĐ
CT
CT
xx
m
xx
,trongđó
C
Đ
CT
x
x
vìhệsốcủa
3
x lớnhơn0.
Đểcựctiểucủađồthịhàmsốnằmbênphảitrụctungthìphảicó:
0
CT
x
,kếthợp
(2)
và
(3)
suyra
(1)
cóhainghiệmtráidấu .00
3
CCĐ T
m
xx m
.
Câu4: NGUYỄNKHUYẾNTPHCMPhươngtrình
2
32
11xxx mx
cónghiệmthựckhivà
chỉkhi:
A.
3
6
2
m
. B.
13m
. C.
3m
. D.
13
44
m
.
Hướngdẫngiải
Sửdụngmáytínhbỏtúi.
2
32432
11 21 0xxx mx mxx m xxm
Chọn
3m
phươngtrìnhtrởthành
43 2
3530xx xx khôngcónghiệmthựcnên
loạiđápánB,C.
Chọn
6m
phươngtrìnhtrởthành
43 2
61360xx xx
khôngcónghiệmthực
nênloạiđápánA.
Kiểmtravới
0m
phươngtrìnhtrởthành
32
00xxx x nênchọnđápánD.
Tựluận
Tacó
32
2
32
42
11
21
x
xx
xxx mx m
xx
1
Xéthàmsố
32
42
21
x
xx
y
xx
xácđịnhtrên
.
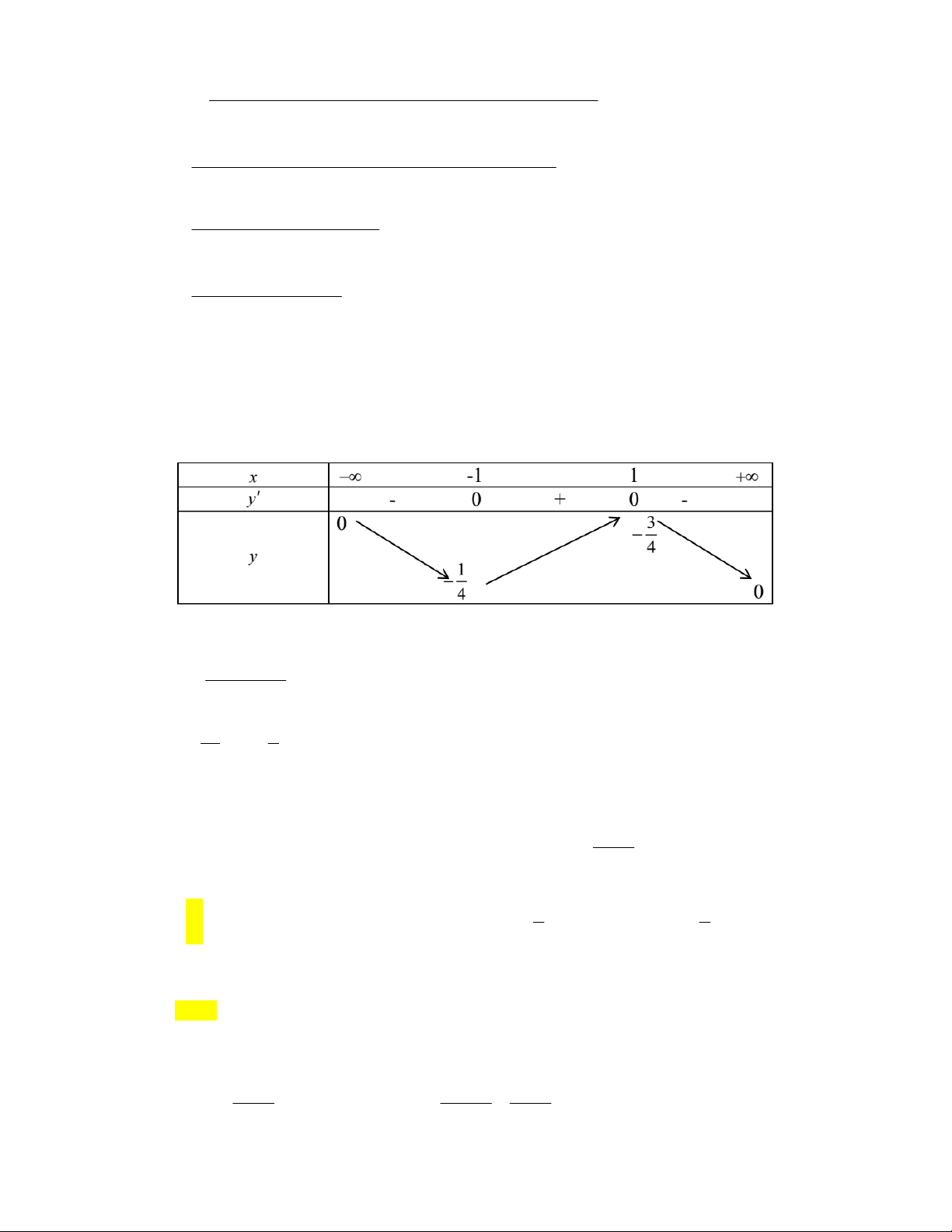
32 4 2 32 4 2
2
42
242323
2
42
6542
2
42
42
2
42
21 21
21
321 21 44
21
221
21
121
21
xxxx x xxxx x
y
xx
xx xx xxxxx
xx
xxxxx
xx
xxx
xx
42
1
01210
1
x
yxxx
x
Bảngbiếnthiên
Phươngtrình1cónghiệmthựckhiđườngthẳng
ym
cắt đồ thị hàm số
32
42
21
x
xx
y
xx
13
44
m
.
ChọnđápánD.
Câu5: NGUYỄN KHUYẾN TPHCM Cho hàm số
9
,
39
x
x
f
xxR
. Nếu
3ab
thì
2fa fb
cógiátrịbằng
A.1. B. 2 . C.
1
4
D.
3
4
.
Hướngdẫngiải
ChọnA
Tacó:
21ba
1
1
993
;21
39 39 39
aa
aaa
fa fb f a

93
21
39 39
a
aa
fa fb
Câu6: T.TDIỆUHIỀNVớigiátrịnàocủa
m thìhaiđiểmcựcđạivàcựctiểucủađồthịhàmsố
32
32yx x mxm nằmvềhaiphíasovớitrụchoành?
A.
3m
. B.
12m
. C.
3m
. D.
23m
.
Hướngdẫngiải
ChọnC.
Tacó:
2
36yx xm
.
Hàmsốcóhaiđiểmcựcđạivàcựctiểunênphươngtrình
0y
có2nghiệmphânbiệt.
Dođó
93 0 3mm
.
Gọi
1
x
,
2
x
làđiểmcựctrịcủahàmsốvà
1
y
,
2
y
làcácgiátrịcựctrịtươngứng.
Ta có:
32
11 2 2
32. 22
33 3 3
yx x mxm y x m x m
nên
11
1ykx
,
22
1ykx
.
Yêu cầu bài toán
2
12 1 2 12 1 2
.0 1 10 10 210 3
3
m
yy k x x xx x x m .
Vậy
3m
thỏamãnbàitoán.
Câu7: TRẦNHƯNGĐẠO–NBTìmtấtcảcácgiátrịcủa
m đểđườngthẳngđiquađiểmcựcđại,
cựctiểucủađồthịhàmsố
3
32yx mx cắtđườngtròntâm
1;1 ,I
bánkínhbằng1tại
2 điểmphânbiệt ,
A
B saochodiệntíchtamgiác IAB đạtgiátrịlớnnhất.
A.
23
2
m
. B.
13
2
m
. C.
25
2
m
. D.
23
3
m
.
Hướngdẫngiải
ChọnA.
Tacó
2
33
y
xm
nên
2
0
y
xm
.
Đồthịhàmsố
3
32yx mx cóhaiđiểmcựctrịkhivàchỉkhi
0m
.
Tacó
32
11
32 3322.22
33
yx mx xx m mx xy mx
.
Đườngthẳngđiquahaiđiểmcựctrịcủađồthịhàmsố
3
32yx mx
cóphươngtrình
:22ymx
Tacó:
111
...sin sin
222
IAB
SIAIBAIBAIB
Δ
H
B
A
I

Diệntíchtamgiác IAB lớnnhấtbằng
1
2
khi
sin 1
A
IB AI BI
.
Gọi
H
làtrungđiểm
A
B tacó:
,
12
22
I
IH AB d
Mà
,
2
212
41
I
m
d
m
Suyra:
2
,
2
212
2
42 24 1
2
41
I
m
dmm
m
2
23
81620
2
mm m
.
Câu8: TRẦNHƯNGĐẠO
–NBTìmtấtcảcácgiátrịthựccủa
m
đểđườngthẳng 1yxm
cắtđồthịhàmsố
21
1
x
y
x
tạihaiđiểmphânbiệt
,
A
B
saocho
23AB
.
A.
410m
. B.
43m
. C.
23m
. D.
210m
.
Hướngdẫngiải
ChọnA.
HoànhđộgiaođiểmlànghiệmPT:
2
220
21
1
1
1
fx x m x m
x
xm
x
x
.
Đườngthẳng
1yxm
cắtđồthịhàmsốtạihaiđiểmphânbiệtkhivàchỉkhiphương
trình
0fx cóhainghiệmphânbiệtkhác 1 ,hay
2
0
2
8120
*
10
6
10
m
mm
f
m
.
Khiđó,gọi
12
,
x
x
làhainghiệmcủaphươngtrình
0fx
,tacó
12
12
2
2
x
xm
xx m
Viète.
Giảsử
11 2 2 2 1
;1,;1 2
A
xx m Bx x m AB x x
.
Theogiảthiết
2
2
21 12 12
23 2 23 4 6 8 6 0AB x x x x x x m m
410m
Kếthợpvớiđiềukiện
*
tađược
410m
.
Câu9: LẠNGGIANGSỐ1Cho
x
,
y
làcácsốdươngthỏamãn
41
x
yy
.Giátrịnhỏnhấtcủa
62
2
ln
xy
x
y
P
x
y
là
lnab
.Giátrịcủatích
ab
là
A.
45
. B.
81
. C.
108
. D.
115
.
Hướngdẫngiải
ChọnB.
,
xy
dươngtacó:
2
41 14 4 1xy y xy y y
04
x
y
.
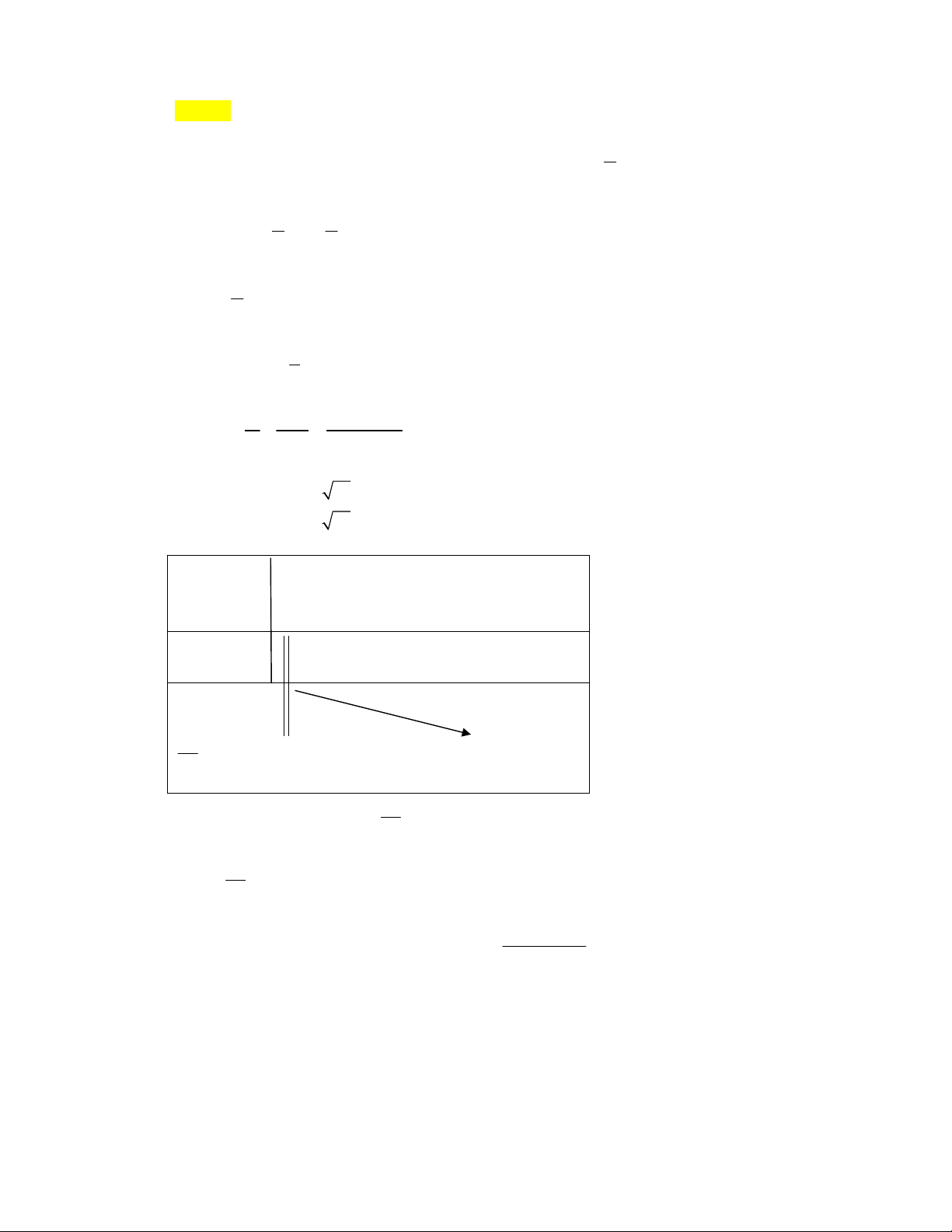
Có
12 6 ln 2
yx
P
xy
.
Đặt
x
t
y
,điềukiện:
04t
thì
6
12 ln 2Pft t
t
2
22
61 612
22
tt
ft
tt tt
321
0
321
t
ft
t
t 04
f
t
P
ft
27
ln 6
2
TừBBTsuyra
27
ln 6
2
GTNN P
khi
4t
27
,6 81
2
abab
.
Câu10: LÝTỰTRỌNG
–TPHCMChohàmsố
2
2
1
49
ax x
y
xbx
cóđồthị
C
,ab
làcáchằngsố
dương,
4ab
.Biếtrằng
C
cótiệmcậnngang
y
c
vàcóđúng1tiệmcậnđứng.Tính
tổng
324Tab c
A.
1.T
B.
4.T
C.
7.T
D.
11.T
Hướngdẫngiải
ChọnD.

lim
4
x
a
y
.Tiệmcậnngang
4
a
yc c
.
(C)
có một tiệm cận đứng nên phương trình
2
490
x
bxcónghiệmkép.
2
01440 12bb .Vì
11
012
312
bb a c
.
Vậy
11T .
Câu11: NGÔGIATỰ‐VPTấtcảcácgiátrịthựccủathamsố
m đểhàmsố
32
23 1 6 2 2017yx m x m x
nghịchbiếntrênkhoảng
;ab
saocho
3ba
là
A.
6m
. B.
9m
. C.
0m
. D.
0
6
m
m
.
Hướngdẫngiải
ChọnD.
Tacó
2
66 16 2yx mx m
Hàmsốnghịchbiếntrên
2
;120;ab x m x m x ab
2
69mm
TH1:
2
0120xmxm x Vôlí
TH2:
03my
cóhainghiệm
12 2 1
,
x
xx x
Hàmsốluônnghịchbiếntrên
12
;
x
x
.
Yêucầuđềbài:
2
2
21 21
3949xx xx S P
2
2
6
14 29 60
0
m
mm mm
m
Câu12: CHUYÊNPHANBỘICHÂUTìmtấtcảcácgiátrịcủa
m đểhàmsố
32
2
x
xmx
y đồngbiến
trên
1, 2
.
A.
1
3
m
. B.
1
3
m
. C.
1m
. D.
8m
.
Hướngdẫngiải
ChọnC.
Tacó
32
2
32 2 ln2
xxmx
yxxm
.
Hàmsốđãchođồngbiếntrên
2
1, 2 ' 0, 1, 2 3 2 0, 1, 2 * yx xxmx
Vì
2
32
f
xxxm
có
1
30, 2
23
b
a
a
nên

12
12
13 0
0
1
0130
3
*1
1
1
11
3
23
1
2
110
10
33
m
m
m
m
xx
m
m
m
xx
Câu13: CHUYÊN PHAN BỘI CHÂU Biết đường thẳng
31 6 3ymxm
cắtđồthịhàmsố
32
31 yx x
tạibađiểmphânbiệtsaochomộtgiaođiểmcáchđềuhaigiaođiểmcònlại.
Khiđó
m
thuộckhoảngnàodướiđây?
A.
(1;0) . B.(0;1) . C.
3
(1; )
2
. D.
3
(;2)
2
.
Hướngdẫngiải.
ChọnA.
Yêucầubàitoántươngđươngphươngtrìnhsaucóbanghiệmphânbiệtlậpthànhcấpsố
cộng
32 32
313163 3 31620 xx mxm xx mxm
.
Giảsửphươngtrình
32
331620 xx mxm cóbanghiệm
123
,,
x
xx
thỏamãn
13
2
(1)
2
xx
x .
Mặtkháctheoviettacó
123
3(2)xxx
.Từ
(1)
và
(2)
suyra
2
1x
.Tức
1x
làmột
nghiệmcủaphươngtrìnhtrên.Thay
1x
vàophươngtrìnhtađược
1
3
m
.
Thửlại
1
3
m
thỏamãnđềbài.
Câu14: CHUYÊN PHAN BỘI CHÂU Số đường tiệm cận đứng và tiệm cận ngang của đồ thị
22
2
4132
xx
y
x
x
là:
A.
2.
B.
3.
C.
4.
D.
1.
Hướngdẫngiải
ChọnA.
Tậpxácđịnh:
11
;;11;
22
D
Tiệmcậnđứng:
22
11
4132
lim lim
1
xx
xx
y
xx
;
22
11
4132
lim lim
1
xx
xx
y
xx
Suyra
1
x
làtiệmcậnđứng.
Tiệmcậnngang:
22
24 2
2
41 2
3
4132
lim lim lim 3
1
1
xx x
xx
xx x
y
xx
x
3y
làtiệmcậnngang

22
24 2
2
41 2
3
4132
lim lim lim 3
1
1
xx x
xx
xx x
y
xx
x
3y
làtiệmcậnngang
Vậyđồthịhàmsốcóhaitiệmcận.
Câu15: SỞ GD HÀ NỘI Cho
22
11
1
1
x
x
fx e
.Biếtrằng
1 . 2 . 3 ... 2017
m
n
f
ff f e
với
,mn
làcácsốtựnhiênvà
m
n
tốigiản.Tính
2
mn .
A.
2
2018mn
. B.
2
2018mn
. C.
2
1mn
. D.
2
1mn
.
Hướngdẫngiải
ChọnD.
Tacó:
2
2
2
22
22
2
1
11 1 1 11
111
11
11
xx
xx
x
xx xx xx
xxx
.
Suyra:
1 . 2 . 3 ... 2017
m
n
f
ff f e
1 2 3 ... 2017
m
ff f f
n
lấylnhaivế
2
1 2018 1
2018
2018 2018
mm
nn
Tachứngminh
2
2018 1
2018
làphânsốtốigiản.
Giảsử
d
làướcchungcủa
2
2018 1
và
2018
Khiđótacó
2
2018 1 d
,
2
2018 2018ddsuyra11dd
Suyra
2
2018 1
2018
làphânsốtốigiản,nên
2
2018 1, 2018mn
.
Vậy
2
1mn
.
Câu16: CHUYÊNHÙNGVƯƠNG
–GLTìmtấtcảcácgiátrịthựccủathamsố m đểđồthịhàmsố
sin cosyxxmxđồngbiếntrên
.
A.
22.m
B.
2.m
C.
22.m
D.
2.m
Hướngdẫngiải
ChọnD.
Tacó:
sin cosyxxmx
'cos sinyxxm
Hàmsốđồngbiếntrên
0, .yx
sin cos , .mxxx
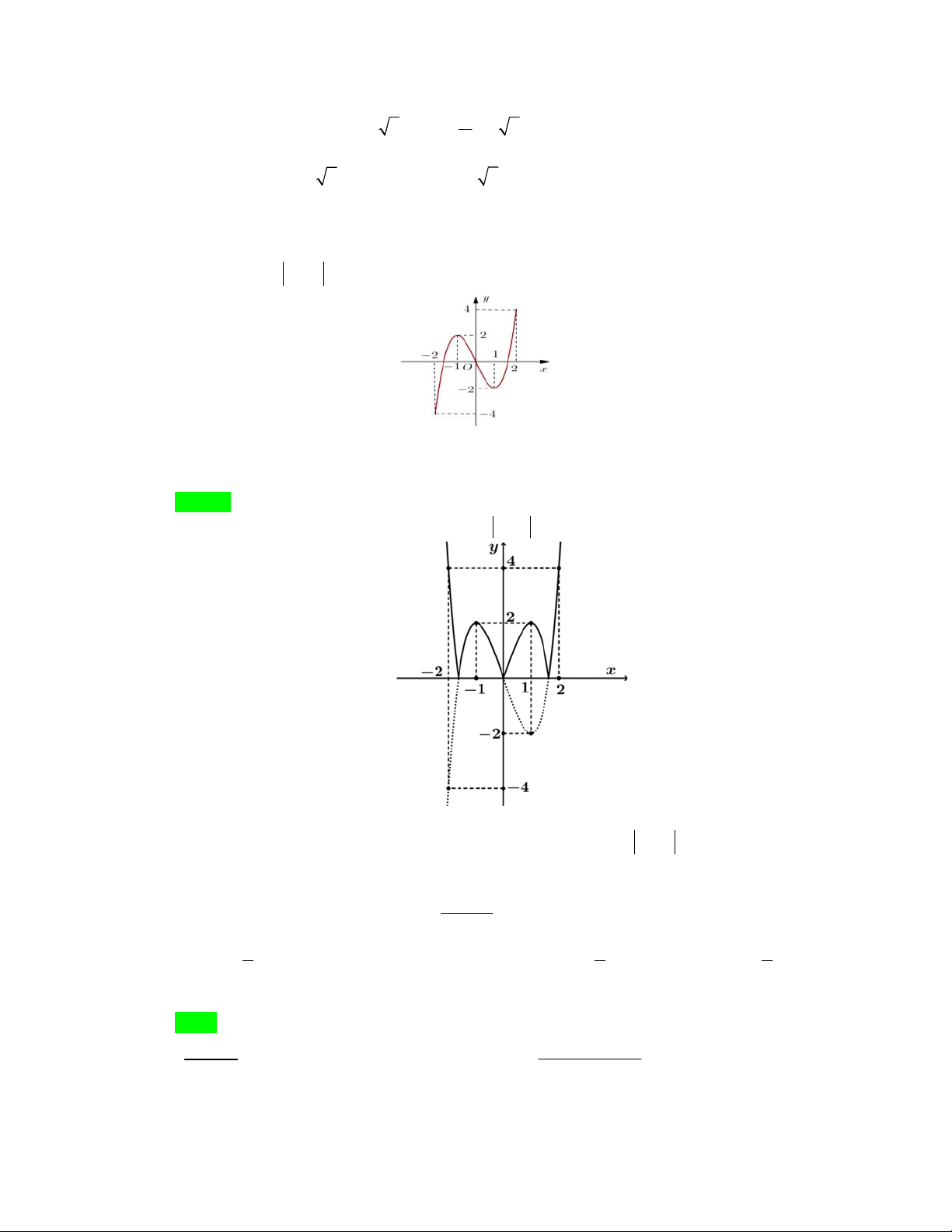
max ,mx
với
sin cos .xxx
Tacó:
sin cos 2 sin 2.
4
xxx x
Dođó:
max 2.x
Từđósuyra
2.m
Câu17: CHUYÊNHÙNGVƯƠNG–GLChohàmsố
()yfx
xácđịnhvàliêntụctrênđoạn
2; 2
vàcóđồthịlàđườngcongtronghìnhvẽbêndưới.Xácđịnhgiátrịcủathamsố
m
để
phươngtrình
fx m
cósốnghiệmthựcnhiềunhất.
A.3. B.6. C.4. D.5.
Hướngdẫngiải
ChọnB.
Dựavàođồthịtacóđồthịcủahàmsố
()yfx
là:
Từđồthịtathấyrằng,vớimthỏa
02m
thìphươngtrình
f
xm
cósốnghiệm
nhiềunhấtlà6.
Câu18: BIÊNHÒA–HÀNAMHàmsố
2
4xx
y
xm
đồngbiếntrên
1;
thìgiátrịcủa
m
là:
A.
1
;2 \ 1
2
m
. B.
1; 2 \ 1m
. C.
1
1;
2
m
. D.
1
1;
2
m
.
Giải
ChọnD.
2
4xx
y
xm
cótậpxácđịnhlà
\Dm
và
2
2
24
'
xmxm
y
xm
.
Hàmsốđãchođồngbiếntrên
2
1
1;
240, 1;
m
xmxm x
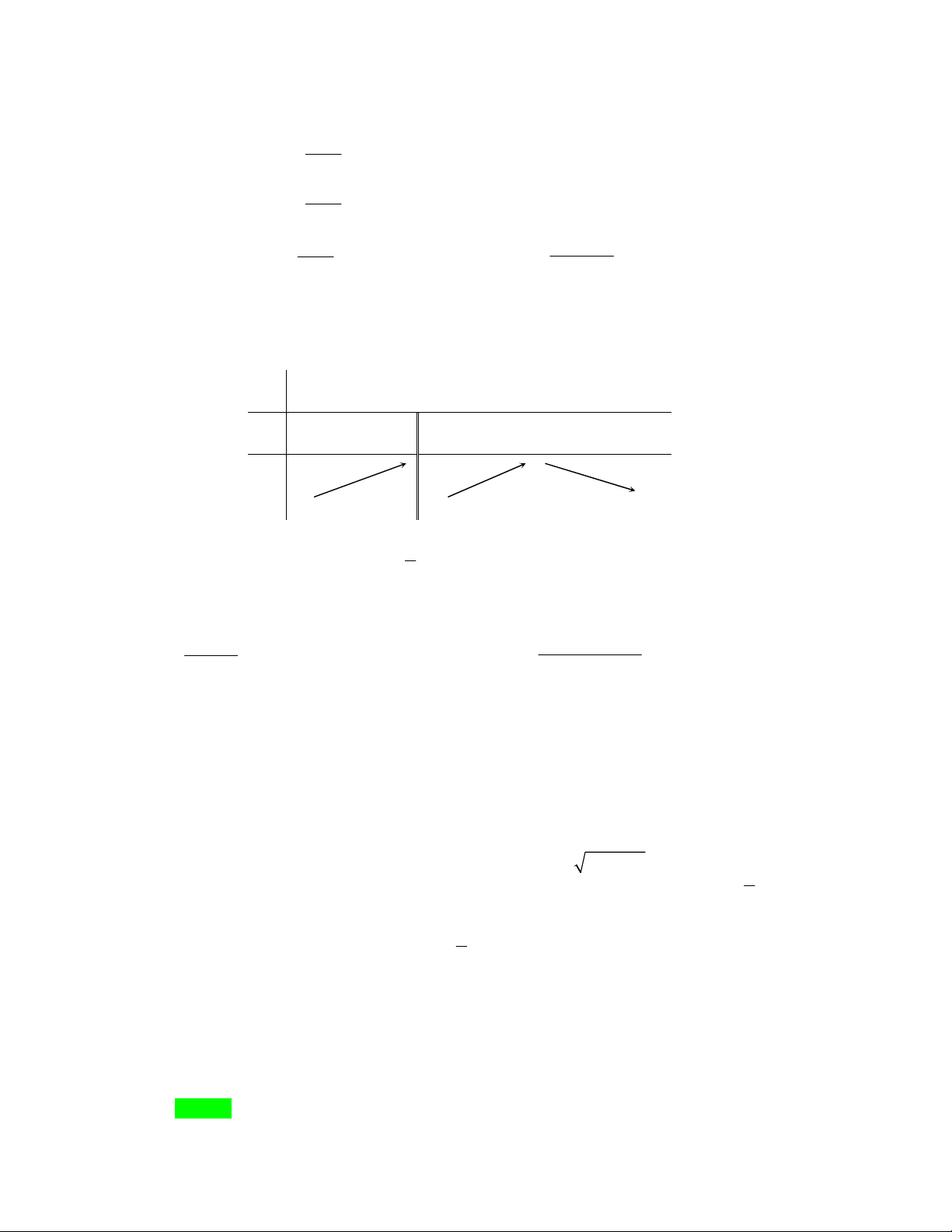
2 2
240, 1; 2 2 , 1;xmxm x mx xx 1
Do
2x
thỏabấtphươngtrình
2
22mx xvớimọi
m
nêntachỉcầnxét
2x
.
Khiđó
2
2
2,1;2
2
1
2,2;
2
x
mx
x
x
mx
x
2
Xéthàmsố
2
2
x
fx
x
trên
1; \ 2 có
2
2
4
2
xx
fx
x
0
0
4
x
fx
x
Bảngbiếnthiên
1
1
21 1
2
28
m
YCBT m m
m
.
Cáchkhác
2
4xx
y
xm
cótậpxácđịnhlà
\
D
m và
2
2
24
'
xmxm
y
xm
.
Hàmsốđãchođồngbiếntrên
2
1
1;
240, 1;
m
xmxm x
2
2
2
2
12
40
0
40
0
4
40
240, 1;
0
1
1
41
1
2
m
m
mm
m
mm
xmxm x
m
xx
mm m
m
Kếthợpvớiđk
1m
tađược
1
1
2
m
.
Câu19: CHUYÊNĐHSPHNChocácsốthực
, , abc
thỏamãn
84 2 0
84 2 0
abc
abc
.Sốgiaođiểm
củađồthịhàmsố
32
y x ax bx c vàtrục
Ox
là
A.
0
. B. 1. C. 2 . D.
3
.
ChọnD.
Tacóhàmsố
32
y x ax bx c xácđịnhvàliêntụctrên
.
x
1
2
4
y
0
y
1
8

Mà
lim
x
y
nêntồntạisố 2
M
saocho
0yM ;
lim
x
y
nêntồntạisố
2m
saocho
0ym ;
2842 0yabc và
2842 0yabc .
Do
.20ym ysuyraphươngtrình 0y cóítnhấtmộtnghiệmthuộckhoảng
;2m .
2. 2 0yysuyraphươngtrình
0y
cóítnhấtmộtnghiệmthuộckhoảng
2; 2 .
2. 0yyM
suyraphươngtrình
0y
cóítnhấtmộtnghiệmthuộckhoảng
2;
M
.
Vậyđồthịhàmsố
32
y
xaxbxc
vàtrục
Ox
có3điểmchung.
Câu20: CHUYÊN ĐHSP HN Tập hợp các giá trị của
m đểđồthịhàmsố
22
21
214 4 1
x
y
mx x x mx
cóđúng1đườngtiệmcậnlà
A.
0. B.
;1 1; .
C.
D.
;1 0 1; .
ChọnA.
Có
lim 0
x
y
.Nênhàmsốluôncó1đườngtiệmcậnngang 0y .Vậytatìmđiềukiệnđể
hàmsốkhôngcótiệmcậnđứng.
Xétphươngtrình:
2
22
2
2 1 0 (1)
214 4 10
44 10 (2)
mx x
mx x x mx
xmx
TH1:Xét
0m
,tađược
2
2
21 1
41
214 1
x
y
x
xx
thỏaycbt
TH2:Xét
0m
.Có:
1
1 m
và
2
2
44m
Th2a.Cả2phươngtrình1và2đềuvônghiệm:
2
10
1
11
440
m
m
m
m
m
Th2b:1vônghiệm,2cónghiệmkép
1
2
x
:tathấytrườnghợpnàyvôlívì
1m
Th2c:2vônghiệm,1cónghiệmkép
1
2
x
:tathấytrườnghợpnàyvôlívì
11m
Câu21: NGÔSĨLIÊNTrênđoạn
2; 2
,hàmsố
2
1
mx
y
x
đạtgiátrịlớnnhấttại
1
x
khivàchỉ
khi
A.
2.m
B.
0.m
C.
2.m
D.
0.m

ChọnB
Cách1:Với
0m
thì 0y nên
2;2
max 0y
khi
1
x
.
Với
0m
.
Đặt
tan
x
t
,tađược
.sin2
2
m
yt
.Với
2; 2x thì
arctan 2;arctan 2t .
Hàmsốđãchođạtgiátrịlớnnhấttại
1
x
tươngứngvới
4
t
.
Khi
0m
thì
arctan2;arctan 2
max
2
m
y
khivàchỉkhi
4
t
.
Khi
0m
thì
arctan2;arctan 2
max
2
m
y
khivàchỉkhi
4
t
.
Vậy
0m
thỏamãnbàitoán.
Cách2:Tacó
2
2
2
1
1
mx
y
x
,
TH1:
00my
làhàmhằngnêncũngcoiGTLNcủanóbằng
0
khi
1
x
TH2:
0m
.Khiđó:
1( )
0
1()
x
n
y
x
n
Vìhàmsốđãcholiêntụcvàxácđịnhnêntacóhàmsốđãchođạtgiátrịlớnnhấttại
1
x
trênđoạn
2; 2 khivàchỉkhi
12
y1 2 0 0
11
yy
ymm
yy
do
0m
Vậy
0m
Chúý:NgoàicáchtrêntrongTH2
0m
,tacóthểxét
0m
,
0m
rồilậpBBTcũngtìm
đượckếtquảnhưtrên.
Câu22: SỞ GD BẮC NINH Tìm các giá trị thực của tham số
m để phương trình
2
21
x
xmxx cóhainghiệmphânbiệt.
A.
23
5; .
4
m
B.
5; 6 .m
C.
23
5; 6 .
4
m
D.
23
5; 6 .
4
m
Hướngdẫngiải
2
21
x
xmxx 1
Điềukiện:
12x
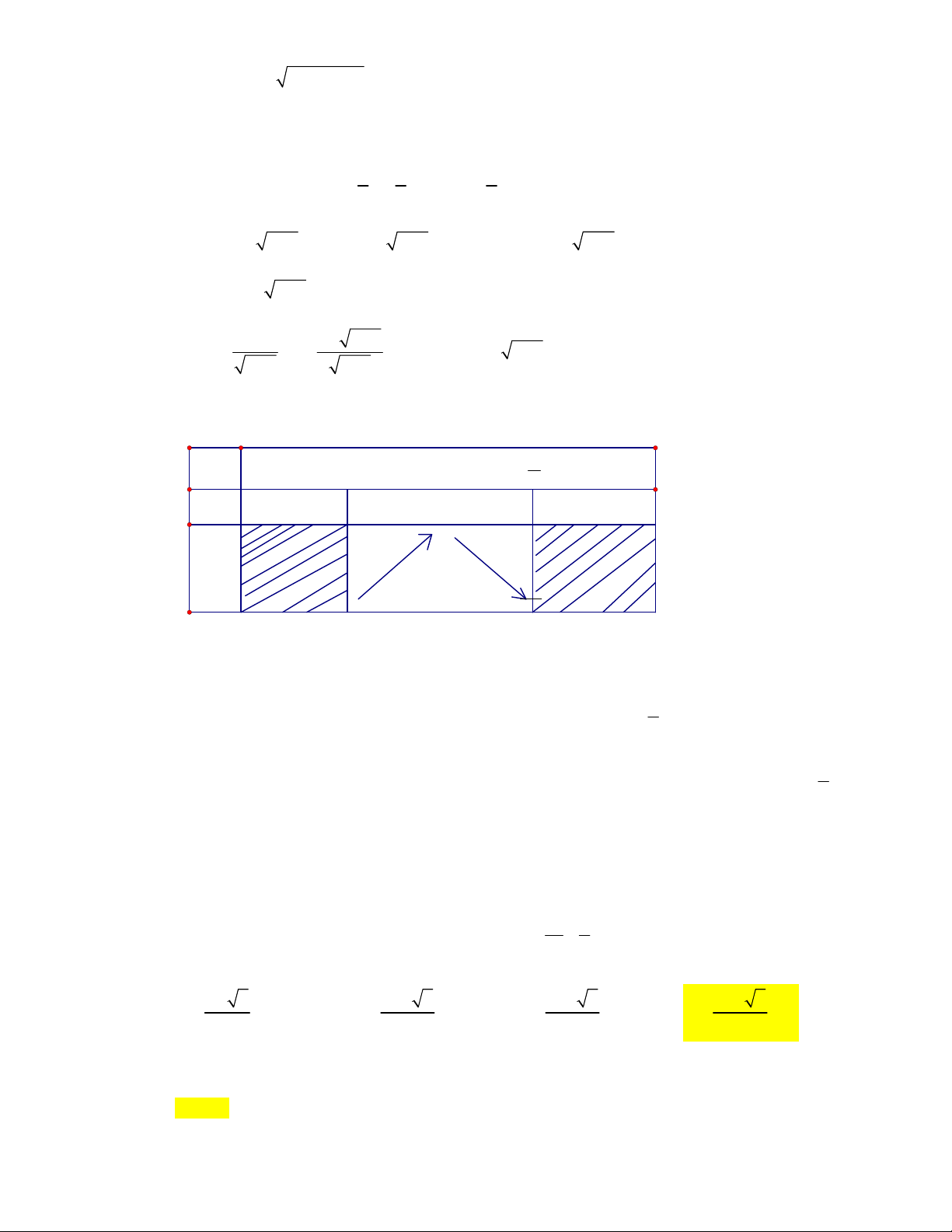
22
132 2
x
xxxm
Đặt:
2
;
x
xt
2
;21
f
xxxfx x
11 1
12,2 2, 2;
24 4
fff t
1322 22 3ttm ttm 223mt t
Đặt
223
f
tt t
112
1
22
t
ft
tt
.
01 20 1ft t t
Bảngbiếnthiên
22
0
x
xt x xt
Đểphươngtrìnhcóhainghiệmphânbiệt
1
14 0
4
tt
Dođóđểphươngtrìnhcóhainghiệmphânbiệtthìphươngtrình
cónghiệm
1
2;
4
t
Từbảngbiếnthiên
5; 6m .
ChọnB
Câu23: CHUYÊNQUANGTRUNGLẦN3Chohàmsố
3
2
3
4 2017
32
x
yxx
.Định m đểphương
trình
2
'
y
mmcóđúnghaingiệmthuộcđoạn
[0; ]m
A.
12
;2
3
.
B.
122
;2
3
.
C.
122
;2
2
.
D.
122
;2
2
.
Hướngdẫngiải
ChọnD
Tacó
:
22 2
'34ymm x x mm
23
4
5
6
+
1
4
-1-2
-
f(t)
f'(t)
t

Đặt
2
34
f
xx x P
Yêucầubàitoán:
2
22
22
2
2
3
3
2
2
7
7
34
4
4
34
4
4
3
2
122
2
122
;2
2
122
2
2
02
m
m
mm
mmm m
mmm m
mm
mm
m
m
m
m
m
m
Câu24: LÊ HỒNG PHONG Tìmtấtcảcácgiátrịcủathamsố
m đểhàmsố
2
ln 16 1 1 2yxmxmnghịchbiếntrênkhoảng
;.
A.
;3.m B.
3; .m C.
;3.m D.
3; 3 .m
Hướngdẫngiải
ChọnB.
Tacó:
2
ln 16 1 1 2yxmxm
2
32
1
16 1
x
ym
x
Hàmsốnghịchbiếntrên
khivàchỉkhi 0,yx
2
32
10,
16 1
x
mx
x
Cách1:
2
32
10,
16 1
x
mx
x
2
32 1 16 1 0,xm x x
2
16 1 32 1 0,mx xm x
2
2
2
16 1 0
1
16 32 240 0
16 16 1 0
m
m
mm
m
1
3.
5
3
m
m
m
m
3
2
2
ym m
7
4
4
3
2
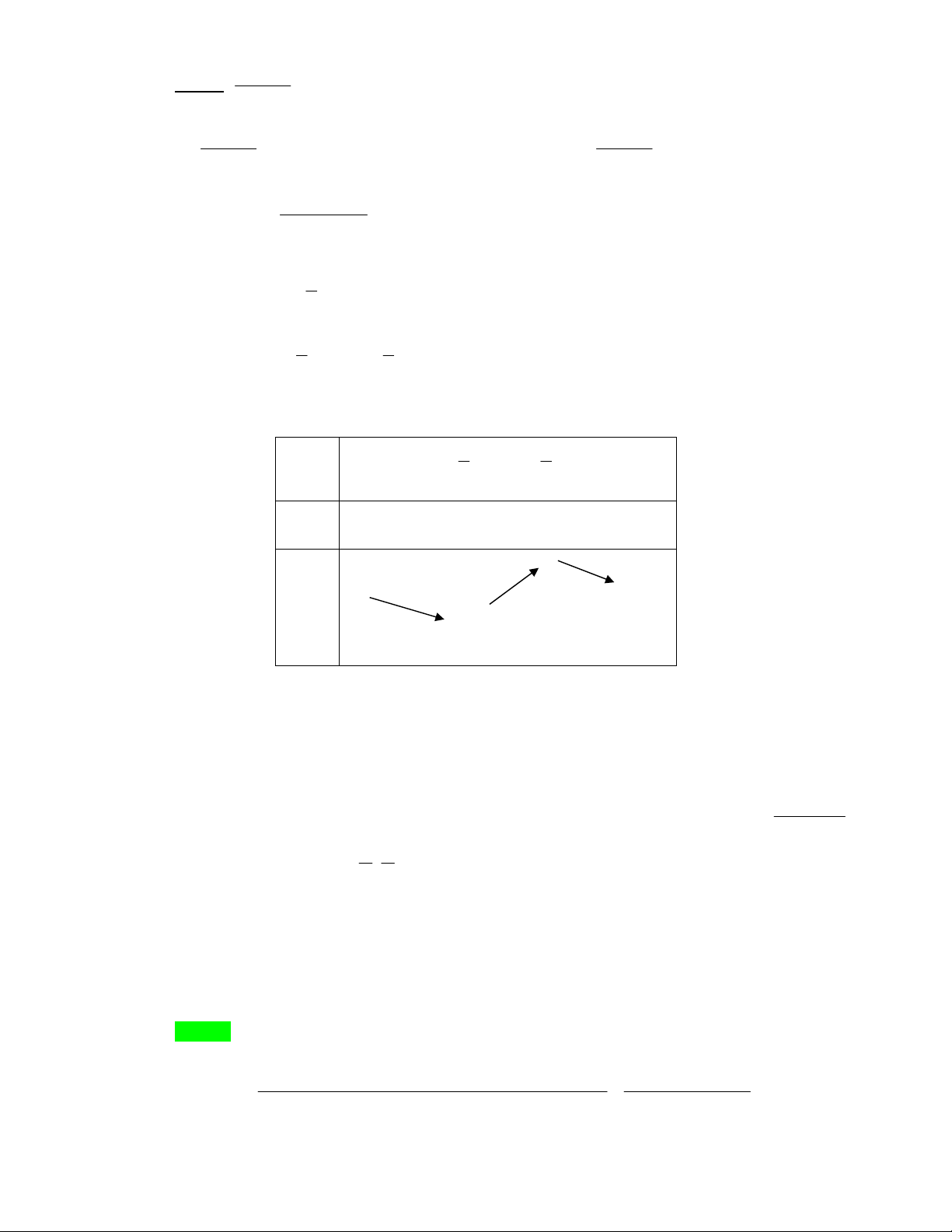
Cách2:
2
32
10
16 1
x
mx
x
2
32
1,
16 1
x
mx
x
1max(),mgx
với
2
32
()
16 1
x
gx
x
Tacó:
2
2
2
512 32
()
16 1
x
gx
x
1
() 0
4
gx x
11
lim ( ) 0; 4; 4
44
x
gx g g
Bảngbiếnthiên:
x
1
4
1
4
g
x
0
0
g
x
4
0
0
4
Dựavàobảngbiếnthiêntacó
max ( ) 4gx
Dođó:
14 3.mm
Câu25: LÊHỒNGPHONGTìmtấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
cot 1
cot 1
x
y
mx
đồngbiếntrênkhoảng
;
42
.
A.
;0 1;m
. B.
;0m
.
C.
1;m
. D.
;1m
.
Hướngdẫngiải
ChọnB.
Tacó:
222
22
1cot cot 1 1cot cot 1 1cot 1
cot 1 cot 1
x
mx m x x x m
y
mx mx
.

Hàmsốđồngbiếntrênkhoảng ;
42
khivàchỉkhi:
2
2
cot 1 0, ;
42
01
0
1cot 1
10
0, ;
42
cot 1
mx x
mm
m
xm
m
yx
mx
.
Câu26: NGUYỄNTRÃI
–HDPhươngtrình
32
23 3 2
2.21024 23 10
xx x
x
xxcótổngcácnghiệm
gầnnhấtvớisốnàodướiđây
A.
0,35.
B.
0,40.
C.
0,50.
D.
0,45.
Hướngdẫngiải
ChọnD
Tacó
32 3 2
23 3 2 23 3 10 2
2 .2 1024 23 10 2 23 2 10
xx x xx x
x
xx xx x
Hàmsố
2
t
f
tt
đồngbiếntrên nên
32
23 3 10 2 3 2
2 23 2 10 23 10 0
xx x
xx x xx x x
hoặc
52
23
x
Tổngcácnghiệmbằng
10
0,4347
23
Mẹo:Khilàmtrắcnghiệmcóthểdùng“
ĐịnhlíVi‐étchophươngtrìnhbậcba
”
Nếuphươngtrình
32
0( 0)ax bx cx d a cóbanghiệm
1
x
,
2
x
,
3
x
thì:
123 122331 13
;;
x
bcd
xxx xxxxxx xxx
aaa
Câu27: HAI BÀ TRƯNG
–HUẾĐường thẳng
:4dy x
cắtđồthịhàmsố
32
234yx mx m x tại3điểmphânbiệt
0; 4 ,
A
B và
C
saochodiện tích tam
giác
M
BC
bằng4,với
1; 3 .M Tìmtấtcảcácgiátrịcủa
m
thỏamãnyêucầubàitoán.
A.
2m
hoặc
3.m
B.
2m
hoặc
3.m
C.
3.m
D.
2m
hoặc
3.m
Hướngdẫngiải
ChọnC.
Phươngtrìnhhoànhđộgiaođiểmcủa
d
vàđồthị
:C
32
2344xmxmx
32
2
0
220
2201
x
xmxm x
xx mxm
Với
0,x
tacógiaođiểmlà
0; 4 .A
d
cắt
C
tại3điểmphânbiệtkhivàchỉkhiphươngtrình1có2nghiệmphânbiệtkhác
0.
2
020
(*)
20
m
mm
Tagọicácgiaođiểmcủa
d
và
C
lầnlượtlà
,;2,;2
BB CC
AB x x C x x
với ,
B
C
x
x là
nghiệmcủaphươngtrình1.
TheođịnhlíViet,tacó:
2
.2
BC
BC
x
xm
xx m
Tacódiệntíchcủatamgiác
M
BC
là
1
,4.
2
SBCdMBC
Phươngtrình
d
đượcviếtlạilà: :4 40.dy x x y
Mà
2
2
134
,, 2.
11
dMBC dMd
Dođó:
2
88
32
,
2
BC BC
dMBC
Talạicó:
22 2
2
232
CB C B CB
BC xx yy xx
22
4. 16 2 4 2 16
BC BC
xx xx m m
2
44240 3; 2.mm mm
Đốichiếuvớiđiềukiện,loạiđigiátrị
2.m
Câu28: Chohàmsố
2
sin , 0;
2
x
yxx
.Hỏihàmsốđồngbiếntrêncáckhoảngnào?
A.
711
0; ;
12 12
và
. B.
711
;
12 12
.
C.
7711
0; ;
12 12 12
và
. D.
711 11
;;
12 12 12
và
.
Hướngdẫn
ChọnA.
TXĐ:
D
.
1
'sin2
2
yx
.Giải
1
12
'0 sin2
7
2
12
x
k
yx
x
k
,
k
Vì
0;x
nêncó2giátrị
7
12
x
và
11
12
x
thỏamãnđiềukiện.
Bảngbiếnthiên:
Hàmsốđồngbiến
7
0;
12
và
11
;
12
Câu29: Tìmtấtcảcácgiátrịthựccủathamsố
m saochohàmsố
() cosyfx xm x
luônđồng
biếntrên
?
x
0
7
12
11
12
y
||
0
0
||
y

A.
1m
. B.
3
2
m
. C.
1m
. D.
1
2
m
.
Hướngdẫn
ChọnA.
Tậpxácđịnh:
D
.Tacó
1sin
ymx
.
Hàmsốđồngbiếntrên
'0, sin 1,yx mxx
Trườnghợp1:
0m
tacó01,x .Vậyhàmsốluônđồngbiếntrên
Trườnghợp2:
0m
tacó
11
sin , 1 1xx m
mm
Trườnghợp3:
0m
tacó
11
sin , 1 1xx m
mm
Vậy
1m
Câu30: Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố (3)(21)cos ym x m xluôn
nghịchbiếntrên
?
A.
2
4
3
m
. B.
2m
. C.
3
1
m
m
. D.
2m
.
Hướngdẫn
ChọnA.
Tậpxácđịnh:
D
.Tacó:
'3(21)sinym m x
Hàmsốnghịchbiếntrên
'0, (2 1)sin 3 ,yx m xmx
Trườnghợp1:
1
2
m
tacó
0
7
2
,x
.Vậyhàmsốluônnghịchbiếntrên
.
Trườnghợp2:
1
2
m
tacó
33
sin , 1
21 21
mm
xx
mm
321 4mm m
Trườnghợp3:
1
2
m
tacó:
33
sin , 1
21 21
mm
xx
mm
2
321
3
mm m
.Vậy
2
4;
3
m
Câu31: Tìmmốiliênhệgiữacácthamsố
a và
b
saochohàmsố
() 2 sin cosyfx xa xbx
luôn
tăngtrên
?

A.
11
1
ab
. B.
223ab
. C.
22
4ab. D.
12
2
3
ab
.
Hướngdẫn
ChọnC.
Tậpxácđịnh
D
.Tacó:
2cos sin
yaxbx
ÁpdụngbấtđẳngthứcSchwartztacó
22 22
22
ab y ab
Yêucầucủabàitoánđưađếngiảibấtphươngtrình
22 22
0, 2 0 4
yx ab ab.
Câu32: Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
32
61
y
xxmx
đồngbiến
trênkhoảng
0; ?
A.
0m
. B. 12m . C.
0m
. D. 12m .
Hướngdẫn
ChọnD.
Cách1:
Tậpxácđịnh:
D
.Tacó
2
312
yx xm
Trườnghợp1:
Hàmsốđồngbiếntrên
0,
yx
30()
12
36 3 0
hn
m
m
Trườnghợp2:Hàmsốđồngbiếntrên
0; 0
y
cóhainghiệm
12
,
x
x
thỏa
12
0xx
*
Trườnghợp2.1:
0
y
cónghiệm
0x
suyra
0m
.Nghiệmcònlạicủa
0
y
là
4x
khôngthỏa*
Trườnghợp2.2:
0
y
cóhainghiệm
12
,
x
x
thỏa
12
0
00
0
xx S
P
36 3 0
40()
0
3
m
vl
m
khôngcó
m .Vậy
12m
Cách2:
Hàmsốđồngbiếntrên
0;
2
12 3 ( ), (0; )mxxgxx .
Lậpbảngbiếnthiêncủa
()
g
x
trên
0;
.
x
0
2
∞
g
0
–
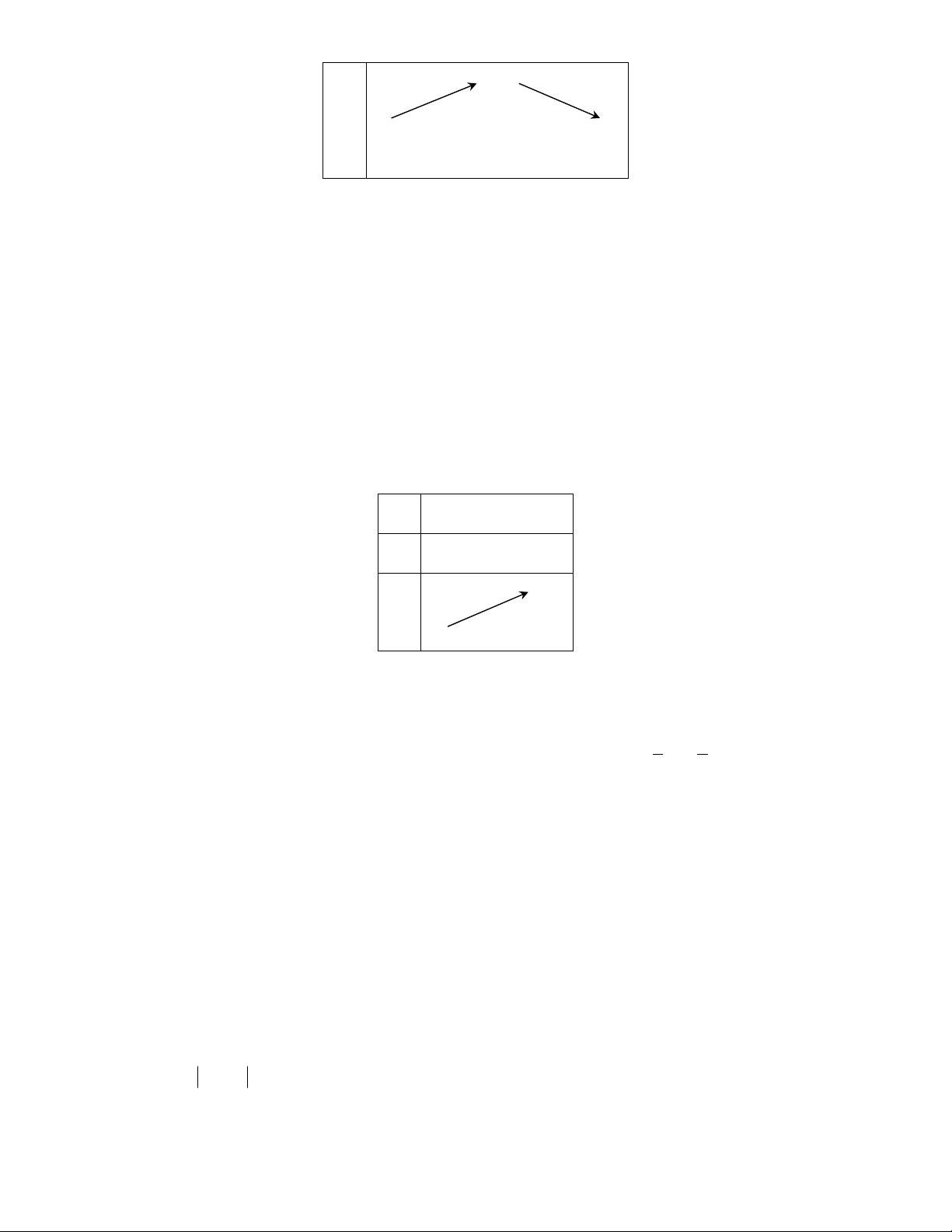
g
0
12
–∞
Câu33: Tìmtấtcảcácgiátrịthựccủathamsố m saochohàmsố
42
2( 1) 2yx m x m đồng
biếntrênkhoảng
(1; 3)
?
A.
5; 2m
. B.
;2m
. C.
2,m
. D.
;5m
.
Hướngdẫn
ChọnB.
Tậpxácđịnh
D
.Tacó
3
'4 4( 1)yx mx.
Hàmsốđồngbiếntrên
(1; 3)
2
'0, (1;3) () 1 , (1;3)yx gxxmx .
Lậpbảngbiếnthiêncủa
()
g
x
trên
(1; 3)
.
x
1
3
g
0
g
2
10
Dựavàobảngbiếnthiên,kếtluận:
min ( ) 2mgxm
.
Câu34: Tìmtấtcảcácgiátrịthựccủathamsố
m saochohàmsố
32
11
234
32
yx mxmxm
nghịchbiếntrênmộtđoạncóđộdàilà3?
A.
1; 9mm. B.
1m
. C.
9m
. D. 1; 9mm .
Hướngdẫn
ChọnA.
Tậpxácđịnh:
D
.Tacó
2
2
yxmx m
Takhôngxéttrườnghợp
0,
yx
vì
10a
Hàmsốnghịchbiếntrênmộtđoạncóđộdàilà3
0
y
có2nghiệm
12
,
x
x
thỏa
2
12
2
2
2
12
080
80
1
3
9
89
949
mm
m hay m
m
xx
m
mm
xx S P

Câu35: Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
tan 2
tan
x
y
x
m
đồngbiếntrên
khoảng
0;
4
?
A.
12m
. B. 0;1 2mm. C.
2m
. D.
0m
.
Hướngdẫn
ChọnB.
Điềukiện
t
an
x
m
.Điềukiệncầnđểhàmsốđồngbiếntrên
0;
4
là
m 0;1
y'
2 m
cos
2
x(tan x m)
2
.
Tathấy:
1
cos
2
x(tan x m)
2
0x 0;
4
;m 0;1
Đểhsđồngbiếntrên
0;
4
y' 0
m (0;1)
m 2 0
m 0;m 1
m 0
hoặc
12m
Câu36: Tìm tất cả các giá trị thực của tham số
m sao cho hàm số
3
2
() 7 14 2
3
mx
yfx mx xm
giảmtrênnửakhoảng
[1; )
?
A.
14
;
15
. B.
14
;
15
. C.
14
2;
15
. D.
14
;
15
.
Hướngdẫn
ChọnB.
Tậpxácđịnh
D
,yêucầucủabàitoánđưađếngiảibấtphươngtrình
2
14 14 0, 1mx mx x,tươngđươngvới
2
14
()
14
g
xm
xx
1
Dễdàngcóđược
()
g
x
làhàmtăng
1;x ,suyra
1
14
min ( ) (1)
15
x
gx g
Kếtluận:1
1
14
min ( )
15
x
g
xm m
Câu37: Tấtcảcácgiátrịthựccủathamsố
m saochohàmsố
42
(2 3)yx mxm
nghịchbiến
trênkhoảng
1; 2
là
;
p
q
,trongđóphânsố
p
q
tốigiảnvà
0q
.Hỏitổng
p
q
là?
A.5. B.9. C.7. D.3.
Hướngdẫn

ChọnC.
Tậpxácđịnh
D .Tacó
3
42(23)
yx mx
.
Hàmsốnghịchbiếntrên
(1; 2)
2
3
0, (1; 2) ( ), (1; 2)
2
yx mx gxx .
Lậpbảngbiếnthiêncủa
()
g
x
trên
(1; 2)
.
() 2 0 0
gx x x
Bảngbiếnthiên
x
1
2
g
0
g
5
2
11
2
Dựavàobảngbiếnthiên,kếtluận:
5
min ( )
2
mgxm
.Vậy 527pq.
Câu38: Hỏicóbaonhiêugiátrịnguyêndươngcủathamsố
m
sao cho hàm số
2
2(1)1
x
mx m
y
xm
đồngbiếntrênkhoảng
(1; )
?
A.3. B.1. C.2. D.0.
Hướngdẫn
ChọnD.
Tậpxácđịnh
\Dm
.Tacó
22
22
24 21 ()
() ()
x
mx m m g x
y
x
mxm
Hàmsốđồngbiếntrên
(1; )
khivàchỉkhi
() 0, 1
g
xx
và
1m
1
Vì
2
2( 1) 0,
g
mmnên1
() 0gx
cóhainghiệmthỏa
12
1xx
Điềukiệntươngđươnglà
2
2(1) 2( 6 1) 0
322 0,2
1
2
gmm
m
S
m
.
Dođókhôngcógiátrịnguyêndươngcủa
m thỏayêucầubàitoán.
Câu39: Tìmtấtcảcácgiátrịthựccủathamsố
m saochophươngtrình
21
x
xm
cónghiệm
thực?
A.
2m
. B.
2m
. C.
3m
. D.
3m
.
Hướngdẫn
ChọnB.
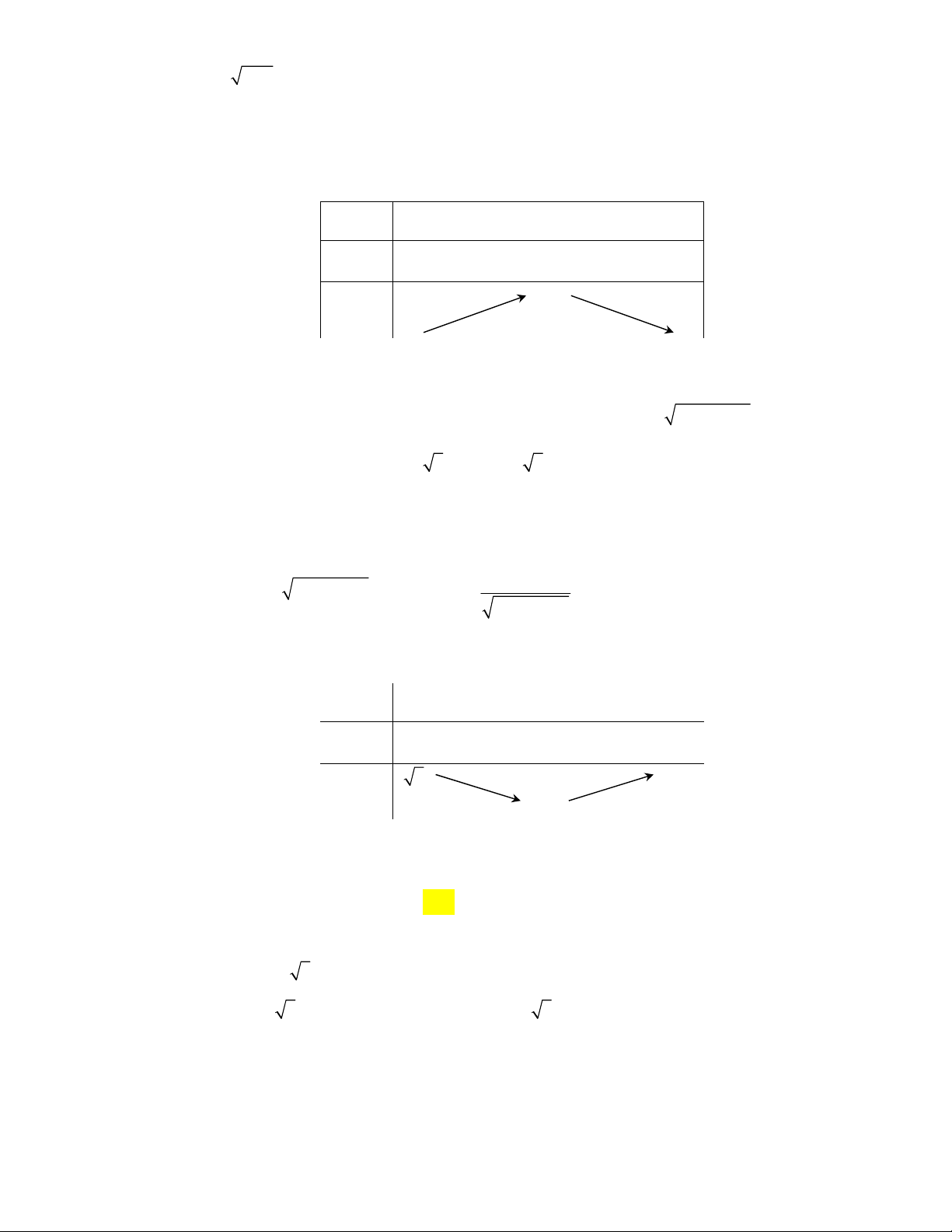
Đặt 1, 0txt.Phươngtrìnhthành:
22
21 21tt m m t t
Xéthàmsố
2
() 2 1, 0; () 2 2
f
tttt ft t
Bảngbiếnthiêncủa
f
t :
Từđósuyraphươngtrìnhcónghiệmkhi
2m
.
Câu40: Tìmtấtcảcácgiátrịthựccủathamsố
m saochophươngtrình
22
45 4
x
xmxx
cóđúng2nghiệmdương?
A.
13m
. B.
35m
. C.
53m
. D.
33m
.
Hướngdẫn
ChọnB
Đặt
2
() 4 5tfx x x.Tacó
2
2
()
45
x
fx
xx
.
() 0 2
fx x
Xét
0x
tacóbảngbiếnthiên
Khiđóphươngtrìnhđãchotrởthành
22
550mt t t t m
1
.
Nếuphươngtrình
1
cónghiệm
12
,tt
thì
12
1tt
.
1cónhiềunhất1nghiệm
1t
.
Vậyphươngtrìnhđãchocóđúng2nghiệmdươngkhivàchỉkhiphươngtrình1cóđúng
1nghiệm
1; 5t
.
Đặt
2
() 5
g
ttt
.
Tađitìmm đểphươngtrình
()
g
tm
cóđúng1
nghiệm
1; 5t
.
Tacó
() 2 1 0, 1; 5
gt t t
.
Bảngbiếnthiên:
x
0 2
f
x
0
f
x
5
1
t
0 1
f
t
0
f
t
1
2
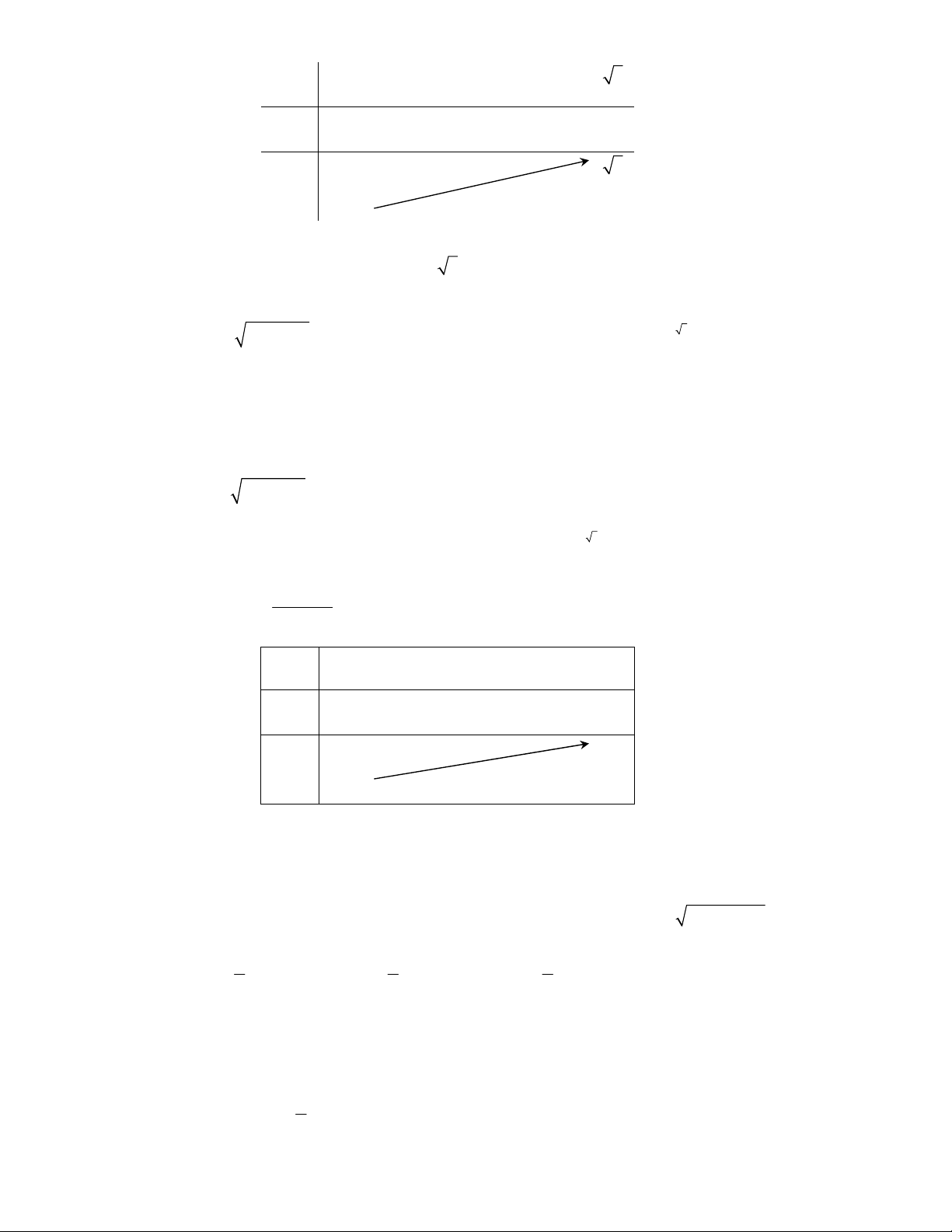
Từbảngbiếnthiênsuyra
35m
làcácgiátrịcầntìm.
Câu41: Tìmtấtcảcácgiátrịthựccủathamsố
m sao cho phương trình:
22
33
log log 1 2 1 0xxmcóítnhấtmộtnghiệmtrênđoạn
3
1; 3
?
A.
13m
. B.
02m
. C.
03m
. D.
12m
.
Hướngdẫn
ChọnB.
Đặt
2
3
log 1tx.Điềukiện:
1t
.
Phươngtrìnhthành:
2
220(*)ttm .Khi
3
1; 3 [1; 2]xt
2
2
(*) ( )
2
tt
f
tm
.Bảngbiếnthiên :
Từbảngbiếnthiêntacó
:02m
Câu42: Tìmtấtcảcácgiátrịthựccủathamsố
m saochophươngtrình
2
22 1
x
mx xcó
hainghiệmthực?
A.
7
2
m
. B.
3
2
m
. C.
9
2
m
. D.
m
.
Hướngdẫn
ChọnC
Điềukiện:
1
2
x
t
1
2
f
t
f
t
0
2
t
1
5
g
t
g
t
3
5
Phươngtrình
2
22 1
x
mx x
2
341 (*)xx mx
Vì
0x
khônglànghiệmnên*
2
341
x
x
m
x
Xét
2
341
()
x
x
fx
x
.Tacó
2
2
31 1
() 0 ; 0
2
x
fx x x
x
Bảngbiếnthiên
Từbảngbiếnthiêntacóđểphươngtrìnhcóhainghiệmthì
9
2
m
.
Câu43: Tìm tất cả các giá trị thựccủa tham số
m saochomọinghiệm của bấtphươngtrình:
2
320xxcũnglànghiệmcủabấtphươngtrình
2
110mx m x m
?
A.
1m
. B.
4
7
m
. C.
4
7
m
. D.
1m
.
Hướngdẫn
ChọnC.
Bấtphươngtrình
2
320xx
12x
.
Bấtphươngtrình
2
110mx m x m
2
2
2
(1)2
1
x
mx x x m
x
x
Xéthàmsố
2
2
()
1
x
fx
x
x
với
12x
.Có
2
22
4x 1
() 0, [1;2]
(1)
x
fx x
xx
Yêucầubàitoán
[1;2]
max ( )mfx
4
7
m
Câu44: Tìmtấtcảcácgiátrịthựccủathamsố
m saochobấtphươngtrình:
3
3
1
32xmx
x
nghiệmđúng
1
x
?
A.
2
3
m
. B.
2
3
m
. C.
3
2
m
. D.
13
32
m
.
x
1
2
0
f
x
+ +
f
x
9
2

Hướngdẫn
ChọnA.
Bpt
32
34
112
32,13 ,1mx x x m x f x x
x
xx
.
Tacó
52 5 2 2
42 2
42 4 2
222 0fx x x
xx x x x
suyra
f
x
tăng.
Ycbt
1
2
3, 1 min 1 2 3
3
x
f
xmx fxf m m
Câu45: Bất phương trình
32
236164 23xxx x
có tập nghiệm là
;ab . Hỏi tổng
ab
cógiátrịlàbaonhiêu?
A.
2
. B.4. C.5. D.3.
Hướngdẫn
ChọnC
Điềukiện:
24x
.Xét
32
() 2 3 6 16 4
f
xxxx x
trênđoạn
2; 4
.
Có
2
32
31
1
() 0, 2;4
24
23616
xx
fx x
x
xxx
.
Dođóhàmsốđồngbiếntrên
2; 4 ,bpt
() (1) 23 1
f
xf x
.
Sovớiđiềukiện,tậpnghiệmcủabptlà
[1; 4] 5.Sab
Câu46: Bất phương trình
22
23 611 3 1
x
xxx xx cótậpnghiệm
;ab
. Hỏi
hiệu
ba
cógiátrịlàbaonhiêu?
A.1. B.2. C.3. D.
1
.
Hướngdẫn
ChọnA.
Điềukiện:
13x
;bpt
22
12 1 3 23
x
xx x
Xét
2
() 2
f
tt t
với
0t
.Có
2
1
'( ) 0, 0
2
22
t
ft t
t
t
.
Dođóhàmsốđồngbiếntrên
[0; )
.1
(1) (3) 13 2fx f x x x
Sovớiđiềukiện,bptcótậpnghiệmlà
(2;3]S
Câu47: Tìmtấtcảcácgiátrịthựccủathamsố
m đểhàmsố
42
3
1
2
ym xmx
chỉcócựctiểu
màkhôngcócựcđại.
A.
1.m
B.
10.m
C.
1.m
D.
10.m

Hướngdẫn
ChọnB
Taxéthaitrườnghợpsauđây:
TH1:
10m
1m
.Khiđó
2
3
2
yx
hàmsốchỉcócựctiểu
0x
màkhôngcó
cựcđại
1m
thỏamãnyêucầubàitoán.
TH2:
10m
1m
.Khiđóhàmsốđãcholàhàmsốtrùngphươngtacó:
32
'4 1 2 4 1
21
m
ymxmxmxx
m
.
Hàmsốchỉcócựctiểumàkhôngcócựcđại
'y
cóđúngmộtnghiệmvàđổidấutừâm
sangdươngkhi
x
điquanghiệmnày
410
0
21
m
m
m
10m
.
Kếthợpnhữnggiátrị
m tìmđược,tacó
10m
.
Câu48: Tìmtấtcảcácgiátrịthựccủathamsố
m đểđồthịhàmsố
32 2
22
23 1
33
yxmx m x
cóhaiđiểmcựctrịcóhoànhđộ
1
x
,
2
x
saocho
12 1 2
21xx x x
.
A.
0.m
B.
2
.
3
m
C.
2
.
3
m
D.
1
.
2
m
Hướngdẫn
ChọnC
Tacó:
2222
'2 2 23 1 2 3 1yxmx m xmxm ,
22
31gx x mx m làtamthứcbậchaicó
2
13 4m .Dođóhàmsốcóhaiđiểmcực
trịkhivàchỉkhi
'y
cóhainghiệmphânbiệt
g
x
cóhainghiệmphânbiệt
0
213
13
213
13
m
m
.1
1
x
,
2
x
làcácnghiệmcủa
g
x nêntheođịnhlýVi‐ét,tacó
12
2
12
31
xx m
xx m
.
Dođó
12 1 2
21xx x x
2
3211mm
2
320mm
0
2
3
m
m
.

Đốichiếuvớiđiềukiện1,tathấychỉ
2
3
m
thỏamãnyêucầubàitoán.
Câu49: Chohàmsố
422
21 1yx mx m .Tìmtấtcảcácgiátrịcủathamsốthực m đểhàm
sốcócựcđại,cựctiểuvàcácđiểmcựctrịcủađồthịhàmsốlậpthànhtamgiáccódiệntích
lớnnhất.
A.
1
.
2
m
B.
1
.
2
m
C.
0.m
D.
1.m
Hướngdẫn
ChọnC
Phươngpháptựluận
32
'4 41yx mx
'0y
22
0
1
x
x
m
Hàmsốcócựcđại,cựctiểukhivàchỉkhi:
1m
Tọađộđiểmcựctrị
0; 1Am
24 2
1; 2Bmmmm
24 2
1; 2Cmmmm
2
21 ;0BC m
Phươngtrìnhđườngthẳng
B
C
:
42
20ym m m
42
,BC 2 1dA m m
,
2
21BC m
24 2
1
.[ , ] 1 2 1
2
ABC
SBCdABCmmm
5
2
11m
VậySđạtgiátrịlớnnhất
0m
.
Phươngpháptrắcnghiệm
24 2
1; 21AB m m m
24 2
1; 21AC m m m

KhiđóS
1
,
2
A
BAC
24 2
121mm m
5
2
11m
VậySđạtgiátrịlớnnhất
0m
.
Câu50: Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđồthịhàmsố
32
23 1 6yx m x mx có
haiđiểmcựctrị ,
A
B saochođườngthẳng
A
B
vuônggócvớiđườngthẳng: 2yx
.
A.
3
.
2
m
m
B.
2
.
3
m
m
C.
0
.
2
m
m
D.
0
.
3
m
m
Hướngdẫn
ChọnC
Phươngpháptựluận
Tacó:
2
66 16yx m xm
1
'0
x
y
x
m
Điềukiệnđểhàmsốcó2điểmcựctrịlà:
1m
Tacó:
1; 3 1Am
32
;3
B
mm m
Hệsốgócđt
A
B
là:
2
1km
Đt
A
B
vuônggócvớiđườngthẳng
2yx
khivàchỉkhi
1k
0
2
m
m
Phươngpháptrắcnghiệm
Bước1:BấmMode2CMPLX
Bước2:
2
32
66161261
'. ''
231 6
18 36
xyxyxy
yy
yxyxyx
a
Bước3:Cacl
x
i ,
1000y
Kếtquả:
1001000 9980001.i
.Hay:
1001000 9980001.yx
Vậyphươngtrìnhđtqua2điểmcựctrị
A
B
là:
2
2
1
y
mmm x
Cóđt
A
B vuônggócvớiđườngthẳng 2yxkhivàchỉkhi
2
11m
0
2
m
m
Câu51: Tìmcácgiátrịcủathamsố
m đểđồthịhàmsố:
32
32yx x mx cóđiểmcựcđạivà
điểmcựctiểucáchđềuđườngthẳngcóphươngtrình:
1yx d
.

A.
0.m
B.
0
.
9
2
m
m
C.
2.m
D.
9
.
2
m
Hướngdẫn
ChọnA
Phươngpháptrắcnghiệm
2
36yxxm
Hàm số có 2 cực trị
3m
,gọi
12
,
x
x
làhainghiệmcủaphươngtrình
0y
, ta có:
12
2xx
Bấmmáytính:
,1000
32 2
1
3236
33
994 2006 1000 6 2000 6 2 6 6
33 3 3 3 3
ximA
x
xxmx xxm
mm
iix
Haiđiểmcựctrịcủađồthịhàmsốlà:
11 2 2
26 6 26 6
;;;
33 33
mm m m
Ax x Bx x
Gọi
I
làtrungđiểmcủa
1;
A
BI m
Đườngthẳngđiquahaiđiểmcựctrịlà:
26 6
33
mm
yx
Yêucầubàitoán
26
9
//
1
3
2
0
11
m
dor d
m
Id
m
m
Kếthợpvớiđiềukiệnthì
0m
.
Câu52: Tìmcácgiátrịcủathamsố
m đểđồthịhàmsố:
4224
21yx mx m cóbađiểmcựctrị.
ĐồngthờibađiểmcựctrịđócùngvớigốcOtạothành1tứgiácnộitiếp.
A.
1.m
B.
1.m
C.Khôngtồntạim. D.
1.m
Hướngdẫn
ChọnA
32
44yy x mx
Hàmsốcó3điểmcựctrịkhi
0m
Khiđó3điểmcựctrịlà:
4
0; 1 , ;1 , ;1
A
mBmCm
GọiIlàtâmđườngtrònngoạitiếpnếucócủatứgiác
A
BOC
.Dotínhchấtđốixứng,ta
có:
,,
A
OI
thẳnghàng
A
O
làđườngkínhcủađườngtrònngoạitiếpnếucócủatứgiác
A
BOC
.
Vậy
24
.0 0AB OB AB OB m m
0
1
m
m
Kếthợpđiềukiện
1m
thỏamãn.
Câu53: Tìmcácgiátrịcủathamsố
m đểđồthịhàmsố:
42
2yx mx m cóbađiểmcựctrị.Đồng
thờibađiểmcựctrịđólàbađỉnhcủamộttamgiáccóbánkínhđườngtrònnộitiếplớn
hơn1.
A.
1.m
B.
2.m
C.
;1 2; .m D.Khôngtồntạim.
Hướngdẫn
ChọnB
Phươngpháptựluận
Hàmsốcó3điểmcựctrịkhi
0m
Bađiểmcựctrịlà
22
0; , ; , ;
A
mB mmm C mmm
Gọi
I
làtrungđiểmcủa
2
0;
B
CImm
2
1
.
2
ABC
SAIBCmm
Chuvicủa
A
BC
là:
4
22pABBCAC mm m
Bánkínhđườngtrònnộitiếp
A
BC
là:
2
4
ABC
S
mm
r
p
mm m
Theobàira:
24
2
4
4
11 1
mm mm m
mm
r
m
mm m
vì
0m
422522
1
20
2
m
mmm m m mm mm mm
m
Sosánhđiềukiệnsuyra
2m
thỏamãn.
Phươngpháptrắcnghiệm

Sửdụngcôngthức
222
23 3 3
4
4162 4161611
bmm
rr
aaab m m
Theobàira:
23
2
3
3
3
11
11 111
11
mm
m
rmm
m
m
332
1
1111 20
2
m
mm mm mm
m
Sosánhđiềukiệnsuyra
2m
thỏamãn.
Câu54: Tìmtấtcảcácgiátrịthựccủathamsố
m đểđồthịhàmsố
32
333ymx mx m cóhai
điểmcựctrị
,
A
B saocho
222
2( )20AB OA OB
Trongđó
O
làgốctọađộ.
A.
1.m
B.
1m
.
C.
1m
hoặc
17
11
m
. D.
1m
hoặc
17
11
m
.
Hướngdẫn
ChọnD
Tacó:
2
(3 6 )
y
mx x
Vớimọi
0m
,tacó
033
0
23
xym
y
xym
.Vậyhàmsốluôncóhaiđiểmcựctrị.
Giảsử
(0;3 3); (2; 3)Am B m.
Tacó:
222 2
1
2( )20116170
17
11
m
AB OA OB m m
m
thỏamãn
Vậygiátrị
m
cầntìmlà:
1
17
11
m
m
.
Câu55: Trongtấtcảcáchìnhchữnhậtcócùngdiệntích48cm
2
,hìnhchữnhậtcóchuvinhỏnhất
bằng:
A.
16 3
cm B.
43
cm C.24cm D.
83
cm
Hướngdẫn
ChọnA.
Cách1
Gọicạnhcủahìnhchữnhật:
a,b
;0
a,b
48
Tacó:
48
48ab b
a
.Chuvi:
48
() 2Pa a
a
2
48
() 21Pa
a
; () 0 43Pa a
Bảngbiếnthiên:
Cách2
ÁpdụngbấtđẳngthứcCôsi:
224883ab ab ab
chuvinhỏnhất:
2( ) 16 3ab
Hìnhchữnhậtcóchuvinhỏnhấtbằng
16 3
khicạnhbằng
43
.
Câu56: Tamgiácvuôngcódiệntíchlớnnhấtlàbaonhiêunếutổngcủamộtcạnhgócvuôngvà
cạnhhuyềnbằnghằngsố
a
a
0?
A.
2
63
a
. B.
2
9
a
. C.
2
2
9
a
. D.
2
33
a
.
Hướngdẫn
ChọnA.
Cạnhgócvuông
,0
2
a
xx;cạnhhuyền: ax
Cạnhgócvuôngcònlạilà:
22
()ax x
Diệntíchtamgiác
2
1
() 2
2
Sx x a ax
.
2
(3)
() ; () 0
3
22
aa x a
Sx Sx x
aax
Bảngbiếnthiên:
x
0
3
a
2
a
Sx
0
Sx
2
63
a
a 0
43
48
P
a
0 +
P
a
16 3

Tamgiáccódiệntíchlớnnhấtbằng
2
63
a
khicạnhgócvuông
3
a
,cạnhhuyền
2
.
3
a
Câu57: Chohàmsố
2
2cos cos 1
.
cos 1
xx
y
x
Gọi
M
làgiátrịlớnnhấtvà
m
làgiátrịnhỏnhấtcủa
hàmsốđãcho.Khiđó
Mm
bằng
A.
–4. B.–5. C.–6. D.3.
Hướngdẫn
ChọnD.
Tậpxácđịnh:
D .Đặt cos , 0 1txt
2
21
() ,0 1
1
tt
y
ft t
t
2
2
24
()
(1)
tt
ft
t
;
0
() 0
20;1
t
ft
t
(0) 1, (1) 2ff
Vậy
min 1, max 2yy
Câu58: Chohàmsố
2
sin 1
.
sin sin 1
x
y
x
x
Gọi
M
làgiátrịlớnnhấtvà
m
làgiátrịnhỏnhấtcủahàm
sốđãcho.Chọnmệnhđềđúng.
A.
2
3
Mm
. B.
1Mm
. C.
3
2
M
m . D.
3
2
Mm
.
Hướngdẫn
ChọnB.
Đặt
sin , 1 1txt
2
1
()
1
t
yft
tt
,
2
2
2
2
()
1
tt
ft
tt
01;1
() 0
21;1
t
ft
t
2
(0) 1, ( 1) 0, (1)
3
ff f
.Vậy
1, 0Mm
Câu59: Chohaisốthực
0, 0xythayđổivàthỏamãnđiềukiện
22
()
x
yxy x y xy
.Giátrị
lớnnhất
M
củabiểuthức
33
11
A
x
y
là:
A.
0.M
B.
0.M
C.
1.M
D.
16.M
Hướngdẫn
ChọnD.
22
33 2 2
3 3 33 33
11 ( )( ) 11x y xyx xyy xy
A
x
yxy xy xy xy
.
Đặt
x
t
y
.Từgiảthiếttacó:
22 3 2 2
() (1) ( 1)
x
yxy x y xy t ty t t y

Dođó
22
2
11
;
1
tt tt
yxty
tt t
.Từđó
2
2
2
2
11 21
1
tt
A
xy t t
.
Xéthàmsố
22
2
2
2
21 3 3
() ()
1
1
tt t
ft f t
tt
tt
.
Lậpbảngbiếnthiêntatìmgiátrịlớnnhấtcủa
A
là:16đạtđượckhi
1
2
xy
.
Câu60: Đồthịhàmsố
2
39
x
y
x
cóđườngtiệmcậnđứnglà
x
a vàđườngtiệmcậnnganglà
yb
.Giátrịcủasốnguyên
m
nhỏnhấtthỏamãn
mab
là
A.
0
. B.
3
. C.
1
. D.
2
.
Hướngdẫn
ChọnD
Tacóđườngtiệmcậnđứnglà
3x
vàđườngtiệmcậnnganglà
1
3
y
Nên
1
3,
3
ab
Dođó
8
2
3
mab m m
Câu61: Chohàmsố
23
()
2
x
yC
x
.Gọi
M
làđiểmbấtkỳtrênC,
d
làtổngkhoảngcáchtừ
M
đếnhaiđườngtiệmcậncủađồthị
C
.Giátrịnhỏnhấtcủa
d
là
A.5. B.10. C.6. D.2.
Hướngdẫn
ChọnD
Tọađộđiểm
M
códạng
0
0
0
23
;
2
x
Mx
x
với
0
2x
Phươngtrìnhtiệmcậnđứng,nganglầnlượtlà
12
20 , 20
x
dy d
.
Tacó
120
0
1
,,2 2
2
ddMd dMd x
x
Câu62: Chohàmsố
32
12
:
33
yxmxxm
cóđồthị
m
C
.Tấtcảcácgiátrịcủathamsố
m
để
m
C
cắttrục
Ox
tạibađiểmphânbiệtcóhoànhđộ
123
, ,
x
xx
thỏa
222
123
15xxxlà
A.
1m
hoặc
1.m
B.
1m
.C.
0m
.D.
1m
.
Hướngdẫn

ChọnA.
Phươngpháptựluận:
Phươngtrìnhhoànhđộgiaođiểmcủa
()C vàđườngthẳng
d
:
32 2
12
01 31320
33
xmxxm x x m xm
2
()
1
31 320 (1)
gx
x
xmxm
m
C
cắt
Ox
tạibađiểmphânbiệt
phươngtrình(1) cóhainghiệmphânbiệtkhác1
2
0
9690
0
10 6 0
g
mm
m
gm
.
Gọi
1
1x
còn
23
,
x
x
lànghiệmphươngtrình
1 nêntheoViettacó
23
23
31
32
xx m
xx m
.
Vậy
2
222
123 23 23
2
2
15 1 2 15
31 2321409 90 1 1
xxx xx xx
mm m mm
Vậychọn
11mm
.
Phươngpháptrắcnghiệm:Takiểmtrangaytrênđápán
Với
2m
,tagiảiphươngtrìnhbậcba:
32
14
20
33
xxx
thuđược3nghiệm
123
6.37..., 1, 0.62...xxx Tachọnnhữnggiátrịnhỏhơncácnghiệmnàyvàkiểm
trađiềukiệncủabàitoán.
Cụthểtatính
22
2
6.4 1 0.63 42.3569 15
loạiC,D.
Với
2m
,talàmtươngtựthuđược3nghiệm
123
6.27..., 1, 1.27...xxx
Tính
2
22
6.2 1 1.3 41.13 15
loạiB.
Vậychọn
11mm
.
Câu63: Chohàmsố
1
21
x
y
x
cóđồthịlà
C .Gọiđiểm
00
;
M
x
y
với
0
1x
làđiểmthuộc
,C biếttiếptuyếncủa
C tạiđiểm
M
cắttrụchoành,trụctunglầnlượttạihaiđiểm
phânbiệt ,
A
B vàtamgiác
OAB
cótrọngtâm
G
nằmtrênđườngthẳng
:4 0dxy
.Hỏi
giátrịcủa
00
2
x
y bằngbaonhiêu?

A.
7
2
. B.
7
2
. C.
5
2
. D.
5
2
.
Hướngdẫn
ChọnA.
Gọi
0
0
0
1
;
21
x
M
xC
x
với
0
1x
làđiểmcầntìm.
Gọi tiếptuyếncủa
C tại
M
tacóphươngtrình.
00
00 0
2
00
0
11
1
:'()() ()
2( 1) 2( 1)
1
xx
yfxxx xx
xx
x
.
Gọi
A
Ox
2
00
21
;0
2
xx
A
và BOy
2
00
2
0
21
0;
2( 1)
xx
B
x
.
Khiđó tạovớihaitrụctọađộ
OAB
cótrọngtâmlà
22
00 00
2
0
21 21
;
66(1)
xx xx
G
x
.
Do
G
thuộcđườngthẳng40xy
22
00 00
2
0
21 21
4. 0
66(1)
xx xx
x
2
0
1
4
1x
vì ,
A
B khôngtrùng
O
nên
2
00
210xx
00
00
11
1
22
13
1
22
xx
xx
.
Vì
0
1x nênchỉchọn
000
113 7
;2
222 2
xM xy
.
Câu64: Chohàmsố
1
21
x
y
x
cóđồthịlà
C
,đườngthẳng
:dy xm
.Vớimọi m taluôncó
d
cắt
C
tại2điểmphânbiệt ,
A
B .Gọi
12
,kk
lầnlượtlàhệsốgóccủacáctiếptuyếnvới
C
tại ,
A
B .Tìm m đểtổng
12
kk
đạtgiátrịlớnnhất.
A.
1m
. B.
2m
. C.
3m
. D.
5m
.
Hướngdẫn
ChọnA.
Phươngtrìnhhoànhđộgiaođiểmcủa
d
và
C là
1
21
x
x
m
x
2
1
2
22 10(*)
x
gx x mx m
.

TheođịnhlíViettacó
12 12
1
;
2
m
xx mxx
.Giảsử
11 2 2
;, ;
A
xy Bxy .
Ta có
2
1
21
y
x
,nêntiếptuyếncủa
C tại
A
và B cóhệsốgóclầnlượtlà
1
2
1
1
21
k
x
và
2
2
2
1
21
k
x
.Vậy
22
12 12
12
2
22
12
12 1 2
2
2
4( ) 4( ) 211
(2 1) (2 1)
42()1
4864122
xx xx
kk
xx
xx x x
mm m
Dấu""xảyra
1m
.
Vậy
12
kk
đạtgiátrịlớnnhấtbằng 2 khi
1m
.
Câu65: Chohàmsố
21
1
x
y
x
cóđồthị
C
.Biếtkhoảngcáchtừ
1; 2I
đếntiếptuyếncủa
C
tại
M
làlớnnhấtthìtungđộcủađiểm
M
nằmởgócphầntưthứhai,gầngiátrịnàonhất?
A.
3e
. B.
2e
. C.e . D.
4e
.
Hướngdẫn
ChọnC.
Phươngpháptựluận
Tacó
2
3
1
y
x
.
Gọi
0
00
0
21
;,1
1
x
Mx C x
x
.Phươngtrìnhtiếptuyếntại
M
là
0
0
2
00
21
3
()
(1) 1
x
yxx
xx
22
000
3( 1) 2 2 10xx y x x
.
0
4
2
0
0
2
0
61
66
,6
9
9( 1)
29
(1)
(1)
x
dI
x
x
x
.
Dấu
""
xảyrakhivàchỉkhi
2
00
2
00
2
0
00
13 23
9
(1) 13
(1)
13 23
x
yL
xx
x
x
yN
.
Tungđộnàygầnvớigiátrị
e nhấttrongcácđápán.
Phươngpháptrắcnghiệm
Tacó
IM
00
121cx d ad bc x

0
0
13 23
13 23
x
yL
x
yN
.
Câu66: Chohàmsố
2
1
x
y
x
cóđồthị
C
.Phươngtrìnhtiếptuyến
củađồthịhàmsố
C
tạo
vớihaiđườngtiệmcậnmộttamgiáccóbánkínhđườngtrònnộitiếplớnnhất.Khiđó,
khoảngcáchtừtâmđốixứngcủađồthị
C
đếnbằng?
A.
3
. B.
26
. C.
23
. D.
6
.
Hướngdẫn
ChọnD.
Phươngpháptựluận
Gọi
0
00
0
2
;,1,1;1
1
x
Mx C x I
x
.Phươngtrìnhtiếptuyếntại
M
códạng
0
0
2
0
0
2
3
:()
1
1
x
yxx
x
x
.
Giaođiểmcủa
vớitiệmcậnđứnglà
0
0
5
1;
1
x
A
x
.
Giaođiểmcủa
vớitiệmcậnnganglà
0
21;1Bx
.
Ta có
0
0
6
,21.12
1
IA IB x IA IB
x
.Bánkínhđườngtròn ngoại tiếp
IAB
là
IAB
Spr
,suyra
22
.. .
23 6
2. 2..
IAB
S
IA IB IA IB IA IB
r
pIAIBAB
IA IB IA IB
IA IB IA IB
.
Suyra
2
0
max 0
0
13 13
23 6 1 3
13 13
M
M
xy
rIAIBx
xy
.
3; 3 6IM IM
.
Phươngpháptrắcnghiệm
IA IB
IAB
vuôngcântại
IIM
.
13 13
112
13 13
MM
MM
MM
xy
cx d ad bc x
xy
6IM
.
Câu67: Chohàmsố
23
2
x
y
x
cóđồthị
C
.Biếtrằngtiếptuyếntạimộtđiểm
M
bấtkỳcủa
C
luôncắthaitiệmcậncủa
C
tại
A
và
B
.Độdàingắnnhấtcủađoạnthẳng
A
B
là
A.
4
. B.
2
.C.
2
. D.
22
.

Hướngdẫn
ChọnD.
Lấyđiểm
1
;2
2
Mm
m
C
với
2m
.Tacó
2
1
'
2
ym
m
.
Tiếptuyếntại
M
cóphươngtrình
2
11
:2
2
2
dy x m
m
m
.
Giaođiểmcủa
d
vớitiệmcậnđứnglà
2
2; 2
2
A
m
.
Giaođiểmcủa
d
vớitiệmcậnnganglà
22;2Bm .
Tacó
2
2
2
1
42 8
2
AB m
m
,suyra
22AB
.Dấu“”xảyrakhi
2
21m ,
nghĩalà
3m
hoặc
1m
.
Câu68: Chohàmsố
2
33
2
xx
y
x
cóđồthị
C
.Tổngkhoảngcáchtừmộtđiểm
M
thuộc
C
đếnhaihaitrụctọađộđạtgiátrịnhỏnhấtbằng?
A.
1. B.
1
2
. C.2 . D.
3
2
.
Hướngdẫn
ChọnD.
Điểm
3
0,
2
M
nằmtrêntrục
Oy
.KhoảngcáchtừMđếnhaitrụclà
3
2
d=
.
Xétnhữngđiểm
M
cóhoànhđộlớnhơn
3
2
3
2
dxy
.
Xétnhữngđiểm
M
cóhoànhđộnhỏhơn
3
2
:
Với
33 3
0
22 2
xy dxy
Với
2
3111
0; 0 1 1 ; ' 0
222
2
xy dxx d
xx
x
.
Chứngtỏhàmsốnghịchbiến.Suyra
3
min 0
2
dy
.
Câu69: Tọađộcặpđiểmthuộcđồthị
()C
củahàmsố
4
2
x
y
x
đốixứngnhauquađườngthẳng
:260dx y
là
A.
4; 4
và
1; 1
. B.
1; 5
và
1; 1
.

C.
0; 2 và
3; 7 . D.
1; 5 và
5;3 .
Hướngdẫn
ChọnB.
Gọiđườngthẳng
vuônggócvớiđườngthẳng
1
:3
2
dy x
suyra
:2yxm
.
Giảsử
cắt
()C
tạihaiđiểmphânbiệt
,
A
B
.Khiđóhoànhđộcủa
,
A
B
lànghiệmcủa
phươngtrình
2
()
4
2
2(3)2
2
40
2
hx
x
x
xm
xmxm
x
.
Điềukiệncần:
Để
cắt
()C
tạihaiđiểmphânbiệtthìphươngtrình
() 0hx
cóhainghiệmphânbiệt
khác
2 ,tứclà
2
0543
10 23 0
(2) 0
60
543
m
mm
h
m
*.
Điềukiệnđủ:
Gọi
I
làtrungđiểmcủa
A
B
,tacó:
3
33 3
4
;
2
3
42
2
2
AB
I
I
II
I
m
xx
x
x
mm
I
m
yxm
ym
.
Để hai điểm
,
A
B
đốixứngnhauqua
:260dx y
khi
Id
333
2. 6 0 3
42
mm
m
thỏađiềukiện*.
Với
3m
phươngtrình
2
11
() 0 2 2 0
15
xy
hx x
xy
Vậytọahaiđiểmcầntìmlà
1; 5
và
1; 1
.
Câu70:
CHUYÊNQUANGTRUNGĐểhàmsố
2
1
x
mx
y
x
m
đạtcựcđạitại
2x
thì m thuộc
khoảngnào?
A.
0; 2
. B.
4; 2
. C.
2;0
. D.
2; 4
.
Hướngdẫngiải
ChọnB.
Tậpxácđịnh:
\Dm
.

x
y
O
3
1
Đạohàm:
22
2
21xmxm
y
xm
.
Hàmsốđạtcựctrịtại
2x
thì
2
2
3
44 1
20 0
1
2
m
mm
y
m
m
.
Với
2
2
2
68
3;0
4
3
x
xx
my y
x
x
.Lậpbảngbiếnthiêntathấyhàmsốđạt
cựcđạitại
2x
nên
3m
tanhận.
Với
2
2
0
2
1;0
2
1
x
xx
my y
x
x
.Lậpbảngbiếnthiêntathấyhàmsốđạtcực
tiểutại
2x
nên
1m
taloại.
Câu71: CHUYÊNVINH–L2Chocácsốthực
,
xy
thỏamãn
23 3xy x y .Giátrịnhỏ
nhấtcủabiểuthức
22
415
P
xy xylà
A.
min 80P
. B.
min 91P
. C.
min 83P
. D.
min 63P
.
Hướngdẫngiải
ChọnC.
Ta có
2
4
2( 3 3) ( ) 4( ) 8 3. 3 4( )
0
xy
xy x y xy xy x y xy
xy
Mặtkhác
2( 3 3) 2 2( ) 8 4;8xy x y xy xy xy
Xétbiểuthức
22 2
4( ) 15 4( ) 7 16( ) 7 7 ( 3) 16 5
P
x y xy xy xy xy xy xy y x .
Mà
30
16(4 ) 5 64 21
4
y
P
xx x
yx
,kếthợpvới
4 3;7 64 21 83xy x x
Vậygiátrịnhỏnhấtcủabiểuthức
P
là
83
Câu72: CHUYÊNVINH–L2Chohàmsốbậcba
yfx
cóđồthịnhưhìnhbên.Tất
cảcácgiátrịcủathamsố
m đểhàmsố
yfxmcóbađiểmcựctrị
là
A.
1m
hoặc
3m
. B.
3m
hoặc
1m
.
C.
1m
hoặc
3m
. D.13m.
Hướngdẫngiải
ChọnA.
Nhậnxét:Đồthịhàmsố
y
fx mgồmhaiphần:
Phần1làphầnđồthịhàmsố
yfxm
nằmphíatrêntrụchoành;
Phần2làphầnđốixứngcủađồthịhàmsố
yfxm
nằmphíadướitrụchoành
quatrụchoành.
Dựavàođồthịcủahàmsố
yf
x đãchohìnhbêntasuyradạngđồthịcủahàmsố
yfxm
.Khiđóhàmsố
y
fx mcóbađiểmcựctrịkhivàchỉkhiđồthịhàmsố
yfxm
vàtrụchoànhtạinhiềunhấthaiđiểmchung
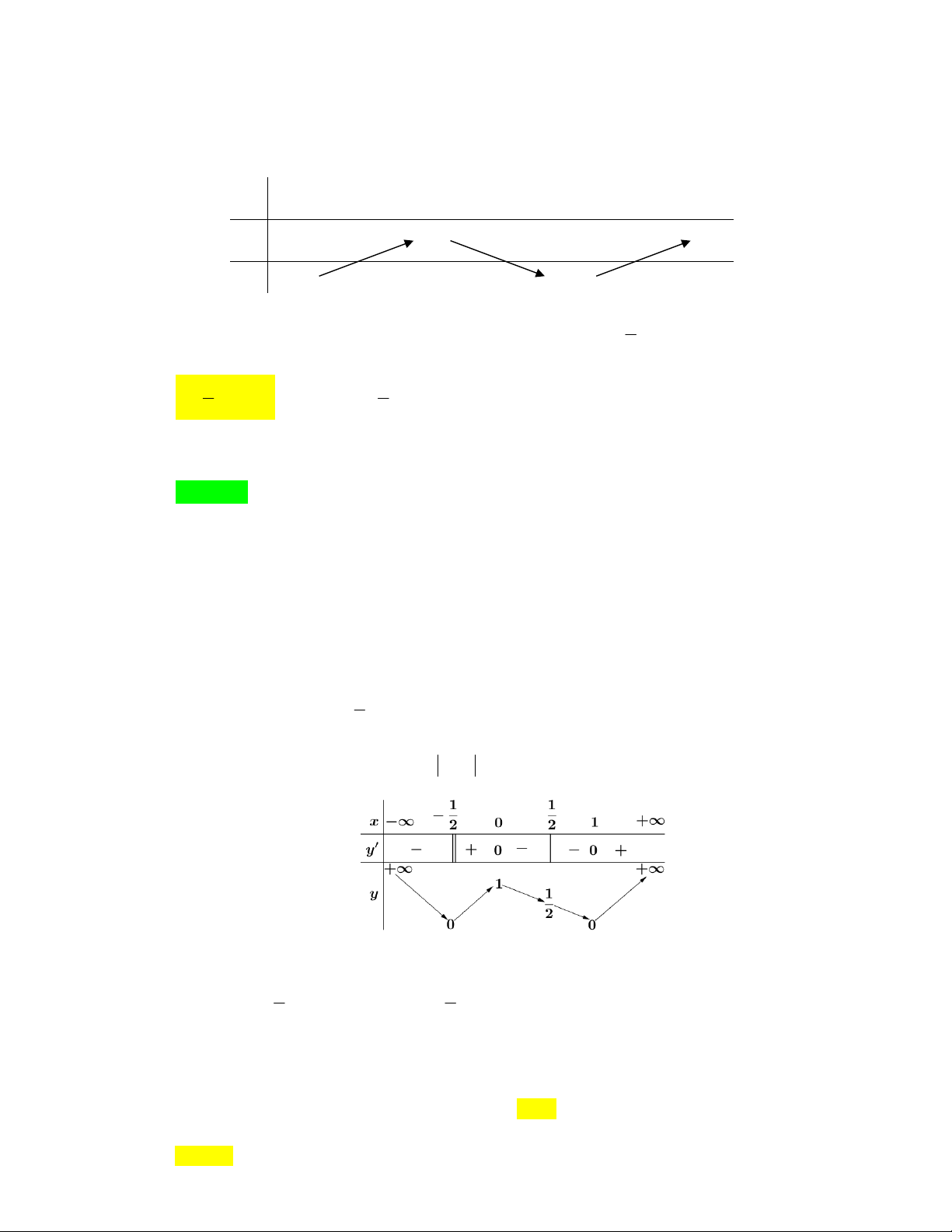
10 1
30 3
mm
mm
.
Câu 73: (CHUYÊN LƯƠNG THẾ VINH – L2) Cho hàm số
32
()yfx axbxcxd có
bảng biến thiên như sau:
Khi đó
|()|fx m
có bốn nghiệm phân biệt
123 4
1
2
xxx x
khi và chỉ khi
A.
1
1
2
m
. B.
1
1
2
m
. C.
01m
. D.
01m
.
Hướng dẫn giải
Chọn A.
Ta có
01
2
10
3
0
00
1
10
f
a
f
b
c
f
d
f
, suy ra
32
() 2 3 1yfx x x.
NX:
0
0
1
2
x
fx
x
.
Bảng biến thiên của hàm số
()yfx
như sau:
Dựa vào bảng biến thiên suy ra phương trình
|()|fx m
có bốn nghiệm phân biệt
123 4
1
2
xxx x
khi và chỉ khi
1
1
2
m
.
Câu 74: (CHUYÊN THÁI BÌNH – L4) Cho hàm số
22 2
() ( 1)( 4)( 9)yfx xx x x
. Hỏi đồ thị
hàm số
()
yfx
¢
=
cắt trục hoành tại bao nhiêu điểm phân biệt?
A.
3.
B.
5.
C.
6.
D.
4.
Hướng dẫn giải
Chọn C
x
0
1
y
0
0
y
1
0

Ta có
22 2 3 42 753
149 1336 144936
fx xx x x x x x x x x x x
64 2
7 70 147 36fx x x x
Đặt
2
,0txt
Xét hàm
32
7 70 147 36gt t t t
Do phương trình
2
21 140 147 0gt t t
có hai nghiệm dương phân biệt và
0360g
nên
0gt
có 3 nghiệm dương phân biệt
Do đó
0fx
có 6 nghiệm phân biệt.
Câu 75: (CHUYÊN THÁI BÌNH – L4) Tìm tất cả các giá trị thực của m để hàm số
33
1ymx x
đồng biến trên
0; 1
.
A.
2.m
B.
2.m
C.
1.m
D.
1.m
Hướng dẫn giải.
Chọn B
+ Tập xác định:
; 1D
.
+
22
23 3 3
33
33
31 . 3 2
21 21
xx
yxx mx xm
xx
.
3
0
0
2
3
x
y
m
x
.
* Trường hợp 1:
2m
, ta có bảng xét dấu:
Dựa vào BXD, ta có
0, x 0; 1y
hàm số nghịch biến trên
0; 1
.
* Trường hợp 2:
2m
.
Để hàm số nghịch biến trên
0; 1
thì
3
2
02
3
m
m
.
Vậy
2m
thì hàm số nghịch biến trên
0; 1
.
Câu 76: (CHUYÊN THÁI BÌNH – L4) Phương trình
sin 2
2017 sin 2 cos
x
xx
có bao nhiêu
nghiệm thực trong
5 ;2017
?
A. vô nghiệm. B.
2017
. C.
2022
. D.
2023
.
Hướng dẫn giải
Chọn D
Ta có hàm số
sin 2
2017 sin 2 cos
x
yxx
tuần hoàn với chu kỳ
2T
.
Xét hàm số
sin 2
2017 sin 2 cos
x
yxx
trên
0; 2
.
Ta có
sin sin
22
2sin .cos sin
cos .2017 .ln 2017 cos cos . 2017 .ln 2017 1
22 cos 1sin
x x
xx x
yx x x
xx
Do vậy trên
0; 2
,
3
0cos 0
22
yxxx
.
2017 1 2 0
2
y
;
31
120
22017
y
Bảng biến thiên
x
0
2
3
2
2
y
0
0
y
0
0
Vậy trên
0; 2
phương trình
sin 2
2017 sin 2 cos
x
x
x có đúng ba nghiệm phân biệt.
Ta có
0y
, nên trên
0; 2
phương trình
sin 2
2017 sin 2 cos
x
x
x có ba nghiệm
phân biệt là
0, , 2
.
Suy ra trên
5 ;2017
phương trình có đúng
2017 5 1 2023
nghiệm.
2
y
3
2
y

Chủđề2.LŨYTHỪA–MŨ–LOGARIT
Câu1: SGDVĨNHPHÚCĐạohàmcủahàmsố
2
ylog 3 1
x
là:
A.
6
31ln2
y
x
B.
2
31ln2
y
x
C.
6
31ln2
y
x
D.
2
31ln2
y
x
Hướngd
ẫngiải
ChọnC.
Điềukiện:
310x
2
31
36
ylog 3 1
31ln2
31ln2 31ln2
x
xy
x
xx
.
Câu2: NGUYỄNKHUYẾNTPHCMBấtphươngtrình
22
2.5 5.2 133. 10
x
xx
cótậpnghiệmlà
;Sab
thì
2ba
bằng
A.
6
B.
10
C.
12
D.
16
Hướngd
ẫngiải
Ta có:
22
2.5 5.2 133. 10 50.5 20.2 133 10
x
xxxxx
chia hai vế bất phương trình
cho
5
x
tađược:
20.2 133 10 2 2
50 50 20. 133.
55 5 5
x
x
xx
xx
1
Đặt
2
,( 0)
5
x
tt
phươngtrình1trởthành:
225
2
20 133 50 0
54
tt t
Khiđ
ótacó:
24
22252 2 2
42
5545 5 5
x
x
x
nên
4, 2ab
Vậy
210ba
BÌNHLUẬN
Phương pháp giải bất phương trình dạng
22
0ma n ab pb
:chia2vếcủabất
phươngtrìnhcho
2
a
hoặc
2
b
.
Câu3: NGUYỄN KHUYẾN TPHCM Cho
a làsốnguyêndươnglớnnhấtthỏamãn
3
32
3log 1 2logaa a
.Tìmphầnnguyêncủa
2
log 2017a
.
A.
14 B. 22 C. 16 D. 19
Hướngd
ẫngiải
BÀI TOÁN VẬN DỤNG (8 - 9 - 10)
_______________________________

Đặt
6
,0tat,từgiảthiếttacó
32 3
32
3log 1 2logtt t
32 2
32
log 1 log 0ft t t t
32
2
32
43
3ln2 2ln3 2ln2 2ln3 2ln3
13 2 21
..
ln 3 1 ln 2
ln 2.ln 3.
tt
tt
ft
tt t
ttt
Vìđềxét
a nguyêndươngnêntaxét
1t
.
Xét
32
3ln2 2ln3 2ln2 2ln3 2ln3gt t t
Tacó
2
84 84
3ln 2ln 3ln 2ln
99 99
gt t t t t
9
2ln
4
00
8
3ln
9
gt t
.
Lậpbảngbiếnthiênsuyrahàmsố
g
t giảmtrênkhoảng
1; .
Suyra
1 5ln 2 6ln 3 0 0gt g f t
.
Suyrahàmsố
f
t luôngiảmtrênkhoảng
1; .
Nên
4t
lànghiệmduynhấtcủaphươngtrình
0ft .
Suyra
6
0 4 4 4 4096ft ft f t a a
.
Nênsốnguyên
a lớnnhấtthỏamãngiảthiếtbàitoánlà
4095a
.
Lúcđó
2
log 2017 22,97764311a
.
Nênphầnnguyêncủa
2
log 2017a
bằng22.
Đápán:B.
Câu4: NGUYỄN KHUYẾN TPHCM Biết
15
2
x
làmộtnghiệmcủabấtphươngtrình
2
2log 23 23 log 2 15
a
a
xxx *.TậpnghiệmT củabấtphươngtrình*là:
A.
19
;
2
T
. B.
17
1;
2
T
. C.
2;8T
. D.
2;19T
.
Hướngdẫngiải
22
2log 23 23 log 2 15 log 23 23 log 2 15
aaa
a
xxx xxx
Nếu
1a
tacó

2
2
2
23 23 2 15
log 23 23 log 2 15 2 19
2150
aa
xxx
xxx x
xx
Nếu
01a
tacó
2
2
12
23 23 2 15
log 23 23 log 2 15
19
23 23 0
aa
x
xxx
xxx
x
x
Mà
15
2
x
làmộtnghiệmcủabấtphươngtrình.ChọnD.
BÌNHLUẬN
‐ Sửdụngtínhchấtcủahàmsốlogarit
log
a
yb
đồngbiếnnếu
1a
nghịchbiếnnếu
01a
‐
1
0
log log
01
0
aa
a
gx
f
xgx
fx gx
a
fx
f
xgx
Câu5: T.TDIỆUHIỀNTìm
m
đểphươngtrình :
2
2
11
22
1
1 log 2 4 5 log 4 4 0
2
mxm m
x
cónghiệmtrên
5
,4
2
A.
7
3
3
m . B.
m
. C.
m
. D.
7
3
3
m .
Hướngdẫngiải
ChọnA.
Đặt
1
2
log 2tx
.Do
5
;4 1;1
2
xt
2
414(5)440mt mtm
2
1510mtm tm
22
151mt t t t
2
2
51
1
tt
m
tt
g
mft
Xét
2
2
51
1
tt
ft
tt
với
1;1t
2
2
2
44
0
1
t
ft
tt
1; 1t
Hàmsốđồngbiếntrênđoạn
1;1
Để phương trình có nghiệm khi hai đồ thị
;
g
mftcắtnhau
1; 1t
7
(1) 1 3
3
fgmf m
BÌNHLUẬN
Đâylàdạngtoánứngdụnghàmsốđểgiảibàitoánchứathamsố.Đốivớibàitoánbiện
luậnnghiệmmàchứathamsốthìphảitìmđiềukiệnđúngchoẩnphụsauđócôlập
m rồi
tìmmax,minhàmsố.
Câu6: LẠNG GIANG SỐ 1 Sốcácgiátrịnguyêndươngđểbấtphươngtrình
22 2
cos sin sin
32 .3
x
xx
m
cónghiệmlà
A.
1
. B.
2
. C.
3
. D.
4
.
Hướngdẫngiải
ChọnA.
Đặt
2
sin
x
t
01t
22 2
1
cos sin sin
32 .3 323
t
x
xx tt
m
2
332
2.3
33
3
t
tt
t
t
mm
Đặt:
32
01
93
t
t
yt
1122
3. .ln .ln 0
9933
tt
y
Hàmsốluônnghịchbiến
Dựavàobảngbiếnthiênsuyra
1m
thìphươngtrìnhcónghiệm
Suyracácgiátrịnguyêndươngcầntìm
1m
.
_
1
1
0
4
f(t)
f'(t)
t
Câu7: LÝ TỰ TRỌNG – TPHCM Cóbaonhiêugiátrịthựccủathamsố m đểphươngtrình
22
32 4 63
.3 3 3
xx x x
mm
cóđúng
3
nghiệmthựcphânbiệt.
A.
1.
B.
2.
C.
3.
D.
4.
Hướngdẫngiải
ChọnA.
Đặt.
2
2
32
63
4
3
.3
3
xx
x
x
u
uv
v
. Khi đó phương trình trở thành
2
32
2
2
2
2
3
2
3
1101 0
1
31
30
1
320
2
4log
4log
xx
x
mu v uv m m u v u u m v
u
vm
mm
x
xx
x
xm
x
m
Đểphươngtrìnhcóbanghiệmthì
2
3
4log
x
m cómộtnghiệmkhác
1; 2
. Tức
3
4log 0 81mm.
ChọnA.
Câu8: LÝTỰTRỌNG–TPHCMCho
2
log log log
log 0;
y
abc b
x
x
pqr ac
.Tính
y
theo
,,
pq
r
.
A.
2
yq pr. B.
2
p
r
y
q
. C.
2yqpr
. D.
2yqpr
.
Hướngdẫngiải
ChọnC.
22
log log
log 2log log log 2 log log log
log 2
yy
bb
xx
ac ac
yx b a cqxpxrx
xqpr
2yqpr
do
log 0x
.
BÌNHLUẬN
Sửdụng
log log log c,log log log ,log log
m
aaaaaaa a
b
bc b b c b m b
c
Câu9: CHUYÊN PHAN BỘI CHÂU Cho hàm số
4
42
x
x
fx
.Tínhgiátrịbiểuthức
1 2 100
...
100 100 100
Af f f
?
A.
50
. B.
49
. C.
149
3
. D.
301
6
.
Hướngdẫngiải

ChọnD.
Cách1.BấmmáytínhCasiofx570theocôngthức
100
100
1
100
4 301
6
42
X
X
X
.
Cách2.Sửdụngtínhchất
11fx f x củahàmsố
4
42
x
x
fx
.Tacó
1
2
1
2
1 99 2 98 49 51 50 100
...
100 100 100 100 100 100 100 100
4 4 301
49
42 6
42
Af f f f f f f f
PS:Chứngminhtínhchấtcủahàmsố
4
42
x
x
fx
.
Tacó
1
1
44 4 4 4 2
11
424 24242.4 4224
xxx x
xxx xx x
fx f x
.
Câu10: THTT
–477Nếu
2
84
log log 5ab
và
2
48
log log 7ab
thìgiátrịcủa
ab
bằng
A.
9
2.
B.
18
2.
C.
8.
D.
2.
Hướngdẫngiải
ChọnA.
Đặt
22
log 2 ; log 2
x
y
xaaybb.
Tacó
2
84
2
48
1
5
log log 5
315 6
3
13213
log log 7
7
3
xy
ab
xy x
xy y
ab
xy
.Suyra
9
22
xy
ab
.
BÌNHLUẬN
Nguyêntắctrongbàinàylàđưavềlogaritcơsố2.
Câu11: THTT
– 477 Cho
1n
làmộtsốnguyên.Giátrịcủabiểuthức
23
11 1
...
log ! log ! log !
n
nn n
bằng
A.
0.
B. .n C.
!.n
D.
1.
Hướngdẫngiải
ChọnD.
!!! !
234
!!
111 1
1, ... log 2 log 3 log 4 ... log
log ! log ! log ! log !
log 2.3.4... log ! 1
nnn n
n
nn
nn n
nnn n
nn
BÌNHLUẬN
Sửdụngcôngthức
1
log
log
a
b
b
a
=
,
log log log
aaa
bc b c=+
,
log 1
a
a =

Câu12: CHUYÊNLƯƠNGVĂNCHÁNHChohaisốthựcdương
,
xy
thỏamãn
22 4
xy
.Tìmgiá
trịlớnnhất
max
P
củabiểuthức
22
22 9
P
xyyx xy .
A.
max
27
2
P . B.
max
18P
. C.
max
27P
. D.
max
12P
.
Hướngdẫngiải
ChọnB.
Tacó
42 2 22 42 2
x y xy xy
xy
.
Suyra
2
1
2
xy
xy
.
Khiđó
22 3322
22 92 410
P
xyyx xy xy xy xy .
22
23210
P
x y x y xy xy xy
22 22
4 4 3 4 10 16 2 2 1 18 xy xy xy xy xyxy
Vậy
max
18P
khi
1
x
y
.
Câu13:
CHUYÊN PHAN BỘI CHÂU Tìmtấtcảcácgiátrịcủa m đểphươngtrình
22
2
1
735 735 2
xx
x
m
cóđúnghainghiệmphânbiệt.
A.
1
16
m
. B.
1
0
16
m
. C.
11
216
m
. D.
1
0
2
1
16
m
m
.
ChọnD.
PT
22
735 735 1
222
xx
m
.
Đặt
2
735
0;1
2
x
t
.KhiđóPT
22
22022ttm mtt gt
1.
Tacó
1
14 0
4
gt t t
.
Suyrabảngbiếnthiên:
PTđãchocóđúng2ng
hiệmphânbiệt
1cóđúng1nghiệm
0;1t
1
1
2
16
8
1
12 0
0
2
m
m
m
m
.
BÌNHLUẬN
Trongbàinàycácemcầnlưuýtìmđiềukiệnđúngcho
t
vàmốiquanhệsốnghiệmgiữa
biếncũvàbiếnmới,tứclàmỗi
0;1t
chotahaigiátrị
x
.
Câu14: CHUYÊNĐHSPHNSốnghiệmthựcphânbiệtcủaphươngtrình
11
44
224
x
x
xx
là
A.
2. B. 3
. C.
1. D. 0.
ChọnD.
Điềukiện
0x
‐
Nếu
1
01
4
xx
x
,dấubằngxẩyrakhi
1
2
x và
1
1
4
x
x
,
dấubằngxẩyrakhi
2x
suyra
11
44
224,0
x
x
xx
x
‐Nếu
1
4
11 1
0112
44 2
x
x
xx x
xx
,dấubằngxẩyrakhi
1
2
x
và
1
4
11 1
112
44 2
x
x
xx
xx
,dấubằngxẩyrakhi
2x
Suyra
11
44
221,0
x
x
xx
x
Vậyphươngtrìnhđãchovônghiệm.
BÌNHLUẬN
SửdụngbấtđẳngthứcCôsichohaisốdương
2ab ab
,dấu“”xảyrakhi .ab
Câu15: CHUYÊNĐHVINHSốnghiệmcủaphươngtrình
22
35
log 2 log 2 2xx xx
là
t 0
1
4
1
g
t
0
g
t
0
1
8
1

A.
3.
B.
2.
C.
1.
D.
4.
Đápán:B.
ĐK:
0; 2xx
.
Đặt
2
2tx x
2
22 2
x
xt
35
log log 2tt.
Đặt
35
log log 2ttu
3
5
log
log 2
tu
tu
3
25
u
u
t
t
523
uu
523
52 3
uu
uu
532
325
uu
uu
532 (1)
.
31
21(2)
55
uu
uu
Xét
1:5 3 2
uu
Ta thấy
0u
là1nghiệm,dùngphươngpháphàmsốhoặcdùngBĐTđểchứngminh
nghiệm
0u
làduynhất.
Với
2
01 210ut xx
,phươngtrìnhnàyvônghiệm.
Xét
31
2: 2 1
55
uu
Tathấy
1u
là1nghiệm,dùngphươngpháphàmsốhoặcdùngBĐTđểchứngminh
nghiệm
1u
làduynhất.
Với
2
03 230utxx
,phươngtrìnhcó2nghiệmphânbiệtthỏa
0; 2xx.
BÌNHLUẬN
Cho
1fx gx
nếu
,
f
xgx
đốinghịchnhaunghiêmngặthoặc
g
x const
và
f
x
tăng,giảmnghiêmngặtthì1cónghiệmduynhất.
Câu16: CHUYÊNTHÁIBÌNHTìmtấtcảcácgiátrịthựccủathamsốmđểphươngtrìnhsaucó
hainghiệmthựcphânbiệt:
2
31
3
log (1 ) log ( 4) 0xxm
.
A.
1
0
4
m
. B.
21
5.
4
m
C.
21
5.
4
m
D.
1
2
4
m
.
ChọnC.
2
2
31
2
2
3
33
1;1
10
log (1 ) log ( 4) 0
log (1 ) log ( 4)
14
x
x
xxm
xxm
xxm
Yê
ucầubàitoán
2
50fx x xm
có2nghiệmphânbiệt
1; 1
Cá
ch1:Dùngđịnhlívềdấutamthứcbậchai.
Để thỏa yêu cầu bài toán ta phải có phương trình
0fx cóhainghiệmthỏa:
12
11xx
.10
50
.1 0
21
30 5
0
4
21 4 0
11
2
af
m
af
mm
m
S
.
Cách2:Vớiđiềukiệncónghiệm,tìmcácnghiệmcủaphươngtrình
0fx rồisosánh
trựctiếpcácng
hiệmvới
1
và
1
.
Cách3:Dùngđồthị
Đườngthẳng
ym
cắtđồthịhàmsố
2
5yx xtạihaiđiểmphânbiệttrongkhoảng
1;1
khivàchỉkhiđườngthẳng
y
m
cắtđồthịhàmsố
2
5yx xtạihaiđiểmphân
bi
ệtcóhoànhđộ
1; 1
.
Cá
ch4:Dùngđạohàm
Xéthàmsố
2
1
5210
2
fx x x f x x x
Có
121
;1 3; 1 5
24
fff
Tacóbản
gbiếnthiên
x
1
1
2
1
f
x
–
0
f
x
5
21
4
3

Dựa vào bảng biến thiên, để có hai nghiệm phân biệt trong khoảng
1;1 khi
21 21
55
44
mm
.
Cách5:DùngMTCT
Saukhiđưavềphươngtrình
2
50xxm ,tanhậpphươngtrìnhvàomáytính.
*Giảikhi
0, 2m
:khôngthỏaloạiA,D.
*Giảikhi
5m
:khôngthỏa
loạiB.
Câu17: Tậptấtcảcácgiátrịcủa
m
đểphươngtrình
2
1
2
22
2. 234. 2 2
xm
x
log x x log x m
cóđúngbanghiệmphânbiệtlà:
A.
13
;1; .
22
B.
13
;1; .
22
C.
13
;1; .
22
D.
13
;1; .
22
Hướngdẫngiải
ChọnD
Tacó
2
1
2
22
2. 234. 2 2
xm
x
log x x log x m
1
2
2
2
1
22
2. 122. 2 2
xm
x
log x log x m
2
Xéthàmsố
2
2. 2 , 0.
t
ft log t t
Vì
0, 0ft t
hàmsốđồngbiếntrên
0;
Khiđó
22
212 12
f
xfxmx xm
2
2
412 03
214
xx m
xm
Phươngtrình
1
cóđúngbanghiệmphânbiệtnếuxảyracáctrườnghợpsau:
PT
3
cónghiệmképkháchainghiệmphânbiệtcủaPT
4
3
2
m
,thayvàoPT
4
thỏamãn
PT
4
cónghiệmképkháchainghiệmphânbiệtcủaPT
3
1
2
m
,thayvàoPT
3
thỏamãn
PT
4
cóhainghiệmphânbiệtvàPT
3
cóhainghiệmphânbiệt,trongđócómột
nghiệmcủahaiPTtrùngnhau
421xm
,với
13
.
22
m
ThayvàoPT
3
tìmđược 1.m
KL:
13
;1; .
22
m
BÌNHLUẬN
B1:Đưaphươngtrìnhvềdạng
f
ufv
với
,uv
làhaihàmtheo
x
.
B2:Xét
hàmsố
,.
f
tt D
B3:Dùngđạohàmchứngminhhàmsố
,
f
tt D
tănghoặcgiảmnghiêmngặttrênD.
B4:
f
ufv uv
Câu18: QUẢNG XƯƠNG I Tấtcảcácgiátrịcủa
m đểbấtphươngtrình
(3 1)12 (2 )6 3 0
xxx
mmcónghiệmđúng
0x
là:
A.
2;
. B.
(;2]
. C.
1
;
3
. D.
1
2;
3
.
Chọn đápánBĐặt 2
x
t .Do
01
x
t
.
Khi đó ta có :
2
(3m 1) t (2 m) t 1 0, t 1
2
22
2
21
(3t t) m t 2 1 t 1 t 1
3
tt
tm
tt
Xéthàmsố
2
2
21
() ê 1;
3
tt
ft trn
tt
2
22
761
'(t) 0 (1; )
(3t t)
tt
ft
BBT
t
1
f'(t)
f(t)
1
3
2
Dođó
1
lim (t) 2
t
mf
thỏamãnyêucầubàitoán
BÌNHLUẬN
Sửdụng
maxf
minf
mfxxD m xxD
mfxxD m xxD
Câ
u19: QUẢNG XƯƠNG I Trong các nghiệm
(; )
x
y
thỏa mãn bất phương trình
22
2
log (2 ) 1
xy
xy
.Giátrịlớnnhấtcủabiểuthức
2Txy
bằng:
A.
9
4
. B.
9
2
. C.
9
8
. D.9.
Chọn đápánB
BấtPT
22
22 22
2
22 22
21 0 21
log (2 ) 1 ( ), ( )
22022
xy
xy xy
x
yIII
xyxy xyxy
.
XétT
2
x
y
TH1:x;ythỏamãnIIkhiđó
22
02 21Txyx y
TH2:x;ythỏamãnI
22 2 2
19
22 (1)(2 )
8
22
xyxyx y
.Khiđó
22 2
1191 199999
22(1)(2 ) (2)(1)(2 ) .
42 42842
222 22
xy x y x y
Suyra:
9
max
2
T
1
(;y) (2; )
2
x
BÌNHLUẬN
‐ Sử dụng tính chất của hàm số logarit
log
a
yb
đồng biến nếu 1a nghịch biến nếu
01a
1
0
log log
01
0
aa
a
gx
f
xgx
fx gx
a
fx
f
xgx
‐ Sử
dụngbấtđẳngthứcBCSchohaibộsố
;,;ab x
y
thì
222 2
ax b
y
abx
y
Dấu“”xảyrak
hi
0
ab
xy
Câ
u20: MINH HỌA L2 Tìm tập hợp các giá trị của tham số thực
m để phương trình
63 2 0
xx
mm
cónghiệmthuộckhoảng
0;1
.
A.
3; 4
. B.
2; 4
. C.
2; 4
. D.
3; 4
.

ChọnC.
Tacó:
63 2 0
xx
mm
1
63.2
21
xx
x
m
Xét hàm số
63.2
21
x
x
x
fx
xácđịnhtrên
, có
2
12 .ln3 6 .ln6 3.2 .ln2
0,
21
xx x
x
fx x nênhàmsố
f
x đồngbiếntrên
Suyra
01 0 12 4 xffxf fx
vì
02, 14.ff
Vậyphươngtrình
1 cónghiệmthuộckhoảng
0;1 khi
2; 4m .
Câu21: CHUYÊNQUANGTRUNGLẦN3Tìm
m đểbấtphươngtrình
22
55
1 log 1 log 4
x
mx x m
thoãmãnvớimọi
x
.
A.
10m
. B.
10m
. C.
23m
. D.
23m
.
Hướngdẫngiải
ChọnC.
BPT thoã mãn với mọi
x
.
2
22
40
51 4
mx x m
x
xmxxm
2
2
40
5450
mx x m
x
mx x m
2
2
0
16 4 0
50
16 4 5 0
m
m
m
m
0
2
2
5
3
7
m
m
m
m
m
m
23m
.
BÌNHLUẬN
SửdụngdấutamthứcbậchaikhôngđổitrênR:
2
2
0
0
0
0
0
0
a
f x ax bx c x R
a
f x ax bx c x R
Câu22: CHUYÊN QUANG TRUNG LẦN 3Cho hàm số
4
2017
y
3x x
em-1e+1
. Tìm m đểhàmsố
đồngbiếntrênkhoảng
1; 2 .
A.
34
31 31eme . B.
4
31me.
C.
23
31 31eme . D.
2
31me.
Hướngdẫngiải
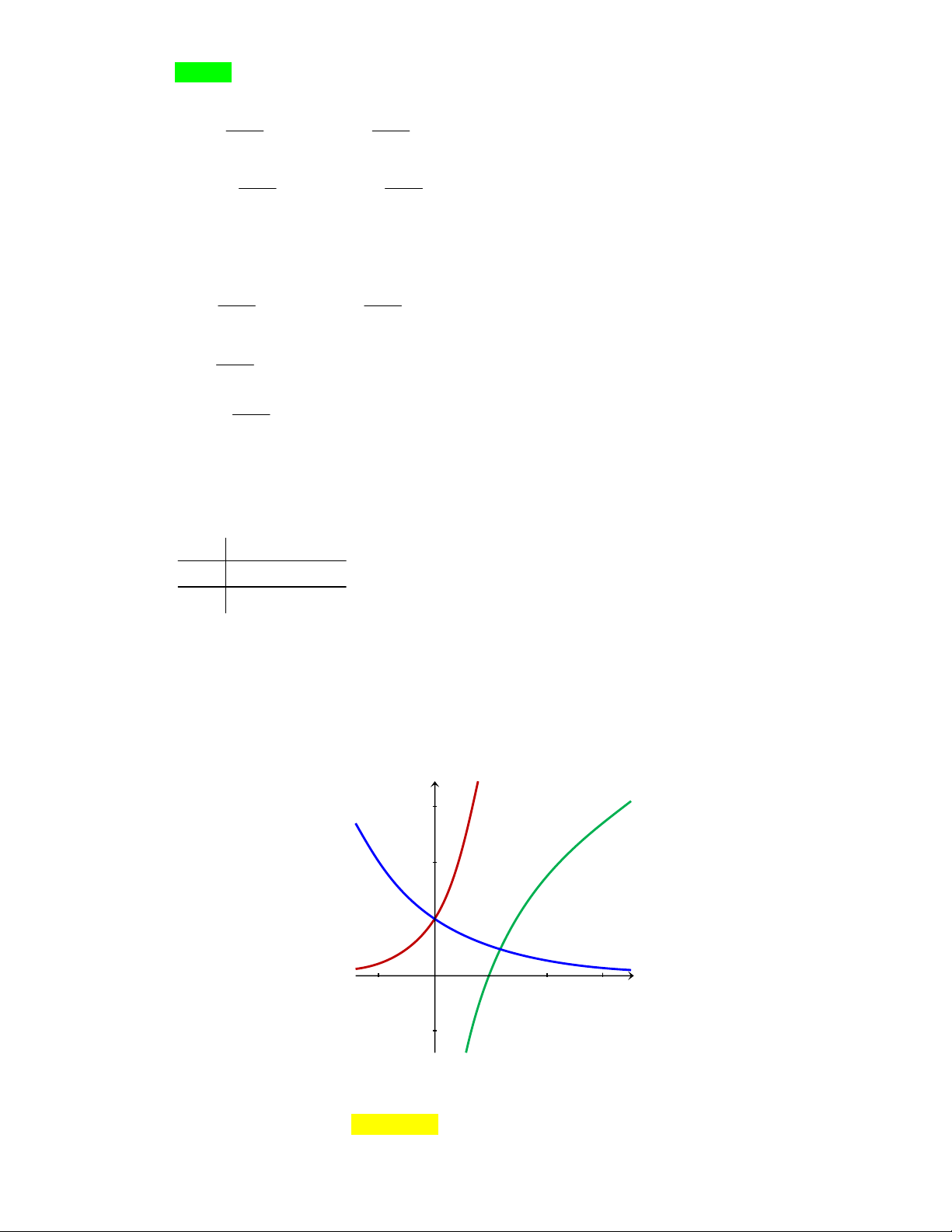
ChọnB.
3
11
3
44
.ln . 1 1
2017 2017
xx
eme
xx
yeme
3
11
3
44
.ln . 3 1
2017 2017
xx
eme
x
x
y
eme
Hàmsốđồngbiếntrênkhoảng
1; 2
3
11
3
44
.ln . 3 1 0, 1;2
2017 2017
xx
eme
xx
yemex
*, mà
3
11
4
0,
2017
4
ln 0
2017
xx
eme
x
. Nên *
3
310,1;2
xx
eme x
2
31, 1;2
x
emx
Đặt
2
31, 1;2
x
gx e x ,
2
3.20, 1;2
x
gx e x
12x
gx
gx
||
||
.Vậy*xảyrakhi
2mg
4
31me
.
BÌNHLUẬN
S
ửdụng
''ln
uu
auaa
và phương pháp hàm số như các bài trên.
Câu23: CHUYÊNBẮCGIANG Tronghình vẽdướiđâycóđồthịcủacáchàmsố
x
y
a
,
x
y
b
,
log
c
yx
.
.
Hãychọnmệnhđềđúngtrongcácmệnhđềsauđây?
A.
.cab
B.
.acb
C.
.bca
D.
.abc
O
1
123
1
2
3
x
y
x
ya
x
yb
log
c
yx

Hướngdẫngiải
ChọnB.
Từđồthị
Tathấyhàmsố
x
ya nghịchbiến
01a
.
Hàmsố
,log
x
c
yby x
đồngbiến 1, 1bc
,abac nênloạiA,C
Nếu
bc
thìđồthịhàmsố
x
yb và
log
c
yx
phảiđốixứngnhauquađườngphângiác
gócphầntưthứnhất
y
x
.Nhưngtathấyđồthịhàmsố
log
c
yx
cắtđường
y
x
nên
loạiD.
Câu24: CHUYÊNBẮCGIANGBiếtrằngphươngtrình
2
log 4 2 3
24.2
x
xx
cóhainghiệm
1
x
,
21 2
x
xx .Tính
12
2
x
x
.
A.1. B.
3
. C.
5
. D. 1 .
Hướngdẫngiải
ChọnD.
Điềukiện
2x
.
Phươngtrìnhthành
22
log 4 log 2 3
24.2
x
xx
2
2log2 3
2. 2 4. 2
x
xx x
hay
2
log 2
24.2
x
xx
.
Lấylôgaritcơsố2haivếtađược
22 2
log 2 .log 2 log 4 2xx x
2
2
22
2
5
log 2 1
log 2 2 log 2
2
log 2 2
6
x
x
xx
x
x
.
Suyra
1
5
2
x
và
2
6.x
Vậy
12
5
22.61
2
xx
.
Câu25: CHUYÊNKHTNL4Cho
,
x
y làsốthựcdươngthỏamãn
2
ln nln l yxxy
.Tìmgiá
trịnhỏnhấtcủa
Pxy
A.
6P
. B.
22 3P
. C.
232P
. D.
17 3P
.
Hướngdẫngiải:
ChọnđápánB.
Từ
22
lnnln l xy xyxxy
y
.Taxét:
Nếu
01x
thì
22
0xyyy
x
x mâuthuẫn.
Nếu
1
x
thì
2
22
1
1
x
xy x y y x x
x
y
.Vậy
2
1
x
xP
x
xy
.

Tacó
2
1
x
fx x
x
xéttrên
1;
.
Có
2
2
22
()
2
2
'0
22
()
41
2
2
1
x
loai
x
fx
x
x
an
x
nh
x
Vậy
1;
22
min 2 2 3
2
fx f
.
Câu26: CHUYÊN KHTN L4 Tìm tập hợp tất cả các tham số
m
sao cho phương trình
22
21 22
4.2320
xx xx
mm
cóbốnnghiệmphânbiệt.
A.
;1 . B.
;1 2; . C.
2;
. D.
2; .
Hướngdẫn
giải
Đặt
2
(1)
2 1
x
tt
Phươngtrìnhcódạng:
2
2320*tmtm
Phư
ơngtrìnhđãchocó4nghiệmphânbiệt
phươngtrình*cóhainghiệmphânbiệtlớnhơn1
2
2
2
2
2
22
1,2
320
320
320
10 2
321
32 1
32 21
mm
mm
mm
mm
xmmm
mm m
mm mm
Ch
ọnđápán:D
BÌNHLUẬN
Trongbàinàydođềbàiyêucầuphươngtrìnhcó4nghiệmphânbiệtnêntacầnchúýmỗi
1t thìtanhậnđượcbaonhiêugiátrị
x
Từ phương trình (*) chúng ta có thể cô lập
m và ứng dụng hàm số để biện luận số
nghiệm của phương trình thỏa đề bài.
Câu27: Tìmtấtcảcácgiátrịthựccủathamsố
m
đểbấtphươngtrình
22
log (5 1).log (2.5 2)
xx
m
cónghiệmvớimọi
1
x
?
A.
6m
. B.
6m
. C.
6m
. D.
6m
.
Hư
ớngdẫngiải
BPT
22 2 2
log (5 1).log (2.5 2) m log (5 1). 1 log (5 1) m
xx x x
Đặt
2
6
log 1txx
do
1
x
2;t

BPT
2
(1 ) ( )ttmttmftm
Với
2
()
f
ttt
,
() 2 1 0ft tvới
2;t
nênhàmđồngbiếntrên
2;t
Nên
() (2) 6Minf t f
Dođóđểđểbấtphươngtrình
22
log(5 1).log(2.5 2) m
xx
cónghiệmvớimọi 1
x
thì:
() 6mMinft m
Câu28: Tìmtấtcảcácgiátrịthựccủathamsố
m
đểphươngtrình
22 2
21 4
2
log log 3 log 3xxmx
cónghiệmthuộc
32;
?
A.
1; 3m
. B.
1; 3m
. C.
1; 3m
. D.
3;1m
.
Hướngdẫngiải
Điềukiện:
0.x
Khiđóphươngtrìnhtươngđương:
2
22 2
log 2 log 3 log 3xxmx .
Đặt
2
logtx
với
22
32 log log 32 5xx
hay
5.t
Phươngtrìnhcódạng
2
2 3 3 *tt mt .
Khiđóbàitoánđượcphátbiểulạilà:“Tìm
m
đểphươngtrình*cónghiệm
5t
”
Với
5t
thì
(*) 3 . 1 3 3. 1 3 0tt mt t tmt
1
130
3
t
tmt m
t
Tacó
14
1.
33
t
tt
Với
44
511 1 3
353
t
t
hay
11
131 3
33
tt
tt
suyra
13.m
Vậyphươngtrìnhcónghiệmvới
13.m
BÌNHLUẬN
Chúngtacóthểdùnghàmsốđểtìmmax,mincủahàmsố
1
,5
3
t
yt
t
Câu29: Tìmtấtcảcácgiátrịthựccủathamsố
m
đểbấtphươngtrình
22
22
log 7 7 log 4 , .xmxxmx
A.
2;5m
. B.
2;5m
. C.
2;5m
. D.
2;5m
.
Hướngdẫngiải
Bấtphươngtrìnhtươngđương
22
77 4 0, xmxxmx
2
2
7 4 7 0 (2)
, .
4 0 (3)
mx x m
x
mx x m
7m
:2khôngthỏa
x
0m
:3khôngthỏa
x

1thỏa
x
2
2
2
3
70
7
5
47 0
2 5.
0
0
2
40
m
m
m
m
m
m
m
m
m
Câu30: Tìmtấtcảcácgiátrịthựccủathamsố
m
saochokhoảng
2;3 thuộctậpnghiệmcủabất
phươngtrình
22
55
log 1 log 4 1 (1)xxxm .
A.
12;13m
. B.
12;13m
. C.
13;12m
. D.
13; 12m
.
Hướngdẫngiải
2
2
2
2
2
4
4()
1
(1)
5
445()
40
xxm
mx xfx
x
mx x gx
xxm
Hệtrênthỏamãn
2;3x
23
23
( ) 12 khi 2
12 13.
( ) 13 khi 2
x
x
mMaxfx x
m
mMinfx x
Câu31: Phươngtrình
2
356
23
x
xx
cóhainghiệm
12
,
x
x
trongđó
12
x
x
,hãychọnphátbiểu
đúng?
A.
12 3
32 log8xx
. B.
12 3
23 log8xx
.
C.
12 3
23 log54.xx
D.
12 3
32 log54.xx
Hướngdẫngiải
Logarithóahaivếcủaphươngtrìnhtheocơsố2tađược:
2
356
22
3 log 2 log 3
x
xx
2
22 2
3 log 2 5 6 log 3 3 2 3 log 3 0xxx xxx
2
22
2
3
30 3
3.1 2log 3 0
1
2
12log3 2log31
log 3
x
xx
xx
x
xx
3333
33 3
log 2 2 log 2 log 9 log 18
xx x
xx x
Câu32: Phươngtrình
33 33 4 4 3
333310
xxxx
cótổngcácnghiệmlà?
A.0. B.2. C.3. D.4.
Hướngdẫngiải
33 33 4 4 3
333310
xxxx
7
333 3
33
27 81 1 1
7 27.3 81.3 10 27. 3 81. 3 10 7'
33 3 3
xx x x
xx x x

Đặt
11
323.2
33
xx
xx
Côsi
t
3
332 33
23 3
11111
3 3 3.3 . 3.3 . 3 3
33333
xxxx x
xxxxx
ttt
Khiđó:
3
333
10 10
7' 27 3 81 10 2
27 3
tt t t t N
Với
10 1 10
3 7''
333
x
x
t
Đặt
30
x
y .Khiđó:
2
3
110
7'' 3 10 3 0
1
3
3
yN
yyy
y
yN
Với
333 1
x
yx
Với
11
31
33
x
yx
Câu33: Phươngtrình
2
32314.350
xx x
x
cótấtcảbaonhiêunghiệmkhôngâm?
A.
1. B. 2. C.
0.
D.
3.
Hướngdẫngiải
2
3 2314.350
xx x
x
2
312314.340
xxx
x
3131 2 4310
xx x
x
325310
xx
x
3250
x
x
Xéthàmsố
325
x
f
xx
,tacó :
10f
.
'3ln320;
x
fx x
.Dođóhàmsố
f
x
đồngbiếntrên
.
Vậynghiệmduynhấtcủaphươngtrìnhlà
1
x
BÌNHLUẬN
Cóthểđặt
30
x
t
sauđótínhdeltatheo
x
Câu34: Gọi
12
,
x
x
làhainghiệmcủaphươngtrình
22
22
21 22
43
22 2 21
xx
xx
.Khiđó,tổng
hainghiệmbằng?
A.
0.
B.
2.
C.
2.
D.
1.
Hướngdẫngiải
22 2 2
222 2
21 22 21 21
431 1
2 2 2 2 1 8.2 2 4.2 4.2 1
xx x x
xxx x

Đặt
2
1
22
x
tt
,phươngtrìnhtrêntươngđươngvới
22 2
8441610310tt t t t t t
vì
2t
.Từđósuyra
2
12
1
22
310
log
2
2310
310
log
2
x
x
x
Vậytổnghainghiệmbằng
0
.
Câu35: Với giá trị của tham số
m
thìphươngtrình
116 2 2 3 4 6 5 0
xx
mmm
cóhai
nghiệmtráidấu?
A.
41.m
B.Khôngtồntại
m
.C.
3
1
2
m
. D.
5
1
6
m
.
Hướngdẫngiải
Đặt
40
x
t
.Phươngtrìnhđãchotrởthành:
2
1223650.
ft
mt mtm
*
Yêucầubàitoán
*
cóhainghiệm
12
, tt
thỏamãn
12
01tt
10 10
110 13120 4 1.
16 5 0 16 5 0
mm
mf m m m
mm mm
BÌNHLUẬN
Tìmmốiquanhệnghiệmgiữabiếncũvàmới,do
4
4
4log
01log0
x
txt
tt
nên
12
01tt
thì
phươngtrìnhcóhainghiệmtráidấu.
Câu36: Vớigiátrịnàocủathamsố
m
thìphươngtrình
1
4.220
xx
mm
cóhainghiệm
12
,
x
x
thoảmãn
12
3xx
?
A.
4m
. B.
2m
. C.
1m
. D.
3m
.
Hướngdẫngiải
Tacó:
2
1
4 .2 2 0 2 2 .2 2 0 *
xx x x
mm mm
Phươngtrình
*
làphươngtrìnhbậchaiẩn
2
x
có:
2
2
'22mmmm
.
Phươngtrình
*
cónghiệm
2
2
20 20
0
m
mm mm
m

ÁpdụngđịnhlýVi‐éttacó:
12 12
2.2 2 2 2
xx xx
mm
Dođó
3
12
322 4xx m m
.
Thửlạitađược
4m thỏamãn.ChọnA.
BÌNHLUẬN
Dophươngtrình
*
làphươngtrìnhbậchaiẩn
20
x
cóthểcónghiệm
20
x
vôlí
nên
khigiảirathamsố
4m
thìphảithửlại.
Câu37: CHUYÊN VINH –L2Tìmtấtcảcácgiátrịcủathamsố
m
đểhàmsố
2
33
1
log 4log 3
y
mx xm
xácđịnhtrênkhoảng
0;
.
A.
;4 1;m
. B.
1;m
.
C.
4;1m
.
D.
1;m
.
Hướngdẫngiải
ChọnA.
Đặt
3
logtx
,khiđó
0;
x
t
.
2
33
1
log 4log 3
y
mx xm
trởthành
2
1
43
y
mt t m
.
Hàmsố
2
33
1
log 4log 3
y
mx xm
xácđịnhtrênkhoảng
0;
khivàchỉkhihàmsố
2
1
43
y
mt t m
xácđịnhtrên
2
430mt t mvônghiệm
2
430 41mm m m
.
Câu38: CHUYÊN VINH –L2Tìmtấtcảcácgiátrịcủathamsố
m đểphươngtrình
3
2
log 1
x
m
x
cóhainghiệmphânbiệt.
A.
01 m
. B.
1m
. C.Khôngtồntạim . D.
10m
.
Hướngdẫngiải
ChọnB.
Điềukiện:
10 1
11 0
xx
xx
Xét hàm số
2
33
22
;1 0,1;00:
log 1 1 .ln 3.log 1
fx x f x x
xxx
Bảngbiếnthiên
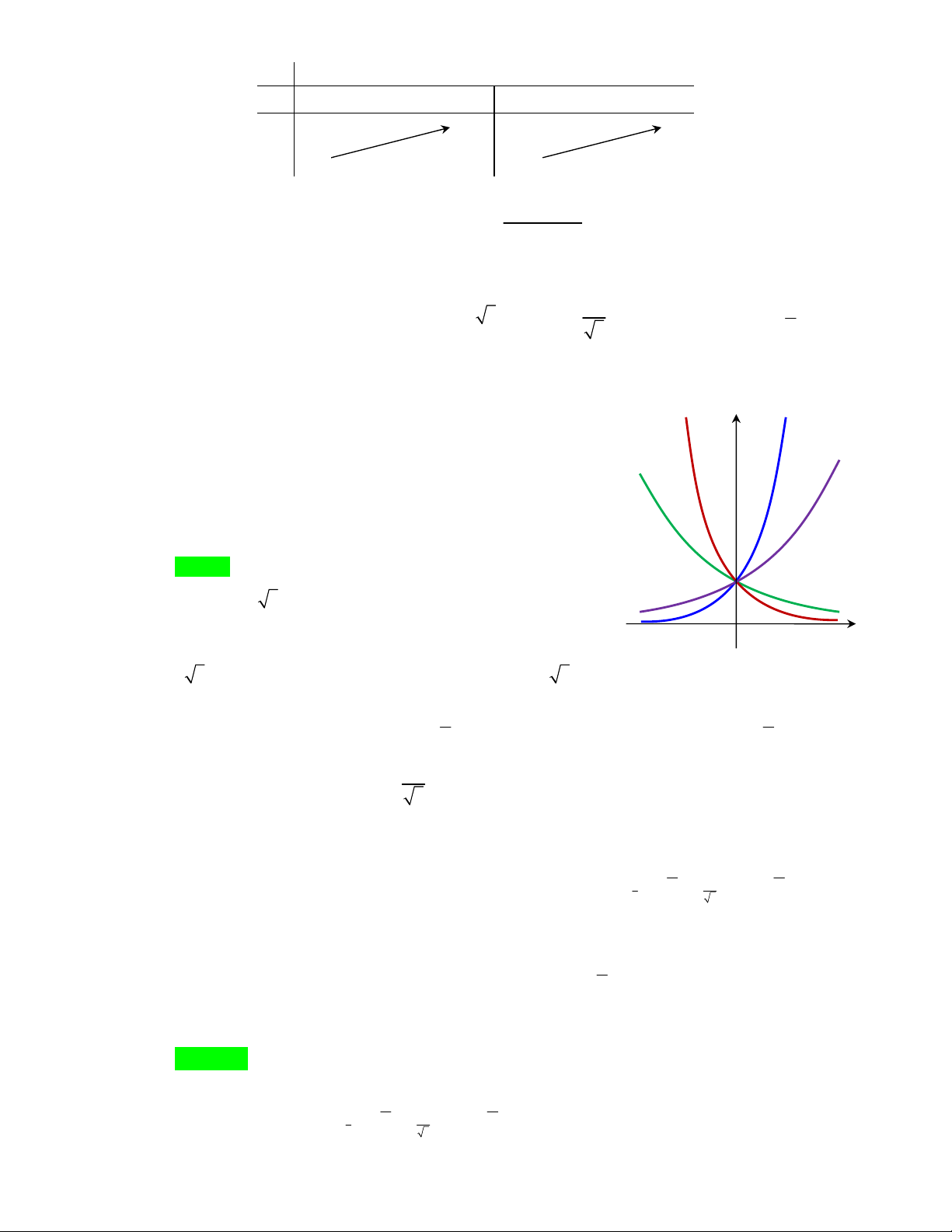
O
x
y
1
C
3
C
4
C
Từbảngbiếnthiênsuyraphươngtrình
3
2
log 1
x
m
x
cóhainghiệmphânbiệtkhivà
chỉkhi
1m
Câu39: TIÊNLÃNG–HPChobốnhàmsố
31
x
y ,
1
2
3
x
y
,
4 3
x
y
,
1
4
4
x
y
có đồ thị là
4
đườngcongtheophíatrênđồthị,thứtựtừtráiquaphảilà
1234
,,,CCCCnhưhìnhvẽbên.
Tươngứnghàmsố‐đồthịđúnglà
A.
2341
1,2,3,4CCCC.
B.
1234
1,2 ,3,4 .CCCC
C.
4132
1,2,3,4CCCC
.
D.
1234
1,2 ,3,4 .CCCC
Hướngdẫngiải
ChọnC.
Tacó
3
x
y và 4
x
y cócơsốlớnhơn1nênhàmđồng
biếnnênnhậnđồthịlà
3
C
hoặc
4
C
.Lấy
2x
tacó
2
2
34 nênđồthị
4
x
y
là
3
C vàđồthị
3
x
y là
4
C .
Tacóđồthịhàmsố
4
x
y và
1
4
x
y
đốixứngnhauqua
Oy
nênđồthị
1
4
x
y
là
2
C
.
Cònlại
1
C
làđồthịcủa
1
3
x
y
.
Vậy
4132
1,2,3,4CCCC
Câu 40: ( CHUYÊN SƠN LA – L2)
Cho phương trình
2
911
3
3
12
4log log log 0
69
xm x xm
( m
là tham số ). Tìm m để phương trình có hai nghiệm
1
x
,
2
x
thỏa mãn
12
.3xx
. Mệnh đề nào
sau đây đúng ?
A.
12m
. B.
34m
. C.
3
0
2
m
. D.
23m
.
Hướng dẫn giải
Chọn C.
Ta có:
2
911
3
3
12
4log log log 0
69
xm x xm
Đk:
0x
x
0
y
+ +
y
1
211
2
2
33
3
12
4 log log log 0
69
xm x xm
2
333
112
4log log log 0
239
xm x xm
2
33
12
log log 0 1
39
xm xm
Đặt
3
logtx
. Khi đó phương trình
1
2
12
02
39
tm tm
Phương trình đã cho có hai nghiệm
12
,xx
thỏa mãn
12
.3xx
31 2
log . 1xx
31 32 1 2
log log 1 1xxtt
(Với
131
logtx
và
232
logtx
)
Áp dụng hệ thức Vi-et cho phương trình
2
Ta có
12
12
11 1
33
b
tt m m
a
Vậy
3
0
2
m
là mệnh đề đúng.
Câu 41: (CHUYÊN LƯƠNG THẾ VINH – L2) Tìm tất cả các giá trị thực của tham số
m để phương trình
31
x
mx
có hai nghiệm phân biệt?
A.
0m
. B.
0
ln 3
m
m
. C.
2m
. D. Không tồn tại m
Hướng dẫn giải
Chọn B
Ta có: Số nghiệm của phương trình
31
x
mx
phụ thuộc vào số giao điểm của đồ
thị hàm số
3
x
y
và đường thẳng
1ymx
.
.ln3 1yx
3
x
y

Ta thấy 1ymx luôn đi qua điểm cố định
0; 1 nên
+Nếu
0m
: phương trình có nghiệm duy nhất
+ Nếu
0m
:
1ymx
là hàm nghịch biến nên có đồ thị cắt đồ thị hàm số 3
x
y
tại m
ộ
t điểm duy nhất.
+
Nếu
0m
:Để thỏa mãn ycbt thì đường thẳng
1ymx
phải khác tiếp tuyến của
đồ thị hàm s
ố
3
x
y
tại điểm
0; 1 , tức là
ln 3m
.
Vậy
0
ln 3
m
m

Chủđề3.NGUYÊNHÀM–TÍCHPHÂN‐ỨNGDỤNG
Câu1: (SGD VĨNH PHÚC)Gọi
St là diện tích hình phẳng giới hạn bởi cácđường
2
1
12
y
xx
,
0y
,
0x
,
( 0)xtt
.Tìm
lim .
t
St
A.
1
ln 2
2
. B.
1
ln 2
2
. C.
1
ln 2
2
. D.
1
ln 2
2
.
Hướngdẫngiải
ChọnB.
Cách1:
*Tìm
,,abc
saocho
2
2
1
1( 2)
12
abxc
xx
xx
2
12 1ax bx c x
22
144ax a x a bx bx cx c
2
144abx abcx ac
01
401
41 3
ab a
abc b
ac c
.
*Vìtrên
0;t
,
2
1
0
12
y
xx
nêntacó:
Diệntíchhìnhphẳng:
22
00
113
dd
1
12 2
tt
x
St x x
x
xx x
2
0
0
11 1 11
dln
12 22
2
t
t
x
x
xx xx
x
11 1
ln ln 2
22 2
t
tt
.
*Vì
11
lim 1 lim ln 0
22
tt
tt
tt
và
1
lim 0
2
t
t
Nê
n
1111
lim lim ln ln 2 ln 2
22 2 2
tt
t
St
tt
.
Cách2:DùngMáytínhcầmtay.
BÀI TOÁN VẬN DỤNG (8 - 9 - 10)
_______________________________

Diệntíchhìnhphẳng:
2
0
1
d
12
t
St x
xx
Cho
100t
tabấmmáy
100
2
0
1
d 0,193
12
x
xx
Dùngmáytínhkiểmtra4kếtquảtađượcđápánB.
Câu2: (NGUYỄNKHUYẾNTPHCM)Chocáctíchphân
0
1
1tan
Idx
x
và
0
sin
cos sin
x
J
dx
x
x
với
0;
4
,khẳngđịnhsailà
A.
0
cos
cos sin
x
Idx
x
x
. B. ln sin osIJ c
.
C.
ln 1 tanI
. D.
IJ
.
Hướngdẫngiải
ChọnC
Tacó
11cos
sin
1 tan cos sin
1
cos
nênAđúng.
0
00
cos sin
cos sin
ln cos sin ln cos sin
cos sin cos sin
dx x
xx
IJ dx x x
xx xx
Bđúng
0
0
IJ dxx
Dđúng.
Câu3: (NGUYỄNKHUYẾNTPHCM)Chohàmsố
3
1
48
x
f
xttdt
.Gọi ,mMlầnlượtlà
giátrịnhỏnhất,giátrịlớnnhấtcủahàmsố
f
x
trênđoạn
0;6
.Tính
M
m
.
A.18 B.12 C.16 D.9
Hướngdẫngiải
3422
1
1
48 4 43
x
x
f
xttdtttxx
,với
0x
.
24; 0 21;6fx x fx x
.
03;2 1;615ff f
.Suyra
15, 1Mm
.Suyra
16Mm
.

Đápán:C.
Câu4: (NGUYỄNKHUYẾNTPHCM)Giảsử
2017
11
1d
ab
xx
x
xx C
ab
với
,ab
là
cácsốnguyêndương.Tính
2ab
bằng:
A.
2017
. B.
2018
. C.
2019
. D.
2020
.
Hướngdẫngiải
Tacó:
2018 2019
2017 2017 2017 2018
11
1d 111d1 1 d
2018 2019
xx
x
xxx xx x x x C
Vậy 2019, 2018 2 2020ab ab.
ChọnD.
Câu5: (NGUYỄNKHUYẾNTPHCM)Cho
Fx
lànguyênhàmcủahàmsố
1
3
x
fx
e
và
1
0ln4
3
F
.Tậpnghiệm
S
củaphươngtrình
3
3ln32Fx x
là:
A.
2S
. B.
2; 2S
. C.
1; 2S
. D.
2;1S
.
Hướngdẫngiải
Tacó:
d1 1
1d ln3
33 3 3
x
x
xx
xe
Fx x x e C
ee
.
Do
1
0ln4
3
F
nên
0C
.Vậy
1
ln 3
3
x
Fx x e .
Dođó:
3ln322
x
Fx e x
ChọnA.
Câu6: (NGUYỄNKHUYẾNTPHCM)Cho
(), ()
f
xgxlàcáchàmsốliêntụctrênđoạn
2;6 và
thỏamãn
366
233
() 3; () 7; () 5f x dx f x dx g x dx
.HãytìmmệnhđềKHÔNGđúng.
A.
6
3
[3() ()] 8gx f x dx
B.
3
2
[3 ( ) 4] 5fx dx
C.
6
ln
2
[2 ( ) 1] 16
e
fx dx
D.
6
ln
3
[4 ( ) 2 ( )] 16
e
fx gxdx
Hướngdẫngiải

36 6
23 2
() () f() 10fxdx fxdx xdx
Tacó:
666
333
[3() ()] 3 () () 15 7 8g x f x dx g x dx f x dx
nên
A
đúng
333
222
[3 () 4] 3f() 4 9 4 5fx dx xdx dx
nên
B
đúng
6
ln 6 6 6
22 22
[2 ( ) 1] [2 ( ) 1] 2 f( ) 1 20 4 16
e
f x dx f x dx x dx dx
nên
C
đúng
6
ln 6 6 6
33 33
[4() 2()] [4() 2()] 4f() 2 () 28 10 18
e
fx gxdx fx gxdx xdx gxdx
Nên
D sai
Chọnđápán
D
Câu7: (NGUYỄN KHUYẾN TPHCM) Giả s ử
23 2 3 2 2
(2 5 2 4) ( )
xx
e x x x dx ax bx cx d e C
.Khiđó
abcd
bằng
A.‐2 B.3 C.2 D.5
Hướngdẫngiải
ChọnB.
Ta có
23 2 3 2 2
(2 5 2 4) ( )
xx
e x x x dx ax bx cx d e C
nên
32 2 2 2 232
32 2
32 2
()'(32)2()
2(32)(22) 2
(2 5 2 4)
xxx
x
x
ax bx cx d e C ax bx c e e ax bx cx d
ax a b x b c x c d e
xxxe
Dođó
22 1
325 1
22 2 2
24 3
aa
ab b
bc c
cd d
.Vậy
3abcd
.
Câu8: (NGUYỄN KHUYẾN TPHCM) Cho biết
5
1
() 15fxdx
. Tính giá trị của
2
0
[(5 3) 7]dxPf x
A.
15P
B.
37P
C.
27P
D.
19P
Hướngdẫngiải

Để tỉnh
P
tađặt
53
3
05
21
dt
txdx
xt
xt
nên
1555
5111
11
[ () 7]( ) [ () 7]dt () 7
33 3
11
.15 .7.(6) 19
33
dt
P
ft ft ftdt dt
chọnđápán
D
Câu9: (NGUYỄN KHU YẾN TPHCM) Cho hàm số
sin 2 cos2
f
xa xb x
thỏa mãn
'2
2
f
và
3
b
a
adx
.Tínhtổng
ab
bằng:
A.
3.
B.
4.
C.
5.
D.
8.
Hướngdẫngiải
ChọnC.
'2cos22sin2
f
xa xbx
'2221
2
faa
1
313 4
bb
a
adx dx b b
Vậy
14 5.ab
Câu10: (TRẦNHƯNGĐẠO–NB)Biếtrằng:
ln 2
0
11 5
dln2ln2ln.
21 2 3
a
x
xxbc
e
Trongđó
,,abc
lànhữngsốnguyên.Khiđó
Sabc
bằng:
A.
2
. B.
3
. C.
4
. D.
5
.
Hướngdẫngiải
ChọnC.
ln 2 ln 2 ln 2
000
11
dd d
21 21
xx
x
xxx x
ee
.
Tính
ln 2
ln 2
22
0
0
ln 2
d
22
x
xx
Tính
ln 2
0
1
d
21
x
x
e
Đặt
d
21d2d d
1
xx
t
te tex x
t
.Đổicận:
ln 2 5, 0 3
x
tx t
.

ln 2 5 5
5
3
033
1d11 5
d d ln 1 ln ln 4 ln 5 ln 2 ln 3 ln 2 ln
21 1 1 3
x
t
xttt
etttt
.
ln 2
2
0
11 5
dln2ln2ln 2,1,1
21 2 3
x
xx abc
e
Vậy
4abc
.
Câu11: (LẠNG GIANG SỐ 1) Diện tích hình phẳng giới hạn bởiđồthị
C của hàm số
2
1
43
2
yxx
vàhaitiếptuyếncủa
C xuấtpháttừ
3; 2M là
A.
8
.
3
B.
5
.
3
C.
13
.
3
D.
11
.
3
Hướngdẫngiải
ChọnA
Tacó
1
24 2
2
yxx
.
Gọi
00
;
x
y
làtọađộtiếpđiểm.Khiđó,
2
000
1
43
2
yxx
và
00
2yx x
.
Phươngtrìnhcủatiếptuyếncủa
C tạiđiểmcótọađộ
00
;
xy
là
2
0000
1
243
2
yx xx x x
Vìtiếptuyếnđiquađiểm
3; 2M
nên
0
2
0000
0
11
1
223 43
5311
2
xyx
xxxx
xyx
Diệntíchhìnhphẳngcầntìm
35
22
13
118
43 1d 43 311d
223
Sxxxxxxxx
Câu12: (LẠNG GIANG SỐ 1) Tích phân
4
0
dln2
1cos2
x
xa b
x
, với
a
,
b
là các số thực .
Tính
16 8ab
A.
4.
B.
5.
C.
2.
D.
3.
Hướngdẫngiải
ChọnA

Đặt
dd
d
1
d
tan
1cos2
2
ux
ux
x
v
vx
x
.Tacó
4
0
11 1 11111
tan tan d ln cos ln ln 2 ,
44
2 2 82 82 84 8 4
2
00
Ixx xx x ab
Dođó,
16 8 4ab
.
Câu13: (LẠNG GIANG SỐ 1) Giả sử
1
0
d3fx x
và
5
0
d9fz z
. Tổng
35
13
dd
f
tt ftt
bằng
A.
12.
B.
5.
C.
6.
D.
3.
Hướngdẫngiải
ChọnC.
Tacó
11
00
d3 d3
f
xx ftt
;
55
00
d9 d9
f
zz ftt
5135 35
0013 13
35
13
9dddd3dd
dd6.
f
tt ftt ftt ftt ftt ftt
ft t ft t
Câu14: (LẠNGGIANGSỐ1)Tíchphân
ln 2
21
0
1
d
x
x
ea
xe
eb
.Tínhtích
.ab
.
A.
1.
B.
2.
C.
6.
D.
12.
Hướngdẫngiải
ChọnB.
ln 2 ln2 ln 2 ln 2 ln 2
21
11
0000 0
1
dddd1d
x
xxx x
x
e
x
ex ex e x e x
e
ln 2
ln 2
1
0
0
11
21
22
x
x
ee ee e
1, 2 2ab ab
.
Câu15: (LÝTỰTRỌNG–TPHCM)Biết
32
3
63
3
sin 3
d3
1
x
xcd
ab
xx
với
,,,abcd
làcácsốnguyên.Tính
abcd
.
A.
28abcd
. B.
16abcd
. C.
14abcd
. D.
22abcd
.

Hướngdẫngiải
ChọnA.
63
33 3
63
66
63
33 3
1sin
sin
1sin
1
1
xx x
x
Idx dxxxxdx
xx
xx
.
Đặt
t x dt dx .Đổicận
33
33
xt
xt
.
333
63 63 6 3
333
1 sin 1 sin 1 sinI t t t dt t t tdt x x xdx
Suyra
33
33
33
22sin sinIxxdxIxxdx
.
3
x
(+)
sin
x
2
3
x
(–)
cos
x
6
x
(+)
sin
x
6(–)
cos
x
0
sin
x
32
32
3
3
3
sin3cos6sin6sin 263
27 3
Ixxxxxx x
Suyra:
27, 3, 2, 6abcd
.Vậy
28abcd
.
Câu16: (NGÔ GIA TỰ ‐ VP) Có bao nhiêu giá trị của
a
trongđoạn ;2
4
thỏa mãn
0
sin 2
d
3
13cos
a
x
x
x
.
A.
2 . B.1. C.4 . D.
3
.
Hướngdẫngiải
ChọnB.
Đặt
2
13cos 13cos 2d 3sind.txtxttxx
Đổicận:+Với
20 tx
+Với
.cos31 Aatax
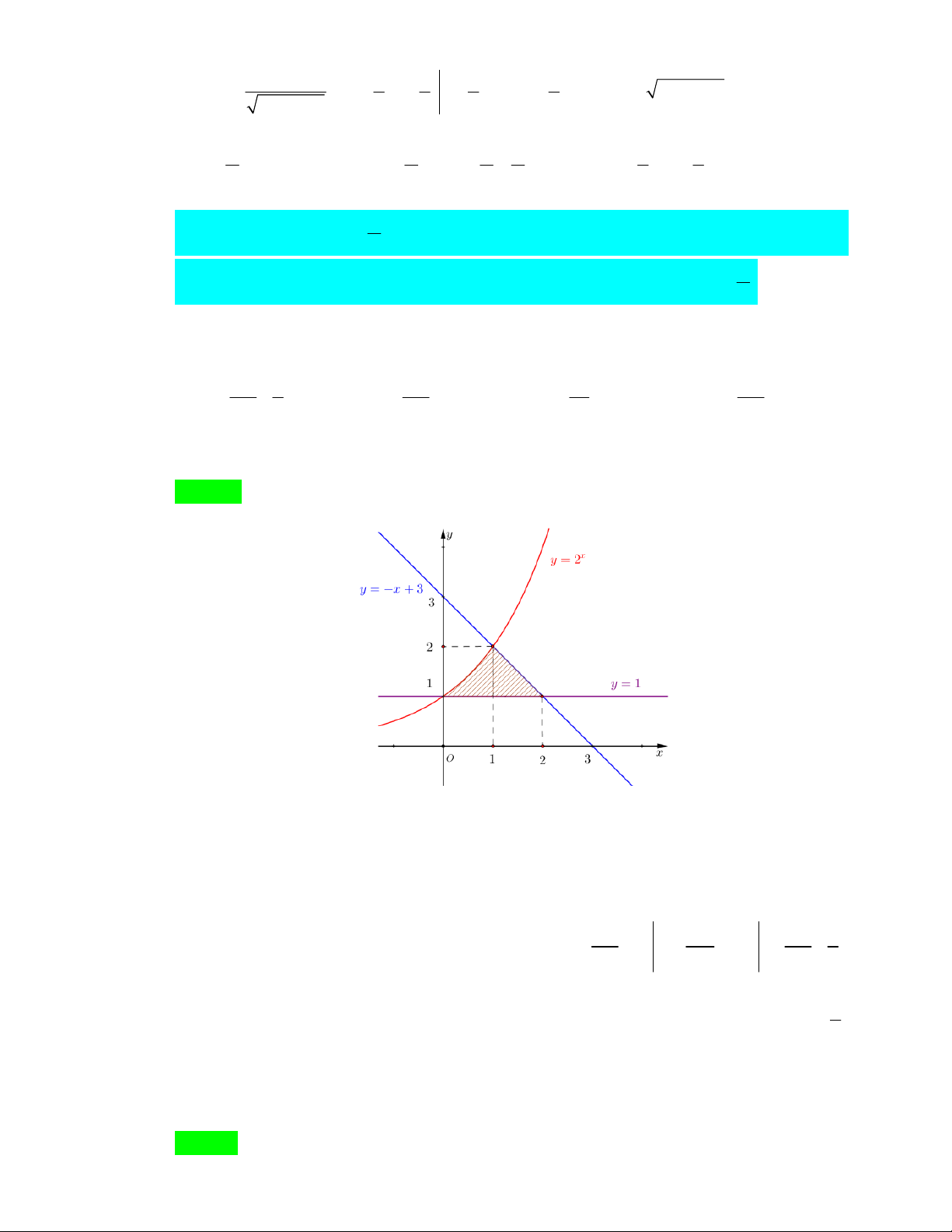
Khiđó
2
2
0
sin 2 2 2 2
dd 2 113cos1cos0
33 3 3
13cos
a
A
A
x
xtt A A a a
x
2
akk
.Do
0
13
;2 2
1
442 42
k
akk
k
.
Bìnhluận:Khicho
2
a
thìtíchphânkhôngxácđịnhvìmẫuthứckhôngxác
định(trongcănbịâm).VậyđápánphảilàB,nghĩalàchỉchấpnhận
2
a
.
Câu17: (NGÔGIATỰ‐VP)Diệntíchmiềnphẳnggiớihạnbởicácđường:
2, 3
x
yyx
và
1y
là:
A.
S
11
ln 2 2
. B.
1
1
ln 2
S
. C.
47
50
S
. D.
1
3
ln 2
S
.
Hướngdẫngiải
ChọnA.
Xétphươngtrìnhhoànhđộgiaođiểmcủacácđường.Tacó:
231
x
x
x
21 0
x
x
31 2xx
Diệntíchcầntìmlà:
12
12
2
01
01
211
21d 31d 2
ln 2 2 ln 2 2
x
x
x
Sxxxx x
Câu18: (CHUYÊNPHANBỘICHÂU)Cóbaonhiêusố
0;20
a saocho
5
0
2
sin sin 2 .
7
a
xxdx
A.
20
. B.
19
. C.
9
. D.
10
.
Hướngdẫngiải
ChọnD

Tacó
56677
0
000
222
sin sin 2 2 sin cos 2 sin sin sin sin .
777
aaa
a
x xdx x xdx xd x x a
Dođó
7
sin 1 sin 1 2
2
aaak. Vì
0;20
a
nên
1
0 2 20 10
22
kkvà
k
nêncó10giátrịcủa
k
Câu19: (THTT–477)Giátrịcủa
1
1
lim d
1
n
x
n
n
x
e
bằng
A.
1.
B.
1.
C.
.e
D.
0.
Hướngdẫngiải
ChọnD.
Tacó:
1
1
d
1
n
x
n
Ix
e
Đặt
1dd
xx
tetex .Đổicận:Khi
1
1; 1 1
nn
x
nt exn t e
Khiđó:
11
1
11
1
1
1
11
111 1
d d ln 1 ln 1 ln
11 1
nn
n
n
nn
ee
n
e
n
e
ee
e
It ttt
tt t t e
Mà
1
1
1
11
1
1
n
n
n
n
e
e
ee
e
e
khin ,Dođó,
1
lim 1 ln 0
n
I
e
Câu20: (THTT–477)Nếu
6
0
1
sin cos d
64
n
xxx
thì
n
bằng
A.
3.
B.
4.
C.
5.
D.
6.
Hướngdẫngiải
ChọnA.
Đặt
sin d cos dtxt xx
.Đổicận:khi
1
00;
62
xtx t
Khiđó:
1
1
1
1
2
2
0
0
11 1
d.
11264
n
n
n
t
Itt
nn
.
Suyra
1
11
264
n
n
cónghiệmduynhất
3n
(tínhđơnđiệu).
Câu21: (SỞ GD HÀ NỘI) Cho hàm số
32
,,, , 0yfx axbx cxdabc a
cóđồthị
C .Biếtrằngđồthị
C tiếpxúcvớiđườngthẳng
4y
tạiđiểmcóhoànhđộâmvà
đồthịhàmsố
yf
x
chobởihìnhvẽdướiđây:
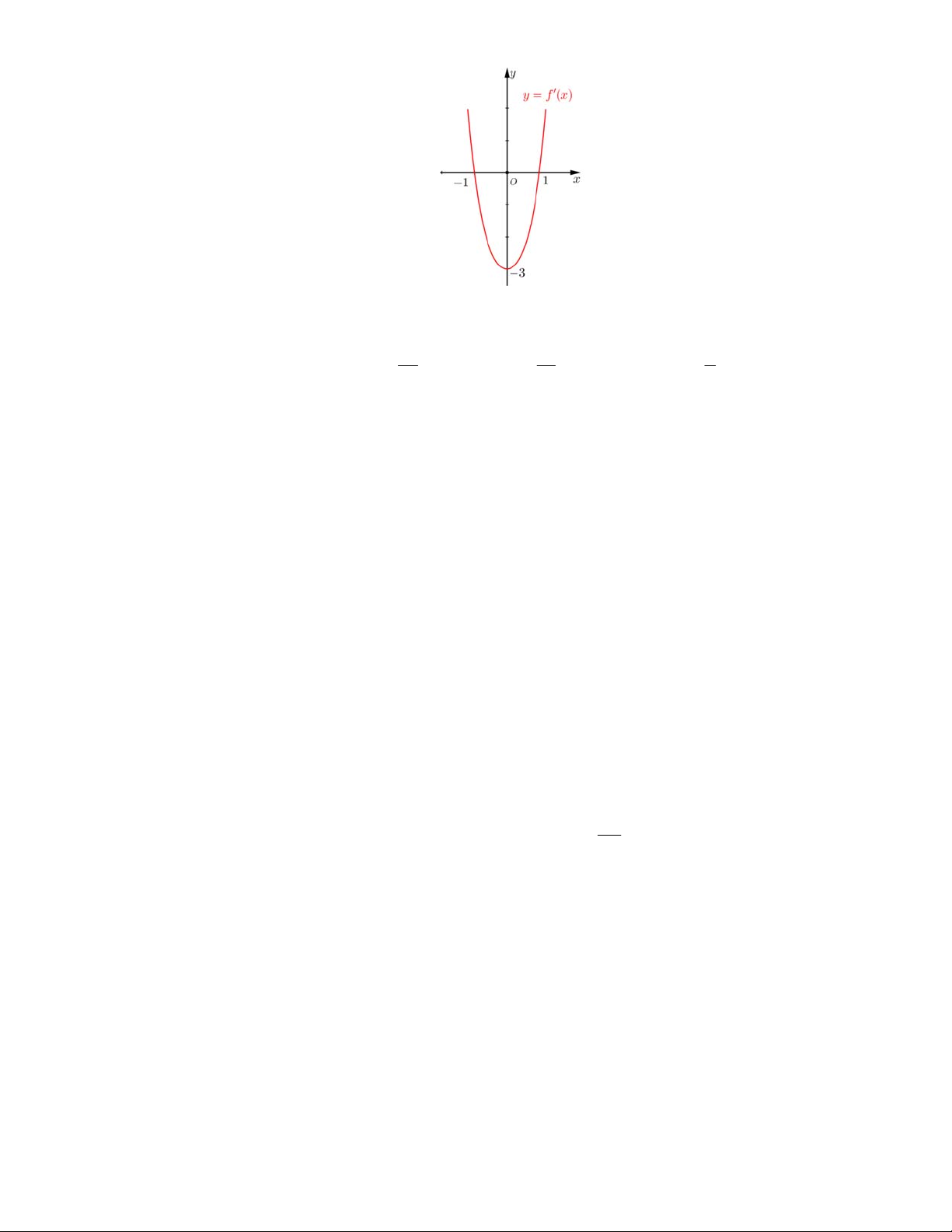
Tínhdiệntích
S
củahìnhphẳnggiớihạnbởiđồthị
C
vàtrụchoành.
A.
9S
. B.
27
4
S
. C.
21
4
. D.
5
4
.
Hướngdẫngiải
ChọnB.
Từđồthịsuyra
2
33fx x
.
23
33 3fx f xdx x dx x x C
.
Do
C
tiếp xúc vớiđường thẳng
4y
tạiđiểm có hoànhđộ
0
x
âm nên
2
00 0
03 30 1fx x x
.
Suyra
14 2fC
3
:32Cyx x
Xétphươngtrình
3
2
320
1
x
xx
x
.
Diệntíchhìnhphẳngcầntìmlà:
1
3
2
27
32
4
xxdx
.
Câu22: (SỞGDHÀNỘI)Cho
yfx
làhàmsốchẵn,cóđạohàmtrênđoạn
6;6 .
Biếtrằng
2
1
d8fx x
và
3
1
2d 3fxx
.Tính
6
1
dIfxx
A.
11.I
B.
5.I
C.
2.I
D.
14.I
Hướngdẫngiải
ChọnD.
Vì
fx
làhàmsốchẵnnên
22
11
d0 d d8
a
a
fx x fx x fx x

33
11
2d 2d 3fxxfxx
Xéttíchphân
3
1
2d 3Kfxx
Đặt
d
2d2dd
2
u
ux u x x
Đổicận:
12;36xux u .
66 6
22 2
11
dd3d6
22
Kfuufxx fxx
Vậy
6626
11 1 2
dddd8614.Ifxxfxxfxxfxx
Câu23: (SỞGDHÀNỘI)Biếtrằng
1
13 2
0
3 ,,
53
x
ab
e dx e e c abc
.Tính
23
bc
Ta
.
A.
6.T
B.
9.T
C.
10.T
D.
5.T
Hướngdẫngiải
ChọnC.
Đặt
2
13 13 2 3txtxtdtdx
Đổicận:+
01
x
t
+
12
x
t
12 2
222
13 22 2
111
01 1
322 2 22 2.
xttttt
edx tedt te edt tee eeee e
10
10
0
a
T
bc
nêncâuCđúng.
Câu24: (SỞGDHÀNỘI)Chohàmsố
yfx
liêntụctrênđoạn
;ab
.Gọi
D
làdiệntích
hình phẳng giới hạn bởiđồthị
:Cyfx
, trục hoành, haiđường thẳng
x
a
,
x
b
(nhưhìnhvẽdướiđây).
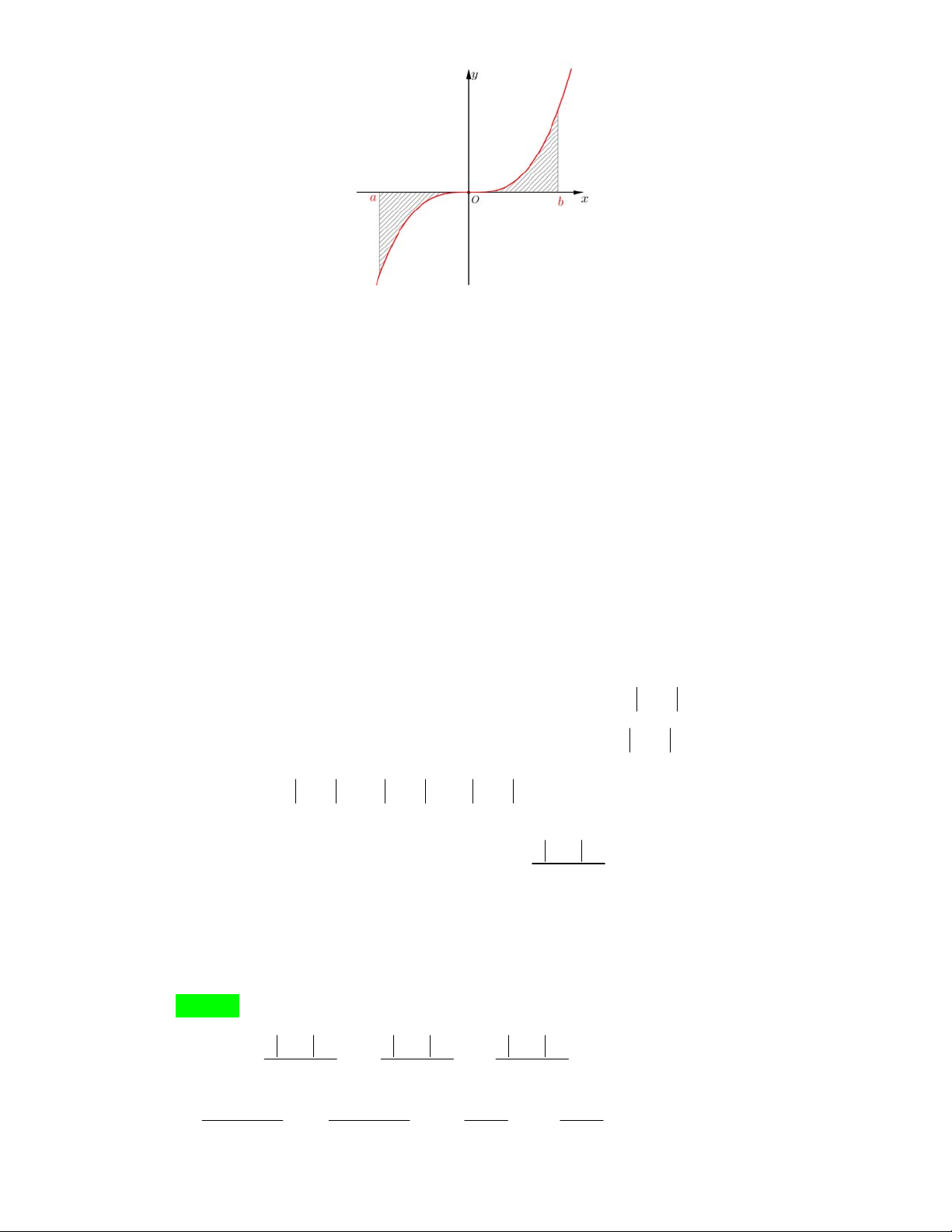
Giảsử
D
S
làdiệntíchhìnhphẳng
D
.ChọncôngthứcđúngtrongcácphươngánA,B,
C,Dchodướiđây?
A.
0
0
dd
b
D
a
Sfxxfxx
. B.
0
0
dd
b
D
a
Sfxxfxx
.
C.
0
0
dd
b
D
a
Sfxxfxx
. D.
0
0
dd
b
D
a
Sfxxfxx
.
Hướngdẫngiải
ChọnB.
+Nhìnđồthịtathấy:
Đồthị
()C
cắttrụchoànhtại
0;0O
Trênđoạn
;0a
,đồthị
()C
ởdướitrụchoànhnên
fx fx
Trênđoạn
0;b
,đồthị
C
ởtrêntrụchoànhnên
fx fx
+Dođó:
00
00
ddd dd
bb b
D
aa a
S fxx fxx fxx fxx fxx
Câu25: (CHUYÊNHÙNGVƯƠNG–GL)Biết
5
1
221
4ln2ln5
x
Idxab
x
,với
,ab
là
cácsốnguyên.Tính
.Sab
A.
9.S
B.
11.S
C.
5.S
D.
3.S
Hướngdẫngiải
ChọnB.
Tacó:
525
112
221 221 221
ddd
xxx
Ixxx
xxx
25
25
12
12
22 1 2 2 1
52 2 3
xx
xx
dx dx dx dx
xxxx
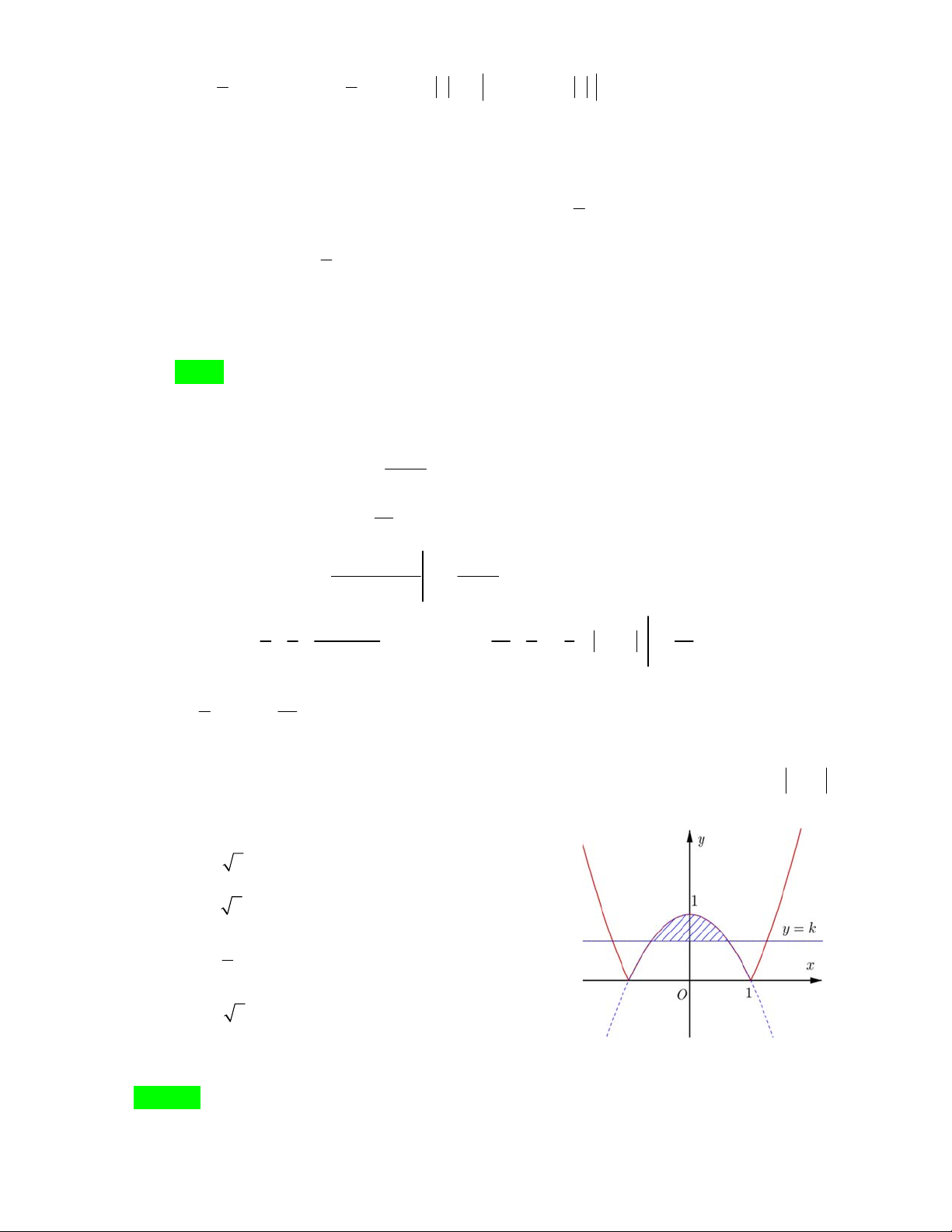
25 2 5
12
12
53
2 5ln 2 3lnxdx dx x x x x
xx
8ln2 3ln5 4
8
11.
3
a
ab
b
Câu26: (BIÊNHÒA–HÀNAM)Biết
4
0
ln 2 1 d ln 3 ,
a
Ix x x c
b
trongđó
, , abc
làcácsố
nguyêndươngvà
b
c
làphânsốtốigiản.Tính
.Sabc
A.
60.S
B.
70.S
C.
72.S
D.
68.S
Hướngdẫngiải
ChọnB.
Tacó
4
0
ln 2 1 dIx x x
Đặt
2
2
ud
ln 2 1
21
dd
2
dx
ux
x
x
vxx
v
4
2
44
2
00
0
ln 2 1
ln 2 1
221
xx
x
Ix xdx dx
x
4
4
2
0
0
11 11 63
8ln9 16ln3 ln 2 1 ln3 3
2442 1 4 4 8 4
xx
dx x x
x
63
63
ln 3 ln 3 3 4 70
4
3
a
a
cbS
b
c
.
Câu27: (PHANĐÌNHPHÙNG–HN)Chohìnhphẳng
H
giớihạnbởicácđường
2
1yx
và
,0 1.yk k
Tìm
k
đểdiệntíchcủahìnhphẳng
H
gấphailầndiệntíchhìnhphẳng
đượckẻsọctronghìnhvẽbên.
A.
3
4.k
B.
3
21.k
C.
1
.
2
k
D.
3
41.k
Hướngdẫngiải
ChọnD.
Dođồthịnhậntrục
Oy
làmtrụcđốixứngnênyêucầubàitoántrởthành:
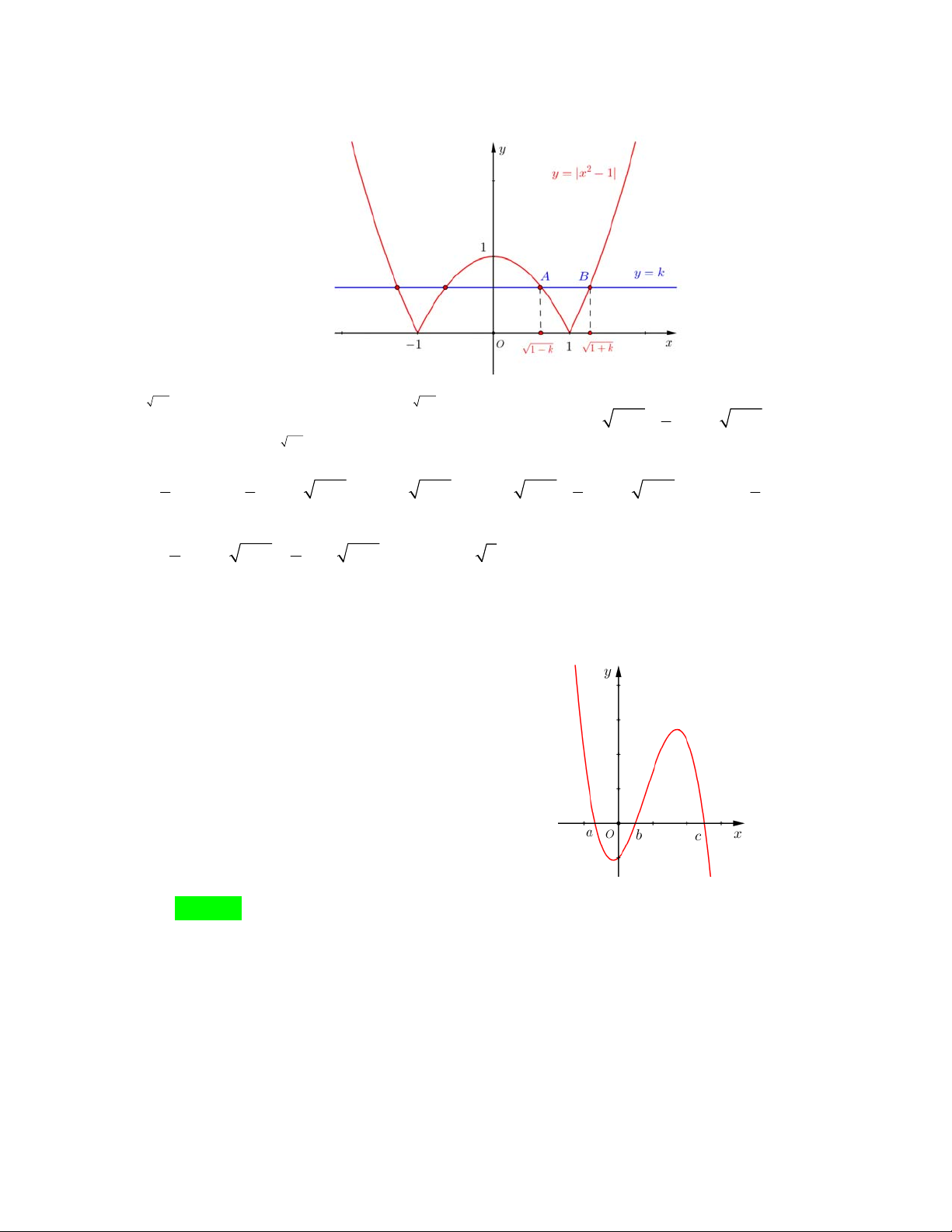
Diệntíchhìnhphẳnggiớihạnbởi
2
1, ,0yxykx
bằngdiệntíchhìnhphẳnggiới
hạnbởi:
22
1, 1, ,0.yxyxykx
111
222
01
1
1
1d 1d 1d1111
3
kk
k
xkx k xx kx x k k k k
11 1 1
1 111111 111
33 3 3
k kkkkkk kkk
24
11
33
kk
3
12k
3
41.k
Câu28: (CHUYÊNTHÁIBÌNH)Chohàmsố
()yfx
cóđồthị
()yfx
cắttrụcOxtạiba
điểmcóhoànhđộ
abc
nhưhìnhvẽ.Mệnhđềnàodướiđâylàđúng?
A.
() () ().fc fa fb
B.
() () ().fc fb fa
C.
() () ().fa fb fc
D.
() () ().fb fa fc
Hướngdẫngiải
ChọnA.
Đồthịcủahàms ố
()yfx
liêntụctrêncác
đoạn
;ab
và
;bc
, lại có
()fx
là một
nguyênhàmcủa
()fx
.
Dođódiệntíchcủahìnhphẳnggiớihạnbởicácđường:
()
0
yfx
y
xa
xb
là:

1
()d ()d
bb
b
a
aa
Sfxx fxxfxfafb
.
Vì
1
0Sfafb
1
Tươngtự:diệntíchcủahìnhphẳnggiớihạnbởicácđường:
()
0
yfx
y
xb
xc
là:
2
()d ()d
cc
c
b
bb
Sfxxfxxfxfcfb
.
2
0Sfcfb
2
.
Mặt khác, dựa vào hình vẽ ta có:
12
S S fa fb fc fb fa fc
3
.
Từ(1),(2)và(3)tachọnđápánA.
(cóthểsosánh
fa
với
fb
dựavàodấucủa
()fx
trênđoạn
;ab
vàsosánh
fb
với
fc
dựavàodấucủa
()fx
trênđoạn
;bc
).
Câu29: Chotamgiácđều
ABC
códiệntíchbằng
3
quayxungquanhcạnh
AC
củanó.Tính
thểtích
V
củakhốitrònxoayđượctạothành.
A.
2.V p=
B.
.V p=
C.
7
.
4
V p=
D.
7
.
8
V p=
Hướngdẫngiải
ĐápánA
32
ABC
SABBCCA= = ==
.Chọnhệtrụcvuônggóc
Oxy
sao cho
()()
()
0;0, 1;0, 0; 3OAB-
với
O
là trungđiểm
AC
.
Phươngtrìnhđường thẳng
AB
là
()
31yx=-
,thể tíchkhối
trònxoaykhiquay
ABO
quanhtrục
AC
(trùng
Ox
)tínhbởi
()
1
0
31Vxdxpp
¢
=-=
ò
. Vậy thể tích cần tìm
22VV p
¢
==
.

Câu30: Trongcácsốdướiđây,sốnàoghigiátrịcủa
2
1
2
2.cos
d
12
x
x
x
x
p
p
-
-
+
ò
A.
1
2
. B.0. C.2. D.1.
Hướngdẫngiải
ChọnA.
Tacó:
() ()
()
22 2
1
00
2
2 cos 2 cos 2 cos
ddd1
12
12.2 12.2
xxx
x
xx
xx x
xxx
pp p
p
-
-
-
=-
+
++
òòò
Đặt
xt=-
tacó
0x =
thì
0, x
2
==-t
p
thì
2
t
p
=
và
ddxt=-
()
()
()
()
() ()
22 2 2
00 0 0
2cos
2 cos cos cos
dd dd
1 2 .2 1 2 .2 1 2 .2 1 2 .2
t
x
xt tx
t
xtx
xttx
pp p p
-
-
-
= - =- =-
++ + +
òò ò ò
Thayvào(1)có
() ()
22 2
1
00
2
2 cos 2 cos cos
dd
12
12.2 12.2
-
-
=+
+
++
òòò
xx
x
xx
xxx
xxdx
pp p
p
()
()
22
2
000
12cos
cos sin 1
dd
222
12.2
+
====
+
òò
x
x
x
xx
xx
pp
p
Vậy
2
1
2
2 cosx 1
d
2
12
x
x
x
p
p
-
-
=
+
ò
Câu31: ( CHUYÊNQUANGTRUNGLẦN 3)Cho
f
,
g
làhaihàmliêntụctrên
1; 3
thỏa:
3
1
3d10fx gx x
.
3
1
2d6fx gx x
.Tính
3
1
d
f
xgx x
.
A.8. B.9. C.6. D.7.
Hướngdẫngiải
ChọnC.
Tacó
333
111
3d10 d3 d10f x gx x f x x gx x
.
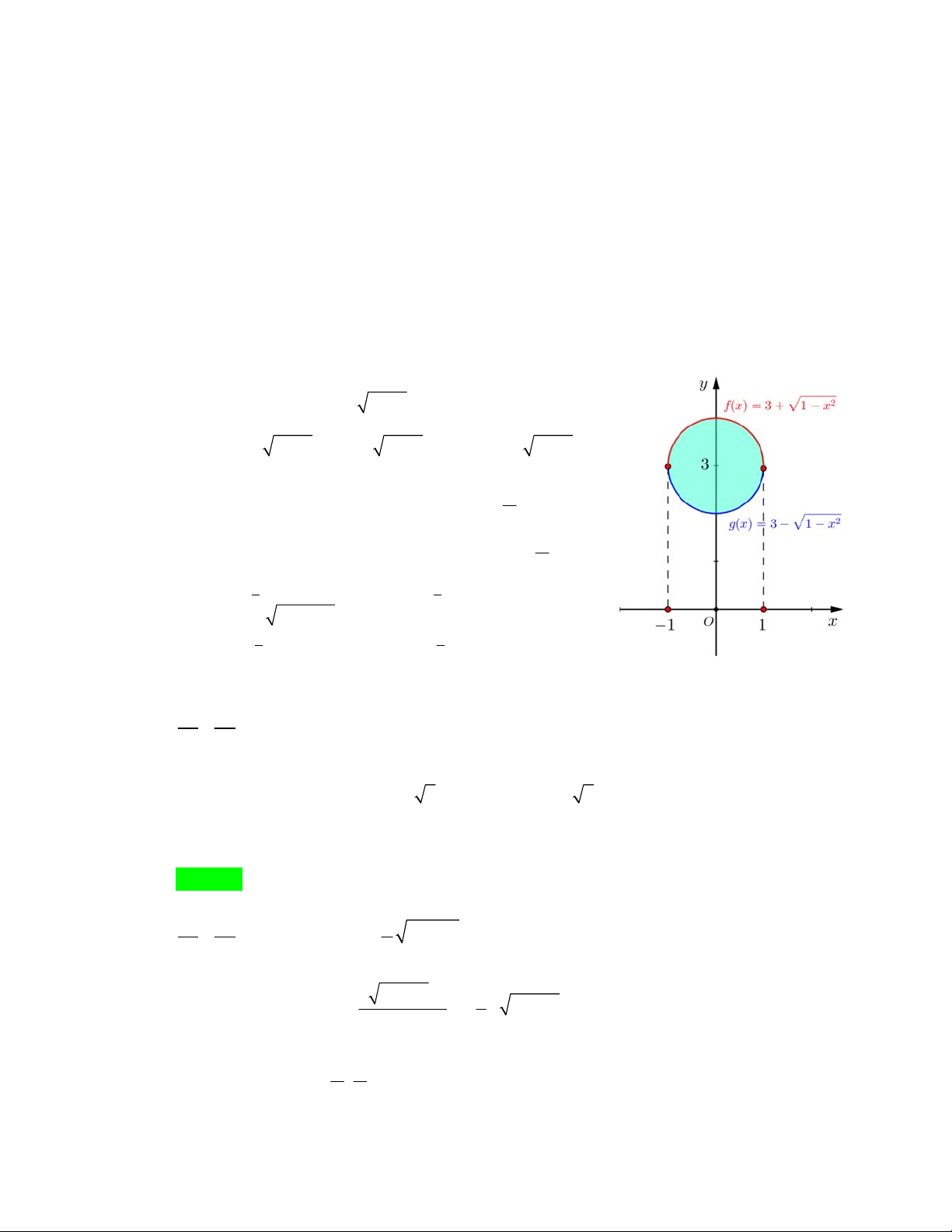
Tươngtự
333
111
2d62dd6f x gx x f x x gx x
.
Xéthệphươngtrình
310 4
26 2
uv u
uv v
,trongđó
3
1
dufxx
,
3
1
dvgxx
.
Khiđó
333
111
ddd426f x gx x f x x gx x
.
Câu32: (PHANĐÌNHPHÙNG) Thểtích
V
củakhốitrònxoayđượcsinhra khi quayhình
phẳnggiớihạnbởiđườngtròn
22
(): ( 3) 1Cx y
xungquanhtrụchoànhlà
A.
6V
. B.
3
6V
. C.
2
3V
. D.
2
6V
.
Hướngdẫngiải
ChọnD.
22 2
(3)1 31xy y x
.
11
22
22 2
11
31 31 12 1
Vxxdxxdx
.
Đặt
sin cos .xtdx tdt
.Với
1
2
11
2
xt
xt
.
22
222
22
12 1 sin .cos 12 cos 6Vttdttdt
.
Câu33: (CHUYÊNĐHKHTNHUẾ)Trongmặtphẳngtọađộ
Oxyz
cho
E
cóphươngtrình
22
22
1, , 0
xy
ab
ab
vàđườngtròn
22
:7.
Cx y
Đểdiệntíchelip
E
gấp7lần
diệntíchhìnhtròn
C
khiđó
A.
7ab
. B.
77ab
. C.
7ab
. D.
49ab
.
Hướngdẫngiải
ChọnD.
22
22
22
1, , 0
xy b
ab y a x
a
ab
.
Diệntích
E
là
d
d
22
22
00
44
aa
E
ba x x b
Saxx
aa
Đặt
tt d tdt
sin , ; cos
22
xa xa
.

Đổicận:
tt
00;
2
xxa
a.costdt 1+cos2tdt
22
00
42
aa
E
b
Sabab
a
Màtacó
2
.7.
C
S π R π
Theogiảthiếttacó
7. 49 49.
EC
S S ab ab
Câu34: (CHUYÊNĐHKHTNHUẾ)Giảsửtíchphân
1
2017
0
.ln 2 1 d ln3
b
xx xa
c
.Vớiphân
số
b
c
tốigiản.Lúcđó
A.
6057.bc
B.
6059.bc
C.
6058.bc
D.
6056.bc
Hướngdẫngiải
ChọnB.
Tacó
11
2017
00
.ln 2 1 d 2017 .ln 2 1 dIx x x x x x
.
Đặt
2
2
dd
ln 2 1
21
1
dd
28
ux
ux
x
x
vxx
v
Dođó
1
11
22
00
0
112
.ln 2 1 d ln 2 1 d
28 2821
xx
x
xx x x
x
1
2
0
33
ln 3 ln 3
848
xx
1
2017
0
3 6051
.ln 2 1 d 2017 ln 3 ln3.
88
Ix x x
Khiđó
6059.bc
Câu35: (NGÔQUYỀN–HP)Gọi
S
làdiệntíchhìnhphẳnggiớihạnbởicácđường
2
2,my x
2
1
,
2
mx y
0m
.Tìmgiátrịcủam để
3S
.
A.
3
.
2
m
B.
2.m
C.
3.m
D.
1
.
2
m
Hướngdẫngiải
ChọnA.
Tacó
22
1
20
2
my x y x
m
(do
0m
).
và
22
20
1
2
2
20
ymx
mx y y mx
ymx
.
Xétphươngtrìnhhoànhđộgiaođiểmcủa
2
2my x
và
2
1
2
mx y
tacó
22 43
0
1
22280
2
2
x
x mxx mmxxmx
xm
m
.
Khiđó
22
22
00
11
2d 2 d
22
mm
S x mx x x mx x
mm
2
32
0
122 4
.
23 3 3
m
xm m
xx
m
.
Để
2
2
493
33
342
m
Smm
(do
0m
).
Câu36: (CHUYÊNKHTNL4)Gọi
H
làphầngiaocủa
haikhối
1
4
hìnhtrụcóbánkính
a
,haitrụchình
trụvuônggócvớinhau. Xemhìnhvẽbên.Tính
thểtíchcủa
H
.
A.
3
2
3
H
a
V
. B.
3
3
4
H
a
V
.
C.
3
2
H
a
V
. D.
3
4
H
a
V
.
Hướngdẫngiải
ChọnđápánA.
Tagọitrụctọađộ
Oxyz
nhưhìnhvẽ.Khiđóphầngiao
H
làm ộtvậtthểcóđáylàmột
phầntưhìnhtròntâm
O
bánkính
a
,thiếtdi ệncủamặtphẳngvuônggócvớitrục
Ox
làmột
hìnhvuôngcódiệntích
22
Sx a x
Thểtíchkhối
H
là
3
22
00
2
3
aa
x
a
Sxdx a dx
.
x
y
Câu37: (CHUYÊN KHTNL4) Với các số nguyên
,ab
thỏa mãn
2
1
3
21lnd ln
2
xxxa b
.
Tínhtổng
Pab
.
A.
27P
. B.
28P
. C.
60P
. D.
61P
.
Hướngdẫngiải
ChọnC.
Đặt
ln
d21d
ux
vx x
tacó
2
1
ddux
x
vx x
22
222
1
11
2
2
2
1
1
1
21lnd ln .d
33
6ln2 1 d 6ln2 6ln2 4 4 ln64
222
xxxxxxxxx
x
x
xx x
46460Pab
.
Câu38: (CHUYÊNVINH–L2)TrongCôngviênToánhọccónhững
mảnhđất manghình dángkhácnhau.Mỗimảnhđược
trồngmộtloàihoavànóđượctạothànhbởimộttrong
nhữngđườngcongđẹp
trongtoánhọc.Ởđócómột
mảnhđất mang tên Bernoulli, nóđược tạo thành từ
đườngLemmiscatecóphươngtrìnhtronghệtọađộ
Oxy
là
22 2
16 25yx x
nhưhìnhvẽbên.
Tínhdiệntích
S
củamảnhđấtBernoullibiếtrằngmỗiđơnvịtronghệtọađộ
Oxy
tươngứngvớichiềudài
1
mét.
A.
2
125
6
Sm
B.
2
125
4
Sm
C.
2
250
3
Sm
D.
2
125
3
Sm
Hướngdẫngiải
ChọnD.
Vìtínhđốixứngtrụnêndiệntíchcủamảnhđấttươngứngvới4lầndiệntíchcủa
mảnhđấtthuộcgócphầntưthứnhấtcủahệtrụctọađộ
Oxy
.
x
y
O
a
M
H
4
K
Từgiảthuyếtbàitoán,tacó
2
1
5
4
yxx
.
Gócphầntưthứnhất
2
1
25 ; 0;5
4
yx xx
Nên
5
23
()
0
1 125 125
25 d ( )
4123
I
Sxxx Sm
Câu39: (CHUYÊN VINH – L2) Gọi
V
là thể tích khối tròn
xoaytạothànhkhiquay hìnhphẳnggiớihạnbởicác
đường
yx ,
0y
và
4x
quanh trục
Ox
.Đường
thẳng
04xa a cắtđồthị hàm
yx
tại
M
(hình vẽ bên). Gọi
1
V
là thể tích khối tròn xoay tạo
thànhkhiquaytamgiác
OMH
quanhtrục
Ox
.Biếtrằng
1
2VV
.Khiđó
A.
2a
. B.
22a
. C.
5
2
a . D.
3a
.
Hướngdẫngiải
ChọnD.
Tacó
00xx
.Khiđó
4
0
d8Vxx
Tacó
;
M
aa
Khiquaytamgiác
OMH quanhtrụcOx tạothànhhaihìnhnóncóchungđáy:
Hìnhnón
1
N
cóđỉnhlà
O
,chiềucao
1
hOKa
,bánkínhđáy
R
MK a
;
Hình nón
2
N
thứ 2 cóđỉnh là
H
, chiều cao
2
4hHK a, bán kínhđáy
R
MK a
Khiđó
22
112
11 4
33 3
VRhRha
Theođềbài
1
4
282. 3
3
VV aa
.
Câu40: (CHUYÊN VINH – L2)Gọi
H
là hình phẳng giới hạn bởiđồthị hàm số:
2
44yx x,trụctungvàtrụchoành.Xácđịnh
k
đểđườngthẳng
d
điquađiểm
0; 4A
cóhệsốgóc
k
chia
H
thànhhaiphầncódiệntíchbằngnhau.
A.
4k
. B.
8k
. C.
6k
. D.
2k
.
Hướngdẫngiải
ChọnC.
Phươngtrìnhhoànhđộgiaođiểmcủađồthịhàmsố
2
44yx xvàtrụchoànhlà:
2
440 2xx x.
O
BI
x
y
d
4
1
Diệntíchhìnhphẳng
H
giớihạnbởiđồthịhàms ố:
2
44
y
xx
,trụctungvàtrục
hoànhlà:
22
22
00
44d 44dSxx x xx x
2
3
2
0
8
24
33
x
xx
.
Phươngtrìnhđườngthẳng
d điquađiểm
0;4A
cóhệsốgóc
k códạng: 4ykx.
Gọi
B làgiaođiểmcủa
d
vàtrụchoành.Khiđó
4
;0
B
k
.
Đườngthẳng
d
chia
H
thànhhaiphầncódiệntích
bằngnhaukhi
BOI
và
14
23
OAB
SS
.
4
02
2
6
1144 6
..4.
223
OAB
k
k
k
k
SOAOB
k
.
Câu41: (CHUYÊN TUYÊN QUANG –L1) Tí nh tích phân
62
42
3
4
1
432
d34
18
xx
xabc
x
.V ới a ,
b
, c làcácsốnguyên.Khiđó
biểuthức
24
ab ccógiátrịbằng
A.
20
. B.241. C.
196
. D.
48
.
Hướngdẫngiải
ChọnB.
Tacó
62 62 62 62
42 2 2
22 22
44 4
11 11
43 1 1
d4d4d d
11 1
xx x x
x
xx xIJ
xx x
.
Tính
62
2
62
2
1
1
4d4 26224Ixx
.
Tính
62 62 62
2
22 2
22
2
4
2
11 1
2
11
11
1
dd d.
1
1
1
2
x
xx
J
xx x
x
x
x
x
x
Đặt
2
11
1d
tx dt x
xx
.Khi
10
62
2
2
xt
xt
.
Khiđó
2
2
2
0
d
2
t
J
t
.Đặt
2
2tan d 2 1 tan dtut uu
. Khi
00
2
4
tu
tu
.
Suyra
2
44
4
2
00
0
21 tan
222
du du
228
21 tan
u
Ju
u
.
Vậy
62
42
2
4
1
16
432
d163164
1
18
ab
xx
x
c
x
.
Vậy
24
241ab c .
Câu 42: (CHU VĂN AN – HN) Cho hai mặt cầu
1
S ,
2
S có cùng bán kính R thỏa mãn
tính chất: tâm của
1
S
thuộc
2
S
và ngược lại. Tính thể tích phần chung
V
của
hai khối cầu tạo bởi
1
()S
và
2
()S
.
A.
3
VR
. B.
3
2
R
V
. C.
3
5
12
R
V
. D.
3
2
5
R
V
.
Hướng dẫn giải
Chọn C
Gắn hệ trục
Oxy
như hình vẽ
Khối cầu
,SOR chứa một đường tròn lớn
là
22 2
:Cx
y
R
Dựa vào hình vẽ, thể tích cần tính là
33
22 2
2
2
5
2d2
312
R
R
R
R
x
R
VRxxRx
.
Câu 43: `(CHU VĂN AN – HN) Cho hàm số
42
3
y
xxm
có đồ thị
m
C với m là tham
số thực. Giả sử
m
C
cắt trục
Ox
tại bốn điểm phân biệt như hình vẽ :
O
R
2
R
22 2
():Cx y R
y
x
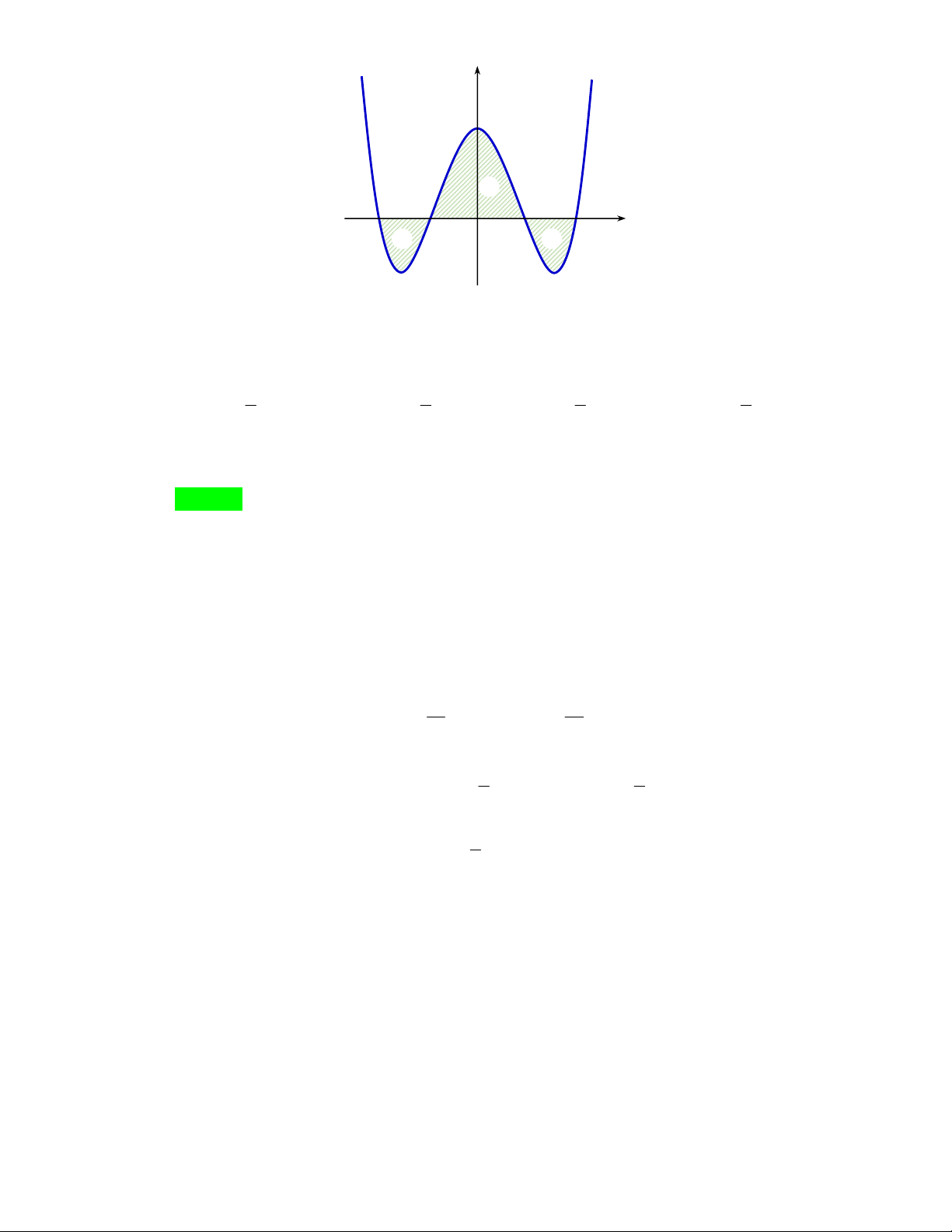
Gọi
1
S
,
2
S
và
3
S
là diện tích các miền gạch chéo được cho trên hình vẽ. Tìm m để
12 3
SS S
.
A.
5
2
m . B.
5
4
m . C.
5
2
m . D.
5
4
m .
Hướng dẫn giải
Chọn D
Giả sử
x
b
là nghiệm dương lớn nhất của phương trình
42
30xxm. Khi đó ta
có
42
30bbm
(1)
Nếu xảy ra
12 3
SS S
thì
54
42 3 2
0
3 d 0 0 0 (2) do 0
55
b
bb
xxmx bmb bm b
Từ (1) và (2), trừ vế theo vế ta được
42 2
45
2 0 (do 0)
52
bb b b .
Thay trở ngược vào (1) ta được
5
4
m .
O
x
y
3
S
1
S
2
S
m
C

Chủđề4.SỐPHỨC
Câu1: (TRẦNHƯNGĐẠO–NB)Chocácsốphức
12
,zz
khácnhauthỏamãn:
12
.zz Chọn
phươngánđúng:
A.
12
12
0
zz
zz
. B.
12
12
zz
zz
làsốphứcvớiphầnthựcvàphầnảođềukhác
0
.
C.
12
12
zz
zz
làsốthực. D.
12
12
zz
zz
làsốthuầnảo.
Hướngdẫngiải
ChọnD.
Phươngpháptựluận:
Vì
12
zz và
12
zz
nêncảhais ốphứcđềukhác
0
.Đặt
12
12
zz
w
zz
và
12
zza,ta
có
22
22
1
1
2121212
12 2
12
12
aa
zz zz z z zz
ww
aa
zz zz
zz
zz
Từđósuyra
w
làsốthuầnảo.ChọnD.
Phươngpháptrắcnghiệm:
Sốphức
12
,zz
khácnhauthỏamãn
12
zz nênchọn
12
1;zzi
,suyra
12
12
1
1
zz
i
i
zz i
làsốth
uầnảo.ChọnD.
Câu2: (TRẦNHƯNGĐẠO–NB)Chosốphức
z thỏamãnđiềukiện 34 2.zi Trong
mặtphẳng
Oxy tậphợpđiểmbiểudiễnsốphức
21wz i
làhìnhtròncódiệntích
A.
9S
. B.
12S
. C.
16S
. D.
25S
.
Hướngdẫngiải
ChọnC.
1
21
2
wi
wz iz
1
34 2 34 2 1 68 4 79 41
2
wi
zi i wii wi
Giảsử
,wxyixy
,khiđó
22
17916xy
Suyratậphợpđiểmbiểudiễnsốphức
wlàhìnhtròntâm
7; 9I ,bánkính
4.r
Vậydiệntíchcầntìmlà
2
.4 16 .S
BÀI TOÁN VẬN DỤNG (8 - 9 - 10)
_______________________________

Câu3: (TRẦNHƯNGĐẠO–NB)Trongcácsốphứcthỏamãnđiềukiện 32.ziz i
Tìmsốphứccómôđunnhỏnhất?
A.
12zi
. B.
12
55
zi
. C.
12
55
zi
. D.
12zi
.
Hướngdẫngiải
ChọnC.
Phươngpháptựluận
Giảsử
,zxyixy
222
2
32 3 21 3 2 1ziz i xy i x y i x y x y
6944214840 210 21yxy xy xy xy
2
2
22 2 2
215
21 5 41 5
555
zxy y y yy y
Suyra
min
5
5
z
khi
21
55
yx
Vậy
12
.
55
zi
Phươngpháptrắcnghiệm
Giảsử
,zxyixy
222
2
32 3 21 3 2 1ziz i xy i x y i x y x y
6944214840 210yxy xy xy
Vậytậphợpcácđiểmbiểudiễnsốphức
z
thỏađiềukiện 32ziz ilàđường
thẳng
:210dx y.
PhươngánA:
12zi
cóđiểmbiểudiễn
1; 2 dnênloạiA.
PhươngánB:
12
55
zi
cóđiểmbiểudiễn
12
;
55
d
nênloạiB.
PhươngánD:
12zi
cóđiểmbiểudiễn
1; 2 dnênloạiB.
PhươngánC:
12
55
zi
cóđiểmbiểudiễn
12
;
55
d
Câu4: (LẠNGGIANGSỐ1)Chosốphức
z
thỏamãn 338zz.Gọi
M
, m lầnlượt
giátrịlớnnhấtvànhỏnhất
.z Khiđó
M
m
bằng
A.
47.
B.
47.
C.
7.
D.
45.
Hướngdẫngiải
ChọnB.
Gọi
zxyi với ;xy .
Tacó
833332 4zzzz zz
.

Dođó 4Mmaxz.
Mà
22
22
338 3 3 8 3 3 8zz xyixyi x yx y
.
ÁpdụngbấtđẳngthứcBunhiacopxki,tacó
22 22
222222
81. 3 1. 3 1 1 3 3
x
yxy xyxy
22 22
822 2 18 22 2 1864xy xy
22 22
777xy xy z
.
Dođó
7Mminz
.
Vậy
47Mm
.
Câu5: (CHUYÊNPHANBỘICHÂU)Chosốphức
z
thỏamãn 23 1 zi.Giátrịlớnnhất
của
1zi
là
A. 13 2 . B. 4 . C.
6
. D. 13 1 .
Hướngdẫngiải
ChọnD
Gọi
zxyitacó
23 23 2 3 zixyiixyi.
Theogiảthiết
22
231xy
nênđiểm
M
biểudiễnchosốphức
z
nằmtrên
đườngtròntâm
2;3I bánkính
1R
.
Tacó
22
1111 11 zixyiix yi x y
.
Gọi
;
M
xyvà
1;1H thì
2
2
11HM x y
.
Do
M
chạytrênđườngtròn,
H
cốđịnhnên
M
H
lớnnhấtkhi
M
làgiaocủa
H
I
với
đườngtròn.
Phươngtrình
23
:
32
x
t
HI
yt
,giaocủa
H
I
vàđườngtrònứngv ới
t
thỏamãn:
22
1
941
13
tt t
nên
32 32
2;3 ,2;3
13 13 13 13
MM
.
Tínhđộdài
M
H
talấykếtquả
13 1HM
.
Câu6: (THTT–477)Cho
123
, , zzz
làcácsốphứcthỏamãn
123
0zzz
và
123
1.zzz
Khẳngđịnhnàodướiđâylàsai?
A.
333 3 3 3
123123
.zzz z z z
B.
333 3 3 3
123 1 2 3
.zzz z z z
C.
333 3 3 3
123 1 2 3
.zzz z z z
D.
333 3 3 3
123 1 2 3
.zzz z z z
Hướngdẫngiải
M
1
I
H
M
2

ChọnD.
Cách1:Tacó:
123 23 1
0zzz zz z
3
333
123 1 23 1213123 2323
33 z z z z z z zz zz z z z zz z z
333
123 123
3zzz zzz
333
123 123
3zzz zzz
.
333
123 123 123
33 3 zzz zzz zzz
Mặtkhác
123
1zzz nên
333
123
3zzz
.VậyphươngánDsai.
Cách2:thaythử
123
1zzz
vàocácđápán,thấyđápánDbịsai
Câu7: (THTT–477)Cho
123
,,zzz
làcácsốphứcthỏa
123
1.zzzKhẳngđịnhnàod ưới
đâylàđúng?
A.
123 122331
.zzz zzzzzz B.
123 122331
.zzz zzzzzz
C.
123 122331
.zzz zzzzzz
D.
123 122331
.zzz zzzzzz
Hướngdẫngiải
ChọnA.
Cách1:Kíhiệu
Re
:làphầnthựccủasốphức.
Tacó
2
123
zzz
222
123 122331
2Rezzz zzzzzz
12 23 31
32Rezz zz zz (1).
2
12 23 31
zz zz zz
222
12 23 31 1223 2331 3112
2Rezz zz zz zzzz zzzz zzzz
22 22 22 2 2 2
12 23 31 123231312
...2Rezz zz zz zzzzzzzzz
13 21 32 12 33 31
32Re 32Rezz zz zz zz zz zz (2).
Từ
1 và
2 suyra
123 122331
zzz zzzzzz .
Cáchkhác:BhoặcCđúngsuyraDđúngLoạiB,C.
Chọn
123
zzz
AđúngvàDsai
Cách2:thaythử
123
1zzz
vàocácđápán,thấyđápánDbịsai
Câu8: (THTT – 477) Cho
P
z là mộtđa thức với hệ số thực.Nếu số phức
z
thỏa mãn
0Pz thì
A.
0.Pz
B.
1
0.P
z
C.
1
0.P
z
D.
0.Pz
Hướngdẫngiải
ChọnD.
Giảsử
P
z códạng
2
01 2 012
... ; ; ;...; ; 0
n
nnn
Pz a az az az a a a a a
22
01 2 01 2
0 ... 0 ... 0
nn
nn
Pz a az az az a az az az
2
01 2
... 0 0
n
n
aazaz az Pz
Câu9: (BIÊNHÒA–HÀNAM)Chosốphức z thỏamãn
1z
.Đặt
2
2
zi
A
iz
.Mệnhđềnào
sauđâyđúng?
A. 1A . B. 1A . C. 1A . D. 1A .
Hướngdẫngiải
ChọnA.
ĐặtCó
22
,, 1aabiab a b (do 1z )
2
2
2
2
221 4 21
2
22
2
abi a b
zi
A
iz b ai
ba
Tachứngminh
2
2
2
2
421
1
2
ab
ba
.
Thậtvậytacó
2
2
22
2222
2
2
421
14 21 2 1
2
ab
ab baab
ba
Dấu“=”xảyrakhi
22
1ab .
Vậy
1A .
Câu10: (CHUYÊNĐHVINH)Chosốphức
z
thỏamãn
2
2
z
vàđiểm
A
tronghìnhvẽbên
làđiểmbiểudiễncủa
z
.Biếtrằngtronghìnhvẽbên,điểmbiểudiễncủas ốphức
1
w
iz
làmột
trongbốnđiểm
M
,
N
,
P
,Q.Khiđóđiểmbiểudiễncủasốphứcwlà
A.điểm
Q. B.điểm
M
.
C.điểm N . D.điểm
P
.
Hướngdẫngiải
Đápán:D.
Dođi ểm
A
làđiểmbiểudiễncủa
z
nằmtronggócphầntưthứnhấtcủamặtphẳng
Oxy nêngọi (, 0)zabiab .
Do
2
2
z
nên
22
2
2
ab
.
Lạicó
22 22
1 ba
wi
iz
ab ab
nênđiểmbiểudiễn wnằmtronggócphầntưthứba
củamặtphẳng
Oxy .
11
22 2
.
wzOA
iz i z
.
Vậyđiểmbiểudiễncủasốphức
wlàđiểm
P
.
O
A
Q
M
N
P
y
x

Câu11: Chosốphức
z
thỏamãn
1z
.Tìmgiátrịlớnnhấtcủabiểuthức
5
1.
i
A
z
A.
5.
B.
4.
C.
6.
D.
8.
Hướngdẫngiải
Tacó:
555
11 16.
ii
A
zz
z
Khi
6.zi A
ChọnđápánC.
Câu12: Gọi
M
làđiểmbiểudiễnsốphức
2
23
2
zzi
z
,trongđó z làsốphứcthỏamãn
23izi iz
. Gọi
N
làđiểm trong mặt phẳng sao cho
,2Ox ON
, trongđó
,Ox OM
làgóclượnggiáctạothànhkhiquaytia
Ox
tớivịtrítia
OM
.Điểm
N
nằmtrong
gócphầntưnào?
A.Gócphầntưthứ(I). B.Gócphầntưthứ(II).
C.Gócphầntưthứ(III). D.Gócphầntưthứ(IV).
Hướngdẫngiải
Tacó:
51 51 1
23 1 ;tan.
44 44 5
izi iz z i w i M
Lúcđó:
2
22
2tan 5 1 tan 12
sin 2 0; cos2 0
13 13
1tan 1tan
.
ChọnđápánA.
Câu13: Chosốphức
z
thỏamãn
1z
.Tìmgiátrịlớnnhất
max
M
vàgiátrịnhỏnhất
min
M
của
biểuthức
23
11.Mz z z
A.
max min
5; 1.MM
B.
max min
5; 2.MM
C.
max min
4; 1.MM
D.
max min
4; 2.MM
Hướngdẫngiải
Tacó:
23
115Mz z z
,khi
max
15 5.zM M
Mặt khác:
33333
3
11111
11,
22 2
1
zzzzz
Mz
z
khi
min
11 1.zMM
ChọnđápánA.
Câu14: Chosốphức z thỏa
2z
.Tìmtíchcủagiátrịlớnnhấtvànhỏnhấtcủabiểuthức
zi
P
z
.

A.
3
.
4
B.
1.
C.
2
. D.
2
.
3
Hướngdẫngiải
Tacó
13
11 .
|| 2
i
P
zz
Mặtkhác:
11
11 .
|| 2
i
zz
Vậy,giátrịnhỏnhấtcủa
P
là
1
2
,xảyrakhi 2;zi giátrịlớnnhấtcủa
P
bằng
3
2
xảy
rakhi
2.zi
ChọnđápánA.
Câu15: Gọi
1234
,
,,zzzz
làcácnghiệmcủaphươngtrình
4
1
1.
2
z
zi
Tínhgiátrịbiểuthức
2222
1234
1111Pzzzz
.
A.
2.P
B.
17
.
9
P
C.
16
.
9
P
D.
15
.
9
P
Hướngdẫngiải
Tacóphươngtrình
44
210.fz z i z
Suy ra:
1234
15fz zz zz zz zz
. Vì
2
111
.
11.
225
fi f i
zziziP
Mà
444
4
15; 3 185.fi i i f i i i
Vậytừ
17
1.
9
P
ChọnđápánB.
Câu16: Chosốphức z thỏamãn
12 3zi
.Tìmmôđunlớnnhấtcủasốphức
2.zi
A.
26 6 17 .
B.
26 6 17 .
C.
26 8 17 .
D.
26 4 17 .
Hướngdẫngiải
Gọi
;; 2 2zxyi x y z ix y i
. Ta có:
22
12 9 1 2 9zi x y
.
Đặt
13sin; 23cos; 0;2 .xty tt
2
22
2 13sin 43cos 266sin 4cos 26617sin ; .zi t t t t t
max
26 6 17 2 26 6 17 2 26 6 17 .zi zi
ChọnđápánA.
Câu17: Chosốphức z thỏamãn 1z .Tìmgiátrịlớnnhấtcủabiểuthức 131.Pz z
A.
315
B.
65
C.
20
D.
220.

Hướngdẫngiải
Gọi
;;zxyi x y .Tacó:
22 2 2
1111;1.zxyyxx
Tacó:
22
22
131 1 31 21 321Pz z xy xy x x .
Xéthàmsố
21 3 21 ; 1;1.fx x x x
Hàmsốliêntụctrên
1;1
vàvới
1;1x
tacó:
13 4
01;1.
5
21 21
fx x
xx
Tacó:
max
4
12; 16; 220 220.
5
ff f P
ChọnđápánD.
Câu18: Chosốphức
z
thỏamãn
1.z
Gọi
M
và
m
lầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏ
nhấtcủabiểuthức
2
11.Pz z z
Tínhgiátrịcủa
.Mm
.
A.
13 3
.
4
B.
39
.
4
C.
33.
D.
13
.
4
Hướngdẫngiải
Gọi
;;zxyi x y
.Tacó:
1.1zzz
Đặt
1tz
,tacó
01112 0;2.zzz t
Tacó
2
2
2
11 1. 22 .
2
t
tzzzzzzxx
Suyra
2
22 2
1.121213zz zzzzzz z x x t
.
Xéthàmsố
2
3, 0;2 .ft t t t
Bằngcáchdùngđạohàm,suyra
13 13 3
max ; min 3 . .
44
ft ft Mn
ChọnđápánA.
Câu19: Gọiđiểm
,
ABl ầnlượtbiểudiễncácsốphức z và
1
;0
2
i
zzz
trênmặtphẳng
tọađộ(
,
,ABC
và
,
,ABC
đềukhôngthẳnghàng).Với
O
làgốctọađộ,khẳngđịnhnào
sauđâyđúng?
A.Tamgiác
OAB
đều.
B.Tamgiác
OAB
vuôngcântại
.O
C.Tamgiác
OAB
vuôngcântại
.B
D.Tamgiác
OAB
vuôngcântại
.A
Hướngdẫngiải

Tacó:
11 2
;...
222
ii
OA z OB z z z z
Tacó:
11 2
..
22 2
ii
BA OA OB BA z z z z z z
Suyra:
222
OA OB AB
và
AB OB OAB
làtamgiácvuôngcântại
.B
ChọnđápánC.
Câu20: Chosốphức
z
thỏamãnđiềukiện
2
42.zz
Khẳngđịnhnàosauđâylàđúng?
A.
31 31
.
66
z
B.
51 51.z
C.
61 61.z
D.
21 21
.
33
z
Hướngdẫngiải
Ápdụngbấtđẳngthức
,uvuv
tađược
22
2
24 44 240 51.zz zzz z
22
22
24424051.zz z z z z z
Vậy,
z
nhỏnhấtlà
51,
khi
5zii
và
z
lớnnhấtlà
51,
khi
5.zii
ChọnđápánB.
Câu21: Chosốphức z thỏamãn
12 2zi
.Tìmmôđunlớnnhấtcủasốphức .z
A.
945.
B.
11 4 5
C.
645
D.
565
Hướngdẫngiải
Gọi
;;zxyi x y
.Tacó:
22
12 2 1 2 4.zi x y
Đặt
12sin; 22cos; 0;2xty tt
.
Lúc đó:
2
22
22
1 2sin 2 2cos 9 4sin 8cos 9 4 8 sin ;zt t tt t
2
945sin 945;945ztz
max
945z
đạtđượckhi
525 1045
.
55
zi
ChọnđápánA.
Câu22: Cho
,
,,ABCDlàbốnđiểmtrongmặtphẳngtọađộtheo thứtự biểudiễn cácsố
phức
1 2;1 3 ;1 3 ;1 2iiii
.Biết
A
BCD
làtứgiácnộitiếptâm
.I
Tâm
I
biểudiễnsố
phứcnàosauđây?

A.
3.z
B.
13.zi
C.
1.z
D.
1.z
Hướngdẫngiải
Ta có
A
B
biểu diễn số phức
3;i
DB
biểu diễn số phức
33i
. Mặt khác
33
3
3
i
i
i
nên
.0AB DB
.Tươngtự(hayvìlídođốixứngqua
Ox
),
.0DC AC
.Từ
đó suy ra
AD
là mộtđường kính củađường trònđi qua
,
,,.ABCD Vậy
1; 0 1.Iz
ChọnđápánC.
Câu23: Trênmặtphẳngtọađộ
,
Oxy
lấyđiểm
M
làđiểmbiểudiễnsốphức
2
24zii
vàgọi
làgóctạobởichiềudươngtrụchoànhvàvectơ
.OM
Tínhcos2 .
A.
425
.
87
B.
475
.
87
C.
475
.
87
D.
425
.
87
Hướngdẫngiải
Tacó:
2
13
2 4 16 13 16;13 tan .
16
zii iM
Tacó:
2
2
1 tan 425
cos2 .
87
1tan
ChọnđápánD.
Câu24: Cho
12
,
zz
làhaisốphứcliênhợpcủanhauvàthỏamãn
1
2
2
z
z
và
12
23.zz
Tính
môđuncủasốphức
1
.z
A.
1
5.z
B.
1
3.z
C.
1
2.z
D.
1
5
.
2
z
Hướngdẫngiải
Gọi
12
;;z a bi z a bi a b
.Khôngmấttínhtổngquáttagọi
0.b
Do
12
23 2 23 3.zz bi b
Do
12
,
zz
làhaisốphứcliênhợpcủanhaunên
12
.zz
,mà
3
3
11
1
22
2
12
.
zz
z
z
zz
Tacó:
3
3322323 2
1
22
0
33 3 0 1.
3
b
z abi a ab abbi abb a
ab
Vậy
22
1
2.zab
ChọnđápánC.
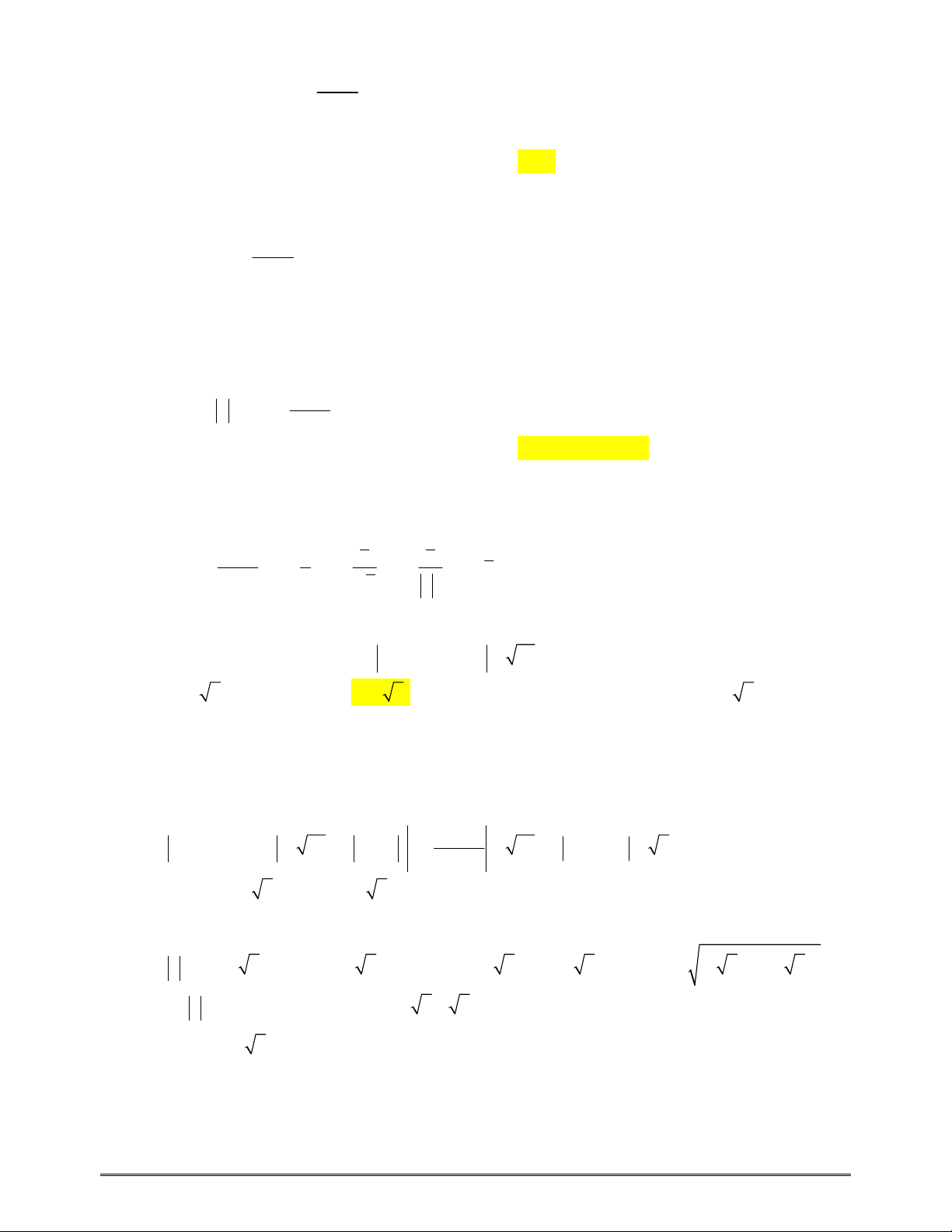
Câu25: Chosốphức
26
,
3
m
i
z
i
m nguyêndương.Cóbaonhiêugiátrị
1; 50m
đểz là
sốthuầnảo?
A.24. B.26. C.25. D.50.
Hướngdẫngiải
Tacó:
26
(2 ) 2 .
3
m
mmm
i
zii
i
z
làsốthuầnảokhivàchỉkhi
21,mk k
(do
*
0;zm
).
Vậycó25giátrị
m thỏayêucầuđềbài.
ChọnđápánC.
Câu26: Nếu
1z
thì
2
1z
z
A.lấymọigiátrịphức. B.làsốthuầnảo.
C.bằng0. D.lấymọigiátrịthực.
Hướngdẫngiải
Tacó:
2
2
11
.
zzz
zz z zz
zzzz
z
làsốthuầnảo.
ChọnđápánB.
Câu27: Chosốphức z thỏamãn
16210iz i
.Tìmmôđunlớnnhấtcủasốphức .z
A.
45
B.
35.
C.
3.
D.
35
Hướngdẫngiải
Gọi
;;zxyi x y
.
Ta có:
22
62
162101. 10 245 2 45.
1
i
iz i i z z i x y
i
Đặt
25sin;45cos; 0;2xtytt
.
Lúcđó:
22 22
2
2 5 sin 4 5 cos 25 4 5 sin 8 5 cos 25 4 5 8 5 sin ;zt t tt t
2
25 20sin 5;3 5ztz
max
35zđạtđượckhi
36.zi
ChọnđápánB.

Câu28: Gọi
,zxyixy
là số phức thỏa mãn haiđiều kiện
22
2226zz
và
33
22
zi
đạtgiátrịlớnnhất.Tínhtích
.xy
A.
9
.
4
xy
B.
13
.
2
xy
C.
16
.
9
xy
D.
9
.
2
xy
Hướngdẫngiải
Đặt
,.zxiyxy
Thayvàođiềukiệnthứnhất,tađược
22
36.xy
Đặt
3cos , 3sin .xtyt
Thayvàođiềukiệnthứhai,tacó
33
18 18sin 6.
4
22
Pz i t
Dấubằngxảyrakhi
33232
sin 1 .
4422
ttz i
ChọnđápánD.
Câu29: Cóbaonhiêusốphứcz thỏa
1
1
z
iz
và
1?
2
zi
z
A.1. B.2. C.3. D.4.
Hướngdẫngiải
Tacó:
1
3
1
1
33
2
.
42 3 3
22
2
1
2
2
z
x
ziz
xy
iz
zi
xy
zi zi z
y
z
ChọnđápánA.
Câu30: Gọiđiểm
,
AB
lầnlượtbiểudiễncácsốphức
1
z
;
212
;.0zzz
trênmặtphẳngtọa
độ(
,
,ABC
và
,
,ABC
đềukhôngthẳnghàng)và
22
1212
.zz zz .Với
O
làgốctọađộ,khẳng
địnhnàosauđâyđúng?
A.Tamgiác
OAB
đều.
B.Tamgiác
OAB
vuôngcântại
.O
C.Tamgiác
OAB
vuôngcântại
.B
D.Diệntíchtamgiác
OAB
khôngđổi.
Hướngdẫngiải
Tacó:
2
22 2
1212 1 121 1 121
.;.zzzz zzzz z zzz
.Do
2
2
121
1
0;
z
zzz
z
(1)
Mặtkhác:
2
2
1
2
1 212 1 212 12
2
.
z
z zzz z zzz zz
z
(do
2
0z
)(2)

Từ(1)và(2)suyra:
22
21
12
12
zz
zz
zz
.Vậytacó:
1221
zzzz OAOBAB
.
ChọnđápánA.
Câu31: Trongcácsốphứcthỏamãnđiềukiện
24 2zizi
.Tìmmôđunnhỏnhấtcủasố
phức
2.zi
A.
5
B.
35.
C.
32
D.
32
Hướngdẫngiải
Gọi
;;zxyi x y
.
Tacó:
22 2
2
24 2 2 4 2 40 4 .zizix y xy xy yx
Tacó:
2
22 2
22 2
2 2 6 2 12 36 2 3 18 18zi x y x x x x x
min
21832zi
khi
3.zi
ChọnđápánC.
Câu32: Tìmđiềukiệncầnvàđủvềcácsốthực
,
mn
đểphươngtrình
42
0zmzn
không
cónghiệmthực.
A.
2
40.mn
B.
2
40mn
hoặc
2
40
0
0
mn
m
n
.
C.
2
40
0.
0
mn
m
n
D.
2
40mn
hoặc
2
40
0
0
mn
m
n
.
Hướngdẫngiải
Phươngtrình
42
0zmzn
khôngcónghiệmthựctrongcáctrườnghợp:
TH1:Phươngtrìnhvônghiệm,tứclà
2
40.mn
TH2:Phươngtrình
42 2
0;tmtn tz
cóhainghiệmâm
2
040
00.
00
mn
Sm
Pn
ChọnđápánD.
Câu33: Nếu
;0zaa
thì
2
za
z
A.lấymọigiátrịphức. B.làsốthuầnảo.
C.bằng0. D.lấymọigiátrịthực.
Hướngdẫngiải

Tacó:
22 2 2
2
.
za a az az
zz z zz
zzzz
z
làsốthuầnảo.
ChọnđápánB.
Câu34:
Chosốphức
z
thỏamãn
12 3zi
.Tìmmôđunnhỏnhấtcủasốphức
1.zi
A.
4.
B.22. C.
2.
D. 2.
Hướngdẫngiải
Gọi
;; 1 11zxyi x y z i x y i
. Ta có:
22
12 9 1 2 9zi x y
.
Đặt
13sin; 23cos; 0;2 .xty tt
2
22
min
13sin13cos106cos2241 2zi t t t zi zi
, khi
1.zi
ChọnđápánC.
Câu35: Gọi
M
làđiểmbiểudiễnsốphức
2
21zz i
zi
,trongđó z làsốphứcthỏamãn
12izi iz
. Gọi
N
làđiểm trong mặt phẳng sao cho
,2Ox ON
, trongđó
,Ox OM
làgóclượnggiáctạothànhkhiquaytia
Ox
tớivịtrítia
OM
.Điểm
N
nằmtrong
gócphầntưnào?
A.Gócphầntưthứ(I). B.Gócphầntưthứ(II).
C.Gócphầntưthứ(III). D.Gócphầntưthứ(IV).
Hướngdẫngiải
Tacó:
7 19 7 19 19
12 3 ;tan.
82 82 82 82 7
izi iz z i w i M
Lúcđó:
2
22
2tan 133 1 tan 156
sin 2 0; cos 2 0
205 205
1 tan 1 tan
.
ChọnđápánC.
Câu36: Biết số phức z thỏa mãnđồng thời haiđiều kiện
34 5zi
và biểu thức
22
2Mz zi
đạtgiátrịlớnnhất.Tínhmôđuncủasốphức
.zi
A.
241zi
B.
35.zi
C.
52zi
D.
41.zi
Hướngdẫngiải

Gọi
;;zxyi x y
.Ta có:
22
34 5 : 3 4 5zi Cx y
: tâm
3;4I
và
5.R
Mặt khác:
22 2 2
22
2 2 1 423 :423 0.Mz zi x y x y x y dx y M
Dosốphức
z thỏamãnđồngthờihaiđiềukiệnnên
d
và
C cóđiểmchung
23
; 5 23 10 13 33
25
M
dId R M M
22
max
42300
5
33 5 4 41.
5
345
xy
x
Mziizi
y
xy
ChọnđápánD.
Câu37: Cácđiểm
,
,ABC
và
,
,ABC
lầnlượtbiểudiễncácsốphức
123
,
,zzz
và
123
,
,zzz
trên mặt phẳng tọađộ(
,
,ABC
và
,
,ABC
đều không thẳng hàng). Biết
123 123
zzz zzz
,khẳngđịnhnàosauđâyđúng?
A.Haitamgiác
ABC
và
ABC
bằngnhau.
B.Haitamgiác
ABC
và
ABC
cócùngtrựctâm.
C.Haitamgiác
ABC
và
ABC
cócùngtrọngtâm.
D.Haitamgiác
ABC
và
ABC
cócùngtâmđườngtrònngoạitiếp.
Hướngdẫngiải
Gọi
111222333
;;;;;1;3
kk
zxyizxyizxyixy k
.
Khiđó:
11 22 33
;; ;; ;Ax y Bx y Cx y
, gọi
G
là trọng tâm
123123
;.
33
xxxyyy
ABC G
Tươngtự,gọi
111222333
;;;;;1;3
kk
zxyizxyizxyixy k
.
Khiđó:
11 22 33
;; ;; ;Axy Bxy Cxy
,
gọi
G
làtrọngtâm
123123
;.
33
xxxyyy
ABC G
Do
123123 123 123 123 123
zzz zzz xxx yyyi xxx yyyi
123 123
123 123
.
xxx xxx
GG
yyy yyy
ChọnđápánC.
Câu38: Trênmặtphẳngtọađộ
,
Oxy
lấyđiểm
M
làđiểmbiểudiễnsốphức
23 1zii
vàgọi
làgóctạobởichiềudươngtrụchoànhvàvectơ
.OM
Tínhsin2 .

A.
5
.
12
B.
5
.
12
C.
12
.
5
D.
12
.
5
Hướngdẫngiải
Tacó:
1
2 3 1 5 5; 1 tan .
5
ziiiM
Tacó:
2
2tan 5
sin 2 .
12
1tan
ChọnđápánA.
Câu39: Chosốphức
,
12
mi
zm
mm i
.Tìmmôđunlớnnhấtcủa
.z
A.1. B.0. C.
1
2
. D.2.
Hướngdẫngiải
Tacó:
22 2
max
1
11;0.
12
11 1
mi m i
zzzzim
mm i
mm m
ChọnđápánA.
Câu40: Chosốphức z có
;0zmm
.Với
;zm
tìmphầnthựccủasốphức
1
.
mz
A. .m B.
1
.
m
C.
1
.
4m
D.
1
.
2m
Hướngdẫngiải
Gọi
Re z làphầnthựccủasốphức .z
Taxét:
2
1111 2
.
mzmz mzz
mz mz mz mz
mzmz
mzzmzmz
2
22111
Re .
2
2
2
mzz mzz
mmzm
mmzz
mmzmz
ChọnđápánD.
Câu41: Chosốphức
12
,zzthỏamãn
1
3z =
,
2
2z =
đượcbiểudiễntrongmặtphẳngphức
lầnlượtlàcácđiểm
,MN.Biết
(
)
,
6
OM ON
p
=
,tínhgiátrịcủabiểuthức
12
12
zz
zz
+
-
.
A.
13
B.
1
C.
73
2
D.
1
13
Hướngdẫngiải
Dựnghìnhbìnhhành
OMPN
trongmặtphẳngphức,khiđóbiểudiễncủa:
12
12
ì
ï
+=
ï
ï
í
ï
-=
ï
ï
î
zz OP
zz MN
()
()
22
0
12 1 2 12
22
0
12 1 2 12
2cos1501
2 cos 30 1
ì
ï
ï
+= + + =
ï
ï
í
ï
ï
-= + - =
ï
ï
î
zz z z zz
zz z z zz
12
12
12
12
1
+
+
==
-
-
zz
zz
zz
zz
.Chọn
B.
Câu42: ( CHUYÊN QUANG TRUNG LẦN 3)Cho thỏa mãn
z
thỏa mãn
10
212iz i
z
.Biếttậphợpcácđiểmbiểudiễnchosốphức
34 12wizi
làđường
tròn
I
,bánkính
R
.Khiđó.
A.
1; 2 .,5IR
B.
1; 2 , .5IR
C.
1; 2 , 5.IR
D.
1; 2 , 5.IR
Hướngdẫngiải
ChọnC.(đãsửađềbài)
Đặt
zabi
và
0zc
,với
;;abc
.
Lạicó
12
34 12
34
wi
wiziz
i
.
Gọi
wxyi
với
;xy
.
Khiđó
12
12
12 5
34 34
wi
wi
zc c c xyi i c
ii
22 22
2
125 1225xy cxy c
.
Vậytậphợpcácđiểmbi ểudiễncủasốphức
w
làđườngtròn
1; 2I
.
KhiđóchỉcóđápánCcókhảnăngđúngvàtheođó
555 1Rcc
.
Thử
1c
vàophươngtrình(1)thìthỏamãn.
Câu43: (CHUYÊNQUANGTRUNGLẦN3)Sốphức
z
đượcbiểudiễntrênmặtphẳngtọa
độnhưhìnhvẽ:
x
O
1
1
y
z
Hỏihìnhnàobiểudiễnchosốphức
i
z
?
A.
B.
B. D.
Hướngdẫngiải
ChọnC.
Gọi
;, .zabiab
Từgiảthiếtđiểmbiểudiễnsốphức
z
nằmởgócphầntưthứnhấtnên ,0ab .
Tacó
22 22 22
ia bi
ii b a
i
abi a b a b a b
z
Do
,0ab nên
22
22
0
0
b
ab
a
ab
điểmbiểudiễnsốphức
nằmởgócphầntưthứhai.
VậychọnC.
Câu44: (CHUYÊNĐHKHTNHUẾ)Trongcácsốphức
z
thỏa
34 2zi++ =
,gọi
0
z
làsốphức
cómôđunnhỏnhất.Khiđó
A.
Khôngtồntạisốphức
0
z
. B.
0
2z =
.
C.
0
7z =
. D.
0
3z =
.
x
y
1
1
O
x
O
1
1
y
x
O
1
1
y
x
O
1
1
y
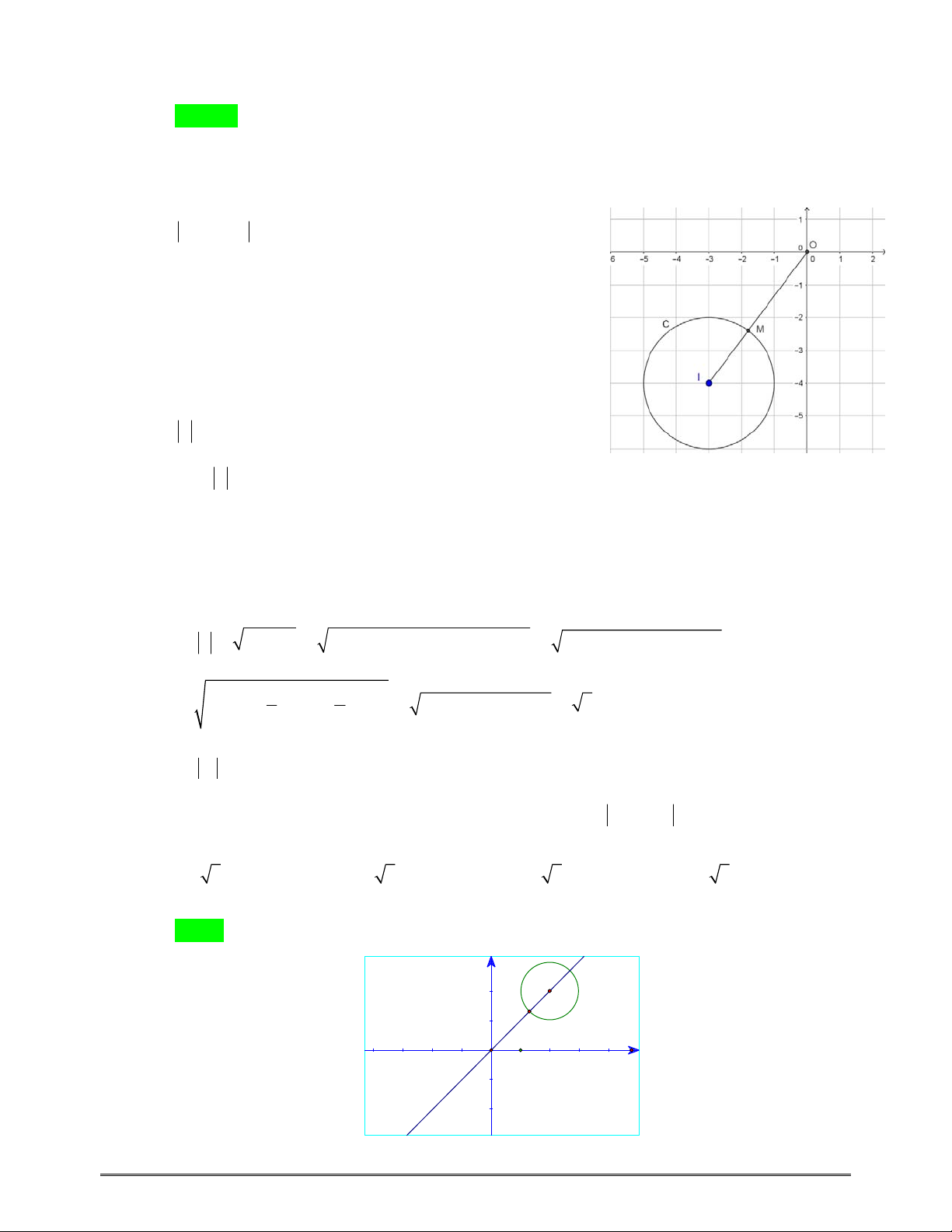
Hướngdẫngiải.
ChọnD
Cách1:
Đặt ( , )zabiab=+ Î . Khiđó
22
34 2 ( 3) ( 4) 4zi a b++ = + + + =
.
Suy ra biểu diễn hình họccủa số phức
z
làđường
tròn
C
tâm
3; 4I
vàbánkính 5R .
Gọi
M
z
làđiểm biểu diễn số phức
z
. Ta có:
M
zC
.
3zOMOIR
.
Vậy
z
bénhấtbằng3khi
M
zCIM
.
Cách2:
Đặt
32cos 32cos
42sin 42sin
aa
bb
jj
jj
ìì
+= =-+
ïï
ïï
íí
ïï
+= =-+
ïï
îî
.
22 2 2
(2cos 3) (2sin 4) 29 12cos 16sinzab jj jj= += - + - = - -
.
34
29 20 cos sin 29 20cos( ) 9
55
jj aj
æö
÷
ç
=- + =- -³
÷
ç
÷
ç
èø
.
0
3z=
Câu45: (NGUYỄN TRÃI – HD) Cho số phức z thỏa mãn: 22 1zi . Số phức zi có
môđunnhỏnhấtlà:
A.
51
B.
51
C.
52
D.
52
.
Hướngdẫngiải
ChọnA.
y
x
1
1
O
I
M

Gọi zxyi , ,xy .
Tacó:
22
2 2 1 ( 2) ( 2) 1 ( 2) ( 2) 1zi x yi x y
Tậphợpcácđiểmtrongmặtphẳng
Oxy biểudiễncủasốphức
z
làđườngtròn ()C
tâm
(2;2)I vàbánkính
1R
.
2
2
1zi x y IM ,với
2; 2I làtâmđườngtròn,
M
làđiểmchạytrênđường
tròn.Khoảngcáchnàyngắnnhấtkhi
M
làgiaođiểmcủađườngthẳngnốihaiđiểm
0;1 , 2; 2NOyI
vớiđườngtròn(C).
min
51IM IN R
Câu46: (HAIBÀTRƯNG–HUẾ)Tìmtậphợpcácđiểm
M
biểudiễnhìnhhọcsốphức
z
trongmặtphẳngphức,biếtsốphức
z
thỏamãnđiềukiện: 4 4 10.zz
A.Tậphợpcácđiểmcầntìmlàđườngtròncótâm
0;0O
vàcóbánkính
4.R
.
B.Tậphợpcácđiểmcầntìmlàđườngelipcóphươngtrình
22
1.
925
xy
C.Tậphợpcácđiểmcầntìmlànhữngđiểm
;
M
xytrongmặtphẳng Oxy thỏamãn
phươngtrình
22
22
4412.xyxy
D.Tậphợpcácđiểmcầntìmlàđườngelipcóphươngtrình
22
1.
25 9
xy
Hướngdẫngiải
ChọnD.
Tacó:Gọi
;
M
xylàđiểmbiểudiễncủasốphức
.zxyi
Gọi
4;0A làđiểmbiểudiễncủasốphức
4.z
Gọi
4;0B làđiểmbiểudiễncủasốphức
4.z
Khiđó:
4 4 10 10.z z MA MB (*)
Hệthứctrênchứngtỏtậphợpcácđiểm
M
làelipnhận ,
A
B làcáctiêuđiểm.
Gọiphươngtrìnhcủaeliplà
22
222
22
1, 0,
xy
ab a b c
ab
Từ(*)tacó:
210 5.aa
222
282 4 9AB c c c b a c
Vậyquỹtíchcácđiểm
M
làelip:
22
:1.
25 9
xy
E
Câu47: (HAIBÀTRƯNG–HUẾ)Tính
2 3 2017
1009 2 3 ... 2017Siii i .
A.
S 2017 1009i.
B.
1009 2017 .i
C.
2017 1009 .i
D.
1008 1009 .i
Hướngdẫngiải
ChọnC
Tacó

2 3 4 2017
4 8 2016 5 9 2017
2 6 10 2014 3 7 11 2015
504 505 504 504
11 1 1
1009 2 3 4 ... 2017
1009 4 8 ... 2016 5 9 ... 2017
2 6 10 ... 2014 3 7 11 ... 2015
1009 4 4 3 4 2 4 1
1009
nn n n
Siiii i
ii i iii i
ii i i ii i i
ni n n i n
509040 509545 508032 508536
2017 1009 .
ii
i
Cáchkhác:
Đặt
2 3 2017
22016
2 3 2017
1 ....
1 2 3 ... 2017
2 3 ... 2017 1
fx x x x x
fx x x x
xf x x x x x
Mặtkhác:
2018
2 3 2017
2017 2018
2
2017 2018
2
1
1 ....
1
2018 1 1
1
2018 1 1
.2
1
x
fx x x x x
x
xx x
fx
x
xx x
xf x x
x
Thay
x
i
vào
1 và
2 tađược:
2017 2018
2
2018 1 1
2018 2018 2
1009 . 1009 2017 1009
2
1
ii i
i
Si i i
i
i
Câu48: Trongmặt phẳng phức Oxy , cácsố phức
z
thỏa
21zi zi
.Tìm số phức
z
đượcbiểudiễnbởiđiểm
M
saocho
M
A
ngắnnhấtvới
1, 3A
.
A.
3 i
. B.
13i
. C.
23i
. D.
23i
.
Hướngdẫngiải
Gọi
,
M
xylàđiểmbiểudiễnsốphức
,zxyixyR
Gọi
1, 2E làđiểmbiểudiễnsốphức
12i
Gọi
0, 1F làđiểmbiểudiễnsốphức
i
Tacó:
21z i z i ME MF
Tậphợpđiểmbiểudiễnsốphức
z
làđường
trungtrục
:20EF x y.
Để
M
A
ngắnnhấtkhi
M
AEF
tại
M
3,1 3
M
zi=>ĐápánA.

Câu49: Trongmặtphẳngphức Oxy ,tậphợpbiểudiễns ốphứcZthỏa
112zi
làhình
vànhkhăn.Chuvi
P
củahìnhvànhkhănlàbaonhiêu?
A.
4P
. B.
P
. B.
2P
. D.
3P
.
Hướngdẫngiải
Gọi
,
M
xylàđiểmbiểudiễnsốphức
,zxyixyR
Gọi
1,1A
làđiểmbiểudiễnsốphức 1 i
112zi
12MA .Tậphợpđiểmbiểudiễnlàhìnhvànhkhăngiớihạnbởi2
đường trònđồng tâm có bán kính lần lượt là
12
2, 1RR
12 1 2
22PPP RR
=>ĐápánC.
Lưuýcầnnắmvữnglýthuyếtvàhìnhvẽcủadạngbàinàykhihọctr ênlớptránhnhầmlẫn
sangtínhdiệntíchhìnhtròn.
Câu50:
Trong mặt phẳng phức Oxy , tập hợp cácđiểm biểu diễn số phức
Z
thỏa mãn
2
2
2
216zz z
làhaiđườngthẳng
12
,dd
.Khoảngcáchgiữa2đườngthẳng
12
,dd
làbao
nhiêu?
A.
12
,2ddd . B.
12
,4ddd . C.
12
,1ddd . D.
12
,6ddd .
Hướngdẫngiải
Gọi
,
M
xylàđiểmbiểudiễnsốphức
,zxyixyR
Tacó:
2
2
2222222
216 2 2 2216zz z xxyiyxxyiyxy
2
416 2xx
12
,4ddd
TachọnđápánB.
Ởđâylưuýhaiđườngthẳngx=2vàx=‐2songsongvớinhau.
Câu51: (CHUYÊN LƯƠNG THẾ VINH – L2)
Cho số phức
z
thỏa mãn
2
25 12 31zz z izi
.
Tính
min | |w ,với
22wz i
.
A.
3
min | |
2
w
. B.min | | 2w . C.min | | 1w . D.
1
min | |
2
w
.
Hướngdẫngiải
ChọnC.
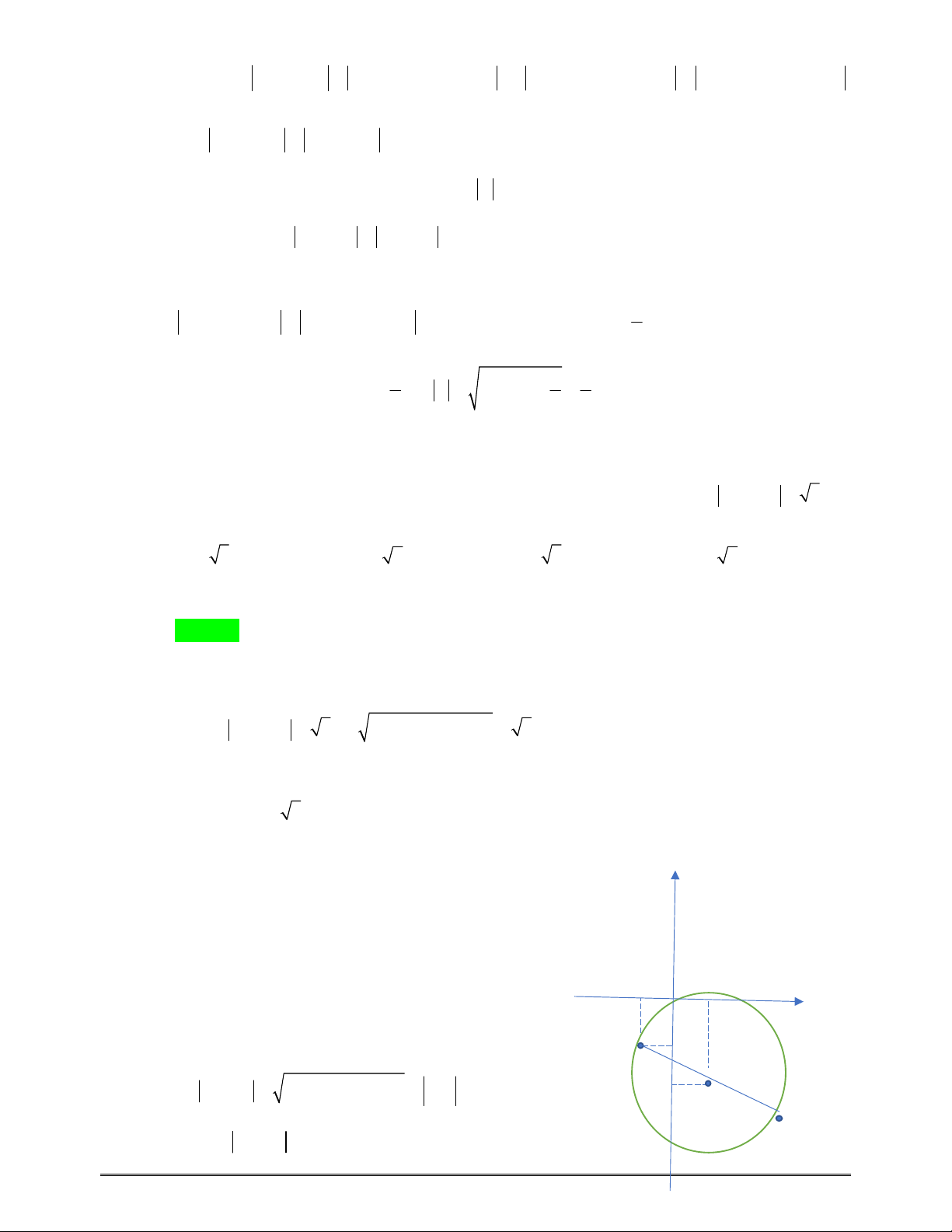
Ta có
2
2 5 12 3 1 12 12 12 3 1zz zizi zizizizi
12 0
12 3 1
zi
zizi
.
Trườnghợp
1:
12 0zi
11ww
1
.
Trườnghợp2:
12 3 1zizi
Gọi
zabi
(với ,ab ) khiđó tađược
22
1
12 1 3 2 3
2
abia bib b b
.
Suyra
2
393
22 2 2
242
wz ia i w a
2 .
Từ
1 ,
2 suyra min | | 1w .
Câu52: ( CHUYÊN SƠN LA – L2) Cho số phức
z
thỏa mãnđiều kiện :
12 5zi
và
1wz i
cómôđunlớnnhất.Sốphức
z
cómôđunbằng:
A.
25. B.
32
. C. 6 . D.
52
.
Hướngdẫngiải:
ChọnB.
Gọi
,1212zxyi xy z i x y i
Tacó:
22 22
12 5 1 2 5 1 2 5zi x y x y
Suyratậphợpđi ểm
;
M
xybiểudiễnsốphức
z
thuộcđườngtròn
C tâm
1; 2I
bánkính
5R
nhưhìnhvẽ:
Dễthấy
OC ,
1; 1NC
Theođềtacó:
;
M
xy C làđiểmbiểudiễnchosố
phức
z
thỏamãn:
1111wz ixyi i x y i
22
111zi x y MN
Suyra
1ziđạtgiátrịlớnnhất
M
N
lớnnhất
O
x
y
1
2
I
1
1
N

Mà
,
M
NC nên
M
N lớnnhấtkhi
M
N làđườngkínhđườngtròn
C
I
làtrungđiểm
2
2
3; 3 3 3 3 3 3 2MN M z i z
Câu53: (CHUYÊNSƠNLA–L2)Giảsử ,
A
Btheothứtựlàđiểmbiểudiễncủasốphức
1
z
,
2
z
.Khiđóđộdàicủa
A
B
bằng
A.
21
zz
. B.
21
zz
. C.
12
zz
. D.
12
zz
.
Hướngdẫngiải.
ChọnB.
Giảsử
1
zabi
,
2
zcdi
,
,,,abcd .
Theođềbàitacó:
;
A
ab ,
;Bcd
22
A
Bcadb.
21
zz ac dbi
22
21
zz ca db .
Câu54: (CHUVĂNAN–HN)Chosốphức
z
thỏamãnđiềukiện
12z
.Tìmgiátrịlớn
nhấtcủa
2Tziz i.
A.
max 8 2T
. B.
max 4T
. C.
max 4 2T
. D.
max 8T
.
Hướngdẫngiải
ChọnB
211 11Tziz i z i z i
.
Đặt
1wz
.Tacó 1w và
11Tw i w i
.
Đặt
.wxyi
.Khiđó
2
22
2wx
y
.
22 22
2222
22
22
11 11
1. 1 1 1. 1 1
11 1 1 1 1
22 2 4 4
Tx yix yi
xy xy
xyxy
xy
Vậy
max 4T
.
Câu55: (CHUVĂNAN–HN)Trênmặtphẳngtọađộ
Oxy
,tìmtậphợpcácđiểmbiểudiễn
cácsốphức
z
thỏamãnđiềukiện 2210zz .

A.Đườngtròn
22
22100xy
. B.Elip
22
1
25 4
xy
.
C.Đườngtròn
22
2210xy
. D.Elip
22
1
25 21
xy
.
Hướngdẫngiải
ChọnD.
Gọi
;
M
xylàđiểmbiểudiễnsốphức zxyi ,
,xy
.
Gọi
A
làđiểmbiểudiễnsốphức
2
Gọi
B
làđiểmbiểudiễnsốphức
2
Tacó:
2 2 10 10zz MBMA .
Tacó
4
A
B
.Suyratậphợpđiểm
M
biểudiễnsốphức
z
làElipvới
2
tiêuđiểmlà
2;0A ,
2;0B , tiêu cự
42AB c
,độdài trục lớn là
10 2a
,độdài trục bé là
22
22 2254221bac.
Vậy,tậphợpcácđiểmbiểudiễncácsốphức
z
thỏamãnđiềukiện 2210zz là
Elipcóphươngtrình
22
1.
25 21
xy
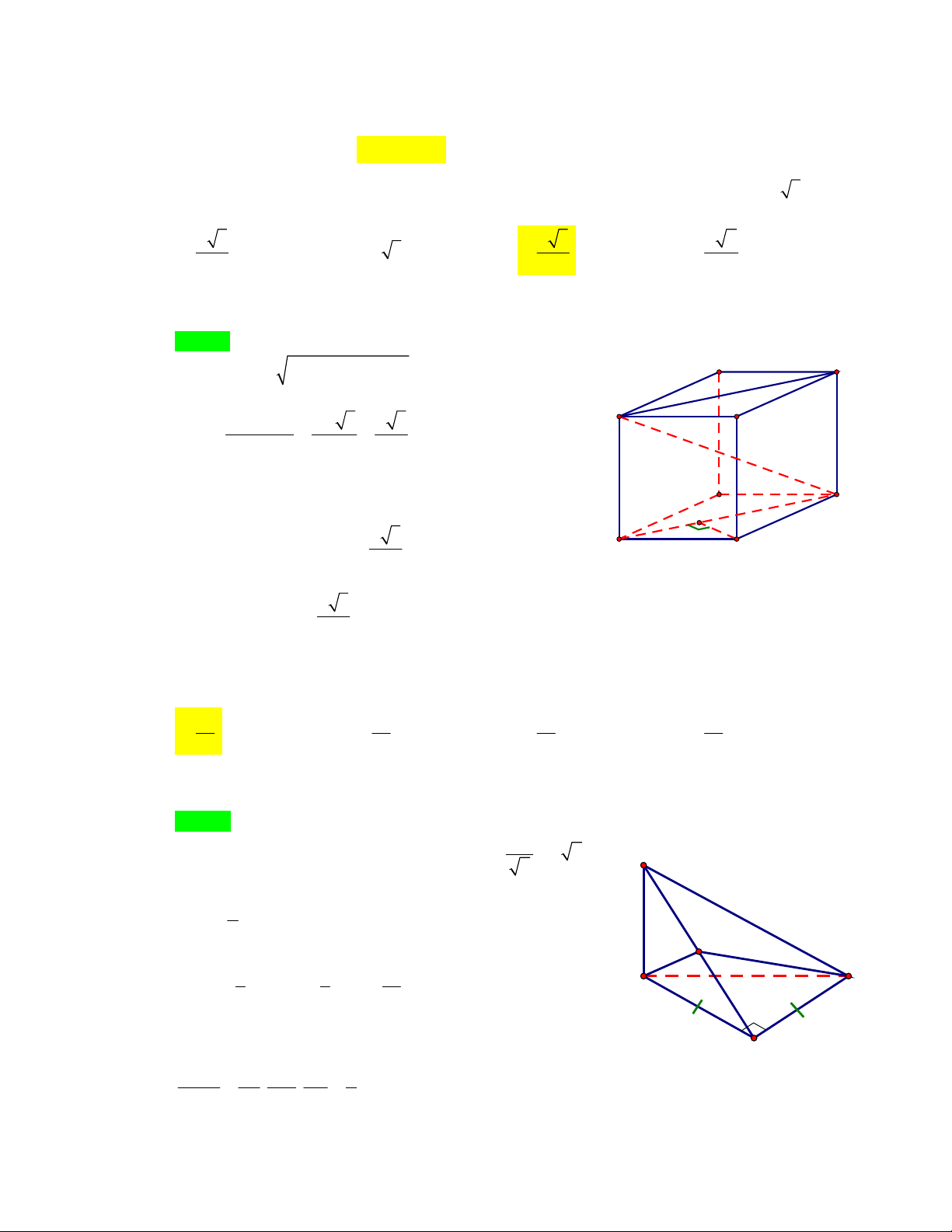
A'
C'
B'
C
A
B
D
D'
H
a
2a
M
A
B
C
S
Chủđề5.KHỐIĐADIỆN
Câu1: SGD VĨNH PHÚC Cho hình hộp chữ nhật
.ABCD A B C D
có
,3.AB a AD a
Tính
khoảngcáchgiữahaiđườngthẳng
BB
và
.AC
A.
3
4
a
. B.
3a
. C.
3
2
a
. D.
2
2
a
.
Hướn
gdẫngiải
ChọnC.
Tacó:
22
2.AC AB BC a
Kẻ
.BH AC
..33
.
22
AB BC aa a
BH
BC a
Vì
//BB ACC A
nên
,,dBBAC dBB ACCA
3
,.
2
a
dBB ACCA BH
Nên
3
,.
2
a
dBBAC
Câu
2: SGDVĨNHPHÚCChohìnhchóp
.S ABC
có
SA ABC
,tamgiác
ABC
vuôngcântại
B
,
2AC a
và
.SA a
Gọi
M
làtrungđiểmcạnh
SB
.Tínhthểtíchkhốichóp
..SAMC
A.
3
6
a
. B.
3
3
a
.
C.
3
9
a
. D.
3
12
a
.
Hướn
gdẫngiải
ChọnA.
Xéttamgiácvuôngcân
ABC
có:
2
2
AC
AB BC a
2
1
.
2
ABC
SABBCa
3
2
.
11
...
333
S ABC ABC
a
VSASaa
Áp
dụngđịnhlíSim‐Sontacó:
.
1
..
2
SAMC
S ABC
V
SA SM SC
VSASBSC
BÀI TOÁN VẬN DỤNG (8 - 9 - 10)
_______________________________
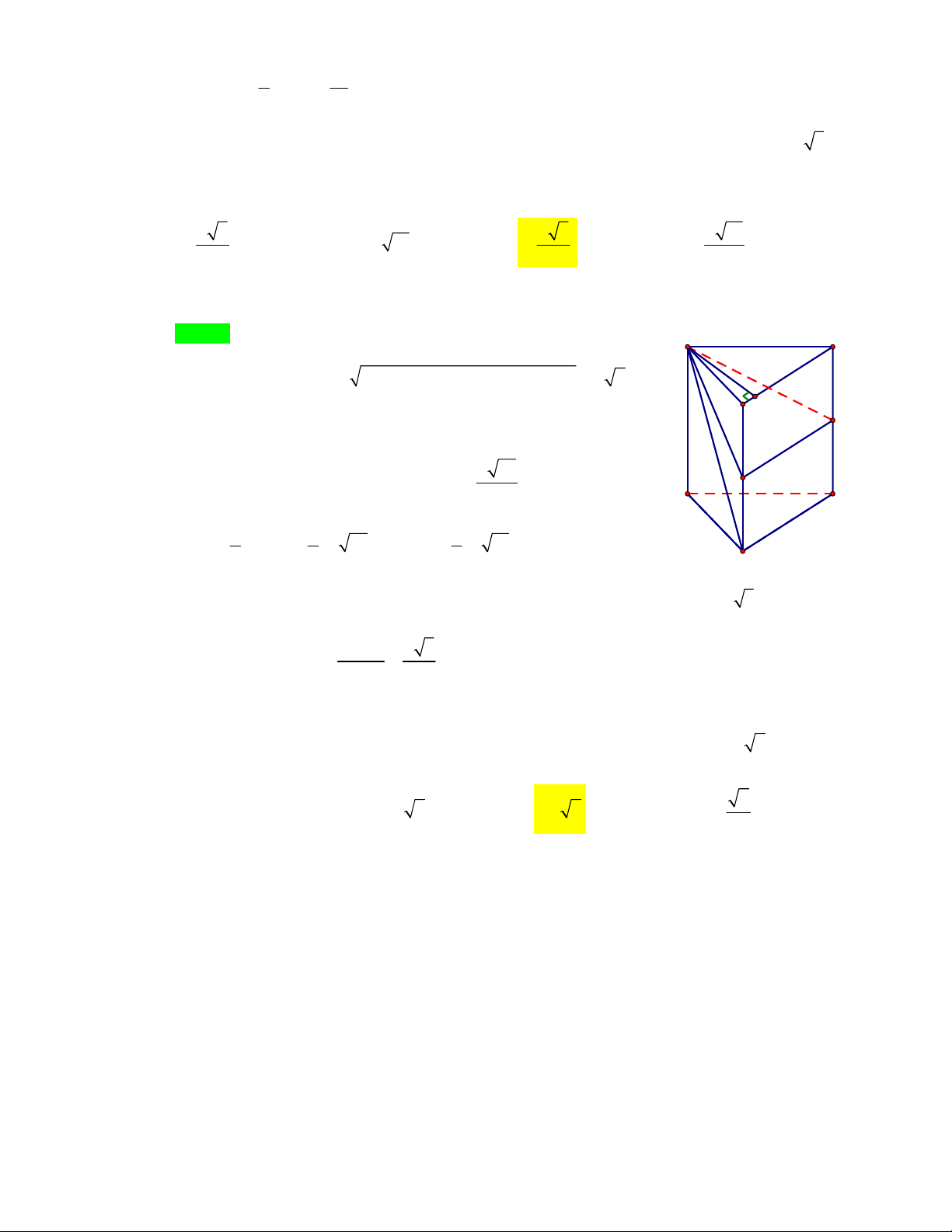
K
I
C
B
C
1
B
1
A
1
A
H
3
..
1
26
SAMC SABC
a
VV
Câu3: SGDVĨNHPHÚCChohìnhlăngtrụđứng
111
.
A
BC A B C
có
A
Ba
,
2
A
Ca
,
1
25
A
Aa
và
120 .BAC
Gọi
K
, I lầnlượtlàtrungđiểmcủacáccạnh
1
CC
,
1
B
B
.Tínhkhoảngcáchtừ
điểm
I đếnmặtphẳng
1
.
A
BK
A.
5
3
a
. B.
15a
. C.
5
6
a
. D.
15
3
a
.
Hướngdẫngiải
ChọnC.
Tacó
22 0
11
2 . . os120 7IK B C BC AB AC AB AC c a
Kẻ
11
A
HBC
khiđó
A
H
làđườngcaocủatứdiện
1
A
BIK
Vì
0
1111111 1
21
. . .sin120
7
a
AH BC AB AC AH
1
23
.
11 1
.35 15()
22 6
IKB A IBK
SIKKBa V advtt
MặtkhácápdụngđịnhlýPitagovàcôngthứcHê‐rôngtatínhđc
1
33
ABK
S a dvdt
Dođó
1
1
1
3
5
,
6
AIBK
ABK
V
a
dI ABK
S
.
Câu4: NGUYỄN KHUYẾN TPHCM Cho hình chóp
.SABCD
có đáy là hình chữ nhật. Tam giác
SAB
vuôngcântại
A
vànằmtrongmặtphẳngvuônggócvớiđáyvà
42SB
.Gọi
M
là
trungđiểmcủacạnh
SD
.Tínhkhoảngcách
l
từđiểm
M
đếnmặtphẳng
SBC
.
A.
2l
B.
22l
C.
2l
D.
2
2
l
Hướngdẫngiải
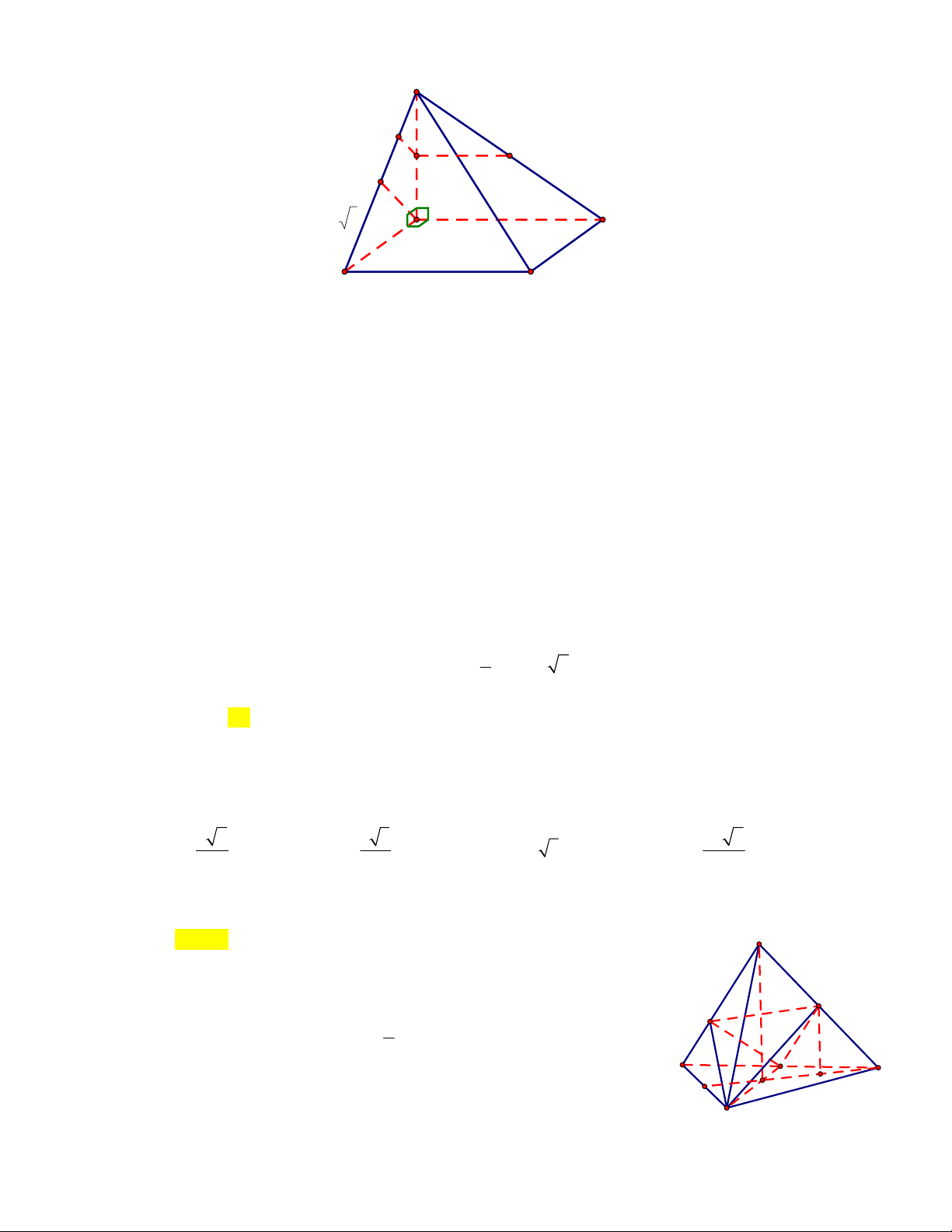
N
M
B
D
C
A
P
Theogiảthiết,tacó
,SAB A BCD SAB ABCD AB
SA AB
SA ABCD .
Gọi
,,NHKlầnlượtlàtrungđiểmcáccạnh ,SA SB vàđoạn
SH
.
Tacó
BC SA
BC SAB BC AH
BC AB
.
Mà
A
HSB
A
BC
cântại
A
có
A
H
làtrungtuyến.
Suyra
A
HSBC ,dođó
K
NSBC vì
||
K
NAH
,đườngtrungbình.
Mặtkhác
|| ||
M
NBC MN SBC
.
Nên
1
,, 22
2
dM SBC dN SBC NK AH
.
Đápán:B.
Câu5: NGUYỄNKHUYẾNTPHCMChotứdiệnđều
A
BCD
cócạnhbằng3.Gọi
,
M
N
lầnlượtlà
trungđiểmcáccạnh
,.
A
DBD
Lấyđiểmkhôngđổi
P
trêncạnh
A
B
khác
,
A
B
.Thểtích
khốichóp
PMNC
bằng
A.
92
16
B.
83
3
C.
33
D.
27 2
12
Hướngdẫngiải
ChọnA
Do
A
BCMN nên
,A,D,d P CMN d CMN d CMN
Vậy
1
4
PCMN DPMN MCND ABCD
VVV V
Dodiệntíchđáyvàchiềucaođềubằngmộtnửa.
42
M
K
N
H
A
B
C
D
S
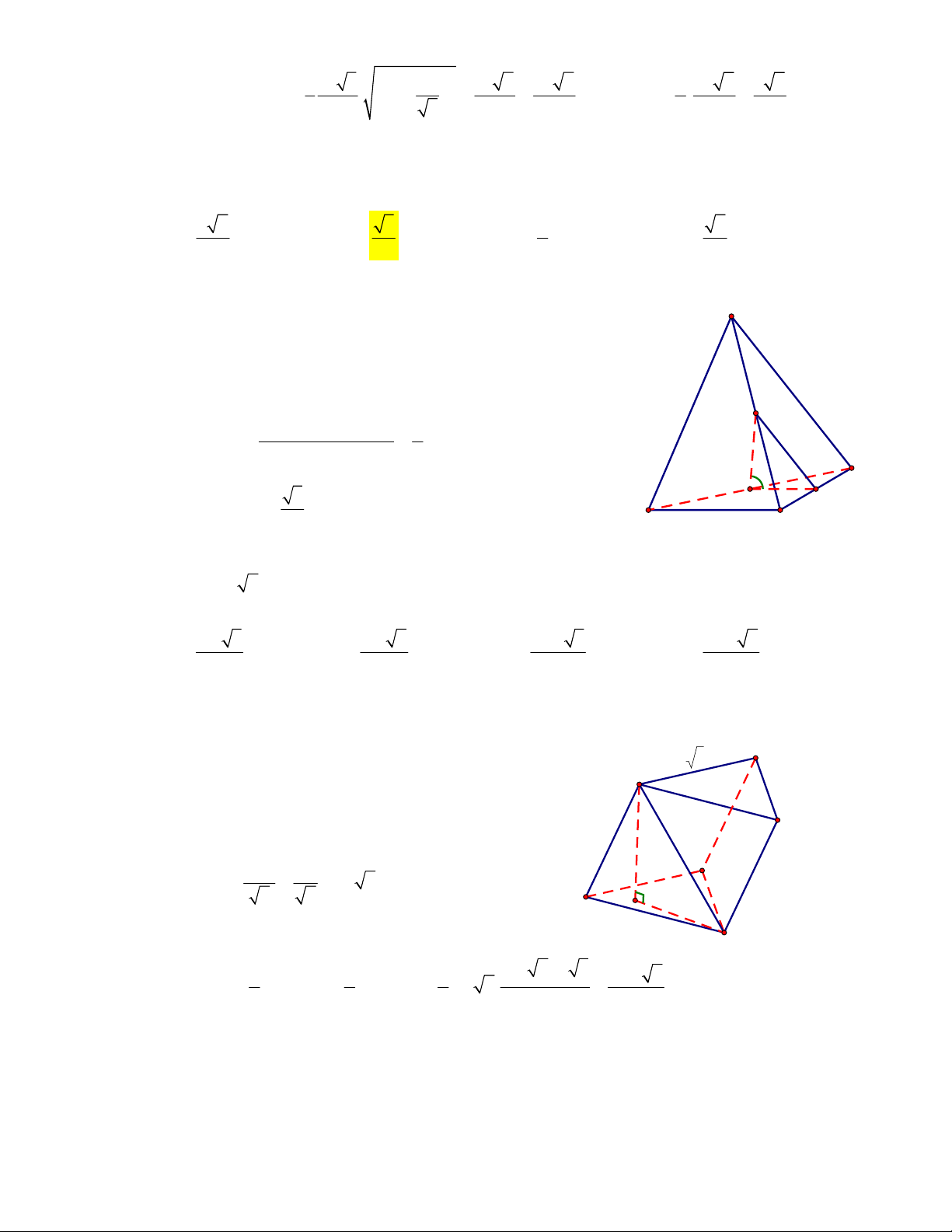
8a
2a 2
C'
B'
A
C
B
A' H
Mặtkhác
2
23
2
13 2272
.
3 4 12 12
3
ABCD
aaa
Va
nên
127 2 92
.
412 16
MCND
V
Câu6: NGUYỄNKHUYẾNTPHCMChotứdiện
A
BCD
có 14, 6AD BC.Gọi ,
M
N lầnlượtlà
trungđiểmcủacáccạnh
,
A
CBDvà
8MN
.Gọi
làgócgiữahaiđườngthẳng
B
C
và
M
N
.Tính
sin
.
A.
22
3
B.
3
2
C.
1
2
D.
2
4
Hướngdẫngiải
Gọi
P
làtrungđiểmcủacạnh
CD
, ta có
,,
M
NBC MNNP
.
Trong tam giác
M
NP
, ta có
222
1
cos
2. 2
MN PN MP
MNP
MN NP
.Suyra
60MNP .
Suyra
3
sin
2
.
Câu7: NGUYỄN KHUYẾN TPHCM Cholăngtrụtamgiác
.'' '
A
BC A B C
cóđáy
A
BC
làđềucạnh
22
A
Ba
.Biết
'8
A
Ca
vàtạovớimặtđáymộtgóc
0
45 .Thểtíchkhốiđadiện
''
A
BCC B
bằng
A.
3
83
.
3
a
B.
3
86
.
3
a
C.
3
16 3
.
3
a
D.
3
16 6
.
3
a
Hướngdẫngiải
Gọi
H
làhìnhchiếucủa
A
lên
'''mp A B C
0
'45HC A
'
A
HC
vuôngcântạiH.
'8
42.
22
AC a
AH a
NX:
2
3
.'' .'''
22.3
222 166
..42. .
333 43
A BCC B ABC A B C ABC
a
a
VV AHSa
ChọnD.
Gọi
H
làhìnhchiếucủa
A
lên
'''mp A B C
0
'45HC A
3
7
14
8
6
M
P
N
B
C
D
A
6 cm
2 cm
3 cm
B
D
C
D'
B'
C'
A'
A
'
A
HC
vuôngcântạiH.
'8
42.
22
AC a
AH a
NX:
2
3
.'' .'''
22.3
222 166
..42. .
333 43
A BCC B ABC A B C ABC
a
a
VV AHSa
Câu8: T.TDIỆUHIỀNChohìnhlậpphương
.'' ' '
A
BCD A B C D
cạnh a .Tínhkhoảngcáchgiữa
haiđườngthẳng
'
B
C
và
'CD
.
A.
2a . B.
3
3
a
. C.
2a
. D.
2
3
a
.
Hướngdẫngiải
ChọnB
Gọi
'' ''OAC BD
vàtừ
'B
kẽ
'
B
HBO
Ta có
'CD
//
('')BA C
nên
'. ' 3
( '; ') ( ';( ' ')) ( '; ( ' ')) '
3
B
BBO a
dBC CD dD BAC dB BAC BH
BO
Câu9: T.TDIỆUHIỀNMộthìnhhộpchữnhật
.
A
BCD A B C D
cóbakíchthướclà
2cm
,
3cm
và
6cm
.Thểtíchcủakhốitứdiện
.
A
CB D
bằng
A.
3
8 cm . B.
3
12 cm . C.
3
6 cm . D.
3
4 cm .
Hướngdẫngiải
ChọnB.
Tacó :
O
B
D
C
D'
A'
C'
B'
A
H

P
N
M
H
K
F
E
A
B
C
D
......
...
...
.. .
..
4
4
1
4.
6
11
.2.
33
A
BCD A B C D B AB C D ACD A B AD C B C D A CB D
ABCD A B C D B AB C A CB D
ACBD ABCD ABCD B ABC
ACBD ABCD ABCD ABCD ABCD
ACBD ABCDABCD
VVVVVV
VVV
VV V
VV V
VV
3
3.6 12cm
Câu10: LẠNGGIANGSỐ1Chokhốitứdiệnđều
A
BCD
cạnhbằng
2.cm
Gọi ,,
M
NPlầnlượtlà
trọngtâmcủabatamgiác
,,.
A
BC ABD ACD Tínhthểtích
V
củakhốichóp
.
A
MNP
A.
3
2
162
Vcm
. B.
3
22
81
Vcm
. C.
3
42
81
Vcm
. D.
3
2
144
Vcm
.
Hướngdẫngiải
ChọnC.
Tamgiác
B
CD
đều
23
3
3
DE DH
22
26
3
AH AD DH
EF
,D,BC
11113
.. . .
22224
K
EFK
SdFKdBC
EF
112632
...
33346
SKFE K
VAHS
.
Mà
2
3
AM AN AP
A
EAKAF
Lạicó:
8842
..
27 27 81
AMNP
AMNP AEKF
AEKF
V
AM AN AP
VV
VAEAKAF
.
Câu11: LÝ TỰ TRỌNG
– TPHCM Cho hình hộp
.
A
BCD A B C D
có
60 , 7, 3,BCD AC a BD a AB AD
,đườngchéo
BD
hợpvớimặtphẳng
A
DD A
góc
30
.Tínhthểtích
V
củakhốihộp
.
A
BCD A B C D
.
A.
3
39 .a
B.
3
39
.
3
a
C.
3
23 .a
D.
3
33 .a
Hướngdẫngiải
ChọnD.
Đặt
ÁpdụngđịnhlýhàmcosvàphângiáctrongtamgiácBCD
và
Với và
VậyVhìnhhộp
Câu12: NGÔGIATỰ‐VPChohìnhchóptứgiácđều
.SABCD
cóthểtích
2
6
V
.Gọi
M
là
trungđiểmcủacạnh
SD
. Nếu
SB SD
thì khoảng cách từ
B
đếnmặtphẳng
M
AC
bằng:
A.
1
2
. B.
1
2
. C.
2
3
. D.
3
4
.
Hướngdẫngiải
ChọnA
Giảsửhìnhchópcóđáy
A
BCD
làhìnhvuôngcạnh a .Khiđó,
2BD a
.
Tamgiác
SBD
vuôngcântại
S
nên
SD SB a
và
2
22
BD a
SO
.
30°
y
x
O
A
C
B
C'
A'
B'
D'
D
;y
x
CD BC x y
222
3axyxy
22 2
5
x
ya
2;
x
aya
22
x
ya
60C
B
DAD
';(ADD'A') 30BD
'3
D
Da
2
.sin60 a 3
ABCD
Sxy
3
33a
O
M
A
S
D
C
B
Suyracáctamgiác ,SCD SAD làcáctamgiácđềucạnh
a
và
SD MAC tại
M
.
Thểtíchkhốichóplà
3
12
..
36
ABCD
a
VSOS
Mà
3
22
1
66
a
a
Vì
O
làtrungđiểm BD nên
1
,,
2
dBMAC dDMAC DM
.
Câu13: THTT
–477Mộthìnhlăngtrụcóđáylàtamgiácđềucạnhbằng
a
,cạnhbênbằng
b
và
tạovớimặtphẳngđáymộtgóc
.Thểtíchcủakhốichópcóđáylàđáycủalăngtrụvà
đỉnhlàmộtđiểmbấtkìtrênđáycònlạilà
A.
2
3
sin .
12
ab
B.
2
3
sin .
4
ab
C.
2
3
cos .
12
ab
D.
2
3
cos .
4
ab
Hướngdẫngiải
ChọnA.
Gọi
H
làhìnhchiếucủa
A
trên
A
BC
.Khiđó
A
AH
.
Ta có
.sin sinAH AA b
nênthểtíchkhốilăngtrụlà
2
.
3sin
.
4
ABC A B C ABC
ab
VAHS
.
Lạicóchiềucaocủachóptheoyêucầuđềbàichínhlàchiềucaocủalăngtrụvàbằng
A
H
nênthểtíchkhốichóplà
2
..
13sin
312
S ABC ABC A B C
ab
VV
.
Câu14: THTT
–477Cácđườngchéocủacácmặtcủamộthìnhhộpchữnhậtbằng
, , abc
.Thể
tíchcủakhốihộpđólà
A.
222222 222
.
8
bcacababc
V
B.
222222222
.
8
bcacababc
V
C.
.Vabc
H'
C
B
A
B'
C'
A'
H
S
D.
.Vabc
Hướngdẫngiải
ChọnA.
Giảsửhìnhhộpchữnhậtcóbakíchthước:
,,
x
yz
.
Theoyêucầubàitoántacó
222 222 222
222 222 22222
22 2 2 22 2 22
xya yax yax
yzc yzc axbxc
xzb zbx zbx
222
2
222 222222
222
2
222
2
2
28
2
abc
y
acbabcbca
abc
xV
bca
z
Câu15: SỞGDHÀNỘIChohìnhlăngtrụ
ABCA B C
cóđáylàtamgiácđềucạnha .Hìnhchiếu
vuônggóccủa
A
lênmặtphẳng
ABC
trùngvớitrọngtâmtamgiác
ABC
.Biếtkhoảng
cách giữahaiđườngthẳng
AA
vàBC bằng
3
4
a
.TínhthểtíchV củakhốilăngtrụ
.ABCA B C
A.
3
3
.
24
a
V
B.
3
3
.
12
a
V
C.
3
3
.
3
a
V
D.
3
3
.
6
a
V
Hướngdẫngiải
ChọnB.
M
làtrungđiểmcủa
BC
thì
BC AA M
.
Gọi
MH làđườngcaocủatamgiácAAM
thì
MH A A
vàHM BC nênHM làkhoảngcách
z
c
b
ax
y
A'
C'
D'
C
B
D
A
B'
H
G
M
B
C
A
C'
B'
A'
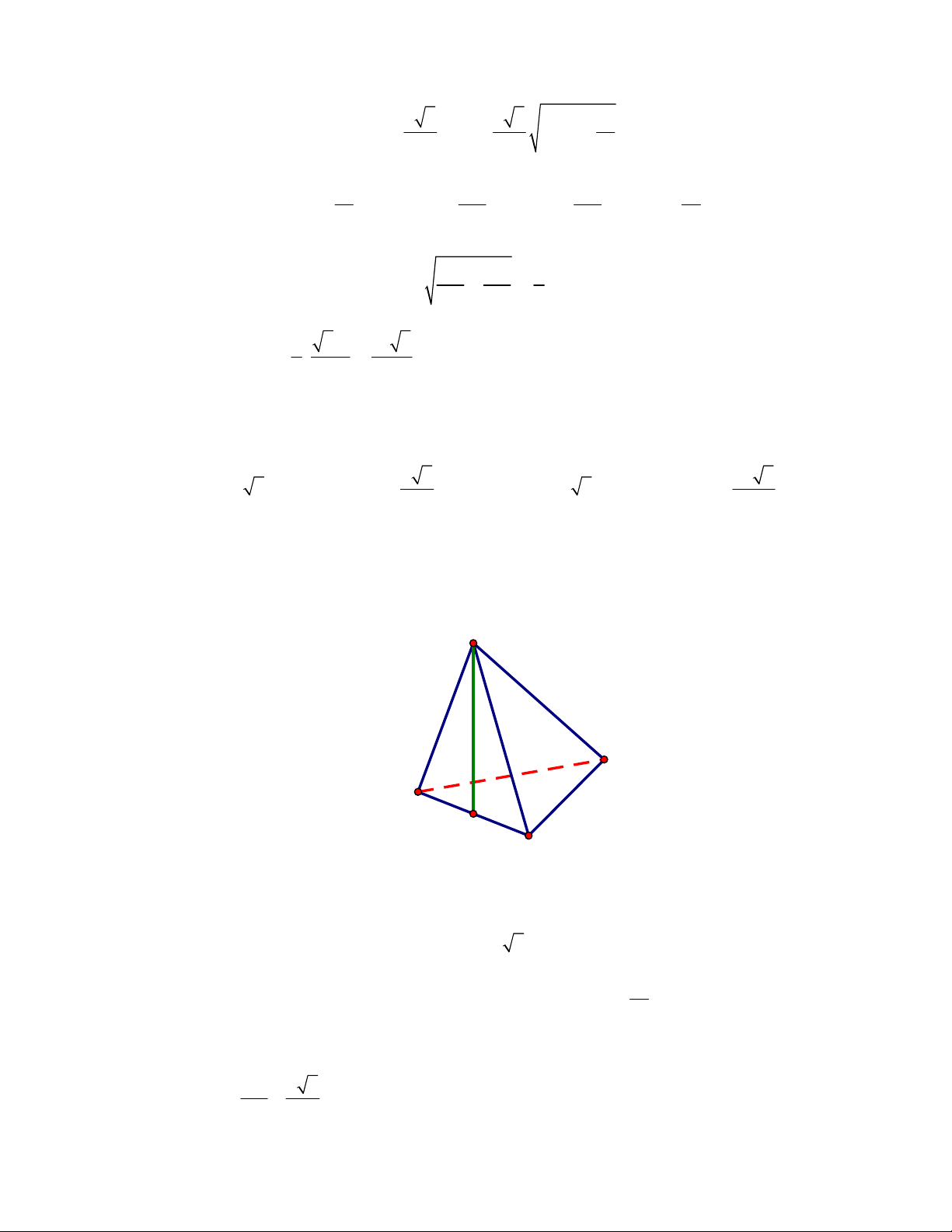
AA
và
BC
.
Tacó
..A A HM A G AM
2
2
33
.
42 3
aa a
AA AA
222
22 2 2
442
43 .
3393
aaaa
AA AA AA AA AA
Đườngcaocủalăngtrụlà
22
43
993
aaa
AG
.
Thểtích
23
33
.
34 12
LT
aaa
V
.
Câu16: SỞGDHÀNỘIChohìnhchóp
.SABC
có
0
60ASB C SB,
0
90ASC ,
SA SB SC a
.
Tínhkhoảngcách
d
từđiểm
A
đếnmặtphẳng
SBC
.
A.
26da
. B.
6
3
a
d
. C.
6da
. D.
26
3
a
d
.
Hướngdẫngiải
ChọnB.
Tacó:
SAB
,
SBC
làcácđềucạnh a nên
A
BBCa
Tacó:
SAC
vuôngcântại
S
nên
2
A
Ca
Tacó:
222
A
CABBCnên
A
BC
vuôngtại
B
có
2
2
ABC
a
S
Gọi
H
làtrungđiểmcủa
A
C
.Tacó:
HA HB HC
và
SA SB SC
nên
SH ABC
và
2
22
AC a
SH
.
H
S
B
C
A
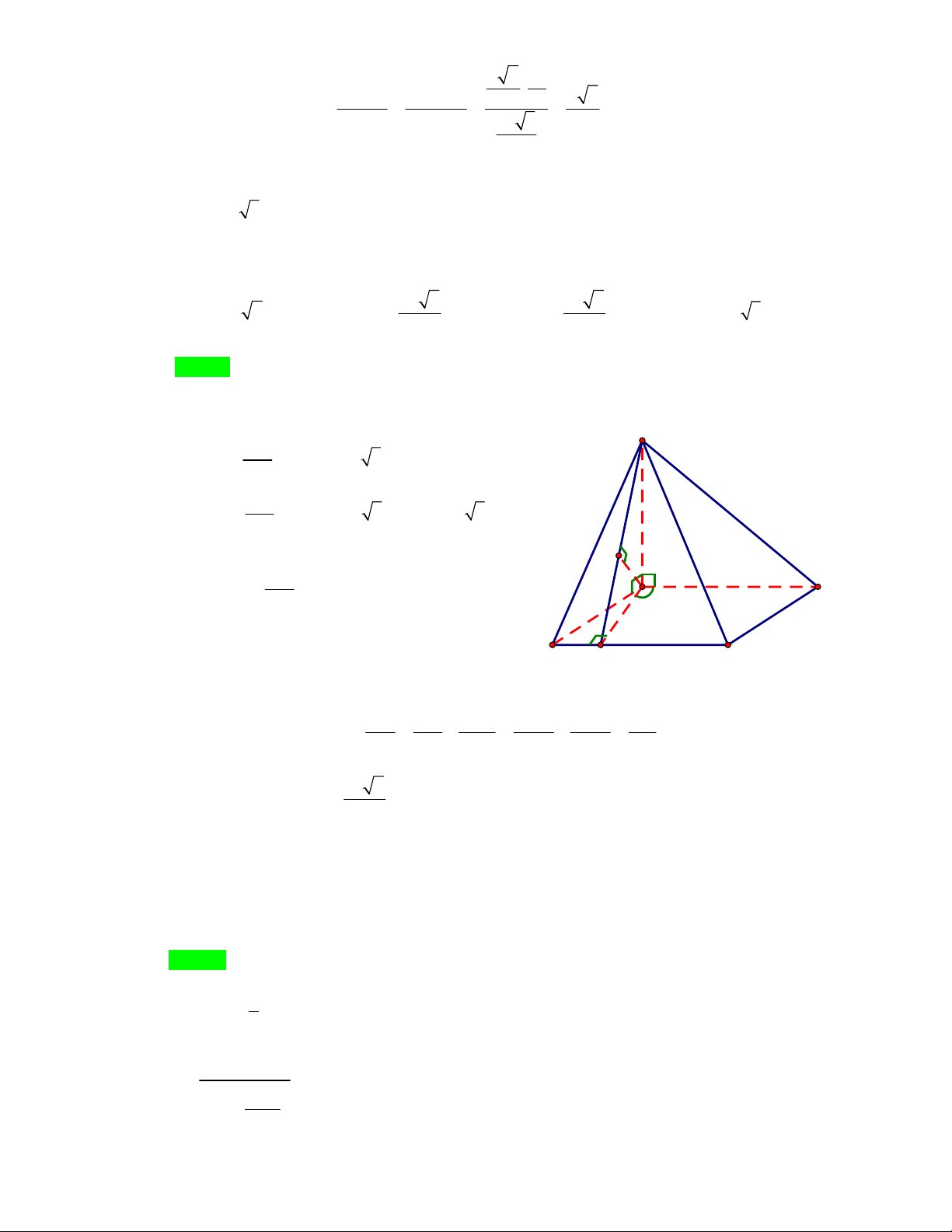
Vậy
2
.
2
2
.
3.
6
22
;
3
3
4
S ABC ABC
SBC SBC
aa
VSHS
a
dASBC
SS
a
Câu17: CHUYÊNHÙNGVƯƠNG
–GLChohìnhchóp
.SABCD
cóđáy
A
BCD
làhìnhthoicạnh
bằng
23a
,góc
BAD
bằng120
0
.Haimặtphẳng
SAB và
SAD cùngvuônggócvới
đáy.Gócgữamặtphẳng
SBC
và
A
BCD
bằng45
0
.Tínhkhoảngcách
h
từ
A
đếnmặt
phẳng
.SBC
A.
22.ha B.
22
.
3
a
h
C.
32
.
2
a
h
D.
3.ha
Hướngdẫngiải
ChọnC.
Gọi
H
làchânđườngcaohạtừ
A
củatamgiác
.
A
BC
Xéttamgiác
:
A
BH
0
sin 2 3.sin 60 3 .
AH
BAHa a
A
B
0
cos 2 3.cos 60 3.
BH
BBHa a
A
B
Xéttamgiác
SAH
vuôngtại
:
A
0
tan 3 tan 45 3 .
SA
SHA SA a a
A
H
Trongtamgiác
SAH
vuôngtại
A
,kẻ
A
ISH
tại
.I
Tacó
A
ISBC
nên
A
I là
khoảngcáchtừ
A
đếnmặtphẳng
.SBC
Xéttamgiác
SAH
,tacó:
22
22 2 2
111 1 1 2
.
9
33
A
ISAAH a
aa
32
,.
2
a
dASBC AI
Câu18: CHUYÊN LƯƠNG VĂN CHÁNH Khi chiều cao của một hình chóp đều tăng lên n lần
nhưngmỗicạnhđáygiảmđi
n lầnthìthểtíchcủanó.
A.Khôngthayđổi. B.Tănglên
n
lần. C.Tănglên
1n
lần. D.Giảmđi
n
lần.
Hướngdẫngiải
ChọnD.
Tacó:
1
..
3
VhS
,với
h
làchiềucao,
S
làdiệntíchđáy
2
0
180
4tan
xa
S
a
với
x
làđộdàicạnhcủađagiácđều, a làsốđỉnhcủađagiácđều.
A
S
D
C
B
H
I
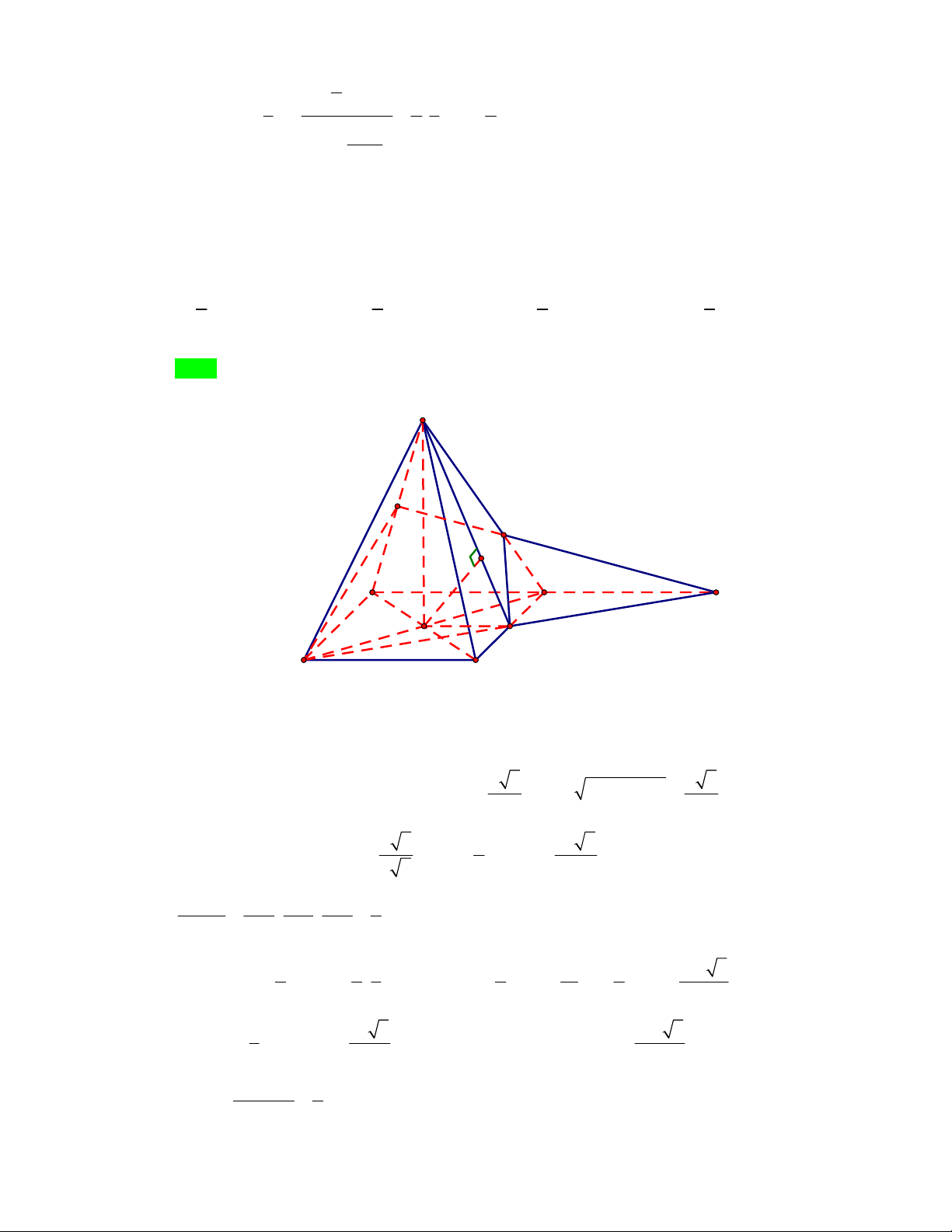
Ycbt
2
1
0
1111
.. ... .
33
180
4tan
x
a
n
Vnh hSV
nn
a
.
Câu19: BIÊNHÒA
–HÀNAMChohìnhchóptứgiácđều
.SABCD
cócạnhđáybằng
a
,cạnhbên
hợpvớiđáymộtgóc
60
.Gọi
M
làđiểmđốixứngcủa
C
qua
D
,
N
làtrungđiểm
.SC
Mặtphẳng
BMN chiakhốichóp
.SABCD
thànhhaiphần.Tỉsốthểtíchgiữahaiphần
phầnlớntrênphầnbébằng:
A.
7
5
. B.
1
7
. C.
7
3
. D.
6
5
.
Hướngdẫngiải
ChọnA.
Giảsửcácđiểmnhưhìnhvẽ.
E
SD M N E làtrọngtâmtamgiác SCM ,
//
D
FBC F
làtrungđiểm
B
M
.
Tacó:
6
,60
2
a
SD ABCD SDO SO
,
22
7
2
a
SF SO OF
2
61 7
,;.
24
27
SAD
aa
dO SAD OH h S SFAD
1
6
MEFD
MNBC
V
ME MF MD
VMNMBMC
3
551 15156
,4
663 2182 72
BFDCNE MNBC SBC SAD
a
VV dMSADShS
33
..
16 76
.
36 36
S ABCD ABCD SABFEN S ABCD BFDCNE
aa
VSOS VVV
Suyra:
7
5
SABFEN
BFDCNE
V
V
E
N
M
FO
AB
C
D
S
H
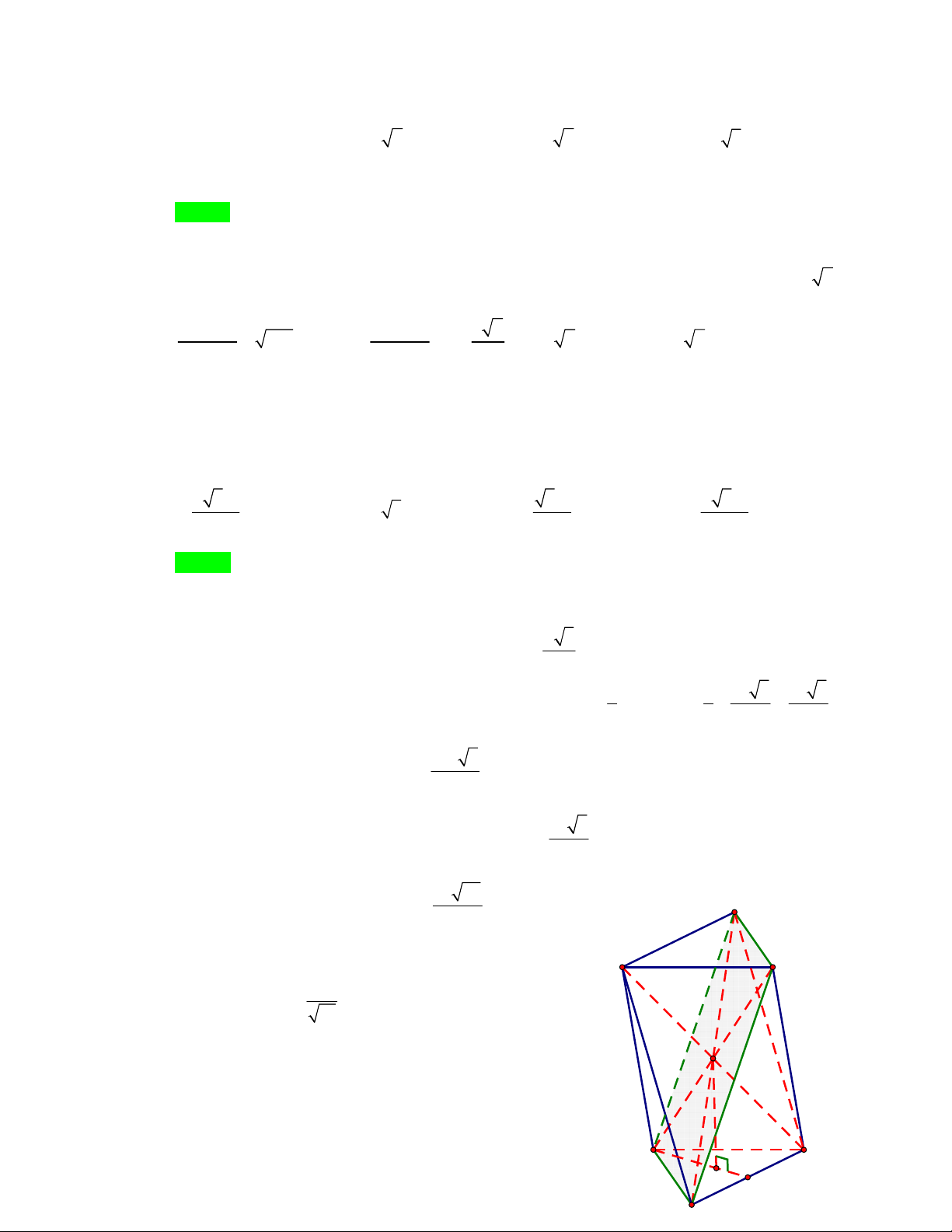
Câu20: CHUYÊNPHANBỘICHÂUChohìnhhộpchữnhật
.
A
BCD A B C D
cótồngdiệntíchcủa
tấtcảcácmặtlà
36
,độdàiđườngchéo
A
C
bằng
6
.Hỏithểtíchcủakhốihộplớnnhấtlà
baonhiêu?
A.
8
. B.
82
. C.
16 2
. D.
24 3
.
Hướngdẫngiải
ChọnC.
Gọichiềudài3cạnhcủahìnhhộpchữnhậtlầnlượtlà:
a ,
b
,
0c
Tacó
22 222
36; 2 2 2 36 ( ) 72 6 2a b c S ab bc cAC a a b c a b c
3
3
3
62
16 2
333
abc abc
abc abc
.Vậy
16 2
Max
V
Câu21: CHUYÊNĐHSPHNChohìnhchópđều
.S ABC
cóđáycạnhbằng a ,gócgiữađườngthẳng
SA
vàmặtphẳng
A
BC
bằng
60
.Gọi
A
,
B
,
C
tươngứnglàcácđiểmđốixứngcủa
A
,
B ,
C
qua
S
.Thểtíchcủakhốibátdiệncócácmặt ,
A
BC
A
BC
,
A
BC
,
B
CA
,
CAB
,
A
BC
,
B
AC
,
CA B
là
A.
3
23
3
a
. B.
3
23a
. C.
3
3
2
a
. D.
3
43
3
a
.
ChọnA.
Cách1:Tatínhthểtíchkhốichóp
.SABC
:
GọiHlàtâmtamgiácABCđềucạnha
3
3
a
CH
.Gócgiữađườngthẳng
SA
vàmặt
phẳng
ABC
bằng
0
60
23
.
1133
60 .S . . .
33412
o
SABC ABC
aa
SCH SH a V H S a
3
.'' .ACS .
23
22.48
3
B ACA C B S ABC
a
VV V V
.
Cách2:Tacóthểtíchkhốichóp
.S ABC
là:
3
.
3
12
S ABC
a
V
.
Diệntíchtamgiác
SBC
là:
2
39
12
SBC
a
S
.
Khoảng cách từ
A
đếnmặtphẳng
SBC
là:
3
,
13
a
dASBC
.
Tứgiác
''
B
CB C
làhìnhchữnhậtvìcóhaiđường
chéobằngnhauvàcắtnhautạitrungđiểmmỗi
đường.
H
B'
A'
C'
C
A
B
S
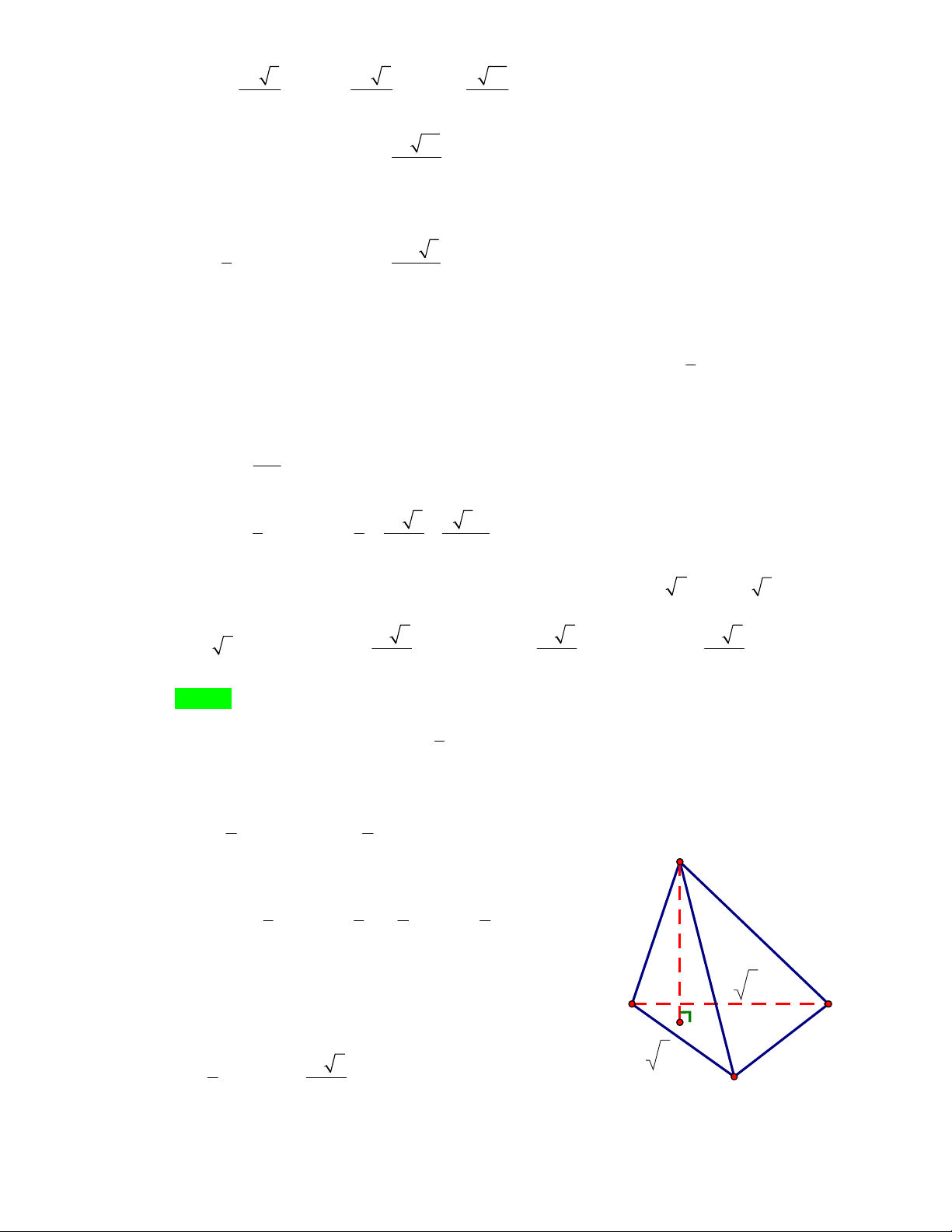
Có
23 23 39
''
33 3
aaa
SB BB B C
.
Diệntích
''
B
CB C
là:
2
''
39
3
BCB C
a
S
.
Thểtíchkhối8mặtcầntìmlà:
3
''
123
2. , . .
33
BCB C
a
VdASBCS
Cách3 ThamkhảolờigiảicủaNgọcHuyềnLB.
Thểtíchkhốibátdiệnđãcholà
''' '. .
1
22.488..
3
A
B C BC A SBC S ABC ABC
VV V V SGS
Ta có:
0
;60.SA ABC SAG
Xét
SGA
vuôngtại
G
:
tan .tan .
SG
SAG SG AG SAG a
A
G
Vậy
23
11323
8. . 8. . . .
3343
ABC
aa
VSGS a
Câu22: CHUYÊNTHÁIBÌNH Chokhốichóp
.SABC
có
SA a
, 2SB a ,
3SC a
.Thểtích
lớnnhấtcủakhốichóplà
A.
3
6a
. B.
3
6
2
a
. C.
3
6
3
a
. D.
3
6
6
a
.
ChọnD.
Gọi
H
làhìnhchiếucủa
A
lên
1
() .
3
SBC
SBC V AH S .
Tacó
A
HSA
;dấu“”xảyrakhi
A
SSBC
.
11
..sin .
22
SBC
S SB SC SBC SB SC, dấu “” xảy ra khi
SB SC
.
Khiđó,
1111
.
3326
SBC
V AH S AS SB SC SA SB SC.
Dấu “” xảy ra khi
,,SA SB SC
đôimộtvuônggócvới
nhau.
Suy ra thể tích lớn nhất của khối chóp là
3
16
..
66
a
VSASBSC
.
a
a2
a3
A
S
B
C
H
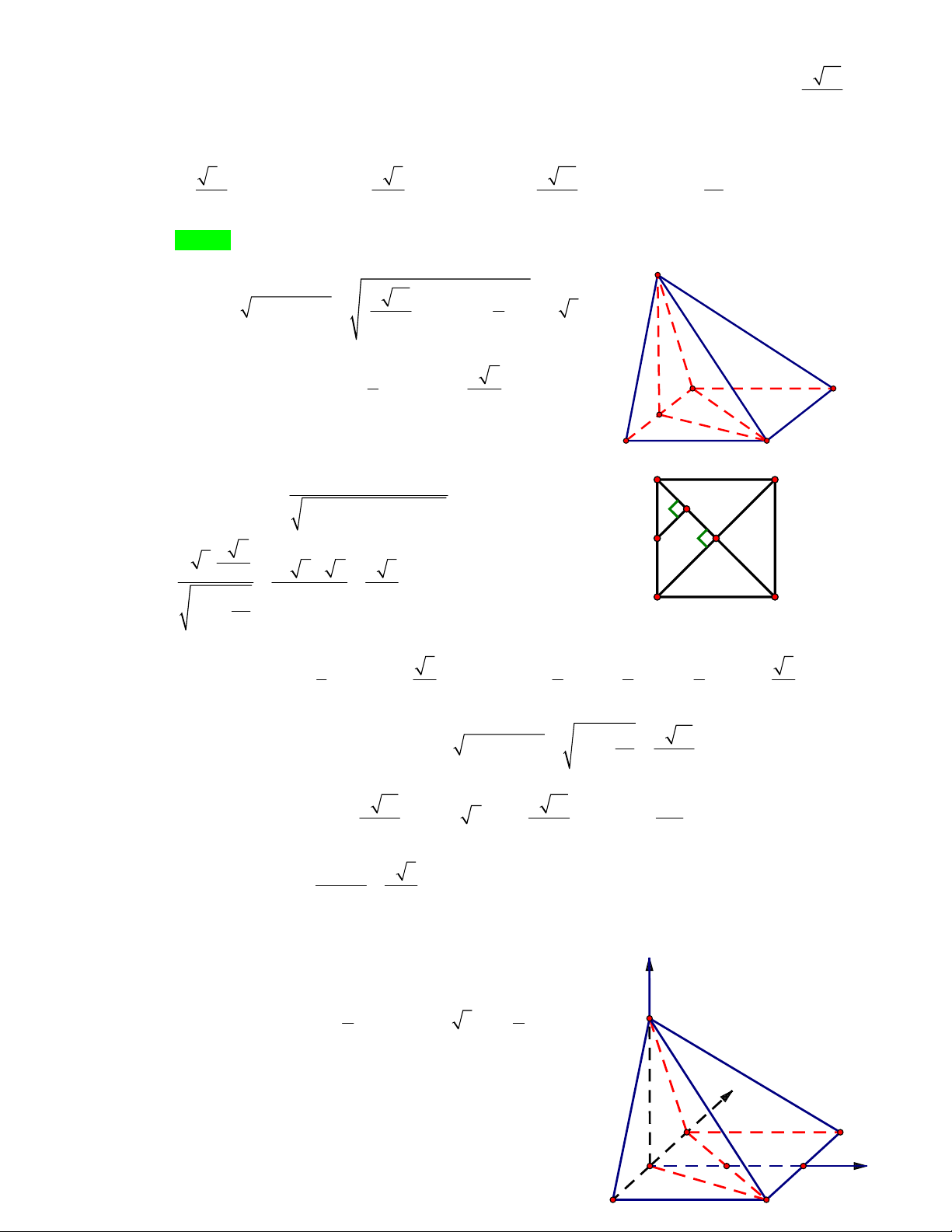
H
I
A D
B C
Câu23: CHUYÊN THÁI BÌNH Cho hình chóp
.SABCD
cóđáylàhìnhvuôngcạnh
a
,
17
2
a
SD
,
hìnhchiếuvuônggóc
H
của
S
lênmặt
A
BCD
làtrungđiểmcủađoạn
A
B .Tínhchiềucao
củakhốichóp
.HSBD
theo
a
.
A.
3
5
a
. B.
3
7
a
. C.
21
5
a
. D.
3a
5
.
ChọnA.
Ta có
SHD
vuôngtại
H
2
2
22 2
17
3
22
aa
SH SD HD a a
.
Cách1.Tacó
12
,,
24
a
d H BD d A BD
.
Chiềucaocủachóp
.HSBD
là
2
2
2
2
2
.,
,
,
2
3.
6.2 2 3
4
.
4.5 5
3
8
SH d H BD
dH SBD
SH d H BD
a
a
aa
a
a
a
Cách2.
3
13
..
33
ABCD
SABCD SHS a
...
3
.
111
2224
3
1
H SBD A SBD S ABC S ABCD
VVVV a
.
Tamgiác
SHB
vuôngtại
H
2
22 2
13
3
42
aa
SB SH HB a
.
Tamgiác
SBD
có
13 17
;2;
22
aa
SB BD a SD
2
5
4
SBD
a
S
.
.
3
3
,.
5
SHBD
SBD
V
a
dH SBD
S
Cách3.Gọi
I
làtrungđiểm
BD
.Chọnhệtrục
Oxyz
với
; ; ; .O H Ox HI Oy HB Oz HS
Tacó
0;0; 0H
; 0; ;0
2
a
B
;
0;0; 3Sa
; ;0;0
2
a
I
Vì
SBD SBI
H
B
S
A
D
C
y
x
O
H
z
I
B
C
D
A
S
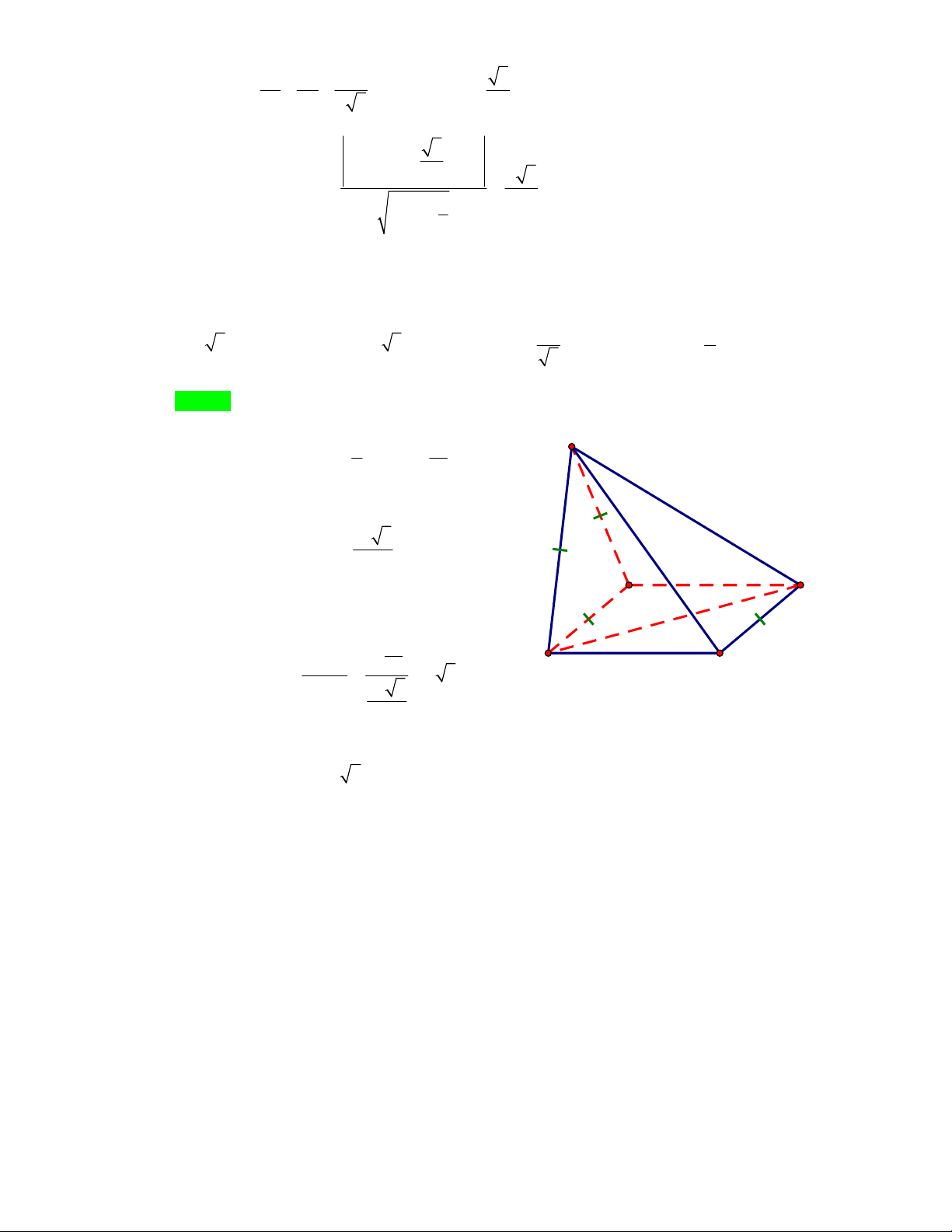
22 3
:1220
3
3
xyz
SBD x y z a
aa
a
.
Suyra
3
2.0 2.0 .0
3
3
,.
5
1
44
3
a
a
dH SBD
Câu24: CHUYÊNPHANBỘICHÂUChokhốichóp
.SABCD
cóthểtíchbằng
3
a
.Mặtbên
SAB
là
tamgiácđềucạnh
a
vàđáy
A
BCD
làhìnhbìnhhành.Tínhtheo
a
khoảngcáchgiữa
SA
và
CD
.
A.
23a
. B.
3a
. C.
2
3
a
. D.
2
a
.
Hướngdẫngiải
ChọnA.
Vìđáy
A
BCD
làhìnhbìnhhành
3
.
1
22
SABD SBCD S ABCD
a
VV V
.
Tacó:
Vìtamgiác
SAB
đềucạnha
2
3
4
SAB
a
S
Vì
CD AB CD SAB
nên
,, ,dCDSA dCD SAB dD SAB
3
2
3.
3
2
23
3
4
SABD
SBD
a
V
a
S
a
.
Câu25: LÝTỰTRỌNG–TPHCMTìm
max
V
làgiátrịlớnnhấtcủathểtíchcáckhốihộpchữnhật
cóđườngchéobằng
32cm
vàdiệntíchtoànphầnbằng
2
18 .cm
A.
3
max
6.Vcm B.
3
max
5.Vcm
C.
3
max
4.Vcm
D.
3
max
3.Vcm
Hướngdẫngiải
ChọnC.
Đặt
,,abc
làkíchthướccủahìnhhộpthìtacóhệ
222
18
9
abc
ab bc ac
.
Suyra
6.abc
CầntìmGTLNcủa
.Vabc
Tacó
69 96.bc a bc abc a a
Do
22
46 496 04.bc bc a a a a
a
A
D
C
B
S
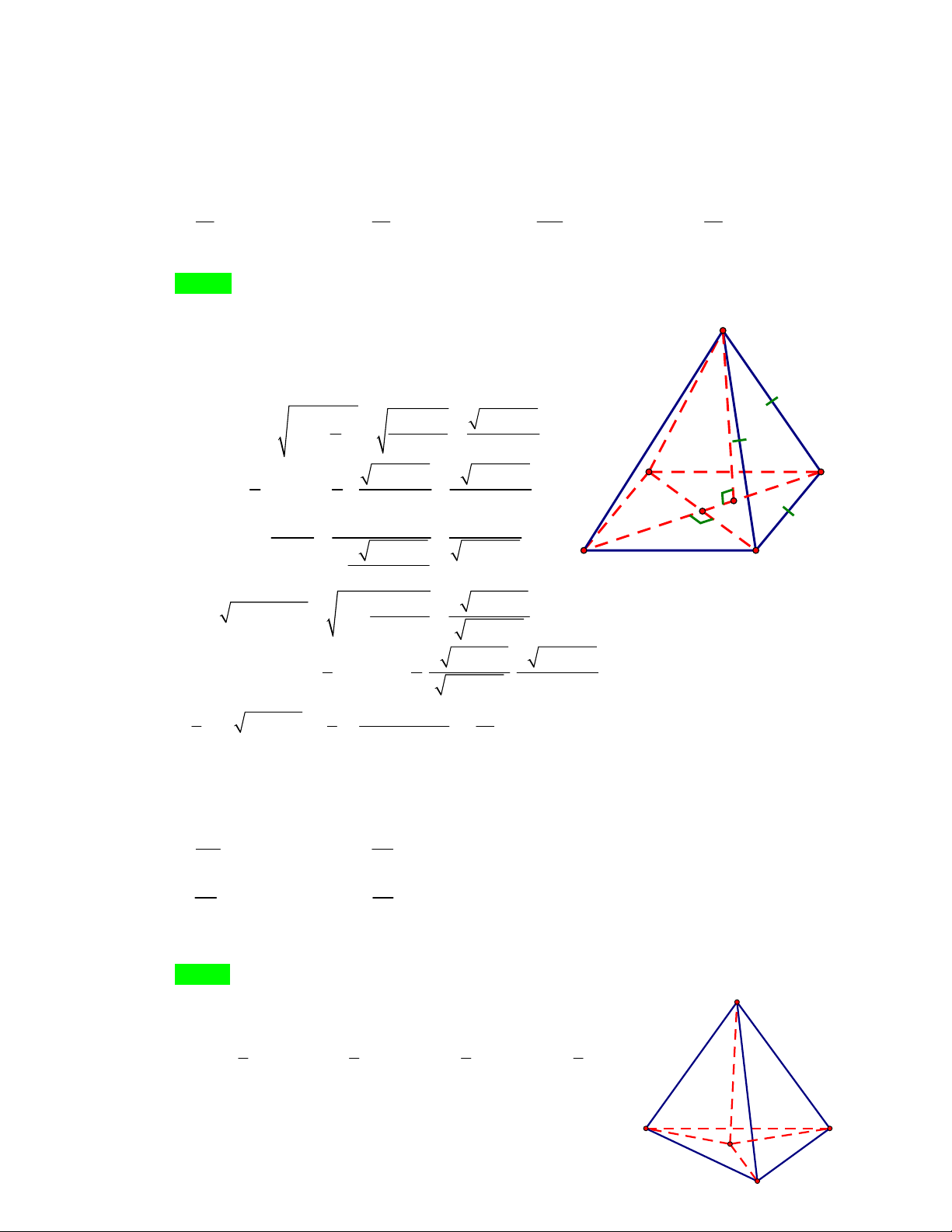
Tươngtự
0,4bc
.
Talạicó
96Va a a
.KhảosáthàmsốnàytìmđượcGTLNcủa
V
là4.
Câu26: CHUYÊN PHAN BỘI CHÂU Khối chóp
.S ABCD
cóđáy
A
BCD
làhìnhthoicạnh
a
.
SA SB SC a
,Cạnh
SD
thayđổi.Thểtíchlớnnhấtcủakhốichóp
.S ABCD
là:
A.
3
8
a
. B.
3
4
a
. C.
3
3
8
a
. D.
3
2
a
.
Hướngdẫngiải
ChọnD.
Khi
SD
thayđổithi
A
C
thayđổi.Đặt
A
Cx
.
Gọi
OACBD
.
Vì
SA SB SC
nênchânđườngcao
SH
trùng
vớitâmđườngtrònngoạitiếptamgiác
A
BC
.
HBO
.
Tacó
2
22 22
2
44
24 2
x
ax ax
OB a
22 22
114 4
..
222 4
ABC
ax xax
SOBACx
22
22 22
..
4
44
4.
4
ABC
aax a x a
HB R
S
x
ax ax
.
422
222
22
22
3
4
4
aaax
SH SB BH a
ax
ax
22 22
..
22
1234
22.. . .
33 4
4
S ABCD S ABC ABC
aa xxa x
VV SHS
ax
222 3
22
113
.3
3322
x
ax a
ax a x a
Câu27: THTT–477Chokhốiđadiệnđều n mặtcóthểtích
V
vàdiệntíchmỗimặtcủanóbằng
.S
Khiđó,tổngcáckhoảngcáchtừmộtđiểmbấtkìbêntrongkhốiđadiệnđóđếncácmặt
củanóbằng
A.
.
nV
S
B. .
V
nS
C.
3
.
V
S
D. .
3
V
S
Hướngdẫngiải
ChọnC.
Xéttrongtrườnghợpkhốitứdiệnđều.
Cáctrườnghợpkháchoàntoàntươngtự.
.1.2.3.4
1111
.; .; .; .
3333
H ABC H SBC H SAB H SAC
V hSV hSV hSV hS
x
a
O
A
S
D
C
B
H
A
C
B
S
H
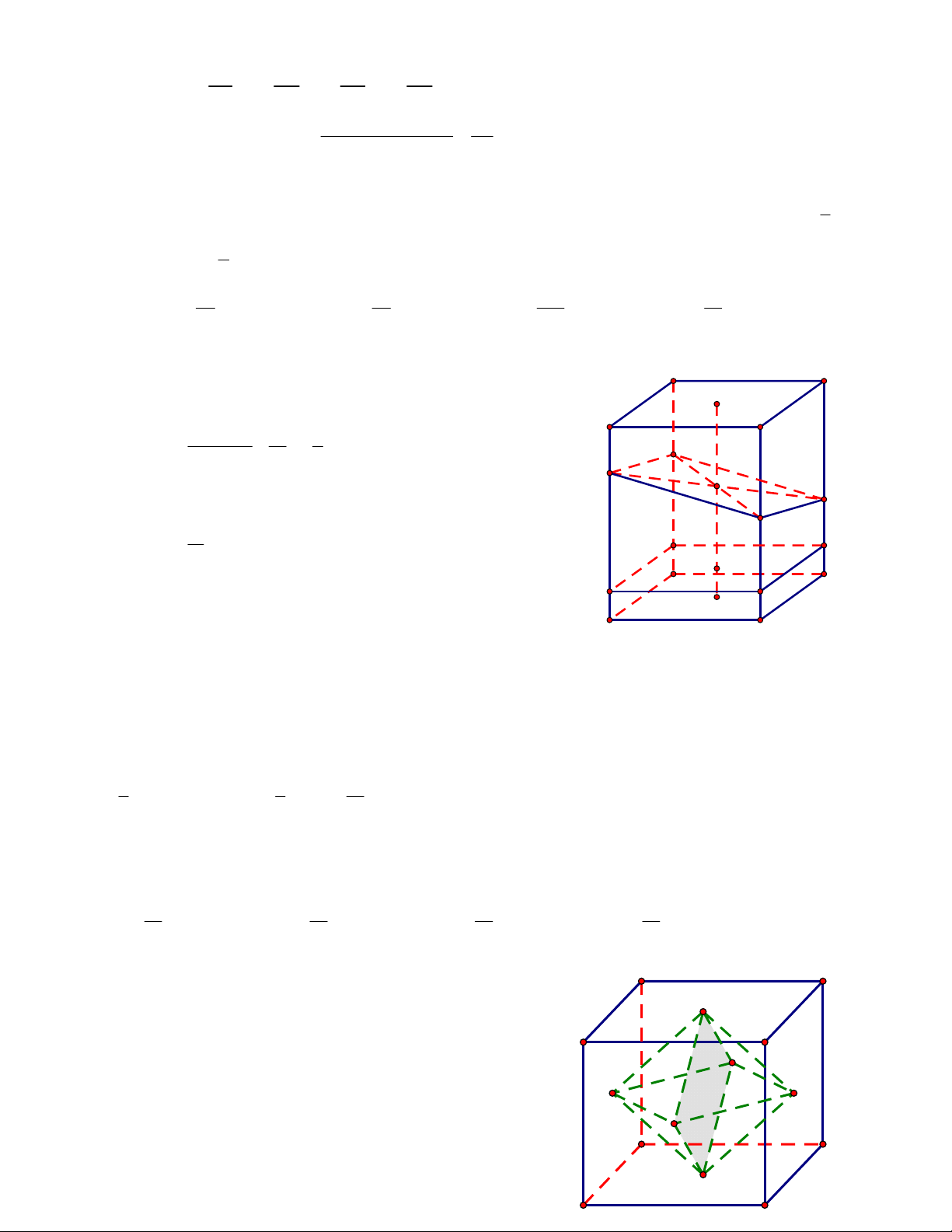
3
12 4
12 3 4
1234
1234
3
33 3
;;;
3
3
V
VV V
hh hh
SSSS
VVVV
V
hhhh
SS
Câu28: LƯƠNG ĐẮC BẰNG Chohìnhlậpphương
.
A
BCD A B C D
cócạnhbằng a , một mặt
phẳng
cắtcáccạnh
A
A
, BB
,
CC
, DD
lầnlượttại
M
,
N
,
P
, Q .Biết
1
3
A
Ma ,
2
5
CP a
.Thểtíchkhốiđadiện
.
A
BCD MNPQ
là:
A.
3
11
30
a
. B.
3
3
a
. C.
3
2
3
a
. D.
3
11
15
a
.
HD:Tứgiác
MNPQ
làhìnhbìnhhànhcótâmlàI
thuộcđoạnOO’.
Tacó:
11
2302
A
MCP a
OI a
GọiO
1
làđiểmđốixứngOquaIthì:
OO
1
2OI
11
15
a
a.VậyO
1
nằmtrongđoạnOO’.
VẽmặtphẳngquaO
1
songsongvớiABCDcắt
cáccạnh
AA’;BB’;CC’;DD’
lầnlượttại
A
1
,B
1
,C
1
,D
1
.
KhiđóIlàtâmcủahìnhhộp
ABCD.AB
1
C
1
D
1
.
VậyVABCD.MNPQVMNPQ.A
1
B
1
C
1
D
1
23
111 1 1
1111
(. )
2230
V ABCD A B C D a OO a
Câu29: CHUYÊNVĨNHPHÚCNgườitagọtmộtkhốilậpphươnggỗđểlấykhốitámmặtđềunội
tiếpnótứclàkhốicócácđỉnhlàcáctâmcủacácmặtkhốilậpphương.Biếtcáccạnhcủa
khốilậpphươngbằnga.Hãytínhthểtíchcủakhốitámmặtđềuđó:
A.
3
a
4
B.
3
a
6
C.
3
a
12
D.
3
a
8
ĐápánB
Dựngđượchìnhnhưhìnhbên
Thấyđượcthểtíchkhốicầntính bằng2lầnthểtíchcủa
hìnhchópS.ABCD
NhiệmvụbâygiờđitìmthểtíchcủaS.ABCD
Q
O
1
I
O'
O
A'
C'
D'
C
B
D
A
B'
N
M
P
B
D
C
S
A
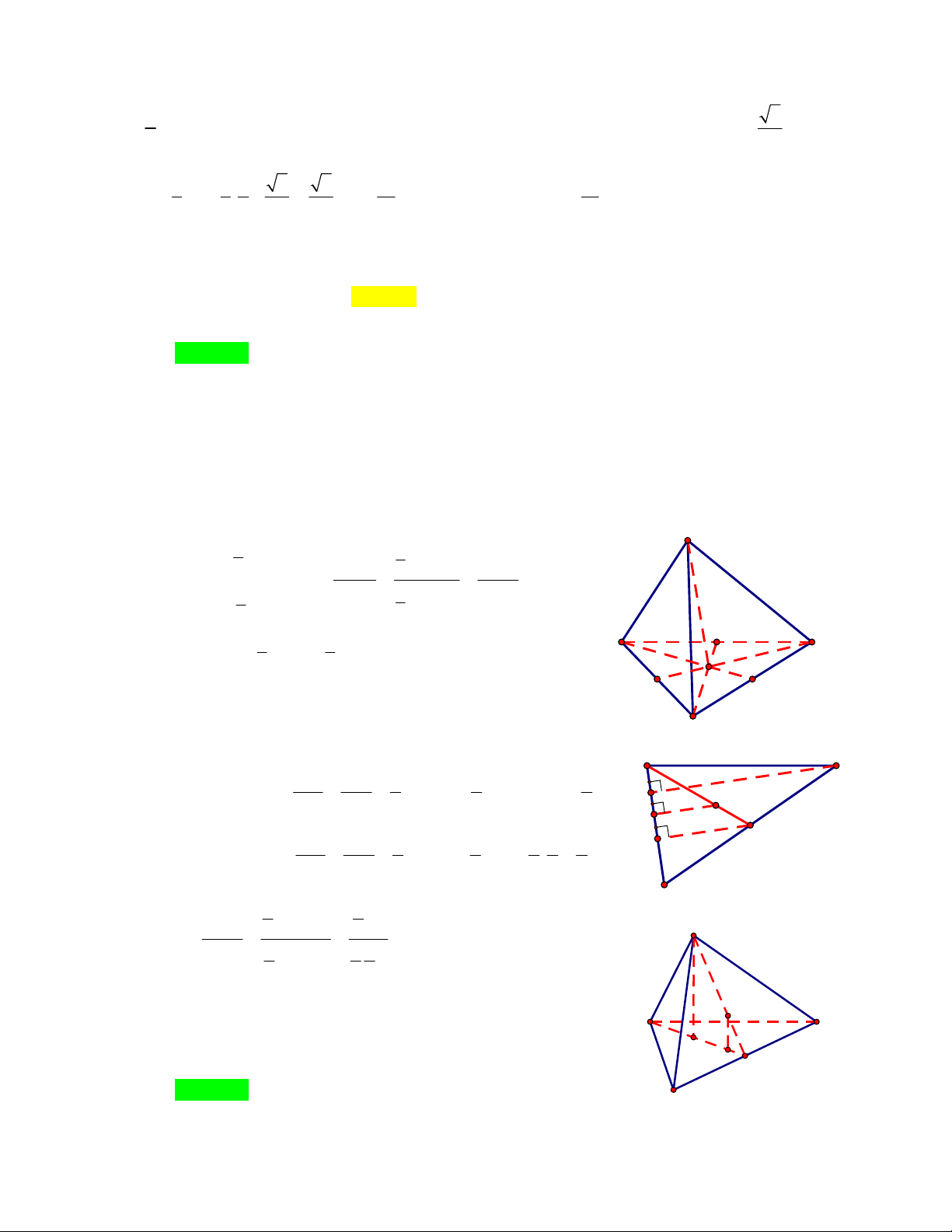
ABCDlàhìnhvuôngcótâmOđồngthờichínhlàhìnhchiếucủaSlênmặtđáy
a
SO
2
;
BD
cạnhcủahìnhlậpphương a .Suyracáccạnhcủahìnhvuông
2
ABCD a
2
3
3
S.ABCD
11122 a
VSh.. a
33222 12
.V
khốiđadiện
3
S.ABCD
a
2.V
6
.
Câu30: Chotứdiện
A
BCD
cóthểtíchbằng12và
G
làtrọngtâmtamgiác
B
CD
.Tínhthểtích
V
củakhốichóp
.
A
GBC
.
A.
3V
. B.
4V
. C.
6V
. D.
5V
.
ChọnB.
Cách1:
Phân tích:tứdiện
A
BCD
và khối chóp
.
A
GBC
cócùng
đườngcaolàkhoảngcáchtừ
A
đếnmặtphẳng
BCD
.Do
G
là trọng tâm tam giác
B
CD
nêntacó
B
GC BGD CGD
SSS 3
B
CD BGC
SS
xem phần chứng
minh.
Ápdụngcôngthứcthểtíchhìnhchóptacó:
.
.
1
1
.
.
3
3
3
1
1
.
.
3
3
ABCD BCD
BCD
ABCD BCD
AGBC GBC
GBC
AGBC GBC
VhS
hS
VS
VS
hS
VhS
.
11
.12 4
33
A GBC ABCD
VV .
Chứngminh:Đặt ;DN h BC a .
Từhìnhvẽcó:
11
//
22 2
M
FCM h
MF ND MF DN MF
DN CD
.
222
// .
33323
GE BG h h
GE MF GE MF
M
FBM
11
.
22
33
11
.
223
BCD
B
CD GBC
GBC
DN BC ha
S
SS
h
S
GE BC a
Chứngminhtươngtựcó
33
B
CD GBD GCD
SSS
B
GC BGD CGD
SSS
.
Cách2:
G
B
C
D
A
H
1
G
I
D
C
B
A
H
F
E
G
M
N
B
C
D
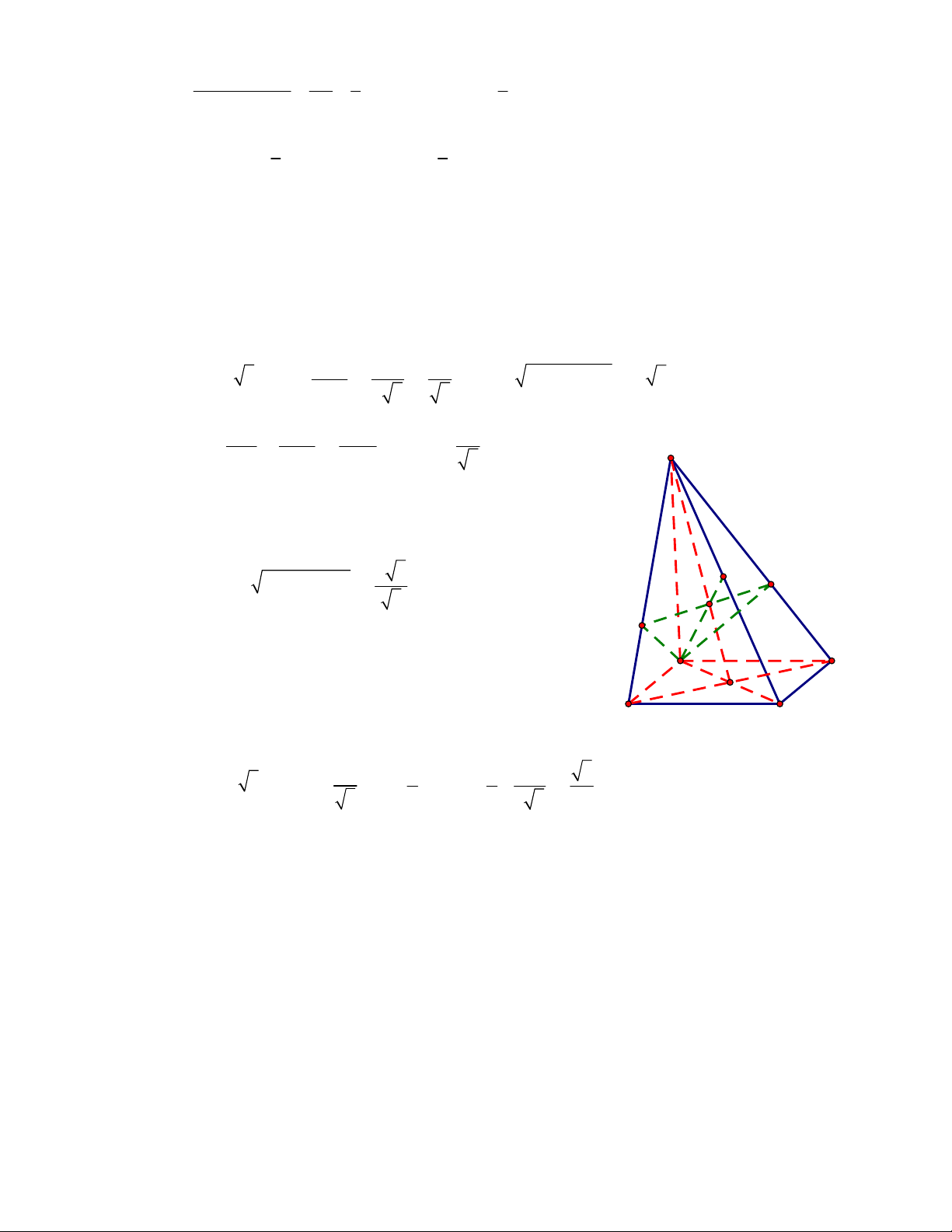
;
11
;;
33
;
d G ABC
GI
d G ABC d D ABC
DI
dD ABC
.
Nên
.
11
;. .4.
33
G ABC ABC DABC
VdGABCSV
Câu31: Mộthìnhtrụcódiệntíchxungquanhbằng 4 ,diệntíchđáybằngdiệntíchcủamặtcầucó
bánkínhbằng
1.TínhthểtíchV khốitrụđó.
A.
4V =
. B.
6V =
. C.
8V =
. D.
10V =
.
ĐápánB
,BD
nhìnAC dướimộtgóc90 .
22
5; ;
55
AD a a
SD a KD
SD
a
====
22
6SC SA A C a=+=
Tacó:
()
22 2
11 1 2
1
5
a
AK
SA AD AK
+==
222
SC SD CD=+
tamgiácSCD vuôngtạiD .
Khiđótamgiác
KDC vuôngtạiD .
22
6
5
a
KC CD KD= + =
Tacó:
22 2
AK KC AC+=
.Vậy
90AKC =
.Tươngtự
0
90AHC =
Vậy
AC
chínhlàđườngkínhmặtcầungoạitiếpkhối
ABCDEHK
.
2
2
a
AC a OA==
.
3
33
44 2
33 3
22
a
VOA app p== =
Câu32: Ghép5khốilậpphươngcạnh
a
đểđượckhốihộpchữthậpnhưhìnhvẽ.
Tínhdiệntíchtoànphần
tp
S
củakhốichữthập
A.
=
2
20
tp
Sa
. B.
=
2
30
tp
Sa
. C.
=
2
12
tp
Sa
. D.
=
2
22
tp
Sa
.
E
O
A
B
C
D
S
H
K
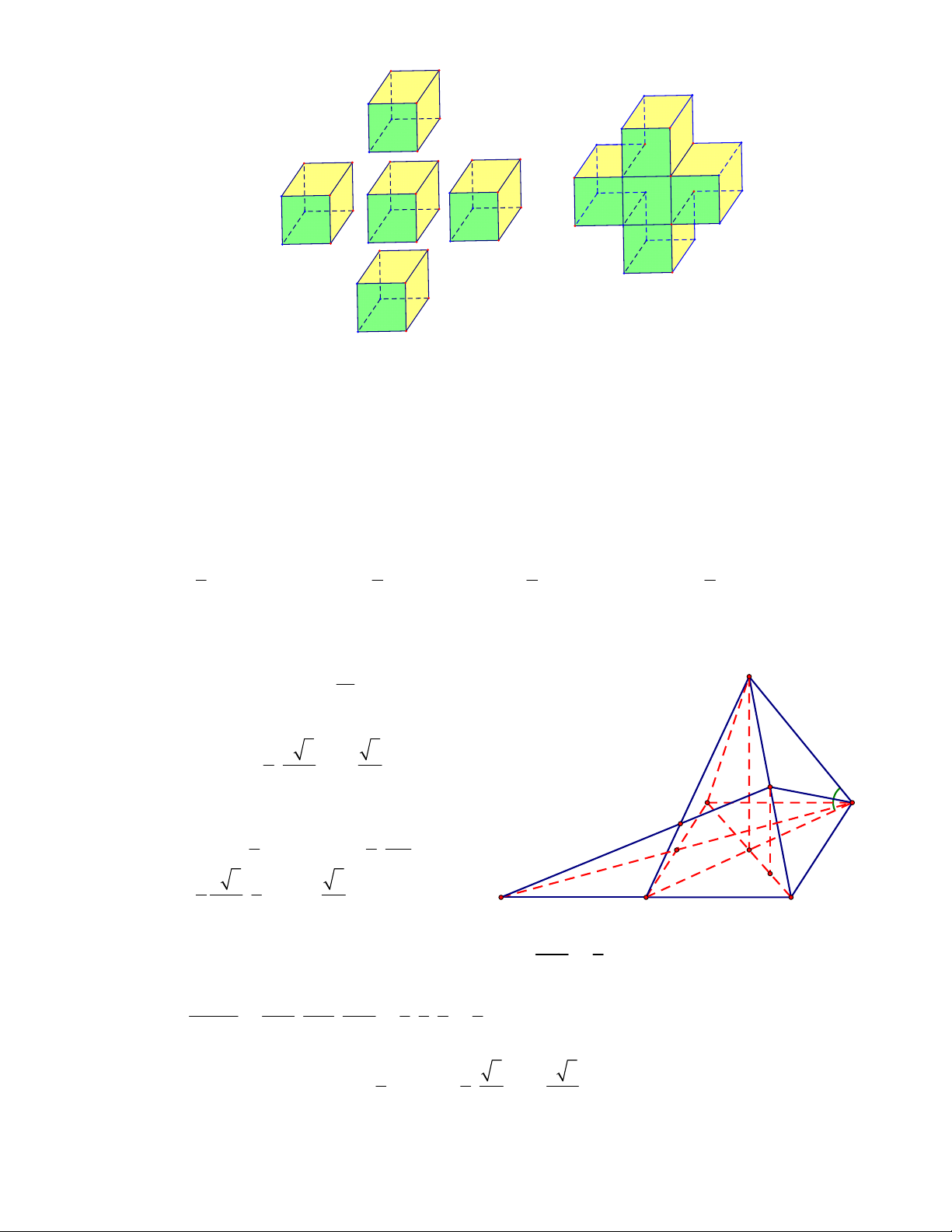
Diệntíchmỗimặtkhốilậpphương:
=
2
1
Sa
Diệntíchtoànphầncáckhốilậpphương:
=
2
2
6Sa
Diệntíchtoànphầnkhốichữthập:
=-=
2
21
5822SS S a
Câu33: Chohìnhchóptứgiácđều
.SABCD
cócạnhđáybằnga ,cạnhbênhợpvớiđáymộtgóc
60
.Gọi
M
làđiểmđốixứngvới
C
qua
D
;
N
làtrungđiểmcủa
SC
,mặtphẳng
BMN
chiakhốichóp
.SABCD
thànhhaiphần.Tínhtỉsốthểtíchgiữahaiphầnđó.
A.
1
5
. B.
7
3
. C.
1
7
. D.
7
5
.
ĐápánD
Đặt
1
1
2
2
?
SABIKN
NBCDIK
VV
V
VV
V
ì
ï
=
ï
=
í
ï
=
ï
î
*
23
.
16 6
.
32 6
SABCD
a
Vaa==
*
.
3
11
.. . .
332
161 6
...2
34 2 12
NBMC BMC BMC
SO
VNHS S
a
aa a
DD
==
==
*NhậnthấyKlàtrọngtâmcủatamgiácSMC
2
3
MK
MN
=
*
.
.
112 1
.. ..
223 6
MDIK
MCBN
V
MD MI MK
VMCMBMN
===
33
2. . .CBN
55656
.
661272
MCBN MDIK M
VV V V a a= - = = =
a
a
60°
H
K
N
M
I
O
A
S
B
C
D
3
33 3
1
1. 2
2
3
76
656 76 7
72
672 72 5
56
72
SABCD
a
V
VV V a a a
V
a
= -= - = = =
Câu34: Chohìnhchóptứgiác
.S ABCD
có
SA ABCD ,
A
BCD
làhìnhthangvuôngtại
A
và B
biết
2
A
Ba
,
33
A
DBCa
.Tínhthểtíchkhốichóp
.SABCD
theo a ,biếtkhoảngcáchtừAđến
mặtphẳng
()SCD bằng
36
4
a
.
A.
3
66a
. B.
3
26a
. C.
3
23a
. D.
3
63a
.
Hướngdẫngiải
Dựng
A
MCD
tại
M
.
Dựng
A
HSM
tại
H
.
Tacó:
36
4
A
Ha .
2
.4
2
ABCD
AD BC
SABa
2
2
22CD AD BC AB a
2
1
.
2
ABC
SABBCa
2
3
ACD ABCD ABC
SS S a
2
132
.
22
ACD
ACD
S
SAMCDAM a
CD
Tacó:
222
22
111 . 36
2
AH AM
A
Sa
AH AM AS
AM AH
3
.
1
.26
3
S ABCD ABCD
VSAS a
Câu35: Cholăngtrụtamgiác
.'' '
A
BC A B C
có
'
B
Ba
,gócgiữađườngthẳng 'BB và
A
BC
bằng
60
,tamgiác
A
BC
vuôngtại
C
vàgóc
60BAC .Hìnhchiếuvuônggóccủađiểm 'B lên
A
BC
trùngvớitrọngtâmcủa
A
BC
.Thểtíchcủakhốitứdiện
'.
A
ABC
theo
a bằng
A.
3
13
108
a
. B.
3
7
106
a
. C.
3
15
108
a
. D.
3
9
208
a
.
Hướngdẫngiải
M
A
D
B
C
S
K
60°
60°
C'
A'
G
M
N
B
C
A
B'
Gọi ,
M
N làtrungđiểmcủa ,
A
BAC
và
G
làtrọngtâmcủa
A
BC
.
'BG ABC
0
', ' 60BB ABC B BG
.
'.
11
..' ...'
36
A ABC ABC
V S BG ACBCBG
Xét
'
B
BG
vuôngtại
G
,có
0
'60BBG
3
'
2
a
BG
.nửatamgiácđều
Đặt
2
A
Bx
.Trong
A
BC
vuôngtại
C
có
0
60BAC
tamgiác
A
BC
lànữatamgiácđều , 3
2
AB
A
CxBCx
Do
G
làtrọngtâm
A
BC
33
24
a
BN BG
.
Trong
B
NC
vuôngtại
C
:
222
BN NC BC
22 2
22
3
213
993
3
16 4 52
213
33
213
a
AC
ax a a
xx x
a
BC
V
ậy,
3
'
13 33 39
...
6 2 208
213213
A ABC
aa a a
V
.
Câu36: Chohìnhlăngtrụđứng
.'' '
A
BC A B C
,biếtđáy
A
BC
làtamgiácđềucạnh
a .Khoảngcách
từ tâm
O
của tam giác
A
BC
đến mặt phẳng
'
A
BC
bằng
6
a
.Tính thể tích khối lăng trụ
.'' '
A
BC A B C
.
A.
3
32
8
a
. B.
3
32
28
a
. C.
3
32
4
a
. D.
3
32
16
a
.
Hướngdẫngiải
Gọi
M
làtrungđiểmcủa
B
C
,
tacó
''
A
AM A BC
theogiao
tuyến
'
A
M
.
Trong
'
A
AM
kẻ
'( ')OH A M H A M
.
'OH A BC
Suyra:
,'
6
a
dO ABC OH.
2
3
4
ABC
a
S
.
Xéthaitamgiácvuông
'
A
AM
và
OHM
cógóc
M
chungnênchúng
đồngdạng.
Suyra:
22 2
2
13
.
13
632
'' ' '
'
3
'
2
aa
OH OM
AA AM AA AA
AA AM
a
AA
.
6
'
4
a
AA
.Thểtích:
23
.'''
6332
.' .
44 16
ABC A B C ABC
aa a
VSAA
.
Câu37: Chohìnhchóptứgiácđều
.SABCDcócạnhđáybằng
a
.Biếtthểtíchkhốichópbằng
3
2
6
a
.Tínhkhoảngcách
h
giữahaiđườngthẳng
BC
và
SA
.
A.
.
6
a
B.
.a
C.
2
.
6
a
D.
.
2
a
Hướngdẫngiải
Gọi
O làtâmhìnhvuông .SABCD, suy ra
(
)
^SO ABCD .
Đặt
=SO x . Ta có
====
3
2
.
1122
.. . .
3362
S ABCD ABCD
aa
VSSOax x
Tacó
BC AD
nên
(
)
BC SAD .Dođó
(
)
(
)
(
)
éùéùéù
éù
===
êú
êúêúêú
ëû
ëûëûëû
,, ,2,d BC SA d BC SAD d B SAD d O SAD
.
Kẻ
^OK SE
.Khiđó
()
éù
== =
êú
ëû
+
22
.
,
6
SO OE a
dO SAD OK
SO OE
.
O
C'
B'
M
A
B
A'
C
H
E
O
C
D
A
B
S
K
Vậy
éù
==
êú
ëû
2
,2 .
6
a
dBCSA OK
ChọnC.
Câu38: ĐỀMINHHỌAQUỐCGIANĂM2017Chohìnhchóptứgiác
.SABCDcóđáylàhình
vuôngcạnhbằng
2.a
Tamgiác
()
SAD
cântạiS vàmặtbên
()
SAD
vuônggócvớimặtphẳng
đáy.Biếtthểtíchkhốichóp
.SABCD
bằng
3
4
.
3
a
Tínhkhoảngcách
h
từ
B
đếnmặtphẳng
(
)
SCD .
A.
=
2
.
3
ha
B.
=
4
.
3
ha
C.
=
8
.
3
ha
D.
=
3
.
4
ha
Hướngdẫngiải
Gọi
H làtrungđiểmAD .
Suyra
()
^^ .SH AD SH ABCD
Đặt
=SH x
.
Tacó
()
===
2
3
14
.. 2 2
33
Vxa axa
.
Tacó
(
)
(
)
éùéù
=
êúêú
ëûëû
,,
dB SCD dA SCD
()
éù
===
êú
ëû
4
2, 2
3
a
dH SCD HK
.ChọnB.
Câu39: Cho hình chóp
.SABCD
cóđáy
ABCD
làhìnhvuôngtâm
O
, cạnh a . Cạnh bên
SA
vuônggócvớiđáy,góc
=
0
60SBD
.Tínhtheo
a
khoảngcáchgiữahaiđườngthẳng
AB
và
SO
.
A.
3
3
a
. B.
6
4
a
. C.
2
.
2
a
D.
5
.
5
a
Hướngdẫngiải
Tacó
D=DSAB SAD
()
--cgc,suyra
=SB SD
.
Lạicó
=
0
60SBD ,suyra
DSBD
đềucạnh == =2SB SD BD a .
Trongtamgiácvuông
SAB ,tacó
=-=
22
SA SB AB a .
Gọi
E
làtrungđiểm
AD
,suyra
OE AB
và
^AE OE
.
Dođó
(
)
(
)
éùéù
éù
==
êú
êúêú
ëû
ëûëû
,, ,.dABSO dAB SOE dA SOE
H
A
B
C
D
S
K
E
O
A
S
B
C
D
K
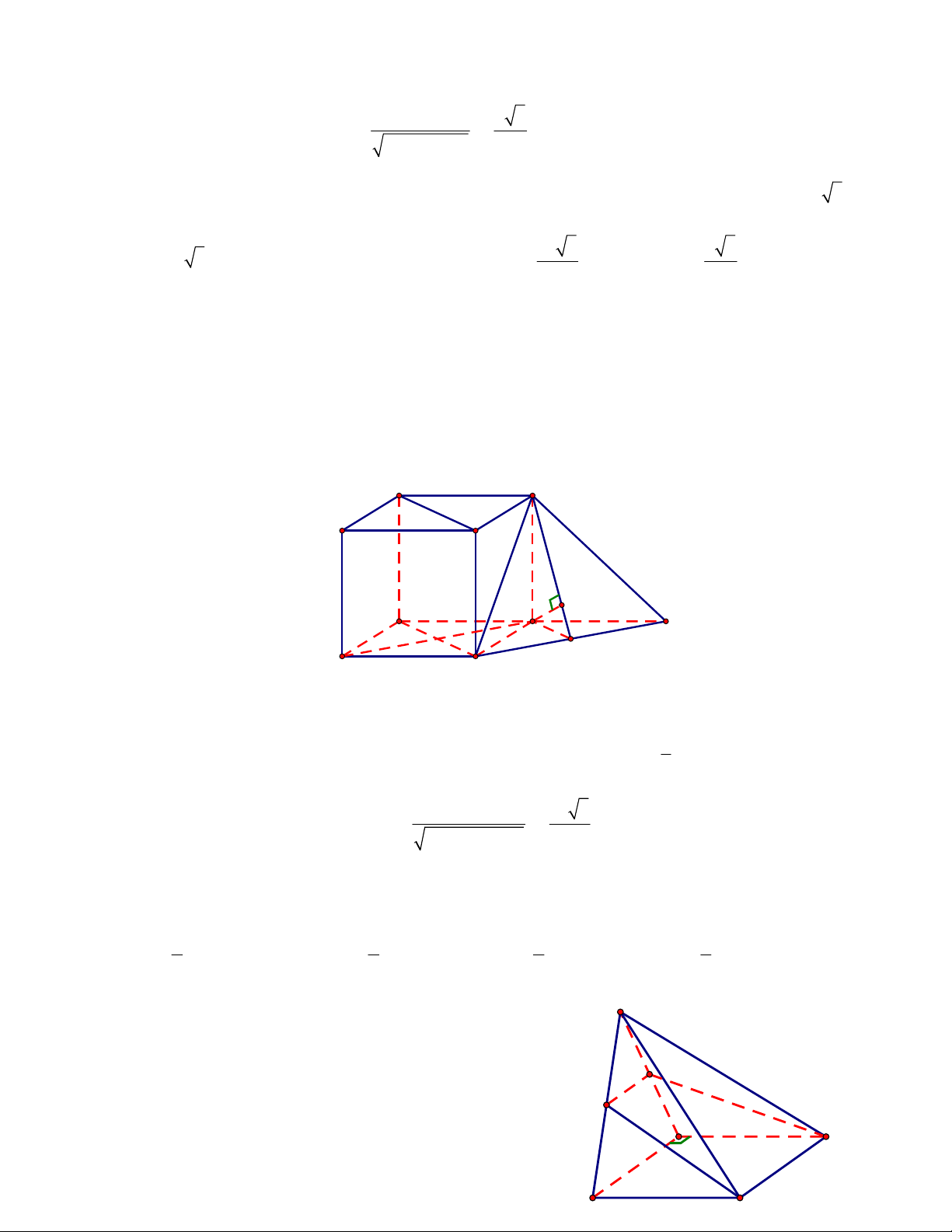
Kẻ
^AK SE
.
Khiđó
()
éù
== =
êú
ëû
+
22
.5
,
5
SA AE a
dA SOE AK
SA A E
.ChọnD.
Câu40: Cho hình hộp chữ nhật
.''''ABCD A B C D cóđáyABCD là hình vuông cạnh
2a
,
='2AA a
.Tínhkhoảngcáchgiữahaiđườngthẳng
BD
và
'CD
.
A.
2.a
B.
2.a
C.
25
.
5
a
D.
5
.
5
a
Hướngdẫngiải
Gọi
I
làđiểmđốixứngcủa
A
qua
D
,suyra
BCID
làhìnhbìnhhànhnên
.BD CI
Dođó
(
)
(
)
éùéù
éù
==
êú
êúêú
ëû
ëûëû
,' , ' , '.dBDCD dBD CDI dD CDI
Kẻ
^DE CI
tại
E
,kẻ
^ 'DK D E
.Khiđó
()
éù
=
êú
ëû
,' .dD CDI DK
Xéttamgiác
IAC ,tacó
DE AC
docùngvuônggócvớiCI vàcó D làtrungđiểmcủa
AI nênsuyraDE làđườngtrungbìnhcủatamgiác.Suyra
==
1
.
2
DE AC a
Tamgiácvuông
'DDE
,có ==
+
22
'. 2 5
.
5
'
DDDE a
DK
DD DE
ChọnC.
Câu41: Chokhốichóptứgiácđều
.SABCD
.Mặtphẳng
(
)
a điqua
, AB
vàtrungđiểm
M
của
SC
.Tỉsốthểtíchcủahaiphầnkhốichópbịphânchiabởimặtphẳngđólà:
A.
1
4
. B.
3
8
. C.
5
8
. D.
3
5
.
Hướngdẫngiải
Kẻ
MN CD
()
ÎNCD, suyrahìnhthang
ABMN
làthiếtdiệncủakhốichóp.
Tacó
=+
...S ABMN S ABM S AMN
VVV.
E
I
B
D
C
D'
B'
C'
A'
A
K
M
N
D
S
C
B
A
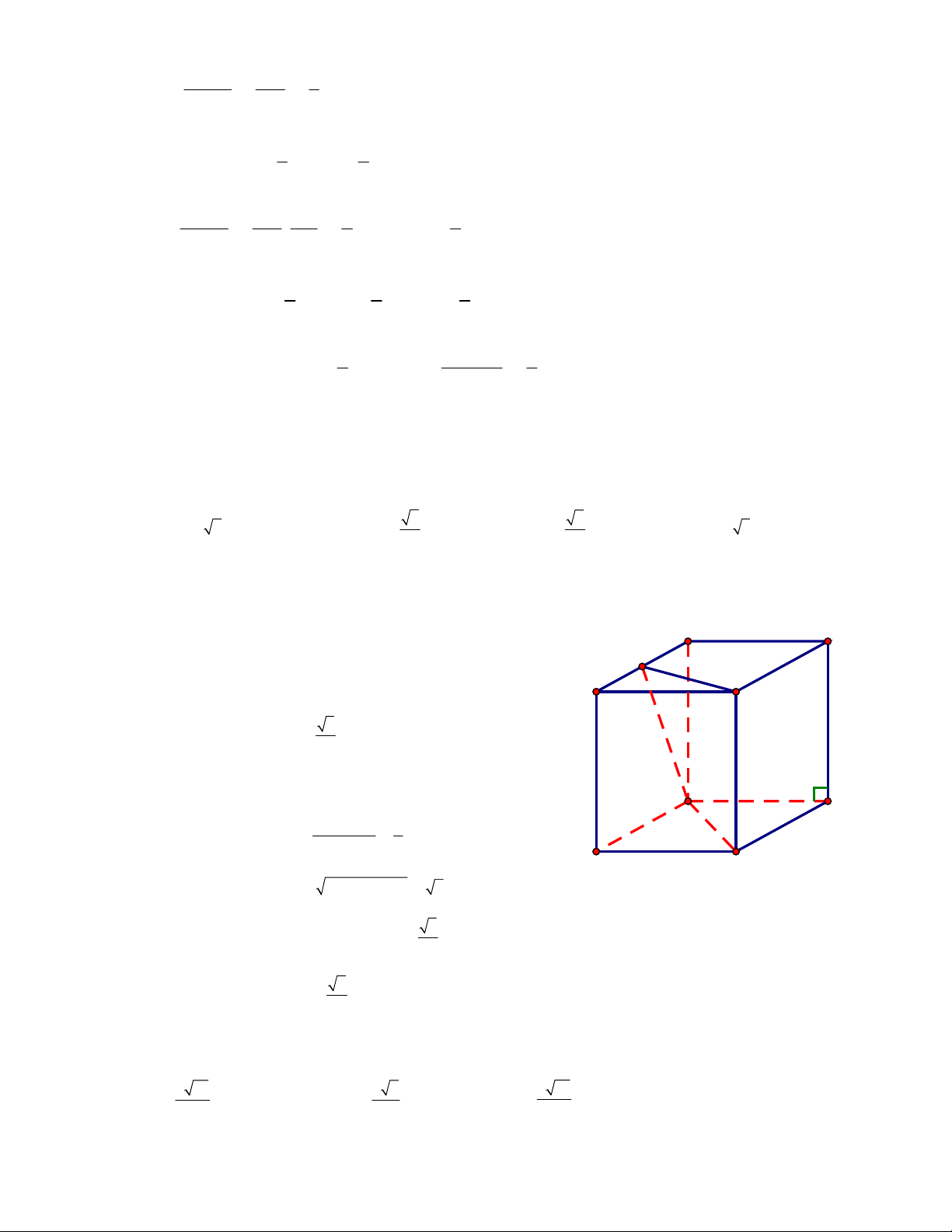
Mà
==
.
.
1
2
SABM
SABC
V
SM
VSC
.
Suyra
==
...
11
.
24
SABM SABC SABCD
VVV
Và
===
.
..
.
11
..
48
SAMN
SAMN SABCD
SACD
V
SM SN
VV
VSCSD
Suyra
=+=
....
113
.
488
SABMN SABCD SABCD SABCD
VVVV
Từđósuyra
=
.
5
8
ABMNDC S ABCD
VV
nên =
.
3
.
5
SABMN
ABMNDC
V
V
ChọnD.
Câu42: Cholăngtrụđứng
.''' 'ABCD A B C D
cóđáylàhìnhthoicạnhbằng 1,
0
120BAD =
.Gócgiữa
đườngthẳng
'AC vàmặtphẳng
()
''
A
DD A
bằng
0
30
.Tínhthểtíchkhốilăngtrụ.
A.
6V = . B.
6
6
V =
. C.
6
2
V =
. D. 3V = .
Hướngdẫngiải
Hìnhthoi
ABCDcó
0
120BAD = ,suyra
0
60ADC = .
Dođótamgiác
ABC và ADC làcáctamgiácđều.
Vì
N
làtrungđiểm ''
A
D nên
'''CN AD^
và
3
'.
2
CN=
Suyra
()
0
30 ', ' ' ', 'AC ADD A AC AN C AN===
.
Tamgiác ,có
'3
2
tan '
CN
AN
CAN
==
.
Tamgiác ,có
22
''2AA AN A N=-=
.
Diệntíchhìnhthoi
2
3
.sin
2
ABCD
SABBAD==
.
Vậy
.''' '
6
.'
2
ABCD A B C D ABCD
VSAA==
đvtt.ChọnC.
Câu43: Chohìnhchóp
.SABCDcóđáy ABCD làhìnhvuôngcạnh
a
,tamgiác SAD đềuvànằm
trongmặtphẳngvuônggócvớiđáy.Tínhkhoảngcáchgiữahaiđườngthẳng
SA và BD .
A.
21
.
14
a
B.
2
.
2
a
C.
21
.
7
a
D.
.a
Hướngdẫngiải
ʹCAN
ʹAA N
N
D
B
C
B'A'
C'
D'
A
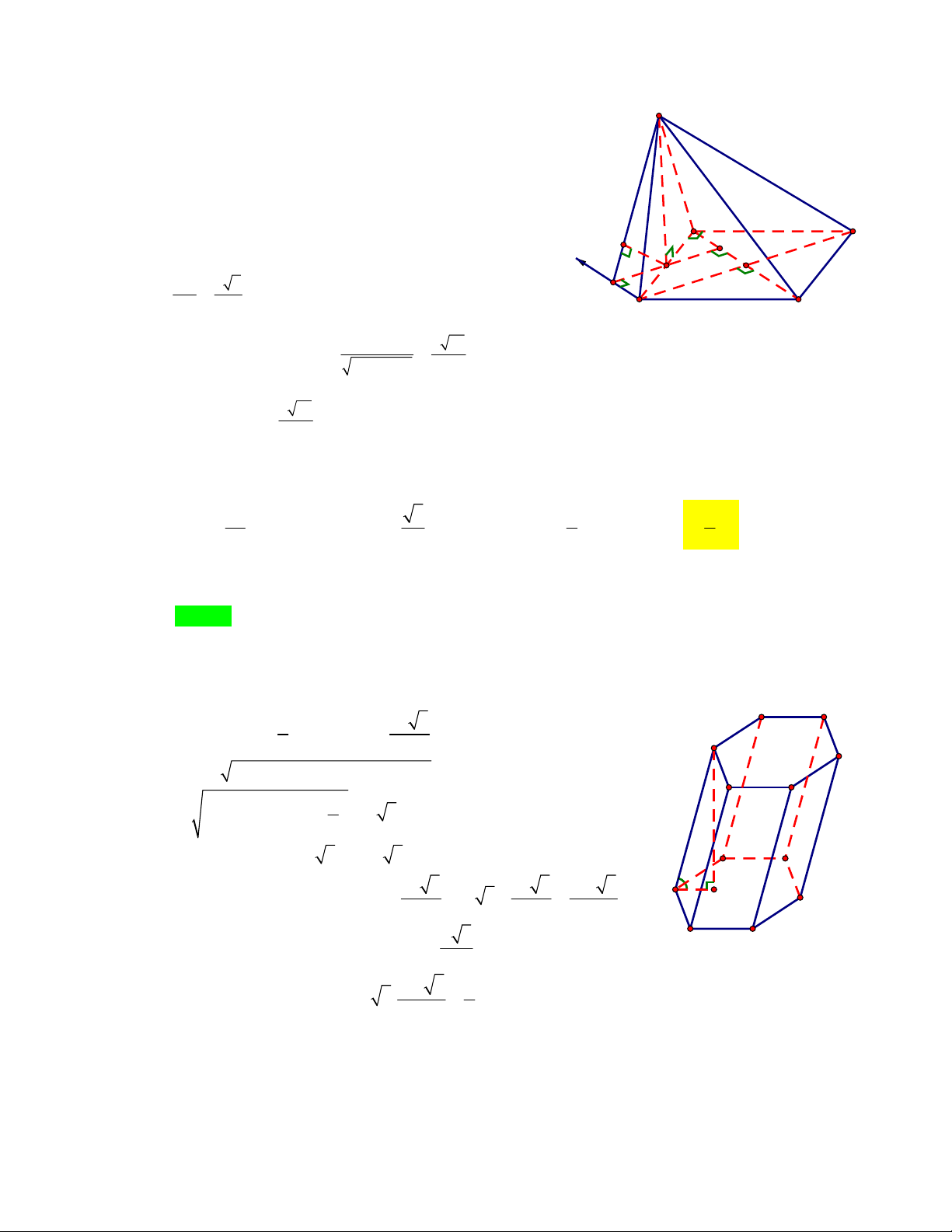
Gọi
I
làtrungđiểmcủa
A
D nênsuyra
()
SI AD SI ABCD^^
.
Kẻ
Ax BD . Do đó
[
]()()()
,, ,2,d BD SA d BD SAx d D SAx d I SAx
éùéùéù
===
ëûëûëû
.
Kẻ
IE A x^
,kẻ
IK SE^
.Khiđó
()
,dI SAx IK
éù
=
ëû
.
Gọi
F làhìnhchiếucủa
I
trên BD , ta có
2
24
AO a
IE IF
== =
.
Tamgiácvuông
SIE ,có
22
.21
14
SI IE a
IK
SI IE
==
+
.
Vậy
[]
21
,2 .
7
a
dBDSA IK==
ChọnC.
Câu44: CHUYÊNQUANGTRUNGLẦN3Chohìnhlăngtrụcótấtcảcáccạnhđềubằng
a ,đáylà
lụcgiácđều,góctạobởicạnhbênvàmặtđáylà
60
.Tínhthểtíchkhốilăngtrụ
A.
3
27
8
Va
. B.
3
3
4
Va
. C.
3
3
2
Va
. D.
3
9
4
a
.
Hướngdẫngiải
ChọnD.
Tacó
A
BCDEF
làlụcgiácđềunêngócởđỉnhbằng
120
.
A
BC
làtamgiáccântại
B
,
DEF
làtamgiáccântại
E
.
2
13
. .sin120
24
ABC DEF
a
SS aa
22
2. . .cos
A
CABBC ABBCB
22
1
2... 3
2
aa aa a
2
.3.3
ACDF
SACAFaaa
222
2
3333
3
442
ABCDEF ABC ACDF DEF
aaa
SSSS a
3
'60' '.sin60
2
a
BBH BH BB
Suyra
Câu45: NGUYỄNTRÃI
–HDMộtcốcnướccódạnghìnhtrụđựngnướcchiềucao
12cm
,đường
kínhđáy
4cm
,lượngnướctrongcốccao
8cm
.Thảvàocốcnước4viênbicócùngđườngkính
2cm
.Hỏinướcdângcaocáchmépcốcbaonhiêuxăng‐ti‐mét?làmtrònsaudấuphẩy2chữsốthập
phân,bỏquađộdàycủacốc
A.
2,67cm
. B.
2,75cm
. C.
2, 25cm
. D.
2,33cm
.
2
3
339
'. 3.
44
ABCDEF
a
VBHS a a
x
E
F
I
O
D
C
B
A
S
K
60°
C'
E'
F'A'
D'
E
F
B
C
D
A
B'
H
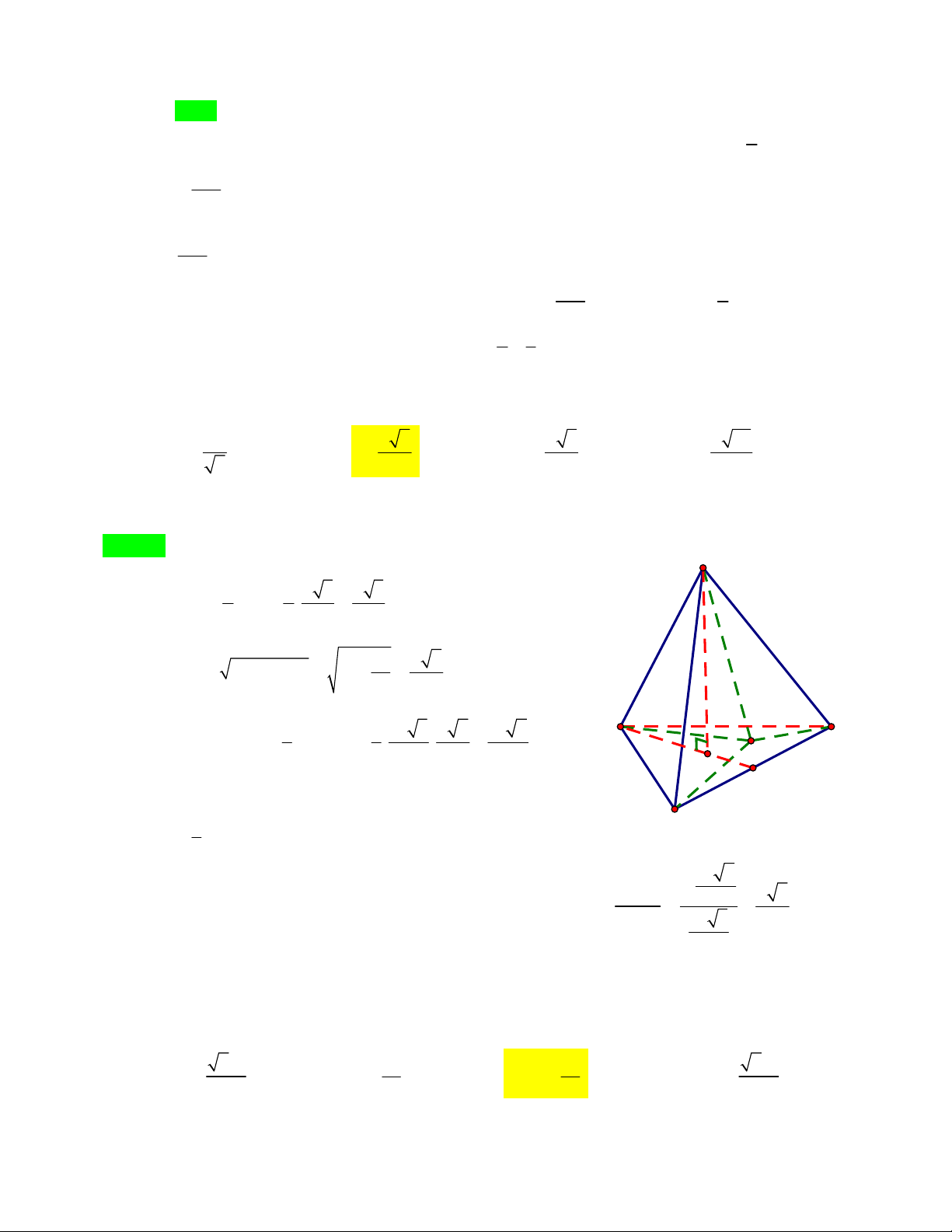
Hướngdẫngiải
ChọnA.
Lượngnướcdânglênchínhlàtổngthểtíchcủa4viênbithảvàobằng
3
4
4.
3
bb
Vr
3
16
cm
3
.
Dễthấyphầnnướcdânglênlàhìnhtrụcóđáybằngvớiđáycốcnướcvàthểtíchlà
3
16
cm
3
.
Chiềucaocủaphầnnướcdânglênlà
d
h
thỏamãn:
2
16
3
d
rh
nên
4
cm
3
d
h .
Vậynướcdângcaocáchmépcốclà
48
12 8 2,67
33
cm.
Câu 46: CHUYÊNBẮCGIANGCho tứ diện đều cạnh
a
và điểm
I
nằm trong tứ diện.
Tính tổng khoảng cách từ
I
đến các mặt của tứ diện.
A.
2
a
. B.
6
3
a
. C.
3
2
a
. D.
34
2
a
.
Hướngdẫngiải
Chọn B
2233
.
3323
aa
AH AM
.
2
222
6
33
aa
SH SA AH a
.
Ta có
23
11362
...
334312
SABC ABC
aa a
VSSH
.
Mặt khác,
SABC ISAB IABC ISAC ISBC
VVVVV
1
.; ; ; ;
3
ABC
S dISAB dIABC dISAC dISBC
3
;; ;;
SABC
A
BC
V
dI SAB dI ABC dI SAC dI SBC
S
3
2
2
3.
6
12
3
3
4
a
a
a
.
Câu 47:
CHUYÊNKHTNL4Cho hình chóp
SABC
có đáy
A
BC
là tam giác vuông cân,
A
BACa
,
SC ABC
và
SC a
. Mặt phẳng qua
C
, vuông góc với
SB
cắt
,SA SB
lần
lượt tại
E
và F . Tính thể tích khối chóp
.SCEF
.
A.
3
2
36
SCEF
a
V
. B.
3
18
SCEF
a
V
. C.
3
36
SCEF
a
V
. D.
3
2
12
SCEF
a
V
.
Hướngdẫngiải
M
C
B
A
S
I
H
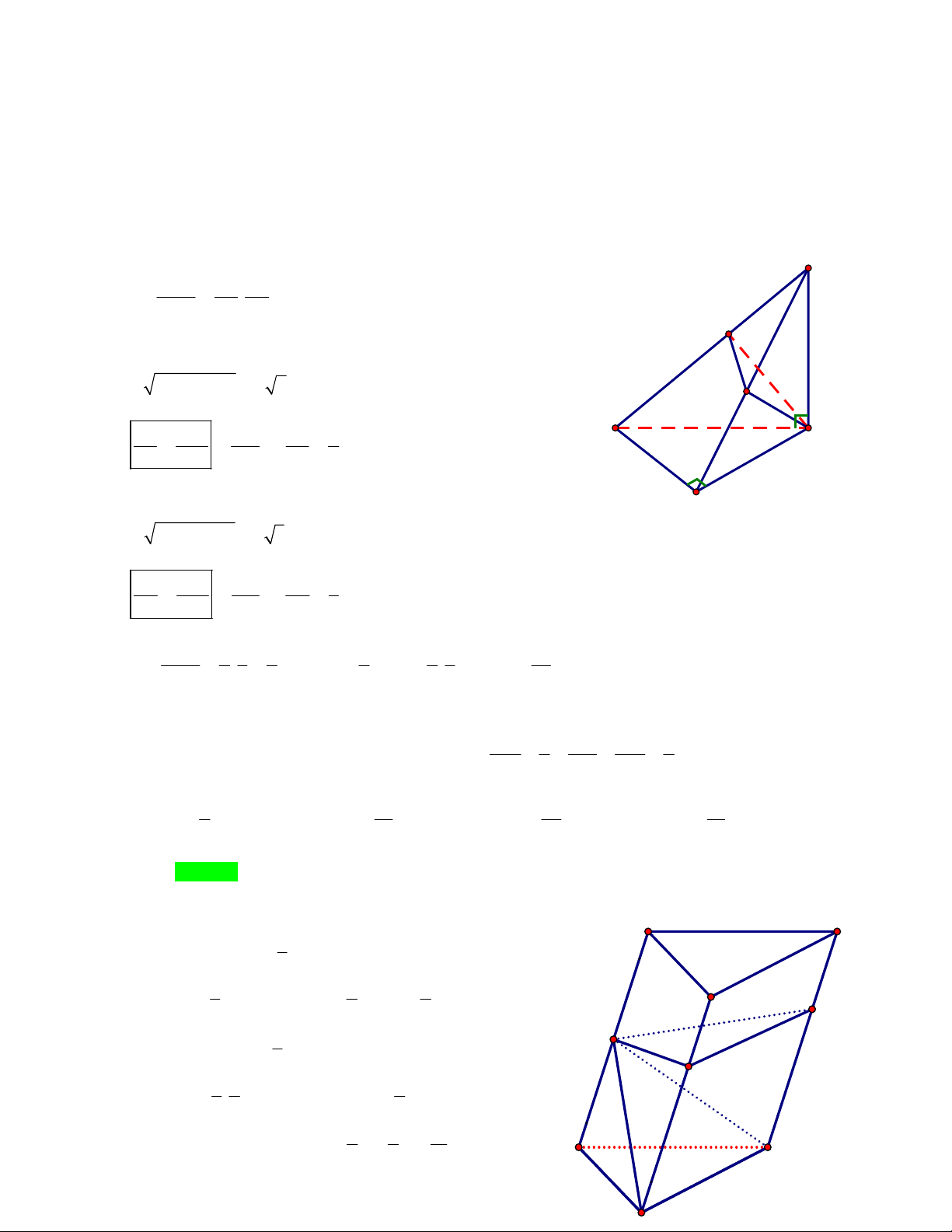
Chọn đáp án C.
Từ
C hạ
,CF SB F SB
,
,CE SA E SA
Ta có
AB AC
A
B SAC AB CE CE SAB CE SB
AB SC
Vậy mặt phẳng qua
C
và vuông góc
SB
là mặt
CEF
.
Ta có
.
SCEF
SCAB
V
SE SF
VSASB
Tam giác vuông
SAC
vuông tại
C
ta có:
22
2SA SC AC a
và
22
22
1
2
2
SE SC a SE
SA SA
SA a
Tam giác vuông
SBC
vuông tại
C
ta có:
22
3SB SC BC a
và
22
22
1
3
3
SF SC a SF
SB SC
SB a
Do đó
3
11 1 1 11 1
...
23 6 6 63 36
SCEF
SCEF SABC ABC
SCAB
V
VV SAS a
V
.
Câu 48: CHUYÊNVINH–L2Cho hình lăng trụ
.
A
BC A B C
có thể tích bằng
V
. Các điểm
M
,
N
,
P
lần lượt thuộc các cạnh
A
A
,
B
B
,
CC
sao cho
1
2
AM
AA
,
2
3
BN CP
BB CC
. Thể tích khối đa diện
.
A
BC MNP
bằng
A.
2
3
V
B.
9
16
V
C.
20
27
V
D.
11
18
V
Hướng dẫn giải
Chọn D.
Đặt
1.
1
,.
3
122
,.
339
M
NPCB NPCB
CC B B
VV dMCCBBS
dM CCBB S V
2.
1
,.
3
11 1
., .
32 6
M
ABC ABC
ABC
VV dMABCS
dA ABC S V
Vậy
.12
2111
96 8
ABC MNP
VVVVVV
a
a
a
B
A
C
S
F
E
M
C
B
A
B'
C'
A'
P
N

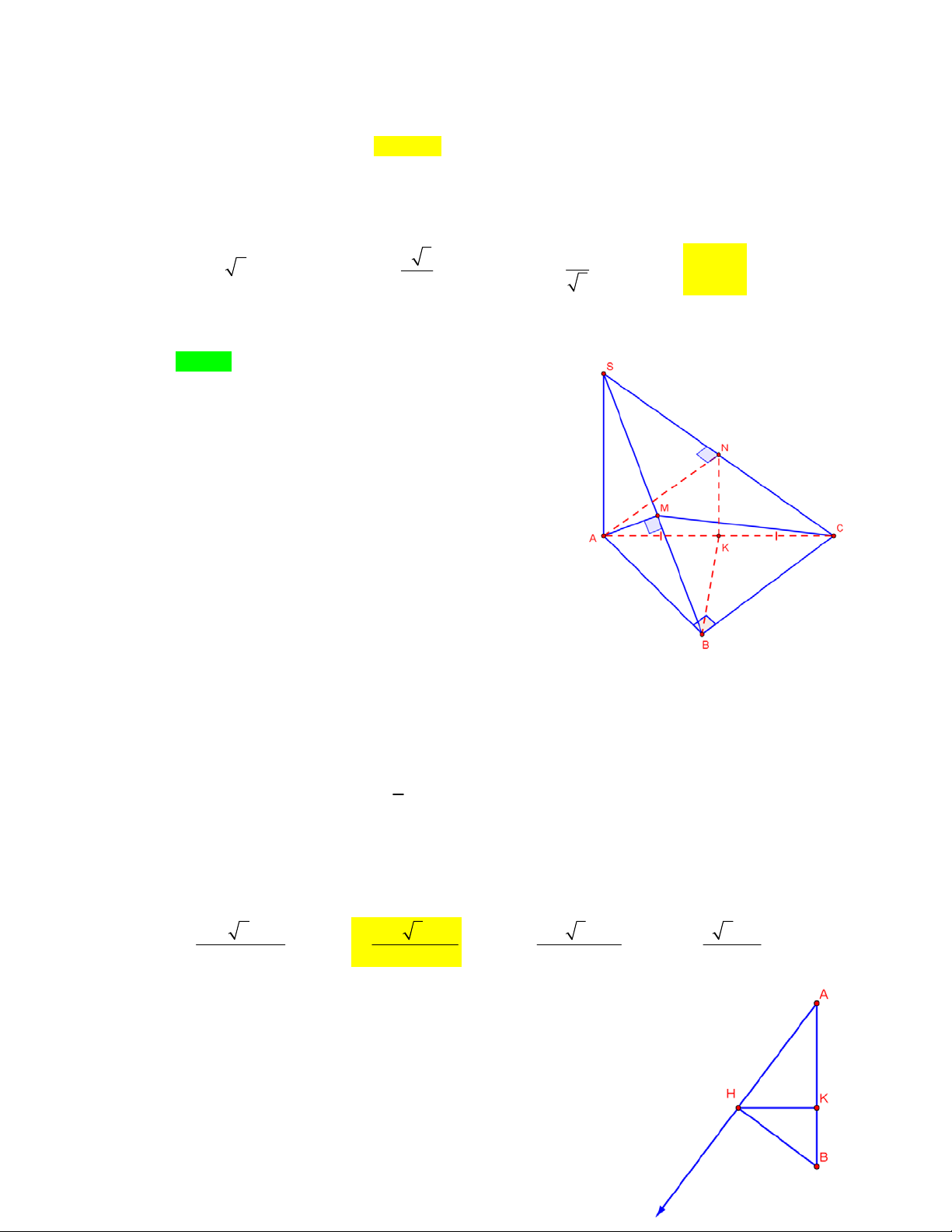
Chủđề6.KHỐITRÒNXOAY
Câu1: SGDVĨNHPHÚCChohìnhchóp
.S ABC
có
SA ABC
,
1AB
,
2AC
và
60 .BAC
Gọi
M
,
N
lầnlượtlàhìnhchiếucủa
A
trên
SB
,
SC
.Tínhbánkính
R
củamặtcầuđiqua
cácđiểm
A
,
B
,
C
,
M
,
N
.
A.
2R
. B.
23
3
R
.
C.
4
3
R . D.
1R
.
Hướn
gdẫngiải
ChọnD.
*Gọi
K
là trung điểm của
AC
suy ra :
1AK AB KC
*Lạ
i có
60 60 ; 30 90 1BAC ABK KBC ABC
*Th
eogiảthiêt
90 2ANC
* Ch
ứngminh
90 3AMC
Th
ậtvậy,tacó:
;BC SA BC AB BC SAB SBC SAB
AM SB AM SBC AM MC
Từ
1;2;3
suyracácđiểm
A
,
B
,
C
,
M
,
N
nội tiếp đường tròn tâm
K
, bán kính
1
1
2
KA KB KC KM KN AC
.
Câu2: NGUYỄNKHUYẾNTPHCMChođoạnthẳngABcóđộdàibằng
2a
,vẽtia
Ax
vềphíađiểm
BsaochođiểmBluôncáchtia
Ax
mộtđoạnbằng
a
.GọiHlàhìnhchiếucủaBlêntia,khi
tamgiácAHBquayquanhtrụcABthìđườnggấpkhúcAHBvẽthànhmặttrònxoaycódiện
tíchxungquanhbằng
A.
2
(2 2)
2
a
B.
2
(3 3)
2
a
C.
2
(1 3)
2
a
D.
2
32
2
a
Hướn
gdẫngiải
C
họnB.
KhiquayquanhtamgiácAHBthìđườnggấpkhúcAHBvẽlên
một mặt tròn xoay. Diện tích mặt tròn xoay này bằng tổng
diệntíchxungquanhhaihìnhnónđườngsinhAHvàBH.
BÀI TOÁN VẬN DỤNG (8 - 9 - 10)
_______________________________
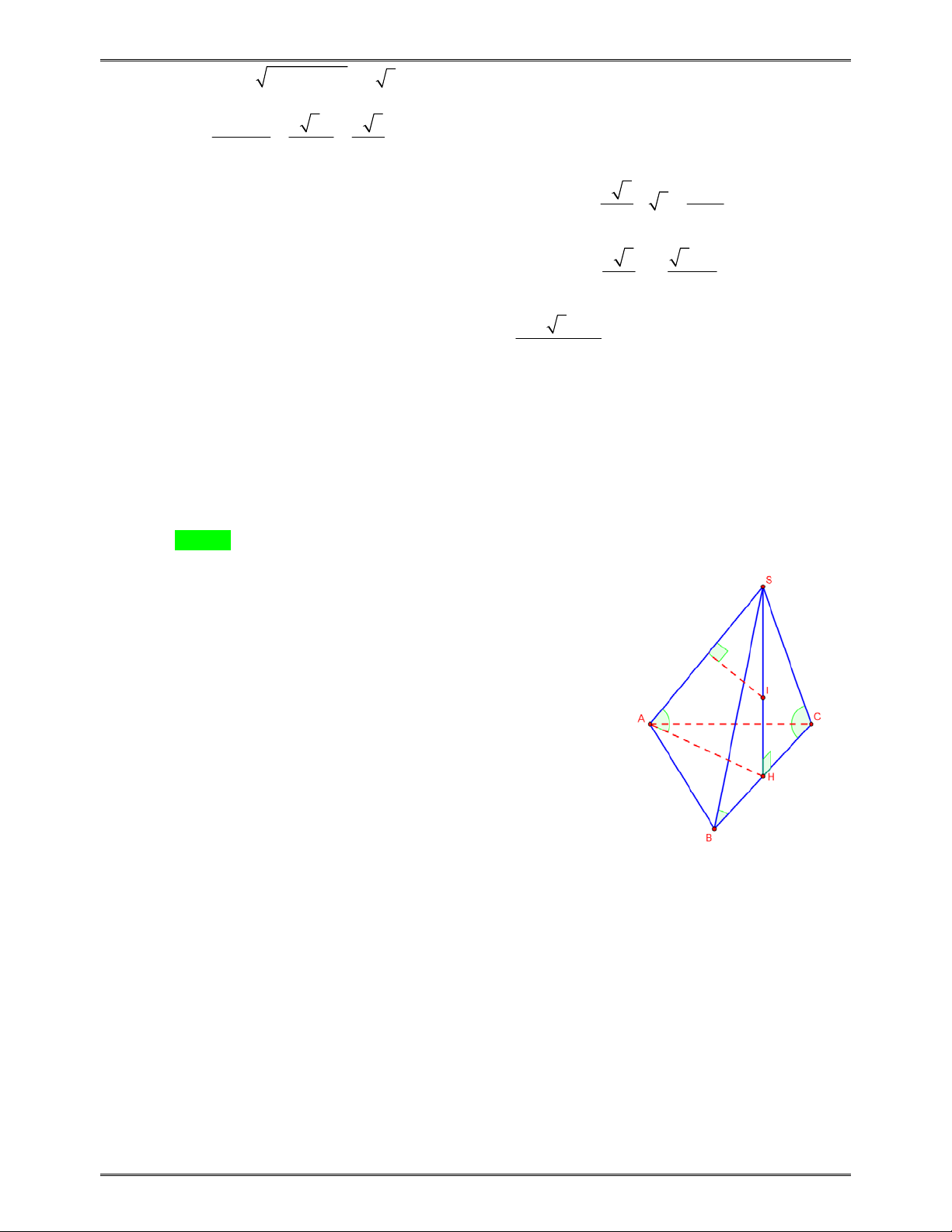
Tacó
22
3
A
HABBHa
.3.3
22
AH BH a a a
HK
AB a
DiệntíchxungquanhhìnhnóncóđườngsinhAHlà
2
1
33
.3
22
aa
Sa
DiệntíchxungquanhhìnhnóncóđườngsinhBHlà
2
2
33
.
22
aa
Sa
Diệntíchmặttrònxoaycầntìmlà
2
12
(3 3)
2
a
SS S
.
Câu3: LÝTỰTRỌNG–TPHCMChohìnhchóp
.SABC
cóđáylàtamgiácvuôngtại
A
,cạnh
huyền
6BC cm
,cáccạnhbêncùngtạovớiđáymộtgóc
60
.Diệntíchmặtcầungoại
tiếphìnhchóp
.SABC
là
A.
2
48 cm
. B.
2
12 cm
. C.
2
16 cm
. D.
2
24cm
.
Hướngdẫngiải
ChọnA.
Gọi
H
làhìnhchiếuvuônggóccủa
S
lênmặtphẳng
A
BC .Gọi
O
làtrungđiểmcủa
B
C
.
Tam giác
A
BC
vuôngtại
A
,
O
làtrungđiểmcủacạnh
huyền
B
C
,suyra
(1)OA OB OC
.
Xétcáctamgiác
,,SHA SHB SHC
có:
90 ( . . ) (2)
60
SH
SHA SHB SHC SHA SHB SHC g c g HA HB HC
SAH SBH SCH
chung
.
Từ
1
và
2
suyra
H
trùng
O
.Khiđó
SH
làtrụcđườngtrònngoạitiếp
A
BC
.
Trong
SAH
dựngtrungtrựccủa
SA
cắt
SH
tại
I
.
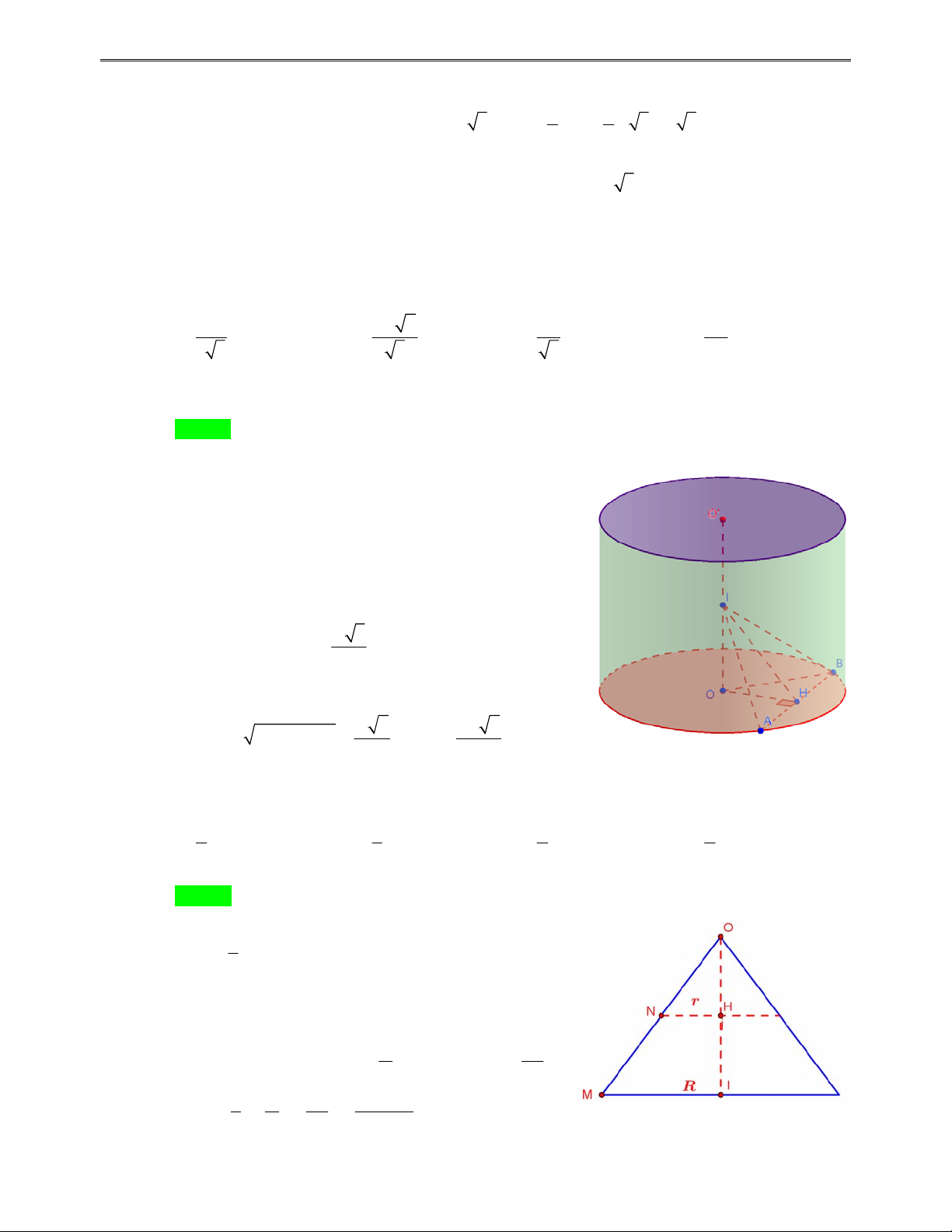
Khiđó
IA IB IC IS
.Vậy
I
làtâmmặtcầungoạitiếphìnhchóp
.SABC
.
SBC
đềucạnhbằng
6 cm
22
33 . .33 23
33
SO SI SO
.
Diệntíchmặtcầungoạitiếphìnhchóp
.SABC
là:
2
2
423 48Scm
.
Câu4: NGÔGIATỰ‐VPChohìnhtrụcóhaiđáylàhaiđườngtròn
O
và
O
,chiềucaobằng
2
R
vàbánkínhđáy
R
.Mộtmặtphẳng
điquatrungđiểmcủa
OO
vàtạovới
OO
mộtgóc
30
,
cắtđườngtrònđáytheomộtdâycung.Tínhđộdàidâycungđótheo
R
.
A.
4
33
R
. B.
22
3
R
. C.
2
3
R
. D.
2
3
R
.
Hướngdẫngiải
ChọnB.
Dựng
OH AB
A
BOIH OIH IAB
IH
làhìnhchiếucủa
OI
lên
I
AB
Theobàitađược
30OIH
Xét tam giác vuông
OIH
vuôngtại
O
3
tan 30
3
R
OH OI
Xét tam giác
OHA
vuôngtại
H
22
626
33
RR
AH OA OH AB
Câu5: CHUYÊNPHANBỘICHÂUChokhốinónđỉnh
O
,trục
OI
.Mătphẳngtrungtrựccủa
OI
chiakhốichópthànhhaiphần.Tỉsốthểtíchcủahaiphầnlà:
A.
1
2
. B.
1
8
. C.
1
4
. D.
1
7
.
Hướngdẫngiải
ChọnD.
Gọi
R
là bán kính đáy của khối nón trục
OI
.
2
1
.
3
VROI
Giảsửmặtphẳngtrungtrựccủa
OI
cắttrục
OI
tại
H
,cắtđườngsinh
OM
tại
N
.Khiđómặtphẳng
nàychiakhốinónthành2phần,phầntrênlàkhối
nónmớicóbánkính
2
R
r ,cóchiềucaolà
2
OI
2
2
1
1..
32 2 24
R
OI R OI
V
.Phầndướilàkhối
nóncụtcóthểtích
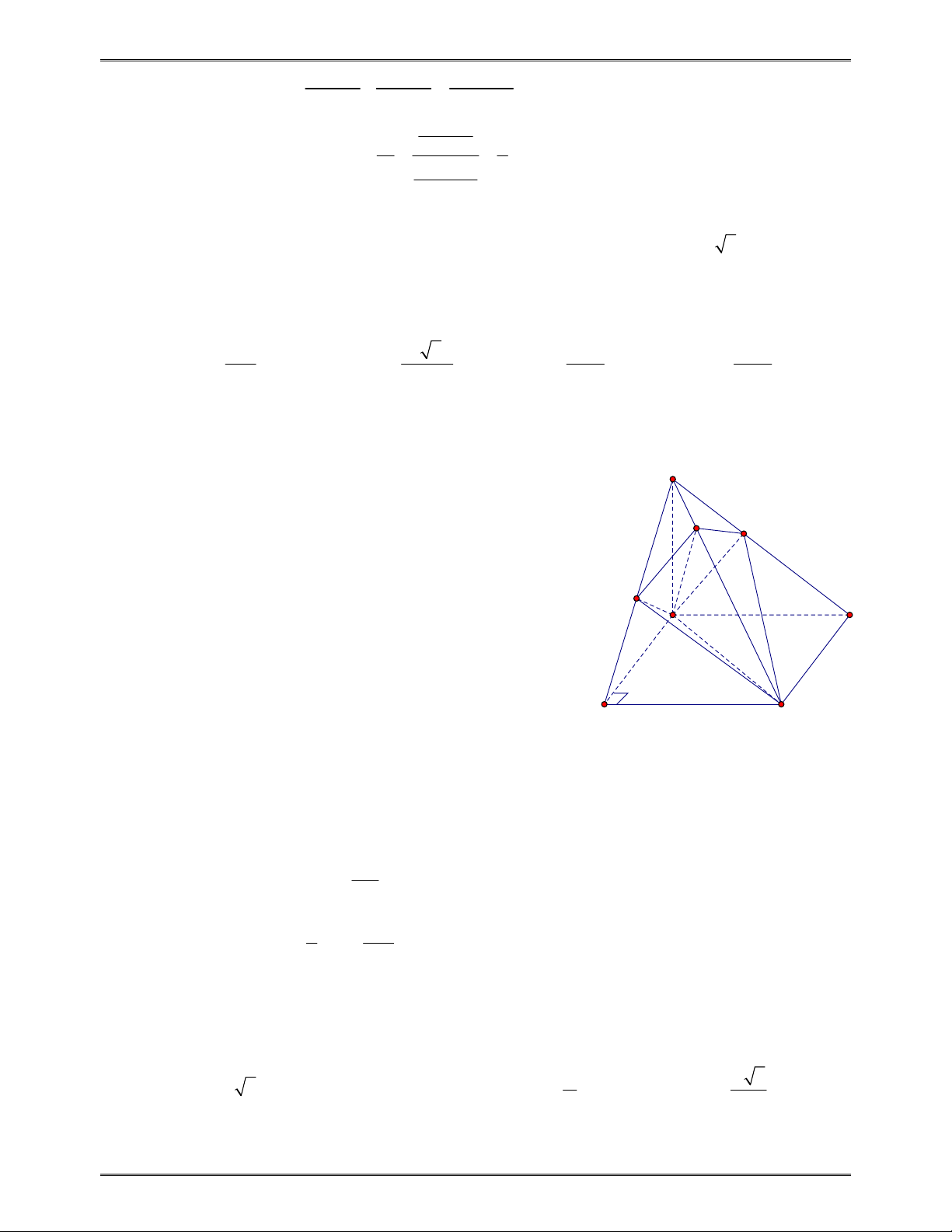
22 2
21
..7.
324 24
R
OI R OI R OI
VVV
.
Vậytỉsốthểtíchlà:
2
1
2
2
.
1
24
7.
7
24
ROI
V
ROI
V
Câu6: SỞGDHÀNỘIChohìnhchóp
.SABCDcóđáylàhìnhvuôngcạnh22,cạnhbên SA
vuônggócvớimặtphẳngđáyvà
3SA .Mặtphẳng
qua
A
vàvuônggócvới SC cắt
cạnh
SB
,
SC
,
SD
lầnlượttạicácđiểm
M
,
N
, P .Thểtích
V
củakhốicầungoạitiếptứ
diện
CMNP
.
A.
32
3
V
.B.
64 2
3
V
.C.
108
3
V
.D.
125
6
V
.
Hướngdẫngiải
ChọnA.
Tacó:
,1CB SAD AM SAB AM CB
,2SC AM AM SC
Từ
1,2 90AM SBC AM MC AMC
.
Chứngminhtươngtựtacó
90APC
Có
90AN SC ANC
Tacó:
90AMC APC APC
khốicầuđườngkính
A
C
làkhốicầungoạitiếptứdiện
CMNP
.
Bánkínhcầunàylà
2
2
AC
r
.
Thểtíchcầu:
3
432
33
Vr
Câu7: SỞGDHÀNỘIChomặtcầu
S
bánkính
R
.Mộthìnhtrụcóchiềucao
h
vàbánkính
đáy r thayđổinộitiếpmặtcầu.Tínhchiềucao
h
theobánkính
R
saochodiệntíchxung
quanhhìnhtrụlớnnhất
A.
2hR
. B.
hR
. C.
2
R
h
. D.
2
2
R
h
.
Hướngdẫngiải
C
A
D
B
S
M
N
P
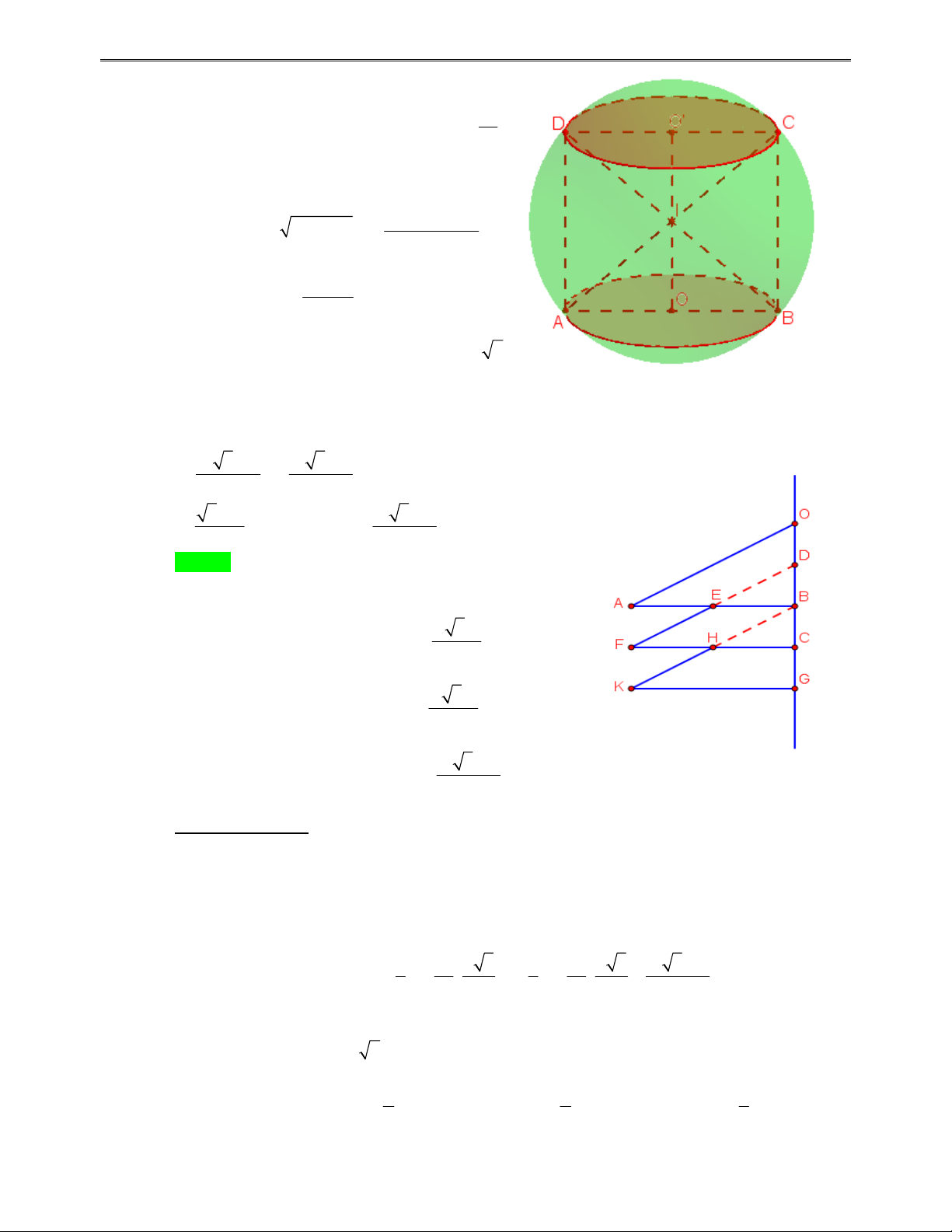
ChọnA.
Tacó
2
22
;,
4
h
OO h IA R AO r r R
.
Diệntíchxungquanhcủahìnhtrụ
222
22
4
24
2
hRh
SrhhRh
,
dùngBĐT
22
2
ab
ab
.
Vậy
22 22
max
24 2SRhRhhR
.
Câu8: BẮCYÊNTHÀNHChobahìnhtamgiácđềucạnhbằng
a
chồnglênnhaunhưhìnhvẽ
cạnhđáycủatamgiáctrênđiquacáctrungđiểmhaicạnhbêncủatamgácdưới.Tính
theo
a
thểtíchcủakhốitrònxoaytạothànhkhiquaychúngxungquanhđườngthẳng
d
.
A.
3
13 3
96
a
.B.
3
11 3
96
a
.
C.
3
3
8
a
. D.
3
11 3
8
a
.
ChọnB.
Nếubahìnhtamgiáckhôngchồnglênnhauthì
thểtíchcủakhốitrònxoaylà
3
1
3
8
a
V
Thểtíchphầnbịchồnglênlà
3
2
3
96
a
V
Thểtíchcầntínhlà
3
12
11 3
96
a
VVV
Hoặclàmnhưsau:
Đặt
1234
;;;VVVVlầnlượtlàthểtích:khốinónsinhbởitamgiác
OAB
quayquanh
OB
,khối
trònxoaysinhbởihình
;BCFE GCHK
,khốinónsinhbởitamgiác
DEB
khiquayquanh
B
C
.Khiđó:Thểtíchkhốicầntìmlà:
223
123 1 4
1313113
32 3 2 .
342 3164 96
aa aa a
VVVV V V
Câu9: CHUYÊNLƯƠNGVĂNCHÁNHChohìnhthangcân
A
BCD
cóđáynhỏ
1
A
B
,đáylớn
3CD
,cạnhbên
2AD
quayquanhđườngthẳng
A
B
.Tínhthểtích
V
củakhốitròn
xoaytạothành.
A.
3V
. B.
4
3
V
. C.
7
3
V
. D.
5
3
V
.
Hướngdẫngiải
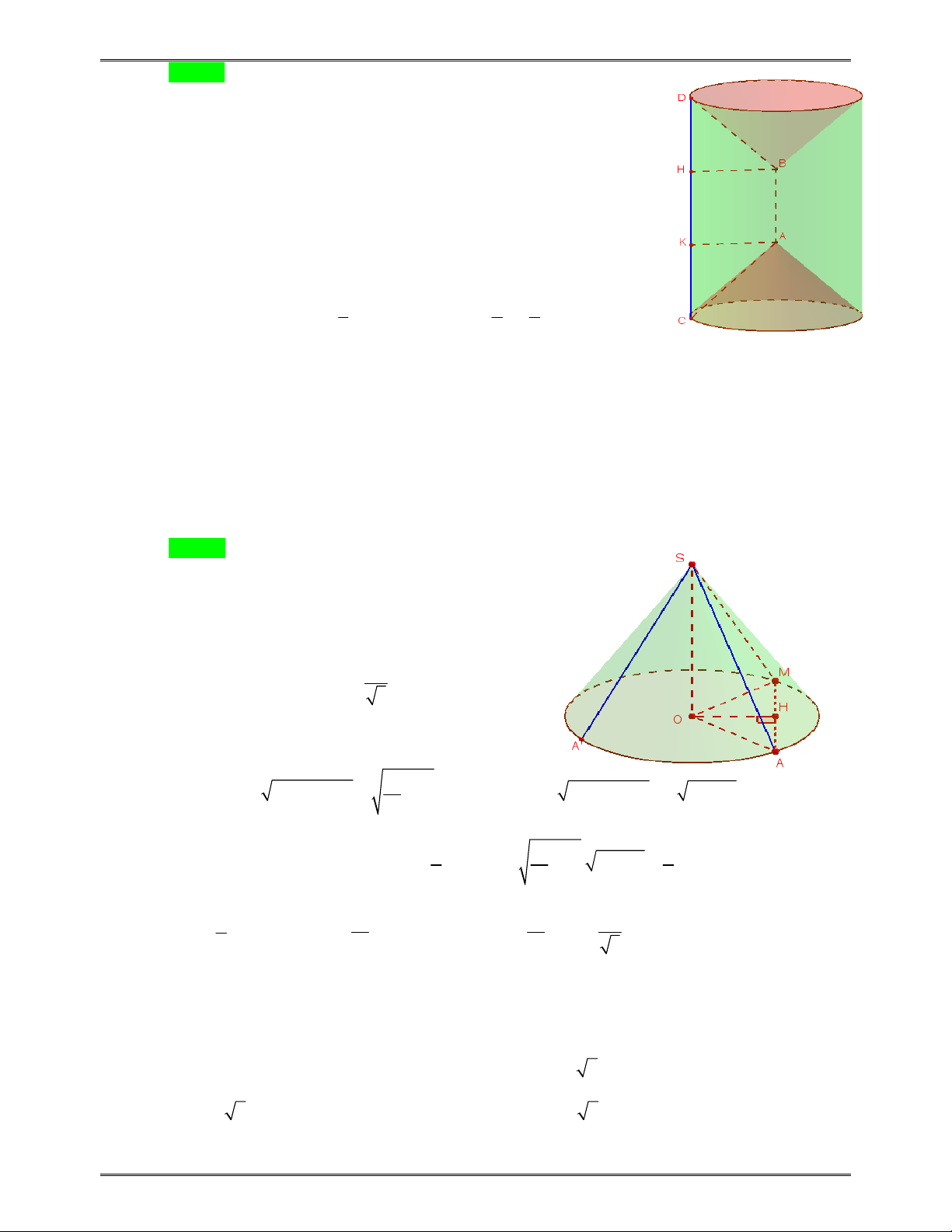
ChọnC.
Theohìnhvẽ:
1
A
HHD.
Thểtíchkhốitrònxoaytạothànhbằngthể
tíchkhốitrụcóbánkính
1rAH
,chiều
cao
3CD
trừđithểtíchhaikhốinónbằng
nhaukhốinónđỉnh
A
,đỉnh
B
vàđáylàđáycủahìnhtrụ.
Vậy
22
127
.. 2... 3
333
VAHCD AHHD
.
Câu10: CHUYÊNLƯƠNGVĂNCHÁNHChohìnhnónđỉnh
S
,đáylàhìnhtròntâm
O
,gócởđỉnh
bằng
120
.Trênđườngtrònđáy,lấyđiểm
A
cốđịnhvàđiểm
M
diđộng.Cóbaonhiêuvị
tríđiểmcủađiểm
M
đểdiệntíchtamgiác
SAM
đạtgiátrịlớnnhất?
A.2. B.3. C.1. D.vôsố.
Hướngdẫngiải
ChọnA.
Gọi
r
làbánkínhđáycủahìnhnón.
Vìgócởđỉnh
120 60ASA ASO
.
Suyra
.cot
3
r
SO OA ASO
.
Gọi
H
làtrungđiểmcủa
A
M vàđặt
x
OH
.
Tacó:
2
22 2
3
r
SH SO OH x
,
22 22
22 2AM AH OA OH r x
.
Diệntíchtamgiác
SAM
bằng
2
222 2
12
...
23 3
r
s
SH AM x r x r
2
max
2
3
s
r
đạtđượckhi
22
222 2
33
3
rrr
xrx x x
.Tứclà
OH SO
.
Theotínhchấtđốixứngcủacủađườngtròntacóhaivịtrícủa
M
thỏayêucầu.
Câu11: PHANĐÌNHPHÙNG
–HNTrongcáchìnhnónnộitiếpmộthìnhcầucóbánkínhbằng3,
tínhbánkínhmặtđáycủahìnhnóncóthểtíchlớnnhất.
A.Đápánkhác. B.
42.R
C.
2.R
D.
22.R
Hướngdẫngiải
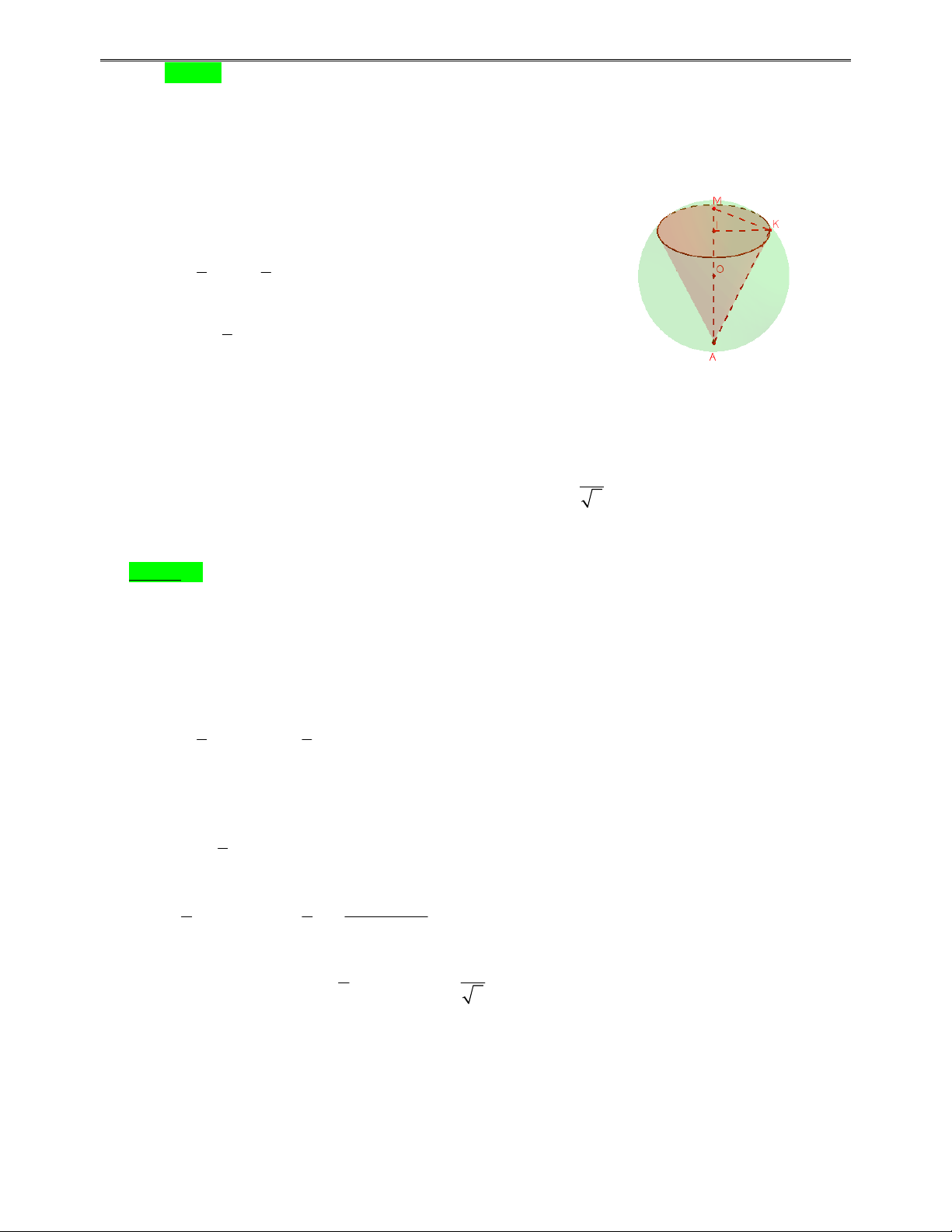
ChọnD.
Giảsửchópđỉnh
A
nhưhìnhvẽlàhìnhchópcóthểtíchlớnnhất.
A
KM
vuôngtại
.K
Tathấy
I
Kr
làbánkínhđáycủachóp,
A
Ih
làchiềucaocủachóp.
22
.6.
I
KAIIMrh h
22
11
606.
33
Vrhhh h
2
max
1
6max
3
Vhh
32
6maxyh h
trên
0;6
Câu12: CHUYÊNĐHVINHChonửađườngtrònđườngkính
2
A
BR
vàđiểmC thayđổitrên
nửađườngtrònđó,đặt
CAB
vàgọi H làhìnhchiếuvuônggóccủa
C
lên
A
B .Tìm
saochothểtíchvậtthểtrònxoaytạothànhkhiquaytamgiác
A
CH quanhtrục
A
B
đạt
giátrịlớnnhất.
A.
60
. B.
45
. C.
1
arctan
2
. D.
30
.
Hướngdẫngiải
Đápán:C.
2
.cos 2 .cos
.sin 2 .cos .sin ;
.cos 2 .cos
AC AB R
CH AC R
A
HAC R
Thểtíchvậtthểtrònxoaytạothànhkhiquaytamgiác
A
CH
quanhtrục
A
B là
2342
18
..cos.sin
33
VAHCH R
.
Đặt
2
cos 0 1tt
32
8
1
3
VRt t
3
33
8822
.. 2 2
663
tt t
Rtt t R
Vậy
V
lớnnhấtkhi
2
3
t
khi
1
arctan
2
.
Chúý:cóthểdùngPPhàmsốđểtìmGTNNcủahàm
2
1
f
tt t
Câu13: SỞGDBẮCNINHChomộthìnhnón
N
cóđáylàhìnhtròntâm
O
.Đườngkính
2a
và
đườngcao
SO a
.Chođiểm
H
thayđổitrênđoạnthẳng
SO
.Mặtphẳng
P
vuônggóc
với SO tại
H
vàcắthìnhnóntheođườngtròn
C
.Khốinóncóđỉnhlà O
vàđáylàhình
tròn
C
cóthểtíchlớnnhấtbằngbaonhiêu?
A.
3
2
.
81
a
B.
3
4
.
81
a
C.
3
7
.
81
a
D.
3
8
.
81
a
Hướngdẫngiải
Gọi
làmặtphẳngquatrụccủahìnhnón
N cắthìnhnón
N theothiếtlàtamgiác
SAB,cắthìnhnónđỉnhSvàcóđáylàđườngtròn
C theothiếtdiệnlàtamgiácSCD,gọiI
làgiaođiểmcủaSOvàCD.Tacó:
2
A
BaOAaSO
.Dođótamgiác
SOA
vuôngcân
tại
S
.Suyratamgiác
SIC
vuôngcântại I .Đặt
(0 )SI AC x x a OI a x
Thểtíchkhốinóncóđỉnhlà
O
vàđáylàhìnhtròn
C
là:
22 32
11 1
.. . .. ( )
33 3
VICOIxax xax
.
2
1
'..32
3
Vx x ax
0
'0 .
2
3
x
Vx
a
x
Bảngbiếnthiên:
ChọnđápánB
Câu14: SỞ GD BẮC NINH Cho hình chóp
.SABC
có
SA
vuông góc với mặt phẳng
,,ABC SA a AB a
,
2,
A
Ca
0
60 .BAC
Tínhdiệntíchhìnhcầungoạitiếphìnhchóp
.S ABC
.
A.
2
5
.
3
a
. B.
2
20 a
. C.
2
20
3
a
. D.
2
5 a
.
Hướngdẫngiải
Gọi
H
làtâmđườngtrònngoạitiếptamgiác
A
BC
,
d
là
đường thẳng đi qua
H vàvuônggóc
v
ới mặt phẳng
()
A
BC
,gọi
làmặtphẳngtrungtrựccủa
SA
,
O
là
giaođiểmcủa
d
và
.Khiđó
O
làtâmcủahìnhcầu
ngoạitiếphìnhchóp
.S ABC
.
Theođịnhlíhàmsốcosintacó
:
22
2
20
2.AC.cos
2 2 .2 .cos60 3
BC AB AC AB BAC
aaaa a

Diệntíchtamgiác
A
BC
:
2
1.3
.AB.AC.sin
22
ABC
a
S BAC
Bánkínhđườngtrònngoạitiếptamgiác
A
BC
:
2
.. .2.a3
4.
3
4.
2
ABC
AB BC AC a a
A
Ha
S
a
Bánkínhcủamặtcầungoạitiếphìnhchóp
.SABC
:
2
2
22
5
22
aa
ROA AH OH a
Diệntíchhìnhcầungoạitiếphìnhchóp
.SABC
2
22
5
44. 5
2
a
SR a
ChọnđápánD
Câu15: CHUYÊNLƯƠNGVĂNCHÁNHChotứdiệnđều
A
BCD
cócạnhbằng
a
.
Tậphợpcácđiểm
M
saocho
222 22
2
M
AMBMCMD a
là
A.Mặtcầucótâmlàtrọngtâmcủatamgiác
A
BC
vàbánkínhbằng
2
2
a
.
B.Mặtcầucótâmlàtrọngtâmcủatứdiệnvàbánkínhbằng
2
4
a
.
C.Mặtcầucótâmlàtrọngtâmcủatứdiệnvàbánkínhbằng
2
2
a
.
D.Đườngtròncótâmlàtrọngtâmtamgiác
A
BC
vàbánkínhbằng
2
4
a
.
Hướngdẫngiải
ChọnB.
Gọi
,
I
J
lầnlượtlàtrungđiểmcủa
,
A
BCD
.Gọi
K
làtrungđiểm
IJ
.Lúcnày,
K
làtrọng
tâmtứdiện.
Ápdụngđịnhlýđườngtrungtuyếntrongtamgiác,tacó:
22
22 2 2
22
22 2 2
22
22
22
22
A
Ba
MA MB MI MI
CD a
MC MD MJ MJ
222 2 222
2
M
AMBMCMD MI MJ a
2
22
22
2
IJ
M
Ka
Tacó:
2
22 2 2 22
22
3
24 4242
IC ID CD a a a a
IJ IC
2
222 2 2
3
4
2
a
MA MB MC MD MK
.
Dođó:
2
222 22 2 2
32
24 2
24
aa
MA MB MC MD a MK a MK
.
Vậytậphợpcácđiểm
M
thoảmãnhệthứcđềbàilàmặtcầutâm
K
,bánkínhbằng
2
4
a
.
Câu16: CHUYÊNLƯƠNGVĂNCHÁNHChohìnhchóp
.SABC
có
,2SA ABC SA a
,tamgiác
A
BC
cântại ,22
A
BC a ,
1
cos .
3
ACB
Tínhdiệntích
S
củamặtcầungoạitiếphình
chóp
..S ABC
A.
2
97
.
4
a
S
B.
2
97
.
2
a
S
C.
2
97
.
3
a
S
D.
2
97
.
5
a
S
Hướngdẫngiải
ChọnA.
Gọi
H
làtrungđiểmcủa
B
C
2
2
BC
HC a
.
Do
A
BC
cântại
A
A
HBC
.
1
cos 3 3 2
3
A
CB AC HC AC a .
22 22
18 2 4
A
HACHC aa a
.
Gọi
M
làtrungđiểm
A
C
,trongmp
A
BC
vẽđườngtrungtrực
A
C
cắt
A
H
tại
O
O
làtâmđườngtrònngoạitiếp
A
BC
.
Tacó
11 22
cos sin cos
33 3
ACH CAH CAH
.
Trong
A
MO
vuôngtại
M
2
3
9
2
4
22
cos
3
a
A
Ma
AO
CAH
Gọi
N
làtrungđiểm
SA
.Trongmp
SAH vẽtrungtrực
SA
cắtđườngthẳngqua
O
và
vuông góc mp
A
BC tại
I
. Chứng minh được
I
là tâm mặt cầu ngoại tiếp hình chóp
..S ABC
Tacó
A
NIO
làhìnhchữnhật
đườngchéo
22
22 2
81 97 97
16 16 4
aa
A
IAOAN a a .
Vậydiệntíchmặtcầungoạitiếphìnhchóp
.SABC
là
2
22
97 97
44
16 4
a
SR a
đvdt.
Câu17: LƯƠNGTÂMChomặtcầu
S Cótâm
I
,bánkính
5R
.Mộtđườngthằng
cắt
S
tại
2
điểm
M
,
N
phânbiệtnhưngkhôngđiqua
I
.Đặt
2
M
Nm
.Vớigiátrịnàocủam
thìdiệntíchtamgiác
IMN
lớnnhất?
A.
52
2
m
. B.
10
2
m
. C.
5
2
m
. D.
52
2
m
.
Hướngdẫngiải
GọiHlàtrungđiểmMN,tacó
:
2
25
I
Hm
DiệntíchtamgiácIMN
:
2
22
22
1
.25
2
25
(25 )
2
IMN
SIHMNmm
mm
mm
Suyra
25
2
IMN
S
.Dấu‘’xãyrakhi
22
5
25
2
mmm
ChọnD
Câu18: Chohìnhchóp
.SABC
cóđáy
ABC
làtamgiácđềucạnhbằng
1
,mặtbên
SAB
làtam
giácđềuvànằmtrongmặtphẳngvuônggócvớimặtphẳngđáy.Tínhthểtích
V
củakhối
cầungoạitiếphìnhchópđãcho.
A.
515
18
V
p
=
. B.
515
54
V
p
=
. C.
43
27
V
p
=
. D.
5
3
V
p
=
.
Hướngdẫngiải
ĐápánB
Gọi
O
làtâmđườngtròntamgiác
ABC
suyra
O
làtrọngtâm,
H
làtrungđiểm
AB
,kẻ
đườngthẳngqua
O
songsong
SH
cắt
SC
tại
N
tađược
()
NO ABC^
,gọi
M
làtrung
điểm
SC
,
HM
cắt
NO
tại
.I
Tacó
HS HC=
nên
HM SC IS IC IA IB r^====
Tacó
0
2266 61
45 , ,
3323 4
6
CN CO
NIM HCS CN SM SN
CS CH
== === == =
Suyra
6
12
NM SM SN=-=
NMID
vuôngtại
M
0
6
tan 45
12
NM
IM NM
IM
===
Suyra
22
5
12
rIC IM MC== + =
Vậy
3
4515
354
Vr
p
p
== .
Cáchkhác:
Gọi
, PQ
lầnlượtlàtrọngtâmcáctamgiác
SAB và ABC
.
Docáctamgiác
SAB và ABC
làcáctamgiácđềucạnhbằng
1
nên
, PQ
lầnlượttâm
đườngtrònngoạitiếptamgiácđó.
Qua
P
đườngthẳngvuônggócvớimặtphẳng
()
,SAB
qua
O
dựngđườngthẳngvuông
gócvớimặtphẳng
()
.ABC
Haitrụcnàycắtnhautại
,I
suyra
IA IB IC IS===
.Vậy
I
làtâmmặtcầungoạitiếphìnhchóp
.SABC
và
RIC=
.
Xét
22
22
13 23 15
:IC . .
32 32 6
IQC IG GC
æöæö
÷÷
çç
÷÷
çç
D=+= +=
÷÷
çç
÷÷
çç
÷÷
çç
èøèø
Vậy
3
4515
354
VR
p
p==
.
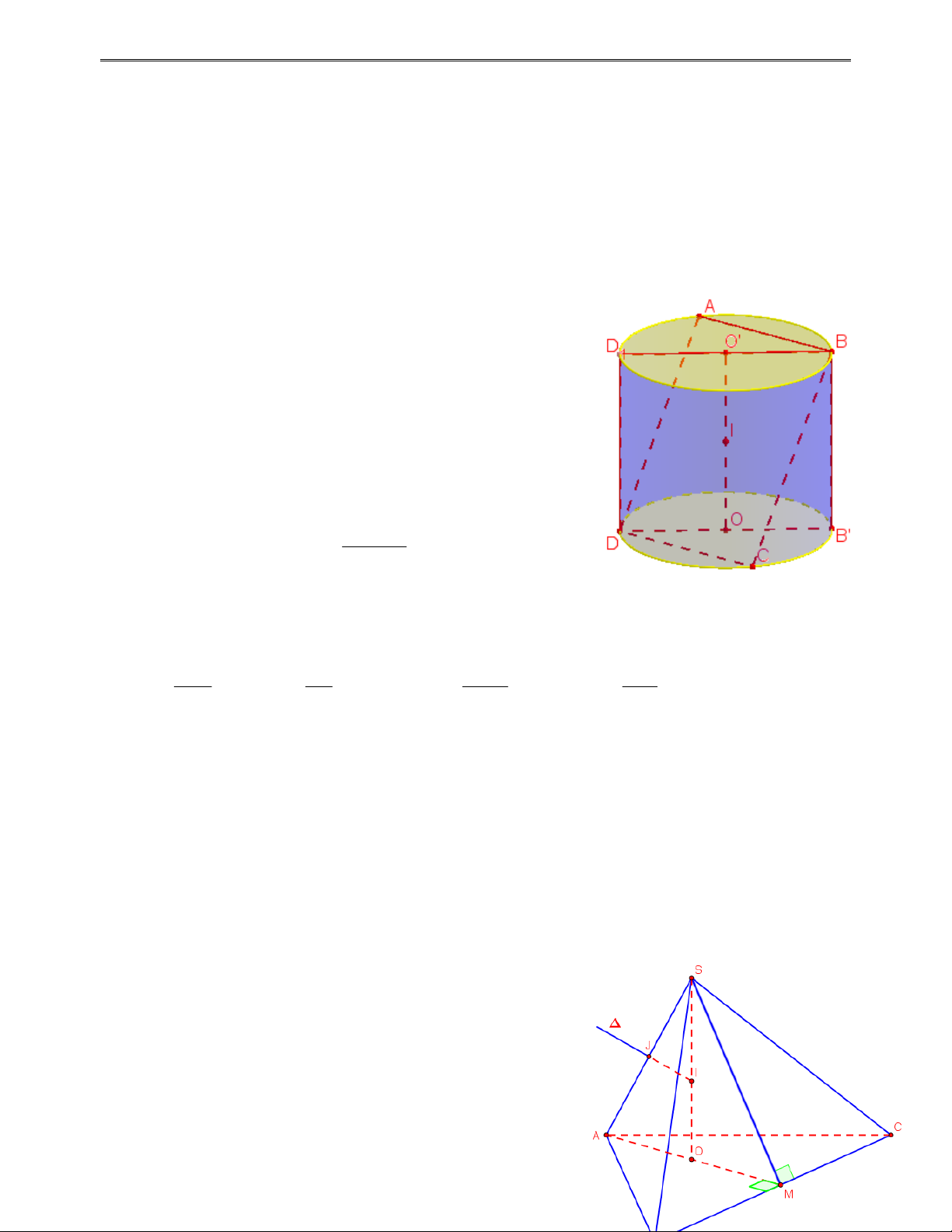
Câu19: Chohìnhtrụcóchiềucao
2,h =
bánkínhđáy
3.r =
Mộtmặtphẳng
(
)
P
khôngvuônggócvới
đáycủahìnhtrụ,lànlượtcắthaiđáytheođoạngiaotuyến
AB
và
CD
saocho
ABCD
làhình
vuông.Tínhdiệntích
S
củahìnhvuông
ABCD
.
A.
12 .S p=
B.
12.S =
C.
20.S =
D.
20 .S p=
Hướngdẫngiải
Kẻđườngsinh
BB’
củahìnhtrụ.Đặtđộdàicạnhcủahìnhvuông
ABCD
là
x
,
x0
.
Do
''
'
CD BC
CD B C B CD
CD BB
ì
ï
^
ï
^ D
í
ï
^
ï
î
vuông tại
C.
Khiđó,
B’D
làđườngkínhcủa
đường
Tròn
()
'O
.Xét
'BCDD
vuôngtại
C
22 2222
''4(1)B D CD CB r x CB=+=+
Xéttamgiác
'CBBD
vuôngtại
B
222222
'' '(2)BC BB CB x h CB=+=+
Từ1và2
22
2
4
20
2
rh
x
+
= =
.
Suyradiệntíchhìnhvuông
ABCD
là
20S =
.
Câu20: Chohình chópđều S.ABC có
AB a
,
SB a 2
.Diệntíchmặtcầungoạitiếphìnhchóp
S.ABClà:
A.
2
3
11
a
S B.
2
3
11
a
S
C.
2
12
11
a
S D.
2
12
11
a
S
Hướngdẫngiải
1Xácđịnhtâmvàbánkínhmặtcầungoạitiếptứdiện.
Xácđịnhtâmmặtcầu
Gọi
O
làtâmđườngtrònngoạitiếptamgiác
A
BC
,
do
.S ABC
làhìnhchópđềunên
SO
làtrụcđườngtròn
ngoạitiếptamgiác
A
BC
.Trongtamgiác
SOA
dựngđườngtrung
trực
củacạnhbên
SA
, cắt
SO
tạiI vàcắt
SA
tạitrungđiểm
J
.
Tacó:
ISO IAIBIC
IA IB IC IS
IIAIS
Vậy
I làtâmcủamặtcầungoạitiếphìnhchóp
.S ABC
.
Tínhbánkínhmặtcầu
Gọi
M
AO BC
thì
M
làtrungđiểmcủa
BC
.
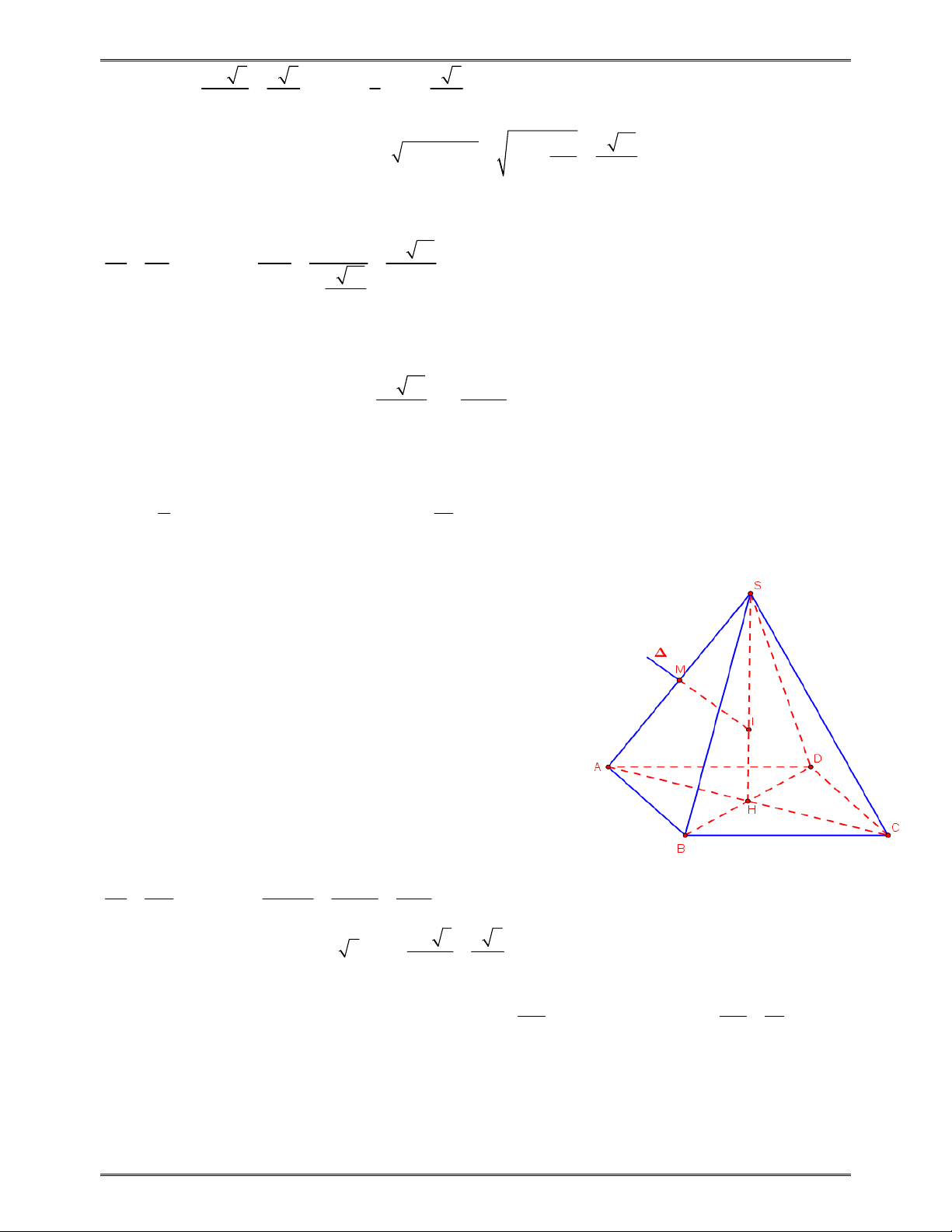
Tacó:
33
22
AB a
AM
23
33
a
AO AM
.
Trongtamgiácvuông
SOA
tacó
2
22 2
333
4
93
aa
SO SA AO a
Xéthaitamgiácvuôngđồngdạng
SJI
và
SOA
tacó:
22
4233
211
33
2.
3
SI SJ SA a a
RSI
SA SO SO
a
2Tínhdiệntíchmặtcầuvàthểtíchkhốicầu
Diệntíchmặtcầulà:
2
2
2
233 12
44
11 11
aa
SR
.
Câu21: ChohìnhchópđềuS.ABCcóđườngcao
SH a
;gócSABbằng45độ.Bánkínhmặtcầu
ngoạitiếphìnhchópS.ABClà
A.
2
a
B.
a
C.
3
2
a
D.
2a
Hướngdẫngiải
GọiIlàtâmcủamặtcầungoạitiếphìnhchopS.ABCD
Khiđó
IA IB IC ID IS
hay
(1)
(2)
IA IB IC ID
IA IS
GọiHlàgiaođiểmcủaACvàBD.Từ1suyra
(*)ISH
TrongmặtphẳngSAHdựngđườngthẳng
làtrungtrựccủaSA.
Từ2,suyra
(2*)
(*) (2*)
I
SH I
GọiMlàtrungđiểmcủaSA,khiđó:
2
...
22
SI SM SM SA SA SA SA
RSI
SA SH SH SH SH
.DoSABcântạiSvàcó
0
45SAB
nênSABvuôngcân
tạiS.Đặt
SA x
,khiđó
36
2;
33
A
Bx
AB x HA
TrongtamgiácvuôngSHAcó:
22
2 2 22 222
633
3
922
x
aa
SA HA SH x a x a R
a
.Đápán
C
Câu22: ChohìnhchópS.ABCD,đáyABCDlàhìnhvuông,cạnh2a,tâmO,mặtbênSABlàtamgiác
đềuvà
SAB ABCD
.Xácđịnhtâmvàbánkínhcủamặtcầungoạitiếphìnhchópđó.
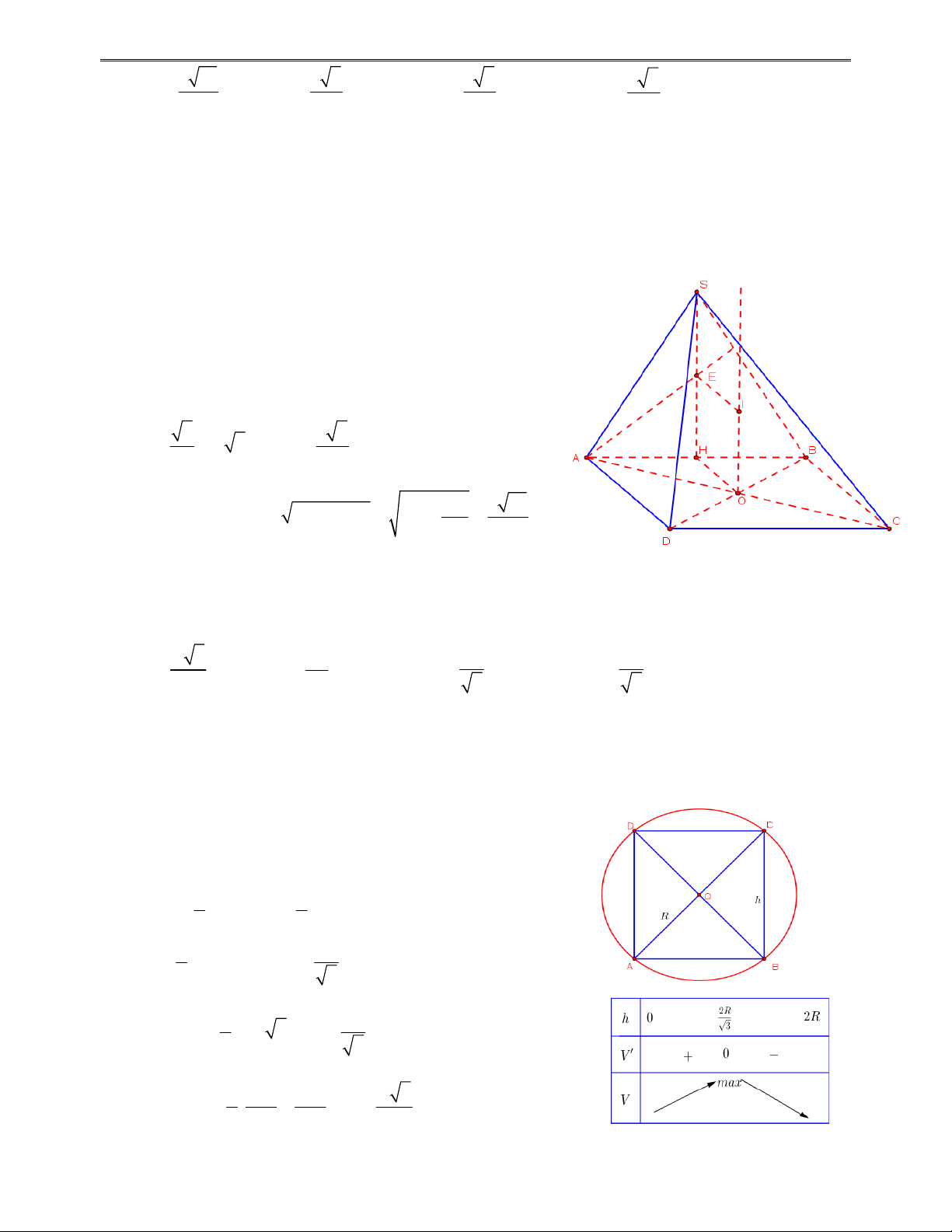
1
2
A.
21
3
a
R
B.
3
3
a
R
C.
3
2
a
R
D.
6
3
a
R
Hướngdẫngiải
QuaO,kẻ
1
ABCD
thì
1
làtrụccủađườngtrònngoạitiếphìnhvuôngABCD.
Do
SAB ABCD nênkẻ
SH AB
thì
SH ABCD
GọiElàtâmđườngtrònngoạitiếptamgiácđềuSABvàkẻ
2
SAB
tạiEthì
2
làtrụccủa
đườngtrònngoạitiếptamgiácSAB.
1
cắt
2
tạiI:tâmcủamặtcầungoạitiếphìnhchópS.ABCD.
TứgiácOHEIcó3gócvuôngO,H,Enênlàhìnhchữnhật
33
2. 3
23
a
SH a a EH
Trong
aa
AIO R AI OA OI a
2
22 2
321
:2
93
.
ĐápánA.
Câu23: ChohìnhcầutâmO,đườngkính2Rvàhìnhtrụtrònxoaynộitiếptronghìnhcầu.Hãytìm
kíchthướccủahìnhtrụkhinócóthểtíchđạtgiátrịlớnnhất.
A.
6
3
R
r
B.
2
3
R
r
C.
2
3
R
r
D.
2
3
R
r
Hướngdẫngiải
Gọihvàrlàchiềucaovàbánkínhđáycủahìnhtrụ.BàitoánquyvềviệctínhhvàrphụthuộctheoR
khihìnhchữnhậtABCDnộitiếptronghìnhtrònO,Rthayđổivề
2
Vrh
đạtgiátrịlớnnhất
Tacó:
222 222
44AC AB BC R r h
22 32
22
11
02
44
32
ʹ
4
3
VRhh hRh hR
R
VhRh
Vậy
3
max
42
3
9
3
R
VV R h
Lúcđó
22
22
14 2 6
.
43 3 3
RR R
rR r
.ChọnA.
h
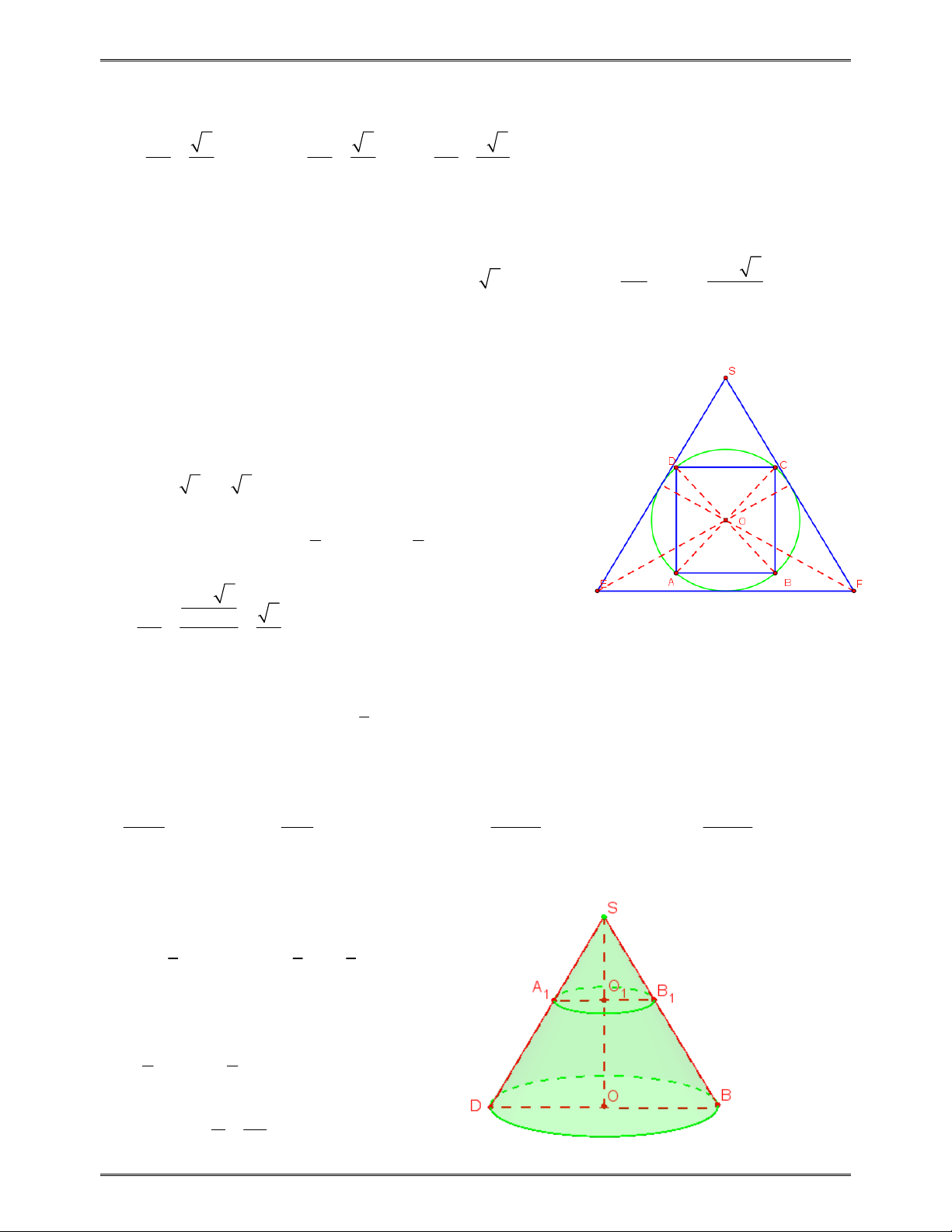
Câu24: ChohìnhcầuStâmO,bánkínhR.HìnhcầuSngoạitiếpmộthìnhtrụtrònxoayTcó
đườngcaobằngđườngkínhđáyvàhìnhcầuSlạinộitiếptrongmộtnóntrònxoayN
cógócởđỉnhbằng
60
.TínhtỉsốthểtíchcủahìnhtrụTvàhìnhnónN.
A.
2
6
T
N
V
V
B.
2
3
T
N
V
V
C.
62
2
T
N
V
V
D.Đápánkhác.
Hướngdẫngiải
BàitoánquyvềhìnhnóntâmOngoạitiếphìnhvuôngABCDvànộitiếptamgiácđềuSEFmàEF//
AB.VìOABlàtamgiácvuôngcânnên
2AB BC R .Suyra
2
3
2
22
T
AB R
VBC
Tathấy,tâmOcủahìnhtròncũngchínhlàtâmcủahìnhvuôngABCDđồngthờicũnglàtrọngtâm
củatamgiácđềuSEF.
Nhưvậy,đườngcaocủatamgiácSEFlà
33SH OH R
TrongtamgiácEOHvuôngtạiH,
30EOH
.Tacó:
.3 3EH O H R
Thểtíchcủahìnhnón
223
11
.3.33
33
N
VEHSHRRR
Vậy
3
3
2
2
2
6
3
T
N
R
V
V
R
.ChọnA.
Câu25: Chohìnhnón
N cóbánkínhđáyR,đườngcaoSO.GọiPmàmặtphẳngvuônggócvới
SOtạiO
1
saocho
1
1
3
SO SO
.Mộtmặtphẳngquatrụchìnhnóncắtphầnkhốinón N
nằmgiữaPvàđáyhìnhnóntheothiếtdiệnlàhìnhtứgiáccóhaiđườngchéovuônggóc.
Tínhthểtíchphầnhìnhnón
N nằmgiữamặtphẳngPvàmặtphẳngchứađáyhình
nón
N .
A.
3
7
9
R
B.
3
9
R
C.
3
26
81
R
D.
3
52
81
R
Hướngdẫngiải
Gọithiếtdiệnthuđượclà
11
A
ABB
Vì
1
1
3
SO SO
nên
11
11
.2
33
A
BAB R
Mặtkhác
11
A
BAB tạiInên
111
11
,
22
I
OABIO AB
Vậy
1
4
33
RR
OO R
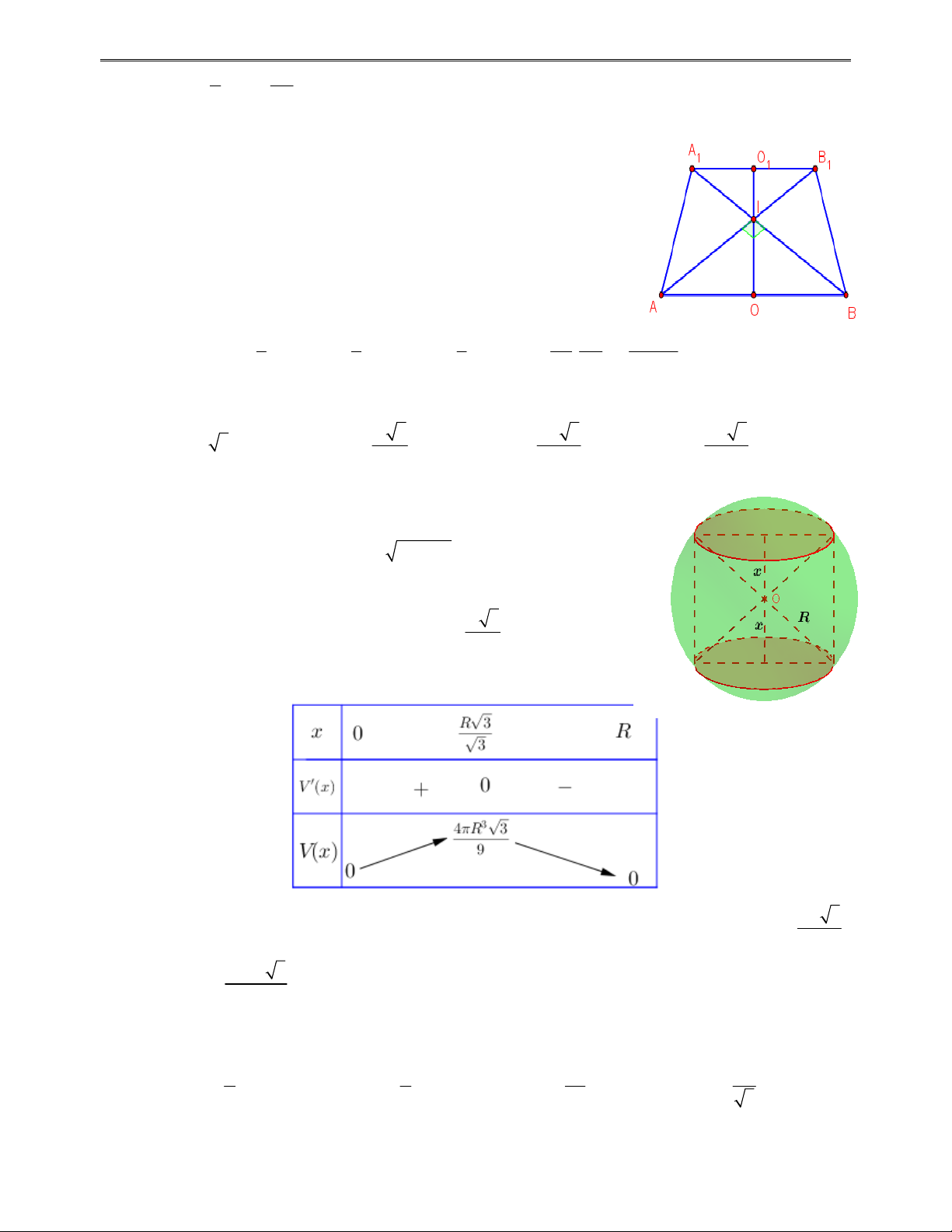
Dễthấy
11
12
23
R
SO OO
Từđó
2SO R
GọithểtíchphầnhìnhnónphảitínhlàV*thì
12
*VVV
,trongđó:
V
1
làthểtíchcủahìnhnón N .
V
2
làthểtíchhìnhnónđỉnhSvàđáylàthiếtdiệncủa
N
đượccắtbởiP.
Tacóthểtíchphầnhìnhnónphảitínhlà
22
12 11 1
11
*..
33
V V V OBSO OBSO
23
2
1252
.2 .
39381
RR R
RR
Câu26: Chiềucaocủakhốitrụcóthểtíchlớnnhấtnộitiếptronghìnhcầucóbánkính
R
là
A.
3
R
. B.
3
3
R
. C.
43
3
R
. D.
23
3
R
.
Hướngdẫngiải
Giảsử
2
x
làchiềucaohìnhtrụ
(0 )
x
R
xemhìnhvẽ
Bánkínhcủakhốitrụlà
22
rRx.Thểtíchkhốitrụlà:
22
()2VRxx
.Xéthàmsố
22
() ( )2,0Vx R x x x R
Tacó:
22
3
'( ) 2 ( 3 ) 0
3
R
Vx R x x
.Bảngbiếnthiên:
Dựa vào BBT, ta thấy thể tích khối trụ lớn nhất khi chiều cao của khối trụ là
23
3
R
;
3
max
43
9
R
V
.
Câu27: Chohìnhnóncóchiềucao
h
.Tínhchiềucao
x
củakhốitrụcóthểtíchlớnnhấtnộitiếp
tronghìnhnóntheo
h
.
A.
2
h
x
. B.
3
h
x
. C.
2
3
h
x
. D.
3
h
x
.
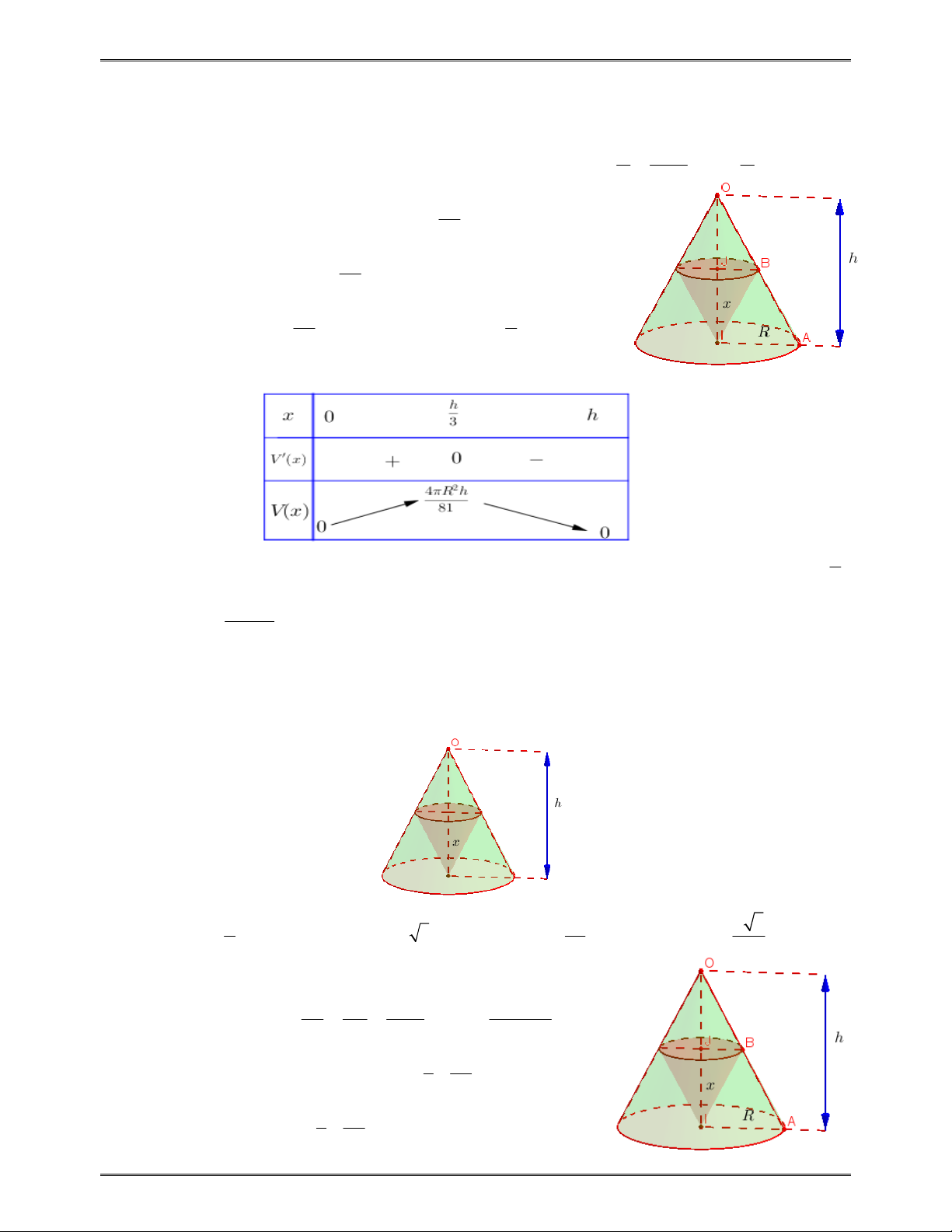
Hướngdẫngiải
Gọi
,rR
theothứtựlàbánkínhđáyhìnhnónvàkhốitrụcầntìm.
O
làđỉnhcủahìnhnón,
I làtâmcủađáyhìnhnón,
J
làtâmcủađáyhìnhtrụvàkhác I .
OA
làmộtđườngsinh
củahìnhnón,
B
làđiểmchungcủa
OA
vớikhốitrụ.Tacó:
()
rhx R
rhx
Rh h
.
Thểtíchkhốitrụlà:
2
22
2
()
R
VxR xhx
h
Xéthàmsố
2
2
2
() ( ),0
R
Vx x h x x h
h
.
Tacó
2
2
'( ) ( )( 3 ) 0 hay .
3
Rh
Vx h xh x x x h
h
Bảngbiếnthiên:
Dựa vào BBT, ta thấy thể tích khối trụ lớn nhất khi chiều cao của khối trụ là
3
h
x
;
2
max
4
27
R
h
V
.
Câu28: Chohìnhnónđỉnh
O
,chiềucaolà
h
.Mộtkhốinónkháccóđỉnhlàtâmcủađáyvàcóđáy
làlàmộtthiếtdiệnsongsongvớiđáycủahìnhnónđỉnh
O
đãchohìnhvẽ.Tínhchiều
cao
x
củakhốinónnàyđểthểtíchcủanólớnnhất,biết
0
x
h
.
A.
3
h
x
. B. 3
x
h . C.
2
3
h
x
. D.
3
3
h
x
.
Hướngdẫngiải
Từhìnhvẽtacó
()
J
BOJ hx Rhx
JB
IA OI h h
.
Thểtíchkhốinóncầntìmlà:
2
2
2
1
()
3
R
Vhxx
h
.
Xéthàmsố
2
2
2
1
() ( ) ,0
3
R
Vx h x x x h
h
.
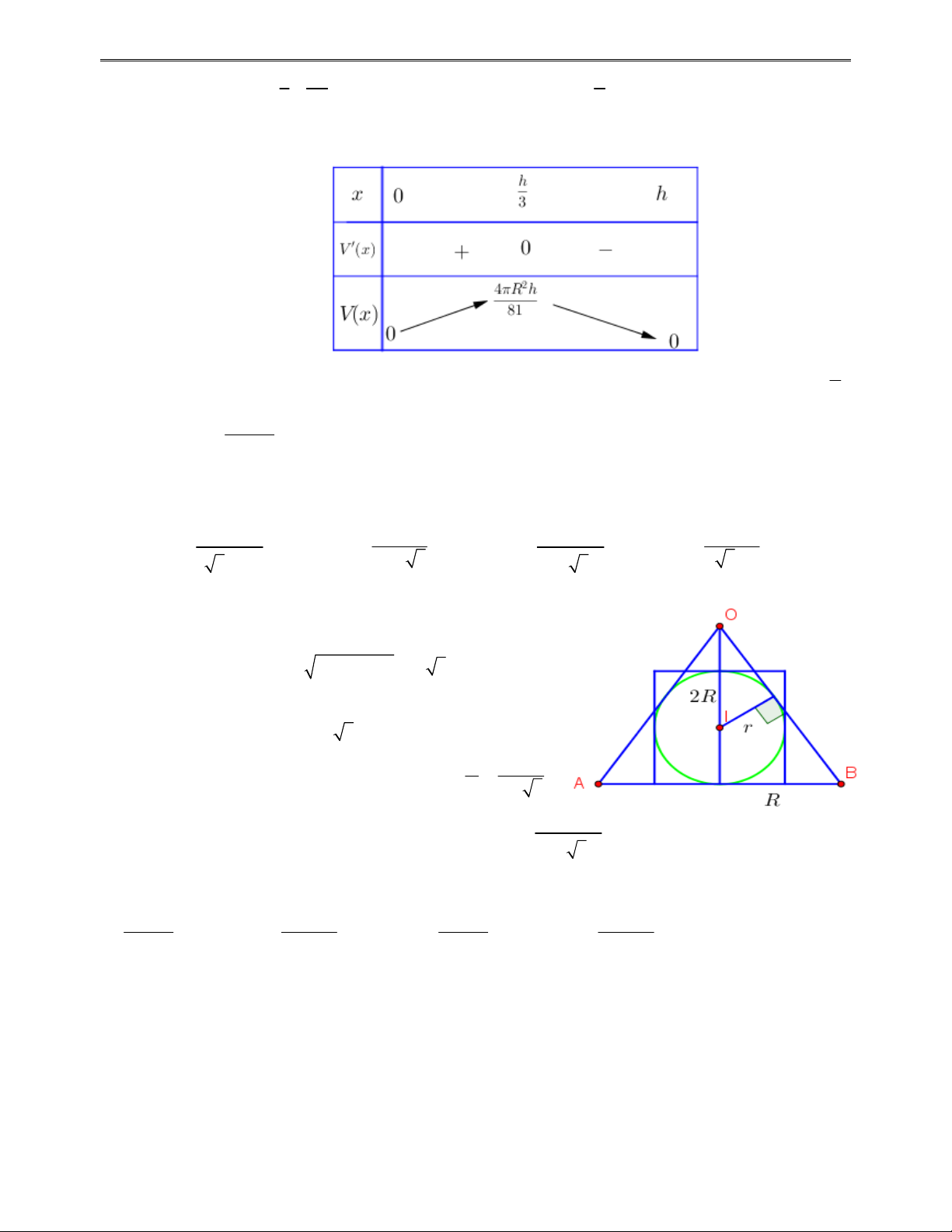
Tacó
2
2
1
'( ) ( )( 3 ) 0 hay .
33
R
h
Vx h xh x x h x
h
Bảngbiếnthiên:
DựavàoBBT,tathấythểtíchkhốinóncầntìmlớnnhấtkhichiềucaocủanólà
3
h
x
;
2
max
4
81
R
h
V
.
Câu29: Chomộthìnhnóncóbánkínhđáylà
R
,chiềucaolà
2
R
,ngoạitiếpmộthìnhcầu
(;)SOr
.
Khiđó,thểtíchcủakhốitrụngoạitiếphìnhcầu
(;)SOr
là
A.
3
3
16
51
R
. B.
3
4
125
R
. C.
3
3
16
15
R
. D.
3
4
25 1
R
.
Hướngdẫngiải
Giảsửhìnhnóncóđỉnh
O
vàđườngkínhđáylà
A
B
.
Tacó
22
(2 ) 5OA OB R R R
.
Tamgiác
OAB
códiệntíchlà
2
2SR
,
chuvilà
22(15)pR
.
Dođóbánkínhkhốicầu
(;)SOr
là
2
15
SR
r
p
.
Thểtíchkhốitrụcầntìmlà:
3
23
3
16
2
15
tru
R
Vrhr
.
Câu30: Hìnhnóncóthểtíchlớnnhấtnộitiếpmộtmặtcầubánkính
R
chotrướcbằng:
A.
3
64
81
R
B.
23
32
81
R
C.
3
32
81
R
D.
23
64
81
R
Hướngdẫngiải
Kíhiệubánkínhđáyhìnhnónlà
x
,chiềucaohìnhnónlà
y
0,02
x
RyR
.Gọi
'SS
là
đườngkínhcủamặtcầungoàitiếphìnhnónthìtacó
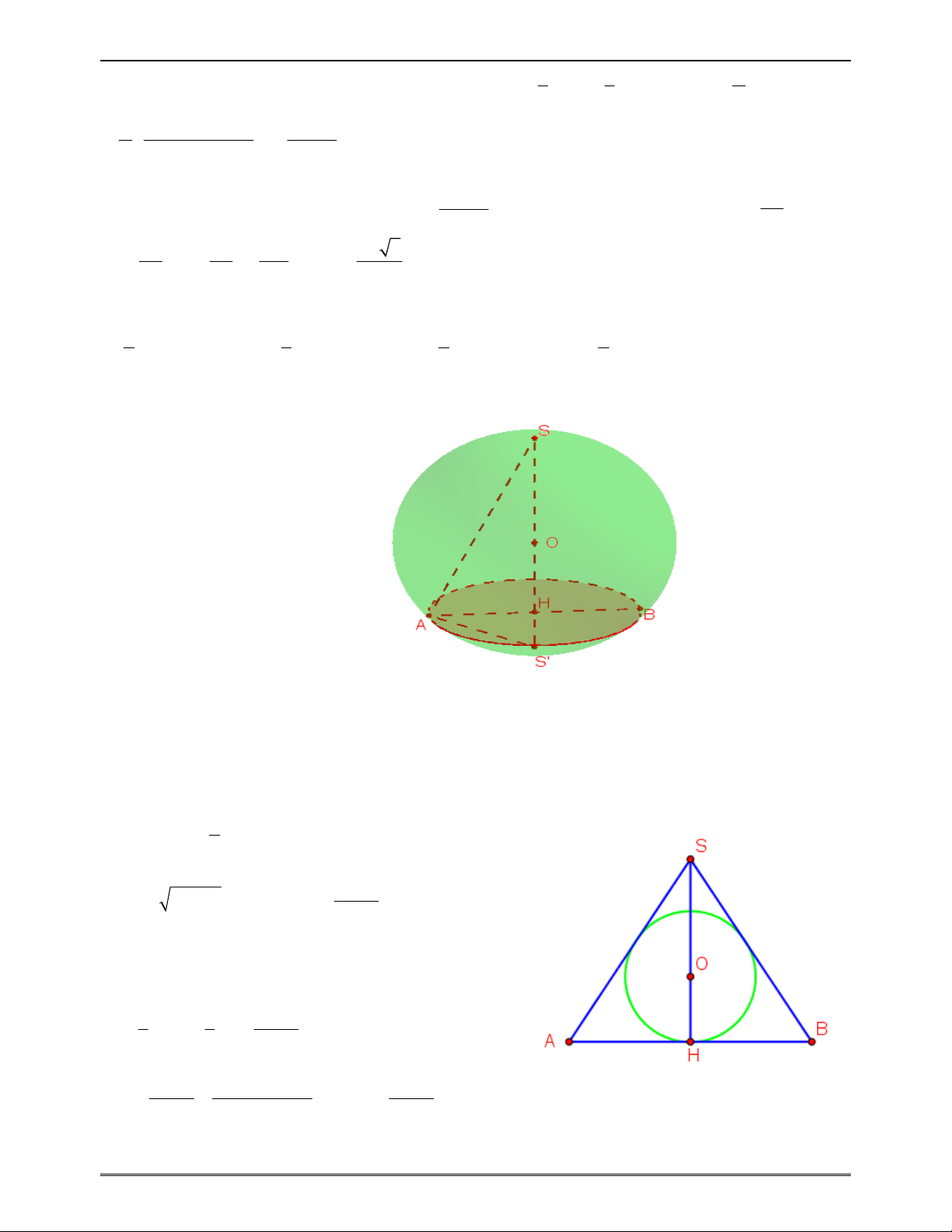
2
2xyRy
.Gọi
1
V là thể tích khối nón thì
2
1
11
.2
33
VxyyyRy
42..
6
Ryyy
3
3
42 32
63 81
R yyy R
Vậy thể tích
1
V đạtgiátrịlớnnhấtbằng
3
32
81
R
khivàchỉkhi
42Ryy
4
3
R
y
, từ đó
2
2
448
2
339
RRR
xR
hay
22
3
R
x
.ChọnC.
Câu31: Tìmhìnhnóncóthểtíchnhỏnhấtngoạitiếpmặtcầubánkính
r
chotrướccóthểtíchbằng:
A.
3
1
6
r
B.
3
8
3
r
C.
3
2
3
r
D.
3
4
3
r
Hướngdẫngiải
Xétmặtphẳngchứatrụccủahìnhnón,mặtphẳngnàycắthìnhnóntheotamgiáccân
SAB
vàcắt
mặtcầunộitiếphìnhnóntheođườngtrònbánkính
r
vàhìnhtrònnàynộitiếptamgiáccân
SAB
.79hb
Kí hiệu bán kính đáy hình nón là
x
,chiềucaohìnhnónlà
0, 2yx y r
thì
1
.
2
AH SA r AB SH
\
Vậythểtíchhìnhnónngoạitiếpmặtcầubánkính
r
là
2
22
2
11
:
33 2
y
Vxyr
yr
Tacó
2222 2
44 4
2
22 2
yyrr r
yr
yr yr yr
2
22 2
2
ry
xxyrxyx
yr

2
4
24
2
r
yr r
yr
2
4
22. 48
2
r
yr rr
yr
Từđó
3
2
1
.8
3
Vr
,tứclà
2
V
đạtgiátrịbénhấtkhivàchỉkhi
2
4
24
2
r
yr y r
yr
từđó 2
x
r
.
Câu32: Gọi
r
và
h
lầnlượtlàbánkínhđáyvàchiềucaocủamộthìnhnón.Kíhiệu
12
,VVlầnlượt
làthểtíchhìnhnónvàthểtíchhìnhcầunộitiếphìnhnón.Khi
r
và
h
thayđổi,tìmgiátrị
bénhấtcủatỉsố
1
2
V
V
A.
2
B.
22
C.
1
3
D.2
Hướngdẫngiải
Gọi
P
làmặtphẳngđiquatrụccủahìnhnónthì
P
cắthìnhnón.Theotamgiáccân
SAB
,cắt
mặtcầutheođườngtrònlớn,đườngtrònnàynộitiếptamgiáccân.Khiđó,bánkính
1
r củahìnhcầu
nộitiếphìnhnónđượctínhbởicôngthức
1
22
rh
r
rhr
3
2
3
2
1
2
2
2
11
11
11
44
h
x
r
V
h
Vx
r
,ởđó
2
2
0
h
x
r
Xét
32
2
11 1 1 221
,'
4
4.2 1
x
xx x
fx f x
x
xx
Vì
2
2
11
0
4.2 1
x
xx
nênkhixétdấucủa
f
x
,tachỉcầnxétdấucủa
221
g
xx x
.
Tacó
1
'1
1
gx
x
.Dễthấy
'0gx
vìkhi
0x
thì
1
1
1x
,đồngthời
08gx x
Vậy
gx
làhàmtăngtrênmiền
0x
và
80g
nên
Với
08x
thì
0;gx
Câu33: Chokhốinóntrònxoaycóđườngcao
20hcm
,bánkínhđáy
25rcm
.Mộtmặtphẳng
Pđiqua2đỉnhcủakhốinónvàcókhoảngcáchđếntâmOcủađáylà12cm.Khiđódiện
tíchthiếtdiệncủaPvớikhốinónbằng:
A.
2
500
cm B.
2
475 cm
C.
2
450
cm D.
2
550
cm
Hướngdẫngiải
GọiSlàđỉnhcủakhốinón.MặtphẳngPđiquađỉnhScắtkhốinóntheohaiđườngsinhbằngnhau
là
SA SB
nêntacóthiếtdiệnlàtamgiáccânSAB.
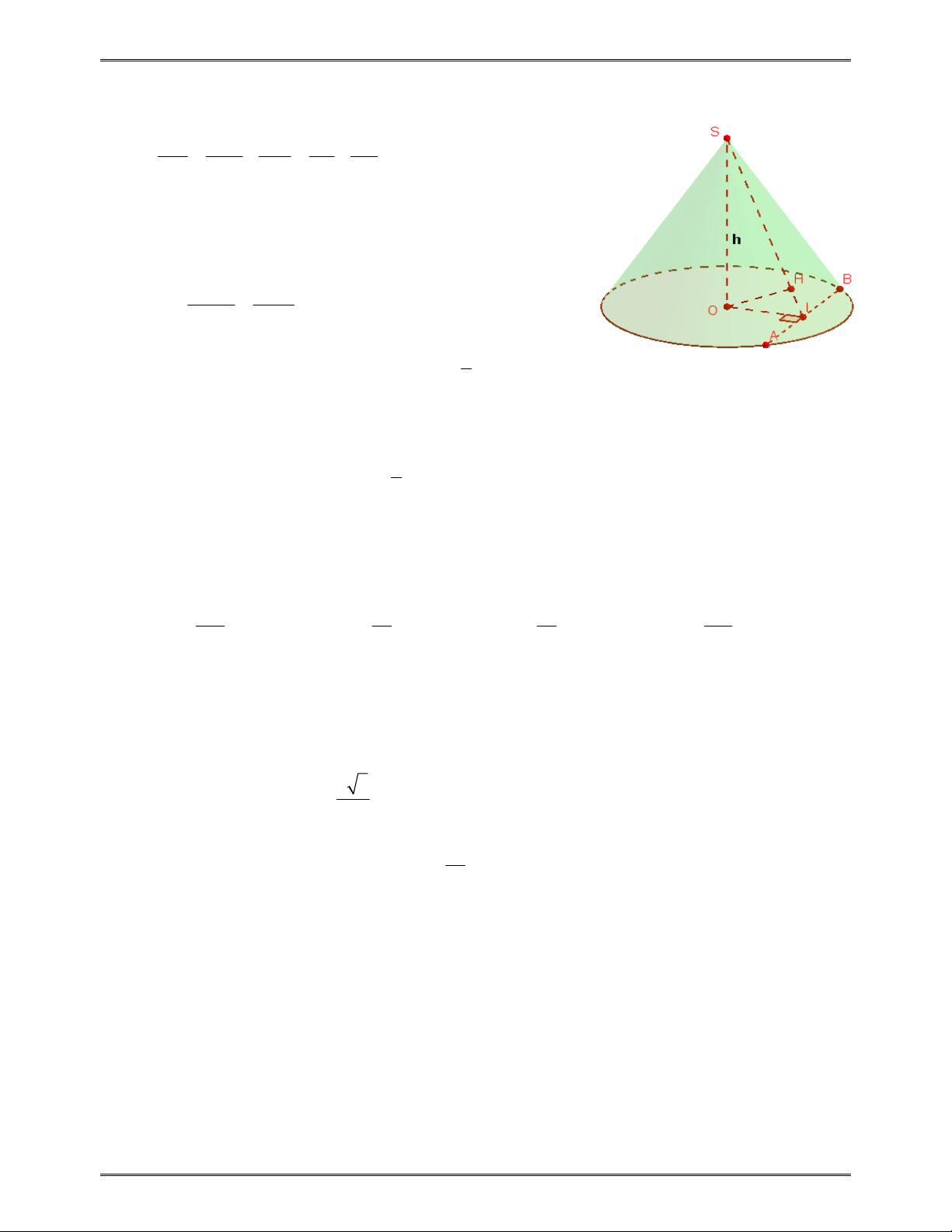
Gọi I là trung điểm của đoạn AB, ta có
OI AB
.TừtâmOcủađáytakẻ
OH SI
tạiH,tacó
OH SAB
vàdođótheogiảthiếttacó
12OH cm
.XéttamgiácvuôngSOItacó:
22222
11111
12 20OI OH OS
15OI cm
Mặtkhác,xéttamgiácvuôngSOItacòncó:
..OS OI SI OH
Dođó
. 20.15
25
12
OS OI
SI cm
OH
GọiS
t
làdiệntíchcủathiếtdiệnSAB.Tacó:
1
.
2
t
SABSI
,trongđó
2AB AI
Vì
222222
25 15 20AI OA OI
nên
20
A
Icm
và
40
A
Bcm
VậythiếtdiệnSABcódiệntíchlà:
2
1
.40.25 500
2
t
Scm
.ChọnA.
Câu34: Cholăngtrụđứng
.'''ABC A B C
cóđáylàtamgiácđềucạnha .Mặtphẳng
()
''AB C
tạo
vớimặtđáygóc
0
60 vàđiểm
G
làtrọngtâmtamgiác
ABC
.Bánkínhmặtcầungoạitiếp
khốichóp
.' ' 'GA B C
bằng:
A.
85
.
108
a
B.
3
2
a
. C.
3
.
4
a
D.
31
.
36
a
Hướngdẫngiải
Gọi
M
làtrungđiểm
''BC
,tacó
()( )
===
0
60 '', ''' ,' 'AB C A B C AM A M AMA
.
Trong
D 'AA M
,có =
3
'
2
a
AM
;
==
3
''.tan '
2
a
AA A M A MA
.
Gọi
'G
làtrọngtâmtamgiácđều
'''ABC
,suyra
'G
cũnglàtâm
đườngtrònngoạitiếp
D '''.ABC
Vìlặngtrụđứngnên
()
^''''GG A B C .
Dođó
'GG
làtrụccủatamgiác
'''ABC
.
Trongmặtphẳng
(
)
''GC G
,kẻtrungtrực
d
củađoạnthẳng
'GC
cắt
'GG
tại
I
.Khiđó
I
làtâm
mặtcầungoạitiếpkhốichóp
.' ' 'GA B C
,bánkính
= .RGI

Tacó
DD =
'
ÿ''
'
GP GG
GPI GG C
GI GC
+
= = = = =
222
.' ' ' '' 31
'2' 2' 36
GP GC GC GG G C a
RGI
GG GG GG
.ChọnD.
Câu35: Chomộthìnhtrụcóbánkínhđáybằng
R
vàcóchiềucaobằng
3.R
Haiđiểm
, AB
lần
lượtnằmtrênhaiđườngtrònđáysaochogócgiữa
AB
vàtrụccủahìnhtrụbằng
0
30
.
Khoảngcáchgiữa
AB
vàtrụccủahìnhtrụbằng:
A.
.R
B.
3.R
C.
3
.
2
R
D.
3
.
4
R
Hướngdẫngiải
Từhìnhvẽkếthợpvớigiảthiết,tacó
=='.OA O B R
Gọi
'AA
làđườngsinhcủahìnhtrụthì
=='' , ' 3OA R AA R và
=
0
'30BAA .
Vì
()
''OO ABA
nên
() () ()
éùé ùé ù
==
êúê úê ú
ëûë ûë û
', ', ' ', ' .dOOAB dOOABA dOABA
Gọi
H
làtrungđiểm
'AB
,suyra
()
ü
ï
^
ï
^
ý
ï
^
ï
þ
''
''
''
OH AB
OH ABA
OH AA
nên
(
)
éù
=
êú
ëû
', ' 'dO ABA O H
.
Tamgiác
'ABA
vuôngtại
'A
nên
==
0
''tan30.BA AA R
Suyratamgiác
''ABO
đềucócạnhbằng
R
nên
=
3
'.
2
R
OH
ChọnC.
Câu36: Chohìnhchóp
.SABC
cóđáy
ABC
làtamgiácđềucạnha ,hìnhchiếuvuônggóccủa
đỉnh
S
trênmặtphẳng
(
)
ABC
làtrungđiểm
H
củacạnh
BC
.Gócgiữađườngthẳng
SA
vàmặtphẳng
()
ABC
bằng
0
60
.Gọi
G
làtrọngtâmtamgiác
SAC
,
R
làbánkínhmặtcầu
cótâm
G
vàtiếpxúcvớimặtphẳng
(
)
SAB
.Đẳngthứcnàosauđâysai?
A.
()
éù
=
êú
ëû
,.RdGSAB
B.
=313 2 .RSH
C.
D
=
2
43
.
39
ABC
R
S
D. = 13.
R
a
Hướngdẫngiải
Tacó
()
===
0
60 , ,SA AB C SA HA SAH
.
Tamgiác
ABC
đềucạnha nên =
3
2
a
AH .
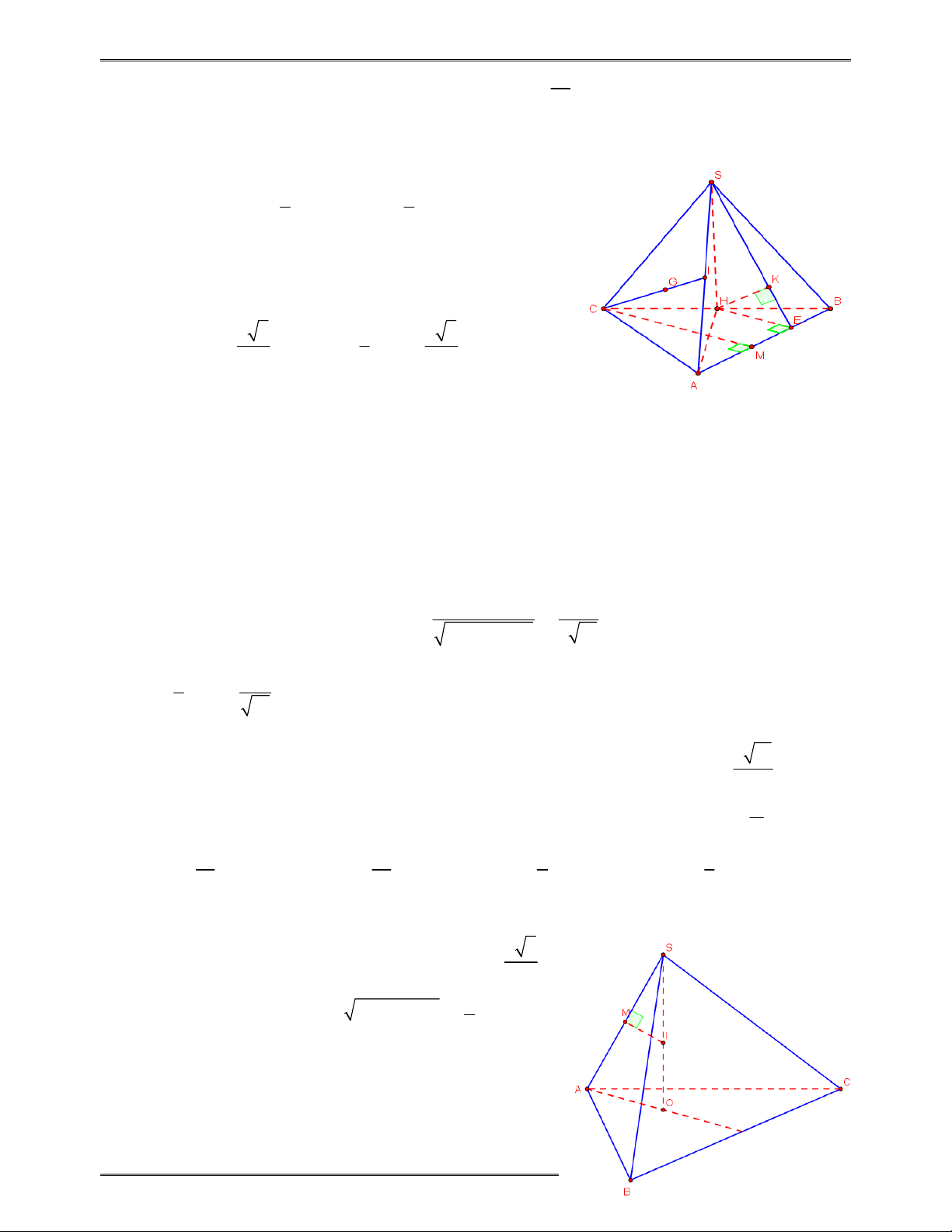
Trongtamgiácvuông
SHA
,tacó
==
3
.tan
2
a
SH AH SAH
.
Vìmặtcầucótâm
G
vàtiếpxúcvới
(
)
SAB
nênbánkínhmặtcầu
()
éù
=
êú
ëû
,.RdGSAB
Tacó
() () ()
éùéùéù
==
êúêúêú
ëûëûëû
12
,,,.
33
dG SAB dC SAB dH SAB
Gọi
, ME
lầnlượtlàtrungđiểm
AB
và
MB
.
Suyra
ì
ï
^
ï
ï
ï
í
ï
=
ï
ï
ï
î
3
2
CM AB
a
CM
và
ì
ï
^
ï
ï
ï
í
ï
==
ï
ï
ï
î
13
24
HE AB
a
HE CM
.
Gọi
K
làhìnhchiếuvuônggóccủa
H
trên
SE
, suy ra
^HK SE
.
()
1
Tacó
()
ì
ï
^
ï
^ ^
í
ï
^
ï
î
.
HE AB
AB SHE AB HK
AB SH
()
2
Từ
()
1
và
()
2
,suyra
(
)
^HK SAB
nên
(
)
éù
=
êú
ëû
,dH SAB HK
.
Trongtamgiácvuông
SHE
,tacó
==
+
22
.3
213
SH HE a
HK
SH HE
.
Vậy
==
2
3
13
a
RHK
.ChọnD.
Câu37: Chohìnhchóptamgiácđều
.SABC
cócạnhđáybằnga vàcạnhbênbằng
21
6
a
.Gọi
h
là
chiềucaocủakhốichópvà
R
làbánkínhmặtcầungoạitiếpkhốichóp.Tỉsố
R
h
bằng:
A.
7
12
B.
7
.
24
C.
7
.
6
D.
1
.
2
Hướngdẫngiải
Gọi
O
làtâm
DABC
,suyra
(
)
^SO ABC
và =
3
.
3
a
AO
Trong
SOA
,tacó == - =
22
.
2
a
hSO SA AO
Trongmặtphẳng
SOA
,kẻtrungtrực
d
củađoạn
SA
cắt
SO
tại
I
,suyra
●
ÎId
nên
=IS IA
.
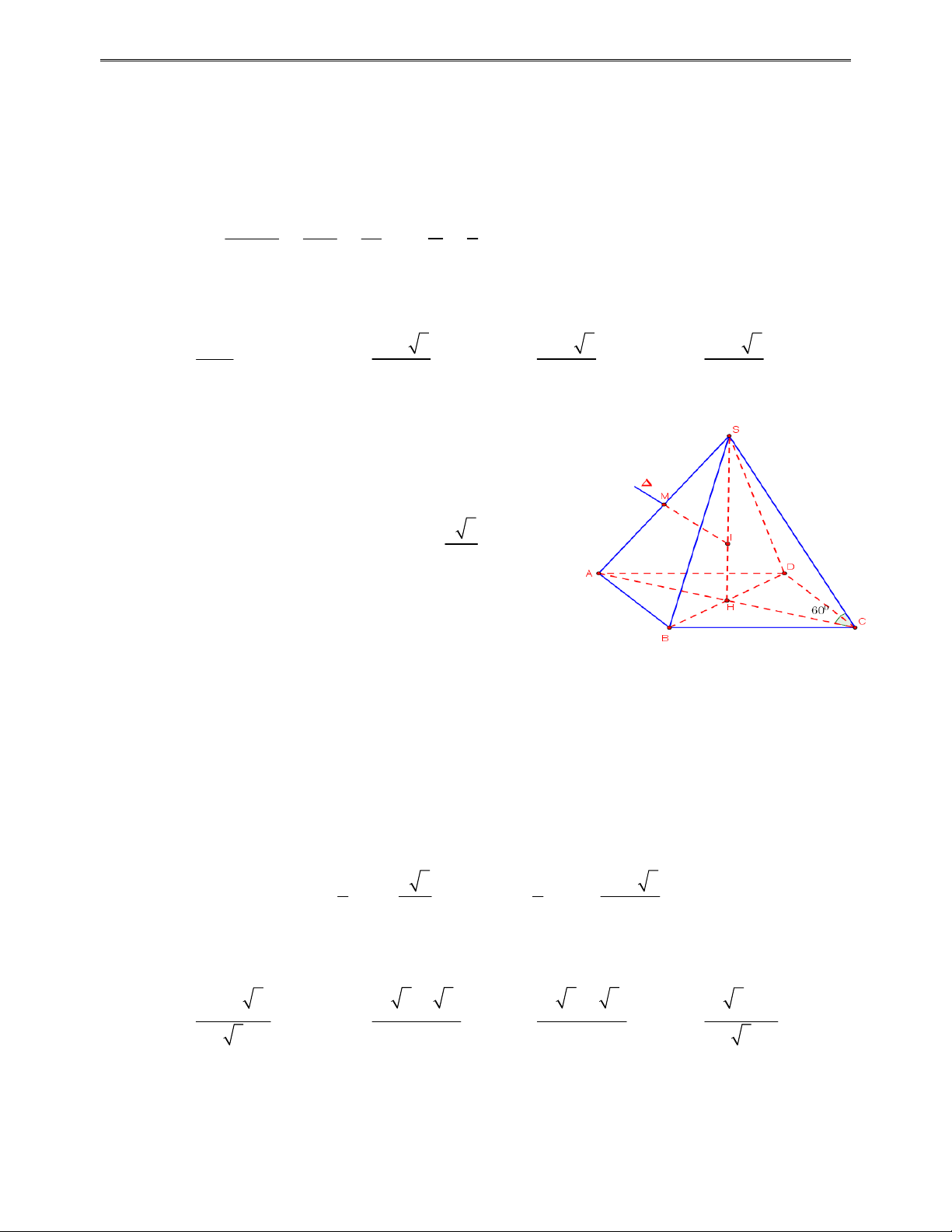
●
ÎISO
nên
==IA IB IC
.
Do đó
===IA IB IC IS
nên
I
là tâm mặt cầu ngoại tiếp khối
chóp
.SABC
.
Gọi
M
làtungđiểm
SA
,tacó
DDÿSMI SOA
nên
== = =
2
.7a
.
212
SM SA SA
RSI
SO SO
Vậy
=
7
.
6
R
h
ChọnC.
Câu38: Chohìnhchóptứgiácđều
.SABCD
cócạnhđáybằnga ,cạnhbênhợpvớimặtđáymột
góc
0
60 .Thểtíchcủakhốicầungoạitiếpkhốichóp
.SABCD
là:
A.
p
3
4
.
3
a
B.
p
3
26
.
9
a
C.
p
3
86
.
9
a
D.
p
3
86
.
27
a
Hướngdẫngiải
Gọi
=ÇOACBD
,suyra
(
)
^SO A BCD
.
Tacó
()
==
0
60 = , ,SB ABCD SB OB SBO
.
Trong
DSOB
,tacó
==
6
.tan
2
a
SO OB SBO
.
Tacó
SO
làtrụccủahìnhvuông
ABCD
.
Trong mặt phẳng
SOB
, kẻ đường trung trực
d
của đoạn
SB
.
Gọi
ìì
ïï
Î===
ïï
=Ç
íí
ïï
Î=
ïï
îî
ISO IAIBIC ID
ISOd
I d IS IB
== ===IA IB IC ID IS R
.
Xét
DSBD
có
ì
ï
=
ï
ï
í
ï
==
ï
ï
î
60
o
SB SD
SBD SBO
DSBD
đều.
Dođó
d
cũnglàđườngtrungtuyếncủa
DSBD
.Suyra
I
làtrọngtâm
DSBD
.
Bánkínhmặtcầu
== =
26
33
a
RSI SO .Suyra
p
p
==
3
3
486
.
327
a
VR
ChọnD.
Câu39: Chohìnhchóptứgiácđều
.SABCD
cócạnhbênbằngcạnhđáybằnga .Khiđómặtcầu
nộitiếphìnhchóp
.SABCD
cóbánkínhbằng:
A.
()
+13
.
2
a
B.
(
)
-62
.
4
a
C.
(
)
+62
.
4
a
D.
()
-31
.
2
a
Hướngdẫngiải
Gọi
H
làtâmcủahìnhvuông
ABCD
.
Tacó
SH
làtrụcđườngtrònngoạitiếpđáy.
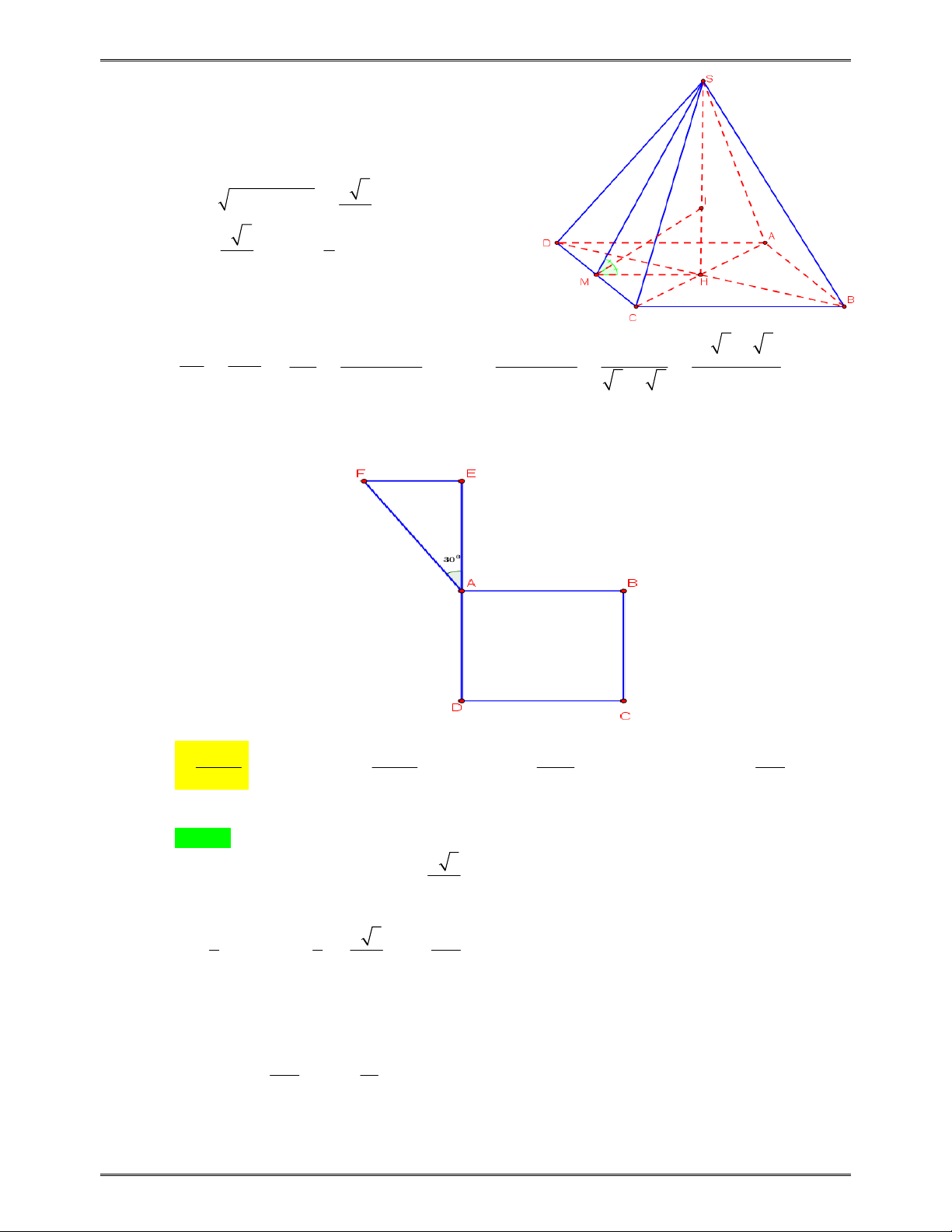
Gọi
M
là trung điểm của
CD
và
I
làchânđườngphângiác
trongcủagóc
Î ()SMH I SH .
Suyra
I
làtâmcủamặtcầunộitiếphìnhchóp,bánkính
=rIH
.
Tacó
=-=
==
22
2
;
2
3
; .
22
a
SH SA AH
aa
SM MH
Dựavàotínhchấtcủađườngphângiáctacó:
=
IS MS
IH MH
(
)
-
+
= = = =
+
+
62
.
.
4
26
a
SH MS MH SH MH a
IH
IH MH MS MH
ChọnB.
Câu40: CHUYÊNQUANGTRUNGLẦN3Tínhthểtíchcủavậtthểtrònxoaykhiquaymôhình
nhưhìnhvẽquanhtrục
DF
A.
3
10
9
a
. B.
3
10
7
a
. C.
3
5
2
a
. D.
3
3
a
.
Hướngdẫngiải
ChọnA.
Tacó
3
.tan .tan30
3
a
EF AF a
Khiquayquanhtrục
DF
,tamgiác
A
EF
tạoramộthìnhnóncóthểtích
2
3
2
1
113
.. . .
3339
aa
VEFAF a
Khiquayquanhtrục
DF
,hìnhvuông
A
BCD
tạoramộthìnhtrụcóthểtích
223
2
.. ..VDCBCaaa
Thểtíchcủavậtthểtrònxoaykhiquaymôhìnhnhưhìnhvẽquanhtrục
DF
là
3
33
12
10
99
a
VVV a a
Câu41: NGÔQUYỀN–HPThểtích
V
củakhốitrònxoaythuđượckhiquayhìnhthang
A
BCD
quanhtrục
OO
,biết
80,OO
24,OD
12,OC
12,OA
6OB
.
A.
43200 .V
B.
21600 .V
C.
20160 .V
D.
45000 .V
Hướngdẫngiải
ChọnC.
Côngthứctínhthểtíchkhốinóncụt
22
1212
1
3
V hRRRR
.
Trongđó
h
làđộdàiđườngcao,
12
;
R
R lầnlượtlàbánkínhhai
đáy.
Gọi
1
V làthểtíchkhốinóncụtkhiquayhìnhthang
A
OO D
quanhtrục
OO
.
Gọi
2
V làthểtíchkhốinóncụtkhiquayhìnhthang
B
OO C
quanhtrục
OO
.
Khiđó
12
VVV.
Tacó
22
1
1
. . . 26880
3
VOOODOAODOA
và
22
2
1
. . . 6720
3
VOOOCOBOCOB
.
Vậy
12
26880 6720 20160VVV
.
Câu42: CHUYÊNBẮCGIANGChohìnhnóncóđộdàiđườngkínhđáylà
2
R
,độdàiđườngsinhlà
17R vàhìnhtrụcóchiềucaovàđườngkínhđáyđềubằng
2
R
,lồngvàonhaunhưhình
vẽ.
.
Tínhthểtíchphầnkhốitrụkhônggiaovớikhốinón
A.
3
5
12
πR
. B.
3
1
3
πR
. C.
3
4
3
πR
. D.
3
5
6
πR
.
Hướngdẫngiải
ChọnD.
Tacó
22 22
17 4 2 ,
2
R
SI SB IB R R R SE R EF
.
Thểtíchkhốinónlớncóđườngcao
SI
là
23
1
14
.4R
33
V πR πR
.
Thểtíchkhốinónnhỏcóđườngcao
SE
là
2
3
2
11
.2
32 6
R
V π R πR
Thểtíchphầnkhốigiaonhaugiữkhốinónvàkhốitrụlà
3
3122
7
6
VVVV πR
.
Thểtíchkhốitrụlàlà
23
4
.2 2V πRR πR
.
Vậythểtíchphầnkhốitrụkhônggiaovớikhốinónlà
3
43
5
6
VVV πR
.
Câu43: CHUYÊNKHTNL4Mộtnútchaithủytinhlàmộtkhốitrònxoay
H
,mộtmặtphẳng
chứatrụccủa
H
cắt
H
theomộtthiếtdiệnnhưtronghìnhvẽbên.Tínhthểtíchcủa
H
đơnvị
3
cm
.
A.
23
H
V
. B.
13
H
V
. C.
41
3
H
V
. D.
17
H
V
.
Hướngdẫngiải:
ChọnđápánC.
Thểtíchkhốitrụlà
2
1. .54 9
tru
VBh
.Thểtíchkhốinónlà
2
1
2.
16
3
4
3
non
V
.
Thểtíchphầngiaolà:
.
2
1
3
2
1.2
3
pgiao
V
.Vậy
16 2 41
3
9
33
H
V
.
Câu44: CHUYÊNKHTNL4Chomộtmặtcầubánkínhbằng
1
.Xétcáchìnhchóptamgiácđều
ngoạitiếpmặtcầutrên.Hỏithểtíchnhỏnhấtcủachúnglàbaonhiêu?
A.
min 8 3V
. B.
min 4 3V
. C.
min 9 3V
. D.
min 16 3V
.
Hướngdẫngiải:
ChọnA.
Hướngdẫngiải
Gọicạnhđáycủahìnhchóplà
a
Tacó
SIJ SMH~
22
2
222
222
2
2
2
1
12 2 0
2
12
12
SI IJ
M
HSH IH IJ SH HM
SM MH
MH SH SH HM
aSHaSH
a
SH a
a
4
2
24
13231
.
112
36126
ABC
a
SSSH
a
aa
.Tacó
24
112 1
48aa
83S
Câu45: CHUYÊNKHTNL4Cắtmộtkhốitrụbởimộtmặtphẳngtađượcmộtkhối
H
nhưhình
vẽbên.Biếtrằngthiếtdiệnlàmộthìnhelipcóđộdàitrụclớnbằng8,khoảngcáchtừđiểm
thuộcthiếtdiệngầnmặtđáynhấtvàđiểmthuộcthiếtdiệnxamặtđáynhấttớimặtđáy
lầnlượtlà8và14xemhìnhvẽ.Tínhthểtíchcủa
H
.
A.
()
192
H
V
.
B.
()
275
H
V
.
C.
()
704
H
V
.
D.
()
176
H
V
.
Hướngdẫngiải
ChọnD.
Đườngkínhđáycủakhốitrụlà
22
10 6 8
Bánkínhđáycủakhốitrụlà
4
R
Thểtíchcủakhốitrụ
1
H
là
22
11
. . .4 .8 128VRh
.
Thểtíchcủakhốitrụ
2
H
là
22
22
.. .4.696VRh
.
ThểtíchcủaHlà
12
11
128 .96 176
22
VV V
.
Câu46: CHUYÊN VINH –L2 Cho lăng trụ
.
A
BC A B C
có
,3
A
BACaBC a
. Cạnh bên
2
A
Aa
.Bánkínhmặtcầungoạitiếptứdiện
A
BCC
bằng
A.
a . B. 2a . C.
5a
. D.
3a
.
Hướngdẫngiải:
ChọnB.
Dễthấytâmmặtcầungoạitiếptứdiện
A
BCC
cũnglàtâmmặtcầungoạitiếpkhốilăng
trụđứngđãcho.
Gọi
O
làtâmđườngtrònngoạitiếptamgiác
A
BC
.
Đườngthẳngqua
O
vuônggócvới
A
BC
cắtmặtphẳngtrungtrựccủa
A
A
tại
I
.
Khiđó
I
làtâmmặtcầungoạitiếp.
Mặtkhác
222
1
cos
2. . 2
AB AC BC
A
AB AC
Tacó:
0
3
2sinA 2sin120
ABC
BC a
R
a
dođó
22 22
2RIA OI OA a a a
.
Câu47: Chokhốichóp
.SABC
có
^ ()SA ABC
;tamgiác
ABC
cântại
A
,
=AB a
;
=120BAC
.
Gọi
,HK
lầnlượtlàhìnhchiếucủaA lên
,SB SC
.Tínhbánkínhmặtcầuđiqua5điểm
,,,,ABC K H
.
A.
= 3Ra B.
=Ra
C.
= 2Ra
D.Khôngtồntạimặtcầunhưvậy
Hướngdẫngiải
Gọi
I làtâmđườngtrònngoạitiếptamgiácABC vàAD làmộtđườngkínhcủađườngtròn
()I
.
Tamgiác
ACD vuôngtạiC ,suyra: ^DC AC mà ^DC SA nên
^ ()DC SAC
.
Talạicó:
ì
ï
^
ï
^
í
ï
^^
ï
î
(()
AK KC
AK KC
AK DC do DC KCD
.
Suyratamgiác
AKD vuôngtạiK ,suyra: ==IA ID IK .
Tươngtựnhưtrêntacũngcó:
==IA I D IH
.
Vậythì
=== =IA IB IC IK IH
,
dođó5điểm
,,,,ABC K H
cùngnằmtrênmộtmặtcầuđpcm.
Bánkính
R
củamặtcầucũnglàbánkínhđườngtrònngoạitiếptamgiácABC .
Ápdụngđịnhlý
cos
tacó:
=+- =
22
2 . .cos120 3BC AB AC AB AC a
.
Ápdụngđịnhlý
sin
tacó:
== = =
3
2
sin 2 sin
3
2.
2
BC BC a
RR a
AA
.ChọnB.
Câu48: Chokhốichóp
.SABCD
có
^ ()SA ABCD
;đáy
ABCD
làhìnhthangvuôngtại
A
và
B
với
==;AB BC a
= 2AD a ; =SA a .Gọi E làtrungđiểmcủa AD .Tìmtâmvàbánkính
mặtcầungoạitiếphìnhchóp
.SECD
.
A.
=
7
2
a
R B.
= 7Ra
C. =
11
2
a
R D. = 11Ra
Hướngdẫngiải
Gọi
O làtrungđiểmcủaCD .
Kẻtia
Ox SA
thì
^ ()Ox ABCD
.
Tacó:
O làtâmđườngtrònngoạitiếptamgiácvuôngCDE và
^ ()Ox ABCD
,nênOx làtrụccủa
đườngtròn
()CD E
.
Gọi
,MN
lầnlượtlàtrungđiểmcủa
,AB SC
.
Tacó:
=+=
22
5
2
a
SM SA AM
; =+=
22
5
2
a
MC MB BC
nênsuyra =SM MC .
Dođótamgiác
SMC cântạiM ,suyra ^MN SC .
Dễthấy
()//()MNO SAD
và
^ ()CE SAD
nênsuyra
^ ()CE MNO
vàdođó ^CE MN .
Vậynên
^ ()MN SEC
,dođóMN làtrụccủađườngtròn
()SEC
.
Gọi
I làgiaođiểmcủaMN vàSO thìI chínhlàtâmmặtcầungoạitiếphìnhchóp .SECD.
Bánkínhmặtcầungoạitiếphìnhchóp
.SECDlà == +
22
RIC IOOC.
Trongđó
=
5
2
a
OC
và
== =
3
33.
22
SA a
IO NP
P làgiaođiểmcủaMO vàAC .
x
x
O
P
M
N
O
C
D
S
B
A
A
B
S
D
C
E
I
E
Vậythì
æö
æö
÷
ç
÷
ç
÷
ç
÷
=+=
ç
÷
ç
÷
÷
ç
÷
ç
ç
÷
èø
ç
èø
2
2
53 11
222
aaa
R
.ChọnC.
Câu49: Chokhốichóp
.SABCcótamgiácABC vuôngtại
,B
biết 1AB = ;
3AC =
.Gọi
M
là
trungđiểm
BC , biết
()SM ABC^
.Tổngdiện tích cácmặtcầungoại tiếp cáctứdiện
SMAB vàb SMAC bằng15
.Diệntíchmặtcầungoạitiếphìnhchóp .SABClà:
A.
21
4
B.
20
C.
25
4
D.
4
Hướngdẫngiải
Dễkiểmtrađược
2
B
Ca
vàtamgiác
M
AB đềucạnh
a
.Đặt
SM h
.
Gọi
12
,RRvà
R
lầnlượtlàbánkínhcácmặtcầungoạitiếpcủacáchình
SMAB
,
SMAC
và
.SABC
.
Gọi
12
,rrvà r lầnlượtlàbánkínhcácđườngtrònngoạitiếpcủacáctamgiác
M
AB
,
M
AC vàABC .
Tacó:
1
3
2
r
và
2
1
2.sin120
AC
r
.
Vì
()SA MAB , ()SA MAC nêndễkiểmtrađược:
2
2
22
11
3
244
hh
Rr
và
2
2
22
22
1
24
hh
Rr
.
Theogiảthiếttổngdiệntíchcácmặtcầuthì:
22
12
415RR
Suyra:
22
315
1
444 4
hh
.Từđâytìmđược
2h
.
Dựngtrungtrựccủa
SC ,cắt SM tại
I
thì
I
làtâmmặtcầungoạitiếpcủa .SABC.
Dễkiểmtra
..SI SM SN SC ,suyra
.5
4
SN SC
RSI
SM
.
Vậythìdiệntíchmặtcầungoạitiếphìnhchóp
.SABClà
2
525
4
44
S
.ChọnC.
N
M
A
B
C
S
I
Câu50: Chohìnhlậpphương
.ABCD A B C D
¢¢¢ ¢
cạnh
.a
Gọi
,
MN
lầnlượtlàtrungđiểmcủacáccạnh
AB vàBC
¢¢
.Mặtphẳng
()DMN
chiahìnhlậpphươngthành2phần.Gọi
1
V
làthểtíchcủa
phầnchứađỉnh
2
,
A
V
làthểtíchcủaphầncònlại.Tínhtỉsố
1
2
V
V
.
A.
2
3
. B.
55
89
. C.
37
48
. D.
1
2
.
Hướngdẫngiải
Gọi
H
AB DN;
M
H
cắt
'
B
B
tại
K
,cắt
'
A
A
tại S ; SD cắt
''
A
D
tại
E
.
Thiếtdiệntươngứnglàngũgiác
D
NKME .
Phầnđadiệnchứa
A
cóthểtíchlà:
1. .' .SADH SAEM KBNH
VV V V
.
Dùngtamgiácđồngdạngkiểmtrađược:
B
ABH
;
4'
A
HAM
;
4'
A
DAE
và
1
'' '
3
SA B K A A
.
Đặtđộdàicạnhhìnhlậpphươngbằng
1
thì:
12
';
33
SA KB
.
Tacó:
.
1114
.. 1 .1.2
6639
SADH
VSAADAH
.
.' .
11
64 144
SAEM SADH
VV
;
..
11
818
KBNH SADH
VV
Vậythìphầnđadiệnchứa
A
cóthểtíchlà:
41 155
9 144 18 144
.
Suyraphầnđadiệnkhôngchứa
A
cóthểtíchlà:
3
55 89
1
144 144
.ChọnB.
E
K
N
M
A'
A
N
M
A'
A
D
C
B
B'
C'
D'
D'
C'
B'
B
C
D
S
H
Chủđề7.TỌAĐỘTRONGKHÔNGGIANOXYZ
Câu1: SGDVĨNHPHÚCTrongkhônggianvớihệ tọađộ
Oxyz
,choba điểm
()
A1;2;0
,
()
B3;4;1
,
(
)
D1;3;2-
.Tìmtọađộđiểm
C
saocho
ABCD
làhìnhthangcóhaicạnhđáy
AB
,
CD
vàcó
góc
C
bằng
45 .
A.
()
C 5;9;5
. B.
()
C1;5;3
.
C.
()
C 3;1;1-
. D.
()
C3;7;4
.
Hướng
dẫngiải
ChọnD.
Cách1.
AB (2;2;1)=
.
Đườngthẳng
CD
cóphươngtrìnhlà
x12t
CD : y 3 2t
z2t
ì
ï
=- +
ï
ï
ï
=+
í
ï
ï
=+
ï
ï
î
.
Suyra
()
C 1 2t;3 2t;2 t-+ + +
;
CB (4 2t;1 2t; 1 t),=- ---
CD ( 2 t; 2t; t)=- - -
.
Tacó
22 2222
(4 2t)( 2t) (1 2t)( 2t) ( 1 t)( t)
cos BCD
(4 2t) ( 1 2t) ( 1 t) ( 2t) ( 2t) ( t)
--+--+---
=
-+-+-- -+-+-
Hay
22 2222
(4 2t)( 2t) (1 2t)( 2t) ( 1 t)( t) 2
2
(4 2t) ( 1 2t) ( 1 t) ( 2t) ( 2t) ( t)
--+--+---
=
- +- +-- -+-+-
1.
Lầnlượtthay t bằng
3; 1; 1; 2
-
thamsố t tươngứngvớitoạđộđiểm
C
ởcácphươngánA,B,
C,D,tathấy
t2=
thoả1.
Cách2.
Ta có
AB (2; 2;1), AD ( 2;1; 2)==-
.
Suyra
AB CD^
và
AB AD=
.Theo
giảthiết,suyra
DC 2AB=
.Kíhiệu
C(a; b; c)
, ta có
DC (a 1;b 3;c 2)=+ - -
,
2AB (4; 4; 2)=
.Từđó
C(3; 7; 4)
.
D
C
B
A
BÀI TOÁN VẬN DỤNG (8 - 9 - 10)
_______________________________
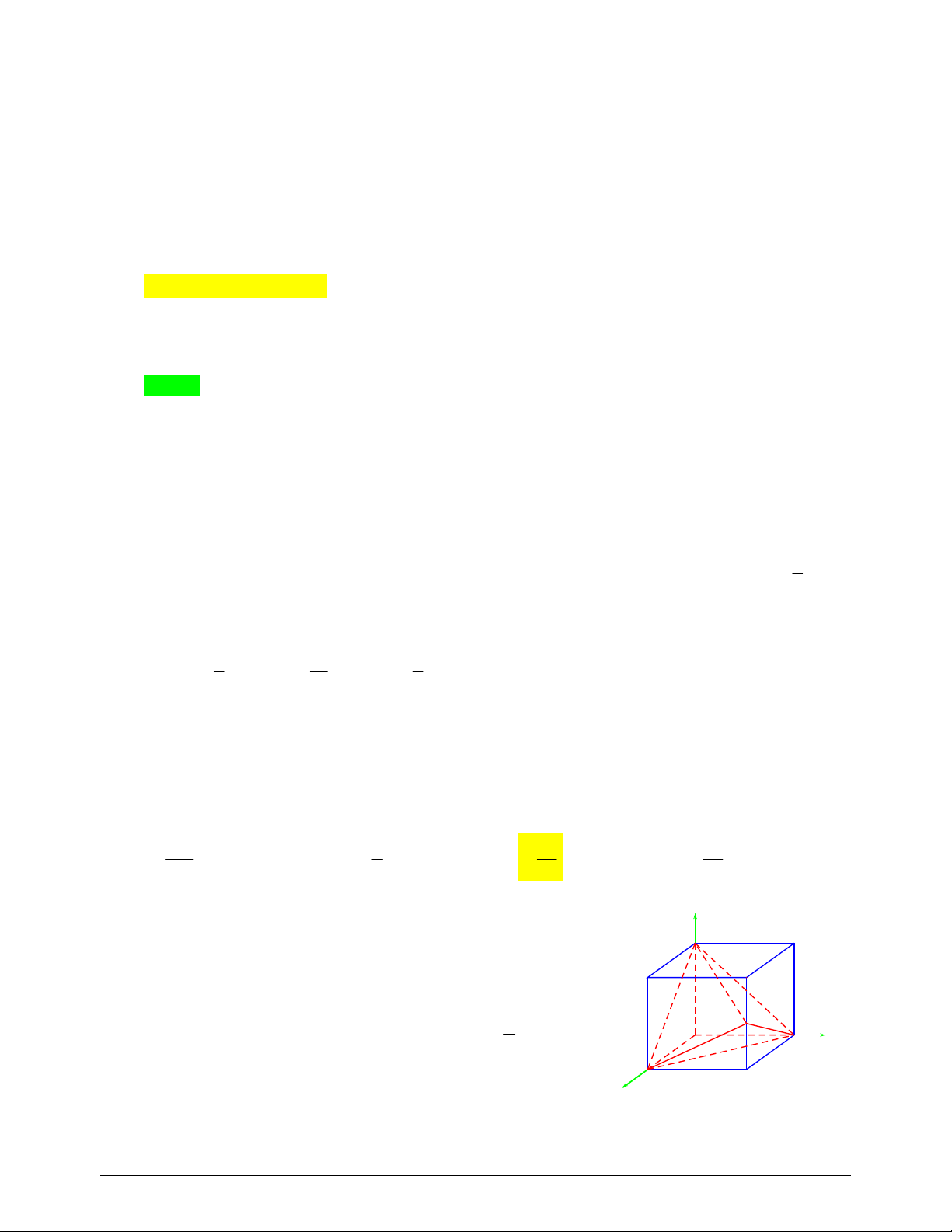
z
y
x
m
n
m
D'
C'
B'
A'
D
C
B
A
O
Câu2: SGD VĨNHPHÚCTrong không gian với hệ tọađộ
Oxyz
,chobađường thẳng
1
1
xt
d:y 0
z0
ì
ï
=
ï
ï
ï
=
í
ï
ï
=
ï
ï
î
,
22
x1
d:y t
z0
ì
ï
=
ï
ï
ï
=
í
ï
ï
=
ï
ï
î
,
3
3
x1
d:y 0
zt
ì
ï
=
ï
ï
ï
=
í
ï
ï
=
ï
ï
î
.Viếtphươngtrìnhmặtphẳngđiquađiểm
(
)
H3;2;1
vàcắtbađường
thẳng
1
d ,
2
d ,
3
d lầnlượttại
A
,
B
,
C
saocho
H
làtrựctâmtamgiác
ABC
.
A.
2x 2y z 11 0++-=
. B.
xyz60++-=
. C.
2x 2y z 9 0+--=
. D.
3x 2y z 14 0++-=
.
Hướngdẫngiải
ChọnA.
Gọi
()
Aa;0;0
,
(
)
B 1;b;0
,
(
)
C1;0;c
.
(
)
(
)
(
)
(
)
AB 1 a;b;0 , BC 0; b;c , CH 2;2;1 c , AH 3 a;2;1=- = - = - =-
.
Yêucầubàitoán
()()()
23
AB,BC .CH 0
2bc 2c a 1 1 c b a 1 0
b0
AB.CH 0 a b 1 9b 2b 0
9
b
c2b
2
BC. AH 0
ì
éù
ï
ï=
êú
ì
ï
ï
+ -+- -=
é
ëû
=
ï
ï
ï
ê
ï
ï
ï
ê
==+ -=
íí
ê
ïï
=
ïï
ê
=
ïï
ë
=
ïï
î
ï
ï
î
Nếu
b0=
suyra
ABº
loại.
Nếu
9
b
2
=
,tọađộ
11
A;0;0
2
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
,
9
B1; ;0
2
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
,
()
C1;0;9
.Suyraphươngtrìnhmặtphẳng
(
)
ABC
là
2x 2y z 11 0++-=
.
Câu3: NGUYỄN KHUYẾN TPHCM Trong không gian với hệ tọa độ
Oxy
,chohìnhhộpchữnhật
ABCD.A B C D
¢¢¢¢
cóA trùngvớigốctọađộO ,cácđỉnh
B(m; 0; 0)
,
D(0; m; 0)
,
A (0; 0; n)
¢
với
m, n 0> và
mn4+=
.Gọi
M
làtrungđiểmcủacạnh
CC
¢
.Khiđóthểtíchtứdiện
BDA M
¢
đạtgiátrịlớnnhấtbằng
A.
245
108
. B.
9
4
. C.
64
27
. D.
75
32
.
Hướngdẫngiải
Tọađộđiểm
n
C (m; m; 0), C (m; m;; n), M m; m;
2
æö
÷
ç
¢
÷
ç
÷
ç
èø
()( )
n
BA m; 0; n , BD m; m; 0 , BM 0; m;
2
æö
÷
ç
¢
÷
=- =- =
ç
÷
ç
èø
()
2
BA , BD mn; mn; m
éù
¢
=---
êú
ëû

2
BDA M
1mn
VBA,BD.BM
64
¢
éù
¢
==
êú
ëû
Tacó
3
2
m m 2n 512 256
m.m.(2n) m n
327 27
æö
++
÷
ç
÷
£=£
ç
÷
ç
èø
BDA M
64
V
27
¢
£
Chọnđápán:C
Câu4: NGUYỄN KHUYẾN TPHCM Trong không gian với hệ tọa độ
Oxyz
, hai mặt phẳng
4x 4y 2z 7 0-+-=
và
2x 2y z 1 0-++=
chứahaimặtcủahìnhlậpphương.Thểtíchkhối
lậpphươngđólà
A.
27
V
8
=
B..
81 3
V
8
=
.
C.
93
2
V
D.
64
27
V
Hướngdẫngiải
Theobàirahaimặtphẳng
44270xyz
và
22 10xyz
chứahaimặtcủahìnhlập
phương.Màhaimặtphẳng
():4 4 2 7 0Pxyz
và
():2 2 1 0Qxyz
songsongvới
nhaunênkhoảngcáchgiữahaimặtphẳngsẽbằngcạnhcủahìnhlậpphương.
Tacó
(0;0; 1) ( )
M
Q
nên
222
27 3
(( ),( )) ( ,( ))
2
4(4)2
dQ P dMP
Vậythểtíchkhốilậpphươnglà:
222 8
..
333 27
V
.
Câu5: NGUYỄN KHUYẾN TPHCM Trong không gian với hệ trục tọa độ
,Oxyz
cho điểm
(2;3;0),A
(0; 2;0),B
6
;2;2
5
M
vàđườngthẳng
:0.
2
xt
dy
zt
Điểm
C
thuộc
d
sao cho chu vi tam
giác
A
BC
lànhỏnhấthìđộdài
CM
bằng
A.
23. B.
4.
C.
2.
D.
26
.
5
Hướngdẫngiải
Do
A
B
cóđộdàikhôngđổinênchuvitamgiác
A
BC
nhỏnhấtkhi
A
CCB
nhỏnhất.
Vì
22
;0;2 2 2 2 9, 2 2 4Cd Ct t AC t BC t
22
222 9 2 2 4.AC CB t t

Đặt
222;3, 2 2;2ut v t
ápdụngbấtđẳngthức
uvuv
22 2
222 9 2 2 4 222 25.ttDấubằngxảyrakhivàchỉ
khi
22
2223 7 7 3 67 3
;0; 2 2 2.
2555 55 5
22
t
tC CM
t
ChọnC.
Câu6: T.TDIỆUHIỀNTrongkhônggianvớihệtrụctọađộ
Oxyz
,cho
1;1;1A
,
0;1;2B
,
2;0;1C
:10Pxyz
.Tìmđiểm
NP
saocho
22 2
2SNANBNC
đạtgiátrịnhỏnhất.
A.
153
;;
244
N
. B.
3; 5;1N . C.
2;0;1N . D.
31
;;2
22
N
.
Hướngdẫngiải
ChọnA.
Gọi
I
làtrungđiểm
BC
và
J
làtrungđiểm
A
I
.Dođó
13
1; ;
22
I
và
35
0; ;
44
J
.
Khiđó
22 2 22 2
11
22 4
22
SNA NI BC NJIJ BC
.
Dođó
S nhỏnhấtkhi NJ nhỏnhất.Suyra J làhìnhchiếucủa N trên
P
.
Phươngtrìnhđườngthẳng
3
:
4
5
4
xt
NJ y t
zt
.
Tọađộđiểm
J
lànghiệmcủahệ:
10
1
2
5
3
4
4
3
5
4
4
xyz
x
xt
y
yt
z
zt
Câu7: LẠNG GIANG SỐ 1 Trong không gian với hệ tọa độ
,Oxyz
chobađườngthẳng
1
1
:1,;
x
dy t
zt
2
2
:,;
1
x
dyuu
zu
11
:.
111
xyz
Viếtphươngtrìnhmặtcầutiếpxúc
vớicả
12
,ddvàcótâmthuộcđườngthẳng
?
A.
22
2
111xyz
. B.
222
1115
2222
xyz
.

C.
222
3131
2222
xyz
. D.
222
5159
44416
xyz
.
Hướngdẫngiải
ChọnA.
Đườngthẳng
1
d
điquađiểm
1
1; 1; 0M vàcóvéctơchỉphương
1
0;0;1
d
u
.
Đườngthẳng
2
d điquađiểm
2
2;0;1M
vàcóvéctơchỉphương
2
0;1;1
d
u
.
Gọi
I làtâmcủamặtcầu.Vì I nêntathamsốhóa
1;;1
I
tt t
,từđó
12
;1 ; 1 , 1 ; ;IM t t t IM ttt
.
Theogiảthiếttacó
12
;;dId dId ,tươngđươngvới
12
12
22
2
12
;;
121
0
1
2
dd
dd
IM u IM u
tt t
t
uu
Suyra
1; 0; 1I
vàbánkínhmặtcầulà
1
;1RdId
.Phươngtrìnhmặtcầucầntìmlà
22
2
111xyz
.
Câu8:
LẠNGGIANGSỐ1Trongkhônggianvớihệtọađộ chohaiđiểm
vàmặtphẳng Tìmtọađộđiểm thuộc saocho nhỏ
nhất?
A. . B. .
C. . D.
21118
;;
555
M
.
Hướngdẫngiải
ChọnD.
Thaytọađộvàophươngtrìnhmặtphẳng ,tađược
haiđiểm
,
A
B
cùngphíavớiđốivớimặtphẳng .
Gọi làđiểmđốixứngcủa
A
qua
P
.Tacó
.
Nên
min
M
AMB AB
khivàchỉkhi
M
làgiaođiểmcủa
A
B
với
P
.
,Oxyz
1; 0; 2 ; 0; 1; 2AB
:22120.Px y z
M
P
M
AMB
2; 2;9M
61825
;;
11 11 11
M
7731
;;
66 4
M
1; 0; 2 ; 0; 1; 2AB
P
0PAPB
P
A
M
AMB MA MB AB
H
M
B
A'
A
P

Phươngtrình điqua vàcóvéctơchỉphương
1; 2; 1
P
n
.
Gọi
H
làgiaođiểmcủa
A
A
trên
P
,suyratọađộcủa
H
là
0; 2;4H ,suyra
1; 4; 6A
,
nênphươngtrình
:13
24
xt
A
B
y
t
zt
.
Vì
M
làgiaođiểmcủa
A
B
với
P
nêntatínhđượctọađộ
Câu9:
LẠNG GIANG SỐ 1 Trong không gian với hệ tọa độ cho đường thẳng
vàmặtphẳng Phươngtrìnhđườngthẳng nằm
trong saocho cắtvàvuônggócvớiđườngthẳng là
A. . B. .
C. . D. .
Hướngdẫngiải
ChọnC.
Vectơchỉphươngcủa ,vectơpháptuyếncủa
P
là
1; 2; 2
P
n
.
Vì .
Tọađộgiaođiểm lànghiệmcủahệ .
Lạicó ,mà .Suyra .
Vậyđườngthẳng điqua vàcóVTCP nêncóphươngtrình
.
Câu10: LÝTỰTRỌNG
–TPHCMTrongkhônggianchođiểm
(1; 3; 2)M
.Cóbaonhiêumặtphẳngđi
qua
M
vàcắtcáctrụctọađộtại
,,
A
BC
mà
0OA OB OC
A.1. B.2. C.3. D.4.
Hướngdẫngiải
ChọnC.
1
:2
22
x
t
A
Ayt
zt
A
A
1; 0; 2A
21118
;;.
555
M
,Oxyz
12
:
11 1
xy z
:2240.Px y z
d
P
d
3
:12
1
xt
dy tt
zt
3
:2
22
xt
dy tt
zt
24
:13
4
xt
dy tt
zt
1
:33
32
xt
dy tt
zt
:1;1;1u
;4;3;1
d
dP
dP
d
uu
uun
dP
un
HP
1
22;1;4
2
2240
xt
yt
tH
zt
xyz
;dPd
HP
H
d
d
2; 1;4H
4; 3;1
d
u
24
:13
4
xt
dy tt
zt

Giảsửmặtphẳng
()
cầntìmcắt
,,Ox Oy Oz
lầnlượttại
(a,0,0),B(0,b,0),C(0,0c)(a,b,c 0)A
(): 1
xyz
abc
;
()
qua
(1; 3; 2)M
nên:
132
(): 1(*)
abc
(1)
(2)
00
(3)
(4)
abc
ab c
OA OB OC a b c
abc
abc
Thay
(1)
vào*tacóphươngtrìnhvônghiệm
Thay
(2),(3),(4)
vào*tađượctươngứng
3
4, 6,
4
aaa
Vậycó3mặtphẳng.
Câu11: LÝ TỰ TRỌNG
–TPHCMTrong không gian với hệ tọa độ
Oxyz
chođiểm
E(8;1;1)
.Viết
phươngtrìnhmặtphẳng
()
quaEvàcắtnửatrụcdương
,,Ox Oy Oz
lầnlượttại
,,
A
BC
sao
cho
OG
nhỏnhấtvới
G
làtrọngtâmtamgiác
A
BC
.
A.
2110 xy z
. B.
866=0xyz
.
C.
2180xyz
. D.
22120xyz
.
Hướngdẫngiải
ChọnD.
Cách1 :
VớiđápánA:
2
11 11 11 11 121
(11;0;0);B(0;11;0);C(0;0; ) ( ; ; ) OG
2336 4
AG
VớiđápánB:
2
33 11 15609
( ;0;0);B(0;66;0);C(0;0;66) ( ;22;22) OG
4416
AG
VớiđápánC:
2
18 18
(9;0;0);B(0;18;0);C(0;0;18) (3; ; ) OG 81
33
AG
VớiđápánD:
2
( 12;0; 0); B(0;6;0);C(0; 0;6) ( 4; 2; 2) OG 24AG
Cách2 :
Gọi
;0;0 , 0; ; 0 , 0;0;
A
aBbCc
với
,, 0abc
.Theođềbàitacó :
811
1
abc
.Cầntìmgiátrị
nhỏnhấtcủa
222
abc
.
Tacó
22
222 222
411 .2 .1 .1 6. 2abc a b c abc abc
Mặtkhác
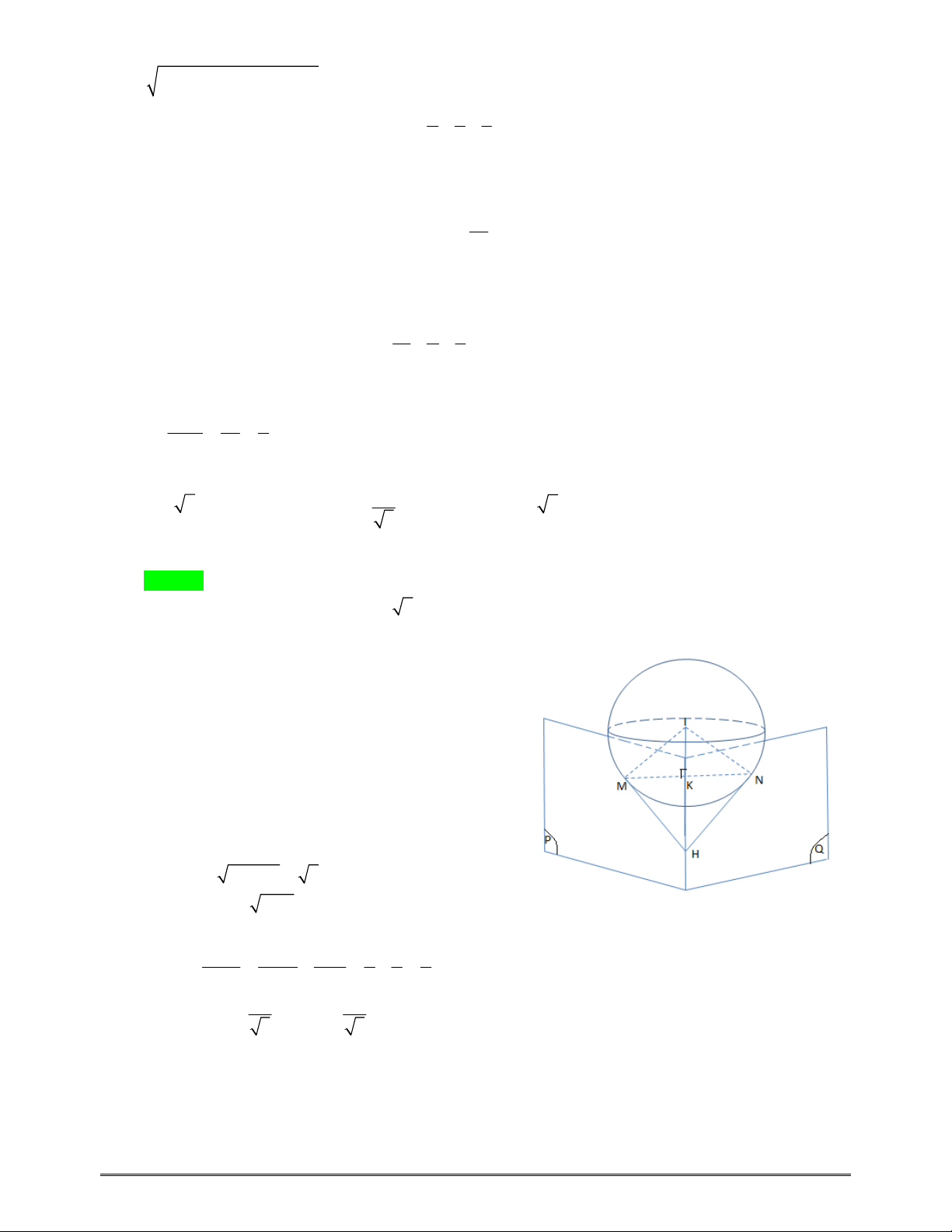
222
2
411 .2 .1 .1
811
2
411 36
abc a b c
abc
abc
Suyra
2223
6abc
.Dấu
'' ''
xảyrakhi
2
22
22.
4
a
bc abc
Vậy
222
abc
đạtgiátrịnhỏnhấtbằng216khi
12, 6abc
.
Vậyphươngtrìnhmặtphẳnglà
:
1
1266
x
yz
hay
22120xyz
.
Câu12: CHUYÊN PHAN BỘI CHÂU Trong không gian với hệ tọa độ
Ox
y
z
, cho đường thẳng
2
:
214
x
yz
d
vàmặtcầu
222
:1 2 12 Sx y z
. Hai mặt phẳng
P
và
Q
chứa
d
vàtiếpxúcvới
S
.Gọi
,
M
N
làtiếpđiểm.Tínhđộdàiđoạnthẳng
.
M
N
A.
22.
B.
4
.
3
C. 6. D.
4.
Hướngdẫngiải
ChọnB.
Mặtcầu
S cótâm
1; 2;1 , 2IR
Đườngthẳng
d
nhận
2; 1; 4
u
làmvectơchỉ
phương
GọiHlàhìnhchiếucủaIlênđườngthẳngd.
22;;4
H
dHt tt
Lạicó:
.0 21; 2;41.2;1;40
IH u t t t
22 1 2 44 1 0 0tt t t
Suyratọađộđiểm
2;0;0H
.
Vậy
141 6IH
Suyra:
62 2HM
Gọi
K
làhìnhchiếuvuônggóccủa
M
lênđườngthẳng
H
I
.
Suyra:
222
111113
424
MK MH MI
.
Suyra:
24
33
MK MN
.
Câu13: CHUYÊNPHANBỘICHÂUTrongkhônggianvớihệtọađộ
Oxyz
,chođiểm
1; 2; 1M
.Mặt
phẳng
P
thayđổiđiqua
M
lầnlượtcắtcáctia
,,Ox Oy Oz
tại
,,ABC
khác
O
.Tínhgiátrị
nhỏnhấtcủathểtíchkhốitứdiện
OABC
.
A.
54.
B.
6.
C.
9.
D.
18.
Hướngdẫngiải
ChọnC.
Gọi
;0;0 , 0; ;0 , 0,0,
A
aBbCcvới
,, 0abc
.
Phươngtrìnhmặtphẳng
P
:
1
xyz
abc
.
Vì:
121
1MP
abc
.
Thểtíchkhốitứdiện
OABC
là:
1
6
OABC
Vabc
ÁpdụngbấtđẳngthứcCauchytacó:
3
121 121
3.
abc abc
Hay
3
254
13 1
abc abc
Suyra:
1
54 9
6
abc abc
Vậy:
9
OABC
V .
Câu14: THTT
–477Chohaiđườngthẳng
1
2
:1
2
x
t
dy t
zt
và
2
22
:3
x
t
dy
zt
.Mặtphẳngcáchđềuhai
đườngthẳng
1
d và
2
d cóphươngtrìnhlà
A.
5 2 12 0.xyz
B.
52120.xyz
C.
5 2 12 0.xyz
D.
52120.xyz
Hướngdẫngiải
ChọnD.
1
d
qua
2;1;0A
vàcóVTCPlà
1
1; 1; 2u
;
2
d qua
2;3;0B
vàcóVTCPlà
2
2;0;1u
.
Có
12
,1;5;2uu
;
0;2;0AB
,suyra
12
,. 10uu AB
,nên
12
;ddlàchéonhau.
Vậymặtphẳng
P
cáchđềuhaiđườngthẳng
12
,ddlàđườngthẳngsongsongvới
12
,ddvàđi
quatrungđiểm
2;2;0I
củađoạnthẳng
AB
.
Vậyphươngtrìnhmặtphẳng
P
cầnlậplà:
52120xyz
.
Câu15: THTT
–477Cho hai điểm
3; 3;1 , 0; 2;1AB
và mặt phẳng
:70xyz
. Đường
thẳng
d
nằmtrên
saochomọiđiểmcủa
d
cáchđều2điểm
, AB
cóphươngtrìnhlà
A.
73.
2
xt
yt
zt
B.
73.
2
xt
yt
zt
C.
73.
2
xt
yt
zt
D.
2
73.
xt
yt
zt
Hướngdẫngiải
A
B
M
P

ChọnA.
Mọiđiểmtrên
d
cáchđềuhaiđiểm ,ABnên
d
nằmtrênmặtphẳngtrungtrựccủađoạn
AB
.
Có
3; 1; 0AB
vàtrungđiểm AB là
35
;;1
22
I
nênmặtphẳngtrungtrựccủa AB là:
35
30370
22
xy xy
.
Mặtkhác
d
nên
d
làgiaotuyếncủahaimặtphẳng:
370 73
70 2
xy y x
xyz z x
.
Vậyphươngtrình
:73
2
xt
dy tt
zt
.
Câu16: SỞGDHÀNỘITrongkhônggian
,Oxyz
chocácđiểm
1; 0; 0 ,A
2;0;3 ,B
0;0;1M
và
0;3;1 .N
Mặtphẳng
P
điquacácđiểm
,
M
N
saochokhoảngcáchtừđiểm
B
đến
P
gấp
hailầnkhoảngcáchtừđiểm
A
đến
.
P
Cóbaomặtphẳng
P
thỏamãnđầubài?
A.Cóvôsốmặtphẳng
.
P
B.Chỉcómộtmặtphẳng
.
P
C.Khôngcómặtphẳng
P
nào. D.Cóhaimặtphẳng
.
P
Hướngdẫngiải
ChọnA.
Giảsử
P
cóphươngtrìnhlà:
222
z0 0ax by c d a b c
Vì
0.
M
Pcd dc
Vì
30NP bcd
hay
0b
vì
0.cd
:0.Paxczc
Theobàira:
,2,dBP dAP
22 22
23
2
acc ac
ac ac
ca ac
Vậycóvôsốmặtphẳng
.
P
Câu17: SỞ GD HÀ NỘI Trong không gian
Ox
y
z
, cho điểm
13
;;0
22
M
vàmặtcầu
222
:8Sx y z
.Đườngthẳng
d
thayđổi,điquađiểm
M
,cắtmặtcầu
S
tạihaiđiểm
,
A
B
phânbiệt.Tínhdiệntíchlớnnhất
S
củatamgiác
OAB
.
A.
7.S B.
4.S
C. 27.S D.
22.S
Hướngdẫngiải
ChọnA.

Cách1:Mặtcầu
S
cótâm
0;0; 0O
vàbánkính
22R
.
Có
2
2
13
1
22
OM
nênMnằmtrongmặtcầu
KhiđódiệntíchAOBlớnnhấtkhiOMAB.Khiđó
22
227AB R OM
và
1
.7
2
AOB
SOMAB
Cách 2:gọiHlàhìnhchiếucủaOxuốngđườngthẳngd,đặt
01OH x x
Khiđó
22 2
228
A
BROH xvà
2
1
.8
2
AOB
SOHABxx
.
Khảosáthàmsố
2
8
f
xx xtrên
0;1 thuđượcgiátrịlớnnhấtcủahàmsốlà
7
Đạt
đượctại
1
x
Câu18: BẮCYÊNTHÀNHCóbaonhiêumặtphẳngđiquađiểm
(1; 9; 4)M
vàcắtcáctrụctọađộtại
cácđiểm
A
,
B
,
C
khácgốctọađộsaocho
OA OB OC
.
A.
1
. B.
2
. C.
3
. D.
4
.
Hướngdẫngiải
ChọnD.
Giảsửmặtphẳng
()
cắtcáctrụctọađộtạicácđiểmkhácgốctọađộlà
(;0;0), (0;;0), (0;0;)Aa B b C c
với
,, 0.abc
Phươngtrìnhmặtphẳng
()
códạng
1.
xyz
abc
Mặtphẳng
()
điquađiểm
(1; 9; 4)M
nên
194
1(1).
abc
Vì
OA OB OC
nên
,abc
dođóxảyra4trườnghợpsau:
TH1:
.abc
Từ
(1)
suyra
194
114,a
aaa
nênphươngtrìnhmp
()
là
14 0.xyz
TH2:
.ab c
Từ
(1)
suyra
194
16,a
aaa
nênptmp
()
là
60.xyz
TH3:
.abc
Từ
(1)
suyra
194
14,a
aaa
nênptmp
()
là
40.xyz
TH4:
.abc
Từ
(1)
có
194
112,a
aaa
nênptmp
()
là
12 0.xyz
Vậycó4mặtphẳngthỏamãn.

Câu19: BIÊN HÒA –HÀNAMTrong không gian với hệ tọa độ
Oxyz
, cho
;0; 0 , 0; ;0 , 0;0;
A
aBbCc
với
,,abc
dương.Biết
,,
A
BC
diđộngtrêncáctia
,,Ox Oy Oz
saocho
2abc
.Biếtrằngkhi
,,abc
thayđổithìquỹtíchtâmhìnhcầungoạitiếptứdiện
OABC
thuộcmặtphẳng
P
cốđịnh.Tínhkhoảngcáchtừ
2016;0;0M
tớimặtphẳng
P
.
A.
2017
. B.
2014
3
. C.
2016
3
. D.
2015
3
.
Hướngdẫngiải
ChọnD.
Gọi
làmặtphẳngtrungtrựccủađoạn
OA
điquađiểm
;0;0
2
a
D
vàcóVTPT
;0;0 1;0;0OA a a
:0
2
a
x
.
Gọi
làmặtphẳngtrungtrựccủađoạn
OB
điquađiểm
0; ;0
2
a
E
vàcóVTPT
0; ;0 0;1;0OB a a
:0
2
a
y
.
Gọi
làmặtphẳngtrungtrựccủađoạn
OC
điquađiểm
0;0;
2
a
F
vàcóVTPT
0;0; 0;0;1OC a a
:0
2
a
z
.
Gọi
I
làtâmmặtcầungoạitiếptứdiện
OABC
;;
222
aaa
II
.
Màtheogiảthiết,
21:1
222
abc
abc I Pxyz
.
Vậy,
2016 1
2015
,
33
dM P
.
Câu20:
SỞ BÌNH PHƯỚC Trong không gian với hệ tọa độ
,Oxyz
chođiểm
;0;0 , 0; ;0 , 0;0; ,
A
aBbCc
trongđó
0a
,
0b
,
0c
và
123
7.
abc
Biếtmặtphẳng
A
BC
tiếp xúc với mặt cầu
222
72
:1 2 3 .
7
Sx y z
Thểtíchcủakhốitứdiện
OABC
là
A.
2
.
9
B.
1
.
6
C.
3
.
8
D.
5
.
6
Hướngdẫngiải
ChọnA.
Cách1:Tacó
:1.
xyz
ABC
abc
Mặtcầu
S
cótâm
1; 2; 3I
vàbánkính
72
.
7
R
Mặtphẳng
A
BC
tiếpxúcvới
222
123
1
72
;.
7
111
abc
S d I ABC R
abc
Mà
222
123 1 1 1 7
7.
2abc a b c
ÁpdụngBĐTBunhiacopskitacó
2
222 2
222 222
111 123 1117
123 7 .
2abc abc abc
Dấu
""
xảyra
123
111
2
2, 1, ,
3
123
7
abc
abc
abc
khiđó
12
.
69
OABC
V abc
Cách2:Tacó
:1,
xyz
ABC
abc
mặtcầu
S
cótâm
72
(1; 2; 3),
7
IR
.
Tacó
A
BC
tiếpxúcvớimặtcầu
S
222
123
1
72
,( )
7
111
abc
dI P R
abc
222 222
222
71
72 1117 111 7
7
72 2
111
abc abc
abc
222
1111237
2abcabc
22 2
11 1 13
10
22abc
2
1
2
3
a
b
c
12
.
69
OABC
Vabc
Cách3:GiốngCách2khiđến
222
1117
2abc
.
Đếnđâytacóthểtìma,b,cbằngbấtđẳngthứcnhưsau:

Tacó
22
2222
222 222
123 1 1 1 1 1 1 1 1 1 7
71.2.3.123
2abc a b c abc abc
Mà
222
1117
2abc
Dấu“”củaBĐTxảyra
111
123
abc
,kếthợpvớigiảthiết
123
7
abc
tađược
2a
,
1b
,
2
3
c
.Vậy:
12
.
69
OABC
Vabc
Tacó
2
1
2
3
a
b
c
12
.
69
OABC
V abc
Cách4:Mặtcầu
S
cótâm
1; 2; 3I
vàbánkính
72
.
7
R
Phươngtrìnhmặtphẳng
(): 1
x
yz
ABC
abc
.
Tacó:
123
123
777
71
abc ab c
nên
123
;;
777
M
ABC
Thaytọađộ
123
;;
777
M
vàophươngtrìnhmặtcầu
()S
tathấyđúngnên
()
M
S
.
Suyra:
()
A
BC
tiếpxúcvới
()S
thì
M
làtiếpđiểm.
Dođó:
()
A
BC
qua
123
;;
777
M
,cóVTPTlà
61218
;; 1;2;3
77 7
MI n
()
A
BC
cóphươngtrình: 2320 1 2
2
21
3
xyz
xyz a,
1b
,
2
3
c
.
Vậy
12
69
Vabc
Câu21: LƯƠNGTÂMPhươngtrìnhcủamặtphẳngnàosauđâyđiquađiểm
1; 2; 3M
vàcắtbatia
Ox
,
Oy
,
Oz
lầnlượttại
A
,
B
,
C
saochothểtíchtứdiện
OABC
nhỏnhất?
A.
632180xyz
. B.
633210xyz
.
C.
633210xyz
. D.
632180xyz
.
Hướngdẫngiải
Giảsử
(;0;0), (0;;0), (0;0;) (,, 0)Aa B b C c abc

ABC:
1
xyz
abc
1
M1;2;3thuộcABC:
123
1
abc
.
ThểtíchtứdiệnOABC:
1
6
V abc
ÁpdụngBDTCôsitacó:
3
1 2 3 6 27.6 1
131 2727
6
abc V
a b c abc abc
Tacó:Vđạtgiátrịnhỏnhất
3
1231
27 6
3
9
a
Vb
abc
c
VậyABC:
632180xyz
.ChọnD
Câu22: PHAN ĐÌNH PHÙNG
–HNTrong không gian với hệ trục tọa độ
,Oxyz
chomặtphẳng
:3 5 0Pxyz
vàhaiđiểm
1; 0; 2A
,
2; 1; 4 .B
Tìmtậphợpcácđiểm
;;
M
xyz
nằm
trênmặtphẳng
P
saochotamgiác
M
AB
códiệntíchnhỏnhất.
A.
7470
.
350
xyz
xyz
B.
74140
.
350
xyz
xyz
C.
7470
.
350
xyz
xyz
D.
37450
.
350
xyz
xyz
Hướngdẫngiải
ChọnC.
Tathấyhaiđiểm
,
A
B
nằmcùng1phíavớimặtphẳng
P
và
A
B
songsongvới
P
.Điểm
M
P
saochotamgiác
A
BM
códiệntíchnhỏnhất
.( ; )
2
ABC
A
Bd M AB
S
nhỏnhất
;dMAB
nhỏnhất,hay
,
M
PQQ
làmặt
phẳngđiqua
A
B
vàvuônggócvới
P
.
Tacó
1; 1; 2AB
,vtptcủa
P
3;1; 1
P
n
Suyravtptcủa
Q
:
,1;7;4
QP
nABn
PTTQ
:1 1 7 4 2 0Qx yz
7470xyz
Quỹtích
M
là
7470
.
350
xyz
xyz
Câu23: CHUYÊN ĐH VINH Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
2; 2;1M
,
1; 2; 3A
vàđườngthẳng
15
:
221
x
yz
d
.Tìmvéctơchỉphương u
củađườngthẳng
điqua
M
,vuônggócvớiđườngthẳng
d
đồngthờicáchđiểm
A
mộtkhoảngbénhất.
A.
2;1;6u
. B.
1; 0; 2u
. C.
3; 4; 4u
. D.
2; 2; 1u
.
Hướngdẫngiải
Đápán:B.
Gọi
P
là mặt phẳng qua
M
và vuông góc với
d
.
Phươngtrìnhcủa
22 90P: x y z
.
Gọi
H,K
lầnlượtlàhìnhchiếuvuônggóccủa
A
trên
,P
.
Tacó
321
K
;;
d( A, ) AH AK
Vậy khoảng cách từ
A
đến
bénhấtkhi
điqua
M
,K
. cóvéctơchỉphương
1; 0; 2u
Câu24: MINH HỌA L2 Trong không gian với hệ tọa độ
,Oxyz
xétcácđiểm
0;0;1A
,
;0;0Bm
,
0; ;0Cn
,
1; 1;1D
với
0; 0mn
và
1.mn
Biếtrằngkhi
m , n thayđổi,tồntạimộtmặt
cầucốđịnhtiếpxúcvớimặtphẳng
A
BC
vàđiqua
d
.Tínhbánkính
R
củamặtcầuđó?
A.
1R
. B.
2
2
R
. C.
3
2
R
. D.
3
2
R
.
Hướngdẫngiải
ChọnA.
Gọi
1; 1; 0I
làhìnhchiếuvuônggóccủa
D
lênmặtphẳng
()Oxy
Tacó:Phươngtrìnhtheođoạnchắncủamặtphẳng
()
A
BC
là:
1
xy
z
mn
Suyraphươngtrìnhtổngquátcủa
()
A
BC
là
0 nx my mnz mn
Mặtkhác
22 22
1
;1
mn
dI ABC
mnmn
vì
1mn
và
1(; .
I
DdIABC
Nêntồntạimặtcầutâm
I
làhìnhchiếuvuônggóccủa
D
lênmặtphẳng
Oxy
tiếpxúcvới
()
A
BC
vàđiqua
D
.Khiđó
1R
.
Câu25: Cho ba điểm
()( )( )
3;1 ; 0 , 0; 1 ; 0 , 0; 0; 6AB C--
. Nếu tam giác
ABC
¢¢¢
thỏamãnhệthức
0AA BB CC
¢¢¢
++=
thìcótọađộtrọngtâmlà:
A.
()
1; 0; 2 .-
B.
(
)
2; 3; 0 .-
C.
(
)
3; 2; 0 .-
D.
()
3; 2;1 .-
Hướngdẫngiải
ĐápánA
*Cáchdiễnđạtthứnhất:
GọiG,G’theothứtựlầnlượtlàtrọngtâmtamgiácABC,A’B’C’.VớimọiđiểmTtrongkhông
giancó:
()
()()( )
1: ' ' ' 0 ' ' ' 0A A B B C C TA TA TB TB TC TC++=-+-+- =
()
''' 2TA TB TC TA TB TC++= + +
d
M
H
K
A
P

Hệthức2chứngtỏ.Nếu
TGº
tứclà
0TA TB TC++=
thìtacũngcó
'''0TA TB TC++=
hay 'TGº hay1làhệthứccầnvàđủđểhaitamgiácABC,A’B’C’có
cùngtrọngtâm.
TacótọađộcủaGlà:
()
300110006
;; 1;0;2
333
G
æö
++ -+ +-
÷
ç
÷
==-
ç
÷
ç
÷
ç
èø
ĐócũnglàtọađộtrọngtâmG’của
'''ABCD
*Cáchdiễnđạtthứhai:
Tacó:
'''0AA BB CC++=
1
()()( )
'' ' '' ' '' ' 0AG GG GA BG GG GB CG GG GC++++++++=
()( )
'' '' '' 3' 0GA GB GC A G B G C G G G+++ + + + =
2
NếuG,G’theothứtựlầnlượtlàtrọngtâmtamgiácABC,A’B’C’nghĩalà
'' '' ''GA GB GC A G B G C G++= + +
thì
()
2'0'GG G G=º
Tómlại1làhệthứccầnvàđủđểhaitamgiácABC,A’B’C’cócùngtrọngtâm.
TacótọađộcủaGlà:
()
300110006
;; 1;0;2
333
G
æö
++ -+ +-
÷
ç
÷
==-
ç
÷
ç
÷
ç
èø
.Đócũnglàtọađộtrọng
tâmG’của
'''ABCD
Câu26: AN LÃOTrongkhônggianvớihệtọađộOxyz,chohaiđiểm
(2;2;1),A
1; 2; 3B
và
đườngthẳng
15
:
221
x
yz
d
.Tìmvectơchỉphương
u
củađườngthẳng
qua
A
,vuông
gócvớidđồngthờicáchđiểmBmộtkhoảngbénhất.
A.
(2;1;6)u
B.
(2;2; 1)u
C.
(25; 29; 6)u
D.
(1; 0; 2)u
Hướngdẫngiải
Cách1Tựluận
GọiPlàmặtphẳngquaAvàvuônggócvớid,B’làhìnhchiếucủaBlênP
Khiđóđườngthẳng
chínhlàđườngthẳngAB’và
B'Au
Tacó
Pd
Qua A( 2; 2;1)
P: (P):2x 2y z 9 0
VTPT n u (2;2; 1)
Gọid’làđườngthẳngquaBvàsongsongd’
x12t
d' y 2 2t
z3t

B’làgiaođiểmcủad’vàP
B'(3;2;1) u B'A (1;0;2)
ChọnD
Cách2:KhôngcầnviếtphươngtrìnhmặtphẳngPquaAvàvuônggócvớid.
Gọid’làđườngthẳngquaBvàsongsongd’
x12t
d' y 2 2t
z3t
B’
d’
B'A 2t 3; 2t 4;t 4
AB’
d
d
u.B'A 0 t 2 u B'A (1;0;2)
ChọnD
Câu27: ANLÃOTrongkhônggianvớihệtọađộOxyz,chođườngthẳng
21
:
121
x
yz
d
.Viết
phươngtrìnhmặtphẳngPchứađườngthẳngdvàcắtcáctrụcOx,OylầnlượttạiAvàBsao
chođườngthẳngABvuônggócvớid.
A.
:2540.Px y z
B.
:2550.Px y z
C.
:2 40.Px yz
D.
:2 3 0.Pxy
Hướngdẫngiải
Cách1Tựluận
ĐườngthẳngdquaM2;1;0vàcóVTCP
1; 2; 1
d
u
Tacó:AB
dvàAB
OznênABcóVTCPlà:
,2;1;0
AB d
uuk
PchứadvàABnênPđiquaM2;1;0,cóVTPTlà:
,1;2;5
dAB
nuu
:2540Px y z
ChọnA
Cách2:Dùngphươngtrìnhmặtphẳngtheođoạnchắn.
Đườngthẳngdqua2điểmM2;1;0vàN3;3;‐1
GiảsửmpPcắtOx,Oy,OzlầnlượttạiAa;0;0,B0;b;0,C0;0;c
:1
x
yz
P
abc
AB
d
.0 2
d
A
Bu a b
1
P
chứadnêndcũngđiquaM,N
21
1
ab
2,
33 1
1
ab c
3

Từ1,2,3a4,b2,c
4
5
:2540Px y z
ChọnA
Câu28: Trongkhônggianvớihệtrụctọađộ
Oxyz
,chobađiểm
3;0;0 , , , 0 , 0; 0;
M
Nmn P p
.Biết
0
13, 60MN MON
,thểtíchtứdiện
OMNP
bằng3.Giátrịcủabiểuthức
22
2
A
mnp
bằng
A.
29.
B.
27.
C.
28.
D.
30.
Hướngdẫngiải
3; 0; 0 , ; ; 0 . 3OM ON m n OM ON m
0
22
.1 1
..cos60
22
.
OM ON m
OM ON OM ON
OM ON
mn
2
2
313MN m n
Suyra
2; 2 3mn
1
, . 63 63 3 3
6
OM ON OP p V p p
Vậy
22.12329.A
Câu29: Trongkhônggianvớihệtọađộ
Oxyz
,chohìnhvuông
ABCD
,
(3;0;8)B
,
(5;4;0)D
.Biếtđỉnh
A
thuộcmặtphẳng
Oxy
vàcótọađộlànhữngsốnguyên,khiđó
CA CB
bằng:
A.
510.
B.
610.
C.
10 6.
D.
10 5.
Hướngdẫngiải
Tacótrungđiểm
BD
là
(1;2;4)I
,
12BD
vàđiểm
A
thuộcmặtphẳng
()Oxy
nên
(;;0)
A
ab
.
ABCD
làhìnhvuông
22
2
2
1
2
AB AD
A
IBD
222 2 2
222
(3) 8(5)(4)
(1)(2)436
ab a b
ab
22
42
(1)(62)20
ba
aa
1
2
a
b
hoặc
17
5
14
5
a
b
A1;2;0hoặc
17 14
;;0
55
A
loại.
Với
(1; 2; 0)A
(3;6;8)C
.
Câu30: Trongkhônggianvớihệtoạđộ
Oxyz
,cho4điểm
(2;4; 1)A
,
(1; 4; 1)B
,
(2;4;3)C
(2;2; 1)D
.
Biết
;;
M
xyz
,để
22 2 2
M
AMBMCMD
đạtgiátrịnhỏnhấtthì
x
yz
bằng
A.
7.
B.
8.
C.
9.
D.
6.
Hướngdẫngiải
Gọi
G
làtrọngtâmcủa
ABCD
tacó:
714
;;0
33
G
.
Tacó:
22 2 2 22222
4
M
AMBMCMD MGGAGBGCGD
22 2 2
GA GB GC GD
.Dấubằngxảyrakhi
M
714
;;0 7
33
Gxyz
.
Câu31: Chohìnhchóp
.SABCD
biết
2; 2;6 , 3;1;8 , 1;0;7 , 1; 2;3ABCD
.Gọi
H
làtrungđiểm
của
,CD
SH ABCD
. Để khối chóp
.SABCD
cóthểtíchbằng
27
2
đvttthìcóhaiđiểm
12
,SS
thỏamãnyêucầubàitoán.Tìmtọađộtrungđiểm
I
của
12
SS
A.
0; 1; 3I
. B.
1; 0; 3I
C.
0;1;3I
. D.
1; 0; 3 .I
Hướngdẫngiải
Tacó
133
1; 1; 2 , 1; 2; 1 ,
22
ABC
AB AC S AB AC
2; 2; 4 , 1; 1; 2 2.DC AB DC AB
ABCD
làhìnhthangvà
93
3
2
ABCD ABC
SS
Vì
.
1
.33
3
S ABCD ABCD
VSHSSH
Lạicó
H
làtrungđiểmcủa
0;1;5CD H
Gọi
; ; ;1 ;5 , 3;3;3 3 ;3 ;3S a b c SH a b c SH k AB AC k k k k
Suyra
222
33 9 9 9 1kkkk
Với
1 3;3;3 3; 2;2kSH S
Với
1 3;3;3 3;4;8kSH S
Suyra
0;1;3I
Câu32: Chođiểm
1; 7; 5I
vàđườngthẳng
16
:
213
x
yz
d
.Phươngtrìnhmặtcầucótâm
I
vàcắt
đườngthẳng
d
tạihaiđiểm
A,B
saochotamgiácdiệntíchtamgiác
IAB
bằng
26015
là:
A.
222
1 7 5 2018. xyz
B.
222
1 7 5 2017. xyz
C.
222
1 7 5 2016. xyz
D.
222
1 7 5 2019. xyz
Hướngdẫngiải
Gọi
H
làhìnhchiếucủa
1; 7; 5I
trên
d
0;0; 4H
;23 IH d I d
2.
8020
2
AIB
AIB
SIH AB
SAB
IH
2
22
2017
2
AB
RIH
Vậyphươngtrìnhmặtcầulà:
222
1 7 5 2017. xyz
LựachọnđápánB.
Câu33: Chođiểm
(0;0;3)I
vàđườngthẳng
1
:2.
2
x
t
dy t
zt
Phươngtrìnhmặtcầu
S
cótâm
I
vàcắt
đườngthẳng
d
tạihaiđiểm
,
A
B
saochotamgiác
I
AB
vuônglà:
A.
2
22
3
3.
2
xy z
B.
2
22
8
3.
3
xy z
C.
2
22
2
3.
3
xy z
D.
2
22
4
3.
3
xy z
Hướngdẫngiải
Gọi
1;2;2
H
tt t d
làhìnhchiếuvuônggóccủa
I
lênđườngthẳng
d
1;2;1
IH t t t
Tacóvectơchỉphươngcủa
d
:
1; 2;1
d
a
và
I
Hd
1227
.0 141 0 260 ;;
3333
d
IH a t t t t t H
222
22223
333 3
IH
Vìtamgiác
I
AB
vuôngtại
I
và
I
AIBR
.Suyratamgiác
I
AB
vuôngcântại
I
,dođóbán
kính:
0
22326
cos 45 2 . 2 2.
233
RIAAB IH IH
Vậyphươngtrìnhmặtcầu
2
22
8
:3
3
Sx y z
.
LựachọnđápánB.
Câu34: Chođiểm
2;5;1A
vàmặtphẳng
():6 3 2 24 0Pxyz
,
H
làhìnhchiếuvuônggóccủa
A
trênmặtphẳng
P
.Phươngtrìnhmặtcầu
()S
códiệntích
784
vàtiếpxúcvớimặtphẳng
P
tại
H
,saochođiểmAnằmtrongmặtcầulà:
A.
222
8 8 1 196.xyz
B.
222
8 8 1 196.xyz
C.
222
16 4 7 196.xyz
D.
222
16 4 7 196.xyz
Hướngdẫngiải
Gọi
d
làđườngthẳngđiqua
A
vàvuônggócvới
P
.Suyra
26
:53
12
x
t
d
y
t
zt
Vì
H
làhìnhchiếuvuônggóccủa
A
trên
P
nên
()Hd P
.
Vì
Hd
nên
26;53;12
H
ttt
.
Mặtkhác,
()HP
nêntacó:
62 6 35 3 21 2 24 0 1 ttt t

Dođó,
4; 2;3H
.
Gọi
,IR
lầnlượtlàtâmvàbánkínhmặtcầu.
Theogiảthiếtdiệntíchmặtcầubằng
784
,suyra
2
4 784 14
RR
.
Vìmặtcầutiếpxúcvớimặtphẳng
P
tại
H
nên
()IH P I d
.
Dođótọađộđiểm
I
códạng
26;53;12
I
ttt
,với
1t
.
Theogiảthiết,tọađộđiểm
I
thỏamãn:
22 2
22 2
62 6 35 3 21 2 24
1
14
(,( )) 14
63(2)
1
3
14
22
63 214
ttt
t
dI P
t
t
AI
t
tt t
Dođó:
8;8; 1I
.
Vậyphươngtrìnhmặtcầu
222
( ) : 8 8 1 196Sx y z
.
LựachọnđápánA.
Câu35: Cho mặt phẳng
:22100Px y z
vàhaiđườngthẳng
1
21
:
11 1
x
yz
,
2
23
:
114
xyz
.Mặtcầu
S
cótâm thuộc
1
,tiếpxúcvới
2
vàmặtphẳng
P
,có
phươngtrình:
A.
222
(1)(1)(2)9 xyz
hoặc
222
11 7 5 81
.
2224
xyz
B.
22 2
(1)(1)(2)9 xyz
hoặc
222
11 7 5 81
.
2224
xyz
C.
222
(1)(1)(2)9. xyz
D.
222
(1)(1)(2)3. xyz
Hướngdẫngiải
1
2
:
1
x
t
yt
zt
;
2
điquađiểm
(2;0; 3)A
vàcóvectơchỉphương
2
(1;1; 4)
a
.
Giảsử
1
(2 ; ;1 )Ittt
làtâmvà R làbánkínhcủamặtcầu
S
.
Tacó:
(;;4 )
A
Itt t
2
,(54;45;0)
A
Ia t t
2
2
2
,
54
;
3
AI a
t
dI
a
2 2 2(1 ) 10
10
(,( ))
3
144
tt t
t
dI P
.
S
tiếpxúcvới
2
và
P
2
(, ) (,( ))dI dI P
54 10tt
7
2
1
t
t
.
Với
7
2
t
11 7 5
;;
22 2
I
,
9
2
R
222
11 7 5 81
:
2224
Sx y z
.

Với
1t
(1; 1; 2), 3IR
222
:( 1) ( 1) ( 2) 9 Sx y z
.
LựachọnđápánA.
Câu36: Trongkhônggianvớihệtoạđộ
Oxyz
,cho
:4260Px y z
,
:2460Qx y z
.Lập
phươngtrìnhmặtphẳng
chứagiaotuyếncủa
,
P
Q
vàcắtcáctrụctọađộtạicácđiểm
,,
A
BC
saochohìnhchóp .O ABC làhìnhchópđều.
A.
60xyz
. B.
60xyz
. C.
60xyz
. D.
30xyz
.
Hướngdẫngiải
Chọn
6;0;0 , 2; 2; 2MN
thuộcgiaotuyếncủa
,
P
Q
Gọi
;0;0 , 0; ;0 , 0;0;
A
aBbCc
lầnlượtlàgiaođiểmcủa
vớicáctrục
,,Ox Oy Oz
:1,,0
xyz
abc
abc
chứa
,
M
N
6
1
222
1
a
abc
Hìnhchóp
.O ABC
làhìnhchópđều
OA OB OC a b c
Vâyphươngtrình
60xyz
.
Câu37: Trong không gian với hệ trục toạ độ
Oxyz
,cho tứ diện
A
BCD
cóđiểm
1; 1; 1 , 2; 0; 2AB
,
1; 1; 0 , 0; 3; 4CD
.Trêncáccạnh
,,
A
BACAD
lầnlượtlấycácđiểm
', ', '
B
CD
thỏa :
4
'''
AB AC AD
A
BACAD
.Viếtphươngtrìnhmặtphẳng
'''BCD
biếttứdiện
'''
A
BCD
cóthể
tíchnhỏnhất?
A.
16 40 44 39 0xyz
. B.
16 40 44 39 0xyz
.
C.
16 40 44 39 0xyz
. D.
16 40 44 39 0xyz
.
Hướngdẫngiải
Ápdụngbấtđẳngthức
A
MGM
tacó:
3
..
43
''' '.'.'
A
BACAD ABACAD
A
BACAD ABACAD
'. '. ' 27
.. 64
AB AC AD
A
BACAD
'''
'. '. ' 27
.. 64
AB C D
ABCD
V
AB AC AD
VABACAD
'''
27
64
A
B C D ABCD
VV
Để
'''
A
BCD
V
nhỏnhấtkhivàchỉkhi
'''3
4
AB AC AD
A
BACAD
3 717
'';;
4 444
AB AB B
Lúcđómặtphẳng
'''BCD
songsongvớimặtphẳng
BCD
vàđiqua
717
';;
444
B
' ' ' :16 40 44 39 0BCD x y z
.
Câu38: Trongkhônggianvớihệtoạđộ
Oxyz
,chomặtphẳng
()
a
điquađiểm
(
)
1; 2; 3M
vàcắtcáctrục
Ox,Oy,Oz
lầnlượttại
A
,
B
,
Ckhácgốctoạđộ Osaocho
M
làtrựctâmtamgiác
A
BC .Mặt
phẳng
()
a
cóphươngtrìnhlà:
A.
23140xyz+ +-=
. B.
10
123
xyz
++-=
.
C.
32 100xyz++-=
. D.
23140xyz+ ++=
.
Hướngdẫngiải
Cách1:
Gọi
H
làhìnhchiếuvuônggóccủa
C
trên
A
B
,
K
làhìnhchiếuvuônggóc
B
trên
A
C
.
M
làtrựctâmcủatamgiác
A
BC khivàchỉkhi
M
BK CH=Ç
Tacó:
()
(1)
AB CH
AB COH AB OM
AB CO
ü
^
ï
ï
^ ^
ý
ï
^
ï
þ
1
Chứngminhtươngtự,tacó:
A
COM^
2.
Từ1và2,tacó:
()
OM ABC^
Tacó:
(
)
1; 2; 3OM
.
Mặt phẳng
()
a
đi qua điểm
(
)
1; 2; 3M
và có một
VTPT
là
(
)
1; 2; 3OM
nêncóphươngtrìnhlà:
()( )()
12 23 3 0 2 3140xyz xyz-+ -+ -=+ +-=
.
Cách2:
Do
CBA ,,
lầnlượtthuộccáctrục
OzOyOx ,,
nên
( ;0;0), (0; ;0), (0;0; )
A
aBbCc
,, 0abc
.
Phươngtrìnhđoạnchắncủamặtphẳng
)(ABC
là: 1
xyz
abc
.
Do
M
làtrựctâmtamgiác
ABC
nên
.0
.0
()
AM BC
BM AC
M
ABC
.Giảihệđiềukiệntrêntađược
,,abc
Vậyphươngtrìnhmặtphẳng:
23140xyz
.
Câu39: Trongkhônggianvớihệtoạđộ
Oxyz
,chođiểm
1; 1;1N
.Viếtphươngtrìnhmặtphẳng
P
cắtcáctrục
,,Ox Oy Oz
lầnlượttại
,,
A
BC
khôngtrùngvớigốctọađộ
O
saocho
N
làtâm
đườngtrònngoạitiếptamgiác
A
BC
A.
:30Pxyz
. B.
:10Pxyz
.
C.
:10Pxyz
. D.
:2 40Px yz
.
M
K
H
O
z
y
x
C
B
A
Hướngdẫngiải
Gọi
;0;0 , 0; ;0 , 0;0;
A
aBbCc
lầnlượtlàgiaođiểmcủa
P
vớicáctrục
,,Ox Oy Oz
:1,,0
xyz
P abc
abc
Tacó:
111
1
11 3 30
11
NP
abc
NA NB a b a b c x y z
NA NC a c
Câu40: Trong không gian với hệ toạ độ
Oxyz
,chohaiđườngthẳng
12
,dd
lần lượt có phương trình
1
223
:
213
x
yz
d
,
2
121
:
214
x
yz
d
.Phươngtrìnhmặtphẳng
cáchđềuhai
đườngthẳng
12
,dd
là:
A.
7240xyz
. B.
72430xyz
.
C.
2330xy z
. D.
14 4 8 3 0xyz
.
Hướngdẫngiải
Tacó
1
d
điqua
2; 2;3A
vàcó
1
2;1;3
d
u
,
2
d
điqua
1; 2; 1B
vàcó
2
2; 1; 4
d
u
12
1;1; 2 ; ; 7; 2; 4
dd
AB u u
;
12
;10
dd
uu AB
nên
12
,dd
chéonhau.
Do
cáchđều
12
,dd
nên
songsongvới
12
,dd
12
;7;2;4
dd
nuu
códạng
724 0xyzd
Theogiảthiếtthì
,,dA dB
21
3
2
69 69
dd
d
:14 4 8 3 0xyz
Câu41: Trong không gian với hệ tọa độ
,Oxyz
gọi
d
đi qua
3; 1;1A
, nằm trong mặt phẳng
:50Pxyz
, đồng thời tạo với
2
:
122
xy
z
mộtgóc
0
45
.Phươngtrìnhđường
thẳng
d
là
A.
37
18.
115
x
t
yt
zt
B.
3
1.
1
x
t
yt
z
C.
37
18.
115
x
t
yt
zt
D.
3
1
1
x
t
yt
z
và
37
18.
115
x
t
yt
zt
Hướngdẫngiải
cóvectơchỉphương
1; 2; 2a
d
cóvectơchỉphương
;;
d
aabc
P
cóvectơpháptuyến
1; 1;1
P
n
00
222
2
222
; 1
,45cos,cos45
22
2
2
3
2 2 2 9 ; 2
dP
dPan bac
dd
abc
abc
abc abc
Từ
1
và
2
,tacó:
2
0
14 30 0
15 7 0
c
cac
ac
Với
0c
,chọn
1ab
,phươngtrìnhđườngthẳng
d
là
3
1
1
x
t
yt
z
Với
15 7 0ac
,chọn
715;8acb
,phươngtrìnhđườngthẳng
d
là
37
18
115
x
t
yt
zt
Câu42: Trong không gian với hệ tọa độ
,Oxyz
gọi
d
điquađiểm
1; 1; 2A
, song song với
:2 3 0Pxyz
,đồngthờitạovớiđườngthẳng
11
:
122
x
yz
mộtgóclớnnhất.
Phươngtrìnhđườngthẳng
d
là.
A.
112
.
157
xyz
B.
112
.
457
xyz
C.
112
.
457
xyz
D.
112
.
157
xyz
Hướngdẫngiải
cóvectơchỉphương
1; 2; 2a
d
cóvectơchỉphương
;;
d
aabc
P
cóvectơpháptuyến
2; 1; 1
P
n
Vì
//dP
nên
.02 0 2
dP dP
a n an abc c ab
2
22
22
54
54
1
cos ,
35 4 2
35 4 2
ab
ab
d
aabb
aabb
Đặt
a
t
b
,tacó:
2
2
54
1
cos ,
35 4 2
t
d
tt

Xéthàmsố
2
2
54
542
t
ft
tt
,tasuyrađược:
153
max
53
ft f
Dođó:
53 1 1
max cos ,
27 5 5
a
dt
b
Chọn
15,7abc
Vậyphươngtrìnhđườngthẳng
d
là
112
157
xyz
Câu43: Trongkhônggianvớihệtọađộ
,Oxyz
gọi
d
điqua
1; 0; 1A
,cắt
1
122
:
21 1
xyz
,
saochogócgiữa
d
và
2
323
:
12 2
xyz
lànhỏnhất.Phươngtrìnhđườngthẳng
d
là
A.
11
.
22 1
xyz
B.
11
.
45 2
xyz
C.
11
.
452
xyz
D.
11
.
221
xyz
Hướngdẫngiải
Gọi
1
12;2 ;2
M
dMttt
d
cóvectơchỉphương
22;2;1
d
aAM t t t
2
cóvectơchỉphương
2
1; 2; 2a
2
2
2
2
cos ;
36 14 9
t
d
tt
Xéthàmsố
2
2
6149
t
ft
tt
,tasuyrađược
min 0 0 0
f
tf t
Dođó
min cos , 0 0 2;2 1dtAM
Vậyphươngtrìnhđườngthẳng
d
là
11
22 1
xy
z
Câu44: Trong không gian với hệ tọa độ
,Oxyz
chohaiđườngthẳng
1
12
:
21 1
xyz
d
và
2
122
:
13 2
xyz
d
.Gọi làđườngthẳngsongsongvới
:70Pxyz
vàcắt
12
, dd
lầnlượttạihaiđiểm
,
A
B
saocho AB ngắnnhất.Phươngtrìnhcủađườngthẳnglà.
A.
12
5.
9
x
t
y
zt
B.
6
5
.
2
9
2
x
t
y
zt
C.
6
5
.
2
9
2
x
yt
zt
D.
62
5
.
2
9
2
x
t
yt
zt
Hướngdẫngiải
1
2
12;;2
1;23;22
Ad A aa a
Bd B b b b
cóvectơchỉphương
2;3 2; 2 4AB b a b a b a

P
cóvectơpháptuyến
1;1; 1
P
n
Vì
//
P
nên
.0 1
PP
A
Bn ABn ba
.Khiđó
1; 2 5; 6
A
Ba a a
222
2
2
1256
6 30 62
54972
6 ;
222
A
Ba a a
aa
aa
Dấu
"" xảyrakhi
559 77
6; ; , ;0;
222 22
aA AB
Đườngthẳng
điquađiểm
59
6; ;
22
A
vàvectơchỉphương
1; 0; 1
d
u
Vậyphươngtrìnhcủa
là
6
5
2
9
2
x
t
y
zt
Câu45: Trong không gian với hệ tọa độ
,Oxyz
chohaiđườngthẳng
1
12
:
211
xy z
d
và
2
12
:1
3
x
t
d
y
t
z
. Phương trình đường thẳng vuông góc với
:7 4 0Pxyz
vàcắthai
đườngthẳng
12
, dd
là:
A.
74
.
211
xyz
B.
21
.
71 4
xyz
C.
21
.
714
xyz
D.
21
.
714
xyz
Hướngdẫngiải
Gọi
d
làđườngthẳngcầntìm
Gọi
12
,
A
ddBdd
1
2
2;1 ;2
12;1 ;3
221; ; 5
Ad Aa a a
Bd B b b
AB a b a b a
P
cóvectơpháptuyến
7;1; 4
P
n

,
p
dP ABn
cùngphương
cómộtsố
k
thỏa
p
A
Bkn
2217 2271 1
02
54 4 5 1
ab k abk a
abk abk b
ak ak k
d
điquađiểm
2;0; 1A
vàcóvectơchỉphương
7;1 4
dP
an
Vậyphươngtrìnhcủa
d
là
21
71 4
xy
z
Câu46: Trong không gian với hệ tọa độ
,Oxyz
chohaiđườngthẳng
1
121
:
312
xy
z
và
2
11
:
123
xy
z
.Phươngtrìnhđườngthẳngsongsongvới
3
:1
4
x
d
y
t
zt
vàcắthaiđường
thẳng
12
;
là:
A.
2
3.
3
x
y
t
zt
B.
2
3.
3
x
y
t
zt
C.
2
3.
3
x
y
t
zt
D.
2
3.
3
x
y
t
zt
Hướngdẫngiải
Gọi
làđườngthẳngcầntìm
Gọi
12
,AB
1
2
13;2 ;12
1;2;13
32;22;232
AAaaa
BBbbb
AB a b a b a b
d
cóvectơchỉphương
0;1;1
d
a
// ,
d
dABa
cùngphương
cómộtsố
k
thỏa
d
A
Bka
320 3 2 1
22 2 2 1
232 23 2 1
ab ab a
ab k abk b
ab k abk k
Tacó
2;3;3 ; 2; 2;2AB
điquađiểm
2;3;3A
vàcóvectơchỉphương
0; 1; 1AB
Vậyphươngtrìnhcủa
là
2
3
3
x
y
t
zt

Câu47: Trongkhônggianvớihệtọađộ
,Oxyz
chođườngthẳng
12 9 1
:,
431
xyz
d
vàmặtthẳng
:3 5 2 0Pxyz
.Gọi
'd
làhìnhchiếucủa
d
lên
.P
Phươngtrìnhthamsốcủa
'd
là
A.
62
25 .
261
x
t
yt
zt
B.
62
25 .
261
xt
yt
zt
C.
62
25 .
261
xt
yt
zt
D.
62
25 .
261
xt
yt
zt
Hướngdẫngiải
Cách1:
Gọi
A
dP
12 4 ;9 3 ;1
30;0;2
A
dA a aa
AP a A
d
điquađiểm
12;9;1B
Gọi
H
làhìnhchiếucủa
B
lên
P
P
cóvectơpháptuyến
3; 5; 1
P
n
BH điqua
12;9;1B
vàcóvectơchỉphương
3; 5; 1
BH P
an
12 3
:95
1
12 3 ;9 5 ;1
78 186 15 113
;;
35 35 7 35
186 15 183
;;
35 7 35
xt
BH y t
zt
HBH H t t t
HP t H
AH
'd
điqua
0;0; 2A
vàcóvectơchỉphương
'
62; 25;61
d
a
Vậyphươngtrìnhthamsốcủa
'd
là
62
25
261
xt
yt
zt
Cách2:
Gọi
Q
qua
d
vàvuônggócvới
P
d
điquađiểm
12;9;1B
vàcóvectơchỉphương
4;3;1
d
a
P
cóvectơpháptuyến
3; 5; 1
P
n
Q
qua
12;9;1B
cóvectơpháptuyến
,8;7;11
QdP
nan
:8 7 11 22 0Qxy z

'd
làgiaotuyếncủa
Q
và
P
Tìmmộtđiểmthuộc
'd
,bằngcáchcho
0y
Tacóhệ
32 0
0;0; 2 '
81122 2
xz x
M
d
xz y
'd
điquađiểm
0;0; 2M
vàcóvectơchỉphương
;62;25;61
dPQ
ann
Vậyphươngtrìnhthamsốcủa
'd
là
62
25
261
xt
yt
zt
Câu48: Trongkhônggianvớihệtọađộ
,Oxyz
chođườngthẳng
12
:24
3
x
t
d
y
t
zt
.Hìnhchiếusongsong
của
d
lênmặtphẳng
Oxz
theophương
162
:
111
xyz
cóphươngtrìnhlà:
A.
32
0.
14
x
t
y
zt
B.
3
0.
12
x
t
y
zt
C.
12
0.
54
x
t
y
zt
D.
32
0.
1
x
t
y
zt
Hướngdẫngiải
Giaođiểmcủadvàmặtphẳng
Oxz
là:
0
(5;0;5)M
.
Trên
12
:24
3
x
t
d
y
t
zt
chọn
M
bấtkỳkhôngtrùngvới
0
(5;0;5)M
;vídụ:
(1; 2; 3)M
.Gọi
A
là
hìnhchiếusongsongcủa
M
lênmặtphẳng
Oxz
theophương
162
:
111
xyz
.
/Lậpphươngtrình
d’
điqua
M
vàsongsonghoặctrùngvới
162
:
111
xyz
.
/ĐiểmAchínhlàgiaođiểmcủa
d’
và
Oxz
/Tatìmđược
(3;0;1)A
Hình chiếu song song của
12
:24
3
x
t
dy t
zt
lênmặtphẳng
Oxz
theo phương
162
:
111
xyz
làđườngthẳngđiqua
0
(5;0;5)M
và (3;0;1)A .
Vậyphươngtrìnhlà:
3
0
12
x
t
y
zt

Câu49: Trong không gian
Oxyz
, cho hai điểm
3; 0; 2A
,
3; 0; 2B
vàmặtcầu
222
(2)(1)25xy z
.Phươngtrìnhmặtphẳng
điquahaiđiểm
A
,
B
vàcắtmặtcầu
S
theomộtđườngtrònbánkínhnhỏnhấtlà:
A.
4 5170xyz
. B.
3 2 7 0xyz
.
C.
4 5130xyz
. D.
3 2 – 1 1 0xyz
.
Hướngdẫngiải
Mặtcầu
S
cótâm
0; 2;1I
,bánkính 5R .Do 17 RIA nên
A
B luôncắt
S
.Dođó
()
luôncắt
S
theođườngtròn
C
cóbánkính
2
2
,rRdI
.Đềbánkính r nhỏ
nhất
,dI P
lớnnhất.
Mặtphẳng
điquahaiđiểm
A
,
B
vàvuônggócvớimp
A
BC
.
Ta có
AB (1;1;1)
, AC (2;3;2)
suyra
A
BC
cóvéctơpháptuyến
,(1;4;5)nABAC
αcóvéctơpháptuyến
,(96;3)3(3;2;1)nnAB
Phươngtrình
: 3 – 2 2 –1 1 – 3 0 3 2 –11 0xyz xyz
.
Câu50: Trongkhônggian
Oxyz
,chođiểm
3; 3; 3A
thuộcmặtphẳng
2–2 1:50xyz
vàmặt
cầu
222
:(x2)(y3)(z5)100S
.Đườngthẳng quaA,nằmtrênmặtphẳng
cắt
()S
tại
A
,
B
.Đểđộdài
AB
lớnnhấtthìphươngtrìnhđườngthẳng
là:
A.
33 3
146
xyz
. B.
33 3
16 11 10
xyz
.
C.
35
3
38
x
t
y
zt
. D.
33 3
11 3
xyz
.
Hướngdẫngiải
Mặtcầu
S
cótâm
2;3;5I
,bánkính
10R
.Do
(I,( )) Rd
nên luôncắt
S
tại
A
,
B
.
Khiđó
2
2
(I, )AB R d
.Dođó,
A
B lớnnhấtthì
,dI
nhỏnhấtnên qua H ,với H
làhìnhchiếuvuônggóccủaIlên
.Phươngtrình
x22t
y3
5
:2
zt
BtH
() 22 2 23–2 5 15 0Httt
2; 7;t2 3H
.

Dovậy
AH (1; 4;6)
làvéctơchỉphươngcủa
.Phươngtrìnhcủa
33 3
146
xyz
Câu51: Trong không gian
Oxyz
, cho mặt phẳng
22 90xyz
vàmặtcầu
222
():( 3) ( 2) ( 1) 100Sx y z
.Tọađộđiểm
M
nằmtrênmặtcầu
()S
saochokhoảng
cáchtừđiểm
M
đếnmặtphẳng
()
P
đạtgiátrịnhỏnhấtlà:
A.
11 14 13
;;
333
M
. B.
29 26 7
;;
333
M
.
C.
29 26 7
;;
33 3
M
. D.
11 14 13
;;
33 3
M
.
Hướngdẫngiải
Mặtcầu
()S
cótâm
(3; 2;1)I
.
Khoảngcáchtừ
I
đếnmặtphẳng
()
P
:
(;( )) 6dI P R
nên
()
P
cắt
()S
.
Khoảngcáchtừ
M
thuộc
()S
đến
()
P
lớnnhất
()
M
d
điqua
I
vàvuônggócvới
()
P
Phươngtrình
32
(): 2 2
1
x
t
dy t
zt
.
Tacó:
() (3 2;2 2;1 )
M
dM t tt
Mà:
()
M
S
1
2
10 29 26 7
;;
3333
10 11 14 13
;;
3333
tM
tM
Thửlạitathấy:
12
(,()) (,())dM P dM P
nên
11 14 13
;;
333
M
thỏayêucầubàitoán
Câu52: Trongkhônggian
Oxyz
,chohìnhhộpchữnhật
.
A
BCD A B C D
cóđiểm
A
trùngvớigốccủa
hệtrụctọađộ,
(;0;0)Ba
,
(0; ;0)
D
a
,
(0;0; )
A
b
(0,0)ab
.Gọi
M
làtrungđiểmcủacạnh
CC
.
Giátrịcủatỉsố
a
b
đểhaimặtphẳng
()
A
BD
và
M
BD
vuônggócvớinhaulà:
A.
1
3
. B.
1
2
. C. 1 . D.1.
Hướngdẫngiải
Tacó
;;0 ' ;; ;;
2
b
AB DC C aa C aab M aa
Cách1.

Tacó 0; ;
2
b
MB a
;
;;0
B
Daa
và
';0;
A
Ba b
Tacó
2
;;;
22
ab ab
uMBBD a
và
222
;;;'BD A aBaa
Chọn
1;1;1v
làVTPTcủa
'
A
BD
2
'.001
22
ab ab a
ABD MBD uv a a b
b
Cách2
.
'' '
A
BAD AX BD
AB AD BC CD a
M
BMD MX BD
với
X
làtrungđiểm
B
D
'; ';
A
BD MBD A X MX
;;0
22
aa
X
làtrungđiểm
B
D
';;
22
aa
A
Xb
;;
222
aab
MX
''
A
BD MBD A X MX
'. 0AXMX
22
2
0
222
aab
1
a
b
Câu53: Trong không gian
Oxyz
, cho mặt phẳng
(): 2 2 4 0Px y z
vàmặtcầu
222
(): 2 2 2 1 0.Sx y z x y z
Giátrịcủađiểm
M
trên
S
saocho
,dM P
đạtGTNN
là:
A.
1; 1; 3
. B.
577
;;
333
.
C.
111
;;
333
. D.
1; 2; 1
.
Hướngdẫngiải
Tacó:
(,())3 2 ()() .dM P R P S
Đườngthẳng
d
điqua
I
vàvuônggócvới
P
cópt:
1
12, .
12
xt
ytt
zt
Tọađộgiaođiểmcủa
d
và
S
là:
577
;;
333
A
,
111
;;
333
B
Tacó:
(,()) 5 (,()) 1.dA P dB P
( ,( )) ( ,( )) ( ,( )).dA P dM P dB P
Vậy:
min
(,()) 1 .dM P M B
Câu54: Trong không gian với hệ trục toạ độ
Oxyz,
chođiểm
10;2;1A
vàđườngthẳng
11
:
213
x
yz
d
.Gọi
P
làmặtphẳngđiquađiểm
A
,songsongvớiđườngthẳng
d
sao
chokhoảngcáchgiữa
d
và
P
lớnnhất.Khoảngcáchtừđiểm
1; 2; 3M
đếnmp
P
là
A.
97 3
.
15
B.
76 790
.
790
C.
213
.
13
D.
329
.
29
Hướngdẫngiải
P
làmặtphẳngđiquađiểm
A
vàsongsongvới
đườngthẳng
d
nên
P
chứađườngthẳng
d
đi
quađiểm
A
vàsongsongvớiđườngthẳng
d
.
Gọi
H làhìnhchiếucủa
A
trên
d
, K làhình
chiếucủa
H
trên
P
.
Tacó
, dd P HK AH
A
H
khôngđổi
GTLNcủa
(,())dd P
là
A
H
, dd P
lớnnhấtkhi
A
H vuônggócvới
P
.
Khiđó,nếugọi
Q
làmặtphẳngchứa
A
và
d
thì
P
vuônggócvới
Q
.
,98;14;70
97 3
:7 5 77 0 , .
15
PdQ
nun
Pxyz dMP
Câu55: Trong không gian với hệ trục toạ độ
,Oxyz
chođiểm
2;5;3A
và đường thẳng
12
:
212
xyz
d
.Gọi
P
làmặtphẳngchứađườngthẳng
d
saochokhoảngcáchtừ
A
đến
P
lớnnhất.Tínhkhoảngcáchtừđiểm
1; 2; 1M
đếnmặtphẳng
P
.
A.
11 18
.
18
B.32. C.
11
.
18
D.
4
.
3
Hướngdẫngiải
d'
d
K
H
A
P
d
H
K
A
P

Gọi
H
làhìnhchiếucủa
A
trên
d
;
K
làhìnhchiếucủa
A
trên
P
.
Tacó
, dAP AK AH
Khôngđổi
GTLNcủa
(,())dd P
là
A
H
⟹
, dAP
lớnnhấtkhi
K
H
.
Tacó
3;1; 4H
,
P
qua
H
và
A
H
:4 30Px yz
Vậy
11 18
,
18
dM P .
Câu56: Trongkhônggianvớihệtrụctoạđộ
,Oxyz
chomặtphẳng
:20Pxyz
vàhaiđường
thẳng
1
:
22
x
t
dyt
zt
;
3
': 1 .
12
x
t
dy t
zt
Biếtrằngcó2đườngthẳngcócácđặcđiểm:songsongvới
P
;cắt
, dd
vàtạovới d góc
O
30 .
Tínhcosingóctạobởihaiđườngthẳngđó.
A.
1
.
5
B.
1
.
2
C.
2
.
3
D.
1
.
2
Hướngdẫngiải
Gọi
làđườngthẳngcầntìm,
P
n
làVTPTcủamặtphẳng
P
.
Gọi
1;;22
M
tt t
làgiaođiểmcủa
và
d
; làgiaođiểmcủa và
Tacó:
Tacó
Vậy,có2đườngthẳngthoảmãnlà .
Khiđó,
Câu57: Trongkhônggianvớihệtrụctoạđộ cho3điểm .Gọi
làmặtphẳngđiqua saochotổngkhoảngcáchtừ và đến lớnnhấtbiếtrằng
khôngcắtđoạn .Khiđó,điểmnàosauđâythuộcmặtphẳng ?
A. B. C. D..
Hướngdẫngiải
3;1;12
M
tt t
'd
'2 ;1 ; 1 2 2
M
Mtttt tt
M
M
//
24;1;32
P
MP
P
tMMttt
MM n
O
2
4
69
3
cos30 cos ,
1
2
36 108 156
d
t
t
MM u
t
tt
12
5
:4;: 1
10
x
xt
yt y
ztzt
12
1
cos , .
2
,Oxyz
1; 0; 1 ; 3; 2; 0 ; 1; 2; 2AB C
P
A
B
C
P
P
BC
P
2; 0; 3.G
3; 0; 2 .F
1;3;1.E
0;3;1H
Gọi làtrungđiểmđoạn ;cácđiểm lần
lượtlàhìnhchiếucủa trên .
Tacótứgiác làhìnhthangvà làđường
trungbình.
Mà với khôngđổi
Dovậy, lớnnhấtkhi
điqua vàvuônggóc với
Câu58: Trongkhônggianvớihệtrụctoạđộ chocácđiểm trongđó
dương và mặt phẳng . Biết rằng vuông góc với và
,mệnhđềnàosauđâyđúng?
A. B.C.D.
Hướngdẫngiải
Tacóphươngtrìnhmp là
Tacó
Từ1và2 .
Câu59: Trongkhônggianvớihệtrụctoạđộ cho3điểm .
Điểm saochogiátrịcủabiểuthức nhỏnhất.
Khiđó,điểm cách mộtkhoảngbằng
A. B. C. D.
Hướngdẫngiải
Gọi .Tacó
với
nhỏnhấtkhi nhỏnhất làhìnhchiếuvuônggóccủa trên
I
BC
, ,
B
CI
, ,
B
CI
P
BCC B
II
, , 2 .dBP dCP BB CC II
II IA
I
A
, , dBP dCP
IA
P
A
I
A
2;0; 1 .I
: 2 1 0 1;3;1 .Pxz E P
,Oxyz
1;0;0 , 0; ;0 , 0;0;
A
Bb C c
,bc
:10Pyz
mp ABC
mp P
1
,
3
d O ABC
1.bc 21.bc 31.bc 33.bc
)
A
BC
1
1
xyz
bc
11
0(1)
A
BC P b c
bc
22
22
11111
,8(2)
33
11
1
dO ABC
bc
bc
1
1
2
bc bc
,Oxyz
1; 2; 3 ; 0; 1; 1 ; 1; 0; 2ABC
:20MPxyz
222
23TMA MB MC
M
:2 2 3 0Qxyz
121
.
54
24.
25
.
3
101
.
54
;;
M
xyz
222
66688631Tx y z xyz
222
2 2 1 145
6
3326
Tx y z
2
145
6
6
TMI
22 1
;;
33 2
I
T
M
I
M
I
P
A
I'
C'
B'
I
C
B
P
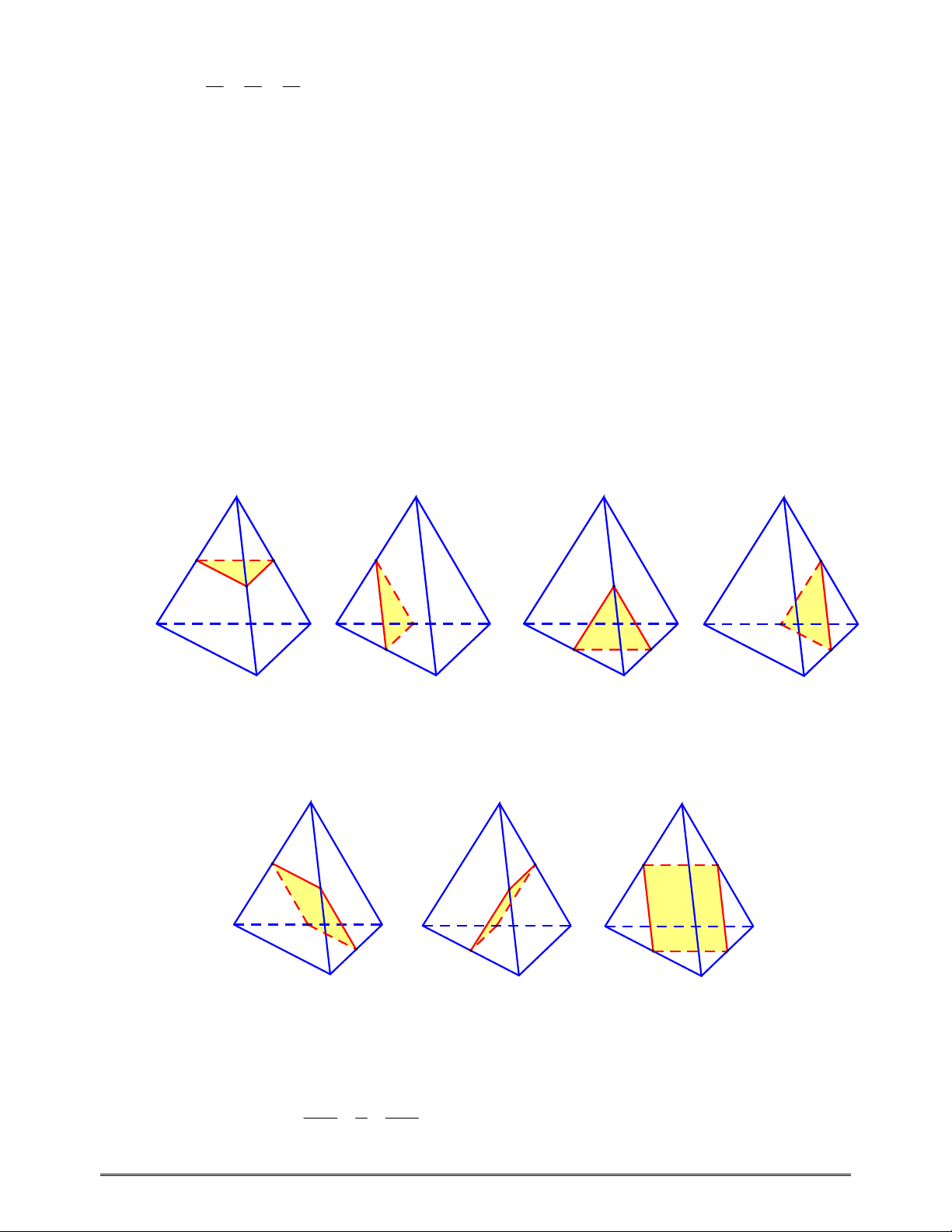
.
Câu60:
Đề minh họa L1
Trong không gian với hệ tọa độ cho bốn điểm
và .Hỏicótấtcảbaonhiêumặtphẳngcáchđều
bốnđiểmđó?
A.
1.
B.4. C.
7.
D. Có vô số mặt
phẳng.
Hướngdẫngiải
Tacó:
Suyra:
4điểm
A
,
B
,
C
,
D
khôngđồngphẳng.
Khiđó,mặtphẳngcáchđềucả4điểm
A
,
B
,
C
,
D
sẽcóhailoại:
Loại1:Có1điểmnằmkhácphíavới3điểmcònlạiđiquacáctrungđiểmcủa3cạnhchung
đỉnh có4mặtphẳngnhưthế.
Loại2:Có2điểmnằmkhácphíavới2điểmcònlạiđiquacáctrungđiểmcủa4cạnhthuộc
haicặpcạnhchéonhau có3mặtphẳngnhưthế.
Vậycótấtcả7mặtphẳngthỏamãnyêucầubàitoán.
ChọnđápánC.
Câu61:
ĐềminhhọaL1
Trongkhônggianvớihệtọađộ chođiểm vàđườngthẳng
cóphươngtrình: .Viếtphươngtrìnhđườngthẳng điqua ,vuônggóc
vàcắt .
5513
;;
18 18 9
M
,
Oxyz
1; 2;0 , 0; 1;1 ,AB
2;1; 1C
3;1; 4D
1;1;1 ; 1; 3; 1 ; 2;3;4 .AB AC AD
,4;0;4,.240AB AC AB AC AD
4
3
2
1
A
B
C
DD
C
B
A
A
B
C
D
D
C
B
A
7
6
5
A
B
C
D
D
C
B
A
A
B
C
D
,
Oxyz
1; 0; 2A
d
11
112
y
xz
A
d

B. .
D. .
Hướngdẫngiải
Do cắt nêntồntạigiaođiểmgiữachúng.Gọi .
Phương trình tham số của : . Do , suy ra
Do nên làvectơchỉphươngcủa .
Theođềbài, vuônggóc nên làvectorchỉphươngcủa .Suyra
.Giảiđược .Vậy
ChọnđápánB.
Câu62:
Đềthửnghiệm2017
Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm và
.Đườngthẳng cắtmặtphẳng tạiđiểm .Tínhtỉsố .
A. . B. . C. . D. .
Hướngdẫngiải
Tacó:
;
;
và
Tacó:
thẳnghàng
và
ChọnđápánA.
Câu63:
Đềthửnghiệm2017
Trongkhônggianvớihệtọađộ
Oxyz
,viếtphươngtrìnhmặtphẳng
songsongvàcáchđềuhaiđườngthẳng và
A. . B. .
C. . D. .
Hướngdẫngiải
Tacó: điquađiểm vàcóVTCP .
12
:
11 1
y
xz
12
:
131
y
xz
d
B
Bd
Bd
d
1
,
1
xt
yt t
zt
Bd
1; ; 1Bt tt
;;2 3AB t t t
,AB AB
d AB u
(1;1;2)u
d
.0AB u
t1
1;1; 1AB
12
:.
11 1
y
xz
2;3;1A
5; 6; 2B
AB
Oxz
M
AM
BM
1
2
A
M
BM
2
A
M
BM
1
3
A
M
BM
3
A
M
BM
;0;MOxz Mxz
;;731 59AB AB
;;23 1AM x z
,,ABM
.AM k AB k
27 9
33 1
10
xkx
kk
zk z
;0;90.M
;; 14 6 2 118 2 .BM BM AB
P
1
2
:
111
y
xz
d
2
1
2
:.
21 1
y
xz
d
:2 2 1 0xPz
:2 2 1 0yPz
:2 2 1 0xPy
:2 2 1 0yPz
1
d
2;0;0A
1
1;1;1u

và điquađiểm vàcóVTCP Vì songsongvớihaiđườngthẳng
và nênVTPTcủa là
Khiđó códạng loạiđápánAvàC.
Lại có cách đều và nên đi qua trung điểm của . Do đó
ChọnđápánB.
Câu64:
Tạp chí THTT Lần 5
Trong không gian với hệ tọa độ cho điểm Viết
phươngtrìnhmặtphẳng điquagốctọađộ vàcách mộtkhoảnglớnnhất.
A. B. C. D.
Hướngdẫngiải
Gọi làhìnhchiếucủa trên vuôngtại
.Khiđó điqua vàvuônggócvới làvectopháp
tuyếncủa phươngtrìnhcủamặtphẳng là
hay
ChọnđápánA.
Câu65:
THPT Hai Bà Trưng Lần 1
Trong không gian với hệ tọa độ cho điểm
Tìmđiểm trongmặtphẳng cócaođộâmsaocho
thểtíchcủakhốitứdiện bằng2vàkhoảngcáchtừ đếnmặtphẳng bằng1.
Khiđócótọađộđiểm thỏamãnbàitoánlà:
A. B.C.D.
Hướngdẫngiải
Vì ,docaođộâmnên
Khoảngcáchtừ đếnmặtphẳng bằng1
Suyratọađộ .Tacó:
Mà .Chọnđápán
ChọnđápánA.
2
d
0;1;2B
2
2; 1; 1 .u
P
1
d
2
d
P
12
,
0;1; 1nuu
P
0yzD
P
1
d
2
d
P
1
0; ;1
2
M
AB
:2 2 1 0yPz
,
Oxyz
1; 2; 1 .M
0;0;0O
M
20.xyz
1.
12 1
y
xz
0.xyz 20.xyz
H
M
()P
MHO
H
MH MO
max
MH
MO
()P
MMO
(1; 2; 1)MO
()P
()P
1( 0) 2( 0) 1( 0) 0xyz
20.xyz
,
Oxyz
2;0; 2 , 3; 1; 4 , 2; 2;0 .AB C
D
Oyz
A
BCD
D
Oxy
D
0;3; 1 .D
0; 3; 1 .D
0;1; 1 .D
0; 2; 1 .D
0; ;
D
Oyz D b c 0.c
0; ;
D
bc
:0Oxy z
11do0.
1
c
cc
0; ; 1Db
1; 1; 2 , 4; 2; 2 ; 2; ;1
A
BACADb
; 2;6;2 ; . 46 26 66 1AB AC AB AC AD b b b
1
;. 1
6
ABCD
VABACADb
0;3; 1
3
212
1
0; 1; 1
ABCD
D
b
Vb
b
D
0;3; 1 .D

Câu66:
THPTHaiBàTrưngLần1
Trongkhônggianvớihệtọađộ chođiểm .Mặt
phẳng điquađiểm cắt tại saocho làtrựctâmcủatamgiác
.Phươngtrìnhcủamặtphẳng là
A.
B.
C.D.
Hướngdẫngiải
Dotứdiện cóbacạnh đôimộtvuônggócnênnếu làtrựctâmcủatam
giác dễdàngchứngminhđược hay .
Vậymặtphẳng điquađiểm vàcóVTPT nênphươngtrình là
ChọnđápánD.
Câu67:
THPTChuyênĐHKHHuếLần1
Trongkhônggianvớihệtọađộ ,chođiểm ,
điểm nằmtrênmặtphẳng và .Gọi làhìnhchiếuvuônggóccủalên
và làtrungđiểmcủa .Biếtđườngthẳng luôntiếpxúcvớimộtmặtcầucốđịnh.
Tínhbánkínhmặtcầuđó.
A. . B. . C. . D. .
Hướngdẫngiải
Tacótamgiác luônvuôngtại .Gọi làtrungđiểmcủa Điểm cốđịnh.
Tacótamgiác vuôngtại có làđườngtrungtuyếnnên
Ta có là đường trung bình của tam giác nên song song với mà
Mặtkháctamgiác cântại .Từđósuyra làđườngtrung
trựccủa
Nên
Vậy luôntiếpxúcvớimặtcầutâm bánkính
ChọnđápánA.
Câu68: CHUYÊNĐHKHTNHUẾTrongkhônggianvớihệtọađộ
Oxyz
,chođiểm
0;0; 4A
,điểm
M
nằ
mtrênmặtphẳng
Oxy
và
MO
.Gọi
D
làhìnhchiếuvuônggóccủa
O
lên
AM
và
E
là
trungđiểmcủa
OM
.Biếtđườngthẳng
DE
luôntiếpxúcvớimộtmặtcầucốđịnh.Tínhbán
kínhmặtcầuđó.
A.
2R
. B.
1R
. C.
4R
. D.
2R
.
Hướngdẫngiải
ChọnA.
Tacótamgiác
OAM
luônvuôngtại
O
.
Gọi
I
làtrungđiểmcủa
OA
Điểm
I
cốđịnh
Tacótamgiác
ADO
vuôngtại
D
có
ID
là
đườngtrungtuyếnnên
1
21
2
ID OA
,
Oxyz
1; 2; 3H
P
,H ,,Ox Oy Oz ,,
A
BC
H
A
BC
P
():3 2 11 0.Pxyz ():3 2 10 0.Pxyz
(): 3 2 13 0.Px y z (): 2 3 14 0.Px y z
OABC
,,OA OB OC
H
A
BC
OH ABC
OH P
P
1; 2; 3H
1; 2; 3OH
P
1 2 2 3 3 0 2 3 14 0.xyz xyz
Oxyz
0;0;4A
M
Oxy
M
O
D
O
A
M
E
OM
D
E
2R
1R 4R
2R
OAM O
I
OA
I
ADO
D
I
D
1
21
2
ID OA
I
E
OAM
I
E
A
M
OD AM OD IE
E
OD
E
I
E
OD
;902DOE ODE IOD IDO IDE IOE ID DE
D
E
I
2
2
OA
R
A
D
I

Tacó
I
E
làđườngtrungbìnhcủatamgiác
OAM
nên
I
E
songsongvới
A
M
mà
OD AM OD IE
Mặt
kháctamgiác
E
OD
cântại
E
.Từđósuyra
I
E làđườngtrungtrựccủa
OD
Nên
;902DOE ODE IOD IDO IDE IOE ID DE
Vậy
D
E
luôntiếpxúcvớimặtcầutâm
I
bánkính 2
2
OA
R
Câu69: CHUYÊN ĐHKHTN HUẾ Cho điểm
(0;8;2)A vàmặtcầu ()S có phương trình
222
():( 5) ( 3) ( 7) 72Sx y z
vàđiểm
(9; 7;23)B
.Viếtphươngtrìnhmặtphẳng
()
P
qua
A
tiếpxúcvới()S saochokhoảngcáchtừ
B
đến ()
P
làlớnnhất.Giảsử (1; ; )
nmn làmột
vectơpháptuyếncủa
()
P
.Lúcđó
A.
.2.mn
B.
.2.mn
C.
.4.mn
D.
.4.mn
Hướngd
ẫngiải
ChọnD.
Mặtphẳng
()P
quaA códạng
(0)(8)(2)0 820a x b y c z ax by cz b c-+ -+ -= ++--=.
Điềukiệntiếpxúc:
222 222
53782 5115
(;( )) 6 2 6 2 6 2
abcbc a bc
dI P
abc abc
-+-- - +
= = =
++ ++
.*
Mà
222 222
972382 91521
(;())
ab cbc a b c
dB P
abc abc
-+ -- - +
==
++ ++
222
51154( 4)abcabc
abc
-++-+
=£
++
222222
222 222 222
5115 4
1(1)4.
4624 182
abc abc
abc
abc abc abc
-+ -+
+- + + +
£+ £+ =
++ ++ ++
.
Dấubằngxảyrakhi
114
abc
==
-
.Chọn 1; 1; 4ab c==-=thỏamãn*.
Khiđó
(): 4 0Pxy z-+ =.Suyra 1; 4mn=- = .Suyra:
.4.mn =-
Câu70: CHUYÊN ĐHKHTN HUẾ Trongkhônggianchođườngthẳng
31
:
123
x
yz
vàđường
thẳng
312
:
312
xyz
d
.Viếtphươngtrìnhmặtphẳng
P
điqua
vàtạovớiđường
thẳng
d
mộtgóclớnnhất.
A.
19 17 2 77 .00xyz
B.
19 17 2 34 .00xyz
C.
31 8 5 91 .0xyz
D.
31 8 5 98 .0xyz
Hướngd
ẫngiải
ChọnD.
Đườngthẳng
d cóVTCPlà
1
3;1; 2u
.
Đườngthẳng
điquađiểm
3; 0; 1M vàcóVTCPlà
1; 2; 3u
.

Do
P
nên
M
P .GiảsửVTPTcủa
P
là
222
;; , 0nABCABC
.
Phươngtrình
P
códạng
310Ax By Cz .
Do
P
nên .0 23 0 23un A B C A B C
.
Gọi
làgócgiữa
d
và
P
.Tacó
1
222 2
22
1
.
32 3 2
32
.
14.
14. 2 3
un
BCBC
AB C
sin
un
ABC
B
CBC
2
22
22
57 57
1
512 10
14
14. 5 12 10
BC BC
B
BC C
BBC C
.
TH1:Với
0C
thì
570
14 14
sin
.
TH2:Với
0C đặt
B
t
C
tacó
2
2
57
1
51210
14
t
sin
tt
.
Xéthàmsố
2
2
57
51210
t
ft
tt
trên
.
Tacó
2
2
2
50 10 112
51210
tt
ft
tt
.
2
8875
5514
0 50 10 112 0
77
0
55
tf
ft t t
tf
.
Và
2
2
57
lim lim 5
51210
xx
t
ft
tt
.
Bảngbiếnthiên
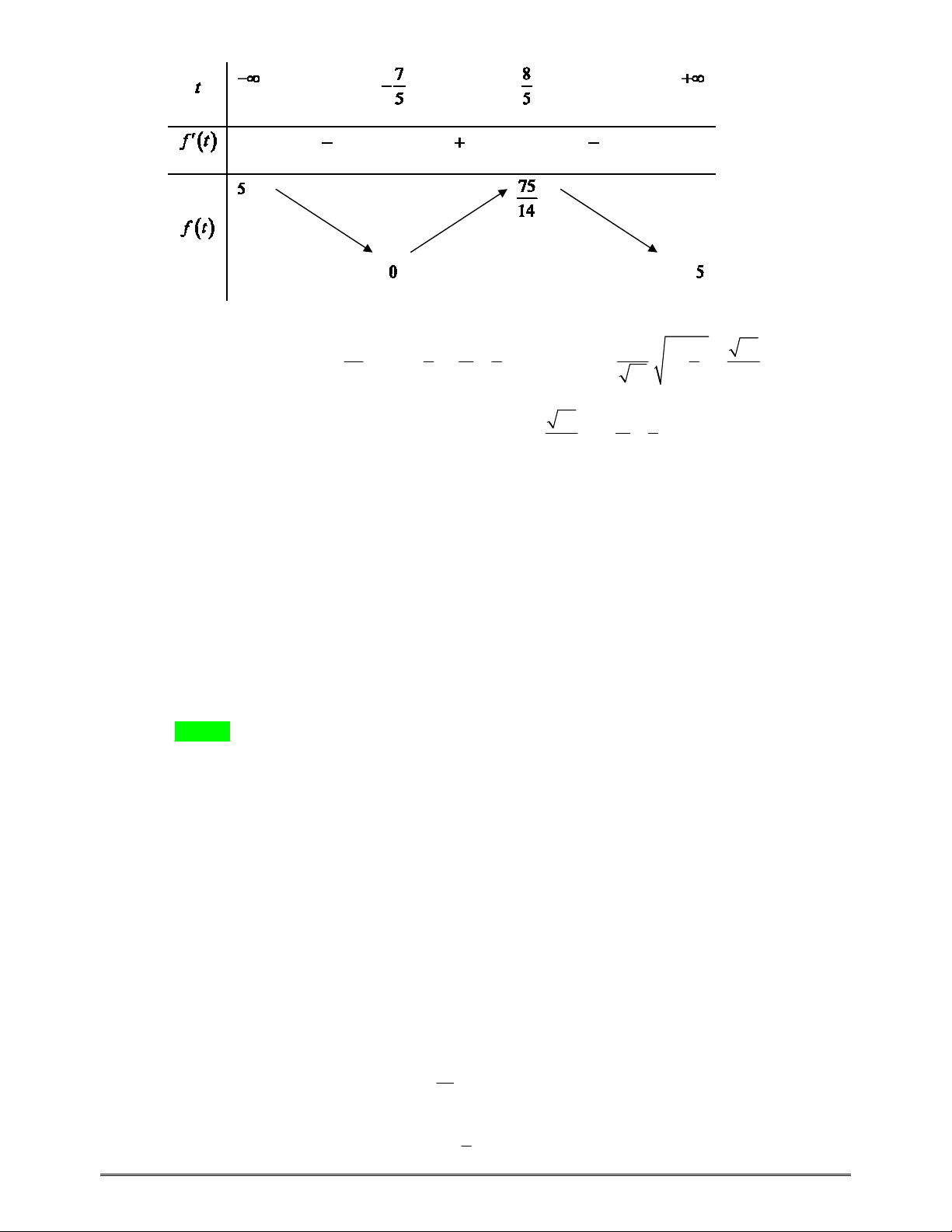
Từđótacó
75
14
Maxf t
khi
88
55
B
t
C
.Khiđó
1875
.
514
14
sin f
.
SosánhTH1vàTh2tacó
s
in
lớnnhấtlà
75
14
sin
khi
8
5
B
C
.
Chọn
8531BCA
.
Phươngtrình
P
là
31 3 8 5 1 0 31 8 5 98 0xyz xyz
.
Câu71: CHUYÊN ĐHKHTN HUẾ Trong không gian
Oxyz
chomặtcầu
222
:1 2 39Sx y zvàmặtphẳng
:2 2 3 0Pxyz
.Gọi
;;
M
abc
làđiểm
trênmặtcầu
S
saochokhoảngcáchtừ
M
đến
P
làlớnnhất.Khiđó
A.
5.abc
B.
6.abc
C.
7.abc
D.
8.abc
Hướngdẫngiải
ChọnC.
Mặtcầu
222
:1 2 39Sx y zcótâm
1; 2; 3I
vàbánkính
3.R
Gọi
d
làđườngthẳngđiqua
1; 2; 3I vàvuônggóc
P
Suyraphươngtrìnhthamsốcủađườngthẳng
d
là
12
22
3
x
t
yt
zt
.
Gọi
,
A
B
lần lượt là giao của d và
S , khi đó tọa độ
,
A
B
ứngvớit lànghiệmcủa
phươngtrình
222
1
12 1 22 2 3 3 9
1
t
ttt
t
Với
13
1 3;0;4 ;( ) .
3
tA dAP
Với
5
11;4;2 ;().
3
tB dBP
0
0

Vớimọiđiểm
;;
M
abc trên
S taluôncó
;( ) ;( ) ;( ) .dBP dM P dAP
Vậykhoảngcáchtừ
M
đến
P
làlớnnhấtbằng
13
3
khi
3; 0; 4M
Dođó
7.abc
Câu72: LÊ HỒNG PHONG Trong không gian với hệ tọa độ
Oxyz , cho đường thẳng
13
:
12 1
xyz
d
vàmặtcầu
S
tâm
I
cóphươngtrình
222
:1 2 118Sx y z .
Đườngthẳng
d
cắt
S tạihaiđiểm
,
A
B
.Tínhdiệntíchtamgiác
I
AB .
A.
811
.
3
B.
16 11
.
3
C.
11
.
6
D.
811
.
9
Hướngdẫngiải
ChọnA.
Đườngthẳng
d
điquađiểm
1; 0; 3C vàcóvectơchỉphương
1; 2; 1u
Mặtcầu
S cótâm
1; 2; 1I ,bánkính 32R
Gọi
H
làhìnhchiếuvuônggóccủa
I
lênđườngthẳng
d
.
Khi đó:
,IC u
IH
u
, với
0; 2; 2IC
;
,6;2;2IC u
Vậy
222
622 66
3
141
IH
Suyra
22 4 6
18
33
HB
Vậy,
116686811
.
22333
IAB
SIHAB
Câu73: HAIBÀTRƯNG
–HUẾChohìnhlậpphương
.ABCD A B C D
cócạnhbằng2.Tínhkhoảng
cáchgiữahaimặtphẳng
và .
A
BD BCD
A.
3
.
3
B.
3.
C.
3
.
2
D.
2
.
3
Hướngdẫngiải
ChọnA.
Tachọnhệtrụctọađộsaochocácđỉnhcủahìnhlập
phươngcótọađộnhưsau:
A
'
D
'
C'
B
'
B
C
D
A

0;0;0 2; 0;0 2; 2;0 0; 2; 0
0;0;2 2; 0; 2 2; 2; 2 0; 2; 2
ABCD
ABCD
2;0; 2 , 0;2; 2 ,
2; 2;0 , 0; 2; 2
AB AD
BD BC
*Mặtphẳng
A
BD
qua
0;0; 0A
vànhậnvéctơ
1
,1;1;1
4
nABAD
làmvéctơ
pháptuyến.Phươngtrình
A
BD
là:
0.xyz
*Mặtphẳng
B
CD
qua
2;0; 0B vànhậnvéctơ
1
,1;1;1
4
mBDBC
làmvéctơ
pháptuyến.
Phươngtrình
B
CD
là:
20.xyz
Suyrahaimặtphẳng
A
BD
và
B
CD
songsongvớinhaunênkhoảngcáchgiữahai
mặt phẳng chính là khoảng cách từ điểm
A
đếnmặtphẳng
B
CD
:
223
,.
3
3
dABCD
Cáchkhác:Thấykhoảngcáchcầntìm
11 23
,.23.
33 3
dABD BCD AC
Câu74: HAI BÀ TRƯNG
–HUẾTrong không gian
Oxyz
, cho điểm
2;0; 2 , 3; 1; 4 , 2; 2;0 .AB C
Điểm D trongmặtphẳng
Oyz
cócaođộâmsaochothể
tíchcủakhốitứdiện
A
BCD
bằng2vàkhoảngcáchtừ D đếnmặtphẳng
Oxy
bằng1.Khiđó
cótọađộđiểm
D
thỏamãnbàitoánlà:
A.
0;3; 1 .D
B.
0; 3; 1 .D
C.
0;1; 1 .D
D.
0; 2; 1 .D
Hướngdẫngiải
ChọnA.
Vì
0; ;DOyz Dbc
,docaođộâmnên
0.c
Khoảng cách từ
0; ;Dbc
đếnmặtphẳng
:0Oxy z
bằng1
11do0.
1
c
cc
Suyratọađộ
0; ; 1Db
.Tacó:
1; 1; 2 , 4; 2; 2 ; 2; ;1
A
BACADb
,2;6;2AB AC
,. 4626661AB AC AD b b b
1
,. 1
6
ABCD
VABACADb
Mà
0;3; 1
3
212
1
0; 1; 1
ABCD
D
b
Vb
b
D
.Chọnđápán
0;3; 1 .D
Câu75: Trongkhônggianvớihệtọađộ
Oxyz
,chođiểm
()
2;11; 5A -
vàmặtphẳng

()
()()
22
:2 1 1 10 0Pmxm ym z+++--=
.Biếtrằngkhi
m
thayđổi,tồntạihaimặtcầucốđịnhtiếpxúc
vớimặtphẳng
()
P
vàcùngđiqua A .Tìmtổngbánkínhcủahaimặtcầuđó.
A.
22. B.52. C.72. D.12 2 .
Lờigiảithamkhảo:
Gọi
()
;; ,I abc rlầnlượtlàtâmvàbánkínhcủamặtcầu.Domặtcầutiếpxúcvới
()
P nêntacó
()
()
()()
()
()
()
22
2
22
21110
210
,
12 12
ma m b m c
bcm mabc
rdIP
mm
+++--
-++--
== =
++
()
()
()
()
()
()
2
22
2
2 2 21001
21012
22 21002
bcr m mabcr
bcm mabc rm
bcr m mabcr
é
+- + +-- - =
ê
ê
+++--=+
ê
++ + +-+ - =
ê
ë
TH1:
()
()
2
2 2 21001bcr m mabcr+- + +-- - =
Domthayđổivẫncómặtcầucốđịnhtiếpxúcvới
()
P
nênyêucầubàitoántrờthànhtìmđiềukiện
,,abc
saocho
()
1 khôngphụthuộcvào
m
.Dođó
()
1 luônđúngvớimọi
20
0
210 0
bcr
a
bcr
ì
ï
+- =
ï
ï
ï
=
í
ï
ï
ï
-- - =
ï
î
250
0
5
br
a
c
ì
ï
=+=
ï
ï
ï
=
í
ï
ï
ï
=-
ï
î
Suyra
()
()
()
()
2
2
22
0;5 2; 5 : 5 2 5Ir Sxyr z r+-=> +-- ++=
.
Lạicó
()
ASÎ
nênsuyra:
()
2
22
22
41152 122400
10 2
r
rrr r
r
é
=
ê
+- - - = - + =
ê
=
ê
ë
TH2:
()
2
22 2100bcr m mabcr++ + +-+ - = làmtươngtựTH1trườnghợpnàykhôngthỏađềbài
Tómlại:Khi
m
thayđổi,tồntạihaimặtcầucốđịnhtiếpxúcvớimặtphẳng
()
P vàcùngđiqua
A
vàcótổngbánkínhlà:
12 2 suyrachọnD
Câu76: Trong không gianvớihệtọađộ
Oxyz
,chobốnđiểm
()()()
3;0;0 , 0;2;0 , 0;0;6ABCvà
()
1;1;1D .Kí
hiệu
d
làđườngthẳngđiqua
D
saochotổngkhoảngcáchtừcácđiểm
, ,
A
BC
đến
d
lớn
nhất.Hỏiđườngthẳng
d
điquađiểmnàodướiđây?
A.
()
1; 2;1M --
. B.
()
5;7;3N
. C.
()
3;4;3P
. D.
()
7;13;5Q
.
Lờigiảithamkhảo:
TacóphươngtrìnhmặtphẳngquaA,B,Clà:
()
:12360
326
xyz
ABC x y z++= + +-=
.
Dễthấy
()
D ABCÎ
.Gọi
', ', '
A
BC
lầnlượtlàhìnhchiếuvuônggóccủa
,,
A
BC
trênd .

Suy ra
()()()
,,,'''dAd dBd dCd AA BB CC AD BD CD++=++£++
.Dấu bằng xảy ra khi
'''
A
BCDººº
.
Haytổngkhoảngcáchtừcácđiểm
, ,
A
BC
đến
d
lớnnhấtkhidlàđườngthẳngquaDvàvuônggóc
vớimặtphẳng
()
12
:13;
1
xt
ABC d y t N d
zt
ì
=+
ï
ï
ï
ï
=> = + Î
í
ï
ï
ï
=+
ï
î
suyrachọnB
Câu77: Trongkhônggian vớihệtọa độ
Oxyz
,chobađiểm
()()( )
5;5;0 , 1;2;3 , 3;5; 1ABC- vàmặtphẳng
()
:50Px yz+++=.Tínhthểtích
V
củakhốitứdiện
SABC
biếtđỉnh
S
thuộcmặtphẳng
()
P và
SA SB SC==
.
A.
145
6
V
=
. B. 145V = . C.
45
6
V =
. D.
127
3
V =
.
Lờigiảithamkhảo:
Gọi
()() ()
;; 5 01S abc P a b cÎ=>+++=
.
Tacó:
()()
22
2
55,AS a b c=-+-+
()()() ()()()
222 222
123, 351BS a b c CS a b c= - +- +- = - +- ++
Do
()()() ()()()
()() ()()()
222 222
22 222
2
123 351
468210
42150
55 351
ab c abc
abc
SA SB SC
ac
abcabc
ì
ï
ï - +- +- = - +- ++
ì
+--=
ï
ï
ïï
==
íí
ïï
+-=
ï
ïî
-+-+= -+-++
ï
ï
î
T
acóhệ:
6
4 68210
23 13 9
42150 6; ;
222
50
9
2
a
abc
ac b S
abc
c
ì
ï
ï
ï
=
ï
ì
+--=
ï
ï
ï
ï
æö
ï
ï
ïï
÷
ç
+-= =- =- -
÷
íí
ç
÷
ç
ïï
èø
ïï
ïï+++=
ï
î
ï
ï
=-
ï
ï
ï
î
.Lạicó:
()()
4; 3;3 , 2;0; 1AB AC-- - -
()
()
.
23 9 145
3; 10; 6 ; 1; ; 145
22 6
S ABC
AB AC AS AB AC AS V
æö
÷
ç
=> = - - = - - => = => =
÷
ç
÷
ç
èø
Câ
u78: ChohìnhchópSABCcóđáylàtamgiácđềucạnhbằng
6cm và
()
43SA SB SC cm===
.GọiDlà
điểmđốixứngcủaBquaC.KhiđóbánkínhmặtcầungoạitiếphìnhchópSABDbằng?
A.
5cm
B. 32cm C.26cm D. 37cm
Lờ
igiảithamkhảo:
Cách1:DựngCGvuônggócvới
()
A
BC ,QuaEdựngmặtphẳngvuônggócvới
SB
,mặtphẳngnàycắt
CGtạiF.SuyraFlàtâmmặtcầungoạitiếphìnhchópS.ABD.Đặt
SF R=
Xéthìnhchữnhật:
()
22
1FGSH FC SH FG SH R CH=> = - = - -
Lạicó:
()
22
2FC R CB=- .Từ1và2suyra
22 22
SH R CH R CB-- =-
()
22 2
612 365120 37RR R Rcm--=---==>= SuyrachọnD
C
ách2:
Chọnhệtrụctọađộnhưhìnhvẽ.

Tacó:
()
()()()
0;0;0 , 3 3; 3;0 , 3 3;3;0 , 2 3;0;6CA B S-- - -
() ()
2
2
0;0; 36 12 6FCG F t FAFS t tÎ=> = +=+-
()
137tSCcm==> =
suyrachọnD

Chủ đề 8. TOÁN THỰC TẾ
Câu1: SGDVĨNHPHÚCSốsảnphẩmcủamộthãngđầuDVDsảnxuấtđượctrong1ngàylàgiátrị
củahàmsố:
21
33
,.
f
mn m n
,trongđó
m
làsốlượngnhânviênvà
n
làsốlượnglaođộng
chính.Mỗingàyhãngphảisảnxuấtđượcítnhất
40
sảnphẩmđểđápứngnhucầukhách
hàng.Biếtrằngmỗingàyhãngđóphảitrảlươngchomộtnhânviênlà
6 USD
vàchomột
laođộngchínhlà
24 USD
.Tìmgiátrịnhỏnhấtchiphítrong1ngàycủahãngsảnxuấtnày.
A.
1720 USD
. B.
720 USD
. C.
560 USD
. D.
600 USD
.
Hướn
gdẫngiải
ChọnB.
Tacógiảthiết:
21
33
.40mn
2
64000mn
với
,mn
.
Tổngsốtiềnphảichitrongmộtngàylà:
32
6 24 3 3 24 3 216 720mnmmn mn
Dấu
""
xảyrakhivàchỉkhi
324mn 8mn
Dođó,
2
64000mn
3
64 64000n
10n
Tachọn
10 80nm
.
Vậychiphíthấpnhấtđểtrảcho80nhânviênvà10laođộngchínhđểsảnxuấtđạtyêucầu
là
720
USD
Câu2: SGDVĨNHPHÚCChohìnhthangcâncóđộdàiđáynhỏvàhaicạnhbênđềubằng
1
mét.
Khiđóhìnhthangđãchocódiệntíchlớnnhấtbằng?
A.
2
33 m
. B.
2
33
2
m
. C.
2
33
4
m
. D.
2
1 m
.
Hướn
gdẫngiải
ChọnC.
Kíhiệu
x
làđộdàiđườngcaosuyra
01x
Tínhđượcđáylớnbằng
2
121x
.
Diệntíchhìnhthang
2
11Sxx
.Xéthàmsố
2
() 1 1fx x x
trên
0;1
.
Tacó:
22
2
211
()
1
xx
fx
x
.
3
() 0
2
fx x
.Lậpbảngbiếnthiên.Suyra
0;1
333
max ( )
24
fx f
BÀI TOÁN VẬN DỤNG (8 - 9 - 10)
_______________________________
Câu3: NGUYỄNKHUYẾNTPHCMChomộtcâynếnhìnhlăngtrụlụcgácđềucóchiềucaovàđộ
dàicạnhđáylầnlượtlà
15cm
và
5cm
.Ngườitaxếpcâynếntrênvàotrongmộthộpcó
dạnghìnhhộpchữnhậtsaochocâynếnnằmkhíttronghộp.Thểtíchcủachiếchộpđó
bằng
A.
1500 ml
. B.
600 6 ml
. C.
1800 ml
. D.
750 3 ml
.
Hướngdẫngiải
Tacó
10 cm,AD=5 3 cmAB
50 3
ABCD
S
. 750 3
ABCD
VS h
Chọnđápán:D
Câu4: NGUYỄNKHUYẾNTPHCMNgườitathay
nướcmóichomộtbểbơidạnghìnhhộpchữnhậtcóđộsâu
1
280hcm
.Giảsử ()ht cmlà
chiềucaocủamựcnướcbơmđượctạithờiđiểm
t giây,bếtrằngtốcđộtăngcủachiềucao
nướctạigiâythứ
t
là
3
1
() 3
500
ht t
.Hỏisaubaolâuthìnướcbơmđược
3
4
độsâucủa
hồbơi?
A.7545, 2
s
. B. 7234,8
s
. C.7200,7
s
. D. 7560,5
s
.
Hướngdẫngiải
Saumgiâymứcnướccủabểlà
4
3
4
3
33
00
0
1333
(m) ( )dt= 3dt= 3 3 3
500 2000 2000
m
mm
t
hht t m
Yêucầubàitoán,tacó
4
3
3
33
3 3 3 280
2000 4
m
3
4
4
3
33
3 140000 3 3 140000 3 3 3 7234,8mm .ChọnB
Câu5: NGUYỄNKHUYẾNTPHCMMộtchấtđiểmchuyểnđộngtheoquyluật
32
617
s
tt t ,
với
t giâylàkhoảngthờigiantínhtừlúcvậtbắtđầuchuyểnđộngvà
s
métlàquãng
đườngvậtđiđượctrongkhoảngthờigianđó.Khiđóvậntốc
v
/ms
củachuyểnđộng
đạtgiátrịlớnnhấttrongkhoảng8giâyđầutiênbằng:
A.
17 /ms
. B.
36 /ms
. C.
26 /ms
D.
29 /ms
.
Hướngdẫngiải
Vậntốccủachấtđiểmlà
2
2
312173 2 2929vs t t t
.
Vậyvậntốccủachuyểnđộngđạtgiátrịlớnnhấtbằng29khi
2t
.
ChọnD.

Câu6: TRẦNHƯNGĐẠO–NBBạnHùngtrúngtuyểnvàođạihọcnhungvìkhôngđủnộptiềnhọc
phíHùngquyếtđịnhvayngânhàngtrong
4
nămmỗinăm
3.000.000
đồngđểnộphọcvới
lãisuất
3%
/năm.SaukhitốtnghiệpđạihọcHùngphảitrảgóphàngthángsốtiềnTkhông
đổicùngvớilãisuất
0, 25% /
thángtrongvòng
5
năm.SốtiềnTmàHùngphảitrảchongân
hànglàmtrònđếnhàngđơnvịlà
A.
232518 đồng. B. 309604đồng. C. 215456 đồng. D. 232289 đồng.
Hướngdẫngiải
ChọnD.
TínhtổngsốtiềnmàHùngnợsau4nămhọc:
Sau1nămsốtiềnHùngnợlà:
3
3r
31 r
Sau2nămsốtiềnHùngnợlà:
2
31 31rr
Tươngtự:Sau4nămsốtiềnHùngnợlà:
432
3 1 3 1 3 1 3 1 12927407,43rrrr A
Tínhsốtiền
T
màHùngphảitrảtrong1tháng:
Sau1thángsốtiềncònnợlà:
1
A
Ar T A r T
.
Sau2thángsốtiềncònnợlà:
2
11.11
A
rT A rTrTA r T rT
Tương tự sau
60
thángsốtiềncònnợlà:
60 59 58
111 1TT
A
rrr TTr
.
Hùngtrảhếtnợkhivàchỉkhi
60 59 58
60 59 58
60
60
60
60
60
60
111 10
111 110
11
10
11
10
1
11
11
232.289
TT T
T
T
Ar r r rT
Ar r r r
r
Ar
r
Ar
Ar r
T
r
T
r
T
r
Câu7: TRẦNHƯNGĐẠO
–NBMộtđámvitrùngtạingàythứ t cósốlượnglà
.
N
t
Biếtrằng
4000
10,5
Nt
t
vàlúcđầuđámvitrùngcó250000con.Hỏisau
10
ngàysốlượngvitrùng
làbaonhiêu?
A.
258 959 con
. B.
253 584 con
. C.
257 167 con
. D.
264 334 con
.
Hướngdẫngiải
ChọnD.
Tacó:
4000
d d 8000.ln 1 0,5
10,5
Nt N t t t t C
t
Màsốlượngvitrùngbanđầubằng
250000
connên
250000C
.
Dođó:
8000.ln 1 0,5 250000Nt t
.
Vậysau
10
ngàysốlượngvitrùngbằng:
10 8000.ln 6 250000 264334N
con.
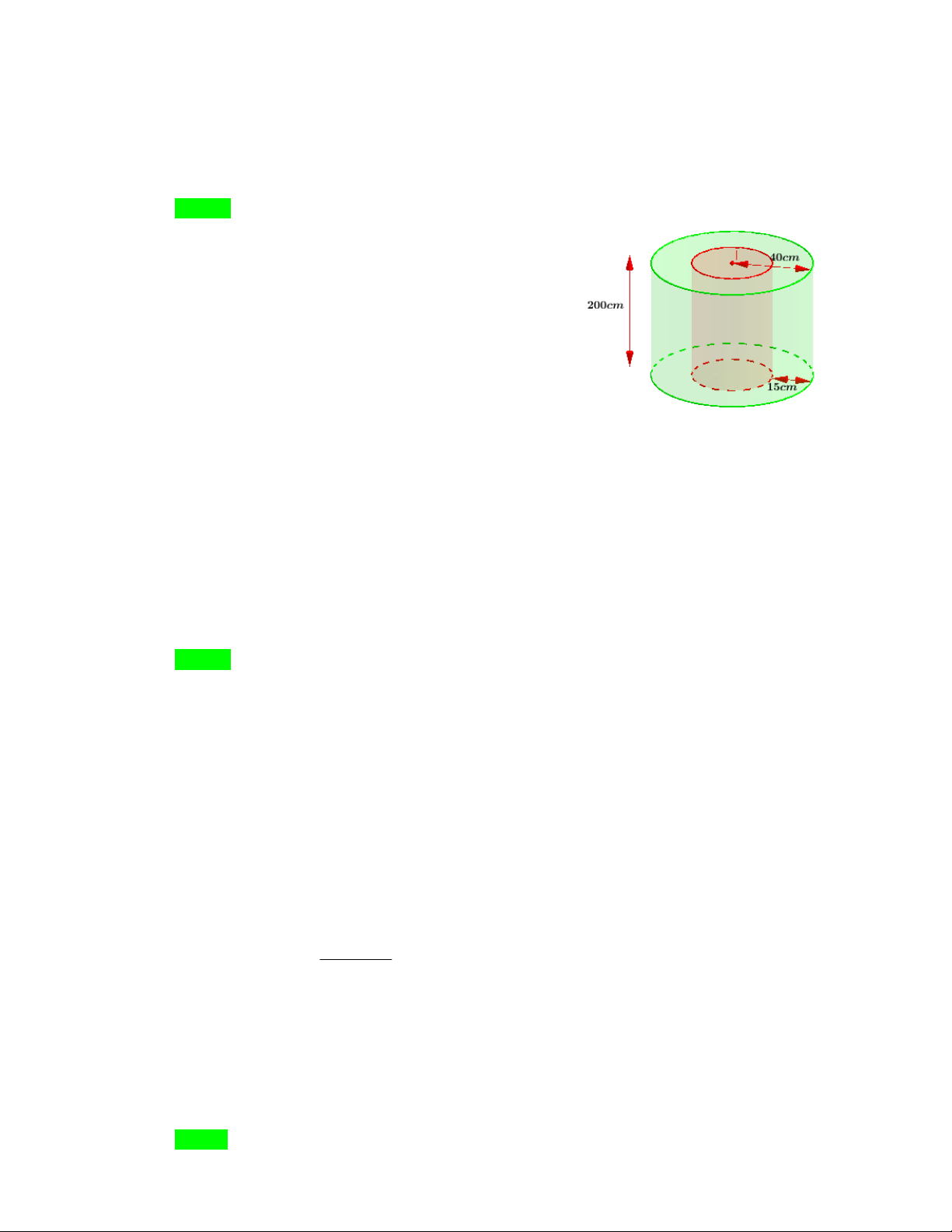
Câu8: TRẦN HƯNG ĐẠO –NBNgười ta cần đổ một ống thoát nước hình trụ với chiều cao
200cm
,độdàycủathànhốnglà
15cm
,đườngkínhcủaốnglà
80cm
.Lượngbêtôngcần
phảiđổlà
A.
3
0,195 m
. B.
3
0,18 m
. C.
3
0,14 m
. D.
3
m
.
Hướngdẫngiải
ChọnA.
Gọi
12
V,V
lầnlượtlàthểtíchcủakhốitrụbênngoài
vàbêntrong
Dođólượngbêtôngcầnphảiđổlà:
22 3 3
12
.40 .200 .25 .200 195000 0,195VVV cm m
Câu9:
LẠNGGIANGSỐ1Mộtngôibiệtthựnhỏcó
10
câycộtnhàhìnhtrụtròn,tấtcảđềucó
chiềucaobằng
4, 2m .Trongđócó 4 câycộttrướcđạisảnhcóđườngkínhbằng
40cm
,
6
câycộtcònlạibênthânnhàcóđườngkínhbằng
26cm
.Chủnhàdùngloại
sơngiảđá
để
sơn
10
câycộtđó.Nếugiácủamộtloạisơngiảđálà
2
380.000 /đ m
kểcảphầnthicông
thìngườichủphảichiítnhấtbaonhiêutiềnđểsơncột
10
câycộtnhàđóđơnvịđồng?
A.
15.845.000.
B.
13.627.000.
C.
16.459.000.
D.
14.647.000.
Hướngdẫngiải
ChọnA.
Diện tích xung quanh
4 câycộttrướcđạisảnhcóđườngkínhbằng
40cm
:
1
4. 2 .0, 2.4, 2S
.
Diệntíchxungquanh6câycộttrướccâycộtcònlạibênthânnhàcóđườngkínhbằng
26cm
:
2
62.0,13.4,2S
.
Sốtiềnđểsơnmườicâycộtnhàlà
12
.380.000SS
15.845.000.
Câu10:
LẠNGGIANGSỐ1Tốcđộpháttriểncủasốlượngvikhuẩntronghồbơiđượcmôhình
bởihàmsố
2
1000
,0
10,3
Bt t
t
,trongđó
Btlàsốlượngvikhuẩntrênmỗi
ml
nước
tạingàythứ
t .Sốlượngvikhuẩnbanđầulà
500
contrênmột
ml
nước.Biếtrằngmứcđộ
antoànchongườisửdụnghồbơilàsốvikhuẩnphảidưới
3000
contrênmỗi
ml
nước.
Hỏivàongàythứbaonhiêuthìnướctronghồkhôngcònantoànnữa?
A.
9
B.
10.
C.
11.
D.
12.
Hướngdẫngiải
ChọnB

Tacó
2
1000 1000
'd d
0,3 1 0,3
10,3
B
tt t C
t
t
Mà
10000 11500
0 500 500
31 0,3.0 3
BCC
Dođó:
10000 11500
31 0,3 3
Bt
t
Nướctronghồvẫnantoànkhichỉkhi
10000 11500
3000 3000 10
31 0,3 3
Bt t
t
Vậykểtừngàythứ10,nướchồkhôngcònantoàn.
Câu11:
LẠNGGIANGSỐ1Mộtlonnướcsoda
80
F
đượcđưavàomộtmáylàmlạnhchứađátại
32
F
.Nhiệtđộcủasodaởphútthứt đượctínhtheođịnhluậtNewtonbởicôngthức
( ) 32 48.(0.9)
t
Tt .Phảilàmmátsodatrongbaolâuđểnhiệtđộlà
50
F
?
A.
1,56.
B.
9,3.
C.
2.
D.
4.
Hướngdẫngiải
ChọnB.
Gọi
o
t
làthờiđiểmnhiệtđộlonnước
80
F
32 48. 0,9 80
o
t
o
Tt
1
Gọi
1
t
làthờiđiểmnhiệtđộlonnước
50
F
1
32 48. 0,9 50
o
t
Tt
2
1
0,9 1
o
t
0
o
t
2
1
3
0,9
8
t
10,9
3
log 9,3
8
t
Câu12:
LẠNGGIANGSỐ1Mộtcôngtybấtđộngsảncó50cănhộchothuê.Biếtrằngnếucho
thuêmỗicănhộvớigiá
2000000
đồngmộtthángthìmọicănhộđềucóngườithuêvàcứ
mỗilầntănggiáchothuêmỗicănhộthêm
50000
đồngmộtthángthìcóthêmmộtcănhộ
bịbỏtrống.Côngtyđãtìmraphươngánchothuêđạtlợinhuậnlớnnhất.Hỏithunhập
caonhấtcôngtycóthểđạtđượctrong1thánglàbaonhiêu?
A.
115 250 000
. B.
101 250 000
. C.
100 000 000
. D.
100 250 000
.
Hướngdẫngiải
ChọnB.
Gọi
x
đồng/tháng
()
0x >
làgiáchothuêmới.
Sốcănhộbịbỏtrốnglà
50 000
x
cănhộ
Sốtiềncôngtythuêđược
() ( )
2 000 000 50
50 000
x
Tx x
æö
÷
ç
=+-
÷
ç
÷
ç
èø
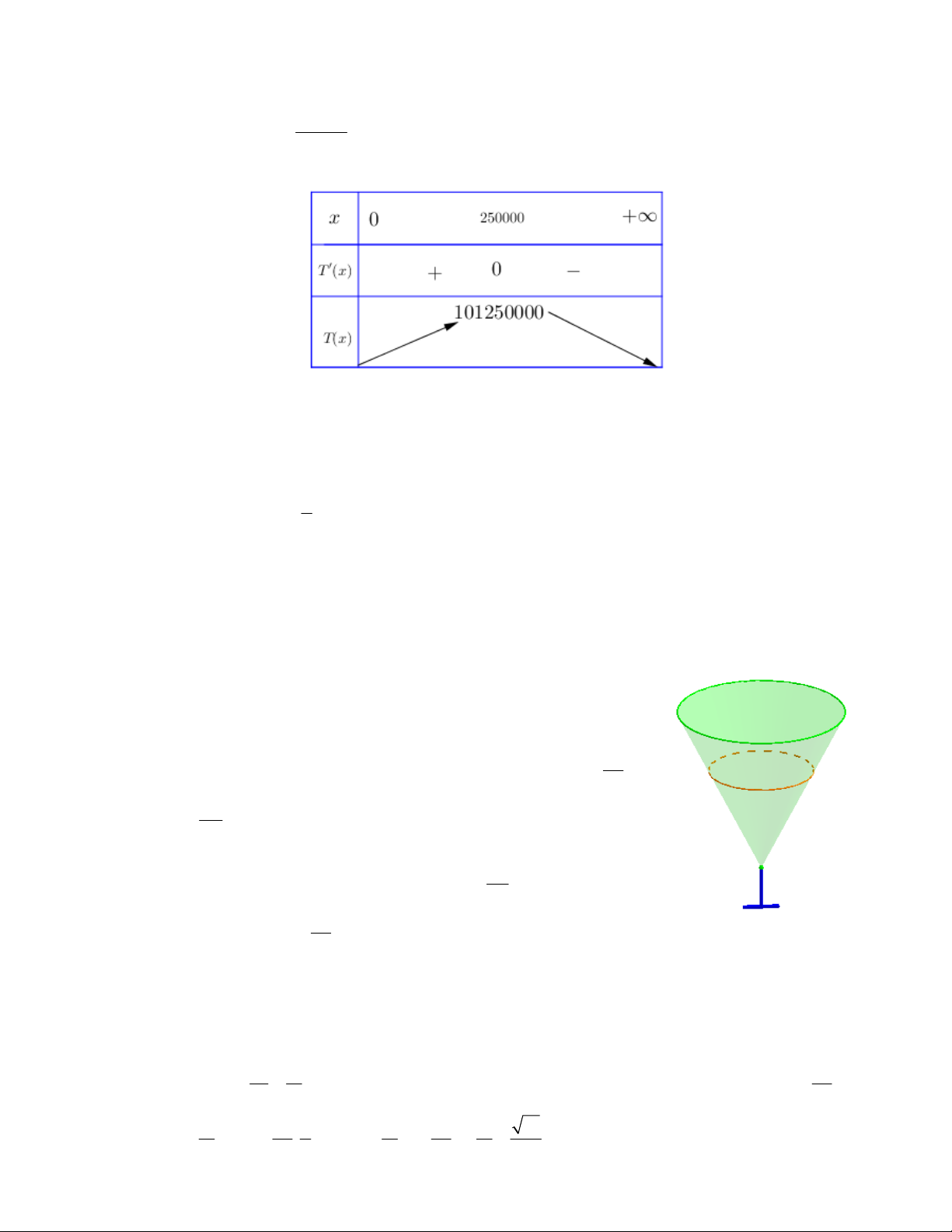
Khảosáthàmsố
(
)
Txtrên
()
0;+¥
()
10
25 000
x
Tx
¢
=-
(
)
0Tx
¢
=
250 000x =
.
Bảngbiếnthiên
Vậythunhậpcaonhấtcôngtycóthểđạtđượctrong1thánglà:
101 250 000T
.
Câu13: LÝTỰTRỌNG
–TPHCMMộtcáilycódạnghìnhnónđượcrótnướcvàovớichiềucao
mựcnướcbằng chiềucaohìnhnón.Hỏinếubịchkínhmiệnglyrồiúpngượclyxuống
thìtỷsốchiềucaomựcnướcvàchiềucaohìnhnónxấpxỉbằngbaonhiêu?
A. . B. . C. . D.
Hướngdẫngiải
ChọnB.
Gọichiềucaovàbánkínhđườngtrònđáycủacáilylầnlượt
là và .
Khiđểcốctheochiềuxuôithìlượngnướctrongcốclàhình
nóncóchiềucaovàbánkínhđườngtrònđáylầnlượtlà
và
Dođóthểtíchlượngnướctrongbìnhlà Phầnkhông
chứanướcchiếm
Khiúpngượclylạithìphầnthểtíchnướctronglykhôngđổivàlúcđóphầnkhôngchứa
nướclàhìnhnónvàtagọi và lầnlượtlàchiềucaovàbánkínhđườngtrònđáycủa
phầnhìnhnónkhôngchứanướcđó.
Tacó vàphầnthểtíchhìnhnónkhôngchứanướclà
2
3
0,33 0,11 0, 21 0,08
h
R
2
3
h
2
.
3
R
8
27
V
19
.
27
V
'h
'
R
''
R
h
R
h
19
27
V
3
3
22
'19 '19'19
.' .. .
3273 27 3
hhhh
RR
hh

Dođótỷlệchiềucaocủaphầnchứanướcvàchiềucaocủacáilytrongtrườnghợpúp
ngượclylà
Câu14: LÝTỰTRỌNG–TPHCMGiảsửvàocuốinămthìmộtđơnvịtiềntệmất10%giátrịso
vớiđầunăm.Tìmsốnguyêndươngnhỏnhấtsaochosau
n năm,đơnvịtiềntệsẽmấtđiít
nhất90%giátrịcủanó?
A.16 B.18. C.20. D.22.
Hướngdẫngiải
ChọnD.
Gọi
0xx làgiátrịtiềntệlúcbanđầu.Theođềbàithìsau1năm,giátrịtiềntệsẽcòn
0,9
x
.
Cuốinăm1còn
0,9
x
Cuốinăm2còn
2
0,9.0,9 0,9
x
x
……………………………
Cuốinăm
n
còn
0,9
n
x
Ycbt
0,9 0,1 21,58
n
xxn.Vì n nguyêndươngnên
22n
.
Câu15: NGÔGIATỰ‐VPMộtngôibiệtthựcó
10
câycộtnhàhìnhtrụtròn,tấtcảđềucóchiều
caobằng
4,2 m
.Trongđó,
4
câycộttrướcđạisảnhcóđườngkínhbằng
40cm
,
6
câycột
cònlạibênthânnhàcóđườngkínhbằng
26cm
.Chủnhàdùngloạisơngiảđáđểsơn
10
câycộtđó.Nếugiácủamộtloạisơngiảđálà
2
380.000 /đ m kểcảphầnthicôngthìngười
chủphảichiítnhấtbaonhiêutiềnđểsơn
10
câycộtnhàđóđơnvịđồng?
A.
15.844.000
. B.
13.627.000
. C.
16.459.000
. D.
14.647.000
.
Hướngdẫngiải
ChọnA.
Diệntíchxungquanhcủamộtcáicộtđượctínhbởicôngthức:
2
xq
SRh
Tổngdiệntíchxungquanhcủa10cáicộtlà:
4. 2 .0, 2.4, 2 6. 2 .0,13.4, 2 13,272
Tổngsốtiềncầnchilà:
13, 272 380.000 15.844.000
.
Câu16: NGÔGIATỰ‐VPMộtđoàntàuchuyểnđộngthẳngkhởihànhtừmộtnhàga.Quãng
đường
s
mét
điđượccủađoàntàulàmộthàmsốcủathờigian
tgiây
,hàmsốđólà
23
6–
s
tt .Thờiđiểm
tgiây
màtạiđóvậntốc
/vms
củachuyểnđộngđạtgiátrịlớn
nhấtlà
A.
4ts
. B.
2ts
. C.
6ts
. D.
8ts
.
Hướngdẫngiải
ChọnB.
Hàmsốvậntốclà
2
312vst t t
,cóGTLNlà
max
12v
tại
2t
Câu17: LÝTHÁITỔ‐HNMộtnhàmáysảnxuấtcầnthiếtkếmộtthùngsơndạnghìnhtrụcónắp
đậyvớidungtích
3
1000cm .Bánkínhcủanắpđậyđểnhàsảnxuấttiếtkiệmnguyênvật
liệunhấtbằng
3
'3 19
1.
3
h
h

A.
3
500
cm
. B.
3
5
10.
cm
. C.
500
cm
. D.
5
10.
cm
.
Hướngdẫngiải
ChọnA.
Gọi
h
cm
làchiềucaohìnhtrụvà R
cm
làbánkínhnắpđậy.
Tacó:
2
1000VRh
.Suyra
2
1000
h
R
.
Đểnhàsảnxuấttiếtkiệmnguyênvậtliệunhấtthìdiệntíchtoànphần
tp
S
củahìnhtrụnhỏ
nhất.
Tacó:
22
2
1000
22 22.
tp
SRRhRR
R
3
22 2
3
1000 1000 1000 1000
2 3. 2 . . 3 2 .1000RR
RR RR
Đẳngthứcxảyrakhivàchỉkhi
2
3
1000 500
2 RR
R
.
Câu18: LÝTHÁITỔ‐HNGiảsửcứsaumộtnămdiệntíchrừngcủanướctagiảm
x
phầntrăm
diệntíchhiệncó.Hỏisau
4
nămdiệntíchrừngcủanướctasẽlàbaonhiêulầndiệntích
hiệnnay?
A.
4
1.
100
x
B.
4
1.
100
x
C.
4
1.
100
x
D.
4
1.
100
x
Hướngdẫngiải
ChọnC
Gọi
0
S
làdiệntíchrừnghiệntại.
Sau
n năm,diệntíchrừngsẽlà
0
1
100
n
x
SS
.
Dođó,sau4nămdiệntíchrừngsẽlà
4
1
100
x
lầndiệntíchrừnghiệntại.
Câu19: CHUYÊNPHANBỘICHÂUMộtcốcnướchìnhtrụcóchiềucao
9cm
,đườngkính
6cm
.
Mặtđáyphẳngvàdày
1cm
,thànhcốcdày
0,2cm
.Đổvàocốc
120ml
nướcsauđóthảvào
cốc5viênbicóđườngkính
2cm
.Hỏimặtnướctrongcốccáchmépcốcbaonhiêu cm .
Làmtrònđếnhaichữsốsaudấuphẩy.
A.
3, 67 cm
. B.
2,67 cm
. C.
3, 28cm
. D.
2,28cm
.
Hướngdẫngiải
ChọnD.
Thànhcốcdày
0,2cm
nênbánkínhđáytrụbằng
2,8cm
.Đáycốcdày
1cm
nênchiềucao
hìnhtrụbằng
8cm
.Thểtíchkhốitrụlà
2
3
. 2,8 .8 197,04
Vcm
.
Đổ
120ml
vàocốc,thểtíchcònlạilà
3
197,04 120 77,04 cm .
Thả5viênbivàocốc,thểtích5viênbibằng
33
4
5. . .1 20,94 ( )
3
bi
Vcm.
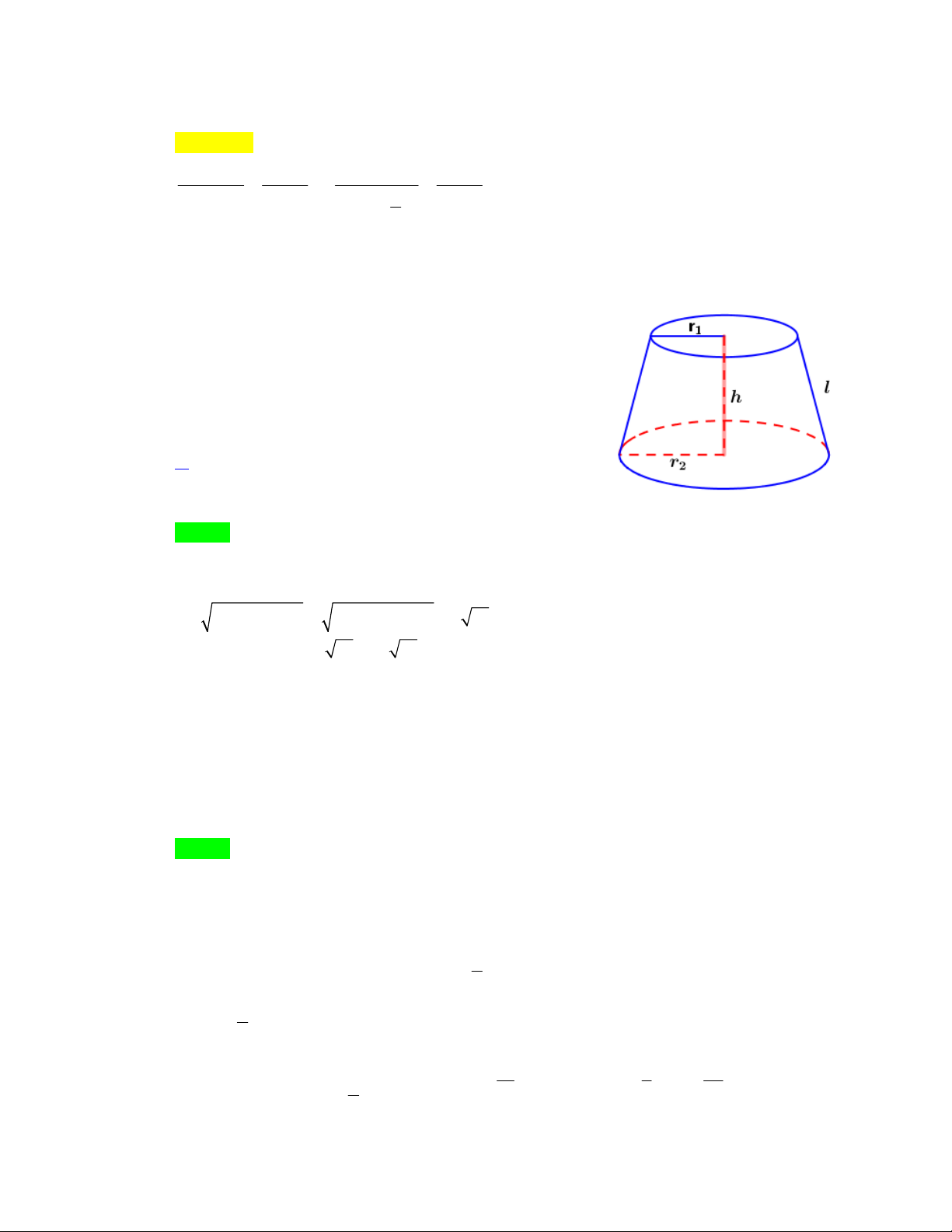
Thểtíchcốccònlại
3
77,04 20,94 56,1cm
.
Tacó
2
56,1 '. . 2,8 ' 2,28
hhcm
.
Cáchkhác:Dùngtỉsốthểtích
2
8. 2,8 .
8
5,72
4
120 5. .
3
Tr coc
nuoc bi
nuoc bi nuoc bi nuoc bi
Vh
h
VVh h
Chiềucaocònlạicủatrụlà
85,72 2,28
.
Vậymặtnướctrongcốccáchmépcốclà
2,28cm
.
Câu20: CHUYÊNPHANBỘICHÂUMộtchiếcxôhìnhnóncụt
đựnghóachấtởphòngthínghiệmcóchiềucao
20 ,cm
đườngkínhhaiđáylầnlượtlà
10cm
và
20cm
.Côgiáo
giaochobạnAnsơnmặtngoàicủaxôtrừđáy.Tính
diện tíchbạn Anphải sơn làm tròn đến hai chữ số
saudấuphẩy.
A.
2
1942,97 .cm
B.
2
561,25 .cm
C.
2
971,48 .cm D.
2
2107,44 .cm
Hướngdẫngiải
ChọnC.
Tacó
12
xq
Srrl
Với
1
5r
,
2
10r
22
22
21
20 10 5 5 17 lhrr
Vậy
5 10 5 17 75 17 971,48
xq
S
Câu21: CHUYÊNPHANBỘICHÂUMộtôtôđangchạyđềuvớivậntốc
15
m/sthìphíatrướcxuất
hiệnchướngngạivậtnênngườiláiđạpphanhgấp.Kểtừthờiđiểmđó,ôtôchuyểnđộng
chậmdầnđềuvớigiatốc
a
2
/ms.Biếtôtôchuyểnđộngthêmđược
20m
thìdừnghẳn.
Hỏi
a thuộckhoảngnàodướiđây.
A.
3; 4
. B.
4;5
. C.
5;6
. D.
6;7
.
Hướngdẫngiải
ChọnC.
Gọi
x
t
làhàmbiểudiễnquãngđường,
vt
làhàmvậntốc.
Tacó:
0
0d
t
vt v a t at
15vt at
.
2
00
1
0d 15d 15
2
tt
x
tx vtt at t at t
2
1
15
2
x
tatt
Tacó:
2
15 0
0
1
15 20
20
2
at
vt
at t
xt
15 8 45
15 20
238
tt t a
.
Câu22: CHUYÊNPHANBỘICHÂUMột nguồn âm đẳng hướng đặt tại điểm
O
cócôngsuất
truyềnâmkhôngđổi.Mứccườngđộâmtạiđiểm
M
cách
O
mộtkhoảng
R
đượctínhbởi
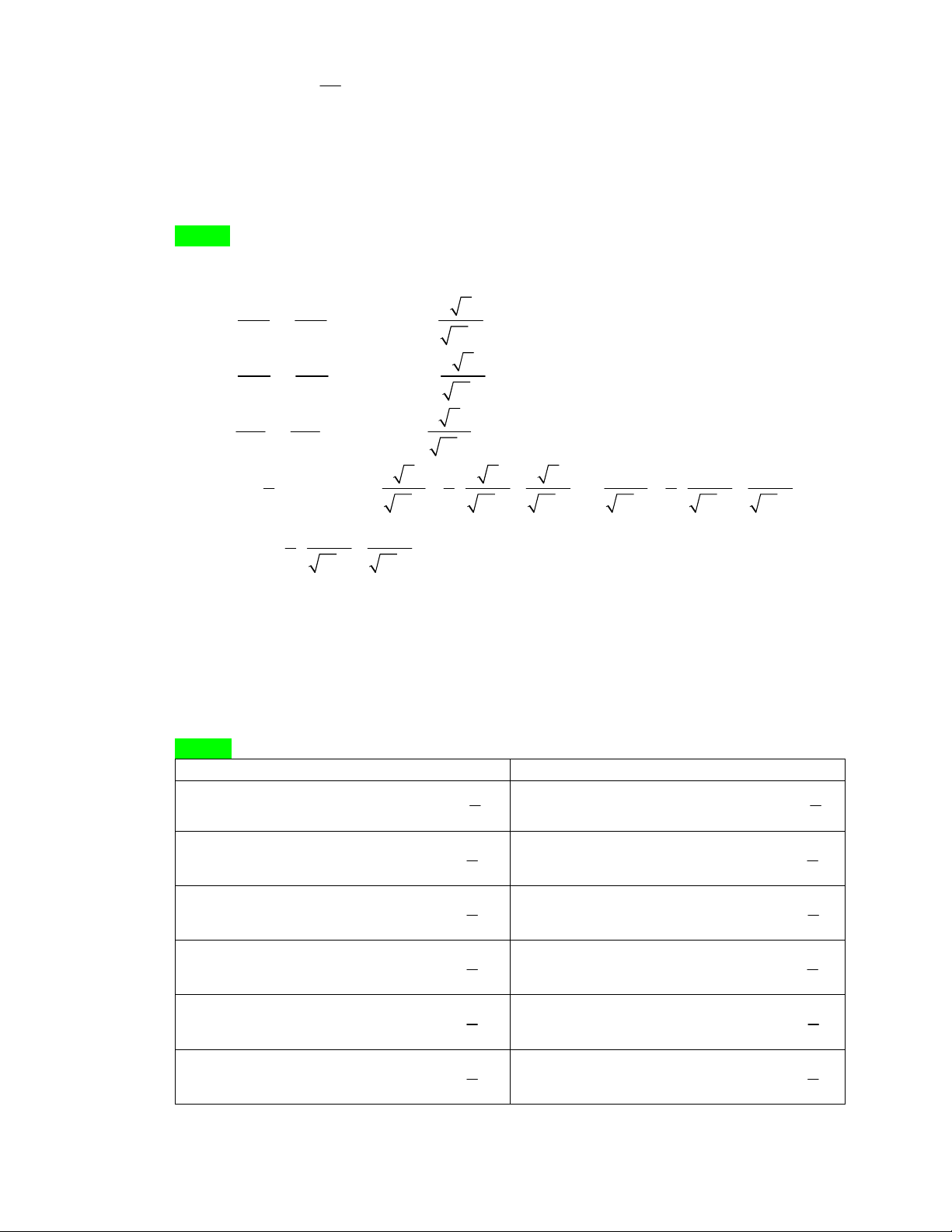
côngthức
2
log
M
k
L
R
Benvới
k
làhằngsố.Biếtđiểm
O
thuộcđoạnthẳng
A
B vàmức
cườngđộâmtại
A
và B lầnlượtlà
3
A
L
Benvà
5
B
L
Ben.Tínhmứccườngđộâm
tạitrungđiểm
A
B làmtrònđến2chữsốsaudấuphẩy.
A.
3,59
Ben. B.
3, 06
Ben. C.
3, 69
Ben. D.
4
Ben.
Hướngdẫngiải
ChọnC.
Tacó:
AB
L
LOAOB
.
Gọi
I
làtrungđiểm
A
B .Tacó:
22
log 10
10
A
A
L
A
L
kk k
LOA
OA OA
22
log 10
10
B
B
L
B
L
kk k
LOB
OB OB
22
log 10
10
I
I
L
I
L
kk k
LOI
OI OI
Tacó:
1
2
OI OA OB
11111
22
10 10 10 10 10 10
IABIAB
LLLLLL
kkk
11 1
2log
2
10 10
AB
I
LL
L
3,69
I
L
.
Câu23: CHUYÊNPHANBỘICHÂUÔngAnbắtđầuđilàmvớimứclươngkhởiđiểmlà1triệu
đồngmộttháng.Cứsau3nămthìôngAnđượctănglương
40%
.Hỏisautròn20nămđi
làmtổngtiềnlươngôngAnnhậnđượclàbaonhiêulàmtrònđếnhaichữsốthậpphân
saudấuphẩy?
A.726,74triệu. B.71674triệu. C.858,72triệu. D.768,37triệu.
Hướngdẫngiải
ChọnD.
Mứclương3nămđầu:1triệu Tổnglương3nămđầu:36.1
Mứclương3nămtiếptheo:
2
1. 1
5
Tổnglương3nămtiếptheo:
2
36 1
5
Mứclương3nămtiếptheo:
2
2
1. 1
5
Tổnglương3nămtiếptheo:
2
2
36 1
5
Mứclương3nămtiếptheo:
3
2
1. 1
5
Tổnglương3nămtiếptheo:
3
2
36 1
5
Mứclương3nămtiếptheo:
4
2
1. 1
5
Tổnglương3nămtiếptheo:
4
2
36 1
5
Mứclương3nămtiếptheo:
5
2
1. 1
5
Tổnglương3nămtiếptheo:
5
2
36 1
5
Mứclương2nămtiếptheo:
6
2
1. 1
5
Tổnglương2nămtiếptheo:
6
2
24 1
5
Tổnglươngsautròn20nămlà
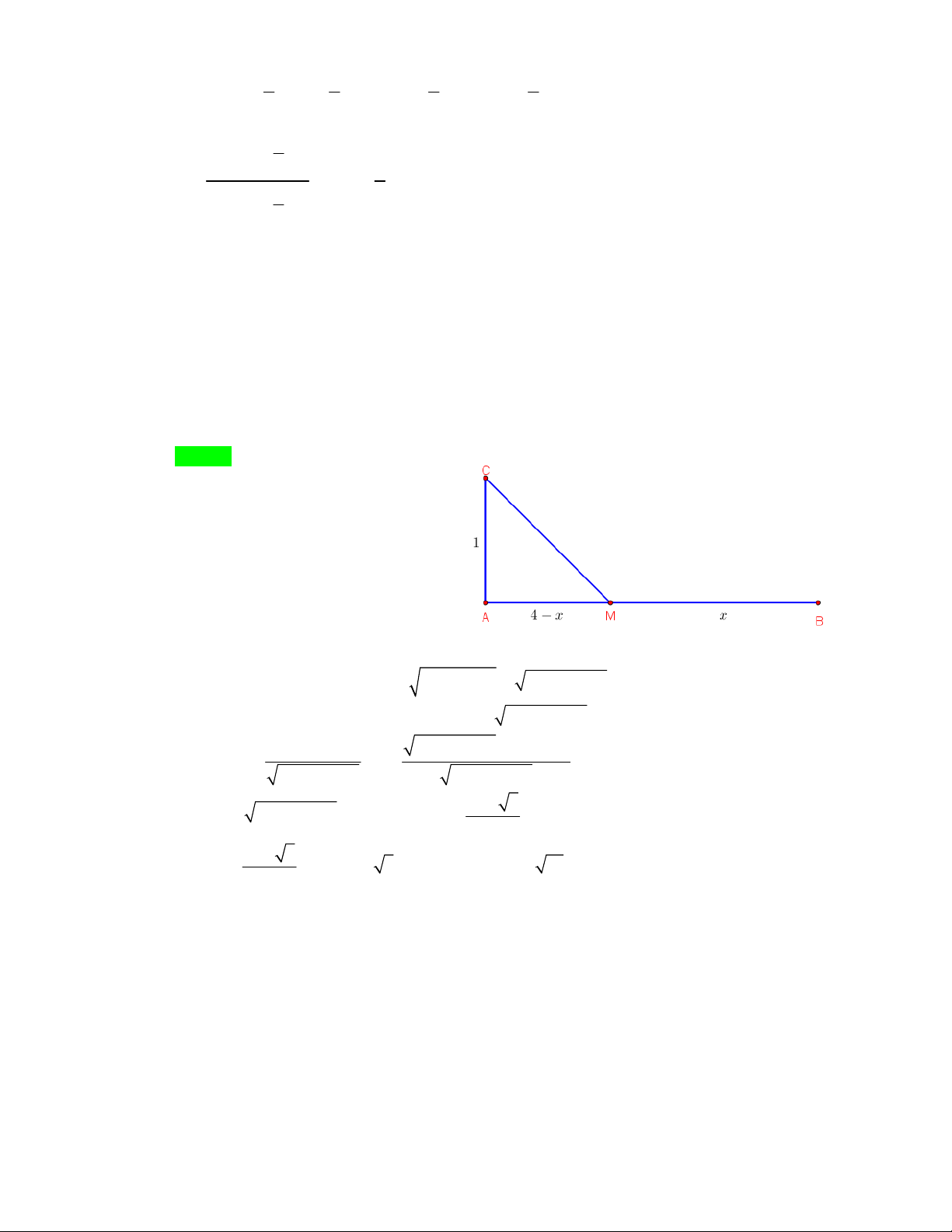
256
6
6
22 2 2
36 1 1 1 ... 1 24 1
55 5 5
2
11 1
5
2
36. 24 1 768,37
2
5
11
5
S
Câu24: CHUYÊNPHANBỘICHÂUMộtđườngdâyđiệnđượcnốitừmộtnhàmáyđiệnở
A
đến
mộthònđảoở
C
nhưhìnhvẽ.Khoảngcáchtừ
C
đến B là1km.Bờbiểnchạythẳngtừ
A
đến
B vớikhoảngcáchlà 4 km.Tổngchiphílắpđặtcho1kmdâyđiệntrênbiểnlà
40
triệuđồng,còntrênđấtliềnlà
20
triệuđồng.Tínhtổngchiphínhỏnhấtđểhoànthành
côngviệctrênlàmtrònđếnhaichữsốsaudấuphẩy.
A.
106,25
triệuđồng. B.
120
triệuđồng.
C.
164,92
triệuđồng. D.
114,64
triệuđồng.
Hướngdẫngiải
ChọnD.
Gọi
M
làđiểmtrênđoạn
A
B
đểlắp
đặtđườngdâyđiệnrabiểnnốivới
điểm
C
.
Đặt
2
2
414178,0;4 BM x AM x CM x x x x
Khiđótổngchiphílắpđặtlà:
2
.20 40 8 17 yx x x
đơnvịlàtriệuđồng.
2
22
8172 4
4
20 40. 20.
817 817
xx x
x
y
xx xx
.
2
12 3
081724
2
yxx xx
Tacó
12 3
80 20 3 114,64; 0 40 17 164,92; 4 120
3
yyy
.
VậytachọnđápánD.
Câu25: SỞGDHÀNỘIÔngViệtdựđịnhgửivàongânhàngmộtsốtiềnvớilãisuất
6,5%
một
năm.Biếtrằng,cứsaumỗinămsốtiềnlãiđượcnhậpvàovốnbanđầu.Tínhsốtiềntối
thiểu
x
triệuđồng,
x
ôngViệtgửivàongânhàngđểsau3nămsốtiềnlãiđủđể
muamộtchiếcxegắnmáytrịgiá
30
triệuđồng
A.
154
triệuđồng. B.
150
triệuđồng. C.
140
triệuđồng. D.
145
triệuđồng.
Hướngdẫngiải
ChọnD.
Ápdụngcôngthứclãikép:
1
n
n
P
xr

Trongđó
n
P
là
tổnggiátrịđạtđượcvốnvàlãi
saunkì.
x
làvốngốc, r làlãisuấtmỗikì.
Tacũngtínhđược
sốtiềnlãi
thuđượcsaunkìlà :
111
nn
n
Pxx r xx r
*
Ápdụngcôngthức*với
3, 6, 5%nr
,sốtiềnlãilà30triệuđồng.
Tađược
3
30 1 6,5% 1 144,27
xx
Sốtiềntốithiểulà145triệuđồng.
Câu26: SỞGDHÀNỘIMộtôtôbắtđầuchuyểnđộngnhanhdầnđềuvớivậntốc
1
() 7vt t
m/s.
Điđược
5
s,ngườiláixepháthiệnchướngngạivậtvàphanhgấp,ôtôtiếptụcchuyển
độngchậmdầnđềuvớigiatốc
70a
m/s
2
.Tínhquãngđường
S
mđiđượccủaôtô
từlúcbắtđầuchuyểnbánhchođếnkhidừnghẳn.
A.
95,70S
m. B.
87,50S
m. C.
94,00S
m. D.
96,25S
m.
Hướngdẫngiải
ChọnD.
Quãngđườngôtôđiđượctừlúcxelănbánhđếnkhiđượcphanh:
5
55
2
11
00
0
( )d 7 d 7 87,5
2
t
Svtt tt
m.
Vậntốc
2
()vt
m/scủaôtôtừlúcđượcphanhđếnkhidừnghẳnthoảmãn
2
( ) ( 70)d = 70vt t t C
,
21
(5) (5) 35 385vv C.Vậy
2
() 70t 385vt .
Thờiđiểmxedừnghẳntươngứngvới
t thoảmãn
2
() 0 5,5vt t
s.
Quãngđườngôtôđiđượctừlúcxeđượcphanhđếnkhidừnghẳn:
5,5 5,5
21
55
( )d ( 70 385)d 8,75Svtt t t
m.
Quãngđườngcầntính
12
96,25SS S
m.
Câu27: SỞGDHÀNỘIMộtcôngtydựkiếnchi
1
tỉđồngđểsảnxuấtcácthùngđựngsơnhình
trụcódungtích
5
lít.Biếtrằngchiphíđểlàmmặtxungquanhcủathùngđólà
100.000
đ/m
2
,chiphíđểlàmmặtđáylà
120.000
đ/m
2
.Hãytínhsốthùngsơntốiđamàcôngtyđó
sảnxuấtđượC.giảsửchiphíchocácmốinốikhôngđángkể.
A.
57582
thùng. B.
58135
thùng. C.
18209
thùng. D.
12525
thùng.
Hướngdẫngiải
ChọnB.
Gọichiềucaohìnhtrụlà
0hh
m.
Bánkínhđáyhìnhtrụlà
0xx
m.
Thểtíchkhốitrụlà:
2
2
55
1000 1000
Vxh h
x
m.
Diệntíchmặtxungquanhlà:
1
2
100
xq
Sxh
x
.
Diệntíchhaiđáylà:
2
2
đ
Sx
Sốtiềncầnlàmmộtthùngsơnlà:
2
1000
240000 0fx x x
x
Tacó:
2
3
1000 1
480000 0
480
fx x fx x
x
.
Bảngbiếnthiên:
x
0
3
1
480
f
x
0
f
x
17201.05
Vậyvớisốtiền
1
tỉđồngthìcôngtycóthểsảnxuấttốiđalà:
9
10
58135
17201.05
thùng.
Câu28: CHUYÊN HÙNGVƯƠNG
–GLMộtbìnhđựng
nướcdạnghìnhnónkhôngcónắpđáy,đựngđầy
nước.Biếtrằngchiềucaocủabìnhgấp3lầnbánkính
đáycủanó.Ngườitathảvàobìnhđómộtkhốitrụvà
đođượcthểtíchnướctràorangoàilà
3
16
()
9
dm
.Biết
rằngmộtmặtcủakhốitrụnằmtrênmặtđáycủahình
nónvàkhốitrụcóchiềucaobằngđườngkínhđáycủa
hìnhnónnhưhìnhvẽdưới.Tínhbánkínhđáy
R
của
bìnhnước.
A.
3( ).Rdm
B.
4( ).Rdm
C.
2( ).Rdm
D.
5( ).Rdm
Hướngdẫngiải

ChọnC.
Gọi ,'hh lầnlượtlàchiềucaocủakhốinónvàkhốitrụ.
,Rrlầnlượtlàbánkínhcủakhốinónvàkhốitrụ.
Theođềtacó:
3,' 2.hRh R
Xéttamgiác
SOA
tacó:
'3 2 1
33
rIM SIhh RR
ROASO h R
1
3
rR
.Talạicó:
23
2
trô
216
'2
999
RR
Vrh R
3
82 .RRdm
Câu29: CHUYÊNHÙNGVƯƠNG
–GLÔngNamgửi
100
triệuđồngvàongânhàngtheothểthức
lãiképkìhạnmộtnămvớilãisuấtlà
12%
mộtnăm.Sau n nămôngNamrúttoànbộtiền
cảvốnlẫnlãi.Tìm
n nguyêndươngnhỏnhấtđểsốtiềnlãinhậnđượchơn
40
triệu
đồng.Giảsửrằnglãisuấthàngnămkhôngthayđổi.
A.
5
. B.
2
. C.
4
. D.
3
.
Hướngdẫngiải
ChọnD
Sốtiềnthuđượccảgốclẫnlãisaunnămlà
100(1 0,12)
n
C
Sốtiềnlãithuđượcsaunnămlà
100(1 0,12) 100
n
L
1,12
77
100(1 0,12) 100 40 1,12 log 2,9740
5
.
5
nn
nL
Câu30: CHUYÊNHÙNGVƯƠNG
–GLMộtchuyếnxebuýtcósứcchứatốiđalà
60
hànhkhách.
Nếumộtchuyếnxebuýtchở
x
hànhkháchthìgiátiềnchomỗihànhkháchlà
2
3
40
x
USD.Khẳngđịnhnàosauđâylàkhẳngđịnhđúng?
A.Mộtchuyếnxebuýtthuđượclợinhuậncaonhấtkhicó
45
hànhkhách.
B.Mộtchuyếnxebuýtthuđượclợinhuậncaonhấtbằng
135
USD.
C.Mộtchuyếnxebuýtthuđượclợinhuậncaonhấtkhicó
60
hànhkhách.
D.Mộtchuyếnxebuýtthuđượclợinhuậncaonhấtbằng
160
USD.
Hướngdẫngiải
ChọnD
Sốtiềnthuđượckhicóxkháchlà
2
() 3
40
x
fx x
Tacó
2
13
'( ) 3 2. 3 3 3 3 3
40 40 40 40 40 20 40 40
x
xxxxxx
fx x
120
3
'( ) 0 3 3 0
40
40 40
x
xx
fx
x
(40) 160
(60) 135
f
f
Vậy
[0;60]
max ( ) (40) 160
x
fx f
.
Câu31: CHUYÊNHÙNGVƯƠNG
–GLMộtviênđạnđượcbắntheophươngthẳngđứngvớivận
tốcbanđầu
29,4
/ms
.Giatốctrọngtrườnglà
9,8
2
/ms.Tínhquãngđường
S
viênđạnđi
đượctừlúcbắnlênchođếnkhichạmđất.
A.
88,2 .Sm
B.
88,5 .Sm
C.
88 .Sm
D.
89 .Sm
Hướngdẫngiải
ChọnA.
Tacócôngthứcliênhệgiữavậntốc,giatốcvàquảngđườngđiđượclà
22
0
2vv as nên
quãngđườngđiđượctừlúcbắnlênđếnkhidừnglạilà
:
22
0
vv s
.
22
2
0
029,4
44,1
2 2.9.8
vv
s
a
Quãngđườngđiđượctừlúcbắnđếnkhichạmđấtlà
44,1.2 88,2Sm
.
Câu32: BẮCYÊNTHÀNHChomộttấmnhômhìnhchữnhật
A
BCD
có
60
A
Dcm
,
40
A
Bcm
.
Tagậptấmnhômtheohaicạnh
M
N
và
P
Q
vàophíatrongchođếnkhi
A
B
và
DC
trùng
nhaunhưhìnhvẽbênđểdượcmộthìnhlăngtrụkhuyếthaiđáy.Khiđócóthểtạođược
khốilăngtrụvớithểtíchlớnnhấtbằng
A.
4000 3
3
cm B.
2000 3
3
cm C.
400 3
3
cm D.
4000 2
3
cm
Hướngdẫngiải
ChọnA.
Đáycủalăngtrụlàtamgiáccâncó
cạnhbênbằng
x
,cạnhđáybằng
60 2
x
Đườngcaotamgiácđólà
2
2
60 2
60 900
2
x
AH x x
,
với
H
làtrungđiểm
NP
Diệntíchđáylà
11
. 60 900. 30 60 900 900 30 900 30
230
ANP
SS AHNP x x x x x
3
2
1 900
100 3
30 3
Scm
Diệntíchđáylớnnhấtlà
2
100 3cm
nênthểtíchlớnnhấtlà
3
40.100 3 4000 3Vcm .
Câu33: BẮCYÊNTHÀNHÔngAgửisốtiền
100
triệuđồngvàongânhàngvớilãisuất
7%
trên
năm,biếtrằngnếukhôngrúttiềnrakhỏingânhàngthìcứsaumỗinămsốtiềnlãisẽđược

nhậpvàovốnbanđầu.sauthờigian
10
nămnếukhôngrútlãilầnnàothìsốtiềnmàôngA
nhậnđượctínhcảgốclẫnlãilà
A.
810
10 .(1 0,07)
. B.
810
10 .0,07
. C.
810
10 .(1 0,7)
. D.
810
10 .(1 0,007)
.
Hướngdẫngiải
ChọnA.
Theocôngthứclãikép
1
N
CA r
vớigiảthiết
8
100.000.000 10 ; 7% 0,07 và 10ArN
.
Vậysốtiềnnhậnđược…
810
10 .(1 0,07) ,nênchọnA.
Câu34: CHUYÊNLƯƠNGVĂNCHÁNHNgườitamuốndùngvậtliệubằngkimloạiđểgòthành
mộtthùnghìnhtrụtrònxoaycóhaiđáyvớithểtích
V
chotrướchaiđáycũngdùng
chínhvậtliệuđó.Hãyxácđịnhchiềucao
h
vàbánkính R củahìnhtrụtheo
V
đểtốnít
vậtliệunhất.
A.
3
22
2
V
Rh
. B.
22
2
V
Rh
. C.
22
2
V
hR
. D.
3
22
2
V
hR
.
Hướngdẫngiải
ChọnD.
Đểvậtliệutốnítnhấtthìdiệntíchtoànphầncủahìnhtrụnhỏnhất.
Tacó:
2
22
tp
SRRh
.
Do
2
VRh
nên
2
V
h
R
.Suyra
32222
3
2
22. 2 3.2..3.2
tp
VVV VV
SRR R R V
RRR RR
.
Đẳngthứcxảyrakhi
2
3
2
2
VV
RR
R
.Khiđó
3
2
2
V
h
.
Câu35: BIÊNHÒA
–HÀNAMMộtviênphấnbảngcódạngmộtkhốitrụvớibánkínhđáybằng
0,5cm
,chiềudài
6cm
.Ngườitalàmmộthìnhhộpchữnhậtbằngcartonđựngcácviên
phấnđóvớikíchthước
656cm cm cm
.Hỏicầnítnhấtbaonhiêuhộpkíchthướcnhư
trênđểxếp
460
viênphấn?
A.
17
. B.
15
. C.
16
. D.
18
.
Hướngdẫngiải
ChọnC.

M
A
B
C
H
1
H
2
H
3
Có3cáchxếpphấntheohìnhvẽdướiđây:
Nếu xếp
theohình
1
H
:vìđườngkínhviênphấnlà2.0,5 1cm nênmỗihộpxếpđượctốiđasố
viênphấnlà:
6.5 30
.
Nếuxếptheohình
2
H
:hàng
6
viênxenkẽhàng
5
viên.Gọisốhàngxếpđượclà
1,nn
.
Tacó
Δ
A
BC
đềucạnhbằng1
3
2
CM
.
Taphảicó
38
2.0,5 . 5
2
3
nn
xếptốiđađược
5
hàngmỗihộpxếpđượctối
đasốviênphấnlà:
3.6 2.5 28
.
Nếuxếptheohình
3H
:hàng
5
viênxenkẽhàng
4
viên.Gọisốhàngxếpđượclà
1,mm
.
Taphảicó
310
2.0,5 . 6
2
3
mm
xếptốiđađược6hàngnênmỗihộpxếp
đượctốiđasốviênphấnlà:
3.5 3.4 27
.
Vậy,xếptheohình
1
H
thìxếpđượcnhiềuphấnnhất,nêncầníthộpnhất.
Tacó
460 :30 15,3
cầnítnhất
16
hộpđểxếphết
460
viênphấn.
Câu36: BIÊNHÒA
–HÀNAMMộtchấtđiểmđangcuyểnđộngvớivậntốc
0
15 /vms
thìtăng
vậntốcvớigiatốc
22
4/at t tm s .Tínhquãngđườngchấtđiểmđóđiđượctrong
khoảngthờigian
3
giâykểtừlúcbắtđầutăngvậntốc.
A.
68,25m
. B.
70,25m
. C.
69,75m
. D.
67,25m
.
Hướngdẫngiải
ChọnC.
232
1
4d 2
3
vt t t t t t C
.Mà
015 15vC
nên
32
1
215
3
vt t t
3
32 4 3 3
0
0
1 1 2 279
2 15 d 15 69,75
31234
St t t t t t t m
.
Câu37: BIÊNHÒA
–HÀNAMMộtnhàmáycầnthiếtkếmộtchiếcbểđựngnướchìnhtrụbằng
tôncónắp,cóthểtíchlà
3
64 m
.Tìmbánkínhđáyr củahìnhtrụsaochohìnhtrụđược
làmratốnítnhiênliệunhất.
A.
3rm . B.
3
16rm
. C.
3
32rm
. D.
4rm .
Hướngdẫngiải

ChọnC.
Gọihìnhtrụcóchiềucao
h
,độdàiđườngsinh
l
,bánkínhđáyr .
Tacó:
2
22 2
64 64 64
Vrhh l
rr r
Đểtốnítnhiênliệunhấtthìdiệntíchtoànphầnnhỏnhất.
Tacó:
22
128
2222
tp day xq
SSS r rlr
r
.
Xéthàmsố
2
128
2fr r
r
với
0r
.
Tacó
3
2
128
4;032fr r fr r
r
.
Lậpbảngbiếnthiêntacó
f
r đạtGTNNkhi
3
32r
.
Câu38: BIÊNHÒA
–HÀNAMMộtngườithả1lábèovàomộtcáiao,sau12giờthìbèosinhsôi
phủkínmặtao.Hỏisaumấygiờthìbèophủkín
1
5
mặtao,biếtrằngsaumỗigiờthìlượng
bèotănggấp10lầnlượngbèotrướcđóvàtốcđộtăngkhôngđổi.
A.
12 log5
giờ. B.
12
5
giờ. C.
12 log 2
giờ. D.
12 ln5
giờ.
Hướngdẫngiải
ChọnA.
Tagọi
i
u
làsốlábèoởgiờthứ
.i
Tacó
0212
012 12
1 10 , 10, 10 ,....., 10 .uuu u
Tacósốlábèođểphủkín
1
5
mặthồlà
12
1
.10
5
thờigianmàsốlábèophủkín
1
5
mặthồ
là
12 log5.
Câu39:
SỞBÌNHPHƯỚCMộtngườinuôicáthìnghiệmtronghồ.Ngườiđóthấyrằngnếumỗi
đơnvịdiệntíchcủamặthồcó
n concáthìtrungbìnhmỗiconcásaumộtvụcânnặng
480 20
P
nn
g
am .Hỏiphảithảbaonhiêucátrênmộtđơnvịdiệntíchcủamặthồđể
saumộtvụthuhoạchđượcnhiềucánhất?
A.
12.
B.
14.
C.
10.
D.
18.
Hướngdẫngiải
ChọnA.
Cách1:Thếđápán:
Sốcátrênmỗiđơn
v
ịdiệntích
12 14 10 18
Sốcânnặng:
2880 2800 2800 2160
480 20 ( )n n gam
Cách 2: Số cân nặng của
n
con cá là:
22
( ) 480 20 20 480 20( 12) 2880 2880fn nn n n n
Vậygiátrịlớnnhấtcủa
()
f
n
là
2880
đạtđượckhi
12n
.
Chúý:hàm
f
nhưmộthàmsốtheobiếnsốthực,chứkhôngphảibiếnsốnguyên
dương
Câu40:
SỞBÌNHPHƯỚCMộtkhốicầucóbánkínhlà
5 dm
,
ngườitacắtbỏhaiphầncủakhốicầubằnghaimặt
phẳngsongsongcùngvuônggócđườngkínhvàcáchtâm
mộtkhoảng
3 dm đểlàmmộtchiếcluđựngnướcnhư
hìnhvẽ.Tínhthểtíchmàchiếcluchứađược.
A.
3
100
3
dm
B.
3
43
3
dm
C.
3
41 dm
D.
3
132 dm
Hướngdẫngiải
ChọnD.
Cách1:Trênhệtrụctọađộ
Oxy ,xétđườngtròn
22
():( 5) 25Cx y
.Tathấynếucho
nửatrêntrục
Ox
của
C quayquanhtrục
Ox
tađượcmặtcầubánkínhbằng5.Nếucho
hình phẳng
H giới hạn bởi nửa trên trục
Ox
của
C , trục
Ox
, hai đường thẳng
0, 2xx
quayxungquanhtrục
Ox
tasẽđượckhốitrònxoaychínhlàphầncắtđicủa
khốicầutrongđềbài.
Tacó
22 2
(5) 25 25(5)xy y x
Nửatrêntrục
Ox
của
C
cóphươngtrình
22
25 ( 5) 10yx xx
Thểtíchvậtthểtrònxoaykhicho
H
quayquanh
Ox
là:
2
2
3
22
1
0
0
52
10 d 5
33
x
Vxxxx
Thểtíchkhốicầulà:
3
2
4 500
V.5
33
Thểtíchcầntìm:
3
21
500 52
2 2. 132
33
VV V dm
Câu41: SỞBÌNHPHƯỚCSựtăngtrưởngcủamộtloạivikhuẩntuântheocôngthức .
rt
SAe ,
trongđó
A
làsốlượngvikhuẩnbanđầu,
r
làtỉlệtăngtrưởng,t
làthờigiantăngtrưởng.
Biếtrằngsốlượngvikhuẩnbanđầulà
100
convàsau
5
giờcó
300
con.Hỏisốconvi
khuẩnsau
10
giờ ?
A.
1000
. B.
850
. C.
800
. D.
900
.
Hướngdẫngiải
ChọnD.
Trướctiên,tatìmtỉlệtăngtrưởngmỗigiờcủaloạivikhuẩnnày.
Từgiảthiếttacó:
5
ln 300 ln100 ln 3
300 100.
55
r
er
Tứctỉlệtăngtrưởngcủaloạivikhuẩnnàylà
ln3
5
r
mỗigiờ.
Sau
10 giờ,từ 100 convikhuẩnsẽcó
ln3
10.
5
100. 900e con.
Câu42:
CHUYÊNPHANBỘICHÂUMộtmiếngbìahìnhtamgiácđều
A
BC
, cạnh bằng
16
. Học sinh Trang cắt một hình chữ nhật
M
NPQ
từmiếngbìatrênđểlàmbiểntrôngxecholớptrong
buổi ngoại khóa với
,
M
N
thuộccạnh
B
C
;
P
,
Q
lầnlượt
thuộccạnh
A
C
và
A
B .Diệntíchhìnhchữnhật
M
NPQ lớn
nhấtbằngbaonhiêu?
A.
16 3.
B.
83.
C.
32 3.
D.
34 3.
Hướngdẫngiải
ChọnC.
Đặt
16
,0 16
2
x
MN x x BM
3
tan60 16
2
QM
QM x
BM
Xéthàmsố
2
33
16 16 max 32 3
22
Sx x x x x S
khi
8x
.
Câu43: CHUYÊN ĐHSP HN Một đám vi trùng tại ngày thứ
t cósốlượng
()Nt
, biết rằng
7000
()
2
Nt
t
vàlúcđầuđámvitrùngcó
300000
con.Sau10ngày,đámvitrùngcókhoảng
baonhiêucon?
A.
302542
con. B.
322542
con. C.
312542
con. D.
332542
con.
Hướngdẫngiải
ChọnC.
Tacó
7000
( ) ( )d d 7000ln | 2 |
2
Nt N t t t t C
t

Do
(0) 300000 300000 7000ln 2NC
Khiđó
(10) 7000ln12 300000 7000ln 2 312542N
.ChọnC
Câu44: CHUYÊNĐHSPHNChuyệnkểrằng:Ngàyxưa,cóôngvuahứasẽthưởngchomộtvị
quanmónquàmàvịquanđượcchọn.Vịquantâu:“HạthầnchỉxinBệHạthưởngchomột
sốhạtthócthôiạ!Cụthểnhưsau:Bàncờvuacó64ôthìvớiôthứnhấtxinnhận1hạt,ô
thứ2thìgấpđôiôđầu,ôthứ3thìlạigấpđôiôthứ2,…ôsaunhậnsốhạtthócgấpđôi
phầnthưởngdànhchoôliềntrước”.Giátrịnhỏnhấtcủa
n
đểtổngsốhạtthócmàvịquan
từ
n
ôđầutiêntừôthứnhấtđếnôthứ
n
lớnhơn1triệulà
A.18. B.19. C.20. D.21.
Hướngdẫngiải
ChọnC.
Bàitoándùngtổngnsốhạngđầutiêncủamộtcấpsốnhân.
Tacó:
21
12
21
... 1 1.2 1.2 ... 1.2 1. 2 1
21
n
nn
nn
Suu u
66
2
2 1 10 log 10 1 19.93.
n
n
Sn
Vậynnhỏnhấtthỏayêucầubàilà20.
Câu45: CHUYÊNĐHSPHNMộtngườigửingânhàng100triệuđồngtheohìnhthứclãikép,lãi
suấtmộtthángkểtừthángthứ2,tiềnlãiđượctínhtheophầntrămtổngtiềncóđược
củathángtrướcđóvàtiềnlãicủathángtrướcđó.Sauítnhấtbaonhiêutháng,ngườiđó
cónhiềuhơn125triệu.
A.
45
tháng. B.
47
tháng. C.
44
tháng. D.
46
tháng.
Hướngdẫngiải
ChọnA.
Ápdụngcôngthứclãiképgửi1lần:
1
n
NA r
,Với
6
100.10A và
0
0
0,5r
.
Theođềbàitatìmnbénhấtsaocho:
86
10 1 0,5% 125.10
n
5
10,5%
4
n
201
200
5
log 44,74
4
n
Câu46: PHANĐÌNHPHÙNG
–HNÁp suất không khí
P
đobằngmilimetthủyngân,kíhiệu
mmHg tại độ cao
x
đobằngmétsovớimựcnướcbiểnđượctínhtheocôngthức
0
x
l
P
Pe ,trongđó
0
760P mmHglàápsuấtkhôngkhíởmứcnướcbiển,
l
làhệsốsuy
giảm.Biếtrằngởđộcao
1000
métthìápsuấtkhôngkhílà
672,71
mmHg.Hỏiápsuấtở
đỉnhFanxipancaométlàbaonhiêu?
A.
22,24 mmHg. B.519,58mmHg.
C.
517,94
mmHg. D.
530,23
mmHg.
Hướngdẫngiải
ChọnD.
Ởđộcao
1000
métápsuấtkhôngkhílà
672,71
mmHg

Nên
1000
672,71 760
l
e
1000
672,71
760
l
e
1 672,71
ln
1000 760
l
ÁpsuấtởđỉnhFanxipan
1 672,71
3143. ln
3143
1000 760
760 760 717,94
l
Pe e
Câu47: CHUYÊNĐHVINHTạimộtnơikhôngcógió,mộtchiếckhícầuđangđứngyênởđộcao
162métsovớimặtđấtđãđượcphicôngcàiđặtchonóchếđộchuyểnđộngđixuống.
Biếtrằng,khícầuđãchuyểnđộngtheophươngthẳngđứngvớivậntốctuântheoquyluật
2
10vt t t
,trongđót phútlàthờigiantínhtừlúcbắtđầuchuyểnđộng,
vt
được
tínhtheođơnvịmét/phút
/mp
.Nếunhưvậythìkhibắtđầutiếpđấtvậntốc
v
củakhí
cầulà
A.
5/vmp
. B.
7/vmp
. C.
9/vmp
. D.
3/vmp
.
Hướngdẫngiải
Đápán:C.
Gọithờiđiểmkhícầubắtđầuchuyểnđộnglà
0t
,thờiđiểmkhinhkhícầubắtđầutiếpđất
là
1
t
.
Quãngđườngkhícầuđiđượctừthờiđiểm
0t
đếnthờiđiểmkhinhkhícầubắtđầutiếp
đấtlà
1
t
là
1
3
22
1
1
0
10 d 5 162
3
t
t
tt t t
493 1093 9t,t,t
Do
00 10vt t nênchọn
9t
.
Vậykhibắtđầutiếpđấtvậntốc
v
củakhícầulà
2
910.99 9/vmp
Câu48: CHUYÊNĐHVINHTrongnôngnghiệpbèohoadâuđượcdùnglàmphânbón,nórấttốt
chocâytrồng.MớiđâycácnhàkhoahọcViệtNamđãpháthiệnrabèohoadâucóthể
dùngđểchiếtxuấtrachấtcótácdụngkíchthíchhệmiễndịchvàhỗtrợđiềutrịbệnhung
thư.Bèohoadâuđượcthảnuôitrênmặtnước.Mộtngườiđãthảmộtlượngbèohoadâu
chiếm
4%
diệntíchmặthồ.Biếtrằngcứsauđúngmộttuầnbèopháttriểnthành3lầnsố
lượngđãcóvàtốcđộpháttriểncủabèoởmọithờiđiểmnhưnhau.Saubaonhiêungày
bèosẽvừaphủkínmặthồ?
A.
3
7log25
. B.
25
7
3 . C.
24
7
3
. D.
3
7 log 24
.
Hướngdẫngiải
Đápán:A.

23 cm
5 cm
Theođềbàisốlượngbèobanđầuchiếm
0,04
diệntíchmặthồ.
Sau7ngàysốlượngbèolà
1
0,04 3
diệntíchmặthồ.
Sau14ngàysốlượngbèolà
2
0,04 3 diệntíchmặthồ.
…
Sau
7 n ngàysốlượngbèolà
0,04 3
n
diệntíchmặthồ.
Đểbèophủkínmặthồthì
3
0,04 3 1 3 25 log 25
nn
n .
Vậysau
3
7log25
ngàythìbèovừaphủkínmặthồ.
Câu49: CHUYÊNNGUYỄNQUANGDIỆUMộtôtôđangchạyvớivậntốc
19 /ms
thìngườiláihãm
phanh,ôtôchuyểnđộngchậmdầnđềuvớivậntốc
38 19 / ,vt t m s trongđót là
khoảngthờigiantínhbằnggiâykểtừlúcbắtđầuhãmphanh.Hỏitừlúchãmphanhđến
khidừnghẳn,ôtôcòndichuyểnbaonhiêumét?
A.
4,75 .m
B.
4,5 .m
C.
4, 25 .m
D.
5.m
Hướngdẫngiải
ChọnA.
Tacóthờigianôtôbắtđầuhãmphanhđếnkhidừnghẳnlà:
1
38 19 0
2
tts .
Trongkhoảngthờigiannàyôtôdichuyểnmộtđoạnđường:
1
1
2
2
2
0
0
19
38 19 d 19 19 4,75
4
s
tx tt m m
.
Câu50: CHUYÊNNGUYỄNQUANGDIỆUMộtcáitụclănsơnnướccó
dạngmộthìnhtrụ.Đườngkínhcủađườngtrònđáylà
5cm
,
chiềudàilănlà
23cm
hìnhbên.Saukhilăntrọn
15
vòng
thìtrụclăntạonênsânphẳngmộtdiệndiệntíchlà
A.
2
1725 .cm
B.
2
3450 .cm
C.
2
1725 .cm
D.
2
862,5 .cm
Hướngdẫngiải
ChọnB.
Diệntíchxungquanhcủamặttrụlà
2
2 2 .5.23 230
xq
SRl cm
.
Saukhilăn15vòngthìdiệntíchphầnsơnđượclà:
2
230 .15 3450Scm
.
Câu51: NGÔSĨLIÊNMộtngườiláixeôtôđangchạyvớivậntốc
20 /ms
thìngườiláixepháthiện
cóhàngràongănđườngởphíatrướccách
45m
tínhtừvịtríđầuxeđếnhàngràovìvậy,
người lái xe đạp phanh. Từ thời điểm đó xe chuyển động chậm dầnđềuvớivậntốc
520vt t
/ms
,trongđó t làkhoảngthờigiantínhbằnggiây,kểtừlúcbắtđầuđạp
phanh.Hỏitừlúcđạpphanhđếnkhidừnghẳn,xeôtôcòncáchhàngràongăncáchbao
nhiêuméttínhtừvịtríđầuxeđếnhàngrào?
A.
5 m
. B.
4 m
. C.
6 m
. D.
3 m
.
Hướngdẫngiải
ChọnA.
Xeđangchạyvớivậntốc
20 /vms tươngứngvớithờiđiểm
0ts
Xeđừnglạitươngứngvớithờiđiểm
4ts
.
Quảngđườngxeđãđilà
4
4
2
0
0
5
5 20 d 20 40
2
Stttt m
.
Vậyôtôcáchhàngràomộtđoạn
45 40 5 m .
Câu52: NGÔSĨLIÊNBiếtthểtíchkhí
2
CO
năm1998là
3
Vm .
10
nămtiếptheo,thểtích
2
CO
tăng
%a
,
10
nămtiếptheonữa,thểtích
2
CO
tăng
%n
.Thểtíchkhí
2
CO
năm
2016
là
A.
10 8
3
2016
36
100 . 100
..
10
an
VV m
B.
18
3
2016
.1 .VVanm
C.
10
3
2016
20
100 100
..
10
an
VV m
D.
18
3
2016
.1 .VVVanm
Hướngdẫngiải
ChọnA.
Tacó:
Sau10nămthểtíchkhí
2
CO
là
10
10
2008
20
100
1
100 10
a
a
VV V
Dođó,8nămtiếptheothểtíchkhí
2
CO
là
10
88
2016 2008
20
10 8 10 8
20 16 36
100
11
100 10 100
100 100 100 . 100
10 10 10
a
nn
VV V
an an
VV
Câu53: NGÔSĨLIÊNChotamgiácđềuvàhìnhvuôngcùngcócạnhbằng
4
đượcxếpchồnglênnhau saochomột đỉnhcủatamgiác đều
trùngvớitâmcủahìnhvuông,trụccủatamgiácđềutrùngvớitrục
củahìnhvuôngnhưhìnhvẽ.Thểtíchcủavậtthểtrònxoaysinh
bởihìnhđãchokhiquayquanhtrục
A
B
là
A.
136 24 3
.
9
B.
48 7 3
.
3
C.
128 24 3
.
9
D.
144 24 3
.
9
Hướngdẫngiải
ChọnD
h
R
'
R
H
C
A
K

KhixoayquanhtrụcABthì:
PhầnhìnhvuôngphíatrêntrởthànhlăngtrụcóbánkínhR2,chiềucaoh4
2
1
2.4 16V
Phầndướitrởthànhhìnhnóncụtvới
23 2 2 3 1hHK AKAH ; 2R
'21 2
'
23 3 3 3
RAH R
R
RAK
Ápdụng
22
24 3 8
' ' ...
1
3
...
9
hR RVRR
Vậy
12
24 3 136
9
VVV
.ĐápánlàcâuD
Câu54: NGÔSĨLIÊNMộtngọnhảiđăngđặtởvịtrí
A
cách
bờ
5km
,trênbờbiểncómộtkhohàngởvịtrí
C
cách
B
mộtkhoảng
7km
.Ngườicanhhảiđăngcóthểchèo
thuyềntừ
A
đến
M
trênbờbiểnvớivậntốc
4/km h
rồiđibộtừ
M
đến
C
vớivậntốc
6/km h
.Xácđịnhđộ
dàiđoạn
BM
đểngườiđóđitừ
A
đếnCnhanhnhất.
A.
32 .km B.
7
.
3
km
C.
25km. D.
7
.
2
km
Hướngdẫngiải
ChọnC.
Gọi
BM x
km
,
07x
.Khiđó:
2
25
A
Mxvà
7
M
Cx
Theođềbàitacó:
2
25 7
46
x
x
fx
2
2
3225
425
x
x
fx
x
Cho
2
2
0
0
0225 3 25
20
25
x
x
fx x x x
x
x
Khiđó:
29
0
12
f
,
74
7
4
f
và
14 5
25
12
f
Vậy
0;7
14 5
min 2 5
12
x
fx f
.
Câu55: CHUYÊNTHÁIBÌNHBạnAcómộtđoạndâydài
20m
.Bạnchiađoạndâythànhhaiphần.
Phầnđầuuốnthànhmộttamgiácđều.Phầncònlạiuốnthànhmộthìnhvuông.Hỏiđộdài
phầnđầubằngbaonhiêuđểtổngdiệntíchhaihìnhtrênlànhỏnhất?
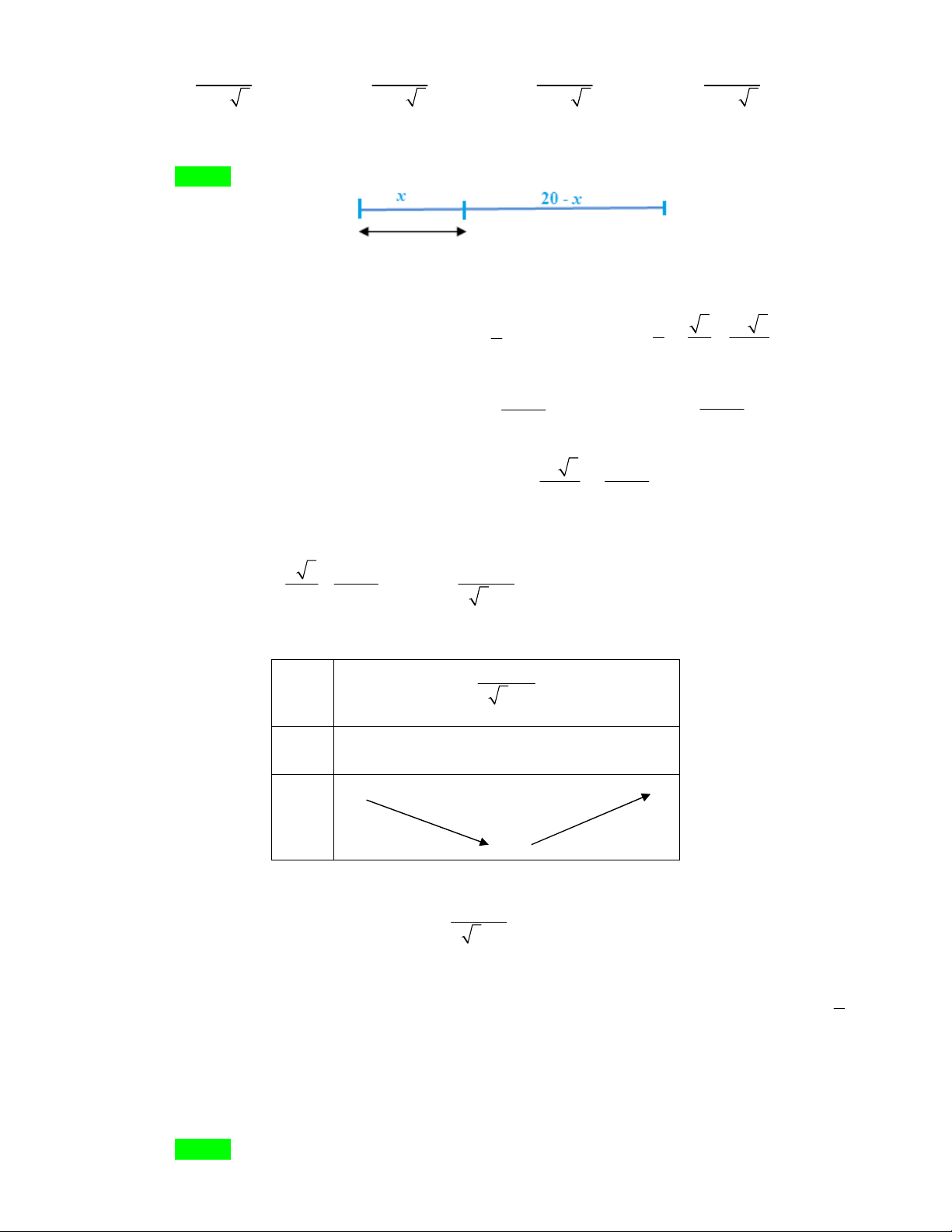
A.
40
.
943
m
B.
180
.
943
m
C.
120
.
943
m
D.
60
.
943
m
Hướngdẫngiải
ChọnB.
BạnAchiasợidâythànhhaiphầncóđộdài
x
m
và
20
x
m
,
020x
nhưhìnhvẽ.
Phầnđầuuốnthànhtamgiácđềucócạnh
3
x
m
,diệntích
2
2
2
1
33
.
34 36
xx
Sm
Phầncònlạiuốnthànhhìnhvuôngcócạnh
20
4
x
m
,diệntích
2
2
2
20
4
x
Sm
Tổngdiệntíchhaihìnhnhỏnhấtkhi
2
2
320
36 4
x
x
fx
nhỏnhấttrênkhoảng
0; 20
.
Tacó:
320 180
'0
18 8
43 9
xx
fx x
.
Bảngbiếnthiên:
x
0
180
43 9
20
f
x
0
f
x
Dựavàobảngbiếnthiêntađược
180
43 9
x
.
Câu56: CHUYÊNTHÁIBÌNHMộtquảbóngbànvàmộtchiếcchénhìnhtrụcócùngchiềucao.
Ngườitađặtquảbónglênchiếcchénthấyphầnởngoàicủaquảbóngcóchiềucaobằng
3
4
chiềucaocủanó.Gọi
1
V
,
2
V
lầnlượtlàthểtíchcủaquảbóngvàchiếcchén,khiđó:
A.
12
98VV . B.
12
32VV . C.
12
16 9VV . D.
12
27 8VV .
Hướngdẫngiải
ChọnA.
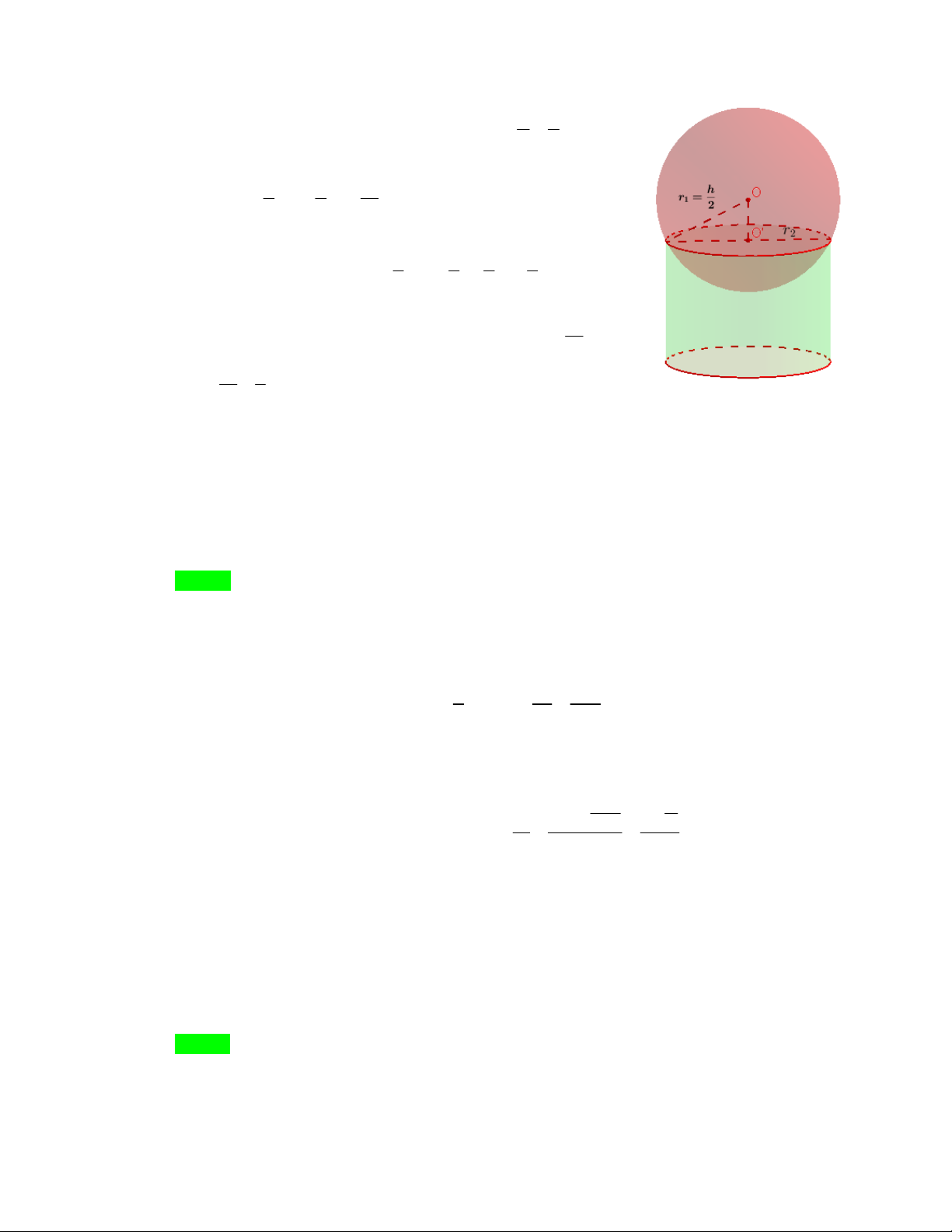
Gọi
1
r
làbánkínhquảbóng,
2
r
làbánkínhchiếcchén,
h
làchiềucaochiếcchén.
Theogiảthiếttacó
11
22hrr h
và
1
24
r
h
OO
.
Tacó
22
22
2
3
2416
hh
rh
.
Thểtíchcủaquảbónglà
3
33
11
44 1
3326
h
Vr h
và thể tích của chén nước là
23
22
3
.
16
VBh rh h
1
2
8
.
9
V
V
Câu57: CHUYÊNTHÁIBÌNHXétmộthộpbóngbàncódạnghìnhhộpchữnhật.Biếtrằnghộp
chứavừakhítbaquảbóngbànđượcxếptheochiềudọc,cácquảbóngbàncókíchthước
nhưnhau.Phầnkhônggiancòntrốngtronghộpchiếm:
A.
65,09% . B. 47,64% . C.82,55% . D.83,3% .
Hướngdẫngiải
ChọnB.
Gọiđườngkínhquảbóngbànlà
d .Khiđókíchthướccủahìnhhộpchữnhậtlà
,,3dd d
.
Vậythểtíchcủahìnhhộpchữnhậtlà
3
1
..3 3Vddd d
Thểtíchcủabaquảbóngbàn:
33
3
2
4
34
382
dd
Vr
.
Thểtíchphầnkhônggiancòntrống:
312
VVV
Phầnkhônggiancòntrốngtronghộpchiếm:
3
3
3
3
1
33
22
47,64%
33
d
d
V
Vd
.
Câu58: CHUYÊNTHÁIBÌNHMộtbểnướccódungtích
1000
lít.Ngườitamởvòichonướcchảy
vàobể,banđầubểcạnnước.Tronggiờđầuvậntốcnướcchảyvàobểlà1lít/1phút.Trong
cácgiờtiếptheovậntốcnướcchảygiờsaugấpđôigiờliềntrước.Hỏisaukhoảngthời
gianbaolâuthìbểđầynướckếtquảgầnđúngnhất.
A.
3,14
giờ. B.
4,64
giờ. C.4,14giờ. D.
3, 64
giờ.
Hướngdẫngiải
ChọnC.
Tronggiờđầutiên,vòinướcchảyđược
60.1 60
lítnước.
Giờthứ2vòichảyvớivậntốc2lít/1phútnênvòichảyđược
60 2 120
lítnước.
Giờthứ3vòichảyvớivậntốc4lít/1phútnênvòichảyđược
60 4 240
lítnước.
Giờthứ4vòichảyvớivậntốc8lít/1phútnênvòichảyđược
60 8 480
lítnước.
r
R
D
C
A
B
R
=5
r
=2
M
C
F
B
E
Trong4giờđầutiên,vòichảyđược:
60 120 240 480 900
lítnước.
Vậytronggiờthứ5vòiphảichảylượngnướclà
1000 900 100
lítnước.
Sốphútchảytronggiờthứ5là
100 :16 6,25
phút
Đổi
6, 25 : 60 0,1
giờ
Vậythờigianchảyđầybểlàkhoảng
4,1
giờ.
Câu59: CHUYÊNTHÁIBÌNHMộtvậtchuyểnđộngchậmdầnvớivậntốc
( ) 160 10 ( / ).vt t m s
Tìmquãngđường
S
màvậtdichuyểntrongkhoảngthờigiantừthờiđiểm 0( )ts đến
thờiđiểmvậtdừnglại.
A.
2560 .Sm
B.
1280 .Sm
C.
2480 .Sm
D.
3840 .Sm
Hướngdẫngiải
ChọnB.
Tacó,vậtdừnglạikhi
() 0 160 10 0 16vt t t s
.
Khiđó,quãngđường
S
màvậtdichuyểntrongkhoảngthờigiantừthờiđiểm
0( )ts
đến
thờiđiểmvậtdừnglạilà
16
0
160 10 1280 .Stdtm
Câu60: SỞGDBẮCNINHPhầnkhônggianbêntrongcủachainướcngọtcóhình
dạngnhưhìnhbên.Biếtbánkínhđáybằng
5,
R
cm
bánkínhcổ
2, 3,rcmABcm 6,
B
Ccm
16 .CD cm
Thểtíchphầnkhônggianbêntrong
củachainướcngọtđóbằng:
A.
3
495 cm
. B.
3
462 cm
.
C.
3
490 cm
. D.
3
412 cm
.
Hướngdẫngiải
Thểtíchkhốitrụcóđườngcao
CD
:
23
1
.400VRCD cm
.
Thểtíchkhốitrụcóđườngcao
A
B :
23
2
.12VrAB cm
.
Tacó
5
4
2
MC CF
MB
M
BBE
Thểtíchphầngiớihạngiữa
B
C
:
22 3
3
..78
3
VRMCrMB cm
.
Suyra:
3
123
490VVV V cm
.
ChọnC
Câu61: SỞGDBẮCNINHMộtcôngtysảnxuấtgỗmuốnthiếtkếcácthùngđựnghàngbêntrong
dạnghìnhlăngtrụtứgiácđềukhôngnắpcóthểtíchlà
2
62,5dm
.Đểtiếtkiệmvậtliệulàm
thùng,ngườitacầnthiếtkếthùngsaochocótổng
S
diệntíchxungquanhvàdiệntích
mặtđáylànhỏnhất,
S
bằng
A.
2
106,25dm
. B.
2
75dm . C.
2
50 5dm
. D.
2
125dm .
I
M
P
N
Q
S
B
A
O
Hướngdẫngiải
Gọi
a làđộdàicạnhđáycủahìnhlăngtrụ.
Theobàitacóchiềucaocủalăngtrụlà
2
62,5
a
.Suyra
22 2 2
3
2
62.5 250 125 125 125 125
4. . 3 . . 75Saaaaa
aaaaaa
.Dấubằngxảyrakhi
3
125 5a .Vậy
S
lànhỏnhấtbằng
75
.
ChọnđápánB
Câu62: SỞGDBẮCNINHChobiếtsựtăngdânsốđượcướctínhtheocôngthức
.
.
Nr
SAe
trong
đó
A
làdânsốcủanămlấylàmmốctính,
S
làdânsốsau
N
năm,
r
làtỉlệtăngdânsố
hàngnăm.Đầunăm2010dânsốtỉnhBắcNinhlà1.038.229người,tínhđếnđầunăm
2015dânsốcủatỉnhlà1.153.600người.Hỏinếutỉlệtăngdânsốhàngnămgiữnguyên
thìđầunăm2025dânsốcủatỉnhnằmtrongkhoảngnào?
A.
1.424.300;1.424.400
. B.
1.424.000;1.424.100
.
C.
1.424.200;1.424.300 . D.
1.424.100;1.424.200 .
Hướngdẫngiải
Gọi
1
S
làdânsốnăm2015,tacó
1
1.153.600, 5, 1.038.229SNA
Tacó:
1
..
1
1
ln
.
5
Nr Nr
S
S
A
SAe e r
A
Gọi
2
S
làdânsốđầunăm2025,tacó
ln
15.
15.
5
2
. 1.038.229. 1.424.227,71
S
A
r
SAe e
ChọnđápánC
Câu63: QUẢNG XƯƠNG I Mộtbìnhđựngnướcdạnghìnhnónkhôngđáy
đựngđầynước.Biếtrằngchiềucaocủabìnhgấp3lầnbánkínhđáy
củanó.Ngườitathảvàođómộtkhốitrụvàđodượcthểtíchnước
trànrangoàilà
3
16
9
dm
.Biếtrằngmộtmặtcủakhốitrụnằmtrênmặt
trêncủahìnhnón,cácđiểmtrên đườngtrònđáy cònlạiđềuthuộccác
đườngsinhcủahìnhnónnhưhìnhvẽvàkhốitrụcóchiềucaobằng
đườngkínhđáycủahìnhnón.Diệntíchxungquanh
x
q
S
củabìnhnướclà:
A.
2
910
2
xq
Sdm
. B.
2
410
xq
Sdm
. C.
2
4
xq
Sdm
. D.
2
3
2
xq
Sdm
.
Hướngdẫngiải
ChọnB
6m
O
Xéthìnhnón:
3hSO r
, ,rOBlSA.Xéthìnhtrụ:
1
2hrNQ
,
1
rONQI
SQI SBO
1
1
33
QI SI r
r
BO SO
Thểtíchkhốitrụlà:
3
2
11
216
26
99
t
r
Vrh r h
22
210lhr
2
410
xq
Srl dm
Câu64: QUẢNGXƯƠNGIMộtmảnhvườnhìnhtròntâm
O
bánkính
6m
.
Ngườitacầntrồngcâytrêndảiđấtrộng
6m
nhận
O
làmtâmđối
xứng, biết kinh phí trồng cây là
70000
đồng
2
/ m
. Hỏi cần bao
nhiêutiền đểtrồngcâytrêndảiđấtđósốtiềnđượclàmtròn
đếnhàngđơnvị
A.
8412322 đồng. B.8142232 đồng.
C.
4821232 đồng. D.4821322 đồng.
Hướngdẫngiải
ChọnD
Xéthệtrụctọađộoxyđặtvàotâmkhuvườn,khiđóphươngtrìnhđườngtròntâmOlà
22
xy 36
.Khiđóphầnnửacungtrònphíatrêntrục
Ox
cóphươngtrình
2
36 (x)
y
x
f
KhiđódiệntíchScủamảnhđấtbằng2lầndiệntíchhìnhphẳnggiớihạnbởitrụchoành,đồthị
(x)yf vàhaiđườngthẳng 3; 3xx
3
2
3
236xdxS
Đặt
6sin 6cos
x
tdx tdt
.Đổicận: 3
6
xt
; 3
6
xt
6
66
2
66
6
2 36cos 36 (cos2t+1)dt 18(sin 2 t 2 t) 18 3 12Stdt
Dođósốtiềncầndùnglà
70000. 4821322S
đồng
Câu65: QUẢNGXƯƠNGIBạnHùngtrúngtuyểnvàotrườngđạihọc
A
nhưngvìdokhôngđủnộp
họcphínênHùngquyếtđịnhvayngânhàngtrong4nămmỗinămvay
3.000.000
đồngđể
nộphọcphívớilãisuất3%/năm.SaukhitốtnghiệpđạihọcbạnHùngphảitrảgóphàng
thángsốtiền
T
khôngđổicùngvớilãisuất0,25%/thángtrongvòng5năm.Sốtiền
T
hàngthángmàbạnHùngphảitrảchongânhànglàmtrònđếnkếtquảhàngđơnvịlà:
A.
232518
đồng. B.
309604
đồng. C.
215456
đồng. D.
232289
đồng.
Hướngdẫngiải
Chọn đápánD
Vậysau4nămbạnHùngnợngânhàngsốtiềnlà:
432
3000000 3% 3% 3% 12927407,43s
LúcnàytacoinhưbạnHùngnợngânhàngkhoảntiềnbanđầulà
12.927.407,43
đồng,
sốtiềnnàybắtđầuđượctínhlãivàđượctrảgóptrong5năm.
Tacócôngthức:
60
60
. 12927407,4 0,0025 .0,0025
232289
0,0025
n
n
Nrr
r
Câu66: QUẢNGXƯƠNGIKhicắtmặtcầu
, SOR
bởimộtmặtkính,tađượchainửamặtcầu
vàhìnhtrònlớncủamặtkínhđógọilàmặtđáycủamỗinửamặtcầu.Mộthìnhtrụgọilà
nộitiếpnửamặtcầu
, SOR
nếumộtđáycủahìnhtrụnằmtrongđáycủanửamặtcầu,
cònđườngtrònđáykialàgiaotuyếncủahìnhtrụvớinửamặtcầu.Biết
1
R
,tínhbán
kínhđáy
r
vàchiềucao h củahìnhtrụnộitiếpnửamặtcầu
, SORđểkhốitrụcóthể
tíchlớnnhất.
A.
36
,
22
rh
. B.
63
,
22
rh
. C.
63
,
33
rh
. D.
36
,
33
rh
.
Hướngdẫngiải
Chọn đápánC.
Hìnhtrụnộitiếpnửamặtcầu,nêntheogiảthiếtđườngtrònđáy
trêncótâmO'cóhìnhchiếucủaOxuốngmặtđáyO'.Suyrahình
trụvànửamặtcầucùngchungtrụcđốixứngvàtâmcủađáydưới
hìnhtrụtrùngvớitâmOcủanửamặtcầu.Tacó:
22 2
hr R
01hR
22
1rh
Thể tích khối trụ là:
22
(1 h ) h (h)Vrh f
2
3
'(h) (1 3 h ) 0 h
3
f
h
0
3
3
1
f'(h)
0
f(h)
23
9
0
0
Vậy:
0;1
23
9
MaxV
đvttkhi
6
3
r
và
3
3
h

Câu67: LƯƠNGĐẮCBẰNGBạnAmuốnlàmmộtchiếcthùnghìnhtrụkhôngđáytừnguyênliệu
làmảnhtônhìnhtamgiácđều
A
BC
cócạnhbằng
90 cm .Bạnmuốncắtmảnhtônhình
chữnhật
M
NPQ từmảnhtônnguyênliệuvới
M
,
N
thuộccạnh
B
C
;
P
vàQ tương
ứngthuộccạnh
A
C
và
A
B
đểtạothànhhìnhtrụcóchiềucaobằng
M
Q
.Thểtíchlớn
nhấtcủachiếcthùngmàbạnAcóthểlàmđượclà:
A.
3
91125
4
cm
. B.
3
91125
2
cm
.
C.
3
108000 3
cm
. D.
3
13500. 3
cm
.
Hướngdẫngiải
GọiIlàtrungđiểmBC.SuyraIlàtrungđiểmMN
ĐặtMNx
090x
;
3
(90 )
2
MQ BM
M
Qx
A
IBI
GọiRlàbánkínhcủatrụ
2
x
R
232
33
() (90) ( 90)
22 8
T
x
Vxxx
Xét
32
3
() ( 90 )
8
f
xxx
với090x .Khiđó:
(0;90)
13500. 3
max ( )
x
fx
khix60.
Câu68: CHUYÊNVĨNHPHÚCMộtngườigửitiếtkiệmngânhàng,mỗithánggửi1triệuđồng,với
lãisuấtkép1%trêntháng.Gửiđượchainăm3thángngườiđócócôngviệcnênđãrút
toànbộgốcvàlãivề.Sốtiềnngườiđóđượcrútlà
A.
27
101. 1,01 1
triệuđồng B.
26
101. 1,01 1
triệuđồng
C.
27
100. 1,01 1
triệuđồng D.
100. 1,01 6 1
triệuđồng
Hướngdẫngiải
ĐápánA
Phươngpháp:Quybàitoánvềtínhtổngcấpsốnhân,rồiápdụngcôngthứctínhtổngcấpsốnhân:
Dãy
123 n
U ; U ;U ;...; U
đượcgọilà1CSNcócôngbộiqnếu:
kk1
UUq
Tổngnsốhạngđầutiên:
n
n12 n1
1q
s u u ... u u
1q
Ápdụngcôngthứctínhtổngcủacấpsốnhân
Cáchgiải:Gọisốtiềnngườiđógửihàngthánglà
a1
triệu
Đầutháng1:ngườiđócóa
Cuốitháng1:ngườiđócó
a. 1 0,01 a.1,01
Đầutháng2ngườiđócó:
aa.1,01
A
B
C
M
N
Q
P
8m
Cuốitháng2ngườiđócó:
2
1, 01 a a.1, 01 a 1, 01 1, 01
Đầutháng3ngườiđócó:
2
a 1 1, 01 1, 01
Cuốitháng3ngườiđócó:
223
a 1 1,01 1,01 .1,01 a 1 1,01 1,01
….
Đếncuốithángthứ27ngườiđócó:
227
a 1 1, 01 1, 01 ... 1, 01
Tacầntínhtổng:
227
a 1 1, 01 1, 01 ... 1, 01
Ápdụngcôngthứccấpsốnhântrênvớicôngbộilà1,01tađược
27
27
11,01
100. 1,01 1
10,01
triệu
đồng.
Câu69: MINHHỌAL2ÔngAncómộtmảnhvườnhìnhelipcóđộdàitrục lớn
bằng
16m
vàđộdàitrụcbébằng
10m
.Ôngmuốntrồnghoa
trênmộtdảiđấtrộng
8m
và nhận trục bé của elip làm
trụcđốixứngnhưhìnhvẽ.Biếtkinhphíđểtrồnghoalà
100.000
đồng/
2
1m . Hỏi ông An cần bao nhiêu tiền để
trồnghoatrêndảiđấtđó?Sốtiềnđượclàmtrònđếnhàng
nghìn.
A.
7.862.000
đồng. B.
7.653.000
đồng. C.
7.128.000
đồng.D.
7.826.000
đồng.
Hướngdẫngiải
ChọnB.
Giảsửelipcóphươngtrình
22
22
1
xy
ab
,với
0ab
.
Từgiảthiếttacó
216 8aa
và
210 5bb
Vậyphươngtrìnhcủaeliplà
2
22
1
2
1
5
64
8
1
5
64 25
64
8
yyE
xy
yyE
Khiđódiệntíchdảivườnđượcgiớihạnbởicácđường
12
;; 4;4 EEx xvàdiện
tíchcủadảivườnlà
44
22
40
55
264d 64d
82
Sxxxx
Tínhtíchphânnàybằngphépđổibiến
8sin
x
t
,tađược
3
80
64
S
Khiđósốtiềnlà
3
80 .100000 7652891,82 7.653.000
64
T
.
X
Y
Câu70: MINHHỌAL2Chohaihìnhvuôngcócùngcạnhbằng5đượcxếpchồng
lênnhausaochođỉnh
X
củamộthìnhvuônglàtâmcủahìnhvuôngcòn
lạinhưhìnhvẽ.Tínhthểtích
V
củavậtthểtrònxoaykhiquaymôhình
trênxungquanhtrục
XY
.
A.
125 1 2
6
V
. B.
125 5 2 2
12
V
.
C.
125 5 4 2
24
V
. D.
125 2 2
4
V
.
Hướngdẫngiải
ChọnC.
Cách1
:
Khốitrònxoaygồm3phần:
Phần1:khốitrụcóchiềucaobằng5,bánkínhđáybằng
5
2
cóthểtích
2
1
5 125
5
24
V
.
Phần2:khốinóncóchiềucaovàbánkínhđáybằng
52
2
cóthểtích
2
2
1 5 2 5 2 125 2
32212
V
Phần3:khốinóncụtcóthểtíchlà
2
2
3
5 2 1 125 2 2 1
1525525
32 2222 24
V
.
Vậythểtíchkhốitrònxoaylà
123
125 2 2 1 125 5 4 2
125 125 2
412 24 24
VVVV
.
Cách2
:
Thểtíchhìnhtrụđượctạothànhtừhìnhvuông
A
BCD
là
2
125
4
T
VRh
Thểtíchkhốitrònxoayđượctạothànhtừhìnhvuông
XEYF là
2
2
2 125 2
36
N
VRh
Thểtíchkhốitrònxoayđượctạothànhtừtamgiác
X
DC
là
2
1125
324
N
VRh
Thểtíchcầntìm
2
542
125
24
TNN
VV V V .
Câu71: Cầnphảixâydựngmộthốga,dạnghìnhhộpchữnhậtcóthểtích
3
Vm ,hệsố
k
cho
trước
k ‐tỉsốgiữachiềucaocủahốvàchiềurộngcủađáy.Gọi ,, 0xyh lầnlượtlà
chiềurộng,chiềudàivàchiềucaocủahốga.Hãyxácđịnh
,, 0xyh xâytiếtkiệmnguyên
vậtliệunhất.
,,
x
yh
lầnlượtlà
A.
3
3
3
2
2
21 21
2
2; ; .
44
21
kV kkV
kV
xyh
k
k
B.
3
3
3
2
2
21 21
2
;;2.
44
21
kV kkV
kV
xyh
k
k
C.
3
3
3
2
2
21 21
2
;2 ; .
44
21
kV kkV
kV
xyh
k
k
D.
3
3
3
2
2
21 21
2
;6 ; .
44
21
kV kkV
kV
xyh
k
k
Hướngdẫngiải
ĐápánC.
Gọi
()
,, ,, 0xyh xyh> lầnlượtlàchiềurộng,chiềudàivàchiềucaocủahốga.
Tacó:
h
khkx
x
==
và
2
VV
Vxyh y
xh
kx
===
.
Nêndiệntíchtoànphầncủahốgalà:
(
)
2
21
22 2
kV
Sxy yh xh kx
kx
+
=+ + = +
x
y
h
ÁpdụngđạohàmtacóSnhỏnhấtkhi
()
3
2
21
4
kV
x
k
+
=
Khiđó
()
()
3
3
2
21
2
2,
4
21
kk V
kV
yh
k
+
==
+
.
Câu72: Khimộtchiếclòxobịkéocăngthêm
x
m sovớiđộdàitựnhiênlà
0,15 m
củalòxothì
chiếclòxotrìlạichốnglạivớimộtlực
800 .
f
xx Hãytìmcông
W
sinhrakhikéolò
xotừđộdàitừ
0,15 m
đến
0,18 .m
A.
2
36.10 .WJ
B.
2
72.10 .WJ
C. 36 .WJ D.72 .WJ
Hướngdẫngiải
ĐápánA.
Côngđượcsinhrakhikéocănglòxotừ0,15mđến0,18mlà:
0,03
20,03 2
0
0
800 .d 400 36.10 .Wxxx J
-
===
ò
Chúý:
Nếulựclàmộtgiátrịbiếnthiênnhưnénlòxovàđượcxácđịnhbởihàm
()
Fxthì
côngsinhratheotrục
Ox
từ
a
tới
b
là
()
d.
b
a
AFxx=
ò
Câu73: Nhânngàyquốctếphụnữ8‐3năm2017,ôngAquyếtđịnhmuatặngvợmộtmónquàvà
đặtnóvàotrongmộtchiếchộpcóthểtíchlà32đvttcóđáyhìnhvuôngvàkhôngcó
nắp.Đểmónquàtrởnênthậtđặcbiệtvàxứngđángvớigiátrịcủanóôngquyếtđịnhmạ
vàngchochiếchộp,biếtrằngđộdạylớpmạtạimọiđiểmtrênhộplànhưnhau.Gọichiều
caovàcạnhđáycủachiếchộplầnlượtlà .Đểlượngvàngtrênhộplànhỏnhấtthìgiá
trịcủa phảilà?
A. B. C. D.
Hướngdẫngiải
ĐápánB.
h;x
h;x
x2;h4== x4;h2==
3
4;
2
==xh
1; 2==xh
x
x
h

Tacó ,đểlượngvàngcầndùnglànhỏ
nhấtthìDiệntíchSphảinhỏnhấttacó
,
Câu74: Mộtđạilýxăngdầucầnlàmmộtcáibồndầuhìnhtrụbằngtôncóthểtích
3
16 m
.Tìm
bánkínhđáy
r
củahìnhtrụsaochohìnhtrụđượclàmraíttốnnguyênvậtliệunhất.
A.
0,8 .m
B.
1, 2 .m
C.
2.m
D.
2,4 .m
Hướngdẫngiải
ĐápánC.
Gọi
()
xmlàbánkínhcủahìnhtrụ
(
)
0x > .Tacó:
2
2
16
..Vxhh
x
p==
Diệntíchtoànphầncủahìnhtrụlà:
() ()
22
32
22 2 ,0Sx x xh x x
x
p
pp p=+=+ >
Khiđó:
()
2
32
'4Sx x
x
p
p=-
,cho
()
'0 2Sx x==.
Lậpbảngbiếnthiên,tathấydiệntíchđạtgiátrịnhỏnhấtkhi
()
2xm=
nghĩalàbánkínhlà
2m
.
Câu75: NhàNamcómộtchiếcbàntròncóbánkínhbằng m.Nammuốnmắcmộtbóngđiệnở
phíatrênvàchínhgiữachiếcbànsaochomépbànnhậnđượcnhiềuánhsángnhất.Biết
rằngcườngđộsángCcủabóngđiệnđượcbiểuthịbởicôngthức làgóctạo
bởitiasángtớimépbànvàmặtbàn,c‐hằngsốtỷlệchỉphụthuộcvàonguồnsáng,
l
khoảngcáchtừmépbàntớibóngđiện.Khoảngcáchnamcầntreobóngđiệntínhtừmặt
bànlà
A.1m B.1,2m C.1.5m D.2m
Hướngdẫngiải
Sxhx
Sx. x x
V
x
Vxhh
x
xx
ì
ï
=+
ï
ï
ï
= + = +
í
ï
===
ï
ï
ï
î
2
22
2
2
22
4
32 128
4
32
() ()
Sxfxfʹ xx x
x
x
=+= =-==
2
2
128 128
204
2
2
sin
Cc
l
Gọihlàđộcaocủabóngđiệnsovớimặtbành0;Đlàbóngđiện;IlàhìnhchiếucủaĐlênmặt
bàn.MNlàđườngkínhcủamặtbàn.nhưhìnhvẽ
Tacó và ,suyracườngđộsánglà: .
LậpbảngbiếnthiêntathuđượckếtquảClớnnhấtkhi ,khiđó
Câu76: AnhPhongcómộtcáiaovớidiệntích
2
50m
đểnuôicádiêuhồng.Vụvừaqua,anhnuôi
vớimậtđộ
2
20con / m
vàthuđược
1, 5
tấncáthànhphẩm.Theokinhnghiệmnuôicácủa
mìnhanhthấycứthảgiảmđi
2
8 con / m
thìmỗiconcáthànhphầmthuđượctăngthêm
0, 5kg
.Đểtổngnăngsuấtcaonhấtthìvụtớianhnênmuabaonhiêucágiốngđểthả?giả
sửkhôngcóhaohụttrongquátrìnhnuôi
A.488con. B.658con. C.342con. D.512con.
Hướngdẫngiải
ĐápánA
SốcáanhPhongthảtrongvụvừaqualà
50.20 1000=
con
Khốilượngtrungbìnhmỗiconcáthànhphầnlà
1500
1, 5 /
1000
kg con=
Gọi
0x >
làsốcáanhcầnthảítđichovụtớinênsẽtăng
0,0625x
kg/con
Tacóphươngtrìnhtổngkhốilượngcáthuđược
() ( )( )
1000 1,5 0,0625Tfx x x== - +
()
()
()
0,125 61 0 488
max 16384 488
0, 125
fx x x
fx x
fx
ì
ï
¢
=- + = =
ï
ï
==
í
ï
¢¢
=-
ï
ï
î
Vậyởvụsauanhchỉcầnthả
1000 488 512-=
concágiống.
2
α
l
N
M
Đ
I
h
sin
h
l
22
2hl
2
3
2
() ( 2)
l
Cl c l
l
2
42
6
'. 0 2
.2
l
Cl c l
ll
'0 6 2Cl l l
6l
Câu77: Vớimộtđĩatrònbằngthéptrángcóbánkính
= 6Rm
phảilàmmộtcáiphễubằngcách
cắtđimộthìnhquạtcủađĩanàyvàgấpphầncònlạithànhhìnhtròn.Cungtròncủahình
quạtbịcắtđiphảibằngbaonhiêuđộđểhìnhnóncóthểtíchcựcđại?
A.
»66
B.
»294
C.
»12,56
D.
»2, 8
Hướngdẫngiải
ĐápánA
Tacóthểnhậnthấyđườngsinhcủahìnhnónlàbánkínhcủađĩatròn.Cònchuviđáycủa
hìnhnónchínhlàchuvicủađĩatrừđiđộdàicungtrònđãcắt.Nhưvậytatiếnhànhgiải
chitiếtnhưsau:
Gọi
()xm
làđộdàiđáycủahìnhnónphầncònlạisaukhicắtcunghìnhquạtcủadĩa.
Khiđó
p
p
==2
2
x
xrr
ChiềucaocủahìnhnóntínhtheođịnhlíPITAGOlà
p
=-=-
2
22 2
2
4
x
hRr R
Thểtíchkhốinónsẽlà:
pp
pp
== -
22
22
22
11
33
44
xx
Vrh R
Đến đây các em đạo hàm hàm
()Vx
tìmđượcGTLNcủa
()Vx
đạtđượckhi
p
p==
2
64
3
xR
Suy ra độ dài cung tròn bị cắt đi là :
pp-24R
pp
a
p
-
= »
00
26 4
360 66
26
Câu78: ChomộttamgiácđềuABCcạnha.Ngườitadựngmột
hìnhchữnhậtMNPQcócạnhMNnằmtrêncạnhBC,hai
đỉnhPvàQtheothứtựnằmtrênhaicạnhACvàABcủa
tamgiác.Xácđịnhgiátrịlớnnhấtcủahình chữ nhật
đó?
A. B.
O
N
6m
2
3
a
8
2
3
a
4
C. D.
Hướngdẫngiải
GọiHlàtrungđiểmcủaBC
BHCH .ĐặtBMx ,tacó:
TamgiácMBQvuôngởM, vàBMx
HìnhchữnhậtMNPQcódiệntích:
SxMN.QM
x
0
S’
0
S
Vậy khix
Câu79: Chomộttấmnhômhìnhvuôngcạnh6cm.Ngườitamuốncắtmộthìnhthangnhưhìnhvẽ.
TìmtổngxyđểdiệntíchhìnhthangEFGHđạtgiátrịnhỏnhất.
A.7 B.5 C. D. .
Hướngdẫngiải
0
2
3
a
2
a
2
a
§iÒu kiÖn 0 x
2
a
MN 2MH 2(BH BM) 2 x a 2x
2
0
B60
QM x 3
2
(a 2x)x 3 3(ax 2x )
aa
S'(x) 3(a 4x); S'(x) 0 x 0;
42
a
4
a
2
2
3
a
8
2
a
x0;
2
3
maxS(x) a
8
a
4
x
cm
y
cm
3cm
2cm
H
G
F
E
D
C
B
A
72
2
42
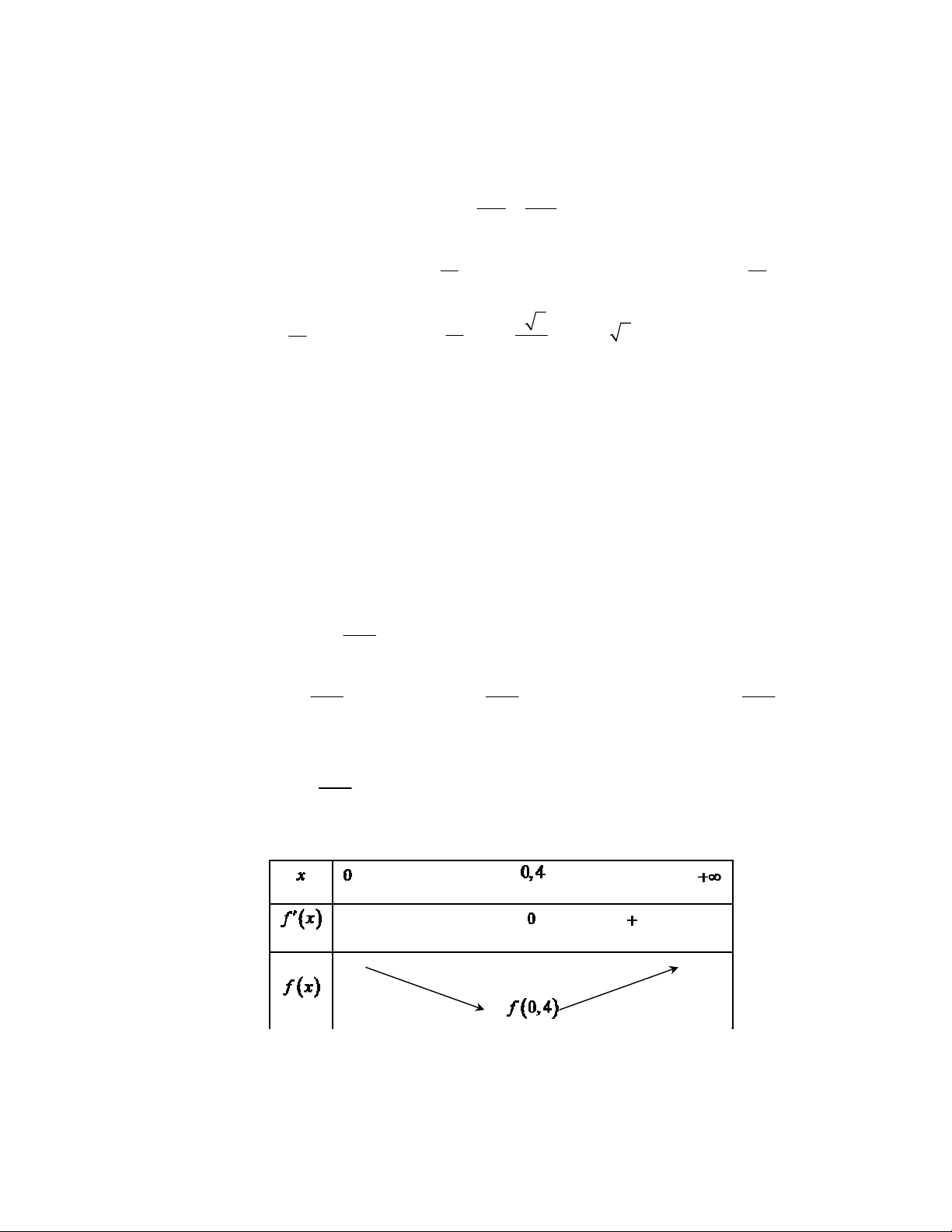
ĐápánC
Tacó nhỏnhất lớnnhất.
Tínhđược 1
Mặtkhác đồngdạng nên 2
Từ1và2suyra .Tacó2Slớnnhấtkhivàchỉkhi nhỏnhất.
Biểuthức nhỏnhất .
Câu80: Đểthiếtkếmộtchiếcbểcáhìnhhộpchữnhậtcóchiềucaolà
60cm ,thểtích
3
96000cm
.
Ngườithợdùngloạikínhđểsửdụnglàmmặtbêncógiáthành
70000
VNĐ/m
2
vàloại
kínhđểlàmmặtđáycógiáthành
100000
VNĐ/m
2
.Tínhchiphíthấpnhấtđểhoànthành
bểcá.
A.
320000 VNĐ. B. 32000 VNĐ. C.832000 VNĐ. D.83200 VNĐ.
Hướngdẫngiải
ĐápánD
Gọi
(
)
(
)
,0,0xym x y>>làchiềudàivàchiềurộngcủađáybể,khiđótheođềtasuyra
0, 16
0,6 0, 096xy y
x
==
.Giáthànhcủabểcáđượcxácđịnhtheohàmsốsau:
()
0, 16 0, 16
2.0,6 .70000 100000fx x x
xx
æö
÷
ç
÷
=+ +
ç
÷
ç
÷
ç
èø
()
0, 16
84000 16000fx x
x
æö
÷
ç
÷
= + +
ç
÷
ç
÷
ç
èø
VNĐ
() ()
2
0, 16
84000 1 , 0 0,4fx fx x
x
æö
÷
ç
¢¢
÷
=- ==
ç
÷
ç
÷
ç
èø
Tacóbảngbiếnthiênsau:
Dựavàobảngbiếnthiênsuyrachiphíthấpnhấtđểhoànthànhbểcálà
()
0,4 83200f =
VNĐ
E
FGH
S
A
EH CGF DGH
SS S S
223(6)(6y)xy4x3y36Sxy x
A
EH
CGF
6
AE AH
xy
CG CF
18
242(4x )S
x
18
4x
x
18
4x
x
18 3 2
422
2
xx y
x
–
Câu81: Mộtvậtchuyểnđộngvớiphươngtrìnhvậntốclà:
()
(
)
()
sin
1
/
2
t
vt m s
p
pp
=+
. Tính
quãngđườngvậtđódichuyểnđượctrongkhoảngthờigian
5
giâylàmtrònkếtquảđến
hàngphầntrăm.
A.
0, 9 .Sm»
B.
0,998 .Sm»
C.
0, 99 .Sm»
D.
1.Sm»
Hướngdẫngiải
ĐápánD
Tacó
(
)
5
0
sin
1
0,99842
2
t
Sdtm
p
pp
æö
÷
ç
÷
ç
=+ »
÷
ç
÷
ç
÷
÷
ç
èø
ò
.
Vìlàmtrònkếtquảđếnhàngphầntrămnên
1Sm»
.
Câu82: Tìmdiệntíchlớnnhấtcủahìnhchữnhậtnộitiếptrongnửađườngtrònbánkính ,
biếtmộtcạnhcủahìnhchữnhậtnằmdọctrênđườngkínhcủađường tròn.
A. B. C. D.
Gọi làđộdàicạnhhìnhchữnhậtkhôngnằmdọctheođườngkínhđườngtròn .
Khiđóđộdàicạnhhìnhchữnhậtnằmdọctrênđườngtrònlà:
Diệntíchhìnhchữnhật:
Tacó
.Suyra làđiểmcựcđạicủahàm .
Vậydiệntíchlớnnhấtcủahìnhchữnhậtlà:
10cm
10cm
x
2
80cm
2
100cm
2
160cm
2
200cm
()
x
cm
(
)
010x<<
(
)
22
210 .
x
cm-
22
210Sx x=-
2
22 2 2
22
2
210 2.10 4
10
x
Sx x
x
¢
=-- =-
-
()
()
é
ê
=
ê
ê
¢
=
ê
ê
=-
ê
ë
10 2
thoûa
2
0
10 2
khoâng thoûa
2
x
S
x
10 2
84020
2
SxS
æö
÷
ç
÷
¢¢ ¢¢
=- =- <
ç
÷
ç
÷
÷
ç
èø
10 2
2
x =
(
)
Sx
()
2
22
10
S 10 2. 10 100
2
cm
=-=
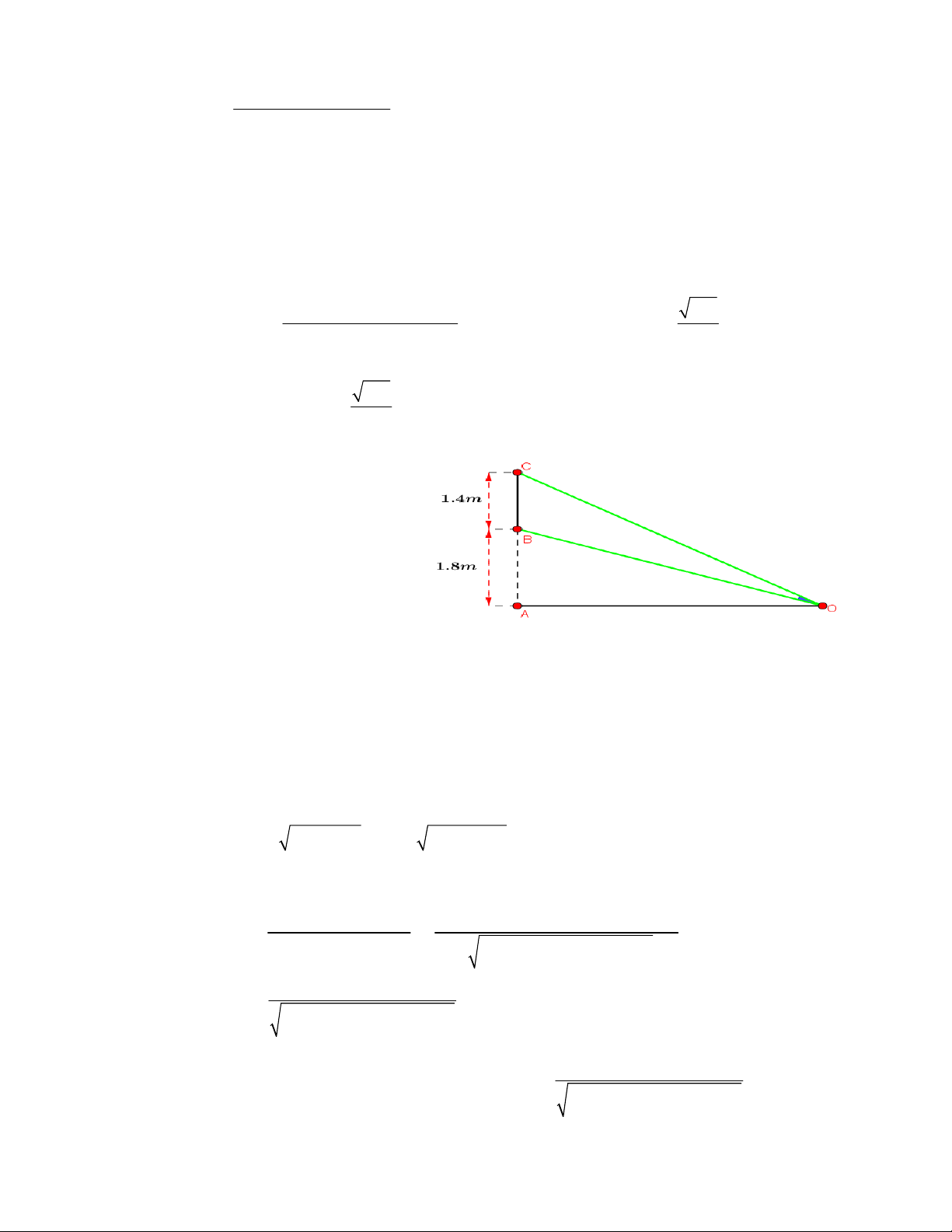
Câu83: LưulượngxeôtôvàođườnghầmHảiVânĐàNẵngđượcchobởicông thức
()
2
290,4 v
0,36 13,2 264
fv
vv
=
++
xe/giây,trongđó
(
)
/vkm h
làvậntốctrungbìnhcủacác
xekhivàođườnghầm.Tínhlưulượngxelàlớnnhất.Kếtquảthuđượcgầnvớigiátrịnào
sauđâynhất?
A.
9 . B.
8, 7
. C.
8, 8
. D.
8, 9
.
Hướngdẫngiải
ĐápánD
Tacó
()
()
()
2
2
2
290,4 0,36 264
'
0, 36 13, 2 264
v
fv
vv
-+
=
++
với
0v >
.
()
264
'0
0, 6
fv v==
Khiđó
()
()
0;
264
8, 9
0, 6
v
Max f v f
Î+¥
æö
÷
ç
÷
ç
=»
÷
ç
÷
ç
÷
ç
èø
xe/giây
Câu84: Một màn ảnh hình chữ nhật
cao
1, 4m
vàđặtởđộcao
1, 4m
sovớitầmmắttínhtừ
đầumépdướicủamànhình.
Đểnhìnrõnhấtphảixácđịnh
vị trí đứng sao cho góc nhìn
lớn nhất. Hãy xác định vị trí
đó?Biếtrằnggóc
BOC
nhọn.
A.
2, 4AO m=
. B.
2AO m=
.
C.
2, 6AO m=
. D.
3AO m=
.
Hướngdẫngiải
ĐápánA
Đặtđộdàicạnh
(
)
(
)
,0AO x m x=>
Suyra
22
3, 24 , 10, 24BO x CO x=+ = +
Tasửdụngđịnhlícosintrongtamgiác
OBC
tacó:
()( )
()( )
22
222
22
3, 24 10, 24 1, 96
cos
2.
23,24 10,24
xx
OB OC BC
BOC
OB OC
xx
++ +-
+-
==
++
()( )
2
22
5, 76
3,24 10,24
x
xx
+
=
++
Vìgóc
BOC
nênbàitoántrởthànhtìmxđể
()
()( )
2
22
5, 76
3,24 10,24
x
Fx
xx
+
=
++
đạtgiátrịnhỏ
nhất.
Đặt
(
)
(
)
2
3, 24 , 3, 24xtt+=>
.Suyra
()
() ()
63
25 63
25
725 7
t
t
Ft
tt tt
+
+
==
++
TađitìmtđểFtđạtgiátrịnhỏnhất.
()
()
()()
()
()
27
25 7 25 63
27
25 63 1
'
25
7
25 7
t
tt t
tt
t
Ft
tt
tt
æö
æö
÷
ç÷
ç
÷
÷
+
ç
ç
÷
÷
ç
ç
+- +
÷
÷
ç
ç
÷
÷
ç
ç
÷
÷
ç
+
÷
ç
÷
ç
ç
+÷
èø
÷
ç
==
÷
ç
÷
ç
÷
+
ç
+
÷
ç
÷
ç
÷
ç
÷
÷
ç
÷
ç
÷
ç
èø
(
)
(
)
(
)
(
)
(
)
(
)
(
)
2
50 7 25 63 2 7
1 1 49 441
25 25
27 7 27 7
tt t t
t
tt tt tt tt
æöæö
÷÷
çç
+- + +
÷÷
-
çç
÷÷
çç
==
÷÷
çç
÷÷
çç
÷÷
++ ++
çç
÷÷
÷÷
çç
èøèø
()
'0 9Ft t==
Bảngbiếnthiên
t
3,249
+¥
()
'Ft
‐0
(
)
Ft
min
F
Thayvàođặttacó:
(
)
22
144
3, 24 9 2, 4 m
25
xx x+== =
Vậyđểnhìnrõnhấtthì
2, 4AO m=
Câu85: Mộtcôngtynhậnlàmnhữngchiếcthùngphikínhayđáyvớithểtích theo yêu cầu là
3
2 mp mỗichiếcyêucầutiếtkiệmvậtliệunhất.Hỏithùngphảicóbánkínhđáy
R
và
chiềucao
h
làbaonhiêu?
A.
1
2,
2
Rmh m==
. B.
1
,8
2
Rmhm==
.C.
1
4,
8
Rmh m==
. D.
1, 2Rmh m==
.
Hướngdẫngiải
ĐápánA
Gọi
R
làbánkínhđáythùng
m
,h :làchiềucaocủathùng
m
.ĐK:
0, 0Rh>>
Thểtíchcủathùnglà:
22
2
2
R2 2Vh Rh h
R
pp====
Diệntíchtoànphầncủathùnglà:
()
2 2
2
22
2R 2R 2R 2R 2
tp
Sh hR R R
R
R
ppp p p
æöæö
÷÷
çç
÷÷
=+= += +=+
çç
÷÷
çç
÷÷
çç
èøèø
Đặt
() ()
2
2
20ft t t
t
p
æö
÷
ç
÷
=+>
ç
÷
ç
÷
ç
èø
với
tR=
()
()
()
3
3
22
41
1
'4 ,'10 1 1
t
ft t f t t
tt
p
p
-
æö
÷
ç
÷
=-= ===
ç
÷
ç
÷
ç
èø
Bảngbiếnthiên:
t
-¥
01
+¥
(
)
'ft
‐0
(
)
ft
Min
Vậytacầnchếtạothùngvớikíchthước
1, 2Rmh m==
Câu86: Mộtcửahàngbánlẻbán
2500 cáitivimỗinăm.Chiphígửitrongkholà
10$
mộtcáimỗi
năm.Đểđặthàngchiphícốđịnhchomỗilầnđặtlà
20$
cộngthêm
9$
mỗicái.Cửahàng
nênđặthàngbaonhiêulầntrongmỗinămvàmỗilầnbaonhiêucáiđểchiphíhàngtồn
kholànhỏnhất?
A.Đặthàng
25 lần,mỗilần100 cáitivi.
B.Đặthàng
20 lần,mỗilần100 cáitivi.
C.Đặthàng
25
lần,mỗilần
90
cáitivi.
D.Đặthàng
20
lần,mỗilần
90
cáitivi.
Hướngdẫngiải
ĐápánA
Gọi
x
làsốtivimàcừahàngđặtmỗilần 1;2500x
éù
Î
êú
ëû
,đơnvịcái
Sốlượngtivitrungbìnhgửitrongkholà
2
x
nênchiphílưukhotươngứnglà
10. 5
2
x
x=
Sốlầnđặthàngmỗinămlà
2500
x
vàchiphíđặthànglà:
()
2500
20 9x
x
+
Khiđóchiphímàcửahàngphảitrảlà:
() ()
2500 50000
20 9x 5x 5x 22500Cx
xx
=++=++
Lậpbảngbiếnthiêntađược:
(
)
min
100 23500CC==
Kếtluận:đặthàng
25
lần,mỗilần
100
cáitivi.

Câu87: Tínhđếnđầunăm
2011
,dânsốtoàntỉnhBìnhPhướcđạtgần
905 300
,mứctăngdânsốlà
1,37% mỗinăm.Tỉnhthựchiệntốtchủtrương
100%
Trẻemđúngđộtuổiđềuvàolớp
1
.
Đếnnămhọc
2024 2025
ngànhgiáodụccủatỉnhcầnchuẩnbịbaonhiêuphònghọccho
họcsinhlớp
1,mỗiphòngdànhcho
35
họcsinh?Giảsửtrongnămsinhcủalứahọcsinh
vàolớp
1
đótoàntỉnhcó
2400
ngườichết,sốtrẻtửvongtrước
6
tuổikhôngđángkể
A.
459
. B.
222
. C.
458
. D.
221
.
Hướngdẫngiải
ĐápánA
Chỉnhữngemsinhnăm2018mớiđủtuổiđihọc6tuổivàolớp1nămhọc2024‐2025.
Ápdụngcôngthức
1
100
n
n
r
SA
đểtínhdânsốnăm2018.
Trongđó:
905300; 1,37; 8Arn
Dânsốnăm2018là:
8
1,37
905300. 1 1009411
100
A
Dânsốnăm2017là:
7
1,37
905300. 1 995769
100
A
Sốtrẻvàolớp1là:
1009411 995769 2400 16042
Sốphònghọccầnchuẩnbịlà
:
16042 : 35 458,3428571
.
Câu88: Một ô tô đang chạy với vận tốc
10 /ms
thìngườiláiđạpphân,từthờiđiểmđó,ôtô
chuyểnđộngchậmdầnđềuvớivậntốc
() ( )
510/vt t m s=- +
,trongđó
t
làkhoảngthời
giantínhbằnggiây,kểtừlúcbắtđầuđạpphanh.Hỏitừlúcđạpphanhđếnkhidừnghẳnô
tôcòndichuyểnbaonhiêumét?
A.
0, 2m
. B.
2m
. C.
10m
. D.
20m
.
Hướngdẫngiải
ĐápánC
Tacóôtôđiđượcthêm
2
giâynữavớivậntốcchậmdầnđều
() ( )
510/vt t m s=- +
ứngdụngtíchphân,tacóquãngđườngcầntìmlà:
() ( ) ()
2
22
2
00
0
5
d510d 1010
2
Svtt t t t t m
æö
÷
ç
÷
==-+=-+=
ç
÷
ç
÷
ç
èø
òò
*Lúcdừngthìtacó:
(
)
05100 2vt t t=-+ ==
Từlúcđạpphanhđếnlúcdừnghẳn,ôtôđiđượcquãngđường:
2
0
1
2
Svt at=+

Với
() ()
2
0
5
1
2 10.2 5 .2 10
2
10
a
tS m
v
ì
ï
=-
ï
ï
ï
== +- =
í
ï
ï
=
ï
ï
î
*Ápdụngcôngthứclý10tacó:
22
21
2. .vv as-=
Tacòncócôngthứcliênhệgiữavậntốcvàgiatốc:
0
.vv at=+
Dựavàophươngtrìnhchuyểnđộngthì
()
2
5/ams=-
Khidừnghẳnthìtacó
(
)
2
0/vms=
Theocôngthứcbanđầu,tađược
(
)
()
22
2
21
010
10
2
2. 5
vv
sm
a
-
-
===
-
.
Câu89: Mộtcôngtybấtđộngsảncó
50
cănhộchothuê.Biếtrằngnếuchothuêmỗicănhộvớigiá
2000.000
đồngmỗithángthìmọicănhộđềucóngườithuêvàcứmỗilầntănggiácho
thuêmỗicănhộ
100.000
đồngmỗithángthìcóthể
2
cănhộbịbỏtrống.Muốncóthu
nhậpcaonhất,côngtyđóphảichothuêvớigiámỗicănhộlàbaonhiêu?
A.
2.250.000.
B.
2.350.000.
C.
2.450.000.
D.
2.550.000.
Hướngdẫngiải
ĐápánA
Gọi
x
làgiáchothuêthựctếcủamỗicănhộ,
x
–đồng; 2000.000x ³ đồng.
Sốcănhộchothuêđượcứngvớigiáchothuê:
() ()
11
50 2000000 90, 1
50000 50.000
xx-- =-+
Gọi
()
Fxlàhàmlợinhuậnthuđượckhichothuêcáccănhộ,
()
Fx:đồng.
Tacó
()
2
11
90 90x
50.000 50.000
Fx x x x
æö
÷
ç
÷
=- + =- +
ç
÷
ç
÷
ç
èø
Bàitoántrởthànhtìmgiátrịlớnnhấtcủa
()
2
1
90x
50.000
Fx x=- +
vớiđiềukiện
2000.000x ³
()
1
'90
25.000
Fx x=- +
()
1
' 0 90 0 2.250.000
25.000
Fx x x=- + ==
Talậpbảngbiếnthiên:
x
2000.000
2.250.000
+¥
()
'Fx
0
-
()
Fx
max
F
Suyra
()
Fx
đạtgiátrịlớnnhấtkhi
2.250.000x =
Vậycôngtyphảichothuêvớigiá
2.250.000
đồngmỗicănhộthìđượclãilớnnhất.
Nhậnxét:
Làmsaotacóthểtìmđượchệsố
1
50000
trongbiểuthức
()
1
?
Tacóthểhiểuđơngiảnnhưsau:Sốcănhộchothuêmỗithángứngvớisốtiềnchothuê;
()
50 2000.000 2.000.000mx x-- =
thìsốcănhộđượcthuêlà
50
.Nếusốtiềnchothuê
tănglênlà
2.100.000x =
thìcó
2
cănhộđểtrống,nghĩalàcó
48
ngườithuê.Tacó:
()
1
50 2.100.000 2.000.000 48
50000
mm
--==
.
Câu90: Cầnphảilàmcáicửasổmà,phíatrênlàhìnhbánnguyệt,phíadưới
là hình chữ nhật, có chu vi là
()am
a
chính là chu vi hình bán
nguyệtcộngvớichuvihìnhchữnhậttrừđiđộdàicạnhhìnhchữ
nhậtlàdâycungcủahìnhbánnguyệt.Hãyxácđịnhcáckíchthước
củanóđểdiệntíchcửasổlàlớnnhất?
A.chiềurộngbằng
p+
2
4
a
,chiềucaobằng
p+4
a
B.chiềurộngbằng
p+4
a
,chiềucaobằng
p+
2
4
a
C.chiềurộngbằng
p+(4 )a
,chiềucaobằng
p+2(4 )a
D.chiềurộngbằng
(4 )-a p
,chiềucaobằng
2(4 )-a p
Hướngdẫngiải
ĐápánA
Gọi
x
làbánkínhcủahìnhbánnguyệt.Tacóchuvicủahìnhbánnguyệtlà
p x
,tổngba
cạnhcủahìnhchữnhậtlà
p-ax
.Diệntíchcửasổlà:
pp
pp
p
--
=+= + =-+ = + -
+
2
2
12
2
2(2)(2)()
22 22
2
2
xaxx
a
SS S x ax x x x
.

Dễthấy
S
lớnnhấtkhi
p
=-
+2
2
a
xx
hay
p
=
+4
a
x
.Cóthểdùngđạohàmhoặcđỉnh
Parabol
Vậyđể
max
S
thìcáckíchthướccủanólà:chiềucaobằng
p+4
a
;chiềurộngbằng
p+
2
4
a
Câu91: Tronglĩnhvựcthuỷlợi,cầnphảixâydựngnhiềumươngdẫnnướcdạng"Thuỷđộnghọc"
KýhiệudiệntíchtiếtdiệnngangcủamươnglàS,
làđộdàiđườngbiêngiớihạncủatiết
diệnnày,
‐đặctrưngchokhảnăngthấmnướccủamương;mươngđựơcgọilàcódạng
thuỷđộnghọcnếuvớiSxácđịnh,
lànhỏnhất.Cầnxácđịnhcáckíchthướccủamương
dẫnnướcnhưthếnàođểcódạngthuỷđộnghọc?nếumươngdẫnnước có tiết diện
nganglàhìnhchữnhật
A.
==4,
4
S
xSy
B.
==4,
2
S
xSy
C.
==2,
4
S
xSy
D.
==2,
2
S
xSy
Hướngdẫngiải
Gọix,ylầnlượtlàchiềurộng,chiềucaocủamương.Theobàira ta có: S xy;
=+= +
2
2
S
yx x
x
.Xéthàmsố =()x
+
2S
x
x
.Tacó
'
()x
-
2
2S
x
1
-
2
2
2xS
x
.
'
()x
0
-==
2
20 2xS x S
,khiđóy
S
x
2
S
.
Dễthấyvớix,ynhưtrênthìmươngcódạngthuỷđộnghọc,vậycáckíchthướccủamươnglà
= 2xS
,y
2
S
thìmươngcódạngthuỷđộnghọc.
Câu92: Mộtthợxâymuốnsửdụng
1
tấmsắtcóchiềudàilà
4m
,chiềurộng
1m
đểuốnthành
2m
khungđúcbêtông,
1khunghìnhtrụcóđáylàhìnhvuôngvà1khunghìnhtrụcóđáylà
hìnhtròn.Hỏiphảichiatấmsắtthành
2
phầntheochiềudàinhưthếnàođểtổngthể
tích
2
khunglànhỏnhất?
A.Khungcóđáylàhìnhvuông,khungcóđáylàhìnhtrònlầnlượtcóchiềudàilà
42
,
44pp
++
.
B.Khungcóđáylàhìnhvuông,khungcóđáylàhìnhtrònlầnlượtcóchiềudàilà
24
,
44
p
pp
++
.
x
y

C.Khungcóđáylàhìnhvuông,khungcóđáylàhìnhtrònlầnlượt có chiều dài là
24 14
,
44
p
pp
+
++
.
D.Khungcóđáylàhìnhvuông,khungcóđáylàhìnhtrònlầnlượt có chiều dài là
4142
,
44
p
pp
+
++
.
Hướngdẫngiải
Gọi
12
,VV
lầnlượtlàthểtíchcủakhunghìnhtrụcóđáylàhìnhvuôngvàkhunghìnhtrụ
cóđáylàhìnhtròn.Gọi
a làchiềudàicủacạnhhìnhvuôngvàr làbánkínhcủahìnhtròn.
Tacó:
22
12
VV a rp+=+
đơnvịthểtích.
Mà
()
12
42 4 2 ,0
2
ar a r r
pp
p
+==- <<
. Suy ra
() ()
2
2
12
1
2
4
Vr V V r r
pp=+= + -
.
() ()()
()
12
22,0
4
4
Vr r rVr rppp
p
¢¢
=- - ==
+
. Lập bảng biến thiên suy ra
min
4
4
V
p
æö
÷
ç
÷
=
ç
÷
ç
÷
ç
+
èø
.
Vậy,phảichiatấmsắtthành
2 phần:phầnlàmlăngtrụcóđáylàhìnhvuônglà
()
()
4
4
m
p
p +
.
Câu93: Mộtcôngtysảnxuấtmộtloạicốcgiấyhìnhnóncóthểtích
3
27cm vớichiềucaolàh và
bánkínhđáylà
r đểlượnggiấytiêuthụlàítnhấtthìgiátrịcủar là:
A.
6
4
2
3
2
r
p
=
. B.
8
6
2
3
2
r
p
=
. C.
8
4
2
3
2
r
p
=
. D.
6
6
2
3
2
r
p
=
.
Hướngdẫngiải
ĐápánB
Thểtíchcủacốc:
22
2
181811
27 .
Vrh rh h
r
p
pp
====
3
Lượnggiấytiêuthụítnhấtkhivàchỉkhidiệntíchxungquanhnhỏnhất.
22
22 2 4
24 22
81 1 81 1
22 2 2
xq
Srlrrhrr r
rr
pp p p
pp
== += + = +
22 22
44
3
22 22 22 22
81 1 81 1 81 1 81 1
223..
22 22
rr
rr rr
pp
pp pp
=++ ³
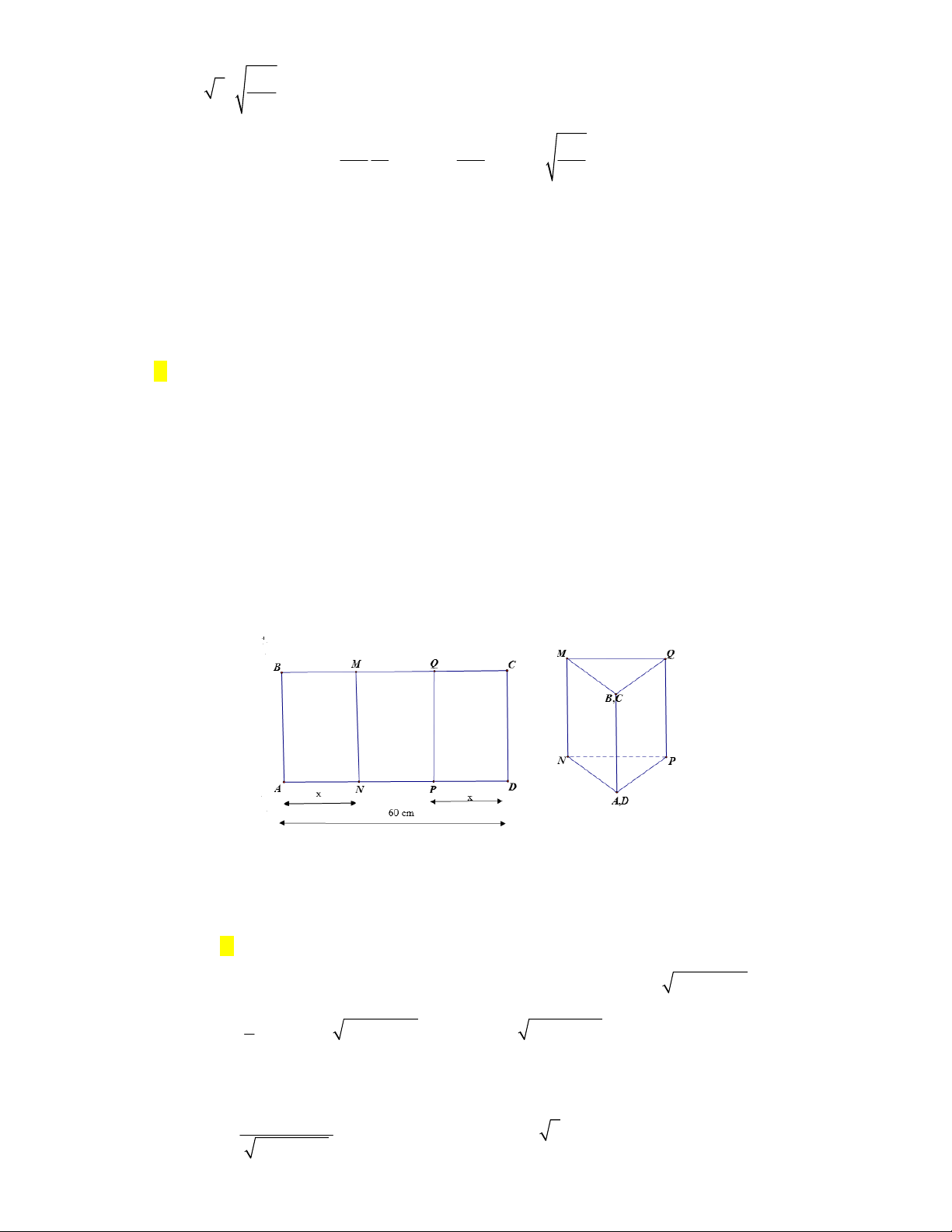
4
6
4
81
23
4
p
p
= theoBĐTCauchy
xq
S
nhỏnhất
288
46
6
22 2 2
81 1 3 3
222
rrr
rppp
= = =
.
Câu94: GiảsửtỉlệlạmphátcủaViệtNamtrong10nămqualà
5%
.Hỏinếunăm2007,giáxănglà
12000 VND/lít
.Hỏinăm2016giátiềnxănglàbaonhiêutiềnmộtlít.
A.
11340,000 VND/lít
.B.
113400 VND/lít
.
C.
18615, 94 VND/lít. D.186160,94 VND/lít .
Hướngdẫngiải
ĐápánC
Giáxăngnăm2008là
(
)
12000 1 0, 05+
Giáxăngnăm2009là
()
2
12000 1 0, 05+
…
Giáxăngnăm2016là
()
9
12000 1 0, 05 18615,94 VND/lit+» .
Câu95: Chomộttấmnhômhìnhchữnhật
A
BCD
có 60AD cm= .Tagấptấmnhômtheo2cạnh
M
N
và
PQ
vàophíatrongđếnkhi
A
B vàDC trùngnhaunhưhìnhvẽdướiđâyđểđược
mộthìnhlăngtrụkhuyếthaiđáy.Tìm
x
đểthểtíchkhốilăngtrụlớnnhất?
A.
20x = . B. 15x = . C.
25x
. D. 30x = .
Hướngdẫngiải
ĐápánA
Tacó
60 2PN x=-,gọiH làtrungđiểmcủaPN suyra 60 900AH x=-
() ()
(
)
()
1
. 60 2 60 900 60 2 15 225
2
ANP
Sxxxxfx
D
=- -=- -=
,dochiềucaocủakhối
lăngtrụkhôngđổinênthểtíchkhốilăngtrụmaxkhi
()
fxmax.
()
(
)
() ()
45 20
' 0 20, 20 100 3, 15 0
15 225
x
fx x f f
x
--
=====
-

()
max f 100 3x = khi
20x =
Câu96: Mộtlãonôngchiađấtchocontraiđểngườiconcanhtácriêng,biếtngườiconsẽđược
chọnmiếngđấthìnhchữnhậtcóchuvibằng
800( )m
.Hỏianhtachọnmỗikíchthướccủa
nóbằngbaonhiêuđểdiệntíchcanhtáclớnnhất?
A.
´200 200mm
B.
´300 100mm
C.
´250 150mm
D.Đápánkhác
Hướngdẫngiải
ĐápánA
Gọichiềudàivàchiềurộngcủamiếngđấtlầnlượtlà: và
Diệntíchmiếngđất:
Theođềbàithì: hay .Dođó: với
Đạohàm: .Cho .
Lậpbảngbiếnthiêntađược: khi .
Kếtluận:Kíchthướccủamiếngđấthìnhchữnhậtlà làhìnhvuông.
Lưuý:CóthểđánhgiábằngBĐTCô‐Sy.
Câu97: Mộttrangchữcủamộttạpchícầndiệntíchlà
2
384cm
.Lềtrên,lềdướilà3cm;lềphải,lề
tráilà2cm.Khiđóchiềungangvàchiềudọctốiưucủatranggiấylầnlượtlà:
A.
24 , 25 .cm cm
B.
15 , 40 .cm cm
C.
20 , 30 .cm cm
D.
22,2 , 27 .cm cm
Hướngdẫngiải
ĐápánC
Gọi
(
)
(
)
,0,0abcm a b>>làđộdàichìudọcvàchìungangcủatrangchữsuyrakích
thướctranggiấylà
6, 4ab++
Tacó:
()
384
.384 1ab b
a
==
Diệntíchtrangsáchlà:
()()
2304
6 4 4 408
Sa b S a
a
=+ += + +
TheobấtđẳngthứcCAUCHYtacó:
2304
2 4 . 408 600Sa
a
³ + =
Suyra
2304
600 4 24
MinS a a
a
== =
,suyrachiềudọcvàchiềungangtốiưulà:
30 ,20cm cm
Câu98: ÔngBìnhmuốnthiếtkếmáichomộtxưởngmaycódiệntích
2
20000
m
cóhaiđồánnhư
sau:
x
y
C=800m
()xm
()(, 0).
y
mxy>
Sxy=
2( ) 800xy+= 400
y
x=-
2
(400 ) 400Sx x x x=-=-+
0x >
ʹ( ) 2 400Sx x=- + ʹ 0 200
y
x==
max
40000S =
200 200xy==
200 200´
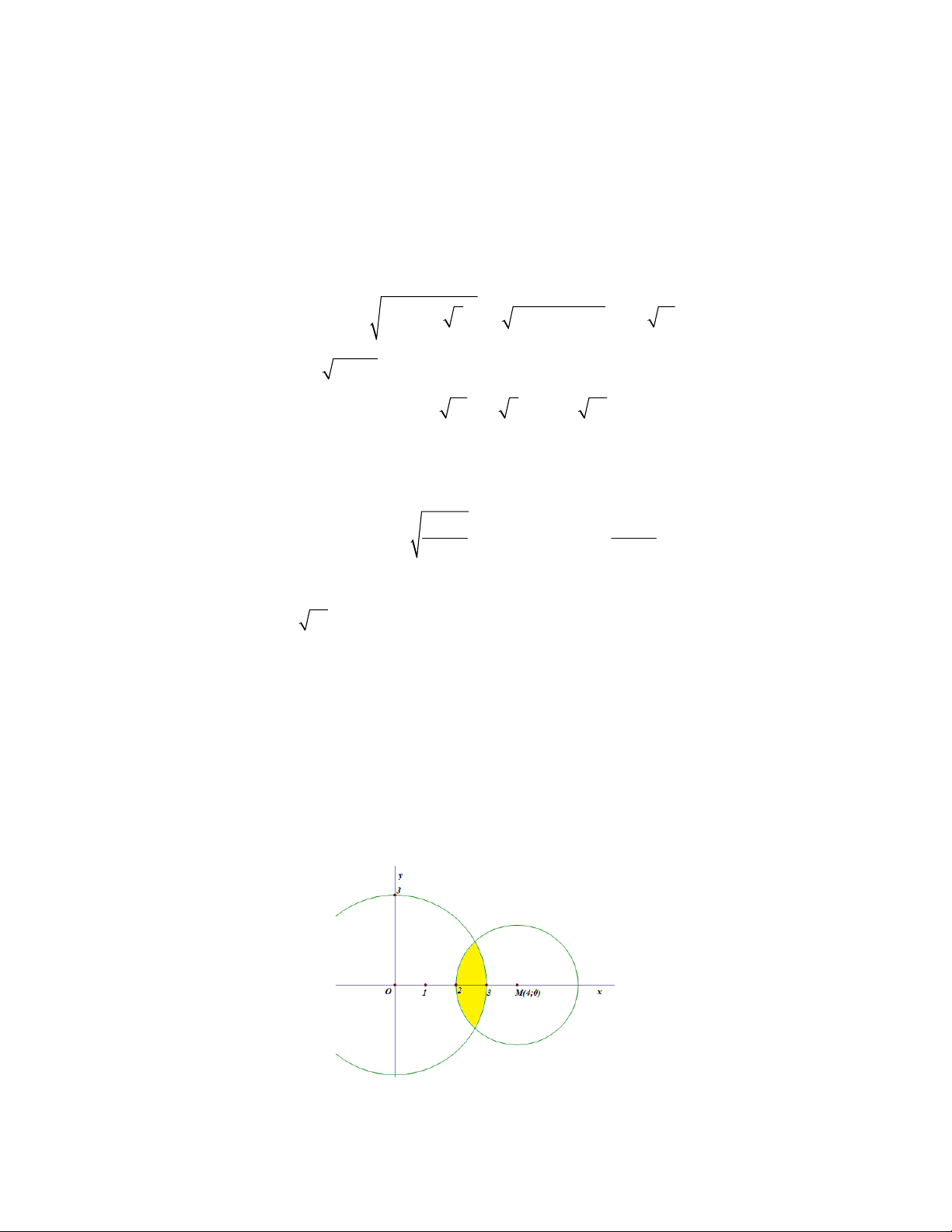
‐CôngtyAthiếtkếdạnghìnhvuôngvớimáilàhìnhchóptứgiácđềucóchiềucaobằng
70m
.
‐CôngtyBthiếtkếdạnghìnhtrònvớimáilànửamặtcầuúpxuống.
HỏithiếtkếcủacôngtyAgiúptiếtkiệmdiệntíchmáihơnbaonhiêu
2
m
?
A.
2
11857 . m
B.
2
20000 .
m C.
2
9000
.m D.
2
5000
.m
Hướngdẫngiải
ĐápánA
PhươngánA:Hìnhchóptứgiácđều
Chiềudàicủacạnhbênlà
()
()
2
2
50 2 4900 5000 30 11 70hh+=+= =
Độdàicạnhđáylà:
20000
chiềucaomặtbên.cạnhđáy
()
2
2.30 11.100 2 6000 22 m==
PhươngánB:Mặtcầu:
Diệntíchhìnhtrònlớnbằng
22 2 2
20000 20000
20000 20000 ; 2 2 40000
mat
mR R S R mppp
pp
= = = = =
Kếtluận:VậyphươngánAgiúptiếtkiệndiệntíchmáihơn
222
40000 6000 22 11857mmm-=
Câu99: Trêncánhđồngcỏcó2conbòđượccộtvào2câycọckhácnhau.Biếtkhoảngcáchgiữa2
cọclà4métcòn2sợidâycột2conbòdài3métvà2mét.Tínhphầndiệntíchmặtcỏlớn
nhấtmà2conbòcóthểănchunglấygiátrịgầnđúngnhất.
A.
1, 034
m
2
B.
1, 5 74
m
2
C.
1,989
m
2
D.
2, 824
m
2
Hướngdẫngiải
Diệntíchmặtcỏănchungsẽlớnnhấtkhi2sợidâyđượckéocăngvàlàphầngiaocủa2
đườngtròn.
Xéthệtrụctọađộnhưhìnhvẽ,gọi
,OM
làvịtrícủacọc.Bàitoánđưavềtìmdiệntích
phầnđượctômàu.

Tacóphươngtrìnhđườngtròntâm
(
)
22 2
:3+=Ox y
vàphươngtrìnhđườngtròntâm
(
)
(
)
2
22
:4 2-+=Mx y
Phươngtrìnhcácđườngcongcủađườngtrònnằmphíatrêntrục
Ox
là:
2
9=-yx
và
()
2
44=--yx
Phươngtrìnhhoànhđộgiaođiểm:
()
2
2
21
449 48169
8
-- = - + -==
xxxx
Diệntíchphầnđượctômàulà:
()
21
3
8
2
2
221
8
24 4 9 1,989
éù
êú
êú
= --+-»
êú
êú
êú
ëû
òò
Sxdxxdx
. Ta có
thểgiảitíchphânnàybằngphépthếlượnggiác,tuynhiênđểtiếtkiệmthờigiannênbấm
máy.ChọnC.
Câu100: Bêntrongmộtcănnhàbỏhoanghìnhlậpphươngthểtích1000m
3
có3chúnhệnconrất
haycãivãnênphảisốngriêng.Mùađôngđến,vìđóirétnênchúngđànhquyếtđịnhhợp
tácvớinhaugiănglướiđểbắtmồi.Bachúnhệntínhtoánsẽgiăngmộtmảnhlướihình
tamgiáctheocáchsau:Mỗichúnhệnsẽđứngởméptườngbấtkìcóthểmépgiữa2bức
tường,giữatườngvớitrần,hoặcgiữatườngvớinềnrồiphóngnhữngsợitơlàmkhung
đếnvịtrícũng2connhệncònlạirồisauđómớiphóngtơdínhđanphầnlướibêntrong.
Nhưngvìvốnđãcóhiềmkhíchtừlâu,nêntrướckhibắtđầu,chúngquyđịnhđểtránhxô
xát,khôngcóbấtkì2connhệnnàocùngnằmtrênmộtmặttường,nềnhoặctrầnnhà.
Tính chu vi nhỏ nhấtcủamảnhlướiđượcgiăngbiếtcácsợitơ khung căngvàkhông
nhùn.
A.
15 6 mét B.230mét C.12 10 mét D.10 2 mét
Hướngdẫngiải
Bàitoánnàytasẽgiảiquyếtbằngcáchứngdụngphươngpháptọađộtrongkhônggian.
Đặthệtrụctọađộnhưhìnhvẽ.Khôngmấttínhtổngquát,vàdựavàoyêucầuvềvịtrí3connhệnta
xácđịnhlàcácđiểm
,,MNP
nằmtrêncáccạnh
'', ',AB CC AD
nhưhìnhvẽ.
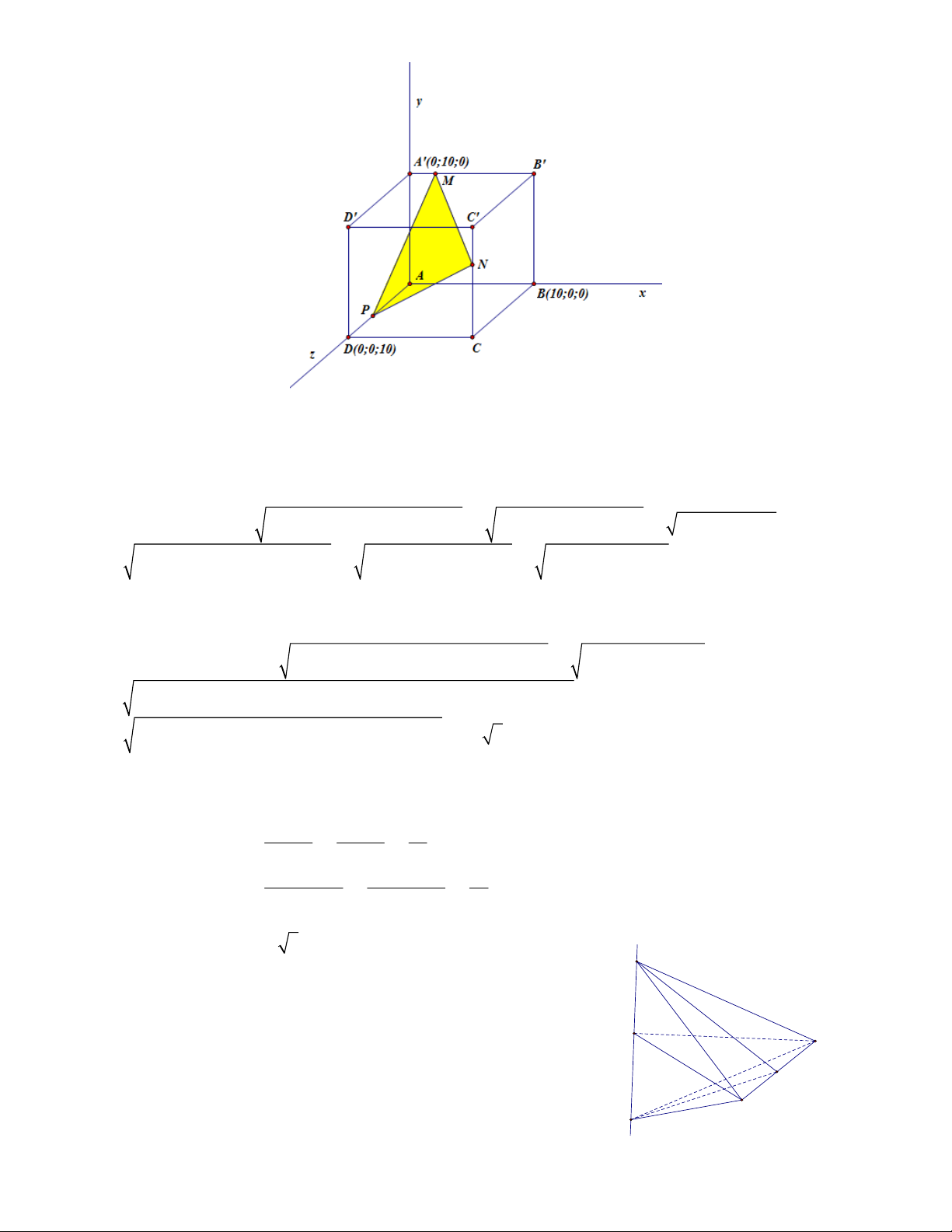
Yêucầubàitoánlàcầntìmtọađộcủa3điểm
,,MNP
đểchuvitamgiác
MNP
nhỏnhất.
Đặt
()()( )
;10; 0 , 0; 0; , 10; ;10Mx P z N y .Chuvitamgiác
MNP
là:
()() ()
(
)
(
)
(
)
(
)
22 2
222 222
22 2 2
22 22 2
10 10 10 10 10 10
10 10 10 10 10 10
++=-+-++ ++- +++
=-+-+++-+++-+
MN NP PQ x y y z x z
xy yz z x
Ápdụngbấtđẳngthứcvecto
:
()() ()
()( )()
()()
22 2
22 2
222
22
10 20 20 10
10 10 10 10 10 10
2 5 450 10 10 10 15 6
MN NP PM x y y z z x
xyz y z x
yzx
++³-+++-+++-+
³ -++ + - +- - + + +
=+--++++³
Dấubằngxảyrakhi
5
10 10 10
25 5
10 10
10
10 20 20
10
ì
ï
ï
ï
+-=
ì
ï
ï
=
ï
ï
ï
ï
--
ï
ï
ï
== -====
íí
ïï
-
ïï
+=
ïï
ïï
-+ +-
î
ï
==
ï
ï
-
ï
î
yzx
yz
xy
yx x y z
yz
xy
xy yz
zx
Vậygiátrịcầntìmlà
15 6
.ChọnA.
Câu101: Mộtngôinhàcónềndạngtamgiácđều
ABC cạnhdài
10 m
đượcđặtsongsongvàcáchmặtđất
()
hm
.Nhà
có3trụtại
,,ABC
vuônggócvới
A
BC
.Trêntrụ
A
ngườitalấyhaiđiểm
,
M
N
saocho
,AM x AN y==
và góc giữa
M
BC
và
(
)
NBC
bằng
90
để là mái và
phầnchứađồbêndưới.Xácđịnhchiềucaothấpnhất
củangôinhà.
(
d
)
10
x
y
B
C
M
A
N
I
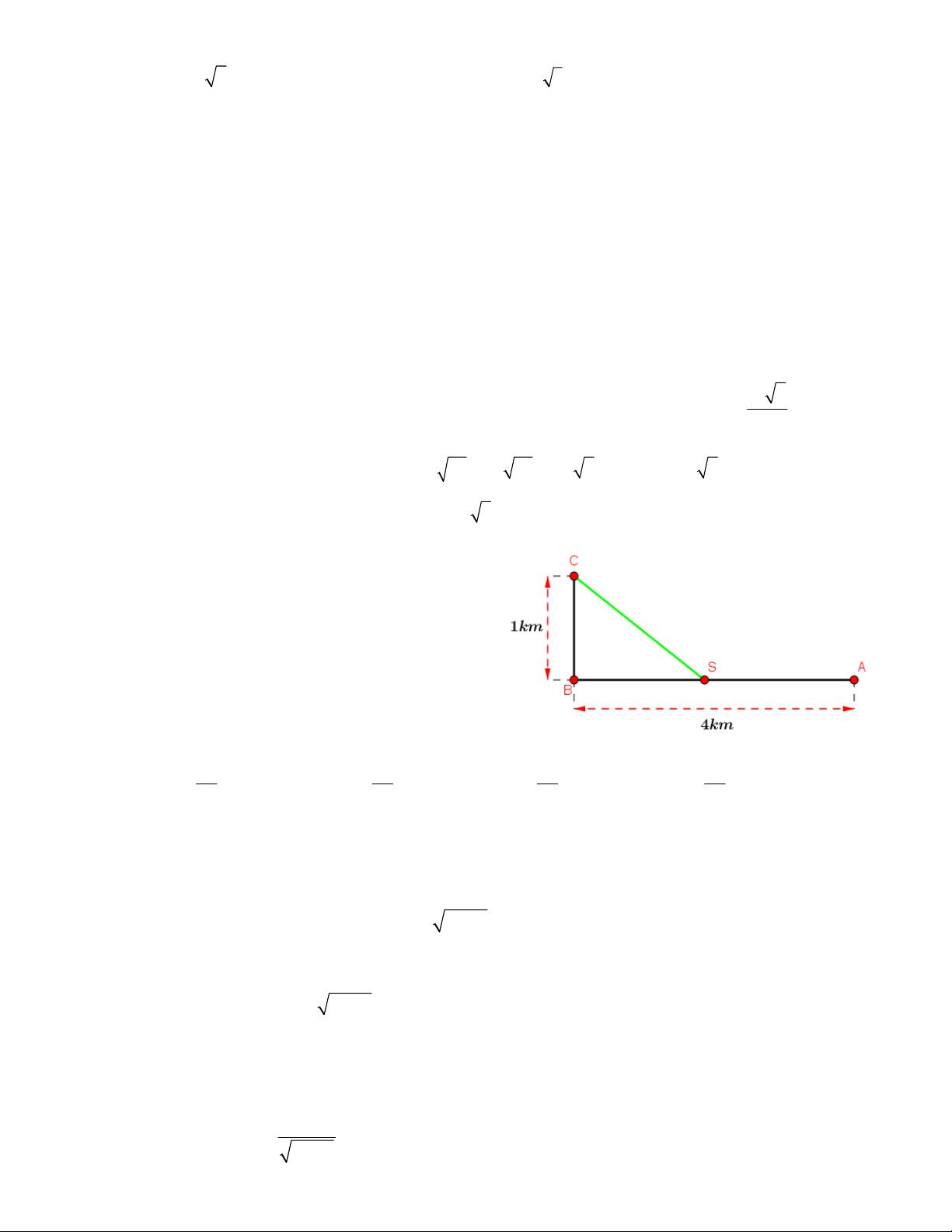
A.
53
. B.
10 3
.
C.
10 . D.12.
Hướngdẫngiải
ĐápánB
Đểnhàcóchiềucaothấpnhấttaphảichọn
N
nằmtrênmặtđất.Chiềucaocủanhàlà
NM x y=+
.
Gọi
I làtrungđiểmcủaBC . Ta có ABCD đều
AI BC^
, vì
(
)
MN ABC MN BC^^
,từđósuyra
()
0
90
MI BC
BC MNI MIN
NI BC
ì
ï
^
ï
^ =
í
ï
^
ï
î
IMND vuôngtạiI nhậnAI làđườngcaonên
2
2
10 3
.75
2
AM AN AI xy
æö
÷
ç
÷
ç
===
÷
ç
÷
ç
÷
ç
èø
TheobấtđẳngthứcCôsi:
2 2.75 103 53xy xy x y+³ = = ==
Dođóchiềucaothấpnhấtcủanhàlà
10 3.
Câu102: NHOQUANAMộtđườngdâyđiệnđược
nốitừmộtnhàmáyđiệnởAđếnmộthòn
đảoởC.khoảngcáchngắnnhấttừCđến
Blà1km.KhoảngcáchtừBđếnAlà4.
Mỗikmdâyđiệnđặtdướinướclàmất
5000 USD, còn đặt dưới đất mất 3000
USD.HỏidiểmStrênbờcáchAbaonhiêu
đểkhimắcdâyđiệntừAquaSrồiđếnC
làíttốnkémnhất.
A.
15
4
km B.
13
4
km C.
10
4
D.
19
4
Hướngdẫngiải
Trướctiên,taxâydựnghàmsố
f
x làhàmsốtínhtổngchiphísửdụng.
Đặt
BS x
thìtađược:
2
4, 1SA x CS x .Theođềbài,mỗikmdâyđiệnđặtdướinước
mất5000USD,cònđặtdướiđấtmất3000USD,nhưvậytacóhàmsố
f
x đượcxácđịnhnhưsau:
2
3000. 4 5000. 1fx x x
với
0;4x
Tacầntìmgiátrịnhỏnhấtcủa
f
x
đểcóđượcsốtiềnítnhấtcầnsửdụngvàtừđóxácđịnhđược
vịtríđiểmS.
2
' 3000 5000. .
1
x
fx
x
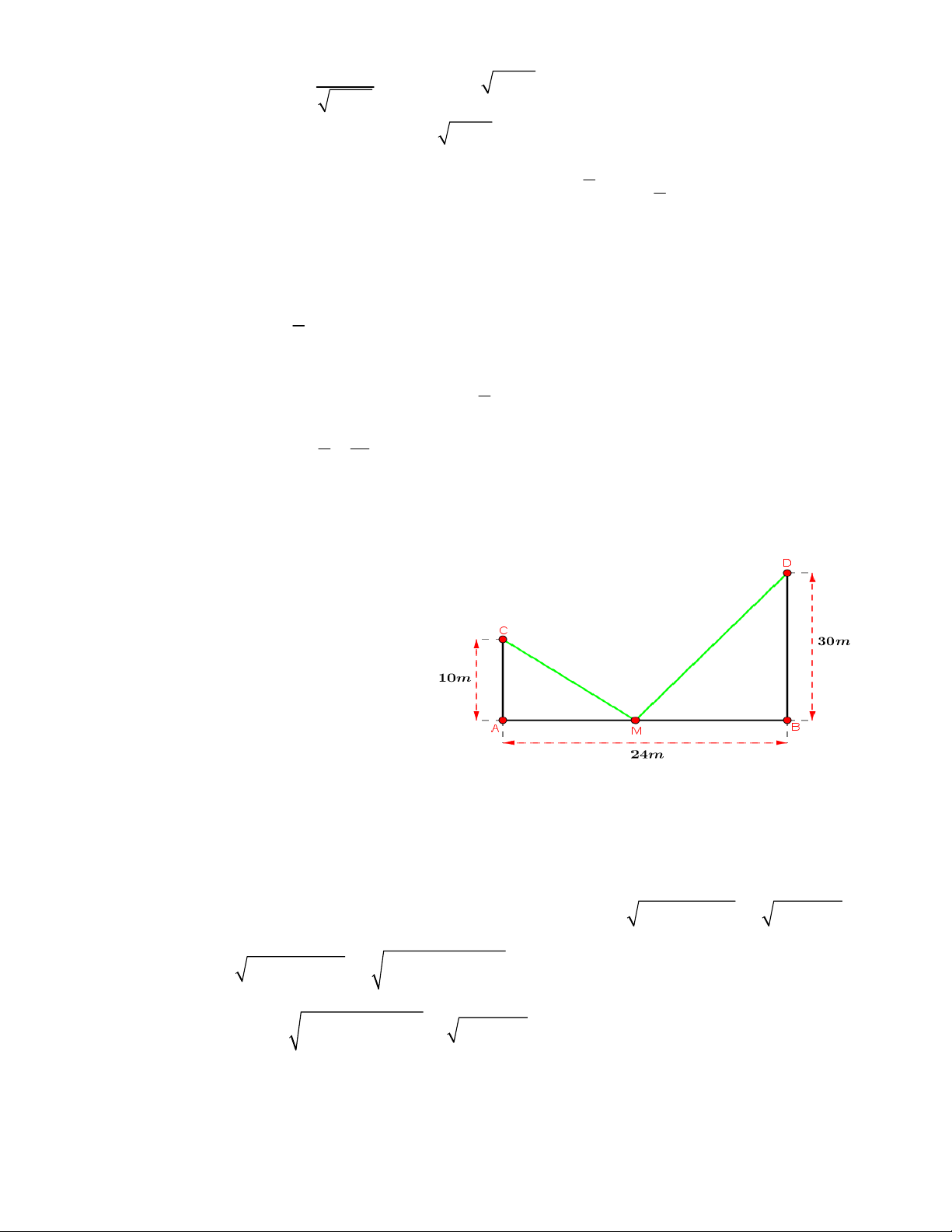
2
2
2
2
' 0 3000 5000. 0 3000 1 5000 0
1
315
3
16 9
3
.
4
4
0
0
x
fx x x
x
xx
x
x
x
x
x
Hàmsố
f
x
liêntụctrênđoạn
0;4 .
Tacó:
3
0 17000, 16000, 4 20615,52813.
4
ff f
Vậygiátrịnhỏnhấtcủa
f
x
là16000vàtại
3
.
4
x
KhiđóchiphílàthấpnhấtvàđiểmSnằmcách
Amộtđoạn
313
44 .
44
SA x
VậyđápánlàB.
Câu103: THTTSỐ673Cóhaichiếccọc
cao
10m
và
30m
lầnlượtđặt
tại hai vị trí
,.AB
Biết khoảng
cách giữa hai cọc bằng
24 m
.
Ngườitachọnmộtcáichốtởvị
trí
M
trênmặtđấtnằmgiữahai
châncộtđểgiangdâynốiđến
haiđỉnh
C
và
D
củacọcnhư
hìnhvẽ.Hỏitaphảiđặtchốtở
vịtrínàođềtổngđộdàicủahai
sợidâyđólàngắnnhất?
A.
6, 18.AM m BM m==
B.
7, 17.AM m BM m==
C.
4, 20.AM m BM m==
D.
12 , 12 .AM m BM m==
Hướngdẫngiải
Đặt
=<< =-(0 24) 24AM x x BM x
.Tacó =+=+
222
100CM CA AM x
()
=+=-+
2
22
24 900MD MB BD x
.Suyratổngđộdàihaisợidâylà:
()
+= -+++= <<
2
2
24 900 100 ( ),(0 24)CM MD x x f x x
Khảosáthàmtađược:
(
)
(
)
==>6=18xm BMm
.ChọnA.
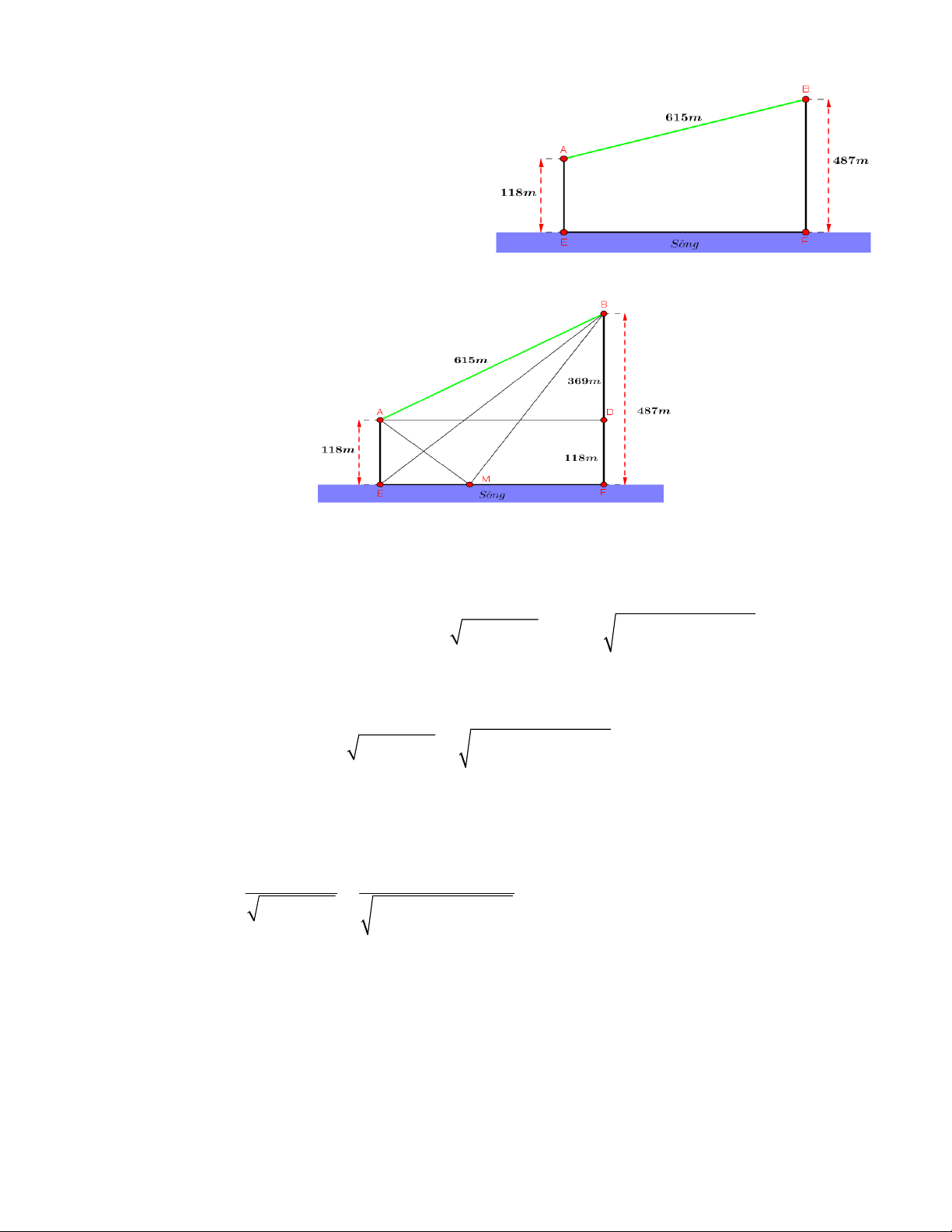
Câu104: HÀNỘI–AMSTERDAMChohaivịtrí
A
,
B
cáchnhau615m,cùngnằmvềmột
phíabờsôngnhưhìnhvẽ.Khoảngcách
từ
A
vàtừ
B
đếnbờsônglầnlượtlà
118mvà487m.Mộtngườiđitừ
A
đến
bờsôngđểlấynướcmangvề
B.
Đoạn
đườngngắnnhấtmàngườiđócóthểđi
là:
A.569,5m B.671,4m C.779,8m D.741,2m
Hướngdẫngiải
GiảsửngườiđóđitừAđếnMđểlấynướcvàđitừMvềB.
dễdàngtínhđược
369, 492.BD EF==
Tađặt
,EM x=
khiđótađược:
()
2
22 2
492 , 118 , 492 487 .MF x AM x BM x=- = + = -+
Nhưvậytacóhàmsố
()
fx
đượcxácđịnhbằngtổngquãngđườngAMvàMB:
() ()
2
22 2
118 492 487fx x x=+ + -+
với
0;492x
éù
Î
êú
ëû
Tacầntìmgiátrịnhỏnhấtcủa
()
fx
đểcóđượcquãngđườngngắnnhấtvàtừđóxácđịnh
đượcvịtríđiểmM.
()
()
22 2
2
492
'.
118
492 487
xx
fx
x
x
-
=-
+
-+
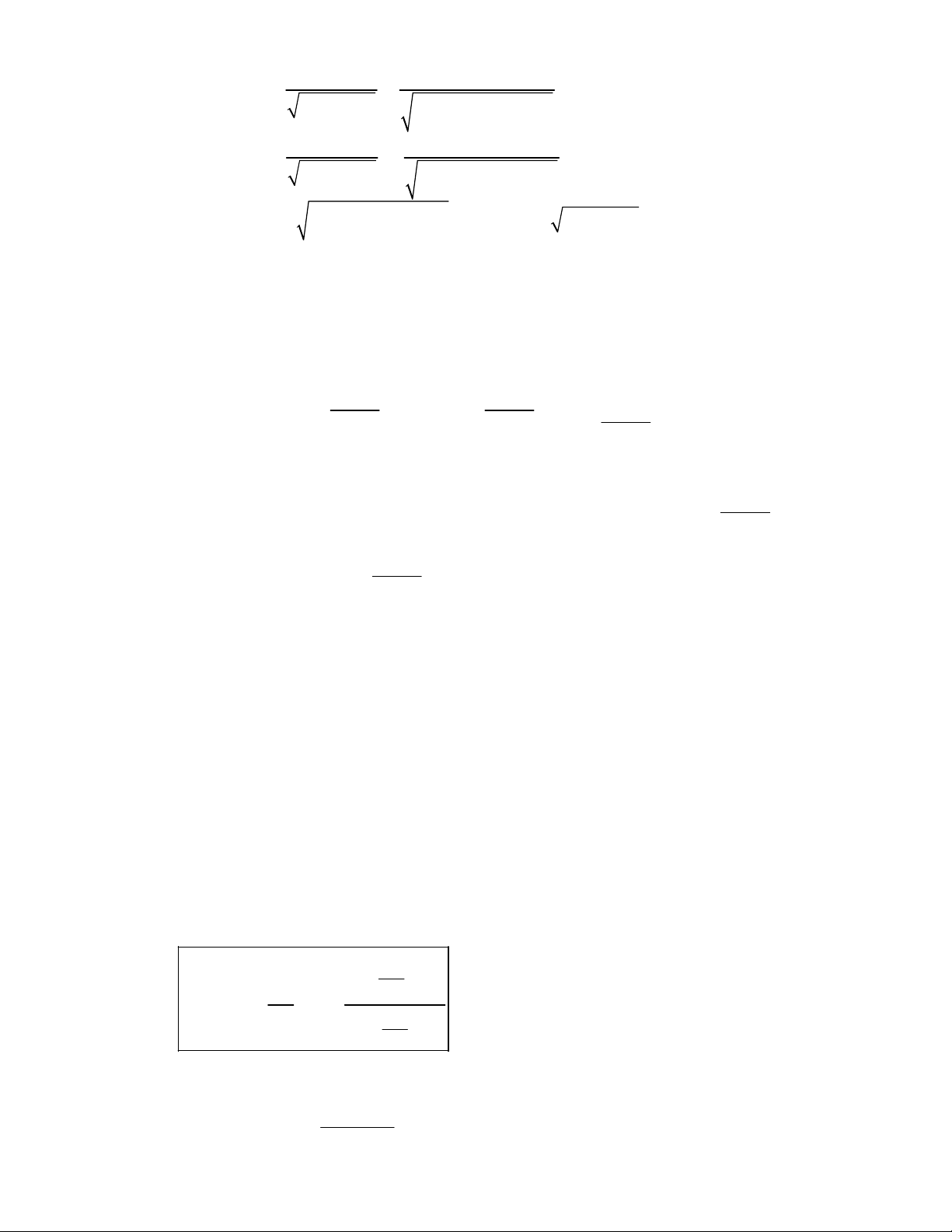
()
()
()
() ()
() ()
()
()( )
22 2
2
22 2
2
2
222
22
2222
22
492
'0 0
118
492 487
492
118
492 487
492 487 492 118
492 487 492 118
0 492
487 58056 118
0 492
58056 58056
605 369
0
xx
fx
x
x
xx
x
x
xx xx
xx xx
x
xx
x
x hay x
x
-
= - =
+
-+
-
=
+
-+
-+=-+
ì
éù
ï
ï
-+ = - +
êú
ï
êú
ëû
í
ï
££
ï
ï
î
ì
ï
ï=-
ï
í
ï
££
ï
ï
î
==-
££
58056
605
492
x
ì
ï
ï
ï
=
í
ï
ï
ï
î
Hàmsố
()
fx
liêntụctrênđoạn
0; 492
éù
êú
ëû
.Sosánhcácgiátrịcủa
(0)
f
,
58056
605
f
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
,
(
)
492f
tacógiátrịnhỏnhấtlà
58056
779, 8
605
fm
æö
÷
ç
÷
»
ç
÷
ç
÷
ç
èø
Khiđóquãngđườngđingắnnhấtlàxấpxỉ779,8m.VậyđápánlàC.
Câu105: AnhTháigửivàongânhàng50triệuđồngvớilãisuất0,6%/tháng.Saumỗitháng,chúTư
đếnngânhàngrútmỗitháng3triệuđồngđểchitiêuchođếnkhihếttiềnthìthôi.Saumột
sốtrònthángthìchúTưrúthếttiềncảgốclẫnlãi.Biếttrongsuốtthờigianđó,ngoàisố
tiềnrútmỗithángchúTưkhôngrútthêmmộtđồngnàokểcảgốclẫnlãivàlãisuấtkhông
đổi.VậythángcuốicùngchúTưsẽrútđượcsốtiềnlàbaonhiêulàmtrònđếnđồng?
A.
1840270
đồng. B.
3000000
đồng.
C.
1840269 đồng. D.1840268 đồng.
Hướngdẫngiải
Phươngpháptựluận
Ápdụngcôngthứctínhsốtiềncònlạisau
n
tháng
()
11
100
19
100
100
n
n
n
r
r
SA X
r
æö
÷
ç
÷
+-
ç
÷
ç
æö
÷
ç
èø
÷
ç
÷
=+ -
ç
÷
ç
÷
ç
èø
Với
50A = triệuđồng,
0, 6r =
và 3X = triệuđồngtađược
1, 0 06 1
50.1, 006 3.
0,006
n
n
n
S
-
=-
.

Đểrúthếtsốtiềnthìtatìmsốnguyêndương
n
nhỏ nhất sao cho
1,006
1, 006 1 500
0 50.1, 006 3. 500 450.1, 006 0 log 18
0,006 450
n
nn
n
Snn
-
< - - <> =
KhiđósốtiềnthángcuốicùngmàAnhTháirútlà
17
17
17
1, 006 1
.1, 006 50.1, 006 3. .1,006 1, 840269833
0,006
S
éù
-
êú
=- »
êú
ëû
triệuđồng
1840270»
đồng
Phươngpháptrắcnghiệm
Nhậplênmànhìnhmáytính
1, 006 1
50.1, 006 3.
0,006
X
X
-
-
,tínhgiátrịchạytừ10đến20với
stepbằng1tađượcbằnggiátrịtươngứngvàsốtiềncònlạinhơhơn3ứngvới
17X =
.
Từ đó tính được số tiền rút ra ở tháng cuối cùng là
17
17
17
1, 006 1
.1, 006 50.1, 006 3. .1, 006 1, 840269833
0, 006
S
éù
-
êú
=- »
êú
ëû
triệuđồng
1840270»
đồng
Câu106: Mộtcôngtyvừatungrathịtrườngsảnphẩmmớivàhọtổchứcquảngcáotrêntruyền
hìnhmỗingày.Mộtnghiêncứuthịtrườngchothấy,nếusau
x
quảngcáođượcphátthìsố
%
ngườixemmuasảnphẩmlà
0.015
100
() , 0
149
x
Px x
e
. Hãy tính số quảng cáo được
pháttốithiểuđểsốngườimuađạthơn
75%
.
A.
333
. B.
343
. C.
330
. D.
323
.
Hướngdẫngiải
Khicó
100
quảngcáophátrathìtỉlệngườixemmuasảnphẩmlà:
1.5
100
100 9.3799%
149
P
e
Khicó
200
quảngcáophátrathìtỉlệngườixemmuasảnphẩmlà:
3
100
200 29.0734%
149
P
e
Khicó
500
quảngcáophátrathìtỉlệngườixemmuasảnphẩmlà:
7.5
100
500 97.3614%
149
P
e
Đápán:A.
Câu107: CHUYÊNQUANGTRUNGLẦN3Trongchươngtrìnhnôngthônmới,tạimộtxãXcóxây
mộtcâycầubằngbêtôngnhưhìnhvẽ.Tínhthểtíchkhốibêtôngđểđổđủcâycầu.
ĐườngcongtronghìnhvẽlàcácđườngParabol.
A.
3
19m
. B.
3
21m
. C.
3
18 .m
D.
3
40m
.
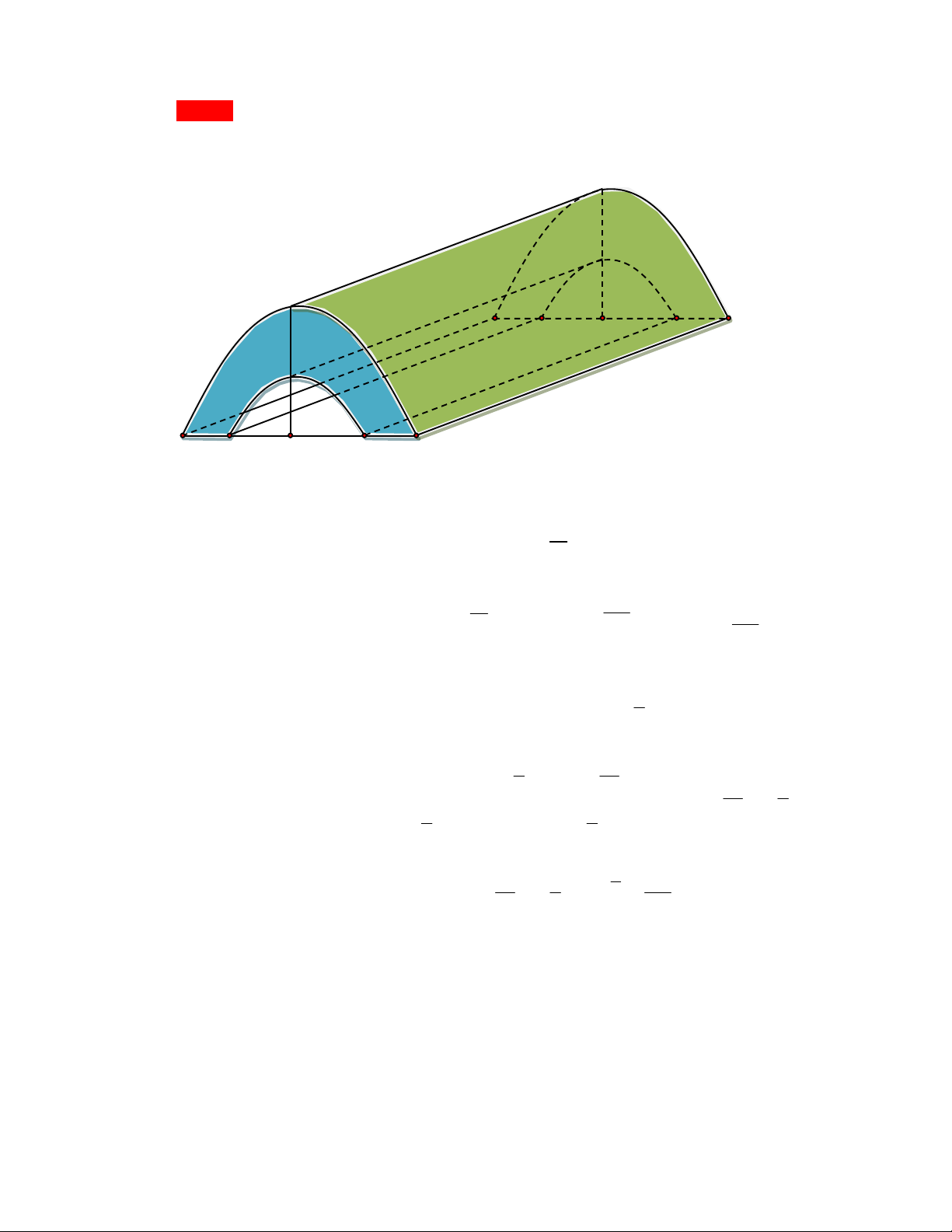
Hướngdẫngiải
ChọnD.
Chọnhệtrục
Ox
y
nhưhìnhvẽ.
Tacó
Gọi
2
1
:
P
yax c
làParabolđiquahaiđiểm
19
;0 , 0;2
2
AB
Nêntacóhệphươngtrìnhsau:
2
2
1
8
19
0. 2
8
:2
361
2
361
2
2
a
a
Py x
b
b
Gọi
2
2
:
Py
ax clàParabolđiquahaiđiểm
5
10;0 , 0;
2
CD
Nêntacóhệphươngtrìnhsau:
2
2
2
1
5
0.10
15
40
2
:
5
5
40 2
2
2
a
a
Py x
b
b
Tacóthểtíchcủabêtônglà:
19
10
223
2
00
15 8
5.2 2 40
40 2 361
Vxdxxdxm
Câu108: NGUYỄNTRÃI
–HDCómộtcáicốclàmbằnggiấy,đượcúpngượcnhưhìnhvẽ.Chiều
caocủachiếccốclà
20cm
,bánkínhđáycốclà
4cm
,bánkínhmiệngcốclà
5cm
.Mộtcon
kiếnđangđứngởđiểm
A
củamiệngcốcdựđịnhsẽbòhaivòngquanhthancốcđểlên
đếnđáycốcởđiểm
B
.Quãngđườngngắnnhấtđểconkiếncóthểthựchiệnđượcdựđịnh
củamìnhgầnđúngnhấtvớikếtquảnàodướcđây?
0,5m 0,5m
19m
5m
2m
0,5m
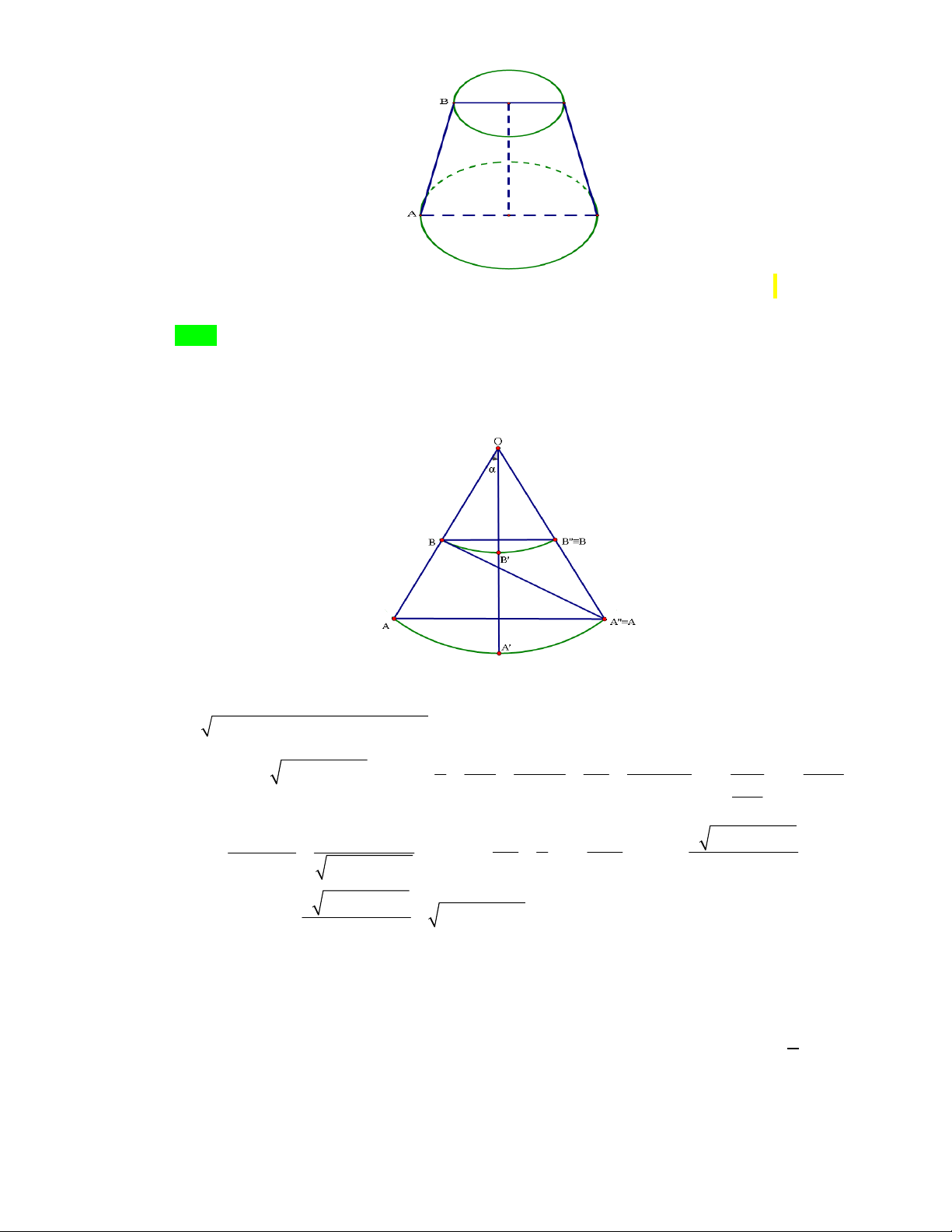
A.
59,98cm
B.
59,93cm
C.
58,67 cm
D.
58,80cm
.
Hướngdẫngiải
ChọnD.
Đặt
,,bah
lầnlượtlàbánkínhđáycốc,miệngcốcvàchiềucaocủacốc,làgóckíhiệu
nhưtrênhìnhvẽ.Ta“trải”hailầnmặtxungquanhcốclênmặtphẳngsẽđượcmộthình
quạtcủamộtkhuyênvớicungnhỏ
"4
B
Bb
vàcunglớn
"4AA a
.
ĐộdàingắnnhấtcủađườngđicủaconkiếnlàđộdàiđoạnthẳngBA”.Ápdụngđịnhlíhàm
sốcosintađược:
22
2. .cos2(1).lBOOA BOOA
22
() .
B
AAB ab h
4() .
11
2
42
(AA )
aalBBOAOBAB AB AB
b
b b OB OB b
l
22
2( ) 2( )
().
()
ab ab
a
AB
ab h
22
()
1()
bab h
AB a a b
OB b
OB b b a b
.
22
22
()
() ().
bab h
OA OB BA a b h c
ab
Thaya,b,cvào1tatìmđược
.l
58,79609 58,80lcm
Ghichú.ĐểtồntạilờigiảitrênthìđoạnBA”phảikhôngcắtcung
BB
tạiđiểmnàokhácB,
tứclàBA”nằmdướitiếptuyếncủa
BB
tạiB.Điềunàytươngđươngvới
1
2cos .
b
a
Tuy
nhiên,tronglờigiảicủathísinhkhôngyêucầuphảitrìnhbàyđiềukiệnnàyvàđềbàicũng
đãchothỏamãnyêucầuđó.

Câu109: NGÔQUYỀN–HPMộtcơsởsảnxuấtkhănmặtđangbánmỗichiếckhănvớigiá
30.000
đồngmộtchiếcvàmỗithángcơsởbánđượctrungbình
3000
chiếckhăn.Cơsởsảnxuất
đangcókếhoạchtănggiábánđểcólợinhậntốthơn.Saukhithamkhảothịtrường,người
quảnlýthấyrằngnếutừmứcgiá
30.000
đồngmàcứtănggiáthêm
1000
đồngthìmỗi
thángsẽbáníthơn
100
chiếc.Biếtvốnsảnxuấtmộtchiếckhănkhôngthayđổilà
18.000
.
Hỏicơsởsảnxuấtphảibánvớigiámớilàbaonhiêuđểđạtlợinhuậnlớnnhất.
A.
42.000
đồng. B.
40.000
đồng. C.
43.000
đồng. D.
39.000
đồng.
Hướngdẫngiải
ChọnD.
Gọisốtiềncầntănggiámỗichiếckhănlà
x
nghìnđồng.
Vìcứtănggiáthêm
1nghìnđồngthìsốkhănbánragiảm
100
chiếcnêntăng
x
nghìn
đồngthìsốxekhănbánragiảm
100
x
chiếc.Dođótổngsốkhănbánramỗithánglà:
3000 100
x
chiếc.
Lúcđầubánvớigiá
30
nghìnđồng,mỗichiếckhăncólãi
12
nghìnđồng.Saukhităng
giá,mỗichiếckhănthuđượcsốlãilà:
12
x
nghìnđồng.Dođótổngsốlợinhuậnmột
thángthuđượcsaukhitănggiálà:
3000 100 12
f
xxx
nghìnđồng.
Xéthàmsố
3000 100 12
f
xxx trên
0; .
Tacó:
2
2
100 1800 36000 100 9 44100 44100fx x x x
.
Dấubằngxảyrakhivàchỉkhi
9x
.
Nhưvậy,đểthuđượclợinhuậncaonhấtthìcơsởsảnxuấtcầntănggiábánmỗichiếc
khănlà
9.000
đồng,tứclàmỗichiếckhănbánvớigiámớilà
39.000
đồng.
Câu110: CHUYÊNVINH–L2Cáckhíthảigâyhiệuứngnhàkínhlànguyênnhânchủyếulàmtrái
đấtnónglên.TheoOECDTổchứchợptácvàpháttriểnkinhtếthếgiới,khinhiệtđộtrái
đất tăng lên thì tổng giá trị kinh tế toàn cầu
giảm.Ngườitaướctínhrằngkhinhiệtđộtrái
đấttăngthêm
2 C
thìtổnggiátrịkinhtếtoàn
cầugiảm3%,cònkhinhiệtđộtráiđấttăngthêm
5 C
thìtổnggiátrịkinhtếtoàncầugiảm
10%
.
Biếtrằngnếu nhiệtđộtráiđấttăngthêm
tC
,
tổnggiátrịkinhtếtoàncầugiảm
f
t % thì
() .
t
f
tka trongđó
,ak
làcáchằngsốdương.
NhiệtđộtráiđấttăngthêmbaonhiêuđộCthìtổnggiátrịkinhtếtoàncầugiảm
20%
?
A.
9,3 C
. B.
7,6 C
. C.
6,7 C
. D.
8, 4 C
.
Hướngdẫngiải
ChọnC.
Theođềbàitacó:
2
5
.3%
1
. 10%
ka
ka
.Cầntìmt thỏamãn
. 20%
t
ka
.

13, 2cm
13,2cm
1cm
1cm
Từ
2
3%
1
k
a
và
3
10
3
a
.Khiđó
. 20%
t
ka
2
2
3% 20
. 20%
3
tt
aa
a
6,7t
.
Câu111: CHUYÊNVINH–L2Mộtxưởngsảnxuấtmuốntạo
ranhữngchiếcđồnghồcátthủytinhcódạnghình
trụ,phầnchứacátlàhainửahìnhcầubằngnhau.Hìnhvẽ
bênvớikíchthướcđãcholàbảnthiếtkếthiếtdiệnqua
trụccủachiếcđồnghồnàyphầngiớihạnbởihìnhtrụvà
phầnhainữahìnhcầuchứacát.Khiđó,lượngthủytinh
làmchiếcđồnghồcátgầnnhấtvớigiátrịnàotrongcác
giátrịsau
A.
3
1070,8 .cm B.
3
602,2 .cm
C.
3
711,6 .cm
D.
3
6021,3 .cm
Hướngdẫngiải
ChọnA.
Tacóthểtíchcủakhốitrụlà
2
1
.13, 2.6,6 1086,4V
.
Đường kính hình cầu là
13, 2 2.1,0 11,2 cm
, suy ra thể tích của hai nửa khối cầu là
3
2
4
.5,6 735,619
3
V
Vậylượngthủytinhlàmchiếcđồnghồgầnnhấtvớigiátrị
3
1070,8 cm .
Bấm Tải xuống để xem toàn bộ.