Giải đề giữa kỳ môn Xác suất thống kê| Trường Đại học Ngoại Thương

HANOI UNIVERSITY OF SCIENCE AND TECHNOLOGY
GIẢI ĐỀ GIỮA KỲ XSTK MI2020 [20181-20201] Tác giả: Tài liệu tham khảo: Made by Team XSTK
•Giáo trình XSTK - Tống Đình Quỳ
•Bài giảng XSTK - Nguyễn Thị Thu Thủ
Hà Nội, 15 tháng 4 năm 2021 Mục lục
Đề 20181 ........................................... 1 Lờig
ải............................................ 2
Đề 20182 ........................................... 4 Lờig
ải............................................ 5
Đề 20183 ........................................... 7 Lờig
ải............................................ 8
Đề 20191 ........................................... 1 Lờig
ải............................................ 12
Đề 20192 ........................................... 14 Lờig
ải............................................ 15
Đề 20193 ........................................... 18 Lờig
ải............................................ 19
Đề 20201 ........................................... 2 Lờig
ải............................................ 23
Hỗ trợ học tập đại cương Xác suất thống kê Đề 1 ĐỀ THI GIỮA KỲ - 20181
Câu 1. Một hộp có 10 mảnh bìa được đánh số thứ tự từ 1 đến 10. Lấy ngẫu nhiên từng mảnh bìa.
a) Tính xác suất để trên 3 mảnh bìa đầu có các số theo thứ tự là 1, 2, 3.
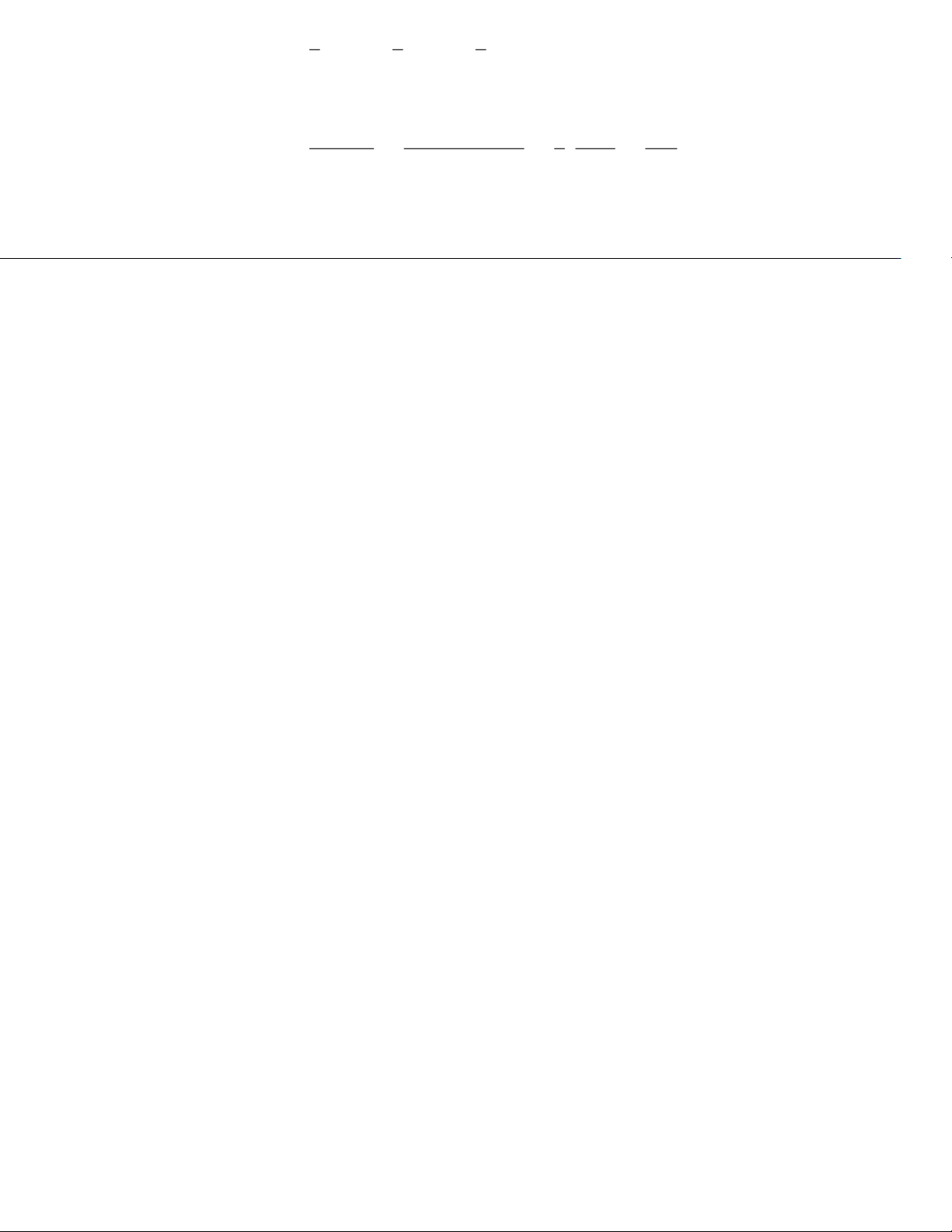
b) Giả sử trên mảnh bìa thứ kcó số thứ tự lớn nhất trong kmảnh đầu tiên. Tính xác suất để số thứ tự đó là số 10.
Câu 2. Một nhóm xạ thủ có 3 người bắn tốt và 4 người bắn khá với xác suất bắn trúng mỗi lần bắn
của mỗi loại tương ứng là 0,9 và 0,8. Chọn ngẫu nhiên 2 xạ thủ và cho mỗi người bắn 1 lần.
a) Tính xác suất để trong 2 lần bắn có đúng 1 người bắn trúng.
b) Biết trong 2 lần đó có ít nhất 1 người bắn trượt, tính xác suất để cả 2 người đó là xạ thủ thuộc nhóm bắn tốt.
Câu 3. Từ một hộp bi có 9 viên bi trắng và 3 bi đỏ lấy ngẫu nhiên lần lượt ra từng viên cho đến khi được 1 viên bi trắng.
a) Lập bảng phân phối xác suất của số viên bi được lấy ra.
b) Tính kỳ vọng và phương sai của số viên bi đỏ trong số bi lấy ra đó.
Câu 4. Cho một biến ngẫu nhiên liên tục Xcó hàm mật độ f(x) = A.e−(x−2)28.
a) Tìm hằng số A, hỏi Xcó phân phối gì?
b) Tính P(0Chúc các bạn qua môn! 1
Hỗ trợ học tập đại cương Xác suất thống kê Giải đề giữa kì 20181 Câu 1.
a) Xét phép thử lấy ngẫu nhiên từng mảnh bìa.
•Tổng số kết cục đồng khả năng là: n=10! cách.
•Gọi A= Trên mảnh bìa thứ k có số thứ tự lớn nhất trong k mảnh đầu tiên.
•Số kết cục thuận lợi cho Alà:m=1.1.1.7! cách. Vậy P(A) = mn=1.1.1.7 1 ! 0 =1 720
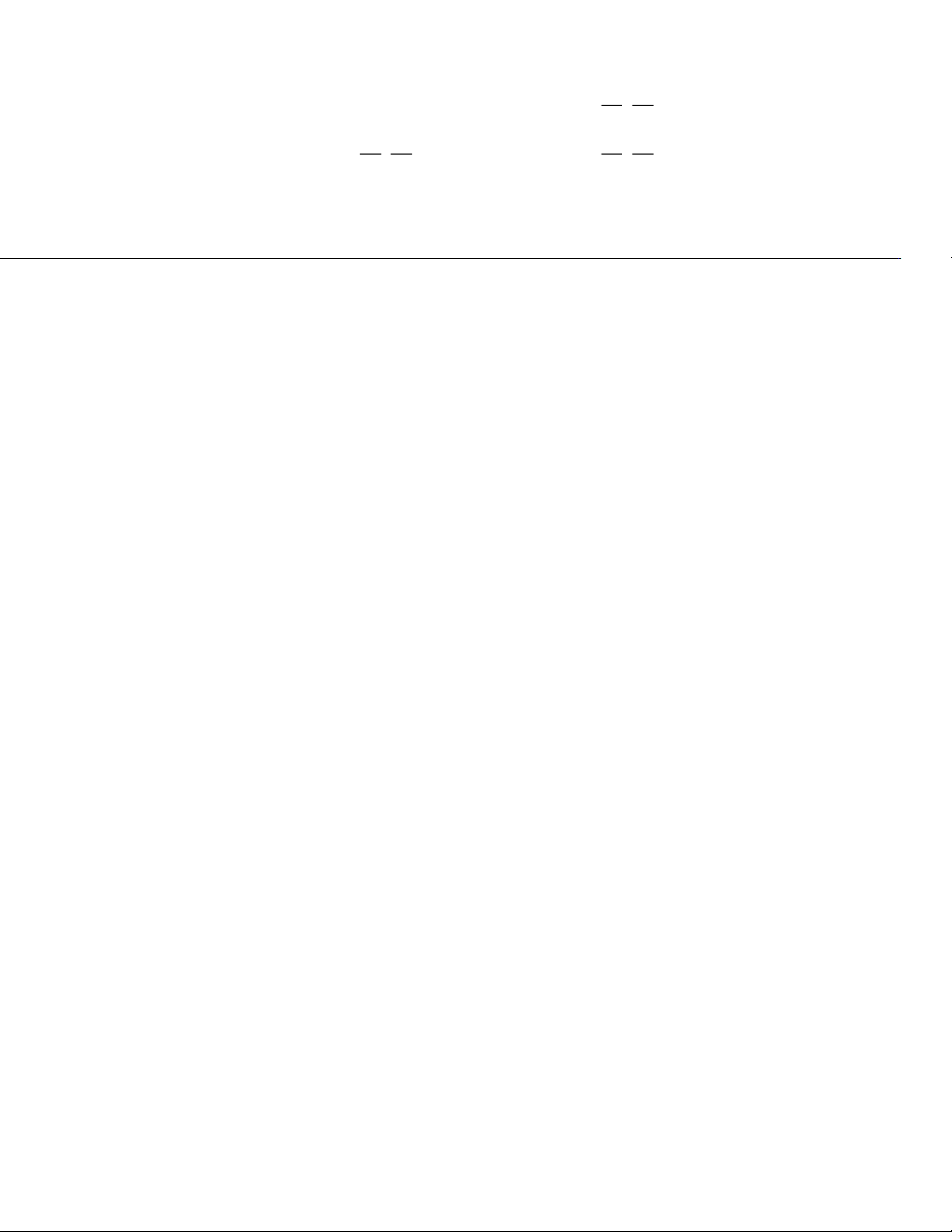
b) Gọi Bk= {Trên mảnh bìa thứ k có số thứ tự lớn nhất trong k mảnh đầu tiên}. P(Bk) = Ck k!=1 10.1.( 1 k 0.−1)! Ck k ⇒P(B10) = 110 Xác suất cần tính là: P(B P(Bk)=P(B10) P(B 10|Bk) = P(B10.Bk) k)=k 10 Câu 2.
Gọi Ai= {Có ingười bắn tốt trong số 2 người bắn}, i=0,1,2.
Hệ {Ai}tạo thành một hệ đầy đủ với: P(A0) = C2 ( 2) = C2 4 =27,P(A1) = 3.4 =47,P A 3 =1 C2 C2 C2 7 7 7 7
a) Gọi H = {Trong 2 lần bắn có đúng một người bắn trúng}.
P(H|A0) = 2.0,2.0,8=0,32; P(H|A1) = 0,1.0,8+0,2.0,9=0,26; P(H|A2) = 2.0,1.0,9=0,18;
Áp dụng công thức xác suất đầy đủ:
P(H) = P(A0)P(H|A0) + P(A1)P(H|A1) + P(A2)P(H|A2)
=27.0,32 +47.0,26 +17.0,18 =0,2657
b) Gọi B = {Trong 2 lần bắn có ít nhất 1 người bắn trượt}.
P(B|A0) = 1−0,8.0,8=0,36; P(B|A1) = 1−0,9.0,8=0,28; P(B|A2) = 1−0,9.0,9=0,19
Áp dụng công thức xác suất đầy đủ:
P(B) = P(A0)P(B|A0) + P(A1)P(B|A1) + P(A2)P(B|A2)
=27.0,36 +47.0,27 +17.0,19 =0,29 Xác suất cần tính là: P(A P(B)=1 7.0,01,9 29 =19 2|B) = P(A P 2 ( B B ) )=P(A2)P(B|A2) 203 =0,0936 Chúc các bạn qua môn! 2
Hỗ trợ học tập đại cương Xác suất thống kê Câu 3.
a) Gọi Xlà biến ngẫu nhiên chỉ số bi được lấy ra, X={1,2,3,4}.
Gọi {Ai}= {Có i bi đỏ có trong số bi được lấy ra}, i=0,1,2,3 P(X=1) = P(A0) = 9 12 =3 4 P(X=2) = P(A1) = 3 12.911 =9 44
P(X=3) = P(A2) = 3 12.211.910 =9 220
P(X=4) = P(A3) = 3 12.211.1 0.9 =1 220
Ta có bảng phân phối xác suất: X1 2 3 4 p3/4 9/44 9/220 1/220
b) Gọi Ylà biến ngẫu nhiên chỉ số bi đỏ được lấy ra, Y=X−1.
E(X) = 1.34+2.9 44 +3.9220 +4.1220 =1,3
E(X2) = 12.34+22.9 44 +32.9220 +42.1220 =2,01 V(X) = E(X2)−(E(X))2 Vậy:
E(Y) = E(X−1) = E(X)−1=1,3−1=0,3 V(Y) = V(X−1) = V(X) = 0,32 Câu 4.
a) Ta thấy Xcó phân phối chuẩn. X∼N(2,22)⇒E(X) = 2,V(X) = 4. A=1 σ√2π=1 2√2π b) P(0Chúc các bạn qua môn! 3
Hỗ trợ học tập đại cương Xác suất thống kê Đề 1 ĐỀ THI GIỮA KỲ - 20182
Câu 1. Lai hai giống hoa ly màu hồng và màu vàng thuần chủng, các cây con ở thế hệ F1 có thể cho
hoa màu trắng, vàng, hồng theo tỷ lệ 1:1:2. Lấy 5 hạt giống thế hệ F1 mang gieo và được 5 cây hoa.
Tính xác suất trong 5 cây hoa đó:
a) Có cây cho hoa màu hồng
b) Có cây cho hoa màu vàng, biết rằng có cây cho hoa màu hồng.
Câu 2. Một kỹ sư nông nghiệp có một hộp đựng hạt giống (trong đó có 6 hạt loại một, 6 hạt loại hai).
Biết rằng hôm trước anh ta đã gieo 3 hạt và hôm sau lấy tiếp 3 hạt để gieo. Hãy tính xác suất để trong
3 hạt giống hôm sau có 2 hạt loại một và 1 hạt loại hai.
Câu 3. Tuổi thọ của một loại bóng đèn là biến ngẫu nhiên X(năm) có hàm mật độ xác suất: f(x) = kx2(4−x)x∈[0; 4] 0x/ ∈[0; 4] a) Tìm kvà tính P(X<2). b) Xác định E(X)và mod(X)
Câu 4. Tại một điểm bán vé máy bay, trung bình trong 10 phút có 4 người đến mua vé.
a) Tính xác suất để trong vòng 10 phút có 7 người đến mua vé.
b) Biết rằng trong vòng 10 phút có người đến mua vé, tính xác suất có đúng 7 người đến mua vé. Chúc các bạn qua môn! 4
Hỗ trợ học tập đại cương Xác suất thống kê Giải đề giữa kì 20182 Câu 1.
a) Gọi A= {Có cây cho hoa màu hồng}.
P(A) = 1−P(A) = 1−0,55=0,9688
b) Gọi B= {Có cây cho hoa màu vàng}. Xác suất cần tính là: P(B|A) = P(BA) P(A) Với:
P(BA) = 1−P(BA) = 1−P(A+B) = 1−[P(A) + P(B)−P(AB)]
=1−(0,55+0,755−0,255) = 0,7324 ⇒P(B|A) = 0,7324 0,9688 Câu 2.
Gọi Ai= {Trong 3 hạt gieo ngày hôm trước có ihạt loại 1}, i=0,1,2,3.
Gọi H= {Trong 3 hạt gieo ngày hôm sau có 2 hạt loại 1 và 1 hạt loại 2} Hệ {Ai}tạo thành một hệ đầy đủ với: P(A0) = C3 C1623=1 11,P(A1) = C16 C.C2 12 6 3=9 22 ,P(A2) = C2 6 C .C1 12 6 3=9 22 ,P(A3) = C3 C1623=1 11
Áp dụng công thức xác suất đầy đủ:
P(H) = P(A0)P(H|A0) + P(A1)P(H|A1) + P(A2)P(H|A2) + P(A3)P(H|A3) với: P(H|A 6.C1 5.C1 0) = C2 3 =15 28 P(H|A1) = C2 4 =10 C3 C3 21 9 9 P(H|A 4.C1 3.C1 2) = C2 5 =514 P(H|A3) = C2 6 =3 C3 C3 14 9 9 Xác suất cần tính là: P(H) = 1 1.15
28 +922.514 +922.514 +111.314 =922 =0,4091 Câu 3.
a) Vì f(x)là hàm mật độ xác suất của Xnên ta có: f(x)>0∀x∈R(1) +∞ Z f(x)dx =1(2) −∞ Chúc các bạn qua môn! 5
Hỗ trợ học tập đại cương Xác suất thống kê
(1)⇔kx2(4−x)>0,x∈[0,4]⇔k>0 +∞ 0 4 +∞
(2)⇔ Z f(x)dx =1⇔ Z 0dx + Z kx2(4−x)dx + Z 0dx −∞ −∞ 0 4 4 ⇔k Z kx2(4−x)dx =1 0 ⇔k.64 3=1 ⇔k=3 64(T M) 3 ⇒f(x) = 64x2(4−x),x∈[0; 4] 0,x/ ∈[0; 4] 2 0 2 P(X<2) = Z f(x)dx = Z f(x)dx + Z f(x)dx −∞ −∞ 0 2 3 = 64x2(4−x)dx =5 Z 16 =0,3125 0 b) +∞ 0 4 +∞ 3 0dx =12
E(X) = Z x f (x)dx =Z 0dx + Z 64x3(4−x) + Z 5=2,4 −∞ −∞ 0 4
mod (X) = {x0|f(x0) = max f(x),x∈[0; 4]} Ta lại có: f0(x) = 364(8x−3x2) f0(x) = 0⇔x=0∨x=8 3
f(0) = 0,f 8 3 =4 9,f(4) = 0⇒max f(x) = 4 9khi x =8 3 ⇒Mod(X) = 83 Câu 4.
Gọi Xlà biến ngẫu nhiên chỉ số người mua vé trong 10 phút. X∼P(4).
a) Gọi A= {Trong 10 phút có 7 người đến mua vé}. P(A) = P(X=7) = e−4.47 7! =0,0595
b) Gọi B= {Trong 10 phút có người đến mua vé}.
P(B) = 1−P(B) = 1−e−4.40 0! =0,9817 Xác suất cần tính là: P(A|B) = P(A P( B B ))=P(A) P(B)=0,0595 0,9817 =0,0606 Chúc các bạn qua môn! 6
Hỗ trợ học tập đại cương Xác suất thống kê Đề 1 ĐỀ THI GIỮA KỲ - 20183
Câu 1. Có 3 tiêu chí phổ biến A,B,Ccho việc chọn một chiếc xe hơi mới tương ứng là hộp số tự động,
động cơ và điều hoà nhiệt độ. Dựa trên dữ liệu bán hàng trước đó ta có P(A) = P(B) = P(C) = 0,7,
P(A+B) = 0,8,P(A+C) = 0,9,P(B+C) = 0,85 và P(A+B+C) = 0,95. Tính xác suất:
a) Người mua chọn cả ba tiêu chí.
b) Người mua chọn chính xác một trong ba tiêu chí.
Câu 2. Có hai lô hàng: lô I có 7 chính phẩm 3 phế phẩm; lô II có 8 chính phẩm 2 phế phẩm. Lấy ngẫu
nhiên từ mỗi lô hàng ra 1 sản phẩm.
a) Tính xác suất để cả 2 sản phẩm lấy ra đều là phế phẩm.
b) Số sản phẩm còn lại trong hai lô hàng dồn vào thành một lô, ký hiệu là lô III. Từ lô III lấy ngẫu
nhiên ra 2 sản phẩm. Tính xác suất để 2 sản phẩm lấy ra từ lô III là phế phẩm.
Câu 3. Biến ngẫu nhiên liên tục X có hàm mật độ xác suất: f(x) = e−x,x>0, 0,x≤0. a) Tính P(X≥5)
b) Xác định hàm phân phối xác suất của biến ngẫu nhiên Y=−2X+5
Câu 4. Có 10 máy sản xuất sản phẩm (độc lập nhau), mỗi máy sản suất ra 2% phế phẩm.
a) Từ mỗi máy sản xuất lấy ngẫu nhiên ra một sản phẩm. Hỏi xác suất lấy được nhiều nhất 2 phế
phẩm trong 10 sản phẩm này là bao nhiêu?
b) Trung bình có bao nhiêu sản phẩm được sản xuất bởi máy đầu tiên trước khi nó tạo ra phế phẩm
đầu tiên (giả sử các sản phẩm sản xuất ra là độc lập)? Chúc các bạn qua môn! 7
Hỗ trợ học tập đại cương Xác suất thống kê Giải đề giữa kì 20183 Câu 1.
a) Gọi A,B,Clần lượt là người chọn mua tiêu chí A,B,C. Gọi Dlà người chọn mua cả 3 tiêu chí. ⇒D=ABC ⇒P(D) = P(ABC) Có: ⇒D=ABC ⇒P(D) = P(ABC) P(AB)
= P(A) + P(B)−P(A+B) = 0,7+0,7−0,8=0,6 P(BC)
= P(B) + P(C)−P(B+C) = 0,7+0,7−0,85 =0,55 P(CA)
= P(C) + P(A)−P(C+A) = 0,7+0,7−0,9=0,5
P(A+B+C) = P(A) + P(B) + P(C)−P(AB)−P(BC)−P(CA) + P(ABC) ⇒P(ABC)
= P(A+B+C)−P(A)−P(B)−P(C) + P(AB) + P(BC) + P(CA)
=0,95 −0,7−0,7−0,7+0,6+0,55 +0,5=0,5 ⇒P(D) = P(ABC) = 0,5
b) Gọi E= {Người mua chọn chính xác một trong ba tiêu chí}. ⇒E=ABC +ABC +ABC
⇒P(E) = P ABC +ABC +ABC =P ABC +P ABC +P ABC Có:
P ABC =P AB −P ABC =P A+B −P A+B+C =1−P(A+B)−[1−P(A+B+C)]
=P(A+B+C)−P(A+B) = 0,95 −0,8=0,15 Tương tự:
P ABC =P(A+B+C)−P(A+C) = 0,95 −0,9=0,05
P ABC =P(A+B+C)−P(B+C) = 0,95 −0,85 =0,1 ⇒P(E) = 0,15 +0,05 +0,1=0,3 Câu 2.
a) Gọi Ai,Bilần lượt là sự kiện có i chính phẩm được lấy ra từ lô I,II.i=0,1. Gọi C= {Cả 2 sản
phẩm lấy ra đều là phế phẩm} ⇒C=AoBo
⇒P(C) = P(AoBo) = P(Ao)P(Bo) = 3 10.210 =0,06
b) Hệ {A0B0,A0B1,A1B0,A1B1}tạo thành một hệ đầy đủ với: P(A0B0) = 0,06 P(A0B1) = 3 10.810 =0,24
P(A1B0) = 710.210 =0,14 P(A1B1) = 7 10.810 =0,56 Chúc các bạn qua môn! 8