
















Preview text:
lOMoAR cPSD| 59735516
Chương 2. GIỚI HẠN
2.1. Giới hạn của dãy số thực
2.1.1. Dãy số hội tụ, các tính chất của dãy hội tụ
Một dãy số thực (dãy số) là một ánh xạ f: N→R.
Ký hiệu {xn} với n N là dãy số, khi ó xn = f(n) với n N.
Một dãy số có thể ược cho bằng một trong hai cách: (1) dưới dạng tường minh xn = f(n); (2) dưới
dạng truy hồi xn+1 = f(xn).
Ví dụ 2.1.1.1. Các dãy số sau ây ược cho dưới dạng tường minh
= f(n) = 1 với n N*,
tức là {xn} cóx1 = f(1) = =1 1, x2 = f(2) = 1 , … + {xn}: xn n 1 2 + {xn}: xn = f(n) = 1+ 1 n
với n N*, tức là {x n} có x1 = f(1) = 1+1 1 = 2, n 1 x2 = f(2) =
1+ 1 2 = 9 , x3 = f(3) = 1+ 1 3 = 64 , … 2 4 3 27 n1khi n + {xn}: x n = f(n) =
= 2k −1 với k N* tức là {xn} có x1 = f(1) = =1 1, n n+ 2 khi n = 2k 1
x2 = f(2) ==, x3 = f(3) =, x4 = f(4) ==, …
Ví dụ 2.1.1.2. Các dãy số sau ây ược cho dưới dạng truy hồi x1 = 2 +
+ {xn}: n = f(x n 1− ) = x 2n 1− 2 với 2 n, tức là {xn} có x1 = 2, x 2x n 1− 3 2 x 2 = f(x )1 = f(2)
= 22 + 2 = , x3 = f(x )2 = f 3 = (3 2)2 + 2 = 17 , … (n 2) a 2.2 2 2.3 2 12 ax − n1 ( n x1 =
+ {xn}: với a > 0, tuy nhiên dãy này có thể biểu diễn dưới dạng tường minh xn =2) lOMoAR cPSD| 59735516 như sau: 1 1 1+ 1 1 1 1 1+ +1 1 1 2
x1 = a = a ,x2 = ax1 = a a2 = a a42 = a 2 22 ,x3 = ax 2 =a a a3= a a a8 4 2 = a 2 22 23 , 1 1 1 1+ + +1 ... 1
…, x n = ax n 1− = a a... a = a 2n ....a 22 a 2 = a 2 22 2n . n
Nhận xét. Trong nhiều trường hợp, dãy số cho dưới dạng truy hồi có thể chuyển về dạng tường minh.
Ví dụ 2.1.1.3. Một cấp số cộng (arithmetic progression hoặc arithmetic sequence) là một dãy số ược
cho dưới dạng truy hồi: Hiệu hai phần tử liên tiếp nhau là một hằng số, hằng số này ược gọi là công sai
của cấp số cộng. Các phần tử của dãy số ược gọi là các số hạng của cấp số cộng. Ký hiệu số hạng ầu và
công sai của một cấp số cộng, tương ứng là a1 và d; khi ó:
- Số hạng thứ n của cấp số cộng ược xác ịnh bằng công thức an = a1 + (n–1)d
- Tổng của n số hạng ầu của cấp số cộng, ược gọi là tổng riêng thứ n của cấp số cộng, ược
xác ịnh bằng công thức S = n a = n(a1 + a )n = n[2a1 + (n −1)d] . n k k 1= 2 2
Ví dụ 2.1.1.4. Một cấp số nhân (geometric progression hoặc geometric sequence) là một dãy số ược
cho dưới dạng truy hồi: Tỷ số của hai phần tử liên tiếp là hằng số, hằng số này ược gọi là công bội của
cấp số nhân. Các phần tử của dãy số ược gọi là các số hạng của cấp số nhân. Ký hiệu số hạng ầu và công
bội của một cấp số nhân, tương ứng là g1 và q; khi ó:
- Số hạng thứ n của cấp số nhân ược xác ịnh bằng công thức gn = g1qn-1
- Tổng của n số hạng ầu của cấp số nhân với công bội q 1, ược gọi là tổng riêng thứ n
của cấp số nhân, ược xác ịnh bằng công thức Sn = n g = g (11 −q )n . k 1 −q k 1=
Ví dụ 2.1.1.5. Tính S( a)
n = +a aa + aaa + +...a...aa+ a...aaa với a ={1, 2, …, 8, 9}. n 1− n Bài giải. = a Ta cóS( a)
n = +a aa +aaa + +...a...aan 1− +a...aaan 9 (9+99+999+ +...
9...99n 1− +9...999)n = a [(101 − +1) (102 − +1) (103 − + +1) ...
(10n 1− − +1) (10n −1)] 9
= a [(101 +102 +103 + +... 10n 1− +10 )n − n] 9 n 18 lOMoAR cPSD| 59735516 =
Ta nhận thấy: 101 +102 +103 + +... 10n 1− +10n 10k là tổng n số hạng ầu của cấp số nhân, k 1=
có số hạng ầu và công bội ều bằng 10, do ó n 10k =10.1 10− n = 10n −10 k 1= 10 S( a) n n = a
9−1 − n = 81a (10n 1+ −9n −10). 9 Định nghĩa 1
- Dãy số {xn} hội tụ ến số hữu hạn a R > 0, n0 N, n > n0 | xn – a | < và ký
hiệu là limx→ n = a hoặc xn → a khi n → . n
Vì xn – a < a – < xn < a + , nên ta còn có thể phát biểu khái niệm dãy số hội tụ như sau:
Dãy số {xn} hội tụ ến a nếu – lân cận của a ều chứa mọi phần tử của dãy số, trừ một số hữu hạn phần tử ầu dãy.
- Dãy số {xn} không hội tụ thì ược gọi là phân kỳ. Định nghĩa 2
- Dãy số {xn} ược gọi là bị chặn trên nếu M: xn M, n N.
- Dãy số {xn} ược gọi là bị chặn dưới nếu m: xn m, n N.
- Dãy số {xn} ược gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới.
Định nghĩa 3 limx→ n =+ A > 0, n0 N, n > n0 xn > A.
n limx→ n =− B < 0, n0 N, n > n0 xn < B. n
Nhận xét. (1) Tất cả các dãy số có giới hạn ều phân kỳ; (2) Mọi dãy số tiến ến + ều bị chặn
dưới; (3) Mọi dãy số tiến ến – ều bị chặn trên.
Ví dụ 2.1.1.6. Dùng Định nghĩa 1 ể chứng minh rằng, dãy số {xn}: xn = f(n) =1n (n N*) hội tụ ến a = 0 tức là limxn = 0. n→ Bài giải.
Ta có xn − =0 1 n − =0 1 n . Giả sử > 0 là một số bé tùy ý cho trước, khi ó xn − =0 1 n 1 n
n 1 và do ó nếu ta lấy n0 = n ( )0 = [1 ] +1 thì với n n0 ta có xn −0 , iều này có
nghĩa là limx→ n = 0( pcm). n
2.1.2. Các tính chất của dãy số hội tụ
(1) Nếu một dãy số hội tụ thì giới hạn của nó là duy nhất. lOMoAR cPSD| 59735516
Nhận xét. Nếu dãy số {xn} hội tụ ến a và với m N*, n N* (m n) ta luôn có limx→ n = a và n lim xm = a . m→
(2) Nếu một dãy số hội tụ thì nó giới nội, tức là tồn tại một khoảng (a,b) chứa mọi phần tử
của dãy số. (3) Giả sử hai dãy số {xn}, {yn} là các dãy số hội tụ, tức là limxn n = x, limy→ n = y . Khi ó → n +
(3.1) nlim(x→ n + y )n = nlimx→ n nlimy→ n = +x y (3.2) nlim(Cx )→
n = Climxn→ n = Cx (C là hằng số) (3.3) nlim(C→
+ x )n = +C nlimx→ n = +C x(C là hằng số) (3.4) nlim(x y )n n = (limx )(limy→ n n→ n ) = xy → n
(3.5)lim 1 = 1 = 1 với yn ≠ 0 và y ≠ 0 n→ yn limy→ n y n = x x n = limxn→ n với yn ≠ 0 và y ≠ 0 (3.6) lim n→ yn limy→ n y n (4)
Giả sử hai dãy số {xn}, {yn} là các dãy số hội tụ, tức là nlimxn = x, limy→ n = y. Khi ó, nếu → n xn yn với n thì x y. (5)
Nguyên lý kẹp. Cho ba dãy số {xn}, {yn} và {zn}. Nếu hai dãy số {xn}, {zn} hội tụ ến cùng
một giới hạn a, tức là nlimx→ n = nlimz→ n = a và xn yn zn với n thì dãy số {yn} cũng hội tụ ến giới
hạn a, tức là limy→ n = a . n
2.1.3. Sự hội tụ của dãy ơn iệu
Dãy số {xn} ược gọi là tăng nếu xn xn+1 với n, là giảm nếu xn xn+1 với n. Dãy số tăng hay
dãy số giảm ược gọi là dãy số ơn iệu.
Nhận xét: Dãy số tăng bị chặn dưới bởi phần tử thứ nhất của nó và dãy số giảm bị chặn trên bởi
phần tử thứ nhất của nó. Ví dụ 2.1.3.1. (a)
Dãy số {xn} với xn = 1/n (n N*) là dãy ơn iệu giảm, bị chặn dưới bởi số 0 và bị chặn trên bởi số 1 x1. 20 lOMoAR cPSD| 59735516 (b)
Dãy số {xn} với xn = n2 (n N) là dãy ơn iệu tăng, bị chặn dưới bởi số 0 x0 và không bị chặn trên. (c)
Dãy số {xn} với xn = (–1)n (n N) là dãy không ơn iệu, tuy nhiên, nó là dãy số bị chặn
dưới bởi số –1 và bị chặn trên bởi số 1.
Định lý (Sự hội tụ của dãy ơn iệu). Dãy số ơn iệu và bị chặn thì hội tụ. Có hai trường hợp (1) Dãy số
ơn iệu tăng và bị chặn trên thì hội tụ; (2) Dãy số ơn iệu giảm và bị chặn dưới thì hội tụ. Ví dụ 2.1.3.2.
Chứng minh dãy số {xn}: xn = 1+ 1 n hội tụ. n Bài giải.
Ta có xn = 1+ 1 n = n C 1nkn k− 1 k = n n! 1 k = n k 0=
n k 0= k!(n −k)! n
1+ n.1 + n(n −1). 12 + +... n(n −1)...(n − +k
1). 1k + +... n(n −1)...(n − +n 1). 1n = n 2! n k! n n! n
= + +1 11 1− 1 + +...1 1− 1 1− 2 ... 1 − k −1 + +... 1 1− 1
1− 2 ... 1 − n −1 2! n k! n n n n! n n n
Tương tự xn 1+ = 1+
1 n 1+ = n 1+ Cn 1k+ 1(n 1) k+ −
1 k = n 1+ (n +1)! 1 k = n +1 k 0=
n +1 k 0= k!(n + −1k)! n +1
1 1+ + 1 1− 1 + +...1 1− 1 1− 2 ... 1 − k −1 + +... 2! n +1
k! n +1 n +1 n +1
1 1− 1 1− 2 ... 1 − n −1 + 1 1− 1 1− 2 ... 1 −
n n! n +1 n +1 n +1 (n +1)! n +1 n +1 n +1
Nếu so sánh xn và xn+1 trong hai khai triển trên, ta thấy khai triển của xn+1 nhiều hơn khai triển
của xn một số hạng, ồng thời từ số hạng thứ ba của mỗi khai triển trở i thì 1 1 n n +1 − − 1 1 1 1
nên các số hạng của xn nhỏ hơn số hạng tương ứng của xn+1, do ó xn+1 > xn với n, n
n +1 suy ra dãy số {xn} là dãy số ơn iệu tăng và bị chặn dưới bởi x1 = 2.
Bây giờ, ta sẽ chứng minh dãy số này bị chặn trên bởi số 3. Thật vậy, ở trên ã có khai triển xn = +
+1 1 1 1− 1 + 1 1− 1 1− 2 + +... 1 1− 1 1− 2 ... 1 − k −1 + +...
2! n 3! n n k! n n n + 1 1
1− 1 1− 2 ... 1 − n −1 và nếu ặt yn = + +1 1 1 + + +1 ... + 1 thì dễ thấy
rằng xn < n! n n n 1! 2! 3! (n −1)! n! lOMoAR cPSD| 59735516
yn, hơn nữa ta thấy 1 = 1 1 = 12 ,..., 1 = 1 1 = 1n 1− nên suy ra 3! 2.3 2.2 2 n! 2.3...n 2.2...2 2 yn + +2 1 12 + +...
1n 1− = +21 1− (1 2)−1 2n 1− = + −2 [1 (1 2)n 1− ] + = 21 3 x n 3. 2 2 2 2 1
Như vậy, dãy {xn} với xn = 1+ 1 n là dãy số tăng và bị chặn trên, nên nó hội tụ, nếu ký hiệu e n
là giới hạn của dãy số này thì ta có lim 1 + 1 n = e. n→ n x1 = a
Ví dụ 2.1.3.3. Cho a > 0 và dãy số {xn} ược cho dưới dạng truy hồi . a + x Chứng − n1
xn =(n 2) minh rằng,
dãy số {xn} này hội tụ và tìm giới hạn của nó. Bài giải.
Hiển nhiên rằng, dãy số {xn} là dãy số tăng và bị chặn dưới bởi x1 = a 0
Ta sẽ chứng minh dãy số này bị chặn trên bằng phương pháp Quy nạp toán học:
- Khi n = 1 ta có x1 = a a +1
- Khi n = 2 ta có x 2 = a + x1 = a + a a + 2 a + =1 ( a +1)2 = a +1
- Giả sử xn +a 1 là úng (giả thiết quy nạp)
- Bây giờ, ta phải chứng minh xn 1+ a 1+ , thật vậy x n 1+ = a + x n a + a +1 (theo giả
thiết quy nạp), mặt khác a + a +1 a + 2 a + =1 ( a +1)2 = a +1 x n 1+ a +1 ( pcm).
Như vậy, theo ịnh lý về sự hội tụ của dãy ơn iệu, dãy số ã cho hội tụ, tức là x (0 x a +1) mà limxn = x . n→
Để tìm giá trị x, ta lấy giới hạn hai vế của ẳng thức truy hồixn 1+ = a + xn = +
limx→ n 1+ lim→ a + xn = a nlimx→ n =x a + x x2 = +a x x2 − − =x a 0, phương n n
trình bậc hai này có hai nghiệm phân biệt là x = 1 1+ 4a và vì x > 0 nên giá trị của giới hạn cần tìm 2 22 lOMoAR cPSD| 59735516 + là x = , tức là limx 4a → n = =x 1+ 12 . 2 n
Ví dụ 2.1.3.4. Tìm giới hạn của mỗi dãy số: (a) xn = n n (2 ≤ n N*), (b)xn = n a (a > 0), (c) = x [ nx] n
(n N*, x R). n Bài giải. n n = = (a) Ta có x k n k− n = n n =n (xn )n = +[1 (xn −1)]n C 1n (xn −1)k C (xkn n −1)k k 0= k 0=
= C0n + C (x1nn − +1)C (x2nn −1)2 + +...C (xnnn −1)n = +1 n(xn − +1) n(n −1) (xn −1)2 + +... (xn −1)n 2 n
n(n −1) (xn −1)2 vì tất cả các số hạng ã bỏ i của ẳng thức trên ều dương. 2
Bất ẳng thức trên tương ương với bất ẳng thức 0 2
xn −1 n2−1 , mà limn→ n −1 = 0 nên
theo Nguyên lý kẹp thì limxn n − =1 0 limx→ n =1 lim→ n n =1(giới hạn này không cần phải chứng → n n minh khi sử dụng).
(b) Theo giả thiết a > 0, ta chứng minh lim n a =1 lần lượt với a = 1, a > 1 và 0 < a < 1. n→
- Khi a = 1 ta có lim n a = lim 1n = lim1=1; n→ n→ n→
- Khi a > 1 thì n a =1 a (n a)n = +[1 (n a −1)]n = C0 n n +C ( a1n − + +1) ... C ( an n n −1)n = +1 n( an − + +1) ...
(n a −1)n n( an −1) do tất cả các số
hạng ã bỏ i ều dương.
Giả sử > 0 là một số bé tùy ý cho trước, từ các bất ẳng thức trên ta thấy 0 n a −1 a n úng
khi n n0 =[a +] 1, iều này có nghĩa là nlim→ n a =1 khi n > n0. - Khi 0 < a < 1 thì 1a 1, theo chứng
minh trên ối với 1a ta ược lim 1 an=1, mặt khác ta n→ n a = lim 1 = 1 nên limn a = =1 1. lOMoAR cPSD| 59735516 có lim n→ n→ n 1 a lim 1 an n→ 1 n→
Vậy lim n a =1 với a > 0 (giới hạn này không cần phải chứng minh khi sử dụng). n→
(c) Ta ã biết 0 − − { } 1 0 [ ] 1 1
[ ] nên nếu ặt = nx (n N*) thì suy ra nx – 1 < [nx] nx
nx −1 [nx] nx −x
1 [nx] x lim x − 1 lim[ nx] limx = x n n n n n n→ n n→ n n→ − 1 = −xlim 1 = − =x 0
x x lim[nx] limx = x Vì lim x n→ n n→ n n→ n n→
Theo Nguyên lý kẹp thì lim[ nx] = x . n→ n
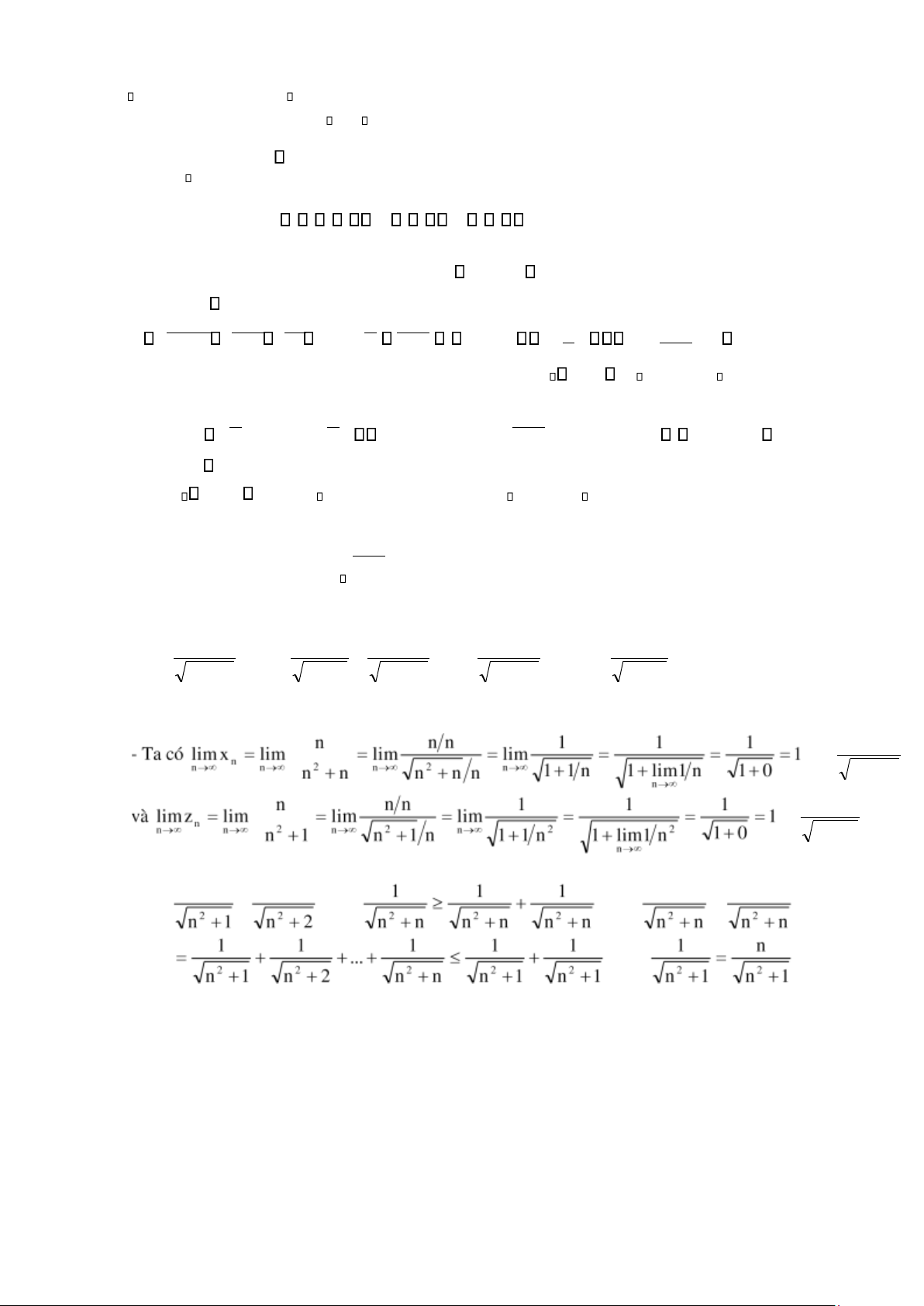
Ví dụ 2.1.3.5. Tìm giới hạn của các dãy số sau xn = n , yn = 12 + 21 + +... 21 và zn = n2 n2 + n n +1 n + 2 n + n n +1 Bài giải. - Mặt khác yn = 1 + 1 + +... + +... 1 = n = xn 2 và yn + ... + = zn 24 lOMoAR cPSD| 59735516
- Suy ra xn yn zn với n, và vì limxn→ n = limzn→ n =1 nên theo Nguyên lý kẹp thì limyn→ n =1.
2.1.4. Giới thiệu tiêu chuẩn Cauchy, giới hạn vô hạn
Dãy số {xn} ược gọi là dãy Cauchy nếu với > 0 bé tùy ý cho trước, n0 = n0( ) N* sao cho
khi với m n0 và n n0 thì xm - xn < .
Định lý (Tiêu chuẩn Cauchy). Dãy số {xn} hội tụ khi và chỉ khi nó là dãy Cauchy.
Dãy số {xn} ược gọi là vô cùng bé (VCB) nếu với > 0 bé tùy ý cho trước, n0=n0( ) N* sao
cho khi n n0 thì xn < và viết limxn = 0. n→
Dãy số {xn} ược gọi là vô cùng lớn (VCL) nếu với A > 0 lớn tùy ý cho trước, n0=n0(A) N* sao
cho khi n n0 thì xn > A và viết limx→ n =+ , khi ó ta nói dãy {xn} có giới hạn vô hạn. n Nhận xét:
- Nếu limx→ n = l thì dãy {xn – l} là một VCB. n
- Nghịch ảo của một VCB là một VCL và ngược lại, nghịch ảo của một VCL là một VCB.
Chú ý. Ta công nhận một số giới hạn sau, ể sử dụng (khi cần)
k n = 0 với a > 1 (khi n→ , an tăng nhanh hơn nk). (a) limn→ an
n a = 0 với a > 0 (khi n→ , n! tăng
nhanh hơn an). (b) lim n→ n! n n!n = 0(khi n→ , nn tăng nhanh hơn n!). (c) lim → n
(d) lim log na = 0 với a > 1 (khi n→ , n tăng nhanh hơn logan), khi a = e thì lim lnn = 0 . n→ n n→ n
(e) limnq n = 0 với q 1. n→
Nhận xét. Nếu thay k = 1 và a = 1/q với q 1 vào (a) thì nhận ược (e).
2.2. Giới hạn của hàm số một biến
2.2.1. Định nghĩa giới hạn hàm số, các tính chất của giới hạn
Xét hàm số y = f(x) với D(f) R và R(f) R tức là ánh xạ f: D(f)→R(f), trong trường hợp tổng quát
nhất thì D(f) = R(f) = R, tương ứng với ánh xạ f: R→R, khi ó ối số x và giá trị hàm số f(x) tương ứng có
thể nhận các giá trị {– , , + }.
Như vậy, có nhiều nhất 9 ịnh nghĩa về giới hạn của hàm số f(x) tương ứng với 9 trường hợp:
x f(x) – L (hữu hạn) +
– 1 2 3 x0 (hữu hạn) 4 5 6 + 7 8 9
(1) lim f(x) =− x→− (2) lim f(x) = L x→− (3) lim f(x) =+ x→− lOMoAR cPSD| 59735516 (4) lim f(x) =− (5) lim f(x) = L (6) lim f(x) =+ x→x0 x→x0 x→x0 (7) lim f(x) =− x→+ (8) lim f(x) = L x→+ (9) lim f(x) =+ x→+
Một cách tự nhiên, trường hợp 5 ược xét ầu tiên.
Định nghĩa. (Trường hợp 5) Giả sử a,b R và a x0 b. Cho hàm số f(x) có D(f) = (a,b) hoặc D(f)
= (a,x0) (x0,b), số hữu hạn L ược gọi là giới hạn của hàm số f(x) tại x0 và viết là limf(x) = L,nếu x→x với 0 > 0
cho trước bé tùy ý, mà tìm ược số = ( ) > 0 sao cho khi x – x0 < thì f(x) – L < .
(ịnh nghĩa giới hạn của hàm số bằng ngôn ngữ “ - ”). Ví dụ 2.2.1.1.
(a) Cho hàm số f(x) = x (f: R→R). Chứng minh rằng lim f(x) = x0 với x0 là một số hữu hạn. x→x0
Ta thấy D(f) = R nên x0 D(f). Giả sử cho trước > 0 bé tùy ý, nếu chọn = ( ) = thì x –
x0 < ồng thời với f(x) – x0 = x – x0 < suy ra theo ịnh nghĩa lim f(x) = x .0 x→x0 + − (b) Cho hàm số f(x) = x x 6 2
. Chứng minh rằng limf(x) = 5. x −2 x 2→
Ta thấy D(f) = R\{2} tức là iểm x0 = 2 D(f). Giả sử cho trước số ε > 0 bé tùy ý, ta phải tìm số
δ = δ(ε) > 0 sao cho khi x − 2 thì x2 + −x 6 −5 . x −2 + −x 6 x −4x + 4 Thật vậy, ta có x2 − =5 2
= (x −2)2 = −x 2 , khi ó ta lấy δ = δ(ε) = ε thì x −2 x −2 x −2 + − x − 2 x 6
. Theo ịnh nghĩa thì limf(x) = lim x2 = 5. x→2 x→2 x − 2
(c) Cho hàm số f(x) = xsin 1 . Chứng minh rằng limf(x) = 0. x x 0→
Ta thấy D(f) = R\{0} tức là iểm x0 = 0 D(f). Giả sử cho trước số ε > 0 bé tùy ý, ta phải tìm số
δ = δ(ε) > 0 sao cho khi x − 0 thì f(x)− =0
xsin 1 − =0 xsin 1 . x x
Thật vậy, ta có xsin 1 = x sin 1 x.1 = x vì sin 1 1với x D(f). Từ ó, nếu |x – 0| = |x| < x x x 26 lOMoAR cPSD| 59735516
thì suy ra f(x)− =0
xsin 1 , nghĩa là ta có thể lấy δ = δ(ε) < ε. x
Theo ịnh nghĩa thì limf(x) = limxsin 1 = 0. x→0 x→0 x
Định nghĩa. (Trường hợp 2) Cho hàm số f(x) với D(f) = (– ,b) (b có thể là số hữu hạn hoặc là + ),
số hữu hạn L ược gọi là giới hạn của hàm số f(x) tại iểm âm vô cùng (– ) và viết là
lim f(x) = L,nếu với > 0 cho trước bé tùy ý, mà tìm ược số N < 0 có |N| ủ lớn sao cho khi x < N x→−
thì f(x) – L < .
Định nghĩa. (Trường hợp 8) Cho hàm số f(x) với D(f) = (a,+ ) (a có thể là – hoặc là số hữu hạn),
số hữu hạn L ược gọi là giới hạn của hàm số f(x) tại iểm dương vô cùng (+ ) và viết là lim f(x) = L,nếu
với > 0 cho trước bé tùy ý, mà tìm ược số N > 0 ủ lớn sao cho khi x > N thì x→+ f(x) – L < .
Nhận xét. Hai ịnh nghĩa trên có thể viết chung như sau: Cho hàm số f(x) với D(f) = (a,b) (a có thể
là – hoặc là số hữu hạn, b có thể là số hữu hạn hoặc là có thể là + , a và b không ồng thời hữu hạn), số
hữu hạn L ược gọi là giới hạn của hàm số f(x) tại iểm vô cùng ( ) và viết là
limf(x) = L, nếu với > 0 cho trước bé tùy ý, mà tìm ược số N > 0 ủ lớn sao cho khi |x| > N thì x→
f(x) – L < . Ví dụ 2.2.1.2. Cho hàm số f(x) = +2 1x . Chứng minh rằng lim f(x) = lim f(x) = 2. x→− x→+
Dễ thấy rằng D(f) = R\{0}. Giả sử cho trước > 0 bé tùy ý, ta có f(x) − =2 (2+1 x)− =2 1 x nên
nếu ta lấy N < 0 mà |N| ủ lớn thì f(x) − =2 1 x . Muốn vậy, ta chỉ cần lấy N sao cho N 1 là ược.
Khi ó, theo ịnh nghĩa thì lim f(x) = 2. Tương tự, ta chỉ cần lấy N sao cho x→− N
1 thì chứng minh ược lim f(x) = 2. x→+
Coi như bài tập, sinh viên tự ịnh nghĩa 6 trường hợp còn lại bằng ngôn ngữ “ - ”.
Các tính chất của giới hạn Từ ây trở i, khi viết limf(x) = Lmà nếu không có lưu ý gì thêm thì ta hiểu rằng L là một số x→a
hữu hạn, còn a có thể là số hữu hạn hoặc là .
Cho limf (x)→ 1= L1, limf (x)→a 2= L2 . Khi ó x a x (1)limCf (x)x 1
= Climf (x)→a 1 = CL1 (C là hằng số) →a x
(2) lim[f (x)x→ 1+f (x)]2= limf (x)→a 1+limf (x)x→a 2= L1 +L2 a x lOMoAR cPSD| 59735516 (3)lim[f (x)f (x)]→a 1 2=[xlimf (x)][limf (x→a 1 x→a 2 )]= L L1 2 x (4) lim f (x)1
= limf (x)x→a 1 = L1 với L2 ≠ 0 x→a f (x)2 limf (x)x→a 2 L2 (5)
Giả sử ba hàm số f(x), g(x), h(x) thỏa mãn f(x) g(x) h(x) với x (a,b). Khi ó với
x0 [a,b] mà limf(x) = lim h(x) = Lthì limg(x) = L(Nguyên lý kẹp ối với hàm số). x→x0 x→x0 x→x0 (6)
Cho f(x) là hàm số tăng (giảm) trên R; khi ó, nếu f(x) bị chặn trên (chặn dưới) nghĩa là
M sao cho f(x) M ( N sao cho f(x) N) với x R thì lim f(x) = L ( lim f(x) = L) với L là một số x→+ x→− hữu hạn. x x
Ví dụ 2.2.1.3. Chứng minh rằng
xlim 1→+ + x1 = e, xlim 1→− + 1 = e và lim1→ ( 0 + x)x1 = e x x Bài giải. x
- Chứng minh lim 1 + 1 = e. x→+ x
Thật vậy, với x > 0 bao giờ cũng n N* sao cho n x < n + 1 1 1 +1 1 1 + +1 1 1 1 n +1 x n n +1 x n + + + Vì 1 1 1 1 1,1 1,1 1 và n x < n + 1 n +1 x n 1 + n x n 1 + 1 n 1+ x n 1+
1 1+ 1 1+ 1
n +1 1+ 1
1+ 1 1+ 1 .
n +1 x n 1+ 1 x n n n +1 1+ 1 n 1+ x n 28 lOMoAR cPSD| 59735516
Mặt khác, khi x→+ thì n → + lim
n +1 lim 1 + 1 lim 1 + 1 1+ 1 n→+ 1 1 x→+
x n→+ n n + n +1
1+ 1 + + n 1 lim 1 + 1 n 1 lim n +1 = →+ n n +1 = e = e →+ Ta có n 1+ n1+1 1+ nlim→+ n1+1 1+ 0 lim 1 n
→+ + n1 n 1+ n1 = nlim 1→+ + n1 n
1+ nlim→+ n1 = e(1+ 0) = e
Theo Nguyên lý kẹp thì lim 1 + 1 x = e ( pcm). x→+ x - Việc chứng minh (
xlim 1 + x1 x = e và lim1x→0 + x)x1 = e coi
như bài tập. →−
Quy ước. Nếu lim f(x) = lim f(x) = L(L là số hữu hạn) thì viết ghép limf(x) = L.Chẳng hạn, ta x→− x→+ x→
viết lim 1 + 1 x = e chung cho lim 1 + 1 x = e và lim 1 + 1 x = e. x→ x x→− x x→+ x 2 2 2 2
Ví dụ 2.2.1.4. Tìm xlim x + x + x − x → 2 2 2 2 2 + 2 + 2 − 2 x x x x
Nhận xét: Để tìm xlim→ x + x + x − x , ta phải tìm xlim→− lOMoAR cPSD| 59735516 2 2 2 2
2 → + , mặt khác trong và
xlim x + x + x − x
. Tuy nhiên, ta thấy rằng, khi x → thì x →+
biểu thức cần tìm giới hạn khi x → chỉ có lũy thừa chẵn của x, do ó ể tránh xét giới hạn tương ứng
với hai trường hợp (x → – , x → + ) ta nên ổi biến t = x2, khi ó x → t → + . Bài giải.
2.2.2. Giới hạn một phía, giới hạn vô cùng
Khi x → x0 có hai khả năng: hoặc x → x0 từ phía trái x0, ược viết là x → x0–0, hoặc x → x0 từ phía
phải x0, ược viết là x → x0+0.
Khi ó, nếu tồn tại các giới hạn lim f(x), lim f(x) thì ta nói rằng ó là các giới hạn một phía, x→ −x0 0 x→ +x0 0
giới hạn trái (nếu lim f(x)) và giới hạn phải (nếu lim f(x)). x→ −x0 0 x→ +x0 0
Định lý. limf(x) = L lim f(x) = lim f(x) = Lvới L là một số hữu hạn. x→x0 x→ −x0 0 x→ +x0 0
Nếu f(x) → – hoặc f(x) → + khi x → x0 (x0 có thể hữu hạn, hoặc là – , hoặc là + ) thì ta nói
hàm f(x) có giới hạn vô cùng (sáu trường hợp còn lại: 1, 3, 4, 6, 7, 9) và viết là f(x) → khi x → x0 lim f(x) = . x→x0 = 1
Ví dụ 2.2.2.1. Tìm các giới hạn trái và phải của hàm f(x)
khi x → 3. Có tồn tại giới hạn 1 x + 2x 3− limf(x)không? x→3 Bài giải. 30 lOMoAR cPSD| 59735516 - Nếu x→3–0 thì 1 →− 2 x − 3 + lim 2 3+ 0 3 → x→ −3 0 x + 2 0 do ó lim 3 x→ −3 0 1 = 1 = 1 = 1 - Nếu x→3+0 thì 1 →+ 1 2 →+ do ó lim = 1 = 1 = 0 x − 3 x→ +3 0+ x + 2x + lim 2
lim f(x) lim f(x) limf(x)không tồn tại. x→ +3 0 x 3 0→ − x 3 0→ + x 3→
2.2.3. Khái niệm vô cùng bé và vô cùng lớn
Hàm số f(x) ược gọi là một vô cùng bé (VCB) khi x → x0 nếu lim f(x) = 0, hàm số f(x) ược x→x0
gọi là một vô cùng lớn (VCL) khi x → x0 nếu lim f(x) =+ với x0 có thể hữu hạn, hoặc là – , hoặc x→x0 là + .
- Nếu lim f(x) = L thì hàm số f(x) – L là một VCB khi x → x0. x→x0
- Nghịch ảo của một VCB là một VCL và ngược lại, nghịch ảo của một VCL là một VCB, tức là,
nếu f(x) là một VCB khi x → x0 thì 1f(x)là một VCL khi x → x0 và ngược lại, nếu f(x) là một
VCL khi x→x0 thì 1f(x)là một VCB khi x → x0.
2.2.4. Các dạng vô ịnh
Các tính chất của giới hạn của hàm số ở trên chỉ úng khi giới hạn L1, L2 tương ứng của các hàm số
f1(x), f2(x) là hữu hạn, tuy nhiên, trong thực tế, các hàm này có thể là VCB hoặc VCL, do ó ta cần phải
xét chi tiết các trường hợp này.
Từ tính chất (2) - phép cộng hai biểu thức, mỗi biểu thức có thể nhận các giá trị (– , ,
+ ), ược viết theo cột thứ nhất và hàng thứ nhất, ta ược + – L2 (hữu hạn) + – – –
? dạng vô ịnh − L1 (hữu hạn) – L1 + L2 + + ? + +
Từ tính chất (3) - phép nhân hai biểu thức, mỗi biểu thức có thể nhận các giá trị (– , ,
+ ), ược viết theo cột thứ nhất và hàng thứ nhất, ta ược – L2 (hữu hạn) + – + ? (khi L2 = 0) – dạng vô ịnh0.
L1 (hữu hạn) ? (khi L1 = 0) L1 L2 ? (khi L1 = 0) + – ? (khi L2 = 0) +
Từ tính chất (4) - phép chia hai biểu thức, mỗi biểu thức có thể nhận các giá trị (– ,, lOMoAR cPSD| 59735516
+ ) ược viết theo cột thứ nhất và hàng thứ nhất, ta ược / – L2 (hữu hạn) + – ? ?
L1 (hữu hạn) 0 ? (khi L1 = L2 = 0) 0 hai dạng vô ịnh 0 , + ? ? 0
Chú ý 2.2.1. Khi tìm giới hạn của một biểu thức, thực chất là khử các dạng vô ịnh. Để khử dạng vô
ịnh − khi tìm giới hạn lim[f(x)−g(x)], trong ó limf(x) = và x→a x→a
limg(x) = , nói chung, ta có thể biến ổi hiệu f(x) – g(x) thành tích
x→a f(x) − g(x) = f(x) 1 −
g(x) hoặc f(x) − g(x) = g(x) f(x) −1 f(x) g(x)
1 − 1 , mà ối với các dạng mới này, có nhiều khả năng dễ hoặc f(x) − g(x) = f(x)g(x) g(x) f(x) tìm giới hạn hơn.
Để khử dạng vô ịnh 0. khi tìm giới hạn lim[f(x)g(x)], trong ólimf(x) = 0 và limg(x) = x→a x→a x→a = =
ta có thể biến ổi tích f(x)g(x) thành f(x)g(x) f(x) (dạng 0 ) hoặc f(x)g(x) g(x) (dạng ). 1 g(x) 0 1 f(x)
Đối với các dạng mới này, có nhiều khả năng dễ tìm giới hạn hơn.
Chú ý 2.2.2. Việc sử dụng ịnh nghĩa khi tìm giới hạn, nói chung là bài toán khó, do ó chủ yếu là
biến ổi biểu thức cần tìm về các dạng giới hạn cơ bản ã biết và áp dụng.
Các giới hạn cơ bản lim =1
lim =1 và lim =1 x→0 x x→0 x x→0 x
lim 1 + 1 x = e lim(1+ x) 1x = e x→ x x→0
limlog (1a + x) = 1 (0 < a ≠ 1) ặc biệt, khi a = e ta ược lim ln(1+ x) =1 x→0 x lna x→0 x lim
ax −1 = lna (0 < a ≠ 1) ặc biệt, khi − a = e ta ược lim e 1 x =1 x→0 x x→0 x (1+ x)a −1 = a lim x→0 x
Chú ý 2.2.3. Bằng cách ổi biến, các giới hạn cơ bản trên có thể ược sử dụng dưới dạng: 32 lOMoAR cPSD| 59735516
sinf(x) =1, lim tanf(x) =1, lim arctanf(x) =1 f(x) 1 lim f (x)→0 f(x) f (x)→0 f(x) f (x)→0 + 1
f(x) = e, lim [1f(x)→0 + f(x)]f(x) = e lim 1
f(x)→ f(x) log [1a + f(x)] = 1 (0 < a ≠ 1), lim ln[1+ f(x)] =1 lim f (x)→0 f(x) lna f (x)→0 f(x) lim af(x) −1 = lna (0 < a ≠ 1), lim ef (x) −1 =1 f(x)→0 f(x) f (x)→0 f(x) [1+ f(x)]a −1 = a lim f (x)→0 f(x)
Chú ý 2.2.4. Ngoài các giới hạn cơ bản trên, ta công nhận một số giới hạn sau, ể sử dụng khi cần:
limax =1(0 < a ≠ 1), lim ax =+ (a > 1), lim ax = 0(a > 1) x→0 x→+
x→− lim x log x→ +0 0 k
a = 0 với a > 1, k > 0 x
với a > 1, k > 0 (khi x→+ , hàm xk tăng nhanh hơn hàm log x→+ xk ax) lim x →+
xk = 0 với a > 1 (khi x→+ , hàm ax tăng nhanh hơn hàm xk) x a −
Ví dụ 2.2.4.1. Tìm các giới hạn (a)lim 4
x→2 x 1− 2 x2 − 4 , (b) xlim ( x→+ 2 + 4x − x), (c)lim 2 − cotx. x→0 sin2x − Bài giải. 4 x→2 x 1− 2
x2 − 4 có dạng vô ịnh − (a)lim lOMoAR cPSD| 59735516
Biến ổi x 1− 2 − x24− 4 = x 1− 2 − (x − 2)(4x + 2) = (xx−+ −2)(2x +42) = (x −x2)(−x2+ 2) = x 1+ 2 4
limx→2 x 1− 2 − x2 − 4 = limx→2 x 1+ 2 = 14 . x→+ x→+ Biến ổi − cotx = 2 − cosx = 1 − cosx = 1− cos x2 = sin x2 2sinxcosx sinx sinxcosx sinx sinxcosx sinxcosx = = tan x lim
2 − cotx= limtan x = 0. x→0 sin2x x→0 x − x
Ví dụ 2.2.4.2. Tìm các giới hạn (a) lim(1− x) tan , (b) lim cot2x cot x→1 2 x→ 4 4 34 lOMoAR cPSD| 59735516 Bài giải. x
(a)lim(1− x) tan có dạng vô ịnh 0. x→1 2 x → →1 u 0 - Đổi biến u = 1 – x (1
− x)tan 2x = utan −(12 u) = utan 2 − 2 u = ucot 2 u 2
lim(1x→1 − x)tan 2x = limucotu→0 2 u = limu→0 1 tan u tan u 2 2 tanu 1 = 2 u = limu→0 u u 1 = 2 1 = 2 . 2 limu→0 2 2 2
− x có dạng vô ịnh 0. (b) lim cot2x cot x→ 4 4 - Đổi biến u = − x 4 x → →4 u 0 cot2xcot
4 − x = cot2 4 −u cotu =
cot 2 − 2u cotu
= tan2ucotu = sin2ucosucos2usinu sin2ucosu
limcot2xcot − x = limcot2 − u cotu = lim sin2ucosu = lim u x→ 4 u→0 4 u→0 cos2usinu u→0 cos2usinu 4 u sin2u sin2u sin2u
= lim u cosu = limu→0 u limcosuu→ 2 2limu→0 2u limcosuu→0 = 2.11 = 2. 0 = u→0 sinu cos2u sinu limcos2u sinu limcos2u 1 1 lOMoAR cPSD| 59735516 lim u→0 lim 2u→0 u u→0 u u→0 u
Ví dụ 2.2.4.3. Tìm các giới hạn x3 + 3x2 −9x − 2 1− x tan x − sinx xx − aa (a)limx→2 x3 − −x 6
, (b)limx→1 1− 3 x , (c)limx→0 x3 , (d)limx→a x − a Bài giải. x3 + 3x2 −9x − 2 0 (a)limx→2 x3 − −x 6 có dạng vô ịnh 0 Biến ổi x3 + 3 2
3x−2x−−9x6 − 2 = ((xx−−2)(2)(xx2 ++25xx ++1)3) = xx 2 2 ++25xx ++13 x
limx3 + 33x− −2x−9x6 − 2 = limx→2 xx22 ++25xx ++13 = xx22 ++25xx ++13 x 2= = 1511 x→2 x 1− x 0
(b)lim có dạng vô ịnh x→1 1− 3 x 0 x → →1 t 1
Đổi biến x = t6 =t6 x 11−− 3 xx = 11−− tt32 = (1(1− t)(1− t)(1+ +t+ t)t )2 = 1+ +1t+ tt2
lim1− x = lim1+ +t t2 = 1+ +t t2 = 3 . x→1 1−
3 x t→1 1+ t 1+ t t 1= 2 tan x − sinx 0 (c)limx 0 3 có dạng vô ịnh → x 0
Biến ổi tanx −3sinx = cosxsinx −3 sinx = sinx −3sinxcosx = sinx(13 − cosx) x x x cosx x cosx 36




