Giải Toán 10 Bài 1: Dấu của tam thức bậc hai CTST

Giải Toán 10 trang 9, 10 Chân trời sáng tạo - Tập 2 Bài 1 trang 9
Đa thức nào sau đây là tam thức bậc hai? Gợi ý đáp án a.
là tam thức bậc hai có a = 4; b = 3; c = 1 b.
không là tam thức bậc hai c.
là tam thức bậc hai có a = 2; b = 4; c = -1 Bài 2 trang 9
Xác định giá trị của m để các đa thức sau là tam thức bậc hai. Gợi ý đáp án
Giá trị của m để các đa thức sau là tam thức bậc hai: a. là tam thức bậc hai khi b.
không là tam thức bậc hai. c.
là tam thức bậc hai với mọi m. Bài 3 trang 10
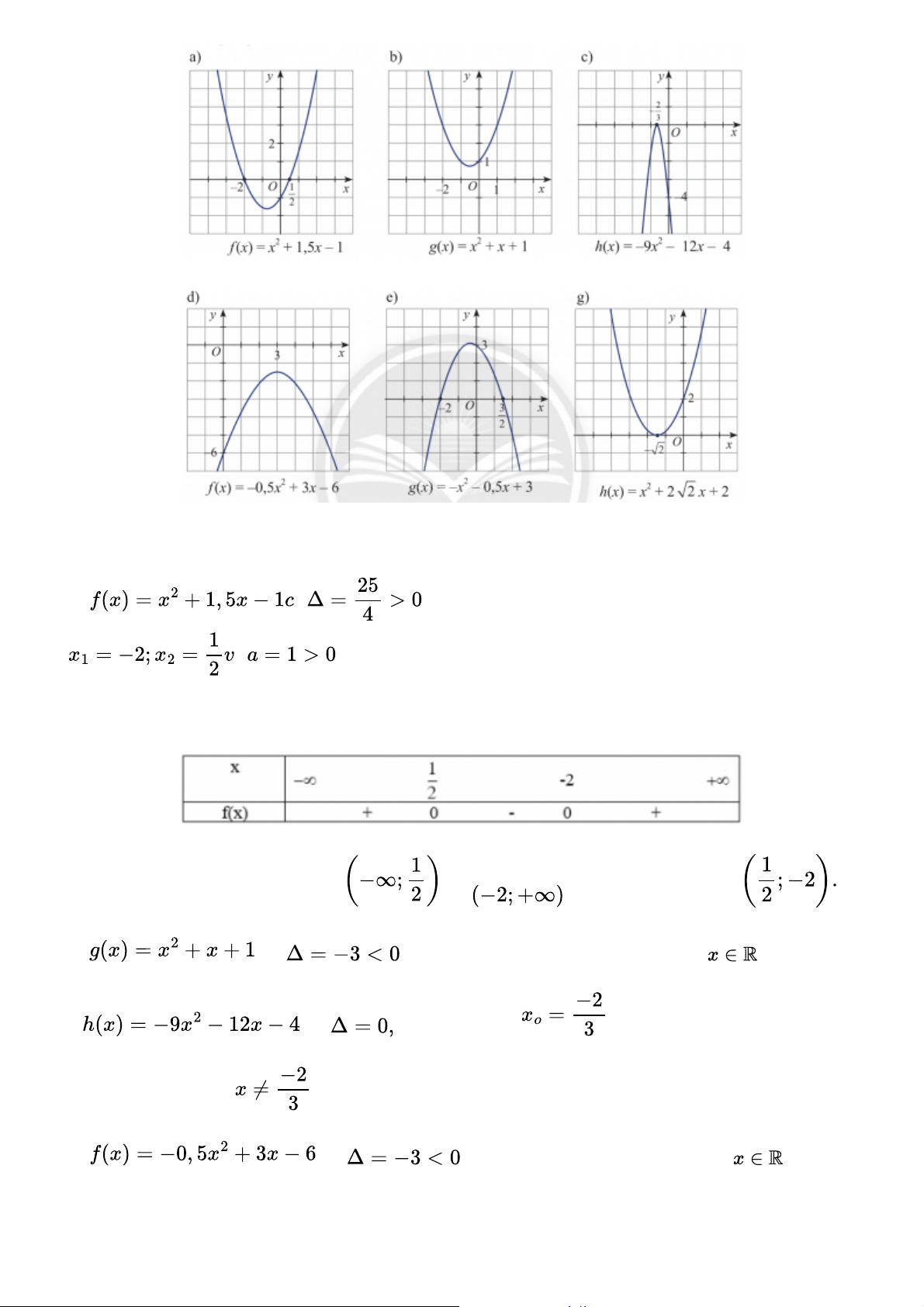
Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng. Gợi ý đáp án ó a.
, hai nghiệm phân biệt là à
Ta có bảng xét dấu f(x) như sau:
Vậy f(x) dương trong hai khoảng và và âm trong khoảng b. có
và a =1 >0 . Vậy f(x) dương với mọi c. có nghiệm kép là và a =-9<0. Vậy f(x) âm với mọi d. có
và a =-0,5 . Vậy f(x) âm với mọi e. có
, hai nghiệm phân biệt là và a = -1 < 0
Ta có bảng xét dấu f(x) như sau:
Vậy f(x) dương trong hai khoảng và và âm trong khoảng g. ó , nghiệm kép là và a = -9 < 0. Vậy f(x) âm với mọi Bài 4 trang 10
Xét dấu của tam thức bậc hai sau đây e. f(x) = (2x+5) (x-3) Gợi ý đáp án a. . Và đa thức có nghiệm
Mặt khác a= 2 > 0 nên f(x) luôn dương với mọi x khác -1 b.
nên phương trình có hai nghiệm phân biệt :
và a= -1 < 0 nên f(x) mang dấu âm khi x nằm trong khoảng
và mang dấu dương với mọi x nằm ngoài khoảng c.
và a= -2 < 0 nên f(x) luôn âm với mọi x .
nên có nghiệm kép là x = -1,5 và a= -4
\Rightarrow f(x) mang dấu âm với mọi x khác -1,5 e. f(x) = 2x^{2} - x - 15.
, và a= 2 > 0 nên f(x) âm Bài 5 trang 10
Độ cao ( tính bằng mét) của quả bóng so với vành rổ khi bóng di chuyển được x mét theo
phương ngang được mô phỏng theo hàm số Trong các khoảng nào
của x thì bóng nằm: cao hơn vành rổ, thấp hơn vành rổ, và ngang vành rổ. Làm tròn kết quả đến hàng phần mười. Gợi ý đáp án Hàm số h(x) có
nên sẽ có hai nghiệm phân biệt : à Vây :
Bóng nằm cao hơn vành rổ khi bóng nằm trong khoảng (1;9)
Bóng nằm thấp hơn vành rổ khi bóng nằm trong khoảng và
Bóng nằm ngang vành rổ khi bóng ở độ cao 1m hoặc 9m Bài 6 trang 10
Một khung dây thép hình chữ nhật có chiều dài 20cm và chiều rộng 15cm được uốn lại thành
khung hình chữ nhật mới có kích thước (20 +x) và (15-x) cm. Với x nằm trong khoảng nào thì
diện tích của khung sau khi uốn: tăng lên, không thay đổi, giảm đi. Gợi ý đáp án
Diện tích của khung dây thép khi chưa uốn là : 20.15 = 300 ( )
Diện tích của khung dây thép khi đã uốn là : . Như vậy
diện tích của khung sau khi uốn tùy thuộc vào giá trị của hàm số Xét hàm số f(x) có
có hai nghiệm phân biệt : và có a = 1 > 0. Nên :
f(x) mang dấu dương khi x thuộc (-5;0)
Diện tích khung hình sau khi uốn nhỏ hơn
trước khi uốn (giảm đi )
f(x) mang dấu âm khi x thuộc à
Diện tích khung hình sau khi uốn
lớn hơn trước khi uốn (tăng lên )
f(x) = 0 khi x = 0 hoặc x = -5
Diện tích khung hình sau khi uốn và trước khi uốn là không thay đổi Bài 7 trang 10
Chứng minh rằng với mọi số thực m ta luôn có : Xét hàm số . Ta có và có a = 9 > 0.
Nên f(m) > 0 với mọi m nghĩa là Bài 8 trang 10
Tìm giá trị của m để : a với mọi b. với mọi Gợi ý đáp án a. Hàm số có . và a= 2 > 0 nên: Để với mọi thì b. Xét hàm số có : Để với mọi ì và