Giải Toán 10 trang 12, 13 Chân trời sáng tạo - Tập 2 Bài 1 trang 12
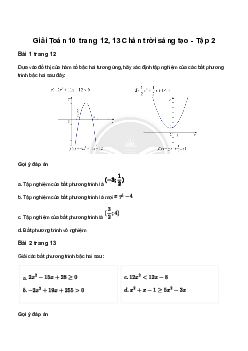
Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau đây: Gợi ý đáp án
a. Tập nghiệm của bất phương trình là
b. Tập nghiệm của bất phương trình là mọi
c. Tập nghiệm của bất phương trình là
d. Bất phương trình vô nghiệm Bài 2 trang 13
Giải các bất phương trình bậc hai sau : a. Gợi ý đáp án a. Xét hàm số . ta có . nên f(x) có hai nghiệm phân biệt :
f(x) có a = 2 > 0 nên f(x) > 0 khi hoặc
Vậy nghiệm của bất phương trình là : hoặc b. Xét hàm số có . Nên f(x) có hai nghiệm phân biệt. f(x) >0 khi c. Xét hàm số có và có a = 12
> 0 nên f(x) luôn lớn hơn 0 với mọi x
Vậy với mọi x ta luôn có : d. Xét hàm số Có
. Vậy f(x) có nghiệm kép x = 0,5 Vậy để thì x = 0,5 Bài 3 trang 13
Kim muốn trồng một vườn hoa trên mảnh đất hình chữ nhật và làm hàng rào bao quanh. Kim
chỉ có đủ vật liệu để làm 30m hàng rào nhưng muốn diện tích vườn hoa ít nhất là 50 m^{2}. Hỏi
chiều rộng của vườn hoa nằm trong khoảng nào? Gợi ý đáp án
Giả sử chiều rộng của vườn hoa là x và chiều dài là y thì theo dữ liệu đề bài ta có : 2(x+y) = 30 (1) và Từ (1) . Thay vào (2) ta có:
Xét tam thức bậc hai một ẩn ta có :
0 nên f(x) có hai nghiệm phân biệt
Và có a = -1 < 0 nên f(x) > 0 khi
Vậy chiều rộng của vườn hoa nằm trong khoảng từ 5 đến 10m. Bài 4 trang 13
Một quả bóng được ném thẳng lên từ độ cao 1,6m so với mặt đất với vận tốc 10m/s.Độ cao
của bóng so với mặt đất (tính bằng m) sau t giây được cho bởi hàm số Hỏi :
a. Bóng có thể cao trên 7m không?
b. Bóng ở độ cao trên 5m trong khoảng thời gian bao lâu? Làm tròn kết quả đến hàng phần trăm Gợi ý đáp án a. Xét hàm có và a=
-4,9 < 0 nên h(t) luôn <0 tức là
Như vậy bóng không thể cao trên 7m b. Xét hàm có nên h(t)
có hai nghiệm phân biệt :
Và có a = -4,9 < 0. nên f(x) > 0 khi
Hay bóng ở độ cao trên 5m trong khoảng thời gian từ 0,55 giây đến 1,5 giây Bài 5 trang 13
Mặt cắt ngang của mặt đường thường có dạng hình parabol để nước mưa dễ dàng thoát sang
hai bên. Mặt cắt ngang của một con đường được mô tả bằng hàm số với gốc
tọa độ đặt tại tim đường và đơn vị đo là mét trong hình 4. Với chiều rộng của đường như thế
nào thì tim đường cao hơn lề đường không quá 15cm. Gợi ý đáp án
Theo dữ liệu của bài ta có : Ta xét có nên f(x) có hai nghiệm phân biệt và a = -0,006 < 0 nên khi x thuộc đoạn từ