Giải Toán 6 Bài tập cuối chương II Cánh diều

Giải Toán 6 trang 88 tập 1 Bài 1
Sử dụng số nguyên âm để thực hiện các tình huống sau: a) Nợ 150 nghìn đồng;
b) 600 m dưới mực nước biển; c) 12 độ dưới 0oC.
Hướng dẫn cách giải
+ Các số – 1, – 2, – 3, ... là các số nguyên âm. Số nguyên âm được nhận biết bằng dấu “–” ở
trước số tự nhiên khác 0.
Ví dụ: – 5, – 10, – 10 000, …. Gợi ý đáp án:
a) Nợ 150 nghìn đồng: – 150 (nghìn đồng)
b)600 m dưới mực nước biển: – 600 (m)
c) 12 độ dưới 0oC: - 12 (ooC) Bài 2
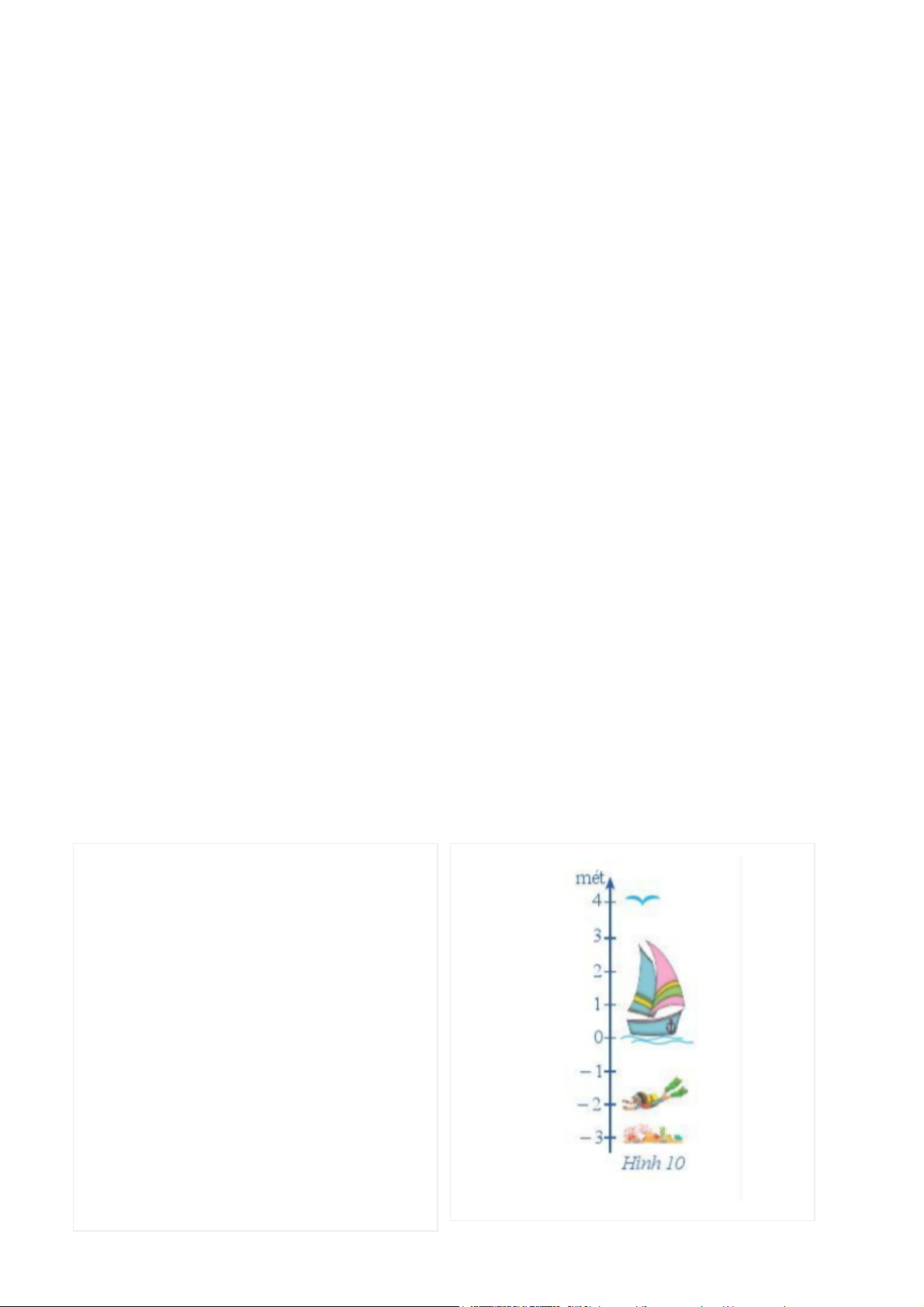
Trong hình 10, hãy tính (theo mét):
a) Khoảng cách giữa rặng san hô và người thợ lặn;
b) Khoảng cách giữa người thợ lặn và mặt nước;
c) Khoảng cách giữa mặt nước và con chim;
d) Khoảng cách giữa rặng san hô và con chim.
Hướng dẫn cách giải
+ Các số – 1, – 2, – 3, ... là các số nguyên âm. Số nguyên âm được nhận biết bằng dấu “–” ở
trước số tự nhiên khác 0.
Ví dụ: – 5, – 10, – 10 000, …. Gợi ý đáp án: Cách 1
a) Khoảng cách giữa rặng san hô và người thợ lặn là: (– 2) – (- 3) = 1 mét
b) Khoảng cách giữa người thợ lặn và mặt nước 0 – (- 2) = 2 mét
c) Khoảng cách giữa mặt nước và con chim là: 4 – 0 = 4 mét
d) Khoảng cách giữa rặng san hô và con chim là: 4 – (- 3) = 7 mét Cách 2
Quan sát Hình 10 trên trục mét, ta thấy:
+ Rặng san hô tương ứng với vị trí – 3 m
+ Người thợ lặn tương ứng với vị trí – 2 m
+ Mặt nước tương ứng với vị trí 0 m
+ Con chim tương ứng với vị trí 4 m Do đó ta có:
a) Khoảng cách giữa rặng san hô và người thợ lặn là: (– 2) – (– 3) = 1 (m)
b) Khoảng cách giữa người thợ lặn và mặt nước là: 0 – (– 2) = 2 (m)
c) Khoảng cách giữa mặt nước và con chim là: 4 – 0 = 4 (m)
d) Khoảng cách giữa rặng san hô và con chim là: 4 – (– 3) = 7 (m). Bài 3
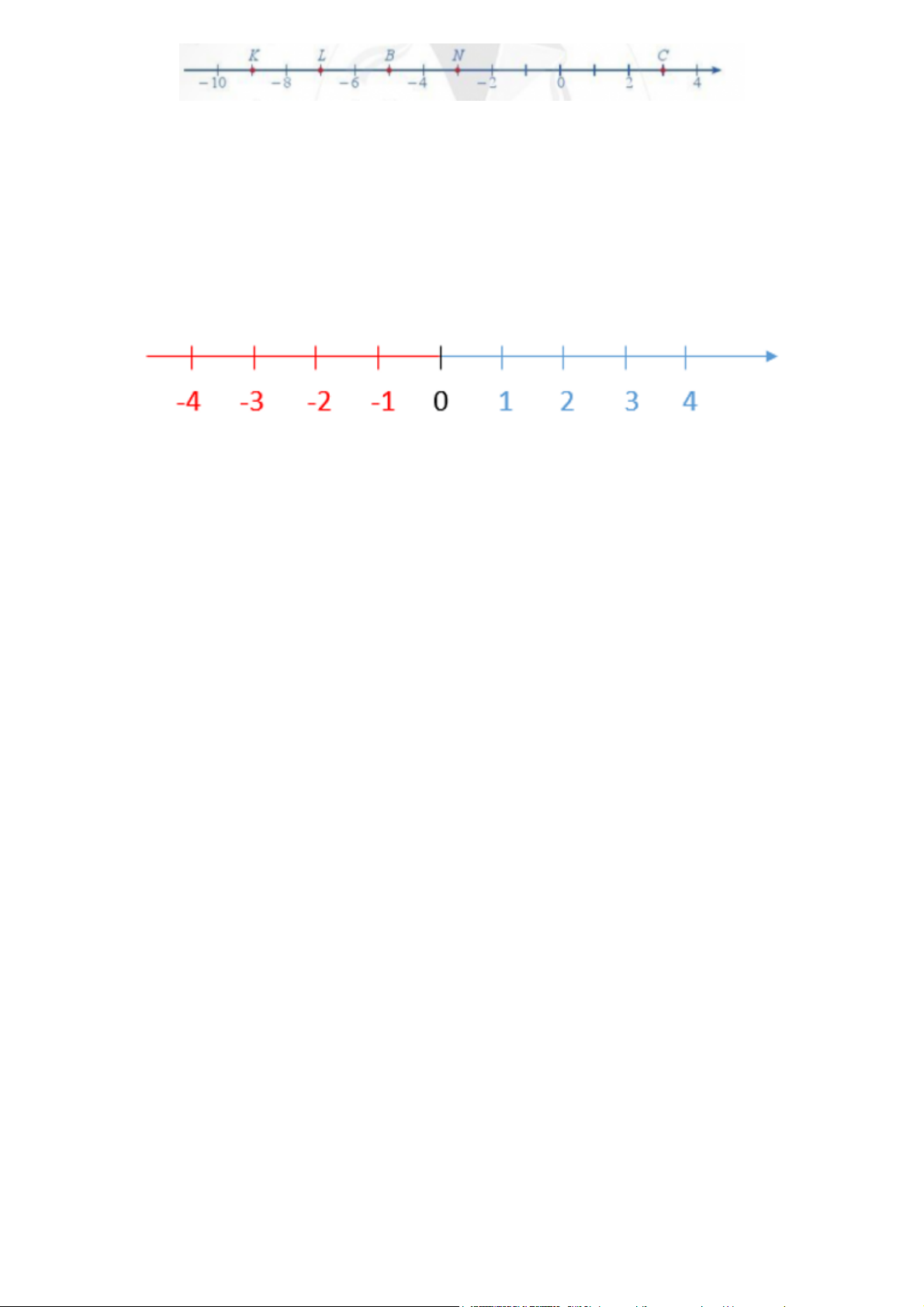
a) Các điểm N, B, C biểu diễn những số nào?
b) Điểm nào biểu diễn số - 7?
Hướng dẫn cách giải
Trên trục số nằm ngang, điểm biểu diễn số nguyên âm nằm bên trái điểm 0, điểm biểu diễn số
nguyên dương nằm bên phải điểm 0. Gợi ý đáp án:
a) Điểm N biểu diễn số - 3
Điểm B biểu diễn số - 5 Điểm C biểu diễn số 3
b) Điểm biểu diễn số - 7 là điểm L. Bài 4
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Giải thích.
a) Kết quả của phép trừ số nguyên dương cho số nguyên dương là số nguyên dương.
b) Kết quả của phép trừ số nguyên dương cho số nguyên âm là số nguyên dương.
c) Kết quả của phép nhân số nguyên dương với số nguyên âm là số nguyên âm.
Hướng dẫn cách giải
- Cách nhận biết dấu của thương: (+) : (+) → (+) (–) : (–) → (+) (+) : (–) → (–) (–) : (+) → (–) Gợi ý đáp án:
a) Kết quả của phép trừ số nguyên dương cho số nguyên dương là số nguyên dương là phát biểu sai.
Ta có thể lấy ví dụ như sau:
Với hai số nguyên dương là 7 và 10 ta thực hiện phép trừ
7 – 10 = 7 + (– 10) = – 3 < 0
Ta được kết quả là – 3, đây là một số nguyên âm, không phải số nguyên dương.
b) Kết quả của phép trừ số nguyên dương cho số nguyên âm là số nguyên dương là phát biểu đúng.
Thật vậy, giả sử ta có số nguyên dương a bất kì đóng vai trò là số bị trừ và số nguyên âm – b
đóng vai trò là số trừ. Khi đó ta thực hiện phép trừ: a – (– b) = a + b
Vì – b là số nguyên âm, nên số đối của nó là b là một số nguyên dương
Do đó tổng a + b là một số nguyên dương, hay kết quả của phép trừ a – (– b) là một số nguyên dương.
c) Ta có tích hai số nguyên khác dấu là số nguyên âm.
Do đó kết quả của phép nhân số nguyên dương với số nguyên âm là số nguyên âm là phát biểu đúng.
i số nguyên âm là số nguyên âm. Bài 5
a) (- 15) . 4 – 240: 6 + 36 : (- 2) . 3;
b) (- 25) + [(- 69) : 3 + 53] . (- 2) – 8.
Hướng dẫn cách giải
Để chia hai số nguyên khác dấu, ta làm như sau:
Bước 1. Bỏ dấu “–” trước số nguyên âm, giữ nguyên số còn lại
Bước 2. Tính thương của hai số nguyên dương nhận được ở Bước 1
Bước 3. Thêm dấu “–” trước kết quả nhận được ở Bước 2, ta có thương cần tìm. Gợi ý đáp án:
a) (– 15) . 4 – 240 : 6 + 36 : (– 2) . 3
b) (– 25) + [(– 69) : 3 + 53] . (– 2) – 8
= – (15 . 4) – 40 + [– (36 : 2) . 3]
= (– 32) + [– (69 : 3) + 53] . (– 2) – 8
= (– 60) – 40 + [(– 18) . 3]
= (– 32) + [ (– 23) + 53] . (– 2) – 8 = (– 60) – 40 + (– 54)
= (– 32) + (53 – 23) . (– 2) – 8
= (– 60) + (– 40) + (– 54)
= (– 32) + 30 . (– 2) – 8 = – (60 + 40 + 54) = (– 32) + (– 60) – 8 = – 154. = – (32 + 60) – 8 = – 92 – 8 = – (92 + 8) = – 100. Bài 6
Tìm số nguyên x, biết: a) 4 . x + 15 = - 5; b) (- 270) : x – 20 = 70. Gợi ý đáp án: a) 4 . x + 15 = – 5 b) (– 270) : x – 20 = 70 4 . x = (– 5) – 15 (– 270) : x = 70 + 20 4 . x = – 20 (– 270) : x = 90 x = (– 20) : 4 x = (– 270) : 90 x = – 5 x = – 3 Vậy x = – 5. Vậy x = – 3. Bài 7
Công ty An Bình có lợi nhuận ở mỗi tháng trong 4 tháng đầu năm là – 70 triệu đồng. Trong 8
tháng tiếp theo lợi nhuận mỗi tháng của công ty là 60 triệu đồng. Sau 12 tháng kinh doanh, lợi
nhuận của công ty An Bình là bao nhiêu tiền? Gợi ý đáp án: Cách 1.
Lợi nhuận của công ty An Bình trong 4 tháng đầu năm là:
– 70 . 4 = – 280 (triệu đồng)
Lợi nhuận của công ty An Bình trong 8 tháng tiếp theo là: 60 . 8 = 480 (triệu đồng)
Sau 12 tháng kinh doanh, lợi nhuận của công ty An Bình là:
(– 280) + 480 = 200 (triệu đồng)
Vậy sau 12 tháng kinh doanh, lợi nhuận của công ty An Bình là 200 triệu đồng. Cách 2. (làm gộp)
Lợi nhuận của công ty An Bình sau 12 tháng kinh doanh là:
(– 70) . 4 + 60 . 8 = 200 (triệu đồng)
Vậy sau 12 tháng kinh doanh, lợi nhuận của công ty An Bình là 200 triệu đồng. Bài 8
Người ta sử dụng biểu thúc T= (I - E) : 12 để biểu diễn số tiền tiết kiệm trung bình mỗi tháng
của một người, trong đó I là tổng thu nhập và E là tổng chi phí trong một năm của người đó.
Bác Dũng có số tiền tiết kiệm trung bình mỗi tháng là 3 triệu đồng và tổng chi phí cả năm là 84
triệu đồng. Tính tổng thu nhập cả năm của bác Dũng. Hướng dẫn giải
Để chia hai số nguyên khác dấu, ta làm như sau:
Bước 1. Bỏ dấu “–” trước số nguyên âm, giữ nguyên số còn lại
Bước 2. Tính thương của hai số nguyên dương nhận được ở Bước 1
Bước 3. Thêm dấu “–” trước kết quả nhận được ở Bước 2, ta có thương cần tìm. Gợi ý đáp án:
Bác Dũng có số tiền tiết kiệm trung bình mỗi tháng là 3 triệu đồng hay T = 3 triệu đồng.
Tổng chi phí cả năm của bác là 84 triệu đồng, hay E = 84 triệu đồng
Ta cần tìm tổng thu nhập I cả năm của bác Dũng.
Khi đó ta có biểu thức T = (I – E) : 12 với T = 3, E = 84
Thay T = 3 và E = 84 vào biểu thức trên ta được: 3 = (I – 84) : 12 Hay (I – 84) : 12 = 3 I – 84 = 3 . 12 I – 84 = 36 I = 36 + 84 I = 120
Vậy tổng thu nhập cả năm của bác Dũng là 120 triệu đồng.
Lý thuyết chương 2 Số nguyên 1. Số nguyên
• Các số tự nhiên khác 0 còn được gọi là các số nguyên dương (đôi khi còn viết +1, +2, +3,…
nhưng dấu “+” thường được bỏ đi).
• Các số -1, -2, -3,…là các số nguyên âm.
• Tập hợp: {...; -3; -2; -1; 1; 2; 3;...} gồm các số nguyên âm, số 0 và các số nguyên dương là tập
hợp các số nguyên. Tập hợp các số nguyên được kí hiệu là Z. Chú ý:
• Số 0 không phải là số nguyên âm và cũng không phải là số nguyên dương.
• Điểm biểu diễn số nguyên a trên trục số gọi là điểm a 2. Số đối
Trên trục số các điểm 1 và -1, 2 và -2, 3 và -3,… cách đều điểm 0 và nằm ở hai phía của điểm
0. Ta nói các số 1 và -1, 2 và -2, 3 và -3,… là các số đối nhau.
Số đối của số 0 là 0.
3. So sánh hai số nguyên
Khi biểu diễn trên trục số (nằm ngang), điểm a nằm bên trái điểm b thì số nguyên a nhỏ hơn số nguyên b.
Chú ý: Số nguyên b gọi là số liền sau của số nguyên a nếu a < b và không có số nguyên nào
nằm giữa a và b (lớn hơn a và nhỏ hơn b). Khi đó ta cũng nói a là số liền trước của b. Nhận xét:
• Mọi số nguyên dương đều lớn hơn số 0.
• Mọi số nguyên âm đều nhỏ hơn số 0.
• Mọi số nguyên âm đều nhỏ hơn bất kỳ số nguyên dương nào.
4. Giá trị tuyệt đối của một số nguyên
Khoảng cách từ điểm a đến điểm 0 trên trục số là giá trị tuyệt đối của số nguyên a.
Giá trị tuyệt đối của số nguyên a kí hiệu là |a| (đọc là “giá trị tuyệt đối của a”). Nhận xét:
• Giá trị tuyệt đối của số 0 là số 0.
• Giá trị tuyệt dối của một số nguyên dương là chính nó.
• Giá trị tuyệt đối của một số nguyên âm là số đối của nó (và là một số nguyên dương).
• Trong hai số nguyên âm, số nào có giá trị tuyệt đối nhỏ hơn thì lớn hơn.
• Hai số đối nhau có giá trị tuyệt đối bằng nhau.