Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam
giác: cạnh - cạnh - cạnh Bài 1
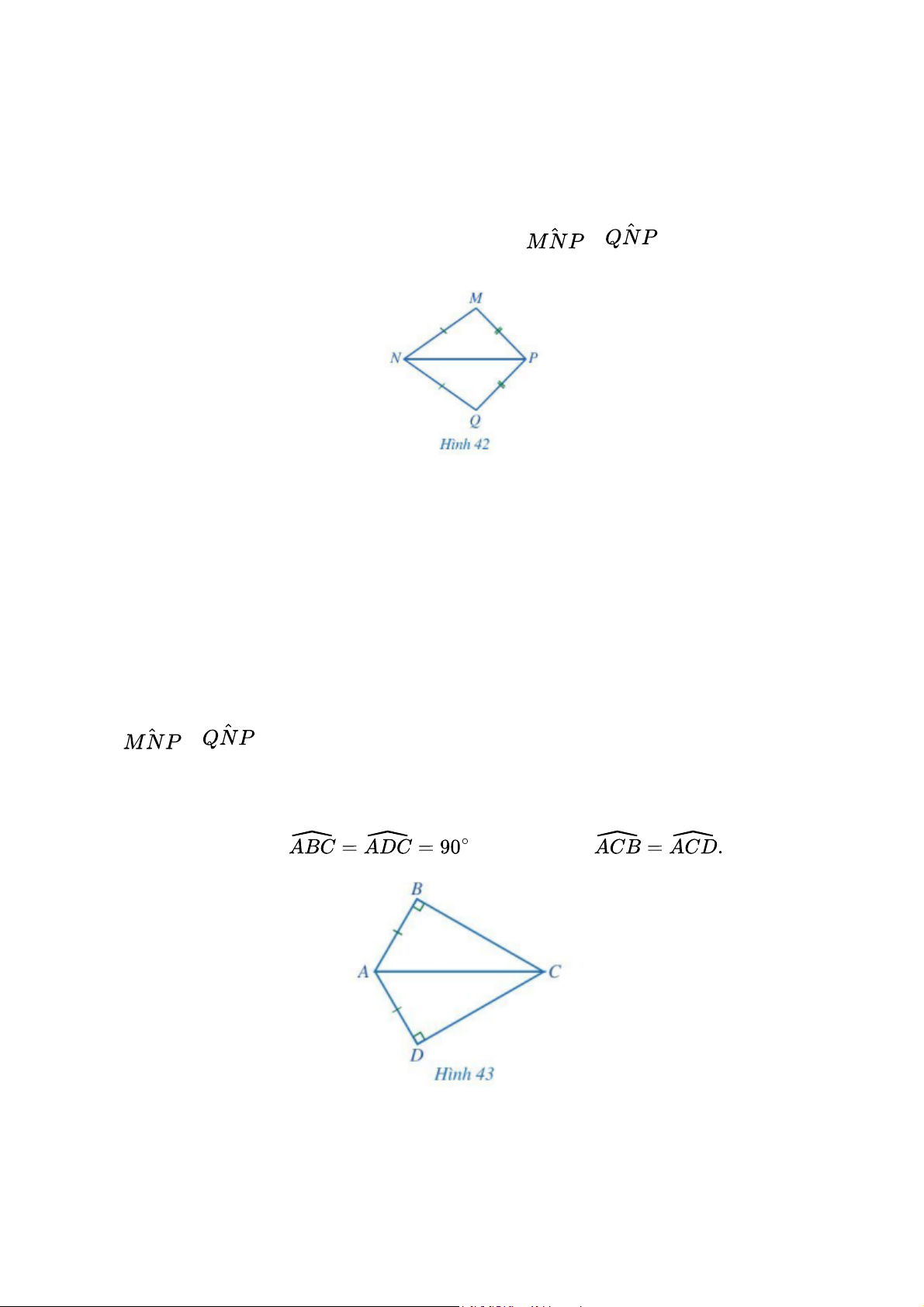
Cho Hình 42 có MN = QN, MP = QP. Chứng minh rằng = Xét ∆MNP và ∆QNP có: MN = QN (theo giả thiết). MP = QP (theo giả thiết). NP chung.
Suy ra ∆MNP = ∆QNP(c - c - c). Do đó = (2 góc tương ứng). Bài 2
Cho Hình 43 có AB = AD, . Chứng minh Gợi ý đáp án
Xét hai tam giác vuông ABC và ADC có: AB = AD, AC chung. Nên
(cạnh huyền - cạnh góc vuông) nên (2 góc tương ứng) Bài 3
Cho Hình 44 có AC = BD, . Chứng minh AD = BC. Gợi ý đáp án
Xét hai tam giác vuông DAB và CBA: AC = BD; AB chung. Nên
(cạnh huyền - cạnh góc vuông)
Nên AD = BC ( 2 cạnh tương ứng) Bài 4
Cho hai tam giác ABC và MNP thỏa mãn: AB = MN, BC = NP, AC = MP, , .
Tính số đo các góc còn lại của hai tam giác. Gợi ý đáp án
Tam giác ABC và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau: AB = MN, BC = NP,
AC = MP). Nên các cặp góc tương ứng trong hai tam giác này bằng nhau: Vậy (vì tổng ba góc
trong một tam giác bằng 180°).