Giải Vật lí 10 Bài 20: Một số ví dụ về cách giải các bài toán thuộc phần động lực học | Kết Nối Tri Thức
Giải Vật lí 10 Bài 20: Một số ví dụ về cách giải các bài toán thuộc phần động lực học sách Kết nối tri thức với cuộc sống giúp các em học sinh lớp 10 có thêm nhiều gợi ý tham khảo để biết cách trả lời các câu hỏi bài học Bài 20 trang 82 thuộc chương 3: Động lực học.
Chủ đề: Chương 3: Động lực học (KNTT)
Môn: Vật Lí 10
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
Một số ví dụ về cách giải các bài toán thuộc phần động lực học Bài 1
Người ta đẩy một cái thùng có khối lượng 55 kg theo phương ngang với lực 220 N làm thùng
chuyển động trên mặt phẳng ngang. Hệ số ma sát trượt giữa thùng và mặt phẳng là 0,35. Tính
gia tốc của thùng. Lấy g = 9,8 m/s2. Gợi ý đáp án
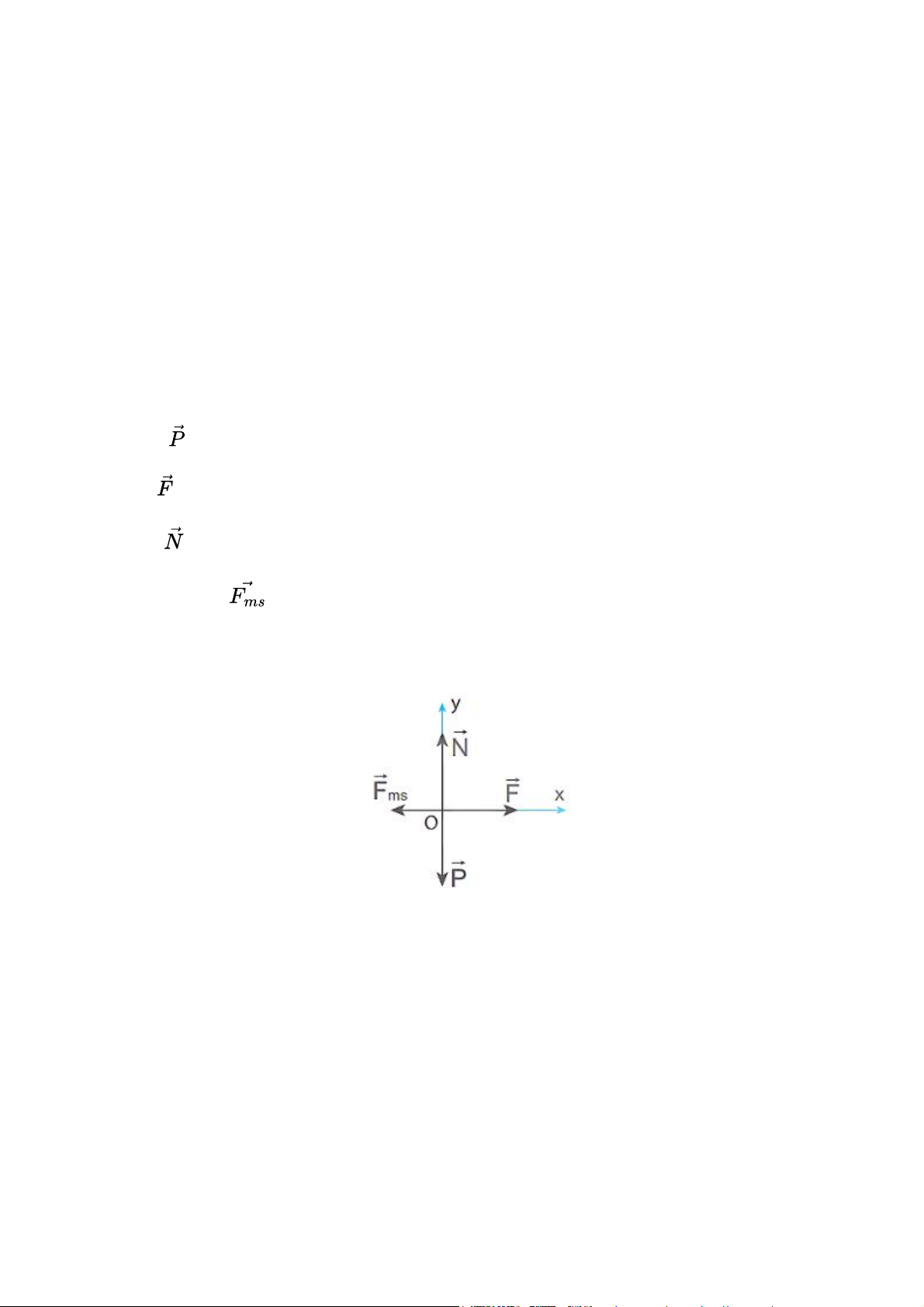
- Thùng chịu tác dụng của bốn lực: + Trọng lực + Lực đẩy + Phản lực + Lực ma sát trượt
- Coi thùng như một chất điểm (hình vẽ) Bài 2
Một quyển sách đặt trên mặt bàn nghiêng và được thả cho trượt xuống. Cho biết góc nghiêng
α = 30o so với phương ngang và hệ số ma sát giữa quyển sách và mặt bàn là µ = 0,3. Lấy g =
9,8 m/s2. Tính gia tốc của quyển sách và quãng đường đi được của nó sau 2 s. Gợi ý đáp án
Coi quyển sách là chất điểm, phân tích các lực tác dụng lên quyển sách tại trọng tâm gồm có:
trọng lực, phản lực, lực ma sát.
Coi như con dốc đủ dài, sau 2s quyển sách vẫn chuyển động trên con dốc.
Chọn hệ trục tọa độ Oxy như hình vẽ:
Quãng đường đi được sau 2s: s = at2 = .2,35.22 = 4,7m Bài 3
Một học sinh dùng dây kéo một thùng sách nặng 10 kg chuyển động trên mặt sàn nằm ngang.
Dây nghiêng một góc chếch lên 30o so với phương ngang. Hệ số ma sát trượt giữa đáy thùng
và mặt sàn là µ = 0,2 (lấy g = 9,8 m/s2). Hãy xác định độ lớn của lực kéo để thùng sách chuyển động thẳng đều. Gợi ý đáp án
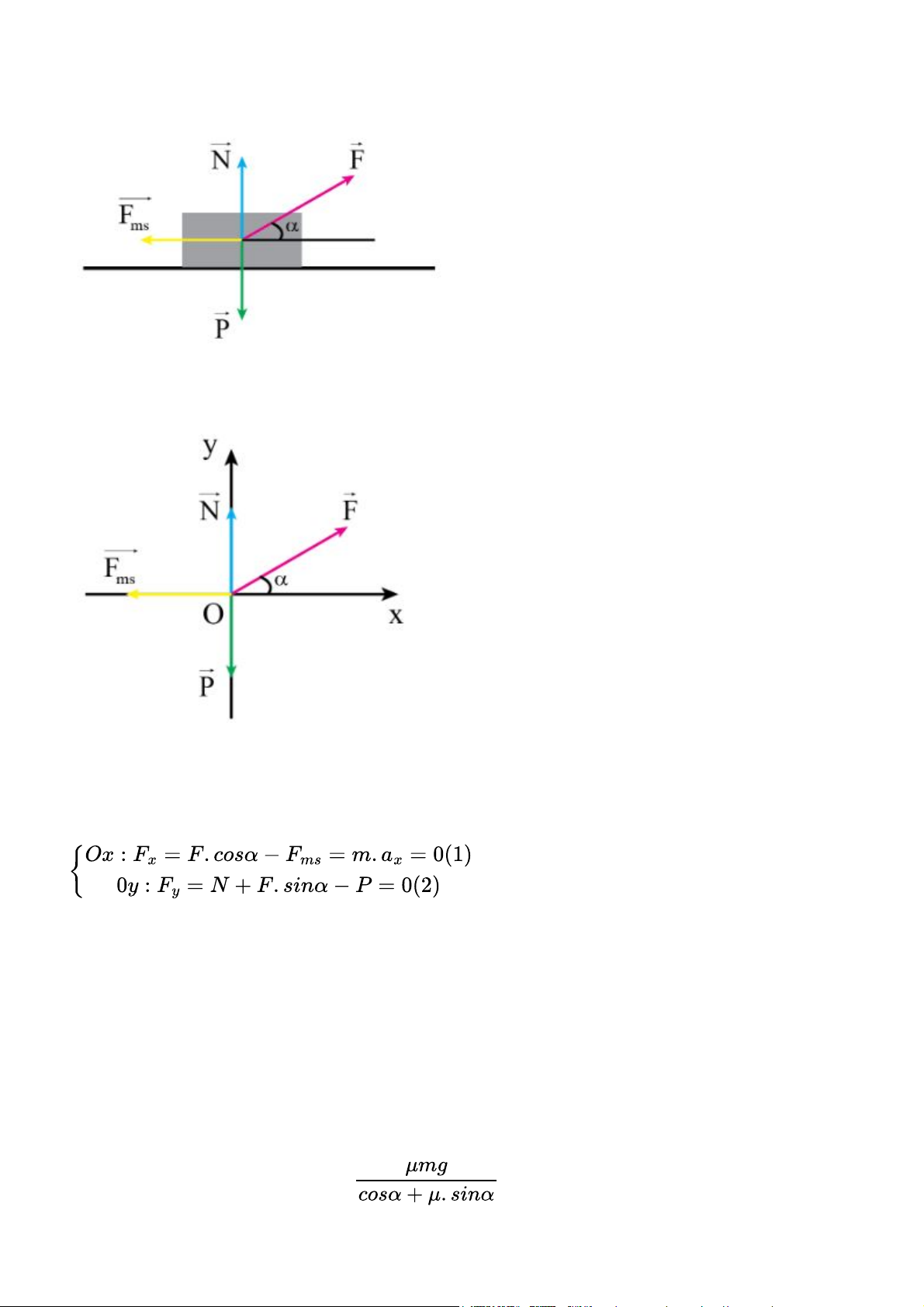
Coi thùng hàng là chất điểm, phân tích các lực tác dụng lên thùng hàng tại trọng tâm gồm có:
lực kéo, trọng lực, phản lực, lực ma sát.
Chọn hệ trục tọa độ Oxy như hình vẽ:
- Vật chuyển động thẳng đều.
- Áp dụng định luật 2 Newton cho chuyển động của vật theo hai trục Ox, Oy: Mà Fms = µ.N
Giải hệ phương trình có:
Từ (2) => N = P - F.sinα = mg - F.sinα
=> Fms = µ.N = µmg - µF.sinα Thay vào (1) ta được:
F.cosα - µmg + µF.sinα = 0 => F = = 20,3N Bài 4
Hai vật có khối lượng lần lượt là m1 = 5 kg và m2 = 10 kg được nối với nhau bằng một sợi dây
không dãn và được đặt trên một mặt sàn nằm ngang. Kéo vật 1 bằng một lực nằm ngang có
độ lớn F = 45 N. Hệ số ma sát giữa mỗi vật và mặt sàn là µ = 0,2. Lấy g = 9,8 m/s2. Tính gia
tốc của mỗi vật và lực căng của dây nối. Gợi ý đáp án
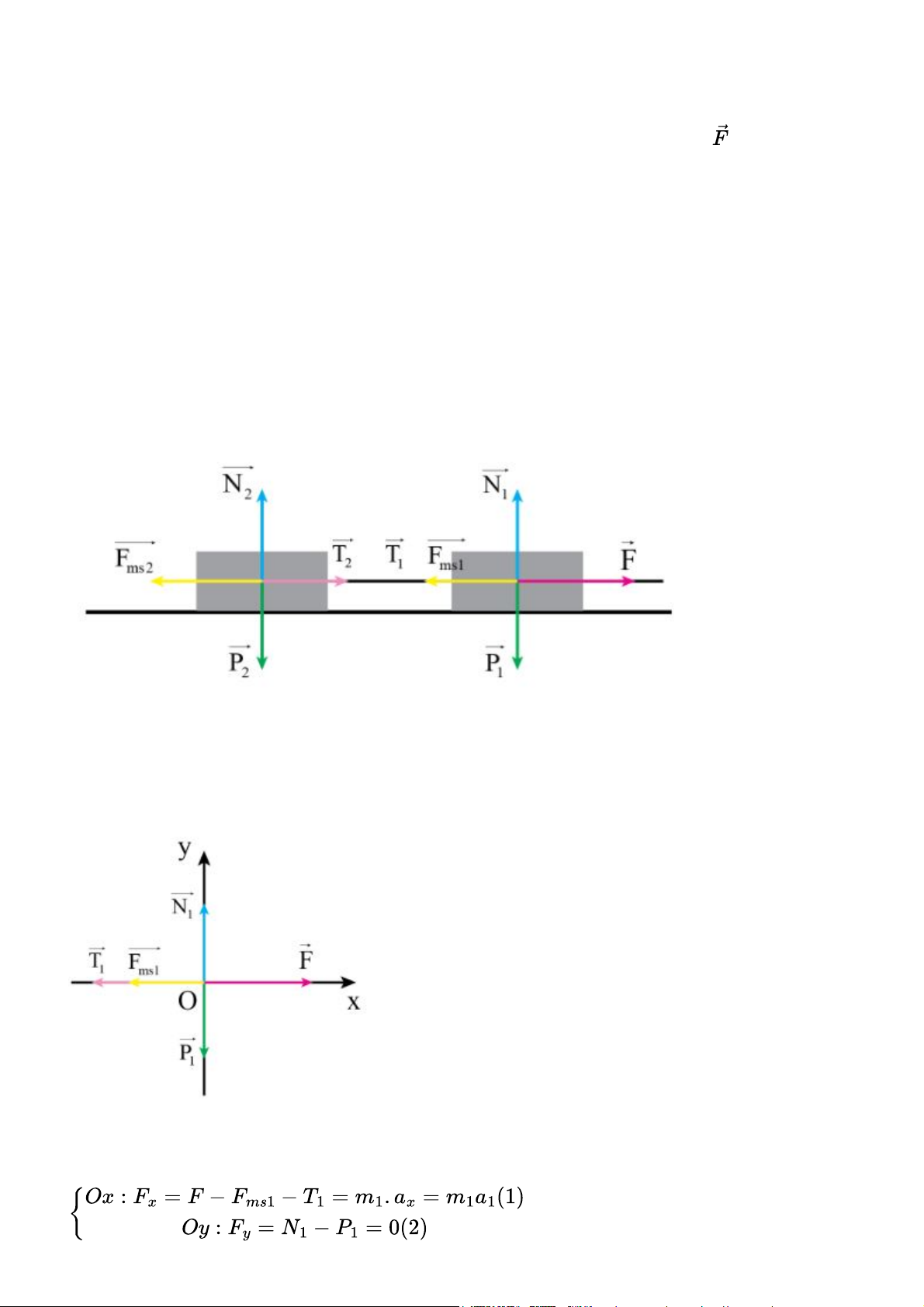
Coi các vật là chất điểm, phân tích các lực tác dụng lên các vật tại trọng tâm của chúng gồm có:
Vật 1: lực kéo, trọng lực, phản lực, lực ma sát, lực căng dây.
Vật 2: lực căng dây, phản lực, lực ma sát, trọng lực.
Chọn hệ trục tọa độ Oxy như hình vẽ: Vật 1:
- Áp dụng định luật 2 Newton cho chuyển động của vật 1 theo hai trục Ox, Oy: Mà Fms1 = µ.N1
Giải hệ phương trình có:
Từ (2) ta được: N1 = P1 = m1g => Fms1 = µ.N1 = µm1g Thay vào (1) ta được:
=> F - µm1g - T1 = m1a1 => T1 = F - µm1g - m1a1 Vật 2: Mà Fms2 = µ.N2
Giải hệ phương trình có:
Từ (4) ta được: N2 = P2 = m2g => Fms2 = µ.N2 = µm2g Thay vào (3) ta được:
=> T2 - µm2g = m2a2 => T2 = µm2g + m2a2
Do hệ 2 vật được nối với nhau bằng một sợi dây không dãn nên ta có:
T1 = T2 => F - µm1g - m1a1 = µm2g + m2a2
Bên cạnh đó hệ hai vật chuyển động với cùng gia tốc nên ta có: a1 = a2 = a
=> F - µm1g - m1a = µm2g + m2a => a = = 1,04m/s2
Lực căng dây nối: T1 = T2 = µm2g + m2a = 30N
Cách khác: có thể viết định luật 2 Newton cho hệ 2 vật vào một phương trình đều được, khi đó
biện luận cho lực căng dây, gia tốc để giải ngắn gọn hơn.