











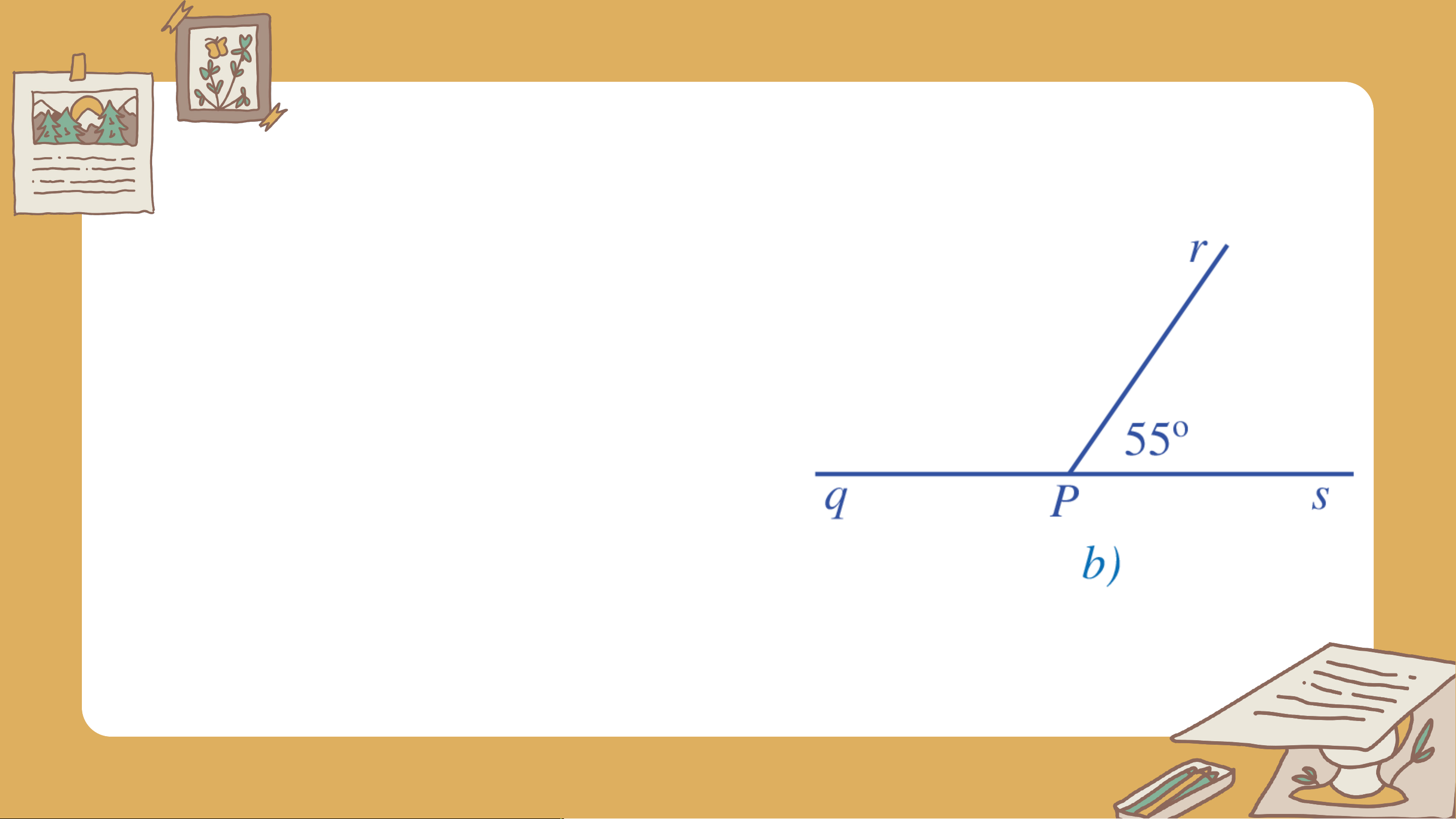




Preview text:
CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC KHỞI ĐỘNG
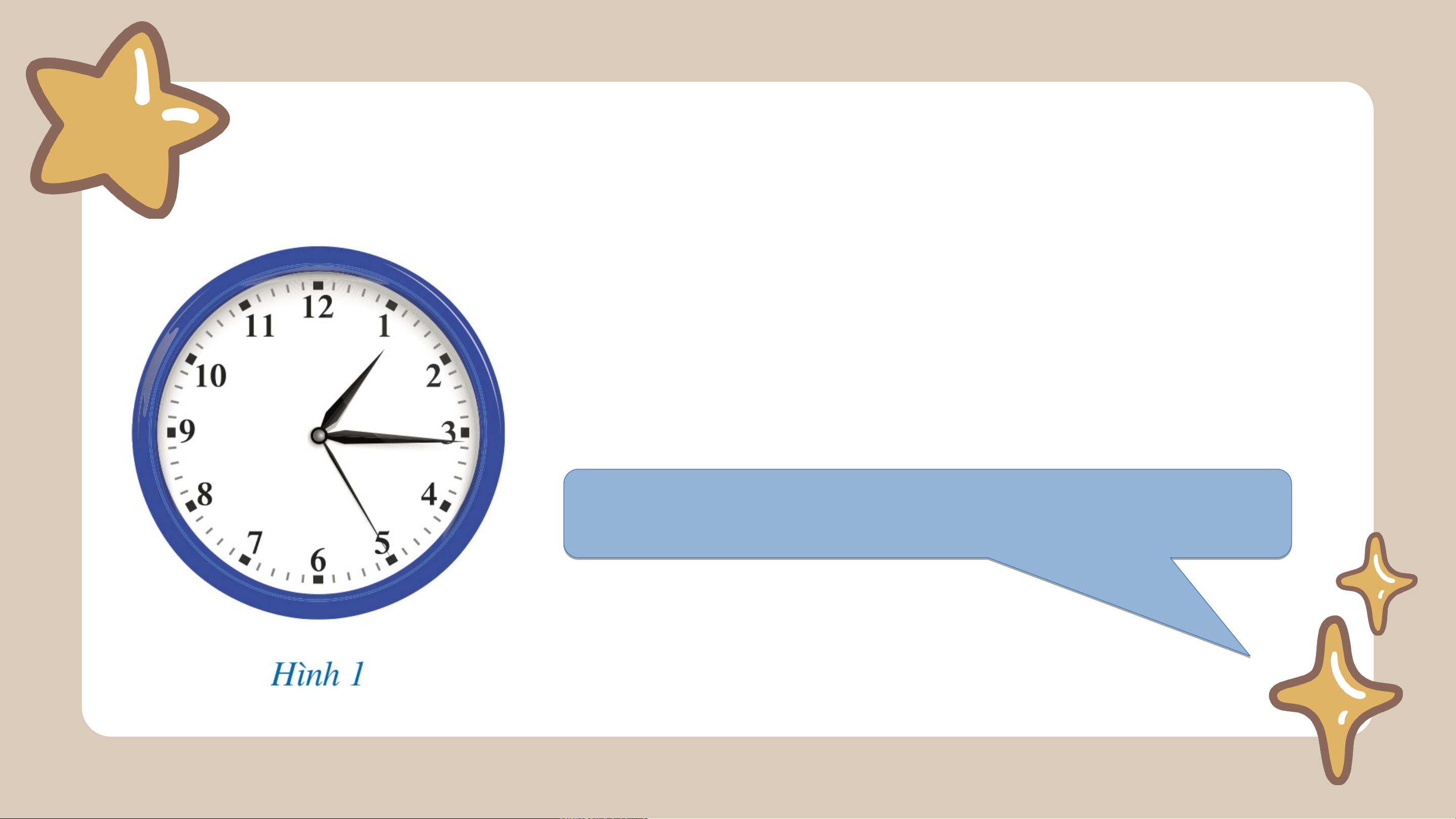
Quan sát hai góc: góc tạo bởi kim giờ và kim
phút; góc tạo bởi kim phút và kim giây. Ha H i a gó g c ó nà n y à có có liên liê h n ệ h ệ gì g đặ đ c ặ biệ b t? iệ CHƯƠNG IV. GÓC.
ĐƯỜNG THẲNG SONG SONG
BÀI 1: GÓC Ở VỊ TRÍ ĐẶC BIỆT NỘI DUNG BÀI HỌC 01 02 03 Hai góc Hai góc bù nhau. Hai góc kề nhau Hai góc kề bù đối đỉnh I. HAI GÓC KỀ NHAU
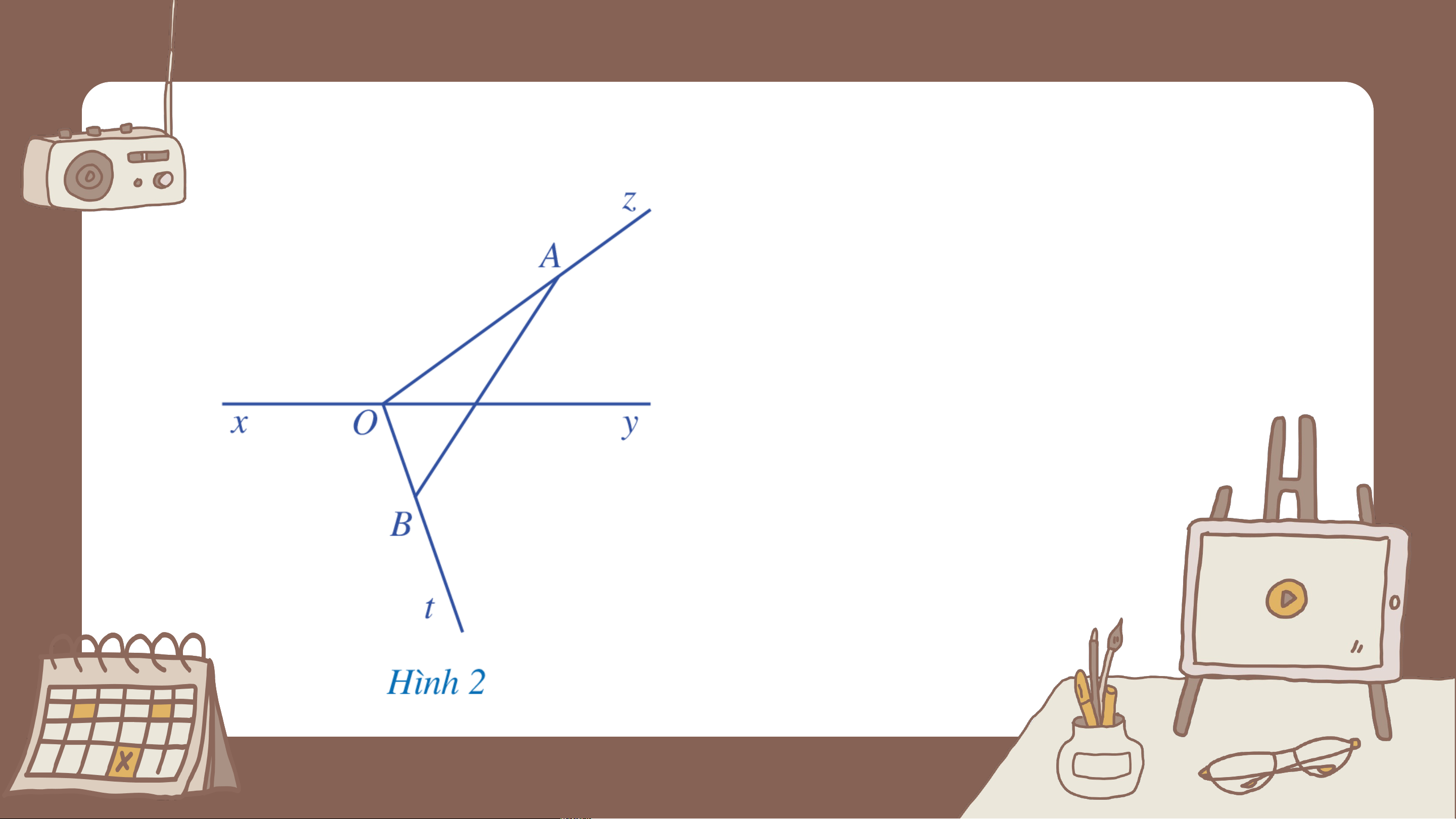
Cho đường thẳng . Từ một điểm trên đường thẳng ta
vẽ hai tia , như Hình 2. HĐ H 1
a) Lấy điểm bất kì trên tia ( khác ), lấy điểm bất kì trên
tia ( khác ), vẽ đoạn thẳng .
b) Đoạn thẳng có cắt đường thẳng hay không? Trả lời Đoạn thẳng cắt đường thẳng . Nhận xét:
Hai tia , ở Hình 2 có tính chất sau:
- Đoạn thẳng nối điểm bất kì trên tia ( khác )
với điểm bất kì trên tia ( khác ) thì cắt đường thẳng .
- Hai tia và như vậy gọi là nằm về hai phía của đường thẳng .
Em hãy chỉ ra trường hợp nào thì có hai tia nằm về hai phía của
một đường thẳng và chỉ rõ đó là hai tia nào nằm về hai phía của đường thẳng nào? HĐ2 Đ
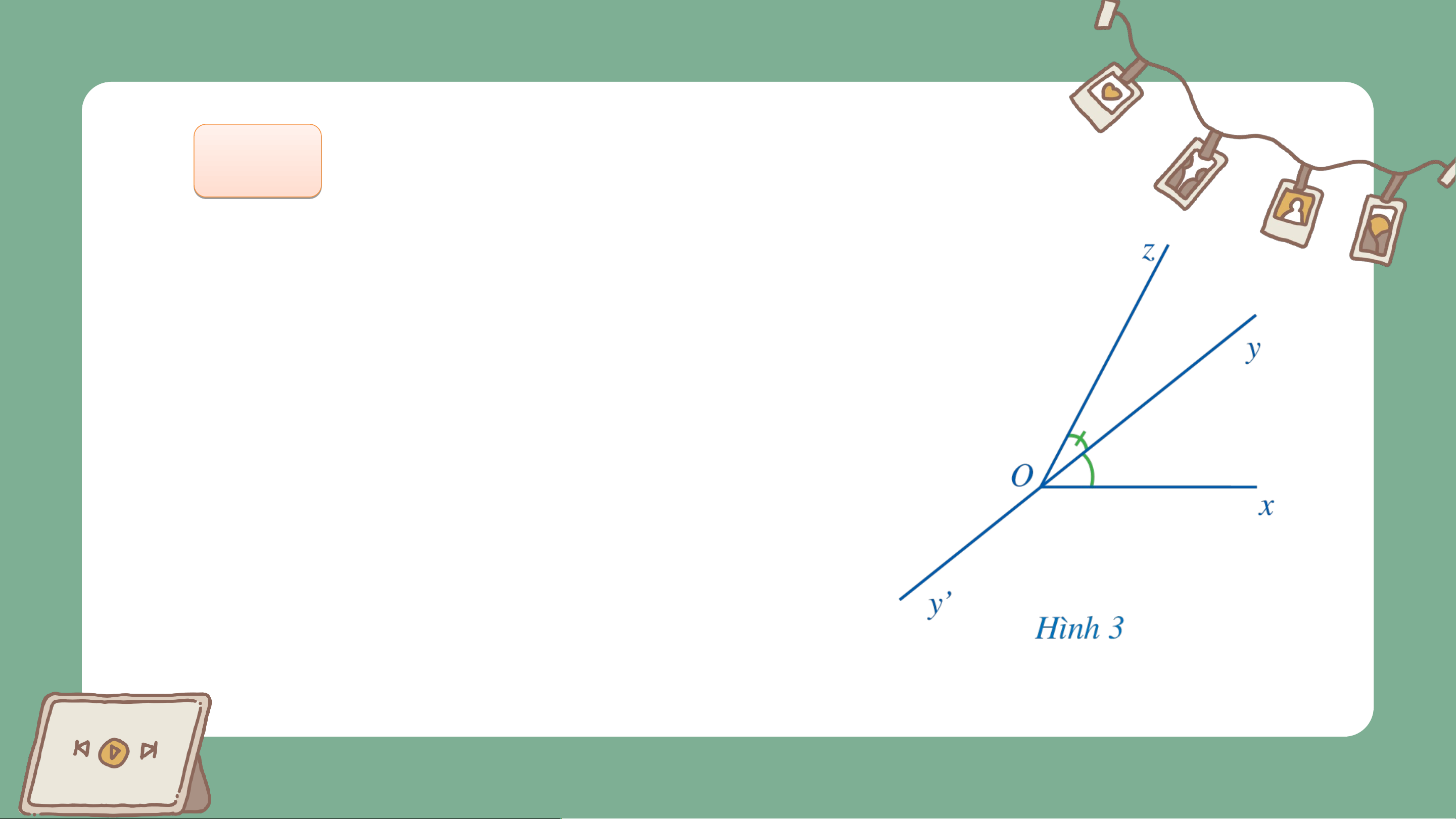
Quan sát hai góc và ở Hình 3.
a) Nêu đỉnh chung và cạnh chung của hai góc và .
b) Vẽ tia đối của tia .
c) Hai tia và có nằm về hai phía
của đường thẳng hay không? Trả lời
a) Đỉnh của góc và cùng là b)
đỉnh ; cạnh chung là cạnh .
c) Hai tia và nằm về hai phía của đường thẳng . Nhận xét:
Hai góc và Ở Hình 3 có tính chất sau:
+ Hai góc đó có đỉnh chung, có một cạnh chung và
hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó.
+ Hai góc và như vậy gọi là hai góc kề nhau.
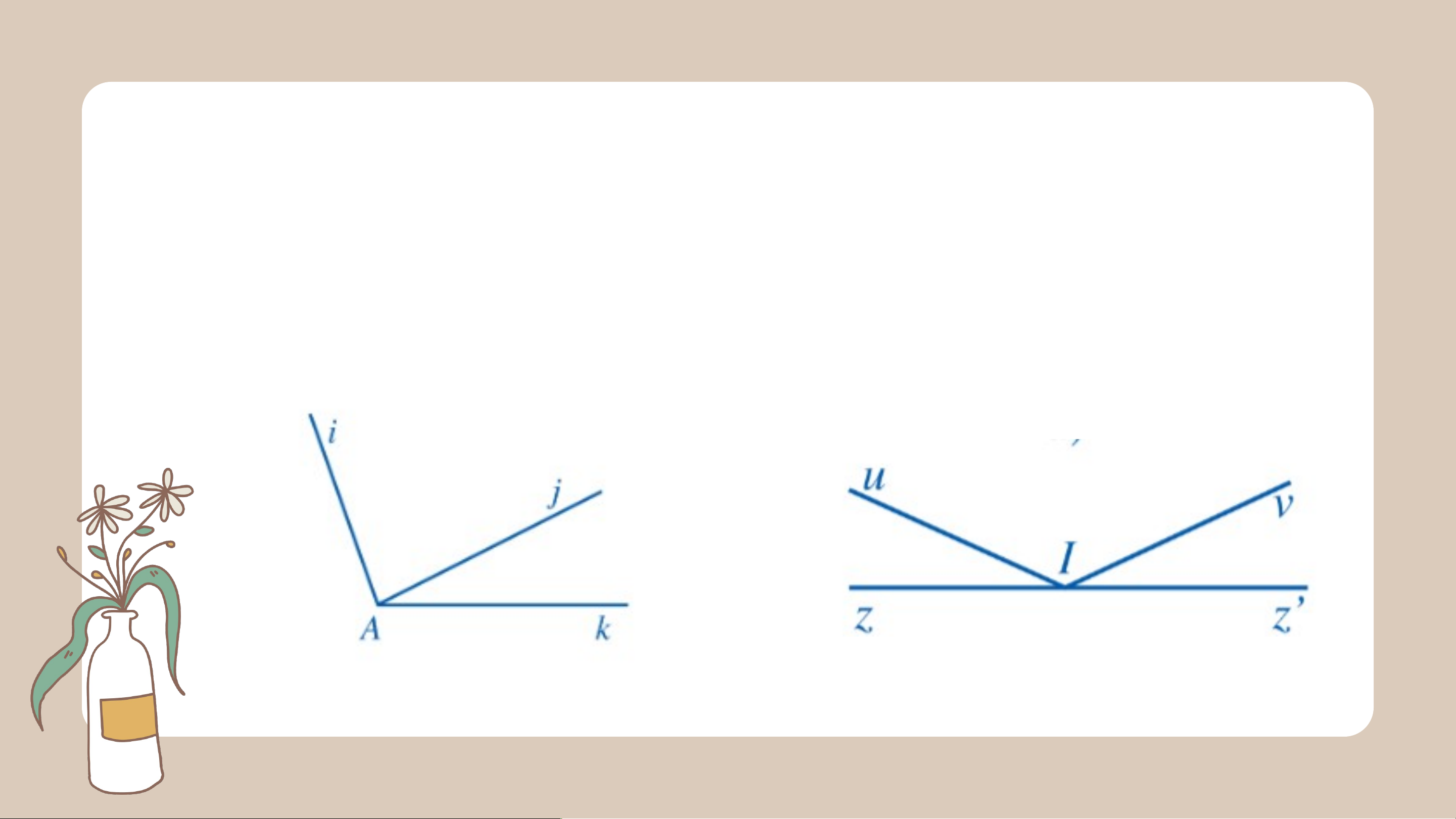
+ Tương tự, hai góc và ở Hình 4 cũng là hai góc kề nhau. Ví dụ dụ 1
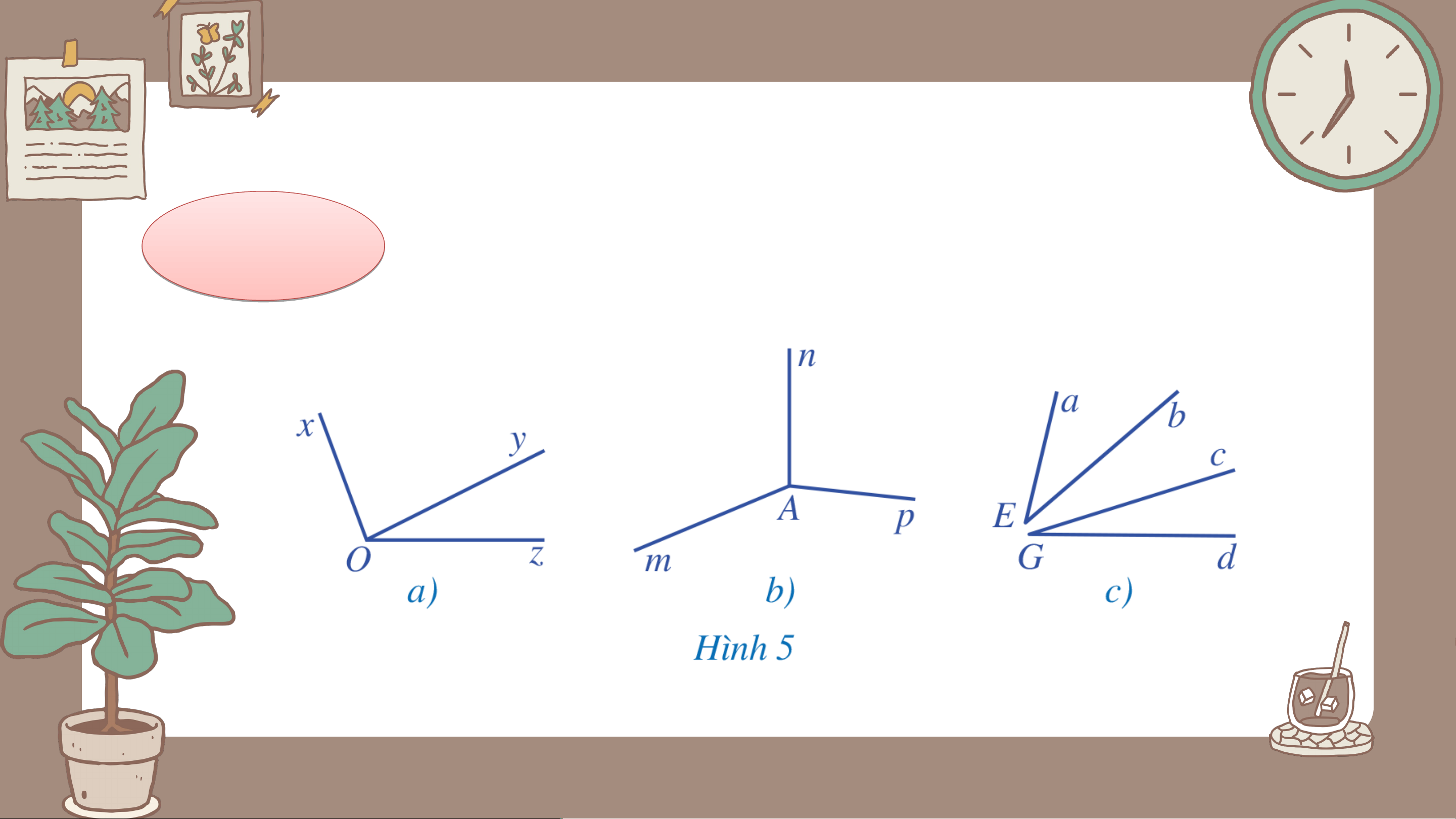
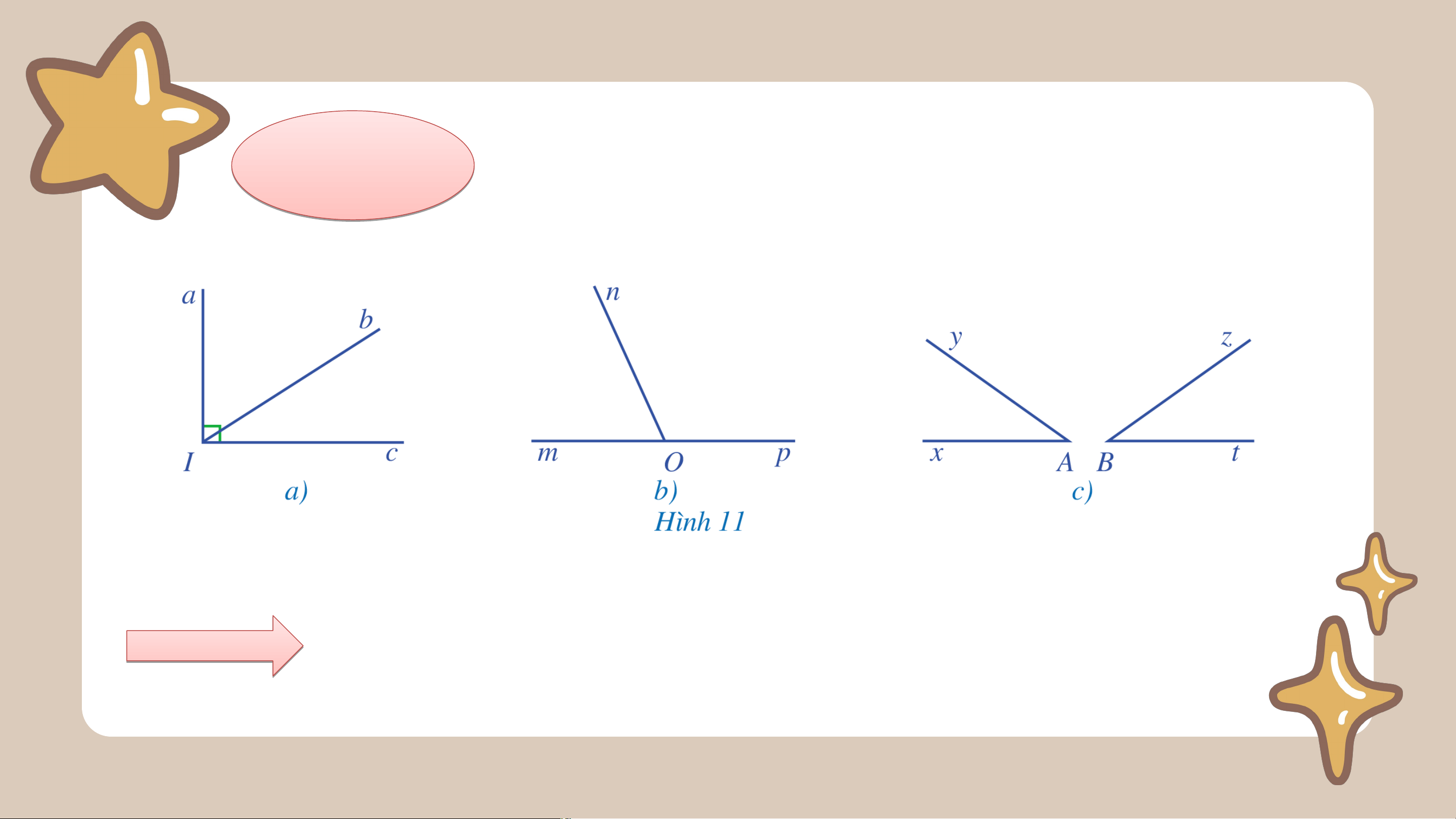
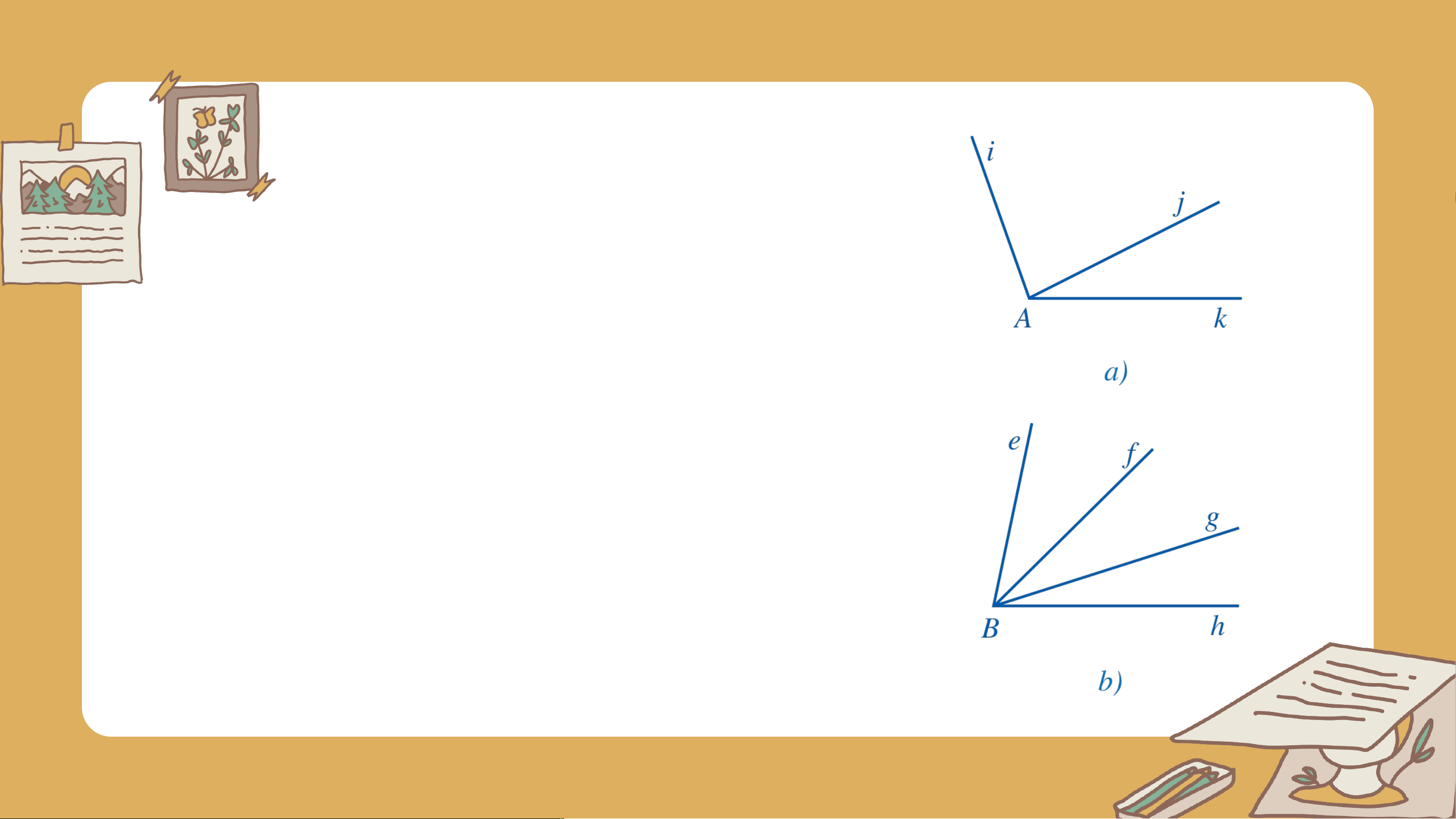
Tìm hai góc kề nhau trong mỗi hình 5a, 5b, 5c: Giải
Các cặp góc kề nhau trong mỗi hình là và và , Không có và , và Chú ý:
Cho góc (khác góc bẹt) và tia nằm trong góc đó,
tức là mỗi điểm ( khác ) của tia đều là điểm trong
của góc . Khi đó hai góc và là hai góc kề nhau và
Nếu góc là góc bẹt thì với mỗi tia (khác hai tia , ), ta cũng có: . Luyệ Luy n ệ n tậ t p 1 ậ
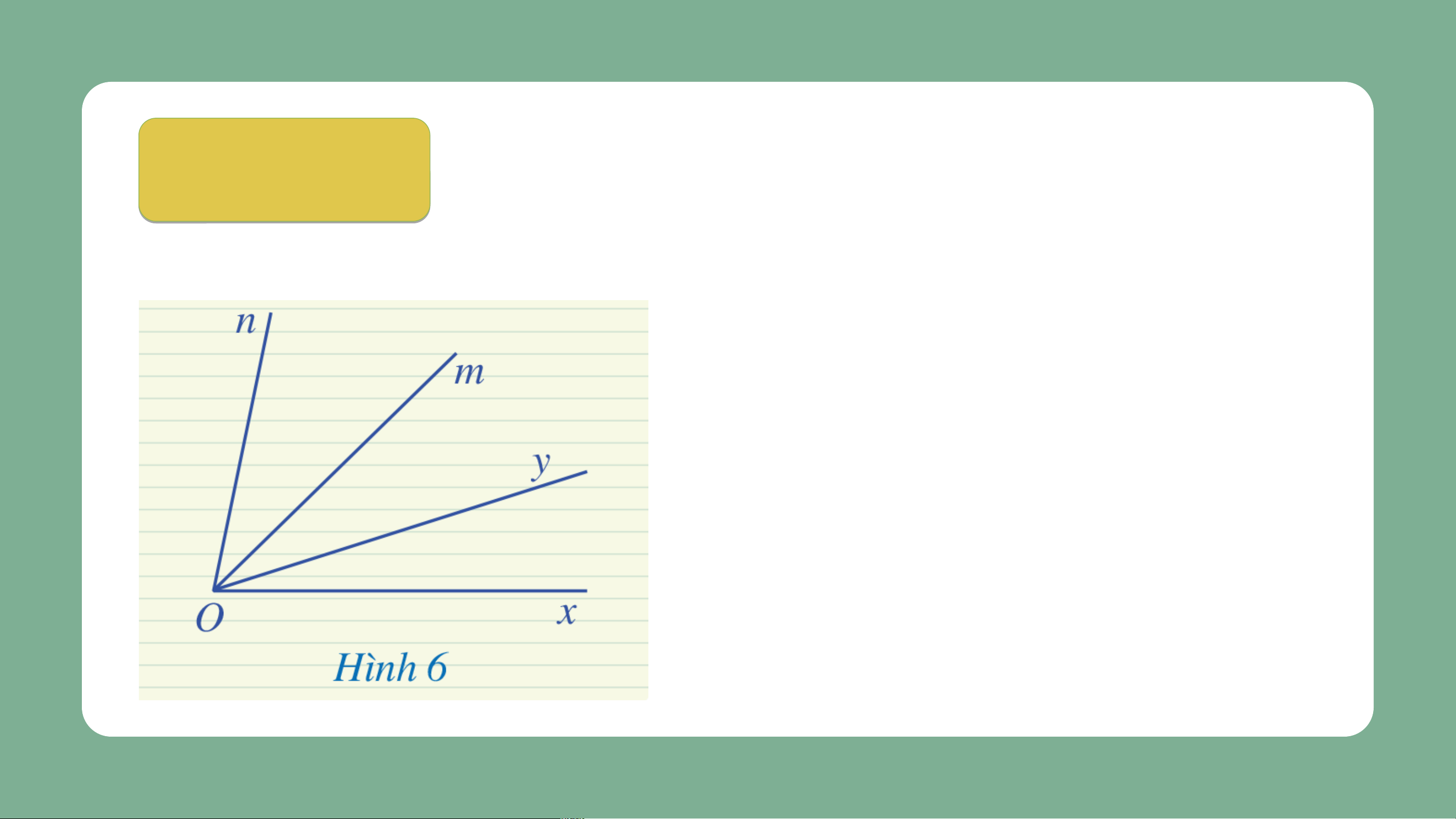
Ở Hình 6, hai góc và có phải là hai góc kề nhau hay không? Vì sao? Giải
Hai góc và không phải là hai góc
kề nhau vì chúng không có cạnh chung. Ví V dụ 2
Nhìn bức ảnh ở Hình 7, bạn Quang
cho rằng cột nhà tạo với thanh vì kèo
bên trái một góc (khoảng) và nó tạo
với thanh vì kèo bên phải một góc
(khoảng) . Theo dự đoán đó của bạn
Quang, hãy tính góc giữa hai thanh
vì kèo của mái nhà đó. Giải
Gọi , lần lượt là hai góc tạo bởi cột nhà với thanh
vì kèo bên trái và bên phải (Hình 8).
Vì và là hai góc kề nhau nên ta có: hay
Vậy góc giữa hai thanh vì kèo của mái nhà là . Luyệ Luy n ệ tậ t p 2 ậ
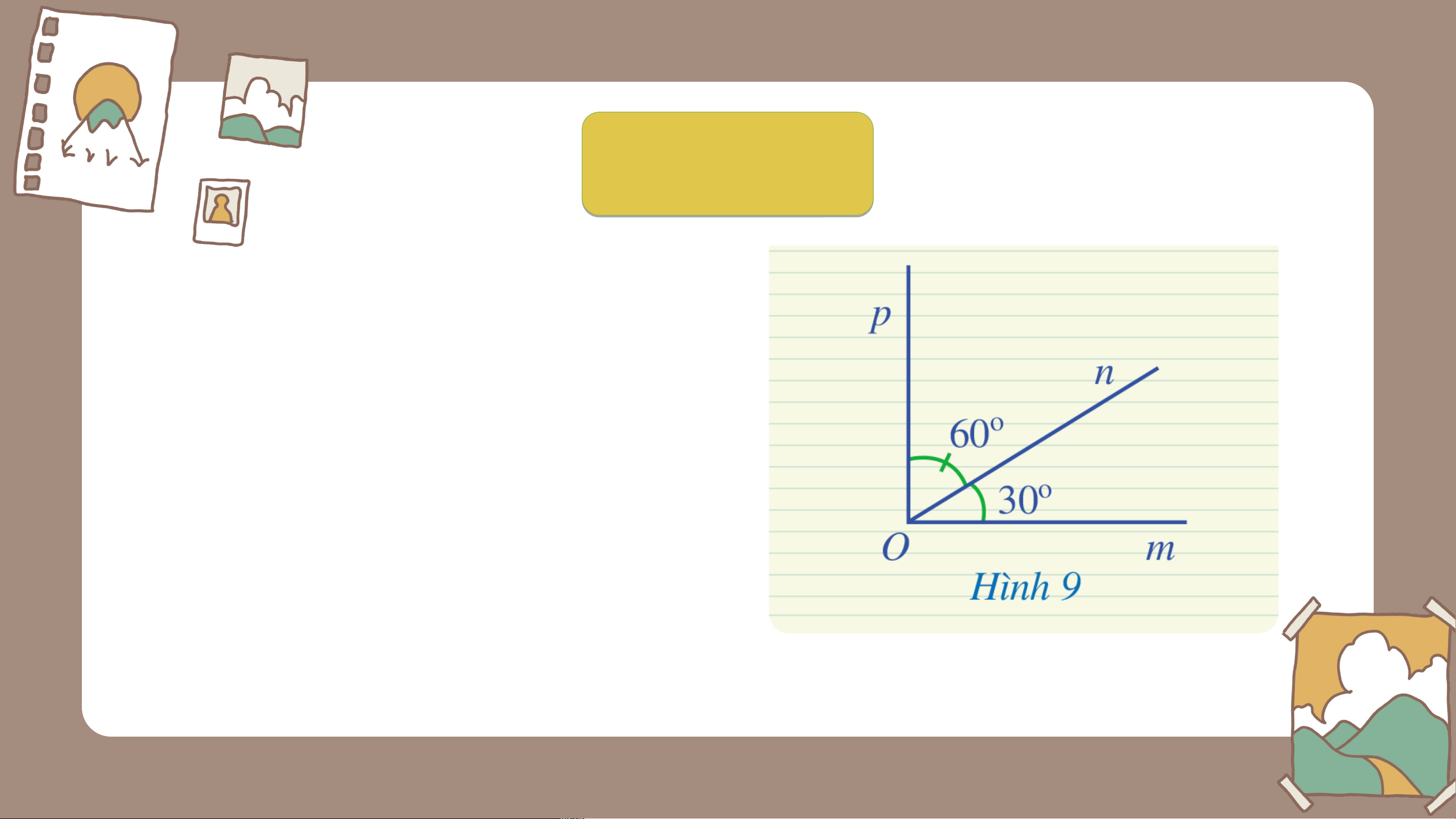
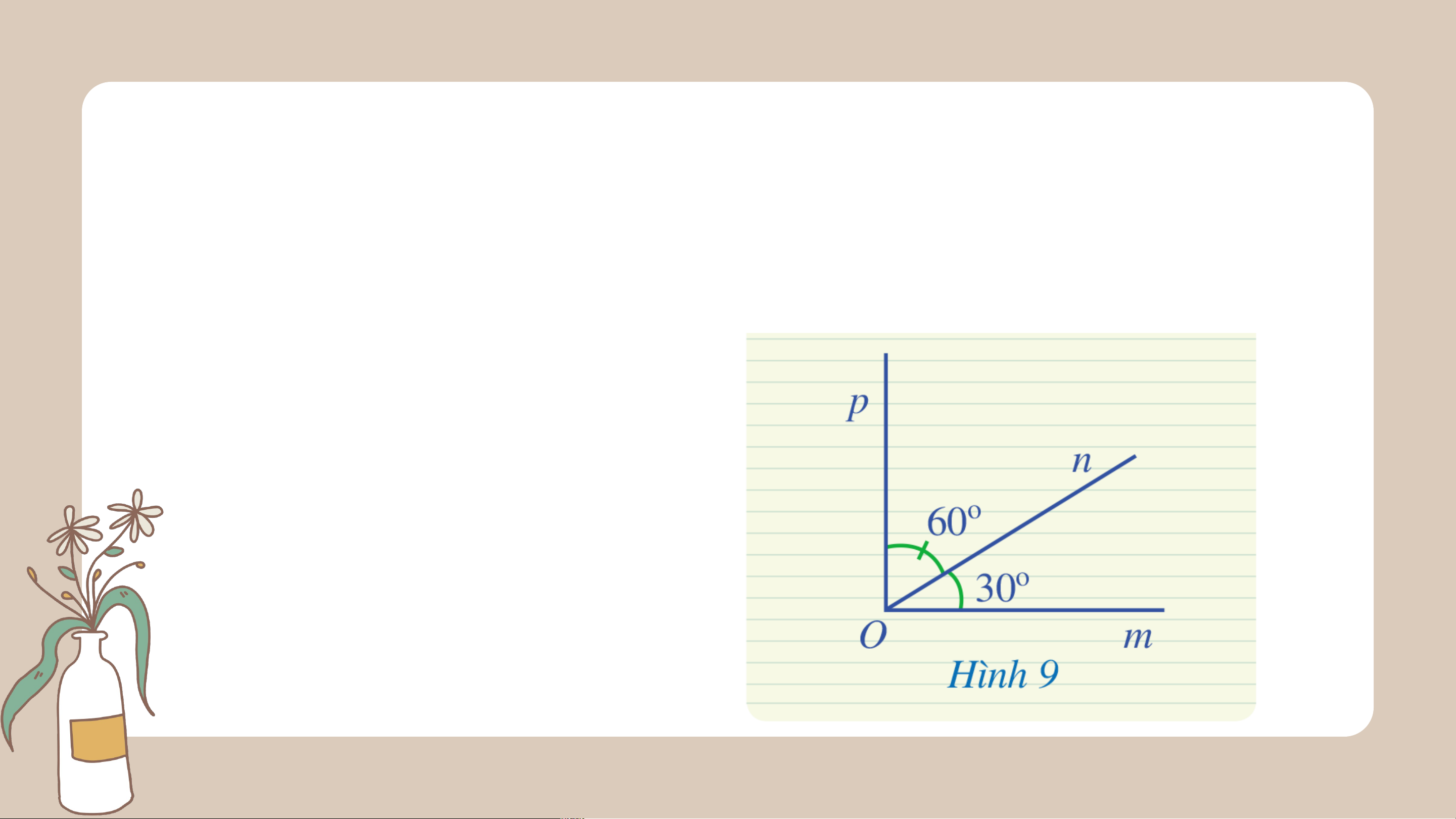
Ở Hình 9, hai góc và có phải là hai góc kề nhau hay không? Tính số đo của góc . Giải
Hai góc và có là hai góc kề nhau vì có đỉnh chung, cạnh chung, 2
cạnh còn lại là và nằm về hai phía so với đường thẳng chứa . Vì nằm trong góc nên Vậy
II. HAI GÓC BÙ NHAU. HAI GÓC KỀ BÙ HĐ3 Đ
Tìm tổng số đo của góc và . Giải
Hai góc có tổng số đo là:
Định nghĩa: Hai góc bù nhau là hai góc có tổng số đo bằng 1800 HĐ4 Đ
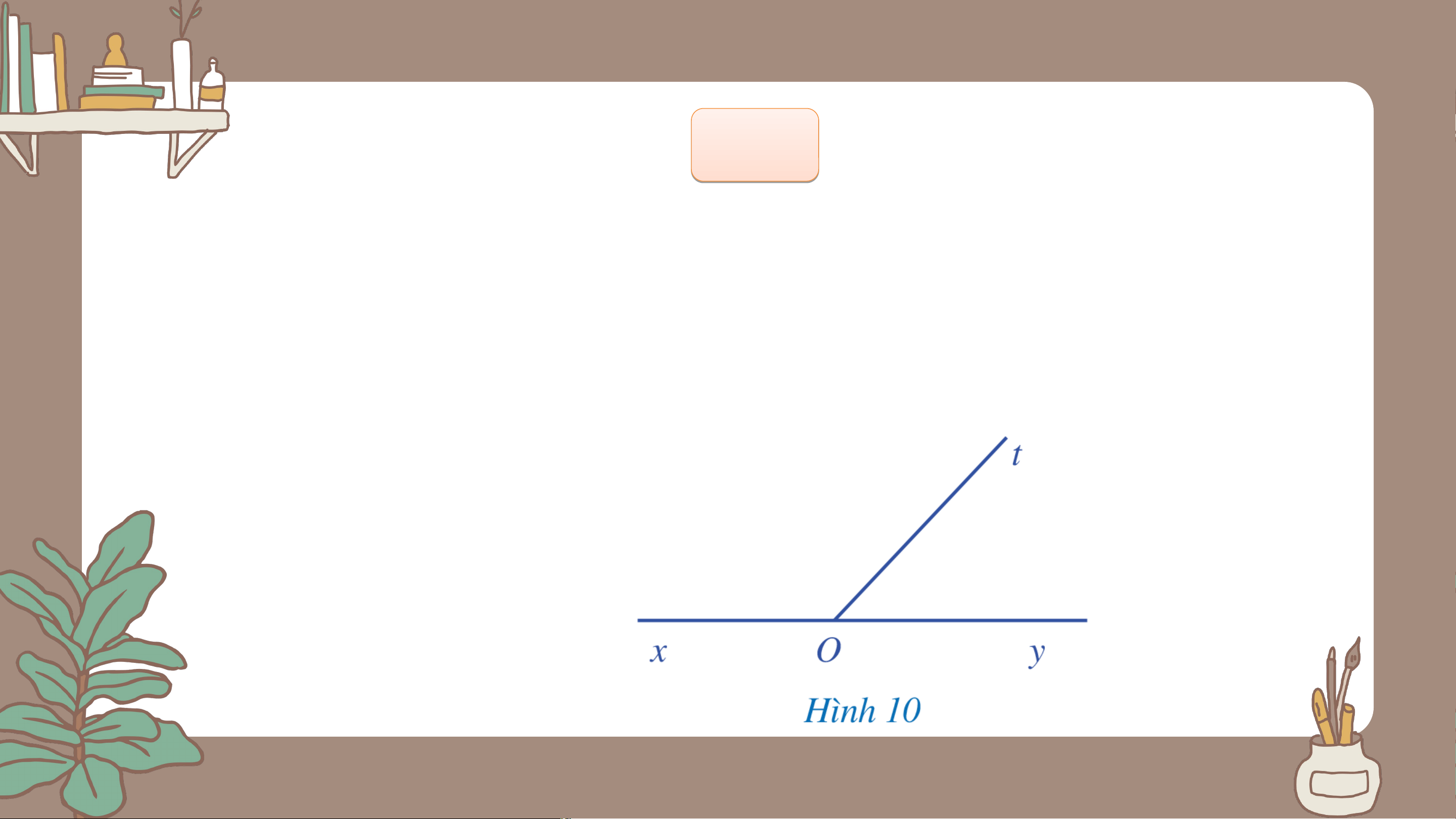
Quan sát hai góc và ở Hình 10, trong đó và là hai tia đối nhau.
a) Hai góc và có kề nhau hay không? b) Tính . Giải
a) Hai góc và là hai góc kề nhau vì có đỉnh chung, cạnh
chung, 2 cạnh còn lại là và nằm về hai phía so với đường thẳng chứa tia .
b) Vì tia nằm trong góc nên: Mà (góc bẹt)
Định nghĩa: Hai góc vừa kề nhau, vừa
bù nhau gọi là hai góc kề bù. Ví V dụ 3
Tìm hai góc kề bù (khác góc bẹt) trong
mỗi hình 11a, 11b, 11c:
Hai góc và ở Hình 11b là hai góc kề bù.
Quan sát hình vẽ và chỉ ra trường hợp nào thì có
hai góc kề bù, giải thích tại sao.
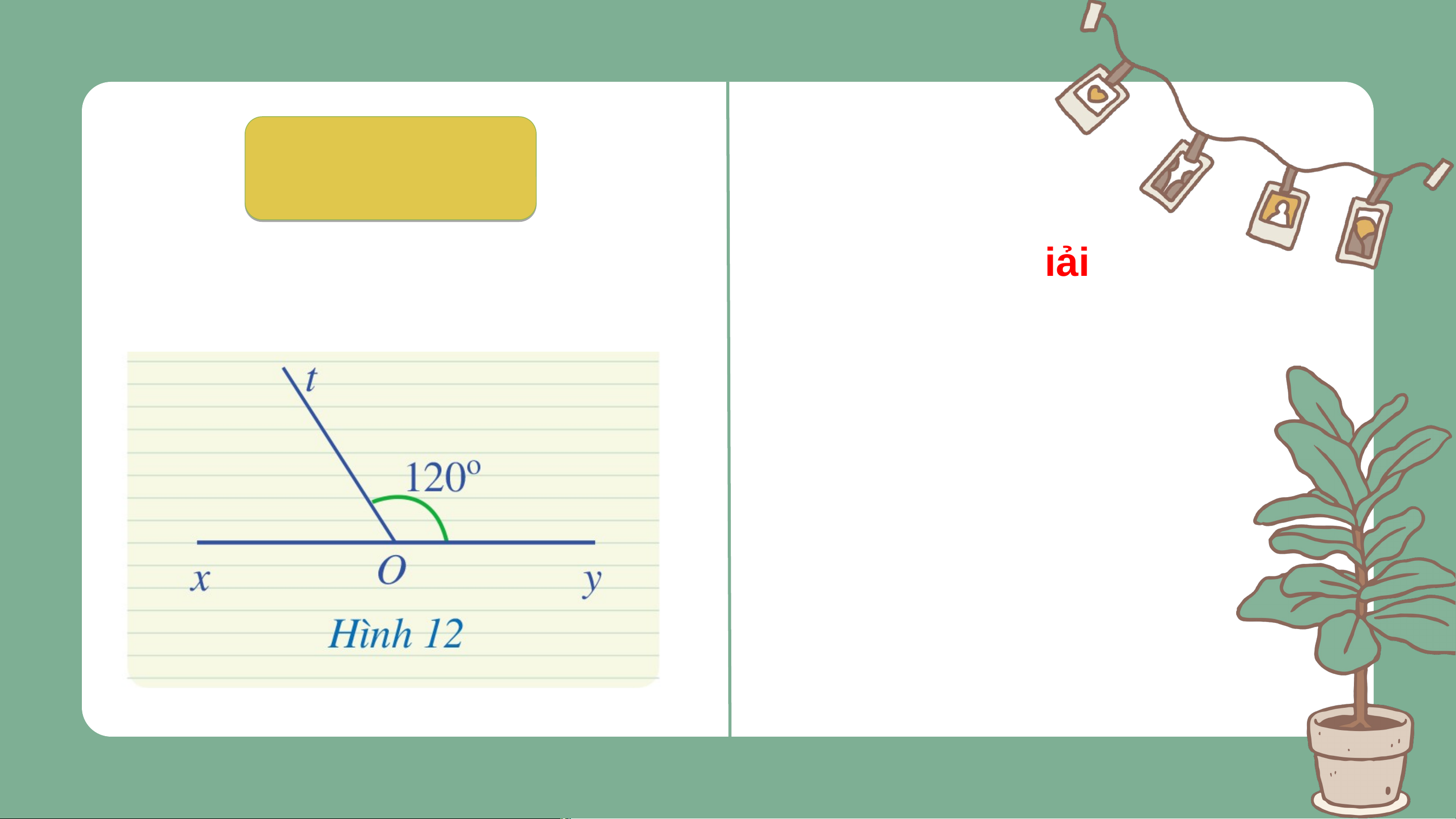
Hai góc có tổng bằng 1800 chưa chắc đã là hai góc kề bù. Luy L ệ uy n ệ n tậ t p 3 ậ Giải
Tính góc trong Hình 12. Ta có:
III. HAI GÓC ĐỐI ĐỈNH HĐ5 Đ
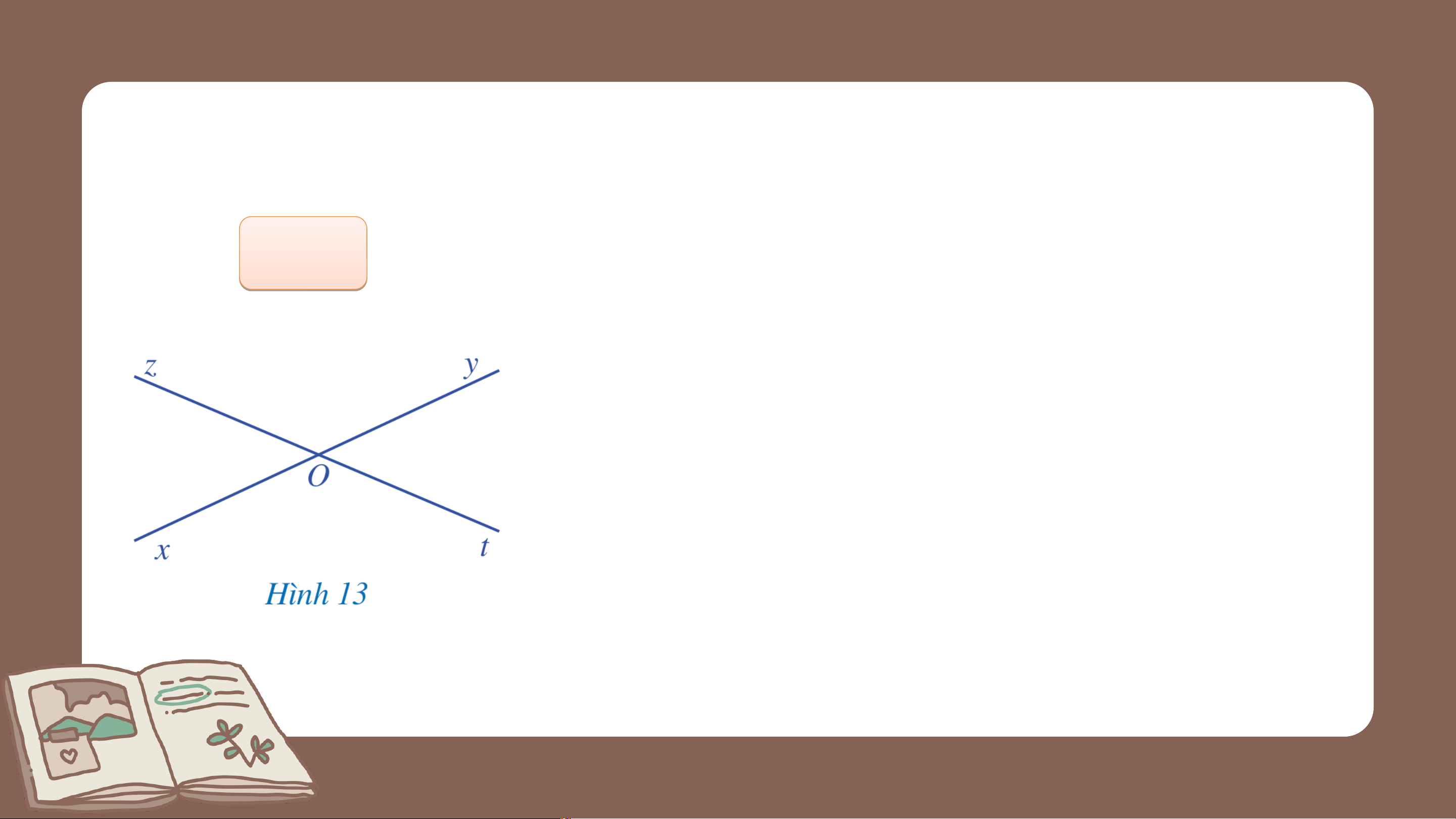
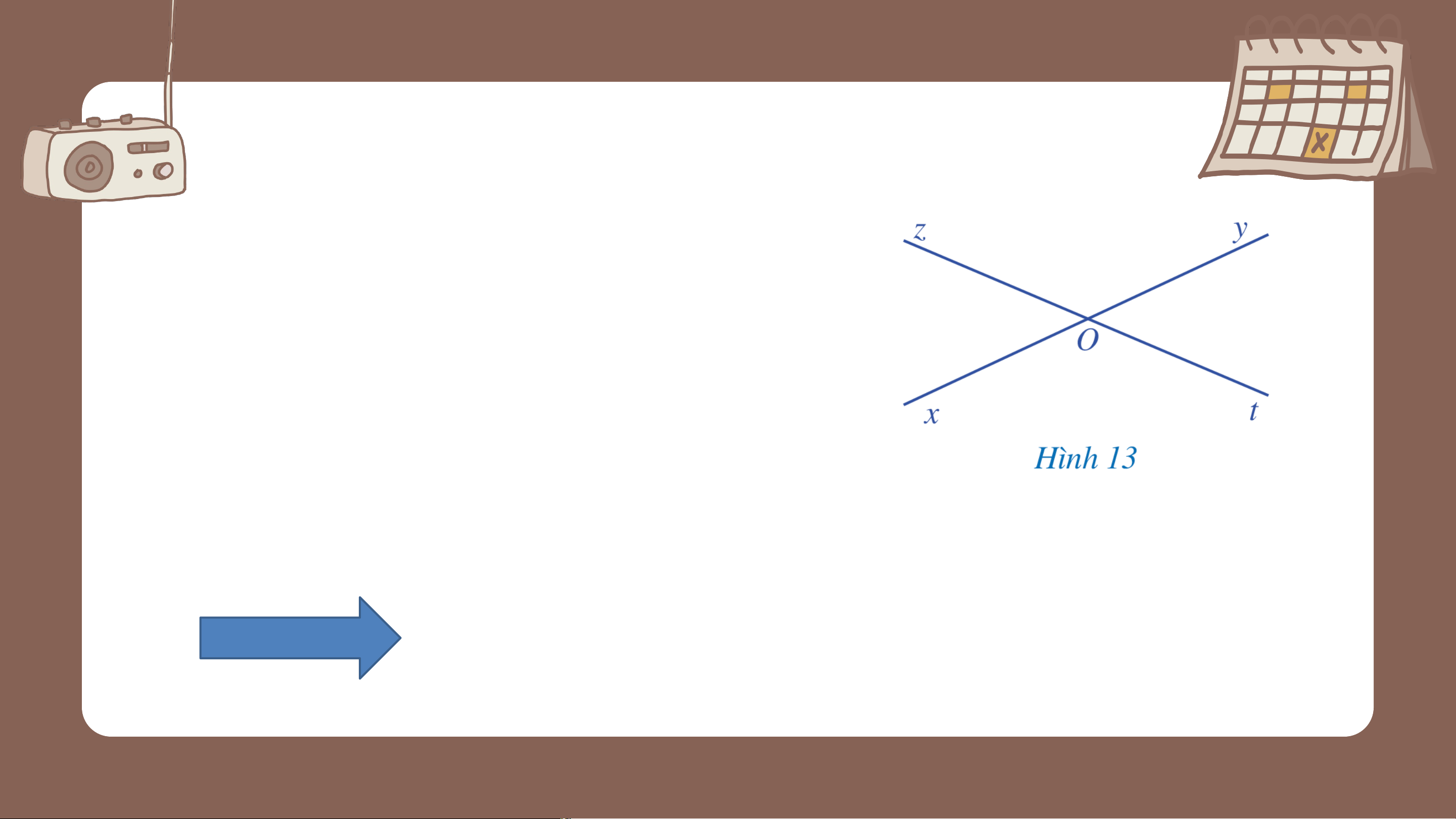
Quan sát hai góc và ở Hình 13, trong đó
và là hai tia đối nhau, và cũng là hai tia đối nhau và cho biết:
a) Cạnh của là tia đối của cạnh nào của .
b) Cạnh của là tia đối của cạnh nào của Giải
a) Cạnh của góc là tia đối của cạnh của góc .
b) Cạnh của góc là tia đối của cạnh của góc .
Hai góc đối đỉnh là hai góc mà mỗi cạnh của
góc này là tia đối của một cạnh của góc kia. Ví V dụ 4
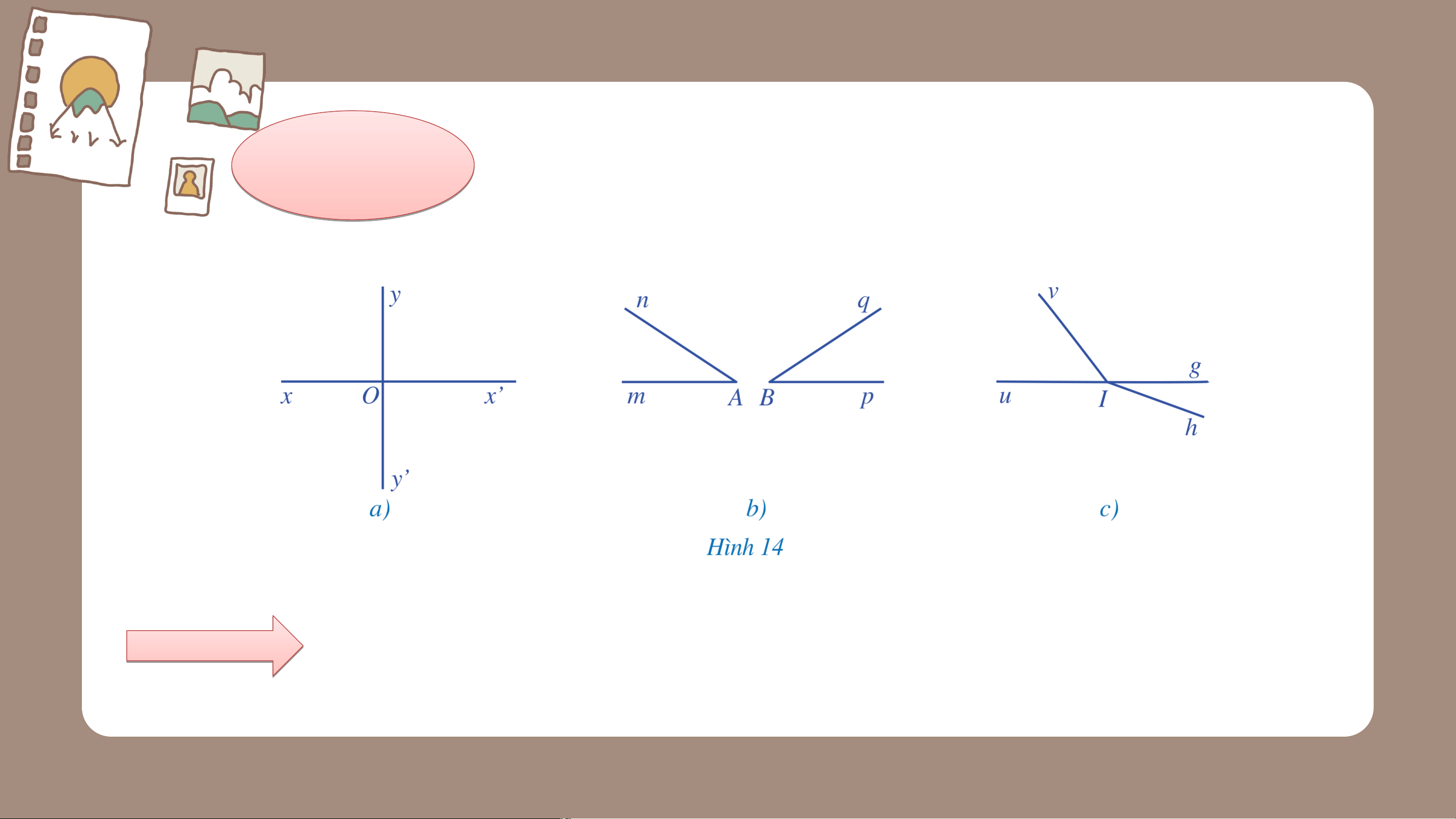
Tìm hai góc đối đỉnh (khác góc bẹt) trong
mỗi hình 14a, 14b, 14c:
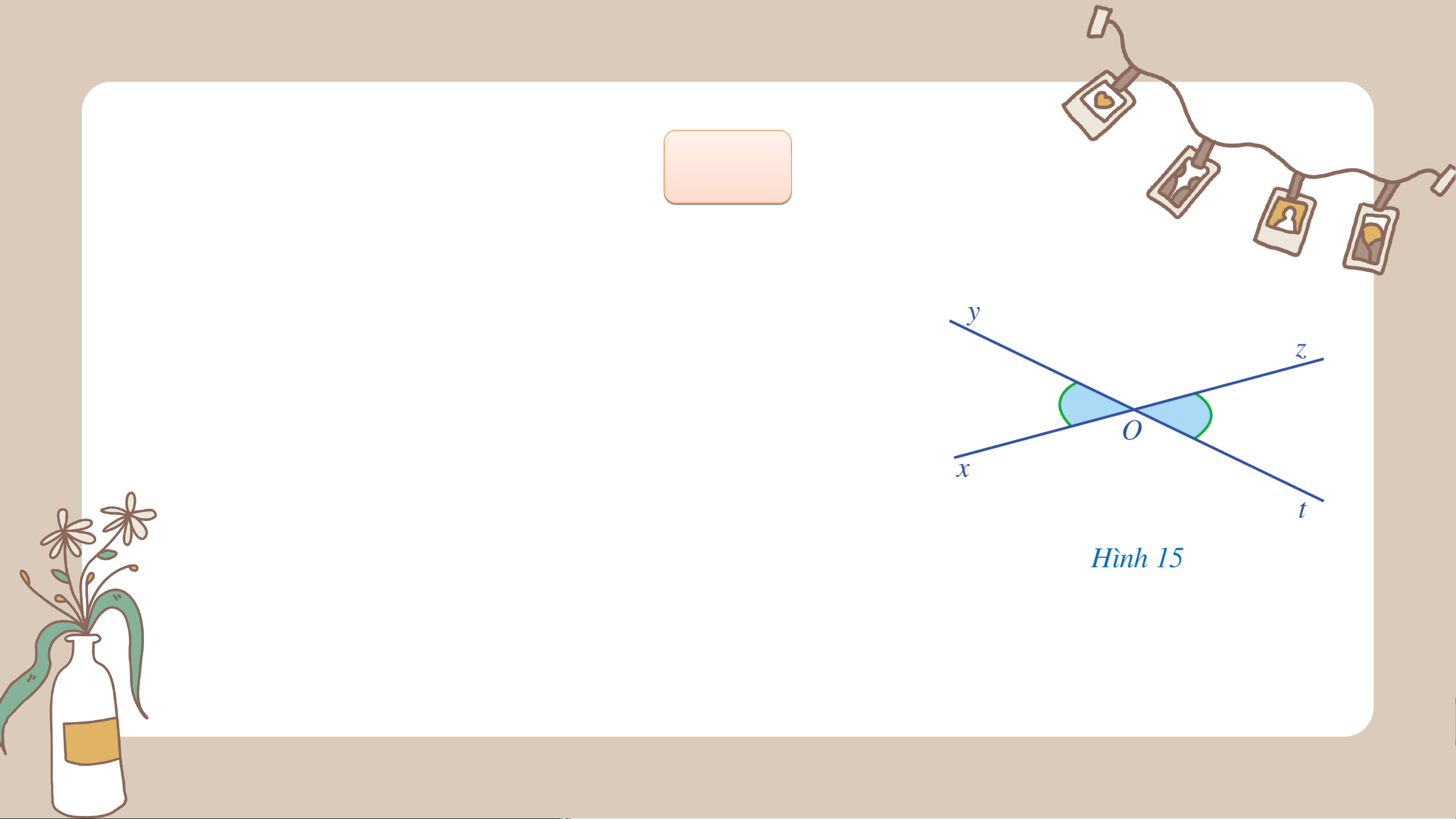
Ở Hình 14a, hai cặp góc và , và là hai cặp góc đối đỉnh. HĐ6
Quan sát Hình 15 và giải thích vì sao:
a) Hai góc và là hai góc kề bù;
b) Hai góc và là hai góc kề bù; c) và Giải
a) Vì 2 góc có chung gốc , chung cạnh , 2 cạnh còn lại là và nằm về
hai phía đối với đường thẳng chứa tia nên hai góc và là hai góc kề nhau.
Hơn nữa, hai góc và có tổng bằng góc nên hai góc và là hai góc bù nhau.
Vậy hai góc và là hai góc kề bù.
b) Vì 2 góc có chung gốc , chung cạnh , 2 cạnh còn lại là và nằm
về hai phía đối với đường thẳng chứa tia nên hai góc và là hai góc kề nhau.
Hơn nữa, hai góc và có tổng bằng nên hai góc và là hai góc bù nhau.
Vậy hai góc và là hai góc kề bù c) Do Vậy Ví V dụ 5
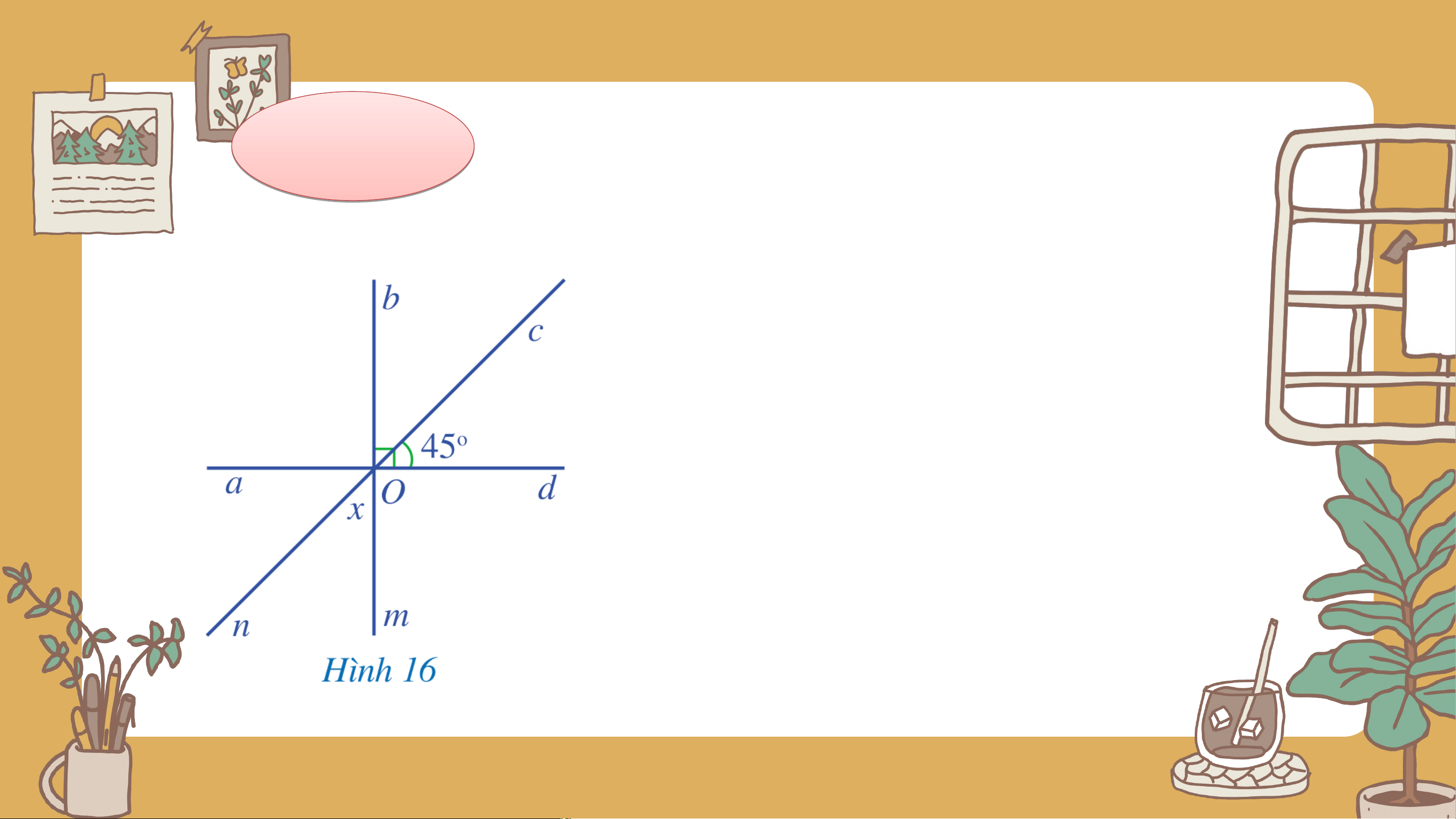
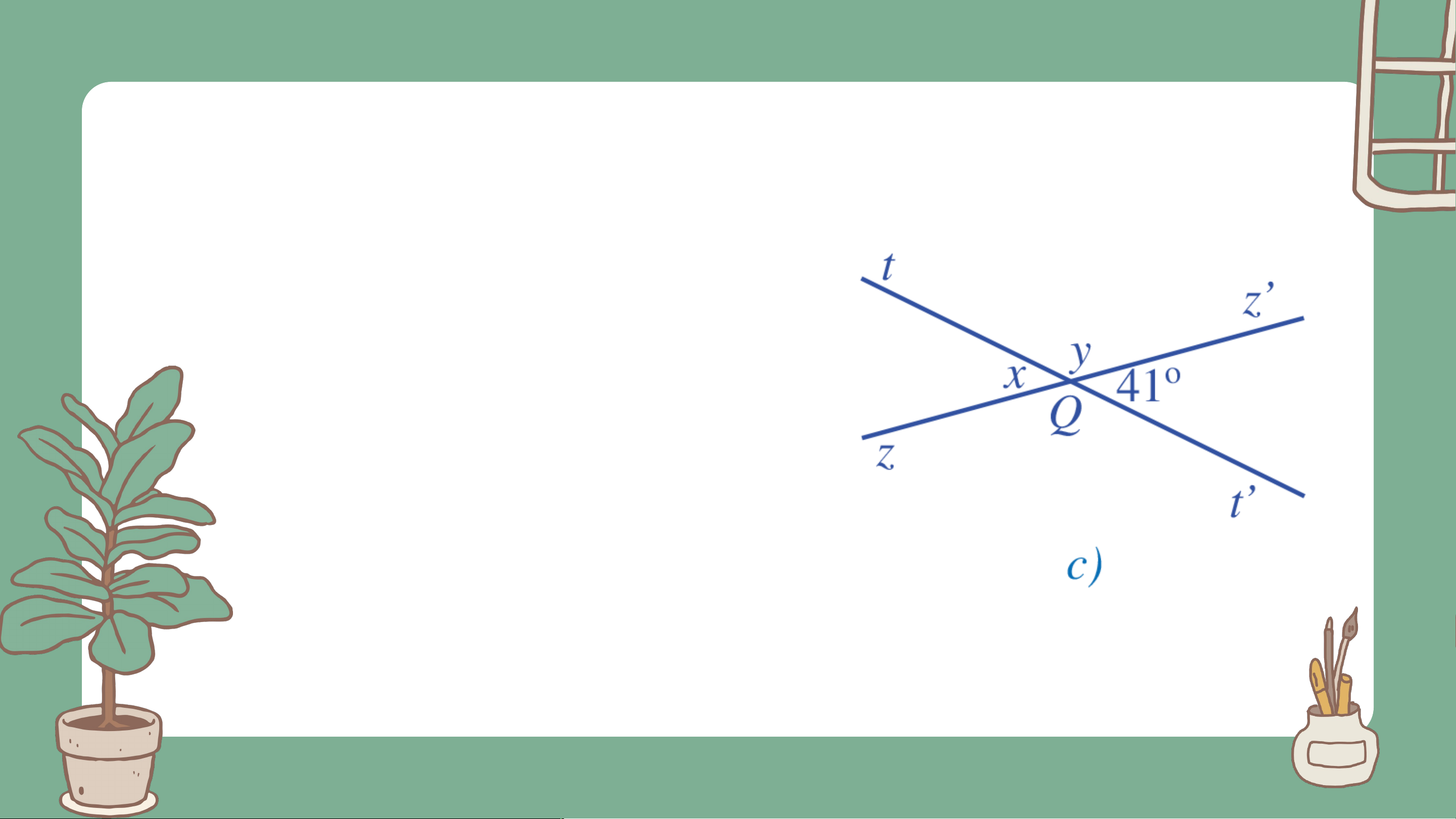
Tìm số đo trong Hình 16. Giải Ta có: (2 góc kề nhau) hay Mà (2 góc đối đỉnh) Vậy . Luy L ệ uy n ệ n tậ t p 4 ậ
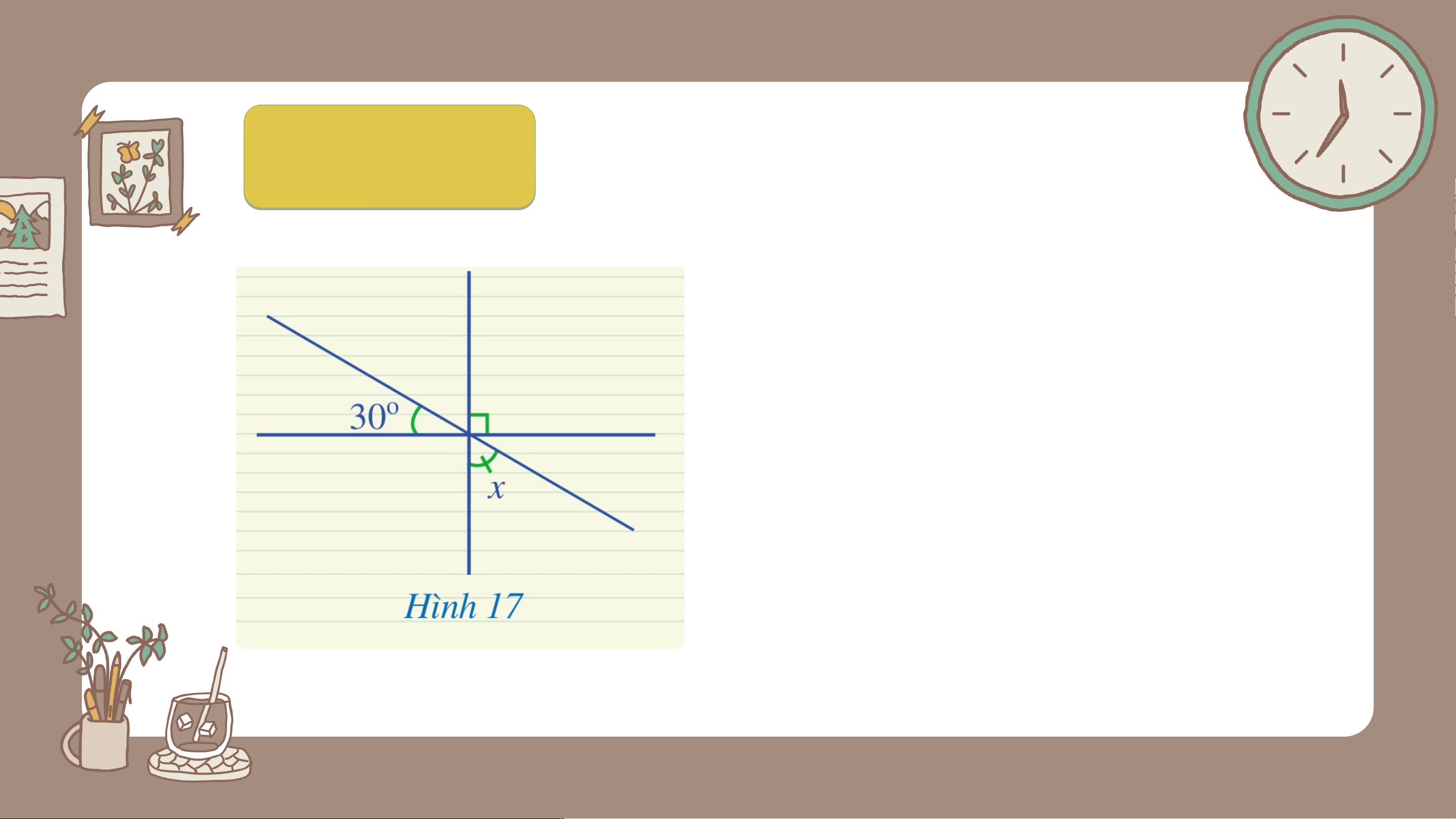
Tính số đo trong Hình 17. Giải
Ta có: (2 góc đối đỉnh) 4 Mà 1𝑂 2 3 Ta có: (kề bù) Vậy LUYỆN TẬP
Bài 1 (SGK – tr.94, 95)
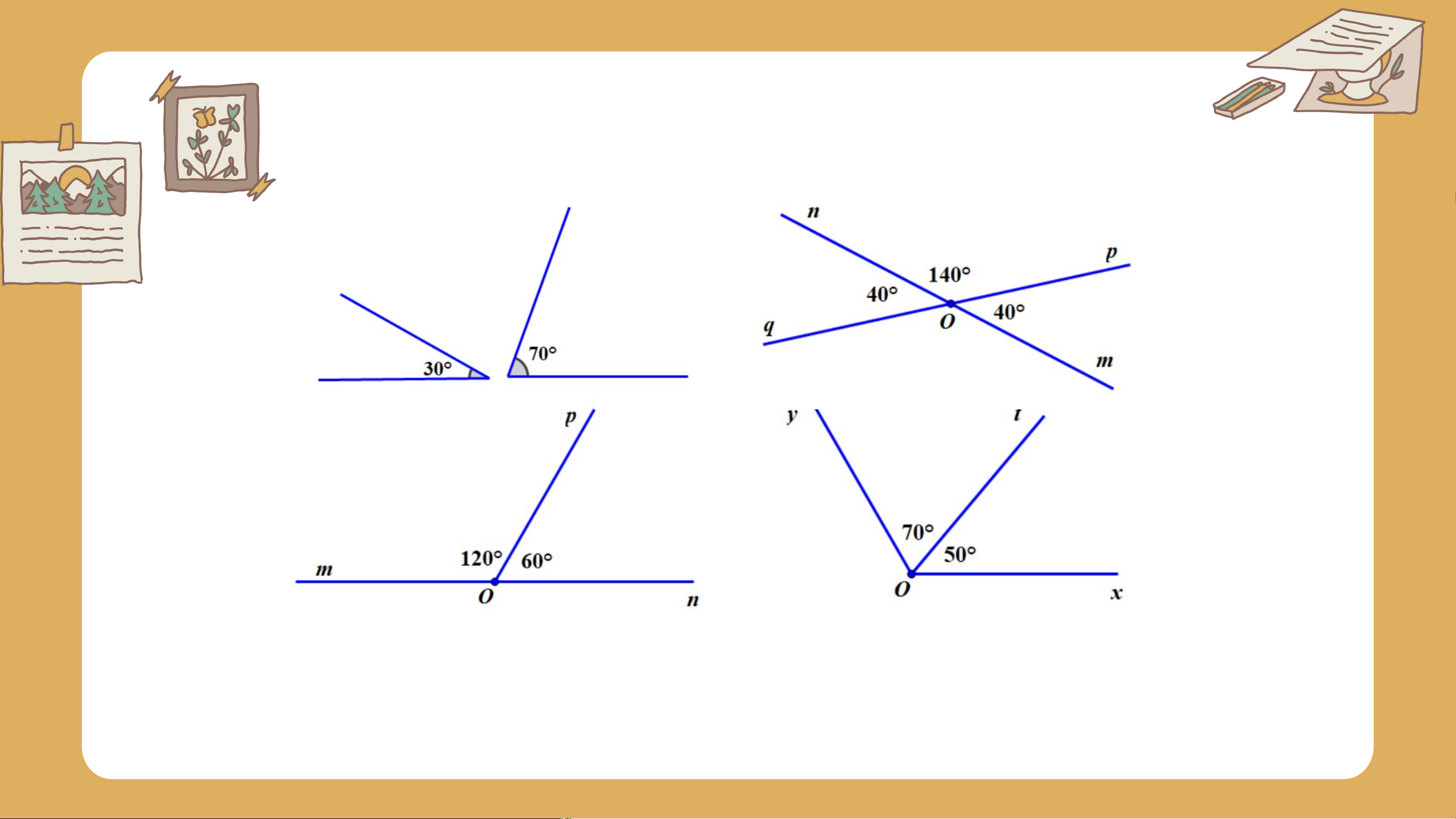
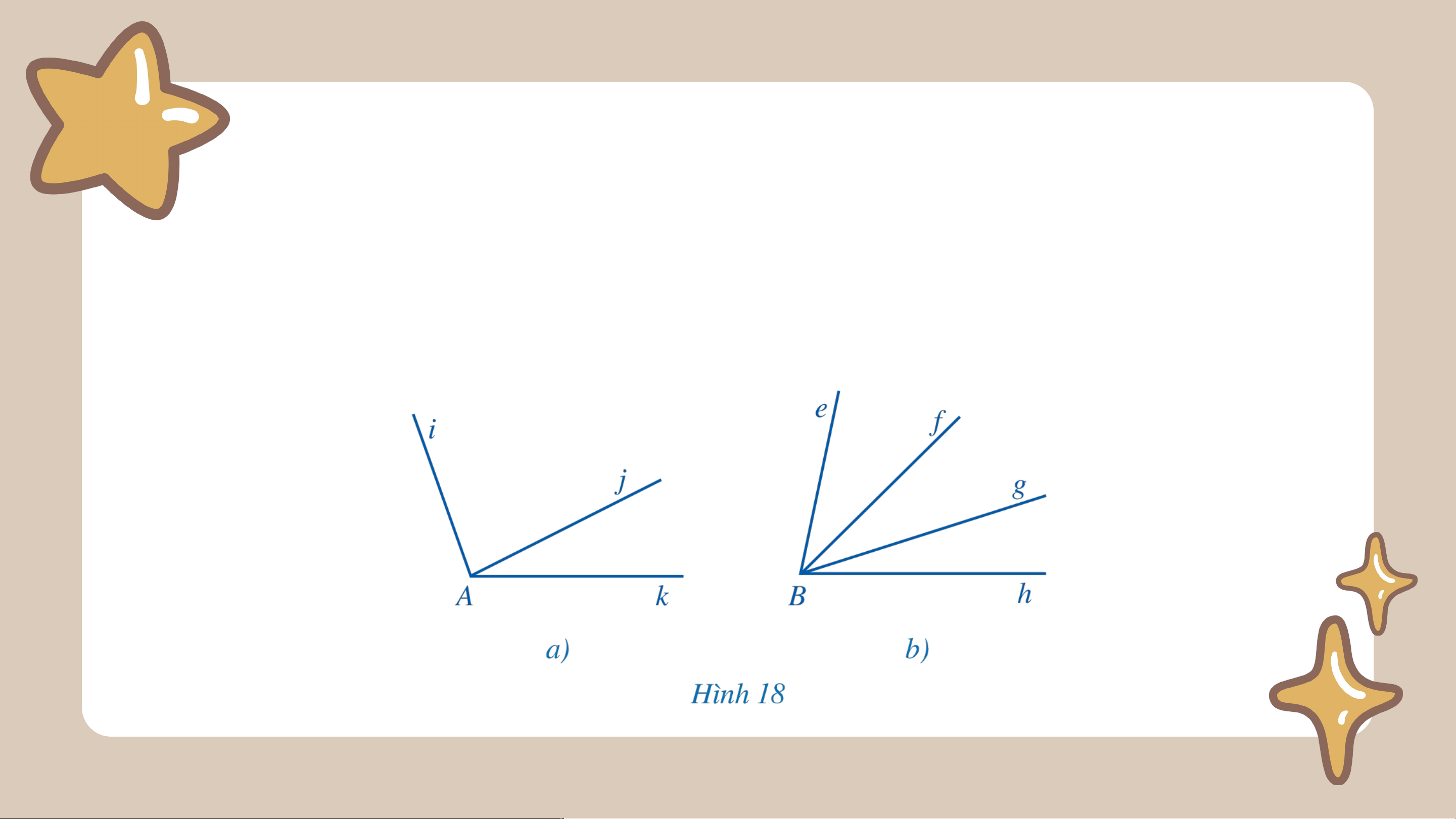
a) Tìm các cặp góc kề nhau trong mỗi hình 18a, 18b: Giải Hai góc kề nhau:
- Trong hình 18a là: góc và góc
- Trong hình 18b là: góc và góc ; góc
và góc ; góc và góc ; góc và góc .
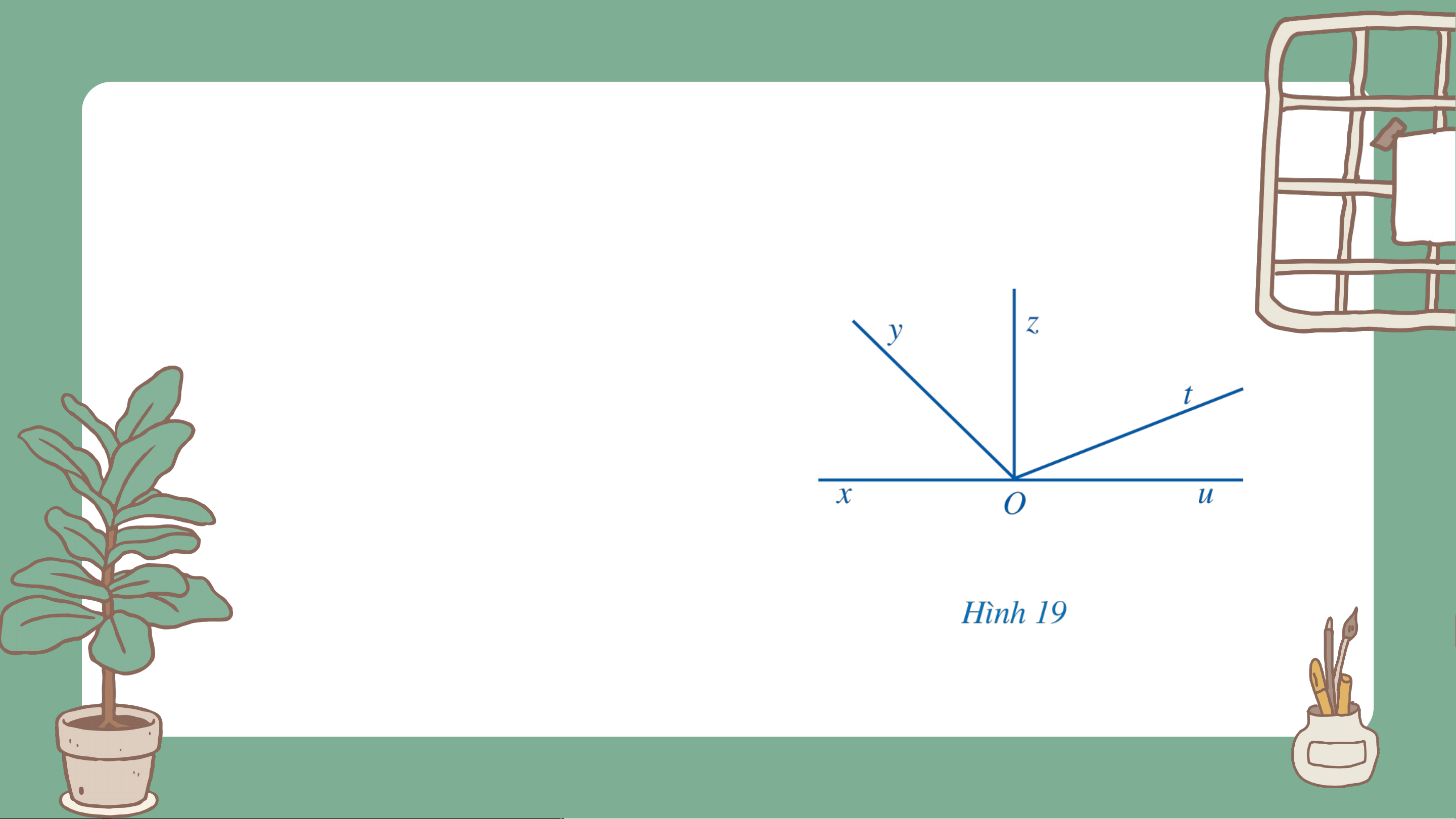
b) Tìm các cặp góc kề bù (khác góc bẹt) ở Hình 19. Giải
Các cặp góc kề bù trong
Hình 19 là: góc và góc ;
góc và góc ; góc và góc .
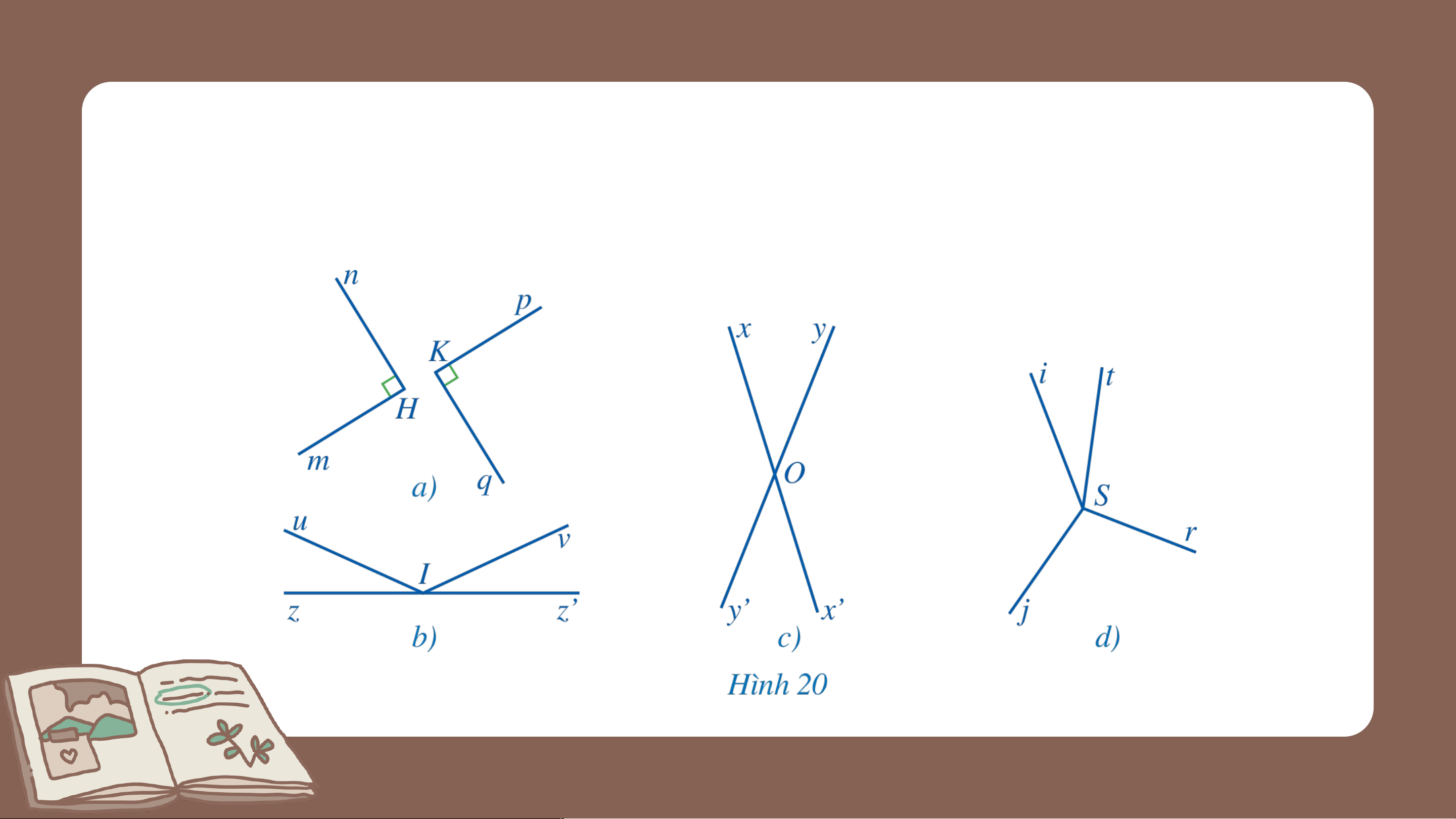
c) Tìm hai góc đối đỉnh (kh20a, 20b, 20c, 20dác góc
bẹt và góc không) trong mỗi hình : Giải
- Trong Hình 20a: Không có vì 2 góc này không có chung đỉnh
- Trong Hình 20b: Không có vì không có 2 góc nào mà mỗi cạnh
của góc này là tia đối của một cạnh của góc kia.
- Trong Hình 20c: góc xOy và góc x’Oy’
- Trong Hình 20d: Không có vì không có 2 góc nào mà mỗi cạnh
của góc này là tia đối của một cạnh của góc kia.
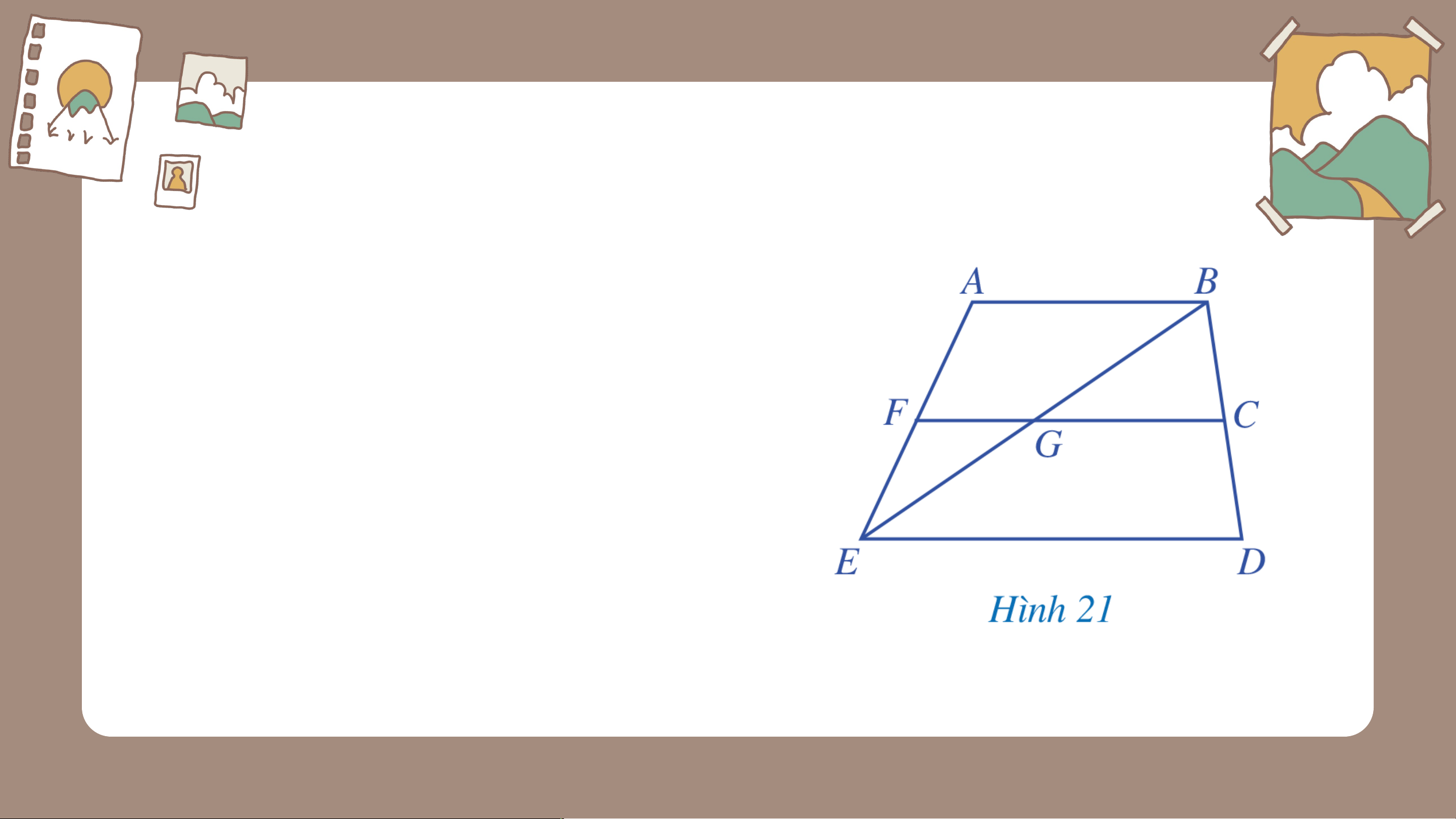
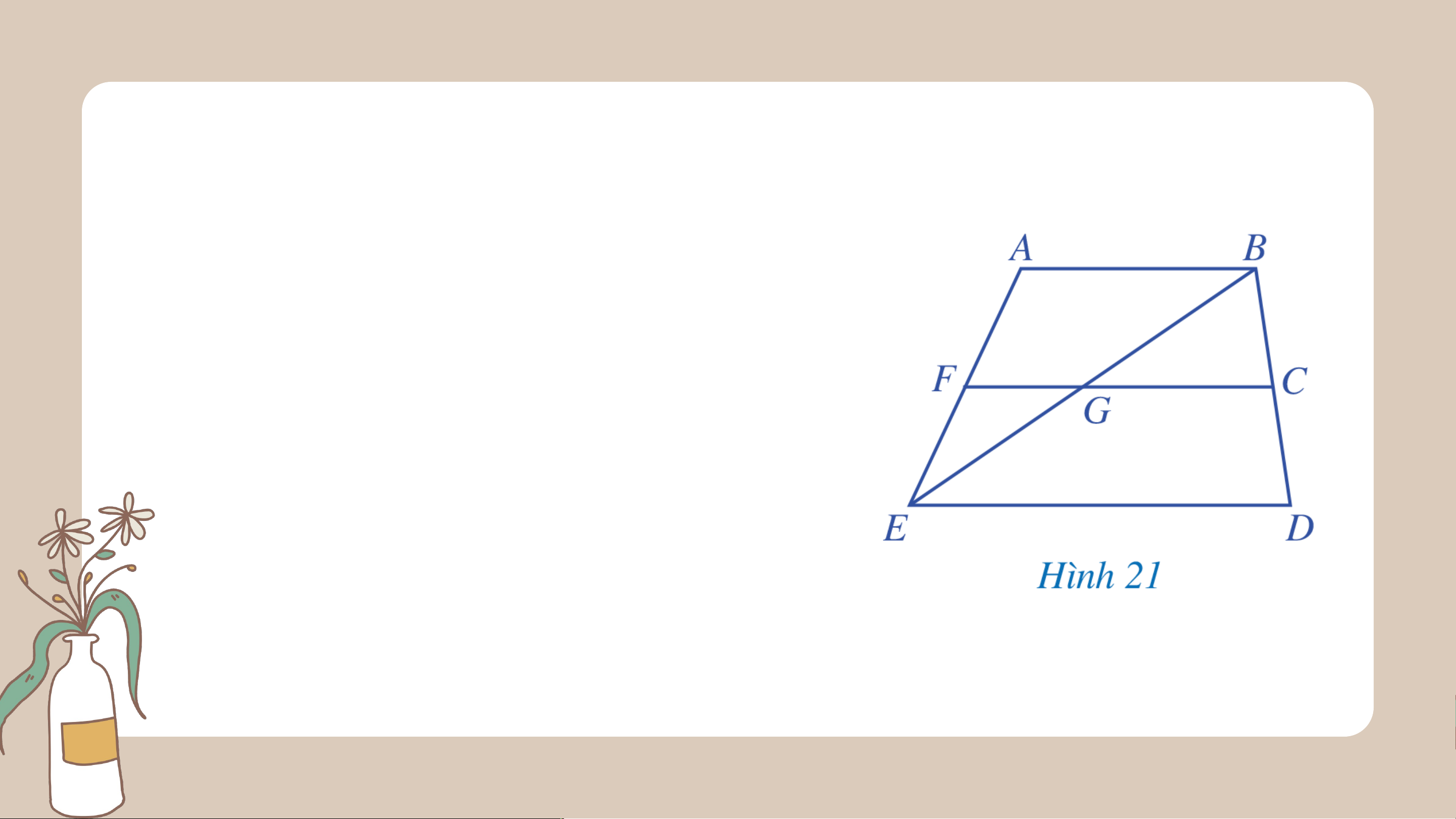
Bài 2 (SGK – tr.95) Quan sát Hình 21 và chỉ ra a) Hai góc kề nhau
b) Hai góc kề bù (khác góc bẹt)
c) Hai góc đối đỉnh (khác góc bẹt và góc không).
a) Hai góc kề nhau là: và ; và ; và ; và ; và ; và ; và ; và .
b) Hai góc kề bù là: và ; và ; và ; và ; và ; và .
c) Hai góc đối đỉnh là: và ; và .
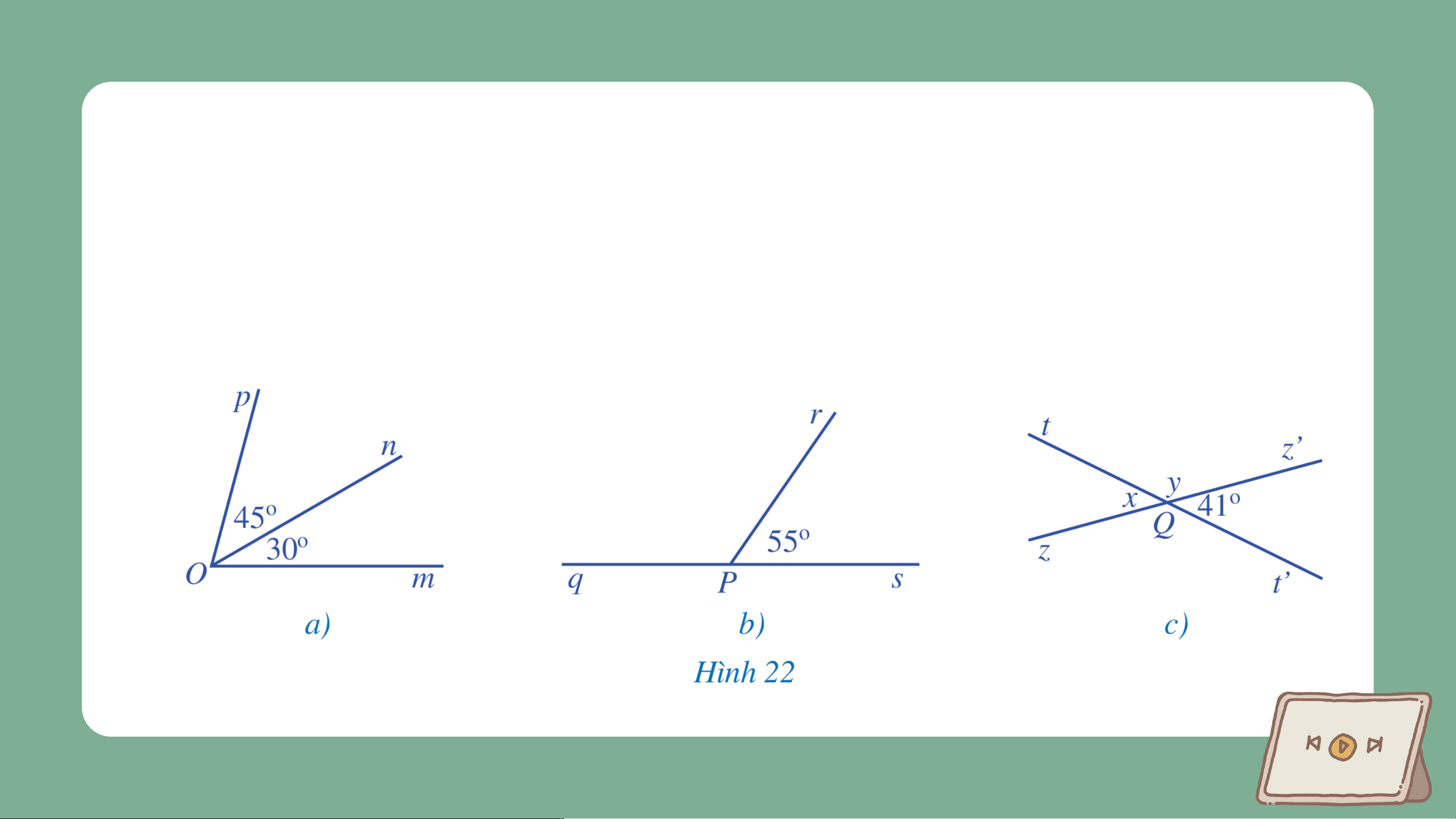
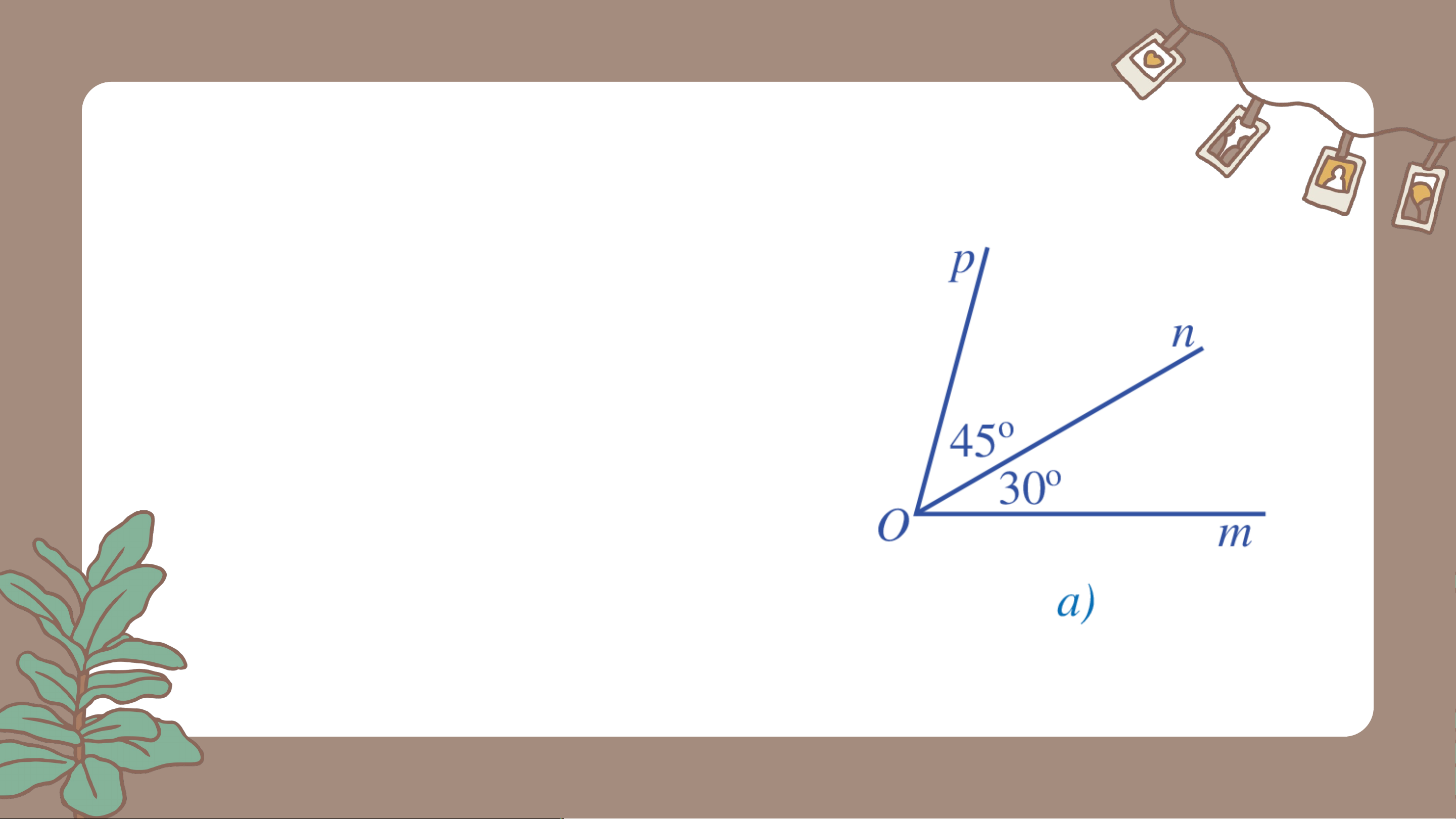
Bài 3 (SGK – tr. 95) Tìm số đo a) Góc trong Hình 22a b) Góc trong Hình 22b c) trong Hình 22c. Giải
a) Vì tia nằm trong góc nên Vậy số đo góc là . b) Ta có: (2 góc kề bù) Vậy số đo góc là . b) Ta có: +) (2 góc đối đỉnh) +) (2 góc kề bù) Vậy , . VẬN DỤNG
Bài 4 (SGK – tr.95) Hình 23 là một mẫu cửa có
vòm tròn của một ngôi nhà. Nếu coi mỗi thanh
chắn vòm cửa đó (ba thanh màu xanh trên hình)
như một cạnh của góc thì các thanh chắn đó tạo
ra các góc kề nhau. Theo em, mỗi góc tạo bởi hai
thanh chắn vòm cửa đó khỏng bao nhiêu độ? Giải
Có 4 góc kề nhau được tạo thành,
xếp thành góc bẹt, mỗi góc tạo bởi 2 thanh chắn vòm cửa Nên mỗi góc có số đo:
HƯỚNG DẪN VỀ NHÀ
Ôn lại tính chất về các loại góc ở vị trí đặc biệt.
Hoàn thành các bài tập trong SBT.
Chuẩn bị bài mới “Bài 2. Tia phân giác của một góc” CẢM ƠN CÁC EM ĐÃ
LẮNG NGHE BÀI GIẢNG
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49




