Giáo án điện tử Toán 7 Bài 1 Cánh diều: Số vô tỉ. Căn bậc hai số học
Bài giảng PowerPoint Toán 7 Bài 1 Cánh diều: Số vô tỉ. Căn bậc hai số học hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 7. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 7
Môn: Toán 7
Sách: Cánh diều
Thông tin:
Tác giả:
Preview text:
CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC Bài toán Tìm , biết: 1 5 1 𝑥2+ : 2 = 8 4 1 5 𝑥2+ . 4 2 = 8 1 5 𝑥2+ 2=2 Có số hữu tỉ nào mà 5 1 bình phương của nó 𝑥2= − 2 2 bằng 2 hay không? 𝑥2=2 Không BÀI 1: SỐ VÔ TỈ.
CĂN BẬC HAI SỐ HỌC (2 tiết) NỘI DUNG BÀI HỌC Số vô tỉ
Căn bậc hai số học Luyện tập I. SỐ VÔ TỈ
1. Khái niệm số vô tỉ
Số vô tỉ là các số không phải là số hữu tỉ. VD: Cách tính, lịch sử hình thành số Pi? 5
2. Số thập phân vô hạn không tuần hoàn
HĐ1 Viết số hữu tỉ dưới dạng số thập phân vô hạn tuần hoàn. 1
3 =0,333 …=0 , (3)
Những số thập phân vô hạn mà phần thập phân của chúng không có
một chu kì nào cả được gọi là số thập phân vô hạn không tuần hoàn. VD:
3. Biểu diễn thập phân của số vô tỉ
Số vô tỉ được viết dưới dạng số thập phân vô hạn không tuần hoàn. Ví dụ ụ 1
Các phát biểu sau đúng hay sai? Vì sao?
a) Nếu thì a không thể là số vô tỉ.
b) Nếu thì a không thể là số vô tỉ.
c) Số thập phân hữu hạn là số vô tỉ. Giải
a) Đúng. Ta có thể giải thích như sau: Nếu thì a là số hữu tỉ và do đó a
được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn,
tức là a không thể là số vô tỉ.
b) Đúng. Ta có thể giải thích như sau: Nếu a là số nguyên thì a cũng là
số hữu tỉ và do đó theo lập luận trên a không thể là số vô tỉ.
c) Sai. Ta có thể giải thích như sau: Số thập phân hữu hạn không thể là
số thập phân vô hạn không tuần hoàn và do đó không thể là số vô tỉ. Luy u ệ y n n tập ậ p 1 1
Phát biểu “Mỗi số vô tỉ đều không thể là
số hữu tỉ” là đúng hay sai? Vì sao?
Khẳng định đúng vì những số không
phải số hữu tỉ là số vô tỉ.
II. CĂN BẬC HAI SỐ HỌC HĐ2 Tính a) 32 ¿ 9
là căn bậc hai số học của b) (0,4 )2 ¿ 0,16
là căn bậc hai số học của Khái niệm
Căn bậc hai số học của số không âm là số sao cho .
Căn bậc hai số học của một số không âm phải là số không âm. Ví dụ:
nhưng không được gọi là căn bậc hai số học của . Chú ý:
Căn bậc hai số học của số được kí hiệu là .
Căn bậc hai số học của số là số , viết là .
Lưu ý: Cho . Khi đó:
o Đẳng thức là đúng nếu và . o . Ví dụ ụ 2 Chứng tỏ rằng:
a) Số là căn bậc hai số học của số
b) Số không phải căn bậc hai số học của Gi G ải
a) Ta có: và nên là căn bậc hai số học của
b) Tuy nhưng nên không phải là căn bậc hai số học của . Ví V dụ d ụ 3 Tìm giá trị của: a) 8 √81 ¿ 9 b) √0,81 ¿0,9 c) √6449 ¿7
Nhận xét: Người ta chứng minh được rằng "Nếu số nguyên dương a
không phải là bình phương của bất kì số nguyên dương nào thì là số
vô tỉ." Như vậy các số, , , , ... đều là số vô tỉ. Lu L y u ện ệ n tập ậ p 2 2 Tìm giá trị của: a) √1600 ¿ 40 b) √0,16 ¿0,4 1 3 c) √2 ¿ 4 ¿ 2 √94 HĐ3
Sử dụng máy tính cầm tay Ví dụ ụ 4
Dùng máy tính cầm tay để tính giá trị trong mỗi trường hợp sau: a) ¿ 1 234 b) √1522 756
√127 . 137 ≈ 68,5492524 III. LUYỆN TẬP a) Đọc các số sau: b) Viết các số sau:
đọc là: căn bậc hai số học của mười
Căn bậc hai số học của viết là: lăm
Căn bậc hai số học của viết là:
đọc là: căn bậc hai số học của hai
Căn bậc hai số học của viết là: mươi bảy phẩy sáu
đọc là: căn bậc hai số học của không phẩy tám mươi hai Chứng tỏ rằng:
a) Số là căn bậc hai số học của
b) Số không phải là căn bậc hai số học của
c) Số là căn bậc hai số học của số nhưng không phải là căn bậc hai số học của số Gi G ải
a) Vì và nên số là căn bậc hai số học của số .
b) Vì tuy nhưng nên số không phải là căn bậc hai số học của số .
c) Vì và nên số là căn bậc hai số học của số . Ngược lại, vì nên không
phải là căn bậc hai số học của số .
Tính giá trị của biểu thức: a) ¿0,7+0,8=1,5 b)
¿0,6−0,9=−0,3 c)
¿ 8. 3 − 8¿ 24 − 8=16 d) ¿0,1.20+0,2.40¿2+8=10 Vận dụng
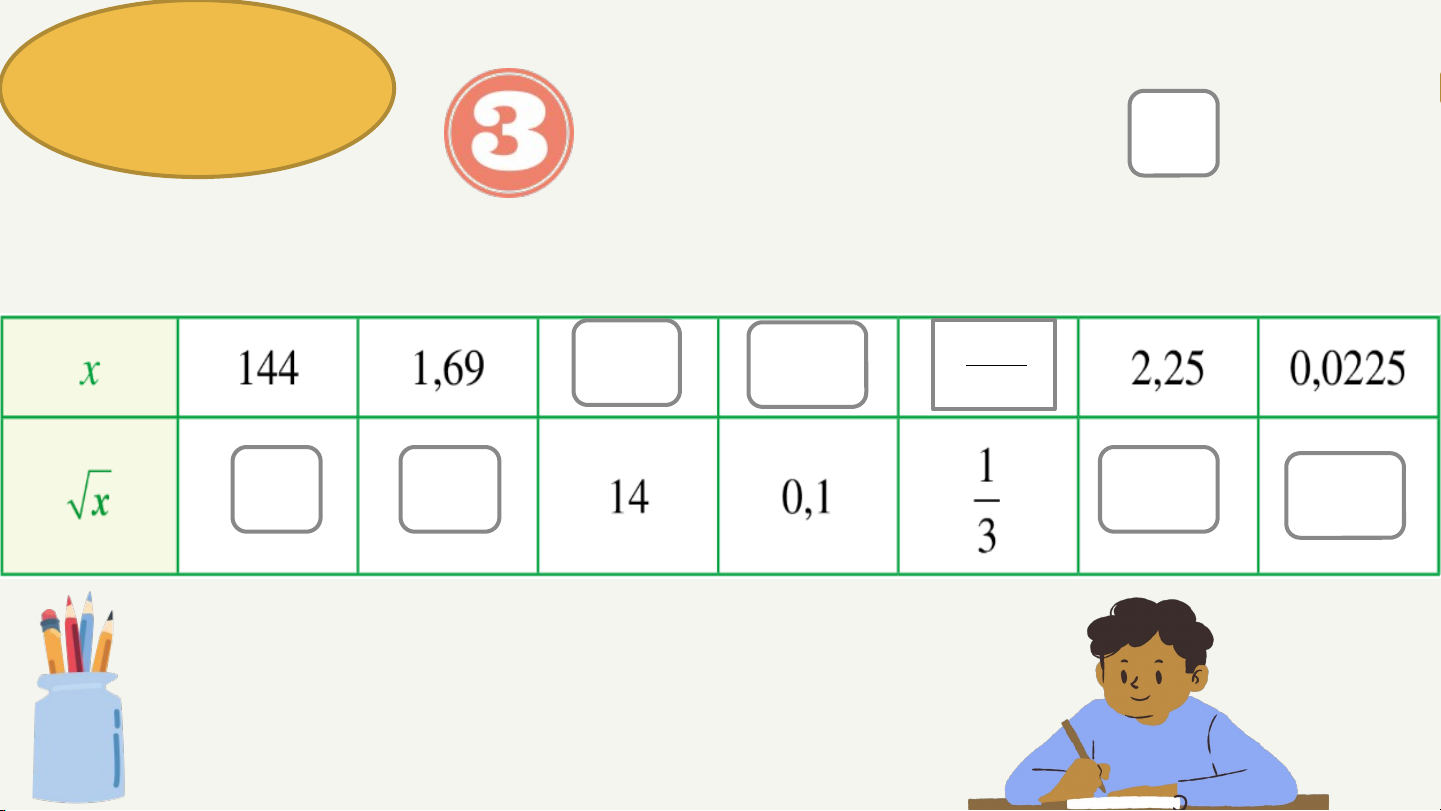
Tìm số thích hợp điền vào ? 1 196 0,01 9 12 1,3 1,5 0,15
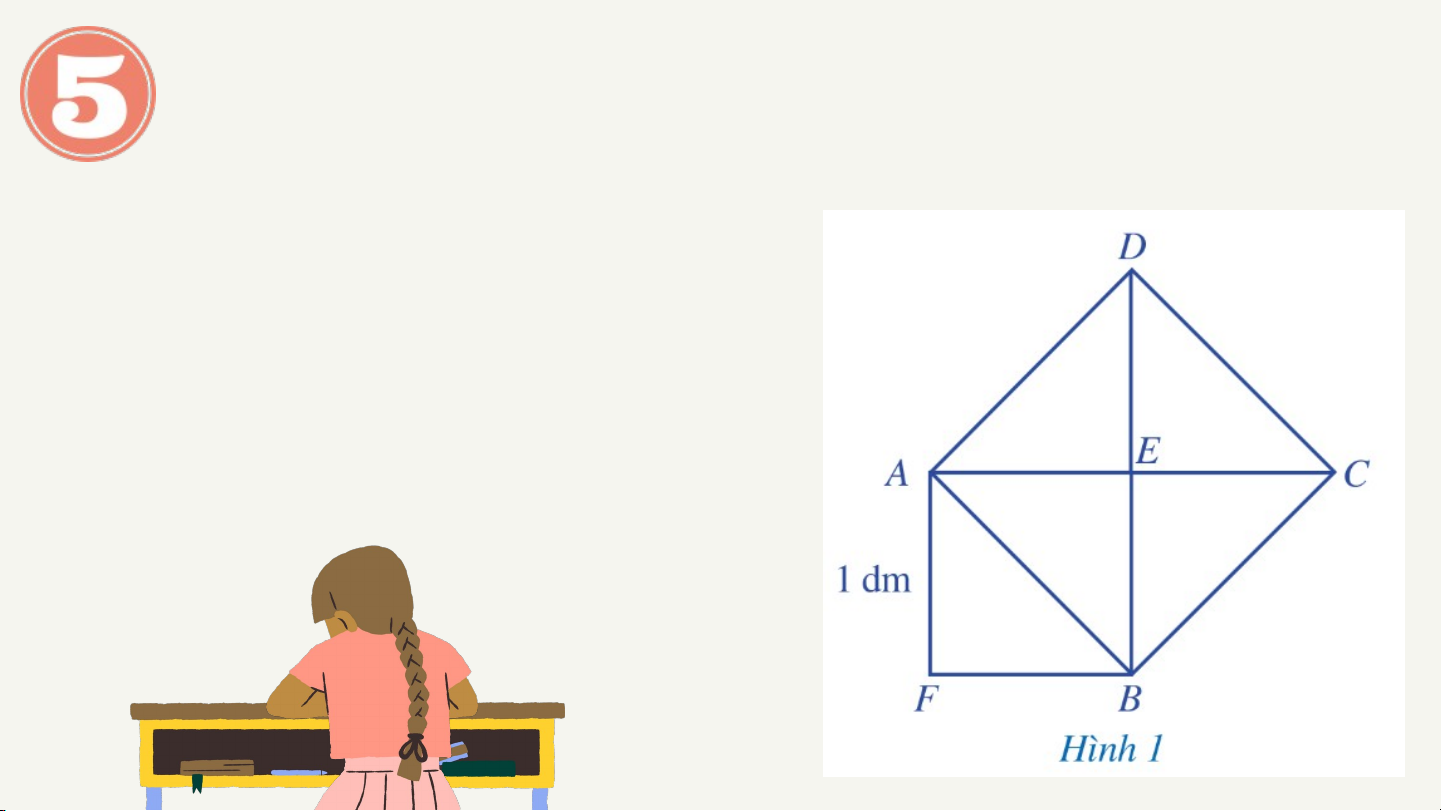
Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 dm,
hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF.
a) Tính diện tích của hình vuông ABCD
b) Tính độ dài đường chéo AB. Gi G ải
a) Diện tích của hình vuông ABCD là:
b) Độ dài đường chéo AB là:
Ghi nhớ: là độ dài đường chéo của hình vuông có độ dài cạnh bằng 1. 0
Phát biểu nào sau đây là sai ? 1 √2∈𝐼 √9∈𝐼 𝜋 ∈ 𝐼 √4 ∈𝑄 0
Số nào trong các số sau không là số hữu tỉ? 2 12 3,(14) √ 3 2 3 0
Trong các số sau đây số nào là số vô tỉ? 3 0,121212… √121 0,12341234…
0,01200120 012… 0
Căn bậc hai số học của 225 là: 4 15 −15 15v à−15 5 0
Chọn câu trả lời sai. Nếu thì bằng: 5 2 2 ( 2 3 ) ( −2 3 ) 2 4 − 9 (− 2 3 ) 0 Nếu thì bằng: 6 3 81 27 9
0 Trong các số số nào không có căn bậc hai là số hữu tỉ. 7 12321 5 , 76 2 ,5 0 , 25
HƯỚNG DẪN VỀ NHÀ Ôn lại kiến thức Hoàn thành các bài
Chuẩn bị bài mới “Tập đã học trong bài tập trong SBT
hợp R các số thực”. CẢM ƠN CÁC EM ĐÃ
LẮNG NGHE BÀI GIẢNG!
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34