Giáo án điện tử Toán 7 Bài 10 Cánh diều: Tính chất ba đường trung tuyến của tam giác
Bài giảng PowerPoint Toán 7 Bài 10 Cánh diều: Tính chất ba đường trung tuyến của tam giác hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 7. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 7
Môn: Toán 7
Sách: Cánh diều
Thông tin:
Tác giả:
Preview text:
TÍNH CHẤT BA ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC Giáo án dạy thêm sưu tầm
I Đường trung tuyến của tam giác
Đường trung tuyến trong tam giác là một đoạn thẳng
nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện.
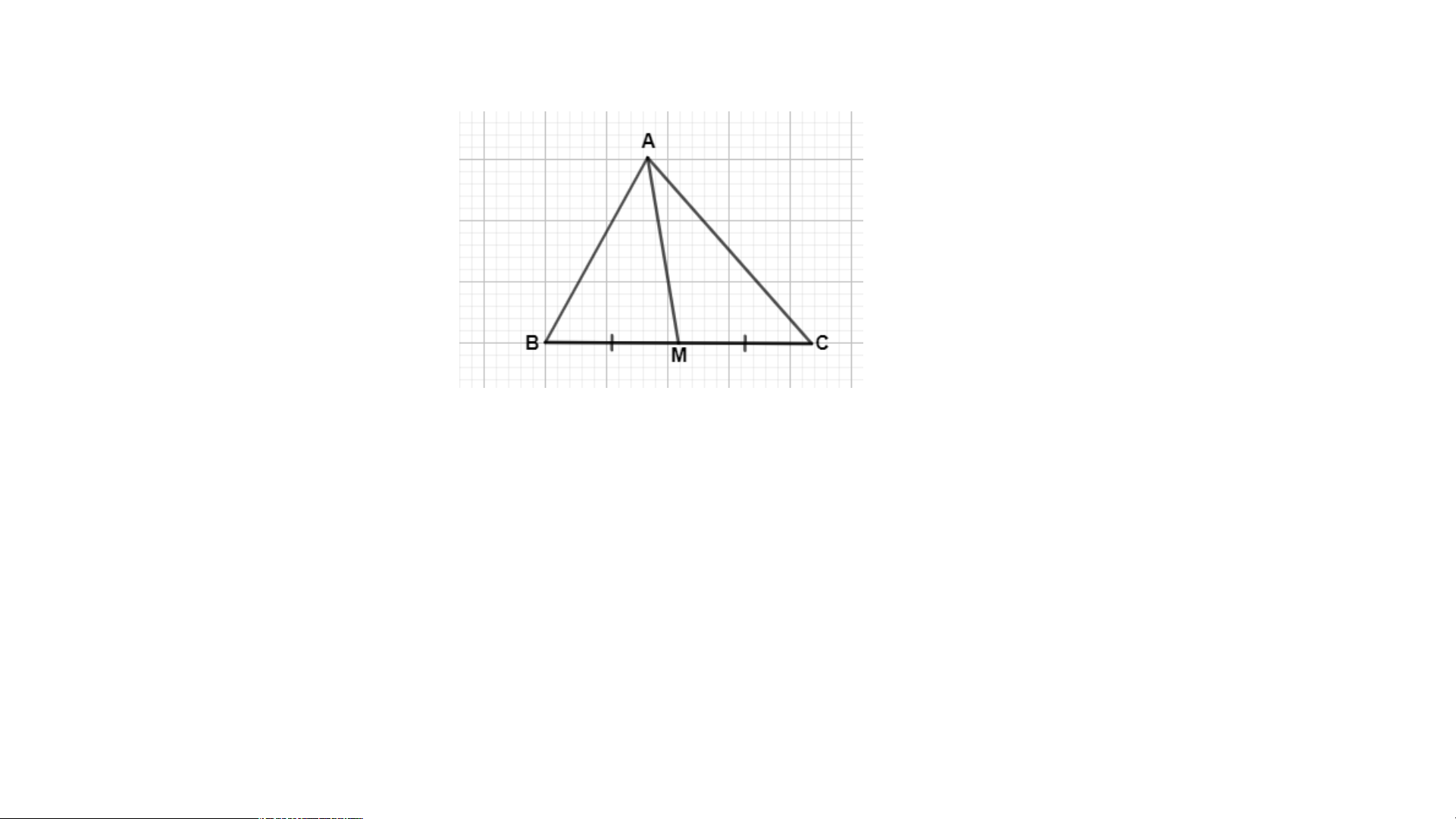
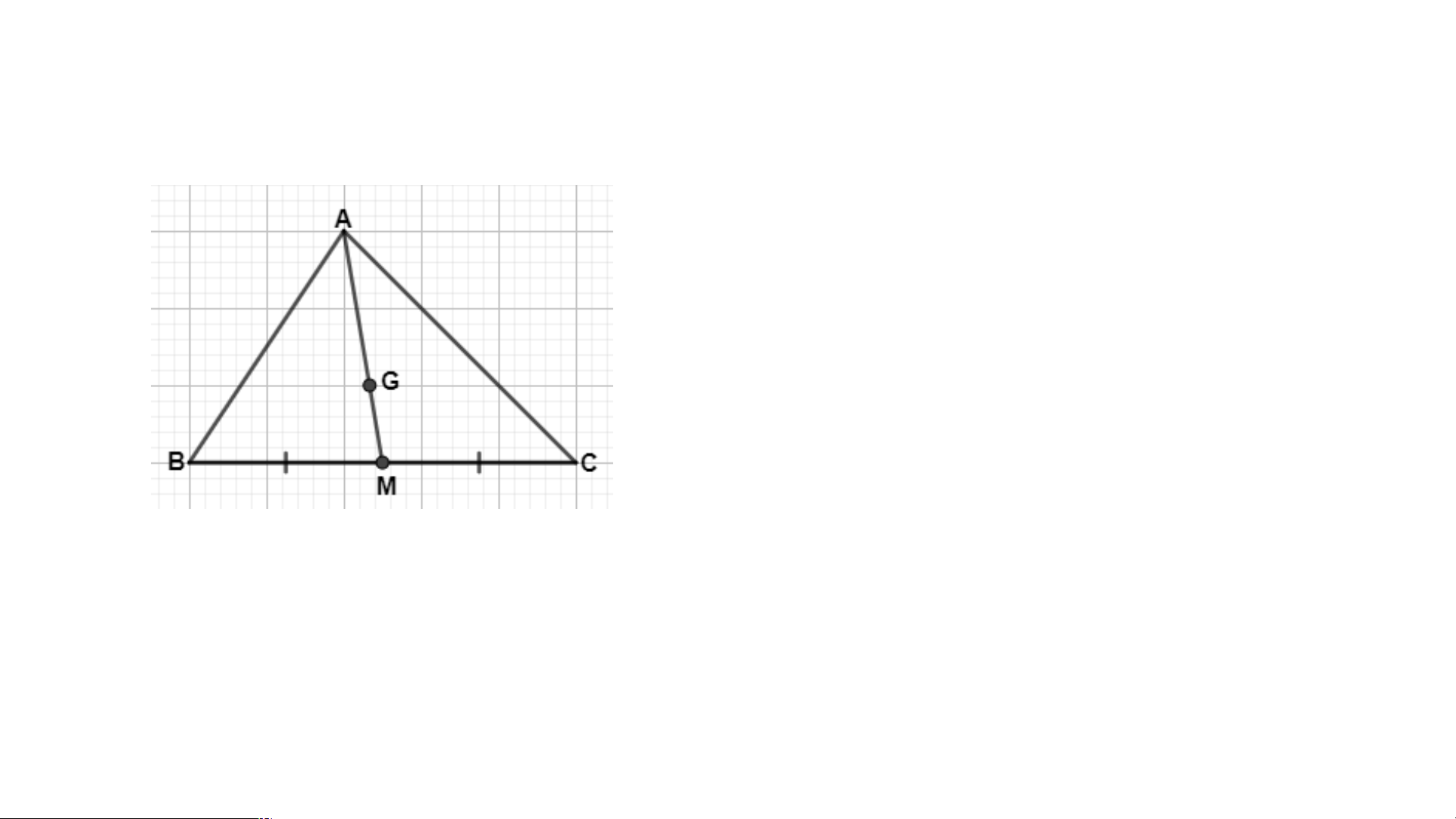
Trong tam giác ABC có AM là đoạn thẳng nối đỉnh
A của tam giác ABC với trung điểm M của cạnh
đối diện BC thì khi đó đoạn AM được gọi là đường
trung tuyến của tam giác ABC
* Nhận xét: Mỗi tam giác có ba đường trung tuyến ứng
với ba đỉnh của tam giác.
Luyện tập 1 trang 105
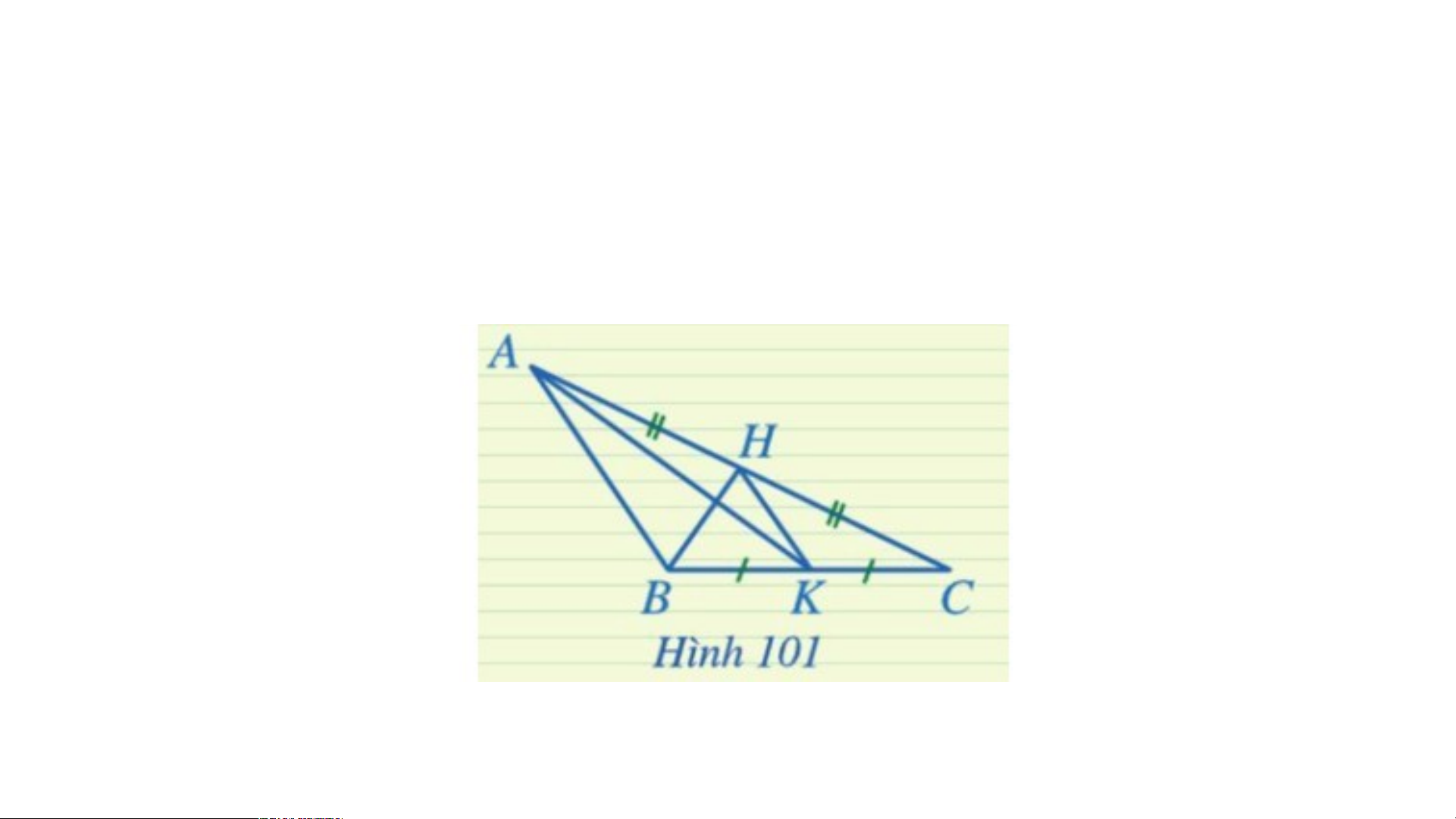
Trong Hình 101, đoạn thẳng HK là đường
trung tuyến của những tam giác nào? Giải
K là đỉnh của tam giác AKC, H là trung điểm của
cạnh AC nên KH là đường trung tuyến của tam giác AKC.
H là đỉnh của tam giác BHC, K là trung điểm của
cạnh BC nên HK là đường trung tuyến của tam giác BHC.
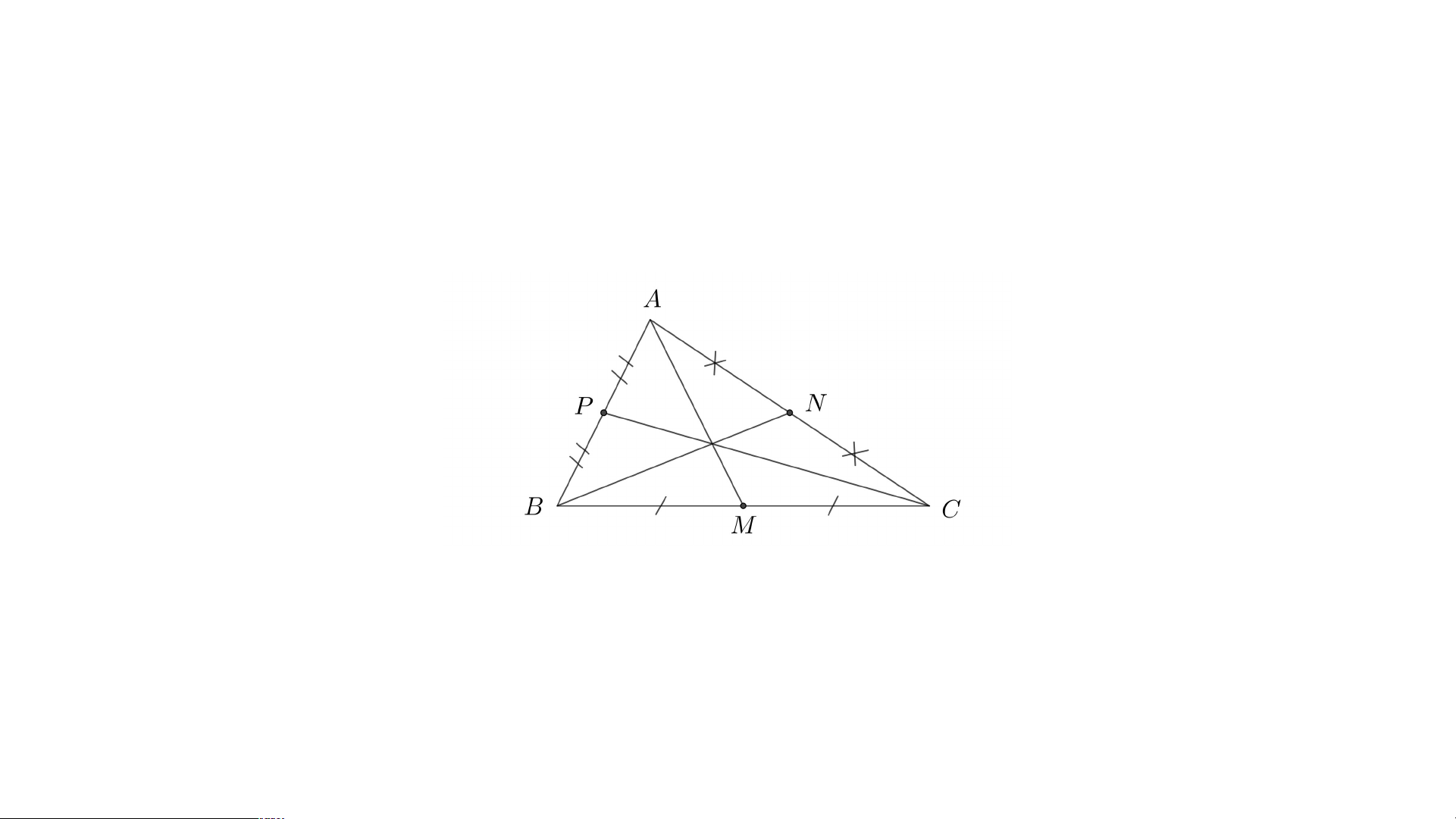
II Tính chất ba đường trung tuyến của tam giác
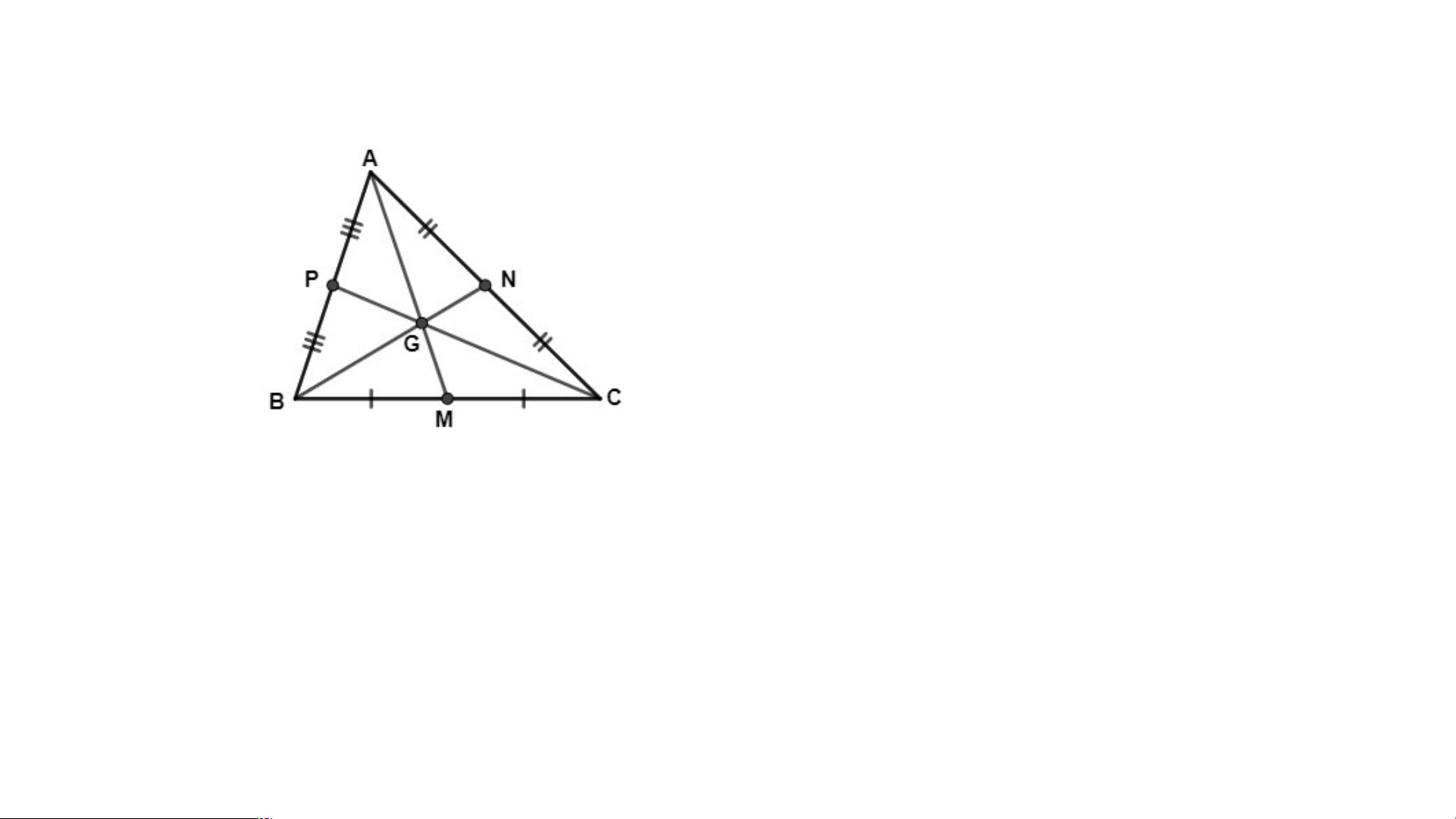
Ba đường trung tuyến của một tam giác cùng đi qua một
điểm. Điểm đó được gọi là trọng tâm của tam giác. Từ đây,
ta quy ước giao điểm ba đường trung tuyến trong tam giác
là điểm G và điểm G được gọi là trong tâm của tam giác.
* Chú ý: Trong tam giác có ba đường trung tuyến cùng đi
qua điểm G, ta còn nói chúng đồng quy tại điểm G. Do đó, để
xác định trọng tâm của một tam giác, ta chỉ cần vẽ hai đường
trung tuyến bất kì và xác định giao điểm của hai đường đó.
Luyện tập 2 trang 105
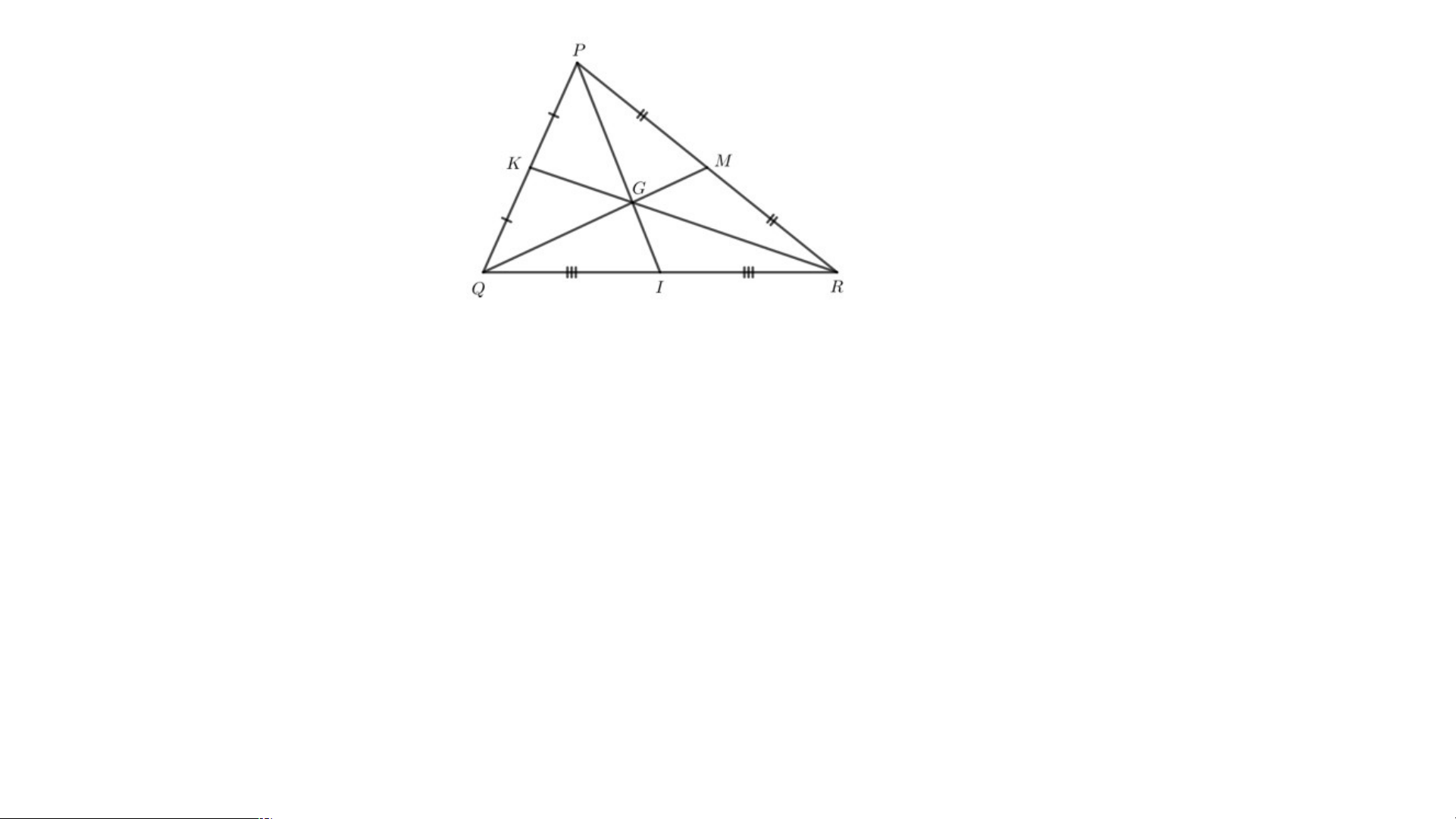
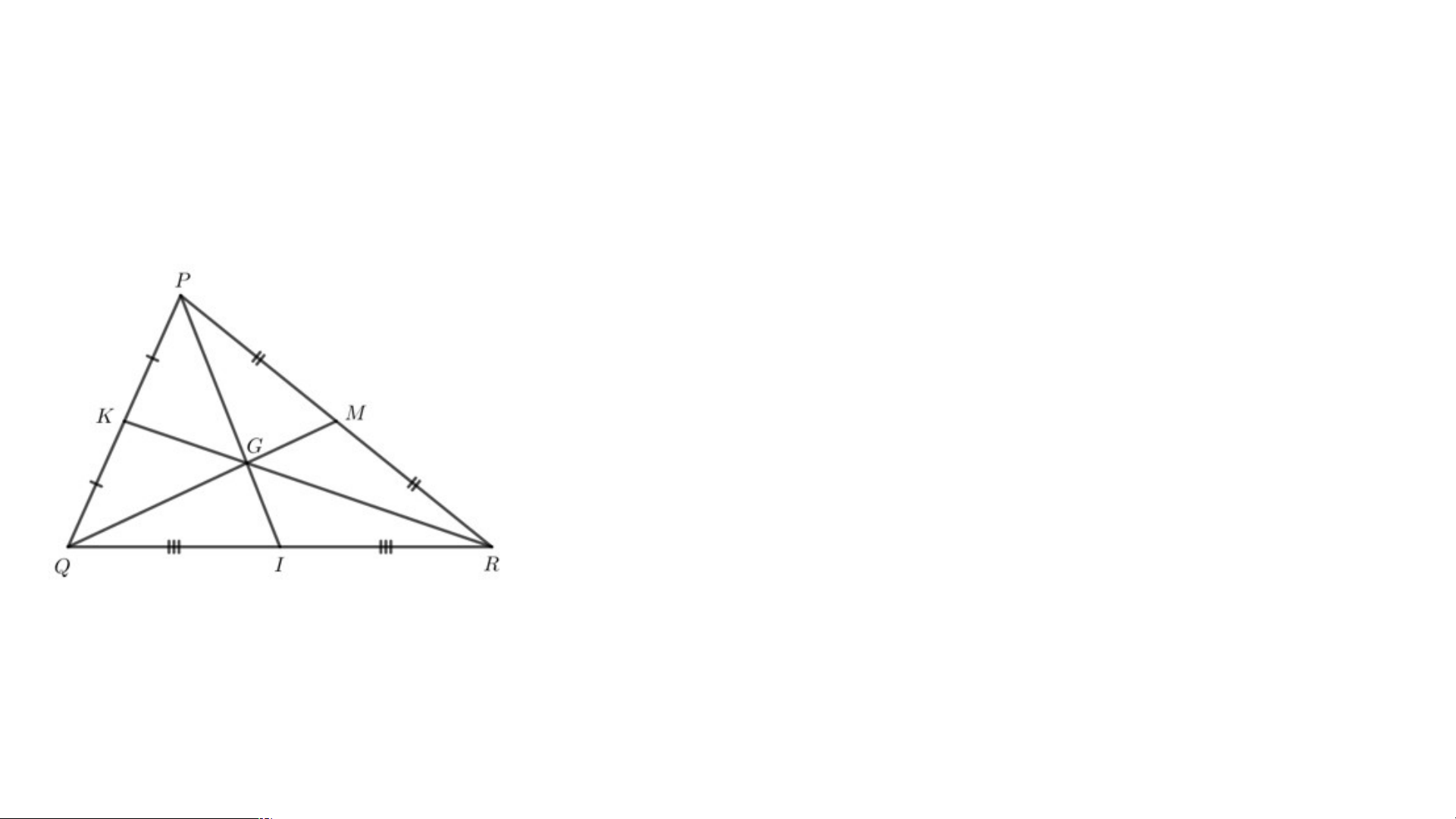
Cho tam giác PQR có hai đường trung tuyến QM và RK
cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng
minh rằng ba điểm P, G, I thẳng hàng.
Phương pháp: Để chứng minh ba điểm P, G, I thẳng
hàng thì ta vận dụng tính chất ba đường trung tuyến Giải
Tam giác PQR có hai đường
trung tuyến QM và RK cắt nhau
tại G nên G là trọng tâm của tam giác PQR.
I là trung điểm của cạnh QR
nên PI là đường trung tuyến của tam giác PQR.
Các đường trung tuyến của
tam giác cùng đi qua trọng
tâm của tam giác nên P, G, I thẳng hàng. * Nhận xét:
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng
độ dài đường trung tuyến đi qua đỉnh ấy.
* Lưu ý: Trong ∆ABC, với AM là đường trung tuyến và G
là trọng tâm thì khi đó điểm G chia đoạn AM thành 3 phần
trong đó đoạn AG chiếm 2 phần còn đoạn GM chiếm 1
phần nên ta có các tỉ số sau:
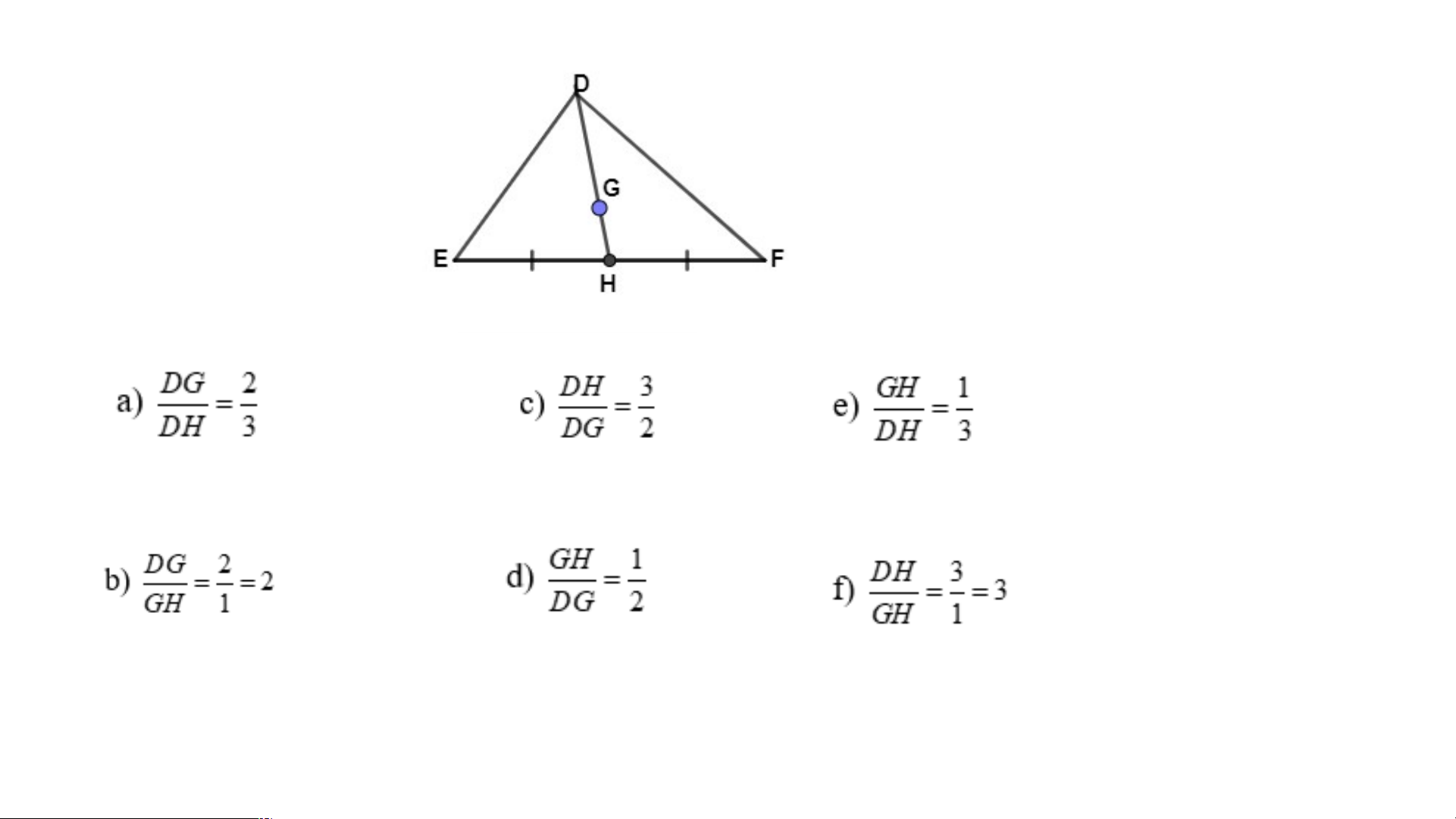
VD: Cho tam giác DEF có đường trung tuyến DH và G là
trọng tâm tam giác. Hãy tính tỉ số: Giải
CÁM ƠN THẦY CÔ, CÁC BẠN ĐÃ LẮNG NGHE
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18