




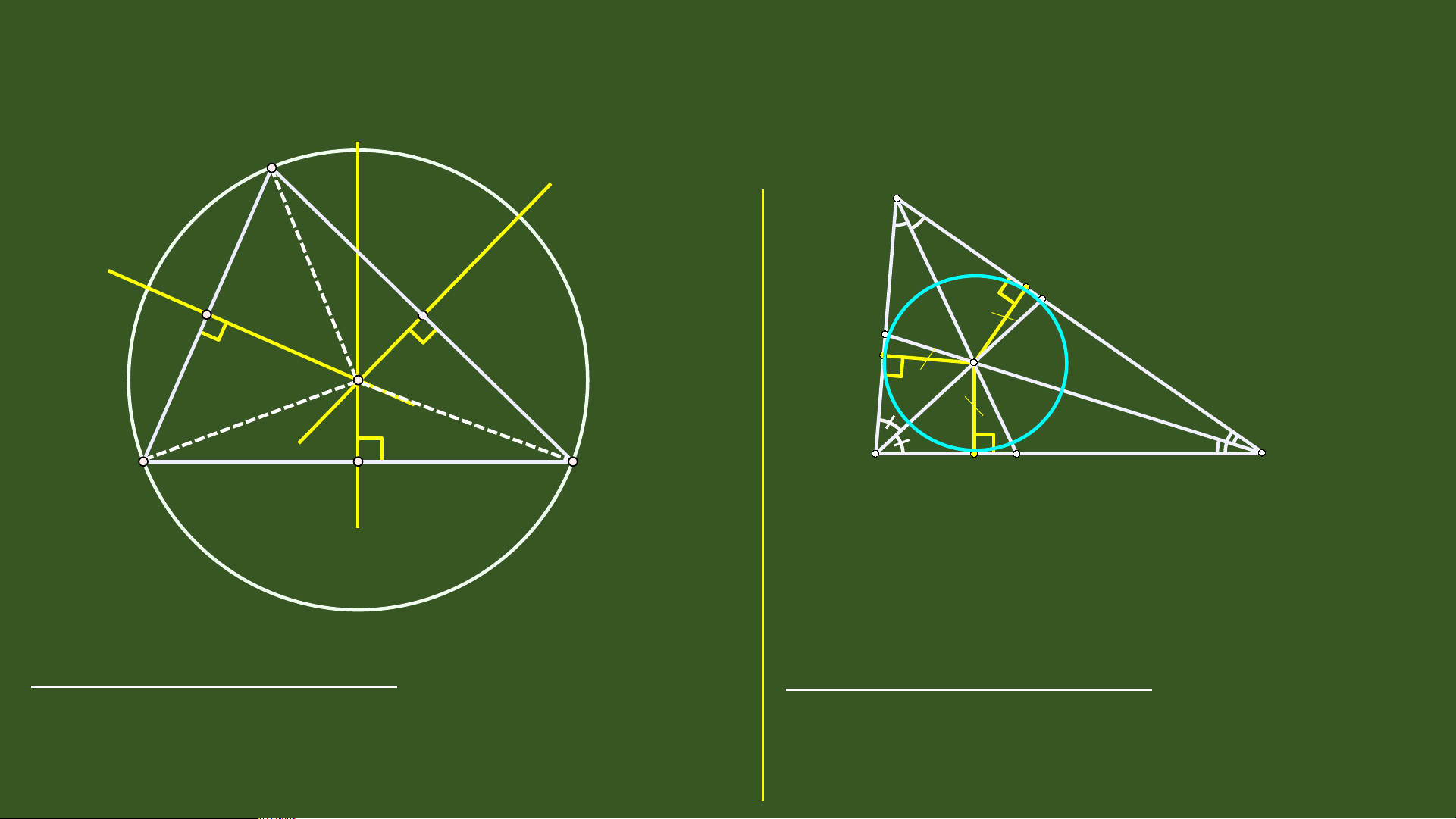
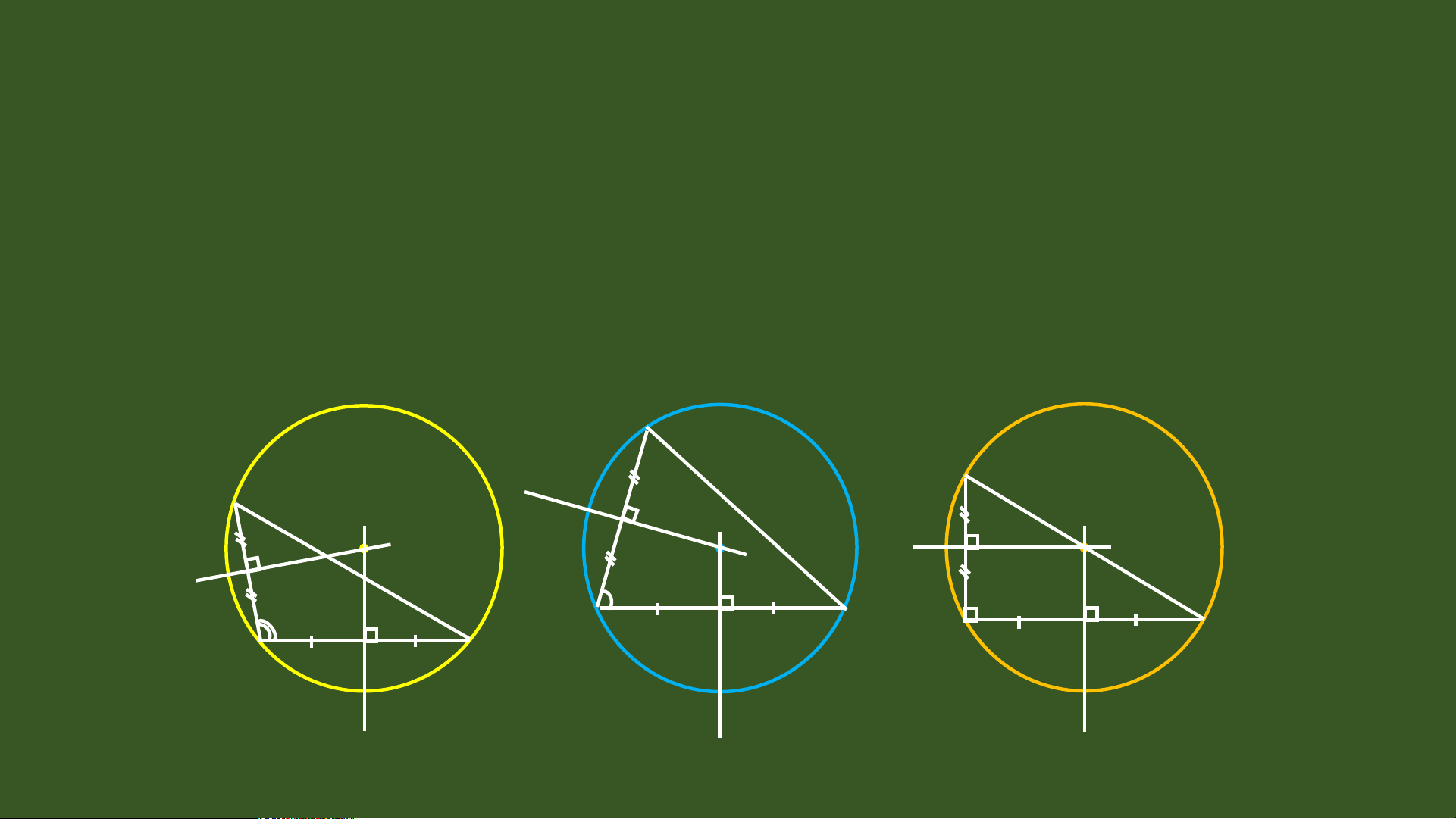



Preview text:
TIẾT 44 – BÀI 12
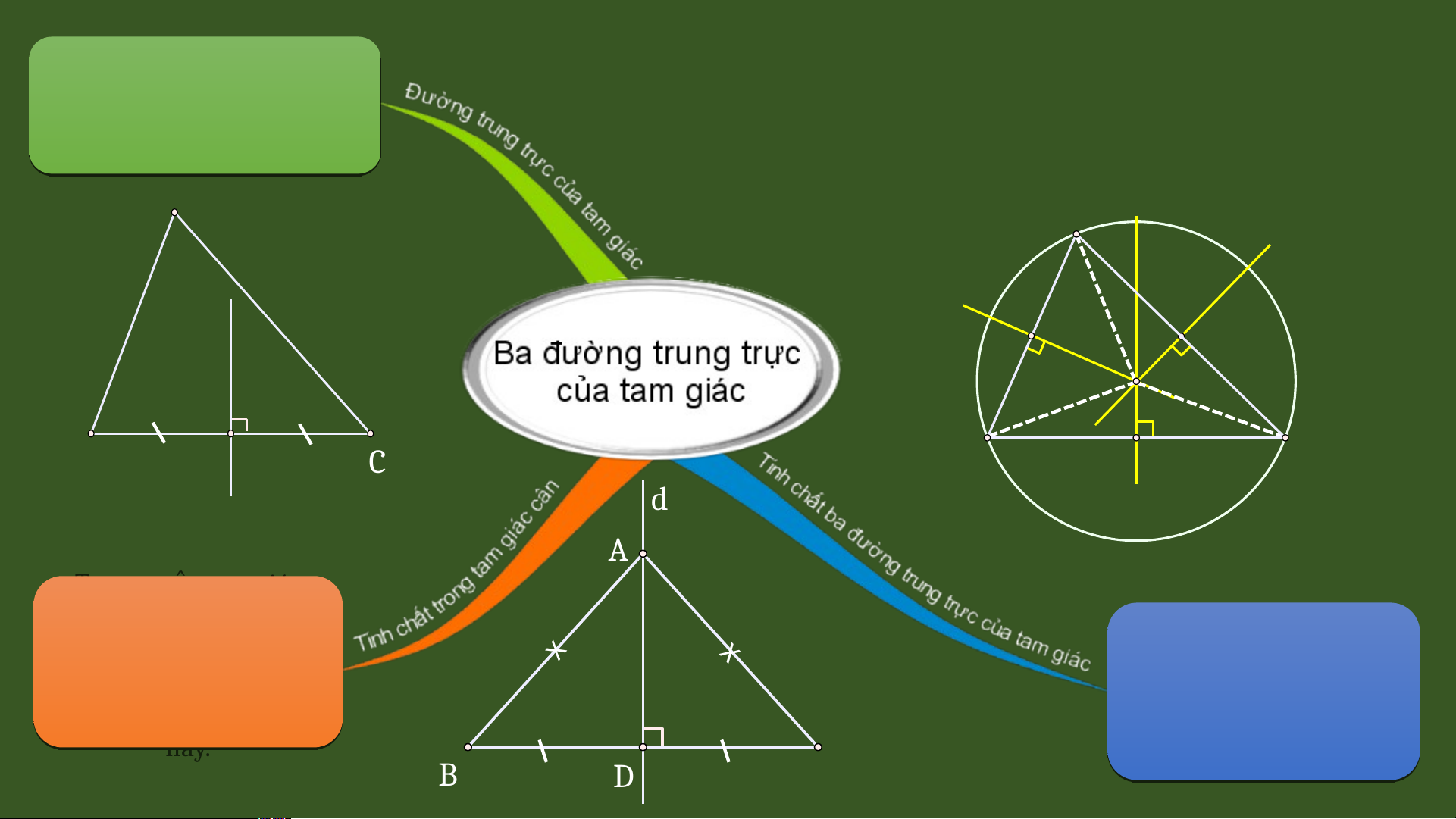
TÍNH CHẤT BA ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC
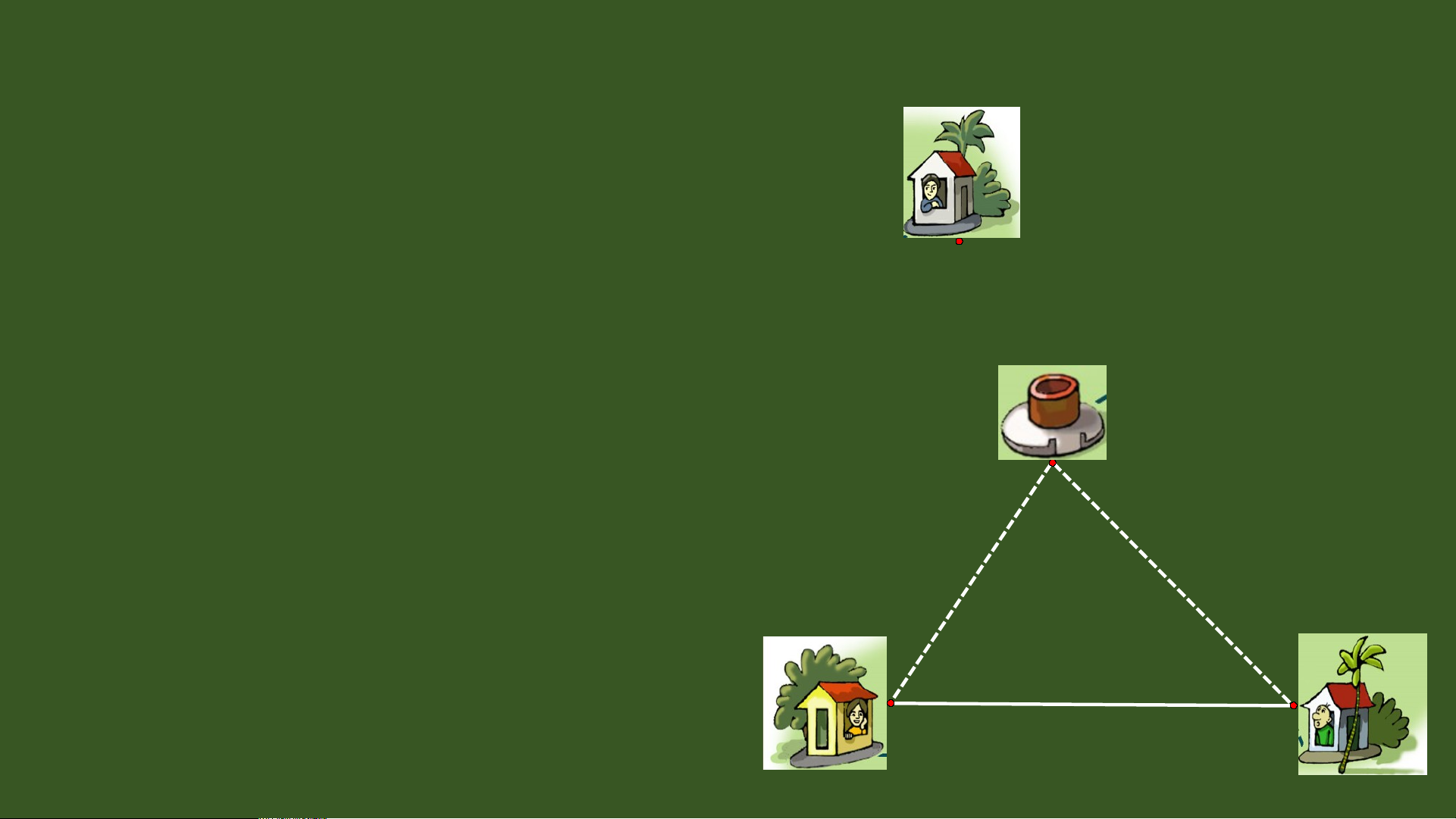
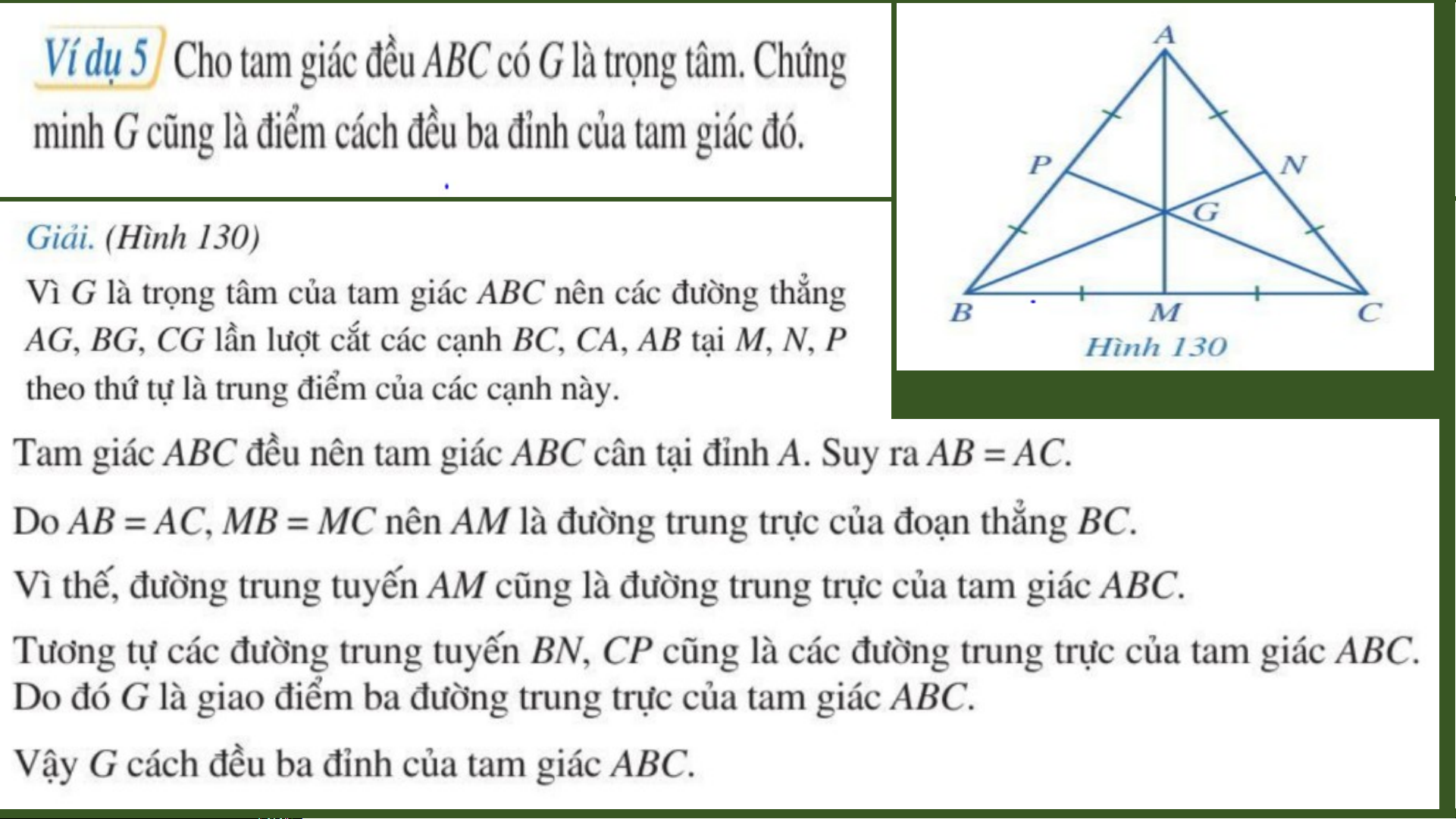
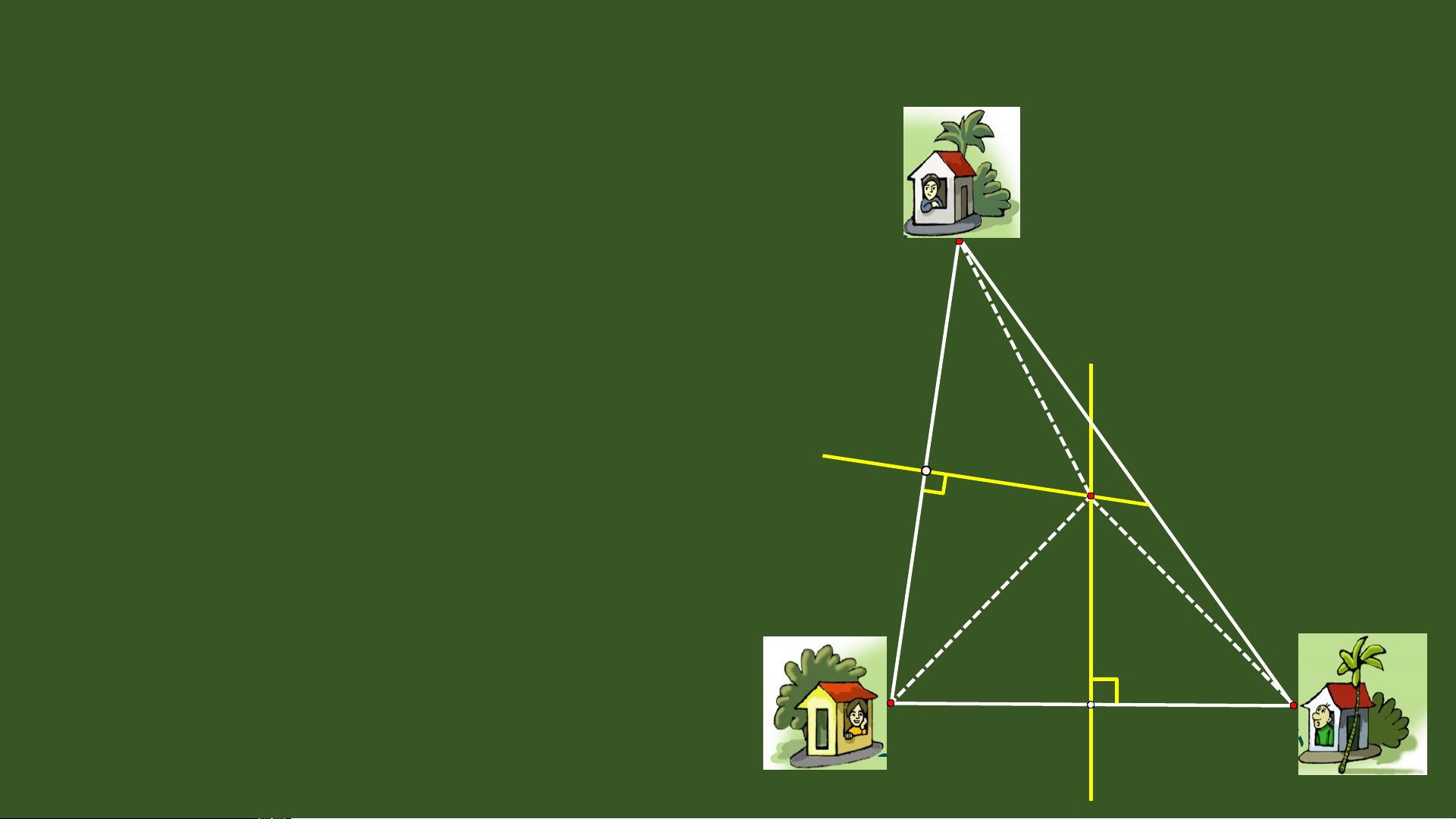
Bài toán: Có ba gia đình A, B và C (nh ư hình vẽ) d ự đ n ị h đào chung m t ộ cái gi n ế g. a) H i ỏ ph i ả ch n ọ v ịtrí c a ủ gi n ế g ở đâu đ ể kho n ả g cách t ừ gi n ế g đ n ế hai nhà A và B C b n ằ g nhau? O A B
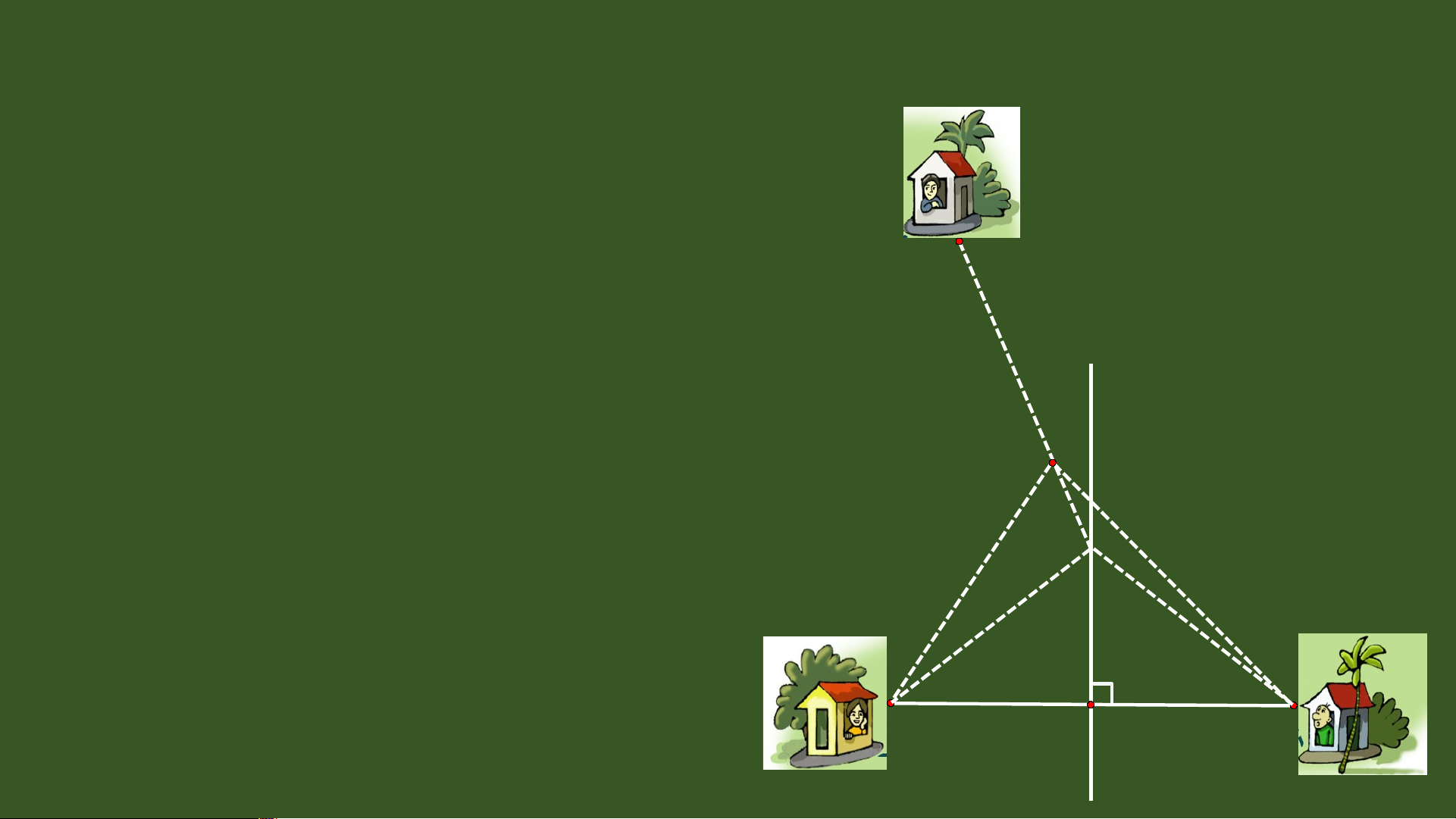
Bài toán: Có ba gia đình A, B và C (nh ư hình vẽ) d ự đ n ị h đào chung m t ộ cái gi n ế g. a) H i ỏ ph i ả ch n ọ v ịtrí c a ủ gi n ế g ở đâu đ ể kho n ả g cách t ừ gi n ế g đ n ế hai nhà A và B C b n ằ g nhau? b) H i ỏ ph i ả ch n ọ v ịtrí c a ủ gi n ế g ở đâu đ ể kho n ả g cách t ừ gi n ế g đ n ế ba nhà b n ằ g nhau? O A I I B TI T Ế 44 0 - TÍNH CH T 1 Ấ BA ĐƯ NG Ờ TRUNG TR C Ự C A Ủ TAM GIÁC I. Đường trung 2 tr c ự c a ủ tam giác A 3 4 d
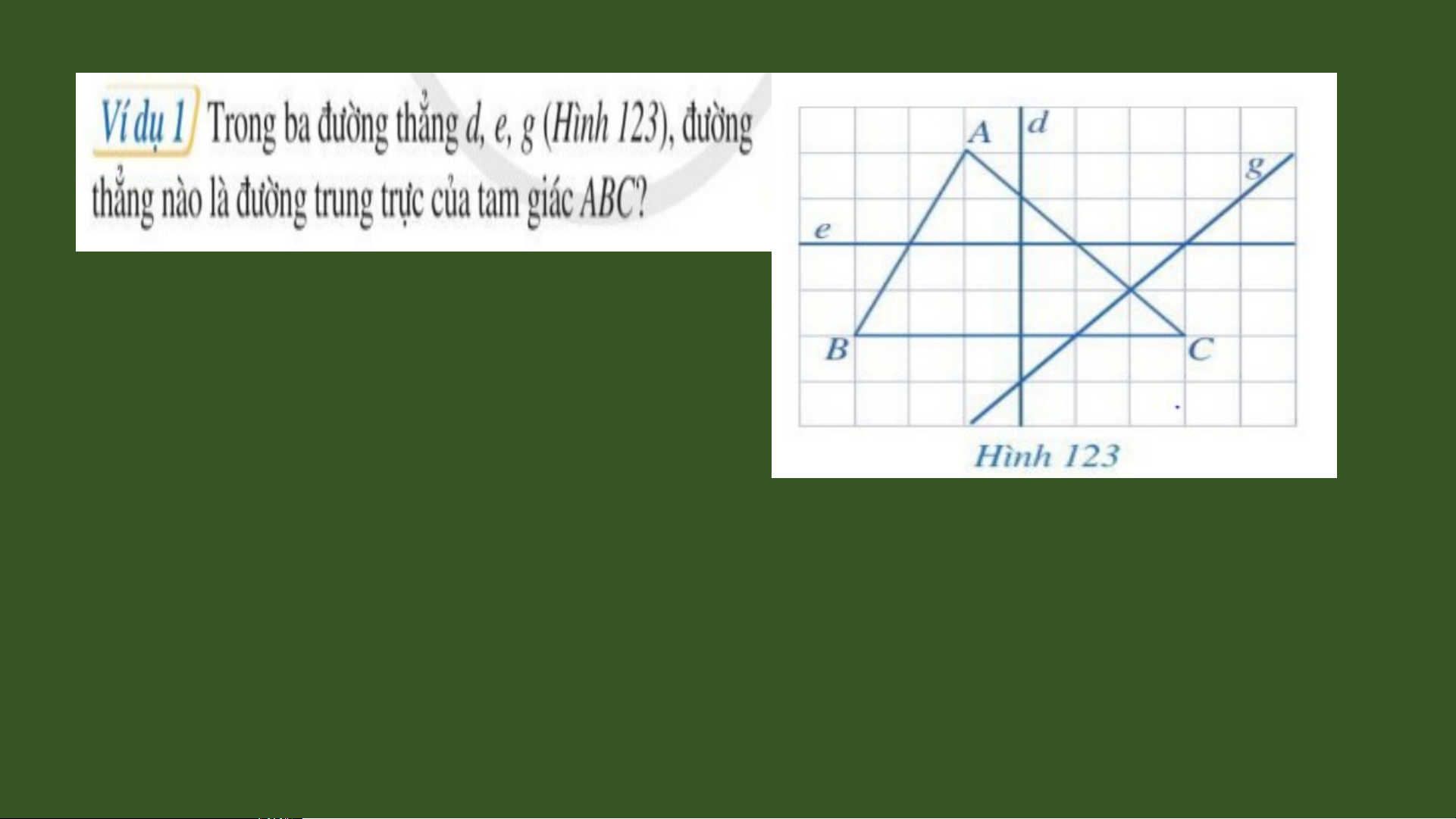
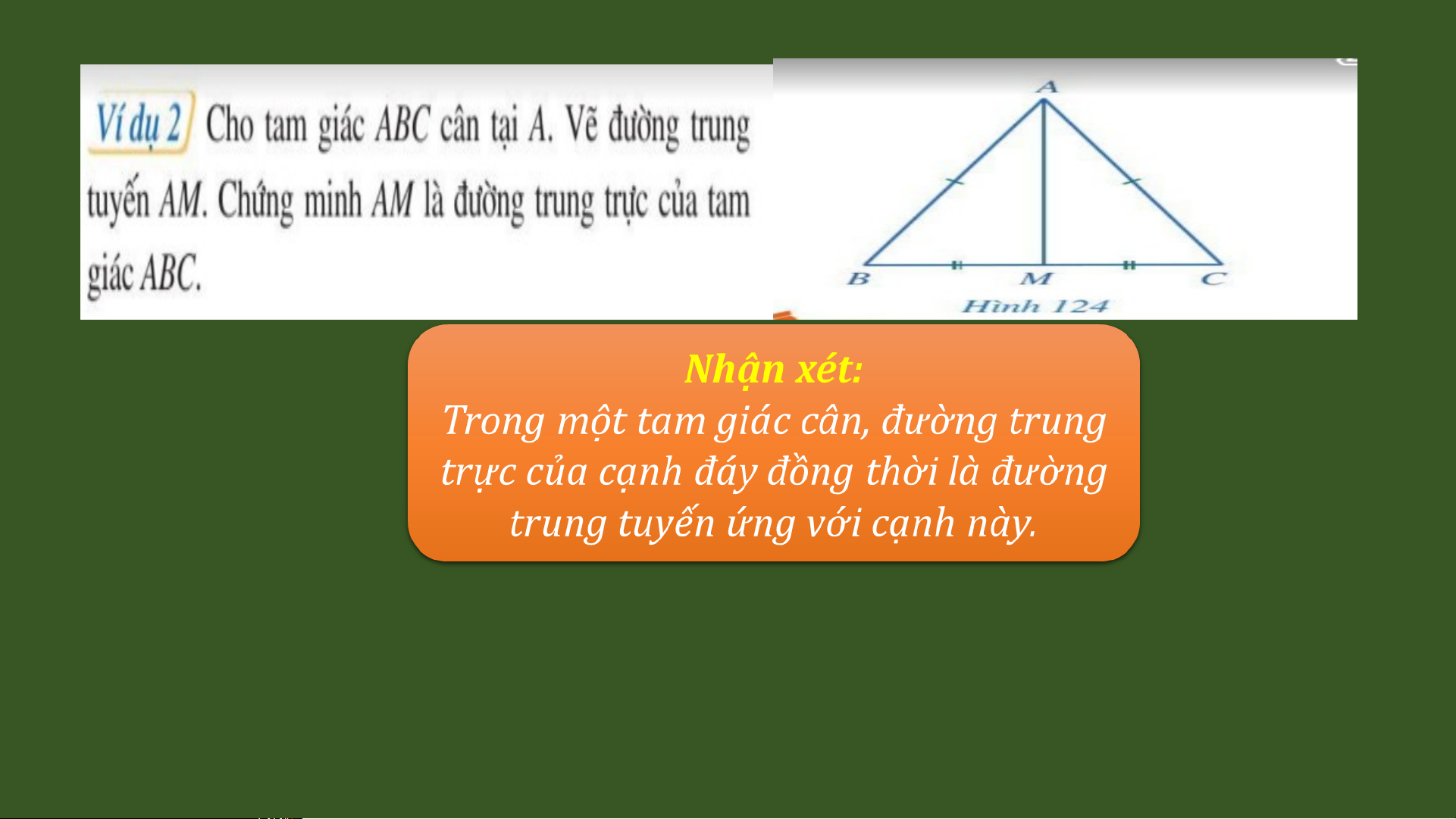
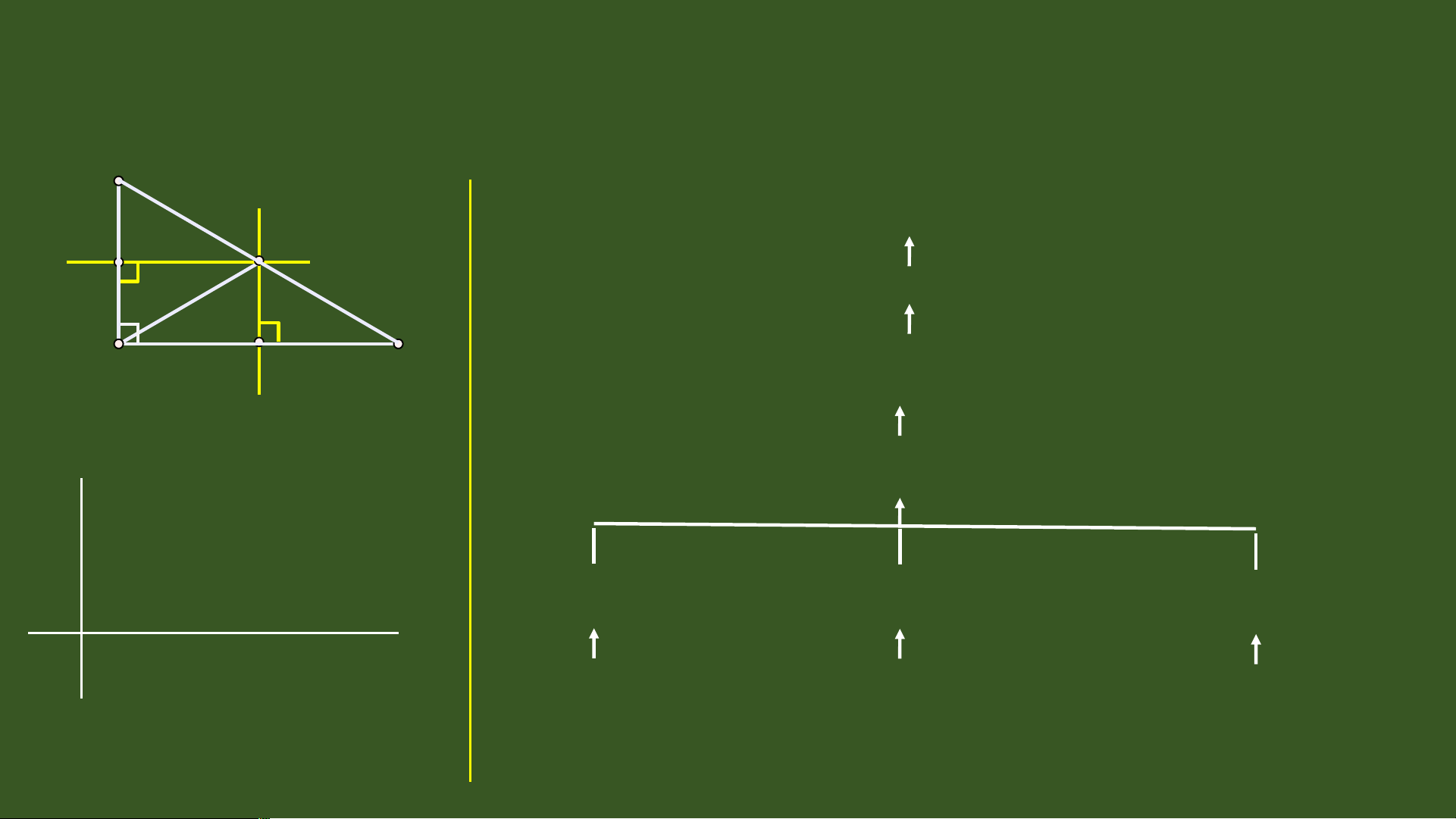
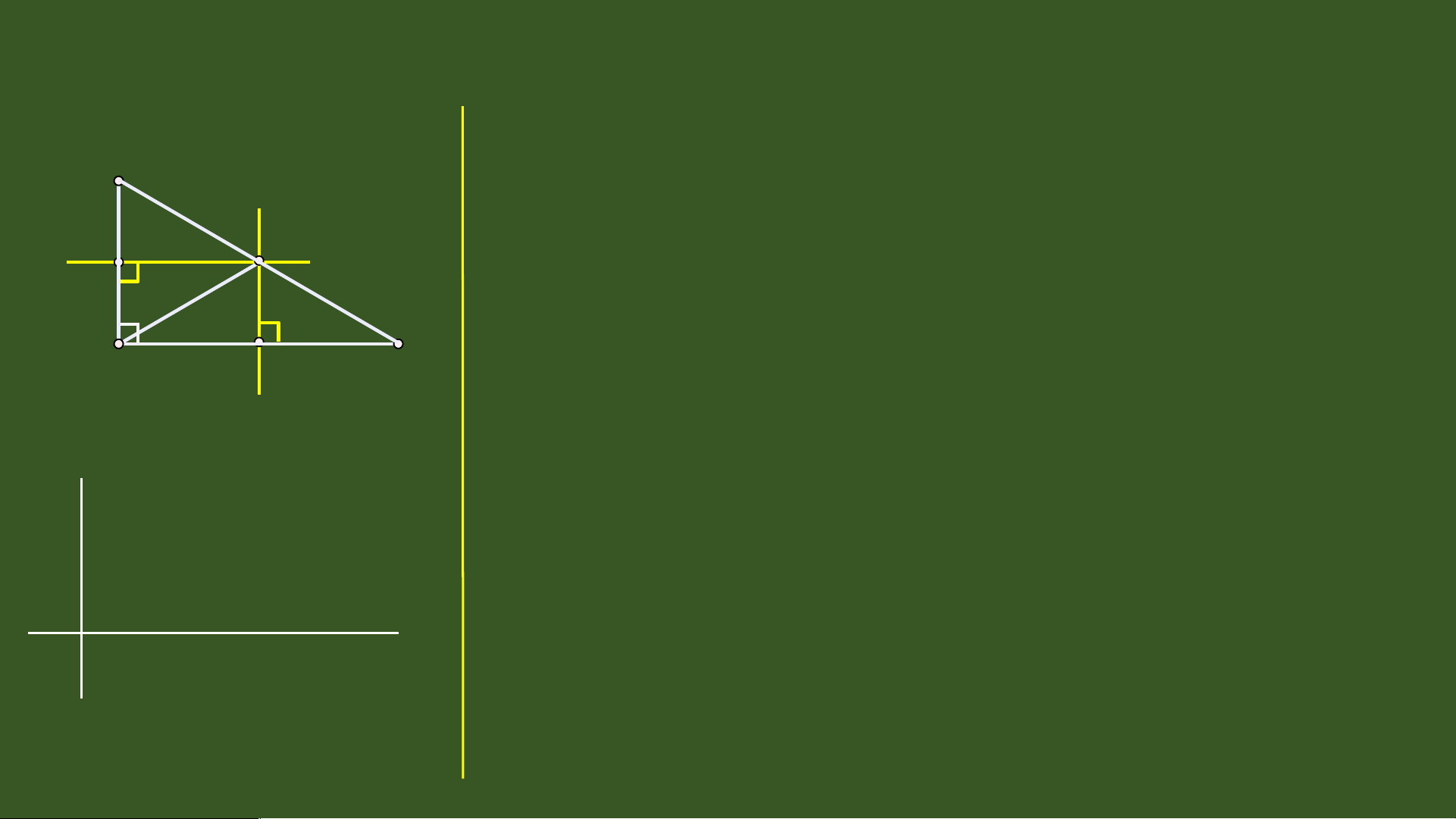
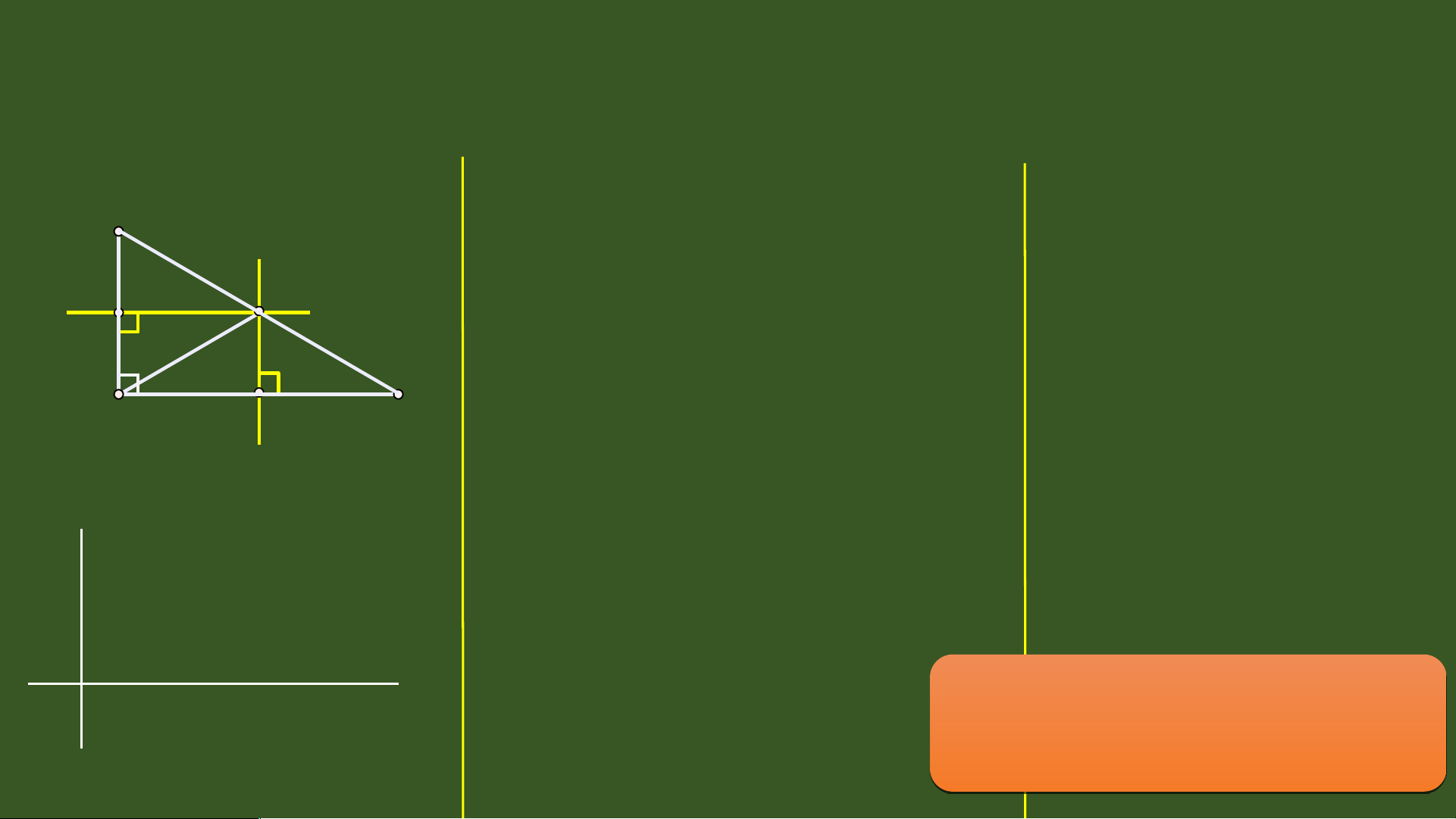
Trong một tam giác, đường trung 6
trực của mỗi cạnh gọi là đường 7 8
trung trực của tam giác đó. 9 10 11 1 I 2 I B 13 D C 14 15 16 17 18 19 20 A B C D TI T Ế 44 0 - TÍNH CH T 1 Ấ BA ĐƯ NG Ờ TRUNG TR C Ự C A Ủ TAM GIÁC I. Đường trung 2 tr c ự c a ủ tam giác A 3 4 5 d X II 6 E 7 F 8 9 II 1 X 0
- Mỗi tam giác có ba đư n ờ g trung tr c ự . 11 1 I 2 I B 13 D C 14 15 16 17 18 19 20 TI T Ế 44- TÍNH CH T Ấ BA ĐƯ N Ờ G TRUNG TR C Ự C A Ủ TAM GIÁC II. Tính ch t ấ ba đư n ờ g trung tr c ự c a ủ tam giác TI T Ế 44- TÍNH CH T Ấ BA Đ NG ƯỜ TRUNG TR C Ự C A Ủ TAM GIÁC A a b Tính chất II X
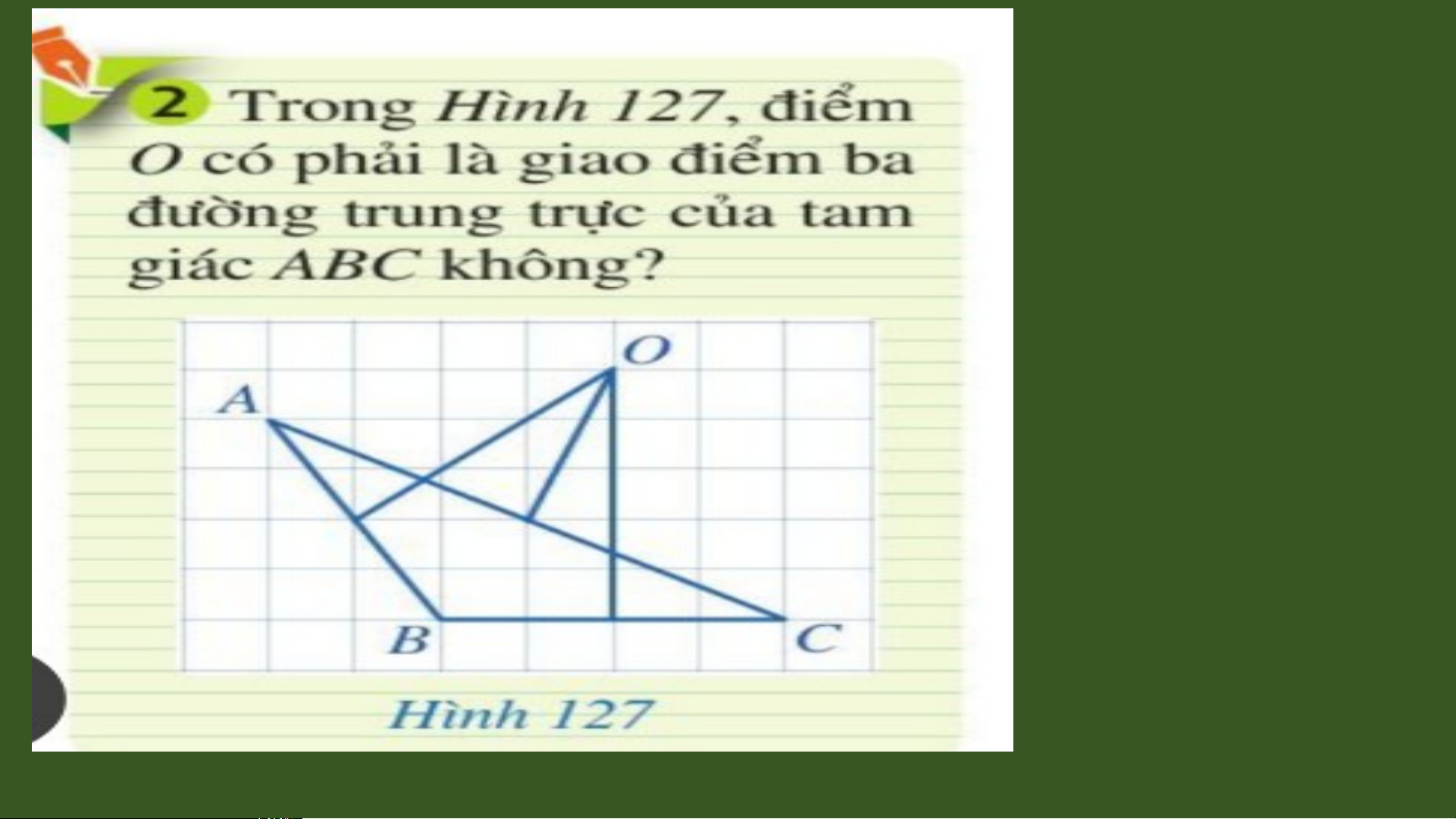
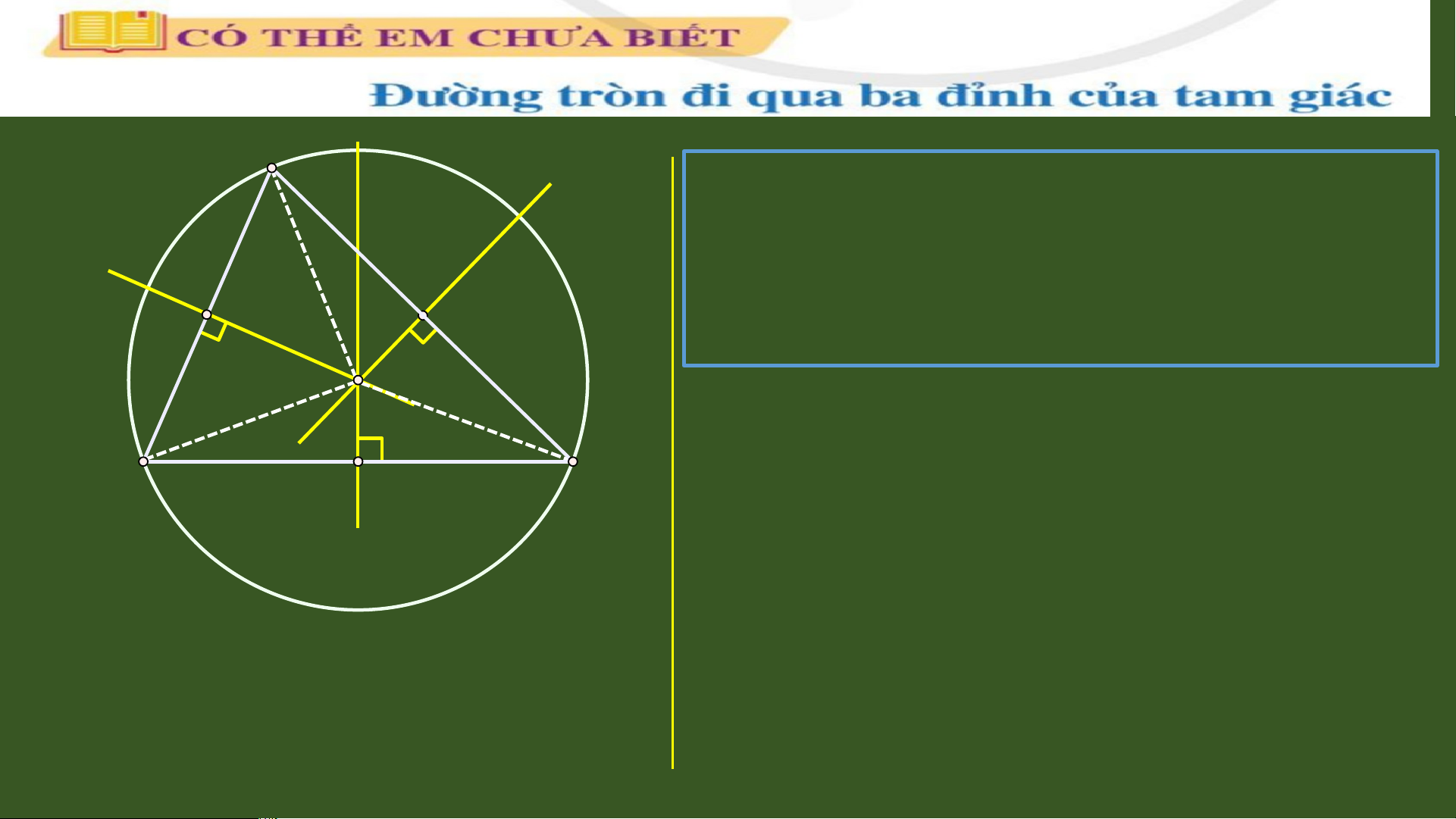
Ba đường trung tr c ự c a ủ m t ộ tam c E F giác cùng đi qua m t ộ đi m ể . Đi m ể này O cách đ u ề ba đỉnh c a t ủ am giác đó. II X Chú ý: B I D I Vì giao đi m ể O c a ủ ba đư n ờ g trung C tr c ự c a ủ cách đ u ề ba đ n ỉ h c a ủ tam giác đó nên có m t ộ đư n ờ g tròn tâm O đi qua ba đỉnh A, B, C. Ta g i ọ đư n
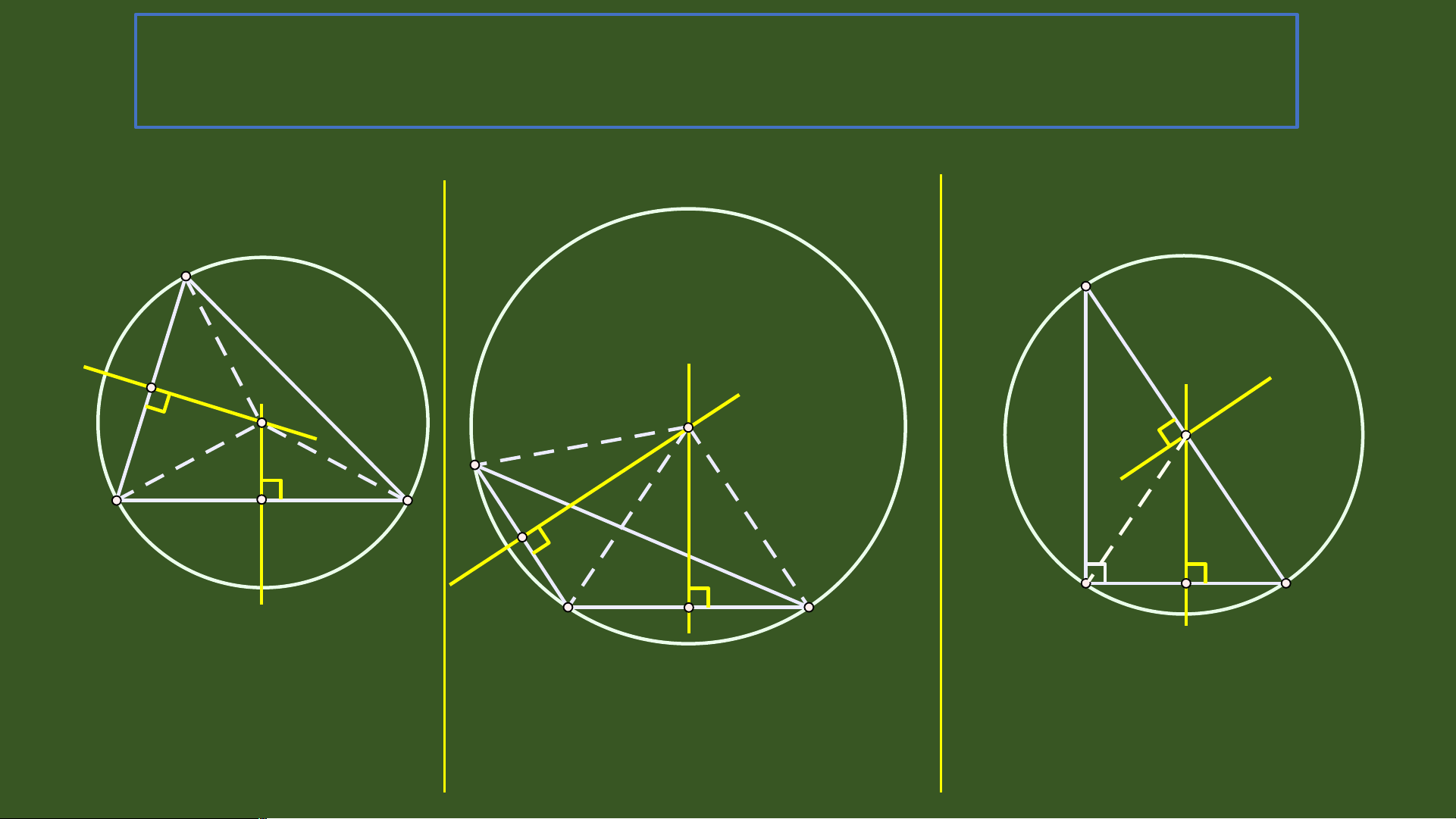
ờ g tròn đó là đư n ờ g tròn ngoại ti p ế . Bài t p ậ Xác đ n ị h v ịtrí giao ba đư n ờ g trung tr c ự và vẽ đư n ờ g tròn đi qua ba đ n ỉ h c a ủ trong các trư n ờ g h p ợ sau: đều nh n ọ
c ¿ ^A =90o b ¿ ^ A >90o A B I E X O I O O B X B I I I D C I E II I A I I I D C A D C Giao đi m ể ba đư ng ờ Giao đi m ể ba đư ng ờ trung Giao đi m ể ba đư ng ờ trung tr c n ự m ằ trong tr c ự n m ằ ngoài trung tr c l ự à trung đi m ể c nh ạ huy n ề BC c a ủ TI T Ế 44TÍNH CH T Ấ BA ĐƯỜNG TRUNG TR C Ự C A Ủ TAM GIÁC44 II, Tính ch t ấ ba đư ng ờ trung tr c ự c a t ủ am giác A a b A II X c E H F E F O I II L X B B I D I C K D C Ba đư ng t ờ rung tr c ự c a ủ m t ộ tam giác Ba đư ng p ờ hân giác c a ủ tam giác cùng đi qua m t ộ đi m ể . Đi m ể này cách đ u ề cùng đi qua m t ộ đi m ể . Đi m ể này cách ba đ n ỉ h c a
ủ tam giác đó. (là tâm đư n ờ g tròn đ u ề ba c nh ạ
của tam giác đó. (là tâm ngo i ti ạ p ế tam giác) đư n ờ g tròn n i ti ộ p ế tam giác)
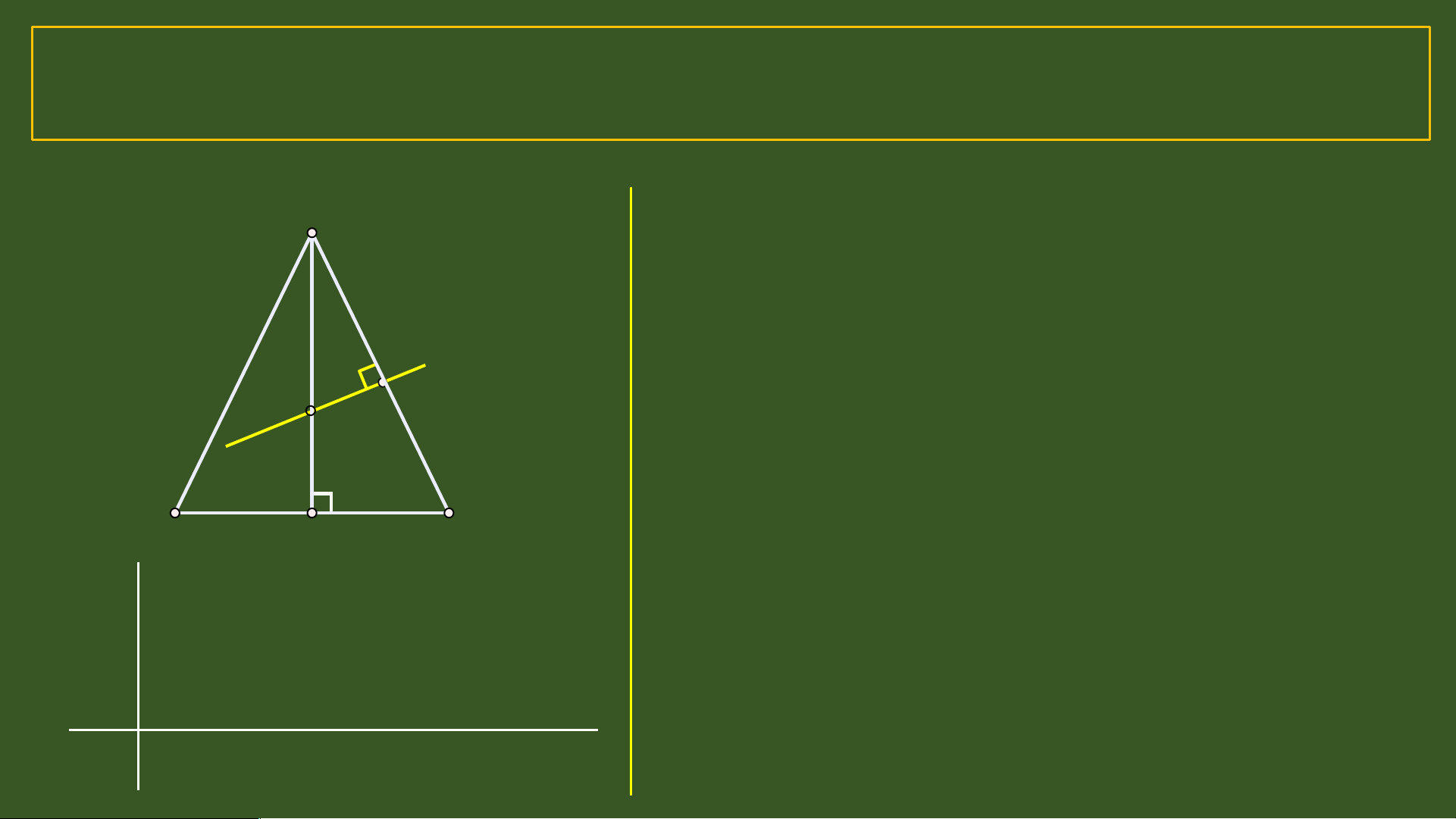
Xác định tâm đường tròn ngoại tiếp tam giác
• Để xác định tâm đường tròn ngoại tiếp tam giác ta chỉ
cần vẽ hai đường trung trực của tam giác. Giao điểm của
chúng là tâm đường tròn ngoại tiếp tam giác. A A A O O O B C B C B C
Bài toán: Có ba gia đình A, B và C (nh ư hình vẽ) d ự định đào chung m t ộ cái gi n ế g. a) Hỏi ph i ả ch n ọ v ịtrí c a ủ gi ng ế ở đâu đ ể kho n ả g cách t ừ gi n ế g đ n ế hai nhà A và B b ng ằ nhau? C b) H i ỏ ph i ả ch n ọ v ịtrí c a ủ gi ng ế ở đâu đ ể kho n ả g cách t ừ gi ng ế đ n ế ba nhà b ng ằ nhau? II HD: Coi ®Þa ®iÓm ba gia O
®×nh lµ ba ®Ønh cña tam gi¸c ABC II
=> VÞ trÝ chän ®Ó ®µo giÕng
lµ giao ®iÓm c¸c ® ưêng
trung trùc cña tam gi¸c ABC I I A B Tr T o r ng m g t ộ tam a giác, giác đ , n ườ g tru tr ng tr g c ự c c a ủ m i ỗ c n ạ h h g i ọ là đ là n ườ g tru tr ng g tr c ự c c a ủ t a am a giác giác đó. A A II X d E F II O X B D C B I D I C d A Tr T o r ng m g t ộ tam a gi m ác ác câ c n â , đư đ n ờ g tr g un u g tr c ự c Ba đ Ba n ườ g tru tr ng g tr c ự c c a ủ c n ạ h đá đ y á đ n ồ g g X X củ c a a m t ộ tam ta giác giác cù c n ù g th i ờ là đư n ờ g g tru tr ng đi qu q a a m t ộ đi đ m. ể Đi m ể tuy tu n ế n n ứ g v g i ớ c n ạ h n này à các c h ác đ u ề ba a đ n ỉ h này à .y B D C củ c a tam a gi g ác á đó.
TIẾT 45 – LUYỆN TẬP
TÍNH CHẤT BA ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC Bµi tr¾c nghiÖm
Điền kí hiệu đúng (Đ) hoặc sai (S) vào ô trống:
1. Đường tròn ngoại tiếp tam giác ABC là đường
tròn đi qua ba đỉnh A, B, C của tam giác đó. §
2. Trong một tam giác, đường trung trực của cạnh
đáy đồng thời là đường trung tuyến ứng với S cạnh này.
3. Ba đường trung trực của một tam giác cùng đi S
qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.
4. Mỗi tam giác có ba đường trung trực. §
5. Tập hợp các điểm cách đều hai mút của một đoạn §
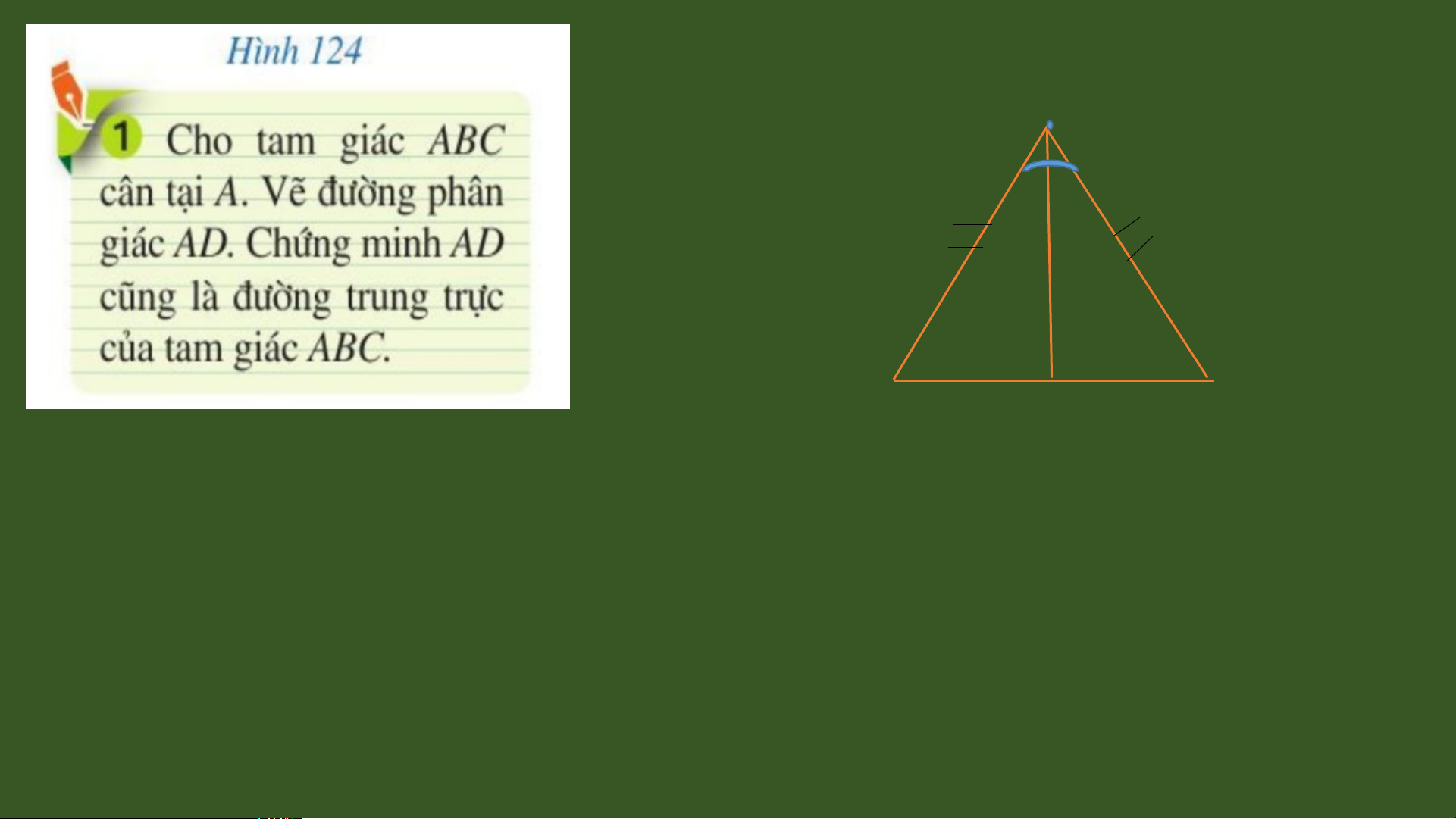
thẳng là đường trung trực của đoạn thẳng đó. Bài 1: Cho có đư n ờ g trung tuy n ế AD đ n ồ g th i ờ là đư n ờ g trung tr c ự n ứ g v i ớ c n ạ h BC c a ủ tam giác. Ch n ứ g minh cân t i ạ A. A
Hướng dẫn giải Vì AD là đư n ờ g trung tr c ự c a ủ đo n ạ BC thu c ộ đư n ờ g trung tr c ự c a ủ đo n ạ BC
(TC đường trung tr c ự của đo n ạ th n ẳ g) cân t i A I I ạ B C D ∆ ABC Đ n ị h lí h : lí N u ế t u a t m g a iá m g c iá có c m ó t đ ộ ư n ờ g n g tru tr ng n g AD là đường trung tuy n ế c a ủ GT tuy tu n ế đ n ồ g n t g h t i là ờ i là đư n ờ g tr g u tr ng n t g r t c ự n ứ g n g v i ớ AD là đường trung tr c ự n ứ g v i ớ cùng m t c ộ n
ạ h thì tam giác đó là m t t ộ am giác c cùng m t c ộ n
ạ h thì tam giác đó là m t t ộ am giá ạnh BC của câ c n â . n KL cân tại A Bài 2: Cho hình vẽ. Ch n ứ g minh ba đi m ể B, C, D th n ẳ g hàng. BI B, D, C th ng ẳ hàng I b D II ^ BDC=180o 1 2 A I I C ^ ADB+^ ADC=180o c ^ ADB ^ BAC + ^
A D C=36 0o− 2( ^ A =90o 1+ ^ A2) c là trung tr c c ự n ạ h AB GT b là trung tr c ự c nh ạ AC ^ A ^ 1 + ^ A2=90o ADB=180o −2 ^ A ^ ADC=180o− 2 ^ A 1 2 b c t ắ c t i D ạ KL B, C, D th ng ẳ hàng ^ BAC=90o cân t i D ạ cân t i ạ D
Bài 55 (SGK/tr80): Cho hình vẽ. Ch n ứ g minh ba đi m B ể , C, D th n ẳ g hàng.
Hướng dẫn giải Vì D thuộc trung tr c ự đo n ạ AB (gt) B (tính ch t
ấ đường trung tr c ự ) II b D cân tại D II ⇒ ^ ADB=180o −2 ^ A (1) 1 1 2 Vì D thuộc trung tr c ự đo n ạ AC (gt) A I I C c (tính ch t
ấ đường trung tr c ự ) cân tại D ^ BAC (2) =90o ⇒ ^
ADC =180o − 2 ^ A2 c là trung tr c c ự n
ạ h AB Từ (1) và (2) ⇒ ^ ADB+^
A D C ¿ 180o− 2 ^ A1+180o − 2 ^ A2 GT b là trung tr c ự c nh ạ AC ¿ 36 0o −2 ^ A −2 ^ A 1 2 b c t ắ c t i D ạ ¿ 36 0o −2( ^ A1+^ A2) Mà KL B, C, D th ng ẳ hàng ⇒ ^ ADB +^
A D C=360o −2. 90o ⇒ ^ ADB +^ A D C=18 0o Hay thẳng hàng (đpcm) Bài 2 Cho hình vẽ. Ch ng ứ minh ba đi m ể B, C, D th ng ẳ hàng. Bài 3 Đi m ể D cách đ u ề ba đ nh ỉ c a A ủ BC vuông t i ạ A. Ch ng ứ minh D là trung đi m ể BC
Hướng dẫn giải Vì D thuộc trung tr c ự đo n ạ AB (gt) B Mà (tính ch t
ấ đường trung trực) II b D cân tại D ⇒ ^ ADB +^
A D C=360o −2.90o II ⇒ ^ ADB=180o −2 ^ A (1) ⇒ ^ ADB +^ A D C=18 0o 1 1 2 Vì D thuộc trung tr c ự đo n ạ AC (gt) Hay A I I C c (tính ch t
ấ đường trung trực) thẳng hàng (3) cân tại D Vì DA = DB và DA = DC (cmt) ^ BAC (2) =90o ⇒ ^
ADC =180o − 2 ^ A2 Þ DB = DC (4) c là trung tr c c ự n ạ h AB Từ (1) và (2) Từ (3) và (4) GT b là trung tr c ự c nh ạ AC ⇒ ^ ADB+^ A D C D là trung điểm BC b c t ắ c t i D ạ ¿ 180o− 2 ^ A1+180o − 2 ^
A2 Nhận nxéxté: :TrTorng m n ột tta t m a gi g ác á vuô vu ng, g KL B, C, D th ng ẳ hàng ¿ 36 0o −2 ^ A −2 ^ A 1 2 đư đ ờng t g ru r ng t n u g t y u ến n n ứ g g vớ v i c i n ạ h n ¿ 36 0o −2( ^ A
huyền bằng một nửa cạnh huyền. 1 + ^ A2)
huyền bằng một nửa cạnh huyền Bài3 Cho cân t i ạ A, đư n ờ g trung tuy n ế AM. Đư n ờ g trung tr c ự c a A ủ C c t ắ AM ở D. Ch n ứ g minh r n ằ g DA = DB. A
Hướng dẫn giải Xét ABC cân t i A ạ , có: II AM là đư n ờ g trung tuy n ế D Þ AM đ ng ồ th i là đ ờ ư ng ờ trung tr c ự c a B ủ C II mà đư ng ờ trung tr c ự c a A ủ C c t ắ AM t i D ạ (gt) I I B C M Þ D là giao đi m ể c a ủ ba đư n ờ g trung tr c ự c a ủ ABC cân tại A Þ D đư ng ờ trung tr c c ự a ủ AB AM là đường trung tuy n ế c a ủ
GT Đường trung trực của AC c t ắ AM
Þ DA = DB (TC đi m t ể hu c đ ộ ư n ờ g trung tr c ự ) tại D KL DA = DB HƯỚNG D N Ẫ VỀ NHÀ - H c ọ thu c ộ lý thuy t ế và ôn các bài t p ậ đã làm
- Làm các bài 3,4,5 (SGK – trang 116)
- Chuẩn b ịbài 13 “Tính ch t ấ ba đư n ờ g cao c a ủ tam giác”
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Xác định tâm đường tròn ngoại tiếp tam giác
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28




