Giáo án điện tử Toán 7 Bài 12 Kết nối tri thức: Tổng các góc trong một tam giác
Bài giảng PowerPoint Toán 7 Bài 12 Kết nối tri thức: Tổng các góc trong một tam giác hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 7. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 7
Môn: Toán 7
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
CHÀO MỪNG QUÝ THẦY CÔ
VỀ DỰ GIỜ LỚP 7B4 MÔN: TOÁN 7
BÀI 12: TỔNG CÁC GÓC TRONG MỘT TAM GIÁC GV: NGUYỄN THỊ HUYỀN CHƯƠNG IV TAM GIÁC BẰNG NHAU 1 1
Tổng các góc trong một tam giác.
Hai tam giác bằng nhau. Trường hợp bằng nhau thứ 2 2 nhất của tam giác. 3 3
Trường hợp bằng nhau thứ hai và thứ ba của tam giác. 4 4
Các trường hợp bằng nhau của tam giác vuông. 5 5
Tam giác cân. Đường trung trực của đoạn thẳng.
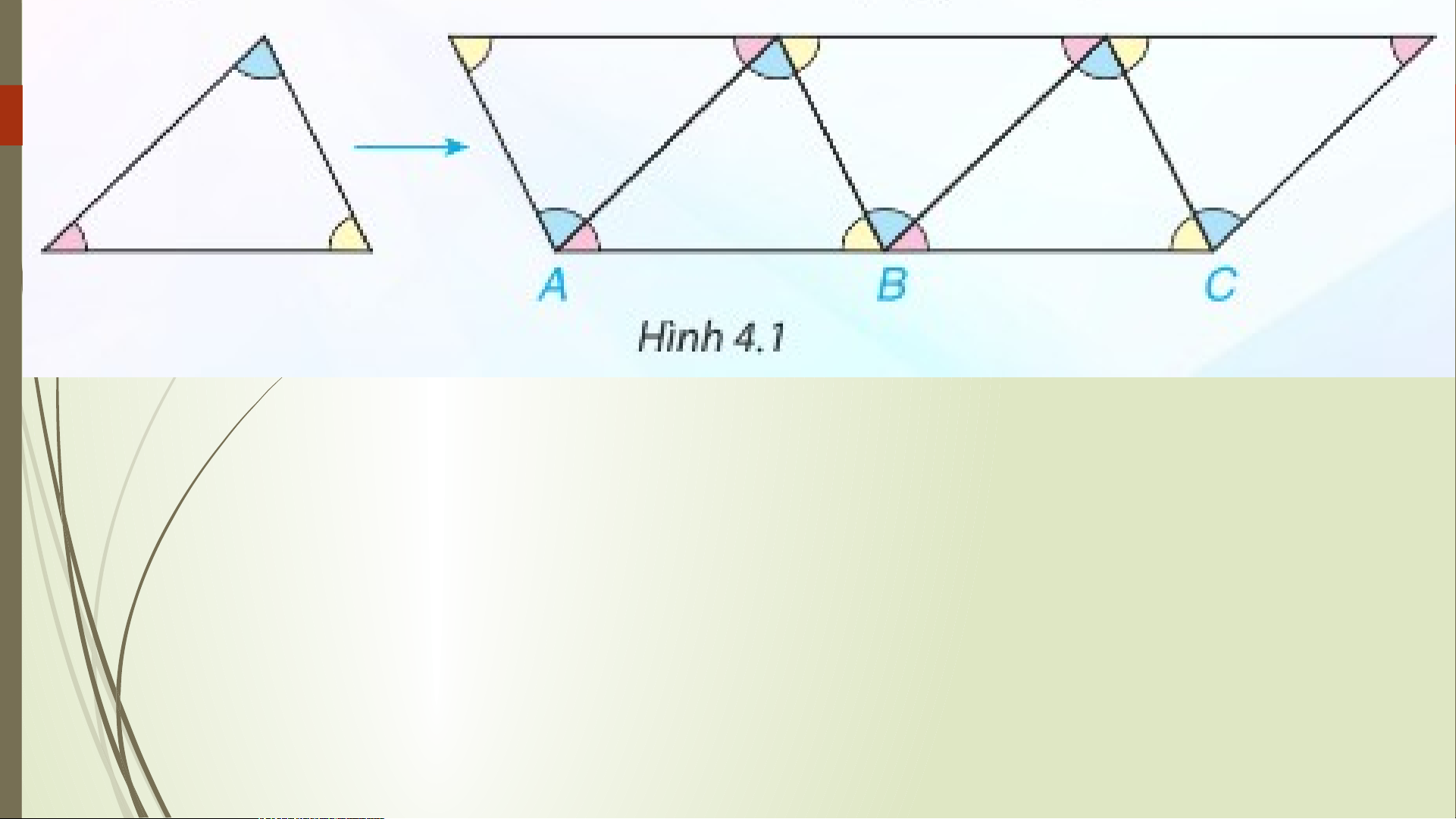
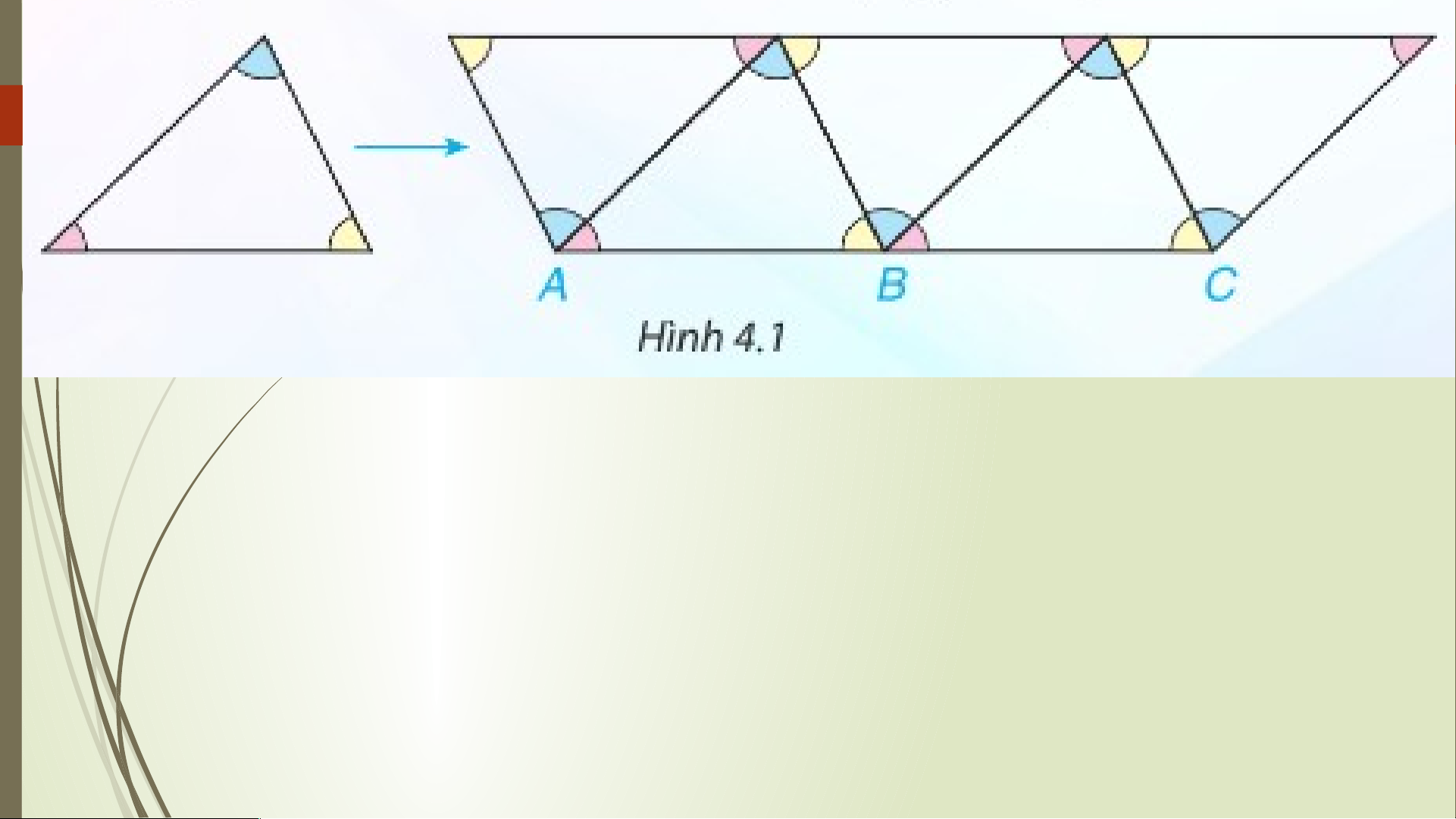
Em có nhận xét gì về ba góc tại mỗi đỉnh chung của
ba tam giác? Từ đó em rút ra kết luận gì về vị trí của ba điểm A, B, C? HOẠT Đ ĐỘNG
Về nhà ( hoạt động cá nhân)
+ Cắt rời một tam giác ABC từ một tờ giấy.
+ Đo các góc của tam giác ABC vừa cắt (ghi số đo vào các góc).
+ Tính tổng số đo ba góc của tam giác ABC. A ...0 B …0 …0 C HOẠT HOẠT ĐỘNG
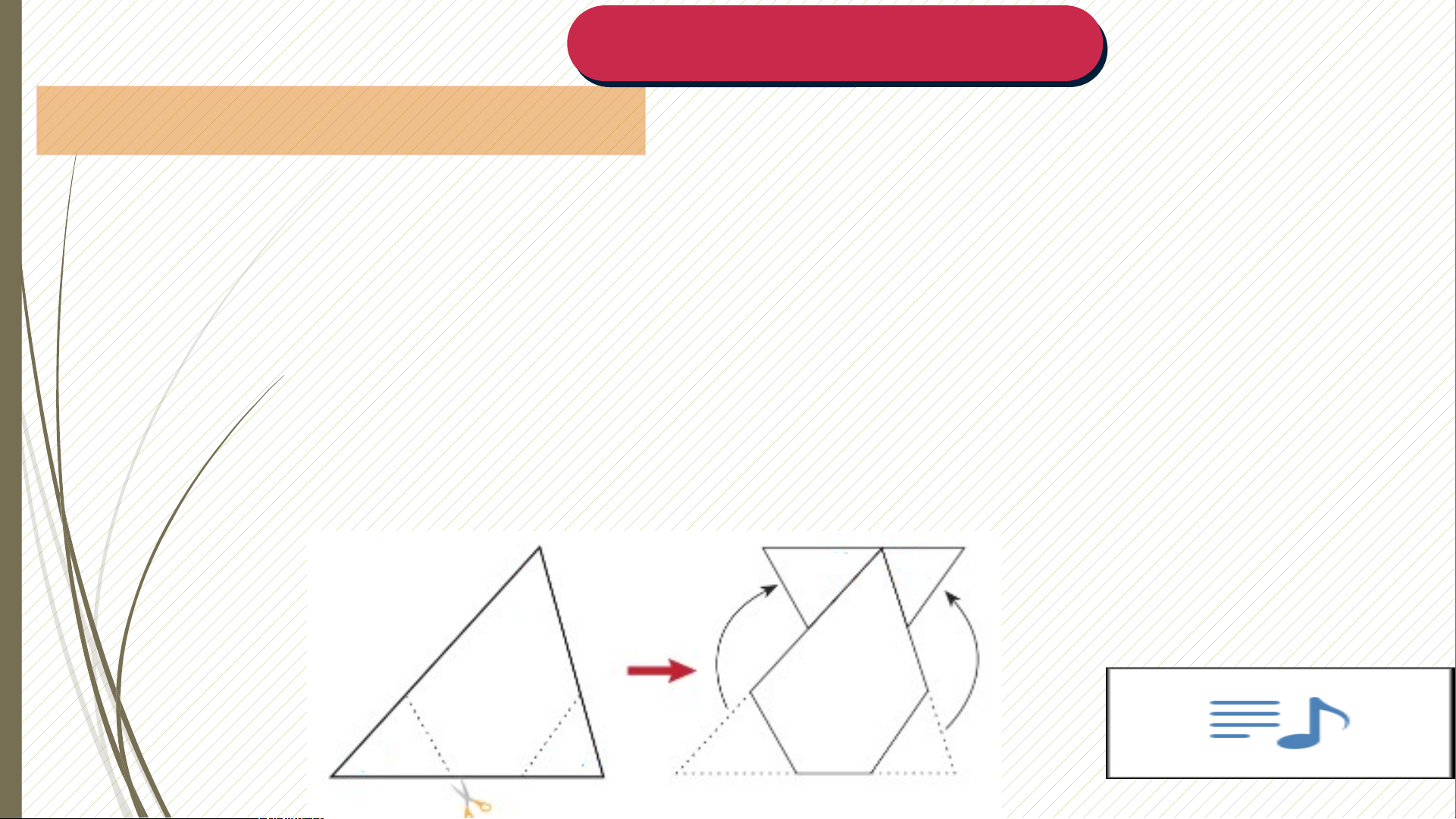
Hoạt động nhóm 4 (3 phút) A
1. So sánh tổng số đo ba góc của mỗi tam giác mà các thành viên B C
trong nhóm đã chuẩn bị. => Rút ra nhận xét.
2. Cắt hai góc B và góc C ghép lên góc A như hình => Dự đoán
tổng số đo các góc của tam giác ban đầu. A B AC B C ĐỊNH LÝ
Tổng ba góc trong một tam giác bằng 1800
Nghiên cứu phần chứng minh – 2 phút Chứng minh:
Qua A kẻ đường thẳng xy song song với BC. xy // BC ⇒ ^ 𝐵=^ 𝐵𝐴𝑥 ; ^ 𝐶=^
𝐶𝐴𝑦 (các cặp góc so le trong) Do đó
Tổng ba góc tại mỗi đỉnh chung của ba tam giác bằng
bao nhiêu độ? Ba điểm A, B, C có thẳng hàng không? Ví dụ 1
Tính số đo các góc A, D, P trong Hình 4.4. A F M 500 900 300 600 B 500 600 C D E N P Giải: Trong ABC có: . Do đó: - - A Chú ý: 700
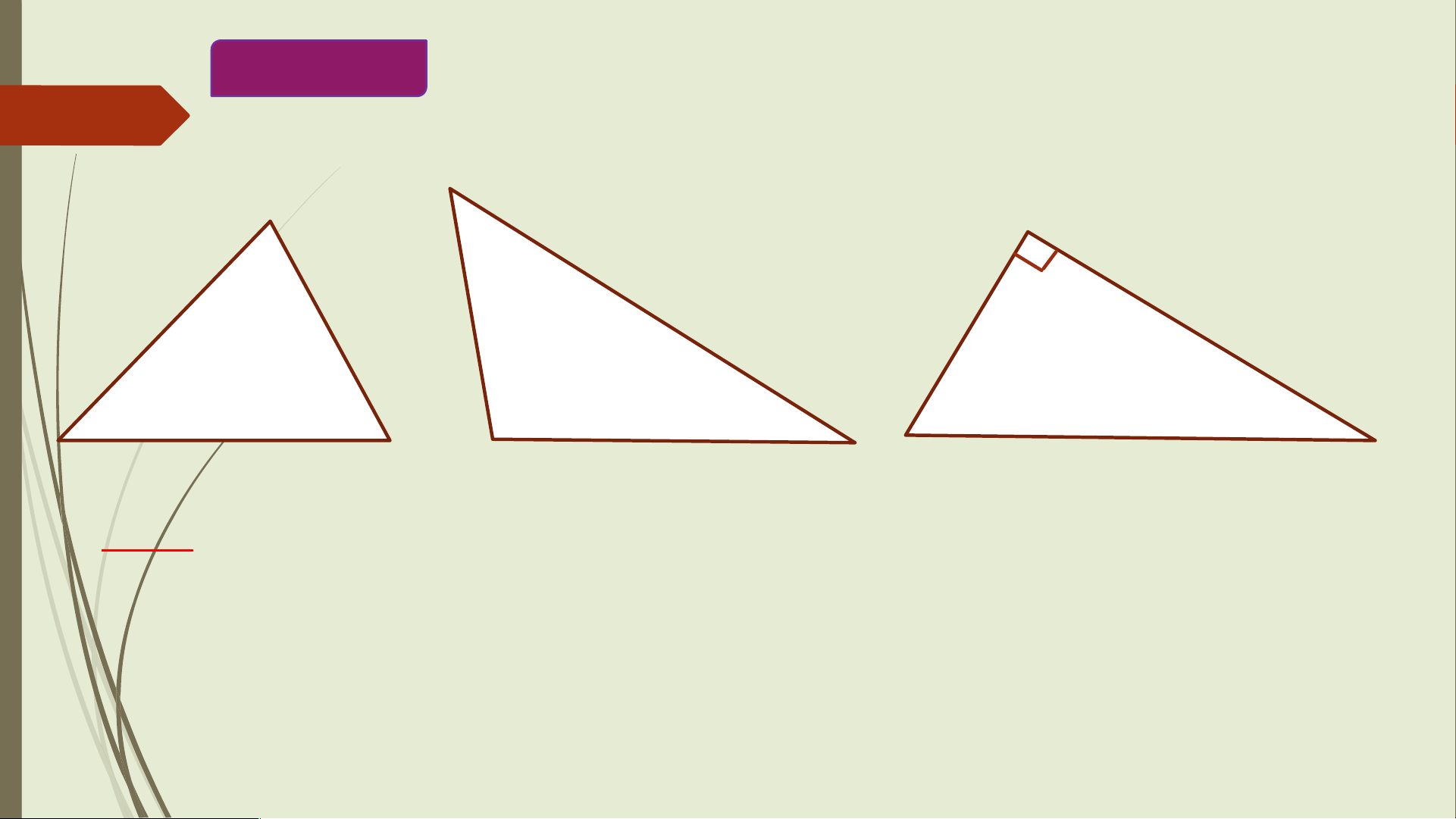
- Tam giác ABC có ba góc đều nhọn
nên gọi là tam giác nhọn B 500 600 C F 500
- Tam giác DEF có một góc tù nên gọi là tam giác tù. 1000 300 D E Chú ý:
- Tam giác MNP có một góc vuông nên gọi là tam giác vuông M Cạnh góc vuông Cạnh góc vuông 900 N P Cạnh huyền MNP vuông tại M. Cho hình vẽ:
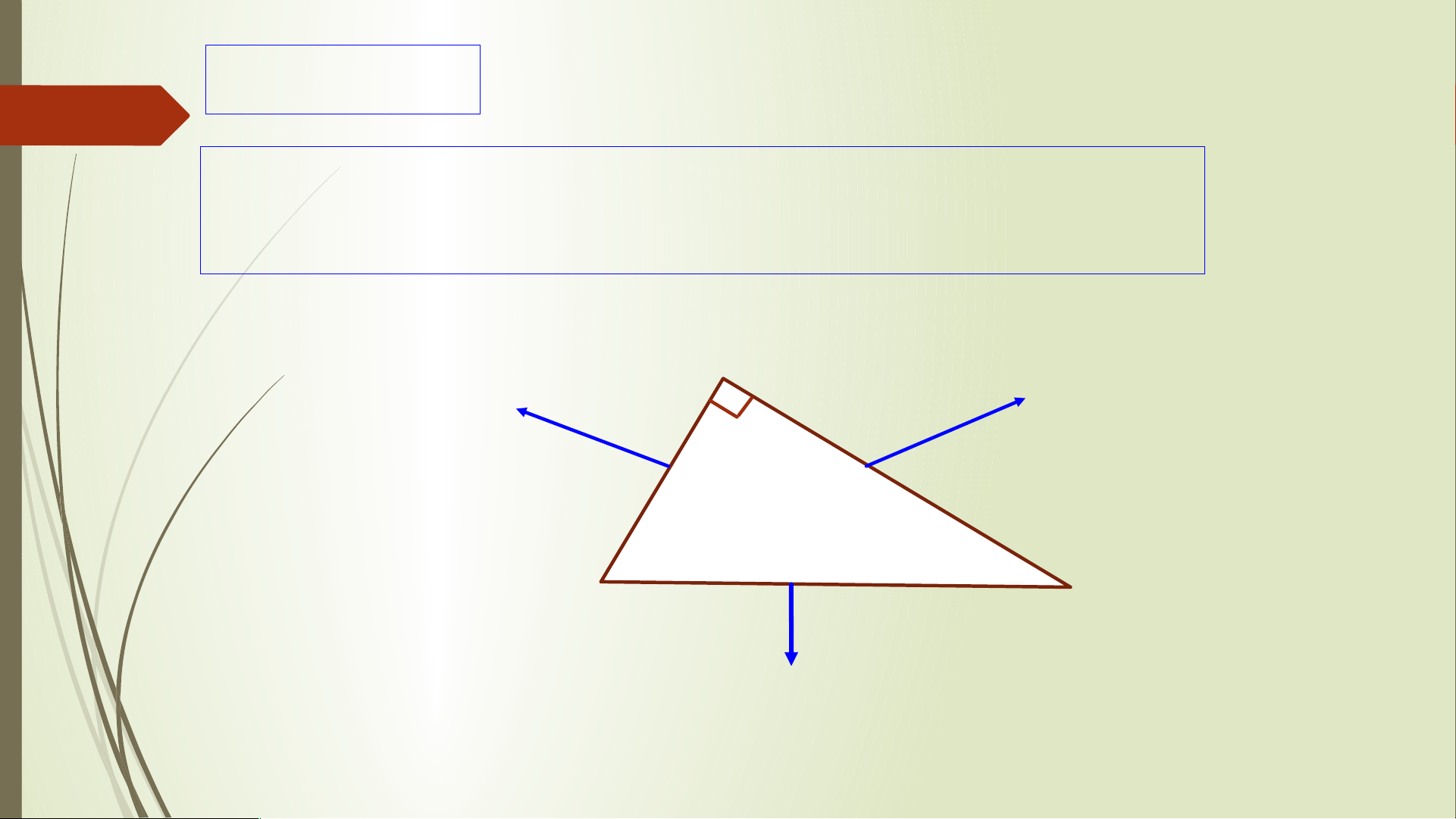
a) Hãy chỉ ra các yếu tố trong tam giác vuông.
b) Cho tam giác ABC vuông tại A. Tính tổng hai góc B và C.
Thảo luận nhóm đôi – 2 phút B A C
Cho tam giác ABC vuông tại A. Tính tổng hai góc B và C. Giải: Trong tam giác ABC ta có: .
Mà tam giác ABC vuông tại A nên Do đó: Nhận xét:
- Hai góc có tổng bằng 900 được gọi là hai góc phụ nhau.
- Trong tam giác vuông, hai góc nhọn phụ nhau. Vận dụng
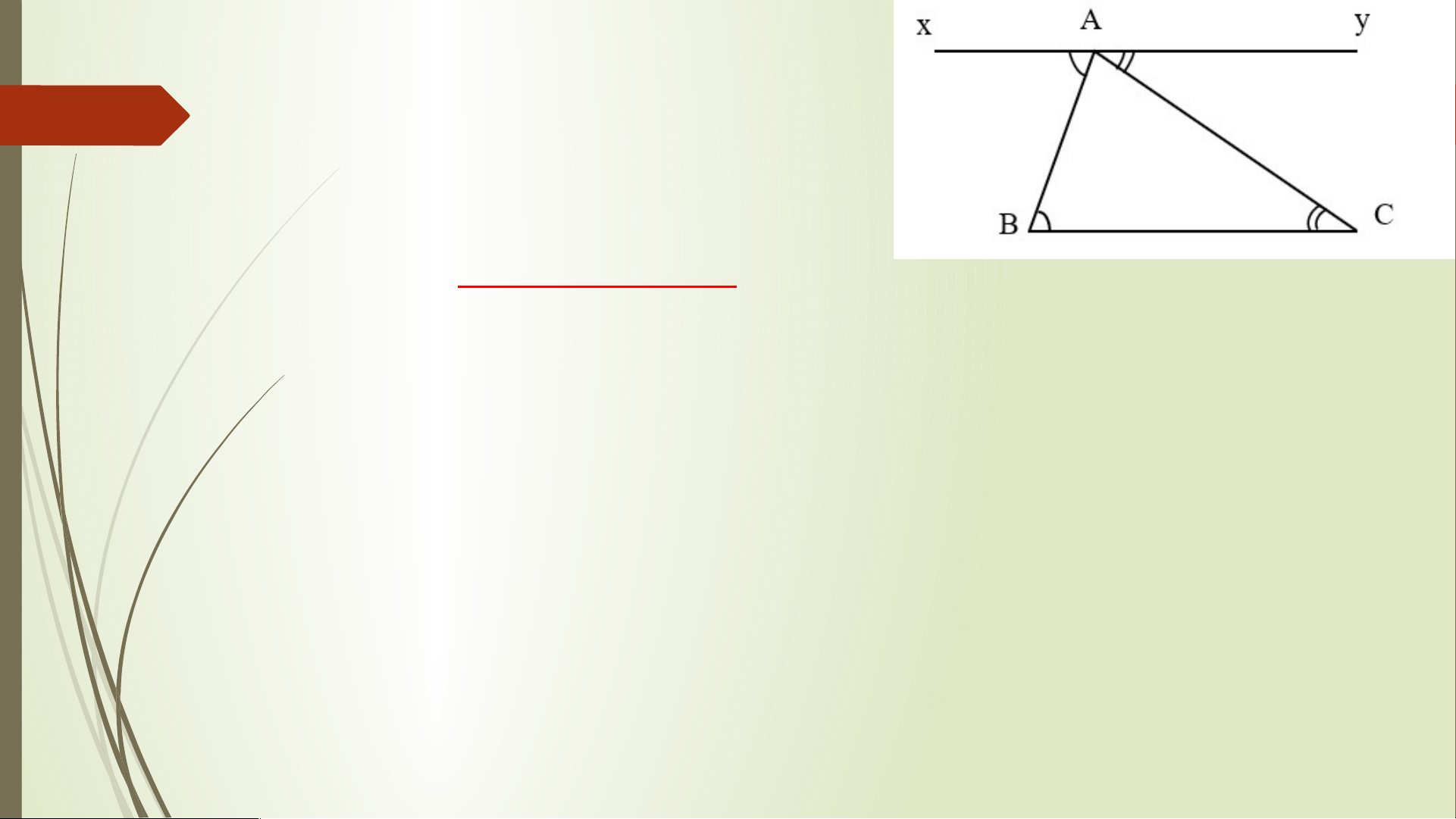
Cho tam giác ABC và Cx là tia đối của tia CB (H.4.5). Chứng minh rằng A
Hoạt động nhóm lớn – 4 phút B C x H.4.5 A B C x
Nhận xét: Góc ACx được gọi là góc ngoài tại C của
tam giác ABC. Góc ACx không kề với góc A và B của tam giác ABC TRÒ CHƠI:
GIẢI CỨU RỪNG XANH
Rừng đang bị tàn phá nghiêm trọng,
hàng trăm loài động vật bị đe dọa.
Các bạn hãy giúp khôi phục lại khu rừng
và đưa các loài động thực vật trở về rừng
bằng cách trả lời đúng các câu hỏi.
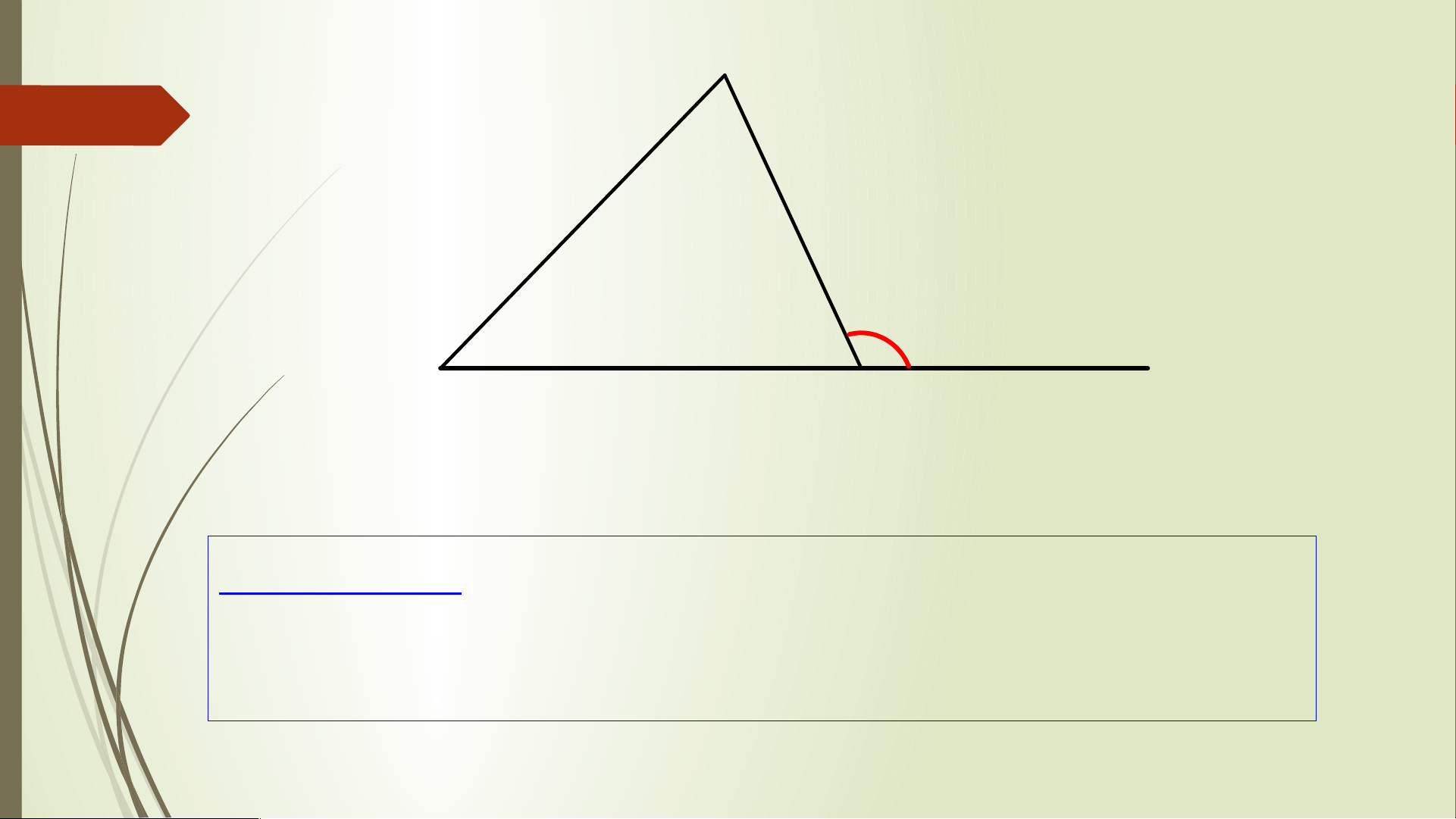
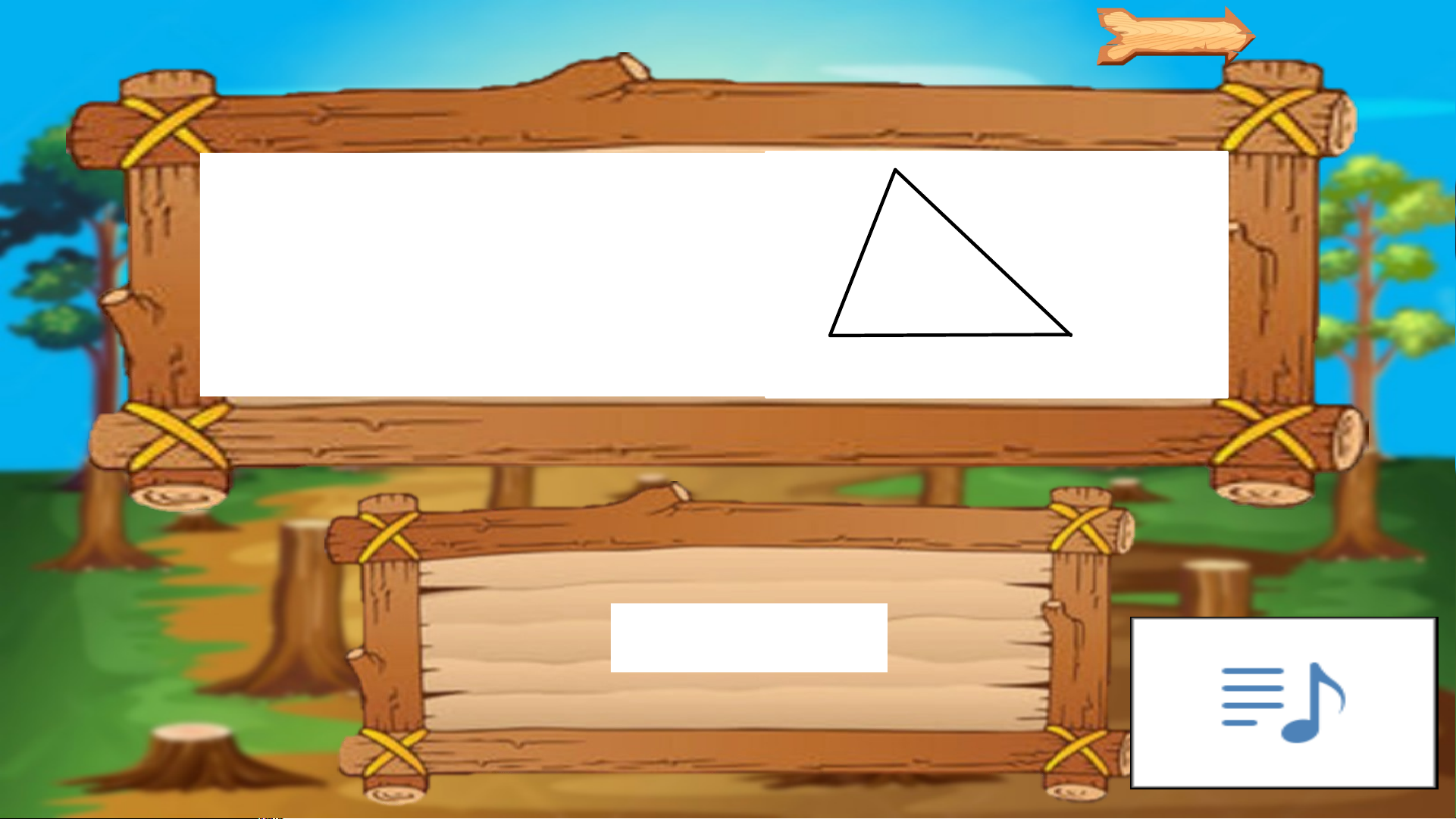
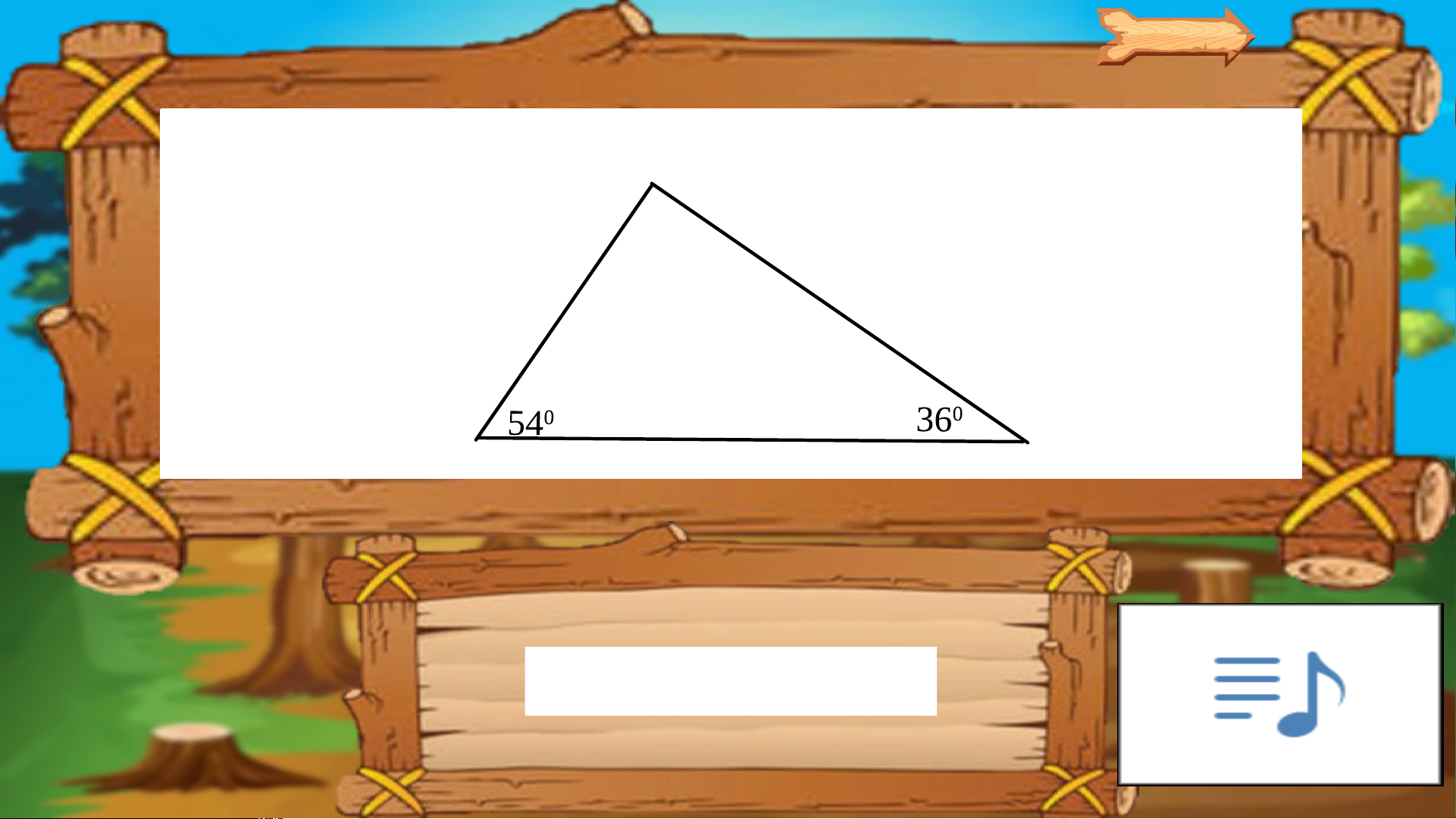
Số đo x trong hình vẽ là: 600 700 x x = 500
Số đo y trong hình vẽ là: 900 550 y x = 350
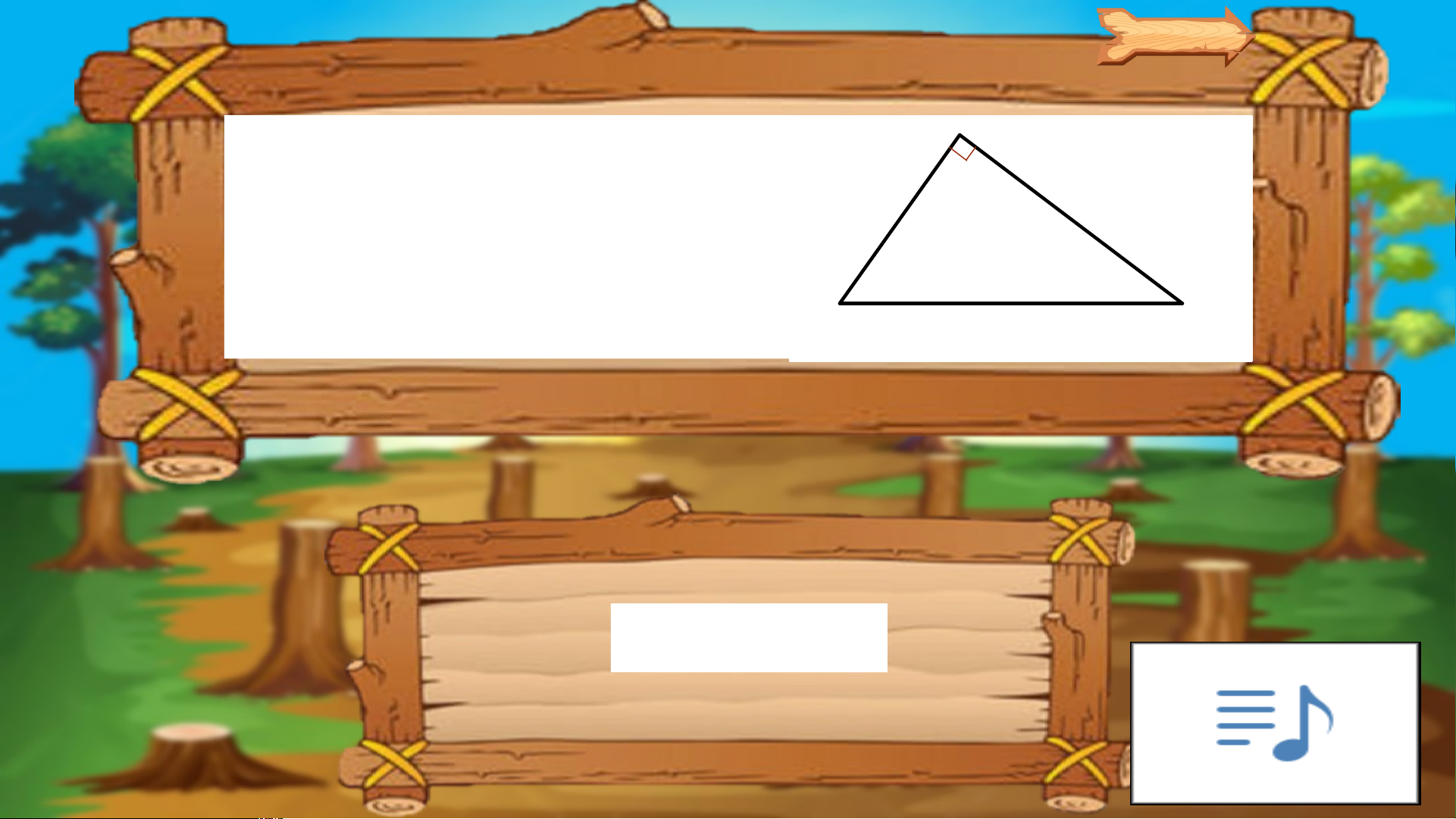
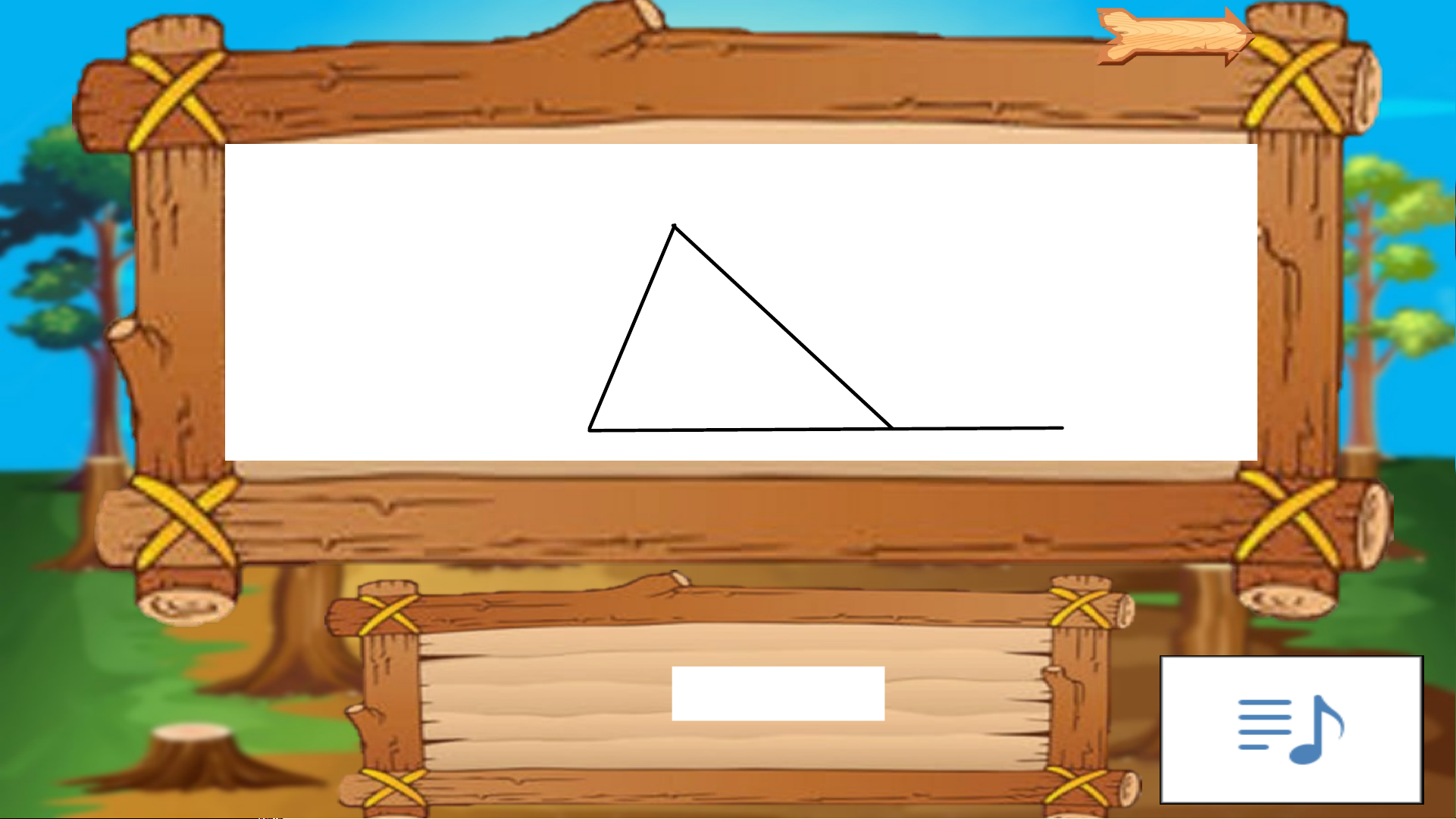
Tam giác trong hình vẽ là tam giác gì? Tam giác vuông
Số đo z trong hình vẽ là: 710 680 z x= 1390
HƯỚNG DẪN VỀ NHÀ -
Học thuộc định lý tổng các góc trong một tam giác. -
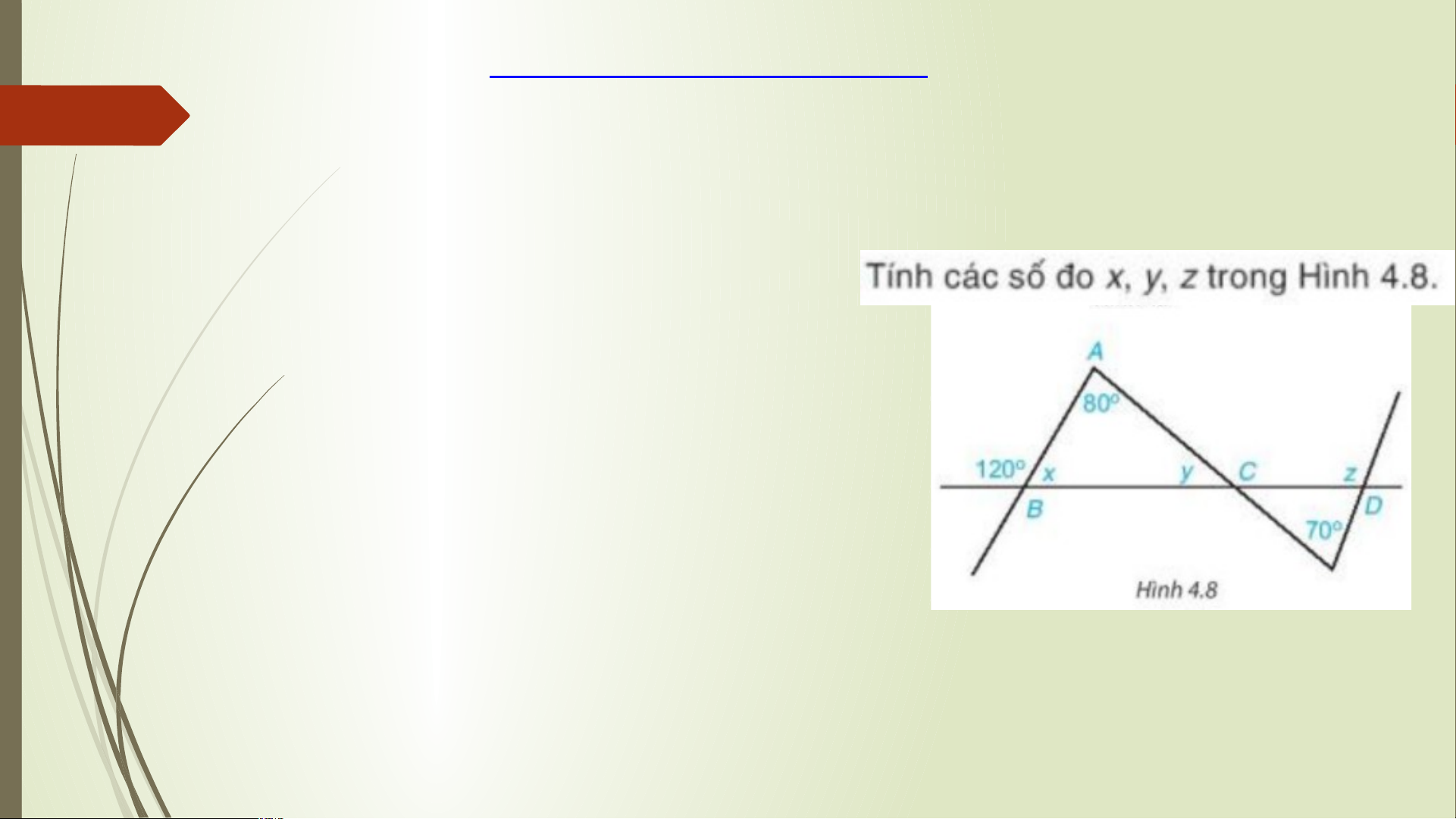
Làm các bài tập trong SGK: 4.1; 4.2; 4.3 trang 62. - Hướng dẫn làm bài 4.3
+ Tính x dựa vào tính chất hai góc kề bù
+ Tính y dựa vào tổng các góc trong một tam giác
+ Tính z: . Tính góc tại đỉnh C dựa vào
tính chất hai góc đối đỉnh.
. Tính z dựa vào tính chất góc ngoài của tam giác.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26