Giáo án điện tử Toán 7 Bài 13 Kết nối tri thức: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Bài giảng PowerPoint Toán 7 Bài 13 Kết nối tri thức: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 7. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 7
Môn: Toán 7
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC TRẮC NGHIỆM
Tổng ba góc trong một tam giác bằng ? SAI A. C. 1000 900 ĐÚNG B. 1200 D. ĐÁP ÁN 1800 SAI TRẮC NGHIỆM
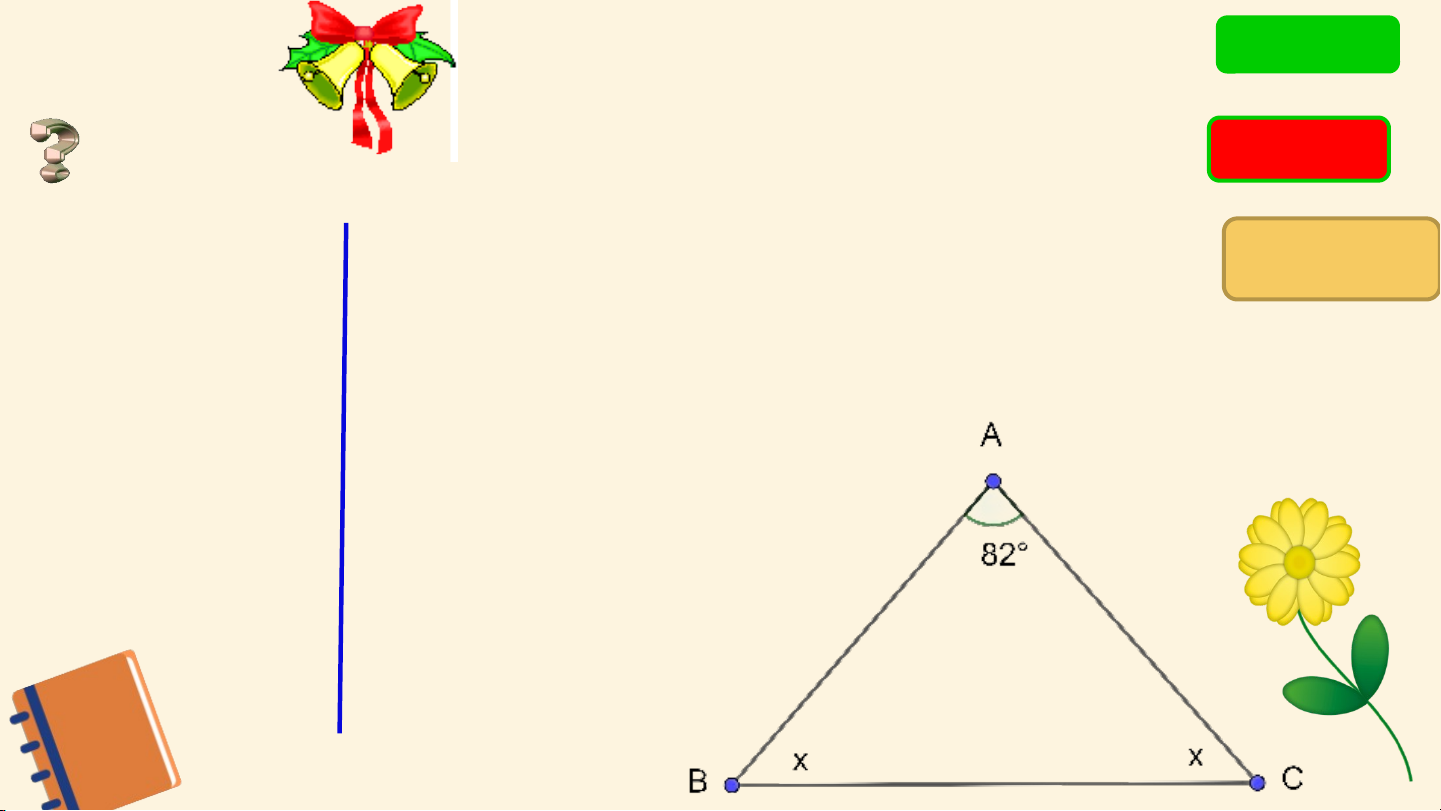
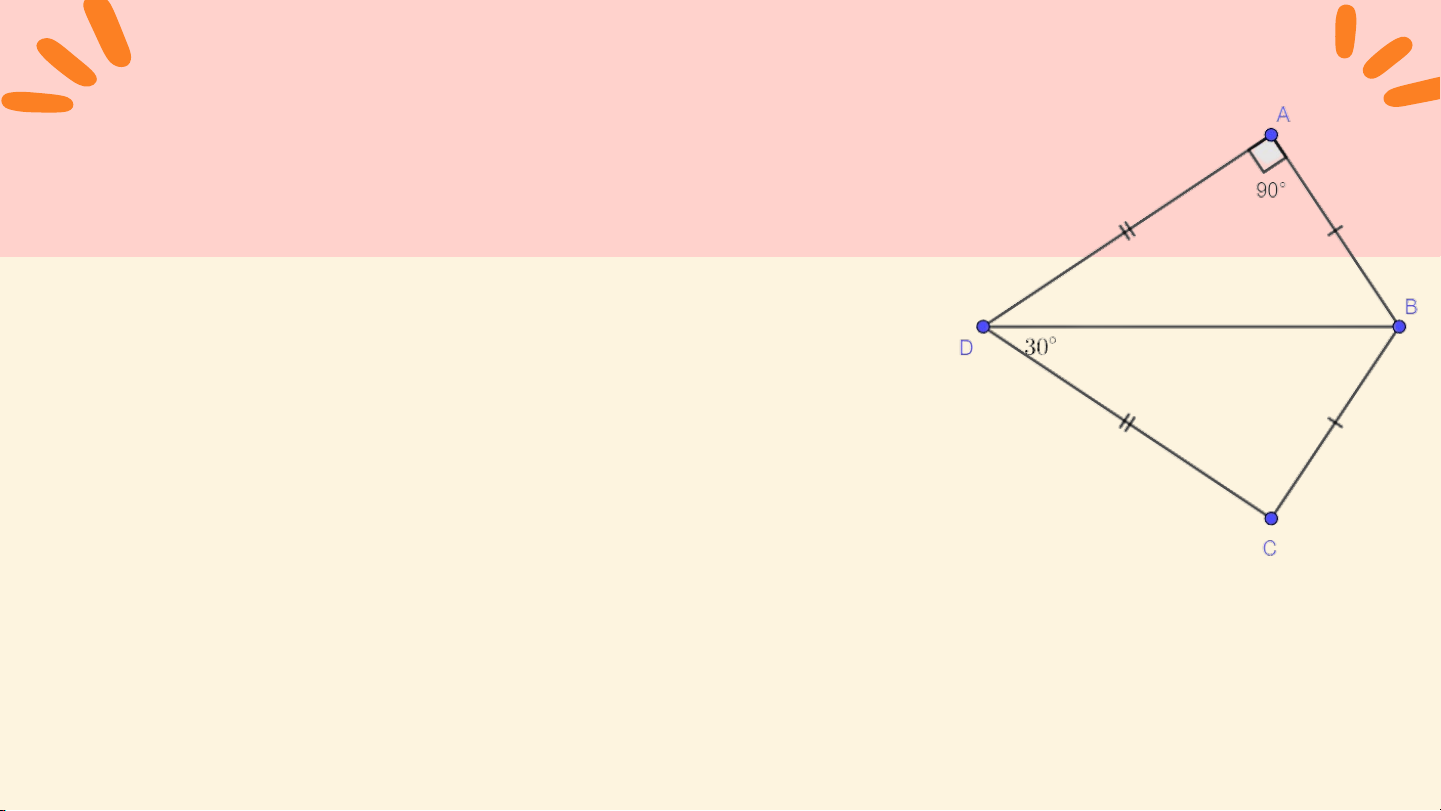
Cho hình vẽ sau, số đo x là ĐÚNG A. 98°; Hướng dẫn ĐÁP ÁN Xét tam giác ABC có: B. 49°; =180° (tổng 3 góc trong tam giác) C. 54°; ⇒ 82°+ x + x = 180° D. 44°; ⇒ 2x = 180°− 82° ⇒ 2x = 98° ⇒ x = 49° KHỞI ĐỘNG
Ta nói hai đoạn thẳng bằng nhau nếu chúng
Thế nào là hai đoạn thẳng bằng nhau ?
có cùng độ dài, hai góc bằng nhau nếu chúng
Thế nào là hai góc bằng nhau ? “
có cùng số đo góc. Vậy hai tam giác như thế
nào thì được gọi là bằng nhau và làm thế nào
để kiểm tra được hai tam giác đó bằng nhau?
BÀI 13: HAI TAM GIÁC BẰNG NHAU.
TRƯỜNG HỢP BẰNG NHAU
THỨ NHẤT CỦA TAM GIÁC NỘI DUNG BÀI HỌC 2 1 Trường hợp bằng nhau Hai tam giác bằng thứ nhất của tam giác nhau Cạnh – cạnh – cạnh
I. HAI TAM GIÁC BẰNG NHAU HĐ1
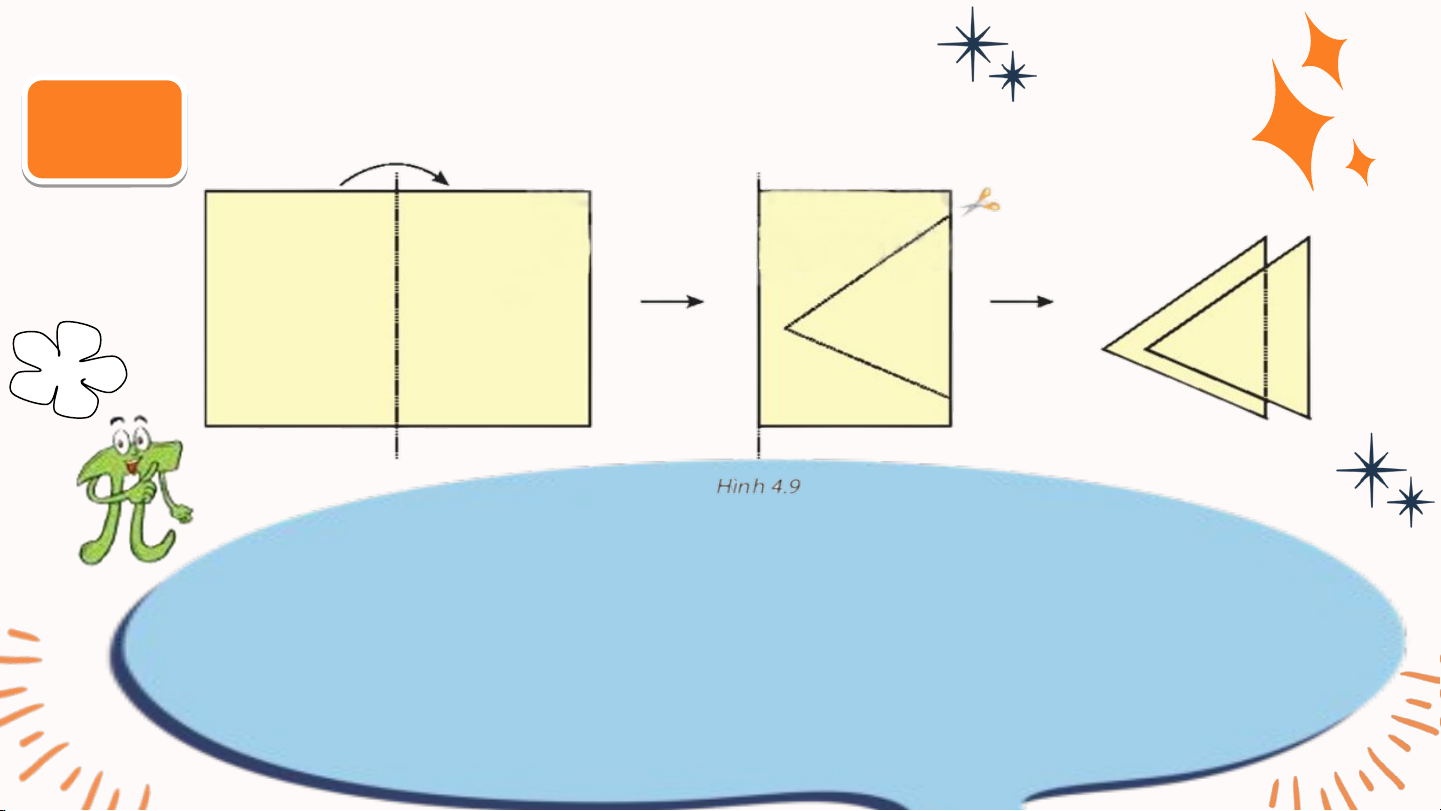
Gấp đôi một tờ giấy như hình 4. 9
Phần được cắt ra là hai tam giác “chồng khít” lên nhau. Theo em:
- Các cạnh tương ứng có bằng nhau không?
- Các góc tương ứng có bằng nhau không? HĐ1 Giải ả
- Các cạnh tương ứng của hai tam giác bằng nhau.
- Các góc tương ứng của hai tam giác bằng nhau. KẾT LUẬN
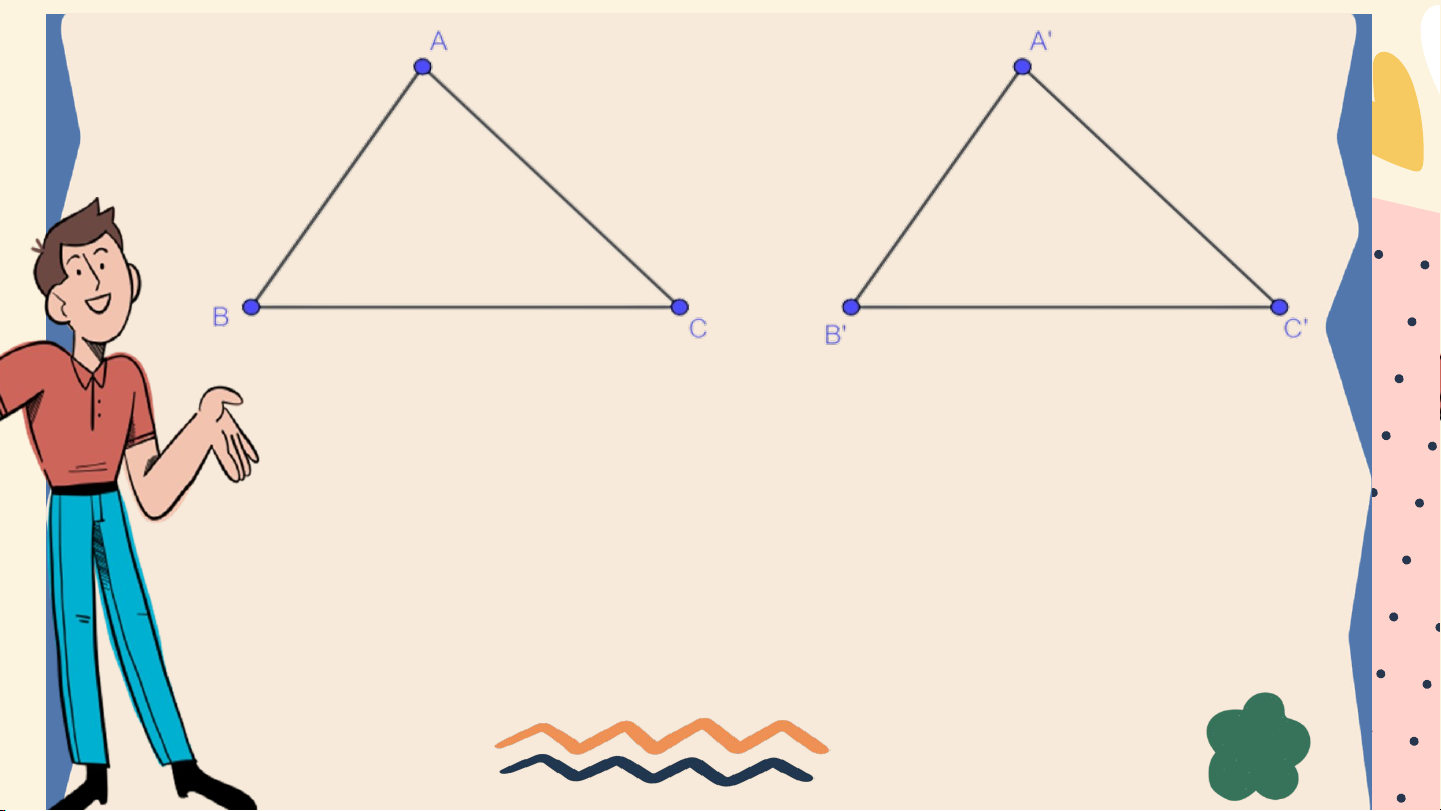
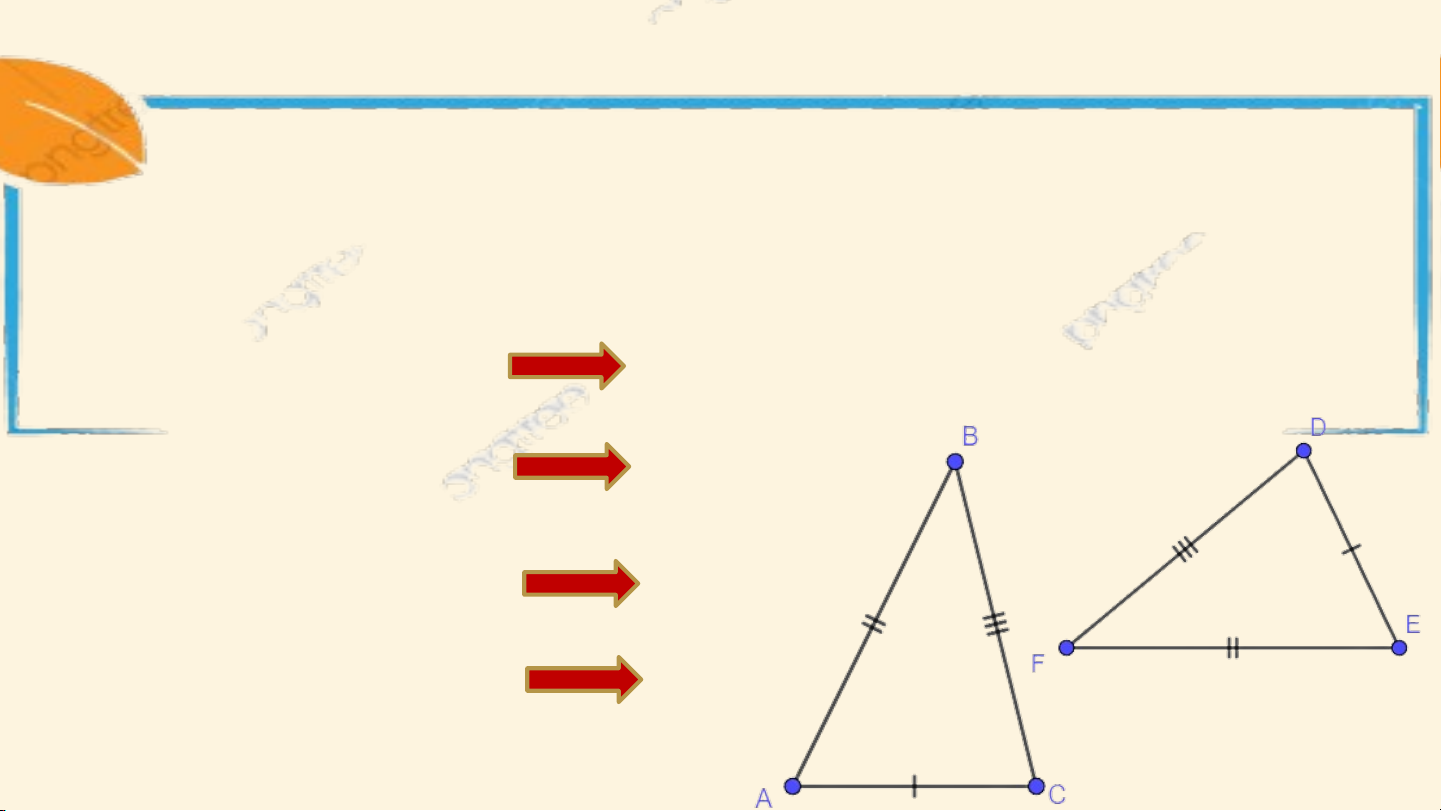
Hai tam giác ABC và A’B’C’ bằng nhau
nếu chúng có các cạnh tương ứng bằng
nhau và các góc tương ứng bằng nhau, nghĩa là: Khi đó ta viết
- Các cặp cạnh tương ứng là: AB và A’B’, AC và A’C’, BC và B’C’.
- Các cặp góc tương ứng là: và , và , và .
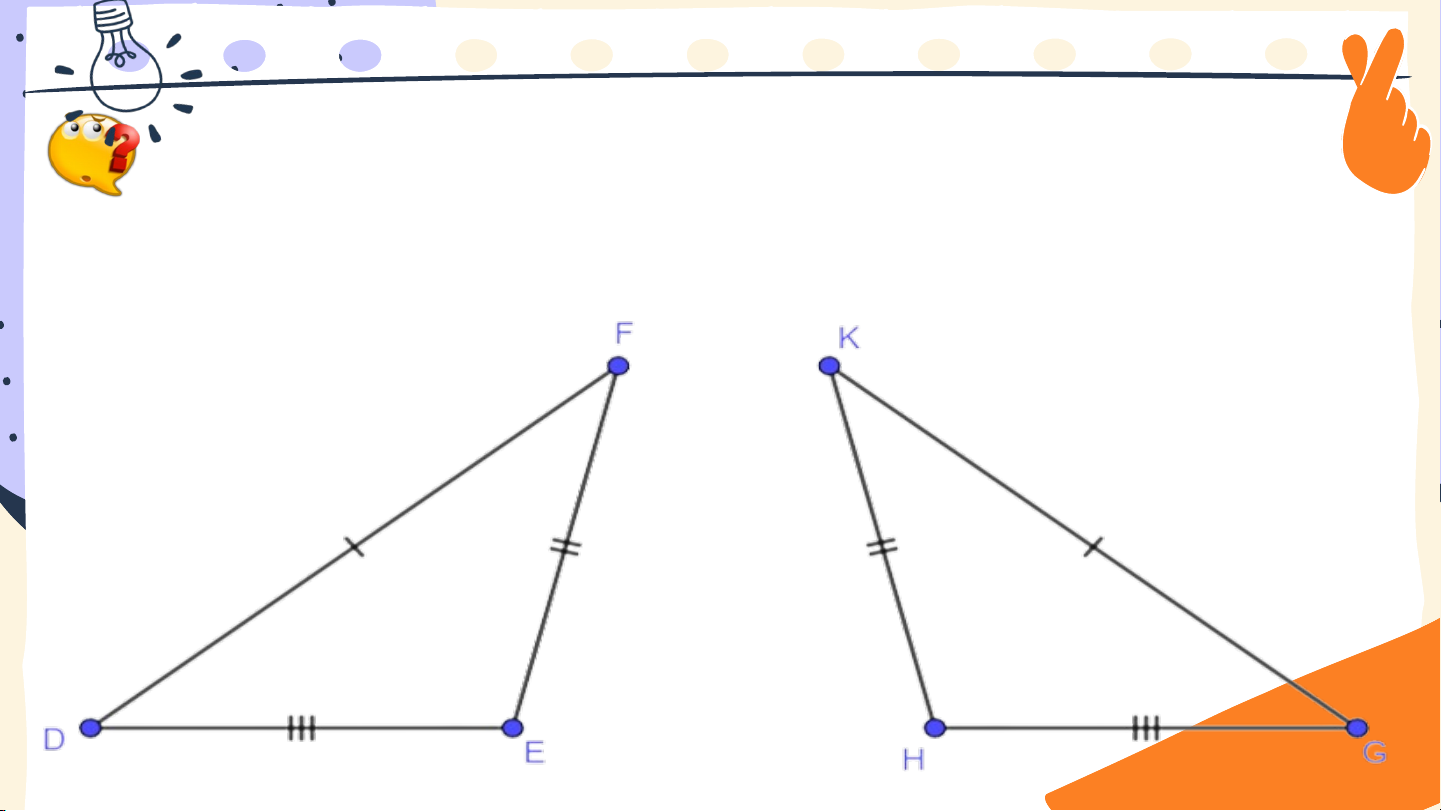
Biết hai tam giác trong hình 4. 11 bằng nhau, em hãy
chỉ ra các cặp cạnh tương ứng, các cặp góc tương ứng và
viết đúng kí hiệu bằng nhau của cặp tam giác đó “ Trả lời
Các cặp cạnh tương ứng: DF và KG, DE và HG, EF và KH
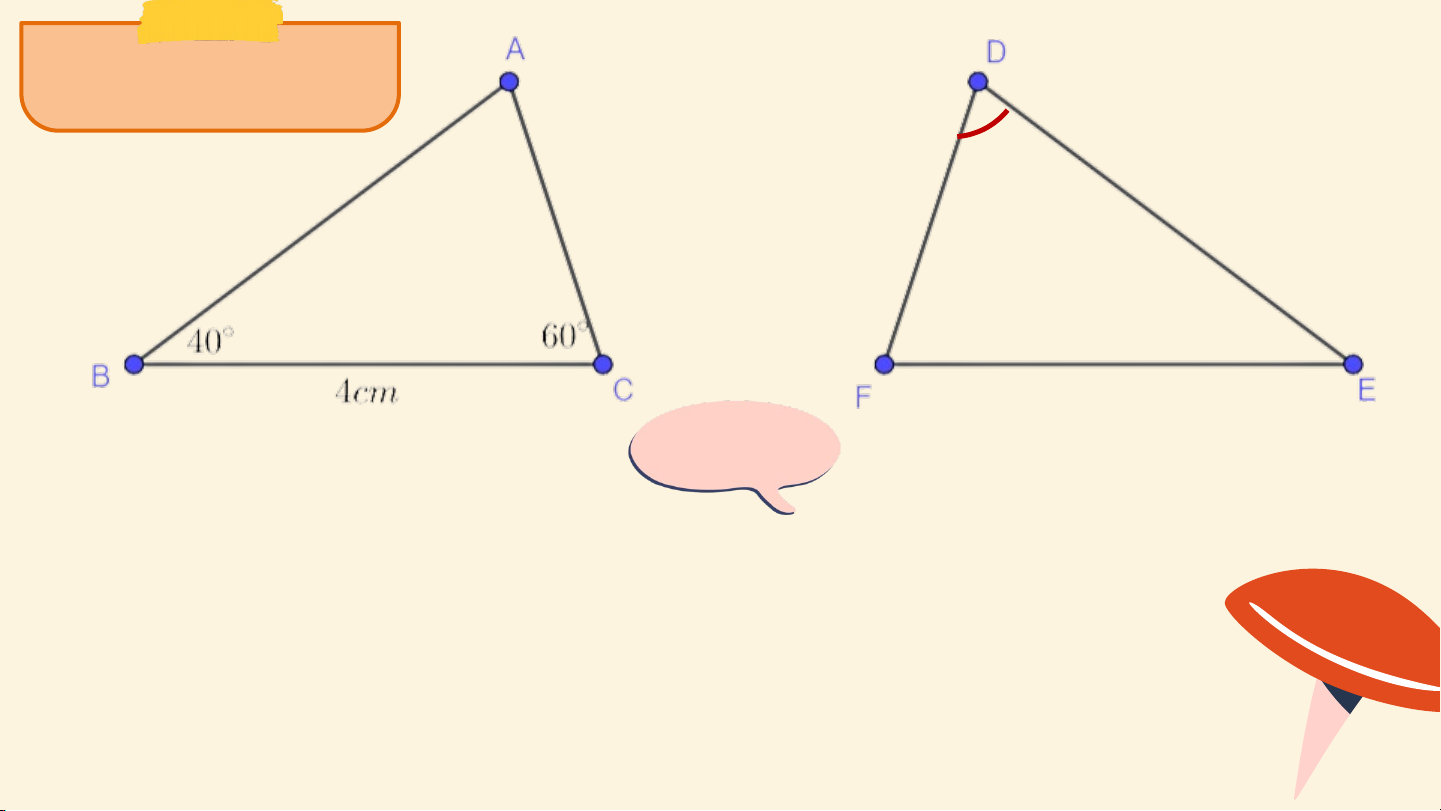
Các cặp góc tương ứng: và , và , và . Kí hiệu: 12 Luyện tập 1 ? ? Giải +) Vì EF = BC = 4cm, +) Ta có: +) .
II. TRƯỜNG HỢP BẰNG NHAU THỨ NHẤT
CỦA TAM GIÁC: CẠNH – CẠNH – CẠNH HĐ 2 SGK Trả lời HĐ 3
- Các góc tương ứng của hai tam giác ABC và A’B’C’ bằng nhau.
- Hai tam giác ABC và A’B’C’ bằng nhau vì có
các cạnh và các góc tương ứng bằng nhau.
Định lí: Trường hợp bằng nhau của canh- cạnh – cạnh (c-c-c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì
hai tam giác đó bằng nhau. GT và AB = A’B’, AC = A’C’, BC = B’C’. KL
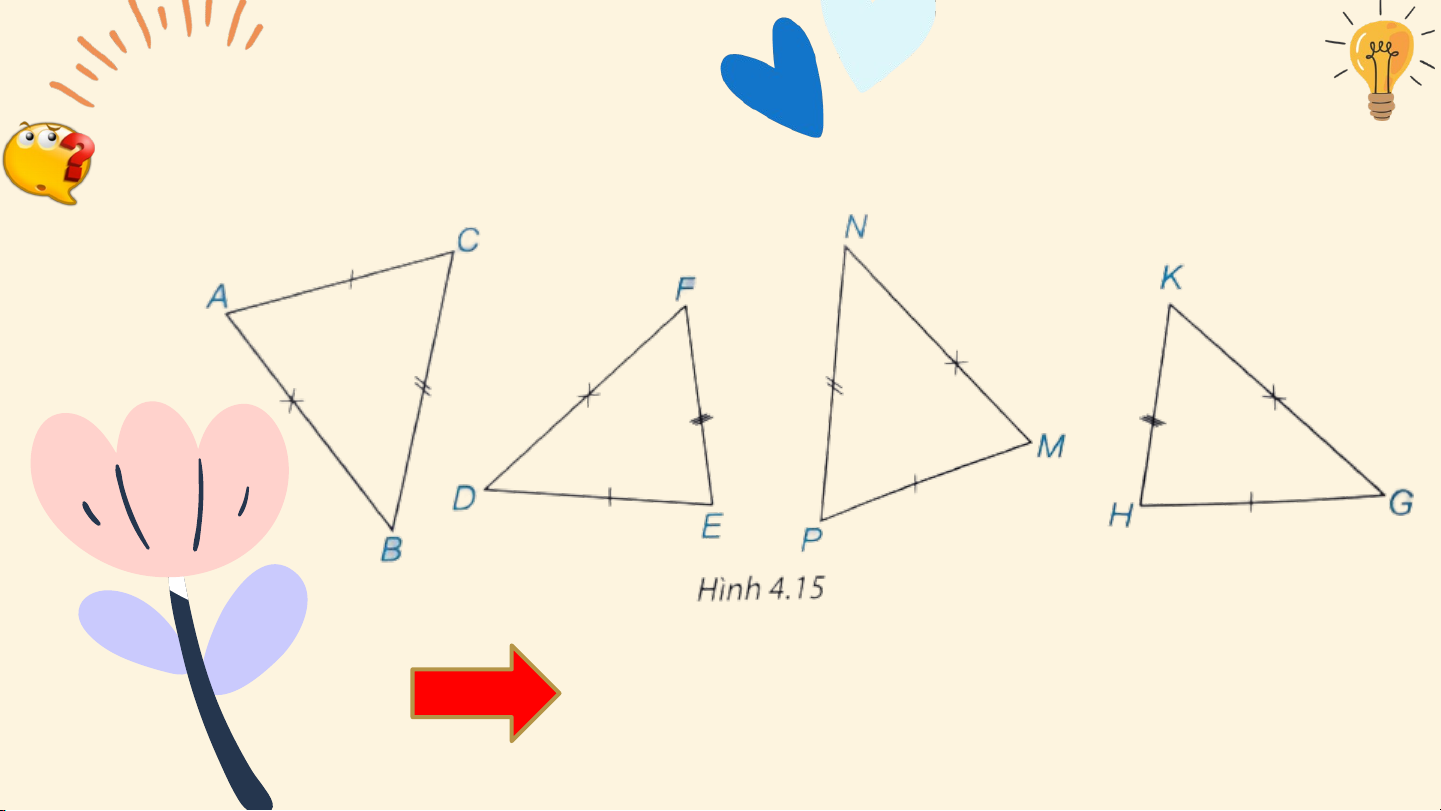
Trong hình 4. 15, những cặp tam giác nào bằng nhau?
𝜟 𝑨𝑩𝑪=𝜟 𝑴𝑵𝑷;𝜟 𝑫𝑬𝑭=𝜟𝑮𝑯𝑲
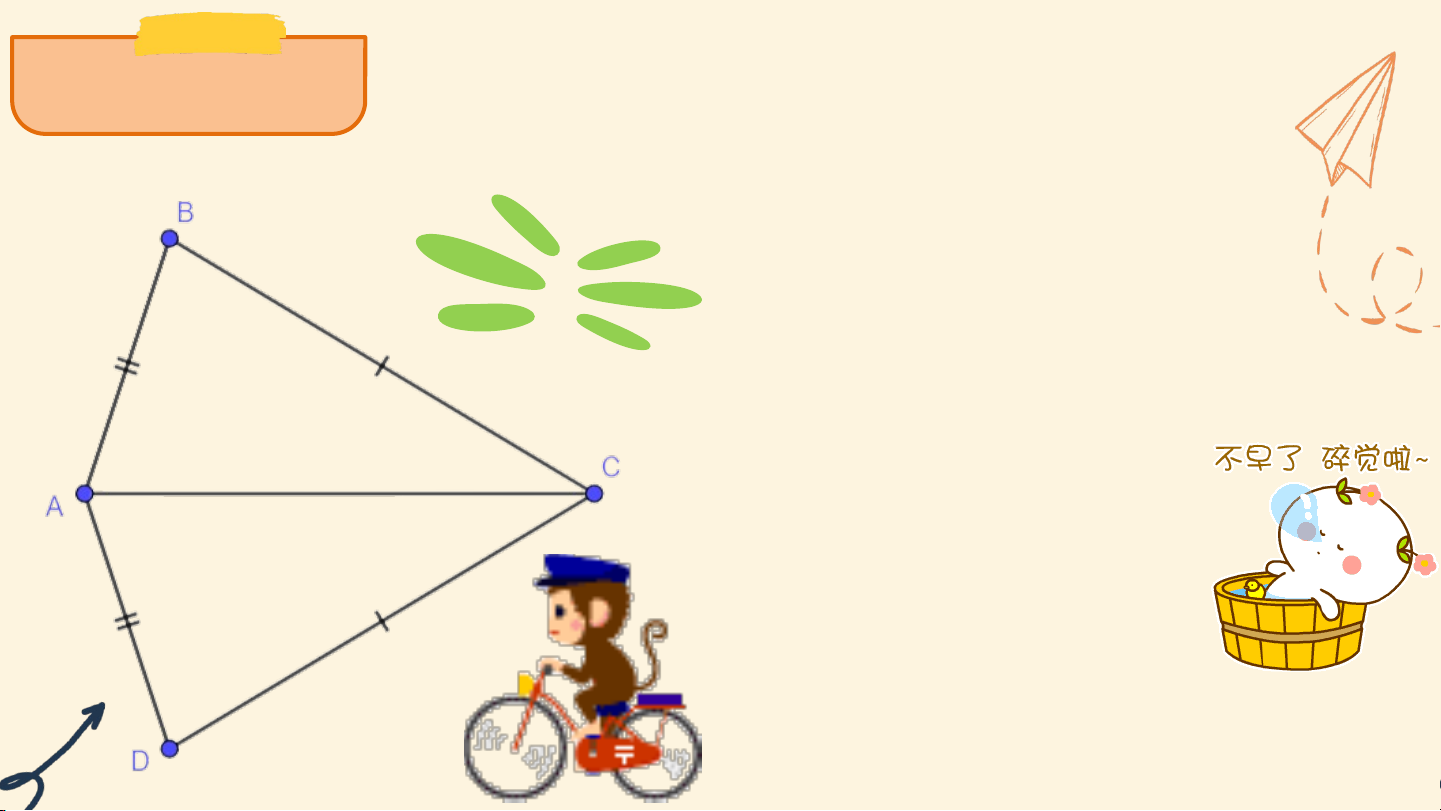
Luyện tập 2 Cho hình 4. 17, biết AB = AD, BC = DC. Chứng minh rằng Giải
Xét tam giác ABC và ADC có: AB = AD CB = CD AC là cạnh chung Vậy Vận dụng Trả lời
Xét tam giác OAM và OBM có: OA = OB AM = BM OM chung Do đó: .
Vậy tia OM là tia phân giác của góc xOy LUYỆN TẬP
Bài 4.4( SGK – tr.67): Cho tam giác ABC và DEF như
hình 4.18. Trong các khẳng định sau, khẳng định nào đúng? (1)ΔABC = ΔDEF Sai (2) ΔACB = ΔEDF Đúng (3) ΔBAC = ΔDFE Sai (4)ΔCAB = ΔDEF Đúng
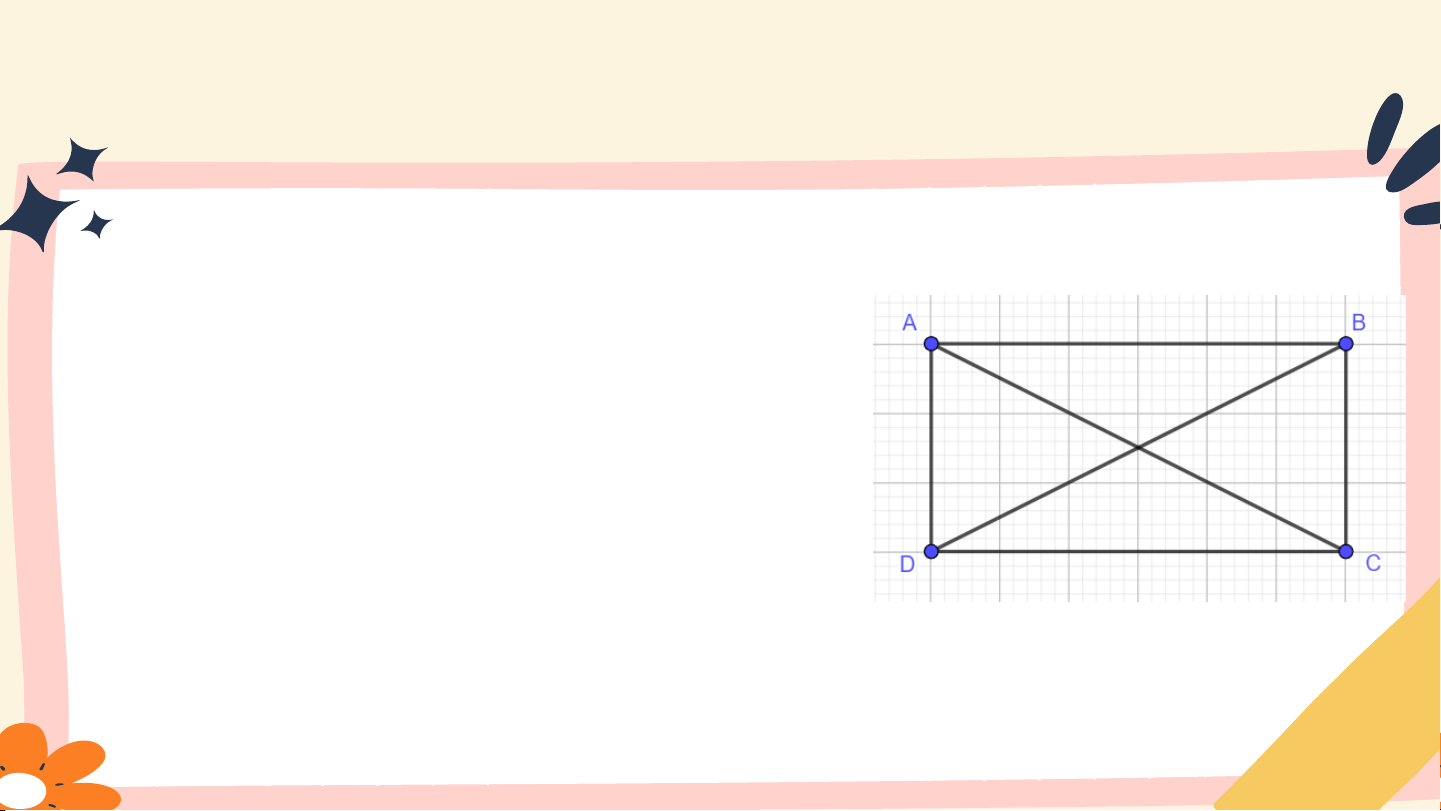
Bài 4.5( SGK – tr.67): Trong Hình 4.19, hãy chỉ ra hai cặp tam giác bằng nhau. Giải
+) Xét ΔABC và ΔCDA có: AB = CD AC chung BC = AD ⇒ΔABC = ΔCDA(c.c.c)
+) Xét ΔABD và ΔCDB có: AB = CD DB chung AD = CB ⇒ΔABD = ΔCDB(c.c.c) Bài 4.6( SGK – tr.67):
a) Chứng minh rằng ΔABD=ΔCBD Xét ΔABD và ΔCBD có: Vậy ΔABD = ΔCBD(c.c.c) b) Tính
Ta có (hai góc tương ứng)
Theo định lí tổng ba góc trong BCD, ta có:
Mà ΔABD = ΔCBD nên ( 2 góc tương ứng) ⇒ ⇒
Bài 1: Cho có XE = 3cm, XF = 4cm, NP = 3,5 cm. Tính chu vi mỗi tam giác. HƯỚNG DẪN Ta có:
Mà XE = 3cm, XF = 4cm, NP = 3,5 cm
Chu vi XEF là: XE + XF + EF = 3 + 4 + 3,5 = 10,5 cm
Chu vi MNP: MN + NP + MP = 3+ 3,5 + 4 = 10,5 cm.
Bài 2: Cho và biết: AB = BC = CA = 3cm;
AD = BD = 2cm (C và D nằm khác phía đối với AB). a) Vẽ và b) Chứng minh rằng . HƯỚNG DẪN a) b) Xét và có: AD = BD CA = CB DC cạnh chung (c.c.c) . 23
HƯỚNG DẪN VỀ NHÀ Ôn lại kiến thức Hoàn thành các bài Chuẩn bị bài mới đã học trong bài tập trong SBT
“Luyện tập chung”. CẢM ƠN CÁC EM ĐÃ “
LẮNG NGHE BÀI GIẢNG!
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25