Giáo án điện tử Toán 7 Bài 2 Cánh diều: Đa thức một biến. Nghiệm của đa thức một biến (tiết 1)
Bài giảng PowerPoint Toán 7 Bài 2 Cánh diều: Đa thức một biến. Nghiệm của đa thức một biến (tiết 1) hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 7. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 7
Môn: Toán 7
Sách: Cánh diều
Thông tin:
Tác giả:
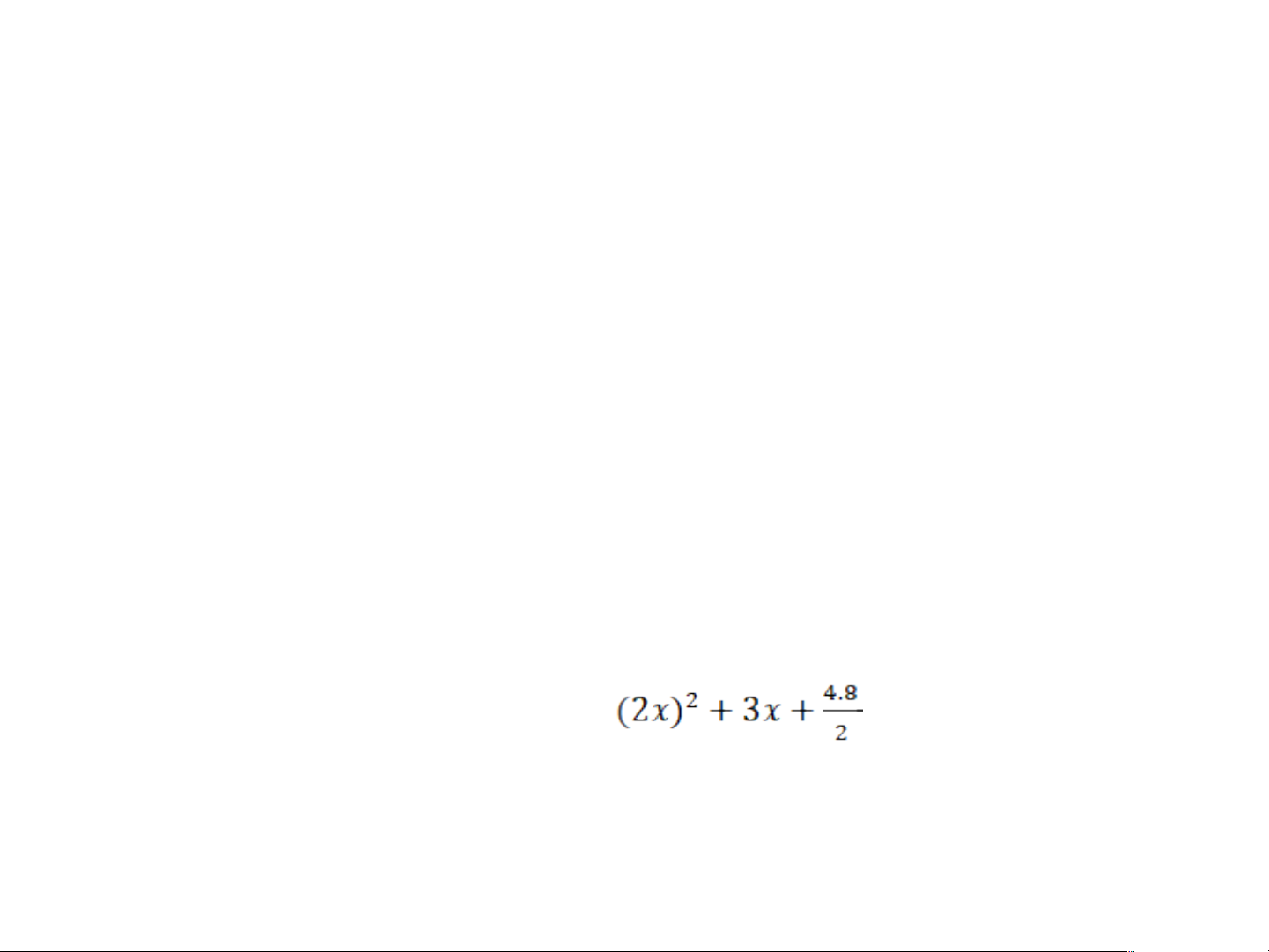
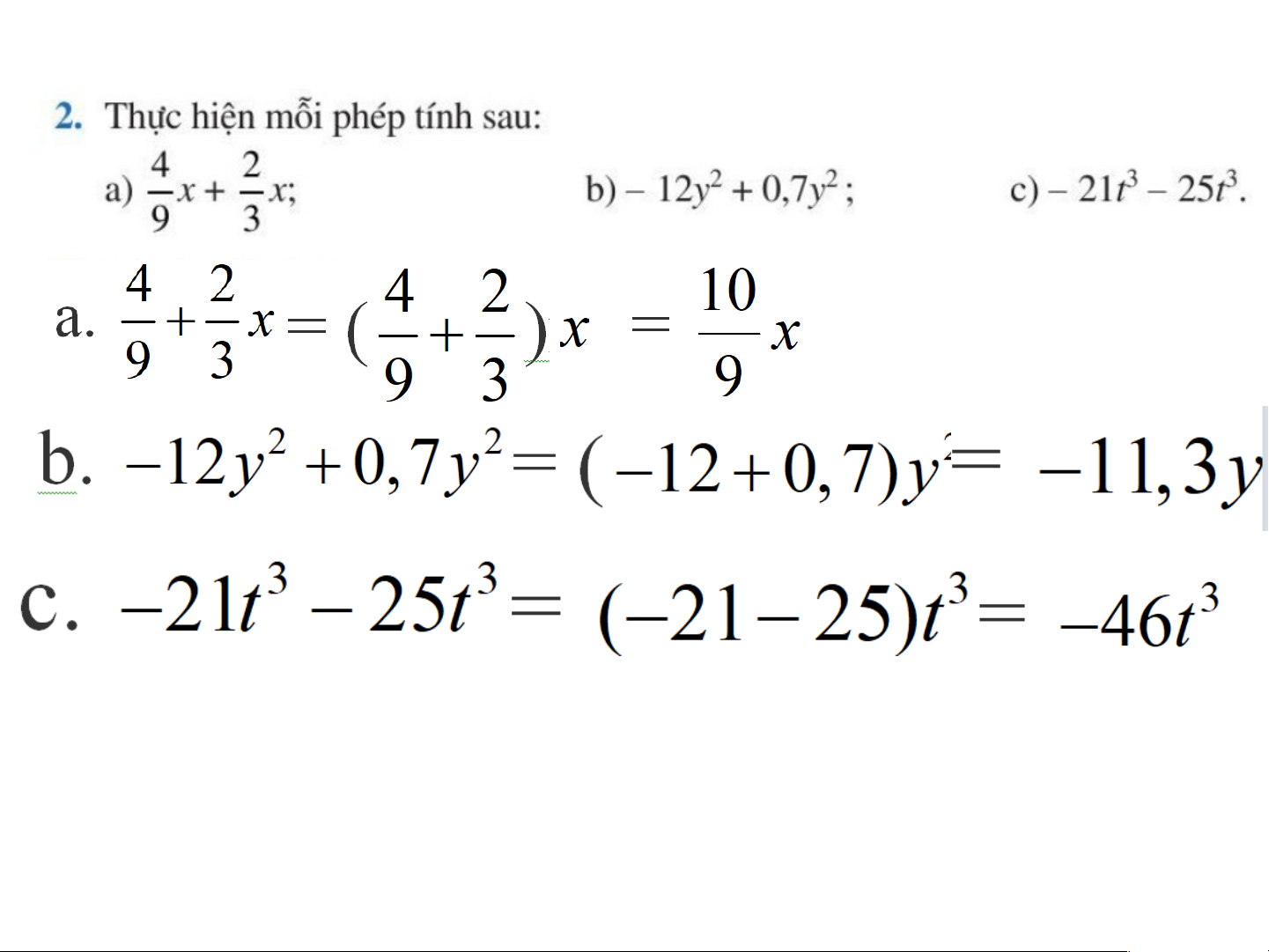
Preview text:
Khởi động
Trong giờ học môn Mĩ thuật, bạn Hạnh dán lên
trang vở hai hình vuông có kích thước lần lượt là
và như ở Hình 1. Tổng diện tích của hai hình vuông đó là .
BÀI 2: ĐA THỨC MỘT BIẾN. NGHIỆM CỦA
ĐA THỨC MỘT BIẾN (3 TIẾT)
I. Đơn thứ một biến. Đa thức một biến NỘI
II. Cộng, trừ đơn thức có cùng số mũ DUNG của biến
III. Sắp xếp đa thức một biến BÀI
VI. Bậc của đa thức một biến HỌC
V. Nghiệm của đa thức một biến
I. Đơn thức một biến. Đa thức một biến Giải a. Biểu thức biểu thị:
- Diện tích của hình vuông có độ dài cạnh là
- Thể tích của hình lập phương có độ dài cạnh 2x là: ¿
b. Các biểu thức trên có dạng là tích của số với lũy thừa
có số mũ nguyên dương của biến.
I. Đơn thức một biến. Đa thức một biến
* Đơn thức một biến là biểu thức đại số chỉ gồm một số hoặc tích
của một số với luỹ thừa có số mũ nguyên dương của biến đó.
Ví dụ: biểu thức , được gọi là đơn thức một biến x. Chú ý
• Mỗi đơn thức (một biến ) nếu không 𝒙𝟐
phải là một số thì có dạng , trong đó 1 là hệ số của
là số thực khác 0 và là số nguyên đơn thức
dương. Lúc đó, số được gọi là hệ số của đơn thức .
𝟖 𝒙𝟑 8 là hệ số
• Để thuận tiện cho việc thực hiện các
phép tính (trên các đơn thức, đa - 2 là đơn thức
thức, ...), một số thực khác 0 được coi -2 = - 2
là đơn thức với số mũ của biến bằng 0 .
I. Đơn thức một biến. Đa thức một biến
* Đơn thức một biến là biểu thức đại số chỉ gồm một số hoặc tích
của một số với luỹ thừa có số mũ nguyên dương của biến đó.
Ví dụ: biểu thức , được gọi là đơn thức một biến x. Chú ý SGK trang 47
a) Viết biếu thức biểu thị:
- Quãng đường ô tô đi được trong thời gian x (h), nếu vận tốc của ô tô là 60 km/h
- Tổng diện tích của các hình; hình vuông có độ dài cạnh là 2x cm;
hình chữ nhật có các kích thước là 3 cm và x cm; hình thoi có độ
dài hai đường chéo là 2x cm và 8 cm
b) Các biểu thức trên có bao nhiêu biến? Mỗi số hạng trong biểu
thức có dạng như thế nào? Giải
- Quãng đường ô tô đi được: S = 60 . x (km).
- Tổng diện tích của các hình: hình vuông có độ dài cạnh là 2x cm;
hình chữ nhật có các kích thước là 3cm và x cm; hình thoi có độ dài
đường chéo là 4 cm và 8 cm: (c = 4x2 + 3x +16 m2).
b. Các biểu thức trên có một biến, mỗi số hạng xuất hiện trong biểu
thức có dạng đơn thức.
I. Đơn thức một biến. Đa thức một biến
* Đơn thức một biến là biểu thức đại số chỉ gồm một số hoặc tích
của một số với luỹ thừa có số mũ nguyên dương của biến đó.
Ví dụ: biểu thức , được gọi là đơn thức một biến x. Chú ý SGK trang 47
* Đa thức một biến là tổng những đơn thức của cùng một biến. Ví dụ: là đa thức của biến * Chú ý
+ Mỗi số được xem là một đa thức (một biến).
+Số 0 được gọi là đa thức không.
+ Mỗi đơn thức cūng là một đa thức.
+ Thông thường ta kí hiệu đa thức một biến là hoặc Ví dụ 1
II. Cộng trừ đơn thức có cùng số mũ của biến Giải
a. Số mũ của biến x trong hai đơn thức bằng nhau (đều bằng 2)
II. Cộng trừ đơn thức có cùng số mũ của biến
*Để cộng (hay trừ) hai đơn thức có cùng số mũ của biến, ta cộng
(hay trừ) hai hệ số với nhau và giữ nguyên phần biến: 5x Giải 9 ( 7)x 16 x b) a) là đa thức một biến x là đa thức một biến x
không phải là đa thức một biến x
không phải là đa thức một biến y là đa thức một biến z là đa thức một biến t
* HƯỚNG DẪN TỰ HỌC Ở NHÀ
- Ghi nhớ kiến thức đã học phần I, II của bài.
- Hoàn thành, làm lại các bài tập đã giải
- Chuẩn bị phần tiếp theo :
+ III. Sắp xếp đa thức một biến (trang 49)
+ IV. Bậc của đa thức một biến ( trang 50)
+ Bài tập 3, 4 sgk trang 52,53
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14