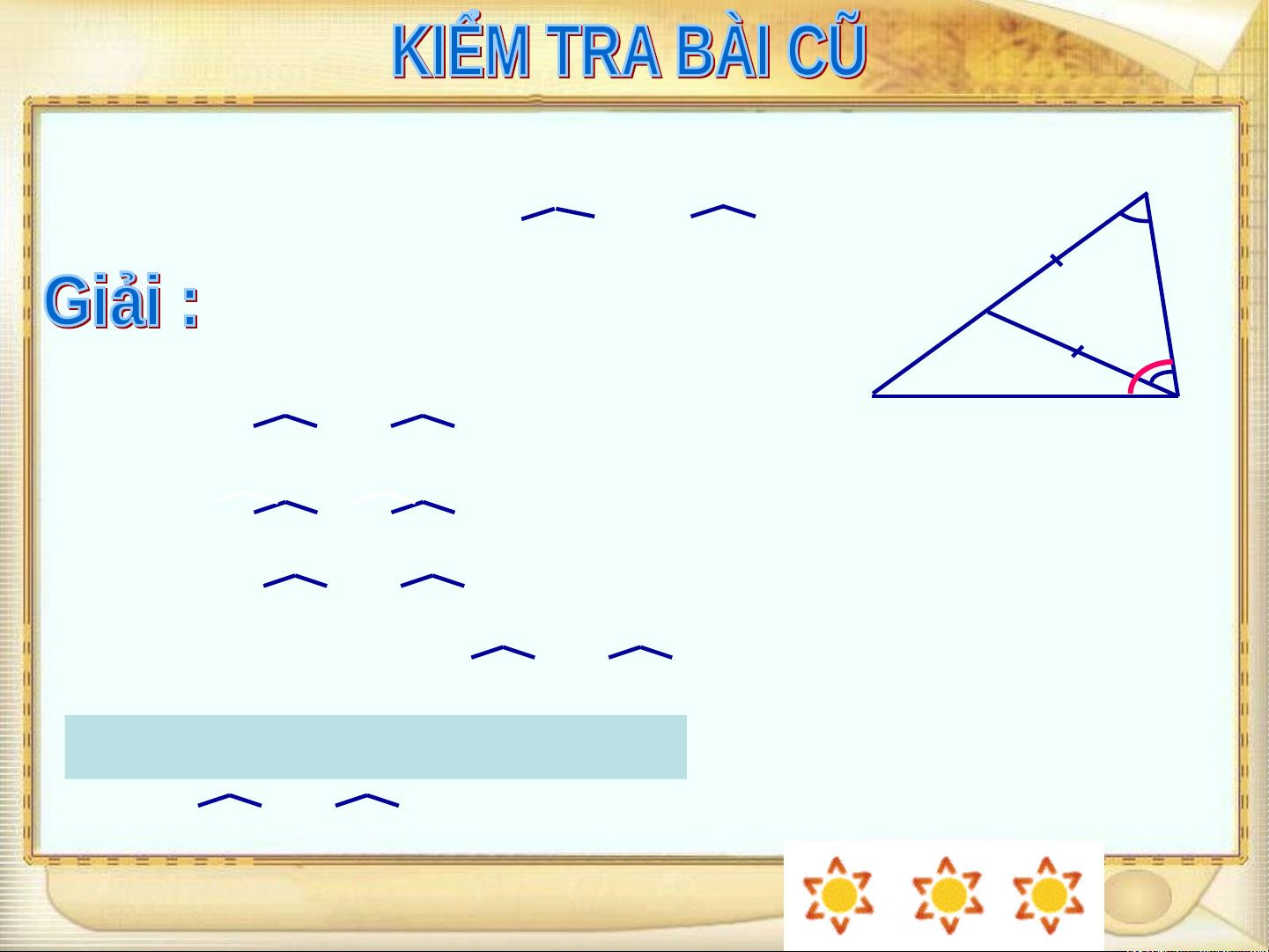
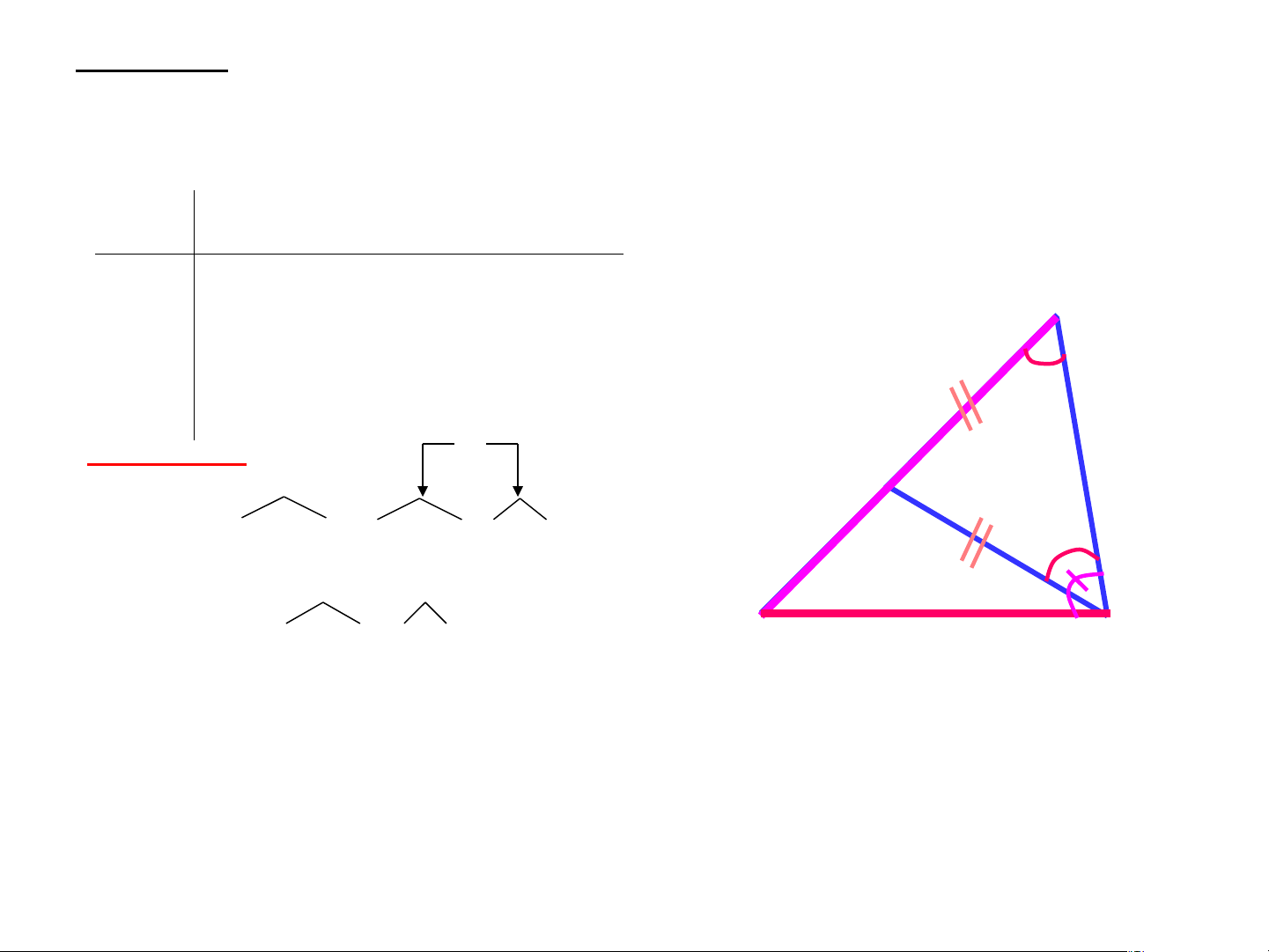
* Hãy nêu quan hệ giữa cạnh và góc đối diện trong tam giác. * Cho hình vẽ D
Biết AD = AC. So sánh BCD và BDC A Ta có : AD = AC (gt) B C nên : ADC = ACD (tam giác ACD cân) hay : BDC = ACD (1)
Mặt khác: BCD > ACD (tia CA nằm giữa hai tia CB và CD) (2)
Từ (1) và (2) suy ra: BCD > BDC
* Em hãy so sánh BD và BC
BDC có BCD > BDC nên BD > BC (qh về cạnh và góc trong tg)
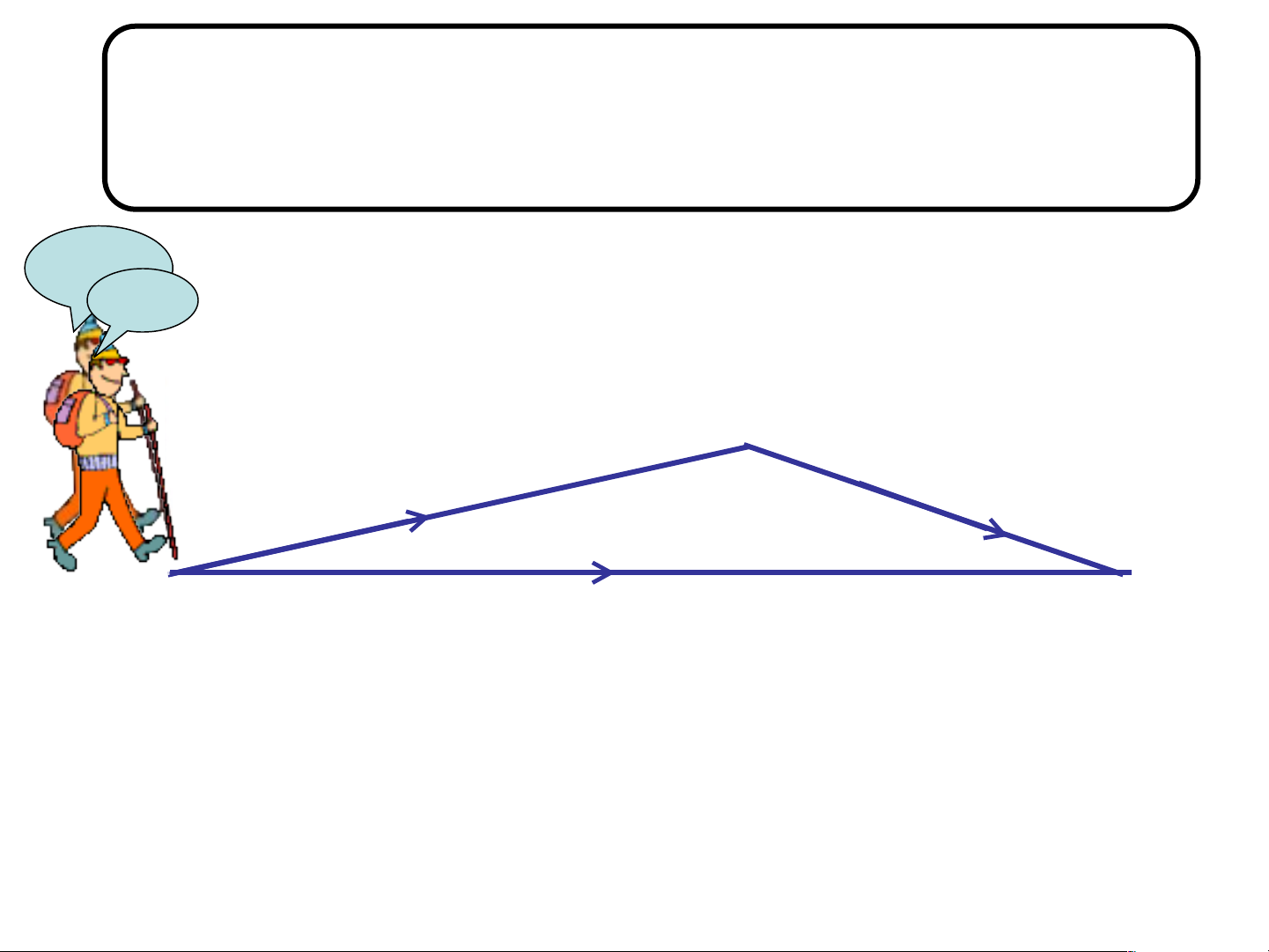
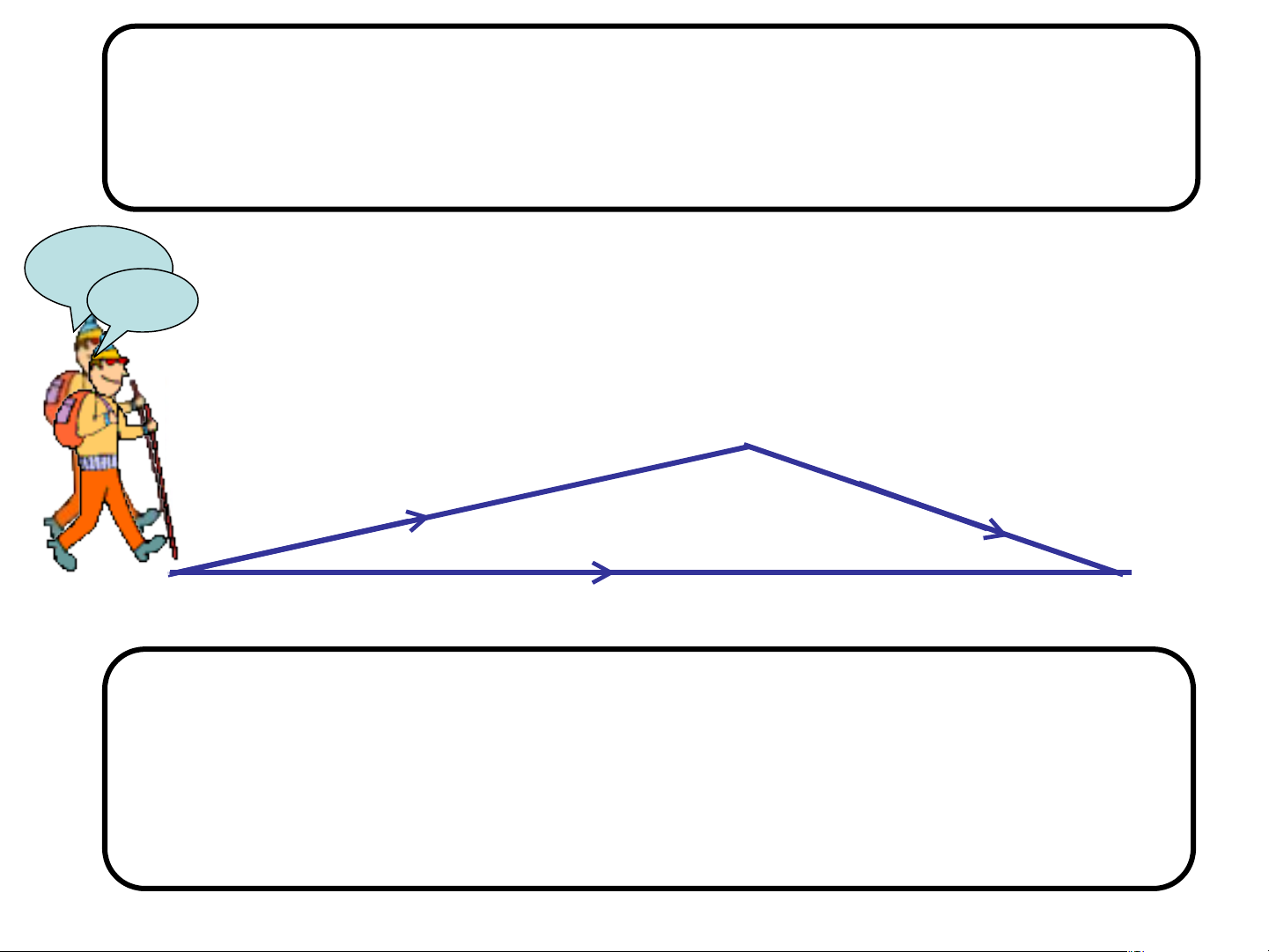
Hòa và Bình cùng xuất phát từ B đi đến C. Hòa đi
theo đường B  C, Bình đi theo đường B  A  C.
Quãng đường đi được của bạn nào ngắn hơn? Bình Hòa A B C
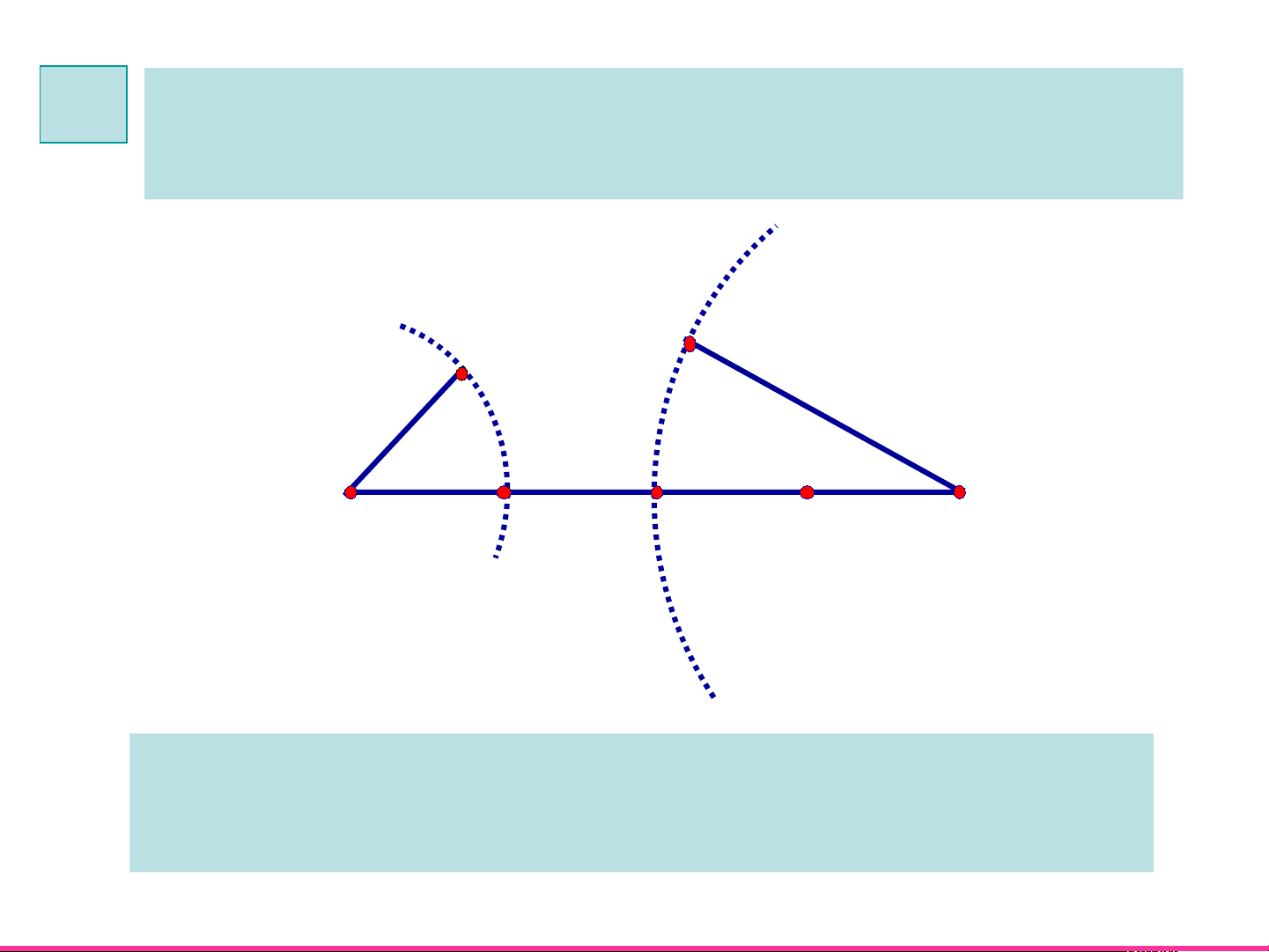
?1 Hãy vẽ tam giác có độ dài 1cm, 2cm, 4cm.
Em có vẽ được không? 2cm 1cm 4
Không vẽ được tam giác có ba cạnh 1cm, 2cm, 4cm
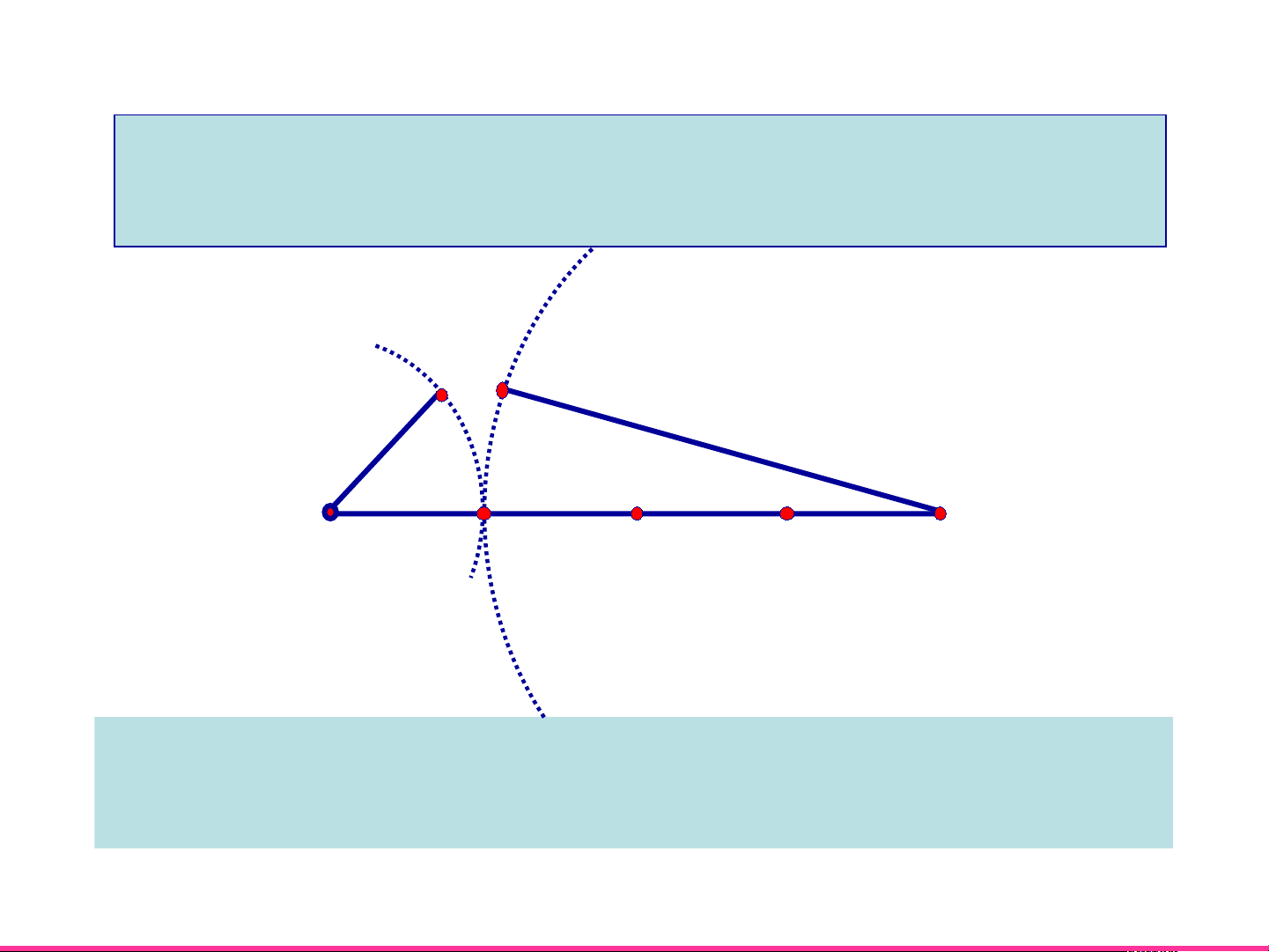
Em hãy thử vẽ một tam giác với các cạnh
có độ dài 1cm, 3cm, 4cm. 3cm 1cm 4cm
Không vẽ được tam giác có ba cạnh 1cm, 3cm, 4cm
Có phải bộ ba số nào
cũng là độ dài ba
cạnh của một tam giác không?
Vậy bộ ba số như thế nào mới là
độ dài ba cạnh của một tam giác? Định lý :
Trong một tam giác, tổng độ dài hai cạnh bất kì bao Ñòn gi h lí ờ c:
ũng lớn hơn độ dài cạnh còn lại. GT ABC D AB + AC > BC KL AB + BC > AC AC + BC ( >  A AC B D cân) Phân tích = A BCA + ACD > D  BCD > D B C  * Các bất đẳng thức BD > BC trong KL của ĐL được 
gọi là các bất đẳng thức  AB + AC > BC tam giác (ñpcm)
Hòa và Bình cùng xuất phát từ B đi đến C. Hòa đi
theo đường B  C, Bình đi theo đường B  A  C.
Quãng đường đi được của bạn nào ngắn hơn? Bình Hòa A B C
Quãng đường của bạn Hòa: BC
Quãng đường của bạn Bình: AB +AC
Quãng đường đi được của bạn Hòa ngắn hơn. Ta thấy: AB+AC > BC A GT G ABC AB + AC > BC AB + BC > AC K L K AC + BC > AB B C
AB + AC > BC  AB > BC – AC ;AC > BC - AB
AB + BC > AC  AB > AC - BC ; BC > AC - AB
AC + BC > AB  AC > AB – BC ; BC > AB - AC
Trong một tam giác, hiệu độ dài hai cạnh
bao giờ cũng nhỏ hơn độ dài cạnh còn lại.
HỆ QUẢ CỦA BẤT ĐẲNG THỨC TAM GIÁC : A GT ABC B C
AB > BC – AC ; AC > BC - AB KL
AB > AC – BC ; BC > AC - AB
AC > AB – BC ; BC > AB - AC
AB + AC > BC ; BC > AC - AB
 AC – AB < BC < AB + AC Nhận xét :
Lưu ý: Khi xét độ dài ba đoạn thẳng có thỏa mãn bất Trođẳ ngng m thức ột t t am am gi g ác, iác độ hay dài kh một ôn cạ g n , h ta ch bao ỉg icần ờ cũ so ng sánh lớn hđộ ơn dà hi i lớn ệu và nh nh ất ỏ hvới ơn ttổng ổng hai các đ đ ộ ộ dà dài i cò của n lại hai , hoặc cạnh so sánh
còn lại độ dài nhỏ nhất với hiệu hai độ dài còn lại.
1/ Điền đúng hoặc sai vào ô trống:
bộ ba nào sau đây là độ dài 3 cạnh của một tam giác : a/ 2cm; 3cm; 6cm sai vì 2 + 3 < 6 b/ 2cm; 4cm; 6cm sai vì 2 + 4 = 6 c/ 3cm; 4cm; 6cm đúng
vì 3 + 4 > 6: thỏa mãn bđt tam giác
2. Cho tam giác ABC với hai cạnh BC = 1cm; AC = 7cm.
a. Hãy tìm độ dài cạnh AB, biết độ dài cạnh này là một số nguyên ?
b. Tam giác ABC là tam giác gì ?
a. Ta có : AC – BC < AB < AC + BC (b.đẳng thức tam giác)
Thay số : 7 - 1 < AB < 7 + 1 6 < AB < 8
Vì độ dài cạnh AB là một số nguyên, nên AB = 7 cm
b. Vì AB = AC nên tam giác ABC là tam giác cân tại A
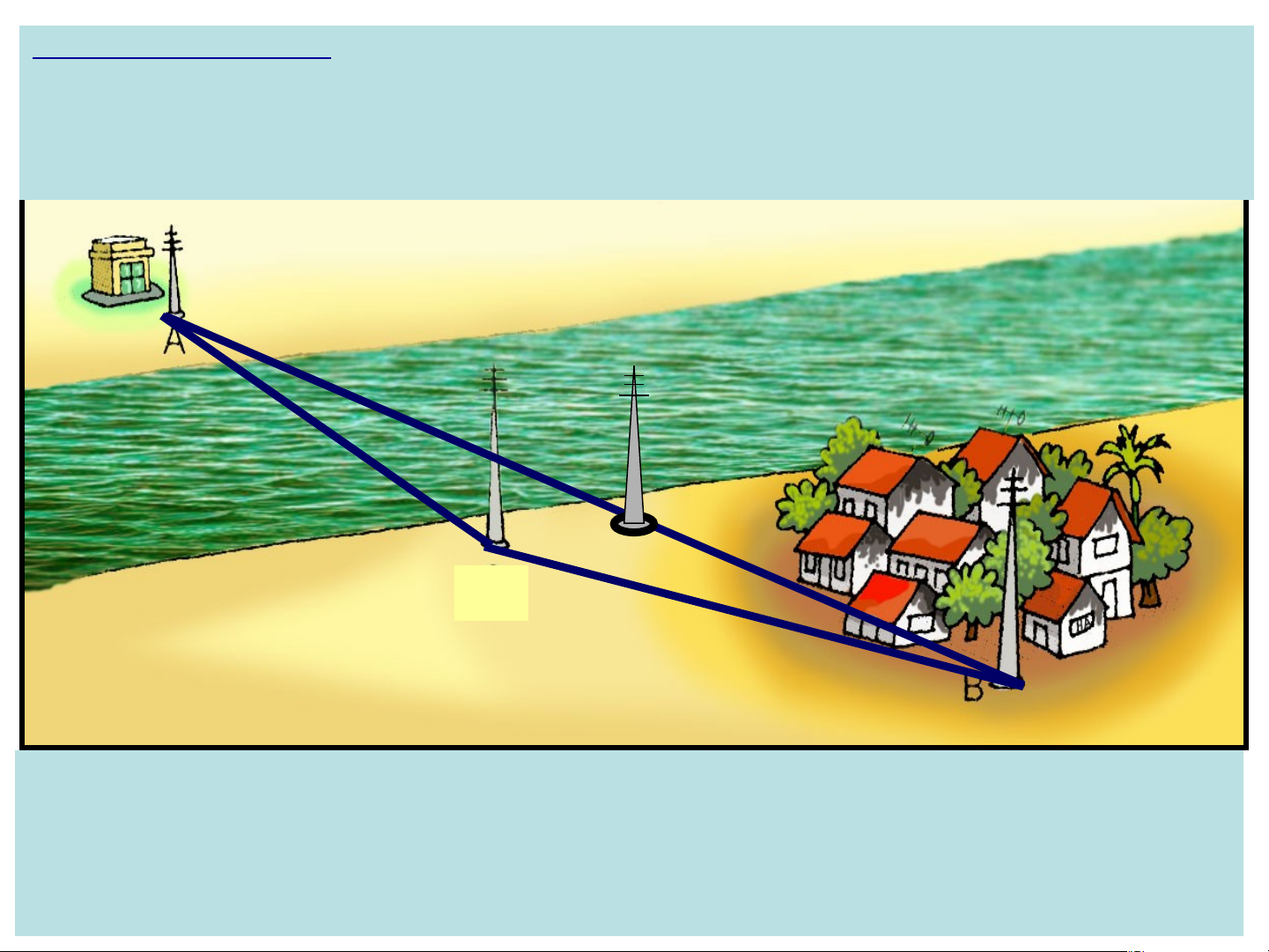
3/ Cho hình vẽ : A: vị trí trạm biến áp. B: Khu dân cư.
C: cột mắc dây điện đưa điện từ trạm biến áp A về khu dân cư B.
Tìm vị trí của C ở gần bờ sông sao cho độ dài đường dây dẫn là ngắn nhất? C D
Địa điểm C thuộc đường thẳng AB và gần bờ sông có khu dân
cư là đường dây dẫn ngắn nhất vì : AC+ BC = AB .
Thật vậy, nếu dựng điểm D khác C thì: AD + DB >AB (bđt tam giác).
* Điền Đ (đúng) hoặc S (sai) vào ô trống
tương ứng với mỗi câu sau: bộ ba nào trong
các bộ ba độ dài sau đây không thể là ba
cạnh của một tam giác 1. 3cm, 4cm, 8cm Đ 2. 3cm, 5cm, 7cm S 3. 2cm, 5cm, 3cm. Đ 4. 5cm, 6cm, 9cm. S
• Hoc kỹ định lí , hệ quả, nhận xét về bất đẳng thức tam giác.
• Xem lại các bài tập đã giải, làm các bài tập
15,17,19 trong sách giáo khoa trang 63-64.
• Chuẩn bị cho tiết “Luyện tập”
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15