Giáo án điện tử Toán 7 Bài 25 Kết nối tri thức: Bậc và các hệ số của một đa thức

Bài giảng PowerPoint Toán 7 Bài 25 Kết nối tri thức: Bậc và các hệ số của một đa thức hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 7. Mời bạn đọc đón xem!

 

12 6 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Bài giảng điện tử Toán 7

Môn: Toán 7

Sách: Kết nối tri thức

Thông tin:

29 trang 3 tháng trước

Tác giả:

Profile Tin Hin


Giáo viên thực hiện: Lương Văn
Thnh

!
"
#
$
%&'()*+,'-.&
/(0&1+23'()*+,'-.&
3'()*+,'-.&'(456&
789.823'()*+,'-.&
:*;*0*(1<=*>3+,'23'()*
5(1+*>323'()*+,'-.&
:*;*0*(1<=*>3+,'23'()*
Đ
i
m
9
Đ
i
m
1
0
(
?
&
'
(
@
A
&
5
Đ
i
m
1
0
V
t
a
y
(
?
&
'
(
@
A
&
5
Đ
i
m
9
V
t
a
y
QUAY
1 2
3
4
VÒNG QUAY
MAY MẮN
B4!3x
5
+ (-5x
5
). 
A. 
B. 
C.
D.


00
0504
03
010607080910
B4 Tnh . B c ca đơn thc nh n đưc l
A.
B.
C.
D.


x x
B4"
 !"#!$%&'()*+,-*#
.#/+
A. -2x
3
– 2x
2
+ x + 1
B. 7x
4
- 2x
3
– 2x
2
+ x + 1
C. -7x
4
- 2x
3
– 2x
2
+ x + 1
D. 2x
3
– 2x
2
+ x + 1


00
0504
03
0607080910
0
1
02 0
P x x x x x x x
B4#3"
40"
5"46789
A. 4x
4
; 3x
2
; x; 1
B. 4x
4
; -3x
2
; x; 1
C. 4x
4
; -3x
2
; x; -1
D. 4x
4
; 3x
2
; x; -1


$
C
D:*;*0*(1<=*>3+,'23'()*
EFG
EFG
:;HI"9
#
J9
K9J!<=7$+>*
7?@*A
:7B-789$C<
!
L&5'M
D
$CA
896-EAFF
DAF<
AF<
$CG896--HIAF<
"
00
0504
03
0607080910
EFG
EFG
:;HI"9
#
J9
K9J!<=7$+>*
7?@*A
:7B-789$C<
!
L&5'M
I"9
#
9
I9 !
D I
$CA
896-EAI"9
#
DA#
AI"
$CG896--HIA!
"
3C
6-
3C6
EJ0
3C6
KL
N

$,M.7.NA
D896-E*-6<
896-E*E
6<
89-I*KL6<
OPQ
O,-2EKL
A(x) = x
5
– 3x
2
+ 8x
4
– 5x
2
– x
5
+ x – 7
'R0&!
O,-2EKL
P
-P
0
0
1 Q
M x x x x x x
2 02 I2 N x x x x
'R0&!
R(M(x)6A-
E41
KLQ
P6A
0
0
1 Q
M x x x x x x
0
0
1 Q
x x x x x
0
1 Qx x x x
'R0&!
R(N(x)6A-
E402
KLJ
-P6A
2 02 I2 N x x x x
02 2 I2 x x x
02 x x
ST
S,T(;!*,+;!U*V,M7!7W<
>**(X8M(0!W
ST
00
0504
03
010607080910
3
3
3
3
3
36-I
36-
3.N6-
36EJ
36KLJ0
0 0
0 Y Q x x x x x x
0
0P x x x
ZA x x
0 0 0B x x x x x x
I ZM x x
ST
7;!
3 36EJ
ZA x x
ST
3
36-
3
36KLJ0
3 36EJ
3
3.N6-
3
36-I
0 0
0 Y Q x x x x x x
0
0P x x x
ZA x x
0 0 0B x x x x x x
I ZM x x
Chú ý
3không.N6-<
$,M2E
!+*.7I[7.76V-HIP<
\ O, -  ,M    
2!+*6<
CUV
]^_`
CUV
]^_`
`>*La*,7(-,V-,U,M-VU<\7(E
-,,b**>,
0
cU<\7(*-,,b**>Z,
0
cU<d
.*+*,7(8($c"c*>2>* ,7(EV,7(*
8(%,I2*>eO-VUf(<
T(*#[-*#c"P-*VBL-V[,
0
P2-*#$H$U.*-,2
$-V62,
0
cU<O,EKL6<
=+W'X(=
1 gi x gi
\7(-,
\7(-,
22x
!$
16x
I2*>
`>*La*,7(-,V-,U,M-VU<\7(E
-,,b**>,
0
cU<\7(*-,,b**>Z,
0
cU<d
.*+*,7(8($c"c*>2>* ,7(EV,7(*
8(%,I2*>eO-VUf(<
T(*#[-*#c"P-*VBL-V[,
0
P2-*#$H$U.*-,2
$-V62,
0
cU<O,EKL6<
PHÂN TCH
Z I2 Y
CUV
]^_`
CUV
]^_`
T(*#[-*#c"P-*VBL-V[,
0
P2-*#$H$U.*-,2
$-V62,
0
cU<O,EKL6<
=+W'X(=-%+;R-Y'ZR&5
1 gi x gi
\7(-,
\7(-,
22x
!$
16x
I2*>
3[-*#cxP-*VBL-V[,
0
PA
=+W'X(=
g
-V
6h ,7(-,%, \7(-,%,I2*>
![ 22x + 16x \
A(x) = 1,5 + 22x + 16x + 8 = 38x + 9,5
Z I2 Y
TRÒ CHƠI
EM TẬP LÀM THỦ MÔN
Câu 1. 
 !"
A. 2
C.
B. #
D.
Câu 2. $ %&'(
)
)
*
)+
),-
A.
C. *
B. ,
D.
B4"i["P@,Tj>*7*k.*A
Di["P-H0<
"
-H"-H<
Ei["P-HJZKL-H0<
A. ./01

+
C. ./01+

B../01+


D. ./01


]^_C
l!.*#
T
-*!
$dmn-*
!dD&7M*
LT
3$U,oA
`5(1+*>323
'()*+,'-.&a
bEcdefCVgF
Tiết học kết thúc !
h
VgFi
| 1/29
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GD & ĐT VĨNH TƯỜNG
TRƯỜNG THCS BÌNH DƯƠNG
Giáo viên thực hiện: Lương Văn Thành
Bài 25. ĐA THỨC MỘT BIẾN
01 Đơn thức một biến
02 Khái niệm đa thức một biến
03 Đa thức một biến thu gọn
04 Sắp xếp đa thức một biến
05 Bậc và các hệ số của ủ một t đa đ thức th
06 Nghiệm của đa thức một biến VÒNG QUAY m ể 9 MAY MẮN i hần 0 1 Đ P m ể i thưởng Đ Điểm 1 2 10 Vỗ a t y Vỗ t h Đ ta ư y P ở h iể 3 4 n ầ g n m 9 QUAY
Câu 1. Tính 3x5 + (-5x5). Hệ số của đơn thức nhận được là A. – 2 B. – 5 C. 3 D. 5 QUAY VỀ 00 05 04 03 01 6 07 08 09 1 1 Câu 2. 5 Tính x   
2 x . Bậc của đơn thức nh n ậ được là 4  1 A. B. 6 2 C. 1 D. 5 QUAY VỀ 7
Câu 3. Cho đa thức Px 4 2 2 4 3 2
  3,5x  5x  3x x x  2x  1 2
Thu gọn và sắp xếp đa thức trên theo lũy thừa giảm của biến ta được kết quả là A. -2x3 – 2x2 + x + 1 B. 7x4 - 2x3 – 2x2 + x + 1 C. -7x4 - 2x3 – 2x2 + x + 1 D. 2x3 – 2x2 + x + 1 QUAY VỀ 00 05 04 03 06 07 08 09 1
Câu 4. Đa thức 4x4 – 3x2 + x – 1 có các hạng tử là A. 4x4; 3x2; x; 1 B. 4x4; -3x2; x; 1 C. 4x4; -3x2; x; -1 D. 4x4; 3x2; x; -1 QUAY VỀ TIẾT 56
BÀI 25. ĐA THỨC MỘT BIẾN
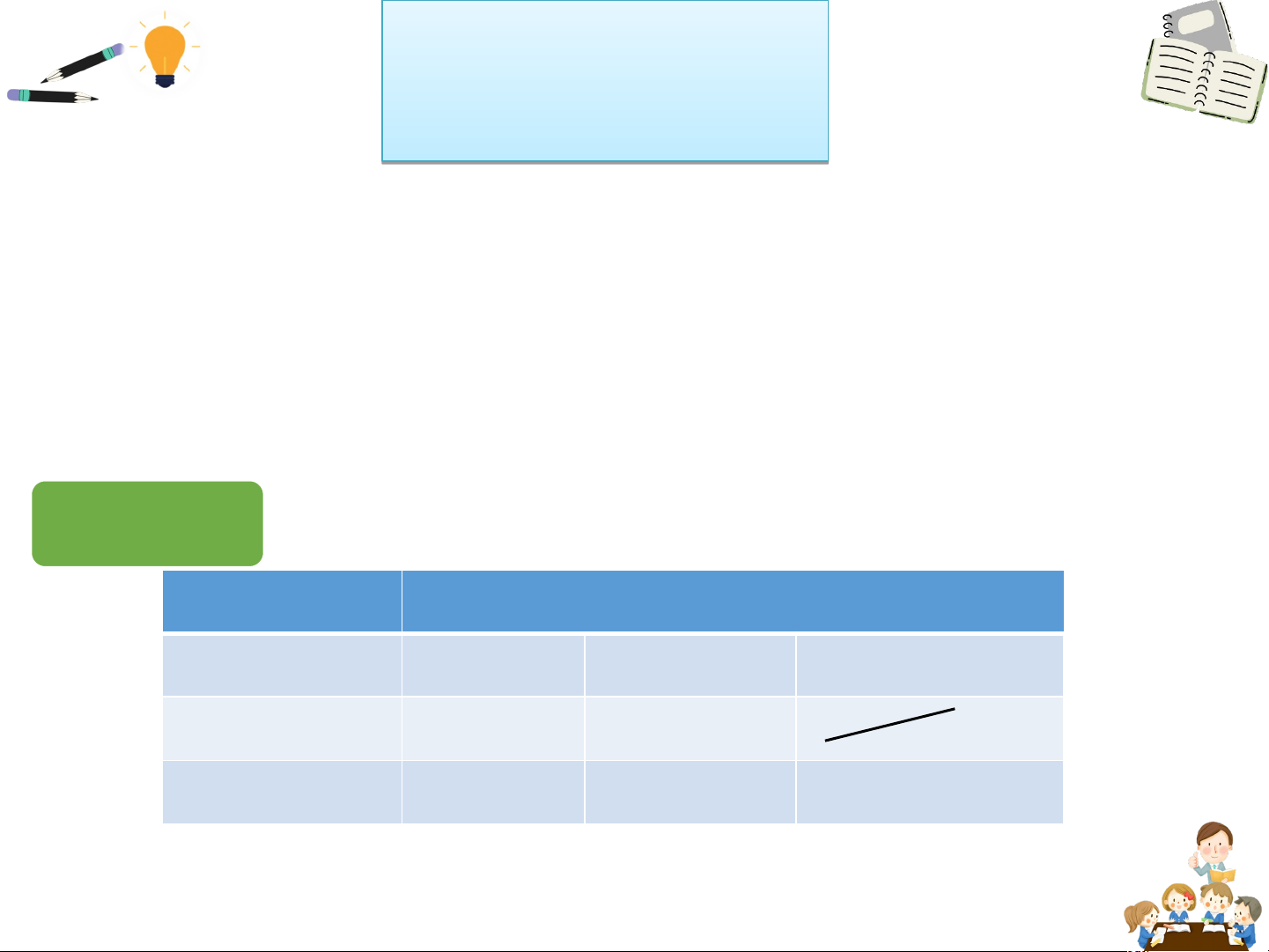
5) Bậc và các hệ số của một đa thức PHIẾU PH HỌC HỌ T ẬP
Xét đa thức P = -3x4 + 5x2 – 2x + 1. Quan sát và trả lời các câu hỏi sau:
1 Xác định bậc của các hạng tử trong P. Hạng tử Bậc Trong đa thức P: 2 Bậc: ….
Hạng tử có bậc cao nhất là: …… Hệ số: ….
3 Trong đa thức P; hạng tử có bậc bằng 0 là: …. 00 05 04 03 06 07 08 09 1 PHIẾU P HỌC H TẬ ỌC P
Xét đa thức P = -3x4 + 5x2 – 2x + 1. Quan sát và trả lời các câu hỏi sau:
Xác định bậc của các hạng tử trong P. 1 Đa thức P có Đa thức P Hạng tử -3x4 5x2 -2x 1
hệ số cao nhất là - 3 có bậc là 4 Bậc 4 2 1 0 2 Trong đa thức P: Bậc: 4
Hạng tử có bậc cao nhất là: -3x4 Hệ số: - 3
3 Trong đa thức P; hạng tử có bậc bằng 0 là: 1 Đa thức P có hệ số tự do là 1 ĐỊNH NGHĨA
Trong một đa thức thu gọn và khác đa thức không:
 Bậc của hạng tử có bậc cao nhất gọi là bậc của đa thức đó.
 Hệ số của hạng tử có bậc cao nhất gọi là hệ số cao nhất của đa thức đó.
 Hệ số của hạng tử bậc 0 gọi hệ số tự do của đa thức đó. Ví dụ
Tìm bậc, hệ số cao nhất và hệ số tự do của đa thức
A(x) = x5 – 3x2 + 8x4 – 5x2 – x5 + x – 7 Bài toán 1
Tìm bậc, hệ số cao nhất và hệ số tự do của đa thức 3 1 a) M x 3 4 2 x
x  7x x  4x  9 2 2 b) N x 2 4 2 1
 ,5x  3, 4x  0,5x  1 Bài toán 1 a) Ta có: 3 1 M x 3 4 2 x
x  7x x  4x  9 2 23 1 4 3 2
 7x x  4x x x  9 2 2 4 3 2
 7x x  4x  2x  9
Vậy đa thức M(x) có: bậc là 4
hệ số cao nhất là – 7 hệ số tự do là 9 Bài toán 1 b) Ta có: N x 2 4 2 1
 ,5x  3, 4x  0,5x  1 4 2 2
 3, 4x 1,5x  0,5x  1 4 2
 3, 4x  2x  1
Vậy đa thức N(x) có: bậc là 4
hệ số cao nhất là – 3,4 hệ số tự do là -1 MẢNH GHÉP
Em hãy ghép hai mảnh ghép với nhau để được một đáp án đúng.
Thời gian suy nghĩ cho hoạt động này là 3 phút MẢNH GHÉP
Đa thức Qx 3 2 3 3
x  4x  8x  5x  4x  5
Đa thức Px 3
 4x  4x  3
Đa thức Ax 4  x 16
Đa thức B x 5 2 2 2 5
 3  2x  3x  2x x  2x  3
Đa thức M x 2 0  x  6
Đa thức có bậc là 0
Đa thức có hệ số cao nhất là - 1
Đa thức có bậc là 2
Đa thức có hệ số tự do là - 3 Đa thức không có bậc 00 05 04 03 01 6 07 08 09 1 MẢNH GHÉP Cách ghép như sau
Đa thức Ax 4  x 16
Đa thức có hệ số cao nhất là - 1 MẢNH GHÉP
Đa thức Qx 3 2 3 3
x  4x  8x  5x  4x Đ a t 5 hức có bậc là 2
Đa thức P x 3
 4x  4x  3 Đa thức có hệ số tự do là - 3
Đa thức Ax 4  x 16
Đa thức có hệ số cao nhất là - 1
Đa thức B x 5 2 2 2 5
 3  2x  3x  2x  Đ x a t  hức 2x không c  3 ó bậc
Đa thức M x 2 0  x  6
Đa thức có bậc là 0 Chú ý
Đa thức không là đa thức không có bậc. 
Trong một đa thức thu gọn, hệ số cao nhất
phải khác 0 (các hệ số khác có thể bằng 0). 
Muốn tìm bậc của một đa thức chưa thu
gọn, ta phải thu gọn đa thức đó. BÀI T I OÁN T TH T ỰC H T ỰC I T ỄN Ễ Người ta dùng g hai máy y bơ bơm để bơm nư nước vào một ột bể chứa nư nước. . Máy y thứ nhất bơm mỗi giờ được 22 22m3 m nư nước. . Máy thứ ha hai bơm mỗi gi giờ được 16 16m3 m nư nước. . Sau khi hi cả ha hai máy chạy y trong ng x g x giờ, , ng người ta tắt máy
y thứ nhất và để máy thứ hai chạy t thêm 0 0,5 ,5 g giờ n nữa t thì hì b bể n nước đầ đầy. y Hãy y vi
viết đa thức (biến x) bi biểu thị du dung g tích của bể (m3
m ), biết rằng trước kh k i hi bơ bơm, trong bể c có 1,5 m3 m n ư nước. Tì
Tìm hệ số cao nhất và hệ số t tự do của đ đa thức đ đó. PHÂN TÍCH Số mét khối 1 giờ x giờ 0,5 giờ Máy bơm 1 22 22x Máy bơm 2 16 16x 16 0  ,5 8  BÀI T I OÁN T TH T ỰC H T ỰC I T ỄN Ễ
Hãy viết đa thức (biến x) biểu thị dung tích của bể (m3), biết rằng trước khi bơm,
trong bể có 1,5 m3 nước. Tìm hệ số cao nhất và hệ số tự do của đa thức đó.
Số mét khối bơm vào bể trong 1 giờ x giờ 0,5 giờ Máy bơm 1 22 22x Máy bơm 2 16 16x 16 0  ,5 8 
Đa thức (biến x) biểu thị dung tích của bể (m3) là:
A(x) = 1,5 + 22x + 16x + 8 = 38x + 9,5 Số mét khối Dung tích Có sẵn
2 máy bơm thêm Máy 2 bơm thêm 0,5 giờ của bể 1,5 22x + 16x 8 TRÒ CHƠI
EM TẬP LÀM THỦ MÔN
Câu 1. Đa thức x2 + 1; hạng tử bậc 1 có hệ số là A. 2 B. 0 C. 1 D. 3
Câu 2. Hệ số cao nhất của đa thức 5x6 + 6x5 + x4 - 3x2 + 7 ? A. 6 B. 7 C. 4 D. 5
Câu 3. Cho đa thức F(x) thỏa mãn đồng thời các điều kiện sau: Bậc của F(x) bằng 3.
Hệ số của x2 bằng hệ số của x và bằng 2.
Hệ số cao nhất của F(x) bằng -6 và hệ số tự do bằng 3. A. F(x) = 3x3 + 2x2 + 2x - 6 B. F(x) = -6x3 + 2x2 + 2x + 3 C. F(x) = -6x2 + 2x + 3 D. F(x) = 6x3 + 2x2 + 2x + 3
HƯỚNG DẪN VỀ NHÀ Ôn tập kiến Hoàn thành bài tập Đọc trước mục: thức đã học trong SGK và bài “Nghiệm của đa tập SBT theo các nội thức một biến” dung đã được học
QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH
Tiết học kết thúc ! CHÚC CÁC EM HỌC TỐT
Document Outline

  • Slide 1
  • Slide 2
  • Slide 3
  • Slide 4
  • Slide 5
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Slide 10
  • Slide 11
  • Slide 12
  • Slide 13
  • Slide 14
  • Slide 15
  • Slide 16
  • Slide 17
  • Slide 18
  • Slide 19
  • Slide 20
  • Slide 21
  • Slide 22
  • Slide 23
  • Slide 24
  • Slide 25
  • Slide 26
  • Slide 27
  • Slide 28
  • Slide 29