CHÀO CÁC EM HỌC SINH
Người thực hiện : Trần Thị Nga
GV TRƯỜNG TH & THCS HUỲNH THÚC KHÁNG Chương I ĐA THỨC
TIẾT 5,6 BÀI 3. PHÉP CỘNG VÀ PHÉP TRỪ ĐA THỨC
Trong buổi sinh hoạt câu lạc bộ Toán học của
lớp, hai bạn tính giá trị của hai đa thức
P = 2x2y – xy2 + 22 và Q = xy2 – 2x2y + 23
tại những giá trị cho trước của x và y.
Kết quả được ghi lại như bảng bên. Ban giám
khảo cho biết một cột chắc chắn có kết quả sai. Bảng 1.1
1 . CỘNG VÀ TRỪ HAI ĐA THỨC
Cho hai đa thức A = 5x2y + 5x – 3 và B = xy – 4x2y + 5x – 1.
Thực hiện phép cộng hai đa thức A và B bằng cách tiến hành các bước sau:
+ Lập tổng A + B = (5x2y + 5x – 3) + (xy – 4x2y + 5x – 1).
+ Bỏ dấu ngoặc và thu gọn đa thức nhận được.
 Thực hiện phép cộng hai đa thức A và B theo các bước sau:
Lập tổng A + B = (5x2y + 5x – 3) + (xy – 4x2y + 5x – 1).
• Bỏ dấu ngoặc và thu gọn đa thức nhận được.
• Bỏ dấu ngoặc và thu gọn đa thức nhận được. 2 2 A B 5
 x y 5x 3 xy 4x y 5x 1  2 2
 5x y 4x 
y  xy  5x 5  x   3  1 2
x y xy10x 4
1 . CỘNG VÀ TRỪ HAI ĐA THỨC
Cho hai đa thức A = 5x2y + 5x – 3 và B = xy – 4x2y + 5x – 1.
Thực hiện phép trừ hai đa thức A và B bằng cách lập hiệu:
A - B = (5x2y + 5x – 3) - (xy – 4x2y + 5x – 1).
Bỏ dấu ngoặc và thu gọn đa thức nhận được. 2 2
 Ta có : A B 
 5x y 5x 
3   xy 4x y5x  1 2 2 5
 x y 5x 3 xy 4x y 5x1  2 2
 5x y 4x 
y  xy  5x 5  x  1  3 2 9
 x y xy 2
1 . CỘNG VÀ TRỪ HAI ĐA THỨC  Chú ý : •
Phép cộng đa thức cũng có các tính chất giao hoán và kết hợp tương
tự như phép cộng các số. •
Với A, B, C là những đa thức tuỳ ý, ta có :
Nếu thì , ngược lại nếu thì
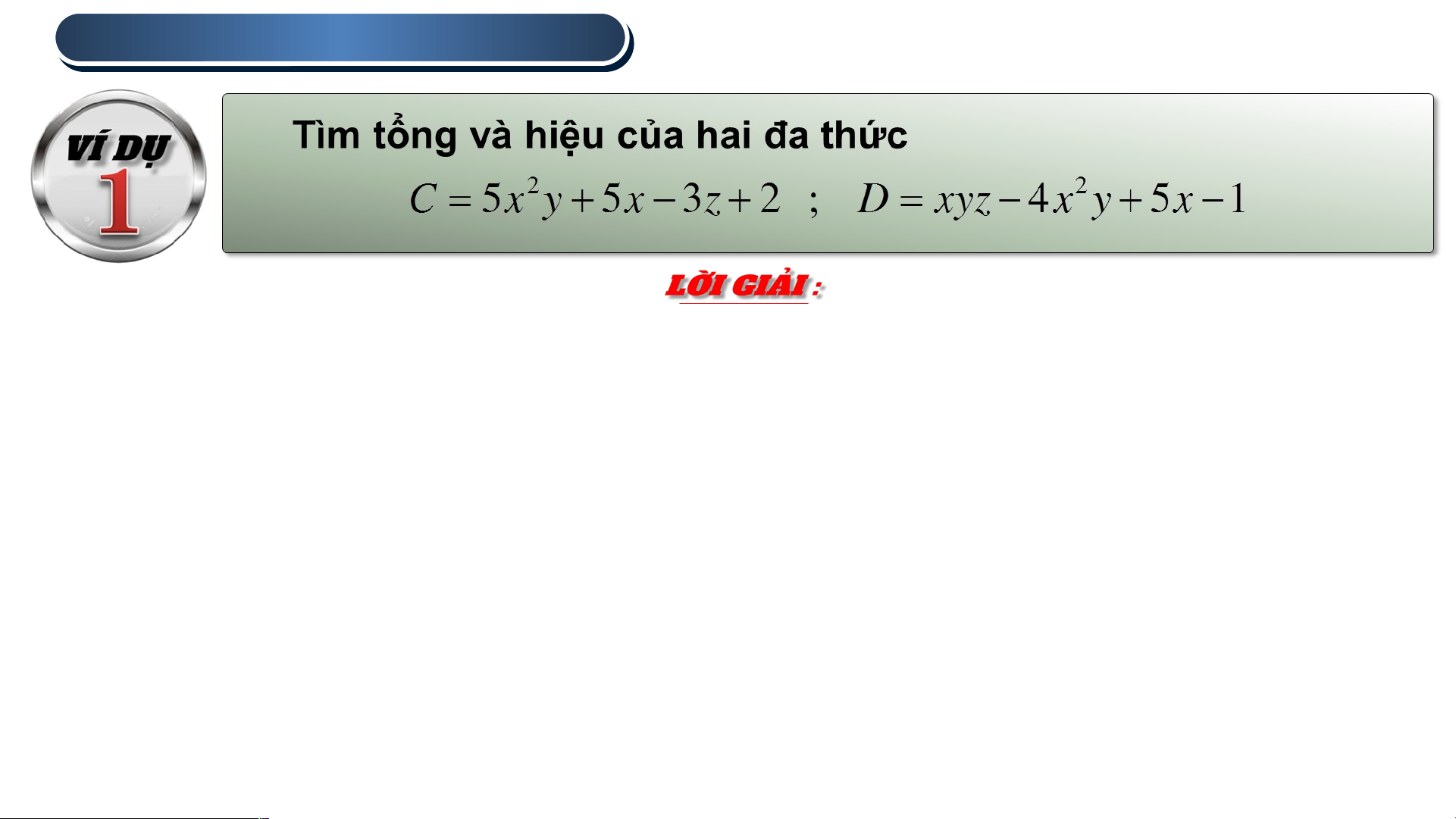
1 . CỘNG VÀ TRỪ HAI ĐA THỨC C  D  2
 x y x z   2 5 5 3 2
xyz 4x y 5x 1 2 2 5
 x y 5x 3z 2 xyz 4x y 5x 1  2 2
 5x y 4x 
y  5x5 
x  3z xyz  2  1 2
x y10x 3z xyz1 C  D  2
 x y x z    2 5 5 3 2
xyz 4x y 5x 1 2 2 5
 x y 5x 3z 2 xyz 4x y 5x1  2 2
 5x y 4x 
y  5x 5 
x  xyz 3z 2  1 2 9
 x y xyz 3z 3
1 . CỘNG VÀ TRỪ HAI ĐA THỨC G  H  2
 x y xy   2 3 3
3x y xy 0,5x  5 2 2
x y 3xy 3 3x y xy 0,5x 5  2 2
 x y 3x 
y   xy 3x 
y  0,5x  5  3 2 4
 x y 2xy 0,5x 2 G  H  2
 x y xy    2 3 3
3x y xy 0,5x  5 2 2
x y 3xy 3 3x y xy 0,5x 5  2 2
 x y 3x 
y   3xy x 
y  0,5x  3  5 2
 2x y 4xy 0,5x 8
1. Cộng và trừ hai đa thức LUYỆN TẬP 2 Lời giải
K = (x2y + 2xy3) – (7,5x3y2 – x3) + (3xy3 – x2y + 7,5x3y2)
= x2y + 2xy3 – 7,5x3y2 + x3 + 3xy3 – x2y + 7,5x3y2
= (x2y – x2y) + (2xy3 + 3xy3) + (7,5x3y2 – 7,5x3y2) + x3 = T 5 h x a y y 3 + x x = 3
2 . và y = −1 vào đa thức thu gọn ở trên, ta được:
K = 5.2.(–1)3 + 23 = 10.(–1) + 8 = –2.
BÀI 1.14. Tính tổng và hiệu của hai đa thức P = x2y + x3 – xy2 + 3 và Q = x3 + xy2 – xy – 6. Lời giải: Ta có:
• P + Q = (x2y + x3 – xy2 + 3) + (x3 + xy2 – xy – 6)
= x2y + x3 – xy2 + 3 + x3 + xy2 – xy – 6
= x2y + (x3 + x3) + (xy2 – xy2) – xy + (3 – 6) = x2y + 2x3 – xy – 3.
• P – Q = (x2y + x3 – xy2 + 3) – (x3 + xy2 – xy – 6)
= x2y + x3 – xy2 + 3 – x3 – xy2 + xy + 6
= x2y + (x3 – x3) – (xy2 + xy2) + xy + (6 + 3) = x2y – 2xy2 + xy + 9.
Vậy P + Q = x2y + 2x3 – xy – 3; P – Q = x2y – 2xy2 + xy + 9.
1.15. Rút gọn các biểu thức sau:
a) (x – y) + (y – z) + (z – x);
b) (2x – 3y) + (2y – 3z) + (2z – 3x). Lời giải:
a) (x – y) + (y – z) + (z – x) = x – y + y – z + z – x
= (x – x) + (y – y) + (z – z) = 0 + 0 + 0 = 0
b) (2x – 3y) + (2y – 3z) + (2z – 3x)
= 2x – 3y + 2y – 3z + 2z – 3x
= (2x – 3x) + (2y – 3y) + (2z – 3z) = –x – y – z.
BÀI 1.16. Tìm đa thức M biết M – 5x2 + xyz = xy + 2x2 – 3xyz + 5. Lời giải:
Ta có M – 5x2 + xyz = xy + 2x2 – 3xyz + 5
Suy ra: M = xy + 2x2 – 3xyz + 5 + 5x2 – xyz
= (5x2 + 2x2) – (3xyz + xyz) + xy + 5 = 7x2 – 4xyz + xy + 5.
Vậy M = 7x2 – 4xyz + xy + 5.
BÀI 1.17. Cho hai đa thức A = 2x2y + 3xyz – 2x + 5 và B = 3xyz – 2 a x2 ) y + Tìm x – cá 4 c . đa thức A + B và A – B;
b) Tính giá trị của các đa thức A và A + B tại x = 0,5; y = −2 và z = 1 L . ời giải: a) Ta có:
• A + B = (2x2y + 3xyz – 2x + 5) + (3xyz – 2x2y + x – 4)
= 2x2y + 3xyz – 2x + 5 + 3xyz – 2x2y + x – 4
= (2x2y – 2x2y) + (3xyz + 3xyz) + (x – 2x) + (5 – 4) = 6xyz – x + 1.
• A – B = (2x2y + 3xyz – 2x + 5) – (3xyz – 2x2y + x – 4)
= 2x2y + 3xyz – 2x + 5 – 3xyz + 2x2y – x + 4
= (2x2y + 2x2y) + (3xyz – 3xyz) – (2x + x) + (5 + 4) = 4x2y – 3x + 9.
Vậy A + B = 6xyz – x + 1; A – B = 4x2y – 3x + 9.
b) Thay x = 0,5; y = −2 và z = 1 vào biểu thức A, ta được:
A = 2 . 0,52 . (−2) + 3 . 0,5 . (−2) . 1 – 2 . 0,5 + 5
= 2 . 0,25 . (−2) + 1,5 . (−2) – 1 + 5
= 0,5 . (−2) – 3 + 4 = −1 – 3 + 4 = 0.
Thay x = 0,5; y = −2 và z = 1 vào biểu thức A + B, ta được:
A + B = 6 . 0,5 . (−2) . 1 – 0,5 + 1
= 3 . (−2) – 0,5 + 1 = −6 + 0,5 = −5,5.
Vậy tại x = 0,5; y = −2 và z = 1 thì A= 0 và A + B = -5,5
THÂN ÁI CHÀO CÁC EM
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17