Giáo án điện tử Toán 7 Bài 34 Kết nối tri thức: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác (tiết 2)
Bài giảng PowerPoint Toán 7 Bài 34 Kết nối tri thức: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác (tiết 2) hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 7. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 7
Môn: Toán 7
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
Bài tập:
Hãy điền từ hoặc cụm từ thích hợp vào chỗ trống trong các câu sau:
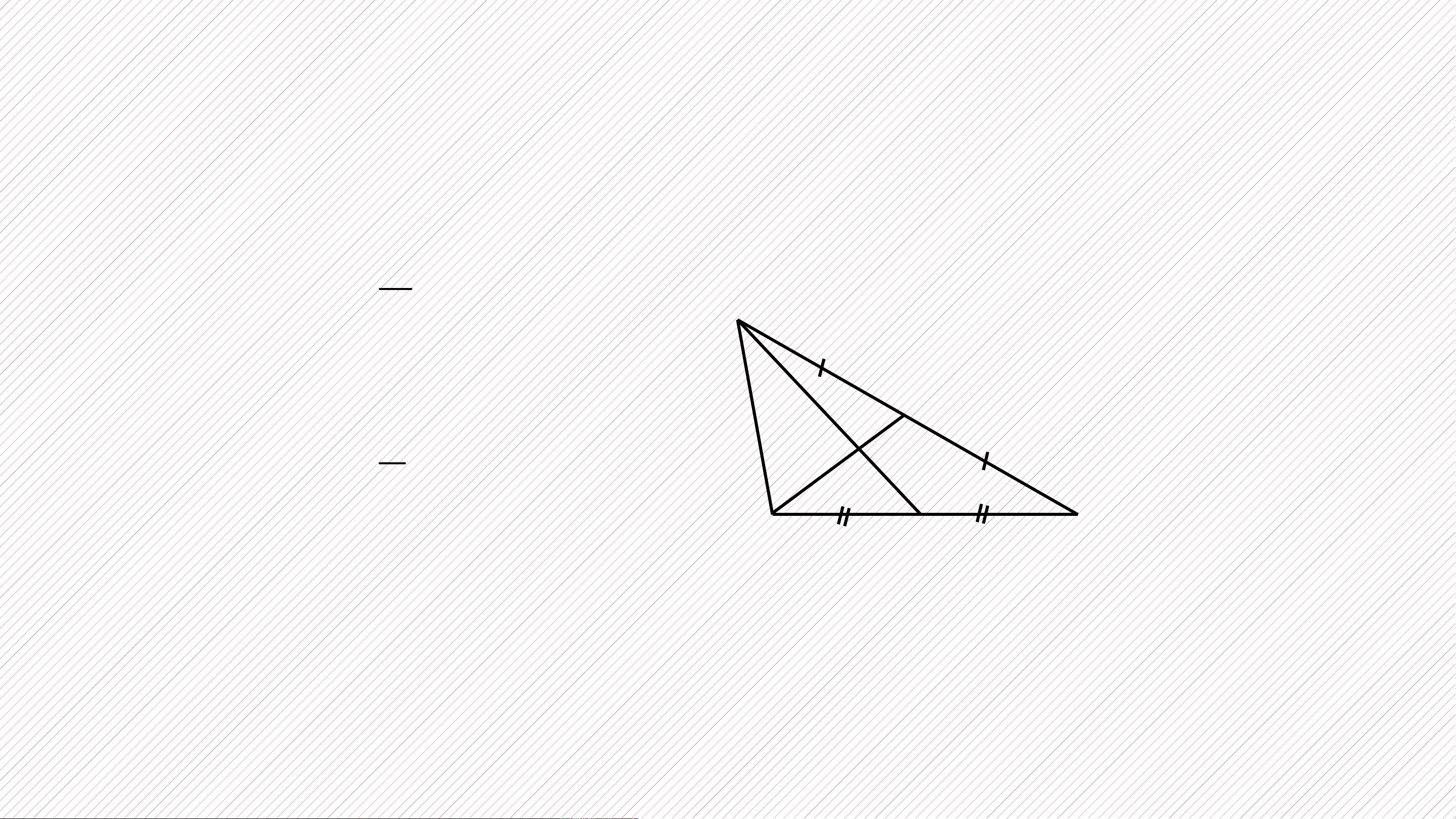
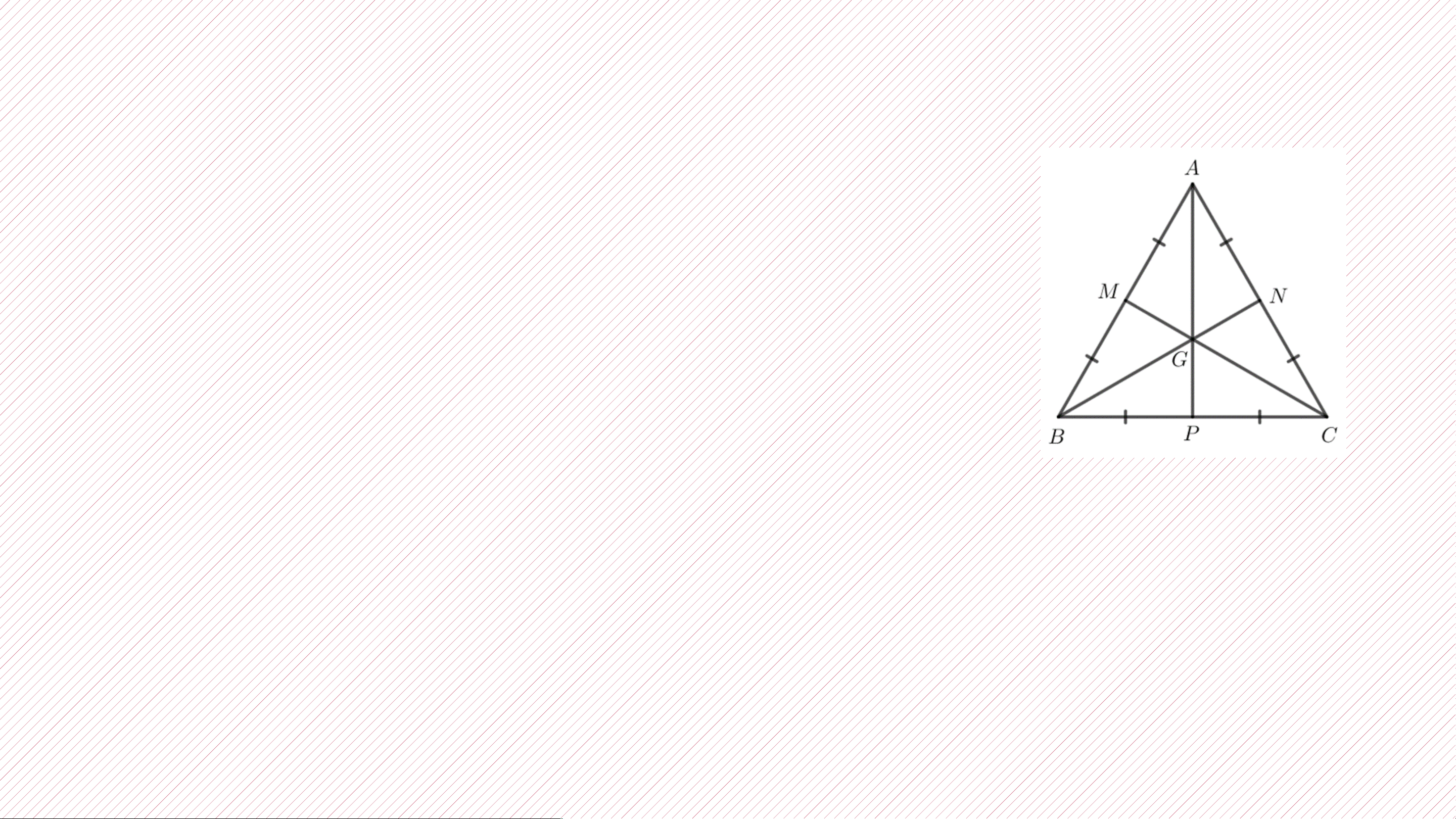
1.Đường trung tuyến của tam giác là đoạn thẳng nối từ … đỉ n của h
tam giác tới ……………………
trung điểm cạnh … đố …… i diện.
2. Ba đường trung tuyến của tam giác cùng đi qua ………... mộ .... t điểm
điểm đó được gọi là …………………………
trọng tâm của tam giác
3. Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng …..
2 độ dài đường trung tuyến……………… đi qua đỉnh 3 ấy. Bài tập:
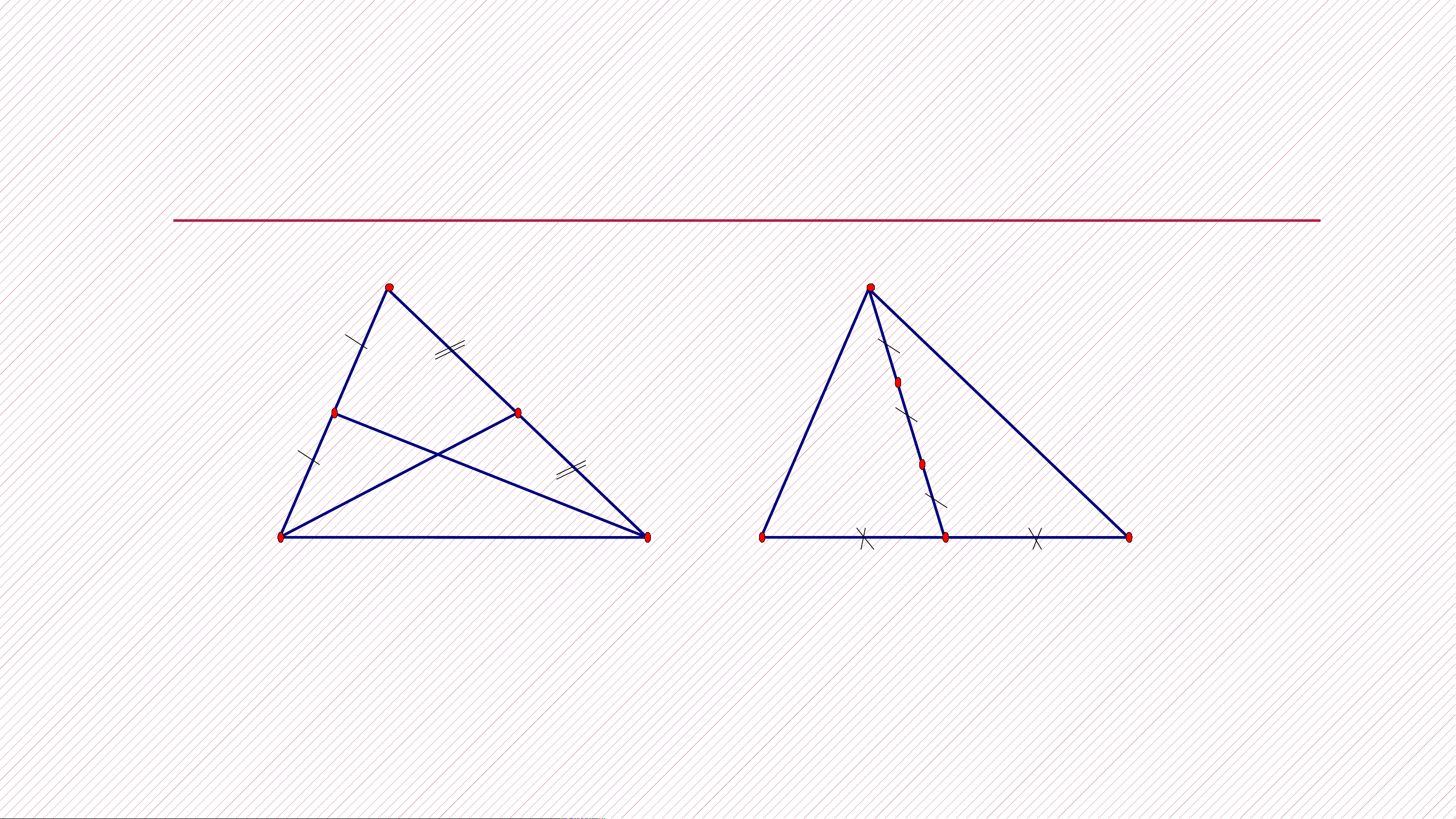
Cho hình vẽ, điền số thích hợp vào chỗ trống: 2 MG = ….MR; M 3 S GR = ….M 1 R; G 3 N R P NG = …GS 2
CÁCH XÁC ĐỊNH TRỌNG TÂM G CỦA TAM GIÁC ABC A A F E G G B C B C D
TIẾT 40 : SỰ ĐỒNG QUY CỦA BA ĐƯỜNG TRUNG TUYẾN,
BA ĐƯỜNG PHÂN GIÁC TRONG MỘT TAM GIÁC (Tiết 2)
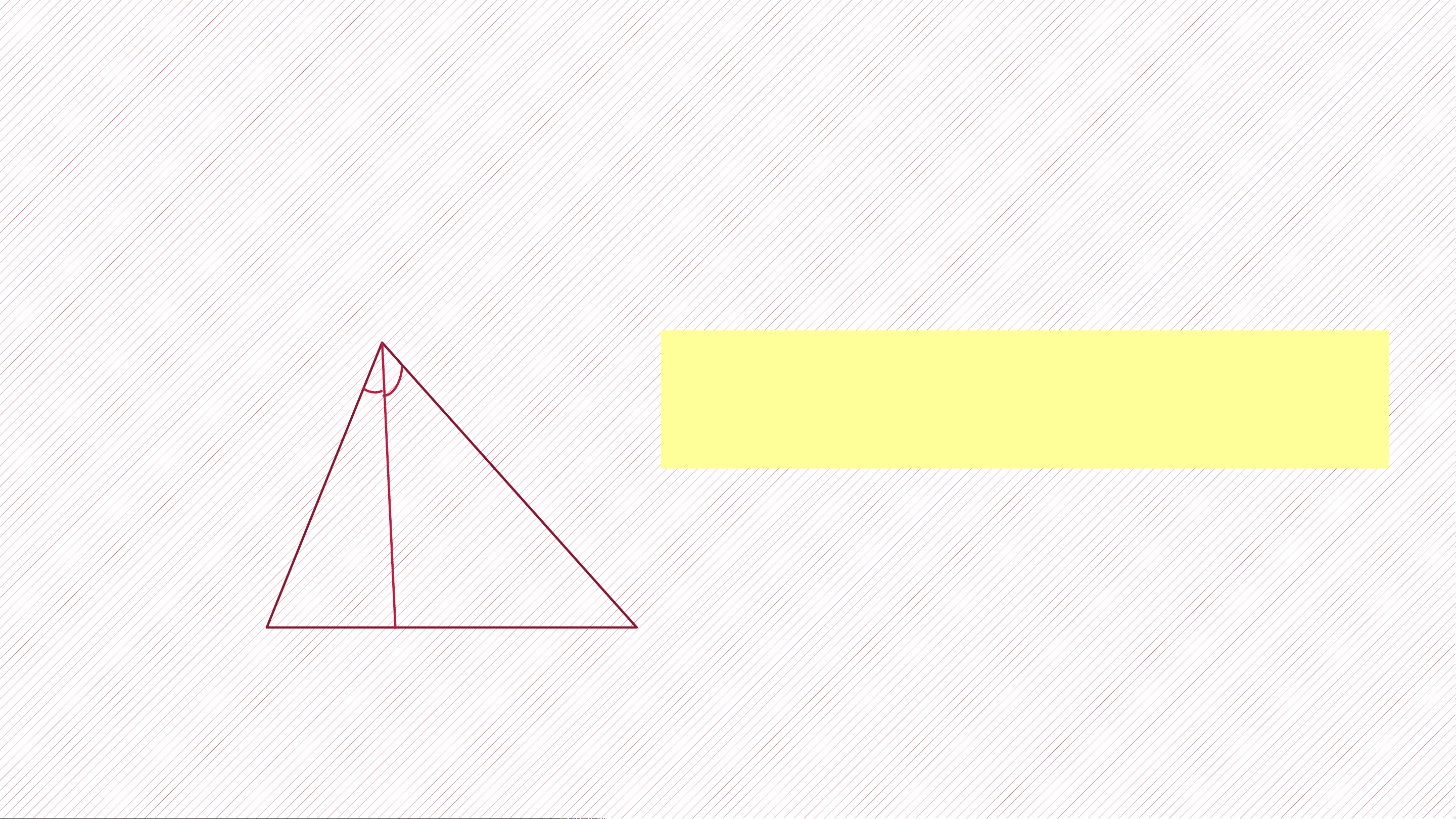
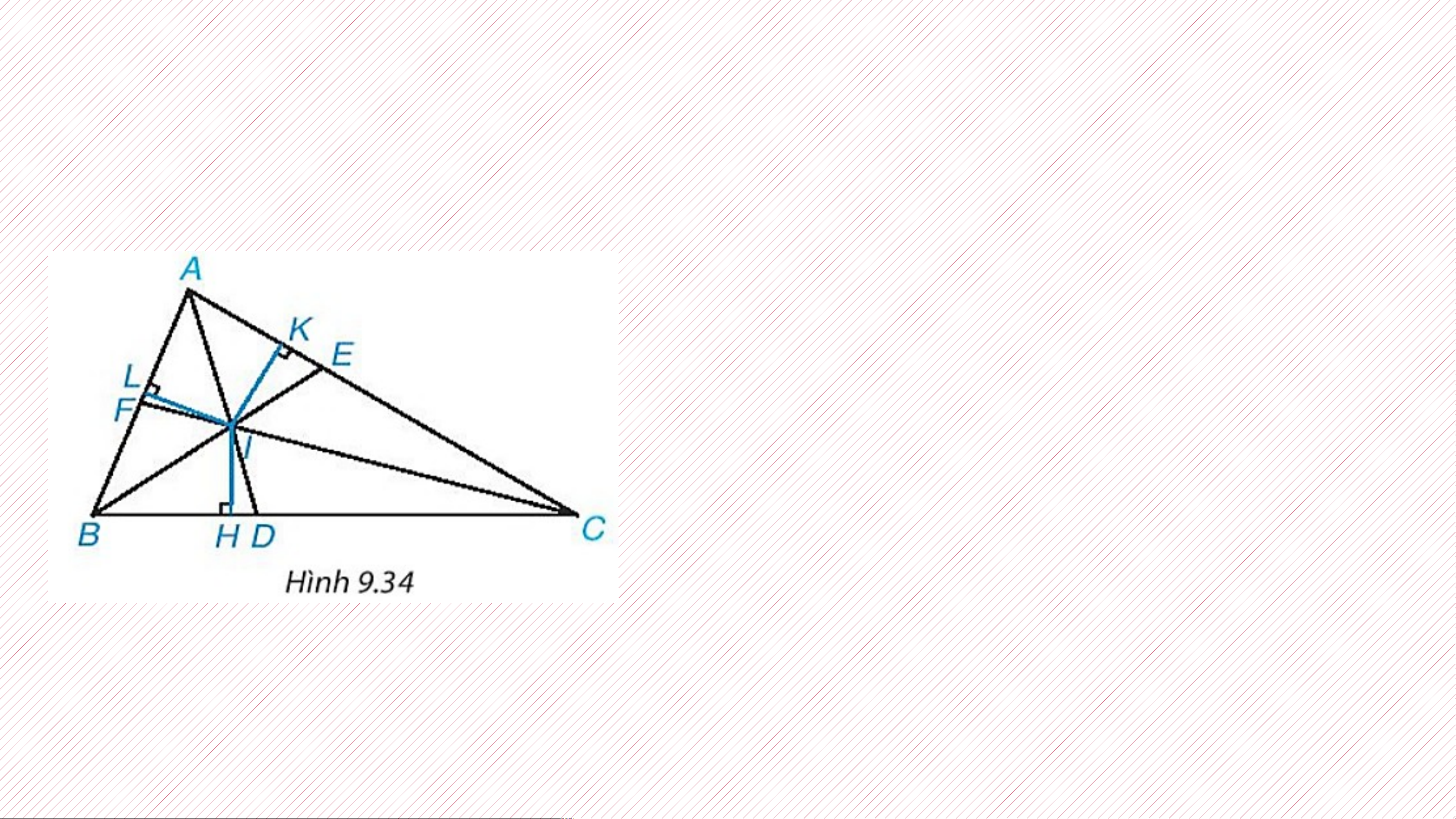
2. Sự đồng quy ba đường phân giác trong tam giác: A
Tia phân giác AD cắt cạnh BC tại điểm D thì
đoạn thẳng AD gọi là đường phân giác của tam giác ABC B C D ?
Mỗi tam giác có mấy đường phân giác? Trả lời:
Mỗi tam giác có 3 đường phân giác.
(Vì từ mỗi đỉnh của tam giác, ta kẻ được 1 đường phân giác của tam
giác nên mỗi tam giác có 3 đường phân giác). Định lí 2:
Ba đường phân giác của một tam giác đồng quy tại Em hãy vẽ 3 đường
một điểm. Điểm này cách đều ba cạnh của tam giác phân giác trong một đó. tam giác?
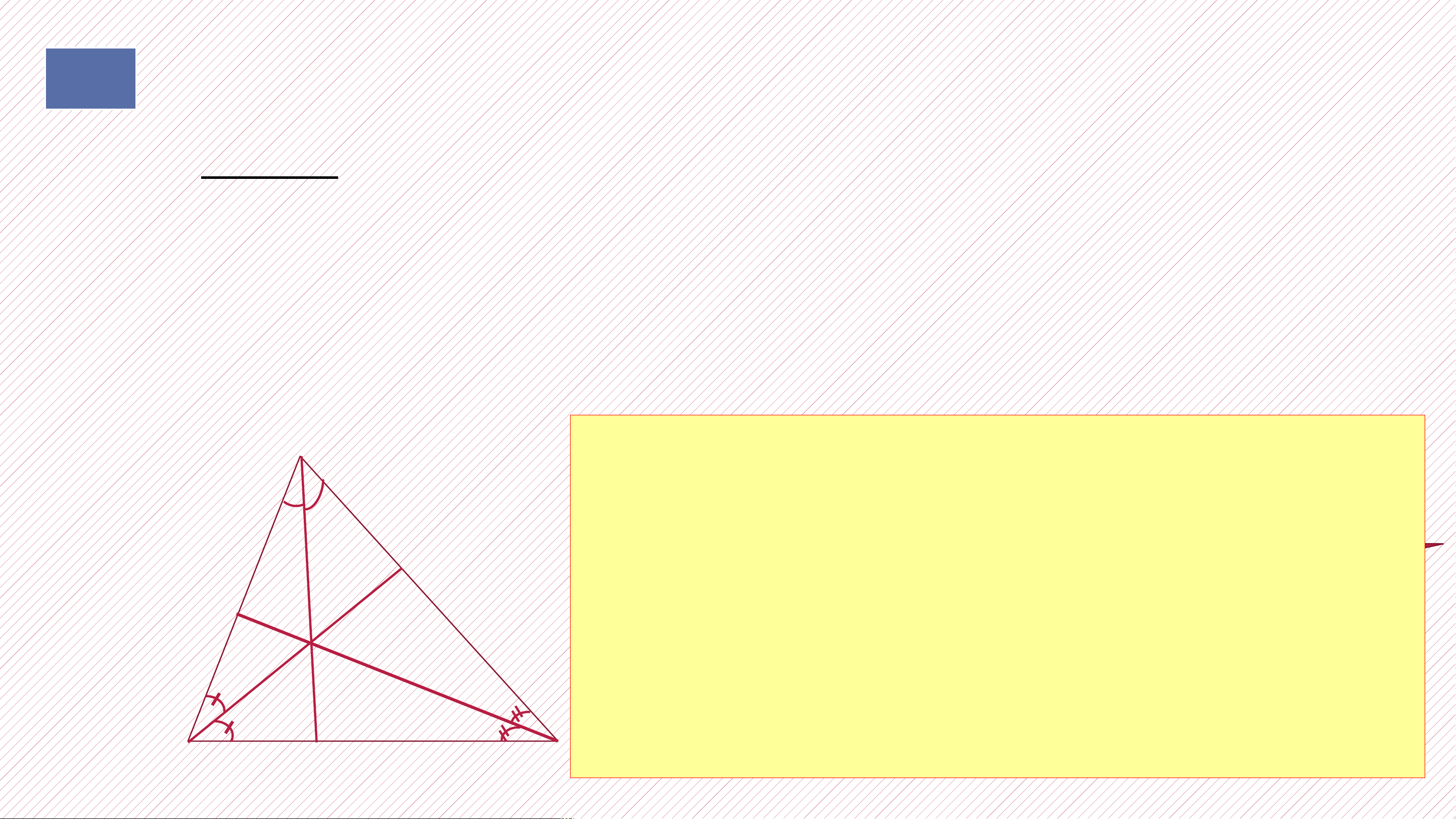
Trong tam giác ABC, các đường phân giác
AD, BE, CF đồng quy tại I và IH = IK = IL. LUYỆN TẬP 2
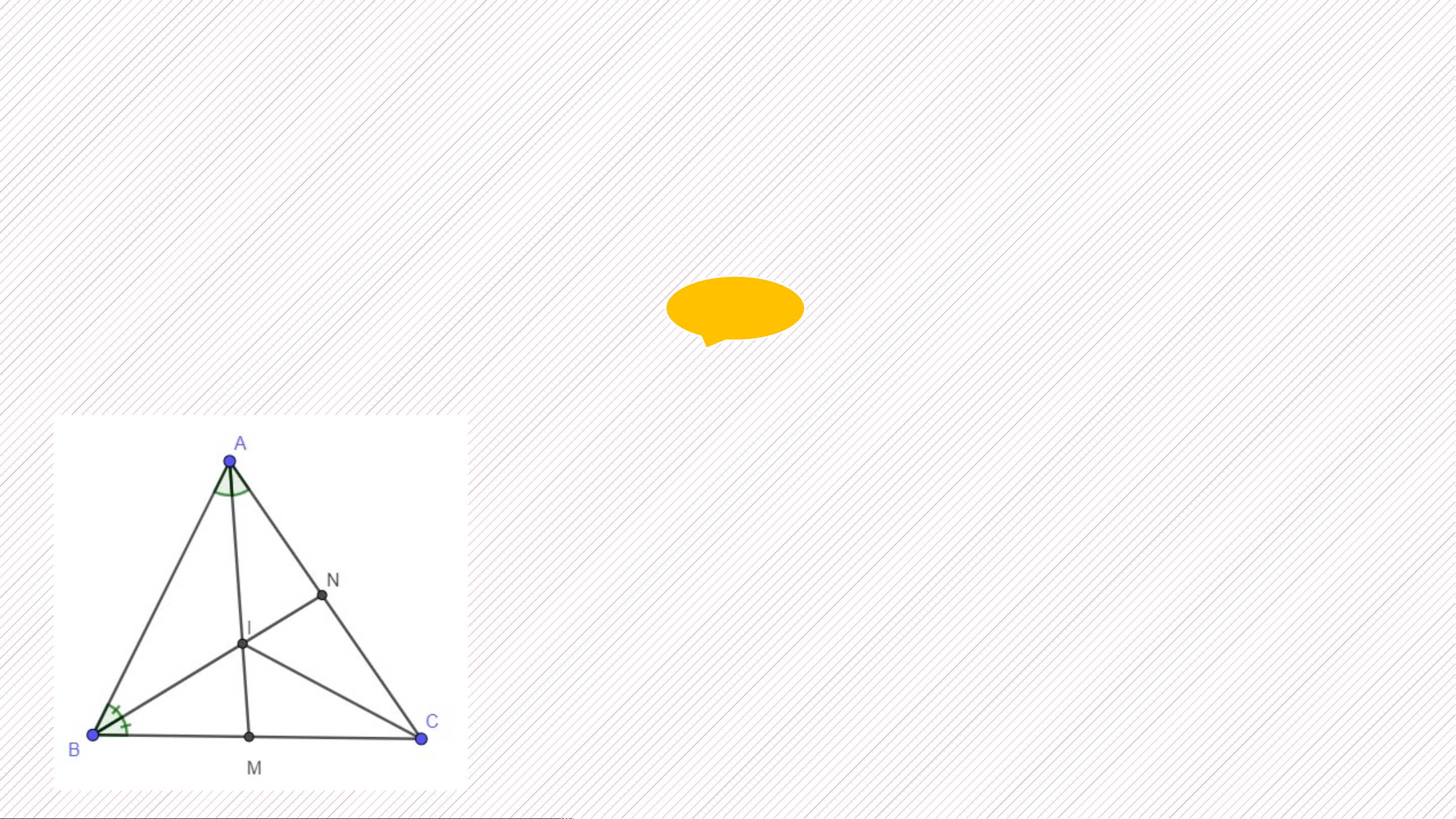
Cho tam giác ABC có hai đường phân giác AM, BN cắt nhau tại điểm I. Hỏi CI có là
đường phân giác của góc C không ? Giả i Xét tam giác ABC có: AM là phân giác BN là phân giác AM cắt BN tại I
CI cũng là đường phân giác của tam giác. (t/c đồng
quy của 3 đường phân giác). CHÚ Ý
• Tam giác đều là tam giác cân tại mỗi đỉnh của nó.
• Trong tam giác đều, hai điểm đồng quy của các đường
trung tuyến và của các đường phân giác trùng nhau. Luyện tập 2:
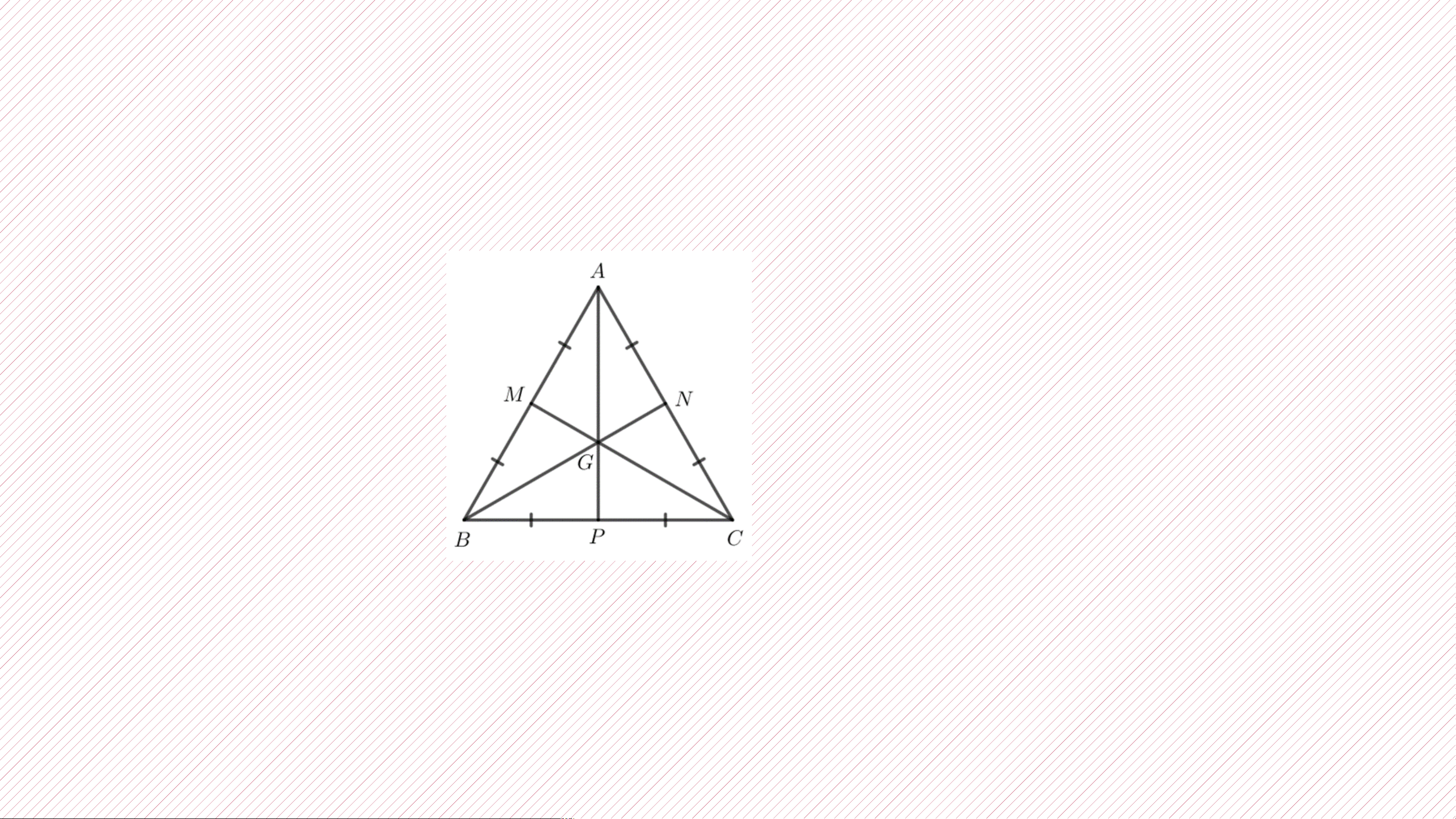
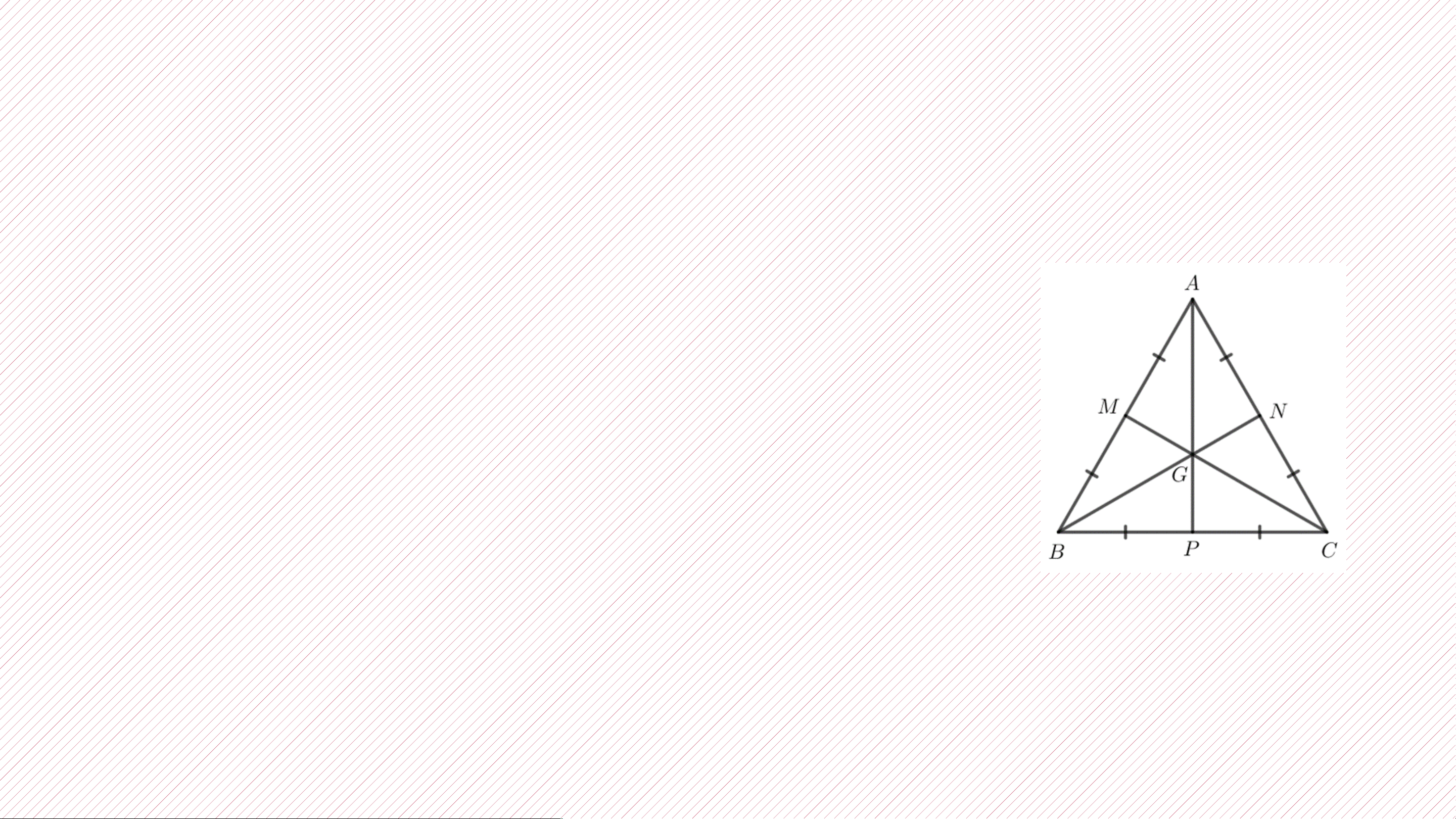
Chứng minh rằng trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó. Giải:
Giả sử tam giác ABC là tam giác đều có M, N, P lần lượt là trung điểm của các cạnh
AB, AC, BC và G là trọng tâm của tam giác.
Khi đó A, G, P thẳng hàng; B, G, N thẳng hang và C, G, M thẳng hàng.
Xét ΔAPB và ΔAPC có:
AB = AC (cmt), AP chung, PB = PC (do P là trung điểm của BC)
⇒ ΔAPB = ΔAPC (c − c −c)
⇒ ˆAPB = ˆAPC (2 góc tương ứng) Mà ˆAPB + ˆAPC = 180° ˆA ⇒ PB = ˆAPC = 90° ⇒ AP B ⊥ C hay GP
⊥ BC hay GP là khoảng cách từ G đến BC
Tương tự ta có GM, GN lần lượt là khoảng cách từ G đến AC, AC.
Do M là trung điểm của AB nên MB = 1/2AB
Do N là trung điểm của AC nên NC = 1/2AC Mà AB = AC nên MB = NC.
Xét ΔMBC và ΔNCB, có:
MB = NC (cmt), ˆMBC = ˆNCB (cmt), BC chung.
⇒ ΔMBC = ΔNCB (c − g − c)
⇒ CM = BN (2 cạnh tương ứng)
ΔABC có G trọng tâm ⇒ CG =2/3CM và BG = 2/3BN ⇒ GM = 1/3CM; GN = 1/3BN Mà CM = BN nên GM = GN.
Chứng minh tương tự ta có GM = GN = GP.
Khi đó trọng tâm G của tam giác đều ABC cách đều ba cạnh của tam giác.
Vậy trong tam giác đều, điểm cách đều ba cạnh của tam giác là
trọng tâm của tam giác đó.
Document Outline
- Slide 1
- Slide 2
- Cách xác định trọng tâm G của tam giác ABC
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11