












Preview text:
KIỂM TRA BÀI CŨ
1. Điểm như thế nào gọi là trung điểm của đoạn thẳng.
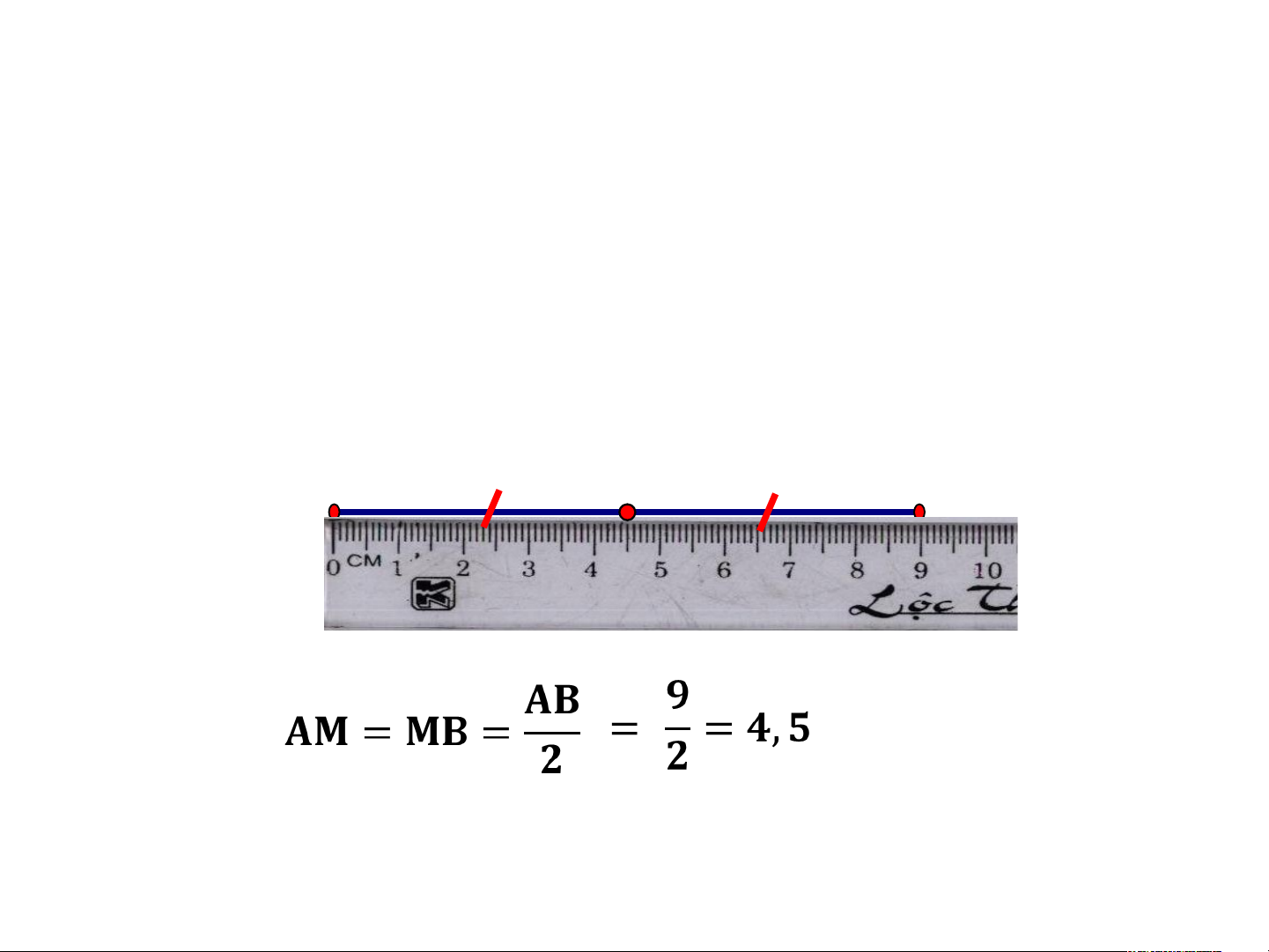
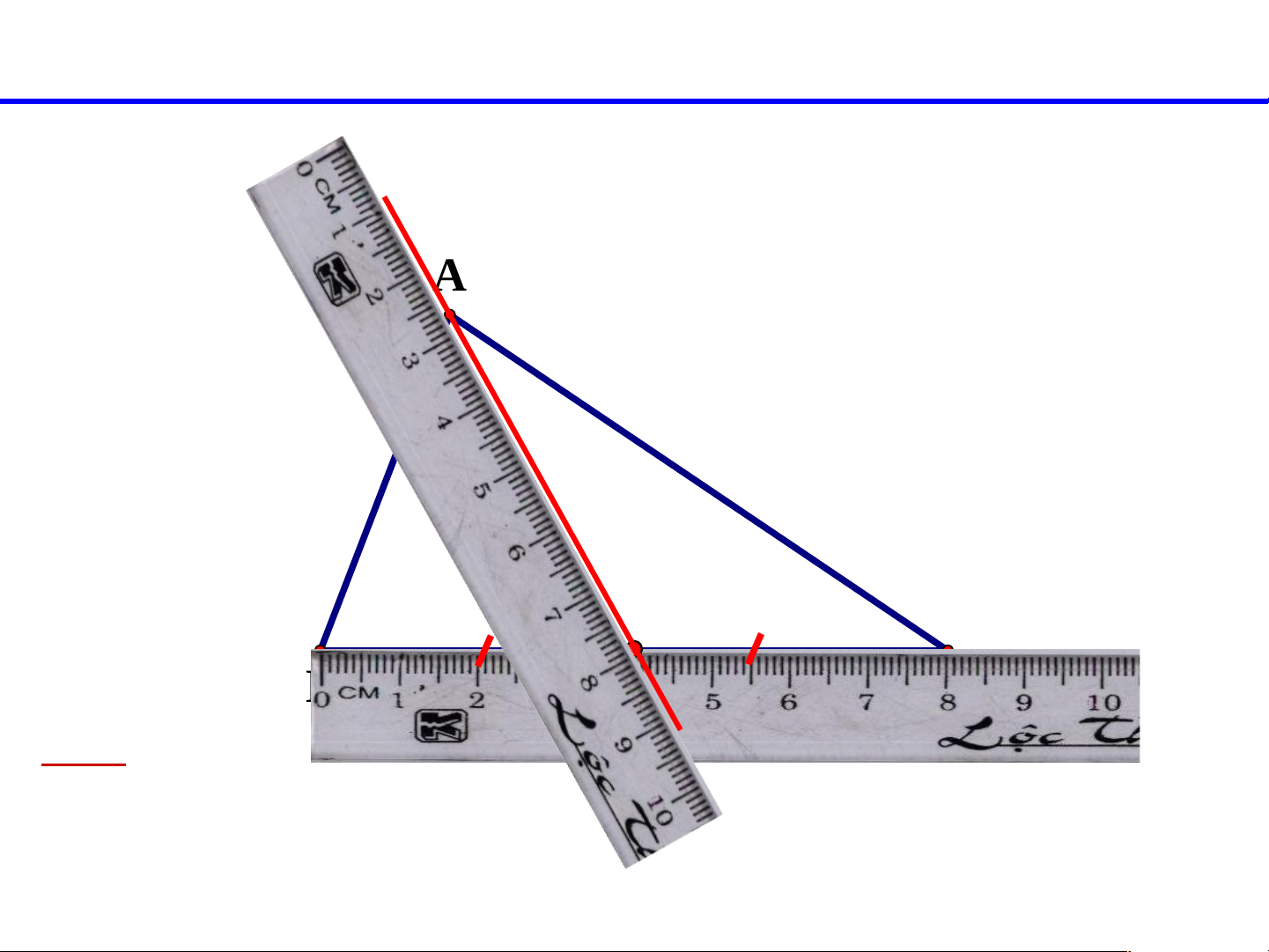
2. Cho đoạn thẳng AB như hình vẽ. Hãy nêu cách xác
định trung điểm M của đoạn thẳng AB. A M B 4,5cm 4,5cm Ta có:
Bài 34. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG
TRUNG TUYẾN, BA ĐƯỜNG PHÂN GIÁC TRONG TAM GIÁC
Tiết 43. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG
TRUNG TUYẾN TRONG TAM GIÁC
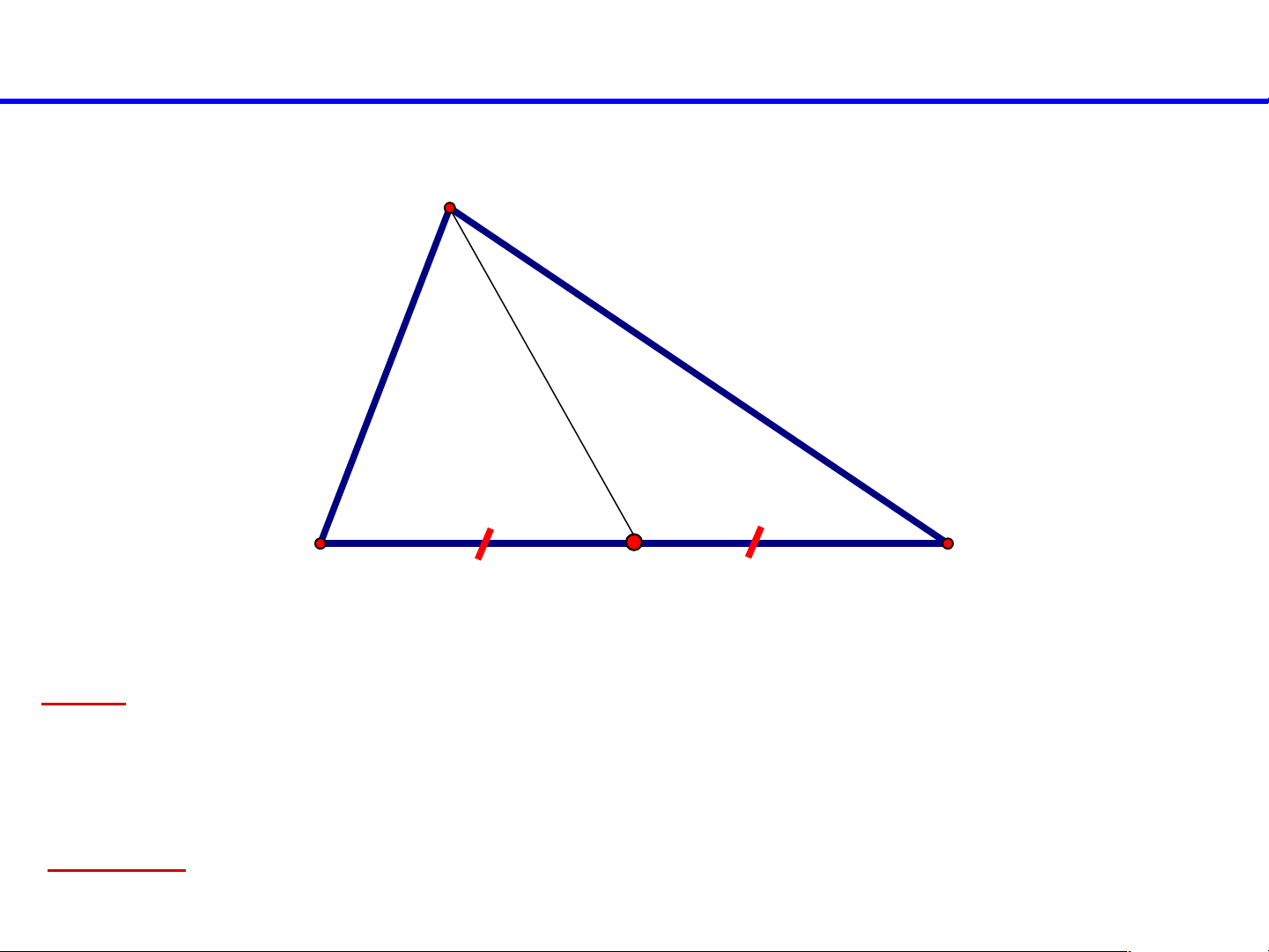
1. Đường trung tuyến của tam giác: A B M C
KN: Đường trung tuyến của tam giác là đoạn thẳng nối
đỉnh của tam giác với trung điểm của cạnh đối diện.
1. Đường trung tuyến của tam giác:
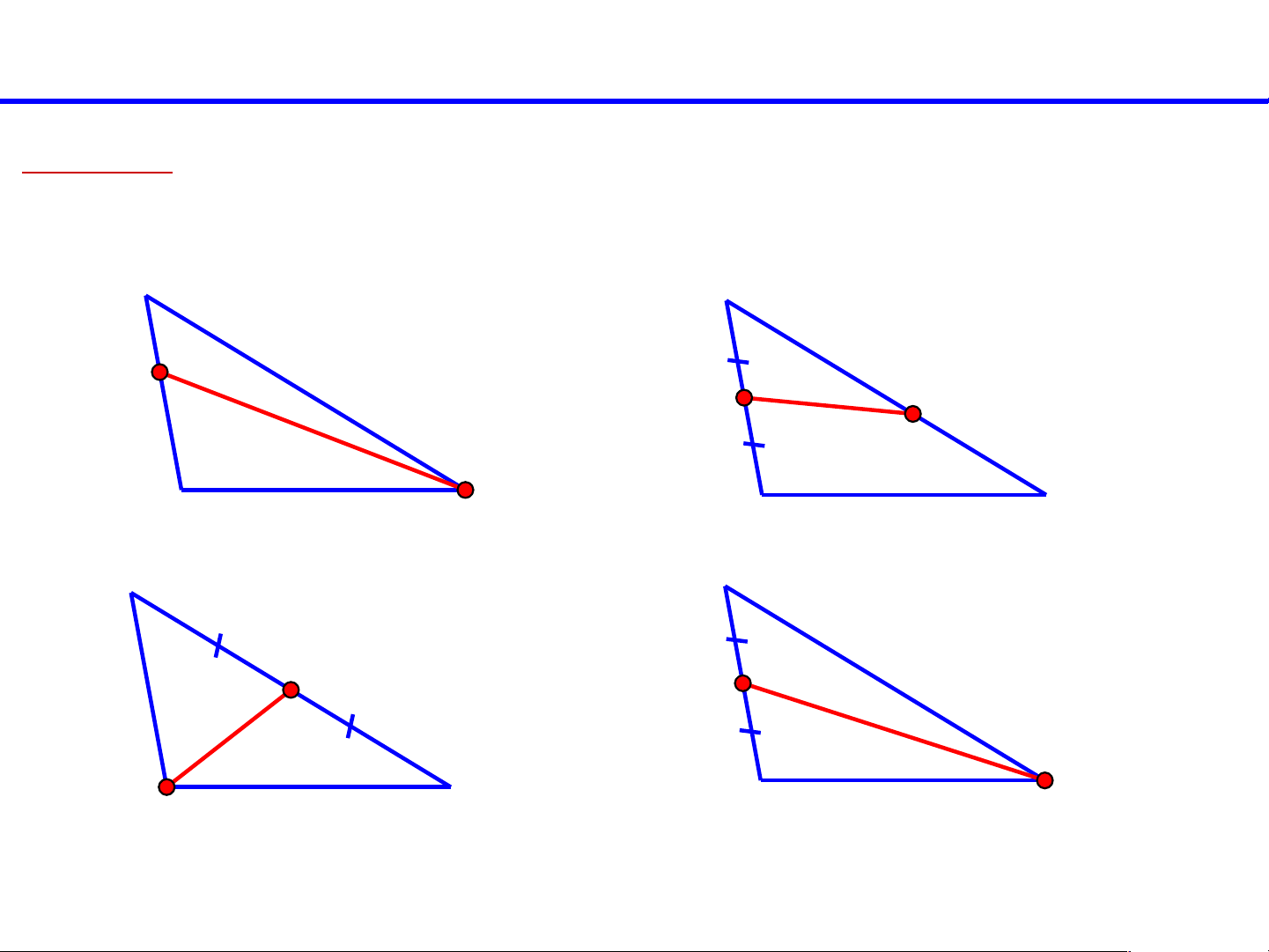
Bài tập: Vẽ đường trung tuyến DH của tam giác DEF.
Hãy chọn phương án đúng trong các hình dưới đây. F F H H E D E D Hình 1 Hình 2 F F H H E D E D Hình 3 Hình 4
1. Đường trung tuyến của tam giác: A B M C
KN: Đường trung tuyến của tam giác là đoạn thẳng nối
đỉnh của tam giác với trung điểm của cạnh đối diện.
Chú ý: Mỗi tam giác có ba đường trung tuyến.
1. Đường trung tuyến của tam giác:
Hãy vẽ tiếp vào hình vẽ hai đường trung tuyến còn lại của tam giác ABC. A B M C
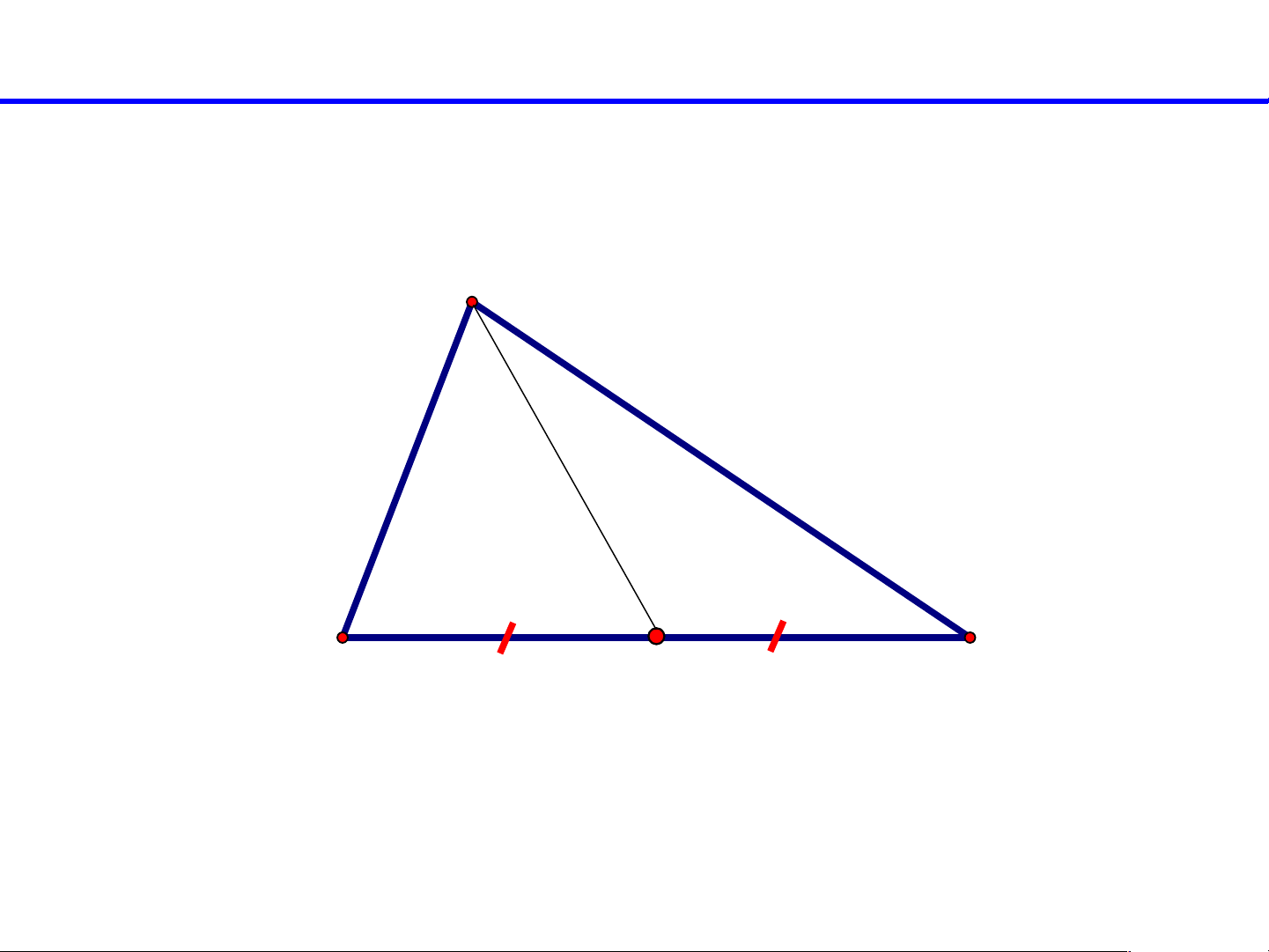
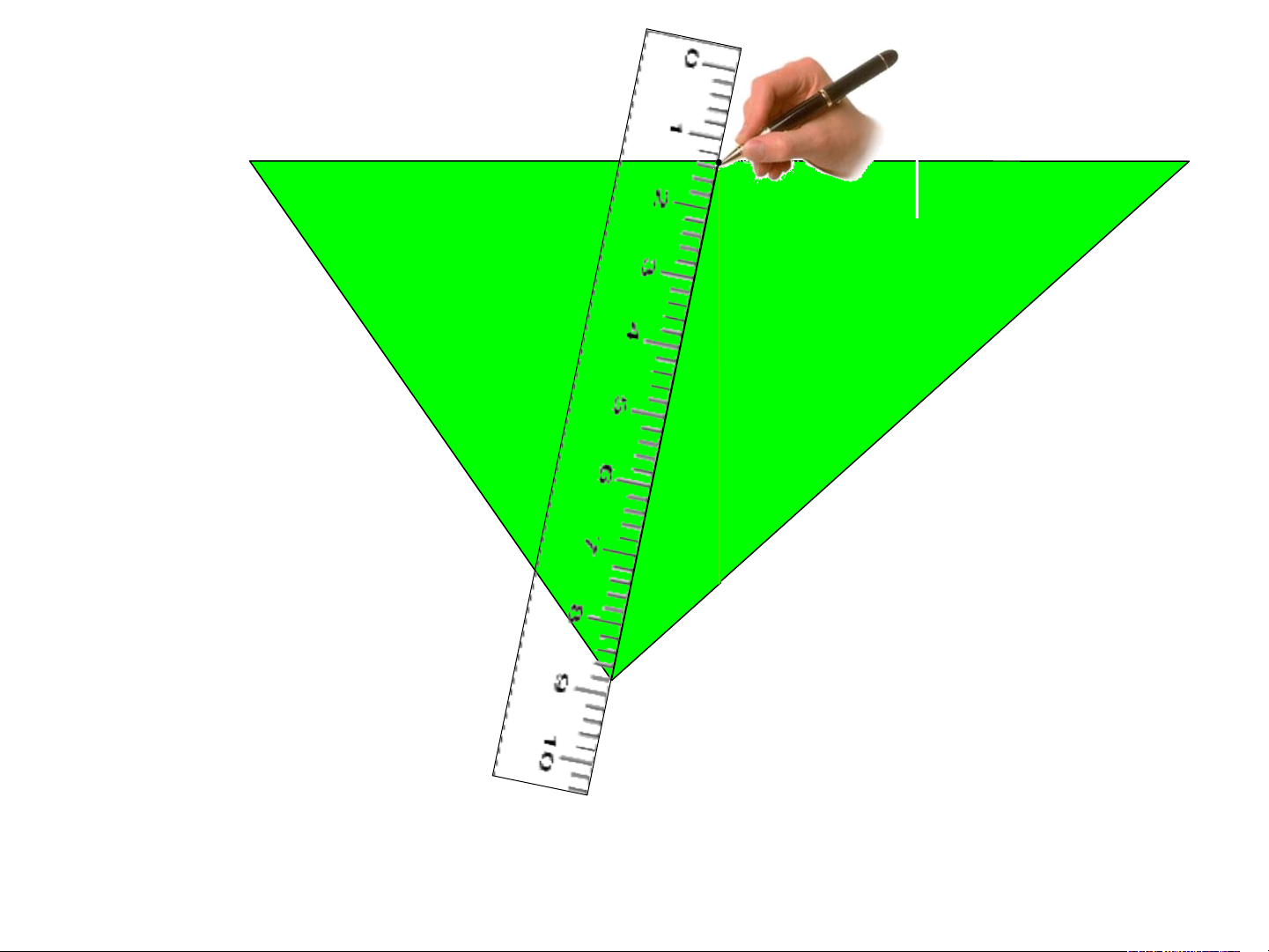
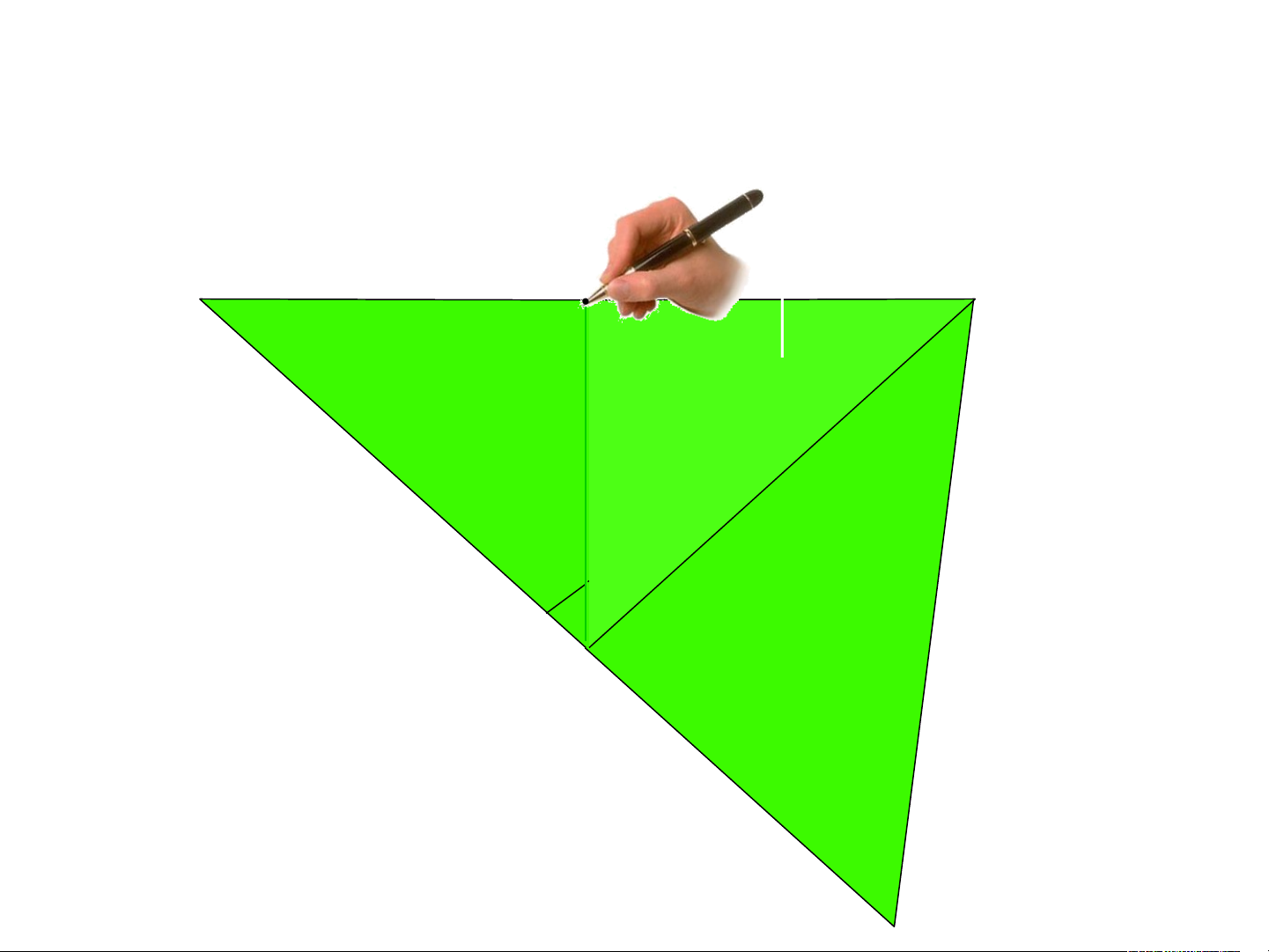
1. Đường trung tuyến của tam giác: *Thực hành:
- Cắt một tam giác bằng giấy.
- Gấp lại để xác định trung điểm một cạnh của nó.
- Kẻ đoạn thẳng nối điểm này với đỉnh đối diện
- Bằng cách tương tự vẽ tiếp hai trung tuyến còn lại. A B C A B C A B C A B C
2. Sự đồng quy của ba đường trung tuyến:
Quan hoạt động thực hành gấp giấy.
Cho biết: Ba đường trung tuyến của
tam giác này có đặc điểm gì ?
Ba đường trung tuyến của tam giác cùng đi qua một điểm.
2. Sự đồng quy của ba đường trung tuyến: F E G
Ba đường trung tuyến của tam giác cùng đi qua một điểm.
Chú ý: Điểm đồng quy của ba đường trung tuyến gọi là trọng tâm của tam giác.
2. Sự đồng quy của ba đường trung tuyến: .A
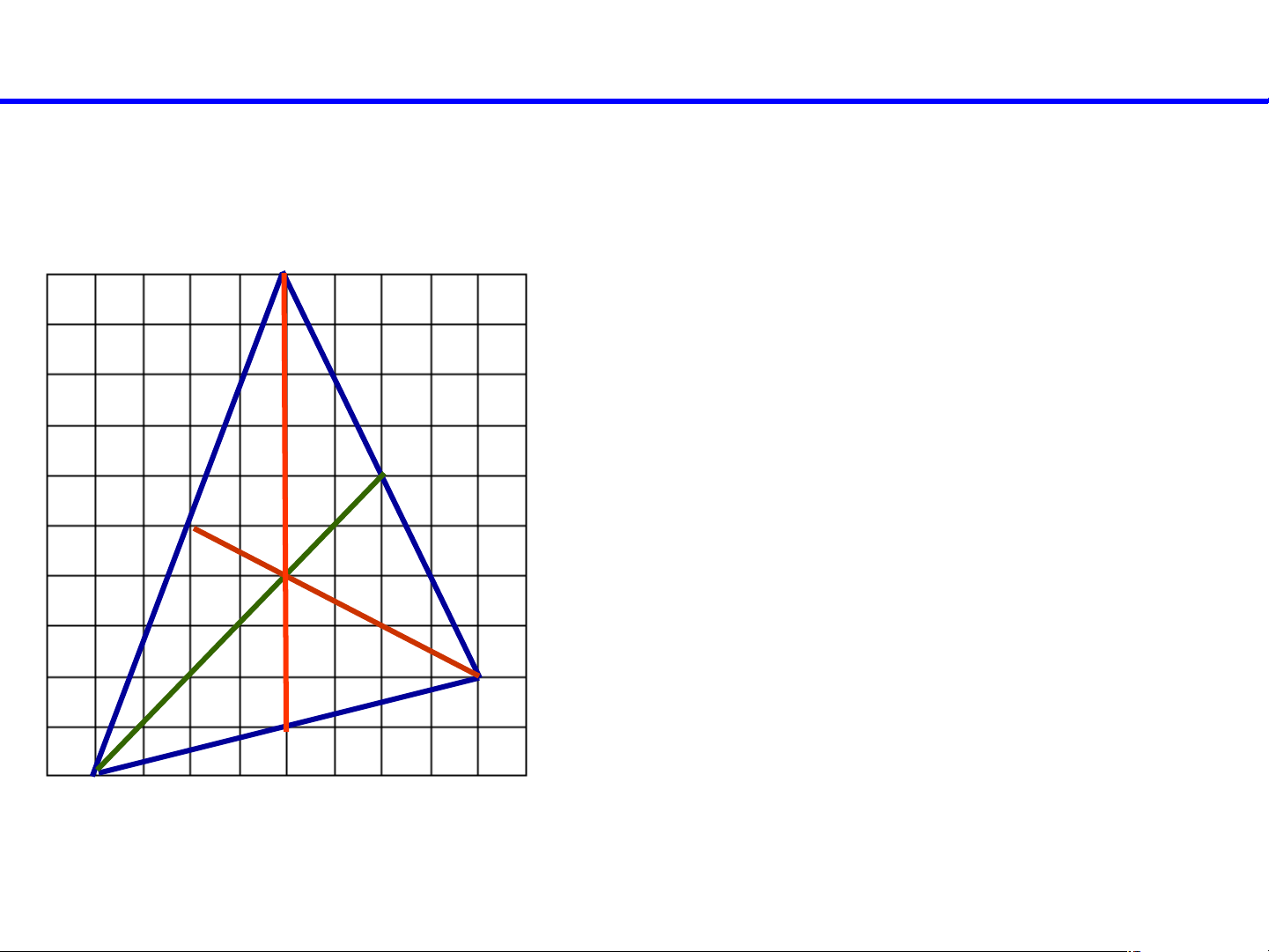
Trên mảnh giấy kẻ ô vuông mỗi chiều
10 ô, em hãy đếm dòng, đánh dấu các .
đỉnh A, B, C rồi vẽ ABC như hình N 9.29 P. . G
Vẽ 2 đường trung tuyến BN và CP,
. chúng cắt nhau tại G. Tia AG cắt cạnh BC tại M. . C .M B Hình 9.29
2. Sự đồng quy của ba đường trung tuyến:
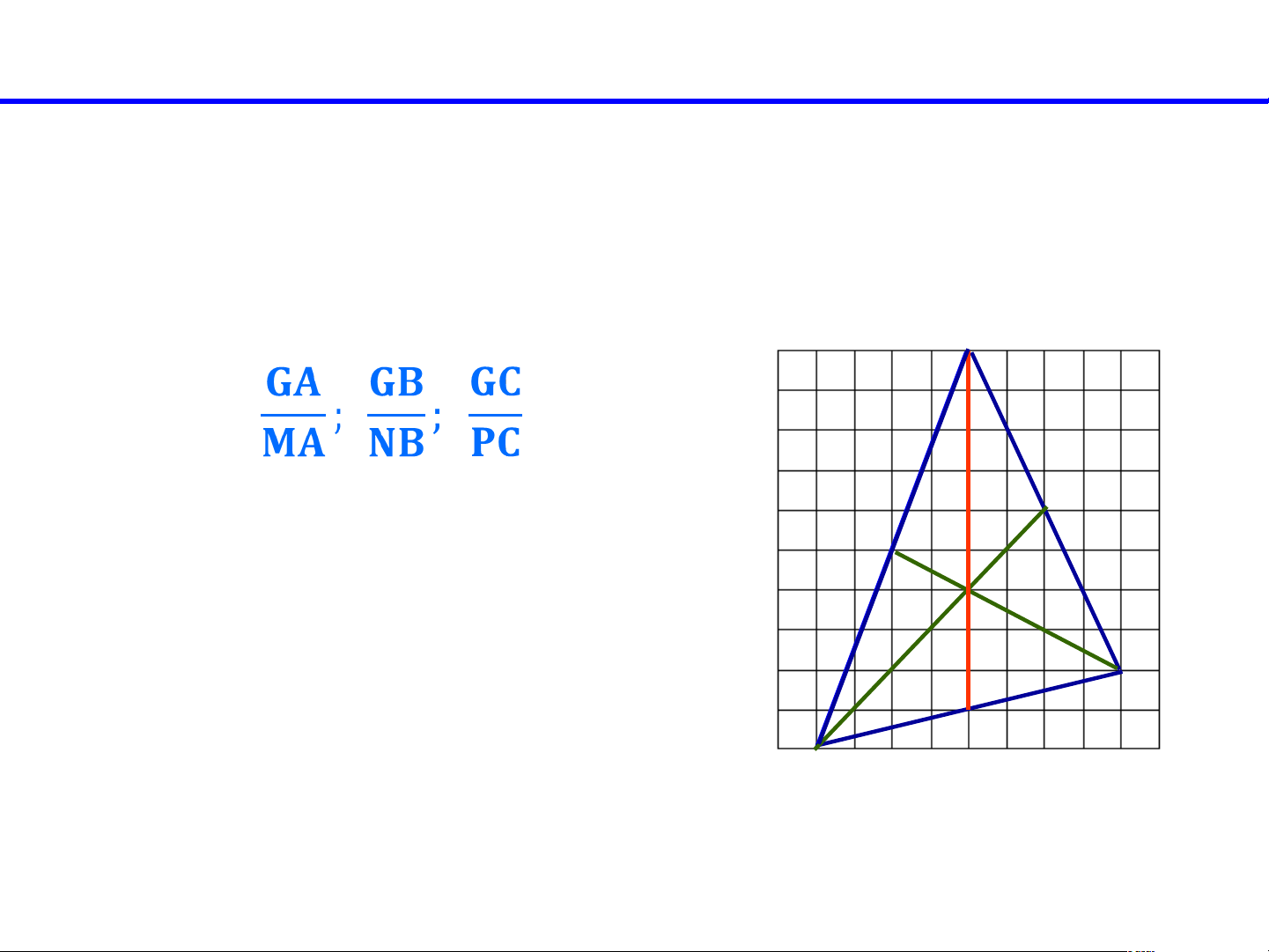
Dựa vào hình 9.29, hãy cho biết:
. AM có là đường trung tuyến của tam giác ABC hay không? .A
. Các tỉ số bằng bao nhiêu? .N . P . G . . C . M B Hình 9.29
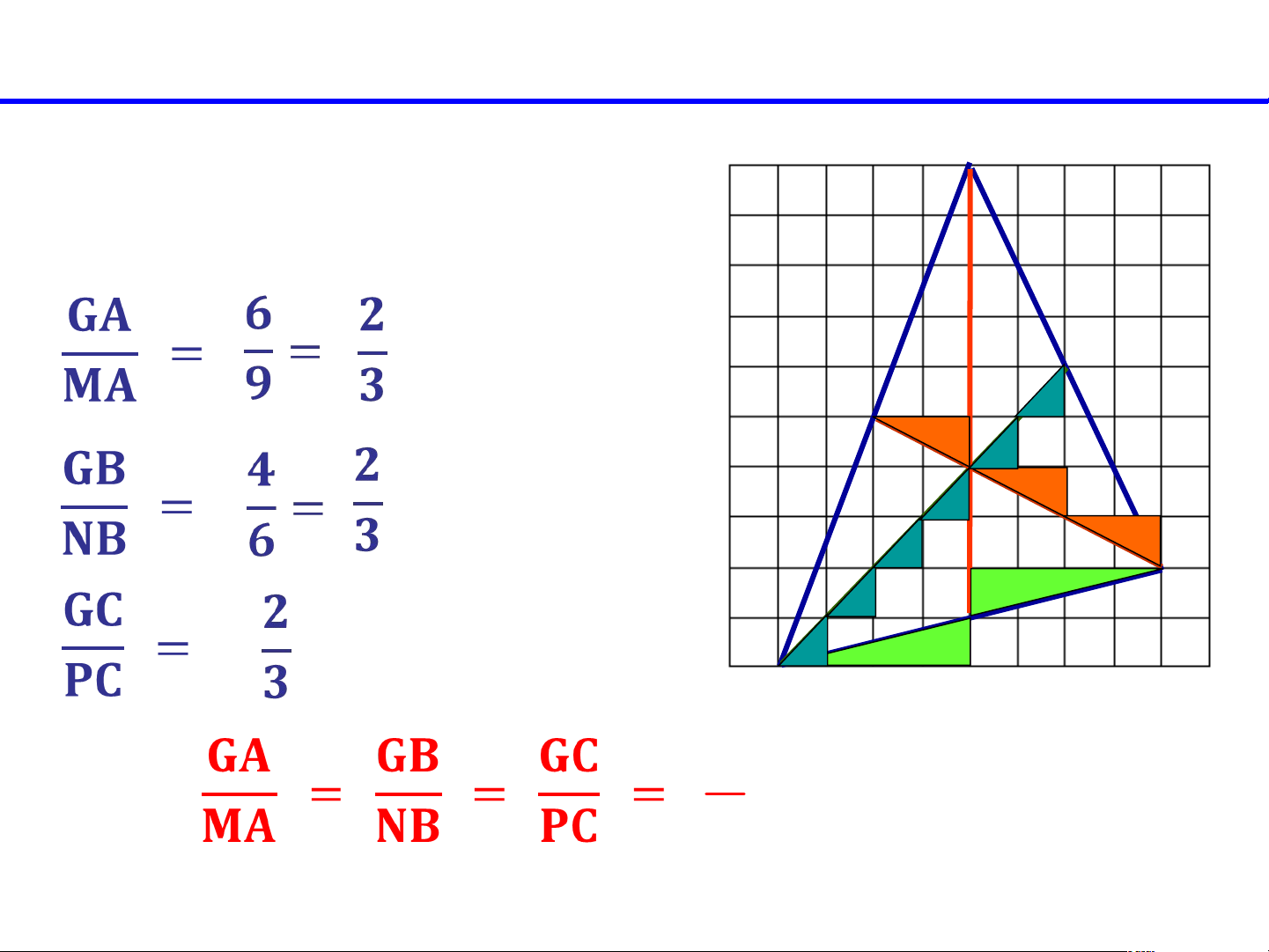
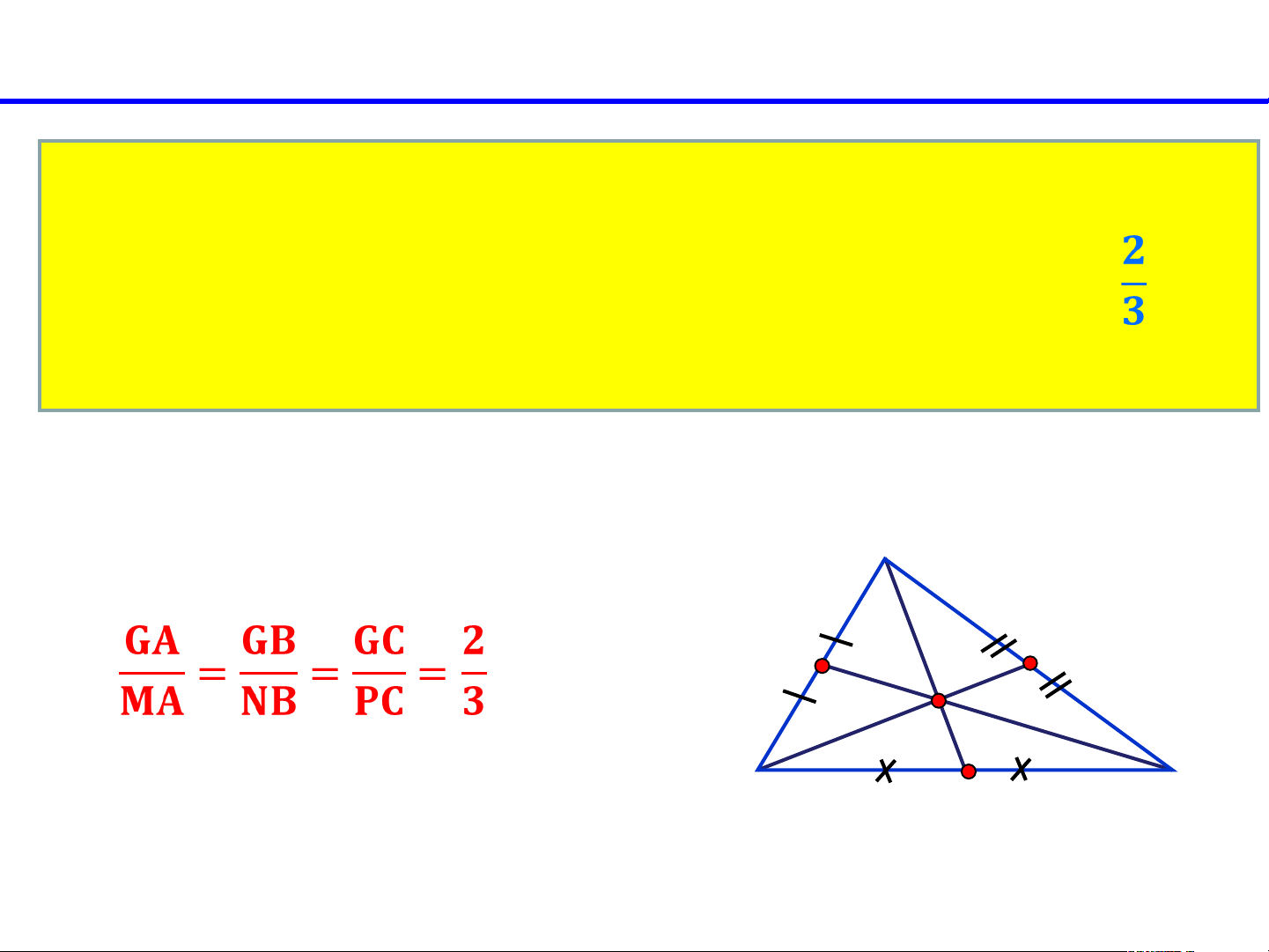
2. Sự đồng quy của ba đường trung tuyến:
*AM là đường trung tuyến của .A tam giác ABC. .N P. .G . . C . M B 2 Suy ra: 3
2. Sự đồng quy của ba đường trung tuyến:
Định lí: Ba đường trung tuyến của tam giác cùng đi qua
một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng độ
dài đường trung tuyến đi qua đỉnh ấy.
Tam giác ABC có AM, BN, CP là ba
trung tuyến đồng quy tại G, ta có: A P N G B C
Điểm G gọi là trọng tâm của M tam giác ABC.
2. Sự đồng quy của ba đường trung tuyến: V í
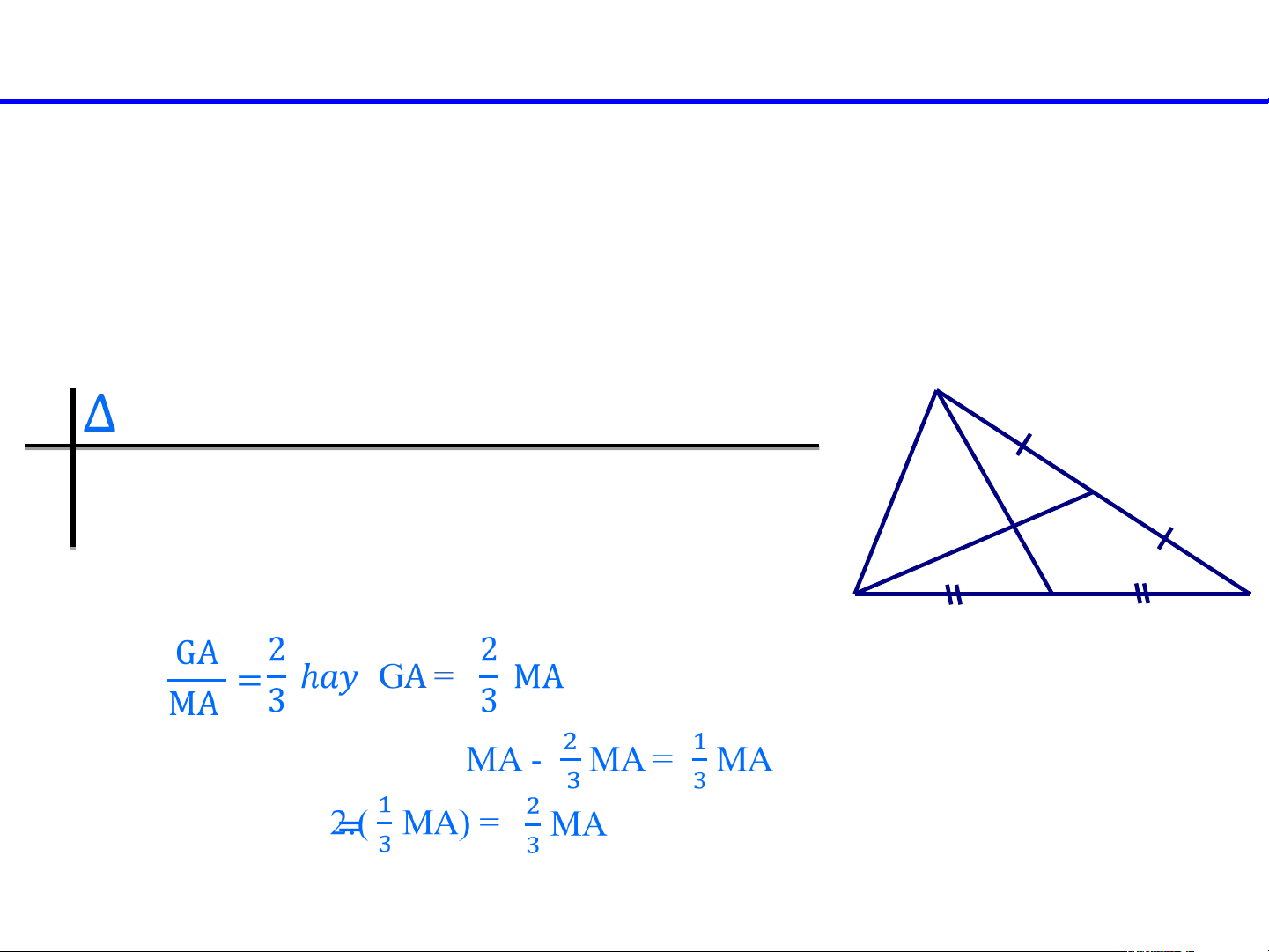
Cho tam giác ABC với AM là trung tuyến và G là trọng tâm d c ụ: ủa tam giác.
a)Chứng minh GA = 2GM. b) Biết GM = 2cm. Tính GA. Giải: A
GT ABC, có AM là trung tuyến, trong a tâm G ) GA = 2GM. KL G b) GM = 2cm. GA = ?.
a) Vì G là trọng tâm tam giác ABC, ta B M C có: Ta có: GM MA – GA = Suy ra: 2 = GM = Vậy GA = 2GM.
b) Khi GM = 2cm, ta có GA = 2GM = 2.2 = 4cm
2. Sự đồng quy của ba đường trung tuyến: V í
Cho tam giác ABC với AM là trung tuyến và G là trọng tâm d c ụ: ủa tam giác.
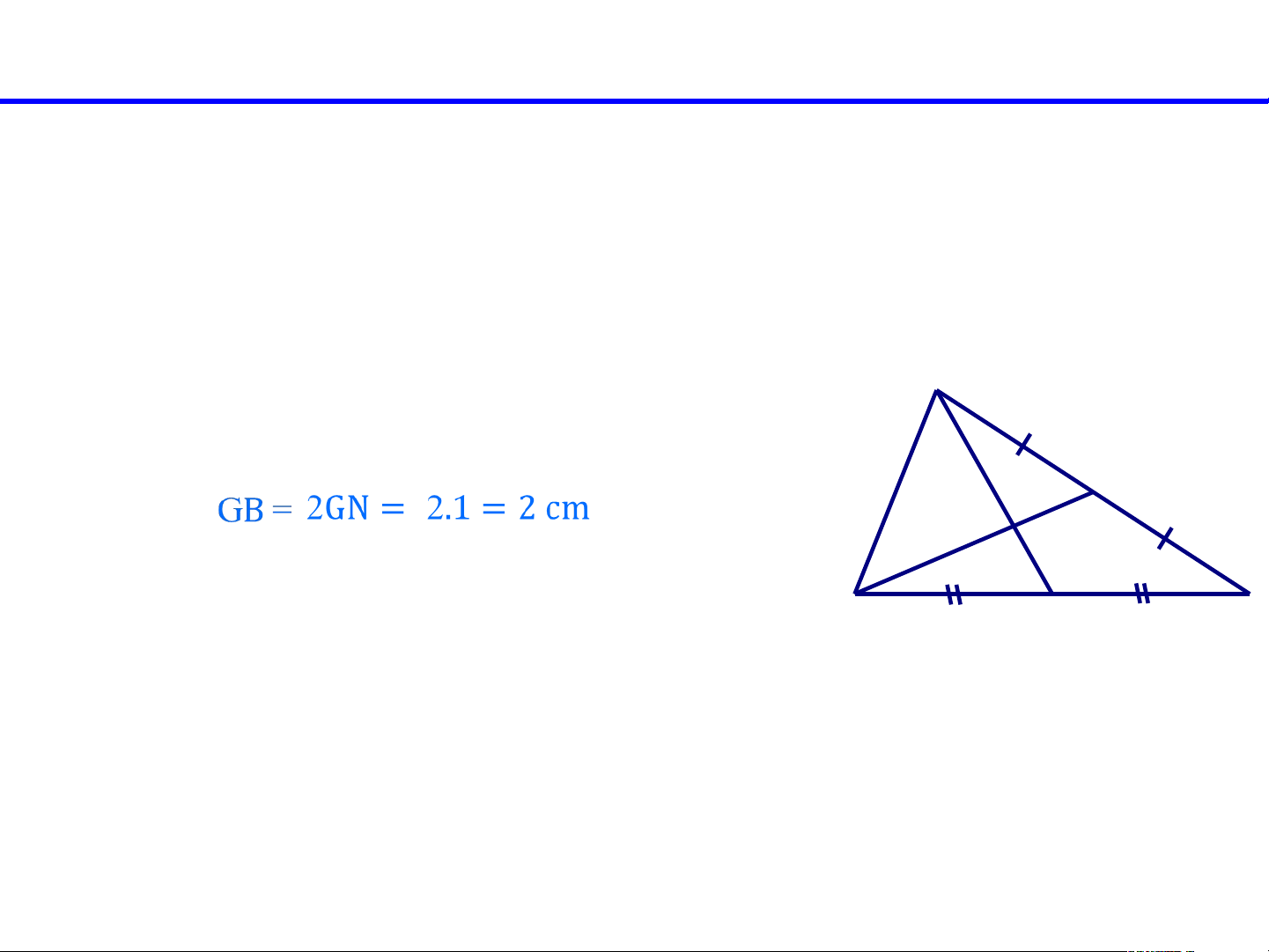
Cho BN là trung tuyến và GN = 1cm. Tính GB và NB Giải: A
- Vì G là trọng tâm tam giác ABC, ta có: N G Ta NB = 3GN = 3.1 = 3 cm B M C có: Bài tập:
Cho hình vẽ, điền số thích hợp vào chỗ trống: 2 MG = ….MR; M 3 S 1 GR = ….MR; G 3 N R P NG = … 2GS
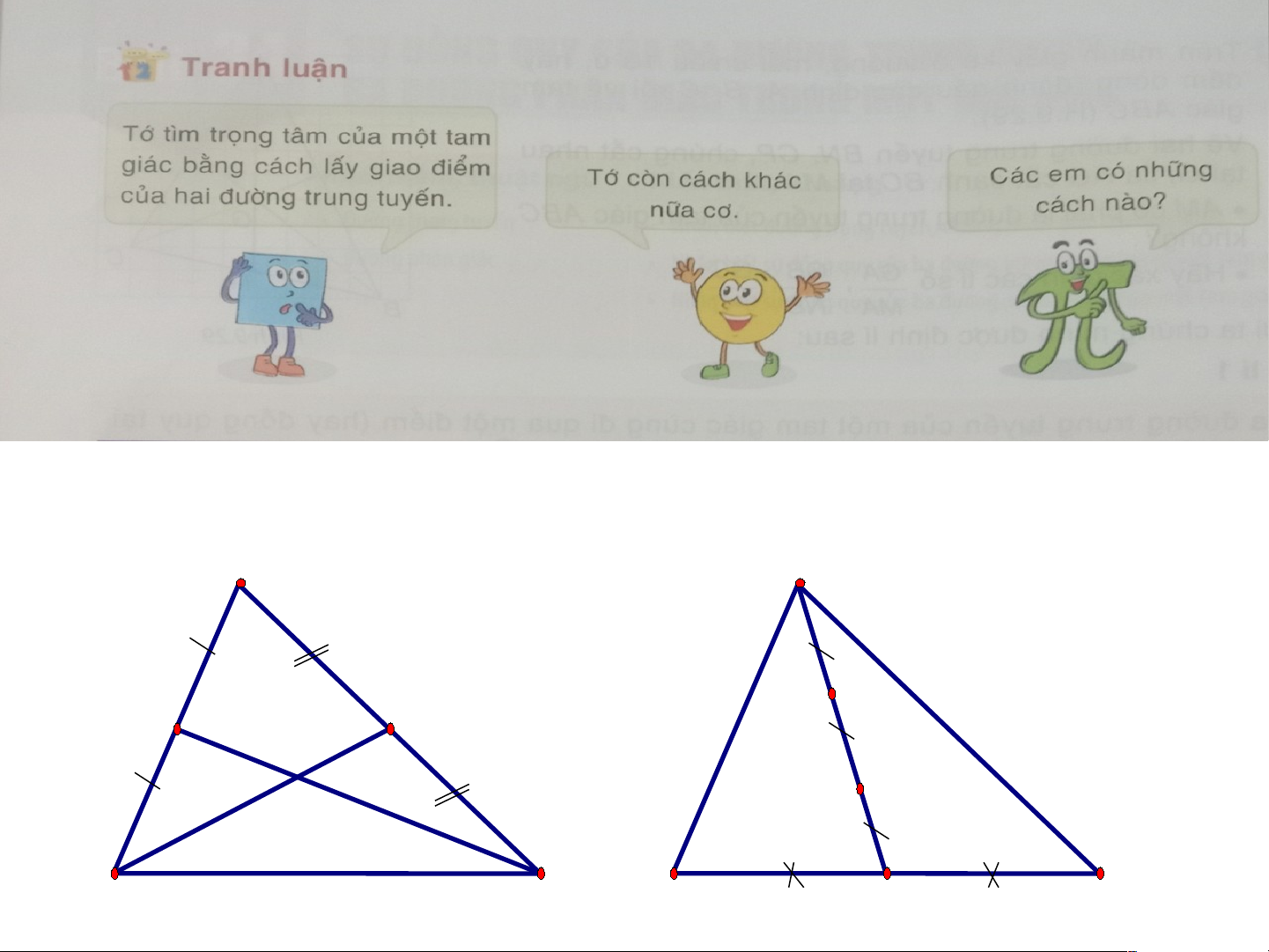
Cách xác định trọng tâm G của tam giác ABC A A F E G G B C B C D
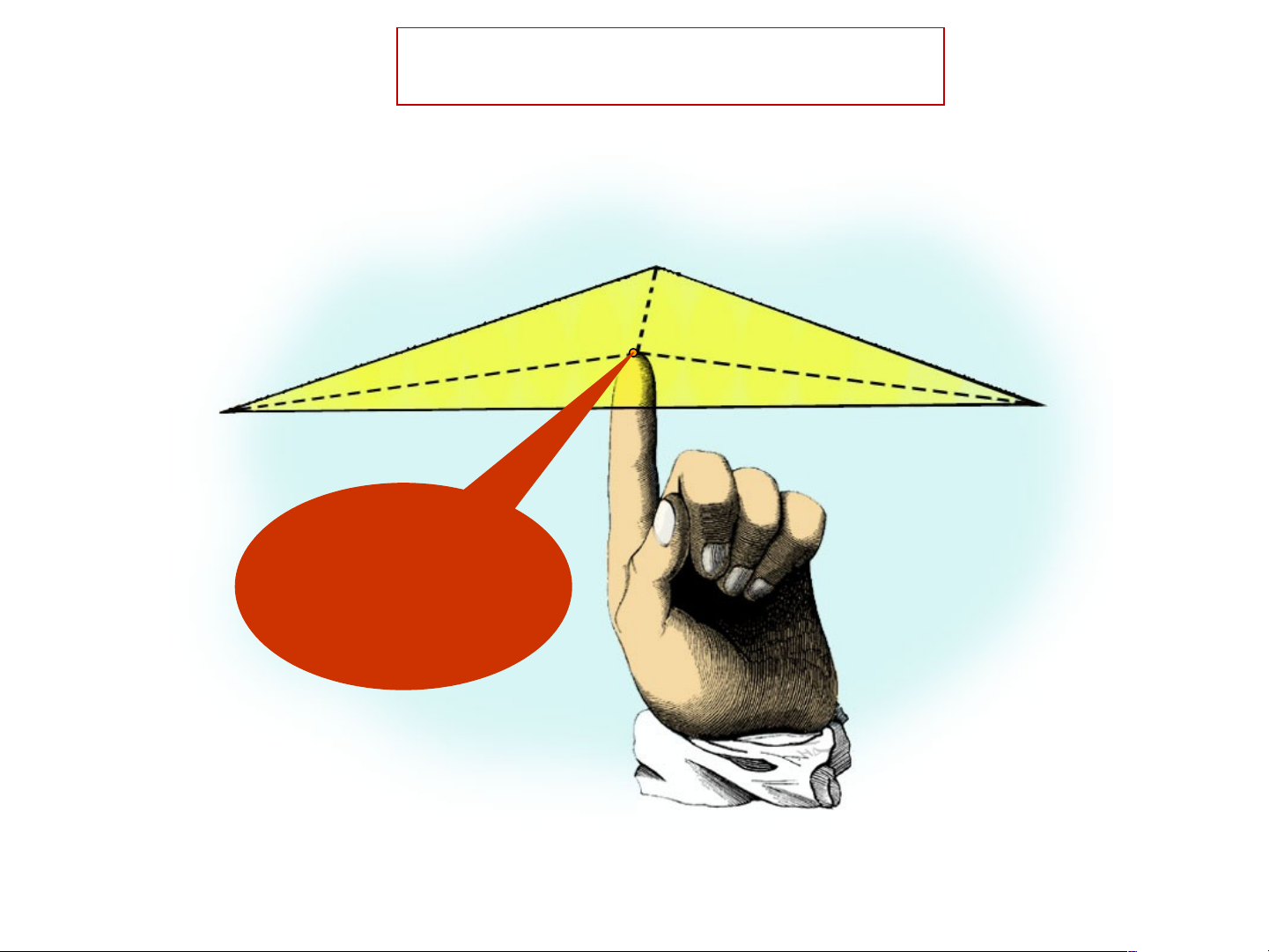
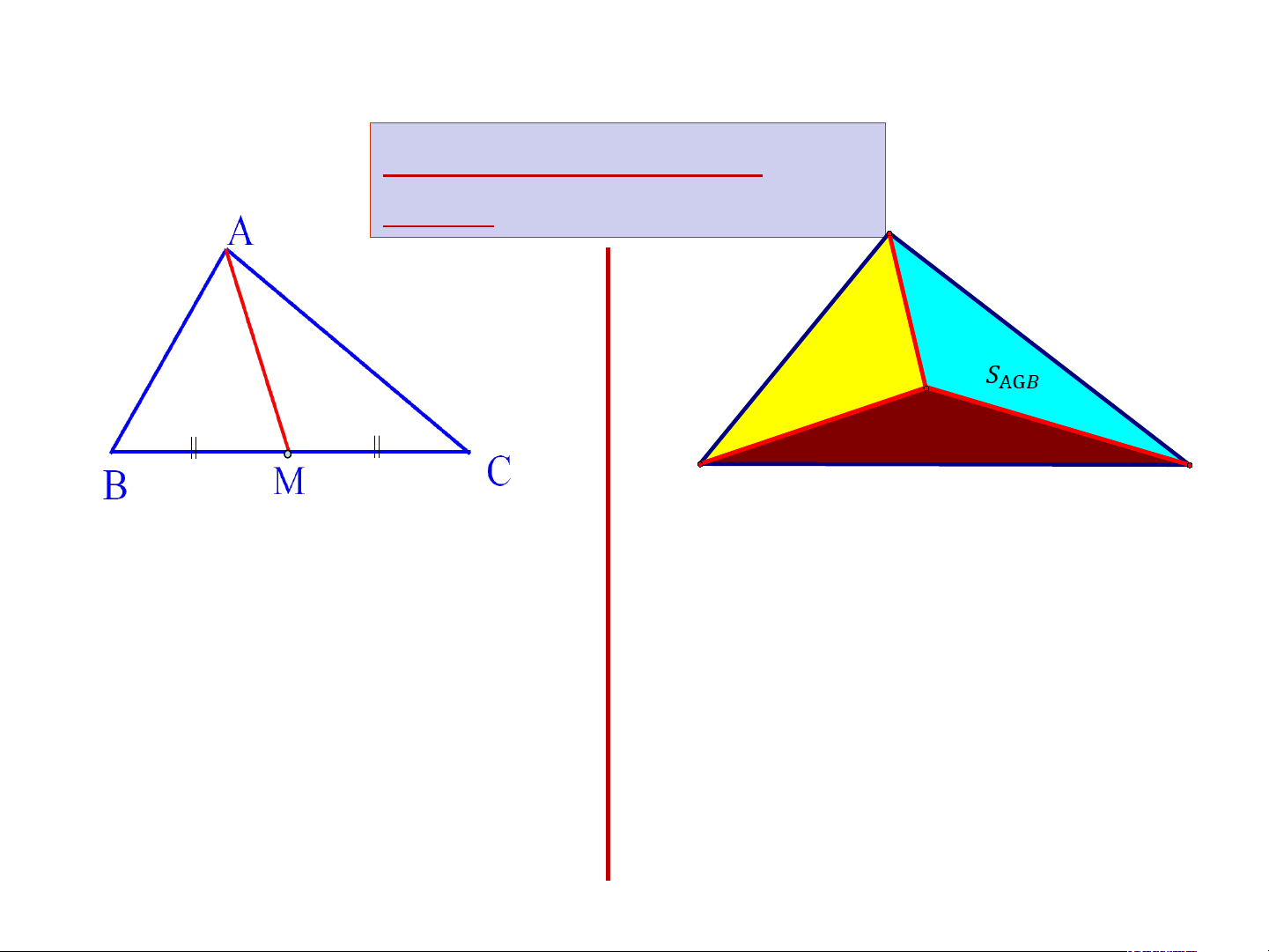
Vận dụng vào thực tế A G C B Điểm G là trọng tâm ΔABC! CÓ THỂ EM CHƯA BIẾT A SAGC G SBGC C B
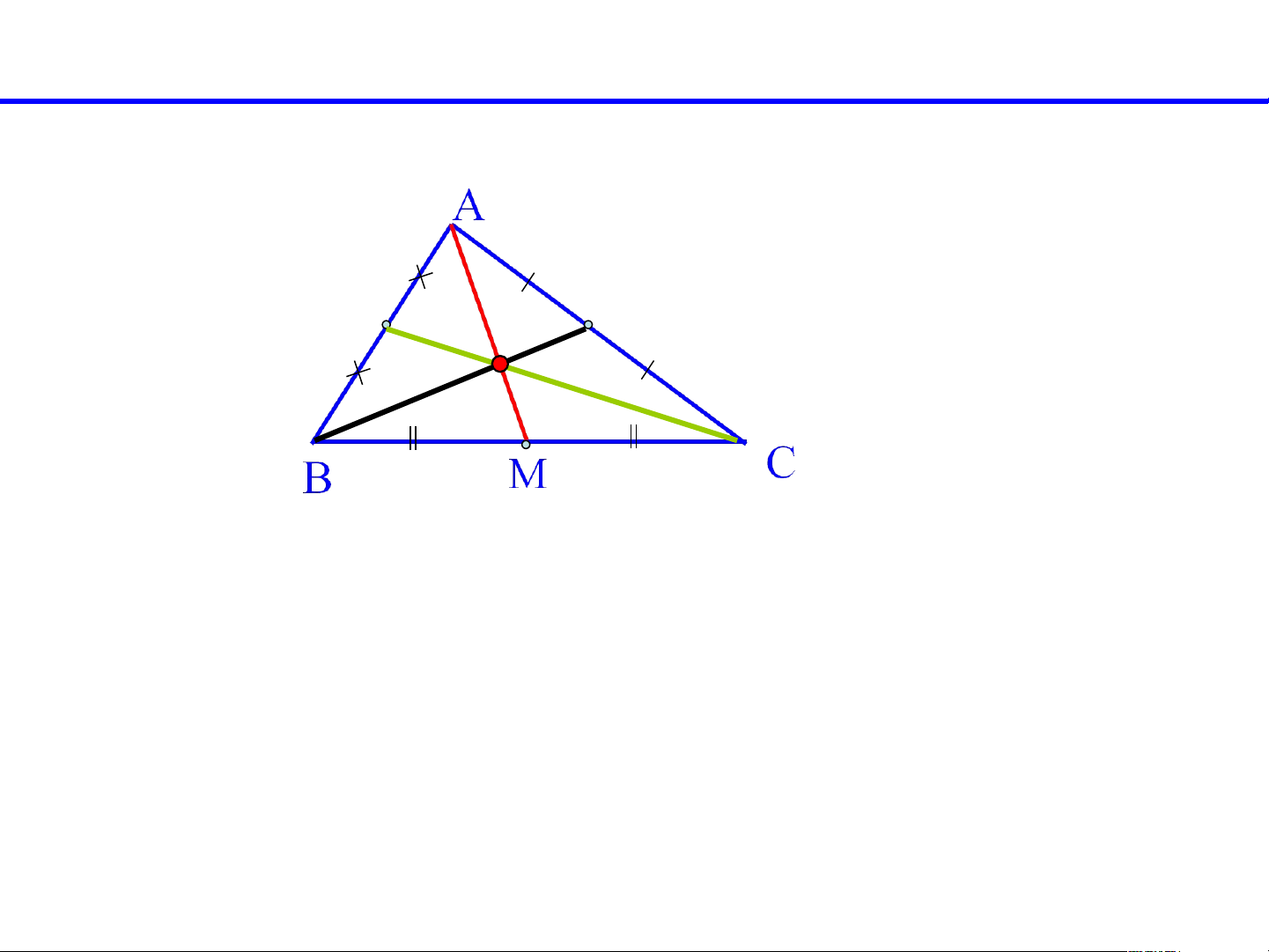
*Mỗi đường trung tuyến chia
* Nếu nối ba đỉnh của một tam giác
tam giác thành hai tam giác có
với trọng tâm của nó thì ta được ba
diện tích bằng nhau.
tam giác nhỏ có diện tích bằng nhau S = = S = S ABM ACM S AGC S AGB BGC Dặn dò về nhà:
- Nắm vững cách vẽ về ba đường trung tuyến.
- Học thuộc khái niệm, tính chất ba đường trung tuyến của tam giác.
- Làm các bài tập: 9.20; 9.21; 9.22 SGK.
- Chuẩn bị tiết sau: “Sự đồng quy của ba đường
phân giác trong tam giác”. Bài tập:
Hãy điền từ hoặc cụm từ thích hợp vào chỗ
trống trong các câu sau:
1. Đường trung tuyến của tam giác là đoạn thẳng nối từ …
đỉn của tam giác tới … t …… run ……… g điểm c ……… ạnh đố …… i diện. 2. Ba
h đường trung tuyến của tam giác cù n g đi q …… ua m …....... ột điểm
điểm đó được gọi là ……… trọng t…… âm c……… ủa tam…… giác
3. Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng ….. đ 2
ộ dài đường trung tuyến……… đi …… qua … đỉnh 3 ấy.
Document Outline
- PowerPoint Presentation
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Cách xác định trọng tâm G của tam giác ABC
- Vận dụng vào thực tế
- Slide 33
- Slide 34
- - Nắm vững cách vẽ về ba đường trung tuyến. - Học thuộc khái niệm, tính chất ba đường trung tuyến của tam giác. - Làm các bài tập: 9.20; 9.21; 9.22 SGK. - Chuẩn bị tiết sau: “Sự đồng quy của ba đường phân giác trong tam giác”.
- Slide 36




