Giáo án điện tử Toán 7 Bài 4 Cánh diều: Định lí
Bài giảng PowerPoint Toán 7 Bài 4 Cánh diều: Định lí hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 7. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 7
Môn: Toán 7
Sách: Cánh diều
Thông tin:
Tác giả:
Preview text:
CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC HÔM NAY KHỞI ĐỘNG
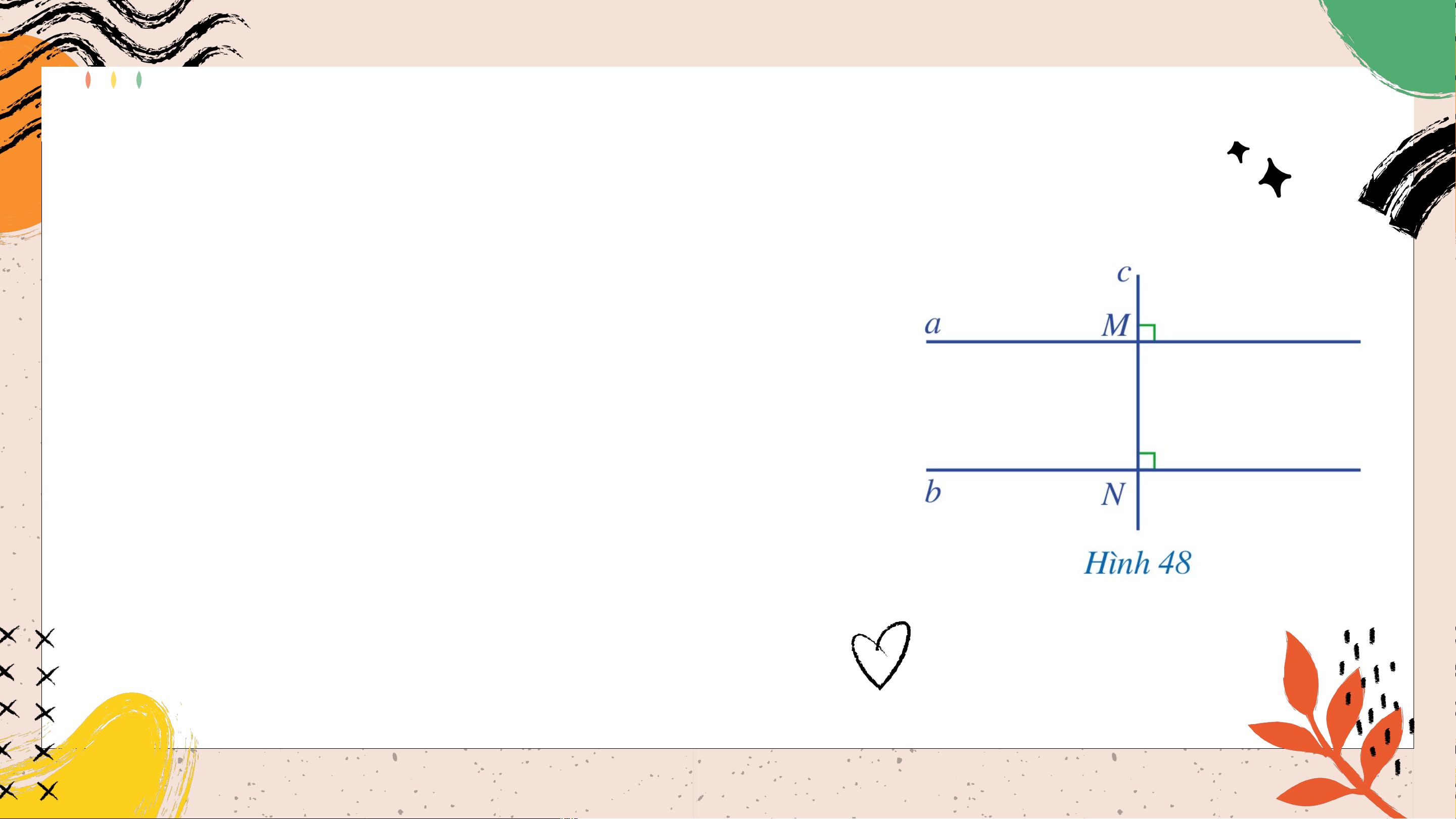
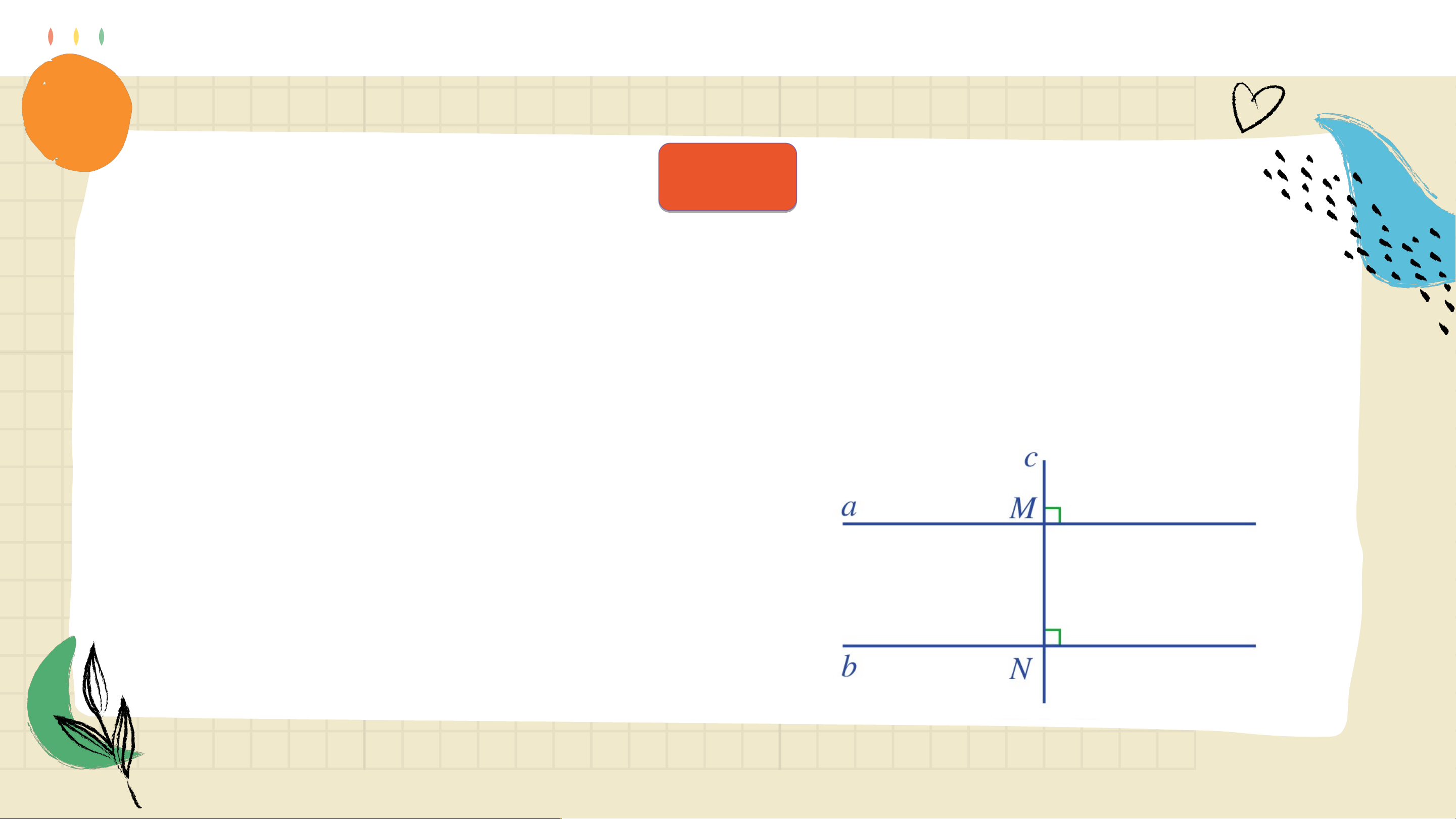
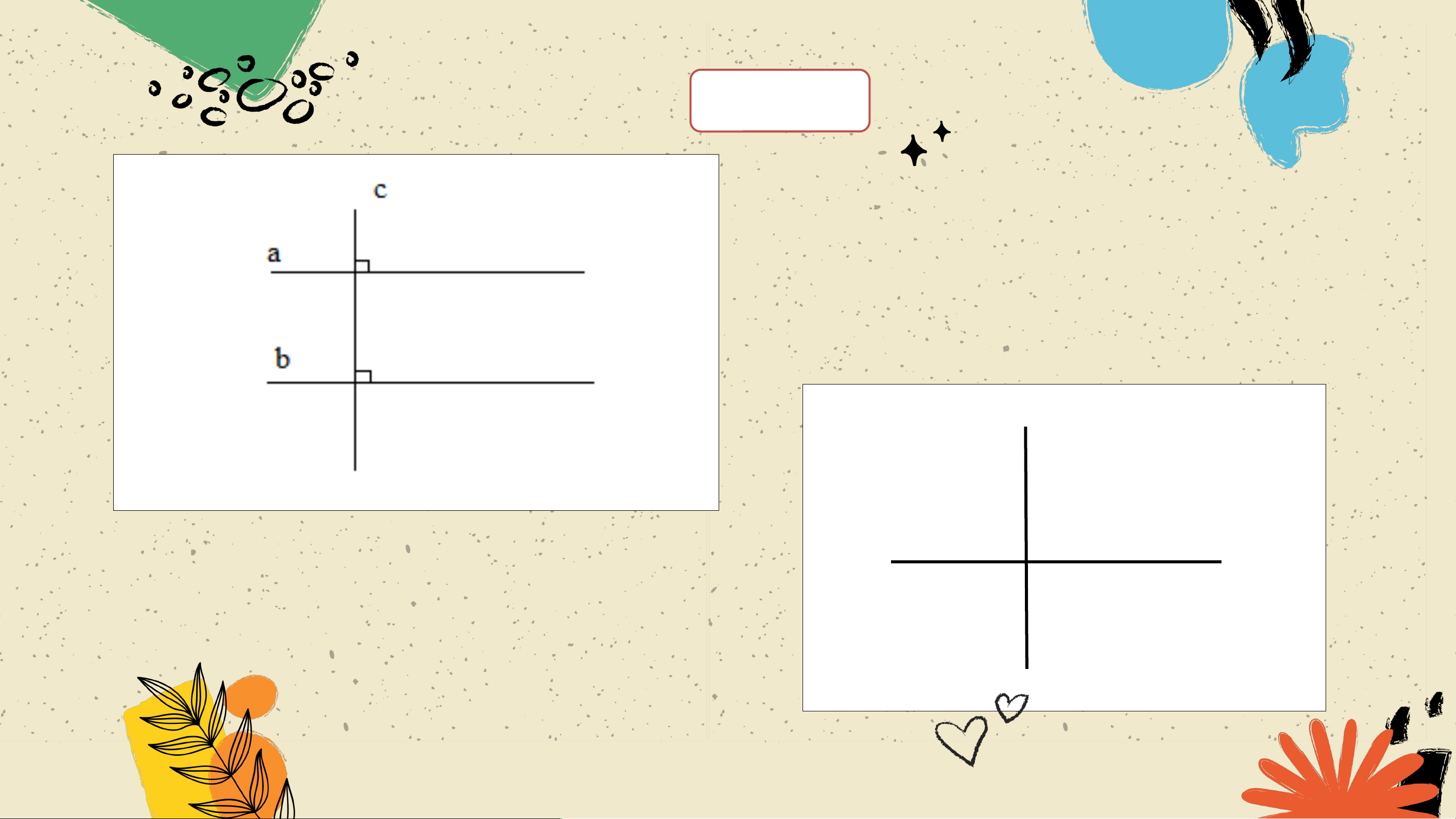
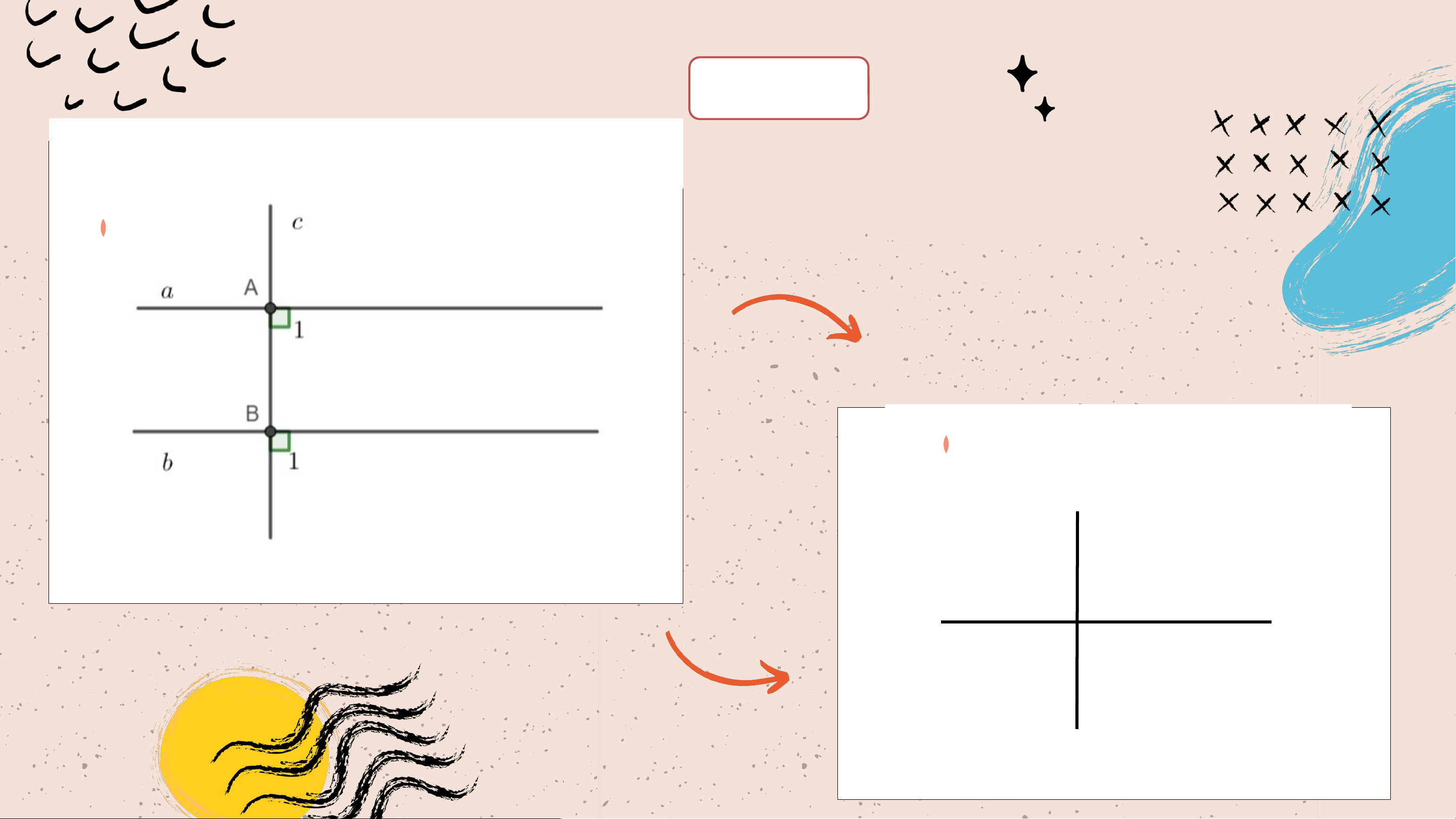
Bạn Ánh vẽ hai đường thẳng (phân biệt) ,
cùng vuông góc với đường thẳng (Hình 48)
và khẳng định với bạn Ngân rằng: “Nếu hai
đường thẳng phân biệt cùng vuông góc với
một đường thẳng khác thì hai đường thẳng đó song song với nhau”.
Em hãy đưa ra một số tính chất
toán học đã biết (đã học) có thể
được phát biểu ở dạng “Nếu … thì...”?
Câu khẳng định có dạng
“Nếu ... thì” trong toán học được gọi là gì? BÀI 4: ĐỊNH LÍ 1 Định lí NỘI DUNG BÀI HỌC 2 Chứng minh định lí I. ĐỊNH LÍ HĐ H 1 Đ
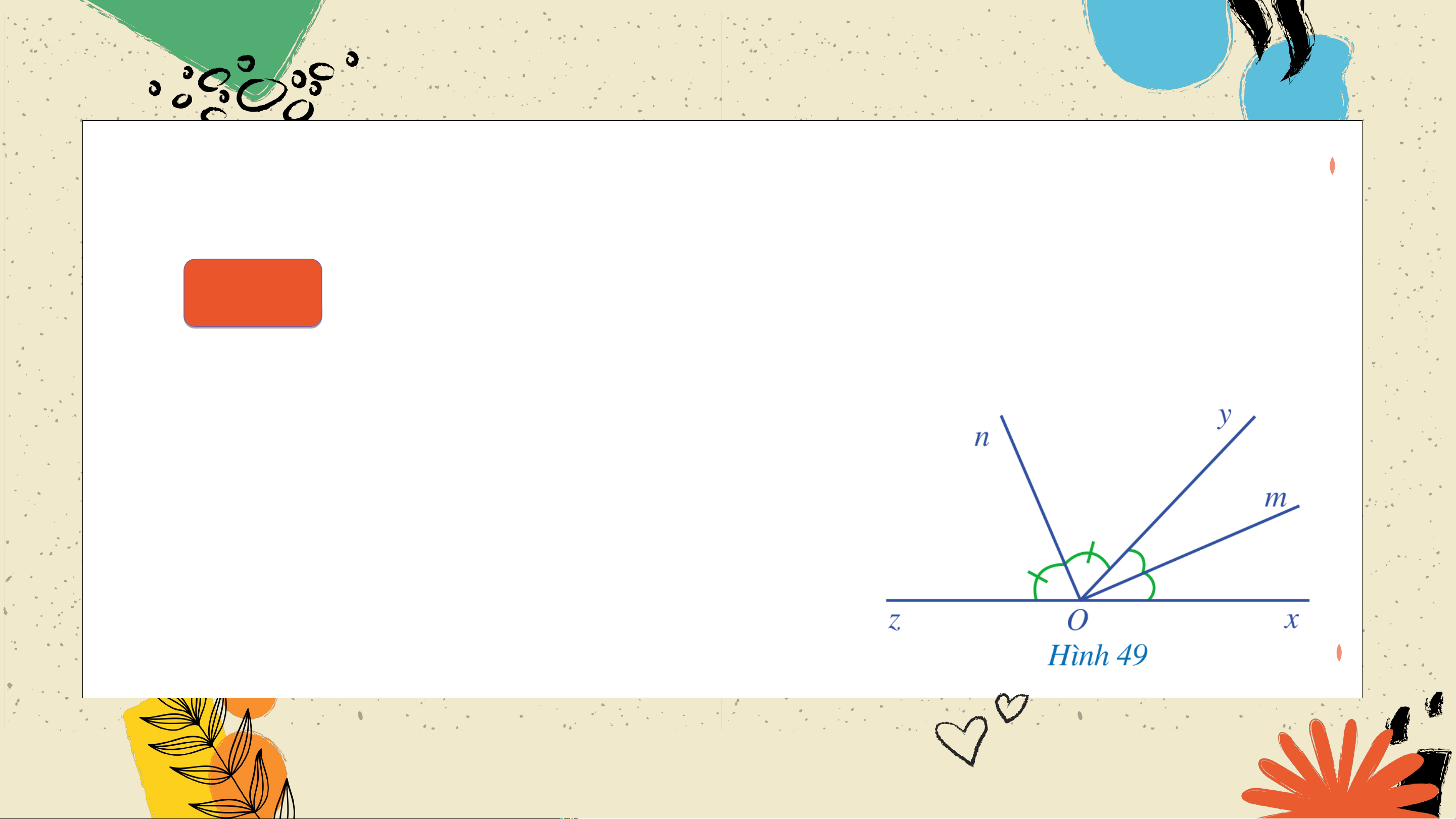
Cho hai góc kề bù là và , và lần lượt là tia phân giác
của góc và góc (Hình 49). Ta thấy và Suy ra
Khẳng định: "Nếu một góc có hai cạnh
là hai tia phân giác của hai góc kề bù
thì góc đó là góc vuông". Nhận xét:
Khẳng định trên có các đặc điểm sau:
- Là một phát biểu về tính chất toán học.
- Tính chất toán học đó đã được chứng tỏ
là đúng không dựa vào các trực giác hay đo đạc,.. Định lí. HĐ H 2 Đ
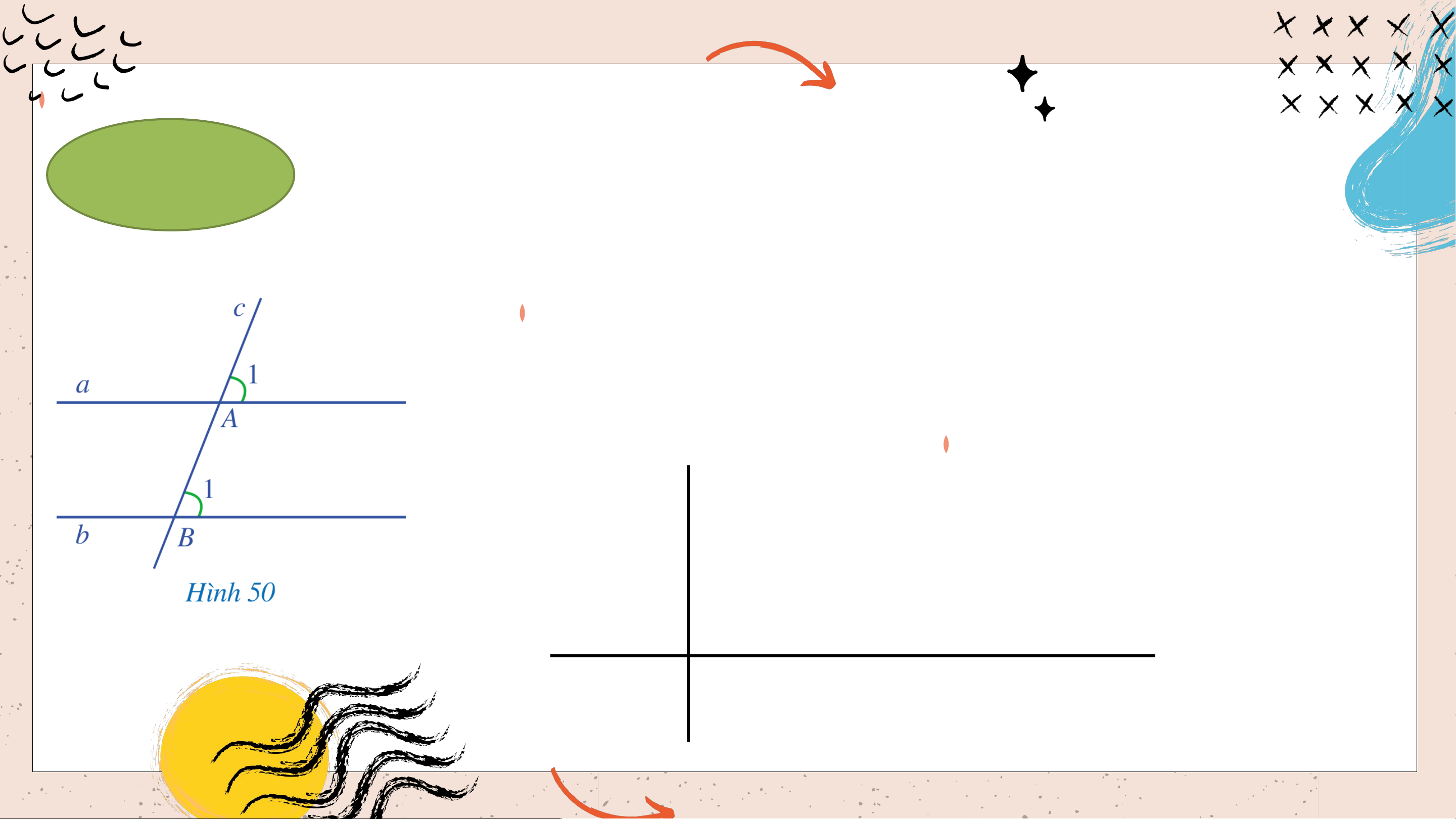
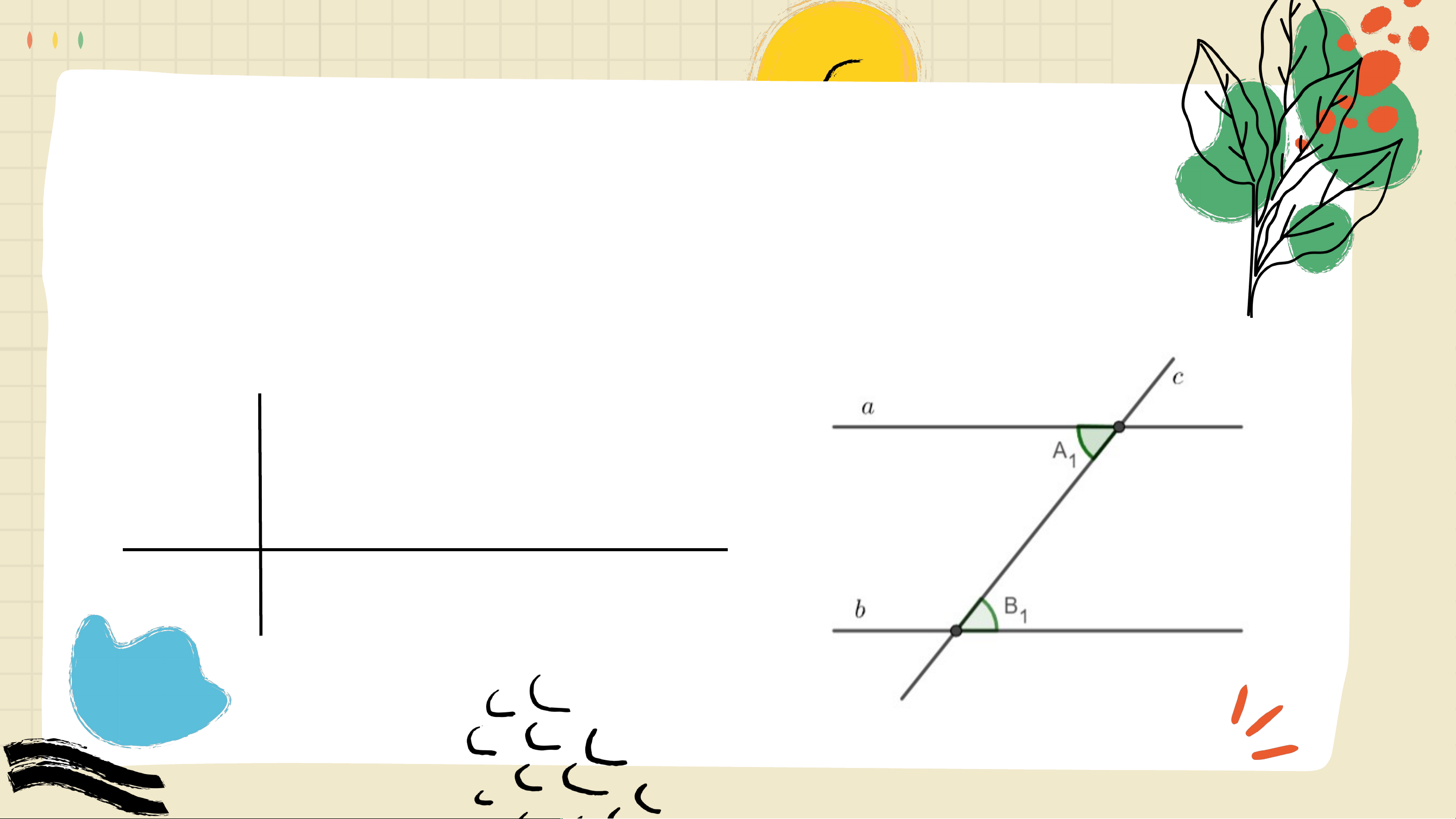
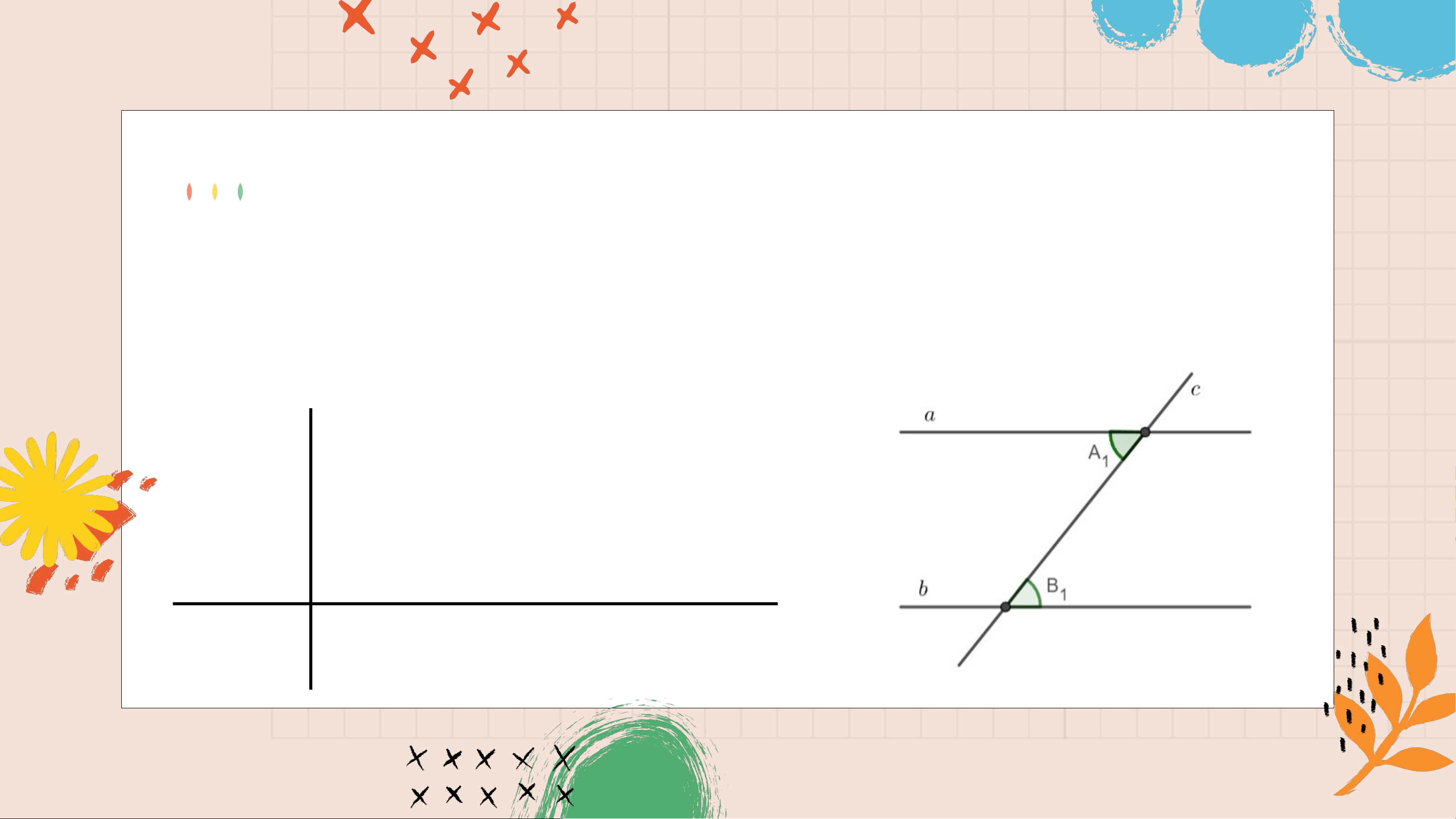
Xét khẳng định “Nếu hai đường thẳng phân biệt cùng vuông góc với một
đường thẳng khác thì hai đường thẳng đó song song với nhau”, ta thấy:
Khẳng định này được phát biểu ở dạng “Nếu … thì…”. Trong khẳng định đó, hãy nêu:
- Phần nằm giữa từ “Nếu” và từ “thì”
- Phần nằm sau từ “thì”. Trả lời
- Phần nằm giữa từ “Nếu” và từ “thì” là:
một đường thẳng cắt hai đường thẳng song song.
- Phần nằm sau từ “thì” là: hai góc so le trong bằng nhau.
Viết giả thiết và kết luận của định lí: “Nếu một đường thẳng cắt Ví dụ 1
hai đường thẳng song song thì hai góc đồng vị bằng nhau” Giải
Giả thiết: Một đường thẳng cắt hai đường thẳng song song.
Kết luận: Hai góc đồng vị bằng nhau. GT cắt tại , cắt tại và là hai góc đồng vị KL ^ 𝐴1=^ 𝐵1 Luy L ệ uy n t ệ ập ậ 1
Viết giả thiết và kết luận của định lí: “Nếu một đường thẳng cắt hai
đường thẳng , và trong số các góc tạo thành có một cặp góc so le trong
bằng nhau thì hai đường thẳng , song song với nhau”. Giải
- Giả thiết: một đường thẳng cắt hai đường thẳng , và trong số các
góc tạo thành có một cặp góc so le trong bằng nhau
- Kết luận: hai đường thẳng , song song với nhau.
II. CHỨNG MINH ĐỊNH LÍ HĐ H 3 Đ a) Vẽ hình minh hoạ nội dung định lí trên.
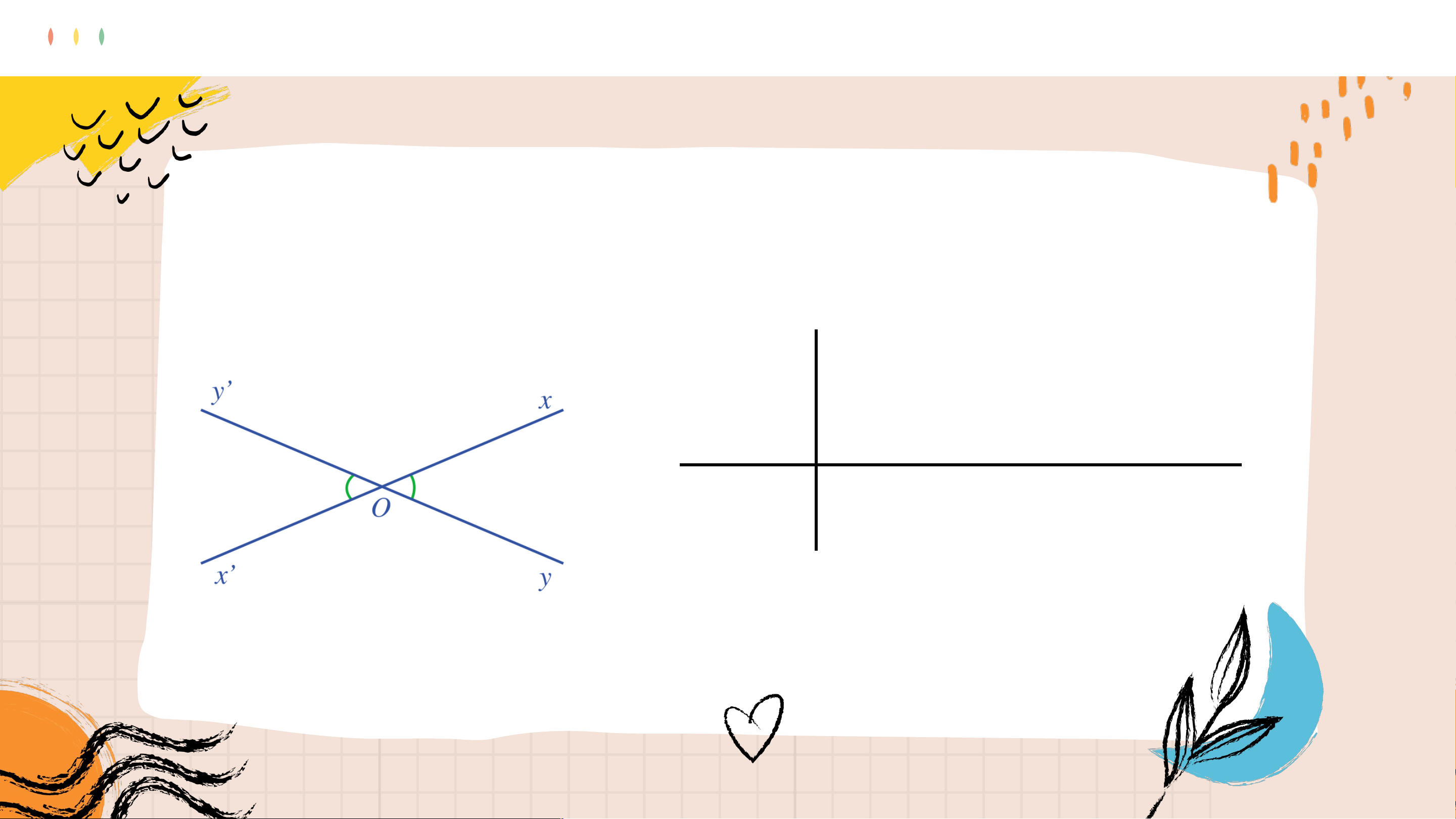
Cho định lí “Nếu hai góc
b) Viết giả thiết và kết
đối đỉnh thì hai góc đó
luận của định lí trên. bằng nhau”.
c) Chứng tỏ định lí trên là đúng. Giải a) b)
và là hai góc đối đỉnh. GT KL ^ 𝑥 𝑂𝑦=^ 𝑥′ 𝑂𝑦 ′ c) Chứng minh định lí: Ta có: (giả thiết) (hai góc đối đỉnh) (cùng bằng ) Mà ; (hai góc kề bù)
Chứng minh định lí: “Nếu một đường thẳng cắt hai đường thẳng Ví dụ 2
phân biệt và trong số các góc tạo thành có một cặp góc so le trong
bằng nhau thì các cặp góc đồng vị bằng nhau”. Giải GT cắt tại , cắt tại KL , , ,
Ta có: (GT); (hai góc đối đỉnh) Suy ra (cùng bằng ).
Hơn nữa các cặp và , và là các cặp góc kề bù nên .
Tương tự, ta chứng minh được và . LUYỆN TẬP
Câu 1. Cho định lí: "Một đường thẳng cắt hai đường thẳng
song song thì tạo thành cặp góc so le trong bằng nhau".
a) Hãy chỉ ra giả thiết và kết luận của định lí.
b) Vẽ hình minh hoạ và ghi giả thiết, kết luận bằng kí hiệu. Giải
a) Giả thiết: một đường thẳng cắt hai đường thẳng song song.
Kết luận: hai góc so le trong tạo thành bằng nhau. b) GT , cắt tại , cắt tại KL ^ 𝐴1= ^ 𝐵1
Câu 2. Cho định lí: “Một đường thẳng cắt hai đường thẳng tạo
thành một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song”.
a) Hãy chỉ ra giả thiết và kết luận của định lí.
b) Vẽ hình minh hoạ và ghi giả thiết, kết luận bằng kí hiệu. Giải
a) Giả thiết: Một đường thẳng cắt hai đường thẳng tạo thành một cặp góc So le trong bằng nhau.
Kết luận: hai đường thẳng đó song song. b) cắt tại , cắt tại , GT
là hai góc so le trong tạo thành và KL 𝑎 / ¿ 𝑏 VẬN DỤNG
Bài 1 (SGK – tr.107) Vẽ hình minh hoạ và viết giả thiết, kết luận cho mỗi định lí sau:
a) Nếu một đường thẳng vuông góc với một trong hai đường
song song thì nó vuông góc với đường thẳng còn lại.
b) Nếu hai đường thẳng phân biệt cùng song song với một đường
thẳng khác thì hai đường thẳng đó song song với nhau.
c) Nếu hai đường thẳng cùng đi qua một điểm và cùng vuông góc
với một đường thẳng khác thì hai đường thẳng đó trùng nhau. Giải a) GT
𝑎/¿𝑏,𝑐⊥𝑎 KL 𝑐⊥𝑏 GT b) KL 𝑎/¿𝑏 GT c) KL 𝑎≡𝑏
Bài 2 (SGK – tr.107) Cho định lí: “Nếu hai đường thẳng phân biệt
cùng vuông góc với một đường thẳng khác thì hai đường thẳng đó song song với nhau”.
a) Vẽ hình minh hoạ nội dung định lí trên.
b) Viết giả thiết, kết luận của định lí trên.
c) Chứng minh định lí trên. Giải a) b) GT , KL 𝑎/¿𝑏 c) Chứng minh định lí:
Ta có: , mà hai góc này ở vị trí đồng vị nên (Dấu
hiệu nhận biết 2 đường thẳng song song)
Như vậy, định lí trên có thể được suy ra trực
tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.
Ôn lại các kiến thức về định lí
trong toán học, cách chứng minh định lí. HƯỚNG DẪN
Hoàn thành các bài tập trong SBT. VỀ NHÀ
Chuẩn bị bài mới “Bài
tập cuối chương IV” CẢM ƠN CÁC EM ĐÃ
LẮNG NGHE BÀI GIẢNG
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29