Giáo án điện tử Toán 7 Bài 5 Cánh diều: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh
Bài giảng PowerPoint Toán 7 Bài 5 Cánh diều: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 7. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 7
Môn: Toán 7
Sách: Cánh diều
Thông tin:
Tác giả:
Preview text:
CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC KHỞI ĐỘNG
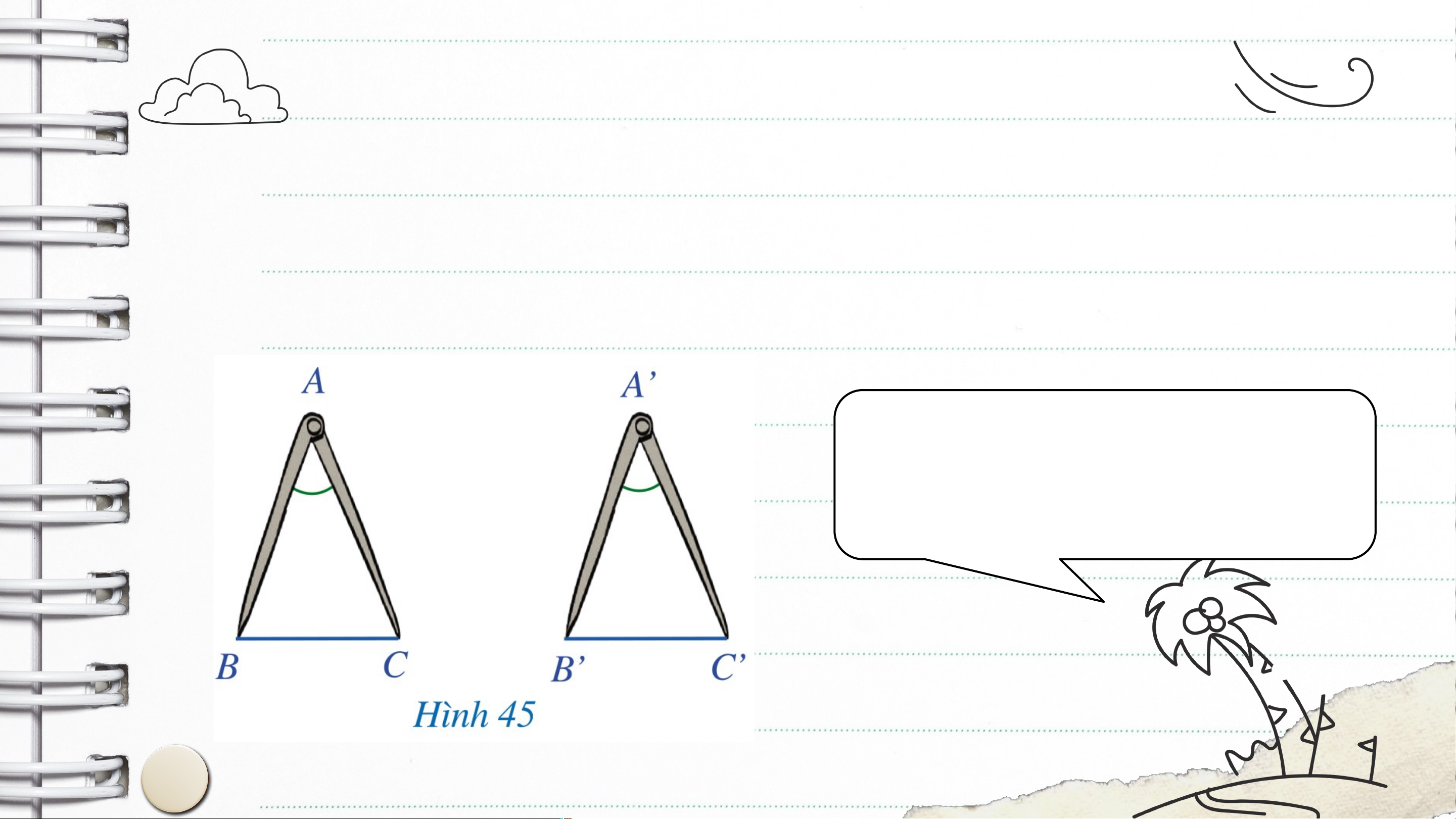
Hai chiếc compa ở Hình 45 gợi nên hình ảnh hai tam giác và có: ; , . Hai tam giác và có bằng nhau hay không ?
BÀI 5: TRƯỜNG HỢP BẰNG
NHAU THỨ HAI CỦA TAM
GIÁC: CẠNH – GÓC – CẠNH NỘI DUNG BÀI HỌC 01 02 Trường hợp bằng nhau
Áp dụng vào trường hợp cạnh – góc – cạnh
bằng nhau về hai cạnh góc vuông của tam giác vuông
I. TRƯỜNG HỢP BẰNG NHAU CẠNH – GÓC – CẠNH
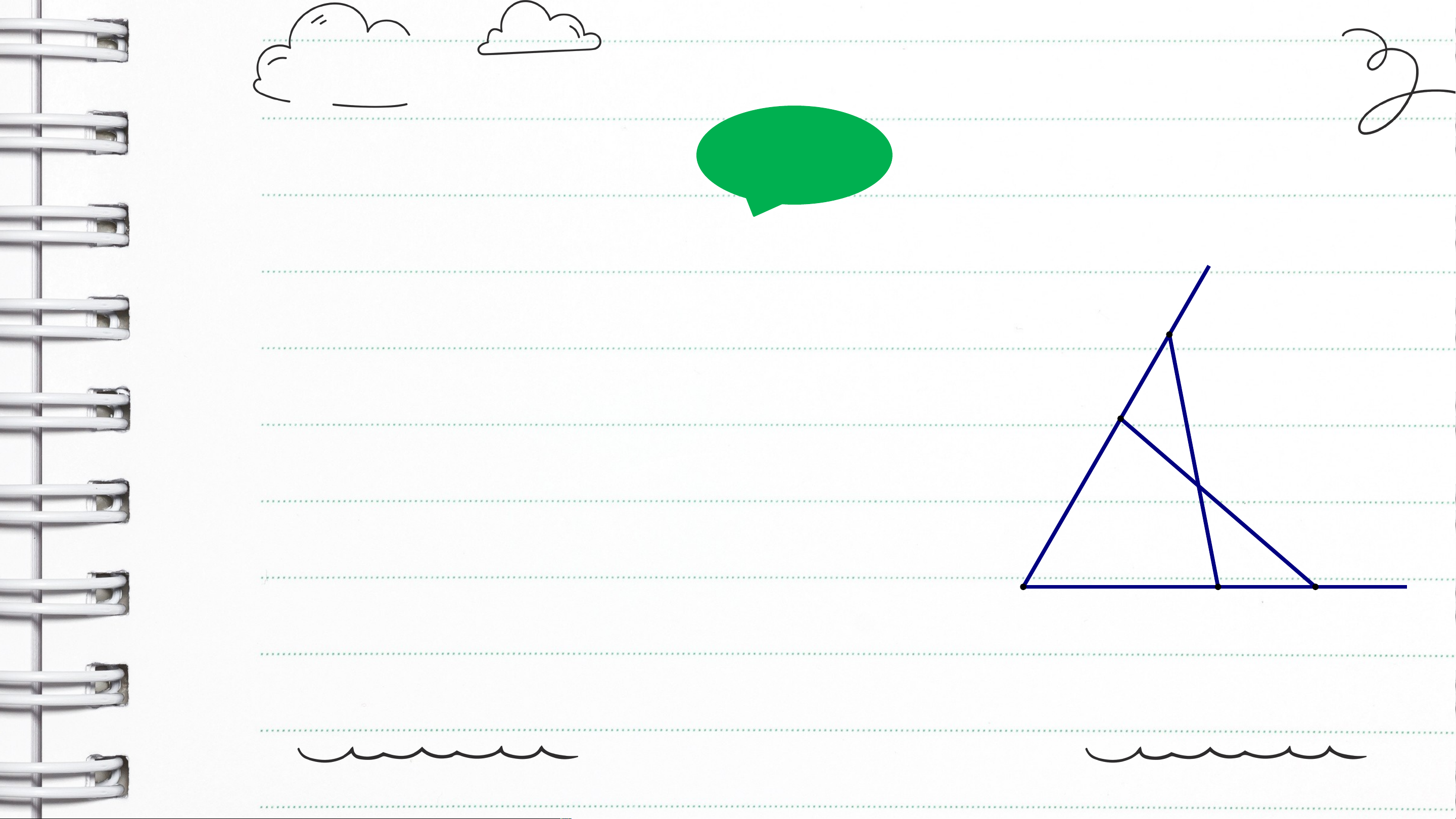
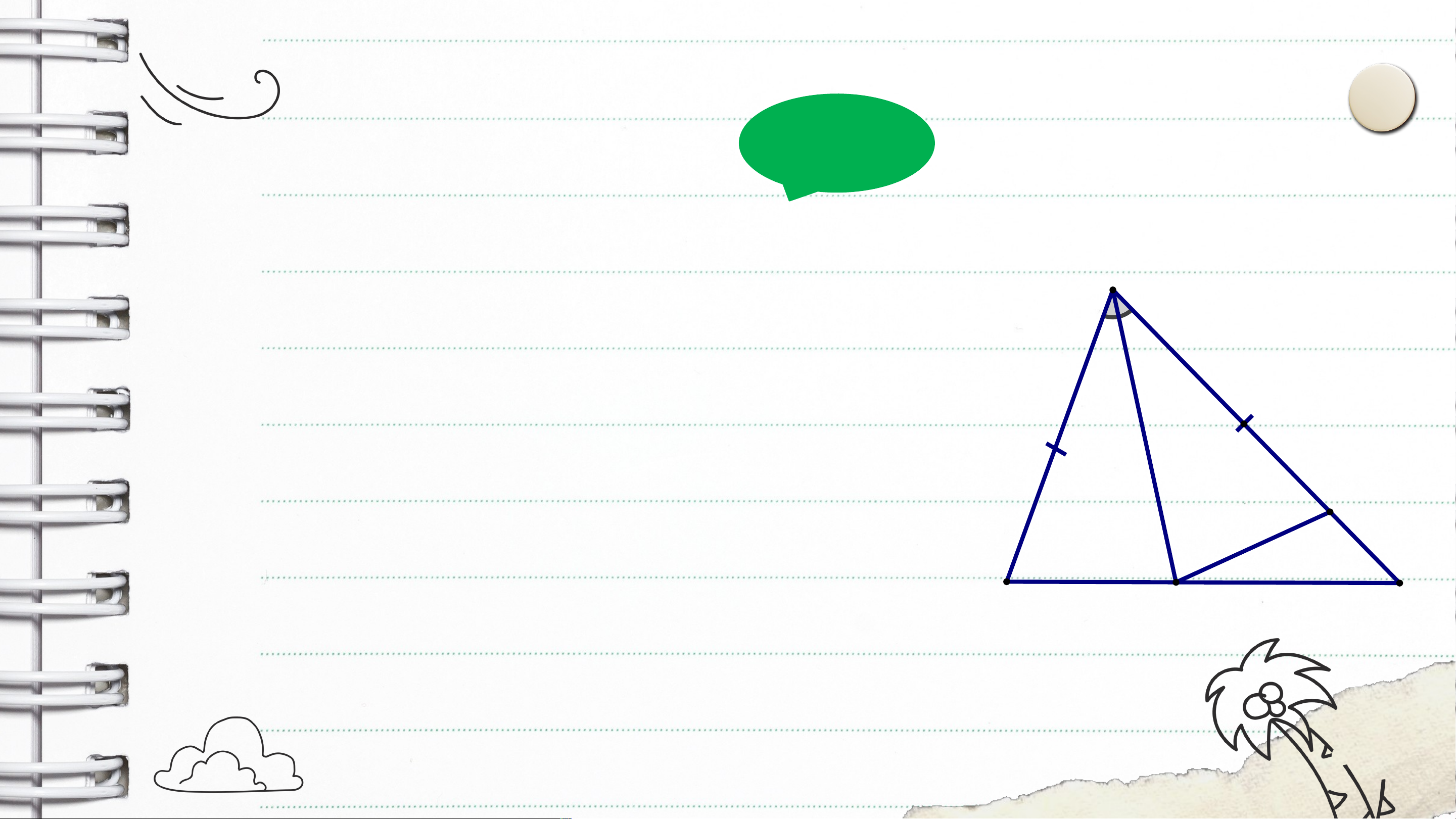
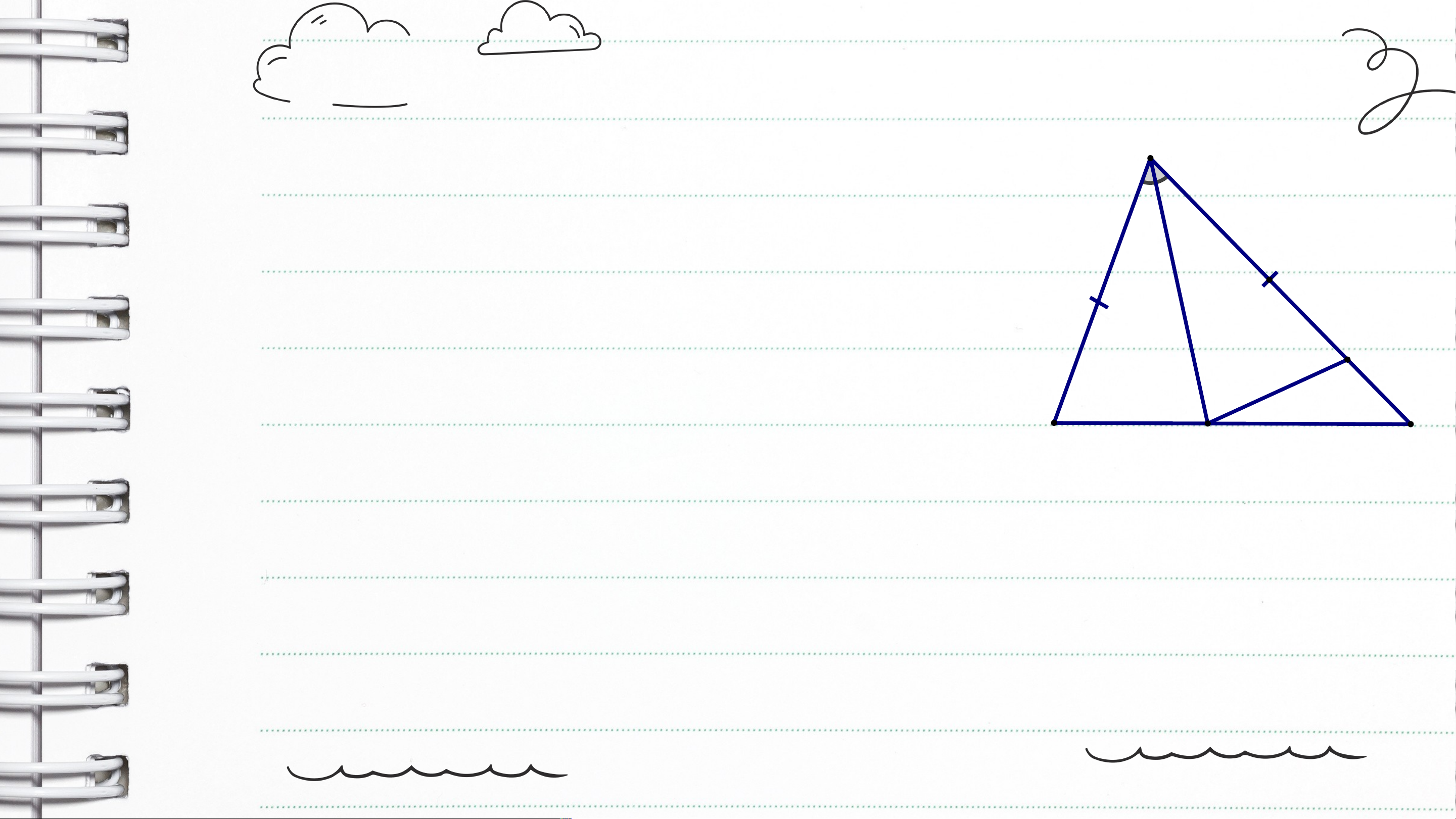
HĐ1 Cho tam giác (Hình 46). Nêu hai cạnh của góc tại đỉnh .
Hai cạnh của góc tại đỉnh là và .
Trong tam giác , ta gọi góc là góc
xen giữa hai cạnh và . HĐ2
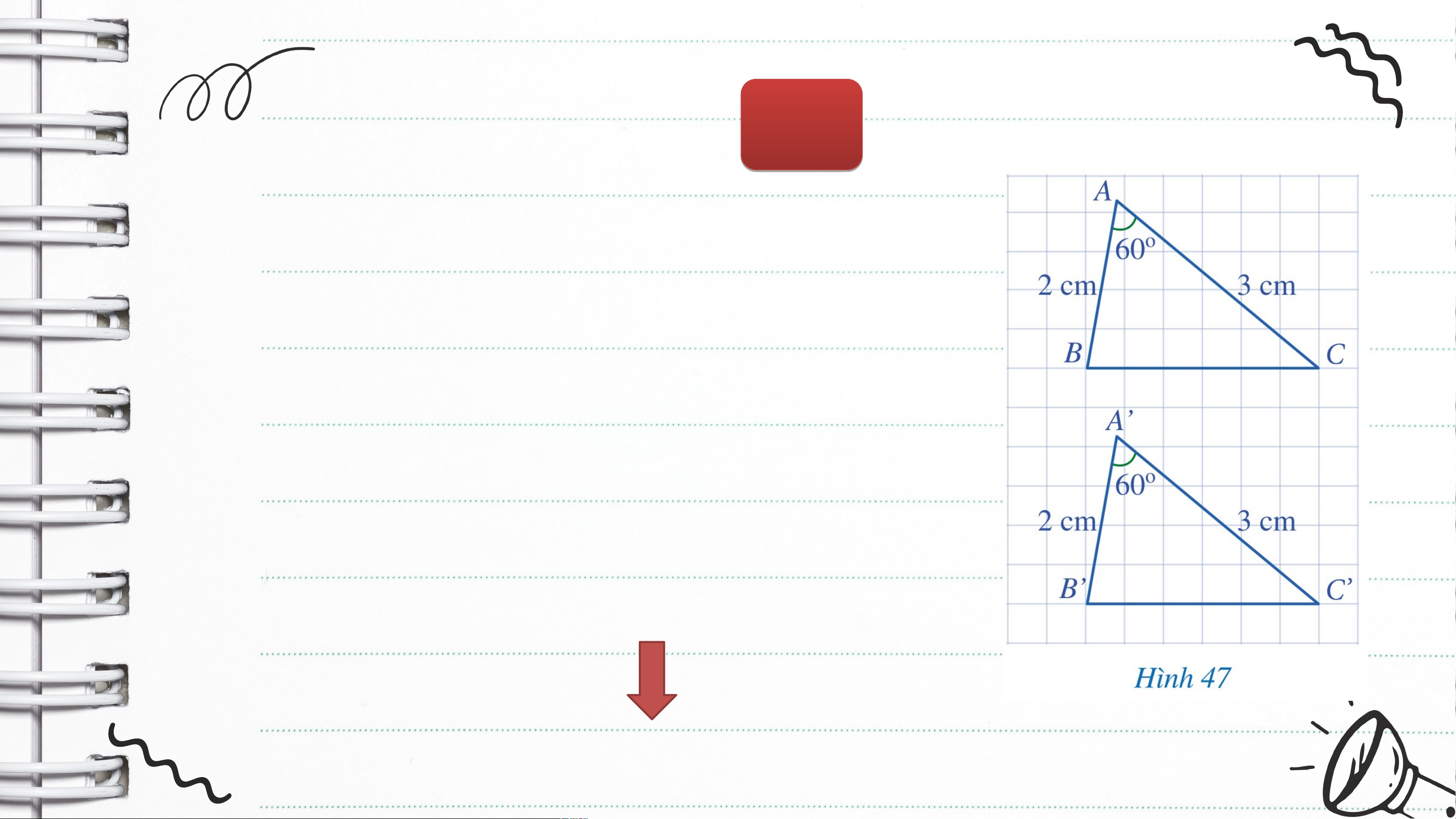
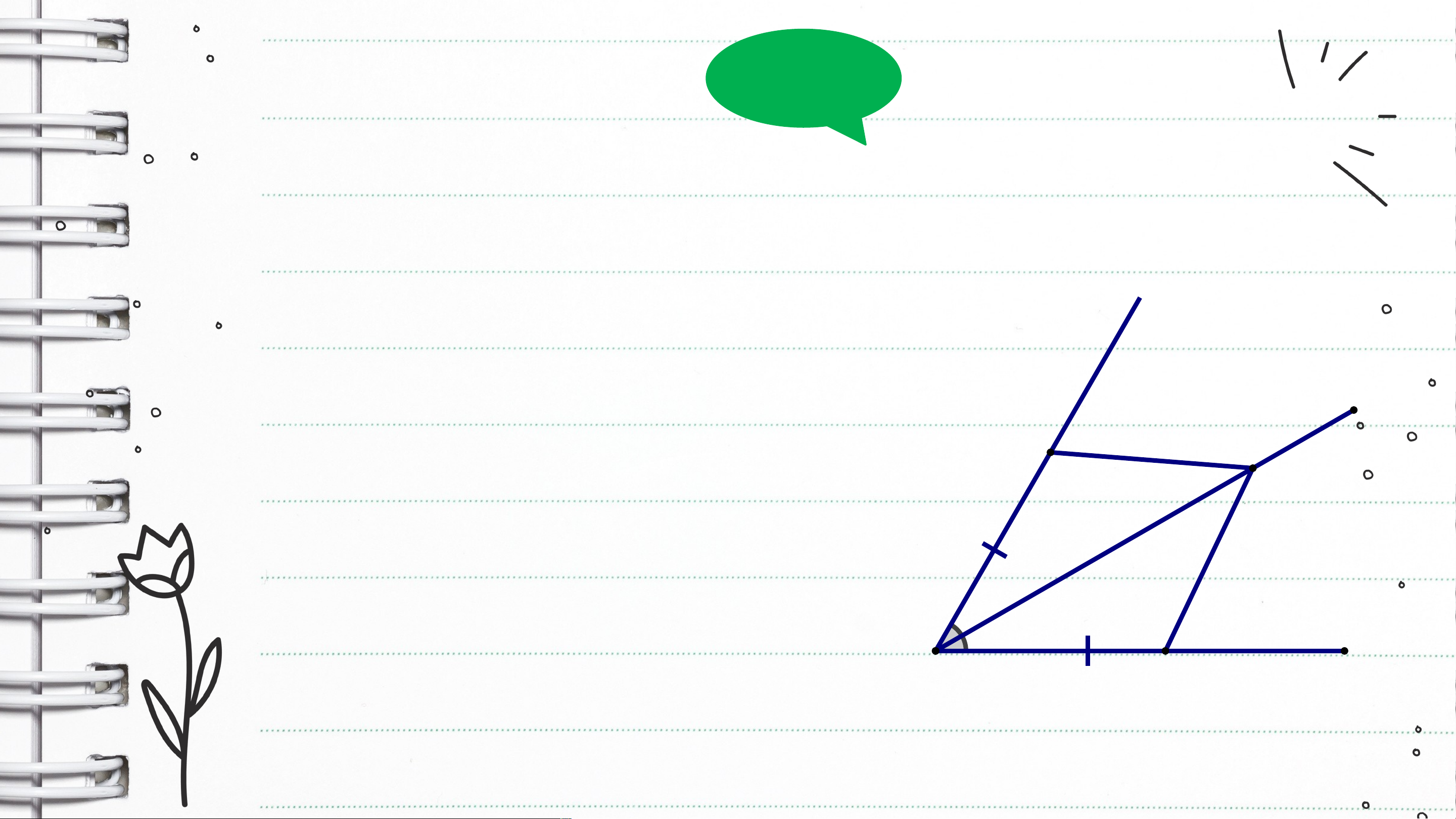
Cho hai tam giác và (Hình 47) có: , , .
Bằng cách đếm số ô vuông, hãy so
sánh và . Từ đó có thể kết luận được
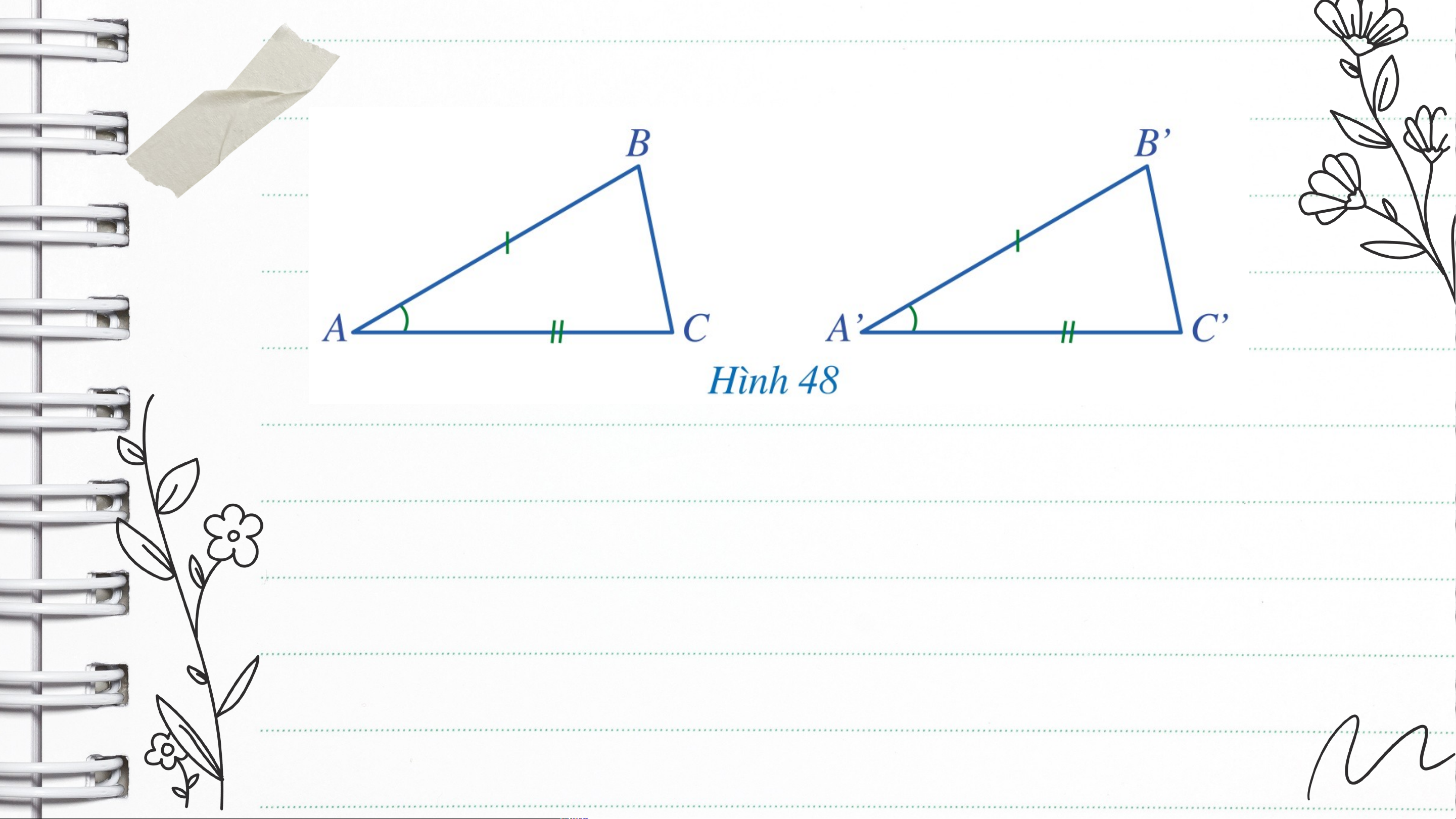
hai tam giác và bằng nhau hay không? và KẾT LUẬN Nếu hai cạ c nh và v gó g c xe x n giữa của tam t giá i c này nà lầ l n lượt lượ bằng hai cạn c h và v góc g xe x n giữa của ta t m giác kia thì hai tam hì hai t giác đó giác đ bằng n hau. Kí hiệu: Nếu , , thì (c.g.c) Ví dụ 1
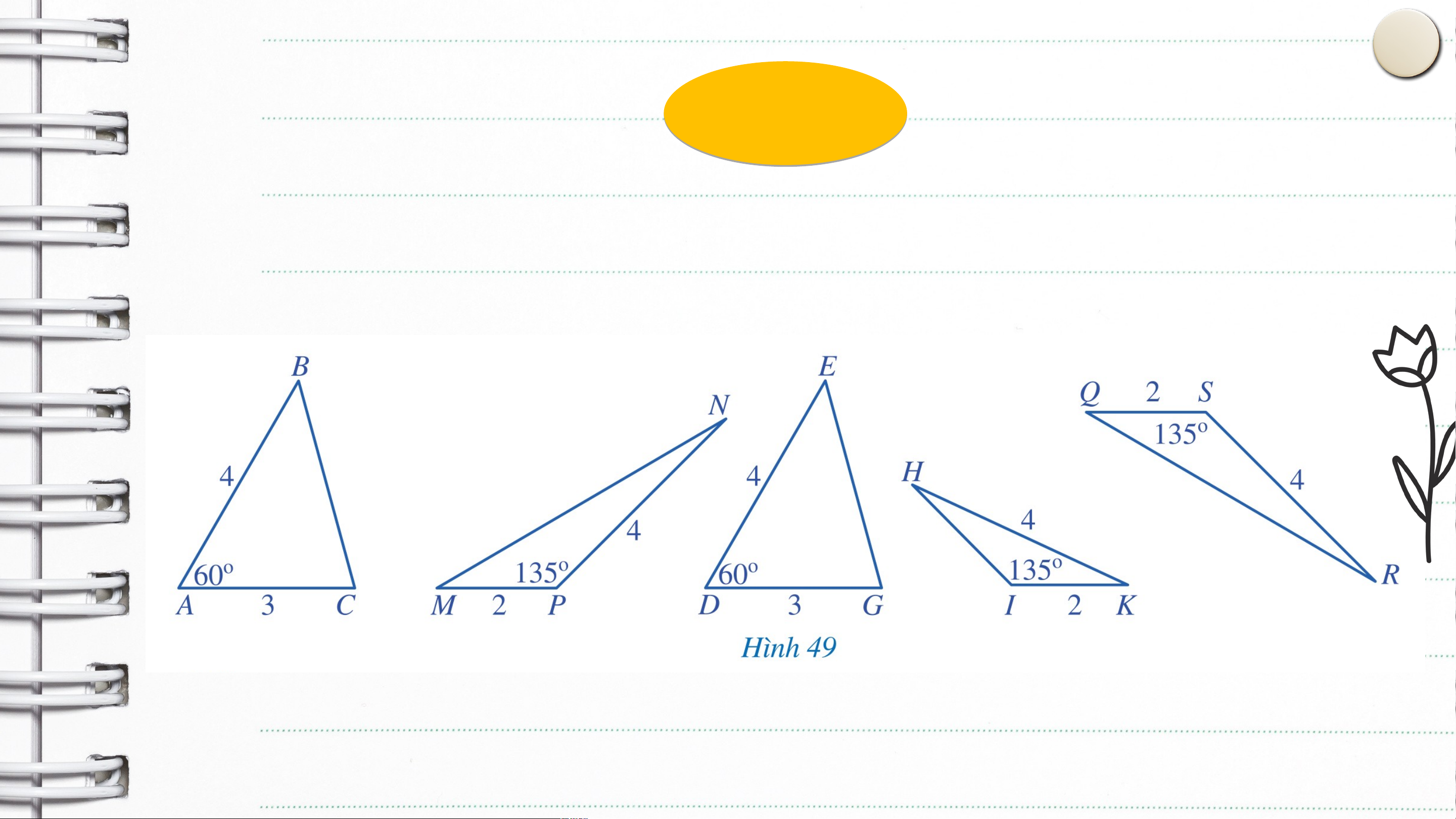
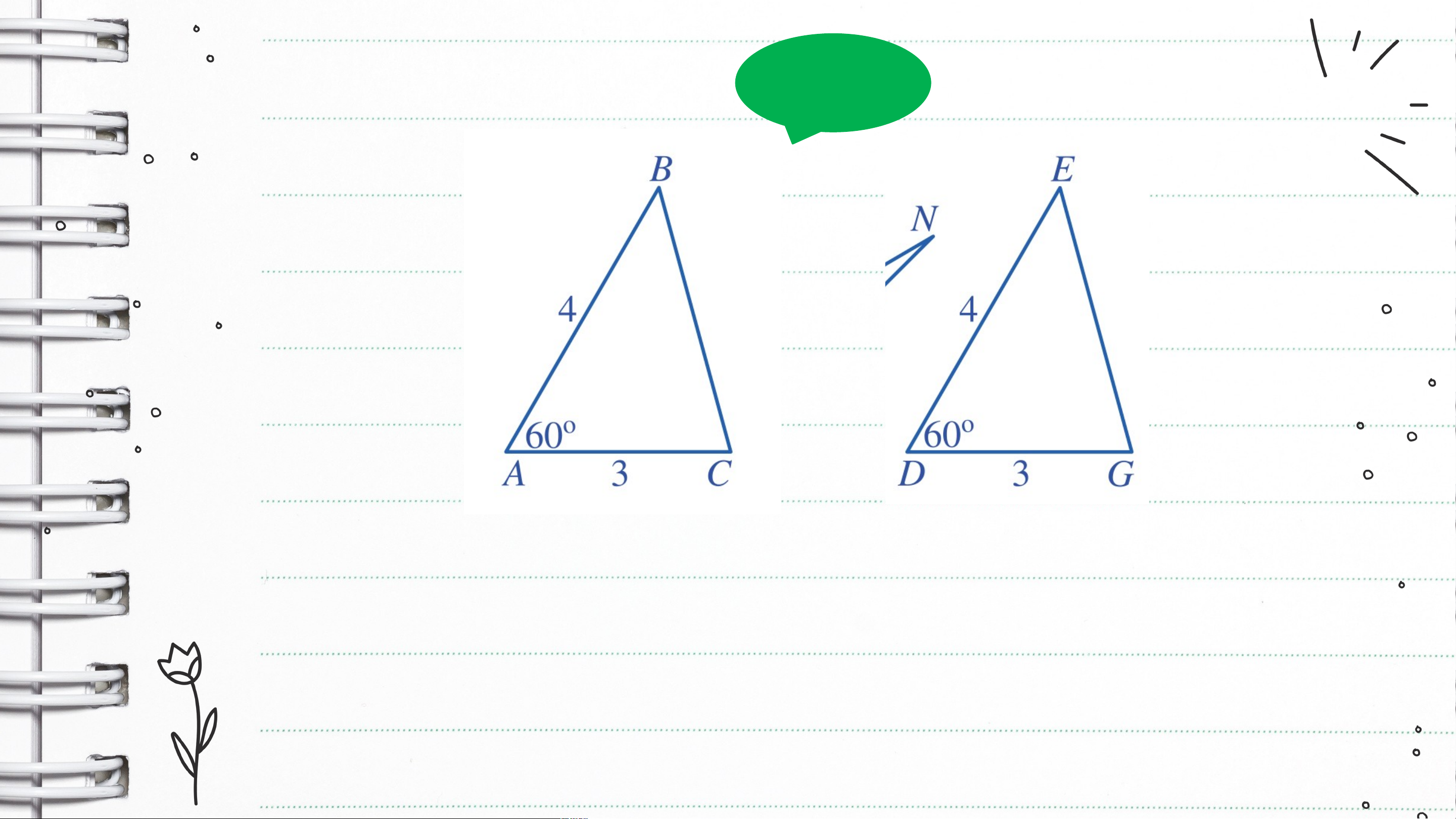
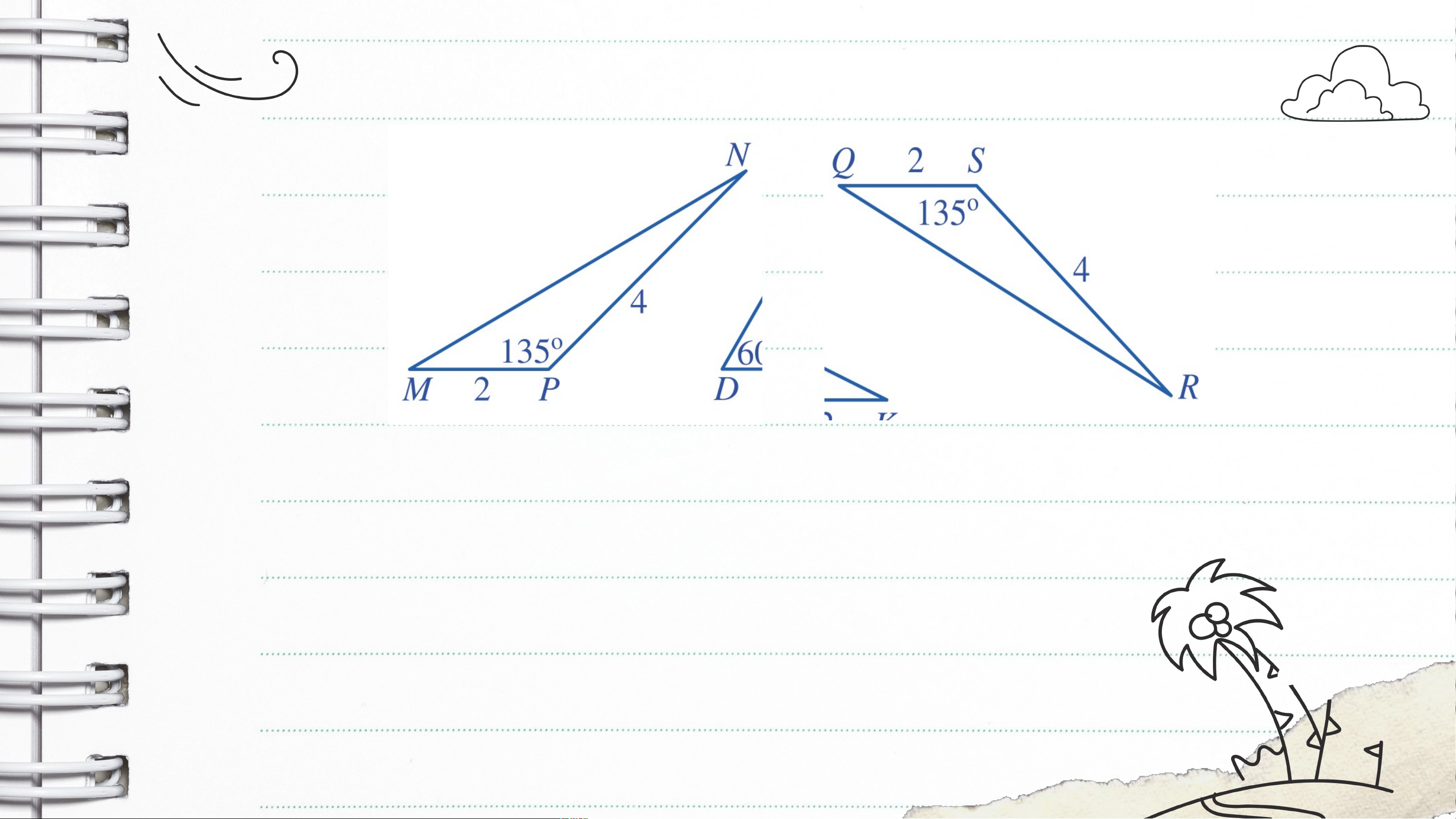
Các cặp tam giác nào ở Hình 49 là bằng nhau? Vì sao? Giải
Xét hai tam giác và , ta có: ; ; Suy ra (c.g.c)
Xét hai tam giác và , ta có: ; ; Suy ra (c.g.c) Ví dụ dụ 2
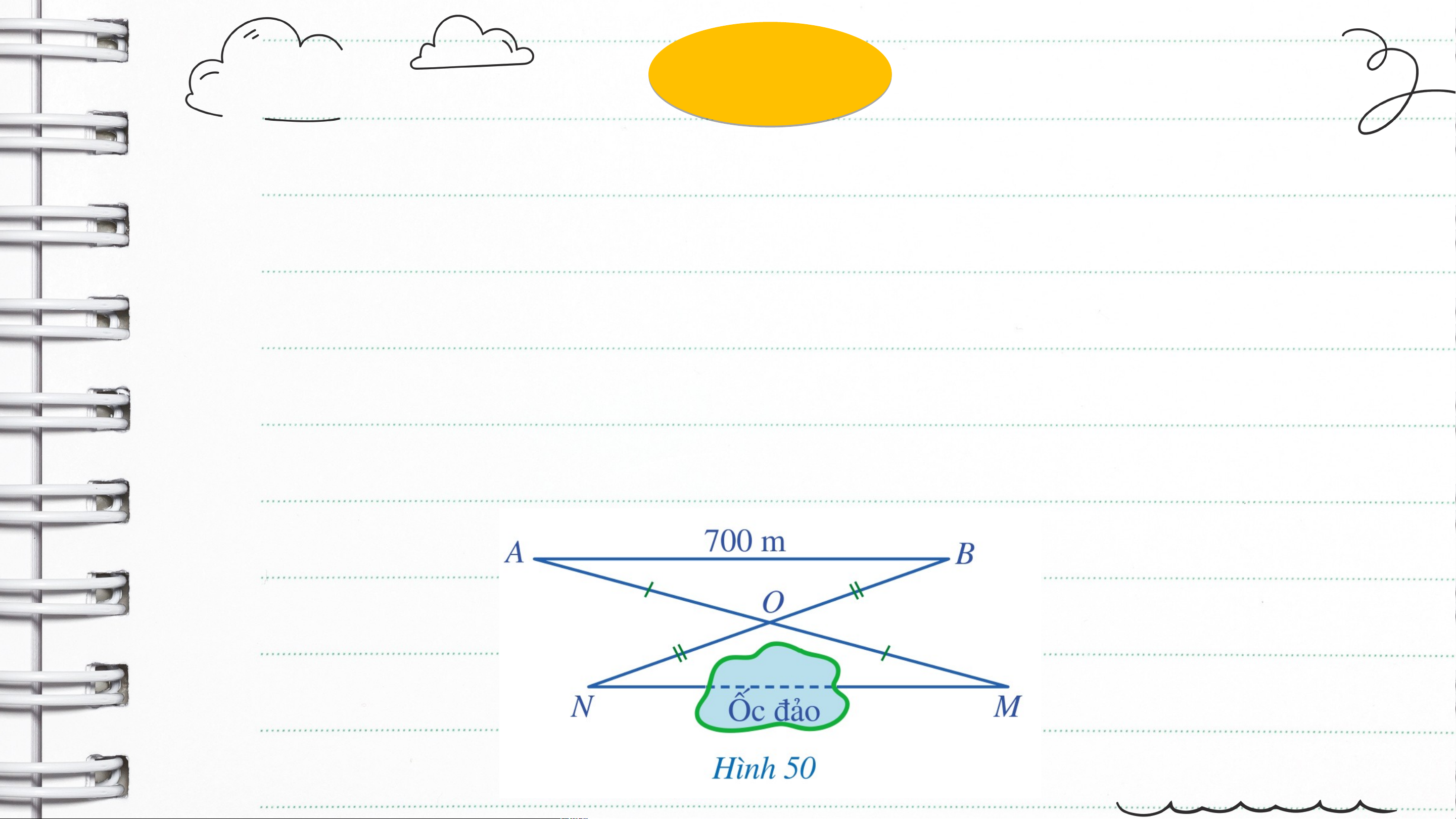
Để đo khoảng cách giữa hai vị trí ở hai phía ốc đảo, người ta
chọn các vị trí bên ngoài ốc đảo sao cho: không thuộc đường
thẳng , khoảng cách là đo được; là trung điểm của cả và
(Hình 50). Người ta đo được . Khoảng cách giữa hai vị trí là bao nhiêu mét? Giải
Xét hai tam giác và , ta có:
(vì là trung điểm của ) (hai góc đối đỉnh)
(vì là trung điểm của ) Suy ra (c.g.c)
Do đó (hai cạnh tương ứng) Luyện tậ Luy p ện tậ 1
Cho góc nhọn . Hai điểm thuộc tia thoả mãn , .
Hai điểm thuộc tia thoả mãn , . Chứng minh . Giải x
Xét hai tam giác và , ta có: N M chung, Suy ra (c.g.c) O P Q y
Do đó: (hai cạnh tương ứng) Luyện t L ập 2 uyện t
Cho góc có là tia phân giác. Hai điểm lần
lượt thuộc và khác thoả mãn , điểm khác và thuộc . Chứng minh . Giải
Vì là tia phân giác của góc
hay (, , lần lượt thuộc tia , , ) x
Xét hai tam giác và , ta có: z (gt) M (cmt) P là cạnh chung Suy ra (c.g.c) O N y
Do đó, (2 cạnh tương ứng)
II. ÁP DỤNG VÀO TRƯỜNG HỢP BẰNG NHAU VỀ
HAI CẠNH GÓC VUÔNG CỦA TAM GIÁC VUÔNG
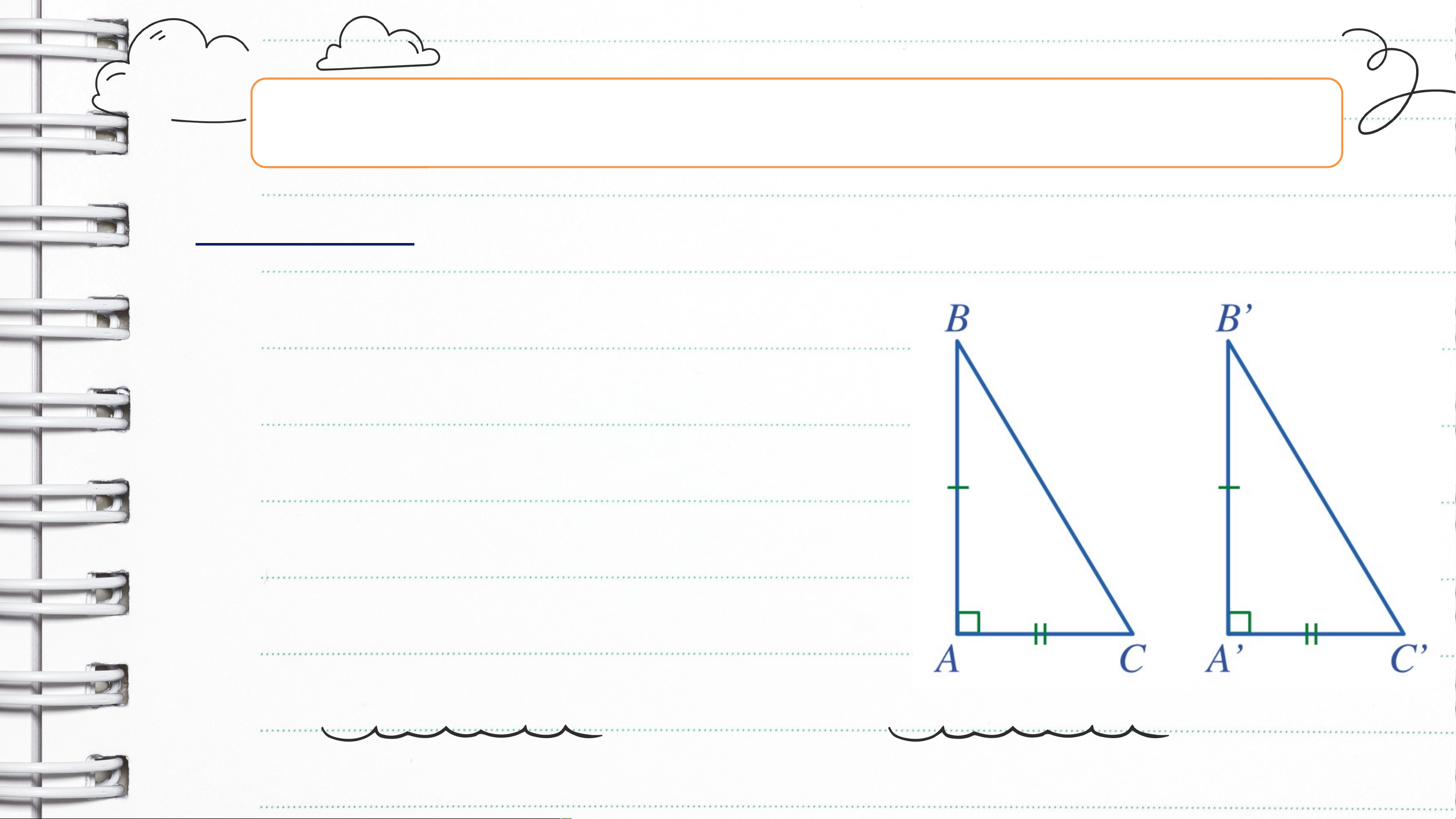
Nếu hai cạnh góc vuông của tam giác vuông này bằng
hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau Nếu , , thì Chứng minh:
Xét hai tam giác vuông và , ta có: Suy ra: (c.g.c) Ví dụ d 3
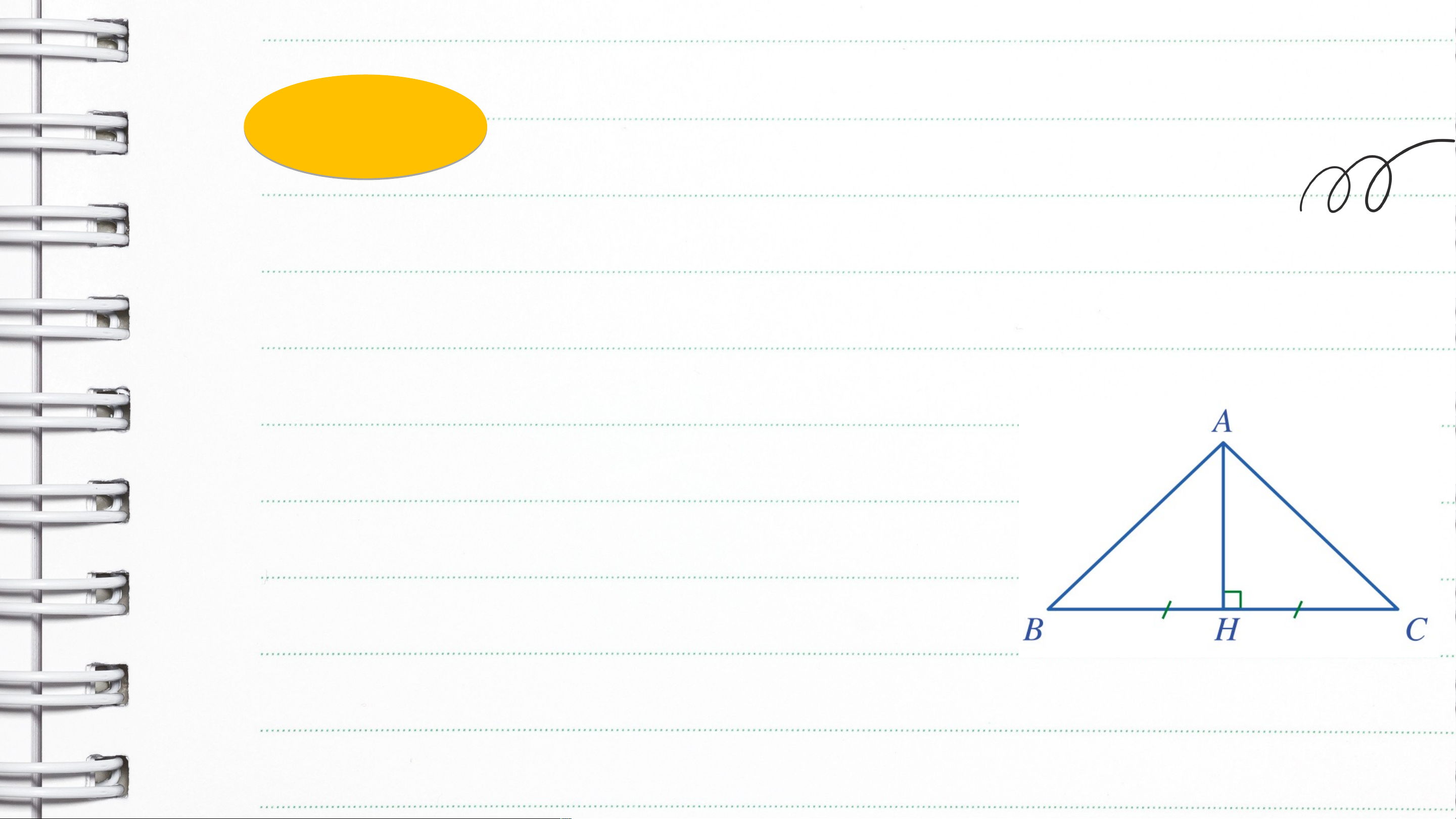
Hai tam giác và vuông tại có . Chứng minh: a) b) Giải
a) Xét hai tam giác vuông và , ta có: là cạnh chung; (gt)
Suy ra (hai cạnh góc vuông) b) Vì nên (hai cạnh tương ứng) LUYỆN TẬP
Bài 1 (SGK – tr.86) Chứng minh định lí: “Trong một tam giác,
góc đối diện với cạnh lớn hơn là góc lớn hơn” thông qua việc giải bài tập sau đây:
Cho tam giác có . Tia phân giác của góc cắt cạnh tại điểm .
Điểm thuộc cạnh thoả mãn . Chứng minh: a) ; b) . Giải A
a) Xét hai tam giác và , ta có: (gt) ( là phân giác góc ) E là cạnh chung Suy ra (c.g.c) B D C A b) Vì (cmt) (hai góc tương ứng) E Có: (hai góc kề bù) B D C
Mà: (tổng 3 góc trong tam giác ) Suy ra: hay (đpcm)
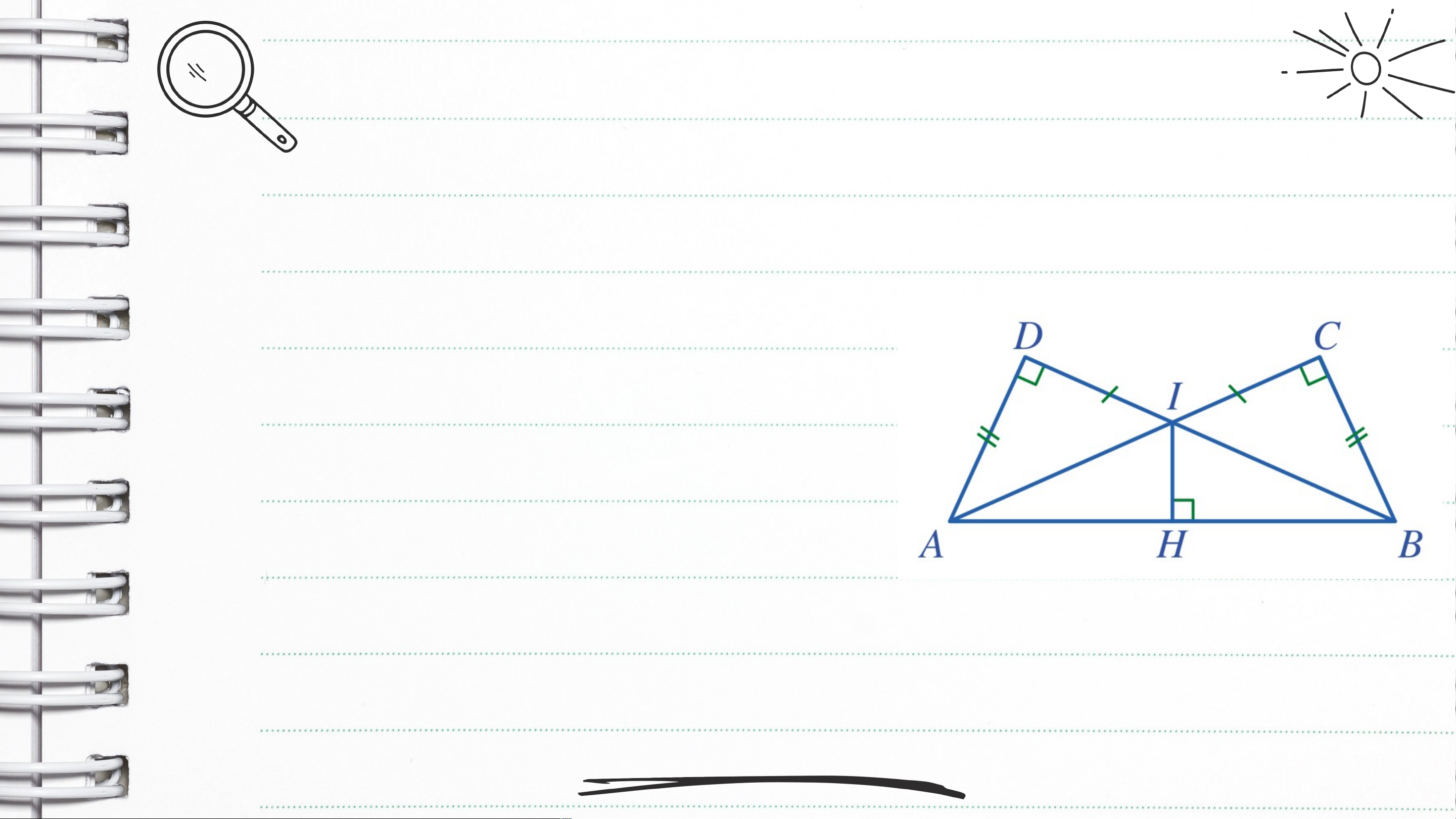
Bài 2 (SGK – tr.86) Cho Hình 53 có , , các góc tại đỉnh là góc vuông. Chứng minh: a) ;
b) là tia phân giác của góc . Giải
a) Xét hai tam giác vuông và , ta có: , Suy ra (c.g.c) (2 cạnh tương ứng)
b) Xét hai tam giác vuông và , ta có: (cmt) là cạnh chung Suy ra (c.g.c) (2 góc tương ứng) là phân giác của góc VẬN DỤNG
Bài 3 (SGK – tr.86) Có hai xã cùng ở một bên bờ sông Lam. Các kĩ
sư muốn bắc một cây cầu qua sông Lam cho người dân hai xã. Để
thuận lợi cho người dân đi lại, các kĩ sư cần phải chọn vị trí của cây
cầu sao cho tổng khoảng cách từ hai xã đến chân cầu là nhỏ nhất.
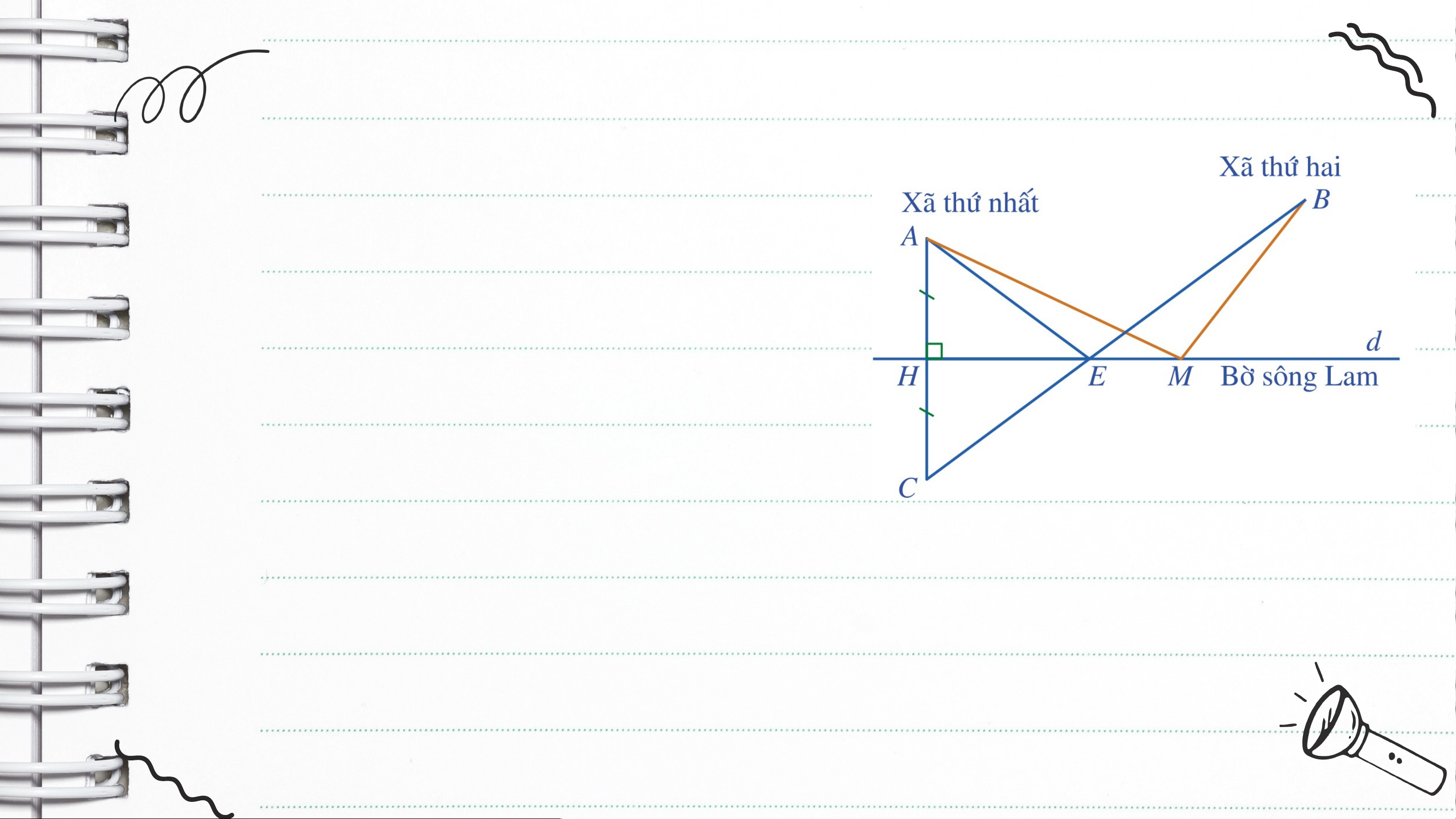
Bạn Nam đề xuất cách xác định vị trí của cây cầu như sau:
+ Điểm chỉ vị trí xã thứ nhất
+ Điểm chỉ vị trí xã thứ hai
+ Đường thẳng chỉ vị trí bờ sông Lam.
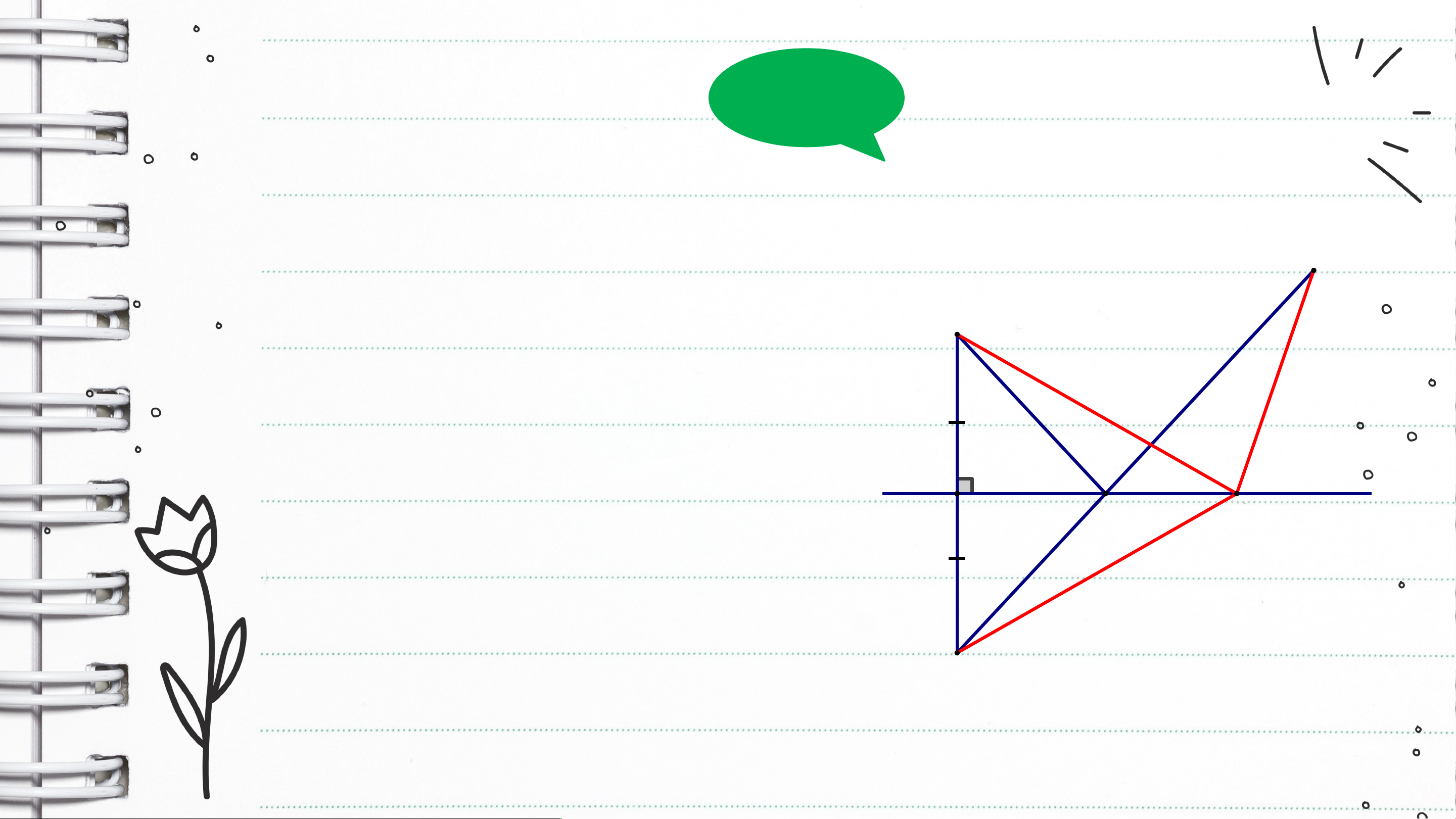
- Kẻ vuông góc với ( thuộc ), kéo dài về phía và lấy điểm sao cho .
- Nối với , cắt đường thẳng tại điểm .
- Khi đó là vị trí của cây cầu.
Bạn Nam nói rằng: Lấy một điểm trên đường thẳng , khác thì .
Em hãy cho biết bạn Nam nói đúng hay sai? Vì sao? Giải
Xét hai tam giác vuông và , ta có: B (gt) A là cạnh chung d Suy ra (c.g.c) H E M (2 cạnh tương ứng) . C
Xét hai tam giác vuông và , ta có: (gt); ; là cạnh chung Suy ra (c.g.c) (2 cạnh tương ứng) . Xét tam giác có:
(hệ thức lượng trong tam giác) Hay Vậy bạn Nam nói đúng. non Ong học việc
Câu 1. Cho tam giác và tam giác có: ; . Cần thêm một điều kiện
gì để tam giác và tam giác bằng nhau theo trường hợp cạnh- góc-cạnh. A. B. C. D.
Câu 2. Cho tam giác và tam giác có , , . Phát biểu nào
trong các phát biểu sau đây đúng A. B. C. D.
Câu 3. Cho tam giác và tam giác có , , , biết , số đo góc là: A. B. C. D.
Câu 4. Cho tam giác có °, tia phân giác của
góc (). Trên cạnh lấy điểm sao cho . Hai góc nào sau đây bằng nhau A. B. C. D.
Câu 5. Cho tam giác vuông tại . Tia phân giác của góc
cắt tại , lấy trên sao cho . Chọn câu đúng A. B. C. D.
HƯỚNG DẪN VỀ NHÀ Ghi nhớ kiến thức Hoàn thành bài tập Chuẩn bị bài mới trong bài. trong SBT “Bài 6”. CẢM ƠN CÁC EM ĐÃ
LẮNG NGHE BÀI GIẢNG
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38