Giáo án điện tử Toán 7 Bài 7 Cánh diều: Đại lượng tỉ lệ thuận
Bài giảng PowerPoint Toán 7 Bài 7 Cánh diều: Đại lượng tỉ lệ thuận hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 7. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 7
Môn: Toán 7
Sách: Cánh diều
Thông tin:
Tác giả:
Preview text:
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN
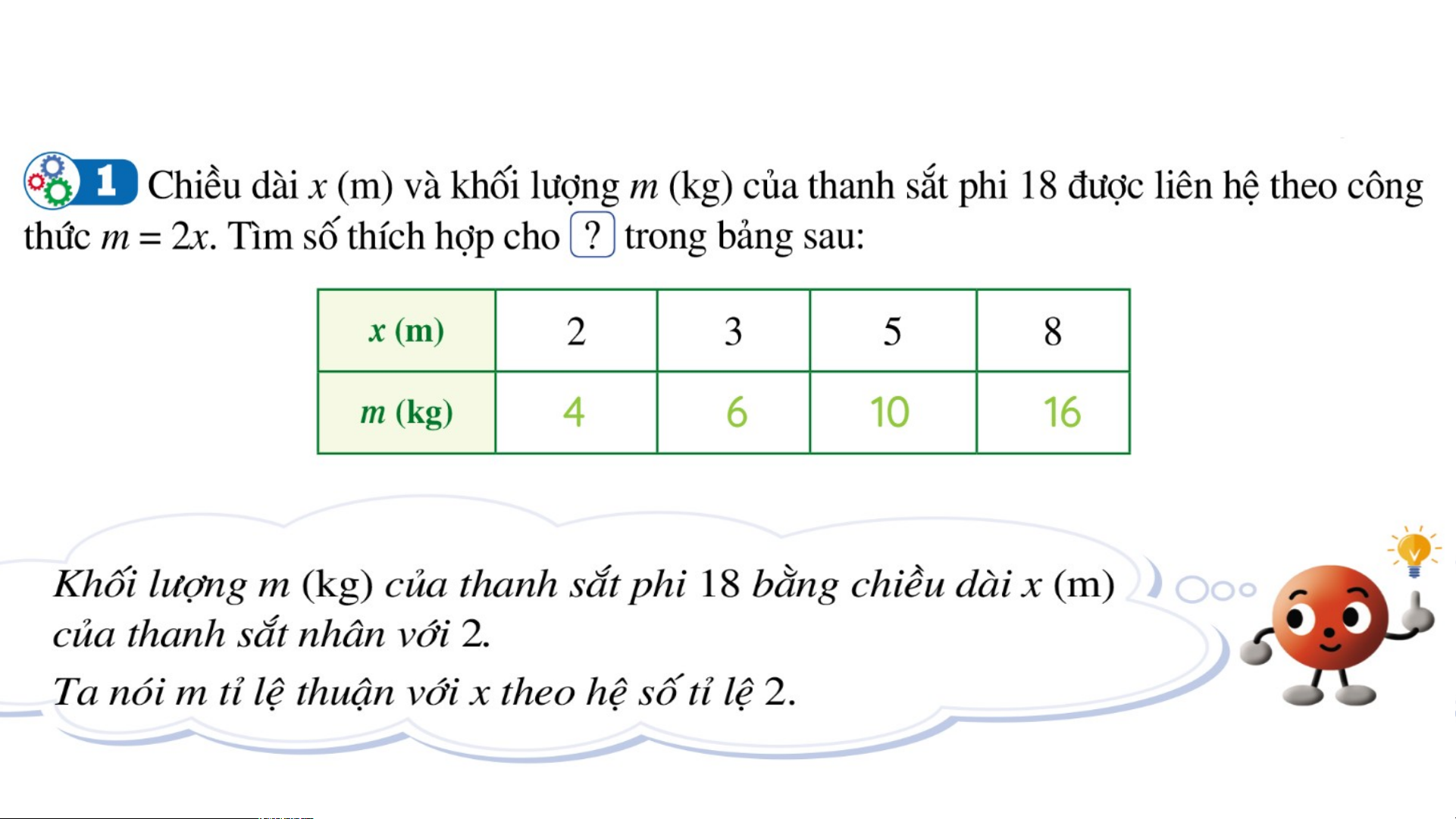
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN KHỞI ĐỘNG
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN I. KHÁI NIỆM
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN I. KHÁI NIỆM
Ví dụ 1: Chu vi đường tròn C có tỉ lệ thuận với đường kính d hay không? Nếu có hãy
xác định hệ số tỉ lệ đó
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN I. KHÁI NIỆM Chú ý 1
Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ k thì x tỉ lệ thuận với y theo hệ số tỉ lệ . Ta
nói x và y là hai đại lượng tỉ lệ thuận với nhau. k
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN I. KHÁI NIỆM
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN I. KHÁI NIỆM Giải
a) Gọi k là hệ số tỉ lệ của y đối với x. Ta có y = kx.
Vì khi x = 1,2 thì y = 0,4 nên 0,4 = k . 1,2 0, 4 4 1 Hay k = 1, 2 12 3 1
b) Ta có công thức tính y theo x là: y x 3
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN I. KHÁI NIỆM
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN I. KHÁI NIỆM
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN I. KHÁI NIỆM Giải
a) Công thức tính quãng đường đi được s (km) theo thời gian t (h) của chuyển động là: s = 65 . t b) Vì s = 65 . t
nên s và t là hai đại lượng tỉ lệ thuận. Hệ số tỉ lệ của s đối với t là: 65 c) Vì s = 65 . t nên
+ Với t = 0,5 thì s = 65 . 0,5 = 32,5 (km) 3 3
+ Với t = thì s = 65 . = 97,5 (km) 2 2
+ Với t = 2 thì s = 65 . 2 = 130 (km) HƯỚNG DẪN VỀ NHÀ
+ Học thuộc phần khái niệm và chú ý.
+ Xem trước phần tính chất
+ Làm bài tập 1; 2 (SGK/T62; 63)
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN (tiết 2)
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN (tiết 2) II. TÍNH CHẤT Giải
a) Vì x và y là hai đại lượng tỉ lệ thuận, khi x = 3 thì y = 9 1 1 nên k = y : x = 9 : 3 = 3 1 1 y 9 y 15 y 21 1 b) Ta có: ; 3 k 2 ; 3 k 3 3 k x 3 x 5 x 7 1 2 3 y y y 1 2 3 Vậy: k x x x 1 2 3 x 3 y 9 3 1 1 c) + Ta có: ; x 5 y 15 5 2 2 x y 1 1 Vậy: x y 2 2 x 3 y 9 3 x y 1 1 1 1 + Ta có: ; x 7 y 21 7 x y 3 3 3 3
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN (tiết 2) II. TÍNH CHẤT
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN (tiết 2) II. TÍNH CHẤT
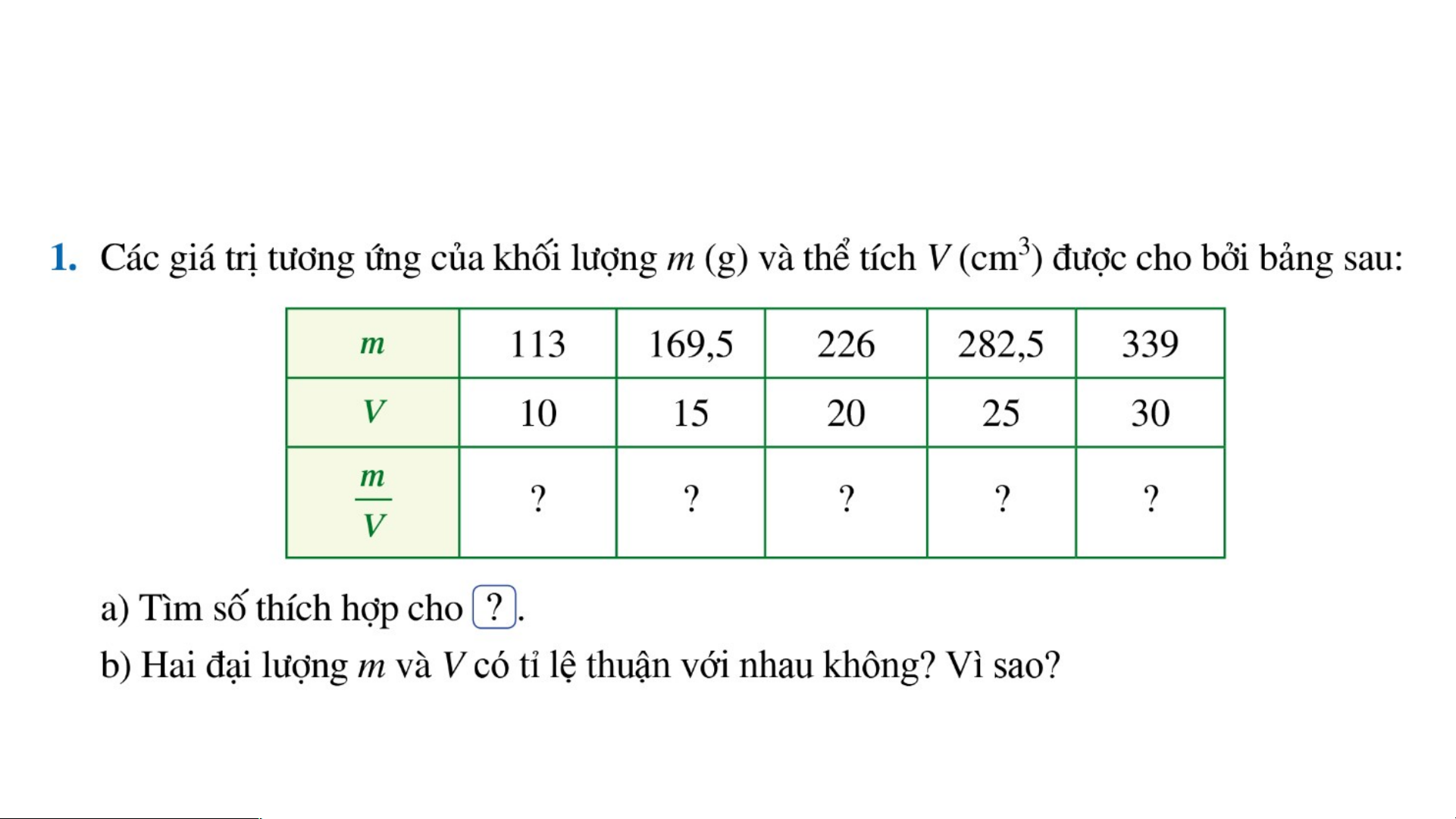
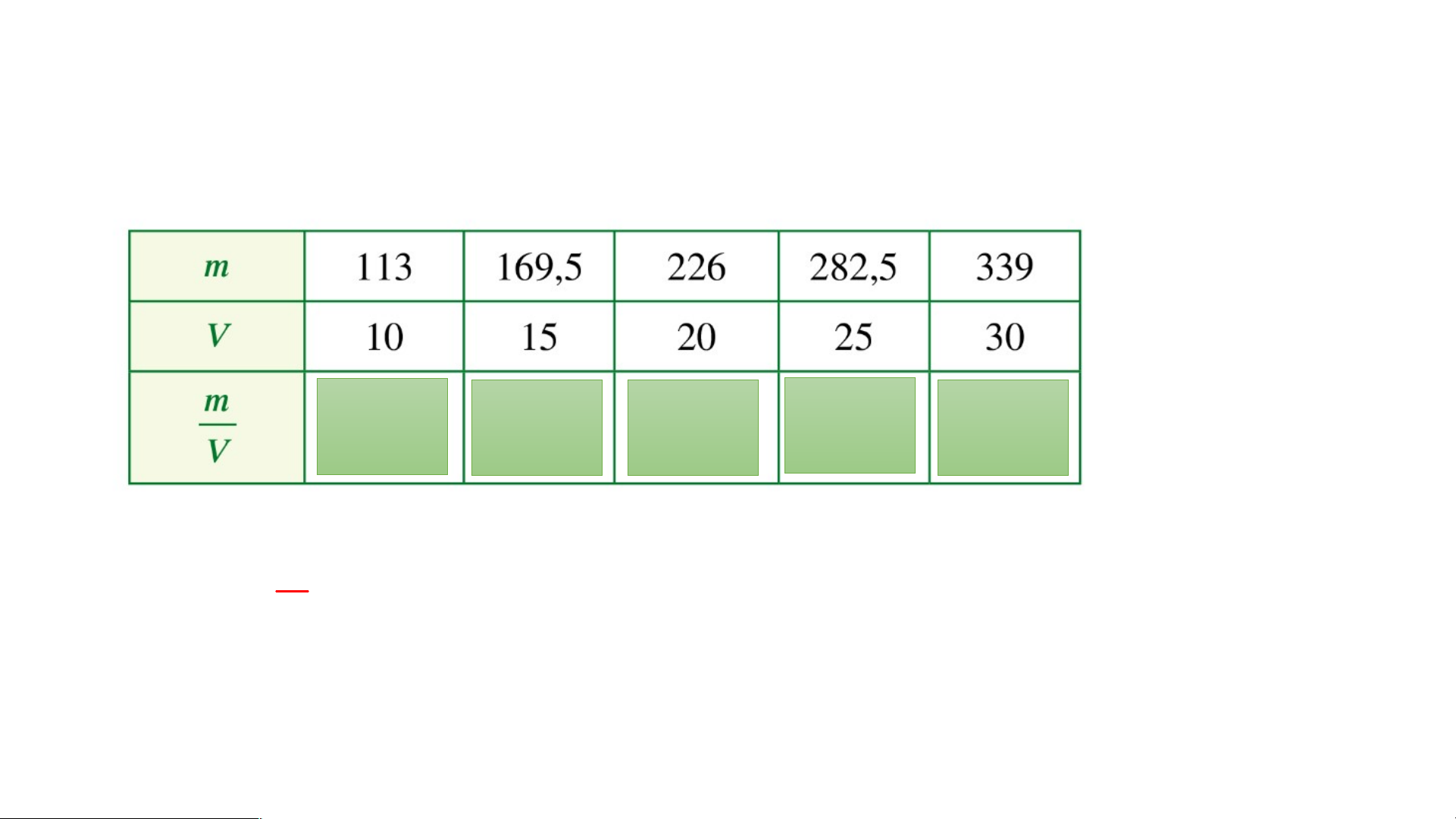
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN (tiết 2) BÀI TẬP Bài 1 (SGK/T62)
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN (tiết 2) BÀI TẬP a) Hoàn thành bảng 11,3 11,3 11,3 11,3 11,3 m
b) Ta thấy tỉ số không đổi nên m và V là hai đại lượng tỉ lệ thuận V
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN (tiết 2) BÀI TẬP Bài 2 (SGK/T63)
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN (tiết 2) BÀI TẬP Giải
a) Gọi k là hệ số tỉ lệ của y đối với x. Ta có y = kx y 4 2 nên k = 1 x 6 3 1 2
Ta có công thức tính y theo x là: y x 3
b) Gọi k là hệ số tỉ lệ của x đối với y. Ta có x = k y 1 1 6 3 nên k1 4 2 3
Ta có công thức tính y theo x là: x y 2
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN (tiết 3)
BÀI 7: ĐẠI LƯỢNG TỈ LỆ THUẬN (tiết 3)
III. MỘT SỐ BÀI TOÁN Luyện tập 2:
Một máy in trong 5 phút in được 120 trang. Hỏi trong 3 phút máy in đó in được bao nhiêu trang Giải
Gọi số trang máy in đó in trong 3 phút là x.
Vì thời gian và số trang in được là hai đại lượng tỉ lệ thuận, theo tính chất của hai đại 120 x 120 . 3
lượng tỉ lệ thuận ta có: x 7 2 5 3 5
Vậy trong 3 phút máy in đó in được 72 trang
III. MỘT SỐ BÀI TOÁN
III. MỘT SỐ BÀI TOÁN
Document Outline
- PowerPoint Presentation
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26