Giáo án điện tử Toán 7 Bài 9 Kết nối tri thức: Hai đường thẳng song song và dấu hiệu nhận biết
Bài giảng PowerPoint Toán 7 Bài 9 Kết nối tri thức: Hai đường thẳng song song và dấu hiệu nhận biết hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 7. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 7
Môn: Toán 7
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
ỦY BAN NHÂN DÂN QUẬN LIÊN CHIỂU
TRƯỜNG THCS NGUYỄN LƯƠNG BẰNG BÀI 9
HAI ĐƯỜNG THẲNG SONG SONG VÀ
DẤU HIỆU NHẬN BIẾT (2 TIẾT) Giáo viên : Hà Duy Ninh Thành phố: Đà Nẵng Sách
: Kết nối tri thức với cuộc sống CHÀO MỪNG CÁC EM
ĐẾN VỚI BÀI GIẢNG HÔM NAY! Tiết 1
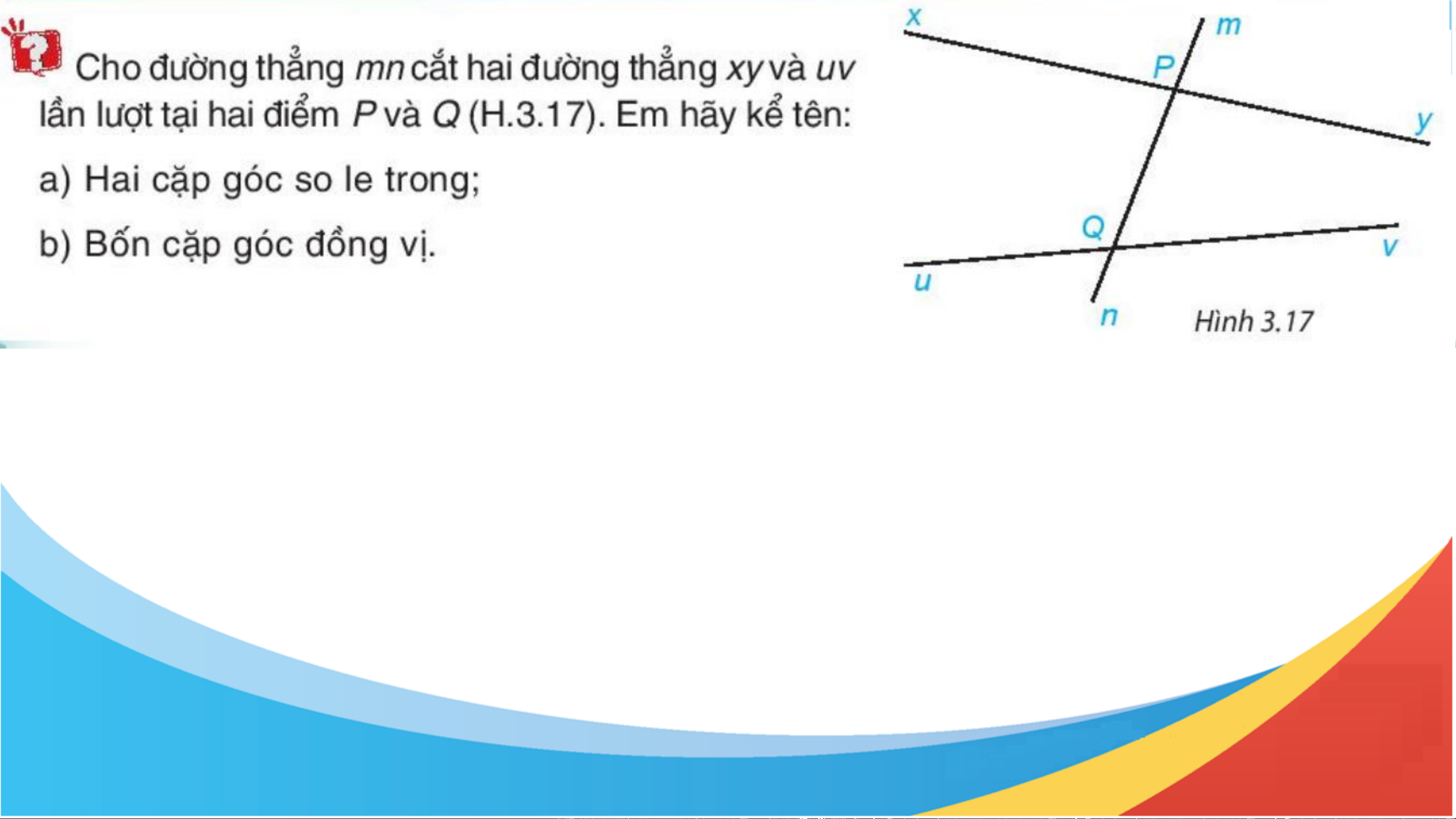
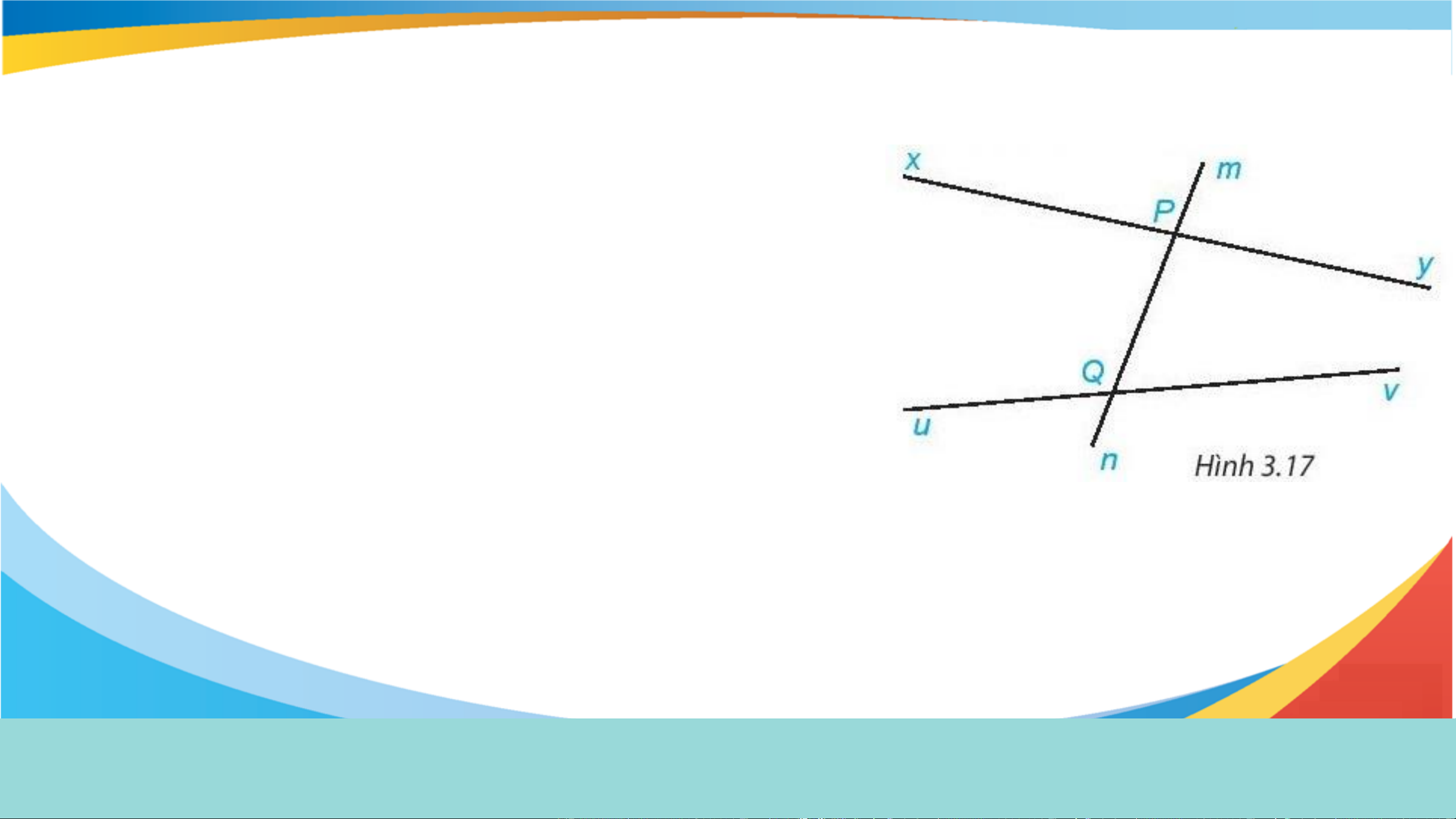
Cho đường thẳng mn cắt đường thẳng xy và uv lần lượt
tại hai điểm P và Q (H.3.17). Em hãy kể tên: a) Hai cặp góc so le trong
b) Bốn cặp góc đồng vị. a) Cặp góc so le trong: Góc xPQ và vQP. b) Cặp góc đồng vị: Góc yPQ và uQP.
Góc mPx và PQu; Góc xPQ và uQn;
Góc mPy và PQv; Góc yPQ và vQn.
Quan hệ giữa các cặp góc so le trong, cặp góc đồng vị
Hoạt động nhóm 4 và thực hiện HĐ1, HĐ2.
Cho biết hai góc so le trong A và B bằng nhau và bằng 60⁰. 1 3 HĐ1
Hãy tính và so sánh hai góc so le trong còn lại A và B . 2 4 𝐴1và 𝐴2 là hai góc kề bù Giải ⇒ 𝐴2 = 180° − 𝐴1 = 180o − 60o = 150o Tương tự 𝐵3 và 𝐵4 là hai góc kề bù ⇒ 𝐵4 = 180° − 𝐵3 = 180o − 60o = 150o
Quan hệ giữa các cặp góc so le trong, cặp góc đồng vị
Hoạt động nhóm 4 và thực hiện HĐ1, HĐ2.
Cho biết hai góc so le trong A và B bằng nhau và bằng 60⁰. 1 3 HĐ2
Chọn hai góc đồng vị rồi tính và so sánh hai góc đó.
Ví dụ hai góc đồng vị: Giải 𝐴1 và 𝐵1. Vì 𝐵1và
𝐵3 là hai góc đối đỉnh nên: 𝐵1 = 𝐵3 = 60𝑜. Vậy 𝐴1 = 𝐵1 = 60𝑜. Luyện tập 1
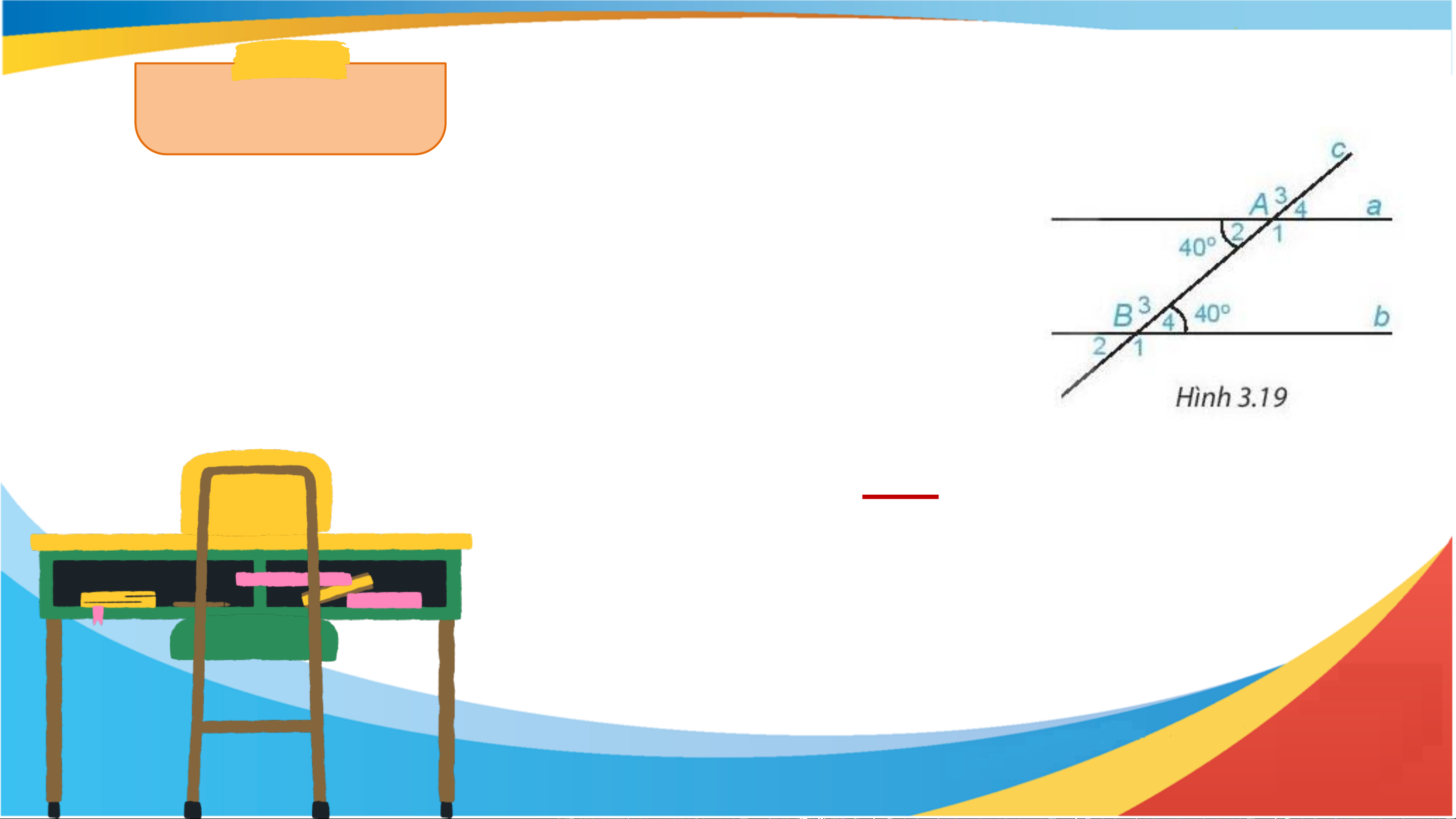
a) Cho hình 3.19, biết góc A = 40°; góc B = 40°. Em 2 4
hãy cho biết số đo các góc còn lại.
b) Các cặp góc A và B ; A và B được gọi là các cặp 1 4 2 3
góc trong cùng phía. Tính tổng: 𝐴1+ 𝐵1 và 𝐴2 + 𝐵3 Giải a) 𝐴1 = 𝐴3 = 140o ; 𝐴2 = 𝐴4 = 40o 𝐵1 = 𝐵3 = 140o; 𝐵2 = 𝐵4 = 40o Luyện tập 1
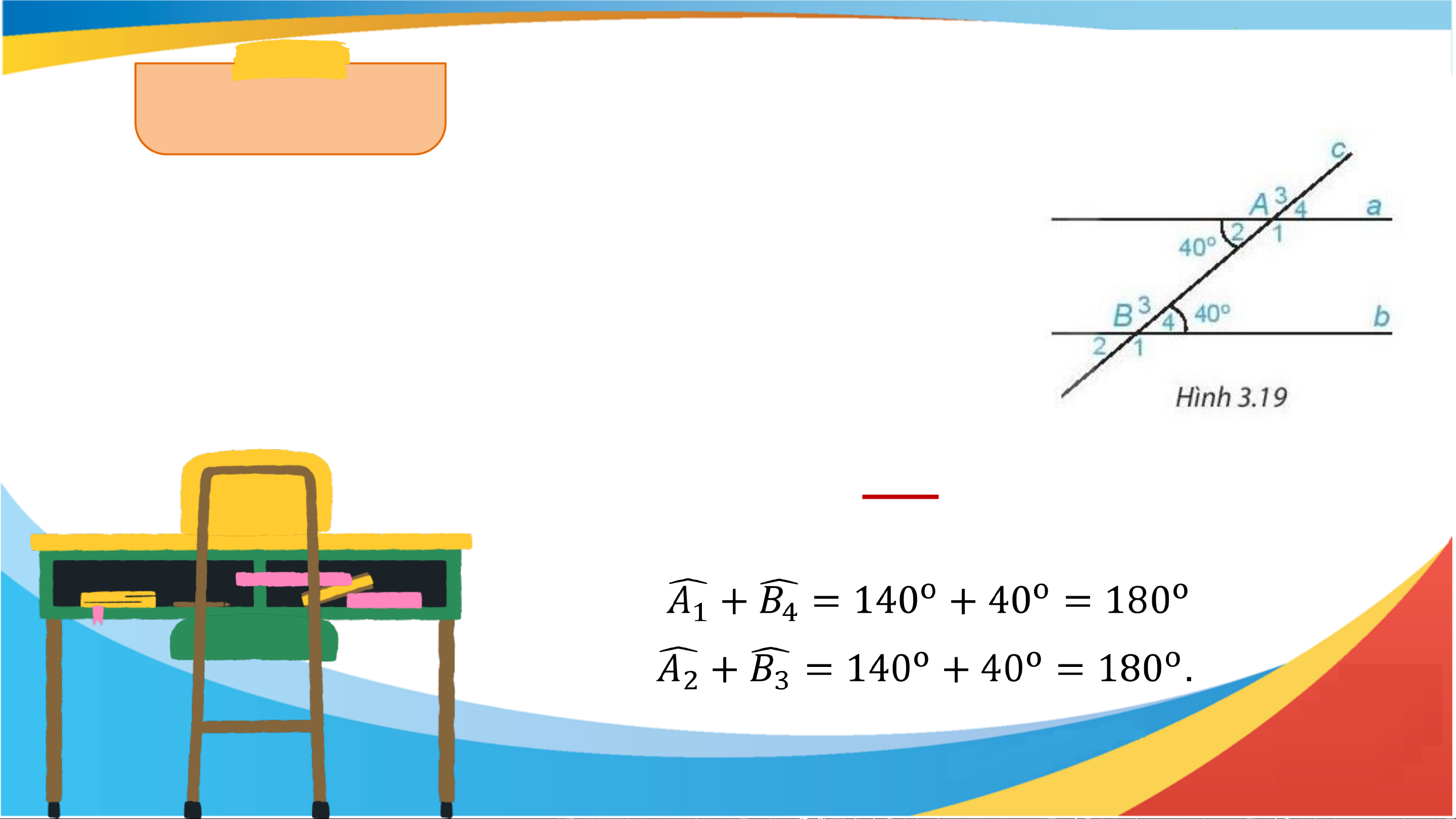
a) Cho hình 3.19, biết góc A =40°; góc B = 40°. Em hãy 2 4
cho biết số đo các góc còn lại.
b) Các cặp góc A và B ; A và B được gọi là các cặp 1 4 2 3
góc trong cùng phía. Tính tổng: 𝐴1+ 𝐵4 và 𝐴2 + 𝐵3 Giải b) LUYỆN TẬP Bài 3.6 (SGK - tr49) Quan sát hình 3.24.
a) Tìm một góc ở vị trí so le trong với góc MNB. Góc NBC
b) Tìm một góc ở vị trí đồng vị với góc ACB. Góc ANM
c) Kể tên một cặp góc trong cùng phía. Góc MBC và BMN
d) Biết MN // BC, em hãy kể tên ba cặp góc bằng nhau trong hình vẽ. 𝐴𝑁𝑀 =
𝐴𝐶𝐵(Á𝑝 𝑑ụ𝑛𝑔 𝑡í𝑛ℎ 𝑐ℎấ𝑡 1) ; 𝐴𝑀𝑁 =
𝐴𝐵𝐶(đề 𝑐ℎ𝑜) ; 𝑀𝑁𝐵 =
𝑁𝐵𝐶(đề 𝑐ℎ𝑜).
HƯỚNG DẪN VỀ NHÀ 02 01 03 Hoàn thành các bài Ôn lại kiến thức tập còn lại SGK và bài đã học Chuẩn bị bài sau tập SBT Tiết 2
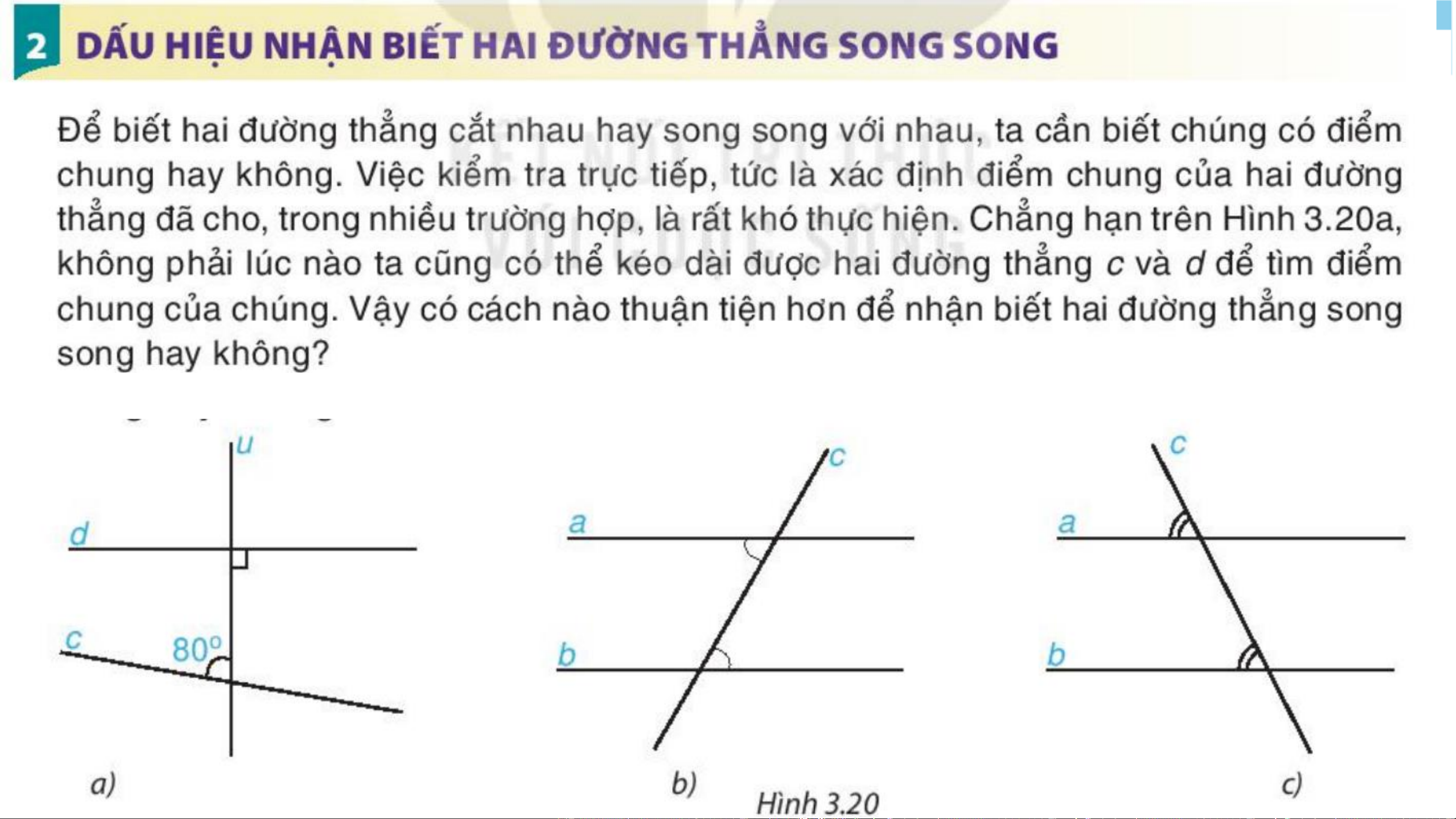
Cho hai đường thẳng a,b. Làm sao để biết được hai đường
thẳng đó song song hay không?
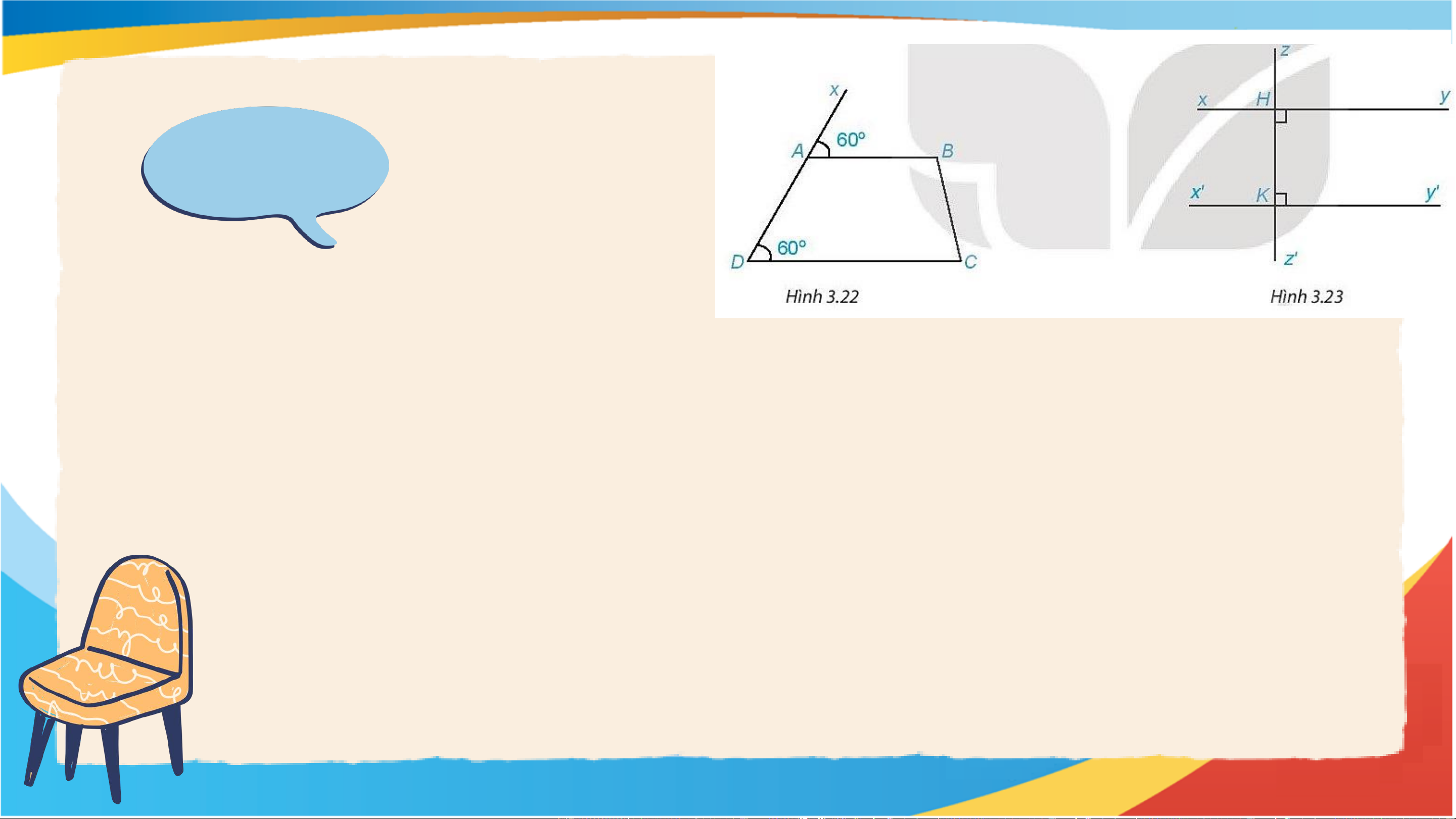
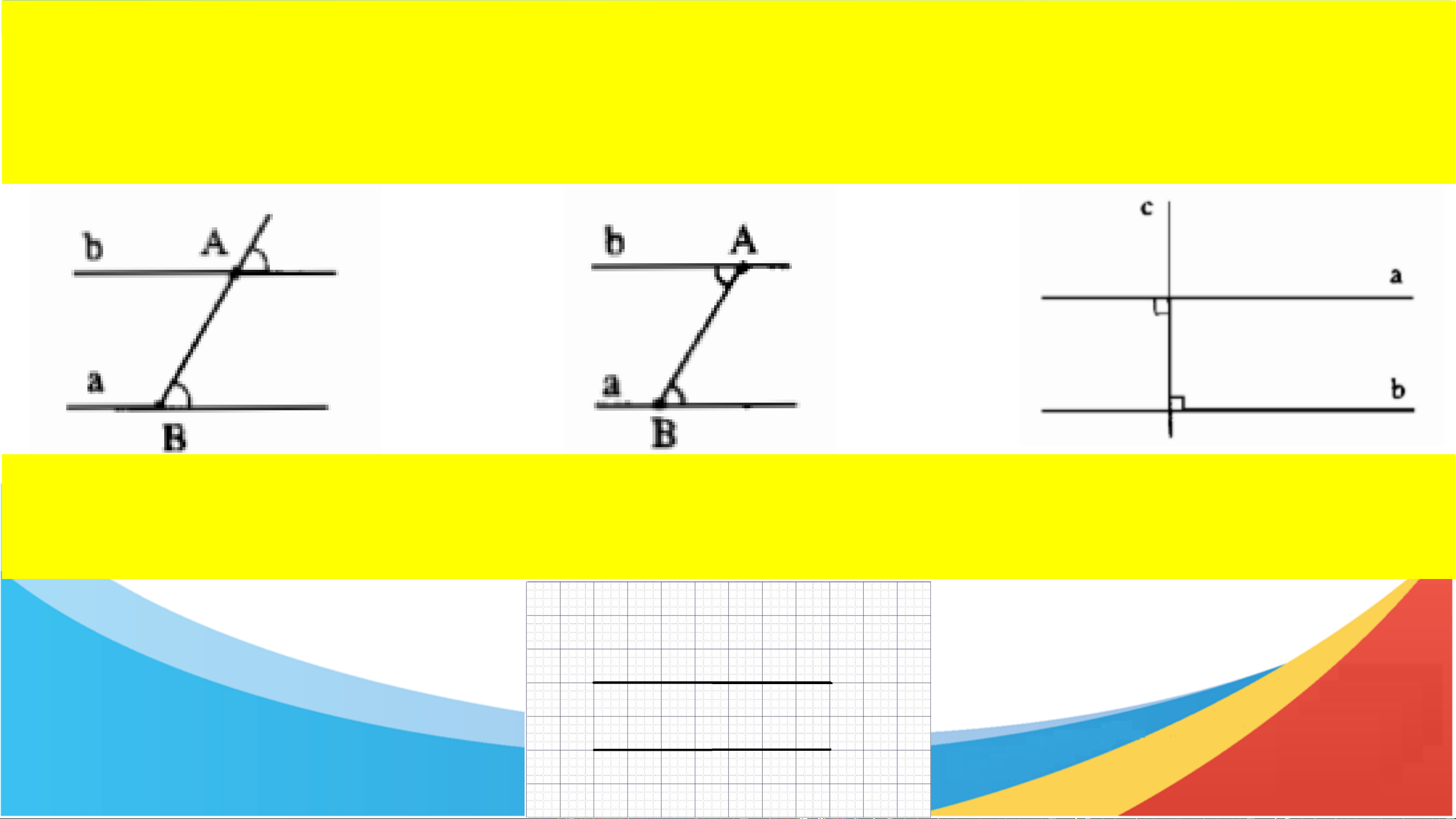
Một học sinh lên kiểm tra hai đường thẳng sau đây
có song song hay không? Lí do?
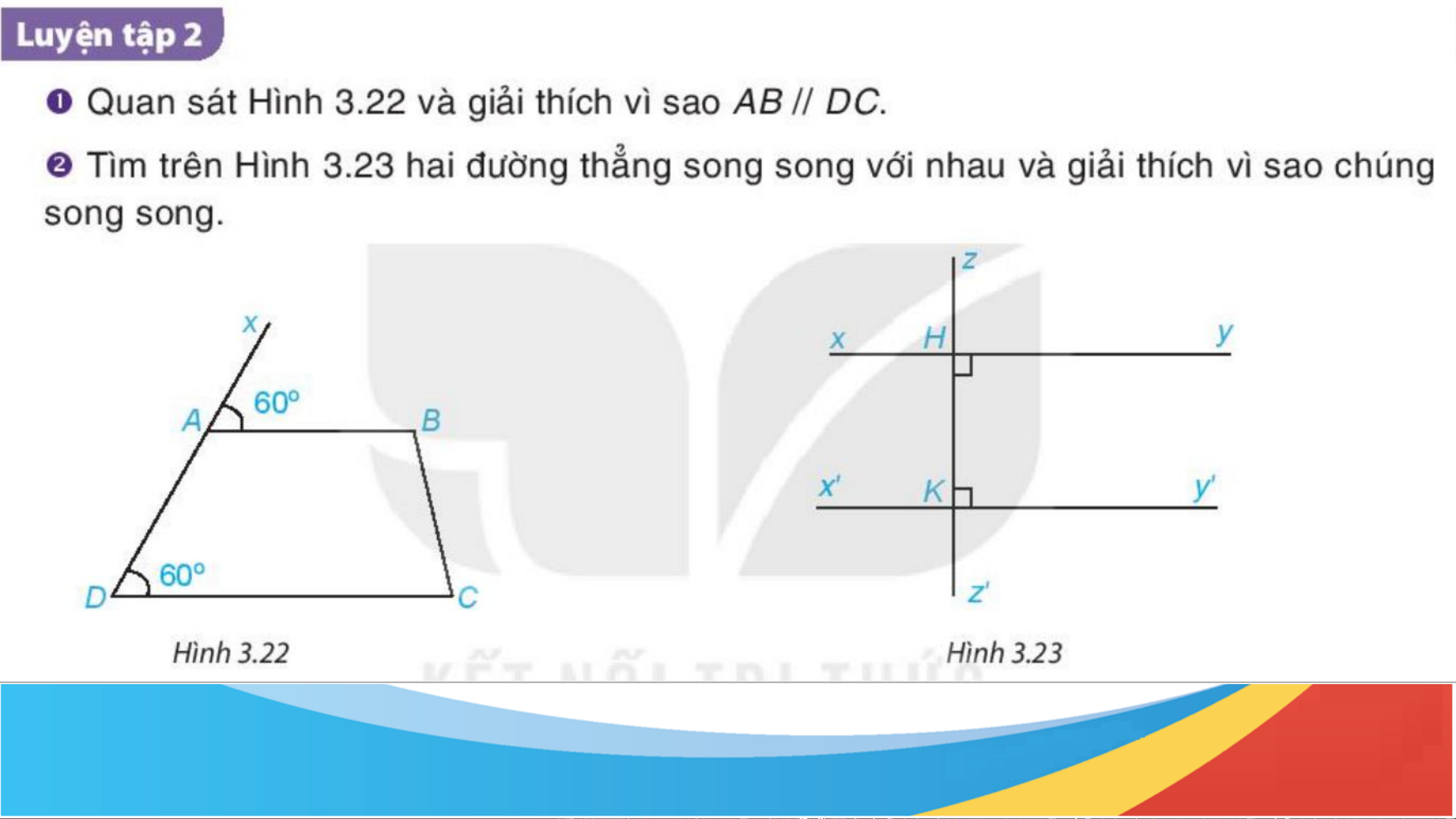
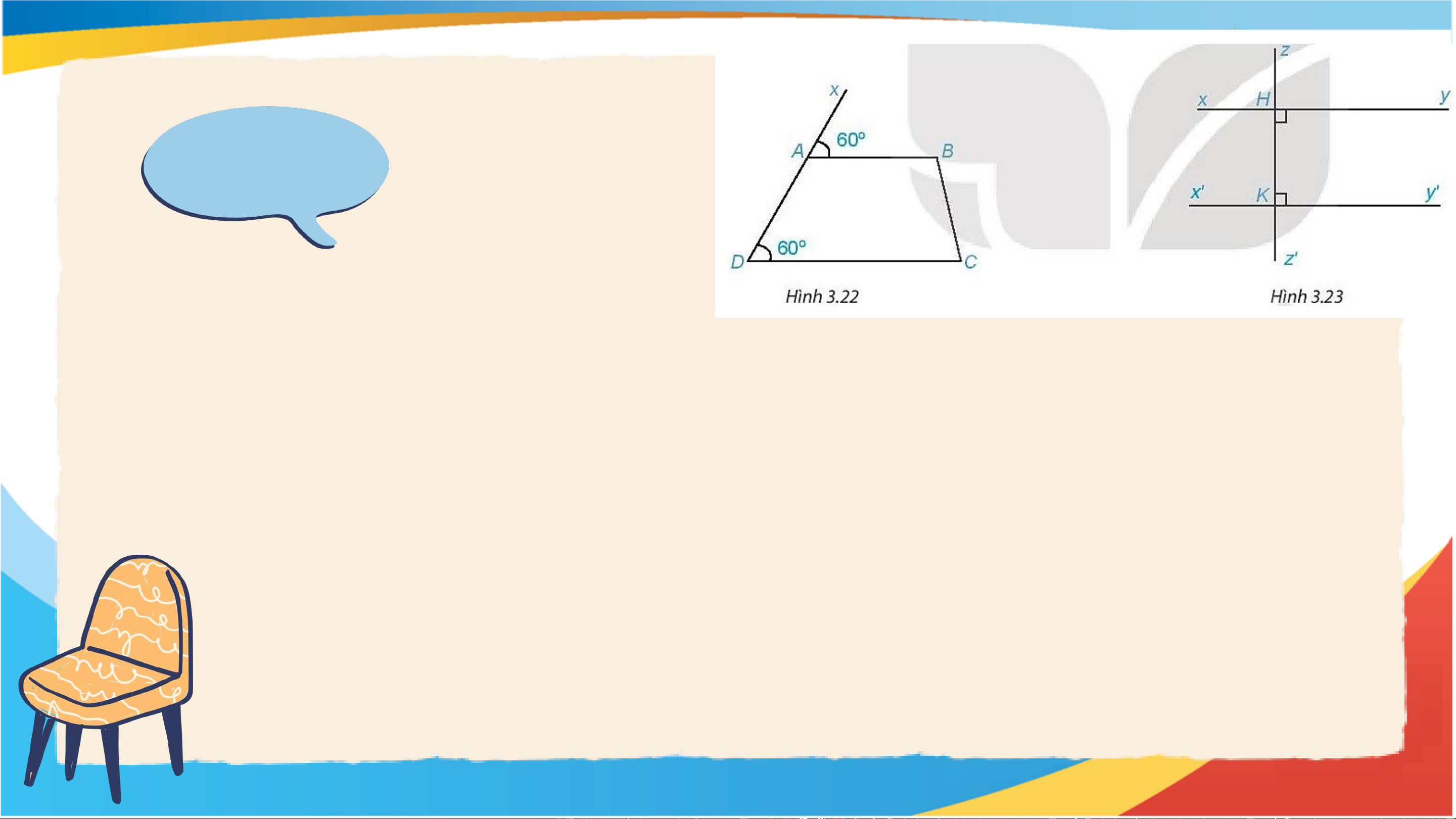
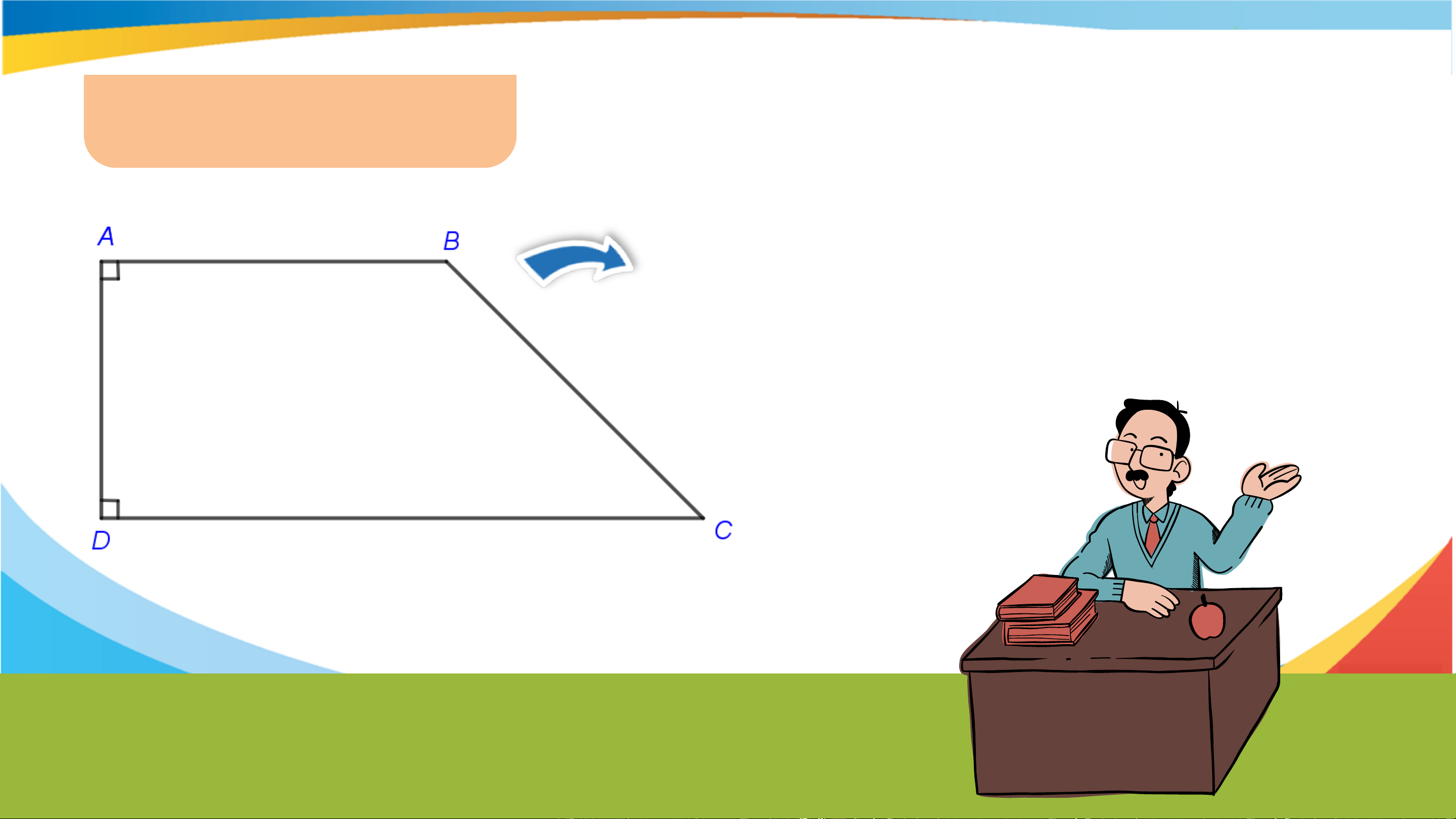
Gợi ý vẽ thêm đường thẳng trung gian cắt hai đường thẳng trên. Giải 1. Ta có: 𝑥𝐴𝐵 = 𝐴𝐷𝐶 = 60°
mà hai góc ở vị trí đồng vị ⇒ AB // DC. 2. Ta có: xy ⊥ zz’⟹ 𝑧𝐻𝑦 = 90° Có 𝑧𝐻𝑦 =
𝐻𝐾𝑦′ = 90° mà hai góc ở vị trí đồng vị ⇒ xx’ // yy’
(Dấu hiệu nhận biết hai đường thẳng song song)
Từ kết quả câu 2 nhận xét nếu hai đường thẳng
phân biệt cùng vuông góc với một đường thẳng thì
chúng sẽ có mối quan hệ gì? Rút ra nhận xét. Nhận xét:
Hai đường thẳng phân biệt cùng vuông góc với một
đường thẳng thứ ba thì chúng song song với nhau.
Em có thể giải Luyện tập 2 câu 2 theo nhận xét? Giải 2. Ta có: xy⊥zz’ x’y’ ⊥zz’ Suy ra: xy//x’y’
EM HÃY TRẢ LỜI CÂU HỎI ĐẶT VẤN ĐỀ TỪ ĐẦU BÀI?
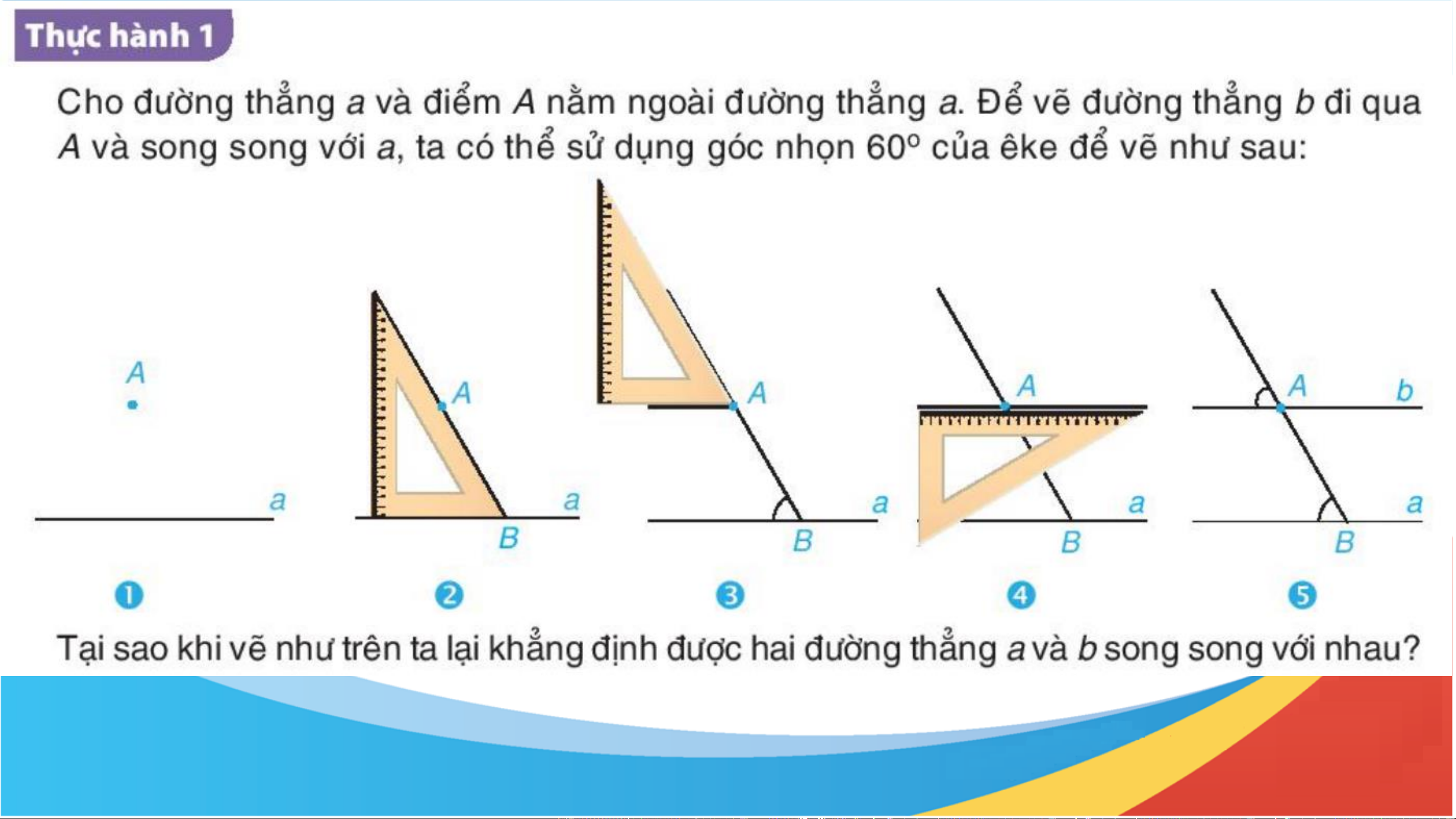
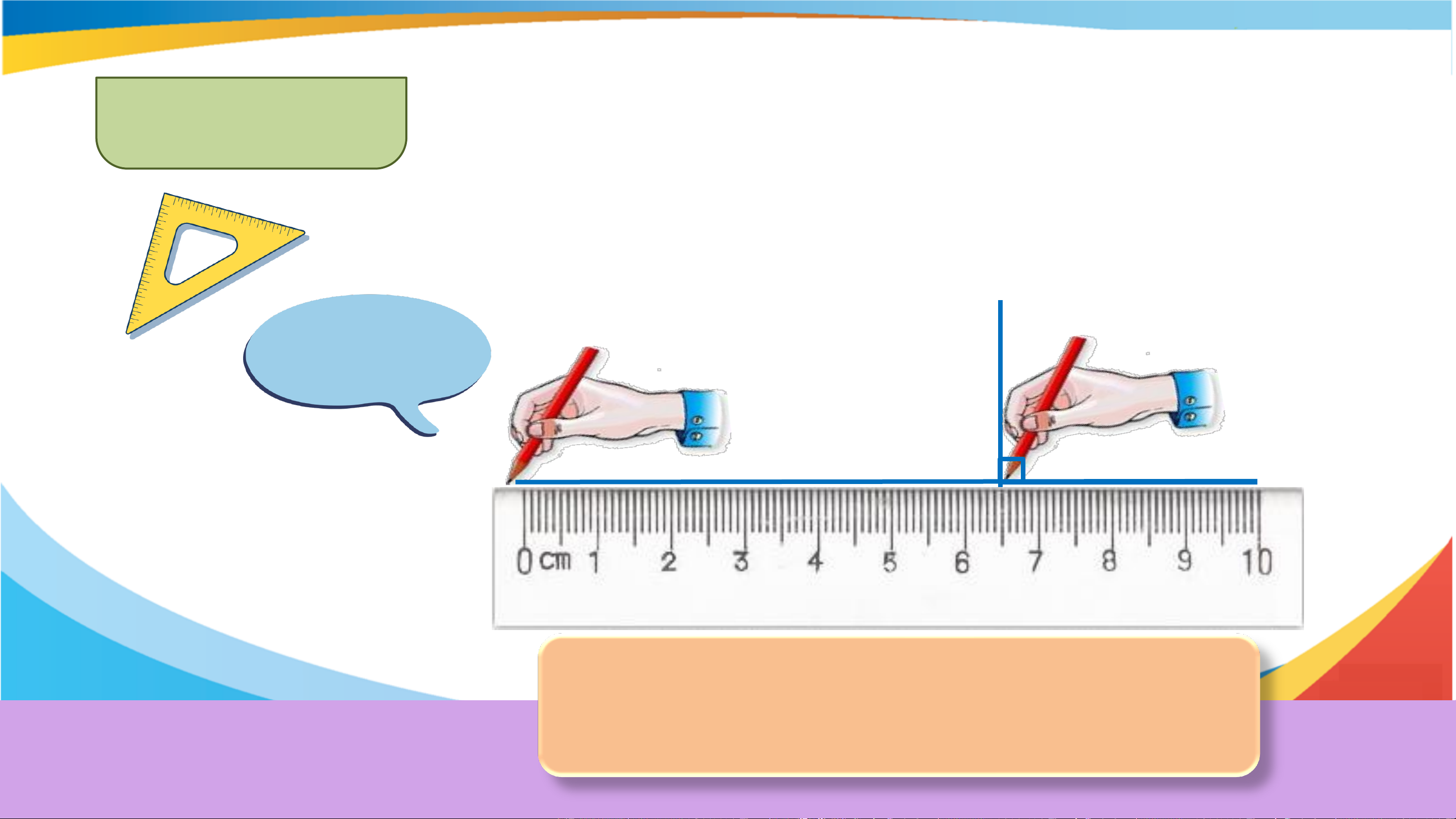
Dùng góc vuông hay góc 30° của êke (thay cho Thực hành 2
góc 60°) để vẽ đường thẳng đi qua A và song
song với đường thẳng a cho trước. Gợi ý Dùng góc vuông A a
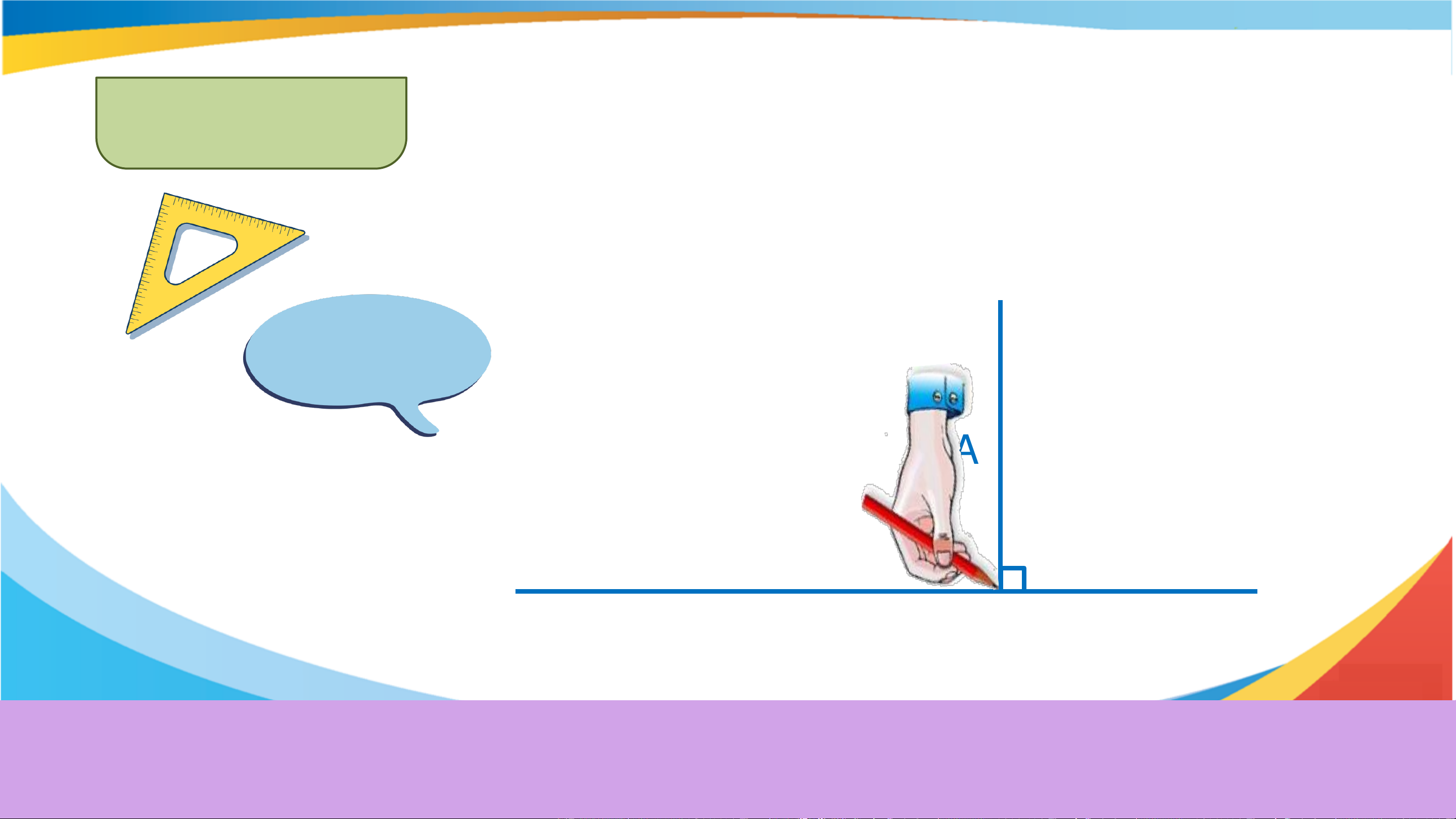
Dùng góc vuông hay góc 30° của êke (thay cho Thực hành 2
góc 60°) để vẽ đường thẳng đi qua A và song
song với đường thẳng a cho trước. c Gợi ý Dùng góc vuông A a
Dùng góc vuông hay góc 30° của êke (thay cho Thực hành 2
góc 60°) để vẽ đường thẳng đi qua A và song
song với đường thẳng a cho trước. c Gợi ý Dùng góc vuông A b a
Vậy ta được đường thẳng b đi qua A
và song song với đường thẳng a.
Chú ý 1: Khi vẽ hai đường thẳng song song phải nêu được lí do song
song khi vẽ hình (Cần có đường thẳng trung gian) không ước lượng, rà
thước, vẽ bằng trực giác…
Chú ý 2: Trường hợp đặc biệt có thể vẽ trên vạch kẻ ô li vở để vẽ hai
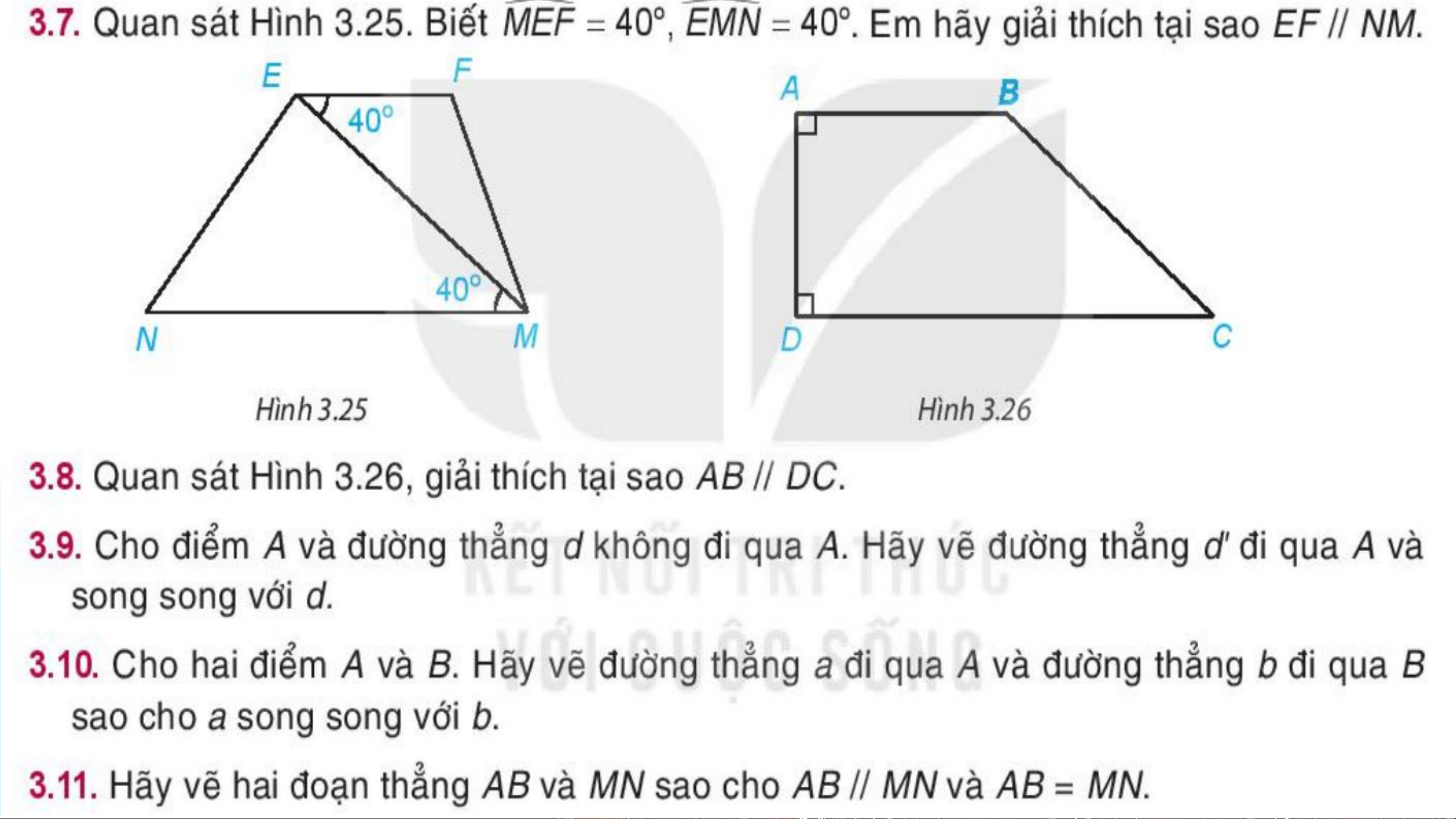
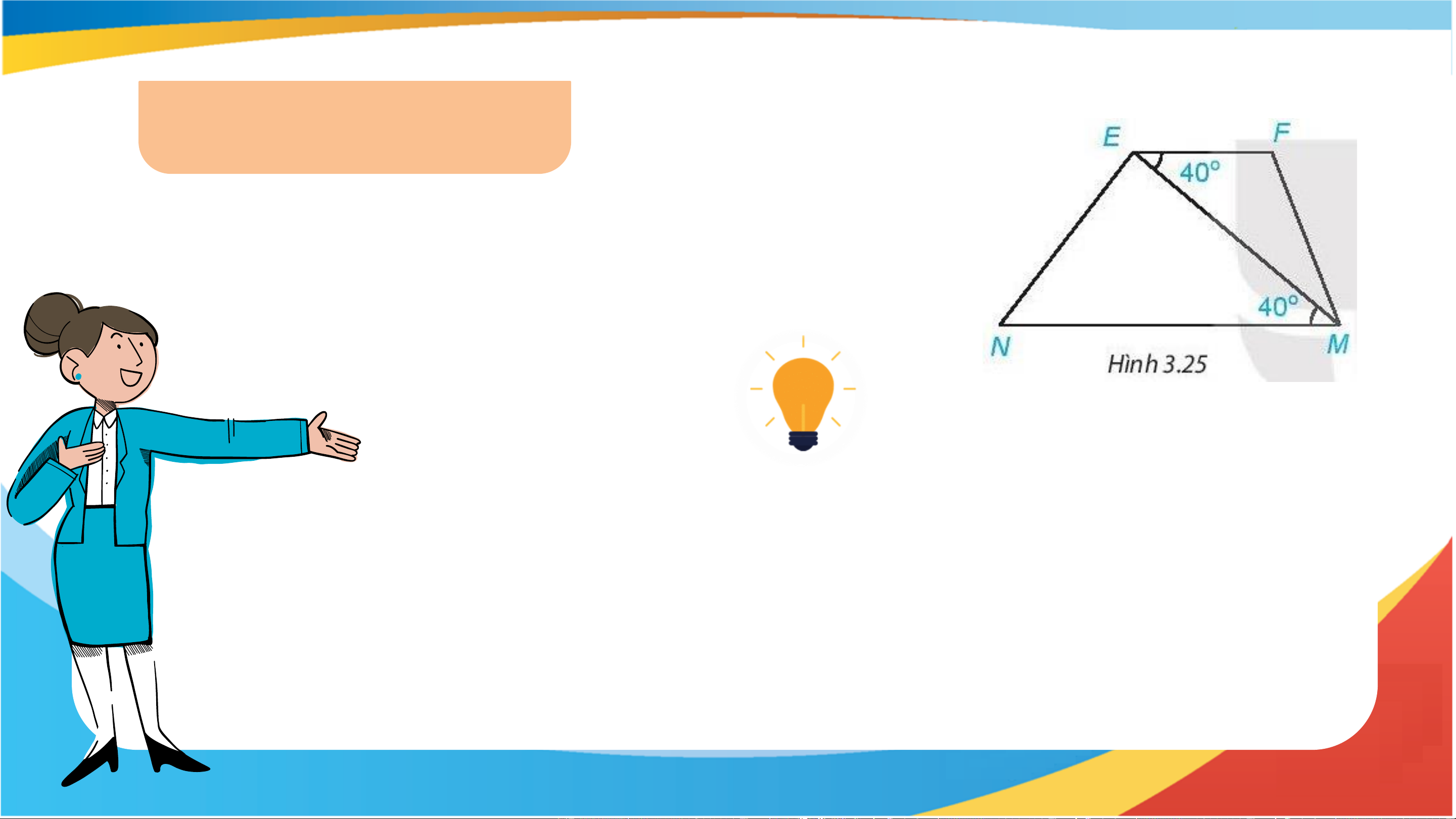
đường thẳng song song. Bài 3.7 (SGK - tr49)
Quan sát Hình 3.25. Biết 𝑀𝐸𝐹 = 40°; 𝐸𝑀𝑁= 40°.
Em hãy giải thích tại sao EF // NM. Ta có 𝑀𝐸𝐹 =
𝐸𝑀𝑁 = 40o mà hai góc này ở vị trí
so le trong, suy ra EF // MN (dấu hiệu nhận biết
hai đường thẳng song song). Bài 3.8 (SGK - tr49)
Quan sát hình 3.26, giải thích vì sao AB // DC.
Ta có: AB ⊥ AD và DC⊥ AD nên AB // DC. Hình 3.26 VẬN DỤNG
Cho điểm A và đường thẳng d không đi qua A. Hãy Bài 3.9 (SGK - tr49)
vẽ đường thẳng d’ đi qua A và song song với d. Hướng dẫn
Em có thể làm tương tự
bài Thực hành 1 hoặc bài Thực hành 2. Bài 3.11 (SGK - tr49)
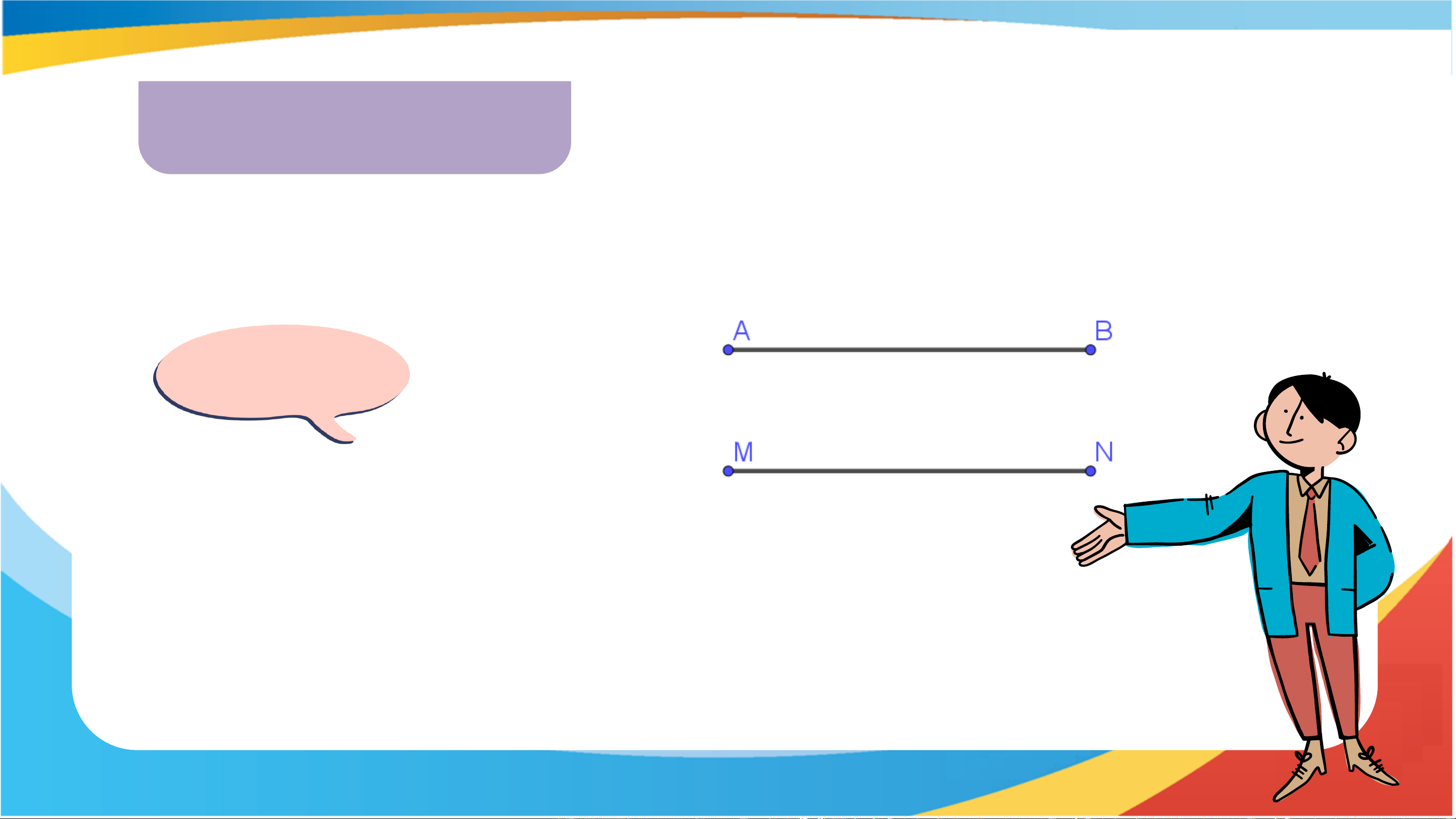
Hãy vẽ hai đoạn thẳng AB và MN sao cho AB // MN và AB = MN Gợi ý
Bước 1: vẽ đoạn thẳng AB.
Bước 2: Vẽ đường thẳng a // AB.
Bước 3: Trên a lấy điểm M và N sao cho MN = AB.
HƯỚNG DẪN VỀ NHÀ 1
Ghi nhớ kiến thức trong bài 2 Hoàn thành bài tập SBT 3 Chuẩn bị bài sau BÀI HỌC KẾT THÚC
CẢM ƠN CÁC EM ĐÃ LẮNG NGHE!
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43