CHÀO MỪNG CÁC EM
ĐẾN VỚI LỚP HỌC KHỞI ĐỘNG
Em hãy nêu trường hợp bằng nhau
thứ hai và thứ ba của hai tam giác?
Các em hãy trả lời nhanh các câu hỏi trắc nghiệm sau
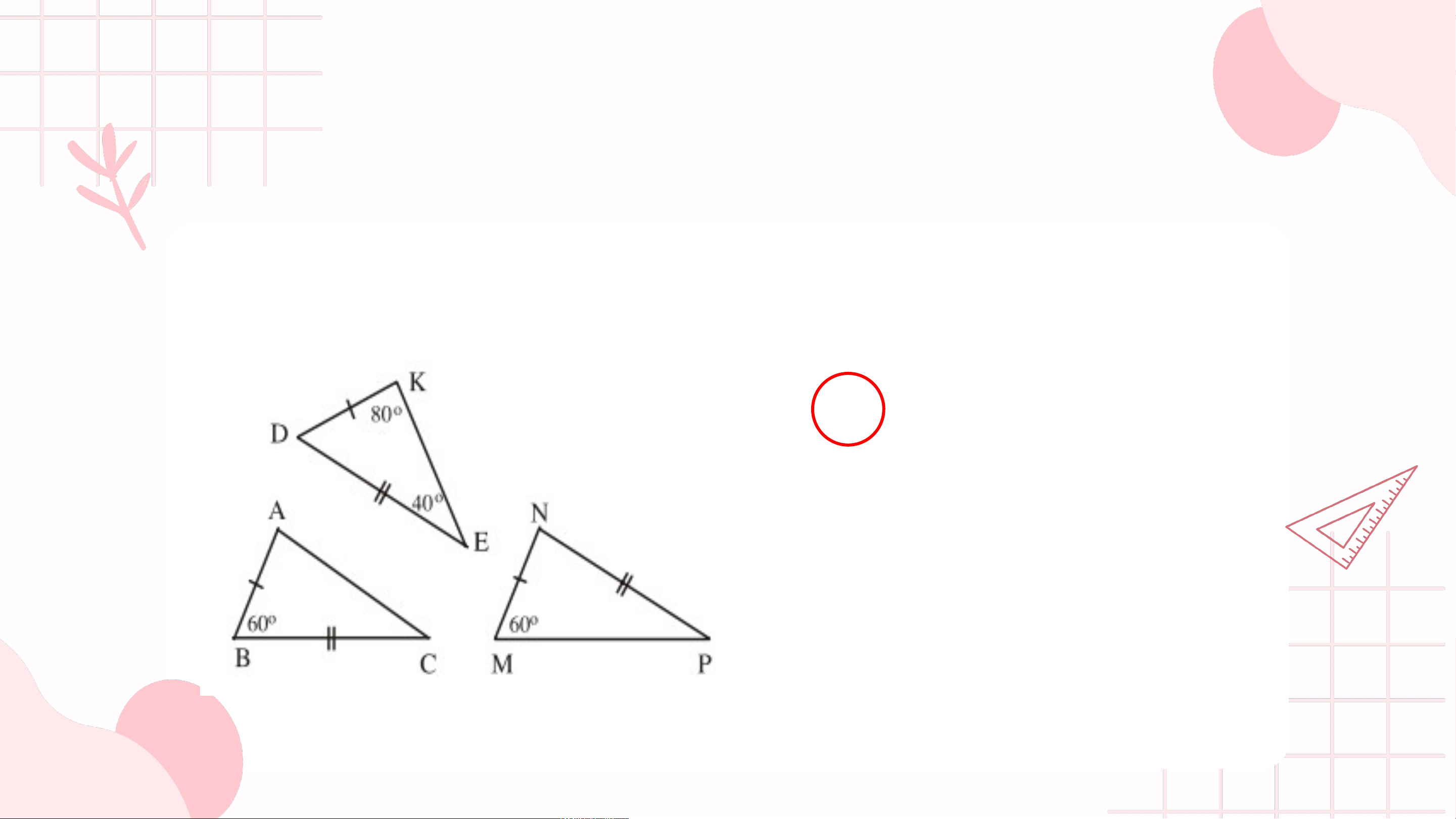
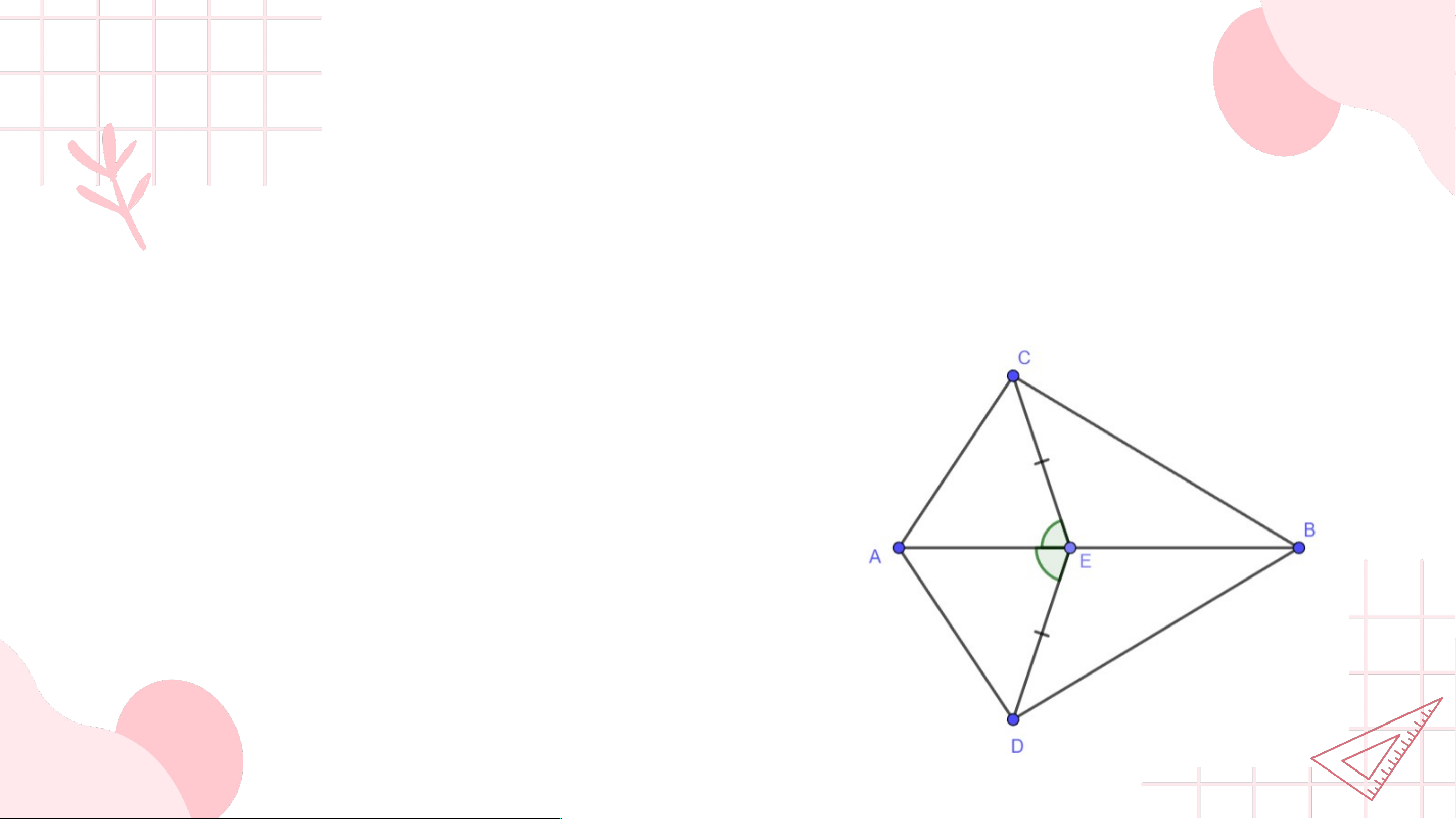
Câu 1: Trên hình sau có các tam giác bằng nhau là: A. B. C. D.
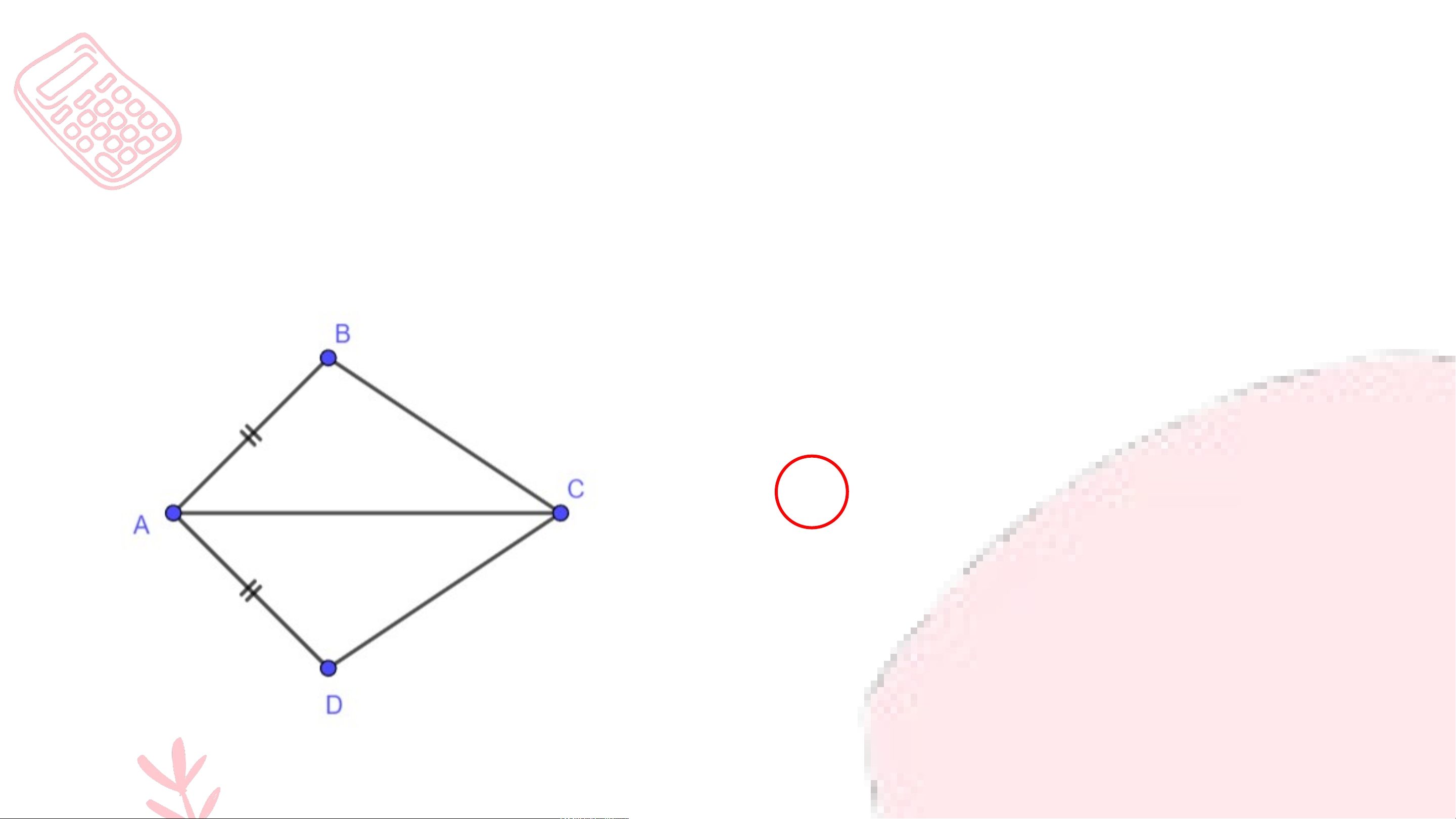
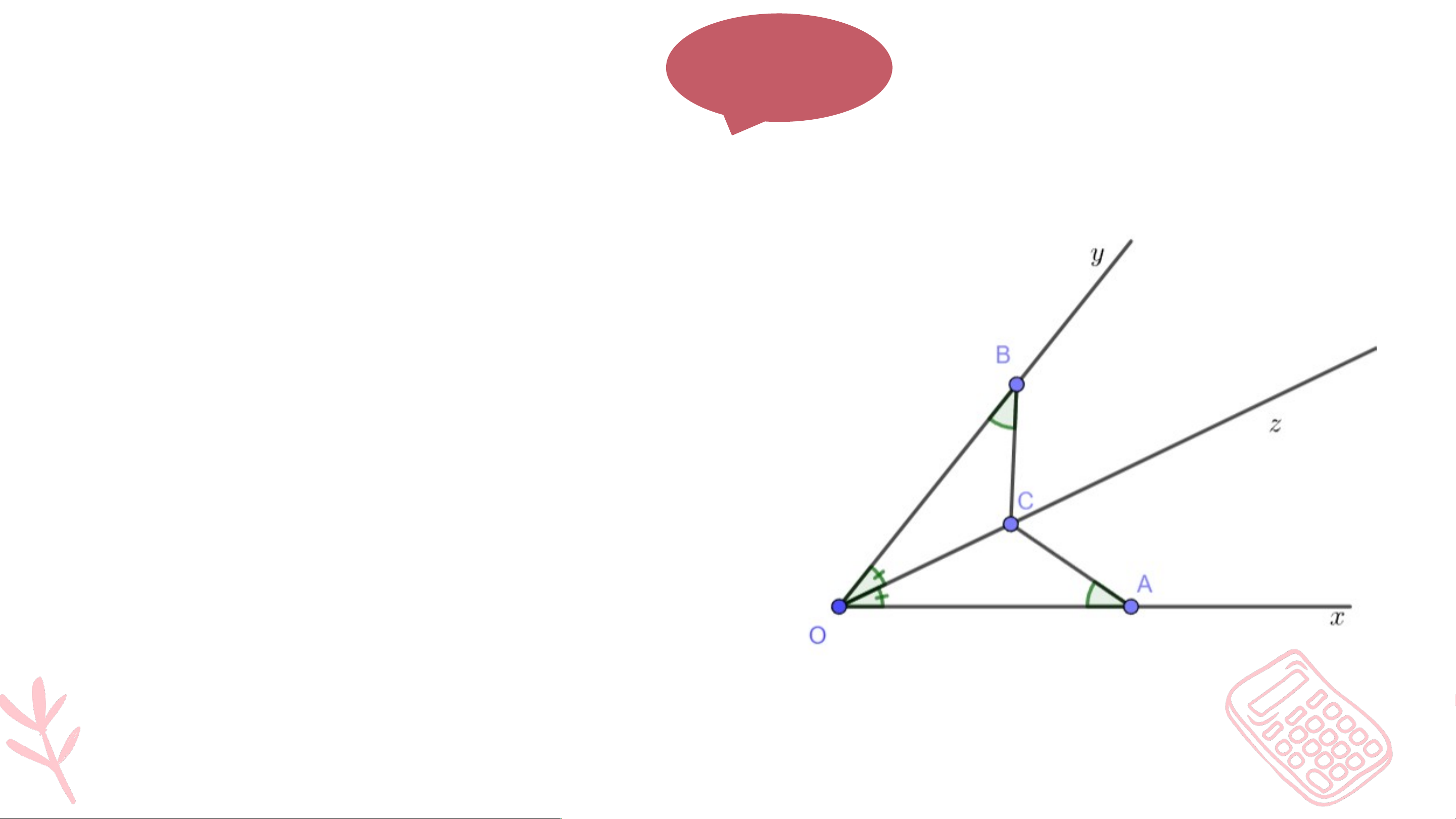
Câu 2: Cho hình vẽ, chọn câu trả lời đúng A. B. C. ; D. Cả đều đúng
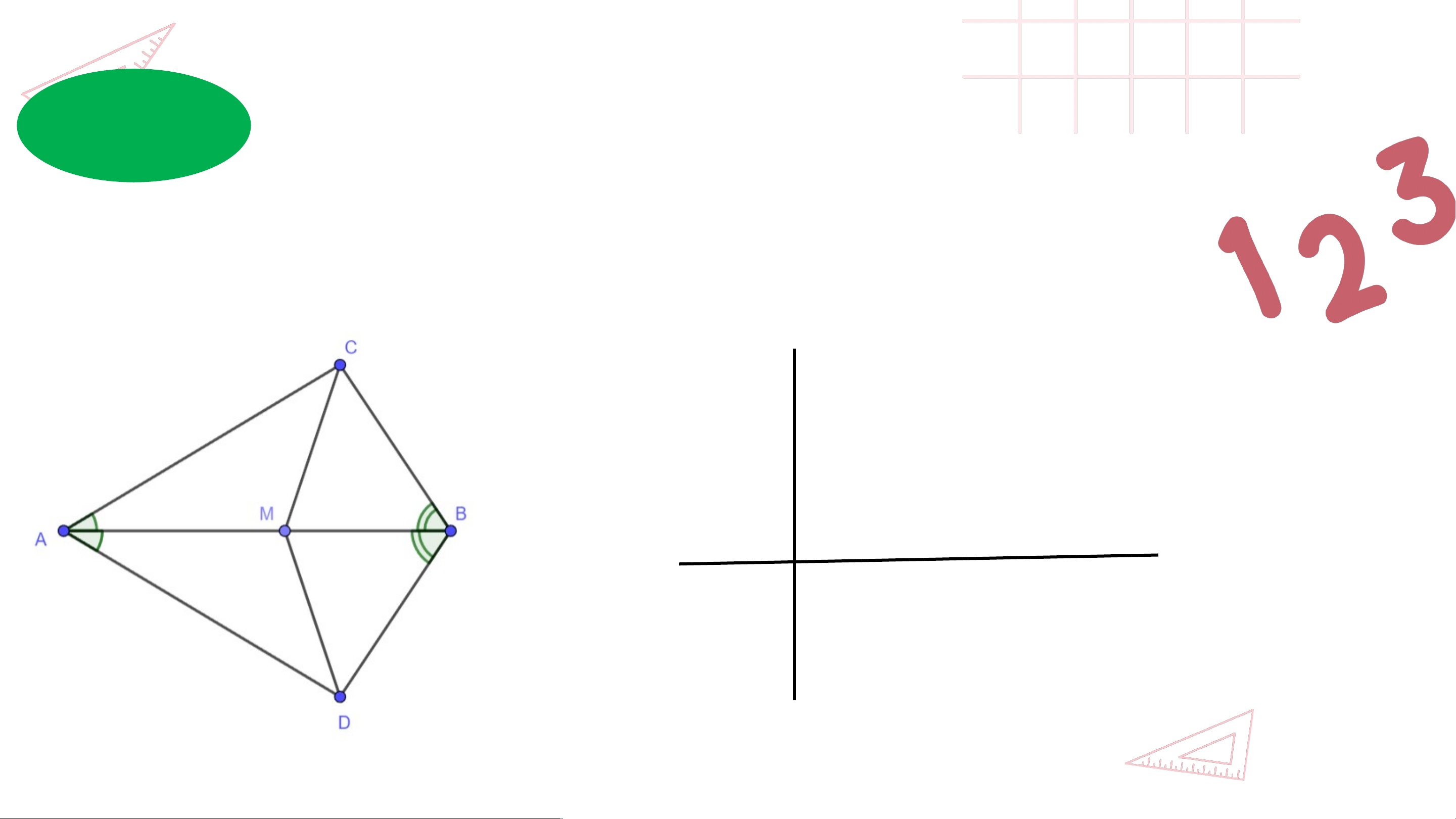
Câu 3: Chọn câu trả lời đúng. Cho hình vẽ:
Cần phải có thêm yếu tố nào để theo trường hợp cạnh – góc – cạnh: A. B. C. D. Cả đều đúng
Câu 4: Cho tam giác có . Tia phân giác của góc cắt tại . Ta có A. B. C. D. Cả đều đúng. LUYỆN TẬP CHUNG
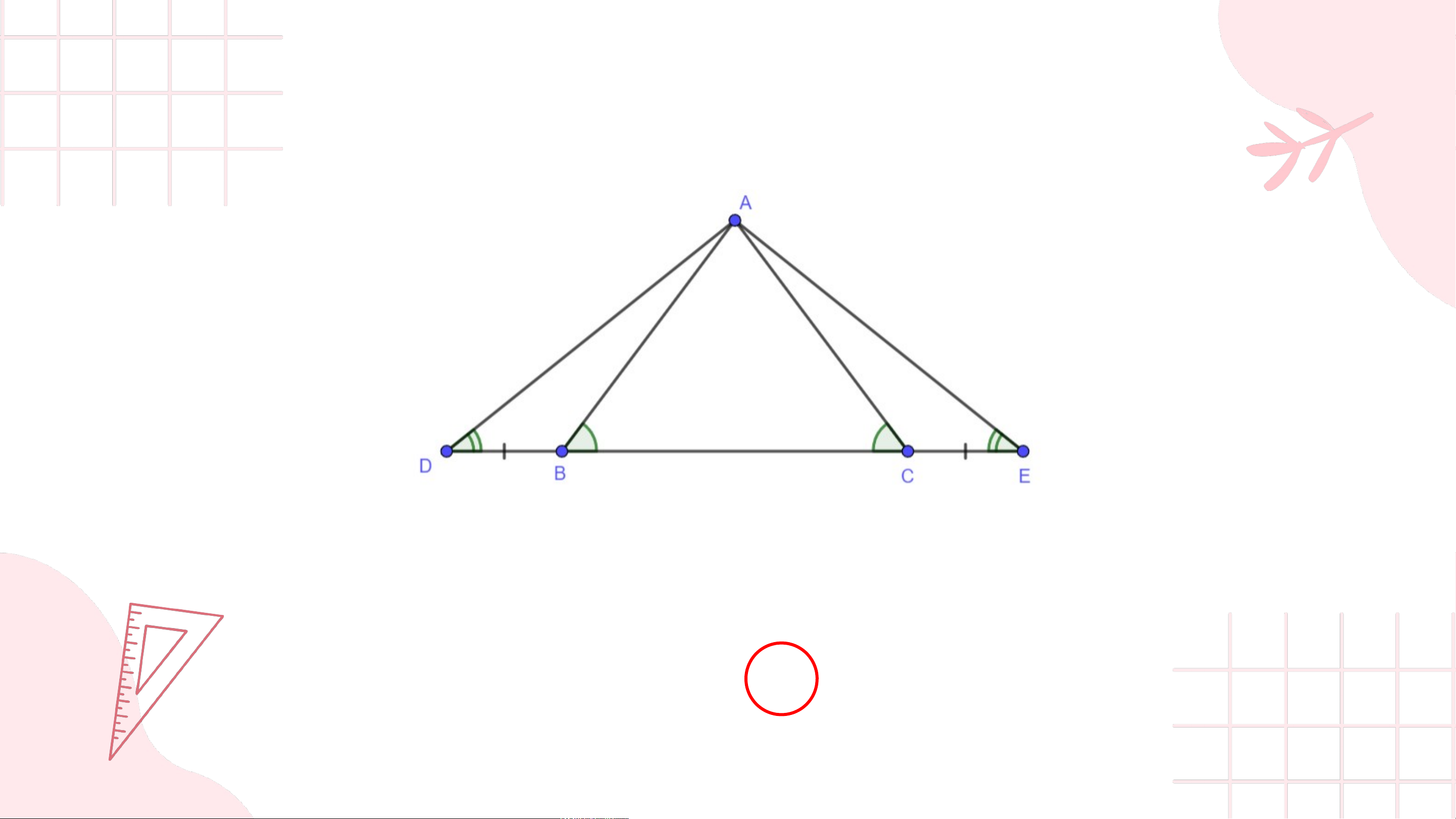
Cho điểm thuộc đoạn thẳng và hai điểm như Hình 4.43 sao Ví dụ cho , . Chứng minh rằng: a) b) . , GT , . KL a) b) . Giải a) Hai tam giác và có: b) Hai tam giác và có: (gt); (gt); là cạnh chung; là cạnh chung; (gt). (vì ). Vậy (g.c.g) Vậy (c.g.c) LUYỆN TẬP
Bài 4.16 (SGK – tr.74) Cho hai tam giác và thoả mãn , , , , .
Tính độ dài cạnh và số đo các góc , , . Giải Xét có: Xét và có: , , (gt) Do đó (c.g.c) suy ra , .
Bài 4.17 (SGK – tr.74) Cho hai tam giác và thoả mãn , , , . Tính độ dài cạnh . Giải Xét và có: (gt), Do đó (g.c.g) suy ra .
Bài 4.18 (SGK – tr.74) Cho Hình 4.44, biết và . Chứng minh rằng a) b) . Giải a) Xét và có: ; ; là cạnh chung. Do đó (c.g.c) VẬN DỤNG
Bài 4.19 (SGK – tr.74) Cho tia là tia phân giác của góc .
Lấy các điểm lần lượt thuộc các tia sao cho . a) Chứng minh rằng .
b) Lấy điểm trên tia đối của tia . Chứng minh rằng . Giải a) Ta có: suy ra . Xét và có: là cạnh chung, . Do đó (g.c.g) b) Ta có: Xét và có: (do là cạnh chung. Do đó c.g.c)
HƯỚNG DẪN VỀ NHÀ Ghi nhớ kiến thức Hoàn thành bài tập Chuẩn bị bài mới trong bài. trong SBT. “Bài 15”.
HẸN GẶP LẠI CÁC EM TRONG TIẾT HỌC SAU!
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18