Giáo án Powerpoint bài Ôn cuối chương 7 Phương pháp tọa độ trong mặt phẳng sách KNTT
Giáo án Powerpoint bài Ôn cuối chương 7 Phương pháp tọa độ trong mặt phẳng sách KNTT theo chương trình chuẩn. Tài liệu được biên soạn dưới dạng file pdf gồm 11 trang chứa nhiều thông tin hay và bổ ích giúp bạn dễ dàng tham khảo và ôn tập đạt kết quả cao. Mời bạn đọc đón xem!
Chủ đề: Chương 7: Phương pháp tọa độ trong mặt phẳng (KNTT)
Môn: Toán 10
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 7: Phương pháp tọa độ trong mặt phẳng (KNTT)
Môn:
Tác giả:
Tài liệu liên quan:
Preview text:
CHƯƠNG I
CHƯƠNG I. MỆNH ĐỀ - TẬP HỢP TOÁN ĐẠI SỐ
ÔN TẬP CUỐI CHƯƠNG VII ➉ A PHẦN TRẮC NGHIỆM B 2 2 3 4 CÂU 7.26. 14 48 6 8
Phương trình nào sau đây là phương trình tham số của đường thẳng? A 𝒙 = 𝟐𝒕
𝟐𝒙 − 𝒚 + 𝟏 = 𝟎. B
C 𝒙𝟐 + 𝒚𝟐 = 𝟏.
D 𝒚 = 𝟐𝒙 + 𝟑. 𝒚 = 𝒕 . Bài giải
Phương trình tham số của đường thẳng có dạng 𝒙 = 𝒙 𝟎 + 𝒂𝒕
, 𝒕 là tham số 𝒚 = 𝒚𝟎 + 𝒃𝒕 CÂU 7.27. 14 48 6 8
Phương trình nào sau đây là phương trình tổng quát của đường thẳng? A 𝒙 = 𝟐 + 𝒕
−𝒙 − 𝟐𝒚 + 𝟑 = 𝟎. B . 𝒚 = 𝟑 − 𝒕 C 𝒙𝟐 𝒚𝟐 𝒚𝟐 = 𝟐𝒙. D + = 𝟏. 𝟏𝟎 𝟔 Bài giải
Phương trình tổng quát của đường thẳng có dạng
𝒂𝒙 + 𝒃𝒚 + 𝒄 = 𝟎, 𝒂𝟐 + 𝒃𝟐 ≠ 𝟎.
CÂU 7.28. Phương trình nào sau đây là phương trình của đường tròn? 14 48 6 8 A
𝒙𝟐 − 𝒚𝟐 = 𝟏 . C
𝒙𝟐 + 𝒚𝟐 = 𝟐.
B 𝒙 − 𝟏 𝟐 + 𝒚 − 𝟐 𝟐 = −𝟒. D 𝒚𝟐 = 𝟖𝒙. Bài giải
Phương trình của đường tròn có tâm 𝑰 𝒂; 𝒃 và bán kính 𝑹 có dạng:
𝒙 − 𝒂 𝟐+ 𝒚 − 𝒃 𝟐 = 𝑹𝟐. CÂU 7.29. 14 48 6 8
Phương trình nào sau đây là phương trình chính tắc của đường elip? 𝒙𝟐 𝒚𝟐 A + = 𝟏. B 𝒙𝟐 𝒚𝟐 𝒙𝟐 𝒚𝟐 + = 𝟏. C − = 𝟏. 𝒙𝟐 𝒚𝟐 D + = 𝟏. 𝟗 𝟗 𝟏 𝟔 𝟒 𝟏 𝟐 𝟏 Bài giải
Phương trình chính tắc của elip có dạng 𝒙𝟐 𝒚𝟐 + = 1, 𝑎 > 𝑏 > 0. 𝒂𝟐 𝒃𝟐 CÂU 7.30. 14 48 6 8
Phương trình nào sau đây là phương trình chính tắc của đường hypebol? 𝒙𝟐 𝒚𝟐 A − = −𝟏 . B 𝒙𝟐 𝒚𝟐 𝒙𝟐 𝒚𝟐 B − = 𝟏. C + = 𝟏. 𝒙𝟐 𝒚𝟐 D + = −𝟏. 𝟑 𝟐 𝟏 𝟔 𝟔 𝟏 𝟐 𝟏 Bài giải
Phương trình chính tắc của đường hypebol có dạng 𝒙𝟐 𝒚𝟐 − = 1, 𝑎, 𝑏 > 0. 𝒂𝟐 𝒃𝟐 CÂU 7.31. 14 48 6 8
Phương trình nào sau đây là phương trình chính tắc của đường parabol? A 𝒙𝟐 = 𝟒𝒚 . B 𝒙𝟐 = −𝟔𝒚. C 𝒚𝟐 = 𝟒𝒙. D 𝒚𝟐 = −𝟒𝒙. Bài giải
Phương trình chính tắc của đường parabol có dạng 𝒚𝟐 = 𝟐𝒑𝒙, 𝒑 > 𝟎. CHƯƠNG I
CHƯƠNG I. MỆNH ĐỀ - TẬP HỢP TOÁN ĐẠI SỐ
ÔN TẬP CUỐI CHƯƠNG VII ➉ B PHẦN TỰ LUẬN B 2 2 3 4
Trong mặt phẳng tọa độ, cho 𝑨 𝟏; −𝟏 , 𝑩 𝟑; 𝟓 , 𝑪 −𝟐; 𝟒 . CÂU 7.32. 14 Tính diện 48
tích tam giác 𝑨𝑩𝑪 6 Bài giải
Cách 1: Ta có 𝑩𝑪 = −𝟓; −𝟏 và 𝑩𝑪 =
−𝟓 𝟐 + −𝟏 𝟐 = 𝟐𝟔.
Đường thẳng 𝑩𝑪 đi qua 𝑩 𝟑; 𝟓 và có một véc tơ pháp tuyến là 𝒏 = 𝟏; −𝟓 nên
đường thẳng 𝑩𝑪 có phương trình là: 𝟏. 𝒙 − 𝟑 − 𝟓. 𝒚 − 𝟓 = 𝟎
⇔ 𝒙 − 𝟓𝒚 + 𝟐𝟐 = 𝟎.
Khoảng cách từ điểm 𝑨 𝟏; −𝟏 đến đường thẳng 𝑩𝑪 là: 𝟏−𝟓. −𝟏 +𝟐𝟐 𝟐𝟖 𝒅 𝑨, 𝑩𝑪 = = . 𝟏𝟐+ −𝟓 𝟐 𝟐𝟔 Diện tích tam giác 𝟏 𝟏 𝟐𝟖
𝑨𝑩𝑪 là: 𝑺𝜟𝑨𝑩𝑪 = 𝒅 𝑨, 𝑩𝑪 . 𝑩𝑪 = . . 𝟐𝟔 = 𝟏𝟒. 𝟐 𝟐 𝟐𝟔 Cách 2:
Ta có: 𝑨 𝒙𝑨; 𝒚𝑨 ; 𝑩 𝒙𝑩; 𝒚𝑩 ; 𝑪 𝒙𝑪; 𝒚𝑪
𝑨𝑪 = 𝒙𝑪 − 𝒙𝑨; 𝒚𝑪 − 𝒚𝑨 Khi đó: = 𝒙 𝟐 𝟐 𝟐; 𝒚𝟐 ⇒ 𝑨𝑪 = 𝒙 + 𝒚 𝑨𝑩 𝒙 𝟐 𝟐 𝟐 𝟐
𝑩 − 𝒙𝑨; 𝒚𝑩 − 𝒚𝑨
= 𝒙𝟏; 𝒚𝟏 ⇒ 𝑨𝑩 = 𝒙𝟏 + 𝒚𝟏
CÂU 7.32. Trong mặt phẳng tọa độ, cho 𝑨 𝟏; −𝟏 , 𝑩 𝟑; 𝟓 , 𝑪 −𝟐; 𝟒 . 14 Tính diện 48
tích tam giác 𝑨𝑩𝑪 6 Bài giải 𝒙 𝒄𝒐𝒔
𝑩𝑨𝑪 = 𝒄𝒐𝒔 𝑨𝑩; 𝑨𝑪 = 𝟏𝒙𝟐+𝒚𝟏𝒚𝟐 . 𝒙𝟐 𝟐 𝟐 𝟐
𝟏+𝒚𝟏 𝒙𝟐+𝒚𝟐 Do 𝒔𝒊𝒏
𝑩𝑨𝑪 > 𝟎 nên 𝒙 𝟐 𝒙
𝟏𝒙𝟐 + 𝒚𝟏𝒚𝟐
𝟏𝒚𝟐 − 𝒙𝟐𝒚𝟏 𝒔𝒊𝒏 𝑩𝑨𝑪 = 𝟏 − 𝒄𝒐𝒔𝟐 𝑩𝑨𝑪 = 𝟏 − = 𝒙𝟐 𝟐 𝟐 𝟐
𝒙𝟐 + 𝒚𝟐 𝒙𝟐 + 𝒚𝟐 𝟏 + 𝒚𝟏 𝒙𝟐 + 𝒚𝟐 𝟏 𝟏 𝟐 𝟐 Vì vậy 𝟏 𝟏
𝑺𝜟𝑨𝑩𝑪 = 𝑨𝑩. 𝑨𝑪. 𝒔𝒊𝒏 𝑩𝑨𝑪 = 𝒙 𝟐 𝟐
𝟏𝒚𝟐 − 𝒙𝟐𝒚𝟏
Diện tích tam giác là 𝟏 𝑺 . 𝜟𝑨𝑩𝑪 = 𝒙 𝟐 𝑩 − 𝒙𝑨
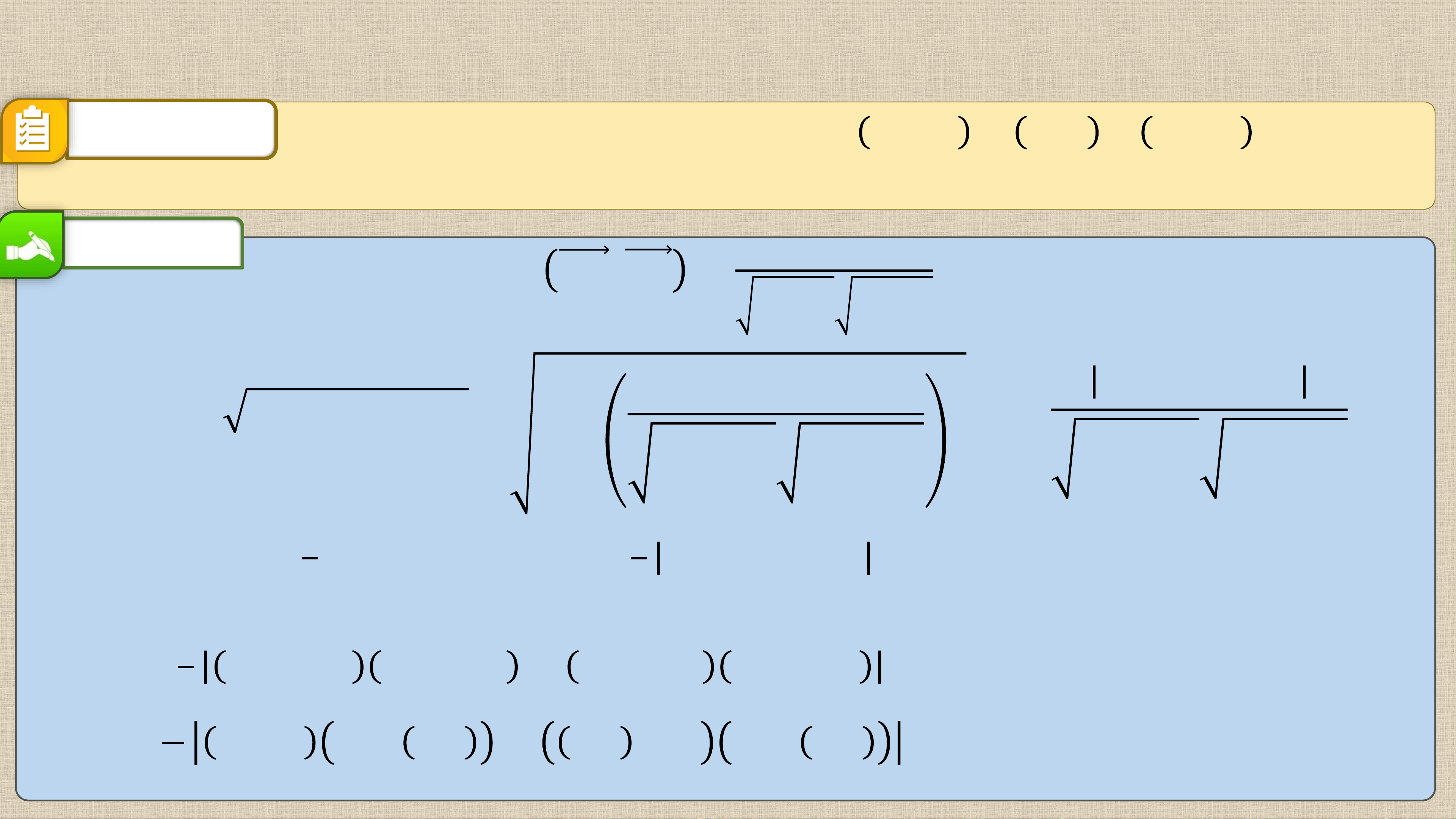
𝒚𝑪 − 𝒚𝑨 − 𝒙𝑪 − 𝒙𝑨 𝒚𝑩 − 𝒚𝑨 𝟏 = 𝟑 − 𝟏 𝟒 − −𝟏 −
−𝟐 − 𝟏 𝟓 − −𝟏 = 𝟏𝟒. 𝟐 CÂU 7.32. 14 48 6
Trong mặt phẳng tọa độ, cho 𝑨 𝟏; −𝟏 , 𝑩 𝟑; 𝟓 , 𝑪 −𝟐; 𝟒 .
Tính diện tích tam giác 𝑨𝑩𝑪 Bài giải Cách 3: Ta có 𝑨𝑩 =
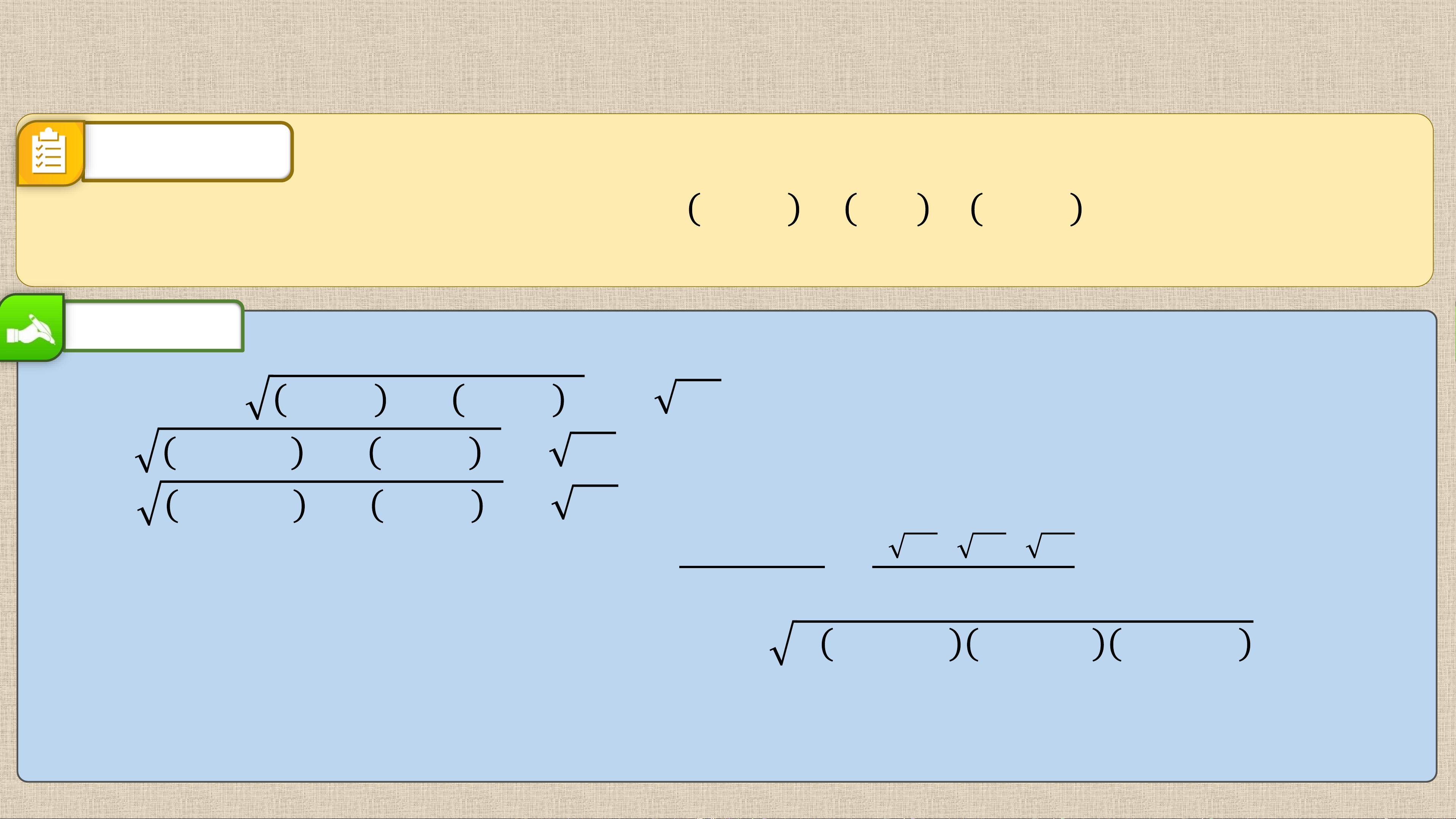
𝟑 − 𝟏 𝟐 + 𝟓 + 𝟏 𝟐 = 𝟐 𝟏𝟎; 𝑨𝑪 =
−𝟐 − 𝟏 𝟐 + 𝟒 + 𝟏 𝟐 = 𝟑𝟒; 𝑩𝑪 =
−𝟐 − 𝟑 𝟐 + 𝟒 − 𝟓 𝟐 = 𝟐𝟔. Tam giác 𝑨𝑩+𝑨𝑪+𝑩𝑪
𝟐 𝟏𝟎+ 𝟑𝟒+ 𝟐𝟔
𝑨𝑩𝑪 có nửa chu vi là: 𝒑 = = 𝟐 𝟐
Áp dụng công thức Heron, ta có 𝑺𝜟𝑨𝑩𝑪 = 𝒑 𝒑 − 𝑩𝑪 𝒑 − 𝑨𝑪 𝒑 − 𝑨𝑩 = 𝟏𝟒.