



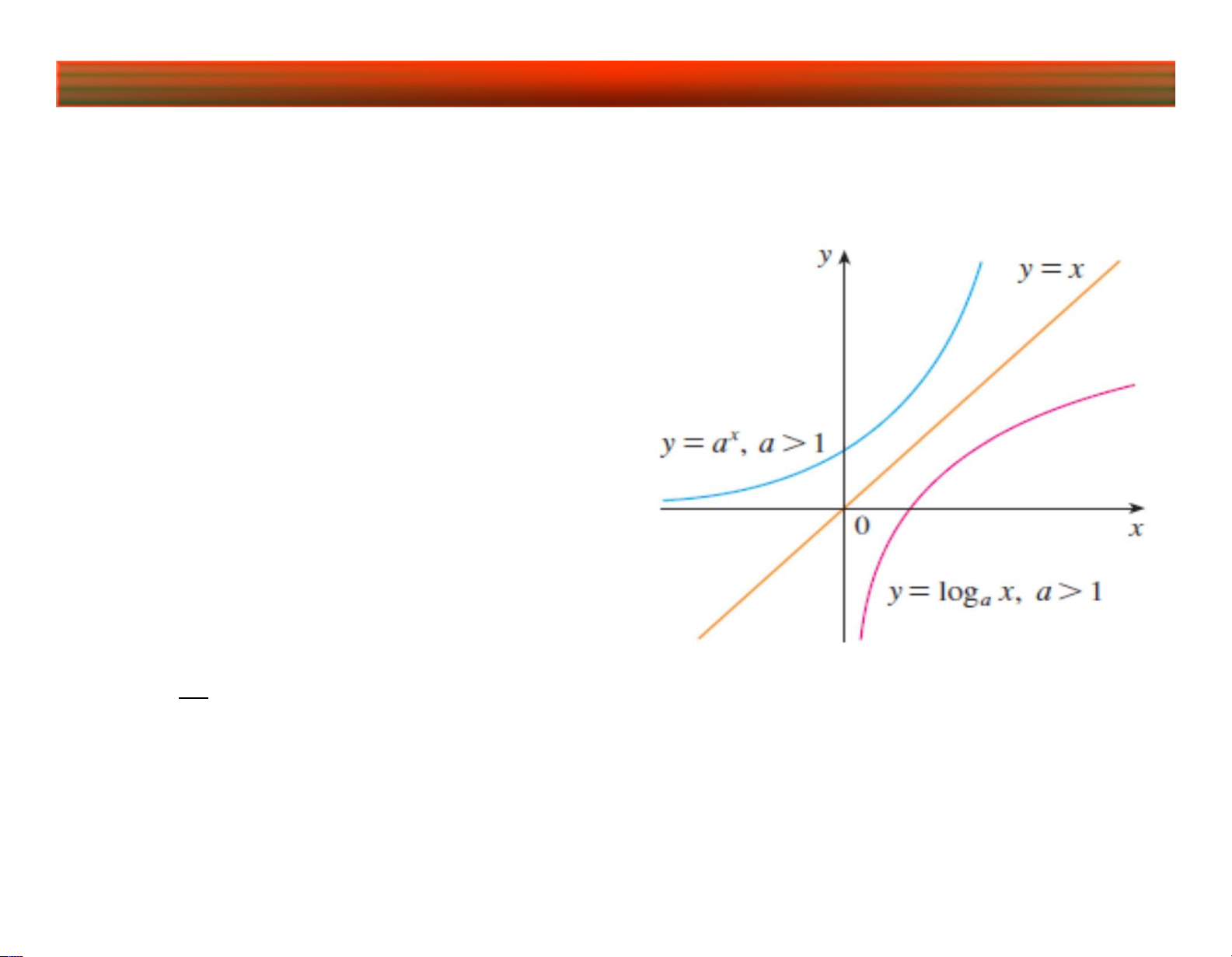



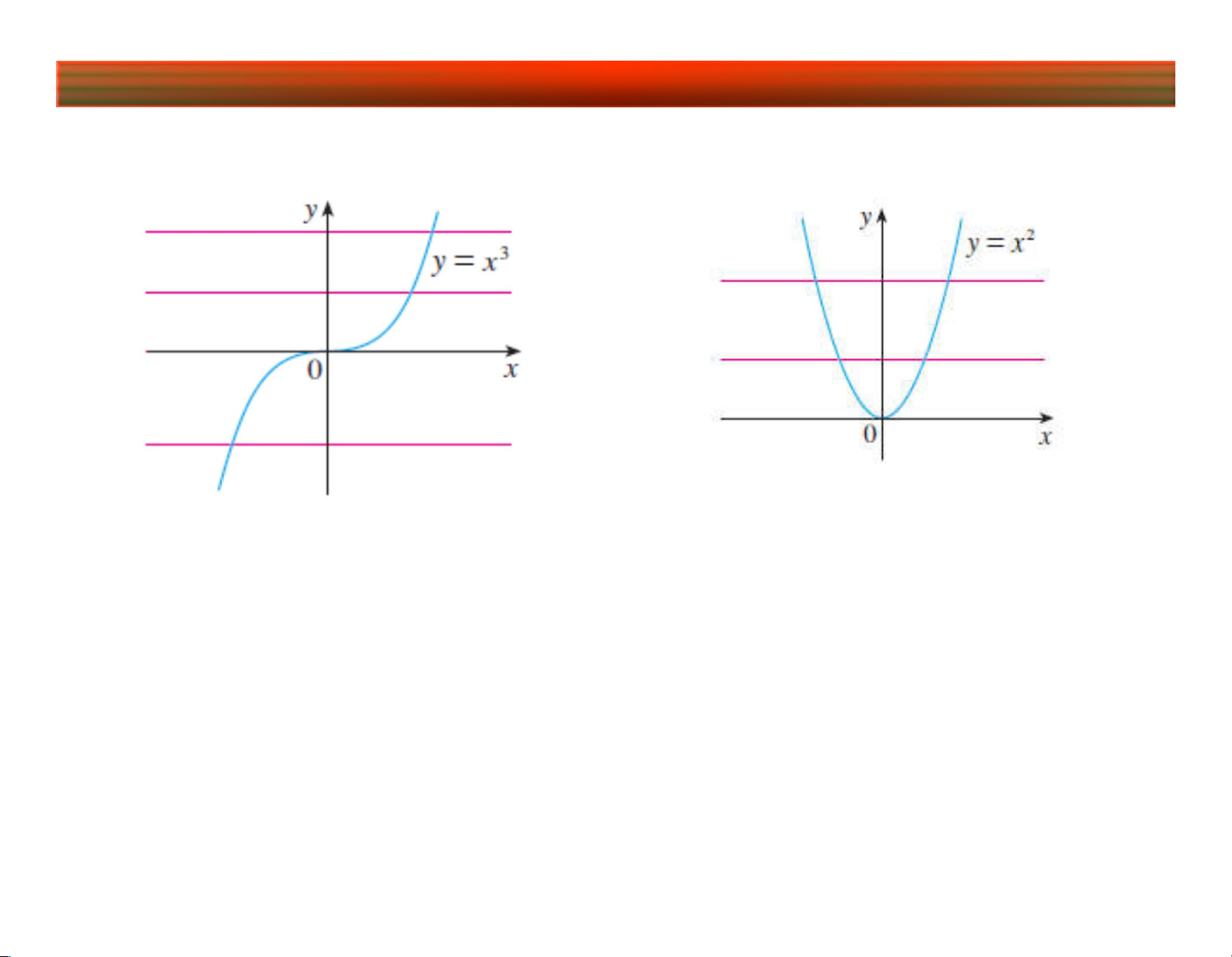



Preview text:
lOMoARcPSD|45315597 lOMoARcPSD|45315597
TRƯỜNG ĐH BÁCH KHOA TP.HCM TOÁN GIẢI TÍCH 1 ĐẠI HỌC
Giảng viên: ThS. Đoàn Thị Thanh Xuân
Email: dtxuan2015@gmail.com lOMoARcPSD|45315597
PHÂN PHỐI CHƯƠNG TRÌNH
45 TIẾT LÝ THUYẾT + 30 TIẾT BÀI TẬP
Ch 1. GIỚI HẠN CỦA DÃY SỐ (BT)
Ch 2. GIỚI HẠN CỦA HÀM SỐ MỘT BIẾN
Ch 3. ĐẠO HÀM VÀ VI PHÂN HÀM MỘT BIẾN
Ch 4. PHÉP TÍNH TÍCH PHÂN CỦA HÀM 1 BIẾN
Ch 5. PHƯƠNG TRÌNH VI PHÂN THƯỜNG lOMoARcPSD|45315597
Chương 2. GIỚI HẠN CỦA HÀM SỐ MỘT BIẾN
Bài 1. HÀM SỐ MỘT BIẾN
Bổ túc về hàm số (xem bài giảng)
1.1. Định nghĩa hàm số-Các hàm số cơ bản 1.2. Hàm số hợp 1.3. Hàm số ngược
1.4. Hàm số Hyperbolic lOMoARcPSD|45315597
Bài 1. Hàm số một biến
Nhắc lại các hàm đã học
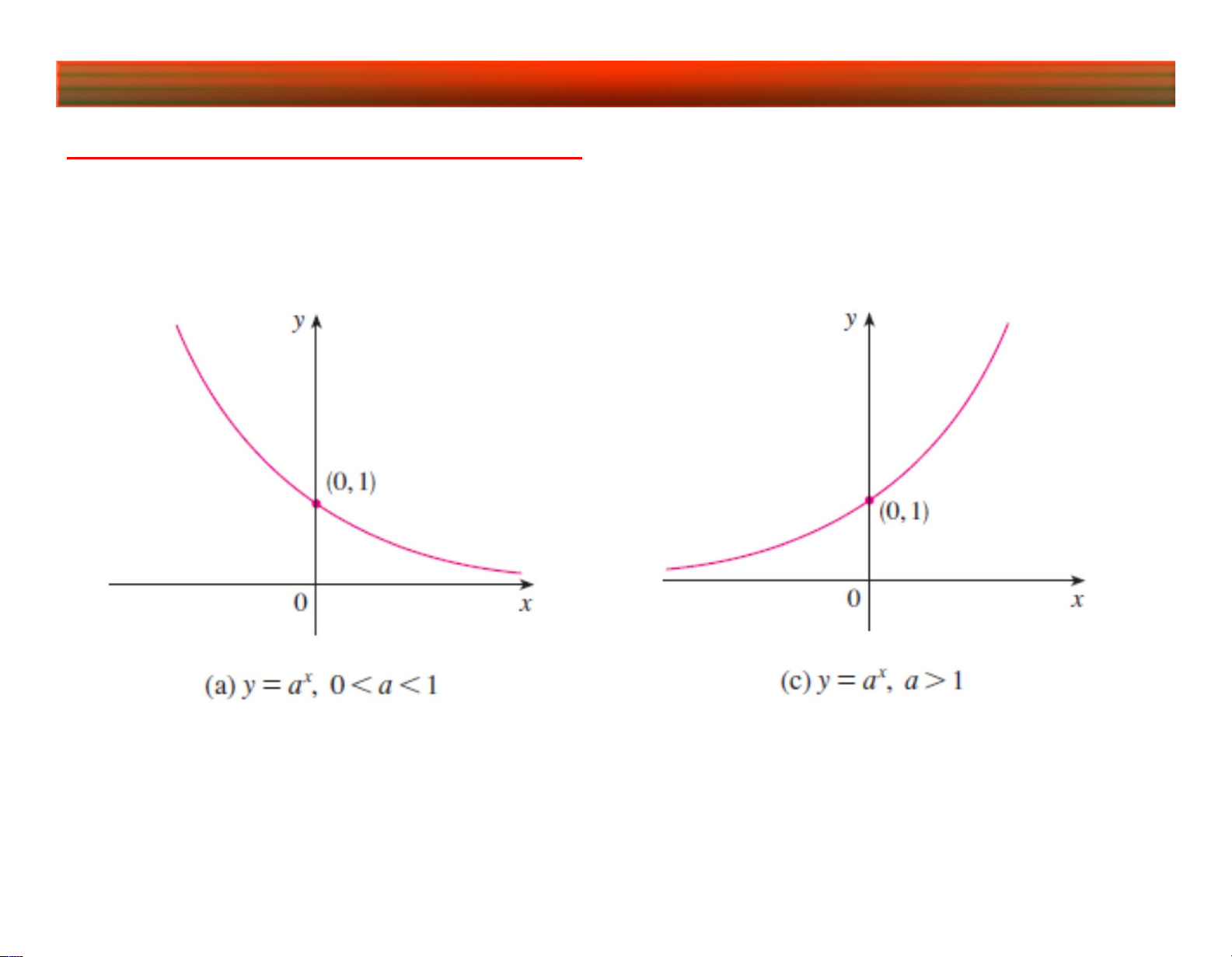
1. Hàm số mũ: y a x , a 0, a 1
MXD: D; MGT :(0;)
• Hàm nghịch biến • Hàm đồng biến
lim a x 0, lim ax
lim a x , lim
ax 0 x x x x lOMoARcPSD|45315597
Bài 1. Hàm số một biến
2. Hàm số logarit: y loga x , a 0, a 1
MXD: D (0;); MGT : a>1: Hàm đồng biến
0 Hàm nghịch biến Tính chất:
log a ( x. y ) log a x loga y x
y loga x x
log a log a x loga y a y y
log a ( x r ) r log a x ,r
log a ( a x ) R
x ,x log a
a x x ,x 0 lOMoARcPSD|45315597
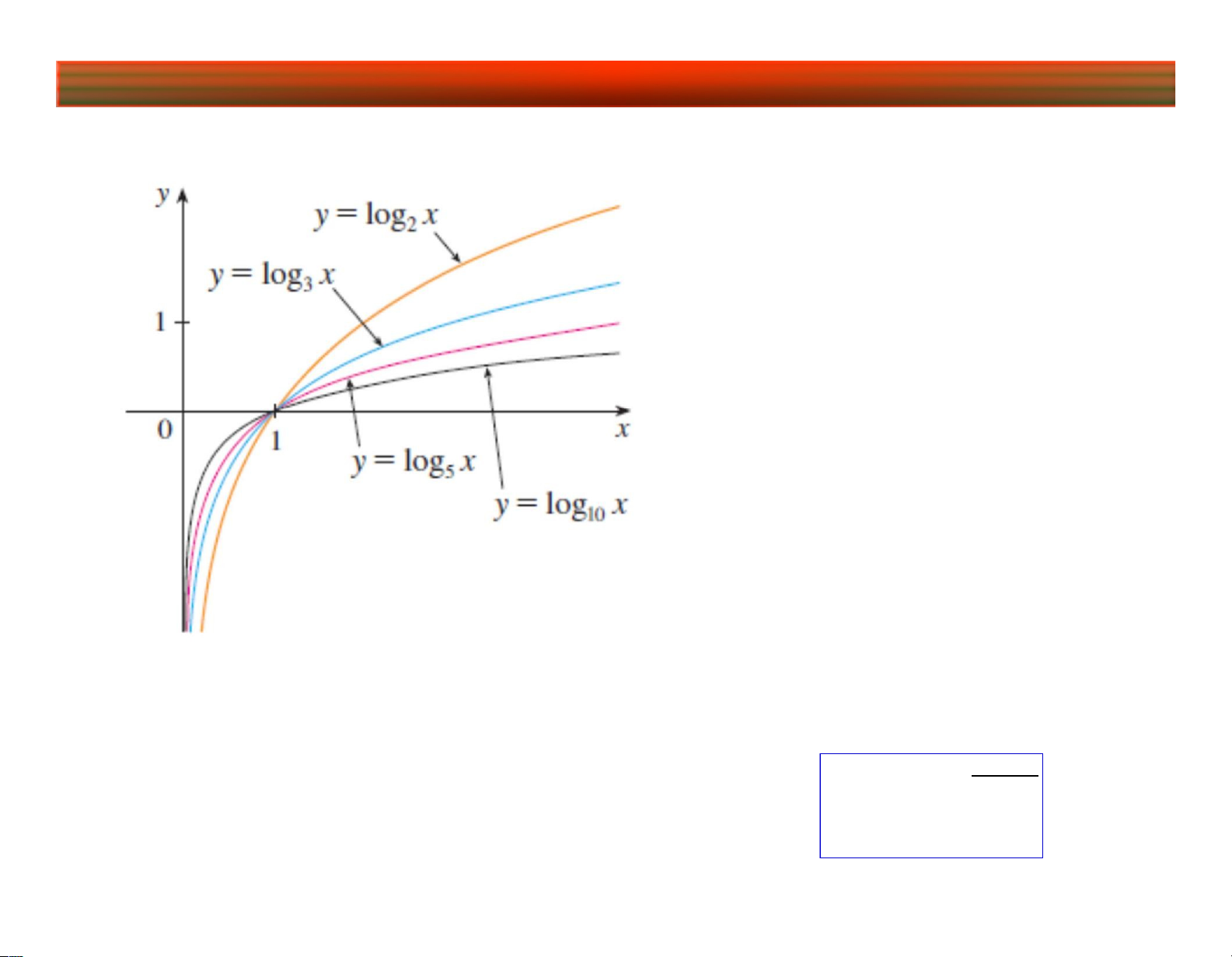
Bài 1. Hàm số một biến So sánh một số hàm
logarit với a>1 cụ thể
Đặc biệt: khi a=e, ta kí hiệu logex = lnx (logarit tự nhiên) loga ln b và ta có công thức b ln a lOMoARcPSD|45315597
Bài 1. Hàm số một biến
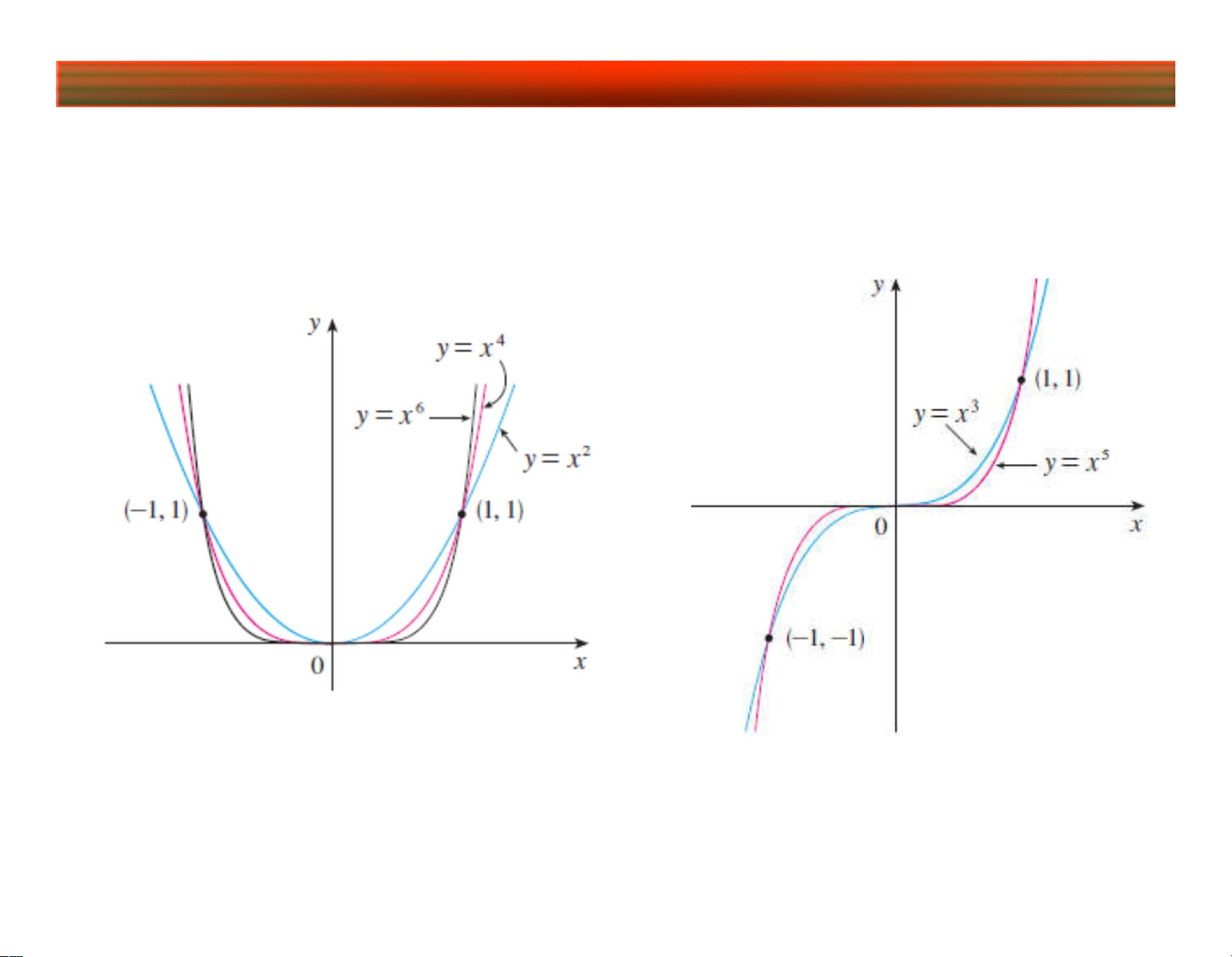
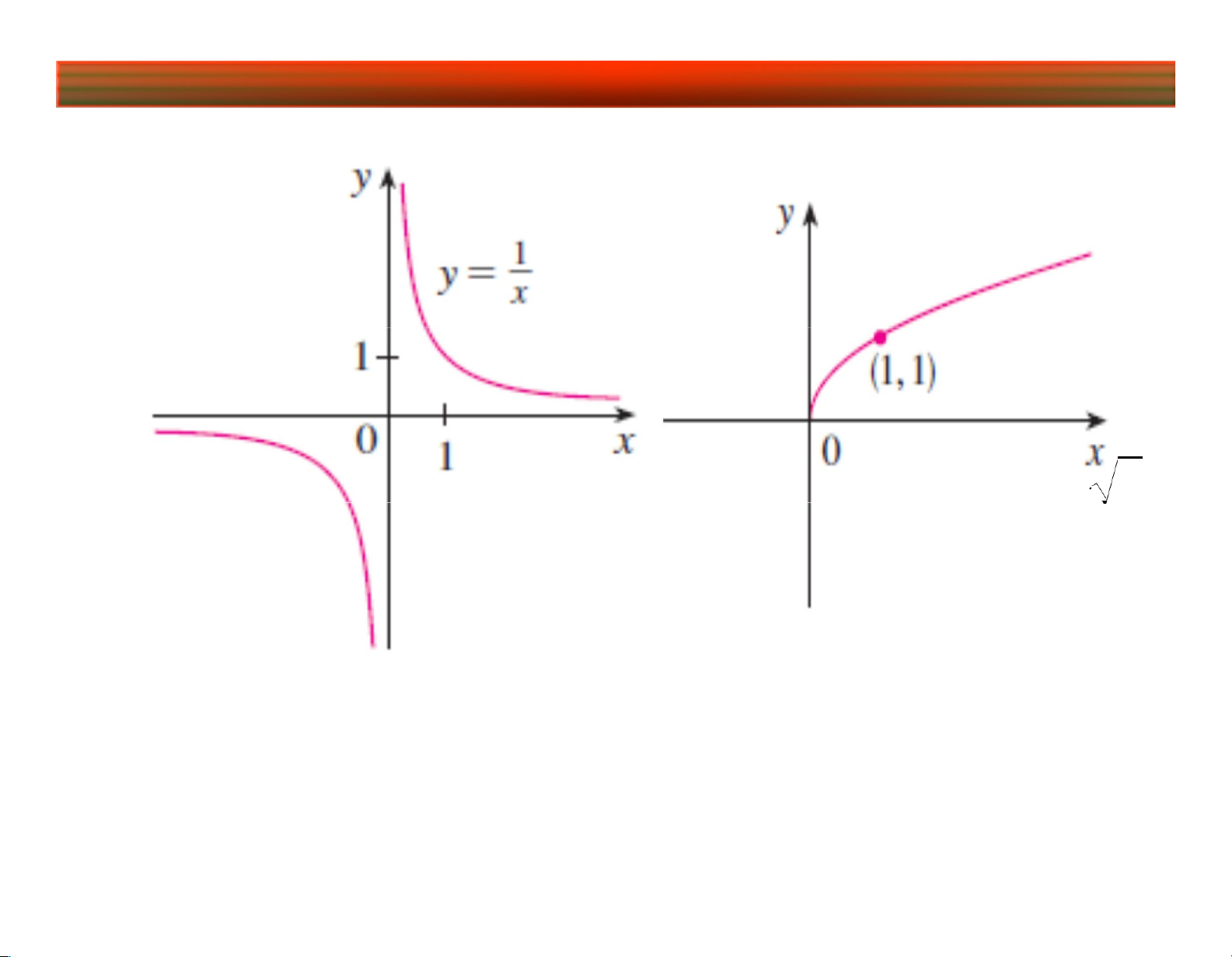
3. Hàm lũy thừa: y x
MXD, MGT: Tùy thuộc vào TH:2, 4,... TH:1, 3,... MXD: . MGT: 0, MXD: . MGT: lOMoARcPSD|45315597
Bài 1. Hàm số một biến
y x TH:1 TH:1/2 MXD: \ 0 . MGT: MXD: 0,
Gọi là đường Hyperbol MGT: 0, lOMoARcPSD|45315597
Bài 1. Hàm số một biến
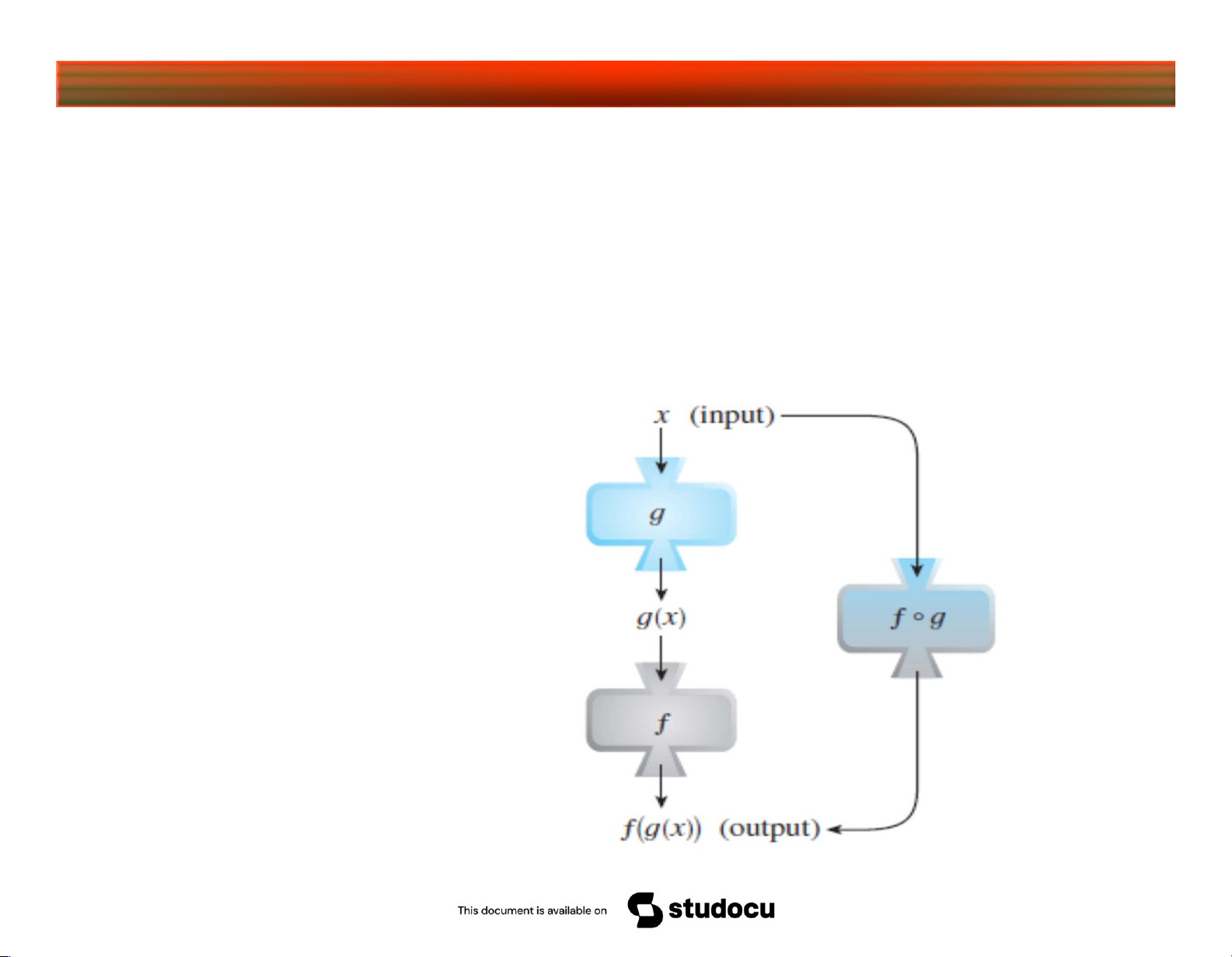
4. Hàm hợp: Giả sử hai hàm số f và g thỏa mãn.
g : X
Y , f :Y Z
Khi đó, hàm số h (x ) ( f g )(x ) f (g (x )) được gọi
là hàm số hợp của f và g . lOMoARcPSD|45315597
Bài 1. Hàm số một biến
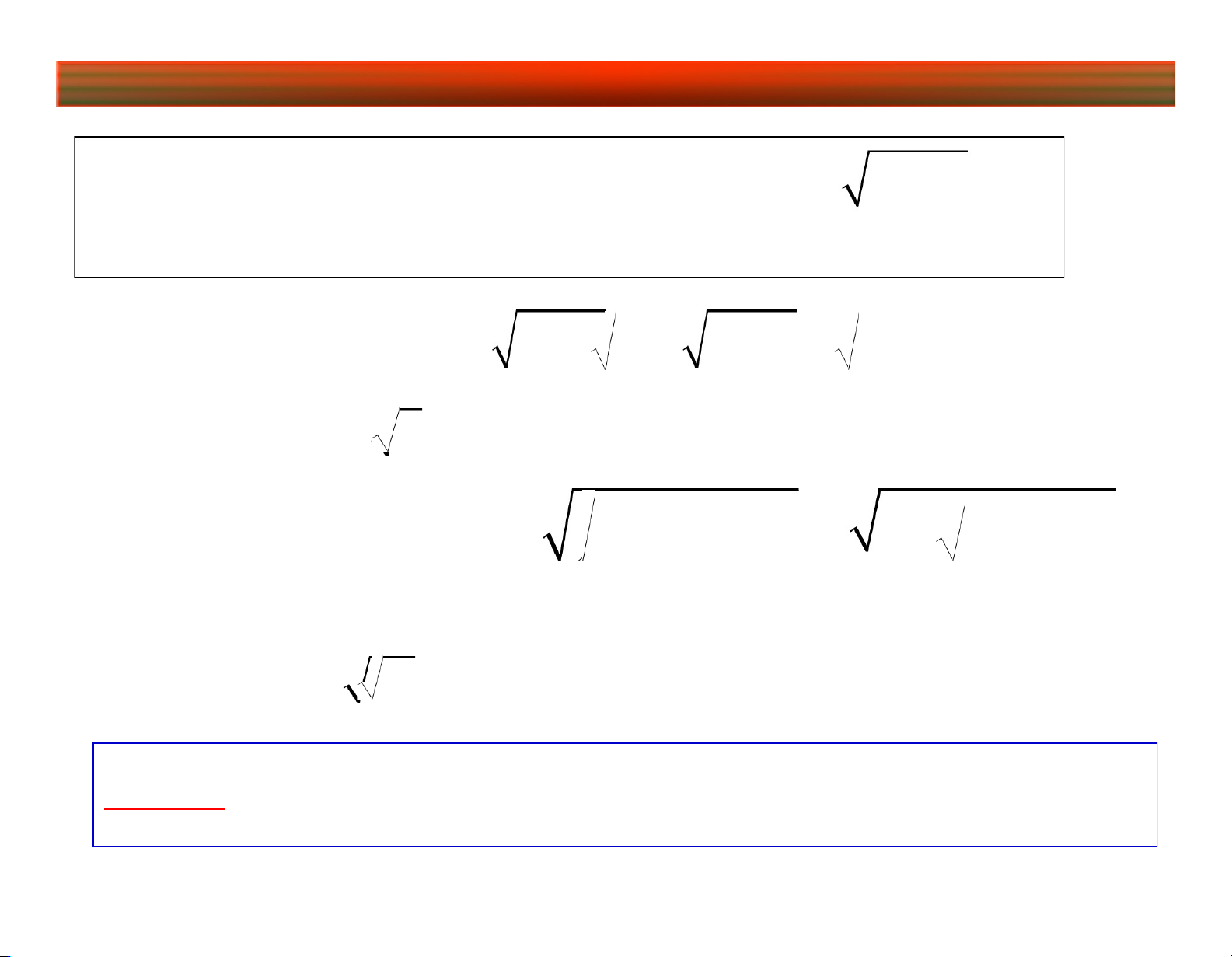
VD: Cho 2 hàm
f ( x ) 2 x 1, g ( x ) x21
Tìm f g , g f
và tính giá trị của chúng tại x = 2
f g ( x) f ( g ( x)) f ( x21) 2 x211
f g(2) 2 51
g f ( x ) g (2 x 1) (2 x 1) 2 1 4 x 2
4 x 2
g f (2) 26
Lưu ý : 2 hàm f
g , g f không bằng nhau lOMoARcPSD|45315597
Bài 1. Hàm số một biến 5. Hàm ngược:
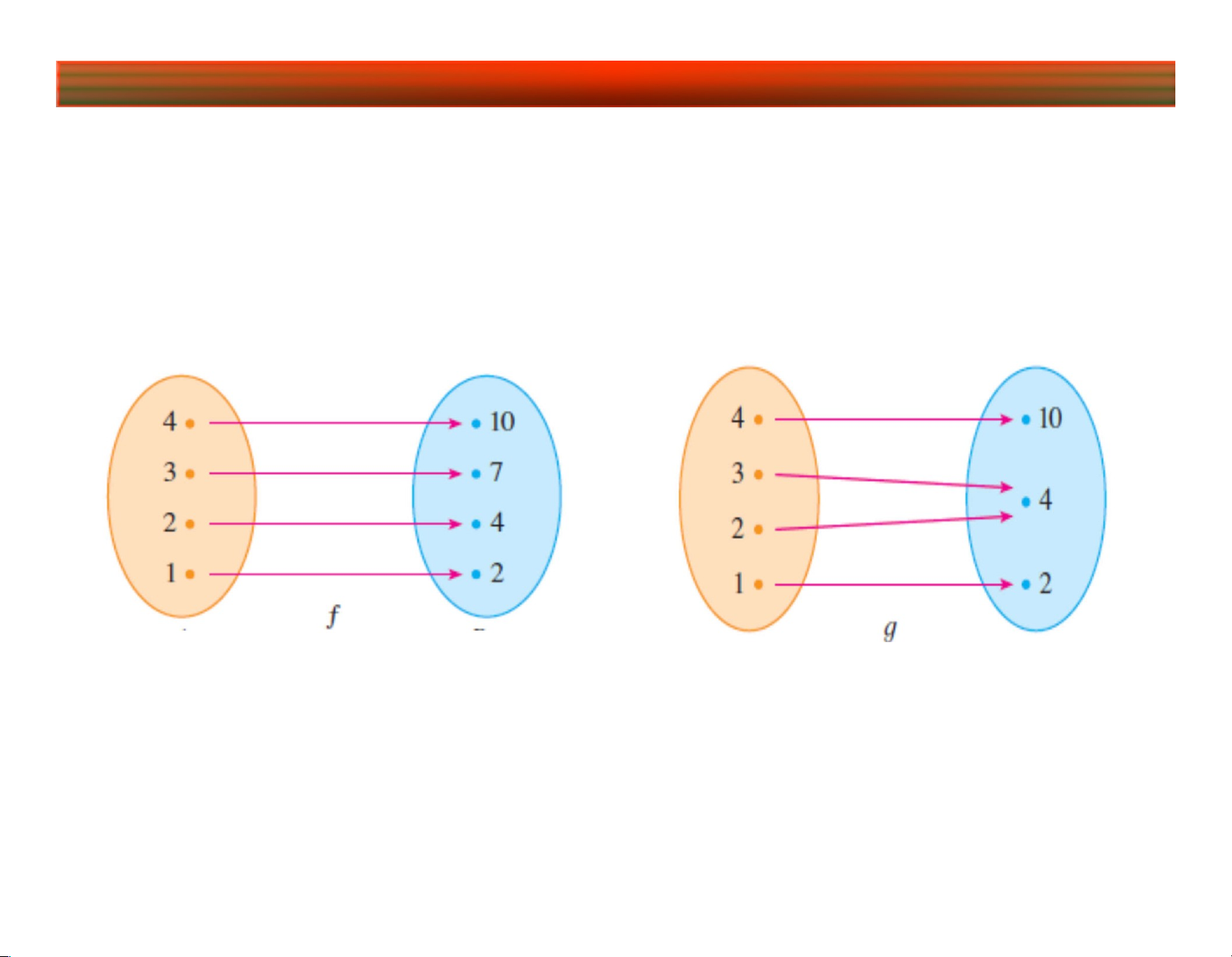
Hàm số f được gọi là song ánh (one-to-one
function) nếu x 1 x 2 f (x 1 ) f (x 2 ).
XY
XY Hàm 1-1 Không là hàm 1-1 lOMoARcPSD|45315597
Bài 1. Hàm số một biến Hàm y=x3 là hàm 1-1
Hàm y=x2 không là hàm 1-1
Hàm 1-1 có đồ thị chỉ cắt mọi đường thẳng y = C,
với C thuộc MGT của hàm tại duy nhất 1 điểm. lOMoARcPSD|45315597
Bài 1. Hàm số một biến
Hàm ngược: Xét hàm song ánh f có MXĐ D và miền
giá trị G . Khi đó, hàm số ngược của f , ký hiệu là f 1,
có MXĐ G và miền giá trị D được định nghĩa
f 1(y ) x f (x ) y (x D, y G). lOMoARcPSD|45315597
Bài 1. Hàm số một biến
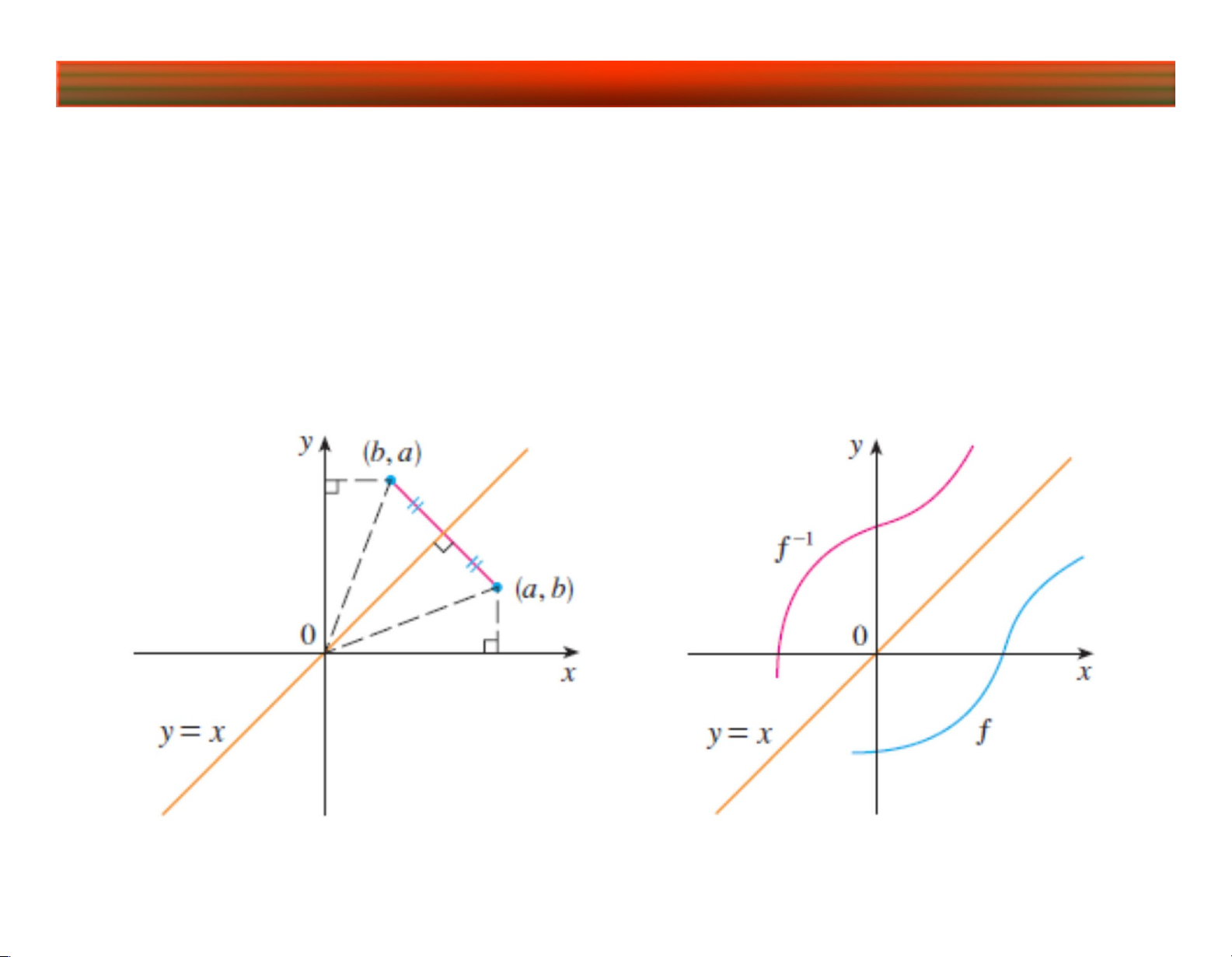
Đồ thị của hàm y f 1(x ) đối xứng với đồ thị
của hàm y f (x ) qua đường thẳng y x . Nếu
điểm (a , b ) thuộc đồ thị hàm f (x ) thì điểm
(b, a) thuộc đồ thị hàm f 1(x ). lOMoARcPSD|45315597
Bài 1. Hàm số một biến
VD: Tìm hàm ngược của hàm y = f(x)= x3 - 1
Ta sẽ tìm hàm y f 1(x ) bằng cách tính x theo y
y x 3 1 x 3 y1
Thay x bởi y, y bởi x, ta được hàm ngược
y f1( x ) 3 x1
f f1(x) f ( f1( x )) f ( 3 x 1) 3 x
131 x
MXĐ và MGT của cả 2 hàm f và f -1 đều là R




