Giáo trình Giải tích 1 - Giải tích 1 | Trường Đại học Bách khoa Thành phố Hồ Chí Minh

lOMoARcPSD|45315597 lOMoARcPSD|45315597 LÊ THÁI THANH
GIÁO TRÌNH GIẢI TÍCH I
(Dành cho chương trình Việt-Pháp) 2024 1 lOMoARcPSD|45315597 Mục lục
Mục lục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1 MỆNH ĐỀ - TẬP HỢP - DÃY SỐ 4
1.1 Mệnh đề . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2 Tập hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.3 Các tập hợp số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.3.1 Số tự nhiên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.3.2 Số nguyên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.3.3 Số hữu tỉ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.3.4 Số thực . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.4 Dãy số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.5 Dãy con . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.6 Một số loại dãy thông thường . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.6.1 Dãy truy hồi tuyến tính cấp một . . . . . . . . . . . . . . . . . . . . . . 16
1.6.2 Dãy truy hồi tuyến tính cấp hai . . . . . . . . . . . . . . . . . . . . . . . 16
2 HÀM SỐ VÀ GIỚI HẠN 22
2.1 Khái niệm hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.1.1 Định nghĩa hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.1.2 Các tính chất của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . 24
2.1.3 Các hàm số sơ cấp cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . 27
2.2 Giới hạn của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.3 Vô cùng bé và vô cùng lớn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
2.4 Tính liên tục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
3 ĐẠO HÀM VÀ VI PHÂN 46
3.1 Đạo hàm và vi phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
3.1.1 Đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
3.1.2 Vi phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
3.1.3 Đạo hàm và vi phân cấp cao . . . . . . . . . . . . . . . . . . . . . . . . . 51
3.2 Các định lý về hàm khả vi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
3.3 Công thức Taylor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
3.4 Sự biến thiên của hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58 2 lOMoARcPSD|45315597
3.5 Khảo sát và vẽ đồ thị đường cong . . . . . . . . . . . ............... 62
3.5.1 Khoảng lồi, lõm và điểm uốn . . . . . . . . . . ............... 62
3.5.2 Vẽ đường cong cho bởi phương trình y “ f pxq ............... 62
3.5.3 Vẽ đường cong cho bởi phương trình tham số ............... 63
3.5.4 Vẽ đường cong trong toạ độ cực . . . . . . . . ............... 65
4 TÍCH PHÂN BẤT ĐỊNH 72
4.1 Định nghĩa và cách tính . . . . . . . . . . . . . . . . ............... 72
4.2 Tích phân các hàm hữu tỉ . . . . . . . . . . . . . . . ............... 76
4.3 Tích phân một số hàm vô tỉ . . . . . . . . . . . . . . ............... 77
4.4 Tích phân các hàm lượng giác . . . . . . . . . . . . . ............... 81
5 TÍCH PHÂN XÁC ĐỊNH 88
5.1 Định nghĩa và các tính chất . . . . . . . . . . . . . . ............... 88
5.2 Các phương pháp tính tích phân xác định . . . . . . ............... 90
5.2.1 Tích phân xác định như là hàm của cận trên . ............... 90
5.2.2 Phương pháp đổi biến . . . . . . . . . . . . . ............... 91
5.2.3 Phương pháp tích phân từng phần . . . . . . ............... 92
5.3 Tích phân suy rộng . . . . . . . . . . . . . . . . . . . ............... 92
5.3.1 Tích phân suy rộng với cận vô hạn . . . . . . ............... 93
5.3.2 Tích phân suy rộng của hàm không bị chặn . ............... 95
5.4 Ứng dụng của tích phân . . . . . . . . . . . . . . . . ............... 97
5.4.1 Tính diện tích hình phẳng . . . . . . . . . . . ............... 97
5.4.2 Tính độ dài cung . . . . . . . . . . . . . . . . ............... 99
5.4.3 Tính thể tích vật thể tròn xoay . . . . . . . . ...............100
6 PHƯƠNG TRÌNH VI PHÂN 106
6.1 Phương trình vi phân cấp một . . . . . . . . . . . . . ...............106
6.1.1 Phương trình tách biến . . . . . . . . . . . . . ...............107
6.1.2 Phương trình đẳng cấp . . . . . . . . . . . . . ...............108
6.1.3 Phương trình tuyến tính . . . . . . . . . . . . ...............109
6.1.4 Phương trình Bernoulli . . . . . . . . . . . . . ...............109
6.2 Phương trình vi phân tuyến tính cấp hai hệ số hằng . ...............110
6.2.1 Phương trình thuần nhất . . . . . . . . . . . . ...............110
6.2.2 Phương trình không thuần nhất . . . . . . . . ...............112 3 lOMoARcPSD|45315597 Chương 1
MỆNH ĐỀ - TẬP HỢP - DÃY SỐ 1.1 Mệnh đề
Định nghĩa 1.1: Mệnh đề hay mệnh đề toán học là những khẳng định có giá trị xác
định: đúng hoặc sai nhưng không thể vừa đúng vừa sai. Ví dụ 1.1:
• "1 ` 1 “ 2" là mệnh đề có giá trị đúng.
• "4 là số nguyên tố" là mệnh đề có giá trị sai.
Ta thường ký hiệu mệnh đề bởi các chữ các in hoa: P, Q, R, . . . ; giá trị đúng là 1
(hoặc T ), giá trị sai là 0 (hoặc F ). Để kiểm tra một mệnh đề là đúng hay sai ta thường lập
bảng giá trị cho mệnh đề đó.
Cho P và Q là hai mệnh đề. Ta xét các phép toán liên kết lôgic các mệnh đề: phép phủ
định (P ), phép kéo theo (P ñ Q), phép tương đương (P ô Q). Giá trị của các phép toán đó
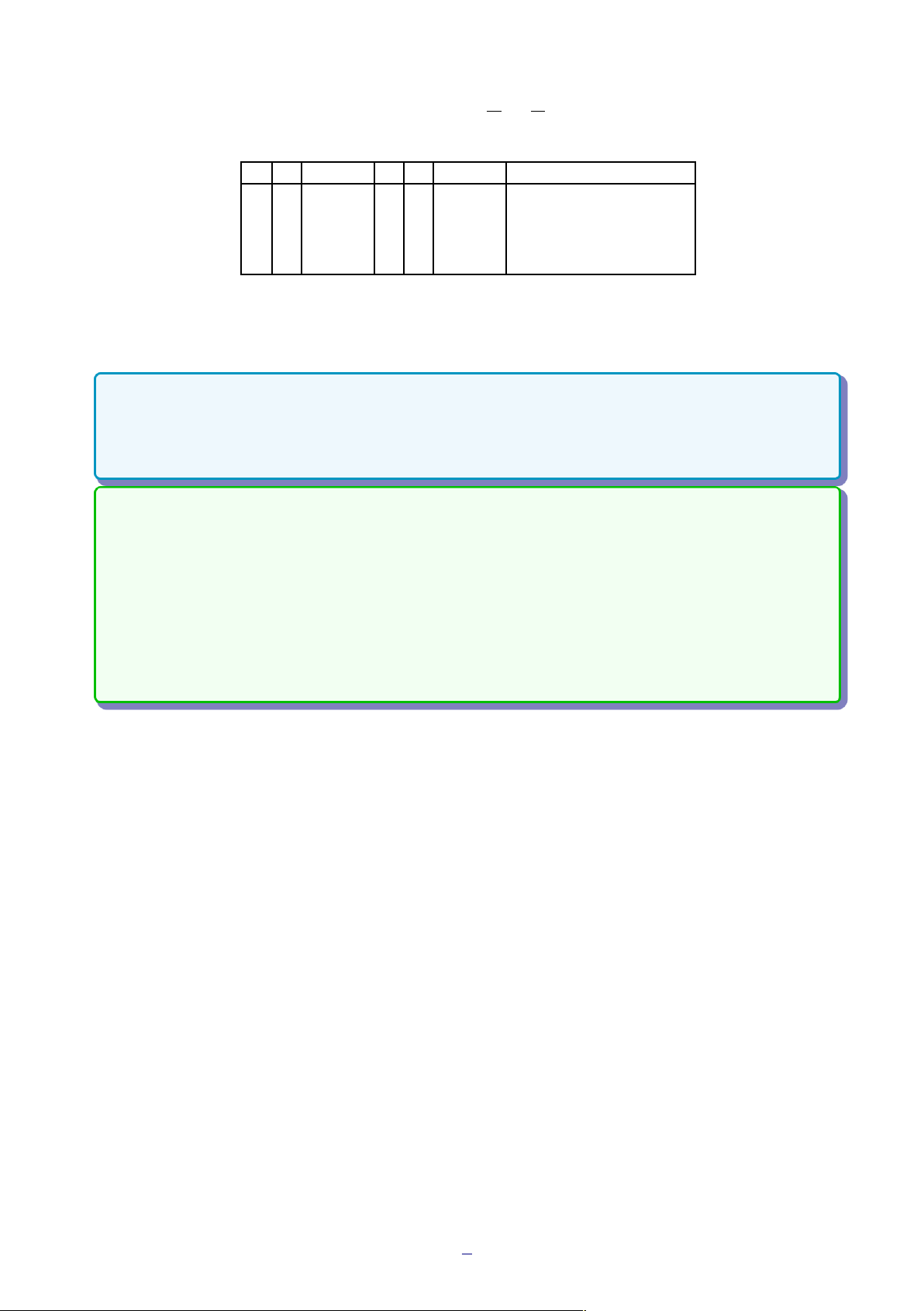
được cho bởi bảng giá trị sau: P Q P P ñ Q P ô Q 1 1 0 1 1 1 0 0 0 0 0 1 1 1 0 0 0 1 1 1
Trong mệnh đề P ñ Q, P được gọi là giả thiết, Q là kết luận. Mệnh đề Q ñ P được gọi
là mệnh đề đảo của mệnh đề P ñ Q; còn mệnh đề Q ñ P được gọi là mệnh đề phản đảo
của mệnh đề P ñ Q.
Mệnh đề P ñ Q có thể đọc theo nhiều cách như sau: nếu P , thì Q; hoặc muốn có Q, thì có
P là đủ; hoặc P là điều kiện đủ của Q; hoặc Q là điều kiện cần của P . Còn mệnh đề P ô Q
có thể đọc như sau: P là điều kiện cần và đủ để có Q; hoặc P nếu và chỉ nếu Q; hoặc P
khi và chỉ khi Q. 4 lOMoARcPSD|45315597
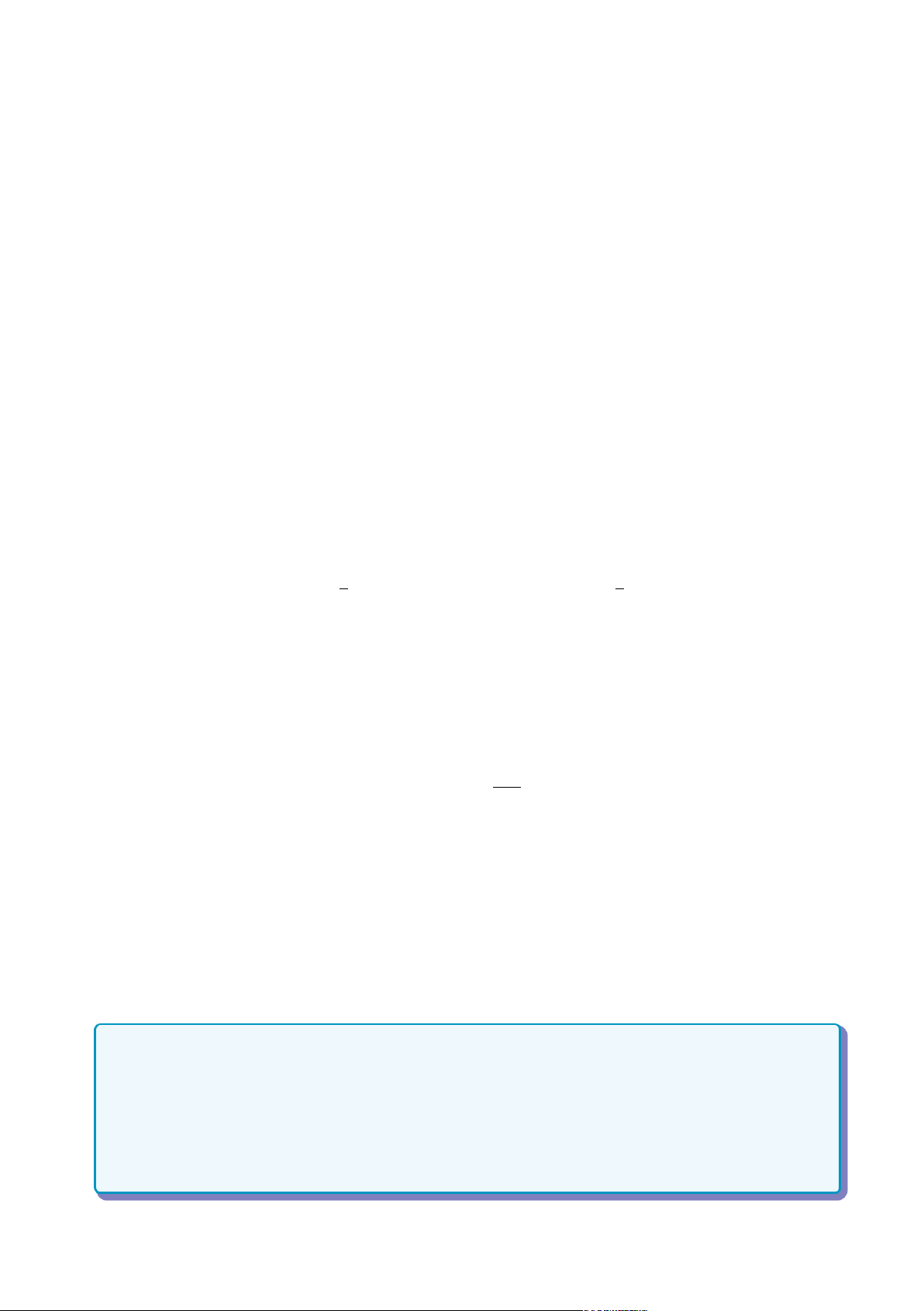
Ta có thể chứng minh mệnh đề pP ñ Qq ô pQ ñ P q luôn luôn đúng bằng cách lập bảng giá trị của nó. P Q P ñ Q Q P Q ñ P
pP ñ Qq ô pQ ñ P q 1 1 1 0 0 1 1 1 0 0 1 0 0 1 0 1 1 0 1 1 1 0 0 1 1 1 1 1
Mệnh đề này là cơ sở của phương pháp phản chứng: để chứng minh P ñ Q là đúng, ta
giả thiết P là đúng và Q là sai, và ta chứng minh rằng điều đó dẫn đến mâu thuẫn; hoặc ta
giả thiết Q là sai và chứng minh P cũng sai.
Định nghĩa 1.2: Mệnh đề chứa biến là một khẳng định P px, y, . . . q phụ thuộc vào một
số biến x, y, . . . sao cho bản thân P px, y, . . . q không phải là mệnh đề, nhưng nếu thay
x, y, . . . bởi những giá trị cụ thể x “ a, y “ b, . . . ta được môt mệnh đề P pa, b, . . . q. Ví dụ 1.2:
• P pnq = "n là một số nguyên tố" là một mệnh đề chứa một biến số tự nhiên n.
Ví dụ, P p3q là mệnh đề đúng, P p4q là mệnh đề sai.
• Qpx, yq = "y ` 2, x ´ y, x ` 2y là các số chẵn" là một mệnh đề chứa hai biến số
nguyên x, y. Ví dụ, Qp4, 2q là mệnh đề đúng. Trong khi Qp5, 2q, Qp4, 7q là những mệnh đề sai.
Giả sử P pxq là một mệnh đề chứa biến x. Ta xét các trường hợp sau:
Trường hợp 1: Khi thay x bởi một phần tử tùy ý a, ta luôn được một mệnh đề đúng P paq. Như vậy
mệnh đề "với mọi x, P pxq" là mệnh đề luôn luôn đúng và ký hiệu bởi "@x, P pxq"
Trường hợp 2: Với một số giá trị a thì P paq là mệnh đề đúng, và với một số giá trị b thì P
pbq là mệnh đề sai. Như vậy, mệnh đề "tồn tại x, P pxq" là mệnh đề đúng và ký hiệu
bởi "Dx, P pxq".
Các ký hiệu @ và D được gọi là các lượng từ với mọi và lượng từ tồn tại. Ngoài ra ta còn
dùng ký hiệu D! với ý nghĩa là tồn tại duy nhất. Chú ý rằng ký tự tác động bởi lượng từ là câm
(nghĩa là có thể thay thế bởi các ký tự khác). Ví dụ: p@x, P pxqq ô p@y, P pyqq hoặc pDx, P
pxqq ô pDy, P pyqq. Hơn nữa, ta không thể thay đổi thứ tự các lượng từ trong một câu. Ví dụ,
@x P N, Dy P N, x ď y là mệnh đề đúng, nhưng Dy P N, @x P N, x ď y là mệnh đề sai. 5 lOMoARcPSD|45315597 1.2 Tập hợp
Định nghĩa 1.3: Tập hợp được hiểu như một tụ tập các đối tượng do một tính chất chung
nào đó hợp thành. Ta ký hiệu tập hợp bởi các chữ cái in hoa như A, B, C, X, Y, ... Nếu x là
một thành phần tạo nên tập hợp X thì ta nói x là phần tử của X và viết x P X .
Nếu y không phải là phần tử của X thì ta viết y R X .
Ta nói tập hợp A là tập con của tập hợp B, ký hiệu là A Ă B, nếu @x P A ñ x P B. Phủ
định của A Ă B được viết là A Ć B. Hai tập hợp A và B được gọi là bằng nhau, A “ B, khi
và chỉ khi A Ă B và B Ă A. Nghĩa là mọi phần tử của A cũng là phần tử của B và ngược lại.
Để xác định một tập hợp, ta có thể liệt kê các phần tử của tập hợp đó X “ tx, y, z, . . . u
hoặc chỉ ra tính chất mà các phần tử của nó có X “ tx | ppx qu hoặc X “ tx : ppxqu. Tập hợp
không chứa phần tử nào được gọi là tập rỗng và ký hiệu H. Ta có với mọi tập X : H Ă X .
Giả sử X là một tập hợp, A, B Ă X . Ta định nghĩa các phép toán trên các tập hợp con của X như sau:
• Phần bù của tập A trong X : CX pAq “ tx P X | x R Au
• Hợp của hai tập hợp A và B: A Y B “ tx P X | x P A hoặc x P Bu
• Giao của hai tập hợp A và B: A X B “ tx P X | x P A và x P Bu
• Hiệu của hai tập hợp A và B: AzB “ A ´ B “ tx P X | x P A và x R Bu
Hai tập hợp A và B được gọi là rời nhau nếu A X B “ H. Các phép toán trên tập hợp có các tính chất sau:
(a) CX pHq “ X, CX pX q “ H, CX pCX pAqq “ A
(b) A Y B “ B Y A, pA Y Bq Y C “ A Y pB Y Cq, A Y B “ B ô A Ă B
(c) A X B “ B X A, pA X Bq X C “ A X pB X Cq, A X B “ B ô B Ă A
(d) CX pA Y Bq “ CX pAq X CX pBq, CX pA X Bq “ CX pAq Y CX pBq
(e) A Y pB X Cq “ pA Y Bq X pA Y Cq, A X pB Y Cq “ pA X Bq Y pA X Cq
(f ) A ´ B “ A X CX pBq “ A ´ pA X Bq, A ´ B “ H ô A Ă B
Giả sử x, y là hai phần tử tương ứng của hai tập hợp X, Y . Ta thành lập một phần tử
mới px, yq gọi là cặp px, yq. Hai cặp px, y q và pu, v q được gọi là bằng nhau nếu x “ u và
y “ v. Nói chung px, yq “ y,p xq. Do đó thứ tự các phần tử trong cặp là quan trọng. Bây giờ
cho hai tập X và Y . Tập tất cả các cặp px, yq với x P X và y P Y được gọi là tích Decartes
của X và Y và ký hiệu là X ˆ Y . Ta có thể mở rộng khái niêm tích Decartes ra cho nhiều
tập hợp. Nếu X “ Y thì tích Decartes X ˆ Y “ X ˆ X được ký hiệu là X 2. 6 lOMoARcPSD|45315597 1.3 Các tập hợp số 1.3.1 Số tự nhiên
Tập các số tự nhiên ký hiệu là N “ t0, 1, 2, . . . . . . u. Trên N có trang bị hai phép toán cộng p`q và nhân p¨q thỏa:
• Phép cộng có tính chất giao hoán, kết hợp, có phần tử trung hòa là 0.
• Phép nhân có tính chất giao hoán, kết hợp, có phần tử trung hòa là 1.
Trên tập N có trang bị một quan hệ thứ tự toàn phần ď pěq tương thích đối với các phép toán cộng và nhân.
Định lý 1.1 (Nguyên lý quy nạp): Nếu một tập con E của N thỏa: 0 P E, @n P E ñ
pn ` 1q P E thì E “ N.
Giả sử P pnq là một mệnh đề phụ thuộc vào một biến tự nhiên n. Khi đó nguyên lý quy
nạp có thể phát biểu dưới dạng sau:
• P pn0q đúng.
• @n P N, n ě n0, giả sử P pnq đúng và P pn ` 1q cũng đúng thì P pnq đúng với mọi n ě n0.
Ví dụ 1.3: Chứng minh công thức n 12 22 n2 i2
npn ` 1qp2n ` 1q (1.1) ÿ “ ` `¨¨¨` “ 6 i“1
Ta chứng minh bằng quy nạp. Dễ thấy (1.1) đúng khi n “ 1. Giả sử (1.1) đúng khi n “ k, nghĩa là: 1 2
` 22 ` ¨ ¨ ¨ ` k2 “ kpk ` 1qp2k ` 1q 6
Ta chứng minh (1.1) cũng đúng khi n “ k ` 1. Ta có k`1 ÿ i2 12 22 k2 k 1 2
kpk ` 1qp2k ` 1q k 1 2 “ ` `¨¨¨` ` p ` q “ 6 ` p ` q i“1
pk ` 1qrkp2k ` 1q ` 6pk ` 1qs
pk ` 1qr2k2 ` 7k ` 6s “ 6 “ 6
pk ` 1qrpk ` 2qp2k ` 3qs
pk ` 1qrpk ` 2qp2pk ` 1q ` 1qs “ 6 “ 6
Công thức (1.1) đúng khi n “ k ` 1. Theo nguyên lý quy nạp công thức (1.1) đúng với mọi n P N. 7 lOMoARcPSD|45315597 1.3.2 Số nguyên
Tập các số nguyên ký hiệu: Z “ t. . . , ´3, ´2, ´1, 0, 1, 2, 3, . . . u và là sự mở rộng của tập các số tự nhiên. 1.3.3 Số hữu tỉ
Tập các số hữu tỉ Q “ tx : x “ pq , p P Z, q P N˚u. Vì a “ a1 nên Z Ă Q. 1.3.4 Số thực
Ta thừa nhận tập hợp các số thực R như là sự mở rộng của tập các số hữu tỷ với hai
phép toán cộng và nhân và một quan hệ thứ tự ď thỏa các tiên đề sau đây:
Tiên đề về trường : pR, `, ¨q là một trường giao hoán, nghĩa là @a, b, c P R
• pa ` bq ` c “ a ` pb ` cq
• a ` b “ b ` a
• D0 P R, a ` 0 “ 0 ` a “ a
• @a P R, Dp´aq P R, a ` p´aq “ p´aq ` a “ 0. Từ đây ta có thể định nghĩa phép trừ
như là phép toán ngược của phép cộng: a ´ b “ a ` p´bq.
• pabqc “ apbcq • ab “ ba
• D1 P R, a ¨ 1 “ 1 ¨ a “ a
• @a P R ´ t0u, Da´1 P R, a ¨ a´1 “ a´1 ¨ a “ 1. Từ đây ta có thể định nghĩa phép chia
như là phép toán ngược của phép nhân: @a P R, @b P R ´ t0u, ab “ a ¨ b´1. Ta
viết 1b thay cho b´1.
• apb ` cq “ ab ` ac và pb ` cqa “ ba ` ca.
Tiên đề thứ tự : ď là một quan hệ thứ tự toàn phần trong R, nghĩa là @a, b, c P R • a ď a
• a ď b ^ b ď a ñ a “ b
• a ď b ^ b ď c ñ a ď c
• @a, b P R ta luôn có hoặc a ď b hoặc b ď a.
Từ quan hệ ď trong R, ta cũng xét quan hệ ě như sau: @a, b P R, a ě b nếu b ď a.
Trong R ta cũng xét hai quan hệ nghiêm ngặt ă và ą: a ă b ô a ď b ^ a “b và a ą b ô a
ě b ^ a “b. 8 lOMoARcPSD|45315597
Ta đưa ra một số định nghĩa:
• Ta nói x P R là cận trên (cận dưới) của tập A Ă R nếu @a P A, a ď x pa ě xq. Nếu A
có một cận trên (cận dưới) thì ta nói nó bị chặn trên (bị chặn dưới). Một tập hợp vừa
bị chặn trên vừa bị chặn dưới được gọi là tập bị chặn.
• Ta nói x P A là phần tử lớn nhất (nhỏ nhất) của tập A Ă R nếu x là một cận trên (cận
dưới) của A. Khi ấy ta viết x “ maxpAq px “ minpAqq.
• Ta nói x là cận trên đúng (cận dưới đúng) của tập A Ă R nếu x là giá trị nhỏ nhất (giá trị
lớn nhất) của tập các cận trên (tập các cận dưới) của A và ký hiệu là sup pAqpinf pAqq.
Định lý 1.2 (Nguyên lý Supremum): Mọi tập con khác rỗng và bị chặn trên của R đều có cận trên đúng.
Định lý 1.3: R là một tập trù mật, nghĩa là với cặp số thực x ă y, luôn có một số thực
z sao cho x ă z ă y.
Bây giờ giả sử A Ă R, M “ suppAq và m “ inf pAq. Từ định nghĩa của cận trên đúng,
cận dưới đúng và tính trù mật của R ta thấy rằng
@ϵ ą 0, Dpx, yq P A2 : M ´ ϵ ă x ď M và m ď y ă m ` ϵ
Định lý 1.4: R là một thể Archimède, nghĩa là:
@ϵ P R˚`, @A P R˚`, Dn P N˚ : nϵ ą A
Từ mệnh đề trên ta cũng suy ra rằng, với mọi x P R, sẽ tồn tại n P Z để cho n ď x ă n ` 1.
Số n như vậy được gọi là phần nguyên của x và ký hiệu là rxs hoặc Epxq. Ví dụ, Ep3, 234q “ 3,
Ep´3, 234q “ ´4.
Ta đưa vào tập R hai phần tử đặc biệt ký hiệu là ´8 và `8 thỏa @x P R, ´8 ă x ă `8.
Trong R ta xét một số tập con đặc biệt sau:
• ra, bs “ tx P R | a ď x ď bu : khoảng đóng hoặc đoạn.
• pa, bq “ tx P R | a ă x ă bu : khoảng mở hoặc khoảng.
• ra, bq “ tx P R | a ď x ă bu : nửa đoạn trái.
• pa, bs “ tx P R | a ă x ď bu : nửa đoạn phải.
• p´8, bs “ tx P R | ´8 ă x ď bu.
• p´8, bq “ tx P R | ´8 ă x ă bu. 9 lOMoARcPSD|45315597
• ra, `8q “ tx P R | a ď x ă `8u.
• pa, `8q “ tx P R | a ă x ă `8u. • R “ p´8, `8q
Ta định nghĩa giá trị tuyệt đối của số thực x là một số thực ký hiệu là |x| xác định bởi: |x| “ # x, nếu x ě 0. x, nếu x 0, ´ ă
Trị tuyệt đối của số thực có các tính chất quan trọng sau: ˇ x
• @x P R, |x| ě 0,|x| “ 0 ô x “ 0 x ˇ k“1 k “ k“1 | k |
• @x, y P R, |xy| “ |x| ¨ |y| ùñ @px1, x2, . . . , xnq P Rn, n ˇ n ˇ ˇ ś nˇ ś n x ˇ ˇ ˇ ˇ k“1 | k |
• @x, y P R, |x ` y| ď |x| ` |y| ùñ @px1, x2
, . . . , xnq P R , k“1 xk ď n ˇ ř ˇ ř 1 ˇ 1 ˇ ˇ ˇ
• @x, y P R, max px, yq “ 2 px ` y ` |x ´ y|q , min px, yq “ 2 px ` y ´ |x ´ y|q
• @x, y P R, ||x| ´ |y|| ď |x ´ y|
Ta có bất đẳng thức Cauchy-Schwarz: ˜ ˜ ¸ ˜ ¸
@n P N˚, @x ¸ 2 ď
1, . . . , xn, y1, . . . , yn P R, k 1 xk yk 2 k 1 xk k 1 yk2 n n n ÿ ÿ ÿ “ “ “
Dấu bằng xảy ra khi xk “ 0 hoặc yk “ αxk , @k “ 1, n. 1.4 Dãy số
Một dãy số là một hàm số từ N vào R. Thay cho ký hiệu u : N Ñ R, ta thường ký hiệu punqnPN nÞÑupnq
hoặc ngắn gọn punq. Ta chỉ xét dãy số thực. Phần tử un được gọi là số hạng thứ n của dãy.
Mỗi hàm số từ tn P N; n ě n0u vào R với n0 P N cố định cũng gọi là một dãy số; phần lớn
các khái niệm được khảo sát chỉ đề cập đến các un "từ một thứ tự nào đó trở đi".
Định nghĩa 1.4: Ta nói dãy số punq có giới hạn là a khi n tiến ra vô cùng khi và chỉ khi:
@ε ą 0, DN P N, @n P N, pn ě N ùñ |un ´ a| ă εq u
Khi đó ta ký hiệu lim un “ a hoặc un ÝÑ a và nói dãy số p n q hội tụ. Ngược lại ta nói n Ñ8 8 n dãy phân kỳ. 10 lOMoARcPSD|45315597 Ví dụ 1.4:
1. Mọi dãy dừng (nghĩa là bằng hằng số từ một thứ tự nào đó trở đi) đều hội tụ. 2. ˇ Dãy ˆ n ˙
hội tụ đến 0 vì @ε ą 0, DN P N, @n P N, pn ě N ùñ ˇ n ´ 0 “ n ă εq 1 1 1 ˇ ˇ N E 1 1 ˇ ˇ nếu chọn “ ˆ ε˙ ` . ˇ ˇ
Định lý 1.5: Giới hạn, nếu có, của dãy số là duy nhất.
Chứng minh: Ta chứng minh bằng phản chứng. Giả sử dãy punq có hai giới hạn là a và b
(a “b). Chọn ε “ 13 |b ´ a|. Theo định nghĩa, tồn tại hai số N1, N2 P N sao cho:
@n P N, #n ą N ùñ| 2
un ´ b | ă ε n N1 un a ε ą ùñ | ´ | ă
Đặt N “ maxpN1, N2q, ta có: |uN ´ a| ă ε và |uN ´ b| ă ε. 2
Suy ra |b ´ a| ď |b ´ uN | ` |uN ´ a| ă 2ε “
3 |b ´ a|. Mâu thuẫn. ■
Định nghĩa 1.5: Cho punq là dãy.
(a) Ta nói punq tiến tới `8 nếu và chỉ nếu @A ą 0, DN P N, @n P
N, pn ě N ùñ un ą Aq
(b) Ta nói punq tiến tới ´8 nếu và chỉ nếu @B ă 0, DN P N, @n P
N, pn ě N ùñ un ă Bq
Chú ý rằng dãy có giới hạn là `8 hoặc ´8 đều phân kỳ.
Định nghĩa 1.6: Dãy punq được gọi là bị chặn nếu và chỉ nếu tồn tại số M P R ` sao cho
@n P N, |un| ď M . Ta còn có khái niệm bị chặn trên và bị chặn dưới. Ta nói dãy thực
punq bị chặn trên nếu và chỉ nếu tồn tại một số A P R sao cho @n P N, un ď A. Ta nói
dãy thực punq bị chặn dưới nếu và chỉ nếu tồn tại một số B P R sao cho @n P N, un ě
B. Chú ý rằng dãy bi chặn khi và chỉ khi nó vừa bị chặn trên, vừa bị chặn dưới.
Định lý 1.6: Mọi dãy hội tụ đều bị chặn.
Chứng minh: Giả sử un ÝÑ a; tồn tại N P N sao cho: @n P N, pn ě N ùñ |un ´ a| ă 1q. n8
Vì vậy với mọi n P N sao cho n ą N , ta có: |un| ď |un ´ a| ` |a| ď 1 ` |a|. Đặt M “ maxp|u0| , . .
. , |uN | , 1 ` |a|q, ta suy ra @n P N, |un| ď M . ■ 11 lOMoARcPSD|45315597
Định lý 1.7: Cho punq, pvnq là hai dãy số; λ, a, b P R. Ta có: ÝÑ |ÝÑ| | ÝÑ ÝÑ ` v ÝÑ ` (a) un 8 a Ñ |un 8 a (c) un 8 a, vn 8 b ñ un n 8 a b n n n n n ÝÑ ô | ÝÑ ÝÑ ñ (b) u ÝÑ n 8 0 | ÝÑ un 8 0 (d) un 8 a, vn 8 b unvn 8 ab n n n n n (e) u ÝÑ ÝÑ “ ñ un a n 8 a, vn 8 b vn ÝÑ b 0 8 n n n Chứng minh:
(a) Sử dụng bất đẳng thức: ||un| ´ |a|| ď |un ´ a|.
(b) Sử dụng đẳng thức: ||un| ´ 0| “ |un| “ |un ´ 0|. ε ε
(c) Lấy ε ą 0 tùy ý. Khi đó sẽ có số N P N sao cho @n ą N ñ |un ´ a| ă 2 và |vn ´ b| ă 2 .
(d) Ta có: |unvn ´ ab| “ |unvn ´ avn ` avn ´ ab| ď |vn| ¨ |un ´ a| ` |a| ¨ |vn ´ b|. Vì pvnq hội
tụ nên nó bị chặn, nghĩa là có một số M ą 0 sao cho @n P N, |vn| ď M . Chọn M sao ε
cho |a| ă M . Khi đó với mọi ε sẽ có số N P N sao cho @n ą N, |un ´ a| ă 2M và ε M ε M ε
|vn ´ b| ă 2M. Vì vậy |unvn ´ ab| ă 2M ` 2M “ ε.
(e) Bây giờ với @n P N, v q ´ p
n ‰ 0, b ‰ 0, ta có: ˇ v v v n ´ b ˇ “ ˇ bvn ˇ “ ´ b vn ´ q ď n ` b ¨ n ˇun a ˇ ˇ bun ´ avn ˇ |bpun a a vn b | |un ´ a|
|a| |vn ´ b| | |¨| | | | | | | | ˇ ˇ ˇ ˇ ˇ ˇ ˇ ˇ b
Vì vn ÝÑ b nên DN1 : @n ą N1 ñ | vn
| |. Lấy ε ą 0 tùy ý, sẽ có hai số N2 , N3 P N | ą 2 n 8 sao cho: n N εb2 2 u a
ε |b| và n N v . Cuối cùng chọn @ ą ñ | n ´ | ă 4 @ ą 3 a ñ | | ¨ | n ´ b| ă 4
N “ maxpN1, N2, N3q, ta có ˇ | ´ b ˇ ă 4 | ¨ b `2“ε ■ ˇ un a ε b 2 ε
@ε ą 0, DN, @n ą N ñ ˇ ˇ | | ˇ ˇ vn ˇ
Định lý 1.8: Cho punq, pvnq là hai dãy số có giới hạn tương ứng là a, b P R. Giả sử
DN0, @n P N, pn ě N0 ùñ un ď vnq. Khi đó a ď b.
Chứng minh: Ta chứng minh bằng phản chứng. Giả sử a ą b. Do #
un ÝÑ a ðñ @ε ą 0, DN1 P N, @n P N, pn ě N1 ùñ |un ´ a| ă εq n8
vn ÝÑ b ðñ @ε ą 0, DN2 P N, @n P N, pn ě N2 ùñ |vn ´ b| ă εq n8
Chọn ε “ a ´3 b và N “ maxpN0, N1, N2q; ta có: vN ă b ` a ´3 b ă a ´ a ´3 b ă uN . Trái với giả thiết. ■ 12 lOMoARcPSD|45315597
Định lý 1.9 (Định lý kẹp): Cho punq, pvnq pwnq là ba dãy số thực sao cho: #
DN0 P N, @n P N, pn ě N0 ùñ un ď vn ď wnq
un ÝÑ a và wn ÝÑ a n8 n8
Khi đó pvnq cũng hội tụ đến a.
Chứng minh: Cho ε ą 0; vì punq và pwnq cùng hội tụ đến a nên tồn tại hai số N1, N2 P N
sao cho @n P N, pn ě N1 ñ |un ´ a| ă εq và @n P N, pn ě N2 ñ |wn ´ a| ă εq. Đặt N “
maxpN0, N1, N2q; ta có
@n P N, n ě N ùñ ´ε ă un ´ a ď vn ´ a ď wn ´ a ă ε ùñ |vn ´ a| ă ε
Vậy pvnq hội tụ đến a. ■
Định nghĩa 1.7: Cho punq là dãy số thực. Ta nói:
• punq là dãy tăng nếu và chỉ nếu @n P N, un ď un`1.
• punq là dãy giảm nếu và chỉ nếu @n P N, un ě un`1.
• punq là dãy đơn điệu nếu và chỉ nếu nó là dãy tăng hoặc là dãy giảm. Định lý 1.10:
(a) Mọi dãy tăng và bị chặn trên đều hội tụ.
(b) Mọi dãy giảm và bị chặn dưới đều hội tụ.
Chứng minh: (a) Giả sử pun q là dãy tăng và bị chặn trên. Tập A “ tun : n P Nu là một tập
con của R không rỗng và bị chăn trên. Vậy tồn tại cận trên đúng a “ suppAq. Cho ε ą 0.
Theo định nghĩa của cận trên đúng, tồn tại N P N sao cho: a ´ ε ă uN ă a. Vì punq tăng nên suy ra:
@n P N, pn ě N ñ un ě uN ñ a ´ ε ă un ă a ă a ` ε ñ |un ´ a| ă εq ùñ un ÝÑ a n8
(b) Áp dụng kết quả phần (a) đối với dãy p´unq. ■
Chúng ta xét một số ví dụ cơ bản sau:
Ví dụ 1.5: Xét dãy tqnu với 0 ď q ă 1. Đây là một dãy giảm và bị chặn dưới. Do đó có
một số a sao cho a “ lim qn “ lim qn`1 “ qa. Vì q ‰ 1 nên a “ 0. nÑ8 nÑ8 ?
Ví dụ 1.6: Xét dãy punq với un “ n n. Áp dụng bất đẳng thức Cauchy đối với n số 13 lOMoARcPSD|45315597
không âm ?n, ?n, 1, 1, . . . , 1 ta được: loooomoooon n´2 số 1 ? n ? n ? n 1 1 2 n n 2 2 2 1 ?n ` ` `¨¨¨` ` ´ 1 1 ď ď n “ n “ ` ? n n ´ n ÝÑ 8 n n Vậy ?n n
1 theo định lý kẹp. Trường hợp ?a n 1, a
0 được chứng minh tương ÝÑ ÝÑ p ą q tự. 8 8 n
Ví dụ 1.7: Xét dãy tunu với un “ 2n . Ta có un 1 u 1 n n ` 1 1 1 ´ n ´ “ 2n ` ˆ 2 ´ ˙ “ 2n lim un 1
nên dãy giảm và bị chặn dưới ñ Da “ nÑ8 un. Do un`1 “ 2
` 2n`1 , nên khi n Ñ 8 ta được a
a 2 và do đó a 0. Vậy n 0. n “ { “ n 2 ÝÑ nk 8 Tổng quát với a 1, k ą P N˚ ta có 0. n n a ÝÑ 8
Ví dụ 1.8: Xét giới hạn của dãy tỉ số hai đa thức theo n. Bằng cách chia tử và mẫu
cho nk với k “ maxpp, qq, ta có công thức sau: 0 nếu p q p p 1 a0n n a0 ă
q ` a1 q ´1 ` ¨ ¨ ¨ ` ap n $ nếu p q b0n b1n ´ bq ÝÑ8 ’ b0 “ ` `¨¨¨` & nếu p q ’ 8 ą % ?
Ví dụ 1.9: Khảo sát sự hội tụ của dãy punq với un “ b 2 ` 2`¨¨¨` 2 . Ta có n`1 “ ` n và ă 1 “
ă nên bằng loooooooooooomoooooooooooon ? adấu căn n u ? 2 u 0u 2 2
qui nạp, ta có thể chứng tỏ rằng
0 ă un ă 2 với mọi n P N˚. Do đó dãy punq bị chặn trên. Mặt khác 2 un 1 un ? ` un 2 un un ´ u 2 p2 ´ u n nqpun ` 1q 0 “ ? ? 2 “ ` ´ “ ` ´ ` un ` un 2 ` un ` un ą
do un ă 2. Vậy nó là dãy tăng; nên dãy hội tụ về số a : 0 ď a ď 2. Trong đẳng thức u ? lim 2 2 ?2 2 ` u ?
n cho n Ñ 8, ta được a “ 2 ` a ùñ a “ 2. Vậy nÑ8 b `¨¨¨` ` a loooooooooooomoooooooooooon n dấu căn
Ví dụ 1.10: Bây giờ ta xét một ví dụ cơ bản về một dãy số thực mà giới hạn của nó là
một số đóng vai trò cực kỳ quan trọng trong giải tích cũng như trong ứng dụng. Xét dãy 14 lOMoARcPSD|45315597 ˆ ˙n 1
số punq với un “ 1 ` n
. Ta có khai triển nhị thức Newton: un 1 n 1 npn ´ 1q 1
npn ´ 1qpn ´ 2q 1 ¨ ¨ “ ` ¨ n ` 1.2 n2 ` 1.2.3 n3 `¨¨¨`
npn ´ 1q . . . pn ´ k ` 1q 1
npn ´ 1q . . . pn ´ n ` 1q 1 ` 1.2 . . . k ¨nk `¨¨¨` 1.2 . . . n ¨ nn
“ 1 ` 1 ` 2! ˆ1 ´ n ˙
` 3! ˆ1 ´ n ˙ ˆ1 ´ n ˙ `¨ ¨` 1 1 1 1 2
`k! ˆ ´ n ˙ ˆ ´ n ˙ ` ¨ ¨ ¨ ` ´ n! ˆ n ˙ ˆ ´ n ˙ 1 1 1 ... 1 k ´ 1 1 1 1 ... 1 n ´ 1 1 1 1 1 1 1
ď 2 ` 2! ` 3! ` ¨ ¨ ¨ ` n ! ď 2 ` 2 2 ` 2 3 ` ¨ ¨ ¨ ` 2 n ă 3 Do đó
punq là dãy bị chặn trên. Mặt khác, xét n ` 1 số không âm: 1 ˙ 1 ˙ ˆ n ,..., ˆ
n , 1 và áp dụng bất đẳng thức Cauchy, ta được: 1 ` 1 `
loooooooooooooomoooooooooooooon n số ` d ˆ ` n ˙ ď
n ` 1 “ ` n ` 1 n n 1 1 n ` 1 ` 1 1 1 1
Do đó un “ ˆ 1 ` n ˙ n ˙ n ` 1 ď ˆ1 ` n ` 1
“ un`1; nên punq là dãy tăng. Theo định lý 1 1
1.4 nó hội tụ về một giới hạn hữu hạn và được ký hiệu là e. Vậy: 1 ˆ nÑ8 1 ` n
˙n “ e « 2, 718281828459045 . . . lim 1.5 Dãy con
Định nghĩa 1.8: Cho dãy số punq. Xét một dãy tăng nghiêm ngặt các số tự nhiên:
pnk q “ n0, n1, . . . , nk , . . . pn0 ă n1 ă ¨ ¨ ¨ ă nk ă . . . q
được xem như một tập con các chỉ số của dãy punq. Chú ý rằng @k P N, nk ą k. Khi
đó dãy punk q được gọi là dãy con của dãy punq.
Định lý 1.11: Nếu dãy punq hội tụ đến a, thì mọi dãy con của nó cũng hội tụ đến a.
Chứng minh: Cho ε ą 0, DN P N sao cho: @k P N, pk ě N ñ |uk ´ a| ă εq. Khi đó ta có:
ą N ñ |unk ´ a| ă εq. Vậy unk ÝÑ a. ■
@k P N, pk ě N ñ nk ą nN n8 15 lOMoARcPSD|45315597
Định lý 1.12: Cho punq là một dãy thực và a P R. Để punq hội tụ đến a, cần và đủ là
các dãy con pu2nq và pu2n`1q cũng hội tụ đến a.
Chứng minh: Cho ε ą 0, ñ DN1, N2 P N sao cho: @p P N, pp ą N1 ñ |u2p ´ a| ă ε q và @p
P N, pp ą N2 ñ |u2p`1 ´ a| ă εq. Đặt N “ maxp2N1, 2N2 ` 1q và xét n P N sao cho
n ą N . Tồn tại p P N sao cho n “ 2p hoặc n “ 2p ` 1. Nếu n “ 2p, ta có p ą N1 và |un ´ a| “ |
u2p ´ a| ă ε. Còn nếu n “ 2p ` 1, ta có p ą N2 và |un ´ a| “ |u2p`1 ´ a| ă ε. Điều này chứng tỏ: un ÝÑ a. ■ n8
Định lý 1.13 (Định lý Bolzano-Weierstrass): Từ mọi dãy thực bị chặn ta đều có thể
trích ra một dãy con hội tụ.
Ta không chứng minh định lý này. 1.6
Một số loại dãy thông thường
1.6.1 Dãy truy hồi tuyến tính cấp một
Xét dãy số thực punq sao cho tồn tại hai số a, b P R thoả:
@n P N, un`1 “ aun ` b, u0 cho trước
Ta dễ dàng tìm được công thức tổng quát sau:
un “ u0an ` bp1 ` a ` a2 ` ¨ ¨ ¨ ` an´1q (1.2) 1.6.2
Dãy truy hồi tuyến tính cấp hai
Xét dãy số thực punq sao cho tồn tại hai số a, b P R thoả:
@n P N, un`2 ` aun`1 ` bun “ 0,
u0, u1 cho trước
Lập phương trình k2 ` ak ` b “ 0 và được gọi là phương trình đặc trưng của dãy truy hồi
tuyến tính cấp hai. Chúng ta xét các trường hợp sau:
(a) Phương trình đặc trưng có hai nghiệm phân biệt k1 và k2. Khi đó ta có:
u “ C kn ` C kn n 1 1 2 2
trong đó các hằng số C1, C2 được xác định từ hệ phương trình (khi cho n “ 0 và n “ 1) " C1 ` C2 “ u0
k1C1 ` k2C2 “ u1
Cuối cùng ta đi đến công thức: ˙ ˆ k ´k ˙ u k1n ` 1 2 k2n (1.3) n “ ˆ k1´ k2 u k u 1 2 0 k1u0 u1 ´ ´ 16 lOMoARcPSD|45315597
(b) Phương trình đặc trưng có duy nhất nghiệm k1. Khi đó ta có: u n n´1
n “ C1k1 ` C2nk1
Bằng cách làm tương tự ta đi đến công thức: u n n´1
n “ u0k1 ` npu1 ´ k1u0qk1 (1.4)
(c) Phương trình đặc trưng có hai nghiệm phức liên hợp. Gọi modul và argument
của hai nghiệm phức là r và θ ‰ kπ. Khi đó ta có:
un “ rnpC1 cospnθq ` C2 sinpnθqq
Bằng cách làm tương tự, ta đi đến công thức: “ „ ` ˆ r sin θ ˙ u u 1 n rn u0 cos nθ
´ ru0 cos θ sin nθ (1.5)
Ví dụ 1.11: Xét dãy Fibonacci pFnq xác định như sau: # n “ N, F F n 2 n 1 Fn F0 0, F1 “ 1 @ P ` “ ` ` ? ?
Phương trình đặc trưng k2 k 1
0 có hai nghiệm thực k1 1 ` 5 và k2 1 ´ 5 . ´ ´ “ “ 2 “ 2
Từ công thức (1.3), ta có F1 ´ k2F0
1 , F1 ´ k1F0 1 và cuối cùng: k ´ “ ? ´ ? 1 k2 5 k 5 1 k2 “ 1 1 ? n 1 ? n ˙ F 5 ´ n “ ? ˆ `2 5 ? 5 ˆ 1 ´2 5 ˙
Ví dụ 1.12: Xét dãy punq xác định như sau: #
u0 “ 0, u1 “ 1
@n P N, un`2 “ 4un`1 ´ 4un
Phương trình đặc trưng k2 ´ 4k ` 4 “ 0 có nghiệm kép k1 “ 2, nên từ (1.4) ta có:
un “ n2n´1.
Ví dụ 1.13: Xét dãy punq xác định như sau:
# n “ N, u “ n 2 2un 1 4un u0 0, u1 1 @ P ` “ ´ ` ´ ?
Phương trình đặc trưng k2 ` 2k ` 4 “ 0 có hai nghiệm phức liên hợp k1,2 “ ´1 ˘ i 3 17 lOMoARcPSD|45315597 2π
với r “ 2 và θ “ 3 , nên từ (1.5) ta có: u 2n 1 ´ ru0 cos θ 1 , và un sin 2nπ r sin θ “ ?3 “ ? 3 3 Bài tập Câu 1. Cho n N˚, x , x , . . . , x
Rn. Với mọi k N˚ ta ký hiệu S n xk . Giả sử S2 S3 S4. Chứng minh rẳng i 1; n, xi 0,1 . P p 1 2 nq P P k “ ř i 1 i “ “ “ @ “ P t u Câu 2. Chứng minh rằng @ P ˚ @p q P p `q 2, ? ` ď ? ` ? . n N , x, y R n x y x n y n
Câu 3. Chứng minh rằng @x, y, z P r0, 1s, 1
minpap1 ´ bq, bp1 ´ cq, cp1 ´ aqq ď 4 $
Câu 4. Giải các hệ phương trình sau với ẩn là x, y, z P R: “ 1 $ (b) y ` 2xz “ y 8z 2 (c) yz ` x “ (a) 1 ` 1 $ x y z
x2 ` 2yz “x xz y 7z ’ 2 ’ ` “
& x ` y “ z &z &x xy y2 1 ’ ` 2xy z “ ? x y x y 56 ’ `y `z “ 12 %x2 % (d) # x ` y y (e) ? 30 2 ` x “ %
#x ` y ` x ` y “ p ´ q “ ` ´ ` ´ “ 3
Câu 5. Chứng minh @x P R, x6 ´ x5 ` x4 ´ x3 ` x2 ´ x ` 4 ą 0.
Câu 6. Chứng minh các bất đẳng thức sau đây và khảo sát các trường hợp xảy ra đẳng thức:
(a) @a, b, c P R, a2 ` b2 ` c2 ě ab ` ac ` bc
(b) @a, b, c P R, abcpa ` b ` cq ď a2b2 ` a2c2 ` b2c2 ď a4 ` b4 ` c4
(c) @a, b, c P R ˚`, 1 b ` 1 b 1 c ` 1 c 1 a ě 3 a 1 1 abc p ` q p ` q p ` q ` P #xy` yz xz3 ´ ď ď 3
Câu 7. Cho x, y, z R sao cho: x y ` z “ 5 . Chứng minh rằng 1 z 13 . ` ` “
Câu 8. Tìm suppEq và inf pEq với (a) E 1 1 n , n N˚ (b) E 1 p´1qn n2 , n N˚
“ " 2n ` p´n q P * “ " ` n ´ P *
Câu 9. Chứng minh rằng:
(a) @x, y P R, x ď y ñ Epxq ď Epyq.(c) @x, y P R, Epx ` yq ´ Epxq ´ Epyq P t0, 1u.
(b) @x P R ´ Z, Ep´xq “ ´Epxq ´ 1. (d) @x P R, @α P Z, Epx ` αq “ Epxq ` α. 18 lOMoARcPSD|45315597
Câu 10. Chứng minh rằng: @n P Z, ´ ¯ 3 ` ˆ 6 ˙ ` ˆ 6 ˙ “ ´2 ¯ ` ˆ 6 ˙ n E E n ` 2 E n ` 4 E n E n ` 3
Câu 11. Chứng minh rằng: @n P N, E ˆˆ 2 n ˙ ą ˆ2 n ˙ ˙ ´ 1 ` 2 . n`1 3 3 1
Câu 12. Cho a, b
R2, un , vn là hai dãy thỏa n P N, un a, vn b và un vn p q Pp q p q @ ď ď p ` q ÝÑ a
b . Chứng minh rằng un a và vn b. n 8 p ` q ÝÑ ÝÑ n 8 n 8 n 1
Câu 13. Chứng minh rằng dãy punq xác định bởi: un “ k“1 k2 hội tụ. ř
Câu 14. Tính giới hạn của dãy punq cho bởi: n ? (a) u 1 “ k k 1 (e) π n u n2 ` 1 ř n n n n “ sin ` ˘ k“ 1 p ` q n 1 (f) un (b) u ˚ n “
? a ` b ` c , pa, b, c P R` q
“ k1 n2? 2k (c) un p´ q ` ř n 1 n n “ ` “ 2 3 (g) n2 “ ? p´2qn`1 ` 3n`1 un k 1 n2 2k (d) un “ ? 3 ` sin n ř ` n “ u
Câu 15. Giả sử un q là một dãy có phần tử thuộc R˚ sao cho n`1 ÝÑ `8 . Chứng minh p ` un 8 rằng ?un . n n ÝÑ `8 n 8 x2
Câu 16. Sử dụng bất đẳng thức @x P R`, x ´ 2 ď lnp1 ` xq ď x, chứng minh sự tồn tại của giới hạn n ˆ 1
k ˙ và tính giới hạn này. n8 k“1 1 ` ` n n2 lim ś m ` n
Câu 17. Cho dãy un n, m p q sao cho: @
P N˚, 0 ď um n ď
. Chứng minh rằng un ÝÑ 0. ` mn n 8 p q
" @n P N, un`1 “ un ` p´1q n
Câu 18. Khảo sát dãy un xác định bởi: u0 P R 2 n . p q
" @n P N, un`2 “ ´un`1 ` un
Câu 19. Cho dãy un xác định bởi: u0 “ 1
. Xác định u1 sao cho tất
cả các số hạng của dãy đều dương. # u0, u1 P R u
Câu 20. Tìm số hạng tổng quát của dãy punq xác định bởi:
@n P N, un`2 “ n`1 ` un và 2
khảo sát sự hội tụ của chúng.
HƯỚNG DẪN VÀ ĐÁP SỐ n
1. Xét tổng ř px2i ´ xiq2