Giáo trình chương 1: Tích phân bội | Đại học Kỹ thuật - Công nghệ Cần Thơ
Giáo trình chương 1: Tích phân bội | Đại học Kỹ thuật - Công nghệ Cần Thơ. Tài liệu được biên soạn dưới dạng file PDF gồm 32 trang, giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem!
Môn: Giải tích 2 (CT)
Trường: Đại học Kỹ thuật - Công nghệ Cần Thơ
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
MỤC LỤC Chương 1. Tích phân bội 1
1.1 Tích phân hai lớp . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1.1 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1.2 Các tính chất . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.1.3 Cách tính tích phân kép . . . . . . . . . . . . . . . . . . . . . 4
1.1.4 Tích phân kép trong tọa độ cực . . . . . . . . . . . . . . . . 9
1.2 Tích phân ba lớp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.2.1 Tích phân của hàm ba biến . . . . . . . . . . . . . . . . . . . 12
1.2.2 Các tính chất . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
1.2.3 Tích phân ba lớp trên một vùng giới hạn chung . . . . . . . 15
1.2.4 Tích phân ba lớp trong tọa độ cong . . . . . . . . . . . . . . 20
1.3 Ứng dụng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
1.3.1 Ứng dụng của tích phân kép . . . . . . . . . . . . . . . . . . 23
1.3.2 Ứng dụng của tích phân bội ba . . . . . . . . . . . . . . . . . 29 i Chương 1. Tích phân bội 1.1 Tích phân hai lớp 1.1.1 Định nghĩa
Tình huống thực tế: Chúng tôi bắt đầu bằng cách xem xét không gian
trên một khu vực hình chữ nhật R. Xét một hàm liên tục f(x, y) ≥ 0 của hai
biến xác định trên hình chữ nhật đóng R :
R = [a, b] × [c, d] = (x, y) ∈ R2 | a ≤ x ≤ b, c ≤ y ≤ d .
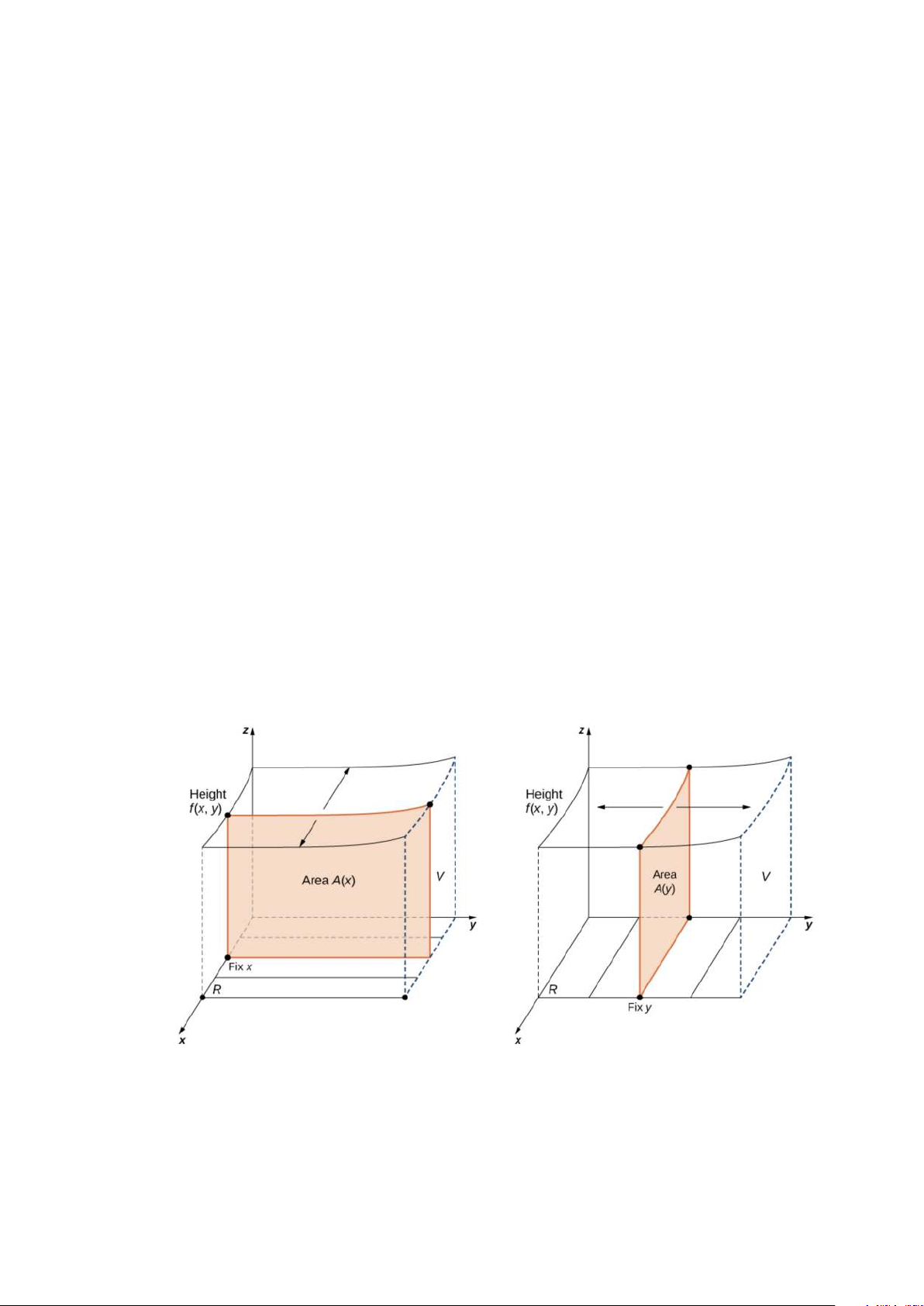
Gọi S là khối rắn nằm trên R và nằm dưới đồ thị của f (Hình 1.1). Đáy của vật
rắn là hình chữ nhật R trong mặt phẳng Oxy. Chúng ta muốn tìm thể tích V của vật rắn S.
Hình 1.1: Đồ thị của f trên miền chữ nhật R.
Bây giờ, chúng ta chia R thành các hình chữ nhật nhỏ Rij, mỗi hình chữ
nhật có diện tích ∆A và có các cạnh ∆x và ∆y (Hình 1.2). Chúng ta làm điều 1
này bằng cách chia khoảng [a, b] thành các khoảng con m và chia khoảng [c, d]
thành các khoảng con n. Do đó, b − a d − c ∆x = , ∆y = và ∆A = ∆x∆y. m n
Hình 1.2: Miền chữ nhật R được chia nhỏ thành R với diện tích ij ∆A.
Hình 1.3: Hình hộp chữ nhật nhỏ bên trên R có chiều cao là ij f (x∗ , y∗ ). ij ij
Thể tích của một hình hộp chữ nhật nhỏ bên trên R ij là f x∗ij, y∗ij ∆A trong đó x∗
là một điểm mẫu tùy ý trong mỗi R ij , y∗ ij
ij như thể hiện trong Hình 1.3. 2
Sử dụng cùng một ý tưởng cho tất cả các hình chữ nhật con, chúng ta thu
được thể tích gần đúng của khối S là m n X X V ≈ f x∗ ij , y∗ ij ∆A. i=1 j=1
Tổng này được gọi là tổng Riemann kép và có thể được sử dụng để tính gần
đúng giá trị thể tích của chất rắn. Ở đây, tổng kép có nghĩa là đối với mỗi hình
chữ nhật con, chúng ta đánh giá hàm tại điểm đã chọn, nhân với diện tích của
mỗi hình chữ nhật, rồi cộng tất cả các kết quả.
Như chúng ta đã thấy trong trường hợp một biến, chúng ta có được giá trị
xấp xỉ tốt hơn với khối lượng thực tế nếu m và n trở nên lớn hơn. m n X X V = lim f x∗ ij , y∗ ij ∆A. m,n→∞ i=1 j=1
Lưu ý rằng, nếu tổng tiến tới giới hạn thì nó là thể tích của vật rắn trên miền
R. Bây giờ chúng ta đã sẵn sàng để định nghĩa tích phân kép.
Định nghĩa 1 Tích phân kép của hàm f(x, y) trên miền hình chữ nhật R trong
mặt phẳng Oxy được định nghĩa là m n Z Z X X f (x, y)dA = lim f x∗ ij , y∗ ij ∆A. m R →∞ i=1 j=1
Nếu f(x, y) ≥ 0, thì thể tích V của vật rắn S, nằm trên R trong mặt phẳng Oxy
và nằm dưới đồ thị của f, là tích phân kép của hàm f(x, y) trên hình chữ nhật
R. Nếu hàm luôn âm, thì tích phân kép có thể được coi là một thể tích "có dấu"
theo cách tương tự như cách chúng ta đã xác định vùng có dấu không âm. 1.1.2 Các tính chất
Giả thiết các tích phân nói dưới đây là tồn tại và (D), (D1) , (D2) là các miền
đóng, bị chặn và có diện tích trong Oxy.
(a) RR kdxdy = k · dt(D), ∀k ∈ R; D
(b) RR [f(x, y) ± g(x, y)]dxdy = RR f(x, y)dxdy ± RR g(x, y)dxdy; D D D
(c) RR kf(x, y)dxdy = k RR f(x, y)dxdy; D D
(d) Nếu f(x, y) ≤ g(x, y) trên (D) thì RR f(x, y)dxdy ≤ RR g(x, y)dxdy; D D 3 (e) RR f (x, y)dxdy |f(x, y)|dxdy; D ≤ RRD
(f) Nếu D = D1 ∪ D2 và dt (D1 ∩ D2) = 0, dt(D) = dt (D1) + dt (D2) thì Z Z Z Z Z Z f (x, y)dxdy = f (x, y)dxdy + f (x, y)dxdy. D D1 D2
1.1.3 Cách tính tích phân kép
Định lý 1 (Định lý Fubini) Giả sử rằng f(x, y) là một hàm hai biến liên tục
trên một miền hình chữ nhật
R = (x, y) ∈ R2 | a ≤ x ≤ b, c ≤ y ≤ d .
Sau đó, chúng ta thấy từ Hình 1.4 rằng tích phân kép của f trên vùng bằng với tích phân lặp, Z Z Z Z Z b Z d Z d Z b f (x, y)dA = f (x, y)dxdy = f (x, y)dydx = f (x, y)dxdy. R R a c c a (1.1.1)
Tổng quát hơn, Định lý Fubini đúng nếu f bị chặn trên R và f chỉ không liên
tục trên một số hữu hạn các đường cong liên tục. Nói cách khác, f phải có thể tích hợp được trên R.
Hình 1.4: Thứ tự tính tích phân theo công thức (1.1.1) 4
Ví dụ 1 Cho D = {(x, y), 0 ≤ x ≤ 1, −2 ≤ y ≤ 2}. Tính RR x2 + y dxdy. D Giải. Z 1 ÇZ 2 å Z 2 ÇZ 1 å I1 = x2 + y dy dx I2 = x2 + y dx dy 0 −2 −2 0 2 1 Z 1 Å y2 ã Z 2 Å ã x3 = yx2 + dx = + xy dy 3 0 2 −2 −2 0 Z 1 Å 22 − (−2)2 ã Z 2 Å 13 − 03 ã = (2 − (−2))x2 + dx = + (1 − 0)y dxy 3 0 2 −2 Z 1 4 Z 2 1 4 = 4x2dx = . = y + dy = . 3 3 0 3 −2
Ví dụ 2 Tính RR x ln ydxdy với D = {(x, y), 0 ≤ x ≤ 4, 1 ≤ y ≤ e}. D Ví dụ 3 Tính I = RR
1 − 6xy2 + 2x dxdy, D = [0, 2] × [−1, 1]. D 5 Định nghĩa 2
(a) Một vùng D trong mặt phẳng Oxy là Loại I nếu nó nằm giữa hai đường
thẳng đứng và đồ thị của hai hàm số liên tục g1(x) và g2(x) (Hình 1.5)
D = {(x, y) | a ≤ x ≤ b, g1(x) ≤ y ≤ g2(x)} .
(b) Miền D trong mặt phẳng Oxy là loại II nếu nó nằm giữa hai đường thẳng
nằm ngang và đồ thị của hai hàm số liên tục h1(y) và h2(y) (Hình 1.6)
D = {(x, y) | c ≤ y ≤ d, h1(y) ≤ x ≤ h2(y)} .
Hình 1.5: Miền D trong mặt phẳng Oxy loại I.
Hình 1.6: Miền D trong mặt phẳng Oxy là loại II. 6
Định lý 2 (Định lý Fubini mạnh)
(a) Đối với hàm số f(x, y) liên tục trên miền D loại I, ta có Z Z Z Z Z b ñZ g ô 2(x) f (x, y)dA = f (x, y)dydx = f (x, y)dy dx. (1.1.2) D D a g1(x)
(b) Tương tự, đối với hàm số f(x, y) liên tục trên miền D loại II, ta có Z Z Z Z Z d ñZ h ô 2(y) f (x, y)dA = f (x, y)dxdy = f (x, y)dx dy. (1.1.3) D D c h1(y)
Ví dụ 4 Cho D = (x, y), −1 ≤ x ≤ 1, 2x2 ≤ y ≤ 1 + x2 . Tính RR (x + 2y)dxdy. D Giải. 1+x2 Z 1 ÇZ 1+x2 å Z 1 I = (x + 2y)dy dx = yx + y2 dx −1 2x2 −1 2x2 Z 1 Ä =
x 1 + x2 − x 2x2 + 1 + x22 − 2x22ä dx −1 Z 1 79 =
−3x4 − x3 + 2x2 + x + 1 dx = . 60 −1
Ví dụ 5 Tính tích phân hai lớp I = R 1 R 4−2x(2y + 1)dydx. 0 2
Ví dụ 6 Tính tích phân hai lớp I = RR x3(y − 1)dxdy với D là miền giới hạn D bởi √ x = y và x = y2. 7 Ví dụ 7 Cho √
D = {(x, y), y/2 ≤ x ≤ y, 0 ≤ y ≤ 4}. Tính RR x2 + y2 dxdy. D Giải. √ √ y Z 4 ÇZ y å Z 4 Å x3 ã I = x2 + y2 dx dy = + xy2 dy 0 y/2 0 3 y/2 Z 4 Ç √y3 å y3 √ y = − + yy2 − y2 dy 0 3 3.23 2 Z 4 Å y3 y3/2 ã 216 = −13 + y5/2 + dy = . 0 24 3 35
Ví dụ 8 Tính tích phân hai lớp I = RR
y2 + x2y − y dxdy với D là miền giới D
hạn bởi y = 0, y = 2x và x = 2.
Ví dụ 9 Tính tích phân hai lớp I = RR xdxdy với D là miền giới hạn bởi D y = 4x − x2 và x + y = 6. 8
1.1.4 Tích phân kép trong tọa độ cực
Định lý 3 (Định lý Fubini) Giả sử rằng f(r, θ) là một hàm hai biến liên tục trên một miền
R = (r, θ) ∈ R2 | r1 ≤ r ≤ r2, α ≤ θ ≤ β . Khi đó, Z Z Z Z Z r2 Z β Z β Z r2 f (r, θ)dA = f (r, θ)(rdr)dθ = f (r, θ)dθ(rdr) = f (r, θ)(rdr)dθ. R R r1 α α r1
Nhận xét 1 Lưu ý rằng biểu thức cho dA được thay thế bằng rdrdθ khi làm việc
trong tọa độ cực. Một cách khác để xem xét tích phân kép cực là thay đổi tích
phân kép trong tọa độ vuông góc bằng cách thay thế. Khi hàm f được cho dưới
dạng x và y, việc sử dụng x = r cos θ, y = r sin θ, dA = (rdr)dθ. sẽ thay đổi nó thành Z Z Z Z f (x, y)dA =
f (r cos θ, r sin θ)(rdr)dθ. R R
Ví dụ 10 Tính tích phân RR 3xdA trên vùng R = {(r, θ) | 1 ≤ r ≤ 3, 0 ≤ θ ≤ π}. R Giải.
Hình 1.7: Phác thảo vùng R = {(r, θ) | 1 ≤ r ≤ 3, 0 ≤ θ ≤ π}.
Ví dụ 11 Phác thảo vùng R = (r, θ) | 1 ≤ r ≤ 2, −π và tính RR xdA. 2 ≤ θ ≤ π 2 R 9
Ví dụ 12 Tính I = RR e−x2−y2dxdy, (D) là hình tròn x2 + y2 ≤ 1. D
Ví dụ 13 Tính I = RR p4 − x2 − y2dxdy, (D) giới hạn bởi nửa trên hình tròn D x2 + y2 − 2x = 0 và y = 0.
Ví dụ 14 Tính tích phân I = RR xy2dxdy, (D) giới hạn bởi phía ngoài đường D
tròn x2 + y2 − 2y = 0 và phía trong đường tròn x2 + y2 − 4y = 0. 10 Ví dụ 15 Tính » I = RR 1 − x2
dxdy, (D) giới hạn bởi Elip x2 + y2 = 1. D a2 − y2 b2 a2 b2
Giải. Đổi sang tọa độ cực suy rộng ® x = arcos θ y = br sin θ
⇒ 0 ≤ r ≤ 1, 0 ≤ θ ≤ 2π, J = abr. Nên Z 2π Z 1 p I = ab dϕ 1 − r2rdr 0 0 Z 2π Z 1 p = ab dφ · 1 − r2rdr. 0 0 Hay I = 2πab. 3
Bài tập 1 Tính các tích phân 2 lớp trên miền hình chữ nhật sau: (a) I = RR
x2 dxdy, (D) = [0, 1] × [0, 1]. D 1+y2
(b) I = RR xy · ex+ydxdy, (D) = [0, 1] × [1, 3]. D
(c) I = RR (x + y)dxdy, (D) = [1, 2] × [1, 4]. D
(d) I = RR x(sin x + cos y)dxdy.(D) = [0, π] × 0, π D 2
Bài tập 2 Tính các tích phân 2 lớp sau:
(a) I = RR sin(x + y)dxdy, (D) giới hạn bởi các đường: y = 0, y = x, x + y = π. D 2 (b) √
I = RR x2ydxdy, (D) giới hạn bởi các đường: y = 0, y = 2ax − x2, a > 0. D
(c) I = RR (x + y)dxdy, (D) giới hạn bởi các đường x = 0, y = 0, x + y = 3. D
(d) I = RR x2(y − x)dxdy, (D) giới hạn bởi các đường: y = x2, x = y2. D
(e) I = RR xy2dxdy, (D) giới hạn bởi các đường: y = x, y = x2. D
(f) I = RR xydxdy, (D) giới hạn bởi các đường: xy = 1, x + y = 5. D 2 (g) I = RR
x2 + y2 dxdy, (D) giới hạn bởi: y = x, y = x + 1, y = 1, y = 3. D (h) √
I = RR xdxdy, (D) giới hạn bởi các đường: y = x, y = 2 − x2, y = 0. D 11 1.2 Tích phân ba lớp
1.2.1 Tích phân của hàm ba biến
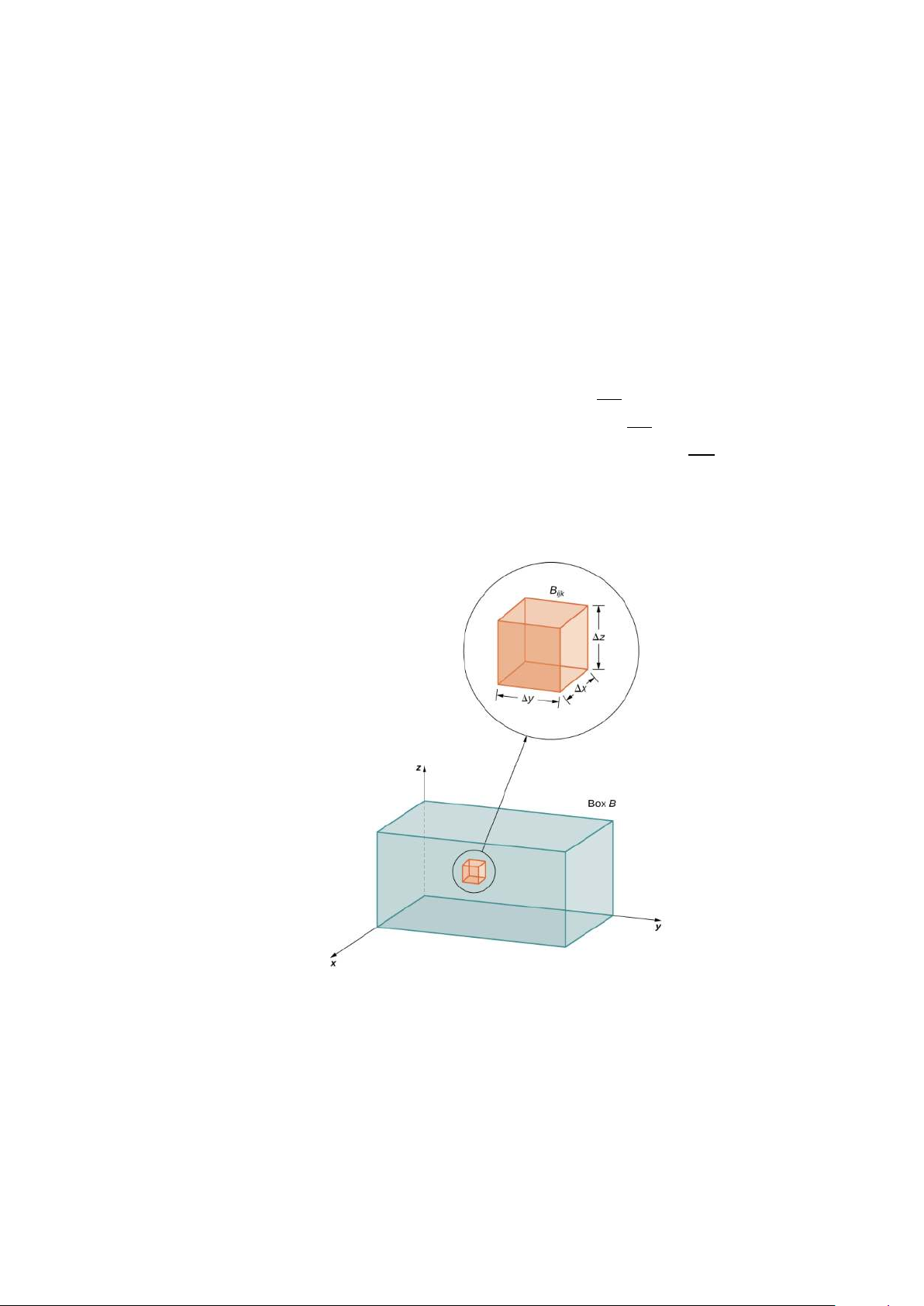
Định nghĩa 3 Chúng ta có thể định nghĩa một hình hộp chữ nhật B trong R3 là
B = {(x, y, z) | a ≤ x ≤ b, c ≤ y ≤ d, e ≤ z ≤ f}.
Chúng ta làm theo quy trình tương tự như những gì chúng ta đã làm trong
Tích phân kép trên Vùng hình chữ nhật. Chúng ta chia khoảng [a, b] thành f các khoảng con [xi , chia khoảng [c, d] thành
−1, xi] có độ dài bằng nhau ∆x = b−a l m các khoảng con [yi và chia khoảng [e, f]
−1, yi] có độ dài bằng nhau ∆y = d−c m thành n các khoảng con [zi . Khi đó, hộp
−1, zi] có độ dài bằng nhau ∆z = f −e n
chữ nhật B được chia thành các hộp con như trong Hình 1.8.
Bijk = [xi−1, xi] × [yi−1, yi] × [zi−1, zi] .
Hình 1.8: Một hộp chữ nhật trong R3 được chia thành các hộp con. Đối với mỗi ä
i, j và k, hãy xem xét một điểm mẫu Äx∗ , y∗ , z∗ trong mỗi ijk ijk ijk
ô phụ Bijk. Chúng ta thấy rằng thể tích của nó là ∆V = ∆x∆y∆z. Lập tổng Riemann nhân ba l m n X X X f x∗ ijk, y∗ ijk, z∗ ijk ∆x∆y∆z. i=1 j=1 k=1 12
Định nghĩa 4 Chúng ta định nghĩa tích phân ba theo giới hạn của tổng Rie-
mann nhân ba, như chúng ta đã làm đối với tích phân kép theo giới hạn của tổng
Riemann nhân đôi. Sự định nghĩa Tích phân ba của hàm f(x, y, z) trên hình hộp
chữ nhật B được định nghĩa là l m n Z Z Z X X X lim f x∗ ijk, y∗ ijk, z∗ ijk ∆x∆y∆z = f (x, y, z)dV l,m,n→∞ i=1 j=1 B k=1
nếu giới hạn này tồn tại. 1.2.2 Các tính chất
Giả thiết các tích phân dưới đây là tồn tại, các tập (V), (V1) , (V2) đóng, bị
chặn và có thể tích trong Oxyz
(a) RRR Cdxdydz = C · tt(V), ∀C ∈ R V
(b) RRR (f ± g)dxdydz = RRR f(x, y, z)dxdydz ± RRR g(x, y, z)dxdydz V V V
(c) RRR Cf(x, y, z)dxdydz = C RRR f(x, y, z)dxdydz, ∀C ∈ R V V
(d) Nếu V = V1 ∪ V2, tt (V1 ∩ V2) = 0 và tt (V ) = tt (V1) + tt (V2). Thì Z Z Z Z Z Z Z Z Z f (x, y, z)dxdydz = f dxdydz + f dxdydz. V V1 V2
(e) Nếu f(x, y, z) ≤ g(x, y, z) trên (V). Z Z Z Z Z Z Thì f (x, y, z)dxdydz ≤ g(x, y, z)dxdydz. V V (f) RRR f (x, y, z)dxdydz |f(x, y, z)|dxdydz. V ≤ RRRV
(g) Nếu m ≤ f(x, y, z) ≤ M trên (V). Thì ∃µ ∈ (m, M) sao cho 1 Z Z Z µ = f (x, y, z)dxdydz. tt(V ) V
Đặc biệt: Nếu f(x, y, z) liên tục trên (V). Thì tồn tại M0 (x0, y0, z0) ∈ (V) sao cho: 1 Z Z Z f (x0, y0, z0) = f (x, y, z)dxdydz. tt(V ) V 13
Định lý 4 (Định lý Fubini cho tích phân ba lớp) Nếu f(x, y, z) liên tục trên một
hình hộp chữ nhật B = [a, b] × [c, d] × [e, f], thì Z Z Z Z f Z d Z b f (x, y, z)dV = f (x, y, z)dxdydz. B e c a
Tích phân này cũng bằng với bất kỳ trong số năm thứ tự có thể có khác cho tích phân bộ ba lặp.
Ví dụ 16 Tính R z=1 R y=4 R x=5 x + yz2 dxdydz. z=0 y=2 x=−1 Giải. Ta có: Z z=1 Z y=4 Z x=5 x + yz2 dxdydz z=0 y=2 x=−1 Z z=1 Z y=4 ï x2 ò x=5 = + xyz2 dydz x=−1 z=0 y=2 2 Z z=1 Z y=4 = 12 + 6yz2 dydz z=0 y=2 Z z=1 ñ y=4ô y2 = 12y + 6 z2 dz z=0 2 y=2 Z z=1 = 24 + 36z2 dz z=0 ï z3 òz=1 = 24z + 36 . 3 z=0
Ví dụ 17 Tính RRR x2yzdV, trong đó B
B = {(x, y, z) | −2 ≤ x ≤ 1, 0 ≤ y ≤ 3, 1 ≤ z ≤ 5}.
Ví dụ 18 Tính RRR z sin x cos ydV, trong đó B n 3π o
B = (x, y, z) | 0 ≤ x ≤ π, ≤ y ≤ 2π, 1 ≤ z ≤ 3 . 2 14
1.2.3 Tích phân ba lớp trên một vùng giới hạn chung
Bây giờ chúng ta mở rộng định nghĩa của tích phân ba lớp để tính tích phân
ba lớp trên một vùng giới hạn tổng quát hơn E trong R3. Các vùng giới hạn
chung mà chúng ta sẽ xem xét có ba loại. Đầu tiên, gọi D là vùng giới hạn là
hình chiếu của E lên mặt phẳng Oxy. Giả sử vùng E trong R3 có dạng
E = {(x, y, z) | (x, y) ∈ D, u1(x, y) ≤ z ≤ u2(x, y)} .
Đối với hai hàm z = u1(x, y) và z = u2(x, y), sao cho u1(x, y) ≤ u2(x, y) với mọi
(x, y) trong D như thể hiện trong hình dưới đây.
Định lý 5 Tích phân ba của một hàm liên tục f(x, y, z) trên một vùng ba chiều tổng quát
E = {(x, y, z) | (x, y) ∈ D, u1(x, y) ≤ z ≤ u2(x, y)}
trong R3, trong đó D là hình chiếu của E lên mặt phẳng Oxy, là Z Z Z Z Z ñZ u ô 2(x,y) f (x, y, z)dV = f (x, y, z)dz dA. E D u1(x,y) 15
Định lý 6 Nếu E = {(x, y, z) | a ≤ x ≤ b, g1(x) ≤ y ≤ g2(x), u1(x, y) ≤ z ≤ u2(x, y)} (xem Hình 1.9) thì Z Z Z Z b Z g2(x) Z u2(x,y) f (x, y, z)dV = f (x, y, z)dzdydx E a g1(x) u1(x,y) Hình 1.9:
Ví dụ 19 Tính tích phân ba lớp Z 1 Z 2x Z x+y I = ydzdydx. 0 x − 0 2 16
Định lý 7 Nếu E = {(x, y, z) | c ≤ y ≤ d, h1(y) ≤ x ≤ h2(y), u1(x, y) ≤ z ≤ u2(x, y)} (xem Hình 1.10) thì Z Z Z Z c Z h2(y) Z u2(x,y) f (x, y, z)dV = f (x, y, z)dzdydx E c h1(y) u1(x,y) Hình 1.10:
Ví dụ 20 Tính tích phân ba lớp Z 1 Z 1−y Z 1−x−y I = (1 − x − y − z)dzdydx 0 0 0 17
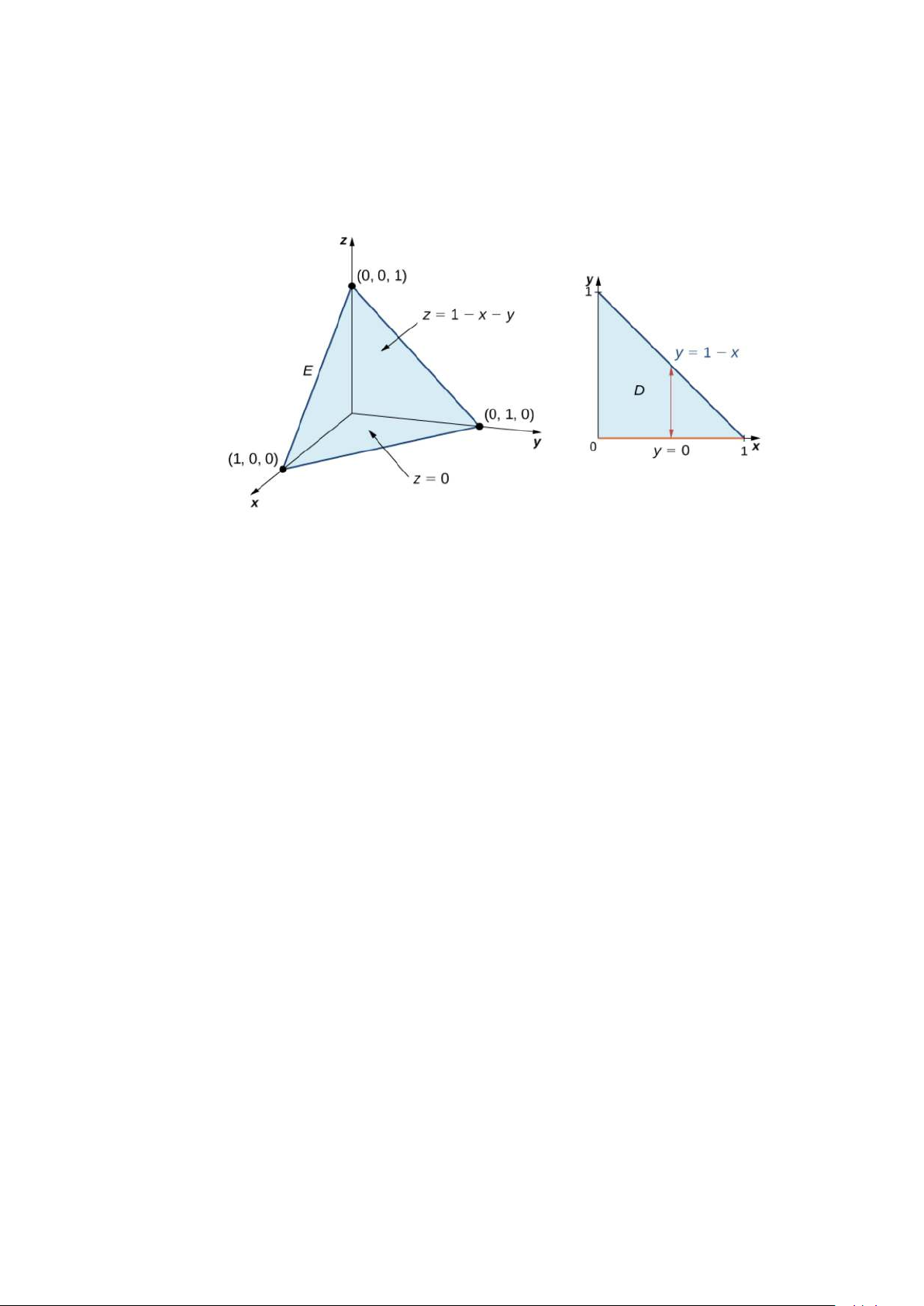
Ví dụ 21 Tính tích phân ba lớp của hàm số f(x, y, z) = 5x − 3y trên tứ diện
giới hạn bởi các mặt phẳng x = 0, y = 0, z = 0, x + y + z = 1. 18
Bài tập 3 Tính tích phân ba lớp Z Z Z 1 I = dxdydz (1 + x + y + z)3 V
với V là miền giới hạn bởi các mặt x = 0, y = 0, z = 0, x + y = 1 và x + y − z = 0.
Bài tập 4 Tính I = R 1 R 0 R y2 dzdydx 0 −1 0
Bài tập 5 Tính I = R 2 R x R xy zdzdydx. 0 0 0 Bài tập 6 Tính Z Z Z I = x2 + y2 dxdydz V
với V xác định bởi 0 ≤ x ≤ 1; 0 ≤ y ≤ 1; và 0 ≤ z ≤ 1. Bài tập 7 Tính Z Z Z 1 I = dxdydz V (1 + x + y + z)3
với V là miền giới hạn bởi mặt x + y + z = 1 và các mặt tọa độ. Bài tập 8 Tính Z Z Z I = (2x + 3y − z)dxdydz V
với V là miền giới hạn bởi z = 0, z = 3, x = 0, y = 0 và x + y = 2. Bài tập 9 Tính Z Z Z I = x2dxdydz V
với V là khối tứ diện có các đỉnh là (0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 0, 0). Bài tập 10 Tính Z Z Z I = xyzdxdydz V
với V là khối tứ diện có các đỉnh là (0, 0, 0), (0, 0, 2), (0, 2, 0), (1, 1, 0). 19
1.2.4 Tích phân ba lớp trong tọa độ cong
Định nghĩa 5 Hệ tọa độ cong trong tích phân ba lớp bao gồm tọa độ trụ và tọa độ cầu.
(a) Trong tọa độ trụ, quan hệ giữa ba biến cũ x, y, z và ba biến mới r, θ, z được cho bởi công thức x = r cos θ, y = r sin θ, z = z .
Kết quả là ta tìm được tích phân mới có dạng Z Z Z Z Z Z f (x, y, z)dxdydz =
r · f(x(r, θ), y(r, θ), z)dzdrdθ (1.2.1) Dxyz Drθz
(b) Trong tọa độ cầu, quan hệ giữa ba biến cũ x, y, z và ba biến mới ρ, θ, φ được cho bởi công thức x = ρ cos θ sin ϕ, y = ρ sin θ sin ϕ, z = ρ cos ϕ .
Kết quả là ta tìm được tích phân mới có dạng Z Z Z Z Z Z f (x, y, z)dxdydz =
ρ2 sin φ · f(ρ, θ, ϕ)dρdθdϕ. (1.2.2) Dxyz Dρθϕ
Vế phải của các phương trình (1.2.1), (1.2.2) được tính theo phương pháp tính
tích phân ba lớp thông thường.
Ví dụ 22 Tính thể tích hình V xác định bởi x2 + y2 ≤ 1 và 1 ≤ z ≤ 2. 20
Ví dụ 23 Tính tích phân ba lớp Z Z Z p I = x2 + y2dxdydz V
với V là miền giới hạn bởi y2 + x2 = z2 và z = 1. 21
Bài tập 11 Tính các tích phân 3 lớp trên miền hình hộp chữ nhật sau:
(a) I = RRR x4y2zdzdydz, trong đó: (V) = [0, 1] × [1, 3] × [4, 8]. V
(b) I = RRR (1 − x − y − z)dxdydz, trong đó: (V) = [0, 1] × [2, 5] × [2, 4]. V (c) I = RRR
xy2 + z3 dxdydz, trong đó (V) = [0, 1] × [0, 1] × [0, 2]. V
Bài tập 12 Tính các tích phân 3 lớp sau:
(a) I = RRR (1 − x − y − z)dxdydz. Trong đó (V) giới hạn bởi các mặt phẳng: V
x = 0, y = 0, z = 0, x + y + z = 1.
(b) I = RRR xdxdydz, (V) xác định bởi x, y ≥ 0, x2 + y2 ≤ z ≤ 4. V 22 1.3 Ứng dụng
1.3.1 Ứng dụng của tích phân kép
Định nghĩa 6 Nếu (D) là hình phẳng trong mặt phẳng Oxy thì Z Z dt(D) = dxdy. (1.3.1) D Ví dụ 24
(a) Tìm diện tích của vùng R = {(x, y) | 0 ≤ x ≤ 3, 0 ≤ y ≤ 2} bằng cách sử dụng tích phân kép.
(b) Tính diện tích Elip (E) : x2 + y2 a2 b2 ≤ 1 với a, b > 0
(c) Tính diện tích (D) giới hạn bởi x = 1, x = 2, y = a2 và y = 2a2 (a > 0). x x 23 Định nghĩa 7
(a) Nếu (V) là thể trụ giới hạn bởi “đáy dưới” là miền (D) đóng, bị chặn, có
diện tích trong mặt phẳng Oxy, “đáy trên” là mặt cong (S) : z = f(x, y) liên
tục, không âm trên (D) thì Z Z tt(V) = f (x, y)dxdy. (1.3.2) D
(b) Nếu (V) là thể trụ giới hạn bởi “đáy dưới” là mặt cong (S) : z = f1(x, y) liên
tục, không âm trên (D), “đáy trên” là mặt cong (S) : z = f2(x, y) liên tục, không âm trên (D) thì Z Z tt(V) = (f2(x, y) − f1(x, y))dxdy. (1.3.3) D
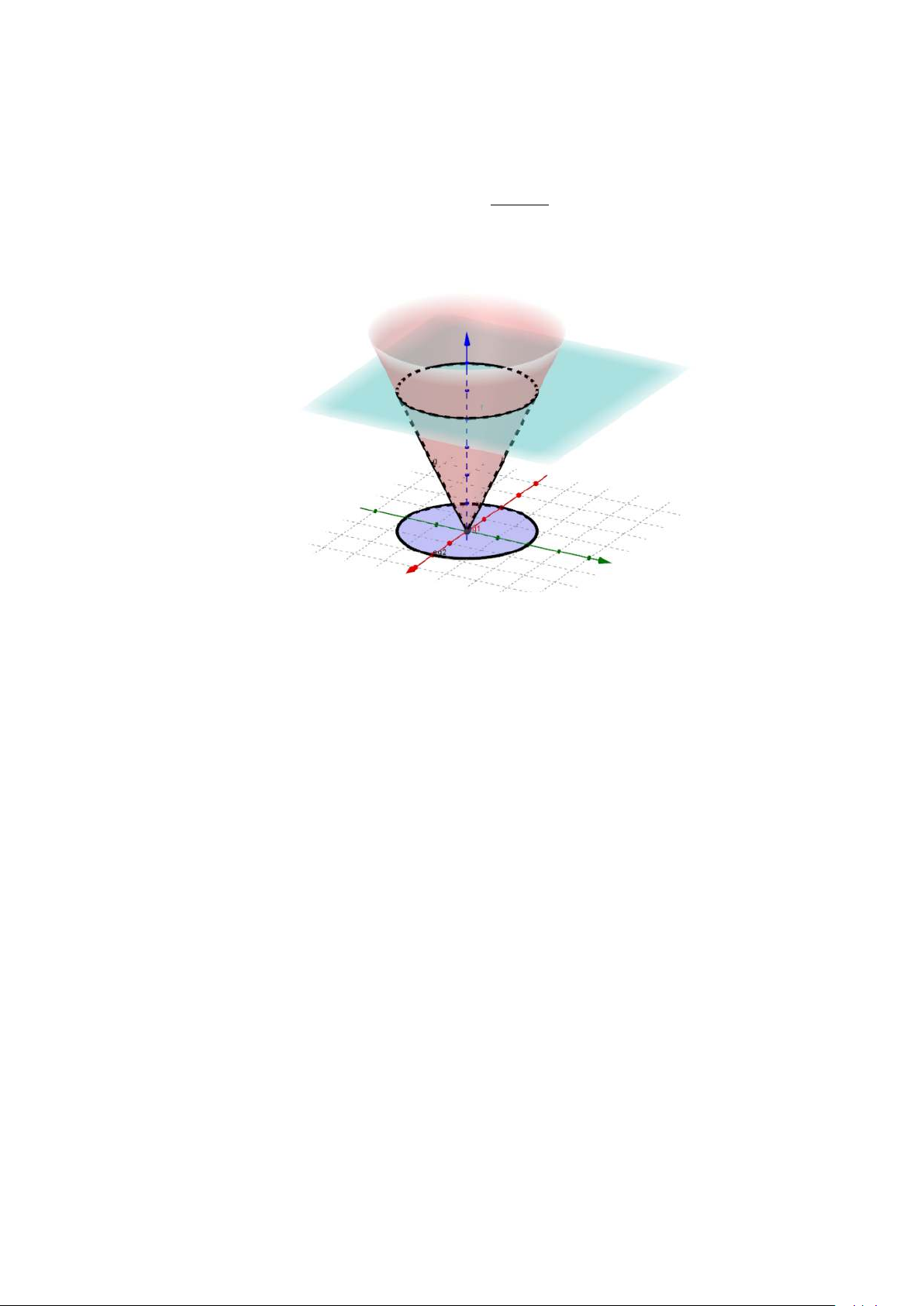
Ví dụ 25 Tính thể tích phần không gian giới hạn bởi phía ngoài mặt nón tròn
xoay z = px2 + y2 và phía trong mặt cầu đơn vị x2 + y2 + z2 = 1. 24
Định nghĩa 8 Nếu mặt cong (S) : z = f(x, y), với f(x, y) là hàm liên tục và có
các đạo hàm riêng liên tục trên (D) đóng, bị chặn, có diện tích trong Oxy. Z Z Å ∂z ã2 Å ∂z ã2 dt(S) = 1 + + dxdy. (1.3.4) ∂x ∂y D
Ví dụ 26 Tính diện tích phần mặt Parabôlôit z = x2 + y2 với z ≤ 1. 25
Định nghĩa 9 Bản phẳng (D) với tỷ khối là một hàm liên tục không âm ρ =
ρ(x, y) trên (D). Khi đó, khối lượng của (D) là Z Z m(D) = ρ(x, y)dxdy. (1.3.5) D
Ví dụ 27 Tính khối lượng của hình tròn (D) tâm O bán kính R > 0, biết ρ(x, y)
tại M(x, y) tỷ lệ với khoảng cách từ tâm đến M. 26
Định nghĩa 10 Bản phẳng (D) có tỷ khối là một hàm liên tục, không âm ρ(x, y) trên (D). Khi đó,
(a) mômen quán tính của bản phẳng đối với trục Ox là Z Z Ix = y2ρ(x, y)dxdy; (1.3.6) D
(b) mômen quán tính của bản phẳng đối với trục Oy là Z Z Iy = x2ρ(x, y)dxdy; (1.3.7) D
(c) mômen quán tính của bản phẳng đối với O là Z Z IO = x2 + y2 ρ(x, y)dxdy. (1.3.8) D
Ví dụ 28 Tính mômen quán tính đối với các trục Ox, Oy và O của bản phẳng
(D) giới hạn bởi các đường sau: y2 = 1 − x, x = 0, y ≥ 0. Biết ρ(x, y) = y. 27
Định nghĩa 11 Bản phẳng (D) có tỷ khối là một hàm liên tục, không âm ρ(x, y) trên (D). Khi đó,
(a) mômen tĩnh của bản phẳng đối với trục Ox là Z Z mx = yρ(x, y)dxdy; (1.3.9) D
(b) mômen tĩnh của bản phẳng đối với trục Oy là Z Z my = xρ(x, y)dxdy; (1.3.10) D
(c) toạ độ trọng tâm H của bản phẳng là m m x y x H = , y . (1.3.11) m( H = D) m(D)
Ví dụ 29 Bản phẳng 4OAB trong Oxy với A(1, 0) và B(0, 1), tỷ khối tại điểm
M (x, y) nằm trong 4OAB là ρ(x, y) = y. Tính mômen tĩnh của bản phẳng đối với các trục tọa độ. 28
1.3.2 Ứng dụng của tích phân bội ba
Định nghĩa 12 Khối (V) với tỷ khối là một hàm liên tục không âm ρ = ρ(x, y, z)
trên (V). Khi đó, khối lượng của (V) là Z Z Z m(D) = ρ(x, y, z)dxdydz. (1.3.12) V
Ví dụ 30 Tính khối lượng của hình lập phương đơn vị (V) : [0, 1] × [0, 1] × [0, 1]
biết tỷ khối tại M(x, y, z) là ρ(x, y, z) = x + y + z. 29
Định nghĩa 13 Khối (V) có tỷ khối là một hàm liên tục, không âm ρ(x, y, z) trên (V). Khi đó,
(a) mômen quán tính của bản phẳng đối với Oxy là Z Z Z Mxy = z2ρ(x, y, z)dxdydz; (1.3.13) V
(b) mômen quán tính của bản phẳng đối với trục Ox là Z Z Z Mx = (y2 + z2)ρ(x, y, z)dxdydz; (1.3.14) V
(c) mômen quán tính của bản phẳng đối với O là Z Z Z MO =
x2 + y2 + z2 ρ(x, y, z)dxdydz. (1.3.15) V
Ví dụ 31 Tính mômen quán tính đối với mặt Oxy, trục Ox và O của vật thể
(V) giới hạn bởi các mặt x + y + z = 1, x = 0, y = 0, z = 0. Biết tỷ khối ρ = 1. 30
Định nghĩa 14 Nếu khối (V) có tỷ khối là một hàm liên tục, không âm ρ(x, y, z) trên (V). Khi đó,
(a) mômen tĩnh của khối đối với mặt Oxy là Z Z Z mOxy = zρ(x, y, z)dxdydz; (1.3.16) D
(b) trọng tâm H của khối là m m m x Oyz Oxz Oxy H = , y , z . (1.3.17) m( H = H = V) m(V) m(V)
Ví dụ 32 Hình cầu x2 + y2 + z2 = 2Rz, tỷ khối tại M bằng OM2. Tính tọa độ
trọng tâm của hình cầu. 31
Document Outline
- Chương Tích phân bội
- Tích phân hai lớp
- Định nghĩa
- Các tính chất
- Cách tính tích phân kép
- Tích phân kép trong tọa độ cực
- Tích phân ba lớp
- Tích phân của hàm ba biến
- Các tính chất
- Tích phân ba lớp trên một vùng giới hạn chung
- Tích phân ba lớp trong tọa độ cong
- Ứng dụng
- Ứng dụng của tích phân kép
- Ứng dụng của tích phân bội ba
- Tích phân hai lớp