Giáo trình Chương 3 Bài toán vận tải | Đại học Kỹ thuật - Công nghệ Cần Thơ

CHƯƠNG 3: BÀI TOÁN VẬN TẢI NỘI DUNG
3.1 Nội dung và đặc điểm bài toán vận tải
3.1.1 Nội dung kinh tế và mô hình toán học
3.1.2 Phương án cực biên
3.1.3 Các tính chất của bài toán vận tải
3.2 Phương pháp tìm phương án cực biên ban đầu
3.2.1 Phương pháp min cước
3.2.2 Phương pháp góc Tây – Bắc 3.2.3 Phương pháp Foghen
3.3 Phương pháp thế vị giải bài toán vận tải
3.3.1 Bài toán đối ngẫu và tiêu chuẩn tối ưu
3.3.2 Thuật toán thế vị NỘI DUNG
3.4 Một số dạng đặc biệt của bài toán vận tải
3.4.1 Bài toán chỉ có hai trạm phát hoặc hai trạm thu
3.4.2 Bài toán vận tải không cân bằng thu phát
3.4.3 Bài toán vận tải cực đại
3.4.4 Bài toán vận tải có ô cấm
3.4.5 Bài toán lập kho trạm hợp lý
3.4.6 Bài toán vận tải theo thời gian GIỚI THIỆU
 Là dạng đặc biệt của bài toán quy hoạch tu y ế n tính.
 Giải quyết vấn đề phân phối hàng hoá từ một số địa điểm
cung cấp (điểm nguồn) đến một số địa điểm tiêu thụ (điểm đích) sao cho:
 Tổng chi phí ít nhất.
 Cự ly vận chuyển nhỏ nhất .
 Hay tổng tiền lời là nhiều nhất.
 Áp dụng để xác định vị trí đặt nhà kho, cửa hàng hay nhà
xưởng mới khi xem xét một số phương án về địa điểm xây dựng.
3.1 NỘI DUNG BÀI TOÁN VÀ CÁC TÍNH CHẤT 3.1.1 Nội dung bài toán
1. Bài toán: Một đơn vị nhận nhiệm vụ vận chuyển một loại hàng
hoá thuần nhất từ m địa điểm phát (kho, nơi sản xuất...) Ai (i = 1,
m ) với khối lượng tương ứng a đơn vị (i = 1, m ) đến n địa điểm i
nhận hàng (điểm thu) B (j = 1, n ) với nhu cầu tiếp nhận là b đơn j j
vị (j = 1, n ). Biết chi phí vận chuyển 1 đơn vị hàng hoá từ điểm
phát A đến điểm thu B là c (i = 1, m ; j = 1, n ). Hãy lập kế hoạch i j ij
vận chuyển thoả mãn yêu cầu giao nhận hàng, sao cho cước phí
vận chuyển tổng cộng là nhỏ nhất, biết rằng tổng số lượng hàng
phát ra đúng bằng lượng hàng thu vào, tức: Bài toán vận tải
2. Mô hình toán học của bài toán
Gọi x là số lượng đơn vị hàng hoá cần vận chuyển trong kế ij
hoạch từ A (i = 1, m ) đến B (j = 1, n ), x >= 0 i j ij
Lượng hàng cần vận chuyển từ m điểm phát A (i = 1...m ) đến n i
điểm thu B (j = 1... n ) thoả mãn điều kiện cân bằng thu phát j
(phát hết hàng từ A , B nhận đủ hàng): i j
Tổng chi phí vận chuyển toàn bộ số lượng hàng hoá từ m điểm
phát A (i = 1, m ) đến n điểm thu B (j = 1, n ) i j
ĐỊNH NGHĨA VÀ MỘT SỐ TÍNH CHẤT
Định nghĩa 1: BTVT TQ có dạng 𝑚 𝑛
(1)𝑓=∑∑𝑐 𝑥→min 𝑖𝑗 𝑖𝑗 𝑖=1 𝑗=1
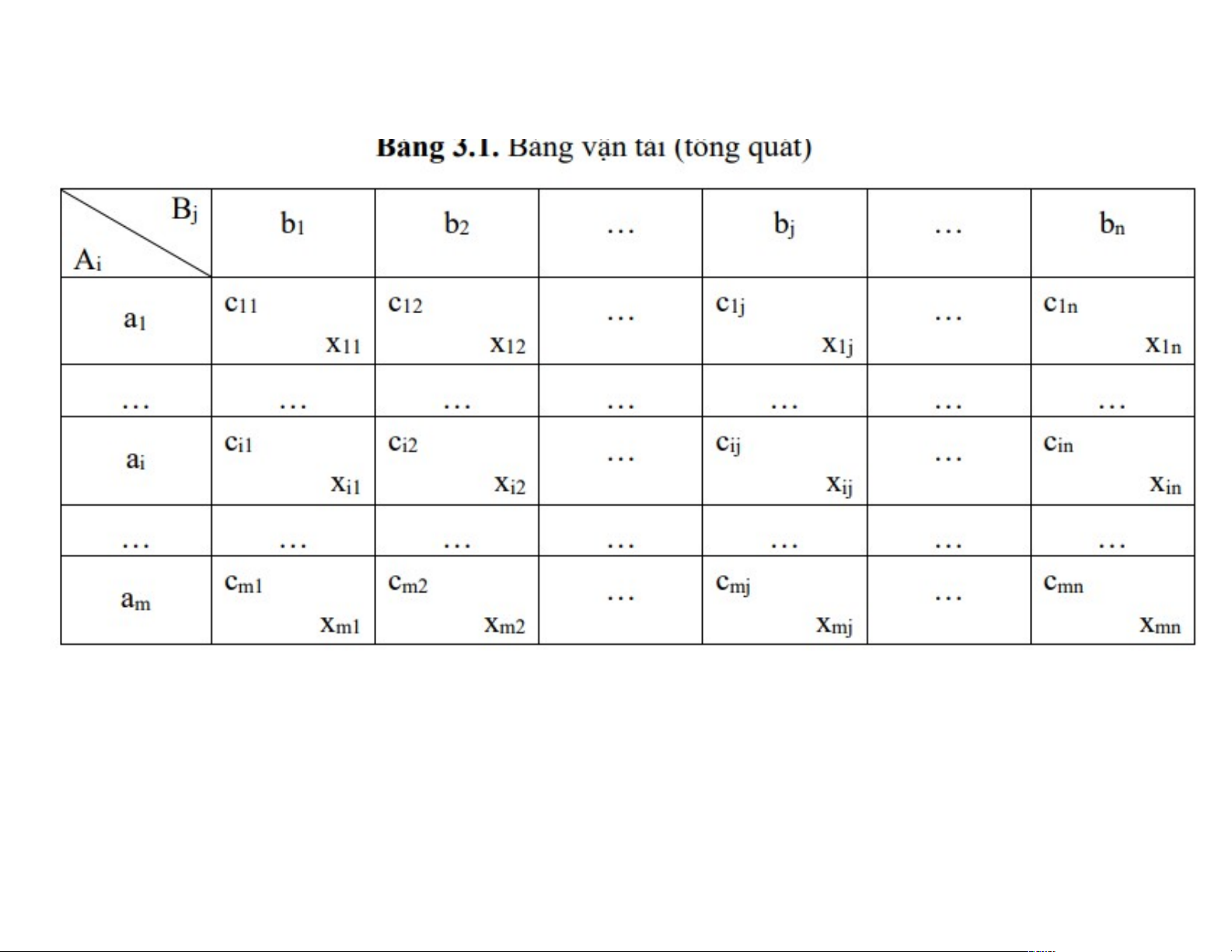
Dạng bảng của BTVT: T B B … B … B 1 2 j n P A c c c c 1 11 12 1j 1n … A c c c c i i1 i2 ij in … A c c C c m m1 m2 mj mn
3. Dạng bảng của bài toán vận tải
Trong mỗi ô (i, j) ghi: - góc trên bên trái là chi phí c ;ij
- góc dưới bên phải là lượng hàng x . ij
Ví dụ 1. Tổng công ty xây dựng X có 3 cơ sở sản xuất đá (A1,
A2, A3) và 3 công trường xây dựng (B1, B2, B3). Công suất
sản xuất đá hàng tuần của các cơ sở lần lượt là 50, 60, 70m3.
Nhu cầu tiêu thụ đá hàng tuần của ba công trường lần lượt là 40, 85, 55m3. 50m3 Cơ sở A1 Công trường B1 40m3 60m3 Cơ sở A2 Công trường B2 85m3 70m3 Cơ sở A3 Công trường B3 55m3 Khả năng cung cấp Luồng vận chuyển Nhu cầu tiêu thụ Điểm nguồn Điểm đích Thu B B B 1 2 3 40 m3 85 m3 55 m3 Phát A1 2 1 5 50 m3 A2 3 4 3 60m3 A3 4 6 6 70 m3 Lưu ý:
+Mỗi hàng A đại diện cho một trạm phát. i
+Mỗi cột B đại diện cho một trạm thu. j
+Ô(i,j) đại diện cho tuyến đường vận tải
hàng từ trạm phát thứ i đến trạm thu thứ j.
+Điều kiện cân bằng thu phát là đk: 𝑚 𝑛
∑ 𝑎 =∑ 𝑏 𝑖 𝑗 𝑖=1 𝑗=1
+ PA của BTVT viết dưới dạng ma trận: ... 𝑥1𝑛
𝑥=(𝑥11... ... ... )=(𝑥ij)𝑚×𝑛
Định lý 1: 𝑥 ... 𝑥 BTVT cân bằ 𝑚n1g thu phát lu 𝑚𝑛 ôn có PATƯ
Định nghĩa 2:
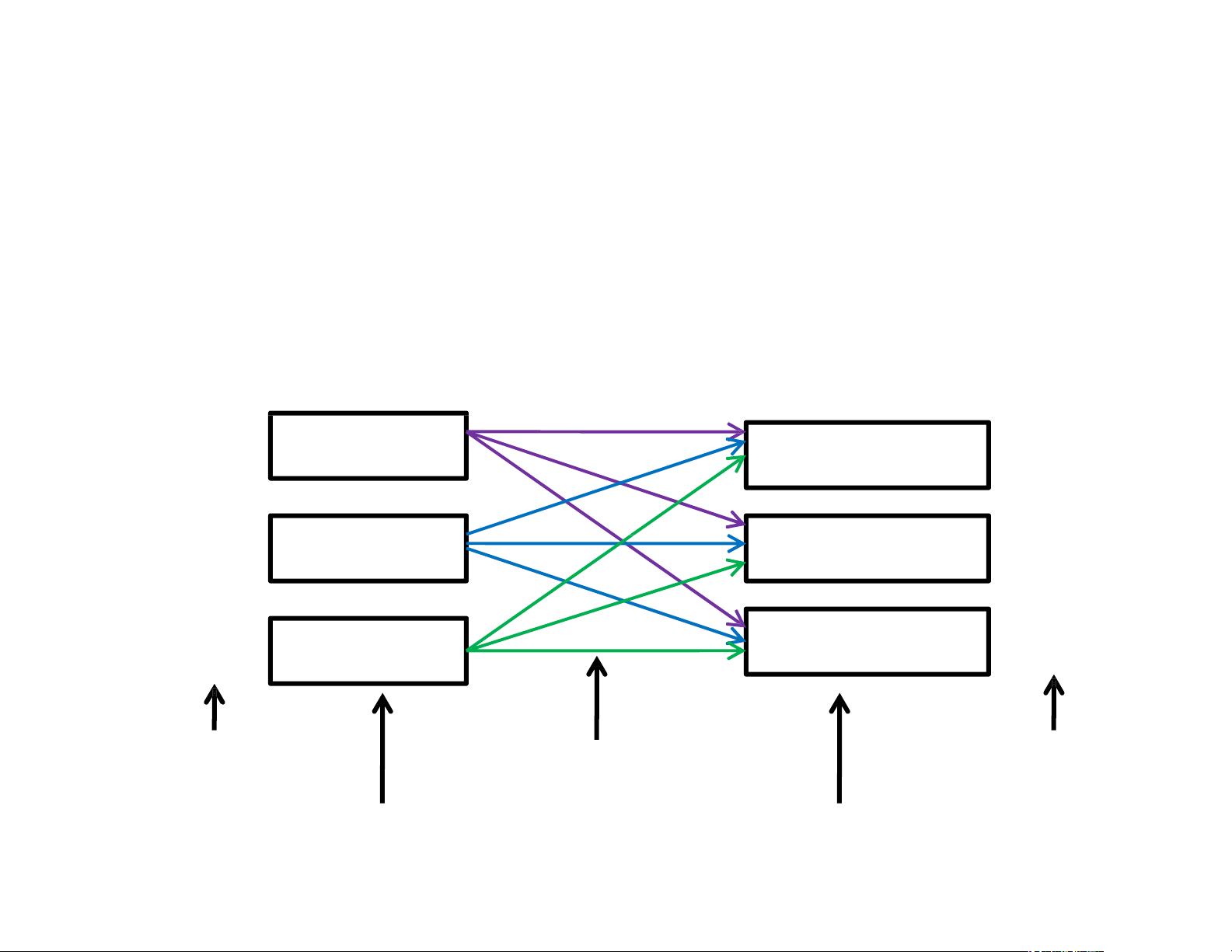
• Tập hợp các ô của bảng vận tải mà cứ hai
ô liên tiếp thì nằm trên cùng một dòng hay
một cột và một dòng hay một cột đó không
chứa quá hai ô được gọi là một đường đi. X X X X X X
• Một đường đi khép kín được gọi là một chu trình. X X X X X X
Định lý 2: Một bảng vận tải m dòng, n cột
thì tập hợp các ô không chứa chu trình có
tối đa là (m+n-1) ô. Các định nghĩa
Nhận xét: - Số ô (ký hiệu là ) trong một chu trình V là một
số ô chẵn. Do tính chất của chu trình, 2 ô kề nhau luôn
cùng nằm trên một hàng (hoặc 1 cột), nên tổng số hàng và
cột các ô của chu trình đi qua phải là số chẵn 2k, trên mỗi
hàng (cột) 1 ô được tính 2 lần vậy số ô của chu trình V là: = 2.2k/2 = 2k và 4
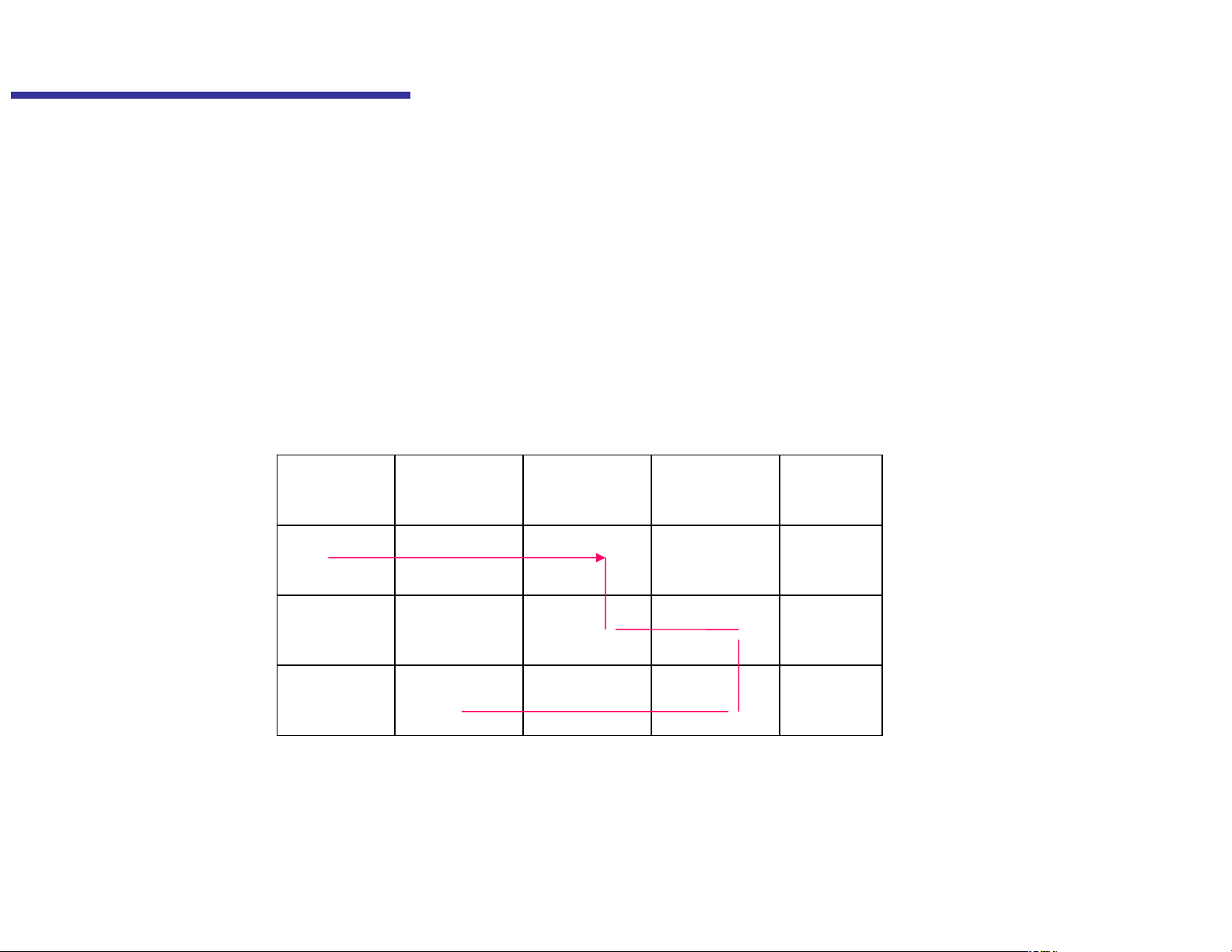
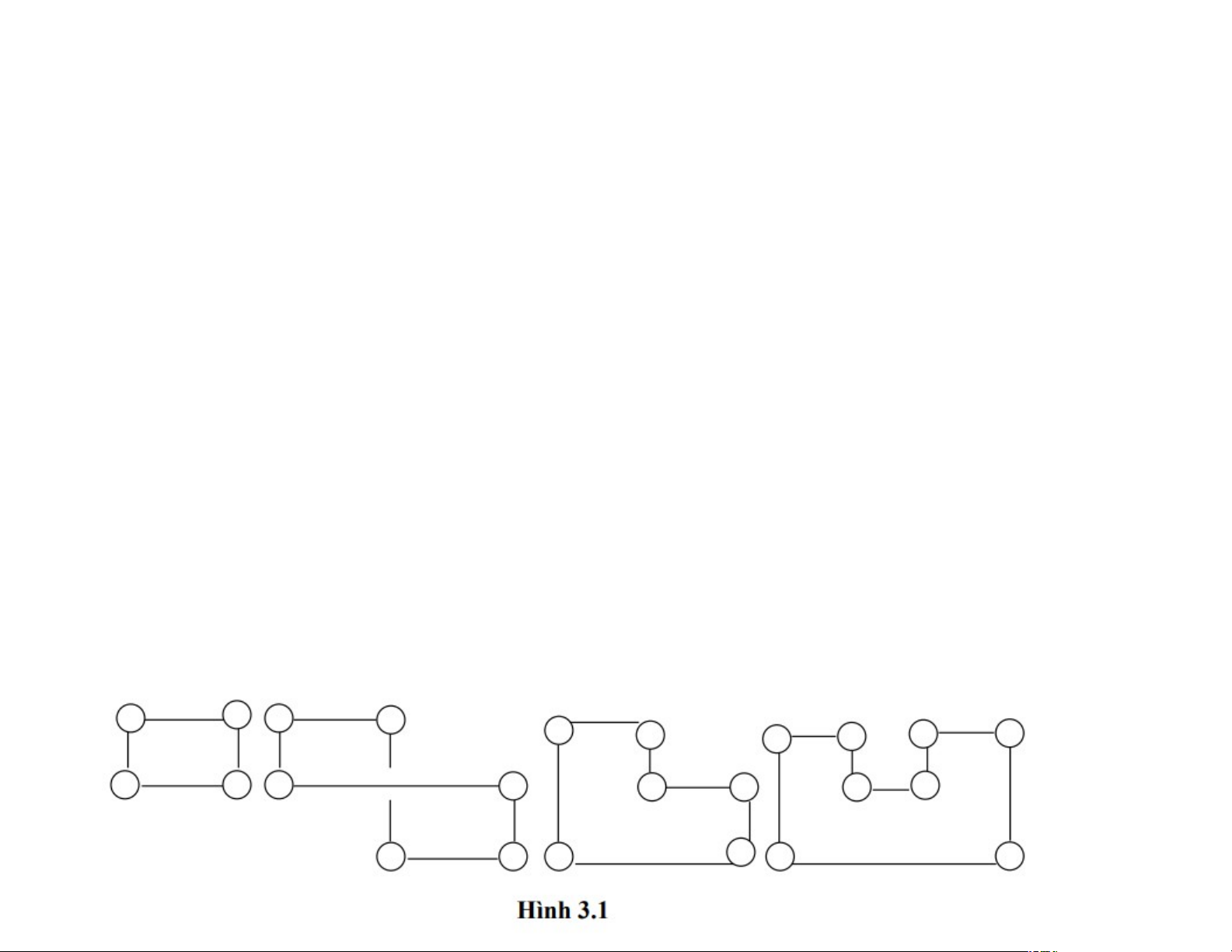
- Ta thấy một số dạng của chu trình thường gặp: dạng hình chu
chữ nhật (hoặc hình vuông), dạng chéo số 8, dạng hình chữ L,
chữ U... Có thể minh hoạ bằng hình 3.1 bằng một số sơ đồ đơn giản sau:
3.1.2 Các tính chất của bài toán vận tải
Định lý 3.1 (đặc điểm PACB của bài toán vận tải đóng):
Phương án x = (x )m.n của bài toán vận tải (3.1) -(3.4) là phương ij
án cực biên khi và chỉ khi tập hợp G các ô sử dụng x > 0 không ij chứa chu trình
♦ Tập ô cơ sở (hay ô chọn) của một PACB là tập hợp m + n – 1
ô không chứa chu trình bao hàm tập ô tương ứng với các
thành phần dương của PACB đó
Các ô thuộc tập ô cơ sở được gọi là các ô cơ sở hay ô chọn,
các ô còn lại gọi là ô phi cơ sở hay ô loại của PACB đó
3.1.2 Các tính chất của bài toán vận tải
♦ Phương án x = (x )m.n của bài toán vận tải (3.1) - (3.4) gọi là ij
PACB không suy biến, nếu số ô chọn của nó đúng bằng m + n - 1.
Tập ô cơ sở là duy nhất.
Ngược lại, phương án x = (x )m.n của bài toán vận tải (3.1) - (3.4) ij
gọi là PACB suy biến, nếu số ô chọn của nó nhỏ hơn m + n - 1.
PACB suy biến có thể có nhiều tập ô cơ sở khác nhau, phần chung
của chúng chính là tập ô ứng với các thành phần dương.
♦ Số ô tối đa không tạo thành chu trình trong bảng m hàng và n cột là m + n – 1
Định nghĩa 3: Trong một PA,
ô có vận tải hàng đi qua ứng với x >0 được ij
gọi là ô chọn. Ô có x =0 gọi là ô loại. ij
Chú ý: ta thường dùng x để chỉ ô chọn.
Định lý 3: X là PACB của btvt khi và chỉ
khi X có tập hợp các ô chọn không chứa chu trình.
Ví dụ: x0 có là PACB không?
Định nghĩa 4: PACB gọi là không suy biến
nếu số ô chọn =m+n-1. PACB gọi là suy
biến nếu số ô chọn <(m+n-1). X X X X X= X X X X X X X
* Đưa PACB suy biến về PACB không suy
biến, ta bổ sung thêm các ô loại cho đủ
(m+n-1) ô chọn không chứa chu trình. Các
ô loại bổ sung đó được gọi là ô chọn 0.