1
GIÁO TRÌNH CƠ HỌC VẬT RẮN BIẾN DẠNG 2
Giáo trình CƠ HỌC VẬT RẮN BIẾN DẠNG 3
GS.TSKH. NGUYỄN ĐÌNH ĐỨC – TS. VŨ THỊ THÙY ANH GIÁO TRÌNH
CƠ HỌC VẬT RẮN BIẾN DẠNG
NHÀ XUẤT BẢN ĐẠI HỌC QUỐC GIA HÀ NỘI – 2022 4
Giáo trình CƠ HỌC VẬT RẮN BIẾN DẠNG
Biên mục trên xuất bản phẩm của Thư viện Quốc gia Việt Nam Nguyễn Đình Đức
Giáo trình Cơ học vật rắn biến dạng / Nguyễn Đình Đức, Vũ Thị Thùy Anh.
- H. : Đại học Quốc gia Hà Nội, 2022. - 376 tr. ; 24 cm ISBN 978-604-369-781-0
1. Cơ học chất rắn 2. Biến dạng 3. Giáo trình 620.1050711 - dc23 DHH0024p-CIP 5 MỤC LỤC
Lời nói đầu ....................................................................................................... 9
Chương 1. ỨNG SUẤT VÀ BIẾN DẠNG
1.1. Hai cách mô tâ chuyển động ................................................................ 12
1.2. Tác động của nội lực và ngoại lực ........................................................ 19
1.3. Ten-xơ ứng suất ................................................................................... 22
1.4. Biểu diễn ten-xơ ứng suất khi biến đổi hệ tọa độ ................................... 27
1.5. Cân bằng lực và mô-men. Tính đối xứng của ten-xơ ứng suất ........... 30
1.6. Ứng suất chính, hướng chính. Các bất biến của ten-xơ ứng suất ............ 33
1.7. Biểu đồ Mohr ....................................................................................... 39
1.8. Phân loại trạng thái ứng suất ................................................................ 41
1.9. Ten-xơ biến dạng hữu hạn Green và Almansi ........................................ 42
1.10. Ý nghïa hình học của các thành phần biến dạng ................................... 44
1.11. Biến dạng thể tích tương đối ................................................................. 51
1.12. Ten-xơ lệch. Ten-xơ quay nhỏ .............................................................. 52
1.13. Biểu diễn chuyển vð qua các thành phần ten-xơ biến dạng nhỏ.
Điều kiện tương thích Saint - Venant ..................................................... 53
1.14. Phương trình cân bằng, biểu diễn ten-xơ ứng suất theo biến Lagrange ... 61
1.15. Biểu diễn công của ngoại lực theo chuyển vð. Thế đàn hồi ......................... 67
1.16. Ý nghïa nhiệt động học của thế đàn hồi ................................................ 71
1.17. Công thức Lagrange và Castigliano. Đðnh lý Clapeyron .............................. 73
1.18. Đðnh luật Hooke .................................................................................... 75
1.19. Đðnh luật Hooke cho môi trường đàn hồi đẳng hướng ............................ 82
Bài tập chương 1 ............................................................................................ 92
Đáp án bài tập chương 1 ................................................................................. 97 6
Giáo trình CƠ HỌC VẬT RẮN BIẾN DẠNG
Chương 2. LÝ THUYẾT ĐÀN HỒI TUYẾN TÍNH
2.1. Các phương trình cơ bân .................................................................... 101
2.2. Điều kiện biên .................................................................................... 107
2.3. Thiết lập bài toán đàn hồi tuyến tính theo chuyển vð ............................ 111
2.4. Đðnh lý Kirchhoff về sự duy nhất nghiệm của bài toán
lý thuyết đàn hồi ............................................................................... 121
2.5. Phương pháp giâi bài toán lý thuyết đàn hồi theo chuyển vð ................. 126
2.6. Đðnh lý Betti về tương hỗ của chuyển dðch .......................................... 128
2.7. Nghiệm riêng của hệ phương trình cân bằng không đồng nhất
theo chuyển vð. Ten-xơ Somilian ......................................................... 130
2.8. Phương pháp giâi bài toán đàn hồi tuyến tính theo ứng suất ............ 135
2.9. Phương pháp giâi hỗn hợp .................................................................. 143
2.10. Trường hợp lực khối là hằng số........................................................... 146
2.11. Cách đặt bài toán thuận và ngược của lý thuyết đàn hồi.
Phương pháp nửa ngược Saint - Venant. lời giâi giâi tích và lời giâi số ........153
2.12. Một số bài toán đơn giân của lý thuyết đàn hồi ................................... 155
Bài tập chương 2 .......................................................................................... 168
Đáp án bài tập chương 2 ............................................................................... 171
Chương 3. BÀI TOÁN PHẲNG CỦA LÝ THUYẾT ĐÀN HỒI
3.1. Trạng thái biến dạng phẳng. Hàm ứng suất Airy .................................. 188
3.2. Trạng thái ứng suất phẳng .................................................................. 195
3.3. Đðnh lý M. Levy .................................................................................. 201
3.4. Nghiệm bài toán phẳng dưới dạng đa thức. Một số bài toán phẳng
trong hệ tọa độ Đề-các ....................................................................... 202
3.5. Hàm ứng suất Prandtl. Hàm vênh ....................................................... 222
3.6. Bài toán phẳng trong hệ tọa độ cực .................................................... 234
3.7. Phương pháp biểu diễn hàm ứng suất dưới dạng hàm biến phức ......... 257
3.8. Phương pháp dùng phép biến đổi tích phân Fourier ............................. 275 Mục lục 7
Bài tập chương 3 .......................................................................................... 282
Đáp án bài tập chương 3 ............................................................................... 289
Chương 4. UỐN TẤM MỎNG
4.1. Các giâ thuyết của Kirchhoff ............................................................... 297
4.2. Phương trình Sophine - Germain ......................................................... 301
4.3. Điều kiện biên đối với bài toán tấm mỏng hình chữ nhật ...................... 304
4.4. Các phương pháp để giâi bài toán tấm mỏng hình chữ nhật ...................... 309
4.5. Bài toán tấm tròn chðu tâi đối xứng trục ............................................... 313
Bài tập chương 4 .......................................................................................... 317
Đáp án bài tập chương 4 ............................................................................... 321
Chương 5. BÀI TOÁN ĐỘNG CỦA LÝ THUYẾT ĐÀN HỒI
5.1. Xây dựng bài toán động của lý thuyết đàn hồi ..................................... 328
5.2. Sóng phẳng và sóng ngang ................................................................ 330
5.3. Sóng phân cực ngang và dọc ............................................................. 335
5.4. Sóng mặt Rayleigh ............................................................................. 337
5.5. Sóng phân cực ngang trong nửa không gian ....................................... 340
5.6. Bài toán phẳng Lamb ......................................................................... 344
5.7. Phương pháp hàm bất biến - giâi pháp của V.I. Smirnov và S.L. Sobolev ..... 352
5.8. Bài toán truyền sóng đàn hồi trong dầm ............................................ 365
Tài liệu tham khâo ........................................................................................ 373 8 9 LỜI NÓI ĐẦU
Tất cả các vật liệu và kết cấu dưới tác động của các lực cơ học và
môi trường vật lý như điện từ, từ trường, nhiệt độ đều bị biến dạng.
Việc tính toán trạng thái ứng suất-biến dạng, độ bền cũng như ổn định
của kết cấu là vô cùng quan trọng. Chính vì vậy, môn Cơ học vật rắn
biến dạng là kiến thức nền tảng của các ngành kỹ thuật. Trong chương
trình đào tạo các ngành có liên quan đến cơ học ở Trường Đại học
Công nghệ - Đại học Quốc gia Hà Nội như Cơ kỹ thuật, Kỹ thuật Xây
dựng… đều có môn học này.
Nếu môn Cơ học môi trường liên tục xem xét các khái niệm và
nguyên lý cơ bản các chuyển động vĩ mô của môi trường ở thể rắn,
lỏng, khí, và quan trọng nhất là giúp thiết lập được các bài toán biên
về Cơ học với các môi trường đó, thì môn Cơ học vật rắn biến dạng
(vật rắn biến dạng) có mục tiêu quan trọng nhất là đưa ra các phương
pháp để giải các bài toán biên đó với môi trường vật rắn.
Nhằm trang bị cho người học và các nhà nghiên cứu liên quan
đến tính toán kết cấu, chúng tôi biên soạn cuốn giáo trình Cơ học vật
rắn biến dạng này nhằm cung cấp cho người đọc những khái niệm,
nguyên lý cơ bản nhất, đồng thời đưa ra những phương pháp và bài
tập áp dụng cụ thể để người đọc hiểu rõ hơn về môn học.
Giáo trình tập trung trình bày nội dung của Cơ học vật rắn biến
dạng trong khuôn khổ Lý thuyết đàn hồi (mà chưa đề cập đến phần
liên quan đến Lý thuyết dẻo) cùng các bài tập ví dụ và bài tập tự giải
kèm theo đáp án hoặc chỉ dẫn nhằm giúp người đọc củng cố kiến thức. 10
Giáo trình CƠ HỌC VẬT RẮN BIẾN DẠNG
Do biên soạn lần đầu nên cuốn sách khó tránh khỏi những sai sót
nhất định. Vì vậy, các tác giả rất mong nhận được sự góp ý của đồng
nghiệp và bạn đọc, cũng như của các em sinh viên để giáo trình ngày càng hoàn thiện.
Các ý kiến đóng góp xin gửi về địa chỉ: Bộ môn Công nghệ Xây
dựng – Giao thông, Phòng 408, Nhà E5, Trường Đại học Công nghệ,
Đại học Quốc gia Hà Nội, 144 Xuân Thủy – Cầu Giấy – Hà Nội. Các tác giả 11 Chương 1
ỨNG SUẤT VÀ BIẾN DẠNG
Các đại lượng vật lý, hình học của Cơ học môi trường liên tục
không phụ thuộc vào sự lựa chọn hệ tọa độ để biểu diễn chúng. Tuy
nhiên, để thuận tiện trong quá trình tính toán, người ta vẫn quy chuẩn
các đại lượng đó trong những hệ tọa độ phù hợp. Tương ứng với mỗi
hệ tọa độ, các đại lượng này được biểu diễn qua một số các giá trị gọi
là thành phần của các đại lượng, khi hệ tọa độ thay đổi, các thành
phần này thay đổi theo, song sự thay đổi đó tuân theo một quy tắc nhất
định. Người ta sử dụng khái niệm “ten-xơ” để biểu diễn những đại
lượng này, hay nói cách khác, ten-xơ như một đối tượng toán học tồn
tại không phụ thuộc vào hệ tọa độ [1]. Thông qua ten-xơ, các định luật
vật lý của Cơ học môi trường liên tục nói chung và Cơ học vật rắn
biến dạng nói riêng được biểu diễn dưới dạng các phương trình ten-xơ,
nếu các phương trình ten-xơ đã đúng trong hệ tọa độ này thì cũng
đúng trong hệ tọa độ khác.
Trong cơ học lý thuyết, khái niệm về vật rắn tuyệt đối được đưa
ra, tức là coi khoảng cách giữa các phần tử trong vật rắn không thay
đổi trong quá trình chuyển động cũng như ở trạng thái cân bằng dưới
tác dụng của ngoại lực. Tuy nhiên trong thực tế, dưới tác dụng của
ngoại lực, mọi vật đều ít nhiều bị biến dạng, do đó khoảng cách giữa
các phần tử bên trong vật cũng bị thay đổi, dẫn đến nội lực tương tác
giữa các phần tử đó cũng thay đổi theo. Người ta nói như vậy trong
vật đã xuất hiện ứng suất. Trên quan điểm vĩ mô, nếu coi môi trường
trong vật rắn là liên tục, dưới tác dụng của lực ngoài, môi trường này
chuyển dịch và thay đổi hình dáng, kích thước, tức là nó biến dạng.
Do tính liên tục, nếu không xét đến sự xuất hiện các vết nứt và lỗ hổng 12
Giáo trình CƠ HỌC VẬT RẮN BIẾN DẠNG
trong quá trình biến dạng, các hạt ở gần nhau sau khi biến dạng cũng
vẫn ở gần nhau. Kết quả của biến dạng, sự sắp đặt các phần tử vật chất
bên trong vật thể thay đổi, giữa các phần tử đó xuất hiện lực tác dụng
tương hỗ. Kết quả này có thể xem như phần lực thêm vào trường lực
sẵn có trong vật thể. Tại mỗi điểm khác nhau, phần lực thêm vào này
là khác nhau, tuy nhiên ta có thể coi nó là trường lực thay đổi đều từ
điểm này sang điểm khác với ý nghĩa trung bình. Điều này cho phép ta
xem ứng suất là hàm số liên tục của các tọa độ và thời gian, và là hàm
khả vi. Trong khi đó, nếu coi tập hợp hàm nào đấy của tọa độ xác định
độ dãn của đoạn vật chất vô cùng nhỏ đi qua điểm cho trước và xác
định sự thay đổi góc giữa hai đoạn vật chất vô cùng bé là một hàm, thì
hàm này sẽ xác định biến dạng lân cận điểm của môi trường [2 - 4].
1.1. HAI CÁCH MÔ TÂ CHUYỂN ĐỘNG
Trong hệ tọa đồ Đề-các vuông góc Ox x x 1 2 3 (hay Oxyz với
x  x , y  x ,z  x 1 2
3 ), giả sử ở trạng thái ban đầu khi chưa biến
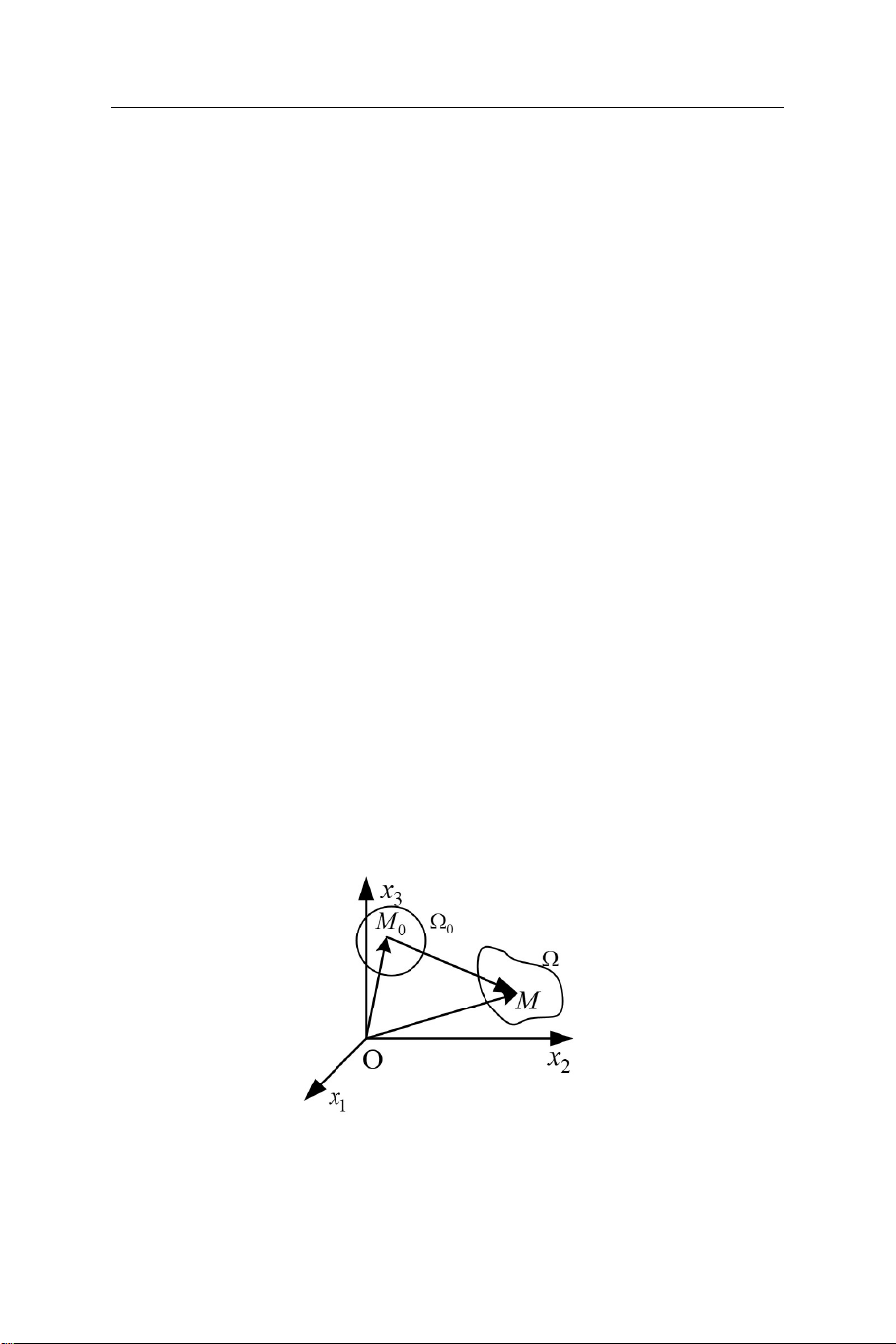
dạng, hình thái ban đầu của vật thể là 0 (hình 1.1). Dưới tác dụng
của lực ngoài, môi trường vật thể chuyển sang hình thái mới tương ứng là  [2, 9].
Hình 1.1. Mô tả quá trình dịch chuyển của điểm 0 M
Chương 1. Ứng suất và biến dạng 13
Như vậy, môi trường chuyển từ trạng thái ban đầu sang trạng thái
mới do sự chuyển động của các hạt (phần tử) vật chất trong môi
trường, các chuyển động này được gọi là chuyển vị.
Gọi u  u ,u ,u 1 2
3  là vec-tơ chuyển vị, từ hình 1.1, ta có:
OM  OM  u . (1.1) 0
Biểu diễn theo tọa độ, biểu thức trên tương ứng:
x    u  , , . i i i (1.2) 1 2 3 
Với cách biểu diễn này, chuyển vị có thể coi là một hàm của k ,
và để thuận tiện hơn, có thể coi sự phụ thuộc này như một hàm:
x  x  , , . i i (1.3) 1 2 3 
Phép biến đổi ngược lại cho tương ứng     , , . i i x x x (1.4) 1 2 3 
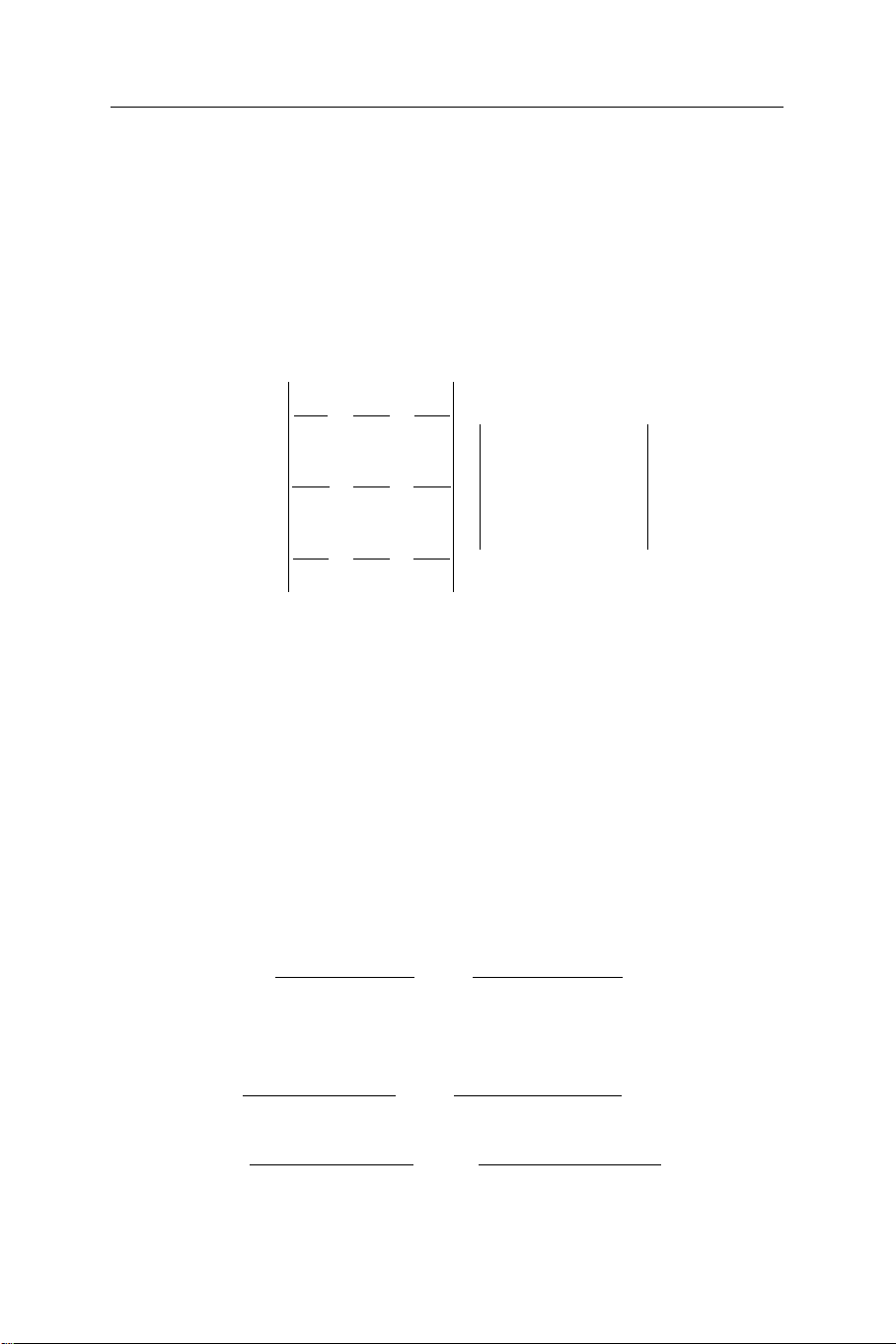
Các hàm này khả vi liên tục một số đủ lần theo các biến, do đó Jacobi: x x x 1 1 1    1 2 3 x x x  i x 2 2 2 J  Det   0.     (1.5) i 1 2 3 x x x 3 3 3    1 2 3
Thay (1.4) vào (1.2), ta có: 14
Giáo trình CƠ HỌC VẬT RẮN BIẾN DẠNG
  x u x ,x ,x . i i i (1.6) 1 2 3  Các hàm x , i
i phải liên tục theo các biến tọa độ. Đồng thời, nếu
xét trên quan điểm chuyển động, các hàm này cũng liên tục theo biến
thời gian. Có hai cách biểu diễn chuyển động của môi trường vật rắn,
theo Lagrange và theo Euler, tùy thuộc vào cách chọn biến số tọa độ
trong phương trình chuyển động là xi hay i .
1.1.1. Mô tả chuyển động theo Lagrange (biến Lagrange)
Phương trình chuyển động theo Lagrange theo thời gian có dạng:
x  x  , , ,t . i i (1.7) 1 2 3 
Với cách mô tả chuyển động này, ta thấy xi xác định vị trí tại
thời điểm t của phần tử tương ứng với điểm i tại vị trí ban đầu. Nếu
i cố định, theo thời gian, (1.7) mô tả chuyển động của một phần tử
xác định (phương trình dưới dạng tham số). Nếu i thay đổi, theo thời
gian, (1.7) cho biết vị trí các phân tố của toàn bộ vật thể tại mỗi thời
điểm t , hay nói cách khác là phương trình mô tả quy luật chuyển
động của vật thể. Tọa độ i được gọi là thông số độc lập hay tọa độ
Lagrange, tọa độ vật chất.
Mô tả chuyển động theo Lagrange dựa trên lịch sử chuyển động
của từng phần tử trong vật rắn, tức là nghiên cứu đến quy luật thay đổi
các đại lượng đặc trưng đối với phần tử cho trước của môi trường. Do
đó, cách mô tả chuyển động theo Lagrange còn được gọi là mô tả theo
tọa độ vật chất, và trong lý thuyết ứng suất và biến dạng nhỏ, phương
pháp này cho kết quả đơn giản và rõ ràng. Hay nói cách khác, trong cơ
học vật rắn biến dạng đa phần các phương trình được biểu diễn trong
tọa độ Lagrange [5 – 7].
Chương 1. Ứng suất và biến dạng 15
1.1.2. Mô tả chuyển động theo Euler (biến Euler)
Ngược lại với Lagrange, mô tả chuyển động theo Euler nghiên
cứu các hiện tượng xảy ra tại điểm sau biến dạng, tức là quan tâm đến
quy luật thay đổi của các đại lượng đặc trưng tại một nơi cho trước.
Phương trình chuyển động theo Euler theo thời gian có dạng:     , , , . i i x x x t (1.8) 1 2 3 
Tọa độ xi được gọi là tọa độ Euler hay tọa độ không gian. Nếu
cố định xi , (1.8) xác định dòng các hạt vật chất lần lượt chuyển tới
điểm M theo thời gian t và quy luật biến đổi của các đại lượng đặc
trưng ứng với từng thời gian t . Do đó, biểu diễn theo Euler còn được
gọi là biểu diễn theo tọa độ không gian.
Hai cách biểu diễn này có quan hệ tương hỗ lẫn nhau, các biến số
có thể quy đổi từ Lagrange theo Euler và ngược lại. Điều kiện cần và
đủ để tồn tại hàm ngược của chúng là các Jacobi J  0 (theo (1.5)).
Khi giải các bài toán tĩnh của cơ học vật rắn biến dạng, chỉ cần
quan tâm tới trạng thái đầu và trạng thái sau của vật thể, tức là xem
xét tới hình thái  , 0
. Khi giải các bài toán động của cơ học vật rắn
biến dạng, tức xem xét tới chuyển động của vật thể theo thời gian t ,
cần phải quan tâm tới vận tốc và gia tốc. Theo cách mô tả chuyển
động theo Lagrange có thể biểu diễn vận tốc và gia tốc dưới dạng:    u v , , ,t   , , ,t , 1 2 3   1 2 3   t (1.9)  u w , , ,t  2       , , ,t . 1 2 3  1 2 3  t 16
Giáo trình CƠ HỌC VẬT RẮN BIẾN DẠNG
Trong khi, theo cách mô tả chuyển động theo Euler:  dv v v v v
w x ,x ,x ,t    v  v  v , (1.10) 1 2 3  1 2 3 dt t x x x 1 2 3 du với v  i ,(i 1,2,3), i hay dt  i
u x ,x ,x ,t
u x ,x ,x ,t 1 2 3  i  1 2 3  v  
v , (i,k 1,2,3). i t  k xk
Khi giải các bài toán động lực học tuyến tính, các chuyển vị và
các đạo hàm của nó theo các biến tọa độ được coi là nhỏ, đại lượng  iv k
v  là vô cùng nhỏ bậc cao, khi đó, sự khác nhau giữa biến xk
Lagrange và Euler không tồn tại.
Chú ý: khi khảo sát chuyển động của môi trường liên tục, cần giả thiết rằng:
- Hai điểm vật chất cạnh nhau trong hình thái ban đầu 0 thì
vẫn ở cạnh nhau trong tất cả các hình thái tiếp theo sau biến dạng.
- Các điểm vật chất chiếm trong hình thái 0 một miền liên
thông nào đấy, thì chúng cũng chiếm miền liên thông cùng cấp trong
 (thể tích, mặt, đường cong), miền vật chất dịch chuyển theo chuyển động.
- Các điểm vật chất nằm bên trong một mặt kín nào đấy trong
0 sẽ luôn nằm bên trong mặt kín dịch chuyển tại mọi thời điểm.
- Mặt biên của môi trường là mặt vật chất.
Thí dụ 1.1. Xác định trường vận tốc và gia tốc theo biến
Lagrange và Euler, biết quy luật chuyển động của môi trường như sau:
Chương 1. Ứng suất và biến dạng 17
x     te  , 1 1 2  1    x     t e  , 2 2 1  1 x    . 3 3  Giải:
Biểu thức Jacobi lập bởi môi trường theo (1.5) có dạng: x x x 1 1 1    t 1 2 3 1 e 1 0 x x x 2 2 2  J   t e 1 1 0  0,    1 2 3 0 0 1 x x x 3 3 3    1 2 3
Theo công thức (1.9), các thành phần vận tốc và gia tốc theo biến Lagrange có dạng: t 
v   e ,v   t e ,v  , 1 2 2 1 3 0 t 
w   e ,w   t e ,w  . 1 2 2 1 3 0
Các thành phần vận tốc theo biến Euler được xác định bằng cách
thay thế các biến  , , x ,x ,x 1 2 3 qua 1 2
3 . Ta có, từ quy luật chuyển
động ban đầu, biến đổi ta có: t  x  x e  x  t x e  1 2  1 2 1  1   ,  ,  x . 1 2 3 3 t t t  e  e  t 1 e  e 1 Do đó:  t 
x  x e  x x  x  t x e 1 2  1 2  1 2 v  ,v  ,v  , 1 2 3 0 t t t  e  e  t 1 e  e 1  t 
x  x e  x x  x  t x e 1 2  1 2  1 2 w  ,w  ,w  . 1 2 3 0 t t t  e  e  t 1 e  e 1 18
Giáo trình CƠ HỌC VẬT RẮN BIẾN DẠNG
Thí dụ 2: Cho trường vận tốc của môi trường như dưới đây.
v  kx ,v  kx ,v  ,k  . 1 2 2 1 3 0 0
Hãy xác định quy luật chuyển động của môi trường đó [12, 13]. Giải:
Từ quy luật của trường vận tốc, ta có: dx dx dx 1 2 3  kx ,  kx ,  . 2 1 0 dt dt dt
Lấy đạo hàm theo t phương trình thứ nhất trong ba phương trình
trên và sử dụng phương trình thứ hai, thu được phương trình mới: 2 d x1 2  k x  . 1 0 2 dt
Phương trình vi phân bậc hai này có nghiệm dạng:
x  C cos kt C sin kt , 1 1   2  
Thay vào hai phương trình còn lại, cho ta:
x  C sin kt  C cos kt , 2 1   2   x  C . 3 3
với C ,C ,C 1 2
3 là các hằng số bất kì.
Xét tại thời điểm ban đầu t  0 với x   , x   , x   . 1 1 2 2 3 3
Thay vào các hệ thức của x , x , x 1 2 3 ở trên cho ta:
C   ,C   ,C   1 1 2 2 3 3 .
Do đó, quy luật chuyển động của môi trường cần tìm có dạng:
x   cos kt   sin kt , 1 1   2   
x   sin kt   cos kt , 2 1   2   x    . 3 3
Chương 1. Ứng suất và biến dạng 19
1.2. TÁC ĐỘNG CỦA NỘI LỰC VÀ NGOẠI LỰC
Giữa các phần tử vật chất luôn có những tương tác. Tại thời điểm
ban đầu, lực tương tác đảm bảo sự không thay đổi hình dáng của vật
thể. Dưới tác động của ngoại lực, vật biến dạng, kéo theo sự thay đổi
lực tương tác bên trong vật thể. Công nhận giả thiết vật thể ở trạng
thái tự nhiên có nghĩa là ở trạng thái cân bằng ban đầu khi chưa có tác
động bên ngoài, nội lực trong hệ bằng không.
Sự biến dạng của vật thể có thể được gây ra dưới tác động của
các lực bên ngoài và mô-men tác dụng lên mặt biên của vật thể; nó là
kết quả của sự tác dụng tương hỗ của vật thể với môi trường bao
quanh (áp suất, lực tiếp xúc…) được gọi là lực mặt; hay tác động lên
mọi điểm của vật thể và phân bố trong toàn thể tích và được gọi là lực
khối (hay lực thể tích). Đây là hai loại của ngoại lực. Ngoại lực tác
dụng lên vật thể biến dạng có thể thay đổi theo thời gian.
Vec-tơ chính của lực khối tác dụng lên một phân tố của vật thể,
được biểu diễn bằng công thức: L    FdV. (1.11) V m dm
trong đó,  - mật độ khối lượng,   lim  , F - lực tác V 0 V dV
dụng trên một đơn vị khối lượng.
Tương ứng, mô-men chính gây ra bởi lực khối có giá trị: M  r   FdV. (1.12) V trong đó r  e i x i
e , i là vec-tơ đơn vị, còn chỉ số lặp i được lấy tổng từ 1 đến 3. 20
Giáo trình CƠ HỌC VẬT RẮN BIẾN DẠNG
Lực hấp dẫn là một lực khối có mật độ lực khối g , hay thường
được gọi là gia tốc trọng trường.
Khi nghiên cứu các bài toán về động lực học, cần quan tâm tới cả
lực quán tính, trong đó mật độ lực khối có cùng giá trị với gia tốc
trong (1.9) với dấu ngược lại. Lực quán tính cũng được xem xét khi
giải các bài toán về trạng thái cân bằng của vật trong hệ tọa độ phi
quán tính, ví dụ trong bài toán về biến dạng của đĩa quay tròn.
Vec-tơ chính của lực mặt tác dụng lên một phần tử mặt của vật
thể với vec-tơ pháp tuyến n , được tính theo công thức: n (1.13) L    dS. S  
trong đó  n là đại lượng đặc trưng cho cường độ lực mặt tác dụng
lên một đơn vị diện tích mặt biên, hay còn được gọi là vec-tơ ứng
suất, được định nghĩa như giới hạn cường độ lực tác dụng lên một đơn
vị diện tích tiết diện S đi qua điểm M thuộc phân tố đó.
Hay nói cách khác, xét phân tố diện tích S chứa điểm M có pháp
tuyến n ở bên trong vật thể. Giả thiết nội lực tác dụng lên diện tích S
đưa về lực tương đương F tại M và ngẫu lực mô-men M .
Khi S  0 (nhưng vẫn chứa điểm M) thì   dF F , còn dS M  0  . S n F dF Đại lượng   lim 
được gọi là vec-tơ ứng suất S 0  S dS
đối với phần tử tiết diện qua điểm M có pháp tuyến n .