Giáo trình Động lực học chất điểm môn Cơ học | Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh
Giáo trình Động lực học chất điểm môn Cơ học | Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem.
Môn: Cơ học (HCMUS) 4 tài liệu
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh 1.1 K tài liệu
Tác giả:
Preview text:
Chương 1. Động lực học chất điểm CƠ HỌC
Cơ học là môn học nghiên cứu về chuyển động (dạng vận động cơ) tức là sự chuyển
dời vị trí của các vật vĩ mô. Cơ học gồm hai phần chính:
Động học nghiên cứu những đặc trưng của chuyển động và những dạng chuyển động khác nhau.
Động lực học nghiên cứu mối liên hệ của chuyển động với sự tương tác giữa các vật,
các định luật về chuyển động. Ngoài các đại lượng động học như vị trí, vận tốc và gia tốc
động lực học còn đưa vào khái niệm lực và khối lượng.
Phần cơ học trình bày trong giáo trình này chủ yếu là cơ học cổ điển của Niutơn, nội
dung chủ yếu của nó bao gồm các định luật cơ bản của động lực học; các định luật Niutơn và
nguyên lý tương đối Galile; ba định luật bảo toàn của cơ học: định luật bảo toàn động lượng,
định luật bảo toàn mô men động lượng và định luật bảo toàn năng lượng; hai dạng chuyển
động cơ bản của vật rắn: chuyển động tịnh tiến và chuyển động quay. CHƢƠNG 1
ĐỘNG LỰC HỌC CHẤT ĐIỂM
Nội dung của chương I nghiên cứu các đặc trưng của chuyển động cơ học (phương
trình chuy ển động , phương trình quỹ đạo , quãng đường dịch chuyển , vận tốc , gia tốc ) và
nguyên nhân gây ra sự thay đổi trạng thái chuyển động.
1.1. ĐỘNG HỌC CHẤT ĐIỂM
1.1.1 Những khái niệm mở đầu
1. Chuyển đô ̣ng.
Theo đi ̣nh nghĩa , chuyển động của một vật là sự chuyển dời vị trí của vật đó đối với
các vật khác trong không gian và theo thời gian . Để xác đi ̣nh vi ̣ trí của mô ̣t vâ ̣t chuyển đô ̣ng ,
ta phải xác đi ̣nh khoảng cách từ vâ ̣t đó đến mô ̣t vâ ̣t (hoă ̣c mô ̣t hê ̣ v ật) khác được qui ước là đứng yên.
Như vâ ̣y, vị trí của một vật chuyển động là vị trí tương đối của vật đó so với một vật
hoă ̣c mô ̣t hê ̣ vâ ̣t được qui ước là đứng yên. Từ đó người ta đưa ra đi ̣nh nghĩa về hê ̣ qui chiếu.
Vật được qui ước là đứng yên dùng làm mốc để xác đi ̣nh vi ̣ trí của các vật trong không
gian đựơc gọi là hê ̣ qui chiếu.
Để xác đi ̣nh thời gian chuyển đô ̣ng của mô ̣t vâ ̣t , người ta gắn hê ̣ qui chiếu với mô ̣t
đồng hồ. Khi mô ̣t vâ ̣t chuyển đô ̣ng thì vi ̣ trí của nó so với hê ̣ qui chiếu thay đổi theo thời gian. 3
Chương 1. Động lực học chất điểm
Vâ ̣y chuyển đô ̣ng của mô ̣t vâ ̣t chỉ có tính chất tương đối tùy theo hệ qui chiếu được
chọn, đối với hê ̣ qui chiếu này nó là chuyển đô ̣ng , nhưng đối với hê ̣ qui chiếu khác nó có thể là đứng yên.
2. Chất điểm, hê ̣ chất điểm, vật rắn.
Bất kỳ vâ ̣t nào trong tự nhiên cũng có kích thước xác đi ̣nh . Tuy nhiên, trong nhiều bài
toán có thể bỏ qua kích thước của vật được khảo sát . Khi đó ta có khái niê ̣m về chất điểm :
Chất điểm là một vật mà kích thước của nó có thể bỏ qua trong bài toán được xét.
Kích thước của một vật có thể bỏ qua được khi kích thước đó rất nhỏ so với kích
thước của các vâ ̣t khác hay rất nhỏ so với khoảng cách từ nó tới các vâ ̣t khác . Vâ ̣y, cũng có thể đi ̣nh nghĩa:
Một vật có kích thước nhỏ không đáng kể so với những khoảng cách , những kích
thước mà ta đang khảo sát được gọi là chất điểm.
Như vâ ̣y, tùy thuộc vào điều kiện bài toán ta nghiên cứu mà có thể xem một vật là chất điểm hay không.
Thí dụ: Khi xét chuyển đô ̣ng của viên đa ̣n trong không khí , chuyển đô ̣ng của quả đất
quay quanh mă ̣t trời , ta có thể co i viên đa ̣n , quả đất là chất điểm nếu bỏ qua chuyển động quay của chúng.
Tâ ̣p hợp các chất điểm được go ̣i là hê ̣ chất điểm. Nếu khoảng cách tương đối giữa các
chất điểm của hê ̣ không thay đổi, thì hệ chất điểm đó được gọi là vật rắn.
3. Phương trình chuyển động của chất điểm
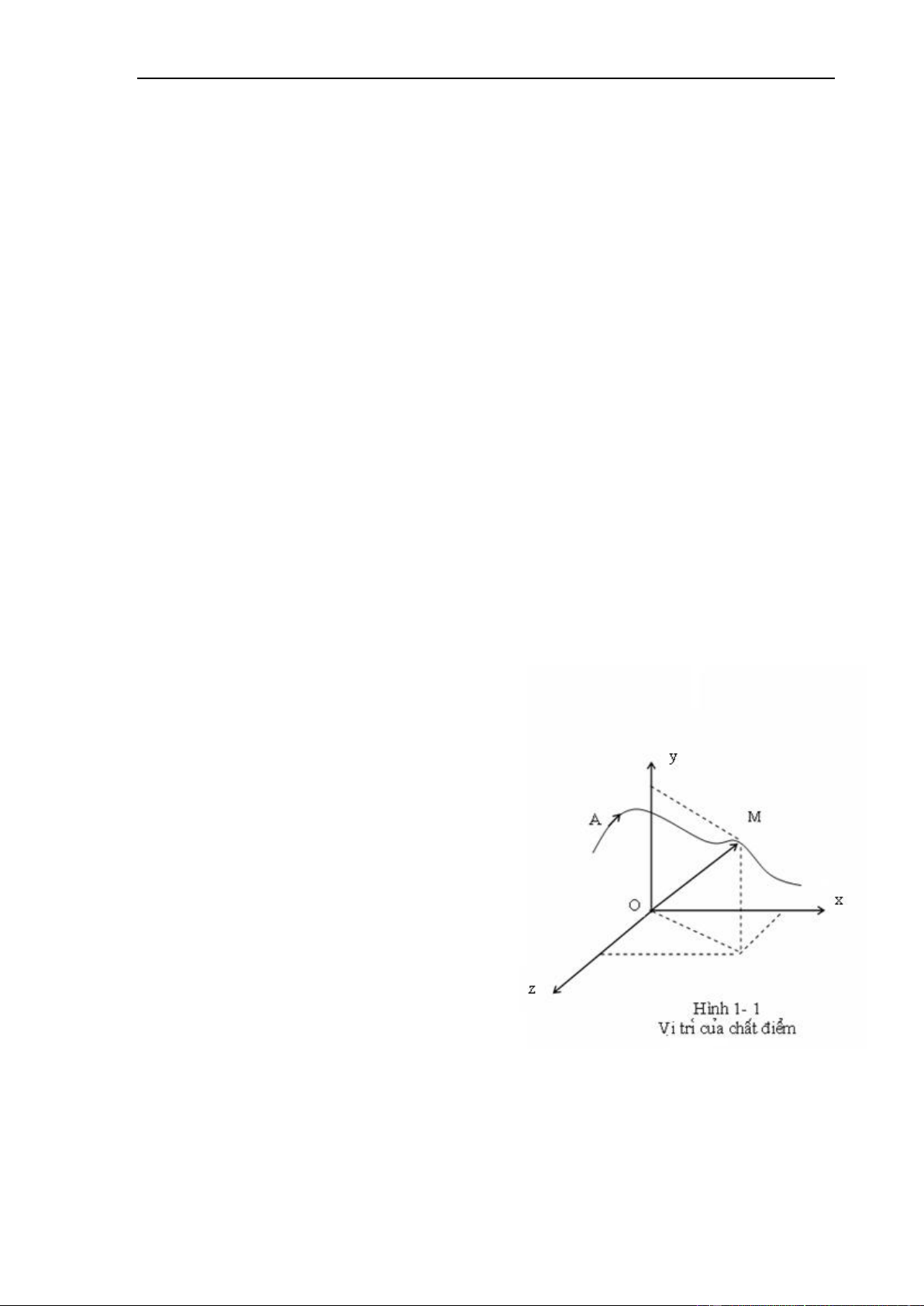
Để xác đi ̣nh chuyển đô ̣ng của mô ̣t chất
điểm, người ta thường gắn vào hê ̣ qui chiếu mô ̣t
hê ̣ to ̣a đô ̣ , chẳng ha ̣n hê ̣ to ̣a đô ̣ Descartes có ba
trục ox, oy, oz vuông góc từng đôi mô ̣t hợp thành
tam diê ̣n thuâ ̣n Oxyz có gốc tọa độ tại O. Hê ̣ qui
chiếu đươ ̣c gắn với gốc O. Như vâ ̣y viê ̣c xét chất
điểm chuyển đô ̣ng trong không gian sẽ được xác
đi ̣nh bằng viê ̣c xét chuyển đô ̣ng của chất điểm đó
trong hê ̣ tọa độ đã chọn . Vị trí M của chất điểm
sẽ được xác định bởi các tọa độ của nó . Với hê ̣
tọa độ Descartes Oxyz, các tọa độ này là x,y,z. Bán kính vectơ M O
r cũng có các tọa độ x,y,z
trên ba tru ̣c ox,oy,oz (hình 1-1), và có mối liên hệ: r x t ( )i y t ( ) j z t ( )k .
Khi chất điểm chuyển đô ̣ng , vị trí M thay đổi theo thời gian , các tọa độ x, y, z của M
là những hàm của thời gian t: 4
Chương 1. Động lực học chất điểm x = x(t) y = y(t) (1-1) z = z(t)
Do đó bán kính vectơ r của chất điểm chuyển động cũng là một hàm của thời gian t:
r r (t ) (1-2)
Các phương trình (1-1) hay (1-2) xác định vị trí của chất điểm tại thời điểm t và
đươ ̣c go ̣i là phương trình chuyển động của chất điểm. Vì ở mỗi thời điểm t, chất điểm có mô ̣t
vị trí xác định, và khi thời gian t thay đổi, vị trí M của chất điểm thay đổi liên tục nên các hàm
x(t), y(t), z(t) hay r (t) là những hàm xác định, đơn tri ̣ và liên tục của thời gian t. 4. Qũy đạo
Quỹ đạo của chất điểm chuyển động là đường cong tạo bởi tập hợp tất cả các vi ̣ trí
của chất điểm trong không gian trong suốt quá trình chuyển động.
Tìm phương trình Quỹ đạo cũng có nghĩa là tìm mối liên hệ giữa các tọa độ x,y,z của
chất điểm M trên quỹ đa ̣o của nó. Muốn vâ ̣y ta có thể khử thời gian t trong các phương trình tham số (1-1) và (1-2).
5. Hoành độ cong
Giả sử ký hiệu quỹ đạo của chất điểm là (C) (Hình 1-1). Trên đường cong (C) ta cho ̣n
điểm A nào đó làm gốc (A đứng yên so với O ) và chọn một chiều dương hướng theo chiều
chuyển đô ̣ng của chất điểm. Khi đó ta ̣i mỗi thời điểm t vị trí M của chất điểm trên đường cong
(C) đươ ̣c xác đi ̣nh bởi tri ̣ đa ̣i số của cung AM, ký hiệu là: AM = s
Người ta gọi s là hoành độ cong của chất điểm chuyển động . Khi chất điểm chuyển
đô ̣ng, s là hàm của thời gian t, tức là: s = s(t) (1-3)
Khi dùng hoành đô ̣ cong, thì quãng đường chất điểm đi được trong khoảng thời gian t=t-t , trong đó s o là s=s-s0
0 là khoảng cách từ chất điểm đến gốc A tại thời điểm ban đầu
(to = 0), s là khoảng cách từ chất điểm đến gốc A tại thời điểm t. Nếu ta ̣i thời điểm ban đầu
chất điểm ở ngay ta ̣i gốc A thì s0 = 0 và s = s, đúng bằng quãng đường mà chất điểm đi
đựơc trong khoảng thời gian chuyển động t. 1.1.2. Vận tốc
Để đă ̣c trưng cho chuyển đô ̣ng về phương , chiều và đô ̣ nhanh châ ̣m , người ta đưa ra
đa ̣i lượng go ̣i là vận tốc. Nói cách khác: vận tốc là một đại lượng đặc trưng cho trạng thái
chuyển động của chất điểm.
1. Vận tốc trung bình và vận tốc tức thời 5
Chương 1. Động lực học chất điểm
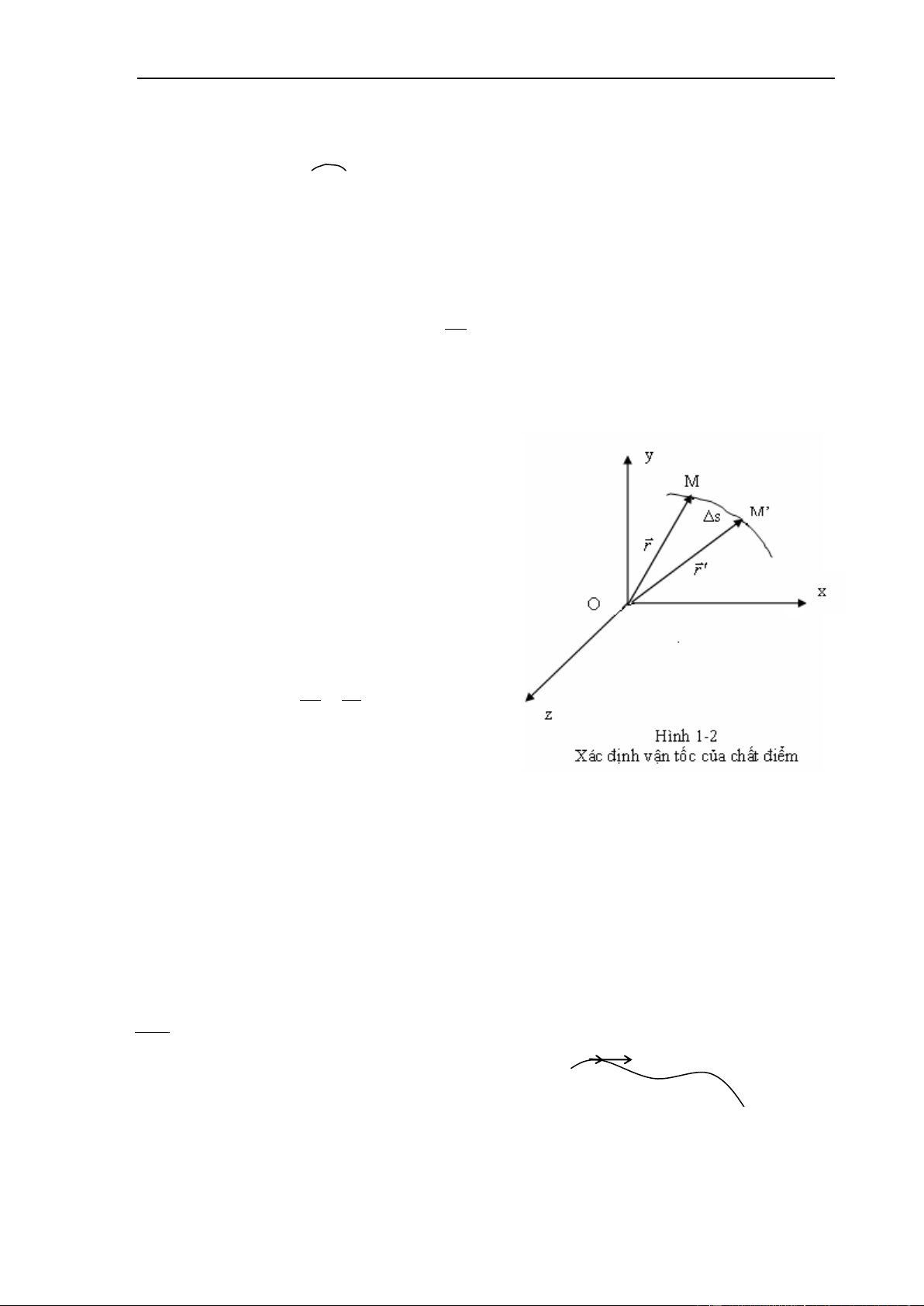
Giả sử ta xét chuyển động của chất điểm trên đường cong (C) (hình 1-2). Tại thời
điểm t, chất điểm ở vị trí M, tại thời điểm t’=t+t chất điểm đã đi được mô ̣t quãng đường s
và ở vị trí M’ Quãng đường đi được của chất điểm trong khoảng thời gian t = t’–t là:
MM’ = s’ – s = s
Tỉ số s/t biểu thi ̣ quãng đường trung bình mà chất điểm đi được trong mô ̣t đơn vi ̣
thời gian từ M đến M’, và được gọi là vận tốc trung bình của chất điểm trong khoảng thời
gian t (hoă ̣c trên quãng đường từ M đến M’) s v (1-4) tb t
Vâ ̣n tốc trung bình chỉ đă ̣c trưng cho đô ̣ nhanh châ ̣m trung bình của chuyển đô ̣ng
trên quãng đường MM’. Trên quãng đường này, nói chung độ nhanh chậm của chất điểm thay
đổi từ điểm này đến điểm khá c. Vì thế để đặc
trưng cho đô ̣ nhanh châ ̣m của chuyển đô ̣ng ta ̣i
từng thời điểm , ta phải tính tỉ số s/t trong
những khoảng thời gian t vô cùng nhỏ , tức là cho t 0.
Theo đi ̣nh nghĩa, khi t 0, M’M, tỉ
số s/t sẽ tiến dần tới một giới hạn gọi là vận tốc
tức thời (gọi tắt là vận tốc ) của chất điểm tại thời điểm t: s ds v lim (1-5) t 0 t dt
Vâ ̣y: Vận tốc của chất điểm chuyển độ ng
bằng đạo hàm hoành độ cong của chất điểm đó theo thời gian.
Số gia s cũng chính là quãng đường mà chất điểm đi được trong khoảng thời gian t
= t-to. Do đó nói chung có thể phát biểu (1-5) như sau:
Vận tốc của chất điể m chuyển động bằng đạo hàm quãng đường đi được của chất
điểm đó theo thời gian.
Biểu thức (1-5) biểu diễn vâ ̣n tốc là mô ̣t lượng đa ̣i số.
Đơn vi ̣ đo của vâ ̣n tốc trong hệ đơn vị SI là : mét (m/s). M giây v s d
2. Vectơ vận tốc v ∫
Để đă ̣c trưng đầ y đủ cả về phương chiều và Hình.1-3
đô ̣ nhanh châ ̣m của chuyển đô ̣ng người ta đưa ra
Để đi ̣nh nghĩa vectơ vâ ̣n tốc
mô ̣t vectơ go ̣i là vectơ vận tốc. 6
Chương 1. Động lực học chất điểm
Đi ̣nh nghĩa:Vectơ vâ ̣n tốc ta ̣i vi ̣ trí M là vectơ có phương nằm trên tiếp tuyến với quĩ
đạo tại M, có chiều theo chiều chuyển động và có đô ̣ lớn được xác đi ̣nh bởi công thức (1-5).
Để có thể viết được biểu thức của vectơ vâ ̣n tốc , người ta đi ̣nh nghĩa vectơ vi phân cung s
d là vectơ nằm trên tiếp tuyến với quỹ đạo tại M, hướng theo chiều chuyển đô ̣ng và
có đô ̣ lớn bằng tri ̣ số tuyê ̣t đối của vi phân hoành đô ̣ cong ds đó. Do đó ta có thể viết lại (1-5) như sau: s d v (1-6) dt
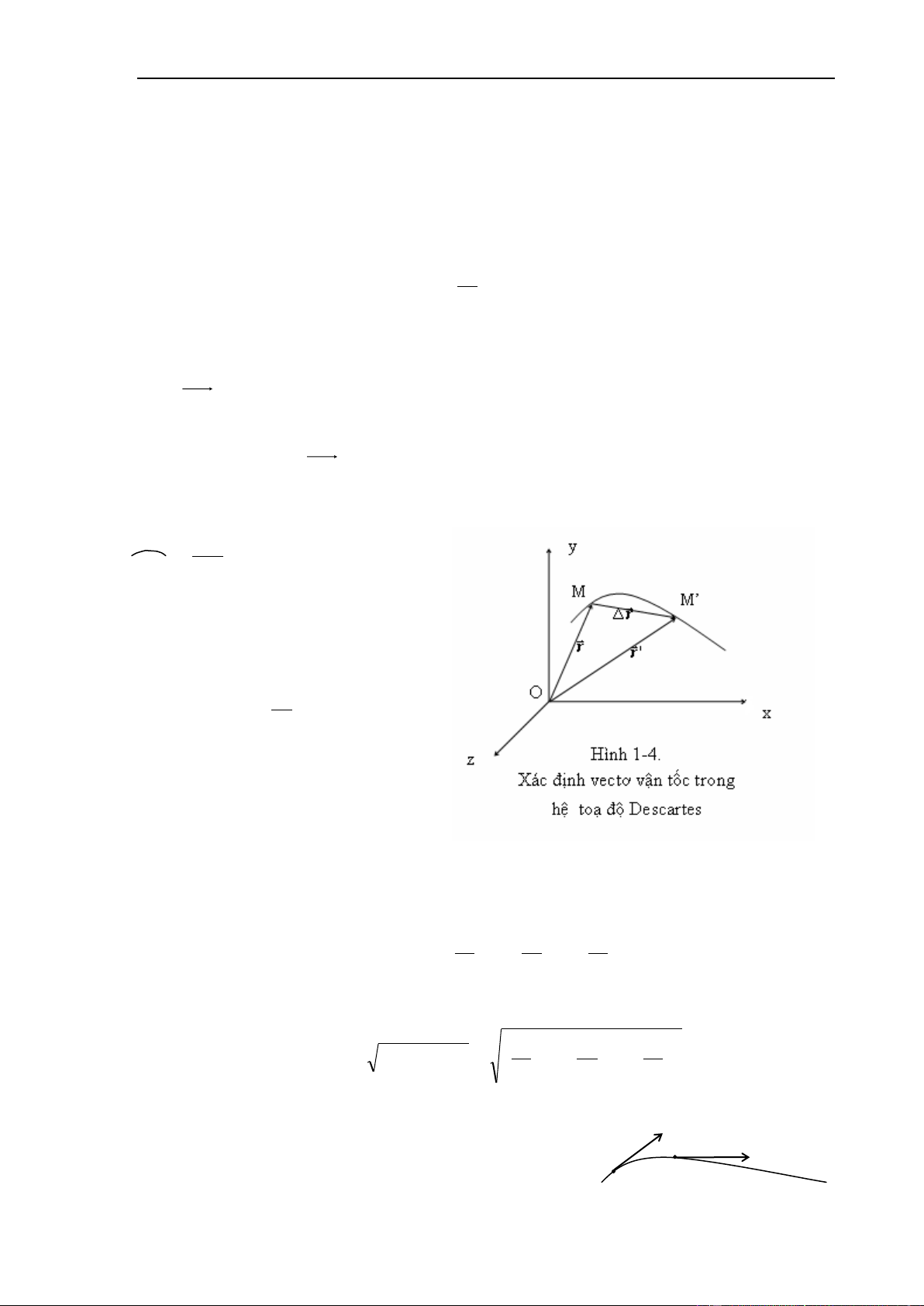
3.Vectơ vâ ̣n tốc trong hê ̣ toa ̣ độ Descartes
Giả sử tại thời điểm t, vị trí của chất điểm chuyển động được xác định bởi bán kính
vectơ OM r (hình1-4). Ở thời điểm sau đó t’=t+t, vị trí của nó đ ược xác định bởi bán kính vectơ:
OM r r Khi t
Δ 0 , M' M , r Δ r d , do đó
MM’ MM ' , r d s d . Hai vectơ r d , s d bằng nhau , do
đó ta có thể viết la ̣i biểu thức (1-6) của vâ ̣n tốc như sau: r d v (1-7) dt
Tức là : Vectơ vận tốc bằng đạo
hàm bán kính vectơ vị trí ch uyển động
của chất điểm theo thời gian.
Gọi ba thành phần v ,v ,v của x y z
véc tơ vận tốc v theo ba trục tọa độ có độ dài đại số lần lượt bằng đạo hàm ba thành phần
tương ứng của bán kính véc tơ theo ba trục tọa độ: dx dy dz v , v , v (1-8) x dt y dt z dt
Độ lớn của vận tốc được tính theo công thức: 2 2 2 dx dy dz 2 2 2 v
v v v (1-9) x y z dt dt dt 1.1.3. Gia tốc v
Để đă ̣c trưng cho sự biến thiên của vectơ vâ ̣n • M v tốc
, người ta đưa ra một đa ̣i lươ ̣ng go ̣i là vectơ gia tốc . M’ Hình 1-5 7
Vận tốc tại những điểm khác nhau
Chương 1. Động lực học chất điểm
Nói cách khác, gia tốc là đại luợng đặc trưng cho sự biến đổi trạng thái chuyển động của chất điểm.
1. Đi ̣nh nghĩa và biểu thức vectơ gia tốc
Khi chất điểm chuyển đô ̣ng , vectơ vâ ̣n t ốc của nó thay đổi cả về phương chiều và độ
lớn. Giả sử tại thời điểm t chất điểm ở điểm M, có vận tốc là v , tại thời điểm sau đó t’ = t+t
chất điểm ở vi ̣ trí M’ có vâ ̣n tốc v v v
(hình 1 -5). Trong khoảng thời gian t=t’- t,
vectơ vâ ̣n tốc của chất điểm biến thiên mô ̣t lượng: v
v v Tỷ số v
xác định độ biến thiên trung bình của vectơ vận tốc trong một đơn vị thời t
gian và được gọi là vectơ gia tốc trung bình của chất điểm chuyển động trong khoảng thời gian t: v a (1-10) tb t
Nhưng nói chung ta ̣i những thời điểm khác nhau trong khoảng thời gian t đã xét, đô ̣
biến thiên vectơ vận tốc trong một đơn vị thời gian có khác nhau . Do đó, để đặc trưng cho độ biến thiên cu v
̉ a vectơ vâ ̣n tốc ta ̣i từng thời điểm , ta phải xác đi ̣nh tỷ số trong khoa ̉ng thời t gian vô cu v
̀ ng nhỏ , nghĩa là cho t 0, khi đó tỷ số
sẽ tiến dần tới giới hạn gọi là vectơ t
gia tốc tức thời (gọi tắt là gia tốc) của chất điểm tại thời điểm t và được ký hiệu là a . v v d a lim (1-11) t 0 t dt
Vâ ̣y: “Vectơ gia tốc của chất điểm chuyển động bằng đạo hàm vectơ vận tốc theo thời gian”.
Nếu phân tích chuyển đô ̣ng của chất điểm thành ba thành phần chuyển đô ̣ng theo ba
trục ox, oy, oz của hệ tọa độ Descartes, ta có: 2 2 2 dv d x dvy d y dv d z a x , a , a z (1-12) x 2 y 2 z 2 dt dt dt dt dt dt
và độ lớn của gia tốc sẽ được tính như sau: 2 2 2 2 2
d x d y d z 2 2 2 a
a a a x y z 2 2 2
dt dt dt
2. Gia tốc tiếp tuyến và gia tốc pháp tuyến
Trường hợp tổng quát , khi chất điểm chuyển đô ̣ng trên quỹ đa ̣o cong , vectơ vâ ̣n tốc
thay đổi cả về phương chiều và đô ̣ lớn . Để đă ̣c trưng riêng cho sự biến đổi về đô ̣ lớn phương
và chiều của vectơ vận tốc người ta phân tích a thành hai thà nh phần: gia tốc tiếp tuyến và gia tốc pháp tuyến. 8
Chương 1. Động lực học chất điểm
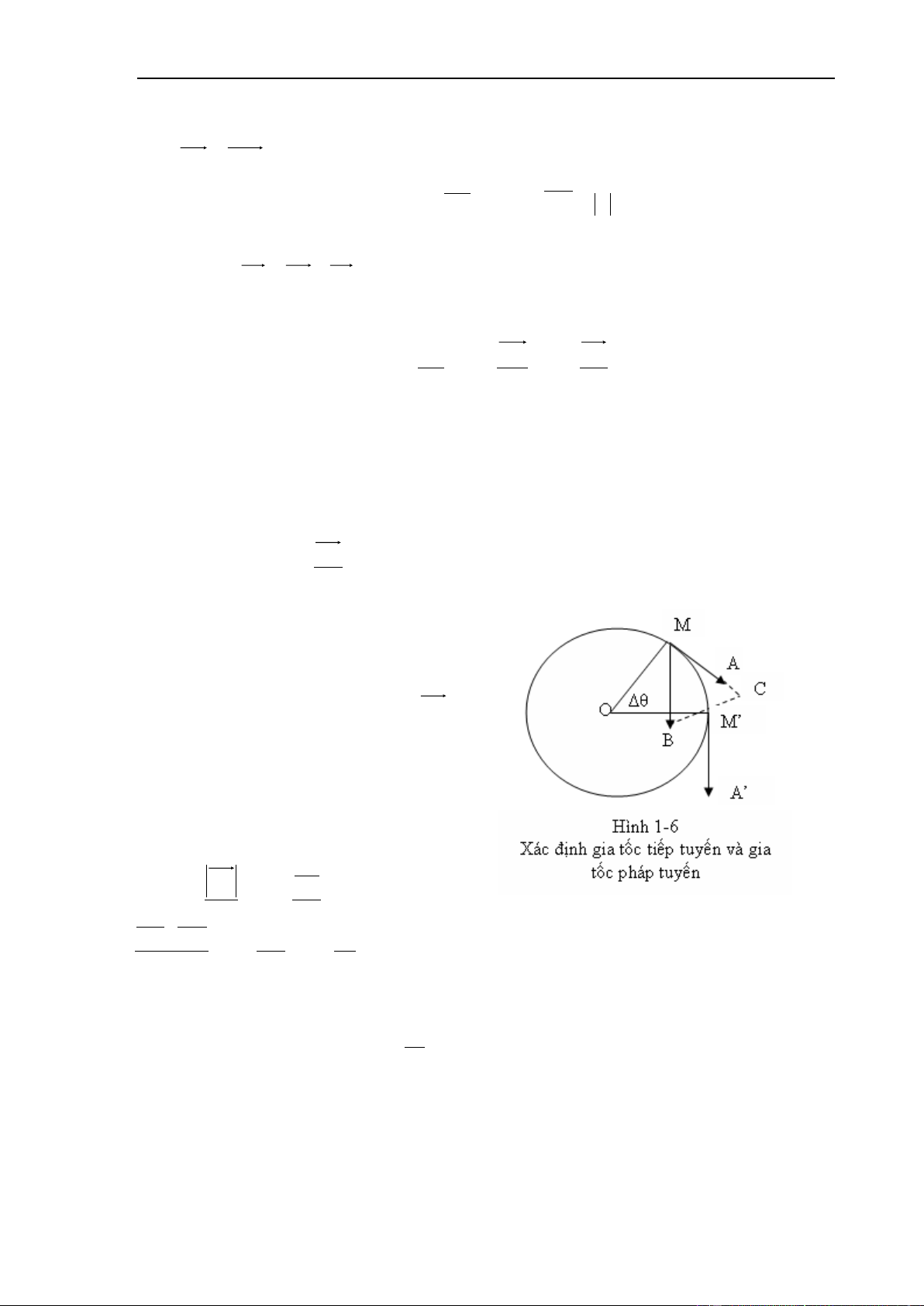
Xét chuyển động của chất điểm trên quỹ đạo tròn (hình 1-6). Tại thời điểm t, chất
điểm ở tại vị trí M có vận tốc v ; Tại thời điểm t’ chất điểm ở vị trí M’, có vận tốc v . Ta vẽ
vectơ MB M
A v ' có gốc tại M.
Ta đă ̣t trên phương MA mô ̣t đoa ̣n MC sao cho MC v' . Khi đó, như trên hình vẽ (1-
6), độ biến thiên vectơ vận tốc trong khoảng thời gian Dt là: v
= AB AC CB
Theo đi ̣nh nghĩa (1-11) về gia tốc, ta có: v Δ AC CB a lim lim lim (1-13) t Δ 0 → t t Δ Δ 0 → t t Δ Δ 0 → t Δ
Theo (1-13), vectơ gia tốc gồm hai thành phần . Sau đây ta sẽ lần lươ ̣t xét các thành phần này.
Gia tốc tiếp tuyến.
Ta ký hiê ̣u thành phần thứ nhất của (1-13) là: AC a lim t t 0 t
Thành phần này luôn cùng phương với
tiếp tuyến của quỹ đa ̣o ta ̣i thờ i điểm t, vì vậy
đươ ̣c go ̣i là gia tốc tiếp tuyến.
Chiều của a trùng chiều với AC . Vì t
vậy khi v' v thì a cùng chiều với v , khi t
v' v , thì a ngươ ̣c chiều với v t
Độ lớn được tính như sau: AC AC a lim lim lim t t Δ 0 t Δ t Δ 0 t Δ Δt 0 M C- M A v -v ' v lim lim t t 0 t 0 t t
Theo định nghĩa đạo hàm: dv a (1-14) t dt
Vâ ̣y: Vectơ gia tốc tiếp tuyến đặc trưng cho sự biến đổi độ lớn của vectơ vận tốc, có:
Phương trùng với tiếp tuyến của qũy đạo, 9
Chương 1. Động lực học chất điểm
Chiều trùng với chiều chuyển động khi vận tốc tăng và ngược chiều chuyển động
khi vận tốc giảm.
Độ lớn bằng đạo hàm trị số vận tốc theo thời gian.
Gia tốc pháp tuyến
Thành phần thứ hai của gia tốc, đươ ̣c ký hiê ̣u là a và theo (1-13), ta có: n CB a lim n t 0 t
Khi t 0, '
v v , CB dần tới vuông góc với AC , tức vuông góc với t iếp tuyến
của quĩ đạo tại M. Vì vậy a được go ̣i là gia tốc pháp tuyến. n
Độ lớn của gia tốc pháp tuyến là: CB a lim n t 0 t
Ta đă ̣t MOM’= CMB = . Trong tam giác cân Δ MCB có: CMB MCB = 2 2 2
Khi t 0, M’ M, 0, MCB
. Vâ ̣y đến giới ha ̣n , CB AC do đó 2
phương của a AC tức là vuông góc với tiếp tuyến của quỹ đa ̣o ta ̣i M. n
Chiều của a luôn hướng về tâm của quĩ đa ̣o , do đó đươ ̣c go ̣i là gia tốc hướng n tâm. CB
Độ lớn của a cho bởi: a lim n n t Δ 0 t Δ
Chú ý rằng các góc : BMC = MOM’= θ. Khi t 0, M’ M, v' v , góc θ rất nhỏ, có thể coi gần đúng: s =MM’Rθ, s CB v '. v'. R CB v' 1 s 1 s lim a lim = lim v' . lim (1-15) n t Δ 0 t Δ R t Δ 0 t Δ Δ 0 R t t Δ 0 t Δ s ds
lim v' v và lim v t Δ 0 t Δ 0 t Δ dt
Thay các kết qủa vừa tính được vào (1-15), cuối cùng ta sẽ được: v 2 a (1-16) n R 10
Chương 1. Động lực học chất điểm
Công thức (1-16) chứng tỏ an càng lớn nếu chất điểm chuyển đô ̣ng càng nhanh và quĩ
đa ̣o càng cong (R càng nhỏ). Với các điều kiện này , phương của vectơ vâ ̣n tốc thay đổi càng
nhiều. Vì thế, gia tốc pháp tuyến đặc trưng cho sự thay đổi phương của vectơ vận tốc.
Tóm lại vectơ gia tốc pháp tuyến đặc trưng cho sự thay đổi phương của vectơ vận tốc, nó có:
Phương: trùng với phương pháp tuyến của quỹ đạo tại M;
Chiều: luôn hướng về phía lõm của quỹ đạo; 2 v
Có độ lớn bằng: a n R Kết luận
Trong chuyển đô ̣ng cong nói chung vectơ gia tốc gồm hai thành phần :
gia tốc tiếp tuyến và gia tốc pháp tuyến, tức là:
a a a (1-17) t n
Gia tốc tiếp tuyến đặc trưng cho sự biến đổ
i về độ lớn của vectơ vận tốc.
Gia tốc pháp tuyến
đặc trưng cho sự biến đổi về phương của vectơ vận tốc. Độ lớn 2 2 2 dv v 2 2 a a a t n dt R
Trong trường hợp tổng quát quỹ đạo của chất điểm là
một đường cong bất kỳ, người ta chứng minh được rằng tại
mỗi vị trí, véc tơ gia tốc tiếp tuyến và pháp tuyến vẫn cho
bới các biểu thức trên, nhưng chú ý rằng trong biểu thức an
thì R là bán kính cong của quỹ đạo tại M (tức là bán kính
của vòng tròn mật tiếp của quỹ đạo tại M)
Chúng ta xét một số trường hợp đặc biệt:
- Khi an = 0, vectơ vâ ̣n tốc không thay đổi phương , chất điểm chuyển động thẳng (quỹ
đa ̣o chuyển đô ̣ng là đường thẳng ).
- Khi at = 0, vectơ vâ ̣n tốc không đổi về tri ̣ số và chiều, nó chuyển động cong đều.
- Khi a = 0 vectơ vâ ̣n tốc không đổi, chất điểm chuyển động thẳng đều.
1.1.4. Một số dạng chuyển động cơ đơn giản
1. Chuyển động thẳng biến đổi đều
Trong trường hợp này an = 0, at = const, nên ta có: Gia tốc 11
Chương 1. Động lực học chất điểm dv a a const (1-18) t dt v t dv a
dv adt dt v 0 0 Từ đó suy ra:
v v at (1-19) o Đường đi: s v v
ds vdt v at dt o 0 v v 0 0 2
chọn gốc tọa độ là vị trí ban đầu ta đươ ̣c at : s v t (1-20) o 2
Từ (1-19) và (1-20), khử thông số t ta sẽ đươ ̣c 2 2
2as v v (1-21) 0
Trong chuyển đô ̣ng thẳng , nếu a = 0, vâ ̣n tốc chuyển đô ̣ng không thay đổi , do đó
chuyển đô ̣ng này được go ̣i là chuyển động thẳng đều. Trong chuyển đô ̣ng thẳng đều: v = const, s = vt
Rơi tự do là chuyển động của vật dưới tác dụng của trọng lực với vận tốc ban đầu
v0 = 0 và gia tốc a = g.
2. Chuyển đô ̣ng tròn
Trong chuyển đô ̣ng , nếu bán kính cong của quỹ đa ̣o không thay đổi (R = const),
chuyển đô ̣ng sẽ được go ̣i là chuyển động tròn.
Trong chuyển đô ̣ng tròn, do có sự thay đổi góc quay của bán kính vectơ OM , ngoài
các đại lượng v, a, at, an, người ta còn đưa ra các đa ̣i lượng vận tốc góc và gia tốc góc.
*Vâ ̣n tốc góc
Giả sử chất điểm M chuyển đô ̣ng trên quỹ đa ̣o tròn tâm O, bán kính R. Trong khoảng
thời gian t = t’ – t chất điểm đi được quãng đường s
bằng cung MM’ ứng với góc quay = MOM’ của bán kính
R = MO (Hình 1-8). Đa ̣i lươ ̣ng /t biểu thi ̣ góc quay M trung bi R
̀nh của bán kính trong mô ̣t đơn vi ̣ thời gian và đươ ̣c
gọi là vận tốc góc trung bình trong khoảng thời gian O t: θ Δ s (1-22) tb t M' Hình 1-8
Nếu cho t 0, tỉ số
sẽ tiến tới giới hạn , ký
Lâ ̣p công thức vâ ̣n tốc t góc 12
Chương 1. Động lực học chất điểm
hiê ̣u là , biểu thi ̣ vâ ̣n tốc góc của chất điểm ta ̣i thời điểm t: Δθ dθ ω lim (1-23) t Δ 0 t Δ dt
Vâ ̣y: “Vận tốc góc bằng đạo hàm góc quay theo thời gian”
Vâ ̣n tốc góc có đơn vi ̣ là radian trên giây (rad/s).
Với chuyển đô ̣ng tròn đều (R= const, = const, v = const) người ta còn đưa ra đi ̣nh
nghĩa chu kỳ và tần số.
Chu kỳ là thời gian cần thiết để chất điểm đi được một vòng tròn. Do chuyển đô ̣ng
tròn đều, góc quay trong khoảng thời gian t là: = .t
Trong mô ̣t chu kỳ t =T, =2π Δθ 2π Và ta suy ra: T . ω ω 2π Vâ ̣y: T ω
Tần số (ký hiệu là f) là số vòng quay được của chất điểm trong một đơn vị thời gian.
Trong khoảng thời gian mô ̣t giây chất điểm đi được cung tròn , mỗi vòng tròn có đô ̣
dài 2π, do đó theo đi ̣nh nghĩa tần số, ta có: ω 1 f 2 π T
Đơn vi ̣ của chu kỳ là giây (s), của tần số là 1/s hoă ̣c còn gọi là Hertz (Hz).
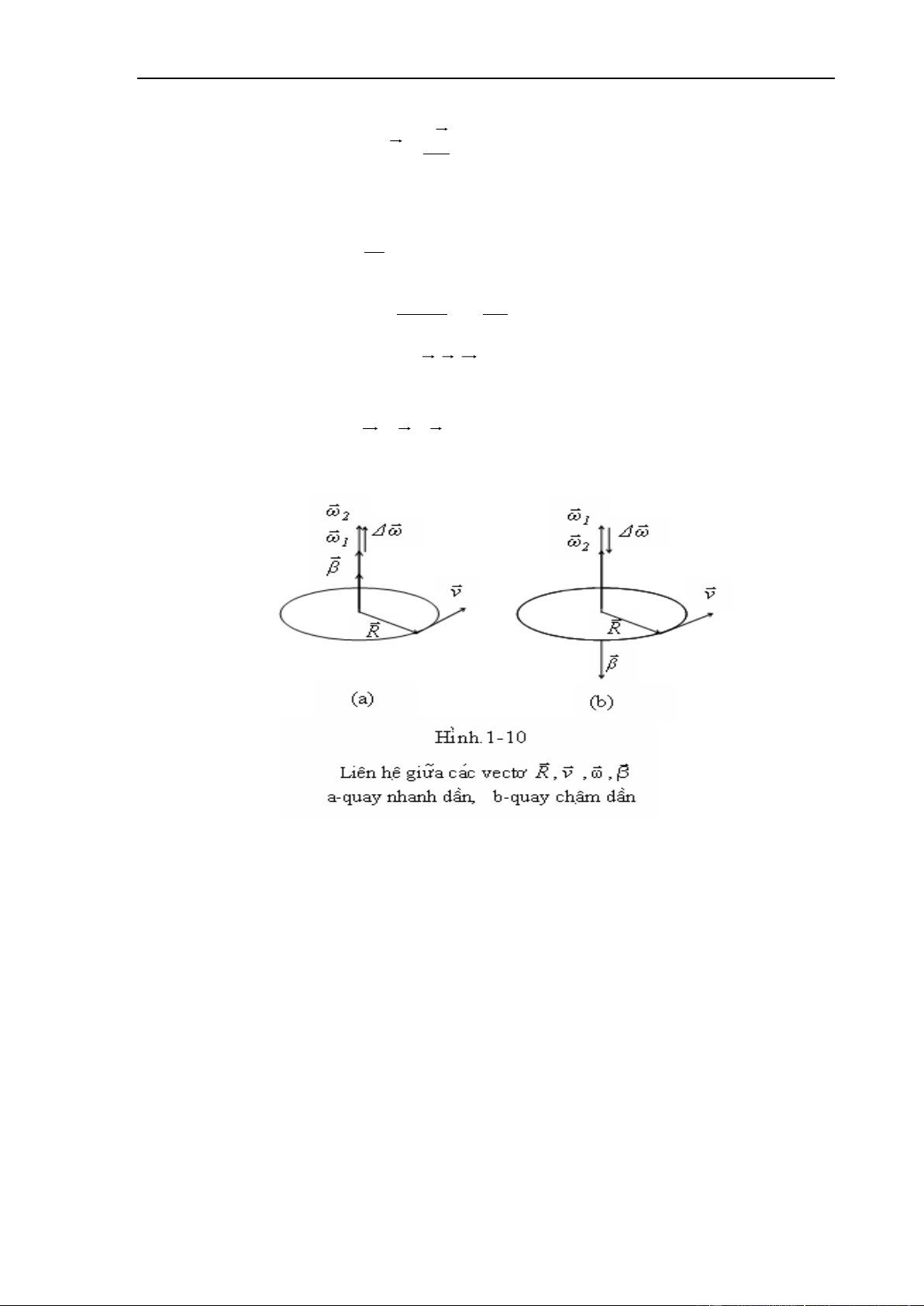
Người ta biểu diễn vận tốc góc bằng véc tơ , nằm trên trục của vòng tròn quỹ đạo, thuận
chiều đối với chiều quay của chuyển động và có giá trị bằng ω.
* Liên hê ̣ giữa các vectơ v và ω . Giữa bán kính R, cung MM’ và góc có mối Δ Δθ liên hê ̣ s
(xem hình 1-8): MM’ = s = R , do đó: R.
Khi t 0, ta đươ ̣c: t Δ t Δ v R ω (1-24)
Nếu đă ̣t OM R (hình 1-9) ta thấy ba ve ctơ , R, v theo thứ tự đó ta ̣o thành mô ̣t
tam diê ̣n thuâ ̣n ba mă ̣t vuông. Ngoài ra theo công thức (1-24) ta có thể viết: v ω R (1-25)
* Liên hê ̣ giữa an và v2 ( R 2 ω ) a 2 ω n =
, v= R, ta suy ra: a = R R n R 13
Chương 1. Động lực học chất điểm a 2 ω R (1-26) n
* Gia tốc góc
Giả sử trong khoảng thời gian t = t’ – t, vâ ̣n tốc góc của chất điểm chuyển đô ̣ng tròn
biến thiên mô ̣t lượng = ’ - . Theo đi ̣nh nghĩa, lượng /t go ̣i là gia tốc góc trung bình
trong khoảng thời gian t, nó biểu thị độ biến thiên trung bình củ a vận tốc góc trong một đơn vi ̣ thời gian: tb t
Nếu cho t 0,gia tốc góc trung bình tiến tới giới ha ̣n go ̣i là gia tốc góc của chất
điểm ta ̣i thời điểm t, ký hiệu là . Do đó: Δω β lim t Δ 0 t Δ
Theo đi ̣nh nghĩa về đa ̣o hàm, ta có: 2 ω d d θ β (1-27) 2 dt dt
Vâ ̣y: “ Gia tốc góc bằng đạo hàm vận tốc góc theo thời gian và bằng đạo hàm bậc
hai của góc quay theo thời gian”.
Gia tốc góc có đơn vi ̣ bằng Radian trên giây bình phương (rad/s2).
Khi > 0, tăng, chuyển đô ̣ng tròn nhanh dần,
Khi < 0, giảm, chuyển đô ̣ng tròn châ ̣m dần.
Khi = 0, không đổi, chuyển đô ̣ng tròn đều.
Khi = const, chuyển đô ̣ng t ròn biến đổi đều (nhanh dần đều hoă ̣c châ ̣m dần
đều). Tương tự như đã chứng minh cho trường hợp chuyển đô ̣ng thẳng biến đổi đều , ta cũng
có thể chứng minh được: t (1-28) 0 1 2
t t (1-29) 0 2
2 2 2 (1-30) 0
Với chú ý là: tại thời điểm ban đầu to = 0, o = 0, vâ ̣n tốc góc có giá tri ̣ o.
Người ta biểu diễn gia tốc góc bằng một véc tơ gọi là véc tơ gia tốc góc, có:
- Phương nằm trên trục của quỹ dạo tròn
- Cùng chiều với khi β > 0 và ngược chiều với khi β < 0 - Có giá trị bằng β 14
Chương 1. Động lực học chất điểm
Vậy ta có thể viết hệ thức sau: d (1-31) dt
* Liên hê ̣ giữa at và dv
Thay v=.R vào a ta đươ ̣c: t dt d R d a R R (1-32) t dt dt
Theo đi ̣nh nghĩa của các vectơ , R,a , ta thấy ba vectơ theo thứ tự đó luôn ta ̣o t
thành tam diện thuận ba mặt vuông; Kết hợp với (1-32) ta có thể viết:
a R (1-33) t 15
Chương 1. Động lực học chất điểm
3. Chuyển đô ̣ng với gia tốc không đổi
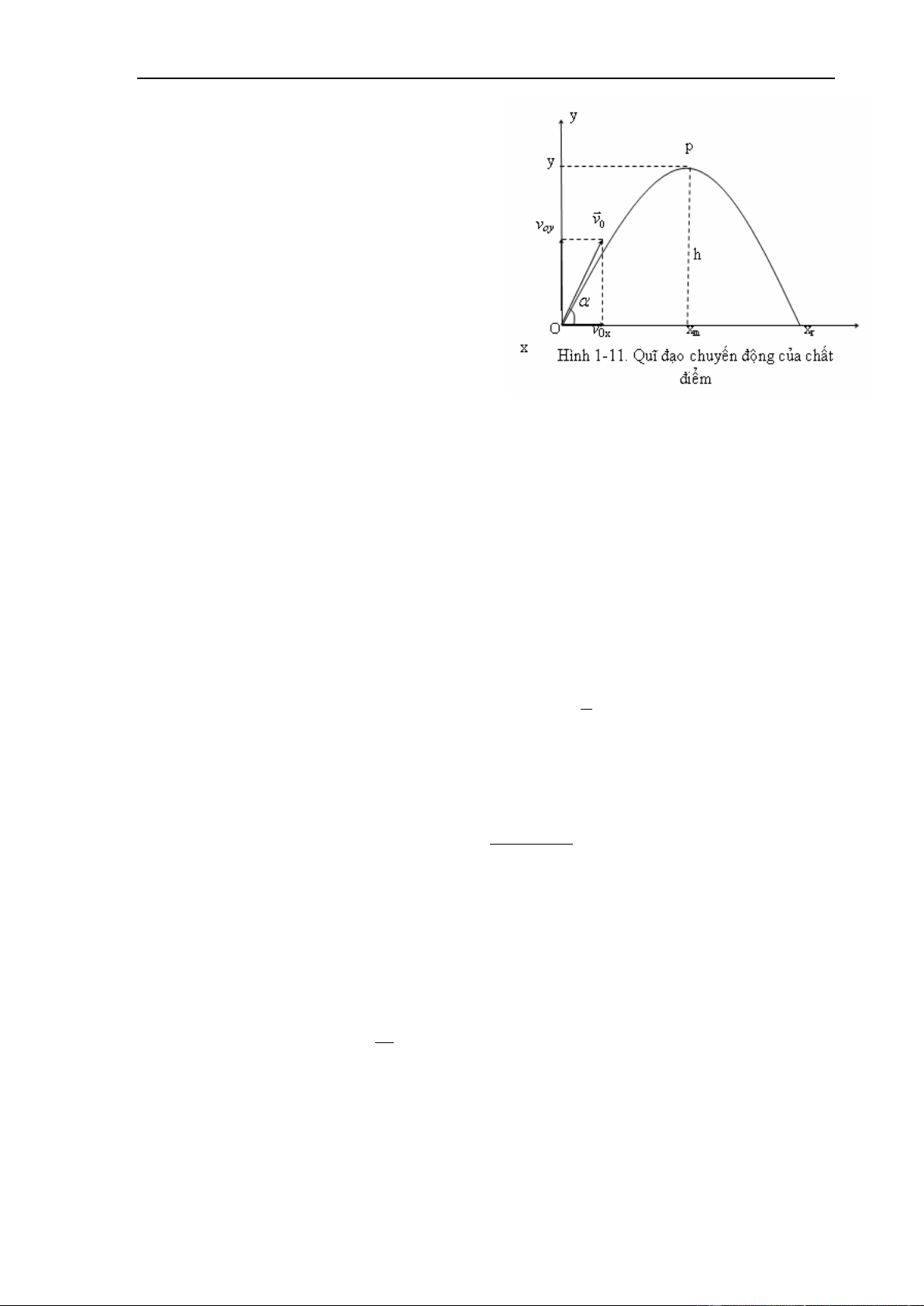
Xét chuyển động của một chất điểm xuất
phát từ một điểm O trên mặt đất với véc tơ vận
tốc ban đầu là v hợp với phương nằm ngang 0
một góc α (hình 1-11) Bỏ qua mọi lực cản không khí.
Chọn mặt phẳng hình vẽ là mặt phẳng
thẳng đứng chứa v , hai trục tọa độ Ox nằm 0
ngang và Oy thẳng đứng hướng lên trên (hình 1-
11). Quỹ đạo của chất điểm sẽ nằm trong mặt phẳng Oxy.
* Phương trình chuyển động
Ta phân tích vectơ vâ ̣n tốc v thành 2 thành phần theo 2 trục Ox, Oy: 0 vox = vocos, voy = vosin
Coi chuyển đô ̣ng gồm hai thành phần: thành phần theo phương Ox, có vận tốc ban đầu
v có gia tốc bằng k ox,
hông ax= 0; thành phần Oy có vận tốc ban đầu voy, gia tốc bằng ay=g, gia
tốc này ngược chiều với tru ̣c Oy. Vâ ̣y phương trình chuyển đô ̣ng của chất điểm là:
x = (vocos)t (1) 1 2
y (v sin )t gt (2) 0 2
* Phương trình quỹ đạo
Khử t từ hai phương trình (1) và (2) ta được: gx 2 y (3) 2 2 2 cos xtg v0
Vâ ̣y quỹ đa ̣o của chất điểm là một parabol
, bề lõm hướng xuống dưới (Hình 1-11).
*. Thời gian rơi
Khi viên đa ̣n rơi cha ̣m đất, y = 0, từ (2) ta được: gt v sin t 0 0 2
Phương trình này có 2 nghiê ̣m:
Nghiê ̣m t1=0 ứng với thời điểm xuất phát , t2 ứng với lúc chạm đất . Vâ ̣y thời gian cần
thiết để chất điểm bay trong không khí là t =t – 2 t1=t2. 16
Chương 1. Động lực học chất điểm v 2 sin t t 0 (4) 2 g
* Độ cao cực đại
Khi đạt đến điểm cao nhất p, vâ ̣n tốc của chất điểm theo phương Oy bằng không: v v gt 0 y 0 y
Thời gian để đạt độ cao nhất: v sin t 0 g
Độ cao lớn nhất mà chất điểm đạt được: gt 2 v2 sin 2 y (5) max v sin 0 t 0 2 2g
*. Tầm bay xa của chất điểm
Khi chất điểm chạm đất, nó cách gốc O mô ̣t khoảng OR = x. Khi đó y=0. v 2 2 cos.sin v2 sin 2
Từ (3) ta được: x 0 0 (6) g g 17
Chương 1. Động lực học chất điểm
1.2. ĐỘNG LỰC HỌC CHẤT ĐIỂM
Động lực học ngh iên cứu mối quan hê ̣ giữa sự biến đổi tra ̣ng thái chuyển đô ̣ng của
các vật với tương tác giữa các vật đó
. Cơ sở của đô ̣ng lực ho ̣c gồm ba
đi ̣nh luâ ̣t Newton và nguyên lý tương đối Galiléo.
1.2.1. Các định luật Newton
Các định luật Newton nêu lên mối quan hệ giữa chuyển động của một vật với tác dụng
từ bên ngoài và quan hê ̣ giữa các tác du ̣ng lẫn nhau giữa các vâ ̣t.
1. Đi ̣nh luật Newton thứ nhất
Chất điểm cô lập : Là chất điểm không tác dụng lên chấ t điểm khác và cũng không
chịu tác dụng nào từ chất điểm khác.
Đi ̣nh luâ ̣t Newton thứ nhất phát biểu như sau:
Một chất điểm cô lập nếu đang đứng yên, sẽ tiếp tục đứng yên, nếu đang chuyển động,
chuyển động của nó là thẳng và đều.
Trong cả hai trường hợp , chất điểm đứng yên ( v 0 ) và chuyển động thẳng đều
( v const ) đều có vận tốc không đổi . Khi vâ ̣n tốc của chất điểm không đổi , ta nói trạng thái
chuyển động của nó được bảo toàn.
Như vâ ̣y theo định luật Newton I : Một chất điểm cô lập luôn bảo toàn trạng thái
chuyển động của nó.
Tính chất bảo toàn trạng thái chuyển động được gọi là quán tính. Vì vậy định luật thứ
nhất của Newton còn được go ̣i là đi ̣nh luật quán tính.
Có thể vận dụng định luật quán tính để giải thích nhiều hiện tượng thực tế .Ví dụ, đoàn
tàu đang đứng yên bỗng chuyển động đột ngột . Khi đó, hành khách đang đứng yên hoặ̣c ngồi
trên tàu sẽ bi ̣ ngã người về phía sau do quán tính . Tương tự, khi đoàn tàu đang chuyển đô ̣ng
thẳng đều bi ̣ dừng đô ̣t ngô ̣t, hành khách sẽ bị chúi người về phía trước.
2. Đi ̣nh luật Newton thứ hai
Đi ̣nh luâ ̣t thứ hai của Newton x ét chất điểm ở trạng thái không cô lập , nghĩa là chịu
tác dụng của những vật khác . Tác dụng từ vật này lên vật khác được đặc trưng bởi một đại
lươ ̣ng là lực, thường ký hiê ̣u bằng vectơ F .
Khi mô ̣t vâ ̣t chịu tác dụng đồng thời của nhiều lực F , F , F ,...thì ta có thể thay tất cả 1 2 3
các lực đó bằng một lực tổng hợp: F F F F .... 1 2 3
Lực tác du ̣ng lên mô ̣t vâ ̣t làm thay đổi tra ̣ng thái chuyển đô ̣ng của vâ ̣t . Vì trạng thái
của một vật được xác định bởi vận tốc và vị trí của nó , do đó khi chi ̣u tác du ̣ng của mô ̣t lực ,
vâ ̣n tốc của vâ ̣t bi ̣ biến đổi , tức là vâ ̣t thu được gia tốc . Lực tác du ̣ng càng lớn , gia tốc mà vâ ̣t 18
Chương 1. Động lực học chất điểm
thu đươ ̣c sẽ c àng lớn. Thí nghiệm chứng tỏ rằng gia tốc của một vật còn phụ thuộc vào quán
tính của vật. Quán tính của mô ̣t vâ ̣t được đă ̣c trưng bởi khối lượng của vâ ̣t, ký hiệu là m.
Ba đa ̣i lượng là lực, khối lượng và gia tốc liên hệ với nhau theo một định luật thực
nghiê ̣m do Newton nêu ra, gọi là định luật Newton thứ II và được phát biểu như sau:
Chuyển động của một chất điểm chi ̣u tác dụng của lực F là một chuyển động có gia tốc a ,
Gia tốc chuyển động của một chất điểm tỷ lê ̣ thuận với lực tác dụng và tỷ lê ̣
nghịch với khối lượng của chất điểm ấy, từ đó có thể viết: F a k (1-34) m
Trong đó , k là một hệ số tỷ lệ phụ thuộc vào cách chọn đơn vị các đại lượng trong
công thức (1-34). Trong hê ̣ đơn vị quốc tế SI, người ta cho ̣n k = 1, do đó: F a m Hoă ̣c có thể viết: F a m (1-35)
Rõ ràng cùng một lực tác dụng lên vật nếu khối lượng m của vật càng lớn thì gia tốc
của vật càng nhỏ , nghĩa là trạng thái chuyển động của vật càng ít thay đổi . Như vâ ̣y khối
lươ ̣ng m của vật đặc trưng cho quán tính của vật.
Thực nghiê ̣m chứng tỏ đi ̣nh luâ ̣t Newton 2 chỉ nghiệm đúng đối với hệ qui chiếu quán
tinh (sẽ được nêu rõ dưới đây).
Biểu thức (1-34) bao gồm cả đi ̣nh luâ ̣t Newton I và II , được go ̣i là phương trình cơ
bản của động lực học chất điểm. Từ phương trình: F a m
Với định luật Newton I:
F 0 a 0 v const
Với định luật Newton II: F F 0 a 0 m
3. Hê ̣ qui chiếu quán tính
Đi ̣nh nghĩa: Hê ̣ qui chiếu trong đó một vật cô lập nếu đang đứng yên sẽ đứng yên mãi
mãi còn nếu đang chuyển động sẽ chuyển động thẳng đều được gọi là hệ qui chiếu quán tính. 19
Chương 1. Động lực học chất điểm
Nói cách khác, hê ̣ qui chiếu trong đó đi ̣nh luật quán tính được nghiê ̣m đúng là hê ̣ qui
chiếu quán tính.
Thực nghiê ̣m cũng chứng tỏ đi ̣nh luâ ̣t Newton II chỉ nghiê ̣m đúng đối với hê ̣ qui chiếu quán tính.
4. Lực tác dụng trong chuyển động cong Trong chuyển đô ̣ng cong , gia tốc của chất a t F điểm gồm hai tha t
̀nh phần gia tốc tiếp tuyến a và t
gia tốc pháp tuyến a . Gia tốc tổng hợp của chất n điểm là a a a n a a a t n F F n
Nhân 2 vế của phương trình này với khối lươ ̣ng cu Hình ̉ a chất điểm 1-12 , ta đươ ̣c:
Lực hướng tâm và lực ly tâm a m a m a m t n
Theo đi ̣nh luâ ̣t Newton II: F a m , F a m , F a m t t n n
ta đươ ̣c: F F F t n
Thành phần F a
m đươ ̣c go ̣i là lực tiếp tuyến , lực tiếp tuyến gây ra gia tốc tiếp t t
tuyến, tức làm thay đổi đô ̣ lớn và chiều của vâ ̣n tốc ; còn thành phần F a m đươ ̣c go ̣i là n n
lực pháp tuyến hay là lực hướng tâm, lực hướng tâm gây ra gia tốc hướng tâm , làm thay đổi
phương của vectơ vâ ̣n tốc.
Như vâ ̣y điều kiê ̣n cần thiết để cho chất điểm chuyển động cong là phải tác dụng lên
nó một lực hướng tâm, có độ lớn: v2
F ma m n n R
5. Định luật Newton thứ ba
Trong tự nhiên không bao giờ có tác đô ̣ng mô ̣t
phía. Newton đã chứng minh rằng khi chất điểm A tác
dụng lên chất điểm B thì ngược la ̣i chất điểm B cũng tác
dụng lên chất điểm A. Newton đã đưa ra đi ̣nh luâ ̣t Newton III phát biểu như sau:
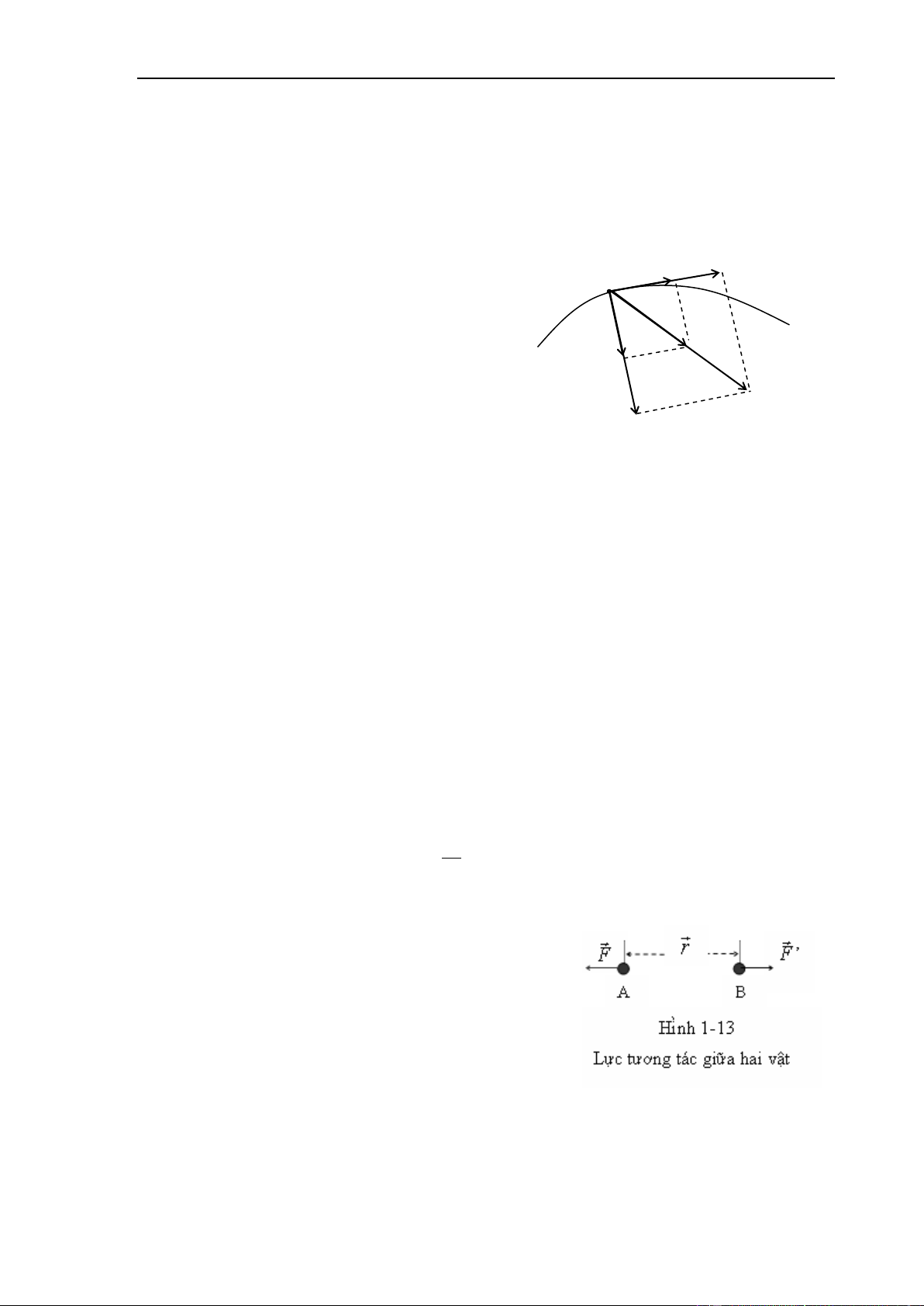
Khi chất điểm A tác dụng lên chất điểm B một lực
F thì đồng thời chất điểm B cũng tác
dụng lên chất điểm A một lực F . Hai lực F và
F đồng thời tồn tại , cùng phương , ngược chiều, cùng cường độ và đặt lên hai chất điểm A
và B khác nhau (hình 1-13): 20
Chương 1. Động lực học chất điểm
F F
Người ta go ̣i F là lực phản tác dụng, thường go ̣i tắt là phản lực. Hai vectơ lực F và
F có điểm đặt khác nhau nên chúng không phải là hai lực cân bằng , tức là không triê ̣t tiêu nhau.
Nếu mô ̣t hê ̣ gồm hai chất điểm A và B tương tác nhau thì các lực tương tác giữa A và
B ( F và F ) khi đó đươ ̣c go ̣i là nội lực tương tác trong hê ̣, tổng hơ ̣p hai vectơ nô ̣i lực này của
hê ̣ bằng không: F F' 0.
Trường hợp tổng quát , nếu hê ̣ có n chất điểm, trong hê ̣ chỉ có các nô ̣i lực tương tác
giữa các chất điểm của hê ̣ (không tương tác với các chất điểm khác ở ngoài hệ ) thì hệ được
gọi là hê ̣ cô lập (hay còn go ̣i là hê ̣ kín). Khi đó nếu xét từng đôi chất điểm của hê ̣ thì tổng hai
lực tương tác giữa chúng bằng không . Do đó nếu xét cả hê ̣ thì : Tổng hợp các nội lực của một
hê ̣ cô lập luôn bằng không.
1.2.2. Các định lý về động lƣợng
Từ đi ̣nh luâ ̣t Newton II ta có thể suy ra mô ̣t số phát biểu khác
, đó là các đi ̣nh lý về đô ̣ng lượng.
1. Đi ̣nh lý 1
Giả sử chất điểm có khối lươ ̣ng m chịu tác dụng của lực F , theo đi ̣nh luâ ̣t Newton
II, chất điểm đó sẽ chuyển đô ̣ng với gia tốc a sao cho: a m F v d Hay m F dt
Giả thiết khối lượng m không đổi, ta có thể viết: d v m F (1-36) dt
Ta đă ̣t: K v
m , và gọi K là vectơ động lượng của chất điể m, do đó có thể viết la ̣i (1- 36) như sau: K d F (1-37) dt
Định lý 1: Đạo hàm động lượng của một chất điểm theo thời gian bằng tổng hợp các
ngoại lực tác dụng lên chất điểm đó.
2. Đi ̣nh lý 2 Từ (1-37) ta suy ra: K d dt F (1-38) 21
Chương 1. Động lực học chất điểm
Độ biến thiên của vectơ K từ thời điểm t có
1 có vectơ động lượng K đến thời điểm t 1 2
vectơ đô ̣ng lượng K có thể tính được như sau: 2 K 2 t2
ΔK K K K d F dt (1-39) 2 1 . K t 1 1 t2
Người ta go ̣i F.dt là xung lượng của lực F trong khoảng thời gian từ t1 đến t2. Biểu 1 t
thức (1-39) được phát biểu thành đi ̣nh lý 2 như sau:
Định lý 2: Độ biến thiên động lượng của mộ t chất điểm trong một khoảng thời gian
nào đó bằng xung lượng của lực tác dụng lên chất điểm trong khoảng thời gian đó.
Trường hợp riêng khi F không đổi theo thời gian, (1-39) trở thành: K F t (1-40) hay: K Δ F (1-41) t Δ
Tức là: Độ biến thiên động lượng của chất điểm trong một đơn vị thời gian bằng lực
tác dụng lên chất điểm đó:
1.2.3. Ý nghĩa của động lƣợng và xung lƣợng
1.Ý nghĩa của động lượng
Đến đây ta có hai đa ̣i lượng đă ̣c trưng cho tra ̣ng thái chuyển đô ̣ng là vâ ̣n tốc và đô ̣ng
lươ ̣ng. Vâ ̣n tốc đă ̣c trưng cho chuyển đô ̣ng về mă ̣t động học. Còn đô ̣ng lượng đă ̣c trưng cho
chuyển đô ̣ng về mă ̣t động lực học, vì động lượng không chỉ liên quan đến vận tốc mà còn liên
quan đến khối lươ ̣ng của chất điểm.
Hơn nữa động lượng còn đặc trưng cho khả năng truyền chuyển động của chất điểm.
Để minh hoa ̣, ta lấy ví du ̣ sau. Mô ̣t quả cầu khối lượng m1 chuyển đô ̣ng với vâ ̣n tốc v 1
đến đập thẳng vào một quả cầu khối lượng m2 đang đứng yên . Sau va cha ̣m , quả cầu m 2 sẽ
chuyển đô ̣ng với vâ ̣n tốc v . Thực nghiê ̣m chứng tỏ v không những phu ̣ thuô ̣c vào v mà 2 2 1 còn phụ thuộc vào m
1, nghĩa là phụ thuộc vào K
m v (đô ̣ng lựơng của qủa cầu thứ nhấ t). 1 1 1
Vâ ̣n tốc v càng lớn nếu m v càng lớn, chứ không phải chỉ riêng do v lớn. 2 1 1 1
Vậy khả năng truyền chuyển động phụ thuộc vào động lượng của vật
2. Ý nghĩa của xung lượng
Xung lươ ̣ng của mô ̣t lực tác du ̣ng trong khoảng thời gian t đă ̣c trưng cho tác du ̣ng
của lực trong khoảng thời gian đó . Thực vâ ̣y, các công thức (1-39) và (1-40) chứng tỏ tác 22
Tài liệu liên quan:
-
Sách Bài tập Cơ học - Tập 1 | Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh
10 5 -
Bài tập Cơ học lưu chất - Cơ học lý thuyết | Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh
316 158 -
Đề thi cuối kỳ học phần Cơ học năm 2024 - 2025 | Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh
153 77