
















































































































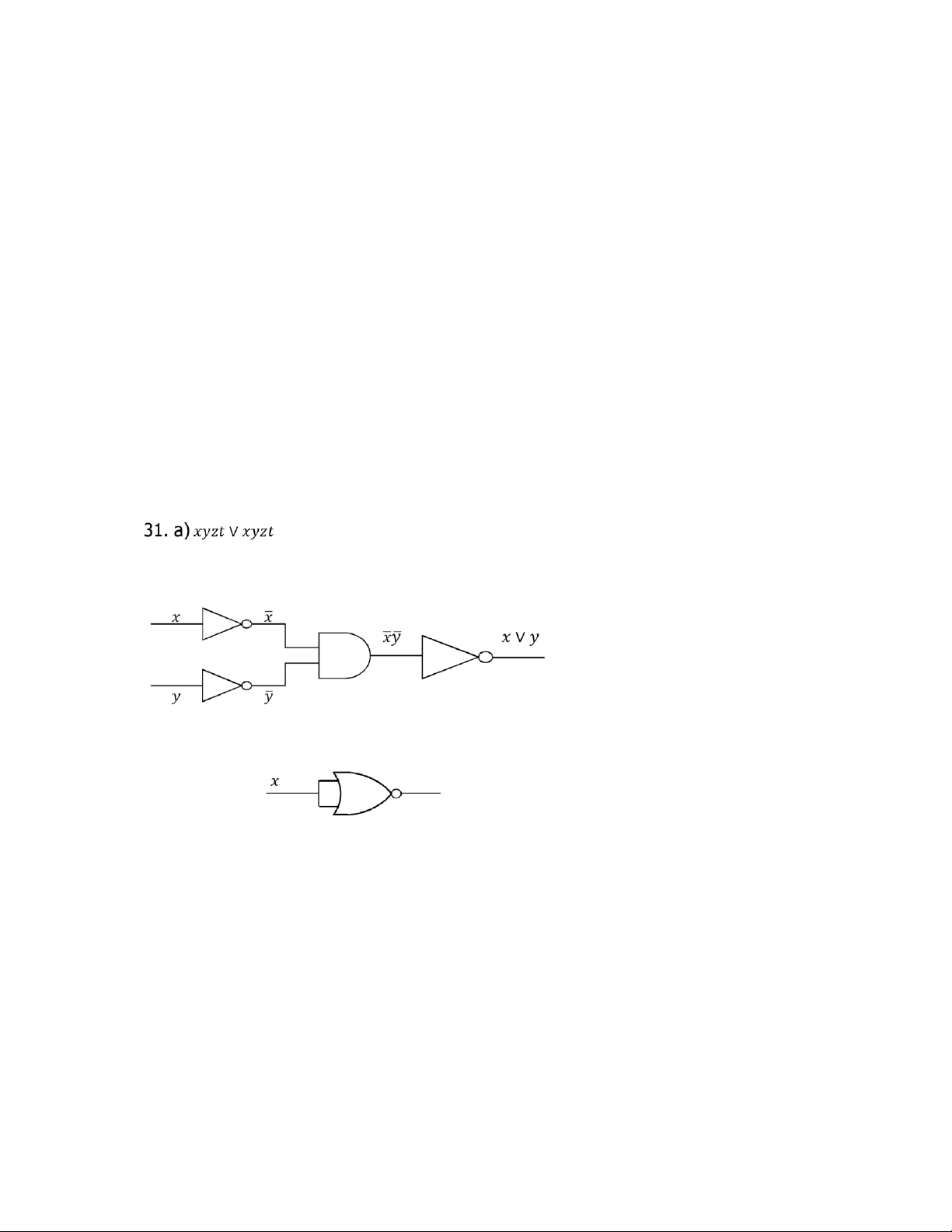

Preview text:
lOMoARcPSD| 36667950 MỤC LỤC
CHƯƠNG 1: CƠ SỞ LOGIC ................................................................................................... 2
§1 PHÁP TÍNH MỆNH ĐỀ .................................................................................................... 2
§2 DẠNG MỆNH ĐỀ ............................................................................................................ 5
§3 QUY TẮC SUY DIỄN ....................................................................................................... 9
§4 VỊ TỪ VÀ LƯỢNG TỪ .................................................................................................... 16
§5 NGUYÊN LÝ QUY NẠP ................................................................................................... 22
BÀI TẬP CHƯƠNG 1 .......................................................................................................... 24
CHƯƠNG 2: PHƯƠNG PHÁP ĐẾM ......................................................................................... 37
§1 TẬP HỢP ..................................................................................................................... 37
§2 ÁNH XẠ ....................................................................................................................... 39
§3 PHÉP ĐẾM ................................................................................................................... 42
§4 GIẢI TÍCH TỔ HỢP ....................................................................................................... 47
§5 NGUYÊN LÝ CHUỒNG BỒ CÂU ....................................................................................... 52
BÀI TẬP CHƯƠNG 2 ........................................................................................................ 53
CHƯƠNG 3: QUAN HỆ ........................................................................................................ 61
§1 QUAN HỆ ..................................................................................................................... 61
§2 QUAN HỆ TƯƠNG ĐƯƠNG ............................................................................................ 64
§3 THỨ TỰ ....................................................................................................................... 66
§4 DÀN ............................................................................................................................ 71
§5 DÀN 2 ......................................................................................................................... 74
§6 DÀN ............................................................................................................................ 75
BÀI TẬP CHƯƠNG 3 .......................................................................................................... 82
CHƯƠNG 4: ĐẠI SỐ BOOL VÀ HÀM BOOL ............................................................................. 89
§1 ĐẠI SỐ BOOL ............................................................................................................... 89
§2 HÀM BOOL .................................................................................................................. 95
§3 MẠNG CÁC CỔNG VÀ CÔNG THỨC ĐA THỨC TỐI TIỂU .................................................... 99
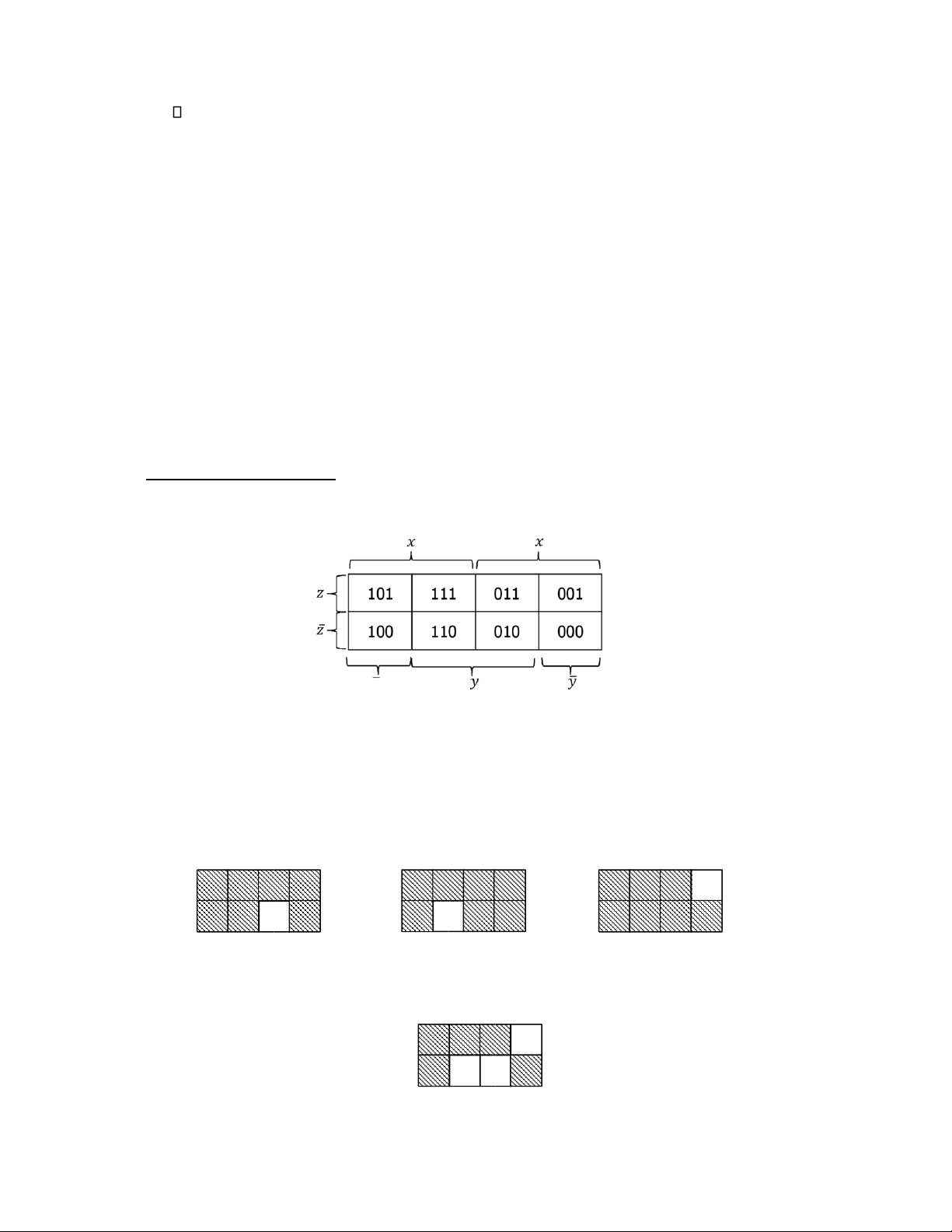
§4 PHƯƠNG PHÁP BIỂU ĐỒ KARNAUGH ........................................................................... 103
§5 PHƯƠNG PHÁP THỎA THUẬN ...................................................................................... 111
BÀI TẬP CHƯƠNG 4 ...................................................................................................... 117
GIẢI ĐÁP MỘT SỐ BÀI TẬP ................................................................................................. 121 lOMoARcPSD| 36667950
CHƯƠNG 1: CƠ SỞ LOGIC
§1 PHÁP TÍNH MỆNH ĐỀ
Trong toán học ta quan tâm ến những mệnh ề có giá trị hân lý xác ịnh ( úng hoặc
sai nhưng không thể vừa úng vừa sai). Các khẳng ịnh như vậy ược gọi là mệnh ề. Các mệnh
ề úng ược nói là có giá trị chân lý úng (hay chân trị úng), các mệnh ề sai ược nói là có chân trị sai. Ví dụ:
1. Các khẳng ịnh sau là mệnh ề:
Môn Toán rời rạc là môn bắt buộc cho ngành Tin học. 1+1=2. 4 là số nguyên tố.
Hai mệnh ề ầu có chân trị 1, mệnh ề thứ ba có chân trị 0.
2. Các khẳng ịnh dưới dạng tán than hoặc mệnh lệnh không phải mệnh ề vì nó không có chân trị xác ịnh.
3. Khẳng ịnh “ là số nguyên tố ” không phải mệnh ề. Tuy nhiên, nếu thay n bằng một số
nguyên cố ịnh thì ta sẽ có một mệnh ề: chẳng hạn với = 3 ta có một mệnh ề úng, trong khi
với = 4 ta có một mệnh ề sai. Khẳng ịnh này ược gọi là một vị từ và cũng là ối tượn khảo sát của logic.
Ta thường ký hiệu các mệnh ề bởi các chữ , , ,… và chân trị úng (sai) ược ký hiệu bởi
1 (0). Đôi khi ta còn dùng các ký hiệu , ể chỉ chân trị úng và dể chỉ chân trị sai.
Phân tích kỹ các ví dụ ta thấy các mệnh ề ược chia ra làm 2 loại:
Các mệnh ề ược xây dựng từ các mệnh ề khác nhờ liên kết chúng lại bằng
các liên từ(và, hay, nếu… thì… ) hoặc trạng từ “không”. Ta nói các mệnh ề
này là mệnh ề phức hợp.
Ví dụ: “Nếu trời ẹp thì tôi i dạo” là một mệnh ề phức hợp.
Các mệnh ề không thể xây dựng từ các mệnh ề khác bằng các liên từ hoặc
trạng từ “không”. Ta nói các mệnh ề này là mệnh ề nguyên thủy hay sơ cấp.
Ví dụ: “Hôm nay trời ẹp”, “3 là số nguyên tố” là các mệnh ề nguyên thủy.
Mục ích của phép tính mệnh ề là nghiên cứu chân trị của một mệnh ề phức hợp từ
chân trị của các mệnh ề ơn giản hơn và các phép nối của những mệnh ề này thể hiện qua
lien từ hoặc trạng từ “không”. Các phép nối:
Phép phủ ịnh: phủ ịnh của mệnh ề P ược ký hiệu bởi ¬ ( ọc là không P). Chân trị của ¬ là
0 nếu chân trị của là 1 và ngược lại.
Ta có bảng sau gọi là bảng chân trị của phép phủ ịnh: ¬ lOMoAR cPSD| 36667950 0 1 1 0
Phép nối liền: mệnh ề nối liền của hai mệnh ề P, Q ược ký hiệu bởi P∧Q ( ọc là
P và Q). Chân trị của P∧Q là 1 nếu cả P lẫn Q ều có chân trị 1. Trong các trường hợp khác, P∧Q có chân trị 0.
Nói cách khác phép nối liền ược xác ịnh bởi bảng chân trị sau: ∧ 0 0 0 0 1 0 1 0 0 1 1 1
Ví dụ: mệnh ề “Hôm nay trời ẹp và trận bóng á sẽ hấp dẫn” ược xem là một mệnh ề úng
nếu cả hai iều kiện “trời ẹp” và “trận bóng á sẽ hấp dẫn” ều xảy ra. Ngược lại nếu một mệnh
ề úng một mệnh ề sai hoặc cả hai mệnh ề ều sai thì mệnh ề là một mệnh ề sai.
Phép nối rời: mệnh ề nối rời của hai mệnh ề P, Q ược ký hiệu bởi P∨Q ( ọc là P hoặc
Q). Chân trị của P∨Q là 0 nếu cả P lẫn Q ều có chân trị 0. Trong các trường hợp khác, P∨Q có chân trị 1.
Nói cách khác phép nối rời ược xác ịnh bởi bảng chân trị sau: ∨ 0 0 0 0 1 1 1 0 1 1 1 1
Ví dụ: “Ba ang ọc báo hay xem tivi” là một mệnh ề úng nếu lúc này ba ọc báo, xem tivi hay
vừa ọc báo vừa xem tivi (!). Ngược lại nếu cả hai việc trên ều không xảy ra, ví dụ Ba ang
làm việc thì mệnh ề là mệnh ề sai. Chú ý rằng trong mệnh ề P∨Q, từ “hay” ược dung theo
nghĩa bao gồm,nghĩa là và có thể ồng thời úng. Tuy nhiên theo ngôn ngữ hằng ngày ta
thường hiểu ∨ theo nghĩa loại trừ, nghĩa là úng hay úng nhưng không ồng thời úng. Để
phân biệt rõ rang, trong trường hợp loại trừ ta sẽ sử dụng từ “hoặc”: “ hoặc ” và ký hiệu ∨
( hay nhưng không ồng thời cả hai). Bảng chân trị của ∨ là: ∨ lOMoAR cPSD| 36667950 0 0 0 0 1 1 1 0 1 1 1 0
Phép kéo theo: nếu P thì Q ược ký hiệu là → (cũng ọc là kéo theo , hay là iều kiện ủ
của , hay là iều kiện ủ của ). Để xác ịnh chân trị cho → ta
hãy xem ví dụ mệnh ề “nếu trời ẹp thì tôi i dạo”. Ta có các trường hợp sau:
trời ẹp và tác giả của khẳng ịnh ang i dạo: khi ấy hiển nhiên là mệnh ề úng.
trời ẹp và tác giả ngồi nhà: mệnh ề rõ ràng sai.
trời xấu và tác giả i dạo: mệnh ề vẫn úng
trời xấu và tác giả ngồi nhà: mặc dù trời xấu nhưng tác giả không vi phạm khẳng ịnh của
mình nên mệnh ề phải ược xem là úng.
Từ ó ta có bảng chân trị của phép kéo theo như sau: → 0 0 1 0 1 1 1 0 0 1 1 1 Chú ý:
1. Với quy ước về chân trị như trên, ta sẽ cò những khẳng ịnh úng rất ngộ nghĩnh như:
“nếu 2=1 thì Quang Trung và Trần Hưng Đạo là một người”
2. Cần phân biệt mệnh ề → với lệnh ℎ trong một số ngôn
ngữ lập trình ví dụ như Pascal, Basic. Trong → thì cả và là mệnh ề còn trong lệnh ℎ ℎì
là một mệnh ề còn là một dãy liên tiếp dòng lệnh sẽ
ược thực hiện nếu mệnh ề P có chân trị 1 và sẽ ược bỏ qua nếu P có chân trị là 0. Nhắc
lại rằng các dòng lệnh là những mệnh lệnh mà máy phải thực hiện nên không phải là
một mệnh dề theo nghĩa ta xét. Dù sao cũng có một sự tương tự giữa hai ối tượng “→” và “ ℎ
”. Hơn nữa có thể lợi dụng các tương ương logic ể thực hiện lệnh “ ℎ ” có hiệu quả.
3. Trong ngôn ngữ hằng ngày, người ta thường hay nhầm lẫn phép kéo theo với kéo
theo hai chiều, chẳng hạn như phát biểu ”giảng viên khoa Toán dạy nghiêm túc” mà viết
theo phép nối là “nếu anh là giáo viên khoa Toán thì anh dạy nghiêm túc” thường bị
phản ứng giáo viên các khoa khác vì họ cho rằng người nói ã ám chỉ “nếu là giảng viên
khoa khác thì dạy không nghiêm túc”. Thật ra khi phát biểu, người nói có khi cũng muốn
ám chỉ “nếu anh là giáo viên khoa Toán thì anh dạy nghiêm túc”. Ở ây nếu viết phát biểu
ban ầu dưới dạng → thì hai phát biểu hiểu nhầm sẽ có dạng (¬ ) → (¬ ) và →. Tuy
nhiên, nếu bao gồm them một trong hai phát biểu sau, thì phát biểu → thành một phép
kéo theo hai chiều theo nghĩa dưới ây.
Phép kéo theo hai chiều: mệnh ề nếu thì và ngược lại ược ký hiệu là ↔ (cũng
ọc là khi và chỉ khi , nếu và chỉ nếu , hay P là iều kiện cần và ủ ể có ). Theo trên, cả hai lOMoARcPSD| 36667950
chiều → và → ều úng nên nếu úng thì cũng úng và ngược lại. Do ó ta có bảng chân trị của
phép kéo theo hai chiều như sau: ↔ 0 0 1 0 1 0 1 0 0 1 1 1
§2 DẠNG MỆNH ĐỀ
Trong Đại số ta có các biểu thức ại số ược xây dựng từ:
các số nguyên, hữu tỉ, thực,… mà ta gọi là hằng số.
các biến , ,… có thể lấy giá trị là các hằng số.
các phép toán thao tác trên các hằng số và các biến theo một thứ tự nhất ịnh.
Khi thay thế các biến trong một biểu thức ại số bởi các hằng số thì kết quả thực hiện
phép toán trong biểu thức sẽ là một hằng số nào ó. Trong phép toán mệnh ề ta cũng có các
“biểu thức logic” tương tự mà ta gọi là các dạng mệnh ề ược xây dựng từ:
các mệnh ề (hằng mệnh ề).
các biến mệnh ề , ,… có thể lấy giá trị là các mệnh ề nào ó.
các phép nối thao tác trên các hằng mệnh ề và biến mệnh ề theo một thứ tự nhất ịnh. Ở ây
thứ tự ược xác ịnh bởi các dấu “()” ể chỉ rõ phép nối thực hiện trên cặp mệnh ề nào, úng ra là
trên các biểu thức con nào. Ví dụ như: ( , , ) → )
là một dạng mệnh ề trong ó , , là các biến mệnh ề còn là một hằng mệnh ề.
Giả sử , là 2 dạng mệnh ề, khi ấy ¬ , ∧
,→,↔ là các dạng mệnh ề. Bằng cách này
ta có thể xây dựng ược các dạng mệnh ề càng ngày càng phức tạp.
Mặt khác, iều ta quan tâm ối với một dạng mệnh ề ( , , ,…) là chân trị của mệnh ề ó có ược
( , , ,…) khi thay các biến mệnh ề , , ,… bởi các hằng mệnh ề
, , ,… có chân trị xác ịnh, nghĩa là sự phụ thuộc của chân trị của ( , , ,…) theo các chân trị
của , , ,… chứ không phải theo các thể hiện cụ thể , , ,… qua các mệnh ề cu thể , , ,… Nói
cách khác mỗi một dạng mệnh ề ( , , ,…) có một bảng chân trị xác ịnh trong ó mỗi dòng cho
biết chân trị của ( , , ,…) theo các chân trị cụ thể của , , ,… Ví dụ:
1. Ta hãy xây dựng bảng chân trị của hai dạng mệnh ề ˅(˄) và
(˅)˄ theo các biến mệnh ề , , . ˄ ˅( ˄ ) ˅ ( ˅ )˄ lOMoAR cPSD| 36667950 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 1 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 0 1 1 1 1 1 0 0 1 1 0 1 1 1 1 1 1 1
Ta thấy hai dạng mệnh ề ˅(˄),(˅)˄ có bảng chân trị khác nhau. Điều này cho thấy
thứ tự thực hiện các phép nối là quan trọng và sự cần thiết của các dấu “()”. Tuy nhiên ta
sẽ quy ước rằng nếu phép nối ¬ i cùng với một phép nối khác mà không có dấu “()” thì phép
nối ¬ sẽ ược ưu tiên thực hiện trước. Ví dụ như ¬ ˅ có nghĩa là thực hiện ¬ trước rồi mới
thực hiện , nói cách khác biểu thức ¬ ˅ và (¬ )˅ là một. Trong trường hợp muốn thực hiện
sau ta phải ặt dấu ngoặc: ¬ (˅).
2. Ta hãy xây dựng bảng chân trị của hai dạng mệnh ề → và ¬ ˅ ¬ → ¬ ˅ 0 0 1 1 1 0 1 1 1 1 1 0 0 0 0 1 1 0 1 1
Như vậy hai dạng mệnh ề → và ¬ ˅ có cùng bảng chân trị. Ta nói chúng tương ương logic theo nghĩa sau
Định nghĩa 1.2.1: hai dạng mệnh ề , ược nói là chúng tương ương logic nếu chúng có cùng
bảng chân trị. Khi ấy ta viết ⟺.
Chú ý rằng nếu và tương ương logic thì dạng mệnh ề ↔ luôn luôn lấy giá trị 1 dù các
biến có lấy giá trị nào i nữa. Định nghĩa 1.2.2: i.
Một dạng mệnh ề ược coi là một hằng úng nếu nó luôn luôn lấy chân trị 1. ii.
Một dạng mệnh ề ược coi là một hằng sai hay mâu thuẫn nếu nó luôn luôn lấy chân trị 0.
Từ nhận xét trên, ta luôn có
Mệnh ề 1.2.1: hai dạng mệnh ề và tương ương logic khi và chỉ khi → là một hằng úng.
Nếu chỉ ể ý ến phép kéo theo một chiều ta có
Định nghĩa 1.2.3: dạng mệnh ề
ược nói là hệ quả logic của mệnh ề nếu → là một hằng
úng. Khi ấy ta viết ⟹. Ta cũng nói là hệ quả logic của .
Như thế nói rằng tương ương logic với có nghĩa là là hệ quả logic của và là hệ quả logic của . lOMoARcPSD| 36667950
Trong phép tính mệnh ề, ta thường không phân biệt các dạng mệnh ề tương ương logic. Ta có
Quy tắc thay thế thứ nhất: trong dạng mệnh ề nếu ta thay thế biểu thức con bởi một
dạng mệnh ề tương ương logic thì dạng mệnh ề thu ược vẫn còn tương dương logic với .
Chú ý: Ta ã sử dụng khái niệm biểu thức con theo một nghĩa hết sức tự nhiên: dạng mệnh
ề “xuất hiện” trong , hay nói cách khác có thể xây dựng từ và một số dạng mệnh ề khác qua các phép nối.
Ví dụ: → (→) tương ương logic với → (¬ ˅) vì trong ó biểu thức con → ã ược thay thế bởi dạng
mệnh ề tương dương logic là ¬ ˅.
Với quy tắc thay thế trên ta có thể “rút gọn” một dạng mệnh ề bằng cách thay một
biểu thức con bởi một dạng mệnh ề tương ương nhưng ơn giản hơn hoặc giúp cho bước rút
gọn tiếp theo dễ dàng hơn. Ngoài ra, cũng cần nhận biết một số hằng úng. Thường các hằng
úng này có thể suy từ một số hằng úng ơn giản nhờ:
Quy tắc thay thế thứ hai: giả sử dạng mệnh ề ( , , ,…) là một hằng úng. Nếu ta thay thế
những nơi p xuất hiện trong E bởi một dạng mệnh ề tùy ý ( ’, ’, ’,…) thì dạng mệnh ề nhận
ược theo các biến , , ,…, ’, ’, ’,… vẫn còn là một hằng úng.
Ngoài hai quy tắc thay thế trên, ta còn sử dụng 10 quy luật logic ược phát biểu dưới dạng
các tương ương logic có thể rút gọn một dạng mệnh ề cho trước. Ta có
Định lý 1.2.2 (Quy luật logic): với , , là các biến mệnh ề, 1 là một hằng úng và 0 là một mâu
thuẫn (hằng sai), ta có các tương ương logic: i.
Phủ ịnh của phủ ịnh: ¬ ¬ ⇔ ii. Quy
tắc De Morgan: ¬ ( ⇔ ¬ ∨ ¬
¬ (∨) ⇔ ¬ ∧ ¬ iii. Luật giao hoán: iv.
Luật kết hợp: v.
Luật phân bố: ) ) vi.
Luật lũy ẳng (Idempotent Rules) vii.
Luật trung hòa: ∧ 1 ⇔ lOMoARcPSD| 36667950
∨ 0 ⇔ viii. Luật về
phần tử bù: ∧ ¬ ⇔ 0 ∨ ¬ ⇔ 1 ix.
Luật thống trị: ∧ 0 ⇔ 0 ∨ 1 ⇔ 1 x.
Luật hấp thụ: ∧ (∨) ⇔ ∨ (∧) ⇔
Chứng minh: ọc giả có thể kiểm tra dễ dàng 10 quy luật logic trên bằng cách lập bảng chân trị
của hai vế của tương ương logic. pcm Ví dụ:
1. Từ quy tắc De morgan ta ược hằng úng ¬ (∧) ⟺ ¬ ∨ ¬
Thay thế p bởi rs ta sẽ ược một hằng úng mới ¬ ( (∧) ∧ ) ⟺ ¬ (∧) ∨ ¬
2. Hãy chứng minh dạng mệnh ề sau là hằng úng [ (→) (→) → → (¬ ∨) (1.2.1)
Muốn vậy ta thay thế r→s bởi p và ¬tu bởi q và ưa về chứng minh dạng mệnh ề sau là hằng úng: ( → ) ] →
Ta sử dụng liên tiếp quy tắc thay thế thứ nhất và ược các tương ương logic sau: ( → ) ] → → → → → ¬ ∨ ¬ ∨ ¬ ∨ 1 1
Do ó 1.2.1 là một hằng úng.
3. Tương tự như trên ta có: (∧) → ¬ ∨ ¬ ∨ ¬ ¬ ∨ ( → ) (1.2.2)
Nếu ta liên kết dạng mệnh ề → với lệnh ℎ trong một số
ngôn ngữ lập trình cấp cao như Pascal, Basic thì dạng mệnh ề (˄) → sẽ ược liên kết với lệnh ˄ ℎ
còn dạng mệnh ề → (→) sẽ ượ liên kết với lệnh ℎ ℎ .
Bây giờ ta hãy xét một ví dụ liên quan ến hay lệnh trên trong một oạn chương trình viết bằng Pascal: a) :=3; lOMoARcPSD| 36667950 For :=1 to 10 do Begin := −; := + 2 ∗ ;
If ( > 0) And ( > 0) Then
Writeln (‘giá trị của + = ’, + ) End; b) :=3; For :=1 to 10 do Begin := −; := + 2 ∗ ; If > 0 Then
If > 0 Then Writeln (‘giá trị của + = ’, + ) End;
Rõ ràng cả hai oạn chương trình trên ều có cùng Output là hai dòng: giá trị của + = 7 giá trị của + = 8
Tuy nhiên trong chương trình a) ta cần 20 lần so sánh (10 lầ so sánh > 0 và 10 lần
so sánh > 0), trong khi chương trình b) ta chỉ cần 12 lần so sánh (10 lần so sánh > 0 và 2
lần so sánh > 0 ứng với = 1,2). Như thế chương trình b) chạy có hiệu quả hơn.
Ví dụ trên ây cho thấy một mặt cần phân biệt → và lệnh ℎ
, mặt khác ta cần nắm rõ các dạng tương ương của dạng mệnh ề ể thực hiện lệnh ℎ
có hiệu quả hơn. Chẳng hạn nhiều chương trình biên dịch lợi
dụng tương ương logic 1.2.2 ể thay lệnh ℎ ( ℎ
). Ở ây lại xảy ra nghịch lý là lệnh (˄) ℎ lại ược thay thế bằng lệnh ℎ ( ℎ ) mà trong ví dụ trên
ta cần ến 20 lần so sánh. Như thế phải cẩn thận khi sử dụng tương ương logic hiển nhiên (luật giao hoán) giữa ˄ và ˄.
§3 QUY TẮC SUY DIỄN
Trong một chứng minh toán học, xuất phát từ một số khẳng ịnh úng p1, p2,…, pn
gọi là tiền ề, ta áp dụng các quy tắc suy diễn ể suy ra chân lý của một khẳng ịnh q mà ta
gọi là kết luận. Nói cách khác, các quy tắc suy diễn ược áp dụng ể suy ra q là hệ quả logic
của p1 p2…pn, hay nói cách khác dạng mệnh ề ( ˄ ˄ …˄) → lOMoARcPSD| 36667950
là một hằng úng, trong ó p1, p2,…, pn, q là các dạng mệnh ề theo một số biến logic nào ó.
Thường thì các biến logic không xuất hiện một cách tường minh mà ược trừu tượng hóa (bỏ
i một phần nội dung cụ thể) từ các mệnh ề nguyên thủy như ví dụ sau ây cho thấy.
Giả sử ta có các tiền ề:
: nếu An học chăm thì An ạt môn Toán rời rạc.
: nếu An không i chơi thì An học chăm.
: An trượt môn Toán rời rạc.
Ta muốn dùng các quy tắc suy diễn ể suy ra kết luận sau là úng: : An hay i chơi.
Muốn vậy ta trừu tượng hóa các mệnh ề nguyên thủy “An học chăm”, “An hay i chơi”,
“An ạt môn toán rời rạc” thành các biến mệnh ề , , . Như vậy các tiền ề bây giờ trở thành các dạng mệnh ề = → = ¬ → = ¬
Ta phải chứng minh dạng mệnh ề sau là một hằng úng: [(→) ∧ (¬ →) →
Ta có thể kiểm tra dễ dàng dạng mệnh ề trên là một hằng úng bằng cách lập ra bảng
chân trị của nó. Tuy nhiên, ây không phải là một phương pháp tốt nếu số biến mệnh ề lớn.
Một phương pháp khác là sử dụng các qui tắc suy diễn ể chia bài toán thành ra các bước
nhỏ, nghĩa là từ các tiền ề suy ra một số kết luận trung gian trước khi tiếp tục áp dụng các
quy tắc suy diễn ể suy ra kết luận. Để tiện ra mô hình hóa phép suy iễn thành sơ ồ sau: . . . n
Dưới ây là một số quy tắc suy diễn thường dùng mà chân lý có thể dược kiểm tra dễ
dàng bằng cách lập bảng chân trị.
Quy tắc Modus Ponens (Phương pháp khẳng ịnh)
Quy tắc này ược thể hiện bởi hằng úng
[(→) ∧ ]→ (1.3.1) hoặc dưới dạng sơ ồ → Ví dụ:
Nếu Minh học chăm thì Minh ạt Toán rời rạc lOMoARcPSD| 36667950 Mà Minh học chăm
Suy ra Minh ạt Toán rời rạc.
Thật ra trong quy tắc Modus Ponens, mệnh ề p→q thường có dạng tổng quát hơn
“với bất kỳ sinh viên X nào, nếu X học chăm thì X ạt Toán rời rạc” và ta ã ặc biệt hóa nó cho
trường hợp X= sinh viên Minh. Các phép ặc biệt hóa sẽ ược xem xét trong phần vị từ và
lượng từ. Một ví dụ cổ iển khác của Qui tắc Modus ponens là:
Mọi người ều chết mà Socrate là người
vậy Socrate sẽ chết.
Thường thì quy tắc Modus Ponens ược áp dụng cùng với quy tắc thay thế ể ơn giản hóa
các bước suy luận. Chẳng hạn ta có phép suy diễn ∨ ) →
Ở ây Quy tắc Modus Ponens (dạng mệnh ề 1.3.1) ược áp dụng cùng với phép thay thế bởi ˅ và q bởi ¬ ˄.
Tam oạn luận (Syllogism) ược thể hiên bởi hằng úng → → → Ví dụ: 1.
Hai tam giác vuông có cạnh huyền bằng nhau và một góc nhọn bằng nhau thì chúng có
một cạnh bằng nhau kèm giữa hai góc bằng nhau.
Hai tam giác có một cạnh bằng nhau kèm giữa hai góc bằng nhau thì chúng bằng nhau.
Suy ra hai tam giác vuông có cạnh huyền bằng nhau và một góc nhọn bằng nhau thì chúng bằng nhau. lOMoAR cPSD| 36667950 2. Xét tam oạn luận
Một con ngựa rẻ thì hiếm Cái gì hiếm thì ắt
Suy ra một con ngựa rẻ thì ắt
Tam oạn luân trên hoàn toàn hợp logic. Tuy nhiên kết luận mâu thuẫn là do dựa trên một tiền ề sai.
3. Ta hãy xét một ví dụ trong ó có sử dụng cả hai quy tắc trên Bình i chơi thì
Bình không học Toán rời rạc
Bình không học Toán rời rạc thì Bình trượt Toán rời rạc Mà Bình thích i chơi
Vậy Bình trượt Toán rời rạc.
Nếu trừu tượng hóa các med nguyên thủy thành các biến mệnh ề p, q, r thì lý luận trên có dạng → ¬ ¬ →
Ta có thể suy luận như sau: → ¬ ¬ → → (Tam oạn luận) mà (Modus Ponens) hoặc là → ¬ ¬ (Modus Ponens) mà ¬ → (Modus Ponens)
Quy tắc Modus Tollens (Phương pháp phủ ịnh)
Phương pháp này ược thể hiện bởi hằng úng [(→) ∨ ¬ ] → ¬ GS. Nguyễn Hữu Anh 14 hay dưới dạng mô hình lOMoARcPSD| 36667950 → ¬ ¬
Ví dụ: xét chứng minh → → ∨ ¬ ¬ ˅ ¬ ¬
Ta có thể suy luận như sau: ta thấy các tiền ề ˅¬ ,¬ ˅ bởi các dạng mệnh ề tương ương → à → . Khi ấy → → → →
→ (Tam oạn luận lập lại nhiều lần) mà ¬
¬ (Phương pháp phủ ịnh)
Tam oạn luận rời: ược thể hiện bởi hằng úng [(∨) ∧ ¬ ] →
Ý nghĩa của quy tắc này là khi chỉ có úng hai trường hợp có thể xảy ra và một trong
hai trường hợp ã ược khẳng ịnh là sai thì trường hợp còn lại là úng.
Quy tắc mâu thuẫn (Chứng minh bằng phản chứng) Ta có tương ương logic [( 1 2 … n )
→ ] ⟺ [( 1 2 … n ¬ ) →0]
Do ó nếu chứng minh ược dạng mệnh ề ở bên phải là một hằng úng thì dạng mệnh ề
ở bên trái cũng là một hằng úng. Nói cách khác nếu thêm giả thiết phụ ¬ vào các tiền ề cho
trước mà dẫn ến một mâu thuẫn thì q là hệ quả logic của các tiền iền cho trước.
Ví dụ: hãy sử dụng phương pháp phản chứng cho chứng minh sau: → ¬ → → ¬ →
Phủ ịnh của kết luận sẽ tương ương với: ¬ (¬ →) ⟺ ¬ (∨)⟺ ¬ ∨ ¬ lOMoARcPSD| 36667950
Như thế ta thêm vào các tiền ề hai giả thiết phụ ¬r và ¬s và tìm cách chứng minh suy luận sau là úng: → ¬ → → ¬ ¬ 0 Ta có các bước sau ây ¬ → → ¬ → mà ( T am o ạ n lu ậ n) ¬ ¬ (¬ ) (Phương pháp phủ ịnh) hay tương ương mà →
(Phương pháp khẳng ịnh)
Kết luận cùng với giả thiết phụ ¬ cho ta: ∧ ¬ ⟺ 0
Do ó theo phương pháp phản chứng, chứng minh ban ầu là úng.
Quy tắc chứng minh theo trường hợp
Quy tắc này ược thể hiện bởi hằng úng sau: [(→) ∧ (→)] → ]
Ý nghĩa của quy tắc này là một giả thiết có thể tách thành hai trường hợp úng hay q
úng, và ta ã chứng minh ược riêng rẻ cho từng trường hợp là kết luận úng, khi ấy cũng úng
trong cả hai trường hợp.
Ví dụ: Để chứng minh rằng ( ) =
+ 2 luôn chia hết cho 3 ta viết ( ) = ( + 2)
và lấy n là một số nguyên tùy ý. Khi ấy có hai trường hợp xảy ra:
chia hết cho 3: khi ấy rõ ràng f(n) cũng chia hết cho 3.
không chia hết cho 3, khi ấy ta có thể viết = 3 ± 1 với một số nguyên k nào ó. Ta có + 2 = (3 ± 1) + 2 = 9 ± 6 + 3 = 3(3 ± 2 + 1) lOMoARcPSD| 36667950 Suy ra 2 ( ) =
( + 2) cũng chia hết cho 3. Như vậy trong mọi trường hợp ( ) chia hết cho 3.
Ta hãy xem một ví dụ trong ó có sử dụng nhiều quy tắc:
Nếu nghệ sĩ Văn Ba không trình diễn hay số vé bán ra ít hơn 50 thì êm diễn sẽ
bị hủy bỏ và ông bầu rất buồn.
Nếu êm biểu diễn bị hủy bỏ thì phải trả lại tiền vé cho người xem.
Nhưng tiền vé ã không ược trả lại cho người xem.
Vậy nghệ sĩ Văn Ba có trình diễn.
Ta thay các mệnh ề nguyên thủy bằng các biến mệnh ề
: “nghệ sĩ Văn Ba ã trình diễn”
: “số vé bán ra ít hơn 50”
: “êm diễn sẽ bị hủy bỏ”
: “trả lại tiền vé cho người xem”
Khi ấy lý luận cần chứng minh là (¬ ∨) → (∧) → ¬
Suy luận trên có thể ược thực hiên theo các bước sau: ¬ (Tiền ề) ∧ →
(hằng úng gọi là phép ơn giản nối liền) → (Tiền ề) ¬ (Tam oạn luân mở rộng) mà ¬ (Tiền ề) ¬ (¬ ∨) (Phương pháp phủ ịnh) hay ∧ ¬
(Quy tắc De Morgan và phủ ịnh của phủ ịnh) mà ∧ ¬ →
(Phép ơn giản nối liền)
(Phương pháp khẳng ịnh) Phản ví dụ
Bây giờ ta hãy xem một bài toán ngược: khi nào một chứng minh (suy luận) là sai,
nghĩa là phải kiểm tra ( 1 2 … n ¬ ) → không phải là một hằng úng. Nói cách khác
tìm các chân trị của biến mệnh ề làm cho các tiền ề ều úng trong khi kết luận q là sai. Ta nói
ví dụ dẫn ến các giá trị của biến mệnh ề như trên là một phản ví dụ của ịnh lý cần chứng minh.
Ví dụ: hãy tìn phản ví dụ cho suy luận dưới ây
Ông Minh ã khẳng ịnh rằng nếu không ược tăng lương thì ông ta sẽ xin nghĩ việc. Mặt
khác nếu ông ta nghỉ việc mà vợ ông ta bị mất việc thì phải bán xe. Biết rằng nếu vợ ông lOMoARcPSD| 36667950
Minh hay i làm trễ thì sẽ mất việc và cuối cùng ông Minh ã ược tăng lương. Suy ra nếu ông
Minh không bán xe thì vợ ông ta không i làm trễ.
Ta ặt các biến mệnh ề như sau:
: Ông Minh ược tăng lương : Ông Minh xin nghỉ việc
: Vợ ông Minh bị mất việc : Ông Minh phải bán xe
: Vợ ông Minh i làm trễ Mô hình suy luận sẽ là ¬ → (∧) → → ¬ → ¬
Để tìm phản ví dụ ta cần tìm các gái trị của các biến mệnh ề sao cho các tiền ề là úng
trong khi kết luận là sai.
Trước hết dể kết luận sai ta cần có ¬ úng và ¬ sai, nghĩa là sai và úng. Khi ấy ể cho
tiền ề thứ tư úng r cũng phải úng. Để tiền ề thứ ba úng ta cần có q sai. Khi ấy p phải úng ể
hai tiền ề ầu là úng. Tóm lại phản ví dụ ừng với các chân trị của biến là = 1, = 0, = 1, = 0 và
= 1. Đó là trường hợp: Ông Minh ược tăng lương ( = 1) và ông Minh không
nghỉ việc ( = 0), vợ ông Minh bị mất việc ( = 1), ông Minh không bán xe ( = 0) và vợ ông Minh hay i làm trễ ( = 1).
§4 VỊ TỪ VÀ LƯỢNG TỪ
Định nghĩa 1.4.1: một vị từ là một khẳng ịnh ( , ,…) trong ó có chứa một số biến , ,… lấy giá
trị trong những tập hợp cho trước , ,… sao cho: i.
bản thân ( , ,…) không phải là mệnh ề ii.
nếu thay , ,… bằng những phần tử cố ịnh nhưng tùy ý , , … ta sẽ ược
một mệnh ề ( , ,…), nghĩa là chân trị của nó hoàn toàn xác ịnh. Các biến , ,… ược nói
là biến tự do của vị từ. Ví dụ: ( ) = “ à ộ ố ê
ố” là một vị từ theo một biến tự do ∈ : với =
1,2,11 ta ược các mệnh ề úng (1), (2), (11), còn với
ta ược các mệnh ề sai (4), (6), (15). lOMoARcPSD| 36667950 ( , ) = “ + 2,−, + 2 à ố
ℎẵ ” là một vị từ với 2 biến tự do , ∈
: chẳng hạn (4,2) là một mệnh ề úng trong khi (5,2), (4,7) là những mệnh ề sai.
Định nghĩa 1.4.2: cho trước các vị từ ( ), ( ) theo một biến ∈ . Khi ấy: i.
Phủ ịnh của p, ký hiệu ¬p là vị từ mà khi thay x bởi một phần tử cố ịnh của thì ta ược mệnh ề ¬ ( ( )) ii.
Phép nối liền (tương ứng nối rời, kéo theo…) của và , ký hiệu bởi ∧ (tương ứng ∨,
→,…) là vị từ theo biến mà khi thay bởi phần tử cố ịnh ∈ ta ược mệnh
ề ( ) ∧ ( ) (tương ứng ( ) ∨ ( ), ( ) → ( ),…)
Giả sử ( ) là một vị từ theo biến ∈
. Khi ấy có 3 trường hợp có thể xảy ra:
Trường hợp 1: khi thay bởi một phần tử a tùy ý trong , ta ược mệnh ề úng ( ).
Trường hợp 2: với một số giá trị ∈
thì ( ) thì mệnh ề úng, một số giá trị ∈ thì ( ) là mệnh ề sai.
Trường hợp 3: khi thay bởi phần tử tùy ý trong , ta ược mệnh ề sai ( ).
Nếu trường hợp 1 xảy ra thì mệnh ề “với mọi
” là một mệnh ề úng. Mệnh
ề này ược ký hiệu bởi ”
”. Như thế mệnh ề này sai nếu trường hợp 2 hay trường hợp 3 xảy ra.
Mặt khác nếu trường hợp 1 hay trường hợp 2 xảy ra thì mệnh ề “tồn tại ∈
, ( )” là một mệnh ề úng. Mệnh ề này ược ký hiệu bởi “ ”. Nếu vậy mệnh
ề này sẽ sai nếu trườgn hợp 3 xảy ra.
Định nghĩa 1.4.2: các mệnh ề “ ” và “
” ược gọi là lượng từ hóa của
vị từ ( ) bởi lượng từ phổ dụng (∀) và lượng từ tồn tại (∃). Chú ý:
1. Trong các mệnh ề lượng từ hóa, biến không còn là tự do nữa. ta nói nó ã bị buộc bởi
các lượng từ ∀ hay ∃.
2. Theo nhận xét trên, phủ ịnh của mệnh ề “
)” là úng nếu trường hợp 2 hay
trường hợp 3 xảy ra. Trường hợp 3 có thể viết lại: khi thay x bởi ∈ tùy ý
thì ¬ ( ) úng. Như thế nếu trường hợp 2 hay trường hợp 3 xảy ra thì mệnh ề “
)” là mệnh ề úng. Nói cách khác, phủ ịnh của mệnh ề “ A, p(x)” là mệnh ề “
)”. Cũng thế phủ ịnh của mệnh ề “ ” là mệnh ề “
” vì cả hai cùng úng nếu trường hợp 3 xảy ra và cùng sai nếu trường hợp
1 hay trường hợp 2 xảy ra.
Bây giờ ta xem một vị từ theo hai biến . Khi ấy nếu thay bằng
một phần tử cố ịnh nhưng tùy ý ị từ theo biến ∈
nên ta có thể lượng tử hóa nó theo biến và ược hai m “
”. Bằng cách này ta ược hai vị từ theo một biến )” và
)”. Nếu lượng tử hóa chúng ta sẽ ược 4 mệnh ề: lOMoARcPSD| 36667950 ) ) ) )
Đương nhiên ta có thể lượng từ hóa theo biến x trước rồi theo biến y sau ể ược 4
mệnh ề nữa. Hãy xét một trong các mệnh ề ó:”
”. Giả sử mệnh ề này úng. Suy ra mệnh ề “
” úng. Rõ ràng iều ngược lại cũng úng nên ta có mệnh ề úng ⟷ )]
Tương tự mệnh ề sau cũng úng: ⟷ )] Hơn nữa ta có
Định lý 1.4.1: nếu ( , ) là một vị từ theo 2 biến
, thì các mệnh ề sau là úng i. ⟷ )] và )] ii. )]
Chứng minh: ta chỉ cần chứng minh ii Giả sử ”
” úng. Khi ấy sẽ tồn tại ∈ sao cho mệnh ề “
” là úng, nghĩa là nếu thay
tùy ý thì ( , ) úng. Như vậy với
tùy ý ta có thể chọn = ể khẳng ịnh rằng “ )” là úng. Do ó “
)” là một mệnh ề úng. pcm
Chú ý: mệnh ề ảo của ii không nhất thiết úng trong trường hợp tổng quát. Thật vậy ta hãy xem một ví dụ
Gọi ( , ) là vị từ theo hai biến thực: “ + = 1”
Ta nhận xét rằng nếu thay y=b là một số thực tùy ý thì ta có thể chọn = 1 − ể
cho x + b = 1 nên mệnh ề “
” là úng. Điều này chứng tỏ mệnh ề “
” úng. Ngược lại nếu thay = tùy ý, ta có thể chọn = − ể nên mệnh ề “
” là sai. Điều này chứng tỏ mệnh ề “
” là sai. Do ó phép kéo theo sau là sai: ⟶ 1) lOMoAR cPSD| 36667950
Các kết quả trên ây có thể ược mở rộng dễ dàng cho các vị từ theo nhiều biến tự do. Đặc biệt ta có:
Định lý 1.4.2: trong một mệnh ề lượng từ hóa từ một vị từ theo nhiều biến ộc lập nếu ta
hoán vị hai lượng từ ứng cạnh nhau thì
Mệnh ề mới vẫn còn tương ương logic với mệnh ề cũ nếu hai lượng từ này cùng loại
Mệnh ề mới sẽ là một hệ quả logic của mệnh ề cũ nếu hai lượng từ trước khi hoán vị có dạng ∃∀.
Ví dụ: một hàm thực liên tục ều trên một khoảng
ược ịnh nghĩa bởi mệnh ề: ∀ > 0,∃ > 0,∀ ∈ ,∀ ∈ ,(|− | < ) ⟶ (| ( ) − ( )| < )
Theo mệnh ề 1.4.2 thì mệnh ề trên có hệ quả logic là
∀ > 0,∀ ∈ ,∃ > 0,∀ ∈ ,(|− | < ) ⟶ (| ( ) − ( )| < ) hay tương ương ∀ ∈ ,∀ > 0,∃ > 0,∀ ∈ ,(|− | < ) ⟶ (| ( ) − ( )| < )
Nói cách khác một hàm liên tục ều trên I thì liên tục.
Để lấy phủ ịnh một mệnh ề lượng từ hóa, chú ý 2 của ịnh nghĩa 1.4.3 có thể ược mở rộng thành
Định lý 1.4.3: phủ ịnh của một mệnh ề lượng từ hóa từ vị từ ( , ,…) có ược bằng cách thay
lượng từ ∀ bởi lượng từ ∃ và lượng từ ∃
bởi lượng từ ∀, và vị từ ( , ,…) bởi phủ ịnh ¬ ( , ,…).
Ví dụ: một hàm thực liên tục tại ∈
ược ịnh nghĩa bởi: ∀ > 0,∃ > 0,∀ ∈ ,(|− | < ) ⟶ (| ( ) − ( )| < )
Do ó lấy phủ ịnh theo ịnh lý 1.4.3 ta sẽ ược ịnh nghĩa của hàm không liên tục tại : ∃ > 0,∀ > 0,∃ ∈ ,(|− | < ) ∨ (| ( ) − ( )| ≥ )
Thông thường các ịnh lý trong toán học ược phát biểu liên quan ến các mệnh ề lượng
từ hóa trong ó có lượng từ phổ dụng. Do ó ngoài các quy tắc suy diễn ta còn sử dụng quy
tắc ặc biệt hóa phổ dụng và quy tắc tổng quát hóa phổ dụng.
Quy tắc ặc biệt hóa phổ dụng: nếu một mệnh ề úng có dạng lượng từ hóa trong ó một
biến ∈ bị buộc bởi lượng từ phổ dụng ∀, khi ấy nếu thay thế bởi ∈ ta sẽ ược một mệnh ề úng. Ví dụ:
1. Khi ta phát biểu “mọi người ều chết”, thực chất là ta ã sử dụng mệnh ề lượng từ hóa: ∀ ,( à ườ ) ⟶ ( ẽ ℎế)
Để áp dụng ược phương pháp khẳng ịnh, ta dùng quy tắc ặc biệt háo phổ dụng với =
(Socrate là người) ⟶ (Socrate sẽ chết)
Do ó kết hợp với tiền ề “Socrate là người”, phương pháp khẳng ịnh cho phép kết luận “Socrate sẽ chết”. lOMoARcPSD| 36667950
2. Trong các ịnh lý tóan học, ví dụ như trường hợp bằng nhau của hai tam giác, khẳng
ịnh là một mệnh ề lượng từ hóa phổ dụng cho một cặp tam giác bất kỳ. khi áp dụng
ta sẽ ặc biệt hóa cho một cặp tam giác cụ thể nào ó.
Bài toán ngược lại là nếu một kết luận có dạng lượng từ hóa phổ dụng thì làm cách
nào suy diễn nó từ các tiền ề. Nếu tập hợp tương ứng A là một tập hợp hữu hạn không quá
nhiều phần tử, ta có thể dùng phương pháp vét cạn bằng cách thay thế biến lần lượt bởi các
phần tử của A và chứng minh mệnh ề là úng. Mặt khác nếu A=N ta thường sử dụng nguyên
lý quy nạp sẽ trình bày ở §5.
Tuy nhiên nếu A vô hạn không ếm ược, hay ngay khi A hữu hạn nhưng số phần tử
của A quá lớn, các phương pháp trên không sử dụng ược và ta phảo sử dụng:
Quy tắc tổng quát hóa phổ dụng: nếu trong một mệnh ề lượng từ hóa, khi thay một biến
buộc bởi lượng từ ∀ bằng một phần tử cố ịnh nhưng tùy ý của tập hợp tương ứng mà mệnh
ề nhận ược có chân trị 1 thì bản thân mệnh ề lượng từ hóa ban ầu cũng có chân trị 1.
Ví dụ: Khi giải phương trình 4− 5 = 15 ta lý luận như sau:
Giả sử 4− 5 = 15 , khi ấy 4 = 20
Giả sử 4 = 20 , khi ấy = 5
Như vậy nếu 4− 5 = 15 thì = 5
Nếu gọi ( ), ( ), ( ) là các vị từ “4− 5 = 15”, “4 = 20”, “ = 5” thì lý luận trên có dạng ∀ , ( ) ⟶ ( ) ∀ , ( ) ⟶ ( ) (1.4.1) ∴ ∀ , ( ) ⟶ ( )
Sự úng ắn của lý luận trên ược cho bởi
Định lý 1.4.4: gọi ( ), ( ), ( ) là các vị từ theo một biến ∈, khi ấy suy luận 1.4.1 là úng.
Muốn vậy ta ặc biệt hóa hai tiền ề và ược hai mệnh ề úng ( ) → ( ) ( ) → ( )
Suy ra ( ) → ( ) theo tam oạn luận. Do ó quy tắc tổng quá hóa phổ dụng cho phép kết
luận ∀ , ( ) → ( ) là một mệnh ề úng.
Ví dụ: Gọi , là 2 hàm thực
Giả sử ( ) liên tục tại = và ( )liên tục tại = = ( ). Khi ấy ℎ( ) = (∘ )( ) liên tục tại = . Suy luận
cần chứng minh có dạng: lOMoAR cPSD| 36667950
Sử dụng phép tổng quát hóa phổ dụng ta bởi một số dương cố ịnh nhưng tùy ý. Để
tiện ta sẽ dùng cùng ký hiệu dể chỉ số cố ịnh trên. Khi ấy ta cần tìm > 0 dể cho mệnh ề sau là úng ∀ ,(|− | < ) → (|∘( ) − ∘ ( )| < )
Dùng phép ặc biệt hóa phổ dụng cho tiền ề thứ hai với > 0 như trên, ta sẽ tìm ược > 0 sao cho: ∀ ,(|− | < ) → (| ( ) − ( )| < ) (1.4.2)
Tiếp theo, ta ặc biệt hóa bởi vừa tìm ược cho tiền ề thứ nhất và tìm ược > 0 sao cho: ∀ ,(|− | < ) → (| ( ) − ( )| < ) (1.4.3)
Thay bởi số thực tùy ý mà ta vẫn ký hiệu là thì 1.4.3 ược ặc biệt hóa bởi
(|− | < ) → (| ( ) − ( )| < ) (1.4.4) Khi ấy ta ặc biệt hóa 1.4.2 với = ( ) ta ược (| ( ) − | < ) → (|∘( ) − ∘ ( )| < ) (1.4.5)
Áp dụng Tam oạn luận cho 1.4.4 và 1.4.5 ta ược lOMoARcPSD| 36667950 (|− | < ) → (|∘( ) − ∘ ( )| < )
Do ó theo phương pháp tổng quát hóa phổ dụng ta có ∀ ,(|− | < ) → (|∘( ) − ∘ ( )| < )
Áp dụng một lần nữa phương pháp tổng quát hóa phổ dụng ta thấy mệnh ề sau là úng ∀ > 0,∃ > 0,∀ ,(|− | < ) → (|∘( ) − ∘ ( )| < )
nghĩa là làm ∘ liên tục tại = .
§5 NGUYÊN LÝ QUY NẠP
Trong nhiều trường hợp, quy tắc tổng quát hóa phổ dụng không cho kết quả, ngay
cả với các vị từ mà biến tự do thuộc N. Tuy nhiên ối với các vị từ này ta có một công cụ rất mạnh là:
Nguyên lý quy nạp: Mệnh ề ∀ ∈ , ( ) là hệ quả của (0) ∧ [∀ ∈ , ( ) → ( + 1)] Chú ý:
Theo ngôn ngữ thông thường ta nói: giả sử (0) úng và nếu ( ) úng thì ( + 1) cũng úng,
khi ấy suy ra ( ) úng với ∈ tùy ý.
Nguyên lý này có thể bắt ầu từ ∈ : nghĩa là ( ) ∧ [∀ ≥ 0, ( ) → ( + 1)] → [∀ ≥ , ( )]
Ví dụ: xét vị từ ( ):
Trước hết (0) úng vì nó có dạng: 0 =
Để chứng minh ∀ , ( ) → ( + 1) ta dùng phép tổng quát hóa phổ dụng, thay bởi , một
số nguyên tùy ý và chứng minh ( ) → ( + 1). Muốn vậy giả sử ( ) úng: Khi ấy nghĩa là (
+ 1) úng. Do ó theo nguyên lý quy nạp “∀ , ( )” là một mệnh ề úng. lOMoAR cPSD| 36667950
Áp dụng: ể kiểm tra một chương trình máy tính có chạy úng ý ịnh cuả người thiết kế khôn,
ta thường tạo ra các số liệu giả ịnh ể chạy thử (Test). Thật ra phương pháp này không thể
khẳng ịnh chắc chắn rằng chương trình chạy có úng không. Hơn nữa trong nhiều trường
hợp, ví dụ như khi chương trình ang xét là một bộ phận của chương trình lớn mà dữ liệu chỉ
có thể sinh ra từ chương trình lớn, thì khi ấy ta không thể tạo ra dữ liệu giả dể chạy chuong
trình con ược. May mắn là trong một số trường hợp ta có thể sử dụng công cụ toán học ể
chứng minh rằng chương trình khi chạy sẽ luôn cho ra kết quả mong muốn. Một trong những
công cụ ó là ngyên lý quy nạp như ví dụ dưới ây cho thấy
Xét oạn chương trình viết bằng Pascal: while < > 0 do Begin ≔ ∗ ; ≔ − 1; End; Kết quả:= ;
Ta muốn kiểm tra rằng khi gọi oạn chương trình trên mà các biến có giá trị , , với là
số nguyên tự nhiên thì khi ra khỏi chương trình , biến sẽ có giá trị . Muốn vậy ta gọi ( ) là vị từ: "ớ ấ ỳ ố ℎự , , ế ℎ ỏ đ ề ℎ ể ℎươ ì ℎ ở ề ò ệ ℎ ℎ ớ á á ị ủ á ế à , , ℎì ℎ ℎỏ ℎươ ì ℎ ế ó á ị "
Ta áp dụng nguyên lý quy nạp như sau:
∗ (0): khi trở về dòng lệnh while với các giá trị của biến là , ,0 thì vòng lặp không ược
thực hiện tiếp và ta ra khỏi chương trình với giá trị của biến là = * với =
là một số nguyên tự nhiên tùy ý. Giả sử ( ) úng, ta sẽ chứng minh
( + 1) úng. Gọi , là các số thực tùy ý và giả sử ta trở về dòng lệnh while với giá trị của các
biến là , , = + 1. Do ≥ 0 nên + 1 > 0. Do ó vòng lặp while ược thực hiện thêm ít nhất một lần
nữa. Sau lần ầu tiên thực hiện ta trở về dòng lệnh while với giá trị của các biến là ∗, , = . Do
( ) úng nên khi ra khỏi chương trình, biến sẽ có giá trị: (∗) ∗ = ∗ ( ) nghĩa là ( + 1) úng.
Do ó “∀ , ( )” úng. Đặc biệt khi ta gọi oạn chương trình trên với các biến , , thì khi ra
khỏi chương trình biến sẽ có giá trị ∗ như mong muốn. lOMoARcPSD| 36667950
BÀI TẬP CHƯƠNG 1
1. Trong các khẳng ịnh sau, cho biết khẳng ịnh nào là mệnh ề: a)
Trần Hưng Đạo là một vị tướng tài. b)
+ 1 là một số nguyên dương. c) 9 là một số chẵn. d)
Hôm nay trời ẹp làm sao! e)
Hãy học Toán rời rạc i. f)
Nếu bạn ến trễ thì tôi sẽ xem bóng á trước.
2. Gọi và là các mệnh ề: : “Minh giỏi Toán” : “Minh yếu Anh văn”
Hãy viết lại các mệnh ề sau dưới dạng hình thức trong ó sử dụng các phép nối a)
Minh giỏi Toán nhưng yếu Anh văn
b) Minh yếu cả Toán lẫn Anh văn
c) Minh giỏi Toán hay Minh vừa giỏi Anh văn vừa yếu Toán
d) Nếu Minh giỏi Toán thì Minh giỏi Anh văn
e) Minh giỏi Toán và Anh văn hay Minh giỏi Toán và yếu Anh văn 3. Gọi , , là các mệnh ề: : “Bình ang học Toán” : “Bình ang học Toán”
: “Bình ang học Anh văn”
Hãy viết lại các mệnh ề sau dưới dạng hình thức trong ó sử dụng các phép nối a)
Bình ang học Toán và Anh văn nhưng không học Tin học
b) Bình ang học Toán và Tin học nhưng không học cùng một lúc Tin học và Anh văn
c) Không úng là Bình ang học Anh văn mà không học Toán
d) Không úng là Bình ang học Anh văn hay Tin học mà không học Toán
e) Bình không học Tin học lẫn Anh văn nhưng ang học Toán
4. Hãy lấy phủ ịnh của các mệnh ề sau: a)
Ngày mai nếu trời mưa hay trời lạnh thì tôi sẽ không ra ngoài b)
15 chia hết cho 3 nhưng không chia hết cho 4 c)
Hình tứ giác này không phải là hình chữ nhật mà cũng không phải là hình thoi d)
Nếu An không i làm ngày mai thì sẽ bị duổi việc e)
Mọi tam giác ều có các góc bằng 600
5. Cho biết chân trị của các mệnh ề sau: a)
= 2 và tổng các góc của một tam giác bằng 1800 b)
= 3.1416 kéo theo tổng các góc của một tam giác bằng 1700 c)
= 3 kéo theo tổng các góc của một tam giác bằng 1700 d)
Nếu 2>3 thì nước sôi ở 1000C e) Nếu 3<4 thì 4<3 f) Nếu 4<3 thì 3<4 lOMoAR cPSD| 36667950
6. Ta ịnh nghĩa một phép nối mới ký hiệu là ↓
ể chỉ mệnh ề: không mà cũng không
. Hãy lập bảng chân trị của phép nối trên.
7. Giả sử và là hai mệnh ề nguyên thủy sao cho →
sai. Hãy xác ịnh chân trị của các mệnh ề sau: a) ∧ b) ¬ ∨ c) → 8. Gọi , , là các mệnh ề sau: : “Bình ang học Toán” : “Bình ang học Toán”
: “Bình ang học Anh văn”
Hãy viết lại các mệnh ề sau theo ngôn ngữ thông thường: a) → b) ¬ → c) ∧ d) →
9. Xác ịnh chân trị của các mệnh ề sau: a)
Nếu 3 + 4 = 12 thì 3 + 2 = 6 b)
Nếu 1 + 1 = 2 thì 1 + 2 = 3 c)
Nếu 1 + 1 = 2 thì 1 + 2 = 4
10. Có bao nhiêu cách ặt dấu “()” khác nhau vào dạng mệnh ề ¬ ∨ ∨ . Lập bảng chân trị cho từng trường hợp.
11. Lập bảng chân trị cho các dạng mệnh ề sau: a) ¬ → (∨) b) ¬ → (¬ ∨) c) (∧) → ¬ d) (∨) → (∨ ¬ ) e) (→) ∨ (→) f) (∨ ¬ ) ∧ (¬ ∨) g) (→ ¬ ) ∨ (→ ¬ ) h) ¬ (¬ ∧ ¬ )
12. Hãy chỉ ra các hằng úng trong các dạng mệnh ề sau: a) (∨) → (∧) b) (∧) → (∨) b) → (¬ →) d) → (→) c) → (→) f) (→) → [(→) → (→)]
13. Trong các khẳng ịnh sau, hãy chỉ ra các khẳng ịnh úng: a) ⇒ → b) ¬ (→) ⟹ c) (∧) ∨ ⟹ ∧ (∨) d) (→) ∧ (→) ⟹ → (→) e) → (→) ⟹ → f) → (∧) ⟹ → g) (∧) → ⟹ (→) ∧ (→) h) → (∨) ⟹ (→) ∨ (→) i) (¬ →) ∨ (→ ¬ ) ⟹ ∧ 14. lOMoAR cPSD| 36667950
a) Giả sử biến mệnh ề có chân trị 1, hãy xác ịnh tất cả các chân trị của các biến mệnh
ề , , ể cho dạng mệnh ề sau lấy chân trị 1:
(→ [(¬ ∨) ∧ ¬ ]) ∧ [¬ → (¬ ∧)]
b) Câu hỏi tương tự cho trường hợp có chân trị 0
15. Có thể nói gì về một dạng mệnh ề: a)
Có hệ quả logic là một mâu thuẫn? b)
Có hệ quả logic là một hằng úng? c)
Là hệ quả logic của một mâu thuẫn? d)
Là hệ quả logic của một hằng úng?
16. Hãy chỉ ra các khẳng ịnh úng trong số các khẳng ịnh sau: a) ∧ (→) ⟺ ∧ b) → ⟺ ¬ ∨ (∧) c) → ⟺ ¬ → ¬ d) ¬ ⟺ ¬ (∨) ∨ (¬ ∧) e)
[(⟷) ∧ (⟷) ∧ (⟷)] ⟺ [(→) ∧ (→) ∧ (→)] f)
(∧) ∨ (∧) ∨ (∧) ⟺ (∨) ∧ (∨) ∧ (∨)
17. Dùng quy tắc thay thế ể kiểm tra các dạng mệnh ề sau là hằng úng: a)
[(∨) → ] ⟷ [¬ → ¬ (∨)] b)
[(∨) → ] ∨ (∨) ⟷ [[[(∨) → ] ∨ ] ∧ [[(∨) → ] ∨ ]]]
18. Đơn giản dạng mệnh ề sau:
[[[(∧) ∧ ] ∨ [(∧) ∧ ¬ ]] ∨ ¬ ] →
19. Lấy phủ ịnh rồi ơn giản các dạng mệnh ề sau: a) ∧ (∨) ∧ (¬ ∨ ¬ ∨) b) (∧) → c) → (¬ ∧) d) ∨ ∨ (¬ ∧ ¬ ∧)
20. Cho biết quy luật logic nào ã ược áp dụng trong mỗi bước tương dương sau: Biểu thức Quy luật logic a) [(∨) ∧ (∨ ¬ )] ∨ ⟺ [∨ (∧ ¬ )] ∨ ⟺ (∨ 0) ∨ ⟺ ∨ b)
¬ (∨) ∨ [(¬ ∧) ∨ ¬ ] ⟺ ¬(∨) ∨ [¬ ∨ (¬ ∧)]
⟺ ¬(∨) ∨ [(¬ ∨ ¬ ) ∧ (¬ ∨)]
⟺ ¬(∨) ∨ [(¬ ∨ ¬ ) ∧ 1] ⟺ ¬(∨) ∨ (¬ ∨ ¬ ) ⟺ ¬(∨) ∨ ¬ (∧) ⟺ ¬[(∨) ∧ (∧)] ⟺ ¬[(∧) ∧ (∨)] ⟺ ¬[∧ [∧ (∨)]] ⟺ ¬(∧) c) (→) ∧ [¬ ∧ (∨ ¬ )] lOMoAR cPSD| 36667950 ⟺ (→) ∧ ¬ ⟺ (¬ ∨) ∧ ¬ ⟺ ¬ ∧ (¬ ∨) ⟺ (¬ ∧ ¬ ) ∨ (¬ ∧) ⟺ (¬ ∧ ¬ ) ∨ 0 ⟺ ¬ ∧ ¬ ⟺ ¬(∨)
21. Hãy iền mệnh ề vào chỗ trống ể cho các suy luận sau ây theo phương pháp khẳng ịnh và phủ ịnh là úng: a)
Nếu xe của Minh không khởi ộng ược thì anh phải kiểm tra bugi. Mà xe của Minh không khởi ộng ược.
Suy ra ............................................................................................... b)
Nếu Hà làm bài úng thì cô ược iểm cao Mà Hà không ược iểm cao
Suy ra ............................................................................................... c)
Nếu ây là vòng lặp REPEAT-UNTIL thì phần thân của vòng lặp phải ược thực hiên ít nhất một lần
Mà ....................................................................................................
Vậy phần thân của vòng lặp ược thực hiên ít nhất một lần. d)
Nếu chiều nay Minh á bóng thì Minh không ược xem tivi buổi tối
Mà ....................................................................................................
Vậy Minh không á bóng chiều nay.
22. Cho biết suy luận nào trong các suy luân dưới ây là úng và quy tắc suy diễn nào ã ược sử dụng? a)
Điều kiện ủ ể CSG thắng trận là ối thủ ừng gỡ lại vào phút cuối Mà CSG ã thắng trận
Vậy ối thủ CSG không gỡ lại vào phút cuối b)
Nếu Minh giải ược bài toán thứ tư thì em ã nộp trước giờ quy ịnh Mà Minh ã
không nộp bài trước giờ quy ịnh
Vậy Minh không giải ược bài toán thứ tư c)
Nếu lãi suất giảm thì số người gửi tiết kiệm sẽ giảm
Mà lãi suất ã không giảm
Vậy số người gửi tiết kiệm không giảm d)
Nếu ược thưởng cuối năm Hà sẽ i Đà Lạt
Nếu i Đà Lạt Hà sẽ thăm Suối vàng
Do ó nếu ược thưởng cuối năm Hà sẽ thăm suối vàng 23.
a) Dùng các quy tắc suy diễn ể suy ra khẳng ịnh sau là úng: (∧) ⟹ (∨)
b) Xét các dạng mệnh ề:
= [∧ (∧)] ∨ ¬ [∨ (∧)]
= [∧ (∨)] ∨ ¬ [∨ (∨)] 24. Xét suy diễn:
[∧ (→) ∧ (∨) ∧ (→ ¬ )] → (∨)
Cho biết các bước suy diễn sau ã sử dụng các quy tắc nào? Bước Quy tắc lOMoARcPSD| 36667950 → ∴ hay ¬ ¬ mà → ¬ ∴ mà ∨ hay ¬ → 25. Xét suy diễn sau: (¬ ∨) → r→ (∨) ¬ ∨ ¬ ¬ → ¬ ∴
Cho biết các quy tắc nào ã ược sử dụng trong các bước sau: Bước Quy tắc ¬ ∧ ¬ ∴ ¬ mà ¬ → ¬ ∴ ¬ mà ¬ nên ¬ ∧ ¬ hay ¬ ( mà → ∨ ∴ ¬ mà (¬ ∨) → hay ∧ ¬ ∴
26. Giải thích các bước của suy luận sau:
[(→) ∧ (¬ ∨) ∧ (∨)] → (¬ →) Bước Quy tắc lOMoARcPSD| 36667950 G.Sử ¬ (¬ →) hay ¬ (∨) hay ¬ ∧ ¬ ∴ ¬ và ¬ mà ¬ ∨ hay → ∴ ¬ → và nên ¬ ∧ ¬ hay ¬ (∨) mà ∨ ∴ 0 Vậy suy luận là úng.
27. Hãy kiểm tra lại các suy luận sau:
a) [(∧ ¬ ) ∧ ] → [(∧) ∨ ]
b) [∧ (→) ∧ (¬ ∨)] →
28. Hãy kiểm tra các suy luận sau: a) → b) → c) → (→) ¬ → ¬ ¬ → ¬ ¬ ∴ ¬ (∨) ∴ ¬ ∴ d) ∧ e) → (→) f) ∨
→ (∧ ) ∨ ¬ ∨ → (∨) → ¬ ¬ s ¬ s ∴ lOMoARcPSD| 36667950 ∴¬ (∨) ∴ ¬ → ¬
29. Tìm phản ví dụ cho các suy luận sau: a) ↔ b) → → ∨ ¬ → (∨ ¬ ) ¬ → ¬ ∨ ¬ ∴¬ (∨) ∴
30. Hãy kiểm tra xem các suy luận sau có úng không
a) Nếu An ược lên chức và làm việc nhiều thì An sẽ ược tăng lương Nếu ược
tăng lương An sẽ mua xe mới Mà An không mua xe mới
Vậy An không ược lên chức hay An không làm việc nhiều.
b) Nếu muốn dự họp sáng thứ ba thì Minh phải dạy sớm Nếu Minh i nghe nhạc
tối thứ hai thì Minh sẽ về trễ
Nếu về trễ và thức dậy sớm thì Minh phải i họp mà chỉ ngủ dưới 7 giờ Nhưng
Minh không thể i họp nếu chỉ ngủ dưới 7 giờ
Do ó hoặc là Minh không i nghe nhạc thối thứ hai hoặc là Minh phải bỏ họp sáng thứ ba.
c) Nếu Bình i làm về muộn thì vợ anh ta sẽ rất giận dữ
Nếu An thường xuyên vắng nhà thì vợ anh ta sẽ rất giận dữ
Nếu vợ Bình hay vợ An giận dữ thì cô Hà bạn họ sẽ nhận ược lời than phiền
Mà Hà không nhận ược lời than phiền Vậy
Bình i làm về sớm và An ít khi vắng nhà. 31. Xét các vị từ ( ):"≤ 5" ( ):" + 3 chẵn"
Trong ó là một biến nguyên. Xét chân trị của các mệnh ề sau: a) (1) b) (2) c) ¬ (2) d) (3) e) (6) ∨ (6) f) ¬ ( (−1) ∨ (−1))
32. Với ( ), ( ) như trên. Xét thêm vị từ: ( ):" > 0"
Tìm chân trị của các mệnh ề sau: a) b) c) → (2)] d) → (3) e) ↔ (1)] f) ↔ (1) 33. Với , , như trên lOMoARcPSD| 36667950
a) Tìm tất cả ể cho ( ) ∧ ( ) ∧ ( ) úng
b) Tìm tất cả nhỏ nhất ể ( ) → [¬ ( ) ∧ ( )] úng 34. Xét vị từ ( ):" − 3
+ 2 = 0". Cho biết chân trị của các mệnh ề sau: a) (0) b) (1) c) (2) e) ∃ , ( ) e) ∀ , ( )
35. Lớp Phân tích Thuật toán có 110 sinh viên ghi tên học trong ó có:
15 sinh viên Toán-Tin học năm thứ 3 5 sinh viên Toán năm thứ 3
25 sinh viên Toán-Tin học năm thứ 4
5 sinh viên Toán năm thứ 4
50 sinh viên Công nghệ Thông tin năm thứ 4
5 sinh viên Toán-Tin học Cao học
5 sinh viên Công nghệ Thông tin Cao học Xét các vị từ: ( ):sinh ê ℎ ê ℎọ ô ℎâ íℎ ℎ ậ á ( ): àsinh ê ă ℎứ 3 ( ): àsinh ê ă ℎứ 4 ( ): àsinh ê ℎọ ( ): àsinh ê ô ℎệ ℎô ( ): àsinh ê á − ℎọ ( ): àsinh ê á
Hãy viết các mệnh ề dưới ây theo dạng lượng từ hóa:
a) Có sinh viên Toán năm thú 3 trong lớp PTTT
b) Có sinh viên trong lớp không phải sinh viên Công nghệ Thông tin
c) Mọi sinh viên trong lớp là sinh viên Toán-Tin học hay Công nghệ Thông tin
d) Không có sinh viên Cao học Toán trong lớp PTTT
e) Mọi sinh viên năm thứ 3 trong lớp thuộc ngành Toán hay ngành Toán-Tin học
f) Có sinh viên ở trường không thuộc ngành Toán-Tin học và cũng không thuộc ngành Công nghệ Thông tin 36. Xét các vị từ: ( , ):" ≥ " ( , ):" + 1 < "
Trong ó , là các biến thực. cho biết chân trị của các mệnh ề sau: a) (2,4) b) (2, ) c) (−3,7) ∧ (1,
d) (−2,1) ∨ ¬ (−1,−1) e) (1,1) → (1,1) f) (2,5) ↔ ¬ (2,5)
37. Xét các vị từ theo biến thực : ( ):" − 5 + 6 = 0" ( ):" − 4− 5 = 0" ( ):" > 0"
Hãy xác ịnh chân trị của các mệnh ề sau: a) ∀ , ( ) → ( ) b) → ¬ ( ) c) ∃ , ( ) → ( ) d) ∃ , ( ) → ¬ ( )
38. Xét vị từ theo hai biến nguyên tự nhiên: ( , ):" à ướ ủ "
Hãy xác ịnh chân trị của các mệnh ề sau: a) (2,3) b) (2,6) c) ∀ , (1, ) lOMoARcPSD| 36667950
d) ∀ , ( , ) e) ∀ ,∃ , ( , ) f) ∃ ∀ , ( , ) e) ∀ ∀ ,( ( , ) ∧ ( , )) → ( = )
d) ∀ ∀ ∀ ,( ( , ) ∧ ( , )) → ( , )
39. Với mỗi mệnh ề dưới ây cho biết chân trị. Phủ ịnh kèm theo có úng không? Nếu không
hãy thay bằng phủ ịnh úng.
a) Với mọi số thực , nếu > thì >
Phủ ịnh: Tồn tại số thực , sao cho > nhưng ≤
b) Với mọi số thực nếu ≠ 0 thì có nghịch ảo
Phủ ịnh: tồn tại số thực khác 0 mà không có nghịch ảo
c) Tồn tại hai số nguyên lẻ có tích là số lẻ
Phủ ịnh: tích của hai số lẻ bất kỳ là số lẻ
d) Bình phương của mọi số hữu tỉ là số hữu tỉ
Phủ ịnh: tồn tại số thực sao cho nếu vô tỉ thì vô tỉ.
40. Lấy phủ ịnh của các mệnh ề sau:
a) Với mọi số nguyên , nếu không chia hết cho 2 thì là số lẻ
b) Nếu bình phương của một số nguyên là lẻ thì số nguyên ấy là lẻ
c) Nếu , , là số nguyên sao cho − và − là số lẻ thì − là số chẵn
d) Nếu là một số thực sao cho > 16 thì < −4 hay > 4
e) Với mọi số thực , nếu |− 3| < 7 thì −4 < < 10
41. Gọi ( ) và ( ) là hai vị từ theo một biến, hãy lấy phủ ịnh và ơn giản các mệnh ề sau: a) ∃ , ( ) ∨ ( ) b) d) ∀ , ( ) → ( ) d) ∃ ,[ ( ) ∨ ( )] → ( )
42. Cho biết chân trị của các mệnh ề sau trong ó , là các biến thực: a) ∃ ∃ , = 1 b) ∃ ∀ , = 1 c) ∀ ∃ , = 1 d) ∀ ∀ , + = + e) ∃ ∃ ,(2 + = 5) ∧ (− 3 = −8) f) ∃ ∃ ,(3− = 7) ∧ (2 + 4 = 3) 43.
a) Sự tồn tại của phần tử 0 trong R ược cho bởi: ∃ ∀ , + =
Hãy viết mệnh ề chỉ sự tồn tại của phần tử ơn vị trong R
b) ′ ược nói là phần tử ối của nếu + = 0
Hãy viết mệnh ề cho biết tồn tại phần tử ối
c) ′ ược nói là nghịch ảo của nếu = 1
Hãy viết mệnh ề cho biết mọi số thực khác 0 ều có nghịch ảo
d) Nếu thu hẹp vào tập hợp các số nguyên thì các mệnh ề trong b) và c) phải ược iều
chỉnh như thế nào ể vẫn còn úng
44. Giả sử ( ) là vị từ theo biến ∈. Khi ấy mệnh ề lượng từ hóa ∃! , ( ) ược ịnh nghĩa như là: ∃ , ( ) ∧ [∀ ∀ ,( ( ) ∧ ( )) → = ] lOMoAR cPSD| 36667950
Nói cách khác tồn tại phần tử sao cho ( ) úng và là phần tử duy nhất của sao cho ( ) úng.
Hãy viết lại các mệnh ề dưới ây dưới dạng hình thức trong ó sử dụng lượng từ ∃!
a) Mọi số thực khác 0 có nghịch ảo duy nhất b) Với mọi ,∈, tổng + là duy nhất
c) Với mọi , tồn tại duy nhất sao cho = 3 + 7
45. Giả sử ( , ) là vị từ = −2 trong ó , là các biến nguyên. Hãy cho biết chân trị của các mệnh ề sau:
a) [∀ ∃! , ( , )] → [∃! ∀, ( , )]
b) [∃! ∀, ( , )] → [∀ ∃! , ( , )]
46. Với vị từ ( , ):" + à ố
ℎẵ ". Hãy cho biết các mệnh ề trong câu 45 có úng không?
47. Xét mệnh ề "∃! , > 1". Hãy tìm tập hợp vũ trụ ể cho mệnh ề trên là úng (tương ứng sai)
48. Hãy iền vào hàng trống dể cho các suy luận sau là úng:
a) Mọi số nguyên là số hữu tỉ
Số thực không phải số hữu tỉ
∴.........................................................
b) Mọi sinh viên Tin học ều học Toán Rời rạc
.........................................................
∴ Minh học Toán Rời rạc
c) .........................................................
Bình là một Giám ốc iều hành
∴ Bình biết cách ủy quyền cho cấp dưới
d) Mọi hình chữ nhật có bốn góc bằng nhau
.........................................................
∴ Tứ giác MNPQ không phải hình chữ nhật
e) Mọi người quan tâm ến Cholesterol ều tránh ăn gan
Minh là một người quan tâm ến Cholesterol
∴ ........................................................
49. Xác ịnh các suy luận úng trong số các suy luận dưới ây. Cho biết quy tắc suy diễn ã ược áp dụng:
a) Mọi người ua thư dều mang theo túi thư
An là một người ưa thư Vậy An mang theo túi thư
b) Mọi công dân tốt ều óng thuế Ông Bình ã dóng thuế
Vậy ông Bình là một công dân tốt
c) Mọi người quan tâm ến môi trường ều ể riêng các túi nhựa bỏ i lOMoARcPSD| 36667950
Hà không quan tâm ến môi trường
Suy ra Hà không ể riêng các túi nhựa bỏ i
d) Mọi sinh viên nghiêm túc ều không nộp bài chưa làm xong
Minh không nộp bài chưa làm xong
Vậy Minh là sinh viên nghiêm túc
50. ( ) và ( ) là hai vị từ theo một biến
Hãy chứng minh các khẳng ịnh dưới dây: a) [∃ , ( ) ∨
( )] ⟺ ∃ , ( ) ∨ ∃ , ( ) b) [∀ , ( ) ∧
( )] ⟺ [∀, ( ) ∧ ∀ , ( ) ] c) ∀, ( ) ∨ ∀ , ( )⟹ [∀ , ( ) ∨ ( )]
d) Hãy tìm phản ví dụ cho phần ảo của c) 51. Xét suy luận:
Hãy cho biết quy tắc suy diễn áp dụng cho mỗi bước sau ây: Bước Quy tắc ∀ , ( ) ∧ ( ) ( ) ∧ ( ) ∴ ( ) và ( ) ∀ , ( ) → ( ( ) ∧ ( )) ( ) → ( ( ) ∧ ∴ ( )) ( ) ∧ ( ) vậy ( ) ∴ ( ) ∧ ( ) như thế ∀ , ( ) ∧ ( ) lOMoARcPSD| 36667950 52. Xét suy luân: ∀ , ( ) → ( ) ∨ ( ) ∃ ,¬ ( ) ∀ ,¬ ( ) ∨ ( )
∀ , ( ) → ¬ ( ) ∴ ∃ ,¬ ( )
Hãy cho biết quy tắc suy diễn áp dụng trong các bước sau: Bước Quy tắc ∃ ,¬ ( ) ¬ ( ) ∀ , ( ) → ( ) ∨ ( ) ( ) ∨ ( ) hay ¬ ( ) → ( ) ∴ ( ) ∀ ,¬ ( ) ∨ ( ) ¬ ( ) ∨ ( ) hay ( ) → ( ) ∴ ( ) ∀ , ( ) → ¬ ( ) ( ) → ¬ ( ) ∴ ¬ ( ) nghĩa là ∃ ,¬ ( )
53. Hãy chứng minh các công thức sau: ) ( ) ) ) ! ) 54. Xét vị từ:
( ): vật bất kỳ thì ồng nhất với nhau trong ó là một biến nguyên, ≥ 1.
Khẳng ịnh: ∀ ≥ 1, ( ) Chứng minh: (1): hiển nhiên
Giả sử (− 1) úng. Xét vật , ,…, Do (− 1) úng nên , ,…,
ồng nhất và ồng thời , ,…, ồng nhất. Suy ra , ,…,
ồng nhất. Nghĩa là ( ) úng. lOMoARcPSD| 36667950
Do ó nguyên lý quy nạp ∀ ≥ 1, ( ) là một mệnh ề úng! Suy luận trên sai do âu? GS. Nguyễn Hữu Anh 34
55. Đặt các số 1,2,…,25 trên một vòng tròn theo thứ tự tùy ý. Chứng minh rằng luôn luôn
có 3 số liên tiếp có tổng ≥ 39
56. Chứng minh các bất ẳng thức sau với ∈ a) Nếu > 3 thì 2 < ! b) Nếu > 4 thì < 2 c) Nếu > 9 thì < 2 57. Xét vị từ ( ):
Chứng minh rằng nếu ( ) úng thì ( + 1) úng với mọi ≥ 1. Từ ó có suy
ra ược ( ) úng với mọi ≥ 1 không? 58. Xét các phương trình 1 = 1 2 + 3 + 4 = 1 + 8 5 + 6 + 7 + 8 + 9 = 8 + 27
10 + 11 + 12 + 13 + 14 + 15 + 16 = 27 + 64
Từ ó suy ra một công thức tổng quát dưới dạng vị từ theo một biến nguyên và chứng minh công thức này.
59. Xét oạn chương trình viết bằng Pascal while < > 0 do Begin ≔ + ; ≔ − 1; End; Ketqua:= ;
Chứng minh rằng khi gọi oạn chương trình trên với các biến , lấy giá trị thực và biến lấy
giá trị nguyên tự nhiên thì khi ra khỏi oạn chương trình, biến Ketqua ược gán giá trị + lOMoARcPSD| 36667950
60. Xét oạn chương trình viết bằng Pascal while < > 0 do Begin ≔ × ; ≔ − 1; End; Ketqua:= ;
Giả sử ta gọi oạn chương trình trên với các biến , lấy giá trị thực và lấy giá trị nguyên
dương. Khi ra khỏi oạn chương trình, biến Ketqua ược gán giá trị nào? Hãy chứng minh khẳng ịnh ó.
CHƯƠNG 2: PHƯƠNG PHÁP ĐẾM
Từ Chương 2 trở i ta sẽ sử dụng các kí hiệu logic quen thuộc ⟹,⟺ ể chỉ các quan
hệ “có hệ quả logic”, “tương ương logic” giữa các mệnh ề mà ta xem như dạng mệnh ề
hằng. Ngoài ra ta cũng dùng các kí hiệu này ể chỉ phép kéo theo và kéo theo hai chiều. Các
kí hiệu ⟶,⟷ ược dành cho các ánh xạ.
§1 TẬP HỢP
Trong chương trước ta ã sử dụng khái niệm tập hợp trong một số ví dụ, ặc biệt trong
ịnh nghĩa của các lượng từ. Trong chương này ta tiếp tục sử dụng khái niệm tập hợp theo
nghĩa trực quan: ó là những ối tượng ược nhóm lại theo một tính chất nào ó. Nếu là một
phần tử của tập hợp , ta viết ∈. Trong trường hợp ngược lại ta viết ∉.
Ở ây khái niệm “tính chất” ược hiểu theo một nghĩa hết sức rộng rãi. Thường thì nó
biểu hiện bởi một vị từ ( ) theo một biến ∈. Khi ấy tập hợp tất cả các phần tử ∈ sao cho ( ) úng ược kí hiệu bởi: = {∈⁄ ( )}
ược gọi là tập hợp vũ trụ. Nếu hiểu ngầm thì có thể viết: = { / ( )} Ví dụ: 1. A = {x ∈ N x⁄ là số nguyên tố} 2. A = {x ∈ Z x⁄ < 5}
Trong ví dụ 2, ta có thể chỉ ra tất cả các phần tử của : -2, -1, 0, 1, 2. Ta viết = {−2,−1,0,1,2}
Ta nói ược mô tả bằng cách liệt ra tất cả các phần tử. Cũng thế = {∈/ ≤ }
có thể ược mô tả bằng cách liệt kê các phần tử: = {0,1,…, }
Với phương pháp mô tả bằng cách liệt kê các phần tử, một tập hợp có thể là: = {1,2,97,100}
Khi này không nhất thiết các phần tử ược nhóm lại theo một tính chất cụ thể nào.
Chú ý rằng tập hợp {∈/ < 0} không có phần tử nào cả. Ta nói nó là tập hợp rỗng và kí hệu bởi ∅. lOMoARcPSD| 36667950
Giả sử , là 2 tập hợp con của tập hợp vũ trụ , ta nói là tập hợp con của (hay ược
bao hàm trong hay bao hàm ) nếu: ∀ ∈ ,(∈) ⟺ (∈)
Sử dụng các phép nối trên mệnh ề và vị từ, ta có thể ịnh nghĩa các phép toán hợp
(∪), giao (∩) và phần bù trên tập hợp.
Định nghĩa 2.1.1: Giả sử , là tập hợp con của tập hợp vũ trụ . Khi ấy ̅ = \ = {∈/ ∉}
̅ ược gọi là phần bù của (trong ). Định lý 2.1.1: ,
, là các tập con tùy ý của , ta có: i. Tính giao hoán: ∪ = ∪ ∩ = ∩ ii. Tính kết hợp: ∪ (∪) = (∪) ∪ ∩ (∩) = (∩) ∩ iii. Luật De Morgan: ∪ = ̅̅ ∩∪ ∩ = iv. Tính phân bố: ∪ (∩) = (∪) ∩ (∪) ∩ (∪) = (∩) ∪ (∩) v. Phần tử trung hòa: ∪ ∅ = ∩ = vi. Phần bù: ∪̅ == ∅ ∩ vii. Tính thống trị: ∪ = ∩ ∅ = ∅
Chứng minh: các tính chất trên suy từ ịnh nghĩa và các qui luật logic (Định lý 1.2.2) mà ta
có thể mở rộng dễ dàng cho các vị từ. pcm
Do tính kết hợp ta có thể dùng ∪ ∪ ể chỉ ∪ (∪) hay (∪) ∪ . Cũng thế, cho trước tập
hợp ∪ ∪ …∪ không phụ thuộc vào thứ tự ặt dấu ngoặc. Ta cũng viết lOMoARcPSD| 36667950 = ∪ ∪ …∪ Tương tự = ∪ ∪ …∪ §2 ÁNH XẠ Định nghĩa 2.2.1: i.
Một ánh xạ từ tập hợp vào tập hợp là phép tương ứng liên kết với mỗi phần tử
của một phần tử duy nhất của mà ta kí hiệu là ( ) và gọi là ảnh của bởi . Ta viết: : ⟶ ⟼ ( ) ii.
Hai ánh xạ , từ vào ược nói là bằng nhau nếu: ∀ ∈ , ( ) = ( ) Định nghĩa 2.2.2: i.
Nếu là một tập hợp con của thì ảnh của bởi là tập hợp: ( ) = { / ∃ ∈ , = ( )} Ta cũng viết: ( ) = { ( )/ ∈} ii.
Nếu là một tập hợp con của thì ảnh ngược (tạo ảnh) của là tập hợp ( ) = {∈/ ( ) ∈ } Chú ý: 1. Nếu thì ta viết ({ }) = ( ). 2. Nếu
( ) = ∅ thì không nằm trong ảnh ( ) của . 3. Nếu
( ) = { }, thì là phần tử duy nhất có ảnh là .
Định nghĩa 2.2.3: Gọi là 1 ánh xạ từ tập hợp vào tập hợp . Khi ấy ta nói
i. là toàn ánh nếu ( ) = ii. là ơn ánh nếu hai phần tử khác nhau bất kỳ của có ảnh khác nhau: ∀ , ∈ , ≠ ′ ⟹ ( ) ≠ ( ) iii.
là song ánh nếu nó ồng thời là ơn ánh và toàn ánh.
Chú ý: nếu là song ánh từ lên , ta viết: :⟷
Khi ấy với ∈ tùy ý, có phần tử duy nhất ∈ sao cho ( lOMoARcPSD| 36667950
ứng ⟼ là 1 ánh xạ từ vào mà ta kí hiệu là −1: ) = . Như thế tương ⟶ : ⟼ ( ) = với ( ) = Ta có: ( ) ∀ ∈ ∀ ∈ ( ) (2.2.1) (2.2.2) Ví dụ:
: ⟶ sao cho ( ) = với ∈ tùy ý là ơn ánh nhưng không phải là toàn ánh vì chẳng hạn không
là ảnh của phần tử nào của .
Giả sử , là hai số thực sao cho ≠ 0. Khi ấy f(x)=ax+b và xác ịnh một song ánh giữa và . Ánh xạ ngược của nó là : ⟶ ⟼ −
Định nghĩa 2.2.4: Cho hai ánh xạ : ⟶ và : ⟶ lOMoARcPSD| 36667950
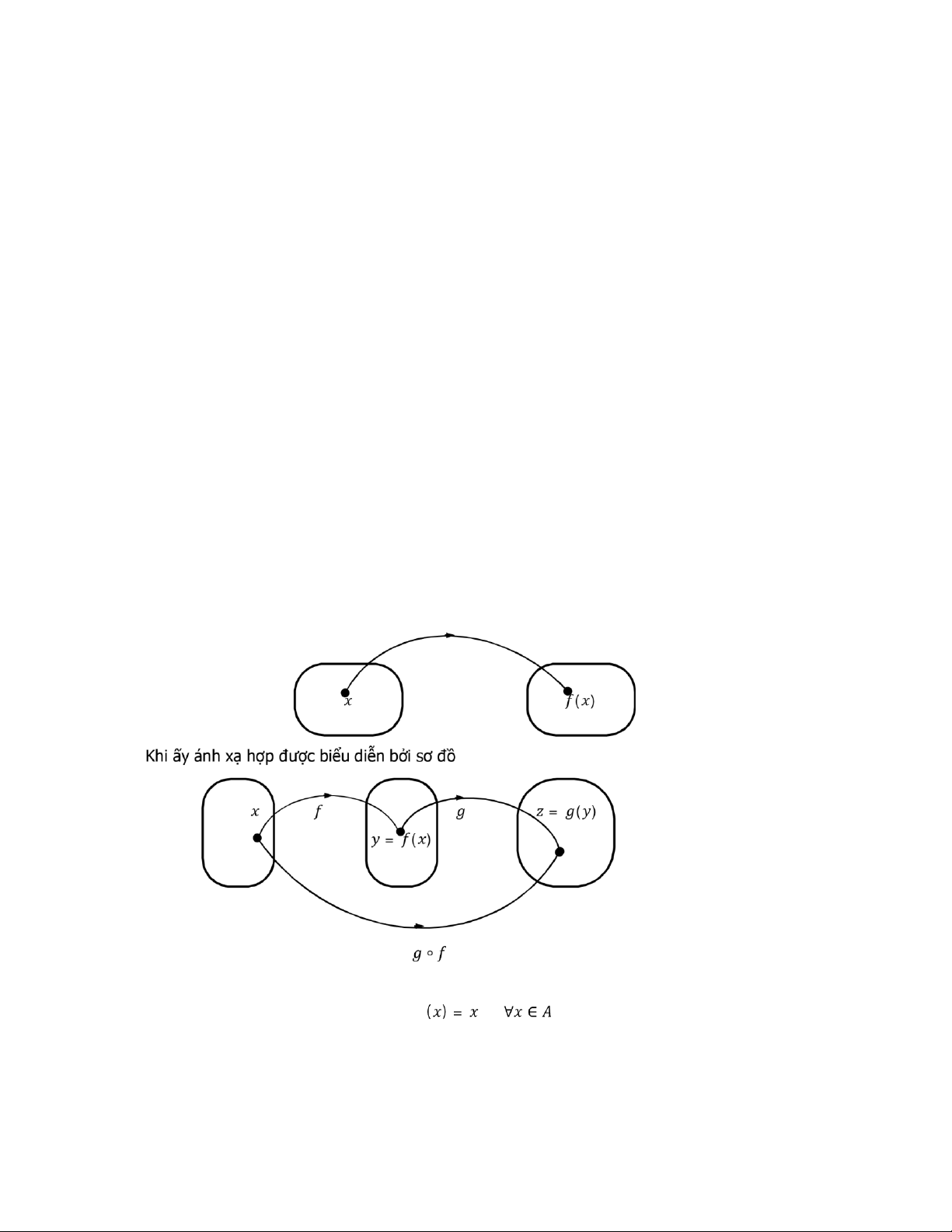
Ánh xạ hợp ℎ là ánh xạ từ vào xác ịnh bởi: ℎ ∶ ⟶ ⟼ ℎ( ) = ( ) Ta viết: ℎ = ∘: ⟶ ⟶ ⟼ ( ) ⟼ ℎ( ) = ( ) Chú ý:
Ta thường biểu diễn một ánh xạ bởi sơ ồ Ký hiệu là ánh xạ ⟶ sao cho
Ta nói là ánh xạ ồng nhất của . tương tự gọi là ánh xạ ồng nhất của . Khi ấy (2.2.1) và (2.2.2) trở thành ∘ = và ∘ = lOMoARcPSD| 36667950
Định lý 2.2.1: Giả sử là một ánh xạ từ vào , và _2 là hai tập con tùy ý của , và
là hai tập con tùy ý của . Ta có: i. ( ∪ ) = ( ) ∪ ( ) ii. ( ∩ ) ⊂ ( ) ∩ ( )
iii. ( ∪ ) = ( ) ∪ ( ) iv. ( ∩ ) = ( ) ∩ ( )
Chứng minh: ta chỉ chứng minh i), các phần còn lại ược lý luận tương tự. Ta có: ∈( ∪ ) ⟺ ∃ ∈ ∪ , = ( ) ⟺ ∈( ) ∨ ∈( ) ⟺ ∈ ( ) ∪ ( )
Chú ý: bao hàm trong ii) có thể là ngặt trong ví dụ sau cho thấy. Xét : ⟶ xác ịnh bởi: ( ) = | |,
Lấy = , = . Ta có ∩ = ∅ nên ( ∩ ) = (∅) = ∅. Trong khi ó ( ) = ( ) = nên ( ) ∩ ( ) ≠ ∅.
§3 PHÉP ĐẾM
Trước hết ta nhận xét rằng phép ếm các phần tử của một tập hợp là một thủ tục gồm có nhiều bước:
Bước 0: nếu = ∅ ta nói số phần tử của bằng 0. Nếu không (≠ ∅) ta qua Bước 1
Bước 1: chọn tùy ý một phần tử ∈ rồi gán tương ứng với phần tử 1 ∈ . Nếu = { } ta nói
là một phần tử. Nếu không ta qua Bước 2
Bước 2: do ≠ { }, tồn tại một phần tử ∈ và ≠. Ta gán b tương ứng với phần tử 2 ∈ .
Nói cách khác ta có một song ánh { , } ⟷ {1,2}. Nếu = { , } ta nói có hai phần tử. Nếu không, ta qua Bước 3.
Cứ tiếp tục thủ tục như trên. Hai trường hợp có thể xảy ra
Trường hợp 1: thủ tục dừng ở một Bước nào ó, nghĩa là tồn tại một song ánh
giữa và {1,2,…, } ⊂ .ta nói rằng có phần tử.
Trường hợp 2: thủ tục không bao giờ dừng. Ta nói có vô số phần tử hay là một
tập hợp vô hạn. Từ nhận xét trên ta có Định nghĩa 2.3.1: i.
Một tập hợp ược nói là hữu hạn và có phần tử nếu tồn tại một song ánh giữa
và tập hợp con {1,2,…, } của . Ta viết | | = . ii.
Nếu không hữu hạn, ta nói vô hạn Chú ý:
1. Do nhận xét trên, phép toán chỉ ra cho ta một thuật toán cụ thể ể xây dựng một
song ánh giữa và {1,2,…, } nếu hữu hạn, trong khi Định nghĩa 2.3.1 chỉ òi hỏi tồn tại một song ánh như vậy.
2. Hai tập hợp hữu hạn , có cùng số phần tử sẽ tương ứng 1 - 1 với nhau, nghĩa là tồn
tại một song ánh ⟷. Ta cũng nói và có cùng lực lượng. Tổng quát hơn ta có Định nghĩa 2.3.2: lOMoAR cPSD| 36667950 i.
Một tập hợp ược nói là có lực lượng bé hơn lực lượng của nếu tồn tại một ơn ánh từ vào . ii.
Hai tập hợp và ược nói là ồng lực lượng nếu có một song ánh ⟷
Chú ý: Giả sử tồn tại một ơn ánh từ vào . Đặt = ( ) và là phần bù của ̅ trong . Chọn một
phần tử ∈ tùy ý. Ta sẽ ịnh nghĩa một ánh xạ : ⟶ như sau:
Nếu ∈ thì tồn tại duy nhất ∈ sao cho = ( ). Ta ặt ( ) = Nếu ∈̅, ta ặt ( ) =
Khi ấy rõ ràng là một ánh xạ từ vào sao cho ( ) = . Suy ra là toàn ánh.
Ngược lại giả sử tồn tại một toàn ánh : ⟶. Khi ấy với ∈ tùy ý, ( ) là một tập con khác
∅ nên ta có thể chọn một phần tử nhất ịnh ∈ ( ). Đặt ( ) = , ta sẽ ược một ánh xạ từ vào .
Do cách xây dựng với ≠’ thì ( ) ∩ ( ) = ∅ nên ( ) = ( ), nghĩa là là ơn ánh. Ở ây ta sử dụng khái
niệm chọn ∈ ( ) một cách trực quan. Theo lý thuyết tập hợp tiên ề thì việc chọn như vậy
không hiển nhiên mà ược dựa trên Tiên ề chọn. Đương nhiên ối với các tập hợp hữu hạn
Tiên ề chọn là không cần thiết. Tóm lại ta ã chứng minh ược.
Mệnh ề 2.3.1: lực lượng của nhỏ hơn lực lượng của khi và chỉ khi tồn tại một tồn ánh từ lên .
Một vấn ề thứ hai là nếu lực lượng của nhỏ hơn lực lượng của và lực lượng của nhỏ
hơn lực lượng của thì liệu và có ồng lực lượng không. Khẳng ịnh này ược chứng minh
trong trường hợp tổng quát, nhưng chứng minh này ra khỏi khuôn khổ của giáo trình Toán Rời rạc.
Tuy nhiên nếu A và B hữu hạn ta có
Định lý 2.3.2: Giả sử và là hai tập hợp hữu hạn. Nếu tồn tại một ơn ánh từ vào và một
ơn ánh từ vào thì và có cùng số phần tử. Hơn nữa mọi ơn ánh (tương ứng với toàn ánh)
từ vào (tương ứng lên) là một song ánh.
Chứng minh: Gọi là một ơn ánh tùy ý từ vào Đặt =
( ) và là phần bù của trong thì Mệnh ề 2.3.3 dưới ây cho: | | = | | + | ̅|
Do f rõ ràng xác ịnh một song ánh giữa và nên ta có | | = | | + | ̅| ≥ | |
Tương tự nếu tồn tại một ơn ánh từ vào ta sẽ có | | ≥ | | Suy ra | | = | | Đặc biệt | ̅| = 0 nghĩa là =
( ) và do ó f là một song ánh giữa và .
Giả sử g là một toàn ánh từ lên . Trên ây ta dang xây dựng một ơn ánh từ vào sao
cho ( ) ∈ ( ) với mọi ∈. Theo chứng minh trên là song ánh nên rõ ràng cũng là song ánh.
Mệnh ề 2.3.3 (Nguyên lý cộng):
Giả sử là một tập hợp con của tập hợp hữu hạn . Gọi là phần bù của trong . Khi ấy ta có: lOMoARcPSD| 36667950 | | = | | + | |
Chứng minh: Gọi , là số phần tử của và tương ứng. Khi ấy tồn tại một song ánh từ lên
{1,2,…, } và một song ánh từ lên {1,2,…, }. Ta ịnh nghĩa ánh xạ ℎ từ vào {1,2,…, + } như sau:
nếu ∈ ta ặt ℎ( ) = ( )
nếu ∈ ta ặt ℎ( ) = ( ) +
Rõ ràng ℎ là một song ánh nên | | = + pcm
Ví dụ: ể chuẩn bị vào giai oạn 2, có 150 sinh viên chương trình 1 ã ghi tên học môn Toán
Rời rạc và 120 sinh viên ghi tên học Vi tích phân 3 ở học kỳ này. Hỏi có bao nhiêu sinh viên
ghi tên học một trong hai môn biết rằng không có sinh viên nào học cả hai môn.
Gọi là tập hợp các sinh viên ghi tên học môn Toán rời rạc và là tập hợp sinh viên
ghi tên học Vi tích phân 3. Khi ấy tập hợp các sinh viên ghi tên học một trong hai môn là ∪
và chính là phần bù của trong ∪ nên ta có
|∪| = | | + | | = 150 + 120 = 270
Qua ví dụ trên, ta thấy quá trình ếm các sinh viên học một trong hai môn có thể ược
thực hiện bằng hai cách: ếm các sinh viên học Toán rời rạc và ếm các sinh viên học Vi tích
phân 3. Hai cách này là loại trừ lẫn nhau theo nghĩa chúng không thể ồng thời xảy ra. Khi
ấy ta cũng có thể phát biểu lại Mệnh ề 2.3.3 dưới dạng:
Nguyên lý cộng: Nếu một quá trình có thể ược thực hiện bằng một trong hai cách loại trừ
lẫn nhau: cách thứ nhất cho kết quả và cách thứ hai cho kết quả. Khi ấy việc thực hiện
quá trình cho + kết quả. Chú ý:
1. Trong ví dụ trên nếu có một số sinh viên ghi tên học cả hai môn, chẳng hạn như 50
thì tập hợp ∩ ≠ ∅ và có 50 phần tử. Trong trường hợp này | | + | | không phải là số
phần tử của |∪| vì |∩| ược tính hai lần trong | | và | |. Do ó ta có dạng mở rộng của nguyên lý cộng là: |∪| = | | + | | − |∩| (2.3.1) = 150 + 120 − 50 = 220
2. Mệnh ề 2.3.3 cũng có thể ược mở rộng theo hướng có nhiều hơn 2 tập hợp. Giả sử
có n tập hợp: , ,…, .Ta nói các tập hợp này ôi một rời nhau nếu ∩ = ∅ nếu ≠. Ta có
Mệnh ề 2.3.4 (Nguyên lý cộng mở rộng): nếu tập hợp hữu hạn có thể viết như là hợp các
tập hợp , ,…, ôi một rời nhau thì | | = | | + | | + ⋯ + | |
Chứng minh: sử dụng Mệnh ề 2.3.3 và Nguyên lý quy nạp trên pcm
Ngoài nguyên lý cộng, một công cụ ếm hữu hiệu là:
Nguyên lý nhân: Nếu một quá trình có thể thực hiện theo hai oạn liên tiếp ộc lập với nhau
sao cho có cách khác nhau ể thực hiện giai oạn 1 và với mỗi cách lựa chọn trong giai oạn
1 ều có cách khác nhau ể thực hiên giai oạn 2. Khi ấy có cách khác nhau ể thực hiên toàn bộ quá trình. lOMoAR cPSD| 36667950
Chú ý: nói rằng hai giai oạn ược thực hiện ộc lập ược thực hiện ( , ) và ( , ) sẽ cho hai kết
quả khác nhau nếu một trong hai trường hợp sau xảy ra:
hai cách thực hiên giai oạn 1 khác nhau ≠ =
và hai cách thực hiện giai oạn 2 khác nhau ≠
Ví dụ: ể chuẩn bị mở một văn phòng ại diện ở nước ngoài, Giám ốc của Công ty X cần
nghe lời cố vấn về pháp luật từ một luật sư chọn trong số 5 luật sư và cố vấn về ịa ốc từ
một chuyên viên ịa ốc chọn trong số 3 chuyên viên ịa ốc. Do ó theo Nguyên lý nhân có tất
cả 5x3=15 phương án ể Giám ốc Công ty X tiếp xúc với hai chuyên viên trong hai lĩnh vực trên.
Trong ví dụ trên, gọi là tập hợp các luật sư và là tập hợp các chuyên viên ịa ốc cần
tham khảo. Khi ấy một phương án tham khảo cố vấn là một cặp có thứ tự ( , ) với ∈,∈. Tập
hợp các phương án tham khảo cố vấn chính là tích Descartes × theo ịnh nghĩa dưới ây.
Định nghĩa 2.3.3: Tích Descartes của 2 tập hợp , ký hiệu bởi × cũng là một tập hợp hữu hạn vả ta có: | × | = | | | |
Chứng minh: Quá trình ếm các phần tử của × ược thực hiên theo hai giai oạn: có | |cách
khác nhau ể chọn 1 phần tử tùy ý của với mỗi cách chọn phần tử ∈, có | | cách chọn một
phần tử tùy ý ∈ ể tạo thành các cặp khác nhau ( , ). Do ó theo nguyên lý nhân có | | | |
cách chọn các cặp ( , ) khác nhau. Nói cách khác | × | = | || |
Để xây dựng một song ánh cụ thể từ × lên {1,2,…, }, trong ó = | |, = | | ta làm như sau: Xét các song ánh: : ⟷ {1,2,…, } và : ⟷ {1,2,…, }
Ta ịnh nghĩa ánh xạ ℎ: × ⟶ {1,2,…, } như sau: ℎ( , ) = ( ( ) − 1) × + ( ) Giả sử ℎ( , ) = ℎ( ,′) Khi ấy
( ( ) − 1) + ( ) = ( ( ) − 1) + (′) (2.3.2) ta có thể giả sử (′) ≤ ( ). Do (2.3.2) ta có: ( ) − ( ) = (′) − ( )
Nhưng 0 ≤ ( ) − ( ) < và (′) − ( ) ≥ nếu (′) − ( ) > 0 Suy ra ( ) = ( ) và (′) − ( ) Do ó ( , ) = ( ,′) vì và là song ánh lOMoARcPSD| 36667950
Sau cùng giả sử là một số nguyên bất kỳ sao cho 1 ≤ ≤
. Gọi là một số nguyên tự nhiên lớn nhất sao cho < . Khi ấy
< ≤( + 1) nên 1 ≤ = − ≤ và 0 ≤ ≤ = Đặt = ( ) và = ( + 1) Rõ ràng ℎ( , ) = ( ( + 1) − 1) + ( ) = + =
Tóm lại ℎ là một song ánh pcm Chú ý: và
cho phép viết và dưới dạng = { , ,…, } và = { , ,…, }
Ta nói các phần tử của (tương ứng ) ã ược ánh chỉ số bởi (tương ứng ). Khi
ấy ánh xạ ℎ có thể viết: ℎ , = (− 1) +
Nói cách khác ta ã “ếm” các phần tử của ×
theo mảng ặt kế tiếp nhau: {( , ),( , ),…,( , )}, {( , ),( , ),…,( , )} …, {( , ),( , ),…,( , )}
Gọi các mảng này lần lượt là , ,…, thì chúng ều tương ứng 1 – 1 với nên có cùng
số phần tử là . Hơn nữa các tập hợp này ôi một rời nhau nên ảnh của ℎ có × phần tử và do ó ℎ là song ánh.
Nguyên lý nhân có thể ược mở rộng cho quá trình nhiều hơn hai giai oạn. Tương tự
Định nghĩa 2.3.3 và Định nghĩa 2.3.5 có thể ược mở rộng cho tích Descartes của nhiều hơn hai tập hợp.
Định nghĩa 2.3.4: có tập hợp không rỗng , ,…,
một bộ phần tử là một họ phần tử có dạng ( , ,…, ), với ∈ , ∈ ,…, ∈ hai bộ ( , ,…, ),( , ,…, )
ược nói là bằng nhau nếu = , = ,…, = tập hợp tất cả các bộ n phần tử ược gọi là tích
Descartes của , ,…, và ký hiệu bởi × × …× × × …× = {( , ,…, )/ ∈ , ∈ ,…, ∈ }
Chú ý: ta cũng ký hiêu tích Descartes bởi Định lý 2.3.6:
nếu A1,A2,…,An hữu hạn thì cũng hữu hạn và ta có lOMoARcPSD| 36667950 = | || | …| | = | |
Chứng minh: dùng Định lý 2.3.5 và nguyên lý quy nạp pcm
Ví dụ: sinh viên Giai oạn 1 thuộc Chương trình 1 của Trường Đại học Khoa học Tự nhiên
cử ra một Ban Đại diện gồm môt sinh viên Toán – Tin, một sinh viên Công nghệ Thông tin,
một sinh viên Vật lý, một sinh viên Hóa học. Hỏi có bao nhiêu cách chọn ra ban Đại diện
biết rằng có 300 sinh viên Toán – Tin, 400 sinh viên Công nghệ Thông tin, 200 sinh viên
Vật lý và 300 sinh viên Hóa? Gọi
lần lượt là tập hợp các sinh viên Giai oạn 1 của các ngành Toán – Tin, 1, 2, 3, 4
Công nghệ thông tin, Lý, Hóa. Khi ấy một Ban Đại diện chính là một bộ 4: ( , , , ), ∈ , ∈ , ∈ , ∈
Do ó theo Định lý 2.3.6 số cách chọn Ban Đại diện là: = | | = 300 × 400 × 200 × 300 = = 7.200.000.000
§4 GIẢI TÍCH TỔ HỢP
Cho trước hai tập hợp và , tập hợp tất cả các ánh xạ từ vào ược ký hiệu bởi . Giả sử | | = , ta có = { , ,…, }
Rõ ràng một ánh xạ từ vào ược xác ịnh hoàn toàn bằng cách chọn ra phần tử = ( ), = ( ),…, = ( )
Nói cách khác ược xác ịnh bởi bộ : ( ( ), ( ),…,
Như vậy ta ược một ánh xạ: : ⟶ với ( ) = ( ( ), ( ),…, ( )) ∈ (2.4.1)
Ngược lại cho trước ( , ,…, ) ∈
thì ta ịnh nghĩa ược một ánh xạ duy nhất ∈ bởi: ( ) = , ( ) = ,…, ( ) =
Như thế ta ã chứng minh:
Mệnh ề 2.4.1: Giả sử | | = với = { , ,…, } thì (2.4.1) xác ịnh một song ánh giữa và . Đặc biệt
nếu hữu hạn thì cũng hữu hạn và ta có: | | = | || |
Chú ý: trong phép tương ứng (2.4.1), là một ơn ánh khi và chỉ khi các phần tử
( ), ( ),…, ( ) là ôi một khác nhau. Từ ó ta có một quá trình bước ể ếm các ơn ánh từ vào .
Bước 1: chọn tùy ý một phần tử ∈ . Ở bước này có cách chọn lOMoAR cPSD| 36667950
Bước 2: chọn tùy ý một phần tử ∈ khác với nghĩa là một phần tử ∈ \ { }. Ở ây \ {
} chỉ phần bù của { } trong . Ta có − 1 cách chọn
.............................................................................................................................
Bước : chọn tùy ý một phần tử ∈ \ { , ,…, }. Do − (− 1) = − + 1, nên có − + 1 cách chọn .
Chú ý rằng ể có thể tiến hành ến Bước thứ ta cần có − + 1 ≥ 1, hay ≥. Do ó áp dụng nguyên lý nhân ta ược
Mệnh ề 2.4.2: Giả sử ≤. Khi ấy số ơn ánh từ vào là: (− 1) …(− + 1) Nếu | | = | | = thì ta có
Hệ quả 1: số song ánh từ lên là : (− 1) …1 = !
Chứng minh: nếu | | = | | thì mọi ơn ánh từ | | vào | | cũng là một song ánh.
Trong trường hợp = thì một song ánh từ lên chính nó còn ược gọi là một phép hoán
vị của . Do ó Hệ quả 1 có thể ược phát biểu lại: lOMoARcPSD| 36667950
Hệ quả 2: số các phép hoán vị của một tập hợp có phần tử là !
Định nghĩa 2.4.1: Đặt = {1,2,…, } i.
Một chỉnh hợp của phần tử chọn là một phép chọn ra phần tử phân biệt trong theo một thứ tự nào ó ii.
Một tổ hợp của phần tử chọn là một phép chọn ra phần tử phân biệt trong không kể thứ tự. Định lý 2.4.1:
i. Số các chỉnh hợp của phần tử chọn là: = − ( 1) …(− + 1)
ii. Số các chỉnh hợp của phần tử chọn là: ( )…( ) = ! Chứng minh:
Với = {1,2,…, } thì một chỉnh hợp của phần tử chọn không gì khác hơn một bộ ( , ,…, ) ∈ ôi
một khác nhau. Do ó số chỉnh hợp ược cho bởi Mệnh ề 2.4.2.
Ta sẽ tính số tổ hợp bằng cách ếm lại số chỉnh hợp theo một quá trình hai bước:
Bước 1: chọn tùy ý một tổ hợp của phần tử chọn , nói cách khác chọn ra một tập hợp
con ’ có m phần tử của . Số cách chọn khác nhau chính là số tổ hợp
Bước 2: với một tập hợp con ’, ta có thể chọn ra m phần tử phân biệt của ’ theo
một thứ tự nhất ịnh: ( , ,…, ). Số cách chọn chính là số phép hoán vị của ’ nên bằng !
Bằng hai bước trên ta ã ếm ược tất cả các chỉnh hợp của phần tử chọn nên: = × ! Suy ra = pcm
Chú ý: Ta thường ký hiệu số tổ hợp bởi và gọi là hệ số nhị thức . Hệ số nhị thức có thể ặt dưới dạng ối xứng: = = = ! (−)!
Dưới dạng trên ta thấy ngay: = −
Định lý 2.4.4: với ≤ ta có + 1 = + − 1 (2.4.2) lOMoARcPSD| 36667950
Chứng minh: Ta sẽ chọn ra các tổ hợp của + 1 phần tử chọn bằng một trong hai cách loại trừ lẫn nhau:
Cách 1: chọn ra một tập hợp con ’ có m phần tử phân biệt trong {1,2,…, + 1}
không chứa + 1. Rõ ràng ’
cũng là một tập hợp con m phần tử của {1,2,…, } nên có cách chọn. GS. Nguyễn Hữu Anh 46
Cách 2: chọn ra một tập hợp con ’’ có m phần tử phân biệt trong {1,2,…, + 1} chứa + 1. Rõ ràng ’’\ {
+ 1} là một tập hợp con − 1 phần tử phân biệt của {1,2,…, } nên có − 1 cách chọn.
Do ó theo nguyên lý cộng, số tổ hợp của + 1 phần tử chọn thỏa (2.4.2) pcm
Để hiểu rõ tại sao số tổ hợp còn ược gọi là hệ số nhị thức, ta hãy chứng minh
công thức dưới ây gọi là Công thức nhị thức Newton Định lý 2.4.5: , là hai biến thực ta có ( + ) = + + ⋯ + 1 (2.4.3) =
Chứng minh: ta hãy khai triển ( + ) = ( + )( + ) …( + ) thành tổng các số hạng có dạng … trong
ó = hay = ,1 ≤ ≤ . Với 0 ≤ ≤ ta gộp tất cả các số hạng trong ó có úng thừa số bằng . Các
số hạng này ều có dạng . Hơn nữa số các số hạng như vậy chính là số cách chọn phần tử
phân biệt của {1,2,…, }: trong ó là số tổ hợp nên (2.4.3) ược chứng minh. pcm Hệ quả: Ta có i. 2 = 1 + + ⋯ + + ⋯ + (2.4.4) 1 ii. 0 = 1 − + ⋯ + (−1) + ⋯ + (−1) 1
Chú ý: Theo nguyên lý cộng, vế phải của (2.4.4) chính là số các tập hợp con của {1,2,…, }
nên ta ếm ược số các tập hợp con của {1,2,…, } chính là 2 . Thật ra ta có thể ếm gián tiếp
số các tập hợp con của một tập hợp có phần tử như sau:
Gọi là một tập hợp con bất kỳ của , ta sẽ ịnh nghĩa hàm ặc trưng của bởi: lOMoARcPSD| 36667950 Rõ ràng
∈ {0,1} . Ngược lại, cho trước ∈ {0,1} . Đặt = (1). Khi ấy rõ ràng
= . Bằng cách này ta ược một song ánh giữa tập hợp ( ) gồm tất cả các tập hợp con của
và {0,1} . Suy ra | ( )| = |{0,1}|| | = 2
Hai tập hợp ( ) và {0,1}^ (ký hiệu là 2 ) là các ại số Bool sẽ ược xét trong chương 4.
Bây giờ ta hãy mở rộng khái niệm tổ hợp trong ó có phép lặp lại. Trước hết ta hãy
xét một ví dụ: một học sinh ến cửa hàng mua 4 cây bút chọn trong 3 màu khác nhau là
xanh, ỏ và vàng. Có bao nhiêu cách khác nhau ể chọn mua hàng?
Trước hết ta hãy liệt kê các trường hợp khác nhau:
4 bút cùng màu: có 3 trường hợp
3 bút cùng màu và bút thứ tư chọn tùy ý trong hai màu còn lại: có 3x2=6
trường hợp (Nguyên lý nhân!)
2 bút cùng màu và 2 bút kia chọn trong 2 màu còn lại: 3 trường hợp 2 cặp
bút cùng màu: có 3 = 3 trường hợp 2
Như vậy tổng cộng có 15 cách mua hàng khác nhau
Tuy nhiên nếu liệt kê như vậy rất khó mở rộng cho trường hợp có nhiều bút và nhiều
màu ể chọn. Thay vì như vậy, ta sẽ biểu diễn mỗi trường hợp bởi 4 dấu “+” và 2 dấu “−” ặt
liên tiếp trên một ường thẳng: số dấu + bên trái dấu – ầu tiên chỉ số bút xanh, số dấu +
nằm giữa 2 dấu – chỉ số bút ỏ và số dấu + nằm bên phải dấu – cuối cùng chỉ số bút màu
vàng. Như vậy trường hợp mua 4 bút xanh ược biểu diễn bởi + + + + − − Cũng thế trường
hợp mua 1 bút xanh và 3 bút vàng ược biểu diễn bởi + − − + + +
Như thế mỗi trường hợp tương ứng với việc lựa chọn vị trí của 2 dấu – trong số 6 ký
hiệu, nói cách khác ứng với 1 tập hợp con 2 phần tử của tập hợp {1,2,…,6} Từ ó suy ra số
cách mua hàng khác nhau chính là 6 == 15 2
Bằng cách này ta có thể tổng quát hóa việc chọn ra vật trong số loại vật khác nhau
trong ó mỗi loại vật có thể ược chọn lại nhiều lần. như trên mỗi trường hợp lựa chọn có thể
ược biểu diễn bằng cách chèn (− 1) dấu – vào trong số dấu + ể chia oạn thẳng thành oạn
tương ứng với số vật mỗi loại. Do ó số cách lựa chọn khác nhau mà ta gọi là số tổ hợp có
lặp lại của n vật chọn chính là: + − 1 = + − 1 − 1 Áp dụng:
Có vật ồng nhất nhau, hỏi bao nhiêu cách chia chúng vào hộp phân biệt nhau?
Ở ây mỗi cách chia cũng chính là một tổ hợp của vật chọn nên số cách chia khác nhau chính là + − 1 Xét phương trình: + + ⋯ + = (2.4.5) lOMoARcPSD| 36667950
trong ó và là các số nguyên không âm cho trước và , ,…, là các ẩn lấy giá trị nguyên không
âm. Ta hãy tìm xem phương trình trên có bao nhiêu lời giải với một cách chia
vật ồng nhất nhau vào n hộp phân biệt: chính là số vật chứa trong hộp thứ .
Do ó số lời giải chính là số tổ hợp có lặp của vật chọn : + − 1
§5 NGUYÊN LÝ CHUỒNG BỒ CÂU
Trong Mệnh ề 2.4.1, ta ã giả sử | | = ≤ | | = ể có thể chọn ra ược một họ phần tử phân
biệt có thứ tự của ; nói cách khác ể chọn ra ược một ơn ánh từ vào
. Trong trường hợp > thì không tồn tại ơn ánh từ vào theo nguyên lý chuồng Bồ câu sau ây
Nguyên lý chuồng Bồ câu: nếu chuồng bồ câu có ít cửa (pigeon hole) hơn số bồ câu thì ít
nhất hai chim bồ câu ở chung trong một cửa. Ví dụ:
1. Trong ví dụ trên, là số bồ câu và là số cửa. Một ánh xạ : ⟶ chính là một cách xếp
chim bồ câu vào các cửa. Nói rằng có 2 chim bồ câu ở chung một cửa có nghĩa là có
2 phần tử phân biệt của có chung ảnh nên không ơn ánh.
2. Trong một nhóm có 367 người sẽ có ít nhất hai người có cùng ngày tháng sinh. Ở ây
số các ngày tháng sinh khác nhau (366 ngày, kể cả ngày 29 tháng 02) chính là số
cửa của chuồng bồ câu.
3. Xét một cơ sở dữ liệu có 500.000 bản tin (record). Hỏi có thể sử dụng một vùng
(thuộc tính) với nhiều nhất 4 ký tự là các mẫu tự làm khóa chính hay không? Ở ây
một vùng ược nói là một khóa chính nếu giá trị của nó xác ịnh bản tin một cách duy
nhất. Để giải áp bài toán trên, ta sẽ sử dụng số các từ ghồm nhiều nhất 4 mẫu tự
làm số cửa của chuồng bồ câu. Số cửa này ược cho bởi Nguyên lý cộng và Nguyên lý nhân: 26 + 26 + 26 + 26 = 475.254
Vì có ến 500.000 bồ câu nên có ít nhất 2 bản tin có cùng giá trị của thuộc tính: không
thể dùng thuộc tính này làm khóa chính ược!
4. Ta hãy dùng Nguyên lý chuồng Bồ câu ể chứng minh rằng mọi tập hợp con có ít nhất 6 phần tử của
= {1,2,…,9} sẽ có hai trong số các phần tử có tổng bằng 10.
Thật vậy, ở ây các cửa của chuồng bồ câu ược chọn là các tập hợp con {1,9},
{2,3}, {3,7}, {4,6}, {5}. Do ó có 5 cửa trong khi số chim bồ câu ≥ 6 nên có ít nhất hai
phần tử phân biệt của thuộc về cùng một tập hợp con trên, hay chính xác hơn thuộc về
cùng một trong bốn tập hợp con ầu tiên. Đó là những cặp có tổng bằng 10.
Chú ý: nghệ thuật ếm khi sử dụng Nguyên lý chuồng Bồ câu là xác ịnh úng âu là số bồ câu
và âu là số cửa như ví dụ sau cho thấy.
Giả sử là một tập hợp con có 6 phần tử của {1,2,…,14}. Hãy chứng minh rằng trong
số các tập hợp con khác ∅ của , có ít nhất 2 tập hợp con mà tổng các phần tử là như nhau.
Giả sử là một tập hợp con khác rỗng bất kỳ của . Gọi là tổng của các phần tử của . Khi ấy ta có lOMoARcPSD| 36667950 1 ≤ ≤ 9 + 10 + ⋯ + 14 = 69
Nếu chọn các số từ 1 ến 69 là số cửa của chuồng bồ câu là số tập hợp con khác rỗng
của là số bồ câu thì số bồ câu là
2 − 1 = 63. Do số bồ câu ít hơn số cửa, ta không thể
áp dụng Nguyên lý chuồng bồ câu ược. Tuy nhiên nếu ta hạn chế chỉ xét các tập hợp con
có tối a năm phần tử thì 1 ≤ ≤ 10 + 11 + ⋯ + 14 = 60
Trong khi số bồ câu bây giờ là 63 − 1 = 62 (trừ 1 tập hợp con 6 phần tử). Do ó theo
Nguyên lý chuồng bồ câu sẽ có hai tập hợp con , ’ có tối a 5 phần tử của A sao cho =
BÀI TẬP CHƯƠNG 2 1. Trong các tập
hợp dưới ây, hãy chỉ ra các tập hợp bằng nhau: a) { , , } b) { , , , } c) { , , , } d) { , , , } 2.
Giả sử = {1,{1},{2}}. Hãy chỉ ra các khẳng ịnh úng trong số các khẳng ịnh dưới ây: a) 1 ∈ A b) {1} ∈ c) {1} ⊂ d) e) { f) {2} ⊂ 3.
Trong số các khẳng dịnh dưới ây, hãy chỉ ra các khẳng ịnh úng: a) ∅ ∈ ∅ b) ∅ ⊂ ∅ c) ∅ ∈ {∅} d) ∅ ⊂ {∅} 4.
Hãy liệt kê ra các phần tử của tập hợp dưới ây: a) {1 + (−1) / ∈} b) { + / ∈ {1,2,3,5,7}} c) {(1/ ( + ))/ ∈, là số lẻ và 5.
Xét các tập hợp con của : = {2 + 1/ ∈} = {2 + 3/ ∈} = {2− 3/ ∈} = {3 + 1/ ∈} = {3 + 2/ ∈} = {2− 2/ ∈}
Hãy xác ịnh các khẳng ịnh úng trong số các khẳng ịnh dưới ây: a) = b) = c) = d) = e) = f) = lOMoARcPSD| 36667950 6.
= {1,2,3,4,5,6,7}. Hãy liệt kê ra: a) Các tập hợp con của b)
Các tập hợp con khác ∅ của c)
Các tập hợp con của chứa 3 phần tử d)
Các tập hợp con của chứa 1,2 e)
Các tập hợp con của chứa 5 phần tử trong ó có 1,2 f)
Các tập hợp con của gồm một số chẵn phần tử g)
Các tập hợp con của gồm một số lẻ phần tử 7.
Trong số các tập hợp dưới ây, tập hợp nào khác ∅ ? a) {∈/ 2 + 7 = 3} b) {∈/ 3 + 5 = 9} c) {∈/ + 4 = 6} d) {∈/ + 4 = 6} e) {∈/ + 5 = 4} f) {∈/ + 3 + 3 = 0} 8.
Xét 4 tập hợp con của tập hợp vũ trụ = {1,2,3,…,10}: = {1,2,3,4,5} = {1,2,3,5,7}
Hãy xác ịnh các tậ hợp dưới ây: a) (∪) ∩ b) ∪ (∩) c) ̅ ∪ d) ∩ e) (∪) ∩ ̅ f) ∪ (∩̅) g) (∩̅) ∩ h) ∩ ∩ i) (∪) ∩ ∩ 9.
Xét các tập hợp con của
Hãy chỉ ra các khẳng ịnh úng trong số các khẳng ịnh dưới ây: a) ⊂ ⊂ b) ⊂ ⊂ c) ⊂ d) ⊂ e) ⊂ f ) ⊂ ̅
10. Với các tập hợp , , ,
, như trong bài tập 9. Hãy xác ịnh các tập hợp dưới ây: a) ∩ b) ∪ c) ∩ d) ∩ e) ̅ f) ∩
11. Xét các tập hợp con tùy ý , , , của tập hợp vũ trụ . Hãy chứng minh các khẳng ịnh dưới ây: a) Nếu ⊂ và ⊂ thì ∩ ⊂ ∩ và ∪ ⊂ ∪ b) Nếu ⊂ và ⊂ thì ∩ ⊂ và ∪ ⊂ c)
⊂ khi và chỉ khi ∩ = ∅ d) ⊂ khi và chỉ khi ̅ ∪ =
12. Trong số các khẳng ịnh dưới ây, cho biết khẳng ịnh nào úng: a) ∀ , ,∈( ),(∩ = ∩) ⟹ ( = ) b) ∀ , ,∈( ),(∪ = ∪) ⟹ ( = ) c) ∀ , ,∈(
),[(∩ = ∩) ∧ (∪ = ∪)] ⟹ ( = )
13. Cho biết khẳng ịnh nào dưới ây là úng: a) (∪) = ( ) ∪ ( ) b) (∩) = ( ) ∩ ( )
14. Xét các tập hợp con , , , của tập hợp vũ trụ , hãy cho biết qui luật nào của Lý thuyết
tập hợp (Định lý 2.1.1) ược sử dụng trong các bước ơn giản tập hợp dưới ây: lOMoAR cPSD| 36667950 Bước Qui luật
(∩) ∪ [∩ ((∩) ∪ (∩))] = (∩) ∪ [∩ (∩ (∩))] = (∩) ∪ [∩ (∩)] = (∩) ∪ (∩) = (∩) ∪ (∩) = ∩ (∪)
15. Dùng các qui luật của Lý thuyết tập hợp ể ơn giản các biểu thức dưới ây: a) ∩ (∩̅) b) (∩) ∪ ( ∩ ∩ ̅ ∩ ) ∪ ( ̅ ∩ ) c) ̅ ∪ ∪ ( ∩ ∩ ̅) d) ̅ ∪ (∩) ∪ ( ∩ ∩ ̅) ∪ ( ∩ ∩ ∩ )
16. Đối với mỗi ánh xạ dưới ây hãy xác ịnh xem nó có là ơn ánh không? Tìm ảnh của miền
xác ịnh của ánh xạ trên. a) : ⟶, ( ) = 2 + 1 b) : ⟶, ( ) = 2 + 1 c) : ⟶, ( ) = − d) : ⟶, ( ) = e) : − , ⟶, ( ) = sin f) :[0, ] ⟶ , ( ) = sin
17. Xét ánh xạ : ⟶ xác ịnh bởi ( ) = . Hãy tìm ( ) ối với mỗi tập hợp dưới ây: a) = {2,3} b) = {−3,−2,2,3} c) = (−3,3) d) = (−3,2] e) = [−7,2] f ) = (−4,−3] ∪ [5,6]
18. Với mỗi ánh xạ : ⟶ dưới ây, hãy xác ịnh xem nó có là ơn ánh hay toàn ánh không? Tìm ( ) a) ( ) = + 7 b) ( ) = 2− 3 c) ( ) = − + 5 e) ( ) = e) ( ) = + f) ( ) =
19. Các câu hỏi tương tự như trong bài tập 18 nhưng bây giờ là một ánh xạ : ⟶
20. Xét 3 ánh xạ : ⟶, : ⟶, ℎ: ⟶. Hãy chứng minh rằng (ℎ ∘ ) ∘ = ℎ ∘ (∘)
21. Xét 3 ánh xạ , ,ℎ từ vào xác ịnh bởi: ( ) = − 1, ( ) = 3 và ℎ( ) = 0 nếu chẵn 1 nếu lẻ a)
Tìm ∘, ∘, ∘ ℎ, ℎ ∘ , ∘ ∘ ℎ b)
Với là số nguyên dương,
ược ịnh nghĩa bằng qui nạp như sau: = , = ∘,…, = ∘ Tương tự cho , ℎ . Hãy xác ịnh , , , ,ℎ ,ℎ ,ℎ
22. Cho trước hai tập hợp con cố ịnh , của . Ta ịnh nghĩa một ánh xạ lOMoARcPSD| 36667950 : ( ) ⟶ ( ) như sau:
( ) = ∩ (∪) với là tập hợp con bất kỳ của . Chứng minh rằng =
23. Với mỗi ánh xạ : ⟶ dưới ây, cho biết nó có ơn ánh, toàn ánh hoặc song ánh
không? Trong trường hợp nó là song ánh, hãy tìm ánh xạ ngược. a) = = , ( ) = + 7 b) = = , ( ) = + 2− 3 c) = [4,9], = [21,96], ( ) = + 7 d) = = , ( ) = 3− 2| | e) = , = (0,+ ∞), ( ) = f) = = , ( ) = ( + 1)
24. Đặt = {1,2,3,4}. Xét hai ánh xạ
: ⟶ và : ⟶ ược xác ịnh bởi ( ) = 2 và
(1) = 2, (2) = 3, (3) = 5, (4) = 7. Hãy tìm ∘. 25.
Xét hai ánh xạ , : ⟶ xác ịnh bởi: ( ) = + và ( ) a) Chứng minh (∘)( ) = 9 − 9 + 3,∀ ∈ . Hãy xác ịnh , . 26. rằng là một
Xét hai ánh xạ , :⟶ xác ịnh bởi: ( ) = + và ( ) = song ánh
trong ó , , , là các hằng số thực. Hãy tìm các hệ thức giữa b) Tìm ∘. 29. Xét hai ánh xạ :
27. Xét ánh xạ : ⟶ ịnh nghĩa bởi: ⟶, : ⟶ + 7 ế ≤ 0 a) Chứn g minh rằng nếu ∘ ( ) = −2 + 5 0 < < 3 ơn ánh thì ơn ánh − 1 3 ≤ = 1 − + . Giả sử a) Tìm (−10), (0), (2), (6)
+ với ∈ tùy ý, , , , ể b)
Tìm nghịch ảnh của các khoảng [−5,−1],[−2,4] 28. cho ∘ =
Xét ánh xạ : ⟶ ịnh nghĩa bởi: ( ) 2− 1 ế > 0 b)
Chứng minh rằng nếu ∘ toàn ánh thì toàn ánh c)
Chứng minh rằng nếu và là song ánh thì ∘ là song ánh. Hãy tìm . d)
Cho ví dụ ể ∘ là song ánh nhưng và khộng phải là song ánh.
30. Xét ánh xạ : ⟶ xác ịnh bởi: ( ): + (−1) a)
Chứng minh rằng và ( ) khác tính chẵn lẻ (một số chẵn và số kia lẻ). b)
Chứng minh rằng là một ơn ánh c)
Tìm . Suy ra biểu thức ơn giản của d)
Giải phương trình 365 = + (−1) , nguyên 31. Xét ánh xạ : ⟶ ịnh nghĩa bởi: ( , ) =
Chứng minh rằng là một song ánh
(Hướng dẫn: sử dụng Nguyên lý Quy nạp ể chứng minh toàn ánh)
32. Hãy ếm số các tập hợp trong mỗi câu hỏi a) - g) của bài tập 6 mà không sử dụng kết quả liệt kê. lOMoARcPSD| 36667950
33. Xét = {1,2,…,10}. Có bao nhiêu con của thỏa: a) | | = 5?
b) | | = 5 và phần tử bé nhất của là 3?
c) | | = 5 và phần tử bé nhất của bé hơn hay bằng 3? 34.
a) Có bao nhiêu tập hợp con của {1,2,…,11} chứa ít nhất một số chẵn?
b) Có bao nhiêu tập hợp con của {1,2,…,12} chứa ít nhất một số chẵn?
c) Tổng quát hóa các kết quả trong a) và b)
35. Giả sử chỉ có một phần tư số tập hợp con năm phần tử của {1,2,…, } chứa số 7. Hãy tìm .
36. Hãy sử dụng các nguyên lý ếm ể chứng minh rằng + 2 = + 2 − 1 + − 2 trong ó ≥ ≥ 2
37. Hãy trình bày một thuật toán và viết chương trình máy tính liệt kê tất cả những tập hợp
con 5 phần tử của {1,2,…,40}. 38. Giả sử ,
, là 3 tập hợp hữu hạn. Hãy chứng minh rằng: | ∪ ∪
| = | | + | | + | | − |∩| − |∩| − |∩| + | ∩ ∩ |
39. Để chọn máy tính trang bị cho phòng LAB, Khoa Toán –Tin học ã xem xét 15 nãn hiệu
máy tính khác nhau dựa theo các tính năng sau: ( ) Có CPU nhanh ( ) Có ổ ĩa cứng tốt
( ) Có màn hình với ộ phân giải cao
Gọi , , lần lượt là các tập hợp những nhãn hiệu thỏa tính năng ( ),( ) hay ( ). Giả
sử | | = | | = | | = 6,|∩| = |∩| = 1,|∩| = 2,| ∩ ∩ | = 0.
a) Có bao nhiêu nhãn hiệu thỏa úng một tính năng?
b) Có bao nhiêu nhãn hiệu không thỏa tính năng nào cả? 40.
a) Trong một lớp học có 7 sinh viên, có bao nhiêu các chia họ thành hai ội? Nếu yêu cầu
mỗi ội có ít nhất 2 sinh viên thì có bao nhiêu cách chia.
b) Trả lời các câu hỏi trong a) khi số sinh viên của lớp là một số nguyên tùy ý .
41. Gọi , ,…, là các số nguyên dương có tổng là . Có bao nhiêu cách chia sinh viên thành
nhóm với số sinh viên của các nhóm là , ,…, .
42. Hãy cho biết các khẳng ịnh dưới ây là úng hay sai
a) Nếu , là hai tập hợp vô hạn thì ∩ cũng vô hạn
b) Nếu vô hạn và ⊂ thì vô hạn
c) Nếu hữu hạn và ⊂ thì hữu hạn
d) Nếu hữu hạn và ⊂ thì vô hạn 43. Xét = {1,2,…,15} lOMoARcPSD| 36667950
a) Có bao nhiêu tập hợp con của chỉ chứa số lẻ
b) Có bao nhiêu tập hợp con của chỉ chứa úng 3 số lẻ
c) Có bao nhiêu tập hợp con 8 phần tử của chứa úng 3 số lẻ
d) Hãy trình bày một thuật toán và viết chương trình máy tính ể liệt kê tất cả các tập
hợp con 8 phần tử của chứa úng 3 số lẻ
44. Lớp thực tập Vật lý có 21 sinh viên phải thực hiện 3 thí nghiệm. Biết rằng tất cả các sinh
viên ều làm ược ít nhất một thí nghiệm , 5 sinh viên không là thí nghiệm thứ nhất, 7 sinh
viên không làm thí nghiệm thứ hai và 6 sinh viên không làm thí nghiệm thứ ba. Ngoài ra
có 9 sinh viên làm cả ba thí nghiệm. hỏi có bao nhiêu sinh viên chỉ làm một thí nghiệm?
45. Theo một mạng lưới hình chữ nhật gồm m mắt lưới theo chiều rộng và n mắt lưới theo
chiều ngang, một con kiến di chuyển từ A ến B dọc theo các cạnh của những mắt lưới
theo qui tắc sau ây: trên một cạnh ngang nó chỉ i từ trái qua phải và trên một cạnh ứng
nó chỉ i từ dưới lên trên. Tìm số các ường i khác nhau khi kiến muốn di chuyển từ A ến B.
(Hướng dẫn: chia mỗi ường i theo các bước nhỏ, trong ó mỗi bước là di chuyển theo
cạnh ngang hoặc cạnh ứng của một mắt lưới) m
46. Có 4 ngăn tiền chứa 4 loại giấy bạc: 1.000 , 2.000 , 5.000 và 10.000 . Hỏi có bao nhiêu
cách chọn 10 tờ giấy bạc từ các ngăn tiền?
47. Tìm số cách chia 10 hòn bi cho 5 ứa trẻ trong các trường hợp sau:
a) Không có hạn chế nào cả
b) Đứa trẻ lớn nhất ược ít nhất 2 hòn bi
c) Mỗi ứa trẻ ược ít nhất 1 hòn bi 48.
a) Tìm ra số cách chia r vật ồng nhất vài hộp phân biệt nếu yêu cầu thêm là không c1 hộp nào ể trống
b) Suy ra số nghiệm của phương trình (2.4.5) nếu ta giả thiết thêm các ẩn , lấy giá trị nguyên dương
49. Tìm số nguyên của phương trình + + + = 32
trong các trường hợp sau: lOMoARcPSD| 36667950 a) , ≥ 5, , ≥ 7 b) ≥ 8,1 ≤ ≤ 4 c) , , > 0,0 < ≤ 25 50.
a) Tìm hệ số của trong phép khai triển của ( + 2 + 3 + + )
b) Có bao nhiêu số hạng khác nhau trong phép khai triển trên? 51. Tính 5
và kiểm tra lại kết quả bằng các liệt kê tất cả các tổ hợp chọn 2 của {1,2,…,5} 2
52. Một Tiểu ban gồm 2 người ược chọn trong số 10 ại biểu nữ và 10 ại biểu nam. Có bao
nhiêu cách chọn? Biết rằng: a) Không có hạn chế nào cả b) Phải có 6 nam 6 nữ
c) Số nữ phải là số chẵn
d) Phải có nhiều nữ hơn nam
e) Phải có ít nhất 8 nam
53. Có bao nhiêu byte khác nhau: a) Chứa úng 2 bit 1 b) Chứa úng 4 bit 1 c) Chứa úng 6 bit 1 d) Chứa ít nhất 6 bit 1
54. Có thể chia 12 quyển sách khác nhau cho 4 ứa trẻ theo bao nhiêu cách? Biết rằng:
a) Mỗi ứa trẻ ược 3 quyển sách
b) Hai ứa lớn nhất ược 4 quyển sách mỗi ứa và hai ứa bé nhất ược 2 quyển mỗi ứa 55.
a) Cho trước 15 iểm trong mặt phẳng sao cho 3 iểm bất kỳ trong số ó không cùng nằm
trên một ường thẳng. Có bao nhiêu ường thẳng i qua hai iểm trong số ó?
b) Cho trước 25 iểm trong không gian sao cho 4 iểm bất kỳ trong số ó không cùng nằm
trong một mặt phẳng. có bao nhiêu tam giác nối 3 iểm bất kỳ trong số ó? Có bao
nhiêu mặt phẳng tạo ược từ các tam giác? Có bao nhiêu tứ diện nối 4 iểm bất kỳ trong số ó?
56. Cho trước một a giác ều n cạnh. Có bao nhiêu tam giác:
a) Tạo ược từ các ỉnh của a giác ều
b) Trong số các tam giác trong a) không có chung cạnh với a giác ều 57. Tìm hệ số của trong: a) ( + ) b) ( + 2 ) c) (2− 3 )
58. Xác ịnh các hệ số của: a) trong ( + + ) b) trong ( + + + ) c) trong (2 − − )
59. Cho trước số nguyên dương và số thực , hãy tính các tổng sau: a) + 2 + ⋯ + 2 + ⋯ + 2 0 1 b) (1 + ) − (1 + ) + (1 + ) + ⋯ + (−1) 1 2 lOMoARcPSD| 36667950 c) d)
60. Chứng minh rằng nếu có m bồ câu và n cửa thỉ ít nhất có bồ câu ở chung trong một
cửa nào ó. Trong ó chỉ số nguyên bé nhất ≥ .
61. Cần phải tung một con xúc sắc bao nhiêu lần ể có một mặt xuất hiện ít nhất: a) 2 lần b) 3 lần c) lần với ≥ 4
62. Chứng minh rằng trong 14 phần tử khác nhau tùy ý của = {1,2,…,25}, có ít nhất 2 phần tử có tổng là 26. 63. a)
Chứng minh rằng trong 11 phần tử khác nhau tùy ý của {1,2,…,100}, có ít nhất
2 phần tử , sao cho 0 < √ − < 1 b)
Hãy tổng quát hóa kết quả trên
64. Chứng minh rằng trong số 10 iểm khác nhau tùy ý bên trong 1 tam giác ều có cạnh bằng
1, có ít nhất 2 iểm mà khoảng cách bé hơn . lOMoARcPSD| 36667950 CHƯƠNG 3: QUAN HỆ §1 QUAN HỆ
Định nghĩa 3.1.1: một quan hệ giữa tập hợp và tập hợp là một tập hợp con ℛ của ×
. Nếu ( , ) ∈ ℛ, ta viết ℛ. Một quan hệ giữa và ược gọi là quan hệ trên Ví dụ: 1. = {1,2,3,4}, = {4,5}
ℛ = {(1,4),(1,5),(3,5),(4,4)} là một quan hệ giữa và . Ta thường biểu
diễn quan hệ ℛ bởi sơ ồ sau: 6 5 ℛ 4 3 2 1 0 0 1 2 3 4 5 2.
Quan hệ “=” trên một tập hợp bất kỳ: ⟺ = 3.
Quan hệ “≤” trên , hay : (ℛ) ⟺ ≤
Trên quan hệ ≤ có thể biểu diễn bởi sơ ồ: 4 3 2 1 0 -3 -2 -1 0 1 2 3 4 -1 -2 -3 4.
Gọi ℒ là tập hợp các ường thẳng trong mặt phẳng. Quan hệ song song ược ịnh nghĩa bởi: ℛ ⟺ / / 5.
Một số nguyên ược nói là chia hết cho số nguyên nếu tồn tại số nguyên
sao cho = . Khi ấy ta cũng nói là ước số của và là bội số của .
Giả sử là một số nguyên >1 và ∈ lOMoARcPSD| 36667950
Xét các bội số không âm của n: 0, ,2 ,…, ,…
Trong số này, các bội số ≤ tạo thành một tập hợp hữu hạn nên ta có thể tìm ược bội số lớn nhất: ≤ < ( + 1) Đặt = = ta có = + ớ 0 ≤ <
Ta nói rằng và là thương số và dư số trong phép chia (có dư) cho .
Chú ý rằng và tồn tại duy nhất. thật vậy,giả sử tồn tại ,′ ∈ sao cho: = + ,0 ≤ <
Ta có thể giả sử ≤. Khi ấy: + = + ′ Suy ra ( − ′) = − ≥ 0 Rõ ràng − < ≤ (− ) nếu − ′ ≥ 1
Cho trước số nguyên > 1, ta ịnh nghĩa quan hệ: ℛ ⟺ − chia hết cho
Quan hệ này ược nói là quan hệ ồng dư modulo . Nếu ℛ ta viết: ≡( )
Rõ ràng khi ấy và có cùng dư số khi chia cho Với = 7 ta có 9 ≡ 2( 7) và 3 ≡ 10( 7) nhưng 3 ≢ 6( 7).
Định nghĩa 3.1.2: cho trước các tập hợp , ,…,
. Khi ấy ánh xạ chiếu lên thành
phần thứ là ánh xạ: : × × …× ⟼ ( , ,…, ) ⟼
1. Ánh xạ chiếu rõ ràng là một toàn ánh
2. Đặc biệt các ánh xạ chiếu , từ × lên và tương ứng là các toàn ánh. Tuy nhiên nếu ℛ
là tập hợp con của × , nghĩa là một quan hệ giữa A và B thì (ℛ) và (ℛ) có thể là tập
hợp con thực sự của A và B tương ứng như các ví dụ sau cho thấy. Ví dụ: 1. = = ,ℛ = {( , )/ = | |}
Quan hệ ℛ ược biểu diễn bởi sơ ồ Ta có (ℛ) = Tuy nhiên (ℛ) = 2. = = ,ℛ = {( , ) ∈ × / = } lOMoARcPSD| 36667950 Rõ ràng (ℛ) = = trong khi
(ℛ) = [0,+ ∞) = {∈/ ≥ 0} 3. × / + ≤ 1} Khi ấy (ℛ) = (ℛ) = = mặc dù ℛ ×
Định nghĩa 3.1.3: một quan hệ trên các tập hợp × × …×
là một tập hợp con của = × × …× Chú ý:
1. Giả sử ℛ là một quan hệ trên , ,…,
. Khi ấy các phần tử của ℛ là những bộ ( , ,… )
2. Xét số nguyên 1 ≤ < < ⋯ < ≤ . Khi ấy ta cũng có thể ịnh nghĩa một ánh xạ chiếu , ,…, : × × …× ⟶ × × …× ( , ,…, ) ⟼ , ,…,
Rõ ràng , ,…, cũng là một toàn ánh.
Định nghĩa 3.1.4: nếu ℛ một quan hệ trên , ,…, thì , ,…,
(ℛ) ược gọi là quan hệ chiếu của ℛ. Chú ý: 1. Quan hệ chiếu , ,…,
(ℛ) là một quan hệ trên × × …× .
2. Trong Lý thuyết về cơ sở dữ liệu mô hình quan hệ, các tập hợp , ,…, ược gọi là các
thuộc tính. Như thế quan hệ chiếu 1, 2,…,
(ℛ) chính là quan hệ ban ầu nhưng
các thuộc tính không thuộc các tập hợp , ,…, ã ược bỏ qua như ví dụ sau cho thấy
Ví dụ: trong cơ sở dữ liệu Môn học ở Đại học Khoa học Tự nhiên, ta có các tập hợp thuộc tính sau: : các mã số môn học : các tên môn học : các Giảng viên
Quan hệ Môn học - Giảng viên ược cho bởi bảng sau: Mã Môn học Tên môn học Giảng viên lOMoARcPSD| 36667950 T001 Vi tích phân Ông Bình T011 Toán Rời rạc Ông An T012 Đại số tuyến tính Ông Minh TH001 Tin học ĐC A1 Cô Hà TH002 Tin học ĐC A2 Cô Hà Quan hệ chiếu
(Môn học-Giảng viên) là quan hệ Môn học ược cho bởi bảng sau: Mã Môn học Tên Môn học T001 Vi tích phân T011 Toán Rời rạc T012 Đại số tuyến tính TH001 Tin học ĐC A1 TH002 Tin học ĐC A2
Mặt khác quan hệ chiếu (Môn học – Giảng viên) chính là quan hệ Giảng viên:
{Ông Bình, Ông An, Ông Minh, Cô Hà}.
§2 QUAN HỆ TƯƠNG ĐƯƠNG
Định nghĩa 3.2.1: một quan hệ ℛ trên tập hợp ược nói là phản xạ nếu: ∀ ∈ ,ℛ Ví dụ:
1. Quan hệ “=” trên một tập hợp bất kỳ, quan hệ “≤” trên , , , quan hệ ống dư trên
Z là phản xạ
2. Quan hệ “// ” trên ℒ là phản xạ. Tuy nhiên quan hệ “⊥” (vuông góc) trên ℒ không
phải là quan hệ phản xạ.
Chú ý: gọi ∆ là ường chéo chính của × : ∆ = {( , )/ ∈}. Khi ấy quan hệ ℛ trên là phản xạ khi và chỉ khi ℛ ⊃ ∆ .
Định nghĩa 3.2.2: quan hệ ℛ trên ược nói là ối xứng nếu: ∀ ,∈, ℛ ⟹ ℛ Ví dụ:
1. Các quan hệ “= ,≡, //, ⊥” là những quan hệ ối xứng
2. Quan hệ “≤” trên ,
, không phải là quan hệ ối xứng
3. Quan hệ ℛ = {(1,2).(2,1),(1,3),(3,1)} trên = {1,2,3,4} là một quan hệ ối xứng nhưng không phản xạ: lOMoARcPSD| 36667950
Chú ý: trong hình vẽ trên ta thấy tập hợp ℛ tự ối xứng qua ường chéo ∆ . Tổng quát hơn
một quan hệ ℛ trên tập hợp bất kỳ là ối xứng khi và chỉ khi ℛ là tự ối xứng qua ∆ Định
nghĩa 3.2.3: một quan hệ ℛ trên ược nói là bắc cầu nếu: ∀ , , ,(ℛ) ∧ (ℛ) ⟹ ℛ Ví dụ:
1. Các quan hệ “= ,≡, //, ≤” là các quan hệ bắc cầu
2. Quan hệ “⊥” trên ℒ không phải là quan hệ bắc cầu
3. Quan hệ {(1,1),(2,3),(3,4),(2,4)} trên = {1,2,3,4} là bắc cầu
Định nghĩa 3.2.4: một quan hệ ℛ trên tập ược gọi là quan hệ tương ương nếu nó phản xạ, ối xứng, bắc cầu. Ví dụ:
1. Các quan hệ “= ,≡, //” là các quan hệ tương ương
2. Quan hệ “≤,⊥” không phải là một quan hệ tương ương
3. Quan hệ ℛ = {(1,1),(2,2),(3,3),(2,3),(3,2)} trên = {1,2,3} là quan hệ tương ương
4. Quan hệ “tương ương logic” trên tập hợp các mệnh ề là một quan hệ tương ương.
5. Cho trước một ánh xạ : ⟶. Ta ịnh nghĩa quan hệ ℛ trên như sau: ℛ ⟺ ( ) = ( )
Khi ó ℛ là một quan hệ tương ương.
Định nghĩa 3.2.5: giả sử ℛ là một quan hệ tương ương trên và ∈. Khi ấy lớp tương ương
chứa là tập hợp con: {∈/ ℛ}
Chú ý: lớp tương ương chứa thường ược ký hiệu bởi ̅ hay [ ] Ví dụ:
Quan hệ ≡ ( 3) có ba lớp tương ương:
0 = {,…,−6,−3,0,3,…} 1 = {,…,−5,−2,1,4,…}
2 = {,…,−4,−1,2,5,…} Để ý rằng: 0 = 3 = 6 = ⋯ 1 = 4 = 7 = ⋯ 2 = 5 = 8 = ⋯
Như thế {0,1,2} là một phân hoạch của , nghĩa là Z là hợp của 3 tập hợp ôi một rời
nhau {0,1,2}. Tỗng quát hơn ta có:
Định nghĩa 3.2.1: giả sử ℛ là một quan hệ tương ương trên . Khi ấy: i. ∀ ∈ , ∈ ̅ ii. ∀ ,∈, ℛ ⟺ iii.
Hai lớp tương ương ̅ và sao cho ̅ ∩ ≠ ∅ thì trùng nhau lOMoARcPSD| 36667950 Chứng minh: i.
Do tính phản xạ, ℛ. Nói cách khác ∈ ̅ ii.
Giả sử ℛ. Gọi là một phần tử bất kỳ của ̅
Ta có: và nên ℛ do tính bắt cầu.Như thế ̅ ⊂. Mặt khác do tính ối xứng ta cũng có ℛ.
Do ó chứng minh tương tự như trên ta có ⊂ ̅.
Ngược lại giả sử ̅ = , do ∈ ̅
. Điều này có nghĩa là iii. Giả
sử ̅ ∩ ≠ ∅. Khi ấy tồn tại ∈ ̅ ∩ , nghĩa là ℛ và ℛ. Do ii) ta có ̅ = ̅ = pcm Ví dụ:
1. Xét quan hệ ℛ trên : ℛ ⟺ =
Theo ví dụ 5 sau Định nghĩa 3.2.4, ℛ là quan hệ tương ương xác ịnh bởi ánh xạ ⟼
từ vào . Các lớp tương ương là {0},{−1,1},{−2,2},…,{− , },… Ở ây ược phân hoạch thành vô
số tập hợp con hữu hạn.
Với ∈, quan hệ ồng dư (mod ) là một quan hệ tương ương với lớp tương ương 0,1,…,−
1. Ta ký hiệu: = {0,1,…,− 1}
Các phần tử của, ược gọi là các số nguyên ồng dư mod .
Với , ∈ , chọn tùy ý ∈ và ∈. Ta có thể kiểm tra ược + không phụ thuộc vào và mà chỉ
phụ thuộc vào và . Do ó ta có thể dùng + ể ịnh nghĩa +
. Đặc biệt ta có thể chọn = và = : + = + Tương tự ta có: =
Bây giờ ta có thẻ kiểm ược 2 phép toán ∙,+ trên
thỏa các tính chất tương tự
như các phép toán ∙,+ trên :
Tính giao hoán: ∀ ̅, , ̅ + = + ̅ và ̅ = ̅
Tính kết hợp: ∀ ̅, ,̅, = (̅ + ) + ̅ và ̅(̅) = (̅)̅
Tính phân bố: ∀ ̅, ,̅,̅( + ̅) = ̅ + ̅ ̅ Phần tử trung hòa: ∀ ̅ ̅ + 0 = ̅ ̅1 = ̅
Phần tử ối: ∀ ̅,̅ + (−) = 0 Ta nói
cũng như là những vành giao hoán có ơn vị
§3 THỨ TỰ
Định nghĩa 3.3.1: một quan hệ ℛ trên tập hợp ược gọi là phản xứng nếu: ∀ , ,(ℛ) ∧ (ℛ) ⟹ = lOMoARcPSD| 36667950 Ví dụ:
Quan hệ “≤” trên , hay R là phản xứng
Quan hệ “ ≡,/ / ” không phản xứng
Chú ý: trái với các quan hệ ối xứng, ối với một quan hệ phản xứng ℛ, mọi bộ phận tự ối
xứng của ℛ ều nằm trong ường chéo ∆ 5 4 3 2 1 0 0 1 2 3 4 5
Định nghĩa 3.3.2: một quan hệ trên tập hợp ược nói là một thứ tự nếu nó phản xạ, phản
xứng và bắc cầu. Khi ấy ta nói là một tập hợp sắp thứ tự (hay có thứ tự) Chú ý:
1. Ta thường ký hiệu một thứ tự bởi ≺. Cặp ( ,≺) là một tập hợp có thứ tự.
2. Giả sử là một tập hợp con của tập hợp có thứ tự ( ,≺). Khi ấy ≺ cảm sinh một thứ tự
trên một cách tự nhiên: với ,∈, ta nói ≺ trong nếu ≺ trong . Ví dụ:
1. (ℛ,≤) là một tập hợp có thứ tự. Thứ tự cảm sinh các thứ tự tự nhiên trên , . 2. Nhắc lại tập hợp ( ) ta có quan hệ: ≺ ⟺ ⊂
Khi ó ≺ là một thứ tự trên ( ) gọi là thứ tự bao hàm. Ký hiêu ⊂ sẽ ược dùng thay vì ≺
Trên tập hợp ℳ các dạng mệnh ề, ta ịnh nghĩa ≺ khi và chỉ khi ⟹, nghĩa là một hệ
quả logic của . Rõ ràng quan hệ trên có tính phản xạ và bắc cầu. Mặt khác nếu ⟹ và ⟹ thì à ươ đươ
. Do ó nếu ta ồng nhất các dạng mệnh ề tương ương
logic thì quan hệ trên trở thành một thứ tự trên ℳ.
Chính xác hơn, ta thấy quan hệ tương ương logic là một quan hệ tương ương trên ℳ
. Ta có một quan hệ trên tập hợp các lớp tương ương như sau: [ ] ≺ [ ] ⟺ là hệ quả logic của
Khi ấy quan hệ trên vẫn còn là phản xạ và bắc cầu.
Giả sử [ ] ≺ [ ] và [ ] ≺ . Khi ấy là hệ quả logic của và ngược lại, nghĩa là và tương
ương logic. Suy ra [ ] = [ ]
Do ó ≺ là một thứ tự trên tập hợp các lớp tương ương của ℳ.
Ví dụ: Gọi là một số nguyên dương. Đặt: = {∈/ | }
Trong ó | có nghĩa là một ước của n hay n chia hết cho a. Trên ta có thể ịnh nghĩa một quan hệ: ≺ ⟺ |
Khi ấy rõ ràng là phản xạ và bắc cầu lOMoARcPSD| 36667950
Giả sử ≺ và ≺. Ta có: = và = với ,∈ Suy ra = ⟹ = 1 ì > 0
Do ,∈ ta phải có = = 1, nghĩa là =
Quan hệ thứ tự trên vẫn ược ký hiệu bởi | Với = 12 ta có = {1,2,3,4,6,12}
Do ó ta có thể liệt kê các cặp thuộc quan hệ trên: {(1,1),(1,2),(1,3),(1,4)(1,6),(1,12),
(2,2),(2,4),(2,6),(2,12),(3,3),(3,6),(3,12),(4,4),(4,12),(6,6),(12,12)}
Tuy nhiên ối với các tập hợp hữu hạn có nhiều phần tử, ta không thể dùng phương pháp liệt
kê như trên mà sẽ sử dụng biểu ồ Hasse
Định nghĩa 3.3.3: Xét một tập hợp có thứ tự ( ,≺) và , là hai phần tử bất kỳ của i.
Nếu ≺ ta nói là trội của hay ược trội bởi ii.
là trội trực tiếp của nếu trội và không tồn tại một trội của sao cho:
Định nghĩa 3.3.4: Biểu ồ Hasse của một tập hợp hữu hạn có thứ tự ( ,≺) bao gồm: i.
Một tập hợp các iểm trong mặt phẳng tương ứng 1 – 1 với , gọi là các ỉnh ii.
Một tập hợp các cung có hướng nối một số ỉnh: hai ỉnh , ược nói lại bởi một cung có
hướng (từ tới ) nếu là trội trực tiếp của . Ví dụ: 1.
Trên ây là biểu ồ Hasse của tập hợp sắp thứ tự { , , , , , } trong ó: ≺ < và ≺ ≺
không so sánh ược với các p hần tử khác, nghĩa là với 1 ≤ ≤ 5 thì ⊀ và ⊀ . 2. Biểu ồ Hasse của ược cho bởi: lOMoARcPSD| 36667950 4 12 2 6 1 3
3. Với = { , , } thì biểu ồ Hasse của ( ( ),⊂) có dạng { , } { , , } { } { , } { } { , } ∅ { }
Ở ây ta quy ước các cung là không chéo nhau. Do ó một cách ể hình dùng dễ dàng
là xem như Biểu ồ Hasse của ( ) gồm các ỉnh và cạnh của một hình lập phương 3 chiều.
4. Biểu ồ Hasse của {1,2,3,4,5} với thứ tự thông thường có dạng một dây chuyền: 1 2 3 4 5
Ta có thể duyệt hết các ỉnh một lần bằng cách i theo các cung mà không quay trở lại
Cũng thế trong vô hạn, ta cũng có thể quy ước biểu diễn thứ tự trên bởi biểu ồ Hasse vô hạn như sau: … … 2 -1 0 1 2
Biểu ồ Hasse trên vẫn còn là một dây chuyền vô hạn
Định nghĩa 3.3.5: một thứ tự trên ược nói là toàn phần nếu hai phần tử bất kỳ ều so sánh
ược, nghĩa là mệnh ề sau là úng: ∀ ,∈,(≺) ∨ (≺) Ví dụ: 1. , ,
, với thứ tự ≤ thông thường là những tập hợp sắp thứ tự toàn phần 2.
Xét một tập hợp hữu hạn không rỗng mà ta gọi là bộ mẫu tự. Giả sử trên có một
thứ tự toàn phần ≺ (ví dụ như thứ tự thông thường nếu là bộ chữ cái:
≺ ≺ ≺ ⋯ ≺ , hay thứ tự xác ịnh bởi mã ASCII nếu là bộ chữ cái ược mở rộng thêm
các ký tự là các số từ 0 ến 9, các dấu+,-,…)
Gọi là tập hợp các chuỗi ký tự có dạng = … và … ∈ với là số nguyên tự nhiên tùy ý.
Với = 0 , ta ược chuỗi rỗng ∅ không có ký tự nào cả. ta sẽ ịnh nghĩa một quan hệ ≺ trên như sau: ∅ ≺ ,∀ ∈
nếu = … và = … là hai chuỗi khác ∅, ta ịnh nghĩa ≺ khi và chỉ khi một trong hai iều kiện sau ược thỏa:
i. tồn tại một chỉ số ,1 ≤ ≤ sao cho: = ,…, = và ii. ≤ và = ,…, = lOMoARcPSD| 36667950
Ta chứng minh ược rằng ≺ là một thứ tự trên gọi là thứ tự tự iển. Hơn nữa với thứ
tự tự iển, là một tập sắp thứ tự toàn phần (Bài tập)
Bây giờ với Định nghĩa 3.3.5, nhận xét trên ây về biểu ồ Hasse có thẻ ược phát biểu
dưới dạng một kết quả tổng quát hơn mà chứng minh là hiển nhiên.
Mệnh ề 3.3.1: biểu ồ Hasse của ( ,≺) là một dây chuyền khi và chỉ khi ≺ là một thứ tự toàn phần trên .
Do Mệnh ề 3.3.1, biểu ồ Hasse của một tập hợp sắp thứ tự toàn phần hữu hạn là một
dây chuyền xuất phát từ một phần tử và chấm dứt bởi 1 phần tử . Rõ ràng là phần tử bé
nhất và là phần tử lớn nhất theo nghĩa: ∀ ∈ , ≺ ≺
Mặt khác, Ví dụ 1 cho thấy phần tử bé nhất và lớn nhất không nhất thiết tồn tại, ngay
cả trong 1 tập hợp sắp thứ tự hữu hạn. Tuy nhiên các phần tử , là những phần tử tối ại và ,
, là những phần tử tối tiểu theo nghĩa sau:
Định nghĩa 3.3.6: trong tập hợp sắp thứ tự ( ,≺), một phần tử ược nói là tối ại (tương ứng
tối tiểu ) nếu không có trội thực sự (tương ứng không là trội thực sự của phần tử nào cả).
Nói cách khác mệnh ề sau là úng: ∀ ∈ ,(≺) ⟹ ( = ) tương ứng
Định lý 3.3.2: trong một tập hợp sắp thứ tự , phần tử lớn nhất , nếu tồn tại, là phần tử tố ại
duy nhất. Suy ra cũng là phần tử lớn nhất duy nhất. Kết luận tương tự cho phần tử bé nhất và phần tử tối tiểu.
Chứng minh: Giả sử là phần tử lớn nhất và tồn tại sao cho ≺. Do lớn nhất, ta cũng có ≺.
Do tính phản xứng, ta có = . Suy ra là một phần tử tối ại.
Mặt khác nếu gọi là một phần tử tối ại tùy ý, do lớn nhất ta có ≺. Nhưng là tối ại, ta phải có =
. Như thế là phần tử tối ại duy nhất và dĩ nhiên cũng là phần tử lớn nhất
duy nhất. Kết luận cho phần tử bé nhất và các phần tử tối tiểu ược chứng minh tương tự
bằng cách ổi chiều các thứ tự (bất ẳng thức). pcm
Sự tồn tại của phần tử tối ại ối với các tập hợp sắp thứ tự hữu hạn ược cho bởi:
Định lý 3.3.3: trong một tập hợp sắp thứ tự hữu hạn thì: i.
mọi phần tử ược trội bởi (tương ứng trội) một phần tử tối ại (tương ứng tối tiểu) ii.
nếu là phần tử tối ại (tương ứng tối tiểu) duy nhất của thì là phần tử lớn nhất
(tương ứng phần tử bé nhất) Chứng minh:
1. Xét một phần tử ∈. Nếu không tối ại sẽ có ∈ sao cho:
Nếu tối ại thì ó là phần tử phải tìm. Nếu không sẽ có ∈ sao cho:
Nếu tối ại thì ó là phần tử phải tìm vì rõ ràng trội . Nếu không ta tiết tiếp tục tìm
ược một trội thực sự của … lOMoARcPSD| 36667950
Do hữu hạn và các phần tử , , ,… ôi một khác nhau, quá trình trên sẽ dừng sau tối a
− 1 bước, trong ó = | |. Phần tử cuối cùng tìm ược chính là phần tử tối ại trội .
2. Giả sử là phần tử tối ại duy nhất của , và là một phần tử tùy ý của . Do i) tồn tại
một phần tử tối ại sao cho: ≺. Do duy nhất ta có: = Suy ra ≺,∀ ∈
Nói cách khác là phần tử lớn nhất.
Chứng minh cho kết luận về phần tử tối tiểu và phần tử bé nhất hoàn toàn tương tự.
Chú ý: Nếu không hữu hạn, Định lý không úng theo cả khi kết luận: 1.
không có phần tử tối a; ví dụ như = với thứ tự thông thường. 2.
có thể có phần tử tối ại duy nhất nhưng không có phần tử lớn nhất như ví dụ sau cho thấy: 0 1 2 3 §4 DÀN
Giả sử là một tập hợp con hữu hạn của tập hợp sắp thứ tự toàn phần , khi ấy phần
tử lớn nhất của tồn tại và ược ký hiệu bởi max . Tương tự, phần tử bé nhất của tồn tại, và ược ký hiệu bởi min .
Đối với các tập hợp sắp thứ tự không toàn phần , khái niệm max, min có thể ược
giảm nhẹ thành khái niệm sup và inf như sau:
Định nghĩa 3.4.1: Giả sử là một tập hợp con của tập hợp sắp thứ tự ( ,≺). Khi ấy
1. Một phần tử ∈ ược nói là chặn trên (tương ứng chặn dưới ) chung của nếu: ∀ ∈ ,≺ (tương ứng ∀ ∈ ,≺) 2. Phần tử bé nhất (tương ứng lớn nhất) của tập hợp {∈/ là chặn trên chung của } (tương ứng {∈/ là chặn dưới chung của
}) ược ký hiệu bởi sup (tương ứng inf ) Ví dụ:
1. Trong một tập hợp sắp thứ tự toàn phần , rõ ràng max của một tập hợp con hữu hạn
chính là sup . Tương tự min chính là inf . 2. Giả sử ℬ = { , ,…,
} là một tâp hợp con hữu hạn của ( ). Khi ấy chính làsup ℬ à chính làinf
Trên tập hợp ℳ các dạng mệnh ề với thứ tự ⟹, xét một tập hợp con hữu hạn ℰ = { ,
,…, }. Khi ấy ∨ ∨ …∨ và ∧ ∧ …∧ chính là sup ℰ và inf ℰ lOMoARcPSD| 36667950 (Bài tập).
Định nghĩa 3.4.2: một tập hợp sắp thứ tự ( ,≺) ược nói là một dàn nếu với hai phần tử bất kỳ , luôn luôn tồn tại.
Ký hiệu: trong một dàn, ta sẽ ký hiệu . Ví dụ:
1. Một tập hợp sắp thứ tự toàn phần là một dàn 2.
( ) với thứ tự bao hàm là một dàn. Ta có:
3. ℳ với thứ tự ⟹ là một dàn: với , là hai dạng mệnh ề, các ký hiệu mới ∨, ∧ dành cho
sup{ , } và inf{ , } trùng với các ký hiệu quen thuộc của phép nối rời và phép nối liền: ∨ và ∧.
4. Tập hợp = { , , , , , } với biểu ồ Hasse dưới ây không phải là một dàn vì { , } không có
sup. Thật vậy các trội chung của { , } là { , , } và tập hợp này không có phần tử bé.
Tương tự ta cũng thấy { , } không có inf.
Định lý 3.4.1: Trong một dàn ( ,≺) các phép toán ∨ và ∧ thỏa các tính chất giao hoán và kết hợp: i. à ∧ ii. à ∧
Chứng minh: i) hiển nhiên nên ta chỉ cần chứng minh ii). Xét 3 phần tử bất kỳ , ,∈.
Khi ấy = ∨ (∨) là một trội chung của và ∨ nên nó cũng là một trội chung của , và thì ∨
≺ vì ∨ là trội chung bé nhất của { , }. Như thế là trội chung của
{ ,∨}. Suy ra = ∨ (∨) ≺ .
Như thế chính là trội chung bé nhất của { , , }. Tương tự ta cũng thấy (∨) ∨ cũng là
trội chung bé nhất của { , , }. Do phần tử bé nhất là duy nhất, ta có: lOMoARcPSD| 36667950 ∨ (∨) = (∨) ∨
Chứng minh của ∧ (∧) = (∧) ∧ hoàn toàn tương tự. pcm
Chú ý: Do tính kết hợp, nếu = , , …,
là một tập hợp con hữu hạn của dàn thì ∨ ∨ …∨
không phụ thuộc vào cách ặt các dấu “( )”. Hơn nữa, chứng minh tương tự
như trong Định lý 3.4.1 ta thấy ∨ ∨ …∨ chính là sup . Tương tự ∧ ∧ …∧ = inf . Đặc biệt nếu hữu hạn ta có:
Mệnh ề 3.4.2: Trong dàn hữu hạn = { , ,…, } thì ∨ ∨ …∨ và ∧ ∧ …∧ chính là phần tử lớn nhất
và phần tử bé nhất của .
Chú ý: Nếu dàn không hữu hạn thì phần tử lớn nhất và bé nhất không nhất thiết tồn tại
như ví dụ của cho thấy.
Định nghĩa 3.4.3: một dàn ược nói là phân bố nếu với mọi , , trong ta có: ∧ (∨) = (∧) ∨ (∧) à ∨ (∧) = (∨) ∧ (∨) Ví dụ:
1. Mọi tập hợp sắp thứ tự toàn phần là một dàn phân bố (Bài tập) 2. Do tính
phân bố của các phép tính tập hợp, dàn ( ) là một dàn phân bố. 3. Do quy
luật phân bố, dàn ℳ các dạng mệnh ề là một dàn phân bố
4. Xét tập hợp sắp thứ tự = { , , , , } với biểu ồ Hasse như sau:
Ta có thể kiểm tra dễ dàng là một dàn. Tuy nhiên không phân bố vì: ∧ (∨) = ∧ = ℎ (∧) ∨ (∧) = ∨ = ≠
Định nghĩa 3.4.4: Giả sử là một dàn với phần tử lớn nhất mà bé nhất mà ta ký hiêu là 1
và 0. Khi ấy một phần tử ̅ ∈ ược nói là phần bù của phần tử ∈ nếu: ∨ ̅ = 1 à ∧ ̅ = 0
Ta nói là một dàn bù nếu mọi phần tử của ều có phần bù.
Chú ý: nếu ̅ là phần bù của thì rõ ràng là phần bù của ̅ Ví dụ: lOMoARcPSD| 36667950
1. Các dàn ( ) và ℳ là dàn bù. Phần bù của ∈( ) chính là phần bù của tập hợp trong , còn
phần bù của dạng mệnh ề chính là phủ ịnh của . 2. Dàn = { , , , , } với biểu ồ Hasse như
dưới ây là một dàn bù §5 DÀN 2
Cho trước hai tập hợp , , nhắc lại rằng
ký hiệu tập hợp các ánh xạ từ vào .
Giả sử ≺ là một thứ tự trên . Khi ấy với ,∈ , ta ịnh nghĩa: ≺ ⟺ ∀ ∈ , ( ) ≺ ( )
Có thể kiểm tra rằng ≺ là một thự tự trên , và hơn nữa ( ,≺) là một dàn nếu ( ,≺ ) là một dàn (Bài tập)
Gọi , là hai phần tử bất kỳ của
,∨ và ∧ là ánh xạ sao cho với mọi ∈: (∨)( ) = ( ) ∨ ( ) à (∧)( ) = ( ) ∧ ( )
trong ó ∨ và ∧ chỉ sup và inf của hai phần tử trong ối với thứ tự ≺ Đặc biệt với
= {0,1}, ta ược dàn {0,1} mà ta ký hiệu là 2 . Với ∈ 2 , ặt = (1). Khi ấy ta có:
Ta nói là hàm ặc trưng của
Hàm ặc trưng của ược ký hiệu bởi . Ta có:
Định lý 3.5.1: tương ứng : ⟼ là một song ánh giữa ( ) và 2 . Hơn nữa với ,
là hai tập hợp con tùy ý của ta có: ⊂ ⟺ ≺ (3.5.1)
Chứng minh: Trên ây ta ã thấy là toàn ánh. Hơn nữa nếu = thì : = (1) = (2) =
Như thế là một song ánh,
Mặt khác, với , là hai tập hợp con tùy ý của , ta có: ⊂ ⟺ ∀ ∈ , ( ) = 1 ⟹ ( ) = 1 ⟺ ≺ lOMoARcPSD| 36667950 pcm
Ta có thể viết lại (3.5.1) như sau: ⊂ ⟺ ( ) ≺ ( )
là ẳng cấu giữa hai tập hợp con có thứ tự ( ) và 2 theo nghĩa sau:
Định nghĩa 3.5.1: môt ẳng cấu giữa hai tập hợp có thứ tự ( ,≺ ),( ,≺ ) là một song ánh : ⟷
sao cho: ∀ , ,(≺ ) ⟺ ( ) ≺ ( ) (3.5.2)
Định lý 3.5.2: Giả sử là một ẳng cấu giữa hai tập hợp có thứ tự ( ,≺ ) và ( ,≺ ) i.
Nếu ( ,≺ ) và ( ,≺ ) là hai dàn, thì với ,∈ tùy ý ta có: (∨) = ( ) ∨ ( )
(3.5.3) và (∧) = ( ) ∧ ( ) (3.5.4) ii.
Nếu là dàn phân bố thì cũng là dàn phân bố iii.
Giả sử có 0 là phần tử bé nhất và 1 là phần tử lớn nhất. Khi ấy (0) và (1) là phần tử
bé nhất và lớn nhất của . iv.
Nếu là dàn bù thì cũng là dàn bù. Hơn nữa nếu ̅ là phần bù của phần tử ∈, thì (̅) là
phần bù của ( ). Nói cách khác (̅) = ( ). Chứng minh: i.
Với ,∈ tùy ý, do (3.5.2) rõ ràng (∨) là chặn trên chung của ( ) và ( ). Suy ra: ( ) ∨ ( ) ≺ (∨) (3.5.5) Mặt khác, cũng do (3.5.2) ( ) ∨
( ) và chặn trên chung của và nên: ∨ ≺ ( ) ∨ ( ) Do ó (∨) ≺ ( ) ∨ ( ) (3.5.6)
Từ (3.5.5) và (3.5.6) ta suy ra (3.5.3)
Chứng minh của (3.5.4) hoàn toàn tương tự.
ii), iii), iv) ược suy ra dễ dàng từ ịnh nghĩa pcm
Hệ quả: nếu , là hai tập hợp con tùy ý của thì ∪ = ∨ à ∩ = trong ó =
∧ là tích của hai hàm theo nghĩa tự nhiên. §6 DÀN
6.1 Ước số chung lớn nhất và bội số chung lớn nhất
Giả sử , là hai số nguyên dương, khi ấy số nguyên dương ược nói là ước số chung
của và nếu là ước số của và là ước số của . Khi ấy 0 ≤ ≤ min( , ). Do ó tập hợp của các
ước số chung của và là một tập hợp hữu hạn và tồn tại một phần tử lớn nhất gọi là ước số
chung lớn nhất của và . Ta viết: = ( , ) lOMoAR cPSD| 36667950
Để tìm ước số chung lớn nhất của 2 số nguyên dương , ta sử dụng thuật toán sau:
Thuật chia Euclide: nếu là ước của , ặt = . Nếu không ta thực hiên lần lượt các phép chia có dư số: + = ,0 ≤ < + = ,0 ≤ < = + ,0 ≤ r < … ………………… ………………… … + ,0 ≤ <
………………… …………………… = … … Do > > > ⋯ >
> ⋯ ≥ 0, thuật chia sẽ ngưng sau một số hữu hạn bước. Gọi
là dư số ầu tiên bằng 0. Ta có: = + , 0 ≤ < = + 0 Ta có:
Định lý 3.6.1: là ước số chung lớn nhất của và . Hơn nữa mọi ước số chung của và là ước số của
Chứng minh: Nếu là ước của thì ước số chung lớn nhất của và chính là = . Nếu không >
0. Giả sử là ước số chung của và . Do = − nên cũng là ước số của với 1 ≤ ≤ . Thật vậy,
giả sử 1 ≤ < và là ước của với 1 ≤ ≤ . Khi ấy do
= − nên cũng là ước của . Như thế theo nguyên lý qui nạp, là ước của . Đặc biệt nếu
gọi là ước số chung lớn nhất của và thì cũng là ước của . Suy ra ≤ lOMoARcPSD| 36667950
Ngược lại, do = nên là ước của . Tương tự như trên, dùng nguyên lý qui nạp , ta thấy là
ước của với 1 ≤ ≤ . Nhưng = + nên cũng là ước của . Cuối cùng do = + , cũng là ước của .
Như thế là ước số chung của và . Suy ra ≤ Tóm lại = pcm
Định lý 3.6.2: Giả sử là ước số chung lớn nhất của và . Khi ấy tồn tại ,∈ sao cho: = +
Chứng minh: với ký hiệu như trong Định lý 3.6.1, ta có = . Như thế: = − = + Nhưng = − Do ó = + ( − ) =
Bằng Nguyên lý qui nạp tương tự như trên ta cũng chứng minh ược tồn tại , ,…, ∈ sao cho: = + = + ( − ) Sử dụng = + = − ta ược: = + ( ) = + pcm
Định nghĩa 3.6.1: hai số nguyên dương , ược nói là một nguyên tố cùng nhau nếu ước số
chung lớn nhất của chúng bằng 1. Khi ấy ta viết ( , ) = 1 lOMoARcPSD| 36667950
Chú ý: Một số nguyên > 1 ược nói là số nguyên tố nếu không có ước nào ngoài 1 và chinh
nó. Nếu là số nguyện tố và không phải là ước của thì và nguyên tố cùng nhau.
Mệnh ề 3.6.3: Giả sử , ,∈ sao cho là ước của và ( , ) = 1. Khi ấy là ước của .
Chứng minh: Do Định lý 3.6.2, tồn tại ,∈ sao cho: 1 = + đó = +
Vì là ước của nên cũng là ước của pcm
Mệnh ề 3.6.4: Giả sử , ,∈ sao cho ( , ) = 1 và ( , ) = 1. Khi ấy ( , ) = 1 Chứng minh: Giả sử ước
số chung lớ nhất của và là > 1. Khi ấy ( , ) = 1 vì nếu không, gọi là ước số chung lớn nhất
của và ta có > 1. Rõ ràng cũng là ước chung của và . Điều này mâu thuẫn với giả thiết ( ,
) = 1. Vậy ( , ) = 1. Do ó theo Mệnh ề 3.6.3 là ước số của . Điều này mâu thuẫn với giả thiết
( , ) = 1. Do ó = 1, nghĩa là ( , ) = 1 pcm
Một số nguyên ược nói là bội số chung của hai số nguyên , nếu ồng thời là bội số của và .
Bổ ề 3.6.5: Cho , ,∈ . Giả sử là bội số chung của , và ( , ) = 1. Khi ấy là bội số chung của .
Chứng minh: Do là bội số của , ta có thể viết =
với là số nguyên. Do Mệnh ề
3.6.3, là ước số của : = , ∈ . Suy ra = ′ pcm
Định lý 3.6.6: Giả sử ,∈ . Gọi là ước số chung lớn nhất của , . Khi ấy là bội số chung của
, . Hơn nữa mọi bội số chung của , ều chia hết cho . Suy ra là bội số chung lớn nhất của và .
Chứng minh: Ta có thể viết = = với , Mặt khác ể ý rằng
và nguyên tố cùng nhau. Thật vậy gọi là ước số chung lớn
nhất của chúng thì cũng là ước số chung của và . Suy ra = 1.
Gọi là bội số chung của và . Áp dụng Bổ ề 3.6.5 cho , , ta thấy là bội số chung của
nên là bội số chung của . pcm
Chú ý: ta ký hiệu bội số chung nhỉ nhất của , bởi ( , )
Giả sử ∈, > 1. Khi ấy nếu gọi là ước bé nhất của sao cho > 1 thì rõ ràng là một số
nguyên tố. Lại tiếp tục xét ta chứng minh ược bằng qui nạp rằng là tích của một số hữu
hạn số nguyên tố. Gộp các thừa số giống nhau lại ta có thể phân tích thành (3.6.1)
thừa số nguyên tố: = … trong ó ∈ , ,…,
là các số nguyên tố ôi một khác nhau và , ,…, GS. Nguyễn Hữu Anh 72
Downloaded by Albedo Lili (albedo0208@gmail.com) lOMoARcPSD| 36667950
Mệnh ề 3.6.7: Biểu diễn (3.6.1) là duy nhất
Chứng minh: xét một phân tích ra thừa số nguyên tố khác của : = … (3.6.2)
Nếu ∉ { , ,…, } thì áp dụng thì áp dụng Mệnh ề 3.6.4 nhiều lần ta i ến kết luận và số
nguyên tố cùng nhau. Điều mâu thuẫn này chứng tỏ ∈ { , ,…, }. Lập luận tương tự cho ,…, , ,…, ta ược: { , ,…, } = { , ,…, } Đặc biệt =
. Sắp xếp thứ tự lại , ,…, ta có thể giả sử = , = ,…, =
. Ta sẽ chứng minh = , = ,…, = bằng qui nạp trên Nếu = 1 thì = = . Suy ra = Giả sử > 1. Nếu < thì = …
rõ ràng nguyên tố cùng nhau với
. Trong khi ó dùng biểu diễn (3.6.2) ta ược: = …
Do − > 0, là ước của. Điều mâu thuẫn này chứng tỏ ≥ . Do và óng vai trò ối xứng ta
cũng có ≤ , nghĩa là = . Khi ấy ta ược 2 biểu iễn của thành thừa số nguyên tố: = … = …
Áp dụng giả thiết qui nạp ta ược = , = ,…, = pcm
Sử dụng phân tích (3.6.1) ta có một phương pháp thứ hai ể tìm ước số chung lớn
nhất và bội số chung nhỏ nhất của hai số nguyên dương. Trước tiên nhận xét rằng nếu và có phân tích = … (3.6.3) = … (3.6.4)
Thì là ước của khi và chỉ khi 2 iều kiện dưới ây ược thỏa: lOMoAR cPSD| 36667950 { , ,…, } ⊂ { , ,…, }. Đặc biệt ≤
Ta sắp xếp thứ tự , ,…, lại sao cho = , = , = . Khi ấy các số mũ thỏa: ≤ , ≤ ,…, ≤ .
Chứng minh của khẳng ịnh trên dựa trên cùng ý tưởng với chứng minh Mệnh ề 3.6.7
nêu ược dành cho ọc giả.
Bây giờ giả sử và có phân tích như trong (3.6.3) và (3.6.4) với các số mũ nguyên
dương. Bằng cách bổ sung thêm vào các thừa số là lũy thừa 0 của những số nguyên tố
trong (3.6.3) và ngược lại, ta có thể giả sử , có dạng: = … = …
Với các số mũ lấy giá trị nguyên dương hay 0. Khi ấy do nhân xét trên ta có: Mệnh ề 3.6.8: ( , ) = … và ( , ) = … ( ) = min , với và = max( , 6.2 Dàn
Nhắc lại rằng tập hợp gồm các ước số dương của ược
sắp thứ tự bởi quan hệ: ≺ ⟺ | ( là ước số của ) Giả sử ,∈. Khi ấy = ( , ) ∈
Rõ ràng ≺ và ≺. Hơn nữa nếu ∈ sao cho ≺ và ≺ thì là ước số chung của , nên theo
Định lý 3.6.1 cũng là ước số của , nghĩa là ≺.
Nói tóm lại chính là inf( , ). Tương tự ( , ) là sup( , ). Với ký hiệu ∧,∨ cho inf và sup ta có: ∧ = ( , ) ∨ = ( , )
Như thế là một dàn phần tử bé nhất là 1, phần tử lớn nhất là .
Hơn nữa nếu gọi , ,…, là các ước số nguyên tố của thì ta có thể biểu diễn 1 phần tử
bất kỳ của dưới dạng (3.6.1) với số mũ thuộc . Xét ba phần tử tùy ý , ,∈ với biểu diễn như trên: = … = … = …
Khi ấy do Mệnh ề 3.6.8 số mũ của trong ∧ (∨) là: )) min( ,max(, )) = max(min( , ) ,min( , lOMoARcPSD| 36667950
Như thế ∧ (∨) = (∧) ∨ (∧) Tương tự ∨ (∧) = (∨) ∧ (∨)
Tóm lại ta ã chứng minh.
Định lý 3.6.9: là một dàn phân bố.
Một số nguyên dương ược nói là không có thừa số chính phương nếu không chia hết cho
bình phương của bất kỳ số nguyên >1 nào. Định lý 3.6.10:
là dàn bù khi và chỉ khi không có thừa số phương.
Chứng minh: Giả sử không có thừa số chính phương và là một phần tử tùy ý của . Khi
ấy và nguyên tố cùng nhau vì nếu không, bất kỳ ước số chung > 1 của chúng cũng ều có
bình phương là ước của . Như thế ∧= 1 Ngoài ra ∨ = , ==
Vậy chính là phần bù của và do ó là một dàn bù.
Ngược lại, giả sử chia hết cho bình phương của số nguyên >1. Gọi là phần bù của trong . Ta có: ∧ = 1 ∨ = Mà
Suy ra = . Nhưng rõ ràng là ước số chung của và nên ∧ ≠ 1. Điều này mâu thuẫn
chứng tỏ không có phần bù và không phài là một dàn bù. Thật ra trong chương 4 ta sẽ
chứng minh rằng nếu có một thứ tự nào ó trên ể nó trở thành một dàn bù thì số phần tử của
phải là một lũy thừa của 2. Trong khi ó số ước của là một lũy thừa của 2 thì trong
phân tích của thành thừa số nguyên tố, các số mũ phải có dạng 2 − 1 (Bài tập). lOMoARcPSD| 36667950
BÀI TẬP CHƯƠNG 3 1. Giả sử = {0,1,2,3,4}, = {1,3,7,12},
= {0,1,2,,4,8,16,} và A_4={-3,-2,-1,0,1,2,3} a) Xét ℛ = {( , , , ) ∈ × × × ; = 0}. Hãy tính |ℛ |. b) Xét ℛ = {( , , , ) ∈ × × × ; < 0}. Hãy tính |ℛ |. 2.
Giả sử = {1,2,3}, = {2,4,5} a) Tính | × | b)
Tìm số quan hệ giữa và c)
Tìm số quan hệ giữa hai ngôi trên d)
Tìm số quan hệ giữa và chứa (1,2),(1,5) e)
Tìm số quan hệ giữa và chứa úng 5 cặp có thứ tự. f)
Tìm số quan hệ giữa hai ngôi trên chứa ít nhất 7 cặp có thứ tự. 3.
Xét hai tập hợp hữu hạn và sao cho | | = 3. Tìm số phần tử của biết rằng có úng 4096 quan hệ giữa và . 4.
Một quan hệ giữa hai tập hợp và ược nếu là một hàm nếu với mọi ∈ (t.ư ∈
), tốn tại duy nhất một phần tử ∈ (t.ư ∈) sao cho ( , ) ∈ ℛ. Khi ấy tương ứng ⟼ (t.ư ⟼)
rõ ràng là một ánh xạ từ vào (t.ư vào ) như ã xét trong Chương 2. Trong các quan hệ
dưới ây, hãy cho biết quan hệ nào là một hàm và tìm ánh xạ tương ứng a) ℛ = {( , ) ∈ / = + 7} b) ℛ = {( , ) ∈ / = } c) ℛ = {( , ) ∈ / = 3 + 1} d) ℛ = {( , ) ∈ / + = 1} e)
ℛ = {( , ) ∈ [0,1] × [0,1]/ + = 1} 5. Giả sử = = . Hãy tìm
(ℛ) và (ℛ) cho các quan hệ ℛ sau ây: a) ℛ = {( , ) ∈ × / = } b) ℛ = {( , ) ∈ × / = cos } c) ℛ = {( , ) ∈ × / + = 1} 6.
Giả sử = { , , , , , } (mã số các loại ngũ cốc), = = = = . Xét quan hệ ℛ giữa các tập , , , , cho bởi bảng dưới ây: L.Vitamin A/ L.Vitamin C/ Mã số Lượng ường/ vtt vtt vtt L.Protein/ vtt U 1 25 25 6 V 7 25 2 4 W 12 25 2 4 X 0 60 40 20 Y 32 25 40 10 Z 2 25 40 10 a)
Hãy tìm quan hệ chiếu của ℛ lên × × b)
Một thuộc tính ược nói là khóa chính của quan hệ ℛ nếu giá trị của nó xác ịnh duy
nhất một bộ 5 thuộc ℛ. Hãy tìm các khóa chính của ℛ. 7.
Giả sử = {1,2}, = { , , }, = = = . Xét quan hệ ℛ giữa , , , , cho bởi bảng dưới ây: lOMoARcPSD| 36667950 Loại viên Loại Vitamin Lượng Vitamin Liều lượng: Vitamin trong viên trong viên số viên/ ngày Số viên trong chai 1 A 10.000 1 100 1 D 400 1 100 1 E 30 1 100 2 A 4.000 1 250 2 D 400 1 250 2 E 15 1 250 a)
Tìm quan hệ chiếu của ℛ lên × và × × b)
Quan hệ này có khóa chính không? c)
Một khóa chính phức hợp là tích Descartes của một số tối thiểu thuộc tính sao cho
nếu gọi ℛ′ là quan hệ chiếu của ℛ lên tích Descartes ó, thì mỗi bộ trong ℛ’ là là
hình chiếu duy nhất của một bộ trong ℛ. Hãy xác ịnh các kháo chính phức hợp của ℛ. 8.
Hãy tìm quan hệ trên = {1,2,3,4} sao cho nó có tính chất a)
Phản xạ và ối xứng nhưng không bắc cầu b)
Phản xạ và bắc cầu nhưng không ối xứng c)
Đối xứng và bắc cầu nhưng không phản xạ 9.
Trong số các quan hệ dưới ây, hãy cho biết quan hệ nào có tính phản xạ, ối xứng, phản xứng, bắc cầu: a)
là một tập con cố ịnh của , xét quan hệ ℛ trên ( ): ℛ ⟺ ∩ ⟺ ∩ b) Quan hệ ℛ trên : ℛ ⟺ + chẵn c) Quan hệ ℛ trên : ℛ ⟺ − lẻ d) Quan hệ ℛ trên ×
: ( , )ℛ( , ) ⟺ ≤ chẵn e) Quan hệ ℛ trên : ℛ ⟺ + chẵn f)
Quan hệ ℛ trên : ℛ ⟺ | | = | | g)
Quan hệ ℛ trên : ℛ ⟺ sin + cos = 1
10. ℛ là một quan hệ trên tập hợp với phần tử. Cho biết các khẳng ịnh dưới ây úng hay
sai. Nếu sai, chỉ ra một phản ví dụ: a) Nếu ℛ phản xạ thì |ℛ| ≥
b) Nếu |ℛ| ≥ thì ℛ phản xạ
c) Nếu ℛ và ℛ là hai quan hệ trên sao cho
phản xạ thì ℛ phản xạ
d) Kết luận tương tự như c) cho tính ối xứng, phản xứng và bắc cầu
e) Nếu ℛ và ℛ là hai quan hệ trên sao cho
phản xạ thì ℛ phản xạ
f) Kết luận tương tự như e) cho tính ối xứng, phản xứng và bắc cầu
11. Giả sử là một quan hệ trên A, quan hệ ối ngẫu của ược ịnh nghĩa bởi: ℛ∗ ⟺ ℛ a)
Quan hệ ối ngẫu của ℛ∗ là gì? b)
Có thể nói gì về ℛ nếu ℛ = ℛ∗ c)
Nếu ℛ bắc cầu thì ℛ∗ có bắc cầu không? Câu hỏi tương tự cho tính ối xứng, phản xứng.
12. = {1,2,3,4}. Xác ịnh số quan hệ trên A có tính chất: a) phản xạ b) ối xứng c) phản xạ và ối xứng lOMoAR cPSD| 36667950 d) phản xứng e) ối xứng và phản xứng f)
phản xạ và ối xứng và phản xứng
13. Giả sử | | = và ℛ là tập hợp con tối ại của × sao cho ℛ là một quan hệ phản xứng. Tìm
số phần tử của ℛ. Có bao nhiêu quan hệ ℛ thỏa iều kiện trên? 14. = {1,2,3,4,5,6},ℛ =
{(1,1),(1,2),(2,1),(2,2),(3,3),(4,4),(4,5),(5,4),(5,5),(6,6)}. a)
Kiểm tra lại ℛ là một quan hệ tương ương b)
Tìm các lớp tương ương [1],[2],[3]. c)
Tìm phân hoạch của thành các lớp tương ương
15. = {1,2,3,4,5}. Tìm quan hệ tương ương ℛ trên sao cho phân hoạch của thành các lớp tương ương có dạng: = {1,2} ∪ {3,4} ∪ {5} 16. = {1,2,3,4,5}, = {1,2}, = {2,3,4},
= {5}. Định nghĩa quan hệ ℛ trên như sau: ℛ ⟺ ∃ :1 ≤ ≤ 3 và ,∈
ℛ có phải là quan hệ tương ương không?
17. Xét quan hệ ℛ trên = sao cho : ( , )ℛ( , ) ⟺ =
a) Kiểm tra lại ℛ là một quan hệ tương ương
b) Chỉ ra các lớp tương ương và cho biết ý nghĩa hình học 18. = {1,2,3,4,5}
× {1,2,3,4,5} và ℛ là quan hệ trên sao cho: ( , )ℛ( , ) ⟺ + = +
a) Kiểm tra lại ℛ là một quan hệ tương ương
b) Xác ịnh các lớp tương ương [(1,3)],[(2,4)] và [(1,1)]
c) Chỉ ra phân hoạch của thành các lớp tương ương 19.
a) Quan hệ ℛ trong 9a) có phải tương ương không?
b) Với = {1,2,3} và = {1,2}. Tìm phân hoạch của ( ) thành các lớp tuong ương
c) Với = {1,2,3} và = {1,2}. Tìm lớp tương ương [{1,3,5}]. Có bao nhiêu lớp tương ương khác nhau?
20. Quan hệ ℛ trên ược ịnh nghĩa bởi: ℛ ⟺ ∃ ∈ : 2 a)
Kiểm tra lại ℛ là một quan hệ tương ương b)
Trong số các lớp tương ương [1], [2], [3], [4] có bao nhiêu lớp ôi một phân biệt? c)
Câu hỏi tương tự như b) sao cho các lớp [6],[7], [21], [24], [25], [35], [42] và [48]
21. Có bao hiêu quan hệ tương ương trên = { , , , , , } sao cho: a)
Có úng hai lớp tương ương với 3 phần từ b)
Có một lớp tương ương với 3 phần tử c)
Có một lớp tương ương với 4 phần tử d)
Có ít nhất một lớp tương ương với ≥ 3 phần tử.
22. Xét một ánh xạ : ⟶. Định nghĩa ℛ trên như sau: ℛ ⟺ ( ) = ( ) a)
Chứng minh rằng ℛ là một quan hệ tương ương b)
Xác ịnh các lớp tương ương lOMoARcPSD| 36667950
23. | | = 30 và ℛ là một quan hệ tương ương trên sao cho ược phân hoạch thành 3 lớp tương
ương , , với cùng số phần tử. Hãy xác ịnh ℛ
24. = {1,2,3,4,5,6,7}. Hãy tìm một quan hệ tương ương ℛ trên sao cho |ℛ| cho các giá trị: 6, 7, 8, 9, 11, 22, 23, 30, 31.
25. Vẽ biểu ồ Hasse cho tập hợp sắp thứ tự ( ( ),⊂) trong ó = {1,2,3,4}
26. Xét hai tập hợp thứ tự tập hợp thứ tự ( ,≺ ) và ( ,≺ ). Với ( , ),( , ) ∈ × ịnh nghĩa: ( , ) ≺ ( , ) ⟺ ( ≺ ) ∧ ( ≺ ) a)
Chứng minh rằng quan hệ trên là một thứ tự b)
Nếu ≺ và ≺ là thứ tự toàn phần thì ≺ có là thứ tự toàn phần không?
27. Cho trước hai tập hợp , và ≺ là một thứ tự trên . ta ịnh nghĩa quan hệ ≺ trên như sau: ≺ ⟺ ∀ ∈ , ( ) ≺ ( ) a)
Chứng minh rằng ≺ là một thứ tự trên b)
Nếu ( ,≺ ) là một dàn, chứng minh rằng ( ,≺) là một dàn
28. Giả sử ℛ là một quan hệ bắc cầu trên . Gọi ℛ∗ là quan hệ ối ngẫu của ℛ như trong bài
tập 11. Chứng minh rằng ℛ là một thứ tự khi và chỉ khi
ℛ ∩ ℛ∗ = ∆ = {( , )/ ∈}
29. Chứng minh rằng thứ tự tự iển trên tập hợp các chuỗi ký tự thật sự là một thứ tự. hơn
nữa S ược sắp thứ tự toàn phần bởi quan hệ trên.
30. Giả sử ≺ là một thứ tự không toàn phần trên , và là một tập hợp con khác ∅ của . Khi
ấy thứ tự cảm sinh trên bởi ≺ có nhất thiết là thứ tự không toàn phần không?
31. Trong các biểu ồ sau, cái nào là biểu ồ Hasse của một tập hợp sắp thứ tự:
32. Có bao nhiêu thứ tự trên tập dưới ây ể cho là một phần tử tối tiểu? a) = { , } b) = { , , }
33. Giả sử = ( ) với = {1,2,3}. Trong tập hợp A với thứ tự bao hàm, hãy tìm sup và inf của tập hợp con ⊂ dưới ây: a) = {1},{2} b) = {1},{2},{3},{1,2} c) = ∅,{1},{2},{1,2} d) = {1},{1,2},{1,3},{1,2,3} e) = {1},{2},{3},{1,2},{1,3},{2,3} f) =
{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3} lOMoAR cPSD| 36667950
34. Giả sử = ( ) với thứ tự bao hàm trong ó = {1,2,3,4,5,6,7}. Xét = {1},{2},{2,3} . Hãy cho biết: a)
Số chặn trên của bao gồm 3,4,5 phần tử của b)
Số tất cả chặn trên của c) sup d)
Số tất cả chặn dưới của e) inf
35. Giả sử ( ,≺) là một tập hợp sắp thứ tự. Cho biết các khẳng ịnh dưới ây úng hay sai? Tại sao? a)
Nếu ( ,≺) là một dàn thì ≺ là thứ tự toàn phần b)
Nếu ≺ là thứ tự toàn phần thì ( ,≺) là một dàn
36. Giả sử ( ,≺) là một dàn và là một phần tử tối ại của . Khi ấy là phần tử lớn nhất. Kết
luận tương tự cho phần tử tối tiểu.
37. Giả sử = { , , , , , , , , , } với thứ tự xác ịnh bởi biểu ồ Hasse dưới ây. Hãy tính: a) inf { , } b) inf { , } c) inf { , } d) sup { , } e) sup { , } f) sup { , } g) sup { , } z x t y v e c d a
38. Với ( ,≺) như trong bài tập 37 a)
có phần tử lớn nhất và bé nhất không không? b)
( ,≺) có là một dàn không?
39. Trên tập hợp ℳ các dạng mệnh ề với thứ tự “có hệ quả logic” (⟹), chứng minh rằng
sup và inf của một tập hợp con hữu hạn ℇ = { , ,…, } chính là các dạng mệnh ề ∨ ∨ …∨
(nối rời) và ∧ ∧ …∧ (nối liền).
40. Một tập hợp thứ tự ≺ trên tập hợp A ược nói là thứ tự tốt nếu mọi tập hợp con A khác ∅
của A ều có phần tử bé nhất. khi ấy ta nói ( ,≺) ược sắp tốt. a)
Chứng minh rằng mọi thứ tự tốt ều là toàn phần. Điều ngược lại có úng không? b)
Chứng minh rằng mọi tập hợp sắp thứ tự tốt có phần tử bé nhất. c)
Cho ví dụ của một tập hợp sắp tốt không có phần tử lớn nhất, và ví dụ của một tập
hợp sắp tốt có phần tử lớn nhất.
41. Trong các tập hợp sắp thứ tự dưới ây, cho biết tập hợp nào sắp thứ tự tốt: a) ( ,≤) b) ( ,≤) c) ( ,≤) d) ( ,≤) lOMoARcPSD| 36667950 e)
( ,≤) trong ó là tập hợp các số nguyên tố f) ( ,≤) trong ó
là tập hợp con hữu hạn của Z g)
( ,≺) trong ó là tập hợp các chuỗi ký tự trên một tập hợp mẫu tự sắp thứ tự toàn
phần và ≺ là thứ tự tự iển.
42. Giả sử ( ,≺) là một tập hợp sắp thứ tự tốt không có phần tử tối ại a)
Chứng minh rằng mỗi phần tử x ều có trội trực tiếp duy nhất ( ) b)
Chứng minh rằng ánh xạ : ⟶ là ơn ánh. Ánh xạ này có toàn ánh không? c)
Giả sử ( ) bằng trừ i một iểm. chứng minh rằng ( ,≺) ẳng cấu với ( ,≤) 43. Tìm ước
số chung lớn nhất của các cặp số sau: a) 43,16 b) 442,276 c) 6234,3312 d) 87657,44441 e) 654321,123456 44.
a) Phân tích 2 số sau ra thừa số nguyên tố: 148.500 và 7.114.800
b) Hãy tìm USCLN và BSCNN của chúng
45. Giả sử số có phân tích ra thừa số nguyên tố: = …
Hãy tìm phân tích ra thừa số nguyên của ,
46. Hãy tìm phân tích ra thừa số nguyên của 8!, 10!, 12! và 15! 47.
a) Hãy tìm ra các ước số dương của 2 5 7
b) Giả sử có phân tích ra thừa số nguyên tố =
Tìm số các ước dương của
c) Tổng quát hóa kết quả trên cho trường hợp có nhiều hơn 3 ước số nguyên tố
d) Suy ra nếu số các ước số dương của là lũy thừa của 2 thì trong phân tích của thành
thừa số nguyên tố, các số mũ ều có dạng 2 − 1,∈ 48. a) Số = 2 3 5 7
11 13 37 có bao nhiêu ước số?
b) Có bao nhiêu ước số dương của chia hết cho 2 3 5 11 37 ?
c) Có bao nhiêu ước số dương của chia hết cho 1.166.400.000
49. Có 200 ồng xu ược ánh số từ 1 ến 200 ặt thành hàng nganh trên bàn và 200 sinh viên
cũng ược ánh số từ 1 ến 200. Sinh viên thứ nhất sẽ lật ngược tất cả các ồng xu lại. Tiếp
theo sinh viên thứ 2 lật ngược ồng xu thứ 2,4,6,… Sinh viên thứ n, 1≤
≤200, lật ngược ồng xu thứ ,2 ,3 ,…
a) Hỏi ồng xu thứ 200 ược lật ngược bao nhiêu lần?
b) Có ồng xu nào có số lần bị lật ngược như ồng xu thứ 200 không? lOMoARcPSD| 36667950
50. Hãy viết một chương trình máy tính cho phép phân tích số nguyên > 1 ra thừa số nguyên tố.
51. Tìm số nguyên dương có úng: a) hai ước số dương b) ba ước số dương c) bốn ước số dương d) năm ước số dương
52. Cho hai số nguyên dương , a) Giả sử ( )) của phương
, ) = 1. Hãy tìm tất cả các lời giải (nghĩa là các cặp ( , trình =
b) Câu hỏi tương tự nhưng không giả thiết , nguyên tố cùng nhau
c) Hãy tìm số các cặp số nguyên , thỏa: + = ( , )
53. Hãy tìm các cặp ( , ) thỏa hệ thức + =
( , ) trong các trường hợp sau: a) = 46, = 16 b) = 124, = 64 c) = 3450, = 331
54. Cho trước số nguyên > 1. Ta nói ∈ khả nghịch (mod ) nếu tồn tại ’ ∈ sao cho: ’ ≡ 1 (mod ) a)
Chứng minh rằng nếu khả nghịch (mod ) thì phương trình ồng dư ≡ (mod
) có nghiệm duy nhất trong b)
Nếu không khả nghịch mod thì sao?
55. Hãy giải các hệ thức ồng dư dưới ây (tìm tất cả các số ồng dư): a) 3≡ 7 (mod 14) b) 5 + 7 ≡ 6 (mod 23) d) 4 + 3 ≡ 7 + 12 (mod 11) d) 3 + 9 ≡ 8 + 61 (mod 64) lOMoARcPSD| 36667950
CHƯƠNG 4: ĐẠI SỐ BOOL VÀ HÀM BOOL
§1 ĐẠI SỐ BOOL
Định nghĩa 4.1.1: Một ại số Bool là tập hợp cùng với hai phép tính (hai ngôi) ∨ và ∧ thỏa mãn các tính chất sau i.
Tính kết hợp: với mọi , ,∈:
∨ (∨) = (∨) ∨ và ∧ (∧) = (∧) ∧ ii. Tính
giao hoán: với mọi , ,∈:
∨ = ∨ và ∧ = ∧ iii. Tính phân bố: với mọi , ,∈:
∨ (∧) = (∨) ∧ (∨) và ∧ (∨) = (∧) ∨ (∧) iv.
Phần tử trung hòa: tồn tại hai phần tử trung hòa 0,1 ối với hai phép toán ∨,∧ sao cho với mọi ∈ ta có: ∨ 0 = và ∧ 1 = v.
Phần tử bù: với mọi ∈, tồn tại ∈ sao cho: ∨ ̅ = 1 và ∧ ̅ = 0 Ví dụ:
1. Một dàn bù phân bố là một ại số Bool với hai phép tính ∨,∧ chính là sup và inf của hai
phần tử. Đặc ( ) là một ại số Bool dối với các phép tính tập hợp ∪ và ∩. Cũng thế ℳ
cũng là một ại số Bool ối với các phép nối rời ∨ và nối liền ∧ của hai dạng mệnh ề. Do
30 không chia hết cho chính phương, là dàn bù phân bố và do ó là một ại số Bool ối với các phép toán : ∨ = ( , ) và ∧ = ( , )
2. Tập hợp = {0,1} là một ại số Bool dối với các phép toán : ∧ = ∨ = + −
Phần bù của chính là ̅ = 1 −
Đại số Bool này óng vai trò quan trọng trong lý thuyết về các hàm Bool.
Chú ý: phần bù ̅ của phần tử là duy nhất và hơn nữa ta có qui tắc De Morgan (Bài tập).
∨ = ̅ ∧ và ∧ = ̅ ∨ Trong các ví dụ trên, các phép toán lOMoARcPSD| 36667950 ại số Bool ược ịnh nghĩa còn tự nhiên hơn cấu trúc thứ tự của dàn bù phân
bố. vấn ề ược ặt ra là liệu có thể suy cấu trúc của dàn bù phân bố từ cấu trúc ại số Bool không? Định lý sau ây là câu trả lời:
Định nghĩa 4.1.1: trong ại số Bool , ịnh nghĩa quan hệ: ≺ ⟺ ∧ =
Khi ấy ≺ là một thứ tự trên sao cho là một dàn bù phân bố ối với thứ tự này.
Hơn nữa, với ,∈ ta có: sup( , ) = ∨ inf( , ) = ∧
Chứng minh: Trước hết ta kiểm tra ≺ là một thứ thự trên . Với mọi ∈ ta có: ∧ ̅ = ∧ ( ∨ ̅) = ∧ 1 = (4.1.1) nghĩa là ≺
Mặt khác với ,∈ sao cho ≺ và ≺ ta có:
Do tính giao hoán của ∧ ta có =
Với , ,∈ sao cho ≺ và ≺ ta có: ∧ = à ∧ = Suy ra ∧ = (∧) ∧ = ∧ (∧) = ∧ = nghĩa là ≺
Tóm lại ≺ là một thứ tự trên . lOMoARcPSD| 36667950 Với ,∈ tùy ý, ta có (∧) ∧ = (∧) ∧ Nhưng nên (∧) ∧ = ∧ nghĩa là ∧ ≺ tương tự ∧ = ∧ ≺
Như thế ∧ là chặn dưới chung của ,
Gọi là một chặn dưới chung bất kỳ của , . Ta có: Do ó ∧ (∧) = (∧) ∧ = ∧ = nghĩa là ≺ ∧ Như thế ∧ = inf( , )
Bây giờ do iv) của Định nghĩa 4.1.1, 1 chính là phần tử lớn nhất. Mặt khác, với ∈ tùy ý: ∧ ̅ = (0 ∨ ̅) ∧
= ̅ ∧ = 0 (4.1.1) nghĩa là 0 là phần tử bé nhất của .
Sau cùng với mọi ,∈, ta có: Mà 0 ∧ nên
∧ (∨) = ∨ 0 = nghĩa là ≺ ∨ Tương tự ≺ ∨ = ∨
Gọi là mộ chặn trên chung của , ta có: nghĩa là ∨ ≺ Như thế ∨ = sup( , )
Tóm lại là một dàn phân bố với phần tử lớn nhất và bé nhất là 1,0. Hơn nữa, do
v) của Định lý 4.1.1 ̅ chính là phần bù của . lOMoARcPSD| 36667950 pcm
Do Định lý 4.1.1, mỗi ại số Bool hữu hạn ược liên kết với một biểu ồ Hasse. Ta hãy
quan sát aho ại số Bool và ({ , , }). Tuy ược ịnh nghĩa khác nhau, các ại số Bool này có hai
biểu ồ Hasse “ ồng dạng” 15 30 { , } { , , } 5 10 { } { , } 3 6 { } { , } 1 ∅ 2 { }
Từ hai biểu ồ trên ta có thể xây dựng một song ánh giữa và ({ , , }) sao cho các ỉnh
tương ứng với nhau 1 ⟼ ∅,2 ⟼ { },3 ⟼ { },… và hai ỉnh ược nối bởi một cạnh của sẽ tương
ứng với hai ỉnh ược nối bởi một cạnh của
({ , , }). Nói cách khác ta có một ẳng cấu giữa
các tập hợp có thứ tự. Do Định lý 3.4.1 sup và inf của hai phần tử , trong tương ứng với
sup, inf của ( ), ( ). Nói cách khác là một ẳng cấu giữa các ại số Bool theo ịnh nghĩa sau:
Định nghĩa 4.1.2: một ẳng cấu giữa hai ại số Bool và ℬ là một song ánh :⟷ ℬ sao cho với mọi ,∈ ta có: (∨) = ( ) ∨ ( ) và (∧) = ( ) ∧ ( )
Mệnh ề 4.1.2: nếu : ⟷ ℬ là một ẳng cấu Đại số Bool thì cũng là ẳng cấu tập hợp có thứ tự
với thứ tự trên và ℬ xác ịnh bởi Định lý 4.1.1. Đặc biệt nếu 0,1 là phần tử trung hòa của ∨,∧
trong ℬ thì (0), (1) là phần tử trung hòa của ∨,∧ trong ℬ.
Chứng minh: giả sử , là hai phần tử trong
sao cho ≺. Khi ấy ta có: ∧ = ⟹( ) ∧ ( ) = ( ) ⟹ ( ) ≺ ( )
Do 0 và 1 cũng là phần tử bé nhất và lớn nhất của , ta thấy (0) và (1) cũng là phần tử
bé nhất và lớn nhất của ℬ, nghĩa là phần tử trung hòa ối với các phép toán ∨,∧ trong ℬ pcm
Trở lại hai ại số Bool và ({ , , }). Sự ẳng cấu của chúng không phải là trường hợp cá biệt. Ta có:
Đinh lý 4.1.3 (Stone): một ại số Bool hữu hạn luôn lương ẳng cấu với ( ), trong ó là một tập hợp hữu hạn.
Hệ quả 1: Số phần tử của một ại số Bool hữu hạn là một ũy thừa của 2.
Hệ quả 2: Hai ại số Bool hữu hạn có cùng số phần tử thì ẳng cấu với nhau. lOMoARcPSD| 36667950
Chứng minh: Thật vậy hai ại số Bool cho trước sẽ ẳng cấu với như sau: : ( ) → ( ) ⟼( )
Khi ấy ta có: (∪) = ( ) ∪ ( ) nghĩa là (∨) = ( ) ∨ ( )
Hơn nữa do là song ánh ta cũng có:
(∩) = ( ) ∩ ( ) nghĩa là (∧) = ( ) ∧ ( ) pcm
Bây giờ ể chứng minh Định lý Stone ta cần tìm tập hợp . Để ý rằng ta có một ơn ánh: : →( ) ⟼ { }
Hơn nữa trong ( ) các tập hợp { } chính là các trội trực tiếp của ∅. Từ ó ta có:
Định nghĩa 4.1.3: trong một ại số Bool
, một trội trực tiếp của phần tử bé nhất ược
sọi là một nguyên tử của .
Bổ ề 4.1.4: Giả sử là một ại số Bool hữu hạn với phần tử bé nhất 0. Khi ấy mọi phần tử ≠ 0
ều có thể viết dưới dạng: = ∨ ∨ …∨ trong ó { , ,…,
} là tập hợp các nguyên tử trội bởi . Hơn nữa nếu , ,…,
là các nguyên tử sao cho: = ∨ ∨ …∨ thì { , ,…, } = { , ,…, }
Chứng minh: Trước hết \ {0} là một tập hợp sắp thứ tự hữu hạn chứa (≠ 0) nên tồn tại một
phần tử tối tiểu ≺. Rõ ràng là một nguyên tử của . Nói cách khác tập hợp { , ,…, } các nguyen
tử trội bởi là không ∅. Đặt = ∨ ∨ …∨ Rõ ràng ≺.
Ta có: = ∧ (∨) = (∧) ∨ (∧) = ∨ (∧) Giả sử (∧) ≠ 0
Khi ấy theo trên tồn tại một nguyên tử ≺
∧ . Như thế = với 1 ≤ ≤ nào ó Đặt = ∨ ∨ …∨ ∨ ∨ …∨ Ta có = ∨ Do ó = ∧ Suy ra : mâu thuẫn.
Như thế (∧) = 0 nghĩa là = Sau cùng giả sử , ,…,
là các nguyên tử trội bởi sao cho = ∨ ∨ …∨ lOMoAR cPSD| 36667950 Ta có : { , ,…, } ⊂ { , ,…, }
Mặt khác, với mỗi cố ịnh, 1 ≤ ≤ ta có: = ∧ = ∧ ∨ ∧ ∨ … ∧
Suy ra tồn tại sao cho 1 ≤ ≤ và 0 ≠ ∧ ≺
Do là nguyên tử ta có: ∧ = nghĩa là ≺ Do
là nguyên tử và ≠ 0 ta có = Như thế { , ,…, } ⊂ { , ,…, } Nghĩa là { , ,…, } = { , ,…, } pcm
Gọi là tập hợp tất cả các nguyên tử của
. Nhờ Bổ ề 4.1.4, ta có một ánh xạ : →
( ) ược ịnh nghĩa như sau: (0) = ∅
nếu ≠ 0 thì ( ) là tập hợp tất cả các nguyên tử trội bởi . Bây giờ Định
lý 4.1.3 là hệ quả của
Định lý 4.1.5: là một ẳng cấu giữa và ( ).
Chứng minh: Giả sử 0 ≠ ≺ . Khi ấy các nguyên tử trội bởi cũng là nguyên tử trội bởi nên ( ) ⊂ ( )
Ngược lại giả sử 0 ≠ ( ) ⊂ ( ) Ta viết ( ) = { , ,…, } và ( ) = { , ,…, } Do Bổ ề 4.1.4 ta có:
= ∨ ∨ …∨ và = ∨ ∨ …∨ Do { , ,…, } ⊂ { , ,…, } nên ≺
Trường hợp = 0 là hiển nhiên.
Tóm lại, ta ã chứng minh: (≺) ⟺ ( ) ⊂ ( ) Đặc biệt nếu ( ) = ( ) thì ≺ và ≺ nên = : là ơn ánh.
Sau cùng, giả sử { , ,…, } ⊂ Đặt = ∨ ∨ …∨ và ( ) = { , ,…, } Do Bổ ề 4.1.4 lOMoARcPSD| 36667950 = ∨ ∨ …∨ và { , ,…, } = { , ,…, }. Như thế là toàn ánh. pcm §2 HÀM BOOL
Xét sơ ồ mạch iện gồm 3 ngắt iện:
Tùy theo các ngắt iện , , ược óng hay mở sẽ có dòng iện i từ ến hay không. Để biết
các ngắt iện iều khiển việc cho dòng iện i qua hay không, ta vẽ ra sơ ồ cho tất cả mọi trường
hợp. Tuy nhiên iều này không thực hiện ược nếu số ngắt iện quá lớn. Ví dụ nếu có 100 ngắt
iện sẽ có 2 sơ ồ khác nhau. Ngay cả trong trường hợp số ngắt iện bé, thì vẫn cần một cách
sắp xếp có hệ thống các sơ ồ ể có thể tra cứu dễ dàng từng trường hợp.
Chẳng hạn ta có thể liên kết với mỗi ngắt iện một biến lấy giá trị 1 nếu ngắt iện óng
và 0 nếu ngắt iện mở. Trong ví dụ về mạch iệm nói trên ta có ba biến , , . Ngoài ra toàn mạch
iện cò ược liên kết với biến lấy giá trị 1 nếu có dòng diện i từ ến và lấy giá trị 0 trong
trường hợp không có dòng diện nào i từ ến . với tương ứng như vậy ta có thể liệt kê tất cả
các trường hợp trong bảng giá trị như sau: 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1
Trong trường ngắt iện lớn thì việc lập bảng giá trị là không thực tế. Ta cần tìm một
công thức cho phép biểu diễn hàm ( , , )
theo các biến , , như các hàm a thức trong
trường hợp hàm biến thực chẳng hạn. Mặt khác ta cũng nhận xét rằng bảng trên rất giống
bảng chân trị của các dạng mệnh ề. Thật ra khi khảo sát các dạng mệnh ề, iều ta quan tâm
không phải là mệnh ề thu ược ( , , ,…) khi ta thay các biến mệnh ề , , ,… lần lượt bởi các mệnh lOMoAR cPSD| 36667950
ề , , ,… mà là sự phụ thuộc chân trị của mệnh ề ( , , ,…) vào chân trị các mệnh ề , , ,… Nói
cách khác ta ồng nhất dạng mệnh ề ( , , ,…) với bảng chân trị của nó. Thực chất ở ây là ta
ang xem xét hàm ( , , ,…) theo các biến
, , ,… trong ó , , ,… và cả ( , , ,…) cũng chỉ lấy hai giá trị 0,1. Đó là các hàm Bool theo ịnh nghĩa dưới ây:
Định nghĩa 4.2.1: một hàm Bool biến là một ánh xạ → , trong ó = {0,1}. Tập hợp các hàm
Bool biến ược ký hiệu bởi ℱ . Chú ý:
1. Các hàm Bool còn ược gọi là hàm logic hay hàm nhị phân
2. Nhắc lại tập hợp là ại số Bool ối với các phép toán ∧ = ∨ = + − = 1 −
3. Các biến xuất hiện trong hàm Bool ược gọi là biến Bool. Mỗi hàm Bool ược liên kết với
một bảng tương tự như bảng trên cho biết sự phụ thuộc của hàm Bool theo giá trị
các biến Bool. Ta cũng gọi bảng giá trị này là Bảng chân trị của hàm Bool.
4. Theo ký hiệu của Chương 3 ℱ chính là tập hợp 2
. Do ó số hàm Bool khác nhau chính là |ℱ | = 2| | = 2( )
Mặt khác trong §1, tương ứng ⟼ là một ẳng cấu của tập hợp có thứ tự ( ) và ℱ
trong ó thứ tự trên ℱ ược xác ịnh như sau: với ,∈ ℱ thì ≺ ⟺ ∀ = ( , ,…, ) ∈ , ( ) ≤ ( )
Khi ấy sup và inf của hai hàm , ược cho bởi: (∨)( ) = ( ) ∨ ( ) = ( ) + ( ) − ( ) ( ),∀ ∈ và (∧)( ) = ( ) ∧ ( ) = ( ) ( ),∀ ∈
và phần bù ̅ của hàm Bool ược cho bởi ̅( ) = ( ) = 1 − ( ),∀ ∈
Ta sử dụng ký hiệu thông thường và 1 − ể chỉ các hàm ∧ và ̅ trong ó 1 chỉ hàm hằng → {1}
Với các phép toán trên, ℱ trở thành một ại số Bool ẳng cấu với ( ). Đặc biệt các nguyên
tử trong ℱ sẽ tương ứng với các nguyên tử trong ( ). mà trong ( ) các nguyên tử chính là các
tập hợp thu về một iểm nên ta có: lOMoAR cPSD| 36667950
Mệnh ề 4.2.1: các nguyên tử trong ℱ là các hàm Bool chỉ khác 0 tại iểm duy nhất, hay nói
cách khác, bảng chân trị của nó chỉ có một dòng duy nhất ở ó hàm khác 0. Các này dược gọi
là các từ tối tiểu của ℱ . Do Định lý Stone ta có:
Định lý 4.2.2: mỗi hàm Bool ều ược viết dưới dạng: = ∨ ∨ …∨ (4.2.1) trong ó , ,…,
là các từ tối tiểu trội bởi .
Do từ tối tiểu chỉ khác 0 ở duy nhất một dòng, sẽ ược trội bởi khi và chỉ khi dòng
mà khác 0 cũng là một trong những dòng mà khác 0. Từ ó ta có qui tắc viết ra công thức
(4.2.1) bằng cách chọn chính là các từ tối tiểu tương ứng với một dòng khác 0 nào ó của .
Chẳng hạn như trong ví dụ về hàm ( , , )
biểu diễn mạch iện ở trên ta có 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 1 0 0 1 0 1 0 0 0 1 0 1 1 0 0 1 0 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 0 0 0 1 Ta có = ∨ ∨ ∨ ∨ (4.2.2)
Bây giờ ể có một công thức tường minh cho một hàm Bool bất kỳ, do (4.2.1) ta cần
tìm một công thức tường minh cho tất cả các từ tối tiểu. Nhắc lại phép chiếu thứ ược cho bởi: :→ ( , ,…, ) ⟼
Rõ ràng bản thân là một hàm Bool biến mà giá trị của nó chỉ phụ thuộc vào biến thứ
. Tương tự như trường hợp các hàm thực, ta sẽ dùng cùng ký hiệu dể chỉ hàm Bool : ( , ,…, ) =
Vớik ý hiệu này thì phần bù ̅ = 1 − cũng là một hàm Bool mà giá trị chỉ phụ thuộc vào
biến thứ . Ta nói ,̅ là các từ ơn. Có tất cả 2 từ ơn.
Mệnh ề 4.2.3: các từ tối tiểu ều có thể viết dưới dạng: = … trong ó = hay = ̅
Chứng minh: giả sử là từ ơn bằng hay ̅ . Ta sẽ chứng minh = … là một từ tối tiểu. Chính
xác hơn gọi = ( , ,…, ) là các phần tử của sao cho = 1 nếu = và = 0 nếu = ̅ . Ta sẽ chứng minh
rằng khác 0 duy nhất tại . lOMoARcPSD| 36667950
Thật vậy với 1 ≤ ≤ ta có: ( ) = ( ) = = 1 nếu = và ( ) = ̅ ( ) = = 1 nếu = ̅
Như thế ( ) = 1 với 1 ≤ ≤ Suy ra ( ) = 1 Mặt khác nếu = ( , ,…,
) ≠ thì tồn tại sao cho 1 ≤ ≤ và ≠ . Khi ấy:
( ) = ( ) = = 0 (vì ≠ ) nếu = và ( ) = ̅ ( ) = = (vì = ) nếu = ̅
Như thế ( ) = 0 và do ó ( ) = 0
Tóm lại là từ tối tiểu tương ứng với iểm .
Ngược lại giả sử là từ tới tiểu khác 0 duy nhất tại iểm = ( , ,…, ). Đặt:
= nếu = 1 và = ̅ nếu = 0
Khi ấy theo chứng minh trên, … là từ tối tiểu tương ứng với iểm = ( , ,…, ) sao cho: = 1 nếu = và = 0 nếu = ̅ nói cách khác Do ó = … pcm Chú ý:
1. Do mỗi có thể lấy hai giá trị , ̅ nên ta tìm lại ược số từ tối tiểu chính là số phần tử của ∶ 2 .
2. Ta có qui tắc ể viết biểu thức của một từ tối tiểu ứng với iểm = ( , ,…, ): viết tích của
tất cả các biến … , sau ó biến thứ mà = 0 sẽ ược gạch ầu. Chẳng hạn trong ví dụ về
mạch iện ở trên các từ tối tiểu , ,…, có biểu diễn như sau: = = ̅ ̅ Do ó (4.2.2) trở thành: = ∨ ̅ ∨ ∨ ̅ ∨
Ở ây ta sử dụng quy ước về thứ tự ưu tiên của phép tính nhân dối với phép toán ∨:
công thức ∨ có nghĩa là phép toán ược thực hiên trước rồi mớit hực hiện phép toán ∨ giữa
và . Nói cách khác ∨ = ( ) ∨
Ngược lại nếu thực hiên phép ∨ trước ta phải viết: (∨)
3. Tổng quát hơn, do (4.2.1) và Mệnh ề 4.2.3 một hàm Bool bất kỳ có thể viết như là
tổng Bool của các từ tối tiểu trội bởi , và mỗi từ tối tiểu này ược viết như là tích của
ủ biến. Công thức này ược gọi là dạng nối rời chính tắc của . lOMoARcPSD| 36667950
4. Thay vì các từ tối tiểu, ta có thể xét các từ tối ại: ó là phần bù của các từ tối tiểu. Khi
ấy do Mệnh ề 4.2.3, mỗi từ tối ại sẽ là tổng Bool của từ ơn. Hơn nữa áp dụng (4.2.1)
cho ̅, ta có thể viết như là tích của các từ tối ại: ây chính là dạng nối liền chính tắc của
hàm Bool . Từ ây ta chỉ ể ý ến dạng nối rời chính tắc và tổng quát hơn các công thức
a thức theo nghĩa dưới ây: Định nghĩa 4.2.1: i.
Một ơn thức là một tích khác 0 của các từ ơn ii.
Một công thức a thức của hàm Bool là công thức biểu diễn dưới dạng tổng Bool của các ơn thức.
Chú ý: Do = và ̅ = 0 nên trong một ơn thức , biến và ̅ có thể xuất hiện nhưng không ồng
thời xuất hiện. Nói cách khác mỗi ơn thức có thể viết như là tích
… trong ó lấy một trong 3 giá trị 1,
,̅ . Do ó số ơn thức khác nhau là 3 . suy ra
mỗi hàm Bool chỉ có một số hữu hạn công thức a thức. Để ý rằng nếu ≠ 1, ta nói là
một thừa số của . Như thế mỗi ơn thức ược viết như là tích của tối a thừa số khác nhau.
§3 MẠNG CÁC CỔNG VÀ CÔNG THỨC ĐA THỨC TỐI TIỂU
Trong ví dụ về mạch iện ở §2, ta ã biểu diễn mạch iện dưới dạng một hàm Bool ể
khảo sát sự phũ thuộc của output (có dòng iện chạy qua hay không) theo các input
, , (ngắt iện tương ứng óng hay mở). Bây giờ ta hãy xét bài toán ngược lại: cho trước một
hàm Bool ( , , ,…). Hãy thiết kế một mạng các thiết bị vật lý cho phép tổng hợp nên hàm Bool
. Ở ây ta không quan tâm ến các thiết bị vật lý cụ thể mà chỉ ể ý ến các nối kết chúng trong
một mạng ể tổng hợp nên hàm Bool. Do Mệnh ề 4.2.2 và 4.2.3, mỗi hàm Bool ều có thể viết
thành một công thức trong ó các biến logic (biến Bool) ược nối kết lại với nhau bởi các phép
toán ∧,∨,−. Do ó ta cần phải tổng hợp các phép toán trên. Thiết bị ể tổng hợp các phép toán
này gọi là các cổng ược biểu diễn bởi các sơ ồ sau: ̅ ∨ Cổng NOT hay ảo iện Cổng AND Cổng OR
Tron các sơ ồ trên, và là hai tín hiệu vào với 2 trạng thái khác nhau cho phép chúng
biểu diễn ược các biến logic với hai giá trị 0,1. Ở ầu ra ta cũng có một tín hiêu biểu diễn cho
một biến logic phụ thuộc vào các input theo các phép toán ∧,∨,−.
Ví dụ: ể tổng hợp hàm Bool =
∨ ̅ , ta có thể sử dụng mạng với các cổng sau: lOMoARcPSD| 36667950
trong ó có hai cổng AND, 1 cổng OR và một cổng NOT.
Mặt khác ta cũng c2o thể viết hàm như sau: == ∨ ̅ ∨∨ ̅̅ ∨ ̅
Đây là dạng nối rời chính tắc của vì các số hạng ều là từ tối tiểu. nếu sử dung công
thức trên ể thiết kế một mạng các tổng hợp f, ta phải sử dụng 8 cổng AND và 3 cổng OR,
không kể một số cổng NOT.
Vấn ề ược ặt ra là làm sao tìm ược một công thứ tối ưu ể tổng hợp một hàm Bool cho trước.
3.1 Bài toán tối ưu ầu tiên là tìm cách giảm số loại cổng từ 3 xuống còn 2, hoặc nếu ược chỉ dùng một loại cổng.
Thật vậy, ta có thể tổng hợp cổng OR từ cổng NOT và cổng AND. Thật ra ta có thể
ặt hai cổng này chung thành một cổng có tên là NAND với sơ ồ:
Khi ấy các cổng NOT và các cổng AND có thể ược tổng hợp như sau:
Từ ó có thể tổng hợp cổng OR mà chỉ dùng cổng NAND như trong bài tập nêu trên.
Suy ra mọi hàm Bool ều ược tổng hợp mà chỉ dùng cổng NAND ta cũng có thể dùng cổng NOR với sơ ồ sau: ∨
Khi ấy ta cũng chứng minh ược mọi hàm Bool ều ược tổng hợp mà chỉ sử dụng cổng NOR.
3.1 Bài toán tối ưu tiếp theo là tối ưu hóa hai mục tiêu: lOMoAR cPSD| 36667950
Cực tiểu hóa thời gian châm trễ (delay): tuy thời gian chậm trễ khi i qua một cổng là
nhỏ nhưng nếu tích lũy qua nhiều lớp cổng thì nó trở thành áng kể, nhất là trong các máy tính có tốc ộ cao.
Cực tiểu hóa số cổng sử dụng
Do thời gian chậm trễ kho i qua cổng NOT là không áng kể, dưới ây khi phân tích các
mạch ta có thể bỏ qua cổng NOT. Nói cách khác các biến ̅, ,̅,… cũng ược xem như là các biến
input tương tự như , , ,…
Thật ra hai mục tiêu trên không thể ồng thời tối ưu hóa ược. Do ó trước hết ta tối ưu
hóa theo thời gian. Ta sẽ thiết kế các mạch chỉ có tối a hai lớp cổng: lớp cổng AND rồi lớp
cổng OR hay lớp cổng OR rồi lớp cổng AND. Tuy nhiên trường hợp sau luôn luôn có thể ưa
ược về trường hợp trước nếu ta xét ̅. Do ó ta chỉ xét các công thức có dạng OR (∨) của các
số hạng là AND (∧) của từ ơn. Đây chính là các công thức a thức
Trong lớp các công thức a thức, ta có một số thuật toán cho phép tìm ược công thức
a thức tối tiểu.
Định nghĩa 4.3.1: Xét hai công thức a thức của hàm Bool : = ∨ ∨ …∨ (4.3.1) = ∨ ∨ …∨ (4.3.2)
Ta nói (4.3.1) ơn giản hơn (4.3.2) nếu tồn tại một ơn ánh :{1,2,…, } → {1,2,…, } sao
cho với 1 ≤ ≤ thì số thừa số là từ ơn của không nhiều hơn số thừa số là từ ơn của . ( ) Chú ý:
1. Nếu (4.3.1) ơn giản hơn (4.3.2) thì ≤
2. Quan hệ “ ơn giản hơn” giữa các công thức a thức của rõ ràng có tính phản xạ và
bắc cầu. Tuy nhiên quan hệ này không phản xứng.
3. Nói rằng (4.3.1) ơn giản hơn (4.3.2) và (4.3.2) ơn giản hơn (4.3.1) có nghĩa là tồn tại các ơn ánh :{1,2,…, } → {1,2,…, } và :{1,2,…, } → {1,2,…, }
sao cho , thỏa Định nghĩa 4.3.1. Khi ấy , là song ánh và với 1 ≤ ≤ thì số thừa số là từ
ơn của không nhiều hơn số thừa số là từ ơn của ∘ . Do ó nếu gọi là số nguyên nhỏ ( ) nhất sao cho
(∘) ∘ (∘) ∘ …∘ (∘) ( ) = và = (∘) ∘ (∘) ∘ …∘ (∘)( )
thì và có thừa số là từ ơn bằng nhau.
Suy ra với 1 ≤ ≤ thì và
có thừa số là từ ơn bằng nhau. Khi ấy ta nói ( )
(4.3.1) và (4.3.2) ơn giản như nhau. Rõ ràng quan hệ ơn giản như nhau là một quan
hệ tương ương. Hơn nữa nếu hai công thức a thức là ơn gản như nhau thì mạng các
cổng tổng hợp chúng sẽ sử dụng cùng số cổng AND và cổng OR.
4. Tương tự như trong Chương 3, nếu chuyển qua các lớp tương ương thì quan hệ ơn
giản hơn trở thành một thứ tự. Tuy nhiên ta cũng có thể khảo sát trực tiếp các
quan hệ chỉ có hai tính chất phản xạ và bắc cầu. ta nói chứng là các quan hệ tiền thứ
tự . Đối với quan hệ tiền thứ tự, khái niệm phần tử tối tiểu và tối ại vẫn còn ý nghĩa.
Chẳng hạn như một công thức a thức ( ) của hàm Bool ược nói là tối tiểu nếu với bất lOMoARcPSD| 36667950
kỳ công thức a thức ( ) của “ ơn giản hơn” ( ) thì ( ) và ( ) ơn giản như nhau. Bây
giờ do tập hợp các công thức a thức của một hàm Bool là hữu hạn, ta chứng minh
ược tương tự như Định lý 3.3.3, cho trước một công thức a thức ( ) của thì sẽ tồ tại
một công thức a thức tối tiểu ( ) của sao cho ( ) ơn giản hơn ( ). Cũng như trường
hợp các tập hợp có thứ tự, một hàm Bool có thể có nhiều công thức a thức tối tiểu.
5. Xét công thức a thức (4.3.1) của hàm . Giả sử tồn tại một dơn thức sao cho ≺. Khi ấy ta có: = ∨ = (∨ ) ∨ ∨ …∨ = ∨ ∨ …∨ (4.3.3) Do ≺ ta có thể viết: =
Như thế mọi thừa số là từ ơn của cũng là một thừa số của . Hơn nữa do
≠ nên có ít nhất một thừa số là từ ơn của không xuất hiện trong . Khi ấy công thức
(4.3.3) rõ ràng ơn giản hơn (4.3.1) nhưng không ơn giản như nhau. Suy ra (4.3.1) không tối tiểu. Ta ã chứng minh.
Mệnh ề 4.3.1: trong một công thức a thức tối tiểu, các số hạng là ơn thức tối dại trội bởi .
Định nghĩa 4.3.2: một ơn thức tối ại trội bởi hàm Bool ược gọi là một tiền ề nguyên tố của .
Do Mệnh ề 4.3.1, ể tìm công thức a thức tối tiểu của một hàm Bool , ta hạn chế tìm
kiếm trong các công thức a thức mà các số hạng là những tiền ề nguyên tố dôi một khác
nhau. Các công thức này là rút gịn theo nghĩa sau:
Định nghĩa 4.3.3: công thức a thức (4.3.1) của hàm ược nói là rút gọn nếu với 1 ≤ ≠ ≤ ,
thì không phải là ước thật sự của .
Ví dụ: Xét hàm Bool theo 3 biến: = ∨ ∨ ̅ ∨ ̅ ̅ ( )
Rõ ràng ( ) là dạng nối rời chính tắc của và là rút gọn. Để có những công thức rút
gọn khác ta sẽ gom tất cả các số hạng lại và sử dụng
Bổ ề 4.3.2: nếu và ℎ là hai hàm Bool thì ℎ ∨ ℎ = ∨ ℎ Chứng minh: ℎ ∨ ℎ = ℎ ∨ (ℎ ∨ ℎ) = ℎ ∨ ℎ ∨ ℎ = ∨ ℎ pcm Từ ( ) ta ược: = ∨(∨) ̅ ∨ ̅ ̅ = ∨ ̅ ∨ ̅ ̅ ( ) Tương tự = ∨ ̅ ∨ ̅ ( ) và = ∨ ̅ ∨ ̅ ̅ ( )
Áp dụng Bổ ề 4.3.2 cho ( ), ( ) và ( ) ta ược: = ( ∨ )̅ ∨ ̅ ̅ = ( ∨ ̅) ∨ ̅ ̅ lOMoARcPSD| 36667950
= ∨ ̅ ∨ ̅ ̅ ( ) Tương tự = ∨ ̅ ∨ ̅ ( ) và = ∨ ̅ ∨ ̅ ( )
Cuối cùng, áp dụng Bổ ề 4.3.2 cho một trong 3 công thức ( ), ( ) hay ( ) ta ược: = ∨ ̅ ∨ ̅ ( )
Tám công thức trên ều là rút gọn và có biểu ồ Hasse: ( ) 3 ( ( ) 3 ( ) 2 ( ) ( ) 8 5
Công thức ( ) là công thức a thức tối tiểu duy nhất nên cũng là công thức ơn 8 giản
nhất. Sử dụng công thức ( ) ể tổng hợp hàm Bool ta chỉ tốn 3 cổng AND và 2 cổng OR thay 8
vì 8 cổng AND và 3 cổng OR nếu dùng ( ). Ta có sơ ồ mạch các cổng ứng với ( ) như sau: 1 8
§4 PHƯƠNG PHÁP BIỂU ĐỒ KARNAUGH
Phương pháp biểu ồ Karnaugh cho phép tìm nhanh công thức a thức tối tiểu của hàm
Bool 3, 4 biến. Trường hợp 3 biến hoàn toàn tương tự nhưng ơn giản hơn trường hợp
4 biến. Do ó ta tập trung trình bày 4 biến. Nhắc lại một hàm Bool 4 biến là một ánh xạ
→ nên ể có thẻ biểu diễn bằng hình ảnh ta sẽ sử dụng một hình vuông gồm có 16 ô vuông
nhỏ ể biểu diễn 16 phần tử của . Khi ấy ta có thể biểu diễn một hàm Bool : → bằng các gạch
chéo các ô ở ó bằng 1.
Như vậy vấn ề chính là ánh dấu 16 ô của hình vuông tương ứng với các phần tử của
. Ta ã biết các phần tử của có thể ược sắp thứ tự theo thứ tự tự iển: 0000,0001,,0010,0011,…,1111
Ta có thể xếp các phần tử của theo thứ tự lần lượt trên các dòng của hình vuông
lớn. tuy nhiên cách này không thuận tiện bằng cách của Veitch và Karnaugh như sau: ̅ lOMoARcPSD| 36667950 1010 1110 0110 0010 1011 1111 0111 0011 1001 1101 0101 0001 1000 1100 0100 0000
Ở ây ký hiệu chỉ cột ở ó biến ầu tiên lấy giá trị 1, ̅ chỉ cột ở ó biến lấy giá trị 0.
Tương tự cho biến thứ hai . Các biến thứ ba và thứ tư , ược gán với các dòng. Ví dụ ở hai
dòng ầu biến lấy giá trị 1 và 2 dòg nsau biến lấy giá trị 0. Tương tự cho biến . Cách biểu
diễn trên của rất thuận tiện cho việc biểu diễn các ơn thức. Thật vậy ta nhận xét rằng 2 ô
liên tiếp nhau chỉ khác nhau một thành phần , ví dụ ô ở dòng 2 cột 2 và ô ở dòng 2 cột 3 chỉ
khác nhau ở thành phần ầu tiên: 1111 và 0111. Mặt khác ô ở dòng 1 cột 1 và dòng 1 cột 4
cũng biểu diễn hai phần tử chỉ khác nhau một thành phần: 1010 và 0010. Ta quy ước rằng
các ô này cũng ược xem như kề nhau theo nghĩa rộng: 2 ô ược nói là kề nhau theo nghĩa rộng
nếu sau khi ta cuốn hình vuông theo chiều rộng hoặc chiều ngang tạo thành hình trụ thì hai
ô ban ầu sẽ trở thành kề nhau trên hình trụ. Với qui ước trên ta thấy rằng hai ô kề nhau
(theo nghĩa thông thường hay nghĩa rộng) khi và chỉ khi chùng biểu diễn hai phần tử của
chỉ khác nhau một thành phần.
Bây giờ ể biểu diễn một hàm Bool 4 biến , ta sẽ gạch chéo các ô của hình vuông lớn
tương ứng với các iểm của ở ó bằng 1. Ta nói hình vẽ ấy là biểu ồ Karnaugh của hàm Bool
. Ví dụ như hình vẽ dưới ây chỉ biểu ồ Karnagh của hàm Bool 4 biến: = ∨̅ ∨ ̅ ∨ ̅ ̅ ∨ ̅ ̅ ̅ ∨ ̅ ̅
Nhận xét rằng hàm Bool chính là các hàm ặc trưng của tập hợp gạch chéo trong biểu
ồ Karnaugh. Do ó sử dụng ẳng cấu giữa 2 ại số Bool ( ) và 2 ta có:
Mệnh ề 4.4.1: Với mọi hàm Bool 4 biến , : lOMoARcPSD| 36667950 i.
Biểu ồ Karnaugh của là tập hợp con của biểu ồ Karnaugh của khi và chỉ khi ≺ ii.
Biểu ồ Karnaugh của ∨ (tương ứng ∧) là hợp (tương ứng giao) của các biểu ồ Karnaugh của và . iii.
Biểu ồ Karnaugh của ̅ là phần bù của biểu ồ Karnaugh của . Chú ý:
1. Sử dụng Mệnh ề 4.4.1 ta có thể vẽ ược biểu ồ Karnaugh của một hàm Bool nếu biết
bảng chân trị của nó hoặc nếu biết ược một công thức biểu diễn hàm Bool dưới dạng
một biểu thức theo các biến và các phép toán ∨,∧,−.
2. Ngược lại nếu biết ược biểu ồ Karnaugh của hàm Bool , ta có thể ọc ngay từ ó dạng
nối rời chính tắc: các từ tối tiểu trội bởi chính là các hàm ặc trưng của mỗi ô nằm
trong biểu ồ Karnaugh. Hơn nữa, công thức cho từ tối tiểu như là tích của bốn từ ơn
ược ọc ngay triong biểu ồ Karnaugh khi xem các dòng và cột chứa ô ang xét: ví dụ
như từ ơn ứng với ô ở dòng 3 cột 2 là ̅ thì các dòng và cột chứa ô này là , ,̅ và .
3. Hai từ tối tiểu ứng với hai ô kề nhau ( theo nghĩa thông thường hoặc nghĩa rộng) hỉ
khác nhau một thừa số là từ ơn, nên ta có thể dùng luật phân bố ể ặt thừa số chung
trong tổng Bool của chúng và ược một ơn thức có 3 thừa số là từ ơn. Ví dụ như: ∨̅ = (∨̅) =
có biểu ồ Karnaugh là một hình chữ nhật theo nghĩa rộng gồm hai ô liên tiếp nhau 1110 và 1111. Tổng quát hơn ta có:
Mệnh ề 4.4.2: biểu ồ Karnaugh của một ơn thức có dạng tích của (1 ≤ ≤ 4) từ ơn là một
hình chũ nhật (theo nghĩa rộng) gồm 2 ô, mà ta gọi là các tế bào. Ví dụ: ̅ ̅ ̅
Do Mệnh ề 4.4.1 và 4.4.2, các tiền ề nguyên tố của một hàm Bool 4 biến có biểu ồ
Karnaugh là một tế bào tối ại nằm trong biểu ồ Karnaugh của . Ta nói các tế bào này là tế
bào lớn của biểu ồ Karnaugh của . Như vậy việc tìm công thức a thức tối tiểu của ưa về việc giải quyết hai vấn ề:
Tìm tất cả các tế bào lớn nằm trong biểu ồ Karnaugh của . lOMoARcPSD| 36667950
Tìm một phép phủ tối tiểu biểu ồ Karnaugh của bằng các tế bào lớn, nghĩa là một
họ tế bào lớn có hợp là biểu ồ Karnaugh của sao cho khi rút bớt một tế bào lớn
thì họ còn lại không phủ kín biểu ồ Karnaugh của . Từ ó ta ược một thuật toán ể
tìm công thức a thức tối tiểu.
Thuật toán: gồm 4 bước
Bước 1: chỉ ra tất cả các tế bào lớn của biểu ồ Karnaugh của .
Sau bước 1 ta sẽ phủ dần biểu ồ Karnaugh bằng các tế bào lớn cho ến khi phủ kín
Bước 2: nếu tồn tại một ô chỉ nằm trong một tế bào lớn duy nhất, ta chọn ra tế bào
này ể phủ. Trong phần còn lại của biểu ồ Karnaugh, nếu có một ô chỉ nằm trong một tế bào
lớn duy nhất, ta chọn ra tế bào này ể phủ, và lặp lại bước 2 cho ến khi không còn ô nào có tính chất trên.
Bước 3: nếu các tế bào lớn chọn trong Bước 2 ã phủ kín biểu ồ Karnaugh của ta qua
thẳng Bước 4. Nếu không, chọn ra một ô còn lại. Trong số các tế bào lớn chứa ô này ta chọn
ra một ô tùy ý dể thêm vào phép phủ và cứ tiếp tục như trên cho phần còn lại cho ến khi
phủ kín biểu ồ Karnaugh của .
Bước 4: ở bước này ta ã chọn ược một số tế bào lớn phủ kín biểu ồ Karnaugh của .
Do trong Bước 3 có sự lựa chọn tùy tế bào lớn chứa một ô , ta thường có nhiều hơn một
phép phủ. Trong số phép phủ nhận ược, loại bỏ các phép phủ không tối tiểu. Sau cùng các
phép phủ còn lại cho ta một công thức a thức của mà ta còn phải so sánh chúng theo Định
nghĩa 4.3.1: loại bỏ những công thức có một công thức khác trong số ó thực sự ơn giản hơn
nó. Các công thức còn lại chính là công thức a thức tối tiểu phải tìm. Chú ý: 1.
Nếu Bước 3 ược bỏ qua thì không có sự lựa chọn tùy ý. Trong trường hợp any2 ta
ược một phép phủ duy nhất tương ứng với công thức a thức tối tiểu duy nhất. 2.
Để thuận tiện cho việc xem xét ta gạch chéo mỗi tế bào lớn ược chọn cho ến khi
phần gạch chéo trùng với biểu ồ Karnaugh của . Đương nhiên hai cách chọn khác nahu sẽ
dẫn ến hai quá trình phủ khác nhau và cho ta hai công thức khác nhau. Ví dụ 1: xét hàm
có biểu ồ Karnaugh như sau:
Bước 1: Biểu ồ Karnaugh của có hai tế bào lớn: ̅ ̅
Bước 2: ô (3,1) nằm duy nhất trong ̅, ô (1,1) nằm duy nhất trong ̅
Hai tế bào lớn này ã phủ kín biểu ồ Karnaugh của nên ta qua thẳng Bước 4
Bước 4: ta chỉ có duy nhất một phép phủ tương ứng với công thức a thức tối tiểu lOMoARcPSD| 36667950 của : = ̅ ∨ ̅
Chú ý: sử dụng cộng thức trên ể tổng hợp hàm Bool bằng một mạng các cổng ta cần 4
cổng AND và một cổng OR (không kể cổng NOT)
Ví dụ 2: xét hàm có biểu ồ Karnaugh như sau:
Bước 1: Biểu ồ Karnaugh của có 4 tế bào lớn:
Bước 2: ô (2,4) nằm trong tế bào lớn duy nhất ̅, ô (4,2) nằm trong tế bào lớn duy nhất ̅
Gạch chéo hai tế bào lớn này ta ược sơ ồ sau:
Còn lại ô (3,3) chưa ược phủ nằm trong hai tế bào lớn nên ta qua Bước 3
Bước 3: ô (3,3) nằm trong 2 tế bào lớn ̅,̅ chọn tùy ý một trong hai tế bào trên ta ều
phủ kín biểu ồ Karnaugh của
Bước 4: ta ược phép phủ tối tiểu tương ứng với hai công thức a thức:
= ̅ ∨ ̅ ∨ ̅ và = ̅ ∨ ̅ ∨ ̅
Cả hai công thức này ều n giản như nhau theo Định nghĩa 4.3.2 nên ta ược 2 công thức a thức tối tiểu.
Chú ý: sử dụng các công thức này ể tổng hợp hàm bằng một mạng các cổng ta cần có 6 cổng AND và 2 cổng OR.
Ví dụ 3: xét hàm với biểu ồ Karnaugh như sau:
Bước 1: Biểu ồ Karnaugh của có 8 tế bào lớn như sau: lOMoARcPSD| 36667950
Bước 2: các ô (1,2) và (2,4) nằm trong các tế bào lớn duy nhất là và tương ứng.
Sau khi chọn các tế bào lớn này thì phần còn lại của biểu ồ Karnaugh của ều có mỗi ô nằm
úng trong hai tế bào lớn nên ta qua Bước 3.
Bước 3: Ta có sơ ồ cách chọn các tế bào lớn còn lại ể phủ kín biểu ồ Karnaugh của
theo các nhánh (của hình cây): Chọn
: còn lại 4 ô chưa phủ
Chọn ̅: còn lại 2 ô chưa phủ
Chọn ̅ ̅: phủ kín biểu ồ Karnaugh của : = ∨ ∨ ∨ ̅ ∨ ̅ ̅ ( )
Không chọn ̅ ̅: ể phủ hai ô (4,3) và (4,4) ta buộc phải chọn ̅ ̅ và ̅: = ∨ ∨ ∨ ̅ ∨ ̅ ̅ ∨ ̅ ( )
Không chọn ̅: ể phủ hai ô (3,2) và (3,3) ta buộc phải chọn và ̅ . Lúc này ̅ chỉ còn lại ô
(4,4). Nếu chọn ̅ ta sẽ ược một phép phủ không tối tiểu vì có thể loại bớt tế bào lớn
mà vẫn còn ược một phép phủ. Do ó ta buộc phải chọn ̅ ̅̅: = ∨ ∨ ∨ ∨ ̅ ̅ ∨ ̅ ̅ ̅ ( )
Không chọn : ể phủ 2 ô (3,1) và (4,1) ta buộc phải chọn các tế bào lớn và ̅. Lúc này còn
lại 2 ô chưa phủ là (3,3) và (4,3).
Chọn ̅ ̅: phủ kín biểu ồ Karnaugh: = ∨ ∨ ∨ ̅ ∨ ̅ ̅ ( ) lOMoARcPSD| 36667950
Không chọn ̅ ̅ : ể phủ hai ô (3,3) và (4,3) ta buộc phải chọn các tế bào lớn ̅ và ̅ ̅̅: = ∨ ∨ ∨ ̅ ∨ ̅ ∨ ̅ ̅ ̅ ( )
Bước 4: ta có 5 công thức a thức. Tuy nhiên ta có thể xây dựng dễ dàng các ơn ánh
trong Định nghĩa 4.3.1 cho thấy công thức ( ) ơn giản hơn ( ), ( ), ( ), ( ) mà không tương
ương ( ơn giản như nhau theo Định nghĩa 4.3.2). Chẳng như ta có ơn ánh: ⟼ ⟼ ⟼ ̅ ⟼ ̅ ̅ ̅ ⟼ ̅ ̅
Trong ó chỉ có hai thừa số là từ ơn trong khi ̅ có 3 thừa số là từ ơn, nghĩa là ( ) thực
sự ơn giản hơn( ). Các ơn ánh khác cũng ược xây dựng tương tự. Tóm lại ta chỉ có duy nhất
một công thức a thức tối tiểu của hàm là: = ∨ ∨ ∨ ̅ ∨ ̅ ̅
Chú ý: sử dụng công thức trên ể tổng hợp bằng mạng các cổng ta cần 6 cổng AND và 4 cổng OR.
Trường hợp hàm 3 biến:
Đối với các hàm Bool 3 biến ta sẽ sử dụng hình chữ nhật có 8 ô dể biểu diễn thay vì hình vuông 16 ô. ̅
Khi ấy ịnh nghĩa biểu ồ Karnaugh ,tế bào, tế bào lớn hoàn toàn tương tự và ta có thể
áp dụng qui trình 4 bước như trên ể tìm công thức a thức tối tiểu.
Ví dụ: Xét hàm Bool = ( ∨ ∨ )( ̅ ∨ ∨ )( ∨ ∨ ̅)
Biểu ồ Karnaugh của ba thừa số là: ∨ ∨ ̅ ∨ ∨ ∨ ∨ ̅
Do ó biểu ồ Karnaugh của có dạng:
Bước 1: có 4 tế bào lớn lOMoARcPSD| 36667950 ̅
Bước 2: ô (1,3) nằm trong tế bào lớn duy nhất , ô (2,4) nằm trong tế bào lớn duy nhất ̅
Chọn các tế bào này cho phép phủ ta ược:
Bước 3: còn lại ô (1,1) nằm trong hai tế bào lớn và . Chọn 1 trong 2 tế bào này ta
ều phủ kín biểu ồ Karnaugh của .
Bước 4: ta có 2 công thức ều là công thức a thức tối tiểu = ∨ ̅ ∨ = ∨ ̅ ∨
Trường hợp 5,6 biến:
Đối với hàm Bool 5 biến, ta dùng 2 lớp hình vuông 16 ô ể biểu diễn 32 ô của , một
lớp tương ứng với giá trị của biến thứ 5 = 0 và lớp ứng với = 1
Biểu ồ Karnaugh của một hàm Bool theo 5 biến , , , , ược thiết lập bằng cách gạch xéo
các ô trong hai lớp trên ứng với các iểm ở ó lấy giá trị 1. Ở ây ngoài các tế bào là những
hình chữ nhat65trong mỗi lớp, ta có các tế bào là 2 hình chữ nhật (tế bào) thuộc 2 lớp có
cùng hình chiếu xuống một mặt phẳng nằm ngang, hay nói cách khác, khối chữ nhật 3 chiều
với chiều cao 2 lớp và áy là một tế bào. Bằng cách này ta ược các tế bào là biểu ồ Karnaugh
của tích của (1 ≤ ≤ 5) thừa số là từ ơn. Tế bào tương ứng sẽ có 2 ô. Phương pháp biểu ồ
Karnaugh ể tìm công thức a thức tối tiểu hoàn toàn tương tự trường hợp 4 biến. lOMoARcPSD| 36667950
Để xử lý trường hợp hàm 6 biến ta sẽ sử dụng 4 lớp 16 ô thay vì 2 lớp. Các lớp kể từ
trên xuống bây giờ ứng với = 1, = 0; = 1, = 1; = 0, = 1; = 0, = 0. Phương pháp tìm công thức a
thức tối tiểu cũng tương tự nhưng hình vẽ phức tạp hơn. Do ó ối với trường hợp này hay
trường hợp nhiều biến hơn ta sẽ dùng phương pháp “Thỏa thuận dưới ây.
§5 PHƯƠNG PHÁP THỎA THUẬN
Nhắc lại hai bài toán chính ể tìm công thức a thức tối tiểu của một hàm Bool :
5.1 Tìm tất cả các tiền ề nguyên tố của
5.2 Tìm cách biểu diễn như là tổng tối tiểu của các tiền ề nguyên tố Để
giải quyết bài toán 5.1 ta sẽ dùng phương pháp thỏa thuận
Định nghĩa 4.5.1: Giả sử là một trong các biến Bool và , là hai ơn thức không chia hết cho
cả lẫn ̅. Khi ấy ược nói là thỏa thuận giữa hai ơn thức và ̅ .
Chú ý: nếu có một biến thứ hai sao cho chia hết cho (hoặc ) và chia hết cho (hoặc ), khi
ấy thỏa thuận rõ ràng bằng 0. Do ó cho trước 3 ơn thức có 3 trường hợp có thể xảy ra:
Trường hợp 1: không tìm ược thỏa thuận của chúng vì không có biến nào như trong Định nghĩa 4.5.1
Trường hợp 2: thỏa thuận của chúng bằng 0 vì có ít nhất hai biến Bool thỏa Định nghĩa 4.5.1
Trường hợp 3: chỉ có một biến Bool thỏa Định nghĩa 4.5.1 và do ó thỏa thuận của
hai ơn thức cho trước là một ơn thức (≠ 0) Ví dụ: 1.
à ̅ không có thỏa thuận 2.
à ̅ có thỏa thuận bằng 0 3. à có thỏa thuận là
Định lý 4.5.1: Thỏa thuận của haqi ơn thức luôn luôn ượ trội bởi tổng Bool của hai ơn thức ấy.
Chứng minh: Xét hai ơn thức và ̅ với thỏa thuận ta có: = ( ∨ ̅) = ∨ ̅ Suy ra: ∨ ∨ ̅ = ( ∨ ) ∨∨ (̅̅ ∨ ̅ ) Nghĩa là ≺ ≺ ̅ pcm
Với khái niệm thỏa thuận ta có phương pháp sau ể xác ịnh tất cả các tiền ề nguyên tố của một hàm Bool .
Bước 1: Viết dưới dạng công thức thu gọn tùy ý (dạng nối rồi chính tắc chẳng hạn): = ∨ ∨ …∨ Đặt = { , ,…, }
Gọi là danh sách các biến theo một thứ tự nhất ịnh nhưng tùy ý. lOMoARcPSD| 36667950
Bước 2: Trong Bước 2 ta sẽ cập nhật dần theo từng biến trong như sau:
i. Giả sử là một biến trong mà ta ã xét tới với ã ược cập nhật theo các biến trước
. Ta phần hoạch thành 3 phần (rời nhau):
gồm các ơn thức chia hết cho
ℬ gồm các ơn thức chia hết cho ̅
gồm các ơn thức không chia hết cho lẫn ̅ ii. Nếu = ∅ hay ℬ = ∅ ta sẽ xét
biến kế tiếp . Nếu không, ta thêm vào tất cả các thỏa thuận của một ơn thức
thuộc và một ơn thức thuộc ℬ. iii. Mỗi lẩn thêm một phần tử mới vào ta phải
duyệt lại và loại bớt những phần tử ược trội thực sự bởi một phần tử khác (kể cả
phần tử mới thêm vào).
Bước 3: Sau khi ã duyệt tất cả các biến trong ta có:
Định lý 4.5.2: Tập hợp sau cùng trong Bước 3 chính là tập hợp tất cả các tiền ề nguyên tố của .
Chứng minh: Gọi là số biến trong , và một là một tiền ề nguyên tố bất kỳ của , ta chứng
minh tập hợp sau cùng sẽ chứa bằng quy nạp trên .
Gọi là biến ầu tiên trong danh sách và ,ℬ, là các tập hợp tương ứng như trong i).
Trường hợp 1: không chia hết cho lẫn ̅, ta có: ≺ ∨ ∨ ∈ ∈ℬ ∈ Ở ây kí hiệu
dùng ể chỉ tổng Bool của tất cả các phần tử của A. Các ký hiệu ∈
khác cũng tương tự. ể ý rằng nếu ∈ ℬ thì chia hia hết cho ̅ nên = 0. Do ó: ≺ / ∨ ∈ ∈ Cho = 1 ta ược ≺ / ∨ ∈ ∈ Tương tự ta có: ≺ / ̅ ∨ ∈ℬ ∈ Suy ra
Giả sử ã ược cập nhật theo biến như trong Bước 2 ở trên. Gọi ′ là tập hợp con của
gồm các ơn thức không chia hết cho lẫn ̅. Gọi ′ là tổng Bool của các ơn thức trong ′ xem như
hàm Bool theo các biến trong = \ { }. Rõ ràng là một tiền ề nguyên tố của ′ nên theo giả thiết
quy nạp, sau khi cập nhật theo biến cuối cùng trong lOMoARcPSD| 36667950
,′ chứa . Nhưng tập hợp ′ sau cùng là tậph ợp con của tập hợp sau khi cập nhật theo biến
sau cùng của ′, vì trong quá trình cập nhật theo các biến của ′, các ơn thức của bị loại i cũng
chính là các ơn thức của ′ bị loại i hoặc là các ơn thức chia hết cho hoặc ̅. Nói tóm lại ta ã
chứng minh ược tậph ợp sau cùng chứa .
Trường hợp 2: chia hết cho hay ̅. Ta có thể giả sử chia hết cho vì trường hợp còn
lại chứng minh tương tự.
Gọi ,ℬ, là 3 tập hợp tạo thành phân hoạch của tương ứng với biến như trong Bước 2. Cho = 1 ta ược: / ≺ ( / )∨ ∈ ∈ Suy ra ≺ ∨ ∈ ∈
Ứng với mỗi hàm Bool theo các biến trong , ta liên kết một hàm Bool ̅ với các biến
trong = \ { } bằng cách cho = 1. Đặt = ∪. Khi ấy ⟼ ̅ là một song ánh giữa ′ và một tập hợp ′
các từ ơn theo các biến trong ′ vì không có phần tử nào của là ước của một phần tử của
(công thức a thức ban ầu của là rút gọn).
Ta có công thức a thức rút gọn: ̅ = ∨ ∈ ∈
Hơn nữa tương ứng ⟼ ̅, nếu thu hệp trên tập ′ ã ược cập nhật ối vối biến sau cùng,
cũng là một song ánh giữa tập hợp này và tập hợp ′ ã ược cập nhật theo biến sau cùng ối
với hàm ̅ , vì nếu có = với ≠ thì một trong hai ơn thức , là tích của ơn thức kia và nên ã ược
loại trong quá trình cập nhật. Rõ ràng ≺, gi̅
ả sử tồn tại ơn thức ′ theo các biến trong ′ sao cho: ≺ ≺ ̅ Ta có: = ≺ ≺ ̅ = ∨ ∈ ∈ ≺
Do là tiền ề nguyên tố, ta có = lOMoARcPSD| 36667950
Suy ra =, nghĩa là là tiền ề nguyên tố của ̅
Như thế theo giả thiết quy nạp, ′, sau khi cập nhật theo biến cuối cùng, sẽ chứa
. Tương tự như trong Trường hợp 1, ta thấy tập hợp sau khi cập nhật ối với biến
cuối cùng, sẽ chứa ′. Suy ra ∈
Cuối cùng do cách cập nhật các ơn thức, trong ơn thức nào trong ược trội thực sự
bởi một ơn thức khác, nghĩa là các phần tử của ều là tiền ề nguyên tố của . pcm Ví dụ 1: = ̅ ∨ ̅ ̅ ∨ ∨ ̅ ∨
Ta có quá trình cập nhật theo các biến trong = [ , , , , ] như sau: Biến : ̅ ̅̅ ̅̅ Thỏa thuận: ̅ Biến : ̅ ̅̅ ̅̅ ̅ Thỏa thuận:
Biến : không có thỏa thuận Biến : ̅ ̅ ̅̅ ̅̅ Thỏa thuận: ̅ ̅ ̅̅ ̅̅ Thỏa thuận: Biến : ̅ ̅ ̅̅ Thỏa thuận: ̅ ̅̅ ̅ Thỏa thuận: ̅̅
Cuối cùng tập hợp các tiền dề nguyên tố là: = {̅̅, ̅, , ̅̅} Thỏa thuận: lOMoARcPSD| 36667950 Thỏa thuận: ̅ Biến : ̅ ̅ ̅̅ Thỏa thuận: Biến : ̅ ̅ ̅ ̅ Thỏa thuận: ̅
Như vậy tập hợp các tiền ề nguyên tố là = {̅,̅,̅,̅}
Bây giờ ta xét bài toán 5.2: biểu diễn hàm Bool như là tổng tối tiểu của các tiền ề
nguyên tố. Trong phương pháp Biểu ồ Karnaugh, bài toán trên chính là bài toán phủ tối tiểu
của biểu ồ Karnaugh của hàm bởi các tế bào lớn. Đó là một họ các tế bào lớn sao cho: i.
Mỗi ô trong biểu ồ Karnaugh nằm trong ít nhất 1 tế bào lớn thuộc ii.
Nếu rút bớt một tế bào lớn thuộc thì phần còn lại không thỏa i)
Do các ô thuộc biểu ồ Karnaugh của chính là biểu ồ Karnaugh của một từ tối tiểu trội
bởi , ta có thể phát biểu bài toán phủ tổng quát như sau:
Bài toán phủ: tìm một họ các tiền ề nguyên tố của sao cho: i.
Mỗi từ tối tiểu trội bởi ược trội bởi một tiền ề thuộc ii.
Họ là từ tối tiểu, nghĩa là nếu rút bớt một phần tử thì phần còn lại không thỏa i) Gọi = ,…,
là tập hợp tất cả các tiền dề nguyên tố của mà ta tìm ược khi giải bài toán 5.1
Ta ưa vào các biến Bool , ,…, và tgiet61 lập một hệ phương trình Bool theo các biến Bool như sau:
Với mỗi từ tối tiểu trội bởi , gọi , ,…, là tất cả các tiền ề nguyên tố của trội . Khi ấy
ta có một phương trình: ∨ ∨ …∨ = 1
Cho chạy khắp các từ tối tiểu trội bởi , ta ược một hệ phương trình trong ó là số
các từ tối tiểu trội bởi . Giải hệ phương trình Bool trên ta ược các nghiệm là bộ : Trong ó , ,…,
là các giá trị cố ịnh bằng 1 hoặc tùy ý. Với các = 1 ta có
= 1, nghĩa là tiền ề nguyên tố ược chọn ể phủ . Để giải hệ phương trình Bool có dạng
trên, ta thực hiên các bước sau:
Bước 1: loại bỏ các phương trình trùng lắp, nói cách khác giả sử có hai phương trình có dạng: ∨ ∨ …∨ = 1 và ∨ ∨ …∨ = 1
sao cho { , ,…, } ⊂ { , ,…, } lOMoAR cPSD| 36667950
Khi ấy phương trình thứ hai là hệ quả của phương trình ầu và do ó có thể ược loại bỏ.
Bước 2: Vì hệ phương trình ồng thời nghiệm úng, ta thấy nó tương ương với một
phương trình duy nhất có vế trái là tích của tất cả các vế trái và vế phải bằng 1 Dùng luật
phân bố khai triển vế trái và ưa nó về dạng một công thức a thức.
Bước 3: Loại bỏ các ơn thức dư thừa, nghĩa là nó là bội của một ơn thức khác. Nói
cách khác ưa vế trái của phương trình ã biến ổi ở Bước 2 về dạng một công thức a thức rút
gọn. Ở ây lưu ý rằng các ơn thức ều là tích của một số biến, không có thừa số ơn nào là
phần bù của biến. Phương trình trở thành: ∨ ∨ …∨ = 1
Bước 4: các lời giải là: = 1 hay = 1 … … hay = 1
Mỗi là tích của một số biến, nên lời giải tương ứng chính là các tiền ề nguyên tố
tương ứng với biến ó.
Ví dụ: trong ví dụ 2 ở trên, ta có 4 tiền ề nguyên tố = ̅, = ̅, = ̅, = ̅, và 5 từ tối tiểu = ̅, = ̅, = ̅ ̅ , = , ̅̅.
Ta có hệ 5 phương trình: = 1 ⎧⎪ ∨ = 1 ∨ = 1 ⎨⎪ ∨ = 1 ⎩ = 1
Phương trình thứ hai là hệ quả của phương trình ầu và phương trình thứ 4 là hệ quả
của phương trình cuối: loại bỏ chúng và lấy tích ta ược phương trình duy nhất: ( ∨ ) = 1 Khai triển ta ược: ∨ = 1
Do ó ta có hai lời giải: = 1 hay = 1
Nói cách khác ta có hai công thức a thức: = ∨ ∨ = ̅ ∨ ̅ ∨ ̅ và = ∨ ∨ = ̅ ∨ ̅ ∨ ̅
Cả hai ều là công thức a thức tối tiểu. lOMoARcPSD| 36667950
BÀI TẬP CHƯƠNG 4
1. Chứng minh rằng trong một ại số Bool
a) Phần bù của một phần tử là duy nhất
b) Suy ra qui tắc De Morgan: ∀ ,∈,∨ = ̅ ∧ và ∧ = ̅ ∨
2. Trong ại số Bool , xét quan hệ thứ tự ≺ xác ịnh bởi ịnh lý 4.1.1. Chứng minh rằng: a) nếu ≺ thì ∨ = b) nếu ≺ thì ≺ ̅
c) nếu ≺ thì ≺ thì ∧ ≺ ∧
d) nếu ≺ thì ≺ thì ∨ ≺ ∨
3. Trong một ại số Bool hãy tìm phần bù của: ∧ ∨ (∧) ( ∧ ̅) ∨ ∧ ∨ (∧)
4. Trong ại số Bool , một tập hợp con ℬ ≠ ∅ củ
a ược nói là một ại số con nếu với mọi
,∈ ℬ thì ∨,∧ và ̅ cũng là phần tử của ℬ. Chứng minh rằng ℬ là một ại số con của .
a) Chứng minh rằng nếu ℬ là một ại số con của thì 0,1 ∈ ℬ b) Với =
({ , , }). Hãy tìm tất cả các ại số con của
c) Giả sử ℬ là một tập hợp con của sao cho với mọi ,∈ ℬ thì ∨ ∈ ℬ và ̅ ∈ ℬ. Chứng minh
rằng ℬ là một ại số con của .
5. là một ại số Bool, ∈. Tập hợp tất cả các phần tử trội bởi có là một ại số Bool không? Nó có là ại số con không?
6. Giả sử : ⟶ ℬ là một ẳng cấu ại số Bool. Chứng minh rằng:
a) nếu là một nguyên tử của
thì ( ) là một nguyên tử của ℬ
b) nếu là một ại số con của thì ( ) là một ại số con của ℬ
7. Gọi là tập hợp các ước dương của 210. Trong ta ịnh nghĩa các phép toán ∨,∧,− như sau: với mọi ,∈ thì: ∨ = ( . ) ∧ = ( , ) ̅ = 210/ Chứng minh rằng là một ại số Bool 8. a) Xét ánh xạ ∶ ⟶ ({ , , , }) Sao cho (2) = { }, (3) = { }, (5) = { } và (7) = { }
Muốn cho là một ảng cấu ại số Bool thì ảnh của 35, 70, 42 là bao nhiêu? b) Có
bao nhiêu ẳng cấu khác nhau từ lên ({ , , , })
9. Giả sử ℬ là một ại số Bool và
là một tập hợp ≠ ∅. Với ,∈ ℬ ịnh nghĩa: ̅
a) Chứng minh rằng ℬ là một ại số Bool với các phép toán trên
b) Chứng minh rằng thứ tự tương ứng trên ℬ chính là thứ tự trong bài tập 27, chương 3 lOMoARcPSD| 36667950
10. Giả sử ,ℬ là hai ại số Bool. Trên × ℬ ịnh nghĩa: ( , ) ∨ ( , ) = (∨,∨) ( , ) ∧ ( , ) = (∧,∧) ( , ) = (̅, )
Chứng minh rằng × ℬ là một ại số Bool với các phép toán trên.
11. Trên ịnh số Bool ịnh nghĩa phép toán ⨁ = ∧∨ (∧) (*)
a) Chứng minh rằng phép toán trên thỏa: ∀ , ,∈ (⨁)⨁ = ⨁(⨁) ⨁ = ⨁ ⨁0 = ⨁ = 0 ∧ (⨁) = (∧)⨁(∧) Nghĩa là ( ,⨂
,∧) là một vành giao hoán.
b) Ngược lại nếu ⨁ là một phép toán trên thỏa các iều kiên trên thì (*) ược thỏa.
12. Cho trước phần tử của Bool . Có thể nói gì về phần tử thỏa một trong các iều kiện sau: a) ∧ = 0 b) ∨ = 1 c) ∧ = 0 và ∨ = 1
13. Trong một ại số Bool
ta khảo sát phương trình: (1)
trong ó a và b là hai phần tử cho trước của và là ẩn.
a) Chứng minh rằng iều kiện cần và ủ ể cho (1) có ít nhất một nghiệm là ≺
b) Đặt = ∨. Chứng minh rằng ∧ = và ∨ = 1
c) Nếu là một nghiệm, chứng minh rằng ∧ ≺ ≺ . Phát biểu và chứng minh phần ảo.
d) Chứng minh rằng nghiệm của (1) gồm tất cả các phần tử có dạng = ∧ với ≻ .
e) Khảo sát tương tự cho phương trình ∧ =
14. Tập hợp có là một ại số Bool không? Có các phép toán nào khác ể trở thành ại số Bool không? 15.
a) Mở rộng ịnh nghĩa trong bài tập 10 cho tích của ại số Bool × × …× .
b) Đặc biệt với = = ⋯ = = ≡ {0,1} hãy xác ịnh thứ tự tương ứng với cấu trúc ại số Bool có
n nguyên tử ều ẳng cấu với
16. Giả sử là một phần tử bất kỳ của ại số Bool có nguyên tử. Gọi ( ) là số ỉnh tối thiểu cần
phải i qua ể i từ 0 ến dọc theo các mũi tên của biểu ồ Hasse ( (0) = 0). a) Tính ( ) khi là một nguyên tử b)
Chứng minh rằng với , tùy ý ta có: (∨) = ( ) + ( ) − (∧) lOMoARcPSD| 36667950
17. Tìm giá trị của các hàm Bool dưới ây khi các biến , ,
và lấy các giá trị 1,1,0 và 0: a) ∨ ̅ b) ∨ ̅ c) ∨ ∨ d) ∨ ∨
e) (∨ ̅) ∨ ∨ (∨)(̅∨)
18. Tìm tất cả các giá trị của y và z ể các biểu thức dưới ây luôn luôn lấy giá trị 1 biết rằng = 1: a) ∨ ∨ b) ∨ c) ̅ ∨ d) ̅ ∨
19. Tìm từ tối tiểu theo 4 biến , , , biết rằng nó lấy giá trị 1 tại: a) = = 0, = = 1 b) = = 1, = = 0 b) = = = 1, = 0 d) = = = = 0 20.
a) Có bao nhiêu hàm Bool 6 biến lấy giá trị 1 tại các iểm có úng hai thành phần có giá
trị 1 (tại các iểm khác hàm Bool có thể bằng 0 hay 1)
b) Có bao nhiêu hàm Bool 6 biến lấy giá trị 1 tại các iểm có ít nhất 2 thành phần có giá
trị 1 (tại các iểm khác hàm Bool có thể bằng 0 hay 1)
c) Có bao nhiêu hàm Bool 6 biến không phụ thuộc biến thứ nhất. Có bao nhiêu hàm
không phụ thuộc 3 biến ầu tiên.
21. Tìm các hàm Bool theo 2 biến sao cho: ,
22. Xác ịnh tất cả các hàm Bool theo 3 biến sao cho: ( , , ) = ( , , ) ∀ , ,
(Hướng dẫn: lập bảng chân trị)
23. Xác ịnh các hàm Bool theo 3 biến biết rằng nó không thay ổi giá trị nếu ta hoán vị 2 biến
bất kỳ? Câu hỏi tương tự cho hàm 4 biến (Hướng dẫn: lập bảng chân trị)
24. Tồn tại hay không một hàm Bool 3 biến khác 0 biết rằng nó ược thay bằng phần bù nếu
ta hoán vị 2 biến bất kỳ? Câu hỏi tương tự cho hàm Bool biến
25. Một hàm Bool biến ược nói là hàm chẵn nếu: ( , ,…, ) = ( , ,…, ), ∀ , ,…, . Có bao nhiêu
hàm chẵn biến? Xác ịnh các hàm này khi = 2 26. Hàm số Bool
biến ược nói là hàm chẵn nếu ( , ,…, ) = (̅ , ,…, ), , ,…,
. Có bao nhiêu hàm lẻ biến? Xác ịnh các hàm này khi = 2
a) Chứng minh rằng mọi hàm Bool theo biến ều ược viết dưới dạng: ( , ,…, ) = [ (1, ,…, )] ∨ [ (0, ,…, )]
b) Sử dụng hệ thức trên ể xây dựng một song ánh giữa ℱ × ℱ và ℱ . Áp dụng ể tìm lại số phần tử của ℱ
c) Sử dụng hệ thức trên ể chứng minh lại sự tồn tại của dạng nối rời chính tắc.
28. Giả sử là tích của từ ơn phân biệt a)
Trong dạng nối rời chính tắc của có bao nhiêu từ tối tiểu xuất hiện b)
Có bao nhiêu hàm Bool trội
29. Tìm dạng nối rời chính tắc của các hàm Bool
theo 4 biến biết rằng thỏa một trong hai iều kiện: a) (1) = {0101,0110,1000,1011} b) }
(0) = {0000,0001,0010,0100,1000,1001,0110 Ở ây ta viết 0101 thay vì (0,1,0,1) ể chỉ ra phần tử của
30. Tìm dạng nối rời chính tắc của hàm Bool theo 3 biến: lOMoARcPSD| 36667950 a) ∨ ̅ b) ( ∨ ̅) b) ∨ ∨ d) (∨) c) ∨ ̅ ̅ f) [ (∨) ∨ ̅] ∨ d) (∨)( ̅ ∨ )̅ h) ∨ ̅ e) (∨)(∨)(∨) j) (̅ ∨)(∨)(̅ ∨)
31. Tìm dạng nối rời chính tắc của hàm Bool theo 4 biến: a) (∨)(∨)(∨)(∨) b) ̅ c) ̅
32. Một bài thi có 4 câu A,B,C,D với số iểm tối a 8,5,4,3.Nếu trả lời úng một câu, sinh viên
ược iểm tối a, trả lời sai ược 0 iểm. Muốn ạt sinh viên phải ược 10 iểm trờ lên. Ta liên kết
với các câu 4 biến Bool a,b,c,d và một hàm Bool (a,b,c,d) lấy giá trị 1 nếu sinh viên ạt và
bằng 0 nếu sinh viên không ạt. Hãy tìm dạng nối rời chính tắc của hàm .
33. Hãy vẽ mạng sử dụng các cổng NOT, AND, OR ể tổng hợp hàm Bool a) (̅ ∨)(∨)(̅ ∨) b) ̅ ∨ ̅ ∨ c) ( ∨ )(̅ ∨ )̅ ̅ d) ∨(̅ ∨)
34. Hãy tổng hợp phép toán ∨ mà chỉ sử dụng cổng AND và cổng NOT 35. Hãy tổng hợp các
cổng AND, OR, NOT mà chỉ sử dụng cổng NOR
36. Viết ra biểu thức hàm tổng hợp bởi mạng các cổng dưới ây:
37. Hãy vẽ một mạch chỉ có cổng NOR tổng hợp các hàm Bool theo 4 biến sao cho lấy giá
trị 1 khi và chỉ khi số biến lấy giá trị 1 là số chẵn. Tương tự ối với cổng NAND.
38. Tìm công thức a tối tiểu của các hàm Bool có biểu ồ Karnaugh dưới ây:
39. Tìm công thức a tối tối tiểu của các hàm sau: a) ̅(∨) ∨ ( ̅ ∨ ̅ ) b) ∨ ̅ ∨ ̅ ∨ ̅ ̅ lOMoARcPSD| 36667950 c) ∨ ̅ ̅ ̅ ∨ ̅ d) ∨ ∨ ̅ ∨ ∨ (̅ ∨̅) e) ̅̅ ∨ ̅ ∨ ̅ ̅ ∨ ̅ ̅ ∨ ̅ ∨ f) (∨)(∨)(∨)(∨) g) (∨) ∨ (̅ ∨) ∨ ̅ h) ∨ ̅ ̅ ∨ ̅ ̅ i) ̅ ∨ ̅ ∨ ̅ ∨ ̅ ∨ ̅ ̅ ̅
40. Tìm các công thức a thức tối tiểu của hàm Bool dưới ây. Cho biết số cổng ể thiết kế các mạng tối ưu tổng hợp a)
là hàm Bool 3 biến và lấy giá trị 1 khi và chỉ khi có úng 2 biến lấy giá trị 1 b)
là hàm Bool 3 biến và lấy giá trị 1 khi và chỉ khi có ít nhất 2 biến lấy giá trị 1 c)
là hàm Bool 4 biến và lấy giá trị 1 khi và chỉ khi số biến lấy giá trị 1 là một số lẻ
GIẢI ĐÁP MỘT SỐ BÀI TẬP CHƯƠNG 1 1. Các mệnh ề là a,c,f
2. a) ∧ b) ¬ ∧ c) ∨ (¬ ∧ ¬ ) d) ⟶ ¬ e) (∧ ¬ ) ∨ (¬ ∧ ¬ ) 3. a) ∧ ∧ ¬ b) ∧
∧ ¬ (∧) c) ¬ (∧ ¬ ) d)¬ [(∨) ∧ ¬ ] e) ¬ ∧ ¬ ∧ 12. b, c, e, f 13. a, b,d, f, h
14. a) Để dạng mệnh ề ã cho lấy chân trị 1, hai dạng mệnh ề sau cần lấy chân trị 1: (¬ ∨) ∧ ¬ , à ¬ ⟶ ¬
Nghĩa là ¬ ,¬ và ¬ ∨ phải lấy chân trị 1.
Tóm lại ta phải chọn: = 1, = 0, = 0 và = 0.
b) Do ¬ ∧ có chân trị 0 ta suy ra ¬ có chân trị 0, nghĩa là có chân trị 1. Trong trường hợp
này và có chân trị tùy ý.
15. Dạng mệnh ề ã cho là : a) Mâu thuẫn b),c) Tùy ý d) Hằng úng
17. a) Thay thế ∨ bởi ta cần chứng minh dạng mệnh ề
(⟶) ⟷ (¬ ⟶ ¬ ) là hằng úng.
Do qui tắc thay thế thứ nhất, dạng mệnh ề trên tương ương logic với: (¬ ∨) ⟷ (∨ ¬ ) ⟺ 1
b) Thay (∨) ⟶ bởi ta cần chứng minh dạng mệnh ề sau là hằng úng:
[∨ (∧)] ⟷ [(∨) ∧ (∨)]
Đây chính là luật phân bố 22. a) Sai b) Đúng, PP phủ ịnh c) Sai d) Đúng, Tam oạn luận 29. a), b) = 1, = 1, = 1, = 0
30. a) Phép suy luận có dạng: (∧) ⟶ lOMoARcPSD| 36667950 ¬⟶ ∴ ¬ ∨ ¬
Sử dụng Tam oạn luận và PP Phủ ịnh b) Phép suy luận có dạng ⟶ ⟶ (∧) ⟶ (∧) ⟶ ¬ ∴ ¬ ∨ ¬ Dùng phép phản chứng.
c) Phép suy luận có dạng: ⟶ ⟶ (∨) ⟶ ¬ ∴ ¬ ∧ ¬ Dùng PP Phủ ịnh 3 lần 34. a) Sai b) Đúng c) Đúng
d) Đúng: chọn = 1 e) Sai: chọn x=0
37. a) Đúng: nếu thay bởi phần tử tùy ý sao cho ( ) úng thì = 2 hay = 3. Khi ó > 0
b) Sai: chọn = 5 thì (5) úng và ¬ (5) sai
c) Đúng: chọn = 0 thì (0) sai nên (0) ⟶ (0) úng
d) Đúng: chọn = 0 thì (0) sai nên (0) ⟶ ¬ (0) úng 38. a) Sai b) Đúng c) Đúng d) Đúng
e) Cho tùy ý, chọn = thì ( , ) úng
f) Sai cì có phủ ịnh úng là: ∀ ∃ ,¬ ( , ) . Thật vậy cho tùy ý, chọn = + 1 thì ¬ ( , ) úng. g) Đúng h) Đúng
39. a) Sai: chọ = −1 và = 0 thì > nhưng <
. Phủ ịnh ã cho ược viết úng.
b) Đúng. Phủ ịnh ã cho ược viết úng.
c) Đúng. 1.3=3 là số lẻ. Phủ ịnh ược viết không chính xác. Phủ ịnh úng là: tích của hai số lẻ bất kỳ là số chẵn.
d) Đúng. Phủ ịnh ược viết không chính xác. Phủ ịnh úng là : tồn tại số hữu tỉ có bình phương là số vô tỉ
40. a) Tồn tại số nguyên sao cho chia hết cho 2 và số chẵn
b) Tồn tại số nguyên chẵn có bình phương là số lẻ
c) Tồn tại các số nguyên ,
, sao cho −,− và − là số lẻ.
d) Tồn tại số thực sao cho > 16 và −4 ≤ ≤ 4
e) Tồn tại số thực sao cho |− 3| < 7 trong khi hay ≥ 10. 41. a) ∀ , ¬ ( ) ∨ ( ) ⟺ ∀ ,¬ ( ) ∧ ¬ ( ) b) ∃ ,¬ ( ) ∧ ¬ ( ) ⟺ ∃ ,¬ ( ) ∨ ( ) ⟺ ∃ , ( ) → ( ) lOMoARcPSD| 36667950 c) ∃ ,¬ ( ) →
( )⟺ ∃,¬ ¬ ( ) ∨ ( )⟺ ∃, ( ) ∧ ¬ ( )
d) ∀ , ( ) ∨ ( ) ∧ ¬ ( ) ⟺ ∀ , ( ) ∧ ¬ ( ) 43. a) ∃ ∀ , = b) c) ∀ ,(≠ 0) → (∃ , = 1)
d) Trong b) vẫn như trên trong khi ó c) phải ược thay bởi ∀ ,(| | = 1) → (∃ , = 1)
44. a) ∀ ∈ , (≠ 0) → ∃! : = 1 . Nếu ược hiểu ngầm thì mệnh ề trên có thể viết: ∀ ≠ 0,∃! : = 1 b) ∀ ∈ ,∀ ∈ ,∃! ∈: = + c) ∀ ,∃! : = 3 + 7 45. ∀ ,∃! ,
= −2 úng trong khi ∃! ,∀ ,
= −2 sai. Thật ra ta cần kiểm tra ∃ ,∀ ,≠
−2 úng. Muốn vậy, ta cho =
tùy ý và chọn = − + 1 thì = −2 + 2 ≠ −2
Với kết quả trên thì a) sai và b) úng 46. Chọn = 0, = 0,
= 2 thì ( , ) và ( , ) úng trong khi ≠ . Như vậy
sai. Suy ra ∃! ∀; ( , ) cũng sai. Từ ó ta thấy cả hai kết luận a) và b) ều úng.
47. Với tập hợp vũ trụ = {1,2} thì mệnh ề “∃! , > 1” úng trong khi với = {1,2} thì mệnh ề trên sai.
49. a) Đúng. Qui tắc ặc biệt hóa phổ dụng và PP khẳng ịnh ã ược sử dụng. b)
Sai. Có thể ông Bình ã óng thuế nhưng vẫn không là công dân tốt (vi phạm luật giao thông chẳng hạn!) c)
Sai. Có thể Hà không quan tâm ến môi trường nhưng vẫn ể riêng các túi nhựa bỏ i
(bị mẹ bắt chẳng hạn!) d)
Sai.Có thể Minh không nộp bài chưa làm xong vì không chịu làm bài (do ó Minh không
phải là sinh viên nghiêm túc). 50. a) b) hiển nhiên.
c) Sử dụng Qui tắc ặc biệt hóa phổ dụng, Qui tắc tổng quát hóa phổ dụng và Phép chứng
minh theo trường hợp, d) Xét hai vị từ trên : ( ):"≥ 0" ( ):"≤ 0" Khi ấy “ ∀ , ( ) ∨
( )” úng trong khi cả “ ∀ , ( )” và “ ∀ , ( )” ều sai.
54.Suy luận sai ngay ngay trong bước qui nạp ầu tiên: (1) → (2).
55. Giả sử 3 số liên tiếp bất kỳ có tổng ≤ 38. Khi ấy ta có: 3.(1 + 2 + ⋯ + 25) ≤ 25.38 nghĩa là 25.39 ≤ 25.38: mâu thuẫn
56. a) Suy ra dễ dàng từ nguyên lý qui nạp.
b) Cần chứng minh bằng qui nạp bất ẳng thứ phụ nếu > 2 thì 2 + 1 < 2 lOMoARcPSD| 36667950
c) Cần chứng minh bằng qui nạp 2 bất ẳng thứ phụ: nếu > 5 thì 6 + 10 < 2 và nếu > 6 thì 3 + 3 + 1 < 2 57. Giả sử Khi ấy:
Tuy nhiên (1) ã sai nên không áp dụng nguyên lý qui nạp ược.
58. Công thức cần chứng minh là ( + 1) + ( + 2) + ⋯ + ( + 1) = + ( + 1) ,≥ 0
Giả sử công thức trên úng với = . Ta có: (( + 1) + 1) + (( + 1) + 2) + ⋯ + ( + 2) lOMoARcPSD| 36667950 = ( + 2 + 1 + 1) + ( + 2 + 1 + 2) + …+ ( + 2 + 1 + 2 + 1) + ( + 1)2 + 2 + 2 + ( + 1)2 + 2 + 3 = ( + 1) + ( + 2) + ⋯ + ( + 1) + (2 + 1).(2 + 1) + 2 + 4 + 5 ) = ( + 1) + + 6 + 12 + 8 = ( + 1) + ( + 2 CHƯƠNG 2
1. Bốn tập hợp bằng nhau. Tuy nhiên 3 cách viết sau không hợp lý vì có những phần tử ược
kể 2 lần trong tập hợp. 2. a) Đúng b) Đúng
c) Đúng do a) d) Đúng do b)
e) Sai. Ta phải viết {2} ⊂ .
f) Sai. Ta phải viết {2} ∈ 3. a) Sai. b) c) d) Đúng. 4. a) {0,2} b) 2, , , , c) , , , , ,
5. a) b) c) e) Đúng. d) và f) Sai
7. Chỉ có d) khác ∅ vì phươn trình tương ứng có nghiệm. 8. a) {1,2,3,5} b) c) và d) e) {4,8} f) {1,2,3,4,5,8} \ {2} g) ∅ h) {1} i) {1,3,4,5,8} 9. a) c) d) Đúng. b) e) f) Sai 10. a) b) c) d) f) e) ̅ = {2 + 1/ ∈}
12. a) Sai, chọn ≠ 0 tùy ý và = = ∅, =
b) Sai, chọn ≠ 0 tùy ý và = ∅, = =
c) Đúng. Ta có: (∩) ∪ (∩) = (∪) ∩ = (∪) ∩ = ∩ ∩ = ∅ Suy ra (∩) ⊂ ∩ (∩) = ∩ ∩ = ∩ ∩ = ∅ Do 11. d) ⊂
. Tương tự ta có ⊂. Nghĩa là = . 13. a) Sai. Chọn = {1}, = {2} b) Đúng ̅ ̅ b) (∩) ∪ ( ∩ ∩ ̅ ∩ ) ∪ ( ̅ ∩ ) =
c) ̅ ∪ ∪ ( ∩ ∩ ̅) = ∩ ∩ d) Tập hợp ã cho bằng ∩ ∩ ∩ 21. a) ∘( ) = 3− 1 và ∘( ) = 3− 0 ế ℎẵ
3 ℎ ∘ ( ) = ℎ(3 ) = ℎ( ); ∘ ℎ( ) = 3 ế ẻ ∘ ∘ ℎ( ) = 3ℎ( ) − 1
b) ( ) = − 2, ( ) = − 3, ( ) = 9 , ( ) = 27 ℎ = ℎ,ℎ = ℎ = ℎ. Bằng qui nạp ℎ = ℎ 22. ( ) = ∩ (∪) = ∩ ∪ ∩ (∪) = ∩ (∪) ∩ (∪) = ∩ (∪) = ( ) lOMoARcPSD| 36667950
23. a) là song ánh. Ánh xạ ngược ( ) = − 7. : → cho bởi b) (1) =
(−3) = 0 nên không ơn ánh GS. Nguyễn Hữu Anh 117
c) Hàm số tăng ngặt trên [4,9] nên là ơn ánh. Mặt khác ([4,9]) ⊂ [21,96]. Hơn nữa với ∈
[21,96] thì phương trình + 2− 3 = có nghiệm duy nhất là . Do ó là song
ánh với ánh xạ ngược là ( ) = −1 + 4 + .
d) là song ánh. Ánh xạ ngược: ế < 5 e) là song ánh. ( ) = ln( ) − 1,∈ (0,+ ∞)
f) là ơn ánh nhưng không toàn ánh vì 1 ∉ ( ) 27. a) (−10) = −3, (0) = 7, (2) = 1, (6) = 5 b) ([−5,−1]) = [2,6], ([−2,4]) = ([−2,0]) ∪ (0.3) ∪ ([3,4]) = (−1,7]
28. a) Chú ý rằng là một song ánh giữa ={1,2,…} va tập hợp các số nguyên tự nhiên lẻ,
cũng như là một song ánh giữa ∪ {0} = {…,−2,−1,0} tập hợp các số nguyên tự nhiên chẵn.
Suy ra là một song ánh giữa và . ế à ố ê ự ℎê ẻ b) ( ) = ế àố ê ự ℎê ℎẵ ⟹ ( ) = ( ) ⟹ = ′
b) Do ∘ toàn ánh nên cho ∈ tùy ý, sẽt tồn tại ∈ sao cho = ∘( ) = ( ) với = ( ) ∈ . Điều này chứng tỏ toàn ánh. c) (∘) = ∘
d) Chọn ( ) = 2 với ∈ và ế à ộ ố ê ự ℎê ℎẵ ( ) = 2 ế à ố ê ự ℎê ẻ 30. a) ( ) =
± 1 nên và ( ) khác tính chẵn lẻ. b) Giả sử ( ) =
( ). Khi ấy và cùng tính chẵn lẻ nên (−1) = (−1) .Suy ra = ∶ là ơn ánh c) ( ) = ( ) + (−1) ( ) = + (−1) − (−1) = ,∀ ∈ Như vậy là song ánh và = .
d) Ta có = (365) = (365) = 365 + (−1) = 364 lOMoARcPSD| 36667950 31. i) Giả sử + < + ′. Khi ấy ≤
Tương tự nếu + < + thì ( + ) < ( , ). Mặt khác nếu + = + ′ và ( , ) = ( , ) thì = , = . Tóm lại là ơn ánh. ii) Đặt = ( ×
). Ta có 0 = (0,0) ∈ GS. Nguyễn Hữu Anh 118
Mặt khác, giả sử = ( , ). Khi ấy + 1 = (− 1, + 1) nếu > 0 và + 1 = ( + 1,0) nếu = 0. Suy ra
( × ) = theo Nguyên lý Qui nạp. 33. a) b) 7 = 35 4 c)
34. a) Đó là các tập hợp có dạng ∪ với là một tập con của ≠ ∅ của {2,4,6,8,10} và ⊂
{1,3,5,7,9,11}. Do ó theo Nguyên lý nhân số tập hợp này là: (2 − 1)2 b) Tương tự như trên,
số tập hợp con có dạng này là 2 (2 − 1)
c) Tổng quát hóa: nếu là một tập hợp số chẵn có phần tử và là một tập hợp số chẵn có
phần tử thì số tập hợp con của ∪ chứa ít nhất một số chẵn là: (2 − 1)2 35. = 20
38. a) Số nhãn hiệu thỏa ít nhất 2 tính năng là:
|(∩) ∪ (∩) ∪ (∩)| = |∩| + |∩| + |∩| = 4
Số nhãn hiệu thỏa ít nhất 1 tính năng là:
|(∩) ∪ (∩) ∪ (∩)| = 18 − 4 = 14
Do ó số nhãn hiệu thỏa úng 1 tính năng là 10.
b) Số nhãn hiệu không thỏa tính năng nào là 15 - 14=1. 40.
a) 2 − 2 = 126;2 − 2 − 7−7 = 112 b) 2 − 2;2 − 2 − 2 1 6 − ! 41. … = ! !… !
44. Gọi , , là tập hợp các sinh viên làm thí nghiệm thứ nhất, thứ hai và thứ ba tương ứng.
Ta có: | | = 21 − 5 = 16, | | = 21 − 7 = 14, | | = 21 − 6 = 15. Áp dụn 38. ta ược |∩| + |∩| + |∩| = 33
Số sinh viên làm ít nhất hai thí nghiệm là:
|(∩) ∪ (∩) ∪ (∩)| = 33 − 3| ∩ ∩ | + | ∩ ∩ | = 15
Do ó có 21 − 15 = 6 sinh viên chỉ làm ược một 1 thí nghiệm. lOMoAR cPSD| 36667950
45. Mỗi ường i ược xác ịnh bởi ký tự ( i ngang) chọn một dãy gồm có + ký tự
và ( i lên). Do ó số các ường i khác nhau là + = + 46. 10 + 4 − 1 = 13 = 286 4 − 1 3 47. a) 10 + 5 − 1 = 14 = 1001 5 − 1 4 b) 12
Chia cho ứa trẻ lớn nhất hai hòn bi, còn lại chia cho 5 ứa: 8 + 5 − 1 = = 495 5 − 1 4 c) 9
Chia 5 hòn bi còn lạc họ ứa: 5 + 5 − 1 = = 126 5 − 1 4
48. a) Cho vào mỗi hợp một vật, còn lại =
− vật chia cho hộp: − + − 1 − 1 − 1 − 1 GS. Nguyễn Hữu Anh 119 b) − 1 − 1
49. a) Đây là số nghiệm ≥ 0 của phương trình + + + = 8 8 + 4 − 1 = 11 = 165 4 − 1 3 b) Chỉ có 1 nghiệm: = = = = 8
c) Chính là số nghiệm của phương trình + + + = 28 với , , ≥ 0,0 ≤ ≤ 24: 31−6 = 4475 3 3
ở ây 6 chính là số nghiệm ≥ 0 của + + + = 3 3
50. a) Theo Nguyên lý nhân, số các số hạng 6 4 (2 ) (3 ) là: 7 × × = 420 2 3 Do ó hệ số của là 420 × 2 × 3 = 15120
b) Số số hạng có dạng là số nghiệm của phương trình + + + + = 7, với ∈ ,1 ≤ ≤ 5: 7 + 5 − 1 = 11 = 330 5 − 1 4 53. a) 8 = 28 b) 8 = 70 c) 8 = 28 lOMoARcPSD| 36667950 2 4 6
d) Đây cũng là số byte có nhiều nhất 2 bit 0: 8 8 8 + + = 37 0 1 2 55. a) 15 = 105 b) 25 = 2300, 25 = 12650 2 3 4 56. a) = ( )( ) 3
b) Có tam giác có chung hai cạnh với a giác ều và (− 4) tam giác có chung một cạnh với a
giác ều. Do ó số tam giác không có cạnh chung là − (− 4) − = ( − 9 + 20) 6 59. a) (1 + 2) = 3 b) (1 + −) = 1 1 c) = = ! d) = (−1) = (1 − 1) = 0
60. Giả sử mỗi cửa có ít hơn bồ câu. Khi ấy ta có: ≤ − 1 < = : mâu thuẫn
61. a) Ít nhất 7 lần: Nguyên lý chuồng bồ câu b)
Gọi là số lần tung. Do 60. Ta cần có: ≥ 3
Do ó giá trị nhỏ nhất của là 13 c) 6(− 1) + 1 GS. Nguyễn Hữu Anh 120
63. a) Ta chọn 10 của chuồng bồ câu: [1,2),[2,3),…,[9,10),{10}. Do nguyên lý chuồng bồ
câu có hai phần tử ≠ có căn bậc hai cùng thuộc một tập hợp, nghĩa là: 0 < √ − < 1.
b) Cho trước một số nguyên > 0. Trong + 1 phần tử khác nhau của {1,2,…, }, có ít nhất 2
phần tử , sao cho: 0 < √ − < 1
64. Vẽ 9 tam giác ều có các cạnh song song với các cạnh của tam giác ều ã cho vaa2 ỉnh
chọn trong số 3 ỉnh, 6 diểm chia các cạnh theo tỉ số và tâm của tam giác ều. Theo Nguyên
lý chuồng bồ câu, có ít nhất 2 trong số 10 iểm ã cho thuộc về cùng một tam giác ều nhỏ.
Khoảng cách của chúng ≤ . Dấu = chỉ xảy ra ối với 2 ỉnh của một tam giác ều nhỏ. Tuy
nhiên chỉ có một ỉnh duy nhất nằm bên trong tam giác ều ã cho. lOMoARcPSD| 36667950 CHƯƠNG 3
1. a) = 0,( , , ) ∈ × × tùy ý: có 4.7 = 196 bộ 4 ≠ 0 tùy ý, = 0,( , ) ∈
× tùy ý: có 4 .7 = 112 bộ 4 ≠ 0 tùy ý, tùy ý, tùy ý, = 0: có 4 .6 = 96 bộ 4
Vậy |ℛ | = 196 + 112 + 96 = 404 b) ≠ 0 tùy ý, tùy ý, tùy ý, = 0 tùy ý Vậy |ℛ | = 4 .6.3 = 288 2. a) | × | = 3 = 9 b) 2| × | = 2 = 512 c) 2| × | = 512
d) Đó là số tập hợp con của × \ {(1,2),(1,5)} = 2 = 128 e) 9
Đó là số tập hợp con 5 phần tử của × : = 126 5 f) 2 − 9−9−9 = 466 0 1 2
3. 2| || | = 4096 = 2 ⟹ 3| | = 12 ⟹ | | = 4 4. a) Quan hệ hàm: : →, ( ) = + 7
b) Quan hệ hàm: : →, ( ) =
c) Quan hệ hàm: : →, ( ) = 3 + 1 hay : →, ( ) = = ( )
d) Không phải là quan hệ hàm e) Quan hệ hàm: :[0,1] ⟶
hay : [0,1] ⟶ [0,1], ( ) = 1 − = ( ) = ( ) b) (ℛ) = , (ℛ) = [−1,1] c) (ℛ) = [−1,1], (ℛ) = [−1,1]
6. a) Quan hệ trên × × trong ó dòng 2 và 3 ồng nhất nên loại bớt 1 và dòng 5
và 6 ồng nhất nên loại bớt 1. b) ×
ều có thẻ dùng làm khóa chính × × ×
gồm 3 cột ầu và ủ 6 dòng. GS. Nguyễn Hữu Anh 121 7. a) Quan hệ chiếu lên
gồm 2 cột ầu và ủ 6 dòng. Quan hệ chiếu lên lOMoARcPSD| 36667950
b) Không có khóa chính vì mỗi cột ều có giá trị lặp lại. c) × , × , × , × , × .
8. a) ℛ = {(1,1),(2,2),(3,3),(4,4),(1,2),(2,1),(2,3),(3,2)}
b) ℛ = {(1,1),(2,2),(3,3),(4,4),(1,2),(2,1),(2,3),(1,3)}
c) ℛ = {(1,1),(2,2),(1,2),(2,1)}
9. a) Phản xạ, ối xứng, bắc cầu. Tuy nhiên không phản xứng trừ trường hợp =
b), e), f), g) Phản xạ, ối xứng, bắc cầu nhưng không phản xứng
c) Đối xứng nhưng không có ba tính chất kia
d) Phản xạ, phản xứng, bắc cầu nhưng không ối xứng
b) ℛ = ℛ∗ khi và chỉ khi ℛ ối xứng
c) bắc cầu, phản xứng khi và chỉ khi ℛ∗ bắc cầu, phản xứng. Theo b) nếu ℛ ối xứng thì ℛ∗ = ℛ cũng ối xứng. 12. a) | ×
| = 16,|∆ | = 4 nên số quan hệ phản xạ là: 2 = 4096
b) Gọi = {( , )/ 1 ≤ < ≤ 4}. Với ⊂ ∪ ∆ thì ∪ {( , )( , ) ∈ } là một quan hệ ối xúng và ngược lại. Do
ó số quan hệ ối xứng là 2∪∆ = 2 = 1024
c) Một quan hệ phản xạ và ối xứng xác ịnh duy nhất bởi tập hợp ⊂ nên số quan hệ phản xạ
và ối xứng là 2| | = 2 = 64.
d) Giả sử ℛ phản xứng, ặt = ℛ ∩ ∆ , = ℛ ∩ và = ℛ∗ ∩ : rõ ràng ℛ ược xác ịnh duy nhất bởi , , .
Do ó số các quan hệ phản xứng là : 6 2 2 = 11.664
e) Đó là quan hệ ℛ ⊂ ∆ : có 2 = 16 quan hệ
f) Quan hệ duy nhất là ℛ = ∆ .
13. Ta viết = { , ,…, }. Đặt = , / < . Ta có | | =
( ) . Tương tự như trên, mỗi quan hệ phản
xứng ℛ tương ứng với các tập con , , . ℛ là tối ại khi và chỉ khi = ∆ và ∪ = , nghĩa là |ℛ| = ( ) + = ( )
Hơn nữa số quan hệ như vậy chính là 2 .
14. a) Trực tiếp từ ịnh nghĩa
b) [1] = {1,2} = [2],[3] = {3}
c) [4] = {4,5} = [5] và [6] = {6}. Do ó ta có phân hoạch của thành các lớp tương ương: = {1,2} ∪ {3} ∪ {4,5} ∪ {6}
15. Ngoài ường chéo chính ∆ , còn chứa các cặp {1,2},{2,1},{3,4},{4,3}. lOMoARcPSD| 36667950 16. Ta có (1,2) và (2,3)
nhưng (1,3) ∉ ℛ nên ℛ không phải là quan hệ tương ương. 17. a) Hiển nhiên
b) [( , )] = {( , )/ ∈ ℛ}. Đấy chính là ường thẳng song song với trục tung và i qua iểm ( , )
19. a) Đó là quan hệ tương ương b) [∅] = ∅,{3} ,[{1}] =
{1},{1,3} ,[{2}] = {2},{2,3} ,[{1,2}] = {1,2},{1,2,3}
c) [{1,3,5}] = {{1,3,4},{1,3,5}}. Mỗi lớp tương ương ều chứa một tập hợp con duy nhất
của nên số lớp tương ương chính là 2| | = 2 = 8 21. a) 6 3 = 10 b) 6 1 + = 80 3 3 1 c) d) 10 + 80 + 30 + = 126
22. a) Suy trực tiếp từ ịnh nghĩa b) { ( )/ ∈( )} 23. ℛ = ( × ) ∪ ( × ) ∪ ( × )
25. Xét = ({1,2,3}) và = {⊂/ 4 ∈ }. Khi ấy biểu ồ Hasse của và là 2 hình lập phương 3 chiều.
Nối mỗi ỉnh ∈ ến ỉnh ∪ {4} ∈ bởi 1 cung có hướng xuất phát từ . Tập hợp các ỉnh trong
và và các cung trong và cùng với các cung mới thêm vào như trên chính là biểu ồ Hasse của ( ).
26. a) Kiểm tra trực tiếp của ịnh nghĩa
b) ≺ không nhất thiết là toàn phần. ví dụ =
= {0,1} và ≺ ,≺ là thứ tự thông thường
27. a) Trực tiếp từ ịnh nghĩa
b) Với ,∈ tùy ý. Định nghĩa ánh xạ ℎ: → bởi ℎ( ) = ( ) ∨ ( ),∀ ∈ . Khi ấy ℎ = sup{ , }
Tương tự ta thấy inf( , ) là ánh xạ →: inf( , ) ( ) = ( ) ∧ ( ),∀ ∈
29. Tính phản xạ hiển nhiên. Gọi là chỉ số sao cho = , = ,…, = và = hoặc nếu < . Gọi
là chỉ số tương tự xác ịnh từ ≺ . Nếu ≥ thì ta có = ,…, = và = hoặc ≺
nếu < . Nếu < thì < nên ta có = ,…, = và ≺ .
Trong cả hai trường hợp ta ều có ≺ và ≺ có tính bắc cầu. Chú ý rằng trong trường hợp trên
nếu = thì trường hợp 2 không xảy ra và khi ó = , nghĩa là ≺ là phản xứng.
Xét hai chuỗi khác rỗng , như trên. Nếu =
với 1 ≤ ≤ min( , ) thì ta có ≺ hay ≺
theo Định nghĩa của ≺. Trong trường hợp ngược lại sẽ có chỉ số bé nhất ể
≠ , nghĩa là = ,…, = . Do thứ tự trên là tòan phần ta có hay . Nói cách khác ≺ hay
≺ . Tóm lại thứ tự trên là toàn phần.
30. Trong 3 biểu ồ ầu, ịnh nghĩa trội trực tiếp bị vi phạm. lOMoARcPSD| 36667950
Ngoài ra trong biểu ồ thứ 2 tính phản xứng cũng bị vi phạm. Chỉ có biểu ồ cuối cùng là biểu ồ Hasse
34. a) Chỉ có một chặn trên gồm 3 phần tử
{1,2,3} Số chặn trên gồm 4 phần tử: 4 = 4
1 Số chặn trên gồm 5 phần tử: 4 = 6 2 b) 4 4 11 + + = 16 3 4 c) {1,2,3}
d) Một chặn dưới duy nhất:∅ e) ∅
35. a) ( ({1,2}),⊂) là 1 dàn nhưng thứ tự ⊂ không toàn phần.
b) Nếu ≺ toàn phần thì với ,∈ tùy ý ta có: sup{ , } = max( , ) à inf{ , } = min( , ) Do ó là một dàn. 37. a) b) c) d) e) f) g)
38. a) là phần tử lớn nhất và là phần tử bé nhất b) ( ,≺) là một dàn
39. Sử dụng các qui luật logic
40. a) ∀ , ,min{ , } tồn tại. Vậy thứ tự tốt toàn phần. Tuy nhiên ≤ là thứ tự toàn phần trên
nhưng không phải là thứ tự tốt. b) Do ịnh nghĩa của thứ tự tốt
c) ≤ là thứ tự tốt trên nhưng không có phần tử lớn nhất. {1,2} là 1 tập hợp sắp tốt có phần tử lớn nhất.
41. a), e), f) là tập hợp sắp tốt.
b) Không phải là tập sắp tốt. Mặt khác tập hợp {1, ,…, ,…} không có phần tử bé nhất nên (
,≤) và ( ,≤) không phải là tập sắp tốt.
g) Giả sử là bộ mẫu tự gồm 2 chữ cái ≺. Khi ấy { , , ,…} là một tập con của không có phần
tử bé nhất nên không phải là tập sắp tốt. 42. a)
chính là trội trực tiếp duy nhất của . b) Giả sử
. Khi ấy nên là ơn ánh. Tuy nhiên
phần tử bé nhất của không thuộc ( ). c)
Định nghĩa ánh xạ : → bởi (0) = , ( ) = ( ), trong ó ( ) ược ịnh nghĩa bằng qui nạp: ( ) =
( ) . Khi ấy là một ẳng cấu giữa hai tập hợp sắp thứ tự ( ,≤) và ( ,≺) 43. a) 1 b) 22 c) 6 d) 11 e) 3 a) 2 .3 .5 .11 và 2 .3.5 .7 .11 b) 47. a) 2 .5 .7 ,0 ≤ ≤ 3,0 ≤ ≤ 2,0 ≤ ≤ 4
b) Các ước số dương của có dạng với 0 ≤ ≤ ,0 ≤ ≤ ,0 ≤ ≤ . Do ó theo Nguyên lý nhân, số
ước số dương là ( + 1)( + 1)( + 1). lOMoARcPSD| 36667950 c) Nếu = thì có ( + 1)(
+ 1) …( + 1) ước số dương.
d) Suy ra + 1 = 2 , nghĩa là = 2 − 1, ∈ ,1 ≤ ≤
49. a) Sinh viên thứ lật 62ng xu thứ 100 khi và chỉ khi là ước số của 200 = 2 .5 . Do ó số lần
mà dồng xu thứ 200 dược lật là 4.3 = 12.
b) Giả sử ồng xu thứ = …< 200 ược lật ngược ( + 1)( + 1)( + 1) …= 12 lần. Khi ấy có thể lấy các giá trị sau: 2 .3 = 96 2 .5 = 160 2 .3 = 72 3 .2 = 108 2 .3.5 = 60 2 .3.7 = 84
2 .3.11 = 132, 2 .3.13 = 156 , 2 .5.7 = 140, 3 .2.7 = 126, 3 .2.11 = 198
52. a) Giả sử ( , ) là một lời giả thì là ước của do Mệnh ề 3.6.3: = . Khi ấy = Ngược lại ( , ),∈ là một lời giả. b) Gọi = ( , ). Ta có =
nên do a) các lời giải có dạng (
c) Gọi = ( , ) = + , ,∈ (Định lý 3.6.2) Do ó nếu , thỏa = + thì (−) = (−) Theo b),
− = ,− = , với ∈ Nghĩa là = + và = − 53. Dùng thuật chia Euclide ể tìm , , : a) = 2, = −1, = 3; = −1 + 8 , = 3 − 23 ,∈ b) = 4, = −1, = 2; = −1 + 16 , = 3 − 31 ,∈ c) = 1,
= −26, = 271; = −26 + 331 , = 271 − 3450 ,∈ 54. a) Giả sử ( ) khi ấy ta có ≡ = ( )
Do ó ′ là nghiệm duy nhất trong
của phương trình ồng dư ã cho.
b) Gọi = ( , ) > 1. Nếu không chia hết cho , thì phương trình dồng dư là vô nghiệm. Mặt khác
giả sử | khi ấy ta ưa về việc giải phương trình ồng dư = : ≡ ( ′)
Theo a) phương trình trên có nghiệm duy nhất trong : ≡ ( ) ớ ′ ≡ 1( )
Đó cũng là nghiệm của phương trình ồng dư ban ầu.
55. a) (3,16)=1. Ta có 3 × 11 ≡ 33 ≡ 1( 16) nên ≡ 11 × 7 ≡ 13( 16) b)
(5,23)=1. Ta có 5 × 14 ≡ 70 ≡ 1(
23) nên ≡ 14(6 − 7) ≡ 9( 23) c)
Phương trình có dạng 3≡ −12 ≡ 10( 11) Mà 3 × 4 ≡ 1( 11) nên ≡ 4 × 10 ≡ 7 (11) d)
Phương trình có dạng 5≡ −52 ≡ 12( 64) lOMoARcPSD| 36667950 Mà 5 × 13 ≡ 65 ≡ 1(
64) nên ≡ 13 × 12 ≡ 28( 64) CHƯƠNG 4
1. a) Giả sử ̅ và ′ là hai phần bù của . Ta có: (̅ ∧) ∨ = 0 ∨ = ′ Mà (̅ ∧) ∨
= (̅ ∨ ) ∧ (∨ ) = (̅ ∨ ) ∧ 1 = ̅ ∨ Suy ra ̅ ≺ ̅ ∨ = ′
Tương tự nếu xét (̅ ∧) ∨ ta cũng có ≺ ̅. Nghĩa là ̅
= ′ b) Kiểm tra trực tiếp từ ịnh nghĩa của phần bù rồi sử dụng a).
2. a) Do ≺ nên là trội chung của và . Hơn nữa nếu là trội chung của , thì ≺ . Như thế = sup{ , } = ∨ b) Do a) ≺ ⟹ ∨ = ⟹ ̅ ∧ = : ≺ ̅ c) ∧ ≺ ≺ và ∧ ≺ ≺ . Suy ra ∧ ≺ ∧ d) ≺ ≺ ∨ và ≺ ≺ ∨ . Suy ra ∨ ≺ ∨ 3. a) ∧ ∨ (∧) = ∨ ∧ nên ∧ ∨ (∧) = ∨ ∨ ̅ = ∧̅ ∨ ̅ b) ( ∧ ̅) ∨ ∧ ∨ (∧) = ( ∧ ̅) ∨ ∨ ∧ ∨
Do ó phần bù của nó là: ∨ ∧
4. a) Xét một phần tử ∈ ℬ. Khi ấy ̅ ∈ ℬ và 0 = ∧ ̅ ∈ ℬ, 1 = ∨ ̅ ∈ ℬ
b) Có 4 ại số con là ,ℬ = ∅,{ },{ , },{ , , } ,ℬ = ∅,{ },{ , },{ , ∅,{ },{ , }.{ , , } . , } ,ℬ =
c) Với ,∈ ℬ tùy ý ta có ̅,∈ ℬ nên ∨ ∈ ℬ. Suy ra ∧ = ̅ ∨ ∈ ℬ. 5.
Đó là ại số Bool với phần tử trung hòa ối với ∧ là . Hơn nữa với ≺ thì ̅ ∧ là phần bù
của . Tuy nhiên nó không phải là ại số con nếu ≠ 1 vì khi ấy nó không chứa 1 6.
a) Giả sử ≺( ), tồn tại sao cho ( ) = . Ta có ( ) ≺ ( ) nên ≺ suy ra = 0 hay = , nghĩa là = 0 hay = .
b) Trực tiếp từ ịnh nghĩa của ại số con.
8. a) Do 35 = (5,7),70 = (35,2) à
42 = (2,3,7) ta phải có (35) = { , }, (70) = { , , }, (42) = { , , }. lOMoARcPSD| 36667950
b) Mỗi ẳng cấu phải biến nguyên tử thành nguyên tử nên ược xác ịnh hoàn toàn bởi một
song ánh giữa {2,3,5,7} và { , , , }. Có tất cả 4! = 24 ẳng cấu khác nhau. 11. a) (⨁)⨁ = ∧ ∨ (∧) ∧ ̅ ∨ (∨) ∧ ∨ ∧ = ∧ ∧
̅ ∨ ( ∧ ∧ ̅) ∨ ( ∧ ∧ ) ∨ ∧ ∧ = ∧(∧) ∨ ∧ ̅ ∨ ∧ ( ∧ ̅) ∨ ∧ = ∧ ⨁ ∨ ( ∧ ⨁ ) = ⨁(⨁) ∧∧ ̅ = ∧ ∧ ( ∨ ̅) ∨ (∧) ∧ ∨ = (∧)⨁(∧)
Các tính chất khác hiển nhiên. b) Đặt = ∧ ∨ (∧) (⨁) ∧ ∧ = ∧ ∧ ⨁ ∧ ∧ = ∧ Suy ra ∧ ≺ ⨁ Tương tự ∧ ≺ ⨁ Vậy ⨁′ ≺ ⨁ Do ó (⨁) ∨ ⨁′ = 1 Mặt khác (⨁) ∧ ⨁′ = ∧ (∨) ∧ ∨ ⨁ ∧ (∨) ∧ ∨ = (∧)⨁(∧) = 0
Như thế ⨁ = ⨁′ = ⨁′ 13. a) ∨ = ⟹ ≺
Mặt khác giả sử ≺. Đặt = ∧. Ta có: ∨ = ∨ =
b) ∧ = (∧) ∨ (∧) = ∨ (∧) = ∨ = ∨ ∨ = ∨ ≻ ∨ = 1 c) Ta có ∧ = ∧ ≺
≺ . Ngược lại giả sử ≺ và ∧ ≺ ≺ . Khi ấy ∨ = ∨ (∧) ≺ ∨ ≺ ∨
Suy ra là nghiệm của (1).
d) Nếu là nghiệm, do b) có dạng ∧ với = ∨ ≺ . Ngược lại nếu = ∧ với ≻ thì ∧ = ∧ ∧ = ∧. Như
thế ∧ ≺ ≺ nên là nghiệm do c). lOMoAR cPSD| 36667950 e) Nghiệm của ∧ =
cũng là nghiệm của ∧ ̅ = nên ta ưa về (1).
14. Do 1728 = 2 .3 chia hết cho chính phương nên không là ại số Bool. Hơn nữa số mũ 6
không có dạng 2 − 1,∈ nên không có thứ tự nào trên ể cho nó trở thành dàn bù phân bố, nghĩa là ại số Bool.
16. a) ( ) = 1 nếu là nguyên tử.
b) Nhận xét rằng nếu là nguyên tử không trội bởi thì ∨ là trội trực tiếp của . Do ó ta có thể
chứng minh bằng qui nạp rằng ( ) = nếu có úng nguyên tử trội bởi . Suy ra (∨) = ( ) + ( ) − (∧) 17. a) 0 b) 0 c) 0 d) 1 e) 1 18. a), b) = 1 ℎ = 1 c), d) = 1, ù ý 19. a) ̅̅ b) ̅̅ c) ̅ d) ̅ ̅ ̅ 20. a) Có 6
= 15 iểm có úng 2 thành phần bằng 1. Còn lại (2 − 15) = 49 iểm, nên có 2
2 hàm Bool thỏa iều kiện này. b) 6 Có 6 +
= 7 iểm ở ó số thành phần có giá trị 1 béhoơn 2, nên tổng số hàm Bool 0 1
thỏa iều kiện này là 2 = 128. c) 2 = 2 và 2 = 2 = 256. 21. Ta có (1,0) =
(0,1) nên các hàm Bool này ều có dạng ∨ ̅ ∨ ( ∨ ̅ ), với
, , là các hằng số bất kỳ thuộc {0,1} 22. Ta có
(1,0,0) = (0,0,1) = (0,1,0) và (1,1,0) = (1,0,1) = (0,1,1)
Do ó các hàm Bool này ều có dạng: ( , , ) = ∨ ̅ ̅ ∨ ( ̅ ∨ ∨ ̅ ) ∨ ( ̅ ∨ ̅ ̅ ∨ ̅
) trong ó là các hằng số tùy ý thuộc {0,1}.
23. Hàm Bool 3 biến không thay ổi giá trị khi ta hoán vị 2 biến bất kỳ chính là các hà m Bool trong 22.
Tương tự một hàm Bool 4 biến khi thay ổi giá trị khi ta hoán vị 2 biến bất kỳ có dạng: ( , , , ) = ∨ ̅ ̅ ̅ ∨ ( ̅ ∨ ̅ ∨ ̅ ∨ ) ∨ ( ̅ ∨ ̅ ∨ ∨
̅ ∨ ∨ ) ∨ ( ̅ ∨ ∨∨ ) với , , , , là các hằng số tùy ý thuộc {0,1}.
24. Xét , ,∈ {0,1} . Khi ấy ít nhất 2 trong số 3 số trên bằng nhau. Giả sử = . Ta có: ( , , ) = ( , , ) ⟹ ( , , ) = 0
Tương tự trong các trường hợp khác ta cũng có = 0.
Nếu > 2 cũng không tồn tại hàm Bool biến ≠ 0 thỏa iều kiện trên. Tuy nhiên nếu = 2 thì các
hàm Bool như vậy có dạng ( , ) = ∨ ̅ với là hằng số tùy ý thuộc {0,1}. lOMoARcPSD| 36667950
25.Lập bảng chân trị. Khi ấy hàm chẵn ược xác ịnh hoàn toàn bởi 2 = 2 dòng ầu tiên. Do ó
hàm chẵn là 2 . Với = 2, ta ược 4 hàm chẵn: ∨ ̅ , ∨ ̅ ,0,1
26. Tương tự trong 25, số hàm lẻ biến là 2 . Với = 2, ta ược 4 hàm lẻ: ,̅, , 27. a) Hai vế bằng nhau khi = 1 hay = 0
b) Xét ánh xạ ℱ × ℱ ⟶ ( , ) ⟼ ℱ
với ( , ,…, ) = ( ,…, ) ∨ ̅ ( ,…, ). Khi ấy ta kiểm ược dễ dàng ánh xạ trên là song ánh. Suy ra |ℱ
| = |ℱ | × |ℱ |.Bằng qui nạp trên ta suy ra |ℱ | = 2 c) Bằng qui nạp trên và tính phân bố
28. a) Viết hàm hằng 1 theo − biến còn lại như là tổng Bool của 2 từ tối tiểu và sử dụng
tính phân bố, ta viết ược như là tổng Bool của 2 từ tối tiểu theo biến.
b) ≺ ⟺ ∃ℎ: = ℎ. Do ó là tích của một số từ ơn xuất hiện trong . Suy ra có 2 hàm Bool trội . 29. a) = ̅ ∨ ̅ ∨ ̅ ∨ b) = ∨ ∨∨ ̅ ∨ ∨ ̅ ∨ ∨̅ ∨ ̅ ∨ ̅ ∨ ∨ ̅
b) ∨̅ ∨ ̅ ∨ ̅ ̅ ∨ ∨ ̅ ∨ ̅ ∨ ̅ ∨ ̅ ̅ ∨ ̅ ∨ ̅ ̅ 32. ∨̅ ∨ ̅ ∨ ̅ ̅ ∨ ∨ ̅ ∨ ̅ ∨ 34.
35. Cổng NOT có thể tổng hợp như sau: ̅
Do ó cổng AND và cổng OR ược tổng hợp nhờ các công thức: = ̅ ∨ và ∨ = ∨ 36. = (∨ ) ∨ ∨ = ̅̅ ∨ ( ∨ ∨ ̅)
37. = ∨ ̅ ̅ ∨ ̅ ∨ ̅ ∨ ̅ ̅ ∨ ̅ ̅ ∨ ̅∨ ̅ ̅ ̅. Ta viết = ̅ ∨ ∨ ̅ ∨ ̅ ể sử dụng một cổng NOR vào tổng hợp từ tối
tiểu này. Tương tự cho các từ tối tiểu khác.
Mặt khác ta có thể viết =̅ ̅ … ể thiết kệ mạng chỉ dùng cổng NAND.
38. a) Các tế bào lớn: ̅, ̅,̅,̅,̅. Dùng phương pháp biểu ồ Karnaugh ta uộc hai công thức: = ̅ ∨ ̅
∨ ̅ , = ̅ ∨ ̅ ∨ ̅ ∨ ̅ , trong ó chỉ cố công thức dầu Là tối tiểu. b) Các tế bào lớn: ̅, ,
,̅,̅,̅. Có 3 công thức a tối tiểu: = ̅ ∨ ∨ ̅ ∨ lOMoAR cPSD| 36667950 , = ̅ ∨ ∨ ̅ ∨ ̅ , = ̅ ∨ ∨ ̅ ∨ ̅
c) Dạng nối rời chính tắc cũng là công thức a thức tối tiểu duy nhất.
d) Các tế bào lớn: ,̅,̅, ̅.
Công thức công thức a thức tối tiểu duy nhất: = ∨̅ ∨ ̅ ∨ ̅ e) Các tế bào lớn: ̅, ̅, ,
. Có 2 công thức a thức tối tiểu: = ̅ ∨ ∨ = ̅ ∨ ∨ ̅ f) Các tế bào lớn: ̅,̅̅,̅, , ,̅
Có 3 công thức a thức tối tiểu: = ̅ ∨ ̅ ∨ ̅ ̅ ∨ = ̅ ∨ ̅ ∨ ̅ ∨ ̅ ∨ ̅ ∨ ̅ ∨ = 39. a) = ̅∨ ̅ ∨ ̅ và = ̅ ∨ ̅ ∨ ̅ b) = ̅ ∨ ∨ ̅ ̅ ∨ ̅ ̅ = ̅ ∨ ∨ ̅ ∨ ̅ ̅ c) = ∨ ̅ ̅ d) = ∨ e)
Dùng phương pháp biểu ồ Karnaugh ược 6 công thức trog ó chỉ có một công thức tối tiểu: = ̅ ̅ ∨ ̅ ∨ ̅ ̅ ∨ ̅ ∨ f) = ∨ g) = ̅ ∨ ̅ ∨ h) = ∨ ̅ ̅ i) = ̅ ∨ ̅ ∨ ̅ ∨ ̅ ̅ ̅
40. a) = ̅ ∨ ∨ ̅ . Đây cũng là công thức a thức tối tiểu duy nhất. mạng tối ưu sử dụng 6 cổng AND và 2 cổng OR. b)
= ∨ ∨ . Đây cũng là công thức a thức tối tiểu duy nhất. Mạng tối ưu sử dụng 3 cổng AND và 2 cổng OR. c)
= ̅ ∨ ̅ ∨ ∨ ̅ ∨ ̅ ̅ ∨ ̅ ̅ ̅ ∨ ̅ ̅ ∨ ̅ ̅ . Đây cũng là công thức a thức tối tiểu duy nhất. Mạng tối ưu
sử dụng 24 cổng AND và 7 cổng OR.



