














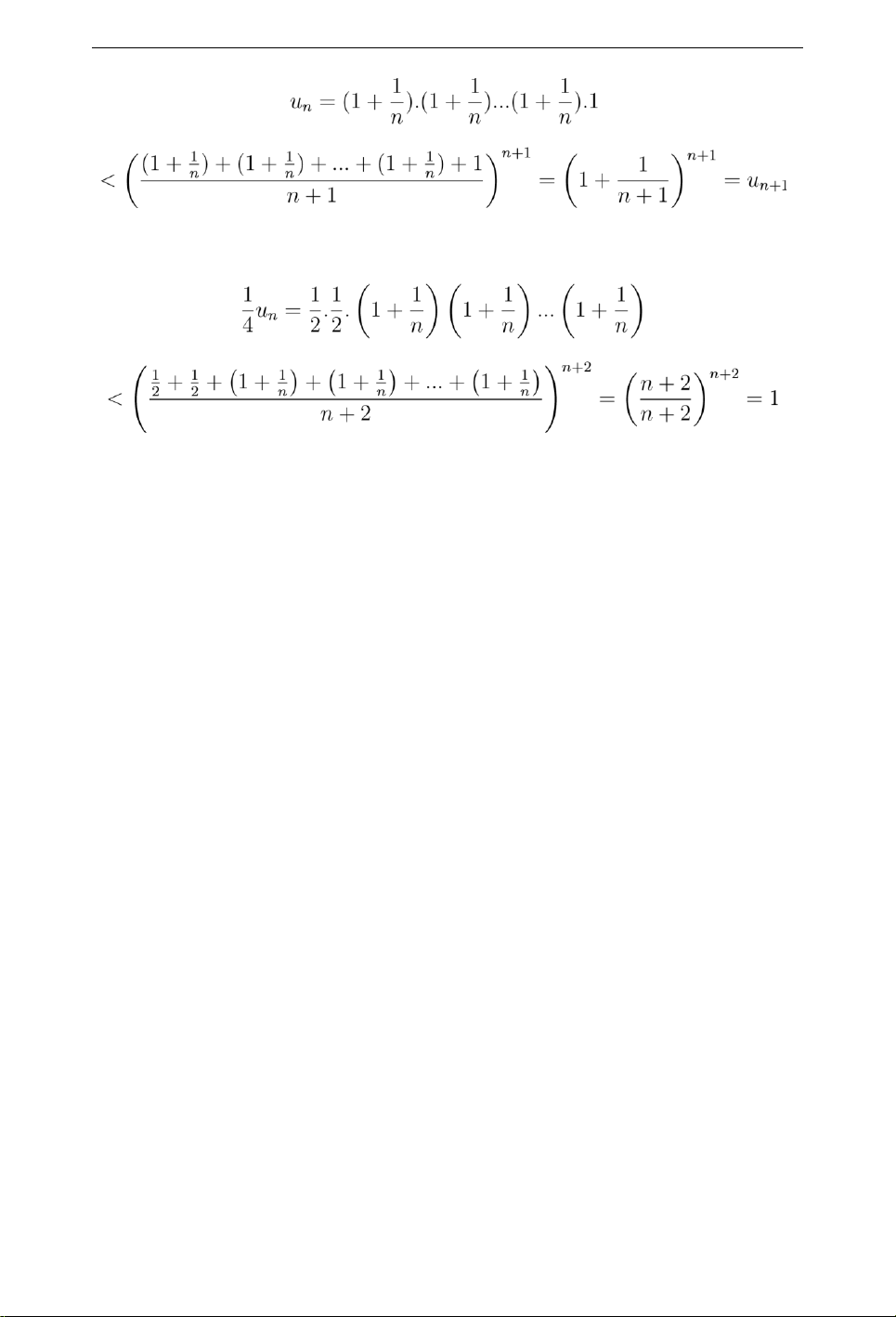



Preview text:
lOMoAR cPSD| 58970315 Lời nói đầu
Toán học được ứng dụng rộng rãi trong hầu hết các ngành, các lĩnh vực
từ Khoa học tự nhiên, khoa học xã hội và các ngành kinh tế học. Việc hiểu và
vận dụng các công cụ toán học để giải quyết các bài toán kinh tế là vô cùng cần
thiết, nó giúp các nhà kinh tế hiểu vấn đề một cách khoa học mà tường minh.
Đối với Sinh viên khối ngành kinh tế của trường Đại học Xây dựng Hà nội, việc
tiếp cận một số mô hình thực tế đơn giản của kinh tế thông qua môn toán và
các ứng dụng sẽ giúp các em dễ dàng hình dung về sự vận hành của các quy luật
kinh tế cũng như mối quan hệ giữa các yếu tố kinh tế như quy luật Cung-Cầu;
Chi phí - Lợi ích; Số lượng sản phẩm - Giá sản phẩm...
Bài giảng này, bên cạnh cung cấp các kiến thức toán học một cách hệ thống
nhưng đơn giản, tập trung vào tính ứng dụng, tác giả cũng giới thiệu và phân
tích thô sơ một vài ví dụ về mô hình kinh tế đơn giản thông qua vận dụng các kiến thức toán học.
Cũng vì tập trung vào tính ứng dụng nên bài giảng không quá đặt nặng các kiến
thức toán học, chủ yếu là trình bày một cách sơ lược các Khái niệm, định nghĩa
đồng thời nêu nội dung các định lý (không chứng minh) và chỉ ra các ứng dụng
thông qua các ví dụ cụ thể. Bài giảng gồm 3 phần:
Phần 1: Phép tính vi phân, tích phân hàm số thực một biến số thực.
Phần 2. Phép tính vi phân và cực trị hàm số thực nhiều biến số thực. Phần 3. Phương trình vi phân.
Bài giảng được đi kèm tập bài tập để sinh viên có thể thực hành từ đó
củng cố các kiến thức toán học và vận dụng tốt các kiến thức toán học trong giải
quyết, phân tích các vấn đề kinh tế.
Đây là bài giảng được viết riêng cho khối ngành Quản lý kinh tế, Lời nói đầu
chỉ lưu hành nội bộ cho Sinh viên Ngành Quản lý Dự án, khoa Kinh tế Xây dựng,
trường Đại học xây dựng Hà nội làm tài liệu học tập, không nhằm mục đích kinh doanh hay thương mại. lOMoAR cPSD| 58970315 2
Bài giảng cũng có sử dụng (có chỉnh lý) một số phần hay ví dụ từ các tài liệu
tham khảo ( được liệt kê trong phần tài liệu tham khảo). Vì được viết lần đầu
tiên, do vậy không tránh được các thiếu sót hoặc có những mô hình mới cần
được bổ sung, cập nhật thường xuyên. Rất mong nhận được những góp ý quý
báu của các Thầy Cô giáo và các bạn Sinh viên. Tác giả TS. Mai Thị Hồng
Bộ Môn Toán - Trường Đại học Xây dựng Hà nội. lOMoAR cPSD| 58970315 Những kí hiệu Trong
cuốn sách này ta dùng những kí hiệu với các ý nghĩa xác định trong bảng dưới đây:
tập hợp số tự nhiên tập hợp số tự nhiên
khác 0 tập hợp số nguyên tập hợp số hữu
tỉ tập hợp số thực tập hợp số phức dấu
đồng dư dương vô cùng (tương đương
với +∞) âm vô cùng tập hợp rỗng tổ hợp
chập k của m phần tử . phép chia hết . không chia hết
ước số chung lớn nhất BCNN bội số chung nhỏ nhất deg bậc của đa thức IMO
International Mathematics Olympiad APMO
Asian Pacific Mathematics Olympiad Mục lục lOMoAR cPSD| 58970315 4 Mục lục
Lời nói đầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 Những kí hiệu
. . . . . . . . . . . . . . . . . . . . . . . . . . . 3 Mục lục 4
1 Số thực và dãy số thực 7
1.1 Tập số thực và Topo trên tập số thực . . . . . . . . . . . . . 7
1.1.1 Lân cận,điểm tụ, điểm cô lập, tập đóng, tập mở và tập bị chặn
. . . . . . . . . . . . . . . . . . . . . . . 7
1.2 Dãy số thực và giới hạn của dãy số thực . . . . . . . . . . . 10
1.2.1 Khái niệm về dãy số . . . . . . . . . . . . . . . . . . 10
1.2.2 Một số dãy số đặc biệt . . . . . . . . . . . . . . . . . 10 1.2.3 Giới hạn dãy số
. . . . . . . . . . . . . . . . . . . . 11
1.2.4 Dãy con và giới hạn riêng của dãy số . . . . . . . . . 13
1.2.5 Tính chất và các phép toán về giới hạn dãy số . . . . 14
2 Phép tính vi phân và tích phân hàm số thực một biến số thực 17
2.1 Hàm số một biến số và sự liên tục của hàm số một biến số . 17
2.1.1 Các khái niệm cơ bản về hàm số một biến số . . . . . 17
2.1.2 Một số hàm số một biến trong phân tích kinh tế . . . 24 2.1.3 Giới hạn hàm số
. . . . . . . . . . . . . . . . . . . . 27
2.1.4 Sự liên tục của hàm số một biến số . . . . . . . . . . 35
2.2 Đạo hàm và vi phân của hàm số một biến . . . . . . . . . . 39
2.2.1 Khái niệm đạo hàm. Ứng dụng đạo hàm trong phân
tích kinh tế . . . . . . . . . . . . . . . . . . . . . . . 39 MỤC LỤC
2.3 Nguyên hàm và tích phân bất định của hàm số một biến . . 59 lOMoAR cPSD| 58970315
2.3.1 Các định nghĩa và ví dụ
. . . . . . . . . . . . . . . . 59
2.3.2 Tính chất của tích phân bất định . . . . . . . . . . . 60
2.3.3 Bảng các tích phân cơ bản . . . . . . . . . . . . . . 60
2.3.4 Các phương pháp tính tích phân bất định . . . . . . 61
2.4 Tích phân xác định. Các ứng dụng của tích phân trong kinh tế 66
2.4.1 Định nghĩa tích phân xác định . . . . . . . . . . . . . 66
2.4.2 Tính chất của tích phân xác định . . . . . . . . . . . 68
2.4.3 Các phương pháp tính tích phân xác định . . . . . . 68
2.4.4 Một số ứng dụng của tích phân trong kinh tế . . . . 73 lOMoAR cPSD| 58970315 6 Chương 1
Số thực và dãy số thực 1.1
Tập số thực và Topo trên tập số thực . . . . . . 7 1.2
Dãy số thực và giới hạn của dãy số thực . . . . . 10 1.1
Tập số thực và Topo trên tập số thực
Phần này giới thiệu các khái niệm cơ bản về topo trên tập số thực được sử
dụng trong giải tích hàm.
1.1.1 Lân cận,điểm tụ, điểm cô lập, tập đóng, tập mở và tập bị chặn
2 Định nghĩa 1.1. Giả sử x0 là điểm thuộc R, δ > 0 là số thực dương tuỳ ý. Ta gọi
khoảng (x0 − δ,x0 + δ), ký hiệu
Uδ(x0) = (x0 − δ,x0 + δ) = {x ∈ R||x − x0| < δ}
là lân cận bán kính δ của điểm x0 ∈ R.
Nếu V ⊂ R và V chứa một lân cận bán kính δ > 0 nào đó của x0 ∈ R thi ta gọi V là
một lân cận của điểm x0.
Ta bổ sung thêm vào tập số thực R hai phần tử đặc biệt là −∞ và ∞ gọi là
tập số thực mở rộng, ký hiệu
R = R ∪ {−∞,∞}. lOMoAR cPSD| 58970315 7 Khi đó ta có:
∀a ∈ R : −∞ < a < ∞.
Do vậy ta có thể mở rộng thêm khái niệm lân cận của điểm vô cùng như sau:
• Lân cận bán kính δ > 0 của điểm −∞ là tập hợp
• Lân cận bán kính δ > 0 của điểm ∞ là tập hợp
2 Định nghĩa 1.2. Điểm a ∈ R được gọi là điểm tụ của tập X ⊂ R nếu mọi lân
cận của a chứa vô số các phần tử của X.
Chú ý rằng, a là điểm tụ của X thì không nhất thiết phải thuộc X và a có thể nhận
các giá trị là ±∞.
• Ví dụ 1.1. Các ví dụ về điểm tụ:
1. Mọi điểm thuộc đoạn [a,b] đều là điểm tụ của (a,b).
2. Mọi điểm a ∈ R đều là điểm tụ của tập số thực R.
2 Định nghĩa 1.3. Điểm a ∈ X không là điểm tụ của X được gọi là điểm cô lập của tập X.
2 Định nghĩa 1.4. Tập H ⊂ R được gọi là tập đóng nếu H chứa mọi điểm tụ (nếu có) của nó.
• Ví dụ 1.2. Một số ví dụ về tập đóng:
1. Người ta quy ước tập ∅ là tập đóng.
2. Tập số thực là tập đóng.
3. Đoạn [a,b] ⊂ R là tập đóng. lOMoAR cPSD| 58970315 8
Số thực và dãy số thực
4. Mọi tập hữu hạn đều là tập đóng.
2 Định nghĩa 1.5. Điểm a ∈ X được gọi là điểm trong của tập X ⊂ R nếu tồn tại
một lân cận của a nằm trọn trong X(Uδ(a) ⊂ X).
1.1 Tập số thực và Topo trên tập số thực
• Ví dụ 1.3. Ví dụ về điểm trong.
1. Mọi điểm a ∈ (a,b) đều là điểm trong của khoảng (a,b).
2. a = 0 và a = 1 không là điểm trong của đoạn [0,1].
2 Định nghĩa 1.6. Tập H ⊂ R được gọi là tập mở nếu mọi phần tử của H đều là
điểm trong của H. Nói cách khác, với mỗi a ∈ H đều tồn tại một lân cận Uδ(a)
của a sao cho Uδ(a) ⊂ H.
• Ví dụ 1.4. Một số ví dụ về tập mở:
1. Người ta quy ước tập ∅ là tập mở.
2. Tập số thực là tập mở.
3. Khoảng (a,b) ⊂ R là tập mở.
4. Đoạn [a,b] ⊂ R không là tập mở.
2 Định nghĩa 1.7. Tập bị chặn:
• Tập X ⊂ R được gọi là tập bị chặn trên nếu tồn tại một số thực K sao cho
∀x ∈ X : x 6 K. K được gọi là cận trên của X. lOMoAR cPSD| 58970315 9
• Tập X ⊂ R được gọi là tập bị chặn dưới nếu tồn tại một số thực k sao cho
∀x ∈ X : x > K. K được gọi là cận dưới của X.
• Tập X ⊂ R được gọi là tập bị chặn nếu X vừa bị chặn trên vừa bị chặn dưới.
Nghĩa là nếu tồn tại một số thực K > 0 sao cho ∀x ∈ X : |x| 6 K.
• Ví dụ 1.5. Một số ví dụ về tập bị chặn:
1. Đoạn [a,b] ⊂ R và khoảng (a,b) ⊂ R là các tập bị chặn.
2. Nửa đoạn (−∞,b] ⊂ R là tập bị chặn trên nhưng không bị chặn dưới.
3. Nửa đoạn [a,∞) ⊂ R là tập bị chặn dưới nhưng không bị chặn trên.
4. R là tập không bị chặn. 1.2
Dãy số thực và giới hạn của dãy số thực 1.2.1 Khái niệm về dãy số
2 Định nghĩa 1.8. Một ánh xạ từ tập các số tự nhiên N∗ =
{1,2,3,...,n,...} vào R u : N∗ → R
được gọi là dãy số thực. Ký hiệu
Phần tử un = u(n),∀n ∈ N∗ được gọi là số hạng thứ n của dãy.
• Ví dụ 1.6. Một số ví dụ về dãy số:
1. Dãy số thực (un) = 1,2,3,4,5.... có u1 = 1;u2 = 2;...;u10 = 10;...un = n...
2. Dãy số thực (un) với un = 3n + 1 có u1 = 4;u2 = 7;...;u10 = 31;...
3. Dãy số Finonaci (un) được xác định bằng công thức truy hồi như sau: u1 =
1;u2 = 1;un = un−1 + un−2 với ∀n > 2.
4. Dãy số thực (un) với un = (−1)n2n có u1 = −2;u2 = 4;...;u10 = 20;... lOMoAR cPSD| 58970315 10
Số thực và dãy số thực 1.2.2
Một số dãy số đặc biệt
2 Định nghĩa 1.9. Dãy số đơn điệu.
• Dãy số thực (un) được gọi là dãy dừng nếu tồn tại một số tự nhiên n0 sao
cho từ số hạng đó trở đi, các phần tử của un đều bằng nhau, nghĩa là un =
a,∀n ≥ n0.
• Dãy số thực (un) được gọi là đơn điệu tăng ( tăng thực sự ) nếu un ≤ un+1 ∀n ∈ N∗
(un < un+1∀n ∈ N∗).
• Dãy số thực (un) được gọi là đơn điệu giảm ( giảm thực sự ) nếu un ≥ un+1 ∀n ∈ N∗
(un > un+1∀n ∈ N∗).
• Dãy số thực tăng hay giảm được gọi chung là dãy đơn điệu.
• Ví dụ 1.7. Ví dụ về dãy đơn điệu: lOMoAR cPSD| 58970315
1.2 Dãy số thực và giới hạn của dãy số thực 11
1. Dãy số thực (un) = 1,2,3,4,5.... là dãy đơn điệu tăng thực sự.
2. Dãy số thực (un) với un = −3n + 1 là dãy đơn điệu giảm thực sự.
3. Dãy số thực (un) với un = (−1)n2n không là dãy đơn điệu.
2 Định nghĩa 1.10. Dãy số bị chặn.
• Dãy số thực (un) được gọi là bị chặn trên nếu tồn tại số thực K sao cho un ≤ K ∀n ∈ N∗.
• Dãy số thực (un) được gọi là bị chặn dưới nếu tồn tại số thực K sao cho un ≥ K ∀n ∈ N∗.
• Dãy số thực được gọi là bị chặn nếu vừa bị chặn trên vừa bị chặn dưới.
Nghĩa là tồn tại số thực dương K > 0 sao cho |un| ≤ K ∀n ∈ N∗.
• Ví dụ 1.8. Ví dụ về dãy số bị chặn:
1. Dãy số thực (un) = 1,2,3,4,5.... là dãy bị chặn dưới nhưng không bị chặn trên.
2. Dãy số thực (un) với un = −3n + 1 là dãy bị chặn trên nhưng không bị chặn dưới.
3. Dãy số thực (un) với un = (−1)n2n không bị chặn trên cũng không bị chặn dưới.
4. Dãy số thực (un) với un = sinn là dãy bị chặn. 1.2.3 Giới hạn dãy số
2 Định nghĩa 1.11. Dãy hội tụ, dãy phân kỳ.
• Cho dãy số un, ta nói dãy hội tụ và có giới hạn là L ∈ mathbbR, ký hiệu
lim un = L n→∞ lOMoAR cPSD| 58970315 12
Số thực và dãy số thực nếu cho trước
nhỏ tuỳ ý, tồn tại một số tự nhiên sao
cho với mọi n ≥ n0 ta có
• Dãy (un) không hội tụ được gọi là dãy phân kỳ.
• Ví dụ 1.9. Một số ví dụ về dãy số. 1.
Dãy dừng (un) = a hội tụ đến a.
lim un = lim a = a n→∞ n→∞ 2. Dãy số thực . Thật vậy, với mỗi
nhỏ tuỳ ý, chọn số tự nhiên ( chú ý
có vô số số tự nhiên như vậy. Kh đó
và với mỗi n ≥ n0 ta có 3. Tương tự, dãy số . 4.
Dãy số thực (un) với un = (−1)n2n không có giới hạn. 2 Định nghĩa
1.12. Dãy có giới hạn vô cùng. • Cho dãy số un, ta nói dãy có giới hạn là +∞, ký hiệu lim un = +∞ n→∞
nếu cho trước K > 0 tuỳ ý, tồn tại một số tự nhiên n0 ∈ N∗ sao cho với mọi n ≥ n0 ta có un > K
• Cho dãy số un, ta nói dãy có giới hạn là −∞, ký hiệu lim un = −∞ n→∞ lOMoAR cPSD| 58970315
1.2 Dãy số thực và giới hạn của dãy số thực 13
nếu cho trước K > 0 tuỳ ý, tồn tại một số tự nhiên n0 ∈ N∗ sao cho với mọi n ≥ n0 ta có un < −K
• Ví dụ 1.10. Về dãy có giới hạn bằng vô cùng.
1. lim (2n + 1) = +∞. n→∞
2. lim (−2n + 1) = −∞. n→∞
4 Định lý 1.1. Nếu dãy un hội tụ và lim un = 0 thì n→∞ Cụ thể hơn:
• Nếu dãy un hội tụ có lim un = 0 và các phần tử của dãy đều là các n→∞ số dương thì .
• Nếu dãy un hội tụ có lim un = 0 và các phần tử của dãy đều là các n→∞ số âm thì . • Ngược lại, nếu . 1.2.4
Dãy con và giới hạn riêng của dãy số
2 Định nghĩa 1.13. Cho dãy số thực (un), giả sử dãy
n1 < n2 < ... < nk < ...
là một dãy tăng thực sự các số tự nhiên nào đó, khi đó dãy số
un1,un2,....,unk... lOMoAR cPSD| 58970315 14
Số thực và dãy số thực
được gọi là dãy con của dãy un và thường ký hiệu là (unk).
Giới hạn của dãy con (nếu có) được gọi là giới hạn riêng của dãy số đã cho. • Ví
dụ 1.11. Một số dãy con hay gặp
1. (u2k) là dãy cón của dãy (un) lấy các phần tử ở vị trí chẵn của dãy
(u2,u4,...,u2k...)
2. (u2k+1) là dãy cón của dãy (un) lấy các phần tử ở vị trí lẻ của dãy.
3. Ngoài ra có thể hay chọn các dãy u3k;u3k+1;u3k+2...
4 Định lý 1.2. Nếu dãy (un) hội tụ và lim un = a thì mọi dãy con (unk) n→∞
cũng hội tụ và có cùng giới hạn.
lim unk = a k→∞
∗ Chú ý: Người ta thường dùng định lý này để chỉ ra một dãy số không có giới
hạn bằng cách chỉ ra dãy có hai giới hạn riêng khác nhau. Cụ thể hơn là chỉ ra
hai dãy con có giới hạn không bằng nhau.
• Ví dụ 1.12. Chỉ ra các dãy không có giới hạn.
1. Dãy un = (−1)n.n. Chọn hai dãy con u2k = (−1)2k.2k = 2k −→ +∞ và u2k+1
= (−1)2k+1.(2k + 1) = −(2k + 1) −→ −∞. 2. Dãy . Chọn hai dãy con
u2k+1 = (−1) .2 k+3 −→ −1. 1.2.5
Tính chất và các phép toán về giới hạn dãy số
Cho dãy số hội tụ (an) với lim an = a Ta có các tính chất sau: n→∞ 3
Tính chất Ta có các tính chất sau:
• lim (an − a) = 0. lOMoAR cPSD| 58970315
1.2 Dãy số thực và giới hạn của dãy số thực 15 n→∞ • Nếu an > 0
∀n > n0 nào đó, khi đó a ≥ 0
• Nếu a > 0, khi đó tồn tại số tự nhiên n0, sao cho với mọi n > n0, an > 0.
4 Định lý 1.3. Các phép toán giữa các dãy hội tụ.
Cho hai dãy số hội tụ (an) và (bn) với lim an = a; lim bn = b. Khi đó các n→∞ n→∞
dãy số (an + bn);(an − bn);(an.bn);(αan) cũng là các dãy hội tụ, đồng thời: • lim
(an + bn) = a + b. n→∞ • lim (an − bn) = a − b. n→∞ • lim (an.bn) = a.b. n→∞ • lim (αan) = αa. n→∞ • Nếu b = 06 thì dãy số cũng hội tụ và .
• lim an = 0 ⇐⇒ lim |an| = 0. n→∞ n→∞
∗ Chú ý: Định lý vẫn đúng trong trường hợp các dãy số có giới hạn vô cùng nếu ta quy ước như sau:
+∞++∞ = +∞;(−∞)+(−∞) = −∞;+∞−(−∞) = +∞;+∞.+∞ = +∞;+∞.(−∞) =
−∞;(−∞).(−∞) = +∞ Các dạng còn lại:
được gọi là các dạng vô định.
4 Định lý 1.4. Cho hai dãy số (an) bị chặn và (bn) hội tụ với lim bn = 0. n→∞
Khi đó dãy số (an.bn) cũng hội tụ và lim (an.bn) = 0 n→∞ 4
Định lý 1.5. Nguyên lý kẹp.
Cho ba dãy số hội tụ (an), (bn) và (cn) thoả mãn các điều kiện
an ≤ bn ≤ cn ∀n ≥ n0 lOMoAR cPSD| 58970315 16
Số thực và dãy số thực
với n0 là số tự nhiên nào đó. Giả thiết thêm rằng
lim an = lim cn = L n→∞ n→∞
. Khi đó các dãy số (bn) cũng là dãy hội tụ và
lim bn = L n→∞
4 Định lý 1.6. Nguyên lý hội tụ của dãy đơn điệu
• Mọi dãy đơn điệu tăng và bị chặn trên đều hội tụ. • Mọi dãy đơn
điệu giảm và bị chặn dưới đều hội tụ.
• Ví dụ 1.13. Dãy số (un) xác định như sau:
a > 0;u1 = √a;un = √a
+ un−1 n > 1
Bằng quy nạp, ta chứng minh được un+1 > un,
n > 1, hay nói cách khác
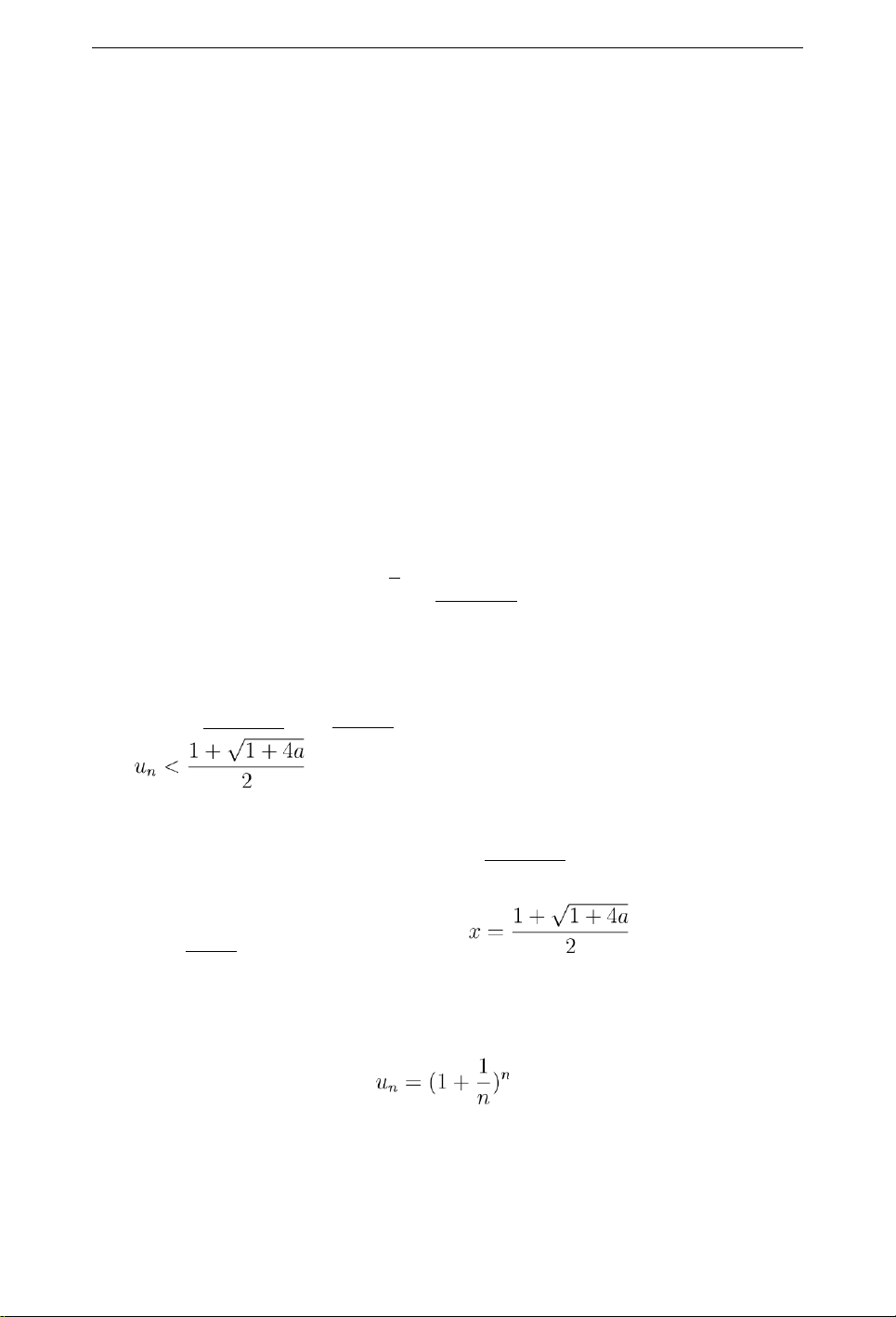
dãy (un) là dãy đơn điệu tăng. Mặt khác un =
√a + un−1 < √a + un ⇒ u2n < a + un hay
do vậy dãy (un) bị trặn trên. Theo nguyên lý trên, dãy số (un) hội tụ.
Giả sử lim un = x, từ đẳng thức un = √a + un−1, cho n −→ ∞ ta được n→∞ x = √a
+ x suy ra dãy có giới hạn
• Ví dụ 1.14. Số e Xét dãy số .
Sử dụng bất đẳng thức Cauchy với tích của n + 1 số dương, ta thấy lOMoAR cPSD| 58970315
1.2 Dãy số thực và giới hạn của dãy số thực 17
hay (un) là dãy đơn điệu tăng.
Để chứng mình (un) là dãy bị chặn, ta có nhiều cách đánh giá, chẳng hạn
suy ra un < 4 ∀n. Vậy dãy (un) đơn điệu và bị chặn, do đó (un) là dãy hội tụ, nói
cách khác tồn tại lim un. Ký hiệu
n→∞ lim un = e n→∞
Người ta chứng minh được số e là số vô tỷ và
e ≈ 2,71828182845....
∗ Chú ý: Ngoài ra còn một số tính chất liên quan đến dãy số và giới hạn dãy số
thực, tuy nhiên trong khuôn khổ bài giảng này chúng tôi không đưa vào. Sinh
viên có thể tham khảo thêm trong Giáo trình Giải tích 1 và các tài liệu về Giải tích hàm một biến. lOMoAR cPSD| 58970315 Chương 2
Phép tính vi phân và tích phân hàm
số thực một biến số thực
2.1 Hàm số một biến số và sự liên tục của hàm số một biến số 2.1.1
Các khái niệm cơ bản về hàm số một biến số 2.1.1.1
Định nghĩa hàm số một biến số
2 Định nghĩa 2.1. Cho X 6= ∅, X ⊆ R, một ánh xạ f từ tập X vào R được gọi là hàm
số một biến số thực, ký hiệu: y = f(x),(x ∈ X).
Tập X được gọi là miền xác định của hàm số f, ký hiệu: Df, tập f(X) = {y ∈ R :
∃ x ∈ X, y = f(x)} được gọi là miền giá trị của hàm số f, ký hiệu: Rf. Trong ký hiệu
y = f(x), x được gọi là biến độc lập hay đối số, y được gọi là biến phụ thuộc hay hàm số.
Đồ thị của hàm số y = f(x),x ∈ X là tập hợp:
Đồ thị của f(x) có thể là một tập điểm rời rạc hữu hạn hoặc vô hạn, cũng có
thể là tập những cung đứt đoạn hay cung liền.
•xnVí dụ 2.1., y = ax, y a) Các hàm số dưới đây đã biết ở bậc học phổ thông:=
loga x, y = lnx, y = sinx, y = cosx, y = tanx, yy == cot .
b) Hàm số cũng có thể được cho bởi nhiều biểu thức, chẳng hạn: lOMoAR cPSD| 58970315
2.1 Hàm số một biến số và sự liên tục của hàm số một biến số 19 .
Tập xác định của hàm số là toàn bộ R, trong khoảng [0,+∞) giá trị của hàm
số tại mỗi điểm x được tính theo công thức f(x) = x, còn trong khoảng (−∞,0)
giá trị của hàm số tại mỗi điểm x được tính theo công thức f(x) = −x.
2.1.1.2 Hàm số đơn điệu, hàm số bị chặn, hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
Ta nói hàm số y = f(x) tăng trên miền X ⊂ Df ⊂ R nếu:
x1, x2 ∈ X,x1 < x2 ⇒ f(x1) ≤ f(x2),
tăng ngặt trên X nếu:
x1, x2 ∈ X,x1 < x2 ⇒ f(x1) < f(x2), giảm trên X nếu:
x1, x2 ∈ X,x1 < x2 ⇒ f(x1) ≥ f(x2),
giảm ngặt trên X nếu:
x1, x2 ∈ X,x1 < x2 ⇒ f(x1) > f(x2).
Các hàm số tăng (tăng ngặt) hay giảm (giảm ngặt) trên X được gọi là các hàm
số đơn điệu (đơn điệu ngặt) trên X.
Hàm số f(x) được gọi là hàm bị chặn trên trong miền X ⊂ R nếu tồn tại hằng số M sao cho:
f(x) ≤ M (∀x ∈ X),
hằng số M được gọi là cận trên của hàm số f(x) trong miền X. lOMoAR cPSD| 58970315 20
Phép tính vi phân và tích phân hàm số thực một biến số thực
Hàm số f(x) được gọi là hàm bị chặn dưới trong miền X ⊂ R nếu tồn tại hằng
số m sao cho: f(x) ≥ m (∀x ∈ X),
hằng số m được gọi là cận dưới của hàm số f(x) trong miền X.
Hàm số f(x) được gọi là hàm bị chặn trong miền X nếu hàm số đó vừa bị
chặn trên vừa bị chặn dưới, tức là tồn tại các hằng số m và M sao cho:
m ≤ f(x) ≤ M (∀x ∈ X).
∗ Chú ý: Dễ thấy hàm số f(x) bị chặn trong miền X khi và chỉ khi tồn tại hằng số
K > 0 sao cho: |f(x)| ≤ K (∀x ∈ X).
Giả sử X ⊂ R, hàm số f : X → R được gọi là hàm chẵn nếu ∀x ∈ X ta luôn có
−x ∈ X và f(−x) = f(x).
Hàm số f : X → R được gọi là hàm lẻ nếu ∀x ∈ X ta luôn có −x ∈ X và f( .
là hàm chẵn nếu n chẵn, là hàm lẻ nếu n lẻ. Đồ thị của
hàm chẵn nhận trục tung làm trục đối xứng. Đồ thị của
hàm lẻ nhận gốc O làm tâm đối xứng.
Giả sử X ⊂ R, hàm số f : X → R được gọi là hàm tuần hoàn nếu tồn tại hằng
số dương T sao cho:
(x ∈ X ⇒ x + T ∈ X
f(x + T) = f(x) (∀x ∈ X),
số T nhỏ nhất (nếu có) thỏa mãn các điều kiện trên được gọi là chu kỳ của f.
• Ví dụ 2.2. a) Hàm số f(x) = x4 + m (x ∈ R) là hàm bị chặn dưới, vì f(x) ≥ m,∀x
∈ R. là hàm bị chặn trên, vì f(x) ≤ M, x ∈ .
c) Hàm số f(x) = sinx là hàm bị chặn, vì −1 ≤ sinx ≤ 1, ∀x ∈ R.
• Ví dụ 2.3. a) Các hàm số y = sinx, y = cosx tuần hoàn với chu kỳ 2π.
