




























































Preview text:
TRƯỜNG ĐẠI HỌC XÂY DỰNG HÀ NỘI KHOA CẦU ĐƯỜNG
BỘ MÔN TRẮC ĐỊA GIÁO TRÌNH
TRẮC ĐỊA ĐẠI CƯƠNG
(DÀNH CHO SINH VIÊN CÁC KHỐI KỸ THUẬT XÂY DỰNG CÔNG TRÌNH)
TS. TRẦN ĐÌNH TRỌNG HÀ NỘI, 2013 Lời nói đầu
Giáo trình Trắc địa đại cương được dùng trong giảng dạy cho chương trình đào tạo
kỹ sư khối ngành kỹ thuật xây dựng, không chuyên về Trắc địa, của trường Đại học Xây
dựng Hà Nội. Do vậy, tác giả cố gắng trình bày một cách đơn giản và dễ hiểu nhất. Nội
dung giáo trình bao gồm các nội dung cơ bản về Trắc địa và Trắc địa ứng dụng trong xây dựng.
Tác giả xin chân thành cảm ơn sự giúp đỡ và đóng góp về chuyên môn của các
thầy, cô trong bộ môn Trắc địa – khoa Cầu đường, đặc biệt TS. Nguyễn Thạc Dũng đã góp
ý và chỉnh sửa giáo trình này. Tác giả MỤC LỤC
CHƯƠNG 1 NHỮNG KHÁI NIỆM CHUNG 1.1 Mở đầu 3
1.2 Hình dáng, kích thước Trái đất 4
1.3 Ảnh hưởng của độ cong Trái đất đến các đại lượng đo 5
1.4 Hệ tọa độ địa lý 6
1.5 Phép chiếu Gauss – Kruger, UTM và hệ tọa độ vuông góc phẳng 7
CHƯƠNG 2 KHÁI NIỆM VỀ SAI SỐ TRONG ĐO ĐẠC
2.1 Đặc điểm tính toán trong Trắc địa 11
2.2 Khái niệm về sai số đo 13
2.3 Các tiêu chuẩn đánh giá độ chính xác 15
2.4 Sai số trung phương hàm các đại lượng đo 17
2.5 Tính và đánh giá kết quả đo 19 CHƯƠNG 3 ĐO GÓC 3.1 Khái niệm 22 3.2 Máy kinh vĩ 22
3.3 Kiểm nghiệm các điều kiện cơ bản của máy kinh vĩ 24 3.4 Đo góc bằng 27
3.5 Sai số trong đo góc bằng 31 3.6. Đo góc đứng 32 CHƯƠNG 4 ĐO KHOẢNG CÁCH 4.1 Khái niệm 33
4.2 Đo khoảng cách bằng thước thép 33
4.3 Đo khoảng cách bằng phương pháp quang học 35
4.4 Hệ thống định vị toàn cầu GPS 38
4.5 Đo khoảng cách điện tử 40 CHƯƠNG 5 ĐO CAO 5.1 Khái niệm 42
5.2 Nguyên lý đo cao hình học 43 5.3 Máy thủy bình 44
5.4 Đo cao hình học hạng IV 47
5.5. Cách loại trừ sai số trong đo cao hình học 49 5.6 Đo cao lượng giác 50
CHƯƠNG 6 LƯỚI KHỐNG CHẾ TRẮC ĐỊA
6.1 Định hướng đường thẳng 51
6.2 Hai bài toán trắc địa cơ bản 53
6.3 Khái niệm lưới khống chế trắc địa mặt bằng 54
6.4 Lưới đường chuyền 56
6.5 Một số phương pháp xây dựng lưới khác 60
6.6 Khái niệm lưới khống chế độ cao 62
6.7 Bình sai gần đùng lưới khống chế độ cao 63
CHƯƠNG 7. BẢN ĐỒ ĐỊA HÌNH VÀ ĐO V¾ BẢN ĐỒ
7.1 Khái niệm về bản đồ 66
7.2 Phân mảnh và đánh số bản đồ 67
7.3 Biểu diễn địa vật, địa hình trên bản đồ 67 7.4 Đo v¿ bản đồ 70
7.5 Đo v¿ mặt cắt địa hình 73 7.6 Sử dụng bản đồ 76
CHƯƠNG 8 TRẮC ĐỊA TRONG XÂY DỰNG
8.1 Bố trí các yếu tố cơ bản 80
8.2 Bố trí điểm mặt bằng 81
8.3 Bố trí đường cong tròn 83
8.4 Tính khối lượng đào đắp 86
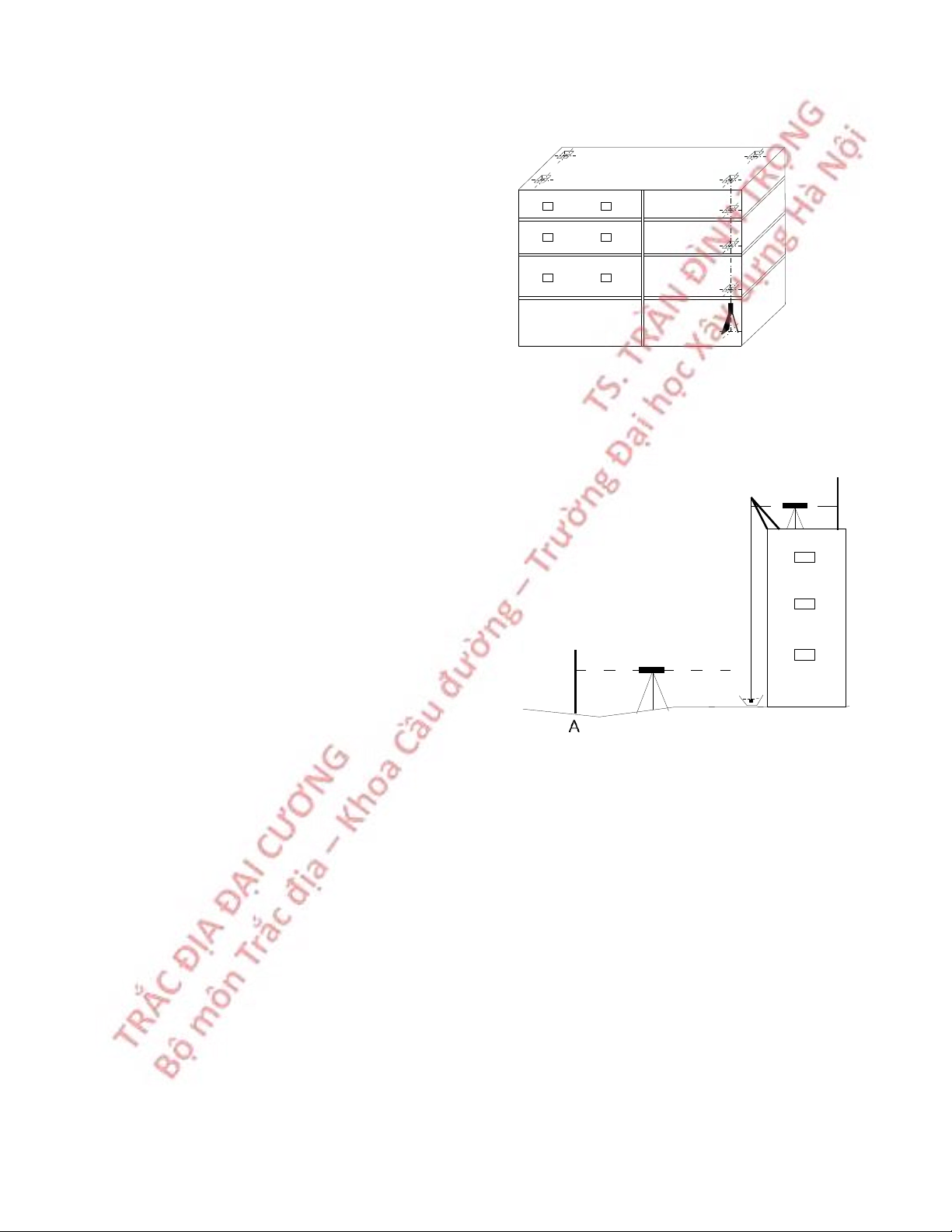
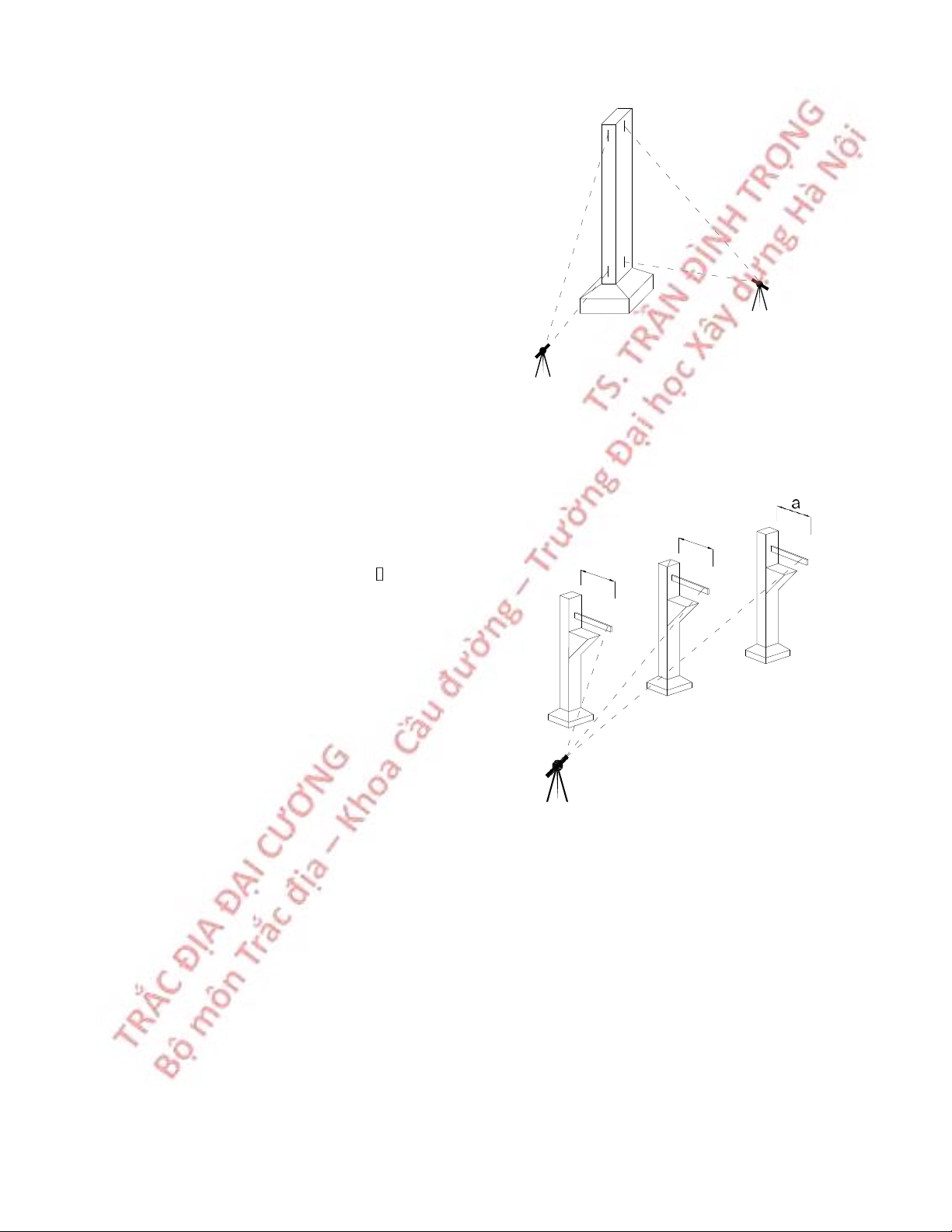
8.5 Công tác trắc địa trong xây dựng 88
8.6 Quan trắc chuyển dịch biến dạng công trình 94 Tài liệu tham kháo 98
CHƯƠNG 1 NHỮNG KHÁI NIỆM CHUNG 1.1 MỞ ĐẦU
Trắc địa là một ngành khoa học về Trái đất, nó nghiên cứu các phép đo thực hiện
trên bề mặt đất, các dụng cụ đo, các phương pháp xử lý số liệu đo nhằm xác định hình
dáng, kích thước Trái đất, biểu diễn bề mặt đất và phục vụ các ngành khoa học khác.
Trong quá trình phát triển, phạm vi nghiên cứu và ứng dụng của môn khoa học này
đã mở rộng và chuyên sâu hơn rất nhiều. Nó không chỉ nghiên cứu các phép đo, các phép
biểu diễn hình dáng Trái đất mà còn nghiên cứu các chuyển động của Trái đất, các tính
chất vật lý của Trái đất, ngoài ra còn nghiên cứu vị trí, bề mặt, chuyển động của các vệ
tinh, hành tinh,... trong vũ trụ.
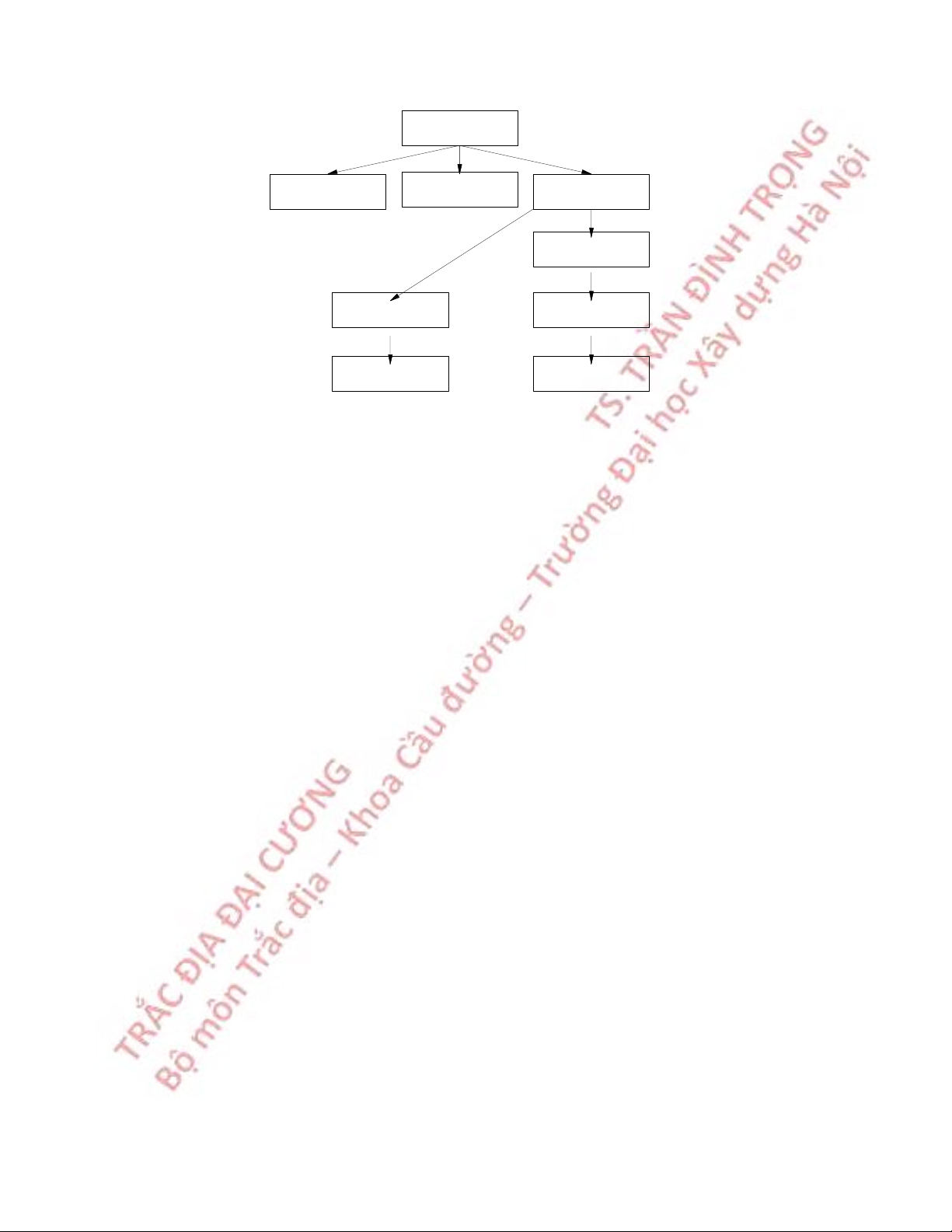
Trắc địa được chia thành 2 mảng lớn là Trắc địa cao cấp, nghiên cứu phạm vi lớn
của bề mặt Trái đất, mảng còn lại gồm các chuyên ngành khác nhau, nghiên cứu trên
phạm vi nhỏ của bề mặt Trái đất (Hình 1).
Trắc địa cao cấp lớn vi ạm
Trắc địa phổ thông Ph Trắc địa ỏ
Trắc địa công trình nh vi Trắc địa ảnh ạm Ph
Trắc địa bản đồ
Hình 1 Các chuyên ngành trong ngành Trắc địa
“Trắc địa đại cương” chủ yếu nằm trong hai chuyên ngành là Trắc địa phổ thông
và Trắc địa công trình.
Nhiệm vụ của môn học: Trong xây dựng công trình, trắc địa tham gia tất cả các
giai đoạn từ khảo sát, thiết kế, thi công đến khi công trình đã đi vào sử dụng. Do đó, kiến
thức về Trắc địa là không thể thiếu đối với mỗi kỹ sư xây dựng. Môn học Trắc địa đại
cương cung cấp những kiến thức cơ bản của Trắc địa, làm cơ sở cho chuyên ngành và thực tế sản xuất. 3
1.2 HÌNH DẠNG, KÍCH THƯỚC TRÁI ĐẤT
1.2.1 Hình dạng tự nhiên của Trái đất
Bề mặt Trái đất có diện tích khoảng 510.106km2, trong đó đại dương chiếm khoảng
71%, lục địa chiếm khoảng 29%. Bề mặt tự nhiên của Trái đất rất phức tạp, lục địa cao
trung bình khoảng 875m, đại dương sâu trung bình khoảng 3800m. Chênh lệch giữa điểm
sâu nhất (vực Marianna sâu 11032m) với điểm cao nhất (đỉnh Everest cao 8884m) khoảng
20km. Bán kính trung bình của Trái đất khoảng 3671km.
Một cách gần đúng, ta có thể coi mô hình Trái đất là quả cầu nước với bán kính
300mm thì vết gợn lớn nhất là 1mm.
1.2.2 Mặt thuỷ chuẩn
Như đã biết, bề mặt Trái đất gồ ghề phức tạp, rất khó để xác định hình dạng thực
của nó. Để đơn giản, người ta tìm một bề mặt có hình dạng gần với hình dáng thực của
Trái đất nhất đó là mặt thuỷ chuẩn (hay còn gọi mặt Geoid, mặt đẳng thế, mặt nước gốc).
Mặt thuỷ chuẩn là mặt nước biển và các đại dương yên tĩnh tưởng tượng kéo dài
xuyên qua các lục địa tạo thành một mặt khép kín sao cho bề mặt tại mọi điểm luôn vuông
góc với phương trọng lực (hay phương dây dọi).
Vật chất trong lòng Trái đất phân bố không đồng đều, do vậy mặt thuỷ chuẩn là mặt
khép kín uốn lượn, không phải là mặt có dạng chính tắc nên không có phương trình toán học để biểu diễn.
Mặt thuỷ chuẩn được chọn làm mặt quy chiếu độ cao. Để xác định được mặt này
phải tiến hành quan trắc mực nước biển trong nhiều năm. Đối với mỗi quốc gia, để phù
hợp nhất với lãnh thổ, thường sử dụng số liệu quan trắc của riêng mình để xây dựng mặt
thuỷ chuẩn riêng gọi là mặt thuỷ chuẩn quốc gia. Ở Việt Nam lấy mặt nước biển trung bình
nhiều năm của trạm nghiệm triều Hòn Dấu – Hải Phòng làm mặt thuỷ chuẩn quốc gia. 1.2.3 Ellipsoid
Để giải các bài toán trắc địa, người ta chọn một mặt toán học đơn giản, gần với mặt
thuỷ chuẩn nhất (tức là gần với bề mặt thực của Trái đất nhất), đó là mặt Ellipsoid
(Ellipsoid được tạo thành khi quay một ellipse quanh trục nhỏ của nó). 4 MÆt ®ất thùc MÆt Geoid MÆt Elipxoid
Hình 1.1 Mặt đất, Geoid và Ellipsoid
Mặt Ellipsoid được chọn thoả mãn:
1. Tâm của Ellipsoid trùng với tâm trọng lực của Trái đất, trục quay của Ellipsoid
trùng với trục quay cả Trái đất.
2. Tổng bình phương khoảng chênh giữa Ellipsoid và Geoid là nhỏ nhất.
Mặt Ellipsoid được chọn làm mặt quy chiếu toạ độ.
Kích thước của Ellipsoid được đặc trưng bởi bán trục lớn a, bán trục bé b hoặc độ
dẹt α (α = a – b ). a
Bảng 1.1 Một số Ellipsoid thông dụng trên thế giới và ở Việt Nam Ellipsoid Năm công bố Bán trục lớn Bán trục bé Độ dẹt a (m) b (m) α Everest 1930 6377276 6356075 1 : 300.8 Kraxovski 1946 6378245 6356760 1 : 298.3 WGS 84 1984 6378137 6356752 1 : 298.3
1.3 ẢNH HƯỞNG ĐỘ CONG TRÁI ĐẤT ĐẾN CÁC YẾU TỐ ĐO
1.3.1 Ảnh hưởng độ cong Trái đất đến đo góc
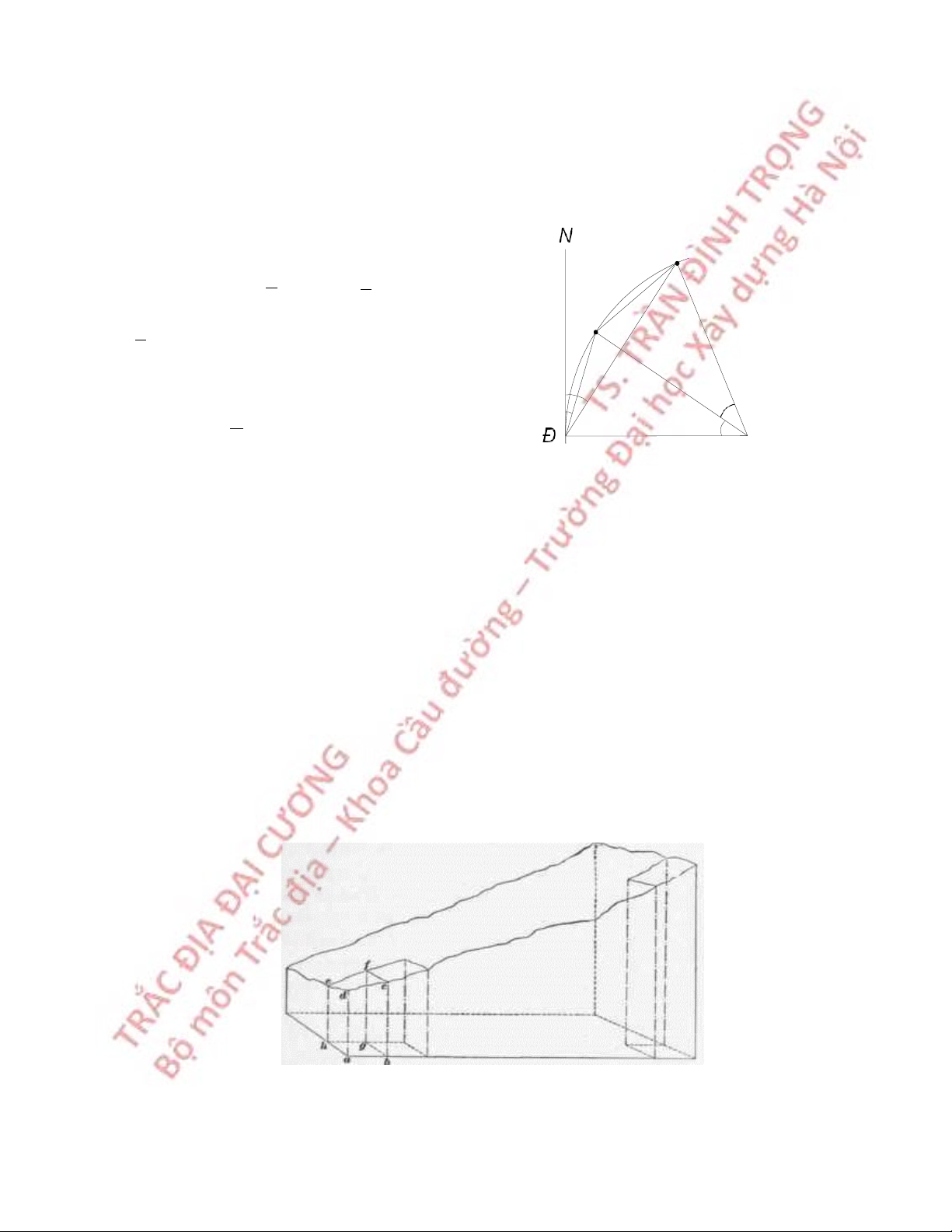
Trắc địa cầu đã chứng minh: tổng các góc trong của đa giác trên mặt phẳng nhỏ
hơn tổng các góc trong của đa giác đó tương ứng trên mặt cầu là ε ε" = p” A/R2 (1.1)
trong đó: A – diện tích đa giác trên mặt cầu, R ≈ 6370km; p” ≈ 206265. 5
Trong phạm vi bán kính 100km, nếu đo góc với độ chính xác mβ = ±1”, có thể coi
Trái đất là mặt phẳng.
1.3.1 Ảnh hưởng độ cong Trái đất đến đo khoảng cách
Khoảng cách S trên mặt đất khi chiếu S MÆt ®ất thùc
lên mặt phẳng ngang và mặt Ellipsoid (hình 1.2) D MÆt ph¼ng
Sai lệch khoảng cách khi thay thế mặt Ellipsoid D' MÆt Elipxoid bởi mặt phẳng: d = D – D’ R Và: D = Rtgα D’= Rα Ta có: d = R(tgα - α) (1.5) a
Khai triển chuỗi Taylor và giữ lại hai số hạng đầu hàm tg α:
Hình 1.2 Khoảng cách trên mặt chiếu tgα = α + α3/3 + … (1.6)
Công thức (1.5) trở thành: d = Rα3/3 (1.7) Thay α ≈ S/R vào (1.7): d = S3/3R2 (1.8)
Nếu lấy R ≈ 6370km, khi đo khoảng cách S = 10km thì sai số này là d = 8.2mm.
Như vậy, nếu đo cạnh với độ chính xác mS = ±10-6S (tức là 10km ± 10mm) thì trong pham
vi bán kính 10km có thể coi Trái đất là mặt phẳng.
1.3.3 Ảnh hưởng độ cong Trái đất đến đo cao
Sai lệch độ cao khi thay mặt cầu bằng mặt phẳng: q = D2/ 2R (1.9)
Nếu đo cao với độ chính xác mh = ±1mm thì trong bán kính 100m có thể coi Trái đất là mặt phẳng.
1.4 HỆ TOẠ ĐỘ ĐỊA LÝ
Hệ toạ độ địa lý được xây dựng dựa trên cơ sở các kinh tuyến, vĩ tuyến và coi Trái đất là hình cầu.
Kinh tuyến là giao giữa mặt cầu với mặt phẳng chứa trục quay Trái đất.
Vĩ tuyến là giao giữa mặt cầu với mặt phẳng vuông góc với trục quay Trái đất. 6
Chọn kinh tuyến đi qua đài thiên văn Greenwich (ngoại ô London, Anh) là kinh tuyến
gốc, mặt phẳng kinh tuyến gốc chia Trái đất làm hai nửa: Đông bán cầu và Tây bán cầu. Vĩ
tuyến nằm trên mặt phẳng chứa tâm của Trái đất (xích đạo) làm vĩ tuyến gốc, mặt phẳng
xích đạo chia Trái đất làm hai nửa: Bắc bán cầu và Nam bán cầu.
Toạ độ địa lý của điểm A được xác định như sau:
- Vĩ độ địa lý (φA): là góc hợp bởi đường dây dọi đi qua A (OA) và mặt phẳng xích
đạo, tính từ xích đạo về hai phía Bắc và Nam bán cầu. Nó có giá trị từ 0 900.
- Kinh độ địa lý (λA): là góc nhị diện hợp bởi
mặt phẳng kinh tuyến gốc với mặt phẳng kinh tuyến A G
đi qua điểm đó, tính từ kinh tuyến gốc về hai phía
Đông và Tây bán cầu. Nó có giá trị từ 0 1800. O jA
Ví dụ: Toạ độ địa lý của một điểm A: lA φA = 210 28’20” N λA = 105o 32’12” E
Hình 1.3 Hệ tọa độ địa lý
Việt Nam nằm hoàn toàn ở Bắc bán cầu và Đông bán cầu nên tất cả các điểm trên
lãnh thổ nước ta đều có vĩ độ Bắc và kinh độ Đông.
1.5 PHÉP CHIẾU GAUSS VÀ UTM - HỆ TOẠ ĐỘ VUÔNG GÓC PHẲNG
Trái đất có hình dạng rất phức tạp và hình học gần đúng với Trái đất nhất là
Ellipsoid. Để dễ dàng thể hiện, tính toán các điểm trên bề mặt Trái đất thì phải chiếu chúng
lên mặt phẳng. Cần phải tìm phép chiếu thích hợp để chuyển từ mặt cong lên mặt phẳng ít bị biến dạng nhất.
Có nhiều phép chiếu khác nhau như: phép chiếu hình nón, phép chiếu hình trụ,
phép chiếu thẳng góc,...
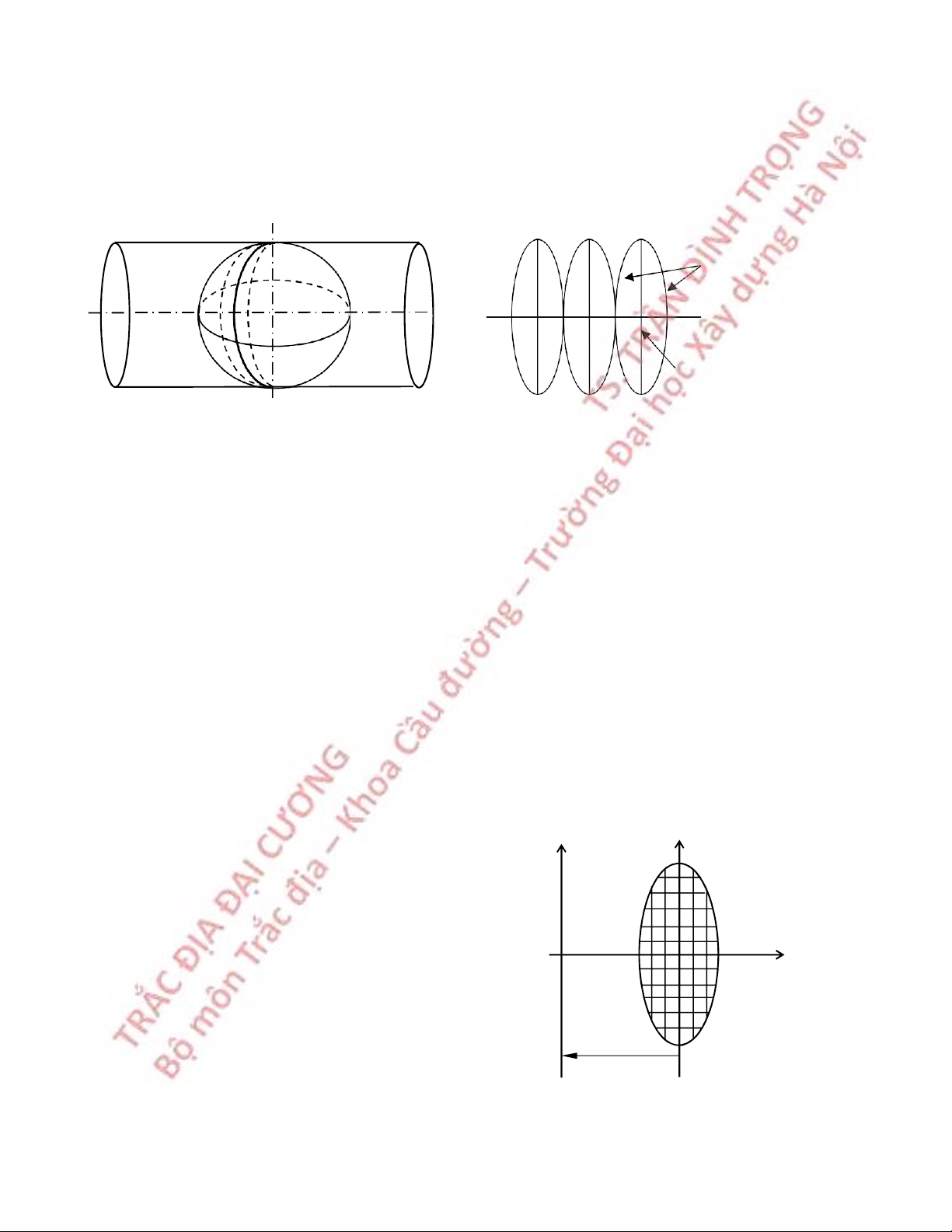
1.5.1 Phép chiếu Gauss - Kruger
Là phép chiếu hình trụ ngang đẳng góc
Chia Ellipsoid thành 60 múi, mỗi múi 60 kinh, đánh số thứ tự từ 1 60 bắt đầu từ
kinh tuyến gốc (λ = 00) theo chiều từ Đông sang Tây. Kinh tuyến giữa của mỗi múi
được gọi là kinh tuyến trục (kinh tuyến giữa múi) có kinh độ được tính theo công thức: 7 L0 = 3(2n –1)
(n là số thứ tự múi chiếu)
Lồng bên ngoài Ellipsoid một hình trụ và tiếp xúc với Ellipsoid tại một kinh tuyến trục
của múi cần chiếu, trục quay của Ellipsoid vuông góc với trục hình trụ (hình 1.4). Kinh tuyến biên O Xích đạo Kinh tuyến trục
Hình 1.4 Phép chiếu Gauss - Kruger
Hình 1.5 Múi chiếu Gauss - Kruger
Lấy tâm O của Ellipsoid làm tâm chiếu, lần lượt chiếu từng múi lên mặt trụ bằng
cách vừa xoay, vừa tịnh tiến. Sau đó, cắt hình trụ theo hai đường sinh và trải phẳng, được
hình chiếu của 60 múi (hình 1.5).
Đặc điểm của phép chiếu Gauss - Kruger:
- Không làm biến dạng về góc nhưng diện tích bị biến dạng.
- Hình chiếu của xích đạo và kinh tuyến trục vuông góc với nhau.
- Kinh tuyến giữa múi là trục đối xứng và không có biến dạng về chiều dài (tỷ lệ biến
dạng bằng 1). Càng xa kinh tuyến trục, biến dạng chiều dài càng tăng (kinh tuyến biên có
tỷ lệ biến dạng bằng 1.0014).
Để giảm tỷ lệ biến dạng, người ta chia nhỏ múi chiếu thành múi 30, thậm chí 1.50.
Phép chiếu Gauss được sử dụng X
để xây dựng hệ toạ độ HN72.
Hệ toạ độ vuông góc phẳng Gaus - Kruger:
Trục X là hình chiếu của kinh tuyến O Y
trục, trục Y là hình chiếu của xích đạo và
giao điểm của hai trục là gốc toạ độ O.
Như vậy, những khu vực ở Bắc bán
cầu, giá trị X luôn dương còn giá trị Y có
thể âm hoặc dương. Để tránh toạ độ Y 500
âm, trục OX dời sang phía Tây 500km (hình 1.8).
Hình 1.8 Hệ tọa độ vuông góc Gauss - Kruger 8
Mỗi múi chiếu, thành lập một hệ toạ độ vuông góc cho múi đó, do đó có thể có điểm
thuộc hai múi chiếu khác nhau lại có cùng giá trị toạ độ. Để tránh trường hợp này, người ta
ghi kèm số thứ tự múi chiếu trước toạ độ Y.
Ví dụ: Toạ độ điểm A: XA = 2 244 900.469m YA = 18 594 655.609m
(Điểm A nằm cách xích đạo 244900.469m về phía Bắc, thuộc múi chiếu thứ 18 và
cách kinh tuyến trục 594655.609 - 500000 = 94655.609m về phía Đông)
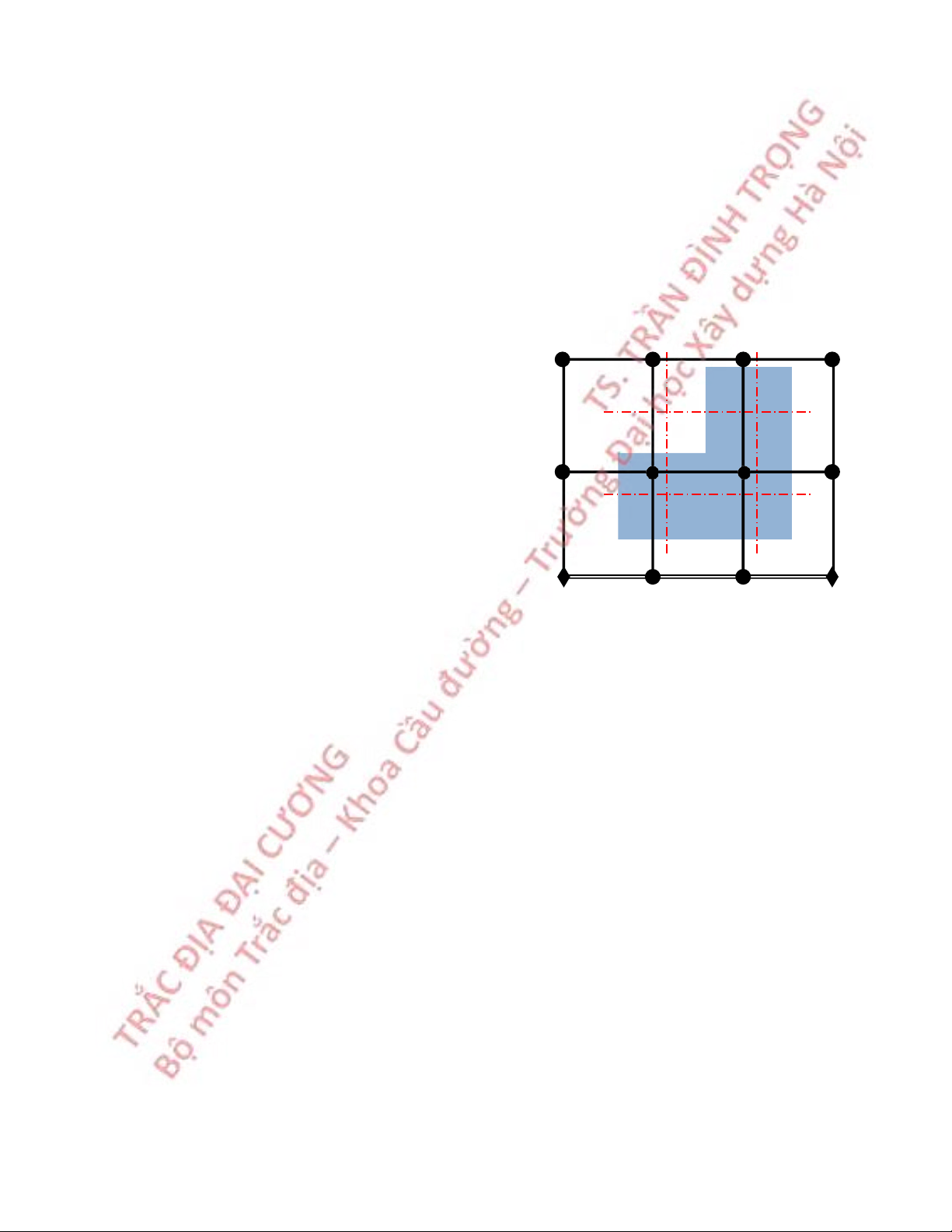
Trên hình chiếu mỗi múi, người ta kẻ thêm những đường thẳng song song với các
trục và cách đều nhau chẵn kilômét, gọi là lưới ô vuông hoặc lưới kilômét của bản đồ.
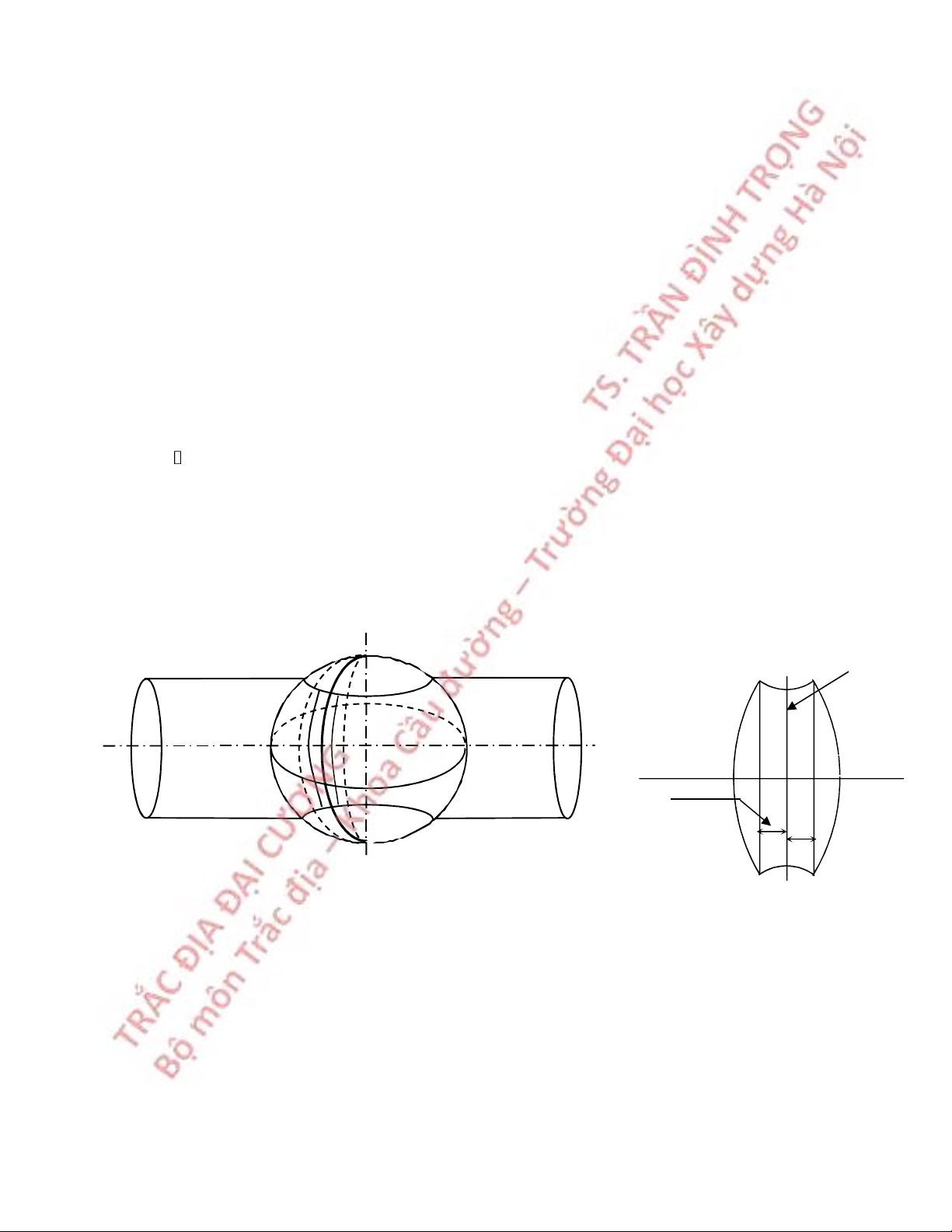
1.5.2 Phép chiếu UTM (Universal Transverse Mercator)
Tương tự như phép chiếu Gauss, Ellipsoid cũng chia thành 60 múi và đánh số thứ
tự từ 1 60 nhưng bắt đầu từ kinh tuyến đối diện với kinh tuyến gốc (λ = 1800) theo chiều từ Tây sang Đông.
Dùng hình trụ ngang cắt Ellipsoid tại hai kinh tuyến cách đều kinh tuyến trục 180km,
lúc này kinh tuyến trục nằm phía ngoài mặt trụ còn hai kinh tuyến biên của múi nằm phía
trong mặt trụ (hình 1.6). Kinh tuyến trục O Xích đạo 180km Hình 1.6 Phép chiếu UTM Hình 1.7 Múi chiếu UTM
Lấy tâm O của Ellipsoid làm tâm chiếu, lần lượt chiếu từng múi lên mặt trụ bằng
cách vừa xoay, vừa tịnh tiến. Sau đó, cắt hình trụ theo hai đường sinh và trải phẳng, được
hình chiếu của 60 múi (hình 1.7).
Đặc điểm của phép chiếu UTM:
- Không làm biến dạng về góc nhưng diện tích bị biến dạng. 9
- Hình chiếu của xích đạo và kinh tuyến trục vuông góc với nhau.
- Tỷ lệ biến dạng về chiều dài tại hai kinh tuyến tiếp xúc bằng 1, tại kinh tuyến trục
bằng 0.9996 (Đối với múi chiếu 30, tỷ lệ này là 0.9999).
So với phép chiếu Gauss, phép chiếu UTM giảm được tỷ lệ biến dạng ngoài biên và
biến dạng là tương đối đều trên phạm vi múi chiếu.
Phép chiếu UTM được sử dụng để xây dựng hệ toạ độ VN-2000.
Hệ toạ độ vuông góc phẳng X UTM:
Hệ toạ độ vuông góc phẳng
UTM tương tự như hệ toạ độ vuông góc phẳng Gauss. O Y
Có thể xem những chú ý khi sử
dụng hệ tọa độ VN-2000 trong [6] 500km
Hình 1.9 Hệ tọa độ vuông góc phẳng UTM
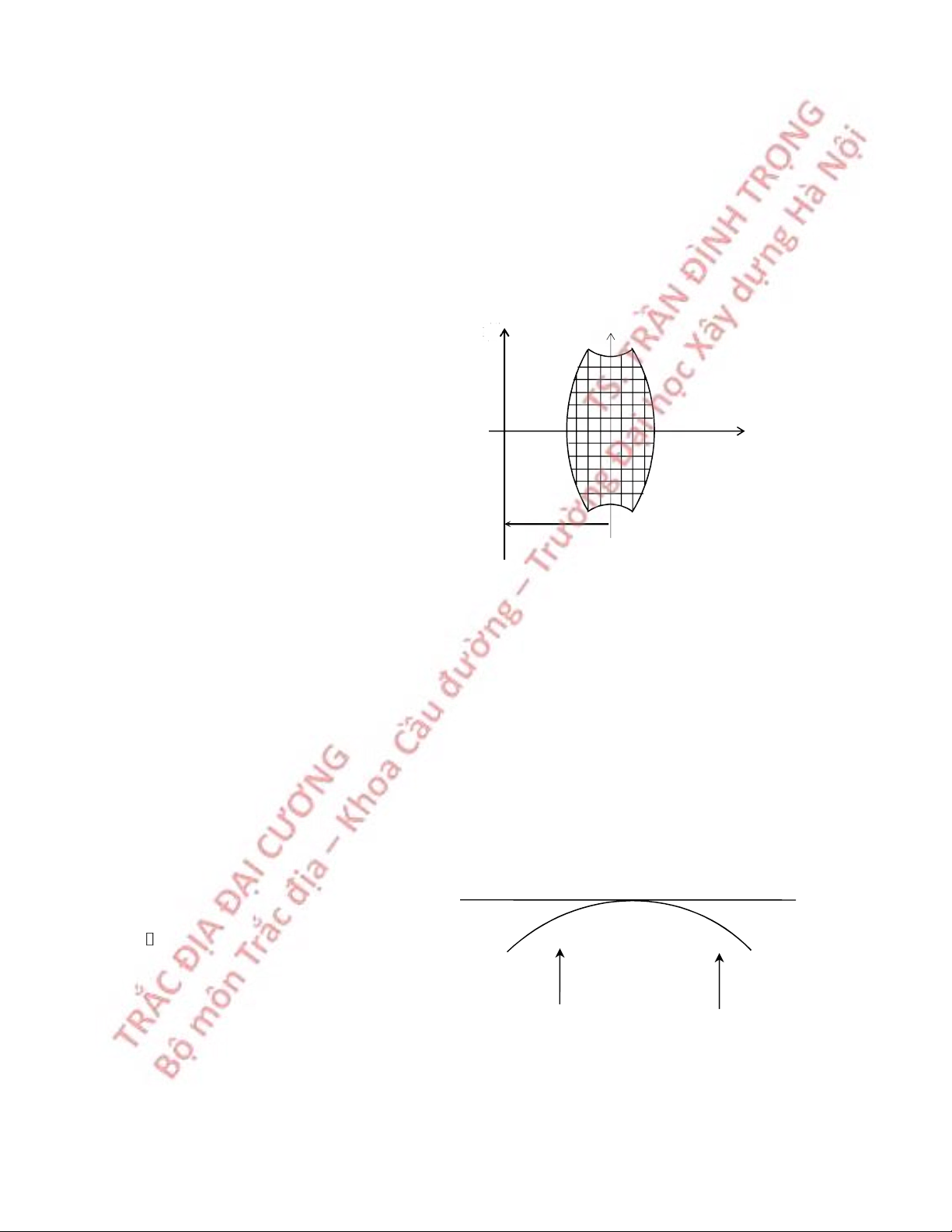
1.5.3 Phép chiếu thẳng góc
Khu vực có phạm vi nhỏ (bán kính nhỏ hơn 10km), có thể sử dụng phép chiếu thẳng góc.
Sử dụng mặt phẳng tiếp xúc với điểm trung tâm khu vực cần chiếu tại điểm trung
tâm, lấy tâm Trái đất làm tâm chiếu. Bán kính Trái đất lớn hơn rất nhiều khoảng cách lớn
nhất trân khu vực cần chiếu nên coi các tia chiếu là song song. (Hình 1.10).
Đặc điểm phép chiếu:
- Tại điểm tiếp xúc, tỷ lệ biến dạng chiều m = 1
dài m = 1. Càng ra xa tỷ lệ biến dạng càng
nhỏ hơn 1, nhưng không đáng kể, có thể coi m 1.
- Góc coi như không bị biến dạng.
Hình 1.10 Phép chiếu thẳng góc 10
CHƯƠNG 2 KHÁI NIỆM VỀ SAI SỐ TRONG ĐO ĐẠC
2.1 ĐẶC ĐIỂM TÍNH TOÁN TRONG TRẮC ĐỊA
2.1.1 Đơn vị đo dùng trong trắc địa
Đơn vị đo độ dài
Đơn vị đo độ dài là mét, kí hiệu là m.
Một mét là chiều dài bằng 1 650 736.73 chiều dài của bước sóng nguyên tử Kripton
86 bức xạ trong chân không, tương đương với quỹ đạo chuyển dời của điện tử giữa hai
mức năng lượng 2p10 và 5d5.
Trong hệ SI (System International), mét được định nghĩa: “mét là khoảng cách ánh
sáng đi được trong chân không trong khoảng thời gian 1/299 792 458s”.
Bội số của mét: 1 mét = 10-1 decamet (dam) = 10-2 hectomet (hm) = 10-3 kilomet (km).
Ước số cuả mét: 1 mét = 10 decimet (dm) = 102 centimet (cm) =103 milimet (mm).
Đơn vị đo diện tích
Đơn vị thường dùng là mét vuông, kí hiệu m2. Bội số của mét vuông:
Are (a), 1a = 102 m2.
Hectare (ha), 1ha = 104 m2.
Kilomet vuông (km2), 1km2 = 106 m2.
Ước số của mét vuông:
Decimet vuông (dm2), 1dm2 = 10-2 m2.
Centimet vuông (cm2), 1cm2 = 10-4 m2.
Milimet vuông (mm2), 1mm2 = 10-6 m2.
Đơn vị đo góc
Trong trắc địa thường dùng ba đơn vị đo góc là độ, grade và radian.
Độ, (o), là góc ở tâm chắn cung có chiều dài bằng 1/360 chu vi đường tròn. Một góc tròn có 3600.
Độ chỉ có ước số, các ước số là phút (’) và giây (”): 10 = 60’, 1’ = 60”. 11
Grade, còn được gọi là gon (g), là góc ở tâm chắn cung có chiều dài bằng 1/400
chu vi đường tròn. Một góc tròn có 400g.
Grade chỉ có ước số, các ước số là centigrade (C) và centi-centigrade (cc). 1g = 100c, 1c = 100cc.
Radian, (rad), là cung có chiều dài bằng bán kính đường tròn đó. Góc ở tâm chắn
cung bằng 1 radian được gọi là góc 1 radian. Một góc tròn có 2ð rad.
Quan hệ giữa các đơn vị đo góc
1 góc tròn = 3600 = 400g = 2 Ã rad. Đặt các hệ số: 1800/Ã = 57,29578 = po po.60 = 3438 = p’ p’.60 = 206265 = p”
Là các hệ số chyển đổi giữa độ và radian.
2.1.2 Đặc điểm tính toán trong trắc địa
Khối lượng tính toán trong trắc địa là rất lớn, thường sử dụng các kết quả đo đạc
ngoài thực địa và hay gặp các phép tính với các số thập phân vô hạn. Trong các phép tính,
nếu lấy sau dấu phảy quá nhiều chữ số s¿ làm việc tính toán nặng nề, tốn kém. Ngược lại,
nếu lấy sau dấu phảy quá ít chữ số thì độ chính xác không đảm bảo và vô tình phủ nhận
độ chính xác của công tác đo đạc ngoài thực địa, một công việc rất vất vả. Do vậy trong
trắc địa có những nguyên tắc tính toán riêng nhằm thoả mãn yêu cầu của từng công việc,
đặc biệt tránh ảnh hưởng của sai số tính toán.
Làm tròn số:
- Khi làm tròn, các số bỏ đi có giá trị nhỏ hơn 5 thì số trước đó giữ nguyên.
- Khi làm tròn, các số bỏ đi có giá trị lớn hơn 5 thì số trước đó cộng thêm 1.
- Khi làm tròn, các số bỏ đi có giá trị đúng bằng 5:
+ Số trước đó giữ nguyên nếu là chẵn
+ Số trước đó cộng thêm 1 nếu là lẻ.
VD: 25.126 ≈ 25.12, 12.132 ≈ 12.13
45.125 ≈ 45.12; 36.135 ≈ 36.14. 12
Lấy đủ các chữ số cần thiết:
Khi tính toán, kết quả tính cần lấy thêm sau dấu phẩy một chữ số so với kết quả đo.
VD: đo khoảng cách chính xác tới cm, kết quả tính lấy tới mm
đo góc chính xác tới giây, kết quả tính lấy tới 1/10 giây.
Giá trị các hàm lượng giác thường là các số thập phân. Đối với từng công việc, số
chữ số sau dấu phảy được lấy khác nhau. Trong trắc địa cao cấp, lấy 7 chữ số (có bảng
tra hàm lượng giác 7 chữ số).
VD: cos 30o12’23” = 0.8642187
Trong trắc địa công trình, lấy 5 chữ số (có bảng tra hàm lượng giác 5 chữ số).
VD: cos 30o12’23” = 0.86422
Riêng đối với các hàm lượng giác của các góc nhỏ, chúng ta có thể tính:
sinε = ε + ε3/3! + ε5/5! + … ≈ ε
tgε = ε + ε3/3 + ε5/5 + … ≈ ε
VD: sin 3” ≈ 3/206265 ≈ 0.0000145 rad
2.2 KHÁI NIỆM VỀ SAI SỐ ĐO 2.2.1 Khái niệm
Đo đạc một đại lượng là đem so sánh nó với một đại lượng cùng loại được chọn làm đơn vị.
Trong Trắc địa, có ba đại lượng đo cơ bản là khoảng cách, góc và độ cao. Khi đo
đạc, do người đo, do môi trường, do dụng cụ mà các kết quả của các lần đo cùng một đại
lượng có khác nhau, điều này chứng tỏ kết quả đo chứa sai số.
Sai số thực (s) là độ lệch giữa giá trị đo (L) và trị thực (X) của đại lượng cần đo. s = L – X (2.1)
Nếu đo n lần trị thực X, ta được dãy n trị đo Li của cùng một đại lượng, tương ứng có các sai số thực si: si = Li - X (2.2) 13
Giá trị sai số s càng nhỏ, kết quả đo càng chính xác. Nghiên cứu các phương pháp
đo, dụng cụ đo, phương pháp xử lý kết quả đo, … nhằm đạt kết quả đo chính xác theo yêu
cầu cũng là nhiệm vụ của Trắc địa.
Theo tính chất, theo quy luật mà sai số phân thành ba loại: sai số thô (sai lầm), sai số
hệ thống, sai số ngẫu nhiên.
2.2.2 Phân loại sai số đo Sai số thô
Sai số thô là các sai số có giá trị lớn, do thiếu cẩn thận, nhầm lẫn trong khi đo gây ra..
Ví dụ: khi đo cạnh, người đo đọc thước được 19.245m nhưng người ghi lại ghi thành 19.425m.
Để tránh sai số này, trong quá trình đo phải cẩn thận, có người kiểm tra và đo nhiều lần.
Sai số hệ thống
Là sai số xuất hiện trong kết quả đo theo một quy luật nào đó do sự thiếu chính xác
của dụng cụ đo, do thói quen của người đo, do ngoại cảnh thay đổi (nhiệt độ, độ ẩm,...).
Ví dụ: sử dụng thước 20m để đo chiều dài, nhưng thực tế thước chỉ dài 19.995m,
như vậy mỗi lần đặt thước sai 5mm.
Sai số hệ thống có thể làm giảm hoặc loại trừ nếu chúng ta tìm ra quy luật của chúng.
Sai số ngẫu nhiên
Là sai số xuất hiện một cách ngẫu nhiên, không có quy luật xuất hiện và không biết
giá trị của nó trong kết quả đo.
Ví dụ: Khi đo khoảng cách bằng thước thép, do đặt đầu thước lệch khỏi điểm cần
đo, do mắt người đo kém nên đọc thước không tốt, … là những nguyên nhân ngẫu nhiên
gây nên sai số ngẫu nhiên.
Sai số ngẫu nhiên không thể tránh được trong quá trình đo đạc. Đây là sai số chính
mà Lý thuyết sai số nghiên cứu.
Sai số ngẫu nhiên tuân theo luật phân bố chuẩn và có các tính chất:: 14
+ Khi số lần đo là vô cùng, số lần xuất hiện của sai số ngẫu nhiên có giá trị dương
xấp xỉ số lần xuất hiện của sai số ngẫu nhiên có giá trị âm. Lim[s ] = 0 (2.3) n→∞
+ Trong cùng điều kiện đo sai số ngẫu nhiên không vượt quá một giới hạn
nào đó và sai số ngẫu nhiên có trị tuyệt đối nhỏ thì khả năng xuất hiện nhiều hơn
sai số ngẫu nhiên có trị tuyệt đối lớn.
2.3 CÁC TIÊU CHUẨN ĐÁNH GIÁ KẾT QUẢ ĐO CÙNG ĐỘ CHÍNH XÁC
2.3.1 Sai số trung bình θ n Σ s i
Sai số trung bình được tính theo công thức: θ = i=1 (2.4) n Trong đó:
si: sai số thực lần đo thứ i, n : số lần đo
Ví dụ: Hai người cùng đo một đoạn thẳng với 9 lần đo và sai số thực của mỗi lần đo:
Người A: 2, 3, -1, -2, -4, 1, -2, 3, 2 (mm)
Người B: 1, 1, -5, 4, 2, -3, -2, 3, -1 (mm)
Sai số trung bình của mỗi người là: θA = 2.2mm θB = 2.2mm
2.3.2 Sai số trung phương m [ss ]
Công thức Gauss tính sai số trung phương: m = ± (2.5) n
Với ví dụ trên: mA = ±2.4mm và mB = ±2.8mm
Ta thấy, qua sai số trung bình thì hai người đo chính xác như nhau, nhưng qua sai
số trung phương người A đo chính xác hơn.
Sai số trung phương khuếch đại được phạm vi biến động của sai số, do đó đánh giá
độ chính xác tốt hơn sai số trung bình nên sai số trung phương thường được dùng để
đánh giá độ chính xác. 15
2.3.3 Sai số xác suất p
Nếu sắp xếp trị tuyệt đối của dãy sai số ngẫu nhiên theo thứ tự tăng dần thì sai số xác suất là:
- Nếu số sai số là số lẻ: p = ± s n+1 (2.6) 2
- Nếu số sai số là chẵn: p = ± 1 ( ÷ s + ÷ n s n 2 +1 (2.7) ø 2 2 ø Với ví dụ trên:
Người A: 1, 1, 2, 2, 2, 2, 3, 3, 4 pA = ± 2mm
Người B: 1, 1, 1, 2, 2, 3, 3, 4, 5 pA = ± 2mm
2.3.4 Sai số giới hạn f
Là sai số mà các sai số ngẫu nhiên không vượt qua giá trị này, nếu vượt qua thì phải loại bỏ.
Thông thường sai số giới hạn được chọn: f = 3m
Trong trường hợp yêu cầu độ chính xác cao, sai số giới hạn được chọn: f = 2m
2.3.5 Sai số trung phương tương đối
Khi đo khoảng cách, ngoài các tiêu chuẩn trên, còn sử dụng sai số trung phương
tương đối 1/T, là tỷ số giữa sai số trung phương với kết quả của đại lượng đo: 1 = m (2.8) T L
Ví dụ: có hai cạnh được đo với kết quả và sai số trung phương như sau: AB = 1000m, mAB = 10mm CD = 800m, mCD = 10mm
Nếu sử dụng sai số trung phương, ta thấy hai cạnh đo chính xác như nhau. Sai số
trung phương tương đối của hai cạnh lần lượt là: 1 = 10 = 1 , 1 = 10 = 1 T 1000000 10000000 T 800000 8000000
Như vậy cạnh AB đo chính xác hơn. 16
2.4 SAI SỐ TRUNG PHƯƠNG CỦA HÀM SỐ CÁC ĐẠI LƯỢNG ĐO
Trong Trắc địa, có rất nhiều đại lượng cần tìm phải tính thông qua các đại lượng đo
khác (đại lượng đo gián tiếp).
VD1: Trong tam giác ABC, chỉ đo hai góc A và B, còn góc C được tính từ hai góc này: C = 1800 – (A + B) (2.9)
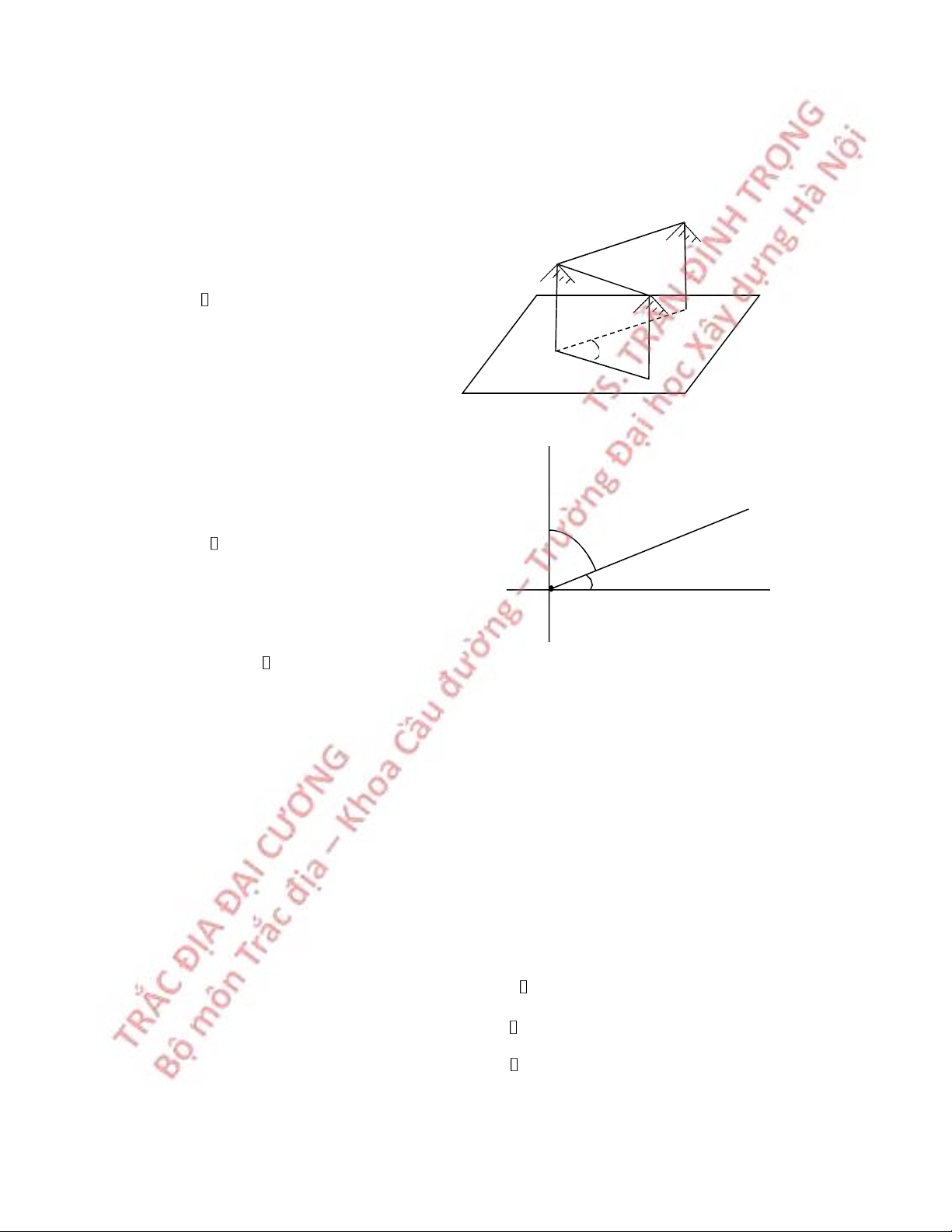
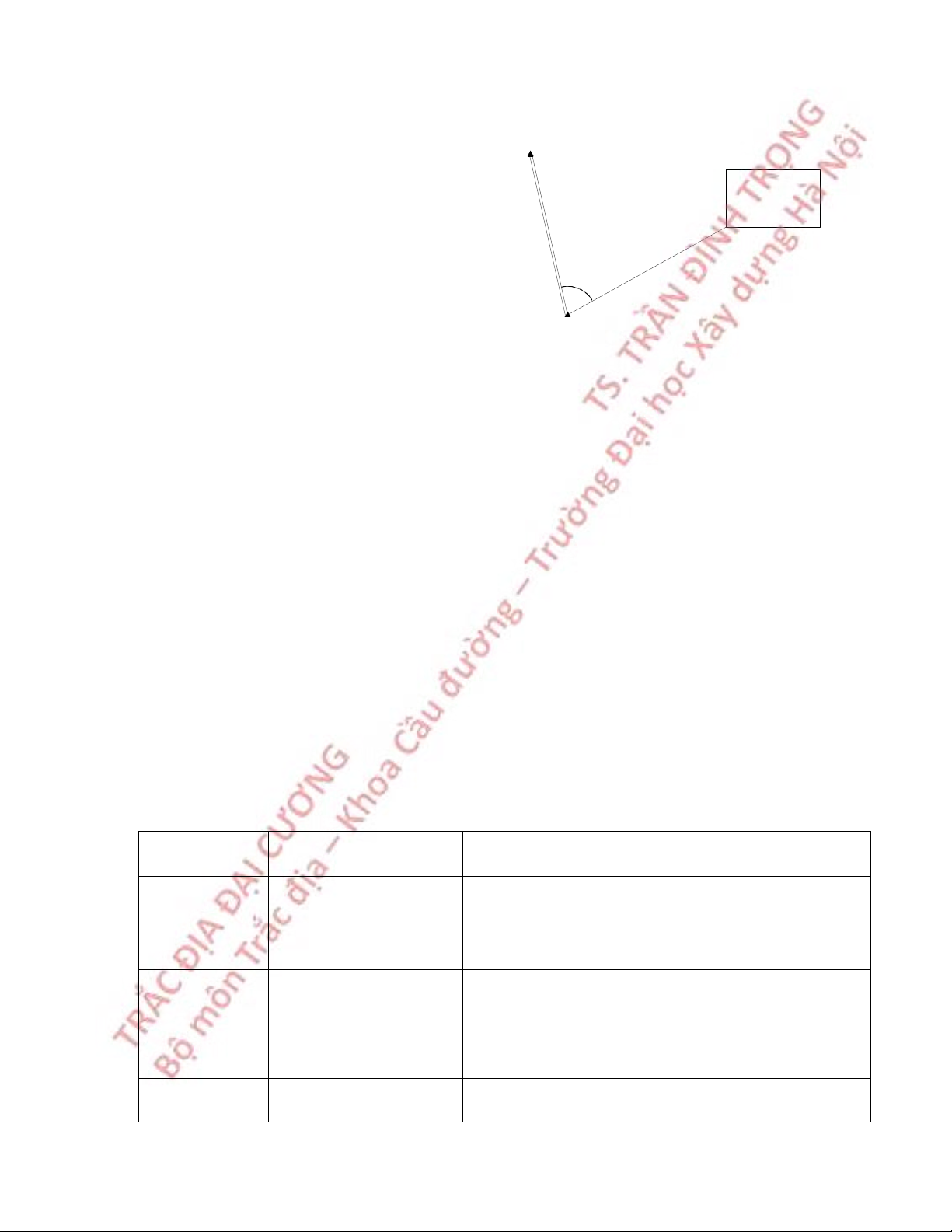
VD2: Trong đo cao lượng giác (hình
2.1), để xác định độ cao h, ta đo khoảng h cách D và góc đứng V: V h = DtgV (2.10) D
Hình 2.1 Đo cao lượng giác
Để đánh giá độ chính xác của các đại lượng đo gián tiếp, phải thông qua hàm số lập được.
2.4.1 Sai số trung phương hàm số dạng tổng quát
Có dãy trị đo Li độc lập nhau, của dãy trị thực Xi, ứng với sai số trung phương mi (i=1, 2, 3, …).
Hàm F được xác định thông qua trị thực Xi: F = f(X1, X2,..., Xn) (2.11) Hay:
F + F = f(L1+s1, L2+s2,..., Ln+ sn) (2.12)
Với F, sI là các sai số thực tương ứng với hàm F và trị đo Li.
Khai triển theo chuỗi Taylor và bỏ qua số hạng phi tuyến tính, nhận được: 6F 6F 6F F + F = f(L1, L2 ,..., L s + s + ... + s (2.13) n ) + 1 6 2 n L 6 6 1 L L 2 n 6F 6F 6F Hay: F = s + s + ... + s (2.14) 6 1 2 n L 6L 6L 1 2 n
Chuyển sang sai số trung phương: 6F 6F 6F m 2 = ( )2 m 2 + ( ) 2 m2 + ... + ( )2 m 2 (2.15) F 6L 1 6L 2 n 1 6L 2 n 17 6F Trong đó:
là đạo hàm riêng phần của hàm F với biến số L 6 i. Li Xét hai ví dụ trên:
VD1: các góc đo: A = 450 12’ 24”, B = 340 22’ 26”. Với sai số mA = mB = m = 3”
Góc C tính được: C = 1800 – (A + B) = 1000 25’ 10”
Độ chính xác m2 = m2 + m2 , mC = 4.2”. C A B
VD2: Đo chiều dài D = 50.12m với độ chính xác mD = ±0.02m. Và góc nghiêng V =
150 30’ 10” ; mV= ±20”. Độ cao h = DtgV = 13.902m,
Theo (2.15), độ chính xác: ( 6 2 2 2 h ( 6h m2 ( D m2 m2 = ÷ ÷ m2 + ÷
÷ V = (tgV )2 m2 + ÷ ÷ V
h ø 6D ø D ø 6V ø p"2
D ø cos2 V ø p"2 Thay số ta được: mh = ±0.007 (m).
2.4.2 Sai số trung phương hàm số dạng đơn giản
Hàm số dạng tổng đại số F = X1 + X2 + … + Xn (2.16) 6F = Vì
1 , theo (2.11): m2 = m2 + m2 +... + m2 = [m2 ] (2.17) 6L F 1 2 n i
Khi các đại lượng trong hàm (2.15) cùng độ chính xác (đo cùng điều kiện ngoại
cảnh, cùng dụng cụ, cùng phương pháp), tức là: m1 = m2 = … = mn = m. thì: m = m n (2.18) F
Hàm số của số trung bình cộng [ Số trung bình cộng: L]
L = L1 + L2 + ... + Ln = (2.19) n n
Sai số trung phương của số trung bình cộng: m 2 = 1 m 2 + 1 m 2 + ... + 1 2 m 1 2 L n 2 n 2 n 2 n m
Nếu m1= m2 =... = mn = m thì: m = L (2.20) n
Như vậy, độ chính xác của số trung bình cộng tăng lên n lần, vì vậy số trung bình
cộng là số đáng tin cậy nhất. 18
Theo (2.20), độ chính xác số trung bình cộng tăng khi số lần đo tăng, nhưng nếu
tăng quá nhiều thì kinh tế, thời gian đo đạc lãng phí, thông thường người ta đo tối đa không quá 24 lần.
2.4.3 Thiết kế độ chính xác đo đạc
Trong Trắc địa, hầu hết các công việc đều đã biết trước yêu cầu độ chính xác, ví dụ
bố trí tim công trình với độ chính xác ±1cm, bố trí cốt (độ cao) với độ chính xác ±0.5cm.
Chúng ta phải thiết kế độ chính xác đo đạc cần thiết để đảm bảo yêu cầu đó.
Để ước tính độ chính xác đo đạc, trong Trắc địa thường sử dụng nguyên tắc đồng
ảnh hưởng: khi một đại lượng được xác định qua các đại lượng đo khác nhau thì coi độ
chính xác của các đại lượng đo ảnh hưởng như nhau tới độ chính xác đại lượng cần xác định.
Áp dụng nguyên tắc đồng ảnh hưởng công thức (2.15): 6F 6F 6F ( )m = ( )m = ... = ( )m = mF 1 2 n 6L n 1 6L2 6Ln Trở lại với VD1:
Để xác định góc C với độ chính xác 5” thì các góc A, B phải đo với độ chính xác là bao nhiêu?
Ta có, độ chính xác xác định góc C: m2 = m2 + m2 C A B
Áp dụng nguyên tắc đồng ảnh hưởng: mA = mB = m 2 Khi đó: = 2m2 , m = mC m C = 3.5" 2
Như vậy, cần phải đo hai góc A, B với độ chính xác 3.5” để góc C xác định với độ chính xác 5”.
2.5 TÍNH VÀ ĐÁNH GIÁ KẾT QUẢ ĐO
2.5.1 Tính kết quả đo cùng độ chính xác – Công thức Bessel
Khi đo đạc các đại lượng đo trong cùng một điều kiện đo, cùng một phương pháp
đo và cùng một dụng cụ đo thì kết quả nhận được có cùng độ chính xác. 19
Giả sử có dãy n trị đo Li, để đánh giá độ chính xác kết quả đo này, chúng ta phải
biết được trị thực (theo công thức 2.4), nhưng trị thực của dãy trị đo trên lại chưa biết (hầu
hết các trị đo trong trắc địa là chưa biết trị thực). Do vậy, để tính và đánh giá kết quả đo chúng ta làm như sau: [
1. Tìm trị tin cậy nhất (số trung bình cộng): L]
L = L1 + L2 + ... + Ln = (2.21) n n
2. Tính sai số (số hiệu chỉnh của các đại lượng đo):
v = L – L (2.22) i i Kiểm tra: [v] = 0.
3. Tính sai số trung phương của một lần đo theo công thức Bessel: m = ± [vv] (2.23) i n –1
4. Tính sai số trung phương của dãy kết quả đo (của số trung bình cộng): m (2.24) m = L n
Ví dụ: Một đoạn thẳng đươc đo 5 lần, kết quả đo trong bảng. Tính kết quả đo và
đánh giá độ chính xác (việc tính toán được thực hiện trong bảng). Lần đo Li (m) vi (cm) vv Kết quả tính 1 45.34 0 0
Kết quả đo: L = 45.340m
Đánh giá độ chính xác: 2 45.33 1 1
- Sai số trung phương một lần đo: mi = 1.6cm 3 45.35 -1 1
- Sai số trung phương kết quả đo: mL = 0.7cm 4 45.36 -2 4
- Sai số trung phương tương đối kết quả đo: 1 5 45.32 2 4 = mL = 1 T L 6400 Σ 0 10
2.5.2 Tính kết quả đo không cùng độ chính xác
Kết quả đo trong điều kiện đo khác nhau, phương pháp đo khác nhau, dụng cụ đo
khác nhau s¿ có độ chính xác khác nhau. 20
Để tính toán và đánh giá độ chính xác của kết quả đo không cùng độ chính xác đó,
sử dụng khái niệm trọng số P: P = c (2.25) i m 2 i Trong đó:
mi: Sai số trung phương của lần đo i c: Hằng số tuỳ chọn
Và trung bình cộng L của dãy trị đo không cùng độ chính xác (trung bình trọng số):
L + P L + ... + P L L = P1 1 2 2 n n = [Pl] (2.26)
P + P + ... + P [P] 1 2 n
Sai số trung phương của kết quả đo không cùng độ chính xác: m = ± [Pvv] (2.27) L (n –1)[P] 21 CHƯƠNG 3 ĐO GÓC 3.1 KHÁI NIỆM
Góc có hai loại: góc bằng β và góc đứng V.
Góc bằng β của hai hướng OA và A
OB là góc nhị diện giữa hai mặt phẳng O
thẳng đứng chứa OA và OB. B β = 00 3600. A'
Góc đứng V (góc nghiêng) của hướ O' β
ng ngắm OA là góc tạo bởi hướng OA B'
với mặt phẳng nằm ngang. Hình 3.1 Góc bằng
Góc đứng V mang giá trị dương khi
hướng OA nằm bên trên mặt phẳng
ngang, âm khi OA nằm bên dưới mặt A phẳng ngang. Z V = 00 ±900.
Trường hợp góc tính từ thiên đỉnh V
(đỉnh trời) theo phương thẳng đứng đi qua O
O tới hướng OA thì góc này gọi là góc
thiên đỉnh Z. Z = 00 1800. Hình 3.2 Góc đứng Z = 900 – V (3.1) 3.2 MÁY KINH VĨ
3.2.1 Khái quát về máy kinh vĩ
Máy kinh vĩ là dụng cụ trắc địa chủ yếu dùng để đo góc, ngoài ra có thể đo khoảng cách và đo cao.
Theo độ chính xác máy kinh vĩ được chia thành 3 loại [5]:
- Máy kinh vĩ độ chính xác cao: mβ = ± 0''5 ±2''
- Máy kinh vĩ độ chính xác: mβ = ± 5'' ±10'' - Máy kinh vĩ kỹ thuật: mβ = ± 15' ±30' .
Theo cấu tạo bàn độ, máy kinh vĩ được chia làm 3 loại: 22
- Máy kinh vĩ kim loại: bàn độ làm bằng kim loại và đọc số bằng kính lúp
- Máy kinh vĩ quang học: bàn độ làm bằng thuỷ tinh, đọc số bằng kính hiển vi
- Máy kinh vĩ điện tử: bàn độ bằng đĩa từ, đọc số nhờ màn hình hiển thị.
3.2.2 Nguyên lý cấu tạo máy kinh vĩ
Máy kinh vĩ gồm ba phần chính:
Giá máy: bằng gỗ hoặc kim loại gồm ba chân.
Các chân có thể thay đổi độ dài.
Đế máy: là bàn đế có 3 ốc cân bằng, chúng để cân bằng máy khi đo.
Thân máy: là phần quan trọng nhất, nó gồm rất nhiều các bộ phận:
- Bàn độ ngang và bàn độ đứng - Ống kính - Ống thuỷ - Bộ phận đọc số
- Các loại ốc khoá, ốc vi động...
Hình 3.3 Máy kinh vĩ điện tử
3.2.3 Một số bộ phận chính Ống kính:
Các bộ phận chính của ống kính
gồm: kính vật, kính mắt, lưới chữ thập.
Đường thẳng nối quang tâm kính
vật với quang tâm kính mắt và đi qua tâm
của màng dây chữ thập là trục ngắm của ống kính.
Hình 3.4 Hình ảnh của lưới chỉ chữ thập
Độ phóng đại của ống kính VX: f VX = v (3.2) fm 23
Trong đó: fv: tiêu cự kính vật, fm: tiêu cự kính mắt .
Bàn độ: có hình tròn, trên đó khắc vạch chia độ (hoặc grad). Có hai loại bàn độ, bàn
độ ngang và bàn độ đứng.
Ống thuỷ: là ống thuỷ tinh bên trong có chứa chất lỏng và bọt khí. Ống thuỷ dùng để
cân bằng máy. Có hai loại ống thuỷ:
- Ống thuỷ dài: Dùng để cân bằng chính xác máy.
Mặt trên của ống thuỷ có các vạch
chia cách nhau 2mm tương ứng với góc
ở tâm (gọi là độ nhậy ống thuỷ). Hình3.5 Ống thuỷ dài
Trục ống thuỷ dài là đường tiếp tuyến với mặt cong phía trong của ống thuỷ và đi
qua điểm giữa ("điểm không").
- Ống thuỷ tròn: Dùng để cân bằng sơ bộ máy.
Mặt trên của ống thuỷ có khắc các
vòng tròn đồng tâm cách nhau 2mm. Mặt
trong của ống thuỷ tròn có dạng chỏm Hình 3.6 Ống thuỷ tròn
cầu, đỉnh chỏm cầu là "điểm không".
3.3 KIỂM NGHIỆM CÁC ĐIỀU KIỆN CƠ BẢN CỦA MÁY KINH VĨ
Máy kinh vĩ là một dụng cụ trắc địa độ chính xác cao, các trục của máy phải luôn
đảm bảo các điều kiện hình học cơ bản, trước khi sử dụng phải kiểm nghiệm các điều kiện này.
Các trục chính của máy kinh vĩ (hình 3.7): - Trục quay máy (TQM - VV)
- Trục quay ống kính (TQOK - HH)
- Trục ống kính (trục ngắm) (TOK - CC)
- Trục ống thuỷ dài (TOT - LL). 24
Các trục trên phải thoả mãn các điệu TQM(V) TOK(C) kiện hình học sau:
- Trục ống thuỷ dài vuông góc với trục quay máy (TOT TQM) TQOK(H) TQOK(H)
- Trục ống kính vuông góc với trục quay ống kính (TOK TQOK) TOT(L) TOT(L)
- Trục quay ống kính vuông góc với trục TOK(C) quay máy TQOK TQM). TQM(V)
Hình 3.7 Các trục chính của máy kinh vĩ
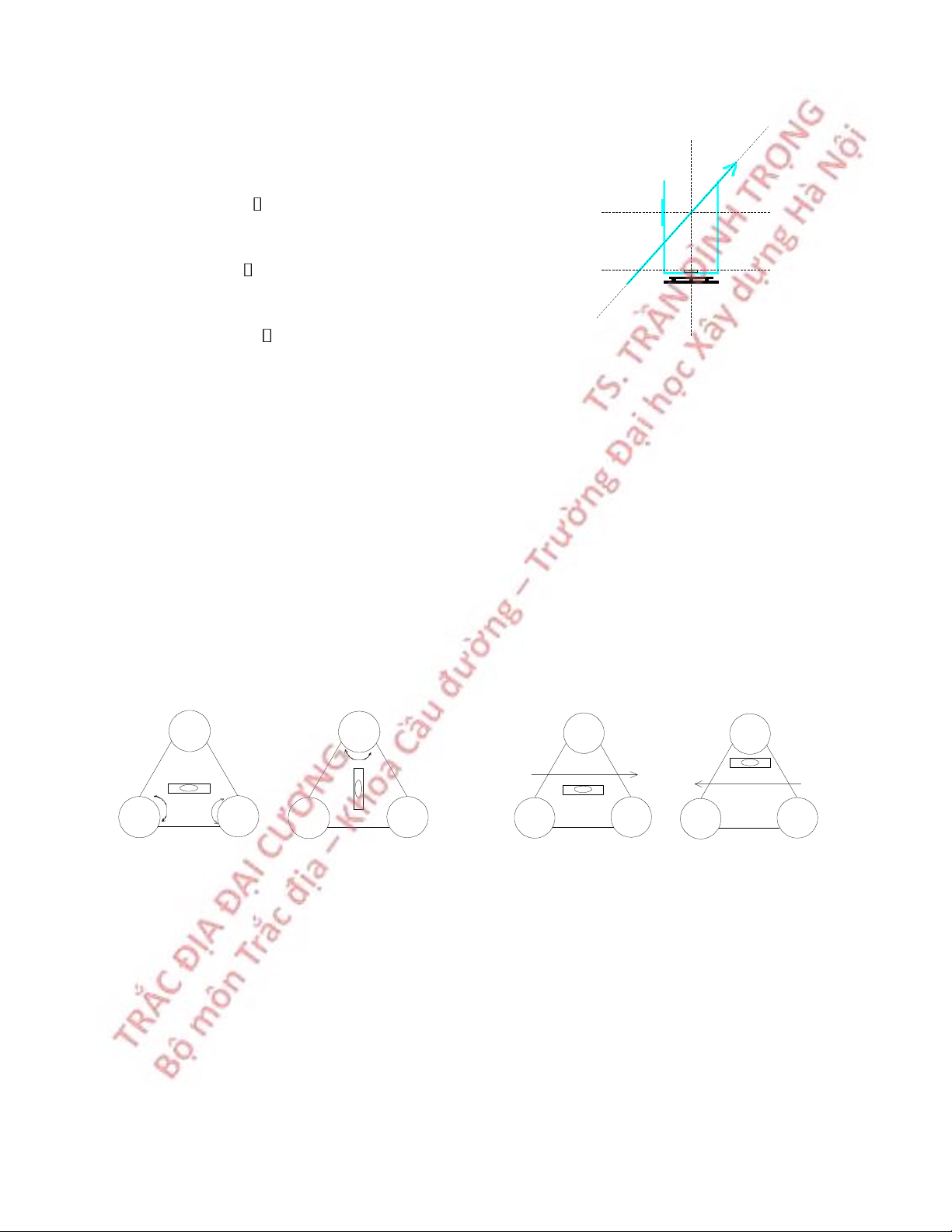
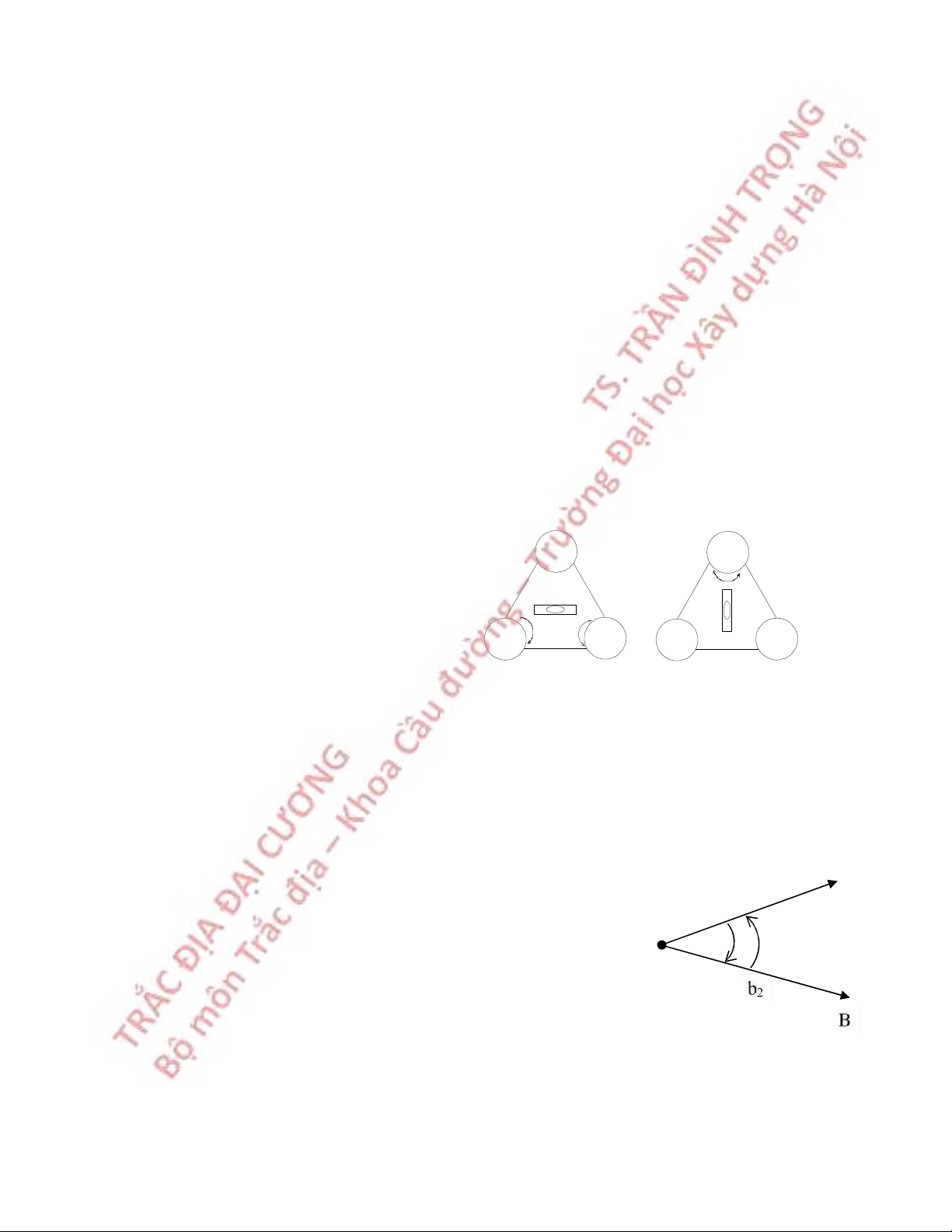
3.3.1 Trục ống thuỷ dài vuông góc với trục quay máy
Sau khi cân bằng máy, quay máy để cho ống thuỷ dài song song với đường nối hai
trong ba ốc cân, xoay hai ốc cân này đồng thời và ngược chiều nhau cho bọt thuỷ vào giữa.
Quay máy 90O , dùng ốc cân thứ ba đưa bọt nước vào giữa.
Quay máy đi 180O, nếu bọt nước không lệch hoặc lệch không quá nửa khoảng chia
thì điều kiện này thoả mãn.
Nếu bọt nước lệch nhiều hơn cần phải điều chỉnh. 3 3 3 3 1 2 1 2 1 2 1 2 Kiểm nghiệm Kiểm tra
Hình 3.8 Kiểm nghiệm trục ống thủy dài vuông góc với trục quay máy
3.3.2 Trục ống kính vuông góc với trục quay ống kính (sai số 2c)
Sau khi cân bằng máy, để bàn độ đứng bên trái (thuận ống kính), ngắm về một
điểm nằm ngang rõ nét và đọc số đọc trên bàn độ ngang, được số đọc T.
Quay máy, đảo ống kính, lúc này bàn độ đứng ở bên tay phải (đảo ống kính), vẫn
ngắm điểm đó, đọc số đọc trên bàn độ ngang được số đọc P. 25
Tính sai số 2c theo công thức: 2c = T – P ± 180O (3.3)
Nếu 2c ±3mĐ (mĐ: sai số đọc số của máy) thì coi như điều kiện này đảm bảo.
Nếu không, cần phải điều chỉnh.
Ví dụ: khi kiểm nghiệm điều kiện này của máy kinh vĩ điện tử T100 (mĐ = 10”), các
số đọc khi kiểm nghiệm: T = 21016’10’’, P = 201015’50’’ Sai số 2c:
2c = 21016’10’’- (201015’50’’ - 1800) = 20’’ < 3x10”
Máy đảm bảo điều kiện.
3.3.3 Trục quay ống kính vuông góc với trục quay máy
Cũng tương tự như kiểm nghiệm điều kiện 3.3.2, chỉ khác chọn mục tiêu trên cao.
Điều kiện này đảm bảo nếu: T – P ± 180O ±3mĐ 3.3.4 Xác định MO
MO là số đọc trên bàn độ đứng khi trục ngắm nằm ngang. MO có giá trị 0 hoặc 900
(nếu máy kinh vĩ đo góc thiên đỉnh). Do chế tạo, do quá trình sử dụng giá trị MO có thể sai
khác, nếu giá trị sai khác này lớn s¿ ảnh hưởng tới độ chính xác đo góc đứng. Cách kiểm nghiệm:
Sau khi cân bằng máy, để bàn độ đứng bên trái (thuận), ngắm về một điểm rβ nét
và đọc số đọc trên bàn độ đứng, được số đọc T.
Quay máy, đảo ống kính, lúc này bàn độ đứng ở bên tay phải (nghịch), vẫn ngắm
điểm đó, đọc số đọc trên bàn độ đứng, được số đọc P. T + P ±1800
Xác định MO theo công thức: MO = (3.4) 2
Nếu MO ±3mĐ (mĐ: sai số đọc số của máy) thì coi như điều kiện này đảm bảo.
Nếu không, cần phải điều chỉnh.
Khi đo góc đứng ở hai vị trí bàn độ trái và phải, góc nghiêng ở hai vị trí thuận và đảo đượ
V = MO – Z c tính: T T (3.5)
V = Z – (180 + MO) P P 0
Góc nghiêng trung bình giữa hai lần đo: V + V
Z – (1800 + MO) + MO – Z Z – Z –1800 V = T P = P T = P T (3.6) 2 2 2
Như vậy, khi đo góc đứng ở hai vị trí ống kính thì kết quả trung bình s¿ không bị
ảnh hưởng của sai số MO. 26 3.4 ĐO GÓC BẰNG
3.4.1 Công tác chuẩn bị tại mỗi trạm đo
Máy đặt lên giá ba chân, vặn chắc chắn ốc nối chân và máy. Đặt máy vào điểm đo
sao cho trục quay máy đi qua tâm điểm đo (định tâm máy) và trục quay thẳng đứng (cân
bằng máy). Các thao tác s¿ được hướng dẫn cụ thể hơn trong quá trình thực tập, ở đây
chỉ giới thiệu sơ bộ các thao tác định tâm và cân bằng máy.
- Định tâm sơ bộ: Sử dụng bộ phận định tâm, di chuyển chân máy để đưa tâm của
bộ phận định tâm trùng với tâm mốc.
- Cân bằng sơ bộ: thay đổi chiều cao chân máy, điều chỉnh bọt thuỷ tròn vào chính giữa.
- Định tâm chính xác: nới lỏng ốc nối, dịch chuyển máy trên đế giá ba chân, điều
chỉnh tâm của bộ phận định tâm quang học trùng với tâm mốc. Vặn chặt ốc nối.
- Cân máy chính xác: 3 3
Quay máy để trục ống thuỷ dài
song song với đường nối hai ốc cân máy,
vặn hai ốc này đồng thời và ngược chiều 1 2 1 2
nhau điều chỉnh bọt thuỷ vào giữa. Hình 3.9 Cân bằng máy
Quay máy đi 900, dùng ốc cân còn lại để điều chỉnh cho bọt nước vào giữa.
Sau khi cân máy chính xác, quay máy đi mọi hướng để kiểm tra tâm và bọt thuỷ,
nếu bị lệch, phải làm lại từ bước định tâm chính xác và cân bằng chính xác.
3.4.2 Đo góc bằng theo phương pháp đo đơn giản
Phương pháp này chỉ áp dụng cho trạm đo có hai A hướng đo. a a 2 1 Thao tác đo: O
Giả sử đo góc tại trạm máy O gồm 2 hướng đo OA, b1
OB (hình 3.10). Máy kinh đã được định tâm và cân bằng
chính xác tại O, tiêu ngắm đặt tại A và B. Hình 3.10 Đo góc đơn 27
- Để bàn độ đứng bên trái (vị trí thuận ống kính), ngắm chính xác điểm A, đọc số
trên bàn độ ngang, được giá trị a1.
Quay máy thuận kim đồng hồ ngắm chính xác điểm B, đọc số trên bàn độ ngang, được giá trị b1.
Giá trị góc khi đo thuận kính: β1 = b1 -a1.
- Quay máy và đảo ống kính để bàn độ đứng bên phải (vị trí đảo ống kính), ngắm
chính xác điểm B, đọc số trên bàn độ ngang, được giá trị b2.
Quay máy ngược chiều kim đồng hồ, ngắm chính xác điểm A, đọc số trên bàn độ
ngang, được giá trị a2.
Giá trị góc khi đo đảo kính: β2 = b2 -a2.
- Nếu β1- β2 3mĐ (mĐ: sai số đọc số của máy), thì tính giá trị góc sau khi đo thuận β 1 – β 2 và đảo ống kính: β = (3.7) 2
Chú ý: Thông thường số đọc a1 (giá trị của hướng ban đầu) được đặt trước và có giá trị
chẵn để dễ tính toán. Để tăng độ chính xác, góc phải được đo nhiều lần (nhiều vòng đo),
mỗi lần đo giá trị hướng ban đầu s¿ khác nhau và giá trị góc là trung bình cộng của các vòng đo.
VD: Ghi sổ và tính toán kết quả đo góc bằng β với 3 vòng đo theo phương pháp đo
cung (giá trị hướng ban đầu mỗi vòng đo khác nhau: 1800/3 = 600):
SỔ ĐO GÓC BẰNG THEO PHƯƠNG PHÁP ĐO CUNG Máy: T100 Số: 893
Người đo: Trần Văn An Ngày đo: 20/09/2006
Người ghi: Nguyễn Văn Hùng
Thời tiết: trời nắng, gió nhẹ
Người tính: Nguyễn Văn Hùng Trạm Hướ Số đọc bàn độ ngang đo ng Góc nửa lần Góc một lần Góc trung đo đo đo bình Lần đo Trái - T Phải - P 1 2 3 4 5 6 7 A 0000’00”(1) 179059’50”(3) 105035’20”[1] O 105035’35”[3] 105035’28”[4] 1 B 105035’20”(2) 285035’40”(4) 105035’50”[2] A 60000’00” 240000’20” 105035’40” O 105035’35” 2 B 165035’40” 345035’50” 105035’30” A 120000’00” 299059’50” 105035’00” O 105035’15” 3 B 25035’00” 45035’20” 105035’30” 28
Tính toán, kiểm tra sổ đo:
Các số trong ngoặc đơn ( ) là các bước đo, các số trong ngoặc vuông [ ] là các bước tính.
1. Giá trị góc bằng nửa vòng đo thuận và nửa vòng đo đảo:
βT = b – a = (2) – (1) = [1] T T
βP = b – a = (3) – (4) = [2] P P 2. Kiểm tra: βT - βP 3mĐ β
3. Tính giá trị trung bình góc một lần đo: i + β β [1] +[2] T P = = = [3] 2 2 n Σ β i
4. Tính giá trị trung bình góc các lần đo: = 1 = [4] β n
3.4.3 Đo góc bằng theo phương pháp đo toàn vòng
Phương pháp này áp dụng cho A
trạm đo có ba hướng đo trở lên. a a 2 1 a' 2 Các thao tác đo: O a' 1 b 1
Giả sử đo góc tại trạm máy O gồm c b 1 2
3 hướng đo OA, OB và OC (hình 3.11). B Máy kinh đã được đị c nh tâm và cân bằng 2
chính xác tại O, tiêu ngắm đặt tại A, B, và C.
Hình 3.11 Đo góc toàn vòng
- Để bàn độ đứng bên trái (vị trí thuận ống kính), ngắm chính xác điểm A, quay máy
thuận chiều kim đồng hồ lần lượt ngắm chính xác các điểm B, C và A, đọc số trên bàn độ
ngang, lần lượt được các giá trị a1, b1, c1, a’1.
- Quay máy và đảo ống kính để bàn độ đứng bên phải (vị trí đảo ống kính), ngắm
chính xác điểm A, quay máy ngược chiều kim đồng hồ lần lượt ngắm chính xác các điểm
C, B và A, đọc số trên bàn độ ngang, lần lượt được các giá trị a2, c2, b2, a’2.
Tương tự như phương pháp đo cung, mỗi lần đo giá trị hướng ban đầu s¿ khác nhau 1800/n.
VD: Ghi sổ và tính toán kết quả đo góc bằng β với 3 vòng đo theo phương pháp đo toàn vòng: 29
SỔ ĐO GÓC BẰNG THEO PHƯƠNG PHÁP ĐO TOÀN VÒNG Máy:T100 Số: 893
Người đo: Trần Văn An Ngày đo: 20/09/2006
Người ghi: Nguyễn Văn Hùng
Thời tiết: trời nắng, gió nhẹ
Người tính: Nguyễn Văn Hùng Trạm đo Hướng Số đọc bàn độ ngang Trung bình Góc trung 2c Quy 0 Lần đo đo hướng bình Trái - T Phải - P 1 2 3 4 5 6 7 A 0000’00”(1) 180000’20”(8) -20” 0000’10”/12”[1] 0000’00”[5] O B 42036’10”(2) 222036’20”(7) -10” 42036’15”[2]
42036’03”[6] 42036’00”[8] 1 C 89020’30”(3) 269020’20”(6) +10” 89020’25”[3]
89020’13”[7] 89020’17”[9] A 0000’10”(4) 180000’20”(5) -10” 0000’15”[4] A 60000’10” 240000’20” -20” 60000’15”/15 00000’00” O B 102036’20” 282036’10” +10” 102036’15” 42036’00” 2 C 149020’40” 329020’30” +10” 149020’35” 89020’20” A 60000’10” 240000’20” -10” 60000’15” 119059’55”/- A 120000’00” 299059’50” +10” 2 00000’00” O B 162035’50” 342036’00” -10” 162035’55” 42035’57” 3 C 209020’10” 29020’20” -10” 209020’15” 89020’17” A 119059’50” 300000’10” -20” 120000’00”
Trình tự và công thức tính sổ đo: 1. Kiểm tra:
Sai số khép hướng ban đầu:
a1 – a’1 ≤ ±3mĐ, a2 – a’2 ≤ ±3mĐ Sai số 2c:
2c = T - ( P ±1800) < ±3mĐ
2. Tính trung bình hướng:
a = a T + a P ± 1800 = (1) + (8) ± 1800 =[1] tb 2 2 b + b ± 1800 b = T P = (2) + (9) ± 1800 =[2] tb 2 2
c + c ± 1800 = (3) + (10) ± 1800 c = T P =[3] tb 2 2 3. Quy không: a 1 + a 2
- Tính giá trị hướng quy không: a = tb
tb = [1] +[4] , giá trị này ghi tương ứng ở [1] 2 2 - Quy 0:
b = bTB – a = [2] – [1] = [6]
c = cTB – a = [3] – [1] = [7]
4. Tính giá trị trung bình góc các lần đo.
Ngoài hai phương pháp cơ bản trên còn có các phương pháp đo lặp, phương pháp tổ hợp... 30
3.5 SAI SỐ TRONG ĐO GÓC BẰNG
3.5.1 Sai số do môi trường
Khi đo góc, môi trường đo ảnh hưởng lớn tới độ chính xác đo góc. Ví dụ: do ánh
nắng chiếu vào máy làm các bộ phận giãn nở; do chiết quang không đều làm tia ngắm bị
bẻ cong,… Cách khắc phục các ảnh hưởng này là không bố trí hướng ngắm dọc hay qua
sông, hồ, …; khi đo sử dụng ô che máy; … 3.5.2 Sai số do máy
Do những điều kiện hình học của máy không được hiệu chỉnh tốt trước khi đo nên
cũng dẫn đến sai số khi đo. Chúng ta có thể loại trừ hoặc làm giảm ảnh hưởng bằng các cách đo hợp lý.
Sai số 2c bị loại trừ nếu đo góc ở hai vị trí bàn độ. Sai số vạch khắc bàn độ không
đều được giảm xuống nếu đặt giá trị hướng ban đầu của mỗi vòng đo khác nhau 180O/n.
3.5.3 Sai số do người đo
1. Sai số định tâm máy A
Giả sử máy bị lệch tâm một khoảng S
em. Khi đó, góc đo bị sai một lượng:
β = β '–β = 2em p β' (3.8) β S O’ O em
Cách hạn chế: sử dụng định tâm chính xác S như B
định tâm quang học, định tâm laser.
Hình 3.12 Sai số định tâm máy
2. Sai số định tâm tiêu A'
Giả sử, tiêu ngắm bị lệch tâm một khoảng
et. Khi đó, góc đo bị sai một lượng: et
δ = β – β ' = et .p (3.9) β A S
Cách hạn chế: đặt tiêu đúng tâm mốc O β β'
và dựng tiêu thẳng, khi đo bắt xuống sát chân tiêu. B
Hình 3.13 Sai số định tâm tiêu 31
3. Sai số ngắm m ng
Sai số ngắm bắt mục tiêu: m = ± 60 (3.10) ng V x
Vx: độ phóng đại của ống kính.
Cách hạn chế: sử dụng máy có độ phóng đại lớn.
4. Sai số đọc số mđ t mđ = (3.11) 2
t: độ chính xác của bộ phận đọc số. 3.6. ĐO GÓC ĐỨNG
Các công tác chuẩn bị cũng tương tự như đo góc bằng.
Giả sử cần đo góc đứng của hướng OA. Các thao tác đo:
- Để bàn độ đứng bên trái (vị trí thuận ống kính), ngắm chính xác điểm A, đọc số
trên bàn độ đứng, được giá trị T.
- Quay máy, đảo ống kính vẫn ngắm chính xác điểm A, đọc số trên bàn độ đứng, được giá trị P.
Ở một vị trí bàn độ, góc đứng được tính theo: V = MO-T (3.12) Hoặc: V = P – (MO + 1800) (3.13) P – T ± 1800
Góc đứng được tính theo hai vị trí bàn độ: V = (3.14) 2
Thông thường góc đứng của một hướng được đo nhiều lần để tăng độ chính xác,
kết quả cuối cùng là trung bình của các lần đo. 32
CHƯƠNG 4 ĐO KHOẢNG CÁCH 4.1 KHÁI NIỆM
Khoảng cách giữa hai điểm trên mặt đất gọi là khoảng cách nghiêng (S) và khoảng
cách giữa hai hình chiếu của chúng trên mặt phẳng nằm ngang gọi là khoảng cách ngang (D). B S A V D AO BO Hình 4.1 Khoảng cách
Quan hệ giữa khoảng cách nghiêng và khoảng cách ngang: D = S cosV (4.1) (V: góc dốc địa hình)
Có nhiều phương pháp đo khoảng cách như: đo bằng thước, phương pháp quang
học, phương pháp điện tử, phương pháp định vị GPS, … Trong chương trình này, chỉ giới
thiệu phương pháp đo bằng thước (thước thép) và phương pháp quang học.
4.2 ĐO KHOẢNG CÁCH BẰNG THƯỚC THÉP 4.2.1 Dụng cụ đo
Thước thép dùng trong Trắc địa thường có chiều dài 20, 30, 50m hoặc lớn hơn,
chiều rộng thước 10 25mm và chiều dày 0.2 0.4mm. Thước được kiểm nghiệm trước khi đo.
4.2.2 Chuẩn bị đường đo
Trước khi đo khoảng cách giữa hai điểm, cần phải dọn dẹp chướng ngại vật thông hướng đường đo. 33
Khi khoảng cách cần đo lớn hơn chiều dài của thước, cần phải đánh dấu các điểm
trung gian trên hướng đo, khoảng cách của hai điểm trung gian kề nhau nhỏ hơn chiều dài
của thước. Gọi là định hướng đường thẳng.
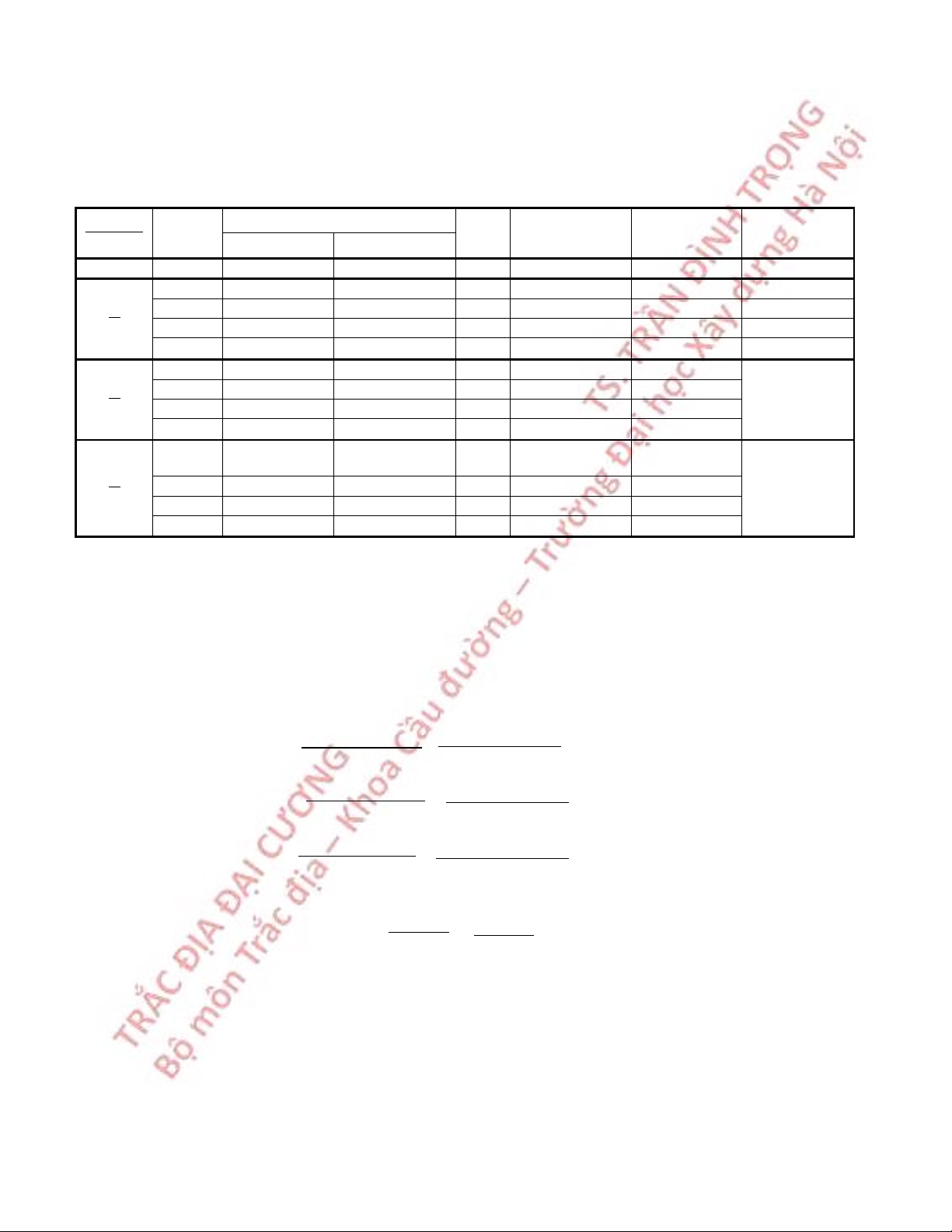
1. Định hướng đường thẳng bằng mắt
Giả sử cần định hướng đường thẳng AB. Dựng sào tiêu ở điểm A và B, một người
đứng sau điểm A và ngắm sao cho hai tiêu này trùng nhau. Điều chỉnh người thứ hai dựng
sào tiêu sao cho ba sào tiêu trùng nhau, đánh dấu điểm. Sào tiêu Sào tiêu Sào tiêu A 1 2 n B
Hình 4.2 Định hướng đường thẳng bằng mắt
Định hướng đuờng thẳng bằng mắt cho độ chính xác không cao. Trong trường hợp
yêu cầu độ chính xác cao, phải định hướng đường thẳng bằng máy kinh vĩ.
2. Định hướng đường thẳng bằng máy kinh vĩ
Đặt máy kinh vĩ ở A, ngắm về sào tiêu đặt ở B, khoá chuyển động ngang của máy.
Lúc này ống kính quay xung quanh trục quay của nó và tạo ra mặt phẳng thẳng đứng
chứa đường thẳng AB. Điều chỉnh và đánh dấu các sào tiêu trong mặt phẳng ngắm, s¿
định hướng được đường thẳng AB. Sào tiêu Sào tiêu Sào tiêu Sào tiêu A 1 2 n B
Hình 4.3 Định hướng đường thẳng bằng máy kinh vỹ
4.2.3 Đo và tính chiều dài
Dùng thước thép đo chiều dài giữa các điểm trung gian kề nhau. Phải tiến hành đo
hai lần, đo đi và đo về, nhằm loại trừ sai số thô và tăng độ chính xác kết quả đo. 34
Kết quả đo là giá trị trung bình giữa hai lần đo: S = (Sđi + Svề)/2 (4.2 S Kiểm tra kết quả đo: = Sđi -Svê 1 . S S 2000
Khoảng cách đo được là khoảng cách nghiêng, cần chuyển về khoảng cách ngang D theo (4.2).
4.2.4 Sai số trong đo khoảng cách bằng thước thép
Sai số kiểm nghiệm thước: l1 = l - l0 (4.3) l: chiều dài thực tế l0: chiều dài danh nghĩa
Sai số do ảnh hưởng của sự thay đổi nhiệt độ: l2 = αl0 t (4.4)
α: hệ số giãn nở vì nhiệt của vật liệu làm thước
t: chênh lệch nhiệt độ giữa khi đo và khi kiểm nghiệm
Ngoài ra còn nhiều sai số khác ảnh hưởng tới đo khoảng cách như sai số do thước
bị nghiêng, sai số do thước bi võng, …
4.3 ĐO KHOẢNG CÁCH BẰNG PHƯƠNG PHÁP QUANG HỌC 4.3.1 Nguyên lý
Khoảng cách S được xác định dựa β S b vào công thức: β
S = 1 b cot g (4.5) 2 2 Trong đó: b: gọi là cạnh đáy
Hình 4.4 Nguyên lý phương pháp quang học β: gọi là góc thị sai.
Máy đo khoảng cách bằng phương pháp quang học được cấu tạo thành hai loại:
Loại có β không đổi, cần đo b: phương pháp đo cạnh đáy
Loại có b không đổi, cần đo β: phương pháp đo góc thị sai. 35
Trong chương trình này, chỉ giới thiệu phương pháp đo cạnh đáy, phương pháp
được áp dụng trong máy kinh vĩ và máy thuỷ bình.
Trên màng dây chữ thập của ống kính
máy kinh vĩ và máy thuỷ bình được khắc chỉ trên (t)
thêm hai vạch ngắm phụ trên (t) và dưới
(d) dùng để đo khoảng cách. chỉ dưới (d)
Hình 4.5 Lưới chỉ chữ thập
Khi đo khoảng cách giữa hai điểm AB, máy kinh vĩ đặt tại A, mia đặt tại B (mia được
làm bằng gỗ hoặc nhôm, dài 3 4m và vạch khắc đến cm). Đọc các số đọc trên mia tương
ứng với hai vạch ngắm phụ, được t và d.
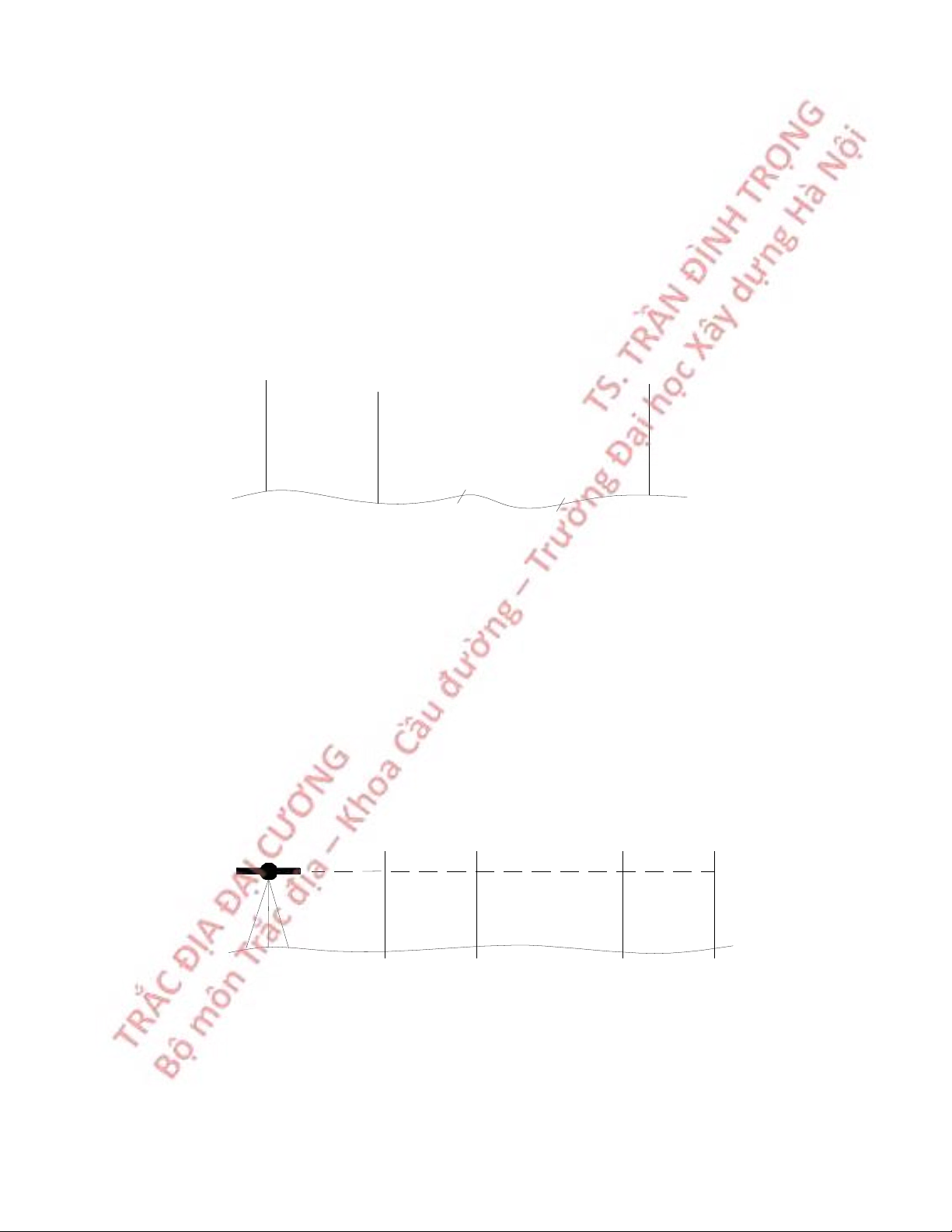
4.3.2 Trường hợp tia ngắm nằm ngang (V = 0) Trục quay máy Mia t t T F Trục ngắm O D d d δ f D' A B D
Hình 4.6 Đo khoảng cách bằng máy kinh vỹ - tia ngắm
Theo hình 4.7, khoảng cách D được tính: D = D’ + f + δ '
Từ hai tam giác đồng dạng CFE và C'F'E' ta có: D = n (4.6) f m
Trong đó, f: tiêu cự kính vật 36
δ: khoảng cách từ kính vật tới trục quay máy
m: khoảng cách giữa hai chỉ trên và dưới
n = t – d (hiệu số đọc trên mia).
f, δ, m được xác định từ khi chế tạo máy. Từ (4.6), ta được:
D' = f .n (4.7) m
Người ta chế tạo máy kinh vĩ sao cho thành phần f + δ = c rất nhỏ (f, δ ngược dấu) f và tỷ số
= k không đổi, thường hằng số k = 100 một số ít máy k = 200. m Thay vào (4.7): D = kn + c (4.8)
Do c rất nhỏ so với khoảng cách cần đo, có thể bỏ qua, khi đó: D = kn (4.9)
4.3.3 Trường hợp tia ngắm nghiêng (V ≠ 0)
Trường hợp tia ngắm nghiêng một t góc V. t'
Khi đó, khoảng cách nghiêng S được S d' d tính: S=kn' (4.11) Mà: n' = n.cosV (4.10) V (n’ = t’- d’, n = t – d) Và khoảng cách ngang: D D = ScosV (4.12)
Hình 4.7 Đo khoảng cách bằng máy kinh vỹ - tia ngắm nghiêng
Thay (4.10) và (4.11) vào (4.12), ta được công thức tính khoảng cách ngang D: D = kncos2V (4.13)
Đây chính là công thức tổng quát của đo khoảng cách bằng phương pháp quang học.
Đo khoảng cách theo phương pháp quang học cho kết quả nhanh nhưng độ chính
xác thấp (chỉ khoảng 1/300). 37
4.4 HỆ THỐNG ĐỊNH VỊ TOÀN CẦU GPS
4.4.1 Hệ thống định vị toàn cầu GPS
Hệ thống định vị toàn cầu GPS (Global Positioning System) được xây dựng và
quản lý bởi Bộ quốc phòng Mỹ xây dựng và quản lý. Năm 1978, vệ tinh GPS đầu tiên
được phóng lên quỹ đạo. Đến năm 1993, đã có 24 vệ tinh và đến nay có 32 vệ tinh trên bay trên 6 quỹ đạo.
Trước năm 1984, GPS chỉ được sử dụng cho mục đích quân sự của Mỹ. Từ năm
này, Mỹ chính thức cho phép sử dụng trong dân sự, nhưng vẫn còn làm nhiễu tín hiệu
nhằm làm giảm độ chính xác định vị, đến năm 2000 thì hủy bỏ việc làm nhiễu này.
GPS bao gồm 3 bộ phận:
Không gian (Space segment): gồm hệ thống các vệ tinh
Điều khiển (Control segment): gồm 5 trạm điểu khiển chính và các trạm theo dõi
khác phân bố đều trên Trái đất. Các trạm điều khiển này có nhiệm vụ duy trì hoạt động của
hệ thống, tính toán lịch vệ tinh.
Sử dụng (User segment): gồm các máy thu GPS phục vụ các mục đích khác nhau
như đạo hàng, định vị, nghiên cứu thời tiết,…
Hình 4.8 Cấu trúc và vệ tinh GPS
Ứng dụng của GPS: Với sự phát triển vượt bậc của khoa học kỹ thuật, chúng ta có
thể thấy GPS ứng dụng rộng rãi trong mọi lĩnh vực đời sống, khoa học. Với một
smartphone có tích hợp chip thu và sử lý tín hiệu GPS, chúng ta có một dụng cụ đạo hàng
đơn giản, tiện lợi. Chúng ta cũng có thể thấy GPS được dùng trong đạo hàng máy bay, tàu
thủy, xe hơi,… Trong khoa học, GPS được ứng dụng trong xây dựng lưới khống chế trắc 38
địa, lưới nghiên cứu địa động học,… với khoảng cách cạnh lưới lên đến hàng nghìn km.
GPS còn được ứng dụng để nghiên cứu dự báo thời tiết, nghiên cứu băng tan, nghiên cứu
trồi sụt của mực nước ngầm,…
4.4.2 Định vị GPS và đo khoảng cách bằng GPS
Bài toán định vị GPS thực chất là bài toán giao hội cạnh, trong đó các vệ tinh GPS
đóng vai trò các điểm gốc. Định vị GPS theo 2 nguyên lý cơ bản: định vị tuyệt đối và định vị tương đối. ρ¯ S S ¯ρ1 P P1 r¯ r¯ ΔR ¯ R¯ R¯ 1 ρ2 O O R¯ 2 P2 Định vị tuyệt đối Định vị tương đối
Hình 4.9 Nguyên lý định vị GPS
Định vị tuyệt đối cho vị trí tuyệt đối R¯ = (x, y, z) của máy thu GPS trong hệ tọa độ địa tâm: R¯ = r¯ − ρ¯ (4.14)
Trong đó khoảng cách từ máy thu tới vệ tinh ρ¯
đo được, vị trí vệ tinh trong hệ tọa độ địa tâm ρ¯ đã biết.
Thu tín hiệu từ 1 vệ tinh cho ta 1 phương trình của 3 ẩn số R¯ = (x, y, z) dạng (4.14),
do vậy cần thu đồng thời tối thiểu 3 vệ tinh để xác định vị trí tuyệt đối của điểm. Với 6 quỹ
đạo chuyển động, trung bình 4 vệ tinh trên 1 quỹ đạo, nên tại mọi điểm trên Trái đất luôn
thu được tối thiểu 4 vệ tinh đồng thời.
Độ chính xác của phương pháp này chỉ khoảng 3 – 30m, nên ít được ứng dụng cho
các mục đính yêu cầu độ chính xác cao.
Định vị tương đối là sử dụng 2 máy thu GPS, đo đồng thời tới các vệ tinh chung để
xác định vị trí tương hỗ (khoảng cách) giữa 2 máy thu này. Với mỗi vệ tinh khoảng cách giữa 2 máy thu là: 39
ΔR¯ = ρ¯1 − ρ¯2 (4.15)
Định vị tương đối không yêu cầu biết vị trí của vệ tinh, và kết quả là hiệu các trị đo
nên các nguồn sai số giống nhau của 2 trị đo bị triệt tiêu nên độ chính xác xác định khoảng
cách giữa 2 máy thu rất cao, cỡ một vài mm trên khoảng cách hàng nghìn km.
Định vị tương đối được ứng dụng trong trắc địa để đo các khoảng cách giữa các
điểm đo (xây dựng lưới khống chế đo cạnh).
4.5 ĐO KHOẢNG CÁCH ĐIỆN TỬ
Nguyên lý đo khoảng cách bằng sóng điện từ
Máy đo khoảng cách điện tử (EDM – electronic distance measurement) và bộ phận
phản xạ (reflector) được đặt tại 2 điểm cần đo khoảng cách. Sóng điện từ lan truyền từ
máy đo tới bộ phận phản xạ và phản xạ lại tới máy đo, lúc này máy đo thu sóng điện từ và
tính toán ra khoảng cách từ máy đo tới bộ phận phản xạ S = 1 vt (4.16) 2
Có 2 kỹ thuật đo khác nhau: đo
trực tiếp thời gian lan truyền của sóng
điện từ (phương pháp đo xung), đo một
đại lượng là tham số (ví dụ pha, tần số)
của sóng điện từ (phương pháp đo hiệu pha).
Hình 4.10 Nguyên lý đo khoảng cách điện tử
Các máy đo khoảng cách điện tử
Giai đoạn đầu của máy đo khoảng cách điện tử, máy đo rất cồng kềnh, khoảng
cách đo được không lớn (hình 4.11a). Nhưng đây thực sự là cuộc cách mạng của kỹ thuật đo đạc. 40 c. Máy đo khoảng
a. Máy đo khoảng cách điện tử
b. Máy toàn đạc điện tử cách cầm tay
Hình 4.11 Các thế hệ máy đo khoảng cách
Ngày nay, các máy đo khoảng cách phát triển theo xu hướng nhỏ gọn, hiện đại và
tích hợp thêm các tính năng và đo đồng thời các trị đo khác. Hình 4.11b là máy toàn đạc
điện tử (đo được khoảng cách và góc) có tích hợp bộ thu GPS, hình 4.11c là máy đo
khoảng cách laser cầm tay.
Các máy đo khoảng cách điện tử ngày nay, cho phép đo khoảng cách rất nhanh, đo
được khoảng cách lớn (cỡ chục km) với độ chính xác rất cao (cỡ mm/km). 41 CHƯƠNG 5 ĐO CAO 5.1 KHÁI NIỆM
Độ cao của một điểm là khoảng cách theo phương thẳng đứng (phương dây dọi) từ
điểm đó tới mặt quy chiếu độ cao (mặt thuỷ chuẩn gốc). A hAB H A B HB MÆt thuû chuẩn Hình 5.1 Đo cao
Hiệu độ cao của hai điểm (chênh lệch độ cao giữa hai mặt thuỷ chuẩn đi qua hai
điểm) được gọi là chênh cao giữa hai điểm: hAB = HB - HA
Đo cao là xác đinh chênh cao giữa hai điểm và từ độ cao của một điểm xác định độ cao của điểm còn lại. Các phương pháp đo cao:
- Đo cao hình học: độ chính xác có thể đạt tới 0.5mm/1km
- Đo cao thuỷ tĩnh: độ chính xác khoảng 2 ÷ 20mm
- Đo cao lượng giác: độ chính xác 2 ÷ 10cm.
Ngoài ra còn rất nhiều phương pháp đo cao khác như đo cao áp kế, đo cao GPS,
đo cao bằng ảnh hàng không, … Trong nội dung chương trình, chỉ giới thiệu hai phương
pháp đo cao cơ bản, chủ yếu sử dụng trong trắc địa, là phương pháp đo cao hình học và
phương pháp đo cao lượng giác. 42
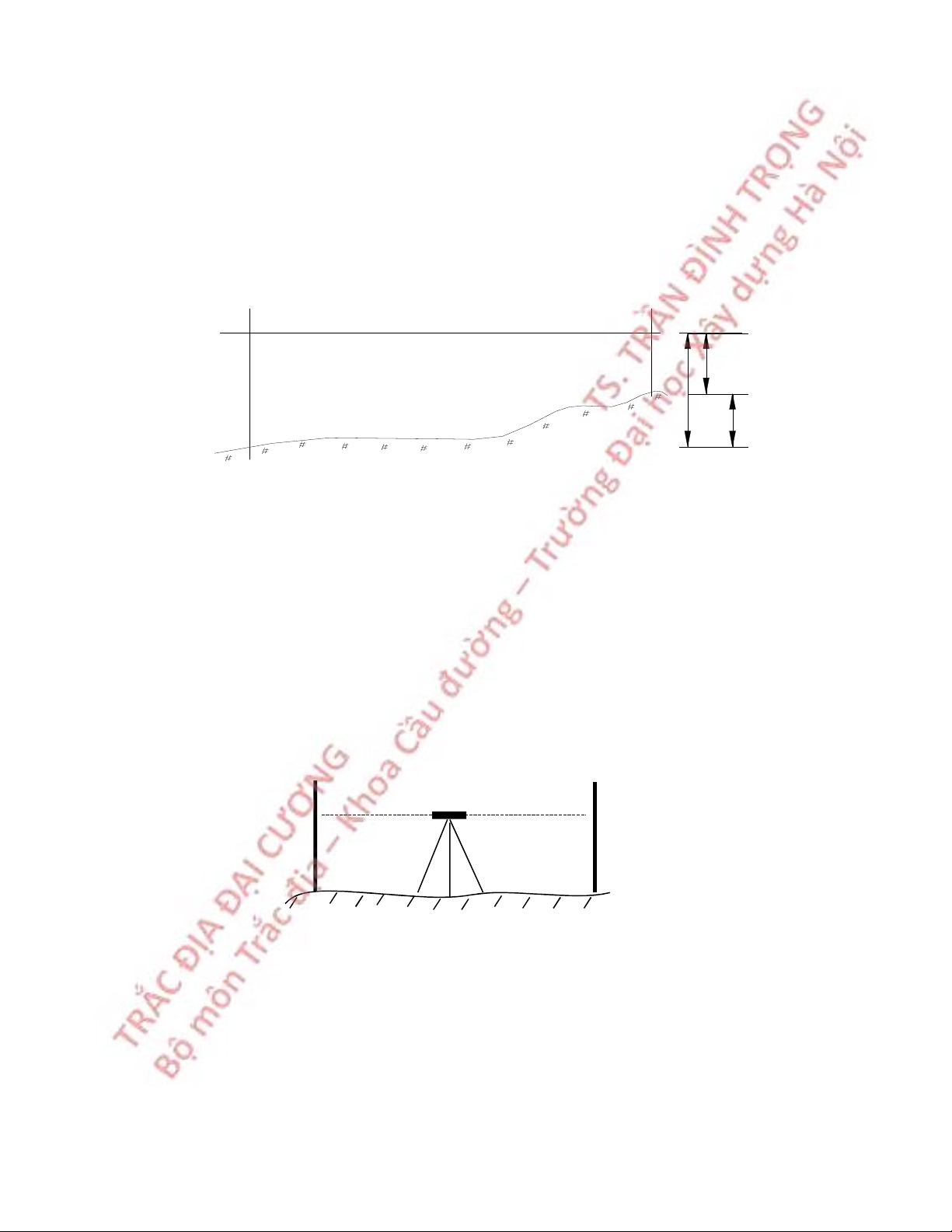
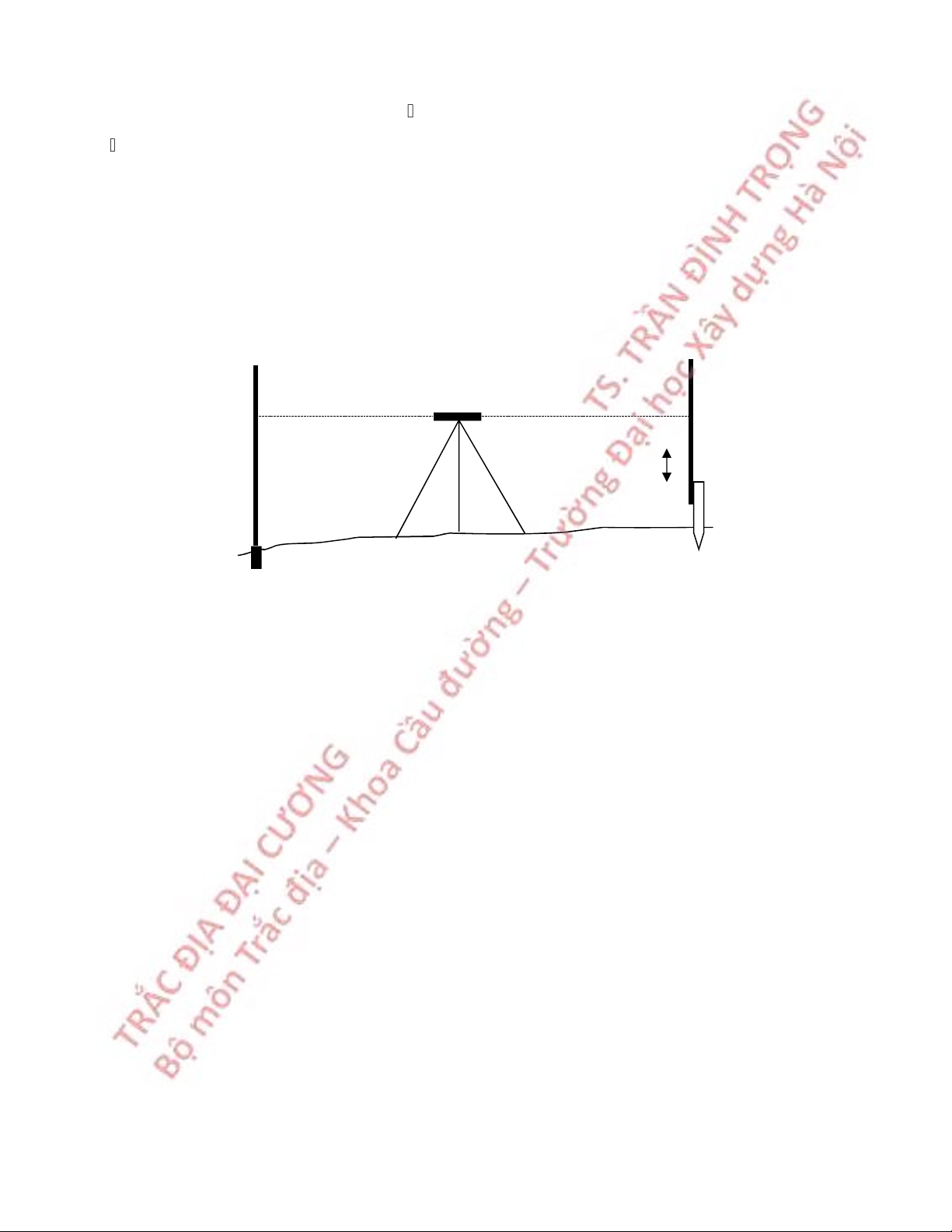
5.2 NGUYÊN LÝ ĐO CAO HÌNH HỌC
Giả sử cần xác định chênh cao giữa hai điểm A và B, tạo một mặt phẳng nằm
ngang và xác định khoảng cách thẳng đứng từ hai điểm tới một mặt phẳng này, giả sử là s
và t (hình 5.2), thì chênh cao giữa chúng là: h = s – t (5.1) MÆt ph¼ng n»m ngang s t t B s h A
Hình 5.2 Nguyên lý đo cao hình học
Dụng cụ để tạo mặt phẳng nằm ngang là máy thuỷ bình (còn gọi là máy thuỷ chuẩn
hay máy Nivo), dụng cụ đặt tại các điểm để đo khoảng cách s, t là mia.
Có các phương pháp đo cao hình học:
- Đo cao hình học phía trước: máy thuỷ bình đặt tại A hoặc tại B (phương pháp này
ít được sử dụng vì độ chính xác không cao).
- Đo cao hình học từ giữa: máy đặt giữa A và B s t A B
Hình 5.3 Đo cao hình học từ giữa
Giả sử điểm A đã biết độ cao HA, điểm B cần xác định độ cao. Mia đặt tại A, điểm
đã biết độ cao gọi là mia sau, mia đặt tại B, điểm chưa biết độ cao gọi là mia trước. Tương
ứng, đọc các số đọc mia sau (s), mia trước (t). Chênh cao giữa hai điểm AB là: hAB = s - t (5.2) 43 Độ cao điểm B: HB = HA + hAB (5.3)
Nếu hai điểm A, B cách xa nhau thì đo liên tiếp nhiều trạm đo (hình 5.4). tn s sn 2 t2 s1 … t B 1 A
Hình 5.4 Tuyến đo cao hình học n Khi đó: h = + + = Σ (5.4) AB h h ... + h h 1 2 n i i=1 n
Trong đó: hi = si – ti.. Độ cao của điểm B là:
H = H + Σ h (5.5) B A i i =1 5.3 MÁY THUỶ BÌNH
5.3.1 Máy thuỷ bình
Máy thuỷ bình là dụng cụ trắc địa
chủ yếu dùng để đo cao, ngoài ra có thể đo góc và đo khoảng cách.
Cũng tương tự như máy kinh vĩ, máy
thuỷ bình gồm ba phần chính:
Giá máy, đế máy và thân máy.
Hình 5.5 Máy thuỷ bình NA720
Máy thuỷ bình có ba trục chính: trục ống kính, trục quay máy và trục ống thuỷ. 44
Hình 5.6 Các trục chính máy thuỷ bình và mia
Theo độ chính xác, máy thuỷ bình được chia làm ba loại [6]:
+ Máy thuỷ bình chính xác cao mh = (0,5 1,0) mm/km
+ Máy thuỷ bình chính xác: mh = (1 10) mm/km
+ Máy thuỷ bình kỹ thuật: mh = (10 30) mm/km.
Theo cấu tạo, máy thuỷ bình chia làm hai loại:
+ Máy thuỷ bình có ốc kích nâng để điều chỉnh tia ngắm nằm ngang
+ Máy thuỷ bình tự động điều chỉnh tia ngắm nằm ngang
+ Máy thuỷ bình điện tử. 5.3.2 Mia đo cao
Mia là một loại thước đặc biệt được dùng trong đo cao. Mia đo cao được làm bằng
gỗ hoặc kim loại dài 3 đến 4m, cả hai mặt đều khắc vạch đến cm (hình 5.6)
Hai mặt mia khắch vạch hai màu đen, đỏ khác nhau và cách nhau một giá trị gọi là
hằng số mia, thường là 4575, 5675,…
Một số mia còn gắn bọt thuỷ tròn để dựng mia được thẳng đứng và thang khắc
vạch làm bằng hợp kim invar, được sử dụng khi yêu cầu độ chính xác cao.
5.3.3 Kiểm nghiệm các điều kiện cơ bản của máy thuỷ bình
Cũng tương tự như máy kinh vĩ, máy thuỷ bình phải thoả mãn các điều kiện hình học cơ bản:
1. Trục ống thuỷ dài vuông góc với trục quay máy 45
2. Dây ngang của dây chữ thập nằm ngang.
3. Trục ống kính song song với trục ống thuỷ dài (sai số góc i).
Hai điều kiện 1 và 2 được kiểm nghiệm tương tự như đối với máy kinh vĩ.
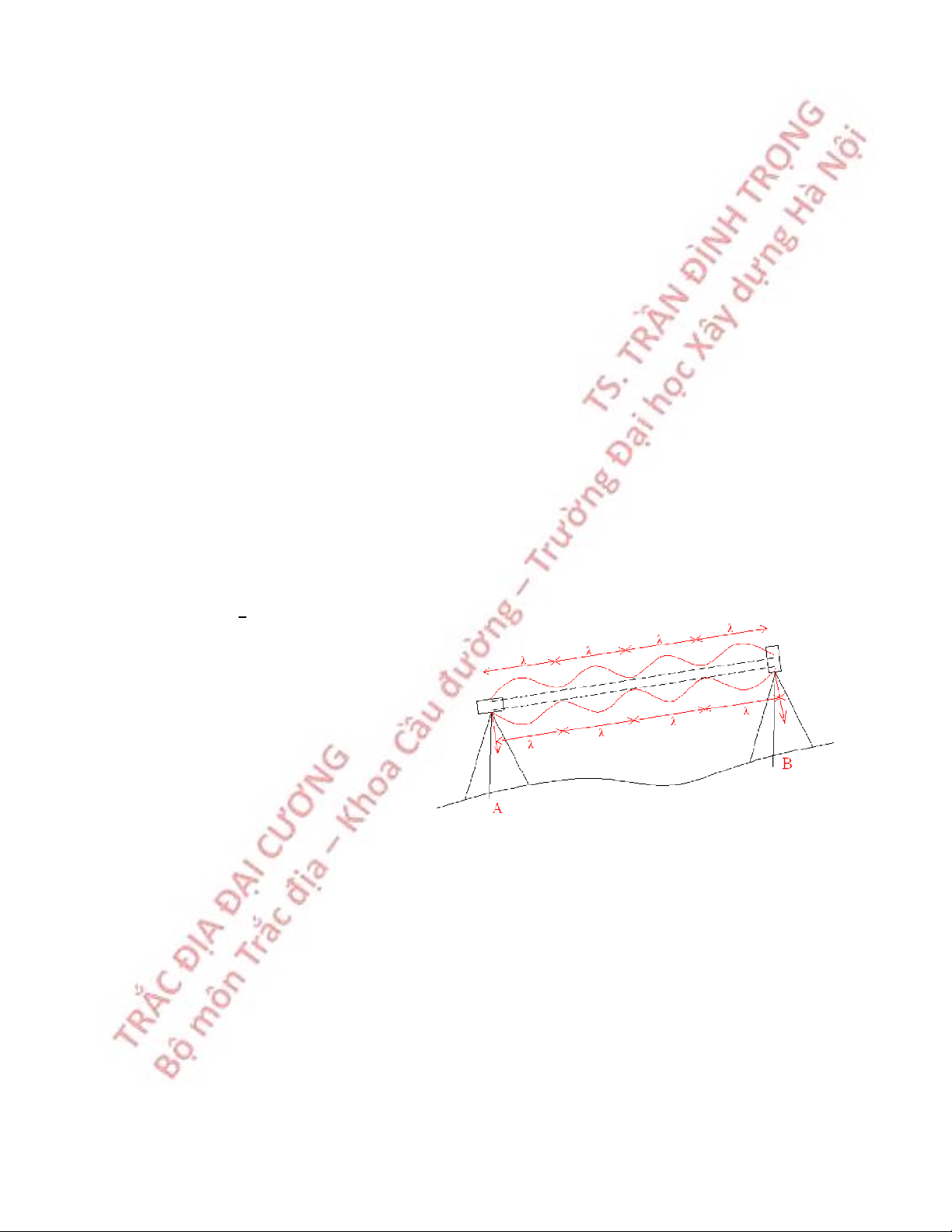
Kiểm nghiệm trục ống kính song song với trục ống thuỷ dài (hay còn gọi điều
kiện trục ống kính nằm ngang hoặc sai số góc i)
Sai số góc i: là góc hợp
bởi trục ngắm ống kính và mặt s' t' phẳng ngang (hình 5.7). s t i
Nếu máy thuỷ bình không
có sai số góc i, các số đọc tương
ứng trên mia A và B là s và t,
chênh cao không chứa sai số h s s A B được xác định: h = s - t (5.6) Hình 5.7 Sai số góc i
Nếu máy tồn tại sai số góc i, các số đọc tương ứng s’ và t’, chênh cao bị ảnh hưởng của sai số góc i là: h’ = s’ – t’ (5.7) Theo hình 5.7:
h’ = (s + s' s ) – (t + t't ) = (s + SAtgi) - (t + SBtgi) (5.8) Hay: h’ = h + (SA – SB)tgi (5.9)
Nếu SA = SB thì h’ = h, tức là máy đặt giữa hai mia thì sai số góc i bị triệt tiêu Kiểm nghiệm: -
Chọn hai điểm A và B trên khoảng đất tương đối bằng phẳng, cách nhau khoảng 40m. i 2x x x i i 3m s s S T
Hình 5.8 Kiểm nghiệm sai số góc i 46
- Đặt máy cách đều hai điểm, cân bằng chính xác. Quay máy đọc số đọc mia tại A,
được giá trị s. Quay máy đọc số đọc mia tại B, được giá trị t.
Chênh cao không chứa sai số góc i: h = s - t
- Chuyển máy cách mia sau 2 - 3m. Đo chênh cao giữa hai điểm A và B lần thứ hai tương tự như trên.
Chênh cao chứa sai số góc i: h’ = s’ – t’
Sai lệch giữa hai giá trị chênh cao h’ và h là do ảnh hưởng của sai số góc i, sai lệch
này phải nhỏ hơn một giá trị nhất định. Ví dụ khi đo cao hạng IV, hiệu (h – h’) ≤ ± 3mm.
5.4 ĐO CAO HÌNH HỌC HẠNG IV
Đo cao hình học được chia thành năm cấp hạng: hạng I, hạng II, hạng III, hạng IV
và cấp Kỹ thuật. Trong đó hai cấp hạng cuối thường được dùng trong xây dựng.
Trình tự đo và ghi sổ: Trạm máy 1:
- Dựng mia thẳng đứng ở hai điểm cần đo, đặt máy ở giữa hai điểm và cân bằng máy.
- Quay máy ngắm mia sau, đọc trên mặt đen các số đọc chỉ trên (1), giữa (2) và dưới (3).
- Quay máy ngắm mia trước, đọc trên mặt đen các số đọc chỉ trên (4), giữa (5) và dưới (6).
- Máy vẫn ngắm mia trước, mia trước quay mặt đỏ, đọc số đọc chỉ giữa (7).
- Quay máy trở lại ngắm mặt đỏ mia sau, đọc số đọc chỉ giữa (8).
(Như vậy, tại một trạm máy, trình tự đo là sau – trước – trước – sau, tương ứng là đen -
đen - đỏ - đỏ).
Kiểm tra các hạn sai đo đạc, tính toán sơ bộ kết quả đo. Nếu đạt, chuyển máy sang trạm đo tiếp theo.
Trạm máy 2: Mia trước vẫn giữ nguyên, và lúc này trở thành mia sau. Mia sau
chuyển đến điểm đo mới và trở thành mia trước. Máy chuyển đến giữa hai mia.
Trình tự đo tương tự như trạm máy 1.
Cứ tiếp tục cho đến hết tuyến đo. 47
SỔ ĐO ĐỘ CAO THUỶ CHUẨN HẠNG IV Máy: NA820 No 56971
Người đo: Trần Văn An Ngày đo: 22- 1- 2006
Người ghi: Nguyễn Phúc Thắng
Thời tiết: Nắng, gió nhẹ
Người tính: Nguyễn Phúc Thắng Hằng số mia: c1 = 4475, c2 = 4575 S Kí hiệu Số đọc mia Chênh cao Chênh cao Trạm đo/ S (m) S mia đen đỏ trung bình tuyến đo T (m) Sau Trước ểS/ÄS Hằng số (mm) hTB (mm) (S) (T) 1 2 3 4 5 6 7 74.2[1] đen trên 1636(1) 2363(4) 77.0[2] đen giữa 1265(2) 1978(5) -713[7] -712.5[10] 1/A-B 151.2/-2.8 đen dưới 0894(3) 1593(6) [3]/[4] đỏ giữa 5741(8) 6553(7) -812[8] c 4476[5] 4575[6] +99[9] 88.8 đen trên 2600 2413 86.0 đen giữa 2156 1983 +173 +174.5 1/B-C đen dưới 1712 1553 174.8/+2.8 đỏ giữa 6730 6454 +276 c 4574 4471 -103 80.8 đen trên 2675 1441 77.0 đen giữa 2271 1056 +1215 +1217.5 1/C-D đen dưới 1867 0671 158.8/+2.2 đỏ giữa 6749 5629 +1120 c 4475 4573 +95 81.4 đen trên 1934 1178 83.0 đen giữa 1527 0763 +764 +762.5 1/D-E đen dưới 1120 0348 164.4/-1.6 đỏ giữa 6099 5238 +861 c 4572 4475 -97 76.0 đen trên 1008 2448 77.0 đen giữa 0629 2062 -1433 -1432.5 1/E-A đen dưới 0248 1678 153.0/-1.0 đỏ giữa 5105 6673 -1532 c 4476 4575 +98 401.2 9853 9843 400.0 7848 7842 +6 9.5 Tổng 5841 5843 801.2/1.2 30424 30547 -87 22573 22669 92
Trình tự tính toán và kiểm tra: Khoảng ngắm: [1] = (1) – (3) [2] = (4) – (6) Tổng khoảng ngắm: [3] = [1] + [2] ≤ 200m
Chênh lệch khoảng ngắm : [4] = [1] – [2] ≤ 5m 48 Hằng số mia: [5] = (8) – (3) [6] = (7) – (6) Chênh cao mặt đen: [7] = (2) – (5) Chênh cao mặt đỏ: [8] = (8) – (7) Kiểm tra: [8] – [7] ≤ ± 5mm Hằng số của cặp mia
[9] = [6] – [5] = [7] – [8] Chênh cao trung bình [10] = [7] + [8] ± 100 2
5.5 CÁCH LOẠI TRỪ SAI SỐ TRONG ĐO CAO HÌNH HỌC
Trong đo cao hình học có rất nhiều sai số ảnh hưởng tới kết quả đo. Tuy nhiên, các
sai số này s¿ bị loại trừ hoặc làm giảm nếu chúng ta sử dụng các thao tác đo hợp lý.
Khi đo, máy đặt giữa s¿ loại trừ được sai số góc i, sai số do ảnh hưởng của độ
cong quả đất, sai số do tia ngắm bị khúc xạ.
Tiến hành đo chênh cao hai lần đi và về trong hai buổi sáng và chiều, kết quả lấy
trung bình s¿ làm giảm được sai số do nhiệt độ môi trường biến đổi, sai số do mia lún.
Đo theo trình tự sau – trước – trước – sau hay đen - đen - đỏ - đỏ s¿ làm giảm
được sai số do máy lún.
Số trạm đo trong một tuyến là chẵn s¿ loại trừ được sai số do vạch “0” của mia bị mòn. ….
Ngoài ra, trong quá trình đo, người đo và người ghi sổ nên hết sức cẩn thận và
kiểm tra lẫn nhau để tránh sai số thô, máy phải được che ô khi đo dưới trời nắng. 49
5.6 ĐO CAO LƯỢNG GIÁC
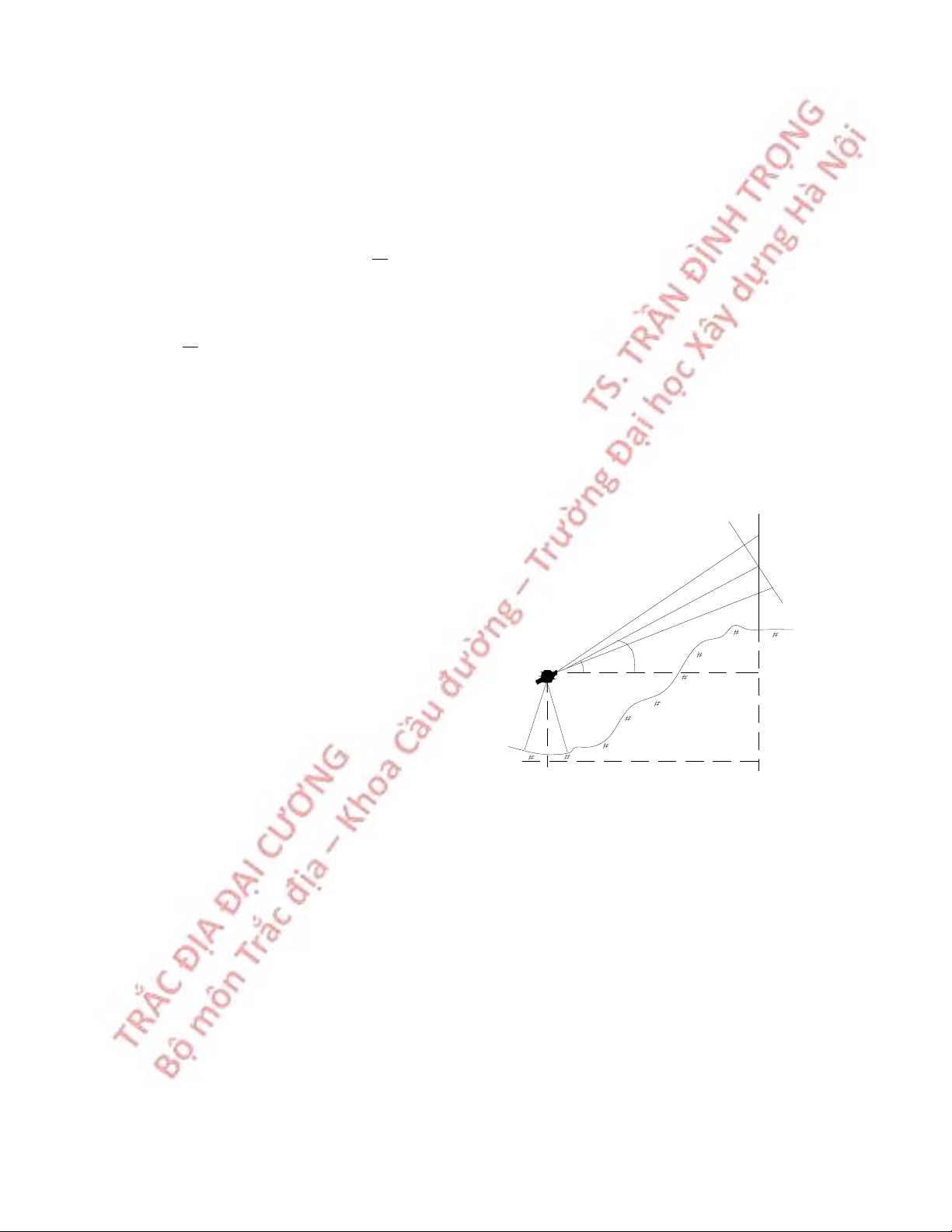
Nguyên lý của đo cao lượng giác là xác định chênh cao h dựa vào mối quan hệ
lượng giác giữa h với các đại lượng đo là góc đứng V, cạnh bằng D. Từ hình 5.9: S h = DtgV + i – r (5.10) r
Nếu khoảng cách AB được đo bằng V D
dây đo khoảng cách (phương pháp quang B học): h i D = Kn cos2V (5.11)
Hình 5.9 Đo cao lượng giác Khi đó: h = Kn cos2VtgV +i – r (5.12) Với: K = 100
n: hiệu số đọc chỉ trên và chỉ dưới
V: góc nghiêng của tia ngắm i: chiều cao máy
r: số đọc chỉ giữa (chiều cao tiêu)
Độ chính xác đo cao lượng giác phụ thuộc vào độ chính xác đo khoảng cách D và góc đứng V. 50
CHƯƠNG 6 LƯỚI KHỐNG CHẾ TRẮC ĐỊA
6.1 ĐỊNH HƯỚNG ĐƯỜNG THẲNG
Định hướng đường thẳng là xác định góc giữa đường thẳng với một hướng được chọn làm hướng gốc.
6.1.1 Góc phương vị thực A
Góc phương vị thực (A) là góc tính từ *
hướng bắc của kinh tuyến thực tới hướng của B¾c y
đường thẳng theo chiều thuận kim đồng hồ. * Góc phương vị A
thực có giá trị từ 00 đến 3600. i+1 a
Do các kinh tuyến thực không song
song với nhau mà hội tụ tại hai cực nên
phương vị thực của một đường thẳng tại các
điểm khác nhau s¿ khác nhau: i+1 A A i i+1 = Ai ± Y (6.1)
Trong đó: Y - độ hội tụ kinh tuyến. i
Hình 6.1 Góc phương vị thực
6.1.2 Góc phương vị từ At
Góc phương vị từ (At) là góc tính từ δ hướ B¾c
ng bắc của kinh tuyến từ (hướng kim
nam châm) tới hướng của đường thẳng A
theo chiều thuận kim đồng hồ. Góc phương i+1
vị từ có giá trị từ 00 đến 3600. a
Kinh tuyến từ các điểm khác nhau
s¿ không song song với nhau. Do đó
phương vị từ tại các điểm khác nhau trên i+1
cùng đường thẳng cũng khác nhau: A i Ati+1 = Ati ± δ (6.2)
Trong đó: δ - độ lệch từ. i
Hình 6.2 Góc phương vị từ
6.1.3 Góc định hướng α
Góc định hướng (α) là góc tính từ hướng bắc của kinh tuyến trục (trục OX) tới
hướng của đường thẳng theo chiều thuận kim đồng hồ. Góc định hướng có giá trị từ 00 đến 3600. 51
Trên cùng một đường thẳng, góc
định hướng không đổi tại các điểm khác Ox
nhau. Do đó trong trắc địa góc định hướng α BA
α được sử dụng chủ yếu. a
Góc định hướng thuận αAB và góc α AB B
định hướng nghịch αBA lệch nhau 1800: αAB = αBA ± 1800 (6.3) A
Hình 6.3 Góc định hướng
6.1.4 Quan hệ giữa góc định hướng và góc bằng
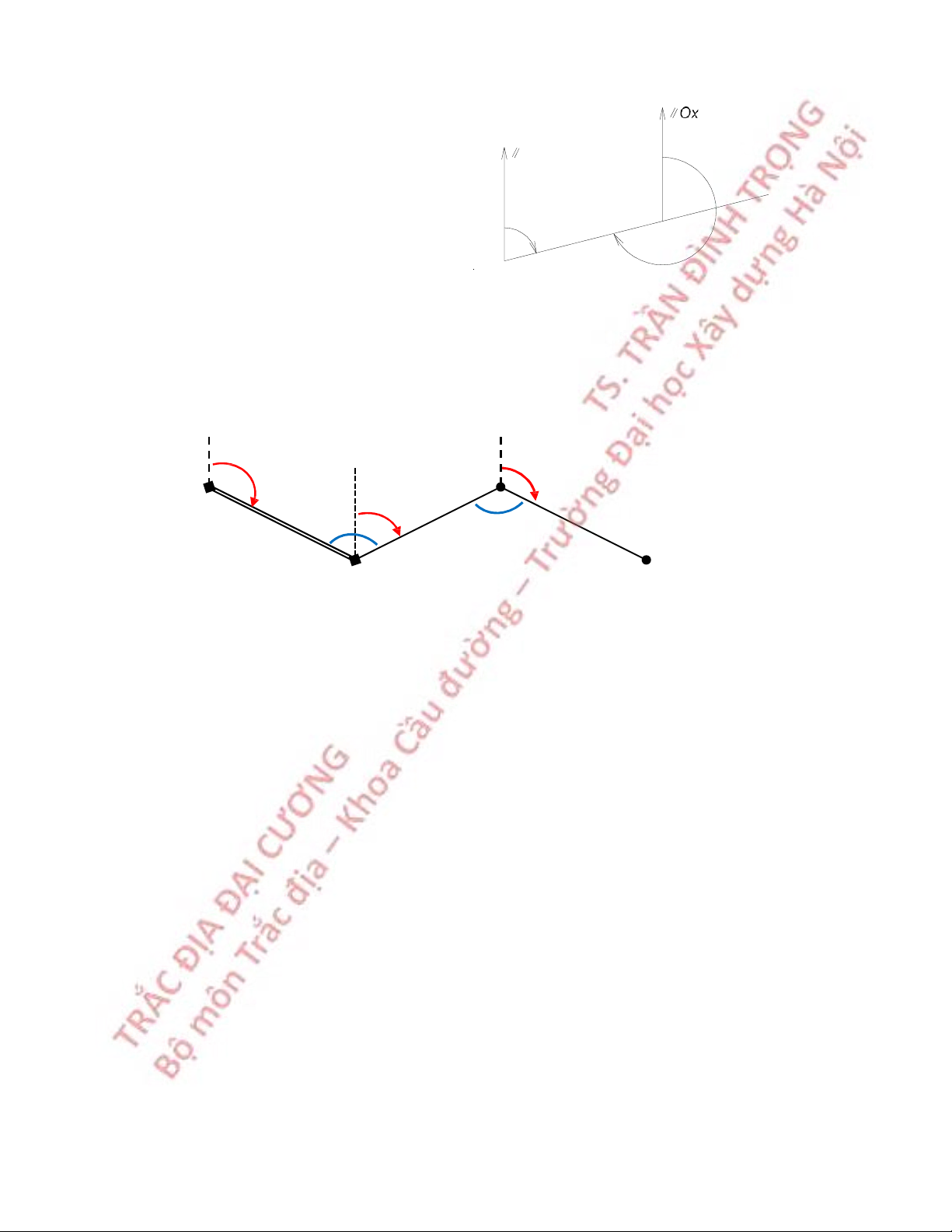
Ký hiệu βi là các góc bằng giữa các đoạn thẳng. Quan hệ giữa góc
định hướng của các đoạn thẳng và các góc bằng như hình 6.4.S α α AB 1 12 α A β1 B1 β2 B 2
Hình 6.4 Góc bằng và góc định hướng
Nếu góc bằng ở bên trái đường tính: αB1 = αAB + β1 ± 1800 (6.4) α12 = αB1 + β2 ± 1800 (6.5)
Nếu góc bằng ở bên phải đường tính: αB1 = αAB - β1 ± 1800 (6.6) α12 = αB1 - β2 ± 1800 (6.7) 52
6.2 HAI BÀI TOÁN TRẮC ĐỊA CƠ BẢN
6.2.1 Bài toán trắc địa thuận
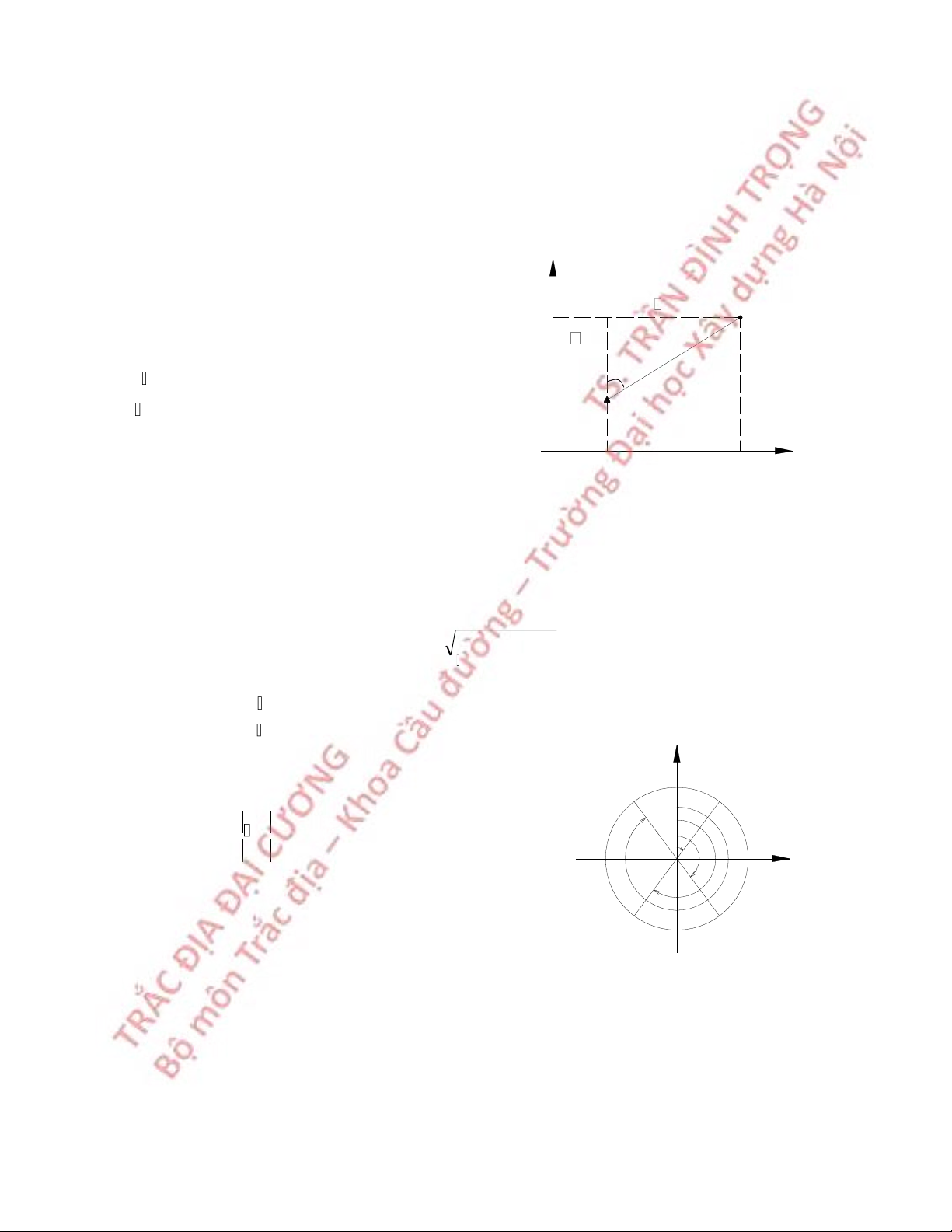
Biết tọa độ điểm A (XA , YA), góc định hướng αAB và đo khoảng cách bằng DAB. Tính
tọa độ của điểm B (XB , YB). Theo hình v¿: X XB = XA + X A B (6.8) Y AB X B Y B B = YA + Y A B X trong đó: AB α AB D X AB AB = DAB cosαAB (6.10) X A YAB = DAB sinαAB A
Thay (6.10), (6.11) vào (6.8), (6.9): XB = XA + DAB cosαAB (6.12) O Y Y A B Y YB = YA + DAB sinαAB (6.13)
Hình 6.5 Bài toán trắc địa cơ bản
6.2.2 Bài toán trắc địa ngược
Biết hai điểm A (XA, YA) và (XB, YB) , tính khoảng cách bằng DAB và góc định hướng αAB. Ta có: D = 2 + Y (6.14) AB 2 X AB AB Trong đó: XAB = XB - XA YAB = YB - YA Để
tính góc định hướng, chúng ta X
phải tính lần lượt như sau: α = 360 o- r IV I Tính góc hai phương: -/+ +/+ α = r Y r = arctg (6.15) X Y
Tính góc định hướng theo dấu của
các gia số toạ độ (hình 6.6) -/- +/- α = 180 o- r α = 180 o+ r III II
Hình 6.6 Tính góc định hướng 53
6.3 KHÁI NIỆM LƯỚI KHỐNG CHẾ MẶT BẰNG 6.3.1 Khái niệm
Lưới khống chế trắc địa mặt bằng là hệ thống các điểm mốc cố định ngoài thực địa,
có toạ độ mặt bằng chính xác trong một hệ thống nhất. Các điểm này được liên kết với
nhau bởi các trị đo góc, khoảng cách hoặc cả hai.
Lưới khống chế được xây dựng theo nguyên tắc từ tổng thể tới chi tiết, từ độ chính
xác cao tới độ chính xác thấp.
Lưới khống chế trắc địa Nhà nước được chia làm bốn hạng với quy mô và độ chính
xác giảm dần và cấp hạng nhỏ là lưới chêm dày cho lưới cấp lớn hơn.
Bảng 6.1 Các chỉ tiêu kỹ thuật của lưới tam giác Nhà nước [8] Chỉ tiêu kỹ thuật Hạng I Hạng II Hạng III Hạng IV
Chiều dài cạnh tam giác (km) 20 30 7 20 5 10 2 6 1 1 1 1
Sai số tương đối đo cạnh đáy 400000 300000 200000 200000
Sai số trung phương đo góc ±0' 7 ±1' 00 ±1' 5 ±2' 5
Góc nhỏ nhất trong tam giác 40O 30O 30O 25O
Mạng lưới Nhà nước tiếp tục được chêm dày bằng các cấp lưới: lưới giải tích cấp
1, cấp 2 hoặc lưới đường chuyền cấp 1, cấp 2 và lưới khống chế đo v¿ nhằm đảm bảo
mật độ điểm khống chế cho các yêu cầu công việc.
Bảng 6.2 Các chỉ tiêu ký thuật của lưới đường chuyền cấp 1, cấp 2 [8] Yêu cầu kỹ thuật Cấp I Cấp II
Chiều dài đường chuyền (km) - Đường đơn 5 3 -
Giữa điểm khởi tính và điểm nút 3 2 - Giữa các điểm nút 2 1,5
Chu vi vòng khép lớn nhất (km) 15 9 Chiều dài cạnh (m) 120 - 800 80 - 350 Góc nhỏ nhất 25o 25o
Số cạnh nhiều nhất trong đường chuyền 15 15
Sai số trung phương đo góc ± 5" ± 10"
Sai số khép góc của đường chuyền ±10" n ±20" n 54
6.3.2 Các phương pháp xây dựng lưới
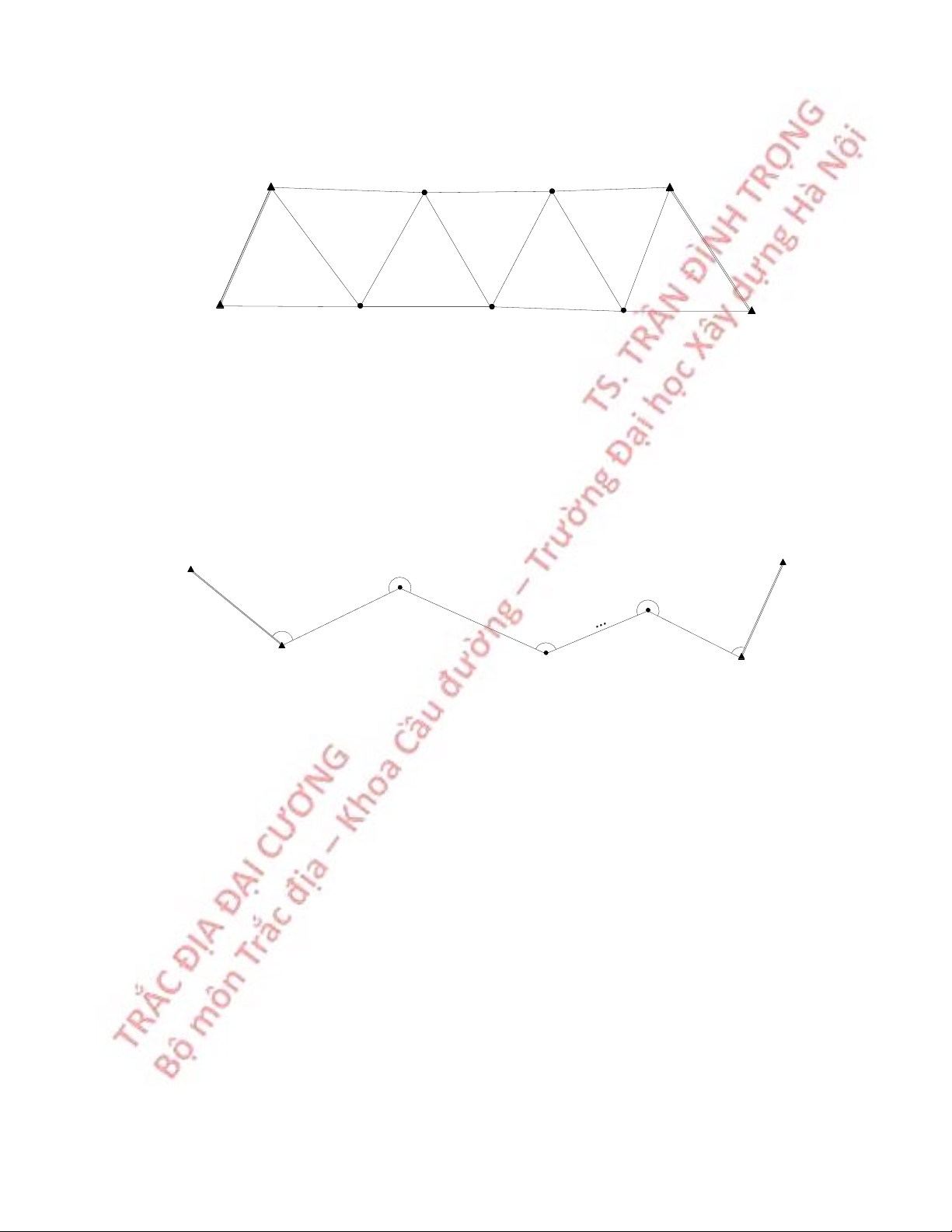
1. Phương pháp tam giác Hình 6.7 Lưới tam giác
Trong đó tất cả các góc hoặc tất cả các cạnh hoặc tất cả góc và cạnh được đo. Các
góc được đo bằng máy kinh vĩ, các cạnh được đo bằng thước thép (hiện nay ít được
dùng), máy đo khoảng cách điện tử (toàn đạc điện tử hiện dùng rất phổ biến để đo góc và
cạnh lưới) hoặc đo bằng định vị GPS tương đối.
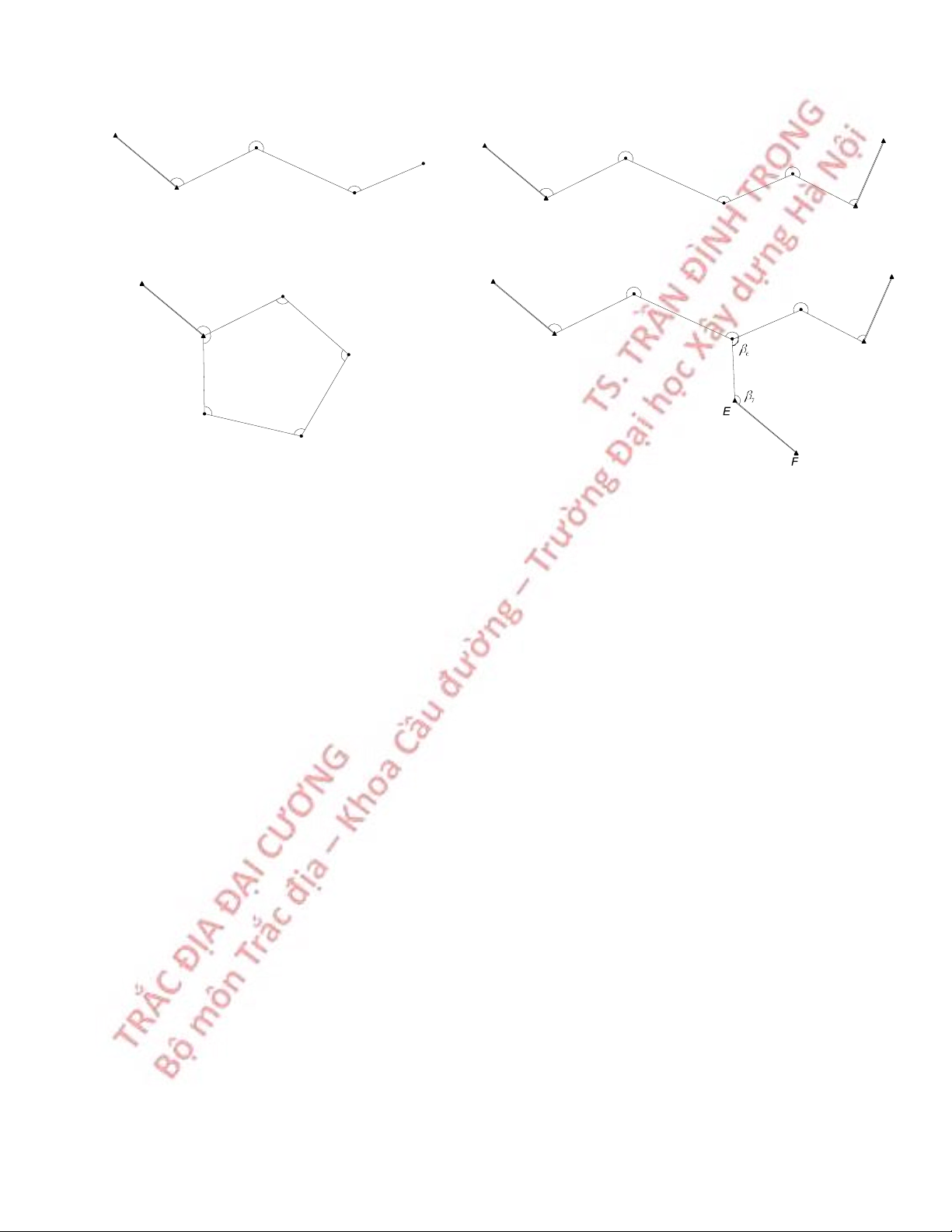
2. Phương pháp đường chuyền β A 2 D β n+1 D 1 1 §2 β 1 β n Dn+1 β 3 n+2 B 2 C
Hình 6.8 Lưới đường chuyền
Trong đó tất cả các góc và tất cả các cạnh. Đường chuyền có các dạng đường
chuyền phù hợp, đường chuyền treo, đường chuyền khép kín, đường chuyền điểm nút.
6.3.3 Các bước xây dựng lưới
Thông thường, các bước xây dựng lưới khống chế trắc địa được thực hiện qua các bước:
- Thiết kế kỹ thuật (ước tính độ chính xác lưới, độ chính xác đo đạc lưới), kinh tế - Chôn mốc - Đo đạc lưới
- Tính toán, bình sai lưới khống chế. 55
6.3.4. Khái niệm về bình sai lưới
Bình sai lưới, công việc bắt buộc và quan trọng của Trắc địa, là phân phối sai số
theo luật phân phối chuẩn dựa vào nguyên lý số bình phương nhỏ nhất (6.16) và tính toán
xác định tọa độ các điểm lưới. [pvv] = min (6.16)
Công tác bình sai lưới được thực hiện khi lưới có trị đo thừa, ví dụ: chỉ cần đo 2 góc
trong một tam giác là đủ (góc còn lại tính từ 2 góc đo), nếu đo cả 3 góc thì có 1 trị đo thừa
mới có thể bình sai được.
Có thể tiến hành bình sai chặt ch¿ (phương pháp bình sai điều kiện, bình sai gián
tiếp,…) hoặc bình sai gần đúng. Phương pháp bình sai gần đúng được sử dụng nếu yêu
cầu độ chính xác không cao (ví dụ lưới đo v¿ bản đồ tỷ lệ nhỏ, lưới khống chế nối các đỉnh
ngoặt khi thi công đường,…)
Trong các tài liệu học tập dành cho chuyên ngành trắc địa như [3], bình sai lưới
được giới thiệu rất kỹ. Giáo trình này, s¿ giới thiệu phương pháp bình sai gần đúng cho một vài dạng lưới.
6.4 LƯỚI ĐƯỜNG CHUYỀN 6.4.1 Khái niệm
Là hệ thống các điểm khống chế mặt bằng tạo thành chuỗi đường chuyền và các
điểm này được liên kết với nhau bởi các trị đo góc và cạnh.
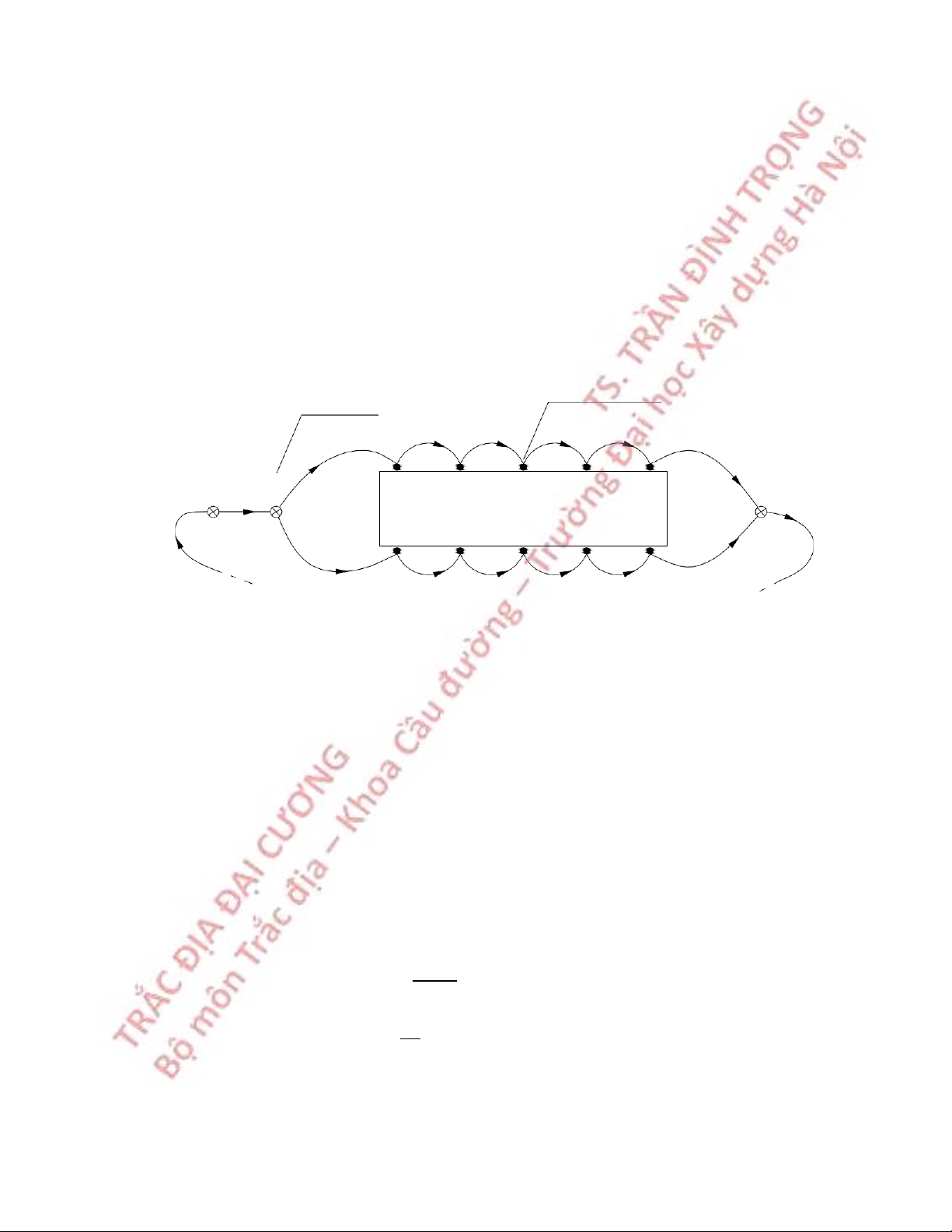
Các dạng đường chuyền: 56 β 2 β A 2 D D 1 β 1 § 4 2 β D 1 1 β 3 3 D D 1 2 β 3 1 D3 3 D4 β 3 β B 5 2 B 2 C §-êng chuyền treo
§-êng chuyền phù hîp β A 1 A 2 β 4 D D 1 D 1 β 1 2 β β 2 D 1 D 1 2 3 3 D4 β 3 β 5 B β B 6 2 C β3 2 D5 D5 D3 β 5 4 β 4 D4 3
§-êng chuyền có ®iểm nót
§-êng chuyền khÐp kÝn
Hình 6.9 Các dạng lưới đường chuyển
Khi xây dựng đường chuyền, chú ý mật độ điểm phải đảm bảo yêu cầu công việc,
chiều dài cạnh, độ lớn góc và sai số đo đạc phải theo đúng các yêu cầu của cấp hạng (bảng 6.2).
6.4.2 Tính toán bình sai gần đúng đường chuyền phù hợp
Giả sử tính toán bình sai gần đúng đường chuyền phù hợp gồm n điểm mới, đo
(n+2) góc và (n+1) cạnh. Trình tự như sau:
1. Bình sai sai số khép góc:
Tổng các góc đo của đường chuyền: [β] = β1 + β2 + … + βn+2 (6.16)
Theo lý thuyết, góc định hướng được tính như sau: αB1 = αAB + β '1 - 1800 α12 = αB1 + β '2 - 1800 … αCD = αnC + β ' n+2 - 1800
Thay các góc định hướng vào:
αCD = αAB + [β'] – (n+2)1800 (6.17) Hay tổng góc lý thuyết:
[β'] = αCD - αAB+ (n+2)1800 (6.18) 57
Sai lệch tổng góc lý thuyết và tổng góc đo, gọi là sai số khép góc (hay sai số khép góc định hướng):
fβ = [β] - [β'] = [β] + αAB - αCD - (n+2)1800 (6.19)
Sai số khép góc này phải nhỏ hơn sai số khép góc cho phép fβcp (cụ thể, đường
chuyền cấp 2 fβcp = ±20" n + 2 , đường chuyền kinh vĩ fβcp = ±60" n + 2 ), nếu không phải đo đạc lại. f β
Tính số hiệu chỉnh góc vβ i: v = – βi (6.20) n Góc sau bình sai: β 'i = βi + vβi (6.21)
2. Tính góc định hướng:
Góc bằng nằm phía trái đườg tính: α '
i,i+1 = α i-1,i + βi – 1800 (6.22)
3. Tính các gia số toạ độ:
X i , i + 1 = Di,i+1.cosαi,i+1 (6.23)
Y i , i + 1 = Di,i+1.sinαi,i+1 (6.24)
4. Bình sai sai số khép toạ độ:
Theo lý thuyết, tổng các gia số toạ độ: [ ’X] = XC - XB (6.26) [ ’Y] = YC - YB (6.27)
Trong khi đó, tổng các gia số toạ độ tính: [ X] = XB1 + X12 + … + XnC (6.28) [ Y] = YB1 + Y12 + … + YnC (6.29)
Sai số khép toạ độ là sai lệch giữa chúng:
fx = [ X] - [ ’X] = [ X] – (XC - XB) (6.30)
fy = [ Y] - [ ’Y] = [ Y] – (YC - YB) (6.31)
Kiểm tra sai số khép toàn phần tương đối: cp f fx2 + fy 2 ( 1 S = ÷ ÷ (6.32) [D] [D] ø T ø
Sai số cho phép đối với đường chuyền kinh vĩ là 1/2000. 58
Tính số hiệu chỉnh gia số tọa độ: v = – fx .D (6.33) Xi,i+1 i,i+1 [D] v = – fy .D (6.34) Y i , i +1 [D] i,i +1
Gia số tọa độ sau bình sai: 'Xi,i+1 = Xi,i+1 + v xi,i+1 (6.35) 'Yi,i+1 = Yi,i+1 + v yi,i+1 (6.36)
5. Tính tọa độ các điểm sau bình sai: Xi+1 = Xi + 'Xi,i+1 (6.37) Yi+1 = Yi + 'Yi,i+1 (6.38)
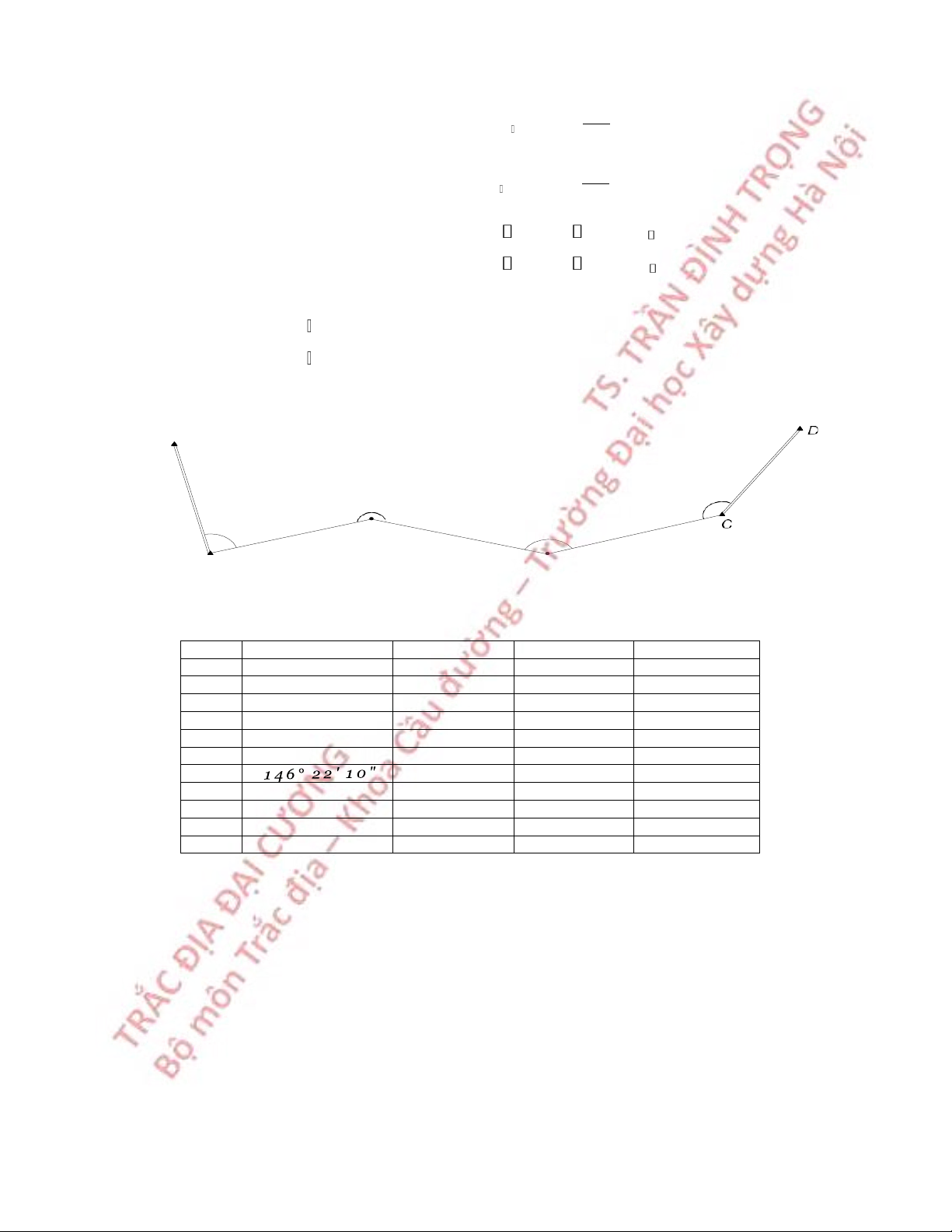
Ví dụ: Bình sai gần đúng đường chuyền kinh vĩ : A β 4 β 2 β 1 1 β 3 D D 3 1 D 2 Hình 6.10 Sơ đồ lưới
S ố liÖ u ® o v à s ố liÖ u g ố c : § iể m β D ( m ) X ( m ) Y ( m ) i i i i A 1 3 8 5 . 5 2 1 1 1 5 6 . 4 2 3 B 8 5 ° 4 6 ' 3 0 " 1 0 0 0 . 3 4 2 1 2 4 2 . 1 0 2 1 0 3 . 3 6 0 1 2 1 2 ° 3 0 ' 4 0 " 1 1 2 . 4 9 9 2 1 1 3 . 6 9 1 C 1 4 0 ° 1 6 ' 3 0 " 1 0 3 4 . 5 0 0 1 5 5 7 . 5 6 2 D 1 2 0 3 . 7 4 4 1 6 6 4 . 8 7 7 59
Các bước tính toán bình sai được thực hiện trong bảng: Góc đo Góc định hướng Cạnh đo Gia số toạ độ Toạ độ sau bình sai Điểm β α i i,i+1 D ΔX i,i+1 (m) (m) ΔY (m) X (m) Y (m) A 1385.521 1156.423 -11” 1670 27’ 34” B 850 46’ 30” -25 + 7 1000.342 1242.102 -11” 730 13’ 53” 103.360 29.820 98.965 1 2120 30’ 40’ -27 + 8 1030.137 1341.074 -11” 1050 44’ 22” 112.499 -30.517 108.281 2 1460 22’ 10’ -27 + 8 999.593 1449.363 -10” 720 06’ 21” 113.691 34.933 108.191 C 1400 16’ 30” 1034.500 1557.562 320 22’ 41” D 1203.744 1664.877 Tổng 5840 55’ 50” 329.550 34.327 315.437 f X = 0.079 m fβ = 43” f 1 D = 0.082 = f f βcp = 60 n + 2 = 120” Y = -0.023 m, [D] 329.550 4000
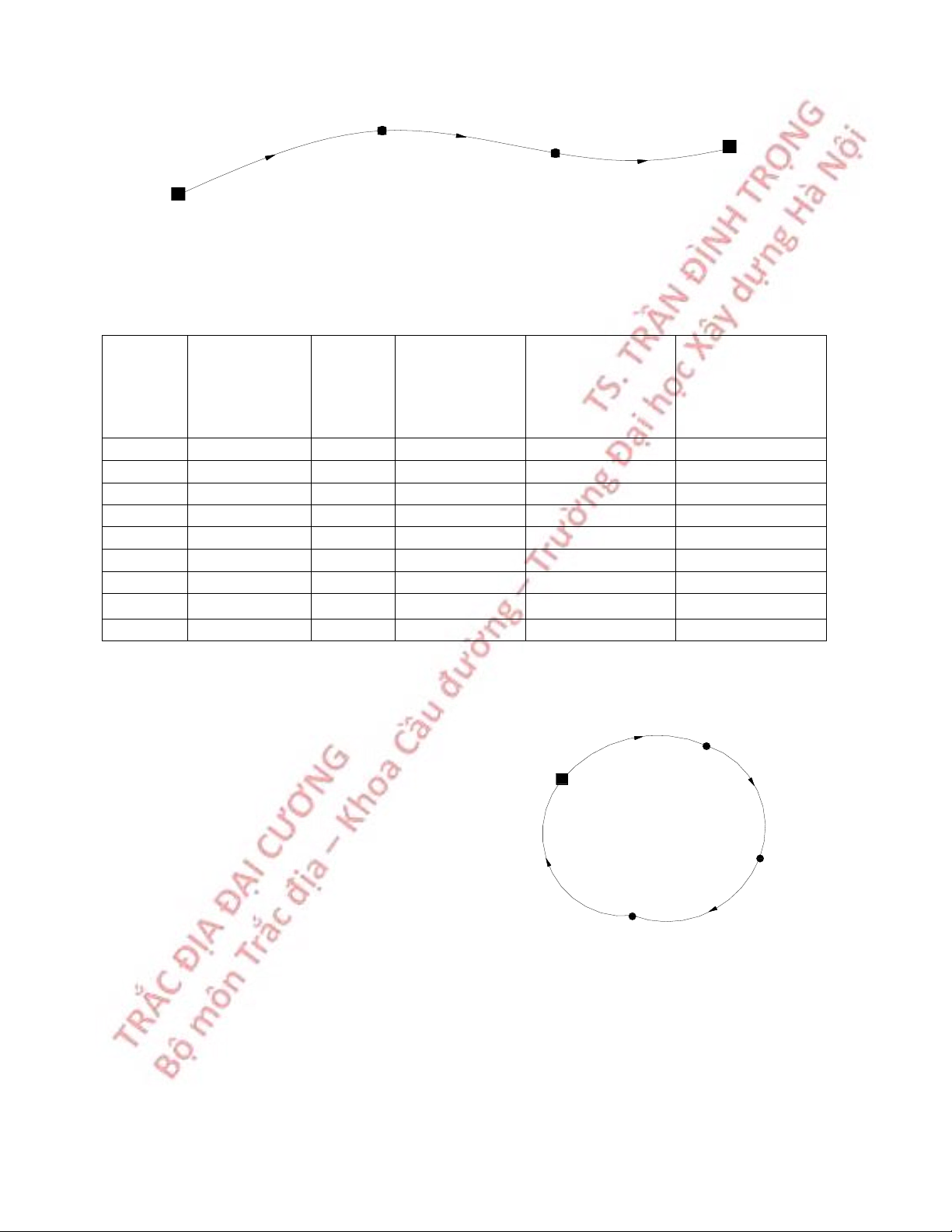
6.4.3 Tính toán bình sai gần đúng đường chuyền khép kín
Xét lưới đường chuyền khép kín n điểm mới, đo (n + 2) góc và (n+1) cạnh.
Khi tính toán bình sai gần đúng, lưu ý, chỉ có các góc trong của đường chuyền,
(n+1) góc, là tham gia bình sai góc, còn một góc ngoài chỉ tham gia tính chuyền phương vị.
Tuần tự tính toán bình sai như đối với đường chuyền phù hợp, chỉ khác các giá trị lý thuyết: [β'] = (n-1)1800 (6.39) Và: [ ’ X ] = 0 (6.40) [ ’ Y ] = 0 (6.41) 60
6.5 MỘT SỐ PHƯƠNG PHÁP XÂY DỰNG LƯỚI MẶT BẰNG KHÁC THƯỜNG DÙNG
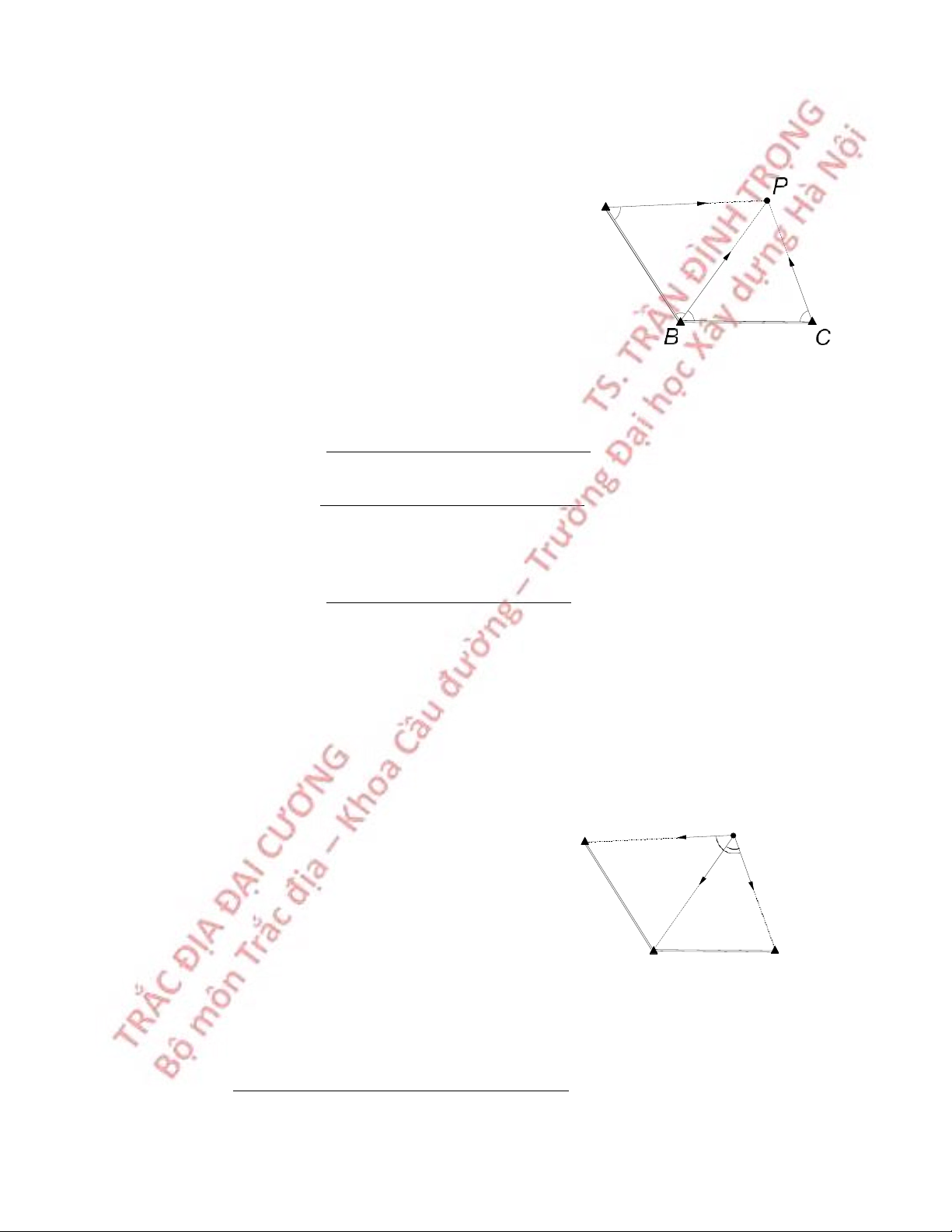
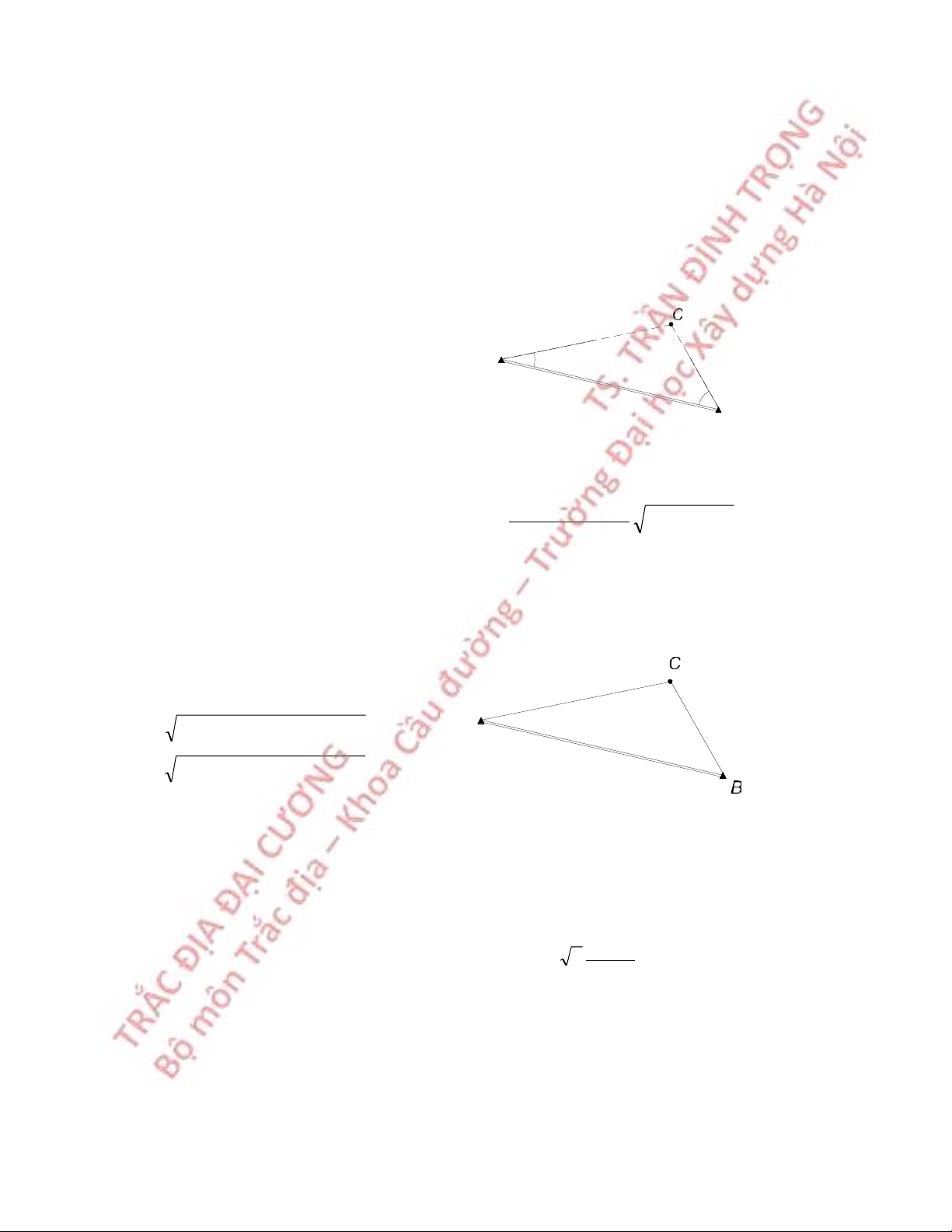
6.5.1 Giao hội góc thuận
Từ hai điểm khống chế đã biết toạ độ A
A, B tiến hành đo góc giao hội β β A, βB tới A
điểm cần xác định toạ độ P (hình 6.11 ). β B β ' β B C
Hình 6.11 Giao hộ góc thuận
Toạ độ điểm P được tính theo công thức (Công thức Iung):
– Y + X cot gβ B + X cot gβ A X = YB A A B P
cot gβ + cot gβ B A (6.42)
– X + Y cot gβ B + Y cot gβ A Y = X A B A B P
cot gβ + cot gβ B A
Hoặc theo công thức Gauss:
tgα AP – X tgα BP + (Y – Y ) X = X A B B A P tgα – tgα (6.43) AP BP
Y = Y + ( X – X )tgα P A B A AP
Để tăng độ chính xác, toạ độ điểm P thường được xác định từ ba điểm đã biết toạ
độ, tạo thành hai tam giác giao hội góc, toạ độ điểm P được tính từ hai tam giác và lấy trung bình.
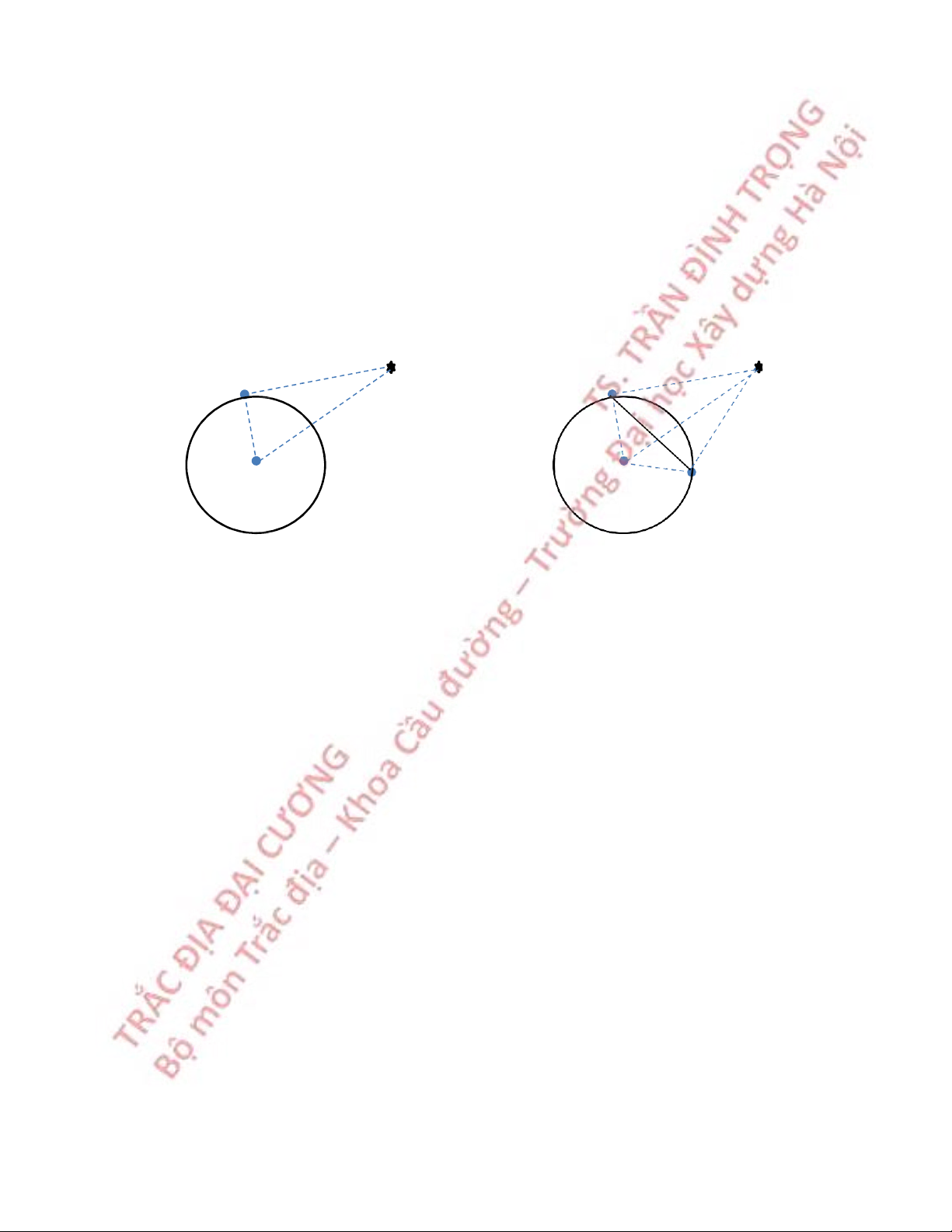
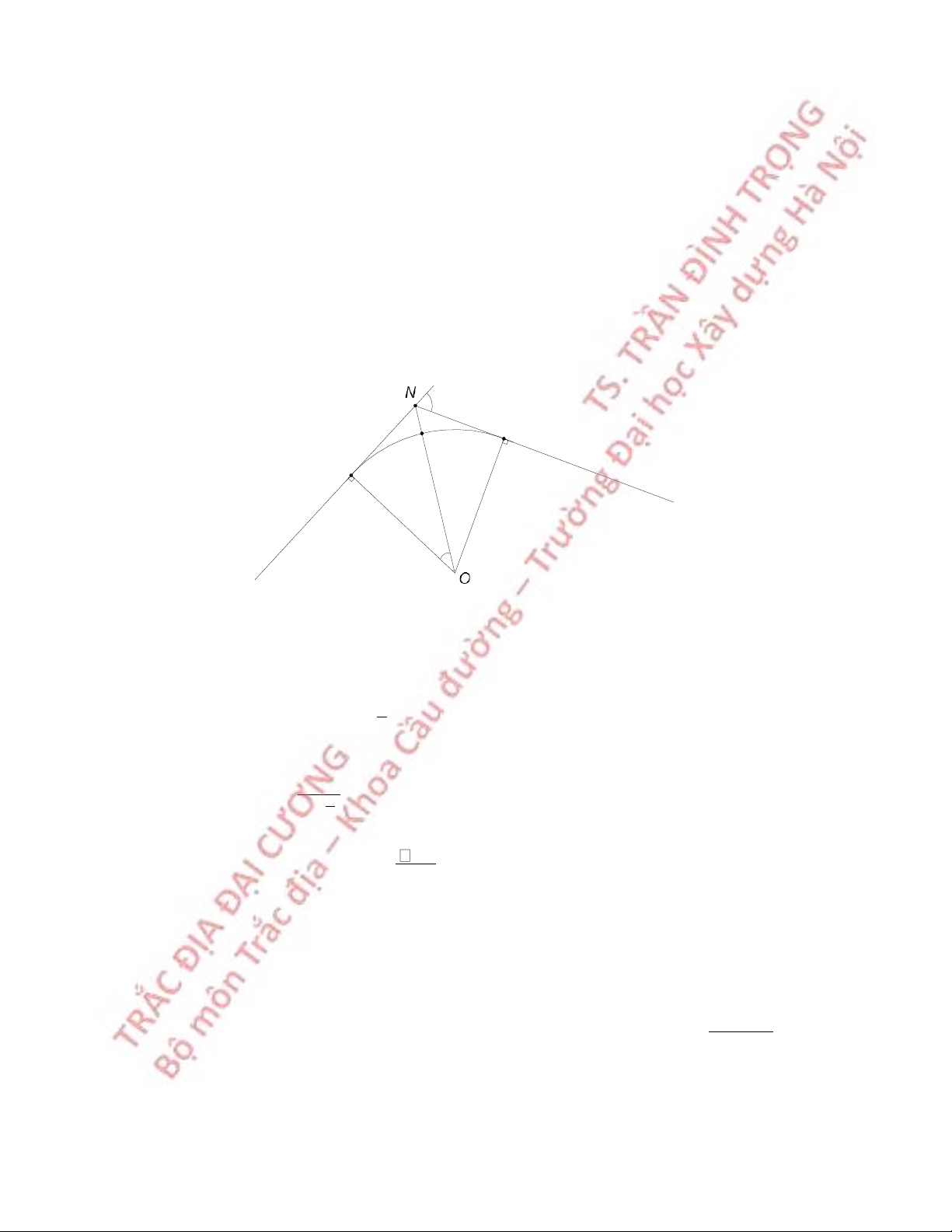
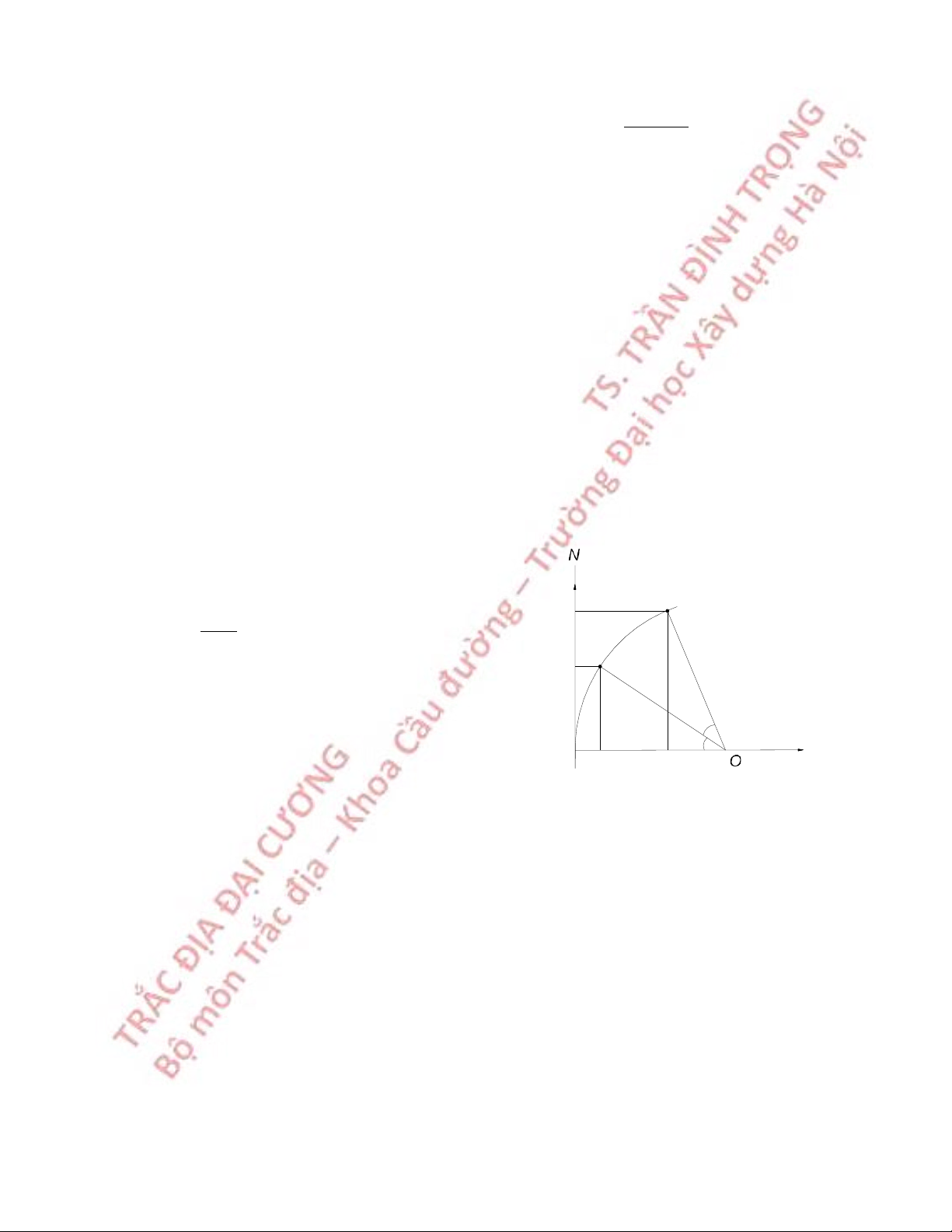
6.5.2 Giao hội góc nghịch
Cần xác định toạ độ điểm P, tại P đo các P
góc β1, β2 tới ba điểm A, B, C đã biết toạ độ C β 2 β (Hình 6.12). 1 Ta có quan hệ: yA - yP = (xA - xP)tgαPA B A
yB - yP = (xB - xP)tg(αPA+β1) y
Hình 6.12 Giao hội góc nghịch
C - yP = (xC - xP)tg(αPA+β2) Biến đổi, ta được: tgα – – – = ( y y )ctgβ y )ctgβ x ) B A 1 – ( yC A 2 + (xC B (6.44) PA (x – x ) B
A )ctgβ1 – (xC – xA )ctgβ2 – ( yC – yB 61
Từ đó xác định các góc định hướng:
α = α + β ± 1800 BP PA 1
α = α + β ± 1800 CP PA 2
Tọa độ điểm P tính theo công thức Gauss (6.43).
Trường hợp điểm P nằm trên vòng tròn ngoại tiếp tam giác ABC thì s¿ có vô số
điểm P thoả mãn các công thức trên, điểm P s¿ là bất định và vòng tròn ngoại tiếp tam
giác ABC được gọi là vòng tròn nguy hiểm.Trường hợp này không được áp dụng phương
pháp giao hội góc nghịch.
6.5.3 Giao hội cạnh
Từ hai điểm A, B đã biết toạ độ, đo P
các khoảng cách tới điểm P: DAP DBP (hình 6.13). D
Góc tại điểm A được xác định theo 1 D1 định lý hàm số cosin: A
= D 2 + D 2 – D 2 B cos A 1 1 AB 2D D 1 1 α = α – Hình 6.13 Giao hội cạnh AP BA A ± 1800
Toạ độ điểm P được xác định từ toạ độ điểm A, góc định hướng và chiều dài cạnh
AP xác định theo bài toán trắc địa thuận.
Để tăng độ chính xác, toạ độ điểm P thường được xác định từ ba điểm đã biết toạ
độ, tạo thành hai tam giác giao hội cạnh, lúc này toạ độ điểm P được tính hai lần và lấy trung bình.
6.6 KHÁI NIỆM LƯỚI KHỐNG CHẾ ĐỘ CAO
Lưới khống chế độ cao là hệ thống các điểm mốc cố định ngoài thực địa, có độ cao
chính xác trong một hệ độ cao thống nhất. Các điểm này được liên kết với nhau bằng các lưới độ cao.
Các nguyên tắc, các bước xây dựng lưới tương tự như đối với lưới khống chế mặt bằng.
Các dạng lưới lưới độ cao cũng có các dạng như lưới đường chuyền trắc địa. 62
Lưới khống chế độ cao được phân thành 5 cấp hạng: hạng I, II, III, IV và cấp kỹ thuật.
Bảng 6.3 Các chỉ tiêu kỹ thuật của các cấp hạng lưới độ cao Cấp hạng Các chỉ tiêu kỹ thuật I II III IV Kỹ thuật
Khoảng ngắm lớn nhất (m) 50 65 75 100 150
Chênh lệch khoảng ngắm (m) 0.5 1.0 2.0 5.0 - Sai số khép độ cao (mm) 3 L 5 L 10 L 20 L 50 L
Sai số trung phương của 1 trạm 0.15 0.30 0.65 3.0 8.0 đo (mm)
6.7 BÌNH SAI GẦN ĐÚNG LƯỚI ĐỘ CAO
6.7.1 Lưới độ cao nối hai điểm gốc
Giả sử có lưới độ cao nối giữa hai điểm gốc A (HA) và B (HB) gồm n điểm cần xác
định độ cao (hình 6.14). Đo (n+1) chênh cao hi với số trạm đo tương ứng ni. 1 n h h n+1 1 2 h ... B 1 n n A 2 n+1 n 1
Hình 6.14 Lưới độ cao nối 2 điểm gốc
Các bước bình sai gần đúng:
-Tính sai số khép độ cao fh: fh = [h] – (HB - HA) (6.45)
(Chú ý: kiểm tra sai số khép so với sai số khép cho phép của cấp hạng lưới) - Tính số hiệu chỉnh: v = – f h n (6.46) hi [n] i Kiểm tra [v] = - fh. - Hiệu chỉnh chênh cao: h (6.47) i' = hi + vhi
- Tính độ cao của các điểm sau bình sai: Hi = Hi-1 + hi' (6.48)
Ví dụ: Bình sai gần đúng lưới độ cao nối hai gốc có sơ đồ và các trị đo như hình 6.15: 63 1 h = 0.819m B 1 2 h = 1.094m 1 h = -1.101m n = 6 1 2 A n = 4 n = 2 1 2 H = 6.013m B H = 5.213m A
Hình 6.15 Sơ đồ lưới độ cao nối 2 điểm gốc
Các bước tính toán bình sai được thực hiện trong bảng: Điểm Chênh cao
Số trạm Số hiệu chỉnh Chênh cao sau Độ cao sau bình sai bình sai hi (m) ni vi (mm) hi (m) Hi (m) A 5.213 1.094 4 - 4 1.090 1 6.303 0.819 6 - 6 0.813 2 7.116 -1.101 2 - 2 -1.103 B 6.013 Σ 0.812 12 -12 0.800 fh = 12mm
6.7.2 Lưới độ cao khép kín
Với dạng lưới độ cao khép kín như h1 1
trên, việc tính toán bình sai hoàn toàn tương A n1 h
tự như đối với lưới độ cao nối hai điểm gốc. 1 n 2
Chỉ khác sai số khép độ cao: f h = [h] (6.49) hn 2 n n ... n
Hình 6.16 Lưới độ cao khép kín 64
6.7.3 Lưới độ cao có điểm nút 1 2 3 B N A h2 1 h n n 2 1 h 4 3 n 3 C
Hình 6.17 Lưới độ cao có điểm nút
Lưới độ cao điểm nút là lưới trong đó có điểm độ cao là giao của ba hoặc nhiều hơn
ba tuyến đo cao (hình 6.17).
Giả sử h1 là tổng chênh cao đo từ điểm A tới điểm nút N, tương ứng với tổng n1 trạm đo.
Tương tự tuyến từ B đến N có h2, n2. Tuyến C đến N có h3, n3.
Đầu tiên tính độ cao điểm nút N, là độ cao trung bình trọng số theo ba tuyến:
H 1 P + H 2 P + H 3 P H = N 1 N 2 N 3 (6.50) N
P + P + P 1 2 3 Trong đó: Trọng số P = 1 (6.51) i n i
Sau đó lần lượt bình sai ba lưới độ cao riêng r¿ như đối với lưới độ cao nối hai điểm đã gốc. 65
CHƯƠNG 7 BẢN ĐỒ ĐỊA HÌNH VÀ ĐO VẼ BẢN ĐỒ
7.1 KHÁI NIỆM VỀ BẢN ĐỒ 7.1.1 Khái niệm
Bản đồ: là hình chiếu thu nhỏ của một khu vực mặt đất lên mặt phẳng ngang theo
một phương pháp chiếu nào đó có kể đến ảnh hưởng độ cong trái đất.
Tuỳ theo mục đích sử dụng và nội dung biểu diễn, bản đồ được chia làm nhiều loại:
bản đồ địa lý, bản đồ du lịch, bản đồ giao thông, bản đồ địa hình,… Trong xây dựng, kiến
trúc và quy hoạch, … chủ yếu sử dụng bản đồ địa hình.
Nội dung thể hiện trong bản đồ địa hình bao gồm [7]: - Cơ sở toán học
- Thủy hệ và các đối tượng liên quan - Địa hình
- Đường giao thông và các đối tượng liên quan
- Dân cư và các đối tượng kinh tế, văn hoá, xã hội - Thực vật
- Biên giới quốc gia, địa giới hành chính
- Ghi chú địa danh và các ghi chú cần thiết khác.
Bình đồ: là hình chiếu thu nhỏ của một khu vực nhỏ mặt đất lên mặt phẳng ngang
theo phương pháp chiếu thẳng góc và không kể đến ảnh hưởng độ cong trái đất.
Mặt cắt : là hình chiếu thu nhỏ của mặt cắt đứng mặt đất theo một hướng nào đó lên mặt đứng.
7.1.2 Tỷ lệ bản đồ
Tỷ lệ bản đồ là tỷ số giữa độ dài của đoạn thẳng trên bản đồ và độ dài tương ứng
của đoạn thẳng đó ngoài mặt đất. Kí hiệu 1:M 1: M = d: D (7.1)
Tỷ lệ bản đồ được thể hiện dưới dạng phân số có tử số bằng 1 và mẫu số chẵn trăm.
VD: 1:M = 1:200, 1:M = 1:500,...
Mắt người chỉ phân biệt được hai điểm cách nhau từ 0.1mm, từ đây người ta lấy làm
cơ sở cho độ chính xác biểu diễn bản đồ: 66 mBĐ = 0.2M (mm) (7.2)
Tức là đoạn thẳng ngoài thực địa có chiều dài lớn hơn 0.2M (mm) mới biểu diễn được trên bản đồ.
7.2 PHÂN MẢNH VÀ ĐÁNH SỐ BẢN ĐỒ
Kích thước tờ bản đồ thường là 50x50cm, và nó chỉ biểu diễn được một khu vực
nhỏ. Để biểu diễn một khu vực lớn, một quốc gia, … phải sử dụng nhiều tờ bản đồ. Để dễ
dàng quản lý và ghép nối, người ta phải phân mảnh và đánh số bản đồ.
Dưới đây trình bày nguyên tắc phân mảnh và đánh số bản đồ trong hệ toạ độ
VN2000 của nước ta [6].
Phân mảnh và đặt phiên hiệu mảnh bản đồ địa hình tỷ lệ 1:1.000.000
Mảnh bản đồ tỷ lệ 1:1.000.000 kích thước 40x60 là giao nhau của múi 60 chia theo
đường kinh tuyến và đai 40 chia theo đường vĩ tuyến.
Ký hiệu múi được đánh số 1, 2, 3,… bắt đầu từ múi số 1 nằm giữa kinh tuyến 1800
Đông và 1740 Tây, ký hiệu múi tăng từ Đông sang Tây.
Ký hiệu đai được đánh bằng các chữ cái Latin A, B, C... (bỏ qua chữ cái O và I để
tránh nhầm lẫn với số 0 và số 1) bắt đầu từ đai A nằm giữa vĩ tuyến 00 và 40 Bắc, ký hiệu
đai tăng từ xích đạo về cực.
Trong hệ thống lưới chiếu UTM quốc tế, người ta đặt trước ký hiệu đai thêm chữ cái
N đối với các đai ở Bắc bán cầu và chữ S đối với các đai ở Nam bán cầu.
Phiên hiệu mảnh bản đồ tỷ lệ 1:1.000.000 trong hệ VN-2000 có dạng X-yy (NX-yy),
trong đó X là ký hiệu đai và yy là ký hiệu múi, phần trong ngoặc là phiên hiệu mảnh theo kiểu UTM quốc tế.
Ví dụ mảnh bản đồ tỷ lệ 1:1.000.000 chứa Hà Nội có phiên hiệu là F-48 (NF-8).
Phân mảnh và đặt phiên hiệu mảnh bản đồ địa hình tỷ lệ 1:500.000
Mỗi mảnh bản đồ tỷ lệ 1:1.000.000 chia thành 4 mảnh bản đồ tỷ lệ 1:500.000, mỗi
mảnh có kích thước 20x30, phiên hiệu mảnh đặt bằng các chữ cái A, B, C, D theo thứ tự từ
trái sang phải, từ trên xuống dưới. 67 1: 1 000 000 2x2 = 4 tê 12x12 = 144 tê 6x6 = 36 tê 1: 500 000 1: 200 000 1: 100 000 2x2 = 4 tê 1: 50 000 16x16 = 256 tê 2x2 = 4 tê 1: 5 000 1: 25 000 3x3 = 9 tê 2x2 = 4 tê 1: 2 000 1: 10 000
S¬ ®ồ chia m¶nh b¶n ®ồ
Hình 7.1 Phân mảnh bản đồ
Các tờ bản đồ tỷ lệ lớn hơn được đánh số theo môt quy luật nhất định (tham khảo
trong các giáo trình chuyên ngành).
7.3 BIỂU DIỄN ĐỊA VẬT, ĐỊA HÌNH TRÊN BẢN ĐỒ
7.3.1 Biểu diễn địa vật
Địa vật là những vật thể do thiên nhiên hay do con người tạo ra như nhà cửa,
đường xá, sông hồ, rừng núi, …
Địa vật được biểu diễn các ký hiệu đơn giản, rβ ràng và thống nhất.
Biểu diễn theo tỷ lệ: đối với những địa vật có hình dáng, kích thước mà khi thu nhỏ
theo tỷ lệ bản đồ vẫn đủ phân biệt hình dáng, kích thước của chúng.
Ví dụ: ao hồ, rừng, làng mạc, thành phố, …
Biểu diễn phi tỷ lệ: đối với những địa vật có kích thước nhỏ mà khi thu nhỏ theo tỷ
lệ bản đồ thì không thể hiện được như cây độc lập, giếng nước, nhà thờ... thì dùng các kí
hiệu đặc trưng. Các kí hiệu này được qui định bởi Cục Đo đạc và Bản đồ Nhà nước. 68 Ví dụ:
Tháp cỗ. §×nh, chùa, ®ền, miếu
Chßi cao. T-îng ®µi, bia t-ëng niÖm
NghÜa ®Þa. Mé x©y ®éc lËp Trg. Tr-êng häc. BÖnh viÖn
Trạm tiếp x¨ng dầu. Lß nung,sấy
Trạm biến thế. Cét anten
§µi phát thanh, truyền h×nh.Trạm b-u ®iÖn
§µi, trạm khÝ t-îng. §iÖn thoại c«ng céng
Ngoài ra người ta kết hợp hai cách biểu diễn trên để biểu diễn những địa vật dạng
tuyến như sông suối, đường giao thông, biên giới,... những địa vật này được thể hiện
chiều dài theo tỷ lệ, chiều rộng phi tỷ lệ.
7.3.2 Biểu diễn địa hình
Địa hình là hình dáng, độ cao thấp của bề mặt đất. Địa hình rất quan trọng trong việc
lựa chọn phướng án quy hoạch, thiết kế, thi công các công trình.
Có nhiều phương pháp để biểu diễn địa hình như: phương pháp kẻ vân, phương
pháp tô màu, … nhưng có nhiều ưu điểm và phổ biến nhất hiện nay là phương pháp
đường đồng mức kết hợp ghi chú độ cao.
Phương pháp đường đồng mức:
Đường đồng mức hay đường bình độ là đường nối liền các điểm có cùng độ cao. 130m 120m 110m 100m
Hình 7.2 Biểu diễn địa hình bằng đường đồng mức 69
Đường đồng mức chính là hình chiếu của giao tuyến giữa mặt đất tự nhiên và mặt
phẳng song song với mặt thuỷ chuẩn.
Các tính chất của đường đồng mức:
- Đường đồng mức là các đường cong trơn, liên tục và khép kín.
- Các đường đồng mức không cắt nhau.
- Các đường đồng mức càng sít nhau, mặt đất càng dốc. Các đường đồng mức càng
xa nhau, mặt đất càng thoải.
- Đường vuông góc ngắn nhất với hai đường đồng mức kề nhau là đường dốc nhất.
Hiệu số độ cao giữa hai đường đồng mức kề nhau là khoảng cao đều h. Khoảng cao
đều càng nhỏ, địa hình càng được biểu diễn chính xác.
Phương pháp đường đồng mức thường được kết hợp ghi chú độ cao để biểu diễn địa
hình, đặc biệt là những nơi độ cao thay đổi như đỉnh núi, yên ngựa, đáy thung lũng,...
7.4 ĐO VẼ BẢN ĐỒ ĐỊA HÌNH 7.4.1 Khái niệm
Đo v¿ bản đồ là đo đạc, tính toán xác định toạ độ của các điểm chi tiết đặc trưng
cho địa vật, địa hình và biểu diễn chúng bằng các kí hiệu (nếu là địa vật) và đường đồng
mức (nếu là địa hình) thành tờ bản đồ.
Để đo v¿ bản đồ cần phải dựa vào các điểm khống chế mặt bằng và khống chế độ
cao Nhà nước và đo các đại lượng góc, cạnh, chênh cao để xác định toạ độ (X,Y,H) của các điểm chi tiết.
Quy phạm về đo v¿ thành lập bản đồ [8] quy định đầy đủ, rõ ràng các yêu cầu kỹ
thuật của công tác đo v¿.
Các phương pháp đo v¿ bản đồ: - Phương pháp toàn đạc - Phương pháp bàn đạc
- Phương pháp ảnh hàng không – viễn thám
Trong khuôn khổ của nội dung, chỉ giới thiệu đo v¿ bản đồ bằng phương pháp toàn đạc. 70
7.4.2 Đo vẽ bản đồ bằng phương pháp toàn đạc
Là phương pháp sử dụng máy kinh vĩ A (X ,Y ,H ) A A A
hoặc máy toàn đạc điện tử đo đạc trực tiếp 2 3 trên khu đo.
Nội dung của phương pháp:
A, B là hai điểm khống chế đã biết 1 4
toạ độ. Xác định toạ độ điểm điểm chi tiết 1 β (X 1 D
1, Y1) bằng phương pháp toạ độ cực, đặt 1
máy kinh vĩ hoặc máy toàn đạc điện tử tại điểm B, đo góc β B (X ,Y ,H ) 1 và khoảng cách D1 B B B
Hình 7.3 Phương pháp toàn đạc
Còn độ cao H1 được xác định bằng phương pháp đo cao lượng giác.
Phương pháp toàn đạc cho độ chính xác cao, thường áp dụng để đo v¿ bản đồ tỷ lệ lớn.
Quy trình đo v¿ bản đồ bằng phương pháp toàn đạc:
- Xây dựng lưới khống chế mặt bằng, độ cao
- Đo chi tiết địa vật, địa hình - Biên tập bản đồ.
1. Xây dựng lưới khống chế mặt bằng, độ cao
Lưới khống chế mặt bằng và độ cao phải đảm bảo đủ mật độ khu vực đo v¿. Công
tác xây dựng lưới khống chế đã được học ở chương trước 6.
2. Đo chi tiết
Các điểm chi tiết đặc trưng cho địa vật là các điểm xác định kích thước, hình dáng
hình học của địa vật. Ví dụ: 4 điểm góc nhà hình chữ nhật xác định được hình dáng, kích thước của nó,...
Bảng 7.1 Mật độ điểm chi tiết [8] Tỷ lệ bản đồ Khoảng cao đều (m)
Khoảng cách tối đa giữa các điểm địa hình (m) 0,5 60 1,0 80 1: 5000 2,0 100 5,0 120 0,5 40 1: 2000 1,0 40 2,0 50 0,5 20 1: 1000 1,0 30 0,5 15 1: 500 1,0 15 71
Các điểm chi tiết đặc trưng cho địa hình là các điểm tại đó độ cao thay đổi như đỉnh
núi, yên ngựa,... Ngoài các điểm đó, chúng ta phải đo các điểm địa hình (độ cao) đảm bảo
mật độ cần thiết để biểu diễn địa hình (bảng 7.1).
Nếu đo bằng máy kinh vĩ, một tổ đo gồm một người đứng máy, một người ghi sổ,
một người sơ hoạ và hai người đi mia. Nếu đo bằng máy toàn đạc điện tử thì không cần
người ghi sổ vì số liệu đo được lưu vào fieldbook.
Trước khi đo máy, mia phải được kiểm nghiệm và hiệu chỉnh, đặc biệt là các sai số 2c và MO.
Trình tự đo chi tiết bằng máy kinh vĩ (hoặc máy toàn đạc điện tử):
- Đặt máy tại điểm khống chế, định tâm, cân bằng máy chính xác - Đo chiều cao máy (i)
- Định hướng 00 0’ 0” tới điểm khống chế lân cận
- Quay máy ngắm mia đặt ở điểm chi tiết đọc chỉ trên (t), chỉ dưới (d) và chỉ giữa.
Đọc góc bằng β trên bàn độ ngang, góc đứng V trên bàn độ đứng. Đối với máy toàn đạc,
mia được thay bằng gương, và chỉ việc ngắm gương, bấm nút đo. Máy s¿ tự đo và lưu
góc bằng, góc đứng và khoảng cách.
Đồng thời người v¿ sơ hoạ theo người đi mia để v¿.
Các số liệu đo được ghi vào sổ đo theo mẫu:
Mẫu sổ đo chi tiết (đo bằng máy kinh vĩ) Trạm đo: A, HA = 171.22m
Người đo: Nguyễn Văn Đoàn Định hướng: B
Người ghi: Nguyễn Tuấn Khanh Chiều cao máy: i = 1.45m
Người v¿ sơ hoạ: Phạm Hồng Văn kn Số đọc Số đọc Số đọc Khoảng Chênh Độ cao Ghi chú (m) chỉ giữa bàn độ bàn độ cách ngang cao (m) (m) Điểm l ngang β đứng (m) h = DtgV + H = Htr + h V D = kncos2V + i - l 1 2 3 4 5 6 7 8 9 1 125.3 1400 10o15'10” 3o31'00” 125.28 1.18 172.40 Cây độc lập 2 60.2 1480 25o22'00” -2o22'00” 60.10 -2.51 168.71 Tụ thuỷ ... 72
3. Biên tập bản đồ (trình bày sơ bộ phương pháp vẽ thủ công)
- V¿ lưới ô vuông: v¿ lưới 4x4 ô vuông kích thước 10x10cm và ghi toạ độ vuông góc tại các góc lưới.
- Chuyển điểm khống chế lên bản v¿ theo toạ độ vuông góc.
- Chuyển các điểm chi tiết lên bản v¿ theo toạ độ cực và ghi độ cao của chúng ở vị
trí tương ứng trên bản v¿.
- Trên cơ sở các điểm chi tiết, v¿ địa vật và v¿ đường đồng mức theo phương pháp ước lượng. - Hoàn thiện bản đồ.
Hiện nay việc biên tập bản đồ được thực hiện trên phần mềm đồ hoạ như
Microstation, Autocad,... cho kết quả nhanh chóng và chính xác. Ở nước ta cũng đã có các
phần mềm biên tập bản đồ chuyên dụng chạy trong môi trường đồ hoạ Autocad như
TOPO (Công ty Hài Hoà), VIMAP (Công ty Vinacad),...
7.5 ĐO VẼ MẶT CẮT ĐỊA HÌNH
Để phục vụ khảo sát, thiết kế và thi công các công trình dạng tuyến như đường
giao thông, kênh mương tưới tiêu, đường ống dẫn nước... phải tiến hành đo v¿ mặt cắt địa hình.
Đo v¿ mặt cắt địa hình gồm các giai đoạn chính sau:
1. Khảo sát chọn tuyến:
Dựa vào các tài liệu bản đồ để tiến hành chọn tuyến công trình. Tuyến được chọn
đánh dấu trên bản đồ bằng các các cọc trăm mét (cọc H), cọc km (cọc K) và cọc đỉnh
ngoặt, điểm đầu, điểm cuối của đường cong.
2. Định tuyến ngoài thực địa:
Từ các điểm đã được chọn để cố định tuyến trên bản đồ, tiến hành bố trí cố định
tuyến trên thực địa bằng các cọc gỗ hoặc cọc bê-tông (định trắc dọc tuyến).
Các đỉnh góc ngoặt sau khi bố trí phải đo góc ngoặt bằng máy kinh vĩ với độ chính xác mβ ±30”.
Các cọc km kí hiệu lần lượt là K1, K2, K3,… Các cọc trăm mét là H1, H2, H3,… 73
Nếu tuyến giao cắt với các công trình khác, phải đánh dấu điểm giao cắt bằng các
cọc và kí hiệu bằng lý trình, ví dụ: H1+23, H4+35,…
Đồng thời với định tuyến trắc dọc, tiến hành định tuyến trắc ngang. Mặt cắt ngang
vuông góc với tuyến và dài từ 20 70m sang mỗi bên. Mặt cắt ngang thường được bố trí
tại các cọc H, cọc K. Đôi khi do yêu cầu, khoảng cách giữa các mặt cắt ngang dày
hơn, khảng 25m một mặt cắt.
3. Đo cao dọc tuyến: C 4 3 4 4 N 3 3 2 Ð 4 H1 1 2 3 2 M0 1 Trạm máy 3 Trạm máy 2 1 2 Trạm máy 1
Hình 7.4 Sơ đồ đo mặt cắt
Xác định độ cao của các điểm trên tuyến bằng đo cao hình học kỹ thuật.
Các điểm cọc chính (cọc H, cọc K, đỉnh ngoặt,…) được đo như các điểm lưới khống chế
độ cao và đo hai mặt đen, đỏ.
4. Tính toán và vẽ mặt cắt:
- Tính toán bình sai độ cao các điểm chính như đường chuyền nối hai điểm gốc, fh≤±50 L (mm).
- Tính độ cao các điểm chi tiết trên mặt cắt dọc và các mặt cắt ngang.
- V¿ mặt cắt. Thông thuờng, mặt cắt dọc có tỷ lệ đứng 1:1 000, tỷ lệ ngang 1:100.
Mặt cắt ngang tỷ lệ đứng bằng tỷ lệ ngang và bằng 1:200. 74 3 2 1 0 -1 -2 Mss:-3.0m -3 6 0 8 8 7 5 5 6 1 3 9 1 0 4 .5 .5 .7 .8 .7 .5 .6 .6 .6 .4 .4 .7 .7 .5 -0 -0 -0 -0 -0 -0 -0 -0 -0 -0 -0 1 1 -0 7 6 5 8 .8 .3 9.83 .9 .5 6.90 3 7 3 5 5 4 6 3 9 2 6 6 6 6 0 3 1 1 .3 .5 .5 .4 .7 .6 .5 .6 .5 .5 .3 .7 .3 .2 0 0 4 8 5 5 9 1 9 1 7 4 4 5 6 6 7 8 8 0 4 3 6 8 8 9 2 2 2 2 2 2 2 3 1 3 6 3 3 3 4 4 4 4 4 4 4 4 3 3 4 4 4 4 4 4 A=58d26'39" L=0.00 T=33.56 P=8.75 R=60.00 K=61.20 8 0 4 8 5 5 9 9 6 7 1 7 4 2 4 5 6 6 7 8 8 1 1 3 6 7 8 8 9 P 2 2 2 2 2 2 0 3 3 3 3 3 3 3 3 + + + + + + + + + + + + + 4 4 4 4 4 4 + 4 4 4 4 4 4 4 4 Hình 7.5 Mặt cắt dọc
7.6 SỬ DỤNG BẢN ĐỒ ĐỊA HÌNH
Tài liệu bản đồ là không thể thiếu khi khảo sát, thiết kế, thi công công trình. Người
kỹ sư xây dựng phải biết sử dụng bản đồ để phục vụ các công việc của mình.
Bản đồ thể hiện địa, vật địa hình càng chính xác, chi tiết và cập nhật sát với thực tế
khi tỷ lệ bản đồ càng lớn, khoảng cao đều đường đồng mức càng nhỏ và thời điểm đo v¿
thành lập bản đồ càng gần hiện tại.
7.6.1 Định hướng bản đồ
Khi sử dụng bản đồ ở trong phòng lẫn ngoài thực địa, đầu tiên chúng ta phải tiến
hành định hướng tờ bản đồ, tức là xoay tờ bản đồ cho đúng hướng thực tế.
Định hướng bằng la bàn: đặt la bàn lên tờ bản đồ và xoay tờ bản đồ cho đến khi
khung đứng của nó song song với kim Bắc – Nam của la bàn. 75
Định hướng theo địa vật: chọn trên bản đồ một địa vật dạng tuyến như đường,
sông,... xoay tờ bản đồ sao cho hướng của địa vật này trên bản đồ trùng với hướng của
địa vật ngoài thực địa.
Sau đây s¿ trình bày cách xác định một số các đại lượng cơ bản trên bản đồ giấy.
7.6.2 Xác định toạ độ của điểm trên bản đồ
1. Xác định tọa độ địa lý của một điểm
Độ kinh, độ vĩ được ghi ở bốn góc khung tờ bản đồ. Trên mỗi cạnh khung có v¿
khoảng đen, trắng liên tiếp biểu thị giá trị độ kinh và độ vĩ chẵn đến phút, gọi là thang chia độ.
Nối các đầu của các đoạn này tương ứng ở các cạnh khung đối diện s¿ được lưới tọa độ địa lý.
Để xác định toạ độ địa lý của điểm P, φ
từ P kẻ một đường thẳng song với cạnh ô 2
kinh tuyến và một đường song song với cạnh d
ô vĩ tuyến. Đo các đoạn thẳng a, b, c, d như
hình 7.6. Toạ độ địa lý của điểm P được xác P đị a b nh: c
φ = φ + c (φ –φ1 ) φ P 1 2 c + d 1
λ = λ + a (λ – λ ) λ1 λ 2 P 1 a + b 2 1 (7.3)
Hình 7.6 Xác định tọa độ địa lý
(φi, λi: vĩ độ, kinh độ của góc ô lưới chứa điểm P)
2. Xác định tọa độ vuông góc của một điểm
Để xác định toạ độ vuông góc của điểm P, từ lưới ô vuông tọa độ trên tờ bản đồ,
xác định toạ độ của bốn góc lưới chứa điểm P là X1, Y1, X2, Y2. Từ P kẻ các đường thẳng
song song với các cạnh lưới, và đo các đoạn thẳng a, b, c, d như hình 7.7.
Toạ độ vuông góc của điểm P được tính: X 2
X = X + c ( X ) d P 1 2 – X 1 c + d a (7.4) P Y = Y + (Y –Y ) a b P 1 a + b 2 1 c X 1 Y Y
Hình 7.7 Xác định tọa độ vuông góc 76
3. Xác định độ cao của một điểm
Để xác định độ cao điểm
P, từ P kẻ đường vuông góc với H hai đường đồ 2 ng mức kề nhau
(H1, H2) và đo các đoạn thẳng a, b như hình 7.8.
Độ cao của điểm A được H tính: 1 b P H = H + a (H ) (7.5) P 1 2 – H1 a a + b
Hình 7.8 Xác định độ cao
7.6.3 Xác định khoảng cách độ dốc của đoạn thẳng
1. Xác định khoảng cách
Độ dài của một đoạn thẳng đựơc xác định bằng cách:
- Dùng thước milimet đo và tính ra khoảng cách thực tế dựa vào tỷ lệ bản đồ.
- Dùng compa đo khoảng cách và kết hợp với thước tỷ lệ (in sẵn bên dưới tờ bản
đồ) tính ra khoảng cách thực tế.
- Xác định toạ độ vuông góc của điểm đầu, điểm cuối và tính ra khoảng cách.
Độ dài của một đoạn cong:
- Chia đường cong thành các đoạn thẳng nhỏ, xác định chiều dài từng đoạn nhỏ và
kết quả là tổng của chúng.
- Dùng máy đo độ dài chuyên dụng (nguyên lý tương tự như đo khoảng cách ở xe máy, ôtô).
2. Xác định độ dốc của đoạn thẳng B
Độ dốc (i) của đoạn thẳng AB chính là
tỷ số giữa chênh cao với khoảng cách h ngang của chúng: – H A i = H A B 100(%) (7.6) D D Hình 7.8 Độ dốc 77
Để xác định độ dốc i, cần xác định độ cao của điểm đầu và điểm cuối, và khoảng cách D
(các xác định các đại lượng này đã giới thiệu ở trên).
7.6.4 Xác định diện tích
Diện tích cần xác định là hình đa giác:
- Tính theo toạ độ các đỉnh của đa 2 (X2,Y2)
giác: (chú ý, đánh số thứ tự các đỉnh theo chiều kim đồng hồ): 3 (X3,Y3) n S = 1 Σ 1 (X X (Y – Y ) (7.7) 1,Y1) 2 i i+1 i–1 i=1 n ... S = 1 Σ
Y ( X – X ) (7.8) 2 i i+1 i–1 i=1 n (Xn,Yn)
Hình 7.9 Xác định diện tích
- Chia đa giác thành các tam giác, xác định diện tính các tam giác bằng cách đo
chiều dài ai, bi, ci các cạnh của các tam giác và tính diện tích theo công thức Heron:
S = p ( p – a )( p – b )( p – c ) (7.9) i i i i i i i i Trong đó: a + b + c p = i i i i 2
Diện tích của đa giác là tổng diện tích các tam giác.
Diện tích cần xác định giới hạn bởi đường cong bất kỳ:
- Xác định bằng lưới ô vuông:
Vạch kẻ lưới ô vuông kích thước 2x2mm hoặc 4x4mm trên tờ giấy trong suốt. Phủ
lưới ô vuông lên hình cần đo, đếm số ô vuông nguyên và ước lượng các ô vuông bị khuyết
ở mép. Diện tích khu đo bằng số ô vuông nhân với diện tích một ô vuông tính theo tỷ lệ bản đồ.
Sử dụng máy đo diện tích: nguyên lý cũng tương tự như máy đo khoảng cách, máy
đo được chiều dài của đường biên, diện tích được tính bằng tích của chiều dài đó với một hằng số của máy. 78
7.6.5 Lập mặt cắt dọc địa hình
Giả sử cần lập mặt cắt dọc địa hình theo hướng AA’ trên bản đồ (hình 7.10).
Hình 7.10 Lập mặt cắt dọc địa hình từ bình đồ
Trên bình đồ, xác định độ cao điểm đầu A, điểm cuối B và các điểm giao nhau với
các đường đồng mức. Xác định khoảng cách giữa các điểm đó. Từ độ cao, khoảng cách
ta v¿ được mặt cắt địa hình theo tỷ lệ. 79
CHƯƠNG 8 TRẮC ĐỊA TRONG XÂY DỰNG
8.1 BỐ TRÍ CÁC YẾU TỐ CƠ BẢN
8.1.1 Khái niệm bố trí công trình
Ngược với đo v¿ bản đồ là đo đạc để chuyển thực địa lên bản đồ, bố trí công trình
là chuyển các các công trình được thiết kế trên bản đồ ra ngoài thực địa.
Bố trí công trình là xác định vị trí mặt bằng, độ cao của các điểm đặc trưng của
công trình ở ngoài thực địa, đảm bảo công trình đúng vị trí, hình dạng, kích thước thiết kế.
Cũng tương tự như đo v¿ bản đồ, bố trí công trình cũng thực hiện theo nguyên tắc
từ tổng quát đến chi tiết.
8.1.2 Bố trí các yếu tố cơ bản
1. Bố trí góc bằng
Từ hướng AB đã xác định (được cố
định bằng các mốc ngoài thực địa), cần xác
định hướng AC tạo với hướng AB một góc β C 1 theo thiết kế. C C2 β
Hình 8.1 Bố trí góc bằng
Đặt máy kinh vĩ ở A, ngắm điểm B được số đọc b trên bàn độ ngang, quay máy để
được số đọc (b + β) (thông thường đặt trước số đọc b = 000’0”). Cố định ống kính, đánh
dấu được điểm C1. Đảo ống kính, thao tác tương tự như trên, đánh dấu được điểm C2.
Trung bình hai hướng là điểm C cần xác định.
2. Bố trí khoảng cách
Trên hướng AC đã định ngoài thực địa, cần bố trí điểm B cách A một đoạn D.
Từ điểm A, theo hướng AC đo sơ bộ một đoạn có chiều dài bằng D, đánh dấu được điểm B'.
Dùng thước thép đo đoạn thẳng AB', giả sử được khoảng cách D’. Tính số hiệu chỉnh: D = D'-D (8.1) 80
Từ B' dịch chuyển một đoạn D theo hướng AB’ ra xa hoặc lại gần tuỳ theo dấu của
D, được điểm B bố trí.
3. Bố trí độ cao
Từ mốc A (đã biết độ cao HA) ngoài thực địa, cần bố trí điểm B (đã có vị trí mặt
bằng ngoài thực địa) với độ cao thiết kế HB. a b B A
Hình 8.2 Bố trí độ cao bằng máy thuỷ bình
Đặt máy thuỷ bình giữa A và B, dựng mia ở A và B. Đọc số đọc trên mia dựng ở A
được a. Giữa số đọc a, độ cao HA và độ cao thiết kế HB, số đọc cần thiết b ở mia B có quan hệ: HA + a = HB + b (8.2) Từ đó: b = HA - HB + a. (8.3)
Quay máy ngắm mia dựng ở B, điều chỉnh mia lên hoặc xuống cho đến khi đọc
được số đọc là b, khi đó đế mia có độ cao HB thiết kế. Đánh dấu hoặc dùng cọc cố định đế mia.
8.2 BỐ TRÍ ĐIỂM MẶT BẰNG
Trên bản v¿ thiết kế có các điểm mặt bằng A(XA, YA), B(XB, YB) và C(XC, YC). Ngoài
thực địa đã có hai mốc A và B, cần phải bố trí điểm C.
8.2.1 Phương pháp tọa độ cực 81
Dụng cụ dùng để bố trí gồm máy kinh vỹ và thước thép hoặc máy toàn đạc điện tử.
Chọn điểm B làm gốc cực, cạnh BA làm cạnh gốc. Tính góc cực β và cạnh cực D
của điểm C cần bố trí: β = α - α BC BA (8.4) A D = ( X ) 2 (8.5)
C – X B )2 + (Y – Y C B C
Việc bố trí điểm C trở thành bố trí góc bằng và β D khoảng cách:
Hình 8.3 Phương pháp tọa độ cực
Đặt máy kinh vĩ tại B, bố trí góc bằng β, cố định chuyển động ngang của máy, lúc
này điểm C nằm trên hướng ống kính. Theo hướng ống kính, dùng thước thép để bố trí
khoảng cách ngang D, được điểm C cần bố trí.
Độ chính xác của phương pháp: m β m = ± 2 m + D 2 ( ) 2 P D (8.6) p
(mβ: sai số bố trí góc; mD: sai số bố trí khoảng cách)
Phương pháp tọa độ cực được sử dụng nhiều nhất trong số các phương pháp.
8.2.2 Phương pháp tọa độ vuông góc
Dụng cụ dùng để bố trí gồm thước thép và máy kinh vỹ hoặc kính chuyên dụng tạo góc vuông.
Tính góc bằng β và cạnh bằng D. Sau đó tính các yếu tố: D A x = Dsinβ (8.7) β x y = Dcosβ (8.8) y P'
Hình 8.4 Phương pháp tọa độ vuông góc
Từ A, theo hướng AB bố trí khoảng cách y được điểm P’. Từ điểm P’, sử dụng máy
kinh vĩ hoặc lăng kính chuyên dụng để xác định hướng vuông góc với hướng AB. Trên
hướng vuông góc, bố trí khoảng cách x xác định được điểm C cần bố trí. m Độ
chính xác của phương pháp: m2 = m2 + m2 + ( )2 x 2 (8.9) P y x p 82
(m┴ : sai số xác định góc vuông)
Phương pháp này thuận lợi hơn nếu thực địa có lưới ô vuông vây dựng và hai điểm
A, B là hai điểm lưới. Phương pháp toạ độ vuông góc ít được áp dụng do yêu cầu có dụng
cụ tạo hướng vuông góc.
8.2.3 Phương pháp giao hội góc
Dụng cụ dùng để bố trí là máy kinh vỹ.
Tính các góc giao hội βA, βB: βA = αAB - αAC A β β A B = αBC - αBA β
Đặt máy kinh vĩ tại A bố trí góc B
bằng βA, tại A bố trí góc bằng βB. Giao B
của hai hướng ngắm là điểm P cần bố
Hình 8.5 Phương pháp giao hội góc trí. m Độ β
chính xác của phương pháp: m = ± 2 D + D 2 C (8.10) p sin(β AC BC A + β B )
Phương pháp này được áp dụng phổ biến, nhất là khi điểm cần bố trí bị ngăn cách bởi sông, hồ, …
8.2.4 Phương pháp giao hội cạnh
Dụng cụ dùng để bố trí là thước thép. D Tính các cạnh giao hội D AC AC, DBC: A D
= ( X – X ) + (Y – Y ) AC C A D 2 2 BC C A D
= ( X – X )2 + (Y – Y )2 BC C B C B Hình 8.6
Dùng hai thước thép có chiều dài lớn hơn khoảng cách DAC, DBC. Đầu 0 của thước
được hai người giữ cố định tại A và B, người thứ ba kéo hai thước để xác định giao điểm
tại số đọc DAC và DBC. Đánh dấu, được điểm C cần bố trí. m
Độ chính xác của phương pháp: m = ± 2 D (8.11) C sin βC
Phương pháp này áp dụng khi khu đo thuận lợi cho việc bố trí khoảng cách. 83
8.3 BỐ TRÍ ĐƯỜNG CONG TRÒN 8.3.1 Khái niệm
Khi xây dựng các công trình dạng tuyến như đường ôtô, đường sắt, kênh mương,...
tại những nơi tuyến đổi hướng cần bố trí các đường cong.
Có các loại đường cong là đường cong tròn và đường cong xoắn. Đường cong tròn
là đường cong có tâm và bán kính không đổi, là dạng cơ bản, thường gặp trong giao thông.
8.3.2 Các yếu tố chính của đường cong tròn θ TC T P Ð C G Ð R θ /2
Hình 8.7 Các yếu tố của đường cong tròn
Các tham số của đường cong: bán kính đường cong R, góc ngoặt θ. Ngoài ra còn các tham số khác: θ
Tiếp cự T: T = T = Rtg (8.12) D = TC 2 1
Phân cự P: P = R( θ –1) (8.13) cos 2
Chiều dài đường cong K: K = Rθ (8.14) 1800
Các điểm chính của đường cong: điểm đầu Đ, điểm cuối C và điểm giữa G.
8.3.3 Bố trí các điểm chính của đường cong
Đặt máy kinh vĩ tại điểm ngoặt N, định hướng về điểm ngoặt của đường cong trước 1800 – θ
đó, bố trí khoảng cách T, được điểm Đ. Quay máy kinh vĩ đi một góc ( ), bố trí 2 84 1800 – θ
khoảng cách P, được điểm G. Tiếp tục quay máy đi một góc ( ), bố trí khoảng cách 2 T, được điểm C.
8.3.4 Bố trí chi tiết đường cong
Khi bố trí đường cong, ngoài các điểm chính, phải bố trí thêm các điểm phụ trên
đường cong. Các điểm phụ có thể cách nhau 5m, 10m, 15m,… tuỳ theo yêu cầu của công
trình. Việc bố trí các điểm phụ gọi là bố trí chi tiết đường cong. Có nhiều phương pháp bố
trí chi tiết: phương pháp toạ độ vuông góc, phương pháp toạ độ cực mở rộng, phương pháp dây cung kéo dài,…
1. Phương pháp tọa độ vuông góc
Giả sử cần bố trí các điểm chi tiết cách đều nhau k (m). Số điểm chi tiết cần bố trí: n = K/k điểm.
Tính toạ độ các điểm chi tiết: Góc ở tâm chắn cung k: x 2 2 1800 x φ = k (8.15) πR 1
Chọn hệ toạ độ với gốc là điểm đầu x1
Đ, trục x trùng với hướng ĐN, trục y trùng
với hướng ĐO. Toạ độ các điểm chi tiết thứ φ 1: φ Ð x y y y 1 1 = Rsinφ (8.16) 2
y1 = R-Rcosφ = R(1-cosφ) = 2Rsin2(φ/2)
Hình 8.8 Phương pháp tọa độ vuông góc (8.17)
Tương tự, tọa độ điểm thứ i: xi = Rsin(iφ ) yi = 2Rsin2(iφ/2) (8.18)
Cách bố trí:
Đặt máy kinh vĩ tại điểm Đ, định hướng về điểm ngoặt N, bố trí các khoảng cách x1,
x2,... xn. Chuyển máy lần lượt tới các điểm vừa bố trí, định hướng tới điểm N mở góc
vuông, bố trí các khoảng cách yi tương ứng, đánh dấu điểm được các điểm i chi tiết của đường cong. 85
Các điểm phụ bố trí một cách độc lập do đó chúng không chịu ảnh hưởng của sai
số lan truyền. Phương pháp này thường được sử dụng ở nơi dễ bố trí chiều dài.
2. Phương pháp tọa độ cực mở rộng
Các điểm chi tiết được xác định nếu 2
biết các góc φi và khoảng cách D (hình 8.9). φ φ Ta có: φ =
, φ = 2 = φ , …, 1 2 2 2 1 D φ φ = i (8.19) i 2 φ D 2 φ φ φ 1 và:
D = 2R sin (8.20) φ O 2
Hình 8.9 Phương pháp tọa độ cực mở rộng
Cách bố trí:
Đặt máy kinh vĩ ở điểm Đ, định hướng về điểm N, bố trí các góc φ1, φ2,... φn và đánh
dấu các hướng. Theo hướng góc φ1, bố trí chiều dài D được điểm 1. Từ điểm 1, dùng
thước thép quay cung bán kính D cắt cạnh góc φ2 được điểm 2,… tiếp tục cho đến hết.
8.4 TÍNH KHỐI LƯỢNG ĐÀO ĐẮP 8.4.1 Nguyên lý
Nguyên tắc của tính khối lượng đào đắp là chia nhỏ khu vực cần tính thành các ô
vuông nhỏ, thể tích của một ô bằng diện tích nhân với độ cao trung bình của ô đó: V = a2.Htb (8.21)
Hình 8.10 Nguyên lý tính khối lượng đào đắp 86
Và hiệu thể tích tính theo độ cao thực tế với thể tích tính theo độ cao thiết kế chính
là khối lượng đào hoặc đắp:
VĐào(đắp) = VThực tế - VThiết kế (8.22)
Việc đo, tính toán có thể thực hiện trên bản đồ hoặc trực tiếp ngoài thực địa.
8.4.2 San nền cân bằng khối lượng đào và khối lượng đắp
Trên khu vực cần san nền, xây dựng một lưới ô vuông (trên bình đồ hoặc trên thực
địa) cạnh a = 5 – 20m, cạnh càng nhỏ độ chính xác tính toán càng cao. 8.42 10.03 8.13 10.03 10.05 10.03 12.68 10.03 +1. 61 +1 .90 -0. 02 - 65 2. 8.93 10.38 10.03
10.84 10.03 11.68 10.03 10.03 +1. 10 -0. 35 -0. 81 - 65 1. 10.87 10.03 9.36 10.03 10.03 9.34 10.03 8.92 -0. 84 +0 .69 +1 .11 +0. 7 6
12.72 10.03 11.08 10.03 10.63 10.03 7.98 10.03 +2. 05 -1.05 -0.60 -2.69
Hình 8.10 Lưới ô vuông đào đắp
Xác định độ cao thực tế của các đỉnh ô vuông (Hđen) trên bình đồ hoặc đo trực tiếp
ngoài thực địa. Độ cao trung bình thực tế của ô vuông bất kỳ: Htbđen = (H1đen + H2đen + H3đen + H4đen )/4 (8.23)
Trong đó: Hiđen: độ cao thực tế của đỉnh i.
Nếu độ cao thiết kế (Hđỏ) của khu vực san nền được cho trước, khi đó khối lượng đào (hoặc đắp) là:
W = Vđen – Vđỏ = a2(∑ Htbđen – ∑Hđỏ) (8.24)
Nếu yêu cầu cân bằng giữa khối lượng đào và khối lượng đắp trên toàn khu thì độ
cao thiết kế (Hđỏ) được tính theo công thức: 87
Hđỏ = (1∑HIđen + 2∑HIIđen + 3∑HIIIđen + 4∑HIVđen)/4n (8.25) Trong đó:
HIđen: Độ cao của đỉnh thuộc một ô vuông HII
đen: Độ cao của đỉnh thuộc hai ô vuông
HIIIđen: Độ cao của đỉnh thuộc ba ô vuông
HIVđen: Độ cao của đỉnh thuộc bốn ô vuông n: số ô vuông.
Độ cao san lấp (độ cao thi công) tại từng đỉnh s¿ bằng độ cao thiết kế trừ đi độ cao đen. Ví dụ hình 8.10:
Từ độ cao đen đẫ đo được ở các đỉnh ô vuông. Xác định độ cao thiết kế để tổng
khối lượng đào bằng tổng khối lượng đắp và tính độ cao thi công tại các đỉnh.
Độ cao của đỉnh thuộc 1 ô vuông: HIđen = 8.42 + 12.68 + 7.98 + 12.72 = 41.72 m
Độ cao của đỉnh thuộc 2 ô vuông: HIIđen = 8.13 + 10.05 + 11.68 + 9.36 + 10.63 +
11.08 + 10.87 + 8.93 = 80.73 m
Độ cao của đỉnh thuộc 4 ô vuông: HIVđen = 10.38 + 10.84 + 8.92 + 9.34 = 39.48 m
Độ cao thiết kế để tổng đào bằng tổng đắp:
Hđỏ = (1x41.72 + 2x80.73 + 4x39.84)/(4x9) = 10.03 m
Độ cao thi công = Hđỏ - Hđen
Độ cao thiết kế (đỏ), độ cao thi công (xanh) được ghi trên mắt lưới hình 8.10 trong
đó: đào mang dấu -, đắp mang dấu +.
8.4.2 San nền theo độ dốc cho trước
Trong xây dựng hay gặp trường hợp san lấp theo độ dốc cho trước để đảm bảo
mục đích cho trước nào đó, ví dụ như đảm bảo thoát nước mưa tự nhiên. Trường hợp này
độ cao đỏ (độ cao thiết kế) s¿ được cho trước ở cọc đầu tiên, học cuối cùng. Độ cao thiết
kế của từng cọc khác s¿ tính dựa vào độ dốc i, kích thước ô vuông a và số thứ tự của cọc j: Hjđỏ = H0đ ỏ - j.i%.a (8.25) 88
8.5 CÔNG TÁC TRẮC ĐỊA TRONG XÂY DỰNG CÔNG TRÌNH
8.5.1 Xây dựng lưới ô vuông xây dựng
Trong xây dựng công trình, các trục của công trình là vuông góc, song song với
nhau và để thuận tiện trong việc bố trí, thi công người ta thường xây dựng trên khu vực
xây dựng một mạng lưới khống chế trắc địa có các điểm tạo thành các ô vuông và các
cạnh lưới song song với trục chính của công trình, gọi là lưới ô vuông xây dựng (hình 8.11).
Lưới ô vuông xây dựng được thiết kế
trên bản v¿ thiết kế công trình, kích thước
thường là 50m, 100m, 200m, … tuỳ theo
quy mô và yêu cầu của công trình. Sau đó
được chuyển ra thực địa và đo đạc bình sai, hoàn nguyên lưới. Hướng ban đầu
Hình 8.11 Lưới ô vuông xây dựng
Việc xây dựng lưới ô vuông gồm các bước:
1. Xác định hướng ban đầu của lưới
Hướng ban đầu của lưới được cố định bởi hai điểm, toạ độ hai điểm này được xác
định trên bản v¿ thiết kế. Các điểm cố định hướng ban đầu của lưới được bố trí dựa vào
các điểm khống chế trắc địa cấp cao hơn đã có trong giai đoạn trước.
Hướng ban đầu còn có thể được bố trí dựa vào các địa vật cố định có trên thực địa
và trên bình đồ thiết kế.
2. Bố trí lưới ô vuông
Từ hướng ban đầu, sử dụng máy kinh vĩ và thước thép lần lượt bố trí các điểm của
mạng lưới, cố định bằng các cọc gỗ.
3. Đo đạc và tính toán bình sai lưới ô vuông xây dựng
Các điểm mép khung lưới được đo đạc, xác định trước theo các phương pháp xây
dựng lưới mặt bằng đã học. 89
Các điểm bên trong lưới ô vuông tạo thành các đường chuyền kinh vĩ duỗi thẳng
với các điểm gốc là các điểm mép khung. Việc đo đạc, tính toán bình sai thực hiện như đối với đường chuyền.
4. Hoàn nguyên, cố định lưới
Từ tọa độ bình sai và tọa độ thiết kế của lưới ô vuông, tính các giá trị (góc, cạnh) để
chuyển các điểm lưới về đúng vị trí thiết kế.
Các điểm lưới được hoàn nguyên về vị trí thiết kế và cố định chắc chắn.
8.5.2 Chuyển trục công trình ra ngoài thực địa (định vị công trình)
Từ các mốc khống chế trắc địa, bố trí các điểm cố định các trục của công trình. Các
điểm này được cố định bằng các cọc gỗ hoặc bê-tông, hoặc được đánh dấu bằng đinh
hoặc vạch sơn trên hệ thống khung định vị (hay còn gọi cọc ngựa - hình 8.12, 8.13). 12 12 E E 6 6 B B 1 1 A A E 12 E 12 B 6 B 6 A 1 A 1
Hình 8.12 Định vị trục công trình
Hình 8.13 Định vị trục công trình
Các điểm này được xác định độ cao bằng đo cao hình học để phục vụ công tác thi công.
Dựa vào các điểm cố định các trục, bố trí các điểm chi tiết của công trình.
8.5.3 Chuyển trục công trình xuống đáy hố móng
Trong trường hợp đáy hố móng không sâu và công trình nhỏ, từ các điểm cố định
các trục, căng dây thép để dóng các trục và dùng quả dọi để chiếu các giao điểm của chúng xuống đáy móng.
Trường hợp ngược lại phải sử dụng máy kinh vĩ để chuyển trục xuống. Đặt máy
kinh vĩ tại cọc định vị trục, định hướng sang điểm định vị đối diện, xác định hướng trục
dưới đáy móng. Làm tương tự ta s¿ chuyển được các trục khác xuống đáy móng. 90
8.5.4 Chuyển độ cao xuống đáy hố móng
Khi cần chuyền độ cao xuống hố móng, trong trường hợp móng nông (nhỏ hơn
3m), sử dụng máy thuỷ bình và mia tiến hành như đo cao hình học thông thường.
Trong trường hợp móng sâu, việc chuyền độ cao phải kết hợp thêm thước thép và tiến hành như hình 8.14 a s Th-íc thÐp A t b
Hình 8.14 Chuyển độ cao xuống đáy hố móng
Độ cao đáy móng được tính theo công thức: Hm = HA + s – (b - a) – t (8.26)
8.5.5 Chuyển trục công trình lên tầng cao
Sau khi xây xong sàn tầng 1, các trục phải được đánh dấu lại trục lên sàn tầng 1
(nếu chuyển trục bằng máy chiếu đứng), hoặc gửi trục ra xa (nếu chuyển trục bằng máy
kinh vĩ) để tiếp tục chuyển các trục lên trên các sàn tầng cao.
Có thể dùng dây dọi để chuyển trục lên tầng với công trình thấp dưới 4 tầng.
Dùng máy kinh vĩ để chuyển trục lên tầng với công trình thấp dưới 10 tầng.
Ví dụ: cần chuyển trục AA, đặt 1 1
máy kinh vĩ tại điểm A, định hướng A
tới điểm thứ hai đánh dấu trục AA
(hình 8.15), cố định bàn độ ngang,
đưa ống kính lên sàn, đánh dấu được điểm A 1. Đảo kính làm tương
tự được điểm A2. Điểm giữa của A1, 1 1 A2 là điểm A. A
Hình 8.15 Chuyển trục công trình lên cao 91 bằng máy kinh vĩ
Đối với nhà cao trên 10 tầng dùng
máy chiếu đứng, khi đó phải để các lỗ trống
20x20cm trên các sàn (hình 8.16), trục s¿
được máy truyền qua các lỗ này lên sàn cần thiết.
Hình 8.16 Chuyển trục công trình lên cao bằng máy chiếu đứng
8.5.6 Chuyển độ cao lên tầng
Chuyển độ cao lên tầng, cũng a t
tương tự như chuyển độ cao xuống đáy móng. Khi đó:
H = HA + s + (a - b) - t (8.27) Th-íc thÐp s b
Hình 8.17 Chuyển độ cao lên tầng
8.5.7 Chỉnh cột thẳng đứng
Khi thi công nhà khung, nhà công nghiệp,... phải đảm bảo các cột thẳng đứng. Nếu
cột không cao, thi công đổ tại chỗ thì có thể dùng dây dọi để chỉnh. 92
Nếu yêu cầu độ chính xác cao
hơn, dùng hai máy kinh vĩ đặt ở hai
hướng vuông góc nhau để chỉnh, tim
cột được đánh dấu ở chân và đỉnh
cột, điều chỉnh cho hai điểm này
cùng nằm trong mặt phẳng ngắm (hình 8.18).
Hình 8.18 Chỉnh cột thẳng đứng bằng máy kinh vĩ
Trường hợp lắp các cột thẳng hàng,
để điều chỉnh thẳng hàng, đặt máy kinh vĩ a
cách dãy cột một đoạn a = 1 1.5m, mia a
đặt ngang trên cột (hình 8.19) và điều chỉnh
cột nhờ số đọc trên mia.
Hình 8.19 Chỉnh các cột thẳng hàng
8.5.8 Đo vẽ hoàn công
Đo v¿ hoàn công công trình là đo đạc và biểu diễn vị trí, kích thước, hình dáng thực
tế của công trình sau khi thi công.
Bản v¿ hoàn công là tài liệu quan trọng để đánh giá chất lượng thi công, là cơ sở
cho việc sửa chữa, mở rộng công trình sau này.
Việc đo v¿ hoàn công có thể thực hiện sau khi xây dựng xong từng phần (móng,
từng tầng nhà...) hoặc toàn bộ công trình và cũng tiến hành tương tự như đo v¿ chi tiết 93
bình đồ về vị trí, ngoài ra còn đo v¿ các kích thước của các hạng mục như đường ống cống ngầm,…
Về nguyên tắc, tất cả các số liệu ghi trên bản thiết kế đều phải đo đạc lại trên thực
tế và thể hiện bản v¿ bình đồ hoàn công.
8.6 QUAN TRẮC CHUYỂN DỊCH BIẾN DẠNG CÔNG TRÌNH 8.6.1 Khái niệm
Trong quá trình thi công công trình, tải trọng của công trình s¿ tăng dần theo thời
gian. Trong quá trình sử dụng, hoạt tải của công trình cũng liên tục thay đổi. Theo thời
gian, các điều kiện ngoại cảnh như biến động của vỏ Trái đất, động đất, ảnh hưởng của
các công trình bên cạnh,… cũng ảnh hưởng tới công trình. Các ảnh hưởng này làm công
trình bị chuyển dịch trong không gian, nếu chuyển dịch không đều s¿ dẫn tới biến dạng và phá huỷ công trình.
Công trình chuyển dịch theo hai phương: phương thẳng đứng (trồi lún) và phương ngang (chuyển vị).
Quan trắc chuyển dịch là đo đạc, phân tích đánh giá và dự báo độ chuyển dịch của
công trình, từ đó có biện pháp xử lý, đề phòng các tai biến có thể xảy ra.
Thực tế, công trình thường chuyển dịch nhỏ và diễn ra theo thời gian, vì vậy phải
sử dụng các phương pháp và dụng cụ có độ chính xác cao để quan trắc. 8.6.2 Quan trắc lún
Trồi lún là chuyển dịch của công trình theo phương thẳng đứng, nguyên nhân chủ
yếu do tải trọng và điều kiện nền móng của công trình. Hầu hết các công trình là bị lún, do
đó quan trắc chuyển dịch thẳng đứng được gọi là quan trắc lún.
Độ lún công trình (S) là sự thay đổi độ cao của công trình theo thời gian: Sj = Hj – Hj – 1 (8.28) Sj = Hj – H0 (8.29)
Trong đó: Hj, Hj-1, H0: độ cao công trình ở thời điểm j, j-1, 0. 94
Như vậy, để quan trắc lún, cần lập lưới độ cao với các mốc là các điểm đặc trưng
của công trình và đo đạc xác định độ cao các điểm đặc trưng ở nhiều thời điểm khác nhau.
1. Lưới độ cao quan trắc lún công trình
Thành lập hai cấp lưới khống chế độ cao độc lập nhau:
- Lưới khống chế cơ sở: bao gồm các mốc có độ cao ổn định trong suốt quá trình
quan trắc (mốc chuẩn), được bố trí nơi có điều kiện địa chất tốt và ngoài khu vực chịu ảnh hưởng của công trình.
Số mốc tối thiểu của lưới là 3, được bố trí thành cụm hoặc riêng biệt. Mốc gốc có
thể chôn sâu tận tầng cuội sỏi, chôn nông hay gắn lên các công trình khác đã ổn định.
- Lưới quan trắc: gồm các mốc được KÕt cÊu chÞu lùc
gắn trực tiếp vào các kết cấu chịu lực của
công trình và chuyển dịch cùng công trình.
Cấu tạo mốc quan trắc lún như hình 8.20.
Hình 8.20 Mốc quan trắc lún
2. Chu kỳ quan trắc lún
Việc đo đạc xác định độ cao các mốc chuẩn và mốc quan trắc lún phải diễn ra theo
từng chu kỳ. Thời gian giữa hai chu kỳ quan trắc phải phù hợp với diễn biến lún của công trình.
- Chu kỳ 0: được thực hiện khi xây xong phần móng công trình.
- Trong giai đoạn thi công: các chu kỳ tiếp theo được thực hiện theo tải trọng công
trình, lần lượt khi công trình đạt 25%, 50%, 75%, 100% tải trọng.
- Trong giai đoạn sử dụng: thời gian giữa các chu kỳ có thể thưa hơn, 2 tháng hoặc 6 tháng một chu kỳ.
Thời gian giữa các chu kỳ có thể thu nhỏ nếu công trình lún nhiều hoặc diễn biến lún phức tạp.
Việc quan trắc lún kết thúc nếu đã có kết luận về thời điểm tắt lún hoặc công trình
lún rất nhỏ, không ảnh hưởng tới việc sử dụng công trình. 95
3. Đo đạc, tính toán
Các phương pháp đo thường được áp dụng là: đo cao hình học, đo cao thuỷ tĩnh,
… Trong đó phổ biến là đo cao hình học.
Độ chính xác đo lún tương đương hạng II, hạng III Nhà nước. Máy sử dụng là máy
thuỷ bình độ chính xác cao có bộ đo cực nhỏ như Ni004, Ni007, …
Tiến hành đo đạc độc lập hai cấp lưới. Việc đo đạc phải tuân thủ nghiêm ngặt các
hạn sai của từng cấp hạng, phải tính toán sổ đo và kiểm tra sai số khép phải thực hiện ngay tại thực địa. Uết cấu chÞu lùc Mốc chuẩn III II 1 2 3 4 5 I Công trình 10 9 8 7 6
Hình 8.21 Sơ đồ mốc quan trắc lún và mốc chuẩn
Sau đó tiến hành bình sai lưới cơ sở và lưới quan trắc lún theo phương pháp chặt
ch¿ (nguyên lý số bình phương nhỏ nhất).
Tính toán các tham số lún:
Độ lún tuyệt đối của các mốc:
- Giữa hai chu kì j và j-1:
S j , j –1 = H j – H j –1 (8.30) i i i - So với chu kỳ 0:
S j ,0 = H j – H 0 (8.31) i i i
Độ lún trung bình của công trình ở chu kỳ j: n ΣSi j = i=1 (8.32) S tb n S j Tốc độ lún: v = tb (8.33) t Lún lệch: Slệch = Smax - Smin (8.34) 96
Ngoài ra, dựa vào các tham số lún trên người ta còn lập biểu đồ lún của các mốc
đặc trưng theo thời gian, biểu đồ lún của các trục, bình độ lún, …
8.6.3 Quan trắc dịch chuyển ngang
Chuyển dịch ngang công trình (chuyển vị) nguyên nhân chủ yếu do các lực phương
ngang tác động lên như áp lực nước tác dụng lên đập thuỷ lợi, thuỷ điện,…
Chuyển dịch ngang là sự thay đổi toạ độ mặt bằng của công trình theo thời gian: q = 2 x + 2 y (8.35)
x = X j – X i j–1 Trong đó: i (8.36)
y = Y j – Y j–1 i i
Tương tự như quan trắc lún, để quan trắc chuyển dịch ngang, cần lập lưới mặt
bằng có các mốc là các điểm đặc trưng của công trình và đo đạc xác định toạ độ các điểm
đặc trưng ở nhiều thời điểm khác nhau.
Việc đo đạc cũng theo từng chu kỳ, thời gian giữa các chu kỳ tuỳ thuộc vào áp lực
tác động lên công trình.
Có nhiều phương pháp để quan trắc chuyển dịch ngang như phương pháp hướng
chuẩn, bằng lưới đo góc cạnh, bằng GPS,… 97
Tài liệu tham khảo
[1] Phạm Văn Chuyên. Trắc địa trong xây dựng. Nhà xuất bản Giáo dục. 1996.
[2] Vũ Thặng. Trắc địa đại cương. Nhà xuất bản Xây dựng. 2000.
[3] Vũ Thặng. Lý thuyết sai số và bình sai. Bài giảng. Trường đại học Xây dựng hà Nội. 2011.
[4] Trần Văn Quảng. Trắc địa đại cương. Nhà xuất bản Xây dựng. 2001.
[5] Nguyen Thac Dung. La topographie en construction. Maison d’édition de l’Education. 1997.
[6] Tổng cục địa chính. Thông tư hướng dẫn áp dụng hệ quy chiếu và hệ toạ độ
quốc gia VN-2000. Số 973/2001/TT-TCĐC. 2001.
[7] Bộ Tài nguyên và môi trường. Quy định kỹ thuật thành lập bản đồ địa hình tỷ lệ
1:10000, 1:25000 và 1:50000 bằng công nghệ ảnh số. Quyết định số 15/2005/QĐ-BTNMT. 2005.
[8] Cục Đo đạc bản đồ Nhà nước. Quy phạm đo v¿ bản đồ địa hình tỷ lệ 1:500, 1:1000,
1:2000, 1:5000. Hà Nội. 1976. 98




