













Preview text:
lOMoAR cPSD| 40551442
Chương 1. HÀM SỐ NHIỀU BIẾN SỐ
Chương 1. HÀM SỐ NHIỀU BIẾN SỐ lOMoAR cPSD| 40551442
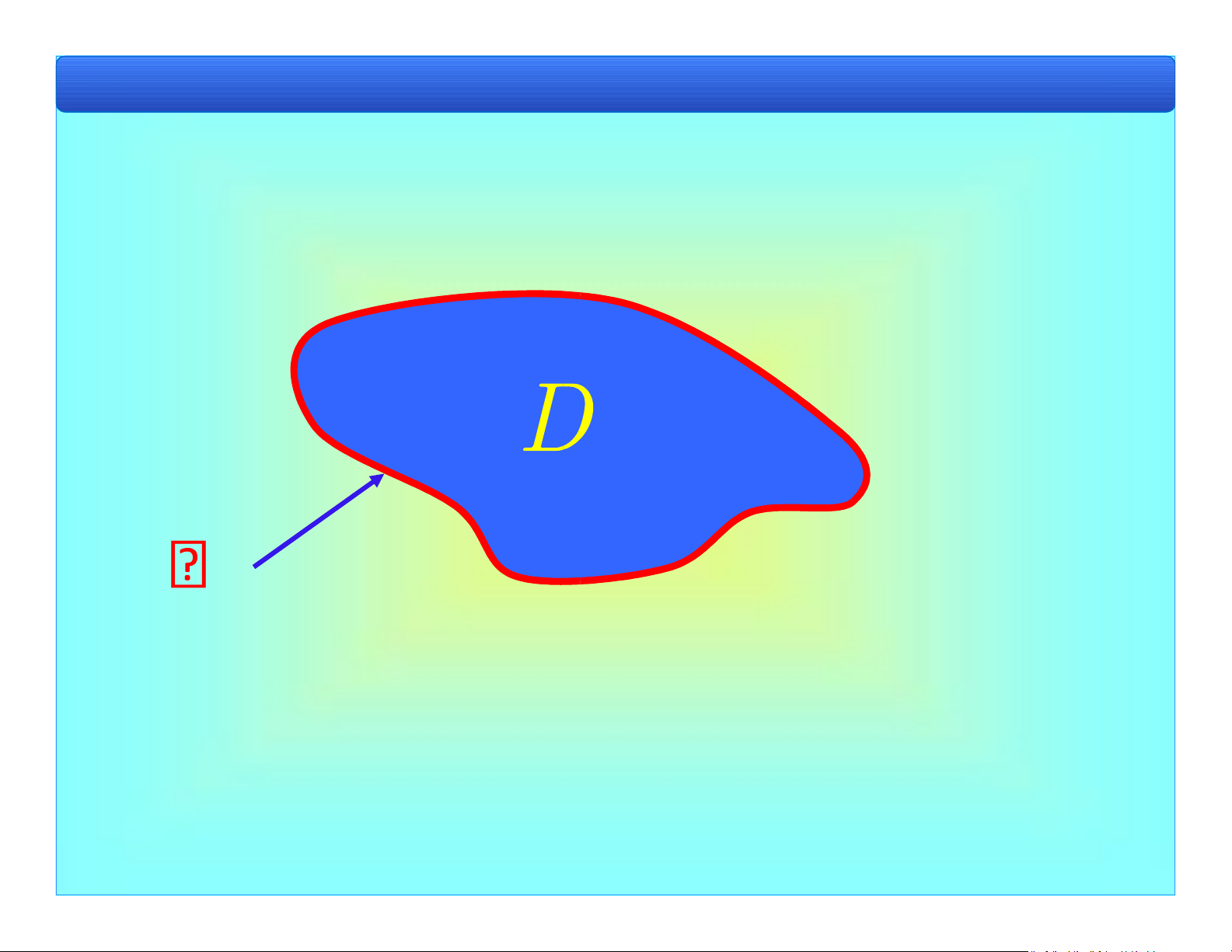
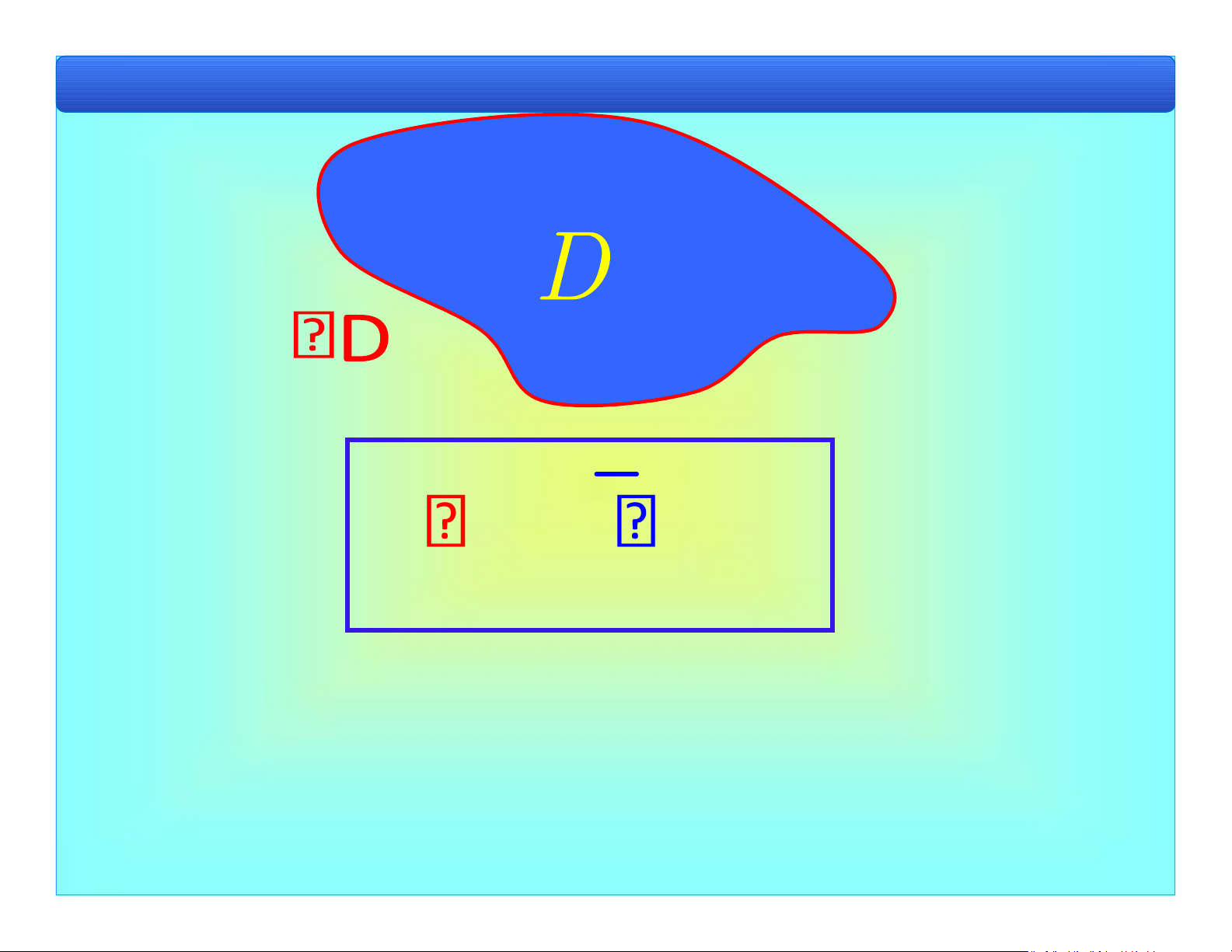
Bài 1. Khái niệm cơ bản lOMoAR cPSD| 40551442 1.1. Các ịnh nghĩa a) Miền phẳng D lOMoAR cPSD| 40551442
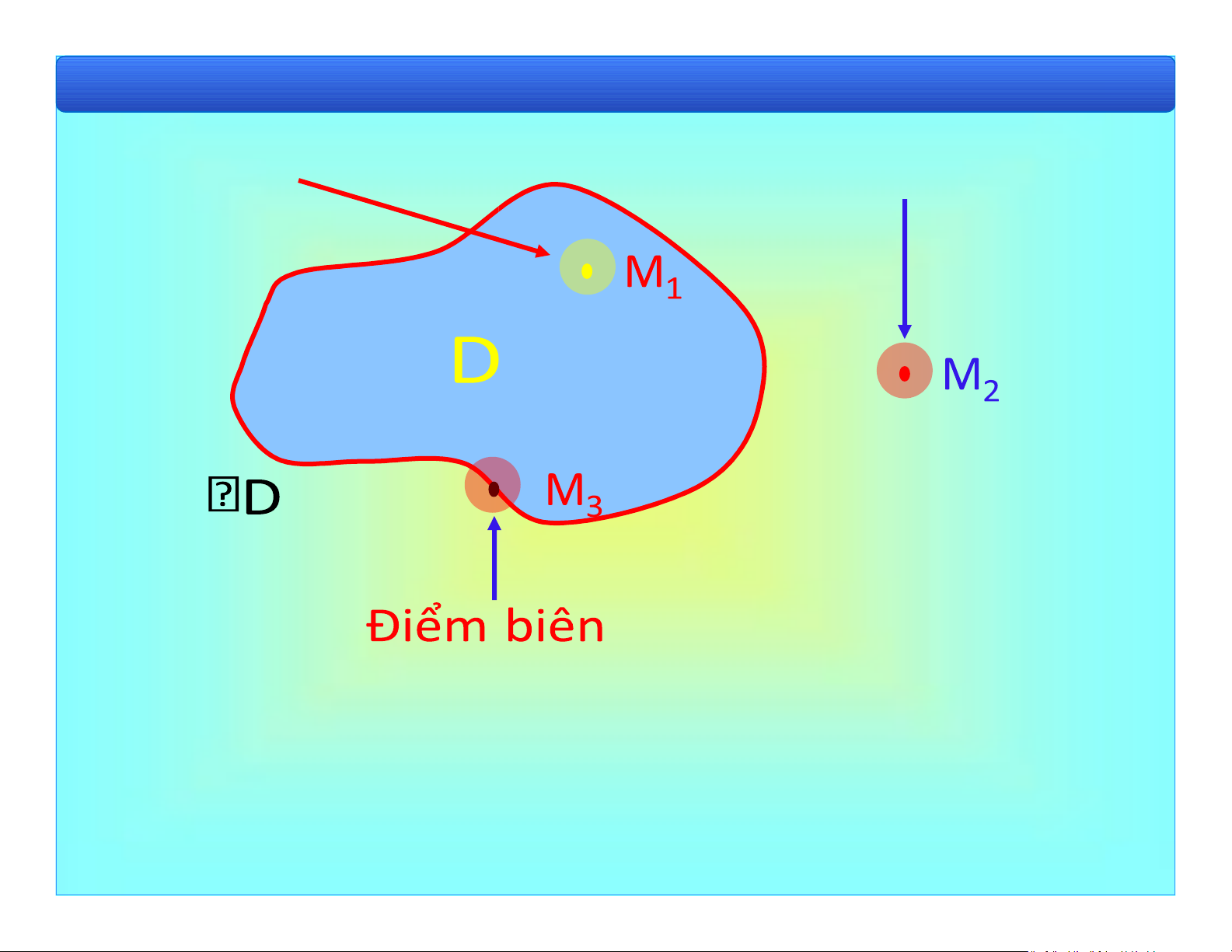
Bài 1. Khái niệm cơ bản Điểm trong Điểm ngoài Miền óng lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản D D D Miền mở lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản D D D\ lOMoAR cPSD| 40551442
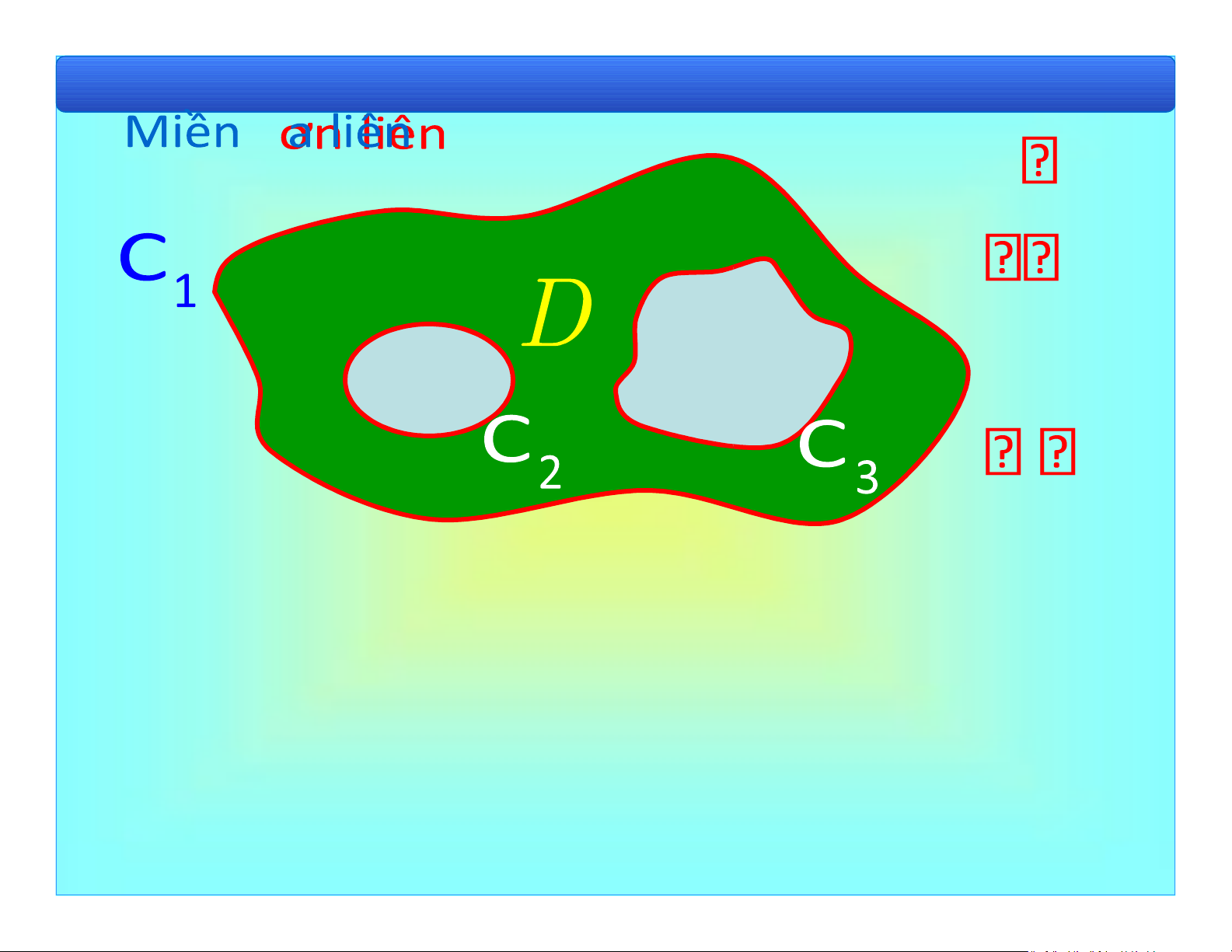
Bài 1. Khái niệm cơ bản D C C CD 1 2 3 lOMoAR cPSD| 40551442
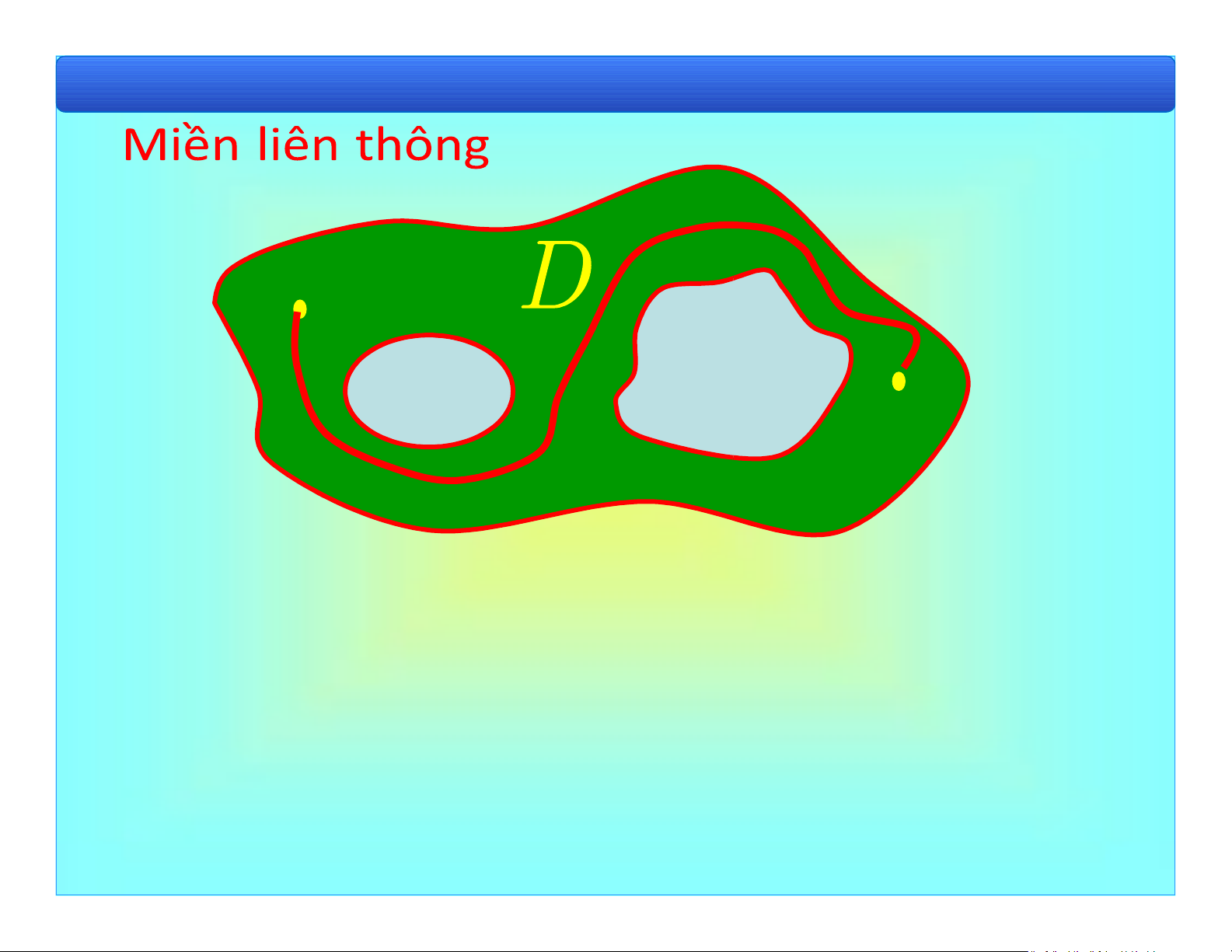
Bài 1. Khái niệm cơ bản Miền không liên thông lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản
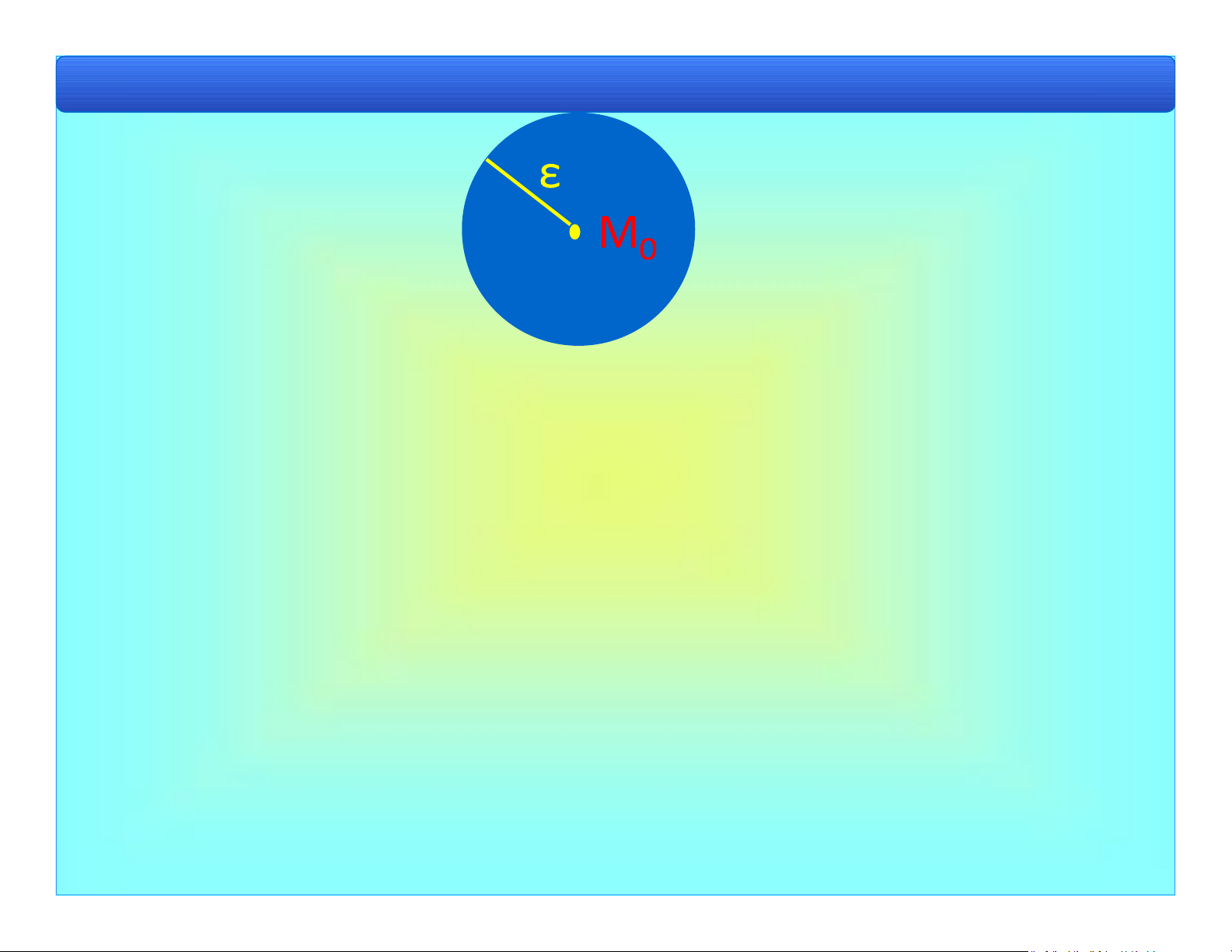
b) Lân cận của một iểm trong mặt phẳng lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản S(M0,ε) lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản M S M ( 0, ) d M M( , • 0) ε H(M0,ε) M0 |x x | M x y( , ) H M( 0, ) |y y 00 | d) Hàm số hai biến số lOMoAR cPSD| 40551442
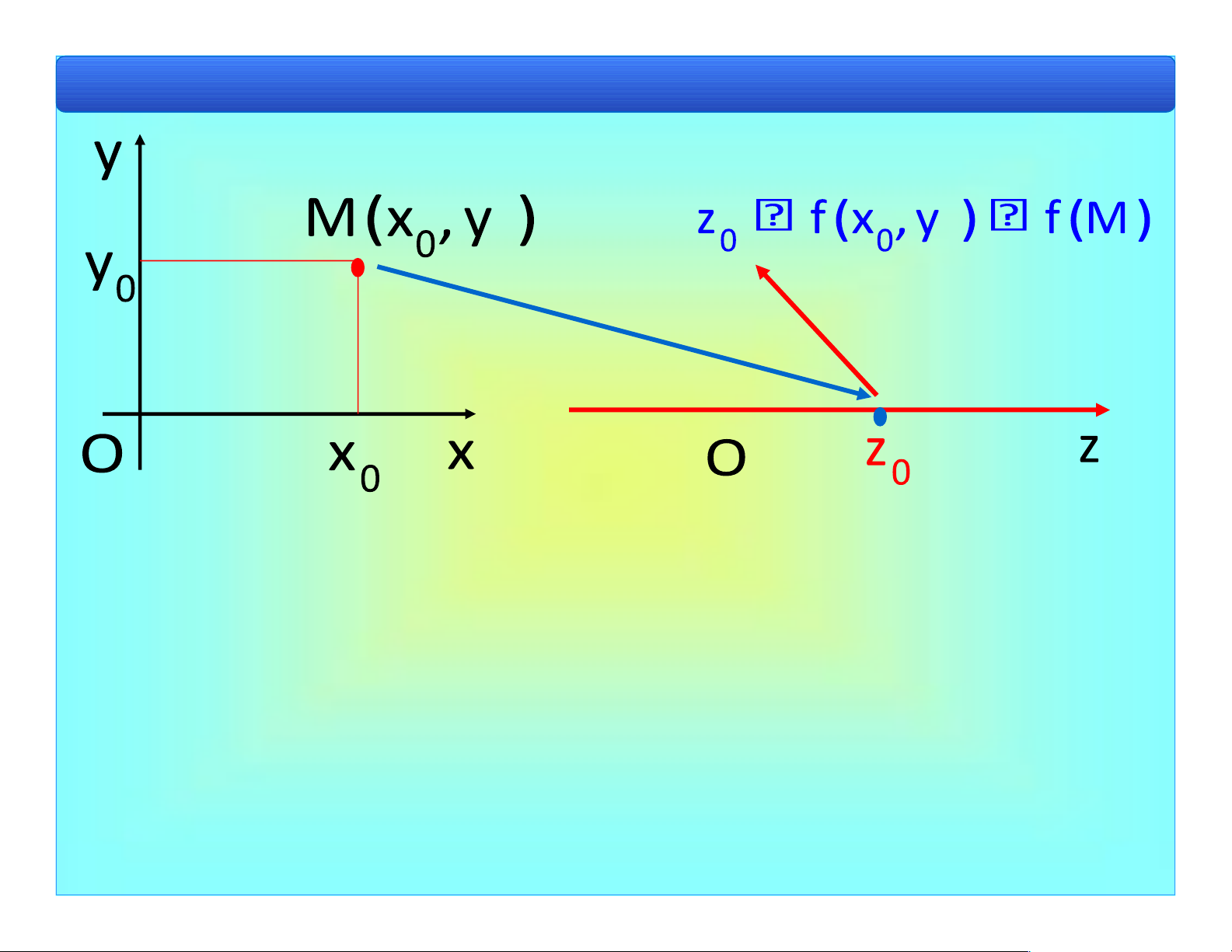
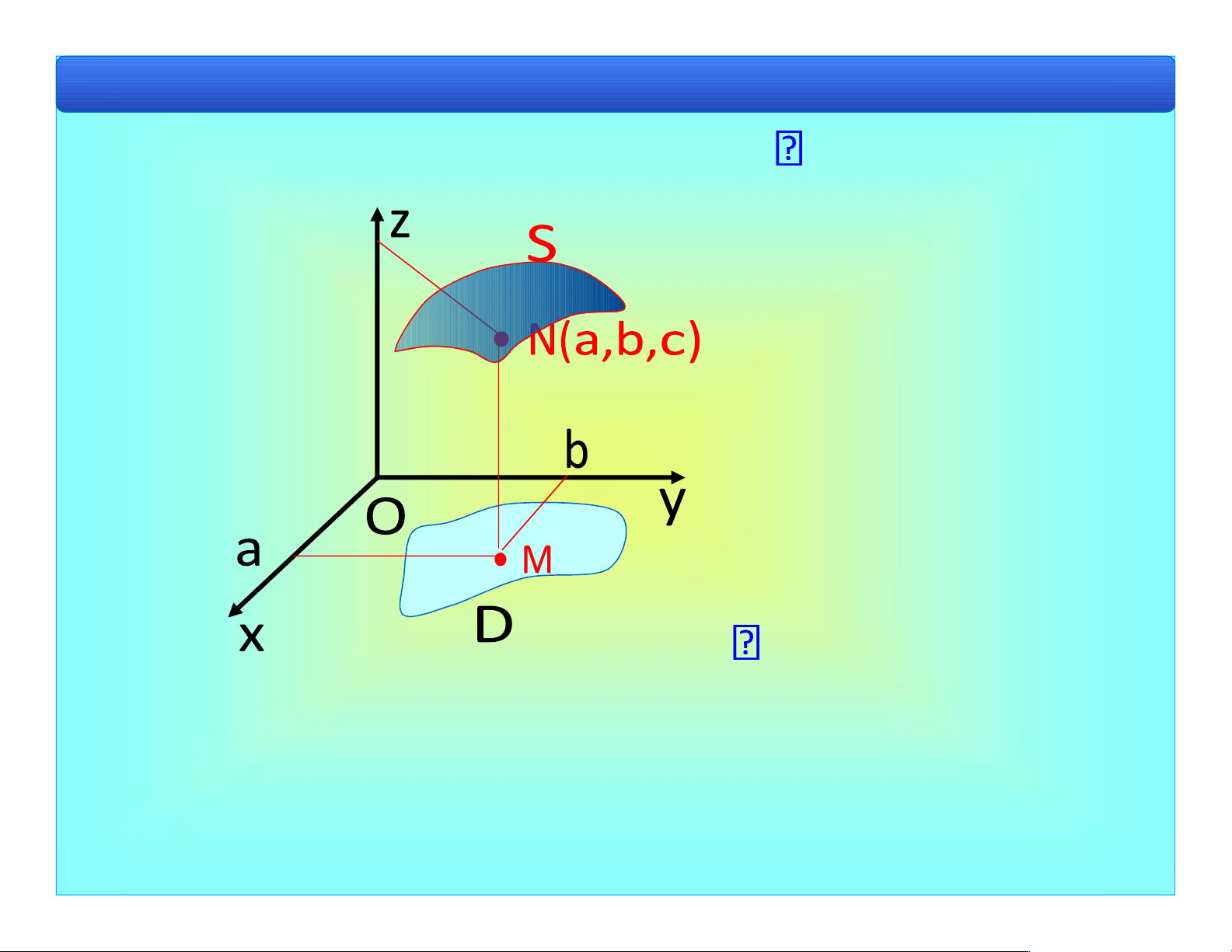
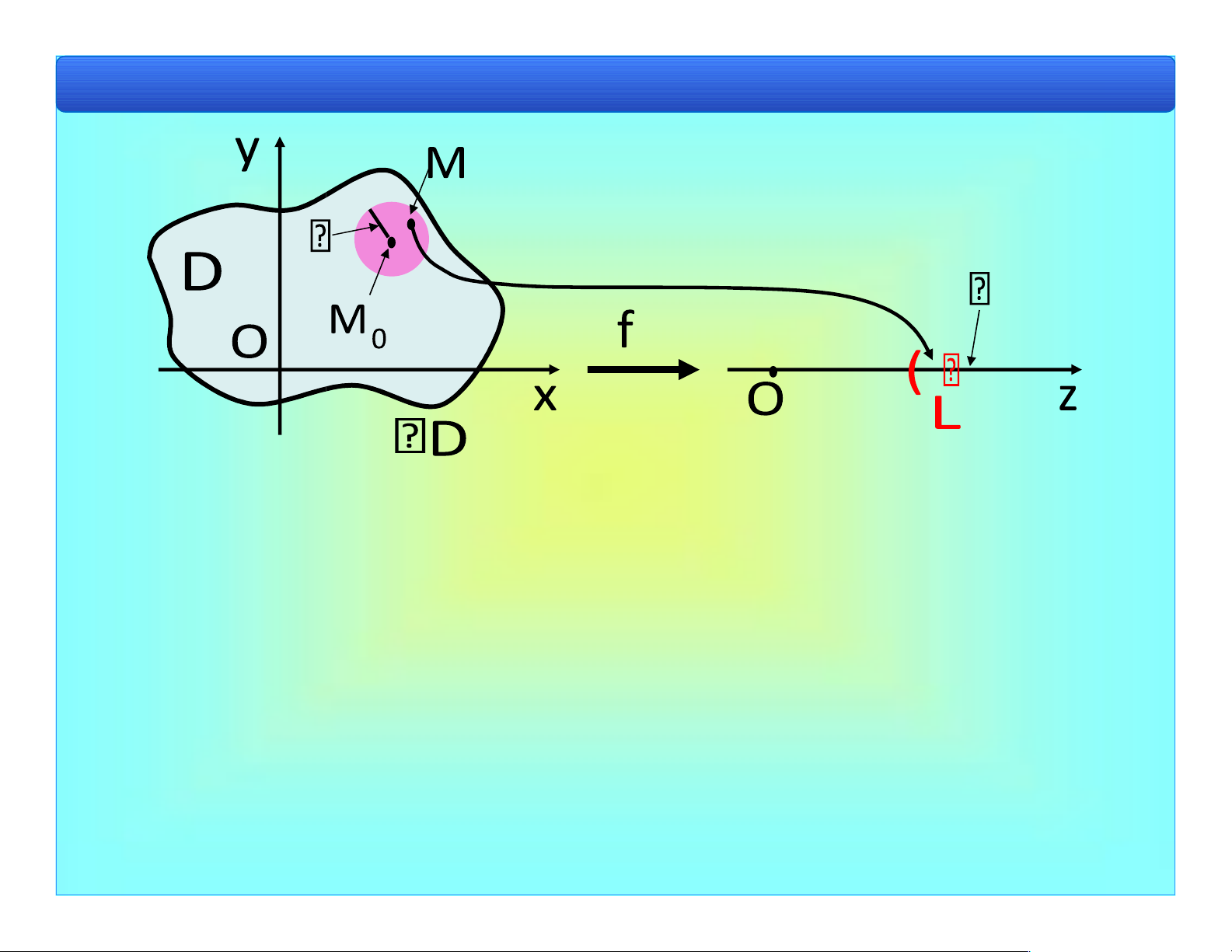
Bài 1. Khái niệm cơ bản f : D 2 (x,y) D z f(x,y) .
• Tập D 2 ược gọi là miền xác ịnh (MXĐ) của hàm
số f x y( , ), ký hiệu là Df . Df {(x y, ) 2 | ( , )f x y }
• z f x y( , ) ược gọi là giá trị của hàm số tại (x y, ). lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản
Đồ thị của hàm số z = f(x,y) f M( ) f(a,b ) c lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản S {(x y f M, , ( ))|M x y( , ) D} VD 1
• Hàm số f x y( , ) 3x y2 cosxy có Df 2.
• Hàm số z 4 x2 y2 có MXĐ là hình tròn óng tâm
O(0; 0), bán kính R 2. Vì M x y( , ) Dz 4 x2 y2 0 lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản x2 y2 4.
• Hàm số z ln(4 x2 y2) có MXĐ là hình tròn mở tâm O(0; 0), bán kính R 2. Vì M x y( , ) Dz 4 x2 y2 0 x2 y2 4. lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản
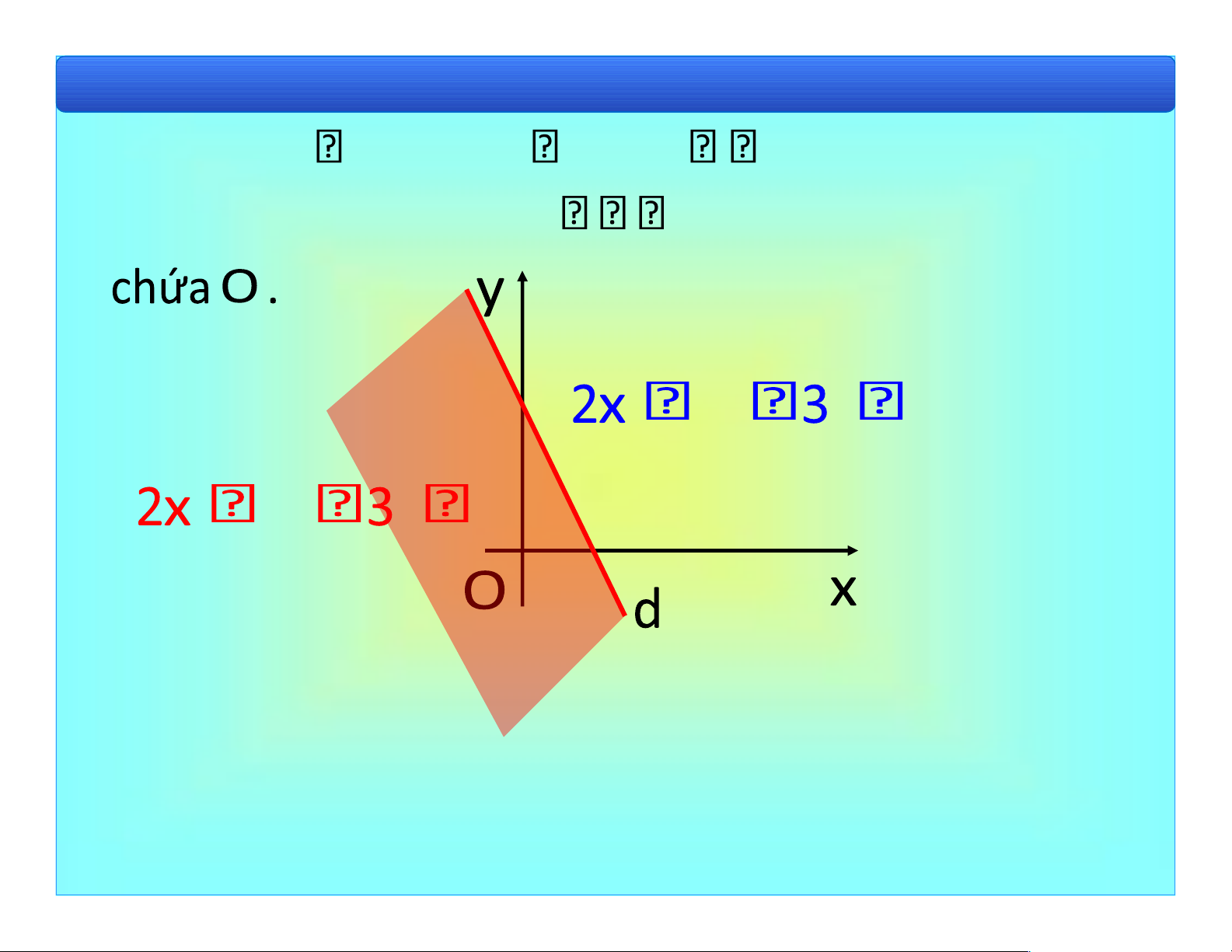
• Hàm số z f x y( , ) ln(2x y 3) có MXĐ là nửa
mp mở có biên d : 2x y 3 0, không lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản
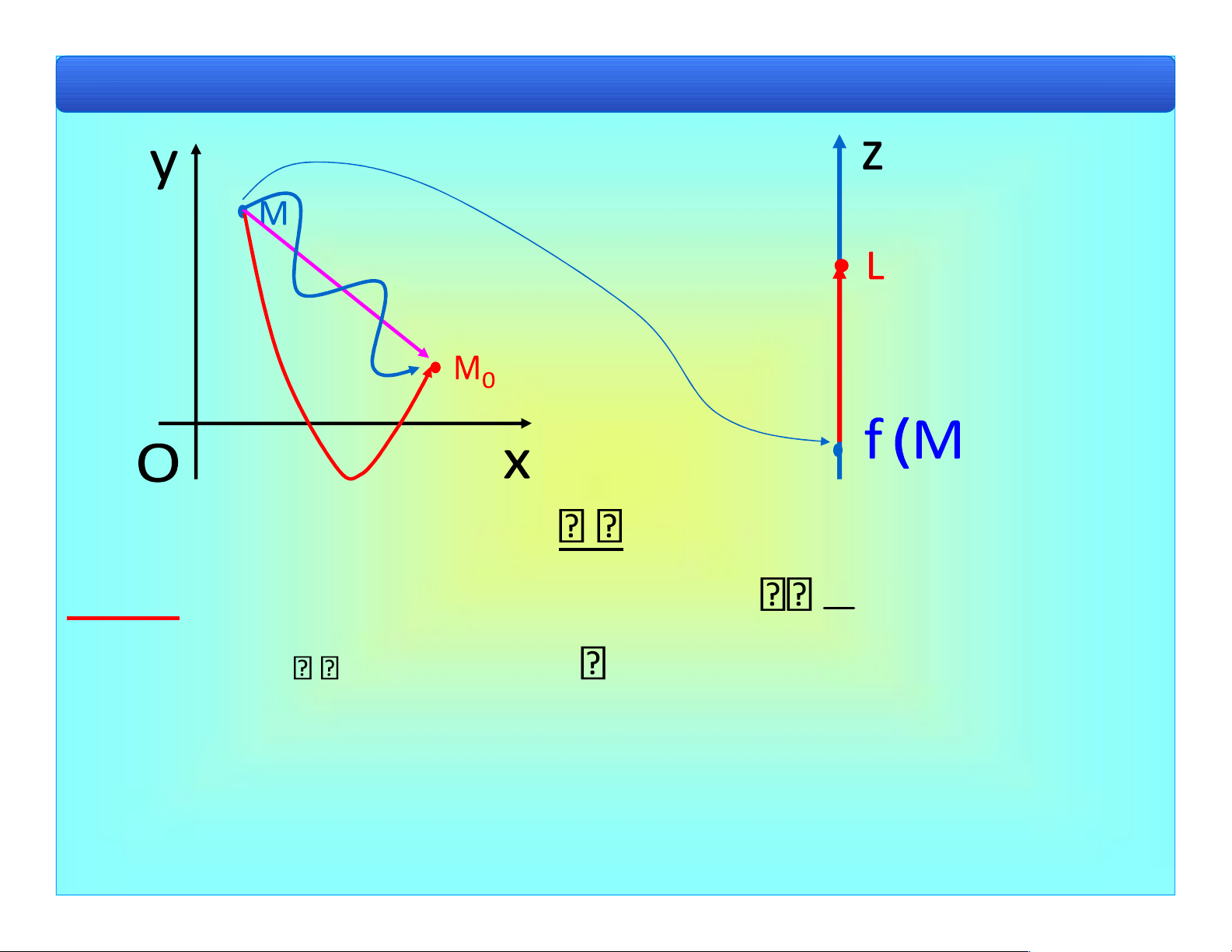
1.2. Giới hạn của hàm số hai biến số a) Điểm tụ • Mn • • • • ••••• •• • • • •
• M••••• 0 • • , lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản
VD. O(0, 0) là iểm tụ của dãy iểm Mn n1 12 . n
b) Định nghĩa giới hạn kép (giới hạn bội) lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản M x y • Điểm
0( 0, 0) ược gọi là giới hạn của dãy iểm M
xn( n, yn), n 1,2,... nếu M x0 0( , y0) là iểm tụ duy nhất của dãy.
Ký hiệu là: lim M M hay M n M . n n 0 n 0 lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản
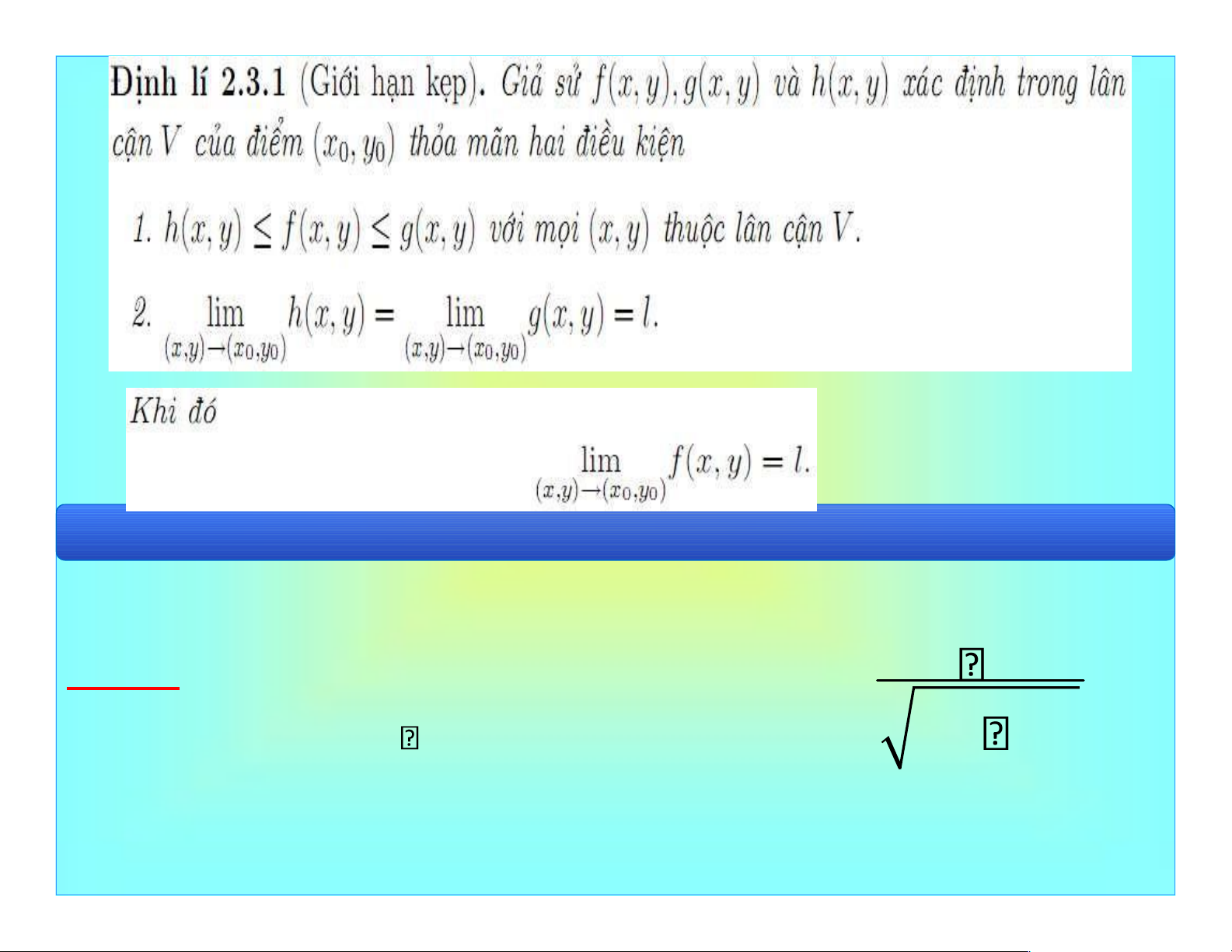
• Hàm số f x y( , ) có giới hạn là L { } khi Mn n M0 nếu nlim f x( n, yn) L.
Ký hiệu là L lim f M( ) M M0 lim f x y( , ) lim f x y( , ). (x y, ) (x y0, 0) x x 0 y y 0 lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản lOMoAR cPSD| 40551442
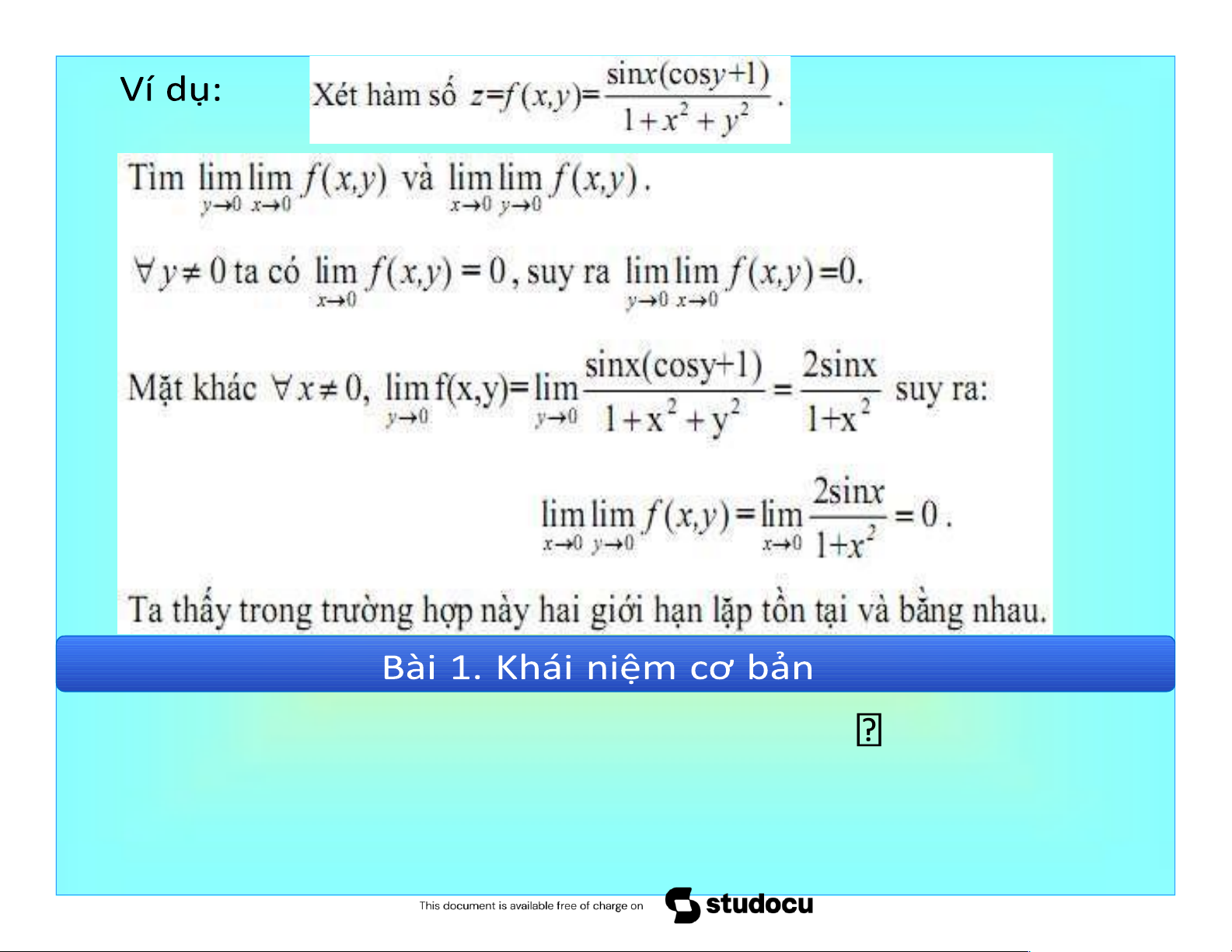
Bài 1. Khái niệm cơ bản 2x y2 3x 1 3 VD 2. lim . (x y, ) (1, 1) xy2 3 2 lOMoAR cPSD| 40551442 Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442 cos
Bài 1. Khái niệm cơ bản sin(x2 y2) VD 4. Tìm lim .
Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442 (x y, ) (0,0) x2 y2
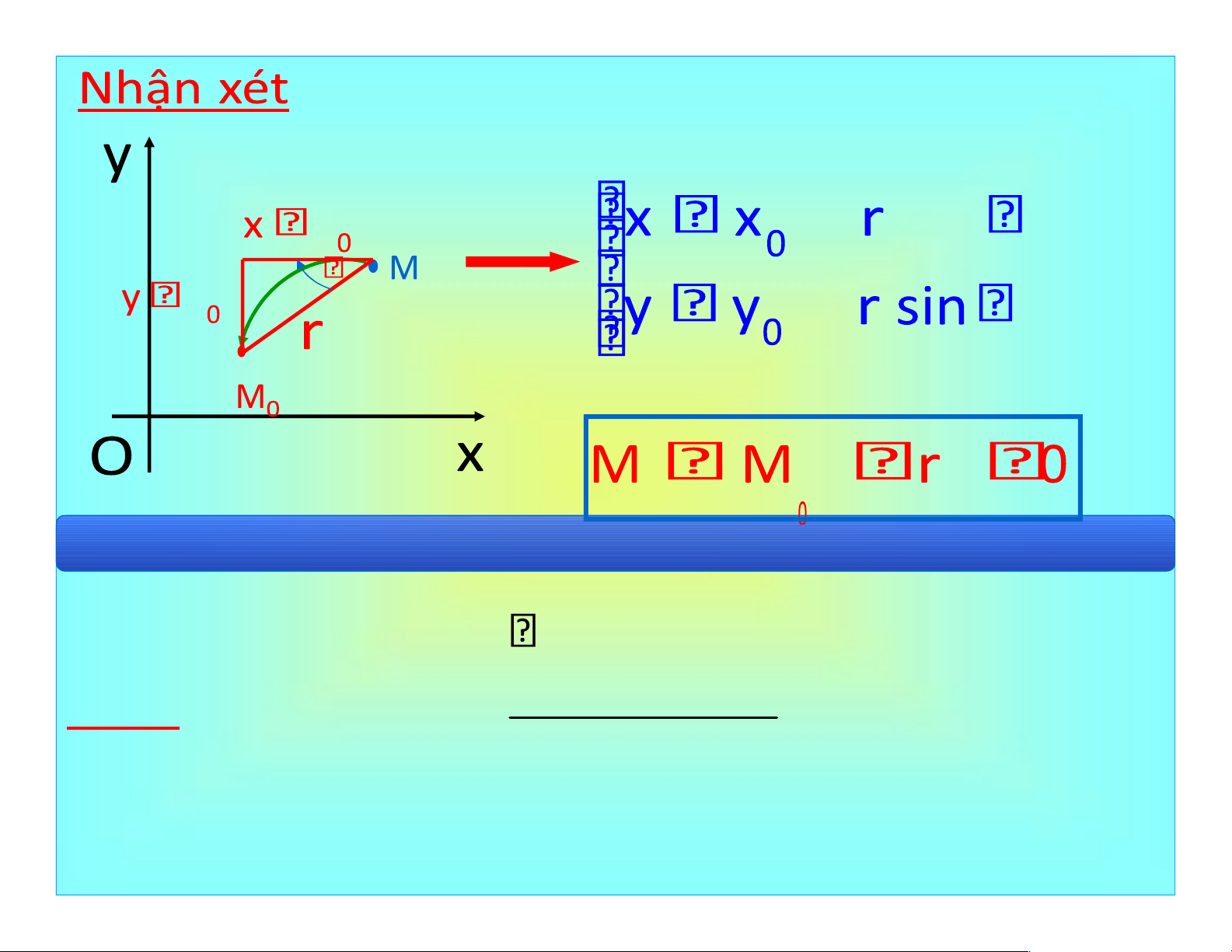
Giải. Đặt x r cos , y r sin , ta có: sin(x2 y2) sinr2 lim lim 1. (x y, ) (0,0) x2 y2 r 0 r2 Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442
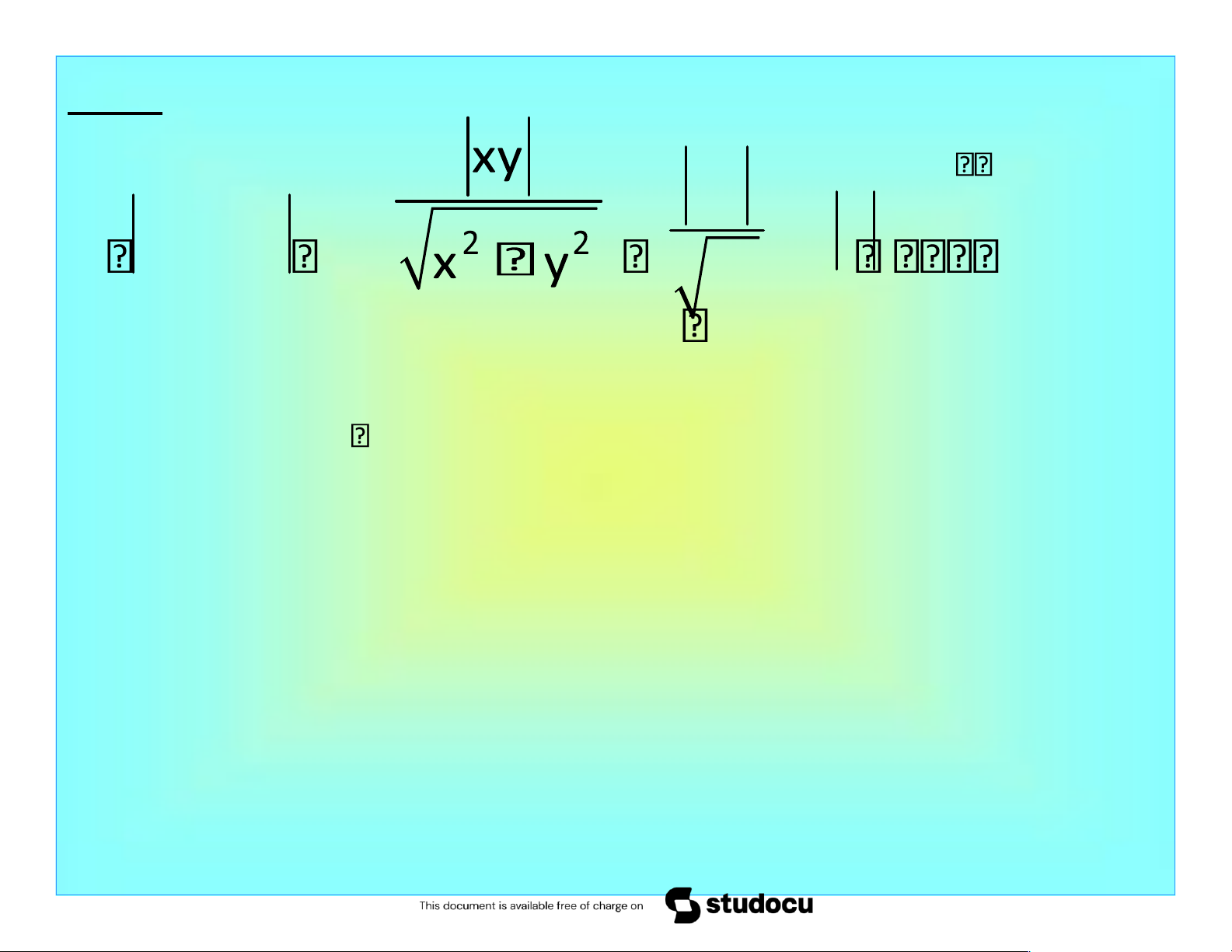
Bài 1. Khái niệm cơ bản xy VD 3. Tìm lim f x y( , ), f x y( , ) . (x y, ) (0,0) x2 y2
Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442 Giải. xyyx 00 0 f x y( , ) x 0. y2 Vậy lim f x y( , ) 0. (x y, ) (0,0) Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442
Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442 2xy Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442
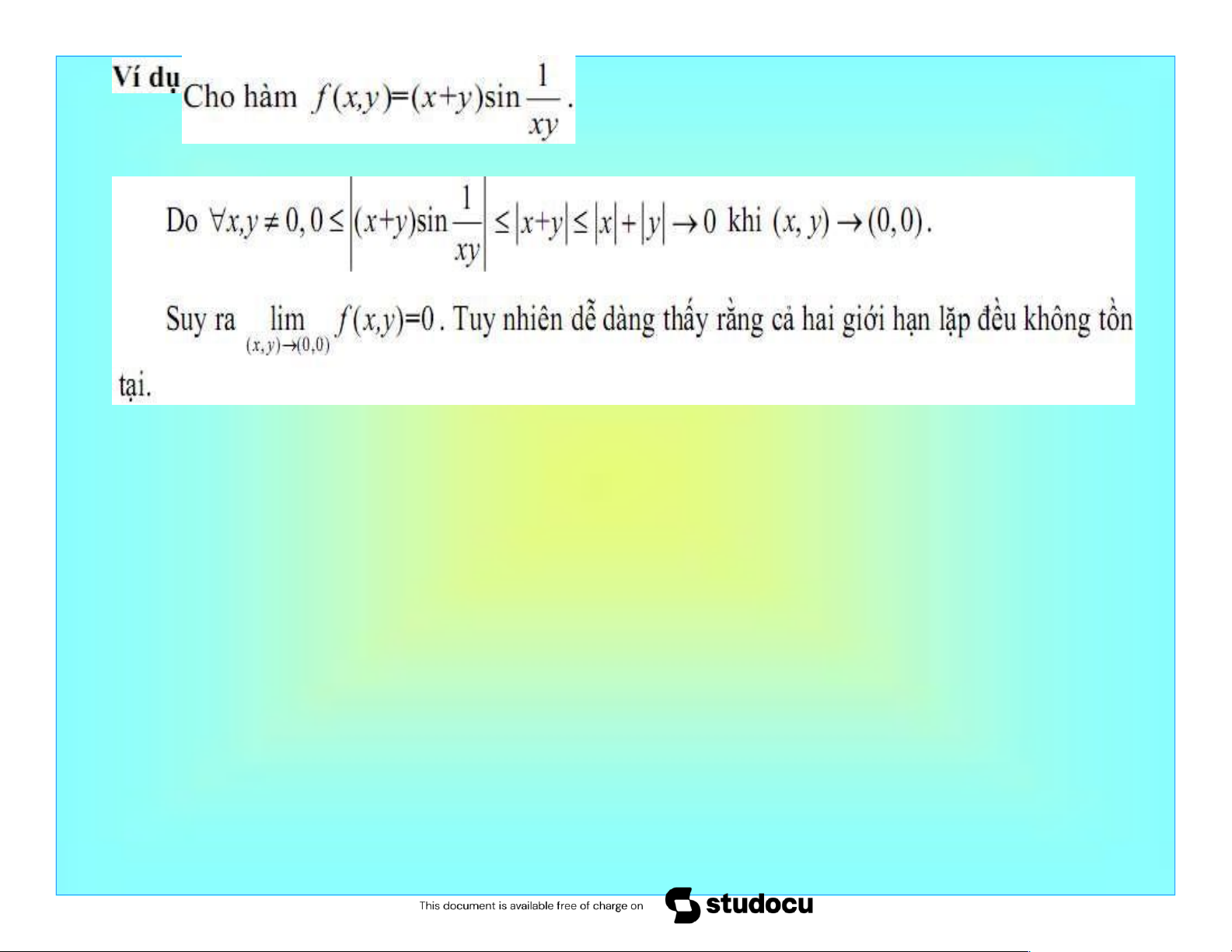
VD 5. Cho hàm số f x y( , ) . x2 y2 Chứng tỏ rằng
lim f x y( , ) không tồn tại. (x y, ) (0,0)
Giải. Đặt x r cos , y r sin , ta có: r2 sin2 lim f x y( , ) lim sin2 . (x y, ) (0,0) r 0 r2
Do giới hạn phụ thuộc vào nên không duy nhất. Vậy
lim f x y( , ) không tồn tại. (x y, ) (0,0)
Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442 c) Giới hạn lặp M x y ( ,
Giới hạn theo từng biến khi dãy iểm n n n) dần
ến M0 của f x y( , ) ược gọi là giới hạn lặp.
• Khi x x0 trước, y y0 sau thì ta viết lim lim ( , )f x y y y 0 x x 0
• Khi y y0 trước, x x0 sau thì ta viết Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442 lim lim ( , )f x y x x0 y y0 Giới hạn lặp
Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442 sinx2 siny2 Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442
VD 6. Xét hàm số f x y( , ) . Ta có: x2 y2 siny2 lim lim ( ,f x y) lim 1, y 0 x 0 y 0 y2 sinx2 lim lim ( , )f x y lim 1. x 0y 0 x 0 x2
Vậy lim lim ( , )f x y lim lim ( ,f x y). y 0x 0 x 0y 0
Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442 Chú ý
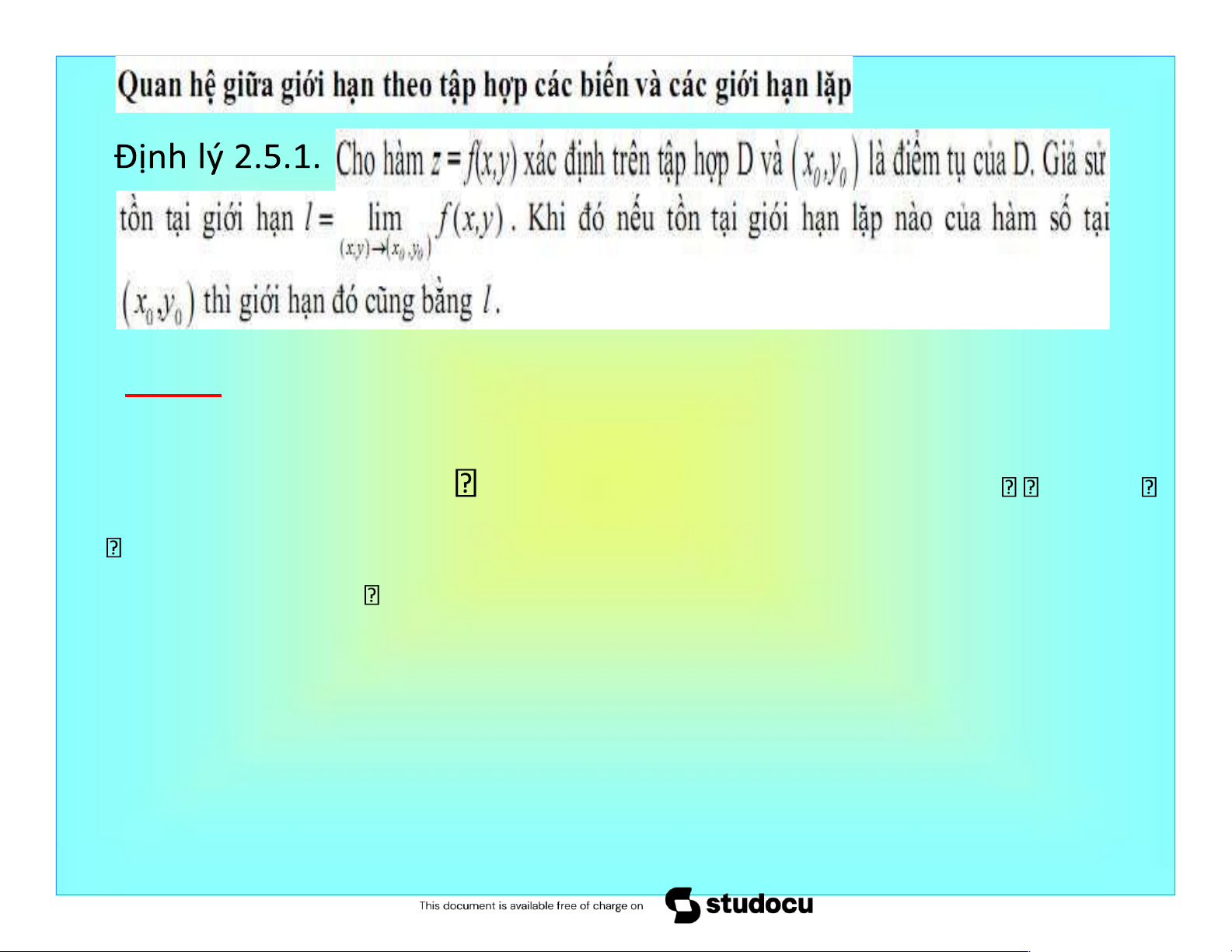
• Nếu lim lim f x y( , ) lim lim f x y( , ) thì không y y x x 0 0 x x y y
0 0 tồn tại lim f x y( , ). (x y, ) (x y0 0, )
• Sự tồn tại giới hạn lặp không kéo theo sự tồn tại của giới hạn bội. Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442
Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442 Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản 1.3. Hàm số liên tục
• Hàm số f x y( , ) liên tục tại M x y0 0 0( , ) D 2 nếu
(xy, )lim (x y0 0,) f x y( , ) f x y( 0, 0)
Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản
• Hàm số f x y( , ) liên tục trên tập D 2 nếu nó liên
tục tại mọi iểm thuộc D. Chú ý
Hàm số f x y( , ) liên tục trên miền óng giới nội D thì
nó ạt giá trị lớn nhất (max) và nhỏ nhất (min) trên D. Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản sinx2 siny2
VD 7. Xét sự liên tục của f x y( , ) . x2 y2 Giải
• Với (x y, ) (0, 0) thì hàm số f x y( , ) xác ịnh nên liên
tục. • Tại (0, 0) thì lim f x y( , ) không tồn tại. (x y, ) (0,0)
Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442
Bài 1. Khái niệm cơ bản
Vậy hàm số f x y( , ) liên tục trên 2 \{(0, 0)}. Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442
Downloaded by H?u h?u Mai mai (abcdefghis@gmail.com) lOMoAR cPSD| 40551442 Ví dụ 3.1.2: f( x,y) x2 y2 ,( x,y) (00, ). 0 ,( x,y) (00, )
………………………………………………………. Downloaded
by H?u h?u Mai mai (abcdefghis@gmail.com)




