



Preview text:
lOMoAR cPSD| 59994889
Một Vi Đặc Tnh Của Ma Phương T Đồng Lời ni ầu
Nhiều hnh thể c ặc tnh ha hợp hiếm thấy trong sinh-học nhưng lại rất dễ xuất
hiện trong toÆn-học. Tỷ dụ cÆc hnh dạng cn ối của hnh-học, cÆc ường tuần
hon của ại-số, cÆc chuỗi số ều ặn của số-học, cÆc quĩ ạo ặc sắc trong cơ-học.
Ma Phương cũng mang một hnh ảnh ha hi ấy. Đy l một ề ti vui tươi, m trŒn
mạng lưới ton cầu hiện nay ª c gần hai triệu trang ´u Mỹ viết về vấn ề ny. Người
ta chœ ến Ma Phương, c lẽ bởi tnh cÆch kỳ lạ hoặc thần b, v ni ến sự thực
dụng th thật sự khng c mấy. C rất nhiều loại Ma Phương, nŒn bi ny chỉ m tả
về hai loại chnh: Ton Ma Phương (Full Magic Square) v BÆn Ma Phương (Semi Magic Square).
Ma Phương ược biết từ thời xa xưa, ở cả bŒn Đng lẫn bŒn Ty. Ma Phương,
hay " vung thần kỳ" l một hnh vung ược chia lm nhiều nhỏ, mỗi chứa một
con số từ 1 trở lŒn, m tổng cộng của cÆc con số trong mọi hng ngang, hng
dọc hay hai ường chØo chnh, gọi l hằng số của Ma Phương, ều bằng nhau.
Loại ny l Ton Ma Phương. Trong một nhm nhỏ của loại ny, ặc biệt cÆc con
số của mọi ường chØo phụ cũng cho một tổng số y hệt, nŒn ta c thể gọi l LiŒn
Ma Phương (Pan Magic Square). C người cn gọi chœng l Quỉ Ma Phương
(Diabolic Magic Square) v tnh cÆch quÆi ản của Ma Phương ny. Ta c thể gọi
chœng l SiŒu Ma Phương hay Super Magic Square.
Một vi cÆch vẽ cho một Ma Phương c thể tm thấy trong những thư mục của
bi ny (1, 2, 3, 4, 5). Ta hªy xØt sơ lược cÆch thiết lập của hai nhm chnh: Ma
Phương lẻ v Ma Phương chẵn, cøng một vi cÆch chuyển hoÆn từ một Ma
Phương ny tới một Ma Phương khÆc. Đối với khoảng 880 Ma Phương chẵn
4-4 (5), ta sẽ tổng kết 12 m hnh ặc biệt của loại Ton Ma Phương ny. ThŒm vo
, sự tạo thnh v những m hnh ặc biệt khÆc trong cÆc BÆn Ma Phương 4-4
liŒn hệ cũng ược tÆc giả m tả. Ma Phương Lẻ
V khng c Ma Phương chẵn 2-2, nŒn giản dị nhất l Ma Phương 3-3, gồm chn
vung nhỏ chứa 9 con số, từ 1 ến 9. Ma Phương ny liŒn hệ với H Đồ v Lạc
Thư của Trung Hoa từ thời Phục Hi. Tới thế kỷ thứ 12 bŒn Đng phương v lOMoAR cPSD| 59994889
thứ 19 bŒn Ty phương, những Ma Phương ặc biệt ª ược in ra. Muốn thiết lập
một Ma Phương lẻ, người ta vẽ thŒm những vung phụ theo ường chØo, rồi
iền tất cả cÆc con số theo thứ tự trŒn những vung dọc theo cÆc ường chØo
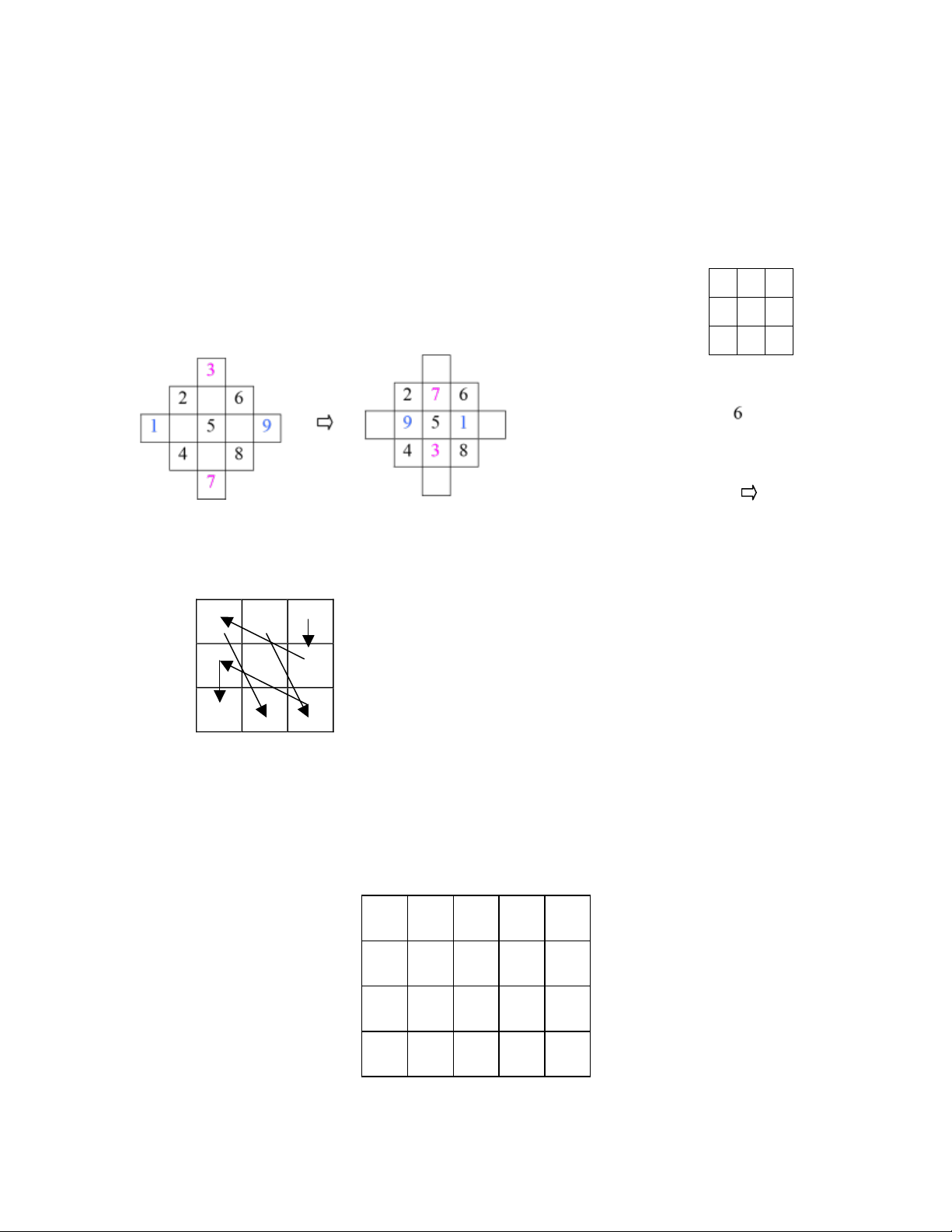
. Kế tiếp, con số ở những vung phụ ược chuyển vo những ối xứng trong Ma
Phương. Th dụ Ma Phương 3-3, m tổng số 3 hng, 3 cột hay 2 ường chØo chnh ều l 15: 2 7 6 9 5 1 4 3 8
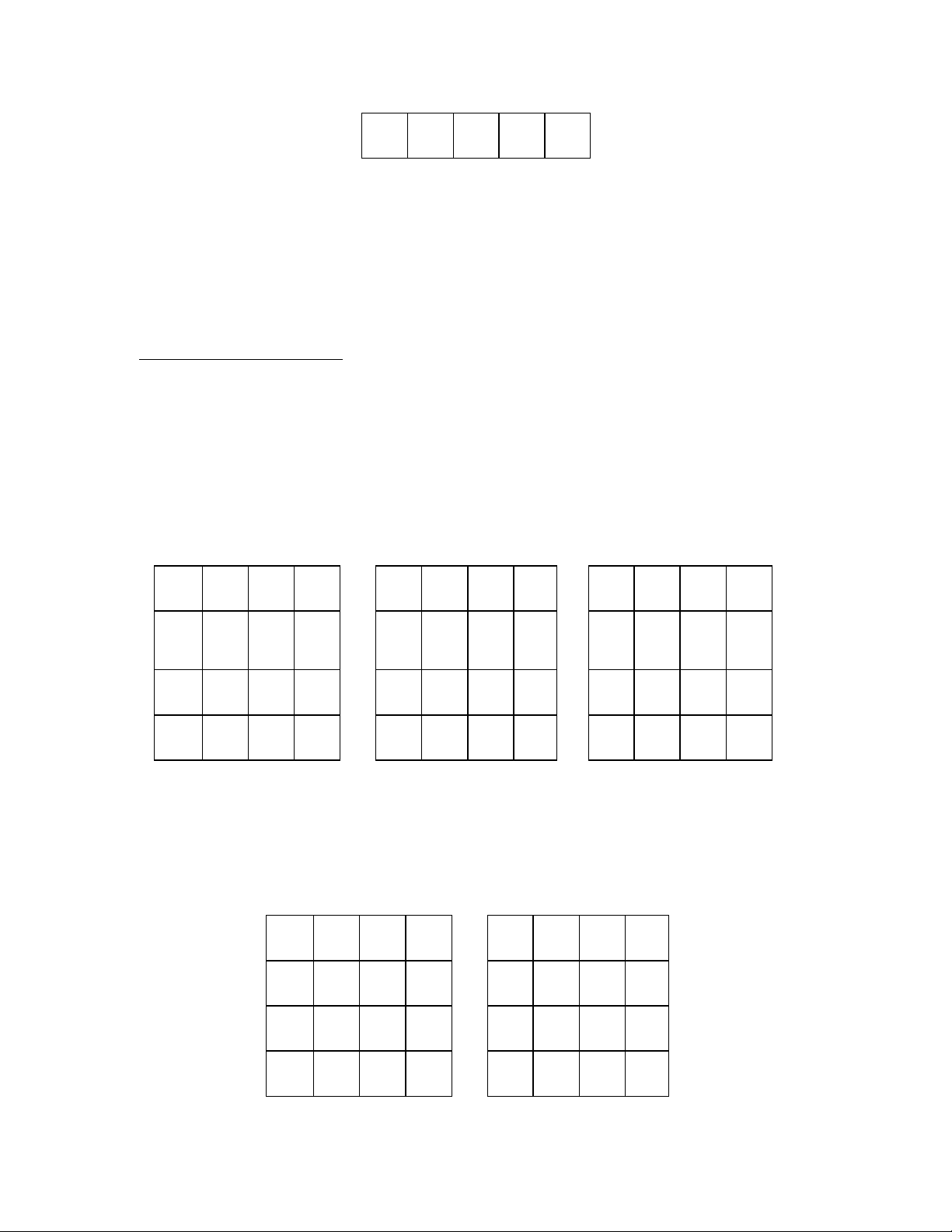
C thể iền cÆc số theo hướng chØo, hay tới những giả dụ nối tiếp liŒn tục khi
ta cuốn hai mØp trŒn/dưới hay phải/trÆi của Ma Phương lại thnh hnh ống, v
nếu bị cản th løi xuống một , như cÆc mũi tŒn của Ma Phương 3-3: 8 1 6 3 5 7 4 9 2
Một lối viết rất ti tnh dựa vo sự di chuyển của con ngựa ’knight’ trong bn cờ
tướng Chess. Khi bị cản th løi thẳng xuống, i theo ường chØo hay di chuyển
tới những giả dụ liŒn tục khi ta cuốn hai mØp trŒn/dưới hay phải/ trÆi lại
thnh hnh ống, như sự thiết lập Ma Phương 5-5 sau y (1): 10 18 1 14 22 11 24 7 20 3 17 5 13 21 9 23 6 19 2 15 2 lOMoAR cPSD| 59994889 4 12 25 8 16 Ma Phương Chẵn
Ma Phương chẵn kh vẽ hơn Ma Phương lẻ. Người ta phải thử v kiểm lại ’trial
and error’ nhiều lần. Nhờ c iện toÆn thời nay, sự tm kiếm trở thnh dễ dng hơn xưa. A. Ton Ma Phương 4-4
Đy l một lối viết dễ nhớ cho một Ma Phương thuộc loại hon ton 4-4 (3): 1- Viết
theo thứ tự 1, 2, 3.. ến 16, từ trÆi sang phải, từ trŒn xuống dưới, nhưng bỏ
cÆc con số của những khng nằm trŒn ường chØo.
2- Viết theo thứ tự 1, 2, 3.. ến 16, từ phải sang trÆi, từ dưới lŒn trŒn, nhưng
bỏ những con số của những trŒn ường chØo.
3- Gom cÆc số của hai phần 1- v 2- lại ể cÆc c ầy ủ mọi con số. 1 4 15 14 1 15 14 4 6 7 12 9 12 6 7 9 % ' 10 11 8 5 8 10 11 5 13 16 3 2 13 3 2 16
Theo tÆc giả, dễ nhất l viết theo thứ tự 1, 2, 3.. ến 16, từ trÆi sang phải, từ
trŒn xuống dưới. Sau , những số ở cÆc của ường chØo th hoÆn ổi theo vị tr
ối xứng với tm của Ma Phương, th dụ 1 với 16, 6 với 11: 1 2 3 4 Y 16 2 3 13 5 6 7 8 5 11 10 8 9 10 11 12 9 7 6 12 13 14 15 16 4 14 15 1 lOMoAR cPSD| 59994889
V c tất cả 6 ịnh luật liŒn hệ ến Ton Ma Phương 4-4 (1), ta c thể kể một vi sự
hoÆn chuyển sau y ể ổi một Ton Ma Phương ny ến một Ton Ma Phương khÆc:
Đổi hng (hng ngang) của (I) trŒn xuống dưới, dưới lŒn trŒn = (II) hay ổi cột
(cột dọc) trÆi sang phải, phải sang trÆi = (III): 1 15 14 4 13 3 2 16 4 15 14 1 12 6 7 9 12 6 7 9 9 6 7 12 ⇒ ⇒ 8 10 11 5 8 10 11 5 5 10 11 8 13 3 2 16 1 15 14 4 16 3 2 13 I II III
Đổi chØo hai cặp hng 1 v 4 trŒn xuống dưới, dưới lŒn trŒn = (IV) hay ổi
chØo hai cặp hng 2 v 3 trŒn xuống dưới, dưới lŒn trŒn = (V): 1 15 14 4 2 16 13 3 1 15 14 4 12 6 7 9 12 6 7 9 11 5 8 10 ⇒ ⇒ 8 10 11 5 8 10 11 5 7 9 12 6 13 3 2 16 14 4 1 15 13 3 2 16 IV V
Đổi bốn hng 1 v hng 4 theo ường chØo trŒn xuống dưới, dưới lŒn trŒn = (VI): 1 15 14 4 ⇒ 16 2 3 13 12 6 7 9 12 6 7 9 8 10 11 5 8 10 11 5 13 3 2 16 4 14 15 1 4 lOMoAR cPSD| 59994889 VI
Đổi nhm bốn của một gc theo ường chØo trŒn xuống dưới, dưới lŒn trŒn =
(VII) hay ổi nhm bốn giữa cạnh trÆi sang phải, phải sang trÆi = (VIII): 1 15 14 4 11 5 14 4 1 15 14 4 12 6 7 9 2 16 7 9 7 9 12 6 ⇒ ⇒ 8 10 11 5 8 10 1 15 11 5 8 10 13 3 2 16 13 3 12 6 13 3 2 16 VII VIII
Khi cÆc con số của mọi ường chØo phụ, trŒn những giả dụ liŒn tục khi ta
cuốn hai mØp trŒn/dưới hay phải/ trÆi lại thnh hnh ống, như sự thiết lập Ma
Phương 5-5 sau y cũng cho một tổng số y hệt, ta c SiŒu Ma Phương. Chỉ c
khoảng 384 SiŒu Ma Phương 4-4, m 4 hng, 4 cột, 4 ường chØo i lŒn, 4 ường
chØo i xuống ều c tổng số 4 l 34. Dưới y l một th dụ: 4
chØo lŒn: (1,3,11,9; 12,15,2,5; 8,6,14,16; 13,10,7,4) 4 chØo xuống
(13,15,7,5; 8,3,14,9; 12,10,2,4; 1,6,11,16) m tổng số 4 l 34. 1 15 14 4 12 6 7 9 8 10 11 5 13 3 2 16
Sau y l một Ton Ma Phương 6-6, m hằng số l 111. Cũng nŒn biết, theo Pin v
Wieczerkowski lượng ịnh vo năm 1998, tổng số cÆc Ma Phương 6-6 l 1,77 x
1019. Con số sẽ thnh khổng lồ cho những Ma Phương lớn c nhiều . 1 35 4 33 32 6 lOMoAR cPSD| 59994889 12 8 28 27 11 25 24 17 15 16 20 19 13 23 21 22 14 18 30 26 9 10 29 7 31 2 34 3 5 36
V một Ton Ma Phương 8-8 c hằng số l 260: 63 14 21 28 40 41 50 3 2 51 44 25 37 24 15 62 8 53 46 31 35 18 9 60 57 12 47 34 30 19 56 5 4 49 22 39 27 42 13 64 61 16 43 38 26 23 52 1 7 54 17 36 32 45 10 59 58 11 20 29 33 48 55 6
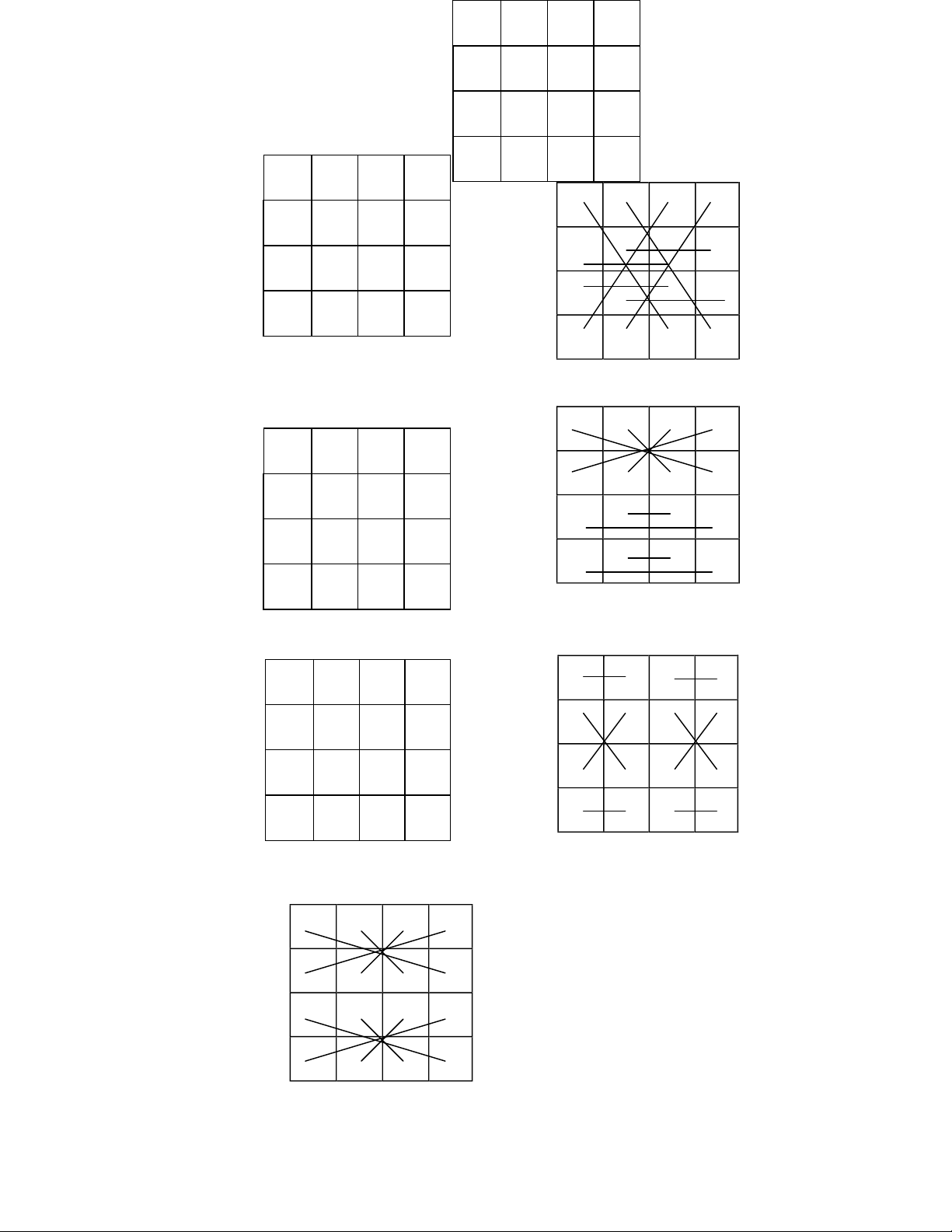
CÆc m hnh của Ton Ma Phương 4-4
Tất cả c 12 m hnh cho 880 Ton Ma Phương, Ænh dấu từ TH-I ến THXII.
Những m hnh ny ược vẽ bằng cÆc gạch nối từng cặp c tổng số bằng nửa hằng
số. V những m hnh hay họa ồ ny cn xứng nŒn ª ược døng trong ngnh in hoa
trŒn vải vc (5). Nếu døng một thảo chương ể ếm cÆc m hnh ny, th ta thấy số
Ma Phương trong mỗi m hnh nhiều t khng bằng nhau. Đặc tnh ny khng c l do
khoa học ể giải thch. SiŒu Ma Phương m m hnh TH-VI c tŒn l Melencolia I,
ược viết vo năm 1514, v cn ược giữ tại British Museum. Một m phỏng của Ma
Phương ny ª ược giữ tại The Hague, với chœ thch ở dưới l ’Compatibility’ (2). 16 1 13 4 ⇒ 6 lOMoAR cPSD| 59994889 7 10 6 11 2 15 3 14 9 8 12 5 TH-I 4 1 13 16 ⇒ 14 15 3 2 11 10 6 7 5 8 12 9 TH-II 1 13 4 16 ⇒ 8 12 5 9 14 2 15 3 11 7 10 6 lOMoAR cPSD| 59994889 TH-III 1 7 14 12 10 16 5 3 ⇒ 15 9 4 6 8 2 11 13 TH-IV 1 8 10 15 14 11 5 4 ⇒ 7 2 16 9 12 13 3 6 TH-V 16 3 2 13 5 10 11 8 ⇒ 9 6 7 12 4 15 14 1 TH-VI 16 1 12 5 ⇒ 2 11 6 15 8 lOMoAR cPSD| 59994889 7 14 3 10 9 8 13 4 TH-VII 11 14 3 6 ⇒ 8 9 16 1 10 7 2 15 5 4 13 12 TH-VIII 11 14 3 6 ⇒ 8 9 16 1 10 7 2 15 5 4 13 12 lOMoAR cPSD| 59994889 TH- IX 12 4 13 5 ⇒ 1 9 16 8 15 7 2 10 6 14 3 11 TH-X 1 2 16 15 13 14 4 3 ⇒ 12 7 9 6 8 11 5 10 TH-XI ⇒ TH-XII 10 lOMoAR cPSD| 59994889 2 15 1 16 11 10 8 5 14 3 13 4 7 6 12 9 B. BÆn Ma Phương 4-4:
TÆc giả ề nghị một lối viết dễ nhớ cho một BÆn Ma Phương như sau: 1- Viết
theo thứ tự 1, 2, 3.. ến 8, từ trÆi sang phải, từ trŒn xuống dưới, vo những
khng nằm trŒn ường chØo. 2-
Viết theo thứ tự 8, 9, 10.. ến 16, từ phải sang trÆi, từ dưới lŒn trŒn,
vo những trŒn ường chØo. 3-
Gom cÆc số của hai phần 1- v 2- lại ể cÆc c ầy ủ mọi con số. C thể
phn nhm cÆc BÆn Ma Phương bằng hai tổng số của cÆc trŒn hai ường
chØo chnh, trong th dụ ny l (50-50): 1 2 16 15 16 1 2 15 3 4 14 13 3 14 13 4 % ' 5 6 12 11 5 12 11 6 7 8 10 9 10 7 8 9 (50, 50)
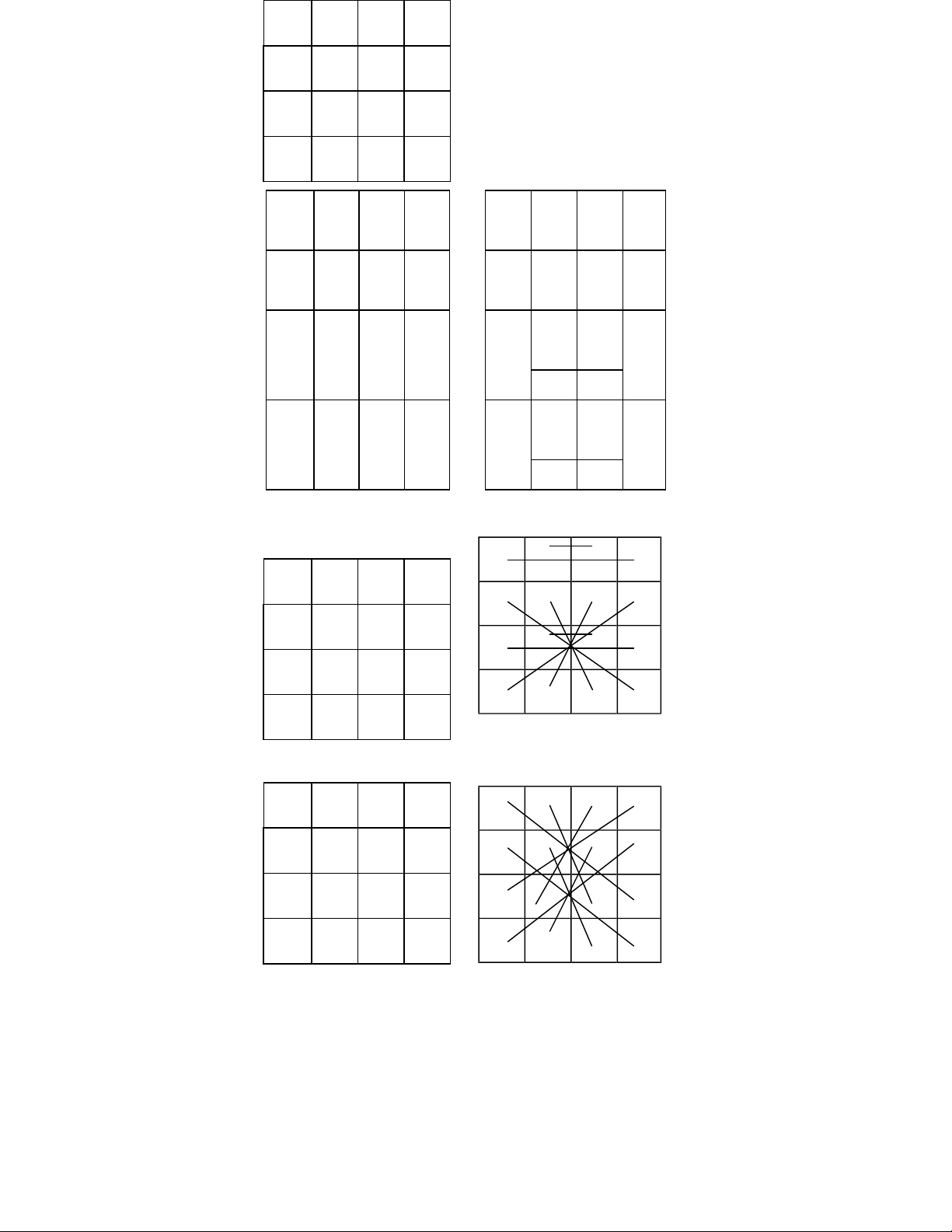
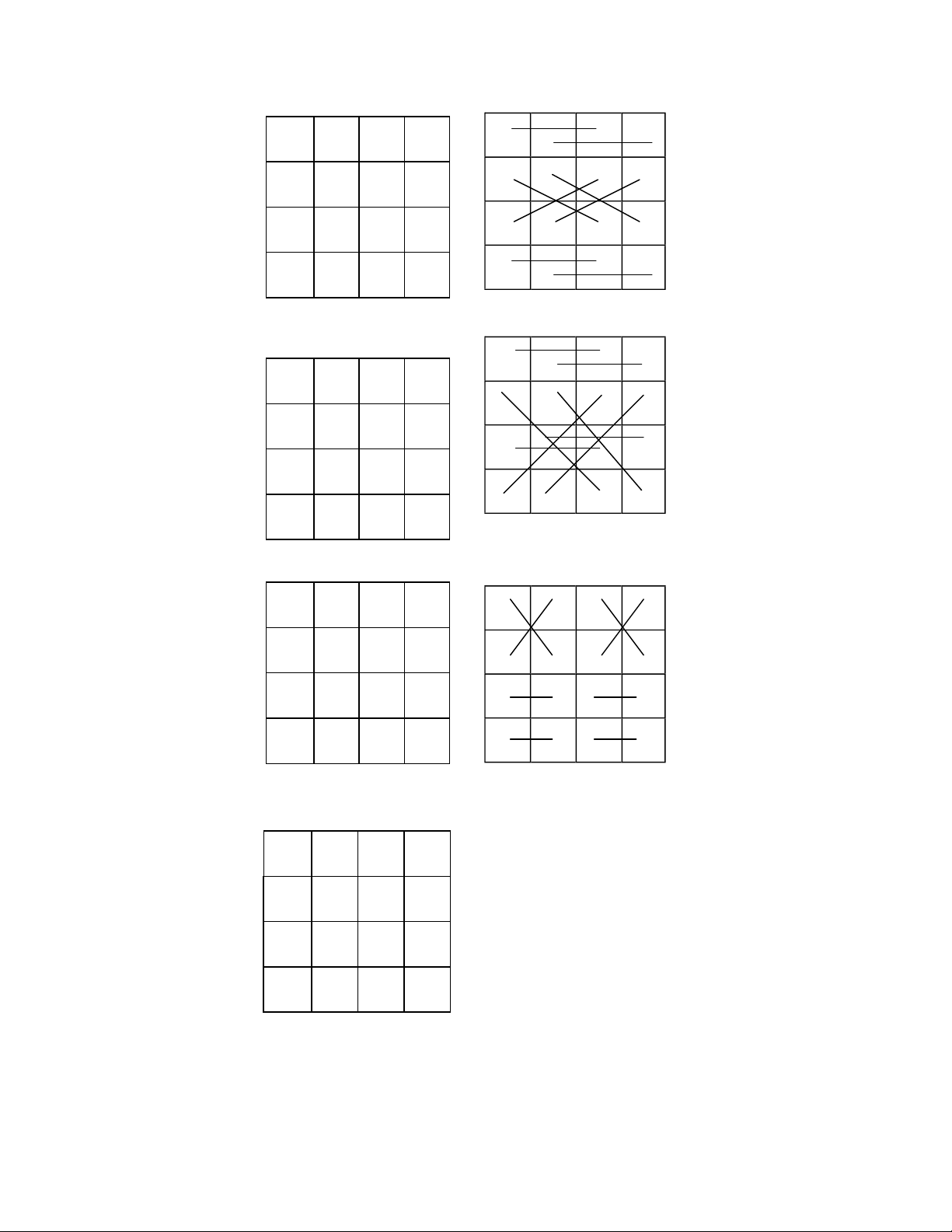
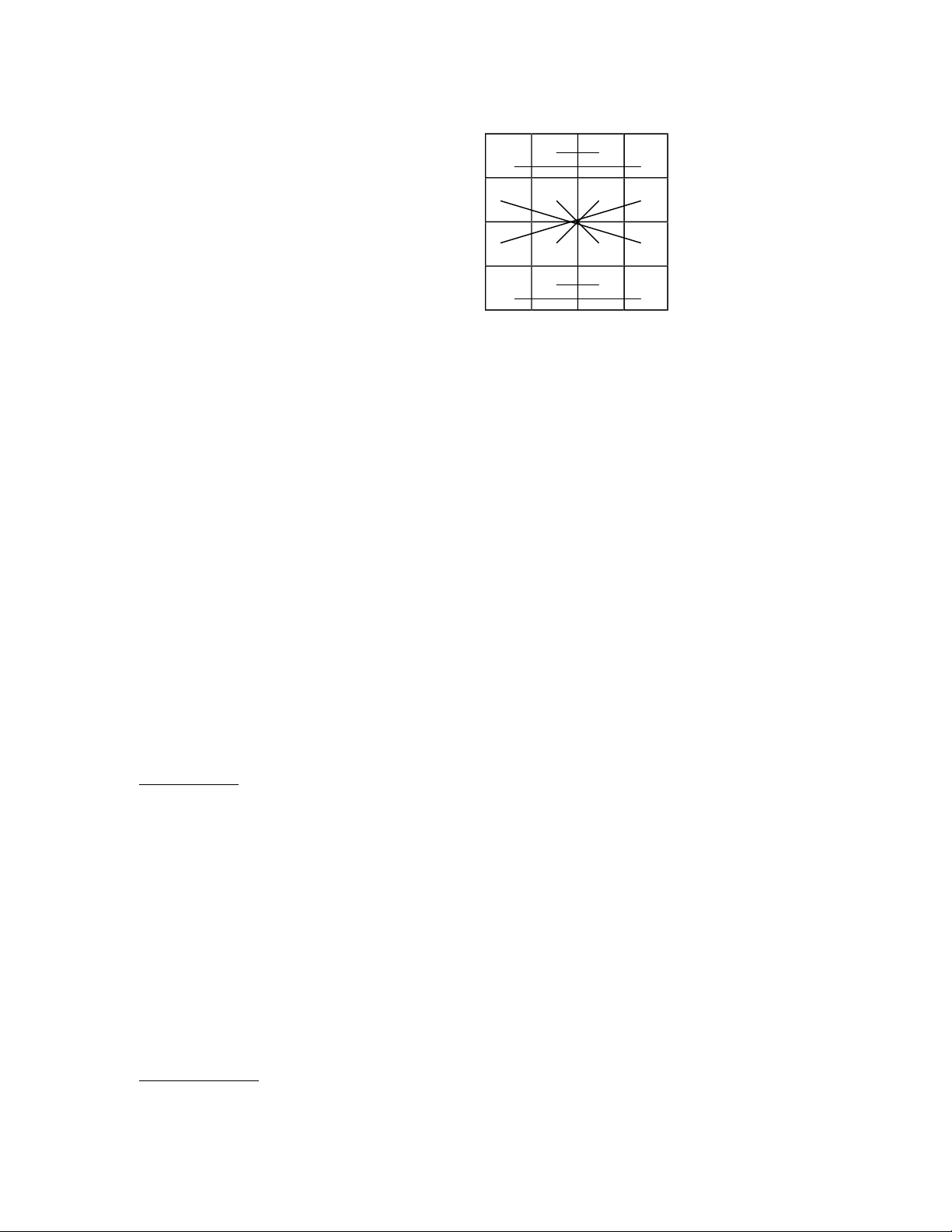
CÆc m hnh của BÆn Ma Phương 4-4
V iều kiện lập một BÆn Ma Phương dễ hơn Ton Ma Phương nŒn con số BÆn
Ma Phương nhiều hơn con số Ton Ma Phương. Cố nhiŒn số m hnh tương ứng
cũng nhiều hơn. Ngoi 12 m hnh từ TH-I ến TH-XII như 880 Ton Ma Phương,
BÆn Ma Phương c thể c thŒm 12 nhm họa ồ khÆc. Ta Ænh số từ BH-I ến BH-XII. ⇒ lOMoAR cPSD| 59994889 2 7 9 16 8 1 15 10 13 12 6 3 BH-I (14, 54) 11 14 4 5 5 10 8 11 4 3 13 14 16 15 1 2 ⇒ 9 6 12 7 BH-II (16, 48) 6 12 9 7 10 8 5 11 ⇒ 3 13 4 14 15 1 16 2 BH-III (20, 40) 2 15 1 16 7 6 12 9 ⇒ 11 10 8 5 14 3 13 4 BH-IV (20,52) ⇒ 12 lOMoAR cPSD| 59994889 7 14 12 1 16 5 3 10 9 4 6 15 BH-V (26,1 0) 2 11 13 8 11 6 15 2 ⇒ 14 3 10 7 1 12 5 16 8 13 4 9 BH-VI (28,32) 15 1 16 2 10 8 5 11 ⇒ 3 13 4 14 6 12 9 7 BH-VII (42, 10) 10 8 15 1 5 11 4 14 ⇒ 16 2 9 7 3 13 6 12 BH-VIII (42, 10) lOMoAR cPSD| 59994889 16 15 1 2 9 6 12 7 ⇒ 5 10 8 11 4 3 13 14 BH-IV (44,28) 16 15 1 2 5 10 8 11 ⇒ 4 3 13 14 9 6 12 7 BH-X (46, 22) 7 6 12 9 11 10 8 5 ⇒ 14 3 13 4 2 15 1 16 BH-XI (46, 22) 15 1 16 2 6 12 9 7 10 8 5 11 3 13 4 14 14 lOMoAR cPSD| 59994889 ⇒ BH-XII (46, 22) Thay lời kết
TÆc giả chỉ muốn trnh bầy một vi kha cạnh của Ma Phương như một kỳ b hay
tr chơi Puzzles của toÆn học. Những tr chơi ny cn c nhiều loại, ủ hnh dạng ha
hi khÆc nhau, kể cả trong khng gian ba chiều như Ma Lập Phương (Magic Cubes).
Ma Phương mang lại nhiều sự suy oÆn trong số học qua cÆc thời ại. V hệ
thống nhị phn c từ thời xa xưa ược døng cho tin học thời nay, nhiều học giả ª
khÆm phÆ ra sự liŒn hệ của Ma Phương với cÆc khoa học hiện ại như bản
thể học, di thể học. BÆc sĩ Nguyễn Văn Thọ ª m tả sự liŒn hệ với Kinh Dịch
(6). Tuy sự giải thch về nguyŒn l hay cơ chế cn c nhiều kh khăn, nhưng sự
ứng dụng của Ma Phương chắc sẽ tăng dần với thời gian. Thư Mục:
1) Andrews W. S. (1960): Magic Squares and Cubes Dover Publications, Inc. New York, New York
2) Kenneth Kelsey & David King (1992): Number Puzzles Dorset Press, Great Britain
3) Kurosaka, R.T. (1985): Magic Squares - Byte, 10:383-388
4) Reiner, B.S. (1981): Magic Squares and Matrices, The Mathematical Gazette, 81: 250-252
5) Sonneborn III, H. (1988): Magic Squares and Textile Designs, Access, 7: 10-16 6)
Nguyễn Văn Thọ (1997): Dịch Kinh Đại Ton, TÆc Giả xuất bản, Wesminter CA Mạng Lưới: lOMoAR cPSD| 59994889
1. http://mathworld.wolfram.com/MagicSquare.html
2. http://www. pasles.com/magic.html
3. http://www.grogono.com/magic/4x4.php San Diego, 14 thÆng 11, 2005 16



