Góc nhọn, góc tù, góc bẹt, góc vuông bao nhiêu độ? 1. Giới thiệu
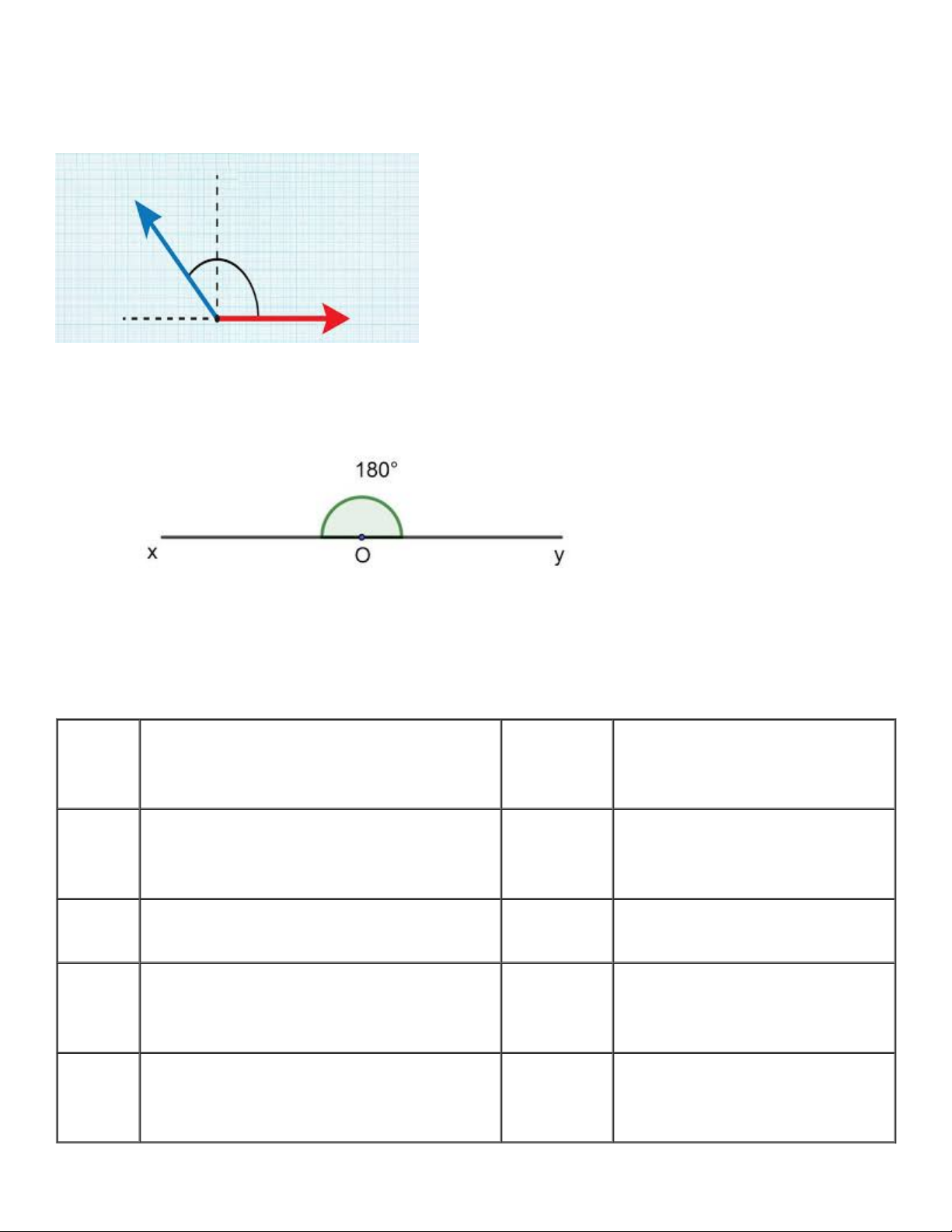
Góc là gì? Góc là hình gồm hai tia chung gốc. Góc chung của hai tia là đỉnh của góc. Hai tia là hai cạnh của góc.
Vai trò của góc trong hình học:
- Đo lường và tính toán: Góc cho phép các nhà toán học và kỹ sư đo lường và tính toán các mối quan hệ
không gian. Chẳng hạn, trong hình học mặt phẳng và không gian, các góc là cơ sở để tính toán diện tích và
thể tích của các hình học phức tạp hơn như tam giác, hình vuông, hình cầu, hay các đa diện khác.
- Mối liên hệ hình học: Góc là công cụ để xác định các mối liên hệ vị trí giữa các đối tượng hình học như
song song, trùng nhau, vuông góc, đối xứng, và nghiêng.
- Ứng dụng trong thiết kế và kiến trúc: Trong thiết kế và kiến trúc, góc là yếu tố quan trọng trong việc xác
định hình dạng, cấu trúc và thẩm mỹ của các công trình, từ các chi tiết nhỏ nhất như mối liên kết trong cấu
trúc, đến thiết kế tổng thể của một tòa nhà.
Việc phân loại góc là một khía cạnh quan trọng trong hình học và có ý nghĩa sâu sắc trong nhiều lĩnh vực
khác nhau từ khoa học tự nhiên đến ứng dụng công nghệ và thậm chí trong đời sống hàng ngày. Bằng cách
phân tích và xác định loại hình góc, chúng ta có thể hiểu rõ hơn về mối quan hệ không gian giữa các đối
tượng và sử dụng những thông tin này để áp dụng vào các bối cảnh khác nhau.
- Trong hình học và toán học:
Xác định tính chất hình học của các hình: Phân loại góc giúp xác định các loại hình học như tam giác, hình
chữ nhật, hình vuông, v.v. Góc vuông chẳng hạn là góc có hai cạnh vuông góc với nhau, còn góc tù là góc
lớn hơn 90 độ nhưng nhỏ hơn 180 độ. Điều này cực kỳ hữu ích trong việc phân biệt và xác định các tính
chất cụ thể của từng hình học.
Tính toán diện tích và thể tích: Trong hình học không gian và tính toán hình học đa chiều, việc phân loại góc
giúp xác định các khối hình và tính toán diện tích, thể tích một cách chính xác hơn. Ví dụ, việc xác định góc
giữa các mặt phẳng trong hình học không gian quyết định đến diện tích bề mặt của một khối hình.
- Trong vật lý và kỹ thuật:
Ứng dụng trong thiết kế và kiến trúc: Phân loại góc giúp các kiến trúc sư và kỹ sư thiết kế các cấu trúc và
công trình như cầu, tòa nhà, hay các bộ phận máy móc một cách chính xác hơn. Các góc vuông, góc tù hay
góc nhọn đóng vai trò quan trọng trong việc đảm bảo tính chính xác và an toàn của công trình.
Ứng dụng trong kỹ thuật điện và điện tử: Việc xác định góc giữa các linh kiện trong thiết kế mạch điện tử
hay các hệ thống điện máy cũng rất quan trọng. Các góc và sự sắp xếp chính xác giúp đảm bảo hiệu suất
hoạt động và tính ổn định của hệ thống.
- Trong cuộc sống hàng ngày và văn hóa:
Hướng dẫn trong định hướng và văn hóa giao thông: Góc được sử dụng để hướng dẫn trong giao thông
đường bộ, đảm bảo sự an toàn và hiệu quả trong việc điều khiển phương tiện.
Sử dụng trong nghệ thuật và thiết kế: Các nghệ sĩ và nhà thiết kế cũng sử dụng góc để sắp xếp, bố trí và
thiết kế các tác phẩm nghệ thuật hay thiết kế sản phẩm một cách hài hòa và thẩm mỹ.
Trong khoa học tự nhiên và nghiên cứu: Nghiên cứu về không gian và hình học: Việc phân loại góc rất quan
trọng trong các nghiên cứu về không gian và hình học, giúp hiểu sâu hơn về các mối quan hệ không gian,
sự chuyển động và tổ hợp.
Tóm lại, việc phân loại góc không chỉ đơn thuần là một khái niệm trong hình học mà còn mang lại nhiều ứng
dụng thực tiễn và có ý nghĩa sâu sắc trong nhiều lĩnh vực khác nhau từ khoa học, công nghệ, thiết kế đến
cuộc sống hàng ngày. Việc hiểu rõ về góc và các tính chất của nó là cơ sở quan trọng cho sự phát triển và
ứng dụng hiệu quả của con người trong nhiều lĩnh vực.
2. Các loại góc cơ bản
Các loại góc cơ bản trong hình học bao gồm góc nhọn, góc vuông, góc tù và góc bẹt. Góc nhọn:
Góc nhọn là góc có số đo lớn hơn 0° và nhỏ hơn 90°. Góc vuông:
Góc vuông là loại góc đơn giản nhất, có số đo là 90°. Góc tù:
Góc tù là loại góc có số đo lớn hơn 90° nhưng nhỏ hơn 180°. Góc bẹt:
Góc bẹt là loại góc có số đo là 180°.
Mỗi loại góc có tính chất và ứng dụng khác nhau trong hình học và các lĩnh vực liên quan đến không gian và hình học phẳng.
3. So sánh và phân biệt các loại góc Số đo (đơn Loại góc Định nghĩa Ví dụ vị) Góc
Góc có độ lớn là 90 độ. 90°
Góc giữa hai cạnh của hình vuông. vuông
Góc nhọn Góc có độ lớn nhỏ hơn 90 độ. < 90°
Góc giữa kim giờ và kim phút.
Góc có độ lớn lớn hơn 90 độ nhưng nhỏ hơn > 90° và <
Góc giữa hai kim của một chiếc Góc tù 180 độ. 180° đồng hồ. Góc
Góc có độ lớn là 180 độ. 180°
Góc giữa hai mặt phẳng. phẳng
4. Ứng dụng của các loại góc trong thực tế
... (Tìm thêm các ví dụ khác)
Các loại góc là những khái niệm cơ bản trong hình học nhưng lại có ứng dụng rộng rãi trong nhiều lĩnh vực
thực tế, từ xây dựng, đồng hồ đến nghệ thuật và các ngành công nghiệp khác: Trong xây dựng:
Góc vuông: Trong xây dựng, góc vuông (90 độ) là một trong những yếu tố quan trọng nhất để đảm bảo tính
chính xác và độ bền của các công trình. Các góc vuông được sử dụng để xác định đường thẳng vuông góc,
cơ sở cho việc xây dựng các tường, móng, đường thẳng chính xác trong thiết kế kiến trúc và cơ sở hạ tầng.
Góc nhọn: Mặc dù ít phổ biến hơn góc vuông, các góc nhọn (nhỏ hơn 90 độ) cũng có ứng dụng trong xây
dựng. Chẳng hạn, trong thiết kế nội thất, các góc nhọn được sử dụng để tạo ra các chi tiết mềm mại, tinh tế
như các cạnh và đường cong. Trong đồng hồ:
Góc vuông: Trên mặt đồng hồ, góc vuông là góc giữa kim giờ và kim phút khi chúng trùng nhau hoặc tạo
thành 90 độ. Đây là góc đặc biệt quan trọng vì nó xác định thời gian chính xác theo từng phút.
Góc nhọn và góc tù: Các góc nhọn và góc tù trên đồng hồ cũng quan trọng trong việc đo lường và phân tích
thời gian. Ví dụ, góc giữa kim giờ và kim phút khi chúng tạo thành góc tù (nhỏ hơn 180 độ) hoặc góc nhọn
(nhỏ hơn 90 độ) có thể dùng để tính toán khoảng cách thời gian giữa các sự kiện. Trong nghệ thuật:
Góc nhìn và phối cảnh: Trên lãnh vực nghệ thuật, các nghệ sĩ sử dụng các góc nhìn và phối cảnh để tạo ra
hiệu ứng thị giác độc đáo. Các góc nhìn không chỉ giúp nghệ sĩ tái hiện lại thế giới xung quanh mà còn tạo
ra cảm giác chiều sâu và sự động trong tác phẩm.
Trong công nghệ và khoa học:
Góc sử dụng trong cảm biến và máy móc: Trong các ứng dụng công nghệ và khoa học, các góc được sử
dụng để điều khiển và đo lường, chẳng hạn như trong cảm biến góc, cơ cấu máy móc, hoặc thiết bị chính xác đo lường.
Trong thiết kế sản phẩm:
Góc và tính chính xác trong sản xuất: Trong lĩnh vực sản xuất và gia công, việc sử dụng góc là rất quan
trọng để đảm bảo tính chính xác và độ chính xác của các chi tiết máy móc, linh kiện điện tử và các sản phẩm công nghiệp khác.
Các loại góc không chỉ là khái niệm hình học trừu tượng mà còn có ứng dụng rất rộng rãi trong cuộc sống
hàng ngày và trong các lĩnh vực chuyên ngành. Việc hiểu và áp dụng chính xác các loại góc là cơ sở quan
trọng để tạo ra các sản phẩm, công trình và tác phẩm nghệ thuật đạt hiệu quả cao và thẩm mỹ.
5. Bài tập vận dụng
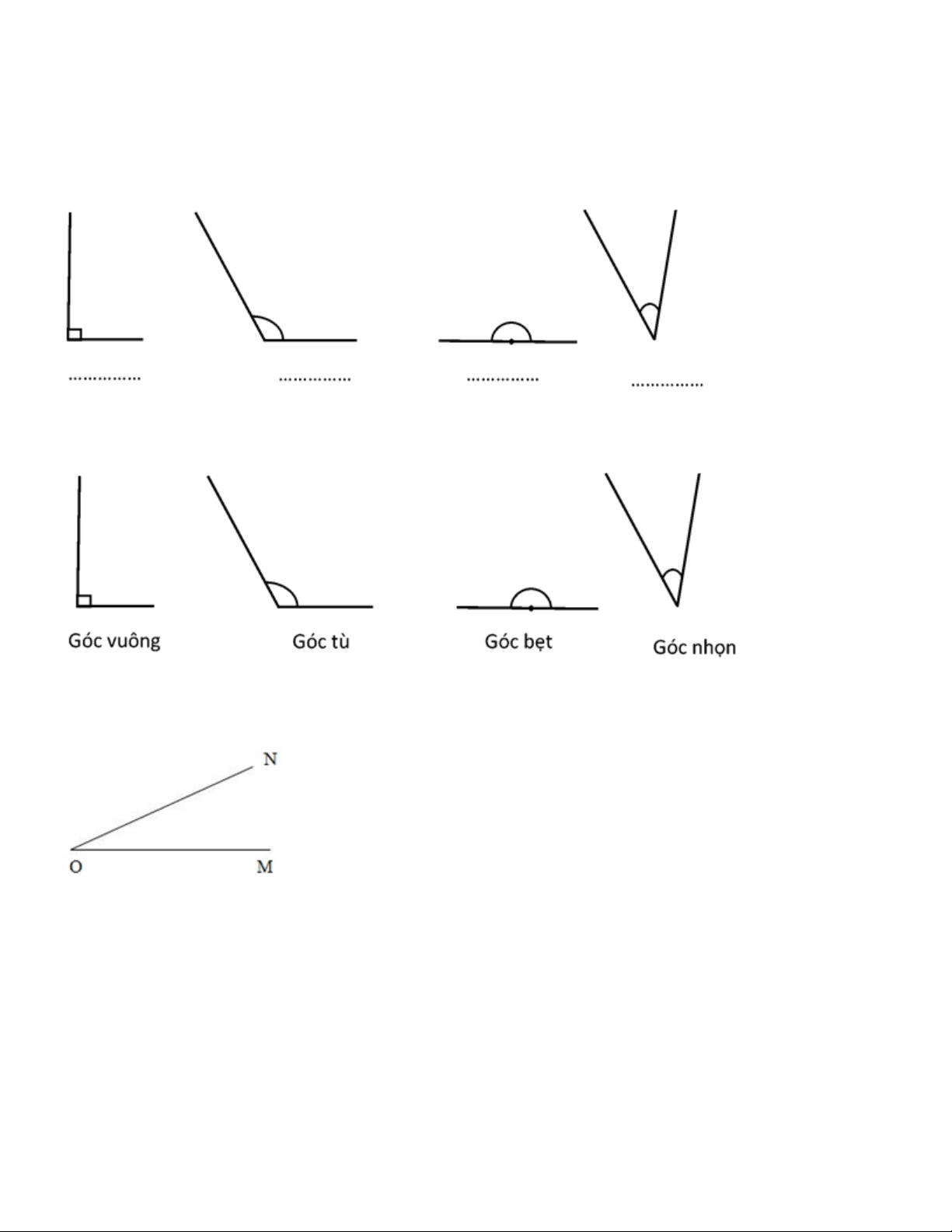
Câu 1: Điền tên góc phù hợp dưới mỗi hình: Trả lời:
Câu 2: Cho hình vẽ như sau: Góc đã cho có đỉnh là: A. Đỉnh O B. Đỉnh M C. Đỉnh N
D. Tất cả các đán án trên đều đúng. Trả lời:
Quan sát hình trên ta thấy góc đã cho có đỉnh O, cạnh OM và ON. Chọn đáp án A
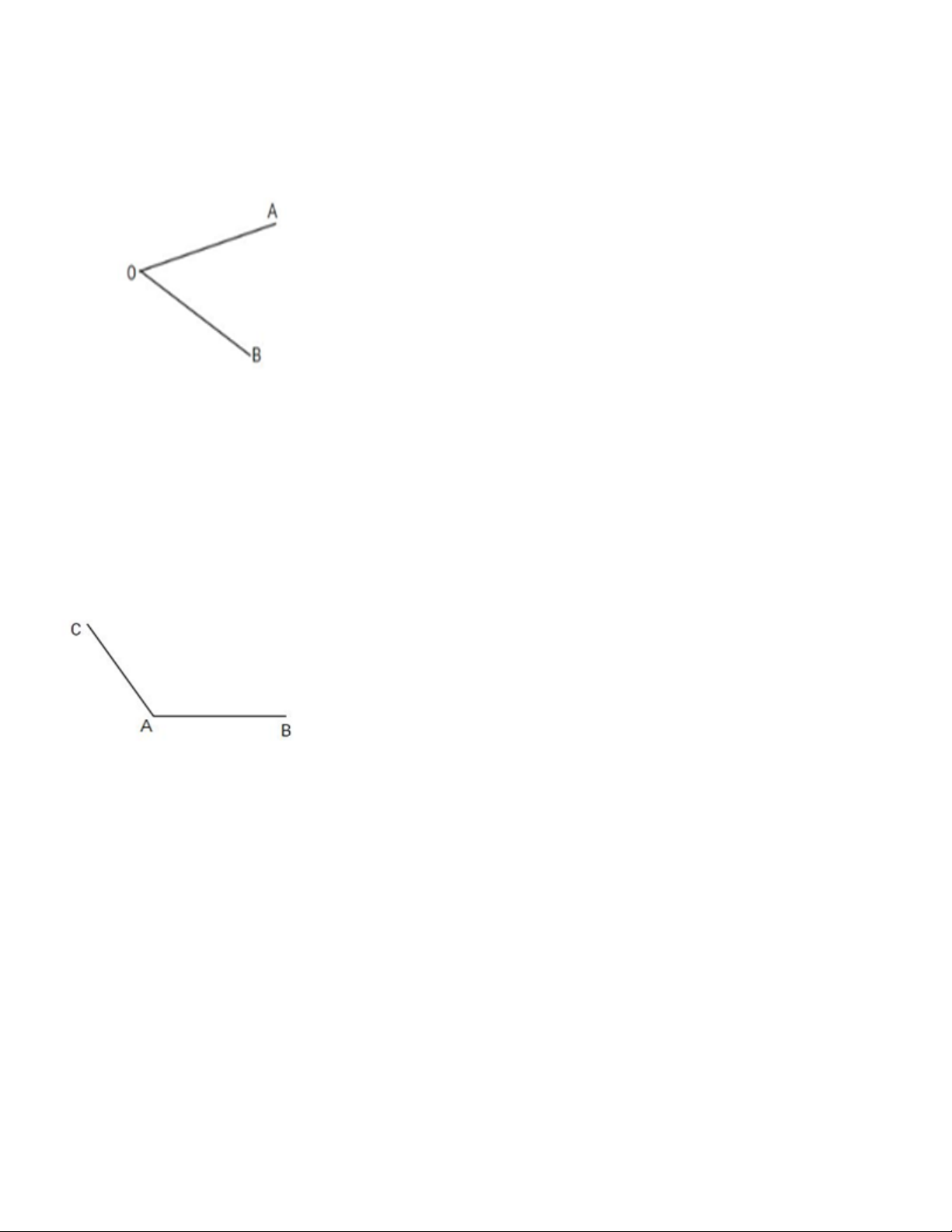
Câu 3: Trong hình dưới đây, góc đỉnh O cạnh OA và OB là góc nhọn. Đúng hay sai? Trả lời:
Nhìn hình trên ta thấy góc đỉnh O cạnh OA và OB là góc nhọn.
Vậy khẳng định đã cho là đúng.
Câu 4: Cho hình vẽ như sau: Góc đỉnh A là góc gì? A. Góc nhọn B. Góc tù C. Góc vuông D. Góc bẹt Trả lời:
Quan sát hình vẽ ta thấy góc đỉnh A cạnh AB, AC là góc tù. Chọn đáp án B
Câu 5: Cho hình vẽ như sau: Góc đã cho có cạnh là: A. Cạnh HDC B. Cạnh DH, HC C. Cạnh DH, DC D. Cạnh DC, HC Trả lời:
Quan sát hình vẽ ta thấy góc đã cho có đỉnh D, cạnh DH, DC. Chọn đáp án C