HD ĐỀ 01 NGÀY 11122025

ĐỀ 01
KIỂM TRA CUỐI HỌC KÌ I - NĂM HỌC 2024 - 2025 NGÀY 11.12.2025 MÔN: TOÁN - LỚP 12
Thời gian làm bài: 90 phút
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án. ax + b
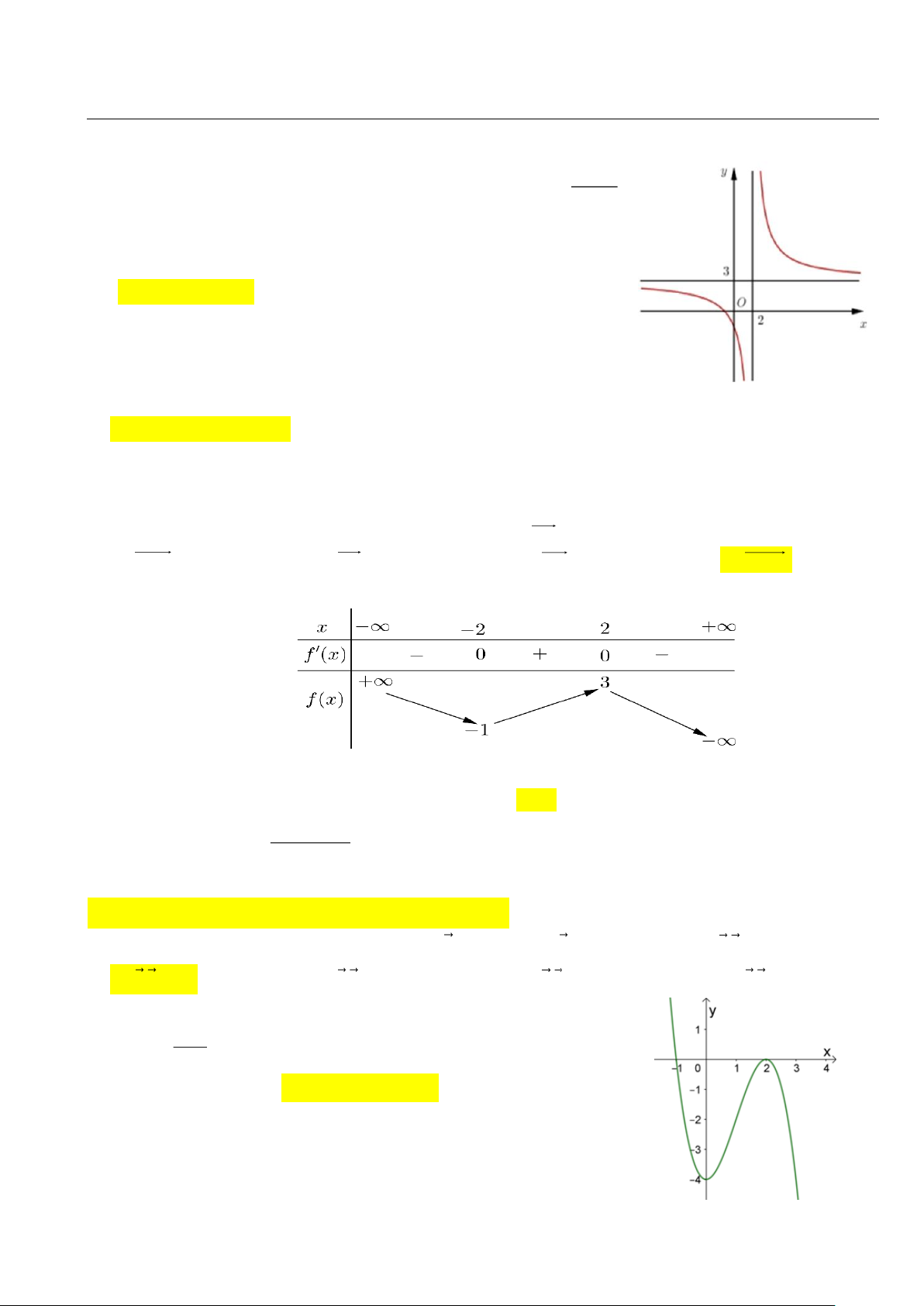
Câu 1. Đường cong ở hình bên dưới là đồ thị của hàm số y = cx + d
với a , b , c , d là các số thực.
Mệnh đề nào dưới đây đúng?
A. y '  0, x   2 .
B. y '  0, x   3.
C. y '  0, x   2 .
D. y '  0 , x   3.
Câu 2. Cho hàm số y = f (x) có lim f (x) = 1và lim f (x) = 1
− . Khẳng định nào đúng? x→+ x→−
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y =1 và y = 1 − .
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x =1 và x = 1 − .
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho không có tiệm cận ngang. 
Câu 3. Cho hình hộp chữ nhật ABC .
D A' B'C ' D' . Khi đó, AB bằng vectơ nào dưới đây?    
A. B' A' . B. BA . C. CD .
D. D'C '.
Câu 4. Cho hàm số y = f ( x) có bảng biến thiên như sau:
Trên khoảng (0;+ ) , giá trị lớn nhất của hàm số đã cho bằng A. 2 . B. 1 − . C. 3 . D. 2 − . 2 x − 2x + 5
Câu 5. Cho hàm số y =
. Mệnh đề nào dưới đây đúng? x −1
A. Hàm số nghịch biến trên khoảng (−1; )
1  (1;3) . B. Hàm số nghịch biến trên khoảng ( 1 − ;3)\  1 .
C. Hàm số nghịch biến trên mỗi khoảng (−1; )
1 và (1;3) . D. Hàm số nghịch biến trên khoảng (−;− ) 1 .   
Câu 6. Trong không gian Oxyz , cho hai vectơ a = (2;1; 0) và b = (−1; 0; −2) . Tính . a b .     A. . a b = −2 B. . a b = 0 . C. . a b = 2 . D. . a b = 5 .
Câu 7. Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? x −1 A. y = . B. 3 2
y = x + 3x − 4. x C. 3
y = −x + 3x − 4 . D. 3 2
y = −x + 3x − 4 .
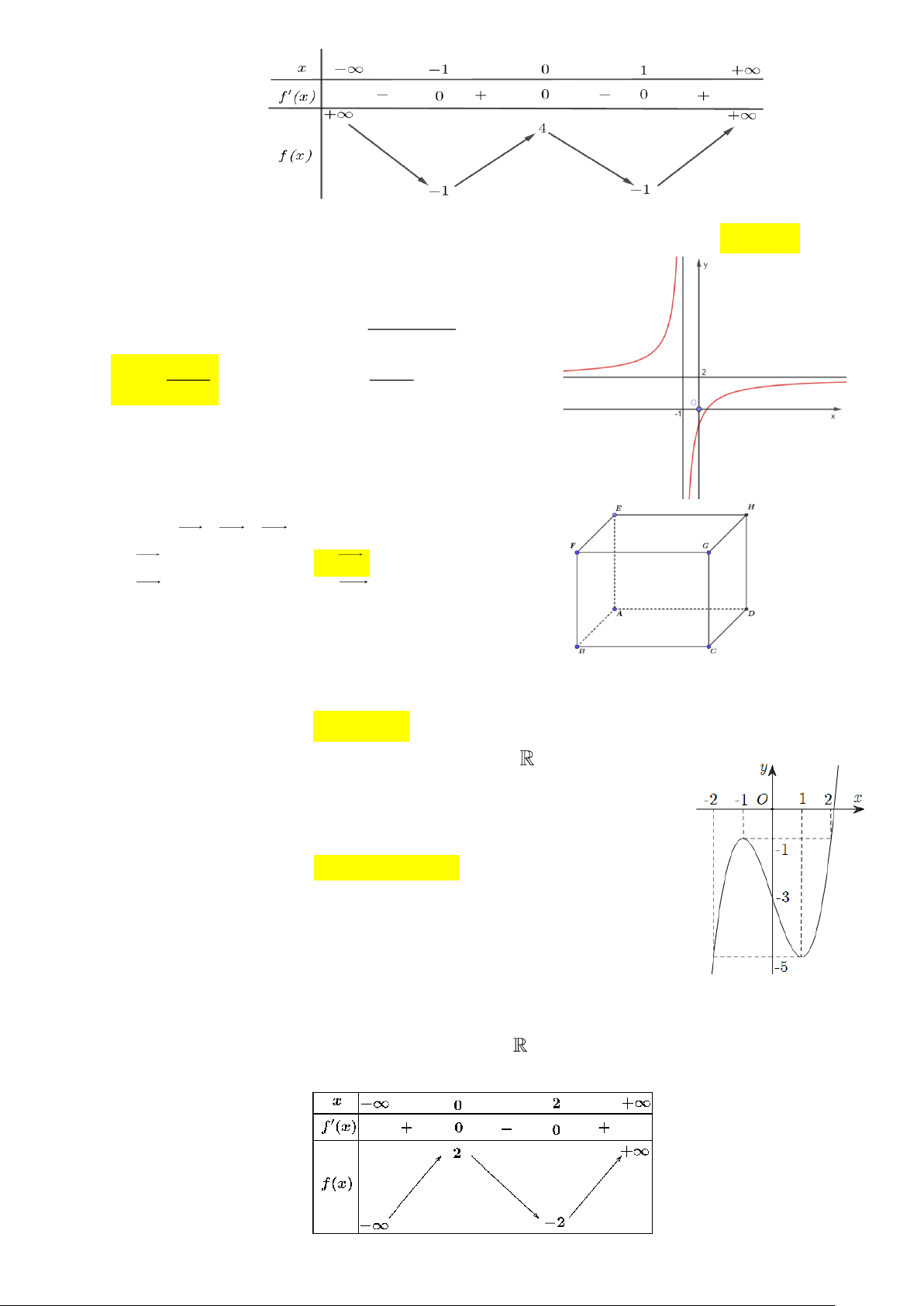
Câu 8. Cho hàm số f ( x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (−;− ) 1 . B. (−1; ) 1 . C. (0; ) 1 . D. (−1;0) .
Câu 9. Đồ thị của hàm số nào dưới đây có dạng như
đường cong trong hình sau. 2 2x + 3x + 2 A. 3
y = x −3x −1. B. y = . x +1 2x −1 2x +1 C. y = . D. y = . x +1 x +1
Câu 10. Cho hình hộp ABC .
D EFGH như hình bên dưới.

Véctơ tổng CB + CD + CG bằng véctơ nào dưới đây?   A. CA . B. CE .   C. CF . D. CH .
Câu 11. Trong không gian Oxyz , hình chiếu vuông góc của điểm M (2;1;− )
1 trên mặt phẳng (Ozx) có tọa độ là A. (0;1;− ) 1 . B. (2;0;− ) 1 . C. (2;1;0) . D. (0;1;0) .
Câu 12. Cho hàm số y = f ( x) xác định và liên tục trên  có đồ thị
như hình vẽ bên dưới . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M
của hàm số y = f ( x) trên đoạn −2;2 . A. m = 2 − ;M = 2. B. m = 5 − ;M = 0 . C. m = 1 − ;M = 0 . D. m = 5 − ;M = 1 − .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số y = f ( x) xác định và liên tục trên  có bảng biến thiên như hình vẽ dưới đây. Xét
tính đúng sai của các khẳng định sau:
a) Hàm số y = f ( x) đồng biến trên khoảng ( ;0 − ) và (2;+).
b) Hàm số g ( x) = 2x − 3 f ( x) nghịch biến trên khoảng (0;2) .  3  c) f ( 2
sin x)  f  .  2 
d) Hàm số y = f (2 − 3x) nghịch biến trên khoảng (0;2) . Hướng dẫn giải
a) Hàm số y = f ( x) đồng biến trên khoảng ( ;0 − ) và (2;+).
b) Ta có g( x) = 2 − 3 f ( x)  0, x
 (0;2) , suy ra hàm số g (x) = 2x − 3 f (x) đồng biến trên khoảng (0;2) .
c) Ta có hàm số y = f ( x) nghịch biến trên khoảng (0;2) . 3  3  Mà 2
0  sin x 1, x   2
 0  sin x  , x     f ( 2 sin x)  f . 2    2 
d) Ta có y = (2 − 3x) 
 f (2 −3x) = 3
− f (2 −3x) .  −  2 x  x 
Hàm số y = f (2 − 3x) nghịch biến y = − f ( − x)   f ( − x) 2 3 0 3 2 3 0 2 3  0     3 . Suy 2 − 3x  2  x  0  2 
ra hàm số y = f (2 − 3x) nghịch biến trên khoảng ( ;0 − ) và ;+   .  3  2
ax + bx + c
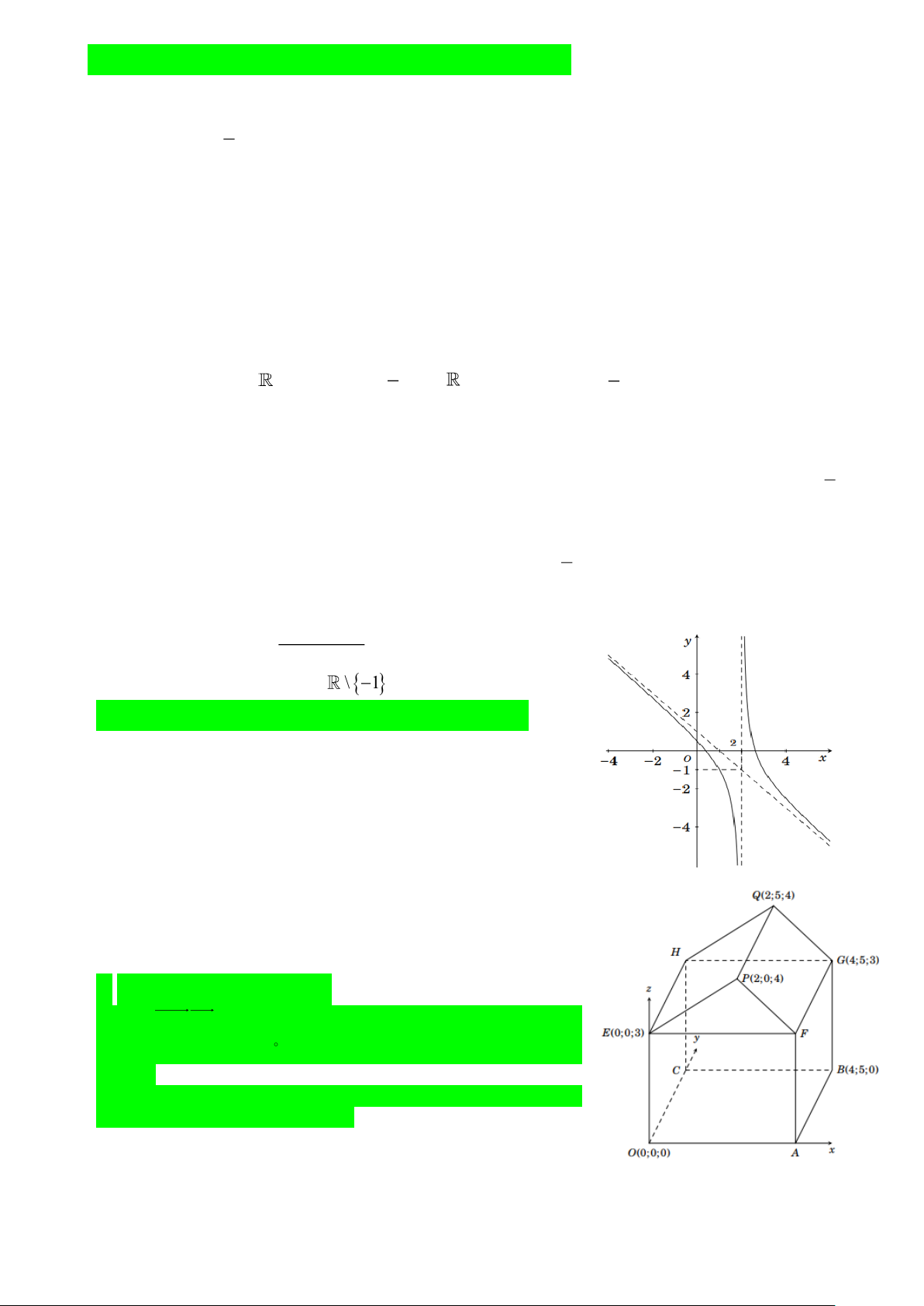
Câu 2. Cho hàm số y =
có đồ thị như hình bên. x − 2
a) Tập xác định của hàm số là  \ −  1 .
b) Hàm số nghịch biến trên các khoảng (−;2) , (2;+) .
c) Điểm I(2;1) là tâm đối xứng của đồ thị hàm số.
d) Hệ số a  0 .
Câu 3. Hình minh họa sơ đồ một ngôi nhà trong hệ trục tọa độ
Oxyz , với độ dài đơn vị trên các trục tọa độ bằng 1m. Trong đó
nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật.
a) Tọa độ của điểm A(5;0;0) .
b) Tọa độ của điểm H (0;5;3) . 
c) Góc (FP,FE) gọi là góc dốc của mái nhà. Số đo của góc dốc
của mái nhà bằng 26,6 (làm tròn kết quả đến hàng phần mười của độ).
d) Chiều cao của ngôi nhà là 4 (m). (Chiều cao ngôi nhà là khoảng
cách từ đỉnh mái nhà đến mặt đất.)
Câu 4. Trong không gian, cho hình lập phương ABC . D A B  C  D
  có cạnh bằng a . Gọi I là tâm hình vuông
ABCD, G là trọng tâm của tam giác AB C  .


  3
a) AB + AD + AA = AC. b) GA + GB + GC = 2GI . c) AB + AD = A C
  . d) BG = a . 3
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 17 đến câu 20.
Câu 1. Trong một nhà hàng, mỗi tuần để chế biến x phần ăn ( x lấy giá trị trong khoảng từ 30 đến 120) thì 7200
chi phí trung bình (đơn vị: nghìn đồng) của một phần ăn được cho bởi công thức: C(x) = 2x − 230 + . x
Tìm số phần ăn sao cho chi phí trung bình của một phần ăn là thấp nhất. ĐS: 60
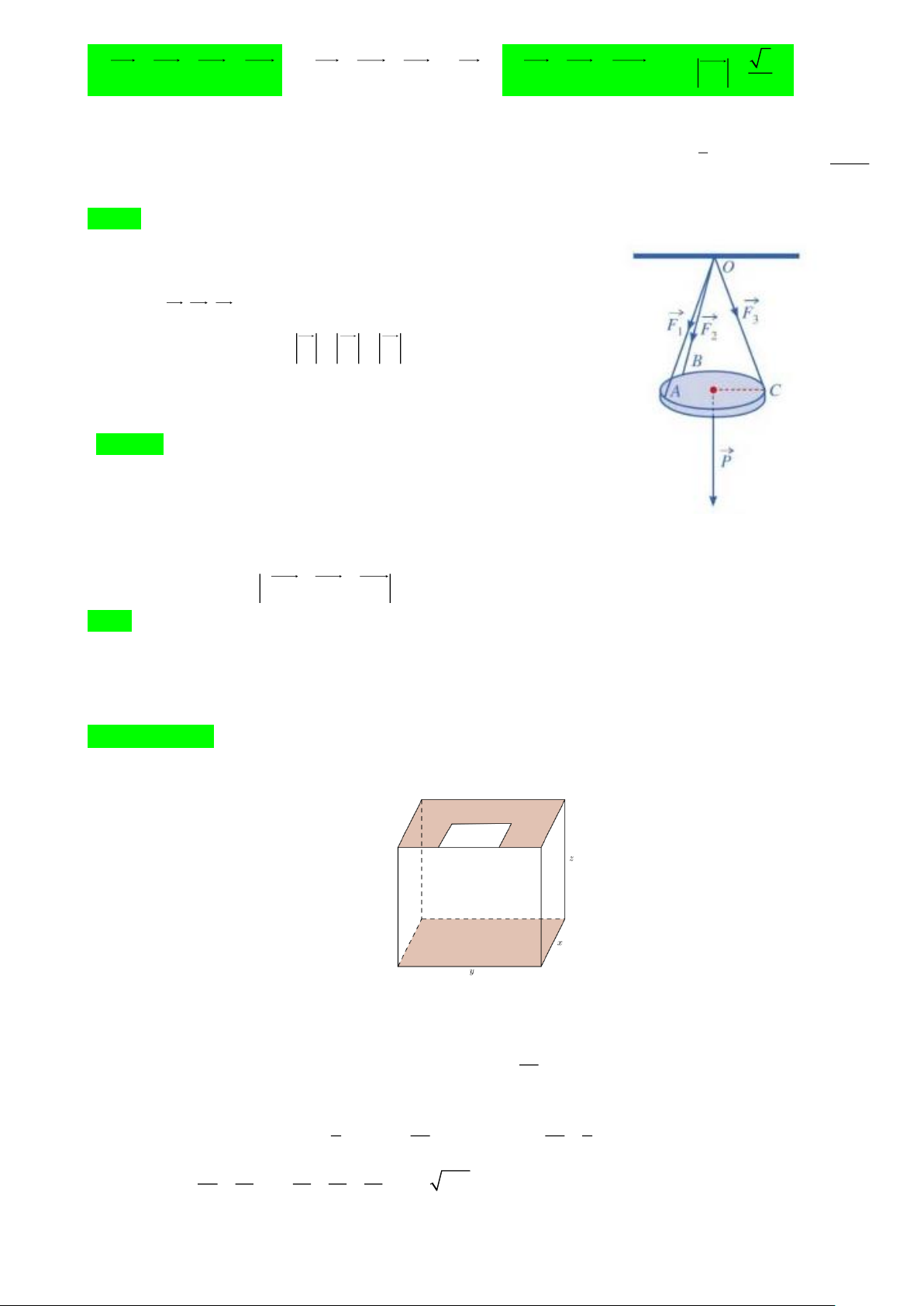
Câu 2. Một tấm gỗ tròn được treo song song với mặt phẳng nằm
ngang bởi ba sợi dây không giãn xuất phát từ điểm O trên trần nhà
và lần lượt buộc vào ba điểm , A ,
B C trên tấm gỗ tròn sao cho các 
lực căng F , F , F OA OB OC 1 2
3 lần lượt trên mỗi dây , , đôi một 
vuông góc với nhau và có F = F = F = 10 N (xem hình vẽ). 1 2 3 ( )
Tính trọng lượng P của tấm gỗ tròn đó (kết quả làm tròn đến chữ
số hàng phần chục). ĐS: 17.3
Câu 3. Trong hệ trục tọa độ Oxyz cho 3 điểm A(6;− 2;0), B(4;5; 2
− ) và C (0;3;2) . Điểm M di động

trên trục Ox . Đặt Q = 2MA + MB + MC . Tìm giá trị nhỏ nhất của Q . ĐS: 4
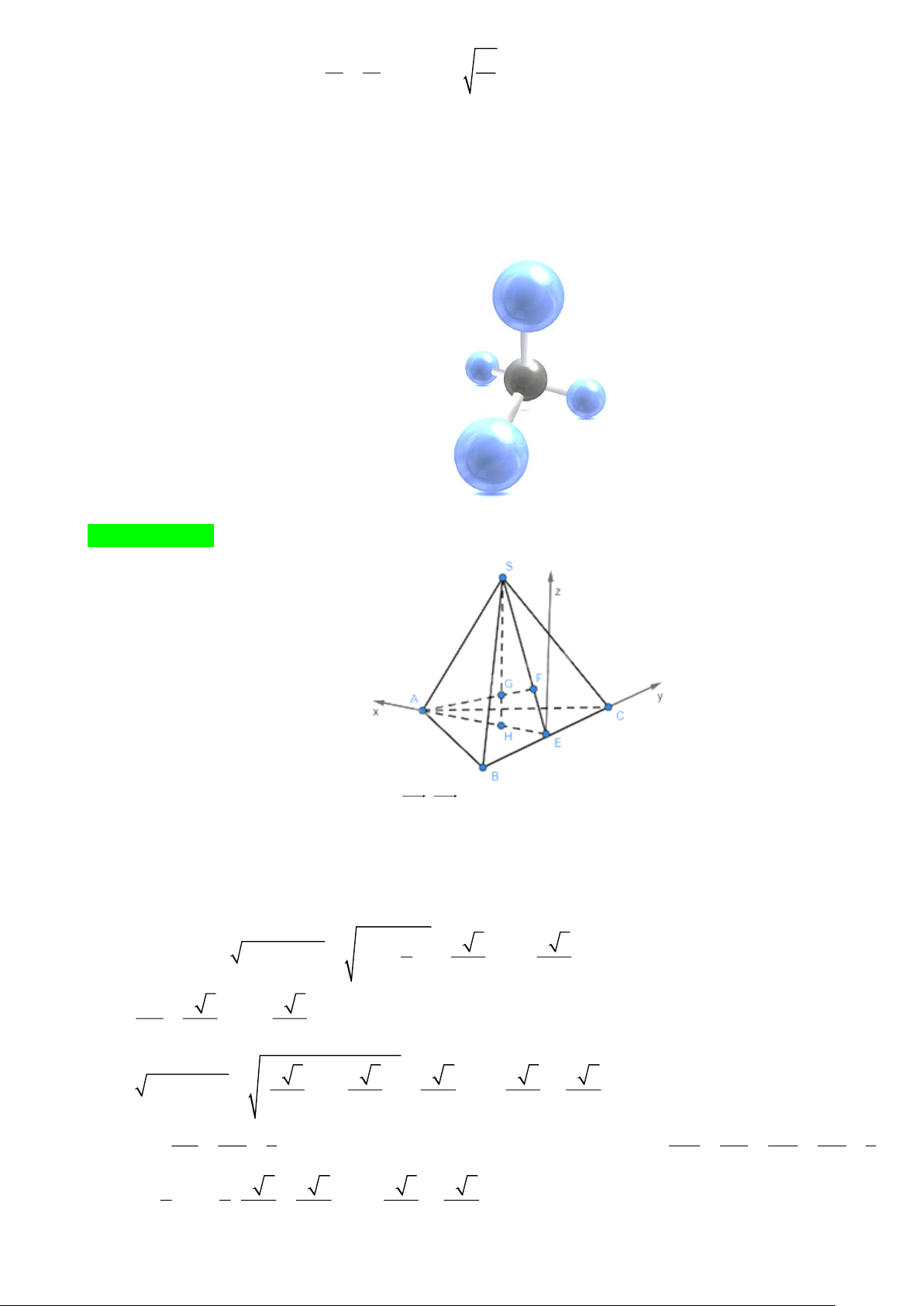
Câu 4. Ông An muốn xây một bể chứa nước dạng hình hộp chữ nhật, phần nắp trên ông để trống một ô có
diện tích bằng 20% diện tích của đáy bể. Biết đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều
rộng, biết bể có thể chứa tối đa 3
10m nước và giá tiền thuê nhân công là 500000 (đồng 2
/m ). Tính số tiền
(triệu đồng) ông An trả ít nhất cho nhân công để xây bể (làm tròn đến chữ số hàng phần chục). HƯỚNG DẪN Gọi ,
x y, z lần lượt là chiều rộng, chiều dài và chiều cao của cái bể ( , x ,
y z 0; y = 2x ).
Đơn vị đo độ dài là mét (m) . Theo đề bài ta có: 2 5
V = xyz = 2x z = 10  z = (m) . 2 x
Diện tích toàn phần cái bể: 1 5 5 1
S = 2xz + 2xy + 2yz − .xy = 2 . x + 2 .2 x x + 2.2 . x − . .2 x x ( 2
m ). (0,25 điểm) 5 2 2 x x 5 30 18 15 15 18 2 2 3 S = + x = + + x  3 810 . x 5 x x 5 Dấu 15 18 75 " = " xảy ra 2  = x 2 3  x =
 S  27,965 (m ). x 5 18
Câu 5. Cho biết bốn đoạn thẳng nối từ một đỉnh của tứ diện đến trọng tâm mặt đối diện luôn cắt nhau tại
một điểm gọi là trọng tâm của tứ diện đó.
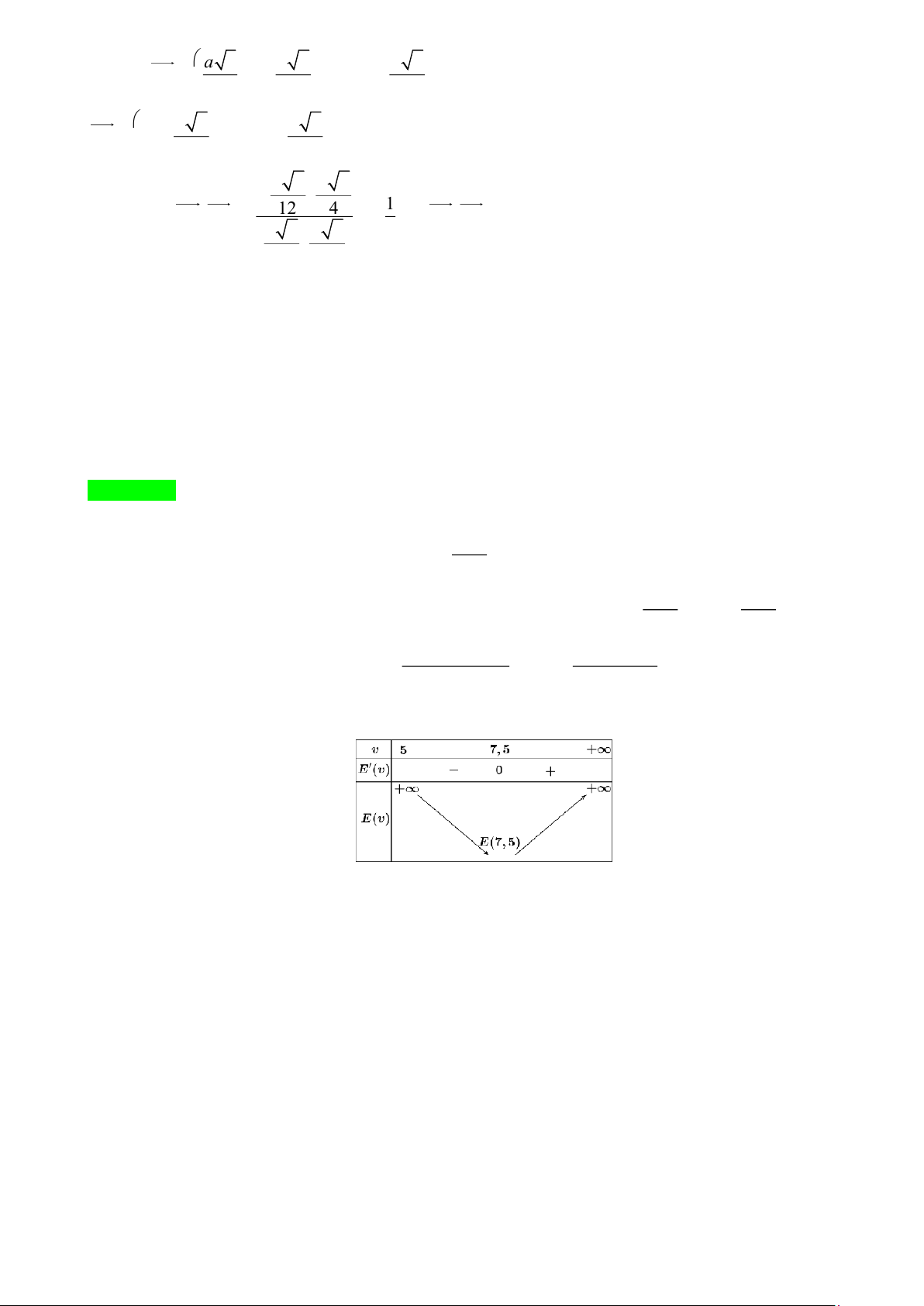
Một phân tử metan CH được cấu tạo bởi bốn nguyên tử hydrogen ở các đỉnh của một tứ diện đều và một 4
nguyên tử carbon ở trọng tâm của tứ diện.
Góc liên kết là góc tạo bởi liên kết H −C − H là góc giữa các đường nối nguyên tử carbon với hai trong
số các nguyên tử hydrogen. Tìm độ lớn góc liên kết nà (làm tròn đến chữ số hàng phần chục). HƯỚNG DẪN 
Từ hình vẽ ta thấy góc liên kết là góc (G , A GS) SH ⊥ AE
Ta có: AE ⊥ BC, SH ⊥ (ABC)  
nên ta có hệ trục tọa độ như hình với với E trùng với SH ⊥ BC gốc tọa độ O
Giả sử các cạnh của tứ diện có độ dài là a 2  a  a 3  a 3  Ta có: 2 2 2
SE = AE = AB − BE = a − =  A    ;0;0 2 2  2      AE a 3  a 3  HE = =  H  ;0;0 3 6  6    2 2       2 2 a 3 a 3 a 6 a 3 a 6
SH = SE − HE =   −   =  S  ;0;   2   6  3  6 3        Lại có: FE HE 1 = =  GH GF FH HE
FH / /SA và AF cắt SH tại G nên 1 = = = = SE AE 3 GS GE SA AE 3 1 1 a 6 a 6  a 3 a 6 
 GH = SH =  =  G  ;0;  4 4 3 12  6 12       Do đó: a 3 a 6 a 6 GA =  ;0;−   GA =  3 12  4     a 6  a 6 GS = 0;0;   GS =  . 4  4   a 6 a 6 − 
 Ta có: 1 12 4 cos(G , A GS) = = −  (G , A GS)  109,5 . a 6 a 6 3  4 4
Câu 6. Một con cá hồi bơi ngược dòng để vượt khoảng cách là 100 km . Vận tốc dòng nước là 5 (km/h) .
Nếu vận tốc bơi của cá khi nước đứng yên là v (km/h) , (v  5) thì năng lượng tiêu hao của cá trong t giờ
được cho bởi công thức ( ) 3
E v = c v t , trong đó c là hằng số dương, E được tính bằng Jun. Biết rằng vận
tốc bơi của cá khi nước đứng yên thuộc khoảng (a;b) thì năng lượng tiêu hao của cá giảm. Hãy tính giá trị
lớn nhất của b − a (kết quả làm tròn tới hàng phần mười). Hướng dẫn giải Trả lời: 2,5
Khi bơi ngược dòng vận tốc của cá là v −5 (km/h). 100
Thời gian để cá vượt khoảng cách 100 km là t = (v  5). v − 5 3 100 v
Năng lượng tiêu hao của cá khi vượt khoảng cách 100 km là E (v) 3 = c v  =100c  . v − 5 v − 5 2 3 2 3v v − 5 − v v (2v −15)
Xét hàm số y = E (v) ta có E(v) ( ) =100c  =  . ( c v − 5) 100 2 (v −5)2
Có E(v) = 0  v = 7,5 (do v  5 ). Ta có bảng biến thiên
Vậy vận tốc bơi của cá khi nước đứng yên thuộc khoảng (5;7,5) thì năng lượng tiêu hoa của cá giảm. Khi
đó giá trị lớn nhất của b − a = 2,5 .
------ HẾT ------