Hệ thống bài tập trắc nghiệm ba đường conic

Tài liệu gồm 66 trang, được biên soạn bởi thầy giáo Lương Tuấn Đức (Giang Sơn), tuyển chọn hệ thống bài tập trắc nghiệm ba đường conic trong chuyên đề phương pháp tọa độ trong mặt phẳng (kết hợp ba bộ sách giáo khoa Toán 10 chương trình mới: Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức Với Cuộc Sống).

129 65 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 7: Phương pháp tọa độ trong mặt phẳng (KNTT)

Môn: Toán 10

Thông tin:

66 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
C
C
H
H
U
U
Y
Y
Ê
Ê
N
N
Đ
Đ
Ề
Ề
P
P
H
H
Ư
Ư
Ơ
Ơ
N
N
G
G
P
P
H
H
Á
Á
P
P
T
T
Ọ
Ọ
A
A
Đ
Đ
Ộ
Ộ
T
T
R
R
O
O
N
N
G
G
M
M
Ặ
Ặ
T
T
P
P
H
H
Ẳ
Ẳ
N
N
G
G
(
(
K
K
Ế
Ế
T
T
H
H
Ợ
Ợ
P
P
3
3
B
B
Ộ
Ộ
S
S
Á
Á
C
C
H
H
G
G
I
I
Á
Á
O
O
K
K
H
H
O
O
A
A
)
)
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM
BA ĐƯỜNG CONIC
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
Đ
Đ
Ư
Ư
Ờ
Ờ
N
N
G
G
E
E
L
L
I
I
P
P
O
O
X
X
Y
Y
(
(
P
P
1
1
–
–
P
P
8
8
)
)
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
Đ
Đ
Ư
Ư
Ờ
Ờ
N
N
G
G
H
H
Y
Y
P
P
E
E
B
B
O
O
L
L
O
O
X
X
Y
Y
(
(
P
P
1
1
–
–
P
P
8
8
)
)
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
Đ
Đ
Ư
Ư
Ờ
Ờ
N
N
G
G
P
P
A
A
R
R
A
A
B
B
O
O
L
L
O
O
X
X
Y
Y
(
(
P
P
1
1
–
–
P
P
8
8
)
)
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
C
C
A
A
O
O
B
B
A
A
Đ
Đ
Ư
Ư
Ờ
Ờ
N
N
G
G
C
C
O
O
N
N
I
I
C
C
(
(
P
P
1
1
–
–
P
P
8
8
)
)
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
;
;
T
T
E
E
L
L
0
0
3
3
9
9
8
8
0
0
2
2
1
1
9
9
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
3
3
/
/
2
2
0
0
2
2
3
3
2
3
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P1)
_____________________________________
Câu 1. Elip
2 2
: 1
25 9
x y
E
có độ dài trục lớn bằng:
A.
5.
B.
10.
C.
25.
D.
50.
Câu 2. Elip
2 2
: 5 25
E x y
có độ dài trục lớn bằng:
A.
1.
B.
2.
C.
5.
D.
10.
C
C
â
â
u
u
3
3
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
h
h
â
â
n
n
g
g
i
i
á
á
c
c
g
g
ó
ó
c
c
p
p
h
h
ầ
ầ
n
n
t
t
ư
ư
t
t
h
h
ứ
ứ
n
n
h
h
ấ
ấ
t
t
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
1
1
Câu 4. Elip
2 2
: 1
100 64
x y
E
có độ dài trục bé bằng:
A.
8.
B.
10.
C.
16.
D.
20.
Câu 5. Elip
2 2
: 1
9 4
x y
E
có tiêu cự bằng:
A.
5.
B.
5.
C.
10.
D.
2 5.
C
C
â
â
u
u
6
6
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
: 1
x y
E
p q
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
í
í
n
n
h
h
2 2
26 5p q
.
A
A
.
.
3
3
2
2
0
0
B
B
.
.
1
1
8
8
0
0
C
C
.
.
2
2
2
2
9
9
D
D
.
.
2
2
5
5
0
0
Câu 7. Elip
2 2
2 2
: 1
x y
E
p q
, với
0p q
có tiêu cự bằng:
A.
p q
. B.
p q
. C.
2 2
p q
. D.
2 2
2
p q
.
Câu 8. Elip
2 2
: 1
100 36
x y
E
có một đỉnh nằm trên trục lớn là:
A.
100;0
. B.
100;0
. C.
0;10
. D.
10;0
.
Câu 9. Elip
2 2
: 1
16 12
x y
E
có một đỉnh nằm trên trục bé là:
A.
4;0
. B.
0;12
. C.
0;2 3
. D.
5;0
.
Câu 10. Elip
2 2
: 1
9 6
x y
E
có một tiêu điểm là:
A.
0;3 .
B.
0 ; 6 .
C.
3;0 .
D.
3;0 .
Câu 12. Cặp điểm nào là các tiêu điểm của elip
2 2
: 1
5 4
x y
E
?
A.
1
1;0
F
và
2
1;0
F
. B.
1
3;0
F
và
2
3;0
F
.
4
C.
1
0; 1
F
và
2
0;1
F
. D.
1
2;0
F
và
2
2;0
F
.
Câu 13. Elip
2 2
: 1
16 9
x y
E
. Tỉ số
e
của tiêu cự và độ dài trục lớn của elip bằng:
A.
1.e
B.
7
.
4
e
C.
3
.
4
e
D.
5
.
4
e
Câu 14. Elip
2 2
: 1
16 8
x y
E
. Tỉ số
k
của tiêu cự và độ dài trục bé của elip bằng:
A.
8k
. B.
8
k
. C.
1k
. D.
1k
.
Câu 15. Cho elip
2 2
: 1
25 9
x y
E
. Trong các khẳng định sau, khẳng định nào sai?
A.
E
có các tiêu điểm
1
4;0
F
và
2
4;0 .
F
B.
E
có tỉ số
4
.
5
c
a
C.
E
có đỉnh
1
5;0 .
A
D.
E
có độ dài trục nhỏ bằng 3.
C
C
â
â
u
u
1
1
6
6
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
: 1
x y
E
p q
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ơ
ơ
s
s
ở
ở
b
b
a
a
o
o
q
q
u
u
a
a
n
n
h
h
e
e
l
l
i
i
p
p
c
c
ó
ó
d
d
i
i
ệ
ệ
n
n
t
t
í
í
c
c
h
h
b
b
ằ
ằ
n
n
g
g
A
A
.
.
4
4
0
0
(
(
đ
đ
v
v
d
d
t
t
)
)
B
B
.
.
3
3
0
0
(
(
đ
đ
v
v
d
d
t
t
)
)
C
C
.
.
4
4
8
8
(
(
đ
đ
v
v
d
d
t
t
)
)
D
D
.
.
3
3
6
6
(
(
đ
đ
v
v
d
d
t
t
)
)
Câu 17. Cho elip
2 2
: 4 1
E x y
. Khẳng định nào sau đây là đúng?
A. Elip có tiêu cự bằng
3.
B. Elip có trục nhỏ bằng
2.
C. Elip có một tiêu điểm là
2
0; .
3
F
D. Elip có trục lớn bằng
4.
Câu 18. Cho elip
2 2
: 4 9 36
E x y
. Tìm mệnh đề sai trong các mệnh đề sau:
A.
E
có trục lớn bằng 6. B.
E
có trục nhỏ bằng 4.
C.
E
có tiêu cự bằng
5.
D.
E
có tỉ số
5
.
3
c
a
Câu 19. Tìm elip nếu nó đi qua điểm
5
2;
3
N
và tỉ số của tiêu cự với độ dài trục lớn bằng
2
3
.
A.
2 2
1.
9 4
x y
B.
2 2
1.
9 5
x y
C.
2 2
1.
9 6
x y
D.
2 2
1.
9 3
x y
Câu 20. Tìm elip nếu nó đi qua điểm
2; 3
A
và tỉ số của độ dài trục lớn với tiêu cự bằng
2
3
.
A.
2 2
1.
16 4
x y
B.
2 2
1.
4 3
x y
C.
2 2
1.
3 4
x y
D.
2 2
1.
4 16
x y
Câu 21. Phương trình chính tắc của elip có hai tiêu điểm
1 2
2;0 , 2;0
F F
và đi qua điểm
2;3
M
là:
A.
2 2
1.
16 12
x y
B.
2 2
1.
16 9
x y
C.
2 2
1.
16 4
x y
D.
2 2
1.
16 8
x y
Câu 22. Cho elip có hai tiêu điểm
1 2
, F F
và có độ dài trục lớn bằng
2a
. Trong các mệnh đề sau, mệnh đề nào
đúng?
A.
1 2
2 .a F F
B.
1 2
2 .a F F
C.
1 2
2 .a F F
D.
1 2
4 .a F F
5
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P2)
_____________________________________
Câu 1. Elip có hai đỉnh là
3;0 ; 3;0
và có hai tiêu điểm là
1;0 ; 1;0
. Phương trình chính tắc của elip là:
A.
2 2
1.
9 1
x y
B.
2 2
1.
8 9
x y
C.
2 2
1.
9 8
x y
D.
2 2
1.
1 9
x y
Câu 2. Elip
2 2
: 4 16 1
E x y
có độ dài trục lớn bằng:
A.
2.
B.
4.
C.
1.
D.
1
.
2
Câu 3. Elip
2 2
: 1
9 4
x y
E
. Tỉ số
f
của độ dài trục lớn và tiêu cự của elip bằng:
A.
3
2
f
. B.
3
5
f
. C.
2
3
f
. D.
5
3
f
.
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
K
K
h
h
o
o
ả
ả
n
n
g
g
c
c
á
á
c
c
h
h
g
g
i
i
ữ
ữ
a
a
h
h
a
a
i
i
t
t
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ủ
ủ
a
a
e
e
l
l
i
i
p
p
đ
đ
ã
ã
c
c
h
h
o
o
b
b
ằ
ằ
n
n
g
g
A
A
.
.
4
4
B
B
.
.
6 3
C
C
.
.
4 2
D
D
.
.
1
1
Câu 5. Lập phương trình chính tắc của elip biết tỉ số giữa độ dài trục nhỏ và tiêu cự bằng
2
, tổng bình
phương độ dài trục lớn và tiêu cự bằng
64
.
A.
2 2
1.
12 8
x y
B.
2 2
1.
8 12
x y
C.
2 2
1.
12 4
x y
D.
2 2
1.
8 4
x y
Câu 6. Tìm elip có một tiêu điểm
2;0
F
và tích độ dài trục lớn với trục bé bằng
12 5
.
A.
2 2
1.
9 5
x y
B.
2 2
1.
36 20
x y
C.
2 2
1.
144 5
x y
D.
2 2
1.
45 16
x y
Câu 7. Tìm elip có độ dài trục lớn bằng
26
và tỉ số của tiêu cự với độ dài trục lớn bằng
12
13
.
A.
2 2
1.
26 25
x y
B.
2 2
1.
169 25
x y
C.
2 2
1.
52 25
x y
D.
2 2
1.
169 5
x y
C
C
â
â
u
u
8
8
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
: 1
x y
E
p q
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
2023
y x
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
1
1
Câu 9. Tìm elip có độ dài trục lớn bằng
6
và tỉ số của tiêu cự với độ dài trục lớn bằng
1
3
.
A.
2 2
+ 1.
9 8
x y
B.
2 2
1.
9 5
x y
C.
2 2
1.
6 5
x y
D.
6
2 2
+ 1.
9 3
x y
Câu 10. Tìm elip có độ dài trục nhỏ bằng
12
và tỉ số của tiêu cự với độ dài trục lớn bằng
4
5
.
A.
2 2
1.
36 25
x y
B.
2 2
1.
25 36
x y
C.
2 2
1.
64 36
x y
D.
2 2
1.
100 36
x y
Câu 11. Elip có tổng độ dài hai trục bằng
18
và tỉ số của tiêu cự với độ dài trục lớn bằng
3
5
. Phương trình chính
tắc của elip là:
A.
2 2
1.
25 16
x y
B.
2 2
1.
5 4
x y
C.
2 2
1.
25 9
x y
D.
2 2
1.
9 4
x y
Câu 12. Elip có tổng độ dài hai trục bằng
10
và tỉ số của tiêu cự với độ dài trục lớn bằng
5
3
. Phương trình chính
tắc của elip là:
A.
2 2
1.
25 16
x y
B.
2 2
1.
5 4
x y
C.
2 2
1.
25 9
x y
D.
2 2
1.
9 4
x y
C
C
â
â
u
u
1
1
3
3
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
í
í
n
n
h
h
g
g
i
i
á
á
t
t
r
r
ị
ị
c
c
ủ
ủ
a
a
b
b
i
i
ể
ể
u
u
t
t
h
h
ứ
ứ
c
c
2 2 2
2a b c
với 2c là tiêu cự của elip.
A
A
.
.
4
4
8
8
B
B
.
.
5
5
4
4
C
C
.
.
6
6
6
6
D
D
.
.
6
6
0
0
Câu 14. Lập phương trình chính tắc của elip, biết elip đi qua hai điểm
7;0
A
và
0;3
B
.
A.
2 2
1.
40 9
x y
B.
2 2
1.
16 9
x y
C.
2 2
1.
9 49
x y
D.
2 2
1.
49 9
x y
Câu 15. Tìm phương trình chính tắc của elip nếu nó có trục lớn gấp đôi trục bé và đi qua điểm
2; 2
M
.
A.
2 2
+ 1.
20 5
x y
B.
2 2
1.
36 9
x y
C.
2 2
1.
24 6
x y
D.
2 2
+ 1.
16 4
x y
Câu 16. Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng
6
và đi qua
5;0
A
.
A.
2 2
1
25 16
x y
. B.
2 2
+ 1
25 16
x y
. C.
2 2
+ 1
25 9
x y
. D.
2 2
+ 1
100 81
x y
.
Câu 17. Trong mặt phẳng
,Oxy
phương trình chính tắc của Elip
E
có một tiêu điểm là
1
2;0
F
và đi qua
điểm
2;3
M
là
A.
2 2
1
16 12
x y
. B.
2 2
1
16 9
x y
. C.
2 2
1
16 4
x y
. D.
2 2
1
4 12
x y
.
Câu 18. Elip qua điểm
5
2;
3
M
và có một tiêu điểm
2;0
F
. Phương trình chính tắc của elip là:
A.
2 2
1
9 5
x y
. B.
2 2
1
9 4
x y
. C.
2 2
1
25 16
x y
. D.
2 2
1
25 9
x y
.
Câu 19. Elip
2
2
: 4
16
x
E y
có tổng độ dài trục lớn và trục bé bằng:
A.
5.
B.
10.
C.
20.
D.
40.
Câu 20. Elip
2 2
: 1
25 16
x y
E
có tiêu cự bằng:
A.3. B. 6. C. 9. D. 18.
_________________________________
7
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P3)
_____________________________________
Câu 1. Cho elip
2 2
: 1
25 9
x y
E
. Hai điểm
, A B
là hai đỉnh của elip lần lượt nằm trên hai trục
Ox
,
Oy
. Khi đó độ
dài đoạn thẳng
AB
bằng:
A.
34.
B.
34.
C.
5.
D.
136.
Câu 2. Elip đi qua các điểm
0;3
M
và
12
3;
5
N
có phương trình chính tắc là:
A.
2 2
1
16 9
x y
. B.
2 2
1
25 9
x y
. C.
2 2
1
9 25
x y
. D.
2 2
1
25 9
x y
.
Câu 3. Một elip
E
có trục lớn dài gấp 3 lần trục nhỏ. Tỉ số
e
của tiêu cự với độ dài trục lớn bằng:
A.
1
.
3
e
B.
2
.
3
e
C.
3
.
3
e
D.
2 2
.
3
e
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
s
s
o
o
n
n
g
g
s
s
o
o
n
n
g
g
v
v
ớ
ớ
i
i
t
t
r
r
ụ
ụ
c
c
h
h
o
o
à
à
n
n
h
h
v
v
à
à
c
c
á
á
c
c
h
h
t
t
r
r
ụ
ụ
c
c
h
h
o
o
à
à
n
n
h
h
m
m
ộ
ộ
t
t
k
k
h
h
o
o
ả
ả
n
n
g
g
b
b
ằ
ằ
n
n
g
g
2
2
,
,
d
d
t
t
ạ
ạ
o
o
v
v
ớ
ớ
i
i
e
e
l
l
i
i
p
p
m
m
ộ
ộ
t
t
d
d
â
â
y
y
c
c
u
u
n
n
g
g
c
c
ó
ó
đ
đ
ộ
ộ
d
d
à
à
i
i
b
b
ằ
ằ
n
n
g
g
A
A
.
.
8 5
3
B
B
.
.
8 6
3
C
C
.
.
10 5
3
D
D
.
.
10 6
3
Câu 5. Một elip
E
có khoảng cách giữa hai đỉnh kế tiếp nhau gấp
3
2
lần tiêu cự của nó. Tỉ số
e
của tiêu cự với
độ dài trục lớn bằng:
A.
5
.
5
e
B.
2
.
5
e
C.
3
.
5
e
D.
2
.
5
e
Câu 6. Cho điểm
2;3
M
nằm trên đường elip
E
có phương trình chính tắc:
2 2
2 2
1
x y
a b
. Trong các điểm sau
đây điểm nào không nằm trên
E
:
A.
1
2;3 .
M
B.
2
2; 3 .
M
C.
3
2; 3 .
M
D.
4
3;2 .
M
Câu 7. Cho elip
2 2
2 2
: 1
x y
E
a b
. Khẳng định nào sau đây là đúng?
A.
E
không có trục đối xứng. B.
E
có một trục đối xứng là trục hoành.
C.
E
có hai trục đối xứng là trục hoành và trục tung. D.
E
có vô số trục đối xứng.
Câu 8. Elip
E
có độ dài trục bé bằng tiêu cự. Tỉ số
e
của tiêu cự với độ dài trục lớn của
E
bằng:
A.
1
e
. B.
2
e
. C.
1
2
e
. D.
1
3
e
.
C
C
â
â
u
u
9
9
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
h
h
â
â
n
n
g
g
i
i
á
á
c
c
g
g
ó
ó
c
c
p
p
h
h
ầ
ầ
n
n
t
t
ư
ư
t
t
h
h
ứ
ứ
n
n
h
h
ấ
ấ
t
t
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
1
1
Câu 10. Elip
E
có hai đỉnh trên trục nhỏ cùng với hai tiêu điểm tạo thành một hình vuông. Tỉ số
e
của tiêu cự
với độ dài trục lớn của
E
bằng:
8
A.
1
e
. B.
2
e
. C.
1
2
e
. D.
1
3
e
.
Câu 11. Elip
E
có độ dài trục lớn bằng
4 2
, các đỉnh trên trục nhỏ và các tiêu điểm của elip cùng nằm trên
một
đường tròn. Độ dài trục nhỏ của
E
bằng:
A.
2.
B.
4.
C.
8.
D.
16.
Câu 12. Cho elip
2 2
16
: 1
9
x y
E
và
M
là một điểm tùy ý trên
E
. Khi đó:
A.
3 4.
OM
B.
4 5.
OM
C.
5.
OM
D.
3.
OM
Câu 13. Elip đi qua các điểm
0;1
A
và
3
1;
2
N
có phương trình chính tắc là:
A.
2 2
1.
16 4
x y
B.
2 2
1.
8 4
x y
C.
2 2
1.
4 1
x y
D.
2 2
1.
2 1
x y
Câu 14. Cho elip
2 2
1
25 4
x y
và
M
là một điểm tùy ý trên
E
. Khi đó:
A.
3 4.
OM
B.
2 5
OM
C.
5.
OM
D.
3.
OM
Câu 15. Cho elip
2 2
: + 1
169 144
x y
E
và điểm
M
nằm trên
E
. Nếu
M
có hoành độ bằng
13
thì khoảng cách từ
M
đến hai tiêu điểm bằng:
A. 10 và 6. B. 8 và 18. C. 13
5
. D. 13
10
.
Câu 16. Cho elip
2 2
: + 1
16 12
x y
E
và điểm
M
nằm trên
E
. Nếu
M
có hoành độ bằng
1
thì khoảng cách từ
M
đến hai tiêu điểm bằng:
A.
3,5
và
4,5
. B.
3
và
5
. C.
4 2
. D.
2
4
2
.
Câu 17. Cho elip
2 2
16
: 1
9
x y
E
. Tính diện tích hình chữ nhật cơ sở.
A.4 B. 24 C. 50 D. 24
Câu 18. Cho elip có phương trình
2 2
16 25 100
x y
. Tính tổng khoảng cách từ điểm
M
thuộc elip có hoành độ
bằng
2
đến hai tiêu điểm.
A.
3.
B.
2 2.
C.
5
. D.
4 3.
C
C
â
â
u
u
1
1
9
9
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
: 1
x y
E
p q
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
2 3 0
x y
theo một dây cung có độ dài bằng
A
A
.
.
8
8
B
B
.
.
4 11
C
C
.
.
2 13
D
D
.
.
6 2
Câu 20. Cho elip có phương trình
2 2
16 25 100
x y
. Tính tổng khoảng cách từ điểm
M
thuộc elip có hoành độ
bằng – 1 đến hai tiêu điểm.
A.
3.
B.
2 2.
C.
5
. D.
4 3.
Câu 21. Cho elip
2 2
: 1
100 36
x y
E
. Qua một tiêu điểm của
E
dựng đường thẳng song song với trục
Oy
và cắt
E
tại hai điểm
M
và
N
. Tính độ dài
MN
.
A.
64
5
. B.
36
5
. C.
25
. D.
25
2
.
_________________________________
9
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P4)
_____________________________________
C
C
â
â
u
u
1
1
.
.
Trong mặt phẳng
,Oxy
cho phương trình Elip
2 2
: 1
100 36
x y
E
. Tọa độ một đỉnh nằm trên trục lớn của
E
đã cho là
A.
100;0
. B.
100;0
. C.
0;10
. D.
10;0
.
C
C
â
â
u
u
2
2
.
.
Trong mặt phẳng
,Oxy
cho Elip
2 2
: 1
25 9
x y
E
. Độ dài trục lớn của Elip đã cho bằng
A.
25.
B.
10.
C.
6.
D.
9.
C
C
â
â
u
u
3
3
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
3
2022 2023 0
x y
tại bao nhiêu điểm
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
1
1
C
C
â
â
u
u
4
4
.
.
Trong mặt phẳng
,Oxy
cho Elip
2 2
: 1
16 9
x y
E
. Độ dài trục bé của Elip đã cho bằng
A.
32
. B.
6
.
C.
8
.
D.
18
.
C
C
â
â
u
u
5
5
.
.
Cho Elip
2 2
: 4 1
E x y
. Tiêu cự của Elip đã cho bằng
A.
5
.
B.
3
.
C.
2 5
.
D.
2 3
.
C
C
â
â
u
u
6
6
.
.
Trong mặt phẳng
Oxy
, cho Elip
2
2
: 4 1
4
x
E y
. Tiêu điểm của
E
là
A.
1 2
2;0 , 2;0
F F
.
B.
1 2
1 1
;0 , ;0
2 2
F F
.
C.
1 2
15 15
;0 , ;0
2 2
F F
.
D.
1 2
17 17
;0 , ;0
2 2
F F
.
C
C
â
â
u
u
7
7
.
.
Phương trình chính tắc của Elip có độ dài trục lớn bằng
16
, độ dài trục bé bằng
12
là
A.
2 2
1
9 16
x y
. B.
2 2
1
64 36
x y
. C.
2 2
1
8 6
x y
. D.
2 2
1
16 9
x y
.
C
C
â
â
u
u
8
8
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
r
r
ò
ò
n
n
2 2
1
x y
tại bao nhiêu điểm
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
1
1
C
C
â
â
u
u
9
9
.
.
Viết phương trình chính tắc của Elip có độ dài trục lớn bằng
2 5
và tiêu cự bằng
2
.
A.
2 2
1
5 4
x y
. B.
2 2
1
20 16
x y
. C.
2 2
1
5 1
x y
. D.
2 2
1
4 5
x y
.
Câu 10. Dây cung của elip
2 2
2 2
: 1
x y
E
a b
0
b a
vuông góc với trục lớn tại tiêu điểm có độ dài bằng:
A.
2
2c
a
. B.
2
2b
a
. C.
2
2a
c
. D.
2
a
c
.
Câu 11. Đường thẳng
: 3 4 12 0
d x y
cắt elip
2 2
: 1
16 9
x y
E
tại hai điểm phân biệt
M
và
N
. Khi đó độ dài
10
đoạn thẳng
MN
bằng:
A.
3.
B.
4.
C.
5.
D.
25.
C
C
â
â
u
u
1
1
2
2
.
.
Trong mặt phẳng tọa độ
Oxy
, viết phương trình chính tắc của Elip biết độ dài trục nhỏ bằng
4
đồng
thời tỉ số giữa tiêu cự và độ dài trục lớn bằng
5
3
.
A.
2 2
1
9 4
x y
. B.
2 2
1
3 2
x y
. C.
2 2
0
9 4
x y
. D.
2 2
1
4 9
x y
.
Câu 13. Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng
2 3
và đi qua
2;1
A
.
A.
2 2
+ 1.
6 3
x y
B.
2 2
1.
8 2
x y
C.
2 2
1.
8 5
x y
D.
2 2
+ 1.
9 4
x y
Câu 14. Elip (E) có các tiêu điểm
1 2
4;0 , 0;4
F F
và một điểm M nằm trên elip sao cho chu vi tam giác
1 2
MF F
bằng 18. Lúc đó tâm sai của elip bằng
A.
4
5
B.
2
3
C.
2
5
D.
5
6
Câu 15. Giá trị của
m
để đường thẳng
: 2 0
x y m
cắt elip
2 2
: 1
4 1
x y
E
tại hai điểm phân biệt là:
A.
2 2.
m
B.
2 2.
m
C.
2 2.
m
D.
2 2 2 2.
m
Câu 16. Cho elip
2 2
1
25 16
x y
với tiêu điểm
1 2
,F F
. Lấy hai điểm A, B thuộc elip (E) sao cho
1 2
8
AF BF
. Khi
đó giá trị biểu thức
2 1
AF BF
bằng
A.10 B. 12 C. 8 D. 14
Câu 17. Cho elip
2 2
: 1
100 36
x y
E
nội tiếp hình chữ nhật cơ sở ABCD. Điểm M nằm trên cạnh AB, tính diện tích
tam giác MCD.
A.120 B. 100 C. 140 D. 80
Câu 18. Tìm chu vi hình chữ nhật cơ sở ngoại tiếp elip có phương trình
2 2
16 25 100
x y
.
20 B. 12 C. 15 D. 9
C
C
â
â
u
u
1
1
9
9
.
.
Trong mặt phẳng
,Oxy
cho Elip
E
đi qua điểm
2 3; 2
M
và
M
nhìn hai tiêu điểm của
E
dưới
một góc vuông. Biết phương trình chính tắc của
E
đã cho có dạng
2 2
2 2
1
x y
a b
. Tính
2 2
S a b
.
A.
24
.
B.
32
.
C.
8
.
D.
25
.
C
C
â
â
u
u
2
2
0
0
.
.
Trong mặt phẳng
Oxy
, cho elip
( )E
có phương trình chính tắc
2 2
1
25 16
x y
. Tìm tọa điểm
M
sao cho
điểm
M
thuộc
( )E
và trục
Ox
.
A.
( 5;0)
hoặc
5;0
. B.
(0; 5)
hoặc
0;5
.
C.
4;0
hoặc
4;0
. D.
0; 4
hoặc
0;4
.
C
C
â
â
u
u
2
2
1
1
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
r
r
ò
ò
n
n
2 2
2 2 1 0
x y x y
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
1
1
C
C
â
â
u
u
2
2
2
2
.
.
Trong mặt phẳng
Oxy
, cho elip
( )E
có phương trình chính tắc
2 2
1
36 9
x y
. Tìm tọa điểm
M
sao cho
điểm
M
thuộc
( )E
và trục
Oy
.
A.
( 6;0)
hoặc
6;0
. B.
(0; 6)
hoặc
0;6
. C.
3;0
hoặc
3;0
. D.
0; 3
hoặc
0;3
.
_________________________________
11
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P5)
_____________________________________
Câu 1. Elip có hai đỉnh là
3;0 ; 3;0
và có một tiêu điểm là
2 2;0
. Phương trình chính tắc của elip là:
A.
2 2
1.
9 1
x y
B.
2 2
1.
8 9
x y
C.
2 2
1.
9 8
x y
D.
2 2
1.
1 9
x y
Câu 2. Tìm phương trình chính tắc của elip nếu trục lớn gấp
6
2
lần trục bé và có tiêu cự bằng
4 3
.
A.
2 2
+ 1.
16 4
x y
B.
2 2
1.
36 9
x y
C.
2 2
1.
36 24
x y
D.
2 2
+ 1.
24 16
x y
Câu 3. Tính diện tích hình chữ nhật cơ sở của elip
2 2
4 25 36
x y
.
A.14,4 B. 15,5 C. 16,5 D. 18
Câu 4. Lập phương trình chính tắc của elip biết độ dài trục lớn hơn độ dài trục nhỏ 4 đơn vị, độ dài trục nhỏ bé
hơn độ dài tiêu cự 2 đơn vị.
A.
2 2
1.
64 60
x y
B.
2 2
1.
25 9
x y
C.
2 2
1.
100 64
x y
D.
2 2
1.
9 1
x y
C
C
â
â
u
u
5
5
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
A
A
B
B
C
C
D
D
n
n
ộ
ộ
i
i
t
t
i
i
ế
ế
p
p
e
e
l
l
i
i
p
p
v
v
à
à
c
c
ó
ó
c
c
á
á
c
c
đ
đ
ỉ
ỉ
n
n
h
h
v
v
ớ
ớ
i
i
t
t
ọ
ọ
a
a
đ
đ
ộ
ộ
n
n
g
g
u
u
y
y
ê
ê
n
n
t
t
h
h
ì
ì
c
c
ó
ó
d
d
i
i
ệ
ệ
n
n
t
t
í
í
c
c
h
h
b
b
ằ
ằ
n
n
g
g
A
A
.
.
2
2
0
0
B
B
.
.
1
1
8
8
C
C
.
.
2
2
4
4
D
D
.
.
1
1
6
6
Câu 6. Lập phương trình chính tắc của elip biết tỉ số giữa độ dài tiêu cự và trục nhỏ bằng
2
, tổng bình
phương độ dài trục lớn và tiêu cự bằng 56
A.
2 2
1.
12 8
x y
B.
2 2
1.
8 12
x y
C.
2 2
1.
12 4
x y
D.
2 2
1.
8 4
x y
Câu 7. Elip (E) đi qua điểm
7
2 3;
2
M
và một tiêu điểm có hoành độ bằng – 3. Độ dài trục lớn của elip bằng
A.6 B. 8 C. 9 D. 10
Câu 8. Tìm elip có độ dài trục lớn bằng
6
và tỉ số của tiêu cự với độ dài trục lớn bằng
1
3
.
A.
2 2
+ 1.
9 8
x y
B.
2 2
1.
9 5
x y
C.
2 2
1.
6 5
x y
D.
2 2
+ 1.
9 3
x y
Câu 9. Tính diện tích hình chữ nhật cơ sở của elip (E) có độ dài trục nhỏ bằng
12
và tỉ số của tiêu cự với độ dài
trục lớn bằng
4
5
.
A.240 B. 260 C. 240 D. 320
Câu 10. Elip (E) có hai tiêu điểm
1 2
2;0 , 2;0
F F
và đi qua điểm
2;3
M
. Khi đó đường tròn
2 2
17
x y
cắt
elip đã cho tại bao nhiêu giao điểm
A.2 B. 1 C. 4 D. 0
Câu 11. Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng
6
và đi qua
5;0
A
.
A.
2 2
1
25 16
x y
. B.
2 2
+ 1
25 16
x y
. C.
2 2
+ 1
25 9
x y
. D.
2 2
+ 1
100 81
x y
.
Câu 12. Tìm elip có tổng độ dài hai trục bằng
18
và tỉ số của tiêu cự với độ dài trục lớn bằng
3
5
.
12
A.
2 2
1.
25 16
x y
B.
2 2
1.
5 4
x y
C.
2 2
1.
25 9
x y
D.
2 2
1.
9 4
x y
C
C
â
â
u
u
1
1
3
3
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
í
í
n
n
h
h
2 2
a b
.
A
A
.
.
1
1
3
3
B
B
.
.
1
1
7
7
C
C
.
.
1
1
0
0
D
D
.
.
1
1
1
1
Câu 14. Tìm elip có tổng độ dài hai trục bằng
10
và tỉ số của tiêu cự với độ dài trục lớn bằng
5
3
.
A.
2 2
1.
25 16
x y
B.
2 2
1.
5 4
x y
C.
2 2
1.
25 9
x y
D.
2 2
1.
9 4
x y
Câu 15. Elip (E) đi qua hai điểm
7;0
A
và
0;3
B
. Tìm số giao điểm của (E) và đường thẳng y = 2x + 7
A.4 B. 3 C. 2 D. 1
Câu 16. Tính khoảng cách lớn nhất từ điểm M (8;0) đến một điểm nằm trên elip
2 2
1.
49 9
x y
A.15 đơn vị B. 14 đơn vị C. 12 đơn vị D. 10 đơn vị
Câu 17. Tìm elip có một tiêu điểm
2;0
F
và tích độ dài trục lớn với trục bé bằng
12 5
.
A.
2 2
1.
9 5
x y
B.
2 2
1.
36 20
x y
C.
2 2
1.
144 5
x y
D.
2 2
1.
45 16
x y
Câu 16. Elip đi qua các điểm
0;3
M
và
12
3;
5
N
. Từ một tiêu điểm của elip dựng đường thẳng vuông góc với
trục hoành cắt elip tại hai giao điểm AB, độ dài đoạn thẳng AB bằng
A.3,6 B. 4,5 C. 7,2 D. Kết quả khác
Câu 18. Elip đi qua các điểm
0;1
A
và
3
1;
2
N
có phương trình chính tắc là:
A.
2 2
1.
16 4
x y
B.
2 2
1.
8 4
x y
C.
2 2
1.
4 1
x y
D.
2 2
1.
2 1
x y
Câu 19. Tìm phương trình chính tắc của elip nếu nó có trục lớn gấp đôi trục bé và đi qua điểm
2; 2
M
.
A.
2 2
+ 1.
20 5
x y
B.
2 2
1.
36 9
x y
C.
2 2
1.
24 6
x y
D.
2 2
+ 1.
16 4
x y
C
C
â
â
u
u
2
2
0
0
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
2
( 1)y k x
tạo với elip một dây cung có độ dài lớn nhất
bằng
A
A
.
.
1
1
4
4
B
B
.
.
8
8
C
C
.
.
1
1
0
0
D
D
.
.
1
1
2
2
Câu 21. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của đoạn thẳng OM, với M là điểm bất ỳ thuộc elip
2 2
1.
16 4
x y
A.5 B. 6 C. 8 D. 4
Câu 22. Elip (E) có tiêu cự bằng
8
và đi qua điểm
15; 1
M
. Đường thẳng y = 1 cắt elip theo một dây cung có
độ dài gần nhất với
A.7,746 B. 7,826 C. 7,725 D. 7,734
Câu 23. Tìm số giao điểm của elip
2 2
1
16 12
x y
và đường parabol
2
2 4 4
y x x
A.4 B. 3 C. 2 D. 1
13
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P6)
_____________________________________
Câu 1. Cho
E
:
2 2
1
16 9
x y
và điểm
M
thuộc Elip. Khi đó độ dài
OM
thỏa mãn:
A.
3
OM
. B.
3 4
OM
. C.
4 5
OM
. D.
5
OM
.
Câu 2. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho elip
2 2
: 1
16 9
x y
E
và đường thẳng
:3 4 12 0
d x y
.
Biết rằng
d
luôn cắt
E
tại hai điểm phân biệt
A
,
B
. Tính độ dài đoạn
AB
.
A.
5
AB
. B.
3
AB
. C.
4AB
. D.
10
AB
.
Câu 3. Cho elip
2 2
2 2
: 1
x y
E
a b
. Khẳng định nào sau đây là đúng?
A.
E
không có tâm đối xứng. B.
E
có đúng một tâm đối xứng.
C.
E
có hai tâm đối xứng. D.
E
có vô số tâm đối xứng.
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
( 2) 1
y k x
tại bao nhiêu điểm (với k là
tham số).
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
1
1
Câu 5. Cặp điểm nào là các tiêu điểm của elip
2 2
: 1
5 4
x y
E
?
A.
1;2
1;0
F
. B.
1;2
5;0
F
. C.
1;2
0; 1
F
. D.
1;2
0; 2
F
.
Câu 7. Cho elip
2 2
: 1
5 4
x y
E
và đường thẳng
2
:
1
x t
d
y t
. Số điểm chung của
E
và
d
là
A.
0.
B.
1.
C.
2.
D.
4.
Câu 8. Viết phương trình chính tắc của elip
E
biết độ dài trục lớn
10
, độ dài trục bé bằng
8
.
A.
2 2
: 1
16 9
x y
E
. B.
2 2
: 1
25 9
x y
E
. C.
2 2
: 1
25 16
x y
E
. D.
2 2
: 1
9 16
x y
E
.
Câu 9. Cho
E
có hai tiêu điểm
1
4;0
F
,
2
4;0
F
và điểm
M
thuộc
E
. Biết chu vi tam giác
1 2
MF F
bằng
18
. Khi đó độ dài trục lớn của
E
bằng
A. 6. B. 10. C. 5. D. 3.
Câu 10. Trong mặt phẳng
(Oxy)
, phương trình nào sau đây là phương trình chính tắc của một elip?
A.
2 2
1
7 6
x y
. B.
2 2
1
7 6
x y
. C.
2 2
1
6 7
x y
. D.
2 2
1
6 7
x y
.
Câu 11. Phương trình chính tắc của
E
có độ dài trục lớn bằng
10
và tiêu cự bằng
6
là:
A.
2 2
1
5 3
x y
. B.
2 2
1
5 3
x y
. C.
2 2
1
25 16
x y
. D.
2 2
1
25 16
x y
.
Câu 12. Có bao nhiêu điểm nguyên (tọa độ đều là số nguyên) nằm trên elip
2 2
1
8 2
x y
A.2 B. 3 C. 4 D. 1
Câu 13. Trong mặt phẳng
(Oxy)
, cho elip
( )E
có một tiêu điểm là
(3;0)
F
, một đỉnh trên trục nhỏ là
(0;4)
B
.
Phương trình chính tắc của
( )E
là
A.
2 2
1
25 9
x y
. B.
2 2
1
16 9
x y
. C.
2 2
1
25 16
x y
. D.
2 2
1
4 1
x y
.
14
C
C
â
â
u
u
1
1
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
2 2
2 3 20
y a b
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
2
2
Câu 15. Trong mặt phẳng
(Oxy)
, cho elip có các đỉnh
1 2
( 7;0), (0;5)
A B
. Phương trình chính tắc của
( )E
là
A.
2 2
1
7 5
x y
. B.
2 2
1
49 25
x y
. C.
2 2
1
7 5
x y
. D.
2 2
1
7 5
x y
.
Câu 16. Elip
2 2
2
( ) : 1
4
x y
E
a
có tiêu cự bằng
6
thì có phương trình chính tắc là
A.
2 2
( ) : 1
7 4
x y
E
. B.
2 2
( ) : 1
169 4
x y
E
. C.
2 2
( ) : 1
5 4
x y
E
. D.
2 2
( ) : 1
13 4
x y
E
.
Câu 17. Trong mặt phẳng
(Oxy)
, cho elip
2 2
2 2
( ) : 1
x y
E
a b
có độ dài trục lớn bằng 4, tiêu cự bằng 2. Phương
trình nào sau đây là phương trình chính tắc của của
( )E
?
A.
2 2
1
4 3
x y
. B.
2 2
1
2 1
x y
. C.
2 2
1
4 1
x y
. D.
2 2
1
16 12
x y
.
C
C
â
â
u
u
1
1
8
8
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
r
r
ò
ò
n
n
2 2 2 2
2 25
x y a b
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
1
1
Câu 19. Cho
2 2
: 1
20 16
x y
E
. Một đường thẳng đi qua điểm
2;2
A
và song song với trục hoành cắt
E
tại hai
điểm phân biệt
M
và
N
. Tính độ dài
MN
.
A.
3 5.
B.
15 2.
C.
2 15.
D.
5 3.
Câu 20. Trong mặt phẳng
(Oxy)
, phương trình nào sau đây là phương trình chính tắc của một elip?
A.
2 2
1
7 6
x y
. B.
2 2
1
7 6
x y
. C.
2 2
1
6 7
x y
. D.
2 2
1
6 7
x y
.
Câu 21. Cho elip
( )E
có hai tiêu điểm là
1 2
,F F
, độ dài các trục lớn là
2a
, trục nhỏ là
2b
, tiêu cự là 2c và M là
điểm nằm trên
( )E
. Khẳng định nào sau đây đúng?
A.
1 2
2MF MF b
. B.
1 2
2MF MF c
.
C.
1 2
2MF MF a
. D.
2 2
1 2
MF MF a b
.
Câu 22. Trong mặt phẳng
Oxy
, phương trình chính tắc của
E
có tiêu cự bằng
6
và đi qua điểm
5;0
A
là
A.
2 2
1
100 81
x y
. B.
2 2
1
15 16
x y
. C.
2 2
1
25 9
x y
. D.
2 2
1
25 16
x y
.
Câu 23. Cho elip
2 2
: 1
169 144
x y
E
và đường tròn
2 2
: 144
C x y
. Elip
E
và đường tròn
C
có bao
nhiêu điểm chung?
A.
0.
B.
1.
C.
2.
D.
4.
_______________________________
15
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P7)
_____________________________________
Câu 1. Cho đường elip
2 2
2 2
1
x y
a b
như hình vẽ bên. Đường elip đã
cho cắt đường thẳng
2023y x
tại bao nhiêu điểm
A. 4 B. 3
C. 2 D. 1
Câu 2. Tìm phương trình chính tắc của elip có tiêu cự bằng 6 và trục lớn bằng 10.
A.
2 2
1.
25 9
x y
B.
2 2
1.
100 81
x y
C.
2 2
1.
25 16
x y
D.
2 2
1.
25 16
x y
Câu 3. Elip có độ dài trục lớn là 10 và có một tiêu điểm
3;0
F
. Phương trình chính tắc của elip là:
A.
2 2
1.
25 9
x y
B.
2 2
1.
100 16
x y
C.
2 2
1.
100 81
x y
D.
2 2
1.
25 16
x y
Câu 4. Trong mặt phẳng
Oxy
, elip
2 2
: 1
100 64
x y
E
có độ dài trục bé bằng
A.
8.
B.
10.
C.
16.
D.
20.
Câu 5. Phương trình chính tắc của Elip
E
đi qua hai điểm
5
; 15
4
M
và
5 3
; 2
2
N
là
A.
2 2
1
25 16
x y
. B.
2 2
1
25 16
x y
. C.
2 2
0
25 16
x y
. D.
2 2
1
16 25
x y
.
Câu 6. Elip có độ dài trục nhỏ là
4 6
và có một tiêu điểm
5;0
F
. Phương trình chính tắc của elip là:
A.
2 2
1.
121 96
x y
B.
2 2
1.
101 96
x y
C.
2 2
1.
49 24
x y
D.
2 2
1.
29 24
x y
Câu 7. Elip có một đỉnh là
5;0
A
và có một tiêu điểm
1
4;0
F
. Phương trình chính tắc của elip là:
A.
2 2
1.
25 16
x y
B.
2 2
1.
5 4
x y
C.
2 2
1.
25 9
x y
D.
1.
5 4
x y
Câu 8. Có bao nhiêu điểm nguyên (tọa độ đều là số nguyên) nằm trên elip
2 2
1
8 2
x y
A.2 B. 3 C. 4 D. 1
Câu 9. Trong mặt phẳng
(Oxy)
, cho elip
( )E
có một tiêu điểm là
(3;0)
F
, một đỉnh trên trục nhỏ là
(0;4)
B
.
Phương trình chính tắc của
( )E
là
A.
2 2
1
25 9
x y
. B.
2 2
1
16 9
x y
. C.
2 2
1
25 16
x y
. D.
2 2
1
4 1
x y
.
Câu 10. Cho đường elip
2 2
2 2
1
x y
a b
như hình vẽ bên.
Đường elip đã cho cắt đường thẳng
2 2
2 3 1
y a b
tại
bao nhiêu điểm
A. 1 B. 3
C. 0 D. 2
Câu 11. Trong mặt phẳng
(Oxy)
, cho elip
2 2
2 2
( ) : 1
x y
E
a b
có độ dài trục lớn bằng 4, tiêu cự bằng 2. Phương
trình nào sau đây là phương trình chính tắc của của
( )E
?
16
A.
2 2
1
4 3
x y
. B.
2 2
1
2 1
x y
. C.
2 2
1
4 1
x y
. D.
2 2
1
16 12
x y
.
Câu 12. Cho đường elip
2 2
2 2
1
x y
a b
như hình vẽ bên.
Đường elip đã cho cắt đường tròn
2 2 2 2
16
x y a b
tại
bao nhiêu điểm
A. 4 B. 3
C. 2 D. 1
Câu 13. Trong mặt phẳng
Oxy
, cho elip
E
có các tiêu điểm
1 2
4;0 , 4;0
F F
và một điểm
M
nằm trên
E
. Biết rằng chu vi của tam giác
1 2
MF F
bằng
18
. Xác định tâm sai e của
.E
A.
4
5
e
. B.
4
18
e
. C.
4
5
e
. D.
4
9
e
.
Câu 14. Phương trình chính tắc của Elip nhận điểm
4;3
M
là một đỉnh của hình chữ nhật cơ sở là
A.
2 2
1
16 9
x y
. B.
2 2
1
16 4
x y
. C.
2 2
1
16 3
x y
. D.
2 2
1
9 4
x y
.
Câu 15. Cho elip
2 2
2 2
: 1
x y
E
a b
với
0.
a b
Gọi
2c
là tiêu cự của
E
. Trong các mệnh đề sau, mệnh đề nào
đúng?
A.
2 2 2
.c a b
B.
2 2 2
.b a c
C.
2 2 2
.a b c
D.
.c a b
Câu 16. Elip qua điểm
5
2;
3
M
và có một tiêu điểm
2;0
F
. Diện tích hình chữ nhật cơ sở của elip là
A.
12 5
B. 24 C. 80 D. 60
Câu 17. Elip (E) có hai tiêu điểm
1 2
2;0 , 2;0
F F
và đi qua điểm
2;3
M
. Khi đó đường tròn
2 2
16
x y
cắt
elip đã cho tại bao nhiêu giao điểm
A.2 B. 4 C. 1 D. 3
Câu 18. Tìm elip nếu nó đi qua điểm
6;0
A
và tỉ số của tiêu cự với độ dài trục lớn bằng
2
2
A.
2 2
+ 1.
36 27
x y
B.
2 2
1.
6 3
x y
C.
2 2
+ 1.
36 18
x y
D.
2 2
+ 1.
6 2
x y
Câu 19. Trong mặt phẳng
Oxy
, cho elip
E
có phương trình
2 2
16 25 100
x y
và điểm
M
thuộc
E
có
hoành độ bằng
2
. Tổng khoảng cách từ
M
đến
2
tiêu điểm của
E
bằng
A.
5
. B.
2 2
. C.
4 3
. D.
3
.
Câu 20. Lập phương trình chính tắc của elip
E
biết
E
có trục lớn bằng
6
và tiêu cự bằng
4
.
A.
2 2
1.
36 16
x y
B.
2 2
1.
6 4
x y
C.
2 2
1.
9 5
x y
D.
2
2
1.
5 4
x y
Câu 21. Tìm elip có độ dài trục lớn bằng
26
và tỉ số của tiêu cự với độ dài trục lớn bằng
12
13
.
A.
2 2
1.
26 25
x y
B.
2 2
1.
169 25
x y
C.
2 2
1.
52 25
x y
D.
2 2
1.
169 5
x y
Câu 22. Trong mặt phẳng tọa độ
Oxy
, Elip có một tiêu điểm
( 2;0)
F
và tích độ dài trục lớn với trục bé bằng
12 5
. Phương trình chính tắc của elip là:
A.
2 2
1
144 5
x y
B.
2 2
1
36 20
x y
C.
2 2
1
9 5
x y
D.
2 2
1
45 16
x y
_____________________________
17
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P8)
_____________________________________
Câu 1. Đường Elip
2 2
1
16 4
x y
có độ dài trục lớn bằng:
A. 16. B. 8. C. 2. D. 4.
Câu 2. Tọa độ tiêu điểm với hoành độ âm của đường Elip
2 2
1
8 4
x y
là
A.
2; 0
. B.
2 2;0
. C.
2 2; 0
. D.
2;0
.
Câu 3. Đường Elip
2 2
1
9 6
x y
có tiêu cự bằng:
A.
2 3
. B.
3
. C. 3. D. 6.
Câu 4. Hãy xác định các tọa độ tiêu điểm của Elip (E):
2 2
4 9 36
x y
?
A.
1 2
5;0 , 5;0
F F
. C.
1 2
5; 5 , 0; 5
F F
.
B.
1 2
5;0 , 0; 5
F F
. D.
1 2
5; 5 , 5; 5
F F
.
Câu 5. Phương trình của elip
E
có độ dài trục lớn bằng 8, độ dài trục nhỏ bằng 6 là:
A.
2 2
9 16 144.
x y
B.
2 2
9 16 1.
x y
C.
2 2
1.
9 16
x y
D.
2 2
1.
64 36
x y
Câu 6. Tìm phương trình chính tắc của elip nếu trục lớn gấp đôi trục bé và có tiêu cự bằng
4 3
.
A.
2 2
+ 1.
16 4
x y
B.
2 2
1.
36 9
x y
C.
2 2
1.
36 24
x y
D.
2 2
+ 1.
24 16
x y
Câu 7. Lập phương trình chính tắc của elip biết độ dài trục lớn hơn độ dài trục nhỏ 4 đơn vị, độ dài trục nhỏ hơn
độ dài tiêu cự 4 đơn vị.
A.
2 2
1.
64 60
x y
B.
2 2
1.
25 9
x y
C.
2 2
1.
100 64
x y
D.
2 2
1.
9 1
x y
Câu 8. Tìm elip nếu nó đi qua điểm
6;0
A
và tỉ số của tiêu cự với độ dài trục lớn bằng
1
2
.
A.
2 2
+ 1.
36 27
x y
B.
2 2
1.
6 3
x y
C.
2 2
+ 1.
36 18
x y
D.
2 2
+ 1.
6 2
x y
Câu 9. Trong mặt phẳng
Oxy
, elip
2 2
: 1
25 9
x y
E
có tâm sai bằng
A.
5
3
. B.
4
5
. C.
4
5
. D.
3
5
.
Câu 10. Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng
8
và đi qua điểm
15; 1
M
.
A.
2 2
1.
12 4
x y
B.
2 2
1.
16 4
x y
C.
2 2
1.
18 4
x y
D.
2 2
1.
20 4
x y
Câu 11. Trong mặt phẳng
Oxy
, elip
E
2 2
1
16 7
x y
có tiêu cự là
A.
18
. B.
6
. C.
9
. D.
3
.
Câu 12. Trong mặt phẳng
Oxy
, cho elip
2 2
1
5 4
x y
. Tỷ số giữa tiêu cự và độ dài trục lớn của elip bằng
A.
3 5
5
. B.
2 5
5
. C.
5
5
. D.
5
4
.
Câu 13. Elip (E) đi qua điểm
5
2;
3
N
và tỉ số của tiêu cự với độ dài trục lớn bằng
2
3
. Tính độ dài dây cung tạo
bởi elip đã cho và đường thẳng x = 2.
18
A.3 B.
10
3
C.
8
3
D.
16
7
Câu 14. Elip (E) có một cạnh nằm trên đường thẳng y = 2 và có độ dài một đường chéo bằng 6. Tìm số giao
điểm của elip đã cho và đường parabol
2
2( 2 )y x x
A.4 B. 1 C. 2 D. 3
Câu 15. Tìm phương trình chính tắc của elip nếu nó có trục lớn gấp đôi trục bé và đi qua điểm
(2; 2)
M
.
A.
2 2
1
36 9
x y
B.
2 2
1
20 5
x y
C.
2 2
1
24 6
x y
D.
2 2
1
16 4
x y
Câu 16. Lập phương trình chính tắc của elip
E
biết
E
đi qua điểm
9
4;
5
M
và
12
3;
5
N
.
A.
2 2
1.
25 9
x y
B.
2 2
1.
4 3
x y
C.
2 2
1.
9 5
x y
D.
2
2
1.
5 4
x y
Câu 17. Trong mặt phẳng
Oxy
, phương trình chính tắc của
E
có độ dài trục lớn gấp
2
lần độ dài trục nhỏ
và đi qua điểm
2; 2
A
là
A.
2 2
1
24 16
x y
. B.
2 2
1
36 9
x y
. C.
2 2
1
16 4
x y
. D.
2 2
1
20 5
x y
Câu 18. Elíp
2 2
( ) : 1
25 9
x y
E
có độ dài trục lớn bằng:
A.
25
. B.
50
. C.
5
. D.
10
.
Câu 19. Phương trình chính tắc của
E
có độ dài trục lớn gấp
2
lần độ dài trục nhỏ và đi qua điểm
2; 2
A
là
A.
2 2
1
36 9
x y
. B.
2 2
1
20 5
x y
. C.
2 2
1
24 16
x y
. D.
2 2
1
16 4
x y
.
Câu 20. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho elip
E
có độ dài trục lớn bằng
12
và độ dài trục bé
bằng
6
. Phương trình nào sau đây là phương trình của elip
E
A.
2 2
1
144 36
x y
. B.
2 2
1
9 36
x y
. C.
2 2
1
36 9
x y
. D.
2 2
0
144 36
x y
.
Câu 21. Tìm phương trình chính tắc của Elip có tâm sai bằng
1
3
và trục lớn bằng
6
.
A.
2 2
1
9 3
x y
. B.
2 2
1
6 5
x y
. C.
2 2
1
9 5
x y
. D.
2 2
1
9 8
x y
.
Câu 22. Trong mặt phẳng
Oxy
, phương trình chính tắc của
E
có độ dài trục lớn gấp
2
lần độ dài trục nhỏ
và tiêu cự bằng
4 3
là
A.
2 2
1
36 9
x y
. B.
2 2
1
36 24
x y
. C.
2 2
1
24 6
x y
. D.
2 2
1
16 4
x y
.
Câu 23. Cho Elip có phương trình
2
2
1
4
x
y
. Một tiêu điểm của Elip có tọa độ là :
A.
0; 3
B
. B.
5;0
C
. C.
3;0
A
. D.
0; 5
D
.
Câu 24. Phương trình chính tắc của (E) biết độ dài 2 trục lớn và nhỏ lần lượt là 10 và 8 là:
A.
2 2
1
25 16
x y
. C.
2 2
1
16 25
x y
.
B.
2 2
0
16 25
x y
. D.
2 2
0
25 16
x y
.
Câu 25. Lập phương trình chính tắc của elip
E
biết
E
có một tiêu điểm
1
4;0
F
và trục lớn bằng 10.
A.
2 2
1.
25 16
x y
B.
2 2
1.
5 4
x y
C.
2 2
1.
25 9
x y
D.
1.
5 4
x y
_____________________________
19
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P1)
_____________________________________
Câu 1. Cho hypebol có phương trình:
2 2
1
16 12
x y
. Tiêu cự của hypebol là:
A.
2 5
. B.
2 3
. C.
4 7
. D.
2 2
.
C
C
â
â
u
u
2
2
.
.
G
G
ọ
ọ
i
i
t
t
ê
ê
n
n
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
o
o
n
n
i
i
c
c
t
t
ạ
ạ
o
o
b
b
ở
ở
i
i
m
m
ặ
ặ
t
t
c
c
ắ
ắ
t
t
v
v
à
à
h
h
a
a
i
i
k
k
h
h
ố
ố
i
i
n
n
ó
ó
n
n
đ
đ
ố
ố
i
i
x
x
ứ
ứ
n
n
g
g
t
t
r
r
o
o
n
n
g
g
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
.
.
A
A
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
t
t
r
r
ò
ò
n
n
B
B
.
.
P
P
a
a
r
r
a
a
b
b
o
o
l
l
C
C
.
.
H
H
y
y
p
p
e
e
b
b
o
o
l
l
D
D
.
.
E
E
l
l
i
i
p
p
Câu 3. Cho đường hypebol có phương trình
2 2
:9 1
H x y
. Khoảng cách giữa hai tiêu điểm là
A.
0
. B.
10
3
. C.
2 2
. D.
2 10
3
.
Câu 4. Trong mặt phẳng tọa độ
Oxy
,cho hypepol
H
có phương trình:
2 2
1.
16 9
x y
Khi đó độ dài trục lớn
bằng
A.
3.
B.
16.
C.
8.
D.
4.
Câu 5. Hypebol có nửa trục thực là
4
, tiêu cự bằng
10
có phương trình chính tắc là:
A.
2 2
1.
16 9
x y
B.
2 2
1.
16 9
y x
C.
2 2
1.
16 9
y x
D.
2 2
1.
16 25
x y
Câu 6. Hypebol (H) đi qua điểm
10;2
N
và hoành độ một giao điểm của (H) với trục hoành bằng 3. Khoảng
cách giữa hai tiêu điểm hypebol bằng
A.6 B.
6 5
C.
8 3
D. 8
Câu 7. Tìm phương trình chính tắc của hyperbol
H
mà hình chữ nhật cơ sở có một đỉnh là
2; 3 .
A.
2 2
1.
2 3
x y
B.
2 2
1.
4 9
x y
C.
2 2
1.
9 3
x y
D.
2 2
1.
2 3
x y
C
C
â
â
u
u
8
8
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
h
h
y
y
p
p
e
e
b
b
o
o
l
l
đ
đ
i
i
q
q
u
u
a
a
đ
đ
i
i
ể
ể
m
m
2 7
4;
3
.
T
T
í
í
n
n
h
h
2 2
2a b
.
A
A
.
.
1
1
6
6
B
B
.
.
1
1
4
4
C
C
.
.
1
1
7
7
D
D
.
.
1
1
3
3
Câu 9. Đường thẳng nào sau đây là trục đối xứng của hypebol
2 2
1.
4 9
x y
A.
0
y
B.
1x
C.
2
x
D.
1
x
Câu 10. Điểm M thuộc hypebol
2 2
1.
16 9
x y
Tính
1 2
MF MF
với
1 2
,F F
là hai tiêu điểm của hypebol.
A.4 B. 8 C. 10 D. 6
Câu 11. Trong mặt phẳng tọa độ
Oxy
, cho hypebol
H
có một tiêu điểm là
2
(6;0)
F
và đi qua điểm
4;0
M
.
Phương trình chính tắc của
H
đó là
A.
2 2
1
20 16
x y
.
B.
2 2
1
16 20
x y
.
C.
2 2
1
20 16
x y
.
D.
2 2
1
16 20
x y
.
Câu 12. Trong mặt phẳng tọa độ
Oxy
, cho hypebol
H
có tiêu cự bằng
26
, hiệu các khoảng cách từ một
20
điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng
24
. Phương trình chính tắc của
H
đó là
A.
2 2
1
144 25
x y
.
B.
2 2
1
25 144
x y
.
C.
2 2
1
144 25
x y
.
D.
2 2
1
144 25
x y
.
C
C
â
â
u
u
1
1
3
3
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
h
h
y
y
p
p
e
e
b
b
o
o
l
l
đ
đ
i
i
q
q
u
u
a
a
đ
đ
i
i
ể
ể
m
m
2 7
4;
3
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
h
h
â
â
n
n
g
g
i
i
á
á
c
c
g
g
ó
ó
c
c
p
p
h
h
ầ
ầ
n
n
t
t
ư
ư
t
t
h
h
ứ
ứ
n
n
h
h
ấ
ấ
t
t
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
0
0
D
D
.
.
1
1
Câu 14. Hai tiêu điểm của hypebol
2 2
9 16 144
x y
đều cách gốc tọa độ một khoảng bằng
A.4 B. 5 C. 6 D. 3
Câu 15. Đường thẳng nào sau đây là trục đối xứng của hypebol
2 2
1
25 144
x y
A.
0
x
B.
1x
C.
2
x
D.
1
x
Câu 16. Điểm
( ; )M x y
thuộc hypebol
2 2
1.
16 9
x y
Giá trị nhỏ nhất của biểu thức
2
Q x y
thuộc khoảng
A.(0;5) B. (17;22) C. (5;10) D. (10;17)
Câu 17. Trong mặt phẳng
,Oxy
viết phương trình chính tắc của hypebol
H
biết
H
có một tiêu điểm là
2
3;0
F
và cắt trục hoành tại điểm có hoành độ bằng
2.
A.
2 2
1
4 5
x y
. B.
2 2
1
4 1
x y
. C.
2 2
1
4 1
x y
. D.
2 2
1.
4 5
x y
Câu 18. Mọi điểm M trên hypebol
2 2
1
25 144
x y
đều cách gốc tọa độ một khoảng nhỏ nhất bằng
A.4 B. 5 C. 6 D. 3
Câu 19. Tìm số giao điểm của hypebol
2 2
1.
16 9
x y
và đường tròn
2 2
9
x y
.
A.3 B. 1 C. 2 D. 0
Câu 20. Đường thẳng nào dưới đây là đường chuẩn của hyperbol
2 2
1
16 12
x y
?
A.
3
0
4
x
. B.
2 0
x
. C.
8 0
x
. D.
8 7
0
7
x
.
Câu 21. Đường hyperbol
2 2
1
20 16
x y
có tiêu cự bằng:
A. 12. B. 2. C. 4. D. 6.
Câu 22. Tiêu cự của hypebol
2 2
7 9 63
x y
bằng
A.8 B. 6 C. 4 D. 10
Câu 23. Có bao nhiêu số nguyên dương m nhỏ hơn 10 để hypebol
2 2
1
20 16
x y
và đường thẳng
y x m
có
điểm chung
A.3 B. 4 C. 8 D. 7
Câu 24. Tìm số giao điểm của hypebol
2 2
1.
16 9
x y
và đường elip
2
2
1
16
x
y
.
A.3 B. 1 C. 2 D. 0
_________________________________
21
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P2)
_____________________________________
Câu 1. Cho hypebol
( )H
có phương trình chính tắc
2 2
1
9 16
x y
. Tìm tọa độ các giao điểm của
( )H
với trục
hoành
A.
9; 0
và
9; 0
.
B.
3; 0
và
3; 0
.
C.
4; 0
và
4; 0
.
D.
16; 0
và
16; 0
.
Câu 2. Tìm số giao điểm của hypebol
2 2
1.
16 9
x y
và đường elip
2 2
25 1
x y
.
A.3 B. 1 C. 2 D. 4
Câu 3. Cho hypebol
H
có phương trình chính tắc
2 2
1
9 16
x y
. Tìm tọa độ điểm thuộc
H
có hoành độ bằng
4 và tung độ âm.
A.
4 7
4;
3
.
B.
7
4;
3
.
C.
8 7
4;
3
.
D.
2 7
4;
3
.
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
h
h
y
y
p
p
e
e
b
b
o
o
l
l
đ
đ
i
i
q
q
u
u
a
a
đ
đ
i
i
ể
ể
m
m
2 7
4;
3
. Có bao nhiêu giá trị m để
đường thẳng
y m
tiếp xúc hypebol đã cho
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
1
1
Câu 5. Điểm M thuộc nhánh phải hypebol
2 2
1
25 144
x y
cách tiêu điểm bên trái một khoảng nhỏ nhất bằng
A.14 B. 18 C. 16 D. 13
Câu 6. Tìm số giao điểm của hypebol
2 2
1.
16 9
x y
và đường tròn
2 2
16
x y
.
A.3 B. 1 C. 2 D. 0
Câu 7. Đường hyperbol
2 2
1.
16 9
x y
có tiêu cự bằng:
A. 12. B. 2. C. 10. D. 6.
Câu 8. Có bao nhiêu số nguyên dương m nhỏ hơn 20 để hypebol
2 2
1.
16 9
x y
và đường thẳng
y x m
có
điểm chung
A.13 B. 14 C. 16 D. 17
Câu 9. Tìm số giao điểm của hai hypebol
2 2
1.
16 9
x y
và
2 2
1
9 4
x y
.
A.3 B. 1 C. 2 D. 4
Câu 10. Cho hypebol
H
có phương trình chính tắc
2 2
1
9 16
x y
. Tìm tọa độ điểm thuộc
H
có hoành độ,
tung độ dương và cách đều hai trục tọa độ.
A.
12 12
;
7 7
.
B.
12 7 12 7
;
7 7
.
C.
12 12
;
5 5
.
D.
12 5 12 5
;
5 5
.
Câu 11. Cho đường hypebol có phương trình chính tắc sau:
2 2
: 1
16 9
x y
H
. Điểm nào sau đây không nằm
trên đường hypebol?
A.
4;0
Q
. B.
4 2;3
N
. C.
4;0
P
. D.
3;1
M
.
22
Câu 12. Trên hypebol
2 2
1.
16 9
x y
có bao nhiêu điểm có tọa độ nguyên
A.3 B. 2 C. 1 D. 4
C
C
â
â
u
u
1
1
3
3
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
1
4 1
x y
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
K
K
h
h
o
o
ả
ả
n
n
g
g
c
c
á
á
c
c
h
h
n
n
g
g
ắ
ắ
n
n
n
n
h
h
ấ
ấ
t
t
g
g
i
i
ữ
ữ
a
a
h
h
a
a
i
i
n
n
h
h
á
á
n
n
h
h
c
c
ủ
ủ
a
a
h
h
y
y
p
p
e
e
b
b
o
o
l
l
b
b
ằ
ằ
n
n
g
g
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
4
4
D
D
.
.
1
1
Câu 14. Đường hypebol nào có tiêu điểm nằm trên đường tròn
2 2
25
x y
A.
2 2
: 1
16 9
x y
H
B.
2 2
: 1
16 20
x y
H
C.
2 2
( ) : 1
25 1
x y
H
D.
2 2
( ) : 1
25 9
x y
H
Câu 15. Cho đường hypebol có phương trình chính tắc sau:
2 2
: 1
25 9
x y
H
. Giao điểm của đường hypebol
với trục hoành là:
A.
5;0 ; 5; 0
A B
. B.
0;5 , 0; 5
M N
. C.
0;3 , 0; 3
P Q
. D.
3;0 , 3;0
C D
.
Câu 16. Tồn tại bao nhiêu điểm
M
thuộc
2 2
: 1
16 20
x y
H
sao cho khoảng cách từ
M
đến trục hoành bằng
khoảng cách từ
M
đến trục tung.
A.3 B. 2 C. 4 D. 1
C
C
â
â
u
u
1
1
7
7
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
1
9 4
x y
như hình vẽ, điểm
( ; )M x y
thuộc hypebol thì
(2 3 )(2 3 )x y x y
bằng
A
A
.
.
4
4
0
0
B
B
.
.
2
2
4
4
C
C
.
.
3
3
6
6
D
D
.
.
1
1
8
8
Câu 18. Cho đường hypebol có phương trình
2 2
1
25 9
x y
. Khoảng cách giữa hai tiêu điểm là
A.
0
. B.10. C.
2 2
. D.
2 34
.
Câu 19. Tìm số giao điểm tối đa của hypebol
2 2
1
25 9
x y
và đường tròn
2 2 2
25
x y m
.
A.3 B. 2 C. 3 D. 0
Câu 20. Tồn tại hai đường thẳng song song và cách trục hoành một khoảng bằng 2, hai đường thẳng này cắt
hypebol
2 2
1
25 144
x y
tại tổng số bao nhiêu giao điểm
A.2 B. 3 C. 4 D. 5
Câu 21. Đường hypebol nào có tiêu điểm có thể nằm trên đường tròn
2 2 2
36
x y m
A.
2 2
1
25 16
x y
B.
2 2
1
25 4
x y
C.
2 2
1
25 49
x y
D.
2 2
2 2
1
15 26
x y
m n
Câu 22. Đường tròn tiếp xúc với cả hai nhánh của hypebol
2 2
: 1
16 20
x y
H
có đường kính nhỏ nhất bằng
A.12 B. 10 C. 6 D. 8
_________________________________
23
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P3)
_____________________________________
Câu 1. Điểm nào sau đây thuộc phương trình đường hypebol
2 2
2 2
1
4 3
x y
?
A.
4;3
M
. B.
4;2
M
. C.
4;0
M
. D.
4;1
M
.
Câu 2. Hypebol nào sau đây có trọng tâm là trọng tâm ABC với
(16;5), ( ;8), ( 1; 13)
A B m C m
?
A.
2 2
: 1
9 16
x y
H
. B.
2 2
: 1
4 5
x y
H
. C.
2 2
: 1
2 1
x y
H
. D.
2 2
:4 1
H x y
.
Câu 3. Cho Hypebol
H
có phương trình
2 2
1
16 3
x y
.Các điểm
M H
có tung độ bằng 3 là
A.
8; 3 , ' 8;3
M M
. B.
8;3 , ' 8;3
M M
.
C.
3;8 , ' 8; 3
M M
. D.
8;3 , ' 8; 3
M M
.
Câu 4. Tìm số giao điểm của hypebol
2 2
1.
16 9
x y
và đường elip
2
2
1
16
x
y
.
A.3 B. 1 C. 2 D. 0
Câu 5. Hypebol nào sau đây có đỉnh bên phải là tâm đường tròn
2 2 2
4 9
x y x m
?
A.
2 2
: 1
9 16
x y
H
. B.
2 2
: 1
4 5
x y
H
. C.
2 2
: 1
2 1
x y
H
. D.
2 2
:4 1
H x y
.
Câu 6. Cho hypebol có phương trình chính tắc
2 2
1
16 9
x y
. Tiêu điểm của hypebol là
A.
1
25;0
F
và
2
25;0
F
. B.
1
5;0
F
và
2
5;0
F
.
C.
1
337;0
F
và
2
337;0
F
. D.
1
337;0
F
và
2
337;0
F
.
C
C
â
â
u
u
7
7
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
c
c
ó
ó
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ơ
ơ
s
s
ở
ở
m
m
ô
ô
t
t
ả
ả
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
B
B
i
i
ế
ế
t
t
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ó
ó
d
d
i
i
ệ
ệ
n
n
t
t
í
í
c
c
h
h
b
b
ằ
ằ
n
n
g
g
8 5
và có một đỉnh nằm trên đường tròn
2 2
4 4 4 0
x y x y
.
T
T
í
í
n
n
h
h
2 2
3a b
.
A
A
.
.
2
2
0
0
B
B
.
.
3
3
0
0
C
C
.
.
1
1
9
9
D
D
.
.
1
1
5
5
Câu 8. Cho hypebol có phương trình chính tắc
2 2
1
4 25
x y
và điểm
M
thuộc hypebol. Khi đó
1 2
MF MF
bằng
A.
4
. B.
8
. C.
6
. D.
10
.
Câu 9. Tìm phương trình chính tắc của hyperbol
H
mà một đỉnh nằm trên đường tròn
2 2
6 4 9 0
x y x y
A.
2 2
: 1
9 16
x y
H
. B.
2 2
: 1
4 5
x y
H
. C.
2 2
: 1
2 1
x y
H
. D.
2 2
:4 1
H x y
Câu 10. Hypebol
2 2
: 1
25 9
x y
H
có hai tiêu điểm là
A.
1 2
4;0 , 4;0
F F
B.
1 2
3;0 , 3;0
F F
.
C.
1 2
5;0 , 5;0
F F
. D.
1 2
34;0 , 34;0
F F
.
Câu 11. Điểm
2
3;0
F
là một tiêu điểm của hypebol có phương trình nào sau đây?
A.
2 2
: 1
9 16
x y
H
. B.
2 2
: 1
4 5
x y
H
. C.
2 2
: 1
2 1
x y
H
. D.
2 2
:4 1
H x y
.
24
Câu 12. Trong mặt phẳng tọa độ
Oxy
, cho hypebol
H
có tiêu cự bằng 10, hiệu các khoảng cách từ một
điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng 6. Phương trình chính tắc của
H
đó là
A.
2 2
: 1
9 16
x y
H
. B.
2 2
: 1
4 5
x y
H
. C.
2 2
: 1
2 1
x y
H
. D.
2 2
:4 1
H x y
.
Câu 13. Cho hypebol có phương trình chính tắc
2 2
2
1
2 5 9
x y
a a
và điểm
M
thuộc hypebol. Khi đó giá trị
nhỏ nhất của biểu thức
1 2
MF MF
bằng
A.
4
. B.
8
. C.
6
. D.
10
.
C
C
â
â
u
u
1
1
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
1
16 9
x y
c
c
ó
ó
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ơ
ơ
s
s
ở
ở
m
m
ô
ô
t
t
ả
ả
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
C
C
h
h
u
u
v
v
i
i
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ơ
ơ
s
s
ở
ở
d
d
à
à
i
i
h
h
ơ
ơ
n
n
t
t
i
i
ê
ê
u
u
c
c
ự
ự
m
m
ộ
ộ
t
t
k
k
h
h
o
o
ả
ả
n
n
g
g
b
b
ằ
ằ
n
n
g
g
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
ơ
ơ
n
n
v
v
ị
ị
đ
đ
ộ
ộ
d
d
à
à
i
i
A
A
.
.
2
2
0
0
B
B
.
.
1
1
4
4
C
C
.
.
1
1
8
8
D
D
.
.
1
1
5
5
Câu 15. Hypebol nào sau đây tiếp xúc với đường elip
2 2
: 1
9 4
x y
E
A.
2 2
: 1
9 16
x y
H
. B.
2 2
: 1
4 5
x y
H
. C.
2 2
: 1
2 1
x y
H
. D.
2 2
:4 1
H x y
.
Câu 16. Trong các phương trình sau, phương trình nào là phương trình chính tắc của hypebol?
A.
2 2
1
16 9
x y
. B.
2
2y x
. C.
2 2
1
16 9
x y
. D.
2 2
1
16 9
y x
.
Câu 17. Hypebol
H
có một tiêu điểm
2
10;0
F
và đi qua điểm
8;0
A
có phương trình chính tắc là
A.
2 2
1
64 36
y x
. B.
2 2
1
64 36
x y
. C.
2 2
1
16 9
x y
. D.
2 2
1
64 36
x y
.
Câu 18. Điểm
( ; )M x y
thuộc hypebol
2 2
1.
16 9
x y
Giá trị nhỏ nhất của biểu thức
2
Q x y
thuộc khoảng
A.(0;5) B. (17;22) C. (5;10) D. (10;17)
Câu 19. Trong mặt phẳng tọa độ
Oxy
, cho hypebol
H
có một tiêu điểm là
2
(6;0)
F
và đi qua điểm
2 5;0
.
Phương trình chính tắc của
H
đó là
A.
2 2
1
20 16
x y
.
B.
2 2
1
16 20
x y
.
C.
2 2
1
20 16
x y
.
D.
2 2
1
16 20
x y
.
Câu 20. Hyperbol
H
2 2
2 2
1
x y
a b
có một tiêu điểm
1
4;0
F
và độ dài trục ảo (
2b
) bằng
28
là
A.
2 2
1.
9 7
x y
B.
2 2
1.
9 7
x y
C.
2 2
1.
3 7
x y
D.
2 2
1.
3
7
x y
Câu 21. Đường hypebol nào có tiêu điểm có thể nằm trên đường tròn
2 2 2
36
x y m
A.
2 2
1
25 16
x y
B.
2 2
1
25 4
x y
C.
2 2
1
25 49
x y
D.
2 2
2 2
1
15 26
x y
m n
Câu 22. Phương trình chính tắc của Hyperbol
H
có một tiêu điểm
2
5;0
F
và độ dài trục thực bằng
8
là
A.
2 2
1.
16 9
x y
B.
2 2
1.
4 3
x y
. C.
2 2
1.
16 9
x y
D.
2 2
0.
16 9
x y
_________________________________
25
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P4)
_____________________________________
Câu 1. Cho đường hypebol có phương trình
2 2
:9 1
H x y
. Khoảng cách giữa hai tiêu điểm là
A.
0
. B.
10
3
. C.
2 2
. D.
2 10
3
.
Câu 2.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
có độ dài trục thực bằng 10 và độ dài trục ảo bằng 8. Tính
2 2
3a b
.
A.73 B. 70 C. 45 D. 60
Câu 3. Hypebol nào có tiêu điểm trùng với tiêu điểm của elip
2 2
: 1
16 9
x y
E
?
A.
2 2
: 1
25 9
x y
H
. B.
2 2
: 1
9 16
x y
H
. C.
2 2
: 1
4 3
x y
H
. D.
2 2
: 1
9 25
x y
H
.
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
c
c
ó
ó
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ơ
ơ
s
s
ở
ở
m
m
ô
ô
t
t
ả
ả
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
B
B
i
i
ế
ế
t
t
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ó
ó
2
2
5
5
%
%
d
d
i
i
ệ
ệ
n
n
t
t
í
í
c
c
h
h
b
b
ằ
ằ
n
n
g
g
2 5
. Tìm giá trị nhỏ nhất của biểu thức
2 2
4a b
.
A
A
.
.
2 5
B
B
.
.
4 5
C
C
.
.
8 5
D
D
.
.
1
1
5
5
Câu 5. Độ dài giữa hai đỉnh (trục lớn) của hypebol
2 2
1.
4 12
x y
bằng đường kính đường tròn nào
A.
2
2
3 25
2 4
x y
B.
2
2
1 9
x y
C.
2 2
3 2 4
x y
D.
2
2
1
16
2
x y
C
C
â
â
u
u
6
6
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
1
9 5
x y
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
K
K
h
h
o
o
ả
ả
n
n
g
g
c
c
á
á
c
c
h
h
n
n
g
g
ắ
ắ
n
n
n
n
h
h
ấ
ấ
t
t
g
g
i
i
ữ
ữ
a
a
h
h
a
a
i
i
n
n
h
h
á
á
n
n
h
h
c
c
ủ
ủ
a
a
h
h
y
y
p
p
e
e
b
b
o
o
l
l
b
b
ằ
ằ
n
n
g
g
A
A
.
.
8
8
B
B
.
.
3
3
C
C
.
.
6
6
D
D
.
.
4
4
Câu 7. Cho hypebol
( )H
có phương trình chính tắc
2 2
1
9 16
x y
. Tìm tọa độ các giao điểm của
( )H
với trục
hoành
A.
9; 0
và
9; 0
.
B.
3; 0
và
3; 0
.
C.
4; 0
và
4; 0
.
D.
16; 0
và
16; 0
.
Câu 8. Phương trình chính tắc của hyperbol
H
có một tiêu điểm
1
4;0
F
và đi qua điểm
2;0
M
là
A.
2 2
1.
4 12
x y
B.
2 2
1.
2 12
x y
C.
2 2
1.
4 12
x y
D.
2 2
1.
2
2 3
x y
Câu 9. Hypebol nào sau đây có hai đỉnh đều nằm trên đường tròn
2
2
3 25
2 4
x y
A.
2 2
: 1
25 9
x y
H
. B.
2 2
: 1
25 16
x y
H
. C.
2 2
: 1
4 25
x y
H
. D.
2 2
: 1
9 25
x y
H
.
26
Câu 10. Tìm số giao điểm của hypebol
2 2
1
4 1
x y
và đường thẳng
3y x
.
A.2 B. 1 C. 3 D. 5
Câu 11. Phương trình của hypebol
H
có một tiêu điểm
1
34;0
F
và đi qua điểm
99
6 ;
25
A
là ?
A.
2 2
: 1
25 9
x y
H
. B.
2 2
: 1
25 16
x y
H
. C.
2 2
: 1
16 25
x y
H
. D.
2 2
: 1
9 25
x y
H
.
Câu 12. Cho điểm
( ; )M x y
thuộc hypebol
2 2
1.
4 12
x y
Giá trị nhỏ nhất của biểu thức
2 2
Q x y y
thuộc
khoảng
A.(3;4) B. (4;5) C. (5;6) D. (6;7)
Câu 13. Tính tổng các giá trị m để hypebol
2 2
2
: 1
4 6 1
x y
H
m m
có tiêu điểm trùng với tiêu điểm của elip
2 2
: 1
16 9
x y
E
.
A.4 B. 2 C. 5 D. 6
Câu 14. Cho hypebol
H
có phương trình
2 2
1
9 4
x y
. Số các điểm
M H
có tọa độ nguyên là
A.
2
. B.
0
. C.
4
. D.
3
.
Câu 15. Tồn tại bốn điểm
M
thuộc
2 2
: 1
16 20
x y
H
sao cho khoảng cách từ
M
đến trục hoành bằng nửa
khoảng cách từ
M
đến trục tung. Bốn điểm M này đều cách gốc tọa độ O một khoảng bằng
A.3 B. 6 C. 4 D. 5
Câu 16. Tìm số giao điểm của hypebol
2 2
1.
16 9
x y
và đường tròn
2 2
16
x y
.
A.3 B. 1 C. 2 D. 0
C
C
â
â
u
u
1
1
7
7
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
p
p
o
o
l
l
2 2
2 2
1
x y
a b
như hình bên, tiêu cự
bằng
2 13
. Có bao nhiêu cặp số (m;n) để hypebol đã cho tiếp
xúc elip
2 2
2 2
: 1
4
81
x y
E
m n
.
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
1
1
Câu 18. Cho
(0;4), (10;4)
A B
. Hypebol nào có hai tiêu điểm là hai đỉnh liên tiếp của hình bình hành
2 1
ABF F
A.
2 2
: 1
25 9
x y
H
. B.
2 2
: 1
9 16
x y
H
. C.
2 2
: 1
16 25
x y
H
. D.
2 2
: 1
9 25
x y
H
.
Câu 19. Tồn tại bao nhiêu cặp số nguyên (m;n) với
20n
để trên đường tròn
2 2
( ) ( 4)
x m y m n
có
thể tồn tại hai tiêu điểm của hypebol
2 2
2 2
1
x y
a b
A.8 B. 4 C. 3 D. 6
Câu 20. Điểm
( ; )M x y
thuộc hypebol
2 2
1.
4 12
x y
Giá trị nhỏ nhất của biểu thức
2 2
2 2023
T x y x
thuộc
khoảng
A.(1954;1975) B. (1975;1986) C. (1986;2000) D. (2000;2023)
Câu 21. Tâm đối xứng của hypebol
2 2
: 1
9 16
x y
H
có tung độ bằng
A.3 B. 2 C. 1 D. 0
_________________________________
27
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P5)
_____________________________________
Câu 1. Trong mặt phẳng tọa độ
Oxy
, cho hypebol
H
có một tiêu điểm là
2
(6;0)
F
và đi qua điểm
2 5;0
.
Phương trình chính tắc của
H
đó là
A.
2 2
1
20 16
x y
.
B.
2 2
1
16 20
x y
.
C.
2 2
1
20 16
x y
.
D.
2 2
1
16 20
x y
.
Câu 2. Cho hypebol
2 2
2 2
1
9 4 9
x y
a a a
. Độ dài ngắn nhất của tiêu cự hypebol đã cho bằng
A.8 B. 10 C. 12 D. 14
Câu 3. Xét điểm
3
;cot
sin
M a
a
với
sin 0
a
, tập hợp các điểm M là hypebol có tiêu cự bằng
A.6 B. 8 C.
2 10
D.
4 5
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
(
(có
tiêu cự
1 2
F F
) thỏa mãn
1 2
6
MF MF
, tam giác
1 2
NA A
là
tam giác vuông cân. Tính diện tích tam giác
1 2
NA A
.
A
A
.
.
1
1
2
2
B
B
.
.
8
8
C
C
.
.
9
9
D
D
.
.
1
1
0
0
Câu 5. Hypebol nào sau đây có đỉnh nào đó nằm trên đường thẳng
5
x y
và tiêu điểm nào đó nằm trên
đường tròn
2 2
41
x y
?
A.
2 2
: 1
25 9
x y
H
. B.
2 2
: 1
25 16
x y
H
. C.
2 2
: 1
16 25
x y
H
. D.
2 2
: 1
9 25
x y
H
.
Câu 6. Điểm
( ; )M x y
là giao điểm của hypebol
2 2
1.
16 9
x y
và đường elip
2 2
2 5 32
x y
. Tính
2 2
x y
.
A.20 B. 16 C. 30 D. 25
Câu 7.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
có độ dài trục thực bằng 12 và độ dài trục ảo bằng 6. Tính
2 2
3a b
.
A.63 B. 50 C. 56 D. 48
C
C
â
â
u
u
8
8
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
c
c
ó
ó
h
h
a
a
i
i
đ
đ
ỉ
ỉ
n
n
h
h
n
n
ằ
ằ
m
m
t
t
r
r
ê
ê
n
n
đ
đ
ồ
ồ
t
t
h
h
ị
ị
h
h
à
à
m
m
s
s
ố
ố
b
b
ậ
ậ
c
c
h
h
a
a
i
i
2
1
( ) ( 5) 4
4
f x x d x
như hình vẽ. Tính
2 2
a d
.
A
A
.
. 60
B
B
.
.
7
7
2
2
C
C
.
. 61
D
D
.
.
6
6
9
9
Câu 9. Điểm M thuộc hypebol
2 2
2
1
9 9
x y
a
. Tìm giá trị nhỏ nhất của
1 2
MF MF
với
1 2
,F F
là hai tiêu điểm của
hypebol.
A.4 B. 8 C. 10 D. 6
C
C
â
â
u
u
1
1
0
0
.
.
Hypebol
2 2
2 2
1
x y
a b
có hai tiêu điểm thuộc đồ thị hàm số bậc hai
2
( ) ( 4) 16
f x x d x
. Tính giá trị
của biểu thức
2 2 2 2
a b c d
với
2c
là tiêu cự của elip.
A.22 B. 30 C. 36 D. 48
C
C
â
â
u
u
1
1
1
1
.
.
Hypebol
2 2
2 2
1
x y
a b
có một đỉnh trùng với đỉnh của đồ thị hàm số
2
( ) 8
f x x x m n
. Tính giá trị của
biểu thức
2
4 4a m n
.
28
A.90 B. 80 C. 76 D. 69
C
C
â
â
u
u
1
1
2
2
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
với
0; 0
a b
c
c
ó
ó
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ơ
ơ
s
s
ở
ở
m
m
ô
ô
t
t
ả
ả
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
B
B
i
i
ế
ế
t
t
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ó
ó
d
d
i
i
ệ
ệ
n
n
t
t
í
í
c
c
h
h
b
b
ằ
ằ
n
n
g
g 48 (đvdt) và có chu vi bằng 32 (đvđd). Tìm giá trị
nhỏ nhất của biểu thức
2
a b
.
A
A
.
. 38
B
B
.
.
28
C
C
.
. 10
D
D
.
.
3
3
0
0
C
C
â
â
u
u
1
1
3
3
.
.
Cho các hypebol
2 2 2 2 2 2 2 2
1 2 3 4
: 1; : 1 : 1 : 1
25 9 16 2 4 3 9 10
x y x y x y x y
H H H H
.
Có bao nhiêu hypebol có tiêu điểm nằm phía bên trong đường elip
2 2
: 1
20 9
x y
E
.
A.1 B. 2 C. 3 D. 4
Câu 14. Hypebol nào sau đây có đỉnh nào đó nằm trên giao điểm của hai đường tròn
2 2 2 2
4; ( 5) 9
x y x y
A.
2 2
: 1
4 1
x y
H
. B.
2 2
: 1
25 16
x y
H
. C.
2 2
: 1
16 25
x y
H
. D.
2 2
: 1
9 25
x y
H
.
Câu 15. Cho hypebol
2 2
2 2
1
9 16
x y
a b
. Độ dài ngắn nhất của tiêu cự hypebol đã cho bằng
A.8 B. 10 C. 12 D. 14
Câu 16. Tìm số giao điểm của hypebol
2 2
1.
16 9
x y
và đường tròn
2 2
15
x y
.
A.3 B. 4 C. 2 D. 0
Câu 17. Điểm
( ; )M x y
thuộc hypebol
2 2
1
4 8
x y
Giá trị nhỏ nhất của biểu thức
2 2
4 2022
T x y x
thuộc khoảng
A.(1954;1975) B. (1975;1986) C. (1986;2000) D. (2000;2020)
C
C
â
â
u
u
1
1
8
8
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
i
i
ể
ể
m
m
M
M
t
t
h
h
u
u
ộ
ộ
c
c
n
n
h
h
á
á
n
n
h
h
p
p
h
h
ả
ả
i
i
h
h
y
y
p
p
e
e
b
b
o
o
l
l
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
1 2 1 2
6; 2 18
MF MF MF MF
Tính
1 2
3
MF MF
.
A
A
.
.
1
1
2
2
B
B
.
.
3
3
0
0
C
C
.
.
1
1
4
4
D
D
.
.
1
1
8
8
Câu 19. Cho hypepol
H
có phương trình:
2 2
1
36 9
x y
Khi đó độ dài trục lớn bằng
A.
3.
B.
16.
C. 12 D.
4.
Câu 20. Hypebol có nửa trục thực là
4
, tiêu cự bằng
2 41
có phương trình chính tắc là:
A.
2 2
1.
16 9
x y
B.
2 2
1.
16 9
y x
C.
2 2
1.
16 9
y x
D.
2 2
1.
16 25
x y
_________________________________
29
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P6)
_____________________________________
C
C
â
â
u
u
1
1
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ứ
ứ
g
g
i
i
á
á
c
c
t
t
r
r
o
o
n
n
g
g
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
l
l
à
à
h
h
ì
ì
n
n
h
h
v
v
u
u
ô
ô
n
n
g
g
.
.
T
T
í
í
n
n
h
h
2 2
a b
.
A
A
.
.
4
4
0
0
B
B
.
.
2
2
5
5
C
C
.
.
3
3
2
2
D
D
.
.
3
3
6
6
Câu 2. Hypebol nào sau đây có đỉnh nào đó nằm trên đường thẳng
5
x y
và tiêu điểm nào đó nằm trên
đường tròn
2 2
34
x y
?
A.
2 2
: 1
25 9
x y
H
. B.
2 2
: 1
25 16
x y
H
. C.
2 2
: 1
16 25
x y
H
. D.
2 2
: 1
9 25
x y
H
.
Câu 3. Điểm
( ; )M x y
là giao điểm của hypebol
2 2
1.
16 9
x y
và đường tròn
2 2
20
x y
. Tính
2 2
3 2x y
.
A.20 B. 18 C. 40 D. 25
Câu 4.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
có độ dài trục thực bằng 8 và độ dài trục ảo bằng 6. Tính
2 2
3a b
.
A.43 B. 50 C. 45 D. 36
C
C
â
â
u
u
5
5
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
c
c
ó
ó
h
h
a
a
i
i
đ
đ
ỉ
ỉ
n
n
h
h
n
n
ằ
ằ
m
m
t
t
r
r
ê
ê
n
n
đ
đ
ồ
ồ
t
t
h
h
ị
ị
h
h
à
à
m
m
s
s
ố
ố
b
b
ậ
ậ
c
c
h
h
a
a
i
i
2
1
( ) ( 9) 3
3
f x x d x
như hình vẽ. Tính
2 2
a d
.
A
A
.
. 80
B
B
.
.
70
C
C
.
. 90
D
D
.
.
6
6
9
9
C
C
â
â
u
u
6
6
.
.
Hypebol
2 2
2 2
1
x y
a b
có một đỉnh trùng với đỉnh của đồ thị hàm số
2
( ) 4
f x x x m n
. Tính giá trị của
biểu thức
2
4 4a m n
.
A.30 B. 32 C. 36 D. 40
C
C
â
â
u
u
7
7
.
.
Cho các hypebol
2 2 2 2 2 2 2 2
1 2 3 4
: 1; : 1 : 1 : 1
25 9 16 4 4 3 9 25
x y x y x y x y
H H H H
.
Có bao nhiêu hypebol có tiêu điểm nằm phía bên trong đường elip
2 2
: 1
20 9
x y
E
.
A.1 B. 2 C. 3 D. 4
C
C
â
â
u
u
8
8
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
c
c
ó
ó
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ơ
ơ
s
s
ở
ở
m
m
ô
ô
t
t
ả
ả
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
B
B
i
i
ế
ế
t
t
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ó
ó
d
d
i
i
ệ
ệ
n
n
t
t
í
í
c
c
h
h
b
b
ằ
ằ
n
n
g
g 32.
Tìm giá trị nhỏ nhất của biểu thức
2 2
9a b
.
A
A
.
.
8 2
B
B
.
.
4 5
C
C
.
. 48
D
D
.
.
3
3
0
0
Câu 9. Điểm
( ; )M x y
thuộc hypebol
2 2
1
4 6
x y
.
Giá trị nhỏ nhất của biểu thức
2 2
8 2023
T x y x
thuộc khoảng
30
A.(1954;1975) B. (1975;1986) C. (1986;2000) D. (2000;2020)
Câu 10. Tồn tại bốn điểm
M
thuộc
2 2
: 1
16 20
x y
H
sao cho khoảng cách từ
M
đến trục hoành bằng
1
5
khoảng cách từ
M
đến trục tung. Bốn điểm M này đều cách gốc tọa độ O một khoảng gần bằng
A.3,86 B. 5,26 C. 5,12 D. 4,14
Câu 11. Tồn tại bao nhiêu cặp số nguyên (m;n) với
40
n
để trên đường tròn
2 2
( ) ( 5) 1x m y m n
có
thể tồn tại hai đỉnh của hypebol
2 2
2 2
1
x y
a b
A.18 B. 13 C. 14 D. 12
C
C
â
â
u
u
1
1
2
2
.
.
Hypebol
2 2
2 2
1
x y
a b
có hai tiêu điểm thuộc đồ thị hàm số bậc hai
2
( ) ( 2) 9f x x d x
. Tính giá trị
của biểu thức
2 2 2 2
a b c d
với
2c
là tiêu cự của elip.
A.22 B. 30 C. 36 D. 29
Câu 13. Hypebol nào có hai đỉnh trùng với tiêu điểm của elip
2 2
: 1
16 7
x y
E
?
A.
2 2
: 1
25 9
x y
H
. B.
2 2
: 1
16 4
x y
H
. C.
2 2
: 1
4 3
x y
H
. D.
2 2
: 1
9 25
x y
H
.
C
C
â
â
u
u
1
1
4
4
.
.
Cho các hypebol
2 2 2 2 2 2 2 2
1 2 3 4
: 1; : 1 : 1 : 1
25 9 16 4 25 16 18 25
x y x y x y x y
H H H H
.
Có bao nhiêu hypebol có đỉnh nằm phía bên trong đường elip
2 2
: 1
40 9
x y
E
.
A.1 B. 3 C. 2 D. 4
Câu 15. Tìm số giao điểm của hypebol
2 2
1.
16 9
x y
và đường tròn
2 2
696
x y
.
A.3 B. 4 C. 2 D. 0
Câu 16. Điểm
( ; )M x y
thuộc hypebol
2 2
1.
4 12
x y
Giá trị nhỏ nhất của biểu thức
2 2
6 4 2023
T x y x
thuộc khoảng
A.(1954;1975) B. (1975;1986) C. (1986;2000) D. (1945;1954)
C
C
â
â
u
u
1
1
7
7
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
p
p
o
o
l
l
2 2
1.
4 12
x y
(có tiêu cự
1 2
F F
)và
đường parabol
2
2 ( 0)
y px p
có hai tiêu điểm nào đó
trùng nhau. Tính giá trị biểu thức
1 2
F F p
.
A.10 B. 12
C. 15 D. 14
C
C
â
â
u
u
1
1
8
8
.
.
Điểm
( ; )M x y
là giao điểm của các hypebol
2 2 2 2
1 2
: 1; : 1
25 9 16 4
x y x y
H H
. Khi đó
A.
1;2
x
y
B.
0;1
x
y
C.
2;3
x
y
D.
4;6
x
y
Câu 19. Trục đối xứng của hypebol
2 2
: 1
9 16
x y
H
không song song với đường thẳng nào
A.
2023
y
B.
2022
x
C.
2021
x
D.
2020y x
Câu 20. Điểm
( ; )M x y
là giao điểm của hypebol
2 2
2 2
1
x y
a b
và đường tròn
2 2
1
x y
. Tính giá trị
2 2 2 2 2 2
( 2) (2 )
b x a y a b
.
A.4 B. 2 C. 5 D. 3
31
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P7)
_____________________________________
Câu 1. Hypebol nào sau đây có đỉnh nào đó nằm trên đường thẳng
5
x y
và tiêu điểm nào đó nằm trên
đường tròn
2 2
41
x y
?
A.
2 2
: 1
25 9
x y
H
. B.
2 2
: 1
25 16
x y
H
. C.
2 2
: 1
16 25
x y
H
. D.
2 2
: 1
9 25
x y
H
.
C
C
â
â
u
u
2
2
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
c
c
ó
ó
h
h
a
a
i
i
t
t
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
,
,
t
t
a
a
m
m
g
g
i
i
á
á
c
c
t
t
r
r
o
o
n
n
g
g
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
l
l
à
à
t
t
a
a
m
m
g
g
i
i
á
á
c
c
đ
đ
ề
ề
u
u
.
.
G
G
i
i
á
á
t
t
r
r
ị
ị
c
c
ủ
ủ
a
a
b
b
i
i
ể
ể
u
u
t
t
h
h
ứ
ứ
c
c
4 4 2 2
2a b a b
gần nhất với
A
A
.
. 22,4
B
B
.
.
2
2
3
3
,
,
5
5
C
C
.
. 21,3
D
D
.
.
2
2
0
0
,
,
5
5
C
C
â
â
u
u
3
3
.
.
Hypebol
2 2
2 2
1
x y
a b
có một đỉnh trùng với đỉnh của đồ thị hàm số
2
( ) 2 8
f x x x m n
. Tính giá trị
của biểu thức
2
4 4a m n
.
A.30 B. 32 C. 36 D. 40
Câu 4. Điểm
( ; )M x y
là giao điểm của hypebol
2 2
1.
16 9
x y
và đường tròn
2 2
17
x y
. Tính
2 2
3 2x y
.
A.34,6 B. 49,2 C. 40,5 D. 38,5
Câu 5. Tìm giá trị nguyên nhỏ nhất của m để đường tròn
2 2
x y m
cắt hypebol
2 2
1.
16 4
x y
A.18 B. 16 C. 20 D. 24
Câu 6.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
có độ dài trục thực bằng 10 và độ dài trục ảo bằng 6. Tính
2 2
3a b
.
A.52 B. 50 C. 45 D. 36
C
C
â
â
u
u
7
7
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
c
c
ó
ó
h
h
a
a
i
i
đ
đ
ỉ
ỉ
n
n
h
h
n
n
ằ
ằ
m
m
t
t
r
r
ê
ê
n
n
đ
đ
ồ
ồ
t
t
h
h
ị
ị
h
h
à
à
m
m
s
s
ố
ố
b
b
ậ
ậ
c
c
h
h
a
a
i
i
2
1
( ) ( 9) 3
3
f x x d x
như hình vẽ. Tính
2 2
a d
.
A
A
.
. 80
B
B
.
.
70
C
C
.
. 90
D
D
.
.
6
6
9
9
C
C
â
â
u
u
8
8
.
.
Cho các hypebol
2 2 2 2 2 2 2 2
1 2 3 4
: 1; : 1 : 1 : 1
25 9 16 4 4 3 9 25
x y x y x y x y
H H H H
.
Có bao nhiêu hypebol có đỉnh nằm phía bên trong đường elip
2 2
: 1
20 4
x y
E
.
A.1 B. 2 C. 3 D. 4
Câu 9. Cho các hypebol
2 2 2 2 2 2 2 2
1 2 3 4
: 1; : 1 : 1 : 1
25 9 16 4 4 3 9 25
x y x y x y x y
H H H H
.
Hypebol nào có đỉnh nào đó gần nhất với tâm đường tròn
2 2
( 5) ( 3) 1
x y
.
A.
2 2
1
: 1
25 9
x y
H
B.
2 2
2
: 1
16 4
x y
H
C.
2 2
3
: 1
4 3
x y
H
D.
2 2
4
: 1
9 25
x y
H
32
Câu 10. Điểm
( ; )M x y
thuộc hypebol
2 2
1
4 2
x y
.
Giá trị nhỏ nhất của biểu thức
2 2
8 2023
T x y x
thuộc khoảng
A.(1954;1975) B. (1975;1986) C. (1986;2000) D. (2000;2020)
Câu 11. Điểm
M
có hoành độ bằng 8 thuộc hypebol
2 2
: 1
16 9
x y
H
thì có các khoảng cách tới hai tiêu điểm
bằng
A.6 và 14 B. 5 và 13 C. 4 và 12 D. 7 và 15
C
C
â
â
u
u
1
1
2
2
.
.
Điểm
( ; )M x y
là giao điểm của các hypebol
2 2 2 2
1 2
: 1; : 1
25 16 9 4
x y x y
H H
. Khi đó
A.
1;2
x
y
B.
0;1
x
y
C.
2;3
x
y
D.
4;6
x
y
Câu 13. Có bao nhiêu số nguyên m để hypebol
2 2
( ) : 1
4 9
x y
H
cắt đường thẳng
y mx
cắt nhau tại hai điểm
phân biệt
A.2 B. 3 C. 4 D. 5
Câu 14. Hai điểm M, N thuộc hai nhánh của hypebol
2 2
25 16 400
x y
, độ dài MN nhỏ nhất bằng
A.12 B. 8 C. 6 D. 10
C
C
â
â
u
u
1
1
5
5
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
c
c
ó
ó
h
h
a
a
i
i
đ
đ
ỉ
ỉ
n
n
h
h
n
n
ằ
ằ
m
m
t
t
r
r
ê
ê
n
n
đ
đ
ồ
ồ
t
t
h
h
ị
ị
h
h
à
à
m
m
s
s
ố
ố
b
b
ậ
ậ
c
c
h
h
a
a
i
i
như hình vẽ. Tính
2 2
a d
.
A
A
.
. 80
B
B
.
.
70
C
C
.
. 90
D
D
.
.
6
6
9
9
Câu 16.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
có độ dài trục thực bằng 8 và độ dài trục ảo bằng 6. Tính
2 2
3a b
.
A.43 B. 50 C. 45 D. 36
Câu 17. Trên hypebol
2 2
1
144 25
x y
(tiêu cự
1 2
F F
) tồn tại điểm N sao cho
1 2
4
NF NF
. Tính
1 2
4
NF NF
.
A.50 B. 64 C. 45 D. 70
Câu 18. Đường tròn đi qua bốn giao điểm của hai đường conic
2 2 2 2
2 6; 8 8
x y x y
có bình phương bán
kính gần nhất với giá trị nào
A.3,65 B. 3,42 C. 3,56 D. 3,28
Câu 19. Trong hệ tọa độ Oxy, điểm
( ; )M x y
có
1
; 3 tan
cos
x y t
t
. Tập hợp các điểm M là hypebol có tiêu
cự bằng
A.6 B. 4 C. 5 D. 3,5
Câu 20. Hypebol
2 2
2 2
1
2 5 2 6
x y
a a b b
có tiêu cự ngắn nhất bằng
A.6 B. 8 C. 10 D. 12
Câu 21. Hypebol
2 2
2 2
1
x y
a b
đi qua
( 5;3)
A
và có
2
c
e
a
(tâm sai) thì độ dài tiêu cự bằng
A.6 B.
4 11
C.
4 13
D.
6 5
Câu 22. Cho hypebol
2 2
8
x y
, elip đi qua điểm
(4;6)
A
và có tiêu điểm trùng với tiêu điểm của hypebol đã
cho. Elip đã cho có độ dài trục bé bằng
A.10 B.
8 5
C.
8 3
D.
12 2
Câu 23. Tìm số giao điểm của hypebol
2 2
1
4 2
x y
và đường tròn
2 2
( 3) ( 1) 1
x y
.
A.3 B. 2 C. 1 D. 4
33
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P8)
_____________________________________
Câu 1. Tìm tiêu cự của hypebol
2 2
2 2
1
4 3
x y
.
A.4 B. 8 C. 10 D. 12
Câu 2. Đường hypebol nào có tiêu điểm có thể nằm trên đường tròn
2 2
2 9
x y m
A.
2 2
1
25 16
x y
B.
2 2
1
25 4
x y
C.
2 2
1
25 49
x y
D.
2 2
2 2
1
15 26
x y
m n
Câu 3. Các giao điểm M của hypebol
2 2
1.
16 9
x y
và đường elip
2 2
1
16 9
x y
đều cách trục tung một khoảng
A.3 B. 1 C. 2 D. 4
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
1
9 1
x y
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
K
K
h
h
o
o
ả
ả
n
n
g
g
c
c
á
á
c
c
h
h
n
n
g
g
ắ
ắ
n
n
n
n
h
h
ấ
ấ
t
t
g
g
i
i
ữ
ữ
a
a
h
h
a
a
i
i
n
n
h
h
á
á
n
n
h
h
c
c
ủ
ủ
a
a
h
h
y
y
p
p
e
e
b
b
o
o
l
l
b
b
ằ
ằ
n
n
g
g
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
6
6
D
D
.
.
4
4
Câu 5. Hyperbol
H
có một tiêu điểm
2
5;0
F
và độ dài trục thực bằng
8
, độ dài trục ảo của (H) là
A.8 B. 6 C. 4 D. 5
Câu 6. Tâm đường tròn
2 2
( 3) 9
x y
một tiêu điểm của hypebol có phương trình nào sau đây?
A.
2 2
: 1
9 16
x y
H
. B.
2 2
: 1
4 5
x y
H
. C.
2 2
: 1
2 1
x y
H
. D.
2 2
:4 1
H x y
.
Câu 7. Tìm độ dài ngắn nhất đối với tiêu cự parabol
2 2
2
: 1
4 4 9
x y
H
m m
.
A.4 B. 8 C. 6 D. 5
Câu 8. Đường conic nào sau đây có trục thực và trục ảo đều có độ dài lớn hơn 5
A.
2 2
1.
16 9
x y
B.
2 2
1.
4 3
x y
C.
2 2
1.
16 9
x y
D.
2 2
0.
16 9
x y
Câu 9. Cho đường hypebol có phương trình
2 2
1
25 9
x y
. Khoảng cách giữa hai tiêu điểm gần nhất với bán kính
đường tròn nào
A.
2 2
100
x y
B.
2 2
2 2 120
x y x y
C.
2 2
4 2 100
x y x y
D.
2 2
8 4 103
x y x y
Câu 10. Điểm
( ; )M x y
thuộc hypebol
2 2
1.
16 9
x y
Giá trị nhỏ nhất của biểu thức
2
1
3
Q x y
thuộc khoảng
A.(0;5) B. (17;22) C. (5;10) D. (10;17)
C
C
â
â
u
u
1
1
1
1
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
1
16 9
x y
c
c
ó
ó
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ơ
ơ
s
s
ở
ở
m
m
ô
ô
t
t
ả
ả
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ó
ó
b
b
á
á
n
n
k
k
í
í
n
n
h
h
k
k
í
í
n
n
h
h
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
r
r
ò
ò
n
n
n
n
g
g
o
o
ạ
ạ
i
i
t
t
i
i
ế
ế
p
p
b
b
ằ
ằ
n
n
g
g
A
A
.
.
6
6
B
B
.
.
7
7
C
C
.
.
5
5
D
D
.
.
8
8
Câu 12. Cho hypebol có phương trình chính tắc
2 2
2
1
4 10 9
x y
a a
có tiêu cự
1 2
F F
và điểm
M
thuộc hypebol.
Khi đó giá trị nhỏ nhất của biểu thức
1 2
MF MF
bằng
34
A.
4
. B.
8
. C.
6
. D.
10
.
Câu 13. Trong mặt phẳng tọa độ Oxy, điểm
( ; )M x y
thỏa mãn
2 2 2 2
( 6) ( 6) 6
x y x y
thì sẽ thuộc
đường hypebol có đỉnh cách gốc tọa độ một khoảng bằng
A.4 B. 2 C. 5 D. 3
Câu 14. Tìm số giao điểm tối đa của hypebol
2 2
1
25 9
x y
và đường tròn
2 2 4
25 4x y m
.
A.3 B. 2 C. 3 D. 0
Câu 15. Tồn tại hai đường thẳng song song và cách trục hoành một khoảng bằng 1, hai đường thẳng này cắt
hypebol
2 2
1
25 144
x y
tại tổng số bao nhiêu giao điểm
A.2 B. 3 C. 4 D. 5
Câu 16. Đường tròn tiếp xúc với cả hai nhánh của hypebol
2 2
2
: 1
16 1
x y
H
a
có đường kính nhỏ nhất bằng
A.12 B. 10 C. 6 D. 8
Câu 17. Hypebol
2 2
1
25 9
x y
có tiêu cự
1 2
F F
, M thuộc hypebol thỏa mãn
1 2
2
MF MF
, tính
1 2
2
MF MF
.
A.24 B. 20 C. 18 D. 16
Câu 18. Trong mặt phẳng tọa độ Oxy, điểm
( ; )M x y
thỏa mãn
2 2 2 2
( 3) ( 3) 4
x y x y
thì sẽ thuộc
đường hypebol có tiêu điểm với hoành độ có thể bằng
A.2 B. 3 C. 4 D. 2,5
Câu 19. Hypebol nào có tiêu điểm trùng với tiêu điểm của elip
2 2
: 1
16 9
x y
E
?
A.
2 2
: 1
4 1
x y
H
. B.
2 2
: 1
9 16
x y
H
. C.
2 2
: 1
5 2
x y
H
. D.
2 2
: 1
9 25
x y
H
.
Câu 20. Tìm số giao điểm của hypebol
2 2
1
4 1
x y
và đường thẳng
4
y x
.
A.2 B. 1 C. 3 D. 5
Câu 21. Tính tổng các giá trị m để hypebol
2 2
2
: 1
4 2 7
x y
H
m m
có tiêu điểm trùng với tiêu điểm của elip
2 2
: 1
16 9
x y
E
.
A.4 B. 2 C. 5 D. 6
Câu 22. Hypebol nào sau đây có hai đỉnh đều nằm trên đường tròn
2 2
25
x y
và độ dài trục thực hơn độ dài
trục ảo 4 đơn vị độ dài
A.
2 2
: 1
25 9
x y
H
. B.
2 2
: 1
25 16
x y
H
. C.
2 2
: 1
4 25
x y
H
. D.
2 2
: 1
9 25
x y
H
.
C
C
â
â
u
u
2
2
3
3
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
c
c
ó
ó
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ơ
ơ
s
s
ở
ở
m
m
ô
ô
t
t
ả
ả
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
B
B
i
i
ế
ế
t
t
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ó
ó
d
d
i
i
ệ
ệ
n
n
t
t
í
í
c
c
h
h
b
b
ằ
ằ
n
n
g
g
16. Tìm giá trị nhỏ nhất của biểu thức
2 2
16a b
.
A
A
.
.
2 5
B
B
.
.
4 5
C
C
.
. 32
D
D
.
.
1
1
5
5
Câu 24. Tâm đối xứng của hypebol
2 2
: 1
9 4
x y
H
có hoành độ bằng
A.3 B. 2 C. 1 D. 0
_______________________________
35
ĐƯỜNG CONIC PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P1)
_____________________________________
C
C
â
â
u
u
1
1
.
.
Phương trình nào dưới dây là phương trình chính tắc của parabol
A.
2
3x y
. B.
2
3x y
. C.
2
3y x
. D.
2
3y x
.
C
C
â
â
u
u
2
2
.
.
Tham số tiêu của parabol
2
6y x
là
A.
3
p
. B.
3
2
p
. C.
6
p
. D.
3
4
p
.
C
C
â
â
u
u
3
3
.
.
Lập phương trình chính tắc của parabol biết khoảng cách từ đỉnh tới tiêu điểm bằng
3.
A.
2
12
x
y
B.
2
3y x
C.
2
12y x
. D.
2
6y x
C
C
â
â
u
u
4
4
.
.
Lập phương trình chính tắc của parabol biết parabol đi qua điểm
(3;3 2)
M
.
A.
2
6y x
B.
2
3y x
C.
2
12y x
D.
2
4y x
C
C
â
â
u
u
5
5
.
.
Cho parabol
P
có phương trình chính tắc
2
4
y
x
. Một đường thẳng đi qua tiêu điểm
F
của
P
cắt
P
tại 2 điểm
A
và
B
. Nếu
1; 2
A
thì tọa độ của
B
là
A.
1;2
. B.
4;4
. C.
1;2
. D.
2;2 2
.
C
C
â
â
u
u
6
6
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
( 2) 1
y k x
tại ít nhất bao
nhiêu điểm (với k là tham số).
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
0
0
C
C
â
â
u
u
7
7
.
.
Tọa độ điểm M thuộc parabol cho
2
: 4P y x
và đường thẳng
: 2 0
d x y
là
A.
0;1
.
B.
0;0
.
C.
0;3
.
D.
0,2
.
C
C
â
â
u
u
8
8
.
.
Cho
2
: 4P y x
điểm nào sao đây thuộc
P
A.
1; 4
A
. B.
1;4
B
. C.
2;8
C
. D.
1;2
D
.
C
C
â
â
u
u
9
9
.
.
Cho parabol
2
:
4
P y
x
. Điểm
M
thuộc
P
và
4MF
(
F
là tiêu điểm của parabol). Khi đó hoành
độ của điểm
M
bằng
A.
1.
B.
3.
C.
2.
D.
3
.
2
C
C
â
â
u
u
1
1
0
0
.
.
Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường parabol?
A.
2
2022
y x
. B.
2
2022
y x
. C.
2
2022
x y
. D.
2
2022
x y
.
C
C
â
â
u
u
1
1
1
1
.
.
Cho parabol
P
có tiêu điểm là
10;0
F
, phương trình đường chuẩn của
P
là
A.
10 0 y
. B.
10 0 x
. C.
5 0 x
. D.
10 0 x
.
C
C
â
â
u
u
1
1
2
2
.
.
Cho parabol
2
: 2P y px
. Có bao nhiêu giá trị nguyên p để đường chuẩn của parapol nằm giữa hai
đường thẳng
1; 5
x x
.
A.1 B. 2 C. 3 D. 4
C
C
â
â
u
u
1
1
3
3
.
.
Cho parabol
P
có phương trình chính tắc
2
20y x
. Tiêu điểm của parabol
P
là
A.
5; 0
F
. B.
10; 0
F
. C.
5; 0
F
. D.
20; 0
F
.
C
C
â
â
u
u
1
1
4
4
.
.
Gọi M là giao điểm của đường chuẩn parabol (conic)
2
6y x
và đường phân giác góc phần tư thứ
nhất. Độ dài đoạn thẳng OM bằng
A.6 B.
5 2
2
C.
5 3
2
D.
3 2
2
C
C
â
â
u
u
1
1
5
5
.
.
Cho parabol
P
có phương trình chính tắc
2
4y x
. Đường chuẩn của
P
là
A.
: 1x
. B.
: 1 0x
. C.
: 1y
. D.
: 1y
.
36
C
C
â
â
u
u
1
1
6
6
.
.
Cho parabol
P
có tiêu điểm là
3; 0
F
. Phương trình chính tắc của parabol
P
là
A.
2
3y x
. B.
2
6y x
. C.
2
12y x
. D.
2
12y x
.
C
C
â
â
u
u
1
1
7
7
.
.
Trong các phương trình sau, phương trình nào là phương trình chính tắc của parabol?
A.
2
2y x
. B.
2
3 0
y x
. C.
2
5y x
. D.
2
4x y
.
C
C
â
â
u
u
1
1
8
8
.
.
Có bao nhiêu điểm trên parabol
2
2y x
mà điểm đó cách đều hai trục tọa độ
A..2 B. 1 C. 4 D. 3
Câu 19. Tìm p để đường chuẩn của parabol
2
2y px
cách đường thẳng
6
x
một khoảng bằng 10 đơn vị độ
dài.
A.
6
p
B.
4
p
C.
8
p
D.
1p
C
C
â
â
u
u
2
2
0
0
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
p
p
o
o
l
l
đ
đ
ã
ã
c
c
h
h
o
o
t
t
ạ
ạ
o
o
v
v
ớ
ớ
i
i
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
2
x
theo một dây cung có
độ dài bằng
A
A
.
.
2
2
B
B
.
.
2 5
C
C
.
.
4
4
D
D
.
.
4 2
C
C
â
â
u
u
2
2
1
1
.
.
Phương trình chính tắc của parabol
P
có tiêu điểm
3
;0
2
F
là
A.
2
3
2
y x
. B.
2
3y x
. C.
2
6y x
. D.
2
3
4
y x
.
C
C
â
â
u
u
2
2
2
2
.
.
Parabol
P
đi qua điểm
2;2
M
. Phương trình chính tắc của parabol
P
là
A.
2
2y x
. B.
2
y x
. C.
2
4y x
. D.
2
1
2
y x
.
C
C
â
â
u
u
2
2
3
3
.
.
Cho Parabol
2
1
:
12
P y x
.
P “ Parabol có phương trình đường chuẩn
3 0
x
”
Q “Parabol có tọa độ tiêu điểm
3;0
F
”
Chọn khẳng định đúng.
A. P đúng, Q sai. B. P sai, Q sai. C. P sai, Q đúng. D. P đúng, Q đúng.
C
C
â
â
u
u
2
2
4
4
.
.
Cho parabol có phương trình
2
4y x
. Tính bán kính qua tiêu của điểm
M
thuộc parabol và có hoành
độ bằng
3.
A.
6
MF
. B.
3
MF
. C.
5
MF
. D.
4MF
.
C
C
â
â
u
u
2
2
5
5
.
.
Cho parabol
2
( ) : 4P y x
. Tìm tọa độ điểm
M
thuộc
( )P
sao cho khoảng cách từ
M
đến tiêu điểm của
( )P
bằng
3
.
A.
(2;2 2)
M
hoặc
(2; 2 2)
M
. B.
(3;3 2)
M
hoặc
(3; 3 2)
M
.
C.
(2;2 2)
M
hoặc
( 2;2 2)
M
. D.
(3;3 2)
M
hoặc
( 3;3 2)
M
.
C
C
â
â
u
u
2
2
6
6
.
.
K
K
h
h
ú
ú
c
c
c
c
u
u
a
a
c
c
ủ
ủ
a
a
m
m
ộ
ộ
t
t
c
c
o
o
n
n
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
ó
ó
d
d
ạ
ạ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
,
,
đ
đ
i
i
ể
ể
m
m
đ
đ
ầ
ầ
u
u
v
v
à
à
o
o
k
k
h
h
ú
ú
c
c
c
c
u
u
a
a
l
l
à
à
đ
đ
i
i
ể
ể
m
m
A
A
,
,
đ
đ
i
i
ể
ể
m
m
c
c
u
u
ố
ố
i
i
l
l
à
à
B
B
,
,
k
k
h
h
o
o
ả
ả
n
n
g
g
c
c
á
á
c
c
h
h
A
A
B
B
=
=
4
4
0
0
0
0
m
m
.
.
Đ
Đ
ỉ
ỉ
n
n
h
h
c
c
ủ
ủ
a
a
p
p
a
a
r
r
b
b
o
o
l
l
(
(
P
P
)
)
c
c
ủ
ủ
a
a
k
k
h
h
ú
ú
c
c
c
c
u
u
a
a
c
c
á
á
c
c
h
h
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
A
A
B
B
m
m
ộ
ộ
t
t
k
k
h
h
o
o
ả
ả
n
n
g
g
2
2
0
0
m
m
v
v
à
à
c
c
á
á
c
c
h
h
đ
đ
ề
ề
u
u
A
A
,
,
B
B
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
(P) khi 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1m trên thực tế là
A
A
.
.
2
1000y x
B
B
.
.
2
200y x
C
C
.
.
2
2000y x
D
D
.
.
2
1500y x
37
ĐƯỜNG CONIC PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P2)
_____________________________________
C
C
â
â
u
u
1
1
.
.
Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường parabol?
A.
2
69y x
. B.
2 2
4( 2 6)y p p x
. C.
2
2022
x y
. D.
2
96x y
.
Câu 2. Với tham số tiêu
0
p
, đường chuẩn của parabol
2
2y px
cách điểm
( ;2023)
M p
một khoảng bằng
A.2p B. 4p C. 1,5p D. 2,5p
C
C
â
â
u
u
3
3
.
.
Cho đường conic
2
: 32P y x
điểm nào sao đây thuộc
P
A.
1; 4
A
. B.
1;4
B
. C.
2;8
C
. D.
1;2
D
.
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
r
r
ò
ò
n
n
2 2
9
x y
tại bao nhiêu điểm
A
A
.
.
1
1
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
0
0
C
C
â
â
u
u
5
5
.
.
Cho
2
: 4P y x
điểm nào sao đây thuộc
P
và thuộc góc phần tư thứ nhất
A.
1; 4
A
. B.
1;4
B
. C.
2;8
C
. D.
4;4
D
.
Câu 6. Tìm p để đường chuẩn của parabol
2
2y px
cách điểm
( ;2023)
M p
một khoảng bằng 12 đơn vị độ dài.
A.
6
p
B.
4
p
C.
8
p
D.
1p
C
C
â
â
u
u
7
7
.
.
Cho parabol
2
2y px
với
0
p
. Điểm
M
thuộc
P
và
4MF
(
F
là tiêu điểm của parabol). Khi đó
hoành độ của điểm
M
bằng
A.
1.
B.
4
2
p
C.
2
p
D.
4
p
C
C
â
â
u
u
8
8
.
.
Cho parabol
P
có tiêu điểm là
5;0
F
, phương trình đường chuẩn của
P
là
A.
10 0 y
. B.
10 0 x
. C.
5 0 x
. D.
10 0 x
.
C
C
â
â
u
u
9
9
.
.
Đường conic
2
: 4P y x
và đường thẳng
4 3 12 0
x y
có bao nhiêu điểm chung
A.2 B. 1 C. 3 D. 0
C
C
â
â
u
u
1
1
0
0
.
.
Cho parabol
2 2
4
y p x
với
0
p
. Điểm
M
thuộc
P
và
4MF
(
F
là tiêu điểm của parabol). Khi đó
hoành độ của điểm
M
có giá trị lớn nhất bằng
A.4 B. 2 C. 1 D. 3
C
C
â
â
u
u
1
1
1
1
.
.
Lập phương trình chính tắc của parabol biết khoảng cách từ đỉnh tới tiêu điểm bằng 1
A.
2
12
x
y
B.
2
4y x
C.
2
12y x
. D.
2
6y x
C
C
â
â
u
u
1
1
2
2
.
.
Cho đường conic
P
có phương trình
2
12y x
. Một đường thẳng đi qua tiêu điểm
F
của
P
cắt
P
tại điểm A thuộc (P) có tung độ bằng 6 thì tạo với (P) một dây cung có độ dài bằng
A.10 B. 12 C.
2 13
D.
4 5
C
C
â
â
u
u
1
1
3
3
.
.
Cho parabol
2
( ) : 4P y x
, điểm
M
thuộc
( )P
sao cho khoảng cách từ
M
đến tiêu điểm của
( )P
bằng
2 thì độ dài đoạn thẳng OM bằng
A.3 B. 2 C.
5
D.
3
C
C
â
â
u
u
1
1
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
3 2
2023
y p p p
tại bao
nhiêu điểm
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
0
0
C
C
â
â
u
u
1
1
5
5
.
.
Cho đường conic
2 2
: 4( 2 8)P y p p x
và các mệnh đề
38
P: “ Parabol có phương trình đường chuẩn cách gốc tọa độ một khoảng lớn hơn 6,5”
Q: “Parabol có tọa độ tiêu điểm
;0
2
p
F
”
Chọn khẳng định đúng
A. P đúng, Q sai. B. P sai, Q sai. C. P sai, Q đúng. D. P đúng, Q đúng.
C
C
â
â
u
u
1
1
6
6
.
.
Cho parabol
2
: 2P y px
. Có bao nhiêu giá trị nguyên dương p để đường chuẩn của parapol cách
trục tung một khoảng bằng 2
A.2 B. 1 C. 0 D. 3
C
C
â
â
u
u
1
1
7
7
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
parabol
2
2y px
với
0
p
có tiêu điểm F
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
M
M
t
t
h
h
u
u
ộ
ộ
c
c
p
p
a
a
r
r
a
a
b
b
o
o
l
l
s
s
a
a
o
o
c
c
h
h
o
o
đ
đ
i
i
ể
ể
m
m
M
M
c
c
á
á
c
c
h
h
đ
đ
ề
ề
u
u
h
h
a
a
i
i
đ
đ
i
i
ể
ể
m
m
H
H
,
,
F
F
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
V
V
ô
ô
s
s
ố
ố
D
D
.
.
1
1
0
0
C
C
â
â
u
u
1
1
8
8
.
.
Cho parabol
2
: 2P y px
. Biết phương trình đường chuẩn của
( )P
là:
3
x
. Tìm tọa độ điểm
( ;1 )A a a
thuộc
( )P
.
A.
(7 4 3; 6 4 3)
A
hoặc
(6 2 6; 5 2 6)
A
.
B.
(7 4 3; 6 4 3)
A
hoặc
(7 4 3; 6 4 3)
A
.
C.
(2 2 6; 5 2 6)
A
hoặc
(7 4 3; 6 4 3)
A
.
D.
( 6 2 6;7 2 6)
A
hoặc
( 6 2 6;7 2 6)
A
.
C
C
â
â
u
u
1
1
9
9
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
parabol
2
2y px
với
0
p
có tiêu điểm F
c
c
ó
ó
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
b
b
ằ
ằ
n
n
g
g
1
1
,
,
đ
đ
i
i
ể
ể
m
m
M
t
t
h
h
u
u
ộ
ộ
c
c
(
(
P
P
)
)
v
v
à
à
c
c
á
á
c
c
h
h
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
1 0
x
một khoảng bằng 2. Độ dài đoạn thẳng MF bằng
A.4 B. 2 C. 1,5 D. 3
C
C
â
â
u
u
2
2
0
0
.
.
Đường parabol
2
( ) : 4P y x
cắt đường tròn
2 2
( 2) 4
x y
tại bao nhiêu điểm
A.2 B. 3 C. 1 D. 4
C
C
â
â
u
u
2
2
1
1
.
.
Trong mặt phẳng tọa độ, cho các parabol
2 2 2 2 2
8 , 16 , 4 , 4( 2 6)y x y x y x y p p x
. Đường
parabol nào có đường chuẩn cách xa gốc tọa độ O nhất
A.
2 2
4( 2 6)y p p x
B.
2
8y x
C.
2
16y x
D.
2
4y x
C
C
â
â
u
u
2
2
2
2
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
parabol
2
2y px
với
0
p
có tiêu điểm F
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
s
s
a
a
o
o
c
c
h
h
o
o
60
HFM
. Tính chu vi tam giác HFM theo
k
biết rằng
2 3 4 9 , 0
MH MF HF k k
.
A
A
.
.
4
4
k
k
B
B
.
.
6
6
k
k
C
C
.
.
3
3
k
k
D
D
.
.
K
K
ế
ế
t
t
q
q
u
u
ả
ả
k
k
h
h
á
á
c
c
C
C
â
â
u
u
2
2
3
3
.
.
Cho parabol
2
( ) : 4P y x
với tiêu điểm F, có bao nhiêu điểm
M
(tọa độ nguyên) thuộc
( )P
thỏa mãn
điều kiện
2 20
MF
.
A.4 B. 6 C. 8 D. 10
C
C
â
â
u
u
2
2
4
4
.
.
Đường parabol nào có thể có đường chuẩn cách xa gốc tọa độ O nhất
A.
2 2
4( 2 6)y p p x
B.
2 2
4 1
y p x
C.
2
16y x
D.
2
4y x
C
C
â
â
u
u
2
2
5
5
.
.
Cho parabol
2
( ) : 4P y x
, đường thẳng d đi qua điểm A (9;9) và tạo với hai trục tọa độ một góc
45
thì
tạo với parabol có tọa độ bằng
A.4 B. 6 C.
6 2
D.
4 2
______________________________
39
ĐƯỜNG CONIC PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P3)
_____________________________________
C
C
â
â
u
u
1
1
.
.
Tham số tiêu của parabol
2
24y x
là
A.
3
p
. B.
3
2
p
. C.
6
p
. D.
12
p
C
C
â
â
u
u
2
2
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
y kx k
tại ít nhất bao nhiêu
điểm (với k là tham số).
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
0
0
C
C
â
â
u
u
3
3
.
.
Phương trình nào dưới dây là phương trình chính tắc của parabol
A.
2
13x y
. B.
2
3x y
. C.
2
3y x
. D.
2
26y x
.
C
C
â
â
u
u
4
4
.
.
Lập phương trình chính tắc của parabol biết khoảng cách từ đỉnh tới tiêu điểm bằng 1,5.
A.
2
12
x
y
B.
2
3y x
C.
2
12y x
. D.
2
6y x
Câu 5. Với
0
p
, khi đường chuẩn của parabol
2
2y px
tiếp xúc đường tròn
2 2
( 1) ( 4) 64
x y
thì giá trị
3
26 5
p p
bằng
A.3113 B. 2540 C. 1265 D. 2045
C
C
â
â
u
u
6
6
.
.
Đường chuẩn của đường conic
2
: 32P y x
tiếp xúc với đường tròn nào sau đây
A.
2 2
8
x y
B.
2 2
( 1) ( 4) 64
x y
C.
2 2
( 3) ( 2) 25
x y
D.
2 2
( 3) ( 4) 25
x y
C
C
â
â
u
u
7
7
.
.
Lập phương trình chính tắc của parabol biết parabol đi qua điểm (8;8).
A.
2
6y x
B.
2
3y x
C.
2
12y x
D.
2
4y x
C
C
â
â
u
u
8
8
.
.
Cho đường parbol (P):
2
y x
và điểm
(0;2)
I
, hai điểm M, N thuộc (P) thỏa mãn
4IM IN
. Tồn tại hai
điểm M, N với tổng hoành độ bằng
A.30 B. 20 C. 24 D. 40
C
C
â
â
u
u
9
9
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
l
l
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
.
.
T
T
ì
ì
m
m
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
đ
đ
i
i
ể
ể
m
m
M
M
n
n
ế
ế
u
u
2 3 16
MH MF
.
A
A
.
.
2
2
,
,
3
3
B
B
.
.
2
2
,
,
4
4
C
C
.
.
2
2
,
,
2
2
D
D
.
.
2
2
Câu 10. Với tham số tiêu
0
p
, đường chuẩn của parabol
2
2y px
cách điểm
(6;2023)
A
một khoảng bằng 12
thì tiêu điểm parabol cách điểm A một khoảng bằng bao nhiêu đơn vị độ dài
A.2023 B. 2000 C. 3000 D. 500
Câu 11. Với tham số tiêu
0
p
, có bao nhiêu số nguyên p để đường chuẩn của parabol
2
2y px
nằm bên phải
đường thẳng
2 7 0
x
.
A.5 B. 3 C. 4 D. 6
C
C
â
â
u
u
1
1
2
2
.
.
Đ
Đường conic
2
: 32P y x
có tham số tiêu p, khi đó hãy tìm số giao điểm của parabol và đường thẳng
2
4x p p
.
A.4 B. 2 C. 3 D. 1
C
C
â
â
u
u
1
1
3
3
.
.
Trong mặt phẳng tọa độ, cho các parabol
2 2 2 2 2
8 , 16 , 4 , 4( 2 6)y x y x y x y p p x
. Có bao
nhiêu đường conic có đường chuẩn nằm bên phải đường thẳng
2 5 0
x
.
A.3 B. 1 C. 2 D. 4
40
C
C
â
â
u
u
1
1
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
l
l
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
.
.
X
X
é
é
t
t
d
d
â
â
y
y
c
c
u
u
n
n
g
g
M
M
N
N
c
c
ó
ó
đ
đ
ộ
ộ
d
d
à
à
i
i
b
b
ằ
ằ
n
n
g
g
4
4
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
,
,
K
K
N
N
s
s
o
o
n
n
g
g
s
s
o
o
n
n
g
g
v
v
ớ
ớ
i
i
M
M
H
H
,
,
t
t
í
í
n
n
h
h
t
t
ổ
ổ
n
n
g
g
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
h
h
a
a
i
i
đ
đ
i
i
ể
ể
m
m
M
M
,
,
N
N
.
.
A
A
.
.
1
1
,
,
9
9
B
B
.
.
2
2
,
,
2
2
C
C
.
.
2
2
D
D
.
.
2
2
,
,
1
1
Câu 15. Tìm p để đường chuẩn của parabol
2
2y px
cách điểm
( ;7)M p
một khoảng bằng 6 đơn vị độ dài.
A.
6
p
B.
4
p
C.
8
p
D.
1p
Câu 16. Đường conic parabol
2
2y px
với
0
p
c
c
ó
ó
m
m
ộ
ộ
t
t
d
d
â
â
y
y
c
c
u
u
n
n
g
g
v
v
u
u
ô
ô
n
n
g
g
g
g
ó
ó
c
c
v
v
ớ
ớ
i
i
t
t
r
r
ụ
ụ
c
c
h
h
o
o
à
à
n
n
h
h
c
c
ó
ó
đ
đ
ộ
ộ
d
d
à
à
i
i
b
b
ằ
ằ
n
n
g
g
2
2
v
v
à
à
k
k
h
h
o
o
ả
ả
n
n
g
g
c
c
á
á
c
c
h
h
t
t
ừ
ừ
g
g
ố
ố
c
c
t
t
ọ
ọ
a
a
đ
đ
ộ
ộ
O
O
đ
đ
ế
ế
n
n
d
d
â
â
y
y
c
c
u
u
n
n
g
g
n
n
à
à
y
y
b
b
ằ
ằ
n
n
g
g
4
4
,
,
g
g
i
i
á
á
t
t
r
r
ị
ị
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
i
i
ê
ê
u
u
p
p
t
t
h
h
u
u
ộ
ộ
c
c
k
k
h
h
o
o
ả
ả
n
n
g
g
A
A
.
.
(
(
0
0
;
;
2
2
)
)
B
B
.
.
(
(
2
2
;
;
4
4
)
)
C
C
.
.
(
(
4
4
;
;
9
9
)
)
D
D
.
.
(
(
9
9
;
;
1
1
5
5
)
)
C
C
â
â
u
u
1
1
7
7
.
.
Trong mặt phẳng tọa độ, cho
2
: 4P y x
. Tìm điểm
M
trên
P
sao cho
M
có tung độ bằng
2
.
A.
2;64
M
. B.
1;2
M
. C.
16;2
M
. D.
2; 8
M
.
C
C
â
â
u
u
1
1
8
8
.
.
Đường chuẩn của parabol
2 2
4 1
y p x
cách xa trục tung nhất một khoảng bằng bao nhiêu đơn vị độ
dài
A.2 B. 1 C. 3 D. 1,5
C
C
â
â
u
u
1
1
9
9
.
.
Trong mặt phẳng tọa độ, cho
2
: 8P y x
. Tìm trên
P
điểm
M
có tung độ dương và có hoành độ
bằng
3
.
A.
3;2 6
M
. B.
3; 2 6
M
. C.
2 6;3
M
. D.
2 6;3
M
.
C
C
â
â
u
u
2
2
0
0
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
l
l
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
.
.
B
B
i
i
ế
ế
t
t
70 , 1,5
HMF HF
, khi đó chu vi tam giác HMF gần nhất với
A
A
.
.
4
4
,
,
2
2
3
3
B
B
.
.
4
4
,
,
5
5
4
4
C
C
.
.
4
4
,
,
1
1
1
1
D
D
.
.
4
4
,
,
4
4
2
2
C
C
â
â
u
u
2
2
1
1
.
.
Cho parabol
2
( ) : 4P y x
với tiêu điểm F, có bao nhiêu điểm
M
(tọa độ nguyên) thuộc
( )P
thỏa mãn
điều kiện
2 35
MF
.
A.4 B. 6 C. 8 D. 10
Câu 22. Đường conic parabol
2
2y px
với
0
p
c
c
ó
ó
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
i
i
ê
ê
u
u
b
b
ằ
ằ
n
n
g
g
6
6
,
,
đ
đ
i
i
ể
ể
m
m
M
M
t
t
h
h
u
u
ộ
ộ
c
c
p
p
a
a
r
r
a
a
b
b
o
o
l
l
c
c
ó
ó
t
t
u
u
n
n
g
g
đ
đ
ộ
ộ
b
b
ằ
ằ
n
n
g
g
6
6
t
t
h
h
ì
ì
c
c
ó
ó
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
b
b
ằ
ằ
n
n
g
g
A
A
.
.
6
6
B
B
.
.
8
8
C
C
.
.
4
4
D
D
.
.
2
2
Câu 23. Đường conic parabol
2
2y px
với
0
p
c
c
ó
ó
m
m
ộ
ộ
t
t
d
d
â
â
y
y
c
c
u
u
n
n
g
g
v
v
u
u
ô
ô
n
n
g
g
g
g
ó
ó
c
c
v
v
ớ
ớ
i
i
t
t
r
r
ụ
ụ
c
c
h
h
o
o
à
à
n
n
h
h
c
c
ó
ó
đ
đ
ộ
ộ
d
d
à
à
i
i
b
b
ằ
ằ
n
n
g
g
8
8
v
v
à
à
k
k
h
h
o
o
ả
ả
n
n
g
g
c
c
á
á
c
c
h
h
t
t
ừ
ừ
g
g
ố
ố
c
c
t
t
ọ
ọ
a
a
đ
đ
ộ
ộ
O
O
đ
đ
ế
ế
n
n
d
d
â
â
y
y
c
c
u
u
n
n
g
g
n
n
à
à
y
y
b
b
ằ
ằ
n
n
g
g
1
1
,
,
g
g
i
i
á
á
t
t
r
r
ị
ị
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
i
i
ê
ê
u
u
p
p
t
t
h
h
u
u
ộ
ộ
c
c
k
k
h
h
o
o
ả
ả
n
n
g
g
A
A
.
.
(
(
0
0
;
;
2
2
)
)
B
B
.
.
(
(
2
2
;
;
4
4
)
)
C
C
.
.
(
(
4
4
;
;
9
9
)
)
D
D
.
.
(
(
9
9
;
;
1
1
5
5
)
)
C
C
â
â
u
u
2
2
4
4
.
.
Đường chuẩn của parabol
2 2
4 8 2y x p p
cách xa trục tung nhất một khoảng bằng bao nhiêu đơn
vị độ dài
A.2 B. 1 C. 3 D. 1,5
C
C
â
â
u
u
2
2
5
5
.
.
Trong mặt phẳng tọa độ, cho các parabol
2 2 2 2 2
8 , 2 , 4 , 4( 2 14)y x y x y x y p p x
. Có bao
nhiêu đường conic có đường chuẩn nằm bên trái đường thẳng
2 7 0
x
.
A.3 B. 1 C. 2 D. 4
C
C
â
â
u
u
2
2
6
6
.
.
Lập phương trình chính tắc của parabol biết khoảng cách từ tiêu điểm đến đường chuẩn bằng 6.
A.
2
12
x
y
B.
2
3y x
C.
2
12y x
. D.
2
6y x
_________________________________
41
ĐƯỜNG PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P4)
_____________________________________
Câu 1. Với
0
p
, khi đường chuẩn của parabol
2
2y px
tiếp xúc đường tròn
2 2
( 1) ( 4) 4
x y
thì giá trị
3
7
p p
bằng
A.75 B. 50 C. 65 D. 40
C
C
â
â
u
u
2
2
.
.
Đường chuẩn của đường conic
2
: 8P y x
tiếp xúc với đường tròn nào sau đây
A.
2 2
8
x y
B.
2 2
( 1) ( 4) 64
x y
C.
2 2
( 3) ( 2) 25
x y
D.
2 2
( 3) ( 4) 25
x y
C
C
â
â
u
u
3
3
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
h
h
a
a
m
m
s
s
ố
ố
t
t
i
i
ê
ê
u
u
c
c
ủ
ủ
a
a
p
p
a
a
r
r
a
a
b
b
o
o
l
l
b
b
ằ
ằ
n
n
g
g
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
0
0
C
C
â
â
u
u
4
4
.
.
Phương trình nào dưới dây luôn là phương trình chính tắc của parabol
A.
2
( 1)y a x
. B.
2
6y x
. C.
2
3 4y x
. D.
2
2 3y x
.
Câu 5. Đường conic parabol
2
2y px
với
0
p
c
c
ó
ó
t
t
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
F
F
,
,
t
t
ì
ì
m
m
t
t
ổ
ổ
n
n
g
g
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
p
p
k
k
h
h
i
i
10
EF
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
i
i
ể
ể
m
m
E
E
(
(
1
1
;
;
3
3
)
)
.
.
A
A
.
.
3
3
B
B
.
.
0
0
C
C
.
.
4
4
D
D
.
.
2
2
C
C
â
â
u
u
6
6
.
.
Lập phương trình của parabol biết khoảng cách từ đỉnh tới tiêu điểm bằng
1
24
.
A.
2
12
x
y
B.
2
3y x
C.
2
12y x
. D.
2
6y x
Câu 7. Đường conic parabol
2
2y px
với
0
p
c
c
ó
ó
m
m
ộ
ộ
t
t
d
d
â
â
y
y
c
c
u
u
n
n
g
g
v
v
u
u
ô
ô
n
n
g
g
g
g
ó
ó
c
c
v
v
ớ
ớ
i
i
t
t
r
r
ụ
ụ
c
c
h
h
o
o
à
à
n
n
h
h
c
c
ó
ó
đ
đ
ộ
ộ
d
d
à
à
i
i
b
b
ằ
ằ
n
n
g
g
8
8
v
v
à
à
k
k
h
h
o
o
ả
ả
n
n
g
g
c
c
á
á
c
c
h
h
t
t
ừ
ừ
g
g
ố
ố
c
c
t
t
ọ
ọ
a
a
đ
đ
ộ
ộ
O
O
đ
đ
ế
ế
n
n
d
d
â
â
y
y
c
c
u
u
n
n
g
g
n
n
à
à
y
y
b
b
ằ
ằ
n
n
g
g
6
6
,
,
g
g
i
i
á
á
t
t
r
r
ị
ị
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
i
i
ê
ê
u
u
p
p
t
t
h
h
u
u
ộ
ộ
c
c
k
k
h
h
o
o
ả
ả
n
n
g
g
A
A
.
.
(
(
0
0
;
;
2
2
)
)
B
B
.
.
(
(
2
2
;
;
4
4
)
)
C
C
.
.
(
(
4
4
;
;
9
9
)
)
D
D
.
.
(
(
9
9
;
;
1
1
5
5
)
)
Câu 8.
T
T
ì
ì
m
m
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
i
i
ê
ê
u
u
c
c
ủ
ủ
a
a
p
p
a
a
r
r
a
a
b
b
o
o
l
l
(
(
P
P
)
)
b
b
i
i
ế
ế
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
c
c
ủ
ủ
a
a
(
(
P
P
)
)
t
t
i
i
ế
ế
p
p
x
x
ú
ú
c
c
v
v
ớ
ớ
i
i
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
r
r
ò
ò
n
n
2 2
( 2) ( 3) 16
x y
.
A.
6
p
B.
4
p
C.
8
p
D.
1p
C
C
â
â
u
u
9
9
.
.
Đường chuẩn của parabol
2 2
4 5 4y x p p
cách xa trục tung nhất một khoảng bằng bao nhiêu đơn
vị độ dài
A.2 B. 3 C. 2,5 D. 1,5
C
C
â
â
u
u
1
1
0
0
.
.
M
M
ộ
ộ
t
t
c
c
h
h
i
i
ế
ế
c
c
đ
đ
è
è
n
n
c
c
ó
ó
m
m
ặ
ặ
t
t
c
c
ắ
ắ
t
t
n
n
g
g
a
a
n
n
g
g
l
l
à
à
h
h
ì
ì
n
n
h
h
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
c
c
h
h
i
i
ề
ề
u
u
r
r
ộ
ộ
n
n
g
g
h
h
a
a
i
i
m
m
é
é
p
p
v
v
à
à
n
n
h
h
l
l
à
à
A
A
B
B
=
=
5
5
0
0
c
c
m
m
v
v
à
à
c
c
h
h
i
i
ề
ề
u
u
s
s
â
â
u
u
h
h
=
=
3
3
0
0
c
c
m
m
(
(
k
k
h
h
o
o
ả
ả
n
n
g
g
c
c
á
á
c
c
h
h
t
t
ừ
ừ
O
O
đ
đ
ế
ế
n
n
A
A
B
B
)
)
,
,
b
b
ó
ó
n
n
g
g
đ
đ
è
è
n
n
n
n
ằ
ằ
m
m
ở
ở
t
t
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
S
S
.
.
T
T
h
h
a
a
m
m
s
s
ố
ố
t
t
i
i
ê
ê
u
u
c
c
ủ
ủ
a
a
p
p
a
a
r
r
a
a
b
b
o
o
l
l
n
n
ằ
ằ
m
m
t
t
r
r
o
o
n
n
g
g
k
k
h
h
o
o
ả
ả
n
n
g
g
A
A
.
.
(
(
4
4
;
;
6
6
)
)
B
B
.
.
(
(
0
0
;
;
4
4
)
)
C
C
.
.
(
(
6
6
;
;
7
7
)
)
D
D
.
.
(
(
7
7
;
;
1
1
2
2
)
)
C
C
â
â
u
u
1
1
1
1
.
.
Cho parabol
2
( ) : 8P y x
với tiêu điểm F, có bao nhiêu điểm
M
(tọa độ nguyên) thuộc
( )P
thỏa mãn
điều kiện
2 20
MF
.
A.3 B. 14 C. 8 D. 10
Câu 12. Có bao nhiêu số nguyên p để là đường conic
2 2
4( 2 2)y p p x
là parabol có đường chuẩn
5
x
.
A.4 B. 2 C. 1 D. 3
C
C
â
â
u
u
1
1
3
3
.
.
Đường parabol nào có thể có đường chuẩn cách xa gốc tọa độ O nhất
A.
2 2
4( 2 6)y p p x
B.
2 2
4 1
y p x
C.
2
16y x
D.
2 2
4(2 )y p x
42
C
C
â
â
u
u
1
1
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
đ
đ
ộ
ộ
d
d
à
à
i
i
d
d
â
â
y
y
c
c
u
u
n
n
g
g
t
t
ạ
ạ
o
o
b
b
ở
ở
i
i
p
p
a
a
r
r
a
a
b
b
o
o
l
l
v
v
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
3 0
x y
.
A
A
.
.
12 5
B
B
.
.
1
1
2
2
C
C
.
.
6 10
D
D
.
.
8
8
C
C
â
â
u
u
1
1
5
5
.
.
Cho parabol
2
( ) : 4P y x
, đường thẳng d đi qua điểm M (5;5) và tạo với hai trục tọa độ một góc
45
thì
tạo với parabol có tọa độ bằng
A.4 B. 6 C.
6 2
D.
4 2
Câu 15. Với tham số tiêu
0
p
, có bao nhiêu số nguyên p để đường chuẩn của parabol
2
2y px
nằm bên phải
đường thẳng
3 11 0
x
.
A.5 B. 3 C. 7 D. 9
Câu 16.
T
T
ì
ì
m
m
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
i
i
ê
ê
u
u
c
c
ủ
ủ
a
a
p
p
a
a
r
r
a
a
b
b
o
o
l
l
(
(
P
P
)
)
b
b
i
i
ế
ế
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
c
c
ủ
ủ
a
a
(
(
P
P
)
)
t
t
i
i
ế
ế
p
p
x
x
ú
ú
c
c
v
v
ớ
ớ
i
i
đ
đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
5 9 45
x y
.
A.
6
p
B.
4
p
C.
8
p
D.
1p
Câu 17. Đường conic parabol
2
2y px
với
0
p
c
c
ó
ó
t
t
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
F
F
,
,
t
t
ì
ì
m
m
đ
đ
ộ
ộ
d
d
à
à
i
i
n
n
g
g
ắ
ắ
n
n
n
n
h
h
ấ
ấ
t
t
c
c
ủ
ủ
a
a
đ
đ
o
o
ạ
ạ
n
n
t
t
h
h
ẳ
ẳ
n
n
g
g
E
E
F
F
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
i
i
ể
ể
m
m
E
E
(
(
1
1
;
;
3
3
)
)
.
.
A.4 B. 2 C. 3 D. 1
C
C
â
â
u
u
1
1
8
8
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
l
l
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
.
.
T
T
ì
ì
m
m
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
đ
đ
i
i
ể
ể
m
m
M
M
n
n
ế
ế
u
u
2 7 22,5
MH MF
.
A
A
.
.
1
1
,
,
8
8
B
B
.
.
1
1
,
,
4
4
C
C
.
.
1
1
,
,
5
5
D
D
.
.
1
1
,
,
6
6
Câu 19. Cổng của một công viên có dạng parabol. Để đo chiều cao h của cổng, một người đo khoảng cách giữa
hai chân cổng được 9m, người đó thấy nếu đứng cách chân cổng 0,5m thì đầu chạm cổng, cho biết người này
cao 1,6m, hỏi chiều cao cổng gần nhất giá trị nào
A.7,66 B. 7,68 C. 7,6 D. 7,62
Câu 20. Có bao nhiêu số nguyên p để là đường conic
2 2
4( 6 5)y p p x
là parabol có đường chuẩn
5
x
.
A.4 B. 2 C. 1 D. 3
Câu 21.
T
T
ì
ì
m
m
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
i
i
ê
ê
u
u
c
c
ủ
ủ
a
a
p
p
a
a
r
r
a
a
b
b
o
o
l
l
(
(
P
P
)
)
b
b
i
i
ế
ế
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
c
c
ủ
ủ
a
a
(
(
P
P
)
)
l
l
à
à
t
t
r
r
ụ
ụ
c
c
đ
đ
ố
ố
i
i
x
x
ứ
ứ
n
n
g
g
c
c
ủ
ủ
a
a
đ
đ
ồ
ồ
t
t
h
h
ị
ị
h
h
à
à
m
m
s
s
ố
ố
b
b
ậ
ậ
c
c
h
h
a
a
i
i
2
( ) 6 3 3
f x x x m
(m là tham số).
A.
6
p
B.
4
p
C.
8
p
D.
1p
Câu 22. Tìm khoảng cách ngắn nhất giữa hai điểm MN với M, N lần lượt thuộc các đường tròn và parabol
2 2 2
10 21 0; 8x y x y x
.
A.3 B. 2 C. 4 D. 2,5
C
C
â
â
u
u
2
2
2
2
.
.
Cho parabol
2
( ) : 4P y x
, tam giác OAB có ba đỉnh thuộc (P), trọng tâm G trùng với tiêu điểm F của
(P), độ dài đoạn thẳng AB bằng
A.2 B. 4 C. 3 D. 5
Câu 23. Tìm tổng các giá trị
0
p
khi đường conic parabol
2
2y px
với
c
c
ó
ó
t
t
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
F
F
t
t
h
h
u
u
ộ
ộ
c
c
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
r
r
ò
ò
n
n
2 2
4 2 3 0
x y x y
.
A.3 B. 2 C. 1 D. 4
Câu 24. Đường conic parabol
2
2y px
có tiêu điểm F thuộc đường elip
2 2
4 4
x y
thì trên parabol có bao
nhiêu điểm nguyên có hoành độ nhỏ hơn 50
A.4 B. 8 C. 5 D. 12
C
C
â
â
u
u
2
2
5
5
.
.
Đường conic parabol
2
( ) : 4P y x
tiếp xúc đường thẳng
4 2 0
x y m
tại điểm có tung độ bằng
A.1 B. 0,5 C. 1,5 D. 2
_________________________________
43
ĐƯỜNG PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P5)
_____________________________________
Câu 1. Trong các đường conic sau, có bao nhiêu đường conic có thể có đường chuẩn
4
x
2 2 2 2 2
4 ; 2 ; 4( 3 2) ; ( 3)y x y px y p p x y p x
A.3 B. 4 C. 1 D. 3
Câu 2. Đường conic parabol
2
2y px
với
0
p
có đường chuẩn
5
x
. Giá trị của p thuộc khoảng
A.(5;7) B. [3;5) C. [7;8) D. [8;11)
Câu 3. Phương trình nào sau đây là phương trình chính tắc của đường conic parabol
A.
2 2
2( 1)y p x
B.
2
2y x
C.
2
6y x
D.
2
2 3y x
C
C
â
â
u
u
4
4
.
.
Tìm khoảng cách ngắn nhất giữa hai điểm MN với M, N lần lượt thuộc các đường tròn và parabol
2 2 2 2
6 0; 4( 2 9)x y x y m m x
.
A.0 B. 2 C. 4 D. 1
Câu 5. Hai điểm A, B thuộc đường conic parabol
2
( ) : 4P y x
lần lượt có tung độ là – 2 và 4. Chu vi của tam
giác OAB (O là gốc tọa độ) gần nhất với
A.15,2 B. 14,6 C. 13,8 D. 16,4
Câu 6. Trong các đường conic sau, có bao nhiêu đường conic có thể có khoảng cách từ đỉnh đến đường chuẩn
lớn hơn 2 đơn vị độ dài
2 2 2 2 2
4 ; 2 ; 4( 2) ; (4 3)y x y px y p p x y p x
A.3 B. 4 C. 1 D. 3
C
C
â
â
u
u
7
7
.
.
Tìm m để đường tròn
2 2
( ) 9
x m y
tiếp xúc với đường conic parabol
2
2y px
với
0
p
.
A.
4
m
B.
9
m
C.
8
m
D. Kết quả khác
C
C
â
â
u
u
8
8
.
.
Cho parabol
2
( ) : 8P y x
, tam giác OAB có ba đỉnh thuộc (P), trọng tâm G trùng với tiêu điểm F của (P),
độ dài đoạn thẳng AB bằng
A.9 B. 8 C. 6 D. 5
Câu 9. Tìm tổng các giá trị
0
p
khi đường conic parabol
2
2y px
c
c
ó
ó
t
t
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
F
F
t
t
h
h
u
u
ộ
ộ
c
c
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
r
r
ò
ò
n
n
2 2
4 2 20
x y x y
.
A.3 B. 2 C. 8 D. 4
C
C
â
â
u
u
1
1
0
0
.
.
Cho parabol
2
( ) : 8P y x
, (P) tiếp xúc với đường thẳng
8 6 5 0
x y m
tại điểm có hoành độ thuộc
khoảng
A.(0;1) B. (1;2) C. (2;3) D. (3;4)
C
C
â
â
u
u
1
1
1
1
.
.
Đường chuẩn của đường conic
2
: 4P y px
với
0
p
trùng với trục đối xứng của đồ thị hàm số bậc
hai
2
( ) 2(3 4) 8
f x x p x p
. Tiêu điểm của (P) cách điểm
(2023;0)
A
một khoảng bằng
A.2023 B. 2020 C. 2022 D. 2021
Câu 12. Đường conic parabol
2
2y px
có tiêu điểm F thuộc đường elip
2 2
6 9
x y
thì trên parabol có bao
nhiêu điểm nguyên có hoành độ nhỏ hơn 50
A.4 B. 8 C. 5 D. 10
C
C
â
â
u
u
1
1
3
3
.
.
Đường conic parabol
2
( ) : 4P y x
tiếp xúc đường thẳng
4 4 2023 0
x y m
tại điểm có tung độ
bằng
A.1 B. 0,5 C. – 3 D. – 2
Câu 14. Trong mặt phẳng tọa độ Oxy, đường conic parabol
2
2y px
với
0
p
có tiêu điểm nằm trên đường
thẳng
2
2023 2002 2023 0
x p y
thì tiếp xúc với đường thẳng nào sau đây
A.
4 2 1 0
x y
B.
2 3 0
x y
C.
2 6 1 0
x y
D.
4 3 0
x y
Câu 15.
T
T
ì
ì
m
m
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
i
i
ê
ê
u
u
c
c
ủ
ủ
a
a
p
p
a
a
r
r
a
a
b
b
o
o
l
l
(
(
P
P
)
)
b
b
i
i
ế
ế
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
c
c
ủ
ủ
a
a
(
(
P
P
)
)
l
l
à
à
t
t
r
r
ụ
ụ
c
c
đ
đ
ố
ố
i
i
x
x
ứ
ứ
n
n
g
g
c
c
ủ
ủ
a
a
đ
đ
ồ
ồ
t
t
h
h
ị
ị
h
h
à
à
m
m
s
s
ố
ố
b
b
ậ
ậ
c
c
h
h
a
a
i
i
2
( ) 8 3 3
f x x x m
(m là tham số).
A.
6
p
B.
4
p
C.
8
p
D.
1p
C
C
â
â
u
u
1
1
6
6
.
.
Điểm
( ; )M x y
parabol
2
( ) : 16P y x
, tìm giá trị nhỏ nhất của biểu thức
2 2
2 6 1958
T x y x
.
A.1789 B. 1945 C. 1979 D. 1858
Câu 17. Hai điểm A, B thuộc đường conic parabol
2
( ) : 4P y x
lần lượt có tung độ là – 2 và 4. Diện tích của tam
giác OAB (O là gốc tọa độ) bằng bao nhiêu đvdt
A.5 B. 6 C. 4 D. 3
C
C
â
â
u
u
1
1
8
8
.
.
Tìm m để đường tròn
2 2
( 2)
x y m
tiếp xúc với đường conic parabol
2
2y px
với
0
p
.
A.
4
m
B.
9
m
C.
8
m
D.
16
m
44
C
C
â
â
u
u
1
1
9
9
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
F
F
c
c
ủ
ủ
a
a
p
p
a
a
r
r
a
a
b
b
o
o
l
l
t
t
h
h
u
u
ộ
ộ
c
c
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
n
n
à
à
o
o
A
A
.
.
3 1 0
x y
B
B
.
.
5y x
C
C
.
.
2 3 2 0
x y
D
D
.
.
6 2 0
x y
Câu 20. Đường conic parabol
2
2y px
với
0
p
có tiêu điểm nằm trên giao điểm hai đường thẳng
3 3 0; 5 (3 1) 5 0
x my x m y
Giá trị tham số p bằng
A.1 B. 0,5 C. 2 D. 1,5
Câu 21. Đường conic parabol
2
2y px
với
0
p
có tiêu điểm F (tọa độ nguyên) nằm trên một trong đường
trung bình của tam giác OAB với O là gốc tọa độ,
(4;4), (4; 6)
A B
. Phương trình đường chính tắc của parapol
là
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
C
C
â
â
u
u
2
2
2
2
.
.
Có bao nhiêu số nguyên
50
m
để parabol
2
( ) : 8P y x
và đường thẳng
8 6 5 0
x y m
không có
điểm chung
A.45 B. 35 C. 20 D. 25
Câu 23. Tìm tổng các giá trị
0
p
khi đường conic parabol
2
4y px
c
c
ó
ó
t
t
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
F
F
c
c
á
á
c
c
h
h
đ
đ
i
i
ể
ể
m
m
(2 5;4)
E p
một
khoảng bằng 5.
A.8 B. 9 C. 10 D. 12
C
C
â
â
u
u
2
2
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
l
l
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
.
.
X
X
é
é
t
t
d
d
â
â
y
y
c
c
u
u
n
n
g
g
M
M
N
N
c
c
ó
ó
đ
đ
ộ
ộ
d
d
à
à
i
i
b
b
ằ
ằ
n
n
g
g
4
4
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
,
,
K
K
N
N
s
s
o
o
n
n
g
g
s
s
o
o
n
n
g
g
v
v
ớ
ớ
i
i
M
M
H
H
,
,
t
t
í
í
n
n
h
h
t
t
ổ
ổ
n
n
g
g
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
h
h
a
a
i
i
đ
đ
i
i
ể
ể
m
m
M
M
,
,
N
N
.
.
A
A
.
.
1
1
,
,
9
9
B
B
.
.
2
2
,
,
2
2
C
C
.
.
2
2
D
D
.
.
2
2
,
,
1
1
C
C
â
â
u
u
2
2
5
5
.
.
Điểm
( ; )M x y
thuộc parabol
2
( ) : 8P y x
, tìm giá trị nhỏ nhất của biểu thức
2 2
16 2023
Q x y x
.
A.1879 B. 1945 C. 1975 D. 1954
Câu 26. Đường conic parabol
2
2y px
với
0
p
có đường chuẩn là một trong các đường trung tuyến của tam
giác ABC với
( 2;3), ( 4; 5), (0; 1)
A B C
. Phương trình đường chính tắc của parapol là
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
C
C
â
â
u
u
2
2
7
7
.
.
Điểm
( ; )M x y
parabol
2
( ) : 16P y x
đồng thời nằm trong góc phần tư thứ nhất của mặt phẳng tọa độ,
tìm giá trị nhỏ nhất của biểu thức
1958
T x y
.
A.1789 B. 1945 C. 1979 D. 1954
C
C
â
â
u
u
2
2
8
8
.
.
Có bao nhiêu số nguyên
50
m
để parabol
2
( ) : 8P y x
và đường thẳng
8 9 10 11 0
x y m
có
điểm chung
A.40 B. 46 C. 20 D. 34
C
C
â
â
u
u
2
2
9
9
.
.
Cho đường parbol
2
( ) : 4P y x
và điểm
(2;0)
I
, hai điểm M, N thuộc (P) thỏa mãn
3 2IM IN
. Tồn
tại hai điểm M, N với tổng hoành độ bằng
A.16 B. 10 C. 10 D. 13
C
C
â
â
u
u
3
3
0
0
.
.
Có bao nhiêu số nguyên m nhỏ hơn 2023 để đường tròn
2 2
( 2)
x y m
có ít nhất một điểm chung
với đường conic parabol
2
2023
y x
.
A.2019 B. 2015 C. 2014 D. 2010
C
C
â
â
u
u
3
3
1
1
.
.
Elip
2 2
2
1
3 5
x y
a a
có đỉnh bên phải trùng với tiêu điểm của parabol
2
( ) : 16P y x
thì có tiêu cự bằng
A.10 B. 6 C. 8 D. 10
_________________________________
45
ĐƯỜNG PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P6)
_____________________________________
Câu 1. Đường conic parabol
2
2y px
với
0
p
có đường chuẩn
2
x
. Giá trị của p thuộc khoảng
A.(0;1) B. [1;2) C. [2;3) D. [3;5)
Câu 2. Phương trình nào sau đây là phương trình chính tắc của đường conic parabol
A.
2
6y x
B.
2
2y x
C.
2
6y x
D.
2
2 3y x
Câu 3. Đường conic parabol nào sau đây có tiêu điểm là tiếp điểm của hai đường tròn
2 2 2 2
4; ( 3) 1
x y x y
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
Câu 4. Trong các đường conic sau, có bao nhiêu đường conic có thể có đường chuẩn
2
x
2 2 2 2 2
4 ; 2 ; 4( 3 2) ; ( 3)y x y px y p p x y p x
A.3 B. 4 C. 1 D. 2
Câu 5. Tính tổng các giá trị p để đường conic
2 2
( ) : 4( 4 2)P y p p x
với
0
p
có tiêu điểm nằm trên đường
thẳng
1y x
.
A.2 B. 3 C. 4 D. 1
Câu 6. Đồ thị hàm số bậc hai
2
( ) 4 3f x x x
cắt trục hoành tại hai điểm A, B. Đoạn thẳng AB nhận tiêu điểm
F của parabol
2
2y px
với
0
p
làm trung điểm. Phương trình đường chính tắc của parapol là
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
C
C
â
â
u
u
7
7
.
.
Cho đường parbol
2
( ) : 4P y x
và điểm
(2;0)
I
, hai điểm M, N thuộc (P) thỏa mãn
2IM IN
. Tồn tại
hai điểm M, N với tổng hoành độ bằng
A.6 B. 8 C. 4 D. 5
C
C
â
â
u
u
8
8
.
.
Cho parabol
2
( ) : 4P y x
, (P) tiếp xúc với đường thẳng
8 6 5 0
x y m
tại điểm có hoành độ thuộc
khoảng
A.
1
0;
2
B.
1 5
;
2 6
C.
5 4
;
6 3
D.
4
;2
3
Câu 9. Parabol nào sau đây có đỉnh cách xa tiêu điểm nhất
A.
2
2y x
B.
2 2
4( 2 8)y p p x
C.
2
4(1 ) (0 1)
y p x p
D.
2
y x
C
C
â
â
u
u
1
1
0
0
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
(
(
P
P
)
)
:
:
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
x
x
é
é
t
t
b
b
a
a
đ
đ
i
i
ể
ể
m
m
, ,A B C
thuộc (P) có tung độ lần lượt là
6;2; 4
.
Trọng tâm tam giác ABC có hoành độ bằng
A
A
.
.
29
6
B
B
.
.
25
6
C
C
.
.
14
3
D
D
.
.
40
9
C
C
â
â
u
u
1
1
1
1
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
có tiêu điểm F cùng với ba điểm
(2;2), (6;2), (5;0)
A B C
tạo
thành hình bình hành
ABCF
. Điểm M trên (P) có tung độ bằng 9 thì có hoành độ thuộc khoảng
A.(9;11) B. (11;15) C. (15;19) D. (19;24)
C
C
â
â
u
u
1
1
2
2
.
.
C
C
h
h
o
o
b
b
a
a
đ
đ
i
i
ể
ể
m
m
(3;6), (4;1), ( 4; 7)
A B C
,
,
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
có tiêu điểm F là trọng tâm
tam giác ABC. Điểm
( ; )M a b
thuộc (P) thì độ dài đoạn thẳng MF bằng
A.
1a
B.
2
a
C.
2 1a
D.
1a
C
C
â
â
u
u
1
1
3
3
.
.
Cho parabol
2
( ) : 4P y x
, tìm hệ số góc k của tiếp tuyến của (P) tại điểm có tung độ bằng 2
A.
1
k
B.
2
k
C.
1
3
k
D.
2
k
Câu 14. Tiêu điểm của parabol
2
2y px
với
0
p
là tâm của đường tròn
2 2 2
6 2 0
x y x my m m
thì
giá trị p thuộc khoảng nào
A.(0;1) B. (1;4) C. (4;7) D. (7;10)
46
Câu 15. Cho ba điểm
(0;4), (0; 4), (4; 4)
A B C
. Tiêu điểm của parabol (P):
2
2y px
với
0
p
là tâm của
đường tròn ngoại tiếp tam giác ABC. Có bao nhiêu điểm M thuộc (P) có tọa độ nguyên dương mà tung độ thuộc
khoảng (1428;1789)
A.128 B. 179 C. 189 D. 148
C
C
â
â
u
u
1
1
6
6
.
.
Có bao nhiêu số nguyên
200
m
để parabol
2
( ) : 2P y x
và đường thẳng
8 6 5 0
x y m
không có
điểm chung
A.180 B. 192 C. 200 D. 175
C
C
â
â
u
u
1
1
7
7
.
.
Tính độ dài dây cung tạo bởi đường conic
2
( ) : 4P y x
và đường thẳng
2 12 0
x y
.
A.10 B.
5 6
C.
5 5
D.
6 3
C
C
â
â
u
u
1
1
8
8
.
.
Điểm
( ; )M x y
thuộc parabol
2
( ) : 8P y x
, tìm giá trị nhỏ nhất của biểu thức
2 2
4 2015
Q x y x
.
A.1979 B. 1945 C. 1975 D. 1954
Câu 19. Đường conic parabol
2
2y px
với
0
p
có đường chuẩn là một trong các đường cao của tam giác
ABC với
5
2; , 5;1 , 0;2
2
A B C
. Phương trình đường chính tắc của parapol là
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
C
C
â
â
u
u
2
2
0
0
.
.
Cho parabol
2
( ) : 8P y x
, tìm hệ số góc k của tiếp tuyến của (P) tại điểm có tung độ bằng 4
A.
1
k
B.
2
k
C.
1
3
k
D.
2
k
C
C
â
â
u
u
2
2
1
1
.
.
Điểm
( ; )M x y
parabol
2
( ) : 16P y x
đồng thời nằm trong góc phần tư thứ nhất của mặt phẳng tọa độ,
tìm giá trị nhỏ nhất của biểu thức
8 2045
T x y
.
A.1789 B. 1945 C. 1979 D. 1954
C
C
â
â
u
u
2
2
2
2
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
(
(
P
P
)
)
:
:
2
2y px
có tiêu điểm
(2;0)
F
,
,
x
x
é
é
t
t
b
b
a
a
đ
đ
i
i
ể
ể
m
m
, ,A B C
thuộc (P) có tung độ lần lượt
là
6;2; 4
. Diện tích tam giác ABC (đvdt) bằng
A.24 B. 15 C. 20 D. 28
C
C
â
â
u
u
2
2
3
3
.
.
A
A
n
n
t
t
e
e
n
n
v
v
ệ
ệ
t
t
i
i
n
n
h
h
p
p
a
a
r
r
a
a
b
b
o
o
l
l
c
c
ó
ó
đ
đ
ầ
ầ
u
u
t
t
h
h
u
u
đ
đ
ặ
ặ
t
t
t
t
ạ
ạ
i
i
t
t
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
,
,
đ
đ
ư
ư
ờ
ờ
n
n
g
g
k
k
í
í
n
n
h
h
m
m
i
i
ệ
ệ
n
n
g
g
a
a
n
n
t
t
e
e
n
n
l
l
à
à
2
2
4
4
0
0
c
c
m
m
,
,
k
k
h
h
o
o
ả
ả
n
n
g
g
c
c
á
á
c
c
h
h
t
t
ừ
ừ
đ
đ
ầ
ầ
u
u
t
t
h
h
u
u
t
t
ớ
ớ
i
i
m
m
i
i
ệ
ệ
n
n
g
g
a
a
n
n
t
t
e
e
n
n
l
l
à
à
1
1
3
3
0
0
c
c
m
m
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
.
.
T
T
í
í
n
n
h
h
k
k
h
h
o
o
ả
ả
n
n
g
g
c
c
á
á
c
c
h
h
(
(
g
g
ầ
ầ
n
n
đ
đ
ú
ú
n
n
g
g
)
)
t
t
ừ
ừ
v
v
ị
ị
t
t
r
r
í
í
đ
đ
ặ
ặ
t
t
đ
đ
ầ
ầ
u
u
t
t
h
h
u
u
đ
đ
ế
ế
n
n
đ
đ
ỉ
ỉ
n
n
h
h
a
a
n
n
t
t
e
e
n
n
A
A
.
.
4
4
9
9
,
,
6
6
c
c
m
m
B
B
.
.
6
6
9
9
,
,
4
4
c
c
m
m
C
C
.
.
4
4
6
6
,
,
9
9
c
c
m
m
D
D
.
.
9
9
6
6
,
,
4
4
c
c
m
m
C
C
â
â
u
u
2
2
4
4
.
.
Cho parabol
2
( ) : 16P y x
, tìm cosin góc tạo bởi hai tiếp tuyến của (P) tại điểm có hoành độ bằng 1
A.0,5 B. 0,6 C. 0,25 D. 0,75
C
C
â
â
u
u
2
2
5
5
.
.
Điểm
( ; )M x y
parabol
2
( ) : 16P y x
đồng thời nằm trong góc phần tư thứ nhất của mặt phẳng tọa độ,
tìm giá trị nhỏ nhất của biểu thức
8 3 2023
T x y
.
A.1789,5 B. 1988,5 C. 1979,5 D. 2018,5
Câu 26. Đường conic parabol nào sau đây có tiêu điểm là điểm đồng quy của ba đường thẳng
3 3; 5; 2 6y x y mx m y nx n
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
C
C
â
â
u
u
2
2
7
7
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
có tiêu điểm cùng với hai điểm
(2;2), (4;6)
A B
tạo thành ba
điểm thẳng hàng. Đường chuẩn của parabol đó có phương trình
A.
1
x
B.
2
x
C.
3
x
D.
1x
Câu 28. Với tham số tiêu
0
p
, đường chuẩn của parabol
2
2y px
cách điểm
(2 ;2023)
M p
một khoảng bằng
A.2p B. 4p C. 1,5p D. 2,5p
C
C
â
â
u
u
2
2
9
9
.
.
Cho parabol
2
( ) : 16P y x
, (P) tiếp xúc với đường thẳng
8 12 4 0
x y m
tại điểm có hoành độ thuộc
khoảng
A.(0;5) B. (8;11) C. (5;8) D. (11;15)
_________________________________
47
ĐƯỜNG PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P7)
_____________________________________
Câu 1. Đường conic parabol
2
2y px
với
0
p
có đường chuẩn
5
2
x
. Giá trị của p thuộc khoảng
A.(0;1) B. [1;2) C. [2;3) D. [3;5]
Câu 2. Phương trình nào sau đây là phương trình chính tắc của đường conic parabol
A.
2
6 1y x
B.
2
2y x
C.
2 2
( 5)y m x
D.
2
2 3y x
Câu 3. Đường conic parabol nào sau đây có tiêu điểm là tiếp điểm của hai đường tròn
2 2 2 2
4; ( 3) 1
x y x y
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
Câu 4. Trong các đường conic sau, có bao nhiêu đường conic có thể có đường chuẩn
2
x
2 2 2 2 2
4 ; 2( ) ; 4( 6 2) ; 6( 3)y x y p q x y p p x y p x
A.2 B. 4 C. 1 D. 3
Câu 5. Cho các đường cong có phương trình
2 2 2 2 2
6 ; ( 20) ; ( 2 5) ; (2 ) ; 2 2y x y m x y m m x y p x y p x
Có bao nhiêu phương trình luôn là phương trình chính tắc của một parabol
A.4 B. 2 C. 3 D. 1
Câu 6. Tính tổng các giá trị p để đường conic
2 2
( ) : 4( 6 2)P y p p x
với
0
p
có tiêu điểm nằm trên
đường thẳng
1y x
.
A.2 B. 3 C. 4 D. 6
Câu 7. Đường conic parabol nào sau đây có tiêu điểm là điểm đồng quy của ba đường thẳng
2
( 9)( 2); 7 2 7; ( 2) 9
y m x y mx n y n x m
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
Câu 8. Đường conic parabol
2
2y px
với
0
p
đi qua điểm
(1; 4)
M
thì có đường chuẩn cách trục tung một
khoảng bằng
A.1 B. 2 C. 1,5 D. 2,5
C
C
â
â
u
u
9
9
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
l
l
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
.
.
T
T
ì
ì
m
m
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
đ
đ
i
i
ể
ể
m
m
M
M
n
n
ế
ế
u
u
2 4MH MF
.
A
A
.
.
1
1
,
,
8
8
B
B
.
.
4
4
C
C
.
.
3
3
D
D
.
.
1
1
,
,
6
6
C
C
â
â
u
u
1
1
0
0
.
.
Cho đường parbol
2
( ) : 4P y x
và điểm
(0;2)
I
, hai điểm M, N thuộc (P) thỏa mãn
2IM IN
. Tồn tại
hai điểm M, N với tổng hoành độ bằng
A.6 B. 8 C. 4 D. 5
C
C
â
â
u
u
1
1
1
1
.
.
Có bao nhiêu số nguyên
200
m
để parabol
2
( ) : 2P y x
và đường thẳng
4 6 10 0
x y m
không
có điểm chung
A.189 B. 185 C. 200 D. 178
C
C
â
â
u
u
1
1
2
2
.
.
Điểm
( ; )M x y
thuộc parabol
2
( ) : 8P y x
, tìm giá trị lớn nhất của biểu thức
2 2
8 1911
Q x y x
.
A.1979 B. 1945 C. 1975 D. 1954
C
C
â
â
u
u
1
1
3
3
.
.
Lập phương trình chính tắc của parabol biết khoảng cách từ đỉnh tới tiêu điểm bằng 0,75.
A.
2
12
x
y
B.
2
3y x
C.
2
12y x
. D.
2
6y x
Câu 14. Đường conic parabol
2
2y px
với
0
p
có đường chuẩn đi qua trung điểm đoạn thẳng AB
với
( 7;10), (3 ;2)
A m B m
. Phương trình đường chính tắc của parapol là
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
C
C
â
â
u
u
1
1
5
5
.
.
Cho đường parbol
2
( ) : 4P y x
, tiếp tuyến tại điểm M thuộc (P) có tung độ bằng 4, hệ số góc của tiếp
tuyến đó bằng
A.1 B. 1,5 C. 0,5 D. 2
C
C
â
â
u
u
1
1
6
6
.
.
Tập hợp các điểm
( ; )M x y
thuộc parabol
2
( ) : 36P y x
đồng thời nằm trong góc phần tư thứ nhất của
mặt phẳng tọa độ người ta gọi là nhánh trên của parabol, phương trình nhánh trên đó là
48
A.
2y x
B.
4y x
C.
6y x
D.
4y x
Câu 17. Đường conic parabol
2
2y px
với
0
p
có khoảng cách từ tiêu điểm đến đường chuẩn bằng 2, điểm
( ; )M x y
nằm trên parabol thì độ dài đoạn thẳng MF bằng
A.
2
x
B.
1x
C.
3x
D.
1x
C
C
â
â
u
u
1
1
8
8
.
.
Cho đường conic parabol
2
( ) : 6P y x
, đường phân giác góc phần tư thứ nhất tạo với parabol một dây
cung có độ dài bằng đường kính của đường tròn nào
A.
2 2
( 4) 24
x y
B.
2 2
( 3) ( 2) 18
x y
C.
2 2
( 3) ( 4) 25
x y
D.
2 2
( 3) ( 1) 20
x y
Câu 19. Đường conic parabol
2
2y px
với
0
p
có khoảng cách từ tiêu điểm đến đường thẳng
10
x
bằng 8
đơn vị độ dài. Phương trình chính tắc đường parabol là
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
Câu 20. Có bao nhiêu số nguyên dương p để
5
(2023 )y p x
là dạng chính tắc của một parabol
A.3 B. 5 C. 4 D. 6
C
C
â
â
u
u
2
2
1
1
.
.
Đường parabol nào có thể có đường chuẩn cách xa gốc tọa độ O nhất
A.
2 2
4( 2 20)y p p x
B.
2 2
4 1
y p x
C.
2
16y x
D.
2
4y x
C
C
â
â
u
u
2
2
2
2
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
l
l
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
.
.
T
T
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
p
p
a
a
r
r
a
a
b
b
o
o
l
l
t
t
r
r
ù
ù
n
n
g
g
v
v
ớ
ớ
i
i
t
t
â
â
m
m
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
r
r
ò
ò
n
n
n
n
à
à
o
o
A
A
.
.
2 2
( 4) 4
x y
B
B
.
.
2 2
( 1) 4
x y
C
C
.
.
2 2
( 1) 4
x y
D
D
.
.
2 2
( 1) ( 2) 1
x y
Câu 23. Tồn tại bao nhiêu giá trị nguyên dương p để tiêu điểm của đường conic
2
2y px
nằm trong khoảng
giữa hai đường thẳng (không nằm trên biên)
1; 3
x x
.
A.4 B. 3 C. 5 D. 2
C
C
â
â
u
u
2
2
4
4
.
.
Cho đường conic parabol
2
( ) : 6P y x
, tiếp tuyến của parabol tại điểm có tung độ bằng 6 đi qua điểm
nào sau đây
A.(8;9) B. (10;16) C. (40;23) D. (50;27)
Câu 25. Đường conic parabol nào sau đây có tiêu điểm là tiếp điểm của hai đường tròn
2 2 22
;( ) )4 34
( 1
x yx y
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
Câu 26.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
có tiêu điểm trùng với tiêu điểm bên phải của hypebol
2 2
16 9 144
x y
. Đường chuẩn của parabol cách trục hoành một khoảng bằng
A.6 B. 10 C. 5 D. 8
C
C
â
â
u
u
2
2
7
7
.
.
Cho đường parbol
2
( ) : 4P y x
, hai điểm M, N thuộc (P) cùng có hoành độ bằng 4, các tiếp tuyến tại M
và N hợp với nhau một góc gần nhất với
A.53 độ B. 54 độ C. 56 độ D. 57 độ
Câu 28. Đồ thị hàm số bậc hai
2 2 2
( ) ( 1)( 2) 1
f x m x m
cắt trục hoành tại hai điểm A, B. Đoạn thẳng AB
nhận tiêu điểm F của parabol
2
2y px
với
0
p
làm trung điểm. Phương trình đường chính tắc của parapol là
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
C
C
â
â
u
u
2
2
9
9
.
.
Tập hợp các điểm
( ; )M x y
thuộc parabol
2
( ) : 4P y x
đồng thời nằm trong góc phần tư thứ nhất của
mặt phẳng tọa độ người ta gọi là nhánh trên của parabol, đường thẳng d là tiếp tuyến của nhánh trên đó và d đi
qua điểm
( 2;0)
A
, hệ số góc của đường thẳng d bằng
A.1 B. 0,5 C. 1,5 D. 2
______________________________
49
ĐƯỜNG PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P8)
_____________________________________
C
C
â
â
u
u
1
1
.
.
Lập phương trình chính tắc của parabol biết parabol đi qua điểm (3;3).
A.
2
6y x
B.
2
3y x
C.
2
12y x
D.
2
4y x
Câu 2. Trong các đường conic sau, có bao nhiêu đường conic có thể có đường chuẩn
2
x
2 2 2 2 2
4 ; 2( ) ; 4( 2 3) ; 4( 3)y x y p q x y p p x y p x
A.1 B. 4 C. 3 D. 2
Câu 3. Trong các phương trình sau
2 2 2
4 ; 2; 2 5 ; 2y x y x y x y x
, có bao nhiêu phương trình là
dạng chính tắc của một đường parabol
A.2 B. 1 C. 3 D. 4
Câu 4. Tính tổng các giá trị p để đường conic
2 3 2
( ) : 4( 2 4 3)P y p p p x
với
0
p
có tiêu điểm nằm trên
đường thẳng
1y x
.
A.0,5 B. 3 C. 2 D. 1
Câu 5. Đường conic parabol nào sau đây có tiêu điểm là điểm đồng quy của ba đường thẳng
2
( 1)( 2); 2 7; ( 2) 4 9
y k x y mx n y n x m
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
C
C
â
â
u
u
6
6
.
.
Đường chuẩn của đường conic
2
: 4P y px
với
0
p
vuông góc với đường thẳng nào sau đây
A.
4y px
B.
3 1y x
C.
2 2022
y m
D.
8 1y x
Câu 7. Có bao nhiêu số nguyên p để
2 2
(9 )y p x
là dạng chính tắc của một parabol
A.4 B. 3 C. 5 D. 6
C
C
â
â
u
u
8
8
.
.
Có bao nhiêu cặp số (m;n) để đường tròn
2 2 2
( 4) ( )
x y m n
tiếp xúc với đường conic parabol
2
2022
y x
.
.
A
A
.
.
5
5
B
B
.
.
2
2
C
C
.
.
3
3
D
D
.
.
4
4
C
C
â
â
u
u
9
9
.
.
Tập hợp các điểm
( ; )M x y
thuộc parabol
2
( ) : 16P y x
đồng thời nằm trong góc phần tư thứ nhất của
mặt phẳng tọa độ người ta gọi là nhánh trên của parabol, phương trình nhánh trên đó là
A.
2y x
B.
4y x
C.
6y x
D.
4y x
Câu 10. Đường conic parabol
2
2y px
với
0
p
c
c
ó
ó
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
i
i
ê
ê
u
u
b
b
ằ
ằ
n
n
g
g
1
1
0
0
,
,
đ
đ
i
i
ể
ể
m
m
M
M
t
t
h
h
u
u
ộ
ộ
c
c
p
p
a
a
r
r
a
a
b
b
o
o
l
l
c
c
ó
ó
t
t
u
u
n
n
g
g
đ
đ
ộ
ộ
b
b
ằ
ằ
n
n
g
g
–
–
1
1
0
0
t
t
h
h
ì
ì
c
c
ó
ó
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
b
b
ằ
ằ
n
n
g
g
A
A
.
.
6
6
B
B
.
.
8
8
C
C
.
.
4
4
D
D
.
.
5
5
C
C
â
â
u
u
1
1
1
1
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ắ
ắ
t
t
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
3 2
2 3 4 2
x p p p
tại
bao nhiêu điểm
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
0
0
C
C
â
â
u
u
1
1
2
2
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
có tiêu điểm cùng với hai điểm
(3;4), (4;6)
A B
tạo thành ba
điểm thẳng hàng. Đường chuẩn của parabol đó có phương trình
A.
1
x
B.
2
x
C.
3
x
D.
1x
C
C
â
â
u
u
1
1
3
3
.
.
C
C
h
h
o
o
b
b
a
a
đ
đ
i
i
ể
ể
m
m
( 3;6), ( 5;1), ( 1; 7)
A B m C m
,
,
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
có tiêu điểm F là
trọng tâm tam giác ABC. Điểm
( ; )M a b
thuộc (P) thì độ dài đoạn thẳng MF bằng
A.
1a
B.
2
a
C.
2 1a
D.
1a
Câu 14. Tìm độ dài dây cung tạo bởi đường thẳng
2 4 0
x y
và đường conic parabol
2
( ) : 4P y x
.
A.4 B.
3 5
C.
6 3
D.
4 7
Câu 15. Tiêu điểm của parabol
2
2y px
với
0
p
là tâm của đường tròn
2 2 2
6 2 15
x y x my m m
thì
giá trị p thuộc khoảng nào
A.(0;1) B. (1;4) C. (4;7) D. (7;10)
50
C
C
â
â
u
u
1
1
6
6
.
.
Điểm
( ; )M x y
parabol
2
( ) : 16P y x
đồng thời nằm trong góc phần tư thứ nhất của mặt phẳng tọa độ,
tìm giá trị nhỏ nhất của biểu thức
8 2033
T x y
.
A.1777 B. 1789 C. 1979 D. 1954
Câu 17. Đường conic parabol
2
2y px
với
0
p
cắt đường phân giác góc phần tư thứ nhất theo một dây
cung có độ dài bằng
5 2
, đường chuẩn của parabol cách tiêu điểm một khoảng bằng
A.2,5 B. 2 C. 3 D. 3,5
C
C
â
â
u
u
1
1
8
8
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
(
(
P
P
)
)
:
:
2
2y px
có tiêu điểm
(1;0)
F
,
,
x
x
é
é
t
t
b
b
a
a
đ
đ
i
i
ể
ể
m
m
, ,A B C
thuộc (P) có tung độ lần lượt
là
6;2; 4
. Diện tích tam giác ABC (đvdt) bằng
A.24 B. 30 C. 32 D. 28
Câu 19. Đường conic parabol nào sau đây có tiêu điểm là điểm đồng quy của ba đường thẳng
7 7; 6 6; ( 1)
y x y x y m x
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
C
C
â
â
u
u
2
2
0
0
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
l
l
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
.
.
T
T
ì
ì
m
m
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
đ
đ
i
i
ể
ể
m
m
M
M
n
n
ế
ế
u
u
2
2 3 44
MH MF
.
A
A
.
.
1
1
,
,
8
8
B
B
.
.
4
4
C
C
.
.
3
3
D
D
.
.
1
1
,
,
6
6
Câu 21. Đường conic parabol
2
2y px
với
0
p
có đường chuẩn đi qua trung điểm đoạn thẳng AB với
(3;6), ( 7;2)
A B
. Phương trình đường chính tắc của parapol là
A.
2
6y x
B.
2
8y x
C.
2
12y x
D.
2
4y x
C
C
â
â
u
u
2
2
2
2
.
.
Cho đường parbol
2
( ) : 4P y x
và điểm
(3;2)
I
, hai điểm M, N thuộc (P) thỏa mãn
2IM IN
. Độ dài
đoạn thẳng MN có thể bằng
A.4 B.
3 5
C.
6 3
D.
4 7
C
C
â
â
u
u
2
2
3
3
.
.
Cho parabol
2
( ) : 4P y x
, (P) tiếp xúc với đường thẳng
8 9 5 0
x y m
tại điểm có hoành độ thuộc
khoảng
A.
1
0;
2
B.
1 5
;
2 6
C.
5 4
;
6 3
D.
4
;2
3
C
C
â
â
u
u
2
2
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
(
(
P
P
)
)
:
:
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
x
x
é
é
t
t
b
b
a
a
đ
đ
i
i
ể
ể
m
m
, ,A B C
thuộc (P) có tung độ lần lượt là
4; 6;8
.
Trọng tâm tam giác ABC có hoành độ bằng
A
A
.
.
29
3
B
B
.
.
25
6
C
C
.
.
14
3
D
D
.
.
40
9
C
C
â
â
u
u
2
2
5
5
.
.
Đường parbol
2
( ) : 4P y x
cắt đường thẳng
2 4
x y
tại hai điểm phân biệt M, N. Độ dài đoạn thẳng
MN bằng
A.4 B.
3 5
C.
6 3
D.
4 7
C
C
â
â
u
u
2
2
6
6
.
.
Đường conic parabol
2
( ) : 4P y x
tiếp xúc đường thẳng
:12 6 0
d x y m
tại điểm M, M có tổng tung
độ và hoành độ bằng
A.2 B. 1 C. 3 D. 2,5
C
C
â
â
u
u
2
2
7
7
.
.
Parabol nào sau đây nhận tiêu điểm là điểm chung của hai đường tròn
2 2 2 2
2 4 3; 8 8 7 0
x y x y x y x y
A.
2
6y x
B.
2
3y x
C.
2
12y x
D.
2
4y x
_________________________________
51
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P1)
_____________________________________
Câu 1. Trong mặt phẳng tọa độ
Oxy
, Elip có tổng độ dài hai trục bằng
18
và tỉ số của tiêu cự với độ dài trục
lớn bằng
3
5
. Phương trình chính tắc của elip là:
A.
2 2
1
25 16
x y
B.
2 2
1
5 4
x y
C.
2 2
1
25 9
x y
D.
2 2
1
9 4
x y
Câu 2. Điểm
( ; )M x y
thuộc elip
2 2
( ) : 4 4
E x y
sao cho
3x y
nhỏ nhất. Tính
xy
.
A.0,2 B. – 0,5 C. – 0,8 D. – 0,6
Câu 3. Elip
2 2
( ) : 1
16 9
x y
E
cắt đường thẳng
3 4 12
x y
tại hai điểm phân biệt A, B. Độ dài đoạn thẳng AB
bằng
A.5 B. 4,9 C. 5,2 D. 4,8
Câu 4. Hai số thực
,x y
thỏa mãn
2 2 2 2
( 3) ( 3) 8
x y x y
. Tổng giá trị lớn nhất, giá trị nhỏ nhất của
biểu thức
2 2
x y
bằng
A.23 B. 24 C. 20 D. 26
C
C
â
â
u
u
5
5
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
( ) :
P y x
. Một góc vuông ở đinh
O cắt parabol tại
1 2
,A A
. Dựng các hình chiếu như hình vẽ,
đường thẳng
1 2
A A
luôn đi qua điểm I cố định có tung độ bằng
A
A
.
.
2
2
B
B
.
.
2
2
,
,
5
5
C
C
.
.
1
1
D
D
.
.
3
3
Câu 6. Tồn tại hai điểm
( ; )M x y
trên đường thẳng
2 4 0
x y
để từ M kẻ được đúng một tiếp tuyến đến
parabol
2
( ) : 4P y x
. Tổng tung độ hai điểm M bằng
A.3 B. 2 C. 1 D.
Câu 7. Elip
2 2
( ) : 1
9 1
x y
E
cắt đồ thị hàm số bậc hai
2
2y x x
tại bốn điểm phân biệt, đường tròn đi qua bốn
điểm này có tâm
( ; )I a b
. Tính
:a b
.
A.2 B. 1 C. 4 D. 3
Câu 8. Điểm M thuộc parabol
2
( ) : 64P y x
sao cho khoảng cách từ M đến đường thẳng
4 3 46 0
x y
đạt
giá trị nhỏ nhất. Khoảng cách OM gần nhất với
A.25,58 B. 25,63 C. 27,43 D. 26,14
Câu 9. Điểm M thuộc elip
2 2
( ) : 1
100 25
x y
E
sao cho
1 2
120
F MF
(
1 2
F F
là tiêu cự). Độ dài đoạn thẳng OM gần
nhất giá trị nào
A.5,11 B. 4,92 C. 4,87 D. 5,25
C
C
â
â
u
u
1
1
0
0
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
l
l
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
.
.
T
T
ì
ì
m
m
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
đ
đ
i
i
ể
ể
m
m
M
M
n
n
ế
ế
u
u
5 3
2 3 . 2256
MH MF MH MF
.
A
A
.
.
1
1
,
,
8
8
B
B
.
.
4
4
C
C
.
.
3
3
D
D
.
.
1
1
,
,
6
6
Câu 11. Trong mặt phẳng tọa độ
Oxy
lập phương trình chính tắc của elip
E
biết nó có một đỉnh và hai tiêu
điểm tạo thành một tam giác đều và chu vi của hình chữ nhật cơ sở của
E
là
12 2 3
.
52
A.
2 2
1
36 27
x y
. B.
2 2
1
36 3
x y
. C.
2 2
1
27 9
x y
. D.
2 2
1
27 36
x y
Câu 12. Cho elip
2 2
( ) : 1
25 16
x y
E
có tiêu cự
1 2
F F
, điểm M thuộc elip sao cho
1 2
2
MF MF
. Điểm M thuộc
đường tròn tâm O có bình phương bán kính bằng
A.20 B.
169
9
C.
100
9
D.
122
9
Câu 13. Trong mặt phẳng tọa độ
Oxy
, cho elip
E
:
2 2
1
9 4
x y
. Từ điểm
A
có tọa độ dương thuộc
E
ta
dựng hình chữ nhật
ABCD
nội tiếp trong
E
có các cạnh song song với các trục tọa độ và diện tích của hình
chữ nhật
ABCD
là lớn nhất. Tìm tọa độ đỉnh
A
.
A.
3 2
; 2
2
A
B.
3;0
A
C.
3;2
A
D.
3 2
; 2
2
A
.
Câu 14. Cho hypebol
H
có hai tiêu điểm
1 2
;F F
nằm trên
Ox
và đối xứng qua gốc tọa độ
O
,
H
đi qua
điểm
M
có hoành độ
5
và
1 2
9 41
;
4 4
MF MF
. Phương trình chính tắc của hypebol
H
là:
A.
2 2
1
9 16
x y
. B.
2 2
1
16 9
x y
. C.
2 2
1
25 16
x y
. D.
2 2
1
25 9
x y
.
Câu 15. Cho hai điểm
(4; 3), (3; 4)
A B
, Điểm
( ; )M x y
thuộc elip
2 2
( ) : 4 4
E x y
sao cho tam giác MAB có
diện tích lớn nhất. Tính
xy
.
A.1 B.
12
13
C.
7
13
D.
3
14
Câu 16. Trong mặt phẳng tọa độ
Oxy
, cho Elip
2 2
: 1
169 144
x y
E
và điểm
M
nằm trên
.E
Tìm tọa độ điểm
M
trên
E
biết rằng bán kính qua tiêu điểm trái gấp hai lần bán kính qua tiêu điểm phải.
A.
169 8 14
;
15 5
và
169 8 14
;
15 5
. B.
169 8 14
;
15 5
và
169 8 14
;
15 5
.
C.
169 8 14
;
15 5
và
169 8 14
;
15 5
. D.
169 8 14
;
15 5
và
169 8 14
;
15 5
.
Câu 17. Parabol
2
2
x
y
chia hình tròn tâm O, bán kính
2 2
R
thành
hai phần có diện tích S và S’ như hình vẽ. Tỉ số
:S S
thuộc khoảng nào ?
A.
2 1
;
5 2
B.
1 3
;
2 5
C.
3 7
;
5 10
D.
7 4
;
10 5
C
C
â
â
u
u
1
1
8
8
.
.
Điểm
( ; )M x y
parabol
2
( ) : 16P y x
đồng thời nằm trong góc phần tư thứ nhất của mặt phẳng tọa độ,
tìm giá trị nhỏ nhất của biểu thức
12 2045
T x x y
.
A.1917 B. 1945 C. 1979 D. 1954
Câu 19. Trong mặt phẳng tọa độ Oxy, cho hình thoi ABCD có A nằm trên trục hoành, AC = 2BD và đường tròn
tiếp xúc với các cạnh hình thoi có phương trình
2 2
4
x y
. Viết phương trình chính tắc của elip (E) đi qua các
đỉnh của hình thoi.
A.
2 2
1
20 5
x y
B.
2 2
1
25 9
x y
C.
2 2
1
64 25
x y
D.
2 2
1
8 4
x y
_________________________________
53
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P2)
_____________________________________
Câu 1. Elip
2 2
2 2
( ) : 1
x y
E
a b
đi qua điểm
(3;0)
M
và thỏa mãn
1 2
2 7
MF MF
(
1 2
F F
là tiêu cự,
2
F
nằm bên phải
trục tung). Tiêu cự của elip bằng
A.6 B. 4 C. 8 D. 10
Câu 2. Đường thẳng d đi qua tiêu điểm parabol
2
( ) : 4P y x
cắt parabol tại hai điểm phân biệt A, B. Tích
khoảng cách từ A, B đến trục hoành là một số không đổi và bằng
A.3 B. 4 C. 6 D. 8
C
C
â
â
u
u
3
3
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
c
c
ó
ó
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ơ
ơ
s
s
ở
ở
m
m
ô
ô
t
t
ả
ả
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
B
B
i
i
ế
ế
t
t
h
h
ì
ì
n
n
h
h
c
c
h
h
ữ
ữ
n
n
h
h
ậ
ậ
t
t
c
c
ó
ó
d
d
i
i
ệ
ệ
n
n
t
t
í
í
c
c
h
h
b
b
ằ
ằ
n
n
g
g 32.
Tìm giá trị nhỏ nhất của biểu thức
9a b
.
A
A
.
.
8 3
B
B
.
.
4 5
C
C
.
.
12 2
D
D
.
.
1
1
5
5
Câu 4. Elip (E) có tiêu điểm với tiêu điểm của hypebol
2 2
9 16 144
x y
và ngoại tiếp hình chữ nhật cơ sở của
(H). tiêu cự của elip bằng
A.
2 55
B.
8 5
C.
10 2
F. 10
Câu 5. Viết phương trình chính tắc của hypebol
H
biết rằng
H
đi qua các điểm
4; 0
M
và
20
; 4
3
N
.
A.
2 2
1
9 16
x y
. B.
2 2
1
16 9
x y
. C.
2 2
1
16 9
x y
. D.
2 2
1
16 25
x y
.
Câu 6. Cho parabol
2
( ) : 4P y x
và hai điểm
(0; 4), ( 6;4)
A B
.
C
là điểm trên
( )P
sao cho tam giác
ABC
có
diện tích bé nhất. Điểm
C
nằm trên đường thẳng nào sau đây?
A.
16 2 6 0
x y
. B.
16 2 6 0
x y
.
C.
16 2 6 0
x y
. D.
16 2 6 0
x y
.
Câu 7. Hai số thực
,x y
thỏa mãn
2 2 2 2
( 1) ( 1) ( 1) ( 3) 6 5
x y x y
. Giá trị lớn nhất của biểu thức
2 2
( 2) ( 3)
x y
bằng
A.125 B. 240 C. 100 D. 120
Câu 8. Điểm
( ; )M x y
nằm trên hypebol (H):
2
2
1
4
x
y
sao cho khoảng cách từ M đến đường thẳng
: 1y x
đạt giá trị nhỏ nhất. Khi đó
A.
4
3
xy
B.
8
3
xy
C.
2
3
xy
D.
7
3
xy
Câu 9. Các hành tinh và các sao chổi khi chuyển động xung quanh mặt trời có quỹ đạo là một đường elip trong
đó tâm mặt trời là một tiêu điểm. Điểm gần mặt trời nhất gọi là điểm cận nhật, điểm xa mặt trời nhất gọi là điểm
viễn nhật. Trái đất chuyển động xung quanh mặt trời theo quỹ đạo là một đường elip có độ dài nửa trục lớn
bằng
93.000.000
dặm. Tỉ số khoảng cách giữa điểm cận nhật và điểm viễn nhật đến mặt trời là
59
61
.
Khoảng cách từ tâm trái đất đến tâm mặt trời khi trái đất ở điểm cận nhật bằng
A.
91.450.000
dặm. B.
91.455.000
dặm. C.
91.000.000
dặm. D.
91.550.000
dặm.
54
Câu 10. Hai thiết bị
A
và
B
dùng để ghi âm một vụ nổ đặt cách nhau
1
dặm, thiết bị
A
ghi được âm thanh
trước thiết bị
B
là 2 giây, biết vận tốc âm thanh là
1100 /feet s
. Tìm các vị trí mà vụ nổ có thể xảy ra ( 1 dặm
5280
feet; 3 feet
0,914m
) .
A.
2 2
1
5280 2200
x y
. B.
2 2
1
5280 2200
x y
.
C.
2 2
2 2
1
5280 1100
x y
. D.
2 2
1
1210000 5759600
x y
.
Câu 11. Điểm M thuộc cung
AB
của đường conic parabol
2
( ) :
P y x
với
(1;1), (2; 2)
A B
. Diện tích lớn nhất
của tam giác MAB khi đó bằng
A.3,25 B. 3,375 C. 3,75 D. 3,425
Câu 12. Trong mặt phẳng
Oxy
cho parabol
2
: 8P y x
. Đường thẳng
Δ
không trùng với trục
Ox
đi qua tiêu
điểm
F
của
P
sao cho góc hợp bởi hai tia
Fx
và
Ft
là tia của
Δ
nằm phía trên trục hoành một góc bằng
0
90
α α
. Biết
Δ
cắt
P
tại hai điểm phân biệt
,M N
và tập hợp trung điểm
I
của đoạn
MN
khi
α
thay
đổi là một Parabol. Phương trình của Parabol là
A.
2
4 8y x
. B.
2
4 4
y x
. C.
2
4 8y x
. D.
2
4 4
y x
.
C
C
â
â
u
u
1
1
3
3
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
i
i
ể
ể
m
m
M
M
t
t
h
h
u
u
ộ
ộ
c
c
n
n
h
h
á
á
n
n
h
h
p
p
h
h
ả
ả
i
i
h
h
y
y
p
p
e
e
b
b
o
o
l
l
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
1 2
6
MF MF
Tìm giá trị lớn nhất của
1 2
(12 )MF MF
.
A
A
.
.
2
2
4
4
B
B
.
.
3
3
0
0
C
C
.
.
3
3
6
6
D
D
.
.
2
2
8
8
Câu 14. Parabol
2
4y x
cắt đường thẳng
0
x y m
tại hai điểm phân biệt A, B sao cho tam giác OAB
vuông tại O, tổng các giá trị m thu được bằng
A.0,8 B. 0,6 C. 0,5 D. 0,7
Câu 15. Điểm M nằm trên hypebol
2 2
( ) : 1
16 9
x y
H
và nhìn hai tiêu điểm dưới một góc vuông. Độ dài đoạn
thẳng OM khi đó bằng
A.4 B. 5 C. 6 D. Kết quả khác
Câu 16. Ông X có một mảnh vườn hình vuông cạnh bằng 8m. Ông dự định
xây một cái bể bơi đặc biệt như hình vẽ bên. Biết AB = 4AM, phần đường
cong đi qua các điểm C, M, N là một phần của đường parabol có trục đối
xứng là MP. Biết kinh phí để làm bể bơi là 5 triệu đồng mỗi mét vuông. Chi
phí ông A phải trả để hoàn thành bể gần nhất với con số nào sau đây ?
A. 95814000 đồng B. 908140000 đồng
C. 94814000 đồng D. 93814000 đồng
Câu 17. Đường thẳng
3 4 12 0
x y
cắt elip
2 2
( ) : 1
16 9
x y
E
tại hai điểm phân biệt A, B. Điểm C thuộc elip
sao cho tam giác ABC có diện tích bằng 6. Bình phương độ dài đoạn thẳng OC khi đó bằng
A.12,5 B. 13,5 C. 14 D. 16,5
Câu 18. Điểm
( ; )M x y
thuộc elip
2 2
( ) : 1
8 2
x y
E
sao cho
2 2
( 2) 4( 3)
M x x
đạt giá trị lớn nhất. Tính giá trị
của biểu thức
2 2
2 3 4x y xy
.
A.11,8 B. 12,5 C. 14,5 D. 16,5
_________________________________
55
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P3)
_____________________________________
Câu 1. Trên mặt phẳng, cho tam giác
ABC
có
2; 2
A
,
2;2
B
,
6;2
C
. Biết tập hợp tất cả các điểm
M
thỏa mãn hệ thức
12
MA MB MA MC
là một elip. Độ dài trục lớn và trục bé của elip là
A.
6
. B.
3 5
. C.
2 3
. D.
6
.
Câu 2. Parabol (P) có tiêu điểm F (3;0), qua điểm
(2;0)
I
kẻ đường thẳng d cắt parabol tại hai điểm phân biệt A,
B, khi đó tích khoảng cách từ A, B đến trục hoành bằng
A.24 B. 25 C. 30 D. 18
C
C
â
â
u
u
3
3
.
.
Điểm
( ; )M x y
parabol
2
( ) : 16P y x
đồng thời nằm trong góc phần tư thứ nhất của mặt phẳng tọa độ,
tìm giá trị nhỏ nhất của biểu thức
1958
T x y
.
A.1789 B. 1945 C. 1979 D. 1954
Câu 4. Trong mặt phẳng với hệ toạ độ Oxy, cho parabol
2
( ) :
P y x
và điểm
A
(5; 0)
. Gọi
M
có tung độ dương
là một điểm trên
P
để đoạn
AM
ngắn nhất. Khi đó
AM
bằng
A.
19
2
. B.
19
2
. C.
9
2
. D.
3 2
2
.
Câu 5. Trong mặt phẳng tọa độ Oxy, tìm diện tích hình tròn tạo bởi đường tròn đi qua bốn giao điểm của elip
2 2
1
9 4
x y
và hypebol
2 2
1
1 4
x y
A.
5
B.
4
C.
8
D.
9
C
C
â
â
u
u
6
6
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
l
l
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
.
.
T
T
ì
ì
m
m
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
đ
đ
i
i
ể
ể
m
m
M
M
n
n
ế
ế
u
u
3
2 7 48,75
MH MF
.
A
A
.
.
1
1
,
,
8
8
B
B
.
.
1
1
,
,
4
4
C
C
.
.
1
1
,
,
5
5
D
D
.
.
1
1
,
,
6
6
Câu 7. Cho
M
là một điểm thuộc Parabol
2
( ) : 64P y x
và
N
là một điểm thuộc đường thẳng
: 4 3 46 0
d x y
. Xác định
,M N
để đoạn
MN
ngắn nhất. Tổng hoành độ hai điểm M và N bằng
A.16,4 B. – 4 C. 4 D. – 16,4
Câu 8. Hai số thực
,x y
thỏa mãn
2 2 2 2
( 2) ( 2) 6
x y x y
. Tổng giá trị lớn nhất, giá trị nhỏ nhất của
biểu thức
2 2
( 1) ( 3)
x y
gần nhất với số nào
A.6,32 B. 7,12 C.5,28 D. 6,24
Câu 9. Cho một cái đèn với chụp bóng đèn có mặt cắt qua trục là parabol với kích thước được thể hiện trên
hình vẽ, giả sử xem dây tóc bóng đèn là một điểm và được đặt ở vị trí tiêu điểm của parabol. Tính khoảng cách
từ dây tóc bóng đèn tới đỉnh của chụp bóng đèn.
A.
45
cm
8
. B.
45
cm
16
. C.
45
cm
4
. D.
45
cm
2
.
Câu 10. Elip (E) có các tiêu điểm là các tiêu điểm của (H):
2 2
1
64 36
x y
và các đỉnh của hình chữ nhật cơ sở của
(H) đều nằm trên elip. Tiêu cực của elip bằng
56
A.20 B. 30 C. 26 D. 24
Câu 11. Vệ tinh nhân tạo đầu tiên được Liên Xô (cũ) phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là
một đường elip nhận tâm Trái Đất là một tiêu điểm có phương trình quỹ đạo là
2 2
2 2 2
2 2
1, 0, 0,
x y
a b c a b
a b
. Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là
583
dặm và xa
nhất là
1342
dặm (1 dặm xấp xỉ
1,609
km). Tìm tỷ số
c
a
, biết bán kính của Trái Đất xấp xỉ
4000
dặm.
A.
0,67
c
a
. B.
0,76
c
a
. C.
0,067
c
a
. D.
0,076
c
a
.
C
C
â
â
u
u
1
1
2
2
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
( ) :
P y x
. Một góc vuông ở đinh
O cắt parabol tại
1 2
,A A
. Dựng các hình chiếu như hình vẽ, tính
1 2
.OB OB
.
A
A
.
.
2
2
B
B
.
.
2
2
,
,
5
5
C
C
.
.
1
1
D
D
.
.
3
3
Câu 13. Từ một điểm M thuộc hypebol
2 2
1
9 16
x y
kẻ các đường thẳng song song với các tiệm cận, ta thu được
hình bình hành OMPQ, diện tích hình bình hành OMPQ bằng bao nhiêu đơn vị diện tích
A.5 B. 6 C. 4 D. 8
Câu 14. Hai số thực
,x y
thỏa mãn
2 2 2 2
( 1) ( 3) ( 2) ( 1) 8
x y x y
. Tổng giá trị lớn nhất, giá trị nhỏ
nhất của biểu thức
2
2
1
1
2
x y
bằng
A.26 B. 25,75 C. 27,25 D. 16,5
Câu 15. Tìm điều kiện của điểm
( ; )M x y
trên đường thẳng
2 4 0
x y
để từ M không kẻ được tiếp tuyến nào
đến parabol
2
( ) : 4P y x
.
A.
1 4
x
B.
0 4
x
C.
1 2
x
D.
2 4
x
Câu 16. Trên bờ biển có hai trạm thu phát tín hiệu
A
và
B
cách nhau
6km
, người ta xây một cảng biển cho
tàu hàng neo đậu là một nửa hình elip nhận AB làm trục lớn và có tiêu cự bằng
2 5 km
. Một con tàu hàng M
nhận tín hiệu đi vào cảng biển sao cho hiệu khoảng cách từ nó đến
A
và
B
luôn là
2 6 km
. Khi neo đậu tại
cảng thì khoảng cách từ con tàu đến bờ biển là bao nhiêu?
A.
126
17
km
. B.
12
17
km
. C.
12
17
km
. D.
126
17
km
.
Câu 17. Hình chữ nhật ABCD nội tiếp elip
2 2
( ) : 1
25 9
x y
E
, có các cạnh song song với các trục tọa độ và có
diện tích lớn nhất, các đỉnh của hình chữ nhật thuộc đường tròn có bình phương bán kính bằng
A.3 B. 2 C. 4 D. 17
Câu 18. Cho elip
2 2
( ) :9 25 225
E x y
. Tồn tại bao nhiêu điểm M thuộc elip thỏa mãn đẳng thức
1 2 1 2
1 1 8
MF MF F F
A. 3 B. 2 C. 4 D. 1
_________________________________
57
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P4)
_____________________________________
Câu 1. Ký hiệu M (x;y) là một điểm thuộc elip
2 2
1
9 4
x y
. Tìm giá trị lớn nhất của biểu thức Q = x + 2y.
A. 4 B.
13
C.
19
D.
11
Câu 2. Cho hypebol
2 2
2 2
1
9 4 16
ax y
a b b
với
0
a
. Độ dài ngắn nhất của tiêu cự hypebol đã cho bằng
A.8 B. 10 C. 12 D. 14
C
C
â
â
u
u
3
3
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
l
l
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
.
.
T
T
ì
ì
m
m
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
đ
đ
i
i
ể
ể
m
m
M
M
n
n
ế
ế
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
b
b
i
i
ể
ể
u
u
t
t
h
h
ứ
ứ
c
c
2
. 12 2023
MH MF MF
đạt giá trị nhỏ nhất.
A
A
.
.
2
2
B
B
.
.
2
2
,
,
4
4
C
C
.
.
1
1
D
D
.
.
1
1
,
,
6
6
Câu 4. Cho hai đường tròn
2 2 2 2
1 2
: 4; : 1
C x y C x y
. Các điểm A, B di động lần lượt trên
1 2
,
C C
sao cho Ox là phân giác của góc
AOB
. Tìm quỹ tích trung điểm M của đoạn thẳng AB.
A. Elip
2
2
4
4 1
9
x
y
B. Elip
2 2
1
25 4
x y
C. Elip
2 2
1
9 4
x y
D. Đường thẳng 2x – 3y + 1 = 0.
Câu 5. Đường thẳng
d
đi qua
(1;1)
I
và cắt elip
2 2
( ) : 1
25 9
x y
E
tại hai điểm phân biệt M, N sao cho I là trung
điểm của đoạn thẳng MN. Hệ số góc của đường thẳng đó bằng
A.
9
25
B.
3
11
C.
2
7
D. 14
Câu 6. Một sân chơi dành cho trẻ em hình chữ nhật có chiều dài
50m và chiều rộng là 30m, người ta làm một con đường nằm
trong sân như hình vẽ. Biết viền ngoài và viền trong của con
đường là hai đường elip và chiều rộng của mặt đường là 3m. Kinh
phí để làm mỗi m
2
đường là 500 nghìn đồng. Tính tổng số tiền
làm con đường đó (làm tròn đến hàng nghìn).
A. 119000000 đồng B. 152000000 đồng C. 119320000 đồng D. 125520000 đồng
Câu 7. Cho elip
2 2
1
25 16
x y
với hai tiêu điểm
1 2
,F F
. Lấy hai điểm A, B thuộc elip (E) sao cho
1 2
AF BF t
. Khi
đó giá trị lớn nhất của biểu thức
1 2 2 1
( )( )AF BF AF BF
bằng
A.90 B. 100 C. 80 D. 96
Câu 8. Hypebol
2 2
( ) : 1
25 16
x y
H
có hai tiêu điểm
1 2
,F F
. Điểm M bất kỳ thuộc hypebol. Tính
2 2
1 2
( ) 4
MF MF OM
A.9 B. 64 C. 16 D. 25
Câu 8.
H
H
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
có độ dài trục thực bằng 6 và phương trình một đường tiệm cận là
5 3x y
. Tính
2 2
a b
.
58
A.40 B. 32 C. 36 D. 24
C
C
â
â
u
u
9
9
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
i
i
ể
ể
m
m
M
M
t
t
h
h
u
u
ộ
ộ
c
c
n
n
h
h
á
á
n
n
h
h
p
p
h
h
ả
ả
i
i
h
h
y
y
p
p
e
e
b
b
o
o
l
l
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
2 3
1 2 1 2
6; 2 136
MF MF MF MF
Tính
1 2
3
MF MF
.
A
A
.
.
1
1
2
2
B
B
.
.
3
3
0
0
C
C
.
.
1
1
4
4
D
D
.
.
1
1
8
8
Câu 10. Đường tròn (C) có bán kính nhỏ nhất tiếp xúc với parabol
2
( ) : 64P y x
và đường thẳng
4 3 46 0
x y
. Tiếp điểm với parabol là điểm M, độ dài đoạn thẳng OM bằng
A.
3 73
B.
8 13
C.
10 17
D.
12 26
Câu 11. Điểm
( ; )M x y
thuộc parabol
2
( ) : 4P y x
.Tìmgiátrịnhỏnhấtcủabiểuthức
2
2
1
3 2023
M xy x
y
.
A.2020 B.2021 C.2023 D.2019
Câu 12. Với M là điểm bất kỳ trên elip
2 2
2 2
( ) : 1
x y
E
a b
, F là tiêu điểm phải của elip. Tính
2
1 1
b
a FM FN
A. 3 B. 2 C. 4 D. 1
Câu 13. Một tháp làm nguội của một nhà máy có mặt cắt là hình
hyperbol có tiêu cự bằng
2 70 m
, độ dài trục ảo bằng
2 42 m
. Biết
chiều cao của tháp là
120m
và khoảng cách từ nóc tháp đến tâm đối
xứng của hypebol là
2
3
khoảng cách từ tâm đối xứng đến đáy. Bán
kính nóc và bán kính đáy của tháp lần lượt là
A.
391m
;
2 871m
. C.
2 391m
;
871m
.
B.
2 391m
;
2 871m
. D.
391m
;
871m
.
Câu 14.
H
H
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
đi qua điểm
(6;3)
M
và góc giữa hai tiệm cận bằng
60
. Khi đó
2 2
2
a b
có thể
bằng
A.14 B. 12 C. 10 D. 15
Câu 15. Trên hypebol
2 2
( ) : 3 4 12
H x y
tồn tại hai điểm P, Q sao cho tam giác OPQ đều, P và Q đều thuộc
đường tròn tâm O có bình phương bán kính bằng
A.8,4 B. 9,6 C. 9 D. 9,2
Câu 16. Trên hypebol
2 2
( ) : 1
16 9
x y
H
có điểm M nhìn hai tiêu điểm dưới một góc 60 độ. Điểm M đó thuộc
đường tròn tâm O có bình phương bán kính bằng
A.36 B. 43 C. 52 D. 48
Câu 17. Đường thẳng
3 4 12 0
x y
cắt elip
2 2
( ) : 1
16 9
x y
E
tại hai điểm phân biệt A, B. Điểm C thuộc elip
sao cho tam giác ABC có diện tích lớn nhất. Bình phương độ dài đoạn thẳng OC khi đó bằng
A.12,5 B. 13,5 C. 14 D. 16,5
Câu 18. Một đường thẳng d qua tiêu điểm F của parabol
2
( ) : 16P y x
và cắt parabol tại hai điểm M, N. Đường
thẳng MN tiếp xúc với đường thẳng nào sau đây
A.
4
x
B.
2
x
C.
0
x
D.
1
x
_________________________________________
59
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P5)
_____________________________________
Câu 1. Trong mặt phẳng tọa độ Oxy, đường cong
2 2
( ) : 5 3 10 12 22 0
H x y x y
được chứng minh là một
đường hypebol, nó có thể đưa về dạng chính tắc trong hệ tọa độ
IXY
trong đó
1
1
x X
y Y
. Tiêu cự hypebol đó
là
A.6 B.
4 2
C.
6 2
D.
8 3
Câu 2. Đường thẳng d (cắt hai trục tọa độ) đi qua điểm
(1;4)
A
và tiếp xúc với hypebol
2 2
( ) : 1
1 4
x y
H
. Đường
thẳng d có hệ số góc gần nhất với
A.2 B. 2,6 C. 2,7 D. 2,8
C
C
â
â
u
u
3
3
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
e
e
l
l
i
i
p
p
2 2
( ) : 1
24 12
x y
E
nội tiếp hình vuông nào ABCD
như hình vẽ. Diện tích hình vuông đó gần nhất với
A
A
.
.
7
7
2
2
B
B
.
.
8
8
0
0
C
C
.
.
7
7
0
0
D
D
.
.
6
6
8
8
Câu 4. Tam giác ABC có A (3;– 2), B (– 3;2), đỉnh C có hoành độ dương và C nằm trên elip
2 2
1
9 4
x y
. Biết
rằng tam giác ABC có diện tích đạt giá trị lớn nhất, khi đó tung độ điểm C là
A. 2 B.
3
C.
2
D.
2
2
Câu 5. Elip
2 2
( ) : 1
25 9
x y
E
cắt đường thẳng
4 5 0
x y m
tại hai điểm phân biệt A, B thì tập hợp trung điểm I
của đoạn thẳng AB là đường thẳng có hệ số góc
k
và hoành độ điểm I thỏa mãn
l x l
. Tính
36kl
.
A.64,8 B. 52,8 C. 70,5 D. 69,6
Câu 6. Elip
2 2
( ) : 1
9 4
x y
E
có tiêu cự
1 2
F F
,
1
F
là tiêu điểm trái điểm M chạy trên elip, phân giác trong của góc
1 2
F MF
cắt trục hoành tại N, H là hình chiếu vuông góc của N trên đoạn
1
MF
. Tính độ dài đoạn MH.
A.3 B.
4
3
C.
5
3
D.
7
6
Câu 7. Trong mặt phẳng tọa độ Oxy, đường cong
2 2
( ) :3 4 6 16 7 0
E x y x y
được chứng minh là một
đường elip, nó có thể đưa về dạng chính tắc trong hệ tọa độ
IXY
trong đó
1
1
x X
y Y
. Tiêu cự của elip đó là
A.6 B.
4 2
C.
6 2
D. 2
C
C
â
â
u
u
8
8
.
.
Cho parabol
2
( ) : 2P y px
, A là điểm trên tia Ox, đường
thẳng qua A vuông góc với tia Ox cắt parabol tại D, gọi B, C là hai
điểm thuộc bánh chứa D của parabol (P) sao cho
DAB DAC
và
2
4 3 .AD AB AC
, số đo góc
BAC
khi đó bằng bao nhiêu độ
A.30 B. 60
C. 45 D. 70
Câu 9. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho elip
2 2
: 1
16 9
x y
E
và đường thẳng
:3 4 12 0
d x y
.
Biết rằng
d
luôn cắt
E
tại hai điểm phân biệt
A
,
B
. Tính độ dài đoạn
AB
.
60
A.
5
AB
. B.
3
AB
. C.
4AB
. D.
10
AB
.
Câu 10. Trong hệ tọa độ Oxy cho điểm C (3;0) và elip
2 2
: 1
9 1
x y
E
. Hai điểm A, B là hai điểm thuộc elip
sao cho tam giác ABC đều. Tính a + c biết rằng
3
;
2 2
a c
A
với
0a
.
A. 2 B. 0 C. – 2 D. – 4
Câu 11. Đường conic parabol
2
( ) : 8P y x
tiếp xúc với đường thẳng
:8 8 0
d x y m n
. Giá trị nhỏ nhất của
biểu thức
2
4 2023
Q n m
gần nhất với số nào
A.1992 B. 1954 C. 1975 D. 2022
C
C
â
â
u
u
1
1
2
2
.
.
Một người kỹ sư thiết kế một đường hầm một chiều có mặt
cắt là một nửa hình elip, chiều rộng của hầm là
12
mét, khoảng
cách từ điểm cao nhất của elip so với mặt đường là
3
mét. Người kĩ
sư này phải đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Một
chiếc xe có chiều rộng bằng
3
mét thì chiều cao lớn nhất có thể đi
qua hầm thuộc khoảng nào sau đây
A.
2,4;2,6
. B.
2,8;3,00
.
C.
3,00;3,20
. D.
2,6;2,8
.
Câu 13. Trong hệ trục tọa độ Oxy, đường cong
1
2
x
y
x
được chứng minh là một hypebol, điểm M thuộc
hypebol thì có tổng khoảng cách đến hai đường thẳng
2; 1x y
đạt giá trị nhỏ nhất bằng
A.2 B.
2 3
C. 4 D.
4 2
Câu 14. Cho hai số
,x y
thỏa mãn
2 2 2 2
( 1) ( 3) 6
x y x y
. Khi đó biểu thức
2 2
( 1) ( 4)
x y
nhận
giá trị nhỏ nhất bằng
A.6 B. 3 C. 4 D. 5
Câu 15. Điểm M thuộc hypebol
2 2
( ) : 1
9 16
x y
H
sao khoảng cách từ M đến tiêu điểm phải nhỏ nhất, tổng tung
độ và hoành độ của M bằng
A.3 B. – 3 C. 0,75 D. 0,75
Câu 16. Cho elip
2 2
( ) : 1
25 9
x y
E
và hai điểm A (– 5;3), B (5;– 3). Tồn tại điểm C (x;y) trên elip sao cho tam
giác ABC có diện tích lớn nhất. Giá trị
2 2
x y
bằng
A. 16 B. 17 C. 20 D. 12
Câu 17. Elip tiếp xúc đồng thời với hai đường thẳng
5 0; 4 10 0
x y x y
thì có tiêu cự bằng
A.8 B.
2 15
C.
4 2
D.
6 2
Câu 18. Cho parabol
2
( ) :
P y x
. Hai điểm A, B di động trên (P) sao cho AB = 2. Gọi S là diện tích hình phẳng
giới hạn bởi parabol (P) và đoạn thẳng AB. Tính diện tích lớn nhất của S.
A.
4
max
3
S
B.
7
max
6
S
C.
5
max
6
S
D.
5
max
3
S
Câu 19. Các điểm M, N chuyển động trên hai tia
,Ox Oy
sao cho đoạn thẳng MN luôn tiếp xúc với đường elip
2 2
( ) : 1
16 9
x y
E
. Giá trị nhỏ nhất của đoạn thẳng MN bằng
A.7 B.6,5 C.7,2 D.6,8
_________________________________
61
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P6)
_____________________________________
Câu 1. Elip
2 2
( ) : 1
4 3
x y
E
có tiêu cự
1 2
F F
, (
2
F
có là tiêu điểm phải), điểm M thuộc elip sao cho
2 2
1 2
7
MF MF
đạt giá trị nhỏ nhất. Tổng tung độ và hoành độ điểm M khi đó bằng
A.3 B. 5 C. 4 D. 2
Câu 2. Để trang trí cho một lễ hội đầu xuân, từ một mảnh vườn
hình elip có chiều dài trục lớn là 10m, chiều dài trục nhỏ là 4m,
Ban tổ chức vẽ một đường tròn có đường kính bằng độ dài trục
nhỏ và có tâm trùng với tâm của elip như hình vẽ. Biết diện tích
hình elip có độ dài trục lớn, trục bé lần lượt là a, b được tính theo
cộng thức
S ab
.
Trên hình tròn người ta trồng hoa với giá 100000 đồng/m
2
, phần còn lại của mảnh vườn người ta trồng cỏ với
giá 60000 đồng/m2 (biết giá trồng hoa và trồng cỏ bao gồm cả công và cây). Hỏi ban tổ chức cần bao nhiêu
tiền để trồng hoa và cỏ (số tiền làm tròn đến hàng nghìn).
A. 2387000 đồng B. 2638000 đồng C. 2639000 đồng D. 2388000 đồng
Câu 3. Cho đường hypebol có một tiêu điểm
( 13;0)
F
và có độ dài trục thực là 6. Tìm điểm
M
thuộc
hypebol biết điểm
M
có tổng hoành độ và tung độ bằng
23
3
. Điểm M có thể có hoành độ bằng
A.22,6 B. 5,5 C. 4 D. 12,5
Câu 4. Điểm M nằm trên elip
2 2
( ) : 1
2013 2012
x y
E
(có tiêu cự
1 2
F F
,
2
F
có là tiêu điểm phải), tính
2
1 2
.
MF MF OM
.
A.2023 B. 4025 C. 2011 D. Kết quả khác
Câu 5. Điểm M nằm trên hypebol
2 2
9 9
x y
và nhìn hai tiêu điểm dưới một góc 60 độ. Điểm M luôn cách gốc
tọa độ một khoảng có bình phương bằng
A.27 B. 28 C. 40 D. 16
Câu 6. Trong hệ trục tọa độ Oxy, tập hợp các điểm
( ; )M x y
thỏa mãn
1
1
x
y
x
là một hypebol, tổng khoảng
cách từ M đến hai trục tọa độ đạt giá trị nhỏ nhất bằng
A.1 B.
2
C.
2 1
D.
3 1
Câu 7. Hình chữ nhật MNPQ nội tiếp elip
2 2
( ) : 1
25 9
x y
E
và có hai đường chéo hợp với nhau góc 60 độ. Điểm
M có thể cách gốc tọa độ một khoảng có bình phương bằng
A.17 B.
75
7
C.
80
7
D.
80
9
Câu 8. Trong hệ trục tọa độ Oxy, tập hợp các điểm
( ; )M x y
thỏa mãn
2 1
mx m
y
x m
là một hypebol, hypebol
này luôn tiếp xúc với một đường thẳng d cố định, khoảng cách từ gốc tọa độ O đến đường thẳng d bằng
A. 1 B.
2
C.
3
D. 0,5
Câu 9. Tam giác ABC vuông cân tại
(3;0)
A
và nội tiếp trong đường elip
2 2
( ) : 1
9 4
x y
E
. Tổng hoành độ và
tung độ điểm B có thể bằng
A.1 B.
9
13
C.
5
13
D.
2
11
Câu 10. Hai điểm A, B nằm trên đường elip
2 2
( ) :9 25 225
E x y
(có tiêu cự
1 2
F F
,
2
F
có là tiêu điểm phải), tứ
giác
1 2
F F BA
có tổng độ dài hai đường chéo bằng 6, chu vi nhỏ nhất của tứ giác bằng
A.49 B. 36 C. 43 D. 38
Câu 11. Đường tròn (C) có tâm thuộc đường thẳng
9 0
x y
, có bán kính nhỏ nhất và đồng thời tiếp xúc với
62
elip
2 2
( ) : 1
16 9
x y
E
. Tung độ tiếp điểm khi đó bằng
A.1 B. – 1,2 C. – 1,8 D. – 2
Câu 12. Điểm M thuộc parabol
2
( ) : 8P y x
và điểm N thuộc đường thẳng
3 0
x y
sao cho độ dài đoạn
thẳng MN ngắn nhất, tung độ điểm M khi đó bằng
A.4 B. – 4 C. – 3,5 D. 2,5
C
C
â
â
u
u
1
1
3
3
.
.
Cho hai điểm
( 2;0), (2;0)
A B
, điểm M chuyển động
sao cho
2MBA MAB
, khi đó M chạy trên một nhánh của
hypebol cố định, tiêu điểm phải của hypebol (sau khi sử
dụng phép đổi hệ trục tọa độ đưa về dạng chính tắc) đó có
hoành độ bằng
A.1 B.
8
3
C.
5
3
D.
7
9
Câu 14. Hai elip
2 2 2 2
1 2
2 2
( ) : 1;( ) : 1
10 6
x y x y
E E
a b
có tung tiêu điểm, elip
2
( )E
đi qua điểm M thuộc đường
thẳng
4 0
x y
đồng thời có độ dài trục lớn nhỏ nhất. Tung độ điểm M khi đó bằng
A.1 B. – 2 C. – 1,5 D. – 1,2
Câu 15. Đường cong (H) bao gồm các điểm
( ; )M x y
thỏa mãn
1xy
là một hypebol, điểm M thuộc hypebol sao
cho độ dài đoạn thẳng AM nhỏ nhất, với
5 5
;
2 2
A
. Giá trị nhỏ nhất ấy bằng
A.5 B.
17
2
C.
13
2
D.
21
2
Câu 16. Điểm M di động trên elip
2 2
( ) : 1
9 4
x y
E
, H và K là hình chiếu vuông góc của M trên hai trục tọa độ và
tứ giác OHMK có diện tích lớn nhất. Điểm M thuộc đường tròn tâm O có bình phương bán kính bằng
A.6,5 B. 5,5 C. 6 D. 7
C
C
â
â
u
u
1
1
7
7
.
.
Một chiếc cốc nằm ngang, có mặt cắt ngang là hình parabol
(hình vẽ). Hình parabol có chiều rộng giữa hai mép cốc là
9cm
AB
và chiều sâu
4cm
h
(
h
bằng khoảng cách từ
S
đến
AB
,
S
là
điểm chính giữa đáy cốc. Viết phương trình chính tắc parabol đó.
A.
2
81
32
y x
. B.
2
81
16
y x
. C.
2
9
4
y x
. D.
2
81
64
y x
Câu 18. Trong hệ trục tọa độ Oxy, tập hợp các điểm
( ; )M x y
thỏa mãn
3
2
x
y
x
là một hypebol, đường thẳng
d: y = 2x + 3m cắt đường hypebol
3
2
x
y
x
tại hai điểm phân biệt A, B thỏa mãn điều kiện
15
.
2
OA OB
 
. Khi đó
đường thẳng d đi qua điểm nào ?
A.
19
2;
2
B. (3;2) C.
1
3;
2
D.
11
3;
2
Câu 19. Điểm M thuộc hypebol
2 2
1
x y
sao cho khoảng cách từ điểm M đến đường thẳng
:5 3 1 0
d x y
đạt giá trị nhỏ nhất. Tung độ điểm M thuộc khoảng nào sau đây
A.
1
0;
3
B.
1 7
;
2 8
C.
1 1
;
3 2
D.
7
;1
8
_________________________________
63
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P7)
_____________________________________
Câu 1. Parabol
2
( ) : 2 ; 0
P y px p
có tiêu điểm là giao điểm của bốn đường tròn
2 2 2 2 2 2 2 2
( 4) ( 3) 18; ( 2) 9; ( 2) 1; ( 4) 9
x y x y x y x y
Đường tròn tiếp xúc đồng thời với parabol và đường thẳng
5y x
thì có bình phương bán kính bằng
A.4 B. 5 C. 2 D. 6
Câu 2. Trong mặt phẳng tọa độ Oxy, đường cong
2 2
( ) : 6 4 24 40 52 0
H x y x y
được chứng minh là một
đường hypebol, nó có thể đưa về dạng chính thức trong hệ tọa độ
IXY
trong đó
2
5
x X
y Y
. Tiêu cự hypebol
đó là
A.
2 10
B.
4 2
C.
6 2
D.
8 3
Câu 3. Có bao nhiêu số nguyên m để hệ phương trình
2 2 2 2
2 2
( 3) ( 4) ( 1) ( 2) 8
( 1) ( 1)
x y x y
x y m
có nghiệm
A.12 B. 14 C. 6 D. 15
Câu 4. Tam giác OAB cân tại O có hai đỉnh A, B thuộc elip
2 2
( ) : 1
4 1
x y
E
và có diện tích lớn nhất. Tính giá trị
của biểu thức
2 2
3
OA OB
.
A.6 B. 5 C. 4 D. 4,5
Câu 5. Cho elip
2 2
1
25 16
x y
, hai điểm A, B thay đổi thuộc elip sao cho
90
AOB
, H là chân đường cao kẻ từ
gốc tọa độ O xuống đoạn thẳng AB, H luôn thuộc đường tròn cố định có bán kính bằng
A.
20
41
B.
10
21
C.
5
11
D. 3,5
C
C
â
â
u
u
6
6
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
t
t
r
r
ò
ò
n
n
2 2
1
x y
cắt trục tung và trục hoành lần lượt tại
(0;1), (0; 1)
A B
. Một đường thẳng
y m
với
1 1; 0
m m
cắt đường
tròn tại T và S, đường thẳng TS cắt đường thẳng AB tại P, tập hợp điểm
P là hypebol có tiêu cự bằng
A
A
.
.
2
2
B
B
.
.
2
2
,
,
5
5
C
C
.
.
K
K
ế
ế
t
t
q
q
u
u
ả
ả
k
k
h
h
á
á
c
c
D
D
.
.
3
3
Câu 7. Cho điểm
(0; 2)
A
. Hai điểm B, C thuộc elip
2 2
( ) : 1
9 4
x y
E
sao cho tam giác ABC có diện tích bằng
9 3
2
. Hai điểm B, C cách gốc tọa độ một khoảng có bình phương bằng
A.5,5 B. 4 C. 6,5 D. 4,5
Câu 8. Hai số
,x y
thỏa mãn
2 2
2 2
2 5 3 4 2 5 3 4 20
x y x y
. Tính tích giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức
2 2
4 3 4 30
Q x y x y
.
A.180 B. 150 C. – 300 D. – 200
Câu 9. Elip
2 2
2 2
( ) : 1
x y
E
a b
có tiêu cự
1 2
F F
, độ dài trục lớn
1 2
4 2
A A
và tứ giác
1 1 2 2
F B F B
nội tiếp đường tròn,
tính giá trị của
2 2
a b
.
A.12 B. 8 C. 4 D. 2
Câu 10. Cho điểm
(2;0)
C
, hai điểm
( ; ), ( ; )A m n B p q
thuộc elip
2 2
( ) : 1
4 1
x y
E
sao cho tam giác ABC vuông
tại C và có diện tích bằng
16
25
. Tính
2 3 4m n p q
.
A.3,2 B. 2,8 C. 3 D. 2,6
64
Câu 11. Hình vẽ bên minh hoạ một phòng thì thầm (whispering gallery) với mă
t cắt ngang là một hình bán elip
với chiều cao 24 feet và chiều rộng 80 feet. Một âm thanh được phát ra từ một tiêu điềm của phòng thì thầm có
thể được C nghe thấy tại tiêu điểm còn lại. Hỏi hai người nói thầm qua lại với nhau thì sẽ cách trung tâm của
phòng bao nhiêu mét? Theo đơn vị đo lường quốc tế, 1 feet
0,3048m
.
A.9,7536 B. 8,5245 C. 8,4525 D. 9,6525
Câu 12. Elip
2 2
2 2
( ) : 1
x y
E
a b
có tiêu cự
1 2
F F
và đi qua điểm
( 2 13; 2)
M
, bán kính đường tròn nội tiếp tam
giác
1 2
MF F
bằng 1. Tính
2 2
2a b
.
A.264 B. 160 C. 36 D. 164
Câu 13. Cho đường conic parabol
2
( ) : 4P y x
và điểm
(1;4)
A
, hai điểm B, C thuộc parabol sao cho
90
BAC
, đường thẳng BC luôn đi qua điểm M cố định có hoành độ bằng
A.15 B. 8 C. 20 D. 17
Câu 14. Có bao nhiêu số nguyên m nhỏ hơn 2023 để hệ bất phương trình sau có nghiệm
2 2 2 2
2 2
( 7) ( 7) 8
5 21 5 14 25
x y x y
x y m
A.2020 B. 2021 C. 1000 D. Kết quả khác
Câu 15. Elip
2 2
( ) : 1
4 3
x y
E
có hai tiêu điểm
1 2
,F F
trong đó
2
F
có hoành độ dương. Tìm giá trị nhỏ nhất của
biểu thức
2 2
1 2
4
MF MF
.
A.13 B. 12 C. 14 D. 12,5
Câu 16. Cho hai điểm
(3;2), (0; 1)
A B
, điểm
( ; )C x y
thuộc hypebol
2 2
( ) : 1
9 4
x y
H
sao cho tam giác ABC có
diện tích nhỏ nhất. Tính
xy
.
A.6,2 B. 7,2 C. 8,5 D. 7,5
Câu 17. Cho hai điểm
(3;4), (5;3)
A B
, điểm C thuộc elip
2 2
( ) : 1
8 2
x y
E
sao cho tam giác ABC có diện tích nhỏ
nhất. Tính tổng hoành độ và tung độ của điểm C.
A.4 C. 3,5 C. 3 D. 2,5
Câu 18. Khi hệ bất phương trình
2 2
2 2 2 2
6 6 18 ,
( 6) ( 6) 4 2
x y x y m
x y x y
có nghiệm duy nhất thì m thuộc
khoảng
A.(0;2) B. (2;4) C. (4;6) D. (6;9)
Câu 19. Cho hình thoi ABCD có
120
ABC
và đường tròn nội tiếp hình thoi có phương trình
2 2
8
x y
. Elip
2 2
2 2
1
x y
a b
đi qua các đỉnh của hình thoi và điểm A thuộc trục hoành, khi đó
2 2
a b
có giá trị thuộc khoảng
A.(100;150) B. (150;250) C. (250;300) D. (300;350)
Câu 20. Hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300km. Tại cùng một thời điểm, hai trạm
cùng phát tín hiệu với vận tốc 292000km/s để một tàu thủy thu và đo độ lệch thời gian. Tín hiệu từ A đến sớm
hơn tín hiệu đến từ B là 0,0005s. Từ thông tin trên ta có thể xác định được tàu thủy thuộc đường hypebol
2 2
2 2
1
x y
a b
, giá trị biểu thức
2 2
3b a
gần nhất số nào
A.1010 B. 1285 C. 1428 D. 1789
65
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P8)
_____________________________________
Câu 1. Hai số thực
,x y
thỏa mãn
2 2 2 2
( 5) ( 5) 6
x y x y
. Tìm giá trị lớn nhất của biểu thức
2x y
A. 4 B.
13
C.
19
D.
11
Câu 2. Cho hypebol
2 2
2 2
1
9 4
ax by
a b
với
0; 0
a b
. Độ dài ngắn nhất của tiêu cự hypebol đã cho bằng
A.
2 10
B.
4 5
C. 12 D. 14
Câu 3. Trong mặt phẳng tọa độ Oxy, đường cong
2 2
( ) :5 3 20 24 53 0
E x y x y
được chứng minh là một
đường elip, nó có thể đưa về dạng chính tắc trong hệ tọa độ
IXY
trong đó
2
4
x X
y Y
. Tiêu cự của elip đó là
A.6 B.
4 2
C.
6 2
D.
2 2
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
p
p
a
a
r
r
a
a
b
b
o
o
l
l
2
2y px
với
0
p
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
,
,
t
t
r
r
o
o
n
n
g
g
đ
đ
ó
ó
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
d
d
l
l
à
à
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
h
h
u
u
ẩ
ẩ
n
n
.
.
T
T
ì
ì
m
m
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
h
h
ỏ
ỏ
n
n
h
h
ấ
ấ
t
t
c
c
ủ
ủ
a
a
2 2
2 . . 7 5 2023
MH MF MH MF MF MH
A
A
.
.
2
2
0
0
0
0
0
0
B
B
.
.
2
2
0
0
1
1
7
7
C
C
.
.
2
2
0
0
0
0
7
7
D
D
.
.
2
2
0
0
1
1
4
4
Câu 5. Cho elip
2 2
1
25 16
x y
, từ điểm M nằm ngoài elip kẻ hai tiếp tuyến
,
MA MB
đến elip với
(1; ), (3; )A a B b
,
đường thẳng OM luôn đi qua điểm C có hoành độ bằng
A.2 B. 3 C. 1 D. 2,5
Câu 6. Cho parabol
2
( ) : 2P y x
và điểm
(2;1)
A
, điểm M chạy trên parabol, N là trung điểm đoạn thẳng AM, khi
đó N chạy trên một parabol cố định, parabol có thể đưa về dạng chính tắc trong hệ tọa độ
IXY
trong đó
1
0,5
x X
y Y
. Đường chuẩn của parabol đó cách trục tung một khoảng bằng
A.0,5 B. 1 C. 1,5 D. 0,75
C
C
â
â
u
u
7
7
.
.
C
C
h
h
o
o
đ
đ
ư
ư
ờ
ờ
n
n
g
g
h
h
y
y
p
p
e
e
b
b
o
o
l
l
2 2
2 2
1
x y
a b
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
i
i
ể
ể
m
m
M
M
t
t
h
h
u
u
ộ
ộ
c
c
n
n
h
h
á
á
n
n
h
h
p
p
h
h
ả
ả
i
i
h
h
y
y
p
p
e
e
b
b
o
o
l
l
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
1 2 1 2
6; 3 2 20
MF MF MF MF
Tính
1 2
3
MF MF
.
A
A
.
.
1
1
2
2
B
B
.
.
3
3
0
0
C
C
.
.
1
1
4
4
D
D
.
.
1
1
8
8
Câu 8. Trong mặt phẳng tọa độ Oxy, tìm diện tích hình tròn tạo bởi đường tròn đi qua bốn giao điểm của elip
2 2
1
9 4
x y
và hypebol
2 2
1
3 5
x y
A.
5
B.
121
19
C.
120
17
D. Kết quả khác
Câu 9. Trong mặt phẳng tọa độ Oxy, đường cong
( ) : 5 2 9 0
H xy x y
được chứng minh là một đường
hypebol, nó có thể đưa về dạng chính tắc trong hệ tọa độ
IXY
trong đó
2
5
x X
y Y
. Tiêu cự hypebol đó là
A.4 B.
4 2
C.
6 2
D.
8 3
66
Câu 10. Đường thẳng
1 0
ax by
tiếp xúc với elip
2 2
( ) : 1
9 4
x y
E
, giá trị lớn nhất của
3 2a b
bằng
A.1 B.
2
C.
3
D.
13
Câu 11. Cho điểm M thuộc hypebol
2 2
2 2
) :
1
(
x y
H
a b
, hai điểm N, P thuộc tiệm cận của hypebol sao cho MNOP
là hình bình hành. Khi đó
A.
2
MNOP
ab
S
B.
3
2
MNOP
ab
S
C.
3
MNOP
ab
S
D.
2
3
MNOP
ab
S
Câu 12. Trong mặt phẳng tọa độ Oxy, đường cong
2 2
( ) :16 9 24 56 108 124 0
P x y xy x y
được chứng
minh là một đường parabol, nó có thể đưa về dạng chính tắc với đường chuẩn là
A.
3 4 1 0
x y
B.
3 4 1 0
x y
C.
3 4 2 0
x y
D.
3 4 0
x y
Câu 13. Cho elip
2 2
1
25 16
x y
, hai điểm A, B thay đổi thuộc elip sao cho
90
AOB
, tìm giá trị lớn nhất của biểu
thức
1 1
OA OB
.
A.1 B.
82
20
C.
41
30
D.
5
3
C
C
â
â
u
u
1
1
4
4
.
.
Hai điểm A, B phân biệt theo thứ tự thuộc hai đường tròn
2 2 2 2
1; 49
x y x y
, sao cho tia Ox luôn là phân giác của góc
AOB
, nếu I là trung điểm đoạn thẳng AB thì tập hợp điểm I là một
hình elip có tiêu cự bằng
A
A
.
.
6
6
B
B
.
.
2 7
C
C
.
.
1
1
0
0
D
D
.
.
2 5
Câu 15. Các điểm M, N chuyển động trên tia Ox, Oy sao cho đoạn thẳng MN luôn tiếp xúc với elip
2 2
( ) : 1
9 4
x y
E
. Giá trị nhỏ nhất của đoạn thẳng MN là
A.8 B. 5 C. 4 D. 6
Câu 16. Cho đường conic parabol
2
( ) : 2P y x
, khoảng cách nhỏ nhất từ điểm
(0;6)
A
đến một điểm trên elip là
A.5 B.
2 5
C.
4 2
D.
3 2
Câu 17. Cho đường conic parabol
2
( ) : 2 ; 0
P y px p
và điểm
27 15
;
8 8
A
. Tồn tại ba điểm M thuộc parabol
sao cho đoạn thẳng AM vuông góc với tiếp tuyến của parabol tại điểm M. Tổng hoành độ ba điểm M này bằng
A.4,625 B. 6,625 C. 5,25 D. 4,425
Câu 18. Hypebol
2 2
( ) : 1
25 16
x y
H
tiếp xúc với đường thẳng
3 0
ax by
, tìm giá trị lớn nhất của
2 2
a b
.
A.5 B. 9 C. 8 D. 10
C
C
â
â
u
u
1
1
9
9
.
.
Cho elip
2 2
( ) : 1
9 4
x y
E
và hai đường thẳng
; 0
ax by bx xy
. Diện tích lớn nhất của tứ giác MPNQ
khi đó gần nhất với
A
A
.
.
1
1
2
2
đ
đ
v
v
d
d
t
t
B
B
.
.
1
1
3
3
đ
đ
v
v
d
d
t
t
C
C
.
.
1
1
1
1
đ
đ
v
v
d
d
t
t
D
D
.
.
1
1
4
4
đ
đ
v
v
d
d
t
t

-----------------------HẾT-----------------------
| 1/66
| | Tải xuống

Có thể bạn quan tâm:

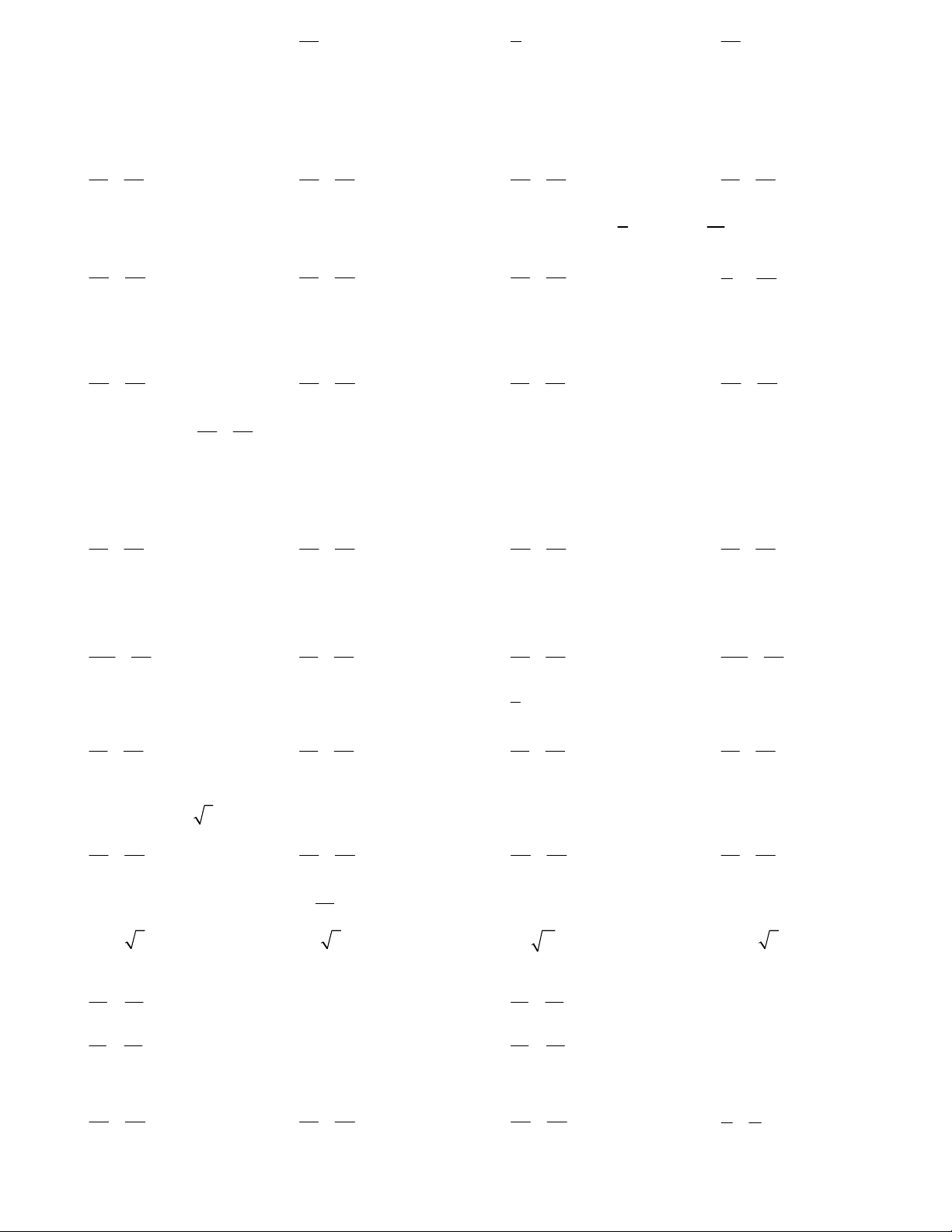
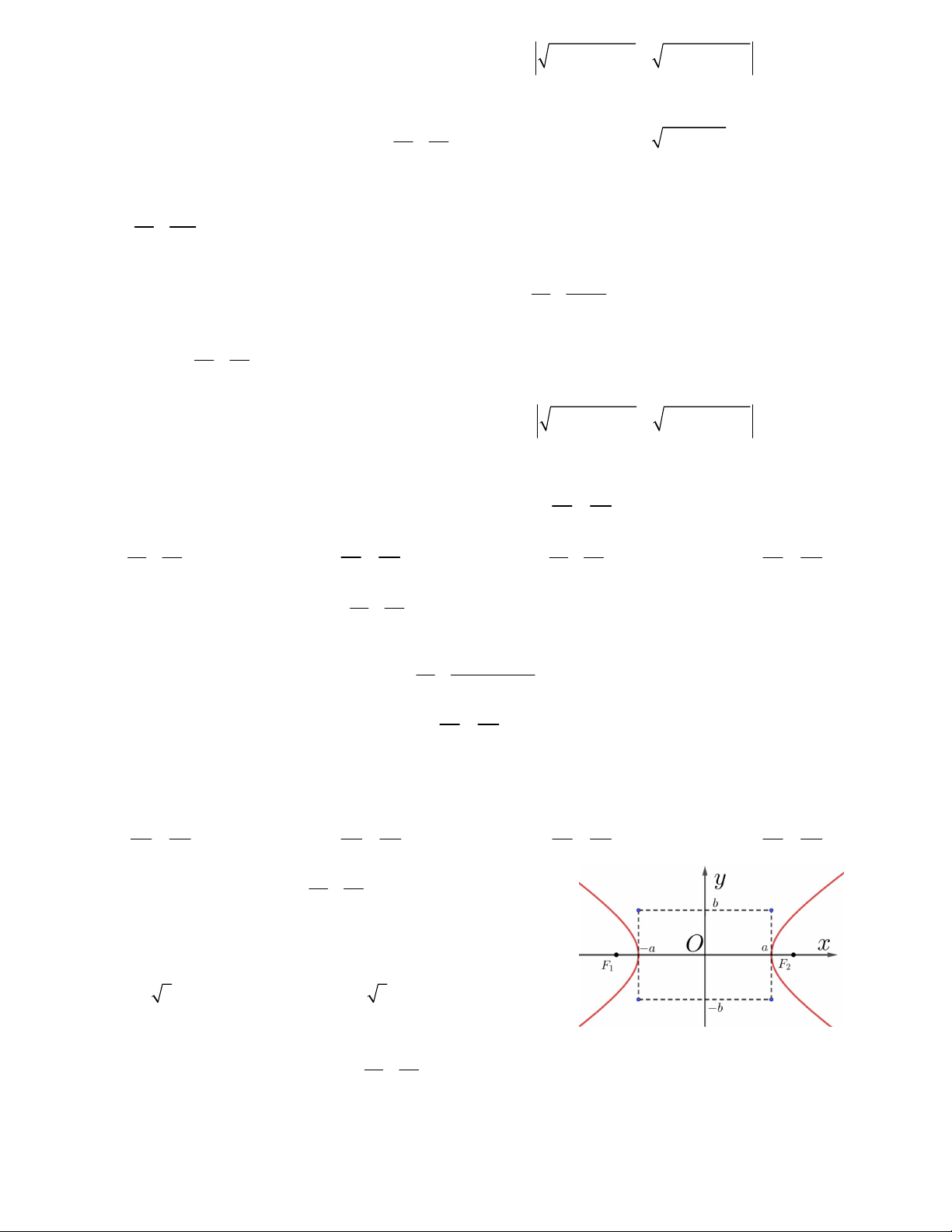
Preview text:


TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
--------------------------------------------------------------------------------------------
CHUYÊN ĐỀ PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM BA ĐƯỜNG CONIC
CƠ BẢN ĐƯỜNG ELIP OXY (P1 – P8)
CƠ BẢN ĐƯỜNG HYPEBOL OXY (P1 – P8)
CƠ BẢN ĐƯỜNG PARABOL OXY (P1 – P8)
VẬN DỤNG CAO BA ĐƯỜNG CONIC (P1 – P8)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 3/2023 1 2
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P1)
_____________________________________ 2 2 x y
Câu 1. Elip  E  : 
 1 có độ dài trục lớn bằng: 25 9 A. 5. B. 10. C. 25. D. 50.
Câu 2. Elip  E  2 2
: x  5 y  25 có độ dài trục lớn bằng: A. 1. B. 2. C. 5. D. 10.
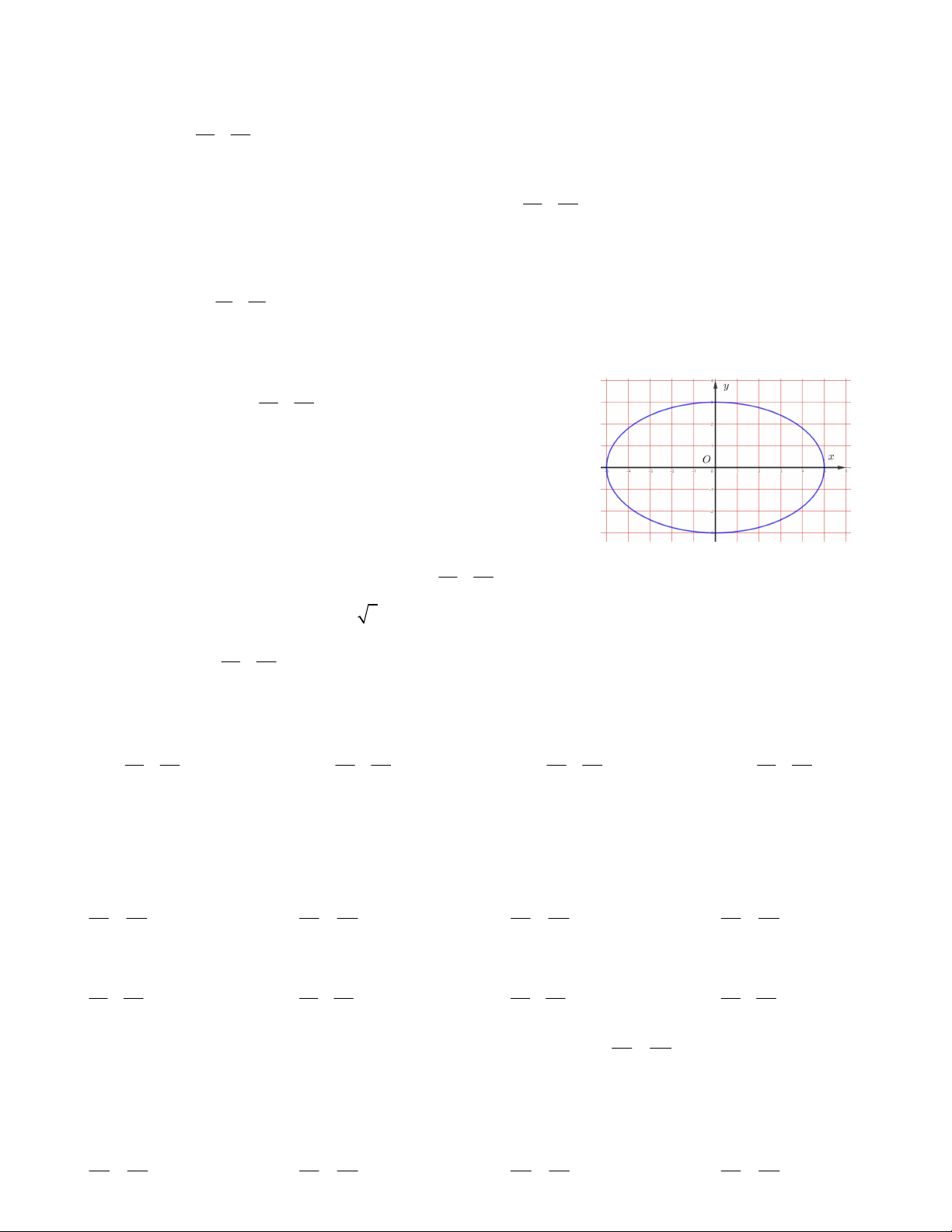
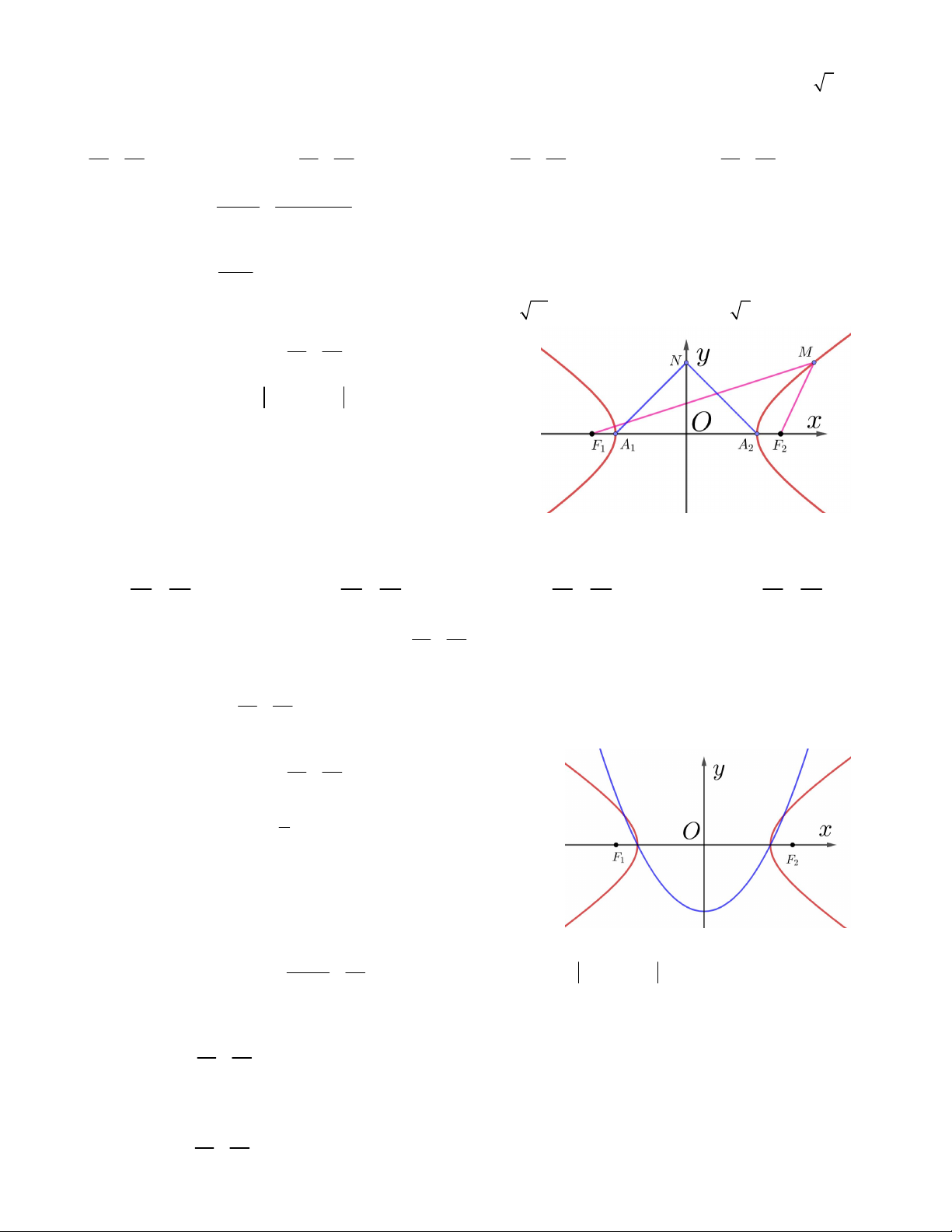
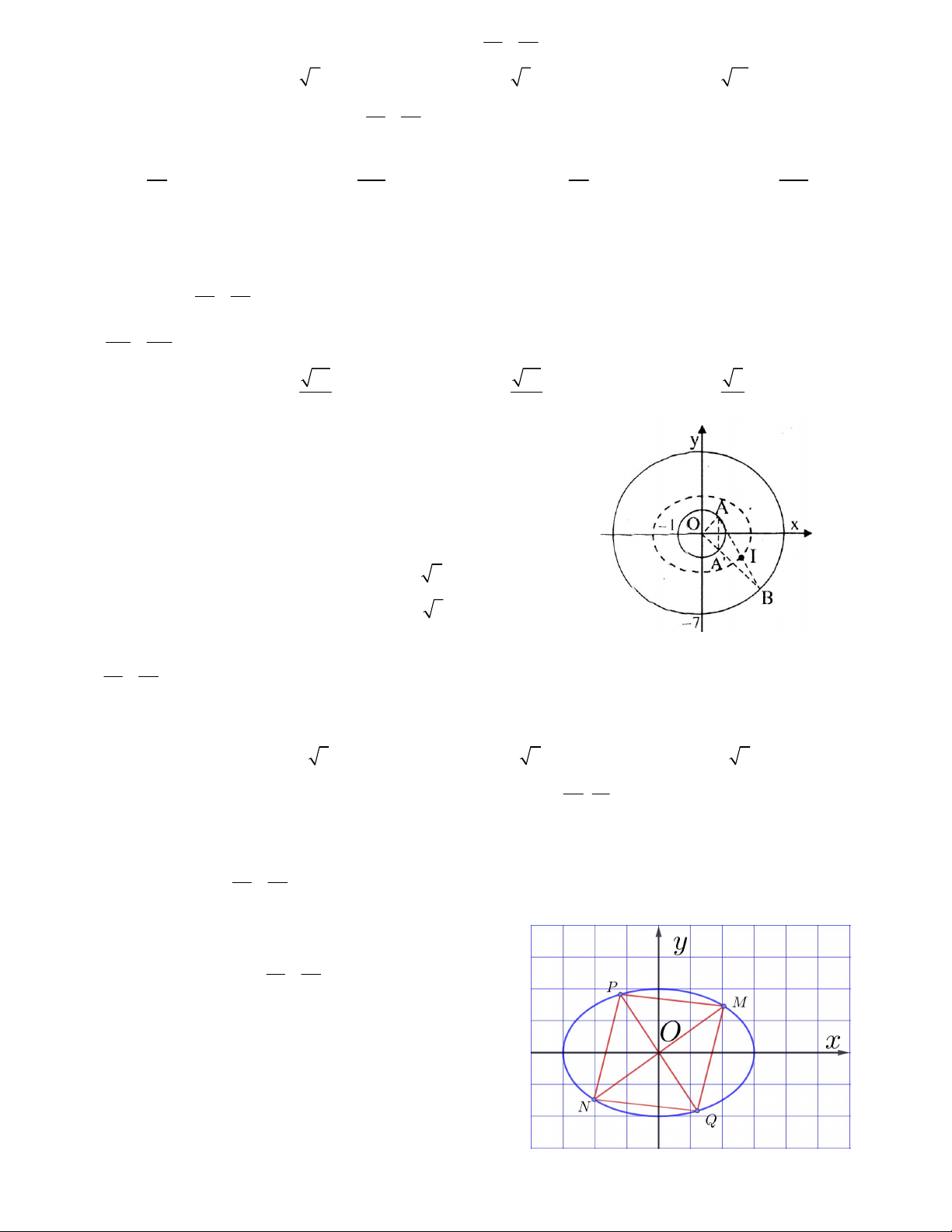
Câu 3. Cho đường elip như hình vẽ bên. Đường elip đã cho cắt
đường phân giác góc phần tư thứ nhất tại bao nhiêu điểm A. 4 B. 3 C. 2 D. 1 2 2 x y
Câu 4. Elip  E  : 
 1 có độ dài trục bé bằng: 100 64 A. 8. B. 10. C. 16. D. 20. 2 2 x y
Câu 5. Elip  E  :   1 có tiêu cự bằng: 9 4 A. 5. B. 5. C. 10. D. 2 5. 2 2 x y
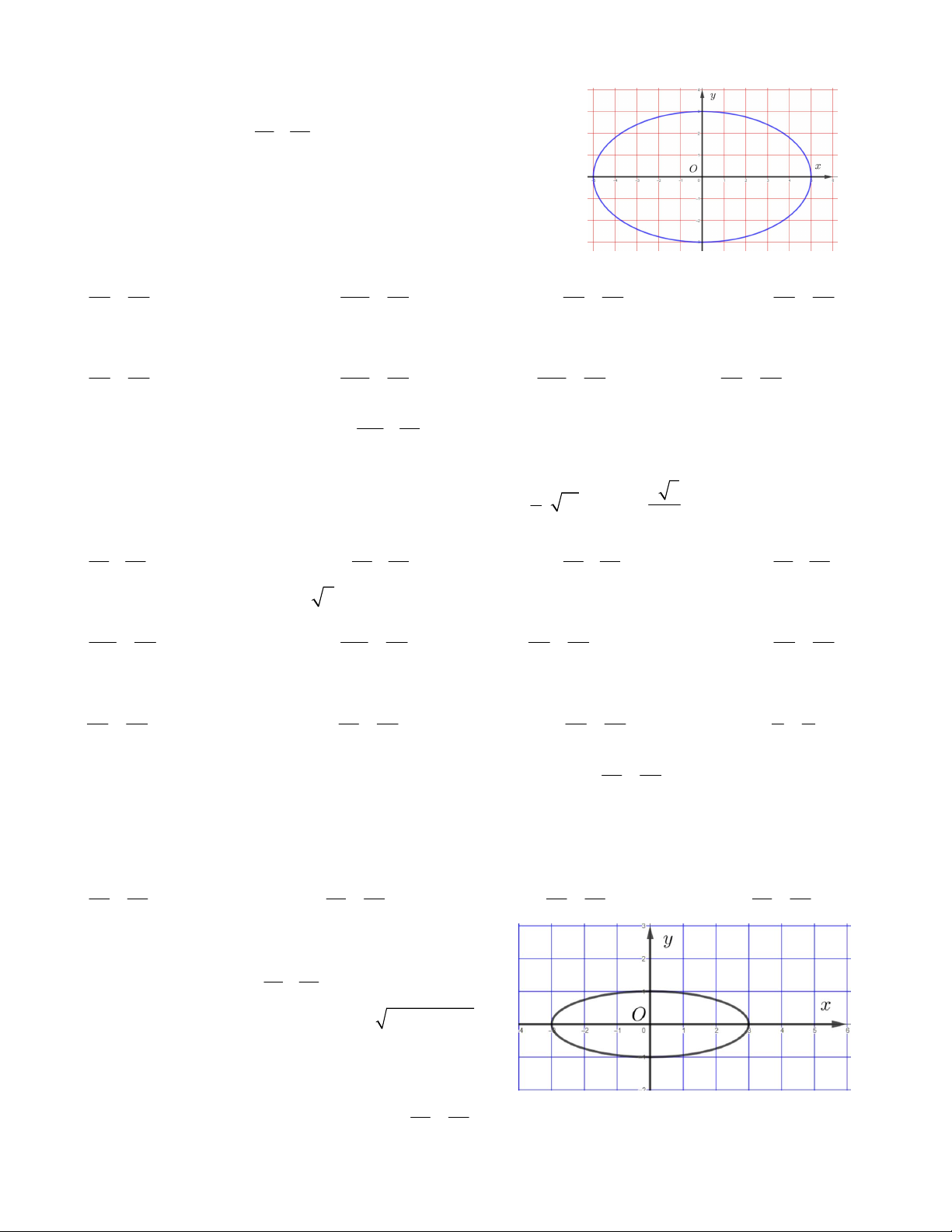
Câu 6. Cho đường elip  E  :   1 như hình vẽ 2 2 p q bên. Tính 2 2
26 p  5q . A. 320 B. 180 C. 229 D. 250 2 2 x y
Câu 7. Elip  E  : 
 1 , với p q  0 có tiêu cự bằng: 2 2 p q A. p q . B. p q . C. 2 2 p q . D. 2 2 2 p q . 2 2 x y
Câu 8. Elip  E  : 
 1 có một đỉnh nằm trên trục lớn là: 100 36 A. 100;0 . B.  1  00;0 . C. 0;10 . D.  10  ;0. 2 2 x y
Câu 9. Elip  E  : 
 1 có một đỉnh nằm trên trục bé là: 16 12 A. 4;0 . B. 0;12 . C. 0;2 3 . D. 5;0 . 2 2 x y
Câu 10. Elip  E  : 
 1 có một tiêu điểm là: 9 6 A. 0;3. B. 0 ; 6 . C.  3;0. D. 3;0. 2 2 x y
Câu 12. Cặp điểm nào là các tiêu điểm của elip  E  :   1? 5 4 A. F 1  ;0 và F 1;0 . B. F 3  ;0 và F 3;0 . 2   1   2   1   3 C. F 0; 1  và F 0;1 . D. F 2  ;0 và F 2;0 . 2   1   2   1   2 2 x y
Câu 13. Elip  E  : 
 1. Tỉ số e của tiêu cự và độ dài trục lớn của elip bằng: 16 9 7 3 5 A. e  1. B. e  . C. e  . D. e  . 4 4 4 2 2 x y
Câu 14. Elip  E  : 
 1. Tỉ số k của tiêu cự và độ dài trục bé của elip bằng: 16 8 A. k  8 . B. k  8 . C. k  1. D. k  1  . 2 2 x y
Câu 15. Cho elip  E  : 
 1. Trong các khẳng định sau, khẳng định nào sai? 25 9 c 4
A.  E  có các tiêu điểm F 4  ;0 và F 4;0 .
B.  E  có tỉ số  . 2   1   a 5
C.  E  có đỉnh A 5  ;0 .
D.  E  có độ dài trục nhỏ bằng 3. 1   2 2 x y
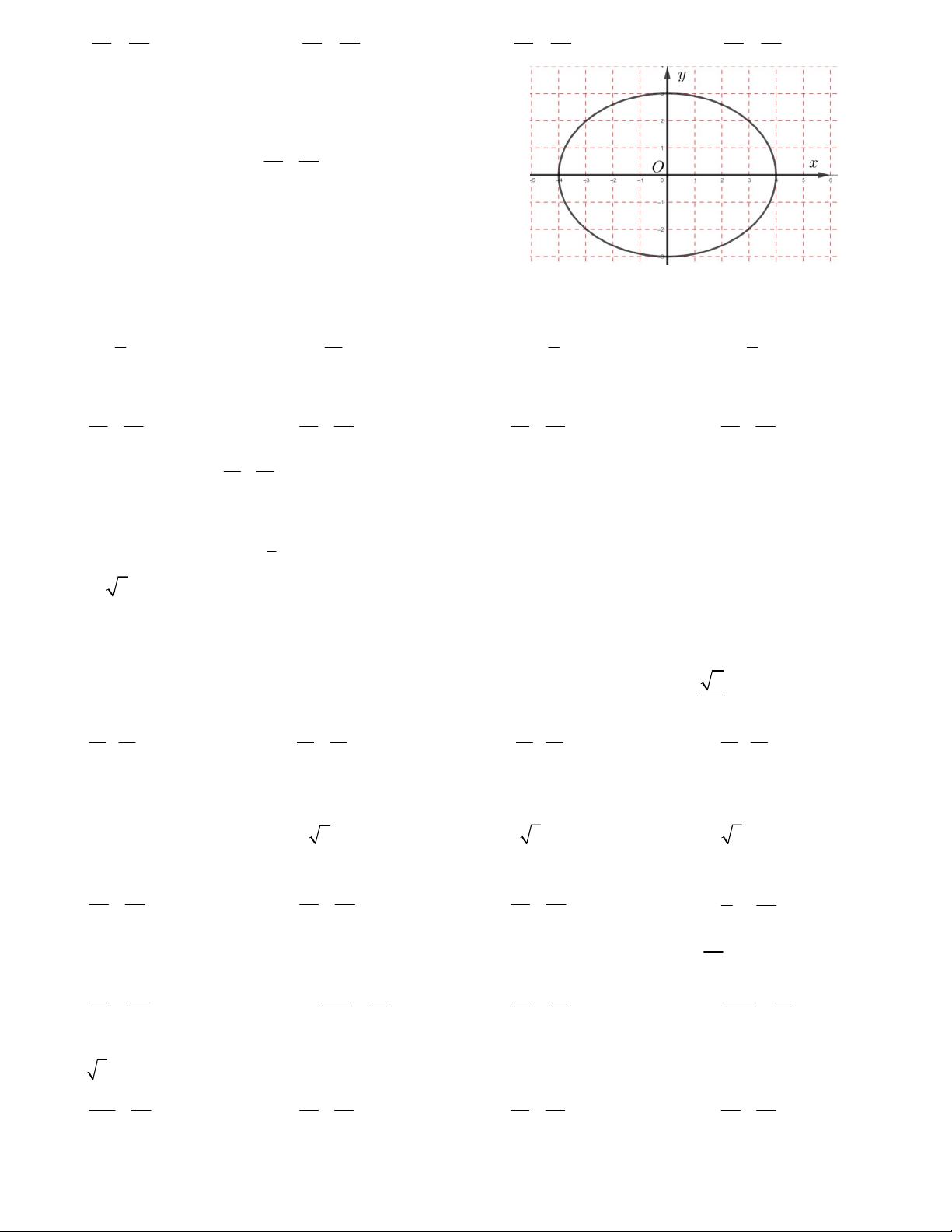
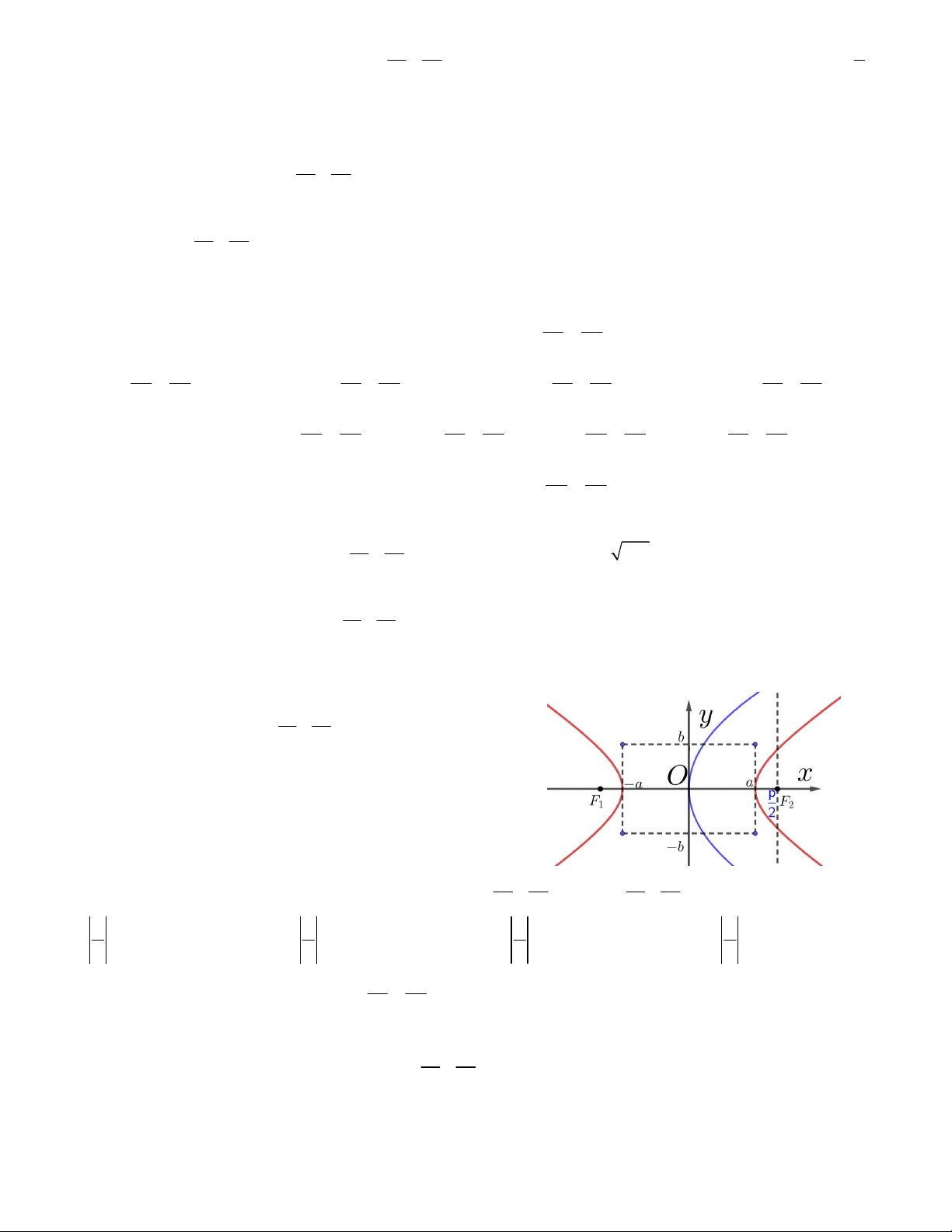
Câu 16. Cho đường elip  E  :   1 như hình vẽ bên. 2 2 p q
Hình chữ nhật cơ sở bao quanh elip có diện tích bằng
A. 40 (đvdt) B. 30 (đvdt)
C. 48 (đvdt) D. 36 (đvdt)
Câu 17. Cho elip  E  2 2
: x  4 y  1. Khẳng định nào sau đây là đúng?
A. Elip có tiêu cự bằng 3.
B. Elip có trục nhỏ bằng 2.  2 
C. Elip có một tiêu điểm là F  0; .
D. Elip có trục lớn bằng 4. 3  
Câu 18. Cho elip  E  2 2
: 4x  9 y  36 . Tìm mệnh đề sai trong các mệnh đề sau:
A.  E  có trục lớn bằng 6.
B.  E  có trục nhỏ bằng 4. c 5
C.  E  có tiêu cự bằng 5.
D.  E  có tỉ số  . a 3  5 2
Câu 19. Tìm elip nếu nó đi qua điểm N 2;    
 và tỉ số của tiêu cự với độ dài trục lớn bằng .  3 3 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 9 4 9 5 9 6 9 3 2
Câu 20. Tìm elip nếu nó đi qua điểm A2; 3 và tỉ số của độ dài trục lớn với tiêu cự bằng . 3 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 16 4 4 3 3 4 4 16
Câu 21. Phương trình chính tắc của elip có hai tiêu điểm F 2
 ;0 , F 2;0 và đi qua điểm M 2;  3 là: 1   2   2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.   1. C.  1. D.   1. 16 12 16 9 16 4 16 8
Câu 22. Cho elip có hai tiêu điểm F , F và có độ dài trục lớn bằng 2a . Trong các mệnh đề sau, mệnh đề nào 1 2 đúng? A. 2a F F .
B. 2a F F .
C. 2a F F . D. 4a F F . 1 2 1 2 1 2 1 2 4
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P2)
_____________________________________
Câu 1. Elip có hai đỉnh là  3
 ;0; 3;0 và có hai tiêu điểm là  1
 ;0; 1;0 . Phương trình chính tắc của elip là: 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 9 1 8 9 9 8 1 9
Câu 2. Elip  E  2 2
: 4x 16 y  1 có độ dài trục lớn bằng: 1 A. 2. B. 4. C. 1. D. . 2 2 2 x y
Câu 3. Elip  E  : 
 1. Tỉ số f của độ dài trục lớn và tiêu cự của elip bằng: 9 4 3 3 2 5 A. f  . B. f  . C. f  . D. f  . 2 5 3 3 2 2 x y
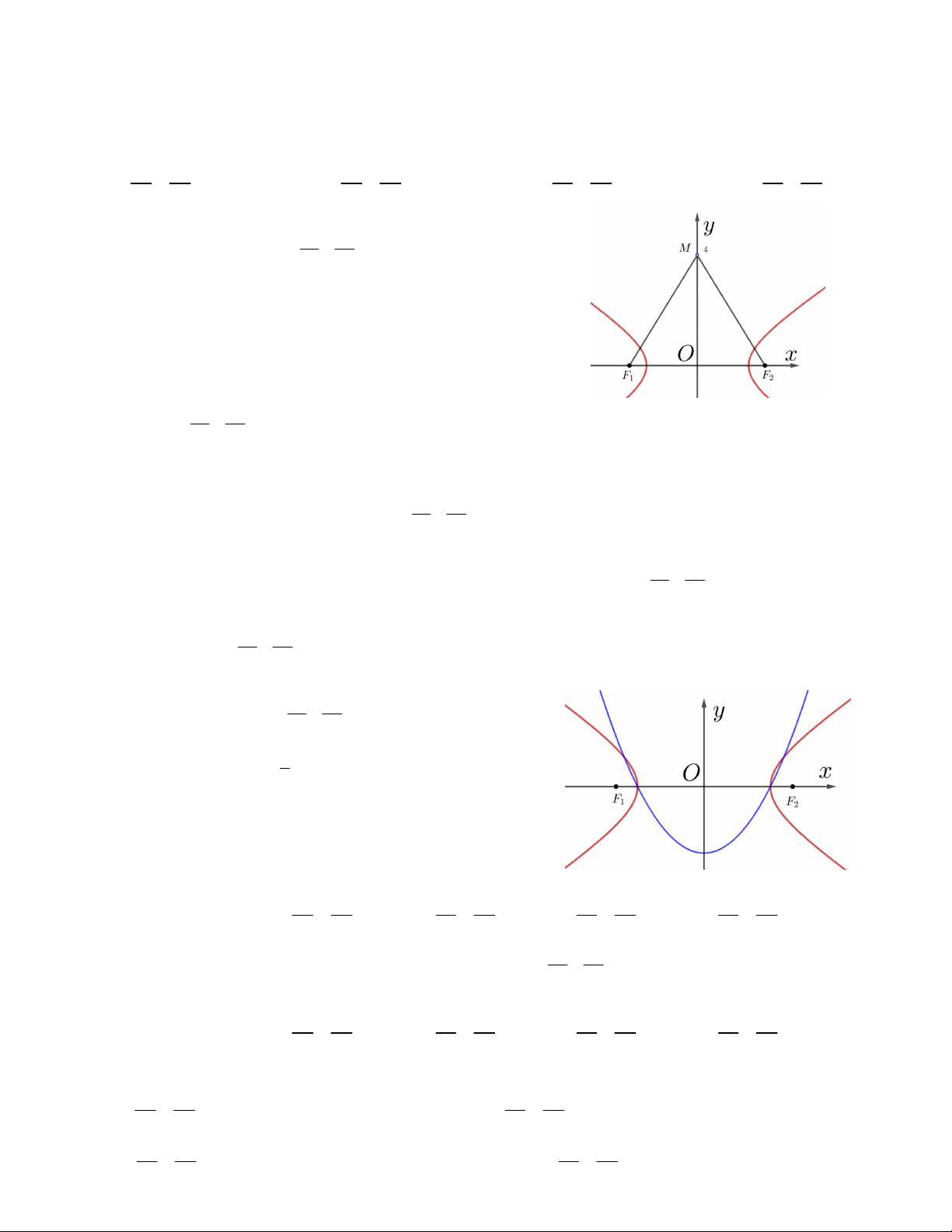
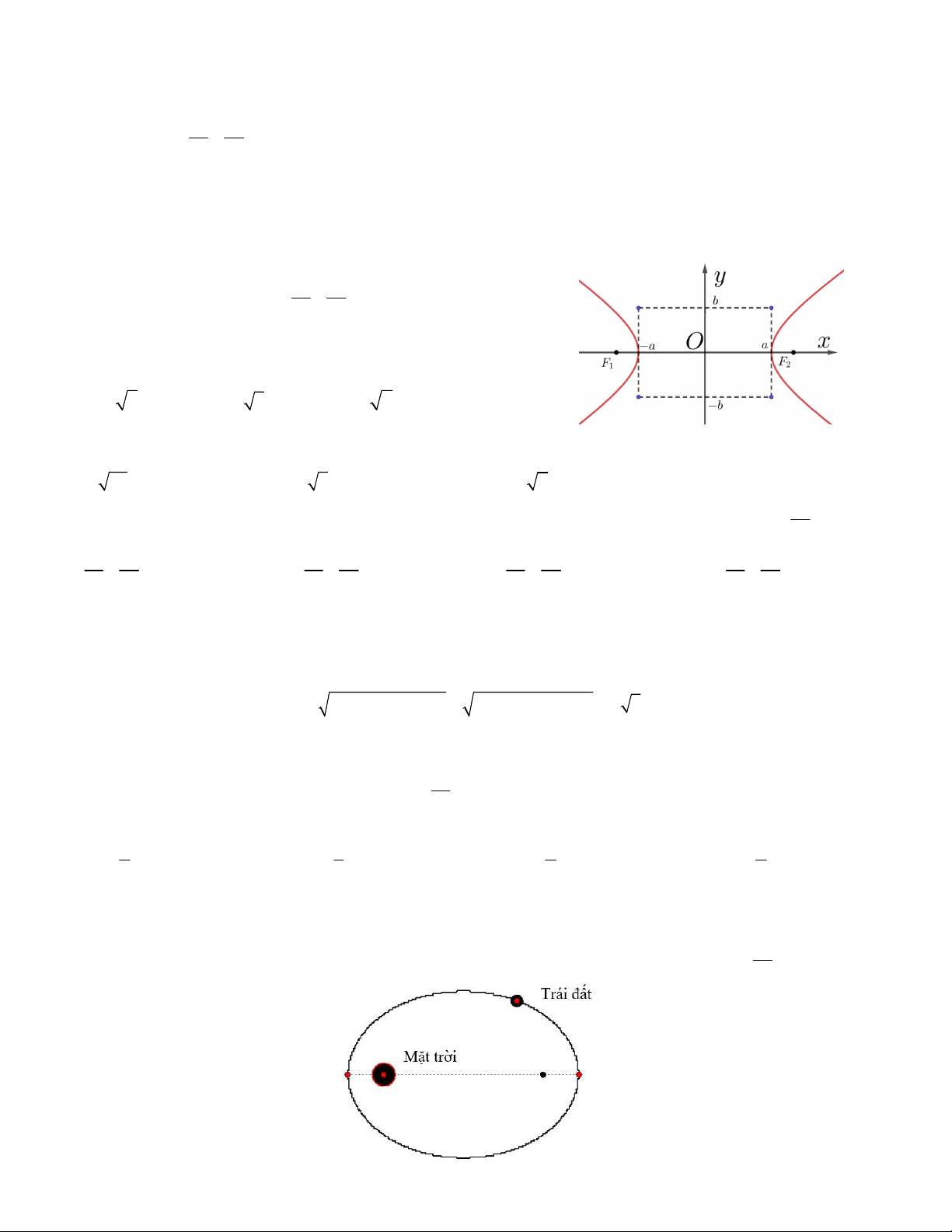
Câu 4. Cho đường elip   1như hình vẽ bên. 2 2 a b
Khoảng cách giữa hai tiêu điểm của elip đã cho bằng A. 4 B. 6 3 C. 4 2 D. 1
Câu 5. Lập phương trình chính tắc của elip biết tỉ số giữa độ dài trục nhỏ và tiêu cự bằng 2 , tổng bình
phương độ dài trục lớn và tiêu cự bằng 64. 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 12 8 8 12 12 4 8 4
Câu 6. Tìm elip có một tiêu điểm F  2
 ;0 và tích độ dài trục lớn với trục bé bằng 12 5 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 9 5 36 20 144 5 45 16 12
Câu 7. Tìm elip có độ dài trục lớn bằng 26 và tỉ số của tiêu cự với độ dài trục lớn bằng . 13 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 26 25 169 25 52 25 169 5 2 2 x y
Câu 8. Cho đường elip  E  :   1 như hình vẽ bên. 2 2 p q
Đường elip đã cho cắt đường thẳng y x 2023 tại bao nhiêu điểm A. 4 B. 3 C. 2 D. 1 1
Câu 9. Tìm elip có độ dài trục lớn bằng 6 và tỉ số của tiêu cự với độ dài trục lớn bằng . 3 2 2 x y 2 2 x y 2 2 x y A. +  1. B.   1. C.   1. D. 9 8 9 5 6 5 5 2 2 x y +  1. 9 3 4
Câu 10. Tìm elip có độ dài trục nhỏ bằng 12 và tỉ số của tiêu cự với độ dài trục lớn bằng . 5 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 36 25 25 36 64 36 100 36 3
Câu 11. Elip có tổng độ dài hai trục bằng 18 và tỉ số của tiêu cự với độ dài trục lớn bằng . Phương trình chính 5 tắc của elip là: 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 25 16 5 4 25 9 9 4 5
Câu 12. Elip có tổng độ dài hai trục bằng 10 và tỉ số của tiêu cự với độ dài trục lớn bằng . Phương trình chính 3 tắc của elip là: 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 25 16 5 4 25 9 9 4 2 2 x y
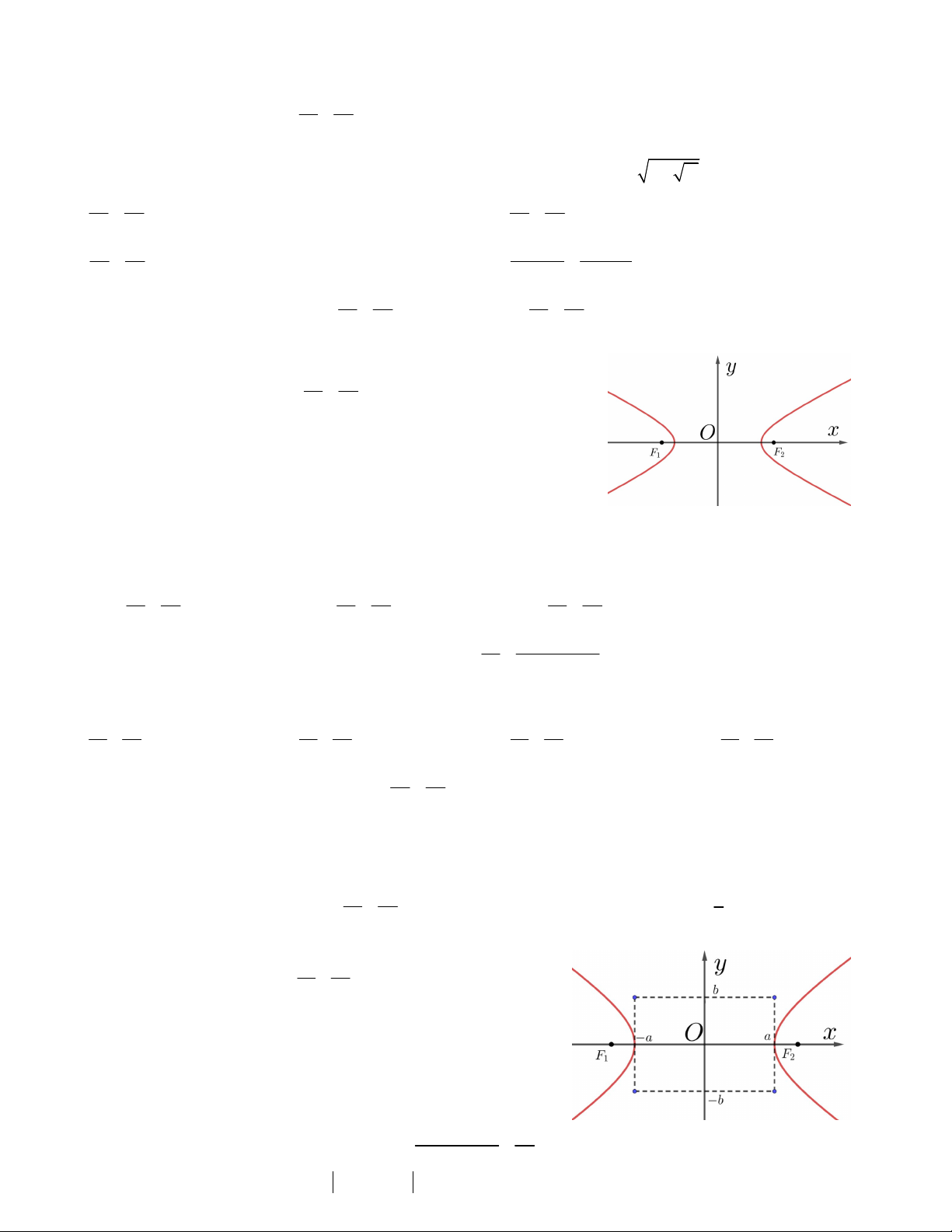
Câu 13. Cho đường elip 
 1như hình vẽ bên. Tính giá trị 2 2 a b của biểu thức 2 2 2
a b  2c với 2c là tiêu cự của elip. A. 48 B. 54 C. 66 D. 60
Câu 14. Lập phương trình chính tắc của elip, biết elip đi qua hai điểm A7;0 và B 0;  3 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 40 9 16 9 9 49 49 9
Câu 15. Tìm phương trình chính tắc của elip nếu nó có trục lớn gấp đôi trục bé và đi qua điểm M 2;2 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A. +  1. B.   1. C.   1. D. +  1. 20 5 36 9 24 6 16 4
Câu 16. Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng 6 và đi qua A5;0. 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B. +  1 . C. +  1 . D. +  1 . 25 16 25 16 25 9 100 81
Câu 17. Trong mặt phẳng Oxy, phương trình chính tắc của Elip  E  có một tiêu điểm là F 2  ;0 và đi qua 1  
điểm M 2;3 là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1 . D.   1. 16 12 16 9 16 4 4 12  5
Câu 18. Elip qua điểm M 2;  
 và có một tiêu điểm F  2
 ;0 . Phương trình chính tắc của elip là:  3 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1 . B.   1 . C.   1 . D.   1 . 9 5 9 4 25 16 25 9 2 x
Câu 19. Elip  E  2 :
y  4 có tổng độ dài trục lớn và trục bé bằng: 16 A. 5. B. 10. C. 20. D. 40. 2 2 x y
Câu 20. Elip  E  :   1 có tiêu cự bằng: 25 16 A.3. B. 6. C. 9. D. 18.
_________________________________ 6
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P3)
_____________________________________ 2 2 x y
Câu 1. Cho elip E:   1 . Hai điểm ,
A B là hai đỉnh của elip lần lượt nằm trên hai trục Ox , Oy . Khi đó độ 25 9
dài đoạn thẳng AB bằng: A. 34. B. 34. C. 5. D. 136.  12
Câu 2. Elip đi qua các điểm M 0;  3 và N 3  ;    
 có phương trình chính tắc là:  5  2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1 . B.  1 . C.   1 . D.   1. 16 9 25 9 9 25 25 9
Câu 3. Một elip E có trục lớn dài gấp 3 lần trục nhỏ. Tỉ số e của tiêu cự với độ dài trục lớn bằng: 1 2 3 2 2 A. e  . B. e  . C. e  . D. e  . 3 3 3 3 2 2 x y
Câu 4. Cho đường elip 
 1như hình vẽ bên. Đường 2 2 a b
thẳng d song song với trục hoành và cách trục hoành một
khoảng bằng 2, d tạo với elip một dây cung có độ dài bằng 8 5 8 6 A. B. 3 3 10 5 10 6 C. D. 3 3 3
Câu 5. Một elip E có khoảng cách giữa hai đỉnh kế tiếp nhau gấp
lần tiêu cự của nó. Tỉ số e của tiêu cự với 2
độ dài trục lớn bằng: 5 2 3 2 A. e  . B. e  . C. e  . D. e  . 5 5 5 5 2 2 x y
Câu 6. Cho điểm M 2; 
3 nằm trên đường elip E có phương trình chính tắc: 
 1 . Trong các điểm sau 2 2 a b
đây điểm nào không nằm trên E : A. M 2  ;3 . B. M 2; 3  . C. M 2  ;3 . D. M 3;2 . 4   3   2   1   2 2 x y
Câu 7. Cho elip E: 
 1 . Khẳng định nào sau đây là đúng? 2 2 a b
A. E không có trục đối xứng.
B. E có một trục đối xứng là trục hoành.
C. E có hai trục đối xứng là trục hoành và trục tung.
D. E có vô số trục đối xứng.
Câu 8. Elip E có độ dài trục bé bằng tiêu cự. Tỉ số e của tiêu cự với độ dài trục lớn của E bằng: 1 1 A. e  1 . B. e  2 . C. e  . D. e  . 2 3
Câu 9. Cho đường elip như hình vẽ bên. Đường elip đã
cho cắt đường phân giác góc phần tư thứ nhất tại bao nhiêu điểm A. 4 B. 3 C. 2 D. 1
Câu 10. Elip E có hai đỉnh trên trục nhỏ cùng với hai tiêu điểm tạo thành một hình vuông. Tỉ số e của tiêu cự
với độ dài trục lớn của E bằng: 7 1 1 A. e  1 . B. e  2 . C. e  . D. e  . 2 3
Câu 11. Elip E có độ dài trục lớn bằng 4 2 , các đỉnh trên trục nhỏ và các tiêu điểm của elip cùng nằm trên một
đường tròn. Độ dài trục nhỏ của E bằng: A. 2. B. 4. C. 8. D. 16. 2 2 x y
Câu 12. Cho elip E: 
 1 và M là một điểm tùy ý trên E . Khi đó: 16 9 A. 3  OM  4. B. 4  OM  5. C. OM  5. D. OM  3.  3
Câu 13. Elip đi qua các điểm A0;  1 và N 1  ;  
 có phương trình chính tắc là:  2  2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 16 4 8 4 4 1 2 1 2 2 x y Câu 14. Cho elip 
 1 và M là một điểm tùy ý trên E . Khi đó: 25 4 A. 3  OM  4. B. 2  OM  5 C. OM  5. D. OM  3. 2 2 x y
Câu 15. Cho elip E: +
 1 và điểm M nằm trên E . Nếu M có hoành độ bằng 13 thì khoảng cách từ 169 144
M đến hai tiêu điểm bằng: A. 10 và 6. B. 8 và 18. C. 13  5 . D. 13  10 . 2 2 x y
Câu 16. Cho elip E: +
 1 và điểm M nằm trên E . Nếu M có hoành độ bằng 1 thì khoảng cách từ M 16 12
đến hai tiêu điểm bằng: 2 A. 3,5 và 4,5 . B. 3 và 5 . C. 4  2 . D. 4  . 2 2 2 x y
Câu 17. Cho elip E: 
 1 . Tính diện tích hình chữ nhật cơ sở. 16 9 A.4 B. 24 C. 50 D. 24
Câu 18. Cho elip có phương trình 2 2
16x  25y  100 . Tính tổng khoảng cách từ điểm M thuộc elip có hoành độ
bằng 2 đến hai tiêu điểm. A. 3. B. 2 2. C. 5 . D. 4 3. 2 2 x y
Câu 19. Cho đường elip  E  :   1 như hình vẽ 2 2 p q bên. Đường elip đã cho cắt đường thẳng
2x  3y  0 theo một dây cung có độ dài bằng A. 8 B. 4 11 C. 2 13 D. 6 2
Câu 20. Cho elip có phương trình 2 2
16x  25y  100 . Tính tổng khoảng cách từ điểm M thuộc elip có hoành độ
bằng – 1 đến hai tiêu điểm. A. 3. B. 2 2. C. 5 . D. 4 3. 2 2 x y
Câu 21. Cho elip E: 
 1 . Qua một tiêu điểm của E dựng đường thẳng song song với trục Oy và cắt 100 36
E tại hai điểm M và N . Tính độ dài MN . 64 36 25 A. . B. . C. 25 . D. . 5 5 2
_________________________________ 8
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P4)
_____________________________________ 2 2 x y
Câu 1. Trong mặt phẳng Oxy, cho phương trình Elip  E  : 
 1. Tọa độ một đỉnh nằm trên trục lớn của 100 36 E đã cho là A. 100;0 . B.  1  00;0 . C. 0;10 . D.  1  0;0 . 2 2 x y
Câu 2. Trong mặt phẳng Oxy, cho Elip  E  : 
 1. Độ dài trục lớn của Elip đã cho bằng 25 9 A. 25. B.10. C. 6. D. 9.
Câu 3. Cho đường elip như hình vẽ bên. Đường elip đã cho cắt đường thẳng 3
x 2022  y 2023  0 tại bao nhiêu điểm A. 4 B. 3 C. 2 D. 1 2 2 x y
Câu 4. Trong mặt phẳng Oxy, cho Elip  E  : 
 1 . Độ dài trục bé của Elip đã cho bằng 16 9 A. 32 . B. 6 . C. 8 . D. 18 .
Câu 5. Cho Elip E x y  . Tiêu cự c ủa Eli   2 2 : 4 1 p đã cho bằng A. 5 . B. 3 . C. 2 5 . D. 2 3 . 2 x
Câu 6. Trong mặt phẳng Oxy , cho Elip  E  2 :
 4 y  1. Tiêu điểm của  E  là 4  1   1  A. 1 F  2  ;0, 2 F 2;0 . B. 1 F  ; 0 ,   2 F ; 0   .  2   2   15   15   17   17  C. 1 F   ;0 , 2 F  ;0  . F   ;0, F  ;0 . 2 2 D. 1 2     2 2    
Câu 7. Phương trình chính tắc của Elip có độ dài trục lớn bằng 16 , độ dài trục bé bằng 12 là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 9 16 64 36 8 6 16 9 2 2 x y
Câu 8. Cho đường elip 
 1như hình vẽ bên. Đường 2 2 a b
elip đã cho cắt đường tròn 2 2
x y  1tại bao nhiêu điểm A. 4 B. 3 C. 2 D. 1
Câu 9. Viết phương trình chính tắc của Elip có độ dài trục lớn bằng 2 5 và tiêu cự bằng 2 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 5 4 20 16 5 1 4 5 2 2 x y
Câu 10. Dây cung của elip E: 
 1 0  b a vuông góc với trục lớn tại tiêu điểm có độ dài bằng: 2 2 a b 2 2c 2 2b 2 2a 2 a A. . B. . C. . D. . a a c c 2 2 x y
Câu 11. Đường thẳng d : 3x  4 y 12  0 cắt elip E : 
 1 tại hai điểm phân biệt M và N . Khi đó độ dài 16 9 9
đoạn thẳng MN bằng: A. 3. B. 4. C. 5. D. 25.
Câu 12. Trong mặt phẳng tọa độ Oxy , viết phương trình chính tắc của Elip biết độ dài trục nhỏ bằng 4 đồng 5
thời tỉ số giữa tiêu cự và độ dài trục lớn bằng . 3 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   0 . D.   1. 9 4 3 2 9 4 4 9
Câu 13. Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng 2 3 và đi qua A2  ;1 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A. +  1. B.   1. C.   1. D. +  1. 6 3 8 2 8 5 9 4
Câu 14. Elip (E) có các tiêu điểm F 4
 ; 0 , F 0; 4 và một điểm M nằm trên elip sao cho chu vi tam giác 1   2  
MF F bằng 18. Lúc đó tâm sai của elip bằng 1 2 4 2 2 5 A. B. C. D. 5 3 5 6 2 2 x y
Câu 15. Giá trị của m để đường thẳng  : x  2 y m  0 cắt elip E : 
 1 tại hai điểm phân biệt là: 4 1 A. m  2  2. B. m  2 2. C. m  2  2. D. 2  2  m  2 2. 2 2 x y Câu 16. Cho elip 
 1 với tiêu điểm F , F . Lấy hai điểm A, B thuộc elip (E) sao cho AF BF  8 . Khi 25 16 1 2 1 2
đó giá trị biểu thức AF BF bằng 2 1 A.10 B. 12 C. 8 D. 14 2 2 x y
Câu 17. Cho elip E: 
 1 nội tiếp hình chữ nhật cơ sở ABCD. Điểm M nằm trên cạnh AB, tính diện tích 100 36 tam giác MCD. A.120 B. 100 C. 140 D. 80
Câu 18. Tìm chu vi hình chữ nhật cơ sở ngoại tiếp elip có phương trình 2 2
16x  25y  100 . 20 B. 12 C. 15 D. 9
Câu 19. Trong mặt phẳng Oxy, cho Elip  E  đi qua điểm M 2 3; 2 và M nhìn hai tiêu điểm của E  dưới 2 2 x y
một góc vuông. Biết phương trình chính tắc của  E  đã cho có dạng   1. Tính 2 2
S a b . 2 2 a b A. 24 . B. 32 . C. 8. D. 25 . 2 2 x y
Câu 20. Trong mặt phẳng Oxy , cho elip (E) có phương trình chính tắc 
 1. Tìm tọa điểm M sao cho 25 16
điểm M thuộc (E) và trục Ox .
A. (5; 0) hoặc 5;0. B. (0; 5) hoặc 0;  5 . C. 4  ;0 hoặc 4;  0 . D.0; 4   hoặc 0;  4 . 2 2 x y
Câu 21. Cho đường elip 
 1như hình vẽ bên. Đường 2 2 a b
elip đã cho cắt đường tròn 2 2
x y  2x  2 y 1  0 tại bao nhiêu điểm A. 4 B. 3 C. 2 D. 1 2 2 x y
Câu 22. Trong mặt phẳng Oxy , cho elip (E) có phương trình chính tắc 
 1 . Tìm tọa điểm M sao cho 36 9
điểm M thuộc (E) và trục Oy . A. (6; 0) hoặc 6;  0 . B. (0; 6) hoặc 0;  6 . C.  3  ;  0 hoặc 3;  0 . D. 0;  3  hoặc 0;  3 .
_________________________________ 10
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P5)
_____________________________________
Câu 1. Elip có hai đỉnh là  3
 ;0; 3;0 và có một tiêu điểm là 2 2;0. Phương trình chính tắc của elip là: 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 9 1 8 9 9 8 1 9 6
Câu 2. Tìm phương trình chính tắc của elip nếu trục lớn gấp
lần trục bé và có tiêu cự bằng 4 3 . 2 2 2 x y 2 2 x y 2 2 x y 2 2 x y A. +  1. B.   1. C.   1. D. +  1. 16 4 36 9 36 24 24 16
Câu 3. Tính diện tích hình chữ nhật cơ sở của elip 2 2
4x  25 y  36 . A.14,4 B. 15,5 C. 16,5 D. 18
Câu 4. Lập phương trình chính tắc của elip biết độ dài trục lớn hơn độ dài trục nhỏ 4 đơn vị, độ dài trục nhỏ bé
hơn độ dài tiêu cự 2 đơn vị. 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 64 60 25 9 100 64 9 1
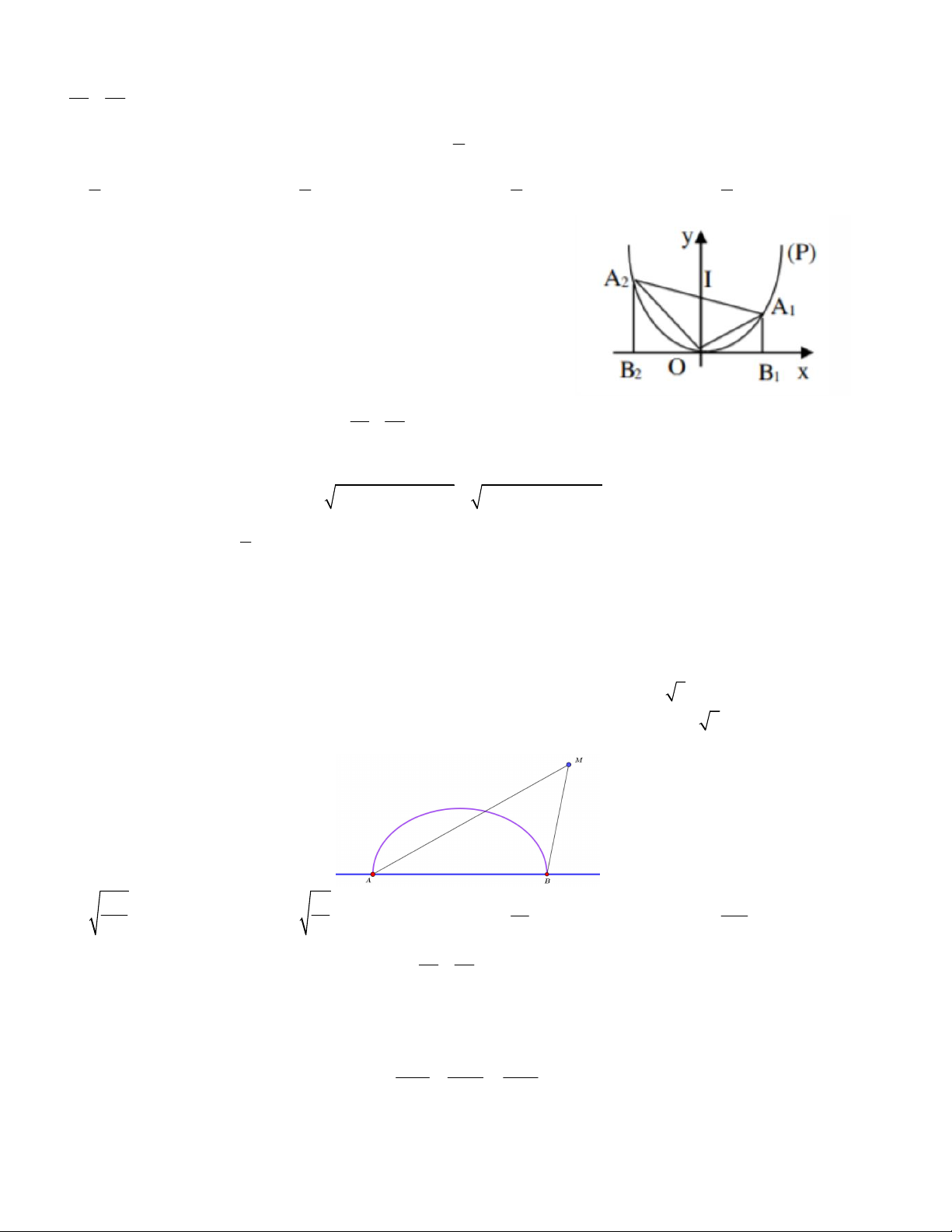
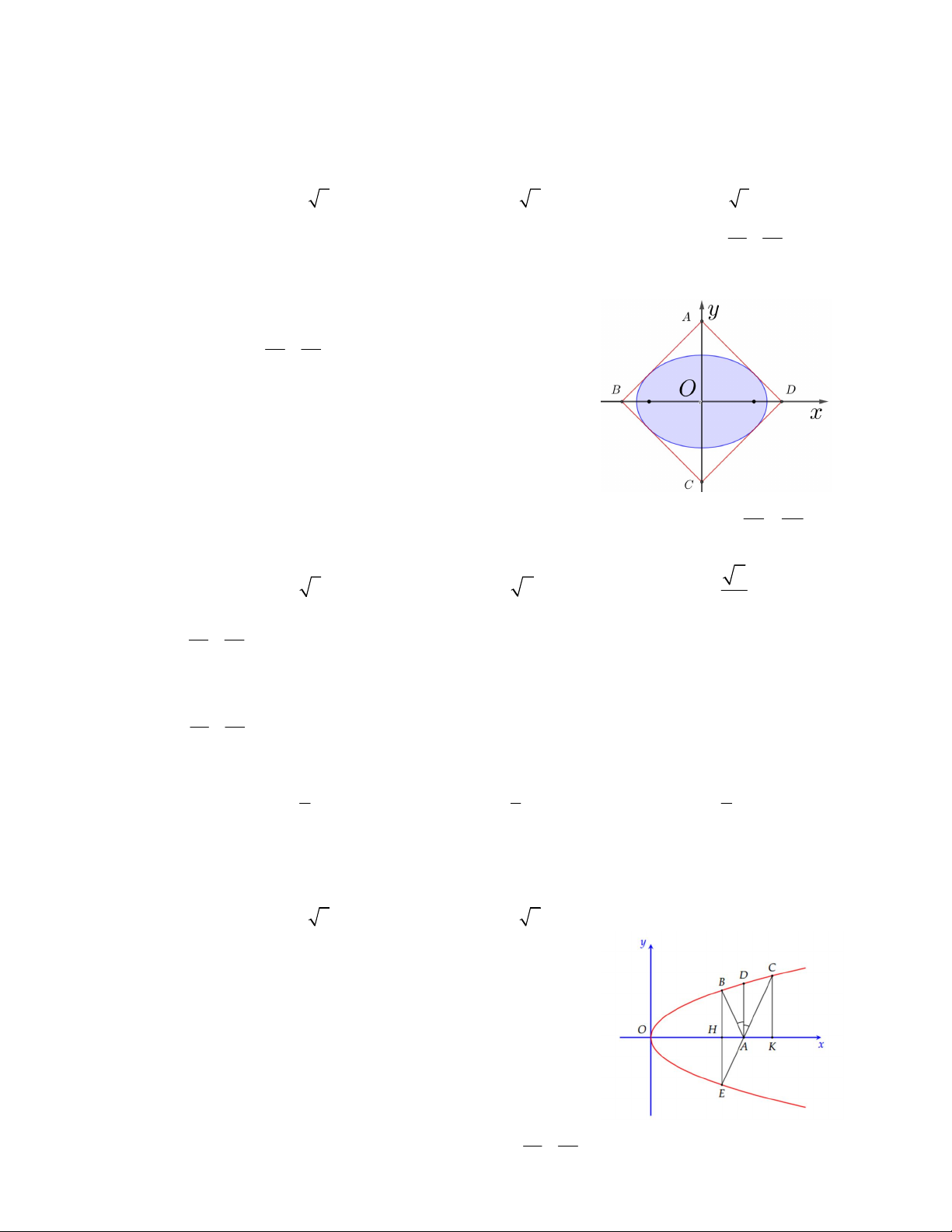
Câu 5. Cho đường elip như hình vẽ bên. Hình chữ nhật ABCD nội
tiếp elip và có các đỉnh với tọa độ nguyên thì có diện tích bằng A. 20 B. 18 C. 24 D. 16
Câu 6. Lập phương trình chính tắc của elip biết tỉ số giữa độ dài tiêu cự và trục nhỏ bằng 2 , tổng bình
phương độ dài trục lớn và tiêu cự bằng 56 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 12 8 8 12 12 4 8 4  7 
Câu 7. Elip (E) đi qua điểm M  2 3;
 và một tiêu điểm có hoành độ bằng – 3. Độ dài trục lớn của elip bằng 2   A.6 B. 8 C. 9 D. 10 1
Câu 8. Tìm elip có độ dài trục lớn bằng 6 và tỉ số của tiêu cự với độ dài trục lớn bằng . 3 2 2 x y 2 2 x y 2 2 x y 2 2 x y A. +  1. B.   1. C.   1. D. +  1. 9 8 9 5 6 5 9 3
Câu 9. Tính diện tích hình chữ nhật cơ sở của elip (E) có độ dài trục nhỏ bằng 12 và tỉ số của tiêu cự với độ dài 4 trục lớn bằng . 5 A.240 B. 260 C. 240 D. 320
Câu 10. Elip (E) có hai tiêu điểm F 2
 ;0 , F 2;0 và đi qua điểm M 2;  3 . Khi đó đường tròn 2 2
x y  17 cắt 1   2  
elip đã cho tại bao nhiêu giao điểm A.2 B. 1 C. 4 D. 0
Câu 11. Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng 6 và đi qua A5;0. 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B. +  1 . C. +  1 . D. + 1 . 25 16 25 16 25 9 100 81 3
Câu 12. Tìm elip có tổng độ dài hai trục bằng 18 và tỉ số của tiêu cự với độ dài trục lớn bằng . 5 11 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 25 16 5 4 25 9 9 4 2 2 x y
Câu 13. Cho đường elip   1như hình vẽ bên. 2 2 a b Tính 2 2
a b . A. 13 B. 17 C. 10 D. 11 5
Câu 14. Tìm elip có tổng độ dài hai trục bằng 10 và tỉ số của tiêu cự với độ dài trục lớn bằng . 3 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.  1. 25 16 5 4 25 9 9 4
Câu 15. Elip (E) đi qua hai điểm A7;0 và B 0; 
3 . Tìm số giao điểm của (E) và đường thẳng y = 2x + 7 A.4 B. 3 C. 2 D. 1 2 2 x y
Câu 16. Tính khoảng cách lớn nhất từ điểm M (8;0) đến một điểm nằm trên elip   1. 49 9 A.15 đơn vị B. 14 đơn vị C. 12 đơn vị D. 10 đơn vị
Câu 17. Tìm elip có một tiêu điểm F  2
 ;0 và tích độ dài trục lớn với trục bé bằng 12 5 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 9 5 36 20 144 5 45 16  12
Câu 16. Elip đi qua các điểm M 0;  3 và N 3  ;    
 . Từ một tiêu điểm của elip dựng đường thẳng vuông góc với  5 
trục hoành cắt elip tại hai giao điểm AB, độ dài đoạn thẳng AB bằng A.3,6 B. 4,5 C. 7,2 D. Kết quả khác  3
Câu 18. Elip đi qua các điểm A0  ;1 và N 1  ;  
 có phương trình chính tắc là:  2  2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.   1. D.   1. 16 4 8 4 4 1 2 1
Câu 19. Tìm phương trình chính tắc của elip nếu nó có trục lớn gấp đôi trục bé và đi qua điểm M 2;2 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A. +  1. B.   1. C.   1. D. +  1. 20 5 36 9 24 6 16 4 2 2 x y
Câu 20. Cho đường elip 
 1như hình vẽ bên. Đường thẳng 2 2 a b 2
y  (k 1)x tạo với elip một dây cung có độ dài lớn nhất bằng A. 14 B. 8 C. 10 D. 12 2 2 x y
Câu 21. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của đoạn thẳng OM, với M là điểm bất ỳ thuộc elip   1. 16 4 A.5 B. 6 C. 8 D. 4
Câu 22. Elip (E) có tiêu cự bằng 8 và đi qua điểm M  15; 
1 . Đường thẳng y = 1 cắt elip theo một dây cung có độ dài gần nhất với A.7,746 B. 7,826 C. 7,725 D. 7,734 2 2 x y
Câu 23. Tìm số giao điểm của elip   1và đường parabol 2
y  2x  4x  4 16 12 A.4 B. 3 C. 2 D. 1 12
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P6)
_____________________________________ 2 2 x y
Câu 1. Cho  E  : 
 1 và điểm M thuộc Elip. Khi đó độ dài OM thỏa mãn: 16 9 A. OM  3 . B. 3  OM  4 . C. 4  OM  5 . D. OM  5 . 2 2 x y
Câu 2. Trong mặt phẳng với hệ trục tọa độ Oxy , cho elip  E  : 
 1 và đường thẳng d : 3x  4 y 12  0 . 16 9
Biết rằng d luôn cắt  E  tại hai điểm phân biệt A , B . Tính độ dài đoạn AB . A. AB  5 . B. AB  3 . C. AB  4 . D. AB  10. 2 2 x y
Câu 3. Cho elip E: 
 1 . Khẳng định nào sau đây là đúng? 2 2 a b
A. E không có tâm đối xứng.
B. E có đúng một tâm đối xứng.
C. E có hai tâm đối xứng.
D. E có vô số tâm đối xứng. 2 2 x y
Câu 4. Cho đường elip 
 1như hình vẽ bên. Đường elip đã 2 2 a b
cho cắt đường thẳng y k (x  2) 1 tại bao nhiêu điểm (với k là tham số). A. 4 B. 3 C. 2 D. 1 2 2 x y
Câu 5. Cặp điểm nào là các tiêu điểm của elip  E :   1? 5 4 A. F  1  ;0 . B. F   5;0 . C. F  0; 1  . D. F  0; 2 . 1;2   1;2   1;2   1;2   2 2 x yx  2t
Câu 7. Cho elip  E  : 
 1 và đường thẳng d : 
. Số điểm chung của  E và d là 5 4 y  1   t  A. 0. B. 1. C. 2. D. 4.
Câu 8. Viết phương trình chính tắc của elip  E biết độ dài trục lớn 10 , độ dài trục bé bằng 8 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  E  :   1. B.  E  :   1. C.  E  :   1. D.  E  :   1. 16 9 25 9 25 16 9 16
Câu 9. Cho  E  có hai tiêu điểm F 4;0 , F 4;0 và điểm M thuộc  E  . Biết chu vi tam giác MF F bằng 2   1   1 2
18 . Khi đó độ dài trục lớn của  E  bằng A. 6. B. 10. C. 5. D. 3.
Câu 10. Trong mặt phẳng (Oxy) , phương trình nào sau đây là phương trình chính tắc của một elip? 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 7 6 7 6 6 7 6 7
Câu 11. Phương trình chính tắc của  E  có độ dài trục lớn bằng 10 và tiêu cự bằng 6 là: 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1 . D.   1. 5 3 5 3 25 16 25 16 2 2 x y
Câu 12. Có bao nhiêu điểm nguyên (tọa độ đều là số nguyên) nằm trên elip   1 8 2 A.2 B. 3 C. 4 D. 1
Câu 13. Trong mặt phẳng (Oxy) , cho elip (E) có một tiêu điểm là F (3; 0) , một đỉnh trên trục nhỏ là ( B 0;4) .
Phương trình chính tắc của (E) là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 25 9 16 9 25 16 4 1 13 2 2 x y
Câu 14. Cho đường elip   1như hình vẽ bên. 2 2 a b Đường elip đã cho cắt đường thẳng 2 2 y
2a  3b  20 tại bao nhiêu điểm A. 4 B. 3 C. 1 D. 2
Câu 15. Trong mặt phẳng (Oxy) , cho elip có các đỉnh A ( 7
 ;0), B (0;5) . Phương trình chính tắc của (E) là 1 2 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.  1. D.   1. 7 5 49 25 7 5  7  5 2 2 x y
Câu 16. Elip (E) : 
 1 có tiêu cự bằng 6 thì có phương trình chính tắc là 2 a 4 2 2 x y 2 2 x y 2 2 x y 2 2 x y A. (E) :   1. B. (E) :   1. C. (E) :   1. D. (E) :   1. 7 4 169 4 5 4 13 4 2 2 x y
Câu 17. Trong mặt phẳng (Oxy) , cho elip (E) : 
 1 có độ dài trục lớn bằng 4, tiêu cự bằng 2. Phương 2 2 a b
trình nào sau đây là phương trình chính tắc của của (E) ? 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 4 3 2 1 4 1 16 12 2 2 x y
Câu 18. Cho đường elip   1như hình vẽ bên. 2 2 a b
Đường elip đã cho cắt đường tròn 2 2 2 2
x y a  2b  25 tại bao nhiêu điểm A. 4 B. 3 C. 2 D. 1 2 2 x y
Câu 19. Cho E: 
 1 . Một đường thẳng đi qua điểm A2;2 và song song với trục hoành cắt E tại hai 20 16
điểm phân biệt M và N . Tính độ dài MN . A. 3 5. B. 15 2. C. 2 15. D. 5 3.
Câu 20. Trong mặt phẳng (Oxy) , phương trình nào sau đây là phương trình chính tắc của một elip? 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 7 6 7 6 6 7 6 7
Câu 21. Cho elip (E) có hai tiêu điểm là F , F , độ dài các trục lớn là 2a , trục nhỏ là 2b , tiêu cự là 2c và M là 1 2
điểm nằm trên (E) . Khẳng định nào sau đây đúng?
A. MF MF  2b .
B. MF MF  2c . 1 2 1 2
C. MF MF  2a . D. 2 2
MF MF a b . 1 2 1 2
Câu 22. Trong mặt phẳng Oxy , phương trình chính tắc của  E  có tiêu cự bằng 6 và đi qua điểm A5;0 là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1 . B.   1. C.   1 . D.   1. 100 81 15 16 25 9 25 16 2 2 x y
Câu 23. Cho elip  E  : 
 1 và đường tròn C 2 2
: x y  144 . Elip  E và đường tròn C có bao 169 144 nhiêu điểm chung? A. 0. B. 1. C. 2. D. 4.
_______________________________ 14
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P7)
_____________________________________ 2 2 x y Câu 1. Cho đường elip 
 1như hình vẽ bên. Đường elip đã 2 2 a b
cho cắt đường thẳng y  2023x tại bao nhiêu điểm A. 4 B. 3 C. 2 D. 1
Câu 2. Tìm phương trình chính tắc của elip có tiêu cự bằng 6 và trục lớn bằng 10. 2 2 2 2 2 2 2 2 x y x y x y x y A.   1. B.   1. C.   1. D.   1. 25 9 100 81 25 16 25 16
Câu 3. Elip có độ dài trục lớn là 10 và có một tiêu điểm F  3
 ;0 . Phương trình chính tắc của elip là: 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 25 9 100 16 100 81 25 16 2 2 x y
Câu 4. Trong mặt phẳng Oxy , elip  E  : 
 1 có độ dài trục bé bằng 100 64 A. 8. B. 10. C. 16. D. 20.  5   5 3 
Câu 5. Phương trình chính tắc của Elip  E đi qua hai điểm M ; 15   và N  ;  2  là  4   2    2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1 . B.   1 . C.   0 . D.   1. 25 16 25 16 25 16 16 25
Câu 6. Elip có độ dài trục nhỏ là 4 6 và có một tiêu điểm F 5;0 . Phương trình chính tắc của elip là: 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 121 96 101 96 49 24 29 24
Câu 7. Elip có một đỉnh là A5;0 và có một tiêu điểm F 4
 ;0 . Phương trình chính tắc của elip là: 1   2 2 x y 2 2 x y 2 2 x y x y A.   1. B.   1. C.   1. D.   1. 25 16 5 4 25 9 5 4 2 2 x y
Câu 8. Có bao nhiêu điểm nguyên (tọa độ đều là số nguyên) nằm trên elip   1 8 2 A.2 B. 3 C. 4 D. 1
Câu 9. Trong mặt phẳng (Oxy) , cho elip (E) có một tiêu điểm là F (3; 0) , một đỉnh trên trục nhỏ là ( B 0;4) .
Phương trình chính tắc của (E) là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 25 9 16 9 25 16 4 1 2 2 x y Câu 10. Cho đường elip   1như hình vẽ bên. 2 2 a b
Đường elip đã cho cắt đường thẳng 2 2
y  2a  3b 1 tại bao nhiêu điểm A. 1 B. 3 C. 0 D. 2 2 2 x y
Câu 11. Trong mặt phẳng (Oxy) , cho elip (E) : 
 1 có độ dài trục lớn bằng 4, tiêu cự bằng 2. Phương 2 2 a b
trình nào sau đây là phương trình chính tắc của của (E) ? 15 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 4 3 2 1 4 1 16 12 2 2 x y Câu 12. Cho đường elip   1như hình vẽ bên. 2 2 a b
Đường elip đã cho cắt đường tròn 2 2 2 2
x y a b 16 tại bao nhiêu điểm A. 4 B. 3 C. 2 D. 1
Câu 13. Trong mặt phẳng Oxy , cho elip  E có các tiêu điểm F 4
 ;0 , F 4; 0 và một điểm M nằm trên 1   2  
E . Biết rằng chu vi của tam giác MF F bằng 18. Xác định tâm sai e của  E. 1 2 4 4 4 4 A. e  . B. e  . C. e   . D. e  . 5 18 5 9
Câu 14. Phương trình chính tắc của Elip nhận điểm M 4;3 là một đỉnh của hình chữ nhật cơ sở là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 16 9 16 4 16 3 9 4 2 2 x y
Câu 15. Cho elip E: 
 1 với a b  0. Gọi 2c là tiêu cự của E. Trong các mệnh đề sau, mệnh đề nào 2 2 a b đúng? A. 2 2 2
c a b . B. 2 2 2
b a c . C. 2 2 2
a b c . D. c a  . b  5
Câu 16. Elip qua điểm M 2;  
 và có một tiêu điểm F  2
 ;0 . Diện tích hình chữ nhật cơ sở của elip là  3 A. 12 5 B. 24 C. 80 D. 60
Câu 17. Elip (E) có hai tiêu điểm F 2
 ;0 , F 2;0 và đi qua điểm M 2;  3 . Khi đó đường tròn 2 2
x y  16 cắt 1   2  
elip đã cho tại bao nhiêu giao điểm A.2 B. 4 C. 1 D. 3 2
Câu 18. Tìm elip nếu nó đi qua điểm A6;0 và tỉ số của tiêu cự với độ dài trục lớn bằng 2 2 2 x y 2 2 x y 2 2 x y 2 2 x y A. +  1. B.   1. C. +  1. D. +  1. 36 27 6 3 36 18 6 2
Câu 19. Trong mặt phẳng Oxy , cho elip  E  có phương trình 2 2
16x  25y  100 và điểm M thuộc  E  có
hoành độ bằng 2 . Tổng khoảng cách từ M đến 2 tiêu điểm của  E  bằng A. 5 . B. 2 2 . C. 4 3 . D. 3 .
Câu 20. Lập phương trình chính tắc của elip  E  biết  E  có trục lớn bằng 6 và tiêu cự bằng 4 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 36 16 6 4 9 5 5 4 12
Câu 21. Tìm elip có độ dài trục lớn bằng 26 và tỉ số của tiêu cự với độ dài trục lớn bằng . 13 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 26 25 169 25 52 25 169 5
Câu 22. Trong mặt phẳng tọa độ Oxy , Elip có một tiêu điểm F ( 2
 ; 0) và tích độ dài trục lớn với trục bé bằng
12 5 . Phương trình chính tắc của elip là: 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1 B.   1 C.   1 D.   1 144 5 36 20 9 5 45 16
_____________________________ 16
ĐƯỜNG ELLIPSE OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P8)
_____________________________________ 2 2 x y Câu 1. Đường Elip 
 1 có độ dài trục lớn bằng: 16 4 A. 16. B. 8. C. 2. D. 4. 2 2 x y
Câu 2. Tọa độ tiêu điểm với hoành độ âm của đường Elip   1 là 8 4 A. 2;  0 . B. 2 2;0. C. 2 2;0. D.  2  ;0. 2 2 x y Câu 3. Đường Elip   1 có tiêu cự bằng: 9 6 A. 2 3 . B. 3 . C. 3. D. 6.
Câu 4. Hãy xác định các tọa độ tiêu điểm của Elip (E): 2 2
4x  9 y  36 ? A. F  5;0 , F 5;0 .
C. F  5; 5 , F 0; 5 . 1   2  1   2  B. F 5;0 , F 0; 5 . D. F 5; 5 , F  5; 5 . 1   2  1   2 
Câu 5. Phương trình của elip  E  có độ dài trục lớn bằng 8, độ dài trục nhỏ bằng 6 là: A. 2 2
9x  16 y  144. B. 2 2
9x  16 y  1. 2 2 x y 2 2 x y C.   1. D.   1. 9 16 64 36
Câu 6. Tìm phương trình chính tắc của elip nếu trục lớn gấp đôi trục bé và có tiêu cự bằng 4 3 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A. +  1. B.   1. C.   1. D. +  1. 16 4 36 9 36 24 24 16
Câu 7. Lập phương trình chính tắc của elip biết độ dài trục lớn hơn độ dài trục nhỏ 4 đơn vị, độ dài trục nhỏ hơn
độ dài tiêu cự 4 đơn vị. 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 64 60 25 9 100 64 9 1 1
Câu 8. Tìm elip nếu nó đi qua điểm A6;0 và tỉ số của tiêu cự với độ dài trục lớn bằng . 2 2 2 x y 2 2 x y 2 2 x y 2 2 x y A. +  1. B.   1. C. +  1. D. +  1. 36 27 6 3 36 18 6 2 2 2 x y
Câu 9. Trong mặt phẳng Oxy , elip  E  :   1 có tâm sai bằng 25 9 5 4 4 3 A. . B. . C.  . D. . 3 5 5 5
Câu 10. Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng 8 và đi qua điểm M  15;  1 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 12 4 16 4 18 4 20 4 2 2 x y
Câu 11. Trong mặt phẳng Oxy , elip  E   1 có tiêu cự là 16 7 A. 18 . B. 6 . C. 9 . D. 3 . 2 2 x y
Câu 12. Trong mặt phẳng Oxy , cho elip 
 1. Tỷ số giữa tiêu cự và độ dài trục lớn của elip bằng 5 4 3 5 2 5 5 5 A. . B. . C. . D. . 5 5 5 4  5 2
Câu 13. Elip (E) đi qua điểm N 2;    
 và tỉ số của tiêu cự với độ dài trục lớn bằng . Tính độ dài dây cung tạo  3 3
bởi elip đã cho và đường thẳng x = 2. 17 10 8 16 A.3 B. C. D. 3 3 7
Câu 14. Elip (E) có một cạnh nằm trên đường thẳng y = 2 và có độ dài một đường chéo bằng 6. Tìm số giao
điểm của elip đã cho và đường parabol 2
y  2(x  2x) A.4 B. 1 C. 2 D. 3
Câu 15. Tìm phương trình chính tắc của elip nếu nó có trục lớn gấp đôi trục bé và đi qua điểm M (2; 2  ) . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1 B.   1 C.   1 D.   1 36 9 20 5 24 6 16 4  9   12 
Câu 16. Lập phương trình chính tắc của elip  E  biết  E đi qua điểm M 4;   và N 3;   .  5   5  2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 25 9 4 3 9 5 5 4
Câu 17. Trong mặt phẳng Oxy , phương trình chính tắc của  E  có độ dài trục lớn gấp 2 lần độ dài trục nhỏ
và đi qua điểm A2; 2 là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1 . C.   1. D.   1 24 16 36 9 16 4 20 5 2 2 x y
Câu 18. Elíp (E) : 
 1 có độ dài trục lớn bằng: 25 9 A. 25 . B. 50. C. 5. D. 10 .
Câu 19. Phương trình chính tắc của  E có độ dài trục lớn gấp 2 lần độ dài trục nhỏ và đi qua điểm A2; 2   là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1 . B.   1. C.   1. D.   1. 36 9 20 5 24 16 16 4
Câu 20. Trong mặt phẳng với hệ trục tọa độ Oxy , cho elip  E có độ dài trục lớn bằng 12 và độ dài trục bé
bằng 6 . Phương trình nào sau đây là phương trình của elip  E  2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1 . B.   1. C.   1 . D.   0 . 144 36 9 36 36 9 144 36 1
Câu 21. Tìm phương trình chính tắc của Elip có tâm sai bằng và trục lớn bằng 6 . 3 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 9 3 6 5 9 5 9 8
Câu 22. Trong mặt phẳng Oxy , phương trình chính tắc của  E  có độ dài trục lớn gấp 2 lần độ dài trục nhỏ và tiêu cự bằng 4 3 là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1 . B.   1 . C.   1. D.   1. 36 9 36 24 24 6 16 4 2 x
Câu 23. Cho Elip có phương trình 2
y  1. Một tiêu điểm của Elip có tọa độ là : 4 A. B 0; 3 . B. C  5;0 . C. A 3;0 . D. D 0; 5.
Câu 24. Phương trình chính tắc của (E) biết độ dài 2 trục lớn và nhỏ lần lượt là 10 và 8 là: 2 2 x y 2 2 x y A.  1. C.  1. 25 16 16 25 2 2 x y 2 2 x y B.   0 . D.   0 . 16 25 25 16
Câu 25. Lập phương trình chính tắc của elip  E  biết  E có một tiêu điểm F 4;0 và trục lớn bằng 10. 1   2 2 x y 2 2 x y 2 2 x y x y A.   1. B.   1. C.   1. D.   1. 25 16 5 4 25 9 5 4
_____________________________ 18
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P1)
_____________________________________ 2 2 x y
Câu 1. Cho hypebol có phương trình: 
 1. Tiêu cự của hypebol là: 16 12 A. 2 5 . B. 2 3 . C. 4 7 . D. 2 2 .
Câu 2. Gọi tên đường conic tạo bởi mặt cắt và hai khối nón đối xứng trong hình vẽ.
A. Đường tròn B. Parabol C. Hypebol D. Elip
Câu 3. Cho đường hypebol có phương trình  H  2 2
: 9x y  1. Khoảng cách giữa hai tiêu điểm là 10 2 10 A. 0 . B. . C. 2 2 . D. . 3 3 2 2 x y
Câu 4. Trong mặt phẳng tọa độ Oxy ,cho hypepol  H  có phương trình: 
 1. Khi đó độ dài trục lớn 16 9 bằng A. 3. B. 16. C. 8. D. 4.
Câu 5. Hypebol có nửa trục thực là 4 , tiêu cự bằng 10 có phương trình chính tắc là: 2 2 x y 2 2 y x 2 2 y x 2 2 x y A.   1. B.   1. C.   1. D.   1. 16 9 16 9 16 9 16 25
Câu 6. Hypebol (H) đi qua điểm N  10;2và hoành độ một giao điểm của (H) với trục hoành bằng 3. Khoảng
cách giữa hai tiêu điểm hypebol bằng A.6 B. 6 5 C. 8 3 D. 8
Câu 7. Tìm phương trình chính tắc của hyperbol  H  mà hình chữ nhật cơ sở có một đỉnh là 2; 3  . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 2 3  4 9 9 3 2 3 2 2 x y
Câu 8. Cho đường hypebol   1 như hình vẽ bên, 2 2 a b  2 7  hypebol đi qua điểm  4;  . Tính 2 2
a  2b .  3    A. 16 B. 14 C. 17 D. 13 2 2 x y
Câu 9. Đường thẳng nào sau đây là trục đối xứng của hypebol   1. 4 9 A. y  0 B. x  1 C. x  2 D. x  1  2 2 x y
Câu 10. Điểm M thuộc hypebol 
 1.Tính MF MF với F , F là hai tiêu điểm của hypebol. 16 9 1 2 1 2 A.4 B. 8 C. 10 D. 6
Câu 11. Trong mặt phẳng tọa độ Oxy , cho hypebol  H  có một tiêu điểm là F (6; 0) và đi qua điểm M 4;0 . 2
Phương trình chính tắc của  H  đó là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 20 16 16 20 20 16 16 20
Câu 12. Trong mặt phẳng tọa độ Oxy , cho hypebol  H  có tiêu cự bằng 26 , hiệu các khoảng cách từ một 19
điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng 24 . Phương trình chính tắc của  H  đó là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1 . B.   1. C.   1. D.   1  . 144 25 25 144 144 25 144 25 2 2 x y
Câu 13. Cho đường hypebol   1 như hình vẽ bên, 2 2 a b  2 7  hypebol đi qua điểm  4;
. Đường hypebol đã cho cắt  3   
đường phân giác góc phần tư thứ nhất tại bao nhiêu điểm A. 2 B. 3 C. 0 D. 1
Câu 14. Hai tiêu điểm của hypebol 2 2
9x 16 y  144 đều cách gốc tọa độ một khoảng bằng A.4 B. 5 C. 6 D. 3 2 2 x y
Câu 15. Đường thẳng nào sau đây là trục đối xứng của hypebol   1 25 144 A. x  0 B. x  1 C. x  2 D. x  1  2 2 x y
Câu 16. Điểm M ( ; x y) thuộc hypebol 
 1. Giá trị nhỏ nhất của biểu thức 2
Q x y thuộc khoảng 16 9 A.(0;5) B. (17;22) C. (5;10) D. (10;17)
Câu 17. Trong mặt phẳng Oxy, viết phương trình chính tắc của hypebol  H  biết  H  có một tiêu điểm là
F 3; 0 và cắt trục hoành tại điểm có hoành độ bằng 2  . 2   2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 4 5 4 1 4 1 4 5 2 2 x y
Câu 18. Mọi điểm M trên hypebol 
 1đều cách gốc tọa độ một khoảng nhỏ nhất bằng 25 144 A.4 B. 5 C. 6 D. 3 2 2 x y
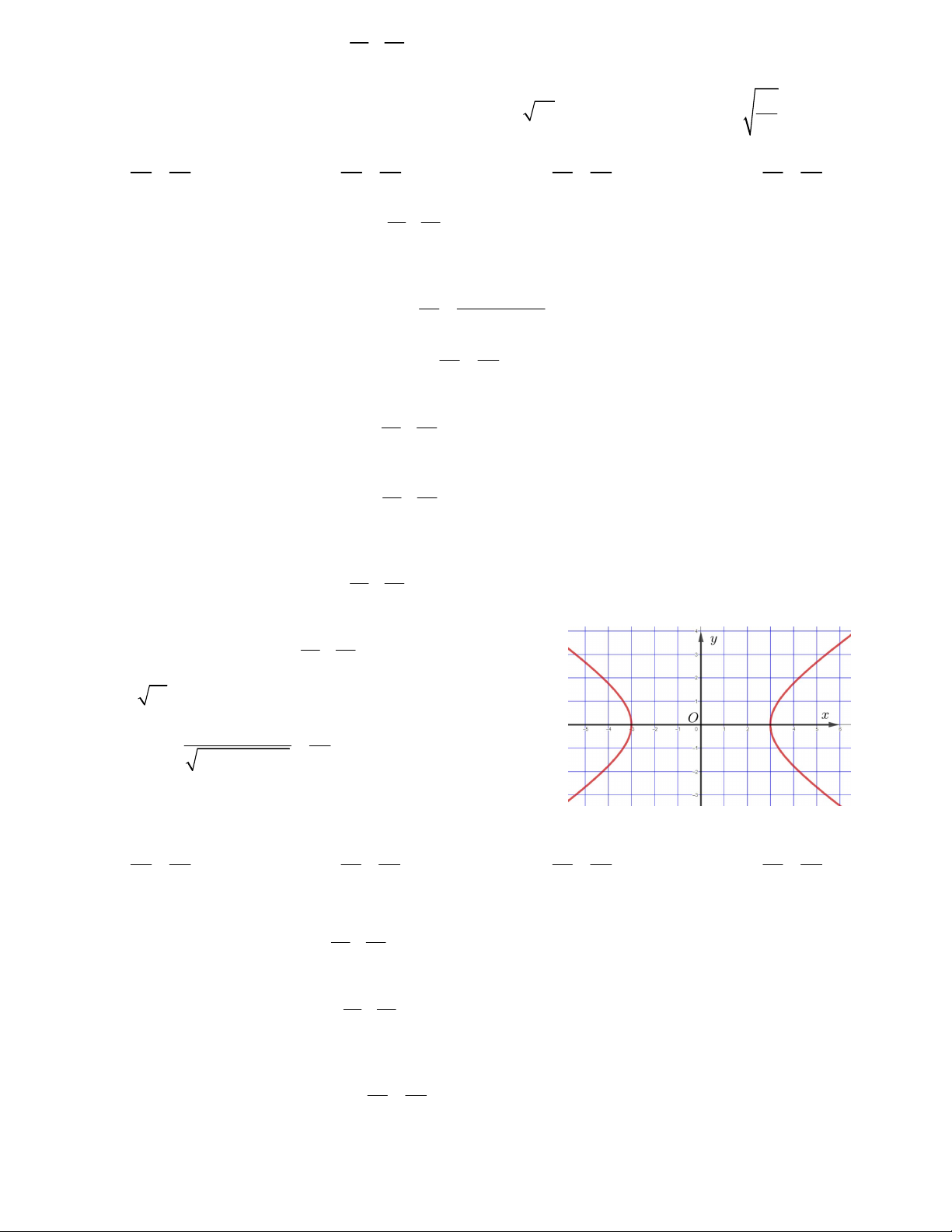
Câu 19. Tìm số giao điểm của hypebol   1.và đường tròn 2 2 x y  9 . 16 9 A.3 B. 1 C. 2 D. 0 2 2 x y
Câu 20. Đường thẳng nào dưới đây là đường chuẩn của hyperbol   1? 16 12 3 8 7 A. x   0 . B. x  2  0 . C. x  8  0 . D. x   0 . 4 7 2 2 x y
Câu 21. Đường hyperbol   1 có tiêu cự bằng: 20 16 A. 12. B. 2. C. 4. D. 6.
Câu 22. Tiêu cự của hypebol 2 2
7x  9 y  63 bằng A.8 B. 6 C. 4 D. 10 2 2 x y
Câu 23. Có bao nhiêu số nguyên dương m nhỏ hơn 10 để hypebol 
 1và đường thẳng y x m có 20 16 điểm chung A.3 B. 4 C. 8 D. 7 2 2 x y 2 x
Câu 24. Tìm số giao điểm của hypebol   1.và đường elip 2  y  1. 16 9 16 A.3 B. 1 C. 2 D. 0
_________________________________ 20
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P2)
_____________________________________ 2 2 x y
Câu 1. Cho hypebol (H ) có phương trình chính tắc 
 1. Tìm tọa độ các giao điểm của (H ) với trục 9 16 hoành A.  9  ; 0 và 9; 0 . B.  3  ; 0 và 3; 0 . C.  4  ; 0 và 4; 0 . D.  1  6; 0 và 16; 0 . 2 2 x y
Câu 2. Tìm số giao điểm của hypebol   1.và đường elip 2 2
x  25 y  1. 16 9 A.3 B. 1 C. 2 D. 4 2 2 x y
Câu 3. Cho hypebol  H  có phương trình chính tắc 
 1. Tìm tọa độ điểm thuộc  H  có hoành độ bằng 9 16 4 và tung độ âm.  4 7   7   8 7   2 7  A.  4;   . B.  4;  . C.  4;  .  4;  .    D.  3          3   3   3   2 2 x y
Câu 4. Cho đường hypebol   1 như hình vẽ bên. 2 2 a b  2 7  hypebol đi qua điểm  4;
 . Có bao nhiêu giá trị m để  3   
đường thẳng y m tiếp xúc hypebol đã cho A. 4 B. 3 C. 2 D. 1 2 2 x y
Câu 5. Điểm M thuộc nhánh phải hypebol 
 1cách tiêu điểm bên trái một khoảng nhỏ nhất bằng 25 144 A.14 B. 18 C. 16 D. 13 2 2 x y
Câu 6. Tìm số giao điểm của hypebol   1.và đường tròn 2 2
x y  16 . 16 9 A.3 B. 1 C. 2 D. 0 2 2 x y
Câu 7. Đường hyperbol   1. có tiêu cự bằng: 16 9 A. 12. B. 2. C. 10. D. 6. 2 2 x y
Câu 8. Có bao nhiêu số nguyên dương m nhỏ hơn 20 để hypebol 
 1.và đường thẳng y x m có 16 9 điểm chung A.13 B. 14 C. 16 D. 17 2 2 x y 2 2 x y
Câu 9. Tìm số giao điểm của hai hypebol   1.và   1. 16 9 9 4 A.3 B. 1 C. 2 D. 4 2 2 x y
Câu 10. Cho hypebol  H  có phương trình chính tắc 
 1. Tìm tọa độ điểm thuộc  H  có hoành độ, 9 16
tung độ dương và cách đều hai trục tọa độ.  12 12   12 7 12 7   12 12   12 5 12 5  A. ;   . B.  ;  . C. ;   . D.  ;  .  7 7      7 7    5 5  5 5   2 2 x y
Câu 11. Cho đường hypebol có phương trình chính tắc sau:  H  : 
 1. Điểm nào sau đây không nằm 16 9 trên đường hypebol? A. Q 4;0 . B. N  4  2;3 . C. P 4;0 . D. M 3  ;1 . 21 2 2 x y Câu 12. Trên hypebol 
 1.có bao nhiêu điểm có tọa độ nguyên 16 9 A.3 B. 2 C. 1 D. 4 2 2 x y
Câu 13. Cho đường hypebol 
 1 như hình vẽ bên. Khoảng 4 1
cách ngắn nhất giữa hai nhánh của hypebol bằng A. 2 B. 3 C. 4 D. 1
Câu 14. Đường hypebol nào có tiêu điểm nằm trên đường tròn 2 2 x y  25 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 B.  H  :   1 C. (H ) :   1 D. (H ) :   1 16 9 16 20 25 1 25 9 2 2 x y
Câu 15. Cho đường hypebol có phương trình chính tắc sau:  H  : 
 1. Giao điểm của đường hypebol 25 9 với trục hoành là:
A. A 5; 0; B 5; 0 .
B. M 0;5, N 0; 5 .
C. P 0;3, Q 0; 3 .
D. C 3; 0, D 3; 0 . 2 2 x y
Câu 16. Tồn tại bao nhiêu điểm M thuộc  H  : 
 1sao cho khoảng cách từ M đến trục hoành bằng 16 20
khoảng cách từ M đến trục tung. A.3 B. 2 C. 4 D. 1 2 2 x y
Câu 17. Cho đường hypebol   1như hình vẽ, điểm 9 4 M ( ;
x y) thuộc hypebol thì (2x  3y)(2x  3y) bằng A. 40 B. 24 C. 36 D. 18 2 2 x y
Câu 18. Cho đường hypebol có phương trình 
 1 . Khoảng cách giữa hai tiêu điểm là 25 9 A. 0 . B.10. C. 2 2 . D. 2 34 . 2 2 x y
Câu 19. Tìm số giao điểm tối đa của hypebol   1 và đường tròn 2 2 2 x y  25  m . 25 9 A.3 B. 2 C. 3 D. 0
Câu 20. Tồn tại hai đường thẳng song song và cách trục hoành một khoảng bằng 2, hai đường thẳng này cắt 2 2 x y hypebol 
 1 tại tổng số bao nhiêu giao điểm 25 144 A.2 B. 3 C. 4 D. 5
Câu 21. Đường hypebol nào có tiêu điểm có thể nằm trên đường tròn 2 2 2
x y  36  m 2 2 x y 2 2 x y A.   1 B.   1 25 16 25 4 2 2 x y 2 2 x y C.   1 D.   1 25 49 2 2 m 15 n  26 2 2 x y
Câu 22. Đường tròn tiếp xúc với cả hai nhánh của hypebol  H  : 
 1có đường kính nhỏ nhất bằng 16 20 A.12 B. 10 C. 6 D. 8
_________________________________ 22
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P3)
_____________________________________ 2 2 x y
Câu 1. Điểm nào sau đây thuộc phương trình đường hypebol   1? 2 2 4 3 A. M 4;3 . B. M 4;2 . C. M 4;0 . D. M 4;  1 .
Câu 2. Hypebol nào sau đây có trọng tâm là trọng tâm ABC với ( A 16;5), B( ;
m 8), C(m 1; 13  ) ? 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1 . C.  H  :   1 . D.  H  2 2
:4x y  1. 9 16 4 5 2 1 2 2 x y
Câu 3. Cho Hypebol  H  có phương trình 
 1.Các điểm M   H  có tung độ bằng 3 là 16 3
A. M 8; 3, M '8;3 .
B. M 8 ;3, M '8;3 .
C. M 3;8, M '8; 3 .
D. M 8; 3, M '8; 3 . 2 2 x y 2 x
Câu 4. Tìm số giao điểm của hypebol   1.và đường elip 2  y  1. 16 9 16 A.3 B. 1 C. 2 D. 0
Câu 5. Hypebol nào sau đây có đỉnh bên phải là tâm đường tròn 2 2 2
x y  4x m  9 ? 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1 . C.  H  :   1 . D.  H  2 2
:4x y  1. 9 16 4 5 2 1 2 2 x y
Câu 6. Cho hypebol có phương trình chính tắc 
 1. Tiêu điểm của hypebol là 16 9 A. F 2  5;0 và F 25;0 . B. F 5  ;0 và F 5;0 . 2   1   2   1  
C. F  337;0 và F 337;0 . D. F 3  37;0 và F 337;0 . 2   1   2   1   2 2 x y
Câu 7. Cho đường hypebol 
 1 có hình chữ nhật cơ sở 2 2 a b
mô tả như hình vẽ bên. Biết hình chữ nhật có diện tích bằng 8 5 và có một đỉnh nằm trên đường tròn 2 2
x y  4x  4 y  4  0 . Tính 2 2 a  3b . A. 20 B. 30 C. 19 D. 15 2 2 x y
Câu 8. Cho hypebol có phương trình chính tắc 
 1 và điểm M thuộc hypebol. Khi đó MF MF bằng 4 25 1 2 A. 4 . B. 8 . C. 6 . D. 10 .
Câu 9. Tìm phương trình chính tắc của hyperbol  H  mà một đỉnh nằm trên đường tròn 2 2
x y  6x  4 y  9  0 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1 . C.  H  :   1 . D.  H  2 2 :4x y  1 9 16 4 5 2 1 2 2 x y
Câu 10. Hypebol  H  : 
 1 có hai tiêu điểm là 25 9 A. F 4  ; 0 , F 4; 0 B. F 3  ; 0 , F 3; 0 . 1   2   1   2   C. F 5  ; 0 , F 5; 0 .
D. F  34; 0 , F 34; 0 . 1   2   1   2  
Câu 11. Điểm F 3; 0 là một tiêu điểm của hypebol có phương trình nào sau đây? 2   2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1 . C.  H  :   1 . D.  H  2 2
:4x y  1. 9 16 4 5 2 1 23
Câu 12. Trong mặt phẳng tọa độ Oxy , cho hypebol  H  có tiêu cự bằng 10, hiệu các khoảng cách từ một
điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng 6. Phương trình chính tắc của  H  đó là 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1 . C.  H  :   1 . D.  H  2 2
:4x y  1. 9 16 4 5 2 1 2 2 x y
Câu 13. Cho hypebol có phương trình chính tắc 
 1 và điểm M thuộc hypebol. Khi đó giá trị 2 a  2a  5 9
nhỏ nhất của biểu thức MF MF bằng 1 2 A. 4 . B. 8 . C. 6 . D. 10 . 2 2 x y
Câu 14. Cho đường hypebol 
 1 có hình chữ nhật cơ sở 16 9
mô tả như hình vẽ bên. Chu vi hình chữ nhật cơ sở dài hơn tiêu
cự một khoảng bằng bao nhiêu đơn vị độ dài A. 20 B. 14 C. 18 D. 15 2 2 x y
Câu 15. Hypebol nào sau đây tiếp xúc với đường elip  E  :   1 9 4 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1 . C.  H  :   1 . D.  H  2 2
:4x y  1. 9 16 4 5 2 1
Câu 16. Trong các phương trình sau, phương trình nào là phương trình chính tắc của hypebol? 2 2 x y 2 2 x y 2 2 y x A.   1. B. 2 y  2x . C.   1. D.   1. 16 9 16 9 16 9
Câu 17. Hypebol  H  có một tiêu điểm F 10;0 và đi qua điểm A8; 0 có phương trình chính tắc là 2   2 2 y x 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1 . C.   1. D.   1 . 64 36 64 36 16 9 64 36 2 2 x y
Câu 18. Điểm M ( ; x y) thuộc hypebol 
 1. Giá trị nhỏ nhất của biểu thức 2
Q x y thuộc khoảng 16 9 A.(0;5) B. (17;22) C. (5;10) D. (10;17)
Câu 19. Trong mặt phẳng tọa độ Oxy , cho hypebol  H  có một tiêu điểm là F (6; 0) và đi qua điểm 2 5;0 . 2
Phương trình chính tắc của  H  đó là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 20 16 16 20 20 16 16 20 2 2 x y
Câu 20. Hyperbol  H  
 1 có một tiêu điểm F 4
 ;0 và độ dài trục ảo ( 2b ) bằng 28 là 1   2 2 a b 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 9 7 9 7 3 7 3 7
Câu 21. Đường hypebol nào có tiêu điểm có thể nằm trên đường tròn 2 2 2
x y  36  m 2 2 x y 2 2 x y A.   1 B.   1 25 16 25 4 2 2 x y 2 2 x y C.   1 D.   1 25 49 2 2 m 15 n  26
Câu 22. Phương trình chính tắc của Hyperbol  H  có một tiêu điểm F 5;0 và độ dài trục thực bằng 8 là 2   2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1.. C.   1. D.   0. 16 9 4 3 16 9 16 9
_________________________________ 24
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P4)
_____________________________________
Câu 1. Cho đường hypebol có phương trình  H  2 2
: 9x y  1. Khoảng cách giữa hai tiêu điểm là 10 2 10 A. 0 . B. . C. 2 2 . D. . 3 3 2 2 x y
Câu 2. Đường hypebol 
 1có độ dài trục thực bằng 10 và độ dài trục ảo bằng 8. Tính 2 2 a  3b . 2 2 a b A.73 B. 70 C. 45 D. 60 2 2 x y
Câu 3. Hypebol nào có tiêu điểm trùng với tiêu điểm của elip  E  :   1 ? 16 9 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1. C.  H  :   1. D.  H  :   1. 25 9 9 16 4 3 9 25 2 2 x y
Câu 4. Cho đường hypebol 
 1 có hình chữ nhật cơ sở 2 2 a b
mô tả như hình vẽ bên. Biết hình chữ nhật có 25% diện tích
bằng 2 5 . Tìm giá trị nhỏ nhất của biểu thức 2 2
a  4b . A. 2 5 B. 4 5 C. 8 5 D. 15 2 2 x y
Câu 5. Độ dài giữa hai đỉnh (trục lớn) của hypebol 
 1.bằng đường kính đường tròn nào 4 12 2  3  25 A. 2 x y    
B. x   y  2 2 1  9  2  4 2 2 2  1 
C.  x  3   y  2  4 D. 2 x y   16    2  2 2 x y
Câu 6. Cho đường hypebol 
 1 như hình vẽ bên. Khoảng cách 9 5
ngắn nhất giữa hai nhánh của hypebol bằng A. 8 B. 3 C. 6 D. 4 2 2 x y
Câu 7. Cho hypebol (H ) có phương trình chính tắc 
 1. Tìm tọa độ các giao điểm của (H ) với trục 9 16 hoành A.  9  ; 0 và 9; 0 . B.  3  ; 0 và 3; 0 . C.  4  ; 0 và 4; 0 . D.  1  6; 0 và 16; 0 .
Câu 8. Phương trình chính tắc của hyperbol  H  có một tiêu điểm F 4
 ; 0 và đi qua điểm M 2;0 là 1   2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.  1. 4 12 2 12 4 12 2 2 3 2  3  25
Câu 9. Hypebol nào sau đây có hai đỉnh đều nằm trên đường tròn 2 x y      2  4 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1. C.  H  :   1. D.  H  :   1. 25 9 25 16 4 25 9 25 25 2 2 x y
Câu 10. Tìm số giao điểm của hypebol 
 1và đường thẳng y x  3 . 4 1 A.2 B. 1 C. 3 D. 5  99 
Câu 11. Phương trình của hypebol  H  có một tiêu điểm F  34;0 và đi qua điểm A 6 ; là ? 1    25   2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1. C.  H  :   1. D.  H  :   1. 25 9 25 16 16 25 9 25 2 2 x y
Câu 12. Cho điểm M ( ; x y) thuộc hypebol 
 1. Giá trị nhỏ nhất của biểu thức 2 2
Q x y y thuộc 4 12 khoảng A.(3;4) B. (4;5) C. (5;6) D. (6;7) 2 2 x y
Câu 13. Tính tổng các giá trị m để hypebol  H  : 
 1có tiêu điểm trùng với tiêu điểm của elip 2 4 m  6m 1 2 2 x yE :   1 . 16 9 A.4 B. 2 C. 5 D. 6 2 2 x y
Câu 14. Cho hypebol  H  có phương trình 
 1. Số các điểm M   H  có tọa độ nguyên là 9 4 A. 2 . B. 0 . C. 4 . D. 3 . 2 2 x y
Câu 15. Tồn tại bốn điểm M thuộc  H  : 
 1sao cho khoảng cách từ M đến trục hoành bằng nửa 16 20
khoảng cách từ M đến trục tung. Bốn điểm M này đều cách gốc tọa độ O một khoảng bằng A.3 B. 6 C. 4 D. 5 2 2 x y
Câu 16. Tìm số giao điểm của hypebol   1.và đường tròn 2 2
x y  16 . 16 9 A.3 B. 1 C. 2 D. 0 2 2 x y
Câu 17. Cho đường hypepol 
 1như hình bên, tiêu cự 2 2 a b
bằng 2 13 . Có bao nhiêu cặp số (m;n) để hypebol đã cho tiếp 2 2 x y xúc elip  E  :   1. 2 2 4 81 m n A. 4 B. 3 C. 2 D. 1 Câu 18. Cho (
A 0; 4), B(10; 4) . Hypebol nào có hai tiêu điểm là hai đỉnh liên tiếp của hình bình hành ABF F 2 1 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1. C.  H  :   1. D.  H  :   1. 25 9 9 16 16 25 9 25
Câu 19. Tồn tại bao nhiêu cặp số nguyên (m;n) với n  20 để trên đường tròn 2 2
(x m)  ( y m  4)  n có 2 2 x y
thể tồn tại hai tiêu điểm của hypebol   1 2 2 a b A.8 B. 4 C. 3 D. 6 2 2 x y
Câu 20. Điểm M ( ; x y) thuộc hypebol 
 1. Giá trị nhỏ nhất của biểu thức 2 2
T x  2 y x  2023 thuộc 4 12 khoảng A.(1954;1975) B. (1975;1986) C. (1986;2000) D. (2000;2023) 2 2 x y
Câu 21. Tâm đối xứng của hypebol  H  :   1có tung độ bằng 9 16 A.3 B. 2 C. 1 D. 0
_________________________________ 26
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P5)
_____________________________________
Câu 1. Trong mặt phẳng tọa độ Oxy , cho hypebol  H  có một tiêu điểm là F (6; 0) và đi qua điểm 2 5;0 . 2
Phương trình chính tắc của  H  đó là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 20 16 16 20 20 16 16 20 2 2 x y Câu 2. Cho hypebol 
 1. Độ dài ngắn nhất của tiêu cự hypebol đã cho bằng 2 2 a  9 a  4a  9 A.8 B. 10 C. 12 D. 14  3 
Câu 3. Xét điểm M ; cot a
 với sin a  0 , tập hợp các điểm M là hypebol có tiêu cự bằng  sin a  A.6 B. 8 C. 2 10 D. 4 5 2 2 x y
Câu 4. Cho đường hypebol 
 1 như hình vẽ bên (có 2 2 a b
tiêu cự F F ) thỏa mãn MF MF  6 , tam giác NA A là 1 2 1 2 1 2
tam giác vuông cân. Tính diện tích tam giác NA A . 1 2 A. 12 B. 8 C. 9 D. 10
Câu 5. Hypebol nào sau đây có đỉnh nào đó nằm trên đường thẳng x y  5 và tiêu điểm nào đó nằm trên đường tròn 2 2
x y  41 ? 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1. C.  H  :   1. D.  H  :   1. 25 9 25 16 16 25 9 25 2 2 x y
Câu 6. Điểm M ( ;
x y) là giao điểm của hypebol   1.và đường elip 2 2
2x  5 y  32 . Tính 2 2 x y . 16 9 A.20 B. 16 C. 30 D. 25 2 2 x y
Câu 7. Đường hypebol 
 1có độ dài trục thực bằng 12 và độ dài trục ảo bằng 6. Tính 2 2 a  3b . 2 2 a b A.63 B. 50 C. 56 D. 48 2 2 x y
Câu 8. Cho đường hypebol 
 1 có hai đỉnh nằm trên đồ 2 2 a b 1 thị hàm số bậc hai 2 f (x) 
x  (d  5)x  4 như hình vẽ. Tính 4 2 2 a d . A. 60 B. 72 C. 61 D. 69 2 2 x y
Câu 9. Điểm M thuộc hypebol 
 1 . Tìm giá trị nhỏ nhất của MF MF với F , F là hai tiêu điểm của 2 a  9 9 1 2 1 2 hypebol. A.4 B. 8 C. 10 D. 6 2 2 x y Câu 10. Hypebol 
 1có hai tiêu điểm thuộc đồ thị hàm số bậc hai 2
f (x)  x  (d  4)x 16 . Tính giá trị 2 2 a b của biểu thức 2 2 2 2
a b c d với 2c là tiêu cự của elip. A.22 B. 30 C. 36 D. 48 2 2 x y Câu 11. Hypebol 
 1có một đỉnh trùng với đỉnh của đồ thị hàm số 2
f (x)  x  8x m n . Tính giá trị của 2 2 a b biểu thức 2
a  4m  4n . 27 A.90 B. 80 C. 76 D. 69 2 2 x y
Câu 12. Cho đường hypebol 
 1với a  0;b  0 có hình 2 2 a b
chữ nhật cơ sở mô tả như hình vẽ bên. Biết hình chữ nhật có
diện tích bằng 48 (đvdt) và có chu vi bằng 32 (đvđd). Tìm giá trị
nhỏ nhất của biểu thức 2
a b . A. 38 B. 28 C. 10 D. 30 2 2 2 2 2 2 2 2 x y x y x y x y
Câu 13. Cho các hypebol  H :   1; H :   1 H :   1 H :   1. 1   2   3   4  25 9 16 2 4 3 9 10 2 2 x y
Có bao nhiêu hypebol có tiêu điểm nằm phía bên trong đường elip  E  :   1. 20 9 A.1 B. 2 C. 3 D. 4
Câu 14. Hypebol nào sau đây có đỉnh nào đó nằm trên giao điểm của hai đường tròn 2 2 2 2
x y  4; (x  5)  y  9 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  H  :   1. B.  H  :   1. C.  H  :   1. D.  H  :   1. 4 1 25 16 16 25 9 25 2 2 x y Câu 15. Cho hypebol 
 1 . Độ dài ngắn nhất của tiêu cự hypebol đã cho bằng 2 2 a  9 b 16 A.8 B. 10 C. 12 D. 14 2 2 x y
Câu 16. Tìm số giao điểm của hypebol   1.và đường tròn 2 2
x y  15 . 16 9 A.3 B. 4 C. 2 D. 0 2 2 x y
Câu 17. Điểm M ( ; x y) thuộc hypebol   1 4 8
Giá trị nhỏ nhất của biểu thức 2 2
T x y  4x  2022 thuộc khoảng A.(1954;1975) B. (1975;1986) C. (1986;2000) D. (2000;2020) 2 2 x y
Câu 18. Cho đường hypebol   1 như hình vẽ bên. 2 2 a b
Điểm M thuộc nhánh phải hypebol thỏa mãn
MF MF  6; 2MF MF  18 1 2 1 2
Tính MF  3MF . 1 2 A. 12 B. 30 C. 14 D. 18 2 2 x y
Câu 19. Cho hypepol  H  có phương trình: 
 1Khi đó độ dài trục lớn bằng 36 9 A. 3. B. 16. C. 12 D. 4.
Câu 20. Hypebol có nửa trục thực là 4 , tiêu cự bằng 2 41 có phương trình chính tắc là: 2 2 x y 2 2 y x 2 2 y x 2 2 x y A.   1. B.   1. C.   1. D.   1. 16 9 16 9 16 9 16 25
_________________________________ 28
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P6)
_____________________________________ 2 2 x y
Câu 1. Cho đường hypebol   1 như hình vẽ bên. 2 2 a b
Tứ giác trong hình vẽ là hình vuông. Tính 2 2
a b . A. 40 B. 25 C. 32 D. 36
Câu 2. Hypebol nào sau đây có đỉnh nào đó nằm trên đường thẳng x y  5 và tiêu điểm nào đó nằm trên đường tròn 2 2
x y  34 ? 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1. C.  H  :   1. D.  H  :   1. 25 9 25 16 16 25 9 25 2 2 x y
Câu 3. Điểm M ( ;
x y) là giao điểm của hypebol   1.và đường tròn 2 2
x y  20 . Tính 2 2 3x  2 y . 16 9 A.20 B. 18 C. 40 D. 25 2 2 x y
Câu 4. Đường hypebol 
 1có độ dài trục thực bằng 8 và độ dài trục ảo bằng 6. Tính 2 2 a  3b . 2 2 a b A.43 B. 50 C. 45 D. 36 2 2 x y
Câu 5. Cho đường hypebol 
 1 có hai đỉnh nằm trên đồ 2 2 a b 1 thị hàm số bậc hai 2 f (x) 
x  (d  9)x  3 như hình vẽ. Tính 3 2 2 a d . A. 80 B. 70 C. 90 D. 69 2 2 x y Câu 6. Hypebol 
 1có một đỉnh trùng với đỉnh của đồ thị hàm số 2
f (x)  x  4x m n . Tính giá trị của 2 2 a b biểu thức 2
a  4m  4n . A.30 B. 32 C. 36 D. 40 2 2 2 2 2 2 2 2 x y x y x y x y
Câu 7. Cho các hypebol  H :   1; H :   1 H :   1 H :   1. 1   2   3   4  25 9 16 4 4 3 9 25 2 2 x y
Có bao nhiêu hypebol có tiêu điểm nằm phía bên trong đường elip  E  :   1. 20 9 A.1 B. 2 C. 3 D. 4 2 2 x y
Câu 8. Cho đường hypebol 
 1 có hình chữ nhật cơ sở 2 2 a b
mô tả như hình vẽ bên. Biết hình chữ nhật có diện tích bằng 32.
Tìm giá trị nhỏ nhất của biểu thức 2 2
a  9b . A. 8 2 B. 4 5 C. 48 D. 30 2 2 x y
Câu 9. Điểm M ( ; x y) thuộc hypebol   1. 4 6
Giá trị nhỏ nhất của biểu thức 2 2
T x y  8x  2023 thuộc khoảng 29 A.(1954;1975) B. (1975;1986) C. (1986;2000) D. (2000;2020) 2 2 x y 1
Câu 10. Tồn tại bốn điểm M thuộc  H  : 
 1sao cho khoảng cách từ M đến trục hoành bằng 16 20 5
khoảng cách từ M đến trục tung. Bốn điểm M này đều cách gốc tọa độ O một khoảng gần bằng A.3,86 B. 5,26 C. 5,12 D. 4,14
Câu 11. Tồn tại bao nhiêu cặp số nguyên (m;n) với n  40 để trên đường tròn 2 2
(x m)  ( y m  5)  n 1có 2 2 x y
thể tồn tại hai đỉnh của hypebol   1 2 2 a b A.18 B. 13 C. 14 D. 12 2 2 x y Câu 12. Hypebol 
 1có hai tiêu điểm thuộc đồ thị hàm số bậc hai 2
f (x)  x  (d  2)x  9 . Tính giá trị 2 2 a b của biểu thức 2 2 2 2
a b c d với 2c là tiêu cự của elip. A.22 B. 30 C. 36 D. 29 2 2 x y
Câu 13. Hypebol nào có hai đỉnh trùng với tiêu điểm của elip  E  :   1 ? 16 7 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1. C.  H  :   1. D.  H  :   1. 25 9 16 4 4 3 9 25 2 2 2 2 2 2 2 2 x y x y x y x y
Câu 14. Cho các hypebol  H :   1; H :   1 H :   1 H :   1. 1   2   3   4  25 9 16 4 25 16 18 25 2 2 x y
Có bao nhiêu hypebol có đỉnh nằm phía bên trong đường elip  E  :   1. 40 9 A.1 B. 3 C. 2 D. 4 2 2 x y
Câu 15. Tìm số giao điểm của hypebol   1.và đường tròn 2 2
x y  696 . 16 9 A.3 B. 4 C. 2 D. 0 2 2 x y
Câu 16. Điểm M ( ; x y) thuộc hypebol   1. 4 12
Giá trị nhỏ nhất của biểu thức 2 2
T x  6 y  4x  2023thuộc khoảng A.(1954;1975) B. (1975;1986) C. (1986;2000) D. (1945;1954) 2 2 x y
Câu 17. Đường hypepol 
 1.(có tiêu cự F F )và 4 12 1 2 đường parabol 2
y  2 px ( p  0) có hai tiêu điểm nào đó
trùng nhau. Tính giá trị biểu thức F F p . 1 2 A.10 B. 12 C. 15 D. 14 2 2 2 2 x y x y
Câu 18. Điểm M ( ;
x y) là giao điểm của các hypebol  H :   1; H :   1. Khi đó 1   2  25 9 16 4 x x x x A.  1; 2 B.  0  ;1 C.  2;3 D.  4;6 y y y y 2 2 x y
Câu 19. Trục đối xứng của hypebol  H  : 
 1không song song với đường thẳng nào 9 16 A. y  2023 B. x  2022 C. x  2021  D. y  2020x 2 2 x y
Câu 20. Điểm M ( ;
x y) là giao điểm của hypebol   1và đường tròn 2 2
x y  1. Tính giá trị 2 2 a b 2 2 2 2 2 2
(b  2)x  (2  a ) y a b . A.4 B. 2 C. 5 D. 3 30
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P7)
_____________________________________
Câu 1. Hypebol nào sau đây có đỉnh nào đó nằm trên đường thẳng x y  5 và tiêu điểm nào đó nằm trên đường tròn 2 2
x y  41 ? 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1. C.  H  :   1. D.  H  :   1. 25 9 25 16 16 25 9 25 2 2 x y
Câu 2. Cho đường hypebol 
 1 có hai tiêu điểm như 2 2 a b
hình vẽ, tam giác trong hình vẽ là tam giác đều. Giá trị của biểu thức 4 4 2 2
a b  2a b gần nhất với A. 22,4 B. 23,5 C. 21,3 D. 20,5 2 2 x y Câu 3. Hypebol 
 1có một đỉnh trùng với đỉnh của đồ thị hàm số 2
f (x)  2x  8x m n . Tính giá trị 2 2 a b của biểu thức 2
a  4m  4n . A.30 B. 32 C. 36 D. 40 2 2 x y
Câu 4. Điểm M ( ;
x y) là giao điểm của hypebol   1.và đường tròn 2 2
x y  17 . Tính 2 2 3x  2 y . 16 9 A.34,6 B. 49,2 C. 40,5 D. 38,5 2 2 x y
Câu 5. Tìm giá trị nguyên nhỏ nhất của m để đường tròn 2 2
x y m cắt hypebol   1. 16 4 A.18 B. 16 C. 20 D. 24 2 2 x y
Câu 6. Đường hypebol 
 1có độ dài trục thực bằng 10 và độ dài trục ảo bằng 6. Tính 2 2 a  3b . 2 2 a b A.52 B. 50 C. 45 D. 36 2 2 x y
Câu 7. Cho đường hypebol 
 1 có hai đỉnh nằm trên đồ 2 2 a b 1 thị hàm số bậc hai 2 f (x) 
x  (d  9)x  3 như hình vẽ. Tính 3 2 2 a d . A. 80 B. 70 C. 90 D. 69 2 2 2 2 2 2 2 2 x y x y x y x y
Câu 8. Cho các hypebol  H :   1; H :   1 H :   1 H :   1. 1   2   3   4  25 9 16 4 4 3 9 25 2 2 x y
Có bao nhiêu hypebol có đỉnh nằm phía bên trong đường elip  E  :   1. 20 4 A.1 B. 2 C. 3 D. 4 2 2 2 2 2 2 2 2 x y x y x y x y
Câu 9. Cho các hypebol  H :   1; H :   1 H :   1 H :   1. 1   2   3   4  25 9 16 4 4 3 9 25
Hypebol nào có đỉnh nào đó gần nhất với tâm đường tròn 2 2
(x  5)  ( y  3)  1 . 2 2 x y 2 2 x y A.  H :   1 B.  H :   1 2  1  25 9 16 4 2 2 x y 2 2 x y C.  H :   1 D.  H :   1 4  3  4 3 9 25 31 2 2 x y
Câu 10. Điểm M ( ; x y) thuộc hypebol   1. 4 2
Giá trị nhỏ nhất của biểu thức 2 2
T x y  8x  2023 thuộc khoảng A.(1954;1975) B. (1975;1986) C. (1986;2000) D. (2000;2020) 2 2 x y
Câu 11. Điểm M có hoành độ bằng 8 thuộc hypebol  H  : 
 1thì có các khoảng cách tới hai tiêu điểm 16 9 bằng A.6 và 14 B. 5 và 13 C. 4 và 12 D. 7 và 15 2 2 2 2 x y x y
Câu 12. Điểm M ( ;
x y) là giao điểm của các hypebol  H :   1; H :   1. Khi đó 1   2  25 16 9 4 x x x x A.  1; 2 B.  0  ;1 C.  2;3 D.  4;6 y y y y 2 2 x y
Câu 13. Có bao nhiêu số nguyên m để hypebol (H ) : 
 1cắt đường thẳng y mx cắt nhau tại hai điểm 4 9 phân biệt A.2 B. 3 C. 4 D. 5
Câu 14. Hai điểm M, N thuộc hai nhánh của hypebol 2 2
25x 16 y  400 , độ dài MN nhỏ nhất bằng A.12 B. 8 C. 6 D. 10 2 2 x y
Câu 15. Cho đường hypebol 
 1 có hai đỉnh nằm trên 2 2 a b
đồ thị hàm số bậc hai như hình vẽ. Tính 2 2 a d . A. 80 B. 70 C. 90 D. 69 2 2 x y
Câu 16. Đường hypebol 
 1có độ dài trục thực bằng 8 và độ dài trục ảo bằng 6. Tính 2 2 a  3b . 2 2 a b A.43 B. 50 C. 45 D. 36 2 2 x y Câu 17. Trên hypebol 
 1(tiêu cự F F ) tồn tại điểm N sao cho NF  4NF . Tính NF  4NF . 144 25 1 2 1 2 1 2 A.50 B. 64 C. 45 D. 70
Câu 18. Đường tròn đi qua bốn giao điểm của hai đường conic 2 2 2 2
x  2 y  6; 8x y  8 có bình phương bán
kính gần nhất với giá trị nào A.3,65 B. 3,42 C. 3,56 D. 3,28 1
Câu 19. Trong hệ tọa độ Oxy, điểm M ( ; x y) có x
; y  3 tan t . Tập hợp các điểm M là hypebol có tiêu cos t cự bằng A.6 B. 4 C. 5 D. 3,5 2 2 x y Câu 20. Hypebol 
 1có tiêu cự ngắn nhất bằng 2 2 a  2a  5 b  2b  6 A.6 B. 8 C. 10 D. 12 2 2 x y c Câu 21. Hypebol   1đi qua (
A 5;3) và có e  
2 (tâm sai) thì độ dài tiêu cự bằng 2 2 a b a A.6 B. 4 11 C. 4 13 D. 6 5 Câu 22. Cho hypebol 2 2
x y  8 , elip đi qua điểm (
A 4; 6) và có tiêu điểm trùng với tiêu điểm của hypebol đã
cho. Elip đã cho có độ dài trục bé bằng A.10 B. 8 5 C. 8 3 D. 12 2 2 2 x y
Câu 23. Tìm số giao điểm của hypebol   1và đường tròn 2 2
(x  3)  ( y 1)  1. 4 2 A.3 B. 2 C. 1 D. 4 32
ĐƯỜNG HYPERBOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P8)
_____________________________________ 2 2 x y
Câu 1. Tìm tiêu cự của hypebol   1. 2 2 4 3 A.4 B. 8 C. 10 D. 12
Câu 2. Đường hypebol nào có tiêu điểm có thể nằm trên đường tròn 2 2
x y  2 9  m 2 2 x y 2 2 x y A.   1 B.   1 25 16 25 4 2 2 x y 2 2 x y C.   1 D.   1 25 49 2 2 m 15 n  26 2 2 x y 2 2 x y
Câu 3. Các giao điểm M của hypebol   1.và đường elip 
 1đều cách trục tung một khoảng 16 9 16 9 A.3 B. 1 C. 2 D. 4 2 2 x y
Câu 4. Cho đường hypebol 
 1 như hình vẽ bên. Khoảng 9 1
cách ngắn nhất giữa hai nhánh của hypebol bằng A. 2 B. 3 C. 6 D. 4
Câu 5. Hyperbol  H  có một tiêu điểm F 5;0 và độ dài trục thực bằng 8 , độ dài trục ảo của (H) là 2   A.8 B. 6 C. 4 D. 5
Câu 6. Tâm đường tròn 2 2
(x  3)  y  9 một tiêu điểm của hypebol có phương trình nào sau đây? 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1 . C.  H  :   1 . D.  H  2 2
:4x y  1. 9 16 4 5 2 1 2 2 x y
Câu 7. Tìm độ dài ngắn nhất đối với tiêu cự parabol  H  :   1. 2 4 m  4m  9 A.4 B. 8 C. 6 D. 5
Câu 8. Đường conic nào sau đây có trục thực và trục ảo đều có độ dài lớn hơn 5 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   0. 16 9 4 3 16 9 16 9 2 2 x y
Câu 9. Cho đường hypebol có phương trình 
 1 . Khoảng cách giữa hai tiêu điểm gần nhất với bán kính 25 9 đường tròn nào A. 2 2 x y  100 B. 2 2
x y  2x  2 y  120 C. 2 2
x y  4x  2 y  100 D. 2 2
x y  8x  4 y  103 2 2 x y 1
Câu 10. Điểm M ( ; x y) thuộc hypebol 
 1. Giá trị nhỏ nhất của biểu thức 2 Q x y thuộc khoảng 16 9 3 A.(0;5) B. (17;22) C. (5;10) D. (10;17) 2 2 x y
Câu 11. Cho đường hypebol 
 1 có hình chữ nhật cơ sở 16 9
mô tả như hình vẽ bên. Hình chữ nhật có bán kính kính đường tròn ngoại tiếp bằng A. 6 B. 7 C. 5 D. 8 2 2 x y
Câu 12. Cho hypebol có phương trình chính tắc 
 1 có tiêu cự F F và điểm M thuộc hypebol. 2 a  4a 10 9 1 2
Khi đó giá trị nhỏ nhất của biểu thức MF MF bằng 1 2 33 A. 4 . B. 8 . C. 6 . D. 10 .
Câu 13. Trong mặt phẳng tọa độ Oxy, điểm M ( ; x y) thỏa mãn 2 2 2 2
(x  6)  y  (x  6)  y  6 thì sẽ thuộc
đường hypebol có đỉnh cách gốc tọa độ một khoảng bằng A.4 B. 2 C. 5 D. 3 2 2 x y
Câu 14. Tìm số giao điểm tối đa của hypebol   1 và đường tròn 2 2 4 x y  25  4m . 25 9 A.3 B. 2 C. 3 D. 0
Câu 15. Tồn tại hai đường thẳng song song và cách trục hoành một khoảng bằng 1, hai đường thẳng này cắt 2 2 x y hypebol 
 1 tại tổng số bao nhiêu giao điểm 25 144 A.2 B. 3 C. 4 D. 5 2 2 x y
Câu 16. Đường tròn tiếp xúc với cả hai nhánh của hypebol  H  : 
 1 có đường kính nhỏ nhất bằng 2 16 a 1 A.12 B. 10 C. 6 D. 8 2 2 x y Câu 17. Hypebol 
 1 có tiêu cự F F , M thuộc hypebol thỏa mãn MF  2MF , tính MF  2MF . 25 9 1 2 1 2 1 2 A.24 B. 20 C. 18 D. 16
Câu 18. Trong mặt phẳng tọa độ Oxy, điểm M ( ; x y) thỏa mãn 2 2 2 2
(x  3)  y  (x  3)  y  4 thì sẽ thuộc
đường hypebol có tiêu điểm với hoành độ có thể bằng A.2 B. 3 C. 4 D. 2,5 2 2 x y
Câu 19. Hypebol nào có tiêu điểm trùng với tiêu điểm của elip  E  :   1 ? 16 9 2 2 2 2 x y x y 2 2 x y 2 2 x y A.  H  :   1. B.  H  :   1. C.  H  :   1. D.  H  :   1. 4 1 9 16 5 2 9 25 2 2 x y
Câu 20. Tìm số giao điểm của hypebol 
 1và đường thẳng y x  4 . 4 1 A.2 B. 1 C. 3 D. 5 2 2 x y
Câu 21. Tính tổng các giá trị m để hypebol  H  : 
 1 có tiêu điểm trùng với tiêu điểm của elip 2 4 m  2m  7 2 2 x yE :   1 . 16 9 A.4 B. 2 C. 5 D. 6
Câu 22. Hypebol nào sau đây có hai đỉnh đều nằm trên đường tròn 2 2
x y  25 và độ dài trục thực hơn độ dài
trục ảo 4 đơn vị độ dài 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  H  :   1 . B.  H  :   1. C.  H  :   1. D.  H  :   1. 25 9 25 16 4 25 9 25 2 2 x y
Câu 23. Cho đường hypebol 
 1 có hình chữ nhật cơ 2 2 a b
sở mô tả như hình vẽ bên. Biết hình chữ nhật có diện tích bằng
16. Tìm giá trị nhỏ nhất của biểu thức 2 2
a 16b . A. 2 5 B. 4 5 C. 32 D. 15 2 2 x y
Câu 24. Tâm đối xứng của hypebol  H  :   1có hoành độ bằng 9 4 A.3 B. 2 C. 1 D. 0
_______________________________ 34
ĐƯỜNG CONIC PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P1)
_____________________________________
Câu 1. Phương trình nào dưới dây là phương trình chính tắc của parabol A. 2 x  3 y . B. 2 x  3  y . C. 2 y  3  x . D. 2
y  3x .
Câu 2. Tham số tiêu của parabol 2 y  6x là 3 3 A. p  3 . B. p  . C. p  6 . D. p  . 2 4
Câu 3. Lập phương trình chính tắc của parabol biết khoảng cách từ đỉnh tới tiêu điểm bằng 3. A. 2 x  12 y B. 2 y  3x C. 2 y  12x . D. 2 y  6x
Câu 4. Lập phương trình chính tắc của parabol biết parabol đi qua điểm M (3;3 2) . A. 2 y  6x B. 2 y  3x C. 2 y  12x D. 2 y  4x
Câu 5. Cho parabol  P có phương trình chính tắc 2
y  4x . Một đường thẳng đi qua tiêu điểm F của  P cắt
P tại 2 điểm A và B . Nếu A1; 2
  thì tọa độ của B là A. 1; 2 . B. 4; 4 . C.  1  ; 2 . D. 2;2 2 .
Câu 6. Cho đường parabol 2
y  2 px như hình vẽ bên. Đường
parabol đã cho cắt đường thẳng y k (x  2) 1 tại ít nhất bao
nhiêu điểm (với k là tham số). A. 2 B. 3 C. 1 D. 0
Câu 7. Tọa độ điểm M thuộc parabol cho  P 2
: y  4x và đường thẳng d : x  2 y  0 là A. 0  ;1 . B. 0;0 . C. 0;3 . D. 0, 2 .
Câu 8. Cho  P 2
: y  4x điểm nào sao đây thuộc  P A. A1; 4 . B. B 1;4 . C. C 2;8 . D. D 1;2 .
Câu 9. Cho parabol  P 2
: y  4x . Điểm M thuộc  P và MF  4 ( F là tiêu điểm của parabol). Khi đó hoành
độ của điểm M bằng 3 A. 1. B. 3. C. 2. D. . 2
Câu 10. Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường parabol? A. 2 y  2  022x . B. 2 y  2022x . C. 2 x  20  22y . D. 2 x  2022 y .
Câu 11. Cho parabol  P  có tiêu điểm là F 10;0 , phương trình đường chuẩn của  P  là A. y  10  0 . B. x 10  0 . C. x  5  0 . D. x 10  0 .
Câu 12. Cho parabol  P 2
: y  2 px . Có bao nhiêu giá trị nguyên p để đường chuẩn của parapol nằm giữa hai
đường thẳng x  1; x  5 . A.1 B. 2 C. 3 D. 4
Câu 13. Cho parabol P  có phương trình chính tắc 2
y  20x . Tiêu điểm của parabol P là A. F 5; 0. B. F 10; 0. C. F 5;  0 . D. F 20; 0.
Câu 14. Gọi M là giao điểm của đường chuẩn parabol (conic) 2
y  6x và đường phân giác góc phần tư thứ
nhất. Độ dài đoạn thẳng OM bằng 5 2 5 3 3 2 A.6 B. C. D. 2 2 2
Câu 15. Cho parabol P  có phương trình chính tắc 2
y  4x . Đường chuẩn của P là A.  : x  1  .
B.  : x  1  0 . C.  : y  1 . D.  : y  1 . 35
Câu 16. Cho parabolP  có tiêu điểm là F 3; 
0 . Phương trình chính tắc của parabolP là A. 2 y  3x . B. 2 y  6x . C. 2 y  12x . D. 2 y  12x .
Câu 17. Trong các phương trình sau, phương trình nào là phương trình chính tắc của parabol? A. 2 y  2  x . B. 2 y  3 x  0 . C. 2 y  5 x . D. 2 x  4 y .
Câu 18. Có bao nhiêu điểm trên parabol 2
y  2x mà điểm đó cách đều hai trục tọa độ A..2 B. 1 C. 4 D. 3
Câu 19. Tìm p để đường chuẩn của parabol 2
y  2 px cách đường thẳng x  6 một khoảng bằng 10 đơn vị độ dài. A. p  6 B. p  4 C. p  8 D. p  1
Câu 20. Cho đường parabol 2
y  2 px như hình vẽ bên. Đường
parapol đã cho tạo với đường thẳng x  2 theo một dây cung có độ dài bằng A. 2 B. 2 5 C. 4 D. 4 2  3 
Câu 21. Phương trình chính tắc của parabol  P có tiêu điểm F ; 0   là  2  3 A. 2 y x . B. 2 3 y  3 x . C. 2 y  6 x . D. 2 yx . 2 4
Câu 22. Parabol  P đi qua điểm M 2; 2 . Phương trình chính tắc của parabol  P là A. 2 y  2x . B. 2 1 yx . C. 2 y  4 x . D. 2 yx . 2 1
Câu 23. Cho Parabol  P 2 : y x . 12
P “ Parabol có phương trình đường chuẩn x  3  0 ”
Q “Parabol có tọa độ tiêu điểm F 3;0 ”
Chọn khẳng định đúng. A. P đúng, Q sai. B. P sai, Q sai. C. P sai, Q đúng. D. P đúng, Q đúng.
Câu 24. Cho parabol có phương trình 2
y  4x . Tính bán kính qua tiêu của điểm M thuộc parabol và có hoành độ bằng 3. A. MF  6 . B. MF  3 . C. MF  5 . D. MF  4 . Câu 25. Cho parabol 2
(P) : y  4x . Tìm tọa độ điểm M thuộc (P) sao cho khoảng cách từ M đến tiêu điểm của (P) bằng 3 .
A. M (2; 2 2) hoặc M (2; 2  2) .
B. M (3;3 2) hoặc M (3; 3  2) .
C. M (2; 2 2) hoặc M ( 2  ; 2 2) .
D. M (3;3 2) hoặc M (3;3 2) .
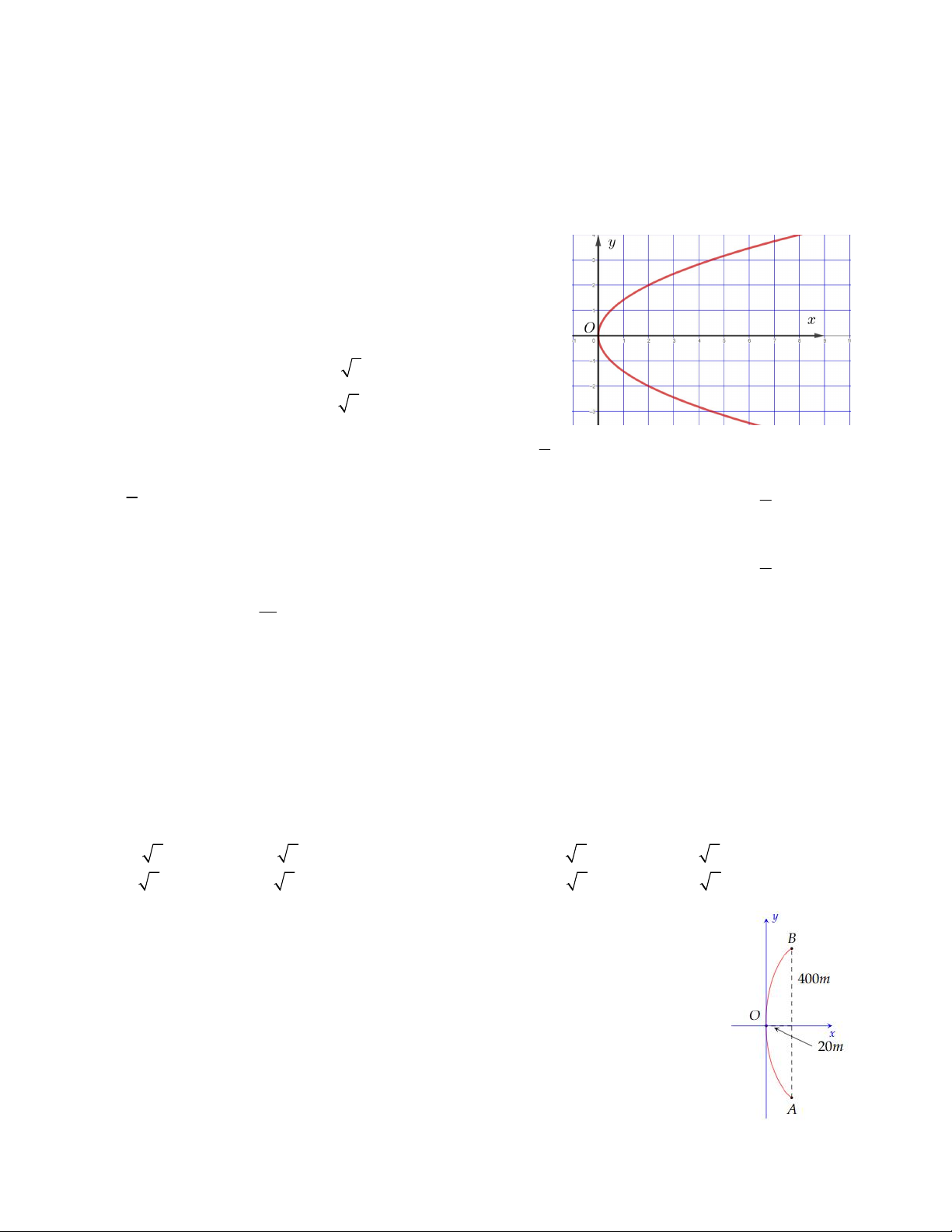
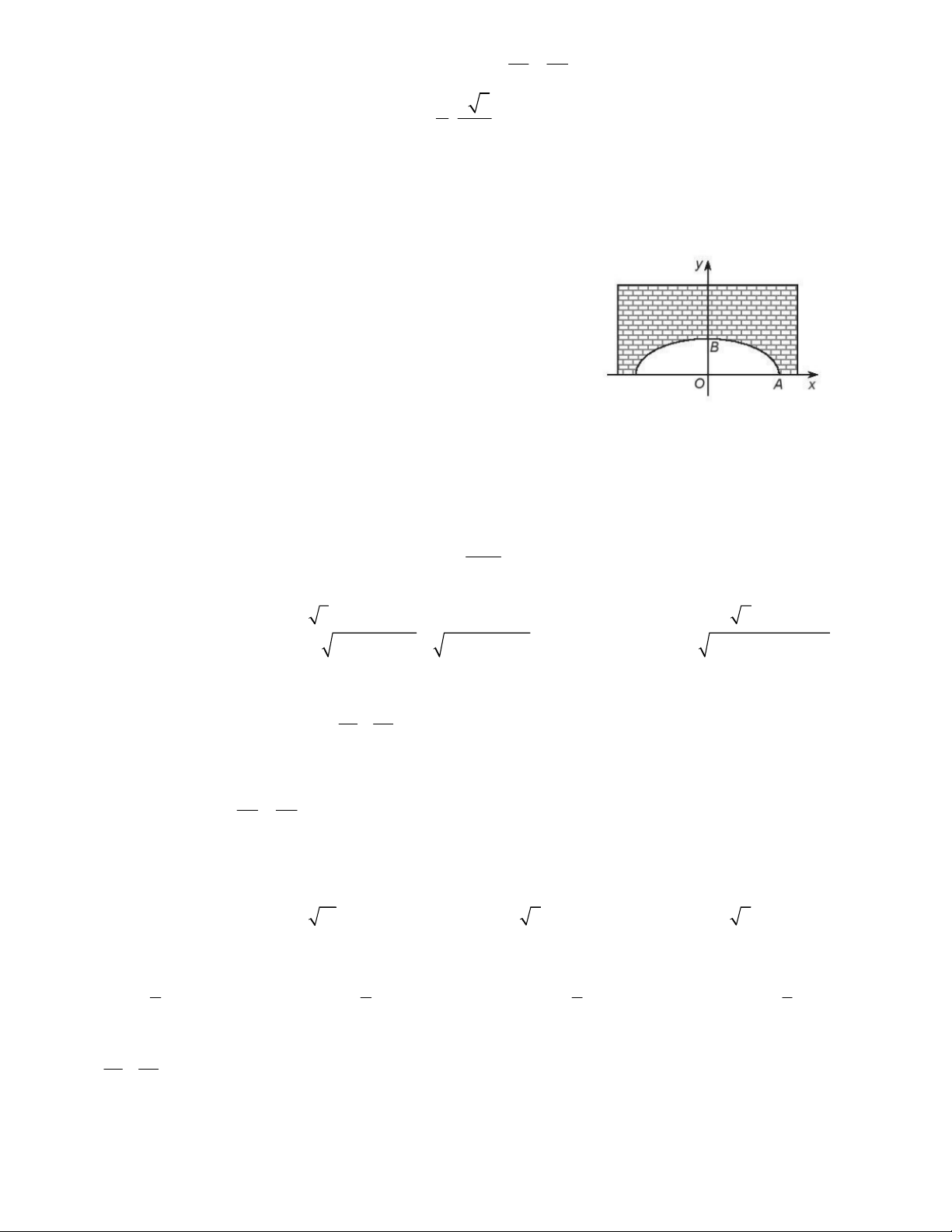
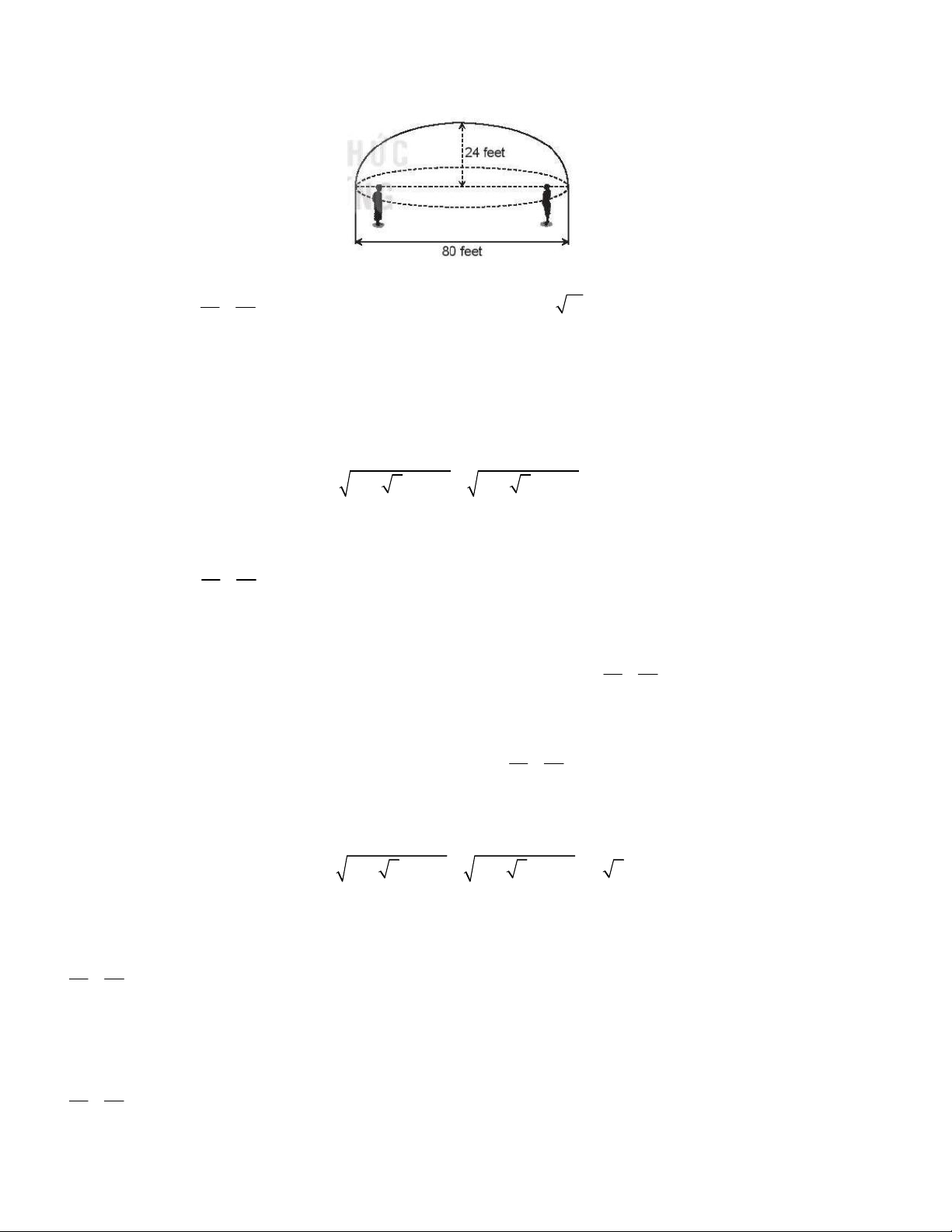
Câu 26. Khúc cua của một con đường có dạng parabol, điểm đầu vào khúc cua là
điểm A, điểm cuối là B, khoảng cách AB = 400m. Đỉnh của parbol (P) của khúc cua
cách đường thẳng AB một khoảng 20m và cách đều A, B. Phương trình đường
parabol (P) khi 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1m trên thực tế là A. 2
y  1000x B. 2 y  200x C. 2
y  2000x D. 2
y  1500x 36
ĐƯỜNG CONIC PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P2)
_____________________________________
Câu 1. Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường parabol? A. 2 y  69x . B. 2 2
y  4( p  2 p  6)x . C. 2 x  20  22 y . D. 2 x  96 y .
Câu 2. Với tham số tiêu p  0 , đường chuẩn của parabol 2
y  2 px cách điểm M ( p; 2023) một khoảng bằng A.2p B. 4p C. 1,5p D. 2,5p
Câu 3. Cho đường conic  P 2
: y  32x điểm nào sao đây thuộc  P A. A1; 4 . B. B 1;4 . C. C 2;8 . D. D 1;2 .
Câu 4. Cho đường parabol 2
y  2 px như hình vẽ bên. Đường
parabol đã cho cắt đường tròn 2 2
x y  9 tại bao nhiêu điểm A. 1 B. 3 C. 2 D. 0
Câu 5. Cho  P 2
: y  4x điểm nào sao đây thuộc  P và thuộc góc phần tư thứ nhất A. A1; 4 . B. B 1;4 . C. C 2;8 . D. D 4; 4 .
Câu 6. Tìm p để đường chuẩn của parabol 2
y  2 px cách điểm M ( ;
p 2023) một khoảng bằng 12 đơn vị độ dài. A. p  6 B. p  4 C. p  8 D. p  1 Câu 7. Cho parabol 2
y  2 px với p  0 . Điểm M thuộc  P và MF  4 ( F là tiêu điểm của parabol). Khi đó
hoành độ của điểm M bằng p A. 1. B. 4  C. 2  p D. 4  p 2
Câu 8. Cho parabol  P  có tiêu điểm là F 5; 0 , phương trình đường chuẩn của  P  là A. y  10  0 . B. x 10  0 . C. x  5  0 . D. x 10  0 .
Câu 9. Đường conic  P 2
: y  4x và đường thẳng 4x  3y 12  0 có bao nhiêu điểm chung A.2 B. 1 C. 3 D. 0 Câu 10. Cho parabol 2 2
y  4 p x với p  0 . Điểm M thuộc  P và MF  4 ( F là tiêu điểm của parabol). Khi đó
hoành độ của điểm M có giá trị lớn nhất bằng A.4 B. 2 C. 1 D. 3
Câu 11. Lập phương trình chính tắc của parabol biết khoảng cách từ đỉnh tới tiêu điểm bằng 1 A. 2 x  12 y B. 2 y  4x C. 2 y  12x . D. 2 y  6x
Câu 12. Cho đường conic  P có phương trình 2
y  12x . Một đường thẳng đi qua tiêu điểm F của  P cắt
P tại điểm A thuộc (P) có tung độ bằng 6 thì tạo với (P) một dây cung có độ dài bằng A.10 B. 12 C. 2 13 D. 4 5 Câu 13. Cho parabol 2
(P) : y  4x , điểm M thuộc (P) sao cho khoảng cách từ M đến tiêu điểm của (P) bằng
2 thì độ dài đoạn thẳng OM bằng A.3 B. 2 C. 5 D. 3
Câu 14. Cho đường parabol 2
y  2 px như hình vẽ bên. Đường
parabol đã cho cắt đường thẳng 3 2
y p p p  2023 tại bao nhiêu điểm A. 2 B. 3 C. 1 D. 0
Câu 15. Cho đường conic  P 2 2
: y  4( p  2 p  8)x và các mệnh đề 37
P: “ Parabol có phương trình đường chuẩn cách gốc tọa độ một khoảng lớn hơn 6,5”  p
Q: “Parabol có tọa độ tiêu điểm F ; 0   ”  2  Chọn khẳng định đúng A. P đúng, Q sai. B. P sai, Q sai. C. P sai, Q đúng. D. P đúng, Q đúng.
Câu 16. Cho parabol  P 2
: y  2 px . Có bao nhiêu giá trị nguyên dương p để đường chuẩn của parapol cách
trục tung một khoảng bằng 2 A.2 B. 1 C. 0 D. 3
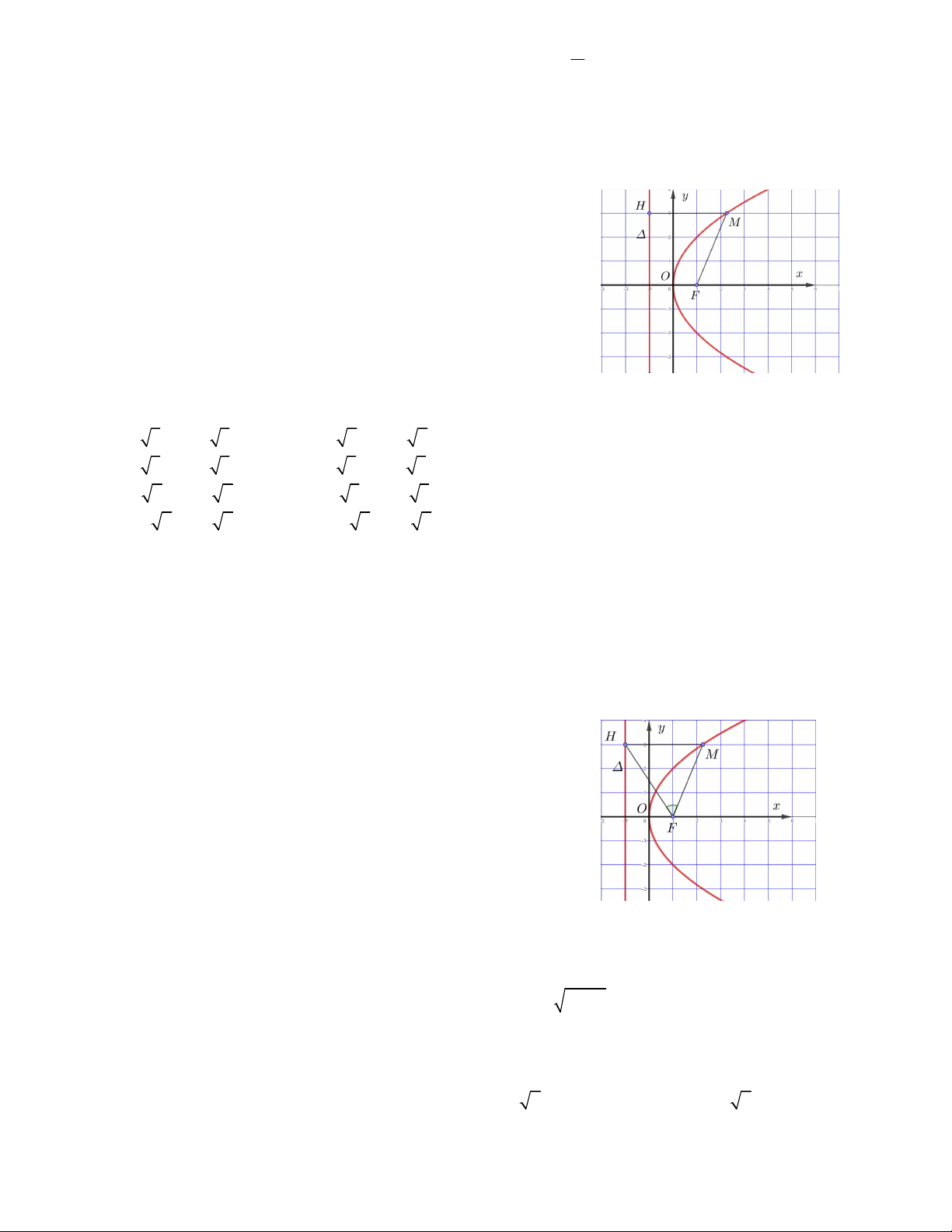
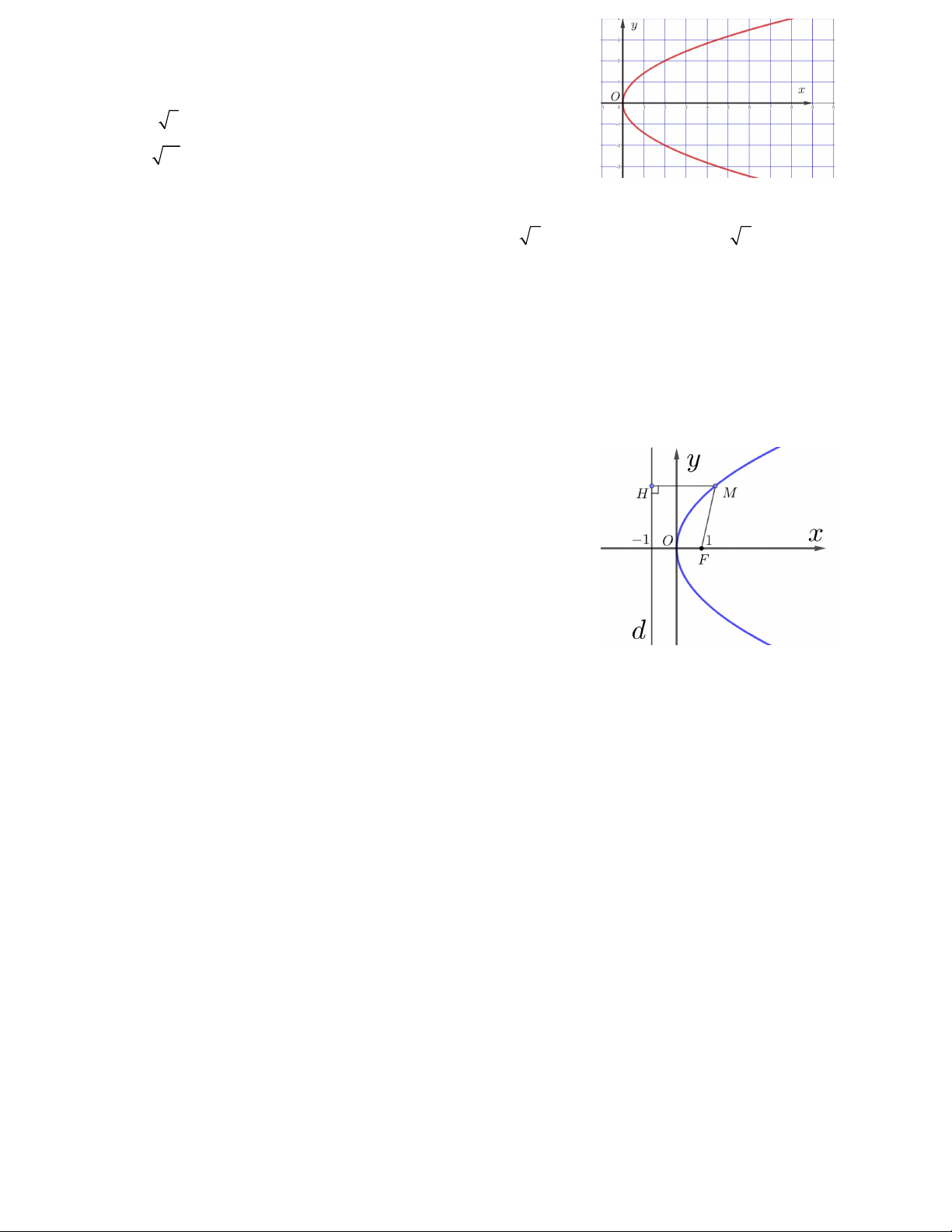
Câu 17. Cho đường parabol 2
y  2 px với p  0 có tiêu điểm F như
hình vẽ bên. Có bao nhiêu điểm M thuộc parabol sao cho điểm M cách đều hai điểm H, F A. 4 B. 3 C. Vô số D. 10
Câu 18. Cho parabol  P 2
: y  2 px . Biết phương trình đường chuẩn của (P) là: x  3
 . Tìm tọa độ điểm (
A a;1  a) thuộc (P) . A. (7 A  4 3; 6   4 3) hoặc ( A 6  2 6; 5   2 6) . B. ( A 7  4 3; 6   4 3) hoặc ( A 7  4 3; 6   4 3) . C. ( A 2  2 6; 5   2 6) hoặc (7 A  4 3; 6   4 3) . D. (
A 6  2 6; 7  2 6) hoặc ( A 6   2 6; 7  2 6) .
Câu 19. Cho đường parabol 2
y  2 px với p  0 có tiêu điểm F có hoành độ bằng 1, điểm M thuộc (P) và cách
đường thẳng x 1  0 một khoảng bằng 2. Độ dài đoạn thẳng MF bằng A.4 B. 2 C. 1,5 D. 3
Câu 20. Đường parabol 2
(P) : y  4x cắt đường tròn 2 2
(x  2)  y  4 tại bao nhiêu điểm A.2 B. 3 C. 1 D. 4
Câu 21. Trong mặt phẳng tọa độ, cho các parabol 2 2 2 2 2
y  8x, y  16x, y  4x, y  4( p  2 p  6)x . Đường
parabol nào có đường chuẩn cách xa gốc tọa độ O nhất A. 2 2
y  4( p  2 p  6)x B. 2 y  8x C. 2 y  16x D. 2 y  4x
Câu 22. Cho đường parabol 2
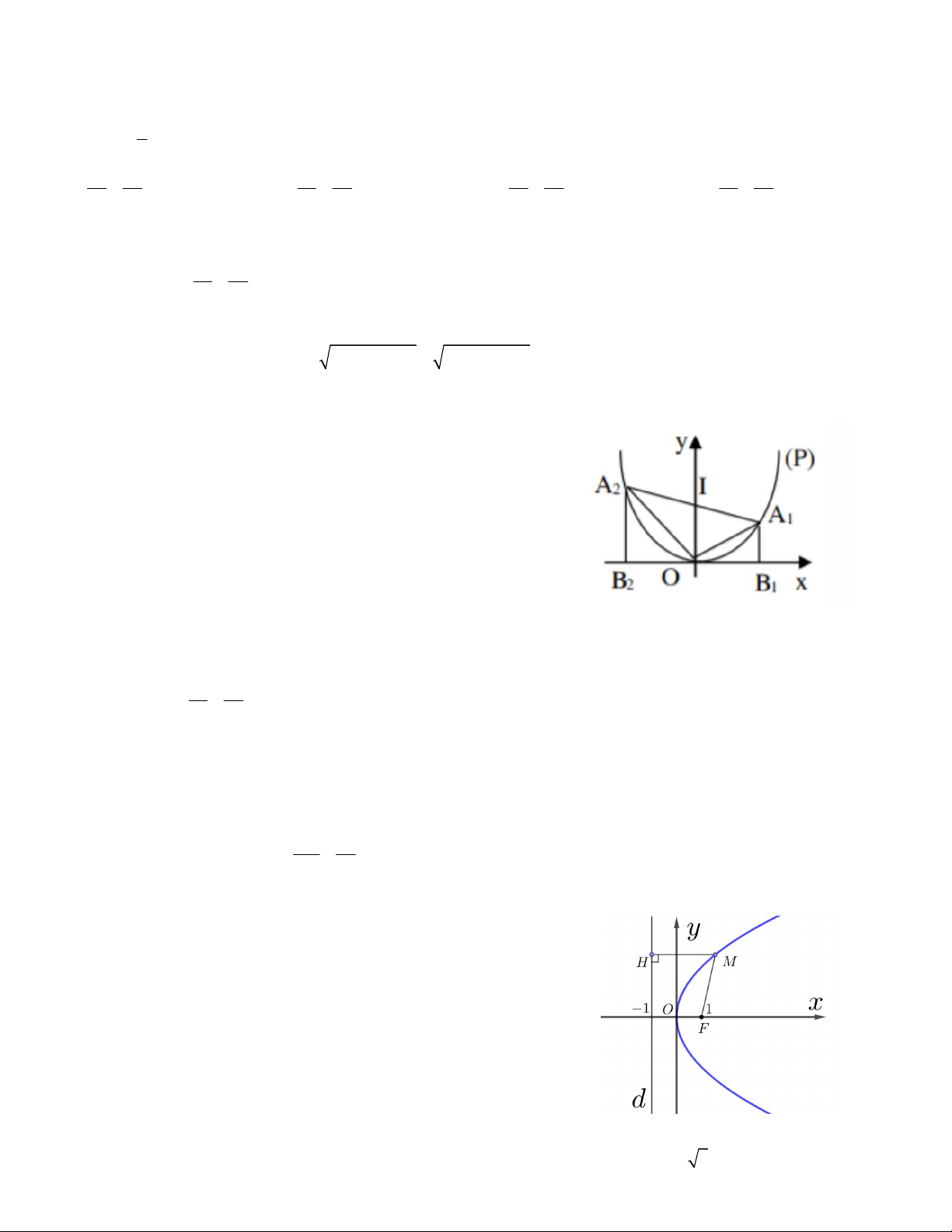
y  2 px với p  0 có tiêu điểm F như  
hình vẽ bên, sao cho HFM  60 . Tính chu vi tam giác HFM theo k
biết rằng 2MH  3MF  4HF  9k, k  0 . A. 4k B. 6k
C. 3k D. Kết quả khác Câu 23. Cho parabol 2
(P) : y  4x với tiêu điểm F, có bao nhiêu điểm M (tọa độ nguyên) thuộc (P) thỏa mãn
điều kiện 2  MF  20 . A.4 B. 6 C. 8 D. 10
Câu 24. Đường parabol nào có thể có đường chuẩn cách xa gốc tọa độ O nhất A. 2 2
y  4( p  2 p  6)x B. 2 2
y  4 1 p x C. 2 y  16x D. 2
y  4x Câu 25. Cho parabol 2
(P) : y  4x , đường thẳng d đi qua điểm A (9;9) và tạo với hai trục tọa độ một góc 45 thì
tạo với parabol có tọa độ bằng A.4 B. 6 C. 6 2 D. 4 2
______________________________ 38
ĐƯỜNG CONIC PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P3)
_____________________________________
Câu 1. Tham số tiêu của parabol 2 y  24x là 3 A. p  3 . B. p  . C. p  6 . D. p  12 2
Câu 2. Cho đường parabol 2
y  2 px như hình vẽ bên. Đường
parabol đã cho cắt đường thẳng y kx k tại ít nhất bao nhiêu
điểm (với k là tham số). A. 2 B. 3 C. 1 D. 0
Câu 3. Phương trình nào dưới dây là phương trình chính tắc của parabol A. 2 x  13y . B. 2 x  3  y . C. 2 y  3  x . D. 2
y  26x .
Câu 4. Lập phương trình chính tắc của parabol biết khoảng cách từ đỉnh tới tiêu điểm bằng 1,5. A. 2 x  12 y B. 2 y  3x C. 2 y  12x . D. 2 y  6x
Câu 5. Với p  0 , khi đường chuẩn của parabol 2
y  2 px tiếp xúc đường tròn 2 2
(x 1)  ( y  4)  64 thì giá trị 3
p  26 p  5 bằng A.3113 B. 2540 C. 1265 D. 2045
Câu 6. Đường chuẩn của đường conic  P 2
: y  32x tiếp xúc với đường tròn nào sau đây A. 2 2 x y  8 B. 2 2
(x 1)  ( y  4)  64 C. 2 2
(x  3)  ( y  2)  25 D. 2 2
(x  3)  ( y  4)  25
Câu 7. Lập phương trình chính tắc của parabol biết parabol đi qua điểm (8;8). A. 2 y  6x B. 2 y  3x C. 2 y  12x D. 2 y  4x  
Câu 8. Cho đường parbol (P): 2
y x và điểm I (0; 2) , hai điểm M, N thuộc (P) thỏa mãn IM  4IN . Tồn tại hai
điểm M, N với tổng hoành độ bằng A.30 B. 20 C. 24 D. 40
Câu 9. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên,
trong đó đường thẳng d là đường chuẩn. Tìm hoành độ điểm M nếu
2MH  3MF  16 . A. 2,3 B. 2,4 C. 2,2 D. 2
Câu 10. Với tham số tiêu p  0 , đường chuẩn của parabol 2
y  2 px cách điểm (
A 6; 2023) một khoảng bằng 12
thì tiêu điểm parabol cách điểm A một khoảng bằng bao nhiêu đơn vị độ dài A.2023 B. 2000 C. 3000 D. 500
Câu 11. Với tham số tiêu p  0 , có bao nhiêu số nguyên p để đường chuẩn của parabol 2
y  2 px nằm bên phải
đường thẳng 2x  7  0 . A.5 B. 3 C. 4 D. 6
Câu 12. Đường conic  P 2
: y  32x có tham số tiêu p, khi đó hãy tìm số giao điểm của parabol và đường thẳng 2
x p  4 p . A.4 B. 2 C. 3 D. 1
Câu 13. Trong mặt phẳng tọa độ, cho các parabol 2 2 2 2 2
y  8x, y  16x, y  4x, y  4( p  2 p  6)x . Có bao
nhiêu đường conic có đường chuẩn nằm bên phải đường thẳng 2x  5  0 . A.3 B. 1 C. 2 D. 4 39
Câu 14. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên,
trong đó đường thẳng d là đường chuẩn. Xét dây cung MN có độ
dài bằng 4 như hình vẽ, KN song song với MH, tính tổng hoành độ hai điểm M, N. A. 1,9 B. 2,2 C. 2 D. 2,1
Câu 15. Tìm p để đường chuẩn của parabol 2
y  2 px cách điểm M ( p; 7) một khoảng bằng 6 đơn vị độ dài. A. p  6 B. p  4 C. p  8 D. p  1
Câu 16. Đường conic parabol 2
y  2 px với p  0 có một dây cung vuông góc với trục hoành có độ dài bằng 2
và khoảng cách từ gốc tọa độ O đến dây cung này bằng 4, giá trị của tham số tiêu p thuộc khoảng A.(0;2) B. (2;4) C. (4;9) D. (9;15)
Câu 17. Trong mặt phẳng tọa độ, cho  P 2
: y  4x . Tìm điểm M trên  P sao cho M có tung độ bằng 2 . A. M 2;6  4 . B. M 1;  2 . C. M 16;  2 . D. M 2; 8 .
Câu 18. Đường chuẩn của parabol 2 2
y  4 1 p x cách xa trục tung nhất một khoảng bằng bao nhiêu đơn vị độ dài A.2 B. 1 C. 3 D. 1,5
Câu 19. Trong mặt phẳng tọa độ, cho  P 2
: y  8x . Tìm trên  P điểm M có tung độ dương và có hoành độ bằng 3 . A. M 3;2 6  .
B. M 3; 2 6  . C. M 2 6;3 . D. M 2 6;3 .
Câu 20. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên, trong đó đường thẳng d là đường chuẩn. Biết 
HMF  70, HF  1, 5 , khi đó chu vi tam giác HMF gần nhất với A. 4,23 B. 4,54 C. 4,11 D. 4,42 Câu 21. Cho parabol 2
(P) : y  4x với tiêu điểm F, có bao nhiêu điểm M (tọa độ nguyên) thuộc (P) thỏa mãn
điều kiện 2  MF  35 . A.4 B. 6 C. 8 D. 10
Câu 22. Đường conic parabol 2
y  2 px với p  0 có tham số tiêu bằng 6, điểm M thuộc parabol có tung độ
bằng 6 thì có hoành độ bằng A.6 B. 8 C. 4 D. 2
Câu 23. Đường conic parabol 2
y  2 px với p  0 có một dây cung vuông góc với trục hoành có độ dài bằng 8
và khoảng cách từ gốc tọa độ O đến dây cung này bằng 1, giá trị của tham số tiêu p thuộc khoảng A.(0;2) B. (2;4) C. (4;9) D. (9;15)
Câu 24. Đường chuẩn của parabol 2 2
y  4x 8  p  2 p cách xa trục tung nhất một khoảng bằng bao nhiêu đơn vị độ dài A.2 B. 1 C. 3 D. 1,5
Câu 25. Trong mặt phẳng tọa độ, cho các parabol 2 2 2 2 2
y  8x, y  2x, y  4x, y  4( p  2 p 14)x . Có bao
nhiêu đường conic có đường chuẩn nằm bên trái đường thẳng 2x  7  0 . A.3 B. 1 C. 2 D. 4
Câu 26. Lập phương trình chính tắc của parabol biết khoảng cách từ tiêu điểm đến đường chuẩn bằng 6. A. 2 x  12 y B. 2 y  3x C. 2 y  12x . D. 2 y  6x
_________________________________ 40
ĐƯỜNG PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P4)
_____________________________________
Câu 1. Với p  0 , khi đường chuẩn của parabol 2
y  2 px tiếp xúc đường tròn 2 2
(x 1)  ( y  4)  4 thì giá trị 3
p p  7 bằng A.75 B. 50 C. 65 D. 40
Câu 2. Đường chuẩn của đường conic  P 2
: y  8x tiếp xúc với đường tròn nào sau đây A. 2 2 x y  8 B. 2 2
(x 1)  ( y  4)  64 C. 2 2
(x  3)  ( y  2)  25 D. 2 2
(x  3)  ( y  4)  25
Câu 3. Cho đường parabol 2
y  2 px như hình vẽ bên. Tham số tiêu của parabol bằng A. 2 B. 3 C. 1 D. 0
Câu 4. Phương trình nào dưới dây luôn là phương trình chính tắc của parabol A. 2
y  (a 1)x . B. 2 y  6x . C. 2 3y  4x . D. 2
2 y  3x .
Câu 5. Đường conic parabol 2
y  2 px với p  0 có tiêu điểm F, tìm tổng các giá trị p khi EF  10 trong đó điểm E (1;3). A.3 B. 0 C. 4 D. 2 1
Câu 6. Lập phương trình của parabol biết khoảng cách từ đỉnh tới tiêu điểm bằng . 24 A. 2 x  12 y B. 2 y  3x C. 2 y  12x . D. 2 y  6x
Câu 7. Đường conic parabol 2
y  2 px với p  0 có một dây cung vuông góc với trục hoành có độ dài bằng 8 và
khoảng cách từ gốc tọa độ O đến dây cung này bằng 6, giá trị của tham số tiêu p thuộc khoảng A.(0;2) B. (2;4) C. (4;9) D. (9;15)
Câu 8. Tìm tham số tiêu của parabol (P) biết đường chuẩn của (P) tiếp xúc với đường tròn 2 2
(x  2)  ( y  3)  16 . A. p  6 B. p  4 C. p  8 D. p  1
Câu 9. Đường chuẩn của parabol 2 2
y  4x 5  p  4 p cách xa trục tung nhất một khoảng bằng bao nhiêu đơn vị độ dài A.2 B. 3 C. 2,5 D. 1,5
Câu 10. Một chiếc đèn có mặt cắt ngang là hình parabol 2
y  2 px với
p  0 như hình vẽ bên, trong đó chiều rộng hai mép vành là AB = 50cm và
chiều sâu h = 30cm (khoảng cách từ O đến AB), bóng đèn nằm ở tiêu điểm S.
Tham số tiêu của parabol nằm trong khoảng A. (4;6) B. (0;4) C. (6;7) D. (7;12) Câu 11. Cho parabol 2
(P) : y  8x với tiêu điểm F, có bao nhiêu điểm M (tọa độ nguyên) thuộc (P) thỏa mãn
điều kiện 2  MF  20 . A.3 B. 14 C. 8 D. 10
Câu 12. Có bao nhiêu số nguyên p để là đường conic 2 2
y  4( p  2 p  2)x là parabol có đường chuẩn x  5  . A.4 B. 2 C. 1 D. 3
Câu 13. Đường parabol nào có thể có đường chuẩn cách xa gốc tọa độ O nhất A. 2 2
y  4( p  2 p  6)x B. 2 2
y  4 1 p x C. 2 y  16x D. 2 2
y  4(2  p )x 41
Câu 14. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên.
Tìm độ dài dây cung tạo bởi parabol và đường thẳng x  3y  0 . A. 12 5 B. 12 C. 6 10 D. 8 Câu 15. Cho parabol 2
(P) : y  4x , đường thẳng d đi qua điểm M (5;5) và tạo với hai trục tọa độ một góc 45 thì
tạo với parabol có tọa độ bằng A.4 B. 6 C. 6 2 D. 4 2
Câu 15. Với tham số tiêu p  0 , có bao nhiêu số nguyên p để đường chuẩn của parabol 2
y  2 px nằm bên phải
đường thẳng 3x 11  0 . A.5 B. 3 C. 7 D. 9
Câu 16. Tìm tham số tiêu của parabol (P) biết đường chuẩn của (P) tiếp xúc với đường elip 2 2
5x  9 y  45 . A. p  6 B. p  4 C. p  8 D. p  1
Câu 17. Đường conic parabol 2
y  2 px với p  0 có tiêu điểm F, tìm độ dài ngắn nhất của đoạn thẳng EF trong đó điểm E (1;3). A.4 B. 2 C. 3 D. 1
Câu 18. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên,
trong đó đường thẳng d là đường chuẩn. Tìm hoành độ điểm M nếu
2MH  7MF  22,5 . A. 1,8 B. 1,4 C. 1,5 D. 1,6
Câu 19. Cổng của một công viên có dạng parabol. Để đo chiều cao h của cổng, một người đo khoảng cách giữa
hai chân cổng được 9m, người đó thấy nếu đứng cách chân cổng 0,5m thì đầu chạm cổng, cho biết người này
cao 1,6m, hỏi chiều cao cổng gần nhất giá trị nào A.7,66 B. 7,68 C. 7,6 D. 7,62
Câu 20. Có bao nhiêu số nguyên p để là đường conic 2 2
y  4( p  6 p  5)x là parabol có đường chuẩn x  5  . A.4 B. 2 C. 1 D. 3
Câu 21. Tìm tham số tiêu của parabol (P) biết đường chuẩn của (P) là trục đối xứng của đồ thị hàm số bậc hai 2
f (x)  x  6x  3m  3 (m là tham số). A. p  6 B. p  4 C. p  8 D. p  1
Câu 22. Tìm khoảng cách ngắn nhất giữa hai điểm MN với M, N lần lượt thuộc các đường tròn và parabol 2 2 2
x y 10x  21  0; y  8x . A.3 B. 2 C. 4 D. 2,5 Câu 22. Cho parabol 2
(P) : y  4x , tam giác OAB có ba đỉnh thuộc (P), trọng tâm G trùng với tiêu điểm F của
(P), độ dài đoạn thẳng AB bằng A.2 B. 4 C. 3 D. 5
Câu 23. Tìm tổng các giá trị p  0 khi đường conic parabol 2
y  2 px với có tiêu điểm F thuộc đường tròn 2 2
x y  4x  2 y  3  0 . A.3 B. 2 C. 1 D. 4
Câu 24. Đường conic parabol 2
y  2 px có tiêu điểm F thuộc đường elip 2 2
x  4 y  4 thì trên parabol có bao
nhiêu điểm nguyên có hoành độ nhỏ hơn 50 A.4 B. 8 C. 5 D. 12
Câu 25. Đường conic parabol 2
(P) : y  4x tiếp xúc đường thẳng 4x  2 y m  0 tại điểm có tung độ bằng A.1 B. 0,5 C. 1,5 D. 2
_________________________________ 42
ĐƯỜNG PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P5)
_____________________________________
Câu 1. Trong các đường conic sau, có bao nhiêu đường conic có thể có đường chuẩn x  4  2 2 2 2 2
y  4x; y  2 ;
px y  4( p  3 p  2) ;
x y  ( p  3)x A.3 B. 4 C. 1 D. 3
Câu 2. Đường conic parabol 2
y  2 px với p  0 có đường chuẩn x  5
 . Giá trị của p thuộc khoảng A.(5;7) B. [3;5) C. [7;8) D. [8;11)
Câu 3. Phương trình nào sau đây là phương trình chính tắc của đường conic parabol A. 2 2
y  2( p 1)x B. 2 y  2x C. 2 y  6x D. 2 2 y  3x
Câu 4. Tìm khoảng cách ngắn nhất giữa hai điểm MN với M, N lần lượt thuộc các đường tròn và parabol 2 2 2 2
x y  6x  0; y  4(m  2m  9)x . A.0 B. 2 C. 4 D. 1
Câu 5. Hai điểm A, B thuộc đường conic parabol 2
(P) : y  4x lần lượt có tung độ là – 2 và 4. Chu vi của tam
giác OAB (O là gốc tọa độ) gần nhất với A.15,2 B. 14,6 C. 13,8 D. 16,4
Câu 6. Trong các đường conic sau, có bao nhiêu đường conic có thể có khoảng cách từ đỉnh đến đường chuẩn
lớn hơn 2 đơn vị độ dài 2 2 2 2 2
y  4x; y  2 px; y  4( p p  2) ;
x y  (4 p  3)x A.3 B. 4 C. 1 D. 3
Câu 7. Tìm m để đường tròn 2 2
(x m )  y  9 tiếp xúc với đường conic parabol 2
y  2 px với p  0 . A. m  4 B. m  9 C. m  8 D. Kết quả khác Câu 8. Cho parabol 2
(P) : y  8x , tam giác OAB có ba đỉnh thuộc (P), trọng tâm G trùng với tiêu điểm F của (P),
độ dài đoạn thẳng AB bằng A.9 B. 8 C. 6 D. 5
Câu 9. Tìm tổng các giá trị p  0 khi đường conic parabol 2
y  2 px có tiêu điểm F thuộc đường tròn 2 2
x y  4x  2 y  20 . A.3 B. 2 C. 8 D. 4 Câu 10. Cho parabol 2
(P) : y  8x , (P) tiếp xúc với đường thẳng 8x  6 y m  5  0 tại điểm có hoành độ thuộc khoảng A.(0;1) B. (1;2) C. (2;3) D. (3;4)
Câu 11. Đường chuẩn của đường conic  P 2
: y  4 px với p  0 trùng với trục đối xứng của đồ thị hàm số bậc hai 2
f (x)  x  2(3 p  4)x p  8 . Tiêu điểm của (P) cách điểm (
A 2023; 0) một khoảng bằng A.2023 B. 2020 C. 2022 D. 2021
Câu 12. Đường conic parabol 2
y  2 px có tiêu điểm F thuộc đường elip 2 2
x  6 y  9 thì trên parabol có bao
nhiêu điểm nguyên có hoành độ nhỏ hơn 50 A.4 B. 8 C. 5 D. 10
Câu 13. Đường conic parabol 2
(P) : y  4x tiếp xúc đường thẳng 4x  4 y m  2023  0 tại điểm có tung độ bằng A.1 B. 0,5 C. – 3 D. – 2
Câu 14. Trong mặt phẳng tọa độ Oxy, đường conic parabol 2
y  2 px với p  0 có tiêu điểm nằm trên đường thẳng 2
2023x  2002 p y  2023  0 thì tiếp xúc với đường thẳng nào sau đây
A. 4x  2 y 1  0
B. x  2 y  3  0
C. 2x  6 y 1  0
D. 4x y  3  0
Câu 15. Tìm tham số tiêu của parabol (P) biết đường chuẩn của (P) là trục đối xứng của đồ thị hàm số bậc hai 2
f (x)  x  8x  3m  3 (m là tham số). A. p  6 B. p  4 C. p  8 D. p  1
Câu 16. Điểm M ( ; x y) parabol 2
(P) : y  16x , tìm giá trị nhỏ nhất của biểu thức 2 2
T x  2 y  6x 1958 . A.1789 B. 1945 C. 1979 D. 1858
Câu 17. Hai điểm A, B thuộc đường conic parabol 2
(P) : y  4x lần lượt có tung độ là – 2 và 4. Diện tích của tam
giác OAB (O là gốc tọa độ) bằng bao nhiêu đvdt A.5 B. 6 C. 4 D. 3
Câu 18. Tìm m để đường tròn 2 2
(x  2)  y m tiếp xúc với đường conic parabol 2
y  2 px với p  0 . A. m  4 B. m  9 C. m  8 D. m  16 43
Câu 19. Cho đường parabol 2
y  2 px như hình vẽ bên. Tiêu
điểm F của parabol thuộc đường thẳng nào
A. 3x y 1  0 B. y  5x
C. 2x  3y  2  0 D. x  6 y  2  0
Câu 20. Đường conic parabol 2
y  2 px với p  0 có tiêu điểm nằm trên giao điểm hai đường thẳng
3x my  3  0; 5x  (3m 1) y  5  0 Giá trị tham số p bằng A.1 B. 0,5 C. 2 D. 1,5
Câu 21. Đường conic parabol 2
y  2 px với p  0 có tiêu điểm F (tọa độ nguyên) nằm trên một trong đường
trung bình của tam giác OAB với O là gốc tọa độ, ( A 4; 4), B(4; 6) 
. Phương trình đường chính tắc của parapol là A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2 y  4x
Câu 22. Có bao nhiêu số nguyên m  50 để parabol 2
(P) : y  8x và đường thẳng 8x  6 y m  5  0 không có điểm chung A.45 B. 35 C. 20 D. 25
Câu 23. Tìm tổng các giá trị p  0 khi đường conic parabol 2
y  4 px có tiêu điểm F cách điểm E(2 p  5; 4) một khoảng bằng 5. A.8 B. 9 C. 10 D. 12
Câu 24. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên,
trong đó đường thẳng d là đường chuẩn. Xét dây cung MN có độ
dài bằng 4 như hình vẽ, KN song song với MH, tính tổng hoành độ hai điểm M, N. A. 1,9 B. 2,2 C. 2 D. 2,1
Câu 25. Điểm M ( ; x y) thuộc parabol 2
(P) : y  8x , tìm giá trị nhỏ nhất của biểu thức 2 2
Q x y 16x  2023. A.1879 B. 1945 C. 1975 D. 1954
Câu 26. Đường conic parabol 2
y  2 px với p  0 có đường chuẩn là một trong các đường trung tuyến của tam giác ABC với ( A 2;3), B( 4  ; 5
 ),C(0; 1) . Phương trình đường chính tắc của parapol là A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2 y  4x
Câu 27. Điểm M ( ; x y) parabol 2
(P) : y  16x đồng thời nằm trong góc phần tư thứ nhất của mặt phẳng tọa độ,
tìm giá trị nhỏ nhất của biểu thức T x y 1958 . A.1789 B. 1945 C. 1979 D. 1954
Câu 28. Có bao nhiêu số nguyên m  50 để parabol 2
(P) : y  8x và đường thẳng 8x  9 y 10m 11  0 có điểm chung A.40 B. 46 C. 20 D. 34  
Câu 29. Cho đường parbol 2
(P) : y  4x và điểm I (2; 0) , hai điểm M, N thuộc (P) thỏa mãn 3IM  2  IN . Tồn
tại hai điểm M, N với tổng hoành độ bằng A.16 B. 10 C. 10 D. 13
Câu 30. Có bao nhiêu số nguyên m nhỏ hơn 2023 để đường tròn 2 2
(x  2)  y m có ít nhất một điểm chung
với đường conic parabol 2 y x 2023 . A.2019 B. 2015 C. 2014 D. 2010 2 2 x y Câu 31. Elip 
 1 có đỉnh bên phải trùng với tiêu điểm của parabol 2
(P) : y  16x thì có tiêu cự bằng 2 a 3a  5 A.10 B. 6 C. 8 D. 10
_________________________________ 44
ĐƯỜNG PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P6)
_____________________________________
Câu 1. Đường conic parabol 2
y  2 px với p  0 có đường chuẩn x  2
 . Giá trị của p thuộc khoảng A.(0;1) B. [1;2) C. [2;3) D. [3;5)
Câu 2. Phương trình nào sau đây là phương trình chính tắc của đường conic parabol A. 2 y  6x B. 2 y  2x C. 2 y  6x D. 2 2 y  3x
Câu 3. Đường conic parabol nào sau đây có tiêu điểm là tiếp điểm của hai đường tròn 2 2 2 2
x y  4; (x  3)  y  1 A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2 y  4x
Câu 4. Trong các đường conic sau, có bao nhiêu đường conic có thể có đường chuẩn x  2  2 2 2 2 2
y  4x; y  2 ;
px y  4( p  3 p  2) ;
x y  ( p  3)x A.3 B. 4 C. 1 D. 2
Câu 5. Tính tổng các giá trị p để đường conic 2 2
(P) : y  4( p  4 p  2)x với p  0 có tiêu điểm nằm trên đường
thẳng y x 1. A.2 B. 3 C. 4 D. 1
Câu 6. Đồ thị hàm số bậc hai 2
f (x)  x  4x  3 cắt trục hoành tại hai điểm A, B. Đoạn thẳng AB nhận tiêu điểm F của parabol 2
y  2 px với p  0 làm trung điểm. Phương trình đường chính tắc của parapol là A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2
y  4x  
Câu 7. Cho đường parbol 2
(P) : y  4x và điểm I (2; 0) , hai điểm M, N thuộc (P) thỏa mãn IM  2IN . Tồn tại
hai điểm M, N với tổng hoành độ bằng A.6 B. 8 C. 4 D. 5 Câu 8. Cho parabol 2
(P) : y  4x , (P) tiếp xúc với đường thẳng 8x  6 y m  5  0 tại điểm có hoành độ thuộc khoảng  1   1 5   5 4   4  A. 0;   B. ;   C. ;   D. ; 2    2   2 6   6 3   3 
Câu 9. Parabol nào sau đây có đỉnh cách xa tiêu điểm nhất A. 2 y  2x B. 2 2
y  4( p  2 p  8)x C. 2 y  4(1
p )x (0  p  1) D. 2 y x
Câu 10. Cho đường parabol (P): 2
y  2 px với p  0 như hình vẽ bên, xét ba điểm ,
A B,C thuộc (P) có tung độ lần lượt là 6; 2; 4  .
Trọng tâm tam giác ABC có hoành độ bằng 29 25 A. B. 6 6 14 40 C. D. 3 9
Câu 11. Cho đường parabol 2
y  2 px với p  0 có tiêu điểm F cùng với ba điểm (
A 2; 2), B(6; 2), C(5; 0) tạo
thành hình bình hành ABCF . Điểm M trên (P) có tung độ bằng 9 thì có hoành độ thuộc khoảng A.(9;11) B. (11;15) C. (15;19) D. (19;24)
Câu 12. Cho ba điểm (3
A ; 6), B(4;1),C( 4
 ; 7) , đường parabol 2
y  2 px với p  0 có tiêu điểm F là trọng tâm
tam giác ABC. Điểm M (a;b) thuộc (P) thì độ dài đoạn thẳng MF bằng A. a 1 B. a  2 C. 2a 1 D. a 1 Câu 13. Cho parabol 2
(P) : y  4x , tìm hệ số góc k của tiếp tuyến của (P) tại điểm có tung độ bằng 2 1 A. k  1 B. k  2 C. k  D. k  2 3
Câu 14. Tiêu điểm của parabol 2
y  2 px với p  0 là tâm của đường tròn 2 2 2
x y  6x  2my m m  0 thì
giá trị p thuộc khoảng nào A.(0;1) B. (1;4) C. (4;7) D. (7;10) 45
Câu 15. Cho ba điểm (
A 0; 4), B(0; 4),  C(4; 4) 
. Tiêu điểm của parabol (P): 2
y  2 px với p  0 là tâm của
đường tròn ngoại tiếp tam giác ABC. Có bao nhiêu điểm M thuộc (P) có tọa độ nguyên dương mà tung độ thuộc khoảng (1428;1789) A.128 B. 179 C. 189 D. 148
Câu 16. Có bao nhiêu số nguyên m  200 để parabol 2
(P) : y  2x và đường thẳng 8x  6 y m  5  0 không có điểm chung A.180 B. 192 C. 200 D. 175
Câu 17. Tính độ dài dây cung tạo bởi đường conic 2
(P) : y  4x và đường thẳng 2x y 12  0 . A.10 B. 5 6 C. 5 5 D. 6 3
Câu 18. Điểm M ( ; x y) thuộc parabol 2
(P) : y  8x , tìm giá trị nhỏ nhất của biểu thức 2 2
Q x y  4x  2015 . A.1979 B. 1945 C. 1975 D. 1954
Câu 19. Đường conic parabol 2
y  2 px với p  0 có đường chuẩn là một trong các đường cao của tam giác  5  ABC với A 2;  , B   5 
;1 ,C 0; 2 . Phương trình đường chính tắc của parapol là  2  A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2 y  4x Câu 20. Cho parabol 2
(P) : y  8x , tìm hệ số góc k của tiếp tuyến của (P) tại điểm có tung độ bằng 4 1 A. k  1 B. k  2 C. k  D. k  2 3
Câu 21. Điểm M ( ; x y) parabol 2
(P) : y  16x đồng thời nằm trong góc phần tư thứ nhất của mặt phẳng tọa độ,
tìm giá trị nhỏ nhất của biểu thức T x  8 y  2045 . A.1789 B. 1945 C. 1979 D. 1954
Câu 22. Cho đường parabol (P): 2
y  2 px có tiêu điểm F (2; 0) , xét ba điểm ,
A B, C thuộc (P) có tung độ lần lượt là 6; 2; 4
 . Diện tích tam giác ABC (đvdt) bằng A.24 B. 15 C. 20 D. 28
Câu 23. Anten vệ tinh parabol có đầu thu đặt tại tiêu điểm, đường
kính miệng anten là 240cm, khoảng cách từ đầu thu tới miệng
anten là 130cm như hình vẽ. Tính khoảng cách (gần đúng) từ vị
trí đặt đầu thu đến đỉnh anten A. 49,6cm B. 69,4cm C. 46,9cm D. 96,4cm Câu 24. Cho parabol 2
(P) : y  16x , tìm cosin góc tạo bởi hai tiếp tuyến của (P) tại điểm có hoành độ bằng 1 A.0,5 B. 0,6 C. 0,25 D. 0,75
Câu 25. Điểm M ( ; x y) parabol 2
(P) : y  16x đồng thời nằm trong góc phần tư thứ nhất của mặt phẳng tọa độ,
tìm giá trị nhỏ nhất của biểu thức T  8x  3y  2023 . A.1789,5 B. 1988,5 C. 1979,5 D. 2018,5
Câu 26. Đường conic parabol nào sau đây có tiêu điểm là điểm đồng quy của ba đường thẳng
y  3x  3; y mx m  5; y nx  2n  6 A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2
y  4x
Câu 27. Cho đường parabol 2
y  2 px với p  0 có tiêu điểm cùng với hai điểm (
A 2; 2), B(4; 6) tạo thành ba
điểm thẳng hàng. Đường chuẩn của parabol đó có phương trình A. x  1  B. x  2  C. x  3  D. x  1
Câu 28. Với tham số tiêu p  0 , đường chuẩn của parabol 2
y  2 px cách điểm M (2 p; 2023) một khoảng bằng A.2p B. 4p C. 1,5p D. 2,5p Câu 29. Cho parabol 2
(P) : y  16x , (P) tiếp xúc với đường thẳng 8x 12 y m  4  0 tại điểm có hoành độ thuộc khoảng A.(0;5) B. (8;11) C. (5;8) D. (11;15)
_________________________________ 46
ĐƯỜNG PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P7)
_____________________________________ 5
Câu 1. Đường conic parabol 2
y  2 px với p  0 có đường chuẩn x  
. Giá trị của p thuộc khoảng 2 A.(0;1) B. [1;2) C. [2;3) D. [3;5]
Câu 2. Phương trình nào sau đây là phương trình chính tắc của đường conic parabol A. 2 y  6x 1 B. 2 y  2x C. 2 2
y  (m  5)x D. 2 2 y  3x
Câu 3. Đường conic parabol nào sau đây có tiêu điểm là tiếp điểm của hai đường tròn 2 2 2 2
x y  4; (x  3)  y  1 A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2 y  4x
Câu 4. Trong các đường conic sau, có bao nhiêu đường conic có thể có đường chuẩn x  2  2 2 2 2 2
y  4x; y  2( p q) ;
x y  4( p  6 p  2)x; y  6( p  3)x A.2 B. 4 C. 1 D. 3
Câu 5. Cho các đường cong có phương trình 2 2 2 2 2 y  6 ;
x y  (m  20) ;
x y  (m  2m  5) ; x y  (2 
p )x; y  2 p  2x
Có bao nhiêu phương trình luôn là phương trình chính tắc của một parabol A.4 B. 2 C. 3 D. 1
Câu 6. Tính tổng các giá trị p để đường conic 2 2
(P) : y  4( p  6 p  2)x với p  0 có tiêu điểm nằm trên
đường thẳng y x 1. A.2 B. 3 C. 4 D. 6
Câu 7. Đường conic parabol nào sau đây có tiêu điểm là điểm đồng quy của ba đường thẳng 2
y  (m  9)(x  2); y  7mx  2n  7; y n(x  2)  m  9 A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2 y  4x
Câu 8. Đường conic parabol 2
y  2 px với p  0 đi qua điểm M (1; 4) 
thì có đường chuẩn cách trục tung một khoảng bằng A.1 B. 2 C. 1,5 D. 2,5
Câu 9. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên,
trong đó đường thẳng d là đường chuẩn. Tìm hoành độ điểm M nếu
2MH MF  4 . A. 1,8 B. 4 C. 3 D. 1,6  
Câu 10. Cho đường parbol 2
(P) : y  4x và điểm I (0; 2) , hai điểm M, N thuộc (P) thỏa mãn IM  2IN . Tồn tại
hai điểm M, N với tổng hoành độ bằng A.6 B. 8 C. 4 D. 5
Câu 11. Có bao nhiêu số nguyên m  200 để parabol 2
(P) : y  2x và đường thẳng 4x  6 y m 10  0 không có điểm chung A.189 B. 185 C. 200 D. 178
Câu 12. Điểm M ( ; x y) thuộc parabol 2
(P) : y  8x , tìm giá trị lớn nhất của biểu thức 2 2
Q  x y  8x 1911. A.1979 B. 1945 C. 1975 D. 1954
Câu 13. Lập phương trình chính tắc của parabol biết khoảng cách từ đỉnh tới tiêu điểm bằng 0,75. A. 2 x  12 y B. 2 y  3x C. 2 y  12x . D. 2 y  6x
Câu 14. Đường conic parabol 2
y  2 px với p  0 có đường chuẩn đi qua trung điểm đoạn thẳng AB với (
A m  7;10), B(3  ;
m 2) . Phương trình đường chính tắc của parapol là A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2 y  4x
Câu 15. Cho đường parbol 2
(P) : y  4x , tiếp tuyến tại điểm M thuộc (P) có tung độ bằng 4, hệ số góc của tiếp tuyến đó bằng A.1 B. 1,5 C. 0,5 D. 2
Câu 16. Tập hợp các điểm M ( ; x y) thuộc parabol 2
(P) : y  36x đồng thời nằm trong góc phần tư thứ nhất của
mặt phẳng tọa độ người ta gọi là nhánh trên của parabol, phương trình nhánh trên đó là 47 A. y  2 x B. y  4 x C. y  6 x D. y  4x
Câu 17. Đường conic parabol 2
y  2 px với p  0 có khoảng cách từ tiêu điểm đến đường chuẩn bằng 2, điểm
M (x; y) nằm trên parabol thì độ dài đoạn thẳng MF bằng A. x  2 B. x 1 C. x  3 D. x 1
Câu 18. Cho đường conic parabol 2
(P) : y  6x , đường phân giác góc phần tư thứ nhất tạo với parabol một dây
cung có độ dài bằng đường kính của đường tròn nào A. 2 2
(x  4)  y  24 B. 2 2
(x  3)  ( y  2)  18 C. 2 2
(x  3)  ( y  4)  25 D. 2 2
(x  3)  ( y 1)  20
Câu 19. Đường conic parabol 2
y  2 px với p  0 có khoảng cách từ tiêu điểm đến đường thẳng x  10 bằng 8
đơn vị độ dài. Phương trình chính tắc đường parabol là A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2 y  4x
Câu 20. Có bao nhiêu số nguyên dương p để 5
y  (2023  p )x là dạng chính tắc của một parabol A.3 B. 5 C. 4 D. 6
Câu 21. Đường parabol nào có thể có đường chuẩn cách xa gốc tọa độ O nhất A. 2 2
y  4( p  2 p  20)x B. 2 2
y  4 1 p x C. 2 y  16x D. 2 y  4x
Câu 22. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên,
trong đó đường thẳng d là đường chuẩn. Tiêu điểm parabol trùng
với tâm đường tròn nào A. 2 2
(x  4)  y  4 B. 2 2
(x 1)  y  4 C. 2 2
(x 1)  y  4 D. 2 2
(x 1)  ( y  2)  1
Câu 23. Tồn tại bao nhiêu giá trị nguyên dương p để tiêu điểm của đường conic 2
y  2 px nằm trong khoảng
giữa hai đường thẳng (không nằm trên biên) x  1; x  3. A.4 B. 3 C. 5 D. 2
Câu 24. Cho đường conic parabol 2
(P) : y  6x , tiếp tuyến của parabol tại điểm có tung độ bằng 6 đi qua điểm nào sau đây A.(8;9) B. (10;16) C. (40;23) D. (50;27)
Câu 25. Đường conic parabol nào sau đây có tiêu điểm là tiếp điểm của hai đường tròn 2 2 2 2 (x  ) 4  y  ; 4 (x  ) 3  y  1 A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2 y  4x
Câu 26. Đường parabol 2
y  2 px với p  0 có tiêu điểm trùng với tiêu điểm bên phải của hypebol 2 2
16x  9 y  144 . Đường chuẩn của parabol cách trục hoành một khoảng bằng A.6 B. 10 C. 5 D. 8
Câu 27. Cho đường parbol 2
(P) : y  4x , hai điểm M, N thuộc (P) cùng có hoành độ bằng 4, các tiếp tuyến tại M
và N hợp với nhau một góc gần nhất với A.53 độ B. 54 độ C. 56 độ D. 57 độ
Câu 28. Đồ thị hàm số bậc hai 2 2 2
f (x)  (m 1)(x  2)  m 1cắt trục hoành tại hai điểm A, B. Đoạn thẳng AB
nhận tiêu điểm F của parabol 2
y  2 px với p  0 làm trung điểm. Phương trình đường chính tắc của parapol là A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2 y  4x
Câu 29. Tập hợp các điểm M ( ; x y) thuộc parabol 2
(P) : y  4x đồng thời nằm trong góc phần tư thứ nhất của
mặt phẳng tọa độ người ta gọi là nhánh trên của parabol, đường thẳng d là tiếp tuyến của nhánh trên đó và d đi qua điểm (
A 2; 0) , hệ số góc của đường thẳng d bằng A.1 B. 0,5 C. 1,5 D. 2
______________________________ 48
ĐƯỜNG PARABOL OXY LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P8)
_____________________________________
Câu 1. Lập phương trình chính tắc của parabol biết parabol đi qua điểm (3;3). A. 2 y  6x B. 2 y  3x C. 2 y  12x D. 2 y  4x
Câu 2. Trong các đường conic sau, có bao nhiêu đường conic có thể có đường chuẩn x  2  2 2 2 2 2 y  4 ;
x y  2( p q) ;
x y  4( p  2 p  3) ;
x y  4( p  3)x A.1 B. 4 C. 3 D. 2
Câu 3. Trong các phương trình sau 2 2 2 y  4 ;
x y x 2; 2 y  5 ; x
y  2 x , có bao nhiêu phương trình là
dạng chính tắc của một đường parabol A.2 B. 1 C. 3 D. 4
Câu 4. Tính tổng các giá trị p để đường conic 2 3 2
(P) : y  4( p  2 p  4 p  3)x với p  0 có tiêu điểm nằm trên
đường thẳng y x 1. A.0,5 B. 3 C. 2 D. 1
Câu 5. Đường conic parabol nào sau đây có tiêu điểm là điểm đồng quy của ba đường thẳng 2
y  (k 1)(x  2); y mx  2n  7; y n(x  2)  4m  9 A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2 y  4x
Câu 6. Đường chuẩn của đường conic  P 2
: y  4 px với p  0 vuông góc với đường thẳng nào sau đây A. y  4 px
B. y  3x 1
C. y m 2  2022
D. y  8x 1
Câu 7. Có bao nhiêu số nguyên p để 2 2
y  (9  p )x là dạng chính tắc của một parabol A.4 B. 3 C. 5 D. 6
Câu 8. Có bao nhiêu cặp số (m;n) để đường tròn 2 2 2
(x  4)  ( y m)  n tiếp xúc với đường conic parabol 2 y x 2022 . A.5 B. 2 C. 3 D. 4
Câu 9. Tập hợp các điểm M ( ; x y) thuộc parabol 2
(P) : y  16x đồng thời nằm trong góc phần tư thứ nhất của
mặt phẳng tọa độ người ta gọi là nhánh trên của parabol, phương trình nhánh trên đó là A. y  2 x B. y  4 x C. y  6 x D. y  4x
Câu 10. Đường conic parabol 2
y  2 px với p  0 có tham số tiêu bằng 10, điểm M thuộc parabol có tung độ
bằng – 10 thì có hoành độ bằng A.6 B. 8 C. 4 D. 5
Câu 11. Cho đường parabol 2
y  2 px như hình vẽ bên. Đường
parabol đã cho cắt đường thẳng 3 2 x
p  2 p  3 p  4  2 tại bao nhiêu điểm A. 2 B. 3 C. 1 D. 0
Câu 12. Cho đường parabol 2
y  2 px với p  0 có tiêu điểm cùng với hai điểm (3
A ; 4), B(4; 6) tạo thành ba
điểm thẳng hàng. Đường chuẩn của parabol đó có phương trình A. x  1  B. x  2  C. x  3  D. x  1
Câu 13. Cho ba điểm (
A 3; 6), B(m  5;1),C(m 1; 7) , đường parabol 2
y  2 px với p  0 có tiêu điểm F là
trọng tâm tam giác ABC. Điểm M (a;b) thuộc (P) thì độ dài đoạn thẳng MF bằng A. a 1 B. a  2 C. 2a 1 D. a 1
Câu 14. Tìm độ dài dây cung tạo bởi đường thẳng 2x y  4  0 và đường conic parabol 2
(P) : y  4x . A.4 B. 3 5 C. 6 3 D. 4 7
Câu 15. Tiêu điểm của parabol 2
y  2 px với p  0 là tâm của đường tròn 2 2 2
x y  6x  2my m m 15 thì
giá trị p thuộc khoảng nào A.(0;1) B. (1;4) C. (4;7) D. (7;10) 49
Câu 16. Điểm M ( ; x y) parabol 2
(P) : y  16x đồng thời nằm trong góc phần tư thứ nhất của mặt phẳng tọa độ,
tìm giá trị nhỏ nhất của biểu thức T x  8 y  2033 . A.1777 B. 1789 C. 1979 D. 1954
Câu 17. Đường conic parabol 2
y  2 px với p  0 cắt đường phân giác góc phần tư thứ nhất theo một dây
cung có độ dài bằng 5 2 , đường chuẩn của parabol cách tiêu điểm một khoảng bằng A.2,5 B. 2 C. 3 D. 3,5
Câu 18. Cho đường parabol (P): 2
y  2 px có tiêu điểm F (1; 0) , xét ba điểm ,
A B,C thuộc (P) có tung độ lần lượt là 6; 2; 4
 . Diện tích tam giác ABC (đvdt) bằng A.24 B. 30 C. 32 D. 28
Câu 19. Đường conic parabol nào sau đây có tiêu điểm là điểm đồng quy của ba đường thẳng
y  7x  7; y  6x  6; y m(x 1) A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2
y  4x
Câu 20. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên,
trong đó đường thẳng d là đường chuẩn. Tìm hoành độ điểm M nếu 2
2MH  3MF  44 . A. 1,8 B. 4 C. 3 D. 1,6
Câu 21. Đường conic parabol 2
y  2 px với p  0 có đường chuẩn đi qua trung điểm đoạn thẳng AB với (3 A ; 6), B( 7
 ; 2) . Phương trình đường chính tắc của parapol là A. 2 y  6x B. 2 y  8x C. 2 y  12x D. 2
y  4x  
Câu 22. Cho đường parbol 2
(P) : y  4x và điểm I (3; 2) , hai điểm M, N thuộc (P) thỏa mãn IM  2IN . Độ dài
đoạn thẳng MN có thể bằng A.4 B. 3 5 C. 6 3 D. 4 7 Câu 23. Cho parabol 2
(P) : y  4x , (P) tiếp xúc với đường thẳng 8x  9 y m  5  0 tại điểm có hoành độ thuộc khoảng  1   1 5   5 4   4  A. 0;   B. ;   C. ;   D. ; 2    2   2 6   6 3   3 
Câu 24. Cho đường parabol (P): 2
y  2 px với p  0 như hình vẽ bên, xét ba điểm ,
A B,C thuộc (P) có tung độ lần lượt là 4; 6  ;8 .
Trọng tâm tam giác ABC có hoành độ bằng 29 25 A. B. 3 6 14 40 C. D. 3 9
Câu 25. Đường parbol 2
(P) : y  4x cắt đường thẳng 2x y  4 tại hai điểm phân biệt M, N. Độ dài đoạn thẳng MN bằng A.4 B. 3 5 C. 6 3 D. 4 7
Câu 26. Đường conic parabol 2
(P) : y  4x tiếp xúc đường thẳng d :12x  6 y m  0 tại điểm M, M có tổng tung độ và hoành độ bằng A.2 B. 1 C. 3 D. 2,5
Câu 27. Parabol nào sau đây nhận tiêu điểm là điểm chung của hai đường tròn 2 2 2 2
x y  2x  4 y  3; x y  8x  8y  7  0 A. 2 y  6x B. 2 y  3x C. 2 y  12x D. 2 y  4x
_________________________________ 50
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P1)
_____________________________________
Câu 1. Trong mặt phẳng tọa độ Oxy , Elip có tổng độ dài hai trục bằng 18 và tỉ số của tiêu cự với độ dài trục 3 lớn bằng
. Phương trình chính tắc của elip là: 5 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1 B.   1 C.   1 D.   1 25 16 5 4 25 9 9 4
Câu 2. Điểm M ( ; x y) thuộc elip 2 2
(E) : 4x y  4 sao cho x y  3 nhỏ nhất. Tính xy . A.0,2 B. – 0,5 C. – 0,8 D. – 0,6 2 2 x y
Câu 3. Elip (E) : 
 1 cắt đường thẳng 3x  4 y  12 tại hai điểm phân biệt A, B. Độ dài đoạn thẳng AB 16 9 bằng A.5 B. 4,9 C. 5,2 D. 4,8
Câu 4. Hai số thực x, y thỏa mãn 2 2 2 2
(x  3)  y  (x  3)  y  8 . Tổng giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2 2 x y bằng A.23 B. 24 C. 20 D. 26
Câu 5. Cho đường parabol 2
(P) : y x . Một góc vuông ở đinh
O cắt parabol tại A , A . Dựng các hình chiếu như hình vẽ, 1 2
đường thẳng A A luôn đi qua điểm I cố định có tung độ bằng 1 2 A. 2 B. 2,5 C. 1 D. 3
Câu 6. Tồn tại hai điểm M ( ;
x y) trên đường thẳng 2x y  4  0 để từ M kẻ được đúng một tiếp tuyến đến parabol 2
(P) : y  4x . Tổng tung độ hai điểm M bằng A.3 B. 2 C. 1 D. 2 2 x y
Câu 7. Elip (E) : 
 1cắt đồ thị hàm số bậc hai 2
y x  2x tại bốn điểm phân biệt, đường tròn đi qua bốn 9 1
điểm này có tâm I (a;b) . Tính a : b . A.2 B. 1 C. 4 D. 3
Câu 8. Điểm M thuộc parabol 2
(P) : y  64x sao cho khoảng cách từ M đến đường thẳng 4x  3y  46  0 đạt
giá trị nhỏ nhất. Khoảng cách OM gần nhất với A.25,58 B. 25,63 C. 27,43 D. 26,14 2 2 x y
Câu 9. Điểm M thuộc elip (E) : 
 1sao cho F MF  120 ( F F là tiêu cự). Độ dài đoạn thẳng OM gần 100 25 1 2 1 2 nhất giá trị nào A.5,11 B. 4,92 C. 4,87 D. 5,25
Câu 10. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên,
trong đó đường thẳng d là đường chuẩn. Tìm hoành độ điểm M nếu 5 3
2MH  3MF MH.MF  2256 . A. 1,8 B. 4 C. 3 D. 1,6
Câu 11. Trong mặt phẳng tọa độ Oxy lập phương trình chính tắc của elip  E  biết nó có một đỉnh và hai tiêu
điểm tạo thành một tam giác đều và chu vi của hình chữ nhật cơ sở của  E  là 122  3 . 51 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1 36 27 36 3 27 9 27 36 2 2 x y
Câu 12. Cho elip (E) : 
 1có tiêu cự F F , điểm M thuộc elip sao cho 2MF MF . Điểm M thuộc 25 16 1 2 1 2
đường tròn tâm O có bình phương bán kính bằng 169 100 122 A.20 B. C. D. 9 9 9 2 2 x y
Câu 13. Trong mặt phẳng tọa độ Oxy , cho elip  E  : 
 1. Từ điểm A có tọa độ dương thuộc  E  ta 9 4
dựng hình chữ nhật ABCD nội tiếp trong  E  có các cạnh song song với các trục tọa độ và diện tích của hình
chữ nhật ABCD là lớn nhất. Tìm tọa độ đỉnh A .  3 2   3 2  A. A  ;  2  B. A3;0 A 3; 2 A  ; 2 .  C.   D.  2      2  
Câu 14. Cho hypebol  H  có hai tiêu điểm F ; F nằm trên Ox và đối xứng qua gốc tọa độ O ,  H  đi qua 1 2 9 41
điểm M có hoành độ 5  và MF  ; MF
. Phương trình chính tắc của hypebol  H  là: 1 2 4 4 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1 . D.   1 . 9 16 16 9 25 16 25 9
Câu 15. Cho hai điểm ( A 4; 3  ), B(3; 4)  , Điểm M ( ; x y) thuộc elip 2 2
(E) : x  4 y  4 sao cho tam giác MAB có
diện tích lớn nhất. Tính xy . 12 7 3 A.1 B. C. D. 13 13 14 2 2 x y
Câu 16. Trong mặt phẳng tọa độ Oxy , cho Elip  E  : 
 1 và điểm M nằm trên  E. Tìm tọa độ điểm 169 144
M trên  E biết rằng bán kính qua tiêu điểm trái gấp hai lần bán kính qua tiêu điểm phải.  169 8 14   169 8 14   169 8 14   169 8 14  A.  ;  và  ;  . B.   ; và   ; .     15 5          15 5   15 5   15 5    169 8 14   169 8 14   169 8 14   169 8 14  C.  ;   và   ; . D.   ; và   ;  .     15 5          15 5   15 5   15 5   2 x
Câu 17. Parabol y
chia hình tròn tâm O, bán kính R  2 2 thành 2
hai phần có diện tích S và S’ như hình vẽ. Tỉ số S : S thuộc khoảng nào ?  2 1   1 3   3 7   7 4  A. ;   B. ;   C. ;   D. ;    5 2   2 5   5 10   10 5 
Câu 18. Điểm M ( ; x y) parabol 2
(P) : y  16x đồng thời nằm trong góc phần tư thứ nhất của mặt phẳng tọa độ,
tìm giá trị nhỏ nhất của biểu thức T x x 12 y  2045 . A.1917 B. 1945 C. 1979 D. 1954
Câu 19. Trong mặt phẳng tọa độ Oxy, cho hình thoi ABCD có A nằm trên trục hoành, AC = 2BD và đường tròn
tiếp xúc với các cạnh hình thoi có phương trình 2 2
x y  4 . Viết phương trình chính tắc của elip (E) đi qua các đỉnh của hình thoi. 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1 B.   1 C.   1 D.   1 20 5 25 9 64 25 8 4
_________________________________ 52
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P2)
_____________________________________ 2 2 x y
Câu 1. Elip (E) : 
 1đi qua điểm M (3; 0) và thỏa mãn 2MF MF  7 ( F F là tiêu cự, F nằm bên phải 2 2 a b 1 2 1 2 2
trục tung). Tiêu cự của elip bằng A.6 B. 4 C. 8 D. 10
Câu 2. Đường thẳng d đi qua tiêu điểm parabol 2
(P) : y  4x cắt parabol tại hai điểm phân biệt A, B. Tích
khoảng cách từ A, B đến trục hoành là một số không đổi và bằng A.3 B. 4 C. 6 D. 8 2 2 x y
Câu 3. Cho đường hypebol 
 1 có hình chữ nhật cơ sở 2 2 a b
mô tả như hình vẽ bên. Biết hình chữ nhật có diện tích bằng 32.
Tìm giá trị nhỏ nhất của biểu thức a  9b .
A. 8 3 B. 4 5 C. 12 2 D. 15
Câu 4. Elip (E) có tiêu điểm với tiêu điểm của hypebol 2 2
9x 16 y  144 và ngoại tiếp hình chữ nhật cơ sở của
(H). tiêu cự của elip bằng A. 2 55 B. 8 5 C. 10 2 F. 10  20 
Câu 5. Viết phương trình chính tắc của hypebol  H  biết rằng  H  đi qua các điểm M 4; 0 và N ; 4   .  3  2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 9 16 16 9 16 9 16 25 Câu 6. Cho parabol 2
(P) : y  4x và hai điểm (0 A ; 4  ), B( 6
 ; 4) . C là điểm trên ( )
P sao cho tam giác ABC có
diện tích bé nhất. Điểm C nằm trên đường thẳng nào sau đây?
A. 16x  2y  6  0 .
B. 16x  2 y  6  0 .
C. 16x  2 y  6  0 .
D. 16x  2 y  6  0 .
Câu 7. Hai số thực x, y thỏa mãn 2 2 2 2
(x 1)  ( y 1)  (x 1)  ( y  3)  6 5 . Giá trị lớn nhất của biểu thức 2 2
(x  2)  ( y  3) bằng A.125 B. 240 C. 100 D. 120 2 x
Câu 8. Điểm M ( ;
x y) nằm trên hypebol (H): 2
y  1sao cho khoảng cách từ M đến đường thẳng 4
 : y x 1đạt giá trị nhỏ nhất. Khi đó 4 8 2 7 A. xy  B. xy  C. xy  D. xy  3 3 3 3
Câu 9. Các hành tinh và các sao chổi khi chuyển động xung quanh mặt trời có quỹ đạo là một đường elip trong
đó tâm mặt trời là một tiêu điểm. Điểm gần mặt trời nhất gọi là điểm cận nhật, điểm xa mặt trời nhất gọi là điểm
viễn nhật. Trái đất chuyển động xung quanh mặt trời theo quỹ đạo là một đường elip có độ dài nửa trục lớn 59
bằng 93.000.000 dặm. Tỉ số khoảng cách giữa điểm cận nhật và điểm viễn nhật đến mặt trời là . 61
Khoảng cách từ tâm trái đất đến tâm mặt trời khi trái đất ở điểm cận nhật bằng A. 91.450.000 dặm. B. 91.455.000 dặm. C. 91.000.000 dặm. D. 91.550.000 dặm. 53
Câu 10. Hai thiết bị A và B dùng để ghi âm một vụ nổ đặt cách nhau 1 dặm, thiết bị A ghi được âm thanh
trước thiết bị B là 2 giây, biết vận tốc âm thanh là 1100 feet / s . Tìm các vị trí mà vụ nổ có thể xảy ra ( 1 dặm
 5280 feet; 3 feet  0,914m ) . 2 2 x y 2 2 x y A.   1 . B.   1. 5280 2200 5280 2200 2 2 x y 2 2 x y C.   1. D.   1. 2 2 5280 1100 1210000 5759600 
Câu 11. Điểm M thuộc cung AB của đường conic parabol 2
(P) : y x với (
A 1;1), B(2; 2) . Diện tích lớn nhất
của tam giác MAB khi đó bằng A.3,25 B. 3,375 C. 3,75 D. 3,425
Câu 12. Trong mặt phẳng Oxy cho parabol  P 2
: y  8x . Đường thẳng Δ không trùng với trục Ox đi qua tiêu
điểm F của  P sao cho góc hợp bởi hai tia Fx và Ft là tia của Δ nằm phía trên trục hoành một góc bằng α  0
α  90  . Biết Δ cắt  P tại hai điểm phân biệt M , N và tập hợp trung điểm I của đoạn MN khi α thay
đổi là một Parabol. Phương trình của Parabol là A. 2
y  4x  8 . B. 2
y  4x  4 . C. 2
y  4x  8 . D. 2
y  4x  4 . 2 2 x y
Câu 13. Cho đường hypebol   1 như hình vẽ bên. 2 2 a b
Điểm M thuộc nhánh phải hypebol thỏa mãn MF MF  6 1 2
Tìm giá trị lớn nhất của MF (12  MF ) . 1 2 A. 24 B. 30 C. 36 D. 28 Câu 14. Parabol 2
y  4x cắt đường thẳng x y m  0 tại hai điểm phân biệt A, B sao cho tam giác OAB
vuông tại O, tổng các giá trị m thu được bằng A.0,8 B. 0,6 C. 0,5 D. 0,7 2 2 x y
Câu 15. Điểm M nằm trên hypebol (H ) : 
 1và nhìn hai tiêu điểm dưới một góc vuông. Độ dài đoạn 16 9 thẳng OM khi đó bằng A.4 B. 5 C. 6 D. Kết quả khác
Câu 16. Ông X có một mảnh vườn hình vuông cạnh bằng 8m. Ông dự định
xây một cái bể bơi đặc biệt như hình vẽ bên. Biết AB = 4AM, phần đường
cong đi qua các điểm C, M, N là một phần của đường parabol có trục đối
xứng là MP. Biết kinh phí để làm bể bơi là 5 triệu đồng mỗi mét vuông. Chi
phí ông A phải trả để hoàn thành bể gần nhất với con số nào sau đây ?
A. 95814000 đồng B. 908140000 đồng
C. 94814000 đồng D. 93814000 đồng 2 2 x y
Câu 17. Đường thẳng 3x  4 y 12  0 cắt elip (E) : 
 1tại hai điểm phân biệt A, B. Điểm C thuộc elip 16 9
sao cho tam giác ABC có diện tích bằng 6. Bình phương độ dài đoạn thẳng OC khi đó bằng A.12,5 B. 13,5 C. 14 D. 16,5 2 2 x y
Câu 18. Điểm M ( ;
x y) thuộc elip (E) :   1 sao cho 2 2
M  (x  2)  4(x  3) đạt giá trị lớn nhất. Tính giá trị 8 2 của biểu thức 2 2
2x  3y  4xy . A.11,8 B. 12,5 C. 14,5 D. 16,5
_________________________________ 54
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P3)
_____________________________________
Câu 1. Trên mặt phẳng, cho tam giác ABC có A 2  ;  2 , B 2
 ; 2 , C 6;2 . Biết tập hợp tất cả các điểm M    
thỏa mãn hệ thức MA MB MA MC  12 là một elip. Độ dài trục lớn và trục bé của elip là A. 6 . B. 3 5 . C. 2 3 . D. 6 .
Câu 2. Parabol (P) có tiêu điểm F (3;0), qua điểm I (2; 0) kẻ đường thẳng d cắt parabol tại hai điểm phân biệt A,
B, khi đó tích khoảng cách từ A, B đến trục hoành bằng A.24 B. 25 C. 30 D. 18
Câu 3. Điểm M ( ; x y) parabol 2
(P) : y  16x đồng thời nằm trong góc phần tư thứ nhất của mặt phẳng tọa độ,
tìm giá trị nhỏ nhất của biểu thức T x y 1958 . A.1789 B. 1945 C. 1979 D. 1954
Câu 4. Trong mặt phẳng với hệ toạ độ Oxy, cho parabol 2
(P) : y x và điểm A(5; 0) . Gọi M có tung độ dương
là một điểm trên  P để đoạn AM ngắn nhất. Khi đó AM bằng 19 19 9 3 2 A. . B. . C. . D. . 2 2 2 2
Câu 5. Trong mặt phẳng tọa độ Oxy, tìm diện tích hình tròn tạo bởi đường tròn đi qua bốn giao điểm của elip 2 2 x y 2 2 x y   1và hypebol   1 9 4 1 4 A. 5 B. 4 C. 8 D. 9
Câu 6. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên,
trong đó đường thẳng d là đường chuẩn. Tìm hoành độ điểm M nếu 3
2MH  7MF  48, 75 . A. 1,8 B. 1,4 C. 1,5 D. 1,6
Câu 7. Cho M là một điểm thuộc Parabol 2
(P) : y  64x và N là một điểm thuộc đường thẳng
d : 4x  3 y  46  0 . Xác định M , N để đoạn MN ngắn nhất. Tổng hoành độ hai điểm M và N bằng A.16,4 B. – 4 C. 4 D. – 16,4
Câu 8. Hai số thực x, y thỏa mãn 2 2 2 2
(x  2)  y  (x  2)  y  6 . Tổng giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2 2
(x 1)  ( y  3) gần nhất với số nào A.6,32 B. 7,12 C.5,28 D. 6,24
Câu 9. Cho một cái đèn với chụp bóng đèn có mặt cắt qua trục là parabol với kích thước được thể hiện trên
hình vẽ, giả sử xem dây tóc bóng đèn là một điểm và được đặt ở vị trí tiêu điểm của parabol. Tính khoảng cách
từ dây tóc bóng đèn tới đỉnh của chụp bóng đèn. 45 45 45 45 A. cm . B. cm . C. cm . D. cm . 8 16 4 2 2 2 x y
Câu 10. Elip (E) có các tiêu điểm là các tiêu điểm của (H): 
 1 và các đỉnh của hình chữ nhật cơ sở của 64 36
(H) đều nằm trên elip. Tiêu cực của elip bằng 55 A.20 B. 30 C. 26 D. 24
Câu 11. Vệ tinh nhân tạo đầu tiên được Liên Xô (cũ) phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là một đường elip nhận tâm Trái Đất là một tiêu điểm có phương trình quỹ đạo là 2 2 x y 2 2 2 
 1, a  0,b  0, c a b . Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa 2 2 a b c
nhất là 1342 dặm (1 dặm xấp xỉ 1, 609 km). Tìm tỷ số
, biết bán kính của Trái Đất xấp xỉ 4000 dặm. a c c c c A.  0, 67 . B.  0, 76 . C.  0, 067 . D.  0, 076 . a a a a
Câu 12. Cho đường parabol 2
(P) : y x . Một góc vuông ở đinh
O cắt parabol tại A , A . Dựng các hình chiếu như hình vẽ, tính 1 2 OB .OB . 1 2 A. 2 B. 2,5 C. 1 D. 3 2 2 x y
Câu 13. Từ một điểm M thuộc hypebol 
 1kẻ các đường thẳng song song với các tiệm cận, ta thu được 9 16
hình bình hành OMPQ, diện tích hình bình hành OMPQ bằng bao nhiêu đơn vị diện tích A.5 B. 6 C. 4 D. 8
Câu 14. Hai số thực x, y thỏa mãn 2 2 2 2
(x 1)  ( y  3)  (x  2)  ( y 1)  8 . Tổng giá trị lớn nhất, giá trị nhỏ 2  1  2
nhất của biểu thức x    y     1 bằng  2  A.26 B. 25,75 C. 27,25 D. 16,5
Câu 15. Tìm điều kiện của điểm M ( ;
x y) trên đường thẳng 2x y  4  0 để từ M không kẻ được tiếp tuyến nào đến parabol 2
(P) : y  4x . A. 1  x  4 B. 0  x  4 C. 1  x  2 D. 2  x  4
Câu 16. Trên bờ biển có hai trạm thu phát tín hiệu A và B cách nhau 6 km , người ta xây một cảng biển cho
tàu hàng neo đậu là một nửa hình elip nhận AB làm trục lớn và có tiêu cự bằng 2 5 km . Một con tàu hàng M
nhận tín hiệu đi vào cảng biển sao cho hiệu khoảng cách từ nó đến A và B luôn là 2 6 km . Khi neo đậu tại
cảng thì khoảng cách từ con tàu đến bờ biển là bao nhiêu? 126 12 12 126 A. km . B. km . C. km . D. km . 17 17 17 17 2 2 x y
Câu 17. Hình chữ nhật ABCD nội tiếp elip (E) : 
 1, có các cạnh song song với các trục tọa độ và có 25 9
diện tích lớn nhất, các đỉnh của hình chữ nhật thuộc đường tròn có bình phương bán kính bằng A.3 B. 2 C. 4 D. 17 Câu 18. Cho elip 2 2
(E) : 9x  25y  225 . Tồn tại bao nhiêu điểm M thuộc elip thỏa mãn đẳng thức 1 1 8   MF MF F F 1 2 1 2 A. 3 B. 2 C. 4 D. 1
_________________________________ 56
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P4)
_____________________________________ 2 2 x y
Câu 1. Ký hiệu M (x;y) là một điểm thuộc elip 
 1. Tìm giá trị lớn nhất của biểu thức Q = x + 2y. 9 4 A. 4 B. 13 C. 19 D. 11 2 2 ax y Câu 2. Cho hypebol 
 1 với a  0 . Độ dài ngắn nhất của tiêu cự hypebol đã cho bằng 2 2 a  9 b  4b 16 A.8 B. 10 C. 12 D. 14
Câu 3. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên,
trong đó đường thẳng d là đường chuẩn. Tìm hoành độ điểm M nếu
giá trị biểu thức 2
MH.MF 12MF  2023 đạt giá trị nhỏ nhất. A. 2 B. 2,4 C. 1 D. 1,6
Câu 4. Cho hai đường tròn C  2 2
: x y  4;C  2 2
: x y  1. Các điểm A, B di động lần lượt trên 1 2 C , C
sao cho Ox là phân giác của góc AOB . Tìm quỹ tích trung điểm M của đoạn thẳng AB. 1   2  2 4x 2 2 x y A. Elip 2  4 y  1 B. Elip   1 9 25 4 2 2 x y C. Elip   1
D. Đường thẳng 2x – 3y + 1 = 0. 9 4 2 2 x y
Câu 5. Đường thẳng d đi qua I (1;1) và cắt elip (E) : 
 1tại hai điểm phân biệt M, N sao cho I là trung 25 9
điểm của đoạn thẳng MN. Hệ số góc của đường thẳng đó bằng 9 3 2 A.  B.  C.  D. 14 25 11 7
Câu 6. Một sân chơi dành cho trẻ em hình chữ nhật có chiều dài
50m và chiều rộng là 30m, người ta làm một con đường nằm
trong sân như hình vẽ. Biết viền ngoài và viền trong của con
đường là hai đường elip và chiều rộng của mặt đường là 3m. Kinh
phí để làm mỗi m2 đường là 500 nghìn đồng. Tính tổng số tiền
làm con đường đó (làm tròn đến hàng nghìn).
A. 119000000 đồng B. 152000000 đồng C. 119320000 đồng D. 125520000 đồng 2 2 x y Câu 7. Cho elip 
 1với hai tiêu điểm F , F . Lấy hai điểm A, B thuộc elip (E) sao cho AF BF t . Khi 25 16 1 2 1 2
đó giá trị lớn nhất của biểu thức ( AF BF )( AF BF ) bằng 1 2 2 1 A.90 B. 100 C. 80 D. 96 2 2 x y
Câu 8. Hypebol (H ) : 
 1có hai tiêu điểm F , F . Điểm M bất kỳ thuộc hypebol. Tính 25 16 1 2 2 2
(MF MF )  4OM 1 2 A.9 B. 64 C. 16 D. 25 2 2 x y Câu 8. Hypebol 
 1có độ dài trục thực bằng 6 và phương trình một đường tiệm cận là 5x  3y . Tính 2 2 a b 2 2 a b . 57 A.40 B. 32 C. 36 D. 24 2 2 x y
Câu 9. Cho đường hypebol   1 như hình vẽ bên. 2 2 a b
Điểm M thuộc nhánh phải hypebol thỏa mãn 2 3
MF MF  6; 2MF MF  136 1 2 1 2
Tính MF  3MF . 1 2 A. 12 B. 30 C. 14 D. 18
Câu 10. Đường tròn (C) có bán kính nhỏ nhất tiếp xúc với parabol 2
(P) : y  64x và đường thẳng
4x  3y  46  0 . Tiếp điểm với parabol là điểm M, độ dài đoạn thẳng OM bằng A. 3 73 B. 8 13 C. 10 17 D. 12 26 1
Câu 11. Điểm M ( ; x y) thuộc parabol 2
(P) : y  4x . Tìm giá trị nhỏ nhất của biểu thức 2
M xy  3x   2023 . 2 y A.2020 B. 2021 C. 2023 D. 2019 2 2 x y 2 b  1 1 
Câu 12. Với M là điểm bất kỳ trên elip (E) : 
 1, F là tiêu điểm phải của elip. Tính  2 2   a b a FM FN  A. 3 B. 2 C. 4 D. 1
Câu 13. Một tháp làm nguội của một nhà máy có mặt cắt là hình
hyperbol có tiêu cự bằng 2 70 m , độ dài trục ảo bằng 2 42 m . Biết
chiều cao của tháp là 120m và khoảng cách từ nóc tháp đến tâm đối 2 xứng của hypebol là
khoảng cách từ tâm đối xứng đến đáy. Bán 3
kính nóc và bán kính đáy của tháp lần lượt là
A. 391 m ; 2 871 m .
C. 2 391 m ; 871 m .
B. 2 391 m ; 2 871 m .
D. 391 m ; 871 m . 2 2 x y
Câu 14. Hypebol
 1đi qua điểm M (6;3) và góc giữa hai tiệm cận bằng 60 . Khi đó 2 2
2a b có thể 2 2 a b bằng A.14 B. 12 C. 10 D. 15 Câu 15. Trên hypebol 2 2
(H ) : 3x  4 y  12 tồn tại hai điểm P, Q sao cho tam giác OPQ đều, P và Q đều thuộc
đường tròn tâm O có bình phương bán kính bằng A.8,4 B. 9,6 C. 9 D. 9,2 2 2 x y
Câu 16. Trên hypebol (H ) : 
 1 có điểm M nhìn hai tiêu điểm dưới một góc 60 độ. Điểm M đó thuộc 16 9
đường tròn tâm O có bình phương bán kính bằng A.36 B. 43 C. 52 D. 48 2 2 x y
Câu 17. Đường thẳng 3x  4 y 12  0 cắt elip (E) : 
 1tại hai điểm phân biệt A, B. Điểm C thuộc elip 16 9
sao cho tam giác ABC có diện tích lớn nhất. Bình phương độ dài đoạn thẳng OC khi đó bằng A.12,5 B. 13,5 C. 14 D. 16,5
Câu 18. Một đường thẳng d qua tiêu điểm F của parabol 2
(P) : y  16x và cắt parabol tại hai điểm M, N. Đường
thẳng MN tiếp xúc với đường thẳng nào sau đây A. x  4  B. x  2  C. x  0 D. x  1 
_________________________________________ 58
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P5)
_____________________________________
Câu 1. Trong mặt phẳng tọa độ Oxy, đường cong 2 2
(H ) : 5x  3y 10x 12 y  22  0 được chứng minh là một x  1 X
đường hypebol, nó có thể đưa về dạng chính tắc trong hệ tọa độ IXY trong đó  . Tiêu cự hypebol đó y  1 Y  là A.6 B. 4 2 C. 6 2 D. 8 3 2 2 x y
Câu 2. Đường thẳng d (cắt hai trục tọa độ) đi qua điểm (
A 1; 4) và tiếp xúc với hypebol (H ) :   1. Đường 1 4
thẳng d có hệ số góc gần nhất với A.2 B. 2,6 C. 2,7 D. 2,8 2 2 x y
Câu 3. Đường elip (E) : 
 1 nội tiếp hình vuông nào ABCD 24 12
như hình vẽ. Diện tích hình vuông đó gần nhất với A. 72 B. 80 C. 70 D. 68 2 2 x y
Câu 4. Tam giác ABC có A (3;– 2), B (– 3;2), đỉnh C có hoành độ dương và C nằm trên elip   1. Biết 9 4
rằng tam giác ABC có diện tích đạt giá trị lớn nhất, khi đó tung độ điểm C là 2 A. 2 B. 3 C. 2 D. 2 2 2 x y
Câu 5. Elip (E) : 
 1cắt đường thẳng 4x  5 y m  0 tại hai điểm phân biệt A, B thì tập hợp trung điểm I 25 9
của đoạn thẳng AB là đường thẳng có hệ số góc k và hoành độ điểm I thỏa mãn l x l . Tính 36kl . A.64,8 B. 52,8 C. 70,5 D. 69,6 2 2 x y
Câu 6. Elip (E) : 
 1có tiêu cự F F , F là tiêu điểm trái điểm M chạy trên elip, phân giác trong của góc 9 4 1 2 1 
F MF cắt trục hoành tại N, H là hình chiếu vuông góc của N trên đoạn MF . Tính độ dài đoạn MH. 1 2 1 4 5 7 A.3 B. C. D. 3 3 6
Câu 7. Trong mặt phẳng tọa độ Oxy, đường cong 2 2
(E) : 3x  4 y  6x 16 y  7  0 được chứng minh là một x  1 X
đường elip, nó có thể đưa về dạng chính tắc trong hệ tọa độ IXY trong đó 
. Tiêu cự của elip đó là y  1 Y  A.6 B. 4 2 C. 6 2 D. 2 Câu 8. Cho parabol 2
(P) : y  2 px , A là điểm trên tia Ox, đường
thẳng qua A vuông góc với tia Ox cắt parabol tại D, gọi B, C là hai  
điểm thuộc bánh chứa D của parabol (P) sao cho DAB DAC và 2  4 AD  3 .
AB AC , số đo góc BAC khi đó bằng bao nhiêu độ A.30 B. 60 C. 45 D. 70 2 2 x y
Câu 9. Trong mặt phẳng với hệ trục tọa độ Oxy , cho elip  E  : 
 1 và đường thẳng d : 3x  4 y 12  0 . 16 9
Biết rằng d luôn cắt  E  tại hai điểm phân biệt A , B . Tính độ dài đoạn AB . 59 A. AB  5 . B. AB  3 . C. AB  4 . D. AB  10. 2 2 x y
Câu 10. Trong hệ tọa độ Oxy cho điểm C (3;0) và elip  E  : 
 1. Hai điểm A, B là hai điểm thuộc elip 9 1  a c 3 
sao cho tam giác ABC đều. Tính a + c biết rằng A ;  với a  0 . 2 2   A. 2 B. 0 C. – 2 D. – 4
Câu 11. Đường conic parabol 2
(P) : y  8x tiếp xúc với đường thẳng d : 8x  8y m n  0 . Giá trị nhỏ nhất của biểu thức 2
Q n  4m  2023 gần nhất với số nào A.1992 B. 1954 C. 1975 D. 2022
Câu 12. Một người kỹ sư thiết kế một đường hầm một chiều có mặt
cắt là một nửa hình elip, chiều rộng của hầm là 12 mét, khoảng
cách từ điểm cao nhất của elip so với mặt đường là 3 mét. Người kĩ
sư này phải đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Một
chiếc xe có chiều rộng bằng 3 mét thì chiều cao lớn nhất có thể đi
qua hầm thuộc khoảng nào sau đây A. 2, 4; 2, 6 . B. 2,8;3, 00 . C. 3,00;3, 20 . D. 2, 6; 2,8 . x 1
Câu 13. Trong hệ trục tọa độ Oxy, đường cong y
được chứng minh là một hypebol, điểm M thuộc x  2
hypebol thì có tổng khoảng cách đến hai đường thẳng x  2; y  1đạt giá trị nhỏ nhất bằng A.2 B. 2 3 C. 4 D. 4 2
Câu 14. Cho hai số x, y thỏa mãn 2 2 2 2
(x 1)  y  (x  3)  y  6 . Khi đó biểu thức 2 2
(x 1)  ( y  4) nhận
giá trị nhỏ nhất bằng A.6 B. 3 C. 4 D. 5 2 2 x y
Câu 15. Điểm M thuộc hypebol (H ) : 
 1sao khoảng cách từ M đến tiêu điểm phải nhỏ nhất, tổng tung 9 16
độ và hoành độ của M bằng A.3 B. – 3 C. 0,75 D. 0,75 2 2 x y
Câu 16. Cho elip (E) : 
 1và hai điểm A (– 5;3), B (5;– 3). Tồn tại điểm C (x;y) trên elip sao cho tam 25 9
giác ABC có diện tích lớn nhất. Giá trị 2 2 x y bằng A. 16 B. 17 C. 20 D. 12
Câu 17. Elip tiếp xúc đồng thời với hai đường thẳng x y  5  0; x  4 y 10  0 thì có tiêu cự bằng A.8 B. 2 15 C. 4 2 D. 6 2 Câu 18. Cho parabol 2
(P) : y x . Hai điểm A, B di động trên (P) sao cho AB = 2. Gọi S là diện tích hình phẳng
giới hạn bởi parabol (P) và đoạn thẳng AB. Tính diện tích lớn nhất của S. 4 7 5 5 A. max S  B. max S  C. max S  D. max S  3 6 6 3
Câu 19. Các điểm M, N chuyển động trên hai tia Ox, Oy sao cho đoạn thẳng MN luôn tiếp xúc với đường elip 2 2 x y (E) : 
 1 . Giá trị nhỏ nhất của đoạn thẳng MN bằng 16 9 A.7 B. 6,5 C. 7,2 D. 6,8
_________________________________ 60
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P6)
_____________________________________ 2 2 x y
Câu 1. Elip (E) : 
 1 có tiêu cự F F , ( F có là tiêu điểm phải), điểm M thuộc elip sao cho 4 3 1 2 2 2 2
MF  7MF đạt giá trị nhỏ nhất. Tổng tung độ và hoành độ điểm M khi đó bằng 1 2 A.3 B. 5 C. 4 D. 2
Câu 2. Để trang trí cho một lễ hội đầu xuân, từ một mảnh vườn
hình elip có chiều dài trục lớn là 10m, chiều dài trục nhỏ là 4m,
Ban tổ chức vẽ một đường tròn có đường kính bằng độ dài trục
nhỏ và có tâm trùng với tâm của elip như hình vẽ. Biết diện tích
hình elip có độ dài trục lớn, trục bé lần lượt là a, b được tính theo
cộng thức S   ab .
Trên hình tròn người ta trồng hoa với giá 100000 đồng/m2, phần còn lại của mảnh vườn người ta trồng cỏ với
giá 60000 đồng/m2 (biết giá trồng hoa và trồng cỏ bao gồm cả công và cây). Hỏi ban tổ chức cần bao nhiêu
tiền để trồng hoa và cỏ (số tiền làm tròn đến hàng nghìn).
A. 2387000 đồng B. 2638000 đồng C. 2639000 đồng D. 2388000 đồng
Câu 3. Cho đường hypebol có một tiêu điểm F ( 13; 0) và có độ dài trục thực là 6. Tìm điểm M thuộc 23
hypebol biết điểm M có tổng hoành độ và tung độ bằng
. Điểm M có thể có hoành độ bằng 3 A.22,6 B. 5,5 C. 4 D. 12,5 2 2 x y
Câu 4. Điểm M nằm trên elip (E) : 
 1(có tiêu cự F F , F có là tiêu điểm phải), tính 2013 2012 1 2 2 2
MF .MF OM . 1 2 A.2023 B. 4025 C. 2011 D. Kết quả khác
Câu 5. Điểm M nằm trên hypebol 2 2
9x y  9 và nhìn hai tiêu điểm dưới một góc 60 độ. Điểm M luôn cách gốc
tọa độ một khoảng có bình phương bằng A.27 B. 28 C. 40 D. 16 x 1
Câu 6. Trong hệ trục tọa độ Oxy, tập hợp các điểm M ( ;
x y) thỏa mãn y
là một hypebol, tổng khoảng x 1
cách từ M đến hai trục tọa độ đạt giá trị nhỏ nhất bằng A.1 B. 2 C. 2 1 D. 3 1 2 2 x y
Câu 7. Hình chữ nhật MNPQ nội tiếp elip (E) : 
 1và có hai đường chéo hợp với nhau góc 60 độ. Điểm 25 9
M có thể cách gốc tọa độ một khoảng có bình phương bằng 75 80 80 A.17 B. C. D. 7 7 9 mx  2m 1
Câu 8. Trong hệ trục tọa độ Oxy, tập hợp các điểm M ( ;
x y) thỏa mãn y  là một hypebol, hypebol x m
này luôn tiếp xúc với một đường thẳng d cố định, khoảng cách từ gốc tọa độ O đến đường thẳng d bằng A. 1 B. 2 C. 3 D. 0,5 2 2 x y
Câu 9. Tam giác ABC vuông cân tại (3
A ; 0) và nội tiếp trong đường elip (E) : 
 1. Tổng hoành độ và 9 4
tung độ điểm B có thể bằng 9 5 2 A.1 B.  C. D.  13 13 11
Câu 10. Hai điểm A, B nằm trên đường elip 2 2
(E) : 9x  25 y  225 (có tiêu cự F F , F có là tiêu điểm phải), tứ 1 2 2
giác F F BA có tổng độ dài hai đường chéo bằng 6, chu vi nhỏ nhất của tứ giác bằng 1 2 A.49 B. 36 C. 43 D. 38
Câu 11. Đường tròn (C) có tâm thuộc đường thẳng x y  9  0 , có bán kính nhỏ nhất và đồng thời tiếp xúc với 61 2 2 x y elip (E) : 
 1. Tung độ tiếp điểm khi đó bằng 16 9 A.1 B. – 1,2 C. – 1,8 D. – 2
Câu 12. Điểm M thuộc parabol 2
(P) : y  8x và điểm N thuộc đường thẳng x y  3  0 sao cho độ dài đoạn
thẳng MN ngắn nhất, tung độ điểm M khi đó bằng A.4 B. – 4 C. – 3,5 D. 2,5
Câu 13. Cho hai điểm (
A 2; 0), B(2; 0) , điểm M chuyển động  
sao cho MBA  2MAB , khi đó M chạy trên một nhánh của
hypebol cố định, tiêu điểm phải của hypebol (sau khi sử
dụng phép đổi hệ trục tọa độ đưa về dạng chính tắc) đó có hoành độ bằng 8 5 7 A.1 B. C. D. 3 3 9 2 2 2 2 x y x y
Câu 14. Hai elip (E ) :   1; (E ) : 
 1có tung tiêu điểm, elip (E ) đi qua điểm M thuộc đường 1 2 2 2 10 6 a b 2
thẳng x y  4  0 đồng thời có độ dài trục lớn nhỏ nhất. Tung độ điểm M khi đó bằng A.1 B. – 2 C. – 1,5 D. – 1,2
Câu 15. Đường cong (H) bao gồm các điểm M ( ;
x y) thỏa mãn xy  1là một hypebol, điểm M thuộc hypebol sao  5 5 
cho độ dài đoạn thẳng AM nhỏ nhất, với A ; 
 . Giá trị nhỏ nhất ấy bằng  2 2  17 13 21 A.5 B. C. D. 2 2 2 2 2 x y
Câu 16. Điểm M di động trên elip (E) : 
 1 , H và K là hình chiếu vuông góc của M trên hai trục tọa độ và 9 4
tứ giác OHMK có diện tích lớn nhất. Điểm M thuộc đường tròn tâm O có bình phương bán kính bằng A.6,5 B. 5,5 C. 6 D. 7
Câu 17. Một chiếc cốc nằm ngang, có mặt cắt ngang là hình parabol
(hình vẽ). Hình parabol có chiều rộng giữa hai mép cốc là AB  9cm
và chiều sâu h  4cm ( h bằng khoảng cách từ S đến AB , S là
điểm chính giữa đáy cốc. Viết phương trình chính tắc parabol đó. 81 81 9 81 A. 2 y x . B. 2 y x . C. 2 y x . D. 2 y x 32 16 4 64 x  3
Câu 18. Trong hệ trục tọa độ Oxy, tập hợp các điểm M ( ;
x y) thỏa mãn y
là một hypebol, đường thẳng x  2 x  3   15
d: y = 2x + 3m cắt đường hypebol y
tại hai điểm phân biệt A, B thỏa mãn điều kiện O . A OB  . Khi đó x  2 2
đường thẳng d đi qua điểm nào ?  19   1   11  A. 2;   B. (3;2) C. 3;   D. 3;    2   2   2 
Câu 19. Điểm M thuộc hypebol 2 2
x y  1sao cho khoảng cách từ điểm M đến đường thẳng
d : 5x  3y 1  0 đạt giá trị nhỏ nhất. Tung độ điểm M thuộc khoảng nào sau đây  1   1 7   1 1   7  A. 0;   B. ;   C. ;   D. ;1    3   2 8   3 2   8 
_________________________________ 62
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P7)
_____________________________________ Câu 1. Parabol 2 (P) : y  2 ; px
p  0 có tiêu điểm là giao điểm của bốn đường tròn 2 2 2 2 2 2 2 2
(x  4)  ( y  3)  18; (x  2)  y  9; (x  2)  y  1; (x  4)  y  9
Đường tròn tiếp xúc đồng thời với parabol và đường thẳng y x  5 thì có bình phương bán kính bằng A.4 B. 5 C. 2 D. 6
Câu 2. Trong mặt phẳng tọa độ Oxy, đường cong 2 2
(H ) : 6x  4 y  24x  40 y  52  0 được chứng minh là một x  2   X
đường hypebol, nó có thể đưa về dạng chính thức trong hệ tọa độ IXY trong đó  . Tiêu cự hypebol y  5  Y  đó là A. 2 10 B. 4 2 C. 6 2 D. 8 3 2 2 2 2 
 (x  3)  ( y  4)  (x 1)  ( y  2)  8
Câu 3. Có bao nhiêu số nguyên m để hệ phương trình  có nghiệm 2 2
(x 1)  ( y 1)  m  A.12 B. 14 C. 6 D. 15 2 2 x y
Câu 4. Tam giác OAB cân tại O có hai đỉnh A, B thuộc elip (E) : 
 1và có diện tích lớn nhất. Tính giá trị 4 1 của biểu thức 2 2 3OA OB . A.6 B. 5 C. 4 D. 4,5 2 2 x yCâu 5. Cho elip 
 1, hai điểm A, B thay đổi thuộc elip sao cho AOB  90 , H là chân đường cao kẻ từ 25 16
gốc tọa độ O xuống đoạn thẳng AB, H luôn thuộc đường tròn cố định có bán kính bằng 20 10 5 A. B. C. D. 3,5 41 21 11
Câu 6. Đường tròn 2 2
x y  1cắt trục tung và trục hoành lần lượt tại ( A 0;1), B(0; 1
 ) . Một đường thẳng y m với 1  m  1; m  0 cắt đường
tròn tại T và S, đường thẳng TS cắt đường thẳng AB tại P, tập hợp điểm
P là hypebol có tiêu cự bằng A. 2 B. 2,5 C. Kết quả khác D. 3 2 2 x y Câu 7. Cho điểm ( A 0; 2) 
. Hai điểm B, C thuộc elip (E) : 
 1 sao cho tam giác ABC có diện tích bằng 9 4
9 3 . Hai điểm B, C cách gốc tọa độ một khoảng có bình phương bằng 2 A.5,5 B. 4 C. 6,5 D. 4,5 2 2
Câu 8. Hai số x, y thỏa mãn  x   2
y   x   2 2 5 3 4 2 5 3
 4 y  20 . Tính tích giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức 2 2
Q x  4 y  3x  4 y  30 . A.180 B. 150 C. – 300 D. – 200 2 2 x y
Câu 9. Elip (E) : 
 1có tiêu cự F F , độ dài trục lớn A A  4 2 và tứ giác F B F B nội tiếp đường tròn, 2 2 a b 1 2 1 2 1 1 2 2 tính giá trị của 2 2 a b . A.12 B. 8 C. 4 D. 2 2 2 x y
Câu 10. Cho điểm C(2; 0) , hai điểm ( A ; m n), B( ;
p q) thuộc elip (E) : 
 1 sao cho tam giác ABC vuông 4 1 16
tại C và có diện tích bằng
. Tính m  2n  3 p  4q . 25 A.3,2 B. 2,8 C. 3 D. 2,6 63
Câu 11. Hình vẽ bên minh hoạ một phòng thì thầm (whispering gallery) với mă̆t cắt ngang là một hình bán elip
với chiều cao 24 feet và chiều rộng 80 feet. Một âm thanh được phát ra từ một tiêu điềm của phòng thì thầm có
thể được C nghe thấy tại tiêu điểm còn lại. Hỏi hai người nói thầm qua lại với nhau thì sẽ cách trung tâm của
phòng bao nhiêu mét? Theo đơn vị đo lường quốc tế, 1 feet  0, 3048 m . A.9,7536 B. 8,5245 C. 8,4525 D. 9,6525 2 2 x y
Câu 12. Elip (E) : 
 1có tiêu cự F F và đi qua điểm M (2 13; 2) , bán kính đường tròn nội tiếp tam 2 2 a b 1 2
giác MF F bằng 1. Tính 2 2 a  2b . 1 2 A.264 B. 160 C. 36 D. 164
Câu 13. Cho đường conic parabol 2
(P) : y  4x và điểm (
A 1; 4) , hai điểm B, C thuộc parabol sao cho 
BAC  90 , đường thẳng BC luôn đi qua điểm M cố định có hoành độ bằng A.15 B. 8 C. 20 D. 17
Câu 14. Có bao nhiêu số nguyên m nhỏ hơn 2023 để hệ bất phương trình sau có nghiệm  2 2 2 2
 (x  7 )  y  (x  7 )  y  8    5x  2
21  5y 142  25m  A.2020 B. 2021 C. 1000 D. Kết quả khác 2 2 x y
Câu 15. Elip (E) : 
 1có hai tiêu điểm F , F trong đó F có hoành độ dương. Tìm giá trị nhỏ nhất của 4 3 1 2 2 biểu thức 2 2 MF  4MF . 1 2 A.13 B. 12 C. 14 D. 12,5 2 2 x y
Câu 16. Cho hai điểm (3
A ; 2), B(0; 1) , điểm C( ;
x y) thuộc hypebol (H ) : 
 1sao cho tam giác ABC có 9 4
diện tích nhỏ nhất. Tính xy . A.6,2 B. 7,2 C. 8,5 D. 7,5 2 2 x y
Câu 17. Cho hai điểm (3
A ; 4), B(5;3) , điểm C thuộc elip (E) : 
 1 sao cho tam giác ABC có diện tích nhỏ 8 2
nhất. Tính tổng hoành độ và tung độ của điểm C. A.4 C. 3,5 C. 3 D. 2,5 2 2
x y  6x  6 y 18  , m
Câu 18. Khi hệ bất phương trình 
có nghiệm duy nhất thì m thuộc 2 2 2 2
 (x  6)  y  (x  6)  y  4 2  khoảng A.(0;2) B. (2;4) C. (4;6) D. (6;9) 
Câu 19. Cho hình thoi ABCD có ABC  120 và đường tròn nội tiếp hình thoi có phương trình 2 2
x y  8 . Elip 2 2 x y
 1 đi qua các đỉnh của hình thoi và điểm A thuộc trục hoành, khi đó 2 2
a b có giá trị thuộc khoảng 2 2 a b A.(100;150) B. (150;250) C. (250;300) D. (300;350)
Câu 20. Hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300km. Tại cùng một thời điểm, hai trạm
cùng phát tín hiệu với vận tốc 292000km/s để một tàu thủy thu và đo độ lệch thời gian. Tín hiệu từ A đến sớm
hơn tín hiệu đến từ B là 0,0005s. Từ thông tin trên ta có thể xác định được tàu thủy thuộc đường hypebol 2 2 x y
 1, giá trị biểu thức 2 2
b  3a gần nhất số nào 2 2 a b A.1010 B. 1285 C. 1428 D. 1789 64
BA ĐƯỜNG CONIC OXY LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P8)
_____________________________________
Câu 1. Hai số thực , x y thỏa mãn 2 2 2 2
(x  5)  y  (x  5)  y  6 . Tìm giá trị lớn nhất của biểu thức x  2 y A. 4 B. 13 C. 19 D. 11 2 2 ax by Câu 2. Cho hypebol 
 1 với a  0;b  0 . Độ dài ngắn nhất của tiêu cự hypebol đã cho bằng 2 2 a  9 b  4 A. 2 10 B. 4 5 C. 12 D. 14
Câu 3. Trong mặt phẳng tọa độ Oxy, đường cong 2 2
(E) : 5x  3y  20x  24 y  53  0 được chứng minh là một x  2  X
đường elip, nó có thể đưa về dạng chính tắc trong hệ tọa độ IXY trong đó 
. Tiêu cự của elip đó là y  4  Y  A.6 B. 4 2 C. 6 2 D. 2 2
Câu 4. Cho đường parabol 2
y  2 px với p  0 như hình vẽ bên,
trong đó đường thẳng d là đường chuẩn. Tìm giá trị nhỏ nhất của 2 2
2MH .MF MH.MF  7MF  5MH  2023 A. 2000 B. 2017 C. 2007 D. 2014 2 2 x y Câu 5. Cho elip 
 1, từ điểm M nằm ngoài elip kẻ hai tiếp tuyến ,
MA MB đến elip với (
A 1; a), B(3;b) , 25 16
đường thẳng OM luôn đi qua điểm C có hoành độ bằng A.2 B. 3 C. 1 D. 2,5 Câu 6. Cho parabol 2
(P) : y  2x và điểm (
A 2;1) , điểm M chạy trên parabol, N là trung điểm đoạn thẳng AM, khi
đó N chạy trên một parabol cố định, parabol có thể đưa về dạng chính tắc trong hệ tọa độ IXY trong đó x  1 X
. Đường chuẩn của parabol đó cách trục tung một khoảng bằng y  0,5  Y  A.0,5 B. 1 C. 1,5 D. 0,75 2 2 x y
Câu 7. Cho đường hypebol   1 như hình vẽ bên. 2 2 a b
Điểm M thuộc nhánh phải hypebol thỏa mãn
MF MF  6; 3MF  2MF  20 1 2 1 2
Tính MF  3MF . 1 2 A. 12 B. 30 C. 14 D. 18
Câu 8. Trong mặt phẳng tọa độ Oxy, tìm diện tích hình tròn tạo bởi đường tròn đi qua bốn giao điểm của elip 2 2 x y 2 2 x y   1và hypebol   1 9 4 3 5 121 120 A. 5 B.  C.  D. Kết quả khác 19 17
Câu 9. Trong mặt phẳng tọa độ Oxy, đường cong (H ) : xy  5x  2 y  9  0 được chứng minh là một đường x  2  X
hypebol, nó có thể đưa về dạng chính tắc trong hệ tọa độ IXY trong đó  . Tiêu cự hypebol đó là y  5  Y  A.4 B. 4 2 C. 6 2 D. 8 3 65 2 2 x y
Câu 10. Đường thẳng ax by 1  0 tiếp xúc với elip (E) : 
 1 , giá trị lớn nhất của 3a  2b bằng 9 4 A.1 B. 2 C. 3 D. 13 2 2 x y
Câu 11. Cho điểm M thuộc hypebol (H ) : 
 1, hai điểm N, P thuộc tiệm cận của hypebol sao cho MNOP 2 2 a b
là hình bình hành. Khi đó ab 3ab ab 2ab A. S  B. S  C. S  D. SMNOP 2 MNOP 2 MNOP 3 MNOP 3
Câu 12. Trong mặt phẳng tọa độ Oxy, đường cong 2 2
(P) :16x  9 y  24xy  56x 108 y 124  0 được chứng
minh là một đường parabol, nó có thể đưa về dạng chính tắc với đường chuẩn là
A. 3x  4 y 1  0
B. 3x  4 y 1  0
C. 3x  4 y  2  0
D. 3x  4 y  0 2 2 x yCâu 13. Cho elip 
 1 , hai điểm A, B thay đổi thuộc elip sao cho AOB  90 , tìm giá trị lớn nhất của biểu 25 16 1 1 thức  . OA OB 82 41 5 A.1 B. C. D. 20 30 3
Câu 14. Hai điểm A, B phân biệt theo thứ tự thuộc hai đường tròn 2 2 2 2
x y  1; x y  49 , sao cho tia Ox luôn là phân giác của góc 
AOB , nếu I là trung điểm đoạn thẳng AB thì tập hợp điểm I là một
hình elip có tiêu cự bằng A. 6 B. 2 7 C. 10 D. 2 5
Câu 15. Các điểm M, N chuyển động trên tia Ox, Oy sao cho đoạn thẳng MN luôn tiếp xúc với elip 2 2 x y (E) : 
 1 . Giá trị nhỏ nhất của đoạn thẳng MN là 9 4 A.8 B. 5 C. 4 D. 6
Câu 16. Cho đường conic parabol 2
(P) : y  2x , khoảng cách nhỏ nhất từ điểm (
A 0; 6) đến một điểm trên elip là A.5 B. 2 5 C. 4 2 D. 3 2  27 15 
Câu 17. Cho đường conic parabol 2 (P) : y  2 ;
px p  0 và điểm A ; 
 . Tồn tại ba điểm M thuộc parabol  8 8 
sao cho đoạn thẳng AM vuông góc với tiếp tuyến của parabol tại điểm M. Tổng hoành độ ba điểm M này bằng A.4,625 B. 6,625 C. 5,25 D. 4,425 2 2 x y
Câu 18. Hypebol (H ) : 
 1 tiếp xúc với đường thẳng ax by  3  0 , tìm giá trị lớn nhất của 2 2 a b . 25 16 A.5 B. 9 C. 8 D. 10 2 2 x y
Câu 19. Cho elip (E) : 
 1 và hai đường thẳng 9 4
ax by; bx xy  0 . Diện tích lớn nhất của tứ giác MPNQ
khi đó gần nhất với
A. 12 đvdt B. 13 đvdt C. 11 đvdt D. 14 đvdt
-----------------------HẾT----------------------- 66