Hệ thống bài tập trắc nghiệm BPT, hệ BPT bậc nhất, bậc hai một ẩn

Tài liệu gồm 49 trang, được biên soạn bởi thầy giáo Lương Tuấn Đức (Giang Sơn), tuyển chọn hệ thống bài tập trắc nghiệm bất phương trình, hệ bất phương trình bậc nhất, bậc hai một ẩn (kết hợp 3 bộ sách giáo khoa Toán 10 chương trình mới: Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức Với Cuộc Sống).

109 55 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số, đồ thị và ứng dụng (KNTT)

Môn: Toán 10

Thông tin:

49 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
C
C
H
H
U
U
Y
Y
Ê
Ê
N
N
Đ
Đ
Ề
Ề
B
B
P
P
T
T
,
,
H
H
Ệ
Ệ
B
B
P
P
T
T
B
B
Ậ
Ậ
C
C
N
N
H
H
Ấ
Ấ
T
T
,
,
B
B
Ậ
Ậ
C
C
H
H
A
A
I
I
M
M
Ộ
Ộ
T
T
Ẩ
Ẩ
N
N
(
(
K
K
Ế
Ế
T
T
H
H
Ợ
Ợ
P
P
3
3
B
B
Ộ
Ộ
S
S
Á
Á
C
C
H
H
G
G
I
I
Á
Á
O
O
K
K
H
H
O
O
A
A
)
)
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM
BPT, HỆ BPT BẬC NHẤT, BẬC HAI MỘT ẨN
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
B
B
P
P
T
T
,
,
H
H
Ệ
Ệ
B
B
P
P
T
T
B
B
Ậ
Ậ
C
C
N
N
H
H
Ấ
Ấ
T
T
M
M
Ộ
Ộ
T
T
Ẩ
Ẩ
N
N
(
(
P
P
1
1
–
–
P
P
6
6
)
)
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
D
D
Ấ
Ấ
U
U
T
T
A
A
M
M
T
T
H
H
Ứ
Ứ
C
C
B
B
Ậ
Ậ
C
C
H
H
A
A
I
I
,
,
B
B
P
P
T
T
B
B
Ậ
Ậ
C
C
H
H
A
A
I
I
M
M
Ộ
Ộ
T
T
Ẩ
Ẩ
N
N
(
(
P
P
1
1
–
–
P
P
6
6
)
)
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
T
T
Ổ
Ổ
N
N
G
G
H
H
Ợ
Ợ
P
P
B
B
P
P
T
T
,
,
H
H
Ệ
Ệ
B
B
P
P
T
T
B
B
Ậ
Ậ
C
C
N
N
H
H
Ấ
Ấ
T
T
,
,
B
B
Ậ
Ậ
C
C
H
H
A
A
I
I
M
M
Ộ
Ộ
T
T
Ẩ
Ẩ
N
N
(
(
P
P
1
1
–
–
P
P
6
6
)
)
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
C
C
A
A
O
O
B
B
P
P
T
T
,
,
H
H
Ệ
Ệ
B
B
P
P
T
T
B
B
Ậ
Ậ
C
C
N
N
H
H
Ấ
Ấ
T
T
,
,
B
B
Ậ
Ậ
C
C
H
H
A
A
I
I
M
M
Ộ
Ộ
T
T
Ẩ
Ẩ
N
N
(
(
P
P
1
1
–
–
P
P
6
6
)
)
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
;
;
T
T
E
E
L
L
0
0
3
3
3
3
3
3
2
2
7
7
5
5
3
3
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
1
1
0
0
/
/
2
2
0
0
2
2
2
2
2
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P1)
________________________________________
Câu 1. Tìm điều kiện tham số m để bất phương trình
2
3 4 3x m mx m
nghiệm đúng với mọi số thực x.
A. m = 4 B. m = 3 C. m = 2 D. m = 1
Câu 3. Tìm điều kiện tham số m để hệ bất phương trình
3( 6) 3
5
7
2
x
x m
có nghiệm.
A. m > – 11 B. m < 11 C. m < – 11 D.
11m
Câu 4. Tập nghiệm của bất phương trình
1 1
1 5x
chứa bao nhiêu số nguyên
A.3 B. 1 C. 2 D. 4
Câu 5. Tìm giá trị tham số m để
2 2
2 5 6 2 3m m x m m x m
với mọi giá trị x.
A. m = 4 B. m = 3 C. m = 2 D. m = 1
Câu 6. Tìm điều kiện tham số m để hệ bất phương trình
3 2 0,
2 0.
x
mx m
có nghiệm.
A. Mọi giá trị m B. Không tồn tại C. m
0 D. m < 1
Câu 7. Cho các bất phương trình
2
1
x m m x m x x
.
Số lượng bất phương trình bậc nhất một ẩn là
A.2 B. 3 C. 1 D. 4
Câu 8. Tập nghiệm của bất phương trình
2
( 1) 0
m x
chứa bao nhiêu số nguyên dương nhỏ hơn 10
A.8 B. 9 C. 7 D. 6
Câu 9. Tìm điều kiện tham số m để bất phương trình
2 2
1 5 1 0
x m m m
có tập nghiệm S = R.
A. m < 2 B. m = – 4 C. m > 1 D. m > 1,5
Câu 10. Tìm điều kiện tham số m để hệ bất phương trình
3 2 0,
3 4 0.
m x m
x
có nghiệm.
A. Mọi giá trị m B. Không tồn tại C. m > – 3 D. m
– 3
Câu 11. Tập nghiệm của bất phương trình
2 2 2
( 1)( 1) 2 0
m m x m
chứa bao nhiêu số nguyên dương
nhỏ hơn 20
A.18 B. 19 C. 17 D. 16
Câu 12. Tập nghiệm của bất phương trình
2
1 26
6 10 5
x x
chứa bao nhiêu số nguyên dương
A.2 B. 1 C. 3 D. 0
Câu 13. Tìm điều kiện tham số m để bất phương trình
2 3
20 4 47 0
m m x m m
có tập nghiệm R.
A. m = 4 B. m = – 4 C. m = 2 D. m = 1,5
Câu 14. Có bao nhiêu số nguyên dương m để hệ bất phương trình
2 1
2
3
3 5
x
x m
có nghiệm ?
A. 5 B. 4 C. 2 D. 1
Câu 15. Tập nghiệm của bất phương trình
2
( 1) 1m x
có thể chứa tối đa bao nhiêu số nguyên dương
A. 2 B. 1 C. 3 D. 0
Câu 16. Tìm điều kiện tham số m để bất phương trình
3 2
3 4 2 2 0
m m x m m
vô nghiệm.
A. m = 4 B. m = 1 C. m = 2 D. m = 1,5
Câu 17. Tìm m để hệ bất phương trình
3
2
4
2( 1) 5
x m
x
có tập nghiệm S = (a;b) thỏa mãn b – a = 2.
A. m = 5,5 B. m = 5 C. m = 8,5 D. m = 2,5
3
Câu 18. Tìm điều kiện tham số m để bất phương trình
2 2
2 5 3 4 5 1m m x m x
vô nghiệm.
A. m = 2 B. m = 2 C. m = 0 D. m = 1,5
Câu 19. Tập nghiệm của bất phương trình
2
1
5
2 3x x
chứa bao nhiêu số nguyên
A.2 B. 0 C. 1 D. 3
Câu 20. Giả sử
2
3 2 3 2 0,a b x a b x
. Mệnh đề nào sau đây có thể sai ?
A. a + b > 2 B. a + b <
2
3
C. 2a + b > 3 D.
3
1
4
a b
Câu 21. Tập nghiệm của bất phương trình
1
0
1x
chứa bao nhiêu số nguyên nhỏ hơn 20
A.19 B. 18 C. 20 D. 10
Câu 22. Tìm điều kiện của m để hệ bất phương trình
3
2
2
2( 1) 5
x m
x
có độ dài tập nghiệm lớn hơn 3.
A. m > 1 B. m < 4 C. m > 0,5 D. 0 < m < 3
Câu 23. Cho các bất phương trình
2
6 5 1 2
2 ( 1) 7; (3 2) 5 1; 0;
5 3 1 5
x x
x m x m x m
x x x
.
Số lượng bất phương trình bậc nhất một ẩn là
A.2 B. 3 C. 1 D. 4
Câu 24. Tìm điều kiện tham số m sao cho
2
1 10 3,m x m x
.
A. m = 1 B. m = 4 C. m = 2 D. m = – 1
Câu 25. Tìm điều kiện tham số m để
2 0, 1mx x
.
A. m > 3 B. m > 2 C. m > 4 D. 5 < m < 6
Câu 26. Tập nghiệm của bất phương trình
2 1 5
x
chứa bao nhiêu số nguyên dương
A.12 B. 13 C. 11 D. 10
Câu 27. Tìm điều kiện tham số m để hệ bất phương trình
3
0,
4
3 1.
x
x
x m
có nghiệm.
A. m < 7 B. m < 8 C. 2 < m < 6 D. 3 < m < 9
Câu 28. Hai tập nghiệm của hai bất phương trình
2 2
1 5
3; 26
2 4 5x x x
có bao nhiêu phần tử nguyên
chung nhau
A.3 B. 2 C. 1 D. 4
Câu 29. Tìm điều kiện tham số m để hai bất phương sau tương đương:
3 0; 4 0x mx m
.
A. m = 0,5 B. m = 4 C. m = 2 D. m = – 2
Câu 30. Tìm tất cả các giá trị m để hai bất phương trình
2 0; 2 1 0
mx m m x m
tương đương.
A. m = 1 B. m = 2 C. m = 4 D. m = – 1
Câu 31. Hàm số
2 1 4 2
2
x
f x x m m
xác định với mọi
0;2
x
khi
;m a b
. Tính a + b.
A. a + b = 3 B. a + b = 5 C. a + b = 2,5 D. a + b = 2
Câu 32. Tìm điều kiện tham số m để hàm số
9
4
2 1
x
y x
x m
xác định trên [7;9].
A. m > 4 hoặc m < 3 B. m > 4 C. m > 9 hoặc m < 7 D. 2 < m < 5
Câu 33. Cho các bất phương trình
2
1
2 ( 3) 1; ( 2) ; 3 8 0; 2
2
x m x m m x m n x x a
x a
.
Số lượng bất phương trình bậc nhất một ẩn là
A.2 B. 3 C. 1 D. 4
______________________
4
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P2)
________________________________________
Câu 1. Xác định giá trị tham số m để bất phương trình
3
16 2
mx x m
có tập nghiệm là
56;

.
A. m = 4 B. m = 2 C. m = 6 D. m = – 2
Câu 2. Cho các bất phương trình
2
2
1
5 4 0; 1; ( 2) 3 1; ( 1)
2 3
x x m x m x m x m
x x
.
Số lượng bất phương trình bậc nhất một ẩn là
A.2 B. 1 C. 3 D. 4
Câu 3. Tìm điều kiện tham số m để hệ bất phương trình
3 2 4 0,
2 3 1 0.
m x m
m x m
có nghiệm nhỏ nhất bằng – 4.
A. m = – 8 B. m = – 9 C. 11m = 4 D. Không tồn tại m
Câu 4. Tập nghiệm của bất phương trình
1 1
2
1x
chứa bao nhiêu số nguyên dương
A.2 B. 1 C. 3 D. 0
Câu 5. Tìm điều kiện tham số m để bất phương trình
2
1 3 2m x m m x
vô nghiệm.
A. m = 1 B. m = 2 C. m = 3 hoặc m = 1 D. m = 1 hoặc m = 2
Câu 6. Tìm điều kiện tham số m để hệ bất phương trình
1 3 0,
3
1.
2 1
m x m
x
x
có nghiệm.
A. Mọi giá trị m B.
1m
C. Không tồn tại m D. m + 1 < 0
Câu 7. Tìm điều kiện tham số m để bất phương trình
2
( 1)
m x m
luôn nghiệm đúng.
A.m > 0 B. m < 0 C. m > 1 D. m > 2
Câu 8. Tìm điều kiện tham số m để bất phương trình
2
1
m x mx
vô nghiệm.
A. m = 0 hoặc m = 1 B. m =
1 C. 0 < m < 1 D. |m| > 1
Câu 9. Có bao nhiêu số nguyên âm m để hệ bất phương trình
2 1
3
3
4(2 1) 9
x m
x
có nghiệm.
A. 10 B. 12 C. 11 D. 16
Câu 10. Cho các bất phương trình
1
5 4 0; 1; ( 2) 3 1; ( 1) ; 1
3 2 2
x m
x x m x m x m x m
mx
.
Số lượng bất phương trình bậc nhất một ẩn là
A.2 B. 1 C. 3 D. 4
Câu 11. Tìm điều kiện tham số m sao cho bất phương trình
2
1 1
m mx m m x
vô nghiệm.
A. m = 7 B. m = 2 C. m = 4 D. m = 0
Câu 12. Tìm điều kiện của tham số m để hai bất phương trình sau tương đương nhau.
1 3 0; 1 2 0
m x m m x m
A. m = 0,5 B. m = 5 C. m = – 6 D. m = – 1
Câu 13. Tìm điều kiện tham số m sao cho
2
1 3 5 2 3
m x m m
.
A. m = 1 B. m = 4 C. m = 2 D. m = – 1
Câu 14. Tìm điều kiện tham số m để hai bất phương trình
1 0; 2 0
mx m m x m
tương đương nhau.
A. m =
3 17
2
B. m =
1 17
4
C. m =
3 17
2
D. m =
3 2 13
2
Câu 15. Tìm điều kiện tham số m để bất phương trình
2
6 4 5 0
x m x m
có tập nghiệm là [1;6].
A.
1
2;
2
m
B. m = 1 C.
1;4
m
D.
1 2
5; ;
2 3
m
5
Câu 16. Tìm điều kiện của m để bất phương trình
2
1 3 1
m m x m
có tập nghiệm S chứa miền (4;5).
A.
1
3
4
m
m
B.
4
3
4
m
m
C.
3
1
4
m
m
D.
2
1
2
m
m
Câu 17. Tìm điều kiện tham số m để bất phương trình
2
3 2
m m x m
có tập nghiệm S chứa miền
(1;5).
A. m > 3 B. 0 < m < 1 C. Mọi giá trị m D. 2 < m < 4
Câu 18. Tìm điều kiện tham số m để bất phương trình
3 1 0
m x m
nhận mọi giá trị x < 2 làm nghiệm.
A. m > 3 B.
3m
C.
5
3
3
m
D. m < – 3
Câu 19. Tìm điều kiện tham số m để
2 0, 2x m x
.
A.
4m
B.
4m
C.
5m
D.
0 4m
Câu 20. Tìm điều kiện tham số m để hệ bất phương trình
2 1 0,
2 1 0.
x m
mx m
có nghiệm duy nhất.
A. m = 2 B. m =
3 17
2
C. m =
3 17
2
D. m =
3 2 13
2
Câu 21. Tìm điều kiện tham số m để bất phương trình
2 1 6
m x m
nghiệm đúng với mọi giá trị x < 7.
A. m > 1 B. 0
m < 1 C. m > 0,5 D. 0,5
m < 1
Câu 22. Tìm điều kiện tham số m để bất phương trình
3 2
m x m
nghiệm đúng với mọi giá trị x < 1.
A. Không tồn tại B. m > – 3 C. Mọi giá trị m D.
3m
Câu 23. Tập nghiệm của bất phương trình
1
5
5x
có bao nhiêu số nguyên dương
A.2 B. 1 C. 0 D. 3
Câu 24. Tìm điều kiện tham số m để hệ bất phương trình
1
0,
2
4 1 .
x
x
x m
vô nghiệm.
A. m < 6 B. m < 5 C. 3 < m < 5 D. 1 < m < 6
Câu 25. Tìm điều kiện m để bất phương trình
2
2 1 2 1
m x m
nhận nghiệm nguyên lớn nhất bằng 2.
A.
1 2m
B.
1 2m
C.
1 2m
D.
1 2m
Câu 26. Có bao nhiêu số nguyên m > – 9 để hệ bất phương trình
3 1
3
2
2(2 1)
x m
x m
có nghiệm ?
A. 3 B. 6 C. 8 D. 5
Câu 27. Tập nghiệm của bất phương trình
26
26
26x
chứa bao nhiêu số nguyên
A.2 B. 1 C. 3 D. 0
Câu 28. Tìm điều kiện tham số m sao cho
2
1 2 15 4,m x m x
.
A. m = 1 B. m = 4 C. m = 2 D. m = – 1
Câu 29. Tìm điều kiện tham số m để hệ bất phương trình
3 2
1
4
5( 4) 6
x m
x
có nghiệm.
A. m < 15,4 B. m < 14,4 C. 2 < m < 5 D. m < 16,6
Câu 30. Có bao nhiêu số nguyên dương m < 10 để
2
( 2)
m x m m
là bất phương trình bậc nhất một ẩn
A.8 B. 9 C. 7 D. 9
_________________________________
6
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P3)
________________________________________
Câu 1. Tìm điều kiện tham số m để hệ bất phương trình
2 0,
2 1 3 0.
mx m
m x m
có nghiệm lớn nhất bằng 1.
A. m = – 2 B. m < 0 C. m = 1 hoặc m = – 2 D. 2m > 1
Câu 2. Tập nghiệm của bất phương trình
2
5 5
26 26
x
chứa bao nhiêu số nguyên
A.2 B. 1 C. 3 D. 4
Câu 3. Tìm điều kiện tham số m để hệ bất phương trình
4
1
3
5( 1) 10
m x
x m
có nghiệm.
A. 1 < m < 2 B. m > 3 C. m > 4 D. Không tồn tại m
Câu 4. Tìm đoạn giá trị của tham số m để hàm số
2 1 2 2
y mx m x m
luôn xác định khi
1x
.
A. [0;1] B. [2;4] C. [3;5] D. [0;4]
Câu 5. Cho các bất phương trình
2 2 2 2
1 1
2 3; ( 1) 2 3; 2 ; ( 3) ( 1) ; ( 1) 4
2
x x m x x m x x m x
x x
.
Có bao nhiêu bất phương trình luôn là bất phương trình bậc nhất một ẩn
A.2 B. 1 C. 3 D. 4
Câu 6. Tìm điều kiện tham số m để bất phương trình
3 2 2
m x m
có miền nghiệm khác rỗng và không
thể chứa miền x < 3.
A.
2
1
3
m
B. 3m > 2 C.
2
2
3
m
D. 5m > 8
Câu 7. Tập nghiệm
S
của hệ bất phương trình
2 0
2 1 2
x
x x
là:
A.
; 3 .
S

B.
;2 .
S 
C.
3;2 .
S
D.
3; .
S

Câu 8. Tìm điều kiện tham số m để hệ bất phương trình
3 2 6,
2 1 4.
x m x
m x m
có nghiệm duy nhất.
A. m = – 1 B. m = – 5 C. m = 1 hoặc m = 5 D. Không tồn tại m
Câu 9. Tìm điều kiện tham số m để bất phương trình
1 7
m x m
có tập nghiệm S chứa miền x < 4
A. 0 < m < 1 B.
1 1m
C. m < – 1 D. m > 7 hoặc m = – 1
Câu 10. Tìm giá trị nguyên nhỏ nhất của m để hệ bất phương trình
4
1
3
5( 3 1) 15
m x
x m
có nghiệm.
A. m = 4 B. m = 3 C. m = 5 D. m = 2
Câu 11. Tìm điều kiện tham số m để bất phương trình
1 5
m x m
có tập nghiệm S chứa miền x > 2.
A. m > – 1 B.
3m
C. 1 < m < 4 C. m = 3
Câu 12. Hệ bất phương trình
3 1
4
2
4(2 3 2) 9
x m
x m
có nghiệm duy nhất. Giá trị m thu được thuộc khoảng nào
A. (0;1) B. (2;5) C. (1;2) D. (5;7)
Câu 13. Tìm điều kiện tham số m để bất phương trình 8x – 4m – 7 < x + 3m có nghiệm nguyên lớn nhất bằng 2.
A.
1 2m
B. m = 7,5 C.
2 3m
D. 1 < m < 2
Câu 14. Tìm điều kiện tham số m để bất phương trình
3 2 2
m x m
có miền nghiệm S chứa miền (3;5).
A.
1m
B. m > 2 C.
1 6m
D.
6
1
7
m
7
Câu 15. Tìm điều kiện tham số m để hệ bất phương trình
2 1,
1 3 1.
mx m x
m x m
có nghiệm duy nhất.
A. 5m = 2 B. 2m = 5 C. 5m + 2 = 0 D. 3m = 4
Câu 16. Tìm điều kiện tham số m để bất phương trình
2 1 1
m x m
có tập nghiệm S chứa miền (2;3).
A. m < 0,5 hoặc m
1 B. m < 0 ,5 hoăc m
2
C. m < 1 hoặc m
3 D. m < 2 hoặc m
4
Câu 17. Tìm điều kiện tham số m sao cho
2
2 3 3 2,m m x m m x
.
A. m = 1 B. m = 4 C. m = 2 D. m = – 1
Câu 18. Tập nghiệm
S
của hệ bất phương trình
2 1
1
3
4 3
3
2
x
x
x
x
là:
A.
4
2; .
5
S
B.
4
; .
5
S

C.
; 2 .
S

D.
2; .
S

Câu 19. Tìm điều kiện của m để x = 2 thuộc miền nghiệm của hệ bất phương trình
2 1
3
2
4( 2) 8
x m
x m
A.
5
3
m
B. m > 9 C. 0 < m < 4 D.
5
9
3
m
Câu 20. Tồn tại bao nhiêu giá trị nguyên của tham số m để bất phương trình
2
5 2 2 2mx x m m
nhận
nghiệm nguyên lớn nhất bằng 1.
A. 2 giá trị B. 3 giá trị C. 4 giá trị D. 1 giá trị
Câu 21. Tổng các nghiệm nguyên của bất phương trình
2 4
4 4
x
x x
bằng:
A.
15
. B.
11
. C.
26
. D.
0
.
Câu 22. Tập nghiệm
S
của bất phương trình
3 2 0
x x
là:
A.
3;S

. B.
3;S

. C.
2 3;S

. D.
2 3;S

.
Câu 23. Bất phương trình
2
3 2 2m m x m x
vô nghiệm khi
A.
1.
m
B.
2.
m
C.
1, 2.
m m
D.
.
m
Câu 24. Có bao nhiêu giá trị thực của tham số
m
để bất phương trình
2
m m x m
vô nghiệm.
A.
0.
B.
1.
C.
2.
D. Vô số.
Câu 25. Tồn tại bao nhiêu giá trị nguyên m < 8 để x = 3 thuộc miền nghiệm của hệ
3 1
4
2
4(2 3 2) 9
x m
x m
A. 6 B. 5 C. 10 D. 4
Câu 26. Tổng tất cả các nghiệm nguyên của bất phương trình
2
2
5 2 4 5
2
x x
x x
bằng:
A.
21.
B.
27.
C.
28.
D.
29.
Câu 27. Tìm điều kiện tham số m để bất phương trình
3 2 2
m x m
nghiệm đúng với mọi giá trị x < 3.
A. 0 < m < 1 B.
2
1
3
m
C.
2
3
m
D. m > 1 hoặc
2
3
m
Câu 28. Hệ bất phương trình
2
1 0
0
x
x m
có nghiệm khi và chỉ khi:
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
_________________________________
8
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P4)
________________________________________
Câu 1. Bất phương trình
2 2
4 2 1 4 5 9 12m x m m x m
nghiệm đúng với mọi
x
khi
A.
1.
m
B.
9
.
4
m
C.
1.
m
D.
9
.
4
m
Câu 2. Cho các bất phương trình
2 2
1
2 1 3 ; ; 6 5 0; 2 1; ( 1) 4
2 2
x
x x a a x x x m m x
x
Số lượng bất phương trình bậc nhất hai ẩn là
A.2 B. 1 C. 3 D. 0
Câu 3. Hệ bất phương trình
2
2
3 7 1
2 8 5
x x x
m x
vô nghiệm khi và chỉ khi:
A.
72
.
13
m
B.
72
.
13
m
C.
1
m
D.
1
m
Câu 4. Tập nghiệm của bất phương trình
2
2
4
2
1 2
a
a
x a
với
a
chứa bao nhiêu số nguyên
A.2 B. 1 C. 3 D. 0
Câu 5. Hệ bất phương trình
2
2 0
1 4
x
m x
có nghiệm khi và chỉ khi:
A.
1.
m
B.
1.
m
C.
1.
m
D.
1 1.
m
Câu 6. Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
3 4
x m m x x
có tập nghiệm là
2;m

.
A.
2.
m
B.
2.
m
C.
2.
m
D.
2.
m
Câu 7. Với
10m
thì tập nghiệm của bất phương trình
2
3 1
( 7) 7
x x
m m
là
A.
7
;
10
m
m

B.
2 7
;
10
m
m

C.
7
;
10
m
m

D.
7
;
10m

Câu 8. Tập nghiệm của hệ bất phương trình
2 2
2
(2 1) 8( 1) (2 3)
6
5 5
x m x
x m m
có độ dài nhỏ nhất bằng
A.3 B. 5 C. 4 D. 2
Câu 9. Bất phương trình
2
9 3 1 6m x m x
nghiệm đúng với mọi
x
khi
A.
3.
m
B.
3.
m
C.
3.
m
D.
3.
m
Câu 10. Tìm điều kiện tham số
m
để bất phương trình
1m x m x
có tập nghiệm là
; 1
m

.
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 11. Tìm tất cả các giá trị thực của tham số
m
để hệ bất phương trình
2
2
3 7 1
2 8 5
x x x
m x
có nghiệm duy
nhất.
A.
72
13
m
. B.
72
13
m
. C.
72
13
m
. D.
72
13
m
.
Câu 12. Tìm tất cả các giá trị của tham số
m
để bất phương trình
1 2 3m x x
có nghiệm.
A.
2
m
. B.
2
m
. C.
2
m
. D.
2
m
.
Câu 13. Tập nghiệm
S
của bất phương trình
2 1 3
2 3 1
x x
x x
là:
A.
3;5 .
S
B.
3;5 .
S
C.
3;5 .
S
D.
3;5 .
S
Câu 14. Có bao nhiêu giá trị thực của tham số
m
để bất phương trình
2
mx x m
vô nghiệm.
9
A.
0.
B.
1.
C.
2.
D. Vô số.
Câu 15. Có bao nhiêu giá trị nguyên m nhỏ hơn 20 để hàm số
( ) (2 1) 4
f x m x m
xác định trên
1;

.
A.18 B. 17 C. 16 D. 15
Câu 16. Tìm tất cả các giá trị của tham số
m
để bất phương trình
1 3m x x
có nghiệm.
A.
1
m
. B.
1
m
. C.
m
. D.
3
m
.
Câu 17. Có bao nhiêu cặp số (a;b) để
2 2
( 3 2) 4 4 ,a b x a b b x
.
A.2 B. 1 C. 3 D. 0
Câu 18. Biết rằng bất phương trình
1 2 3
5 3
3
2
3 5
x x
x
x
x x
có tập nghiệm là một đoạn
;a b
. Hỏi
a b
bằng:
A.5,5 B.
8.
C. 4,5 D. 4,7
Câu 19. Biểu diễn hình học của bất phương trình
3 4 0, 1mx m x
có dạng
A.Một đoạn thẳng B. Một tia C. Hình chữ nhật D. Hình vuông
Câu 20. Có bao nhiêu số nguyên m nhỏ hơn 10 để
2 2 0, 1mx m x
.
A.7 B. 8 C. 6 D. 9
Câu 21. Tìm giá trị thực của tham số
m
để hệ bất phương trình
2 1 3
4 3 4
m x x
mx x
có nghiệm duy nhất.
A.
5
.
2
m
B.
3
.
4
m
C.
3 5
; .
4 2
m m
D.
1.
m
Câu 22. Có bao nhiêu cặp số (a;b) để
2 2
( 3 2 5) 2 4 4 ,a b x a b b x
.
A.2 B. 1 C. 3 D. 4
Câu 23. Tìm điều kiện tham số m để bất phương trình
( )
m x m x m
có tập nghiệm
; 1
S m

.
A. m < 1 B. m = 1 C.
1m
D.
1m
Câu 24. Hệ bất phương trình
2
2
2
4 2
1
2
2
( 1)( 1) 0
x x
x
x
x x x
có bao nhiêu nghiệm nguyên
A.3 B. 2 C. 1 D. 4
Câu 25. Có bao nhiêu số nguyên m nhỏ hơn 10 để
3 4 0, 1mx m x
.
A.7 B. 8 C. 6 D. 9
Câu 26. Cho các bất phương trình
2 2
1
2 1 5 ; ; ( 2) 6 5 0; 2 1; ( 1) 4
2 2
x
x x a a x x x x m m x m
x
Số lượng bất phương trình bậc nhất hai ẩn là
A.2 B. 1 C. 3 D. 0
Câu 27. Tìm điều kiện tham số m để bất phương trình
2
4 3 2 1
m x m
có tập nghiệm S chứa miền
7
1;
5
A. m > 2 B.
3
4
m
C.
2
0,8
m
m
D.
4
5
m
Câu 28. Miền nghiệm của hệ bất phương trình
2 2
2 2
( 1) 4 5
2 2
x x a
x a x a
là một khoảng có độ dài nhỏ nhất bằng
A.2 B. 1 C. 1,5 D. 3
Câu 29. Có bao nhiêu số nguyên dương m để
1( 2 2) 0, 2;3
x x m x
.
A.2 B. 1 C. 3 D. 4
Câu 30. Có bao nhiêu giá trị nguyên m nhỏ hơn 20 để hàm số
( ) 5 8
f x mx m
xác định trên
1;

.
A.18 B. 17 C. 16 D. 15
_________________________________
10
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P5)
________________________________________
Câu 1. Tìm điều kiện tham số m sao cho
2
4 3 2,m x m x
.
A. m = 3 B. m = 4 C. m = 2 D. m = – 2
Câu 2. Tìm điều kiện tham số m để hệ bất phương trình
2 0,
4.
x
mx m
có nghiệm.
A.
0
4
m
m
B.
0
5
m
m
C.
1
7
m
m
D. m < 0
Câu 3. Tìm số nghiệm nguyên của bất phương trình
2 2
(1 )( 1) 0
x x x
.
A.3 B. 2 C. 4 D. 1
Câu 4. Tìm điều kiện tham số m để bất phương trình
2 2
4 2 1 1 3 4 4m m x m x m
vô nghiệm.
A. m = 2 B. m = 1 C. m = 0 D. m = 1,5
Câu 5. Tìm điều kiện tham số m để
1 1 0,m x m x
.
A. m = 1 B. m = 3 C. Không tồn tại D. m = 2
Câu 6. Tìm số nghiệm nguyên của bất phương trình
2
2
1 2x
.
A.3 B. 2 C. 1 D. 4
Câu 7. Tìm điều kiện tham số m để hệ bất phương trình
3 5 0,
2 3 .
x
mx m
có độ dài tập nghiệm bằng 2.
A. m = 1 B. m =
9
25
C. m – 2 D. m =
7
26
Câu 8. Tồn tại các giá trị a và b để
2
2 1 3 2 0,a b x a b x
. Khi đó điều kiện tham số b là
A.
2
0,5
b
b
B.
3
0
b
b
C.
1
0,75
b
b
D.
4
0,25
b
b
Câu 9. Tìm điều kiện tham số m để bất phương trình
3
9 10 4 0
m m x m
có tập nghiệm S = R.
A. m = 4 B. m = – 4 C. m = 1 D. m = 1,5
Câu 10. Bất phương trình
0
ax b
vô nghiệm khi:
A.
0
.
0
a
b
B.
0
.
0
a
b
C.
0
.
0
a
b
D.
0
.
0
a
b
Câu 11. Tìm số nghiệm nguyên của hệ bất phương trình
2 2
2
( 1) ( 2)
( 3)( 2 3) 0
x x
x x x
A.3 B. 2 C. 4 D. 1
Câu 12. Gọi
S
là tập nghiệm của bất phương trình
6 2 3mx x m
với
2
m
. Hỏi tập hợp nào sau đây là
phần bù của tập
S
?
A.
3;

. B.
3;

. C.
;3

. D.
;3

.
Câu 13. Tìm giá trị thực của tham số
m
để bất phương trình
2 1 2 1m x x
có tập nghiệm là
1; .
A.
3
m
B.
1
m
C.
1
m
D.
2.
m
Câu 14. Hệ bất phương trình
3 6 3
5
7
2
x
x m
có nghiệm khi và chỉ khi:
A.
11.
m
B.
11.
m
C.
11.
m
D.
11.
m
Câu 15. Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
1
m x mx m
có nghiệm.
A.
1.
m
B.
0
m
. C.
0; 1.
m m
D.
m
.
Câu 16. Tìm giá trị thực của tham số
m
để bất phương trình
2 3 1
x m x
có tập nghiệm là
4; .
11
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 17. Cho bất phương trình
2
2
3
3 2
1 8 4
2 6 13 9
x x x
x x x x
. Tổng nghiệm nguyên lớn nhất và nghiệm nguyên
nhỏ nhất của bất phương trình bằng:
A.
2.
B.
3.
C.
6.
D.
7.
Câu 18. Tìm số nghiệm nguyên của bất phương trình
1
0
1
x
x x
.
A.2 B. 1 C. 3 D. 4
Câu 19. Tìm tất cả các giá trị của tham số
m
để hệ bất phương trình
2
6
3 1 5
m x x
x x
có nghiệm duy nhất.
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Câu 20. Miền nghiệm của hệ bất phương trình
2 2
2 2
( 1) 4 5
2 2
x x a
x a x a
là một khoảng có độ dài nhỏ nhất bằng
A.2 B. 1 C. 1,5 D. 3
Câu 21. Tìm số nghiệm nguyên của hệ bất phương trình
2
( 1)( 4 5) 0
0
x x x
x x
A.2 B. 1 C. 3 D. 4
Câu 22. Tập nghiệm của bất phương trình
2
( 2 2) 5
m m x
có thể chứa tối đa bao nhiêu số nguyên dương
A.3 B. 2 C. 1 D. 4
Câu 23. Xác định giá trị tham số m để bất phương trình
2
1 6 0
m x m m
có tập nghiệm là
0;

.
A. m = 0,5 B. m = 3 C. m = 2 D. m = – 4
Câu 24. Tập nghiệm
S
của bất phương trình
2 2
3 3 2
x x
là:
A.
3
; .
6
S

B.
3
; .
6
S

C.
3
; .
6
S

D.
3
; .
6
S

Câu 25. Tìm tất cả các giá trị của tham số
m
để bất phương trình
4 0
mx
nghiệm đúng với mọi
8
x
.
A.
1 1
; .
2 2
m
B.
1
; .
2
m

C.
1
; .
2
m

D.
1 1
;0 0; .
2 2
m
Câu 26. Hệ bất phương trình
1 2
2 2 1
m mx
m mx m
có nghiệm khi và chỉ khi:
A.
1
.
3
m
B.
1
0 .
3
m
C.
0.
m
D.
0.
m
Câu 27. Miền nghiệm của hệ bất phương trình
2 2 2
2 2
( 1) 2 4 8
2( 1) 2 3 2
x x x a a
x a x a
là một khoảng có độ dài nhỏ
nhất bằng
A.2 B. 3 C. 1,5 D. 4
Câu 28. Tìm điều kiện tham số m sao cho bất phương trình
2 2
4 3 0
m m x m m
nhận tập nghiệm R.
A. m = 0,5 B. m = 4 C. m = – 3 D. m = – 1
Câu 29. Tìm số nghiệm nguyên của hệ bất phương trình
2
2
( 2)( 2 5) 0
( 1)( 3) 0
x x x
x x
A.3 B. 1 C. 2 D. 4
Câu 30. Có bao nhiêu cặp số (a;b) để bất phương trình
2 2
( 2 1) 2 1 0
a b x a b b
luôn nghiệm đúng
với mọi giá trị x
A.2 B. 1 C. 3 D. 4
_________________________________
12
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P6)
________________________________________
Câu 1. Tập
3
1;
2
S
là tập nghiệm của hệ bất phương trình sau đây ?
A.
2( 1) 1
.
1
x
x
B.
2( 1) 1
.
1
x
x
C.
2( 1) 1
.
1
x
x
D.
2( 1) 1
.
1
x
x
Câu 2. Tìm số nghiệm nguyên của bất phương trình
1
0
2
x
x
.
A.2 B. 1 C. 1 D. 3
Câu 3. Bất phương trình
0
ax b
có tập nghiệm là
khi:
A.
0
.
0
a
b
B.
0
.
0
a
b
C.
0
.
0
a
b
D.
0
.
0
a
b
Câu 4. Tìm giá trị thực của tham số
m
để hệ bất phương trình
3
3 9
mx m
m x m
có nghiệm duy nhất.
A.
1.
m
B.
2.
m
C.
2.
m
D.
1.
m
Câu 5. Tập nghiệm
S
của bất phương trình
2
5 1 3
5
x
x
là:
A.
.
S
B.
;2 .
S 
C.
5
; .
2
S

D.
20
; .
23
S

Câu 6. Hệ bất phương trình
2 7 8 1
5 2
x x
m x
vô nghiệm khi và chỉ khi:
A.
3.
m
B.
3.
m
C.
3.
m
D.
3.
m
Câu 7. Hệ bất phương trình
2 2
2 2 2
( 1) 2 1
( 1)( 1) ( 1)( 2)
x x a
x x x a
có miền nghiệm M với độ dài nhỏ nhất bằng
A.2 B. 1 C. 3 D. 4
Câu 8. Bất phương trình
3 5 2
1
2 3
x x
x
có bao nhiêu nghiệm nguyên lớn hơn
10?
A.
4.
B.
5.
C.
9.
D.
10.
Câu 9. Hệ bất phương trình
3 4 9
1 2 3 1
x x
x m x
vô nghiệm khi và chỉ khi:
A.
5
.
2
m
B.
5
.
2
m
C.
5
.
2
m
D.
5
.
2
m
Câu 10. Tổng các nghiệm nguyên của bất phương trình
2 7 6 1
x x x x x
trên đoạn
10;10
bằng:
A.
5.
B.
6.
C.
21.
D.
40.
Câu 11. Bất phương trình
2
2 1 3 3 1 1 3 5
x x x x x x
có tập nghiệm
A.
2
; .
3
S

B.
2
; .
3
S

C.
.
S
D.
.
S
Câu 12. Tập nghiệm
S
của bất phương trình
2 2 2
2
1 3 15 4
x x x x
là:
A.
;0 .
S 
B.
0; .
S

C.
.
S
D.
.
S
Câu 13. Hệ bất phương trình
2 2
3 5 1
2 1 9
1 2
x x
x x
mx m x m
vô nghiệm khi và chỉ khi:
A.
3.
m
B.
3.
m
C.
3.
m
D.
3.
m
Câu 14. Tập nghiệm
S
của bất phương trình
2 2 2
x x x
là:
A.
2
.b ac
B.
;2 .
S 
C.
2 .
S
D.
2; .
S

13
Câu 15. Tìm tất cả các giá trị thực của tham số
m
để hệ bất phương trình
2 1 3
0
x
x m
có nghiệm duy nhất.
A.
2
m
. B.
2
m
. C.
2
m
. D. m > 1
Câu 16. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để bất phương trình
2
6 2
m m x m x
vô
nghiệm. Tổng các phần tử trong
S
bằng:
A.
0.
B.
1.
C.
2.
D.
3.
Câu 17. Hệ bất phương trình
2 3 5 4
1 1
x x
mx x
vô nghiệm khi và chỉ khi:
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 18. Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
6 1
m m x m
có nghiệm.
A.
2
m
. B.
2
m
và
3
m
. C.
m
. D.
3
m
.
Câu 19. Tập nghiệm của hệ bất phương trình
2 2 2
( 2) 2 5 4
2( 1) 2 1
x a x x
x x a
chứa tối đa bao nhiêu số nguyên
A.2 B. 1 C. 3 D. 4
Câu 20. Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
2
2 5 0
m x mx x
nghiệm đúng
với mọi
2018;2
x
.
A.
7
2
m
. B.
7
2
m
. C.
7
2
m
. D.
m
.
Câu 21. Tìm điều kiện của tham số
m
để bất phương trình
2
2 0
m x m x
có nghiệm
1;2
x
A.
2
m
. B.
2
m
. C.
1
m
. D.
2
m
.
Câu 22. Tập nghiệm
S
của hệ bất phương trình
1
1
2
5 2
3
2
x
x
x
x
là:
A.
1
; .
4
S

B.
1; .
S

C.
1
;1 .
4
S
D.
.
S
Câu 23. Tìm điều kiện tham số m để hệ bất phương trình
3 2 4 0,
2 3 1 0.
m x m
m x m
có nghiệm nhỏ nhất bằng 3.
A. m = 1 B. 6m = 5 C. Không tồn tại m D. 6m = – 5
Câu 24. Cho các bất phương trình
2 2
1 1
1; ( 2) 5; 5 4 0; 2
2
m x x x x m x m
x x
.
Số lượng bất phương trình bậc nhất một ẩn là
A.2 B. 1 C. 3 D. 0
Câu 25. Tìm điều kiện tham số m để bất phương trình (m – 2)x > m có nghiệm nguyên nhỏ nhất bằng 4.
A.
3m
B.
8
3
3
m
C.
8
3
m
D. m < 3
Câu 26. Số nghiệm nguyên của hệ bất phương trình
5
6 4 7
7
8 3
2 25
2
x x
x
x
là:
A. Vô số. B.
4
. C.
8.
D.
0.
Câu 27. Bất phương trình
2
1 9 3m x x m
nghiệm đúng với mọi
x
khi
A.
1.
m
B.
3.
m
C.
.
m
D.
1.
m
Câu 28. Hệ bất phương trình
2 1 0
2
x
x m
có nghiệm khi và chỉ khi:
A.
3
.
2
m
B.
3
.
2
m
C.
3
.
2
m
D.
3
.
2
m
_________________________________
14
DẤU TAM THỨC BẬC HAI, BẤT PHƯƠNG TRÌNH BẬC HAI LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P1)
________________________________________________________
Câu 1. Tìm điều kiện tham số m để
2
2 6 0,x x m x
.
A. m > 5 B. m > 8 C. m > 7 D. m < 10
Câu 2. Tìm số nghiệm nguyên của bất phương trình
2
8 7 0
x x
.
A.2 B. 1 C. 7 D. 6
Câu 3. Tìm điều kiện tham số m để bất phương trình
2
3 4x x m
nghiệm đúng với mọi x thuộc đoạn [1;2].
A.
2m
B.
7
2
4
m
C.
7
4
m
D.
7
4
m
Câu 4. Tìm điều kiện tham số m để bất phương trình
2
2 1 3 0
x m x m
có nghiệm.
A. Mọi giá trị m B. m > 0,5 C. 0 < m < 1 D.
2m
Câu 5. Tìm số nghiệm nguyên của bất phương trình
2 2
( 2 5)( 3 2) 0
x x x x
.
A.2 B. 1 C. 3 D. 4
Câu 6. Tìm điều kiện tham số m để hàm số
2
5
4 12 7
y
x x m
luôn xác định trên R.
A. m > 3 B. m > 19 C. m > 2 D. 1 < m < 4
Câu 7. Tìm số nghiệm nguyên của bất phương trình
2
5 4
0
7
x x
x
A.3 B. 2 C. 4 D. 1
Câu 9. Tìm điều kiện tham số k để
2
2 8 8 0
x k
với mọi số thực x.
A. k < 1 B. k > 8 C. k < 8 D. k < 6
Câu 10. Tìm số nghiệm nguyên của bất phương trình
2 2
2
( 8 7)( 2)
0
1
x x x
x x
A.5 B. 7 C. 4 D. 6
Câu 11. Có bao nhiêu số nguyên
10;10
m
để bất phương trình
2
5 20 0
mx mx
nhận x = 1 là nghiệm
A.15 B. 12 C. 14 D. 16
Câu 12. Hàm số bậc hai
2
( )
f x ax bx c
có đồ thị
như hình vẽ. Tìm độ dài tập nghiệm của bất phương
trình
( ) 0
f x
.
A.3 B. 4
C.2 D. 1
Câu 13. Tồn tại bao nhiêu số nguyên m < 10 để hàm số
2017
10 2 10
y
x x m
xác định trên R ?
A. 7 giá trị B. 8 giá trị C. 10 giá trị D. 6 giá trị
Câu 14. Tìm điều kiện tham số m để
2 2
2 5 0,x mx m m x
.
A. m > 5 B. m > 4 C. m > 2 D. m > 7
Câu 15. Tìm số nghiệm nguyên của bất phương trình
2 2
4
(3 4 1)( 1)
0
5
x x x
x
.
A.3 B. 2 C. 1 D. 4
Câu 16. Tìm điều kiện tham số m để hàm số
2 2
10 25 2
y x mx m m
có tập xác định là R.
A. m
1 B. m
6 C. m
2 D. m
7
Câu 17. Tìm số nghiệm nguyên của bất phương trình
4 2
10 9 0
x x
A.4 B. 3 C. 7 D. 6
Câu 18. Tìm điều kiện tham số m để
2 2
2 3 9 0,x mx m m x
.
A. m > 4 B. m > 3 C. m > 2,5 D. m > 1
15
Câu 19. Tồn tại bao nhiêu giá trị nguyên m nhỏ hơn 40 để hàm
2
2018
9 12 6
y
x x m
luôn xác định trên R ?
A. 17 giá trị B. 28 giá trị C. 30 giá trị D. 29 giá trị
Câu 20. Tìm điều kiện tham số m để
2 2
4 4 3 12 0,x mx m m x
.
A. m > 4 B. m > 3 C. m > 2,5 D. m > 1
Câu 21. Tìm điều kiện tham số m để bất phương trình
2 2
2 4 1 1 0
x m x m
có ít nhất một nghiệm lớn
hơn 2017.
A. Mọi giá trị m B. m > 1 C. m < 1 D. m > 0
Câu 22. Cho hàm số bậc hai
2
y ax bx c
có đồ
thị như hình vẽ. Mệnh đề nào đúng
A.
2
0; 4 0; 0
a b ac c
B.
2
0; 4 0; 0
a b ac c
C.
2
0; 4 0; 0
a b ac c
D.
2
0; 4 0; 0
a b ac c
Câu 23. Tìm giá trị nhỏ nhất của tham số m để
2 2
12 3 1 0,x mx m m x
.
A. m = 1 B. m = 2 C. m = 3 D. m = 4
Câu 24. Tìm điều kiện tham số m để hàm số
2 2
4 4 7
y x mx m m
có tập xác định là R.
A. m
1 B. m
6 C. m
2 D. m
7
Câu 25. Tìm giá trị nhỏ nhất của tham số m để bất phương trình
2
2
2 7 5
5 7
x x
m
x x
luôn đúng với mọi x.
A. m = 2 B. m = 5 C. m = 6 D. m = 3
Câu 26. Bất phương trình
2
2
2
1
3 4
x mx
x x
luôn luôn đúng trên R khi và chỉ khi nào ?
A. m < – 4 hoặc m
0 B. m < – 3 hoặc m
0
C. m < 2 hoặc m > 5 D. m < – 6 hoặc m
1
Câu 27. Tìm m để bất phương trình kép
2
2
1
3
1
x mx
x x
có tập nghiệm là R.
A. – 5 < m < 1 B. 0 < m
1 C. 0
m < 4 D. 0
m
6
Câu 28. Tìm số nghiệm nguyên của bất phương trình
2
( 1)( 9 8) 0
x x x
.
A.64 B. 8 C. 18 D. 30
Câu 29. Biết rằng
2
0,f x ax bx c x
. Mệnh đề nào sau đây đúng ?
A. a + b + c > 0 B. a – 2b + c > 0 C. 2a + b – c > 0 D. 4a – 3b + 9c > 0
Câu 30. Tìm điều kiện tham số m để
2 2
6 9 12 0,x mx m m x
.
A. m > 12 B. m > 3 C. m > 2,5 D. m > 1
Câu 31. Tìm điều kiện của m sao cho
2
2
4 9
0,
( 1) 4
x x
x
x m x
.
A. Mọi giá trị m B.
5; 3
m
C.
4; 2
m
D. m > 0
Câu 32. Tìm điều kiện tham số m để hàm số
2 2 2
4 4 5
y x mx m m m
luôn xác định trên R.
A. m
5 hoặc m = 0 B. m
6 hoặc m = 0
C. m
2 hoặc m = 0 D. m
7 hoặc m = 0
Câu 33. Tìm điều kiện tham số m để
2 2
6 8 4 0,x mx m x
.
A. – 2 < m < 2 B. 1 < m < 2 C. m > 2,5 D. 3 < m < 4
Câu 34. Bất phương trình
2 2
2 2 1 0
x x x
có bao nhiêu nghiệm nguyên dương?
A.
0
. B.
1
. C.
2
. D. Nhiều hơn 2
Câu 35. Biết rằng
2
0,f x ax bx c x
. Mệnh đề nào sau đây đúng ?
A. a + b + 2c > 0 B. 9a – 2b + c > 0 C. 4a – 2b + c > 0 D. 4a – 3b + 7c > 0
_________________________________
16
DẤU TAM THỨC BẬC HAI, BẤT PHƯƠNG TRÌNH BẬC HAI LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P2)
________________________________________________________
Câu 1. Biết rằng
2
0,f x ax bx c x
. Mệnh đề nào sau đây đúng ?
A. a + 3b + 2c > 0 B. 9a – 3b + c > 0 C. 4a – 3b + c > 0 D. a + b + c < 0
Câu 2. Tìm điều kiện của m để tam thức
2
( ) 2 3f x x mx
có giá trị dương tại x = 2.
A.m > 2 B. m > 1 C. m > 2,5 D. m > 0
Câu 3. Tồn tại bao nhiêu số nguyên m < 7 để hàm số
2 2
4 4 2 1
y x mx m m
luôn xác định trên R ?
A. 4 giá trị B. 3 giá trị C. 5 giá trị D. 6 giá trị
Câu 4. Tìm điều kiện tham số m để
2 2
6 10 3 0,x mx m m x
.
A. – 1 < m < 2 B. 0 < m < 3 C. – 1 < m < 1 D. 3 < m < 4
Câu 5. Tam thức bậc hai
2
( ) ( 1) 3 1f x m x x
có nghiệm duy nhất. Giá trị m thu được thuộc khoảng nào
A.(0;1) B. (1;2) C. (2;3) D. (3;4)
Câu 6. Tìm điều kiện của tham số m để hàm số
2
3 2 10
2 10
f x
x mx m
luôn xác định trên tập hợp số thực.
A. 0 < m < 10 B. 0 < m < 6 C. 1 < m < 9 D. 2 < m < 5
Câu 7. Tìm số nghiệm nguyên của bất phương trình
2
2
10 9
0
1
x x
x
.
A.4 B. 8 C. 9 D. 7
Câu 8. Tồn tại bao nhiêu số nguyên m nhỏ hơn 6 để
2 2
25 10 6 3 0,x mx m m x
?
A. 4 giá trị B. 2 giá trị C. 5 giá trị D. 6 giá trị
Câu 9. Tồn tại bao nhiêu giá trị nguyên của m để hàm
2 2
16 8 6
y x mx m m
luôn xác định trên R ?
A. 14 giá trị B. 13 giá trị C. 11 giá trị D. 16 giá trị
Câu 10. Tìm điều kiện tham số m để bất phương trình
2
5 0
x mx
nhận x = 1 làm nghiệm.
A.m > 4 B. m > 2 C. m < 3 D. 0 < m < 1
Câu 11. Tìm số nghiệm nguyên của bất phương trình
3 2
0
1
x x
x
.
A.3 B. 2 C. 4 D. 1
Câu 12. Có bao nhiêu số nguyên m để tam giác bậc hai
5 2
( ) 2 3f x m x mx
không đổi dấu trên R
A.2 B. 0 C. 1 D. 3
Câu 13. Tìm điều kiện tham số m để hàm số
2 2
4
3
3 2 2 5 2
y
x m x m m
xác định với mọi x thực.
A. – 5 < m < 1 B. – 4 < m < 1 C. – 6 < m < – 2 D. 0 < m < 3
Câu 14. Tìm điều kiện tham số m để biểu thức
2
10 5Z mx x
không dương với mọi x thực.
A. m
- 5 B. m
- 2 C. 2 < m
- 7 D. m < 0
Câu 15. Có bao nhiêu giá trị nguyên m để tam thức bậc hai
2 2
( ) 2( 1) 2 3
f x x m x m m
vô nghiệm
A.3 B. 20 C. Vô số D. 30
Câu 16. Tồn tại bao nhiêu số nguyên m nhỏ hơn 17 để hàm
2
2
6
3 6
2 8 1
x x
T x
x m x m
xác định trên R?
A. 12 giá trị B. 16 giá trị C. 15 giá trị D. 8 giá trị
Câu 17. Tìm điều kiện tham số m để
2 2 2
6 9 6 ,x mx m m m x
.
A. – 2 < m < 3 B. 0 < m < 3 C. – 1 < m < 1 D. 0 < m < 6
Câu 18. Tồn tại bao nhiêu giá trị nguyên của m nhỏ hơn 30 để hàm số
2 2
4 40 25 8 16
y x mx m m
luôn xác định trên R ?
A. 12 giá trị B. 28 giá trị C. 29 giá trị D. 26 giá trị
Câu 19. Tìm điều kiện tham số m để bất phương trình
2
2 5x x m
nghiệm đúng với mọi x thuộc đoạn [2;4].
A.
4m
B.
5 13m
C.
5m
D.
4 13m
Câu 20. Tồn tại bao nhiêu số m để hàm số
2
2
2
3
10
y x mx m
x
có tập xác định D = R ?
A. 2 giá trị B. 9 giá trị C. 10 giá trị D. 6 giá trị
17
Câu 21. Tìm điều kiện của m để biểu thức
2 2 2
4 4 6
P x mx m m m
luôn không âm với mọi số thực x.
A. m = 0 hoặc m
6 B. m = 0 hoặc m
2. C. m = 0 hoặc m
5. D. m
6
Câu 22. Bất phương trình
2
2
5
0
1 2 1 4
x x
m x m x
luôn đúng với mọi x khi và chỉ khi
A.
1 3m
B.
1 4m
C. – 1 < m < 6 D. – 1 < m < 2
Câu 23. Tìm số nghiệm nguyên của bất phương trình
4 2
2
0
5 6
x x
x x
A.3 B. 1 C. 2 D. 4
Câu 24. Biết rằng
2
0,f x ax bx c x
. Mệnh đề nào sau đây sai ?
A. a + b + c > 0 B. 5a – b + 2c > 0 C. 10a – 2b + 2c > 0 D. 11a – 3b + 5c > 0
Câu 25. Hàm số bậc hai
2
( )
f x ax bx c
có đồ thị
như hình vẽ. Tìm số nghiệm nguyên dương nhỏ hơn
30 của bất phương trình
A. 29
B. 25
C. 24
D. 29
Câu 26. Tìm điều kiện tham số m để giá trị biểu thức
2
5Q mx mx
luôn luôn âm với mọi số thực x.
A. – 20 < m
0 B. – 10
m < 0 C. – 5
m < 2 D. – 12 < m
4
Câu 27. Tập xác định của hàm số
2
2
2
5 4
( ) 25
2 3 1
x x
f x x
x x
chứa bao nhiêu số nguyên
A.5 B. 8 C. 7 D. 10
Câu 28. Tìm số nghiệm nguyên nhỏ hơn 40 của bất phương trình
2
( ) 2 5 0
x x x x
.
A.40 B. 34 C. 28 D. 18
Câu 29. Có bao nhiêu số nguyên m để bất phương trình
2
2
10
0
(2 1) 9
x x
x m x
nghiệm đúng với mọi x ?
A. 2 B. 3 C. 4 D. 5
Câu 30. Tìm điều kiện tham số m để hàm số
2
1
6 1
y
x x m
luôn xác định trên R.
A. m > 1 B. m > 9 C. m > 10 D. 3 < m < 8
Câu 31. Hàm số bậc hai
2
( )
f x ax bx c
có đồ thị
như hình vẽ. Mệnh đề nào sau đây đúng
A.
0;5 0
a a b
B.
0;5 2 0
a a b
C.
0;4 0
a a b
D.
0;5 0
a a b
Câu 32. Tìm điều kiện tham số m để bất phương trình
2
7 6 0
x m x m
có tập hợp nghiệm S sao cho
S và tập hợp (5;7) có phần tử chung.
A. m > – 1 B. m > – 2 C. m > 0 D. 0 < m < 2
Câu 33. Tìm điều kiện tham số m để bất phương trình
2
2 2 1 3 0
m x m x m
có tập nghiệm S =
[a;b] thỏa mãn điều kiện b = 2a.
A. m = 8 B. m = – 7 hoặc m = 8 C. Không tồn tại D. m = – 7
Câu 34. Hàm số bậc hai
2
( )
f x ax bx c
thỏa mãn điều kiện
4 ; 3 ; 0
b a c a a
. Tìm độ dài tập
nghiệm của bất phương trình
0
f x
.
A.3 B. 4 C. 2 D. 3,5
_________________________________
18
DẤU TAM THỨC BẬC HAI, BẤT PHƯƠNG TRÌNH BẬC HAI LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P3)
________________________________________________________
Câu 1. Có bao nhiêu số nguyên m > – 10 để biểu thức
2 2
3 2 1 1K m x m x
luôn luôn dương ?
A. 16 giá trị B. 9 giá trị C. 14 giá trị D. 10 giá trị
Câu 2. Tìm giá trị nguyên lớn nhất của m để hàm số
4
1 2 1 2
g x m x m x m
không thể xác
định với mọi giá trị x.
A. m = 3 B. m = 0 C. m = 2 D. m = 1
Câu 3. Tìm số nghiệm nguyên
10;10
của bất phương trình
2
2 5 1
0
6 7 3
x
x x x
.
A.11 B. 10 C. 8 D. 9
Câu 4. Tìm điều kiện tham số m để
2
1 2 , 2;3
x m x
.
A.
1
4
m
B.
2m
C.
3m
D.
6m
Câu 5. Tìm điều kiện tham số m để hàm số
2
3 7
1 2 5 9
h x
m x mx m
xác định trên tập số thực.
A. m < 1 B. m < 0,5 C. m < 2 D. 1 < m < 2
Câu 6. Tìm điều kiện tham số m để bất phương trình
2
2 3 6 0x mx m
nhận x = 1 làm nghiệm.
A.m > 3 B. m > 4 C. m > 5 D. 0 < m < 6
Câu 7. Tìm điều kiện tham số m để
2 2
6 9 5,x mx m m x
.
A. – 2 < m < 4 B. 3 < m < 5 C. m < 5 D. 3 < m < 4
Câu 8. Tìm số nghiệm nguyên của bất phương trình
2
5 4
0
4 6
x x
x x
.
A.15 B. 16 C. 20 D. 10
Câu 9. Cho mệnh đề:
2 2
1 2 3 1 0,m x m x x
.
Tồn tại bao nhiêu số nguyên m lớn hơn – 10 để mệnh đề trên đúng ?
A. 5 giá trị B. 17 giá trị C. 10 giá trị D. 8 giá trị
Câu 10. Tìm điều kiện tham số m để
3 , 4;9
x x m x
.
A. m
- 8 B. m
0 C. m
- 2 D. m
1
Câu 11. Tìm điều kiện tham số m để biểu thức
2
2 2 2 2
E m x m x
không dương với mọi x.
A. Không tồn tại B. m > 4 C. 1 < m < 2 D. m < – 2
Câu 12. Tồn tại bao nhiêu số nguyên m nhỏ hơn 3 để hàm số
4
2
2
5
x x
y
x x m
xác định trên tập số thực ?
A. 1 giá trị B. 2 giá trị C. 4 giá trị D. 5 giá trị
Câu 13. Tồn tại bao nhiêu giá trị nguyên m để
2
1 4 1 1 0,m x m x m x
?
A. 1 B. 2 C. 3 D. 0
Câu 14. Tìm điều kiện cần và đủ của tham số m để bất phương trình
2 2
2 8 1 ,x m x m n n
có
nghiệm thực x.
A. 0 < m < 5 B.
6 33 6 33
m
C.
6 2 33 6 2 33
m
D.
9 2 5 9 2 5
m
.
Câu 15. Có bao nhiêu số nguyên m để hàm số
2
2 2
2 4
2 8 2 2 2
x x
y
m m x m x
xác định trên R ?
A. 5 giá trị B. 4 giá trị C. 3 giá trị D. 6 giá trị
Câu 16. Tìm điều kiện tham số a để bất phương trình kép
2
2
3 5
1 6
2 1
x ax
x x
luôn luôn đúng.
A. 0 < a
5 B. 1
a < 4 C. 2
a < 6 D. 0
a < 7
19
Câu 17. Tam thức bậc hai
2 2
( ) 2( 1) 6 5
f x x m x m m
không đổi dấu qua điểm
A.x = 0 B. x = 1 C. x = 2 D. x = 3
Câu 18. Hàm số
2
11 13
2 2 1 2 1
m
y
x m x m
có tập xác định là R khi và chỉ khi
A.
1 2;1 2
m
B.
3 2;3 2
m
C.
3 2 2;3 2 2
m
D.
5 2;5 2
m
Câu 19. Xét tam thức bậc hai
2
6 7
f x x x m
. Tìm giá trị nguyên nhỏ nhất của tham số m để bất
phương trình
0
f x
vô nghiệm.
A. m = 3 B. m = 2 C. m = 1 D. m = 4
Câu 20. Tìm điều kiện tham số m để bất phương trình
2
7 6 0
x m x m
có tập hợp nghiệm S sao cho
S và tập hợp (8;10) có phần tử chung.
A. Mọi giá trị m B. 0 < m < 7 C. m < 4 D. 2 < m < 3
Câu 21. Tìm số nghiệm nguyên
10;10
của bất phương trình
2
2
5 6 1
5 6
x x x
x x x
.
A.15 B. 17 C. 16 D. 9
Câu 22. Tìm điều kiện tham số m để bất phương trình
2 2 2
1 2 2 0
x m x m
có ít nhất một nghiệm âm.
A. Mọi giá trị m B. m > 0 C. 1 < m < 2 D. 0 < m < 3
Câu 23. Tìm tất cả các giá trị m để
2
1 1 1 2 0,m x m x m x
.
A.
5
1
9
m
B. 2 < m < 3 C.
1
2
9
m
D.
1 4m
Câu 24. Giá trị biểu thức
2 2
1
2 2
Q x m x m
m
luôn dương khi nào ?
A. 2 < m < 6 B. 4 < m < 9 C. 0 < m < 2 D. 1 < m < 4
Câu 25. Tìm điều kiện tham số m để
2
2
3 6
9 6
1
x mx
x x
xảy ra với mọi số thực.
A. – 2 < m < 4 B. – 3 < m < 6 C. 1 < m < 5 D. – 1 < m < 7
Câu 26. Tìm số nghiệm nguyên không âm của bất phương trình
2 2
3 1 2
4 2 2
x x
x x x x
.
A.2 B. 1 C. 3 D. 4
Câu 27. Hàm số bậc hai
2
( )
f x ax bx c
có đồ thị
như hình vẽ. Mệnh đề nào sau đây đúng
A.
( ) 0,f x x
B.
( ) 2,f x x
C.
2
( ) ( 1) 2
f x a x
D.
2
( ) ( 1)
f x a x
Câu 28. Tìm điều kiện tham số m để
2
2
3 2 9,x m m x
.
A. – 2 < m < 6 B. 2 < m < 5 C. – 3 < m < 3 D. 1 < m < 7
Câu 29. Tìm giá trị bé nhất của tham số m để bất phương trình
2
1 2 1 3 3 0
m x m x m
vô nghiệm.
A. m = 2 B. m = 4 C. m = 3 D. m = 1
Câu 30. Tìm điều kiện tham số m để
2
2
3 2
1, 2;2
2 3 4
x x m
x
x x
.
A. m
- 6 B. m
13
6
C. m
13
2
D. m
17
4
_________________________________
20
DẤU TAM THỨC BẬC HAI, BẤT PHƯƠNG TRÌNH BẬC HAI LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P4)
________________________________________________________
Câu 1. Tìm số nguyên m lớn nhất để tam thức
2 2
2 2 2 1 2 1
x m x m m
luôn âm với mọi giá trị thực x.
A. m = 0 B. m = 2 C. m = 1 D. m = 3
Câu 2. Tìm điều kiện tham số m để hàm số
2
6
2
3 10
2 2 3
x x
y
m x x m
xác định trên tập số thực.
A. m > 0 B. m > 3 C. m > 1 D. m > 2
Câu 3. Tìm số nghiệm nguyên của bất phương trình
3 2
0
1
x x
x
.
A.4 B. 1 C. 2 D. 3
Câu 4. Cho mệnh đề: Hàm số
2
2 2 2 4
F m x m x m
luôn luôn xác định trên R.
Tồn tại bao nhiêu giá trị nguyên m không vượt quá 2017 để mệnh đề trên đúng ?
A. 2018 giá trị B. 2017 giá trị C. 2020 giá trị D. 2015 giá trị
Câu 5. Hàm số
2
6
3 10
2 2 2 4
x
L
m x m x m
luôn xác định trên R khi nào ?
A.
2m
B. m > 3 C. m > 2 D. 3 < m
5
Câu 6. Tìm số nguyên a nhỏ nhất sao cho
2
,
1
x
a x
x
.
A. a = 3 B. a = 1 C. a = 4 D. a = 2
Câu 7. Tìm số nghiệm nguyên của bất phương trình
2 2
1 1
5 2 3 5x x x x
.
A.3 B. 2 C. 1 D. 4
Câu 8. Tìm điều kiện tham số m để
2
2
5 49,x m m x
.
A. – 2 < m < 6 B. – 6 < m < 6 C. – 7 < m < 7 D. 1 < m < 7
Câu 9. Tìm tất cả các giá trị tham số m để biểu thức
2
3 10 2 23 24
S m x m x m
nhận giá trị
không âm với mọi giá trị thực x.
A.
2;5
m
B. 2 < m < 7 C.
1
2;
2
m
D.
1;6
m
Câu 10. Hàm số bậc hai
2
( )
f x ax bx c
có đồ thị
như hình vẽ. Tìm số nghiệm nguyên của bất phương
trình
3
f x
.
A. 3 B. 2
C. 4 D. 5
Câu 11. Tìm tất cả các giá trị tham số m để hàm số
2
2
4
y
mx x m
có tập xác định D = R.
A. m > 2 B. m > 1 C. m > 0 D. m < 3
Câu 12. Tìm m để bất phương trình kép
2
2
3 5
1 6
2 1
x mx
x x
có tập nghiệm là D = R.
A. 0 < m < 4 B. 0 < m
5 C. 0
m < 6 D. 0
m
8
Câu 13. Xác định tất cả các giá trị tham số m để
2
2
4
2
4
x x
x mx
với mọi số thực x.
A.
2;5
m
B.
1
2;
2
m
C.
1;6
m
D.
5 3
;
2 2
m
21
Câu 14. Tìm điều kiện tham số m để
2
2
2 1 3
,
3 1 2
x mx
x
x x
.
A.
1
4
2
m
B.
1 4
2 3
m
C.
5
4
2
m
D.
5 7
2 2
m
Câu 15. Tìm đoạn giá trị của tham số m để hàm số
2
1
x m
y
x x
có tập giá trị K = [– 1;1].
A. [0;1] B. [1;2] C. [4;5] D. [6;8]
Câu 16. Khoảng (a;b] là điều kiện cần và đủ của tham số m để biểu thức sau luôn luôn âm với mọi số thực x.
2
4 5 20 2 1
f x m x m x m
.
Tính M = 11a + 3b.
A. M = 30 B. M = 25 C. M = 44 D. M = 57
Câu 17. Tìm điều kiện tham số m để biểu thức
2
2 2 4m x x
luôn luôn âm với mọi số thực x.
A. m = 2 hoặc m < 1,75 B. m = 2 hoặc m < 1
C. m = 2 hoặc m > 3 D. m = 1 hoặc m > 6,5
Câu 18. Tìm số nghiệm nguyên của bất phương trình
1 2
4 3 8
x x x x
.
A.8 B. 10 C. 12 D. 6
Câu 19. Tồn tại bao nhiêu số nguyên lẻ m để
2
8 2 8 8 1 0,m m x m x m x
?
A. 3 số nguyên lẻ B. 4 số nguyên lẻ C. 7 số nguyên lẻ D. 5 số nguyên lẻ
Câu 20. Tìm giá trị nhỏ nhất của m để bất phương trình
2
2 1 2 0
mx m x m
vô nghiệm.
A. m = 0,5 B. m = 2 C. m = 1 D. m = 0,25
Câu 21. Nửa khoảng (a;b] là điều kiện của m để bất phương trình kép
2
2
5
1 7
2 3 2
x x m
x x
luôn nghiệm đúng
với mọi số thực x. Tính H = 3a + 10b + 13.
A. H = 26 B. H = 15 C. H = 18 D. H = 24
Câu 22. Đoạn [p;q] là điều kiện của m để
2
2
3 12
2,
4
x x
x
x mx
. Tính G = 4a + 8b + 48.
A. G = 40 B. G = 50 C. G = 36 D. G = 28
Câu 23. Tìm điều kiện của tham số m để hàm số
3
2
11 5
1 2 5 9
m
y
m x mx m
xác định với mọi số thực x.
A. m > 0,5 B. m > 2 C. m > 0 D. m > 1
Câu 24. Tồn tại bao nhiêu giá trị nguyên m để hàm số
2
4 2
3
4 6
x mx m
y
x x
có tập xác định D = R.
A. 5 giá trị B. 20 giá trị C. 12 giá trị D. 9 giá trị
Câu 25. Tìm điều kiện tham số m để bất phương trình
2
4 3x x m
nghiệm đúng với mọi x thuộc đoạn [0;3].
A.
2m
B.
7
2
4
m
C.
1m
D.
3m
Câu 26. Ký hiệu S là nghiệm của bất phương trình
2
1 0
x m x m
. Tìm độ dài L của S khi biểu diễn S
thành đoạn thẳng trên trục số.
A. L = |m – 2| B. L = |m + 1| C. L = |m| D. L = |m – 1|
Câu 27. Hàm số bậc hai
2
( )
f x ax bx c
có đồ thị
như hình vẽ. Tìm số nghiệm nguyên của bất phương
trình
2
2 6
f x x
.
A. 8 B. 5
C. 7 D. 9
Câu 28. Tìm điều kiện tham số m để bất phương trình
2 2 3
2 2 2 4 0
x m m x m m
có ít nhất một
nghiệm dương.
A. Mọi giá trị m B. m > 0 C. 1 < m < 2 D. 0 < m < 3
22
DẤU TAM THỨC BẬC HAI, BẤT PHƯƠNG TRÌNH BẬC HAI LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P5)
________________________________________________________
Câu 1. Tồn tại bao nhiêu giá trị nguyên m để hàm số
2
2016 2017
3 4 9
f x
x m m x
xác định trên R.
A. 7 giá trị B. 8 giá trị C. 9 giá trị D. 10 giá trị
Câu 2. Tìm số nghiệm nguyên của bất phương trình
2
2
4 10
0
4 3
x x
x x
.
A.3 B. 1 C. 2 D. 4
Câu 3. Tìm điều kiện tham số m để bất phương trình
2 2
3 2 2 1
x x m
có nghiệm x trong khoảng [0;2].
A.
7m
B.
1
5
m
C.
3m
D.
0,2 7m
Câu 4. Tìm điều kiện tham số m để hàm số
2
11
10 19
y
x m
luôn xác định trên R.
A. m > 1 B. m > 19 C. m > 10 D. 3 < m < 4
Câu 5. Tìm điều kiện tham số m để
2
10 24 0,x x m x
.
A. m > 5 B. m > 1 C. m > 7 D. m < 10
Câu 6. Tồn tại bao nhiêu giá trị nguyên của tham số của m để hàm số
2
17 3
6 7 2
f x
x mx m m
xác
định trên R ?
A. 12 giá trị B. 6 giá trị C. 5 giá trị D. 8 giá trị
Câu 7. Hàm số bậc hai
2
( )
f x ax bx c
có đồ thị
như hình vẽ. Tìm số nghiệm nguyên của bất phương
trình
8
f x
.
A. 8 B. 4
C. 6 D. 7
Câu 8. Tìm điều kiện tham số m để hàm số
2
15
3 2 1
f x
x m
luôn xác định trên R.
A. m > 1 B. m > 19 C. m > 2 D. 3 < m < 8
Câu 9. Tìm số nghiệm nguyên của bất phương trình
2
( 5 4) 0
x x x
.
A.4 B. 5 C. 1 D. 2
Câu 10. Tồn tại bao nhiêu giá trị nguyên của tham số m để
2 2
9 12 4 4 ,x mx m m x
.
A. 5 giá trị B. 4 giá trị C. 3 giá trị D. 7 giá trị
Câu 11. Tồn tại bao nhiêu số nguyên m để hàm số
2
2
1 4
y x m m
có tập xác định là R.
A. 6 giá trị B. 2 giá trị C. 5 giá trị D. 4 giá trị
Câu 12. Tìm số nghiệm nguyên
10;10
của bất phương trình
2 3
2 1 2 1
1 1 1
x
x x x x
.
A.4 B. 11 C. 10 D. Kết quả khác
Câu 13. Tìm điều kiện tham số m để bất phương trình
2
1 2 1 0
m x m x m
có nghiệm.
A.
1
0
m
m
B. Mọi giá trị m C.
1
1
2
m
m
D.
1
1
2
m
Câu 14. Bất phương trình:
2 2
3 4 5 0
x x x
có bao nhiêu nghiệm nguyên dương?
A.
0
. B.
1
. C.
2
. D. Nhiều hơn 2
23
Câu 15. Tính tổng các giá trị m để tam thức bậc hai
3 2 3
( ) 2( 1) 8f x m x m x
là bình phương của một nhị
thức
A.4 B. 3 C. 5 D. 2
Câu 16. Tìm điều kiện tham số m để
2
9
5 3 2 2 , ;4
4
x x m x
.
A. m
15
4
B. m
6 C. m
- 1 D. m
- 1
Câu 17. Tìm điều kiện tham số m để bất phương trình
2
1 2 3 0
m x mx m
vô nghiệm.
A.
1 7 1 7
;
2 2
m
B.
1 17 1 17
;
2 2
m
C.
1 37 1 37
;
2 2
m
D.
1 57 1 57
;
2 2
m
Câu 18. Tồn tại bao nhiêu số nguyên m lớn hơn – 8 để hàm số
2 2
4 40 25 3
y x mx m m
luôn xác định
trên R ?
A. 7 giá trị B. 18 giá trị C. 11 giá trị D. 26 giá trị
Câu 19. Tìm điều kiện tham số m để
2
4 2 5 ,x x m m m x
.
A. – 2 < m < 4 B. 0 < m < 2 C. – 1 < m < 1 D. 0 < m < 2,5
Câu 20. Tồn tại bao nhiêu giá trị nguyên m để biểu thức
2
2 2 2 2
M x m x m
luôn luôn âm với mọi x
thực ?
A. 7 giá trị B. 1 giá trị C. 6 giá trị D. 14 giá trị
Câu 21. Tìm số nghiệm nguyên của bất phương trình
2
3 4
0
1
x x
x x
.
A.3 B. 2 C. 5 D. 1
Câu 22. Tồn tại bao nhiêu giá trị m để tam thức bậc hai
3 2 3
( ) 2( 1) 1f x m x m x
không đổi dấu tại một
điểm nào đó.
A.3 B. 2 C. 6 D. 4
Câu 23. Tìm điều kiện của tham số m để bất phương trình
2 2
2 1 6 0
x m x m m
có miền nghiệm
chứa khoảng (1;5).
A.
4
0
11
m
B.
6
1
m
m
C.
2
7
m
m
D.
9
0
m
m
Câu 24. Tìm điều kiện tham số m để bất phương trình
2 2
2 1 6 0
x m x m m
có ít nhất một nghiệm
nhỏ hơn 2018.
A. Mọi giá trị m B. m > 1 C. m < 1 D. m = 0
Câu 25. Hàm số bậc hai
2
( )
f x ax bx c
có bảng
biến thiên như hình vẽ. Tìm giá trị nhỏ nhất k thỏa mãn
, 3;4
f x k x
.
A. k = 14 B. k = 18
C. k = 20 D. k = 24
Câu 26. Tìm điều kiện tham số m để
2 2
6 9 2 2 0,x mx m m x
.
A. – 5 < m < 3 B. 1 < m < 5 C. m < 1 D. 1 < m < 2,5
Câu 27. Tìm điều kiện tham số m để bất phương trình
2 2
2 2 3 4 4 0
x m x m m
có nghiệm.
A. Mọi giá trị m. B.
4
0
11
m
C.
2m
D.
7
2
2
m
Câu 28. Tìm số nghiệm nguyên < 100 của bất phương trình
2
( 4 ) 3 0
x x x
A.85 B. 40 C. 96 D. 97
24
DẤU TAM THỨC BẬC HAI, BẤT PHƯƠNG TRÌNH BẬC HAI LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P6)
________________________________________________________
Câu 1. Tồn tại bao nhiêu giá trị nguyên của tham số m lớn hơn – 7 để hàm số
2 2
9 90 25 50
y x mx m m
luôn xác định trên R ?
A. 19 giá trị B. 8 giá trị C. 15 giá trị D. 14 giá trị
Câu 2. Tìm điều kiện tham số m để
2 2
4 4 2 1 0,x mx m m x
.
A. – 4 < m < 2 B. 0 < m < 4 C. – 1 < m < 1 D. m < 0,5
Câu 3. Tìm điều kiện tham số m để hàm số
2
1
4 1
y
x x m
luôn xác định trên R.
A. m > 6 B. m > 1 C. m > 5 D. 3 < m < 8
Câu 4. Tồn tại bao nhiêu số nguyên m thuộc đoạn [– 10;10] để hàm số
2
2 2 2
g x m m x mx
xác
định trên tập hợp số thực.
A. 15 giá trị B. 17 giá trị C. 14 giá trị D. 18 giá trị
Câu 5. Tìm điều kiện tham số m để
2 2
10 25 5 10 0,x mx m m x
.
A. – 3 < m < 7 B. 0 < m < 5 C. m < 1 D. 0 < m < 4
Câu 6. Hãy tìm đoạn giá trị của tham số m để bất phương trình
2 2
3 2 2 5 2 0
x m x m m
có tập
nghiệm là R.
A. [2;6] B. [3;5] C. [1;4] D. [0;2]
Câu 7. Hàm số bậc hai
2
y ax bx c
có đồ thị
như hình vẽ. Mệnh đề nào đúng ?
A. a < 0; b < 0; c > 0
B. a > 0; b > 0; c < 0
C. a > 0; b < 0; c < 0
D. a > 0; b > 0; c > 0
Câu 8. Tìm giá trị nhỏ nhất của tham số m để bất phương trình
2
1 2 1 3 3 0
m x m x m
vô nghiệm.
A. m = 1 B. m = 2 C. m = 3 D. m = 4
Câu 9. Tìm m để bất phương trình kép
2
2
1
2
1
x mx
x
có tập nghiệm là
.
A. – 2 < m < 2 B. 0 < m
1 C. 0
m < 3 D. 2
m
3
Câu 10. Tìm giá trị nhỏ nhất của m để bất phương trình
2 2
2 3 2 1 1 0
m m x m x
vô nghiệm.
A. m = 3 B. m = 2 C. m = 5 D. m = 1
Câu 11. Tìm điều kiện tham số m để tam thức
2
2 1 4
f x mx m x
không âm với mọi giá trị thực x.
A.
3 8 3 8
m
B.
3 2 8 3 2 8
m
C.
3 5 3 5
m
D.
3 4 5 3 4 5
m
Câu 12. Tìm đoạn giá trị của tham số m để hàm số
2
2
4
2
4
x x
y
x mx
có tập xác định là tập số thực.
A. [2;3] B. [0;3] C. [1;4] D.
5 3
;
2 2
Câu 13. Tìm điều kiện tham số m để
2
4 6 0,x x m x
.
A. m > 3 B. m > 8 C. m > 10 D. m < 10
Câu 14. Tìm điều kiện tham số k để
2
4 9 0x x k
với mọi số thực x.
A. k < 5 B. k < 4 C. k < 2 D. k > 10
Câu 15. Tìm điều kiện tham số m để hàm số
2
1 2 1 3 3
y a x a x a
xác định với mọi giá trị thực
x.
A. a > 5 B. a > 2 C. a > 4 D. a > 1
25
Câu 16. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 8 để
2
1 2 2 6
h x m x m x m
không dương
với mọi số thực x.
A. 8 giá trị B. 15 giá trị C. 9 giá trị D. 16 giá trị
Câu 17. Tìm điều kiện tham số m để
2
2
5 2 25,x m m x
.
A. – 5 < m < 5 B. 0 < m < 5 C. – 5 < m < 6 D. 1 < m < 3
Câu 18. Tìm điều kiện tham số m để hàm số
2
2 2
1
2 2
x x
f x
x mx m m
xác định với mọi số thực x.
A. m > 2 B. m < 1 C. m > 4 D. m > 4
Câu 19. Tìm điều kiện tham số m để hàm số
4 3 2
2
2 2 4 5
2 1 4
x x x x
f x
mx m x m
xác định với mọi x.
A.
1
3 1
m
m
B.
2
3 2
m
m
C.
3
7 2
m
m
D.
6
7 3
m
m
Câu 20. Hàm số bậc hai
2
y ax bx c
có đồ thị
như hình vẽ. Mệnh đề nào đúng ?
A. a < 0; b < 0; c > 0
B. a > 0; b > 0; c < 0
C. a > 0; b < 0; c < 0
D. a > 0; b > 0; c > 0
Câu 21. Tìm điều kiện tham số m để hệ bất phương trình
2
2
3 3 2 1,
2 2 .
x x x
m x m
có nghiệm.
A. Mọi giá trị m. B. m > 2 C.
1 2m
D. 1 < m < 2
Câu 22. Tìm điều kiện của tham số m để bất phương trình
2 2
4 4 8 0x x m m
có ít nhất một nghiệm lớn
hơn 5.
A. Mọi giá trị m B. m > 1 C. m < 1 D. m > 0
Câu 23. Tìm tất cả các giá trị của tham số m để hệ bất phương trình
3 2 2,
3 2 4.
x x
x x m
có nghiệm.
A. m > – 4 B. m < – 8 C. m > 2 D. 0 < m < 4
Câu 24. Tìm điều kiện của tham số m để bất phương trình
2 2
2 1 6 0
x m x m m
không nhận x = 5
làm nghiệm.
A. m < 5 B. 2 < m < 7 C. 3 < m < 8 D. 0 < m < 5
Câu 25. Tìm điều kiện tham số m để
2
1 2 1 3 3 0,m x m x m x
.
A. m
2 B. m
1 C. m
3 D. m
4
Câu 26. Tìm điều kiện tham số m sao cho hàm số
2 2
2
3 10 4
2 8 1
x x
y
x m x m
có tập xác định D = R.
A. 0 < m < 5 B. 0 < m < 28 C. 1 < m < 67 D. 2 < m < 10
Câu 27. Tìm điều kiện tham số m để bất phương trình
2
2 1 4 0
mx m x m
có tập nghiệm S = [a;b]
thỏa mãn đẳng thức 4a + b = 3.
A. m = 8 hoặc m = 0,5 B. m = 8 hoặc m = 1
C. m = 0,5 hoặc m = 3 D. m = 2 hoặc m = 2,5
Câu 28. Tính tổng tất cả các giá trị tham số m để bất phương trình
2 2
2 1 6 0
x m x m m
có miền
nghiệm S = [a;b] thỏa mãn đẳng thức
3 3
35
a b
.
A. – 1 B. 3 C. 2 D. 0
Câu 29. Ký hiệu S là tập hợp nghiệm của bất phương trình
2 2 2
2 7 2 6 0
x m m x m m
. Giả sử L
là độ dài đoạn thẳng miền nghiệm trên trục số. Tìm giá trị tham số để L ngắn nhất.
A. m = 2 B. m = 0 C. m = 1 D. m = – 2
26
CƠ BẢN BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI (MỘT ẨN) LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG HỢP P1)
________________________________________
Câu 1. Tìm điều kiện tham số m để bất phương trình
2
3 4 3x m mx m
nghiệm đúng với mọi số thực x.
A. m = 4 B. m = 3 C. m = 2 D. m = 1
Câu 2. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình
2 1x y
?
A.
2;1
. B.
3; 7
. C.
0;1
. D.
0;0
.
Câu 3. Biết rằng
2
0,f x ax bx c x
. Mệnh đề nào sau đây đúng ?
A. a + b + 2c > 0 B. 9a – 2b + c > 0 C. 4a – 2b + c > 0 D. 4a – 3b + 7c > 0
Câu 4. Bất phương trình
2
3 2
0
1
x x
x
có bao nhiêu nghiệm nguyên
A.3 B. 2 C. 1 D. 4
Câu 5. Cho bất phương trình
2
3 2(2 1) 4 0
x m x m
. Tìm số giá trị nguyên của
m
để bất phương trình
trên có tập nghiệm là R
A. 3. B. 2. C. 4. D. 5.
Câu 6. Với
x
thuộc tập hợp nào dưới đây thì
2
1
4 3
x
f x
x x
không dương?
A.
;1
S

. B.
3; 1 1;S

.
C.
; 3 1;1
S
. D.
3;1
S
.
Câu 7. Có bao nhiêu số nguyên dương m để hệ bất phương trình
2 1
2
3
3 5
x
x m
có nghiệm ?
A. 5 B. 4 C. 2 D. 1
Câu 8. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình
4 5 0
x y
?
A.
5;0
. B.
2;1
. C.
1; 3
. D.
0;0
.
Câu 9. Với
x
thuộc tập hợp nào dưới đây thì nhị thức
2
1
f x x x
không âm?
A.
; 1 1;
 
. B.
1;0 1;

. C.
; 1 0;1

. D.
1;1
.
Câu 10. Tìm điều kiện tham số m để hệ bất phương trình
3( 6) 3
5
7
2
x
x m
có nghiệm.
A. m > – 11 B. m < 11 C. m < – 11 D.
11m
Câu 11. Tam thức
2
3 4f x x x
nhận giá trị âm khi và chỉ khi
A.
–4
x
hoặc
–1
x
. B.
1x
hoặc
4
x
. C.
–4 –4
x
. D. Mọi x
Câu 12. Cho tam thức
2
( ) 12 13
f x x x
. Có bao nhiêu giá trị nguyên của x để f(x) nhận giá trị âm
A.
12
. B.
14
C.
15
. D.
13
.
Câu 13. Tìm điều kiện tham số m để bất phương trình
2 2
1 5 1 0
x m m m
có tập nghiệm S = R.
A. m < 2 B. m = – 4 C. m > 1 D. m > 1,5
Câu 14. Biểu thức nào dưới đây là nhị thức bậc nhất?
A.
2
6 3f x x
. B.
2 1f x x
. C.
5
f x
. D.
3
2 1
f x x
.
Câu 15. Cho biểu thức
1 2 2
f x m x x
. Tìm
m
để biểu thức
f x
là nhị thức bậc nhất
A.
2.
m
B.
2.
m
C.
1.
m
D.
1.
m
Câu 16. Nhị thức nào sau đây nhận giá trị âm với mọi số nhỏ hơn
3
2
?
A.
( ) 2 3f x x
. B.
( ) 2 3f x x
. C.
( ) 3 2
f x x
. D.
( ) 2 3f x x
.
Câu 17. Bất phương trình
0
ax b
nghiệm đúng với mọi
x
khi
A.
0
0
a
b
. B.
0
0
a
b
. C.
0
0
a
b
. D.
0
0
a
b
27
Câu 18. Với giá trị nào của
a
thì bất phương trình
2
0
ax x a
có tập nghiệm là
A.
0
a
. B.
0
a
. C.
1
0
2
a
. D.
1
2
a
.
Câu 19. Bất phương trình
2
( 1)
0
3
x x
x
có số nghiệm nguyên là
A.4 B. 3 C. 2 D. 1
Câu 20. Tìm
m
để bất phương trình
2
1 0
m x mx m
có tập nghiệm là
?
A.
1
m
. B.
1
m
. C.
4
3
m
. D.
4
3
m
.
Câu 21. Bất phương trình
2 2
2 2 1 0
x x x
có bao nhiêu nghiệm nguyên dương?
A.
0
. B.
1
. C.
2
. D. Nhiều hơn 2
Câu 22. Tìm số giá trị nguyên
k
để bất phương trình
2 2
2 4 1 15 2 7 0
x k x k k
nghiệm đúng với mọi x
A.
3
. B.
1
. C.
4.
D.
2.
.
Câu 23. Tìm giá trị tham số m để
2 2
2 5 6 2 3m m x m m x m
với mọi giá trị x.
A. m = 4 B. m = 3 C. m = 2 D. m = 1
Câu 24. Tìm số nghiệm nguyên lớn hơn – 20 của bất phương trình
4 2
( 1) ( 2 3) 0
x x x x
A.20 B. 21 C. 18 D. 15
Câu 25. Tìm số giá trị nguyên m để phương trình
2
( 5) ( 1) 0
m x m x m
có 2 nghiệm
1 2
,x x
thỏa mãn
điều kiện
1 2
2
x x
.
A. 3. B. 2. C. 4. D. 1.
Câu 26. Tập nghiệm của bất phương trình
2
2 6 9
x x x
là:
A.
1
;
2

. B.
1
;
2

. C.
3;

. D.
1
;
2

.
Câu 27. Bất phương trình:
2 2
3 4 5 0
x x x
có bao nhiêu nghiệm nguyên dương?
A.
0
. B.
1
. C.
2
. D. Nhiều hơn 2
Câu 28. Tìm điều kiện tham số m để bất phương trình
2 2
2 4 1 1 0
x m x m
có ít nhất một nghiệm lớn
hơn 2017.
A. Mọi giá trị m B. m > 1 C. m < 1 D. m > 0
Câu 29. Tìm điều kiện tham số m để bất phương trình
2
4 3x x m
nghiệm đúng với mọi x thuộc đoạn [0;3].
A.
2m
B.
7
2
4
m
C.
1m
D.
3m
Câu 30. Tìm điều kiện của
m
để bất phương trình
2 2
2( 2) 2 3 0
x m x m m
có nghiệm
A.Mọi x B.
1 4
m
. C.
;1 3;m
 
D.
.
Câu 31. Tìm giá trị nhỏ nhất của tham số m để hệ bất phương trình
2
2 2
2
4 1,
2
9 1 .
x
x
x m x m
vô nghiệm.
A. m = 14 B. m = 8 C. m = 12 D. m = 6
Câu 32. Với mọi giá trị tham số m, bất phương trình
2
2 1 3 0
x m x m
luôn có tập nghiệm S = (a;b).
Tìm hệ thức liên hệ giữa a và b độc lập với tham số m.
A.
2 2a b ab
B.
2 4a b ab
C.
2 4a b ab
D.
3a b ab
Câu 33. Bất phương trình
2
2
4 9
2 3.
2( 4)
x
x
x
có bao nhiêu nghiệm nguyên thuộc [ -21; 22]? ?
A.
22
. B.
20
. C.
21
. D.
23
.
Câu 34. Có bao nhiêu số nguyên m để phương trình
2 3 2
( 1) 5 0
x m x m m
có nghiệm âm
A.Vô số B. 10 C. 22 D. 14
Câu 35. Tìm số nghiệm nguyên của bất phương trình
10 9 0
x x
A.81 B. 9 C. 10 D. 24
28
CƠ BẢN BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI (MỘT ẨN) LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG HỢP P2)
________________________________________
Câu 1. Với giá trị nào của
m
thì bất phương trình
2
1 0
x mx
có tập nghiệm là
A.
2 2
m
B.
1
m
. C.
2
m
D.
1 3
m
Câu 2. Tìm tập xác định của hàm số
2
2 5 2
y x x
.
A.
1
;
2

. B.
2;

. C.
1
; 2;
2
 
. D.
1
;2
2
.
Câu 3. Tìm giá trị nhỏ nhất của tham số m để hệ bất phương trình
2
2 2
2
4 1,
2
9 1 .
x
x
x m x m
vô nghiệm.
A. m = 14 B. m = 8 C. m = 12 D. m = 6
Câu 4. Cho
2
0 .
f x ax bx c a
Điều kiện để
0,f x x
là
A.
0
.
0
a
B.
0
.
0
a
C.
0
.
0
a
D.
0
.
0
a
Câu 5. Tìm điều kiện tham số m để bất phương trình
3
9 10 4 0
m m x m
có tập nghiệm S = R.
A. m = 4 B. m = – 4 C. m = 1 D. m = 1,5
Câu 6. Tìm điều kiện tham số m để hệ bất phương trình
3 5 0,
2 3 .
x
mx m
có độ dài tập nghiệm bằng 2.
A. m = 1 B. m =
9
25
C. m – 2 D. m =
7
26
Câu 7. Cho
2
0
f x ax bx c a
. Điều kiện để
0,f x x
là
A.
0
0
a
. B.
0
0
a
C.
0
0
a
D.
0
0
a
.
Câu 8. Bất phương trình:
3 2
x x
có tập nghiệm là:
A.
2; 1 .
B.
1;2 .
C.
2;3 .
D.
–1;2 .
Câu 9. Tồn tại bao nhiêu giá trị nguyên m để hàm
2 2
1 2
8 59 10
f x
x mx m m
xác định trên R.
A. 2 giá trị B. 4 giá trị C. 3 giá trị D. 1 giá trị
Câu 10. Tìm tất cả các giá trị thực của tham số
m
sao cho ptrình
2
1
1 0
3
x m x m
có nghiệm ?
A.
.
m
B.
1.
m
C.
3
1.
4
m
D.
3
.
4
m
Câu 11. Xác định tất cả các giá trị m để hệ bất phương trình sau có tập nghiệm là một đoạn trên trục số có độ
dài bằng 1 đơn vị
2
3 2 12
3 4,
1 6.
x x
x
x
m x m
A. m = 3 B. m = 2 C. m = – 6 D. m = – 2
Câu 12. Phương trình
2
2( 2) 2 1 0
x m x m
(
m
là tham số) có nghiệm khi
A.
1
.
5
m
m
B.
5 1.
m
C.
5
.
1
m
m
D.
5
.
1
m
m
Câu 13. Cho hàm số
2
2
f x x x m
. Với giá trị nào của tham số
m
thì
0,f x x
.
A.
1
m
. B.
1
m
. C.
0
m
. D.
2
m
.
Câu 14. Tìm tất cả các giá trị của tham số
m
để tam thức f(x) =
2
2 8 1 0
x m x m
.
x
A.
0;28
m
. B.
;0 28;m
 
. C.
;0 28;m

. D.
0;28
m
.
29
Câu 15. Tìm điều kiện tham số m để hệ bất phương trình
3 2 0,
3 4 0.
m x m
x
có nghiệm.
A. Mọi giá trị m B. Không tồn tại C. m > – 3 D. m
– 3
Câu 16. Có bao nhiêu số nguyên
m
để với mọi x biểu thức
2
2 8 1
f x x m x m
luôn nhận giá trị
dương.
A.
27
. B.
28
. C. Vô số. D.
26
.
Câu 17. Tìm
x
để
2
5 6
1
x x
f x
x
không âm.
A.
1;3
. B.
1;2 3;

. C.
2;3
. D.
;1 2;3

.
Câu 18. Bất phương trình
2 2
3 6 3 .x x x x
có tập nghiệm là
; ; ;( , , , )
a b c d a b c d
. Tính tổng a + b
+ c + d
A.
4
. B.
0
. C.
1
. D.
6
.
Câu 19. Tìm giá trị bé nhất của tham số m để hệ bất phương trình
2
2
3 7 1,
2 8 5 .
x x x
m x
vô nghiệm.
A. m = 6,5 B. m = 7,5 C. m = – 6 D. m = – 2
Câu 20. Dấu của tam thức bậc 2:
2
( ) 5 6f x x x
được xác định như sau
A.
0
f x
với
2 3
x
và
0
f x
với
2
x
hoặc
3
x
.
B.
0
f x
với
3 2
x
và
0
f x
với
3
x
hoặc
2
x
.
C.
0
f x
với
2 3
x
và
0
f x
với
2
x
hoặc
3
x
.
D.
0
f x
với
3 2
x
và
0
f x
với
3
x
hoặc
2
x
.
Câu 21. Tập nghiệm của bất phương trình
2
6 0
x x
là:
A.
; 3 2;
 
. B.
3;2
. C.
2;3
. D.
; 2 3;
 
.
Câu 22. Tìm điều kiện tham số m để
1 1 0,m x m x
.
A. m = 1 B. m = 3 C. Không tồn tại D. m = 2
Câu 23. Giá trị nào là nghiệm nguyên âm lớn nhất của bất phương trình
2
5 6 0
x x
?
A.
3
. B.
1
. C.
2
. D. 0 .
Câu 24. Gọi
S
là tập nghiệm của bất phương trình
2
6 0
x x
, S có tập con nào sau đây ?
A.
;0

. B.
1;7
. C.
2;2
. D.
6;
.
Câu 25. Tập xác định của hàm số
2
2
5 6
y
x x
là:
A.
; 6 1;
 
. B.
6;1
. C.
; 6 1;
 
. D.
; 1 6;
 
.
Câu 26. Tìm tất cả các giá trị của tham số m để hệ bất phương trình
2
12 0,
1 2 .
x x
x x m
vô nghiệm.
A.
4m
B.
4m
C. m > 4 D.
3m
Câu 27. Bất phương trình
2
2 2 3 0
mx m x m
có tập nghiệm S = [a;b] thỏa mãn điều kiện
2 2
1a b
. Giá trị tham số m tìm được nằm trong khoảng nào ?
A. (0;1) B. (4;6) C. (1;3) D. (6;8)
Câu 28. Bất phương trình:
2 3
x x
có tập nghiệm là:
A.
3;

B.
; 1 3;
 
C.
; 1
D. R
Câu 29. Giá trị nào không là nghiệm của bất phương trình
2
6 0
x x
?
A.
2
. B.
1
. C.
2
. D. 0 .
Câu 30. Tìm điều kiện của m sao cho
2
2
4 9
0,
( 1) 4
x x
x
x m x
.
A. Mọi giá trị m B.
5; 3
m
C.
4; 2
m
D. m > 0
_________________________________
30
CƠ BẢN BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI (MỘT ẨN) LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG HỢP P3)
________________________________________
Câu 1. Tìm điều kiện tham số m để hàm số
2
11
10 19
y
x m
luôn xác định trên R.
A. m > 1 B. m > 19 C. m > 10 D. 3 < m < 4
Câu 2. Cho
2
( ) 1 2 1 4
f x m x m x
. Tập hợp tất cả các giá trị m để giá trị của hàm số không âm [a;b].
Tính giá trị
2 2
a b
.
A.
4
B.
10
C.
9
D.
3
Câu 3. Tìm điều kiện tham số m để hệ bất phương trình
2
3
,
1 2.
x x
x
x
m x
có duy nhất nghiệm.
A. m = 3 B. m = 1 C. m = – 6 D. m = – 3
Câu 4. Cho
2
0
f x ax bx c a
. Điều kiện để
0,f x x
là
A.
0
0
a
. B.
0
0
a
C.
0
0
a
D.
0
0
a
.
Câu 5. Với
x
thuộc tập hợp nào dưới đây thì
2
2 3f x x x
luôn dương?
A.
. B. R. C.
; 1 3;
 
. D.
1;3
.
Câu 6. Tìm điều kiện của m để hệ bất phương trình
3
2
2
2( 1) 5
x m
x
có độ dài tập nghiệm lớn hơn 3.
A. m > 1 B. m < 4 C. m > 0,5 D. 0 < m < 3
Câu 7. Tìm điều kiện tham số m để
3 7, 2
m x x
.
A. m < 0,5 B. m > 1 C. m > 0,5 D. m < 4
Câu 8. Với
x
thuộc tập hợp nào dưới đây thì tam thức
2
6 8f x x x
không dương?
A.
2;3
. B.
;2 4;

. C.
2;4
. D.
1;4
.
Câu 9. Tam thức
2
( ) 2 3f x x x
nhận giá trị dương khi và chỉ khi
A.
–3
x
hoặc
–1
x
. B.
–1
x
hoặc
3
x
. C.
–2
x
hoặc
6
x
. D.
–1 3
x
.
Câu 10. Tổng các nghiệm nguyên dương của bất phương trình
2 4
4 4
x
x x
.
A.
21
. B.
15
. C.
13
. D.
11
.
Câu 11. Số nghiệm nguyên của bất phương trình
3 2 5 0
x x
là
A.
6
. B.
5
. C.
0
. D. Vô số.
Câu 12. Cho
2
0
f x ax bx c a
. Điều kiện để
0,f x x
là
A.
0
0
a
. B.
0
0
a
C.
0
0
a
D.
0
0
a
.
Câu 13. Với giá trị nào của
m
thì bất phương trình
2
(2 1) 3( 1) 1 0
m x m x m
(1). có nghiệm.
A.
[-5; 1]
m
B.
. ( 5; 2)
m
C.
; 5 1;m
 
D.
[7; )
m

Câu 14. Bất phương trình
2
2
2 2
1
x mx m
x x
có tập nghiệm là R khi và chỉ khi
A.
2 2
m
. B.
2 10
m
. C.
2 10
m m
. D.
2 10
m
.
Câu 15. Bất phương trình
1 2
x
có tập nghiệm là
A.
; 1 3;S
. B.
; 1 3;S
.
C.
1;3
S
. D.
1;3
S
.
Câu 16. Tìm tất cả các giá trị của tham số
m
để hệ sau có nghiệm
2
2 0
2 0
x
x x m
.
A.
1
m
B.
2
m
C.
1
m
D.
m
31
Câu 17. Tìm điều kiện tham số m sao cho
2
4 3 2,m x m x
.
A. m = 3 B. m = 4 C. m = 2 D. m = – 2
Câu 18. Cho bất phương trình
2
2 4 5 0
x x m
. Tìm
m
để bất phương trình nghiệm đúng với
3x
?
A.
11m
. B.
11m
. C.
11m
. D.
11m
.
Câu 19. Cặp số
2;3
là nghiệm của bất phương trình nào sau đây?
A.
2 – 3 –1 0
x y
. B.
– 0
x y
. C.
4 3x y
. D.
– 3 7 0
x y
.
Câu 20. Giá trị nào là một nghiệm của bất phương trình
2
6 0
x x
:
A.
4
. B.
1
. C.
2
. D. 3 .
Câu 21. Tồn tại bao nhiêu số nguyên m < 10 để hàm số
2017
10 2 10
y
x x m
xác định trên R ?
A. 7 giá trị B. 8 giá trị C. 10 giá trị D. 6 giá trị
Câu 22. Tìm số nghiệm nguyên thuộc
9;9
của bất phương trình
2
2
4 4
0
4 5
x x
x x
A.16 B. 18 C. 17 D. 5
Câu 23. Giá trị nào không là nghiệm của bất phương trình
2
8 16 0
x x
:
A.
4
. B.
1
. C.
4
. D. 3 .
Câu 24. Tìm tất cả các giá trị của tham số m để hệ bất phương trình
2
12 0,
1 2 .
x x
x x m
vô nghiệm.
A.
4m
B.
4m
C. m > 4 D.
3m
Câu 25. Tìm m để bất phương trình
( 1) 3( 1)
m x m
vô nghiệm.
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Câu 26. Biết rằng bất phương trình
2
( ) 1 2 3 0
f x m x mx m
vô nghiệm. Tổng các giá trị nguyên của
m thỏa mãn
( ) 0
f x
với mọi giá trị x là
A.
1
. B.
2
. C.
0
. D.
1
.
Câu 27. Tìm điều kiện xác định của bất phương trình
2
2
2
x
x
x
.
A.
2 0
x
. B.
2
x
. C.
2
0
x
x
. D.
0
x
.
Câu 28. Điều kiện xác định của bất phương trình
2
2 1
0
4
1
x
x
x
là:
A.
2
1
x
x
. B.
2
1
x
x
. C.
2
1
x
x
. D.
2
1
x
x
.
Câu 29. Bất phương trình
2 1 2 6 1
x x
có bao nhiêu nghiệm nguyên?
A.
10
. B.
8
. C.
11
. D.
9
.
Câu 30. Tìm điều kiện tham số m để hệ bất phương trình
3
0,
4
3 1.
x
x
x m
có nghiệm.
A. m < 7 B. m < 8 C. 2 < m < 6 D. 3 < m < 9
Câu 31. Tập nghiệm của bất phương trình
2 5 7
x
có bao nhiêu số nguyên?
A.
12
. B.
13
. C.
10
. D.
11
.
Câu 32. Tìm giá trị nhỏ nhất của tham số m để bất phương trình
2
2
2 7 5
5 7
x x
m
x x
luôn đúng với mọi x.
A. m = 2 B. m = 5 C. m = 6 D. m = 3
Câu 33. Để bất phương trình
2
( 5)(3 ) 2
x x x x a
nghiệm đúng
5;3
x
, tham số
a
phải thỏa điều
kiện nào sau đây
A.
3
a
. B.
4
a
. C.
5
a
. D.
6
a
.
_________________________________
32
CƠ BẢN BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI (MỘT ẨN) LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG HỢP P4)
________________________________________
Câu 1. Tam thức nào dưới đây luôn dương với mọi giá trị của
x
?
A.
2
10 2x x
. B.
2
2 10
x x
. C.
2
2 10
x x
. D.
2
2 10
x x
.
Câu 2. Có bao nhiêu giá trị nguyên dương của
x
thỏa mãn
2 2
3 1 2
4 2 2
x x
x x x x
?
A.
0.
B.
2.
C.
1.
D.
3.
Câu 3. Có tất cả bao nhiêu giá trị nguyên của
m
để ptrình
2 2
2 2 2 3 4 0
x m x m m
có nghiệm ?
A.
3.
B.
4.
C.
2.
D.
1.
Câu 4. Các giá trị
m
để phương trình
2
2 8 1 0
x m x m
có hai nghiệm phân biệt ?
A.
0
m
hoặc
28.
m
B.
0
m
hoặc
28.
m
C.
0 28.
m
D.
0.
m
Câu 5. Tìm điều kiện tham số m để
2
2
2 3
1, 2;2
2 2
x x m
x
x x
.
A.
8
3
m
B. m
13
6
C. m
2 D. m
- 1
Câu 6. Tìm điều kiện tham số m để
4
5 4 , ;9
9
x x m x
.
A. m
- 8 B. m
4
3
C. m
- 5 D. m
4
3
Câu 7. Tập nghiệm của bất phương trình
2
6 9 0
x x
là:
A.
3;

. B.
.
C.
\ 3
.
D.
3
.
Câu 8. Với giá trị nào của
m
thì bất phương trình
2
2
0
4 5
x x m
x x
có tập nghiệm là
A.
1
m
. B.
1
m
. C.
1
4
m
. D.
1
4
m
.
Câu 9. Gọi
S
là tập nghiệm của bất phương trình
2
8 7 0
x x
. Tập hợp nào là tập con của
S
?
A.
;0

. B.
1;7
. C.
0;2
. D.
6;
.
Câu 10. Tìm tất cả các giá trị của tham số m để hệ bất phương trình
2
2 2 5 ,
3 3 .
x x
x x m
có nghiệm.
A. m
1 B. m < 2 C. 0
m
3 D. m < 5
Câu 11. Tập nghiệm của bất phương trình
1 3 2
x x
A.
5 7
;
2 4
. B.
5 7
;
2 4
. C.
7
;
4

. D.
5
;
2

.
Câu 12. Giá trị của m để
( ) 1 0
f x mx
với
x
là:
A.
1
m
. B.
0
m
. C.
0
m
. D.
0
m
.
Câu 13. Với giá trị nào của
m
thì
2 f x mx m x
luôn dương?
A.
0
m
. B.
2
m
. C.
2
m
. D.
m
.
Câu 14. Bất phương trình
3 5 2
1
2 3
x x
x
có bao nhiêu nghiệm nguyên lớn hơn
10
?
A. 10. B. 5. C. 9. D. 4.
Câu 15. Tìm m để bất phương trình
2
3 4
m x mx
có nghiệm
A.
0
m
B.
1
m
C.
1
m
hoặc
0
m
D.
m
Câu 16. Hệ bất phương trình
2
1 0
0
x
x m
vô nghiệm khi:
A.
1
m
B.
1
m
C.
1
m
D.
1
m
Câu 17. Bất phương trình:
2 4
x x
có nghiệm nguyên nhỏ nhất là:
33
A.
3
. B.
1.
C.
0.
D.
2.
Câu 18. Tìm tất cả giá trị thực của tham số
m
để hệ bất phương trình
3 5 7
3
x x
m x
vô nghiệm.
A.
9
m
B.
3
m
C.
9
m
D.
3
m
Câu 19. Tìm điều kiện tham số m để hàm số
2 2 2 1
f x x m m mx
xác định với mọi
1x
.
A. m = 0 hoặc m
- 1 B. m = 0 hoặc m
- 2
C. m = 1 hoặc m
0 D. m = 2 hoặc m
1.
Câu 20. Tìm điều kiện tham số m để hệ bất phương trình
1
0,
2
4 1 .
x
x
x m
có nghiệm duy nhất.
A. m = 6 B. m = 5 C. 3 < m < 5 D. m = 2
Câu 21. Nghiệm nguyên dương nhỏ nhất của bất phương trình:
2 1 3x x
là:
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 22. Bất phương trình
2
2 2 3 0
mx m x m
có tập nghiệm S = [a;b] thỏa mãn điều kiện
2 2
1a b
. Giá trị tham số m tìm được nằm trong khoảng nào ?
A. (0;1) B. (4;6) C. (1;3) D. (6;8)
Câu 23. Tìm tất cả các giá trị của tham số
m
để hệ bất phương trình
3 4 0
2 5 0
x
m x
vô nghiệm
A.
7
3
m
. B.
7
3
m
. C.
7
3
m
. D.
7
3
m
.
Câu 24. Với mọi giá trị tham số m, bất phương trình
2
2 1 3 0
x m x m
luôn có tập nghiệm S = (a;b).
Tìm hệ thức liên hệ giữa a và b độc lập với tham số m.
A.
2 2a b ab
B.
2 4a b ab
C.
2 4a b ab
D.
3a b ab
Câu 25. Bất phương trình:
2
8 2
x x
có tập nghiệm là:
A.
2; 2 2 .
B.
2; 2 2 .
C.
3; 2 2 .
D.
–3;2 .
Câu 26. Tồn tại bao nhiêu giá trị nguyên m nhỏ hơn 40 để hàm
2
2018
9 12 6
y
x x m
luôn xác định trên R ?
A. 17 giá trị B. 28 giá trị C. 30 giá trị D. 29 giá trị
Câu 27. Hàm số bậc hai
2
y ax bx c
có đồ thị
như hình vẽ. Tìm số nghiệm nguyên của bất phương
trình
( ) 0
f x
A. 1 B. 2
C. 3 D. 4
Câu 28. Tồn tại bao nhiêu giá trị nguyên của tham số m để
2 2
9 12 4 4 ,x mx m m x
.
A. 5 giá trị B. 4 giá trị C. 3 giá trị D. 7 giá trị
Câu 29. Bất phương trình:
2
2 15 3x x x
có tập nghiệm là:
A.
5
x
. B.
5 6
x
. C.
3 6
x
. D.
3 5
x
.
Câu 30. Tìm điều kiện tham số m để hàm số
2 2
6 9 2
y x mx m m
có tập xác định là R.
A. m
1 B. m
6 C. m
2 D. m
7
Câu 31. Tìm điều kiện của m sao cho
2
2 5 2 , 1;0
x x m x
.
A.
2m
B.
2 9m
C.
9m
D.
9
8
m
Câu 32. Tìm tất cả các giá trị của tham số m để hệ bất phương trình
2
4 3 0,
1 2 3 .
x x
x x m
vô nghiệm.
A. m
0 B. m
1 C. m
3 D. m
6
_________________________________
34
CƠ BẢN BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI (MỘT ẨN) LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG HỢP P5)
________________________________________
Câu 1. Tồn tại các giá trị a và b để
2
2 1 3 2 0,a b x a b x
. Khi đó điều kiện tham số b là
A.
2
0,5
b
b
B.
3
0
b
b
C.
1
0,75
b
b
D.
4
0,25
b
b
Câu 2. Tìm điều kiện tham số m sao cho
2
1 10 3,m x m x
.
A. m = 1 B. m = 4 C. m = 2 D. m = – 1
Câu 3. Tìm điều kiện tham số m để
2 0, 1mx x
.
A. m > 3 B. m > 2 C. m > 4 D. 5 < m < 6
Câu 4. Tìm điều kiện tham số m để hệ bất phương trình
2 0,
4.
x
mx m
có nghiệm duy nhất.
A. m = 3 B. m = 4 C. m = 2 D. m = 0
Câu 5. Với
x
thuộc tập hợp nào dưới đây thì biểu thức
2
1
1
f x
x
âm?
A.
; 1
. B.
; 1 1;
. C.
1;
. D.
1;1
.
Câu 6. Tập nghiệm của bất phương trình
5 4 6
x
có dạng
; ;S a b
 
. Tính tổng
5
P a b
.
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 7. Bất phương trình
3mx m x
vô nghiệm khi
A.
3.
m
B.
0.
m
C.
3.
m
D.
.
m
Câu 8. Tìm m để phương trình
2
1 2 2 3 0
m x m x m
có hai nghiệm trái dấu.
A.
1, 3
m m
. B.
2, 3
m m
. C.
1 3
m
. D.
3
m
.
Câu 9. Tìm giá trị của tham số m để phương trình
2 2
2 4 0
x m x m m
có hai nghiệm trái dấu.
A.
2.
m
B.
0 4.
m
C.
2.
m
D.
0
m
hoặc
4.
m
Câu 10. Hệ bất phương trình
3
3 9
mx m
m x m
có nghiệm duy nhất khi và chỉ khi
A.
1
m
. B.
2
m
. C.
1
m
. D.
2
m
.
Câu 11. Tìm giá trị của tham số m để phương trình
2
1 0
x mx
có hai nghiệm phân biệt.
A.
1
m
hoặc
1
m
. B. Không có giá trị m.
C.
2
m
hoặc
2
m
. D.
2
m
hoặc
2
m
.
Câu 12. Tìm điều kiện xác định của bất phương trình sau
2
1
6 3 5
2 3
x
x
x x
A.
2
3
x
x
. B.
2 3
x
. C.
2
1
x
x
. D.
3
1
x
x
.
Câu 13. Bất phương trình nào sau đây tương đương với bất phương trình
5 0
x
A.
2
5 0
x x
. B.
5 5 0
x x
. C.
2
1 5 0
x x
. D.
5 5 0
x x
.
Câu 14. Điều kiện để bất phương trình
2
0;
ax bx c
với
0
a
có tập nghiệm bằng
là
A.
0
. B.
0
C.
0
D.
0
.
Câu 15. Tập nghiệm của bất phương trình
2
1 0
x
là:
A.
1;

. B.
1;

. C.
1;1
. D.
; 1 1;
 
.
Câu 16. Nghiệm nguyên dương nhỏ nhất của bất phương trình
2
1 0
x x
là:
A.
0
. B.
1
. C.
2
. D. 3 .
Câu 17. Tập nghiệm của bất phương trình
2
4 4 0
x x
là:
A.
2;

. B.
.
C.
\ 2
.
D.
\ 2
.
Câu 18. Tập nghiệm của bất phương trình
2
4 2 8 0
x x
là:
A.
;2 2

. B.
\ 2 2
. C.
. D.
.
35
Câu 19. Cho pt
2
5 2 1 0
m x m x m
1
. Tìm số giá trị nguyên của
m
để pt (1) có 2 nghiệm
1 2
,x x
thỏa
1 2
2
x x
A. 3. B. 2. C. 4. D. 1.
Câu 20. Cho bất phương trình
2 2
(2 2) 2 0
x m x m m
. Tìm
m
để bất phương trình nghiệm đúng với mọi
x
thuộc đoạn
0;1
?
A.
1 0m
. B.
0
1
m
m
. C.
1 0m
. D.
1
2
m
m
.
Câu 21. Bất phương trình nào sau đây vô nghiệm
A.
2
8 16 0
x x
B.
2
2 5 4 0
x x
C.
2
2 7 9 0
x x
D.
2
10 24 0
x x
Câu 22. Điều kiện để bất phương trình
2
0 0 ,
ax bx c a
có tập nghiệm bằng
là
A.
0
0
a
. B.
0
0
a
C.
0
0
a
D.
0
0
a
.
Câu 23. Bất phương trình:
2
6 5 8 2x x x
tương đương với hệ nào sau đây ?
A.
2
8 2 0
6 5 8 2
x
x x x
. B.
2
2
6 5 0
6 5 8 2
x x
x x x
C.
2
8 2 0
6 5 8 2
x
x x x
. D.
2
8 2 0
6 5 8 2
x
x x x
Câu 24. Bất phương trình:
2 1 3x x
tương đương với hệ nào sau đây ?
A.
2
3 0
.
2 1 3
x
x x
. B.
2
3 0
.
2 1 3
x
x x
C.
2
2 1 0
3 0
2 1 3
x
x
x x
. D.
2
2 1 0
3 0
2 1 3
x
x
x x
.
Câu 25. Bất phương trình
2 4 3
2.
x x
x
có bao nhiêu nghiệm nguyên thuộc [ -21; 22]?
A.
22
. B.
20
. C.
21
. D.
23
.
Câu 26. Hàm số bậc hai
2
y ax bx c
có đồ thị
như hình vẽ. Tập nghiệm của bất phương trình
( ) 0
f x
có bao nhiêu số nguyên
A. 2 B. 1
C. 3 D. 4
Câu 27. Bất phương trình
2
2
2
1
3 4
x mx
x x
luôn luôn đúng trên R khi và chỉ khi nào ?
A. m < – 4 hoặc m
0 B. m < – 3 hoặc m
0
C. m < 2 hoặc m > 5 D. m < – 6 hoặc m
1
Câu 28. Bất phương trình
2
3 4 2
2.
x x
x
có bao nhiêu nghiệm nguyên?
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 29. Tìm tất cả các giá trị của tham số m để hệ bất phương trình
2
2 3,
1 4 3 .
x x
x x m
vô nghiệm.
A. m <
4
3
B. m
2
3
C. m
1 D. m
4
3
Câu 30. Tìm điều kiện của m sao cho
2
2 5 2 , 1;0
x x m x
.
A.
2m
B.
2 9m
C.
9m
D.
9
8
m
36
CƠ BẢN BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI (MỘT ẨN) LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG HỢP P6)
________________________________________
Câu 1. Tồn tại bao nhiêu giá trị nguyên m trong khoảng (– 19;19) để
2
4
2 2
4 19
2 2 1 1
x x
y
m x m x
xác định
với mọi giá trị thực x ?
A. 15 giá trị B. 20 giá trị C. 17 giá trị D. 19 giá trị
Câu 2. Tìm điều kiện tham số m để hàm số
2 2
10 25 2
y x mx m m
có tập xác định là R.
A. m
1 B. m
6 C. m
2 D. m
7
Câu 3. Bất phương trình
2
2
8 7
0
2 3
x x
x x
có số nghiệm nguyên là
A.6 B. 3 C. 8 D. 7
Câu 4. Tìm giá trị nhỏ nhất của tham số m để
2 2
12 3 1 0,x mx m m x
.
A. m = 1 B. m = 2 C. m = 3 D. m = 4
Câu 5. Tìm số nghiệm nguyên của bất phương trình
2
4
9
0
1
x
x
.
A.7 B. 6 C. 5 D. 10
Câu 6. Tìm tất cả các giá trị của tham số m để hệ bất phương trình
2
4 3 0,
1 2 3 .
x x
x x m
vô nghiệm.
A. m
0 B. m
1 C. m
3 D. m
6
Câu 7. Tìm điều kiện tham số m để hàm số
2 2
6 9 2
y x mx m m
có tập xác định là R.
A. m
1 B. m
6 C. m
2 D. m
7
Câu 8. Tìm điều kiện tham số m để
2 2
4 3 5 ,x mx m m x
.
A. – 5 < m < 6 B. 0 < m < 5 C. – 1 < m < 2 D. 0 < m < 6
Câu 9. Tìm điều kiện tham số m để bất phương trình
2 2
2 3 1 0
x m x m
có nghiệm.
A. Mọi giá trị m. B.
4
0
11
m
C.
2m
D.
7
2
2
m
Câu 10. Tập nghiệm của bất phương trình
2
2
4 4
0
2 3 4
x x
x x x
là
A.
. B.
2
. C.
. D.
\ 2
.
Câu 11. Tập nghiệm của bất phương trình
2
4 5 1 0
x m x m
là một khoảng có độ dài bằng 10. Tính
tổng L bao gồm tất cả các giá trị của m xảy ra.
A. L = 12 B. L = 19 C. L = 10 D. L = 20
Câu 12. Tìm điều kiện tham số m để bất phương trình
2 2
1 0
x m x
có tập hợp nghiệm S sao cho S và
tập hợp (5;10) có phần tử chung.
A. |m| < 3 B. |m| > 2 C. |m| < 4 D. 1 < |m| < 5
Câu 13. Tìm điều kiện tham số m để hệ bất phương trình
2
2
7 4
1,
1
2 2 4 0.
x
x x
x m x m m
có nghiệm.
A.
5m
B. m
5 C. Mọi giá trị m. D. 2
m
3
Câu 14. Tìm đoạn giá trị của tham số m để hệ bất phương trình
8
1,
3
3 .
x
x mx
vô nghiệm.
A.
8
;0
5
B.
1
;2
5
C.
3
;2
5
D.
4
;3
5
Câu 15. Tìm điều kiện tham số m để bất phương trình
2
2 2 0x mx m
có tập nghiệm với độ dài bằng 2.
A. m = 3 B. m = 1 hoặc m = – 2
C. m – 1 hoặc m = 2 D. Không tồn tại m.
37
Câu 16. Tìm điều kiện tham số m để hệ bất phương trình
2
2,
5 1.
x x
x
x x m
có nghiệm.
A. m < 5 B. m < 4 C. m < 0 D. m > 7
Câu 17. Tìm điều kiện tham số m để
3 7, 2
m x x
.
A. m < 0,5 B. m > 1 C. m > 0,5 D. m < 4
Câu 18. Tìm điều kiện tham số m để hệ bất phương trình
2 0,
4.
x
mx m
có nghiệm duy nhất.
A. m = 3 B. m = 4 C. m = 2 D. m = 0
Câu 19. Tồn tại bao nhiêu số m nhỏ hơn 30 để hàm số
2 2 2
3
12 36 9
f x
x mx m m m
luôn xác định
trên tập hợp số thực ?
A. 21 giá trị B. 22 giá trị C. 20 giá trị D. 25 giá trị
Câu 20. Tìm số nghiệm nguyên của bất phương trình
2
4 3
2 2
x x
x x
.
A. 1 nghiệm B. 2 nghiệm C. 4 nghiệm D. 3 nghiệm
Câu 21. Hai bất phương trình
1
0; 2 0
1
x
x m
x
có tập nghiệm lần lượt là A và B. Tồn tại bao nhiêu số
nguyên m thuộc [– 10;10] để
A B
?
A. 12 B. 9 C. 10 D. 8
Câu 22. Hàm số bậc hai
2
y ax bx c
có đồ thị
như hình vẽ. Tập nghiệm của bất phương trình
( ) 5
f x
có bao nhiêu số nguyên
A. 3 B. 1
C. 5 D. 4
Câu 23. Cho tam thức
2
( ) ( 2) 3 3
f x x m x m
. Tập hợp S bao gồm tất cả các số nguyên dương m để
( ) 0, 5
f x x
. Tổng tất cả các phần tử của tập hợp S là
A. 6 B. 15 C. 11 D. 21
Câu 24. Giả sử
2
0,f x ax bx c x
. Mệnh đề nào sau đây đúng ?
A.
4 2 0a b c
B.
9 3 1 2a b c
C.
3 0a b c
D.
2 1a b c
Câu 25. Tìm điều kiện tham số m để bất phương trình
2
4 1 5 0
x m x m
có tập nghiệm là [2;4].
A.
1
2;
2
m
B. m = 3 C. m = 2 D.
1
2; ;0
2
m
Câu 26. Tìm điều kiện tham số m để bất phương trình
2
3 2 1 5 0
m x m x m
có tập nghiệm S =
[a;b] thỏa mãn điều kiện
2 2
39a b ab
.
A.
49
4;
19
m
B. m = 49 C.
49
19
m
D. Không tồn tại m.
Câu 27. Tìm số nghiệm nguyên của bất phương trình
2 3 1
0
2 3 1
x x
x x
.
A.1 B. 2 C. 3 D. Kết quả khác
Câu 28. Tìm điều kiện tham số m để
2
2
2 3
1, 0;4
2
x x m
x
x
.
A. m <
17
4
B. m < 0 C. m
1 D. m
- 6
_________________________________
38
BPT + HỆ BPT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P1)
_____________________________
Câu 1. Tìm điều kiện tham số m để
2
2
3 6 3
2, 5;2
2 2
x x m
x
x x
.
A. m
17
8
B. m
13
6
C. m
16
3
D. m
17
4
Câu 1. Tìm số nghiệm nguyên lớn hơn – 40 của bất phương trình
2 4
4 2 4x x x x
.
A.30 B. 24 C. 28 D. 40
Câu 2. Tìm giá trị của a để hệ bất phương trình
2
2
2
1 0,
1 0,
0.
ax x
x ax
x x a
có nghiệm duy nhất.
A. a = – 4 B. a = – 2 C. a = 1 D. a > 5
Câu 3. Tìm điều kiện tham số m để phương trình
2
3
0
1 2
x x m
x
có nghiệm.
A.
9
4
m
B.
9
4
m
C.
2m
D.
2m
Câu 4. Tìm điều kiện của m để bất phương trình
4 3 2 2
4 2 4 4 0
x x m x mx m
có nghiệm duy nhất.
A. m = 2 B. m = 0 C. m = 3 D. m = 1
Câu 5. Tìm điều kiện tham số m để
2
2
4 5
1, 3;3
2 2
x x m
x
x x
.
A. m
0 B. m
- 7 C. m
1
4
D. m
17
4
Câu 1. Tìm số nghiệm nguyên của bất phương trình
2
4 4
2 2
1 2 6 3 2 7 3 2 1x x x x x x x
.
A.3 B. 1 C. 2 D. 4
Câu 6. Tìm điều kiện tham số m để bất phương trình
2
2
2 6
4
4
x x m
x x
có nghiệm x thuộc đoạn [4;5].
A. m
0 B. m
- 7 C. m
- 24 D. m
- 6
Câu 7. Ký hiệu S là tập hợp nghiệm của bất phương trình
2 2 2
3 2 0
x m m x m m
. Giả sử L là độ
dài đoạn thẳng miền nghiệm trên trục số. Tìm giá trị tham số để L ngắn nhất.
A. m = 2 B. m = 0 C. m = 1 D. m = 0,5
Câu 1. Tìm số nghiệm nguyên nhỏ hơn 30 của bất phương trình
2
2 3 5 4 8 2 21 10x x x x x x x
.
A.29 B. 28 C. 18 D. 15
Câu 2. Tồn tại bao nhiêu giá trị nguyên của tham số m trong đoạn [– 30;10] để phương trình sau có nghiệm ?
5 6 8 9
x x x x m
.
A. 13 giá trị B. 26 giá trị C. 14 giá trị D. 10 giá trị
Câu 9. Ký hiệu S là tập hợp nghiệm của bất phương trình
2 2
8 1 15 3 0
x m x m m
. Tìm điều kiện của
m để khi biểu diễn trên trục số, độ dài của S lớn hơn 3.
A.
2
6
m
m
B.
3
7
m
m
C.
1
1
m
m
D.
1
11
m
m
Câu 10. Tìm điều kiện cần và đủ của các tham số a, b, c để hệ bất phương trình
2
2
2
0,
0,
0.
ax bx c
bx cx a
cx ax b
có nghiệm.
A. a + b + c > 0 B. a + b + c > 1 C. 2 < a + b + c < 3 D. 2a + b – c > 4
39
Câu 11. Tìm điều kiện của tham số m để bất phương trình
2 2
2 2 1 4 3 0
x m x m m
có tập nghiệm S
=
1 2
;x x
thỏa mãn điều kiện
2 2
1 2
2 2 1 4 3 2x m x m m
.
A. m = – 3 B. m = 2 C. m = 1 D. Không tồn tại m.
Câu 12. Tìm điều kiện tham số m sao cho
2 2
1 1 3 1 2 0,x x m x m m x
.
A.
1
1;
2
m
B.
1
1;
5
m
C.
6
3;
5
m
D.
1m
Câu 13. Tìm điều kiện của tham số m để
2 2
3
4 10 1 2 1 3 3 0,x x a x a x a x
.
A. a > 5 B. a > 2 C. a > 4 D. a > 1
Câu 14. Tìm điều kiện của tham số m để
3
2 2 2
2 7 2 2 0
x x x mx m m
với mọi số thực x.
A. m > 2 B. m < 1 C. m > 4 D. m > 4
Câu 15. Tìm điều kiện tham số m để bất phương trình
2
2 2
5 4 3 5 4
x x x x m
có nghiệm.
A.
9
4
m
B.
3
2
m
C.
1m
D.
1 10m
Câu 1. Tìm số nghiệm nguyên nhỏ hơn 80 của
bấtphươngtrình
2
3 4 9x x x x x
.
A.40 B.70 C.60 D.65
Câu 19. Tồn tại bao nhiêu giá trị nguyên của tham số m trong đoạn [– 30;40] để bất phương trình sau nghiệm
đúng với mọi giá trị thực x ?
2 2 2
2 4 3 4
x x x x mx
.
A. 38 giá trị B. 41 giá trị C. 61 giá trị D. 37 giá trị
Câu 23. Tam thức bậc hai
2
0,f x ax bx c x
và b > c > a. Tìm giá trị lớn nhất của biểu thức
9 2 7 3 3
b c c a
F
a c a b c
.
A. F max = 0,2 B. F max =
5
6
C. F max =
1
3
D. F max =
2
5
Câu 21. Tìm điều kiện tham số m để bất phương trình
2 2
2 6 6 5 2x x x x m
có nghiệm.
A.
16m
B.
79
16
m
C.
10m
D.
6m
Câu 1. Tìm số nghiệm nguyên của bất phương trình
2
4 6 10 27x x x x x
.
A.3 B. 2 C. 1 D. 4
Câu 22. Tìm giá trị lớn nhất của k để bất phương trình
2
x x k
có nghiệm.
A. k = 2
2
B. k = 2 C. k = 3 D. k =
5
Câu 23. Với mọi số thực x, luôn tồn tại a và b để
2
2
2 3
1
x x
a b
x
. Tính giá trị biểu thức a + b.
A.
5
3
B. 1 C. 2 D.
2
5
Câu 24. Tìm điều kiện của tham số m để hệ
3
2
2 2
1 1 3 2,
3 2 .
x x
x x x x m
có nghiệm duy nhất.
A. m = 1 hoặc m = 3 B. m = 0 hoặc m = 5
C. m = 6 hoặc m = 2 D. m = 4 hoặc m = 2
Câu 25. Tìm số nghiệm nguyên của bất phương trình
2
1
1 2( 1)
x x
x x
.
A.3 B.2 C.1 D.0
_________________________________
40
ÔN TẬP BPT + HỆ BPT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P2)
________________________________________
Câu 1. Tìm điều kiện tham số m để bất phương trình
2
2 2
3 2 2 3 2
x x x x m
có nghiệm.
A.
9m
B.
1m
C.
1m
D.
3 2m
Câu 2. Tìm số nghiệm nguyên nhỏ hơn 30 của bất phương trình
3
2 6
3 2 2
1 1 1 1x x x x x x x x x
.
A.19 B. 31 C. 26 D. 40
Câu 3. Tìm điều kiện tham số m để phương trình
2
3
0
3 4
x x m
x x
nghiệm đúng với mọi giá trị x thuộc [3;4].
A.
4 3m
B.
4m
C.
3 0m
D.
0 4m
Câu 4. Giả sử
2
4 3 3 2 0,a b x a b x
. Mệnh đề nào sau đây sai ?
A.
2
4 6
0
2 3 3
a b
a b
B.
1
0
16 11
b
b
C.
1
0
4 1
a
a
D.
1 1
2
4 1 16 11
a b
a b
Câu 5. Tìm điều kiện tham số m để hệ bất phương trình
2
2
2 1 0,
4 6 6 0.
x x m
x x m
có nghiệm duy nhất.
A. m = 1 B. m = 2 C. m = 0 D. m = 3
Câu 6. Tìm độ dài tập nghiệm của
b
b
ấ
ấ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
8 3 2 1 4 1 1815x x x x
.
A.2,75 B. 3,75 C. 1,25 D. 2
Câu 7. Khoảng giá trị [p;q] là điều kiện cần và đủ của tham số m để hệ bất phương trình sau có nghiệm.
2
3 2
3 4 0,
3 15 0.
x x
x x x m m
Tính S = q – p.
A. S = 17 B. S = 20 C. S = 10 D. S = 12
Câu 8. Tìm điều kiện tham số m để bất phương trình
2 2
6 6 5 2
x x x x m
có nghiệm.
A.
7m
B. m > 9 C.
7 13m
D.
27
4
m
Câu 9. Tìm điều kiện tham số m để bất phương trình
2
4 5 6 10 12 3
x x x x mx
có nghiệm thực.
A.
9
4
m
B.
1
3
m
C.
5
12
m
D.
1
18
m
Câu 10. Có bao nhiêu số nguyên x thỏa mãn bất phương trình
2 2 3 2
2 1 2 1 5 2 1x x x x x x x x x
.
A.1 B. 0 C. 2 D. 5
Câu 11. Tìm giá trị lớn nhất của tham số m để bất phương trình
2 11
x x k
nghiệm đúng với mọi x
thuộc đoạn [2;11].
A. m =
2
B. m = 3 C. m =
6
D. m = 4
Câu 12. Tìm điều kiện tham số m để hệ bất phương trình
2
2 2
8 7 0,
2 1 0.
x x
x m x m m
có nghiệm duy nhất.
A. m = 0 hoặc m = 8 B. m = 0 hoặc m = 7 C. m = 1 hoặc m = 2 D. m = 4 hoặc m = 6
Câu 13. Tìm giá trị nhỏ nhất của tham số m để bất phương trình
4 3 2
2 2 1 0x x mx x
có nghiệm thực.
A. m = – 1 B. m = – 2 C. m = – 4 D. m = – 7
Câu 14. Tìm điều kiện của tham số m để hệ sau đây có nghiệm
2
2
3 ,
2 3 2 6.
x x x x m
x x x
A. m = 1 B. m = – 4 C. m = – 6 D. m = 7
41
Câu 15. Tìm điều kiện của m để bất phương trình
4 3 2 2
8 2 16 8 0
x x m x mx m
có nghiệm duy nhất.
A. m = 2 B. m = 0 C. m = 3 D. m = 4
Câu 16. Hàm số
2
2
2 4 5
1
x x
y
x
có tập giá trị H = [a;b]. Tính giá trị biểu thức M = 2a + 3b.
A. M = 0 B. M = 1 C. M = 0,5 D. M = 2
Câu 17. Tìm điều kiện của m để hệ bất phương trình
4 2
2 2
5 4 0
2 1 2 0.
x x
x m x m m
có nghiệm duy nhất.
A. 2 < m < 3 hoặc – 4 < m < – 3 B. 3 < m < 5 hoặc 0 < m < 4
C. 1 < m < 4 hoặc m < – 2 D. 2 < m < 5 hoặc 7 < m < 8
Câu 18. Tìm độ dài miện nghiệm của bất phương trình
2
(4 14) 2 ( 1) 2 1 6 14 0
x x x x x
.
A.0,5 B.
2
7
C.
1
6
D.
1
3
Câu 19. Ký hiệu S là nghiệm của bất phương trình
2 2
2 3 3 2 0
x m x m m
. Tìm điều kiện của tham
số m sao cho
1;4
S
.
A. m = 4 B. m < 3 C. 3 < m < 5 D. Không tồn tại m.
Câu 20. Tìm điều kiện tham số m để bất phương trình
2
2 1 0
x m x
có tập nghiệm chứa miền (1;3).
A. m > 2 B. m < 1 C. m < 0 hoặc m > 2 D.
1m
Câu 21. Khoảng giá trị [p;q] là điều kiện cần và đủ của m để hệ bất phương trình
2
2
5 4 0,
3 16 0.
x x
x mx x
có
nghiệm. Tính Z = q – p.
A. Z = 1 B. Z = 2 C. Z = 5 D. Z = 8
Câu 22. Khoảng (a;b] là điều kiện cần và đủ của tham số m để biểu thức sau luôn luôn âm với mọi số thực x.
5
4 2
1 4 5 20 2 1
f x x x m x m x m
.
Tính M = 11a + 3b.
A. M = 30 B. M = 25 C. M = 44 D. M = 57
Câu 23. Ký hiệu S là nghiệm của bất phương trình
2 2
2 5 5 6 0
x m x m m
. Tìm độ dài L khi biểu
diễn S trên trục số.
A. L = 3 B. L = 2 C. L = 1 D. L = 4
Câu 24. Tìm điều kiện của m để tập hợp nghiệm của bất phương trình
2 2 3 2
2 2 0
x m x m m m
chứa khoảng (1;2)
A. m < 1 B. 0 < m < 4 C. m < 0 D. m > 1 hoặc m < 0
Câu 25. M là độ dài miền nghiệm của bất phương trình
2 2
2 3( 2 2)
x x x x x
. Khi đó M gần
nhất với giá trị nào sau đây
A.3,87 B. 2,56 C. 3,23 D. 4,48
Câu 26. Tìm điều kiện của các tham số a, b, c để
1
a b x c b a
với mọi số thực x.
A. a = b và
0 1c
B. a = b và c < 1 C. a = b và c > 0 D. a = b và 0 < c < 2
Câu 27. Tìm tất cả các giá trị tham số m để bất phương trình
2
9 9
x x x x m
nghiệm đúng với
mọi giá trị x thuộc đoạn [0;9].
A.
9
4
m
B.
9
0
4
m
C.
1
4
m
D.
0 1m
Câu 28. Ký hiệu S là nghiệm của bất phương trình
2 2
2 5 5 6 0
x m x m m
. Tìm điều kiện tham số m
để S chứa miền [p + 3; p + 10] với p là hằng số thực.
A. m = 3 B. m = 0 C. m = 1 D. Không tồn tại
Câu 29. Tìm điều kiện tham số m sao cho
3 2
2 2 1 0,x x x mx x
.
A. m = 2 B. m = 1 C. m = 0 D. m = – 1
_________________________________
42
BPT + HỆ BPT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P3)
________________________________________
Câu 1. Tam thức bậc hai
2
0,f x ax bx c x
và b > c > a. Tìm giá trị lớn nhất của biểu thức
4 2 3 5 2
b c c a
P
a b c c b
.
A. P max = 0,5 B. P max =
6
7
C. P max =
1
3
D. P max =
2
5
Câu 2. Tìm số thực p nhỏ nhất sao cho
2 2
1 0
a b x p a b
với mọi số thực x.
A. p = 2 B. p = 1 C. p = 0 D. p = 3
Câu 3. Tìm điều kiện tham số m để hệ sau đây có nghiệm
3
2
2
4 2 2
4
5,
2
8 16 16 32 16 0.
x
x
x
x x mx m m
A. m = 4 B. m = 3 C. m = – 2 D. m = – 1
Câu 4. Tìm điều kiện tham số m để hệ
2
3 2
1 1 ,
2 2 1 0.
x x x
x mx x m
có nghiệm duy nhất.
A. m = – 1 hoặc m = – 2 B. m = 0 hoặc m = – 3
C. m = 1 hoặc m = – 2 D. m = – 1 hoặc m = 2
Câu 5. Tìm số thực m nhỏ nhất sao cho
2 2 2
1 9 10
x y y z z x m
với mọi giá trị x, y, z làm biểu thức
xác định.
A.10 B. 11 C. 12 D. 12,5
Câu 6. Tìm điều kiện tham số m để hệ bất phương trình
2
2
2 2 0,
7 7 0.
x m x m
x m x m
có nghiệm.
A. m < 4 B. m < 0 C. 1 < m < 4 D. 8 < m < 10
Câu 7. Tìm độ dài tập nghiệm (tính cả biên) của bất phương trình
2 2
9 2 2 3 6 5 48 68x x x x x x x x x
.
A.1 B. 0,5 C.
2
3
D. Kết quả khác
Câu 8. Tìm tất cả các giá trị tham số k để bất phương trình
2 2
1
6
x k
k x
đúng với mọi x thỏa mãn |x| < 1.
A.
7 3 5
2
k
B.
7 3 5
3
k
C.
7 5
3
k
D.
7 5
4
k
Câu 9. Tìm điều kiện tham số m để bất phương trình
2 2
2 2 1 0
x mx x m m
có nghiệm.
A.
1 1
;
2 2
m
B.
1
1;
2
m
C.
5 3
;
2 2
m
D.
5 7
;
2 2
m
Câu 10. Ký hiệu S là tập hợp nghiệm của bất phương trình
2 2 2
4 4 0
x m x m m m
. Giả sử L là
độ dài đoạn thẳng miền nghiệm trên trục số. Giá trị nhỏ nhất L đạt được là
A. L min = 3 B. L min = 2 C. L min = 3 D. L min = 1
Câu 11. Ký hiệu k là giá trị lớn nhất của tham số m để bất phương trình
4 3 2
7 7 7 1 0x x mx x
có nghiệm
thực. Mệnh đề nào sau đây đúng ?
A. m =
57
28
B. m = 1 C. m =
11
23
D. m =
25
13
Câu 12. Số nghiệm nguyên âm của bất phương trình
2
2
8 12
8 12
5 5
x x
x x
x x
là
A. 3 B. Vô số C. 2 D. 0
43
Câu 13. Ký hiệu k là giá trị nhỏ nhất của tham số m để bất phương trình
4 3 2
5 1 0x x mx x
có nghiệm
thực. Mệnh đề nào sau đây đúng ?
A. m = 1 B. m =
9
20
C. m =
11
13
D. m =
25
14
Câu 14. Ký hiệu S là nghiệm của bất phương trình
2
6 2 8 0
x m x m
. Tìm điều kiện của m để khi biểu
diễn trên trục số, độ dài của S lớn hơn 5.
A.
6
2
m
m
B.
3
7
m
m
C.
4
3
m
m
D.
5
1
m
m
Câu 15. Tìm giá trị lớn nhất của tham số m để bất phương trình sau nghiệm đúng với mọi số thực x
2 3 4 5
x x x x m
.
A. m = – 4 B. m = – 2 C. m = – 1 D. m = 2
Câu 16. Bất phương trình
2
1 3
2 5 1
5 1
x
x x
x
có tập nghiệm
;
a
S
b

với a, b nguyên dương và
nguyên tố cùng nhau. Tính a + b.
A. 10 B. 11 C. 15 D. 18
Câu 17. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 sao cho
2 2
4 5 3 2 3 2 0,x x m x m x m x
.
A. 10 giá trị B. 6 giá trị C. 8 giá trị D. 7 giá trị
Câu 18. Tìm điều kiện của tham số m để hệ sau đây có nghiệm
2
2
3
2
2
1 2 3 2 3 ,
1 1
0.
1
x x x x x m
x x
x x
A. m = 2 B. m = 3 C. m = – 4 D. m = 5
Câu 19. Tìm giá trị nguyên lớn nhất của tham số m để bất phương trình
3 31 4 6
x x m
nghiệm đúng
với mọi giá trị x thuộc đoạn [6;31].
A. m = 11 B. m = 15 C. m = 25 D. m = 10
Câu 20. Hàm số bậc hai f (x) có bảng biến thiên như hình vẽ. Có bao nhiêu số
nguyên m nhỏ hơn 10 để bất phương trình sau có nghiệm:
( cos2 2)
f x m
.
A. 7 B. 8
C. 6 D. 10
Câu 21. Tìm điều kiện của tham số m để bất phương trình
2 2
2 2 1 4 3 0
x m x m m
có tập nghiệm S
=
1 2
;x x
thỏa mãn điều kiện
2 2
1 2
4 2 2 1 4 3 1
x m x m m m
.
A. m = – 3 B. m = 2 C. m = 1 D. m = 0
Câu 22. Tìm điều kiện của tham số m để bất phương trình
4 3 2 2
10 2 25 10 0
x x m x mx m
có
nghiệm duy nhất.
A. m =
9
4
B. m = 0 C. m =
25
4
D. m = 1
Câu 23. Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình
2 4 2
( 1) ( 1) 6( 1) 0
m x m x x
có nghiệm
S
. Tổng tất cả các phần tử thuộc S bằng
A. – 1,5 B. 1 C. – 0,5 D. 0,5
Câu 24. Độ dài tập nghiệm của bất phương trình
2 3
4 25 14 3 31 30
x x x x
gần nhất với số nào
A.3,28 B. 4,26 C. 3,65 D. 2,85
_________________________________
44
BPT + HỆ BPT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P4)
_____________________________
Câu 1. Tìm điều kiện tham số m để hệ bất phương trình
2
2 2
2 4 3 0,
2 1 0.
x mx m
x m x m m
vô nghiệm.
A. 2 < m < 3 hoặc – 4 < m < – 3 B. 3 < m < 5 hoặc 0 < m < 4
C.
2 2 2 2
m
D. 2 < m < 5 hoặc 7 < m < 8
Câu 2. Tìm độ dài tập nghiệm (tính cả biên) của bất phương trình
2 2 3 2
2 1 3 2 1 8 5 8 5 0x x x x x x x x x x
.
A.3 B. 4 C. 3,5 D. Kết quả khác
Câu 3. Tìm điều kiện tham số m để bất phương trình
2 2 2
2 3 1 2 5 1
x x x x mx
có nghiệm thực.
A.
7 4 2
m
B.
5 4 2
m
C.
5 3 2
m
D.
3 2
m
Câu 4. Tính tổng tất cả các giá trị tham số m để hệ bất phương trình
2
2
4 4 0,
2 3 3 0.
x x m
x x m
có tập hợp nghiệm
là một đoạn có độ dài bằng 1.
A. – 6 B. – 6,5 C. – 4 D. – 7
Câu 5. Tìm điều kiện tham số m để bất phương trình
2 2
3 3 5
x x x x m
có nghiệm.
A.
1
0
2
m
B.
35
4
m
C.
35
5
4
m
D.
19
1
4
m
Câu 6.
T
T
ậ
ậ
p
p
n
n
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
b
b
ấ
ấ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
2
1
2 5 9 1
x x
x x
chứa bao nhiêu số nguyên nhỏ hơn 40.
A.20 B. 37 C. 40 D. 16
Câu 7. Tìm điều kiện tham số m để phương trình
2
6
0
1 5
x x m
x x
có nghiệm.
A.
4 3m
B.
9m
C.
3 0m
D.
3m
Câu 8. Tồn tại các hằng số a và b sao cho
3 3 4 22 , 22;3
a x x b x
. Tính Q = a + b.
A. Q = 45 B. Q = 38 C. Q = 50 D. Q = 40
Câu 9. Tìm điều kiện tham số m để hệ bất phương trình
2
2
3 2 0,
1 0.
x x
m x mx m
vô nghiệm.
A. m > 3 B. m > 4/7 C. 1 < m < 3 D. 2 < m < 2,5
Câu 10. Tìm điều kiện tham số m để bất phương trình
4 2
x x m
nghiệm đúng với mọi giá trị
1x
.
A. m > 4 B.
5
m
C.
6
m
D.
2
m
Câu 11. Tìm điều kiện tham số m để bất phương trình
2
2 3 2 0
mx m x x
có nghiệm.
A. Mọi giá trị m B. Không tồn tại m C. m > 0 D.
0m
Câu 12. Tồn tại bao nhiêu giá trị nguyên m trong đoạn [– 30;60] để bất phương trình sau có nghiệm ?
2
4 3 1 2 1
x x x m
.
A. 33 giá trị B. 26 giá trị C. 61 giá trị D. 55 giá trị
Câu 13. Ký hiệu k là giá trị nhỏ nhất của tham số m để bất phương trình
4 3 2
2 11 2 0x x mx x
có
nghiệm thực. Mệnh đề nào sau đây đúng ?
A. k =
2
11
B. k =
3
13
C. k =
4
15
D. k =
7
17
Câu 14. Tìm tất cả các giá trị m để hệ bất phương trình
2
1 4 5 5 28,
3 2 2.
x x x x
m x
vô nghiệm.
45
A.
16 5
27 6
m
B.
11 5
27 6
m
C.
16
1
27
m
D.
16 5
27 6
m
Câu 15. Tìm điều kiện tham số m để phương trình
2
2 2
6 9 4 9
x x mx x x
có nghiệm thực.
A.
9
4
m
B.
9
4
m
C.
25
4
m
D.
9
16
m
Câu 16. Tìm độ dài tập nghiệm của bất phương trình
4 3 2
3 5 8 3 7 3 0x x x x x x
.
A.2 B. 1,5 C. 1 D. Kết quả khác
Câu 17. Tìm giá trị lớn nhất của tham số m để hệ bất phương trình
7 1 3 18 2 7,
2 2 3 7.
x x x
x m x m
có nghiệm.
A. m = 6 B. m = 3 C. m = 10 D. m = 7
Câu 18. Tìm giá trị lớn nhất m để bất phương trình
1 3 5 7
x x x x m
đúng với mọi số thực x.
A. m = – 16 B. m = – 12 C. m = – 14 D. m = – 17
Câu 19. Ký hiệu S là tập hợp nghiệm của bất phương trình
2 2 2
5 4 0
x m x m
. Tìm độ dài nhỏ nhất
khi biểu diễn S thành một đoạn thẳng trên trục số.
A. 4 B. 3 C. 2 D. 5
Câu 20. Tìm điều kiện của m để tập nghiệm của bất phương trình
2
3 3 0
x m x m
chứa khoảng (– 2;0)
A.
2m
B. m
0 C. m
1 D.
2 0m
Câu 21. Tìm điều kiện tham số m để hệ bất phương trình
2
2 2
8 2 6 3 ,
1 2 2 1.
x x x
m m x m m
có nghiệm.
A. m > 0 B. m < 3 C. Mọi giá trị m. D. Không tồn tại m.
Câu 22. Tam thức bậc hai
2
0,f x ax bx c x
và b > c > a. Tìm giá trị lớn nhất của biểu thức
16 2 5 3 5
b c c a
H
a b c a b c
.
A. H max =
7
12
B. H max =
5
6
C. H max =
6
7
D. H max =
4
5
Câu 23.
T
T
ậ
ậ
p
p
n
n
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
b
b
ấ
ấ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3
3
1 1
3 10 4 0
x x
x x
chứa tất cả bao nhiêu số nguyên
nhỏ hơn 40
A.39 B. 40 C. 30 D. 28
Câu 24. Biết rằng bất phương trình
2
2 2 1 3 0
m x m x m
có tập nghiệm S = [a;b] thỏa mãn điều
kiện
9 10
ab a b
. Giá trị m thu được nằm trong khoảng nào ?
A. (0;3) B. (4;6) C. (6;9) D. (0;5)
Câu 25. Tìm điều kiện tham số m để hệ bất phương trình
2
2
42
1 ,
1
4 1 2 2 1 0.
x x
x x
x m x m m
có nghiệm.
A. m > – 1 B. Mọi giá trị m B. m < 1 C. – 1 < m < 1
Câu 26. Tìm điều kiện tham số m để bất phương trình sau nghiệm đúng với mọi số thực x
2
48 6 1 1 3 4
x x x m
.
A.
2401m
B. m < 2401 C.
168m
D.
48m
Câu 27. Tìm điều kiện tham số m để bất phương trình
2
5 4
0
5 2 4 3
x x m
x x
nghiệm đúng với mọi
4
3
x
.
A.
9
0
4
m
B.
5
2
3
m
C.
8
9
m
D.
9
0
4
m
Câu 28. Tập nghiệm bất phương trình
2
2 2
4 5 2 9 12 10 2
x x x x x
chứa bao nhiêu số nguyên
A.2 B. 3 C. 1 D. 4
46
BPT + HỆ BPT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P5)
_____________________________
Câu 1. Tìm điều kiện tham số m sao cho
3 2
2 6 3 1 3 0,x x x m x x
.
A. m = 0 B. m = 1 C. m = 2 D. m = – 1
Câu 2. Tập nghiệm của bất phương trình
2 2
3 2 3x x x x
chứa bao nhiêu số nguyên
100;100
A.196 B. 120 C. 150 D. 90
Câu 3. Tìm điều kiện tham số m để hệ
2
4 3 2 2
2 2 3 2,
2 2 2 3 2.
x x x
x x mx m x m
có nghiệm duy nhất.
A. m = 1 hoặc m = – 3 B. m = 0 hoặc m = – 5
C. m = – 6 hoặc m = – 2 D. m = – 4 hoặc m = 2
Câu 4. Tìm điều kiện m để bất phương trình
4 3 2 2
14 2 49 14 0
x x m x mx m
có nghiệm duy nhất.
A. m = 2 B. m =
25
4
C. m = 3 D. m =
49
4
Câu 5. Tìm điều kiện tham số m để phương trình
2
2 2 1
0
3
x x m
x x
có nghiệm.
A.
1 2
3 3
m
B. m > 1 C.
1m
D.
3m
Câu 6. Tìm điều kiện của tham số m để hệ sau đây có nghiệm
2
2
3
4 3 1 1,
5 2 1 2 0.
x x x
x x x x x m
A. m =
7
2
B. m =
2
5
C. m = – 1 D. m =
7
8
Câu 7. Tìm điều kiện của tham số m để phương trình
2
5 5 4 1
x x x x m
nghiệm đúng với mọi x
thuộc đoạn [1;4].
A.
19 23
4 4
m
B.
39
16
4
m
C.
19
4
m
D.
0 1m
Câu 8. Tập nghiệm của bất phương trình
2
2
4 17
2
8
x x
x x
x
chứa bao nhiêu số nguyên
100;100
A.190 B. 198 C. 100 D. 96
Câu 9. Định m để hệ bất phương trình
2
2 2
5 6 0,
3 2 2 7 12 0.
x x
x mx m m
vô nghiệm.
A.
2,5
3
m
m
B.
3,5
5
m
m
C. 2 < m < 5 D.
6,5
6
m
m
Câu 10. Tìm tất cả các giá trị tham số m để bất phương trình
2
3 5 9
x x m
nghiệm đúng với mọi giá trị x
thuộc tập xác định.
A.
10
m
B. m > 4 C.
5
m
D.
5
m
Câu 11. Tìm giá trị lớn nhất của tham số m để bất phương trình
2 8
x x k
nghiệm đúng với mọi x
thuộc đoạn [2;8].
A. k =
2
B. k =
5
C. k =
6
D. k = 4
Câu 12. Tồn tại bao nhiêu giá trị nguyên nhỏ hơn 100 của tham số m để bất phương trình sau nghiệm đúng với
mọi giá trị x thuộc đoạn [5;34].
2 34 5 5
x x m
A. 71 giá trị B. 52 giá trị C. 49 giá trị D. 63 giá trị
Câu 13. Tìm điều kiện tham số m để bất phương trình
2
2 2
2 3 4 3 3 4
x x x x m
có nghiệm.
47
A.
9
4
m
B.
9
8
m
C.
1m
D.
25
4
m
Câu 14. Tìm giá trị nhỏ nhất của tham số m để bất phương trình
2
1 1
4 3 1
x x m
x x
có nghiệm.
A. m = 10 B. m = 11 C. m = 13 D. m = 18
Câu 15. Tìm giá trị lớn nhất của tham số m để bất phương trình sau nghiệm đúng với mọi số thực x
3 5 8
x x x x m
.
A. m = – 4 B. m =
225
4
C. m =
25
4
D. m =
123
4
Câu 16. Bất phương trình
17 26 2 1 14 1 3 5
x x x x
có tập nghiệm
;M a b
. Tính
6b a
.
A.5 B. – 2 C. – 6 D. 1
Câu 17. Tìm điều kiện tham số m để hệ bất phương trình
2
2
1 0,
2 1 2 0.
x
x m x
có nghiệm.
A. – 3 < m < 5 B. 2 < m < 3 C. 5 < m < 8 D. 10 < m < 12
Câu 18. Tìm giá trị lớn nhất của m sao cho phương trình
1
3 1 4 3
3
x
x x x m
x
có nghiệm thực.
A. m = – 4 B. m = 2 C. m = 4 D. m = 3
Câu 19. Tìm điều kiện tham số m để bất phương trình
2
2
3 4 3
0
1 5
x x m
x x x
có nghiệm.
A.
5
2
3
m
B.
5
3
m
C. m > 4 D. 0 < m < 2
Câu 20. Tìm độ dài miền nghiệm của bất phương trình
2
2 2
3 1 3 7 13 10 2 0x x x x x
.
A.0 B. 2 C. 4 D. 5,5
Câu 21. Ký hiệu k là giá trị nhỏ nhất của tham số m để bất phương trình
4 3 2
8 28 48 27x x x x m
có tập
nghiệm S = R. Giá trị k nằm trong khoảng nào ?
A. (0;4) B. (4;9) C. (– 7;– 4) D. (– 3;– 1)
Câu 22. Tồn tại bao nhiêu số nguyên m trong đoạn [– 10;10] để bất phương trình sau có nghiệm ?
1 2 3
x x x x m
.
A. 13 giá trị B. 12 giá trị C. 14 giá trị D. 15 giá trị
Câu 23. Tìm giá trị nhỏ nhất của tham số m để bất phương trình
2
1 1
3 2 5
x x m
x x
có nghiệm.
A. m = 10 B. m = 12 C. m = 13 D. m = 18
Câu 24. Tìm tổng các giá trị tham số m xảy ra khi bất phương trình
2
2 1 3
x m x m
có tập nghiệm S =
1 2
;x x
thỏa mãn đẳng thức
2
1 2
1
2 1 3
2
m
x m x m
.
A. 4 B. 2,5 C. 1,25 D. 3,25
Câu 25. Tìm điều kiện tham số m để hệ bất phương trình
2
2
1 0,
2 2 0.
x x m m
x mx m
có nghiệm duy nhất.
A. m = 5 B. m = 6 C. m = 2 D. m = 1
Câu 26. Biết rằng
3 6 3 6 , 3;6
a x x x x b x
. Giá trị biểu thức b – a gần nhất với
giá trị nào ?
A. 3,25 B. 4,25 C. 5,67 D. 8,61
Câu 27. Tìm điều kiện tham số m để bất phương trình sau nghiệm đúng với mọi số thực x
1 2 3 4
x x x x m
.
A. m
- 1 B. m
- 2 C. m
3 D. m
- 5
_________________________________
48
BPT + HỆ BPT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P6)
_____________________________
Câu 1. Khoảng giá trị [p;q] là điều kiện cần và đủ của m để hệ
2
2
10 9 0,
12 0.
x x
x mx x
có nghiệm. Tính q – p.
A. 4 B.
4 6
13
3
C.
4 2
17
3
D.
6
11
3
Câu 2. Ký hiệu k là giá trị nhỏ nhất của tham số m để bất phương trình
4 3 2
4 11 14 10x x x x m
có
nghiệm thực. Giá trị k nằm trong khoảng nào ?
A. (0;3) B. (2;9) C. (– 7;– 4) D. (– 3;– 1)
Câu 3. Tập nghiệm của bất phương trình
2
2 2 1 3 2 13 25
x x x x x
chứa bao nhiêu số nguyên
A.4 B. 2 C. 3 D. 1
Câu 4. Tồn tại bao nhiêu số nguyên m trong khoảng (– 10;10) để phương trình
2
2 5 2 1 0
x m x m
có
tập nghiệm
1 2
;x x
thỏa mãn điều kiện
2
1 2
2 5 2 1
x m x m m
.
A. 14 giá trị B. 16 giá trị C. 15 giá trị D. 18 giá trị
Câu 5. Tìm điều kiện tham số m để phương trình
2
1 3
1
2 2
x m x m
có tập nghiệm
1 2
;x x
thỏa mãn
điều kiện
1 2
2 3 5
x x
.
A.
7
1
2
m
B.
9
2
2
m
C.
15
4
2
m
D.
2 6m
Câu 6. Tìm điều kiện tham số m để bất phương trình
2 2
1 1 0
x m x m m
có tập nghiệm
2 1
;x x
thỏa mãn đồng thời các điều kiện
1 2
x x
và
2 2
1 2 1
1 2 7
x x x m x m m
.
A. 0 < m < 3 B. m > 1 C. m > 2 D. m < 4
Câu 7. Tập nghiệm của bất phương trình
3 2 4 3 2
3 4 1 4 3 4 3 4
11 5 7 11 5 7
x x x x x x x
x x
chứa bao nhiêu số nguyên
A.3 B. 2 C. 7 D. 0
Câu 8. Bất phương trình
2
2 3 0x mx
có tập nghiệm
1 2
;x x
. Tồn tại bao nhiêu giá trị nguyên m thỏa mãn
bất đẳng thức
2 2
1 1 2 2
2 3 2 3 5x mx m x mx m m
?
A. 3 giá trị B. 5 giá trị C. 4 giá trị D. 2 giá trị
Câu 9. Tìm điều kiện của tham số m để hệ sau đây có nghiệm
2
4 2 2
2 3 4 3 5 9 6 13,
2 1 2 2 .
x x x x
x m x m x m
A. m = 3 B. m = 0 C. m = 2 hoặc m = – 1 D. m = 4
Câu 10. Tính tổng các giá trị m để hệ bất phương trình
2
2
3 2 0,
6 6 0.
x x
x x m m
có nghiệm duy nhất.
A. 8 B. 10 C. 7 D. 8
Câu 11. Tìm giá trị nhỏ nhất của tham số m để bất phương trình
2
1 1
4 3 1
x x m
x x
có nghiệm.
A. m = 10 B. m =
7
16
C. m =
13
15
D. m = 1
Câu 12. Tìm tất cả các giá trị nguyên của m để bất phương trình
2
1 4
x m m m
có nghiệm nguyên
nhỏ nhất bằng 4.
A. m = 1 hoặc m = 2 B. m = 3 hoặc m = 2 C. m = 4 hoặc m = 1 D. m = 5 hoặc m = 0
Câu 13. Tìm độ dài miền nghiệm của
b
b
ấ
ấ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
4
2 2
4 3 3 4
4 3 4 3
x x x
x
x x x x
.
A.1 B. 3 C. 2 D. Kết quả khác
49
Câu 14. Ký hiệu S là nghiệm của bất phương trình
2
8 3 15 0
x m x m
. Tìm điều kiện của m để khi
biểu diễn trên trục số, độ dài của S lớn hơn 4.
A.
2
6
m
m
B.
3
7
m
m
C.
1
1
m
m
D.
1
11
m
m
Câu 15. Tồn tại bao nhiêu số nguyên m thuộc đoạn [0;30] để bất phương trình
2
2 3 3 1
m m x m
có tập
nghiệm S chứa miền (1;7).
A. 15 giá trị B. 31 giá trị C. 23 giá trị D. 10 giá trị
Câu 16. Tìm điều kiện tham số m để hệ bất phương trình
2
2 2
2 1 2 0,
2 1 2 0.
x m x m
x m x m m
có nghiệm.
A. m < 0 B. m
3 C. m
1
2
D. Mọi giá trị m.
Câu 17. Tính tổng tất cả các giá trị nguyên của m để bất phương trình
2
3 2 3 2 1
x m m m
có
nghiệm nguyên nhỏ nhất bằng 1.
A. 30 B. 21 C. 40 D. 32
Câu 18. Tìm độ dài miền nghiệm của bất phương trình
4
1 1 32 50
x x x x
.
A.2 B. 1 C. 0,5 D. Kết quả khác
Câu 19. Tìm tất cả các giá trị tham số m để biểu thức sau nhận giá trị không âm với mọi giá trị thực x.
2
3
2 2
3 8 3 10 2 23 24
S x x m x m x m
.
A.
2;5
m
B. 2 < m < 7 C.
1
2;
2
m
D.
1;6
m
Câu 20. Với a, b, c là các tham số thực dương sao cho
3 3
1 2,a b x c a b x
. Tìm giá trị lớn
nhất của biểu thức
3 3
2
3 2 3
3
2 2
2
a b
Q c c
a a b b
.
A. Q max = 16 B. Q max = 38 C. Q max = 20 D. Q max = 42
Câu 21. Tìm số gần nhất với độ dài miền nghiệm bất phương trình
2
2
2
1
. 3 2 2 3
2 12 13
x x
x x x
x x
.
A.10 B. 8 C. 9 D. 11
Câu 22. Tìm điều kiện tham số m để hệ bất phương trình
2
2 2
2 2 4 5 0,
2 5 5 6 0.
x m x m
x m x m m
vô nghiệm.
A.
2
m
B. m
3 C. m
1
2
D. Mọi giá trị m.
Câu 23. Tìm điều kiện của m để bất phương trình
2
6 5 1 0
x x m x x
có nghiệm thực.
A.
5m
B. 2 < m < 5 C. m > 5 D. 6 < m < 7
Câu 24. Tập nghiệm của bất phương trình
2
2(8 7) (4 3)( 1) 7
x x x
có độ dài bằng
A.1 B.
2
2
C.
3 2
2
D.
2 3
3
Câu 25. Bất phương trình
2
2 5 0
x m x
có tập nghiệm
2 1
,x x
thỏa mãn đồng thời các điều kiện
1 2
x x
. Tìm giá trị nhỏ nhất của biểu thức
2 2
1 2 1 2
2 2 4 3 3K m x m x m m x x
.
A. Kmin =
63
8
B. Kmin =
2
25
C. Kmin =
11
4
D. Kmin =
13
5
Câu 26. Có bao nhiêu số nguyên
100
x
thỏa mãn bất phương trình
3 2
3 2 1 2 2x x x x x x
.
A.90 B. 98 C. 68 D. 54
____________HẾT____________
| 1/49
| | Tải xuống

Có thể bạn quan tâm:

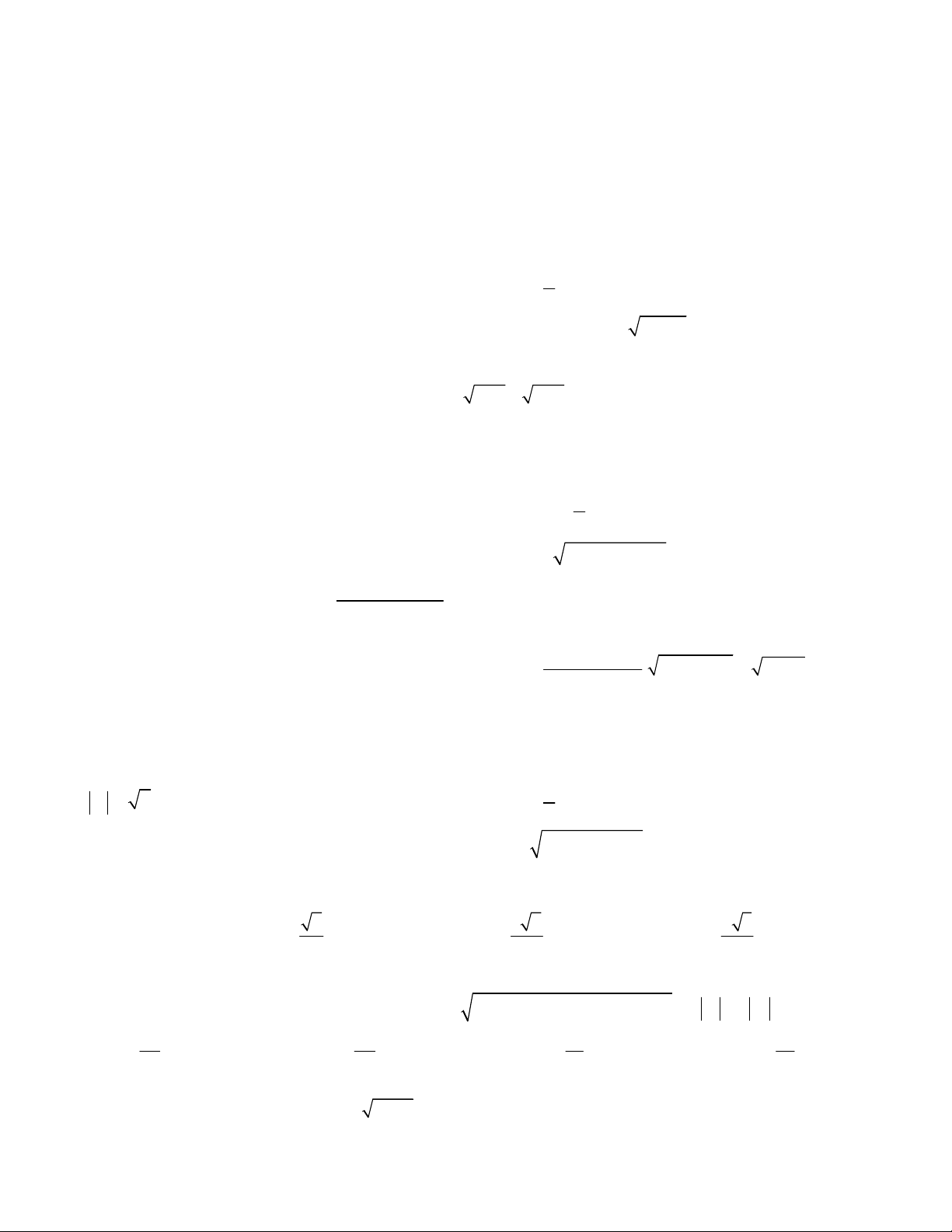
Preview text:


TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
--------------------------------------------------------------------------------------------
CHUYÊN ĐỀ BPT, HỆ BPT BẬC NHẤT, BẬC HAI MỘT ẨN
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM
BPT, HỆ BPT BẬC NHẤT, BẬC HAI MỘT ẨN
CƠ BẢN BPT, HỆ BPT BẬC NHẤT MỘT ẨN (P1 – P6)
CƠ BẢN DẤU TAM THỨC BẬC HAI, BPT BẬC HAI MỘT ẨN (P1 – P6)
CƠ BẢN TỔNG HỢP BPT, HỆ BPT BẬC NHẤT, BẬC HAI MỘT ẨN (P1 – P6)
VẬN DỤNG CAO BPT, HỆ BPT BẬC NHẤT, BẬC HAI MỘT ẨN (P1 – P6)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
GACMA1431988@GMAIL.COM (GMAIL); TEL 0333275320
THÀNH PHỐ THÁI BÌNH – THÁNG 10/2022 1
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P1)
________________________________________
Câu 1. Tìm điều kiện tham số m để bất phương trình 2
3x m mx  4m  3 nghiệm đúng với mọi số thực x. A. m = 4 B. m = 3 C. m = 2 D. m = 1 3  (x  6)  3  
Câu 3. Tìm điều kiện tham số m để hệ bất phương trình 5x m có nghiệm.  7   2 A. m > – 11 B. m < 11 C. m < – 11 D. m  11 1 1
Câu 4. Tập nghiệm của bất phương trình 
chứa bao nhiêu số nguyên x 1 5 A.3 B. 1 C. 2 D. 4
Câu 5. Tìm giá trị tham số m để  2
m mx m   2 2 5
m  6 x  2  3m với mọi giá trị x. A. m = 4 B. m = 3 C. m = 2 D. m = 1 3   2x  0,
Câu 6. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm.
mx m  2  0.  A. Mọi giá trị m B. Không tồn tại C. m  0 D. m < 1 1
Câu 7. Cho các bất phương trình 2
2x m 1; (m  2) x m 1; x  6x  5  0;  4 . x  2
Số lượng bất phương trình bậc nhất một ẩn là A.2 B. 3 C. 1 D. 4
Câu 8. Tập nghiệm của bất phương trình 2
(m 1) x  0 chứa bao nhiêu số nguyên dương nhỏ hơn 10 A.8 B. 9 C. 7 D. 6
Câu 9. Tìm điều kiện tham số m để bất phương trình  2 x   2 1
m m  5  m 1  0 có tập nghiệm S = R. A. m < 2 B. m = – 4 C. m > 1 D. m > 1,5  
m  3 x m  2  0,
Câu 10. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm. 3  x  4  0.  A. Mọi giá trị m B. Không tồn tại C. m > – 3 D. m  – 3
Câu 11. Tập nghiệm của bất phương trình 2 2 2
(m m 1)(x 1)  m  2  0 chứa bao nhiêu số nguyên dương nhỏ hơn 20 A.18 B. 19 C. 17 D. 16 1 26
Câu 12. Tập nghiệm của bất phương trình 
chứa bao nhiêu số nguyên dương 2 x  6x 10 5 A.2 B. 1 C. 3 D. 0
Câu 13. Tìm điều kiện tham số m để bất phương trình  2 m m   3
20 x m  4m  47  0 có tập nghiệm R. A. m = 4 B. m = – 4 C. m = 2 D. m = 1,5  2x 1   2
Câu 14. Có bao nhiêu số nguyên dương m để hệ bất phương trình  3 có nghiệm ? 3
x m  5  A. 5 B. 4 C. 2 D. 1
Câu 15. Tập nghiệm của bất phương trình 2
(m 1)x  1có thể chứa tối đa bao nhiêu số nguyên dương A. 2 B. 1 C. 3 D. 0
Câu 16. Tìm điều kiện tham số m để bất phương trình  3 m m   2 3
4 x m  2m  2  0 vô nghiệm. A. m = 4 B. m = 1 C. m = 2 D. m = 1,5 3x m   2
Câu 17. Tìm m để hệ bất phương trình  4
có tập nghiệm S = (a;b) thỏa mãn b – a = 2. 2(x 1)  5  A. m = 5,5 B. m = 5 C. m = 8,5 D. m = 2,5 2
Câu 18. Tìm điều kiện tham số m để bất phương trình  2 m m   2 2 5 3 x  4m  5
x 1vô nghiệm. A. m = 2 B. m = 2 C. m = 0 D. m = 1,5 1
Câu 19. Tập nghiệm của bất phương trình
 5 chứa bao nhiêu số nguyên 2 x  2x  3 A.2 B. 0 C. 1 D. 3
Câu 20. Giả sử a b   2 3
2 x a  3b  2  0, x
   . Mệnh đề nào sau đây có thể sai ? 2 3 A. a + b > 2 B. a + b < C. 2a + b > 3 D.
a b  1 3 4 1
Câu 21. Tập nghiệm của bất phương trình
 0 chứa bao nhiêu số nguyên nhỏ hơn 20 x 1 A.19 B. 18 C. 20 D. 10 3x m   2
Câu 22. Tìm điều kiện của m để hệ bất phương trình  2 
có độ dài tập nghiệm lớn hơn 3. 2(x 1)  5  A. m > 1 B. m < 4 C. m > 0,5 D. 0 < m < 3
Câu 23. Cho các bất phương trình 2 x  6x  5 1 2
2x  (m 1)x  7; (3m  2) x  5m 1;  0;  . x  5 3x 1 x  5
Số lượng bất phương trình bậc nhất một ẩn là A.2 B. 3 C. 1 D. 4
Câu 24. Tìm điều kiện tham số m sao cho  2 m  
1 x m 10  3, x    . A. m = 1 B. m = 4 C. m = 2 D. m = – 1
Câu 25. Tìm điều kiện tham số m để mx  2  0, x   1. A. m > 3 B. m > 2 C. m > 4 D. 5 < m < 6
Câu 26. Tập nghiệm của bất phương trình
2x 1  5 chứa bao nhiêu số nguyên dương A.12 B. 13 C. 11 D. 10  x  3   0,
Câu 27. Tìm điều kiện tham số m để hệ bất phương trình  x  4 có nghiệm. 3
x m  1.  A. m < 7 B. m < 8 C. 2 < m < 6 D. 3 < m < 9 1 5
Câu 28. Hai tập nghiệm của hai bất phương trình  3; 
26 có bao nhiêu phần tử nguyên 2 2 x  2 x  4x  5 chung nhau A.3 B. 2 C. 1 D. 4
Câu 29. Tìm điều kiện tham số m để hai bất phương sau tương đương: x  3  0; mx m  4  0 . A. m = 0,5 B. m = 4 C. m = 2 D. m = – 2
Câu 30. Tìm tất cả các giá trị m để hai bất phương trình mx  2  m  0;m  2 x 1 m  0tương đương. A. m = 1 B. m = 2 C. m = 4 D. m = – 1 x
Câu 31. Hàm số f x  x  2m 1  4  2m
xác định với mọi x 0;2 khi m  ; a b. Tính a + b. 2 A. a + b = 3 B. a + b = 5 C. a + b = 2,5 D. a + b = 2 x  9
Câu 32. Tìm điều kiện tham số m để hàm số y
 4x xác định trên [7;9]. x  2m 1 A. m > 4 hoặc m < 3 B. m > 4 C. m > 9 hoặc m < 7 D. 2 < m < 5
Câu 33. Cho các bất phương trình 1 2
2x  (m  3)x m 1; (m  2) x m  ;
n 3x  8x a  0;  2 . x  2a
Số lượng bất phương trình bậc nhất một ẩn là A.2 B. 3 C. 1 D. 4 ______________________ 3
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P2)
________________________________________
Câu 1. Xác định giá trị tham số m để bất phương trình mx    3 16
2 x m  có tập nghiệm là  56  ;  . A. m = 4 B. m = 2 C. m = 6 D. m = – 2 1
Câu 2. Cho các bất phương trình 2
x  5x  4  0;
 1; (m  2)x  3m x 1; (m 1) x m . 2 x  2x  3
Số lượng bất phương trình bậc nhất một ẩn là A.2 B. 1 C. 3 D. 4   3m  2 
x m  4  0,
Câu 3. Tìm điều kiện tham số m để hệ bất phương trình 
có nghiệm nhỏ nhất bằng – 4. m  2 
x  3m 1  0.  A. m = – 8 B. m = – 9 C. 11m = 4 D. Không tồn tại m 1 1
Câu 4. Tập nghiệm của bất phương trình 
chứa bao nhiêu số nguyên dương x 1 2 A.2 B. 1 C. 3 D. 0
Câu 5. Tìm điều kiện tham số m để bất phương trình 2
m x 1  m  3m  2 x vô nghiệm. A. m = 1 B. m = 2 C. m = 3 hoặc m = 1 D. m = 1 hoặc m = 2   m  
1 x m  3  0, 
Câu 6. Tìm điều kiện tham số m để hệ bất phương trình  x  3 có nghiệm.  1.   2x 1 A. Mọi giá trị m B. m  1  C. Không tồn tại m D. m + 1 < 0
Câu 7. Tìm điều kiện tham số m để bất phương trình 2
(m 1)x m luôn nghiệm đúng. A.m > 0 B. m < 0 C. m > 1 D. m > 2
Câu 8. Tìm điều kiện tham số m để bất phương trình 2 m x   1  mx vô nghiệm. A. m = 0 hoặc m = 1 B. m =  1 C. 0 < m < 1 D. |m| > 1
 2x m 1   3 
Câu 9. Có bao nhiêu số nguyên âm m để hệ bất phương trình  3  có nghiệm.  4(  2x 1)  9  A. 10 B. 12 C. 11 D. 16
Câu 10. Cho các bất phương trình 1 x m
x  5 x  4  0;
 1; (m  2)x  3m x 1; (m 1) x  ; m   1. mx  3 2 2
Số lượng bất phương trình bậc nhất một ẩn là A.2 B. 1 C. 3 D. 4
Câu 11. Tìm điều kiện tham số m sao cho bất phương trình 2 m mx  
1  m 1 mx vô nghiệm. A. m = 7 B. m = 2 C. m = 4 D. m = 0
Câu 12. Tìm điều kiện của tham số m để hai bất phương trình sau tương đương nhau. m  
1 x  3  m  0;m  
1 x  2  m  0 A. m = 0,5 B. m = 5 C. m = – 6 D. m = – 1
Câu 13. Tìm điều kiện tham số m sao cho  2 m  
1 x  3m  5  2m  3. A. m = 1 B. m = 4 C. m = 2 D. m = – 1
Câu 14. Tìm điều kiện tham số m để hai bất phương trình mx m 1  0;m  2 x m  0 tương đương nhau. 3   17 1 17 3   17 3   2 13 A. m = B. m = C. m = D. m = 2 4 2 2
Câu 15. Tìm điều kiện tham số m để bất phương trình  x  2 6
m  4 x  5m  0có tập nghiệm là [1;6].    1   1 2  A. m  2;  B. m = 1 C. m 1;  4 D. m  5  ; ;   2   2 3  4
Câu 16. Tìm điều kiện của m để bất phương trình  2 m m  
1 x  3m 1có tập nghiệm S chứa miền (4;5). m  1 m  4 m  3 m  2 A.     3 B. 3 C. 1 D. 1 m  m  m  m   4  4  4  2
Câu 17. Tìm điều kiện tham số m để bất phương trình  2
m m  3 x m  2 có tập nghiệm S chứa miền (1;5). A. m > 3 B. 0 < m < 1 C. Mọi giá trị m D. 2 < m < 4
Câu 18. Tìm điều kiện tham số m để bất phương trình m  3 x m 1  0 nhận mọi giá trị x < 2 làm nghiệm. 5 A. m > 3 B. m  3 C.  m  3 D. m < – 3 3
Câu 19. Tìm điều kiện tham số m để x m  2  0, x   2 . A. m  4 B. m  4 C. m  5 D. 0  m  4
2x 1 m  0,
Câu 20. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm duy nhất.
mx  2m 1  0.  3   17 3   17 3   2 13 A. m = 2 B. m = C. m = D. m = 2 2 2
Câu 21. Tìm điều kiện tham số m để bất phương trình 2m  
1 x m  6 nghiệm đúng với mọi giá trị x < 7. A. m > 1 B. 0  m < 1 C. m > 0,5 D. 0,5  m < 1
Câu 22. Tìm điều kiện tham số m để bất phương trình 3m  2 x m nghiệm đúng với mọi giá trị x < 1. A. Không tồn tại B. m > – 3 C. Mọi giá trị m D. m  3 1
Câu 23. Tập nghiệm của bất phương trình
 5 có bao nhiêu số nguyên dương x  5 A.2 B. 1 C. 0 D. 3  x 1   0,
Câu 24. Tìm điều kiện tham số m để hệ bất phương trình  x  2 vô nghiệm. 4x 1  . m  A. m < 6 B. m < 5 C. 3 < m < 5 D. 1 < m < 6
Câu 25. Tìm điều kiện m để bất phương trình  m   2 2
1 x  2m 1nhận nghiệm nguyên lớn nhất bằng 2. A. 1  m  2 B. 1  m  2 C. 1  m  2 D. 1  m  2 3x m 1   3 
Câu 26. Có bao nhiêu số nguyên m > – 9 để hệ bất phương trình  2  có nghiệm ?  2(
 2x 1)  m  A. 3 B. 6 C. 8 D. 5 26
Câu 27. Tập nghiệm của bất phương trình 
26 chứa bao nhiêu số nguyên x  26 A.2 B. 1 C. 3 D. 0
Câu 28. Tìm điều kiện tham số m sao cho  2 m  
1 x  2m 15  4, x    . A. m = 1 B. m = 4 C. m = 2 D. m = – 1  3
x m  2   1
Câu 29. Tìm điều kiện tham số m để hệ bất phương trình  4 có nghiệm. 5(x  4)  6  A. m < 15,4 B. m < 14,4 C. 2 < m < 5 D. m < 16,6
Câu 30. Có bao nhiêu số nguyên dương m < 10 để 2
(m  2)x m m là bất phương trình bậc nhất một ẩn A.8 B. 9 C. 7 D. 9
_________________________________ 5
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P3)
________________________________________
mx m  2  0, 
Câu 1. Tìm điều kiện tham số m để hệ bất phương trình
có nghiệm lớn nhất bằng 1.   2m   
1 x  3  m  0.  A. m = – 2 B. m < 0 C. m = 1 hoặc m = – 2 D. 2m > 1 5 5
Câu 2. Tập nghiệm của bất phương trình 
chứa bao nhiêu số nguyên 2 x  26 26 A.2 B. 1 C. 3 D. 4
m  4  x   1
Câu 3. Tìm điều kiện tham số m để hệ bất phương trình  3  có nghiệm.  5
 (x m 1)  10   A. 1 < m < 2 B. m > 3 C. m > 4 D. Không tồn tại m
Câu 4. Tìm đoạn giá trị của tham số m để hàm số y
mx  2m 1  2x m  2 luôn xác định khi x  1. A. [0;1] B. [2;4] C. [3;5] D. [0;4]
Câu 5. Cho các bất phương trình 1 1 2 2 2 2
x  2  x  3;
(m 1) x  2x  3; m  2   ;
(x  3)  (x 1) ;
(m 1)x  4 . x x  2
Có bao nhiêu bất phương trình luôn là bất phương trình bậc nhất một ẩn A.2 B. 1 C. 3 D. 4
Câu 6. Tìm điều kiện tham số m để bất phương trình 3m  2 x m  2 có miền nghiệm khác rỗng và không thể chứa miền x < 3. 2 2 A.  m  1 B. 3m > 2 C.  m  2 D. 5m > 8 3 3 2  x  0
Câu 7. Tập nghiệm S của hệ bất phương trình  là:
2x 1  x  2  A. S   ;  3  . B. S   ;  2. C. S   3  ; 2. D. S   3  ; . 3
x m  2x  6, 
Câu 8. Tìm điều kiện tham số m để hệ bất phương trình có nghiệm duy nhất.   2m    1 x m  4.  A. m = – 1 B. m = – 5 C. m = 1 hoặc m = 5 D. Không tồn tại m
Câu 9. Tìm điều kiện tham số m để bất phương trình m  
1 x m  7 có tập nghiệm S chứa miền x < 4 A. 0 < m < 1 B. 1  m  1 C. m < – 1 D. m > 7 hoặc m = – 1
m  4  x   1
Câu 10. Tìm giá trị nguyên nhỏ nhất của m để hệ bất phương trình  3  có nghiệm.  5
 (x  3m 1)  15   A. m = 4 B. m = 3 C. m = 5 D. m = 2
Câu 11. Tìm điều kiện tham số m để bất phương trình m  
1 x m  5 có tập nghiệm S chứa miền x > 2. A. m > – 1 B. m  3 C. 1 < m < 4 C. m = 3 3x m 1   4
Câu 12. Hệ bất phương trình  2 
có nghiệm duy nhất. Giá trị m thu được thuộc khoảng nào  4(
 2x  3m  2)  9  A. (0;1) B. (2;5) C. (1;2) D. (5;7)
Câu 13. Tìm điều kiện tham số m để bất phương trình 8x – 4m – 7 < x + 3m có nghiệm nguyên lớn nhất bằng 2. A. 1  m  2 B. m = 7,5 C. 2  m  3 D. 1 < m < 2
Câu 14. Tìm điều kiện tham số m để bất phương trình 3m  2 x m  2 có miền nghiệm S chứa miền (3;5). 6 A. m  1 B. m > 2 C. 1  m  6 D.  m  1 7 6
mx  2m x 1, 
Câu 15. Tìm điều kiện tham số m để hệ bất phương trình có nghiệm duy nhất.   m    1 x  3m 1.  A. 5m = 2 B. 2m = 5 C. 5m + 2 = 0 D. 3m = 4
Câu 16. Tìm điều kiện tham số m để bất phương trình 2m  
1 x m 1có tập nghiệm S chứa miền (2;3). A. m < 0,5 hoặc m  1 B. m < 0 ,5 hoăc m  2 C. m < 1 hoặc m  3 D. m < 2 hoặc m  4
Câu 17. Tìm điều kiện tham số m sao cho  2
m  2m  3 x m  3m  2, x    . A. m = 1 B. m = 4 C. m = 2 D. m = – 1
 2x 1  x 1   3
Câu 18. Tập nghiệm S của hệ bất phương trình  là: 4  3x   3  x   2  4   4  A. S  2; .   B. S  ;  .   C. S   ;  2  . D. S   2  ; .  5   5 
 2x m 1   3
Câu 19. Tìm điều kiện của m để x = 2 thuộc miền nghiệm của hệ bất phương trình  2  4( 
x m  2)  8  5 5 A. m  B. m > 9 C. 0 < m < 4 D.  m  9 3 3
Câu 20. Tồn tại bao nhiêu giá trị nguyên của tham số m để bất phương trình 2
5mx  2x  2m m  2 nhận
nghiệm nguyên lớn nhất bằng 1. A. 2 giá trị B. 3 giá trị C. 4 giá trị D. 1 giá trị x  2 4
Câu 21. Tổng các nghiệm nguyên của bất phương trình  bằng: x  4 x  4 A. 15 . B. 11. C. 26 . D. 0 .
Câu 22. Tập nghiệm S của bất phương trình  x  3 x  2  0 là:
A. S  3;  .
B. S  3;  . C. S    2 3;  . D. S    2  3;  .
Câu 23. Bất phương trình  2
m  3mx m  2  2x vô nghiệm khi A. m  1. B. m  2.
C. m  1, m  2. D. m  . 
Câu 24. Có bao nhiêu giá trị thực của tham số m để bất phương trình  2
m mx m vô nghiệm. A. 0. B. 1. C. 2. D. Vô số. 3x m 1   4
Câu 25. Tồn tại bao nhiêu giá trị nguyên m < 8 để x = 3 thuộc miền nghiệm của hệ  2   4(
 2x  3m  2)  9  A. 6 B. 5 C. 10 D. 4 5
x  2  4x  5 
Câu 26. Tổng tất cả các nghiệm nguyên của bất phương trình  bằng: x    x  22 2  A. 21. B. 27. C. 28. D. 29.
Câu 27. Tìm điều kiện tham số m để bất phương trình 3m  2 x m  2 nghiệm đúng với mọi giá trị x < 3. 2 2 2 A. 0 < m < 1 B.  m  1 C. m
D. m > 1 hoặc m  3 3 3 2 x 1  0
Câu 28. Hệ bất phương trình 
có nghiệm khi và chỉ khi: x m  0  A. m  1. B. m  1. C. m  1. D. m  1.
_________________________________ 7
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P4)
________________________________________
Câu 1. Bất phương trình 2
m x     2 4 2 1
4m  5m  9 x 12m nghiệm đúng với mọi x khi 9 9 A. m  1.  B. m  . C. m  1. D. m   . 4 4
Câu 2. Cho các bất phương trình 1 x 2 2
2x 1  3x  ; a  ; a
x  6x  5  0;
 2 x m 1; (m 1)x  4 x  2 2
Số lượng bất phương trình bậc nhất hai ẩn là A.2 B. 1 C. 3 D. 0    x  2 2 3
x  7x 1
Câu 3. Hệ bất phương trình 
vô nghiệm khi và chỉ khi:
2m  8  5x  72 72 A. m  . B. m  . C. m  1 D. m  1 13 13 2 4a
Câu 4. Tập nghiệm của bất phương trình
 2a với a   chứa bao nhiêu số nguyên 2 x 1  2a A.2 B. 1 C. 3 D. 0 x  2  0 
Câu 5. Hệ bất phương trình
có nghiệm khi và chỉ khi:   2 m    1 x  4  A. m  1. B. m  1. C. m  1. D. 1  m  1.
Câu 6. Tìm tất cả các giá trị thực của tham số m để bất phương trình  x mm x  3x  4 có tập nghiệm là
m  2; . A. m  2. B. m  2. C. m  2. D. m  2. 3x x 1
Câu 7. Với m  10 thì tập nghiệm của bất phương trình  là 2 (m  7) m  7  m  7   2m  7   m  7   7   A. ;    B. ;    C. ;    D. ;     m 10   m 10   m 10   m 10  2 2
(2x 1)  8(m 1)  (2x  3) 
Câu 8. Tập nghiệm của hệ bất phương trình 2  x m m  6
có độ dài nhỏ nhất bằng    5 5 A.3 B. 5 C. 4 D. 2
Câu 9. Bất phương trình  2
m  9 x  3  m1 6x nghiệm đúng với mọi x khi A. m  3. B. m  3. C. m  3.  D. m  3. 
Câu 10. Tìm điều kiện tham số m để bất phương trình m x m  x 1 có tập nghiệm là  ;  m   1 . A. m  1. B. m  1. C. m  1. D. m  1.    x  2 2 3
x  7x 1
Câu 11. Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình  có nghiệm duy
2m  8  5x  nhất. 72 72 72 72 A. m  . B. m  . C. m  . D. m  . 13 13 13 13
Câu 12. Tìm tất cả các giá trị của tham số m để bất phương trình m x  
1  2x  3 có nghiệm. A. m  2 . B. m  2 . C. m  2 . D. m  2 . 2   x   1  x  3
Câu 13. Tập nghiệm S của bất phương trình  là:
2x  3 x    1  A. S   3  ;5. B. S   3  ;5. C. S  3;5. D. S   3  ;  5 .
Câu 14. Có bao nhiêu giá trị thực của tham số m để bất phương trình mx  2  x m vô nghiệm. 8 A. 0. B. 1. C. 2. D. Vô số.
Câu 15. Có bao nhiêu giá trị nguyên m nhỏ hơn 20 để hàm số f (x) 
(2m 1)x m  4 xác định trên 1; . A.18 B. 17 C. 16 D. 15
Câu 16. Tìm tất cả các giá trị của tham số m để bất phương trình m x  
1  3  x có nghiệm. A. m  1. B. m  1. C. m   . D. m  3 .
Câu 17. Có bao nhiêu cặp số (a;b) để 2 2
(a  3b  2)x a b  4  4b, x  . A.2 B. 1 C. 3 D. 0
x 1  2x  3  5  3x
Câu 18. Biết rằng bất phương trình 
x  3 có tập nghiệm là một đoạn  ;
a b . Hỏi a b bằng: 2  3
x x  5  A.5,5 B. 8. C. 4,5 D. 4,7
Câu 19. Biểu diễn hình học của bất phương trình 3mx m  4  0, x   1có dạng A.Một đoạn thẳng B. Một tia C. Hình chữ nhật D. Hình vuông
Câu 20. Có bao nhiêu số nguyên m nhỏ hơn 10 để 2mx m  2  0, x   1 . A.7 B. 8 C. 6 D. 9 
2m x   1  x  3
Câu 21. Tìm giá trị thực của tham số m để hệ bất phương trình  có nghiệm duy nhất.
4mx  3  4x  5 3 3 5 A. m  . B. m  . C. m  ; m  . D. m  1.  2 4 4 2
Câu 22. Có bao nhiêu cặp số (a;b) để 2 2
(a  3 b  2  5)x  2a b  4  4 , b x  . A.2 B. 1 C. 3 D. 4
Câu 23. Tìm điều kiện tham số m để bất phương trình m(x m)  x m có tập nghiệm S   ;  m   1 . A. m < 1 B. m = 1 C. m  1 D. m  1 2  x x 1 2  x  2 
Câu 24. Hệ bất phương trình 2  x  2
có bao nhiêu nghiệm nguyên  4 2
(x 1)(x x 1)  0  A.3 B. 2 C. 1 D. 4
Câu 25. Có bao nhiêu số nguyên m nhỏ hơn 10 để 3mx m  4  0, x   1 . A.7 B. 8 C. 6 D. 9
Câu 26. Cho các bất phương trình 1 x 2 2
2x 1  5x  ; a  ; a
x(x  2)  6x  5  0;
 2 x m 1; (m 1)x  4m x  2 2
Số lượng bất phương trình bậc nhất hai ẩn là A.2 B. 1 C. 3 D. 0  7 
Câu 27. Tìm điều kiện tham số m để bất phương trình  m   2 4
3 x  2m 1có tập nghiệm S chứa miền 1;    5  3 m  2 4 A. m > 2 B. m  C.  D. m  4 m  0,8  5 2 2 
(x 1)  x  4a  5
Câu 28. Miền nghiệm của hệ bất phương trình 
là một khoảng có độ dài nhỏ nhất bằng 2 2
2x  2a x a  A.2 B. 1 C. 1,5 D. 3
Câu 29. Có bao nhiêu số nguyên dương m để
x 1(x  2m  2)  0, x  2;  3 . A.2 B. 1 C. 3 D. 4
Câu 30. Có bao nhiêu giá trị nguyên m nhỏ hơn 20 để hàm số f (x) 
5mx m  8 xác định trên 1; . A.18 B. 17 C. 16 D. 15
_________________________________ 9
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P5)
________________________________________
Câu 1. Tìm điều kiện tham số m sao cho  2
m  4 x m  3  2, x    . A. m = 3 B. m = 4 C. m = 2 D. m = – 2 x  2  0,
Câu 2. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm. mx m  4.  m  0 m  0 m  1 A.  B.  C.  D. m < 0 m  4  m  5  m  7 
Câu 3. Tìm số nghiệm nguyên của bất phương trình 2 2
(1  x )(x x  1)  0 . A.3 B. 2 C. 4 D. 1
Câu 4. Tìm điều kiện tham số m để bất phương trình  2
m m   x    2 4 2 1 1
3m  4 x  4m vô nghiệm. A. m = 2 B. m = 1 C. m = 0 D. m = 1,5
Câu 5. Tìm điều kiện tham số m để
m 1 x   1  m  0, x    . A. m = 1 B. m = 3 C. Không tồn tại D. m = 2 2
Câu 6. Tìm số nghiệm nguyên của bất phương trình  2 . x 1  2 A.3 B. 2 C. 1 D. 4 3  x  5  0,
Câu 7. Tìm điều kiện tham số m để hệ bất phương trình 
có độ dài tập nghiệm bằng 2. 2mx  3  . m  9 7 A. m = 1 B. m =  C. m – 2 D. m =  25 26
Câu 8. Tồn tại các giá trị a và b để a b   2 2
1 x a  3b  2  0, x
   . Khi đó điều kiện tham số b là b  2 b  3 b  1 b  4 A.  B.  C.  D.  b  0,5  b  0  b  0, 75  b  0, 25 
Câu 9. Tìm điều kiện tham số m để bất phương trình  3
m  9m 10 x m  4  0 có tập nghiệm S = R. A. m = 4 B. m = – 4 C. m = 1 D. m = 1,5
Câu 10. Bất phương trình ax b  0 vô nghiệm khi: a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  . b  0  b  0  b  0  b  0  2 2 
(x 1)  (x  2)
Câu 11. Tìm số nghiệm nguyên của hệ bất phương trình  2
(x  3)(x  2x  3)  0  A.3 B. 2 C. 4 D. 1
Câu 12. Gọi S là tập nghiệm của bất phương trình mx  6  2x  3m với m  2 . Hỏi tập hợp nào sau đây là
phần bù của tập S ? A. 3;  . B. 3;  . C.  ;  3 . D.  ;   3 .
Câu 13. Tìm giá trị thực của tham số m để bất phương trình m 2x  
1  2x 1 có tập nghiệm là 1; . A. m  3 B. m  1 C. m  1 D. m  2.  3
  x  6  3 
Câu 14. Hệ bất phương trình 5x m
có nghiệm khi và chỉ khi:  7   2 A. m  11.  B. m  11.  C. m  11.  D. m  11. 
Câu 15. Tìm tất cả các giá trị của tham số m để bất phương trình 2
m x 1  mx m có nghiệm. A. m  1. B. m  0 .
C. m  0; m  1. D. m   .
Câu 16. Tìm giá trị thực của tham số m để bất phương trình 2x m  3 x  
1 có tập nghiệm là 4; . 10 A. m  1. B. m  1. C. m  1.  D. m  1.   1 x  2 2
 8  4x x
Câu 17. Cho bất phương trình 
. Tổng nghiệm nguyên lớn nhất và nghiệm nguyên   x  23 3 2
x  6x 13x  9 
nhỏ nhất của bất phương trình bằng: A. 2. B. 3. C. 6. D. 7. x 1
Câu 18. Tìm số nghiệm nguyên của bất phương trình  0 . x x 1 A.2 B. 1 C. 3 D. 4 2
m x  6  x
Câu 19. Tìm tất cả các giá trị của tham số m để hệ bất phương trình  có nghiệm duy nhất.
3x 1  x  5  A. m  1. B. m  1. C. m  1. D. m  1. 2 2 
(x 1)  x  4a  5
Câu 20. Miền nghiệm của hệ bất phương trình 
là một khoảng có độ dài nhỏ nhất bằng 2 2
2x  2a x a  A.2 B. 1 C. 1,5 D. 3 2
(x 1)(x  4x  5)  0 
Câu 21. Tìm số nghiệm nguyên của hệ bất phương trình 
x x  0  A.2 B. 1 C. 3 D. 4
Câu 22. Tập nghiệm của bất phương trình 2
(m  2m  2)x  5 có thể chứa tối đa bao nhiêu số nguyên dương A.3 B. 2 C. 1 D. 4
Câu 23. Xác định giá trị tham số m để bất phương trình m   2
1 x m m  6  0 có tập nghiệm là 0; . A. m = 0,5 B. m = 3 C. m = 2 D. m = – 4 2 2
Câu 24. Tập nghiệm S của bất phương trình  x  3   x  3  2 là:  3   3   3   3  A. S   ;  . B. S   ;  . C. S    ;   . D. S    ;  . 6         6   6   6  
Câu 25. Tìm tất cả các giá trị của tham số m để bất phương trình mx  4  0 nghiệm đúng với mọi x  8 .  1 1   1  A. m   ; .  B. m   ;  .  2 2      2   1   1   1  C. m   ;  .   D. m   ; 0  0; .      2   2   2    m mx   1  2
Câu 26. Hệ bất phương trình 
có nghiệm khi và chỉ khi: m
 mx  2  2m 1  1 1 A. m  . B. 0  m  . C. m  0. D. m  0. 3 3 2 2 2 
(x 1)  x x  2a  4a  8
Câu 27. Miền nghiệm của hệ bất phương trình 
là một khoảng có độ dài nhỏ 2 2
2(x 1)  2a x  3a  2  nhất bằng A.2 B. 3 C. 1,5 D. 4
Câu 28. Tìm điều kiện tham số m sao cho bất phương trình  2 m m   2 4
3 x m m  0 nhận tập nghiệm R. A. m = 0,5 B. m = 4 C. m = – 3 D. m = – 1 2 
(x  2)(x  2x  5)  0
Câu 29. Tìm số nghiệm nguyên của hệ bất phương trình  2
(x 1)(x  3)  0  A.3 B. 1 C. 2 D. 4
Câu 30. Có bao nhiêu cặp số (a;b) để bất phương trình 2 2
(a  2b  1)x a b  2b  1  0 luôn nghiệm đúng với mọi giá trị x A.2 B. 1 C. 3 D. 4
_________________________________ 11
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P6)
________________________________________  3 
Câu 1. Tập S  1; 
 là tập nghiệm của hệ bất phương trình sau đây ?  2  2(x 1)  1 2(x 1)  1 2(x 1)  1 2(x 1)  1 A.  . B.  . C.  . D.  . x  1   x  1   x  1   x  1   x 1
Câu 2. Tìm số nghiệm nguyên của bất phương trình  0 . x  2 A.2 B. 1 C. 1 D. 3
Câu 3. Bất phương trình ax b  0 có tập nghiệm là  khi: a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  . b  0  b  0  b  0  b  0 
mx m  3 
Câu 4. Tìm giá trị thực của tham số m để hệ bất phương trình có nghiệm duy nhất.   m  3 
x m  9  A. m  1. B. m  2.  C. m  2. D. m  1.  2x
Câu 5. Tập nghiệm S của bất phương trình 5x 1   3 là: 5  5   20  A. S  .  B. S   ;  2. C. S   ;  .   D. S  ;  .    2   23 
2x  7  8x 1
Câu 6. Hệ bất phương trình 
vô nghiệm khi và chỉ khi: m  5  2x  A. m  3.  B. m  3. C. m  3. D. m  3. 2 2 
(x 1)  x  2a 1
Câu 7. Hệ bất phương trình 
có miền nghiệm M với độ dài nhỏ nhất bằng 2 2 2
(x 1)(x 1)  (x 1)(a  2)  A.2 B. 1 C. 3 D. 4 3x  5 x  2
Câu 8. Bất phương trình 1 
x có bao nhiêu nghiệm nguyên lớn hơn 10 ? 2 3 A. 4. B. 5. C. 9. D. 10. 3
x  4  x  9
Câu 9. Hệ bất phương trình 
vô nghiệm khi và chỉ khi:
1 2x m  3x 1  5 5 5 5 A. m  . B. m  . C. m  . D. m  . 2 2 2 2
Câu 10. Tổng các nghiệm nguyên của bất phương trình x 2  x  x 7  x  6 x   1 trên đoạn  10  ;10 bằng: A. 5. B. 6. C. 21. D. 40.
Câu 11. Bất phương trình  x   x    x    x   x   2 2 1 3 3 1 1
3  x  5 có tập nghiệm  2   2  A. S   ;   .   B. S   ;  .    C. S  . D. S  .   3   3  2 2 2
Câu 12. Tập nghiệm S của bất phương trình  x     x   2 1 3
15  x   x  4 là: A. S   ;  0.
B. S  0; . C. S  .  D. S  .  3
x  5  x 1  2 2
Câu 13. Hệ bất phương trình 
x  2   x  
1  9 vô nghiệm khi và chỉ khi:
mx 1 m  2 x m  A. m  3. B. m  3. C. m  3. D. m  3.
Câu 14. Tập nghiệm S của bất phương trình x
x  2  2  x  2 là:
A.   b2  . ac B. S   ;  2. C. S    2 .
D. S  2; . 12 2x 1  3
Câu 15. Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình  có nghiệm duy nhất. x m  0  A. m  2 . B. m  2 . C. m  2 . D. m > 1
Câu 16. Gọi S là tập hợp tất cả các giá trị thực của tham số m để bất phương trình  2
m mx m  6x  2 vô
nghiệm. Tổng các phần tử trong S bằng: A. 0. B. 1. C. 2. D. 3. 
2  x  3  5 x  4
Câu 17. Hệ bất phương trình 
vô nghiệm khi và chỉ khi:
mx 1  x 1  A. m  1. B. m  1. C. m  1. D. m  1.
Câu 18. Tìm tất cả các giá trị của tham số m để bất phương trình  2
m m  6 x m 1 có nghiệm. A. m  2 .
B. m  2 và m  3 . C. m   . D. m  3 . 2 2 2
(x  2)  a  2x  5x  4
Câu 19. Tập nghiệm của hệ bất phương trình 
chứa tối đa bao nhiêu số nguyên
2(x 1)  x  2a 1  A.2 B. 1 C. 3 D. 4
Câu 20. Tìm tất cả các giá trị thực của tham số m để bất phương trình 2
m x  2  mx x  5  0 nghiệm đúng
với mọi x  201  8; 2 . 7 7 7 A. m  . B. m  . C. m  . D. m   . 2 2 2
Câu 21. Tìm điều kiện của tham số m để bất phương trình 2
m x  2  m x  0 có nghiệm x 1;2 A. m  2 . B. m  2  . C. m  1  . D. m  2 .
x 1  x 1   2
Câu 22. Tập nghiệm S của hệ bất phương trình  là: 5  2x 3   x    2  1   1  A. S   ;   .  
B. S  1;. C. S   ;1 .   D. S  .   4   4    3m  2 
x m  4  0,
Câu 23. Tìm điều kiện tham số m để hệ bất phương trình 
có nghiệm nhỏ nhất bằng 3. m  2 
x  3m 1  0.  A. m = 1 B. 6m = 5 C. Không tồn tại m D. 6m = – 5 1 1
Câu 24. Cho các bất phương trình 2 2 
1; (m  2)x x  5; x  5x  4  0; m x m  2 . x x  2
Số lượng bất phương trình bậc nhất một ẩn là A.2 B. 1 C. 3 D. 0
Câu 25. Tìm điều kiện tham số m để bất phương trình (m – 2)x > m có nghiệm nguyên nhỏ nhất bằng 4. 8 8 A. m  3 B.  m  3 C. m  D. m < 3 3 3  5 6x   4x  7   7
Câu 26. Số nghiệm nguyên của hệ bất phương trình  là: 8x  3   2x  25   2 A. Vô số. B. 4 . C. 8. D. 0.
Câu 27. Bất phương trình 2 m x  
1  9x  3m nghiệm đúng với mọi x khi A. m  1. B. m  3.  C. m  .  D. m  1.  2x 1  0
Câu 28. Hệ bất phương trình 
có nghiệm khi và chỉ khi: x m  2  3 3 3 3 A. m   . B. m   . C. m   . D. m   . 2 2 2 2
_________________________________ 13
DẤU TAM THỨC BẬC HAI, BẤT PHƯƠNG TRÌNH BẬC HAI LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P1)
________________________________________________________
Câu 1. Tìm điều kiện tham số m để 2
x  2x m  6  0, x    . A. m > 5 B. m > 8 C. m > 7 D. m < 10
Câu 2. Tìm số nghiệm nguyên của bất phương trình 2
x  8x  7  0 . A.2 B. 1 C. 7 D. 6
Câu 3. Tìm điều kiện tham số m để bất phương trình 2
x  3x  4  m nghiệm đúng với mọi x thuộc đoạn [1;2]. 7 7 7 A. m  2 B.  m  2 C. m  D. m  4 4 4
Câu 4. Tìm điều kiện tham số m để bất phương trình 2
x  2m  
1 x m  3  0 có nghiệm. A. Mọi giá trị m B. m > 0,5 C. 0 < m < 1 D. m  2
Câu 5. Tìm số nghiệm nguyên của bất phương trình 2 2
(x  2x  5)(x  3x  2)  0 . A.2 B. 1 C. 3 D. 4 5
Câu 6. Tìm điều kiện tham số m để hàm số y  luôn xác định trên R. 2
4x 12x m  7 A. m > 3 B. m > 19 C. m > 2 D. 1 < m < 4 2 x  5x  4
Câu 7. Tìm số nghiệm nguyên của bất phương trình  0 7  x A.3 B. 2 C. 4 D. 1
Câu 9. Tìm điều kiện tham số k để   x  2 2 8
k  8  0 với mọi số thực x. A. k < 1 B. k > 8 C. k < 8 D. k < 6 2 2
(x  8x  7)(x  2)
Câu 10. Tìm số nghiệm nguyên của bất phương trình  0 2 x x 1 A.5 B. 7 C. 4 D. 6
Câu 11. Có bao nhiêu số nguyên m   10 
;10 để bất phương trình 2
mx  5mx  20  0 nhận x = 1 là nghiệm A.15 B. 12 C. 14 D. 16
Câu 12. Hàm số bậc hai 2
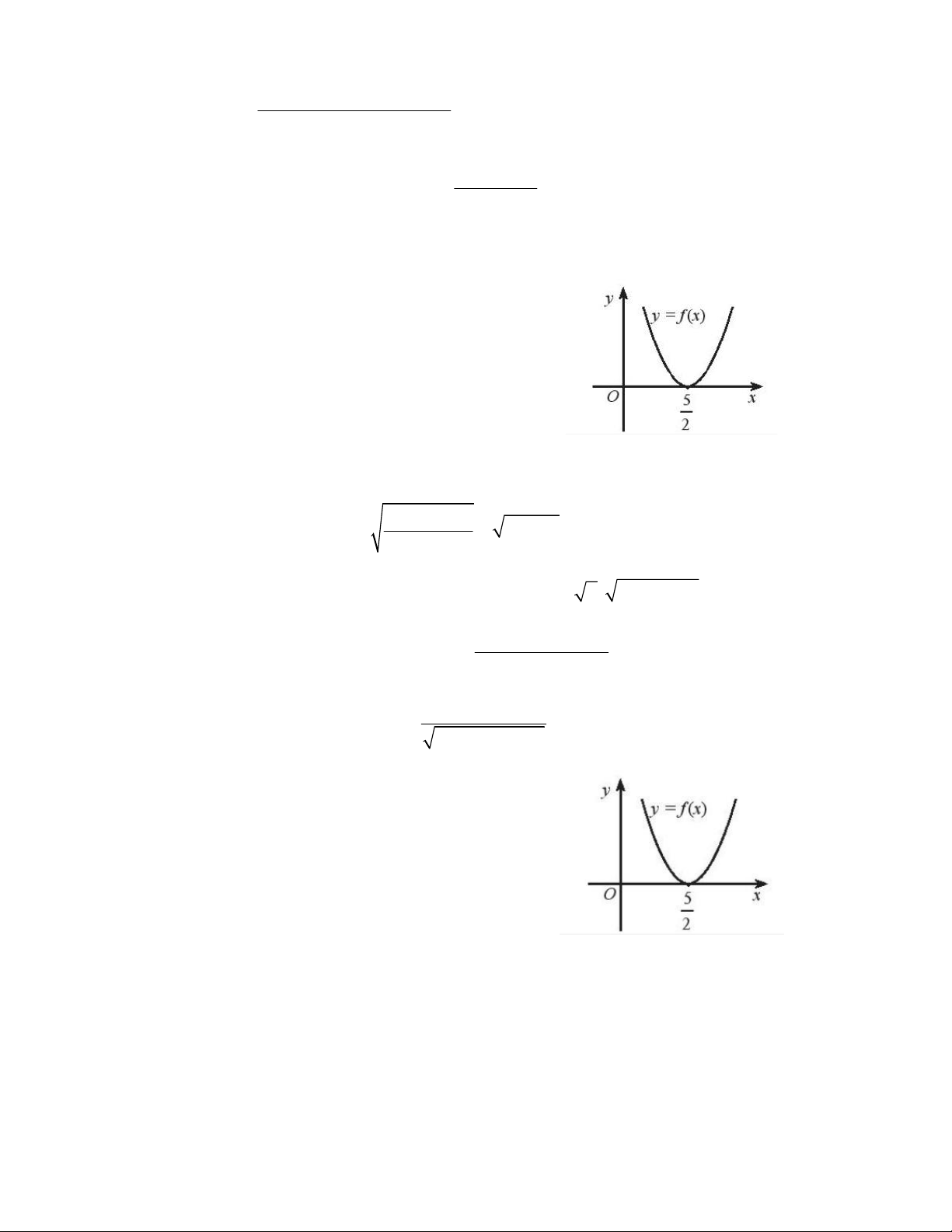
f (x)  ax bx c có đồ thị
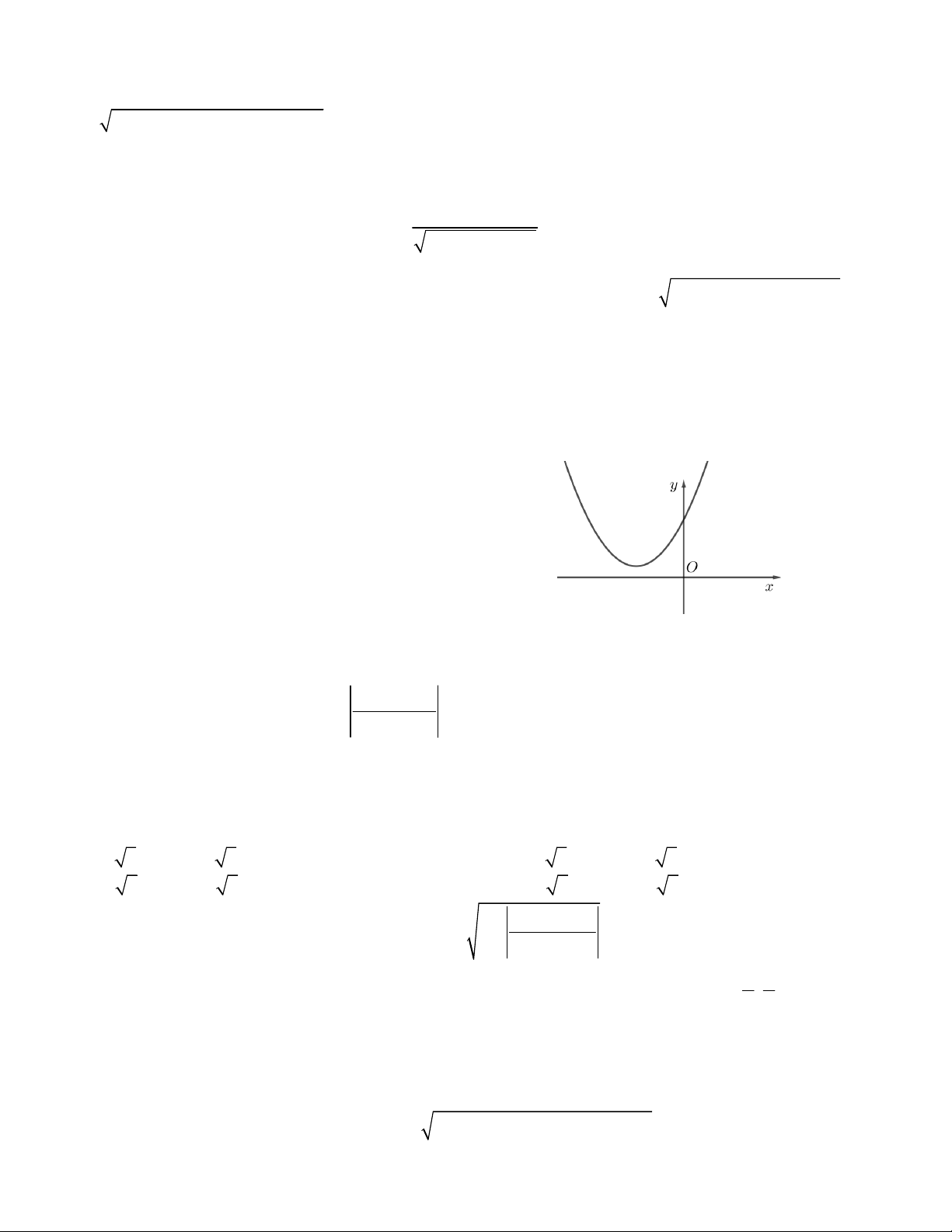
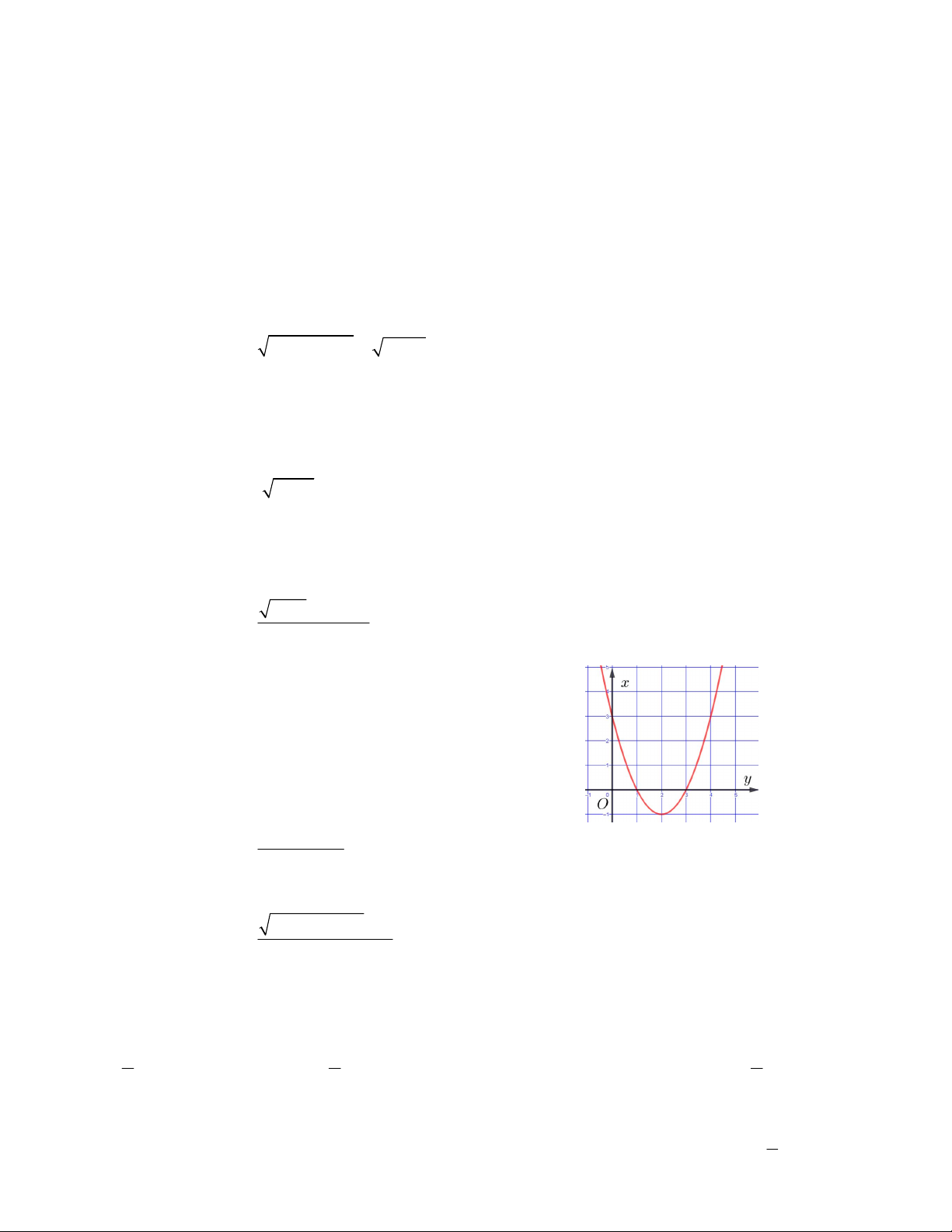
như hình vẽ. Tìm độ dài tập nghiệm của bất phương
trình f (x)  0 . A.3 B. 4 C.2 D. 1 2017
Câu 13. Tồn tại bao nhiêu số nguyên m < 10 để hàm số y  xác định trên R ?
x x 10  2m 10 A. 7 giá trị B. 8 giá trị C. 10 giá trị D. 6 giá trị
Câu 14. Tìm điều kiện tham số m để 2 2
x  2mx m m  5  0, x    . A. m > 5 B. m > 4 C. m > 2 D. m > 7 2 2
(3x  4x 1)(x 1)
Câu 15. Tìm số nghiệm nguyên của bất phương trình  0 . 4 x  5 A.3 B. 2 C. 1 D. 4
Câu 16. Tìm điều kiện tham số m để hàm số 2 2 y
x 10mx  25m m  2 có tập xác định là R. A. m  1 B. m  6 C. m  2 D. m  7
Câu 17. Tìm số nghiệm nguyên của bất phương trình 4 2
x 10x  9  0 A.4 B. 3 C. 7 D. 6
Câu 18. Tìm điều kiện tham số m để 2 2
x  2mx m  3m  9  0, x    . A. m > 4 B. m > 3 C. m > 2,5 D. m > 1 14 2018
Câu 19. Tồn tại bao nhiêu giá trị nguyên m nhỏ hơn 40 để hàm y  luôn xác định trên R ? 2
9x 12x m  6 A. 17 giá trị B. 28 giá trị C. 30 giá trị D. 29 giá trị
Câu 20. Tìm điều kiện tham số m để 2 2
x  4mx  4m  3m 12  0, x    . A. m > 4 B. m > 3 C. m > 2,5 D. m > 1
Câu 21. Tìm điều kiện tham số m để bất phương trình 2
x   m   2 2 4
1 x m 1  0 có ít nhất một nghiệm lớn hơn 2017. A. Mọi giá trị m B. m > 1 C. m < 1 D. m > 0
Câu 22. Cho hàm số bậc hai 2
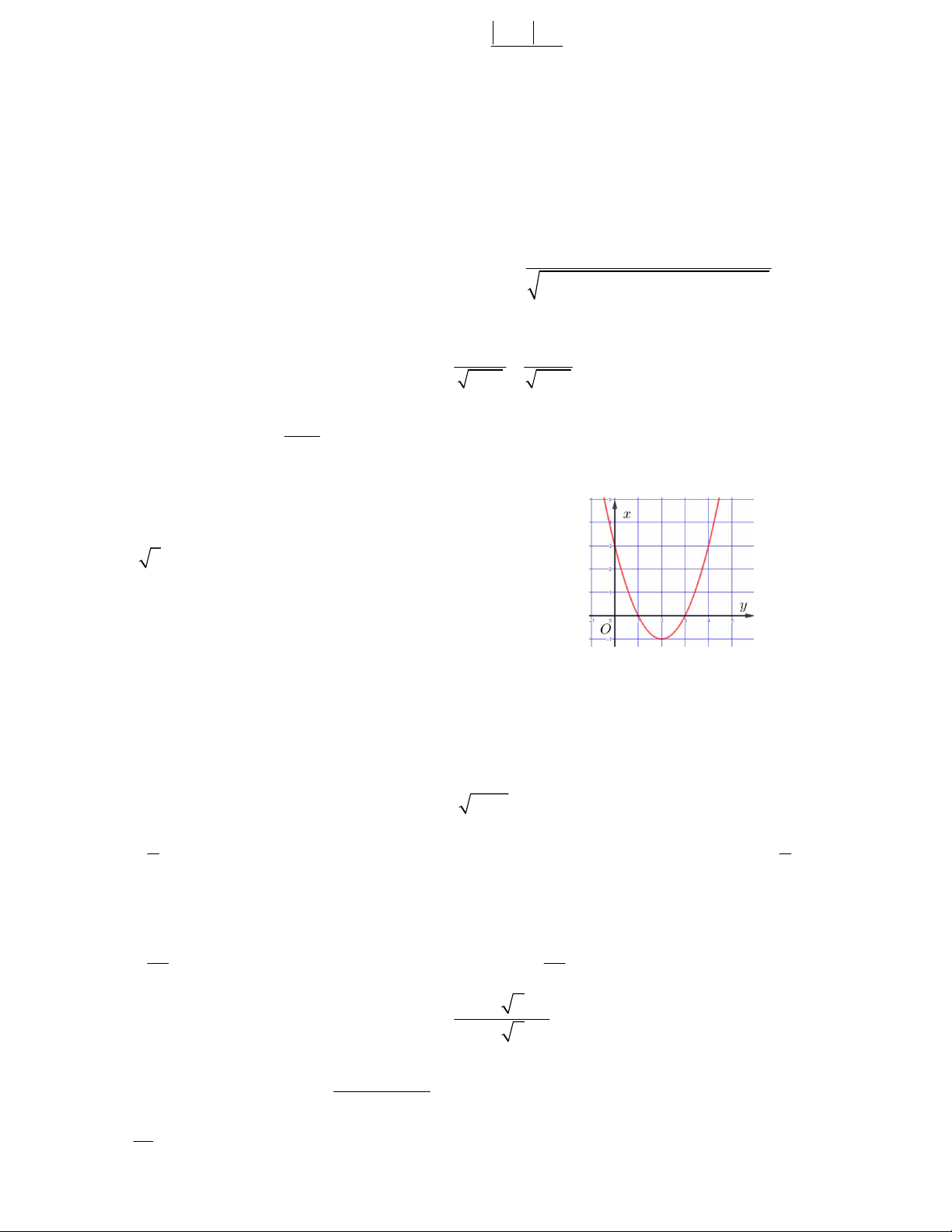
y ax bx c có đồ
thị như hình vẽ. Mệnh đề nào đúng A. 2
a  0;b  4ac  0; c  0 B. 2
a  0;b  4ac  0; c  0 C. 2
a  0;b  4ac  0; c  0 D. 2
a  0;b  4ac  0; c  0
Câu 23. Tìm giá trị nhỏ nhất của tham số m để 2 2
x 12mx  3m m 1  0, x    . A. m = 1 B. m = 2 C. m = 3 D. m = 4
Câu 24. Tìm điều kiện tham số m để hàm số 2 2 y
x  4mx  4m m  7 có tập xác định là R. A. m  1 B. m  6 C. m  2 D. m  7 2 2x  7x  5
Câu 25. Tìm giá trị nhỏ nhất của tham số m để bất phương trình
m luôn đúng với mọi x. 2 x  5x  7 A. m = 2 B. m = 5 C. m = 6 D. m = 3 2 x mx  2
Câu 26. Bất phương trình  1
 luôn luôn đúng trên R khi và chỉ khi nào ? 2 x  3x  4
A. m < – 4 hoặc m  0
B. m < – 3 hoặc m  0 C. m < 2 hoặc m > 5
D. m < – 6 hoặc m  1 2 x mx 1
Câu 27. Tìm m để bất phương trình kép
 3 có tập nghiệm là R. 2 x x 1 A. – 5 < m < 1 B. 0 < m  1 C. 0  m < 4 D. 0  m  6
Câu 28. Tìm số nghiệm nguyên của bất phương trình 2
(x 1)(x  9 x  8)  0 . A.64 B. 8 C. 18 D. 30
Câu 29. Biết rằng f x 2
ax bx c  0, x
   . Mệnh đề nào sau đây đúng ? A. a + b + c > 0 B. a – 2b + c > 0 C. 2a + b – c > 0 D. 4a – 3b + 9c > 0
Câu 30. Tìm điều kiện tham số m để 2 2
x  6mx  9m m 12  0, x    . A. m > 12 B. m > 3 C. m > 2,5 D. m > 1 2
x  4x  9
Câu 31. Tìm điều kiện của m sao cho  0, x    . 2
x  (m 1)x  4 A. Mọi giá trị m B. m  5  ;   3 C. m  4  ; 2   D. m > 0
Câu 32. Tìm điều kiện tham số m để hàm số 2 2 2 y
x  4mx  4m m m  5 luôn xác định trên R. A. m  5 hoặc m = 0 B. m  6 hoặc m = 0 C. m  2 hoặc m = 0 D. m  7 hoặc m = 0
Câu 33. Tìm điều kiện tham số m để 2 2
x  6mx  8m  4  0, x    . A. – 2 < m < 2 B. 1 < m < 2 C. m > 2,5 D. 3 < m < 4
Câu 34. Bất phương trình  2 x x   2 2
2x 1  0 có bao nhiêu nghiệm nguyên dương? A. 0 . B. 1. C. 2 . D. Nhiều hơn 2
Câu 35. Biết rằng f x 2
ax bx c  0, x
   . Mệnh đề nào sau đây đúng ? A. a + b + 2c > 0 B. 9a – 2b + c > 0 C. 4a – 2b + c > 0 D. 4a – 3b + 7c > 0
_________________________________ 15
DẤU TAM THỨC BẬC HAI, BẤT PHƯƠNG TRÌNH BẬC HAI LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P2)
________________________________________________________
Câu 1. Biết rằng f x 2
ax bx c  0, x
   . Mệnh đề nào sau đây đúng ? A. a + 3b + 2c > 0 B. 9a – 3b + c > 0 C. 4a – 3b + c > 0 D. a + b + c < 0
Câu 2. Tìm điều kiện của m để tam thức 2
f (x)  2x mx  3 có giá trị dương tại x = 2. A.m > 2 B. m > 1 C. m > 2,5 D. m > 0
Câu 3. Tồn tại bao nhiêu số nguyên m < 7 để hàm số 2 2 y
4x  4mx m  2m 1 luôn xác định trên R ? A. 4 giá trị B. 3 giá trị C. 5 giá trị D. 6 giá trị
Câu 4. Tìm điều kiện tham số m để 2 2
x  6mx  10m  3m  0, x    . A. – 1 < m < 2 B. 0 < m < 3 C. – 1 < m < 1 D. 3 < m < 4
Câu 5. Tam thức bậc hai 2
f (x)  (m 1)x  3x 1có nghiệm duy nhất. Giá trị m thu được thuộc khoảng nào A.(0;1) B. (1;2) C. (2;3) D. (3;4) 3  2  10
Câu 6. Tìm điều kiện của tham số m để hàm số f x 
luôn xác định trên tập hợp số thực. 2
x  2mx 10m A. 0 < m < 10 B. 0 < m < 6 C. 1 < m < 9 D. 2 < m < 5 2 x 10x  9
Câu 7. Tìm số nghiệm nguyên của bất phương trình  0 . 2 x 1 A.4 B. 8 C. 9 D. 7
Câu 8. Tồn tại bao nhiêu số nguyên m nhỏ hơn 6 để 2 2
25x 10mx m  6m  3  0, x    ? A. 4 giá trị B. 2 giá trị C. 5 giá trị D. 6 giá trị
Câu 9. Tồn tại bao nhiêu giá trị nguyên của m để hàm 2 2
y  16x  8mx m  6  m luôn xác định trên R ? A. 14 giá trị B. 13 giá trị C. 11 giá trị D. 16 giá trị
Câu 10. Tìm điều kiện tham số m để bất phương trình 2
x mx  5  0 nhận x = 1 làm nghiệm. A.m > 4 B. m > 2 C. m < 3 D. 0 < m < 1 x  3 x  2
Câu 11. Tìm số nghiệm nguyên của bất phương trình  0 . x 1 A.3 B. 2 C. 4 D. 1
Câu 12. Có bao nhiêu số nguyên m để tam giác bậc hai 5 2
f (x)  m x  2mx  3 không đổi dấu trên R A.2 B. 0 C. 1 D. 3 3
Câu 13. Tìm điều kiện tham số m để hàm số y
xác định với mọi x thực. 2
x  3m  2 2 4
x  2m  5m  2 A. – 5 < m < 1 B. – 4 < m < 1 C. – 6 < m < – 2 D. 0 < m < 3
Câu 14. Tìm điều kiện tham số m để biểu thức 2
Z mx 10x  5không dương với mọi x thực. A. m  - 5 B. m  - 2 C. 2 < m  - 7 D. m < 0
Câu 15. Có bao nhiêu giá trị nguyên m để tam thức bậc hai 2 2
f (x)  x  2(m 1)x  2m m  3vô nghiệm A.3 B. 20 C. Vô số D. 30 2 x  3x  6
Câu 16. Tồn tại bao nhiêu số nguyên m nhỏ hơn 17 để hàm T x  xác định trên R? 2
6 x  m  2 x  8m 1 A. 12 giá trị B. 16 giá trị C. 15 giá trị D. 8 giá trị
Câu 17. Tìm điều kiện tham số m để 2 2 2
x  6mx  9m m  6 , m x    . A. – 2 < m < 3 B. 0 < m < 3 C. – 1 < m < 1 D. 0 < m < 6
Câu 18. Tồn tại bao nhiêu giá trị nguyên của m nhỏ hơn 30 để hàm số 2 2 y
4x  40mx  25m  8m 16
luôn xác định trên R ? A. 12 giá trị B. 28 giá trị C. 29 giá trị D. 26 giá trị
Câu 19. Tìm điều kiện tham số m để bất phương trình 2
x  2x  5  m nghiệm đúng với mọi x thuộc đoạn [2;4]. A. m  4 B. 5  m  13 C. m  5 D. 4  m  13 2
Câu 20. Tồn tại bao nhiêu số m để hàm số 2 y
x mx m  3 có tập xác định D = R ? 2 x 10 A. 2 giá trị B. 9 giá trị C. 10 giá trị D. 6 giá trị 16
Câu 21. Tìm điều kiện của m để biểu thức 2 2 2
P x  4mx  4m m m  6 luôn không âm với mọi số thực x. A. m = 0 hoặc m  6 B. m = 0 hoặc m  2. C. m = 0 hoặc m  5. D. m  6 2 x x  5
Câu 22. Bất phương trình
 0 luôn đúng với mọi x khi và chỉ khi m   2
1 x  2m   1 x  4 A. 1   m  3 B. 1   m  4 C. – 1 < m < 6 D. – 1 < m < 2 4 2 x x
Câu 23. Tìm số nghiệm nguyên của bất phương trình  0 2 x  5x  6 A.3 B. 1 C. 2 D. 4
Câu 24. Biết rằng f x 2
ax bx c  0, x
   . Mệnh đề nào sau đây sai ? A. a + b + c > 0 B. 5a – b + 2c > 0 C. 10a – 2b + 2c > 0 D. 11a – 3b + 5c > 0
Câu 25. Hàm số bậc hai 2
f (x)  ax bx c có đồ thị
như hình vẽ. Tìm số nghiệm nguyên dương nhỏ hơn
30 của bất phương trình A. 29 B. 25 C. 24 D. 29
Câu 26. Tìm điều kiện tham số m để giá trị biểu thức 2
Q mx mx  5 luôn luôn âm với mọi số thực x. A. – 20 < m  0 B. – 10  m < 0 C. – 5  m < 2 D. – 12 < m  4 2 x  5x  4
Câu 27. Tập xác định của hàm số 2 f (x) 
 25  x chứa bao nhiêu số nguyên 2 2x  3x 1 A.5 B. 8 C. 7 D. 10
Câu 28. Tìm số nghiệm nguyên nhỏ hơn 40 của bất phương trình 2
(x x ) x  2x  5  0 . A.40 B. 34 C. 28 D. 18 2 x x 10
Câu 29. Có bao nhiêu số nguyên m để bất phương trình
 0 nghiệm đúng với mọi x ? 2
x  (2m 1)x  9 A. 2 B. 3 C. 4 D. 5 1
Câu 30. Tìm điều kiện tham số m để hàm số y  luôn xác định trên R. 2
x  6x m 1 A. m > 1 B. m > 9 C. m > 10 D. 3 < m < 8
Câu 31. Hàm số bậc hai 2
f (x)  ax bx c có đồ thị
như hình vẽ. Mệnh đề nào sau đây đúng
A. a  0;5a b  0
B. a  0;5a  2b  0
C. a  0; 4a b  0
D. a  0;5a b  0
Câu 32. Tìm điều kiện tham số m để bất phương trình 2
x  m  7 x m  6  0có tập hợp nghiệm S sao cho
S và tập hợp (5;7) có phần tử chung. A. m > – 1 B. m > – 2 C. m > 0 D. 0 < m < 2
Câu 33. Tìm điều kiện tham số m để bất phương trình m   2
2 x  2m  
1 x m  3  0 có tập nghiệm S =
[a;b] thỏa mãn điều kiện b = 2a. A. m = 8 B. m = – 7 hoặc m = 8 C. Không tồn tại D. m = – 7
Câu 34. Hàm số bậc hai 2
f (x)  ax bx c thỏa mãn điều kiện b   4 ; a c  3 ;
a a  0 . Tìm độ dài tập
nghiệm của bất phương trình f x  0 . A.3 B. 4 C. 2 D. 3,5
_________________________________ 17
DẤU TAM THỨC BẬC HAI, BẤT PHƯƠNG TRÌNH BẬC HAI LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P3)
________________________________________________________
Câu 1. Có bao nhiêu số nguyên m > – 10 để biểu thức K   2 m   2
3 x  2m  
1 x 1luôn luôn dương ? A. 16 giá trị B. 9 giá trị C. 14 giá trị D. 10 giá trị
Câu 2. Tìm giá trị nguyên lớn nhất của m để hàm số g x 4  m  
1 x  2m  
1 x m  2 không thể xác
định với mọi giá trị x. A. m = 3 B. m = 0 C. m = 2 D. m = 1 2x  5 1
Câu 3. Tìm số nghiệm nguyên   10 
;10của bất phương trình   0 . 2 x  6x  7 x  3 A.11 B. 10 C. 8 D. 9 2
Câu 4. Tìm điều kiện tham số m để  x   1  2  , m x  2;  3 . 1 A. m   B. m  2 C. m  3 D. m  6 4 3  7
Câu 5. Tìm điều kiện tham số m để hàm số h x 
xác định trên tập số thực. 1 m 2
x  2mx  5  9m A. m < 1 B. m < 0,5 C. m < 2 D. 1 < m < 2
Câu 6. Tìm điều kiện tham số m để bất phương trình 2
x  2mx  3m  6  0 nhận x = 1 làm nghiệm. A.m > 3 B. m > 4 C. m > 5 D. 0 < m < 6
Câu 7. Tìm điều kiện tham số m để 2 2
x  6mx  9m m  5, x    . A. – 2 < m < 4 B. 3 < m < 5 C. m < 5 D. 3 < m < 4 x  5 x  4
Câu 8. Tìm số nghiệm nguyên của bất phương trình  0 . 2 x  4x  6 A.15 B. 16 C. 20 D. 10
Câu 9. Cho mệnh đề:  2 m   2
1 x  2m  3 x 1  0, x    .
Tồn tại bao nhiêu số nguyên m lớn hơn – 10 để mệnh đề trên đúng ? A. 5 giá trị B. 17 giá trị C. 10 giá trị D. 8 giá trị
Câu 10. Tìm điều kiện tham số m để x  3 x m, x  4;9. A. m  - 8 B. m  0 C. m  - 2 D. m  1
Câu 11. Tìm điều kiện tham số m để biểu thức E  m   2
2 x  2m  2 x  2 không dương với mọi x. A. Không tồn tại B. m > 4 C. 1 < m < 2 D. m < – 2 4 x x  2
Câu 12. Tồn tại bao nhiêu số nguyên m nhỏ hơn 3 để hàm số y
xác định trên tập số thực ? 2
5x x m A. 1 giá trị B. 2 giá trị C. 4 giá trị D. 5 giá trị
Câu 13. Tồn tại bao nhiêu giá trị nguyên m để m   2
1 x  4m  
1 x m 1  0, x    ? A. 1 B. 2 C. 3 D. 0
Câu 14. Tìm điều kiện cần và đủ của tham số m để bất phương trình 2
x  m   2
2 x  8m 1  n , n   có nghiệm thực x. A. 0 < m < 5
B. 6  33  m  6  33
C. 6  2 33  m  6  2 33
D. 9  2 5  m  9  2 5 . 2 x  2x  4
Câu 15. Có bao nhiêu số nguyên m để hàm số y  xác định trên R ?  2
m  2m  8 2
x  2m  2 x  2 A. 5 giá trị B. 4 giá trị C. 3 giá trị D. 6 giá trị 2 3x ax  5
Câu 16. Tìm điều kiện tham số a để bất phương trình kép 1   6 luôn luôn đúng. 2 2x x 1 A. 0 < a  5 B. 1  a < 4 C. 2  a < 6 D. 0  a < 7 18
Câu 17. Tam thức bậc hai 2 2
f (x)  x  2(m 1)x m  6m  5 không đổi dấu qua điểm A.x = 0 B. x = 1 C. x = 2 D. x = 3 11  m 13
Câu 18. Hàm số y
có tập xác định là R khi và chỉ khi 2
2x  2m   1 x  2m 1
A. m  1 2;1 2 
B. m  3  2;3  2 
C. m  3  2 2;3  2 2 
D. m  5  2;5  2 
Câu 19. Xét tam thức bậc hai f x 2
x  6x m  7 . Tìm giá trị nguyên nhỏ nhất của tham số m để bất
phương trình f x  0 vô nghiệm. A. m = 3 B. m = 2 C. m = 1 D. m = 4
Câu 20. Tìm điều kiện tham số m để bất phương trình 2
x  m  7 x m  6  0có tập hợp nghiệm S sao cho
S và tập hợp (8;10) có phần tử chung. A. Mọi giá trị m B. 0 < m < 7 C. m < 4 D. 2 < m < 3 2 x  5x  6 x 1
Câu 21. Tìm số nghiệm nguyên   10 
;10của bất phương trình  . 2 x  5x  6 x A.15 B. 17 C. 16 D. 9
Câu 22. Tìm điều kiện tham số m để bất phương trình 2 x   2 m   2
1 x  2m  2  0 có ít nhất một nghiệm âm. A. Mọi giá trị m B. m > 0 C. 1 < m < 2 D. 0 < m < 3
Câu 23. Tìm tất cả các giá trị m để m   2
1 x  m  
1 x 1 2m  0, x    . 5 1 A.  m  1 B. 2 < m < 3 C.  m  2 D. 1  m  4 9 9 1
Câu 24. Giá trị biểu thức 2 Q
x  2m  2 2
x m luôn dương khi nào ? m A. 2 < m < 6 B. 4 < m < 9 C. 0 < m < 2 D. 1 < m < 4 2 3x mx  6
Câu 25. Tìm điều kiện tham số m để 9  
 6 xảy ra với mọi số thực. 2 x x 1 A. – 2 < m < 4 B. – 3 < m < 6 C. 1 < m < 5 D. – 1 < m < 7 x  3 1 2x
Câu 26. Tìm số nghiệm nguyên không âm của bất phương trình   . 2 2 x  4 x  2 2x x A.2 B. 1 C. 3 D. 4
Câu 27. Hàm số bậc hai 2
f (x)  ax bx c có đồ thị
như hình vẽ. Mệnh đề nào sau đây đúng
A. f (x)  0, x    B. f (x)  2  , x    C. 2
f (x)  a(x  1)  2 D. 2
f (x)  a(x 1)
Câu 28. Tìm điều kiện tham số m để   x m2 2 3 2  m  9, x    . A. – 2 < m < 6 B. 2 < m < 5 C. – 3 < m < 3 D. 1 < m < 7
Câu 29. Tìm giá trị bé nhất của tham số m để bất phương trình m   2
1 x  2m  
1 x  3m  3  0 vô nghiệm. A. m = 2 B. m = 4 C. m = 3 D. m = 1 2
3x  2x m
Câu 30. Tìm điều kiện tham số m để  1, x   2  ; 2 . 2   2x  3x  4 13 13 17 A. m  - 6 B. m   C. m   D. m   6 2 4
_________________________________ 19
DẤU TAM THỨC BẬC HAI, BẤT PHƯƠNG TRÌNH BẬC HAI LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P4)
________________________________________________________
Câu 1. Tìm số nguyên m lớn nhất để tam thức 2
x   m   2 2 2 2
1 x  2m m 1luôn âm với mọi giá trị thực x. A. m = 0 B. m = 2 C. m = 1 D. m = 3 2 x  3x 10
Câu 2. Tìm điều kiện tham số m để hàm số y  6
xác định trên tập số thực. m  2 2
x  2 3x m A. m > 0 B. m > 3 C. m > 1 D. m > 2 x  3 x  2
Câu 3. Tìm số nghiệm nguyên của bất phương trình  0 . x 1 A.4 B. 1 C. 2 D. 3
Câu 4. Cho mệnh đề: Hàm số F  m   2
2 x  2m  2 x m  4 luôn luôn xác định trên R.
Tồn tại bao nhiêu giá trị nguyên m không vượt quá 2017 để mệnh đề trên đúng ? A. 2018 giá trị B. 2017 giá trị C. 2020 giá trị D. 2015 giá trị 3x 10
Câu 5. Hàm số L
luôn xác định trên R khi nào ? m  2 2 6
x  2m  2 x m  4 A. m  2 B. m > 3 C. m > 2 D. 3 < m  5 x
Câu 6. Tìm số nguyên a nhỏ nhất sao cho  a, x    . 2 x 1 A. a = 3 B. a = 1 C. a = 4 D. a = 2 1 1
Câu 7. Tìm số nghiệm nguyên của bất phương trình  . 2 2 x x  5 2x  3x  5 A.3 B. 2 C. 1 D. 4
Câu 8. Tìm điều kiện tham số m để   x m2 2 5  m  49, x    . A. – 2 < m < 6 B. – 6 < m < 6 C. – 7 < m < 7 D. 1 < m < 7
Câu 9. Tìm tất cả các giá trị tham số m để biểu thức S  m   2
3 x 10m  2 x  23m  24 nhận giá trị
không âm với mọi giá trị thực x.  1  A. m 2;5 B. 2 < m < 7 C. m  2  ;  D. m 1;6 2   
Câu 10. Hàm số bậc hai 2
f (x)  ax bx c có đồ thị
như hình vẽ. Tìm số nghiệm nguyên của bất phương
trình f x  3 . A. 3 B. 2 C. 4 D. 5 2
Câu 11. Tìm tất cả các giá trị tham số m để hàm số y  có tập xác định D = R. 2
mx  4x m A. m > 2 B. m > 1 C. m > 0 D. m < 3 2 3x mx  5
Câu 12. Tìm m để bất phương trình kép 1 
 6 có tập nghiệm là D = R. 2 2x x 1 A. 0 < m < 4 B. 0 < m  5 C. 0  m < 6 D. 0  m  8 2 x x  4
Câu 13. Xác định tất cả các giá trị tham số m để
 2 với mọi số thực x. 2 x mx  4  1   5 3  A. m 2;5 B. m  2  ;  C. m 1;6 D. m   ; 2       2 2  20 2 2 x mx 1 3
Câu 14. Tìm điều kiện tham số m để   , x    . 2 3 x x 1 2 1 1 4 5 5 7 A.  m  4 B.  m  C.  m  4 D.  m  2 2 3 2 2 2 x m
Câu 15. Tìm đoạn giá trị của tham số m để hàm số y
có tập giá trị K = [– 1;1]. 2 x x 1 A. [0;1] B. [1;2] C. [4;5] D. [6;8]
Câu 16. Khoảng (a;b] là điều kiện cần và đủ của tham số m để biểu thức sau luôn luôn âm với mọi số thực x.
f x  m   2
4 x  5m  20 x  2m 1. Tính M = 11a + 3b. A. M = 30 B. M = 25 C. M = 44 D. M = 57
Câu 17. Tìm điều kiện tham số m để biểu thức m   2
2 x  2x  4 luôn luôn âm với mọi số thực x. A. m = 2 hoặc m < 1,75 B. m = 2 hoặc m < 1 C. m = 2 hoặc m > 3 D. m = 1 hoặc m > 6,5 1 2
Câu 18. Tìm số nghiệm nguyên của bất phương trình  . x x  4 3x x  8 A.8 B. 10 C. 12 D. 6
Câu 19. Tồn tại bao nhiêu số nguyên lẻ m để m m   2
8 x  2m  8 x  8m 1  0, x    ? A. 3 số nguyên lẻ B. 4 số nguyên lẻ C. 7 số nguyên lẻ D. 5 số nguyên lẻ
Câu 20. Tìm giá trị nhỏ nhất của m để bất phương trình 2
mx  2m  
1 x m  2  0 vô nghiệm. A. m = 0,5 B. m = 2 C. m = 1 D. m = 0,25 2
x  5x m
Câu 21. Nửa khoảng (a;b] là điều kiện của m để bất phương trình kép 1   7 luôn nghiệm đúng 2 2x  3x  2
với mọi số thực x. Tính H = 3a + 10b + 13. A. H = 26 B. H = 15 C. H = 18 D. H = 24 2 3x x 12
Câu 22. Đoạn [p;q] là điều kiện của m để  2, x
   . Tính G = 4a + 8b + 48. 2 x mx  4 A. G = 40 B. G = 50 C. G = 36 D. G = 28 3 11 m  5
Câu 23. Tìm điều kiện của tham số m để hàm số y
xác định với mọi số thực x. m   2
1 x  2mx  5  9m A. m > 0,5 B. m > 2 C. m > 0 D. m > 1 2
x mx m  3
Câu 24. Tồn tại bao nhiêu giá trị nguyên m để hàm số y
có tập xác định D = R. 4 2 x  4x  6 A. 5 giá trị B. 20 giá trị C. 12 giá trị D. 9 giá trị
Câu 25. Tìm điều kiện tham số m để bất phương trình 2
x  4x  3  m nghiệm đúng với mọi x thuộc đoạn [0;3]. 7 A. m  2 B.  m  2 C. m  1 D. m  3 4
Câu 26. Ký hiệu S là nghiệm của bất phương trình 2
x  m  
1 x m  0 . Tìm độ dài L của S khi biểu diễn S
thành đoạn thẳng trên trục số. A. L = |m – 2| B. L = |m + 1| C. L = |m| D. L = |m – 1|
Câu 27. Hàm số bậc hai 2
f (x)  ax bx c có đồ thị
như hình vẽ. Tìm số nghiệm nguyên của bất phương trình f x 2 2  x  6 . A. 8 B. 5 C. 7 D. 9
Câu 28. Tìm điều kiện tham số m để bất phương trình 2 x   2 m m   3 2
2 x  2m  4m  0 có ít nhất một nghiệm dương. A. Mọi giá trị m B. m > 0 C. 1 < m < 2 D. 0 < m < 3 21
DẤU TAM THỨC BẬC HAI, BẤT PHƯƠNG TRÌNH BẬC HAI LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P5)
________________________________________________________ 2016  2017
Câu 1. Tồn tại bao nhiêu giá trị nguyên m để hàm số f x  xác định trên R. 2
x m 3m  4x  9 A. 7 giá trị B. 8 giá trị C. 9 giá trị D. 10 giá trị 2 x  4x 10
Câu 2. Tìm số nghiệm nguyên của bất phương trình  0 . 2 x  4x  3 A.3 B. 1 C. 2 D. 4 2 2
Câu 3. Tìm điều kiện tham số m để bất phương trình 3x  2  2x   1
m có nghiệm x trong khoảng [0;2]. 1  A. m  7 B. m  C. m  3 D. 0, 2  m  7 5 11
Câu 4. Tìm điều kiện tham số m để hàm số y  luôn xác định trên R.
x 102  m 19 A. m > 1 B. m > 19 C. m > 10 D. 3 < m < 4
Câu 5. Tìm điều kiện tham số m để 2
x 10x m  24  0, x    . A. m > 5 B. m > 1 C. m > 7 D. m < 10 17  3
Câu 6. Tồn tại bao nhiêu giá trị nguyên của tham số của m để hàm số f x  xác 2
x  6mx  7mm  2 định trên R ? A. 12 giá trị B. 6 giá trị C. 5 giá trị D. 8 giá trị
Câu 7. Hàm số bậc hai 2
f (x)  ax bx c có đồ thị
như hình vẽ. Tìm số nghiệm nguyên của bất phương
trình f x  8 . A. 8 B. 4 C. 6 D. 7 15
Câu 8. Tìm điều kiện tham số m để hàm số f x  luôn xác định trên R.
3x  22  m 1 A. m > 1 B. m > 19 C. m > 2 D. 3 < m < 8
Câu 9. Tìm số nghiệm nguyên của bất phương trình 2
(x  5x  4) x  0 . A.4 B. 5 C. 1 D. 2
Câu 10. Tồn tại bao nhiêu giá trị nguyên của tham số m để 2 2
9x 12mx  4m  4  m , x    . A. 5 giá trị B. 4 giá trị C. 3 giá trị D. 7 giá trị
Câu 11. Tồn tại bao nhiêu số nguyên m để hàm số y   x  2 2
1  4m m có tập xác định là R. A. 6 giá trị B. 2 giá trị C. 5 giá trị D. 4 giá trị 2 1 2x 1
Câu 12. Tìm số nghiệm nguyên   10 
;10của bất phương trình   . 2 3 x x 1 x 1 x 1 A.4 B. 11 C. 10 D. Kết quả khác
Câu 13. Tìm điều kiện tham số m để bất phương trình m   2
1 x  2m  
1 x m  0 có nghiệm. m  1 m  1 1 A.   B. Mọi giá trị m C. 1 D.  m  1 m  0  m  2  2
Câu 14. Bất phương trình:  2 x x   2 3 4
x  5  0 có bao nhiêu nghiệm nguyên dương? A. 0 . B. 1. C. 2 . D. Nhiều hơn 2 22
Câu 15. Tính tổng các giá trị m để tam thức bậc hai 3 2 3
f (x)  m x  2(m 1) x  8 là bình phương của một nhị thức A.4 B. 3 C. 5 D. 2 2  9 
Câu 16. Tìm điều kiện tham số m để  x  5  3 x  2  2  , m x   ; 4  . 4    15 A. m  B. m  6 C. m  - 1 D. m  - 1 4
Câu 17. Tìm điều kiện tham số m để bất phương trình m   2
1 x  2mx m  3  0 vô nghiệm. 1 7 1 7  1 17 1 17  A. m  ;   B. m  ;   2 2   2 2   1 37 1 37  1 57 1 57  C. m  ;   D. m  ;   2 2   2 2  
Câu 18. Tồn tại bao nhiêu số nguyên m lớn hơn – 8 để hàm số 2 2 y
4x  40mx  25m m  3 luôn xác định trên R ? A. 7 giá trị B. 18 giá trị C. 11 giá trị D. 26 giá trị
Câu 19. Tìm điều kiện tham số m để x x m 2 4  2m  5  , m x    . A. – 2 < m < 4 B. 0 < m < 2 C. – 1 < m < 1 D. 0 < m < 2,5
Câu 20. Tồn tại bao nhiêu giá trị nguyên m để biểu thức 2 M  2
x  2m  2 x m  2 luôn luôn âm với mọi x thực ? A. 7 giá trị B. 1 giá trị C. 6 giá trị D. 14 giá trị 2 x  3x  4
Câu 21. Tìm số nghiệm nguyên của bất phương trình  0 . x x 1 A.3 B. 2 C. 5 D. 1
Câu 22. Tồn tại bao nhiêu giá trị m để tam thức bậc hai 3 2 3
f (x)  m x  2(m 1) x 1không đổi dấu tại một điểm nào đó. A.3 B. 2 C. 6 D. 4
Câu 23. Tìm điều kiện của tham số m để bất phương trình 2
x   m   2 2
1 x m m  6  0 có miền nghiệm chứa khoảng (1;5). 4 m  6 m  2  m  9 A. 0  m  B.  C.  D.  11 m  1  m  7  m  0 
Câu 24. Tìm điều kiện tham số m để bất phương trình 2
x   m   2 2
1 x m m  6  0 có ít nhất một nghiệm nhỏ hơn 2018. A. Mọi giá trị m B. m > 1 C. m < 1 D. m = 0
Câu 25. Hàm số bậc hai 2
f (x)  ax bx c có bảng
biến thiên như hình vẽ. Tìm giá trị nhỏ nhất k thỏa mãn
f x  k, x  3;4. A. k = 14 B. k = 18 C. k = 20 D. k = 24
Câu 26. Tìm điều kiện tham số m để 2 2
x  6mx  9m  2m  2  0, x    . A. – 5 < m < 3 B. 1 < m < 5 C. m < 1 D. 1 < m < 2,5
Câu 27. Tìm điều kiện tham số m để bất phương trình 2
x  m   2 2
2 x  3m  4m  4  0 có nghiệm. 4 7 A. Mọi giá trị m. B. 0  m  C. m  2  D. 2  m  11 2
Câu 28. Tìm số nghiệm nguyên < 100 của bất phương trình 2
(x  4 x ) x  3  0 A.85 B. 40 C. 96 D. 97 23
DẤU TAM THỨC BẬC HAI, BẤT PHƯƠNG TRÌNH BẬC HAI LỚP 10 THPT
(LỚP BÀI TOÁN CƠ BẢN P6)
________________________________________________________
Câu 1. Tồn tại bao nhiêu giá trị nguyên của tham số m lớn hơn – 7 để hàm số 2 2
y  9x  90mx  25m m  50 luôn xác định trên R ? A. 19 giá trị B. 8 giá trị C. 15 giá trị D. 14 giá trị
Câu 2. Tìm điều kiện tham số m để 2 2
x  4mx  4m  2m 1  0, x    . A. – 4 < m < 2 B. 0 < m < 4 C. – 1 < m < 1 D. m < 0,5 1
Câu 3. Tìm điều kiện tham số m để hàm số y  luôn xác định trên R. 2
x  4x m 1 A. m > 6 B. m > 1 C. m > 5 D. 3 < m < 8
Câu 4. Tồn tại bao nhiêu số nguyên m thuộc đoạn [– 10;10] để hàm số g x  mm   2
2 x  2mx  2 xác
định trên tập hợp số thực. A. 15 giá trị B. 17 giá trị C. 14 giá trị D. 18 giá trị
Câu 5. Tìm điều kiện tham số m để 2 2
x 10mx  25m  5m 10  0, x    . A. – 3 < m < 7 B. 0 < m < 5 C. m < 1 D. 0 < m < 4
Câu 6. Hãy tìm đoạn giá trị của tham số m để bất phương trình 2
x   m   2 3
2 x  2m  5m  2  0 có tập nghiệm là R. A. [2;6] B. [3;5] C. [1;4] D. [0;2]
Câu 7. Hàm số bậc hai 2
y ax bx c có đồ thị
như hình vẽ. Mệnh đề nào đúng ?
A. a < 0; b < 0; c > 0
B. a > 0; b > 0; c < 0
C. a > 0; b < 0; c < 0
D. a > 0; b > 0; c > 0
Câu 8. Tìm giá trị nhỏ nhất của tham số m để bất phương trình m   2
1 x  2m  
1 x  3m  3  0 vô nghiệm. A. m = 1 B. m = 2 C. m = 3 D. m = 4 2 x mx 1
Câu 9. Tìm m để bất phương trình kép
 2 có tập nghiệm là  . 2 x 1 A. – 2 < m < 2 B. 0 < m  1 C. 0  m < 3 D. 2  m  3
Câu 10. Tìm giá trị nhỏ nhất của m để bất phương trình  2
m m   2 2
3 x  2m  
1 x 1  0 vô nghiệm. A. m = 3 B. m = 2 C. m = 5 D. m = 1
Câu 11. Tìm điều kiện tham số m để tam thức f x 2
mx  2m  
1 x  4 không âm với mọi giá trị thực x.
A. 3  8  m  3  8
B. 3  2 8  m  3  2 8
C. 3  5  m  3  5
D. 3  4 5  m  3  4 5 2 x x  4
Câu 12. Tìm đoạn giá trị của tham số m để hàm số y  2 
có tập xác định là tập số thực. 2 x mx  4  5 3  A. [2;3] B. [0;3] C. [1;4] D.  ;  2 2   
Câu 13. Tìm điều kiện tham số m để 2
x  4x m  6  0, x    . A. m > 3 B. m > 8 C. m > 10 D. m < 10
Câu 14. Tìm điều kiện tham số k để 2
x  4x k  9  0 với mọi số thực x. A. k < 5 B. k < 4 C. k < 2 D. k > 10
Câu 15. Tìm điều kiện tham số m để hàm số y  a   2
1 x  2a  
1 x  3a  3 xác định với mọi giá trị thực x. A. a > 5 B. a > 2 C. a > 4 D. a > 1 24
Câu 16. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 8 để h x  m   2
1 x  2m  2 x m  6 không dương với mọi số thực x. A. 8 giá trị B. 15 giá trị C. 9 giá trị D. 16 giá trị
Câu 17. Tìm điều kiện tham số m để   x m2 2 5 2  m  25, x    . A. – 5 < m < 5 B. 0 < m < 5 C. – 5 < m < 6 D. 1 < m < 3 2 x x 1
Câu 18. Tìm điều kiện tham số m để hàm số f x 
xác định với mọi số thực x. 2 2
x  2mx m m  2 A. m > 2 B. m < 1 C. m > 4 D. m > 4 4 3 2
x  2x  2x  4x  5
Câu 19. Tìm điều kiện tham số m để hàm số f x  xác định với mọi x. 2
mx  2m   1 x  4mm  1  m  2  m  3  m  6  A.  B.  C.  D.  3m  1  3m  2  7m  2  7m  3 
Câu 20. Hàm số bậc hai 2
y ax bx c có đồ thị
như hình vẽ. Mệnh đề nào đúng ?
A. a < 0; b < 0; c > 0
B. a > 0; b > 0; c < 0
C. a > 0; b < 0; c < 0
D. a > 0; b > 0; c > 0 2
 3  3x x  2x 1, 
Câu 21. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm.  2 m  2   x  2 . m  A. Mọi giá trị m. B. m > 2 C. 1  m  2 D. 1 < m < 2
Câu 22. Tìm điều kiện của tham số m để bất phương trình 2 2
x  4x m  4m  8  0 có ít nhất một nghiệm lớn hơn 5. A. Mọi giá trị m B. m > 1 C. m < 1 D. m > 0 
x  3  x  2  2,
Câu 23. Tìm tất cả các giá trị của tham số m để hệ bất phương trình  có nghiệm. 3
x  2x m  4.  A. m > – 4 B. m < – 8 C. m > 2 D. 0 < m < 4
Câu 24. Tìm điều kiện của tham số m để bất phương trình 2
x   m   2 2
1 x m m  6  0 không nhận x = 5 làm nghiệm. A. m < 5 B. 2 < m < 7 C. 3 < m < 8 D. 0 < m < 5
Câu 25. Tìm điều kiện tham số m để m   2
1 x  2m  
1 x  3m  3  0, x    . A. m  2 B. m  1 C. m  3 D. m  4 2 2 x  3  x 10  4
Câu 26. Tìm điều kiện tham số m sao cho hàm số y  có tập xác định D = R. 2
x  m  2 x  8m 1 A. 0 < m < 5 B. 0 < m < 28 C. 1 < m < 67 D. 2 < m < 10
Câu 27. Tìm điều kiện tham số m để bất phương trình 2
mx  2m  
1 x m  4  0 có tập nghiệm S = [a;b]
thỏa mãn đẳng thức 4a + b = 3. A. m = 8 hoặc m = 0,5 B. m = 8 hoặc m = 1 C. m = 0,5 hoặc m = 3 D. m = 2 hoặc m = 2,5
Câu 28. Tính tổng tất cả các giá trị tham số m để bất phương trình 2
x   m   2 2
1 x m m  6  0 có miền
nghiệm S = [a;b] thỏa mãn đẳng thức 3 3
a b  35 . A. – 1 B. 3 C. 2 D. 0
Câu 29. Ký hiệu S là tập hợp nghiệm của bất phương trình 2 x   2 m m   2 2
7 x m  2m  6  0 . Giả sử L
là độ dài đoạn thẳng miền nghiệm trên trục số. Tìm giá trị tham số để L ngắn nhất. A. m = 2 B. m = 0 C. m = 1 D. m = – 2 25
CƠ BẢN BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI (MỘT ẨN) LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG HỢP P1)
________________________________________
Câu 1. Tìm điều kiện tham số m để bất phương trình 2
3x m mx  4m  3 nghiệm đúng với mọi số thực x. A. m = 4 B. m = 3 C. m = 2 D. m = 1
Câu 2. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 2x y  1? A.  2  ;  1 . B. 3; 7   . C. 0;  1 . D. 0;0 .
Câu 3. Biết rằng f x 2
ax bx c  0, x
   . Mệnh đề nào sau đây đúng ? A. a + b + 2c > 0 B. 9a – 2b + c > 0 C. 4a – 2b + c > 0 D. 4a – 3b + 7c > 0 2 x  3x  2
Câu 4. Bất phương trình
 0 có bao nhiêu nghiệm nguyên x 1 A.3 B. 2 C. 1 D. 4
Câu 5. Cho bất phương trình 2
3x  2(2m 1) x m  4  0 . Tìm số giá trị nguyên của m để bất phương trình
trên có tập nghiệm là R A. 3. B. 2. C. 4. D. 5. x 1
Câu 6. Với x thuộc tập hợp nào dưới đây thì f x  không dương? 2 x  4x  3 A. S   ;   1 . B. S   3  ;   1 1;  . C. S   ;  3    1  ;  1 . D. S   3   ;1 .  2x 1   2
Câu 7. Có bao nhiêu số nguyên dương m để hệ bất phương trình  3 có nghiệm ? 3
x m  5  A. 5 B. 4 C. 2 D. 1
Câu 8. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình x  4 y  5  0 ? A.  5  ; 0 . B.  2   ;1 . C. 1; 3   . D. 0;0 .
Câu 9. Với x thuộc tập hợp nào dưới đây thì nhị thức f x  x  2 x   1 không âm? A.  ;    1 1;  . B.  1
 ; 01;  . C.  ;    1 0;  1 . D.  1  ;  1 . 3  (x  6)  3 
Câu 10. Tìm điều kiện tham số m để hệ bất phương trình 5x m có nghiệm.  7   2 A. m > – 11 B. m < 11 C. m < – 11 D. m  11
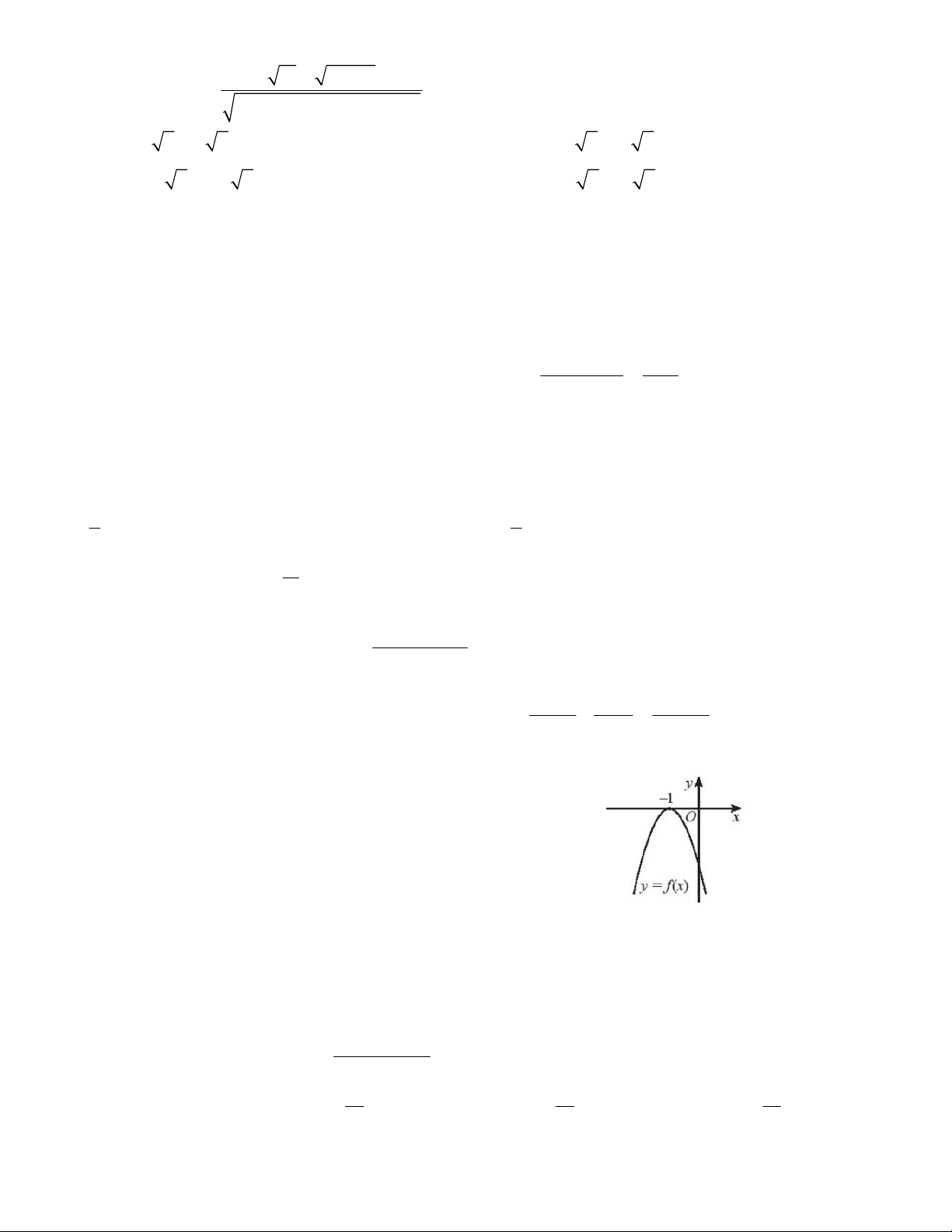
Câu 11. Tam thức f x 2
 x  3x  4 nhận giá trị âm khi và chỉ khi
A. x  –4 hoặc x  –1.
B. x  1 hoặc x  4 .
C. –4  x  –4 . D. Mọi x
Câu 12. Cho tam thức 2
f (x)  x 12x 13 . Có bao nhiêu giá trị nguyên của x để f(x) nhận giá trị âm A. 12 . B. 14 C. 15 . D. 13 .
Câu 13. Tìm điều kiện tham số m để bất phương trình  2 x   2 1
m m  5  m 1  0 có tập nghiệm S = R. A. m < 2 B. m = – 4 C. m > 1 D. m > 1,5
Câu 14. Biểu thức nào dưới đây là nhị thức bậc nhất? A. f x 2  6  3x .
B. f x  2x 1.
C. f x  5. D. f x 3  2x 1.
Câu 15. Cho biểu thức f x   m  1 x  2 x  2 . Tìm m để biểu thức f x  là nhị thức bậc nhất A. m  2. B. m  2. C. m  1. D. m  1. 3
Câu 16. Nhị thức nào sau đây nhận giá trị âm với mọi số nhỏ hơn  ? 2 A. f ( ) x  2x  3. B. f (x)  2  x  3. C. f ( ) x  3  x  2 . D. f ( ) x  2  x  3 .
Câu 17. Bất phương trình ax b  0 nghiệm đúng với mọi x khi a  0 a  0 a  0 a  0 A.  . B.  . C.  . D.  b  0  b  0  b  0  b  0  26
Câu 18. Với giá trị nào của a thì bất phương trình 2
ax x a  0 có tập nghiệm là  1 1 A. a  0 . B. a  0 . C. 0  a  . D. a  . 2 2 2 x(x 1)
Câu 19. Bất phương trình
 0 có số nghiệm nguyên là x  3 A.4 B. 3 C. 2 D. 1
Câu 20. Tìm m để bất phương trình m   2
1 x mx m  0 có tập nghiệm là  ? 4  4 A. m  1. B. m  1. C. m  . D. m  . 3 3
Câu 21. Bất phương trình  2 x x   2 2
2x 1  0 có bao nhiêu nghiệm nguyên dương? A. 0 . B. 1. C. 2 . D. Nhiều hơn 2
Câu 22. Tìm số giá trị nguyên k để bất phương trình 2
x   k   2 2 4
1 x 15k  2k  7  0 nghiệm đúng với mọi x A. 3 . B. 1. C. 4. D. 2..
Câu 23. Tìm giá trị tham số m để  2
m mx m   2 2 5
m  6 x  2  3m với mọi giá trị x. A. m = 4 B. m = 3 C. m = 2 D. m = 1
Câu 24. Tìm số nghiệm nguyên lớn hơn – 20 của bất phương trình 4 2
x(x 1) (x  2x  3)  0 A.20 B. 21 C. 18 D. 15
Câu 25. Tìm số giá trị nguyên m để phương trình 2
(m  5)x  (m 1)x m  0 có 2 nghiệm x , x thỏa mãn 1 2
điều kiện x  2  x . 1 2 A. 3. B. 2. C. 4. D. 1.
Câu 26. Tập nghiệm của bất phương trình 2 x  2 
x  6x  9 là:  1   1   1  A. ;    . B. ;   . C. 3;  . D. ;    .  2   2   2 
Câu 27. Bất phương trình:  2 x x   2 3 4
x  5  0 có bao nhiêu nghiệm nguyên dương? A. 0 . B. 1. C. 2 . D. Nhiều hơn 2
Câu 28. Tìm điều kiện tham số m để bất phương trình 2
x   m   2 2 4
1 x m 1  0 có ít nhất một nghiệm lớn hơn 2017. A. Mọi giá trị m B. m > 1 C. m < 1 D. m > 0
Câu 29. Tìm điều kiện tham số m để bất phương trình 2
x  4x  3  m nghiệm đúng với mọi x thuộc đoạn [0;3]. 7 A. m  2 B.  m  2 C. m  1 D. m  3 4
Câu 30. Tìm điều kiện của m để bất phương trình 2 2
x  2(m  2) x  2m  3m  0 có nghiệm A.Mọi x B. 1  m  4 . C. m   
;1  3;  D. . 2
x  2  4x 1, 
Câu 31. Tìm giá trị nhỏ nhất của tham số m để hệ bất phương trình 2  vô nghiệm. 
x m  92  x m  2 1 .  A. m = 14 B. m = 8 C. m = 12 D. m = 6
Câu 32. Với mọi giá trị tham số m, bất phương trình 2
x  2m  
1 x m  3  0 luôn có tập nghiệm S = (a;b).
Tìm hệ thức liên hệ giữa a và b độc lập với tham số m.
A. a b  2ab  2
B. a b  2ab  4
C. a b  2ab  4
D. a b ab  3 2 4x 9
Câu 33. Bất phương trình
 2x 3. có bao nhiêu nghiệm nguyên thuộc [ -21; 22]? ? 2 2(x  4) A. 22 . B. 20 . C. 21. D. 23.
Câu 34. Có bao nhiêu số nguyên m để phương trình 2 3 2
x  (m 1)x m m  5  0 có nghiệm âm A.Vô số B. 10 C. 22 D. 14
Câu 35. Tìm số nghiệm nguyên của bất phương trình x 10 x  9  0 A.81 B. 9 C. 10 D. 24 27
CƠ BẢN BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI (MỘT ẨN) LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG HỢP P2)
________________________________________
Câu 1. Với giá trị nào của m thì bất phương trình 2
x mx 1  0 có tập nghiệm là  A. 2  m  2 B. m  1 . C. m  2 D. 1  m  3
Câu 2. Tìm tập xác định của hàm số 2
y  2x  5x  2 .  1   1   1  A.  ;   . B. 2; . C.  ;  2;    . D. ; 2 . 2        2   2  2
x  2  4x 1, 
Câu 3. Tìm giá trị nhỏ nhất của tham số m để hệ bất phương trình 2  vô nghiệm. 
x m  92  x m  2 1 .  A. m = 14 B. m = 8 C. m = 12 D. m = 6
Câu 4. Cho f x  2
ax bx c a  0. Điều kiện để f x 0, x    là a   0  a   0  a  0 a   0 A.  .    B.  . C.  D.    . . 0    0    0    0 
Câu 5. Tìm điều kiện tham số m để bất phương trình  3
m  9m 10 x m  4  0 có tập nghiệm S = R. A. m = 4 B. m = – 4 C. m = 1 D. m = 1,5 3  x  5  0,
Câu 6. Tìm điều kiện tham số m để hệ bất phương trình 
có độ dài tập nghiệm bằng 2. 2mx  3  . m  9 7 A. m = 1 B. m =  C. m – 2 D. m =  25 26
Câu 7. Cho f x 2
ax bx ca  0 . Điều kiện để f x 0, x   là a   0 a   0 a   0 a   0 A.  . B.  C.  D.  .       0    0    0    0 
Câu 8. Bất phương trình: 3x  2  x có tập nghiệm là: A. 2;  1 . B. 1; 2. C. 2;3. D.  –1; 2. 1 2
Câu 9. Tồn tại bao nhiêu giá trị nguyên m để hàm f x  xác định trên R. 2 2
x  8mx  59m 10m A. 2 giá trị B. 4 giá trị C. 3 giá trị D. 1 giá trị 1 2
Câu 10. Tìm tất cả các giá trị thực của tham số m sao cho ptrình x m   1 x m   0 có nghiệm ? 3 3 3 A. m  .  B. m  1. C.   m 1. D. m   . 4 4
Câu 11. Xác định tất cả các giá trị m để hệ bất phương trình sau có tập nghiệm là một đoạn trên trục số có độ dài bằng 1 đơn vị 2
3x  2x 12   3x  4,  x
mx   1  m  6.  A. m = 3 B. m = 2 C. m = – 6 D. m = – 2
Câu 12. Phương trình 2
x  2(m  2)x  2m 1  0 ( m là tham số) có nghiệm khi m  1 m  5 m  5 A.  .        B. 5 m 1. C. . D. . m  5  m  1  m  1 
Câu 13. Cho hàm số f x 2
x  2x m . Với giá trị nào của tham số m thì f x  0, x    . A. m  1 . B. m  1. C. m  0 . D. m  2 .
Câu 14. Tìm tất cả các giá trị của tham số m để tam thức f(x) = 2
x  m  2 x  8m 1  0 . x    A. m 0; 28 .
B. m  ;0  28;   . C. m  ;0  28;  . D. m  0; 28 . 28  
m  3 x m  2  0,
Câu 15. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm. 3  x  4  0.  A. Mọi giá trị m B. Không tồn tại C. m > – 3 D. m  – 3
Câu 16. Có bao nhiêu số nguyên m để với mọi x biểu thức f x 2
x  m  2 x  8m 1 luôn nhận giá trị dương. A. 27 . B. 28 . C. Vô số. D. 26 . 2 x  5x  6
Câu 17. Tìm x để f x  không âm. x 1 A. 1;  3 .
B. 1;2 3;  . C. 2;3 . D.  ;   1 2;  3 .
Câu 18. Bất phương trình 2 2
x  3x  6 x 3 .
x có tập nghiệm là  ; a b ; c d ; (a, , b ,
c d  ) . Tính tổng a + b + c + d A. 4 . B. 0 . C. 1. D. 6  .    x  2 2 3
x  7x 1,
Câu 19. Tìm giá trị bé nhất của tham số m để hệ bất phương trình  vô nghiệm. 2m  8  5 . x  A. m = 6,5 B. m = 7,5 C. m = – 6 D. m = – 2
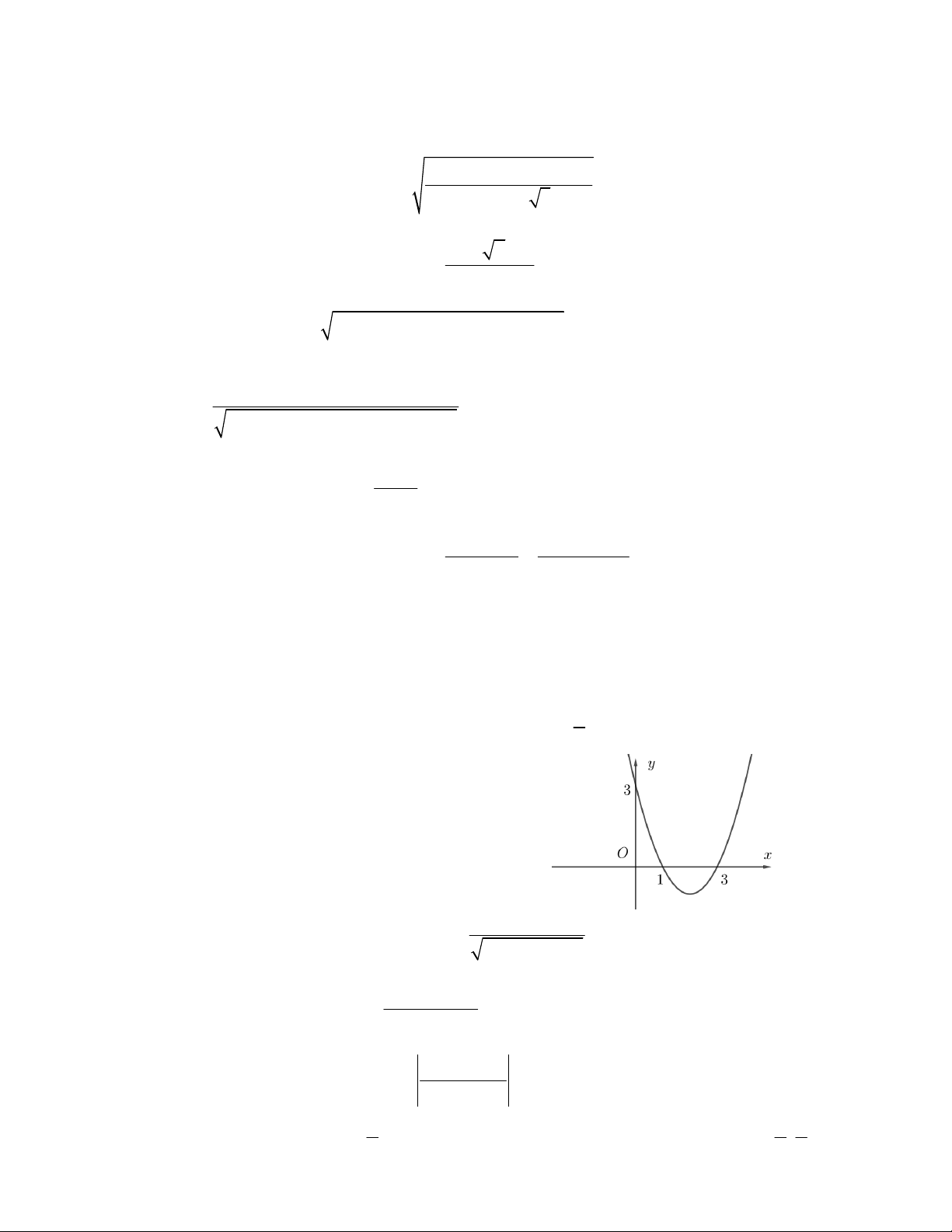
Câu 20. Dấu của tam thức bậc 2: 2 f ( )
x  x  5x  6 được xác định như sau
A. f x  0 với 2  x  3 và f x  0 với x  2 hoặc x  3.
B. f x  0 với 3   x  2
 và f x  0 với x  3  hoặc x  2  .
C. f x  0 với 2  x  3 và f x  0 với x  2 hoặc x  3.
D. f x  0 với 3   x  2
 và f x  0 với x  3  hoặc x  2  .
Câu 21. Tập nghiệm của bất phương trình 2
x x  6  0 là: A.  ;  3    2;  . B.  3  ; 2 . C.  2  ;3 . D.  ;  2    3;  .
Câu 22. Tìm điều kiện tham số m để
m 1 x   1  m  0, x    . A. m = 1 B. m = 3 C. Không tồn tại D. m = 2
Câu 23. Giá trị nào là nghiệm nguyên âm lớn nhất của bất phương trình 2
x  5x  6  0 ? A. 3 . B. 1. C. 2 . D. 0 .
Câu 24. Gọi S là tập nghiệm của bất phương trình 2
x x  6  0 , S có tập con nào sau đây ? A.  ;  0 . B. 1;7 . C.  2  ; 2 . D. 6; . 2
Câu 25. Tập xác định của hàm số y  là: 2 x  5x  6 A.  ;  6
 1;  . B.  6  ;  1 . C.  ;  6    1;  . D.  ;    1  6; . 2
x x 12  0,
Câu 26. Tìm tất cả các giá trị của tham số m để hệ bất phương trình  vô nghiệm.
x 1  2x  . m  A. m  4 B. m  4 C. m > 4 D. m  3
Câu 27. Bất phương trình 2
mx  2m  2 x m  3  0 có tập nghiệm S = [a;b] thỏa mãn điều kiện 2 2
a b  1. Giá trị tham số m tìm được nằm trong khoảng nào ? A. (0;1) B. (4;6) C. (1;3) D. (6;8)
Câu 28. Bất phương trình: 2x  3  x có tập nghiệm là: A. 3;  B. ;   1  3;  C.  ;    1 D. R
Câu 29. Giá trị nào không là nghiệm của bất phương trình 2
x x  6  0 ? A. 2 . B. 1. C. 2 . D. 0 . 2
x  4x  9
Câu 30. Tìm điều kiện của m sao cho  0, x    . 2
x  (m 1)x  4 A. Mọi giá trị m B. m  5  ;   3 C. m  4  ; 2   D. m > 0
_________________________________ 29
CƠ BẢN BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI (MỘT ẨN) LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG HỢP P3)
________________________________________ 11
Câu 1. Tìm điều kiện tham số m để hàm số y  luôn xác định trên R.
x 102  m 19 A. m > 1 B. m > 19 C. m > 10 D. 3 < m < 4
Câu 2. Cho f x  m   2 ( )
1 x  2 m  
1 x  4 . Tập hợp tất cả các giá trị m để giá trị của hàm số không âm [a;b]. Tính giá trị 2 2 a b . A. 4 B. 10 C. 9 D. 3 2
x x  3   x,
Câu 3. Tìm điều kiện tham số m để hệ bất phương trình  x có duy nhất nghiệm. mx   1  2.  A. m = 3 B. m = 1 C. m = – 6 D. m = – 3
Câu 4. Cho f x  2
ax bx ca  0 . Điều kiện để f x  0, x   là a   0 a   0 a   0 a   0 A.  . B.  C.  D.  .       0    0    0    0 
Câu 5. Với x thuộc tập hợp nào dưới đây thì f x 2
x  2x  3 luôn dương? A.  . B. R. C.  ;    1  3; . D.  1  ;3 . 3x m   2
Câu 6. Tìm điều kiện của m để hệ bất phương trình  2 
có độ dài tập nghiệm lớn hơn 3.  2(  x 1)  5  A. m > 1 B. m < 4 C. m > 0,5 D. 0 < m < 3
Câu 7. Tìm điều kiện tham số m để m  3 x  7, x   2 . A. m < 0,5 B. m > 1 C. m > 0,5 D. m < 4
Câu 8. Với x thuộc tập hợp nào dưới đây thì tam thức f x 2
x  6x  8 không dương? A. 2;3 . B.  ;  24;  . C. 2; 4 . D. 1;4. Câu 9. Tam thức 2
f (x)  x  2x  3 nhận giá trị dương khi và chỉ khi
A. x  –3 hoặc x  –1.
B. x  –1 hoặc x  3 .
C. x  –2 hoặc x  6 . D. –1  x  3 . x  2 4
Câu 10. Tổng các nghiệm nguyên dương của bất phương trình  . x  4 x  4 A. 21 . B. 15 . C. 13 . D. 11.
Câu 11. Số nghiệm nguyên của bất phương trình 3  x 2x  5  0 là A. 6 . B. 5 . C. 0 . D. Vô số.
Câu 12. Cho f x 2
ax bx ca  0 . Điều kiện để f x 0, x   là a  0 a   0 a   0 a  0 A.  . B.  C.  D.  .        0   0    0     0
Câu 13. Với giá trị nào của m thì bất phương trình 2
(2m 1)x  3(m 1)x m 1  0 (1). có nghiệm. A. m [-5; 1] B. .m  (5; 2) C. m   ;  5    1  ;  D. m [7; ) 2
x mx m
Câu 14. Bất phương trình 2  
 2 có tập nghiệm là R khi và chỉ khi 2 x x 1 A. 2   m  2 . B. 2   m  10 .
C. m  2  m  10 . D. 2  m  10 .
Câu 15. Bất phương trình x 1  2 có tập nghiệm là
A. S   ;   1  3;    .
B. S   ; 1  3;    .
C. S  1;3 .
D. S  1;3 . x  2  0
Câu 16. Tìm tất cả các giá trị của tham số m để hệ sau có nghiệm  . 2
x  2x m  0  A. m  1 B. m  2 C. m  1 D. m  30
Câu 17. Tìm điều kiện tham số m sao cho  2
m  4 x m  3  2, x    . A. m = 3 B. m = 4 C. m = 2 D. m = – 2
Câu 18. Cho bất phương trình 2
2x  4x m  5  0 . Tìm m để bất phương trình nghiệm đúng với x  3 ? A. m  11 . B. m  1  1. C. m  1  1. D. m  11 .
Câu 19. Cặp số 2;3 là nghiệm của bất phương trình nào sau đây?
A. 2x – 3y –1  0 .
B. x – y  0 . C. 4x  3y .
D. x – 3y  7  0 .
Câu 20. Giá trị nào là một nghiệm của bất phương trình 2
x x  6  0 : A. 4 . B. 1. C. 2 . D. 3 . 2017
Câu 21. Tồn tại bao nhiêu số nguyên m < 10 để hàm số y  xác định trên R ?
x x 10  2m 10 A. 7 giá trị B. 8 giá trị C. 10 giá trị D. 6 giá trị 2 x  4x  4
Câu 22. Tìm số nghiệm nguyên thuộc  9
 ;9 của bất phương trình  0 2 x  4x  5 A.16 B. 18 C. 17 D. 5
Câu 23. Giá trị nào không là nghiệm của bất phương trình 2
x  8x 16  0 : A. 4 . B. 1. C. 4 . D. 3 . 2
x x 12  0,
Câu 24. Tìm tất cả các giá trị của tham số m để hệ bất phương trình  vô nghiệm.
x 1  2x  . m  A. m  4 B. m  4 C. m > 4 D. m  3
Câu 25. Tìm m để bất phương trình (m 1)x  3(m 1) vô nghiệm. A. m  1. B. m  1. C. m  1. D. m  1.
Câu 26. Biết rằng bất phương trình f x  m   2 ( )
1 x  2mx  m  3  0 vô nghiệm. Tổng các giá trị nguyên của
m thỏa mãn f (x)  0 với mọi giá trị x là A. 1. B. 2 . C. 0 . D. 1.
Câu 27. Tìm điều kiện xác định của bất phương trình x  2  x  2. 2 xx  2  A. 2   x  0 . B. x  2  . C.  . D. x  0 . x  0  2x 1
Câu 28. Điều kiện xác định của bất phương trình   0 là: 2 x 1 x  4 x  2   x  2 x  2  x  2 A.  . B.  . C.  . D.  . x  1  x  1  x  1  x  1 
Câu 29. Bất phương trình 2x 1  x  2  6  
1 có bao nhiêu nghiệm nguyên? A. 10 . B. 8 . C. 11. D. 9 .  x  3   0,
Câu 30. Tìm điều kiện tham số m để hệ bất phương trình  x  4 có nghiệm. 3
x m  1.  A. m < 7 B. m < 8 C. 2 < m < 6 D. 3 < m < 9
Câu 31. Tập nghiệm của bất phương trình 2  5  x  7 có bao nhiêu số nguyên? A. 12 . B. 13 . C. 10 . D. 11 . 2 2x  7x  5
Câu 32. Tìm giá trị nhỏ nhất của tham số m để bất phương trình
m luôn đúng với mọi x. 2 x  5x  7 A. m = 2 B. m = 5 C. m = 6 D. m = 3
Câu 33. Để bất phương trình 2
(x  5)(3  x)  x  2x a nghiệm đúng x   5  ; 
3 , tham số a phải thỏa điều kiện nào sau đây A. a  3 . B. a  4 . C. a  5 . D. a  6 .
_________________________________ 31
CƠ BẢN BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI (MỘT ẨN) LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG HỢP P4)
________________________________________
Câu 1. Tam thức nào dưới đây luôn dương với mọi giá trị của x ? A. 2
x 10x  2 . B. 2
x  2x 10 . C. 2
x  2x 10 . D. 2
x  2x 10 . x  3 1 2x
Câu 2. Có bao nhiêu giá trị nguyên dương của x thỏa mãn   ? 2 2 x  4 x  2 2x x A. 0. B. 2. C. 1. D. 3.
Câu 3. Có tất cả bao nhiêu giá trị nguyên của 2 2
m để ptrình 2x  2m  2 x  3  4m m  0 có nghiệm ? A. 3. B. 4. C. 2. D. 1. 2
Câu 4. Các giá trị m để phương trình x m  2 x  8m 1  0 có hai nghiệm phân biệt ?
A. m  0 hoặc m  28.
B. m  0 hoặc m  28. C. 0  m  28. D. m  0. 2
x  2x  3m
Câu 5. Tìm điều kiện tham số m để  1, x   2  ; 2 . 2   2x x  2 8 13 A. m   B. m   C. m  2 D. m  - 1 3 6  4 
Câu 6. Tìm điều kiện tham số m để x  5 x  4  m, x   ;9  . 9    4 4 A. m  - 8 B. m  C. m  - 5 D. m  3 3
Câu 7. Tập nghiệm của bất phương trình 2
x  6x  9  0 là: A. 3;  . B.  . C.  \   3 . D.   3 . 2
x x m
Câu 8. Với giá trị nào của m thì bất phương trình
 0 có tập nghiệm là  2 x  4x  5 1 1 A. m  1 . B. m  1 . C. m  . D. m  . 4 4
Câu 9. Gọi S là tập nghiệm của bất phương trình 2
x  8x  7  0 . Tập hợp nào là tập con của S ? A.  ;  0 . B. 1;7 . C. 0;2. D. 6; . 2
2x  2  5x,
Câu 10. Tìm tất cả các giá trị của tham số m để hệ bất phương trình  có nghiệm.
x  3  3x  . m  A. m  1 B. m < 2 C. 0  m  3 D. m < 5
Câu 11. Tập nghiệm của bất phương trình x  1  3 x  2  5 7   5 7   7   5  A.  ;    . B.  ;   . C.  ;    . D. ;    .  2 4   2 4   4   2 
Câu 12. Giá trị của m để f (x)  mx 1  0 với x là: A. m  1. B. m  0 . C. m  0 . D. m  0 .
Câu 13. Với giá trị nào của m thì f x  mx m  2x luôn dương? A. m  0 . B. m  2 . C. m  2  . D. m  . 3x  5 x  2
Câu 14. Bất phương trình  1 
x có bao nhiêu nghiệm nguyên lớn hơn 1  0? 2 3 A. 10. B. 5. C. 9. D. 4.
Câu 15. Tìm m để bất phương trình 2
m x  3  mx  4 có nghiệm A. m  0 B. m  1
C. m  1 hoặc m  0 D. m    2 x 1  0
Câu 16. Hệ bất phương trình  vô nghiệm khi: x m  0  A. m  1 B. m  1 C. m  1 D. m  1
Câu 17. Bất phương trình:
x  2  4  x có nghiệm nguyên nhỏ nhất là: 32 A. 3 . B. 1. C. 0. D. 2. 3
x  5  x  7
Câu 18. Tìm tất cả giá trị thực của tham số m để hệ bất phương trình  vô nghiệm. m x  3  A. m  9 B. m  3 C. m  9 D. m  3
Câu 19. Tìm điều kiện tham số m để hàm số f x  2x m  2  2m 1 mx xác định với mọi x  1. A. m = 0 hoặc m  - 1 B. m = 0 hoặc m  - 2 C. m = 1 hoặc m  0 D. m = 2 hoặc m  1.  x 1   0,
Câu 20. Tìm điều kiện tham số m để hệ bất phương trình  x  2 có nghiệm duy nhất. 4x 1  . m  A. m = 6 B. m = 5 C. 3 < m < 5 D. m = 2
Câu 21. Nghiệm nguyên dương nhỏ nhất của bất phương trình: 2x 1  3  x là: A. 1 . B. 2 . C. 0 . D. 3 .
Câu 22. Bất phương trình 2
mx  2m  2 x m  3  0 có tập nghiệm S = [a;b] thỏa mãn điều kiện 2 2
a b  1. Giá trị tham số m tìm được nằm trong khoảng nào ? A. (0;1) B. (4;6) C. (1;3) D. (6;8) 3  x  4  0
Câu 23. Tìm tất cả các giá trị của tham số m để hệ bất phương trình  vô nghiệm
m  2x  5  0  7 7 7 7 A. m   . B. m  . C. m   . D. m   . 3 3 3 3
Câu 24. Với mọi giá trị tham số m, bất phương trình 2
x  2m  
1 x m  3  0 luôn có tập nghiệm S = (a;b).
Tìm hệ thức liên hệ giữa a và b độc lập với tham số m.
A. a b  2ab  2
B. a b  2ab  4
C. a b  2ab  4
D. a b ab  3
Câu 25. Bất phương trình: 2 8  x
x  2 có tập nghiệm là: A. 2;  2 2 . B. 2; 2 2 . C. 3;  2 2 . D.  –3; 2. 2018
Câu 26. Tồn tại bao nhiêu giá trị nguyên m nhỏ hơn 40 để hàm y  luôn xác định trên R ? 2
9x 12x m  6 A. 17 giá trị B. 28 giá trị C. 30 giá trị D. 29 giá trị
Câu 27. Hàm số bậc hai 2
y ax bx c có đồ thị
như hình vẽ. Tìm số nghiệm nguyên của bất phương
trình f (x)  0 A. 1 B. 2 C. 3 D. 4
Câu 28. Tồn tại bao nhiêu giá trị nguyên của tham số m để 2 2
9x 12mx  4m  4  m , x    . A. 5 giá trị B. 4 giá trị C. 3 giá trị D. 7 giá trị
Câu 29. Bất phương trình: 2
x  2x 15  x  3 có tập nghiệm là: A. x  5 . B. 5  x  6 . C. 3  x  6 . D. 3  x  5 .
Câu 30. Tìm điều kiện tham số m để hàm số 2 2 y
x  6mx  9m m  2 có tập xác định là R. A. m  1 B. m  6 C. m  2 D. m  7
Câu 31. Tìm điều kiện của m sao cho 2
2x  5x  2  m, x  1;0. 9 A. m  2 B. 2  m  9 C. m  9 D. m   8 2
x  4x  3  0,
Câu 32. Tìm tất cả các giá trị của tham số m để hệ bất phương trình  vô nghiệm.
x 1  2x  3 . m  A. m  0 B. m  1 C. m  3 D. m  6
_________________________________ 33
CƠ BẢN BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI (MỘT ẨN) LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG HỢP P5)
________________________________________
Câu 1. Tồn tại các giá trị a và b để a b   2 2
1 x a  3b  2  0, x
   . Khi đó điều kiện tham số b là b  2 b  3 b  1 b  4 A.  B.  C.  D.  b  0,5  b  0  b  0, 75  b  0, 25 
Câu 2. Tìm điều kiện tham số m sao cho  2 m  
1 x m 10  3, x    . A. m = 1 B. m = 4 C. m = 2 D. m = – 1
Câu 3. Tìm điều kiện tham số m để mx  2  0, x   1. A. m > 3 B. m > 2 C. m > 4 D. 5 < m < 6 x  2  0,
Câu 4. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm duy nhất. mx m  4.  A. m = 3 B. m = 4 C. m = 2 D. m = 0 2
Câu 5. Với x thuộc tập hợp nào dưới đây thì biểu thức f x  1 âm? 1 x A.  ;    1 . B.  ;    1  1;  . C. 1;   . D.  1  ;  1 .
Câu 6. Tập nghiệm của bất phương trình 5x  4  6 có dạng S   ;  a ;
b  . Tính tổng P  5a b . A. 1. B. 2 . C. 3 . D. 0 .
Câu 7. Bất phương trình mx m  3x vô nghiệm khi A. m  3. B. m  0. C. m  3  . D. m  . 
Câu 8. Tìm m để phương trình m   2
1 x  2 m  2 x m  3  0 có hai nghiệm trái dấu.
A. m  1, m  3.
B. m  2, m  3 . C. 1  m  3 . D. m  3 .
Câu 9. Tìm giá trị của tham số m để phương trình 2
x  m   2
2 x m  4m  0 có hai nghiệm trái dấu. A. m  2. B. 0  m  4. C. m  2.
D. m  0 hoặc m  4.
mx m  3 
Câu 10. Hệ bất phương trình
có nghiệm duy nhất khi và chỉ khi   m  3 
x m  9  A. m  1. B. m  2  . C. m  1  . D. m  2 .
Câu 11. Tìm giá trị của tham số m để phương trình 2
x mx 1  0 có hai nghiệm phân biệt.
A. m  1 hoặc m  1.
B. Không có giá trị m.
C. m  2 hoặc m  2 .
D. m  2 hoặc m  2 . x 1
Câu 12. Tìm điều kiện xác định của bất phương trình sau 6  3x   5 2 x  2x  3  x  2  x  2  x  3 A.  . B. 2  x  3 . C.  . D.  . x  3   x  1   x  1  
Câu 13. Bất phương trình nào sau đây tương đương với bất phương trình x  5  0 A. 2
x x  5  0 . B.
x  5  x  5  0 . C.  x  2 1  x  5  0 . D.
x  5  x  5  0 .
Câu 14. Điều kiện để bất phương trình 2
ax bx c  0; với a  0 có tập nghiệm bằng  là A.   0 . B.   0 C.   0 D.   0 .
Câu 15. Tập nghiệm của bất phương trình 2 x 1  0 là: A. 1; . B.  1  ;  . C.  1  ;  1 . D.  ;    1  1; .
Câu 16. Nghiệm nguyên dương nhỏ nhất của bất phương trình 2
x x 1  0 là: A. 0 . B. 1. C. 2 . D. 3 .
Câu 17. Tập nghiệm của bất phương trình 2
x  4x  4  0 là: A. 2;  . B.  . C.  \   2  . D.  \   2 .
Câu 18. Tập nghiệm của bất phương trình 2
x  4 2x  8  0 là: A.  ;  2 2  . B.  \ 2 2. C.  . D.  . 34 2
Câu 19. Cho pt m 
5 x  2m 
1 x m  0  
1 . Tìm số giá trị nguyên của m để pt (1) có 2 nghiệm x , x thỏa 1 2 x 2 x 1 2 A. 3. B. 2. C. 4. D. 1.
Câu 20. Cho bất phương trình 2 2
x  (2m  2)x m  2m  0 . Tìm m để bất phương trình nghiệm đúng với mọi x thuộc đoạn 0;1   ? m   0   m  1  A. 1  m  0 . B. . C. 1   m  0 . D. . m   1       m 2 
Câu 21. Bất phương trình nào sau đây vô nghiệm A. 2
x  8x 16  0 B. 2
2 x  5x  4  0 C. 2
2x  7x  9  0 D. 2
x 10x  24  0
Câu 22. Điều kiện để bất phương trình 2
ax bx c  0a  0, có tập nghiệm bằng  là a   0 a   0 a   0 a   0 A.  . B.  C.  D.  .       0    0    0    0 
Câu 23. Bất phương trình: 2
x  6x  5  8  2x tương đương với hệ nào sau đây ? 8   2x  0 2 
x  6x  5  0 A.  . B.  2
x  6x  5  8  2x 2 
x  6x  5  8  2x  8   2x  0 8   2x  0 C.  . D.  2
x  6x  5  8  2x 2 
x  6x  5  8  2x
Câu 24. Bất phương trình: 2x 1  3  x tương đương với hệ nào sau đây ? 2x 1  0 2x 1  0 3   x  0  3   x  0      A. . . B. . C. 3   x  0 . D. 3   x  0 . 2x 1   3 x2  2x 1   3  x2    2x 1   3  x2  2x 1   3 x2 
2  x  4x 3
Câu 25. Bất phương trình
 2. có bao nhiêu nghiệm nguyên thuộc [ -21; 22]? x A. 22 . B. 20 . C. 21. D. 23.
Câu 26. Hàm số bậc hai 2
y ax bx c có đồ thị
như hình vẽ. Tập nghiệm của bất phương trình
f (x)  0 có bao nhiêu số nguyên A. 2 B. 1 C. 3 D. 4 2 x mx  2
Câu 27. Bất phương trình  1
 luôn luôn đúng trên R khi và chỉ khi nào ? 2 x  3x  4
A. m < – 4 hoặc m  0
B. m < – 3 hoặc m  0 C. m < 2 hoặc m > 5
D. m < – 6 hoặc m  1 2 3
x x  4  2
Câu 28. Bất phương trình
 2. có bao nhiêu nghiệm nguyên? x A. 0 . B. 2 . C. 1. D. 3 . 2
x  2x  3,
Câu 29. Tìm tất cả các giá trị của tham số m để hệ bất phương trình  vô nghiệm.
x 1  4x  3 . m  4 2 4 A. m < B. m  C. m  1 D. m  3 3 3
Câu 30. Tìm điều kiện của m sao cho 2
2x  5x  2  m, x   1  ;0. 9 A. m  2 B. 2  m  9 C. m  9 D. m   8 35
CƠ BẢN BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI (MỘT ẨN) LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG HỢP P6)
________________________________________ 2 x  4x 19
Câu 1. Tồn tại bao nhiêu giá trị nguyên m trong khoảng (– 19;19) để y  4 xác định  2 m  2 2
x  2m   1 x 1
với mọi giá trị thực x ? A. 15 giá trị B. 20 giá trị C. 17 giá trị D. 19 giá trị
Câu 2. Tìm điều kiện tham số m để hàm số 2 2 y
x 10mx  25m m  2 có tập xác định là R. A. m  1 B. m  6 C. m  2 D. m  7 2 x  8x  7
Câu 3. Bất phương trình
 0 có số nghiệm nguyên là 2 x  2x  3 A.6 B. 3 C. 8 D. 7
Câu 4. Tìm giá trị nhỏ nhất của tham số m để 2 2
x 12mx  3m m 1  0, x    . A. m = 1 B. m = 2 C. m = 3 D. m = 4 2 x  9
Câu 5. Tìm số nghiệm nguyên của bất phương trình  0 . 4 x 1 A.7 B. 6 C. 5 D. 10 2
x  4x  3  0,
Câu 6. Tìm tất cả các giá trị của tham số m để hệ bất phương trình  vô nghiệm.
x 1  2x  3 . m  A. m  0 B. m  1 C. m  3 D. m  6
Câu 7. Tìm điều kiện tham số m để hàm số 2 2 y
x  6mx  9m m  2 có tập xác định là R. A. m  1 B. m  6 C. m  2 D. m  7
Câu 8. Tìm điều kiện tham số m để 2 2
x  4mx  3m  5  m, x    . A. – 5 < m < 6 B. 0 < m < 5 C. – 1 < m < 2 D. 0 < m < 6
Câu 9. Tìm điều kiện tham số m để bất phương trình 2
x  m   x   2 2 3m   1  0 có nghiệm. 4 7 A. Mọi giá trị m. B. 0  m  C. m  2  D. 2  m  11 2 2 x  4x  4
Câu 10. Tập nghiệm của bất phương trình  0 là 2
2x  3x  4  x A.  . B.   2  . C. . D.  \   2 .
Câu 11. Tập nghiệm của bất phương trình 2
x  m  4 x  5m  
1  0 là một khoảng có độ dài bằng 10. Tính
tổng L bao gồm tất cả các giá trị của m xảy ra. A. L = 12 B. L = 19 C. L = 10 D. L = 20
Câu 12. Tìm điều kiện tham số m để bất phương trình 2 x   2 m  
1 x  0 có tập hợp nghiệm S sao cho S và
tập hợp (5;10) có phần tử chung. A. |m| < 3 B. |m| > 2 C. |m| < 4 D. 1 < |m| < 5  7x  4 1, 
Câu 13. Tìm điều kiện tham số m để hệ bất phương trình 2 x x 1  có nghiệm. 2
x  2m  2 x mm  4  0.  A. m  5 B. m  5 C. Mọi giá trị m. D. 2  m  3  8   1,
Câu 14. Tìm đoạn giá trị của tham số m để hệ bất phương trình 3  x vô nghiệm.
x  3  m . x   8   1   3   4  A.  ; 0  B.  ; 2 C.  ; 2 D.  ;3 5           5   5   5 
Câu 15. Tìm điều kiện tham số m để bất phương trình 2
x  2mx m  2  0 có tập nghiệm với độ dài bằng 2. A. m = 3 B. m = 1 hoặc m = – 2 C. m – 1 hoặc m = 2 D. Không tồn tại m. 36
x  2  x   2,
Câu 16. Tìm điều kiện tham số m để hệ bất phương trình  x có nghiệm. 5
x x m 1.  A. m < 5 B. m < 4 C. m < 0 D. m > 7
Câu 17. Tìm điều kiện tham số m để m  3 x  7, x   2 . A. m < 0,5 B. m > 1 C. m > 0,5 D. m < 4 x  2  0,
Câu 18. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm duy nhất. mx m  4.  A. m = 3 B. m = 4 C. m = 2 D. m = 0 3
Câu 19. Tồn tại bao nhiêu số m nhỏ hơn 30 để hàm số f x  luôn xác định 2 2 2
x 12mx  36m m m  9
trên tập hợp số thực ? A. 21 giá trị B. 22 giá trị C. 20 giá trị D. 25 giá trị 2 x  4x 3
Câu 20. Tìm số nghiệm nguyên của bất phương trình  . x  2 x  2 A. 1 nghiệm B. 2 nghiệm C. 4 nghiệm D. 3 nghiệm x 1
Câu 21. Hai bất phương trình
 0;  2x m  0 có tập nghiệm lần lượt là A và B. Tồn tại bao nhiêu số x 1
nguyên m thuộc [– 10;10] để A B ? A. 12 B. 9 C. 10 D. 8
Câu 22. Hàm số bậc hai 2
y ax bx c có đồ thị
như hình vẽ. Tập nghiệm của bất phương trình
f (x)  5 có bao nhiêu số nguyên A. 3 B. 1 C. 5 D. 4
Câu 23. Cho tam thức 2
f (x)  x  (m  2)x  3m  3. Tập hợp S bao gồm tất cả các số nguyên dương m để
f (x)  0, x
  5 . Tổng tất cả các phần tử của tập hợp S là A. 6 B. 15 C. 11 D. 21
Câu 24. Giả sử f x 2
ax bx c  0, x
   . Mệnh đề nào sau đây đúng ?
A. 4a  2b c  0
B. 9a  3b c  1  2
C. a b c  3  0
D. a b c  2  1
Câu 25. Tìm điều kiện tham số m để bất phương trình  x  2 4 m  
1 x  5m  0 có tập nghiệm là [2;4].    1   1  A. m  2;  B. m = 3 C. m = 2 D. m  2; ;0  2   2 
Câu 26. Tìm điều kiện tham số m để bất phương trình m   2
3 x  2m  
1 x m  5  0 có tập nghiệm S =
[a;b] thỏa mãn điều kiện 2 2
a b ab  39 .  49  49 A. m  4;  B. m = 49 C. m  D. Không tồn tại m.  19  19 2x  3 x 1
Câu 27. Tìm số nghiệm nguyên của bất phương trình  0 . 2x  3 x 1 A.1 B. 2 C. 3 D. Kết quả khác 2
2x  3x m
Câu 28. Tìm điều kiện tham số m để  1, x   0; 4 . 2   x  2 17 A. m <  B. m < 0 C. m  1 D. m  - 6 4
_________________________________ 37
BPT + HỆ BPT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P1) _____________________________ 2
3x  6x  3m
Câu 1. Tìm điều kiện tham số m để  2, x   5  ; 2 . 2   2x x  2 17 13 16 17 A. m   B. m   C. m   D. m   8 6 3 4
Câu 1. Tìm số nghiệm nguyên lớn hơn – 40 của bất phương trình 2 4
x  4x  2  x  4  x   . A.30 B. 24 C. 28 D. 40 2
ax x 1  0, 
Câu 2. Tìm giá trị của a để hệ bất phương trình 2
x ax 1  0, có nghiệm duy nhất.  2
x x a  0.  A. a = – 4 B. a = – 2 C. a = 1 D. a > 5 2
x  3x m
Câu 3. Tìm điều kiện tham số m để phương trình  0 có nghiệm. x 1  2 9  9 A. m  B. m  C. m  2  D. m  2  4 4
Câu 4. Tìm điều kiện của m để bất phương trình 4 3
x x   m   2 2 4 2
4 x  4mx m  0 có nghiệm duy nhất. A. m = 2 B. m = 0 C. m = 3 D. m = 1 2
x  4x  5m
Câu 5. Tìm điều kiện tham số m để  1, x   3  ;3 . 2   2x x  2 1 17 A. m  0 B. m  - 7 C. m   D. m   4 4
Câu 1. Tìm số nghiệm nguyên của bất phương trình 2
x  4   x  4   2
x x     2 1 2 6 3 2
7 x  3x  2  1  x   . A.3 B. 1 C. 2 D. 4 2
2x  6x m
Câu 6. Tìm điều kiện tham số m để bất phương trình
 4 có nghiệm x thuộc đoạn [4;5]. 2 x x  4 A. m  0 B. m  - 7 C. m  - 24 D. m  - 6
Câu 7. Ký hiệu S là tập hợp nghiệm của bất phương trình 2 x   2 m m   2
3 x m m  2  0 . Giả sử L là độ
dài đoạn thẳng miền nghiệm trên trục số. Tìm giá trị tham số để L ngắn nhất. A. m = 2 B. m = 0 C. m = 1 D. m = 0,5
Câu 1. Tìm số nghiệm nguyên nhỏ hơn 30 của bất phương trình
x   x    x   2 2 3 5 4
x  8  2x  21x 10  x   . A.29 B. 28 C. 18 D. 15
Câu 2. Tồn tại bao nhiêu giá trị nguyên của tham số m trong đoạn [– 30;10] để phương trình sau có nghiệm ?
x  5 x  6 x  8 x  9  m . A. 13 giá trị B. 26 giá trị C. 14 giá trị D. 10 giá trị
Câu 9. Ký hiệu S là tập hợp nghiệm của bất phương trình 2
x   m   2 8
1 x 15m  3m  0 . Tìm điều kiện của
m để khi biểu diễn trên trục số, độ dài của S lớn hơn 3. m  2 m  3 m  1 m  1 A.  B.  C.  D.  m  6   m  7   m  1   m  11   2
ax bx c  0, 
Câu 10. Tìm điều kiện cần và đủ của các tham số a, b, c để hệ bất phương trình 2 bx
cx a  0, có nghiệm.  2
cx ax b  0.  A. a + b + c > 0 B. a + b + c > 1 C. 2 < a + b + c < 3 D. 2a + b – c > 4 38
Câu 11. Tìm điều kiện của tham số m để bất phương trình 2
x  m   2 2 2
1 x m  4m  3  0 có tập nghiệm S
= x ; x thỏa mãn điều kiện 2
2x  2 m 1 x  4m  3  2  m . 1   2 1 2  2 A. m = – 3 B. m = 2 C. m = 1 D. Không tồn tại m.
Câu 12. Tìm điều kiện tham số m sao cho  2
x x   m   2 1
1 x  3m  
1  m  2  0, x      .  1   1   6  A. m  1;  B. m  1;   C. m  3;   D. m  1 2     5   5 
Câu 13. Tìm điều kiện của tham số m để  2 x x   a   2 3 4 10
1 x  2a  
1 x  3a  3  0, x    . A. a > 5 B. a > 2 C. a > 4 D. a > 1
Câu 14. Tìm điều kiện của tham số m để  x x   x mx m m  3 2 2 2 2 7 2 2
 0 với mọi số thực x. A. m > 2 B. m < 1 C. m > 4 D. m > 4 2
Câu 15. Tìm điều kiện tham số m để bất phương trình  2
x x     2 5 4
3 x  5x  4  m có nghiệm. 9 3 A. m   B. m   C. m  1 D. 1  m  10 4 2
Câu 1. Tìm số nghiệm nguyên nhỏ hơn 80 của bất phương trình  x   2 3
x x  4x  9  x   . A.40 B. 70 C. 60 D. 65
Câu 19. Tồn tại bao nhiêu giá trị nguyên của tham số m trong đoạn [– 30;40] để bất phương trình sau nghiệm
đúng với mọi giá trị thực x ?  2
x x   2 x x   2 2 4 3 4  mx . A. 38 giá trị B. 41 giá trị C. 61 giá trị D. 37 giá trị
Câu 23. Tam thức bậc hai f x 2
ax bx c  0, x
   và b > c > a. Tìm giá trị lớn nhất của biểu thức b c c a F   . 9a  2c
7a  3b  3c 5 1 2 A. F max = 0,2 B. F max = C. F max = D. F max = 6 3 5
Câu 21. Tìm điều kiện tham số m để bất phương trình  2 x x  2 2 6
 6x x  5  2m có nghiệm. 79 A. m  16 B. m  C. m  10 D. m  6 16
Câu 1. Tìm số nghiệm nguyên của bất phương trình 2
x  4  6  x x 10x  27  x   . A.3 B. 2 C. 1 D. 4
Câu 22. Tìm giá trị lớn nhất của k để bất phương trình
x  2  x k có nghiệm. A. k = 2 2 B. k = 2 C. k = 3 D. k = 5 2
x  2x  3
Câu 23. Với mọi số thực x, luôn tồn tại a và b để a
b . Tính giá trị biểu thức a + b. 2 x 1 5 2 A. B. 1 C. 2 D. 3 5   x  3 1 1  3x  2, 
Câu 24. Tìm điều kiện của tham số m để hệ  có nghiệm duy nhất.
x  3x  2   x x m2 2 2 .  A. m = 1 hoặc m = 3 B. m = 0 hoặc m = 5 C. m = 6 hoặc m = 2 D. m = 4 hoặc m = 2 x x
Câu 25. Tìm số nghiệm nguyên của bất phương trình  1 . 2
1 2(x x 1) A.3 B. 2 C. 1 D. 0
_________________________________ 39
ÔN TẬP BPT + HỆ BPT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P2)
________________________________________ 2
Câu 1. Tìm điều kiện tham số m để bất phương trình  2
x x     2 3 2
2 x  3x  2  m có nghiệm. A. m  9  B. m  1 C. m  1 D. 3  m  2
Câu 2. Tìm số nghiệm nguyên nhỏ hơn 30 của bất phương trình
x   x x  3  x x x   x  2   x  6 3 2 2 1 1 1 1  x   . A.19 B. 31 C. 26 D. 40 2
x  3x m
Câu 3. Tìm điều kiện tham số m để phương trình
 0 nghiệm đúng với mọi giá trị x thuộc [3;4].
x  3  4  x A. 4  m  3  B. m  4 C. 3  m  0 D. 0  m  4
Câu 4. Giả sử a b   2 4
3 x a  3b  2  0, x
   . Mệnh đề nào sau đây sai ? a  4b  6 b 1 A.  0 B.  0 2 2a  3b  3 16b 11 a 1 a 1 b 1 C.  0 D.   2 4a 1
4a 1 16b 11 2 
x  2x m 1  0,
Câu 5. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm duy nhất. 2
x  4x  6m  6  0.  A. m = 1 B. m = 2 C. m = 0 D. m = 3 2
Câu 6. Tìm độ dài tập nghiệm của bất phương trình 8x  3 2x   1 4x   1  1815  x  . A.2,75 B. 3,75 C. 1,25 D. 2
Câu 7. Khoảng giá trị [p;q] là điều kiện cần và đủ của tham số m để hệ bất phương trình sau có nghiệm. 2
x  3x  4  0,   3 2
x  3x x m 15m  0.   Tính S = q – p. A. S = 17 B. S = 20 C. S = 10 D. S = 12
Câu 8. Tìm điều kiện tham số m để bất phương trình 2 2
6x x  6x x  5  m  2 có nghiệm. 27 A. m  7 B. m > 9 C. 7  m  13 D. m  4
Câu 9. Tìm điều kiện tham số m để bất phương trình  x   x   x   x   2 4 5 6 10
12  3mx có nghiệm thực. 9 1 5 1 A. m   B. m   C. m   D. m   4 3 12 18
Câu 10. Có bao nhiêu số nguyên x thỏa mãn bất phương trình  2
x xx   2 x   3 2 2 1
2x 1  5x x  2x 1  x   . A.1 B. 0 C. 2 D. 5
Câu 11. Tìm giá trị lớn nhất của tham số m để bất phương trình
x  2  11  x k nghiệm đúng với mọi x thuộc đoạn [2;11]. A. m = 2 B. m = 3 C. m = 6 D. m = 4 2
x  8x  7  0, 
Câu 12. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm duy nhất. 2 x   2m   2
1 x m m  0.  A. m = 0 hoặc m = 8 B. m = 0 hoặc m = 7 C. m = 1 hoặc m = 2 D. m = 4 hoặc m = 6
Câu 13. Tìm giá trị nhỏ nhất của tham số m để bất phương trình 4 3 2
x  2x mx  2x 1  0 có nghiệm thực. A. m = – 1 B. m = – 2 C. m = – 4 D. m = – 7
Câu 14. Tìm điều kiện của tham số m để hệ sau đây có nghiệm x
  x     x x m2 2 3 , 
 2x  3  x  2x  6.  A. m = 1 B. m = – 4 C. m = – 6 D. m = 7 40
Câu 15. Tìm điều kiện của m để bất phương trình 4 3
x x   m   2 2 8 2
16 x  8mx m  0 có nghiệm duy nhất. A. m = 2 B. m = 0 C. m = 3 D. m = 4 2 2x  4x  5
Câu 16. Hàm số y
có tập giá trị H = [a;b]. Tính giá trị biểu thức M = 2a + 3b. 2 x 1 A. M = 0 B. M = 1 C. M = 0,5 D. M = 2 4 2
x  5x  4  0 
Câu 17. Tìm điều kiện của m để hệ bất phương trình  có nghiệm duy nhất. 2 x   2m   2
1 x m m  2  0. 
A. 2 < m < 3 hoặc – 4 < m < – 3
B. 3 < m < 5 hoặc 0 < m < 4
C. 1 < m < 4 hoặc m < – 2
D. 2 < m < 5 hoặc 7 < m < 8
Câu 18. Tìm độ dài miện nghiệm của bất phương trình 2
(4x 14) 2  x  (x 1) 2x 1  6x 14  0 . 2 1 1 A.0,5 B. C. D. 7 6 3
Câu 19. Ký hiệu S là nghiệm của bất phương trình 2
x   m   2 2
3 x m  3m  2  0 . Tìm điều kiện của tham
số m sao cho 1;4  S . A. m = 4 B. m < 3 C. 3 < m < 5 D. Không tồn tại m.
Câu 20. Tìm điều kiện tham số m để bất phương trình 2
x  2m  
1 x  0 có tập nghiệm chứa miền (1;3). A. m > 2 B. m < 1 C. m < 0 hoặc m > 2 D. m  1 2
x  5x  4  0, 
Câu 21. Khoảng giá trị [p;q] là điều kiện cần và đủ của m để hệ bất phương trình  có 2 3
x mx x 16  0.  nghiệm. Tính Z = q – p. A. Z = 1 B. Z = 2 C. Z = 5 D. Z = 8
Câu 22. Khoảng (a;b] là điều kiện cần và đủ của tham số m để biểu thức sau luôn luôn âm với mọi số thực x. 5
f x   4
x x   m   2 1
4 x  5m  20 x  2m 1   . Tính M = 11a + 3b. A. M = 30 B. M = 25 C. M = 44 D. M = 57
Câu 23. Ký hiệu S là nghiệm của bất phương trình 2
x   m   2 2
5 x m  5m  6  0 . Tìm độ dài L khi biểu diễn S trên trục số. A. L = 3 B. L = 2 C. L = 1 D. L = 4 Câu 24. Tìm điều kiện của m để tập hợp nghiệm của bất phương trình 2 x   2 m   3 2
2 x m m  2m  0 chứa khoảng (1;2) A. m < 1 B. 0 < m < 4 C. m < 0 D. m > 1 hoặc m < 0
Câu 25. M là độ dài miền nghiệm của bất phương trình 2 2 x x
x  2  3(x  2x  2) . Khi đó M gần
nhất với giá trị nào sau đây A.3,87 B. 2,56 C. 3,23 D. 4,48
Câu 26. Tìm điều kiện của các tham số a, b, c để a bx c b a  1với mọi số thực x.
A. a = b và 0  c  1 B. a = b và c < 1 C. a = b và c > 0 D. a = b và 0 < c < 2
Câu 27. Tìm tất cả các giá trị tham số m để bất phương trình 2
x  9  x
x  9x m nghiệm đúng với
mọi giá trị x thuộc đoạn [0;9]. 9 9 1 A. m   B.   m  0 C. m  D. 0  m  1 4 4 4
Câu 28. Ký hiệu S là nghiệm của bất phương trình 2
x   m   2 2
5 x m  5m  6  0 . Tìm điều kiện tham số m
để S chứa miền [p + 3; p + 10] với p là hằng số thực. A. m = 3 B. m = 0 C. m = 1 D. Không tồn tại
Câu 29. Tìm điều kiện tham số m sao cho  3 2
x x  2x  2mx   1  0, x    . A. m = 2 B. m = 1 C. m = 0 D. m = – 1
_________________________________ 41
BPT + HỆ BPT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P3)
________________________________________
Câu 1. Tam thức bậc hai f x 2
ax bx c  0, x
   và b > c > a. Tìm giá trị lớn nhất của biểu thức b c c a P   .
4a  2b  3c 5c  2b 6 1 2 A. P max = 0,5 B. P max = C. P max = D. P max = 7 3 5
Câu 2. Tìm số thực p nhỏ nhất sao cho a b 2 2
x p a b 1  0 với mọi số thực x. A. p = 2 B. p = 1 C. p = 0 D. p = 3
Câu 3. Tìm điều kiện tham số m để hệ sau đây có nghiệm 3  4x 2 x   5,    x  22  4 2 2
x  8x 16mx 16m  32m 16  0.  A. m = 4 B. m = 3 C. m = – 2 D. m = – 1
x  1 x  1 x, 
Câu 4. Tìm điều kiện tham số m để hệ  có nghiệm duy nhất.
2x  2mx x  m  2 3 2 1  0.  A. m = – 1 hoặc m = – 2 B. m = 0 hoặc m = – 3 C. m = 1 hoặc m = – 2 D. m = – 1 hoặc m = 2
Câu 5. Tìm số thực m nhỏ nhất sao cho 2 2 2
x 1 y y 9  z z 10  x m với mọi giá trị x, y, z làm biểu thức xác định. A.10 B. 11 C. 12 D. 12,5 2 x  
m  2 x  2m  0,
Câu 6. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm. 2 x  
m  7 x  7m  0.  A. m < 4 B. m < 0 C. 1 < m < 4 D. 8 < m < 10
Câu 7. Tìm độ dài tập nghiệm (tính cả biên) của bất phương trình 2 x   2 9
x  2x  2 x  3  x  6  x 5  x  48x  68  x   . 2 A.1 B. 0,5 C. D. Kết quả khác 3 2 2 x k
Câu 8. Tìm tất cả các giá trị tham số k để bất phương trình
 1đúng với mọi x thỏa mãn |x| < 1. k 6  x 7  3 5 7  3 5 7  5 7  5 A. k  B. k  C. k  D. k  2 3 3 4
Câu 9. Tìm điều kiện tham số m để bất phương trình 2
x  mx x  2 2
 2m m 1  0 có nghiệm.  1 1   1   5 3   5 7  A. m   ;  B. m  1; C. m   ; D. m   ; 2 2           2   2 2   2 2 
Câu 10. Ký hiệu S là tập hợp nghiệm của bất phương trình 2 x   2
m   x m 2 4
m m  4  0 . Giả sử L là
độ dài đoạn thẳng miền nghiệm trên trục số. Giá trị nhỏ nhất L đạt được là A. L min = 3 B. L min = 2 C. L min = 3 D. L min = 1
Câu 11. Ký hiệu k là giá trị lớn nhất của tham số m để bất phương trình 4 3 2
x  7x  7mx  7x 1  0 có nghiệm
thực. Mệnh đề nào sau đây đúng ? 57 11 25 A. m = B. m = 1 C. m = D. m = 28 23 13 2 2 x  8x 12 x  8x 12
Câu 12. Số nghiệm nguyên âm của bất phương trình  là 5  x 5  x A. 3 B. Vô số C. 2 D. 0 42
Câu 13. Ký hiệu k là giá trị nhỏ nhất của tham số m để bất phương trình 4 3 2
x x  5mx x 1  0 có nghiệm
thực. Mệnh đề nào sau đây đúng ? 9 11 25 A. m = 1 B. m =  C. m =  D. m =  20 13 14
Câu 14. Ký hiệu S là nghiệm của bất phương trình 2
x  m  6 x  2m  8  0 . Tìm điều kiện của m để khi biểu
diễn trên trục số, độ dài của S lớn hơn 5. m  6 m  3 m  4 m  5 A.  B.  C.  D.  m  2   m  7   m  3   m  1  
Câu 15. Tìm giá trị lớn nhất của tham số m để bất phương trình sau nghiệm đúng với mọi số thực x
x  2 x  3 x  4 x  5  m . A. m = – 4 B. m = – 2 C. m = – 1 D. m = 2 2 1 3xa
Câu 16. Bất phương trình
x  2  5x 1 có tập nghiệm S  ;  
 với a, b nguyên dương và 5x 1  b
nguyên tố cùng nhau. Tính a + b. A. 10 B. 11 C. 15 D. 18
Câu 17. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 sao cho  2
x x   m   2 4 5
3 x  2m  3 x m  2  0, x      . A. 10 giá trị B. 6 giá trị C. 8 giá trị D. 7 giá trị
Câu 18. Tìm điều kiện của tham số m để hệ sau đây có nghiệm
x1 xx  2x  3  2x m  32 2 ,    x  3 1  2 x   1   0. 2   x 1  x A. m = 2 B. m = 3 C. m = – 4 D. m = 5
Câu 19. Tìm giá trị nguyên lớn nhất của tham số m để bất phương trình 3 31  x  4 x  6  m nghiệm đúng
với mọi giá trị x thuộc đoạn [6;31]. A. m = 11 B. m = 15 C. m = 25 D. m = 10
Câu 20. Hàm số bậc hai f (x) có bảng biến thiên như hình vẽ. Có bao nhiêu số
nguyên m nhỏ hơn 10 để bất phương trình sau có nghiệm:
f ( cos 2x  2)  m . A. 7 B. 8 C. 6 D. 10
Câu 21. Tìm điều kiện của tham số m để bất phương trình 2
x  m   2 2 2
1 x m  4m  3  0 có tập nghiệm S
= x ; x thỏa mãn điều kiện 2 4  2
x  2 m 1 x m  4m  3  1 m 1   2 1 2  2   . A. m = – 3 B. m = 2 C. m = 1 D. m = 0
Câu 22. Tìm điều kiện của tham số m để bất phương trình 4 3 x x   m   2 2 10 2
25 x 10mx m  0 có nghiệm duy nhất. 9 25 A. m = B. m = 0 C. m = D. m = 1 4 4
Câu 23. Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình 2 4 2
m (x 1)  m(x 1)  6(x 1)  0 có nghiệm S   . Tổng tất cả các phần tử thuộc S bằng A. – 1,5 B. 1 C. – 0,5 D. 0,5
Câu 24. Độ dài tập nghiệm của bất phương trình 2 3
4x  25x 14  3 x  31x  30 gần nhất với số nào A.3,28 B. 4,26 C. 3,65 D. 2,85
_________________________________ 43
BPT + HỆ BPT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P4) _____________________________ 2
x  2mx  4m  3  0, 
Câu 1. Tìm điều kiện tham số m để hệ bất phương trình  vô nghiệm. 2 x   2m   2
1 x m m  0. 
A. 2 < m < 3 hoặc – 4 < m < – 3
B. 3 < m < 5 hoặc 0 < m < 4 C. 2  2  m  2  2
D. 2 < m < 5 hoặc 7 < m < 8
Câu 2. Tìm độ dài tập nghiệm (tính cả biên) của bất phương trình  2
x x   x    2 x x   3 2 2 1 3 2 1
8  x x  5x  8x  5  0  x   . A.3 B. 4 C. 3,5 D. Kết quả khác
Câu 3. Tìm điều kiện tham số m để bất phương trình  2
x x   2 x x   2 2 3 1 2 5
1  mx có nghiệm thực.
A. m   7  4 2 
B. m   5  4 2 
C. m   5  3 2  D. m  3 2 2 
x  4x  4  m  0,
Câu 4. Tính tổng tất cả các giá trị tham số m để hệ bất phương trình  có tập hợp nghiệm 2
x  2x  3  3m  0. 
là một đoạn có độ dài bằng 1. A. – 6 B. – 6,5 C. – 4 D. – 7
Câu 5. Tìm điều kiện tham số m để bất phương trình 2 2
3x x  3x x m  5 có nghiệm. 1 35 35 19 A. 0  m  B. m  C. 5  m  D. 1  m  2 4 4 4 2  x x
Câu 6. Tập nghiệm của bất phương trình
 1 chứa bao nhiêu số nguyên nhỏ hơn 40. 2 2
x  5x  9 1 A.20 B. 37 C. 40 D. 16 2
x  6x m
Câu 7. Tìm điều kiện tham số m để phương trình  0 có nghiệm.
x 1  5  x A. 4  m  3  B. m  9  C. 3  m  0 D. m  3
Câu 8. Tồn tại các hằng số a và b sao cho a  3 3  x  4 x  22  b, x   22  ;  3 . Tính Q = a + b. A. Q = 45 B. Q = 38 C. Q = 50 D. Q = 40 2
x  3x  2  0, 
Câu 9. Tìm điều kiện tham số m để hệ bất phương trình  vô nghiệm. m    2
1 x mx m  0.  A. m > 3 B. m > 4/7 C. 1 < m < 3 D. 2 < m < 2,5
Câu 10. Tìm điều kiện tham số m để bất phương trình
x  4  x  2  m nghiệm đúng với mọi giá trị x  1. A. m > 4 B. m  5 C. m  6 D. m  2
Câu 11. Tìm điều kiện tham số m để bất phương trình mx m   2 2
3x  2x  0 có nghiệm. A. Mọi giá trị m B. Không tồn tại m C. m > 0 D. m  0
Câu 12. Tồn tại bao nhiêu giá trị nguyên m trong đoạn [– 30;60] để bất phương trình sau có nghiệm ?  x  2 4 3  x   1 2x   1  m . A. 33 giá trị B. 26 giá trị C. 61 giá trị D. 55 giá trị
Câu 13. Ký hiệu k là giá trị nhỏ nhất của tham số m để bất phương trình 4 3 2
2x x 11mx x  2  0 có
nghiệm thực. Mệnh đề nào sau đây đúng ? 2 3 4 7 A. k = B. k = C. k = D. k = 11 13 15 17  
x   x   2 1
4  5 x  5x  28,
Câu 14. Tìm tất cả các giá trị m để hệ bất phương trình  vô nghiệm. 
 3m  2 x  2.  44 16 5 11 5 16 16 5 A.  m  B.  m  C.  m  1 D.  m  27 6 27 6 27 27 6 2
Câu 15. Tìm điều kiện tham số m để phương trình  2
x x    mx 2 6 9
x  4x  9 có nghiệm thực. 9 9 25 9 A. m   B. m  C. m  D. m  4 4 4 16
Câu 16. Tìm độ dài tập nghiệm của bất phương trình 4 3 2
x  3x  5x  8x  3  7  3x  0  x   . A.2 B. 1,5 C. 1 D. Kết quả khác 
 7x 1  3x 18  2x  7,
Câu 17. Tìm giá trị lớn nhất của tham số m để hệ bất phương trình  có nghiệm.
2x m  2  x  3m  7.  A. m = 6 B. m = 3 C. m = 10 D. m = 7
Câu 18. Tìm giá trị lớn nhất m để bất phương trình  x  
1  x  3 x  5 x  7  m đúng với mọi số thực x. A. m = – 16 B. m = – 12 C. m = – 14 D. m = – 17
Câu 19. Ký hiệu S là tập hợp nghiệm của bất phương trình 2 x   2 m   2
5 x m  4  0 . Tìm độ dài nhỏ nhất
khi biểu diễn S thành một đoạn thẳng trên trục số. A. 4 B. 3 C. 2 D. 5
Câu 20. Tìm điều kiện của m để tập nghiệm của bất phương trình 2
x  m  3 x  3m  0 chứa khoảng (– 2;0) A. m  2  B. m  0 C. m  1 D. 2  m  0 2
 8  2x x  6  3x, 
Câu 21. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm.  2 m m    2
1 x  2m  2m 1.  A. m > 0 B. m < 3 C. Mọi giá trị m. D. Không tồn tại m.
Câu 22. Tam thức bậc hai f x 2
ax bx c  0, x
   và b > c > a. Tìm giá trị lớn nhất của biểu thức b c c a H   .
16a b  2c
5a  3b  5c 7 5 6 4 A. H max = B. H max = C. H max = D. H max = 12 6 7 5  1   1 
Câu 23. Tập nghiệm của bất phương trình 3 3 x  10 x   4  0 
chứa tất cả bao nhiêu số nguyên 3     x   x  nhỏ hơn 40 A.39 B. 40 C. 30 D. 28
Câu 24. Biết rằng bất phương trình m   2
2 x  2m  
1 x m  3  0 có tập nghiệm S = [a;b] thỏa mãn điều
kiện 9 ab a b   10 . Giá trị m thu được nằm trong khoảng nào ? A. (0;3) B. (4;6) C. (6;9) D. (0;5)  42 x   x   1  ,
Câu 25. Tìm điều kiện tham số m để hệ bất phương trình 2 x x 1  có nghiệm. 2
x  4m  
1 x  2m2m   1  0.  A. m > – 1 B. Mọi giá trị m B. m < 1 C. – 1 < m < 1
Câu 26. Tìm điều kiện tham số m để bất phương trình sau nghiệm đúng với mọi số thực x  x  2 48 6 1  x  
1 3x  4  m . A. m  24  01 B. m < 2401 C. m  16  8 D. m  48  2
x  5x m  4 4
Câu 27. Tìm điều kiện tham số m để bất phương trình
 0 nghiệm đúng với mọi x  .
5  2x  4  3x 3 9 5 8  9 A.   m  0 B.  m  2 C. m  D.   m  0 4 3 9 4
Câu 28. Tập nghiệm bất phương trình  x x   x x      x2 2 2 4 5 2 9 12 10 2
chứa bao nhiêu số nguyên A.2 B. 3 C. 1 D. 4 45
BPT + HỆ BPT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P5) _____________________________
Câu 1. Tìm điều kiện tham số m sao cho  3 2
2x  6x x  3 m  
1 x  3  0, x      . A. m = 0 B. m = 1 C. m = 2 D. m = – 1
Câu 2. Tập nghiệm của bất phương trình 2
x    x   2 3 2
x  3x chứa bao nhiêu số nguyên   100  ;100 A.196 B. 120 C. 150 D. 90 2 
x  2x  2  3x  2,
Câu 3. Tìm điều kiện tham số m để hệ  có nghiệm duy nhất. 4 3 2
x  2x  2mx   2m  3 2 x m  2.  A. m = 1 hoặc m = – 3 B. m = 0 hoặc m = – 5 C. m = – 6 hoặc m = – 2 D. m = – 4 hoặc m = 2
Câu 4. Tìm điều kiện m để bất phương trình 4 3 x x   m   2 2 14 2
49 x 14mx m  0 có nghiệm duy nhất. 25 49 A. m = 2 B. m = C. m = 3 D. m = 4 4 2
x  2x  2m 1
Câu 5. Tìm điều kiện tham số m để phương trình  0 có nghiệm. x  3  x 1 2 A.  m  B. m > 1 C. m  1 D. m  3 3 3
Câu 6. Tìm điều kiện của tham số m để hệ sau đây có nghiệm 2
4x  3x x 1 1,   2
x x  52x   1   3
x  2x m  0.  7 2 7 A. m = B. m = C. m = – 1 D. m = 2 5 8
Câu 7. Tìm điều kiện của tham số m để phương trình x   x 2 5
 5x x  4  m 1nghiệm đúng với mọi x thuộc đoạn [1;4]. 19 23 39 19 A.  m  B.  m  16 C. m  D. 0  m  1 4 4 4 4 2 x  4x 17
Câu 8. Tập nghiệm của bất phương trình 2 
x x  2 chứa bao nhiêu số nguyên  100;100 x  8 A.190 B. 198 C. 100 D. 96 2 
x  5x  6  0,
Câu 9. Định m để hệ bất phương trình  vô nghiệm. 2 2 3
x  2mx  2m  7m 12  0.  m  2  ,5 m  3  ,5 m  6,5 A.  B.  C. 2 < m < 5 D.  m  3  m  5  m  6 
Câu 10. Tìm tất cả các giá trị tham số m để bất phương trình 2
3x  5  9x m nghiệm đúng với mọi giá trị x thuộc tập xác định. A. m  10 B. m > 4 C. m   5 D. m  5
Câu 11. Tìm giá trị lớn nhất của tham số m để bất phương trình
x  2  8  x k nghiệm đúng với mọi x thuộc đoạn [2;8]. A. k = 2 B. k = 5 C. k = 6 D. k = 4
Câu 12. Tồn tại bao nhiêu giá trị nguyên nhỏ hơn 100 của tham số m để bất phương trình sau nghiệm đúng với
mọi giá trị x thuộc đoạn [5;34].
2 34  x  5 x  5  m A. 71 giá trị B. 52 giá trị C. 49 giá trị D. 63 giá trị 2
Câu 13. Tìm điều kiện tham số m để bất phương trình  2
x x     2 2 3 4
3 x  3x  4  m có nghiệm. 46 9 9 25 A. m   B. m   C. m  1 D. m   4 8 4 2  1   1 
Câu 14. Tìm giá trị nhỏ nhất của tham số m để bất phương trình 4 x   3 x  1  m     có nghiệm.  x   x  A. m = 10 B. m = 11 C. m = 13 D. m = 18
Câu 15. Tìm giá trị lớn nhất của tham số m để bất phương trình sau nghiệm đúng với mọi số thực x
x x  3 x  5 x  8  m . 225 25 123 A. m = – 4 B. m =  C. m =  D. m =  4 4 4
Câu 16. Bất phương trình 17x  26 2x 1  14 x   1
3x  5 có tập nghiệm M   ;
a b . Tính b  6a . A.5 B. – 2 C. – 6 D. 1 2 x 1  0, 
Câu 17. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm. 2 2x   m   1 x  2  0.  A. – 3 < m < 5 B. 2 < m < 3 C. 5 < m < 8 D. 10 < m < 12 x 1
Câu 18. Tìm giá trị lớn nhất của m sao cho phương trình  x  3 x   1  4 x  3
m có nghiệm thực. x  3 A. m = – 4 B. m = 2 C. m = 4 D. m = 3 2
3x  4x m  3
Câu 19. Tìm điều kiện tham số m để bất phương trình  0 có nghiệm. 2
x x 1  5  x 5 5 A.  m  2 B. m  C. m > 4 D. 0 < m < 2 3 3 2
Câu 20. Tìm độ dài miền nghiệm của bất phương trình  2 x   2 3
1 3x  7x 13 102  x  0  x   . A.0 B. 2 C. 4 D. 5,5
Câu 21. Ký hiệu k là giá trị nhỏ nhất của tham số m để bất phương trình 4 3 2
x  8x  28x  48x  27  m có tập
nghiệm S = R. Giá trị k nằm trong khoảng nào ? A. (0;4) B. (4;9) C. (– 7;– 4) D. (– 3;– 1)
Câu 22. Tồn tại bao nhiêu số nguyên m trong đoạn [– 10;10] để bất phương trình sau có nghiệm ? x x  
1  x  2 x  3  m . A. 13 giá trị B. 12 giá trị C. 14 giá trị D. 15 giá trị 2  1   1 
Câu 23. Tìm giá trị nhỏ nhất của tham số m để bất phương trình 3 x   2 x   5  m     có nghiệm.  x   x  A. m = 10 B. m = 12 C. m = 13 D. m = 18
Câu 24. Tìm tổng các giá trị tham số m xảy ra khi bất phương trình 2
x  2m  
1 x m  3 có tập nghiệm S = m 1
x ; x thỏa mãn đẳng thức 2
x  2 m 1 x m  3  . 1   1 2  2 2 A. 4 B. 2,5 C. 1,25 D. 3,25 2
x x m  1 m  0,
Câu 25. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm duy nhất. 2
x  2mx  2  m  0.  A. m = 5 B. m = 6 C. m = 2 D. m = 1
Câu 26. Biết rằng a
x  3  6  x   x  36  x  , b x   3
 ;6. Giá trị biểu thức b – a gần nhất với giá trị nào ? A. 3,25 B. 4,25 C. 5,67 D. 8,61
Câu 27. Tìm điều kiện tham số m để bất phương trình sau nghiệm đúng với mọi số thực x  x  
1  x  2 x  3 x  4  m . A. m  - 1 B. m  - 2 C. m  3 D. m  - 5
_________________________________ 47
BPT + HỆ BPT MỘT ẨN LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P6) _____________________________ 2
x 10x  9  0, 
Câu 1. Khoảng giá trị [p;q] là điều kiện cần và đủ của m để hệ  có nghiệm. Tính q – p. 2
x mx x 12  0.  4 6 4 2 6 A. 4 B. 13  C. 17  D. 11  3 3 3
Câu 2. Ký hiệu k là giá trị nhỏ nhất của tham số m để bất phương trình 4 3 2
x  4x 11x 14x 10  m có
nghiệm thực. Giá trị k nằm trong khoảng nào ? A. (0;3) B. (2;9) C. (– 7;– 4) D. (– 3;– 1)
Câu 3. Tập nghiệm của bất phương trình  x   x    x   2 2 2 1 3 2
x x 13  25 chứa bao nhiêu số nguyên A.4 B. 2 C. 3 D. 1
Câu 4. Tồn tại bao nhiêu số nguyên m trong khoảng (– 10;10) để phương trình 2
x  2m  5 x  2m 1  0 có
tập nghiệm x ; x thỏa mãn điều kiện 2
x  2m  5 x  2m 1  m . 1   1 2  2 A. 14 giá trị B. 16 giá trị C. 15 giá trị D. 18 giá trị 1 3
Câu 5. Tìm điều kiện tham số m để phương trình 2
x  m   1 x m
có tập nghiệm x ; x thỏa mãn 1 2  2 2
điều kiện 2x  3x  5 . 1 2 7 9 15 A. 1  m  B. 2  m  C. 4  m  D. 2  m  6 2 2 2
Câu 6. Tìm điều kiện tham số m để bất phương trình 2
x  m   2
1 x m m 1  0 có tập nghiệm x ; x 2 1 
thỏa mãn đồng thời các điều kiện x x và 2 x x
x m 1 x  2m m  7 . 1 2 1   2 1 2 A. 0 < m < 3 B. m > 1 C. m > 2 D. m < 4 3 2 4 3 2
3x  4x x 1
4x  3x  4x  3x  4
Câu 7. Tập nghiệm của bất phương trình 
chứa bao nhiêu số nguyên 11 x  5  7 11 x  5  7 A.3 B. 2 C. 7 D. 0
Câu 8. Bất phương trình 2
x  2mx  3  0 có tập nghiệm x ; x . Tồn tại bao nhiêu giá trị nguyên m thỏa mãn 1 2  bất đẳng thức  2
x  2mx m  3 2
x  2mx m  3  5m ? 1 1 2 2  A. 3 giá trị B. 5 giá trị C. 4 giá trị D. 2 giá trị
Câu 9. Tìm điều kiện của tham số m để hệ sau đây có nghiệm 2 
2 3x  4  3 5x  9  x  6x 13,  4 x   2m   2
1 x  2m  2 2 x m .  A. m = 3 B. m = 0 C. m = 2 hoặc m = – 1 D. m = 4 2
x  3x  2  0, 
Câu 10. Tính tổng các giá trị m để hệ bất phương trình  có nghiệm duy nhất. 2
x  6x m  6  m  0.  A. 8 B. 10 C. 7 D. 8 2  1   1 
Câu 11. Tìm giá trị nhỏ nhất của tham số m để bất phương trình 4 x   3 x  1  m     có nghiệm.  x   x  7 13 A. m = 10 B. m = C. m = D. m = 1 16 15
Câu 12. Tìm tất cả các giá trị nguyên của m để bất phương trình x m   2
1  m m  4 có nghiệm nguyên nhỏ nhất bằng 4. A. m = 1 hoặc m = 2 B. m = 3 hoặc m = 2 C. m = 4 hoặc m = 1 D. m = 5 hoặc m = 0 4 4x  3 x  3x  4
Câu 13. Tìm độ dài miền nghiệm của bất phương trình   x   . 2 2 4  3x x 4  3x x A.1 B. 3 C. 2 D. Kết quả khác 48
Câu 14. Ký hiệu S là nghiệm của bất phương trình 2
x  m  8 x  3m 15  0 . Tìm điều kiện của m để khi
biểu diễn trên trục số, độ dài của S lớn hơn 4. m  2 m  3 m  1 m  1 A.  B.  C.  D.  m  6   m  7   m  1   m  11  
Câu 15. Tồn tại bao nhiêu số nguyên m thuộc đoạn [0;30] để bất phương trình  2
2m m  3 x  3m 1có tập
nghiệm S chứa miền (1;7). A. 15 giá trị B. 31 giá trị C. 23 giá trị D. 10 giá trị 2 x   2m  
1 x  2m  0,
Câu 16. Tìm điều kiện tham số m để hệ bất phương trình  có nghiệm. 2 x  2  m   2
1 x m  2m  0.  1 A. m < 0 B. m  3 C. m  D. Mọi giá trị m. 2
Câu 17. Tính tổng tất cả các giá trị nguyên của m để bất phương trình
x   m   2 3 2 3
2  m m 1có
nghiệm nguyên nhỏ nhất bằng 1. A. 30 B. 21 C. 40 D. 32
Câu 18. Tìm độ dài miền nghiệm của bất phương trình 4
1 x  1 x x  32x  50 . A.2 B. 1 C. 0,5 D. Kết quả khác
Câu 19. Tìm tất cả các giá trị tham số m để biểu thức sau nhận giá trị không âm với mọi giá trị thực x.
S   x x  2 3 2 m   2 3 8
3 x 10m  2 x  23m  24   .  1  A. m 2;5 B. 2 < m < 7 C. m  2  ;  D. m 1;6 2   
Câu 20. Với a, b, c là các tham số thực dương sao cho a b 3 3
x c a b 1  2, x
   . Tìm giá trị lớn 3 3 3a b nhất của biểu thức 2
Q c  2c  2  . 3 2 3
a a b  2b A. Q max = 16 B. Q max = 38 C. Q max = 20 D. Q max = 42 2 x x 1
Câu 21. Tìm số gần nhất với độ dài miền nghiệm bất phương trình 2
. x  3x  2  2x  3 . 2 2x 12x 13 A.10 B. 8 C. 9 D. 11 2 x  2 
m  2 x  4m  5  0,
Câu 22. Tìm điều kiện tham số m để hệ bất phương trình  vô nghiệm. 2 x   2m  5 2
x m  5m  6  0.  1 A. m  2 B. m  3 C. m  D. Mọi giá trị m. 2
Câu 23. Tìm điều kiện của m để bất phương trình 2
x  6x m   x  51 x  0 có nghiệm thực. A. m  5 B. 2 < m < 5 C. m > 5 D. 6 < m < 7
Câu 24. Tập nghiệm của bất phương trình 2
2(8x  7) (4x  3)(x 1)  7 có độ dài bằng 2 3 2 2 3 A.1 B. C. D. 2 2 3
Câu 25. Bất phương trình 2
x  m  2 x  5  0 có tập nghiệm x , x thỏa mãn đồng thời các điều kiện 2 1 
x x . Tìm giá trị nhỏ nhất của biểu thức 2 2 K  2m
x m  2 x m m  4  3 x  3 x . 1   2   1 2 1 2 63 2 11 13 A. Kmin = B. Kmin = C. Kmin = D. Kmin = 8 25 4 5
Câu 26. Có bao nhiêu số nguyên x  100 thỏa mãn bất phương trình  x   3 2 3
2x 1  x x  2x  2  x   . A.90 B. 98 C. 68 D. 54
____________HẾT____________ 49