Hệ thống bài tập trắc nghiệm đại cương hàm số

Tài liệu gồm 25 trang, được biên soạn bởi thầy giáo Lương Tuấn Đức (Giang Sơn), tuyển chọn hệ thống bài tập trắc nghiệm đại cương hàm số, (kết hợp 3 bộ sách giáo khoa Toán 10 chương trình mới: Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức Với Cuộc Sống).

113 57 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số, đồ thị và ứng dụng (KNTT)

Môn: Toán 10

Thông tin:

25 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
C
C
H
H
U
U
Y
Y
Ê
Ê
N
N
Đ
Đ
Ề
Ề
H
H
À
À
M
M
S
S
Ố
Ố
V
V
À
À
Đ
Đ
Ồ
Ồ
T
T
H
H
Ị
Ị
(
(
K
K
Ế
Ế
T
T
H
H
Ợ
Ợ
P
P
3
3
B
B
Ộ
Ộ
S
S
Á
Á
C
C
H
H
G
G
I
I
Á
Á
O
O
K
K
H
H
O
O
A
A
)
)
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM ĐẠI CƯƠNG HÀM SỐ
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
Đ
Đ
Ạ
Ạ
I
I
C
C
Ư
Ư
Ơ
Ơ
N
N
G
G
H
H
À
À
M
M
S
S
Ố
Ố
(
(
P
P
1
1
–
–
P
P
6
6
)
)
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
C
C
A
A
O
O
Đ
Đ
Ạ
Ạ
I
I
C
C
Ư
Ư
Ơ
Ơ
N
N
G
G
H
H
À
À
M
M
S
S
Ố
Ố
(
(
P
P
1
1
–
–
P
P
6
6
)
)
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
;
;
T
T
E
E
L
L
0
0
3
3
3
3
3
3
2
2
7
7
5
5
3
3
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
1
1
0
0
/
/
2
2
0
0
2
2
2
2
2
CƠ BẢN HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN ĐẠI CƯƠNG HÀM SỐ - P1)
__________________________________
Câu 1. Hàm số nào sau đây là hàm số bậc nhất?
A.
2
y x
B.
2
1
y x
C.
2 1
y x
D.
4
x
Câu 2. Bảng biến thiên trong hình bên là của hàm số nào sau đây?
A.
4 5y x
B.
4
y x
C.
6
y x
D.
7 1
y x
Câu 3. Tìm tập xác định của hàm số
2
x x
y
.
A.
\ 3
B.
1;

C.
1;

D.
\ 1
Câu 4. Cho hàm số
( 0)
y ax b a
. Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến khi
0
a
B. Hàm số đồng biến khi
0
a
C. Hàm số nghịch biến khi
b
x
a
D. Hàm số nghịch biến khi
b
x
a
Câu 5. Đồ thị của hàm số nào dưới đây có dạng như đường thẳng trong hình vẽ bên?
A.
2 3
y x
B.
3
y x
C.
3
y x
D.
2 3
y x
Câu 6. Tìm m để hàm số
3
2
8
m
y x x
x
là hàm số lẻ.
A. m = 8 B. m = 2 C. m = 1 D. m = 6
Câu 7. Tập xác định D của hàm số
2
5 ; 5
3 1 ; 3
x x x
f x
x x
có bao nhiêu phần tử nguyên trên đoạn [0;10] ?
A. 5 phần tử B. 9 phần tử C. 8 phần tử D. 10 phần tử
Câu 8. Tìm giá trị nhỏ nhất của hàm số
2
4 8y x x
trên R.
A. miny = 2 B. miny = 4 C. miny = 3 D. miny = 5
Câu 9. Hàm số nào sau đây là hàm số lẻ
A.
3y x
B.
6
2
y x
C.
2 4
1
y x x
D.
4
y x x
Câu 10. Với giá trị nào của tham số
m
để
1 2y m x
là hàm số bậc nhất?
A.
1
m
B.
1
m
C.
1
m
D.
0
m
Câu 11. Điểm nào sau đây không thuộc đồ thị hàm số
2 3y x
?
A.
1;1
M
B.
3;9
A
C.
1;5
B
D.
0;4
C
Câu 12. M (a;b) là giao điểm nằm bên phải trục tung của hai đồ thị
2
6; 2 6y x x y x
. Tính a + b.
A. a + b = 14 B. a + b = 15 C. a + b = 10 D. a + b = 9
Câu 13. Với giá trị nào của
m
thì đồ thị hàm số
2 2021
y x m
đi qua điểm
1; 2
M
?
A.
2025
B.
2025
C.
2021
D.
2021
Câu 14. Tìm tập giá trị W của hàm số
2 6
y x x
.
A.
1;

B. [1;3] C.
4;

D. [2;6]
Câu 15. Cho hai đường thẳng
1
: 2 3d y x
và
2
: 1d y x
. Mệnh đề nào sau đây đúng?
A.
1
d
song song với
2
.d
B.
1
d
trùng với
2
.d
C.
1
d
vuông góc với
2
.d
D.
1
d
cắt
2
d
nhưng không vuông góc với
2
.d
3
Câu 16. Cho hàm số
1y x
có đồ thị là đường thẳng
.
Đường thẳng
tạo với hai trục tọa độ một tam giác
có diện tích bằng:
A.
1
.
2
B.
1.
C.
2.
D.
3
.
2
Câu 17. Đồ thị hàm số nào nằm hoàn toán phía trên trục hoành ?
A. y = 6x B.
1
y
x
C.
2
4 3y x x
D.
2
2
3
1
x
y
x x
Câu 18. D là tập xác định của hàm số
2
3
2
5 4 1
3 1
x x
y x
x x
. Hỏi D có chứa bao nhiêu giá trị nguyên ?
A. 5 B. 4 C. 2 D. 3
Câu 19. Hàm số nào sau đây đồng biến trên R ?
A.
3
4y x x
B.
2
6 10
y x x
C.
4
y x
D.
5 1y x
Câu 20. Tìm m để đồ thị hàm số
2
2 2
1
7 2
x x
y
m m x
nhận Oy làm trục đối xứng.
A. m = 0;m = 7 B. m = 1;m = 2 C. m = 3;m = 7 D. m = 7
Câu 21. Có bao nhiêu đồ thị có tâm đối xứng O trong các đồ thị hàm số
2
3 3
3 8
; ; 8
x
y x y y x
x x
?
A. 0 B. 1 C. 2 D. 3
Câu 22. Tìm m để đồ thị hàm số
2
2 3
4 4 5
y x x m x
có trục đối xứng Oy.
A. m = 4 B. m = 17 C. m = 12 D. m = 8
Câu 23. Quỹ tích các điểm P (3m; 6m – 7) là đường thẳng d, d có hệ số góc là
A. 5 B. 4 C. 2,5 D. 2
Câu 24. Tìm số giao điểm nằm phía trên trục hoành của hai đồ thị
2
13 9; 10 9y x x y x
.
A. 1 B. 2 C. 3 D. 4
Câu 25. Có bao nhiêu số nguyên m thuộc (– 9;9) để hàm số
3 2
3
9
f x x x m
x
không chẵn, không lẻ ?
A. 19 B. 15 C. 17 D. 2
Câu 26. Giá trị nhỏ nhất của hàm số
1
4 1
y x
x
trên
0;

là
A. 5 B. 2 C. 4 D. 8
Câu 27. Có bao nhiêu số nguyên m lớn hơn – 5 để hàm số
2
3 1 2019
y m x
đồng biến trên R ?
A. 6 B. 9 C. 10 D. 8
Câu 28. Tập giá trị của hàm số
2
11
2 2
y
x x
là
A. (0;8) B. (1;7] C. (0;11] D.
;11

Câu 29. Tìm số giao điểm của hai đồ thị hàm số
4
y x
x
và đường thẳng y + 3 = 0.
A. 2 B. 1 C. 4 D. 0
Câu 30. Tập xác định D của hàm số
3
1
4
2 1
x
y x
x x
chứa bao nhiêu phần tử nguyên nhỏ hơn 8 ?
A. 5 B. 8 C. 6 D. 7
Câu 31. Trên đồ thị hàm số
19
1
x
y
x
có bao nhiêu điểm nguyên ? (các tọa độ x, y đều nguyên).
A. 13 B. 10 C. 14 D. 12
Câu 32. Tìm số giao điểm của hai đồ thị hàm số
3 2
11 ; 6 6
y x x y x
.
A. 4 B. 2 C. 3 D. 1
Câu 33. Tìm tập xác định của hàm số
4
2 1
x
y
x x
.
A.
1
; \ 1
2

B.
1
;
2

C.
1;

D.
\ 1
_________________________________
4
CƠ BẢN HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN ĐẠI CƯƠNG HÀM SỐ - P2)
__________________________________
Câu 1. Tìm m để hàm số
3
4
2
m
y x x
x
là hàm số lẻ.
A. m = 2 B. m = 1 C. m = 3 D. m = 4
Câu 2. Tồn tại bao nhiêu giá trị m để hàm số
4 2 2
4 5 6 8y x x m m x
là hàm số chẵn.
A. 2 giá trị B. 3 giá trị C. 1 giá trị D. 0 giá trị
Câu 3. Tìm số giao điểm của đồ thị hàm số
2
2
3 ; 0
4 7 ; 0
x x
y
x x x
và đường thẳng y = 4.
A. 2 B. 1 C. 3 D. 4
Câu 4. Tìm tập giá trị của hàm số
1 3
y x x
.
A. [1;3] B.
2;

C.
1;

D. (1;3)
Câu 5. Hàm số y = f (x) có bảng biến thiên như hình vẽ. Có
bao nhiêu số nguyên m thuộc khoảng (– 10;10) để phương
trình f (x) – 2 = m có hai nghiệm phân biệt
A. 11 B. 8
C. 10 D. 9
Câu 6. Hàm số nào sau đây đồng biến trên R ?
A.
3
y x x
B.
2 1y x
C.
1
y
x
D.
2
4 5y x x
Câu 7. Tồn tại bao nhiêu giá trị nguyên m để hàm số
2
9 4
y m x
đồng biến trên R ?
A. 3 B. 2 C. 1 D. 5
Câu 8. Tồn tại bao nhiêu giá trị nguyên m để hàm số
4 2 5
2
1
3 4 1 2
y x m m x
x
là hàm số chẵn ?
A. 2 B. 3 C. 1 D. 4
Câu 9. Giả sử D là tập xác định của hàm số
2
2
1
4 3
2
f x x x
x x
. D chứa bao nhiêu giá trị
nguyên x ?
A. 3 B. 2 C. 1 D. 4
Câu 10. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 7 để hàm số
2
2 1
y x x m
có tập xác định D = R.
A. 5 B. 6 C. 7 D. 2
Câu 11. Trên đồ thị hàm số
3 1
3 2
x
y
x
có bao nhiêu điểm có tọa độ nguyên (điểm nguyên) ?
A. 1 B. 2 C. 3 D. 4
Câu 12. Tồn tại bao nhiêu giá trị m để hàm số
3
1 1
3 4 4
x x
y
m m x
là hàm số chẵn ?
A. 2 B. 3 C. 1 D. 4
Câu 13. Tồn tại bao nhiêu số nguyên m nhỏ hơn 10 để hàm số
2
1
2 4
y
x x m
xác định trên R ?
A. 3 B. 4 C. 2 D. 5
Câu 14. Hàm số nào sau đây đồng biến trên R ?
A.
2
2 4
y x x
B.
2
1 4
y m x
C.
2
y x
D.
3 2
3y x x x
Câu 15. Tìm số giao điểm nằm phía bên phải trục tung của hai đồ thị hàm số
3
4 1; 5 1y x y x x
.
A. 1 B. 2 C. 3 D. 0
Câu 16. Tồn tại bao nhiêu điểm trên đồ thị hàm số
2
1 ; 1
4 ; 1
x x
y
x x x
có tung độ bằng 4.
A. 1 B. 2 C. 3 D. 4
5
Câu 17. Tồn tại bao nhiêu hàm số lẻ trong các hàm số
3 4 2
1
; 5 3; 2 1y x y x x y x
x
?
A. 2 B. 1 C. 3 D. 0
Câu 18. Hàm số nào sau đây đồng biến trên từng khoảng xác định ?
A.
2
3 2
y x
B.
7 2y x
C.
3
4 5y x x
D.
4
3
x
y
x
Câu 19. Tìm điều kiện tham số m để hàm số
3 1x
y
x m
xác định với mọi x thuộc khoảng (1;2).
A.
2
1
m
m
B. m > 0 C. 1 < m < 2 D.
1;2
m
C
C
â
â
u
u
2
2
0
0
.
.
H
H
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
í
í
n
n
h
h
t
t
ổ
ổ
n
n
g
g
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
m
m
x
x
ả
ả
y
y
r
r
a
a
k
k
h
h
i
i
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2f x m
c
c
ó
ó
b
b
a
a
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
.
.
A
A
.
.
2
2
B
B
.
.
4
4
,
,
5
5
C
C
.
.
3
3
,
,
2
2
5
5
D
D
.
.
5
5
,
,
5
5
Câu 21. Gọi d là quỹ tích các điểm K (2m; 7m – 1). Khi đó d là đường thẳng có hệ số góc là
A. 3 B. 2 C. 3,5 D. 7
Câu 22. Tìm tất cả các giá trị của m để hàm số
2 1
x m
y
m x
xác định trên
1;

.
A. m
0 B. m > 2 C. 0 < m < 1 D. 0,5 < m < 3
Câu 23. Ký hiệu D là tập xác định của hàm số
2
2
5 6 1
2
2 1
x x
f x
x
x x
. Tập hợp D có bao nhiêu
số nguyên nhỏ hơn 10 ?
A. 4 B. 8 C. 9 D. 7
Câu 24. Tìm tập hợp giá trị của hàm số
1
2y x
x
với x > 0.
A.
2 2;

B. [1;2] C. [0;4] D.
0;

Câu 25. Trên đồ thị hàm số
3
2
5 ; 0
3 8 ; 0
x x x
y
x x x
tồn tại bao nhiêu điểm có tung độ bằng 6 ?
A. 2 B. 1 C. 3 D. 4
Câu 26. Tìm điều kiện tham số m để hàm số
2
y x m
xác định với mọi
0;2
x
.
A.
0m
B. m < 0 C. m > 1 D. m > 0
Câu 27. Tồn tại bao nhiêu giá trị nguyên m để hàm số
2
4 27
y m x m
đồng biến ?
A. 2 B. 1 C. 3 D. 4
Câu 28. Tìm số giao điểm của đồ thị hàm số
2
; 3
7 5 ; 3
x x
y
x x x
với đường thẳng y = 13.
A. 3 B. 1 C. 2 D. 4
Câu 29. Đường thẳng nào sau đây đi qua điểm
2; 1
M
và song song với đường thẳng
2 1y x
?
A.
2 3.
y x
B.
2 3.
y x
C.
2 3.
y x
D.
1
2
2
y x
Câu 30. Biết đường thẳng
y ax b
đi qua điểm
4; 2
M
và vuông góc với đường thẳng
4 3y x
. Tính
4 3P a b
A.
4.
P
B.
2P
C.
2P
D.
4P
_________________________________
6
CƠ BẢN HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN ĐẠI CƯƠNG HÀM SỐ - P3)
__________________________________
Câu 1. Hàm số y = f (x) có bảng biến thiên như hình
vẽ. Hàm số f (x) đồng biến trên khoảng nào
A. (1;3) B. (0;3)
C. (– 1;4) D. (0;2)
Câu 2. Cho hàm số f (x) = 3x + 5. Mệnh đề nào sau đây đúng ?
A. f (2007) < f (2008) B. f (2006) = f (2005) C. f (4) < f (3) + 4 D. f (2006) > f (2009)
Câu 3. D là tập xác định của hàm số
2 3
2 5
x
y
x
. Hỏi D chứa bao nhiêu số nguyên ?
A. 5 B. 4 C. 2 D. 6
Câu 4.
Với giá trị nào của tham số thực m thì hàm số
3 1
y m x m
là hàm số bậc nhất?
A.
1
m
. B.
1
m
. C.
3
m
. D.
3
m
.
Câu 5.
Hàm số nào sau đây có khoảng nghịch biến là các khoảng
;3 , 3;
A.
2
2y x x
B.
1
2
y
x
C.
2
3
y
x
D.
2
2 1
y
x
Câu 6.
Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
2
2y x x
. B.
2
2y x x
. C.
2
2y x x
. D.
1y x
.
Câu 7.
Biết rằng khi
0
m m
thì hàm số
3 2 2
1 2 1
f x x m x x m
là hàm số lẻ. Khẳng định nào sau
đây đúng?
A.
0
1
;3
2
m
. B.
0
1
;0
2
m
. C.
0
1
0;
2
m
. D.
0
3;m

.
Câu 8. Có bao nhiêu số nguyên m
(– 9;9) để hàm số
5 3
2
1
2 5
m
y x x x
x
không chẵn, không lẻ ?
A. 10 B. 2 C. 16 D. 12
C
C
â
â
u
u
9
9
.
.
T
T
r
r
ê
ê
n
n
m
m
i
i
ề
ề
n
n
[
[
–
–
3
3
;
;
6
6
]
]
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
G
G
i
i
á
á
t
t
r
r
ị
ị
l
l
ớ
ớ
n
n
n
n
h
h
ấ
ấ
t
t
c
c
ủ
ủ
a
a
h
h
à
à
m
m
s
s
ố
ố
y f x
t
t
r
r
ê
ê
n
n
đ
đ
o
o
ạ
ạ
n
n
[
[
–
–
3
3
;
;
6
6
]
]
l
l
à
à
A
A
.
.
2
f
B
B
.
.
6f
C
C
.
.
1f
D
D
.
.
2
f
Câu 10. Gọi T là tập hợp giá trị của hàm số
2 1y x x
. Hỏi T có bao nhiêu phần tử nguyên ?
A. 1 B. 2 C. 3 D. 4
Câu 11. Khi x, y đều là các số nguyên thì F (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên
đồ thị hàm số
5 9
5 1
x
y
x
?
A. 2 điểm nguyên. B. 6 điểm nguyên. C. 4 điểm nguyên. D. 8 điểm nguyên.
Câu 12. Cho các hàm số
4 2 2 4
3 ; 8 9 5; 2 10 ; 25 1y x y x x y x x y x x
.
Hỏi có bao nhiêu hàm số chẵn ?
A. 2 B. 3 C. 4 D. 5
Câu 13. Tìm số giao điểm giữa hai parabol
2 2
6 5; 10 8y x x y x x
.
A. 1 giao điểm. B. 2 giao điểm. C. 3 giao điểm. D. 4 giao điểm.
Câu 14. Tính tổng tất cả các số nguyên thuộc tập xác định của hàm số
3
4 2
x
y
x x
.
A. 4 B. 6 C. 7 D. 5
7
Câu 15. Tìm số giao điểm giữa đồ thị hàm số
4 9
y x
và đường thẳng y = 2x – 5.
A. 2 giao điểm. B. 4 giao điểm. C. 3 giao điểm. D. 1 giao điểm.
Câu 16. Tồn tại bao nhiêu giá trị nguyên của m trong khoảng (– 19;19) để đường thẳng
2y x m
cắt đường
thẳng
4 3
1
x
y
x
tại hai điểm phân biệt.
A. 31 giá trị. B. 33 giá trị. C. 38 giá trị. D. 13 giá trị.
Câu 17. Tìm số giao điểm của hai đồ thị hàm số
2
y x x
và
2
y
.
A. 3 B. 2 C. 1 D. 4
Câu 18. Trong các hàm số
3 4 2 3 2
4
; 4 1; 1;
2
x
y x x y x x y x x y
x
, có bao nhiêu đồ thị có tâm
đối xứng ?
A. 4 B. 2 C. 1 D. 3
Câu 19. Tồn tại bao nhiêu giá trị nguyên m trong khoảng (– 7;7) sao cho đường thẳng
1
1
x
y
x
cắt đường
thẳng
y x m
tại hai điểm phân biệt.
A. 13 giá trị. B. 15 giá trị. C. 12 giá trị. D. 5 giá trị.
Câu 20. Tìm m để hàm số
9
2 1
x
y
x m
xác định trên đoạn [3;5].
A. m > 2 hoặc m < 1 B. m > 3 hoặc m < 0 C. m > 4 hoặc m < 1 D. m > 5 hoặc m < 0
C
C
â
â
u
u
2
2
1
1
.
.
H
H
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
đ
đ
i
i
ề
ề
u
u
k
k
i
i
ệ
ệ
n
n
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
f x m
c
c
ó
ó
b
b
a
a
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
.
.
A
A
.
.
1
1
<
<
m
m
<
<
5
5
B
B
.
.
2
2
<
<
m
m
<
<
6
6
C
C
.
.
0
0
<
<
m
m
<
<
4
4
D
D
.
.
3
3
<
<
m
m
<
<
4
4
Câu 22. Hàm số nào sau đây đồng biến trên khoảng (1;4) ?
A.
2
4 5y x x
B.
5
1
x
y
x
C.
4
y x
D.
4 2
8 10
y x x
Câu 23. Tìm số giao điểm giữa đồ thị hàm số
2
2 3 7
y x x
và đường thẳng y = x + 2.
A. 4 giao điểm. B. 2 giao điểm. C. 3 giao điểm. D. 1 giao điểm.
Câu 24. Tính tổng các giá trị
m
để ba đường thẳng
1
: 2
y x
,
2
: 4y x
và
2
3
: 2 4
y x m
đồng
quy.
A.
0.
B.
3.
C.
9.
D.
3.
Câu 25. Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
: 3 2 7 1
d y m x m
vuông góc với
đường thẳng
: 2 1.
y x
A.
0.
m
B.
5
.
6
m
C.
5
.
6
m
D.
1
.
2
m
Câu 26. Tìm tất cả các giá trị m để hàm số
1
2 6
y m x
x m
xác định trên (– 1;0)
A.
1m
B.
3 1m
C. 0 < m < 2 D. 2 < m < 3
Câu 27. Tập giá trị của hàm số
4 2
4 6
y x x
là
A.[1;3] B. [4;6] C.
2;

D.
4;

Câu 28. Tìm phương trình đường thẳng
: .d y ax b
Biết đường thẳng
d
đi qua điểm
2;3
I
và tạo với hai
trục
,Ox Oy
một tam giác vuông cân.
A.
5.
y x
B.
5.
y x
C.
5.
y x
D.
5.
y x
____________________________________
8
CƠ BẢN HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN ĐẠI CƯƠNG HÀM SỐ - P4)
__________________________________
Câu 1. Tìm điều kiện tham số m để hàm số
3
8 8
y x x m
không chẵn, không lẻ.
A.
8m
B. m = 9 C. m = 8 D. m > 10
Câu 2. Tồn tại bao nhiêu số nguyên m nhỏ hơn 5 để hàm số
2
1 9y m x
đồng biến trên R ?
A. 12 B. 10 C. 13 D. 14
Câu 3. Cho hai hàm số
3 2 2 4 2 3 2
4 3 5; 1 5 10
f x x m m x x g x x m x x
. Tìm điều
kiện tham số m để đồ thị hàm số
f x
có tâm đối xứng và đồ thị hàm số
g x
có trục đối xứng.
A. m = 3 B. m = 2 C. m = 1 D. m = 4
Câu 4. Hàm số bậc hai f (x) có bảng biến thiên như
hình vẽ. Tìm điều kiện của m để phương trình f (x) = m
có nghiệm dương.
A. m < 3 B. m < 2
C. 0 < m < 4 D. m > 1
Câu 5. Tìm số giao điểm của đồ thị hàm số
2
3 4 4
y x x
và đồ thị hàm số
2y x
.
A. 1 B. Không cắt nhau C. 2 D. 3
Câu 6. Gọi T là tập hợp giá trị của hàm số
3
3
y x
x
với x > 0 và Q là tập hợp giá trị của hàm số
2
26
y x
. Hỏi tập hợp
T Q
có bao nhiêu phần tử nguyên ?
A. 4 B. 3 C. 5 D. 2
Câu 7. Hàm số bậc hai
2
f x ax bx c
có đồ thị như hình
vẽ. Tính
3 3
2 2
f a f a
với a là tham số.
A. 0 B. 2
C. 3 D. 1
Câu 8. Tìm điều kiện tham số m để hàm số
2 2
3 3 3y x x m x
là hàm số chẵn.
A. m = 4 B. m = 1 C. m = 0 D. m = 3
Câu 9. Gọi A và B tương ứng là tập giá trị của hàm số
2 2
5; 4 6y x x y x x
. Mệnh đề nào sau đây
đúng ?
A.
A B
B.
B A
C. A = B D.
A
Câu 10. Cho các hàm số
3 5 3 4
2
3
1; ; ; 2 4
y x x y x x y x y x
x
. Có bao nhiêu hàm số mà đồ
thị của chúng có tâm đối xứng ?
A. 3 B. 2 C. 1 D. 0
Câu 11. Tìm điều kiện m để đồ thị hàm số
2
4y x x
cắt đường thẳng y = m tại hai điểm phân biệt.
A. m > – 4 B. m > 2 C. m > – 1 D. m > – 5
Câu 13. Gọi D là tập xác định của hàm số
2
3
2 1
3 1
3 4
x x
f x x
x x
. Hỏi D chứa bao nhiêu số nguyên
nhỏ hơn 10 ?
A. 8 B. 2 C. 7 D. 6
Câu 14. Tìm số giao điểm của đồ thị hàm số
3
5 4; 11 4
y x x y x
.
A. 2 B. 3 C. 4 D. 1
Câu 15. Tìm tập hợp giá trị của hàm số
1 2 3 4
y x x x x
.
A.
2;

B.
1;

C.
3;

D.
4;

Câu 16. Hàm số nào sau đây có trục đối xứng là trục tung ?
9
A.
4
4
3
1
y x
x
B.
2 1 3 2 1y x x
C.
2 2 3
1 2
y x x x x x
D.
2
1
3
y x
x
C
C
â
â
u
u
1
1
7
7
.
.
H
H
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
đ
đ
i
i
ề
ề
u
u
k
k
i
i
ệ
ệ
n
n
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
1
f x m
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
c
c
ù
ù
n
n
g
g
d
d
ư
ư
ơ
ơ
n
n
g
g
.
.
A
A
.
.
0
0
<
<
m
m
<
<
4
4
B
B
.
.
1
1
<
<
m
m
<
<
5
5
C
C
.
.
2
2
<
<
m
m
<
<
3
3
D
D
.
.
3
3
<
<
m
m
<
<
4
4
Câu 18. Hàm số nào sau đây nghịch biến trên R ?
A.
2
2
1
y x x
B.
4
2
x
y
x
C.
3
2 1
y x
D.
3
4 1y x x
Câu 19. Tồn tại bao nhiêu điểm nguyên (x;y) trên đồ thị hàm số
3 1
1
x
y
x
?
A. 4 B. 2 C. 1 D. 3
Câu 20. Hàm số nào sau đây là hàm số lẻ ?
A.
4
3
1 1
x
y
x x
B.
3
1 4y x x
C.
2 4
y x
D.
3
2
10 1
y x
Câu 21. Tồn tại bao nhiêu điểm trên M có tung độ bằng 2 nằm trên đồ thị hàm số
3
3
1
y x
x
?
A. 1 điểm. B. 2 điểm. C. 3 điểm. D. 4 điểm.
Câu 22. Đường cong
4 2
1
x
y
x
cắt đường thẳng
3 4y x
tại các điểm P, Q. Gọi a;b tương ứng là tung độ
của P, Q. Tính giá trị biểu thức S = a + b.
A. S = 11 B. S = 10 C. S = 11 D. S = 12
Câu 23. Đường cong
2 5
1
x
y
x
cắt đường thẳng
1y x
tại hai điểm phân biệt A, B. Tìm tọa độ trung điểm I
của đoạn thẳng AB.
A. I (0;1) B. I (0;2) C. I (4;5) D. I (– 2;2)
Câu 24. Hàm số
2 2
9
4 3 25
x x
y
x x x
có tập xác định
\ ; ; ;a b c d
. Tính a + b + c + d.
A. 4 B. 5 C. 6 D. 7
Câu 25. Biết đồ thị hàm số
y ax b
đi qua điểm
4; 1
N
và vuông góc với đường thẳng
4 1 0.
x y
Tính
tích
.P ab
A.
0.
P
B.
1
.
4
P
C.
1
.
4
P
D.
1
.
2
P
Câu 26. Điểm
A
có hoành độ bằng
1
và thuộc đồ thị hàm số
2 3.
y mx m
Tìm
m
để điểm
A
nằm trong
nửa mặt phẳng tọa độ phía trên trục hoành.
A.
0.
m
B.
0.
m
C.
1.
m
D.
0.
m
Câu 27. Tìm tất cả các giá trị của tham số
m
để hàm số
2 1
y x m
có giá trị nhỏ nhất trên
1;3
bằng 3?
A.
6.
m
B.
4.
m
C.
0.
m
D.
1.
m
Câu 28. Đường thẳng
: 3 2 1
d y m x m
cắt hai trục tọa độ tại hai điểm
A
và
B
sao cho tam giác
OAB
cân. Khi đó, số giá trị của
m
thỏa mãn là:
A.
1.
B.
0.
C.
3.
D.
2.
_________________________________
10
CƠ BẢN HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN ĐẠI CƯƠNG HÀM SỐ - P5)
__________________________________
Câu 1. Tập xác định của hàm số
4 2y x
là
A.
2; .
D

. B.
;2 .
D 
. C.
.
D
. D.
\ 2 .
D
.
Câu 2. Tìm điều kiện của m để hàm số
9
3 4
x
y
m x m
có tập xác định
D
.
A. m = 4 B. m = 3 C. m > 2 D. 1 < m < 3
Câu 3. Tập xác định của hàm số
2
x x
y
x
là
A.
.
D
. B.
0; .
D
. C.
\ 0 .
D
. D.
;0 .
D 
.
Câu 4. Điểm nào sau đây thuộc đồ thị hàm số
5 2.
y x
A.
1
3;1 .
M
B.
1
2;0
M
. C.
1
0;2
M
. D.
1
1;3 .
M
.
Câu 5. Cho hàm số
2
3 khi 0
1 khi 0
x x x
y f x
x x
. Tính
1 .
f
A.
4.
. B.
2.
. C.
2.
. D.
0.
.
Câu 6. Tìm tập xác định của hàm số
2
10
2 1
2
x
y x
x x
.
A. D =
1;2 \ 0
B. D =
0;

C. D =
0; \ 1

D. D =
1
;
2

Câu 7. Tìm tất cả các giá trị của a để hàm số
2
2 1
6 2
x
y
x x a
có tập xác định
D
.
A. a > 11 B. a > 8 C. 7 < a < 9 D. 1 < a < 3
Câu 8. Trong các hàm số
4 2 5
2 3
3
2 3
2 1 1
; ; 2 ;
4
1
x x x
y y y x x y x
x x x
x
tồn tại a hàm số chẵn, b
hàm số lẻ. Tính 5a + 4b.
A. 13 B. 12 C. 18 D. 14
Câu 9. Cho hàm số
1y f x x
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số
y f x
đồng biến trên
. B. Hàm số
y f x
đồng biến trên
;1
.
C. Hàm số
y f x
đồng biến trên
1;
. D. Hàm số nghịch biến trên
.
Câu 10. Tìm tập giá trị của hàm số
2
1
y x
.
A.
1;

. B.
0;

. C.
1;

. D.
.
Câu 11. Có bao nhiêu điểm trên đồ thị hàm số
2
2 ; 0
( )
2 ; 0
x x x
f x
x x
có tung độ bằng 4.
A.2 B. 1 C. 3 D. 4
Câu 12. Hàm số nào sau đây đồng biến trên
?
A.
5y x
. B.
3y x
. C.
3y x
. D.
2 5y x
.
Câu 13. Đồ thị của hàm số
2 1y x
song song với đồ thị hàm số nào trong các hàm số sau đây?
A.
2 1y x
. B.
2 1y x
. C.
1
1
2
y x
. D.
2x 1
y
.
Câu 14. Tập giá trị của hàm số
4 2
4 5
y x x
có phần tử nguyên nhỏ nhất là
A.2 B. 1 C. 3 D. 4
Câu 15. Cho hàm số
2 1
y x m
. Tìm giá trị
m
để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
4
.
A.
3
m
. B.
3
m
. C.
0
m
. D.
1
m
.
Câu 16. Hàm số nào sau đây có tập xác định là
R
?
11
A.
2
3
1
x
y
x
. B.
2
1
x
y
x
. C.
2
1
x
y
x
. D.
2
1
1
x
y
x
.
Câu 17. Đồ thị hàm số
y ax b
cắt trục
Ox
tại điểm
2
x
. Tính
2
a b
.
A.
0
. B.
2
. C.
4
. D.
2
.
Câu 18. Tìm m để hàm số
4 3 2 2
( ) ( 2) 5 ( 4) 3f x x m x x m x
là hàm số lẻ.
A.2 B. 1 C. 3 D. 4
Câu 19. Hàm số nào sau đây là hàm số chẵn? .
A.
4
3y x x
. B.
4
2y x x
. C.
2
2y x x
. D.
4 2
2y x x
.
Câu 20. Cho hàm số
y f x
có đồ thị như sau
Hàm số đã cho đồng biến trên khoảng:
A.
0;

. B.
;0

. C.
;2

. D.
2;

.
Câu 21. Tìm số giao điểm của hai đồ thị hàm số
2
5 ; 6
y x x y
.
A.3 B. 2 C. 1 D. 0
Câu 22. Tập xác định
D
của hàm số
1 1y x x
.
A.
1;D

. B.
1;D

. C.
D
. D.
1;1 .
D
.
Câu 23. Hàm số nào dưới đây nghịch biến trên
?
A.
2
y x
. B.
y x
. C.
2
y x
. D.
y x
.
Câu 24. Cho đường thẳng
:
d y ax b
đi qua điểm
1;2
I
và tạo với các tia
Ox
,
Oy
một tam giác có diện
tích bằng
4
. Tính giá trị của biểu thức
.P a b
A.
2P
. B.
6
P
. C.
4P
. D.
2P
.
Câu 25. Tìm giá trị lớn nhất của hàm số
2
6
y x x
.
A.3 B. – 9 C. 1 D. – 4
Câu 26. Đồ thị hàm số
y ax b
nào sau đây đi qua hai điểm
2;1 , 1; 2
A B
.
A.
1.y x
. B.
1.2y x
. C.
1.y x
. D.
2 1.y x
.
Câu 27. Đồ thị của hàm số nào dưới đây có dạng như đường thẳng trong hình vẽ bên?
A.
2 1
y x
B.
2 1
y x
C.
2
y x
D.
3y x
Câu 28. Cho các hàm số
4
2 4
8 1
; 6 1; 9 1; 1
x
y y x y x x y x
x
. Có bao nhiêu đồ thị hàm số
có trục đối xứng ?
A. 3 B. 2 C. 4 D. 1
Câu 29. Khi x, y đều là các số nguyên thì M (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên
đồ thị hàm số
10
1
x
y
x
?
A. 6 điểm nguyên. B. 5 điểm nguyên. C. 4 điểm nguyên. D. 8 điểm nguyên.
_________________________________
12
CƠ BẢN HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN ĐẠI CƯƠNG HÀM SỐ - P6)
__________________________________
Câu 1. Hàm số nào sau đây đồng biến trên
?
A.
2
y x
. B.
y x
. C.
2 5y x
. D.
2
y x
.
Câu 2. Tìm số giao điểm của hai đồ thị hàm số
3 ; 2 1y x y x
.
A.2 B. 3 C. 1 D. 4
Câu 3. Tập xác định của hàm số
2
4 10
y x x
chứa bao nhiêu số nguyên dương
A.3 B. 2 C. 4 D. 1
Câu 4. Tìm tất cả các giá trị của tham số
m
để hàm số
1 2
y m x m
nghịch biến trên
.
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Câu 5. Tìm tập giá trị của hàm số
2
2 5
y x x
.
A.[1;4] B. [1;5] C.
2;

D.
3;

Câu 6. Khi x, y đều là các số nguyên thì M (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên
đồ thị hàm số
10
1
x
y
x
?
A. 6 điểm nguyên. B. 5 điểm nguyên. C. 4 điểm nguyên. D. 8 điểm nguyên.
C
C
â
â
u
u
7
7
.
.
H
H
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
( ) 50
f x
.
A.3 B. 4
C. 6 D.5
Câu 8. Đồ thị của hàm số nào dưới đây vuông góc với đường thẳng
2y x
?
A.
4 1
y x
B.
5
y x
C.
1
y x
D.
2 3
y x
Câu 9. Tìm tung độ giao điểm của đường cong
2 3
3
x
y
x
và đường thẳng
1y x
.
A. 0 B. 1 C. 2 D. – 1
Câu 10. Đường cong
2 5
1
x
y
x
cắt đường thẳng
1y x
tại hai điểm phân biệt A, B. Tìm tọa độ trung điểm I
của đoạn thẳng AB.
A. I (0;1) B. I (0;2) C. I (4;5) D. I (– 2;2)
Câu 11. Đồ thị hàm số nào sau đây cắt đường thẳng
y x
A.
2
4
y x x
B.
2
4 4
y x x
C.
1
4
y x
x
D.
5
y x
Câu 12. Tồn tại bao nhiêu giá trị nguyên m trong khoảng (– 7;7) sao cho đường thẳng
1
1
x
y
x
cắt đường
thẳng
y x m
tại hai điểm phân biệt.
A. 13 giá trị. B. 15 giá trị. C. 12 giá trị. D. 5 giá trị.
Câu 13. Tập xác định của hàm số
2
1 1
3 5
y x
x x
chứa bao nhiêu số nguyên dương nhỏ hơn 100
A.80 B. 98 C. 95 D. 90
Câu 14. Tìm
m
để đồ thị của hàm số
2
2 2
y m m x m
song song với đường thẳng
3 1y x
?
A.
1
m
B.
3
m
C.
1
m
hoặc
3
m
D.
3
m
Câu 15. Bảng biến thiên trong hình bên là của hàm số nào sau đây?
13
A.
4 5
y x
B.
2 .y x
C.
6
y x
D.
1
y x
Câu 16. Hàm số
f x
có tập xác định
và có đồ thị như hình vẽ
Mệnh đề nào sau đây sai ?
A. Hàm số đồng biến trên khoảng (1;4) B. Hàm số nghịch biến trên khoảng (– 3;0).
C.
2 5 15
f f
D.
10 26
f
.
Câu 17. Đường cong
2 8
x
y
x
cắt đường thẳng
y x
tại hai điểm M, N. Tính độ dài đoạn thẳng MN.
A. MN = 4 B. MN =
2 5
C. MN =
4 2
D. MN =
6 2
Câu 18. Tìm điều kiện của m để hàm số
4 3 3 2
2 8 8
y m x x m x x
là hàm lẻ.
A. m = 8 B. m = 2 C. m = 3 D. m < 2,5
Câu 19. Hàm số nào sau đây không phải là hàm số bậc nhất?
A.
3
y
B.
2 1
y x
C.
1
y x
D.
2
1 3
y m x
Câu 20. Tìm tập hợp điểm biểu diễn điểm P (m; 2m
2
– m + 2).
A. Parabol y = 2x
2
– x + 2. B. Đường thẳng 3x – y + 1 = 0.
C. Đường thẳng y = 2x – 2. D. Parabol y = 3x
2
– 4x + 1.
Câu 21. Hàm số nào sau đây nghịch biến trên miền
4;

A.
1
4
y
x
B.
6
4
x
y
x
C.
2
1
4
y
x
D.
5
4
y
x
Câu 22. Hàm số nào dưới đây nghịch biến trên
?
A.
3
y x
B.
1
y x
C.
2 5
y x
D.
3 1
y x
Câu 23. Với giá trị nào của tham số
m
để hàm số
2 2021
y m x
đồng biến trên
?
A.
2
m
B.
2
m
C.
2
m
D.
2
m
Câu 24. Tìm tập xác định của hàm số
2
3
1 9
3 5
x
y
x x x
.
A.
3;

B.
5;

C.
0;

D.
0; \ 3
Câu 25. Cho các hàm số
2 4
4 2 4 2
2
1 2 1 3
; ; ; 6 ; 2 5
1 1
x x
y x x y y y x y x x
x x x
. Tồn tại bao nhiêu
hàm số chẵn ?
A. 2 B. 3 C. 4 D. 1
Câu 26. Tìm số giao điểm giữa đồ thị hàm số
3 4
y x
và đường thẳng y = x – 3.
A. 2 giao điểm. B. 4 giao điểm. C. 3 giao điểm. D. 1 giao điểm.
Câu 27. Phương trình đường thẳng đi qua giao điểm của 2 đường thẳng
2 1; 3 4
y x y x
và song song với
đường thẳng
2 15.
y x
A.
2 11 5 2.
y x
B.
5 2.
y x
C.
2 2 5.
y x
D.
4 2.
y x
14
ĐẠI CƯƠNG HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P1)
____________________________
Câu 1. Tìm điều kiện m để hàm số
3
y x m
xác định trên [1;7].
A.
3
m
B. m < 4 C. 2 < m < 4 D. 0 < m
1
Câu 2. Giá trị nhỏ nhất của hàm số
4
4
6
f x x
x
trên miền
0;

là
A. 11 B. 10 C. 13 D. 17
C
C
â
â
u
u
3
3
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
4 3 2
f x x
.
.
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
2
2
Câu 4. Tập giá trị của hàm số
1 2 5 6
y x x x x
chứa bao nhiêu phần tử nguyên nhỏ hơn 10 ?
A. 15 B. 14 C. 12 D. 16
Câu 5. Khi x, y đều là các số nguyên thì F (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên đồ
thị hàm số
3
8 1
1
x x
y
x
?
A. 2 điểm nguyên. B. 6 điểm nguyên. C. 8 điểm nguyên. D. 12 điểm nguyên
Câu 6. Đường cong
4 2
1
x
y
x
cắt đường thẳng
3 4y x
tại các điểm P, Q. Gọi a;b tương ứng là tung độ
của P, Q. Tính giá trị biểu thức S = a + b.
A. S = 11 B. S = 10 C. S = 11 D. S = 12
Câu 7. Ký hiệu X, Y tương ứng là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
2
2 2
2 2
x x
y
x x
trên R. Tính giá
trị biểu thức K = X + Y.
A. K = 6 B. K = 3 C. K = 2 D. K = 4
Câu 8. Tập giá trị W của hàm số số
1 2 3
y x x x
là
A. [5;10] B.
2;

C.
3
;
2

D.
5;

Câu 9. Hàm số
2 1 4 2
2
x
f x x m m
xác định với mọi
0;2
x
khi
;m a b
. Tính a + b.
A. a + b = 3 B. a + b = 5 C. a + b = 2,5 D. a + b = 2
Câu 10. Trên đồ thị hàm số
2
2
2
x
y
x
có bao nhiêu điểm có tọa độ nguyên ?
A. 4 B. 2 C. 3 D. 6
Câu 11. Cho hàm số
f x
thỏa mãn
3
3 3 1f x x x
. Tính
3
f x
.
A.
3
3 6 3 6 1
f x x x
. B.
3
3 2 3 2 1
f x x x
.
C.
3
3 2 2 3 2 1
f x x x
D.
3
3 4 2 3 2 1
f x x x
.
Câu 12. Tìm điều kiện tham số m để hàm số
3 2
5
y
x mx x m
có tập xác định D = R\{a;b}.
A. 0 < m < 2 B.
0 1
m
C. m > 3 D.
0 3
m
Câu 13. Hàm số nào sau đây đồng biến trên từng khoảng xác định ?
A.
5
3
x
y
x
B.
3 2
2 10y x x x
C.
3
9y x x
D.
2
4
y x
Câu 14. Gọi A là giao điểm có hoành độ < 1 của đường cong
3 1
1
x
y
x
cắt đường thẳng
1y x
. Tính OI.
A. OI = 1 B. OI = 2 C. OI = 3 D. OI =
2
15
Câu 15. Điểm M (x;y) gọi là điểm nguyên khi x, y đều là các số nguyên. Tìm số giao điểm nguyên của hai đồ thị
hàm số
7 2 ; 5 3 2
y x y x x
.
A. 1 giao điểm. B. 2 giao điểm. C. 3 giao điểm. D. 4 giao điểm.
Câu 16. Đồ thị hàm số
2 4
y x x
cắt đồ thị hàm số
2
6 11
y x x
tại bao nhiêu điểm ?
A. 1 giao điểm. B. 2 giao điểm. C. 3 giao điểm. D. 4 giao điểm.
Câu 17. Hàm số
2
2
2 2 2
2 3
x x
y
x
có tập giá trị K = [a;b]. Tính giá trị biểu thức a + b.
A.
5
3
B. 1 C. 2 D.
2
5
Câu 18. Tìm số giao điểm của đồ thị hàm số
2
3 2
3 2
x
y x
x
và đường thẳng
1y x
.
A. 1 điểm. B. 2 điểm. C. 3 điểm. D. 4 điểm.
Câu 19. Hàm số
8 4 6 5
y x x
đạt giá trị lớn nhất và giá trị nhỏ nhất tương ứng tại x = a; x = b. Tính
giá trị biểu thức Q = |25a – b + 2|.
A. Q = 50 B. Q = 48 C. Q = 71 D. Q = 31
C
C
â
â
u
u
2
2
0
0
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
3 2 0
f x f x
.
.
A
A
.
.
1
1
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
2
2
Câu 21. Tìm giá trị của m để đường cong
2
1
x
y
x
cắt đường thẳng
1
2
y x m
tại hai điểm phân biệt nằm
về hai phía của trục tung.
A. m > 2 B. m > 3 C. 0 < m < 1 D. 2 < m < 4
Câu 22. Tìm hàm số
f x
thỏa mãn
2
1 4 3
2
x
f x f
x x
.
A.
2
x
f x
B.
2
3
1
f x x
x
C.
3
1
1
f x x
x
D.
1
2f x x
x
.
Câu 23. Tìm tập hợp điểm biểu diễn điểm L (3m – 1;m
2
– 2m + 2).
A. Đường thẳng y = x. B. Parabol
2
4 13
9
x x
y
.
C. Đường cong y = 2x
3
+ 5x
2
+ 2x – 1. D. Đường thẳng 8y = 3x + 3.
Câu 24. Cho các hàm số
2
3 2
4 7 1 2 2
8 1; ; 4 ; 3;
1 2 1
x x x
y x y y x x y x x y
x x
. Số lượng
hàm số đồng biến trên tập xác định tương ứng là
A. 2 B. 5 C. 3 D. 4
Câu 25. Tìm điều kiện tham số m để hàm số
9
4
2 1
x
y x
x m
xác định trên [7;9].
A. m > 4 hoặc m < 3 B. m > 4 C. m > 9 hoặc m < 7 D. 2 < m < 5
Câu 26. Cho các hàm số
2 2 2
2
1 4 1 2 5
; ; 1;
3 3
2
x x x x x x
y y y x y
x x x
x
. Có bao nhiêu đồ thị
hàm số nằm hoàn toàn phía trên trục hoành ?
A. 2 B. 4 C. 1 D. 3
Câu 27. Tồn tại bao nhiêu giá trị nguyên của m trong khoảng (– 20;20) để đường thẳng
3y x m
không cắt
đường thẳng
2
1
x
y
x
.
A. 1 giá trị. B. 3 giá trị. C. 2 giá trị. D. 4 giá trị.
_________________________________
16
ĐẠI CƯƠNG HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P2)
_____________________________
Câu 1. Tồn tại bao nhiêu điểm có tung độ bằng 29 nằm trên đồ thị hàm số
3
2
2
2 ;2 4
2 21 ; 4
29 ; 2
x x
y x x
x x x
A. 3 B. 2 C. 1 D. 4
Câu 2. Tồn tại bao nhiêu số nguyên dương m để hàm số
4
4 8
y x x m
xác định trên R ?
A. 5 B. 2 C. 3 D. 4
Câu 3. Cho hàm số
f x
thỏa mãn
2
4 1 4 1f x x x
. Giá trị biểu thức
2
f
gần nhất với giá trị nào ?
A. 2,2 B. 1,5 C. 3,7 D. 4,1
Câu 4. Giả sử hàm số
2
2 4 3 1 3
f x x x x x
có tập giá trị W = [a;b]. Hãy tính giá trị của biểu
thức K = a
2
+ b
2
.
A. K = 145 B. K = 144 C. K = 143 D. K = 169
Câu 5. Khi x, y đều là các số nguyên thì F (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên đồ
thị hàm số
4
3 16
1
x x
y
x
?
A. 8 điểm nguyên. B. 6 điểm nguyên. C. 10 điểm nguyên. D. 12 điểm nguyên
Câu 6. Tập giá trị của hàm số
2018 2 1y x x
chứa bao nhiêu phần tử nguyên ?
A. 68 B. 56 C. 37 D. 43
C
C
â
â
u
u
7
7
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
4 0
f x x
.
.
A
A
.
.
1
1
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
2
2
Câu 8. Có bao nhiêu cặp số nguyên dương (m;n) với m < 6, n < 6 để hàm số
5 3
3 4
f x x x x m n
không chẵn, không lẻ ?
A. 20 B. 22 C. 21 D. 10
Câu 9. Tính độ dài khi biểu diễn trên trục số của tập xác định hàm số
2
5
2 3 1
x x
y
x x x
.
A. 5 B. 4 C. 3 D. 2,5
Câu 10. Hàm số
2
2 2 4
y x x x
có tập giá trị [a;b]. Tổng giá trị a + b gần nhất với giá trị nào ?
A. 2,8 B. 3 C. 2 D. 4
Câu 11. Giá trị nhỏ nhất của hàm số
2
4
3
f x x x
là
A. 3 B. 4 C. 5 D. 7
Câu 12. Tìm hàm số
f x
thỏa mãn
3
3
1 1
f x x
x x
.
A.
3
3f x x x
B.
2
6 1f x x x
C.
3
f x x x
D.
1
2f x x
x
.
Câu 13. Tìm hàm số
f x
thỏa mãn đẳng thức
2
2 6 4
f x x x
. Khi đó, hãy tìm giá trị nhỏ nhất của
hàm số
4 2
4 30 28
g x f x x x x
.
A. 11 B. 14 C. 12 D. 20
Câu 14. Tồn tại bao nhiêu điểm nguyên trên đồ thị hàm số
2
2
1
1
x x
y
x x
?
A. 4 B. 3 C. 2 D. 1
Câu 15. Có bao nhiêu số nguyên m trong khoảng (– 2018;2018) để đường thẳng
2y x m
cắt đường cong
17
2
1
x
y
x
tại hai điểm phân biệt.
A. 2018 B. 4000 C. 4035 D. 2346
Câu 16. Hàm số
2
2
1 2 2 4
2 1
a x a x a
g x
x x
có giá trị nhỏ nhất M. Có bao nhiêu tự nhiên a để M < 4 ?
A. 2 B. 4 C. 5 D. 3
Câu 17. Tìm giá trị lớn nhất m để hàm số
2 1
y x m x m
xác định với số dương x.
A. m = – 1 B. m = 2 C. m = – 3 D. m = 4
Câu 18. Trên đồ thị hàm số
2018
3
y
x
có bao nhiêu điểm có tung độ nguyên ?
A. 670 điểm B. 2018 điểm C. 672 điểm D. 520 điểm
Câu 19. Tập giá trị của hàm số
1 2 3
y x x x x
là
A. [0;3] B.
2;

C. [1;4] D.
1;

Câu 20. Cho hàm số
3 2
5 7 3f x x x x
. Phương trình
2
( 3 2) 0
f x x
có bao nhiêu nghiệm ?
A. 4 B. 3 C. 2 D. 1
Câu 21. Tìm tập hợp điểm biểu diễn điểm E (4m;5m
2
+ 3).
A. Parabol
2
5
3
16
y x
. B. Đường thẳng 3x – 7y + 6 = 0.
C. Đường thẳng 9y = 2x – 2. D. Parabol y = 5x
2
– 4x + 3.
C
C
â
â
u
u
2
2
2
2
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 3 2
f x x
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
2
2
.
Câu 23.
Hàm số
f x
thỏa mãn
2
2 1
f x f x x
. Tính f(0).
A.
1
0
3
f
B.
2
0
3
f
C.
5
0
3
f
D.
4
0
3
f
.
Câu 24. Tìm tập giá trị W = [a;b] của hàm số hai biến
2 2
2 2
x xy y
y
x xy y
.
A. W = [2;3] B. W = [0;2] C. W =
1
;3
3
D. W =
2
;2
3
.
Câu 25. Đường cong
2 8
x
y
x
cắt đường thẳng
y x
tại hai điểm M, N. Tính độ dài đoạn thẳng MN.
A. MN = 4 B. MN =
2 5
C. MN =
4 2
D. MN =
6 2
Câu 26. Đường cong
8
3y
x
cắt đường thẳng
6y x
tại hai điểm phân biệt H, K. Tính diện tích S của tam
giác OHK với O là gốc tọa độ.
A. S = 21 B. S = 23 C. S = 41 D. S = 14
Câu 27. Hàm số
2
2
2 4
x mx n
y
x x
có tập giá trị T =
1
;3
3
. Tính tổng tất cả các giá trị có thể xảy ra của m và n.
A. 20 B. 21 C. 10 D. 15
Câu 28. Tồn tại bao nhiêu giá trị nguyên của m trong khoảng (– 19;19) để đường thẳng
2y x m
cắt đường
thẳng
3 1
2
x
y
x
tại hai điểm phân biệt có hoành độ trái dấu.
A. 18 giá trị. B. 17 giá trị. C. 13 giá trị. D. 16 giá trị.
18
ĐẠI CƯƠNG HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P3)
____________________________
Câu 1. Tìm tập hợp giá trị của hàm số
4 4
6 8
f x x x
.
A. [2;9] B.
2;

C.
1;

D.
3
;
2

Câu 2. Tồn tại bao nhiêu giá trị m để hàm số
2
2 2 3
2 9
y x x m x
là hàm số chẵn.
A. 2 B. 1 C. 3 D. 0
Câu 3. Tìm số giao điểm của đồ thị hàm số
2
4 8 1y x x
và đường thẳng
1y x
.
A. 2 B. 3 C. 1 D. 4
Câu 4. Trên đồ thị hàm số
2
6 1
1
x x
y
x
có bao nhiêu điểm M (x;y) mà x, y đều nguyên ?
A. 4 B. 2 C. 6 D. 8
Câu 5. Tồn tại bao nhiêu số nguyên m nhỏ hơn 11 để hàm số
2
1
4 5
f x
x x m
có tập xác định D = R.
A. 5 B. 9 C. 2 D. 1
Câu 6. Có bao nhiêu giá trị nguyên m lớn hơn – 7 để hàm số
2
6 9
g x x x m
xác định trên R ?
A. 14 B. 7 C. 5 D. 10
Câu 7. Hàm số
2
2
3 2 1
2 3
x x
y
x x
có tập giá trị S = [a;b]. Tính giá trị biểu thức a
2
+ b
2
+ ab.
A. 5 B. 2 C. 4 D. 3
Câu 8. Hàm số y = |ax + b| có đồ thị như hình vẽ bên.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
trên miền [0;3] là
A. 2 B. 1
C. 3 D. 4
Câu 9. Tìm số giao điểm của đồ thị hàm số
2
3 2
3 2
x
y x
x
và đường thẳng
1y x
.
A. 1 điểm. B. 2 điểm. C. 3 điểm. D. 4 điểm.
Câu 10. Tính giá trị biểu thức a + b + 2c + 4d, trong đó hai đoạn rời nhau [a;b] và [c;d] (a < c) là tập hợp tất cả
các giá trị m để hàm số sau xác định trên (0;1):
4 3 3 1
2
5 2
x m x
y
x m
m x
.
A. 3 B. 2 C. 6 D. 3,5
Câu 11. Hàm số y = |ax + b| có đồ thị như hình vẽ bên.
Với m là tham số thực, tính tổng các nghiệm của
phương trình |x – 2| = f (10 – m) – f (m – 8) + 7.
A. 2 B. 1
C. 3 D. 4
Câu 12. Tồn tại bao nhiêu điểm có hoành độ bằng 1 thuộc đồ thị hàm số
3 3
5 7 5 12
y x x
?
A. 1 điểm. B. 2 điểm. C. 3 điểm. D. 4 điểm.
Câu 13. Tìm điều kiện tham số m để hàm số
2 1
y x m x m
xác định với mọi x > 0.
A.
1m
B.
2 2m
C. m
0 D. m
1
Câu 14. Hàm số
3 6 3 6
y x x x x
có tập giá trị W = [a;b]. Giá trị biểu thức b – a gần nhất
với giá trị nào ?
A. 3,25 B. 4,25 C. 5,67 D. 8,61
Câu 15. Tồn tại bao nhiêu điểm có hoành độ bằng 5 thuộc đồ thị hàm số
2 2
5 8 4
y x x x x
?
A. 1 điểm. B. 2 điểm. C. 3 điểm. D. 4 điểm.
19
Câu 16. Tìm điều kiện tham số a để tập hợp giá trị của hàm số
2
1
x a
y
x
chứa đoạn [0;1].
A. Mọi a B. a
2 C. a
0,75 D. a < 2
Câu 17. Tìm điều kiện của tham số m để hàm số
4
1
6 9 3
2
y m x
x m
xác định trên đoạn [0;1].
A. – 1 < m < 2 B.
1 2m
C. 0 < m < 1 D. 2 < m < 3
Câu 18. Hàm số f (x) có tập xác định D = R với đồ thị như hình vẽ bên,
O là tâm đối xứng của đồ thị. Tính giá trị
2017 2017
f f
.
A. 2 B. 1
C. 3 D. 0
Câu 19. Hai tập xác định của các hàm số
2
2
9 3| | ;
| | 4
9 1
x x
y x y
x x
x
khi giao nhau sẽ chứa bao
nhiêu phần tử nguyên ?
A. 4 B. 5 C. 6 D. 7
Câu 20. Tìm giá trị của m để đường cong
2
1
x
y
x
cắt đường thẳng
1
2
y x m
tại hai điểm phân biệt nằm
về hai phía của trục tung.
A. m > 2 B. m > 3 C. 0 < m < 1 D. 2 < m < 4
Câu 21. Đường cong
3 3
2
x
y
x
cắt đường thẳng
1y x
tại hai điểm phân biệt D, E. Tính diện tích S của
tam giác ODE với O là gốc tọa độ.
A. S =
2
B. S = 1 C. S = 3 D. S = 1,5
Câu 22. Tồn tại bao nhiêu điểm nguyên (x;y) trên đồ thị hàm số
2
2
1
1
x x
y
x x
?
A. 4 B. 3 C. 2 D. 1
Câu 23. Đoạn [a;b] là tập hợp tất cả các giá trị m để hàm số
2 1 4 2 0,5f x x m m x
xác định
với mọi
0;2
x
. Tính a + b.
A. 3 B. 2 C. 4 D. 5
Câu 24. Cho hàm số
3 2
6 9 3f x x x x
. Phương trình
3
4 0
f x f x
có bao nhiêu nghiệm ?
A. 7 B. 8 C. 5 D. 6
Câu 25. Gọi M là tập hợp giá trị của hàm số
2
2
1
1
x x
f x
x x
, M chứa bao nhiêu phần tử nguyên ?
A. 4 B. 2 C. 3 D. 4
Câu 26. Hàm số f (x) có đồ thị như hình vẽ bên, biết rằng trên các miền
x < 0 và x > 2, đồ thị hàm số là đường thẳng, không gấp khúc. Tìm giá
trị lớn nhất của tham số m để hàm số
2
g x f x m
luôn xác
định với mọi x.
A. m = 4 B. m = 3
C. m = 2,5 D. m = 5
Câu 27. Tồn tại bao nhiêu giá trị nguyên m để hàm số
( 1) 2 3
y m x m
xác định trên [– 3;– 1] ?
A. 2 B. 3 C. 1 D. Vô số
Câu 28. Có mấy số nguyên dương m để hàm số
1
2 1
y x m
x m
xác định trên (1;2) hoặc
4;

?
A. 6 B. 7 C. 8 D. 9
20
ĐẠI CƯƠNG HÀM SỐ THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P4)
_____________________________
Câu 1. Tìm m để hàm số
2
4
x
y
x x m
có tập xác định là R \{a}, a là hằng số thực.
A. m = 4 B. m = 3 C. m = 2 D. m = 5
Câu 2. Hàm số
2
2 2
3 6 3 9
y x x x x
có tập giá trị W chứa bao nhiêu phần tử nhỏ hơn 10 ?
A. 12 B. 1 C. 10 D. 8
Câu 3. Trên đồ thị hàm số
2
2
x
y
x
có bao nhiêu điểm nguyên
A.3 B. 2 C. 4 D. 1
Câu 4. Có bao nhiêu số nguyên m < 10 để hàm số
1999 3sin 4cos
( )
4 sin(1993 )
x x m
f x
x
có tập xác định
?
A. 9 B. 8 C. 5 D. 13
Câu 5. Với a là tham số thực bất kỳ, tìm số giao điểm của hai đường cong
4 2 2
; 7 4
y x y x a
.
A. 4 B. 1 C. 3 D. 2
Câu 6. Tìm giá trị m để hàm số
2
1
4 5
f x
x x m
có tập xác định D = R.
A. m > 0 B. m < 2 C. 4 < m < 5 D. m < 1
Câu 7. Giá trị nhỏ nhất của hàm số
2
2 2
2 4 2 1
y x x x x
trên R là
A. – 2 B. – 3 C. 1 D. 0
Câu 8. Tìm điều kiện của m để hàm số
2 2
2 6 1
y x x m x
luôn luôn xác định.
A. m
4 B. m
2 C. m
5 D. m
8
C
C
â
â
u
u
9
9
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
s
s
á
á
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
2
2 2 0
f x m f x m
A
A
.
.
4
4
B
B
.
.
2
2
C
C
.
.
5
5
D
D
.
.
3
3
Câu 10. Gọi K là tập giá trị của hàm số
3 4
y x x
. K chứa bao nhiêu số nguyên nhỏ hơn 10 ?
A. 4 B. 8 C. 9 D. 10
Câu 11. Tìm tất cả các giá trị của m để hàm số
1
1
3 1
y x m
m x
xác định trên [0;2]
A. m > 0,5 B.
1
1
3
m
C. m > 1 D. – 2 < m < 0
Câu 12. Tìm hàm số
f x
thỏa mãn
3 2
1
f x x x x
. Tìm
1
f x
.
A.
3 2
1 5 7f x x x x
B.
3 2
1 5 7f x x x x
C.
3 2
1 5 4f x x x x
D.
3 2
1 3 2f x x x x
.
Câu 13. Tìm điều kiện của tham số m để hàm số
1
2 4
y a x
x a
xác định trên (0;1).
A.
3
0
2
a
B. 1 < a < 2 C. 0 < m < 1 D.
3
2
a
Câu 14. Tìm phương trình đường thẳng
: .d y ax b
Biết đường thẳng
d
đi qua điểm
1;3 ,
I
cắt hai trục
,Ox Oy
và cách gốc tọa độ một khoảng bằng
5.
21
A.
2 5.
y x
B.
2 5.
y x
C.
2 5.
y x
D.
2 5.
y x
Câu 15. Có bao nhiêu số tự nhiên m < 2018 để hàm số
2
( ) 2( 1) 2 1
f x x m x m
đồng biến trên (2;4).
A.2016 B. 2018 C. 2015 D. 2017
C
C
â
â
u
u
1
1
6
6
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
.
.
H
H
ỏ
ỏ
i
i
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
3 2
2 14 17 17
f x x x
.
.
A
A
.
.
4
4
B
B
.
.
2
2
C
C
.
.
5
5
D
D
.
.
3
3
Câu 17. Tồn tại bao nhiêu số nguyên m lớn hơn – 19 để hàm số
2
3
y x x m
có tập xác định D = R ?
A. 13 B. 16 C. 11 D. 15
Câu 18. Cho hàm số
3
( ) 2 1f x x x
. Đặt
3
2 2
2 2 2 3 2
3 3 8 4
2. ;
1 1 ( 1) 1
x x
A B
x x x x
.
Khẳng định nào sau đây là đúng và đầy đủ nhất
A.
f A f B
B.
f A f B
C.
f A f B
D.
f A f B
Câu 19. Tìm điều kiện tham số m để hàm số
4 3 2
4 ( 5) 4 4
y x x m x x m
xác định trên R.
A.
0m
B.
0m
C.
0m
D.
0m
Câu 20. Tìm điều kiện của m để hàm số
3 2
1 1 5
y x x m x x
là hàm số chẵn.
A. m = 1 B. m = 5 C. m > 2 D. 1,5 < m < 2
Câu 21. Khi x, y đều là các số nguyên thì F (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên
đồ thị hàm số
3
2 12
1
x x
y
x
?
A. 2 điểm nguyên. B. 4 điểm nguyên. C. 6 điểm nguyên. D. 8 điểm nguyên
Câu 22. Hàm số
2 2
4 21 3 10
f x x x x x
có tập giá trị T = [a;b]. Giá trị biểu thức T = 3a + 2b gần
nhất với giá trị nào ?
A. 12,24 B. 32,14 C. 45,12 D. 52,21
C
C
â
â
u
u
2
2
3
3
.
.
Hàm số
3 2
f x ax bx cx d
có đồ thị
như hình dưới đây. Với m là tham số thực thuộc đoạn
[2;3], hỏi phương trình sau có tối đa bao nhiêu nghiệm
thực ?
2 3
f x m m
.
A
A
.
.
6
6
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
4
4
Câu 24. Tìm tập giá trị K của hàm số
2
4 3
1
x
y
x
.
A. K = [– 1;4] B. K = [0;2] C. K = [– 2;5] D. K = [3;7]
Câu 25. Cho hàm số
3 2
7 14 8f x x x x
. Phương trình
2
( 9 ) 0
f x
có bao nhiêu nghiệm thực ?
A. 4 B. 3 C. 2 D. 1
Câu 26. Tìm hàm số
f x
thỏa mãn
2
1 6 4f x x x
.
A.
2
5 2
f x x x
B.
2
4f x x x
C.
2
8 11
f x x x
D.
2
6 1f x x x
.
_________________________________
22
ĐẠI CƯƠNG HÀM SỐ THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P5)
_____________________________
Câu 1. Hàm số
f x
thỏa mãn
3
3
1 1
f x x
x x
. Tìm số nghiệm của phương trình
8 2
( )
3 6
f x
x x
x
.
A. 2 B. 3 C. 1 D. 2.
Câu 2. Trên đồ thị hàm số
3
3
1
2
x
y
có bao nhiêu điểm
( ; )M x y
thỏa mãn
5 2 2 5
( ) 2x x y x y xy y
.
A.2 B. 1 C. 3 D. 4
Câu 3. Có bao nhiêu giá trị nguyên m để hàm số
( ) 1
f x x x m
là hàm số lẻ
A.1 B. 0 C. 2 D. 4
Câu 4. Tìm điều kiện của m để hàm số
4
3 1 3 1
2 6
x x
y
m x m x
là hàm chẵn.
A. m = 4 B. m = 6 C. m = 3 D. m < 2
Câu 5. Tìm tập hợp điểm biểu diễn điểm J (3m; 27m
3
+ 9m
2
+ 6m).
A. Parabol
2
4 13
9
x x
y
. B. Parabol y = 2x
2
.
C. Đường cong y = x
3
+ x
2
+ 2x. D. Đường thẳng y = 3x + 3.
Câu 6. Có bao nhiêu số nguyên m < 10 để hàm số
265 3sin 4cos
( )
5 sin(2000 )
x x m
f x
x
có tập xác định
?
A. 9 B. 8 C. 5 D. 13
Câu 7. Tìm số giao điểm của hai đồ thị hàm số
2
( ) ; ( ) 2 2
1 1
x
f x g x x x
x
.
A.3 B. 2 C. 4 D. 1
Câu 8. Khi x, y đều là các số nguyên thì F (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên đồ
thị hàm số
3
2 7 34
1
x x
y
x
?
A. 8 điểm nguyên. B. 12 điểm nguyên. C. 4 điểm nguyên. D. 10 điểm nguyên
Câu 9. Hàm số
3 6 3 6
y x x x x
có tập giá trị W = [a;b]. Giá trị biểu thức b – a gần nhất
với giá trị nào ?
A. 3,25 B. 4,25 C. 5,67 D. 8,61
Câu 10. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Đặt hàm số
3
( ) (2 1)
y g x f x x m
. Tìm m để
[0;1]
max ( ) 10
g x
.
A. m = - 13 B. m = - 12 C. m = - 1 D. m = 3
Câu 11. Hàm số
2
2
2 2 2
2 3
x x
y
x
có tập giá trị K = [a;b]. Tính giá trị biểu thức a + b.
A.
5
3
B. 1 C. 2 D.
2
5
Câu 12. Tồn tại bao nhiêu giá trị nguyên của m trong khoảng (– 6;6) để đường thẳng
2y x m
cắt đồ thị hàm
số
6 1
2 1
x
y
x
tại hai điểm phân biệt nằm về hai phía của trục tung ?
A. 4 giá trị. B. 3 giá trị. C. 6 giá trị. D. 5 giá trị.
Câu 13. Cho hàm số
( )f x
nhận giá trị nguyên với mọi giá trị nguyên x. Phương trình sau có bao nhiêu nghiệm
nguyên:
3
( ) 3 2 ( ) 1 0
x xf x x f x
.
A.3 B. 4 C. 1 D. 2
23
Câu 14. Tìm số giao điểm của hai đồ thị hàm số
2
3 1 5 4; 3 3y x x y x x
.
A.3 B. 2 C. 1 D. 4
Câu 15. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Tìm số
nghiệm
2;5
của phương trình
3 2
( ) 6 ( ) 11 ( ) 6
0
( ) 4
f x f x f x
f x
A. 4 B. 5
C. 6 D. 3
Câu 16. Trên đồ thị hàm số
2000
3( 2)
y
x
có bao nhiêu điểm có tọa độ nguyên
A.2 B. 1 C. 0 D. 3
Câu 17. Tập giá trị của hàm số
3 2
( ) ( 6 11 6)
f x x x x x
chứa bao nhiêu số nguyên nhỏ hơn 20
A.21 B. 18 C. 10 D. 13
Câu 18. Tồn tại bao nhiêu giá trị nguyên m < 10 để hai đồ thị hàm số
( ) 3 2 2; ( ) 2 4f x x m g x x m m
cắt nhau tại hai điểm phân biệt.
A. 9 B. 6 C. 5 D. 4
Câu 19. Có bao nhiêu giá trị m để hàm số
2 2 2 3
4 2
( 2 ) ( 4) 2 5
( )
2 10
x x m x mx
f x
x x
là hàm số lẻ
A.1 B. 2 C. 3 D. 4
Câu 20. Tìm số giao điểm của hai đồ thị hàm số
2 2
( ) 2 3 ( 1) 6; ( ) ( 2) 2 9
f x x x x g x x x x
.
A.3 B. 2 C. 1 D. 0
Câu 21. Có bao nhiêu giá trị nguyên
2018;2019
m
để hàm số
2 1
y x m x m
có tập xác định
0;

.
A.4038 B. 2018 C. 2019 D. 2020
Câu 22. Cho hàm số
3 2
( ) 3 6 1f x x x x
. Tìm số nghiệm của phương trình
( ) 1 1 ( ) 2
f f x f x
.
A. 4 B. 6 C. 7 D. 9
Câu 23. Có bao nhiêu số nguyên m để phương trình
1 2 2
x x x m
có hai nghiệm phân biệt
0;2
.
A.2 B. 1 C. 3 D. 0
Câu 24. Có bao nhiêu giá trị nguyên m để hàm số
( 1) 2 3
y m x m
xác định trên
3; 1
.
A.2 B. 1 C. Vô số D. 3
Câu 25. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Có bao
nhiêu giá trị nguyên m để phương trình sau có số
2;5
nghiệm
đạt tối đa:
3 2 2
( ) 3 ( ) 2 0
f x m mf x m m
.
A. 4 B. 2
C. 1 D. 3
Câu 26. Để tập xác định của hàm số
2
16 2017 2018y x x m
có đúng 1 phần tử thì
a
m
b
(phân số
tối giản). Tính giá trị a + b.
A.3025 B. – 3025 C. 5043 D. – 5043
Câu 27. Tìm điều kiện của m để hàm số
2
2
1
3
x x
y
m x mx m
có tập xác định
\D a
.
A.
12;12
m
B. m = 2 C.
4;0
m
D. m = 3
Câu 28. Cho hàm số
y f x
thỏa mãn
2 ( ) (2 ) 3f x f x x
. Tính
2 (0) 3 (2)f f
.
A.8 B. 4 C. 6 D. 5
24
ĐẠI CƯƠNG HÀM SỐ THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P6)
_____________________________
Câu 1. Tìm tập xác định của hàm số
2
23
8
3 2
4 3
x
y x x
x x
.
A.
3
; \ 1;3
4

B.
3
; \ 1;2;3
4

C.
\ 1;3
D.
1;2
Câu 2. Hàm số
f x
thỏa mãn
2
4 1 4 1f x x x
. Giá trị biểu thức
2
f
gần nhất với giá trị nào
A. 2,2 B. 1,5 C. 3,7 D. 4,1
Câu 3. Tập giá trị của hàm số
( 1)( 2)( 3)( 4)
y x x x x
có bao nhiêu số nguyên nhỏ hơn 10
A.10 B. 11 C. 9 D. 8
Câu 4. Hàm số
f x
thỏa mãn
2
2 ( ) (1 ) 2 1
f x f x m m
. Tìm giá trị nhỏ nhất của
7 (0) 4 (1)f f
.
A. Kết quả khác B. 1,5 C.
7
8
D.
2
3
C
C
â
â
u
u
5
5
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
.
.
V
V
ớ
ớ
i
i
m
m
l
l
à
à
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
h
h
ự
ự
c
c
,
,
h
h
ỏ
ỏ
i
i
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
1
13
2
f
x m
.
.
A
A
.
.
4
4
B
B
.
.
2
2
C
C
.
.
5
5
D
D
.
.
3
3
Câu 6. Cho hàm số
f x
thỏa mãn
2
2 1 5 6
f x x x
. Tính
3 1
f x
.
A.
2
3 3 14 16
3 1
4
x x
f x
B.
2
3 14 16
3 1
4
x x
f x
.
C.
2
6 18
3 1
4
x x
f x
. D.
2
6 5 18
3 1
4
x x
f x
.
Câu 7. Hàm số
4
1
2 2
5 9
y x m
m x
xác định với x thuộc nửa khoảng (0;4].
A.
1 1m
B.
2 1m m
C. m > 2 D. 0 < m < 3
Câu 8. Trên đồ thị hàm số
4y x
có bao nhiêu điểm
( ; )M x y
thỏa mãn điều kiện
6 5 0
y y x x
.
A.4 B. 2 C. 3 D. 1
Câu 9. Tìm giá trị nhỏ nhất của tham số m để hàm số
1
2 5
m x
y
x m
xác định trên khoảng (1;5).
A. m = 5 B. m = 6 C. m = 4 D. m = 2
Câu 10. Cho hàm số
( ) 2 1f x x
. Tìm giá trị nhỏ nhất của
2
( ) ( ) ( ( )) 2022
g x f x f f x
.
A.2022 B. 2015 C. 1999 D. 2000
Câu 11. Hàm số bậc nhất y = ax + b có đồ thị d như
hình vẽ bên. Giá trị của m là
A. 0,75 B. 0,7
C. 0,8 D. 0,9
Câu 12. Tìm điều kiện của m để hàm số
3 2
4 3 9 8
x x
y
x m m x
xác định với mọi x thuộc (5;21,5).
A.
0 1m
B. 1 < m < 2 C.
0,5 2m
D.
1,5 2m
Câu 13. Cho các hàm số
25
4 4
3 3
1 1
; 3 5; 4 4 ; 2 2
1 1
x x
y y x y x x y x x x x
x x
Số lượng hàm số chẵn là
A. 2 B. 3 C. 4 D. 1
Câu 14. Tìm điều kiện của m để hàm số
2
1 1 2
y x x mx
là hàm số lẻ.
A. m = 0 B. m = 2 C. m > 3 D. 0 < m < 1
Câu 15. Tìm số giao điểm của hai đồ thị hàm số
3 2 3
2 10 3; (3 5) 3
y x x x y x x x
.
A.3 B. 2 C. 1 D. 4
Câu 16. Tìm tất cả các giá trị của m và n để hàm số
2 4 3 2
3 3 4
y m m x x m x x n
là hàm lẻ.
A. m = 3 và n = 4. B. m = 3; n = 2 C. m = 0; n = 2 D. m > 4; n > 3
Câu 17. Trên đồ thị hàm số
5 2
2
3 2 ; 3
5 1 3 ; 3
x x x x
y
x x x x
có bao nhiêu điểm
( ; )M x y
thỏa mãn đẳng
thức
3 3 2
3( 3 5 ) 14 0
x y x y y
.
A.3 B. 2 C. 1 D. 4
Câu 18. Tìm tập hợp điểm biểu diễn điểm L (3m – 1;m
2
– 2m + 2).
A. Đường thẳng y = x. B. Parabol
2
4 13
9
x x
y
.
C. Đường cong y = 2x
3
+ 5x
2
+ 2x – 1. D. Đường thẳng 8y = 3x + 3.
Câu 19. Khi x, y đều là các số nguyên thì F (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên
đồ thị hàm số
4
3 16
1
x x
y
x
?
A. 8 điểm nguyên. B. 6 điểm nguyên. C. 10 điểm nguyên. D. 12 điểm nguyên
Câu 20. Hàm số
2
1 1 1
y x x x
có giá trị lớn nhất A và giá trị nhỏ nhất B. Tính tỷ số k = A : B.
A. k =
2
B. k = 2 C. k = 4 D. k = 2,4
C
C
â
â
u
u
2
2
1
1
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
1 3 2
2 ( ) ( )
f x m f x m
c
c
ó
ó
n
n
h
h
i
i
ề
ề
u
u
h
h
ơ
ơ
n
n
5
5
n
n
g
g
h
h
i
i
ệ
ệ
m
m
?
?
A
A
.
.
3
3
B
B
.
.
2
2
C
C
.
.
5
5
D
D
.
.
4
4
Câu 22. Giả sử d là đường thẳng đi qua điểm C (3;6) và cắt hai tia Ox, Oy tại A, B sao cho
2 2
1 1
OA OB
đạt giá
trị nhỏ nhất. Tính diện tích S của tam giác OAB khi đó.
A. S = 56,25 B. S = 60,75 C. S = 12,65 D. S = 14,75
Câu 23. Tìm m để hàm số
2
3 2
41
12 47
x
y
x x x m
có tập xác định
\ ; ; ;
D a b c a b c
, đồng thời thỏa
mãn điều kiện a < b < c; a + c = 2b.
A. m = 16 B. m = 60 C. m = 32 D. m = 54
Câu 24. Hàm số
f x
thỏa mãn
2
2 1
f x f x x
. Tính f(0).
A.
1
0
3
f
B.
2
0
3
f
C.
5
0
3
f
D.
4
0
3
f
.
Câu 25. Trong mặt phẳng tọa độ Oxy, tồn tại Q (x;y) nằm trên đường phân giác góc phần tư thứ nhất sao cho
biểu thức
2 2
2 2 4
K x y x y
đạt giá trị nhỏ nhất. Tính giá trị biểu thức H = 3x + 6y.
A. H = 1 B. H = 2 C. H = 0,5 D. H = 1,5
________________________________
| 1/25
| | Tải xuống

Có thể bạn quan tâm:

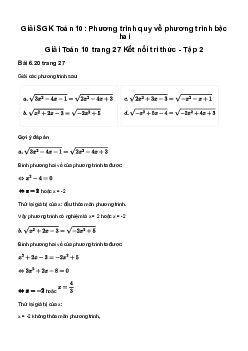
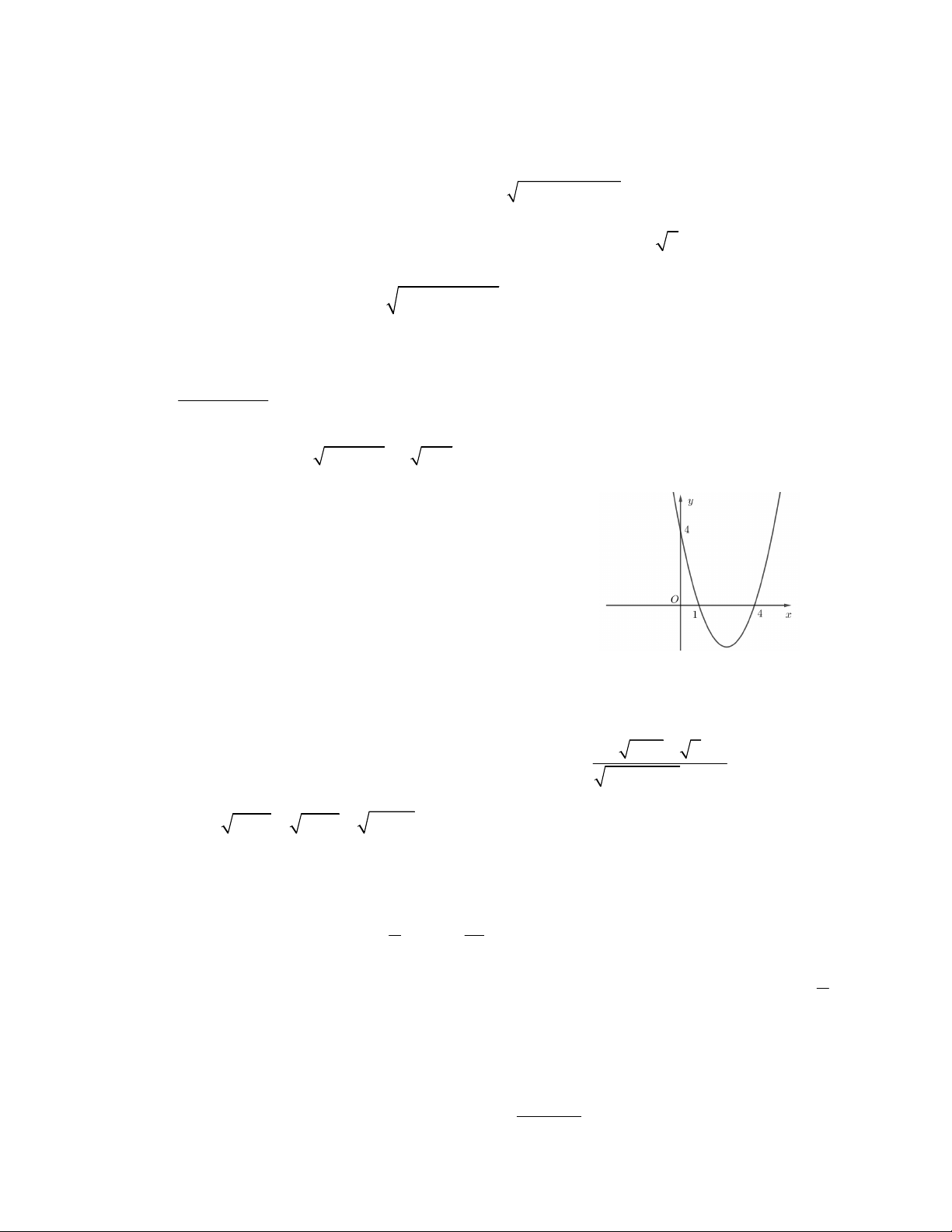
Preview text:


TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
--------------------------------------------------------------------------------------------
CHUYÊN ĐỀ HÀM SỐ VÀ ĐỒ THỊ
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM ĐẠI CƯƠNG HÀM SỐ
CƠ BẢN ĐẠI CƯƠNG HÀM SỐ (P1 – P6)
VẬN DỤNG CAO ĐẠI CƯƠNG HÀM SỐ (P1 – P6)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
GACMA1431988@GMAIL.COM (GMAIL); TEL 0333275320
THÀNH PHỐ THÁI BÌNH – THÁNG 10/2022 1
CƠ BẢN HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN ĐẠI CƯƠNG HÀM SỐ - P1)
__________________________________
Câu 1. Hàm số nào sau đây là hàm số bậc nhất? A. 2 y x  B. 2
y  x 1
C. y  2x 1 D. x  4 
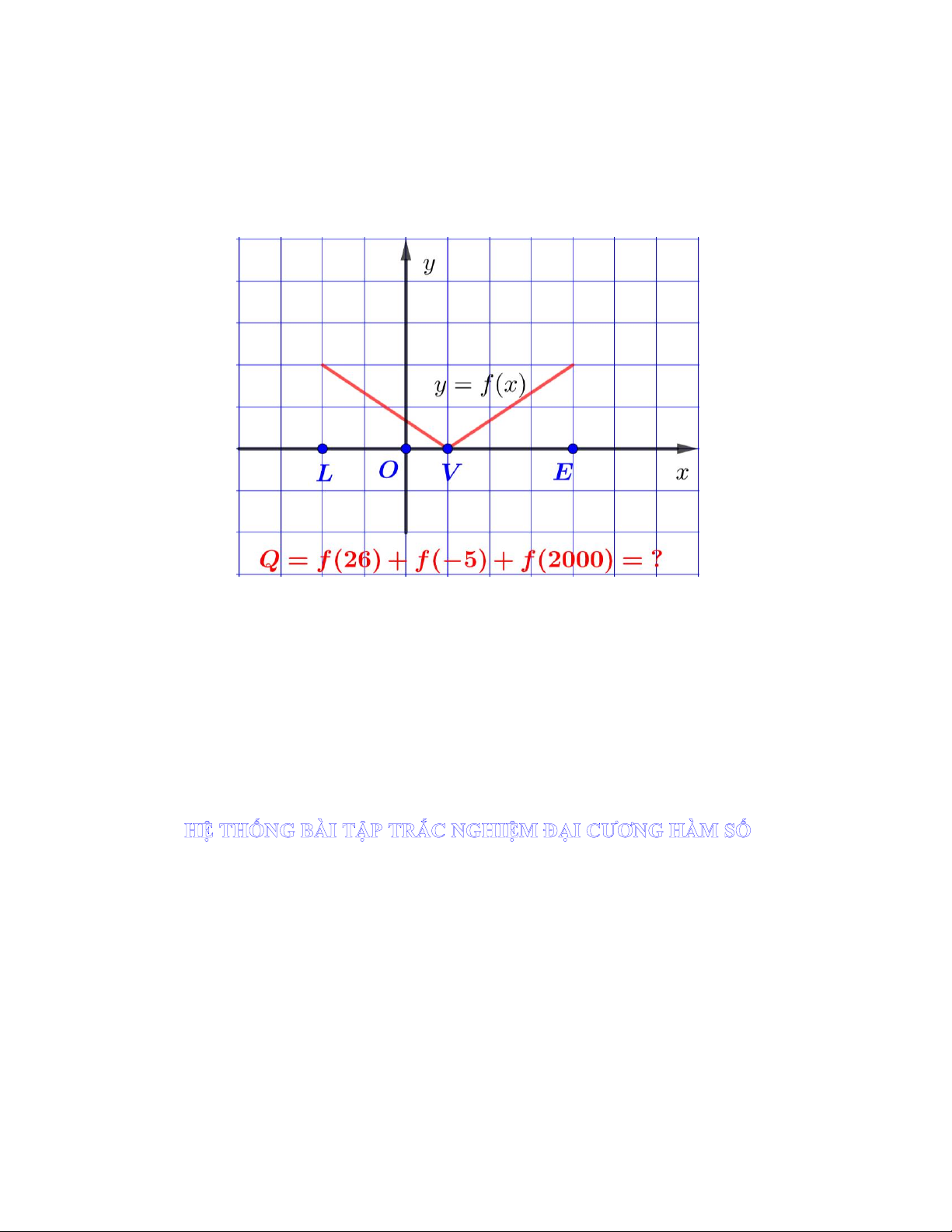
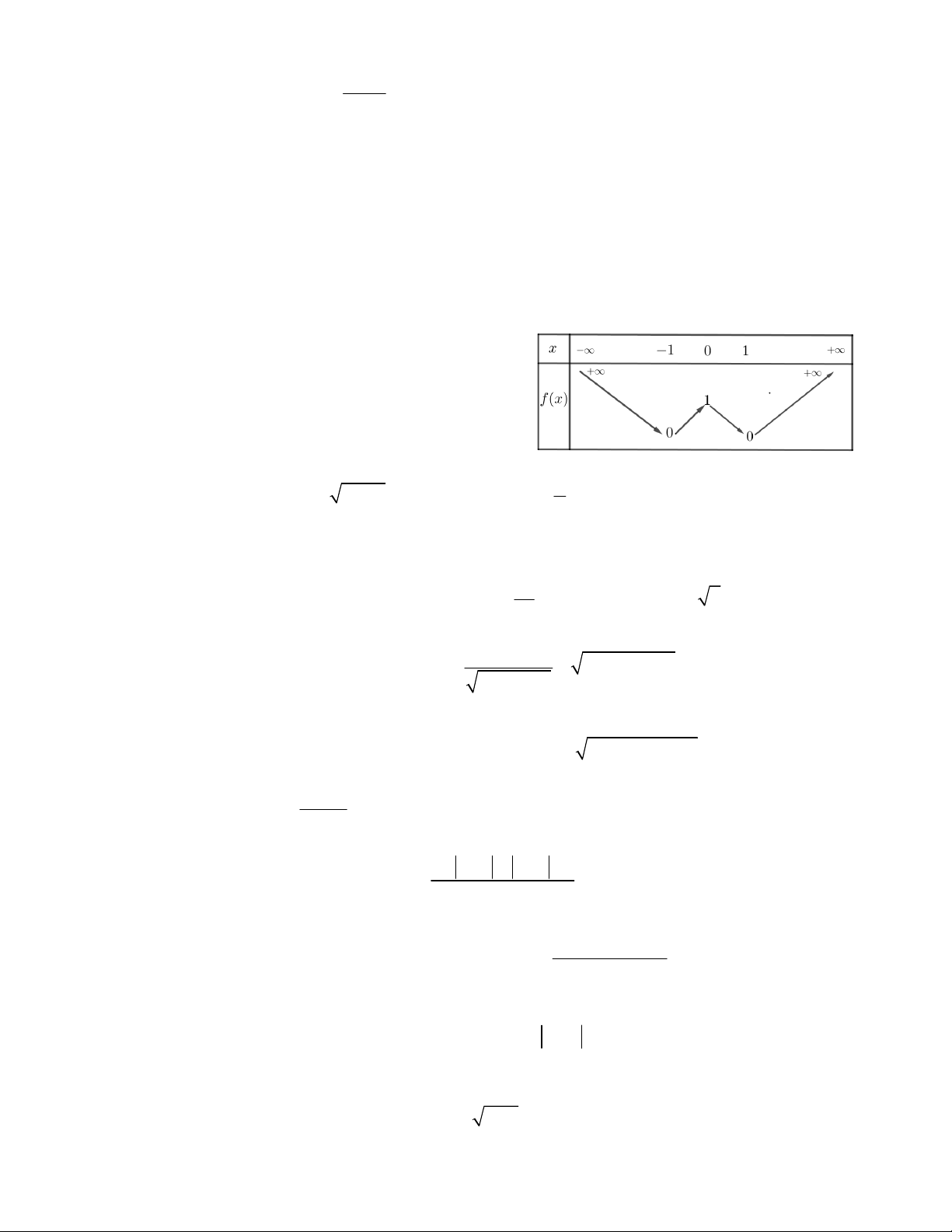
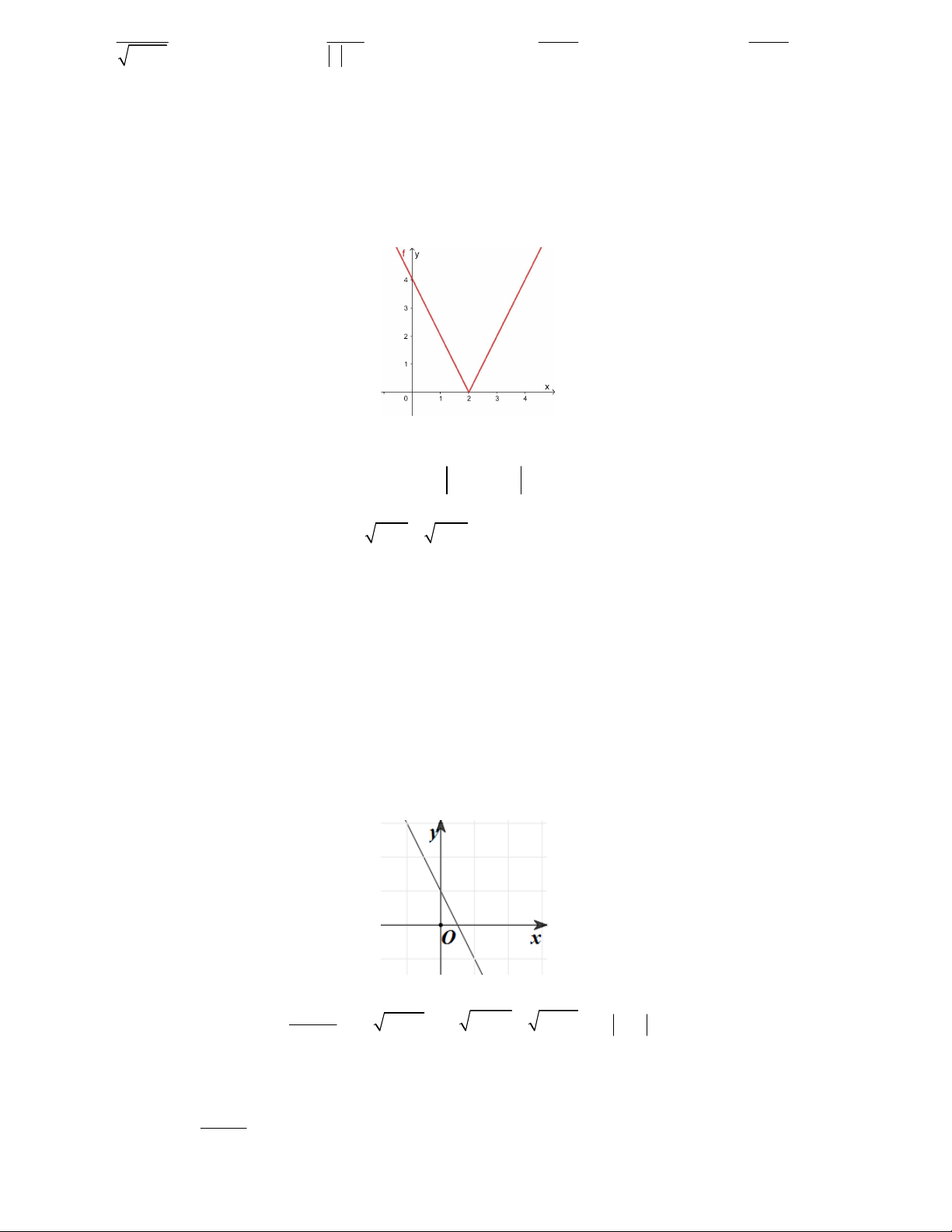
Câu 2. Bảng biến thiên trong hình bên là của hàm số nào sau đây?
A. y  4  5x
B. y x  4 
C. y  x  6  D. y  7  x 1 2 x x 1
Câu 3. Tìm tập xác định của hàm số y  . x  3 A.  \   3 B. 1; C. 1;  D.  \   1
Câu 4. Cho hàm số y ax b (a  0) . Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến khi a  0 
B. Hàm số đồng biến khi a  0  b b
C. Hàm số nghịch biến khi x  
D. Hàm số nghịch biến khi x   a a
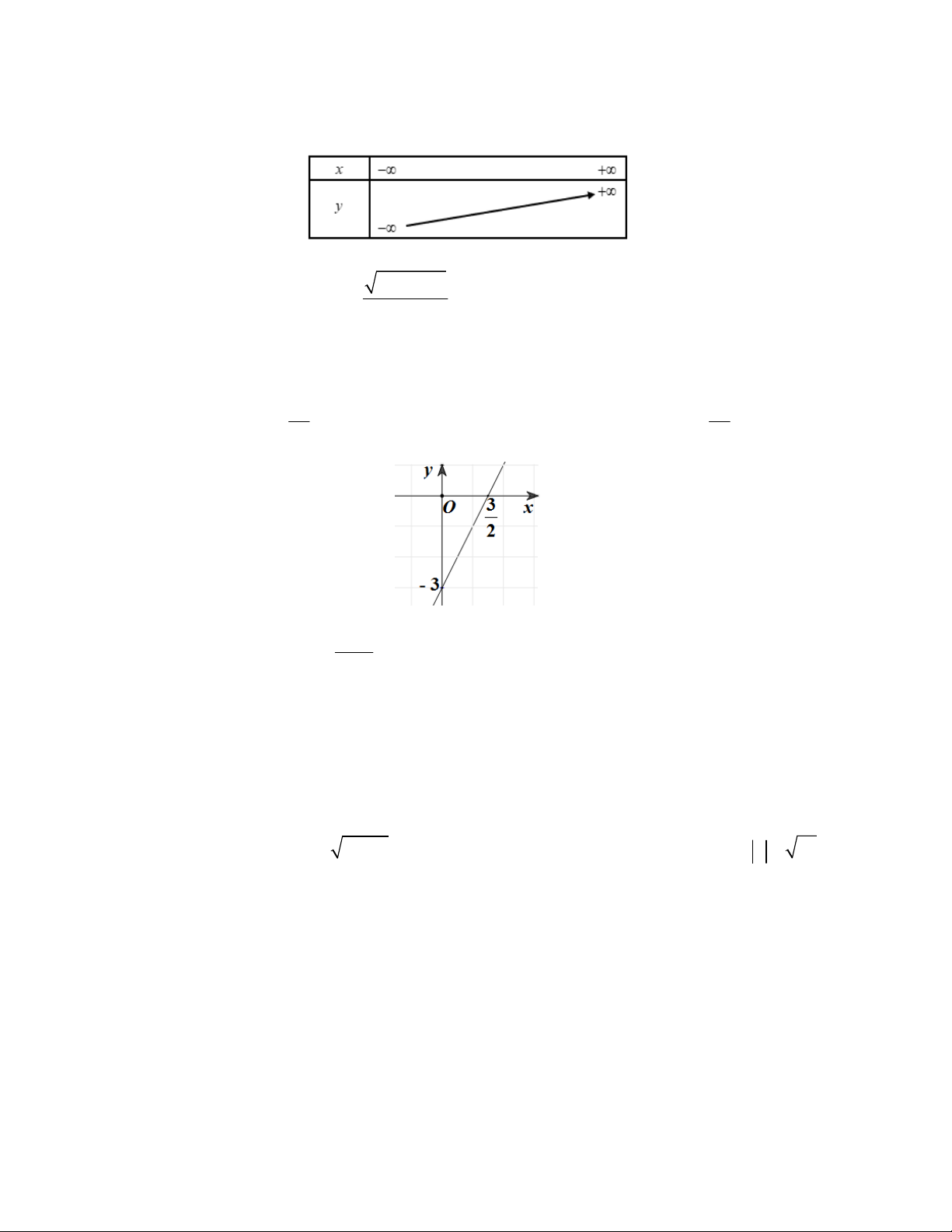
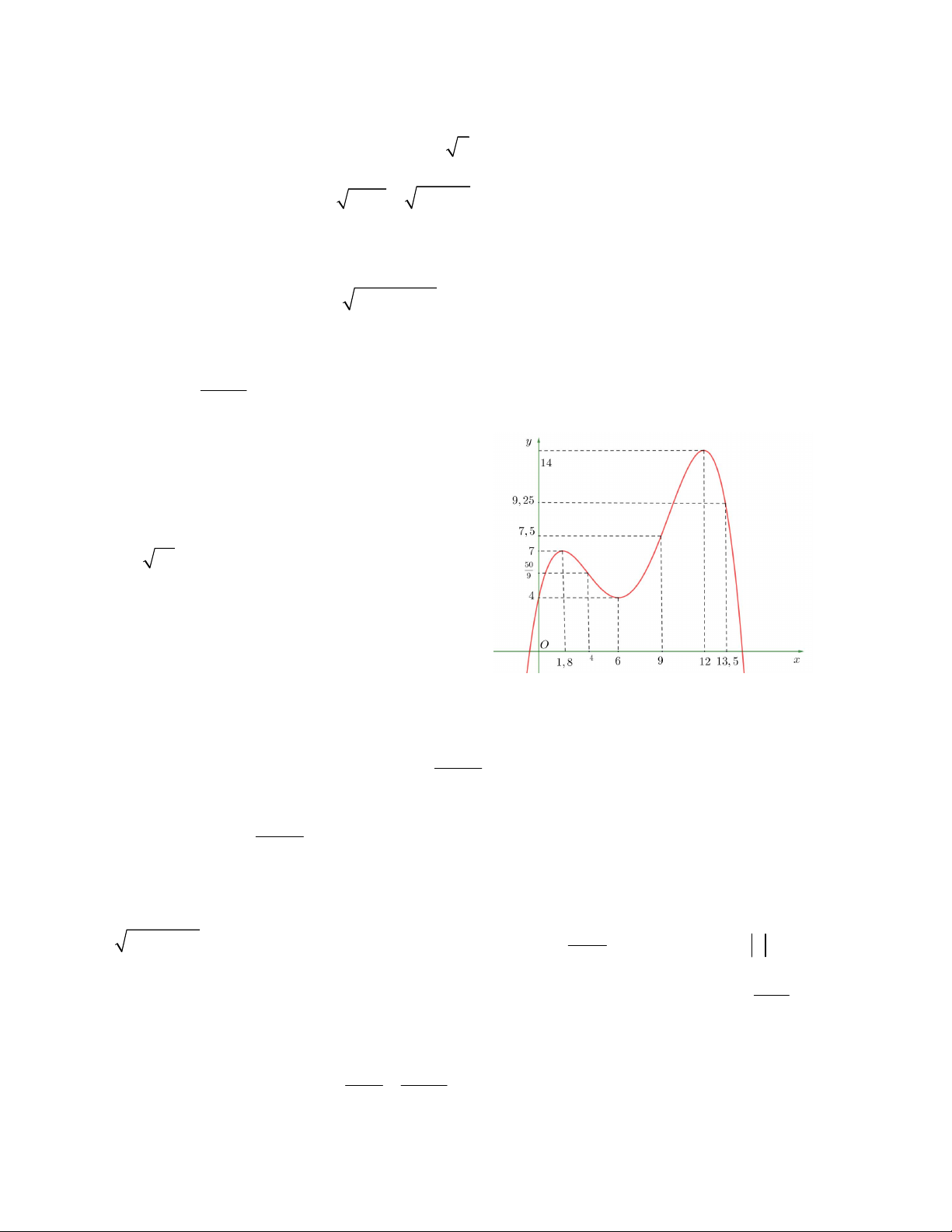
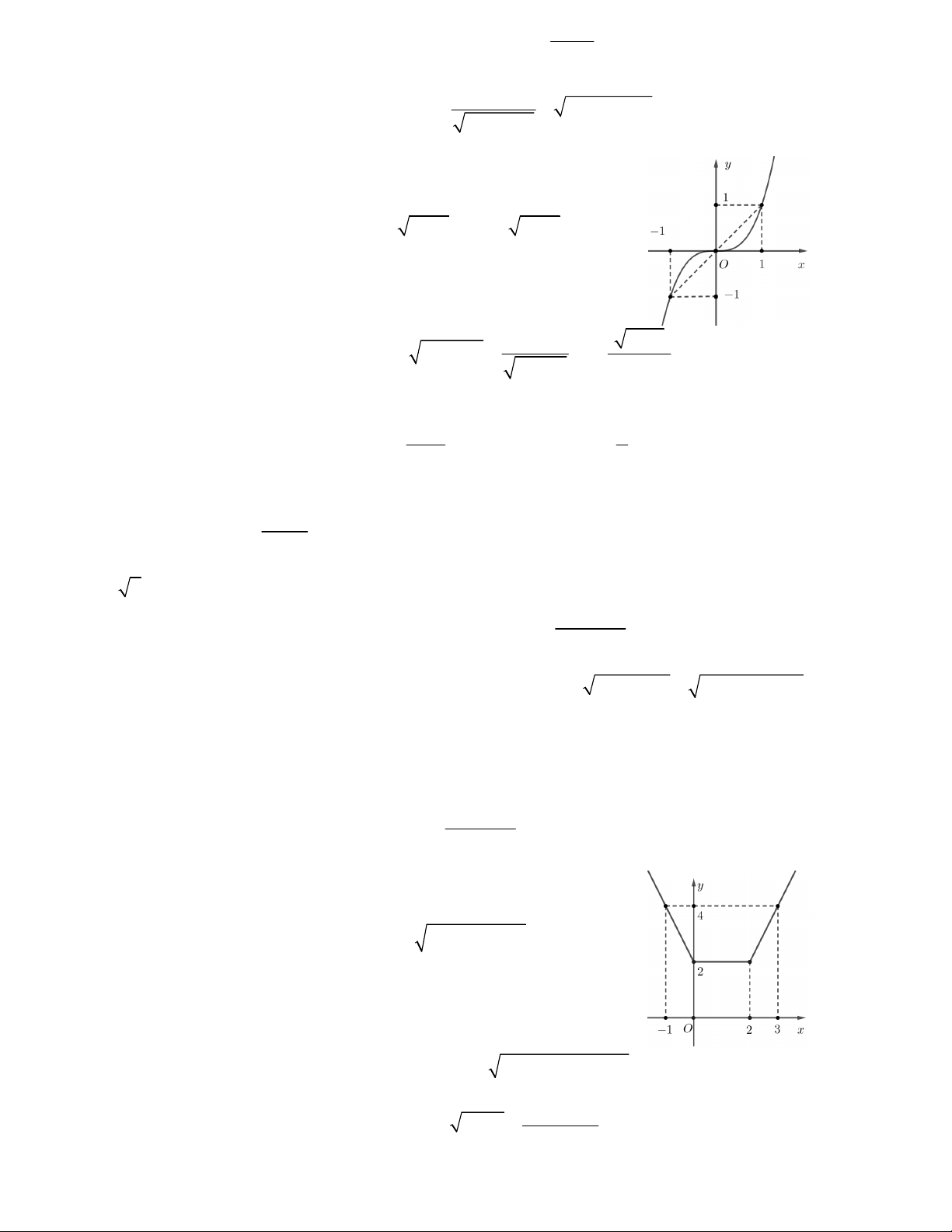
Câu 5. Đồ thị của hàm số nào dưới đây có dạng như đường thẳng trong hình vẽ bên?
A. y  2x  3
B. y  x  3
C. y x  3
D. y  2x  3 m  8
Câu 6. Tìm m để hàm số 3
y x x  là hàm số lẻ. 2 x A. m = 8 B. m = 2 C. m = 1 D. m = 6 2 x  5x ; x  5
Câu 7. Tập xác định D của hàm số f x  
có bao nhiêu phần tử nguyên trên đoạn [0;10] ? 3x 1 ; x  3  A. 5 phần tử B. 9 phần tử C. 8 phần tử D. 10 phần tử
Câu 8. Tìm giá trị nhỏ nhất của hàm số 2
y x  4x  8 trên R. A. miny = 2 B. miny = 4 C. miny = 3 D. miny = 5
Câu 9. Hàm số nào sau đây là hàm số lẻ A. y  3x B. 6 y x  2 C. 2 4
y  1 x x D. 4 y x x
Câu 10. Với giá trị nào của tham số m để y  m  
1 x  2 là hàm số bậc nhất? A. m  1 B. m  1 C. m  1 D. m  0 
Câu 11. Điểm nào sau đây không thuộc đồ thị hàm số y  2x  3 ? A. M 1  ;1  B. A3;9  C. B 1;5  D. C 0; 4
Câu 12. M (a;b) là giao điểm nằm bên phải trục tung của hai đồ thị 2
y x x  6; y  2x  6 . Tính a + b. A. a + b = 14 B. a + b = 15 C. a + b = 10 D. a + b = 9
Câu 13. Với giá trị nào của m thì đồ thị hàm số y  2x m  2021 đi qua điểm M 1; 2 ? A. 2025  B. 2  025 C. 2021 D. 2  021
Câu 14. Tìm tập giá trị W của hàm số y   x  2 x  6 . A. 1;  B. [1;3] C. 4;  D. [2;6]
Câu 15. Cho hai đường thẳng d : y  2x  3 và d : y  x 1 . Mệnh đề nào sau đây đúng? 1 2 A. d d .
B. d trùng với d . 1 song song với 2 1 2 C. d d . D. d
d nhưng không vuông góc với d . 1 vuông góc với 2 1 cắt 2 2 2
Câu 16. Cho hàm số y x 1 có đồ thị là đường thẳng .
 Đường thẳng  tạo với hai trục tọa độ một tam giác có diện tích bằng: 1 3 A. . B. 1. C. 2. D. . 2 2
Câu 17. Đồ thị hàm số nào nằm hoàn toán phía trên trục hoành ? 1 2 x  3 A. y = 6x B. y  C. 2
y x  4x  3 D. y x 2 x x 1 2
x  5x  4 1
Câu 18. D là tập xác định của hàm số 3 y
x . Hỏi D có chứa bao nhiêu giá trị nguyên ? 2 3x x 1 A. 5 B. 4 C. 2 D. 3
Câu 19. Hàm số nào sau đây đồng biến trên R ? A. 3
y x  4x B. 2
y x  6x 10
C. y x  4
D. y  5x 1
x  2  x  2
Câu 20. Tìm m để đồ thị hàm số y
1nhận Oy làm trục đối xứng.  2
m  7mx  2 A. m = 0;m = 7 B. m = 1;m = 2 C. m = 3;m = 7 D. m = 7 2 3 x  8
Câu 21. Có bao nhiêu đồ thị có tâm đối xứng O trong các đồ thị hàm số 3 3 y x  ; y  ; y x  8 ? x x A. 0 B. 1 C. 2 D. 3 2
Câu 22. Tìm m để đồ thị hàm số y   2
x x  m   3 4
4 x  5 có trục đối xứng Oy. A. m = 4 B. m = 17 C. m = 12 D. m = 8
Câu 23. Quỹ tích các điểm P (3m; 6m – 7) là đường thẳng d, d có hệ số góc là A. 5 B. 4 C. 2,5 D. 2
Câu 24. Tìm số giao điểm nằm phía trên trục hoành của hai đồ thị 2
y x 13x  9; y  10  x  9 . A. 1 B. 2 C. 3 D. 4 3
Câu 25. Có bao nhiêu số nguyên m thuộc (– 9;9) để hàm số f x 3 2  x x
m  9 không chẵn, không lẻ ? x A. 19 B. 15 C. 17 D. 2 1
Câu 26. Giá trị nhỏ nhất của hàm số y  4x  1trên 0;  là x A. 5 B. 2 C. 4 D. 8
Câu 27. Có bao nhiêu số nguyên m lớn hơn – 5 để hàm số y   2   3m  
1 x  2019 đồng biến trên R ? A. 6 B. 9 C. 10 D. 8 11
Câu 28. Tập giá trị của hàm số y  là 2 x  2x  2 A. (0;8) B. (1;7] C. (0;11] D.   ;11  4
Câu 29. Tìm số giao điểm của hai đồ thị hàm số y x
và đường thẳng y + 3 = 0. x A. 2 B. 1 C. 4 D. 0 1 x
Câu 30. Tập xác định D của hàm số 3 y  
x  4 chứa bao nhiêu phần tử nguyên nhỏ hơn 8 ? 2x 1  x A. 5 B. 8 C. 6 D. 7 x 19
Câu 31. Trên đồ thị hàm số y
có bao nhiêu điểm nguyên ? (các tọa độ x, y đều nguyên). x 1 A. 13 B. 10 C. 14 D. 12
Câu 32. Tìm số giao điểm của hai đồ thị hàm số 3 2 y x 11 ;
x y  6x  6 . A. 4 B. 2 C. 3 D. 1 x  4
Câu 33. Tìm tập xác định của hàm số y  . 2x 1  x  1   1  A. ;  \      1 B. ;    C. 1;  D. \   1  2   2 
_________________________________ 3
CƠ BẢN HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN ĐẠI CƯƠNG HÀM SỐ - P2)
__________________________________ m  2
Câu 1. Tìm m để hàm số 3
y x x  là hàm số lẻ. 4 x A. m = 2 B. m = 1 C. m = 3 D. m = 4
Câu 2. Tồn tại bao nhiêu giá trị m để hàm số 4 2
y x x   2 4
m  5m  6 x  8là hàm số chẵn. A. 2 giá trị B. 3 giá trị C. 1 giá trị D. 0 giá trị 2  x  3 ; x  0
Câu 3. Tìm số giao điểm của đồ thị hàm số y   và đường thẳng y = 4. 2
x  4x  7 ; x  0  A. 2 B. 1 C. 3 D. 4
Câu 4. Tìm tập giá trị của hàm số y   x   1  x  3 . A. [1;3] B.  2  ;  C.  1  ;  D. (1;3)
Câu 5. Hàm số y = f (x) có bảng biến thiên như hình vẽ. Có
bao nhiêu số nguyên m thuộc khoảng (– 10;10) để phương
trình f (x) – 2 = m có hai nghiệm phân biệt A. 11 B. 8 C. 10 D. 9
Câu 6. Hàm số nào sau đây đồng biến trên R ? 1 A. 3
y x x B. y  2x 1 C. y   D. 2
y x  4x  5 x
Câu 7. Tồn tại bao nhiêu giá trị nguyên m để hàm số y   2
9  m x  4 đồng biến trên R ? A. 3 B. 2 C. 1 D. 5 1
Câu 8. Tồn tại bao nhiêu giá trị nguyên m để hàm số 4 y x    2
3m  4m   5
1 x  2 là hàm số chẵn ? 2 x A. 2 B. 3 C. 1 D. 4 1
Câu 9. Giả sử D là tập xác định của hàm số f x 2 
 x  4x  3 . D chứa bao nhiêu giá trị 2 x x  2 nguyên x ? A. 3 B. 2 C. 1 D. 4
Câu 10. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 7 để hàm số 2 y
x  2x 1  m có tập xác định D = R. A. 5 B. 6 C. 7 D. 2 3x 1
Câu 11. Trên đồ thị hàm số y
có bao nhiêu điểm có tọa độ nguyên (điểm nguyên) ? 3x  2 A. 1 B. 2 C. 3 D. 4
x 1  x 1
Câu 12. Tồn tại bao nhiêu giá trị m để hàm số y  là hàm số chẵn ?  3
m  3m  4 x  4 A. 2 B. 3 C. 1 D. 4 1
Câu 13. Tồn tại bao nhiêu số nguyên m nhỏ hơn 10 để hàm số y  xác định trên R ? 2
x  2x m  4 A. 3 B. 4 C. 2 D. 5
Câu 14. Hàm số nào sau đây đồng biến trên R ? A. 2
y x  2x  4 B. y m  2 x   1  4
C. y x  2 D. 3 2
y x x  3x
Câu 15. Tìm số giao điểm nằm phía bên phải trục tung của hai đồ thị hàm số 3
y  4x 1; y x  5x 1 . A. 1 B. 2 C. 3 D. 0   x 1 ; x  1
Câu 16. Tồn tại bao nhiêu điểm trên đồ thị hàm số y   có tung độ bằng 4. 2 x x  4 ; x  1  A. 1 B. 2 C. 3 D. 4 4 1
Câu 17. Tồn tại bao nhiêu hàm số lẻ trong các hàm số 3 4 2 y x
; y x  5x  3; y  2x 1 ? x A. 2 B. 1 C. 3 D. 0
Câu 18. Hàm số nào sau đây đồng biến trên từng khoảng xác định ? x  4
A. y   x  2 3 2
B. y  7  x 2 C. 3
y x  4x  5 D. y x  3 3x 1
Câu 19. Tìm điều kiện tham số m để hàm số y
xác định với mọi x thuộc khoảng (1;2). x mm  2 A.  B. m > 0 C. 1 < m < 2 D. m 1;2 m  1 
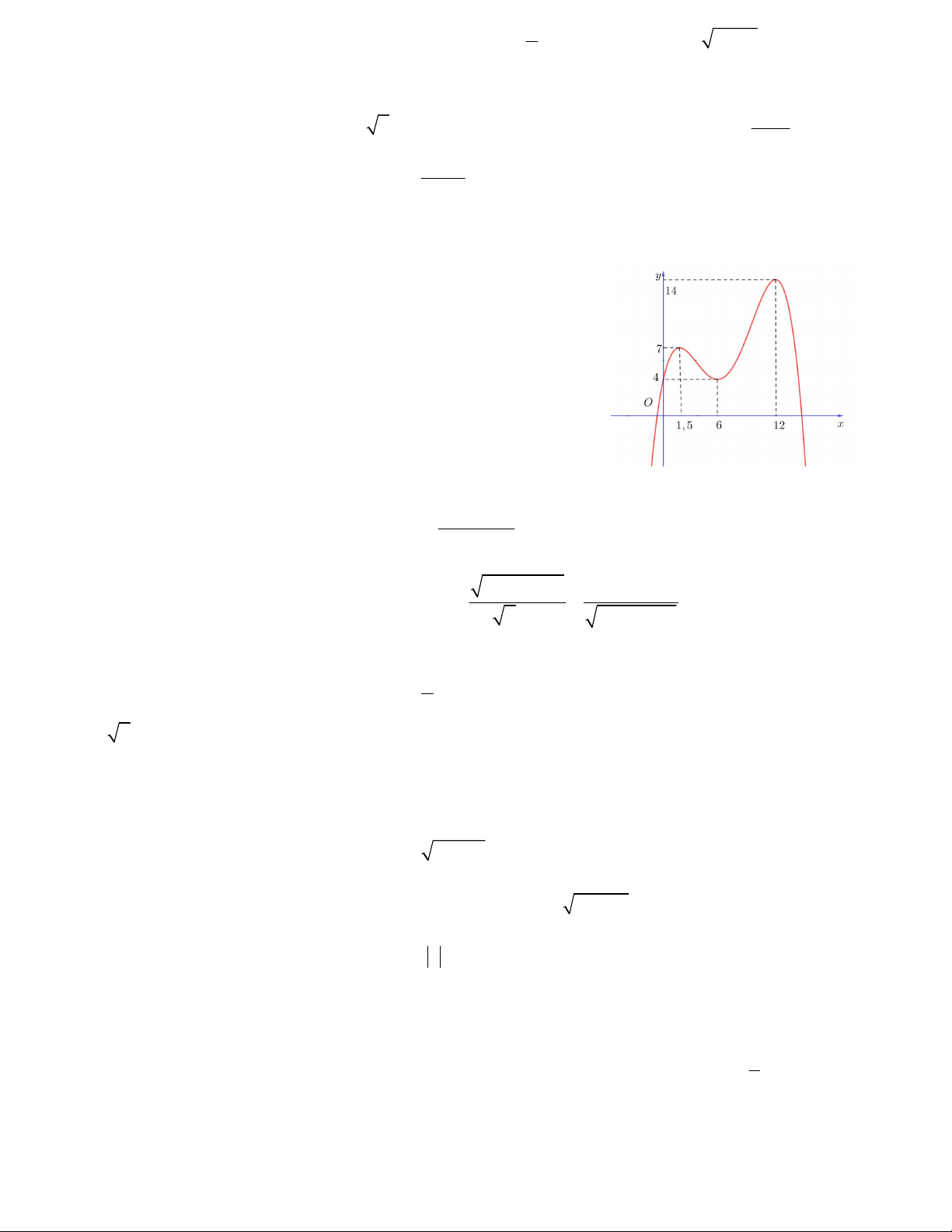
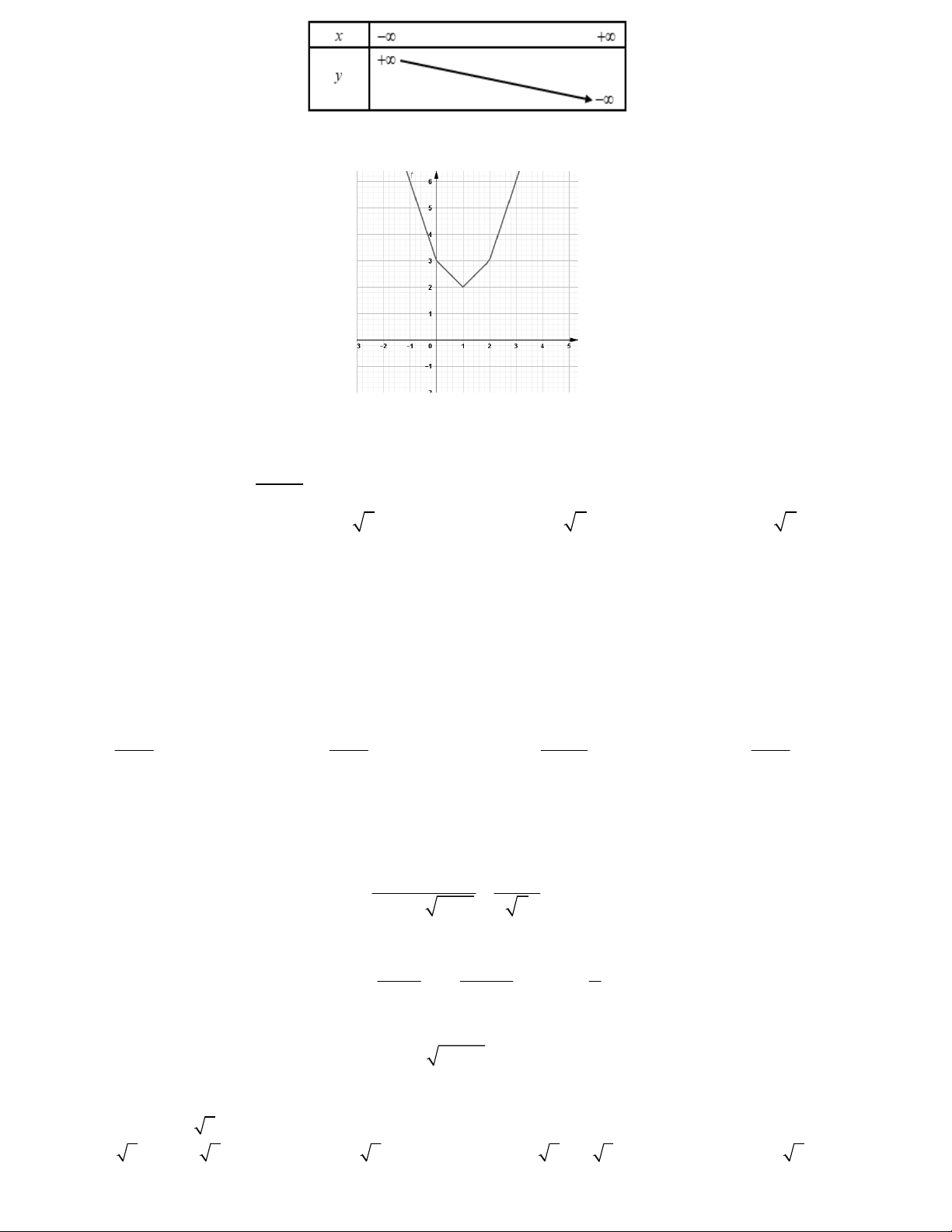
Câu 20. Hàm số y f x có đồ thị như hình vẽ bên. Tính tổng các giá
trị m xảy ra khi phương trình f x  2m có ba nghiệm phân biệt. A. 2 B. 4,5 C. 3,25 D. 5,5
Câu 21. Gọi d là quỹ tích các điểm K (2m; 7m – 1). Khi đó d là đường thẳng có hệ số góc là A. 3 B. 2 C. 3,5 D. 7 x m
Câu 22. Tìm tất cả các giá trị của m để hàm số y
xác định trên 1; . 2m 1 x A. m  0 B. m > 2 C. 0 < m < 1 D. 0,5 < m < 3 2 x  5x  6 1
Câu 23. Ký hiệu D là tập xác định của hàm số f x  
. Tập hợp D có bao nhiêu 2 x  2 x  2x 1 số nguyên nhỏ hơn 10 ? A. 4 B. 8 C. 9 D. 7 1
Câu 24. Tìm tập hợp giá trị của hàm số y  2x  với x > 0. x A. 2 2;  B. [1;2] C. [0;4] D. 0;    3  x  5x ; x  0
Câu 25. Trên đồ thị hàm số y  
tồn tại bao nhiêu điểm có tung độ bằng 6 ? 2
x  3x  8 ; x  0  A. 2 B. 1 C. 3 D. 4
Câu 26. Tìm điều kiện tham số m để hàm số y
2x m xác định với mọi x  0;2 . A. m  0 B. m < 0 C. m > 1 D. m > 0
Câu 27. Tồn tại bao nhiêu giá trị nguyên m để hàm số y  m   2
4 x  27  m đồng biến ? A. 2 B. 1 C. 3 D. 4  x ; x  3 
Câu 28. Tìm số giao điểm của đồ thị hàm số y  
với đường thẳng y = 13. 2
x  7x  5 ; x  3  A. 3 B. 1 C. 2 D. 4
Câu 29. Đường thẳng nào sau đây đi qua điểm M 2;  
1 và song song với đường thẳng y  2  x 1? 1 A. y  2  x  3.
B. y  2x  3. C. y  2  x  3. D. y x  2  2
Câu 30. Biết đường thẳng y ax b đi qua điểm M 4; 2 và vuông góc với đường thẳng y  4x  3 . Tính
P  4a  3b A. P  4. B. P  2  C. P  2  D. P  4 
_________________________________ 5
CƠ BẢN HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN ĐẠI CƯƠNG HÀM SỐ - P3)
__________________________________
Câu 1. Hàm số y = f (x) có bảng biến thiên như hình
vẽ. Hàm số f (x) đồng biến trên khoảng nào A. (1;3) B. (0;3) C. (– 1;4) D. (0;2)
Câu 2. Cho hàm số f (x) = 3x + 5. Mệnh đề nào sau đây đúng ? A. f (2007) < f (2008) B. f (2006) = f (2005) C. f (4) < f (3) + 4 D. f (2006) > f (2009) 2x  3
Câu 3. D là tập xác định của hàm số y
. Hỏi D chứa bao nhiêu số nguyên ? 2  5  x A. 5 B. 4 C. 2 D. 6
Câu 4. Với giá trị nào của tham số thực m thì hàm số y  3 
m x m 1 là hàm số bậc nhất? A. m  1  . B. m  1  . C. m  3 . D. m  3 .
Câu 5. Hàm số nào sau đây có khoảng nghịch biến là các khoảng  ;  3,3; 1 2 2 A. 2
y x  2x B. y  C. y  D. y x  2 x  3 2x 1
Câu 6. Trong các hàm số sau, hàm số nào là hàm số chẵn? 2 A. 2
y x  2x . B. 2
y x  2 x .
C. y x  2x .
D. y x 1.
Câu 7. Biết rằng khi m m thì hàm số f x 3  x   2 m   2
1 x  2x m 1 là hàm số lẻ. Khẳng định nào sau 0 đây đúng?  1   1   1  A. m  ;3 . B. m   ; 0 . C. m  0; . D. m  3;  . 0   0   0   0    2   2   2  m 1
Câu 8. Có bao nhiêu số nguyên m (– 9;9) để hàm số 5 3
y x  2x
 5x không chẵn, không lẻ ? 2 x A. 10 B. 2 C. 16 D. 12
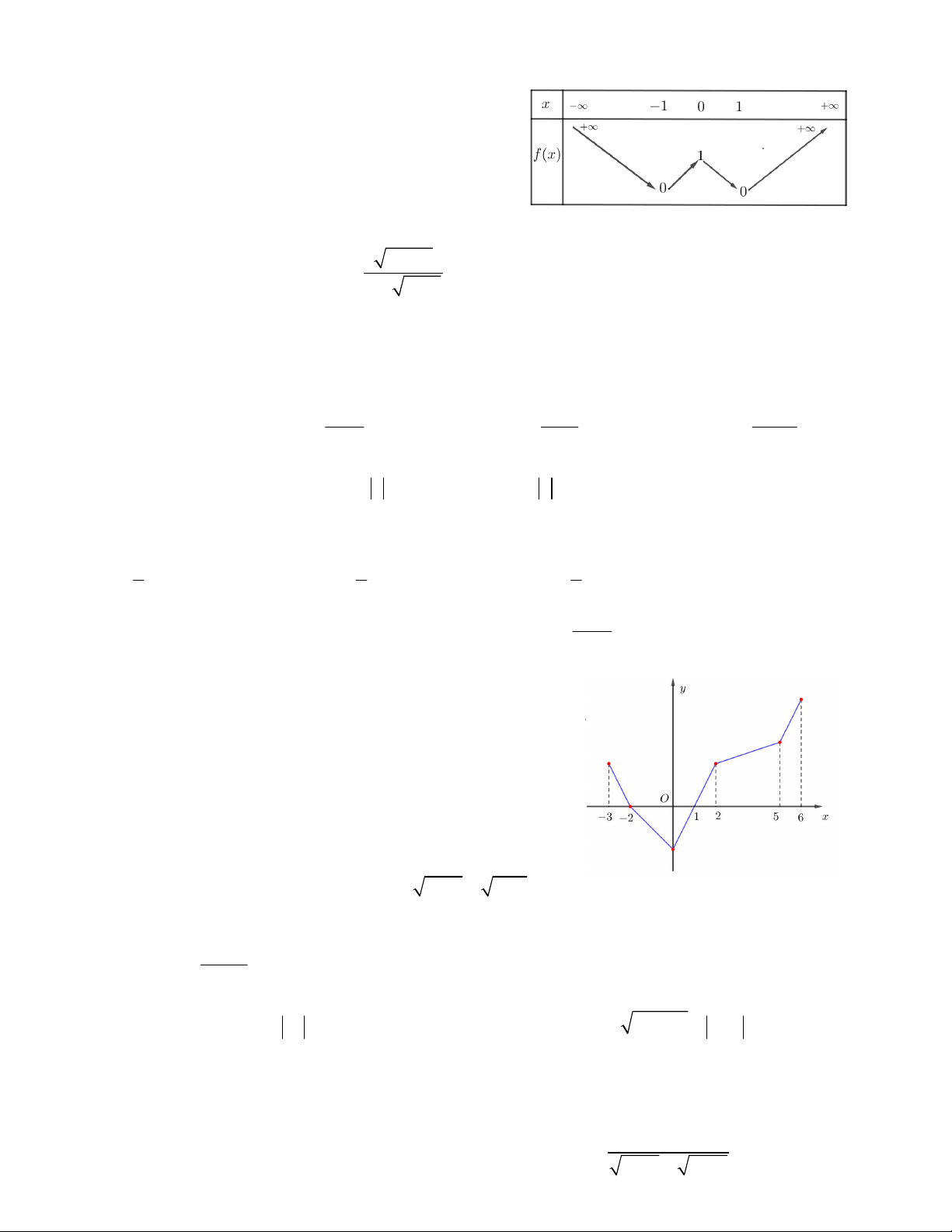
Câu 9. Trên miền [– 3;6] hàm số y f x có đồ thị như hình vẽ
bên. Giá trị lớn nhất của hàm số y f x trên đoạn [–3;6] là A. f  2   B. f 6 C. f   1 D. f 2
Câu 10. Gọi T là tập hợp giá trị của hàm số y  2  x
x 1 . Hỏi T có bao nhiêu phần tử nguyên ? A. 1 B. 2 C. 3 D. 4
Câu 11. Khi x, y đều là các số nguyên thì F (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên 5x  9
đồ thị hàm số y  ? 5x 1 A. 2 điểm nguyên. B. 6 điểm nguyên. C. 4 điểm nguyên. D. 8 điểm nguyên.
Câu 12. Cho các hàm số 4 2 2 4
y  3x ; y  8
x  9x  5; y  2x 10 ; x y
x  25  x 1 .
Hỏi có bao nhiêu hàm số chẵn ? A. 2 B. 3 C. 4 D. 5
Câu 13. Tìm số giao điểm giữa hai parabol 2 2
y x  6x  5; y x 10x  8 . A. 1 giao điểm. B. 2 giao điểm. C. 3 giao điểm. D. 4 giao điểm. 3 x
Câu 14. Tính tổng tất cả các số nguyên thuộc tập xác định của hàm số y  . 4  x x  2 A. 4 B. 6 C. 7 D. 5 6
Câu 15. Tìm số giao điểm giữa đồ thị hàm số y
4x  9 và đường thẳng y = 2x – 5. A. 2 giao điểm. B. 4 giao điểm. C. 3 giao điểm. D. 1 giao điểm.
Câu 16. Tồn tại bao nhiêu giá trị nguyên của m trong khoảng (– 19;19) để đường thẳng y x  2m cắt đường 4x  3 thẳng y
tại hai điểm phân biệt. x 1 A. 31 giá trị. B. 33 giá trị. C. 38 giá trị. D. 13 giá trị.
Câu 17. Tìm số giao điểm của hai đồ thị hàm số y  2  x x và y  2 . A. 3 B. 2 C. 1 D. 4 x  4
Câu 18. Trong các hàm số 3 4 2 3 2 y x  ;
x y x  4x 1; y x x 1; y
, có bao nhiêu đồ thị có tâm x  2 đối xứng ? A. 4 B. 2 C. 1 D. 3 x 1
Câu 19. Tồn tại bao nhiêu giá trị nguyên m trong khoảng (– 7;7) sao cho đường thẳng y  cắt đường x 1
thẳng y x m tại hai điểm phân biệt. A. 13 giá trị. B. 15 giá trị. C. 12 giá trị. D. 5 giá trị. x  9
Câu 20. Tìm m để hàm số y
xác định trên đoạn [3;5]. x  2m 1 A. m > 2 hoặc m < 1 B. m > 3 hoặc m < 0 C. m > 4 hoặc m < 1 D. m > 5 hoặc m < 0
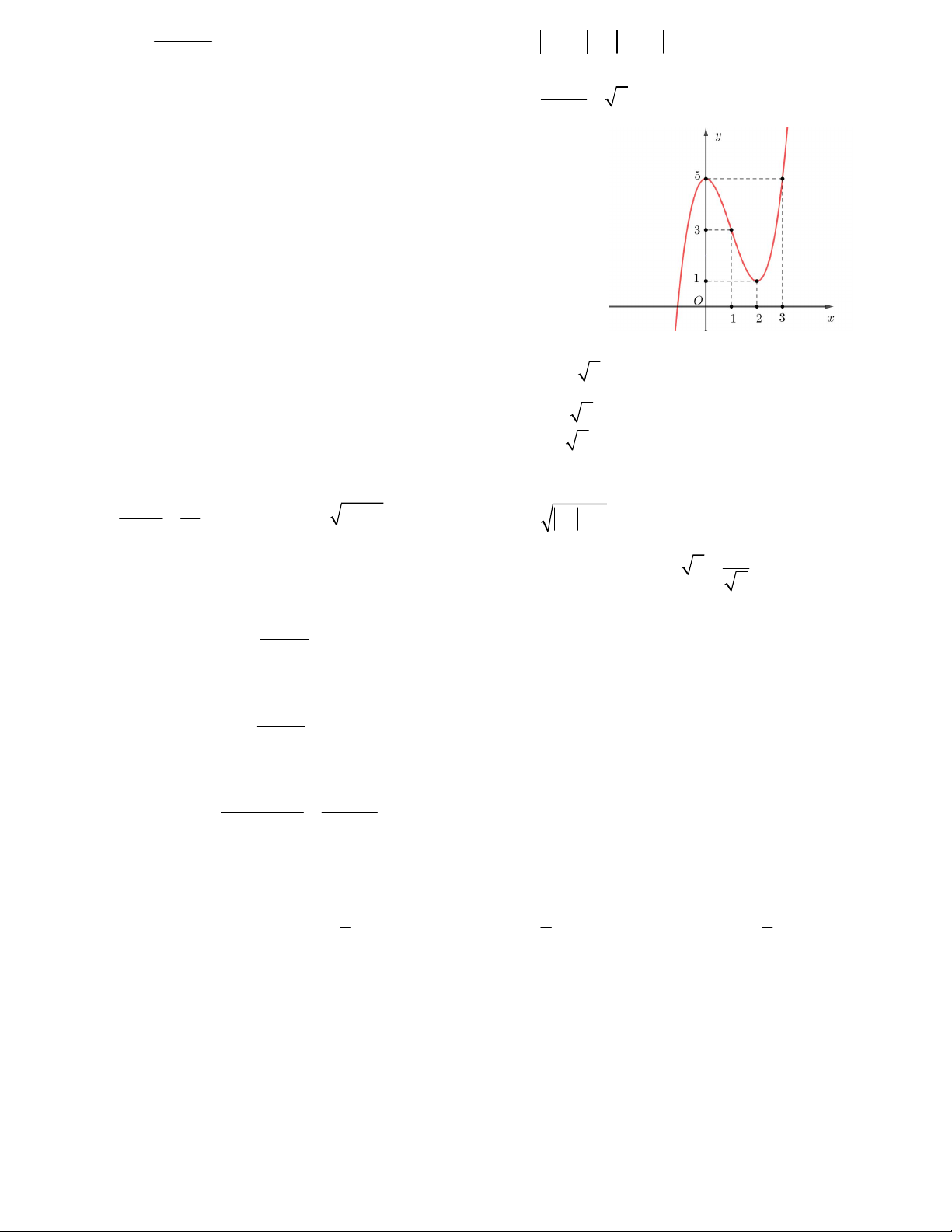
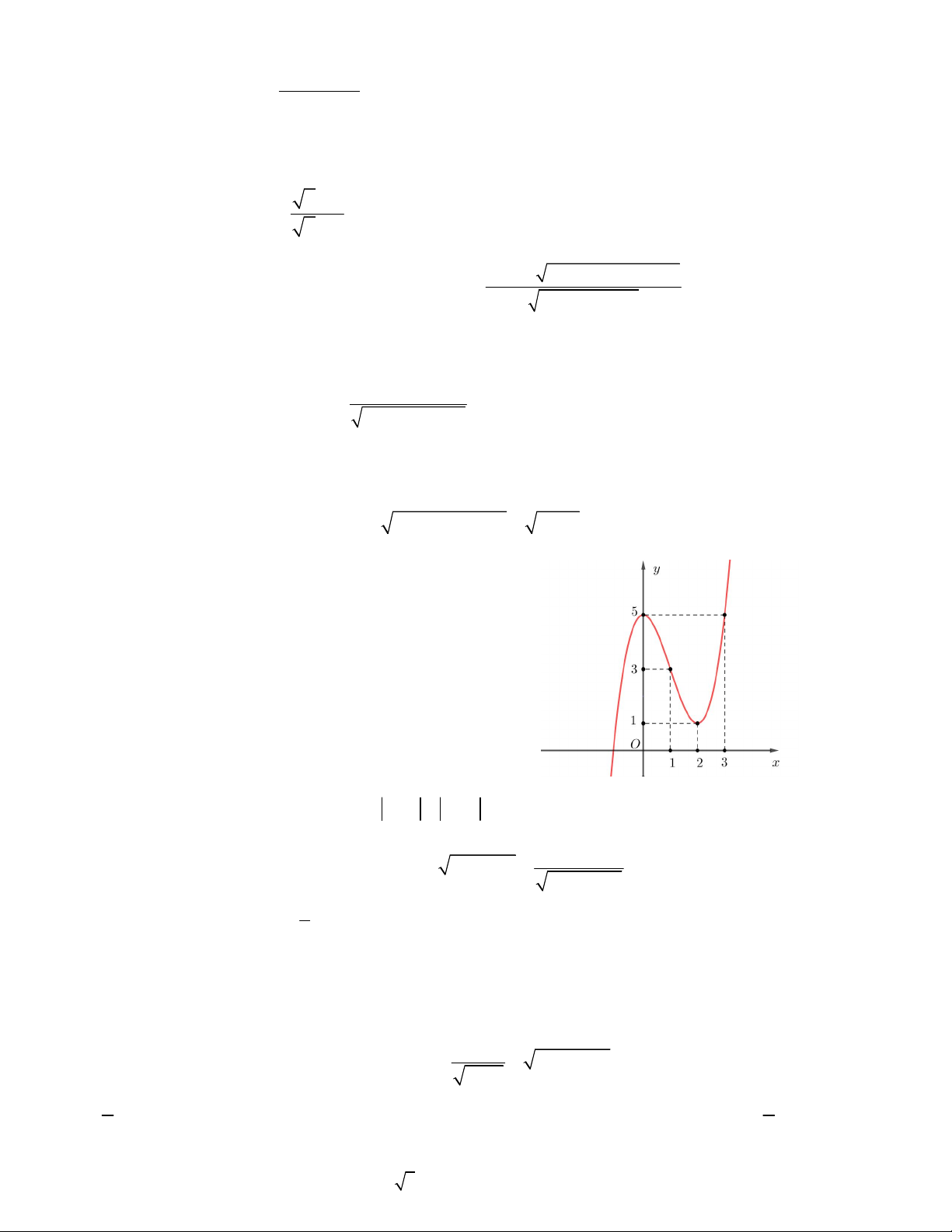
Câu 21. Hàm số y f x có đồ thị như hình vẽ bên. Tìm điều
kiện tham số m để phương trình f x  m có ba nghiệm phân biệt.
A. 1 < m < 5 B. 2 < m < 6
C. 0 < m < 4 D. 3 < m < 4
Câu 22. Hàm số nào sau đây đồng biến trên khoảng (1;4) ? x  5 A. 2
y x  4x  5 B. y  C. y  4  x D. 4 2
y x  8x 10 x 1
Câu 23. Tìm số giao điểm giữa đồ thị hàm số 2 y
2x  3x  7 và đường thẳng y = x + 2. A. 4 giao điểm. B. 2 giao điểm. C. 3 giao điểm. D. 1 giao điểm.
Câu 24. Tính tổng các giá trị m để ba đường thẳng  : y x  2 ,  : y  x  4 và 2
 : y  2x m  4 đồng 1 2 3 quy. A. 0. B. 3. C. 9. D. 3.
Câu 25. Tìm tất cả các giá trị thực của tham số m để đường thẳng d : y  3m  2 x  7m 1 vuông góc với
đường thẳng  : y  2x 1. 5 5 1 A. m  0. B. m   . C. m  . D. m   . 6 6 2 1
Câu 26. Tìm tất cả các giá trị m để hàm số y
 2m  6  x xác định trên (– 1;0) x m A. m  1 B. 3  m  1 C. 0 < m < 2 D. 2 < m < 3
Câu 27. Tập giá trị của hàm số 4 2
y x  4x  6 là A.[1;3] B. [4;6] C. 2;  D. 4; 
Câu 28. Tìm phương trình đường thẳng d : y ax  .
b Biết đường thẳng d đi qua điểm I 2;3 và tạo với hai
trục Ox, Oy một tam giác vuông cân.
A. y x  5.
B. y  x  5.
C. y  x  5.
D. y x  5.
____________________________________ 7
CƠ BẢN HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN ĐẠI CƯƠNG HÀM SỐ - P4)
__________________________________
Câu 1. Tìm điều kiện tham số m để hàm số 3
y x  8x m  8 không chẵn, không lẻ. A. m  8 B. m = 9 C. m = 8 D. m > 10
Câu 2. Tồn tại bao nhiêu số nguyên m nhỏ hơn 5 để hàm số y   2   m  
1 x  9 đồng biến trên R ? A. 12 B. 10 C. 13 D. 14
Câu 3. Cho hai hàm số f x 3  x   2
m m   2 x x g x 4  x   2 m   3 2 4 3 5;
1 x  5x 10 . Tìm điều
kiện tham số m để đồ thị hàm số f x có tâm đối xứng và đồ thị hàm số g x có trục đối xứng. A. m = 3 B. m = 2 C. m = 1 D. m = 4
Câu 4. Hàm số bậc hai f (x) có bảng biến thiên như
hình vẽ. Tìm điều kiện của m để phương trình f (x) = m có nghiệm dương. A. m < 3 B. m < 2
C. 0 < m < 4 D. m > 1
Câu 5. Tìm số giao điểm của đồ thị hàm số 2
y  3x  4x  4 và đồ thị hàm số y x  2 . A. 1 B. Không cắt nhau C. 2 D. 3 3
Câu 6. Gọi T là tập hợp giá trị của hàm số 3 y x
với x > 0 và Q là tập hợp giá trị của hàm số x 2 y
26  x . Hỏi tập hợp T Q có bao nhiêu phần tử nguyên ? A. 4 B. 3 C. 5 D. 2
Câu 7. Hàm số bậc hai   2
f x ax bx c có đồ thị như hình vẽ. Tính f  3
a   f  3 2
2  a  với a là tham số. A. 0 B. 2 C. 3 D. 1
Câu 8. Tìm điều kiện tham số m để hàm số 2 2
y  3  x  3  x  m  3 x là hàm số chẵn. A. m = 4 B. m = 1 C. m = 0 D. m = 3
Câu 9. Gọi A và B tương ứng là tập giá trị của hàm số 2 2
y x x  5; y x  4x  6 . Mệnh đề nào sau đây đúng ? A. A B B. B A C. A = B D.   A 3
Câu 10. Cho các hàm số 3 5 3 4
y x x 1; y x   x ; y x  ; y
2x  4 . Có bao nhiêu hàm số mà đồ 2 x
thị của chúng có tâm đối xứng ? A. 3 B. 2 C. 1 D. 0
Câu 11. Tìm điều kiện m để đồ thị hàm số 2
y x  4x cắt đường thẳng y = m tại hai điểm phân biệt. A. m > – 4 B. m > 2 C. m > – 1 D. m > – 5 2 x  2x 1
Câu 13. Gọi D là tập xác định của hàm số f x 3 
 3x 1 . Hỏi D chứa bao nhiêu số nguyên 3x  4  x nhỏ hơn 10 ? A. 8 B. 2 C. 7 D. 6
Câu 14. Tìm số giao điểm của đồ thị hàm số 3 y
x  5x  4; y  11x  4 . A. 2 B. 3 C. 4 D. 1
Câu 15. Tìm tập hợp giá trị của hàm số y   x  
1  x  2 x  3 x  4 . A. 2;  B.  1  ;  C.  3  ;  D.  4  ; 
Câu 16. Hàm số nào sau đây có trục đối xứng là trục tung ? 8 3 A. 4 y x
B. y  2x 1  3 2x  1  x  4 1 1 C. y   2 x   2 x x   3 1 2  x x D. y   x 2 x  3
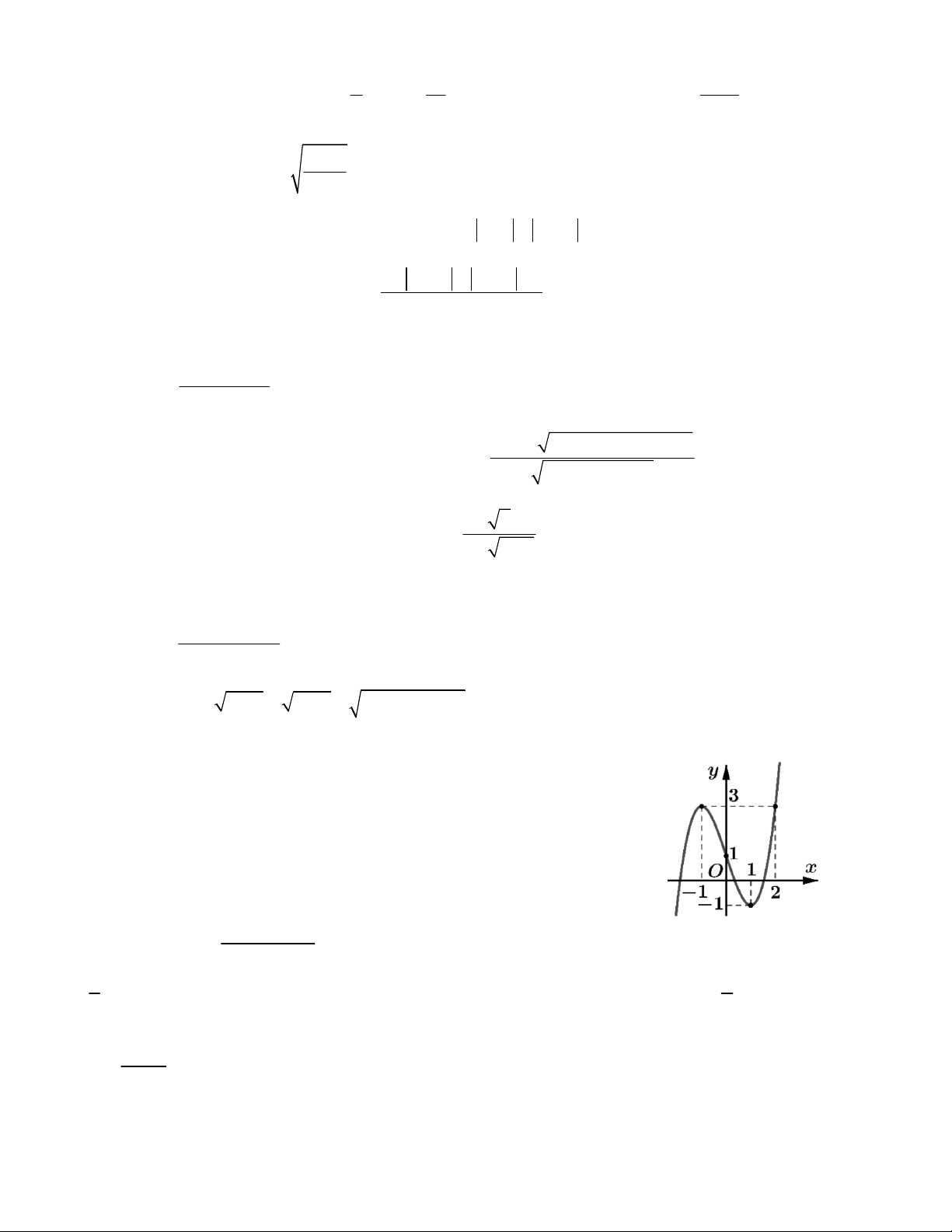
Câu 17. Hàm số y f x có đồ thị như hình vẽ bên. Tìm điều kiện
tham số m để phương trình f x 1  m có hai nghiệm phân biệt cùng dương.
A. 0 < m < 4 B. 1 < m < 5
C. 2 < m < 3 D. 3 < m < 4
Câu 18. Hàm số nào sau đây nghịch biến trên R ? x  4
A. y   x  2 2 1  x B. y  C. y     3 2 x 1 D. 3
y x  4x  1 x  2 3 x 1
Câu 19. Tồn tại bao nhiêu điểm nguyên (x;y) trên đồ thị hàm số y  ? x 1 A. 4 B. 2 C. 1 D. 3
Câu 20. Hàm số nào sau đây là hàm số lẻ ? 4 x 1 1 A. y   B. 3 y x 1  4x C. y  2x  4 D. y    x  3 2 10 1 3 x x 1
Câu 21. Tồn tại bao nhiêu điểm trên M có tung độ bằng 2 nằm trên đồ thị hàm số 3 y x  ? 3 x A. 1 điểm. B. 2 điểm. C. 3 điểm. D. 4 điểm. 4x  2
Câu 22. Đường cong y
cắt đường thẳng y  3x  4 tại các điểm P, Q. Gọi a;b tương ứng là tung độ x 1
của P, Q. Tính giá trị biểu thức S = a + b. A. S = 11 B. S = 10 C. S = 11 D. S = 12 2x  5
Câu 23. Đường cong y
cắt đường thẳng y x  1tại hai điểm phân biệt A, B. Tìm tọa độ trung điểm I x 1 của đoạn thẳng AB. A. I (0;1) B. I (0;2) C. I (4;5) D. I (– 2;2) x  9 x
Câu 24. Hàm số y  
có tập xác định  \  ; a ; b ;
c d. Tính a + b + c + d. 2 2 x  4x  3 x  25 A. 4 B. 5 C. 6 D. 7
Câu 25. Biết đồ thị hàm số y ax b đi qua điểm N 4;  
1 và vuông góc với đường thẳng 4x y 1  0. Tính tích P  . ab 1 1 1 A. P  0. B. P   . C. P  . D. P   . 4 4 2
Câu 26. Điểm A có hoành độ bằng 1 và thuộc đồ thị hàm số y mx  2m  3. Tìm m để điểm A nằm trong
nửa mặt phẳng tọa độ phía trên trục hoành. A. m  0. B. m  0. C. m  1. D. m  0.
Câu 27. Tìm tất cả các giá trị của tham số m để hàm số y  2x m 1 có giá trị nhỏ nhất trên 1;  3 bằng 3? A. m  6. B. m  4. C. m  0. D. m  1.
Câu 28. Đường thẳng d : y  m  3 x  2m 1 cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB
cân. Khi đó, số giá trị của m thỏa mãn là: A. 1. B. 0. C. 3. D. 2.
_________________________________ 9
CƠ BẢN HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN ĐẠI CƯƠNG HÀM SỐ - P5)
__________________________________
Câu 1. Tập xác định của hàm số y  4  2x là
A. D  2; ..
B. D  ; 2.. C. D  .  . D. D   \   2 . . x  9
Câu 2. Tìm điều kiện của m để hàm số y
có tập xác định D   .
m  3 x m  4 A. m = 4 B. m = 3 C. m > 2 D. 1 < m < 3 2 x x
Câu 3. Tập xác định của hàm số y  là x A. D  .  .
B. D  0;.. C. D   \   0 .. D. D   ;  0..
Câu 4. Điểm nào sau đây thuộc đồ thị hàm số y  5x  2. A. M 3  ;1 . B. M 2  ;0 . C. M 0; 2 . D. M 1;3 . . 1   1   1   1   2
x  3x khi x  0
Câu 5. Cho hàm số y f x   . Tính f   1 . 1 x khi x  0  A. 4. . B. 2  . . C. 2. . D. 0. . x 10
Câu 6. Tìm tập xác định của hàm số y   2x 1 . 2 x x  2  1  A. D = 1  ; 2 \   0 B. D = 0; 
C. D = 0;  \   1 D. D =  ;     2  2x 1
Câu 7. Tìm tất cả các giá trị của a để hàm số y
có tập xác định D   . 2
x  6x a  2 A. a > 11 B. a > 8 C. 7 < a < 9 D. 1 < a < 3 4 2 5 x x  2 x 1 1
Câu 8. Trong các hàm số 2 3 y  ; y
; y x  2 ; x y x  
tồn tại a hàm số chẵn, b 2 3 3 x  4 x 1 x x
hàm số lẻ. Tính 5a + 4b. A. 13 B. 12 C. 18 D. 14
Câu 9. Cho hàm số y f x  x  1 . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số y f x đồng biến trên  .
B. Hàm số y f x đồng biến trên ;1 .
C. Hàm số y f x đồng biến trên 1;   .
D. Hàm số nghịch biến trên  .
Câu 10. Tìm tập giá trị của hàm số 2 y x 1. A. 1;  . B. 0;  . C. 1;  . D.  . 2 x x  2 ; x  0 
Câu 11. Có bao nhiêu điểm trên đồ thị hàm số f (x)   có tung độ bằng 4. x  2 ; x  0   A.2 B. 1 C. 3 D. 4
Câu 12. Hàm số nào sau đây đồng biến trên  ?
A. y x  5 .
B. y  x  3 . C. y  3  x . D. y  2  x  5 .
Câu 13. Đồ thị của hàm số y  2
x 1 song song với đồ thị hàm số nào trong các hàm số sau đây? 1 A. y  2  x 1.
B. y  2x 1. C. y x 1 . D. y  2  x 1. 2
Câu 14. Tập giá trị của hàm số 4 2
y x  4x  5 có phần tử nguyên nhỏ nhất là A.2 B. 1 C. 3 D. 4
Câu 15. Cho hàm số y  2x m 1. Tìm giá trị m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 4 . A. m  3  . B. m  3 . C. m  0 . D. m  1  .
Câu 16. Hàm số nào sau đây có tập xác định là R ? 10 2 x 2x x x 1 A. y  . B. y  . C. y  . D. y  . 3 2 2 x 1 x 1 x 1 x 1
Câu 17. Đồ thị hàm số y ax b x  
cắt trục Ox tại điểm 2 . Tính 2a b . A. 0 . B. 2  . C. 4  . D. 2 .
Câu 18. Tìm m để hàm số 4 3 2 2
f (x)  x  (m  2)x  5x  (m  4)x  3 là hàm số lẻ. A.2 B. 1 C. 3 D. 4
Câu 19. Hàm số nào sau đây là hàm số chẵn? . A. 4
y x  3x . B. 4
y x  2x . C. 2
y x  2x . D. 4 2
y x  2x .
Câu 20. Cho hàm số y f x có đồ thị như sau
Hàm số đã cho đồng biến trên khoảng: A. 0; . B. ;0 . C. ; 2 . D. 2;  .
Câu 21. Tìm số giao điểm của hai đồ thị hàm số 2
y x x  5 ; y  6 . A.3 B. 2 C. 1 D. 0
Câu 22. Tập xác định D của hàm số y
x 1  x 1 . A. D  1  ;   . B. D   1  ;   . C. D   . D. D   1   ;1 . .
Câu 23. Hàm số nào dưới đây nghịch biến trên  ? A. 2 y  x .
B. y   x . C. y  2   x . D. y x .
Câu 24. Cho đường thẳng d : y ax b đi qua điểm I 1; 
2 và tạo với các tia Ox , Oy một tam giác có diện
tích bằng 4 . Tính giá trị của biểu thức P a  . b A. P  2  . B. P  6 . C. P  4 . D. P  2 .
Câu 25. Tìm giá trị lớn nhất của hàm số 2
y  6x x . A.3 B. – 9 C. 1 D. – 4
Câu 26. Đồ thị hàm số y ax b A 2  ;1 , B 1; 2 
nào sau đây đi qua hai điểm     .
A. y  x 1. .
B. y  2x  1..
C. y x  1. .
D. y  2x 1..
Câu 27. Đồ thị của hàm số nào dưới đây có dạng như đường thẳng trong hình vẽ bên? A. y  2  x 1
B. y  2x 1
C. y x  2  D. y  3x  4 8x 1
Câu 28. Cho các hàm số 2 4 y
; y  6x 1; y
x  9  x 1; y x 1 . Có bao nhiêu đồ thị hàm số x có trục đối xứng ? A. 3 B. 2 C. 4 D. 1
Câu 29. Khi x, y đều là các số nguyên thì M (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên x 10
đồ thị hàm số y  ? x 1 A. 6 điểm nguyên. B. 5 điểm nguyên. C. 4 điểm nguyên. D. 8 điểm nguyên.
_________________________________ 11
CƠ BẢN HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN ĐẠI CƯƠNG HÀM SỐ - P6)
__________________________________
Câu 1. Hàm số nào sau đây đồng biến trên  ? A. 2 y x . B. y  x .
C. y  2x  5 . D. 2 y  x .
Câu 2. Tìm số giao điểm của hai đồ thị hàm số y  3 x; y  2x  1. A.2 B. 3 C. 1 D. 4
Câu 3. Tập xác định của hàm số 2 y  4  x
x 10 chứa bao nhiêu số nguyên dương A.3 B. 2 C. 4 D. 1
Câu 4. Tìm tất cả các giá trị của tham số m để hàm số y  m  
1 x m  2 nghịch biến trên  . A. m  1. B. m  1. C. m  1. D. m  1.
Câu 5. Tìm tập giá trị của hàm số 2 y
x  2x  5 . A.[1;4] B. [1;5] C. 2;  D. 3;
Câu 6. Khi x, y đều là các số nguyên thì M (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên x 10
đồ thị hàm số y  ? x 1 A. 6 điểm nguyên. B. 5 điểm nguyên. C. 4 điểm nguyên. D. 8 điểm nguyên.
Câu 7. Hàm số y f x có đồ thị như hình vẽ
bên. Tìm số nghiệm của phương trình f (x)  50 . A.3 B. 4 C. 6 D.5
Câu 8. Đồ thị của hàm số nào dưới đây vuông góc với đường thẳng y x  2 ?
A. y  4x 1
B. y  x  5
C. y x 1
D. y  2x  3 2x  3
Câu 9. Tìm tung độ giao điểm của đường cong y
và đường thẳng y x 1. x  3 A. 0 B. 1 C. 2 D. – 1 2x  5
Câu 10. Đường cong y
cắt đường thẳng y x  1tại hai điểm phân biệt A, B. Tìm tọa độ trung điểm I x 1 của đoạn thẳng AB. A. I (0;1) B. I (0;2) C. I (4;5) D. I (– 2;2)
Câu 11. Đồ thị hàm số nào sau đây cắt đường thẳng y x 1 A. 2 y x x  4 B. 2
y x  4x  4 C. y x
D. y x  5 x  4 x 1
Câu 12. Tồn tại bao nhiêu giá trị nguyên m trong khoảng (– 7;7) sao cho đường thẳng y  cắt đường x 1
thẳng y x m tại hai điểm phân biệt. A. 13 giá trị. B. 15 giá trị. C. 12 giá trị. D. 5 giá trị. 1 1
Câu 13. Tập xác định của hàm số y  
x chứa bao nhiêu số nguyên dương nhỏ hơn 100 2 x  3 x  5 A.80 B. 98 C. 95 D. 90
Câu 14. Tìm m để đồ thị của hàm số y   2
m  2mx m  2 song song với đường thẳng y  3x 1? A. m  1 B. m  3  
C. m  1 hoặc m  3   D. m  3
Câu 15. Bảng biến thiên trong hình bên là của hàm số nào sau đây? 12
A. y  4x  5  B. y  2  . x
C. y x  6 
D. y  x 1
Câu 16. Hàm số f x có tập xác định  và có đồ thị như hình vẽ
Mệnh đề nào sau đây sai ?
A. Hàm số đồng biến trên khoảng (1;4)
B. Hàm số nghịch biến trên khoảng (– 3;0).
C. f 2  f 5  15 D. f 10  26 . 2x  8
Câu 17. Đường cong y
cắt đường thẳng y  x tại hai điểm M, N. Tính độ dài đoạn thẳng MN. x A. MN = 4 B. MN = 2 5 C. MN = 4 2 D. MN = 6 2
Câu 18. Tìm điều kiện của m để hàm số y  m   4 3
x x   3 m   2 2 8
8 x x là hàm lẻ. A. m = 8 B. m = 2 C. m = 3 D. m < 2,5
Câu 19. Hàm số nào sau đây không phải là hàm số bậc nhất? A. y  3
B. y  2x 1
C. y  1 x  D. y   2 m   1 x  3
Câu 20. Tìm tập hợp điểm biểu diễn điểm P (m; 2m2 – m + 2). A. Parabol y = 2x2 – x + 2.
B. Đường thẳng 3x – y + 1 = 0.
C. Đường thẳng y = 2x – 2.
D. Parabol y = 3x2 – 4x + 1.
Câu 21. Hàm số nào sau đây nghịch biến trên miền 4;  1 6x 1 5 A. y  B. y  C. y  D. y x  4 x  4 2 x  4 x  4
Câu 22. Hàm số nào dưới đây nghịch biến trên  ?
A. y x  3
B. y  1 x
C. y  2x  5
D. y  3x 1
Câu 23. Với giá trị nào của tham số m để hàm số y  2  mx  2021 đồng biến trên  ? A. m  2  B. m  2  C. m  2  D. m  2  2 1 x  9
Câu 24. Tìm tập xác định của hàm số y   .  x  3 3 x  5 x A. 3;  B. 5;  C. 0;  D. 0;  \   3 2 4 x 1 2x 1 3
Câu 25. Cho các hàm số 4 2 4 2
y x x ; y  ; y  ; y  6x
; y x  2x  5 . Tồn tại bao nhiêu 2 x 1 x 1 x hàm số chẵn ? A. 2 B. 3 C. 4 D. 1
Câu 26. Tìm số giao điểm giữa đồ thị hàm số y
3x  4 và đường thẳng y = x – 3. A. 2 giao điểm. B. 4 giao điểm. C. 3 giao điểm. D. 1 giao điểm.
Câu 27. Phương trình đường thẳng đi qua giao điểm của 2 đường thẳng y  2x 1; y  3x  4 và song song với đường thẳng y  2x  15.
A. y  2x  11 5 2.
B. y x  5 2. C. y  2x  2 5.
D. y  4x  2. 13
ĐẠI CƯƠNG HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P1) ____________________________
Câu 1. Tìm điều kiện m để hàm số y  3x m xác định trên [1;7]. A. m  3 B. m < 4 C. 2 < m < 4 D. 0 < m  1 4
Câu 2. Giá trị nhỏ nhất của hàm số f x 4  x
 6 trên miền 0;  là x A. 11 B. 10 C. 13 D. 17
Câu 3. Cho hàm số y f x có đồ thị như hình vẽ bên. Tìm số nghiệm
thực của phương trình f  2
x  4x  3   2  . A. 4 B. 3 C. 1 D. 2
Câu 4. Tập giá trị của hàm số y   x  
1  x  2 x  5 x  6 chứa bao nhiêu phần tử nguyên nhỏ hơn 10 ? A. 15 B. 14 C. 12 D. 16
Câu 5. Khi x, y đều là các số nguyên thì F (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên đồ 3 x  8x 1 thị hàm số y  ? x 1 A. 2 điểm nguyên. B. 6 điểm nguyên. C. 8 điểm nguyên. D. 12 điểm nguyên 4x  2
Câu 6. Đường cong y
cắt đường thẳng y  3x  4 tại các điểm P, Q. Gọi a;b tương ứng là tung độ x 1
của P, Q. Tính giá trị biểu thức S = a + b. A. S = 11 B. S = 10 C. S = 11 D. S = 12 2 x  2x  2
Câu 7. Ký hiệu X, Y tương ứng là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  trên R. Tính giá 2 x  2x  2
trị biểu thức K = X + Y. A. K = 6 B. K = 3 C. K = 2 D. K = 4
Câu 8. Tập giá trị W của hàm số số y x 1  x  2  x  3 là  3  A. [5;10] B. 2; C. ;    D. 5;  2  x
Câu 9. Hàm số f x  x  2m 1  4  2m
xác định với mọi x 0;2 khi m  ; a b . Tính a + b. 2 A. a + b = 3 B. a + b = 5 C. a + b = 2,5 D. a + b = 2 x  2
Câu 10. Trên đồ thị hàm số y
có bao nhiêu điểm có tọa độ nguyên ? 2 x  2 A. 4 B. 2 C. 3 D. 6
Câu 11. Cho hàm số f x thỏa mãn f x   3
3  x  3x 1. Tính f x  3 . 3 3
A. f x  3   x  6  3 x  6 1.
B. f x  3   x  2  3 x  2 1. 3 3
C. f x  3  2 x  2  3 x  2 1
D. f x  3  4 x  2  3 x  2 1. 5
Câu 12. Tìm điều kiện tham số m để hàm số y
có tập xác định D = R\{a;b}. 3 2
x mx x m A. 0 < m < 2 B. 0  m  1 C. m > 3 D. 0  m  3
Câu 13. Hàm số nào sau đây đồng biến trên từng khoảng xác định ? x  5 A. y  B. 3 2
y x  2x 10x C. 3
y x  9x D. 2 y x  4 x  3 3x 1
Câu 14. Gọi A là giao điểm có hoành độ < 1 của đường cong y
cắt đường thẳng y x  1. Tính OI. x 1 A. OI = 1 B. OI = 2 C. OI = 3 D. OI = 2 14
Câu 15. Điểm M (x;y) gọi là điểm nguyên khi x, y đều là các số nguyên. Tìm số giao điểm nguyên của hai đồ thị
hàm số y  7  2x ; y  5  3x x  2 . A. 1 giao điểm. B. 2 giao điểm. C. 3 giao điểm. D. 4 giao điểm.
Câu 16. Đồ thị hàm số y
x  2  4  x cắt đồ thị hàm số 2
y x  6x  11tại bao nhiêu điểm ? A. 1 giao điểm. B. 2 giao điểm. C. 3 giao điểm. D. 4 giao điểm. 2 2x  2x  2
Câu 17. Hàm số y
có tập giá trị K = [a;b]. Tính giá trị biểu thức a + b. 2 2x  3 5 2 A. B. 1 C. 2 D. 3 5 2 x
Câu 18. Tìm số giao điểm của đồ thị hàm số y
 3x  2 và đường thẳng y  1 x . 3x  2 A. 1 điểm. B. 2 điểm. C. 3 điểm. D. 4 điểm.
Câu 19. Hàm số y  8 x  4  6 5  x đạt giá trị lớn nhất và giá trị nhỏ nhất tương ứng tại x = a; x = b. Tính
giá trị biểu thức Q = |25a – b + 2|. A. Q = 50 B. Q = 48 C. Q = 71 D. Q = 31
Câu 20. Cho hàm số y f x có đồ thị như hình vẽ bên. Tìm số
nghiệm thực của phương trình 2
f x  3 f x  2  0 . A. 1 B. 3 C. 5 D. 2 x  2 1
Câu 21. Tìm giá trị của m để đường cong y
cắt đường thẳng y  
x m tại hai điểm phân biệt nằm x 1 2
về hai phía của trục tung. A. m > 2 B. m > 3 C. 0 < m < 1 D. 2 < m < 4 2  1  4x  3
Câu 22. Tìm hàm số f x thỏa mãn 2 f x  f    .  x x 2 5x  2 3 1 1
A. f x  B. f x 2  x  1 C. f x 3  x
D. f x  2x  . 3x x x 1 x
Câu 23. Tìm tập hợp điểm biểu diễn điểm L (3m – 1;m2 – 2m + 2). 2 x  4x 13 A. Đường thẳng y = x. B. Parabol y  . 9
C. Đường cong y = 2x3 + 5x2 + 2x – 1.
D. Đường thẳng 8y = 3x + 3. 2 4x  7 1 x  2x  2
Câu 24. Cho các hàm số 3 2
y  8x 1; y  ; y  4x  ; x y x x  3; y  . Số lượng x 1 2 x 1
hàm số đồng biến trên tập xác định tương ứng là A. 2 B. 5 C. 3 D. 4 x  9
Câu 25. Tìm điều kiện tham số m để hàm số y
 4x xác định trên [7;9]. x  2m 1 A. m > 4 hoặc m < 3 B. m > 4 C. m > 9 hoặc m < 7 D. 2 < m < 5 2 2 2 x 1  x x x  4 1 x  2x  5
Câu 26. Cho các hàm số y  ; y  ; y x  1; y  . Có bao nhiêu đồ thị 2 x  2 x  3 x 3x
hàm số nằm hoàn toàn phía trên trục hoành ? A. 2 B. 4 C. 1 D. 3
Câu 27. Tồn tại bao nhiêu giá trị nguyên của m trong khoảng (– 20;20) để đường thẳng y x  3m không cắt 2x đường thẳng y  . x 1 A. 1 giá trị. B. 3 giá trị. C. 2 giá trị. D. 4 giá trị.
_________________________________ 15
ĐẠI CƯƠNG HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P2) _____________________________ 3 x  2 ; 2  x  4 
Câu 1. Tồn tại bao nhiêu điểm có tung độ bằng 29 nằm trên đồ thị hàm số 2
y  2x  21 ; x  4  2
x x  29 ; x  2  A. 3 B. 2 C. 1 D. 4
Câu 2. Tồn tại bao nhiêu số nguyên dương m để hàm số 4 y
x  4x  8  m xác định trên R ? A. 5 B. 2 C. 3 D. 4
Câu 3. Cho hàm số f x thỏa mãn f x   2 4
1  x  4x 1. Giá trị biểu thức f  2 gần nhất với giá trị nào ? A. 2,2 B. 1,5 C. 3,7 D. 4,1
Câu 4. Giả sử hàm số f x 2
 x  2x  4 3  x x  
1  3 có tập giá trị W = [a;b]. Hãy tính giá trị của biểu thức K = a2 + b2. A. K = 145 B. K = 144 C. K = 143 D. K = 169
Câu 5. Khi x, y đều là các số nguyên thì F (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên đồ 4 x  3x 16 thị hàm số y  ? x 1 A. 8 điểm nguyên. B. 6 điểm nguyên. C. 10 điểm nguyên. D. 12 điểm nguyên
Câu 6. Tập giá trị của hàm số y
2018  x  2 x 1 chứa bao nhiêu phần tử nguyên ? A. 68 B. 56 C. 37 D. 43
Câu 7. Cho hàm số y f x có đồ thị như hình vẽ bên.
Tìm số nghiệm của phương trình f  2
x  4x  0 . A. 1 B. 3 C. 5 D. 2
Câu 8. Có bao nhiêu cặp số nguyên dương (m;n) với m < 6, n < 6 để hàm số f x 5 3
x  3x x m n  4 không chẵn, không lẻ ? A. 20 B. 22 C. 21 D. 10 5  x x
Câu 9. Tính độ dài khi biểu diễn trên trục số của tập xác định hàm số y  . 2
x  2x  3  x 1 A. 5 B. 4 C. 3 D. 2,5 Câu 10. Hàm số 2
y  2  x  2  x  4  x có tập giá trị [a;b]. Tổng giá trị a + b gần nhất với giá trị nào ? A. 2,8 B. 3 C. 2 D. 4
Câu 11. Giá trị nhỏ nhất của hàm số f x  x   x  2 4 3 là A. 3 B. 4 C. 5 D. 7  1  1
Câu 12. Tìm hàm số f x thỏa mãn 3 f x   x    . 3  x x 1 A. f x 3  x  3x B. f x 2
x  6x 1 C.   3
f x x x
D. f x  2x  . x
Câu 13. Tìm hàm số f x thỏa mãn đẳng thức f x   2
2  x  6x  4 . Khi đó, hãy tìm giá trị nhỏ nhất của
hàm số g x  f x 4 2
x  4x  30x  28 . A. 11 B. 14 C. 12 D. 20 2 x x 1
Câu 14. Tồn tại bao nhiêu điểm nguyên trên đồ thị hàm số y  ? 2 x x 1 A. 4 B. 3 C. 2 D. 1
Câu 15. Có bao nhiêu số nguyên m trong khoảng (– 2018;2018) để đường thẳng y  2x m cắt đường cong 16 x  2 y
tại hai điểm phân biệt. x 1 A. 2018 B. 4000 C. 4035 D. 2346 a   2
1 x  2a  2 x a  4
Câu 16. Hàm số g x 
có giá trị nhỏ nhất M. Có bao nhiêu tự nhiên a để M < 4 ? 2 x  2x 1 A. 2 B. 4 C. 5 D. 3
Câu 17. Tìm giá trị lớn nhất m để hàm số y
x m  2x m 1 xác định với số dương x. A. m = – 1 B. m = 2 C. m = – 3 D. m = 4 2018
Câu 18. Trên đồ thị hàm số y
có bao nhiêu điểm có tung độ nguyên ? x  3 A. 670 điểm B. 2018 điểm C. 672 điểm D. 520 điểm
Câu 19. Tập giá trị của hàm số y x x  
1  x  2 x  3 là A. [0;3] B. 2;  C. [1;4] D. 1; 
Câu 20. Cho hàm số f x 3 2
x  5x  7x  3. Phương trình 2
f ( x  3x  2)  0 có bao nhiêu nghiệm ? A. 4 B. 3 C. 2 D. 1
Câu 21. Tìm tập hợp điểm biểu diễn điểm E (4m;5m2 + 3). 5 A. Parabol 2 y x  3.
B. Đường thẳng 3x – 7y + 6 = 0. 16
C. Đường thẳng 9y = 2x – 2.
D. Parabol y = 5x2 – 4x + 3.
Câu 22. Cho hàm số y f x có đồ thị như hình vẽ bên.
Tìm số nghiệm thực của phương trình
f  2x  3  x   2  A. 4 B. 3 C. 1 D. 2 .
Câu 23. Hàm số f x thỏa mãn f x  f   x 2 2 1  x . Tính f(0). 1 2 5 4 A. f 0   B. f 0   C. f 0   D. f 0   . 3 3 3 3 2 2
x xy y
Câu 24. Tìm tập giá trị W = [a;b] của hàm số hai biến y  . 2 2
x xy y 1   2  A. W = [2;3] B. W = [0;2] C. W = ;3  D. W = ; 2 . 3       3  2x  8
Câu 25. Đường cong y
cắt đường thẳng y  x tại hai điểm M, N. Tính độ dài đoạn thẳng MN. x A. MN = 4 B. MN = 2 5 C. MN = 4 2 D. MN = 6 2 8
Câu 26. Đường cong y  3 
cắt đường thẳng y x  6 tại hai điểm phân biệt H, K. Tính diện tích S của tam x
giác OHK với O là gốc tọa độ. A. S = 21 B. S = 23 C. S = 41 D. S = 14 2
x mx n 1 
Câu 27. Hàm số y  có tập giá trị T =
;3 . Tính tổng tất cả các giá trị có thể xảy ra của m và n. 2 x  2x  4 3    A. 20 B. 21 C. 10 D. 15
Câu 28. Tồn tại bao nhiêu giá trị nguyên của m trong khoảng (– 19;19) để đường thẳng y x  2m cắt đường 3x 1 thẳng y
tại hai điểm phân biệt có hoành độ trái dấu. x  2 A. 18 giá trị. B. 17 giá trị. C. 13 giá trị. D. 16 giá trị. 17
ĐẠI CƯƠNG HÀM SỐ LỚP 10 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P3) ____________________________ 4 4
Câu 1. Tìm tập hợp giá trị của hàm số f x   x  6   x  8 .  3  A. [2;9] B. 2;  C. 1;  D. ;     2 
Câu 2. Tồn tại bao nhiêu giá trị m để hàm số y   x x2 2 2 3 2
m x  9 là hàm số chẵn. A. 2 B. 1 C. 3 D. 0
Câu 3. Tìm số giao điểm của đồ thị hàm số 2
y  4x  8x 1 và đường thẳng y x 1. A. 2 B. 3 C. 1 D. 4 2 x  6x 1
Câu 4. Trên đồ thị hàm số y
có bao nhiêu điểm M (x;y) mà x, y đều nguyên ? x 1 A. 4 B. 2 C. 6 D. 8 1
Câu 5. Tồn tại bao nhiêu số nguyên m nhỏ hơn 11 để hàm số f x  có tập xác định D = R. 2
x  4x m  5 A. 5 B. 9 C. 2 D. 1
Câu 6. Có bao nhiêu giá trị nguyên m lớn hơn – 7 để hàm số g x 2 
x  6x  9  m xác định trên R ? A. 14 B. 7 C. 5 D. 10 2 3x  2x 1
Câu 7. Hàm số y
có tập giá trị S = [a;b]. Tính giá trị biểu thức a2 + b2 + ab. 2 x  2x  3 A. 5 B. 2 C. 4 D. 3
Câu 8. Hàm số y = |ax + b| có đồ thị như hình vẽ bên.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên miền [0;3] là A. 2 B. 1 C. 3 D. 4 2 x
Câu 9. Tìm số giao điểm của đồ thị hàm số y
 3x  2 và đường thẳng y  1 x . 3x  2 A. 1 điểm. B. 2 điểm. C. 3 điểm. D. 4 điểm.
Câu 10. Tính giá trị biểu thức a + b + 2c + 4d, trong đó hai đoạn rời nhau [a;b] và [c;d] (a < c) là tập hợp tất cả x  4m  3 3x 1
các giá trị m để hàm số sau xác định trên (0;1): y   . x  2m 5  2m x A. 3 B. 2 C. 6 D. 3,5
Câu 11. Hàm số y = |ax + b| có đồ thị như hình vẽ bên.
Với m là tham số thực, tính tổng các nghiệm của
phương trình |x – 2| = f (10 – m) – f (m – 8) + 7. A. 2 B. 1 C. 3 D. 4
Câu 12. Tồn tại bao nhiêu điểm có hoành độ bằng 1 thuộc đồ thị hàm số 3 3
y  5x  7  5x 12 ? A. 1 điểm. B. 2 điểm. C. 3 điểm. D. 4 điểm.
Câu 13. Tìm điều kiện tham số m để hàm số y
x m  2x m 1 xác định với mọi x > 0. A. m  1 B. 2  m  2 C. m  0 D. m  1
Câu 14. Hàm số y
x  3  6  x   x  36  x có tập giá trị W = [a;b]. Giá trị biểu thức b – a gần nhất với giá trị nào ? A. 3,25 B. 4,25 C. 5,67 D. 8,61
Câu 15. Tồn tại bao nhiêu điểm có hoành độ bằng 5 thuộc đồ thị hàm số 2 2 y
x x  5 
x  8x  4 ? A. 1 điểm. B. 2 điểm. C. 3 điểm. D. 4 điểm. 18 x a
Câu 16. Tìm điều kiện tham số a để tập hợp giá trị của hàm số y  chứa đoạn [0;1]. 2 x 1 A. Mọi a B. a  2 C. a  0,75 D. a < 2 1
Câu 17. Tìm điều kiện của tham số m để hàm số 4 y
 6m  9  3x xác định trên đoạn [0;1]. x m  2 A. – 1 < m < 2 B. 1  m  2 C. 0 < m < 1 D. 2 < m < 3
Câu 18. Hàm số f (x) có tập xác định D = R với đồ thị như hình vẽ bên,
O là tâm đối xứng của đồ thị. Tính giá trị f  2017   f  2017  . A. 2 B. 1 C. 3 D. 0 x x  2
Câu 19. Hai tập xác định của các hàm số y  9  3 | x |  ; y  khi giao nhau sẽ chứa bao 2 x | x | 4 9x 1   nhiêu phần tử nguyên ? A. 4 B. 5 C. 6 D. 7 x  2 1
Câu 20. Tìm giá trị của m để đường cong y
cắt đường thẳng y  
x m tại hai điểm phân biệt nằm x 1 2
về hai phía của trục tung. A. m > 2 B. m > 3 C. 0 < m < 1 D. 2 < m < 4 3x  3
Câu 21. Đường cong y
cắt đường thẳng y x 1tại hai điểm phân biệt D, E. Tính diện tích S của x  2
tam giác ODE với O là gốc tọa độ. A. S = 2 B. S = 1 C. S = 3 D. S = 1,5 2 x x 1
Câu 22. Tồn tại bao nhiêu điểm nguyên (x;y) trên đồ thị hàm số y  ? 2 x x 1 A. 4 B. 3 C. 2 D. 1
Câu 23. Đoạn [a;b] là tập hợp tất cả các giá trị m để hàm số f x  x  2m 1  4  2m  0,5x xác định
với mọi x 0; 2. Tính a + b. A. 3 B. 2 C. 4 D. 5
Câu 24. Cho hàm số f x 3 2
x  6x  9x  3. Phương trình 3
f x  4 f x  0 có bao nhiêu nghiệm ? A. 7 B. 8 C. 5 D. 6 2 x x 1
Câu 25. Gọi M là tập hợp giá trị của hàm số f x 
, M chứa bao nhiêu phần tử nguyên ? 2 x x 1 A. 4 B. 2 C. 3 D. 4
Câu 26. Hàm số f (x) có đồ thị như hình vẽ bên, biết rằng trên các miền
x < 0 và x > 2, đồ thị hàm số là đường thẳng, không gấp khúc. Tìm giá
trị lớn nhất của tham số m để hàm số g x 
f x  m  2 luôn xác định với mọi x. A. m = 4 B. m = 3 C. m = 2,5 D. m = 5
Câu 27. Tồn tại bao nhiêu giá trị nguyên m để hàm số y
(m 1)x  2m  3 xác định trên [– 3;– 1] ? A. 2 B. 3 C. 1 D. Vô số 1
Câu 28. Có mấy số nguyên dương m để hàm số y x m
xác định trên (1;2) hoặc 4;  ? 2x m 1 A. 6 B. 7 C. 8 D. 9 19
ĐẠI CƯƠNG HÀM SỐ THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P4) _____________________________ x
Câu 1. Tìm m để hàm số y
có tập xác định là R \{a}, a là hằng số thực. 2
x  4x m A. m = 4 B. m = 3 C. m = 2 D. m = 5 2
Câu 2. Hàm số y   2
x x   2 3
6 x  3x  9 có tập giá trị W chứa bao nhiêu phần tử nhỏ hơn 10 ? A. 12 B. 1 C. 10 D. 8 x  2
Câu 3. Trên đồ thị hàm số y
có bao nhiêu điểm nguyên x  2 A.3 B. 2 C. 4 D. 1
1999  3sin x  4 cos x m
Câu 4. Có bao nhiêu số nguyên m < 10 để hàm số f (x)  có tập xác định  ? 4  sin(1993x) A. 9 B. 8 C. 5 D. 13
Câu 5. Với a là tham số thực bất kỳ, tìm số giao điểm của hai đường cong 4 2 2
y x ; y  7x a  4 . A. 4 B. 1 C. 3 D. 2 1
Câu 6. Tìm giá trị m để hàm số f x  có tập xác định D = R. 2
x  4x  5  m A. m > 0 B. m < 2 C. 4 < m < 5 D. m < 1 2
Câu 7. Giá trị nhỏ nhất của hàm số y   2
x x   2 2
4 x  2x 1trên R là A. – 2 B. – 3 C. 1 D. 0
Câu 8. Tìm điều kiện của m để hàm số 2 2 y
x  2x  6  m
x 1 luôn luôn xác định. A. m  4 B. m  2 C. m  5 D. m  8
Câu 9. Cho hàm số y f x có đồ thị như hình vẽ.
Có bao nhiêu số nguyên m để phương trình sau có
sáu nghiệm thực phân biệt 2
f x  m  2 f x  2m  0 A. 4 B. 2 C. 5 D. 3
Câu 10. Gọi K là tập giá trị của hàm số y x  3  x  4 . K chứa bao nhiêu số nguyên nhỏ hơn 10 ? A. 4 B. 8 C. 9 D. 10 1
Câu 11. Tìm tất cả các giá trị của m để hàm số y x 1 m  xác định trên [0;2] 3m 1 x 1 A. m > 0,5 B.  m  1 C. m > 1 D. – 2 < m < 0 3
Câu 12. Tìm hàm số f x thỏa mãn f x   3 2
1  x x x . Tìm f x   1 .
A. f x   3 2
1  x  5x  7x
B. f x   3 2
1  x  5x  7x
C. f x   3 2
1  x  5x  4x
D. f x   3 2
1  x  3x  2x . 1
Câu 13. Tìm điều kiện của tham số m để hàm số y
 2a  4  x xác định trên (0;1). x a 3 3 A.   a  0 B. 1 < a < 2 C. 0 < m < 1 D. a   2 2
Câu 14. Tìm phương trình đường thẳng d : y ax  .
b Biết đường thẳng d đi qua điểm I 1;3, cắt hai trục
Ox, Oy và cách gốc tọa độ một khoảng bằng 5. 20
A. y  2x  5. B. y  2  x  5.
C. y  2x  5. D. y  2  x  5.
Câu 15. Có bao nhiêu số tự nhiên m < 2018 để hàm số 2
f (x)  x  2(m 1)x  2m 1 đồng biến trên (2;4). A.2016 B. 2018 C. 2015 D. 2017
Câu 16. Cho hàm số y f x có đồ thị như hình
vẽ. Hỏi phương trình sau có bao nhiêu nghiệm thực ? f  3 2
x  2x 14x  17   17 . A. 4 B. 2 C. 5 D. 3
Câu 17. Tồn tại bao nhiêu số nguyên m lớn hơn – 19 để hàm số 2 y
x  3x m có tập xác định D = R ? A. 13 B. 16 C. 11 D. 15 3 2 2  x  3  x  3 8 4 Câu 18. Cho hàm số 3
f (x)  x  2x 1. Đặt A   2. ; B    . 2  2 2 3 2 x 1 x 1 (x 1) x 1  
Khẳng định nào sau đây là đúng và đầy đủ nhất
A. f A  f B
B. f A  f B
C. f A  f B
D. f A  f B
Câu 19. Tìm điều kiện tham số m để hàm số 4 3 2 y
x  4x  (m  5)x  4x m  4 xác định trên R. A. m  0 B. m  0 C. m  0 D. m  0
Câu 20. Tìm điều kiện của m để hàm số y x
x   m   3 2 1 1
5 x x là hàm số chẵn. A. m = 1 B. m = 5 C. m > 2 D. 1,5 < m < 2
Câu 21. Khi x, y đều là các số nguyên thì F (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên 3 x  2x 12
đồ thị hàm số y  ? x 1 A. 2 điểm nguyên. B. 4 điểm nguyên. C. 6 điểm nguyên. D. 8 điểm nguyên
Câu 22. Hàm số f x 2 2
 x  4x  21  x  3x 10 có tập giá trị T = [a;b]. Giá trị biểu thức T = 3a + 2b gần
nhất với giá trị nào ? A. 12,24 B. 32,14 C. 45,12 D. 52,21 Câu 23. Hàm số   3 2
f x ax bx cx d có đồ thị
như hình dưới đây. Với m là tham số thực thuộc đoạn
[2;3], hỏi phương trình sau có tối đa bao nhiêu nghiệm thực ?
f x  m  2  3  m . A. 6 B. 3 C. 5 D. 4 4x  3
Câu 24. Tìm tập giá trị K của hàm số y  . 2 x 1 A. K = [– 1;4] B. K = [0;2] C. K = [– 2;5] D. K = [3;7]
Câu 25. Cho hàm số f x 3 2
x  7x 14x  8 . Phương trình 2
f ( 9  x )  0 có bao nhiêu nghiệm thực ? A. 4 B. 3 C. 2 D. 1
Câu 26. Tìm hàm số f x thỏa mãn f x   2
1  x  6x  4 . A. f x 2
x  5x  2 B. f x 2  x  4x C. f x 2
x  8x 11 D. f x 2
x  6x 1.
_________________________________ 21
ĐẠI CƯƠNG HÀM SỐ THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P5) _____________________________  1  1 f (x)
Câu 1. Hàm số f x thỏa mãn 3 f x   x   
. Tìm số nghiệm của phương trình 8 2
x  3x  6 . 3  x x x A. 2 B. 3 C. 1 D. 2. 3 x 1
Câu 2. Trên đồ thị hàm số 3 y
có bao nhiêu điểm M ( ; x y) thỏa mãn 5 2 2 5
x x y (x y)  xy  2 y . 2 A.2 B. 1 C. 3 D. 4
Câu 3. Có bao nhiêu giá trị nguyên m để hàm số f (x)  x  1  x m là hàm số lẻ A.1 B. 0 C. 2 D. 4
3x 1  3x 1
Câu 4. Tìm điều kiện của m để hàm số y  là hàm chẵn. m  2 4
x  m  6 x A. m = 4 B. m = 6 C. m = 3 D. m < 2
Câu 5. Tìm tập hợp điểm biểu diễn điểm J (3m; 27m3 + 9m2 + 6m). 2 x  4x 13 A. Parabol y  . B. Parabol y = 2x2. 9
C. Đường cong y = x3 + x2 + 2x.
D. Đường thẳng y = 3x + 3.
265  3sin x  4cos x m
Câu 6. Có bao nhiêu số nguyên m < 10 để hàm số f (x)  có tập xác định  ? 5  sin(2000x) A. 9 B. 8 C. 5 D. 13 x
Câu 7. Tìm số giao điểm của hai đồ thị hàm số 2 f (x) 
; g(x)  x  2x  2 . 1 1  x A.3 B. 2 C. 4 D. 1
Câu 8. Khi x, y đều là các số nguyên thì F (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên đồ 3 2x  7x  34 thị hàm số y  ? x 1 A. 8 điểm nguyên. B. 12 điểm nguyên. C. 4 điểm nguyên. D. 10 điểm nguyên
Câu 9. Hàm số y
x  3  6  x   x  36  x có tập giá trị W = [a;b]. Giá trị biểu thức b – a gần nhất với giá trị nào ? A. 3,25 B. 4,25 C. 5,67 D. 8,61
Câu 10. Cho hàm số y f x có đồ thị như hình vẽ bên. Đặt hàm số 3
y g(x)  f (2x x 1)  m . Tìm m để max g(x)  1  0 . [0;1]
A. m = - 13 B. m = - 12 C. m = - 1 D. m = 3 2 2x  2x  2
Câu 11. Hàm số y
có tập giá trị K = [a;b]. Tính giá trị biểu thức a + b. 2 2x  3 5 2 A. B. 1 C. 2 D. 3 5
Câu 12. Tồn tại bao nhiêu giá trị nguyên của m trong khoảng (– 6;6) để đường thẳng y  2x m cắt đồ thị hàm 6x 1 số y
tại hai điểm phân biệt nằm về hai phía của trục tung ? 2x 1 A. 4 giá trị. B. 3 giá trị. C. 6 giá trị. D. 5 giá trị.
Câu 13. Cho hàm số f (x) nhận giá trị nguyên với mọi giá trị nguyên x. Phương trình sau có bao nhiêu nghiệm nguyên: 3
x xf (x)  3x  2 f (x) 1  0 . A.3 B. 4 C. 1 D. 2 22
Câu 14. Tìm số giao điểm của hai đồ thị hàm số 2
y  3x 1  5x  4; y  3x x  3 . A.3 B. 2 C. 1 D. 4
Câu 15. Cho hàm số y f x có đồ thị như hình vẽ bên. Tìm số nghiệm  2
 ;5 của phương trình 3 2
f (x)  6 f (x) 11 f (x)  6  0 f (x)  4 A. 4 B. 5 C. 6 D. 3 2000
Câu 16. Trên đồ thị hàm số y
có bao nhiêu điểm có tọa độ nguyên 3( x  2) A.2 B. 1 C. 0 D. 3
Câu 17. Tập giá trị của hàm số 3 2
f (x)  x(x  6x 11x  6) chứa bao nhiêu số nguyên nhỏ hơn 20 A.21 B. 18 C. 10 D. 13 Câu 18. Tồn tại bao nhiêu giá trị nguyên m < 10 để hai đồ thị hàm số
f (x)  3 x  2m  2; g(x)  x  2m  4m cắt nhau tại hai điểm phân biệt. A. 9 B. 6 C. 5 D. 4 2 2 2 3
(x  2x)  (m  4)x  2mx  5
Câu 19. Có bao nhiêu giá trị m để hàm số f (x)  là hàm số lẻ 4 2 x  2x 10 A.1 B. 2 C. 3 D. 4 Câu 20. Tìm số giao điểm của hai đồ thị hàm số 2 2
f (x)  2x  3  (x 1) x  6; g(x)  (x  2) x  2x  9 . A.3 B. 2 C. 1 D. 0
Câu 21. Có bao nhiêu giá trị nguyên m  2018 
; 2019để hàm số y x m  2x m 1 có tập xác định 0; . A.4038 B. 2018 C. 2019 D. 2020 Câu 22. Cho hàm số 3 2
f (x)  x  3x  6x  1. Tìm số nghiệm của phương trình
f f (x)  
1 1  f (x)  2 . A. 4 B. 6 C. 7 D. 9
Câu 23. Có bao nhiêu số nguyên m để phương trình x 1  2 x  2x m có hai nghiệm phân biệt 0;2 . A.2 B. 1 C. 3 D. 0
Câu 24. Có bao nhiêu giá trị nguyên m để hàm số y
(m 1)x  2m  3 xác định trên  3  ;   1 . A.2 B. 1 C. Vô số D. 3
Câu 25. Cho hàm số y f x có đồ thị như hình vẽ bên. Có bao
nhiêu giá trị nguyên m để phương trình sau có số  2  ;5 nghiệm đạt tối đa: 3 2 2
f (x m)  3mf (x m)  2m  0 . A. 4 B. 2 C. 1 D. 3 a
Câu 26. Để tập xác định của hàm số 2
y  16  x  2017x  2018m có đúng 1 phần tử thì m  (phân số b
tối giản). Tính giá trị a + b. A.3025 B. – 3025 C. 5043 D. – 5043 2 x x 1
Câu 27. Tìm điều kiện của m để hàm số y
có tập xác định D   \   a . m  3 2
x mx m A. m  12  ;1  2 B. m = 2 C. m  4  ;  0 D. m = 3
Câu 28. Cho hàm số y f x thỏa mãn 2 f (x)  f (2  x)  3x . Tính 2 f (0)  3 f (2) . A.8 B. 4 C. 6 D. 5 23
ĐẠI CƯƠNG HÀM SỐ THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO P6) _____________________________ 2 x  8
Câu 1. Tìm tập xác định của hàm số 3 2 y
x  3x  2 . 4x  3  x  3   3  A. ;  \    1;  3 B. ;  \   1; 2;  3 C. \ 1;  3 D. 1;2  4   4 
Câu 2. Hàm số f x thỏa mãn f x   2 4
1  x  4x 1. Giá trị biểu thức f  2 gần nhất với giá trị nào A. 2,2 B. 1,5 C. 3,7 D. 4,1
Câu 3. Tập giá trị của hàm số y  (x 1)(x  2)(x  3)(x  4) có bao nhiêu số nguyên nhỏ hơn 10 A.10 B. 11 C. 9 D. 8
Câu 4. Hàm số f x thỏa mãn 2
2 f (x)  f (1 x)  2m m 1. Tìm giá trị nhỏ nhất của 7 f (0)  4 f (1) . 7 2 A. Kết quả khác B. 1,5 C. D. 8 3
Câu 5. Cho hàm số y f x có đồ thị như hình vẽ. Với m là tham số
thực, hỏi phương trình sau có bao nhiêu nghiệm thực ?  1  f  13   .  2x m  A. 4 B. 2 C. 5 D. 3
Câu 6. Cho hàm số f x thỏa mãn f x   2 2
1  x  5x  6 . Tính f 3x   1 .  2
3 3x 14x 16 2 3x 14x 16
A. f 3x   1 
B. f 3x   1  . 4 4 2 6x x 18 2 6x  5x 18
C. f 3x   1  .
D. f 3x   1  . 4 4 1
Câu 7. Hàm số y
x  2m  2 
xác định với x thuộc nửa khoảng (0;4]. 4 5m  9  x A. 1  m  1
B. m  2  m  1 C. m > 2 D. 0 < m < 3
Câu 8. Trên đồ thị hàm số y x  4 có bao nhiêu điểm M ( ;
x y) thỏa mãn điều kiện y  6 y x  5x  0 . A.4 B. 2 C. 3 D. 1 m x 1
Câu 9. Tìm giá trị nhỏ nhất của tham số m để hàm số y
xác định trên khoảng (1;5). x  2m  5 A. m = 5 B. m = 6 C. m = 4 D. m = 2
Câu 10. Cho hàm số f (x)  2x 1. Tìm giá trị nhỏ nhất của 2
g(x)  f (x )  f ( f (x))  2022 . A.2022 B. 2015 C. 1999 D. 2000
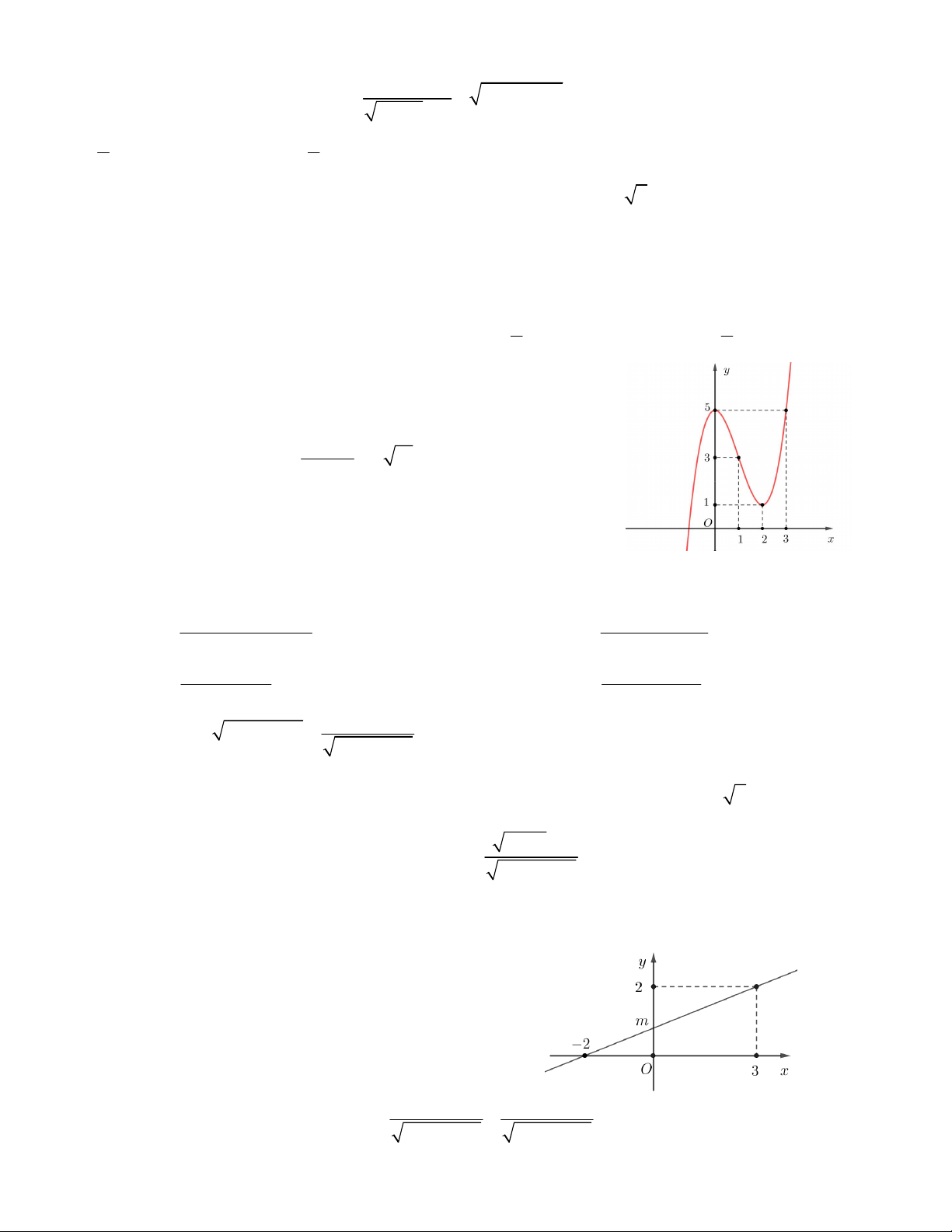
Câu 11. Hàm số bậc nhất y = ax + b có đồ thị d như
hình vẽ bên. Giá trị của m là A. 0,75 B. 0,7 C. 0,8 D. 0,9 x  3 x  2
Câu 12. Tìm điều kiện của m để hàm số y  
xác định với mọi x thuộc (5;21,5). x  4m  3 9m  8  x A. 0  m  1 B. 1 < m < 2 C. 0,5  m  2 D.1,5  m  2
Câu 13. Cho các hàm số 24
x 1  x 1 3 4 3 4 y
; y  3x  5; y x  4  x  4 ; y x  2x x  2x
x 1  x 1
Số lượng hàm số chẵn là A. 2 B. 3 C. 4 D. 1
Câu 14. Tìm điều kiện của m để hàm số 2
y  1 x  1  x  2mx là hàm số lẻ. A. m = 0 B. m = 2 C. m > 3 D. 0 < m < 1
Câu 15. Tìm số giao điểm của hai đồ thị hàm số 3 2 3
y  2x x 10x  3; y  (3x  5) 3x x . A.3 B. 2 C. 1 D. 4
Câu 16. Tìm tất cả các giá trị của m và n để hàm số y   2 m m 4 3
x x  m   2 3
3 x x n  4 là hàm lẻ. A. m = 3 và n = 4. B. m = 3; n = 2 C. m = 0; n = 2 D. m > 4; n > 3 5 2
x x  3x  2 ; x  3 
Câu 17. Trên đồ thị hàm số y  
có bao nhiêu điểm M ( ;
x y) thỏa mãn đẳng 2
x  5x 1 
x  3 ; x  3  thức 3 3 2
x y  3(x  3y  5 y)  14  0 . A.3 B. 2 C. 1 D. 4
Câu 18. Tìm tập hợp điểm biểu diễn điểm L (3m – 1;m2 – 2m + 2). 2 x  4x 13 A. Đường thẳng y = x. B. Parabol y  . 9
C. Đường cong y = 2x3 + 5x2 + 2x – 1.
D. Đường thẳng 8y = 3x + 3.
Câu 19. Khi x, y đều là các số nguyên thì F (x;y) được gọi là điểm nguyên. Tồn tại bao nhiêu điểm nguyên trên 4 x  3x 16
đồ thị hàm số y  ? x 1 A. 8 điểm nguyên. B. 6 điểm nguyên. C. 10 điểm nguyên. D. 12 điểm nguyên Câu 20. Hàm số 2
y  1 x  1 x  1  x có giá trị lớn nhất A và giá trị nhỏ nhất B. Tính tỷ số k = A : B. A. k = 2 B. k = 2 C. k = 4 D. k = 2,4
Câu 21. Cho hàm số y f x có đồ thị như hình vẽ. Có bao nhiêu giá 1 3 2
trị nguyên của m để phương trình   có nhiều
2 f (x)  m f (x) m hơn 5 nghiệm ? A. 3 B. 2 C. 5 D. 4 1 1
Câu 22. Giả sử d là đường thẳng đi qua điểm C (3;6) và cắt hai tia Ox, Oy tại A, B sao cho  đạt giá 2 2 OA OB
trị nhỏ nhất. Tính diện tích S của tam giác OAB khi đó. A. S = 56,25 B. S = 60,75 C. S = 12,65 D. S = 14,75 2 x  41
Câu 23. Tìm m để hàm số y
có tập xác định D   \  ; a ; b
c ; a b c , đồng thời thỏa 3 2
x 12x  47x m
mãn điều kiện a < b < c; a + c = 2b. A. m = 16 B. m = 60 C. m = 32 D. m = 54
Câu 24. Hàm số f x thỏa mãn f x  f   x 2 2 1  x . Tính f(0). 1 2 5 4 A. f 0   B. f 0   C. f 0   D. f 0   . 3 3 3 3
Câu 25. Trong mặt phẳng tọa độ Oxy, tồn tại Q (x;y) nằm trên đường phân giác góc phần tư thứ nhất sao cho biểu thức 2 2
K x  2 y  2x y  4 đạt giá trị nhỏ nhất. Tính giá trị biểu thức H = 3x + 6y. A. H = 1 B. H = 2 C. H = 0,5 D. H = 1,5
________________________________ 25