Hệ trục tọa độ trong không gian - Tài liệu tham khảo | Đại học Hoa Sen
Hệ trục tọa độ trong không gian - Tài liệu tham khảo | Đại học Hoa Sen và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả
Môn: Nguyên lý Kế toán (KT 204DV02) 40 tài liệu
Trường: Đại học Hoa Sen 4.8 K tài liệu
Tác giả:
Preview text:
Trường THPT Marie Curie
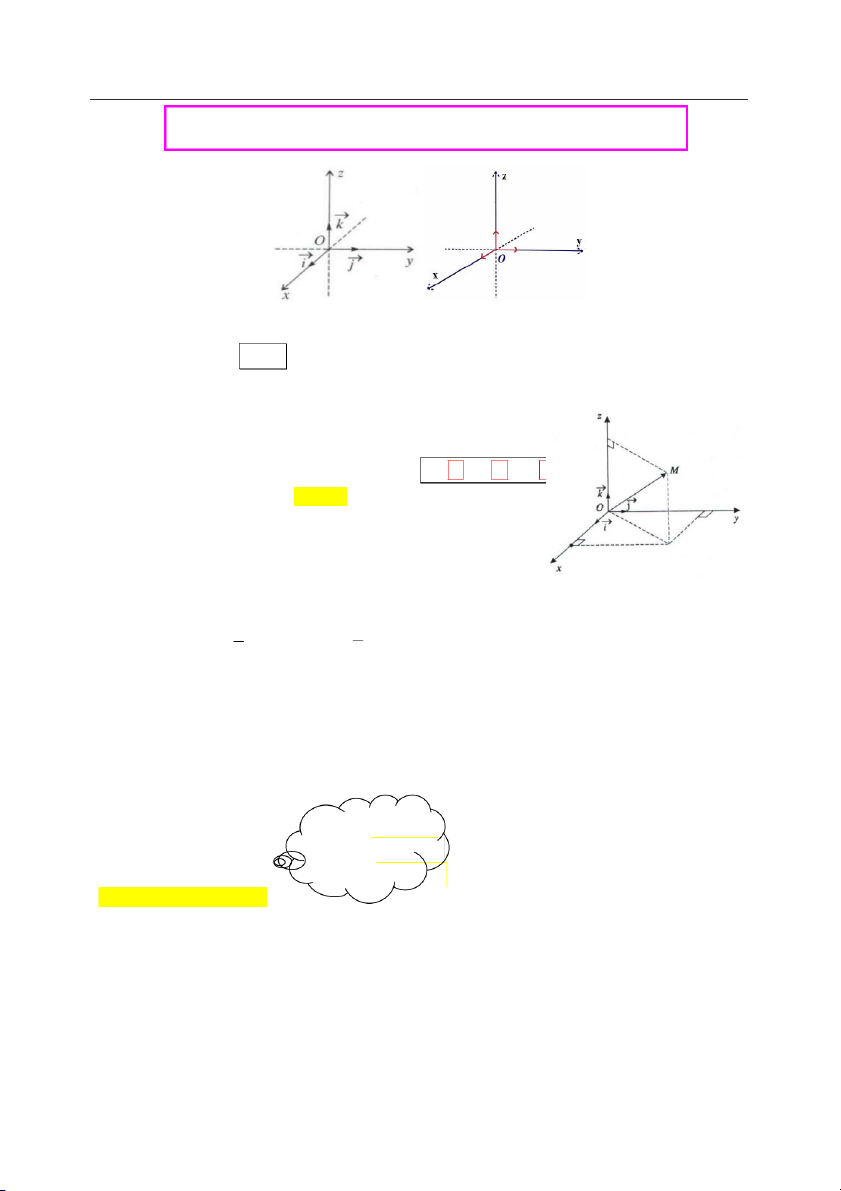
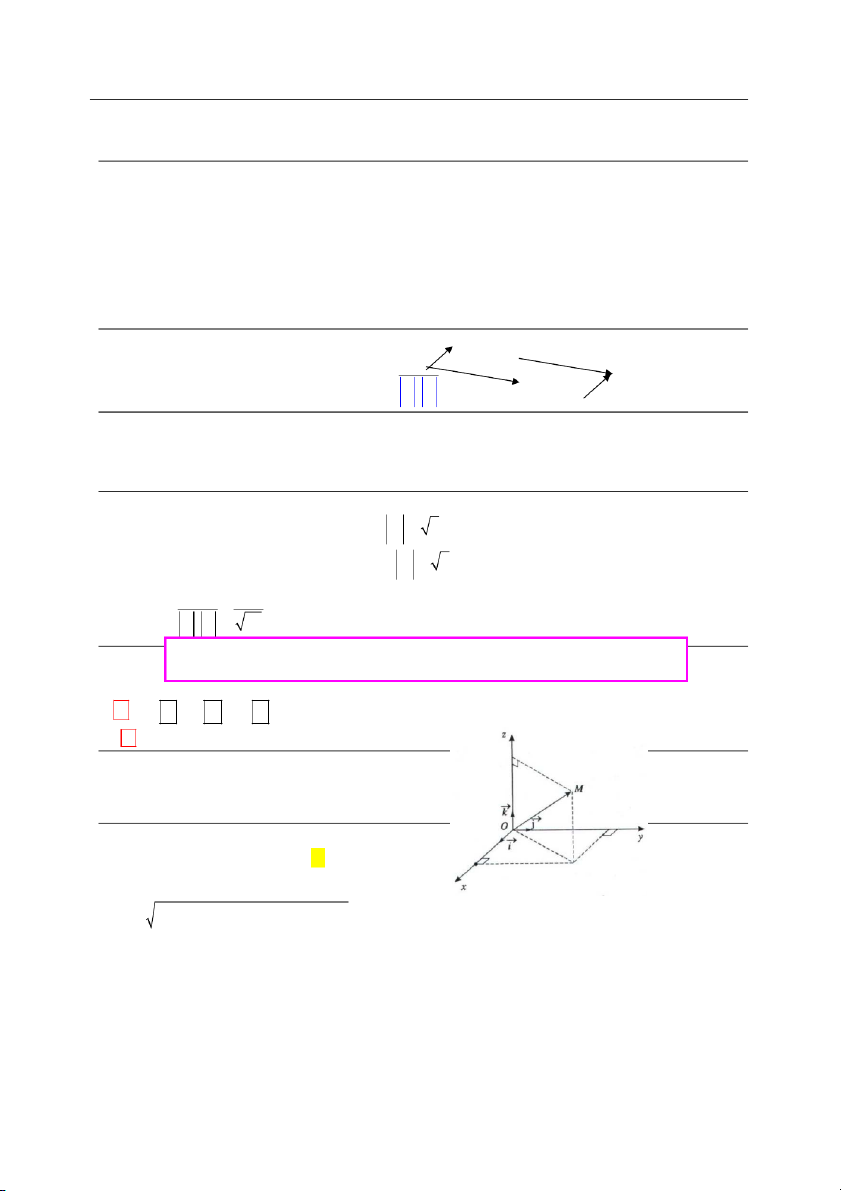
1. Hệ tọa độ trong không gian Oxyz
Gồm 3 trục O ; x O ;
y Oz vuông góc từng đôi một.
Véctơ đơn vị : i , j ,k trên các trục O , x O , y Oz .
Các trục O ,
x Oy, Oz lần lượt là trục hoành, trục tung và trục cao.
Các mặt phẳng Ox ; y Oy ;
z Oxz gọi là các mặt tọa độ . 2. Tọa độ véctơ ur
Trong không gian Oxyz, cho vectơ a tùy ý.
Khi đó luôn tồn tại bộ số a ;a ;a thỏa a a . i a . j a 1 2 3 1 2 ur
Ta nói bộ số a ;a ;a là tọa độ của vectơ 1 2 3 a ur ur
Ký hiệu : a
a ;a ;a hay a a ;a ;a . 1 2 3 1 2 3 ur r ur ur ur
Ví dụ: a i
3 2 j k a ; 3 ; 2 1 ur r ur ur r Ví dụ: a i 2j . 0 k a ; 1 ; 2 0 ur r ur ur r
Ví dụ: a i 5 .
0 j k a ; 5 ; 0 1 ur ur ur r Ví dụ: a j 1 2 k 1 a ; 0 ; 2 2 2 ur u r u r ur r u r u r ur
Ví dụ: a . 2b c
3 d a ; 2 ; 3
1 , Vì bộ b ;c ;d không phải là vectơ đơn vị
Ví dụ: a i 2 j k a 1; 2;1 Ví dụ: a 3
k 2 j a 0; 2;3 . Cẩn thận
Ví dụ: c 2;3; 2 c 2
.i 3 j 2k
Ví dụ: Biểu diễn b 2;4;
1 theo i , j ,k . Giải: b 2.i 4 j k Như vậy:
i = 1. i + 0. j + 0. k i 1;0;0
j = 0.i + 1. j + 0. k j 0; ;10
k = 0.i + 0. j + 1. k k 0;0 1 ;
3. C6c phép to6n : ( cộng, trừ theo thành phần) ur ur
Trong không gian Oxyz, cho vectơ a
a ;a ;a ; b
b ;b ;b 1 2 3 1 2 3 - 1 - Trường THPT Marie Curie
Cộng hai véctơ :
" h+h ; t+t ; c+c" ur u r a b
a b ;a b ;a b 1 1 2 2 3 3
Trừ hai véctơ : " hh
; t t ; c c " ur u r a b
a b ;a b ;a b 1 1 2 2 3 3 a 2;1; 1 ,
Ví dụ: Trong không gian Oxyz , cho hai vectơ b 1;4; 3 ur ur ur ur
Tính tổng a b và hiệu a b .
Giải: a 2;1; 1, b 1;4; 3
a b 3; 5 ; 4
a b 1; 3;2
Một số nhân véctơ : “là 1 véctơ ”.
Trong không gian Oxyz, cho vectơ a
a ;a ;a và số thực k 1 2 3 ur ka
ka ;ka ;ka 1 2 3 Ví dụ: a
5;2; 4 2a 10; 4;8 u r u r Vd: b ; 5 ; 2 1 b 3 1 ; 5 ; 6 3
a cung chieu b k 0
Lưu ý: a k .b
a nguoc chieu b k 0
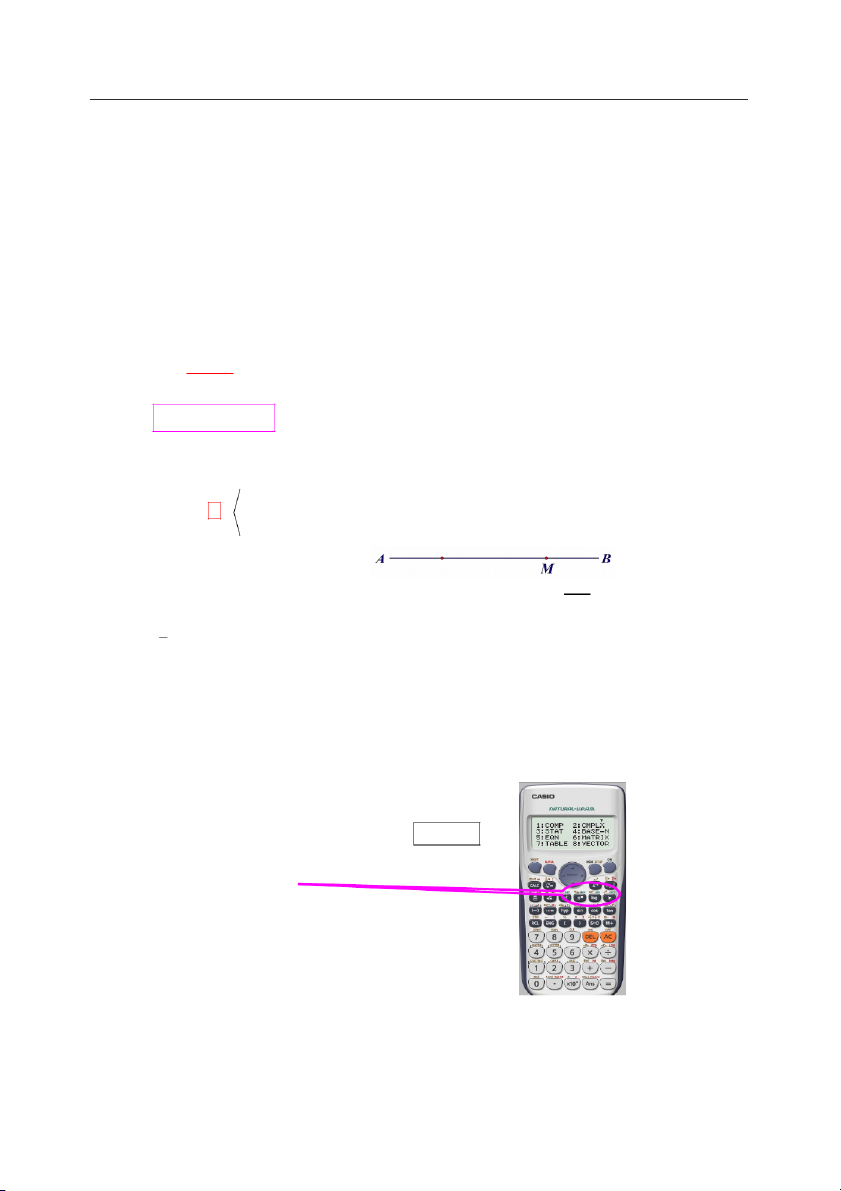
Vd: Cho đoạn thẳng AB và
điểm M nằm giữa hai điểm A,B
sao cho AM 3MB (như hình vẽ). Mệnh đề nào sau đây sai?
A. AM 3BM . B. AB 4 MB . C. 1
MA MB . D. 4AM 3 AB . 3 Giải C
Ví dụ: Trong không gian Oxyz , a 2; 1;3 , b 4; 1;0 , c 2; 2; 5 . TNnh x 2
a 3.b 4c Giải: 2a 4; 2;6 3b 12;3; 0 4c 8; 8; 20
Cộng theo vế ta được : x 2
a 3b 4c 0; 7; 14
Hướng dẫn dùng m6y tính Casio 570 Mode 811: nhập VtcA
Shift 5221: Nhập VtcB Shift 5231: Nhập VtcC - 2 - Trường THPT Marie Curie
Bấm AC. Kết thúc việc nhập Gọi lại véctơ
Bấm shift 5 …. . Bấm số tương ứng véctơ cần
Ví dụ: Cho ba vectơ Za ( ; 2 ; 1 1 , ) b ( ; 2 ; 1 3, ) c ( ; 1 ; 1 ) 1
Tọa độ của vectơ 2Za b 3c bằng
A. 2; 6;9 . B. 9;6;2 .
C. 9; 6; 2 .
D. 9; 6;2 .
Tích vô hướng = 1 số
Trong không gian Oxyz, cho hai vectơ a a ;a ;a , b b ;b ;b 1 2 3 1 2 3 ur u r
a .b a
b a b a b ¡ 1 1 2 2 3 3
Ví dụ: Trong không gian Oxyz, cho hai vectơ Za ( ; 2 ; 1 1,)b ( ; 2 ; 1 ) 3 . TNch bằng uru r a b bằng A. 2 . B. 8. C. 7 . D. 3 . Giải: r u ru ( ; 2 ; 1 ) 1, ( ; 2 b ; 1 ) 3 u r u r a b 2 . 2 1 1 . 1 3 8
Vd: Trong không gian Oxyz, cho hai vectơ a ( 2;0; 1),b (
m 1;2; m)
Tìm m để a .b 3 Giải: a .b 3
2(m 1) 0 m 3 m 5 / 3
Vd: Trong không gian Oxyz, cho hai vectơ a
2 ;m 1;3 , b
m 3; 2 ;m .
Tìm m để a .b 2 Giải: a .b .
h h t.t . c c 2 2 ( m 3 ) 2( m 1) 3 m 2 m = 2/3
Ví dụ: Cho a (2;1; 1),b(2 m 1;3; )
m . Tìm m để . a b 3 Giải: ab 2 2 m 1 3m3 m 2 5
Độ dài véctơ : “ khoảng c6ch giữa điểm gốc và ngọn” - 3 - Trường THPT Marie Curie
h 2 tung 2 ao2 a hoan c = 1 số 0
Trong không gian Oxyz, cho vectơ a
a ;a ;a 1 2 3
2 a a
a 2 a 2 2 2 3
Ví dụ: Trong không gian Oxyz, a = (2;1;1) . Tính độ dài vectơ a
Giải: a 2 2 2 2 1 1 6
Ví dụ: Trong không gian Oxyz, cho hai vectơ Za ( ; 2 ; 1 1 , ) b ( ; 2 ; 1 ) 3 . ur u r
Biểu thức a b 2 bằng. A. 101 . B. 2 5 . C. 37 . D. 94. Giải: ur u r ur u r a b 2 ; 6 ; 3 7 a b 2 36 9 49 94 uuu r
Nhớ: AB AB . Là khoảng cách giữa hai điểm A, B r r r
Ví dụ: Trong không gian Oxyz,cho ba vectơ a ; 2 ; 0 1 , b ; 2 ; 2 3 ,c ; 2 ; 1 3 r r r
Tính a b 2 c 4 461
Ví dụ: Trong không gian Oxyz, cho a = (2;1;1),
b = (1;2;1) , c = (1;1;2)
Tính 2a b 2c 70 Nhập véctơ
Mode 811: nhập VtcA; Shift 5221: Nhập VtcB
Shift 5231: Nhập VtcC; Bấm AC.
Kết thúc việc nhập Gọi lại véctơ
Bấm shift 5 …. . Bấm số tương ứng véctơ cần
2a b 2c
3; 6;5 2a b 2c 9 36 25 70
M6y shift hyp shift56 ấn 2x = 70
Ví dụ: Trong không gian Oxyz,cho a = (2;3;1),
b = (1;3;2),
c =(1;2;2)
Tính 2a b 3c 109
Ví dụ: Cho a ( ; m 1;1),b ( 1;2;m)
Tìm m để a 2b 30 - 4 - Trường THPT Marie Curie a ( ; m 1;1), Giải: a 2b
m 2; 5;1 2m
2b (2; 4; 2m)
a 2b 30 2 m 2 ( 2) 25 (1 2 ) m 30 2 m 2 ( 2) 25 (1 2 )
m 30 m0.
Vd: Cho a (1; 2;2 ) m ,b(0; ; m5), c ( 2; 1 ;3 )
m . Tìm m để a 3b c 281 Giải: a (1 ; 2 ;2 ) m , 3b(0 ; 3 ; m 15),
a 3b c (3; 1 3 ; m 16)
c (2;1; 3 ) m m 2
a 3b c 281 2 m 2 3 1 3 16 281 1 m 5 / 3
Ví dụ: Cho b(2 m 1;3 ; )
m . Tìm m để b 19 Giải: b m 2 9 2 19 2 1 m 9 1 0 m 1 2 m m 2 4 4
1 9 m 19 m 9 / 5 h h
Hai véctơ bằng nhau a = b t t c c
" các thành phần bằng nhau"
Hai véctơ cùng chiều, cùng độ lớn
Ví dụ: Cho ABC đều. Mệnh đề nào sai?
A. AB AC
B. AB AC
C. AB BC.
D. AB AC BC .
Ví dụ: Cho hình bình hành
Chỉ ra các cặp véctơ bằng ?
Giải: AB DC ; AD BC - 5 - Trường THPT Marie Curie
Tích có hướng hai véctơ = 1 véctơ
Véctơ này vuông góc đồng thời với 2 véctơ đã cho.
Trong không gian Oxyz, cho hai vectơ a
a ;a ;a , 1 2 3 b
b ;b ;b 1 2 3 a a a a a a 2 3 3 1 1 2
a ,b ; ; b b b b b b 2 3 3 1 1 2
a b a b ; a b a b ;a b a b 2 3 3 2 3 1 1 3 1 2 2 1
Vd: Trong không gian Oxyz,
a = (2;1 ;1), b = (0; 2 ;1) 1 1 a ,b 1 1 2 2 ; ; 2 1 1 0 0 2
= (12; 02; 4+0) = (3; 2 ;4) DÙNG CASIO Nhập véctơ Mode 811: nhập VtcA
Shift 5221: Nhập VtcB
Bấm AC. Kết thúc việc nhập
shift53shift54 = (3; 2;4)
Vd: a 1;m ;1 2 , b 1;2; 1 . Tìm m để a ,b 35 Giải: m 1 2 2 1 1 m 1
,a b ; ; 2 1 1 1 1 2 m 5; 3; m 1
a b m 2 ( 3) m 2 2 , 5 1 35
“bình phương hai vế, thu gọn” m 0 2 2m 8m 0 m 4
Vd: Trong không gian Oxyz, cho ba vectơ a 2;1;0 , b 1; 1; 3 , c ; m m 1; 2
Tìm m để a,b c 2 - 6 - Trường THPT Marie Curie
Giải: a,b 3; 6; 3
a,b c 3
m 6 m 1 6 2 m 2 / 3
Vd: Trong không gian Oxyz, cho ba vectơ a 2;1; 0 , b 1; 1; 3 , c 3;0; 2
Biểu thứca,b c bằng
Vd: Trong không gian Oxyz , cho a 2;1; 2 , b 1; 1; 3 ,c 3;1; 2
Tính a,b 2c ?
Vd: Trong không gian Oxyz , cho a 2;0; 2 , b 1; 1; 3 , c x 1;2; 3 r r r
Tìm x để a,b c 21 Giải: r r , a b ; ; 2 4 2 r r r , a b c x ; ; 1 2 1 r r r 2
a,b c x 1 41 21 x 3 x2 x
2 150 x 5
Lưu ý: a ,b b ,a .
Vd: Trong không gian Oxy ,
z cho hai vectơ a 2;0; 2 , b 1; 1; 3
Nhập a , b
shift53shift54= a ,b = (2;4;2)
shift54shift53= b ,a = (2; 4; 2)
Như vậy ta thấy a ,b b ,a
Ví dụ: Trong không gian Oxy ,
z cho a (1; 1;2),b ( 0;1;m).
Tìm các giá trị m để a,b 35 Giải: 1 2 2 1 1 1 a,b ; ; 1 m m 0 0 1 - 7 - Trường THPT Marie Curie a,b m 2; ; m 1 a,b m 2 2 2
m 1 170 0 …. Các em tự giải phương trình này nhé!
Quan hệ vuông góc, cùng phuơng, đồng phẳng.
Điều kiện vuông góc a b a .b 0
“hai véctơ vuông góc thì tích vô hướng = SỐ 0”
Vd: Trong không gian Oxy , z Cho a 2;1; 2 , b
m 2; m;m 1 .
Tìm m để a b .
Giải: a b a .b 0 . hh . t t . c c 0 2( m ) 2 m 2 m 1 0 m6. Vậy b 4; 6; 7
a ,b 0
Đk hai véctơ cùng phương h t c
a cùng phương b h t c
a k .b
Hai véctơ có gi6 song song hoặc trùng nhau. Ví dụ: Cho a 1; 2; 3 ,b
m ; 2 n; 3 . Tìm ,
m n để a cùng phương b . Giải: m n 3
a cùng phương b 2 1 2 3 m 3 m 1 m 1 1 3
b 1;2; 3 2 n 3 2 n 2 n 0 2 3
Đk ba véctơ đồng phẳng : a ,b .c 0 o véct Ví dụ: a 2 ( ; 1;1 , ) b 0 ( ;2 ; 3 , ) c(1;1 ; ) 5
A. 3 véctơ đồng phẳng.
B. 3 véctơ không đồng phẳng. Giải: - 8 - Trường THPT Marie Curie
a ,b .c 13 0 o véct Ví dụ: a 2 ( ; 1;1 , ) b 0 ( ;2 ; ) 3 ,c(1 ; 1; m ) 1 .
Tìm m để a , b , c đồng phẳng. Giải: a,b 1;6; 4 , c 1 ( ; 1; m ) 1 a,b c 0 1 6 4 m 1
0 m9/ 4 . a b
Góc giữa hai véctơ : co s a;b a .b
Ví dụ: Trong không gian Oxy , z cho a 2;1; 0 , b 1 ; 1; 2
TNnh cos(a ; b ) = ? a 2;1; 0 a 5
a.b 2 1 01 b 1; 1; 2 b 6
a .b a b 1 cos ; a .b 30
O M x . i y . j z . k M x ; y ; z 0 0 0 0 0 0
O là gốc tọa độ. Vd: O B i
j 3k B( ; 1 ; 1 3 )
Vd: OM i 3k M 1;0;3 AB
x x ; y y ;z z “BA” B A B A B A
AB BA “ngược chiều”
AB x x 2 y y 2 z z 2 B A B A B A - 9 - Trường THPT Marie Curie
chính là độ dài véctơ 2 2 2
AB h t c
Vd: A2;1;1, B 0;2;3 . TNnh AB ?
AB x x 2 y y 2 z z 2 3 B A B A B A uuu r
Hoặc là AB ; 2 ; 1 2 AB 4 1 4 3
Vd: Trong không gian Oxy ,
z Cho tam giác ABC , A 2;0; 0 ,Z B 0;0 ;2 , C 0 ( ; 2 ) ;0 TNnh chu vi ABC . Giải: AB
2;0;2 AB 8
AC 2; 2;0 AC 8 BC
0; 2; 2 BC 8
Cv AB BC AC 6 2
Vd: Trong không gian Oxy ,
z tìm M Oz sao cho AM 3, ( A 2;1; ) 3
M Oz M 0;0; z , ( A 2;1; 3) 2 AM
2 ; 1; z 3 , "M A " AM 4 1 z 3 3 z
z 2 4 1 3 9 2
z 6z 50 ( mode53) 1 z 5 Vậy M ( ; 0 ; 0 ) 1 ; M ( ; 0 ; 0 ) 5 1 2
Vd: Trong không gian Oxy ,
z cho A 3;1;–2 , B –1;2;
1 . Tìm COx sao cho tam
giác ABC vuông tại . A
COx C ; x 0; 0
AB 4;1;3 , AC x 3 ; 1; 2
ABC vuông tại A A . B AC 0 4 x
3 1( 1) 3(2) 0 x 17/ 4 Vậy C 17/ 4;0; 0 .
Vd: Trong không gian Oxy ,
z cho ABC , A ; 4 ; 5 0 , B ; 1 ; 0 1 , C ; 2 ; 1 1 .
Chứng tỏ ABC vuông. TNnh diện tNch tam giác này. uuu r Giải: AB
; ; AB2 3 5 1 35 uuu r AC
; ; AC2 2 6 1 41 uuu r BC ; ; BC 2 1 1 2 6 - 10 - Trường THPT Marie Curie
BC2 AB2 AC2
ABC vuông tại B. 1 210 S AB.BC ABC 2 2
Công thức trung điểm M của AB x x A B x M 2 x 2 x x x 2 x x A M B B M A y y A B y y 2
y y
y 2y y M A M B B M A 2 z 2z z z 2z z z z A M B B M A A B z M 2
Vd: Trong không gian Oxy ,
z Cho ABC , A ; 2 ; 1 1 , B( ; 4 ; 3 ) 1 , C( ; 2 ; 3 ) 7 .
TNnh độ dài trung tuyến AM. ( vẽ hình) Giải: x x B C x 3 M 2 y y B C y 0 M 3;0; 3 M 2 z z B C z 3 M 2 AM
1; 1;2 AM 1 1 4 6
Vd: Trong không gian Oxy ,
z cho ABC , A(2;1;1), B(0;2;2), C(1;1;1)
a) TNnh AB , AC
. b) TNnh độ dài trung tuyến MB. c) Tìm N Oy sao cho CN=3. Giải: AB 2; 1;1
AB , AC
2; 1; 5 AC 1;2;0
b) Gọi M là trung điểm AC , ( A ; 2 ; 1 ) 1 ,C ; 1 ; 1 1 x x A C x ; y ; z M 2 M M 3 M ;0;1 , ( B 0; 2;2) 2
3 9 29
MB ; 2;1 BM 41 2 4 2
c) Tìm N Oy sao cho CN = 3.
N Oy N 0; y;0 ; C1;1; 1 CN
1; y 1; 1 - 11 - Trường THPT Marie Curie 2
CN 1 (y 1) 1 3 2 y 2y 6 0 y 1
7 . Vậy N 0;1 7;0 , N 0;1 7;0 2 2
Công thức trọng tâm G của ABC
x x x A B C x G 3
y y y A B C y
G = {giao 3 trung tuyến}. G 3
z z z A B C z G 3
Điều kiện A, B, C thẳng hàng
AB , AC 0
AB cùng phương AC h t c h t c
Vd: Trong không gian Oxy ,
z A 2;3; 2 , B –1;2; 4 . Tìm tọa độ giao
điểm M của đường thẳng AB với mặt phẳng Ox . y M x
O y M ; x y; 0
AM
x 2;y 3; 2 "M A" AB 3 ; 1 ;2 x 2 y 3 2
M,A,B thẳng hàng 3 1 2 x 2 2 x 3 2 5
Vậy M 5;4;0 y 3 2 y 4 1 2 Diện tích 1 ABC : S A , B AC ABC 2 Ve t c o
Vd: Trong không gian Oxy , z ( A ; 2 ; 0 ) 1 , B( ; 0 ; 2 ) 1 ,C( ; 3 ; 2 ) 0 .
TNnh diện tNch tam giác ABC . uuu r uuu r Giải: AB ; 2 ; 2 2 ; AC ; 1 ; 2 1 uuu r uuu r
AB, AC ; ; 2 4 6 1 1 S
AB, AC 4 16 36 14 B A C 2 2 V ecto - 12 - Trường THPT Marie Curie
Vd: Trong không gian Oxy , z ( A ; 2 ; 2 ) 1 , B( ; 0 ; 2 ) 1 ,C( ; 3 ; 2 ) 1
a) TNnh diện tNch ABC b) TNnh đường cao AH? c) TNnh cosB? uuu r uuu r Giải: AB ; 2 ; 0 2 ; AC ; 1 ; 0 2 uuu r uuu r A , B AC ; ; 0 6 0 1 S A , B AC 3 ABC 2 1 6 S AH.BC 3 AH ABC 2 BC uuu r BC ; 3 ; 0
0 BC 3 AH 2 - 13 - Trường THPT Marie Curie c) Tính cosB? uur uuu r . BA BC 6 2 cos B . BA BC . 8 9 2 uur uuu r BA ; 2 ; 0 2 ; BC ; 3 ; 0 0
Vd: Trong không gian Oxy , z A ; 2 ; 1 1 , B( ; 0 ; 2 1 , ) C( ; 1 ; 1 ) 1
Chứng tỏ A, B, C là 3 đỉnh của tam giác. TNnh diện tNch ABC ? Giải:
Giải: AB = (2; 1 ;2) , AC = (1; 0; 2) AB, AC ( ; 2 2 ; ) 1 0
AB không cùng phương AC
A, B, C là 3 đỉnh của tam giác 1 1 3 S A , B AC 4 4 1 ABC 2 2 2
Vd: Trong không gian Oxy ,
z cho ABC , A 3;4;– 1 , B 2;5
;1 và C –1;1;– 2 . TNnh độ
dài đường cao AH của tam giác ABC . Giải: 1 1 S AH. C B A , B C A ABC 2 2 AB, AC AH C B AB
1;1;2, AC 4; 3; 1 ,
AB, AC 5;9; 7 AB, AC 155 BC 3; 4; 3 BC 34 A , B AC 155 AH BC 34
Vd: Trong không gian Oxy , z cho (
A 2; 1;1), B(0;3; 2),C(2; 1;0)
Chứng minh: A, B, C không thẳng hàng . TNnh d , A BC (2; A
1;1), B(0;3; 2),C(2; 1;0) AB 2;4; 3 , AC 0;0; 1
BC 2; 4; 2
AB, AC 4; 2;0 0 - 14 - Trường THPT Marie Curie
A, B, C không thẳng hàng AB, AC d A BC 20 30 , BC 24 6
Điều kiện A, B, C, D đồng phẳng
AB, AC AD 0
Thể tích tứ diện 1 ABCD : V A , B AC . AD ABCD 6 1 SO
Vd: Trong không gian Oxy ,
z Cho A 2;0;
1 , B 1;1; 2 ,C 1;3;3 , D 2; 2; 1 .
Chứng tỏ ABCD là tứ diện. TNnh thể tNch tứ diện ABCD . Giải:
AB = (3;1;3),
AC = (1;3;2),
AD =(0;2;2)
Nhập 3 véctơ . Xong bấm AC
( shift53shift54)shift57shift55 = 34
AB, AC .AD 34 0
ABCD là tứ diện 1 1 V
AB AC AD = 17 (đvtt) ABCD , . . 34 6 6 3
Vd: Trong không gian Oxy ,
z cho A 2;0;0 , B 0;0; 2 ,C 0;3;0 , D 2;1; 1
Chứng tỏ ABCD là tứ diện. TNnh V ? ABCD
Tứ gi6c ABCD là hình bình hành
x x x x B A C D
AB DC y y y y ... B A C D
z z z z B A C D
Vd: Trong không gian Oxy ,
z A 2;0;0 , B 0;0; 2 ,C 0;3;0 . Tìm D để ABCD là
hình bình hành. TNnh diện tNch hình bình hành đó? Giải: uuu r uuu r AB ; 2 ; 0 2 , AC ; 2 ; 3 0 uuur uuur r A , B AC ; 6 ; 4 6 0 - 15 - Trường THPT Marie Curie
x x x x B A C D
D để ABCD là hình bình hành AB DC y y y y D 2;3;2 B A C D
z z z z B A C D 1 uuu r uuu r S S 2 . 2
AB, AC 2 22 ABCD ABC 2 - 16 -