Hình chóp tam giác đều là gì? Mặt bên chóp tam giác đều là hình gì?
Hình chóp tam giác đều là kiến thức quan trọng mà bất kỳ ai cũng được làm quen trong chương trình
Toán học 8. Dù đã được tìm hiểu, thực hành nhiều bài tập nhưng vẫn có không ít bạn học sinh không
nhớ được chính xác khái niệm, tính chất, công thức tính. Vậy nên, trong bài viết này Luật Minh Khuê
cung cấp cho bạn các thông tin quan trọng về hình chóp tam giác đều.
1. Khái quát về hình chóp tam giác đều
1.1 Khái niệm chóp tam giác đều
- Hình chóp tam giác đều là hình chóp có đáy là tam giác đều, các mặt bên (cạnh bên) đều bằng nhau
hay hình chiếu của đỉnh chóp xuống đáy trùng với tâm của tam giác đều.
- Dưới đây là một số ứng dụng thực tế của hình chóp tam giác đều:
+ Kiến trúc và xây dựng: Hình chóp tam giác đều được sử dụng rộng rãi trong kiến trúc và xây dựng. Ví
dụ, nó có thể được sử dụng làm dạng cấu trúc của các tòa nhà, như nhà thờ, pháo đài, hoặc đài tưởng
niệm. Hình chóp tam giác đều cũng được sử dụng để tạo ra các đỉnh núi nhân tạo trong công trình cảnh quan.
+ Đồ họa máy tính và thiết kế 3D: Trong lĩnh vực đồ họa máy tính và thiết kế 3D, hình chóp tam giác
đều được sử dụng để mô phỏng và tạo ra các hình dạng và cấu trúc phức tạp. Nó có thể được sử dụng
để tạo ra mô hình các công trình kiến trúc, trò chơi điện tử, hoặc trong sản xuất phim hoạt hình.
+ Đo lường và tính toán: Hình chóp tam giác đều cũng có ứng dụng trong các lĩnh vực đo lường và tính
toán. Ví dụ, bề mặt hình chóp tam giác đều có thể được sử dụng để tính toán diện tích và thể tích của
các hình dạng và vật thể khác. Nó cũng có thể được sử dụng để giải quyết các vấn đề liên quan đến
hình học và không gian.
+ Trò chơi và giải trí: Hình chóp tam giác đều cũng được sử dụng trong các trò chơi và giải trí. Ví dụ, nó
có thể xuất hiện là hình dạng của các đồ vật trong các trò chơi như bóng bay, các khối xếp hình, hay
trong các trò chơi xây dựng. Nó cũng có thể được sử dụng làm phần của các đồ họa và hiệu ứng trong
các bộ phim, video và sản phẩm giải trí khác. 1.2. Tính chất
- Đáy của hình chóp này là một tam giác đều
- Các cạnh bên đều bằng nhau
- Các mặt bên của hình chóp này là tam giác cân, không nhất thiết phải là tam giác đều.
- Chân đường cao trùng với tâm đáy (tâm đáy là trọng tâm tam giác)
- Góc được tạo bởi mặt bên và mặt đáy đều bằng nhau
- Góc được tạo bởi cạnh bên và mặt đáy đều bằng nhau.
1.3. Mặt bên chóp tam giác đều là hình gì?
Hình chóp đều có các mặt bên là các hình tam giác cân bằng nhau có chung đỉnh, đỉnh này gọi là đỉnh
của hình chóp và các đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy gọi là đường cao của
hình chóp và hình chóp còn được bao bởi mặt đáy là đa giác đều (tam giác đều, hình vuông,…).
Trong hình học, một hình chóp là một khối đa diện được hình thành bằng cách kết nối một điểm của
một đa giác và một điểm, được gọi là đỉnh. Mỗi cạnh cơ sở và đỉnh tạo thành một hình tam giác, được
gọi là mặt bên. Hình chóp đều được bao bọc bởi mặt đáy là 1 hình đa giác và các mặt bên là các hình
tam giác cân bằng nhau có chung đỉnh. Trên hình chóp đều S. ABCD:
+ Chân đường cao H là tâm của đường tròn đi qua các đỉnh của mặt đáy
+ Đường cao vẽ từ đỉnh S của mỗi mặt bên của hình chóp đều được gọi là trung đoạn của hình chóp đó.
Do vậy có thể thấy rằng hình chóp tứ giác đều có các tính chất sau: Đáy là hình vuông; Các cạnh bên
bằng nhau; Tất cả các mặt bên là các tam giác cân bằng nhau; Chân đường cao trùng với tâm mặt đáy
(tâm đáy là giao điểm 2 đường chéo); Tất cả các góc tạo bởi cạnh bên và mặt đáy bằng nhau. Hình
chóp tam giác đều có các tính chất như sau: Hình chóp tam giác đều có 3 mặt phẳng đối xứng; Đáy là
tam giác đều; Các cạnh bên bằng nhau; Tất cả các mặt bên là các tam giác cân bằng nhau; Chân đường
cao trùng với tâm mặt đáy (tâm đáy là trọng tâm của tam giác); Tất cả các góc tạo bởi các mặt bên và
mặt đáy đều bằng nhau; Tất cả các góc tạo bởi cạnh bên và mặt đáy đều bằng nhau.
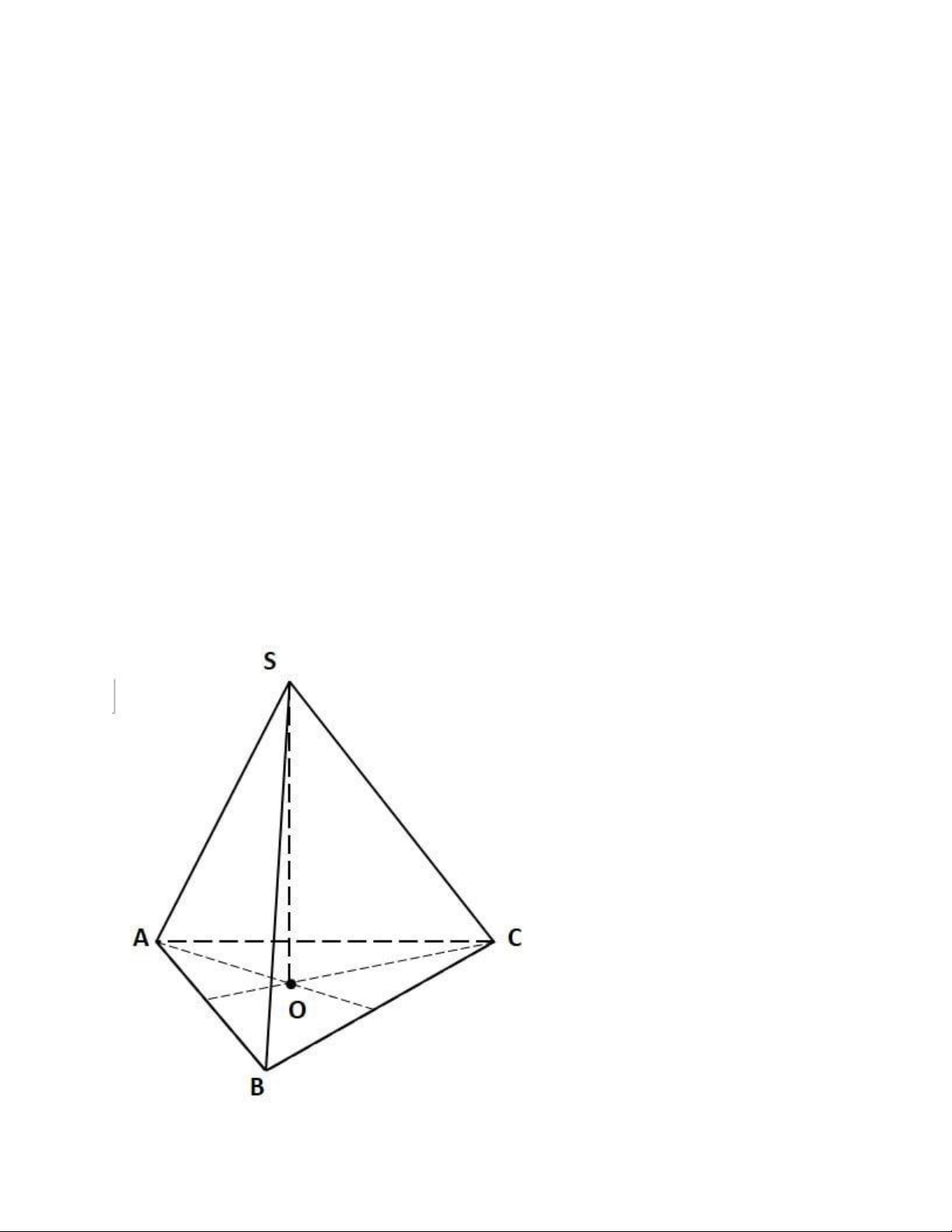
Ví dụ: Hình chóp tam giác đều S. ABC thì:
△ABC đều có tâm O. SO ⊥ (ABC). SA = SB = SC.
((SAB); (ABC)) = ((SBC); (ABC)) = ((SAC); (ABC)). (SA; (ABC)) = (SB; (ABC)) = (SC; (ABC)).
2. Phân biệt chóp tam giác đều và tứ diện đều
Có không ít người nhầm lẫn, không phân biệt được đâu là hình chóp tam giác đều, đâu là hình chóp
tứ giác đều. Vậy nên, Luật Minh Khuê giúp bạn phân biệt hình chóp tam giác đều và hình chóp tứ giác đều dễ nhớ nhất.
- Hình chóp tam giác đều là hình chóp đều có đáy là tam giác (mặt bên là tam giác cân, chưa đều) Hình
chóp tứ giác đều là hình chóp đều có đáy là tứ giác, lúc này đáy là hình vuông, mặt bên là tam giác
cân. Hình chóp tam giác đều có cạnh bên chưa chắc bằng cạnh đáy, chóp tam giác đều có thêm điều
kiện là cạnh bên bằng cạnh đáy là tứ diện đều. Hình tứ diện đều là một hình chóp tam giác đều là
trường hợp đặc biệt có thêm cạnh bên bằng cạnh đáy.
- Tứ diện đều cũng chính là chóp tam giác đều, tuy nhiên trong tứ diện đều, cạnh bên bằng cạnh đáy
nói cách khác ở tứ diện đều tất cả các mặt đều là tam giác đều.
3. Hướng dẫn vẽ dựa vào tính chất hình chóp đều
Hình chóp đều là một trong những kiến thức hình học không gian trọng tâm trong chương trình trung
học phổ thông. Để vẽ được chúng cần phụ thuộc vào các đặc tính cụ thể của loại hình này. Đối với hình
chóp tứ giác đều cũng như tam giác đều thì các vẽ sẽ khá giống nhau và được thực hiện như sau:
Bước 1: Tiến hành vẽ đáy hình chóp là hình vuông hoặc hình tam giác. Đối với hình chóp tứ giác đều
thì vẽ đáy là hình vuông và hình chóp tam giác đều thì vẽ đáy là hình tam giác đều.
Bước 2: Xác định tâm của mặt phẳng đáy, tâm của mặt phẳng đáy cũng chính là chân đường cao theo
như tính chất hình chóp đều.
Bước 3: Từ chân đường cao hình chóp kéo một đường thẳng nhất định để xác định đỉnh của hình chóp đều.
Bước 4: Tiến hành vẽ những cạnh bên sao cho chúng đều bằng nhau. Vẽ cạnh bên bằng cách nối từ
đỉnh hình chóp xuống góc đáy của hình chóp để tạo thành những cạnh bên là những tam giác đều và bằng nhau.
Bước 5: Những góc tạo được bởi mặt đáy và cạnh bên của mặt đáy là bằng nhau
4. Các công thức tính liên quan
4.1 Cách tính diện tích của hình chóp đều
Diện tích xung quanh hình chóp đều
Dựa vào tính chất hình chóp đều ta có công thức tính diện tích xung quanh của hình chóp đều là tích
của trung đoạn của hình chóp đều nhân với nửa chu vi đáy. Công thức tổng quát tính diện tích xung
quanh của hình chóp đều: Sxq=p×d Trong đó: d là trung đoạn
p là nửa chu vi đáy.
Sxq: Diện tích xung quanh
Diện tích toàn phần hình chóp đều
Dựa vào tính chất hình chóp đều ta có công thức tính diện tích toàn phần của hình chóp đều là tổng
của diện tích xung quanh và diện tích đáy. Công thức tổng quát tính diện tích toàn phần của hình chóp đều:
Stp=Sxq+Sđáy Trong đó:
Sđáy là diện tích mặt đáy
Sxq: Diện tích xung quanh
Stp: Diện tích toàn phần
Đối với diện tích đáy cần tùy thuộc vào dạng đáy mà áp dụng những công thức tính khác nhau.
4.2 Cách tính thể tích hình chóp đều
Để tính được thể tích hình chóp đều cần phụ thuộc vào các đặc tính của loại hình này như đã được
nêu ở phía trên bài viết. Theo đó công thức tính thể tích hình chóp đều là tích của ⅓ diện tích đáy
nhân với chiều cao. Công thức tổng quát tính thể tích hình chóp đều cụ thể là:
V = 1/3 S.h Trong đó:
S là diện tích đáy và tùy thuộc vào mỗi hình đáy mà có những công thức tính diện tích đáy khác nhau. h là chiều cao. V là thể tích.
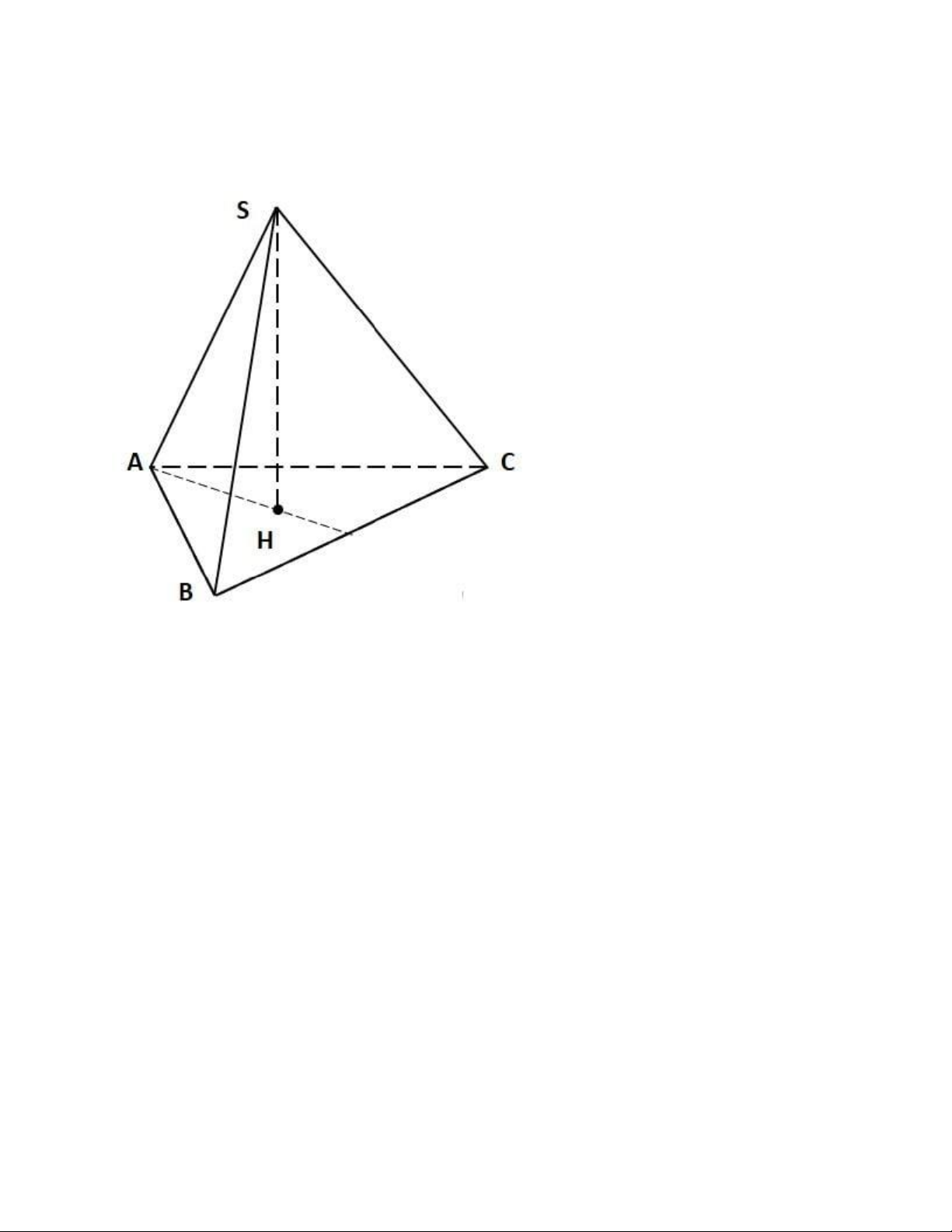
Ví dụ: Cho hình chóp đều S. ABC. Chứng minh rằng: Mỗi cạnh bên của hình chóp đó vuông góc với
cạnh đối diện, mỗi mặt phẳng chứa một cạnh bên và đường cao của hình chóp đều vuông góc với cạnh đối diện.
* S. ABC là hình chóp đều
⇒ △ABC là tam giác đều ⇒ SA = SB = SC.
Do đó khi ta vẽ SH ⊥ (ABC)
⇒ H là trọng tâm của △ABC đều và có AH ⊥ BC.
Theo định lý ba đường vuông góc ⇒ SA ⊥ BC
Chứng minh tương tự ta được SB ⊥ AC và SC ⊥ AB.
* Vì BC ⊥ AH và BC ⊥ SH ⇒ BC ⊥ (SAH)
Chứng minh tương tự ta có CA ⊥ (SBH) và AB ⊥ (SCH).