Preview text:
lOMoAR cPSD| 59735516
Chương 1: Những khái niệm tổng quát 1.1.
Mục đích và yêu cầu:
-Mục đích: Bản vẽ là văn kiện kỹ thuật cơ bản để chỉ đạo sản xuất. Bản vẽ được
xây dựng nhờ những phương phảp biểu diển vả cảc hệ thống qui ước. Nghiên cứu
các phương pháp biểu diển làm cơ sở lý luận cho việc xây dựng cảc bản vẽ là nguồn
gốc lịch sử và là môt trong những nội dung cuả Hình học họa hình.
Để biểu diễn cảc đối tượng cụ thể như môt bộ phận máy móc, một công trình
xây dựng, trước hết phải biết cách biểu diễn các không giản hình học chứa những
đối tượng cụ thể ấy.
Nói rõ hơn, Hình học họa hình lả môt môn hoc nghiên cứu cách biểu diễn cảc
không gian bằng những yếu tố hình học của một không gian có chiều thấp hơn, phổ
biển nhất lả mặt phẳng, rồi dùng các hình biểu diễn ấy để nghiên cứu các không gian ban đầu.
Hình học họa hình nhờ bảo đảm đươc tính trưc quản vả chính xác nên đã được
dùng nhiều trong thực tế để xây dựng các bản vẽ kỹ thuật và nó là một trong những
môn học cơ sơ của chương trình đào tạo kỹ sư.
-Yêu cầu của hình biểu diễn: Muốn đạt được mục đích trên, các hình biểu diễn
phải đạt đươc các yêu cầu sau;
+ Đơn giản, rõ ràng, chính xác.
+ Thoả mãn tính tương đương hình hoc hay tính phản chuyển cuả bản vẽ. 1.2. Các phép chiếu:
1.2.1 Phép chiếu xuyên tâm:
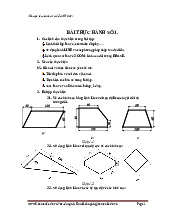
-Trong không gian lấy một mặt phẳng P làm mặt phẳng hình chiếu, lấy một
điểm S không thuộc mặt phẳng P làm tâm chiếu. - Hình chiếu xuyên tâm của điểm
A bất kỳ trong không gian lên mặt phẳng P là giao điểm A’ của đường thẳng SA với mặt phẳng P.
+ P: Là mặt phẳng hình chiếu. Ký hiệu bằng chữ hoa.
+ S: Là tâm chiếu. Ký hiệu bằng chữ in hoa. + SA: Là tia chiếu. 1 lOMoAR cPSD| 59735516
-Tính chất 1: Hình chiếu xuyên tâm của đường thẳng không đi qua tâm chiếu là đường thẳng.
- Tính chất 2: Hình chiếu xuyên tâm của các đường thẳng song song nói chung
là các đường thẳng đồng quy.
1.2.2 Phép chiếu song song:
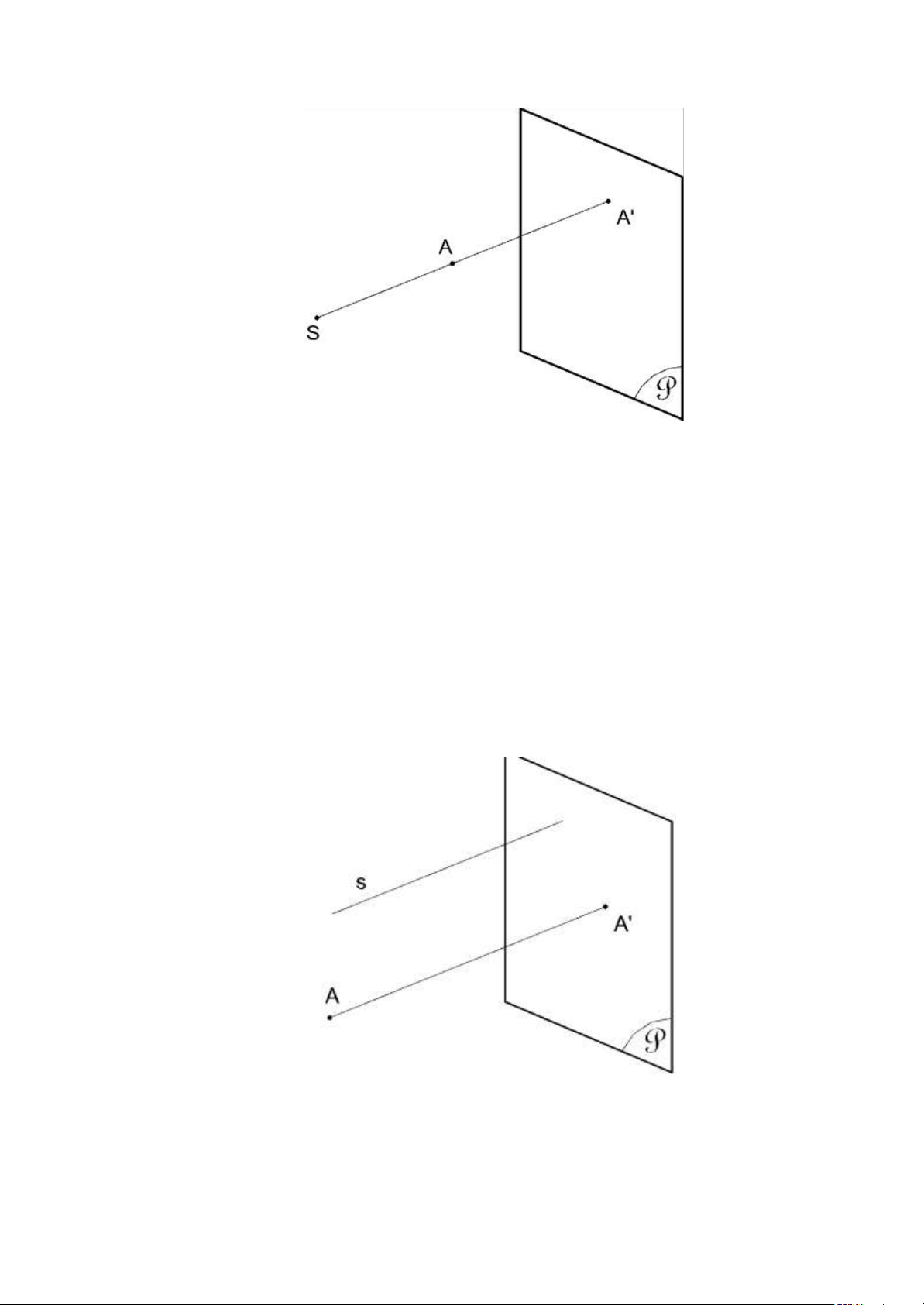
Trong không gian lấy mặt phẳng P làm mặt phẳng hình chiếu và đường thẳng
s không song song với P làm hướng chiếu.
Hình chiếu song song của điểm A là giao điểm A’ của đường thẳng qua A,
song song với s, và mặt phẳng P. P: là mặt phẳng hình chiếu. s: là hướng chiếu. AA’: là tia chiếu
A’: là hình chiếu song song của điểm A
Phép chiếu song song là trường hợp đặc biệt của phép chiếu xuyên tâm khi
tâm chiếu ớ xa vô tận, do đó no có các tinh chất của phép chiếu xuyên tâm.
Phép chiếu song song còn có 2 tinh chất sau: 2 lOMoAR cPSD| 59735516
- Tính chất 1: Hình chiếu song song của các đường thẳng song song là các đường thẳng song song.
- Tính chất 2: Tỉ số hai hình chiếu song song của hai đoạn thẳng song song
bằng tỷ số của hai đoạn thẳng đó.
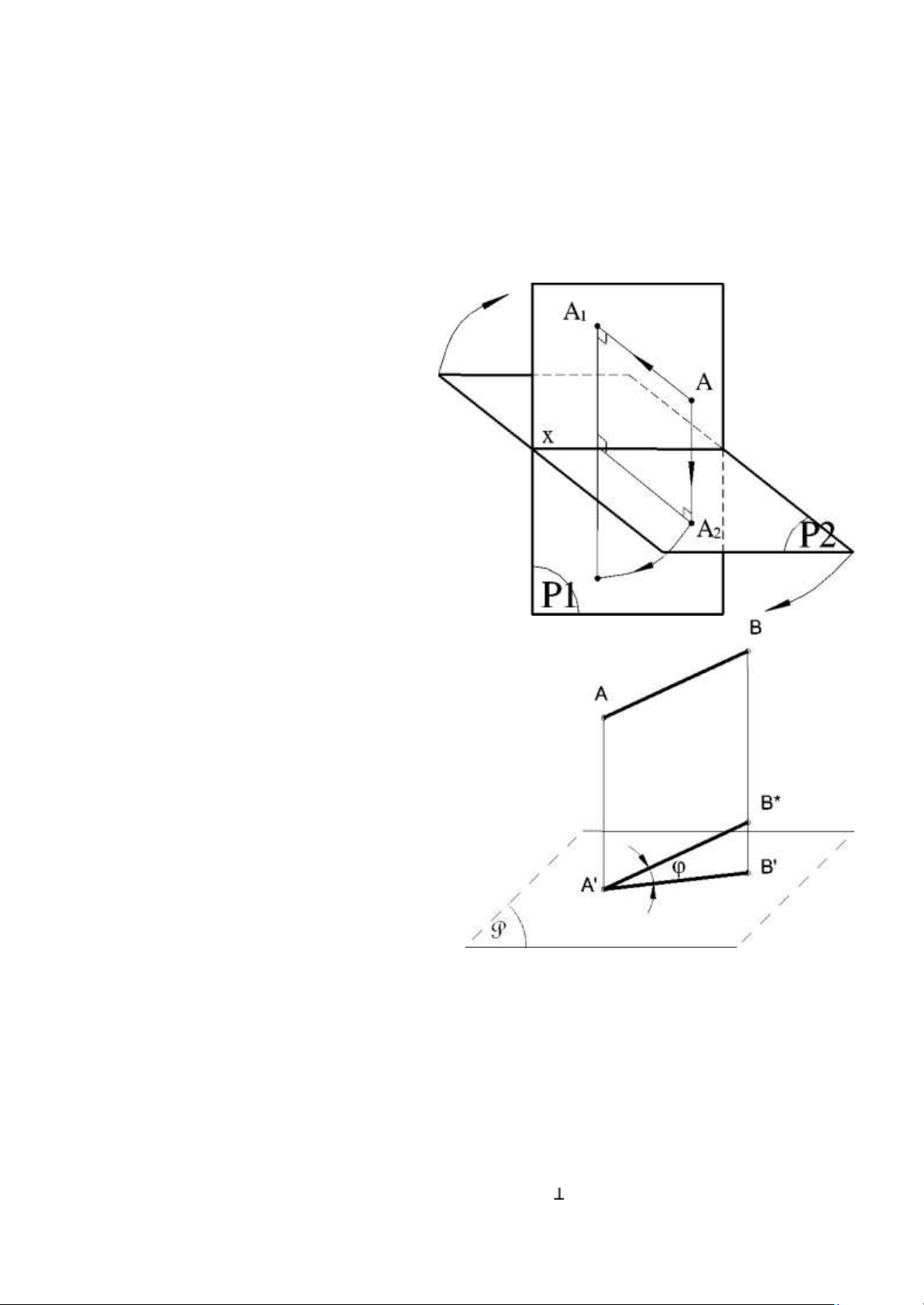
1.2.2 Phép chiếu thẳng góc: Phép chiếu thẳng góc
là trường hợp đặc biệt của phép
chiếu song song khi hớng chiếu
vuông góc với mặt phẳng hinh chiếu.
Phép chiếu thẳng góc là trờng
hợp đặc biệt của phép chiếu song
song nên nó có tất cả các tính chất
của phép chiếu song song, ngoài ra
nó còn có tính chất sau:
- Đô dài hình chiếu thẳng góc
của một đoạn thẳng bằng độ dài của
đoạn thẳng đó nhân với cosφ, là góc
hợp bởi đoạn thẳng đó và mặt phẳng hình chiếu.
Kết luận Các phép chiếu trên
đây cho ta vẽ đợc hình chiếu của các
đối tợng trong không gian lên mặt
phẳng. Nhng ngợc lại, chúng cha
thiết lập quan hệ một đối một giữa
các yếu tố trong không gian với các
yếu tố trên mặt phẳng.
Để xây dựng bản vẽ thoả mãn
điều kiện phản chuyển, trong kỹ
thuật thường dùng các phòng pháp sau: - Phương pháp các hình chiếu thẳng góc. - Phương
pháp hình chiếu trục đo.
- Phương pháp hình chiếu phối cảnh. - Phương pháp hình chiếu có số.
1.3. Biểu diễn điểm:
1.3.1 Dùng 2 mặt phẳng hình chiếu
a. Cách xây dựng đồ thức.
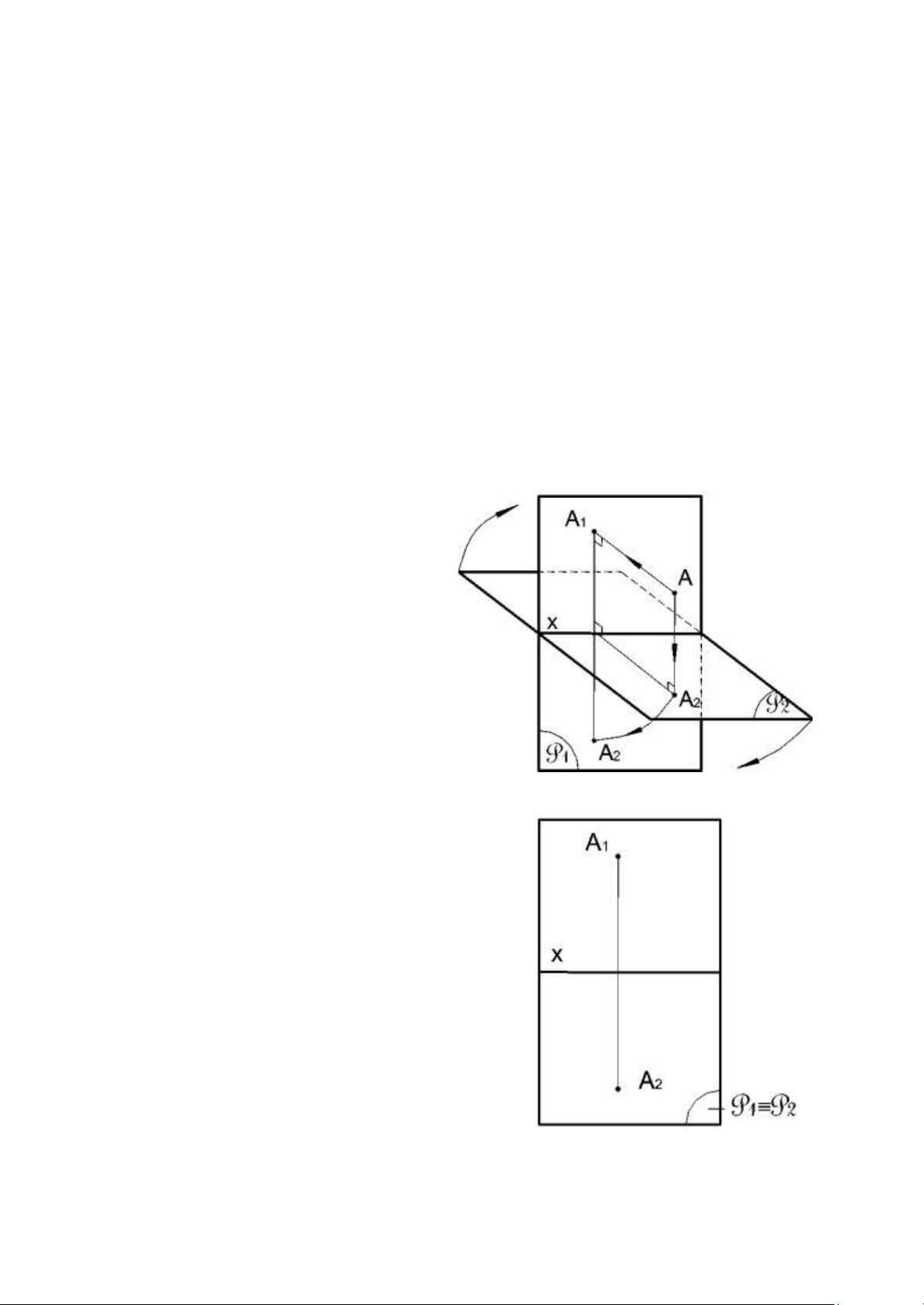
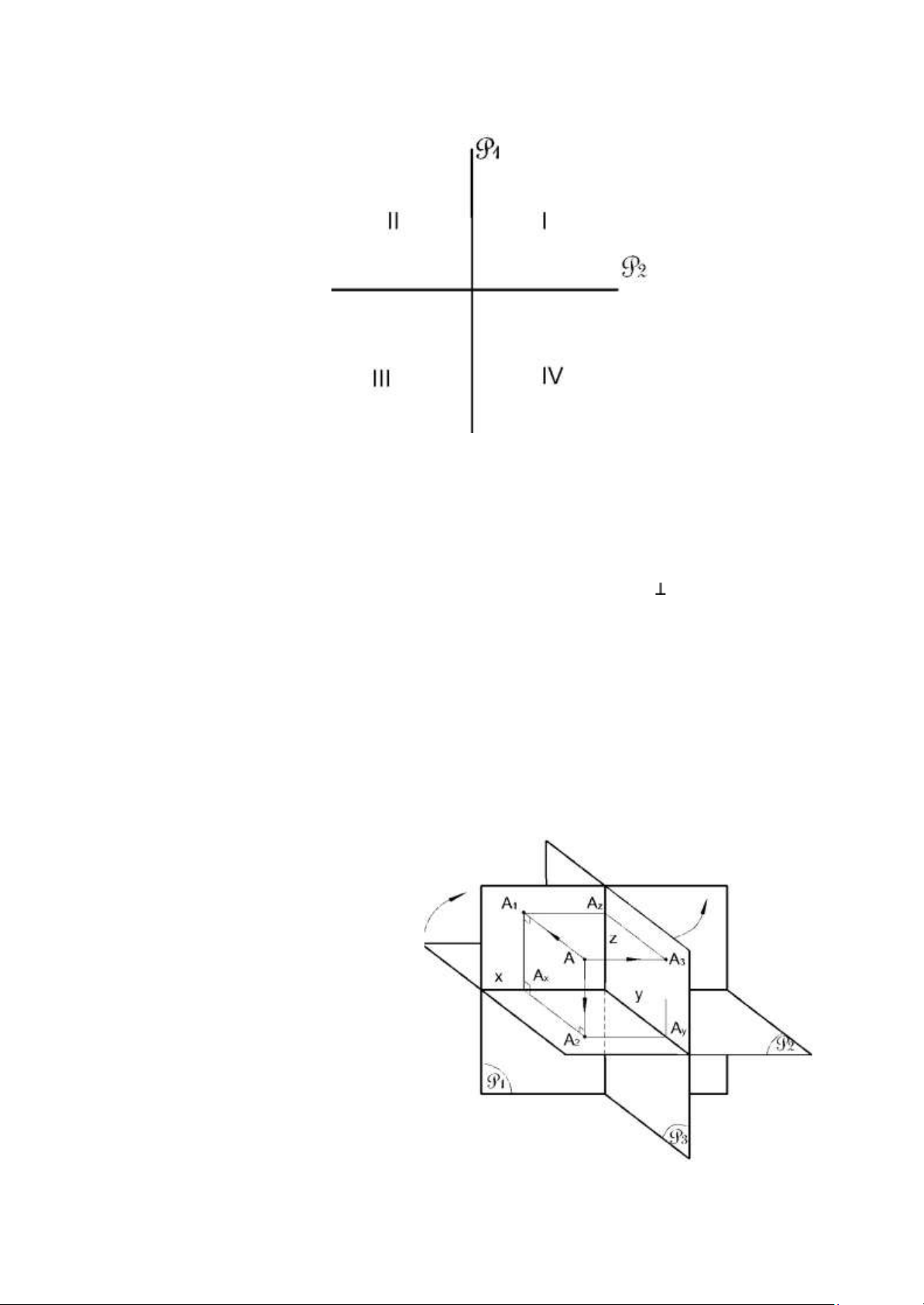
- Trong không gian lấy 2 mặt phẳng P1 P2, làm hai mf hình chiếu. 3 lOMoAR cPSD| 59735516
- Chiếu điểm A lên 2 mặt phẳng P1 và P2 được 2 hình chiếu là A1 và A2.
- Xoay mặt phẳng P2 xung quanh giao tuyến x của 2 mặt phẳng theo
chiều mũi tên như hình vẽ để mặt phẳng P2 trùng với mặt phẳng P1.
Kết quả trên mặt phẳng P1 = P2 ta được hai hình chiếu thẳng góc của điểm A.
Hình thu được bằng cách làm như vậy gọi là đổ thức của điểm A. b. Các định nghĩa:
- P1 thường lấy thẳng đứng - gọi là mặt phẳng hình chiếu đứng.
- P2 thờng lấy nằm ngang - gọi là mặt phẳng hình chiếu bằng.
- A1 gọi là hình chiếu đứng của điểm A.
- A2 gọi là hình chiếu bằng của điểm A.
- Giao tuyến x = P1 x P2 gọi là trục hình chiếu.
Khoảng cách từ A đến P1 gọi là độ xa của điểm A, với quy ước:
Nếu A nằm phía trước mặt phẳng P1 thì độ xa > 0.
Nếu A nằm phía sau mặt phẳng P1 thì độ xa < 0.
Nếu A nằm thuộc mặt phẳng P1 thì độ xa = 0.
- Khoảng cách từ A đến
P2 gọi là độ cao của điểm A.
Nếu A nằm phía trên mặt phẳng P2 thì độ cao > 0.
Nếu A nằm phía dưới mặt phẳng P2 thì độ cao < 0.
Nếu A thuộc mặt phẳng P2 thì độ cao = 0.
- Hai mặt phẳng P1 và P2 chia
không gian làm 4 phần gọi là 4 góc t.
+ Góc t I là phần không gian nằm phía
truớc mặt phẳng P1 và phía trên mặt phẳng
P2 (Điểm thuộc góc I có độ xa > 0, độ cao > 0).
+ Góc t II là phần không gian nằm phía
sau mặt phẳng P1 và phía trên mặt phẳng P2
(Điểm thuộc góc II có độ xa < 0, độ cao > 0).
+ Góc t III là phần không gian nằm phía
sau mặt phẳng P1 và phía dưới mặt phẳng P2
(Điểm thuộc góc III có độ xa < 0, độ cao < 0).
+ Góc t IV là phần không gian nằm phía trớc mặt phẳng P1 và phía dưới mặt
phẳng P2 Điểm thuộc góc IV có độ xa > 0, độ cao < 0). 4 lOMoAR cPSD| 59735516
- Mặt phẳng chia đôi góc t I và III gọi là mặt phẳng phân giác I.
- Mặt phẳng chia đôi góc t II và IV gọi là mặt phẳng phân giác II. c. Các tính chất.
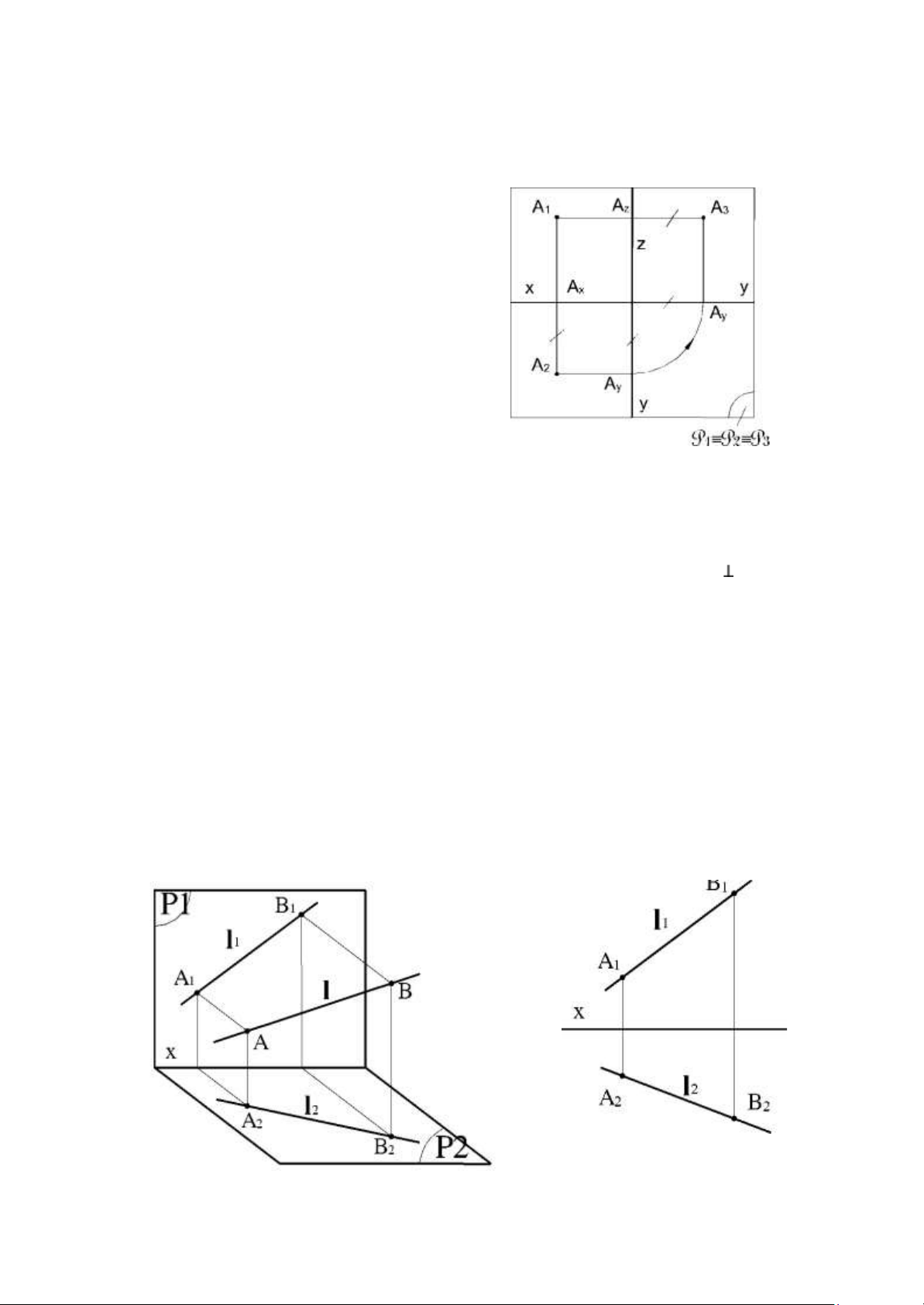
- Gọi Ax là giao điểm của trục x với mặt phẳng xác định bởi 3 điểm A, A1 A2.
Thì trên đổ thức 3 điểm A1, Ax, A2 thẳng hàng và đường thẳng nối ba điểm đó
vuông góc với trục x- Gọi là đường dóng thẳng đứng (A1 Ax A2 x) - Độ dài A1 Ax
bằng trị tuyêt đối độ cao của điểm A.
Nếu A1, nằm phía trên trục x thì độ cao > 0
Nếu A1, thuộc trục x thì độ cao = 0
Nếu A1 nằm phía dưới trục x thì độ cao < 0 - Độ dài
A2 Ax bằng trị tuyêt đối độ xa của điểm A.
Nếu A2 nằm phía dưới trục x thì độ xa > 0
Nếu A2 thuộc trục x thì độ xa = 0
Nếu A2 nằm phía trên trục x thì độ xa < 0
-Nếu A thuộc mf phân giác I
-thì A1 đối xứng với A2 qua trục x
-Nếu A thuộc mf phân giác II- thì A1 trùng A2
1.3.2 Dùng 3 mặt phẳng hình chiếu
a. Cách xây dựng đồ thức:
- Trong không gian lấy 3 mặt
phẳng đôi một vuông góc với nhau P1, P2, P3.
- Chiếu thẳng góc điểm A
lần lượt lên 3 mặt phẳng P1, P2, P3 được A1, A2, A3. 5 lOMoAR cPSD| 59735516
- Xoay mặt phẳng P2 quanh trục x theo chiều mũi tên để mặt phẳng P2 ≡ P1. -
Xoay mặt phẳng P3 quanh trục z theo chiều mũi tên để mặt phẳng P3 ≡ P1.
- Kết quả trên mặt phẳng P1 ≡ P2 ≡ P3 ta được ba hình chiếu thẳng góc của
điểm A, đó là đồ thức của điểm A trên ba mặt phẳng hình chiếu. b. Các định nghĩa:
Các yếu tố thuộc mặt phẳng P1, P2
được định nghĩa như dùng 2 mặt phẳng hình
chiếu. Các yếu tố còn lại định nghĩa nh sau:
- P3: Là mặt phẳng hình chiếu cạnh
- A3: Là hình chiếu cạnh của điểm A.
- Khoảng cách từ A -đến P3 goi là độ xa
cạnh của điểm A c. Các tính chất:
Ngoài các tính chất nh đã nêu trong trờng hợp dùng hai mặt phẳng hình chiếu,
còn có các tính chất sau:
Goi Az là giao điểm của trục z với mặt phẳng A A1 A3
- Thì trên đổ thức, ba điểm A1, Az, A3 thẳng hàng và đường thẳng nối ba
điểm đó vuông góc với trục Z- goi là đờng dóng nằm ngang (A1 A2 A3 z). -
A3Az = A2Ax = AA1 (độ xa của điểm A).
1.3. Đồ thức của đường thẳng
Trong không gian đờng thẳng được xác định bởi hai điểm và hình chiếu của
một đờng thẳng là một đường thẳng. Vì vậy đổ thức của đường thẳng được xác
định khi biết đổ thức của hai điểm thuộc đờng thẳng ấy.
1.3.1 Biểu diễn đường thẳng
Đổ thức của một đường thẳng l(A, B) là một cặp đường thẳng l1(A1B1) và
l2(A2,B2) trên mặt phẳng đổ thức P1 - P2 6 lOMoAR cPSD| 59735516
Ta gọi đường thẳng bất kỳ là đường thẳng có hướng không song song hoặc
vuông góc với mặt phẳng hình chiếu. Trên đổ thức, các hình chiếu của đường thẳng
bất kỳ cũng có hướng bất kỳ.
1.3.2 Các đường thẳng đặc biệt
1.3.2.1 Các đường đồng mức.
Đường đổng mức là đường thẳng song song với một mặt phẳng hình chiếu
Gồm có: Đường bằng, đường mặt, đường cạnh. a. Đường bằng
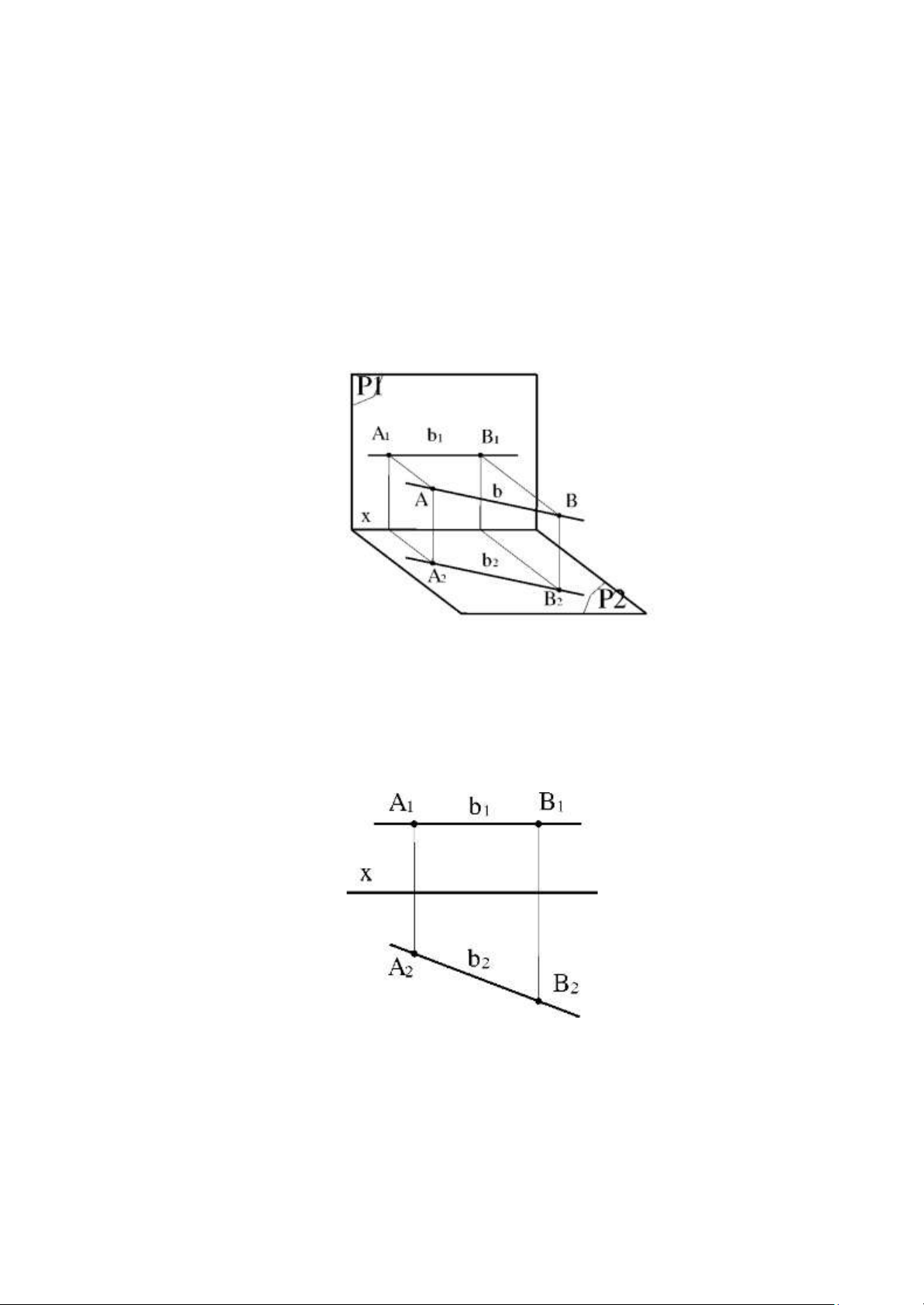
Đĩnh nghĩa: Đường bằng là đường thẳng song song với mặt phẳng hình chiếu bằng P2 Tính chất:
- Hình chiếu đứng b song song với trục x.
- Hình chiếu bằng của bất kì đoạn thẳng nào thuộc đường bằng cũng có độ
dài bằng chính nó: A2B2 = AB.
- Góc của hình chiếu bằng của đờng bằng với trục x chính là góc giữa đường
thẳng đó với mặt phẳng hình chiếu đứng P1 . b. Đường mặt 7 lOMoAR cPSD| 59735516
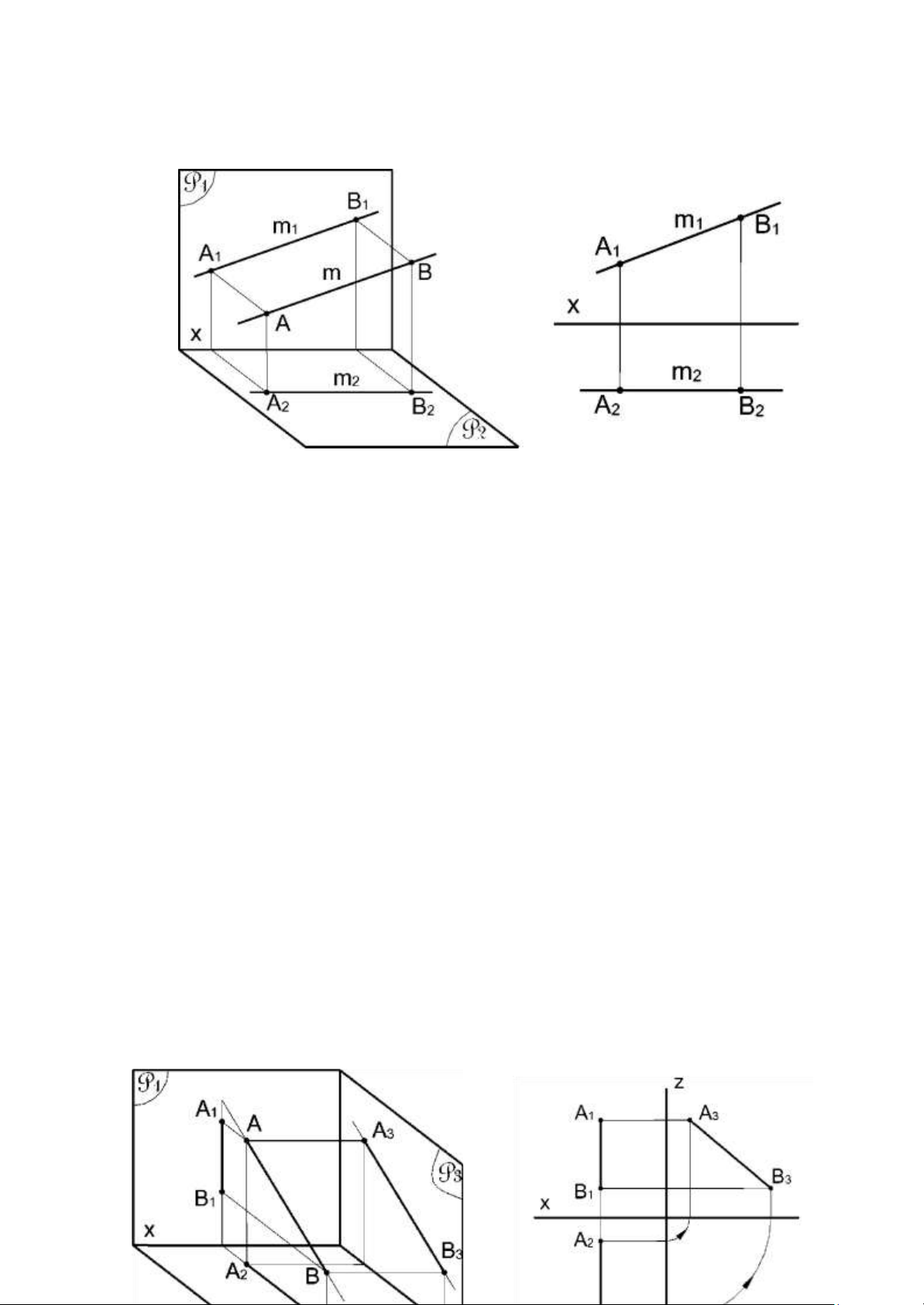
Định nghĩa: Đường mặt là đường thẳng song song với mặt phẳng hình chiếu đứng P1. Tính chất:
- Hình chiếu bằng m2 song song với trục x.
- Hình chiếu đứng của bất kì đoạn thẳng nào thuộc đường mặt cũng có độ dài bằng chính nó: A1B1 = AB.
- Góc của hình chiếu đứng của đường mặt với trục x chính là góc giữa đờng
thẳng đó với mặt phẳng hình chiếu bằng P2. c. Đường cạnh
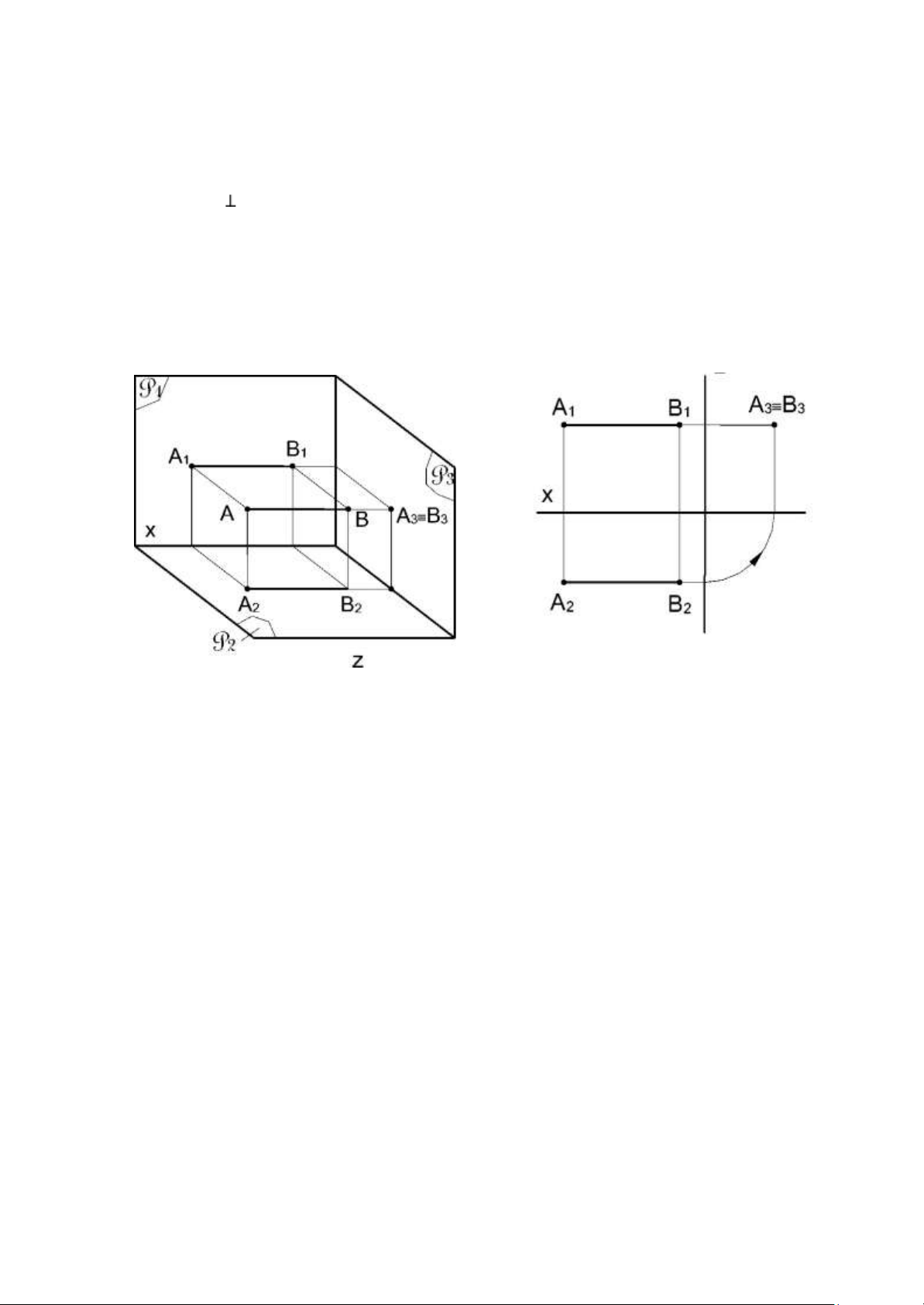
Đinh nghĩa: Đường cạnh là đường thẳng song song với mặt phẳng hình chiếu cạnh Tính chất:
- Hình chiếu đứng và hình chiếu bằng (A1B1, A2B2) cùng nằm trên đường
dóng thẳng đứng và vuông góc với trục x.
- Hình chiếu cạnh của đoạn thẳng bất kì thuộc đường cạnh A3B3 cũng có độ dài bằng chính nó.
- Góc giữa hình chiếu cạnh của đường cạnh với trục z là góc giữa đờng thẳng
đó với mặt phẳng hình chiếu đứng P1.
- Góc giữa hình chiếu cạnh của đường cạnh với trục y là góc giữa đờng thẳng
đó với mặt phẳng hình chiếu bằng P2.
1.3.2.2 Các đường thẳng chiếu.
đường thẳng chiếu là đường thẳng vuông góc với mặt phẳng hình chiếu. 8 lOMoAR cPSD| 59735516
Gồm các: Đường thẳng chiếu bằng, đường thẳng chiếu đứng, đường thẳng chiếu cạnh. d.
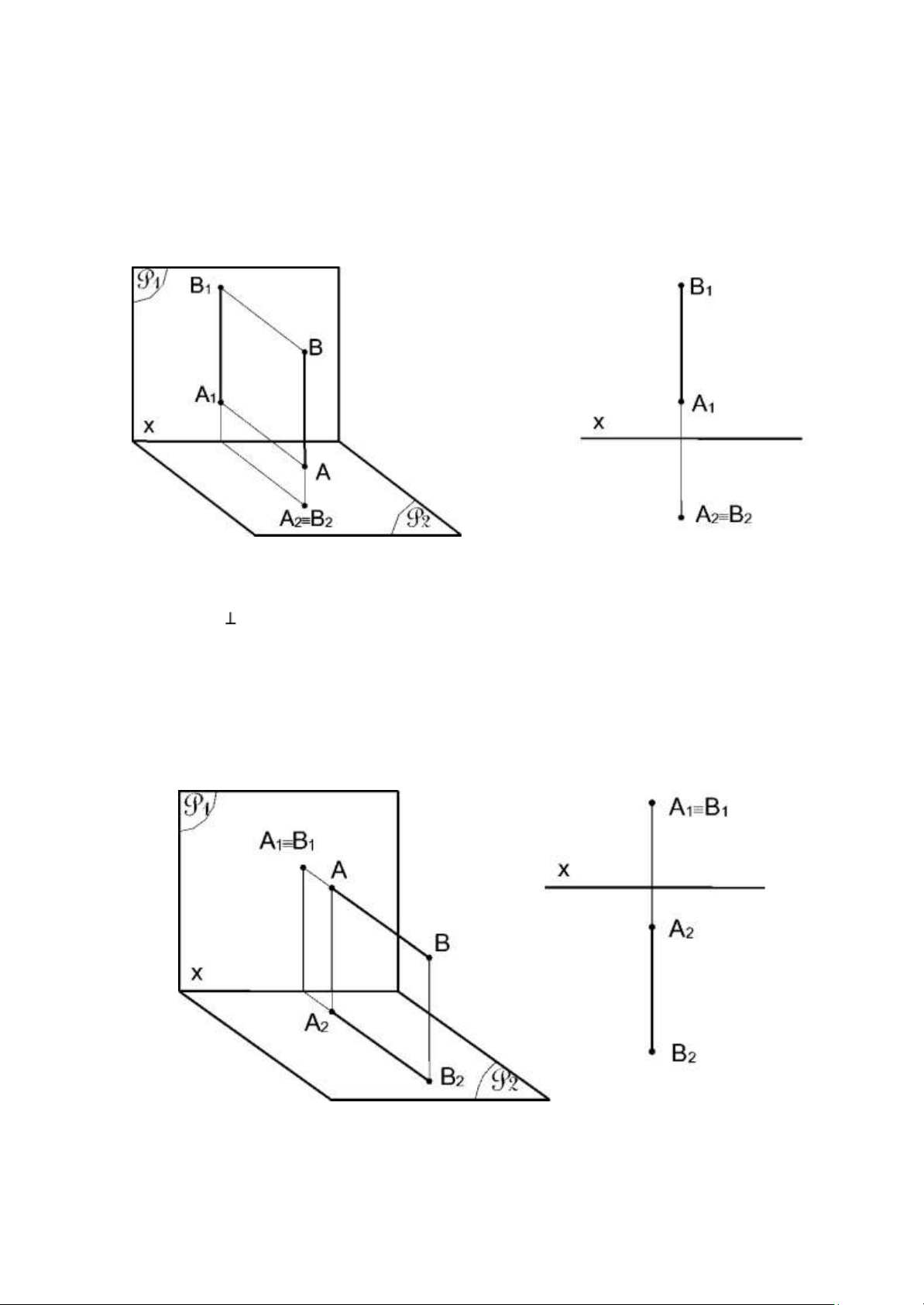
Đường thẳng chiếu bằng
Định nghĩa: Đường thẳng chiếu bằng là đường thẳng vuông góc với mặt
phẳng hình chiếu bằng P2 Tính chất:
- Hình chiếu bằng suy biến thành một điểm: A2 ≡ B2
- Hình chiếu đứng là đờng thẳng vuông góc với trục x: A1B1 x
- Hình chiêu đứng và hình chiếu cạnh của bất kì đoạn thẳng nào thuộc
đường thẳng chiếu bằng cũng có độ dài bằng độ dài thật. A1B1 = AB = A3B3. e.
Đường thẳng chiếu đứng
Định nghĩa: Đường thẳng chiếu đứng là đường thẳng vuông góc với mặt
phẳng hình chiếu đứng. . 9 lOMoAR cPSD| 59735516 Tính chất: -
Hình chiếu đứng suy biến thành một điểm: A1 ≡ B1 - Hình chiếu bằng
là đờng thẳng vuông góc với trục x: A2B2 x. -
Hình chiếu bằng và hình chiếu cạnh của bất kì đoạn thẳng nào thuộc
đt chiếu đứng cũng có độ dài bằng độ dài thật: A2B2 = AB = A3B3.
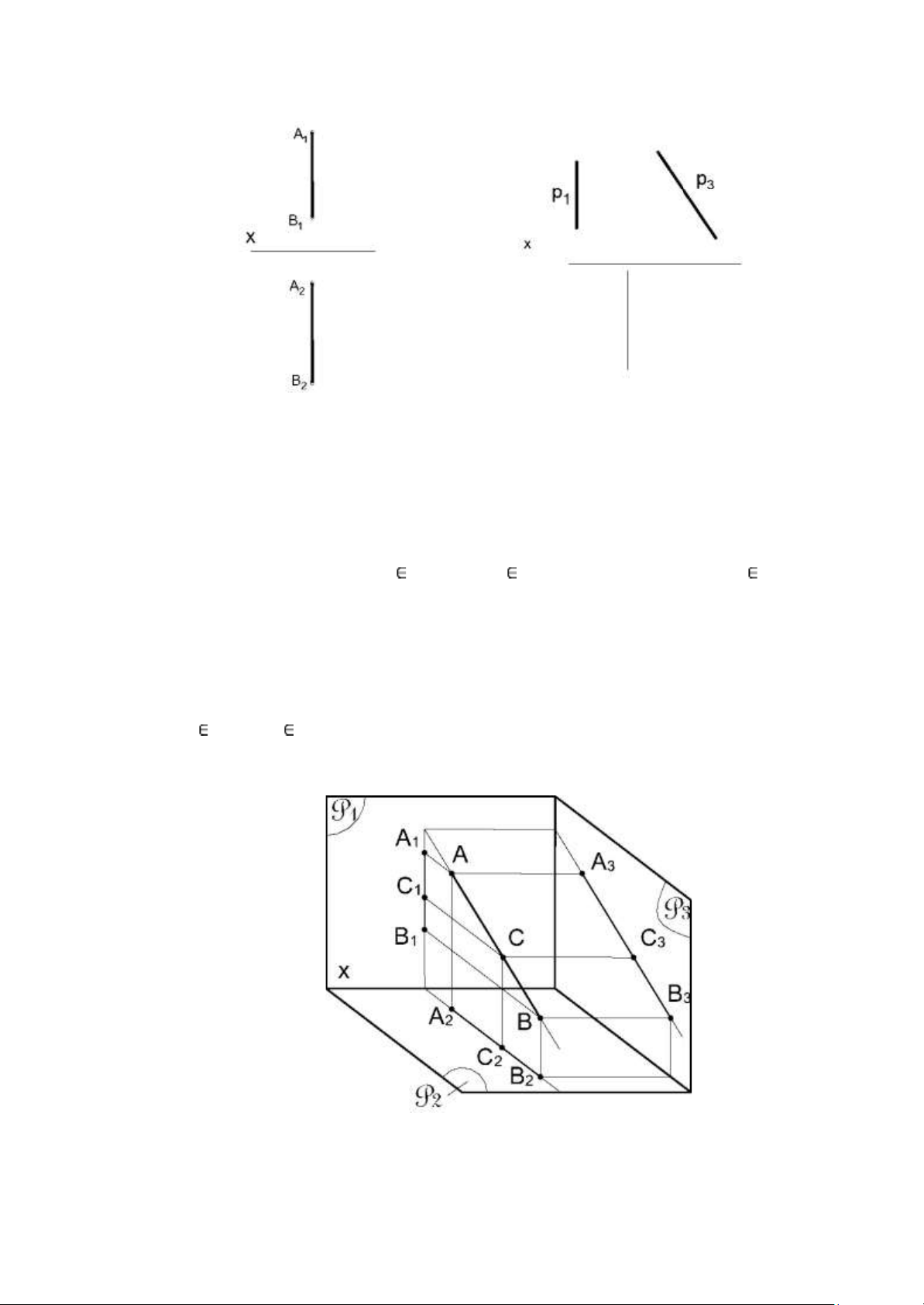
f.Đường thẳng chiếu cạnh
Đinh nghĩa: Đường thẳng chiếu cạnh là đường thẳng vuông góc với măt phẳng hình chiếu canh. Tính chất: -
Hình chiếu cạnh suy biến thành một điểm: A3 ≡B3. -
Các hình chiếu đứng và hình chiếu bằng cùng song song với trục x: A1B1 // x // A2B2 -
Hình chiếu đứng và hình chiếu bằng của bất kì đoạn thẳng nào thuộc
đường thẳng chiếu cạnh cũng bằng độ dài thật. Chú ý: -
Đường thẳng không phải là đường cạnh hoàn toàn được xác định khi
biết hình chiếu đứng và hình chiếu bằng của nó.
-Trờng hợp đường cạnh, khi biết hình đứng và hình bằng , đường thẳng đó
cha được xác định: Bởi mặt phẳng đi qua hai hình chiếu đó và tưong ứng vuông
góc với mặt phẳng hình chiếu đứng và mặt phẳng hình chiếu bằng sẽ trùng nhau.
Do đó, muốn xác định đường cạnh trên hai hình chiếu thì phải cho đổ thức của hai
điểm của đờng cạnh. Hoặc cho hình chiếu cạnh với hình chiếu đứng hoặc hình chiếu bằng của nó
1.3.3 Điểm thuộc đường thẳng. 10 lOMoAR cPSD| 59735516
1.3.3.1. Trường hợp đường thẳng không phải là đường cạnh.
Điều kiện cần và đủ để một điểm thuộc đường thẳng là: hình chiếu đứng của
điểm thuộc hình chiếu đứng của đường thẳng, hình chiếu bằng của điểm thuộc hình
chiếu bằng của đường thẳng.
1.3.3.2. Trường hợp đường thẳng là đường cạnh.
- Từ hai hình chiếu với: C1 A1B1, và C2 A2B2 chưa đủ để kết luận C AB. Vì
mọi điểm thuộc mặt phẳng chứa đường thẳng AB và song song với P3 đều có hình
chiếu đứng và bằng nằm trên A1B1 và A2B2 .
-Vậy để xem một điểm có thuộc đường cạnh không thì hoặc dựa vào hc cạnh:
điều kiện là hc đứng của điểm thuộc hc đứng của đờng cạnh và hình chiếu cạnh của
điểm thuộc hình chiếu cạnh của đường cạnh. C1 A1B1; C3 A3B3
-Hoặc (Nếu chỉ biết hc đứng và hc bằng), ta dựa vào tính chất không đổi của
tỉ số đơn của 3 điểm thẳng hàng trong phép chiếu song song.
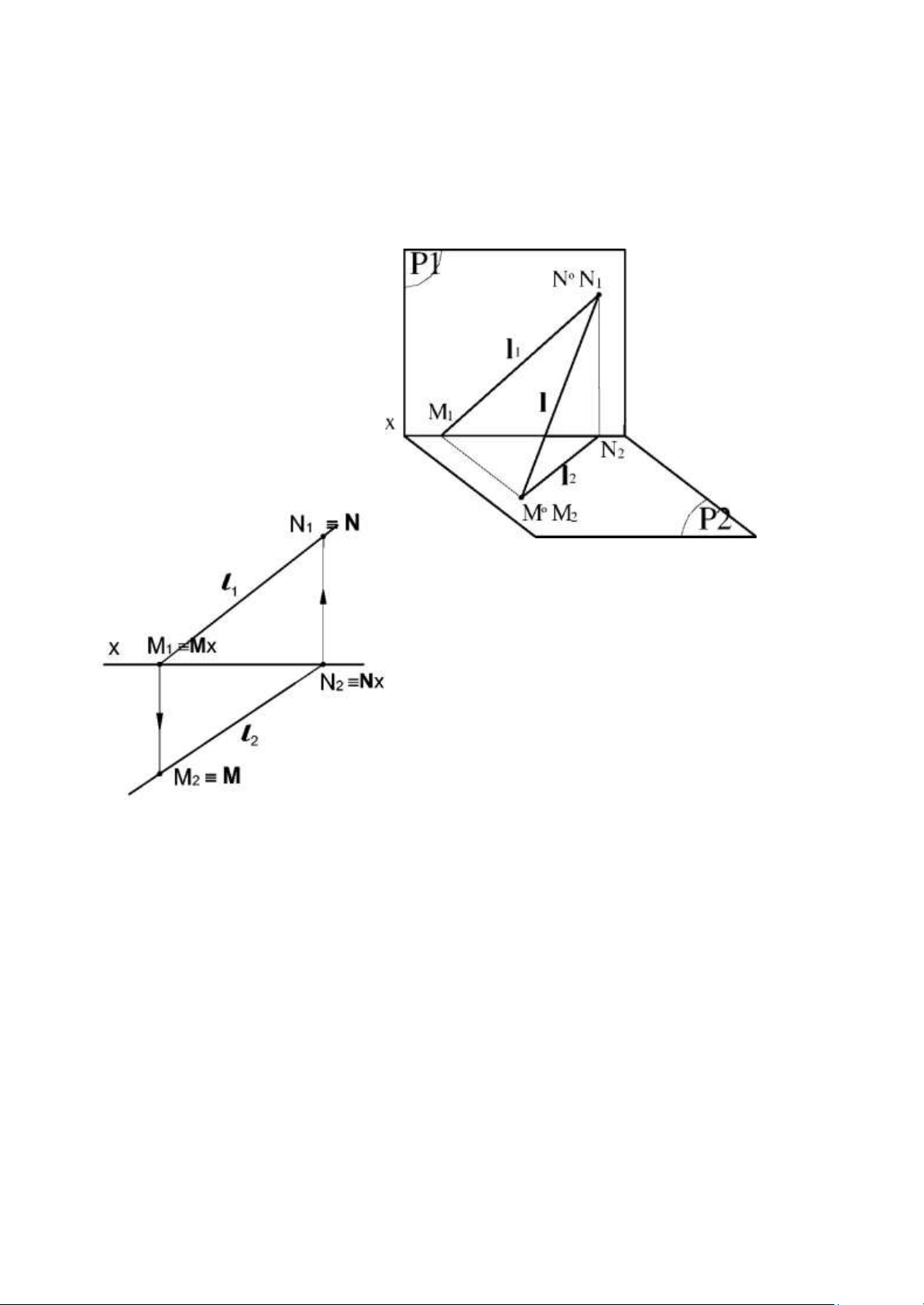
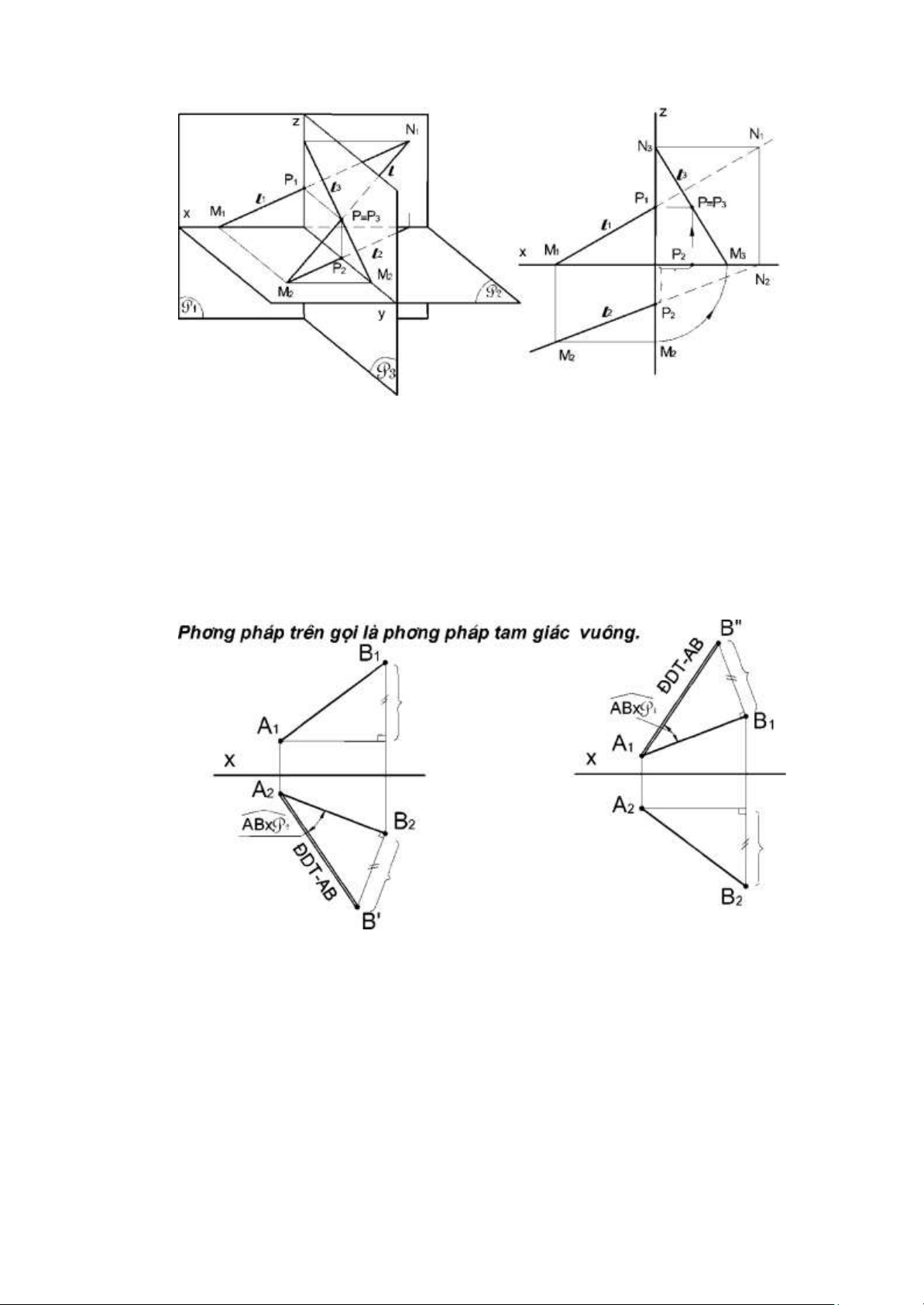
1.3.3.3. Vết của đường thẳng. Định nghĩa. 11 lOMoAR cPSD| 59735516
- Vết của đường thẳng là giao điểm của đường thẳng với mặt phẳng hình chiếu.
- Vết đứng là giao điểm của đường thẳng với mặt phẳng hình chiếu đứng P1. Thường kí hiệu là N. - Vết
bằng là giao điểm của đường thẳng với mặt phẳng hình chiếu bằng P2. Thường kí hiệu là M. - Vết cạnh là giao điểm của đường thẳng với mặt phẳng hình chiếu cạnh P3. Thường kí hiệu là P. Cách xác định vết.
+ Kéo dài hình chiếu bằng l2 cắt trục x tại N2=
Nx. Từ N2 kẻ đường dóng thẳng đứng cắt l1 tại N1 = N.
+ Tương tự, kéo dài 11 cắt trục x tại M1= Mx.
Từ điểm này kẻ đờng dóng thẳng đứng cắt 12 tại M2 = M.
Cách xác định vết cạnh:
+ Kéo dài hình chiếu bằng l2 của đường
thẳng cắt trục yz tại một điểm ta được hình chiếu bằng P2 của vết cạnh.
+ Dùng cách xác định hình chiếu cạnh tìm được P2 trên trục x. Từ P2 kẻ đường
dóng song song với trục z, cắt hình chiếu cạnh 13 của đường thẳng tại điểm P3 chính
là hình chiếu cạnh hay vết cạnh của đờng thẳng l. 12 lOMoAR cPSD| 59735516
1.3.3.4. Tìm độ dài thật của đoạn thẳng và góc của nó với các mặt phẳng hình chiếu.
- Lấy hình chiếu bằng làm một cạnh góc vuông, vẽ tam giác vuông có độ dài
canh góc vuông còn lại là hiệu độ cao của hai đầu đoạn thẳng, thì cạnh huyền bằng
độ dài thật của đoạn thẳng AB và góc kề hc bằng là góc nghiêng của AB với P
- Tương tự, vẽ tam giác vuông có một cạnh là hình chiếu đứng, cạnh còn lại là
hiệu độ xa của 2 đầu đoạn thang AB, thì cạnh huyền của tam giác là ĐDT của AB,
góc đối diện với cạnh hiệu độ xa là góc nghiêng giữa AB với mặt phẳng P. Chú ý:
- Nếu chỉ cần xác định độ lớn thật của một đoạn thẳng thì tam giác vuông
dựng ỏ hình chiếu nào cũng được.
- Nếu muốn xác định góc của đoạn thẳng với mặt phẳng hình chiếu nào thì
phải dựng tam giác trên hình chiếu đó.
- Với đường cạnh, góc của nó với P1 và P2 là 2 góc phụ nhau. Nếu không phải
là đường cạnh thì 2 góc với P1 và P2 là 2 góc độc lập nhau.
1.3.4 Vị trí tương đối của hai đường thẳng. 13 lOMoAR cPSD| 59735516
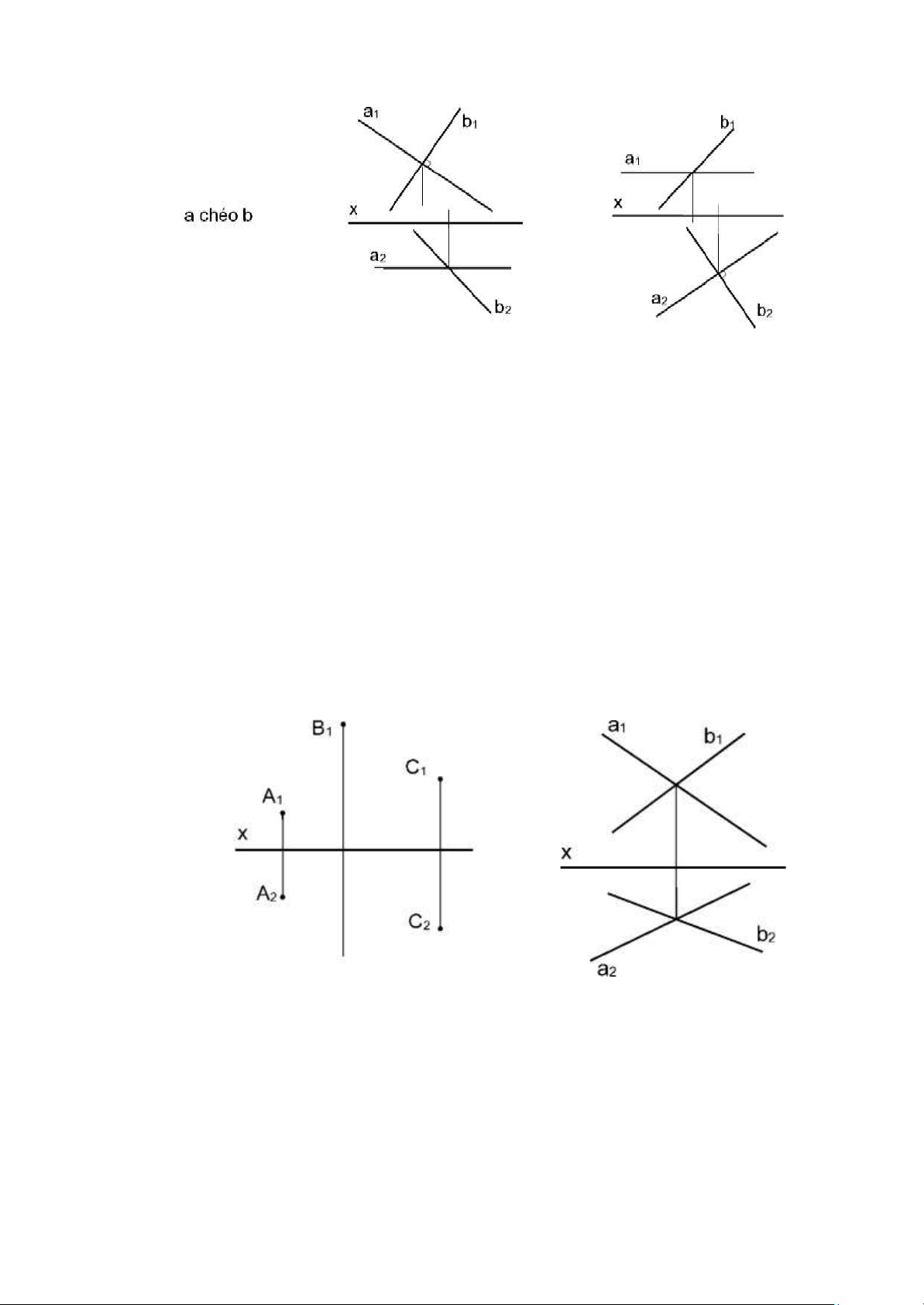
Trong không gian hai đường thẳng có
thể cắt nhau, song song và chéo nhau. Ta đi
xét các trong hợp này trên đổ thức.
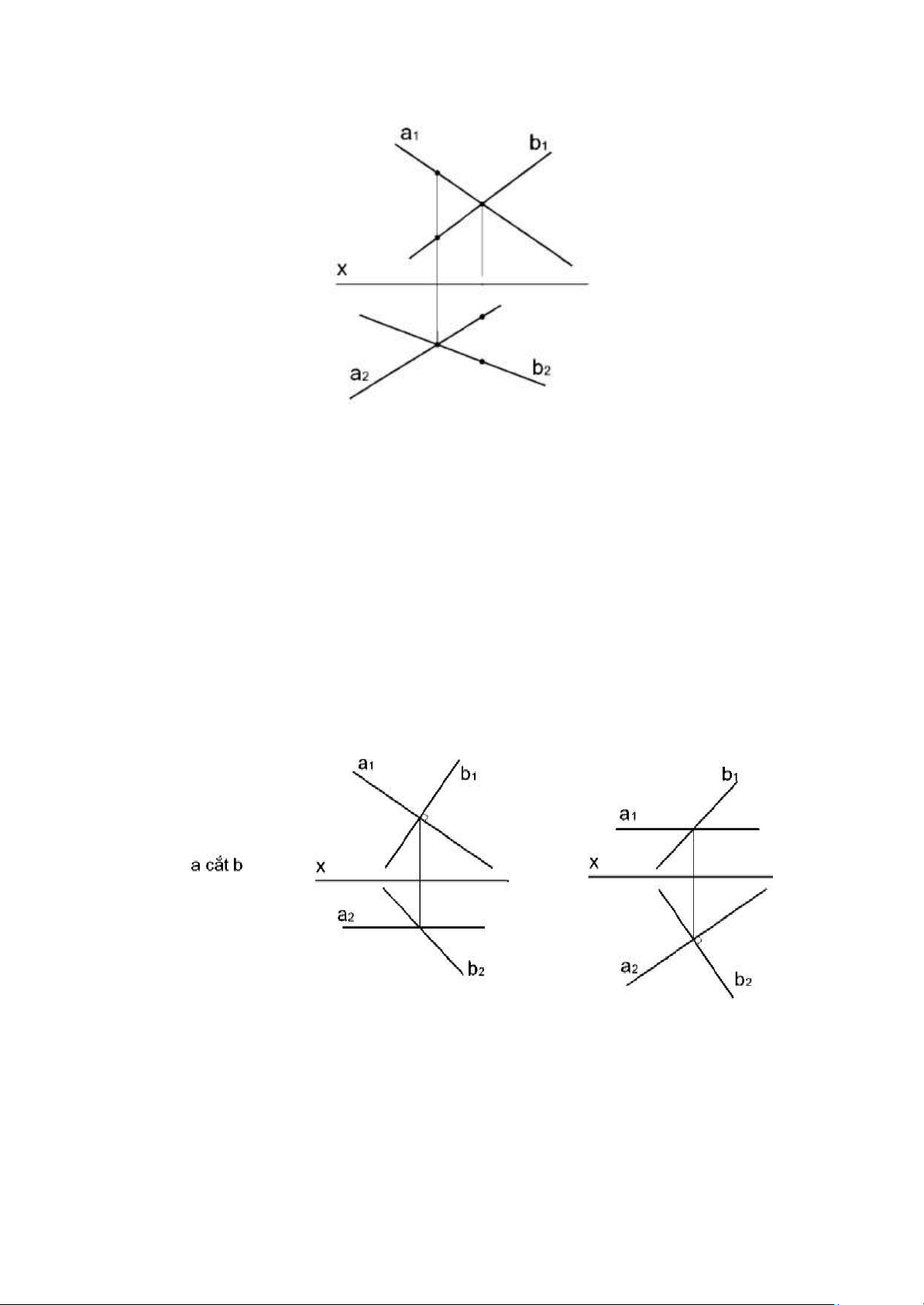
1.3.4.1. Hai đường thẳng cắt nhau.
a. Trường hợp hai đường thẳng
không phải là đường cạnh.
Đình lý: Điêu cần và đủ để 2 đưong
thẳng cắt nhau là các hình chiếu đứng của
chúng cắt nhau, các hình chiếu bằng cua
chúng cắt nhau và hai giao điểm phải cùng
nằm trên một đường dóng.
b. Trường hợp có đường thẳng là đường cạnh.
- Giả thiết cho đường thẳng m và
đường cạnh AB, mặc dù các hình chiếu
bằng và đứng của chúng cắt nhau, và
các giao điểm ấy nằm trên cùng một
đường dóng, nhưng trong không gian chưa chắc m cắt AB.
- Giả sử m1 x A1B1 = I1 m2 x A2B2 = I2
- Ta thấy điểm I đã thuộc m. Bài toán trở
về xét xem I có thuộc đường cạnh AB hay không, có 2 phương pháp:
+Dựa vào hình chiếu cạnh. +
Dựa vào tỷ số đơn của 3 điểm (A1I1B1) và (A2I2B2).
Nếu I thuộc AB thì đường thẳng m cắt đường cạnh AB. Nếu
I không thuộc AB, thì m và AB chéo nhau.
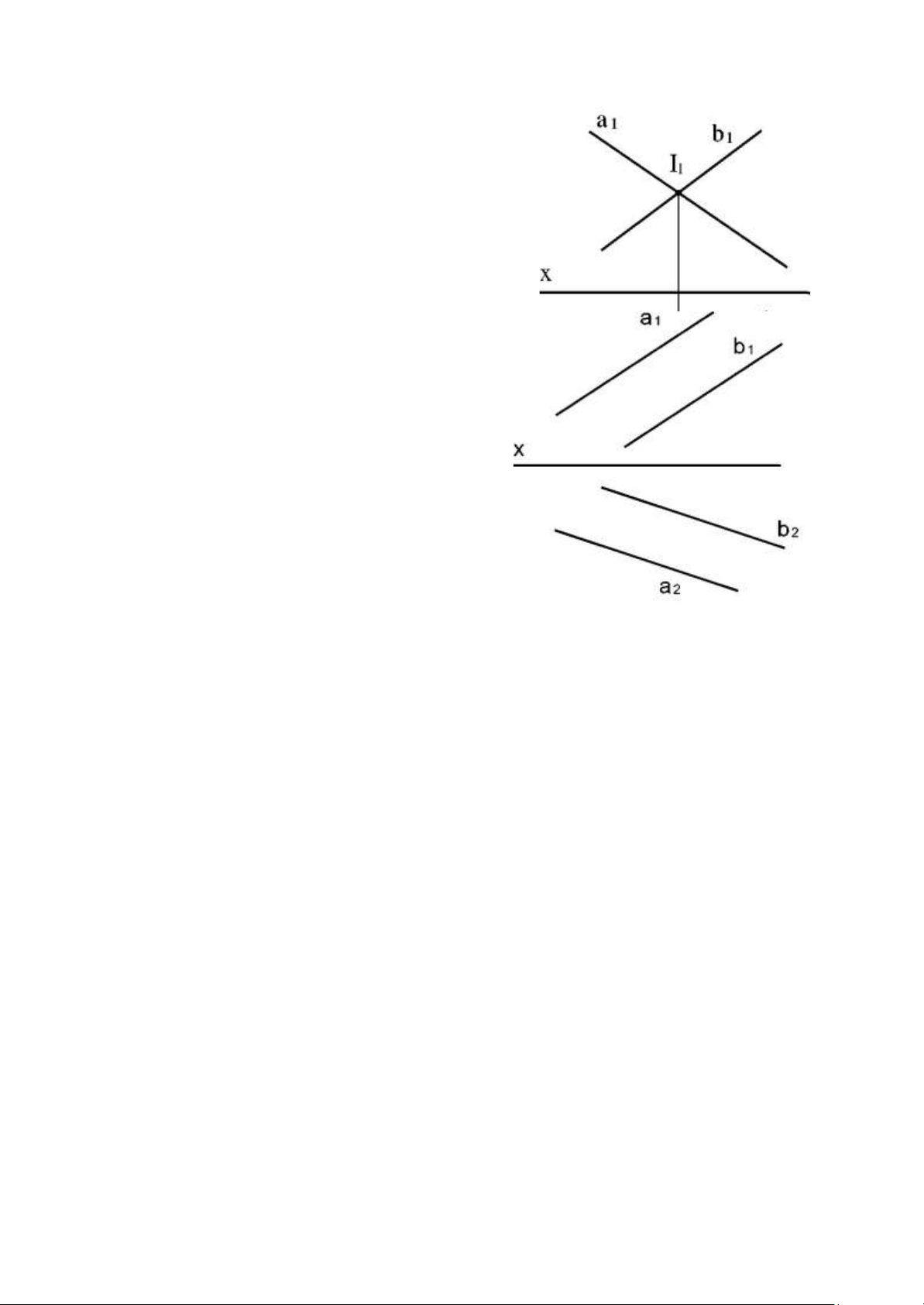
1.3.4.2. Hai đường thẳng song song.
a. Trường hợp hai đường thẳng không phải là đường cạnh.
Định lý: Điều kiện cần và đủ để hai đường thẳng song song với nhau là các
hình chiếu cùng tên của chúng song song với nhau.
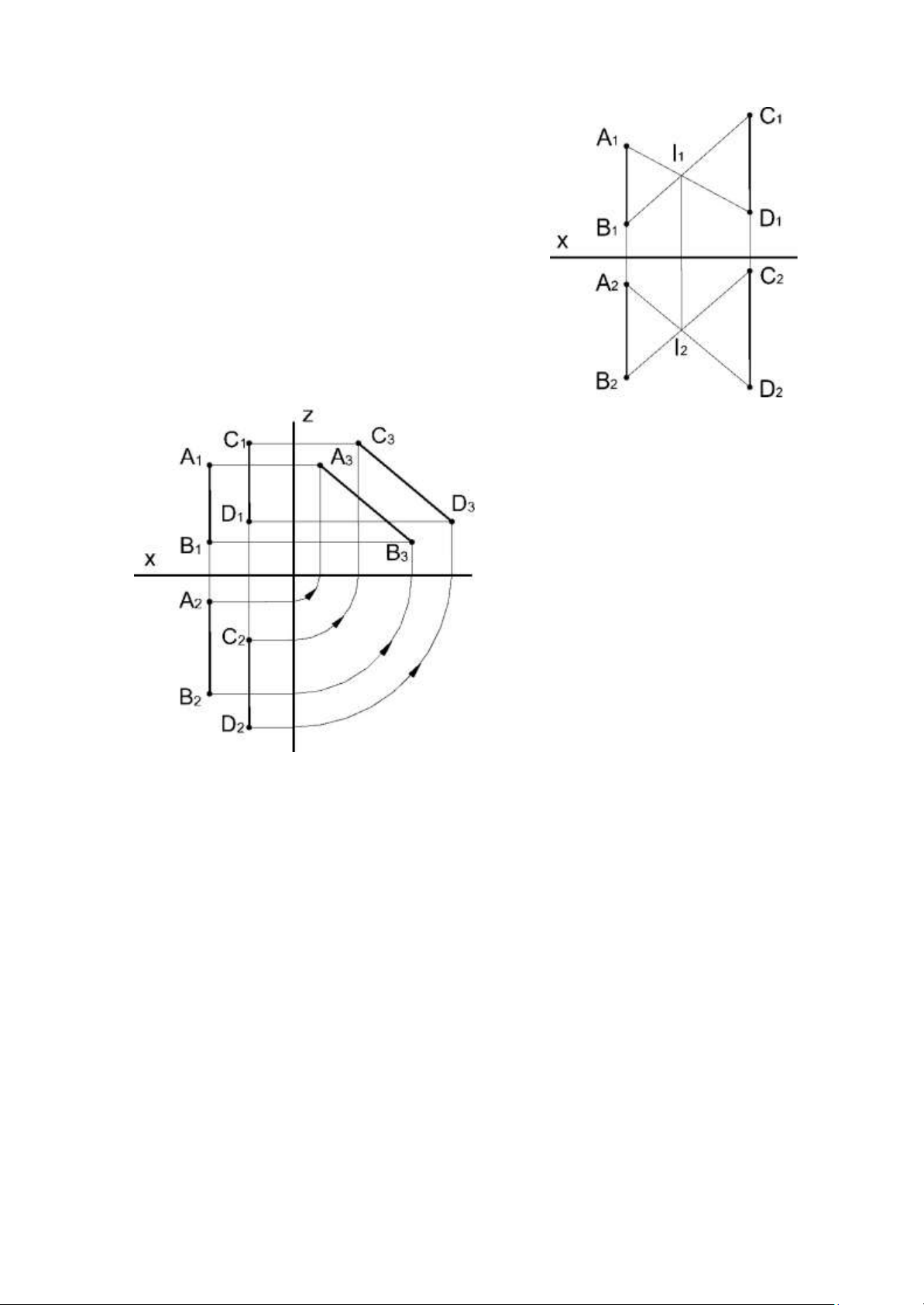
b. Trường hợp có đường thẳng là đường cạnh. -
Để 2 đường cạnh song song ngoài điều kiên trên thì hình chiếu
cạnh của 2 đường thẳng đó phải song song với nhau. 14 lOMoAR cPSD| 59735516 -
Nếu hai đờng cạnh AB // CD thì tổn tại một mặt phẳng a(AB //
CD).Nếu ta vẽ thêm các đờng phụ AD và BC, thì chúng hoặc song song , hoặc cắt chau
Trên đổ thức: Hình chiếu đứng và hình chiếu bằng của hai đờng thẳng AD,
BC cắt nhau tại các giao điểm nằm trên một đờng dóng thẳng đứng.
1.3.4.2. Hai đường thẳng chéo nhau.
Hai đường thẳng chéo nhau là hai đường thẳng không cắt nhau và không song song với nhau. 15 lOMoAR cPSD| 59735516
1.3.4.3. Hai đường thẳng vuông góc.
Hình chiếu của một góc vuông nói chung không là một góc vuông. -
Điều kiện đẽ một góc vuông chiếu thẳng góc vẫn là một góc
vuông là ít nhất một cạnh của nó song song với mặt phăng hình chiếu,
còn cạnh kia không vuông góc với mặt phẳng hình chiếu. -
Hai đường thẳng vuông góc cắt nhau hoặc chéo nhau chiếu
xuống mặt phẳng hình chiếu bằng mà các hình chiếu vẫn vuông góc với
nhau khi có ít nhất 1 đường là đường bằng còn đường kia không phải là
đường thẳng chiếu bằng. -
Hai đường thẳng vuông góc cắt nhau hoặc chéo nhau chiếu lên
mặt phẳng hình chiếu đứng vẫn vuông góc khi có ít nhất 1 đường là
đường mặt còn đường kia không phải là đường thẳng chiếu đứng. 16 lOMoAR cPSD| 59735516 1.4. Mặt phẳng:
Trong không gian, một mặt phẳng được xác định bởi một trong các cách sau:
- Ba điểm không thẳng hàng.
- Một điểm và một đường thẳng không đi qua điểm đó.
- Hai đường thẳng cắt nhau.
- Hai đường thẳng song song.
Do đó đồ thức của mặt phẳng cũng được xác định bằng:
- Đồ thức của ba điểm không thẳng hàng.
- Đồ thức của một điểm và một đường thẳng không đi qua nó.
- Đồ thức của hai đường thẳng cắt nhau.
- Đồ thức của hai đường thẳng song song. Chú ý:
- Có thể chuyển từ cách xác định này sang cách xác định khác một cách dễ dàng. 17 lOMoAR cPSD| 59735516
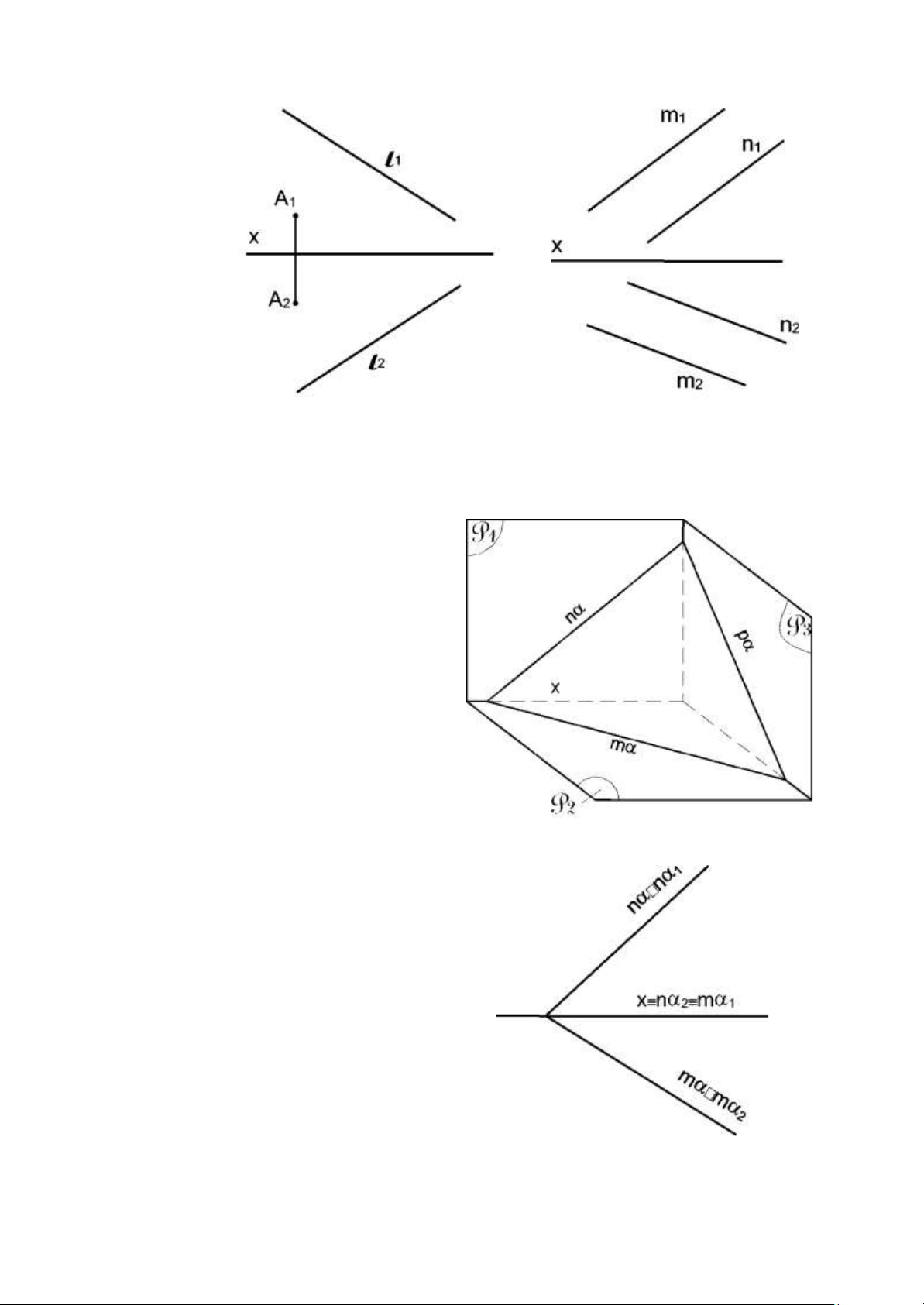
1.4.1 Các vết của mặt phẳng: a. Định nghĩa:
- Vết của mặt phẳng là giao tuyến
của mặt phẳng với các mặt phẳng hình chiếu.
- Vết đứng của mặt phẳng là giao
tuyến của mặt phẳng với mặt phẳng
hình chiếu đứng, (nếu mặt phẳng là α,
vết đứng kí hiệu là nα).
- Vết bằng của mặt phẳng là giao
tuyến của mặt phẳng với mặt phẳng
hình chiếu bằng (nếu mặt phẳng là α,
vết bằng ký kí hiệu là mα).
- Vết cạnh của mặt phẳng là giao
tuyến của mặt phẳng với mặt phẳng
hình chiếu cạnh (nếu mặt phẳng là α, vết cạnh kí hiệu là pα).
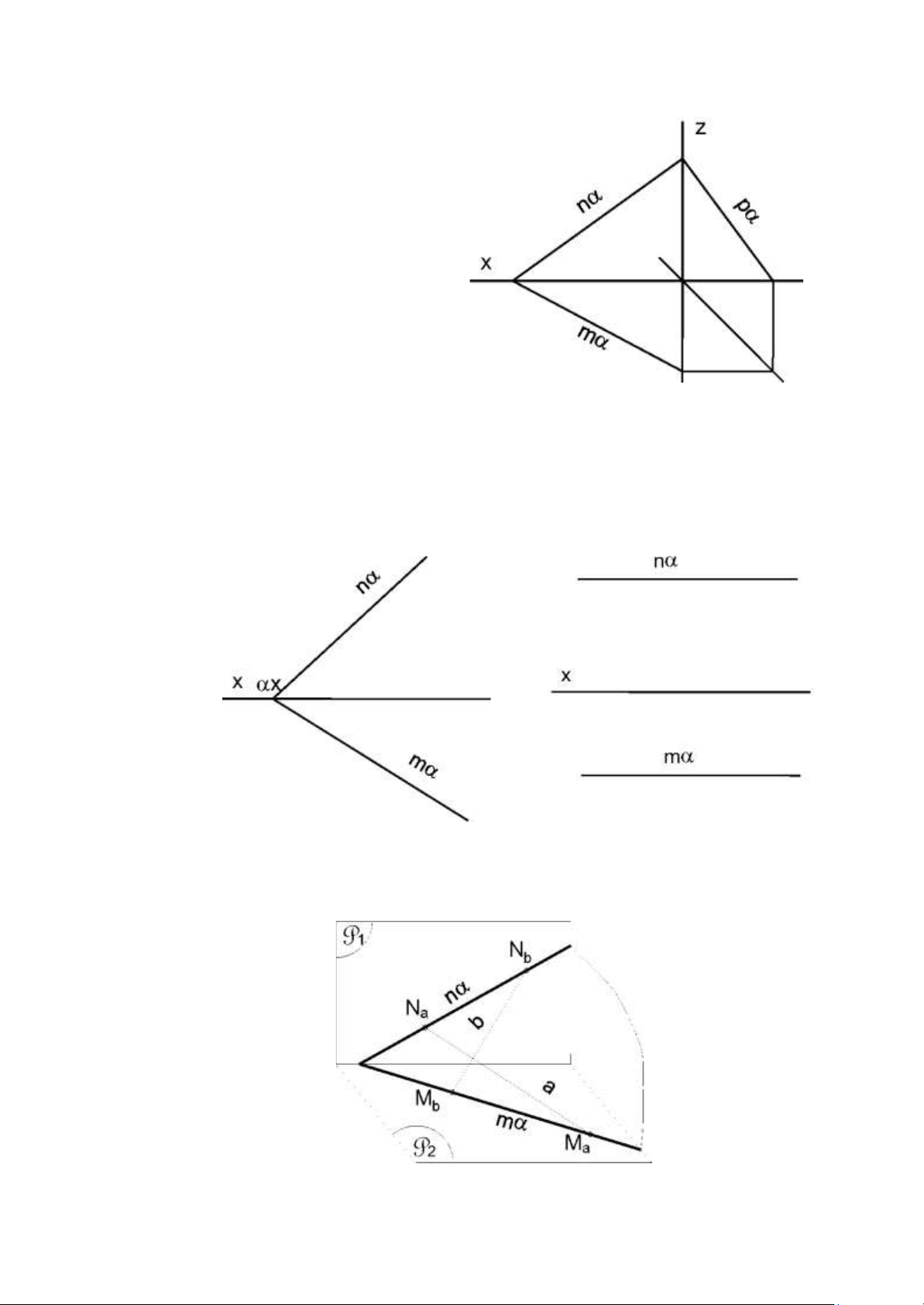
b. Các hình chiếu của vết: -Vết đứng:
Hình chiếu đứng của vết đứng là n(α)1 = n(α) Hình
chiếu b»ng của vết đứng là n(α)2 = x -Vết bằng: Hình
chiếu bằng của vết bằng là m(α)2 = m(α)
Hình chiếu đứng của vết bằng là m(α), = x - Vết cạnh: 18 lOMoAR cPSD| 59735516
Hình chiếu cạnh của vết cạnh là p(α)3 = p(α)
Hình chiếu đứng và hình chiếu
bằng là p(α)1 = z, p(α)2 = y Nhân xét:
- Trong không gian cũng như trên
đồ thức vết đứng và vết bằng của mặt
phẳng phải cắt nhau trên trục x (hoặc
song song vơí trục x). Vết đứng và vết
cạnh phải cắt nhau trên trục z (hoặc
cùng song song với trục z). Còn
vết bằng và vết cạnh trong không gian
cắt nhau trên trục y (hoặc cùng song song với trục y).
- Một mặt phẳng hoàn toàn được xác định bởi 2 vết. Vì vây có thể cho mặt
phẳng bằng hai vết của nó. Đây chính là cách cho mặt phẳng bằng hai đường thẳng cắt nhau hoặc song song.
- Nếu một đường thẳng thuộc một mặt phẳng thì vết của đường thẳng phải
thuộc vết tương ứng của mặt phẳng. 19 lOMoAR cPSD| 59735516
1.4.2 Các mặt phẳng đặc biệt:
- Mặt phẳng đặc biệt là mặt phẳng vuông góc, hoặc song song với mặt phẳng hình chiếu.
1.4.2.1. Các mặt phẳng chiếu.
Các mặt phẳng chiếu là các mặt phẳng vuông góc với một mặt phẳng hình chiếu Bao gổm có:
Mặt phẳng chiếu bằng, mặt phẳng chiếu đứng, mặt phẳng chiếu cạnh. a.
Mặt phẳng chiếu bằng:
Đinh nghĩa: mf chiếu bằng là mặt phẳng vuông góc với mf hình chiếu bằng. Tính chất:
- Hình chiếu bằng của mặt phẳng chiếu bằng suy biến thành một đường thẳng
trùng với vết bằng của nó. Đây là tinh chất đặc trưng cho mf chiếu bằng, vì biết hc
bằng thì mf này cũng hoàn toàn được xác định.
- Vết đứng của mặt phẳng chiếu bằng vuông góc với trục x.
- Góc giữa hình chiếu bằng của măt phẳng chiếu bằng với trục x chính là góc
giữa mặt phẳng đó với mặt phẳng hình chiếu đứng. b.
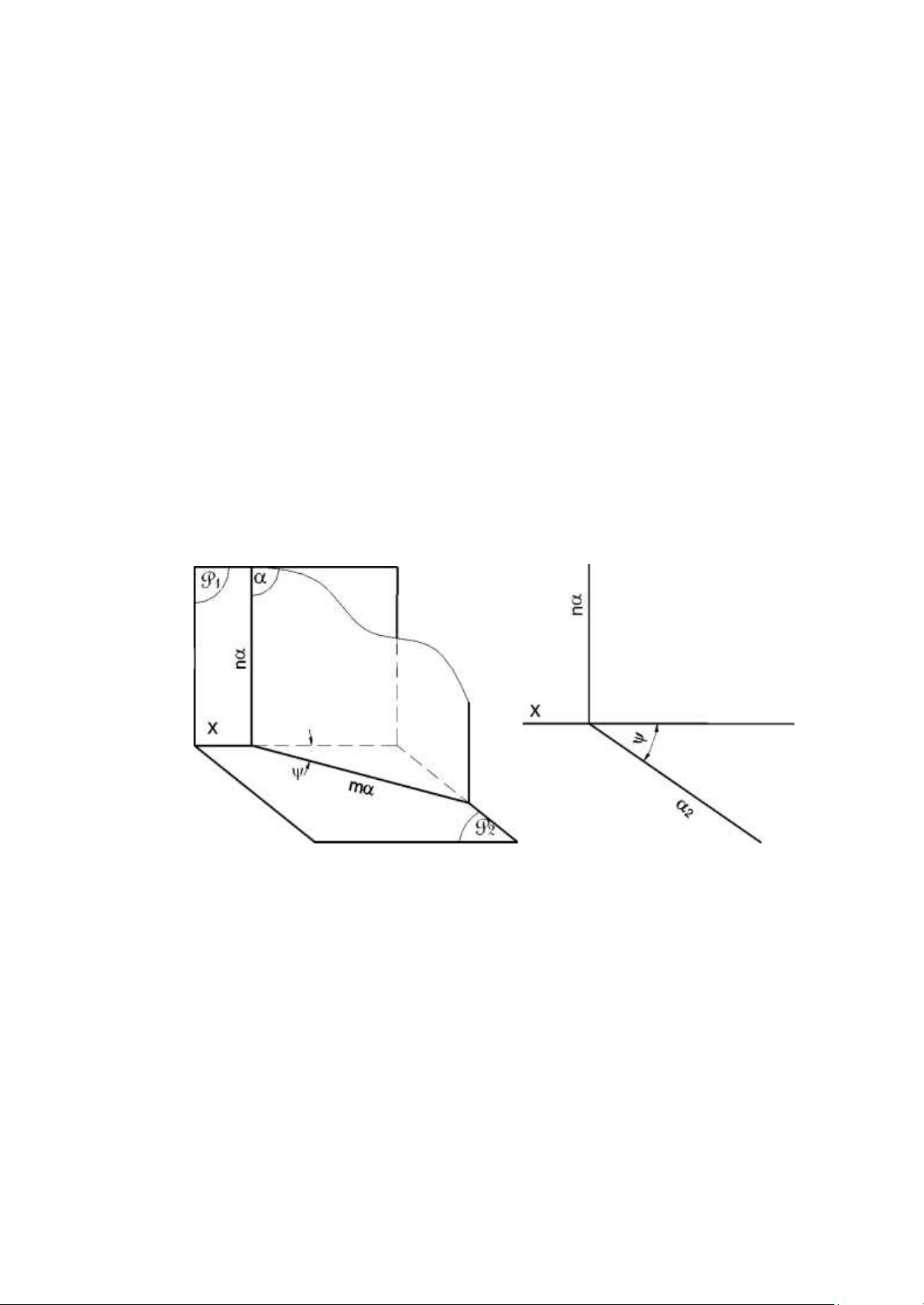
Mặt phẳng chiếu đứng:
Đinh nghĩa: Mặt phẳng chiếu đứng là mặt phăng vuông góc với mặt phẳng hình chiếu đứng. Tính chất:
- Hình chiếu đứng của mặt phẳng chiếu đứng suy biến thành đường thẳng
trùng với vết đứng của nó.
- Vết bằng của mặt phẳng chiếu đứng vuông góc với trục x.
- Góc giữa hình chiếu đứng của mặt phẳng chiếu đứng với trục x chính là góc
giữa mặt phẳng đó với mặt phẳng hình chiếu bằng. 20