Hình học Oxy: Elip và các bài toán liên quan – Nguyễn Thanh Tùng

Tài liệu Hình học Oxy – Elip và các bài toán liên quan của thầy Nguyễn Thanh Tùng gồm các dạng bài toán về đường Elip trong hình học tọa độ phẳng. Tài liệu được chia thành 3 phần:

I. Kiến thức cơ sở
Để giải quyết tốt các lớp bài toán liên quan tới Elip (tìm điểm và viết phương trình tắc của elip) trước tiên chúng ta cần nắm được các kiến thức cơ bản qua sơ đồ tư duy trong tài liệu. Dựa trên các kiến thức cơ bản này, kết hợp với các bài toán trước các bạn đã được tìm hiểu, sẽ giúp ta giải quyết dễ dàng các lớp bài toán liên quan tới elip

101 51 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 7: Phương pháp tọa độ trong mặt phẳng (KNTT)

Môn: Toán 10

Thông tin:

23 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
I. KIẾN THỨC CƠ SỞ
Để giải quyết tốt các lớp bài toán liên quan tới Elip (tìm điểm và viết phương trình tắc của elip) trước tiên
chúng ta cần nắm được các kiến thức cơ bản qua sơ đồ sau:
Dựa trên các kiến thức cơ bản này, kết hợp với các bài toán trước các bạn đã được tìm hiểu, sẽ giúp ta giải
quyết dễ dàng các lớp bài toán liên quan tới elip. Cụ thể:
+) Khi gặp bài toán “Tìm điểm thuộc thỏa mãn điều kiện (*) cho trước ” thì về cơ bản ta cần thiết lập
được hai dấu “=” mà ở đó dữ kiện điểm thuộc luôn cho ta được một dấu “=” đầu tiên. Các dữ kiện còn
lại sẽ giúp ta tìm ra dấu “=” thứ hai. Nếu cần, trong một số bài toán ta có thể tham số hóa điểm thuộc
theo một ẩn. Ví như: .
+) Khi gặp bài toán “Viết phương trình chính tắc của elip (E)” cần cắt nghĩa chính xác dữ kiện của bài toán
dựa trên các kiến thức cơ bản liên quan tới elip và tính đối xứng của elip (elip nhận hai trục tọa độ làm hai trục
đối xứng và gốc tọa độ làm tâm đối xứng).
II. CÁC VÍ DỤ MẪU
Ví dụ 1. Trong mặt phẳng tọa độ , viết phương trình chính tắc của elip biết rằng có tâm sai
bằng và hình chữ nhật cơ sở của có chu vi bằng .
( )
E
( )
E
( )
E
2 2
2 2
( ): 1
x y
M E
a b
( sin ; cos )
Oxy
( )
E
( )
E
5
3
( )
E
20
ELIP VÀ CÁC BÀI TOÁN LIÊN QUAN
GV: Nguyễn Thanh Tùng
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
Giải:
Gọi phương trình chính tắc của elip có dạng:
Ta có và (với )
Khi đó ta có: hoặc (loại)
Với . Vậy phương trình chính tắc của elip là:
Ví dụ 2. Trong mặt phẳng với hệ tọa độ , cho elip có phương trình . Tìm điểm
M
nằm trên elip
sao cho , trong đó lần lượt là các tiêu điểm trái, phải của elip.
Giải:
Từ phương trình Elip :
Cách 1: Gọi
0 0
( ; )
M x y
, suy ra
1 0 0
2 0 0
3
5
5
3
5
5
c
MF a x x
a
c
MF a x x
a
Khi đó
1 2 0 0 0
3 3
4 5 4 5 5
5 5
MF MF x x x
Do đó
2
2
0
0 0
5
(5; ) ( ) 1 0
25 16
y
M y E y
Vậy
(5;0)
M
Cách 2:
Gọi , khi đó
Thay (2) vào (1) ta được : .
Vậy
Ví dụ 3. Trong mặt phẳng tọa độ , cho elip điểm . Viết phương trình
đường thẳng qua cắt tại hai điểm sao cho .
( )
E
2 2
2 2
1
x y
a b
5 5
3 3
c
e c a
a
2.(2 2 ) 20 5 5
a b a b b a
0 5
a
2
2 2 2 2 2 2
5
(5 ) 18 45 0 3
3
a b c a a a a a a
15
a
3 2
a b
( )
E
2 2
1
9 4
x y
Oxy
2 2
1
25 16
x y
1 2
4
MF MF
1 2
,
F F
( )
E
2 2
1
25 16
x y
2 2
5
3
4
a
c a b
b
1
2
( 3;0)
(3;0)
F
F
0 0
( ; )
M x y
2 2 2 2
0 0 0 0
2
2 2 2 2
2
0 0 0 0 0
( )
1 1 (1)
25 16 25 16
4
( 3) 4 6 5 (2)
x y x y
M E
MF
x y y x x
2 2
0 0 0
6 5
1
25 16
x x x
0 0
2
0 0
2
0 0
5 0
3 50 175 0
35 640
0
3 9
x y
x x
x y
(5;0)
M
Oxy
2
2
( ): 1
4
x
E y
2 2
;
3 3
M
M
E
,
A B
2
MA MB
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
Giải:
+) Gọi (1)
+) Do nằm trong nên từ
+) Mà (2)
+) Từ (1) và (2) ta được hệ:
Với ; Với
Vậy hoặc .
Ví dụ 4. Trong mặt phẳng tọa độ , cho elip . Đường thẳng cắt tại
hai điểm . Tìm tọa độ điểm trên sao cho tam giác có diện tích lớn nhất
Giải:
+) Do nên cố định hay độ dài không đổi
Suy ra diện tích lớn nhất khi khoảng cách lớn nhất
+) Phương trình tham số của : nên gọi
Khi đó
Dấu“ =” xảy ra khi: ( )
+) Với +) Với
Vậy hoặc .
Nhận xét : Ngoài cách để dưới dạng chính tắc , trong nhiều bài toán các bạn có thể chuyển
nó về dạng tham số sau : để việc tham số hóa điểm thuộc elip được dễ dàng hơn.
2
2 2 2
0
0 0 0 0 0
( ; ) ( ) 1 4 4 0
4
x
B x y E y x y
M
( )
E
2
MA MB
0
0
0 0
0
0
2 2
2
2 2
3 3
2 (2 2 ;2 2 )
2 2
2 2
2
3 3
A
A
A
A
x x
x x
MA MB A x y
y y
y y
2
2 2 2
0
0 0 0 0 0
(2 2 )
( ) (2 2 ) 1 4 2 8 4 0
4
x
A E y x y x y
2 2
0 0
0 0
2 2
0 0
0 0 0 0
(0;1)
0; 1
4 4 0
8 3
8 3
;
;
4 2 8 4 0
5 5
5 5
B
x y
x y
B
x y
x y x y
(0;1) : 2 2 0
B x y
8 3
; : 14 10 0
5 5
B x y
2 2 0
x y
14 10 0
x y
Oxy
2 2
( ): 1
8 4
x y
E
: 2 0
x y
( )
E
,
B C
A
( )
E
ABC
( ) ;
E B C
,
B C
BC
ABC
( , )
h d A
( )
E
2 2sin
2cos
x t
y t
2 2 sin ;2cos
A t t
4sin
2 2 sin 2 2 cos 2 2 sin cos
4
4
( , )
3 3 3 3
t
t t t t
h d A
3
sin 1
2
4
4
sin 1
4
2
sin 1
4
4
t
t k
t
t k
t
k
3
2 2; 2
4
t k A
2 2; 2
4
t k A
2; 2
A
2; 2
A
( )
E
2 2
2 2
1
x y
a b
sin
cos
x a t
y b t
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
III. BÀI TẬP TỰ LUYỆN
Bài 1. Trong mặt phẳng tọa độ , viết phương trình chính tắc của elip có tâm sai bằng và độ dài
đường chéo hình chữ nhật cơ sở bằng .
Giải:
+) Gọi phương trình chính tắc của elip có dạng:
với
Tâm sai .
Độ dài đường chéo hình chữ nhật
+) Khi đó
Vậy trình chính tắc của elip cần lập là:
Bài 2. Trong mặt phẳng tọa độ , cho elip có phương trình và . Một đường
thẳng d đi qua cắt tại sao cho lớn nhất. Tìm tọa độ .
Giải:
+) thuộc miền trong của
nên luôn cắt tại
Gọi phương trình đường thẳng có dạng: với .
+) Gọi . Trong đó là nghiệm của phương trình:
Theo hệ thức Vi – et ta có:
+) Khi đó
Mặt khác , do đó lớn nhất khi và chỉ khi
Khi đó đường thẳng có dạng : , suy ra tọa độ giao điểm của và là nghiệm của hệ:
hoặc .
Vậy hoặc .
Oxy
( )
E
3
3
2 5
( )
E
2 2
2 2
1
x y
a b
0
a b
2
2
3
3 3
c a
e c
a
2 2 2 2 2 2
(2 ) (2 ) 2 5 5 5
a b a b b a
2
2 2 2 2 2 2
5 3
3
a
a b c a a a
2
2
b
( )
E
2 2
1
3 2
x y
Oxy
( )
E
2 2
1
8 4
x y
(1; 1)
M
M
( )
E
,
A B
.
MAMB
,
A B
(1; 1)
M
( )
E
d
( )
E
,
A B
d
1
1
x mt
y nt
2 2
, 0
t m n
1 1 2 2
(1 ; 1 ), (1 ; 1 )
A mt nt B mt nt
1 2
,
t t
2 2
2 2 2
(1 ) ( 1 )
1 2 2( 2 ) 5 0
8 4
mt nt
m n t m n t
1 2
2 2
5
2
t t
a b
2 2
2 2 2 2
2 2
1 1 2 2 1 2
2
2 2
2 2
5( ) 5
. .
2
2
m n
MA MB mt nt mt nt m n t t
m
m n
m n
2
2 2
0 1
m
m n
.
MA MB
2
2 2
1 0
m
n
m n
d
1
y
,
A B
d
( )
E
2 2
2
6; 1
6
1 6
8 4
1
1
6; 1
1
x y
A
x
x
y
y
B
y
6; 1
6; 1
A
B
6; 1
6; 1
A
B
6; 1
6; 1
A
B
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
Bài 3. Trong mặt phẳng tọa độ . Lập phương trình chính tắc của elip trong mặt phẳng Oxy biết điểm
thuộc elíp và tam giác vuông tại , trong đó là hai tiêu điểm của elíp.
Giải:
+) Gọi phương trình chính tắc của elip có dạng:
với và
Khi đó (1)
+) Với , khi đó tam giác vuông tại nên ta suy ra:
(2)
+) Thay (2) vào (1) ta được:
Vậy phương trình chính tắc của elip cần lập là:
Bài 4. Trong mặt phẳng tọa độ . Viết phương trình chính tắc của elip biết rằng elip có hai tiêu
điểm và với và có một điểm thuộc sao cho tam giác vuông tại và có diện
tích bằng .
Giải:
+) Gọi phương trình chính tắc của elip có dạng:
với
Với , suy ra hay (1)
+) Gọi
Khi đó
Ta có
+) Mặt khác (2)
Thay (1) vào (2) ta được: (do )
Vậy phương trình chính tắc của elip cần lập là:
Bài 5. Trong mặt phẳng tọa độ . Viết phương trình chính tắc của elíp đi qua điểm và tiêu điểm
của elip nhìn trục nhỏ với một góc .
Oxy
8 1
;
3 3
M
1 2
F MF
M
1 2
,
F F
( )
E
2 2
2 2
1
x y
a b
0
a b
2 2 2
a b c
2 2 2 2
2 2
8 1 8 1
; ( ) 1 8 3
3 3 3 3
M E a b a b
a b
1 2
( ;0), ( ;0)
F c F c
1 2
F MF
M
2 2
2 2 2 2 2
1 2 1 2
8 1 8 1
4 3
3 3 3 3
MF MF F F c c c c
2 2 2 2
3
a b c b
2 2 2 2 4 2 2
3 8 3 3 1 1 4
b b b b b b a
( )
E
2
2
1
4
x
y
Oxy
( )
E
( )
E
1
F
2
F
1
3;0
F
M
( )
E
1 2
F MF
M
1
( )
E
2 2
2 2
1
x y
a b
0
a b
1
3;0
F
3
c
2 2 2
3
a b c
2 2
3
a b
0 0
( ; )
M x y
1 0 0
2 0 0
3 ;
3 ;
MF x y
MF x y
0 2 2 2 2
1 2 1 2 0 0 0 0
90 . 0 3 0 3
F MF MF MF x y x y
1 2
2 2
1 2 0 0 0 0
1 1 1 8
( , ). .2 3 3 1
2 2 3 3
F MF
S d M Ox F F y y y x
0 0
( ; ) ( )
M x y E
2 2
0 0
2 2 2 2
8 1
1 1
3 3
x y
a b a b
4
2 2
8 1
1 3 3 1
3( 3) 3
b b
b b
0
b
2
4
a
( )
E
2
2
1
4
x
y
Oxy
3
1;
2
M
0
60
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
Giải:
+) Gọi phương trình chính tắc của elip có dạng:
với
Gọi là tiêu điểm của và là hai đỉnh thuộc trục nhỏ của
+) Do cân tại và , suy ra đều
Khi đó (1)
+) Với (2)
Thay (1) vào (2) ta được :
Vậy phương trình chính tắc của elip cần lập là:
Bài 6. Trong mặt phẳng tọa độ , cho elip có phương trình . Giả sử là hai tiêu điểm
của elip, trong đó có hoành độ âm. Tìm tọa độ điểm trên sao cho .
Giải:
+) có phương trình
+) Gọi
+) Khi đó
+) Với
Vậy hoặc .
Bài 7. Trong mặt phẳng tọa độ , cho elip có phương trình . Tìm điểm thuộc elip sao cho
góc
với là hai tiêu điểm của elip.
Giải:
+) Elip :
( )
E
2 2
2 2
1
x y
a b
0
a b
1
( ;0)
F c
( )
E
1 2
(0; ), (0; )
B b B b
( )
E
1 1 2
F B B
1
F
0
1 1 2
60
B F B
1 1 2
F B B
2 2 2 2 2 2 2
1 1 1 2 1 1 1 2
F B B B F B B B c b b c b
2 2 2 2
4
a b c b
2 2
3 1 3
1; ( ) 1
2 4
M E
a b
2 2
2 2
1 3
1 1 4
4 4
b a
b b
( )
E
2
2
1
4
x
y
Oxy
( )
E
2 2
1
8 4
x y
1 2
,
F F
1
F
M
( )
E
1 2
2
MF MF
( )
E
2 2
1
8 4
x y
2 2
2 2
2
2
a
b
c a b
0 0
1
0 0 1 2 0
0 0
2
2
2 2
2 2
( ; ) ( ) 2
2
2 2
2 2
cx x
MF a
a
M x y E MF MF x
cx x
MF a
a
1 2 0 0
2 2 2 2
MF MF x x
2
0
2
0
0 0
0
3
2
2 4 1 4 1 3
8 8
3
y
x
x y
y
2; 3
M
2; 3
M
Oxy
2 2
1
25 9
x y
M
1 2
F MF
0
90
1 2
,
F F
( )
E
2 2
1
25 9
x y
2 2
5; 3
4
a b
c a b
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
+) Gọi với
Do nên suy ra :
+) Thay vào (*) ta được:
Vậy , , .
Bài 8. Trong mặt phẳng tọa độ . Viết phương trình chính tắc của elip, biết hai tiêu điểm cùng với hai đỉnh
trên trục bé xác định một hình vuông và phương trình hai đường chuẩn là .
Giải:
+) Ta có hai tiêu điểm và hai đỉnh thuộc trục nhỏ xác định một hình vuông
nên ta có . Elip có phương trình đường chuẩn
+) Khi đó:
+) Suy ra phương trình chính tắc của elip là: .
Bài 9. Trong mặt phẳng tọa độ , cho elip có hai tiêu điểm . Tìm tọa độ điểm
thuộc sao cho bán kính đường tròn nội tiếp tam giác bằng .
Giải:
+) Từ
+) Suy ra diện tích tam giác
là:
+) Mặt khác ta có:
+) Vì
Vậy hoặc .
Bài 10. Trong mặt phẳng tọa độ . Viết phương trình chính tắc của elip biết rằng khi điểm thay đổi
trên thì độ dài nhỏ nhất của bằng và độ dài lớn nhất của bằng , với là tiêu điểm có
1 0 0 2 0 0
0 0
2 2
0 0
4 4
5 ; 5
5 5
( ; ) ( )
1 (*)
25 9
c c
MF a x x MF a x x
a a
M x y E
x y
0
0
x
0
1 2
90
F MF
2 2
2 2 2 2
1 2 1 2 0 0 0 0
4 4 5 14
5 5 64 8 175
5 5 4
MF MF F F x x x x
0
5 14
4
x
2
2
0
0 0
7 9 3 2
1
8 9 8 4
y
y y
5 14 3 2
;
4 4
M
5 14 3 2
;
4 4
M
5 14 3 2 5 14 3 2
; , ;
4 4 4 4
M M
Oxy
8
x
1 2
( ;0), ( ;0)
F c F c
1 2
(0; ), (0; )
B b B b
b c
2 2
2
8 8
a a a
x a c
e c c
2
2 2 2 2 2
32
8 4 0
4
a
a b c c c c c
b
2 2
1
32 16
x y
Oxy
2 2
( ): 1
25 9
x y
E
1 2
,
F F
M
( )
E
1 2
MF F
4
3
2 2
2 2
5
( ): 1 3
25 9
4
a
x y
E b
c a b
1 2
1 2 1 2
2 2
9
2 2
MF F
MF MF F F
a c
p a c
1 2
MF F
1 2
4
9. 12
3
MF F
S pr
1 2
1 2
1 2
1 1 12
. ( , ). . .2 4 3
2 2 4 4
MF F
MF F M M M
S
S d M Ox F F y c y y
2
(0;3)
9
( ; ) ( ) 1 0
(0; 3)
25 9
M
M M M
M
x
M x y E x
M
(0;3)
M
(0; 3)
M
Oxy
( )
E
M
( )
E
OM
4
1
MF
8
1
F
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
hoành độ âm.
Giải:
+) Gọi phương trình chính tắc của elip cần lập là: với
Gọi
Suy ra độ dài lớn nhất bằng : (1)
+) Lại có:
Suy ra độ dài nhỏ nhất của bằng (2)
Từ (1) và (2) ta được:
Vậy phương trình elip cần lập là:
.
Bài 11. Trong mặt phẳng tọa độ , cho elip . Viết phương trình đường thẳng cắt tại
hai điểm phân biệt có tọa độ là các số nguyên.
Giải:
Gọi (*) (vì )
+) Với thay vào (*) ta được: (thỏa mãn)
+) Với thay vào (*) ta được: (loại)
Suy ra 4 điểm có tọa độ nguyên trên là:
Khi đó ta sẽ lập được 6 phương trình đường thẳng thỏa mãn yêu cầu đề bài là:
.
Nhận xét: Ở ví dụ trên nếu ta tiếp cận theo cách thông thường là giả sử dạng phương trình của rồi tìm
giao điểm, sau đó sử dụng điều kiện tọa độ nguyên thì chúng ta sẽ gặp khó khăn. Song nếu ta làm theo chiều
nghịch thì bài toán sẽ trở nên “nhẹ nhàng” hơn rất nhiều. Bởi ở những bài toán liên quan tới elip (hay cả
đường tròn) ta hoàn toàn có thể chặn điều kiện cho khá đơn giản. Vì vậy việc yêu cầu tọa độ nguyên của
bài toán, giúp ta nghĩ tới ngay giải pháp trên.
Bài 12. Trong mặt phẳng tọa độ , cho elip . Tìm tọa độ điểm trên sao cho bán
kính qua tiêu của tiêu điểm này bằng 3 lần bán kính qua tiêu của tiêu điểm kia.
Giải:
( )
E
2 2
2 2
1
x y
a b
0
a b
0
0 0 1
0
1
( ; ) ( )
a x a
M x y E a c MF a c
cx
MF a
a
1
MF
8
a c
2 2
0 0
2 2 2 2 2 2
2
2 2
0 0 0 0 0 0
0 0
2 2 2 2 2 2
2 2
0 0
2 2
( ; ) ( ) 1
1
x x
a b
x y x y x y
OM
a b
M x y E OM b
a b b b b b
x y
a b
OM
4
b
2
8 5
16 8
4 4
4
a c a
a a
b b
b
( )
E
2 2
1
25 16
x y
Oxy
2 2
( ): 1
8 2
x y
E
d
( )
E
2 2
0 0
0 0
( ; ) ( ) 1
8 2
x y
M x y E
2
0 0
2 1;0;1
y y
0
y
0
1
y
0
2
x
0
0
y
0
2 2
x
( )
E
1 2 3 4
(2;1), (2; 1), ( 2;1), ( 2; 1)
M M M M
d
2; 2; 1; 1; 2 0; 2 0
x x y y x y x y
d
,
x y
Oxy
2
2
( ): 1
9
x
E y
M
( )
E
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
+) Từ
+) Gọi
Từ giả thiết ta có:
+) Mặt khác
Vậy hoặc hoặc hoặc
Nhận xét: Trong giải toán ta biết , và ta thường chỉ quen với chiều biến đổi thuận. Nhưng
trong nhiều trường hợp, việc biến đổi theo chiều ngược lại sẽ giúp giải bài toán ngắn gọn hơn rất nhiều, mà ví
dụ trên là một điển hình.
Bài 13. Trong mặt phẳng tọa độ , cho điểm , đường elip đi qua điểm và khoảng cách
giữa hai đường chuẩn của là 6. Lập phương trình chính tắc của .
Giải:
+) Gọi phương trình chính tắc của elip là: với
+) Elip có hai phương trình đường chuẩn là và
Do đó khoảng cách giữa hai đường chuẩn là:
(1)
+) Mặt khác (2)
Thay (1) vào (2) và rút gọn ta được:
Vậy phương trình cần lập là:
2
2
2 2
3
2 2
( ): 1 1
9 3
2 2
a
x c
E y b e
a
c a b
1 0
0 0
2 0
( ; ) ( )
MF a ex
M x y E
MF a ex
1 2 1 2
1 2 2 1
2 1 2 1
3 3 0
3 3 0
3 3 0
MF MF MF MF
MF MF MF MF
MF MF MF MF
2
2 2
1 2 1 2 1 2 1 2
10 . 3 0 16 . 3 0
MF MF MF MF MF MF MF MF
2
2 2 2 2
0 0 0
16 . 3. 2 0 16( ) 12
a ex a ex a a e x a
2 2
2
0 0
2
2
3 81 9 2
4 32 8
2 2
4.
3
a
x x
e
2
2
0
0 0
23 46
( ) 1
9 32 8
x
M E y y
9 2 46
;
8 8
M
9 2 46
;
8 8
M
9 2 46
;
8 8
M
9 2 46
;
8 8
M
0
. 0
0
A
A B
B
Oxy
3;1
M
( )
E
M
( )
E
( )
E
( )
E
2 2
2 2
1
x y
a b
0
a b
( )
E
a
x
e
a
x
e
2 2 4
2 4 2 2 2 2
2 9
2 6 3 9 9( )
9
a a a a
a c a c a b b
e c
2 2
3 1
3;1 ( ) 1
M E
a b
4 2 2 2
12 36 0 6 2
a a a b
( )
E
2 2
1
6 2
x y
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
Bài 14. Trong mặt phẳng tọa độ . Lập phương trình chính tắc của elip biết rằng có một đỉnh và hai
tiêu điểm của tạo thành một tam giác đều và chu vi hình chữ nhật cơ sở của là .
Giải:
+) Gọi phương trình chính tắc của elip có dạng:
với
Ta có chu vi hình chữ nhật cơ sở: (1)
+) Không mất tính tổng quát giả sử đỉnh và hai tiêu điểm tạo thành tam giác đều
Do luôn cân tại , nên đều khi
+) Khi đó (2) (do )
Thay (2) vào (1) ta được :
+) Vậy phương trình chính tắc của elip cần lập là:
Bài 15. Trong mặt phẳng tọa độ , cho elip có hai tiêu điểm và đi qua điểm
. Lập phương trình chính tắc của và với mọi điểm thuộc , hãy tính giá trị biểu thức
Giải:
+) Gọi phương trình chính tắc của elip có dạng:
với
có hai tiêu điểm , suy ra
+) Khi đó
+) Với
Vậy phương trình chính tắc của là : .
+) Gọi
Khi đó
Oxy
( )
E
( )
E
( )
E
12 2 3
( )
E
2 2
2 2
1
x y
a b
0
a b
4( ) 12 2 3 3 2 3
a b a b
(0; )
B b
1 2
( ;0), ( ;0)
F c F c
1 2
BF F
B
1 2
BF F
2
2 2 2 2 2 2
1 1 2 1 1 2
4
3
b
BF F F BF F F c b c c
2 2 2 2 2
4 2 3
3 3
a b c a b a b
, 0
a b
2 3
3 2 3 3 2 3 9 2 3 3 3 6
3
b b b b a
( )
E
2 2
1
36 27
x y
Oxy
( )
E
1 2
3;0 , 3;0
F F
1
3;
2
A
( )
E
M
( )
E
2 2 2
1 2 1 2
3 .
P MF MF OM MF MF
( )
E
2 2
2 2
1
x y
a b
0
a b
( )
E
1 2
3;0 , 3;0
F F
3
c
2 2 2 2 2
3 3
a b c a b
2 2
2 2
( ): 1
3
x y
E
b b
4 2 2 2 2 2
2 2
1 3 1
3; ( ) 1 4 3 0 (4 3)( 1) 0 1 4
2 3 4
A E b b b b b a
b b
( )
E
2
2
1
4
x
y
1 0 2 0
0 0
2
2 2 2 2
0
0 0 0
;
( ; ) ( )
; 1
4
c c
MF a x MF a x
a a
M x y E
x
OM x y y
2 2
2 2
0 0 0 0 0 0
3
c c c c
P a x a x x y a x a x
a a a a
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
Vậy .
Bài 16. Trong mặt phẳng tọa độ , cho elip có phương trình với hai tiêu điểm
(hoành độ của âm). Tìm tọa độ điểm thuộc elip sao cho
=
Giải:
+) có phương trình , suy ra
+)
Ta có
+) Thay vào (*) ta được: . Vậy hoặc .
Bài 17 (A – 2012). Trong mặt phẳng tọa độ , cho đường tròn . Viết phương trình chính
tắc elip , biết rằng có độ dài trục lớn bằng và cắt tại bốn điểm tạo thành bốn đỉnh của một
hình vuông.
Giải:
Gọi phương trình chính tắc của elip có dạng:
+) (E) có độ dài trục lớn bằng 8
+) (E) cắt tại bốn điểm phân biệt tạo thành bốn đỉnh của một hình vuông nên 4 đỉnh nằm trên hai đường
phân giác thuộc góc phần tư thứ nhất và thứ hai .
Ta giả sử là một giao điểm của (E) và thuộc đường phân giác .
+) Gọi ( ). Ta có: (vì )
+) Mà .
22
2 2 2 2 2 2 2 2
0
0 0 0 0 0 0 0
2
3 9
3 4 3 4 3 4 3 1
4 4
x
c
a x x y x x y y
a
1
P
Oxy
( )
E
2 2
1
9 5
x y
1 2
,
F F
1
F
M
1 2
MF F
0
60
( )
E
2 2
1
9 5
x y
2
2 2
2
9
2
5
a
c a b
b
1
2
( 2;0)
(2;0)
F
F
1 0 0 2 0 0
0 0
2 2
0 0
2 2
3 ; 3
3 3
( ; ) ( )
1 (*)
9 5
c c
MF a x x MF a x x
a a
M x y E
x y
2 2 2
2 1 1 2 1 1 2 1 2
2 . .cos
MF MF F F MF F F MF F
2 2
2 0
0 0 0
2 2 2
3 3 4 2. 3 .4.cos60
3 3 3
x x x
0 0
3
4 3
4
x x
0
3
4
x
2
0 0
75 5 5
16 4
y y
3 5 5
;
4 4
M
3 5 5
;
4 4
M
Oxy
2 2
( ): 8
C x y
( )
E
( )
E
8
( )
E
( )
C
( )
E
2 2
2 2
1
x y
a b
2 8 4
a a
( )
C
A
( )
C
:
y x
( ; )A t t
0
t
2 2
( ) 8 2
A C t t t
0
t
(2;2)
A
( )
A E
2 2
2
2 2
2 2 16
1
4 3
b
b
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
Vậy phương trình chính tắc của elip (E) là:
Bài 18 (B – 2012). Trong mặt phẳng tọa độ , cho hình thoi có và đường tròn tiếp xúc
với các cạnh của hình thoi có phương trình . Viết phương trình chính tắc của elip đi qua các
đỉnh của hình thoi. Biết thuộc trục .
Giải:
Gọi phương trình chính tắc của elip :
( với )
Vì (E) đi qua các đỉnh A, B, C, D và nên không mất tính tổng quát giả sử: và .
Mà hình thoi ABCD có AC = 2BD
(vì ) hay và
Gọi là hình chiếu của lên
( vì đường tròn
tiếp xúc với các cạnh của hình thoi)
Xét tam giác ta có: hay
Vậy phương trình chính tắc của elip là:
Bài 19. Trong mặt phẳng tọa độ . Lập phương trình chính tắc của elip có tâm sai bằng , biết diện
tích của tứ giác tạo bởi các tiêu điểm và các đỉnh trên trục bé của bằng 24.
Giải:
+) Gọi phương trình chính tắc của elip có dạng:
với và
Ta có tâm sai
2 2
1
16
16
3
x y
Oxy
ABCD
2
AC BD
2 2
4
x y
( )
E
, , ,
A B C D
A
Ox
( )
E
2 2
2 2
1
x y
a b
0
a b
A Ox
( ;0)
A a
(0; )
B b
2 4 2
OA OB OA OB
2
a b
0
a b
(2 ;0)
A b
(0; )
B b
H
O
AB
2
OH R
2 2
4
x y
OAB
2 2 2
1 1 1
OH OA OB
2
2 2
1 1 1
5
4 4
b
b b
2 2
4 20
a b
( )
E
2 2
1
20 5
x y
Oxy
( )
E
3
5
( )
E
( )
E
2 2
2 2
1
x y
a b
0
a b
2 2 2
a b c
3 5
5 3
c
e a c
a
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
+) Gọi là các tiêu điểm và là các đỉnh trên trục bé.
Suy ra là hình thoi , khi đó:
Khi đó (do )
Suy ra . Vậy phương trình chính tắc của elip cần lập là:
Bài 20. Trong mặt phẳng tọa độ , cho elip có tâm sai , đường tròn ngoại tiếp hình chữ nhật cơ
sở của elip có phương trình . Viết phương trình chính tắc của elip và tìm tọa độ điểm thuộc
sao cho nhìn hai tiêu điểm của dưới một góc vuông và có hoành độ dương.
Giải:
+) Gọi phương trình chính tắc của elip có dạng:
với
Ta có tâm sai
Vì đường tròn ngoại tiếp hình chữ nhật cơ sở có bán kính
Khi đó .
Vậy phương trình chính tắc của elip cần lập là:
Bài 21. Trong mặt phẳng tọa độ , cho elip có hai tiêu điểm và với có hoành
độ âm. Tìm tọa độ điểm thuộc sao cho đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Giải:
+) Ta có , suy ra
1 2
( ;0), ( ;0)
F c F c
1 2
(0; ), (0; )
B b B b
1 2 2 1
F B F B
1 2 2 1
1 2 1 2
1 1 12
. .2 .2 2 24 12
2 2
F B F B
S F F B B c b bc bc b
c
2 2
2 2 2 2 4 4 4
5 12
25 1296 9 81 3
3
a b c c c c c c c
c
0
c
5; 4
a b
( )
E
2 2
1
25 16
x y
Oxy
( )
E
4
5
e
2 2
34
x y
M
( )
E
M
( )
E
M
( )
E
2 2
2 2
1
x y
a b
0
a b
4 4
5 5
c
e c a
a
34
R
2 2
34
a b
2 2
34
b a
2
2 2 2 2 2 2
4
34 25 5; 3; 4
5
a b c a a a a a b c
( )
E
2 2
1
25 9
x y
Oxy
2 2
( ):4 9 36
E x y
1
F
2
F
1
F
M
( )
E
2 2
1 2
2
MF MF
2 2
2 2
( ):4 9 36 1
9 4
x y
E x y
2 2
3; 2
5
3
5
a b
c
e
a
c a b
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
+) Gọi với
Khi đó
+) Xét hàm với
Ta có ;
Từ bảng biến thiên suy ra khi
+) Thay vào (*) ta được:
Vậy đạt giá trị nhỏ nhất khi hoặc .
Bài 22. Trong mặt phẳng tọa độ , cho elip và điểm . Lập phương trình đường
thẳng đi qua , cắt tại hai điểm phân biệt sao cho là trung điểm của .
Giải:
+) thuộc miền trong của
nên luôn cắt tại
Gọi phương trình đường thẳng có dạng: với .
+) Gọi . Trong đó là nghiệm của phương trình:
Theo hệ thức Vi – et ta có:
+) là trung điểm của khi
1 0 2 0
2 2
0 0
0 0
;
( ; ) ( )
1 (*)
9 4
MF a ex MF a ex
M x y E
x y
0
3 3
x
2 2
2 2 2 2 2 2
1 2 0 0 0 0 0 0
5 6 81
2 2 3 2 3
3 5
5
P MF MF a ex a ex a aex e x x x
2
0 0 0
6 81
( )
5
5
f x x x
0
3;3
x
0 0
6
'( ) 2
5
f x x
0 0
3
'( ) 0 3;3
5
f x x
0
0 0
[ 3;3]
108 5
min ( ) min ( ) 36
5 3
x
f x P f x
0
3
5
x
0
3
5
x
2
0 0
16 4
5
5
y y
2 2
1 2
2
MF MF
3 4
;
5 5
M
3 4
;
5 5
M
Oxy
2 2
( ): 1
16 9
x y
E
(1;2)
I
d
I
( )
E
,
A B
I
AB
(1;2)
I
( )
E
d
( )
E
,
A B
d
1
2
x mt
y nt
2 2
, 0
t m n
1 1 2 2
(1 ;2 ), (1 ;2 )
A mt nt B mt nt
1 2
,
t t
2 2
2 2 2
(1 ) (2 )
1 9 16 2(9 32 ) 71 0
16 9
mt nt
m n t m n t
1 2
2 2
2(9 32 )
9 16
m n
t t
m n
I
AB
1 2
1 2
2 2 ( ) 2
2 4 ( ) 4
A B I
A B I
x x x m t t
y y y n t t
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
(do )
Với , ta chọn
Suy ra phương trình hay
Bài 23. Trong mặt phẳng tọa độ , cho điểm và elip . Tìm tọa độ các điểm
thuộc sao cho tam giác vuông cân tại .
Giải:
+) Ta có thuộc và tam giác vuông cân tại . Mặt khác và elip nhận
làm các trục đối xứng nên sẽ đối xứng nhau qua trục . Do đó gọi với
+) Suy ra , khi đó
Suy ra
+) Với (loại)
+) Với , suy ra hoặc
Bài 24. Trong mặt phẳng tọa độ , cho điểm và elip . Tìm tọa độ các điểm
thuộc sao cho tam giác vuông cân tại , biết điểm có tung độ dương.
Giải:
+) Do ; và cân tại nên đối xứng nhau qua trục hoành
2 2
1 2
1 2
2 2
2 (9 32 )
0
( ) 0
9 16
9 32 0
( ) 0 2 (9 32 )
0
9 16
m m n
m t t
m n
m n
n t t n m n
m n
2 2
0
m n
9 32 0 9 32
m n m n
32
9
m
n
1 32
:
2 9
x t
d
y t
9 32 73 0
x y
Oxy
(3;0)
A
2
2
( ): 1
9
x
E y
,
B C
( )
E
ABC
A
,
B C
( )
E
ABC
A
(3;0)
A Ox
( )
E
,
Ox Oy
,
B C
Ox
( ; )
( ; )
B m n
C m n
0
n
( 3; )
( 3; )
AB m n
AC m n
2 2
2 2
2 2 2 2
, ( )
1 1
9 9
. 0
( 3) 0 ( 3)
m m
B C E
n n
AB AC
m n n m

2
2 2
3
( 3) 1 5 27 36 0
12
9
5
m
m
m m m
m
3 0
m n
12 3
5 5
m n
12 3
;
5 5
12 3
;
5 5
B
C
12 3
;
5 5
12 3
;
5 5
B
C
Oxy
(3;0)
A
2
2
( ): 1
9
x
E y
,
B C
( )
E
ABC
A
B
(0;3) ( )
A E
, ( )
B C E
ABC
A
,
B C
Ox
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
Khi đó gọi và với
Gọi là trung điểm của
+) Ta giác vuông cân tại nên:
(do )
+) Do có tung độ dường nên ta có: và .
Bài 25. Trong mặt phẳng tọa độ , cho . Tìm điểm có hoành độ dượng thuộc sao
cho , trong đó là các tiêu điểm.
Giải:
+) .
+) Gọi
Vì tam giác vuông tại nên :
+) Do có hoành độ dường nên ta được: hoặc
.
Bài 26. Trong mặt phẳng tọa độ , cho elip có tâm sai , đường tròn ngoại tiếp hình chữ nhật cơ
sở của elip có phương trình . Viết phương trình chính tắc của elip và tìm tọa độ điểm thuộc elip
sao cho nhìn hai tiêu điểm dưới một góc vuông và có hoành độ dương.
Giải:
+) Gọi phương trình chính tắc của elip có dạng: với
+) Vì đường tròn ngoại tiếp hình chữ nhật cơ sở có bán kính nên
Khi đó ta có hệ :
Vậy phương trình chính tắc của elip là:
0 0 0 0
( ; ) ( ; )
B x y C x y
2
2
0
0
1
9
x
y
0
3
x
H
0
( ;0)
BC H x
2
0 0
0 0
2
2 9
3
3 3
BC y x
AH x x
ABC
A
2
0 0 0
1 1 2 12
3 . 9
2 2 3 5
AH BC x x x
0
3
x
2
0 0
9 3
25 5
y y
B
12 3
;
5 5
B
12 3
;
5 5
C
Oxy
2 2
( ): 1
25 9
x y
E
M
( )
E
0
1 2
90
F MF
1 2
,
F F
2 2
( ): 1
25 9
x y
E
2 2
5
4
3
a
c a b
b
2 2
0 0
0 0
1 0 2 0
1
25 9
( ; ) ( )
4 4
5 ; 5
5 5
x y
M x y E
MF x MF x
1 2
F MF
M
2 2 2
1 2 1 2
MF MF F F
2 2
2
0 0 0
4 4 175
5 5 64
5 5 16
x x x
2
0
81
16
y
M
5 7 9
;
4 4
M
5 7 9
;
4 4
M
Oxy
( )
E
4
5
e
2 2
34
x y
M
( )
E
M
M
( )
E
2 2
2 2
1
x y
a b
1
a b
34
R
2 2
34
a b
2 2
2 2 2
2 2
2 2
4
25( ) 16 5
4
5
3
34
34
c a b
a b a a
e
c
a a
b
a b
a b
( )
E
2 2
1
25 9
x y
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
+) Gọi
Vì tam giác vuông tại nên :
+) Do có hoành độ dường nên ta được: hoặc
.
Bài 27. Trong mặt phẳng tọa độ , cho đường thẳng và elip . Viết
phương trình đường thẳng vuông góc với và cắt tại hai điểm sao cho diện tích tam giác
bằng 3.
Giải:
+) Đường thẳng vuông góc với đường thẳng nên có dạng:
Khi đó phương trình hoành độ giao điểm của và là:
(*)
Ta có cắt tại hai điểm khi và chỉ khi (*) có hai nghiệm phân biệt hay
(2*)
+) Đường thẳng cắt tại hai điểm phân biệt
với là nghiệm của (*) và . Khi đó:
, suy ra:
(thỏa mãn (2*))
Vậy phương trình đường thẳng cần lập là hoặc .
Bài 28. Trong mặt phẳng tọa độ , cho biết elip có chu vi hình chữ nhật cơ sở bằng , đồng
thời một đỉnh của tạo với hai tiêu điểm một tam giác đều. Viết phương trình đường tròn có tâm là gốc
tọa độ và cắt tại bốn điểm là bốn đỉnh của một hình vuông.
Giải:
2 2
0 0
0 0
1 0 2 0
1
25 9
( ; ) ( )
4 4
5 ; 5
5 5
x y
M x y E
MF x MF x
1 2
F MF
M
2 2 2
1 2 1 2
MF MF F F
2 2
2
0 0 0
4 4 175
5 5 64
5 5 16
x x x
2
0
81
16
y
M
5 7 9
;
4 4
M
5 7 9
;
4 4
M
Oxy
:3 4 0
d x y
2 2
( ): 1
9 4
x y
E
d
( )
E
,
A B
OAB
:3 4 0
d x y
3 0
x y c
( )
E
2 2 2 2
4 ( ) 36 5 2 36 0
x x c x cx c
d
( )
E
,
A B
2
' 180 4 0 3 5 3 5
c c
( )
E
1 2
1 2
; , ;
3 3
x c x c
A x B x
1 2
,
x x
1 2
2
1 2
2
5
36
5
c
x x
c
x x
2
2 2
2
2 1
2 1 1 2 1 2
10 10
4 720 16
3 3 15
x x
AB x x x x x x c
( , )
10
c
d O
2
1 1 10
3 . ( , ) 3 . 720 16 . 3
2 2 15
10
OAB
c
S AB d O c
4 2
3 10
16 720 8100 0
2
c c c
2 6 3 10 0
x y
2 6 3 10 0
x y
Oxy
( )
E
16 2 3
( )
E
( )
T
( )
E
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
+) Gọi phương trình chính tắc của elip có dạng: với
Ta có chu vi hình chữ nhật cơ sở là (1)
+) Gọi là đỉnh của mà là tam giác đều, khi đó:
(2)
Mặt khác ta có : (3)
Thay (1), (2) vào (3) ta được:
Vậy phương trình
+) Phương trình đường tròn có dạng:
Đường tròn cắt tại bốn điểm phân biệt .
Do và đều nhận làm các trục đối xứng nên là hình chữ nhật
Gọi
Khi đó hình chữ nhật thành hình vuông thì
Do nên thỏa mãn:
Vậy phương trình đường tròn cần lập là .
Bài 29. Trong mặt phẳng tọa độ , cho elip và điểm . Viết phương trình đường
thẳng đi qua cắt tại hai điểm sao cho trung điểm của đoạn thẳng nằm trên đường thẳng
.
Giải:
( )
E
2 2
2 2
1
x y
a b
0
a b
4( ) 16 2 3 4 2 3
a b a b
(0; )
M b
( )
E
1 2
MF F
1 2
3
3
2
3
F F
b
MO b c c
2 2 2
a b c
2
2
2
4 2 3 4 3 8
3
b
b b b a
2 2
( ): 1
64 48
x y
E
( )
T
2 2 2
x y R
( )
T
( )
E
, , ,
A B C D
( )
T
( )
E
,
Ox Oy
ABCD
( ; )
( ; )
( ; )
B x y
A x y
C x y
ABCD
2 2
2 2
AB BC x y x y
( ) ( )
A T E
,
x y
2 2 2
2
2 2
2 2
2
2 2
2 2
384
2
1
64 48 7
1
2.64 2.48
x y R
R
x y
x y
R
R R
x y
( )
T
2 2
384
7
x y
Oxy
2 2
( ): 1
25 9
x y
E
(2;1)
M
d
M
( )
E
,
A B
AB
: 2
y x
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
+) Do nên nằm trong , suy ra mọi đường thẳng qua đều cắt tại hai điểm phân biệt
+) Nếu đi qua và song song với hay có phương trình
thì trung điểm của là điểm không thuộc đường thẳng (loại)
Do đó gọi phương trình đường thẳng đi qua có hệ số góc có dạng:
Khi đó tọa độ là nghiệm của hệ:
+) Gọi . Ta có:
: là trung điểm của
+) Khi đó
Vậy phương trình đường thẳng cần lập là hoặc .
Bài 30. Trong mặt phẳng tọa độ , cho elip ngoại tiếp tam giác đều . Tính diện tích
tam giác , biết nhận làm đỉnh và trục tung làm trục đối xứng.
Giải:
+) Do là tam giác đều và nên đối xứng nhau qua trục tung
nên gọi với
+) Độ dài tam giác đều là và chiều cao
Khi đó
+) Ta có
Vậy .
2 2
2 1
1
25 9
M
( )
E
M
( )
E
d
(1;2)
M
Ox
d
1
x
AB
(1;0)
I
2
y x
d
(2;1)
M
k
( 2) 1
y k x
,
A B
2 2
2 2 2
( 2) 1
2 1
(25 9) 50 (2 1) 25(2 1) 225 0 (*)
1
25 9
y k x
y kx k
x y
k x k k x k
1 1 2 2
( ; ), ( ; )
A x y B x y
1 2
2
2 2
1 2
2
50 (2 1)
25 (2 1) 9 18
25 9
;
2(9 18 )
25 9 25 9
25 9
k k
x x
k k k
k
I
k
k k
y y
k
AB
2 2
1 1
:
9 18 50 (2 1)
2 2
(2 1)(50 9) 0
9 9 34
25 9 25 9
:
50 50 25
k d y x
k k k
I k k
k k
k d y x
d
1
2
y x
9 34
50 25
y x
Oxy
2 2
( ): 1
16 4
x y
E
ABC
ABC
( )
E
(0;2)
A
ABC
(0;2)
A
,
B C
0 0 0 0
( ; ) ( ; )
B x y C x y
0
0
x
ABC
0
2
a x
0
2
h y
0 0 0 0 0 0
3
2 3 2 3 ;2 3
2
a
h y x y x B x x
2
2
0
0
0 0
0
2 3
16 3 16 3
0
( ) 1
16 4 13 13
x
x
x
B E x x

0
0
32 3
2
16 3 22 1 768 3
13
;
13 13 2 169
48
2
13
ABC
a x
B S ah
h y
768 3
169
ABC
S
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
Bài 31. Trong mặt phẳng tọa độ , cho elip . Tìm các điểm thuộc sao cho
, trong đó là hai tiêu điểm của .
Giải:
+) Elip có .
+) Gọi
Khi đó ta có:
+) Thay vào (*) ta được:
Vậy hoặc .
Bài 32. Trong mặt phẳng tọa độ , cho đường thẳng và hai elip có phương trình
và ( ). Biết hai elip này có cùng tiêu điểm và đi qua điểm
thuộc đường thẳng . Tìm tọa độ điểm sao cho elip có độ dài trục lớn nhỏ nhất.
Giải:
Oxy
2 2
( ): 1
100 25
x y
E
M
( )
E
0
1 2
120
F MF
1 2
,
F F
( )
E
( )
E
2 2
10
5 3
5
a
c a b
b
1 2
2 10 3
F F c
2 2
0 0
0 0
1 0 0 2 0 0
1 (*)
100 25
( ; ) ( )
3 3
10 ; 10
2 2
x y
M x y E
c c
MF a x x MF a x x
a a
2 2 2
1 2 1 2 1 2 1 2
2 . .cos
F F MF MF MF MF F MF
2 2
2
0
0 0 0 0
3 3 3 3
10 3 10 10 2 10 10 .cos120
2 2 2 2
x x x x
2 2 2
0 0 0 0
3 3
300 200 100 0 0
2 4
x x x x
0
0
x
2
0 0
25 5
y y
(0;5)
M
(0; 5)
M
Oxy
: 5 0
x y
2 2
1
( ) : 1
25 16
x y
E
2 2
2
2 2
( ): 1
x y
E
a b
0
a b
2
( )
E
M
M
2
( )
E
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
+) Elip có hai tiêu điểm . Dễ thấy nằm cùng phía với
Vì và nhận là hai tiêu điểm nên ta có:
Khi đó elip có độ dài trục lớn nhỏ nhất khi và chỉ khi nhỏ nhất
+) Gọi đối xứng với qua . Khi đó ta có phương trình là:
+) Ta có . Suy ra nhỏ nhất khi
Vậy tọa độ điểm là nghiệm của hệ :
Vậy .
Bài 33. Trong mặt phẳng tọa độ , cho elip và hai điểm . Tìm trên
điểm có tọa độ dương sao cho diện tích tam giác lớn nhất.
Giải:
+) Phương trình đường thẳng là:
+) Gọi với . Do
Khi đó (1)
Mặt khác theo Bất đẳng thức Bu – nha ta có:
(2)
Từ (1) và (2) suy ra
+) Dấu “=” xảy ra khi : . Vậy .
Bài 34. Trong mặt phẳng tọa độ . Lập phương trình chính tắc của elip , biết điểm nhìn hai
tiêu điểm của dưới một góc vuông và hình chữ nhật cơ sở của nội tiếp đường tròn có phương trình
.
Giải:
+) Gọi phương trình chính tắc của elip là với
Do nên (1)
+) Hình chữ nhật cơ sở của nội tiếp đường tròn : (2)
1
( )
E
1 2
( 3;0), (3;0)
F F
1 2
,
F F
2
( )
M E
2
( )
E
1 2
,
F F
1 2
2
MF MF a
2
( )
E
1 2
MF MF
N
1
( 3;0)
F
( 5;2)
N
2
NF
4 3 0
x y
1 2 2 2
68
MF MF MN MF NF
1 2
MF MF
2
M NF
M
17
4 3 0
17 8
5
;
5 0 8
5 5
5
x
x y
M
x y
y
17 8
;
5 5
M
Oxy
2 2
( ): 1
9 4
x y
E
(3; 2), ( 3;2)
A B
( )
E
C
ABC
AB
2 3 0
x y
0 0
( ; )
C x y
0 0
, 0
x y
2 2
0 0
( ) 1
9 4
x y
C E
0 0
0 0
2 3
1 1
. ( , ) . 52. 2 3
2 2
13
ABC
x y
S AB d C AB x y
2
2 2
2 2
0 0 0 0 0 0
0 0
2 1 1 2 2 3 6 2
9 4 3 2 3 2
x y x y x y
x y
6 2
ABC
S
2 2
0 0
0
0 0
0
3 2
1
3 2
9 4
; 2
2
2
2
3 2
x y
x
C
x y
y
3 2
; 2
2
C
Oxy
( )
E
1; 3
M
( )
E
( )
E
2 2
20
x y
( )
E
2 2
2 2
1
x y
a b
0
a b
0
1 2
90
F MF
1 2
1
2
OM F F
2 2
2 4
OM c a b
( )
E
2 2
20
x y
2 2
20
a b
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
Từ (1) và (2) suy ra . Vậy elip cần lập là:
Bài 35. Trong mặt phẳng tọa độ , cho elip có hai tiêu điểm . Tìm tọa độ điểm
thuộc sao cho bán kính đường tròn nội tiếp tam giác bằng .
Giải:
+) Ta có
Khi đó
+) Mặt khác . Vậy hoặc .
Bài 36. Trong mặt phẳng tọa độ , cho điểm . Viết phương trình chính tắc của elip đi qua
điểm , sao cho nhìn hai tiêu điểm của dưới một góc vuông.
Giải:
+) Gọi phương trình chính tắc của elip là với
Do (1)
+) Mặt khác nên (2)
Từ (1) và (2) suy ra . Vậy elip cần lập là: .
Bài 37. Trong mặt phẳng tọa độ , cho điểm và elip
2
2
( ): 1
4
x
E y
. Tìm các điểm
,
A B
trên
( )
E
sao cho và tam giác
CAB
có diện tích lớn nhất.
Giải:
+) Theo giả thiết ta có là đỉnh nằm trên trục lớn của elip .
Do , suy ra đối xứng nhau qua trục hoành
2 2
12; 8
a b
( )
E
2 2
1
12 8
x y
Oxy
2 2
( ): 1
25 9
x y
E
1 2
,
F F
M
( )
E
1 2
MF F
4
3
2 2
( ): 1
25 9
x y
E
1 2 1 2
2 2
5
3 9
2
4
a
MF MF F F
b p
c a b
1 2
1 2
1 2
4
2.9.
1 2
3
( , ). ( , ) 3 3
2 8
MF F M M
pr
S pr d M Ox F F d M Ox y y
F F
( ) 0
M
M E x
(0;3)
M
(0; 3)
M
Oxy
2 3;2
M
( )
E
M
M
( )
E
( )
E
2 2
2 2
1
x y
a b
0
a b
2 2
12 4
( ) 1
M E
a b
0
1 2
90
F MF
1 2
1
4
2
OM F F c c
2 2
16
a b
2 2
24; 8
a b
( )
E
2 2
1
24 8
x y
Oxy
(2;0)
C
CA CB
C
( )
E
CA CB
,
A B
GV: Nguyễn Thanh Tùng HOCMAI.VN facebook.com/ ThayTungToan
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
Gọi với
Khi đó
(1)
Mặt khác áp dụng BĐT Cauchy ta có:
(2)
Từ (1) và (2) suy ra:
Dấu “=” xảy ra khi
Vậy hoặc .
CẢM ƠN CÁC BẠN ĐÃ QUAN TÂM !
GV: Nguyễn Thanh Tùng
2
2
0
0
0 0
0 0
1
( ; ) ( )
4
( ; )
x
y
A x y E
B x y
0
( 2;2)
x
0 0 0 0
1 1
( , ). 2 . 2 (2 )
2 2
ABC
S d C AB AB x y x y
2 3
2 2 2 2
0 0 0
0 0 0
(2 ) (2 )
(2 ) . (2 ) . 1
4 4
ABC
x x x
S x y x
3
3
0 0 0 0 0
4
0 0 0
2 2 2 (2 ) .(2 )
4 2 4. (2 ) .(2 ) 27
3 3 3 27
x x x x x
x x x
2
27 3 3
4 2
ABC ABC
S S
0
0 0 0
3 3
1; , 1;
2 2
2 3
2 1 1
3 2
3 3
1; , 1;
2 2
A B
x
x x y
A B
3 3
1; , 1;
2 2
A B
3 3
1; , 1;
2 2
A B
| 1/23
| | Tải xuống

Có thể bạn quan tâm:

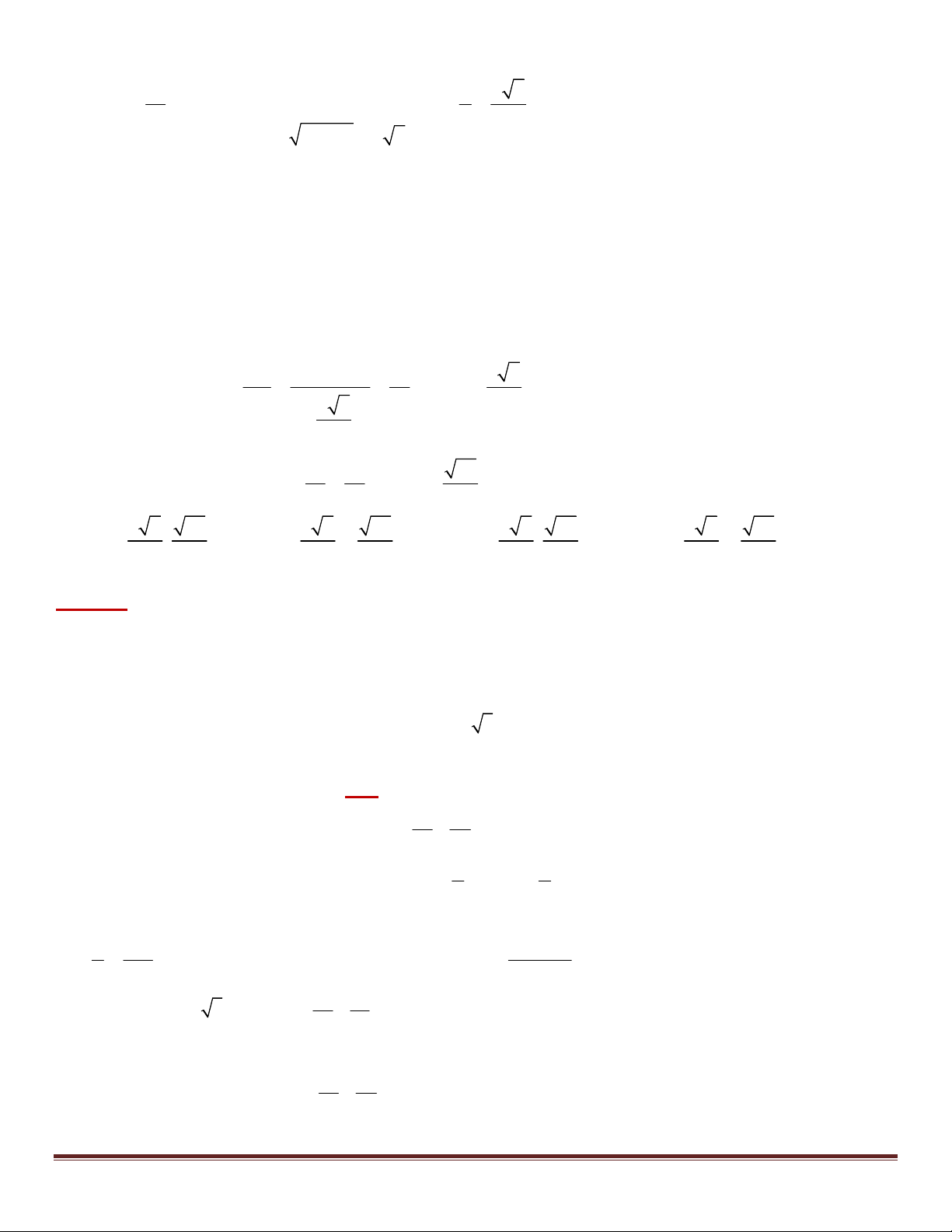
Preview text:

GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan
ELIP VÀ CÁC BÀI TOÁN LIÊN QUAN
GV: Nguyễn Thanh Tùng
I. KIẾN THỨC CƠ SỞ
Để giải quyết tốt các lớp bài toán liên quan tới Elip (tìm điểm và viết phương trình tắc của elip) trước tiên
chúng ta cần nắm được các kiến thức cơ bản qua sơ đồ sau:
Dựa trên các kiến thức cơ bản này, kết hợp với các bài toán trước các bạn đã được tìm hiểu, sẽ giúp ta giải
quyết dễ dàng các lớp bài toán liên quan tới elip. Cụ thể:
+) Khi gặp bài toán “Tìm điểm thuộc (E) thỏa mãn điều kiện (*) cho trước ” thì về cơ bản ta cần thiết lập
được hai dấu “=” mà ở đó dữ kiện điểm thuộc (E) luôn cho ta được một dấu “=” đầu tiên. Các dữ kiện còn
lại sẽ giúp ta tìm ra dấu “=” thứ hai. Nếu cần, trong một số bài toán ta có thể tham số hóa điểm thuộc (E) 2 2 x y
theo một ẩn. Ví như: M  (E) : 
 1  M (a sin t;b cos t) . 2 2 a b
+) Khi gặp bài toán “Viết phương trình chính tắc của elip (E)” cần cắt nghĩa chính xác dữ kiện của bài toán
dựa trên các kiến thức cơ bản liên quan tới elip và tính đối xứng của elip (elip nhận hai trục tọa độ làm hai trục
đối xứng và gốc tọa độ làm tâm đối xứng). II. CÁC VÍ DỤ MẪU
Ví dụ 1. Trong mặt phẳng tọa độ Oxy , viết phương trình chính tắc của elip (E) biết rằng (E) có tâm sai 5 bằng
và hình chữ nhật cơ sở của (E) có chu vi bằng 20 . 3
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan Giải: 2 2 x y
Gọi phương trình chính tắc của elip (E) có dạng:   1 2 2 a b c 5 5 Ta có e    c
a và 2.(2a  2b)  20  a b  5  b  5  a (với 0  a  5) a 3 3 2  5  Khi đó ta có: 2 2 2 2 2 2
a b c a  (5  a)  
a   a 18a  45  0  a  3 hoặc a 15 (loại)  3    2 2 x y
Với a  3  b  2 . Vậy phương trình chính tắc của elip (E) là:   1 9 4 2 2 x y
Ví dụ 2. Trong mặt phẳng với hệ tọa độ Oxy , cho elip có phương trình 
 1. Tìm điểm M nằm trên elip 25 16
sao cho MF  4MF , trong đó F , F lần lượt là các tiêu điểm trái, phải của elip. 1 2 1 2 Giải: 2 2 x ya  5 F (3; 0)
Từ phương trình Elip (E) :   1 2 2  1 
c a b  3   25 16 b  4  F (3; 0)  2  c 3 MF a x  5  x 1 0 0   a 5
Cách 1: Gọi M (x ; y ) , suy ra 0 0  c 3
MF a x  5  x 2 0 0   a 5 3  3 
Khi đó MF  4MF  5  x  4 5  xx  5 1 2 0  0  0 5  5  2 2 5 y Do đó 0
M (5; y )  (E)    1  y  0 0 0 25 16 Vậy M (5; 0) Cách 2: 2 2 2 2  x yx y 0 0 0 0 M  (E)    1    1 (1)
Gọi M (x ; y ) , khi đó   25 16  25 16 0 0 2 MF  4  2 2 2 2 2 (x 3) y 4    
y  x  6x  5 (2)  0 0  0 0 0
x  5  y  0 2 2 x x  6x  5 0 0
Thay (2) vào (1) ta được : 0 0 0   1 2 3x 50x 175 0       . 35 640 25 16 0 0 2  x   y    0 0 0  3 9 Vậy M (5; 0) 2 x  2 2 
Ví dụ 3. Trong mặt phẳng tọa độ Oxy , cho elip 2 (E) :
y  1 điểm M ; . Viết phương trình   4  3 3 
đường thẳng  qua M cắt E tại hai điểm ,
A B sao cho MA  2MB .
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan Giải: 2 x +) Gọi 0 2 2 2
B(x ; y )  (E) 
y  1  x  4 y  4  0 (1) 0 0 0 0 0 4
+) Do M nằm trong (E) nên từ MA  2MB  2  2  x   2 x   A  0     3  3 
x  2  2x A 0  MA  2  MB      (
A 2  2x ; 2  2 y ) 0 0 2  2  y  2  2 y   A 0 y   2 y A  0   3   3  2 (2  2x ) +) Mà 0 2 2 2 A  (E) 
 (2  2 y )  1  x  4 y  2x  8 y  4  0 (2) 0 0 0 0 0 4
x  0; y  1 B(0;1) 2 2 0 0 
x  4 y  4  0
+) Từ (1) và (2) ta được hệ: 0 0     8 3   8 3  2 2
x  4 y  2x  8y  4  0 x  ; y   B ;  0 0 0 0 0 0    5 5   5 5   8 3 
Với B(0;1)   : x  2 y  2  0 ; Với B ;
  : x 14 y 10  0    5 5 
Vậy x  2 y  2  0 hoặc x  14 y 10  0 . 2 2 x y
Ví dụ 4. Trong mặt phẳng tọa độ Oxy , cho elip (E) : 
 1 . Đường thẳng  : x  2 y  0 cắt (E) tại 8 4
hai điểm B,C . Tìm tọa độ điểm A trên (E) sao cho tam giác ABC có diện tích lớn nhất Giải:
+) Do   (E)   ;
B C nên B,C cố định hay độ dài BC không đổi
Suy ra diện tích ABC lớn nhất khi khoảng cách h d ( , A ) lớn nhất 
x  2 2 sin t
+) Phương trình tham số của (E) :
nên gọi A 2 2 sin t; 2 cos t   
y  2 cos t     t tt t  4sin t 2 2 sin 2 2 cos 2 2 sin cos      4  4
Khi đó h d ( , A )     3 3 3 3     3 sin t   1    t   k 2 4   
Dấu“ =” xảy ra khi: 4 sin t 1         ( k  )  4    sin t   1
t    k2      4  4  3 +) Với t
k 2A 2;  2 +) Với t  
k 2A 2  ; 2     4 4
Vậy A 2;  2 hoặc A 2; 2 .     2 2 x y
Nhận xét : Ngoài cách để (E) dưới dạng chính tắc
 1 , trong nhiều bài toán các bạn có thể chuyển 2 2 a b
x a sin t
nó về dạng tham số sau :
để việc tham số hóa điểm thuộc elip được dễ dàng hơn.
y bcost
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan
III. BÀI TẬP TỰ LUYỆN 3
Bài 1. Trong mặt phẳng tọa độ Oxy , viết phương trình chính tắc của elip (E) có tâm sai bằng và độ dài 3
đường chéo hình chữ nhật cơ sở bằng 2 5 . Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) có dạng: 
 1 với a b  0 2 2 a b 2 c 3 a Tâm sai 2 e    c  . a 3 3
Độ dài đường chéo hình chữ nhật 2 2 2 2 2 2
(2a)  (2b)  2 5  a b  5  b  5  a 2 a +) Khi đó 2 2 2 2 2 2
a b c a  5  a   a  3 2  b  2 3 2 2 x y
Vậy trình chính tắc của elip (E) cần lập là:   1 3 2 2 2 x y
Bài 2. Trong mặt phẳng tọa độ Oxy , cho elip (E) có phương trình 
 1 và M (1; 1) . Một đường 8 4
thẳng d đi qua M cắt (E) tại , A B sao cho M .
A MB lớn nhất. Tìm tọa độ , A B .
Giải:
+) M (1; 1) thuộc miền trong của (E) nên d luôn cắt (E) tại , A B x  1 mt
Gọi phương trình đường thẳng d có dạng: với 2 2
t  , m n  0 .  y  1   nt  +) Gọi ( A 1 mt ; 1
  nt ), B(1 mt ; 1 nt ) . Trong đó t , t là nghiệm của phương trình: 1 1 2 2 1 2 2 2 (1 mt) ( 1   nt)   1   2 2 m  2n  2
t  2(m  2n)t  5  0 8 4 5
Theo hệ thức Vi – et ta có: t t   1 2 2 2 a  2b 2 2 2 2 2 2 5(m n ) 5 +) Khi đó M .
A MB  mt    nt  . mt    nt    2 2 m n t t   1 1 2 2  1 2 2 2 2 m  2n m 2  2 2 m n 2 m 2 m Mặt khác 0   1, do đó .
MA MB lớn nhất khi và chỉ khi  1  n  0 2 2 m n 2 2 m n
Khi đó đường thẳng d có dạng : y  1
 , suy ra tọa độ giao điểm ,
A B của d và (E) là nghiệm của hệ: 2 2  x y   2 A 6;  1    1      6 A x x   6;   1 6  8 4      hoặc .   y  1     y  1  B y    6; 1 1 B  6;  1     A 6;  A 6;  1  1 Vậy hoặc .   B  6;  1 B  6;  1  
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan
Bài 3. Trong mặt phẳng tọa độ Oxy . Lập phương trình chính tắc của elip trong mặt phẳng Oxy biết điểm  8 1  M  ;
 thuộc elíp và tam giác F MF vuông tại M , trong đó F , F là hai tiêu điểm của elíp.  3 3  1 2 1 2  
Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) có dạng: 
 1 với a b  0 và 2 2 2
a b c 2 2 a b  8 1  8 1 Khi đó 2 2 2 2 M  ;   (E)  
 1  a  8b  3a b (1) 2 2  3 3  3a 3b   +) Với F ( ; c 0), F ( ;
c 0) , khi đó tam giác F MF vuông tại M nên ta suy ra: 1 2 1 2 2 2  8  1  8  1 2 2 2 2 2
MF MF F F  2 2 2 2  c      c   
 4c c  3  a b c b  3 (2) 1 2 1 2  3  3  3  3    
+) Thay (2) vào (1) ta được: 2 2
b   b   2 b   2 4 2 2 3 8 3
3 b b  1  b  1  a  4 2 x
Vậy phương trình chính tắc của elip (E) cần lập là: 2  y  1 4
Bài 4. Trong mặt phẳng tọa độ Oxy . Viết phương trình chính tắc của elip (E) biết rằng elip (E) có hai tiêu
điểm F và F với F  3; 0 và có một điểm M thuộc (E) sao cho tam giác F MF vuông tại M và có diện 1   1 2 1 2 tích bằng 1 .
Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) có dạng: 
 1 với a b  0 2 2 a b
Với F  3; 0 , suy ra c  3 2 2 2
a b c  3 hay 2 2
a b  3 (1) 1   
MF   3  x ;  y 1   0 0 
+) Gọi M (x ; y )   0 0  MF  3  x ;  y 2  0 0  
  Khi đó  0 2 2 2 2
F MF  90  MF .MF  0  x  3  y  0  x y  3 1 2 1 2 0 0 0 0 1 1 1 8 Ta có 2 2 S
d (M , Ox).F F
y .2 3  3 y  1  y   x F MF 1 2 0 0 0 0 1 2 2 2 3 3 2 2 x y 8 1
+) Mặt khác M (x ; y )  (E) 0 0    1    1 (2) 0 0 2 2 2 2 a b 3a 3b 8 1
Thay (1) vào (2) ta được: 4 
 1  3b  3  b  1 (do b  0 ) 2  a  4 2 2 3(b  3) 3b 2 x
Vậy phương trình chính tắc của elip (E) cần lập là: 2  y  1 4  3 
Bài 5. Trong mặt phẳng tọa độ Oxy . Viết phương trình chính tắc của elíp đi qua điểm M 1;  và tiêu điểm  2   
của elip nhìn trục nhỏ với một góc 0 60 .
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan
Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) có dạng: 
 1 với a b  0 2 2 a b Gọi F ( ;
c 0) là tiêu điểm của (E) và B (0; b
 ), B (0;b) là hai đỉnh thuộc trục nhỏ của (E) 1 1 2 +) Do  F
B B cân tại F và 0
B F B  60 , suy ra FB B đều 1 1 2 1 1 1 2 1 1 2 Khi đó 2 2 2 2 2 2 2
F B B B F B B B c b  (2 ) bc  3b 2 2 2 2
a b c  4b (1) 1 1 1 2 1 1 1 2  3  1 3 +) Với M 1;   (E)    1 (2) 2 2  2  a 4b   1 3
Thay (1) vào (2) ta được : 2 2 
 1  b  1  a  4 2 2 4b 4b 2 x
Vậy phương trình chính tắc của elip (E) cần lập là: 2  y  1 4 2 2 x y
Bài 6. Trong mặt phẳng tọa độ Oxy , cho elip (E) có phương trình   .
1 Giả sử F , F là hai tiêu điểm 8 4 1 2
của elip, trong đó F có hoành độ âm. Tìm tọa độ điểm M trên (E) sao cho MF MF  2 . 1 1 2
Giải: a  2 2 2 2 x y
+) (E) có phương trình   1  b   2 8 4  2 2 c a b  2   cx 2 x 0 0 MF a   2 2  1   a 2 2
+) Gọi M (x ; y )  (E)  
MF MF  2x 0 0 1 2 0 cx 2x 0 0 MF a   2 2  2   a 2 2
+) Khi đó MF MF  2  2x  2  x  2 1 2 0 0 2  x   2  y  3  +) Với 2 0 0 x  2  y  4 1  4 1  3     0 0   8    8   y   3  0 Vậy M 2; 3 hoặc M 2;  3 .     2 2 x y
Bài 7. Trong mặt phẳng tọa độ Oxy , cho elip có phương trình 
 1. Tìm điểm M thuộc elip sao cho 25 9 góc F MF 0
 90 với F , F là hai tiêu điểm của elip. 1 2 1 2
Giải: 2 2 x ya  5; b  3  +) Elip (E) :   1   25 9 2 2 c a b  4 
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToanc 4 c 4 MF a x  5  x ; MF a x  5  x 1 0 0 2 0 0   a 5 a 5
+) Gọi M (x ; y )  (E)  với x  0 0 0  2 2 x y 0  0 0   1 (*)   25 9 2 2  4   4  5 14 Do  0
F MF  90 nên suy ra : 2 2 2 2
MF MF F F  5  x  5  x
 64  8x  175  x   1 2 1 2 1 2  0   0  0 0  5   5  4 5 14 2 7 y 9 3 2 +) Thay x   vào (*) ta được: 0 2   1  y   y   0 4 0 0 8 9 8 4  5 14 3 2   5 14 3 2   5 14 3 2   5 14 3 2  Vậy M  ;  , M  ;   , M   ;  , M   ;  .  4 4          4 4   4 4 4 4    
Bài 8. Trong mặt phẳng tọa độ Oxy . Viết phương trình chính tắc của elip, biết hai tiêu điểm cùng với hai đỉnh
trên trục bé xác định một hình vuông và phương trình hai đường chuẩn là x  8  .
Giải:
+) Ta có hai tiêu điểm F ( ; c 0), F ( ;
c 0) và hai đỉnh B (0; b
 ), B (0;b) thuộc trục nhỏ xác định một hình vuông 1 2 1 2 2 2 a a a
nên ta có b c . Elip có phương trình đường chuẩn 2 x     
 8  a  8c e c c 2 a  32 +) Khi đó: 2 2 2 2 2
a b c  8c c c c  4  0  b  4  2 2 x y
+) Suy ra phương trình chính tắc của elip là:   1 . 32 16 2 2 x y
Bài 9. Trong mặt phẳng tọa độ Oxy , cho elip (E) : 
 1 có hai tiêu điểm F , F . Tìm tọa độ điểm M 25 9 1 2 4
thuộc (E) sao cho bán kính đường tròn nội tiếp tam giác MF F bằng . 1 2 3
Giải: a  5 2 2 x y
MF MF F F 2a  2c +) Từ (E) :   1  b  3 1 2 1 2  p  
a c  9 25 9 MF F 1 2  2 2 2 2 c a b  4  4
+) Suy ra diện tích tam giác MF F là: Spr  9.  12 1 2 MF F 1 2 3 1 1 SMF F 12 +) Mặt khác ta có: 1 2 S
.d (M , Ox).F F  . y .2c  4 yy    3 MF F 1 2 M M M 1 2 2 2 4 4 2 x 9 M (0;3)
+) Vì M (x ; y )  (E) M    1  x  0  M M  25 9 M M (0; 3  ) 
Vậy M (0;3) hoặc M (0; 3) .
Bài 10. Trong mặt phẳng tọa độ Oxy . Viết phương trình chính tắc của elip (E) biết rằng khi điểm M thay đổi
trên (E) thì độ dài nhỏ nhất của OM bằng 4 và độ dài lớn nhất của MF bằng 8 , với F là tiêu điểm có 1 1
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan hoành độ âm.
Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) cần lập là: 
 1 với a b  0 2 2 a b
a x a 0 
Gọi M (x ; y )  (E)  
a c MF a c 0 0 cx 1 0 MF a   1  a
Suy ra độ dài MF lớn nhất bằng : a c  8 (1) 1 2 2  x x 0 0 a b    2 2 2 2 2 2 2 2 2  a b x y x y x y OM +) Lại có: 0 0 0 0 0 0
M (x ; y )  (E)    1        OM b 0 0 2 2 2 2 2 2 2 2 x y a b b b b b  0 0   1 2 2   a b
Suy ra độ dài nhỏ nhất của OM bằng b  4 (2) 2 a c  8 
a a 16  8 a  5
Từ (1) và (2) ta được:      b  4  b  4 b  4   2 2 x y
Vậy phương trình elip (E) cần lập là:   1. 25 16 2 2 x y
Bài 11. Trong mặt phẳng tọa độ Oxy , cho elip (E) : 
 1. Viết phương trình đường thẳng d cắt (E) tại 8 2
hai điểm phân biệt có tọa độ là các số nguyên.
Giải: 2 2 x y Gọi 0 0
M (x ; y )  (E)    1 (*) 2
y  2  y  1; 0;1 y   0 0   (vì ) 0 0 8 2 0 +) Với y  1
 thay vào (*) ta được: x  2  (thỏa mãn) 0 0
+) Với y  0 thay vào (*) ta được: x  2  2 (loại) 0 0
Suy ra 4 điểm có tọa độ nguyên trên (E) là: M (2;1), M (2; 1), M ( 2  ;1), M (2; 1  ) 1 2 3 4
Khi đó ta sẽ lập được 6 phương trình đường thẳng d thỏa mãn yêu cầu đề bài là:
x  2; x  2; y  1; y  1; x  2 y  0; x  2 y  0 .
Nhận xét: Ở ví dụ trên nếu ta tiếp cận theo cách thông thường là giả sử dạng phương trình của d rồi tìm
giao điểm, sau đó sử dụng điều kiện tọa độ nguyên thì chúng ta sẽ gặp khó khăn. Song nếu ta làm theo chiều
nghịch thì bài toán sẽ trở nên “nhẹ nhàng” hơn rất nhiều. Bởi ở những bài toán liên quan tới elip (hay cả
đường tròn) ta hoàn toàn có thể chặn điều kiện cho x, y khá đơn giản. Vì vậy việc yêu cầu tọa độ nguyên của
bài toán, giúp ta nghĩ tới ngay giải pháp trên. 2 x
Bài 12. Trong mặt phẳng tọa độ Oxy , cho elip 2 (E) :
y  1. Tìm tọa độ điểm M trên (E) sao cho bán 9
kính qua tiêu của tiêu điểm này bằng 3 lần bán kính qua tiêu của tiêu điểm kia.
Giải:
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToana  3 2 xc 2 2 +) Từ 2 (E) :
y  1  b  1  e   9 a 3  2 2 c a b  2 2 
MF a ex +) Gọi 1 0
M (x ; y )  (E)  0 0
MF a ex  2 0 MF  3MF
MF  3MF  0 Từ giả thiết ta có: 1 2 1 2     MF 3MF MF  3MF  0 1 2   2 1  MF  3MF MF  3MF  0  2 1  2 1
 10MF .MF  3 MF MF
 0  16MF .MF  3 MF MF  0 1 2  1 2  1 2  1 2 2 2 2
 16 a ex . a ex  3. 2a  0  16(a e x ) 12a 0   0   2 2 2 2 2 0 2 2 a 3 81 9 2 2  x     x   0 2 2 0 4e 32 8  2 2  4.  3   2 x 23 46 +) Mặt khác 2 0
M  (E)  y  1   y   0 0 9 32 8  9 2 46   9 2 46   9 2 46   9 2 46  Vậy M  ;  hoặc M  ;   hoặc M   ;  hoặc M   ;    8 8          8 8   8 8   8 8    A  0
Nhận xét: Trong giải toán ta biết . A B  0 
, và ta thường chỉ quen với chiều biến đổi thuận. Nhưng B  0 
trong nhiều trường hợp, việc biến đổi theo chiều ngược lại sẽ giúp giải bài toán ngắn gọn hơn rất nhiều, mà ví
dụ trên là một điển hình.
Bài 13. Trong mặt phẳng tọa độ Oxy , cho điểm M  3;1 , đường elip (E) đi qua điểm M và khoảng cách  
giữa hai đường chuẩn của (E) là 6. Lập phương trình chính tắc của (E) . Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) là:  
1 với a b  0 2 2 a b a a
+) Elip (E) có hai phương trình đường chuẩn là x  và x   e e
Do đó khoảng cách giữa hai đường chuẩn là: 2 2 4 a 2a 9a a 2 4 2 2 2 2 2 
 6  a  3c a  9c  9(a b )  b  (1) e c 9 3 1
+) Mặt khác M  3;1  (E)    1 (2)   2 2 a b
Thay (1) vào (2) và rút gọn ta được: 4 2 2 2
a 12a  36  0  a  6  b  2 2 2 x y
Vậy phương trình (E) cần lập là:   1 6 2
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan
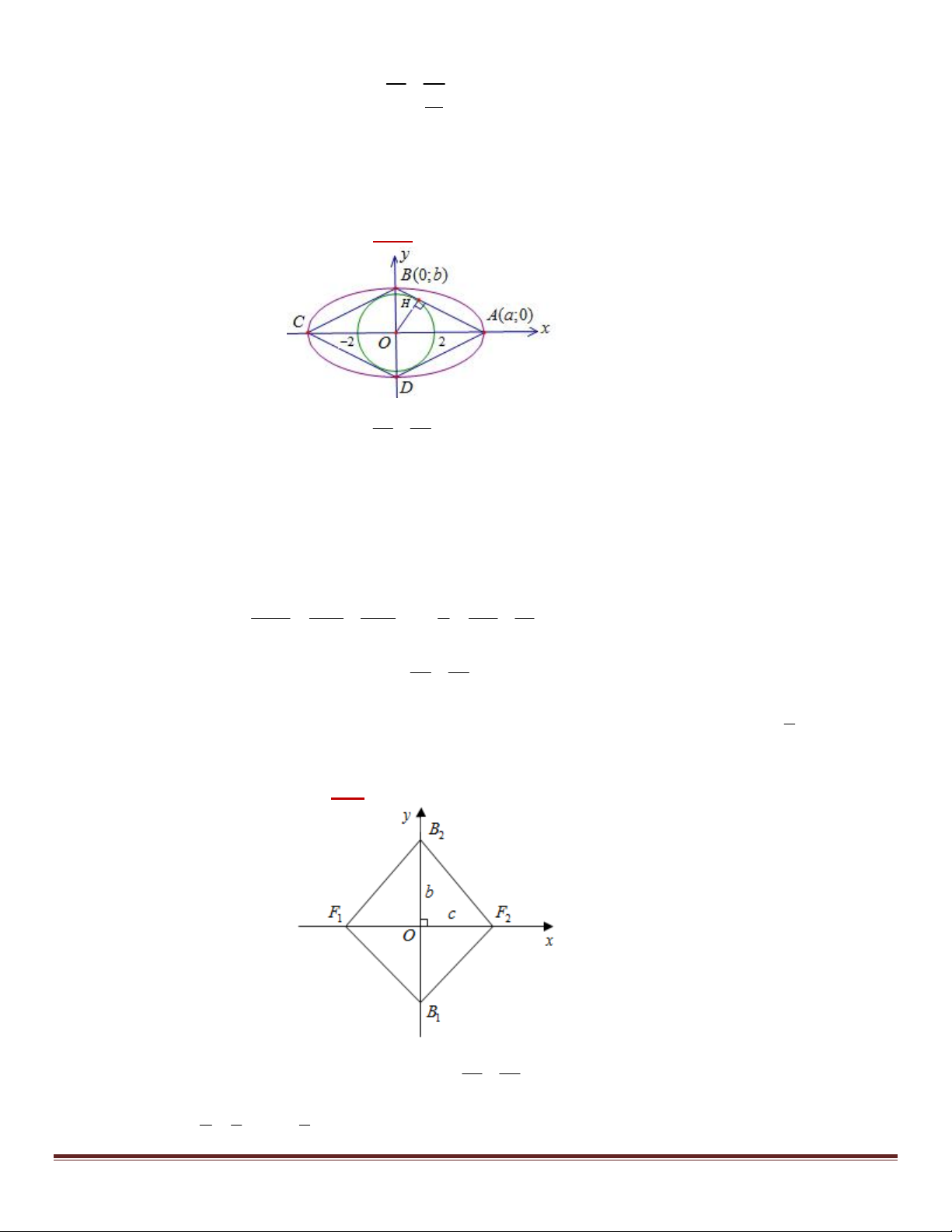
Bài 14. Trong mặt phẳng tọa độ Oxy . Lập phương trình chính tắc của elip (E) biết rằng có một đỉnh và hai
tiêu điểm của (E) tạo thành một tam giác đều và chu vi hình chữ nhật cơ sở của (E) là 12 2  3 .   Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) có dạng: 
 1 với a b  0 2 2 a b
Ta có chu vi hình chữ nhật cơ sở: 4(a b)  12 2  3  a b  3 2  3 (1)    
+) Không mất tính tổng quát giả sử đỉnh B(0;b) và hai tiêu điểm F ( ; c 0), F ( ;
c 0) tạo thành tam giác đều 1 2 2 b Do B
F F luôn cân tại B , nên BF F đều khi 2 2 2 2 2 2
BF F F BF F F c b  4c c  1 2 1 2 1 1 2 1 1 2 3 4 2 3 +) Khi đó 2 2 2 2 2
a b c a b a
b (2) (do a, b  0 ) 3 3 2 3
Thay (2) vào (1) ta được :
b b  3 2  3 
3b 2  3  9 2  3  b  3 3  a  6       3 2 2 x y
+) Vậy phương trình chính tắc của elip (E) cần lập là:   1 36 27
Bài 15. Trong mặt phẳng tọa độ Oxy , cho elip (E) có hai tiêu điểm F  3;0 , F 3; 0 và đi qua điểm 1   2    1  A 3;
. Lập phương trình chính tắc của (E) và với mọi điểm M thuộc (E) , hãy tính giá trị biểu thức    2  2 2 2
P MF MF  3OM MF .MF 1 2 1 2 Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) có dạng: 
 1 với a b  0 2 2 a b
(E) có hai tiêu điểm F  3;0 , F 3; 0 , suy ra c  3 1   2   2 2 x y +) Khi đó 2 2 2 2 2
a b c  3  a b  3  (E) :   1 2 2 b  3 b  1  3 1 +) Với 4 2 2 2 2 2 A 3;  (E)  
 1  4b b  3  0  (4b  3)(b 1)  0  b  1  a  4   2 2  2  b  3 4b 2 x
Vậy phương trình chính tắc của (E) là : 2  y  1. 4  c c MF a x ; MF a x 1 0 2 0   a a
+) Gọi M (x ; y )  (E)  0 0  2 x 2 2 2  0 2
OM x y ;  y  1 0 0 0   4 2 2  c   c   c   c
Khi đó P a xa x  3      2 2 x ya x a x 0 0 0 0   0   0   a   a   a   a
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan 2 2 3c 9  x  2 2  a
x  3 x y  4 
x  3 x y  4  3  y  4  3  1 2 0  2 2 0 0  2 0  2 2 0 0  0 2  0  a 4 4   Vậy P  1 . 2 2 x y
Bài 16. Trong mặt phẳng tọa độ Oxy , cho elip (E) có phương trình 
 1 với hai tiêu điểm F , F 9 5 1 2
(hoành độ của F âm). Tìm tọa độ điểm M thuộc elip sao cho MF F = 0 60 1 1 2 Giải: 2 2 x y 2  a  9 F ( 2  ;0)
+) (E) có phương trình   1, suy ra 2 2 1   c
a b  2   9 5 2 b   5  F (2;0)  2  c 2 c 2 MF a x  3  x ; MF a x  3  x 1 0 0 2 0 0   a 3 a 3
+) M (x ; y )  (E)   0 0 2 2 x y  0 0   1 (*)   9 5 Ta có 2 2 2 
MF MF F F  2MF .F F .cos MF F 2 1 1 2 1 1 2 1 2 2 2  2   2   2  3 2 0  3  x  3  x  4  2. 3  x .4.cos 60  4x  3   x    0   0   0  0 0  3   3   3  4 3 75 5 5  3 5 5   3 5 5 
+) Thay x   vào (*) ta được: 2 y   y   . Vậy M   ; hoặc M   ; . 0   4 0 0 16 4  4 4      4 4  
Bài 17 (A – 2012). Trong mặt phẳng tọa độ Oxy , cho đường tròn 2 2
(C) : x y  8 . Viết phương trình chính
tắc elip (E) , biết rằng (E) có độ dài trục lớn bằng 8 và (E) cắt (C) tại bốn điểm tạo thành bốn đỉnh của một hình vuông. Giải: 2 2 x y
Gọi phương trình chính tắc của elip (E) có dạng:   1 2 2 a b
+) (E) có độ dài trục lớn bằng 8  2a  8  a  4
+) (E) cắt (C) tại bốn điểm phân biệt tạo thành bốn đỉnh của một hình vuông nên 4 đỉnh nằm trên hai đường
phân giác thuộc góc phần tư thứ nhất và thứ hai .
Ta giả sử A là một giao điểm của (E) và (C) thuộc đường phân giác  : y x . +) Gọi (
A t;t)   ( t  0 ). Ta có: 2 2
A  (C)  t t  8  t  2 (vì t  0 )  ( A 2; 2) 2 2 2 2 16 +) Mà A  (E) 2    1  b  . 2 2 4 b 3
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan 2 2 x y
Vậy phương trình chính tắc của elip (E) là:   1 16 16 3
Bài 18 (B – 2012). Trong mặt phẳng tọa độ Oxy , cho hình thoi ABCD có AC  2BD và đường tròn tiếp xúc
với các cạnh của hình thoi có phương trình 2 2
x y  4 . Viết phương trình chính tắc của elip (E) đi qua các đỉnh ,
A B, C, D của hình thoi. Biết A thuộc trục Ox . Giải: 2 2 x y
Gọi phương trình chính tắc của elip (E) : 
 1 ( với a b  0 ) 2 2 a b
Vì (E) đi qua các đỉnh A, B, C, D và AOx nên không mất tính tổng quát giả sử: ( A ;
a 0) và B(0;b) .
Mà hình thoi ABCD có AC = 2BD  2OA  4OB OA  2OB
a  2b (vì a b  0 ) hay A(2b;0) và B(0;b)
Gọi H là hình chiếu của O lên AB
OH R  2 ( vì đường tròn 2 2
x y  4 tiếp xúc với các cạnh của hình thoi) 1 1 1 1 1 1
Xét tam giác OAB ta có:   hay 2    b  5 2 2
a  4b  20 2 2 2 OH OA OB 2 2 4 4b b 2 2 x y
Vậy phương trình chính tắc của elip (E) là:   1 20 5 3
Bài 19. Trong mặt phẳng tọa độ Oxy . Lập phương trình chính tắc của elip (E) có tâm sai bằng , biết diện 5
tích của tứ giác tạo bởi các tiêu điểm và các đỉnh trên trục bé của (E) bằng 24. Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) có dạng: 
 1 với a b  0 và 2 2 2
a b c 2 2 a b c 3 5 Ta có tâm sai e    a c a 5 3
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan +) Gọi F ( ; c 0), F ( ;
c 0) là các tiêu điểm và B (0; b
 ), B (0;b) là các đỉnh trên trục bé. 1 2 1 2 1 1 12
Suy ra F B F B là hình thoi , khi đó: SF F .B B  .2 .
c 2b  2bc  24  bc  12  b  1 2 2 1 F B F B 1 2 1 2 1 2 2 1 2 2 c 2 2  5   12  Khi đó 2 2 2 2 4 4 4
a b c c
c  25c  1296  9c c  81  c  3 (do c  0 )      3   c  2 2 x y
Suy ra a  5;b  4 . Vậy phương trình chính tắc của elip (E) cần lập là:   1 25 16 4
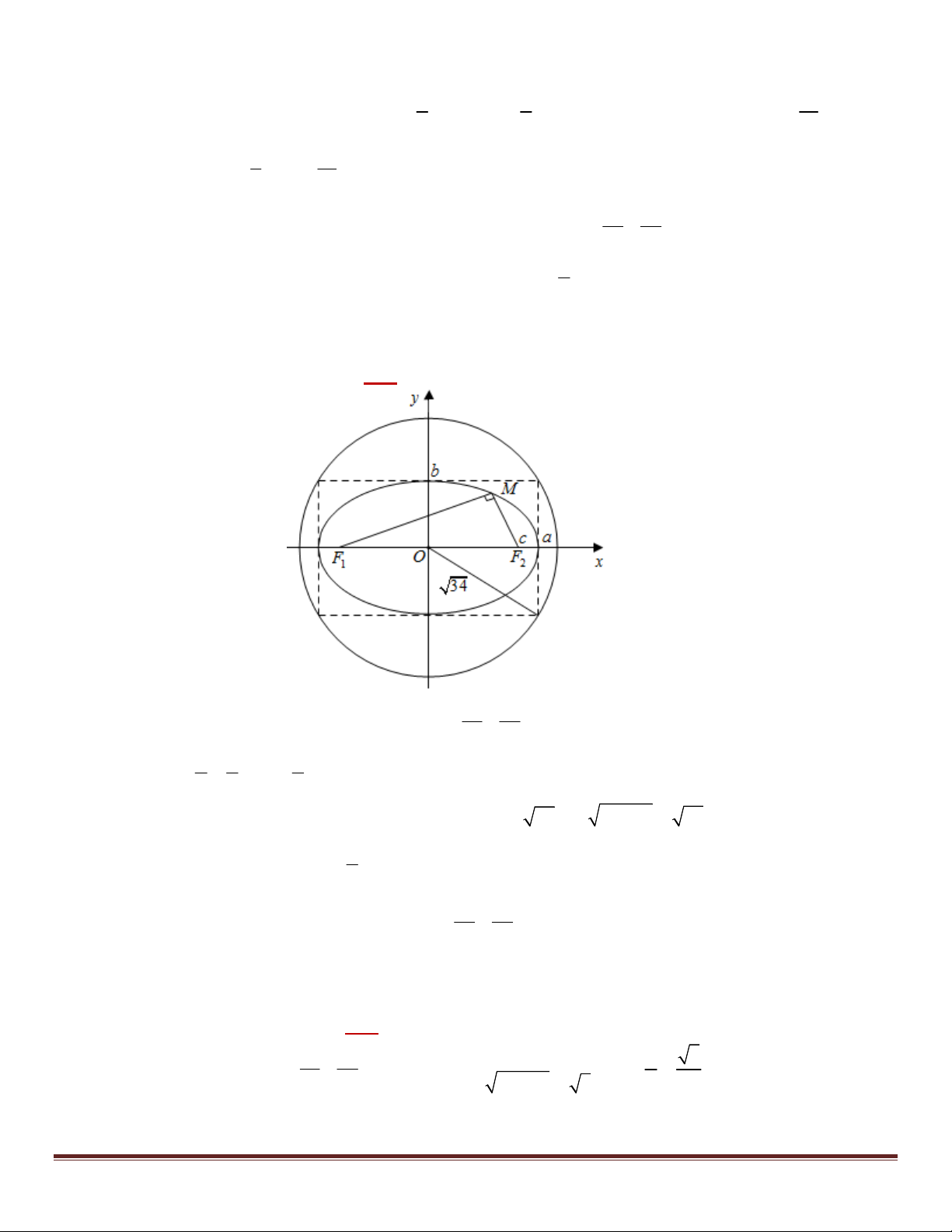
Bài 20. Trong mặt phẳng tọa độ Oxy , cho elip (E) có tâm sai e
, đường tròn ngoại tiếp hình chữ nhật cơ 5
sở của elip có phương trình 2 2
x y  34 . Viết phương trình chính tắc của elip và tìm tọa độ điểm M thuộc
(E) sao cho M nhìn hai tiêu điểm của (E) dưới một góc vuông và M có hoành độ dương. Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) có dạng: 
 1 với a b  0 2 2 a b c 4 4 Ta có tâm sai e    c a a 5 5
Vì đường tròn ngoại tiếp hình chữ nhật cơ sở có bán kính R  34 2 2
a b  34 2 2
b  34  a 2  4  Khi đó 2 2 2 2 2 2
a b c a  34  a a
a  25  a  5; b  3; c  4 .    5  2 2 x y
Vậy phương trình chính tắc của elip (E) cần lập là:   1 25 9
Bài 21. Trong mặt phẳng tọa độ Oxy , cho elip 2 2
(E) : 4x  9 y  36 có hai tiêu điểm F và F với F có hoành 1 2 1
độ âm. Tìm tọa độ điểm M thuộc (E) sao cho 2 2
MF  2MF đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó. 1 2 Giải: 2 2 x y
a  3; b  2  c 5 +) Ta có 2 2
(E) : 4x  9 y  36    1, suy ra   e   9 4 2 2 c a b  5 a 3 
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan
MF a ex ;
MF a ex 1 0 2 0  +) Gọi 2 2
M (x ; y )  (E)  với 3   x  3 0 0  x y 0 0 0   1 (*)   9 4 2 2 5  6 81  Khi đó 2 2
P MF  2MF a ex  2 a ex
 3a  2aex  3e x x x  1 2  0   0  2 2 2 2 0 0  0 0  3  5 5  6 81 +) Xét hàm 2
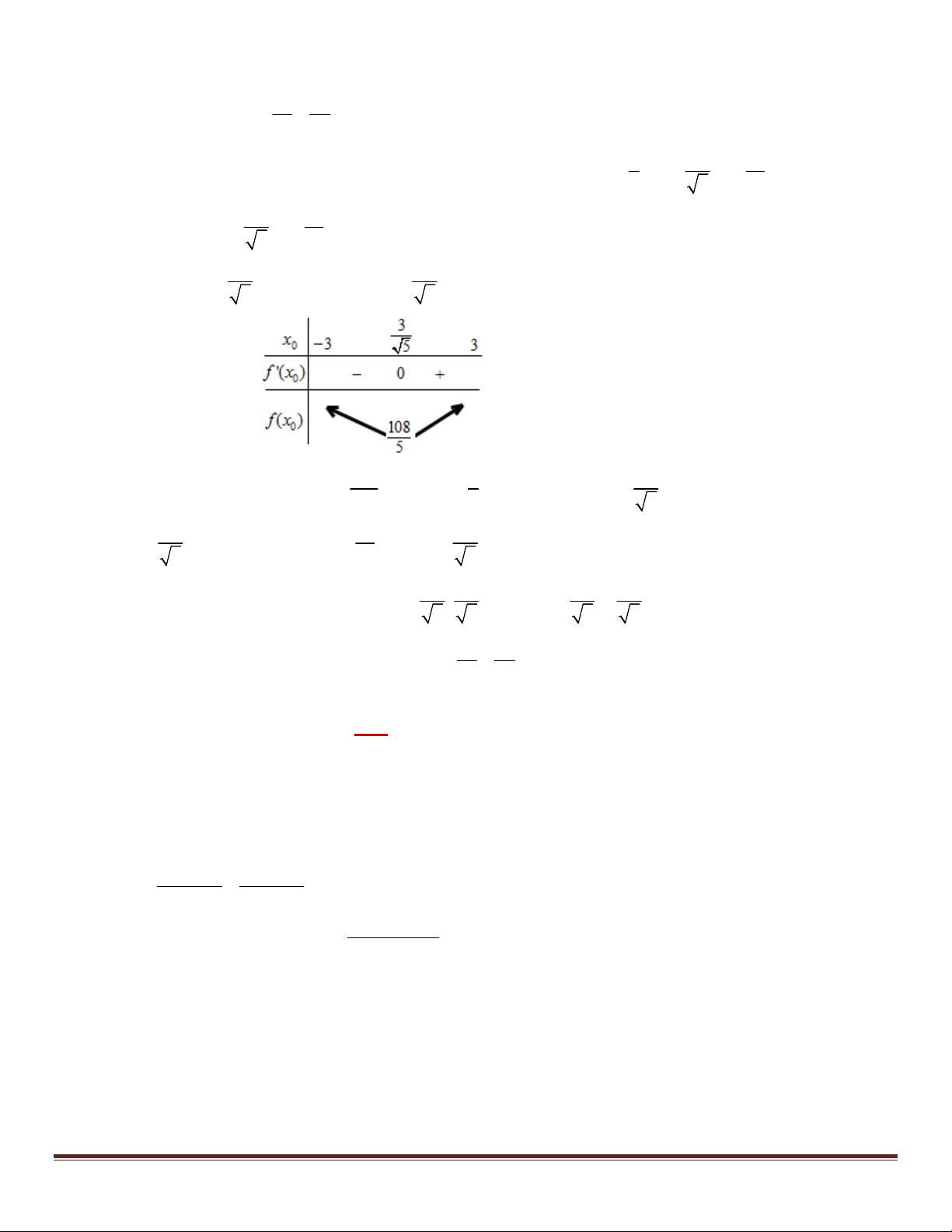
f (x )  x x  với x  3;3 0   0 0 0 5 5 6 3
Ta có f '(x )  2x
; f '(x )  0  x   3  ;3 0 0   0 0 5 5 108 5 3
Từ bảng biến thiên suy ra min f (x )   min P
f (x )  36 khi x  0 0 0 x   5 3 5 0 [ 3;3] 3 16 4 +) Thay x  vào (*) ta được: 2 y   y   0 0 0 5 5 5  3 4   3 4  Vậy 2 2
MF  2MF đạt giá trị nhỏ nhất khi M ; hoặc M ;  . 1 2      5 5   5 5  2 2 x y
Bài 22. Trong mặt phẳng tọa độ Oxy , cho elip (E) : 
 1 và điểm I (1; 2) . Lập phương trình đường 16 9
thẳng d đi qua I , cắt (E) tại hai điểm phân biệt ,
A B sao cho I là trung điểm của AB . Giải:
+) I (1; 2) thuộc miền trong của (E) nên d luôn cắt (E) tại , A B x  1 mt
Gọi phương trình đường thẳng d có dạng: với 2 2
t  , m n  0 .
y  2  nt  +) Gọi (
A 1 mt ; 2  nt ), B(1 mt ; 2  nt ) . Trong đó t , t là nghiệm của phương trình: 1 1 2 2 1 2 2 2 (1 mt) (2  nt)   1   2 2 9m 16n  2
t  2(9m  32n)t  71  0 16 9 2(9m  32n)
Theo hệ thức Vi – et ta có: t t   1 2 2 2 9m 16n
x x  2x
2  m(t t )  2
+) I là trung điểm của AB khi A B I 1 2  
y y  2 y
4  n(t t )  4  A B I  1 2
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan  2 (
m 9m  32n)   0     2 2 ( m t t ) 0  9m  16n 1 2  2 2   
 9m  32n  0 (do m n  0 ) (
n t t )  0 2 (
n 9m  32n)  1 2   0 2 2   9m 16nm  32
Với 9m  32n  0  9m  32n , ta chọn n  9 
x  1 32t
Suy ra phương trình d : hay 
9x  32 y  73  0 y  2  9t  2 x
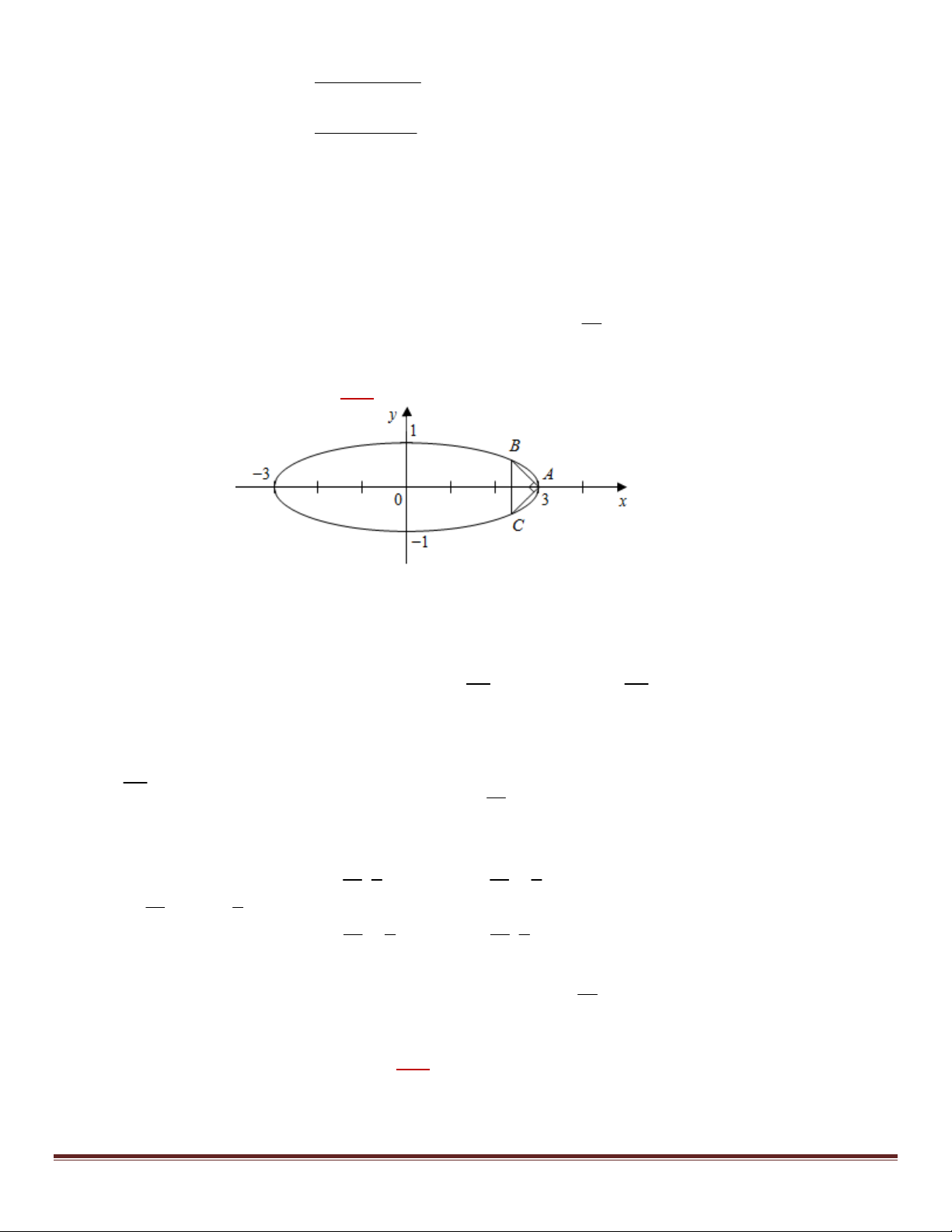
Bài 23. Trong mặt phẳng tọa độ Oxy , cho điểm A(3; 0) và elip 2 (E) :
y  1. Tìm tọa độ các điểm B, C 9
thuộc (E) sao cho tam giác ABC vuông cân tại A . Giải:
+) Ta có B, C thuộc (E) và tam giác ABC vuông cân tại A . Mặt khác A(3; 0)  Ox và elip (E) nhận Ox, Oy B( ; m n)
làm các trục đối xứng nên B, C sẽ đối xứng nhau qua trục Ox . Do đó gọi với n  0 C( ; m n)   2 2  mm  2 2
AB  (m  3; n)
B, C  (E)    n  1   n  1 +) Suy ra 
, khi đó     9   9 
AC  (m  3; n)  A . B AC  0  2 2 2 2 (m 3) n 0     n  (m  3)   m  3 2 m Suy ra 2 2 (m 3) 1 5m 27m 36 0          12 9 m   5
+) Với m  3  n  0 (loại)   12 3    12 3  B ;    B ;     12 3   5 5    5 5  +) Với m   n   , suy ra hoặc   5 5  12 3   12 3  C  ;     C ;      5 5     5 5  2 x
Bài 24. Trong mặt phẳng tọa độ Oxy , cho điểm A(3; 0) và elip 2 (E) :
y  1. Tìm tọa độ các điểm B, C 9
thuộc (E) sao cho tam giác ABC vuông cân tại A , biết điểm B có tung độ dương.
Giải:
+) Do A(0;3)  (E) ; B, C  (E) và A
BC cân tại A nên B, C đối xứng nhau qua trục hoành Ox
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan 2 x
Khi đó gọi B(x ; y )  C(x ;  y ) và 0 2
y  1 với x  3 0 0 0 0 0 9 0  2 2 BC  2 y  9  x  Gọi 0 0
H là trung điểm của BC H (x ; 0)  3 0 
AH  3  x  3  x 0 0 
+) Ta giác ABC vuông cân tại A nên: 1 1 2 12 9 3 2 AH
BC  3  x  .
9  x x  (do x  3 ) 2  y   y   0 0 0 2 2 3 5 0 0 0 25 5  12 3   12 3 
+) Do B có tung độ dường nên ta có: B ; và C ;  .      5 5   5 5  2 2 x y
Bài 25. Trong mặt phẳng tọa độ Oxy , cho (E) : 
 1. Tìm điểm M có hoành độ dượng thuộc (E)sao 25 9 cho  0
F MF  90 , trong đó F , F là các tiêu điểm. 1 2 1 2
Giải: 2 2 x ya  5 +) (E) :   1 2 2  
c a b  4 . 25 9 b  3  2 2  x y 0 0   1   +) Gọi 25 9
M (x ; y )  (E)  0 0  4 4
MF  5  x ; MF  5  x 1 0 2 0   5 5
Vì tam giác F MF vuông tại M nên : 1 2 2 2  4   4  175 81 2 2 2
MF MF F F 2  5  x  5  x  64  x  2  y  1 2 1 2  0   0  0 0  5   5  16 16  5 7 9   5 7 9 
+) Do M có hoành độ dường nên ta được: M  ;  hoặc M  ;   .  4 4      4 4   4
Bài 26. Trong mặt phẳng tọa độ Oxy , cho elip (E) có tâm sai e
, đường tròn ngoại tiếp hình chữ nhật cơ 5
sở của elip có phương trình 2 2
x y  34 . Viết phương trình chính tắc của elip và tìm tọa độ điểm M thuộc elip
(E) sao cho M nhìn hai tiêu điểm dưới một góc vuông và M có hoành độ dương.
Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) có dạng:  
1 với a b  1 2 2 a b
+) Vì đường tròn ngoại tiếp hình chữ nhật cơ sở có bán kính R  34 nên 2 2 a b  34 2 2  c a b 4 2 2 2 e    
25(a b)  16aa  5 Khi đó ta có hệ :       c  4 a a 5 2 2 
a b  34 b  3   2 2 a b  34  2 2 x y
Vậy phương trình chính tắc của elip (E) là:   1 25 9
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan 2 2  x y 0 0   1   +) Gọi 25 9
M (x ; y )  (E)  0 0  4 4
MF  5  x ; MF  5  x 1 0 2 0   5 5
Vì tam giác F MF vuông tại M nên : 1 2 2 2  4   4  175 81 2 2 2
MF MF F F 2  5  x  5  x  64  x  2  y  1 2 1 2  0   0  0 0  5   5  16 16  5 7 9   5 7 9 
+) Do M có hoành độ dường nên ta được: M  ;  hoặc M  ;   .  4 4      4 4   2 2 x y
Bài 27. Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : 3x y  4  0 và elip (E) :   1. Viết 9 4
phương trình đường thẳng  vuông góc với d và cắt (E) tại hai điểm ,
A B sao cho diện tích tam giác OAB bằng 3.
Giải:
+) Đường thẳng  vuông góc với đường thẳng d : 3x y  4  0 nên có dạng: x  3 y c  0
Khi đó phương trình hoành độ giao điểm của  và (E) là: 2 2 2 2
4x  (x c)  36  5x  2cx c  36  0 (*)
Ta có d cắt (E) tại hai điểm ,
A B khi và chỉ khi (*) có hai nghiệm phân biệt hay 2
 '  180  4c  0  3 5  c  3 5 (2*)  x c   x c
+) Đường thẳng  cắt (E) tại hai điểm phân biệt 1 2 A x ; , B x ;  1   2   3   3   2c x x   1 2   5
với x , x là nghiệm của (*) và . Khi đó: 1 2  2 c  36 x x  1 2   5 2  x x  10 10
AB   x x 2 2 1   x x  4 x x  720 16c 2 1    1 2  2 2 1 2  3  3 15 c 1 1 10 c d (O, )  , suy ra: 2 S  3  A .
B d (O, )  3  . 720 16c .  3 OAB 10 2 2 15 10 3 10 4 2
 16c  720c  8100  0  c   (thỏa mãn (2*)) 2
Vậy phương trình đường thẳng  cần lập là 2x  6 y  3 10  0 hoặc 2x  6 y  3 10  0 .
Bài 28. Trong mặt phẳng tọa độ Oxy , cho biết elip (E) có chu vi hình chữ nhật cơ sở bằng 16 2  3 , đồng  
thời một đỉnh của (E) tạo với hai tiêu điểm một tam giác đều. Viết phương trình đường tròn (T ) có tâm là gốc
tọa độ và cắt (E) tại bốn điểm là bốn đỉnh của một hình vuông.
Giải:
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan 2 2 x y
+) Gọi phương trình chính tắc của elip (E) có dạng: 
 1 với a b  0 2 2 a b
Ta có chu vi hình chữ nhật cơ sở là 4(a b)  16 2  3  a  4 2  3  b (1)    
+) Gọi M (0;b) là đỉnh của (E) mà MF F là tam giác đều, khi đó: 1 2 3F F b 1 2 MO
b  3c c  (2) 2 3 Mặt khác ta có : 2 2 2
a b c (3) 2 2 b
Thay (1), (2) vào (3) ta được: 2 4 2 3 b    b
b  4 3  a  8     3 2 2 x y
Vậy phương trình (E) :   1 64 48
+) Phương trình đường tròn (T ) có dạng: 2 2 2
x y R
Đường tròn (T ) cắt (E) tại bốn điểm phân biệt ,
A B, C, D .
Do (T ) và (E) đều nhận Ox, Oy làm các trục đối xứng nên ABCD là hình chữ nhật B( ; x y) Gọi ( A ; x y) 
C( ;xy) 
Khi đó hình chữ nhật ABCD thành hình vuông thì 2 2
AB BC  2x  2 y x y 2 2 2  2
x y RR 2 2  x y  2 2 x y    2 384
Do A  (T )  (E) nên x, y thỏa mãn: 2    1    R  2 2 64 48 R R 7     1 2 2 x y   2.64 2.48  384
Vậy phương trình đường tròn (T ) cần lập là 2 2 x y  . 7 2 2 x y
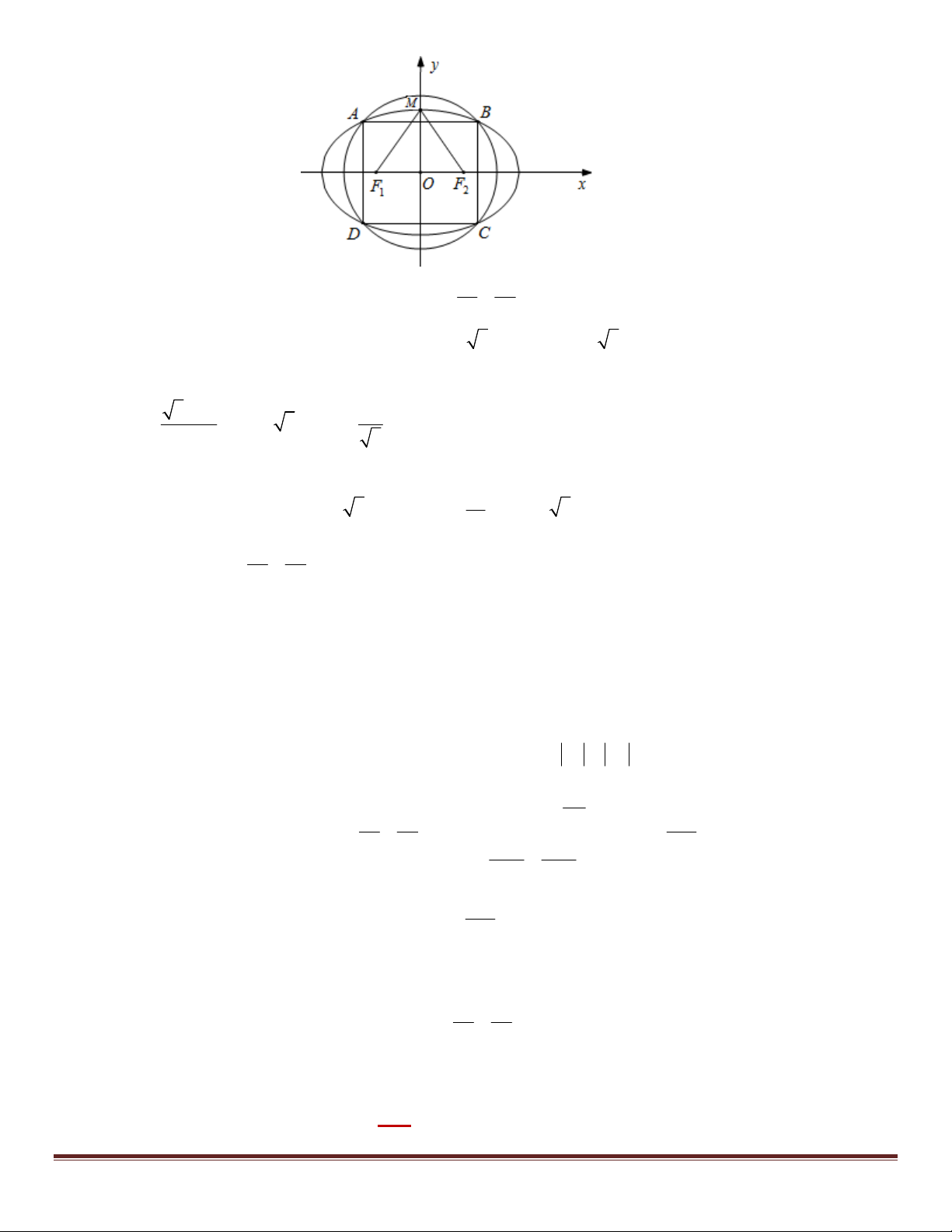
Bài 29. Trong mặt phẳng tọa độ Oxy , cho elip (E) : 
 1 và điểm M (2;1) . Viết phương trình đường 25 9
thẳng d đi qua M cắt (E) tại hai điểm ,
A B sao cho trung điểm của đoạn thẳng AB nằm trên đường thẳng
 : y  2x .
Giải:
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan 2 2 2 1 +) Do 
 1 nên M nằm trong (E) , suy ra mọi đường thẳng qua M đều cắt (E) tại hai điểm phân biệt 25 9
+) Nếu d đi qua M (1; 2) và song song với Ox hay d có phương trình x  1
thì trung điểm của AB là điểm I (1; 0) không thuộc đường thẳng y  2 x (loại)
Do đó gọi phương trình đường thẳng d đi qua M (2;1) có hệ số góc k có dạng: y k( x  2) 1 Khi đó tọa độ ,
A B là nghiệm của hệ:
y k (x  2) 1 
y kx  2k 1 2 2   x y  2 2 2   1
(25k  9)x  50k (2k 1)x  25(2k 1)  225  0 (*)    25 9 +) Gọi (
A x ; y ), B(x ; y ) . Ta có: 1 1 2 2  50k(2k 1) x x  1 2  2  25k  9
 25k (2k 1) 9 18k    I ;
: là trung điểm của AB  2 2  2(9 18k)  25k  9 25k  9   y y  1 2 2   25k  9  1  1 k d : y x 9 18k 50k(2k 1)  2    2
+) Khi đó I    
 (2k 1)(50k  9)  0     2 2 25k  9 25k  9 9 9 34 k    d : y   x   50  50 25 1 9 34
Vậy phương trình đường thẳng d cần lập là y
x hoặc y   x  . 2 50 25 2 2 x y
Bài 30. Trong mặt phẳng tọa độ Oxy , cho elip (E) : 
 1 ngoại tiếp tam giác đều ABC . Tính diện tích 16 4
tam giác ABC , biết (E) nhận A(0; 2) làm đỉnh và trục tung làm trục đối xứng.
Giải:
+) Do ABC là tam giác đều và (
A 0; 2) nên B, C đối xứng nhau qua trục tung
nên gọi B(x ; y )  C(x ; y ) với x  0 0 0 0 0 0
+) Độ dài tam giác đều ABC là a  2x và chiều cao h  2  y 0 0 a 3 Khi đó h
 2  y  3x y  2  3x B x ; 2  3x 0 0 0 0  0 0  2 2 3x x 2 2 0 16 3 x 0 16 3 +) Ta có 0 0 B  (E)    1  x    x  0 0 16 4 13 13  32 3 a  2x   0  16 3 22   1 768 3 13  B  ;      Sah   13 13 ABC  48 2 169  
h  2  y  0   13 768 3 Vậy S  . ABC 169
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan 2 2 x y
Bài 31. Trong mặt phẳng tọa độ Oxy , cho elip (E) : 
 1. Tìm các điểm M thuộc (E) sao cho 100 25  0
F MF  120 , trong đó F , F là hai tiêu điểm của (E) . 1 2 1 2
Giải: a  10 +) Elip (E) có 2 2   c
a b  5 3  F F  2c  10 3 . b  5 1 2  2 2  x y 0 0   1 (*) 1  00 25
+) Gọi M (x ; y )  (E)  0 0   c 3 c 3 MF a x  10  x ; MF a x  10  x 1 0 0 2 0 0   a 2 a 2 Khi đó ta có: 2 2 2 
F F MF MF  2MF .MF .cos F MF 1 2 1 2 1 2 1 2 2 2 2  3   3   3   3  0  10 3  10  x   10  x   210  x 10  x .cos120   0 0 0 0  2   2   2   2          3 3 2 2 2  300  200  x 100 
x x  0  x  0 0 0 0 0 2 4
+) Thay x  0 vào (*) ta được: 2
y  25  y  5  0 0 0
Vậy M (0;5) hoặc M (0; 5) .
Bài 32. Trong mặt phẳng tọa độ Oxy , cho đường thẳng  : x y  5  0 và hai elip có phương trình 2 2 x y 2 2 x y (E ) :   1 và (E ) : 
 1 ( a b  0 ). Biết hai elip này có cùng tiêu điểm và (E ) đi qua điểm M 1 25 16 2 2 2 a b 2
thuộc đường thẳng  . Tìm tọa độ điểm M sao cho elip (E ) có độ dài trục lớn nhỏ nhất. 2
Giải:
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan
+) Elip (E ) có hai tiêu điểm F (3;0), F (3; 0) . Dễ thấy F , F nằm cùng phía với  1 1 2 1 2
Vì M  (E ) và (E ) nhận F , F là hai tiêu điểm nên ta có: MF MF  2a 2 2 1 2 1 2
Khi đó elip (E ) có độ dài trục lớn nhỏ nhất khi và chỉ khi MF MF nhỏ nhất 2 1 2
+) Gọi N đối xứng với F ( 3
 ; 0) qua   N (5; 2) . Khi đó ta có phương trình NF là: x  4 y  3  0 1 2
+) Ta có MF MF MN MF NF  68 . Suy ra MF MF nhỏ nhất khi M   NF   1 2 2 2 1 2 2  17 x  
x  4 y  3  0   5  17 8 
Vậy tọa độ điểm M là nghiệm của hệ :     M  ;  
x y  5  0 8   5 5   y    5  17 8  Vậy M  ; .    5 5  2 2 x y
Bài 33. Trong mặt phẳng tọa độ Oxy , cho elip (E) :   1 và hai điểm (
A 3; 2), B(3; 2) . Tìm trên (E) 9 4
điểm C có tọa độ dương sao cho diện tích tam giác ABC lớn nhất. Giải:
+) Phương trình đường thẳng AB là: 2x  3y  0 2 2 x y
+) Gọi C(x ; y ) với x , y  0 . Do 0 0 C  (E)    1 0 0 0 0 9 4 1 1 2x  3y Khi đó 0 0 SA .
B d (C, AB)  . 52.
 2x  3y (1) ABC 0 0 2 2 13
Mặt khác theo Bất đẳng thức Bu – nha ta có: 2 2 2  x y   x y x y 2   2 2 1  1  0 0 0 0 0 0      
2  2x  3y  6 2 (2)     0 0 9 4    3 2  3 2
Từ (1) và (2) suy ra S  6 2 ABC 2 2  x y 0 0 1    3 2   9 4 x   3 2   3 2 
+) Dấu “=” xảy ra khi : 0    2  C  ; 2  . Vậy C  ; 2  . x y  2     2 0 0   y  2      0   3 2
Bài 34. Trong mặt phẳng tọa độ Oxy . Lập phương trình chính tắc của elip (E) , biết điểm M 1; 3 nhìn hai  
tiêu điểm của (E) dưới một góc vuông và hình chữ nhật cơ sở của (E) nội tiếp đường tròn có phương trình 2 2
x y  20 .
Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) là 
 1 với a b  0 2 2 a b 1 Do  0
F MF  90 nên OM F F 2 2
OM c  2  a b  4 (1) 1 2 1 2 2
+) Hình chữ nhật cơ sở của (E) nội tiếp đường tròn : 2 2 x y  20 2 2
a b  20 (2)
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan 2 2 x y Từ (1) và (2) suy ra 2 2
a  12;b  8. Vậy elip (E) cần lập là:   1 12 8 2 2 x y
Bài 35. Trong mặt phẳng tọa độ Oxy , cho elip (E) : 
 1 có hai tiêu điểm F , F . Tìm tọa độ điểm M 25 9 1 2 4
thuộc (E) sao cho bán kính đường tròn nội tiếp tam giác MF F bằng . 1 2 3
Giải: a  5 2 2 x y
MF MF F F +) Ta có (E) :   1 1 2 1 2  b   3  p   9 25 9 2  2 2 c a b  4  4 2.9. 1 2 pr Khi đó 3 Spr
d (M , Ox).F F d (M , Ox)    3  yy  3  MF F 1 2 M M 1 2 2 F F 8 1 2
+) Mặt khác M  (E)  x  0 . Vậy M (0;3) hoặc M (0; 3) . M
Bài 36. Trong mặt phẳng tọa độ Oxy , cho điểm M 2 3; 2 . Viết phương trình chính tắc của elip (E) đi qua  
điểm M , sao cho M nhìn hai tiêu điểm của (E) dưới một góc vuông.
Giải: 2 2 x y
+) Gọi phương trình chính tắc của elip (E) là 
 1 với a b  0 2 2 a b 12 4
Do M  (E)    1 (1) 2 2 a b 1 +) Mặt khác  0
F MF  90 nên OM
F F c c  4 2 2
a b  16 (2) 1 2 1 2 2 2 2 x y Từ (1) và (2) suy ra 2 2
a  24;b  8 . Vậy elip (E) cần lập là:   1. 24 8 2 x
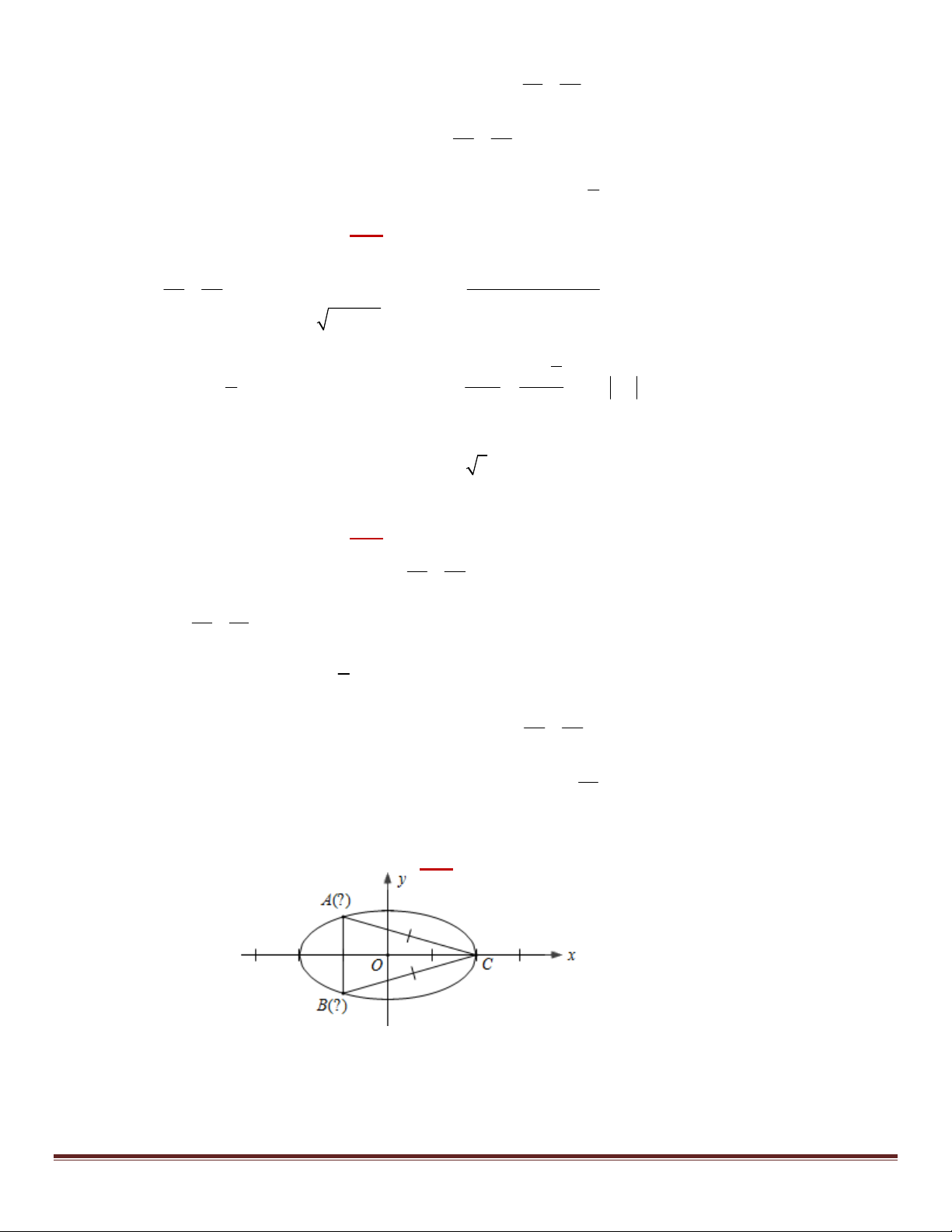
Bài 37. Trong mặt phẳng tọa độ Oxy , cho điểm C(2; 0) và elip 2 (E) :
y  1. Tìm các điểm , A B trên (E) 4
sao cho CA CB và tam giác CAB có diện tích lớn nhất.
Giải:
+) Theo giả thiết ta có C là đỉnh nằm trên trục lớn của elip (E) .
Do CA CB , suy ra ,
A B đối xứng nhau qua trục hoành
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !
GV: Nguyễn Thanh Tùng HOCMAI.VN
facebook.com/ ThayTungToan 2  x0 2   y  1 Gọi 0 (
A x ; y )  (E)   4 với x  ( 2  ; 2) 0 0 0
B(x ; y )  0 0 1 1 Khi đó S
d (C, AB).AB
2  x . 2 y  (2  x ) y ABC 0 0 0 0 2 2 2 3  x
(2  x ) (2  x ) 2 2 2 2 0 0 0  S
 (2  x ) .y  (2  x ) . 1  (1) ABC 0 0 0   4 4  
Mặt khác áp dụng BĐT Cauchy ta có: 3 2  x 2  x 2  x
(2  x ) .(2  x ) 0 0 0 0 0 3 4 4     2  x  4.
 (2  x ) .(2  x )  27 (2) 0 0 0 3 3 3 27 27 3 3 Từ (1) và (2) suy ra: 2 S   SABC 4 ABC 2   3   3   A 1;  , B  1;    2   2  2  x 3      Dấu “=” xảy ra khi
0  2  x  1  x  1  y    0 0 0 3 2   3   3   A1;  , B  1  ;    2   2        3   3   3   3  Vậy A 1  ;  , B  1  ;   hoặc A  1  ;   , B  1  ;  .  2   2          2 2    
CẢM ƠN CÁC BẠN ĐÃ QUAN TÂM !
GV: Nguyễn Thanh Tùng
Tham gia các khóa học môn Toán của Thầy Lê Anh Tuấn – Thầy Nguyễn Thanh Tùng trên HOCMAI.VN
tự tin chinh phục thành công kì thi THPTQG sắp tới !