

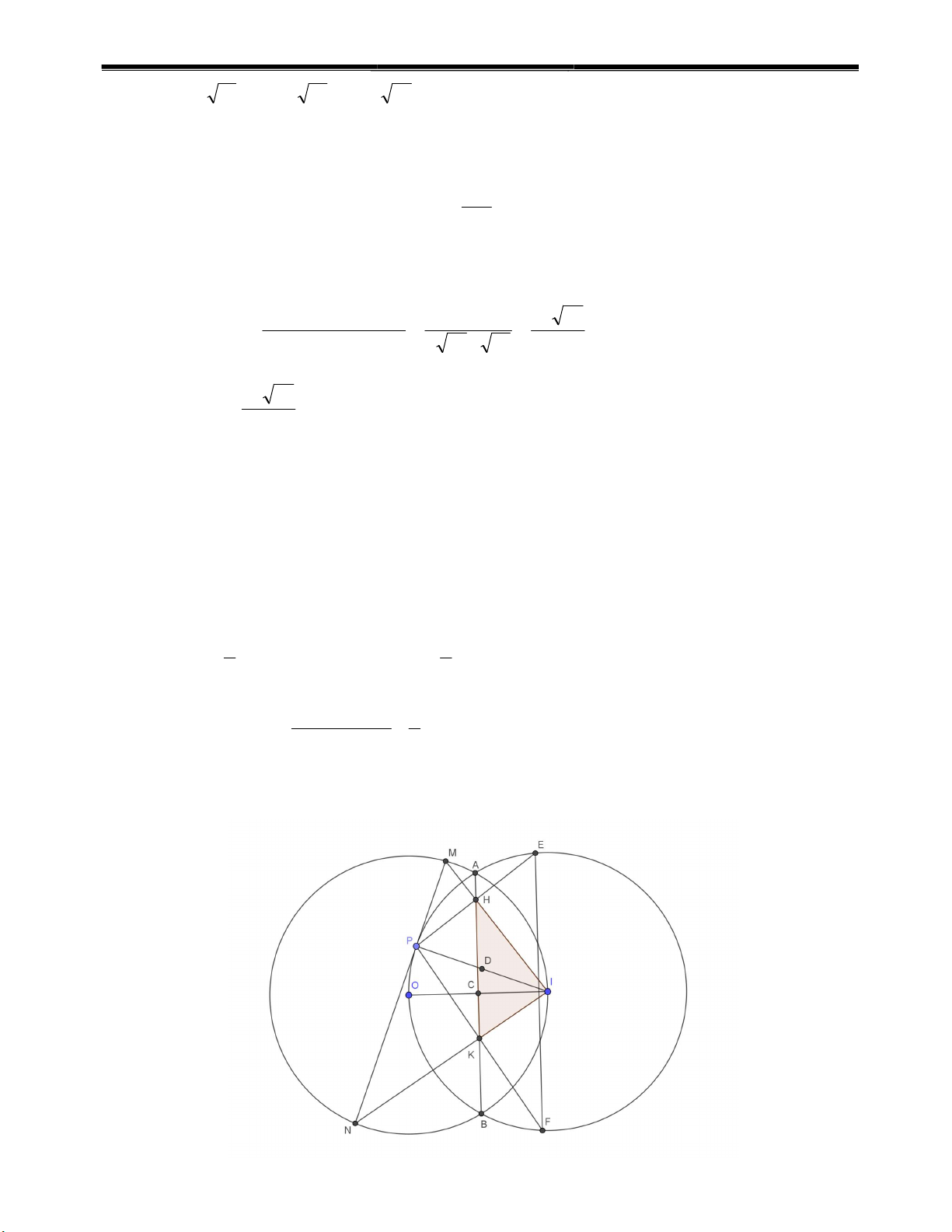

Preview text:
CLB Toán Cơ Sở
Đăng ký học Online Toán 6789 (Khá, Phòng Nội Dung
Chuyên, Nâng cao) qua Zalo: 0989.15.2268
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT HƯNG YÊN NĂM HỌC 2025-2026 Môn thi: TOÁN (CHUYÊN) ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút Câu I. (2,0 điểm) 1 3 x 10 x 4 x 4 Cho biểu thức M 2 . x 4
x x 2x 4 x 8 4 x
1) Tìm điều kiện xác định và rút gọn biểu thức M. 2) Đặt N M . 9
( x 2 x 4) . Tìm giá trị nhỏ nhất của biểu thức N. Câu II. (2,0 điểm)
1) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d) : y x m và parabol 2
(P) : y 2x . Tìm tất cả giá trị
của tham số m sao cho đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ x , x thỏa mãn 1 2 (2 2 x x m)2 (2 2 x x m)2 4 . 1 2 2 1 3 x 2 x 2 xy 2 (x 2 y )3
2) Giải hệ phương trình . 56 2 x 20( 2 x 2 y ) 3 4x 8 ( x ) 1 2 Câu III. (2,0 điểm)
1) Tìm tất cả nghiệm nguyên (x, y) của phương trình ( 2 x ) 3 2
y (x 2 y)(x 2y ) 1 25x 2y 169 .
2) Một thùng có 40 quả bóng có kích thước và khối lượng như nhau, trong đó có một số quả bóng màu đỏ,
một số quả bóng màu xanh, còn lại là những quả bóng màu khác. Lấy ngẫu nhiên một quả bóng trong thùng. 3 3
Xác suất để lấy được quả bóng màu đỏ là
, xác suất để lấy được quả bóng màu xanh là . Tìm số quả 10 8
bóng có màu khác màu đỏ và màu xanh.
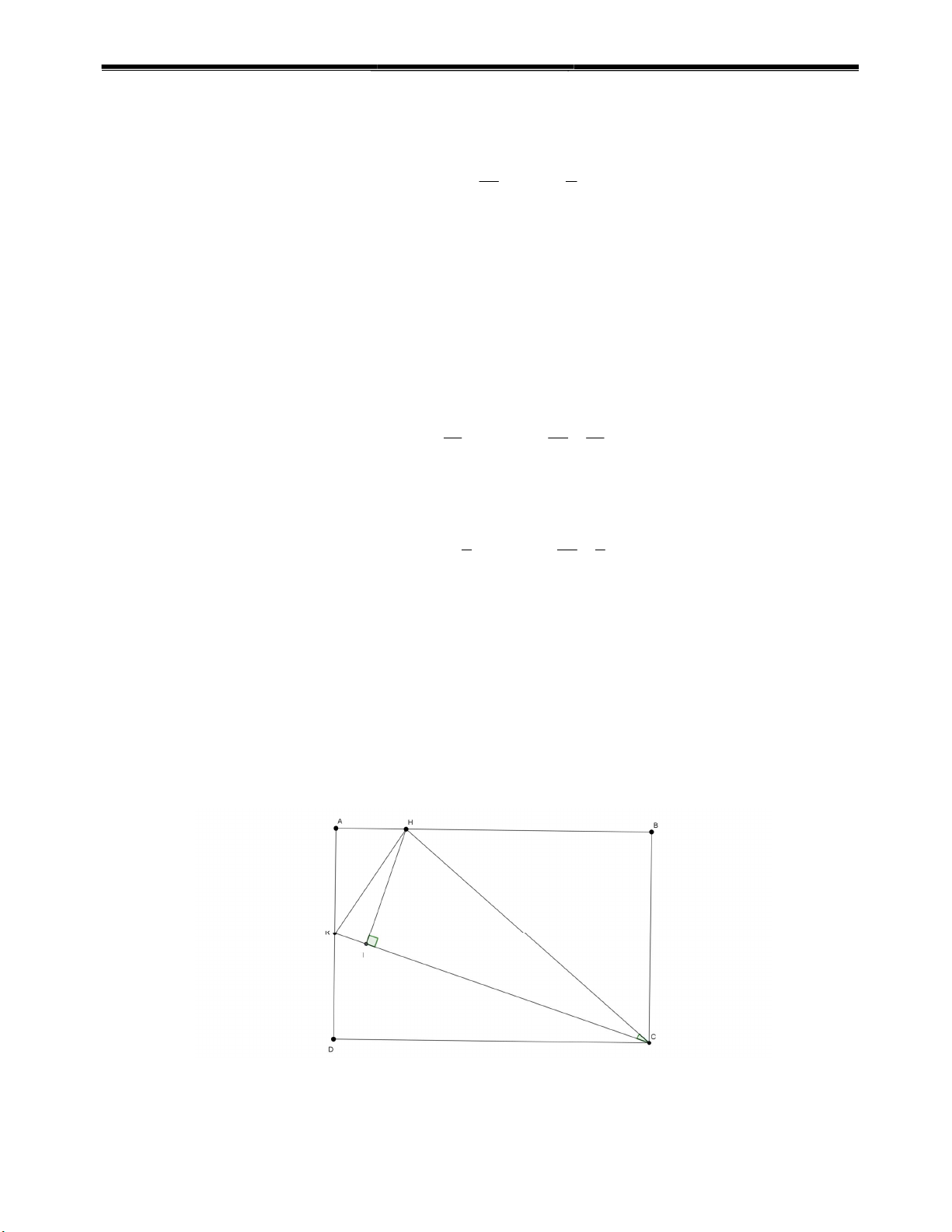
Câu IV. (1,0 điểm) Cho hình chữ nhật ABCD, có AB=9cm, BC = 6cm. Gọi K là trung điểm của AD. Trên
cạnh AB lấy điểm H sao cho AH = 2cm. Tính cos HCK .
Câu V. (2 điểm). Cho đường tròn (O; R) và điểm I cố định nằm trên đường tròn (O; R). Gọi A, B là các
giao điểm của hai đường tròn (O; R) và (I; R), P là điểm thay đổi trên cung nhỏ đã của đường tròn (I; R).
Đường thẳng qua P và vuông góc với IP cắt đường tròn (O; R) tại M, N. Kè PH vuông góc với IM tại H, PK vuông góc với IN tại K.
1) Chứng minh rằng bốn điểm I, H, P, K cũng thuộc một đường tròn và HK vuông góc với OI.
2) Khi P thay đổi trên cung nhỏ AB của đường tròn (I; R), tìm giá trị lớn nhất của diện tích tam giác IHK.
Câu VI (1,0 điểm) Cho các số thực dương x, y, z. Tìm giá trị nhỏ nhất của biểu thức 2x2 2xy y2 2y2 2yz z2 2z2 2zx x2 P . x 2y y 2z z 2x -----HẾT----- 1 CLB Toán Cơ Sở
Đăng ký học Online Toán 6789 (Khá, Phòng Nội Dung
Chuyên, Nâng cao) qua Zalo: 0989.15.2268
HƯỚNG DẪN GIẢI ĐỀ THI CHUYÊN TOÁN TỈNH HƯNG YÊN 2025 Câu I. x 4 0 x 4
a. Điều kiện xác định: x x 2x 4 x 8 0 (
x 4)( x 2) 0 x , 0 x 4. x , 0 x 0 x 0 Ta có: 1 3 x 10 x 4 x 4 M 2
x 4 x x 2x 4 x 8 4 x x 2 3 x 10 x 4 x 4
(x 4)( x 2) (x 4)( x 2) 4 x 4 x 8 ( x 2)2 1 . . ( x 2)2 ( x 2) 4 x x 1 Vậy M , x , 4 x 0. x 9x 2 x 4 4 2 2 b. Ta có: N M . 9 ( x 2 x ) 4 9 x 2 34 x 10 1 . 0 4 x x x Như vậy min N 1 .
0 Dấu bằng xảy ra khi và chỉ khi 2 2 4 34 x x x . 4 x 3 9 Câu II.
a. Giả sử (d) cắt (P) tại hai điểm phân biệt. Khi đó phương trình hoành độ x2 2 x m có hai nghiệm phân biệt x , x . 1 2 Ta có: 2 2
x x m 0 có hai nghiệm phân biệt x , x khi 1 8m . 0 1 2 Khi đó: 2 2 x x m 0 2 2
x x m x x . Tương tự 2 2 x x m x x . 1 1 1 2 1 2 2 1 2 1 1 m
Theo định lý Viet thì x x , x x . 1 2 2 1 2 2 Như vậy 4 (2 2 x x m)2 (2 2
x x m)2 (x x )2 (x x )2 (x x )2 2. 1 2 2 1 1 2 2 1 1 2 2 1 7
Hay là: 2 (x x ) 4x x 2m m . Thử lại ta thấy thoả mãn. 1 2 1 2 4 8 2 CLB Toán Cơ Sở
Đăng ký học Online Toán 6789 (Khá, Phòng Nội Dung
Chuyên, Nâng cao) qua Zalo: 0989.15.2268 7
Vậy m là giá trị cần tìm thoả mãn yêu cầu bài toán. 8 b. Điều kiện: 2 x y . 0 Ta có: Đặt 2
a x y 0 . Từ (1) khi đó 3 x x( 2 x y ) 2 ( 2 x y )3 0 3 2 x ax 2 3 a 0 (x a)( 2 x 2ax 2 2 a ) 0. Mà 2 x 2ax 2 2 a (x a)2 2 a . 0 Suy ra 2
x a x x y , x . 0 (*)
Ta bình phương hai vế (*) lên ta có: 2 2
y x x . Thay vào (2) thì 56 2 x 2 ( 0 2 2 x x x ) 4x 8 ( x ) 1 2 96 2 3 x 20x 2 3 4x 8 ( x ) 1 . Ta có: 63 4x 8 ( x ) 1 33 . 2 16 . x 8 ( x ) 1 24x . 3 Và 6. 9 ( 6 2 x 20x ) 2 5 ( 76 2 x 144x ) 9 24x 3 (24x )
3 2 24x 3 24x 3. Như vậy 2 3 96x 20x 2 4x 8 ( x )
1 , đẳng thức xảy ra khi và chỉ khi 1
2 16x 8x 1 x . (tm) 8 1 7 1 7 2 2 7 7 Suy ra y x x y . Thử lại các cặp , , , đều thoả mãn. 64 8 8 8 8 8 1 7 1 7
Vậy hệ phương trình có các nghiệm là: , , , . 8 8 8 8 Câu III.
1. Giả sử phương trình ( 2 x ) 3 2
y (x 2y)(x 2 y )
1 25x 2y 169(*) có nghiệm nguyên. Ta có
phương trình (*) tương đương 2 2 x y 7 2 2
y x x 2y 25x 2y 169 ( 2 x 7) 2 2
y x 26x 169 (x 1 ) 3 2. Như vậy 2
x 7 là số chính phương. Đặt x2 7 z2, z là số nguyên dương.
Khi đó 7 (z x)(z x). Do z x z x 2z 0. Ta xét hai trường hợp: 3 CLB Toán Cơ Sở
Đăng ký học Online Toán 6789 (Khá, Phòng Nội Dung
Chuyên, Nâng cao) qua Zalo: 0989.15.2268 z x 1 x 3 Trường hợp 1: . Suy ra 2 y 16 y 4 . z x 7 z 4 z x 7 x 3 2 25 5 Trường hợp 2: . Suy ra y y . (loại) z x 1 z 4 4 2
Như vậy phương trình (*) có các nghiệm (x, y) thoả mãn là , 3 ( 4), , 3 ( 4 ).
2. Gọi số quả bóng có màu đỏ, màu xanh trong thùng lần lượt là: x, . y
Số cách lấy ngẫu nhiên một quả bóng từ trong thùng là 40 (cách).
Số cách để lấy được một quả bóng màu đỏ là: x (cách). 3 x 3
Vì xác suất để lấy được quả bóng màu đỏ là . Như vậy x 12. 10 40 10
Số cách để lấy được một quả bóng màu xanh là: y (cách). 3 y 3
Vì xác suất để lấy được quả bóng màu xanh là . Như vậy x 15. 8 40 8
Do đó số quả bóng có màu khác trong thùng là 40 - 12 - 15 = 13.
Vậy số quả bóng có màu khác xanh và đỏ là 13 (quả). Câu IV.
Kẻ đường cao HI của tam giác HKC. Do K là trung điểm AD nên AK = KD = 3 (cm). Ta có:
BH AB AH 9 2 7(cm).
Áp dụng định lý Pitago cho các tam giác vuông KAH, BHC, KDC thì 2 2 2 KH AH AK 1 , 3 2 2 2 KC KD DC 9 , 0 2 2 2 HC HB BC 85. 4 CLB Toán Cơ Sở
Đăng ký học Online Toán 6789 (Khá, Phòng Nội Dung
Chuyên, Nâng cao) qua Zalo: 0989.15.2268
Suy ra KH 13, KC 3 10, HC 85(cm). Ta có: 2 2 2 2 2
KH HI KI HC IC (KC IC)2 2 2 HC KC 2KC.IC. IC
Mà tam giác HIC vuông tại I nên cos H CK IC HC.cos HCK. HC Như vậy 2 2 2
KH HC KC 2KC.HC.cos H CK. 2 2 2 HC KC KH 85 90 13 27 34 Do đó: cosHCK . 2KC.HC 2 85 3 . 10 170 27 34 Vậy cosHCK . 170 Câu V.
1) Gọi C là giao điểm của OI và HK, và D là trung điểm của IP.
Do tam giác IPK vuông tại K và tam giác IPH vuông tại H nên DK = DP = DI = DH.
Như vậy bốn điểm P, K, I, H thuộc cùng một đường tròn. 1 1 Ta có: I KH I DH HPI P MI NOI. 2 2 180 NOI 1 Suy ra CIH IKH NOI 90 . 2 2
Vậy HK vuông góc OI tại C. 5 CLB Toán Cơ Sở
Đăng ký học Online Toán 6789 (Khá, Phòng Nội Dung
Chuyên, Nâng cao) qua Zalo: 0989.15.2268
2) Ta gọi giao của PH, PK với (I,R) lần lượt là E, F.
Do tam giác IPE cân tại I có IH vuông góc EP nên H là trung điểm PE.
Giả sử AH cắt (O,R) tại B’ thì H . A HB' HM. 2 HI HP H . P H . E
Như vậy tứ giác APB’E nội tiếp. Hay B’ thuộc (I,R) nên B’ trùng B.
Do đó H thuộc AB, tương tự thì K cũng thuộc AB.
Như vậy A,H,K,B thẳng hàng.
Ta có AO = AI, BO = BI nên AB là đường trung trực của OI nên C là trung điểm OI. 1 1 2 R R Ta có: S IC.HK .I . O HK .IP
(do IP là đường kính của đường tròn (D, DI)) HIK 2 4 4 4 1
Dấu bằng xảy ra khi và chi khi R IP HK EF. Tức là EF là đường kính của (I,R). Hay P 2 trùng với O. 2 R Vậy GTLN của S là khi P trùng với O. HIK 4 Câu VI. C S Ta có: ( 5 2 2 x 2 2
xy y ) 22 12 (x y)2 2
x 2(x y) x2 (3x 2y)2. x y 2 2 x 2 2 xy y x y x 2 2 3 ( 2 )2 Suy ra 3 2 1 2 (x y) x hay 1 . 5 x 2 y 5(x 2 y) 5 x 2 y
Chứng minh tương tự ta cũng có: 2 2 y 2 2 yz z 1 2y 2 2 z 2 2 zx x 1 2z 1 , 1 . y 2z 5 y 2 z z 2x 5 z 2x
Khi đó ta cộng vế theo vế và áp dụng bất đẳng thức cộng mẫu thì 3 2 x y z 3 2 2 2 2 x y z P 5
5 x 2y y 2z z 2 x 5 5 2 x 2 2 xy y 2 2 yz z 2 zx 3 2 (x y z)2 3 2 . 5. 5 5 2 2 2
x y z 2xy 2 yz 2zx 5 5
Vậy min P 5. Dấu bằng xảy ra khi và chi khi x = y = z. 6


