GI¶i ®Ò thi CKC F1_§H GTVT HN ĐỀ SỐ 12
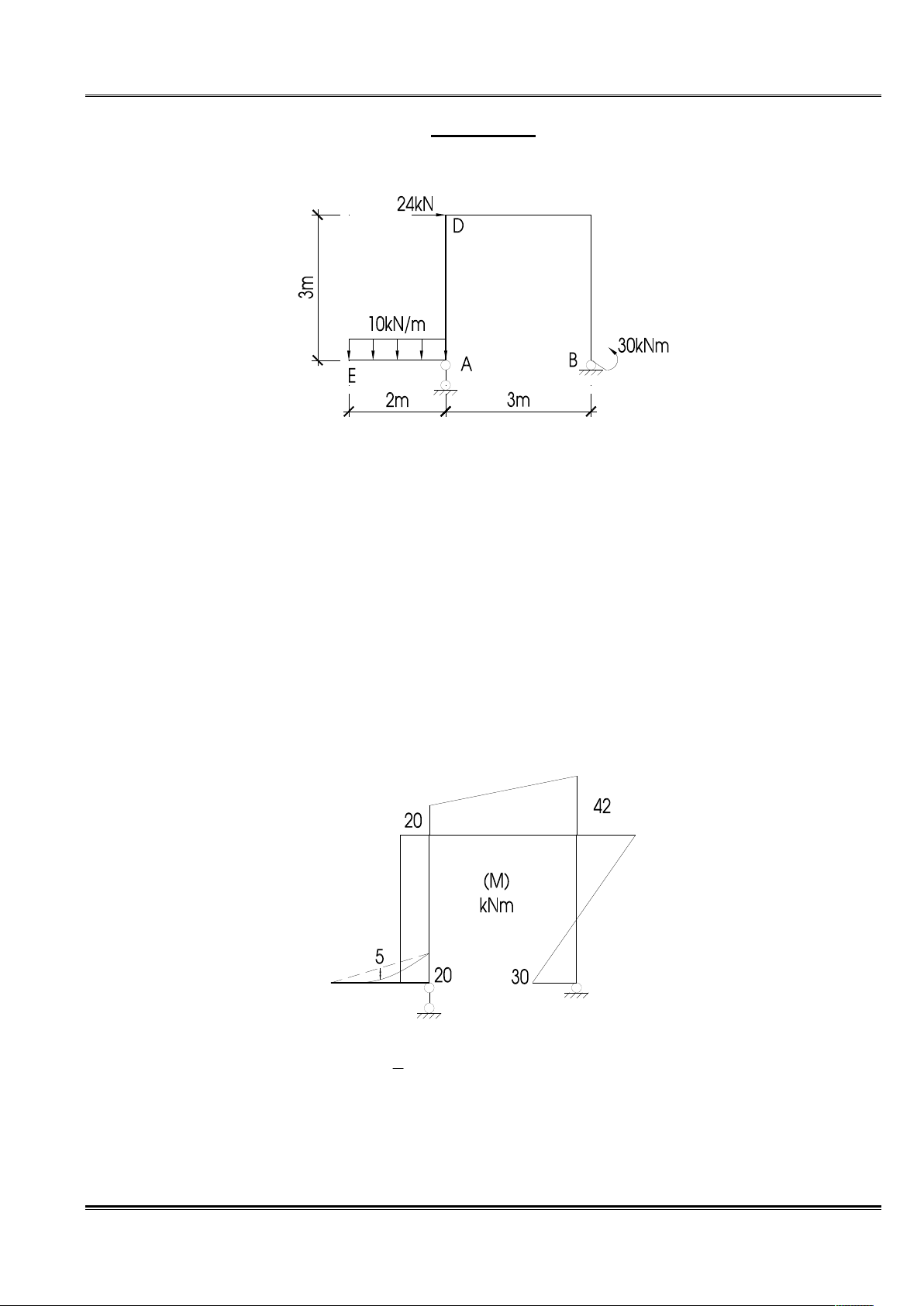
Câu 1. Cho EJ = Const, tính chuyển vị thẳng đứng tại E và chuyển vị góc xoay tại D.
Tổng hình chiếu theo phương ngang ta có HB = 24 kN, tổng mômen tại A ta được RB = 22/3 kN.
Lúc này ta vẽ ngay được biểu đồ mômen bằng cách nhận xét.
 Đoạn BC – biểu đồ có dạng đường xiên, tại gối B do có mômen tập trung nên MB = 30 kN.m
(Căng trái), tại C ta có MC = 24.3 – 30 = 42 kNm (Căng phải).
 Đoạn CD – biểu đồ có dạng đường xiên, tại C xét cân bằng nút C ta có MC = 42 kNm (căng
trên), tại D ta có MD = (22/3).3 + 30 – 24.3 = - 20 kNm (Căng trên).
 Đoạn EA – biểu đồ có dạng đường cong bậc hai, tại E có ME = 0, tại gối A ta có MA = -10.22/2
= - 20 kNm (Căng trên). Tung độ treo = 10.22/8 = 5 kNm.
 Đoạn AD – biểu đồ có dạng đường thẳng song song với đường chuẩn, tại gối A xét cân bằng
nút ta có MA = 20 kNm (Căng trái), tại D xét cân bằng nút D ta có MD = 20 kN (Căng trái).
Vậy ta vẽ được biểu đồ mômen như sau:
1. Tính chuyển vị thẳng đứng tại E.
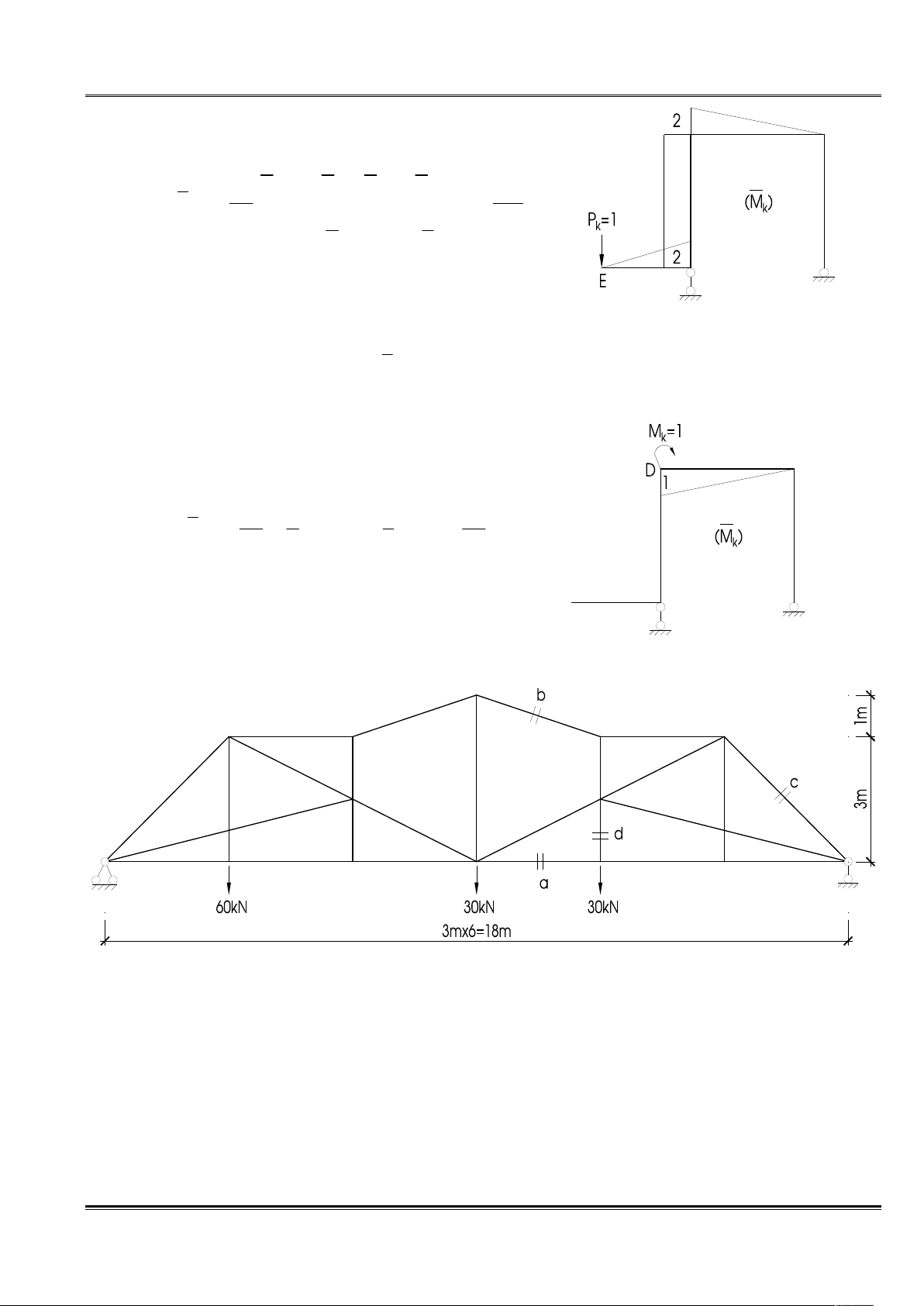
Ta lập trạng thái “k” và vẽ biểu đồ M do tải trọng đơn vị P k
k = 1 đặt tại E theo phương thẳng đứng.
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN 1 2 2 1   .20.2. .2 - .5.2. .2  1 2 3 3 2  143 y = M M =   = E   k EJ  1  1    EJ
+20.2 + .2.3.20 + .22  2  3   
2. Tính chuyển vị góc xoay tại D.
Ta lập trạng thái “k” và vẽ biểu đồ M do tải trọng đơn vị M k
k = 1 đặt tại D theo chiều kim đồng hồ. 1  1  1  41 φ = M M =
 .1.3.20 + .22 = - D
  k EJ  2  3  EJ  
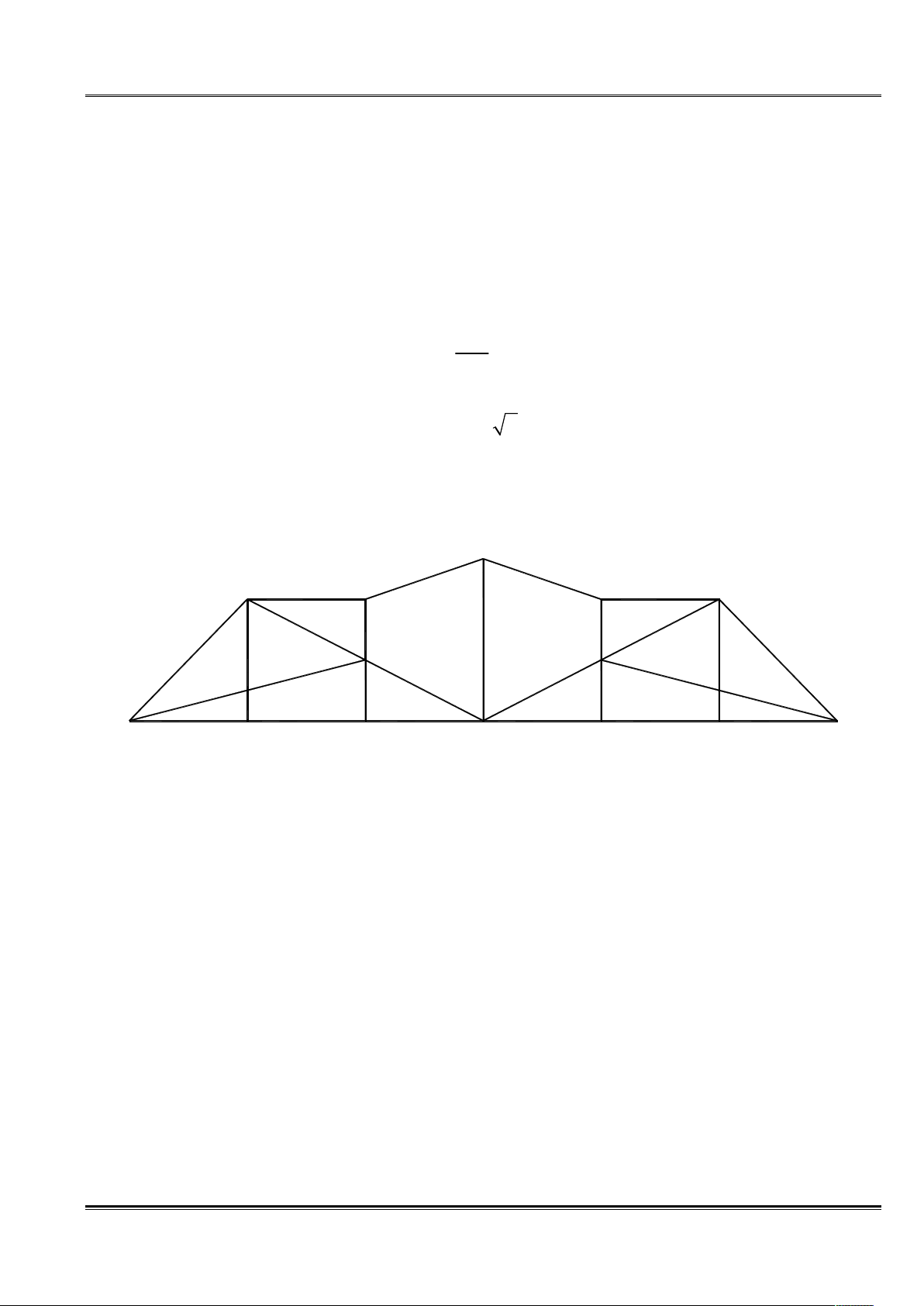
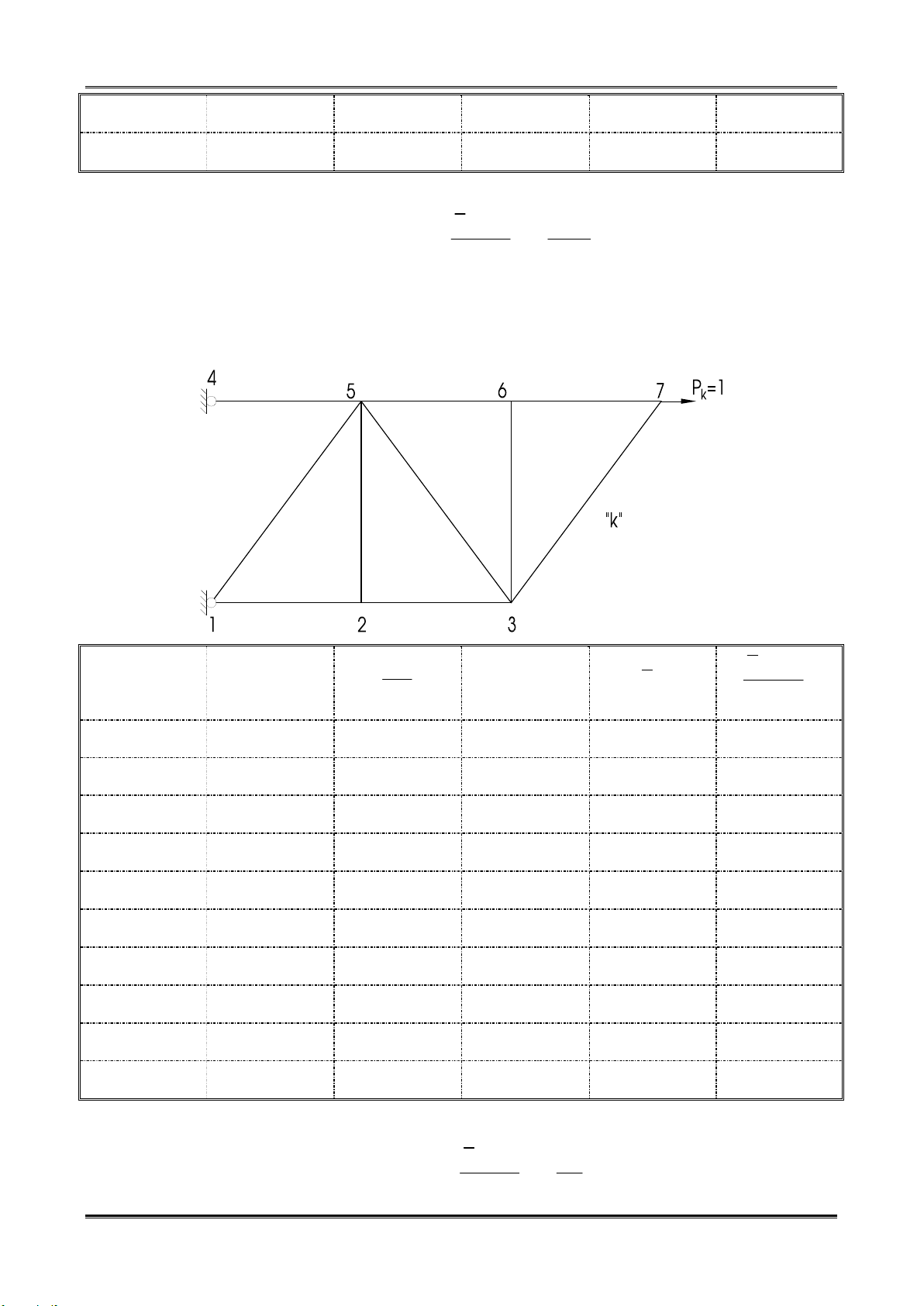
Câu 2. Thanh a, c – giải tích; b, d – đah.
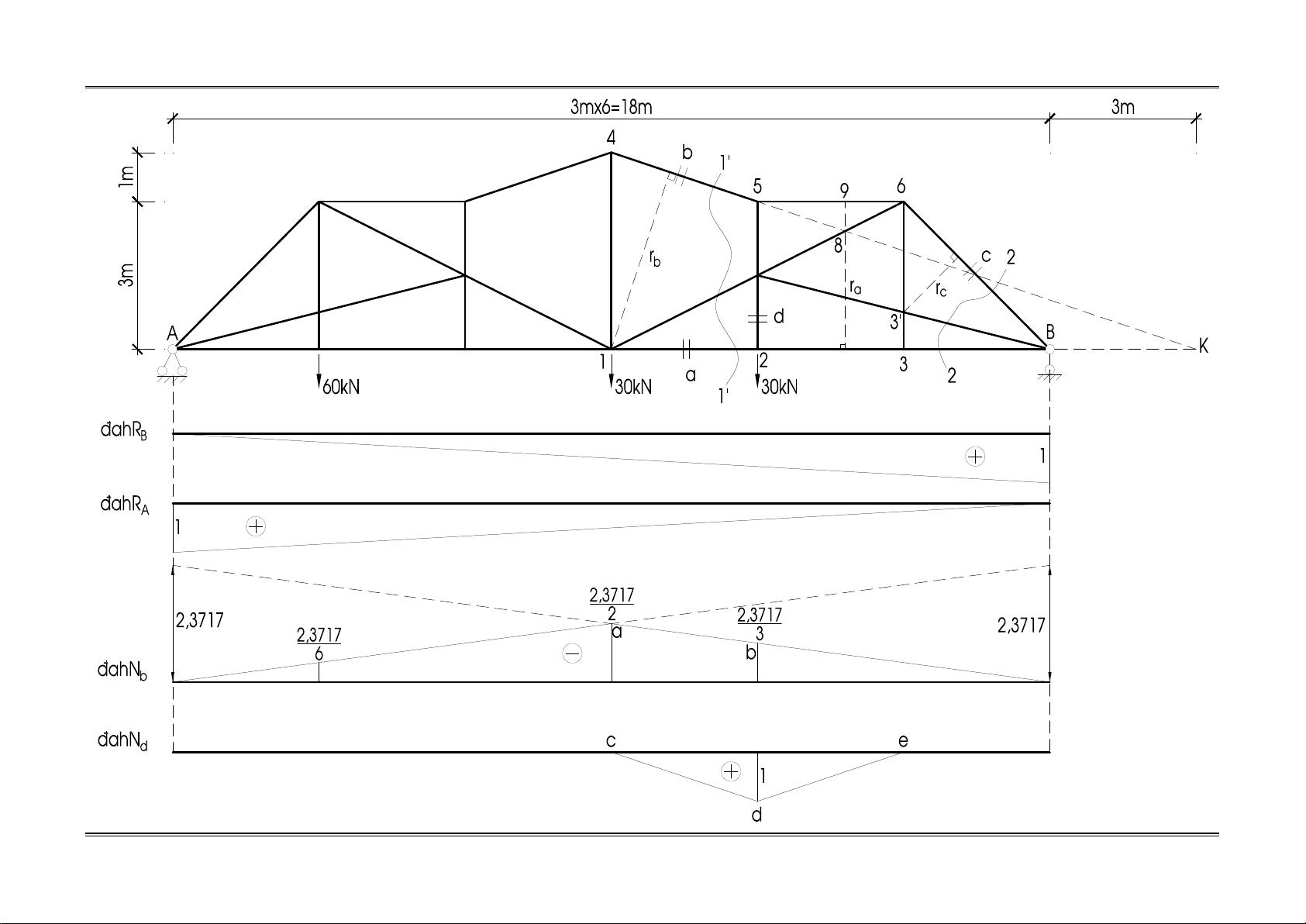
Xác định phản lực gối
M = 0 R .3.6-60.3-30.3.3-30.3.4 = 0 R = 45 kN A B B  Y = 0  R = 75 kN A
1. Tính thanh a – giải tích.
Ta dùng mặt cắt 1’-1’ xét cân bằng phần bên phải và lấy mômen tại điểm 8, ta có:
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN MPh¶i 405  6  8 = 0 N .r - 30.59 - 45. 59 = 0 N = kN a a   a 4 9 r 6 3    59 89  a Víi 
 59 1,8m  89  0,6m  r  2, 4m a 3 9    96 3- 59 
XÐt tû sè ®ång d¹ng trong  567 ta cã 89 = =       2 2 
2. Tính thanh c – giải tích
Ta thấy lực trong thanh 2-3 = nội lực trong thanh 3-B và bằng nội lực thanh a = 405 kN . 4
Ta dùng mặt cắt 2-2, xét cân bằng phần bên phải ta có: MPh¶i 405  .3  37,12 3' = 0 N .r - 0,75 + 45 = 0 N = kN c c a 4     2 2  o  o Víi r  3'B.sin3'B6 = 3 + 0 0,75 ,75 .sin45 - arctan = 14 2'    = 1,5911m c   3    3. Thanh b – đah.
Ta vẽ ngay đah 2 phản lực gối như trên hình vẽ. Ta dùng mặt cắt 1’-1’
Nếu P = 1 di động bên trái mặt cắt, ta xét cân bằng phần bên phải, ta có: Ph¶i -9 M   ® ® ® 1 = 0 N .r + R .9 = 0 ahN = ahR = -2,3717 ahR b b B b B B rb  3  o o
Víi tan1K4= 1K4 18 26'  r  12sin18 26'  3,794733m. b 9
Nếu P = 1 di động bên phải mặt cắt, ta xét cân bằng phần bên trái, ta có: Tr¸i -9 M   ® ® ® 1 = 0 N .r + R .9 = 0 ahN = ahR = -2,3717 ahR b b A b A A rb  3  o o
Víi tan1K4= 1K4 18 26'  r  12sin18 26'  3,794733m. b 9
Nếu P = 1 di động trong khoang bị cắt 1-2, thì theo nguyên tắc của hệ thống truyền lực ta có
đường nối ab như hình vẽ.
Từ đah ta có nội lực trong thanh c được xác định: 2,3717 2,3717 2,3717 N = - .60 - .30 - .30 = -83,0095kN b 6 2 3 4. Thanh d – đah.
Ta dùng mặt cắt kín đi qua nút 2:
Nếu P = 1 đặt tại nút 2 thì ta có Nd = 1.
Nếu P = 1 di động ngoài khoang bị cắt thì ta có Nd = 0.
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN
Nếu P = 1 di động trong khoang bị cắt 1-2, thì theo nguyên tắc của hệ thống truyền lực ta có
đường nối cd như hình vẽ.
Nếu P = 1 di động trong khoang bị cắt 2-3, thì theo nguyên tắc của hệ thống truyền lực ta có
đường nối de như hình vẽ.
Từ đah ta có nội lực trong thanh d được xác định: N = 1.30 = 30kN d
Kết luận: Vậy nội lực trong các thanh là. N = 405 kN a 4 N = -83,0095kN b N  35 2 kN c N = 30kN d
“Kết quả chạy bằng Midas Civil 2011” -83. -83.0 0 -78.7 -78.7 14.0 58.7 -26.2 - -26.3 3 52.5 7 60.0 0.0 . - 1 -93.7 77 -36.1 . 3 - 25.2 -25.2 -7 0.0 7 -36.1 .3 101.2 101.2 101.2 101.2 30.0 101.2 0.0 101.2 60.0
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN ĐỀ SỐ 15 Câu 1. Tính và vẽ M.
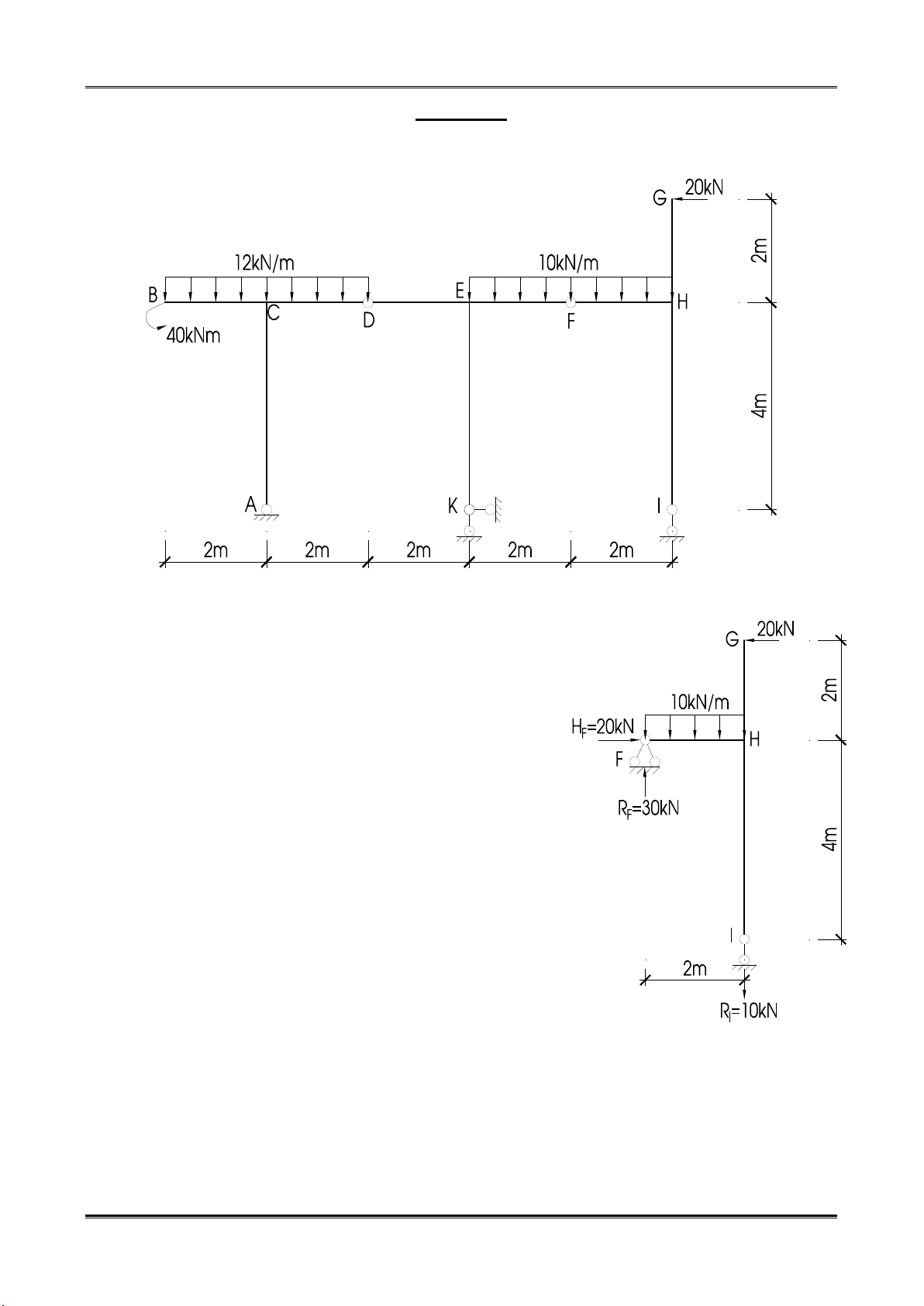
1. Xét phần kết cấu phụ thuộc FGHI
Tổng mômen tại F ta có RI.2 – 20.2 – 10.2.1 = 0 → RI = 30 kN.
Tổng hình chiếu theo phương đứng ta có RF = 40 kN.
Tổng hình chiếu theo phương ngang ta có HF = 20 kN.
 Đoạn GH – biểu đồ mômen có dạng đường xiên,
MG = 0, MH(GH) = 20.2 = 40 kNm (Căng phải)
 Đoạn IH – không có mômen.
 Đoạn FH – biểu đồ có dạng đường cong bậc 2, mômen
tại khớp F MF =0. Tại H ta xét cân bằng nút H ta có
MH(HF) = 40 kNm (Căng dưới), tung độ treo = 10.22/8 = 5 kNm.
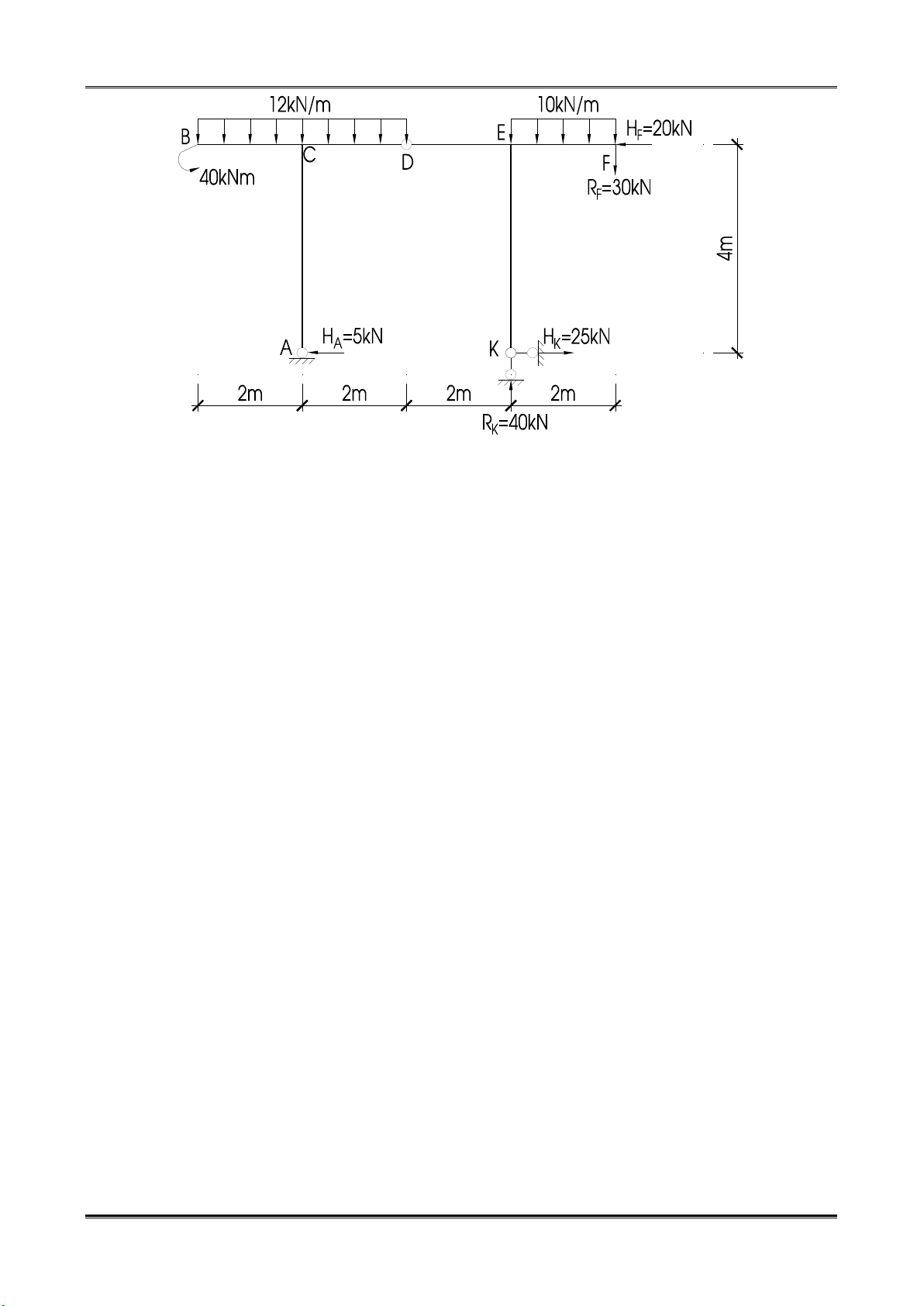
2. Xét phần kết cấu cơ bản ABCDEFK.
Tổng mômen tại A ta có RK.4 + 20.4 + 40 – 30.6 – 10.2.5 = 0 → RK = 40 kN.
Dùng mặt cắt qua khớp D, lấy tổng mômen tại DPhải = 0 → HK.4 + 40.2 – 30.4 – 10.2.3 = 0 → HK = 25 kN.
Tổng hình chiếu theo phương ngang ta có HA = 5 kN.
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN
 Đoạn EF – biểu đồ mômen có dạng đường cong bậc hai, mômen tại khớp F có MF = 0,
mômen tại E ME(EF) = –30.2 – 10.2.1 = - 80 kNm (Căng trên). Tung độ treo = 10.22/8 = 5 kNm.
 Đoạn KE – biểu đồ mômen có dạng đường xiên, mômen tại gối K có MK = 0, mômen tại
E ME(KE) = 25.4 = 100 kNm (Căng trái).
 Đoạn DE – biểu đồ mômen có dạng đường xiên, tại khớp D có MD = 0, tại E ta xét cân
bằng nút E ta có ME(DE) = 100 – 80 = 20 kNm (Căng dưới).
 Đoạn BC – biểu đồ mômen có dạng đường cong bậc hai, tại B có MB = -40 kNm (Căng
trên), tại C ta có MC(BC) = -40 – 12.22/2 = -64 kNm (Căng trên). Tung độ treo = 12.22/8 = 6 kNm.
 Đoạn AC – biểu đồ mômen có dạng đường xiên, tại gối A có MA = 0, tại C ta có MC(AC) = 5.4 = 20 kNm (Căng phải).
 Đoạn CD – biểu đồ mômen có dạng đường cong bậc hai, mômen tại khớp D có MD = 0,
xét cân bằng nút C ta có mômen tại C MC(CD) = 64 – 20 = 44 kNm (Căng trên). Tung độ treo = 12.22/8 = 6 kNm.
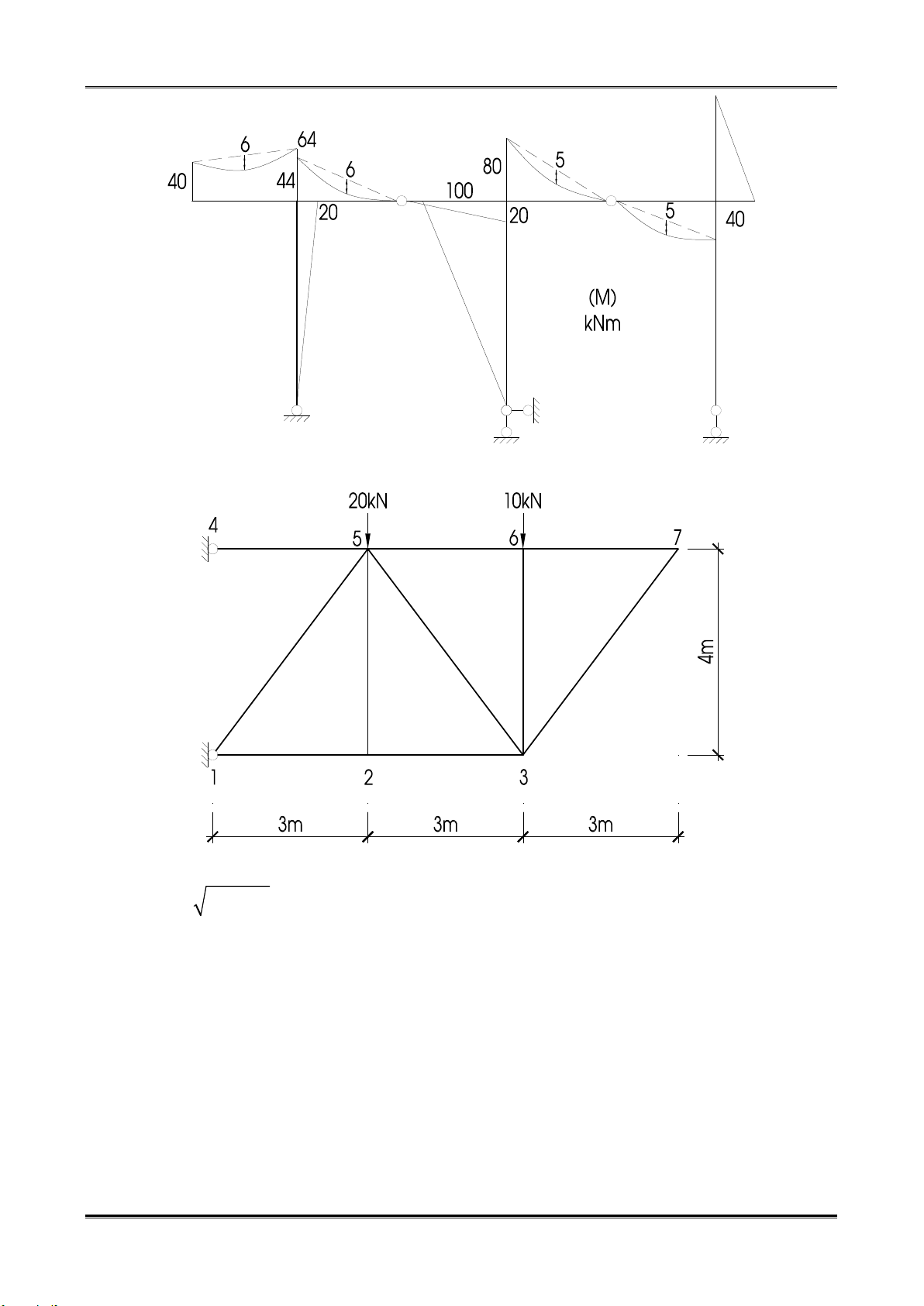
Vậy ta vẽ được biểu đồ mômen như sau:
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN
Câu 2. Tính chuyển vị toàn phần tại 7, EF = Const.
Gọi y7 là chuyển vị thẳng đứng tại 7 và x7 là chuyển vị ngang tại 7→ Chuyển vị toàn phần tại 7 là Δ = 2 x  2 y 7 7 7
1. Xác định chuyển vị thẳng đứng tại điểm 7
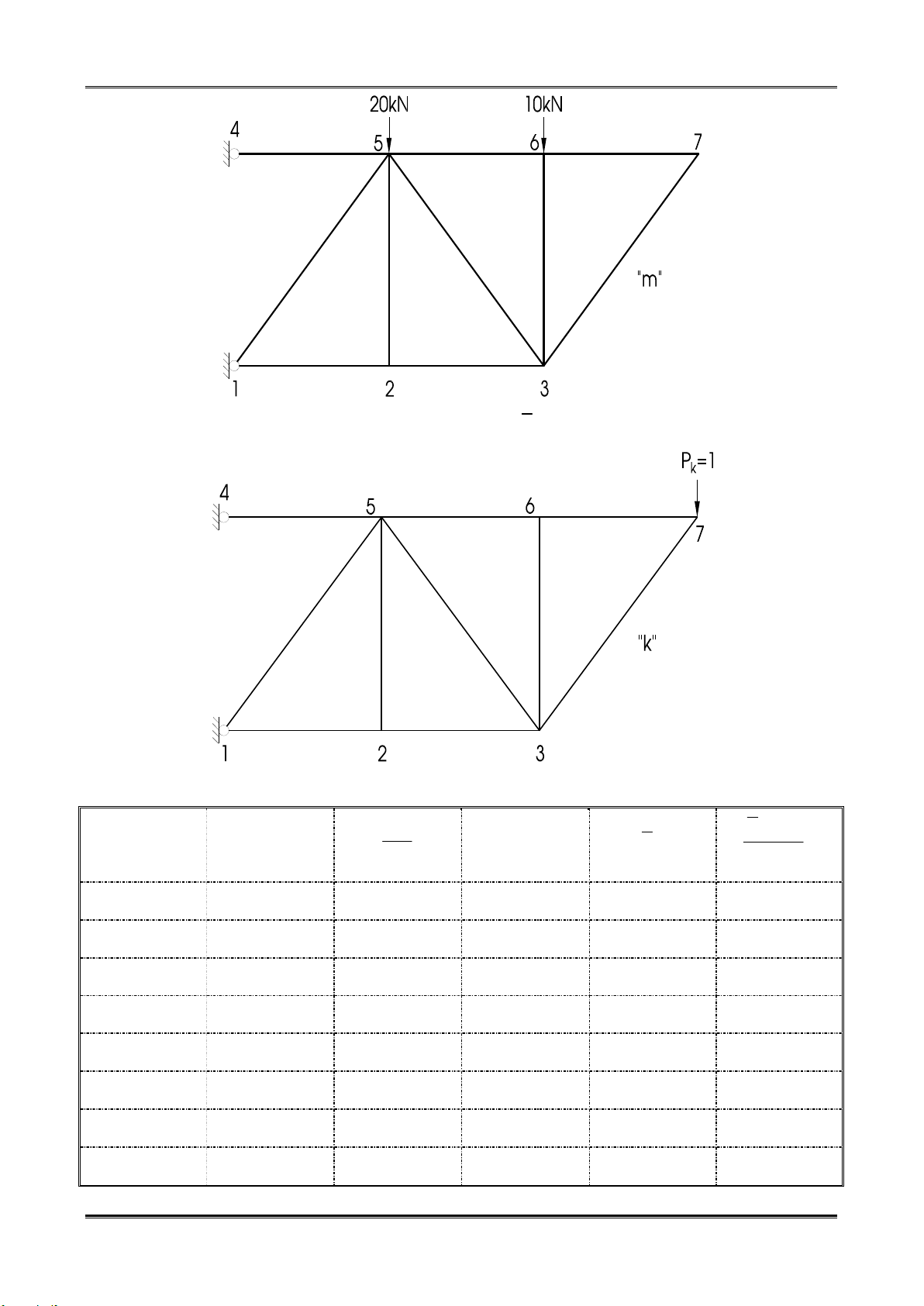
Trạng thái “m” do tải trọng, ta xác định Nim ( Thống kê trong bảng)
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN
Trạng thái “k” do tải trọng đơn vị Pk = 1, ta xác định N ( Thống kê trong bảng). ik
Kết quả tính toán được thống kê trong bảng sau: 1 N N Thanh l i (m) l EF Nim N ik im ik i EF i i 1-2 3 1/EF -30/4 -6/4 33,75/EF 1-5 5 1/EF -75/2 -5/4 234,375/EF 2-3 3 1/EF -30/4 -6/4 33,75/EF 2-5 4 1/EF 0 0 0 3-5 5 1/EF 50/4 5/4 78,125/EF 3-6 4 1/EF -10 0 0 3-7 5 1/EF 0 -5/4 0 4-5 3 1/EF 30 9/4 202,5/EF
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN 5-6 3 1/EF 0 3/4 0 6-7 3 1/EF 0 3/4 0
Chuyển vị thẳng đứng tại 7 được xác định như sau: N N 1165 ik im y = Δ =  .l = 7 km i EF 2EF i
2. Xác định chuyển vị ngang tại điểm 7
Lập trạng thái “k” bằng cách đặt lực Pk = 1 theo phương ngang tại điểm 7 và xác định lực dọc trong giàn 1 N N Thanh l i (m) l EF Nim N ik im ik i EF i i 1-2 3 1/EF -30/4 0 0 1-5 5 1/EF -75/2 0 0 2-3 3 1/EF -30/4 0 0 2-5 4 1/EF 0 0 0 3-5 5 1/EF 50/4 0 0 3-6 4 1/EF -10 0 0 3-7 5 1/EF 0 0 0 4-5 3 1/EF 30 1 90/EF 5-6 3 1/EF 0 0 0 6-7 3 1/EF 0 0 0 Chuyển vị ngang tại 7 N N 90 ik im x = Δ =  .l = 7 km i EF EF i
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN  90 2 11652
Vậy chuyển vị toàn phần tại 7 là Δ = 2 589, 41 x  2 y    7 7          7 EF  2EF  EF ĐỀ SỐ 18
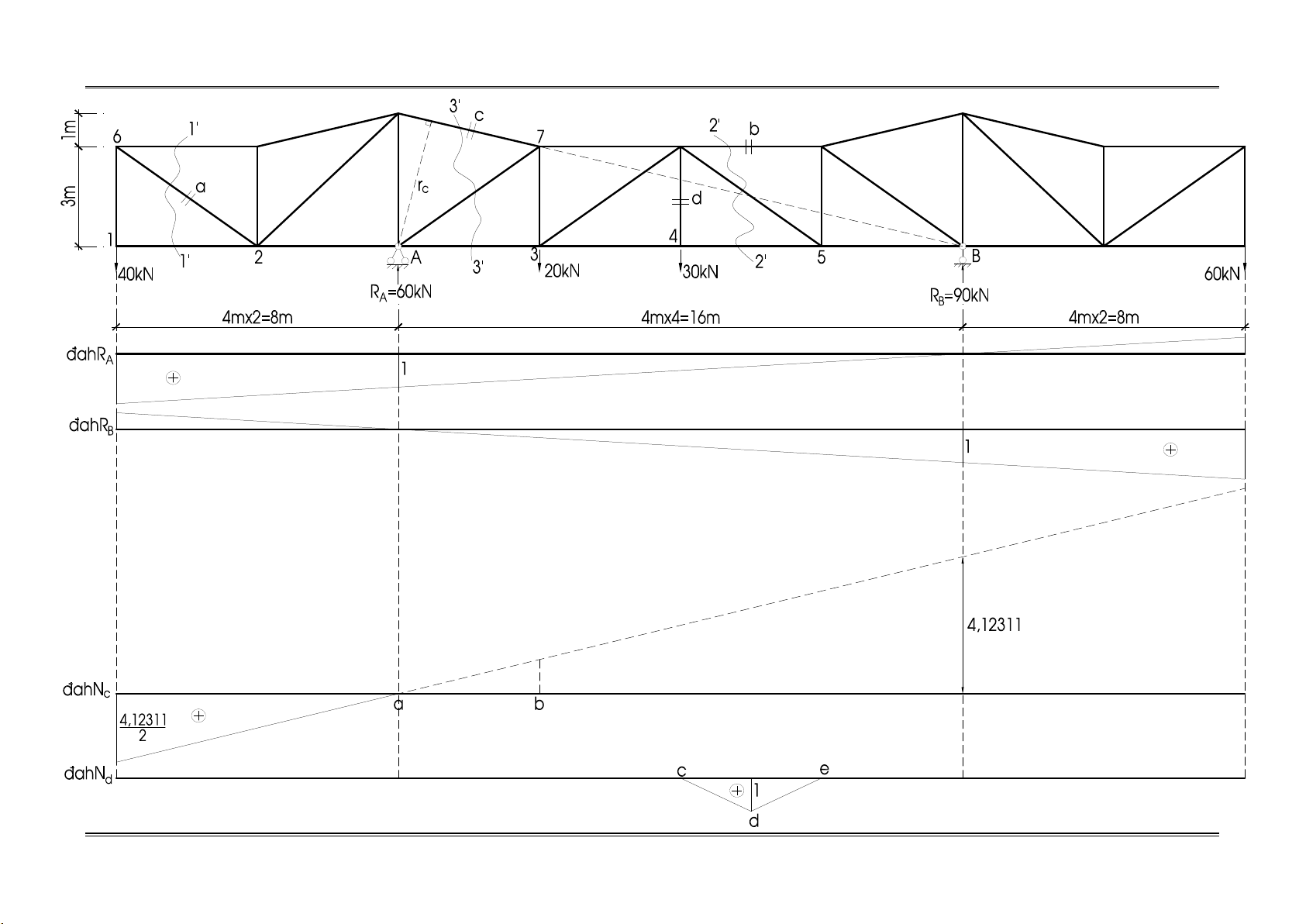
Câu 1. Tính a, b – giải tích; c,d – đah.
Xác định phản lực gối
M = 0 R .4.4-60.4.6-30.4.2-20.4+40.4.2 = 0 R = 90 kN A B B  Y = 0  R = 60 kN A 1. Thanh a – giải tích
Dùng mặt cắt 1’-1’ xét cân bằng phần bên trái, ta có: 3 200
Y = 0 N . + 40 = 0  N = - kN a a 5 3
2. Tính thanh b – giải tích.
Ta dùng mặt cắt 2’-2’ xét cân bằng phần bên phải và lấy mômen tại điểm 5, ta có: MPh¶i   90.4  60.4.3  120 5 = 0 N .3 = 0 N = kN b b 3. Thanh c – đah.
Ta vẽ ngay đah 2 phản lực gối như trên hình vẽ. Ta dùng mặt cắt 3’-3’
Nếu P = 1 di động bên trái mặt cắt, ta xét cân bằng phần bên phải, ta có: P ¶ h i -16
M = 0 N .r + R .16 = 0 a ® hN = a ® hR = -4,12311 a ® hR A c c B c B B rc  3  o o Víi tan3B7=
 3B7 14 2'  r  16sin 14 2'  3, 88057 m. c 12
Nếu P = 1 di động bên phải mặt cắt, ta xét cân bằng phần bên trái, ta có: MTr¸i = 0  N = 0 A c
Nếu P = 1 di động trong khoang bị cắt A-3, thì theo nguyên tắc của hệ thống truyền lực ta
có đường nối ab như hình vẽ.
Từ đah ta có nội lực trong thanh c được xác định: N = 4,12311.40 = 82,4622kN c 2 4. Thanh d – đah.
Ta dùng mặt cắt kín đi qua nút 4:
Nếu P = 1 đặt tại nút 4 thì ta có Nd = 1.
Nếu P = 1 di động ngoài khoang bị cắt thì ta có Nd = 0.
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN
Nếu P = 1 di động trong khoang bị cắt 3-4, thì theo nguyên tắc của hệ thống truyền lực ta có
đường nối cd như hình vẽ.
Nếu P = 1 di động trong khoang bị cắt 4-5, thì theo nguyên tắc của hệ thống truyền lực ta có
đường nối de như hình vẽ.
Từ đah ta có nội lực trong thanh d được xác định: N = 1.30 = 30kN d
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN 82 55.0 . 8 5 2 . 123.7 5 53.3 80.0 120.0 80.0 5 - .0 - .0 6 6 6 5 . . 6 7 0. 0.0 0.0 0. 0 0 40.0 37.7 13.3 -60 20.0 30.0 30.0 -90 20.0 -100.0 60.0 0.0 -80.0 -80.0 -80.0 -80.0 -120.0 -120.0 0.0
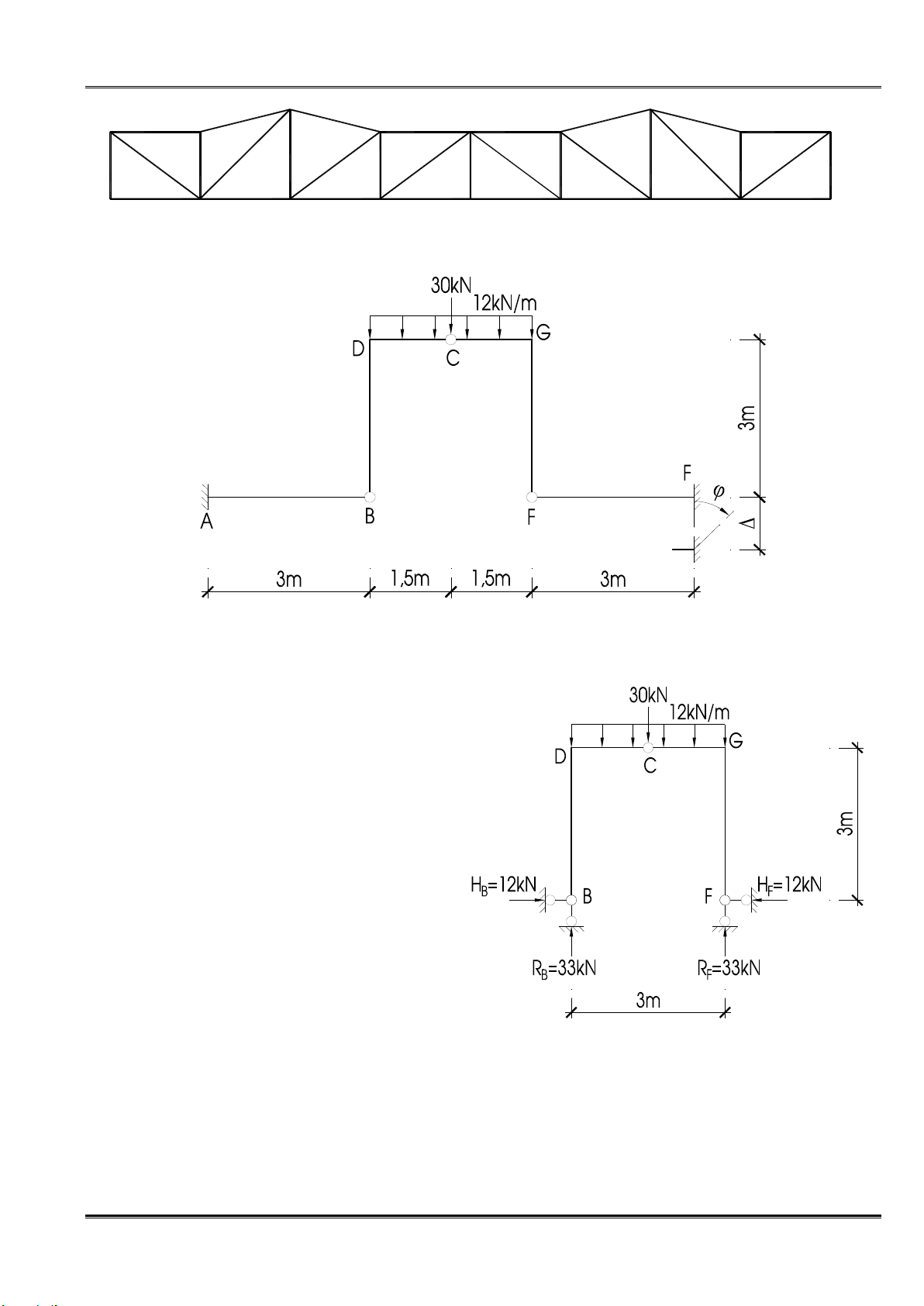
Câu 2. Tính chuyển vị thẳng đứng tại C, góc xoay tại D. Giả thiết EJ = Const, ∆ = 0,04 m, φ = 0,02 rad. 1. Vẽ biểu đồ mômen.
 Ta xét phần kết cấu phụ thuộc
Tổng mômen tại B ta có RE .3 – 30.1,5 – 12.3.1,5 = 0 → RE = 33 kN.
Tổng hình chiếu theo phương thẳng đứng → RB = 33 kN.
Dùng mặt cắt qua khớp C, xét cân bằng phần
bên phải ta có HE.3 + 12.1,52/2 – 33.1,5 = 0→ HE = 12 kN.
Tổng hình chiếu theo phương ngang → HB = 12 kN.
Do tính chất đối xứng nên ta chỉ xét ½ kết cấu.
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN
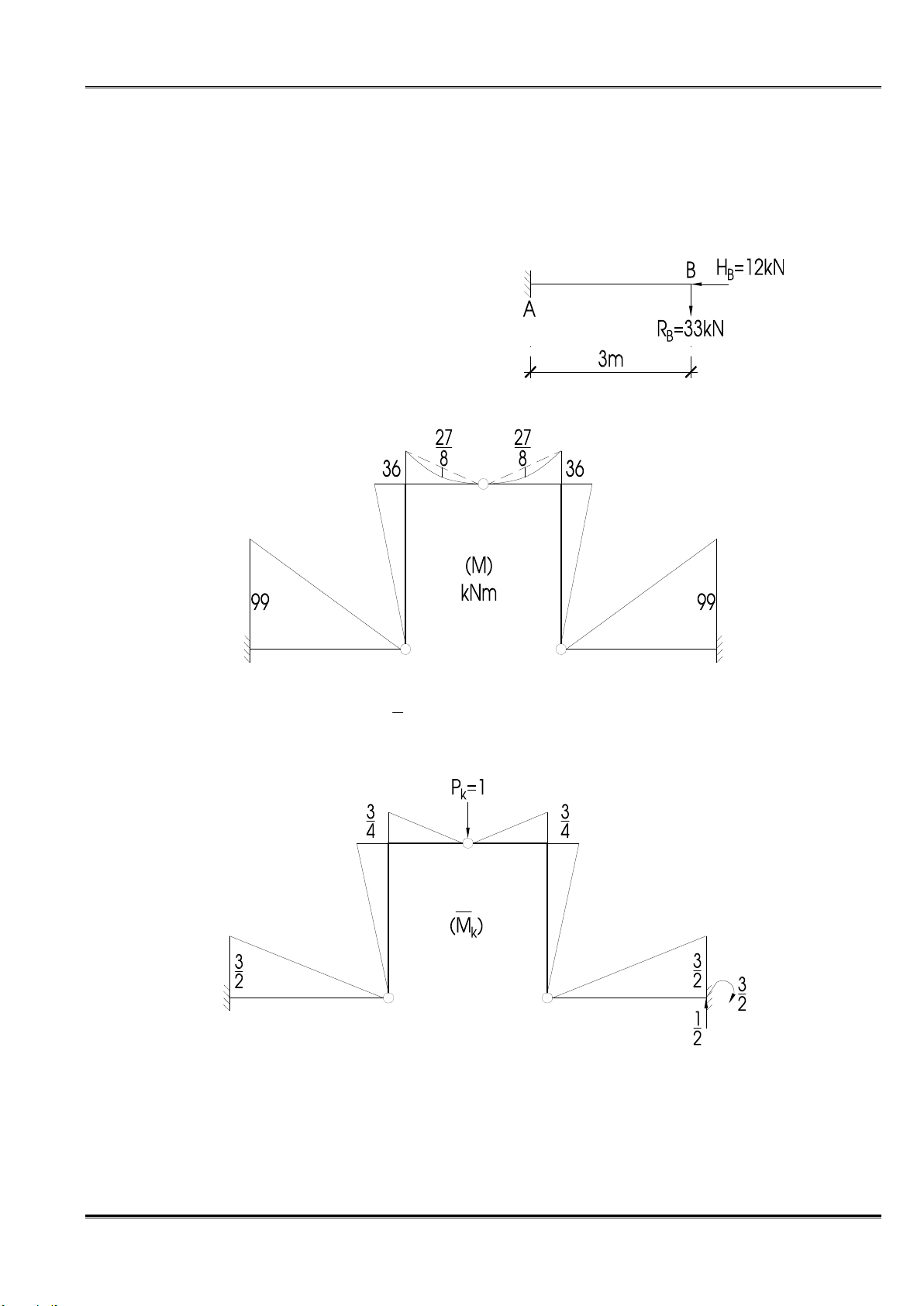
 Đoạn BD – biểu đồ có dạng đường xiên, tại khớp B có MB = 0, tại D ta có MD(BD) = 12.3 = 36 kNm (Căng trái).
 Đoạn DC – biểu đồ có dạng đường cong bậc hai, tại khớp C có MC = 0, tại D ta xét cân bằng
nút ta có MD(DC) = 36 kNm (Căng trên). Tung độ treo = 12.1,52/8 = 27/8.
 Ta xét phần kết cấu cơ bản (do tính chất đối xứng ta chỉ xét ½ kết cấu).
Đoạn AB – biểu đồ mômen có dạng đường
xiên, tại khớp B có MB = 0, tại A ta có MA = -99 kNm (Căng trên).
Ta vẽ được biểu đồ mômen như sau:
2. Tính chuyển vị thẳng đứng tại C.
Ta lập trạng thái “k” và vẽ biểu đồ M do tải trọng đơn vị P k
k = 1 đặt tại C theo phương thẳng đứng.
NORTH SAINT_buddha93uct@gmail.com 
GI¶i ®Ò thi CKC F1_§H GTVT HN  1 2 3     .36.1,5. .   1 1 2 3 1 2 3   2 3 4   y = M M + =
 .99.3. . .2 + .36.3. . .2 +   .2 C   k Z EJ 2 3 2 2 3 4  2 27 1 3   . .1,5. .           3 8 2 4   1 3  12015     φ  0,01  2 2  32EJ
3. Tính chuyển vị góc xoay tại D.
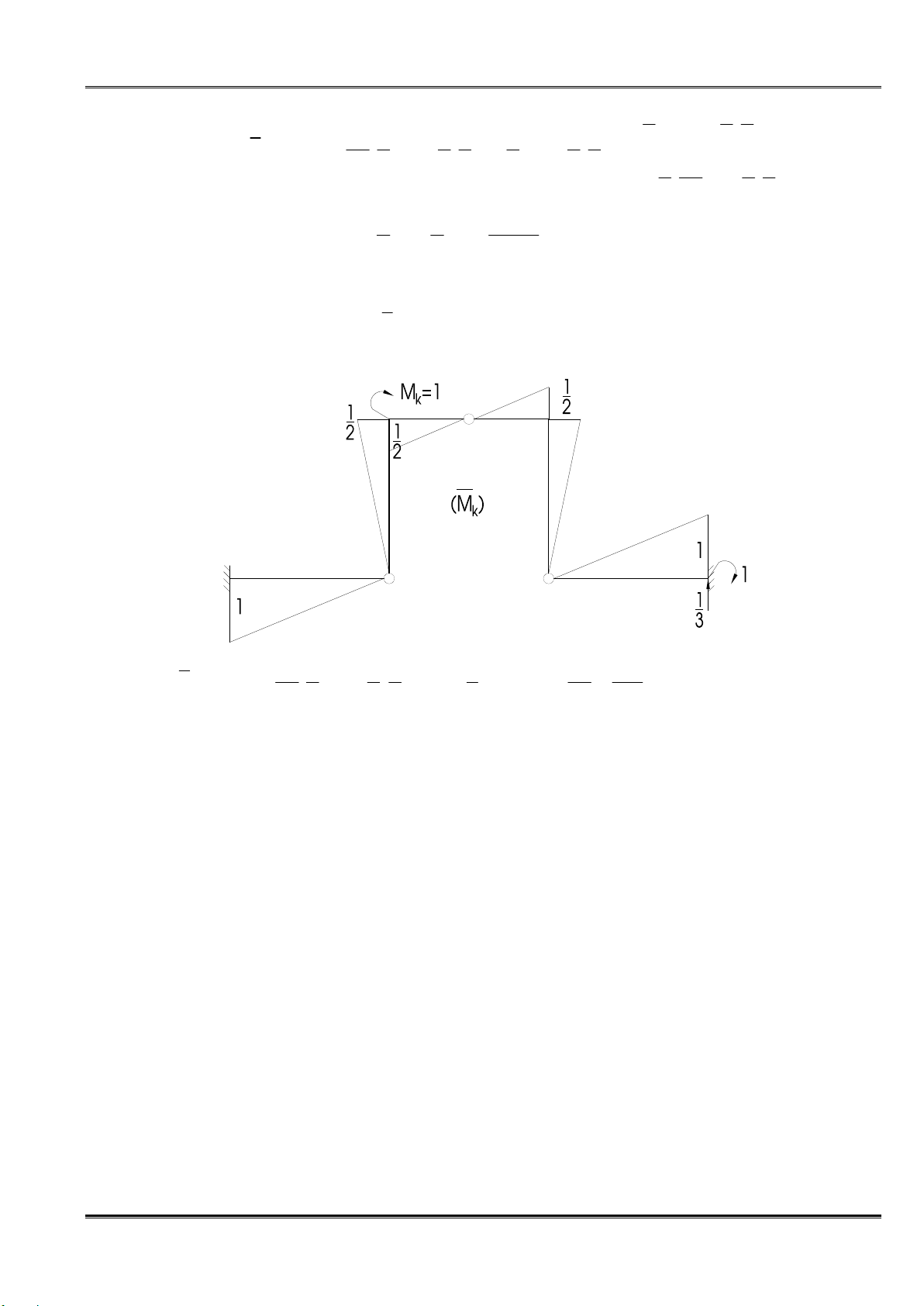
Ta lập trạng thái “k” và vẽ biểu đồ M do tải trọng đơn vị M k
k = 1 đặt tại D theo chiều kim đồng hồ. 1 1 2 1   1  36 1 φ = M M +  =  .36.3. . .2     1 =  D   k Z EJ 2 3 2   3    EJ 150
NORTH SAINT_buddha93uct@gmail.com 