Hướng dẫn giải toán VDC trong các đề thi thử TN THPT 2022 môn Toán

Tài liệu gồm 98 trang, được biên soạn bởi tác giả Trần Minh Quang, hướng dẫn giải toán vận dụng cao (VDC) trong các đề thi thử tốt nghiệp THPT năm 2022 môn Toán. Mời các bạn đón xem

41 21 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

ĐỀ LIÊN TRƯỜNG NGHỆ AN LẦN 1

Câu 46. Một bình thủy tinh hình trụ không có nắp, trong bình được xếp vào ba viên bi bằng nhau có bán

kính

sao cho các viên bi đều tiếp xúc với đáy, đôi một tiếp xúc nhau và tiếp xúc với đường sinh của

bình. Người ta đổ đầy nước vào rồi đặt lên miệng bình một khối lập phương .

ABCD A B C D

   

đặc, sao cho

đường chéo



có phương vuông góc với mặt đáy của bình và các cạnh , ,

AA AB AD



tiếp xúc với miệng

bình (xem hình vẽ). Sau đó quan sát thấy lượng nước tràn ra ngoài bằng

lượng nước ban đầu có trong

bình. Giả sử chiều dày của vỏ bình không đáng kể, hỏi thể tích của bình thủy tinh gần nhất với số nào sau

đây ?





276, 41

. B.





319,94

. C.





350,31

. D.





275, 44

Lời giải

Đầu tiên ta có hình vẽ sau đây.

Hình 1 Hình 2

Chú thích: hình 2 là hình mặt cắt khối hình 1 qua khối trụ và ba khối cầu trong khối trụ đó.

Gọi các cạnh , ,

AA AB AD



tiếp xúc với miệng bình lần lượt là các điểm

, ,

M N P

Theo hình 1, ta có:

Nhận xét: do đường chéo



có phương vuông góc với mặt đáy của bình nên ta suy ra khối tứ diện

AMNP

là một khối tam diện vuông có ba cạnh , ,

AA AB AD



bằng nhau và bằng





x dm

, thể tích bằng

 

3 3

x dm

. Khi đó

, ,

M N P

đều nằm trên đường tròn đáy của khối trụ tức bán kính đường tròn đáy của

trụ





cũng chính bằng bán kính đường tròn ngoại tiếp tam giác đều

MNP



, suy ra

 

2 2

3 3 3

MNP

MN AM x

R R dm

    . (1)

Do đổ nước đầy bình sau khi bỏ ba quả cầu nên ta có thể tích nước ban đầu bằng:





 

2 2 3

3. 3 12 3

V R h R h dm

   

   

với

là chiều cao của khối trụ.

Theo hình 2, ta có:

Gọi

, ,

D E F

lần lượt là tâm đường tròn mặt cắt tử ba quả cầu và

là tâm đường tròn ngoại tiếp

DEF



Tiếp đến ta gọi

, ,

I J K

là các điểm tiếp xúc của đường tròn mặt cắt với đường tròn ngoài có bán kính

bằng

. Ta có

DEF



đều có cạnh bằng





2 3

nên suy ra

 

2 3

OF dm

 

Suy ra:





2 3

R OK OF FK dm

    

(2)

Từ (1) và (2) ta có được:

 

2 3

2 3 6

3 2

x dm

    

Theo giả thiết thì thể tích phần nước tràn (tức thể tích khối tứ diện

AMNP

bằng

lượng nước ban đầu

có trong bình nên ta có phương trình sau:

   

3 2 2

1 1 1 3 1

12 3 6 12 3

6 16 6 16

x R h R h

   

 

     

 

 

Giải phương trình ta thu được





7,312

h dm

 .

Vậy thể tích khối trụ cần tìm là:





 

2 3

2 3 7,312 319,94

tru

V R h dm

 

   

. Chọn B

Câu 50. Xét các số thực dương

, ,

x y z

thỏa mãn

 

2 3 27 2 3

y z

y z xy xz



 

    

 

 

. Tìm giá trị nhỏ nhất

của biểu thức

 

2 2 2 2 2

5 5

1 3 6

log log 3 3

y z

P y z y z



 

    

 

 



. B.



. C.

4 log 3

 . D.

3 log 5



Lời giải

Giả thiết ban đầu suy ra:

   

1 1

2 2

2 3 27 2 3 3 27

x x

y z y z

y z x y z x

y z

 

   

        

   



   

3 3

y z



   



. Xét hàm số





y f t t

  

trên







có









3 ln 3 1 0, 0;

f t t



     

Suy ra





f t

đồng biến trên







tức

y z





Ta có:





   

2 2

2 2 2 2 2 2 2 2

3 2

3 6

3 3 3 3 2 3 3 4 4 2

y z

y z y z y z y z y z yz y z

x x



             

Cùng với:

   

2 2

4 1 5

y y z

y z



    (Svac-xo) nên

 

5 5

log log 2

5 4

y z

P y z



   .

Đặt

2 0

t y z

  

ta suy ra:

 

2 2

5 5 5

1 1

log log log 1 2 2

5 4 2

P t t

 

      

 

 

. Vậy

min

 

khi

t y z

  

. Chọn B

ĐỀ THCS – THPT NGUYỄN KHUYẾN TPHCM

Câu 43. Cho hàm số





y f x

 có





3 1 1

 

và









, ,

f x ax bx c a b c R



    . Đồ thị hàm số





y f x



 như sau:

Số điểm cực trị của

   

 









2 8 3

f x f x

g x f f x f x

 



    

 

 

là

. B.

. C.

. D.

Lời giải

Đầu tiên, dễ dàng giải hệ

, ,

a b c

ra được

   

2 2

2 2 2

f x x x f x x x C



         

Với





3 1 1

 

ta suy ra

2 3

C  

, tức

 

2 2 3

3 3

f x x x     

Ta có:

   

 

   

6 9 1

2 8 3 1

f x f x

g x f f x f x

 

  

 

     

 

 

 

3 1

3 5 8 3 1

f x

f f x f x

 

 

 

      

 

 

Đặt

 

3 0

u f x

  

khi đó

 

4 3

2 2

5 8 2 5 8 0

8 8 2

u u

g u f u u g u uf u

 

          

   

2 2 2

2 2

4 2 2 2 2

5 3 . . 3 5 3

4 4 4

u u u

f u f u

u u u u u

 

           

(đánh giá Cauchy 3 số không âm).

Khi đó:

   

 

   

 

2 2

5 2 5 2 3

2 2 0 3 2

2 2

u u

u u f x

f x x x

u f x

 







      

 

 



        

 



   

 



 





Suy ra:

   

2 2 3 1

3 3

3 4 1

2 2 3 1

3 3

x x

f x f x

x x



     



     



      





(1)

Thử bằng máy tính casio ta thấy (1) có 5 nghiệm bội lẻ nên ta suy ra





g x

có tất cả 5 điểm cực trị.

Câu 45. Cho hàm số





3 2

y f x x bx cx

    

có đồ thị như hình sau:

Hình phẳng





giới hạn bởi





, 0, 0, 4

y f x y x x

   

quay quanh

sinh ra một khối tròn

xoay có thể tích bằng

. Khẳng định đúng là

3072





. B.

3073





. C.

3074





. D.

3076





Lời giải

Giả thiết ban đầu suy ra:





3 2

f x x x

   . Suy ra

 

4 4

2 3 2

0 0

3072

V f x dx x x dx



 

    

 

Câu 48. Cho hàm số





3 2

y f x ax bx cx



   

có đồ thị hàm số





y f x



 như sau

Và





0 0



. Số điểm cực trị của hàm





















g x f xf x xf x

  bằng

. B.

. C.

. D.

Lời giải

Giả thiết ban đầu suy ra:

     

3 2 2 3

3 3

f x x x x x f x x



        

với





0 0



Ta có:

   

 

ln 0

g x f xf x xf x xf x f xf x

xf x

 



    

 

 

. Cho





g x





   

 





 

3 1 1

(1)

(2)

f x

f x xf x

f x x x x

f xf x

xf x

f xf x

xf x





   



  







 



















Tại (1) phương trình tương đương với:

3 1 1 4 1

0 0

4 4

x x x x x

     

 

Xét hàm số

 

4 1

h x

x x

 



có

 

4 1

h x



   



tức





h x

nghịch biến trên từng khoảng xác

định.

Vậy phương trình (1) có nghiệm duy nhất



(nhận).

Tại (2) phương trình tương đương với: (đặt





t xf x

 )

 

3 2

0.764

1 1

2.961

f t t t

t t







      







Suy ra:

 

0.764 0.764

2.961 2.961

f x f x

x x

f x f x

x x

 

 

 



 

 

 

 

. Khảo sát sự tương giao của đồ thị





y f x

 và hai đường cong

lần lượt là

0.764



và

2.961



ta thấy có 6 nghiệm bội lẻ (2).

Từ (1) và (2) ta kết luận hàm số





g x

có tổng cộng 7 điểm cực trị.

Câu 49. Cho

       

1 2

: ; : 4

C y g x C y f x x bx c

     





tiếp xúc

tại

 

 

 

và





qua





2;1

B . Giá trị nhỏ nhất của

 

4 2

2. 2 3

1 2

x f x

g x x

f x x

 

 

 

 

 

 

trên đoạn





0;2

bằng

và

2 2

a b







Khẳng định đúng là





2;0

M   . B.





0;1

M  . C.





1;2

M  . D.





2;4

M  .

Lời giải

Ta có:





f x x b



 

. Do





tiếp xúc

tại

 

 

 

nên

 

 

 

là điểm cực trị của đồ thị





 

   

12 0 12

4 12 9 2 3 0

16 2 1 9

2 1

b b

y f x x x x

b c c



 





   

 

  

          

 

  

   

 







Tiếp đến, ta có:





 













 

2 1 2

4 2

2 1 1 1

2 1

1 2 1 2

2 3 1

f x x

x f x

f x x f x x

  

 

    

 

   

 



Khi đó, suy ra:

 

2 2

4 2

2. 2 3 2. 2 2 3

1 1

1 2

2 3 1

x f x

P g x x x

f x x

 

 

     

 

 

 



 

 



 

 

Đặt

   

 

2 2

; ; 2 3 ; 2 ; 4 3

a b x x y a a

 

    

 

 

. Do





0;2

x

nên









0;1 , 0;3

a b 

-Nếu



thì





 

  

4 3 1

1 2 1 0

4 3 1

1 2 1 0

a a



 

  



   



  

  



(vô lí do





0;1

a 

)

-Nếu

0 1

 

thì ta có:

2 2

1 1

P ab

a b

 



 

Đến đây ta có bất đẳng thức (*) sau:

a b



thỏa

0 1

 

thì ta có:

2 2

1 1 2

1 1 1

a b ab

 

  

Thật vậy, bất đẳng thức (*) tương đương với:

 

2 2

1 1 1 1

0 0

1 1 1 1

ab a ab b

a ab b ab

 

       

   

 





 





   

2 2

1 1 0 1 0

a b a b b b a a b a ab

          

luôn đúng với

0 1

 

Như vậy (*) đúng, suy ra

 

2 2

2 2 1 2 2

P ab ab ab

     



Như vậy giá trị nhỏ nhất của

bằng

khi



. Chọn đáp án B.

Câu 50. Cho hàm số





y f x

 liên tục trên

, có









3 2

0, ;

f x x x x



   và có đồ thị





y f x

 như hình

dưới đây

Gọi

   

 





 

 

0 0

0 0 0 3

1 ; ; ; 0

f f x f x

f x xf f x f f x m n x x

 





 



     

 

 

 

 

. Khi giá trị

nhỏ nhất của

  

2 1 4

1 4 1 2 4 1

m n

S mn

m n mn



  

  

trên





3 2

;

x x x

 bằng

và

















0 0

T k f x k f x x

   

. Khẳng định đúng là





0;1

T  . B.





2;3

T  . C.





4;5

T  . D.





5;6

T  .

Lời giải

Từ đồ thị ta có:









1 1 3

; 0

f x x f x

 

-Trên





x thì





f x



(dựa vào đồ thị)









   

 

 

0 0 3

0 1

0 1 1 3

0, ;0

f x x x

f x x

f x f x x x



 



  



  





-Vì









3 2

0, ;

f x x x x



   nên theo bất đẳng thức tiếp tuyến, với mọi









0 3

f x x thì





























   

 

   

 

   

0 0 0

0 0 0 0 0 0 0

0 0 0 0

1 1

1 1 1

f x f f x x f x f f x

f x xf f x f f x f f x x f x f f x xf f x f f x

f x xf f x f f x f f x f x



  

  

         

 

     

-Lại có









3 2

0, ;

f x x x x



   nên suy ra





f x



đồng biến và liên tục trên





3 2

;

x x





0 3

x x nên





1 0

x f x

 

(suy ra từ nhìn nhận đồ thị)













0 1

f f x f x

 

  

(do

x x



là điểm cực trị của đồ thị hàm số).

Mà mặt khác





f x



nên suy ra

 





 

0 0

2 4

f f x f x

f f x f x n

 







   

 

 

Kéo theo

   

 

0 0

1 1

f x xf f x f f x m

 



    

 

Đặt









; 4 ;

m n a b

 thì khi đó

, 1

a b



và

a b



Ta có:

     

2 1 4 2 1 1

1 4 1 2 4 1 1 1 2 1 2

m n a b

S mn ab

m n mn a b ab

 

     

     

, 1

a b



nên ta có:





























1 1 0 1 1 1 1 2 1

a b ab a b a b ab a b ab

               

Suy ra:

    

 

2 1 1

1 1 1

1 2 1 2

2 1

a b ab ab ab

a b

S ab

ab ab

    



   

 



Đến đây ta cần chứng minh

    

 

2 1 1

2 1

a b ab ab ab

    





(**)

           

2 1 1 3 1 1 1 3 1

a b ab ab ab ab a b ab ab ab ab

              

Ta nhận thấy: do 1

ab a b

  

nên

        

1 1 1 2 1

a b ab ab ab a b ab ab ab ab ab

          

Đến đây ta cần chứng minh





2 1 3 1

ab ab ab ab

   

(*). Thật vậy, ta có:

(*) tương đương với:

 

2 2

1 0

2 1 3 1

t ab

t t t t



 



   



   





và luôn đúng với mọi



Như vậy bất đẳng thức (*) đúng, tức kéo theo (**) đúng, từ đó suy ra

min

S k

 

Dấu bằng xảy ra khi và chỉ khi

0 1

x x x

 

và





0 0

f x x



Suy ra:

 

   

2 2 2 2 2 2

0 0 0 0 0 0

9 9

2;3

4 4

T k f x k f x x k f x x x x           

ĐỀ THPT ĐÔ LƯƠNG 1 NGHỆ AN

Câu 46. Cho hai số thực

và

thỏa mãn





3 3

2 log log 5

x y  . Biết giá trị nhỏ nhất của biểu thức

P  

là

log

a c



trong đó

, ,

a b c

là các số tự nhiên,

b c

là số nguyên tố. Tính giá trị của biểu thức

2 3

T a b c

  



. C.



Lời giải

Ta thực hiện biến đổi biểu thức P như sau:

 

3 3

log 5 log 5

log 5

log log 5

3 3

log 3 log 5

log log 5

log 5 log 5

log 5

1 1 5 3

3 3 3 3 3 log 5

5 5 log 5 3

5 3

x x x x x

y x x

x x



 

           

 

 

Đặt

log 5

 

, xét hàm số

 

log 5

y f t t

  

có

 

log 5 1

log 5 0 1

f t t t



 



    

 

 

Mà





1 0





nên ta suy ra









min min 1 1 log 5

P f x f    .

Đồng nhất hệ số ta suy ra

1, 3, 5

a b c

  

. Vậy

2 3 22

T a b c

   

Chọn đáp án A.

Câu 47. Cho hình lăng trụ tam giác đều

1 1 1

ABC A B C

có cạnh đáy



. Gọi

M N

thứ tự là trung

điểm của

1 1

A B

và

. Biết rằng hình chiếu của

lên đường thẳng

C N

là đoạn thẳng có độ

dài bằng

và chiều



. Tính thể tích của khối lăng trụ

1 1 1

ABC A B C

125 3

. B.

125 3

. C.

25 3

. D.

125 3

Lời giải

Ta kẻ

1 1

;

BE C N MF C N

  thì khi đó ta thu được hình chiếu của

lên đường thẳng

C N

chính là đoạn

. Mặt khác, khi ta dựng hình bình hành

NC KM

và kẻ

BE KM

 tại

thì hình chiếu lúc này chính là

, ta nhận thấy cả hai trường hợp này đều cho ra 2 đoạn hình chiếu song song và bằng nhau.

Khi đó ta suy ra

EF ME

BE BE



 











. Đặt

AA x

 

2 2

1 1

; 25 ; 25

4 4

BM x C N BN BC x

       

Tiếp đến ta có:

   

 

2 2 2

1 1 1 1

1 1 1

5 3

; ;

3 75

4 25

; . .

d N BC d A B C

BE BE ME MB BE

d N BC BC BE C N



 





     











1 1 1

1 . 1

25 3 75 5 125 3

25 5

4 4 25 2 4

ABC A B C ABC

x x AA V AA S

 



 

         

 



 

. Chọn đáp án D.

Câu 48. Cho hàm số





f x x

 

và









3 2 2

1 2

g x x mx m x

    

. Gọi M là giá trị lớn nhất của hàm số









y g x f x

 

trên đoạn





0;1

. Khi M đạt giá trị nhỏ nhất thì giá trị của m bằng?

C. 21 D. 5

Lời giải

Ta có:





















10 2 10 ln10 2 10 2

x x x

y h x g x h x g x

 

      

Xét









2 2

3 2 1

g x x mx m



   

có

 





2 2 2

3 1 2 3 0

3 0

g x

m m m







       











nên suy ra hàm số





g x

luôn đồng

biến trên đoạn





0;1

tức giá trị lớn nhất của hàm số





h x

tại



Khi đó ta có:

   





 

3 2 2 2

1 12 12 12 12 1 2 12 144 1738 12 6 1306 1306

h g m m m m m            

Như vậy dấu bằng xảy ra khi

6 0 6

m m

   

. Chọn đáp án B.

Câu 49. Cho hàm số





y f x

 liên tục trên





1;1

 và thỏa mãn

f x

 

 2 

x  t

 

f t

 





với





1;1

x  

Khi đó

 

I f x dx







bằng



Lời giải

Chú ý trong tích phân lấy theo biến t do đó x trong tích phân lúc này là tham số các em nhé, nên không đặt

m  x t

 

f t

 





được:

f x

 

2

x t

 

f t

 

1





xf t

 

1



 tf t

 

1

















x f t

 

1





tf t

 

1



Do đó

 f x

 

2 ax b; a 

f t

 

1



;b 

tf t

 

1















Thay ngược lại đẳng thức đã cho

ax b 

x at  b2

 







t at b2

 







x ´2 b 2

 



a  3 b2

 

x a



a  3 b2





b  a











 a  b  3 f x

 

 3x 1 f x

 

1



 3x 1

 

1



 2.

Chọn đáp án C.

Câu 50. Trong không gian với hệ trục tọa độ

Oxyz

cho đường tròn





là giao tuyến của mặt phẳng tọa

độ





xOy

với mặt cầu

       

2 2 2

: 6 6 3 41

S x y z

     

. Gọi

là đường thẳng đi qua các điểm





0;0;12

A và





0;4;8

B . Với

M N

là các điểm thay đổi thứ tự trên





và

. Giá trị nhỏ nhất của độ dài

đoạn thẳng

là

2 17

 . B.

. C.

1 2 5

 . D.

Lời giải

Đầu tiên ta có phương trình

     

2 2

: 6 6 32

C x y

   

với tâm





6;6

I và bán kính

4 2

R 

Gọi





F d Oy

  ,

IK Oy







D IK C

  ,





G IF C

  ,

ML Oy



. Như vậy để

đạt giá trị nhỏ nhất

thì

phải thuộc cung nhỏ



Kẻ

   

 

;

6 6

; 3 2

NL FL

KH d NL d

x x

KH FK

NL KH

LK x

KH d K d





 

 

 

   

 









 



Cùng với

 





2 2 2 2

6 ; 6 32 6 32

LM R d I ML KL x

        

Suy ra

 

2 2

2 2 2 2

6 32 6 32

MN ML LN x x f x



 

          

 

 

Xét hàm số

 





6 32 , 4 2;4 2

y f x x x



 

       

 

. Có

       

0 12 6 32 0 3,5145 4 2; 4 2 min 3,5145 2.35488

f x x x x x x f x f

 



             

 

Như vậy giá trị nhỏ nhất của

bằng xấp xỉ

2.35488

. Chọn đáp án E.

ĐỀ THI THỬ LẦN 2 SỞ HẢI DƯƠNG

Câu 46. Cho hàm số





y f x

 có đạo hàm trên

. Biết hàm số





y f x



 là hàm bậc 3 có đồ thị như hình

vẽ bên dưới

Có bao nhiêu giá trị nguyên của tham số

để hàm số

 





2 3 1

g x f x x m

   

có đúng 5 điểm

cực trị.

. B.

. C.

. D.

Lời giải

Đầu tiên ta thấy





f x





có ba nghiệm lần lượt là

2; 2;6



Tiếp đến, ta có:

 













 

3 3

2 3 1 2 3 1

g x f x x m f x x m g x

            nên suy ra





g x

là hàm chẵn

tức đồ thị hàm số





g x

đối xứng qua

. Suy ra để hàm số





g x

có đúng 5 điểm cực trị thì hàm số









2 3 1

h x f x x m

   

phải có 2 điểm cực trị dương.

Tức













2 3

6 3 2 3 1 0

h x x f x x m

 

     

phải có nghiệm dương bội lẻ. Phương trình tương đương với:

 





 

3 3 3

2 3 3

2 3 1 2

2 3 1 0 2 3 1 2 2 3 1

2 3 1 8

2 3 7

m x x u x

x x m

f x x m x x m m x x u x

x x m

m x x u x



   



    





             



   

   





. Khi đó ta có bảng biến thiên

gộp từ ba hàm













1 2 3

, ,

u x u x u x

như sau:

Vậy để thỏa yêu cầu đề bài thì

1 3

  

tức có 4 giá trị nguyên

thỏa. Chọn đáp án A.

Câu 47. Có bao nhiêu số nguyên

thuộc đoạn





2022; 2022

 sao cho tồn tại

x R



thỏa mãn

12 3 12.2 2 3

x x

y y

  

2028

2027

C. 2021 D. 2022

Lời giải

Ta có:

12 3 12.2 2 3

x x

y y

  

. Đặt

3 12.2

u y 

khi đó phương trình ban đầu trở thành:

12 2 3

3 12.2

u y



 





 





. Lấy hai phương trình cộng vế theo vế ta có được phương trình mới như sau:

3 3

12 2 12.2

x x

u u    . Xét hàm số





y f t t t

   có





3 12 0,

f t u u R



    

. Như vậy ta suy ra

hàm số





f t

đồng biến trên R. Khi đó:

2 12.2

2 3 12.2 2

x x

x x x

u y y



     

Xét hàm số

 

2 12.2

x x

y g x



 

có





8 ln 2 4.2 ln 2 0 1

x x

g x x



    

Như vậy để tồn tại

x R



thì tham số

phải thỏa:

 

 

2022;2022

16 16

1 2022

3 3

y g y

 

     

Như vậy có tất cả

2022 ( 5) 1 2028

   

giá trị

nguyên thỏa mãn. Chọn đáp án A.

Câu 48. Cho đồ thị hai hàm số





y f x

 và





y g x

 như hình vẽ bên dưới

Biết đồ thị của hàm số





y f x

 là một Parabol đỉnh

có tung độ bằng



và





y g x

 là một

hàm số bậc ba. Hoành độ giao điểm của hai đồ thị là

1 2 3

, ,

x x x

thỏa mãn

1 2 3

x x x

 

. Diện tích hình phẳng

giới hạn bởi hai đồ thị hàm số





y f x

 và





y g x

 gần nhất với giá trị nào dưới đây ?

C. 5 D. 8

Lời giải

Từ hình trên ta quy ước hoành độ giao điểm giữa hai hàm số từ trái qua phải là

1 2 3

, ,

x x x

Đầu tiên ta dễ dàng tìm được

 

f x x

 

với



, khi đó ta suy ra

1 3

x x

 

Gọi





3 2

g x ax bx cx d

   







. Nhận ra điểm

cũng chính là điểm uốn của hàm số





y g x

 nên ta

suy ra

 

1 0

6 2 0

a b c d

a b



 

    

 



 

 





 



Tiếp theo, xét phương trình hoành độ giao điểm của





y f x

 và





y g x

 , ta có:

 

3 2 3 2

1 0

2 2

ax bx cx d x ax b x c x d

 

           

 

 

(1)

Biết rằng phương trình (1) có ba nghiệm phân biệt

1 2 3

, ,

x x x

nên theo định lí Viét ta có được:

1 2 3

6 6

x x x d a



    

. Từ đó ta giải hệ 4 ẩn ra được:

1 3 3

, , 0,

8 8 4

a b c d

     

Suy ra:

   

3 2

1 3 3

8 8 4

f x g x x x x

     

kéo theo phương trình









f x g x



có nghiệm là

1 7



 











Vậy

   

1 7

6, 22

S f x g x dx





  



gần với 6. Chọn đáp án A.

Câu 49. Xét các số phức

z w

thỏa mãn

2 2 1

z i

  

và

2 3

w i w i

   

. Khi

3 3

z w w i

   

đạt giá

trị nhỏ nhất. Tính

z w



2 5

2 13

Lời giải

Gọi

M N

lần lượt là các điểm biểu diễn số phức

z w

Qua biến đổi đại số, ta suy ra:

       

   

2 2

: 2 2 1

: 1 0

M z C x y

N w d x y



    





   





. Gọi





3; 3



, khi đó ta có:

3 3

P z w w i MN NA MN NB MB

          trong đó





4; 2



là điểm đối xứng với

qua





Như vậy

 

min min

6 1 5

P MB MI R

     

với





2; 2

 

là tâm đường tròn





Dấu bằng xảy ra khi





1; 2

 

và





3; 2



. Vậy

2 2 61

z w OM ON   

 

Chọn đáp án A.

Câu 50. Trong không gian

Oxyz

, cho hai điểm





1;1; 3



và





2;3;1

B  . Xét hai điểm

M N

thay đổi thuộc

mặt phẳng





Oxz

sao cho



. Giá trị nhỏ nhất của

AM BN



bằng

Lời giải

Đầu tiên ta có hình vẽ như sau:

Xét mặt phẳng





: 1

P y



. Dựng đường tròn





tâm

, bán kính

AA MN



 

với





A C



 sao cho

AA NM



là hình bình hành. Đến đây ta nhận thấy

A B



đều cùng phía với mặt phẳng





Oxz

nên ta suy ra:

AM BN A N BN A N B N A B

    

     

với





2; 3;1



  là điểm đối xứng với

qua





Oxz

Gọi





2;1;1

H  là hình chiếu của



lên





khi đó ta suy ra



đạt giá trị nhỏ nhất khi ba điểm

, ,

A H A



thẳng hàng với

nằm giữa

và



. Ta có:



nên suy ra

min

HA AA AH MN AH

 

    

Vậy

 

2 2 2 2

min

3 4 5

AM BN A B B H A H

   

      

. Chọn đáp án A.

ĐỀ THI THỬ LẦN 1 SỞ HÀ NỘI

Câu 42. Cho bất phương trình:













2 3 3

8 3 .4 3 2 2 1 2 1

x x x

x x m x m x

      

. Số các giá trị nguyên của

tham số

để bất phương trình trên có đúng năm nghiệm nguyên dương phân biệt là

Lời giải

Đầu tiên ta có bất phương trình tương đương với:









   









   

2 3

3 3

2 3

8 3 . 2 3 .2 2 2 2 2 2 2 2

x x x x x x

x x x x mx mx x x mx mx

            

Xét hàm đặc trưng





y f t t t

  

có





3 2 0

f t t



  

với mọi

t R



nên





f t

luôn đồng biến trên

Từ đó ta suy ra









2 2

x x

f x f mx x mx

    

(*)

Với



thì bất phương trình (1) tương đương với

 

. Xét hàm số

   

1, 0;

y g x x

     

thì ta có:





0 1, 44

g x x x



   

, cùng với





g x





nên suy ra

x x



là điểm cực tiểu.









1 2 3

g g

 

nên để có 5 nghiệm nguyên dương phân biệt thì

Suy ra để thỏa yêu cầu đề bài thì













4 6 7,4 11,6 8;9;10;11

g m g m m



      



tức có 4 giá trị

nguyên

thỏa mãn yêu cầu đề bài. Chọn đáp án B.

Câu 43. Trong không gian

Oxyz

cho điểm





1; 2;3

. Đường thẳng





đi qua điểm





cắt tia

tại

và cắt mặt phẳng





Oyz

tại

sao cho

MA MB



. Độ dài đoạn thẳng

bằng

3 17

5 17

Lời giải

Ta có:





;0;0

A a

và





0; ;

B b c

cùng với

là điểm thỏa

MA MB O

 

  

Suy ra

 

2 2 2

9 3 17

; ; 6 2 ; ; 3;3;

2 2 2 2 2

9 2

A B A B A B

x x y y z z

M b a b c AB





  



 

     



  

 







Chọn đáp án A.

Câu 44. Có bao nhiêu số phức

thỏa mãn

z z



là số thực và

 





2 2

z z i

  là số thuần ảo ?

Lời giải

Cách 1:

Đầu tiên ta đặt





z a bi a b R

  

Điều kiện:

 

     

2 2

2 2 2

2 0

2 0 2 2 2 0 0 ; 2;0

2 2 0

a b a

z z a b a ab b i i a b

ab b



  

            



 



 





 

2 2

2 2 2

a bi a b a ab b i

z z

a b a ab b

 

    

 





   

là số thực nên suy ra

 

2 2 2 3

2 2

2 2 2 0 4 0

a ab b b a b a ab a b b

b a a





          



 



(1)

Tiếp theo ta có:

 





   

2 2 2 2 4

z z i z i a bi a bi i

       

, do

 





2 2

z z i

  là số thuần ảo nên suy ra

2 2

2 2 0

a b b a

   

(2). Từ (1) và (2) ta xét hai trường hợp như sau:

TH1:



loại

TH2:

2 2

b a a

 

thì thế vào (2) suy ra

b a



. Đưa về hình học

Oxy

thì số nghiệm





;

a b

chính là số giao

điểm giữa đường tròn

     

2 2

: 1 1 2

C x y

   

có tâm





1;1 , 2

I R 

và đường thẳng





: 3

d y x



Nhận thấy









;

d I d R



nên suy ra





cắt





tại 2 điểm tức có 2 số phức tồn tại là





0;0

(L) và

2 6

;

5 5

 

 

 

Tổng hợp ta kết luận có tất cả 1 số phức thỏa mãn yêu cầu đề bài. Chọn đáp án A.

Cách 2:

Điều kiện:



. Nhận xét: số phức

là một số thực thì khi đó ta luôn có:

w w



. Từ đó, ta có:

 

2 2 2

2 2 2 2 0

z z

z z z z z z z z z z z

z z

z z z

z z







          



 







Đặt





z a bi a b R

  

thì khi đó phương trình tương đương với:

2 2

a b a







 



 





2 2

z z i

  là số thuần ảo, khi đó ta có:

2 2

2 2 0

a b a b

   

Chuyển về xét tương giao trên hệ trục tọa độ

Oxy

, ta có:

   

     

2 2

: 1 1

; 0

: 1 1 2

C x y



  







   





Từ đó ta có hình vẽ như sau:

Đối chiếu với điều kiện



nên ta suy ra chỉ có 1 số phức thỏa mãn, tức điểm

. Chọn đáp án A.

Câu 45. Cho hàm số





y f x



. Đồ thị





y f x





trên





3;0



có hình vẽ như sau (phần đường cong của đồ

thị là một phần của parabol

y ax bx c

  

)

Cho





f x







, giá trị





bằng



Lời giải

Đầu tiên từ đồ thị trên ta dễ dàng có được:

 

4 3, 3 1

2 2 , 1 0

x x x

y f x

x x



      





 



   





Khi đó ta có:





     

3 3

1 1 0

ln ln

e e

f x

dx f x d x f x dx

 



  

  

Đặt









u f x du f x dx

dv dx v x



  

 



 

  

 

 

Suy ra

                 

0 0 1 0

3 3 3 1

3 0 3 3 0 3 3

f x dx f x f x dx f x f x dx x f x dx



   

  

        

   

   

 

    

1 0

3 1

3 0 3 4 3 3 2 2 3 0 4

f x x x dx x x dx f



 

          

 

. Suy ra

 



. Chọn đáp án C.

Câu 46. Trong không gian

Oxyz

, cho ba điểm













1;1;1 , 1; 2; 2 , 0;0;4

A B I

. Mặt cầu





đi qua hai điểm

A B

và tiếp xúc với mặt phẳng





Oxy

tại điểm

. Giá trị lớn nhất của độ dài đoạn

là

2 3

3 2

Lời giải

Cách 1: Nhận xét: để tồn tại mặt cầu





đi qua hai điểm

A B

thì tâm





; ;

K a b c

của mặt cầu đó phải nằm

trên mặt phẳng trung trực của đoạn thẳng

, tức mặt phẳng





Mặt phẳng





đi qua trung điểm

nhận



là pháp tuyến có phương trình là:





: 3 0

P y z

  

Ta có

là hình chiếu của

lên mặt phẳng

Oxy

với





; ;0

C a b

. Từ đó ta có phương trình sau:

       

2 2 2

2 2 2 2 2

1 1 1 3 2

KA KC a b c c a b a b c

             

(1)

Mặt khác ta lại có

thuộc mặt phẳng





nên

3 0

b c

  

(2)

Từ (1) và (2) ta suy ra

   

2 2 2

3 2 3 1 4

a b a a b

       

tức điểm

thuộc đường tròn tâm





1;0

và bán kính



. Tiếp theo ta có:

2 2 2

IC IO OC OC

   

tức khi

max thì

cũng max

Mà

max 1

2 2 4

OC OI R

    

nên suy ra

max

16 3 5

  

. Chọn đáp án A.

Cách 2: Sử dụng phương tích

Ta có phương trình đường thẳng

có dạng:

 

: 1

AB y t

z t







 





 



. Gọi





M AB Oxy

 

nên suy ra





1;0;0

Từ đó ta có được

 

2 2

. 4 1 4

MC MA MB x y

     

với





1;3

x 

Suy ra:

2 2 2

16 2 19 2.3 19 25 5

max

IC x y x IC

         

. Chọn đáp án A.

Câu 47. Cho hàm số





y f x



có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của tham số

thuộc đoạn

 

10;10

để hàm số

   

h x f x m 

có đúng 3

điểm cực trị ?

A. 19 B.

C. 18 D.

Lời giải

Để hàm số

 

h x

có đúng 3 điểm cực trị thì phương trình

 

f x m

phải có 1 nghiệm bội lẻ.

Dễ dàng thấy rõ với





0;1

m

thì





h x

có đúng 5 điểm cực trị nên suy ra để thỏa yêu cầu đề bài thì











. Mà

m

nên suy ra

 

10;10m 

tức có 21 giá trị nguyên thỏa mãn. Chọn đáp án D.

Câu 48. Cho hai số phức

,z w

phân biệt thỏa mãn

4z w 

và

 

z i w i  là số thực. Giá trị nhỏ nhất của

z w

bằng

A. 8 B.

2 3

C. 2 15 D.

2 14

Lời giải

Cách 1: Đầu tiên ta đặt ẩn dạng lượng giác như sau:

4cos 4 sin

z u i u

w v i v

 





 



Suy ra ta có:

 

  

4cos 4 sin 4 cos 4 sinz i w i u i u i v i v i       mà do là số thực nên ta có được

phương trình sau:

 

cos cos 4 sin 0 2sin sin 4 cos 0

2 2 2

u v u v u v

u v u v

  

 

       

 

 

Cùng với

,z w

là hai số phức phân biệt nên ta suy ra

sin 4cos

2 2

u v u v

 

   



   

   

Ta có:

 

1 1 1

sin 1;1 cos ; cos 0;

2 2 4 4 2 16

u v u v u v   

         

     

     

   

         

Suy ra:

     

2 2 2

16 16. sin sin cos cos 16. 2 2 sin sin cos cos

z w

z w u v u v u v u v



 

         

 

 

2 2

32. 1 cos 32 1 2 cos 1 32 2 2 cos 32 2 2 60

2 2 16

u v u v

u v

 

     

     

          

 

     

   

     

   

 

Vậy

60 2 15z w  

. Chọn đáp án C.

Cách 2: Đầu tiên ta đặt ẩn như sau:

a z i

b w i

 





 



thì khi đó ta có:

4a i b i   

 

      

1z i w i a bi i c di i ac bd b d a c ad bc i               

Mà do

 

z i w i  là số thực nên suy ra

a b

a c ad bc

c d



     



. Gọi

,A B

lần lượt là điểm biểu

diễn số phức

,z w

và điểm

 

0;1C

Từ đó ta suy ra với hệ thức trên ta có được

, ,A C B

thẳng hàng. Khi đó ta có hình vẽ như sau:

–

∞

+ ∞

–

∞

+ ∞

Ta suy ra

2 2

max

2 4 1 2 15z w AB    

. Chọn đáp án C.

Cách 3: Sử dụng cách thuần đại số

Ta có:

 

        

1 1z i w i z i w i z i w i R z i k w i k i kw z k                 

Suy ra:

   

2 2

1 16 1k kw z kw z k       . Mà vì

1k 

nên suy ra

0k 

Do đó

 

   

 

2 2 22

2 2

1 15 1 2k kw z k w z k zw zw k zw zw k k             

Tiếp theo, ta nhận thấy:

 

2 2

15 1 15 30 15 0 15 1 2 28k k k k k k           

nên suy ra

   

 

28 28 0k zw zw k zw zw k        . Từ đó ta có được:

 

32 32 28 60 2 15z w zw zw z w          . Chọn đáp án C.

Câu 50. Cho hàm số

 

y f x

là hàm đa thức bậc bốn. Đồ thị hàm số

 

y f x





được cho trong hình vẽ

dưới đây

Đặt hàm số

   

3 2

4 4

x x

g x f x x   

. Tập hợp tất cả các giá trị thực của tham số

để hàm số

 

y g x m 

nghịch biến trên khoảng







là

 

1;  B.

 

5; 1 





; 5  D.

 

1; 

Lời giải

Ta có:

     

2 2

3 3

1 0 1

4 2 4 2

x x x x

g x f x f x

  

        

Xét tương giáo giữa hai đồ thị





y f x





và

4 2

x x

  

thì khoảng

làm cho





g x





là các khoảng

2 0

  









Tiếp đến, ta có:

   

2 0

0 , 3 2 , 3 max 2 1

x m

y g x m x m x x m x m

x m

   



 

                



 



Giải thích: trường hợp

2 0

x m

   

bị loại vì

 

bị sai. Chọn đáp án A.

ĐỀ THI THỬ CHUYÊN SƠN LA LẦN 1

Câu 39. Cho hàm số xác định trên





\ 2;1

R 

thỏa mãn

       

1 1

, 3 3 0, 0

2 3

f x f f f

x x



    

 

. Giá trị

của biểu thức













4 1 4

f f f   

bằng

1 1

ln 2

3 3



1 1

ln 20

3 3



ln 80 1



1 8

ln 1

3 5



Lời giải

Ta có:

   

  

 

1 1

ln , ; 2

3 2

1 1

ln , 2;1

2 1 2 3 2

1 1

ln , 1;

3 2

C x

dx dx x

f x f x dx C x

x x x x x

C x

 

    











       



    





   







  

Trên





; 2

 

ta có:

 

ln 4

f C

  

. Trên





2;1



, ta có

 

2 2

l 1 1 1 ln 2

0 ln

3 2 3 3

f C C



    

Từ đó suy ra:

 

2 ln 2 1



 

. Trên







ta có:

 

1 2

3 ln

3 5

f C

  

. Mà









3 3 0

f f

  

nên

1 3

ln10

C C



 

       

1 2 3 2 1 3

1 5 ln 2 ln 2 1 5 2 ln 2

4 1 4 ln ln

3 2 3 3 3 2 3

f f f C C C C C C

               

1 5 2 ln 2 1 ln 2 ln10 1 1

ln ln 2

3 2 3 3 3 3 3



     

. Chọn đáp án A.

Câu 40. Trong không gian

Oxyz

, cho đường thẳng

1 2 2

3 2 2

x y z

  

 



và mặt phẳng





: 3 2 2 0

P x y z

   

. Đường thẳng



song song với





, đi qua





2; 2; 4

và cắt đường thẳng

có

phương trình là

2 2 4

9 7 6

x y z

  

 



2 2 4

9 7 6

x y z

  

 



2 2 4

9 7 6

x y z

  

 

 

2 2 4

9 7 6

x y z

  

 

 

Lời giải

Đầu tiên ta loại đáp án C,D đi vì vector chỉ phương nhân vô hướng với vector pháp tuyến mặt phẳng





khác 0. Tiếp đến do đường thẳng



qua





2; 2; 4

nên ta khoanh B. Chọn đáp án B.

Câu 42. Bà Hương nhận làm 100 chiếc nón lá giống nhau có độ dài đường sinh là

. Ở phần mặt trước

của mỗi chiếc nón (từ A đến B như hình vẽ) bà Hương thuê người sơn và vẽ hình trang trí. Biết

20 2

AB cm



và giá tiền công để sơn trang trí

là 50000 đồng. Tính số tiền (làm tròn đến hàng nghìn)

mà bà Hương phải thuê sơn trang trí cho cả đợt làm nón

128.000

đồng B.

257.000

đồng C.

384.000

đồng D.

209.000

đồng

Lời giải

Đầu tiên theo tính chất góc ở tâm bằng hai lần góc nội tiếp chắn cung tương ứng nên ta suy ra:



2 120

AOB AIB 



. Sử dụng đính li Cosin ta có:





2 2 2 2

2 . cos120 3 20 2

AB OA OB OA OB R    



Từ đó suy ra

 

20 6

R cm



. Tiếp theo, ta gọi đỉnh của hình nón là

, sau đó ta trải phẳng mặt xung

quanh của nón ra, khi ấy diện tích mặt cần sơn và trang trí chính là phần hình quạt

SAB

Ta có độ dài cung



là

 

2 20 6 40 6

3 3 9

l cm

 

 

. Từ đó ta tính được diện tích hình quạt

SAB

là:

   

2 4 2

. 1 40 6 1200 6 1200 6

.30. .10

2 2 9 18 18

l SA

S cm m

  



   

. Mà giá tiền công để sơn trang trí

là

50000 đồng nên giá tiền công sơn 100 cái nón là:

1200 6

.10 .50.000.100 256.509







(đồng).

Như vậy tổng tiền này gần với đáp án B nhất. Chọn đáp án B.

Câu 43. Cho hàm số





f x

có đồ thị như hình vẽ . Đặt













g x f f x

 

. Tìm số nghiệm của phương trình





g x





Lời giải

Ta có:

     

 









 

0 1

. 1 0

1 0 2

f x

g x f x f f x

f f x







  

   





 





Nhìn vào đồ thị, dễ thấy (1) có 3 nghiệm.

(2) tương đương với:









 

   









 

   

1 1;0 1 0;1 2

1 1 2 2

1 1; 2 1 2;3 2

f x a f x a n

f x f x n

f x b f x b n

        

 

    

 

      

 

. Tổng là 6 nghiệm.

Như vậy hàm số cần tìm có tất cả 9 nghiệm. Chọn đáp án A.

Câu 44. Có bao nhiêu giá trị nguyên của

thuộc đoạn





0;2022

để bất phương trình

 

1 4 2 1 4 0

x x

m m x



 

      

 

 

nghiệm đúng với mọi

thuộc





0;1

2021

1011

2022

Lời giải

Đầu tiên ta xét





4 4

4 0, 0;1

x x



     

, do





4 4, 0;1

x x  

nên bất phương trình tương đương

với:

 

1 4 2 1 0

m m

    

. Đặt





4 1; 4

t  

, khi bất phương trình trở thành:

     









2 2

1 2 1 0 1 2 1 2 0, 1; 4 , 1;4

t t

m t m m t m t t m t

t t t

 

                



Xét hàm số

 





, 1; 4

t t

y f t t

t t

 

   



có

 

3 4 4

0 2

t t

f t t

t t

 



   



Mà

     

1 4

2 7 1

lim ; lim ; 2

3 12 2

t t

f t f t f

 

 

  

nên ta suy ra được

 

f t



tức

 

min

f t



Suy ra để bất phương trình có nghiệm đúng trên tập cho trước thì

 

min

m f t m

  

Với





0;2022

m

ta thu được

 



 

 

tức có 1 giá trị nguyên

thỏa mãn. Chọn đáp án D.

Câu 45. Có bao nhiêu số phức

thỏa mãn

2 2

z i

  

và

 





3 1 3

w z i z i

     là số thực ?

Lời giải

Đầu tiên ta đặt





z a bi a b R

  

 





     

3 1 3 1 3 3 6 8

w z i z i z i a bi i a bi i

             

. Do

là số thực nên ta suy ra





Im 3 3 8 2 2 8 0

w b a b a a b

        

. Cùng với

2 2

z i

  

ta quy về hình học

Oxy

nên số các số

phức

thỏa chính là số giao điểm giữa đường tròn

     

2 2

: 2 1 4

C x y

   

với tâm





2;1 , 2

I R

 

và

đường thẳng

4 0

x y

  

Ta nhận thấy





d I d R



nên





cắt





tại 2 điểm tức có 2 số phức thỏa mãn. Chọn đáp án B.

Câu 46. Cho ba số phức

1 2 3

, ,

z z z

thỏa mãn

1 2 1 2

1, 7, 2

z z z z   

và giá trị lớn nhất của biểu thức

1 2 3

3 2

z z z

 

bằng 78. Giá trị

bằng

78 53

 B.

78 73

 D.

Lời giải

Ta có:

2 2 2

1 2 1 2 1 2 1 2

2 2 3

z z z z z z z z

      

, khi đó ta suy ra:

2 2

1 2 1 2 1 2

3 2 9 4 12 9 4.7 12.3 73

z z z z z z       

Mà theo bất đẳng thức Mincopski ta có:





1 2 3 1 2 3 3

3 2 3 2 73 78

z z z z z z z

       

nên ta suy ra:

Giá trị của

78 73

z  

. Thử lại dấu bằng xảy ra tại bất đẳng thức trên ta thấy

1 2

z z

không tồn tại dấu

bằng thỏa mãn nên ta kết luận không có đáp án nào đúng.

Câu 47. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

 

1 3

: 2

2 3 1

x a at

y t

z a a t



  



   





   



. Biết rằng khi

thay đổi thì luôn tồn tại một mặt cầu cố định đi qua điểm





1;1;1

và tiếp xúc với đường thẳng



. Tìm bán

kính của mặt cầu đó.

6 3

5 3

7 3

4 3

Lời giải

Ta có:

 

1 3

: 2 3

2 3 1

x a at

y t x y z

z a a t



  



        





   



. Thế

 

vào ta thu được:







 





 



Khi đó ta suy ra rằng



luôn qua điểm





1; 5; 1

 

cố định, và nằm trong mặt phẳng





: 3 0

P x y z

   

Mặt cầu tiếp xúc với đường thẳng



với mọi

nên mặt cầu tiếp xúc với mặt phẳng





tại

Đường thẳng

vuông góc với





có phương trình là:

 

5 1 ; 5 ; 1

x t

y t I t t t

z t

 





        





  



Mà

IA IM



nên

     

2 2

2 2 2 2

6 2 5 6;0; 6 5 3

t t t t t t t I R IM             

Vậy bán kính của mặt cầu cần tìm là bằng

5 3

. Chọn đáp án B.

Câu 48. Có bao nhiêu giá trị nguyên

để bất phương trình

2 2

14 2 3

2 11

2 2

m x x

x x m

  



  

 

nghiệm đúng

với mọi giá trị thực của

Lời giải

Bất phương trình tương đương với:

2 2

14 3 2 3 3 2 2

2 .2 2 .2 2 11

m x x x x

x x m

    

    













2 2 2 2

17 6 2 2 17 2 6 2

2 2 2 11 2 17 2 6

m x x x m x x x

x x m m x x x

       

             

Xét hàm đặc trưng





y f t t

  

có





2 ln 2 1 0

f t



  

với mọi

t R



Suy ra hàm số





f t

đồng biến trên R.

Từ đó kéo theo:





2 2 2 2 2

17 6 2 11 0 1 11 0 10 10

m x x x x x m m m



                    





nên





3;3

m 

tức có 7 giá trị nguyên

thỏa mãn đề bài. Chọn đáp án C.

Câu 49. Cho hàm đa thức





y f x



. Hàm số





y f x





có đồ thị như hình vẽ sau:

Có bao nhiêu giá trị của

để

 

0;6 ,2m m 

để hàm số









2 1 2

g x f x x x m

    

có đúng 9 điểm

cực trị.

A. 6 B. 5 C. 7 D. 3

Lời giải

Ta có:

 





1 2 1 1

g x f x x m

     

Đồ thị hàm số

 

y g x

nhận đường thẳng

1x 

làm trục đối xứng và hàm số

 

y g x

luôn có một điểm

cực trị là

1x 

Xét trường hợp

1x 

, ta có:

 

4 2g x f x x m   

   

 

2 4 . 4 2g x x f x x m

 

    

 

4 2 0 *

4 2 0

0 4 2 1 4 1 1

4 2 2

4 2

4 2 3

4 1 3

x x m

g x x x m x x m

x x m



 











   





          



   

  



   



   



Phương trình

 

nếu có nghiệm thì các nghiệm này sẽ là nghiệm bội chẵn của

 

0g x





nên hàm số

 

g x

không đạt cực trị tại các nghiệm này.

Đồ thị các hàm số 4 1y x x



    , 4y x x



   , 4 1y x x



    trên khoảng

 

1; 

được cho bởi hình

dưới đây:

Hàm số

 

y g x

có 9 cực trị



Hàm số

 

y g x

có 4 cực trị

1x 



Phương trình

 

0g x





có 4 nghiệm phân biệt

1x 

3 4 6 2 8

2 2 4

m m

   

 

 

 

 

 

Kết hợp với điều kiện

2m

và

0 2 12m 

ta được:

 

2 0;1;2;3; 4;7m

, tức là

1 3 7

0; ;1; ; 2;

2 2 2

 



 

 

Vậy có 6 giá trị của

thỏa mãn yêu cầu bài toán. Chọn đáp án A.

Câu 50. Cho hàm số bậc ba

 

y f x

có đồ thị là đường cong như hình bên. Biết hàm số

 

f x

đạt cực trị

tại hai điểm

1 2

,x x thỏa mãn

2 1

2x x  và









1 2

f x f x

 

. Gọi

1 2

,S S là diện tích hình phẳng được gạch

như hình bên và

S là diện tích phần tô đậm. Tính tỉ số

Lời giải

Cách 1:

Ta thực hiện tịnh tiến điểm gốc tọa độ vào trùng với tọa độ trung điểm hai hoành độ

1 2

x x

. Khi đó diện

tích của các phần cần tính không thay đổi và hàm số





 





 

 

 

 



 

 

 

 

y f x y g x

y h x y h x

 Ta thấy

và

trở thành

và

tương ứng không thay đổi giá trị.

 Ta thấy







y g x

là hàm lẻ









    

y g x ax bx a

có hai điểm cực trị

và

thỏa mãn

 

2 1

' '

x x

Mặt khác

 



  







2 1

' 1

' ' 2

' 1

x x

 Ta có





 

' 3

g x ax b

có nghiệm

 

' 1

và



' 1





     

' 1 0 3

g b a





  

g x ax ax



Tại

 

' 1

thì





 

1 2

g a

 

 

       

 

0 0

1 1

3 5

' 3

4 2 2

a a a

S g x ax ax dx

 

 

 

      

 

 

0 0

1 1

' 2 2 3

S a g x dx a ax ax dx

Do đường thẳng





h x

cắt





g x

tại ba điểm trong đó có điểm uốn nên suy ra hai hoành độ còn lại lần lượt

là

 

2 ' 2

và



2 ' 2

với









  

1 2 2

g g a

, suy ra









 

h x ax a

Suy ra:

   

 

         

  

2 2 2

3 3

3 1

0 0 0

' 3 4 4

S h x g x dx ax ax ax dx ax ax dx a

Vậy tỉ số

2 2

3 1 3

4 4 16

S S a

S a



  



. Chọn đáp án D.

Cách 2: Chọn









3 ,

y g x x x y h x x

    

để tính toán cho gọn

ĐỀ THI THỬ CHUYÊN KHTN – HÀ NỘI LẦN 1

Câu 42. Cho số phức

thỏa mãn



. Tìm giá trị lớn nhất của biểu thức 1

P z z i

   

8 4 2



2 2 2



2 2

Lời giải

Đặt





, ,

z a bi a b R

   và gọi

là điểm biểu diễn của số phức

thỏa mãn



Khi đó điểm

chạy trên đường tròn tâm

, bán kính



. Đặt









1;0 , 0;1

A B , ta suy ra

P z z i MA MB

      . Gọi

1 1

;

2 2

 



 

 

là trung điểm của

. Theo công thức đường trung tuyến ta

có:





 

2 2 2

2 2 2 2 2 2

2 4 4 2

MA MB AB

MC MA MB MC AB MC

 

      

Suy ra:





2 2 2

2 4 2

P MA MB MC

   

. Mà theo hình dưới thì

max khi

M M

 với

M C CO R   

nên suy ra

4 1 2 2 2 2

 

    

 

 

. Chọn đáp án C.

Câu 45. Cho hàm số





y f x

 là hàm đa thức bậc bốn. Biết hàm số





y f x



 có đồ thị





như hình vẽ và

diện tích hình phẳng giới hạn bởi đồ thị





và trục hoành bằng 9. Gọi

và

lần lượt là giá trị lớn nhất

và giá trị nhỏ nhất của hàm số





y f x

 trên đoạn





3; 2

 . Khi đó, giá trị

M m



bằng

Lời giải

Đầu tiên, từ đồ thị trên ta dễ dàng suy ra:

     

1 2 3 2

f x a x x ax ax a



     

với



Khi đó, ta có:

   

 

4 2

3 2 2

4 2

ax ax

f x f x dx ax ax a dx ax C



       

 

Mà diện tích hình phẳng giới hạn bởi đồ thị





và trục hoành bằng 9 nên ta suy ra:

       

3 4

9 1 2 9 2 4 6 4 9

4 2 3

a a

f x dx f f a C a a a C a



 



               

 

 



Khi đó ta suy ra:

 

3 3

f x x x C

   

, ta có bảng biến thiên trên đoạn





3; 2

 như sau:

Với

, 8

M C m C

    

ta suy ra

 

8 32

3 3

M m C C

 

      

 

 

. Chọn đáp án B.

Câu 46. Trong không gian với hệ tọa độ

Oxyz

, cho hai đường thẳng lần lượt có phương trình là:

1 2

1 2 2 1 1

: , :

1 2 1 2 1 1

x y z x y z

d d

    

   

và mặt phẳng





: 2 5 0

P x y z

   

. Lập phương trình đường

thẳng song song với mặt phẳng





và cắt

1 2

d d

lần lượt tại

A B

sao cho độ dài

đạt giá trị nhỏ nhất ?

1 2 2

1 1 1

x y z

  

 

 

1 2 2

1 1 1

x y z

  

 

1 2 2

1 1 1

x y z

  

 



1 2 2

1 1 1

x y z

  

 

Lời giải

Đầu tiên ta có:





 

1 ; 2 2 ;

3 2 ;3 2 ;1

2 2 ;1 ;1

A a a a

A d d

AB b a b a b a

B d d

B b b b

   

 





        

 

 

  









(1)

Mặt phẳng





: 2 5 0

P x y z

   

có vector pháp tuyến





1;1; 2

 



cùng với





AB P



nên ta có:













. 0 3 2 3 2 2 1 0 4

AB n b a b a b a a b

             

 

(2)

Từ (1) và (2) ta suy ra:

       

2 2 2 2

2 2

3 2 3 2 1 2 8 35 2 2 27 27

AB b a b a b a b b b

               

Khi đó dấu bằng xảy ra khi và chỉ khi









2 2 3; 3; 3 1;1;1

b a AB k         



Như vậy phương trình đường thẳng

là . Chọn đáp án B.

Câu 47. Trong không gian với hệ tọa độ

Oxyz

, cho điểm





1; 1;3

A  và hai đường thẳng lần lượt có phương

trình là:

1 2

4 2 1 2 1 1

: , :

1 4 2 1 1 1

x y z x y z

d d

     

   

 

. Viết phương trình đường thẳng

đi qua điểm

vuông góc với đường thẳng

và cắt đường thẳng

1 1 3

2 1 1

x y z

  

 

1 1 3

2 1 1

x y z

  

 

1 1 3

2 1 1

x y z

  

 



1 1 3

2 1 1

x y z

  

 

 

Lời giải

Đầu tiên, ta gọi

B d d

 

tức

B d



, khi đó ta có:









2 ; 1 ;1 1 ; ; 2

B t t t AB t t t

        



khi đó



chính là vector chỉ phương của đường thẳng

. Mà

d d



với vector chỉ phương

là





1;4; 2

 



nên

suy ra:













1. 1 4 2 2 0 1 2; 1; 1

t t t t AB

          



Vậy phương trình đường thẳng

là:

1 1 3

2 1 1

x y z

  

 

 

. Chọn đáp án D.

1 2 2

1 1 1

x y z

  

 

Câu 48. Biết rằng có đúng một số phức

thỏa mãn

2 2 4

z i z i

   

và

z i





là số thuần ảo. Tính tổng

phần thực và phần ảo của



Lời giải

Đặt





, ,

z a bi a b R

   . Khi đó ta có:

     

2 2 2

2 2 4 2 2 4 4

z i z i a b a b b a

             

(1)

















 

   

 

2 2

1 1

1 2 1

1 1

a b i a b i

a b a b i

z i

a b a b

   

   



 



   

là số thuần ảo, khi đó

 

1 1

a b

  

(2)

Thế (1) vào (2) ta có:

 

a a a

    

. Vậy tổng cần tìm là

2 4 1

a b a

    

. Chọn đáp án D.

Câu 49. Cho hàm số





f x

có đạo hàm trên

và thỏa mãn





3 2

f x x x

  

với mọi số thực

. Từ đó hãy

tính

 

x f x dx





219

357

Lời giải

Đầu tiên, ta thế



vào phương trình





3 2

f x x x

  

thu được





4 3



Ta gọi tích phân cần tìm là

 

I x f x dx







. Đặt

 

du xdx

u x

v f x

dv f x dx









 



 











Suy ra:

       

4 4 4

0 0 0

16 4 2 48 2

I x f x dx f xf x dx xf x dx



    

  

Đặt





 

    

3 2

4 1

2 3 3

0 0

3 3 3

2 2 3 3 3 3

: 0 1

x t t dx t dt

xf x dx t t t f t t dt



    



    









 

   

2 3 2

165

2 3 3 3 2

t t t t dt    



. Vậy

165 27

4 4

I   

. Chọn đáp án A.

Câu 50. Có bao nhiêu số nguyên dương

để phương trình sau đây có ít nhất một nghiệm thực.





log

log log

1 2 2

x x

a a x

   

Lời giải

Điều kiện ban đầu:



của phương trình (1)

Đầu tiên ta xét hai trường hợp cơ bản nhất như sau:

-Trường hợp 1: Nếu



thì (1) trở thành:

2 2 2 2

x x

   

(thỏa mãn)

-Trường hợp 2: Nếu



thì ta luôn có:

log 0



. Khi đó ta đặt

log 0 10

t a a   

Phương trình (1) trở thành:

 





   

log log

10 1 10 2 2 1 2 2

x x t

t t t t

x x x x

        

(2)

Đặt

1 0

x y

y x



  

  







. Khi ấy phương trình (2) trở thành:

1 2 2

y y x

    





log

log log

1 2 2

x x

a a x

   

Từ đó ta có hệ sau:

2 1

x y

y x y



 





  





. Trừ hai phương trình theo vế ta thu được phương trình mới tương

ứng là:

2 2 2 2

t t t t

x y y x x x y y

       (3)

-Nếu

x y

 

thì ta luôn có









3 3

VT VP . Tương tự nếu

y x

 

thì ta luôn có









3 3

VP VT

Như vậy, để dấu bằng phương trình (3) xảy ra thì ta phải có:





 

log 1

log

x y

x x t

y x







    



 







2 0 log 1 log

x x x

     nên ta suy ra:





 

 

log 1

log 1 10 2;9

log

a t a a







      



Vậy có tất cả 9 giá trị nguyên dương

thỏa mãn. Chọn đáp án D.

ĐỀ THI THỬ CÂU LẠC BỘ TOÁN LIM ++

Câu 42. Tính thể tích của hình trụ bị cắt bởi hai mặt phẳng song song (hình vẽ) dưới đây. Biết rằng

ABCD

là hình thoi cạnh bằng 4 và



ABC 





Lời giải

Đầu tiên ta có hình vẽ như sau:

Ta kẻ ,

AE BC CF AD

 

. Khi đó ta gọi

là thể tích giới hạn bởi đường tròn đường kính

, elip trục

lớn

và đường cao

là thể tích giới hạn bởi đường tròn đường kính

, elip trục lớn

và

đường cao , và

là thể tích khối trụ có đường tròn đáy đường kính

và đường sinh

sin 60 2 3; 2

2 2

BC AB

AE CF AB AF CE

      



(do

ABC



đều).

Nhận thấy rằng

1 2

V V V

V V

 









nên suy ra

1 2

V V

 

, lúc này thể tích của khối tròn xoay cần tìm là:

1 2

2 2 . 2.2 .3 12

V V V V V AF

  

 

      

 

 

. Chọn đáp án A

Câu 43. Xét trên tập số phức phương trình:

2 2

2 2 4 0

z mz m m

    

(với

là tham số thực). Có bao

nhiêu giá trị thực của

để phương trình trên có hai nghiệm phân biệt

1 2

;

z z

sao cho

2 2

1 2

z z

 

Lời giải

Ta có

2 2 4

m m



   

. Phương trình có hai nghiệm phân biệt





0 1;2



      . Nên để phương

trình đó có hai nghiệm phân biệt

thỏa mãn

2 2

1 2

z z

 

Khi đó ta có:

   





 

2 2

1 2 1 2 1 2

2 2 2 2

1 2 1 2 1 2

4 8 2

20 2 4 8 2 2 2 5

z z z z z z m m

z z z z z z m m m m m m



      





              





. Từ đó ta suy ra:

2 0

1 2 7

3 2 4 5

1 2 7 1 2 7

;1;

3 3

2 0

2 4 5

m m





  











  

 





 



  



   

 





    

 















   







Vậy có duy nhất 3 giá trị thực

thỏa mãn yêu cầu đề bài. Chọn đáp án C.

Câu 44. Có 6 vị khách tham gia bữa tiệc trong đó có Phượng và Hòa, cần phải sắp xếp họ ngồi quanh một

bàn tròn có 6 ghế phân biệt. Có bao nhiêu cách xếp để Phượng và Hòa không ngồi cạnh nhau ?

600

280

576

432

Lời giải

Số cách để xếp 6 người (trong đó có Phượng và Hòa) vào 1 bàn tròn ghế bất kì là:

(cách) (do 6 ghế đã

phân biệt nên cách xếp xem như tương tự với xếp 1 hàng ngang).

Ta sẽ giải phần bù tức tìm số cách xếp để Phượng và Hòa ngồi cạnh nhau

Coi Phượng và Hòa là một phần tử ngồi cạnh nhau, 2 bạn tự hoán đổi nhau trong lúc xếp nên có 2! cách,

như vậy có tất cả 6 cách để xếp phần tử này vào 6 ghế cố định.

Còn 4 vị trí còn lại cho 4 người, có tất cả 4! cách.

Suy ra số cách xếp để Phượng và Hòa ngồi cạnh nhau là

2.6.4!

cách

Suy ra số cách xếp cần tìm là

6! 2.6.4! 432

 

cách. Chọn đáp án D.

Câu 45. Có bao nhiêu số nguyên dương

sao cho ứng với mỗi

tồn tại ít nhất 6 số nguyên





12;12

b 

để bất phương trình





1 1

1 1 ln 0

x x b

a xe x be

  

 

   

 

có nghiệm

1210

890

1211

891

Lời giải

Ta có bất phương trình tương đương với:

 





 

1 1 1

1 1

1 1 ln

1 1 ln 0 0 1 ln 0

x b

x x b x b

x x

xe x

a xe x be a a e x x be

e e



 

    

 

 

 

   

           

 

   

 

(1)

Tiếp theo ta xét hàm số:









1 ln

y f x e x x



    có

   

1 1

1 1 1

ln ;

x x

f x e x f x e

x e x

 



 

      

Ta nhận thấy với

 

thì

e x





nên suy ra

1 1

e x





tức

 

0, 0

f x e x





    

Khi đó suy ra





f x

là hàm lõm và





f x





có nhiều nhất một cực trị trên





0;1

Khi đó ta suy ra

0.08

x x  với





2,79

f x  . Với

















1 1

0 1

lim 1 ln ; lim 1 ln 2

x x

e x x e e x x

 

 

 

     

Từ đó ta có bảng biến thiên như sau:

Từ bảng biến thiên trên, với

 









0;1

min 1 2

f x f

 

ta suy ra (1) 2 0 2

b b

a be a be

 

     

Như vậy với



thì hàm số





y g b be



   luôn đồng biến, tức

có nghĩa, mà theo đề bài ứng với

mỗi

tồn tại ít nhất 6 số nguyên





12;12

b 

nên suy ra





12; 6

  

kéo theo





6 0

 

với





h x a be



  , tương đương

6 6

2 6 0 3 1 1210

a e a e a





      



Vậy có tất cả 1210 số nguyên dương

thỏa mãn yêu cầu bài toán. Chọn đáp án A.

Câu 46. Cho hàm số





3 2

y f x x bx cx d

    

có hai điểm cực trị

1 2

x x

thỏa mãn

2 1

x x

 









1 2

3 0

f x f x

 

và đồ thị





y f x



luôn đi qua điểm









1 2

M x f x



. Gọi





y g x



là hàm bậc 2 có đồ

thị đi qua 2 điểm cực trị của





f x

và đi qua

. Tính diện tích hình phẳng giới hạn bởi hai đồ thị









f x g x

Lời giải

Gọi

là hoành độ trung điểm giữa hai hoành độ

1 2

x x

tức hoành độ điểm uốn của đồ thị .





y f x



Đầu tiên, ta dễ dàng nhận ra

1 2

, ,

x x x

và

1 0 2

, ,

x x x

lần lượt là các cấp số cộng có công sai lần lượt là

và

Khi đó ta xem như

1 1 0 2

1 1 2, 3, 4

x x x x x

      

và diện tích hình phẳng giới hạn bởi hai đồ thị









f x g x

không thay đổi. Từ đó ta có hệ sau:





 

3 2

3 18 2 0

9 24

2 12 4 0

f b

f x x x x d

f b c



  



    





   





(1)

Ta lại có:













2 3 1 0 20 3 16 14

f f d d d

        

. Như vậy ta suy ra





3 2

9 24 14

f x x x x

   

. Tiếp theo, ta đặt:









g x ax dx e a

   

, khi đó ta có hệ phương trình sau:





 

1 3

2 4 2 9 10 2 10 6

4 16 4 3

g a d e

g a d e b g x x x

g a d e

   



 





          

 

 

 

   



. (2)

Từ (1) và (2), ta suy ra diện tích cần tìm là:

   

S f x g x dx  



. Chọn đáp án C.

Câu 47. Tính thể tích vật thể khi quay hình tròn





, đường kính

2 8

AB R

 

quanh trục

. Biết hình

tròn tiếp xúc với

tại





0;8;0

, mặt





Oyz

chứa tâm

vuông góc với mặt phẳng chứa hình tròn. Hình

tròn nghiêng 1 góc



so với đáy





Oxy

(xem hình vẽ).

32 2



64 2



160 2



128 2



Lời giải

Đầu tiên ta có hình vẽ như sau: (Xét mặt phẳng cắt hình tròn





và vuông góc với trục

)

Do hình tròn nghiêng 1 góc



so với đáy





Oxy

nên dễ dàng tính được tâm





0;8 2 2; 2 2

I 

Đặt

OA PB z

 

, khi đó

2 2 4

IQ BQ IB PB IB z

     

Suy ra:

 

2 2

16 2 4

QN IN IQ z     . Do dùng mặt cắt vuông góc với

và hình tròn ta thu được

chính là đoạn

ta suy ra thiết diện mặt cắt của khối tròn xoay chính là hình vành khăn tâm

Tức ta có diện tích thiết diện cần tìm là:

 









2 2 2 2

16 2 4 8 2 2

S AN AQ QN z z z

   

 

       

 

 

Từ đó ta suy ra thể tích khối tròn xoay cần tìm với thiết diện

chạy từ cao độ

đến

4 2

là:

 

4 2 4 2

0 0

128 2

8 2 2

V S dx z z dx



   

 

. Chọn đáp án D.

Câu 48. Trong không gian Oxyz cho các điểm

   

 

2;0;0 , 2;0;0 , 4;1; 2A B C  và

 

1; 2; 4D 

. Điểm

thay đổi thỏa mãn 2 3MA MB  . Giá trị nhỏ nhất của biểu thức

2 2

2T MC MD  thuộc khoảng nào dưới

đây ?





; 40







40; 41





41; 42





42;



Lời giải

Cách 1: Phương pháp hình học

Gọi tọa độ điểm

là





; ;

M x y z

, khi đó ta có:

Xét riêng trên mặt phẳng

 

Oxy

ta nhận thấy quỹ tích điểm

để thỏa đẳng thức 2 3MA MB  là một

elip chính tắc có tiêu cự là 2 2 2AB c  và độ dài trục lớn là 2 2 3a  , từ đó suy ra hệ số 1b  , tức

phương trình elip là:

 

(1).

Tương tự xét riêng trên mặt phẳng

 

Oxz

ta cũng thu được phương trình:

z 

(2).

Từ (1) và (2) ta sẽ thu được quỹ tích chính thức của điểm

như hình dưới đây.

Gọi

là điểm thỏa 2 0IC ID 

  

từ đó suy ra

 

3;0;0

C D



 

(tâm tỉ cự)

Như vậy biểu thức

min khi

min, mà I Ox nên ta suy ra giá trị nhỏ nhất của

là:

min 0

3 3

MI OM   

với

 

3;0;0M M .

Vậy ta suy ra

 

2 2

min

2 40.7 40; 41T MC MD   

. Chọn đáp án B.

Cách 2: Phương pháp đại số

Ta có:

 





 

2 2

2 2 2 2 2 2

12 2 . 2 2

MA MB

MA MB MA MA MB MB MA MB MA MB MA MB

MA MB



           



Tiếp theo ta đặt

 

; ;M x y z

, khi đó ta có:

 

2 2 2

MA x y z

MB x y z



   







   



. Từ đó ta suy ra:

 

2 2 2 2 2 2 2

2 2 ; 4 2MA MB x y z MB MA x      

. Thế vào phương trình trên ta suy ra được:

 

2 2 2 2 2 2 2 2 2 2

32 2

12 4 2 3 2 3 3 3

12 3

x y z x y z x x y z

              

Như vậy điểm





; ;

M x y z

dao động trên đường cong khép kín

 

2 2 2 2 2

: 3 3 3 1

T x y z y z

      

     





     

 

2 2 2 2 2 2

2 2

2 2 2 2 2

2 2 4 1 2 1 2 4

3 18 63 3 1 18 63 2 18 66

T MC MD x y z x y z

x y z x x x x x

             

 

            

 

 

Mà

2 2 2

3 3 3

x y z

  

nên suy ra

3; 3

 

 

 

. Xét hàm số





2 18 66

y f x x x

   

trên

3; 3

 



 

 

4 18 0, 3; 3

f x x x

 



     

 

nên





 

3 72 18 3 40,82 40; 41

T f     . Chọn đáp án B.

Câu 49. Cho hình chóp .

S ABC

có

vuông góc với đáy, các cạnh

, 2

AB a AC a

 

và góc



120

BAC 



. Gọi

M N

lần lượt là hình chiếu của

lên các cạnh

SB SC

. Gọi



là góc giữa hai mặt phẳng





AMN

và





ABC

sao cho

cos





. Tính cosin góc giữa hai mặt phẳng





SAB

và





SBC

Lời giải

Đầu tiên ta có hình vẽ như sau: (chuẩn hóa



Dựng đường kính

của đường tròn ngoại tiếp tam giác

ABC

, khi đó ta có:



ABD ACD 



Mà





SA ABC



nên suy ra





 

BD SAB

AM BD

AN CD

CD SAC











 









mà

AM SB

AN SC











nên





 

AM SBD

AN SCD













Suy ra





 

SD AMN

SA ABC













tức

   

 



 



; ;AMN ABC SD SA ASD



  

, suy ra:

tan



  (1).

Mà :

2 2

2 7

2 . cos120 7; 2

sin120

BC AB AC AB AC AD R      



nên

SA AD 

Khi đó ta có:

1 21 1 7

. . .sin120 ; . ; 2 2; 11

6 6 2 2

S ABC SAB

V SA AB AC S SA AB SB SC     



Suy ra:

   

 



13; ;

6 7

sin cos

2sin .

13 13

3 6

SBC

SAB SBC

SABC

S SAB SBC

S S



 





 



 



   





 



. Chọn đáp án A.

Câu 50. Cho số phức

thỏa mãn tồn tại các số phức

1 2

w w

sao cho









1 1 2 2

w w w w

  

trong đó ta có

1 2

2 2

;

4 16

z z

w w

z z

 

 

. Ngoài ra

4 4

z i m

  

(với

là tham số thực). Có bao nhiêu giá trị thực của tham

số

sao cho tồn tại đúng 5 số phức

như vậy ?

D. Vô số.

Lời giải

Đầu tiên ta có điều kiện ban đầu là:

4 0 4

16 0

z z

z i



  







 

 

 





. Tiếp theo ta có:

  

1 1

1 1 2 2

2 2

w w

w w w w

w w





   



 





như vậy ta suy ra: với





, ,

z a bi a b R

   

ta có hệ sau:

 

2 2

4 0

. 4 . 4

16 0

. 16 . 16

z z

z z z

a b

z z z z z z

z z

z z z

z z z z z z

a b

 









 



  



 



  

   



   

   





  

   

   



 





 



 









Chuyển về hệ trục tọa độ





Oxy

ta có được hình vẽ như sau:

z i







 



nên ta loại các điểm

, ,

A B C

đi (như hình vẽ).

Phương trình

4 4

z i m

  

biểu diễn số phức

thuộc đường tròn





tâm





4;4

có bán kính

R m



Với đúng 5 số phức

thỏa mãn ta nhận thấy qua hình vẽ đường tròn





qua tiếp xúc ngoài với đường

tròn

2 2

x y

 

, đi qua





0;2

và đi qua





0; 2



Với ba đường tròn thỏa mãn ta suy ra có 3 giá trị nguyên

thỏa mãn. Chọn đáp án B.

ĐỀ THI THỬ CHUYÊN BIÊN HÒA – HÀ NAM

Câu 39. Cho hàm số





y f x



là hàm đa thức và có đồ thị









f x f x



như hình vẽ bên dưới. Có bao nhiêu

giá trị nguyên của tham số

để giá trị lớn nhất của hàm số dưới đây trên đoạn





2;3



không vượt quá

4044:

   

 

5 4 2 2

1 1

3 1 4 2022

5 2 3

g x f x x x m m x x        

Lời giải

Ta có:

















4 3 2 2

2 3 2 1 4

g x f x x x m x m x

 

       

 





   

2 2

2 1 1

f x x x mx x x



        

 

 

. Nhận thấy khi tịnh tiến thêm 2 đơn vị theo chiều dương

của đồ thị





f x



thì đồ thị





f x





luôn dương trên đoạn





2;3



Mà





   

 

2 2

1 1 0, 2;3

x x mx x x x          nên suy ra









0, 2;3

g x x



   

tức hàm số





g x

luôn đồng biến trên đoạn





2;3



Khi đó ta có được

 

     

2 2

2;3

20601 1687 20601

max 3 3 9 9 9 9 4044

10 200 10

g x g f m m m m



         

Suy ra:





14.32 15.32 14;15

m m



     



tức có 30 giá trị nguyên

thỏa. Chọn đáp án B.

Câu 41. Trong không gian

Oxyz

cho hai đường thẳng

1 2

1 2 2 1 1

: , :

1 2 1 2 1 1

x y z x y z

d d

    

   

và mặt

phẳng





: 2 5 0

P x y z

   

. Tìm phương trình đường thẳng

song song với mặt phẳng





và cắt .

1 2

d d

. lần lượt tại

và

sao cho

AB  và điểm

có hoành độ dương.

1 2 2

2 4 3

x y z

  

 

 

2 4 3

x y z

  

 

1 2 2

2 4 3

x y z

  

 



1 2 2

2 4 3

x y z

  

 



Lời giải

Đầu tiên ta có

A B

lần lượt là các điểm thuộc

1 2

d d

nên ta suy ra:





 

1 ; 2 2 ;

2 2 ;1 ;1

A a a a

B b b b

   





  









2 3; 2 3;1

AB a b a b a b

         



mà





d P



nên ta suy ra

AB n



 

với





1;1; 2

 



là vector pháp

tuyến của





. Khi đó:













2 3 2 3 2 1 0 4 4

a b a b a b a b b a

                  

(1).

Ta có:

         

2 2 2 2 2

2 3 2 3 1 5 1 9 29

AB a b a b a b a a

                

thế từ (1).

Giải phương trình suy ra





 





 

0;0;1 2;4;3

2;4;3 0;0;0

A A

A B



 







 















 

. Chọn đáp án B.

Câu 42. Tính tổng các nghiệm nguyên thuộc





5;10



của bất phương trình sau đây:





2 2

2 3 6 6 7 29 34

x x

x x x x



    

Lời giải

Bất phương trình tương đương với:









2 2 2

2 12 24 24 7 29 34

x x

x x x x

 

     (1)

Ta nhận thấy:













2 2 2 2

12 24 24 7 29 34 5 5 10 5 2

x x x x x x x x

          

nên (1) trở thành:

   

2 2

12 24 24 7 29 34

2 2

5 5

2 12 24 24 2 7 29 34

x x x x

   

     

Xét hàm số

 

y f t t

  có

 

5 5

2 2 ln 2 0

t t

f t



  

với mọi số thực

nên suy ra hàm số





f t

luôn

đồng biến trên tức

2 2 2

12 24 24 7 29 34 2 0

x x x x x x





         



 



Mà





5;10

x  

nên









5; 2 1;10

x   

. Suy ra tổng nghiệm nguyên của bất phương trình (1) là:

2 10

5 1

k k

S X X



 

  

 

. Chọn đáp án D.

Câu 44. Cho hàm số

 

4 3 2

y f x ax x x bx

     

và hàm số





3 2

y g x cx dx x

   

(với , , ,

a b c d R



)

là các hàm số có đồ thị như hình vẽ bên dưới. Gọi

1 2

S S

là diện tích hình phẳng tô màu trong hình vẽ, biết

S 

. Tính

143

133

153

163

Lời giải

Ta nhận thấy









   

2 1 0

g g

f f

  





 

  





, Giải 2 hệ ta lần lượt ra được:

 

4 3

3 2

4 3

x x

f x x

g x x x x



   







  



Suy ra:

   

 

1 1

4 3

0 0

2 133

2 2 2

4 3 60

x x

S f x g x dx x x dx

 

       

 

 

 

. Chọn đáp án B.

Câu 45. Trong không gian với hệ tọa độ , cho mặt cầu

     

2 2 2

( ) : 1 2 3 48

S x y z

     

và đường

thẳng

1 2 3

1 1

x y z

  

  . Điểm

( ; ; ), ( 0)

M a b c a



nằm trên đường thẳng sao cho từ kẻ được ba

tiếp tuyến , ,

MA MB MC

đến mặt cầu

( ),( , ,

S A B C

là các tiếp điểm) và



0 0 0

60 , 90 , 120

AMB BMC CMA   .

Tính

Q a b c

  

6 4 2

Q  

10 4 2

Q  

9 4 2

Q  

9 4 2

Q  

Lời giải

Mặt cầu





có tâm





1; 2;3

I 

, bán kính

4 3

R  .

Gọi





là đường tròn giao tuyến của mặt phẳng





ABC

và mặt cầu





Đặt

MA MB MC x

  

khi đó

, 2, 3

AB x BC x CA x

  

do đó

ABC



vuông tại

nên trung điểm

của

là tâm đường tròn





và

, ,

H I M

thẳng hàng.

Vì



120

AMC  nên

AIC



đều do đó

3 4

x R x AM

   

suy ra

2 2 8

IM AM x

  

Lại có

M d



nên





1 ; 2 ;3 2 ,( 1)

M t t t t

    

Mà



nên

   

2 2

2 64 3; 6;3 4 2 6 4 2

t t t M a b c





          



 



. Chọn đáp án A.

Câu 47. Xét hai số phức

1 2

z z

thỏa mãn

 













1 1 1

2 2 2 3 3

z i i z z i

     

và

2 2

1 2

z i z i

   

. Giá

trị nhỏ nhất của

1 2

z z



bằng

2 6

2 2

Lời giải

Đặt





1 2

; , , , ,

z a bi z c di a b c d R

     . Khi đó ta có:

 

   

 

2 2

1 1 1 1 1 1

1 2

2 2 2 3 3 2 2 2 1

z i i z z i z i z z a b b b

 

                 

Tiếp đến ta có:

2 2

1 2 2 0

z i z i c d

       

Từ đó ta suy ra:

     

2 2

2 2 2 2

1 2

4 5 1 4 5

2 2

2 2 2

a a a a

z z a c b d a c c a c c

   

   

              

   

   

 

1 2

1 4 5 1

2 4 8 2 2

2 2 2 2

a a

a z z

 



 

 

        

 

 

. Chọn đáp án D.

Oxyz

Câu 49. Có bao nhiêu số nguyên

sao cho ứng với mỗi

có không quá 255 giá trị nguyên

thỏa mãn









5 4

log log

x y x y

  

3 7

3 8

4 0

3 6

Lời giải

Cách 1:

Ta có

x x x

   



nên điều kiện:

y x

 

mà





nên

y x

 

tức





 

là nghiệm đầu tiên của

tham số

(tức

)

Tiếp theo ta có bất phương trình tương đương với:









4 5

log log 0

x y x y

   

Xét hàm số













4 5

log log

f y x y x y

   

có:

 

1 1

ln 4

ln 5

f y

x y



  



. Từ đó ta suy ra hàm

số





f y

luôn đồng biến trên tập xác định. Ta có bảng biến thiên như sau:

Ta có bất phương trình là:





f y



Do đề bài cần không qua 255 giá trị nguyên

nên ta chỉ nhận đúng 255 giá trị, tức từ

đến

255

để





f y



, suy ra tại giá trị

256

phải làm cho





f y



tức ta có điều kiện cần và đủ để tồn tại nghiệm thỏa

là:













256 4 5

256 0 log 256 log 256 0

x x

f y f x x x

        









log 2562 2

5 4

log 256 log 256 256 5 0 18.72 19.72

x x x x x            

Mà





nên ta suy ra

1 8 1 9

  

tức có





19 18 1 38

   

giá trị nguyên

thỏa mãn. Chọn đáp án B.

Cách 2:

Đầu tiên, với

,x y





ta luôn có:





















4 4

log log

2 2 2

5 4

log log 5 5

x y x y

x y x y x y x x x y

 

          

(*)

Đặt

t x y

 

. Xét hàm số





log

y f t t

  

có

 

log

5 1 0

ln 5

f t



  

với mọi













Từ đó ta suy ra bất phương trình (*) tương đương với:





1 2

x y f x x



   

Ta có nhận xét sau: khi giá trị nguyên của

không quá 255 thì giá trị nguyên của

t x y

 

cũng không quá

255 giá trị, tức













1 2 1 2 2

1 256 256 256

x y f x x f x x x x f

 

          

4 4

log 256 log 256

2 2

5 256 5 256 0 18.72 19.72

x x x x x           

Mà





nên ta suy ra

1 8 1 9

  

tức có





19 18 1 38

   

giá trị nguyên

thỏa mãn. Chọn đáp án B.

Câu 50. Có bao nhiêu số nguyên dương

để phương trình

 

2 2

3 0z a z a a    

có hai nghiệm phức

1 2

,z z sao cho thỏa mãn

1 2 1 2

z z z z  

Lời giải

Ta chia hai trường hợp như sau:

Trường hợp 1: Hai nghiệm là hai số phức

z và

z có phần ảo khác không

Để phương trình bậc hai với hệ số thực có hai nghiệm phức có phần ảo khác không khi

 

2 2

3 4 0 3 10 9 0a a a a a          

2 13 5 2 13 5

; ;

3 3

   

  

    

   

   

Giả sử

b i

  



;

b i

  



. Ta có

1 2 1 2

3 3 10 9z z z z a a a        

 

3 3 10 9 1

a a a a

 





        







so với điều kiện ta nhận được

9a  

;

1a 

Trường hợp 2: Hai nghiệm là hai số thực

z và

z .

2 2

1 2 1 2

4 0

z z z z S S P P





        



 



. Thử lại thỏa mãn.

Vậy ta suy ra

 

9; 1; 0;1

S   

tức có 4 giá trị nguyên

thỏa mãn. Chọn đáp án B.

ĐỀ THI THỬ SỞ THANH HÓA LẦN 2

Câu 40. Cho hàm số bậc bốn

 

y f x

có bảng biến thiên như hình sau:

Có bao nhiêu giá trị nguyên của tham số





2022;2022

m 

để phương trình sau có đúng 5 nghiệm phân

biệt:

 

   

 

2 2 2 2 2

2 14 4 1 36 0f x x m m f x x m        

4 0 4 3

4 0 4 4

Lời giải

Đầu tiên, từ bảng biến thiên đã cho ta dễ dàng tìm được





4 2

3 6 3

f x x x

  

Ta có phương trình tương đương với:

 

   

 

2 2 2 2 2

2 14 4 1 36 0f x x m m f x x m        

Đặt

 

2 2

t f x x 

thì khi đó phương trình trở thành:

       

4 1 4 9 4 0t t m t t       

   

 

2 2 2

4 9 1 0 0

9 1

2 10 0 *

f x x

t t m f x

t m

f x x m m







 



        



  

    





–

∞

+ ∞

–

+ ∞

Ta để ý rằng hàm số

y x

 

là phương trình nửa trên đường tròn có tâm là gốc tọa độ nên từ đó ta

nhận thấy

 

f x x

 

có 4 nghiệm phân biệt.

Do hàm số









2 2 2

2 10

y f x x m m    

là hàm số chẵn nên có 2 nghiệm, suy ra

 

, thử lại ta thấy

phương trình (*) có 3 nghiệm. Mặt khác ta nhận thấy (1) có 4 nghiệm phân biệt nên suy ra (2) phải có duy

nhất 1 nghiệm nên ta kết luận không có giá trị

nào thỏa mãn. Chọn đáp án A.

Câu 41. Cho hàm số





y f x



có đạo hàm





2 1,

f x e x x R



    

và





0 1



. Biết





F x

là một nguyên

hàm của hàm số





f x

thỏa mãn





F e



. Tính







Lời giải

Ta có:













2 1

x x

f x f x dx e x dx e x x C



       

 

mà





0 1



nên



. Suy ra:

     

3 2

x x

f x e x x F x f x dx e C



        



mà





F e



nên



 

nên ta suy ra:

   

3 2

5 1

3 2 6 6

x x

F x e F

     

. Chọn đáp án A.

Câu 42. Cho hàm số









4 3 2

, , ,

y f x x ax bx cx d a b c d R

      

thỏa mãn

 

min

f x f

 

 



 

 

và hàm

số

 





f x

g x





. Biết đồ thị hàm số





y g x



có 3 điểm cực trị là

























; , 0; 0 , 1; 1

A m g m B g C g

. Gọi





y h x



là hàm số bậc hai có đồ thị đi qua 3 điểm

A C

và





2; 5

D b



. Diện tích hình phẳng giới hạn bởi

hai đồ thị hàm số





y f x



và













1 1

y x h x x

   

bằng

4 6

1 5

6 4

1 5

5 6

1 5

4 4

1 5

Lời giải

Ta có:

 





 

3 2

12 6 2

4 3 2

24 6

f x x ax b

y f x x ax bx c

f x x a





  





     





 





. Mà

 

min

f x f

 

 



 

 

nên ta suy ra:





 

4 3 2

3 2

0 6 6 0 1

4 3 2

f x x x bx cx d

f a a

f x x x bx c



    



 



       



 



   

 





Tiếp đến ta có:

 













 

1 2

x f x xf x

g x



 



 



. Từ giả thiết đề bài ta suy ra:





 

0 0

1 0























   

 

   

4 3 2 4 3 2

0 0

1 1 1

2 1

1 1

f x x x bx b x x b x

b d b

f f











            

 

  











Khi đó:

 









4 3 2

4 3

2 2

1 1

x x b x

x x

g x b

x x

   

 

  

 

Ta nhận thấy ba điểm

, ,

A B C

cùng nằm trên đồ thị





 

3 2

4 3 2 3

2 2

f x

x x bx

y x x b



 

    





. Mặt khác

điểm





2; 5

D b



cũng thuộc đồ thị tương ứng nên ta suy ra: đồ thị của hàm số





y h x



cũng có dạng là:

 

h x x x b

  

. Suy ra:

 

2 2 2

1 1 1 2 1

y x h x x x x x b x u x

 

          

 

 

Xét phương trình hoành độ giao điểm của





u x

và





f x

, ta có:

   

4 3 2 2 2 4 3 2

3 1 1

1 1 1 2 1 2 0 1

2 2 2

x x b x x x x b x x x x x x

 

                  

 

 

Suy ra:

   

1 1

4 3 2

1 1

1 1 44

2 2 15

S u x f x dx x x x x dx

 

       

 

. Chọn đáp án D.

Câu 43. Trong không gian

Oxyz

cho hai đường thẳng

1 2

1 2 2

: , : 3

2 1 2

x t

x y z

d d y t

z t

 



  



   







 



(

là tham số)

và mặt phẳng





: 6 0

P x y z

   

. Đường thẳng





song song với mặt phẳng





và cắt









1 2

d d

lần

lượt tại

và

sao cho

3 6

AB  . Phương trình của





là

5 2

1 1 2

x y z

 

 



1 3 4

2 1 1

x y z

  

 



2 3 4

1 1 2

x y z

  

 

 

4 1

1 1 2

x y z

 

 

 

Lời giải

Ta chia hai trường hợp như sau:

Đầu tiên ta có

A B

lần lượt là các điểm thuộc

1 2

d d

nên ta suy ra:





 

1 2 ; 2 ; 2 2

2 ;3 ;4

A a a a

B b b b

   





  









1 2 ; 5;2 2

AB a b b a a b

       



mà





d P



nên ta suy ra

AB n



 

với





1; 1;1

n  



là vector pháp

tuyến của





. Khi đó:













1 2 5 2 2 0 2 2

a b b a a b a b b a

              

(1).

Ta có:

       

2 2 2 2

2 2

1 2 5 2 2 3 3 9 9 54

AB a b b a a b a a

             

thế từ (1).

Giải phương trình suy ra

 

   

1; 3;4 6;3; 3 2;1; 1

1; 3

2; 0

0;5;6

3;3;6 1; 1; 2

A AB k

a b

AB k



     



   





 



 



    









Mà đường thẳng tại phương án B nằm trong





nên ta chọn đáp án D.

Câu 44. Cho hình trụ

và



là tâm của hai đáy. Xét hình chữ nhật

ABCD

có

A B

cùng thuộc đường tròn





và

C D

cùng thuộc đường tròn







sao cho

3 3, 6

AB BC

 

, đồng thời mặt phẳng





ABCD

tạo với

mặt phẳng đáy hình trụ góc



. Thể tích khối trụ bằng

3 3



2 7 3



9 3



8 1



Lời giải

Đầu tiên ta có hình vẽ như sau:

Gọi

là trung điểm



và kẻ

OH AB



tại

khi đó ta suy ra



IHO 



. Cùng với

 

, ta suy

ra:

3 3

2 3 3

sin 60

9 27

cos 60

4 4 4

OO IO

IO IH

OA OH

OH IH





 





 

    

 

 









. Như vậy, khối trụ có đường sinh

3 3



 và bán kính đáy



có thể tích là:

27 3

V R h

 

  . Chọn đáp án B.

Câu 45. Trong không gian

Oxyz

cho mặt phẳng





: 2 10 0

P x y z

   

và hai điểm









1; 1; 2 , 2;0; 4

A B

 

Gọi





; ;

M a b c

là điểm thuộc đoạn thẳng

sao cho luôn tồn tại hai mặt cầu có bán kính

R  tiếp xúc

với mặt phẳng





, đồng thời tiếp xúc với đoạn thẳng

tại

. Gọi





;

T m n



là tập giá trị của biểu thức

2 2 2

25 2

a b c

  . Tổng

m n



bằng

1 2 3 7 1

7 6

8 6

1 4 0

1 3 4 0

1 9

Lời giải

Đầu tiên, ta nhận thấy:

A B

đều nằm cùng phía với mặt phẳng





Phương trình





có dạng là:

1 1 2

1 1 6

x y z

  

 



Gọi

1 2

I I

lần lượt là tâm của hai mặt cầu cố định đó. Suy ra

1 2

2 6

I I  và

1 2

MI I

là tam giác cân tại

Gọi





là mặt phẳng chứa

và vuông góc với





, suy ra:





: 2 0

Q x y

  

Gọi





là giao tuyến của hai mặt phẳng





và





, suy ra:

 

1 3

1 1 1

x y z

 

 

Gọi mặt phẳng





: 2 4 0

R x y z

   

và

là trung điểm của

1 2

I I

. Ta có hình vẽ như sau:

Vì

thuộc giao tuyến





và





nên tọa độ là:





1 ; 3 ;

N a a a

   

Ta có:









1 ; 1 ;2 6

M AB M t t t

     

. Mà

là điểm thuộc đoạn thẳng

nên





0;1

t 

Suy ra:





2; 2; 6 2

MN a t a t a t

      



. Mà

vuông góc với

nên ta có:

     

19 21 21 7

. 0 2 2 6 6 2 0 2 ; ;

2 2 2 2

t t t t

MN u a t a t a t a MN

 

                   

 

 

  

Suy ra điều kiện để tồn tại hai mặt cầu cố định thỏa đề bài là:

6 6

MN MN

  

2 2 2

21 21 7 24

2 2 2 931

t t t

     

        

     

     

Lại có:

2 2 2 2

25 2 98 34

T a b c t

    

nên suy ra:

98 34 34

694

34;

98 34 98. 34

931

T t



  



 

 







   

 





Vậy ta suy ra

694 1340

19 19

m n   

. Chọn đáp án D.

Câu 46. Có bao nhiêu số nguyên

thỏa mãn





2 2 5

log 5 log 6 3 log 0

x x x

    

6 4

6 5

Lời giải

Đầu tiên ta có điều kiện:

0 125

3 log 0





  



 



Trường hợp 1:

 

2 2 5

2 2

125

log 5 log 6 3 log 0

log 5 log 6 0

; 64

x x x

x x











      



   

 





Trường hợp 2:





2 2 5

log 5log 6 3 log 0

x x x

    

++Trường hợp 2a:

2 2

log 5log 6 0

3 log 0

125

x x



   

 

 



 

 









. So với điều kiện, ta nhận.

++Trường hợp 2b:

2 2

log 5log 6 0

3 log 0

x x



   



 



 





.So với điều kiện, ta loại.

Vậy, tổng 2 trường hợp ta suy ra:

 

;64 125

 

 

 

 

tức có 65 giá trị nguyên

thỏa mãn. Chọn đáp án C.

Câu 47. Cho hàm số





y f x



có đạo hàm





3 2,

f x x x x R



    

. Có bao nhiêu giá trị nguyên của tham

số





30;30

m 

để hàm số





4 2

y f x x m

   có đúng 7 điểm cực trị ?

1 6

1 7

Lời giải

Ta có

     

3 2 1 2 0 1

f x x x x x x



         

(nghiệm kép) hoặc



(nghiệm đơn).

Đặt

 





4 2

y g x f x x m

    . Ta có:

 









 

4 2 3

4 2

8 4 16

8 0

x x x x

g x f x x m

f x x m

x x

 



 

 

     



  







Vì hàm số





g x

không xác định tại

0, 2

x x

  

và đổi dấu khi

qua điểm

0, 2

x x

  

nên ta suy ra





g x

đạt cực trị tại

0, 2

x x

  

. Suy ra hàm số





g x

có 5 điểm cực trị là

0, 2, 2

x x x

    

Tiếp đến ta có:

 

4 2

8 1 1

8 0

8 2 2

x x m

f x x m

x x m



   





   



  



, các nghiệm của (1) (nếu có) là nghiệm bội

chẵn nên không phải là cực trị của hàm số.

Từ (2) ta suy ra:

4 2

8 2

x x m

  

. Xét hàm số





4 2

y h x x x

  

có

 

h x







 



 



Từ đó ta có bảng biến thiên như sau:

Như vậy để





g x

có 7 điểm cực trị thì (2) phải có 2 nghiệm phân biệt





2; 2;0

x    tức ta có được





30;30

16 2 14 30 14

m m m

 

         

. Như vậy có tất cả 17 giá trị nguyên

thỏa mãn đề bài.

Chọn đáp án C.

Câu 48. Trên tập hợp các số phức, xét phương trình

2 2 0

z z m

   

(

là tham số thực). Gọi

là tập

hợp các giá trị của

để phương trình trên có hai nghiệm phân biệt được biểu diễn hình học bởi hai điểm

A B

trên mặt phẳng tọa độ sao cho diện tích tam giác

ABC

bằng

2 2

, với





1;1

C 

. Tổng các phần tử trong

bằng



Lời giải

Gọi

1 2

z z

là 2 nghiệm của phương trình đề cho. Khi đó ta có:

1 0



   

. Sau đó ta xét 2 trường hợp sau:

Trường hợp 1:

1 0

 

, tức

1 2

z z

là 2 số thực. Khi đó ta có:

1,2

1 1

z m

  

tức ,

A B Ox



Suy ra:

 

1 2

2 1 . . ; 1 2 2 9

ABC

AB z z m S AB d C Ox m m



          

(1)

Trường hợp 2:

1 0

 

, tức

1 2

z z

là 2 số phức. Khi đó ta có:

1,2

1 1

z i m

  

mà





, : 1

A B d x

 

nên suy

ra:

 

1 2

2 1 . . ; 2 1 2 2 1

ABC

AB z z m S AB d C Ox m m



           

(2)

Từ (1) và (2) ta suy ra tổng các phần tử

bằng





9 1 8

  

. Chọn đáp án C.

Câu 49. Có tất cả bao nhiêu cặp số nguyên dương với



thỏa mãn những

4 3 2 2 2

2022

log 2 2

y y x y y x



   



3 8 0

2 0 0

4 2 0

2 1 0

Lời giải

Ta có bất phương trình tương đương với:

 

2 2 2 2

2022

log 2

y y x y y x



    



   

 

   

 

       





2 2

2022 2022 2022

log 1 1 1 1 log 1 log 1 1 1 (*)

y y x y x x y y y x



               



Xét hai trường hợp sau: (



luôn đúng)

- 1 1

x y x y

    

thì









* *

VT VP

nên ta loại trường hợp này.

 

1 1 1; 2;...;

x y

x y x y





     







. Suy ra số cặp





;

x y

thỏa mãn yêu cầu đề bài là

210





(cặp).

Vậy có tất 210 cặp số nguyên dương





;

x y

thỏa mãn đề bài. Chọn đáp án D.

Câu 50. Xét các số phức

1 2

, ,

z z z

thỏa mãn

1 2

4 5 1 1

z i z

    

và

4 8 4

z i z i

   

. Tính

1 2

M z z

 

khi

biểu thức

1 2

P z z z z

   

đạt giá trị nhỏ nhất.

4 1

M 



2 5

M 

2 1 3

M 

Lời giải

Ta có như sau:

4 5 1

z i

   

tập hợp điểm

biểu diễn số phức

là đường tròn





có tâm





4;5 ,

bán kính



1 1

  

tập hợp điểm

biểu diễn số phức

là đường tròn





có tâm





1;0 ,

bán kính



Đặt

z a bi

 





, .

a b 



Ta có

     

2 2 2

4 8 4 4 8 4

z i z i a b a b           

a b

  

. Suy

ra tập hợp điểm

biểu diễn số phức

nằm trên đường thẳng

: 4.

x y

  

Khi đó

1 2

.P z z z z CA CB     

Gọi

là điểm đối xứng của J qua đường thẳng , khi đó ta tìm được





4; 3K

 

phương trình đường thẳng : 4.IK x  Do đó

min

P khi và chỉ khi C IK   và

   

o giua

A CI C A CI

B CJ C B CJ

 





 





   

1 2

4;4 , 2;0 2 13.A B M z z    

Chọn đáp án D.

ĐỀ THI THỬ THPT QUỐC HỌC HUẾ LẦN 1

Câu 2. Cho số nguyên dương n và số phức z thỏa mãn

    

10 1 6 8

n n

iz i z i    . Chứng minh rằng z là

một số thực.

Lời giải

Đặt cos sinz i

 

  , khi đó phương trình trở thành:

 

  

10 1 cos sin 6 8 cos sin

i i i i i

   

     

Câu 3. Cho hàm số f nhận giá trị dương, có đạo hàm trên R và thỏa mãn

 

2022 4 1 ,

f t

f x x dt x R

 

    

 



 



Tính giá trị của





Lời giải

Ta có phương trình tương đương với:

   

2 2

2022 1 ,

4 4

f x f t

dt x R

x t

 

   

 

 

 



(1)

Đặt

 

f x

g x





thì (1) trở thành:

   

2022 1 ,

g x g t dt x R

 

   

 

 



(2)

Thay 0x  vào (2) ta dễ dàng có được





0 2022

g 

Tiếp theo, ta đạo hàm hai vế cho phương trình (2) thu được:

   

2022g x g x









 





 

2022 2022 ln 2022

g x g x

dx x g x x C

g x g x

 

      



Thay 0x  vào, cùng với

 

0 2022g 

ta thu được

 

ln 0 ln 2022C f 

Suy ra:

   

2022

ln 2022 ln 2022 2022

g x x g x e   

. Với

 





f x

g x





ta suy ra:

 

2 2022

2022 4

f x x e 

. Vậy

 

2022

1 10110f e

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

ĐỀ CHUYÊN QUỐC HỌC HUẾ LẦN 1

Câu 36. Cho hai số phức phân biệt

1 2

z z

thỏa mãn

1 2

z z





là số ảo và

1 1

 

. Giá trị lớn nhất của

1 2

z z



bằng

. B.

2 2

. C.

. D.

Lời giải

Gọi

A B

lần lượt là điểm biểu diễn số phức

1 2

z z

, khi đó

1 2

OC z z

 



và

1 2

BA z z

 



1 2

z z





là số ảo nên

OC BA



. Ta cũng có:

     

1 2

1 1

z z

ki k ki z ki z

z z



      





1 2 1 2

1 1

ki z ki z z z

     

. Suy ra

OACB

là hình thoi và

1 2

z z AB

 

Trường hợp 1:

và

đối xứng nhau qua trục tung, khi đó

C Oy



, suy ra

đạt max khi

và

nằm

trên trục hoành, nhưng loại vì khi đó

1 2

z z





là số thực.

Trường hợp 2:

và

đối xứng nhau qua trục hoành, khi đó

C Ox



, suy ra

đạt max khi tâm đường

tròn số phức

là trung điểm

tức

1 2 max

max 2 2

z z AB R

   

. Chọn đáp án D.

Câu 42. Cho tứ diện

ABCD

có

AB AC BC CD BD a

    

. Gọi

M N

lần lượt là trung điểm

BD CD

Góc giữa hai đường thẳng

và

là



. B.



. C.



. D.



Lời giải

Dễ nhận thấy ,

ABC BCD

 

đều. Gọi

là trung điểm

thì khi đó

 

AI BC

BC AID AD BC

DI BC





   







. Mà

MN BC



(tính chất đường trung bình)

Nên

MN AD



tức góc giữa hai đường thẳng

và

là



. Chọn đáp án C.

Câu 48. Trong không gian

Oxyz

, cho hình chóp tam giác đều

S ABC

có tọa độ đỉnh





6; 2;3

S 

, thể tích



và





AB a a

 

. Đường thẳng

có phương trình là

1 1

1 2 1

x y z

 

 

. Gọi





là mặt cầu tiếp

xúc với mặt phẳng





ABC

tại

và tiếp xúc với cạnh

. Khi đó bán kính của mặt cầu





thuộc khoảng

nào sau đây ?





2;3

. B.





4;5

. C.





3;4

. D.





5;6

Lời giải

Gọi

là trung điểm

khi đó ta dễ dàng có

   

1 ; 1 2 ;E t t t t   



Ta có:

 

SO BC

BC SOE SE BC

OE BC





   







tức





. 0 1 2;1;1 29

SE u t E SE     

 

Ta có:





2 2

1 1 3

2 6

. . 29 . 18

3 3 12 4

ABC

AB BC a a

a a

a AB

V SO S

SO SE OE

   



 



     

 





   







Gọi

là bán kính mặt cầu với

là tâm.

Ta có





, ,

IA ABC BS IH IA IH R

   

và

là tâm đường tròn ngoại tiếp tam giác

ABC

Tiếp đến gọi

là hình chiếu của

lên

, khi đó,

IKOA

là hình chữ nhật

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

IA IH R

 

nên





BHI BAI ch cgv BH BA

     

Ta lại có:

 

2 2

2 6

29 3 3

; 3 3 ; 35 2 6

SK SO IA R HS BH BS BA BS

SB SE EB





  

         





  



Vì

2 2 2 2

IH HS IK SK

   nên ta suy ra













2 2 2

35 2 6 2 2 3 3

R R

    

. Giải phương trình trên ta

suy ra được





3, 26.... 3; 4

R  

. Chọn đáp án C.

Câu 49. Cho hình nón đỉnh

có góc ở đỉnh bằng



và có độ dài đường sinh

l cm



. Gọi

là một

đường kính cố định của đáy hình nón,

là một dây cung thay đổi của đường tròn đáy và luôn vuông

góc với

. Biết rằng tâm đường tròn ngoại tiếp của tam giác

SMN

luôn thuộc một đường tròn





cố

định. Tính bán kính của đường tròn





6 2

. B.

. C.

3 2

. D.

2 3

Lời giải

Gọi

là giao điểm của

và

. Theo đề bài ta có được

MN AB



tại

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Gọi



là tâm đường tròn ngoại tiếp của

SAB



và



là điểm cố định.

Lúc này ta có được

O E O F O A O S

   

  

, (do



nằm trên mặt phẳng trung trực của

Vẽ tiếp





O K SMN





khi đó ta giả sử

là trung điểm

(1), thì khi đó

O E SN





Mà





O K SN SN SMN



 

nên





SN KO E





, suy ra

KE SN



(2)

Từ (1) và (2) ta suy ra

là tâm đường tròn ngoại tiếp tam giác

SMN

với

K SJ







K SAB



và nhìn

O S



dưới một góc vuông nên điểm

sẽ di động trên đường tròn đường kính

O S



Tới đây ta có:



2 60 30 cos 12cos30 6 3

ASB ASO ASO SO SA ASO       

  

Khi đó ta suy ra

2 2

4 3

2.6 3

SAB

R S O



   

Vậy điểm

sẽ di động trên đường tròn





bán kính là

2 3

O S



 

. Chọn đáp án D.

Câu 50. Số các giá trị nguyên của





2021;2022

m 

để

log log

5 3 log 2

a b

b a

a b m b

  

với mọi





1;b

 

là

4044

. B.

2020

. C.

2021

. D.

2022

Lời giải

Ta đặt

log 0

b x

 

. Khi đó bất phương trình ban đầu trở thành:

 

log log

2 2

5 3 log 2 5 3 2 5 3 2

a b

b a

x x x x

a b m b a a mx a a mx m



             

(1)

Xét hàm số

 

2 2

y f x



 

với mọi



, ta có

 





 

2 ln 2

0, 0;

a x a

f x x





    

Suy ra hàm số





f x

luôn đồng biến trên







Từ đó ta nhận thấy để (1) có nghĩa thì









min 2 ln

m f x a



 

Mà do

ln 0, 1

a a

  

nên suy ra









2021;2022

0 2021;0

m m

 

   

tức có tất cà 2021 giá trị nguyên

thỏa mãn yêu cầu đề bài. Chọn đáp án C.

SỞ BÌNH PHƯỚC LẦN 1

Câu 46. Trong không gian

Oxyz

, cho mặt cầu

     

2 2

: 1 2 9

S x y z

    

và điểm





2; 1;2

A 

. Từ

kẻ

ba tiếp tuyến bất kì

, ,

AM AN AP

đến





. Gọi

là điểm thay đổi trên mặt phẳng





MNP

sao cho từ

kẻ được hai tiếp tuyến vuông góc với nhau đến





và cả hai tiếp tuyến này đều nằm trong mặt phẳng





MNP

Khoảng cách từ điểm

đến giao điểm của đường thẳng

 

: 2

1 3

x t

y t

z t

  





  





 



với mặt phẳng





MNP

có

giá trị nhỏ nhất bằng

27 3 3 5

16 2



. B.

27 3 3 5

16 2



. C.

27 3 3 5

8 2



. D.

27 3

Lời giải

Đầu tiên ta có mặt cầu





tâm





0;1; 2



, bán kính



Ta có tiếp phương trình mặt cầu





với tâm là trung điểm

và bán kính

là

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

   

2 2

: 1 12

S x y z

   

thì khi đó phương trình mặt phẳng





MNP

chính là kết quả của phép trừ vế

theo vế của phương trình mặt cầu





và





tức





: 2 2 4 1 0

MNP x y z

   

Tiếp đến gọi





là đường tròn thiết diện của mặt cầu





và mặt phẳng





MNP

và tâm là

Khi đó ta có

2 2

9 3 3 1 1

. 5 3 0 ; ;

5 4 4 2

2 6

R MI IE IA IE EI EA E

 

          

 

 

 

Khi đó đường tròn





sẽ có tâm

3 1 1

; ;

4 4 2

 



 

 

và bán kính

2 2

3 10

r R IE  

Tiếp theo, do hai tiếp tuyến qua

và vuông góc với nhau nên đoạn

luôn bằng

lần

tức ta có quỹ

tích điểm

là đường tròn





có tâm

3 1 1

; ;

4 4 2

 



 

 

là bán kính

3 10 3 5

2 2

4 2

r r  

Mặt khác, ta dễ dàng tìm được giao điểm của







và





MNP

là

17 33 13

; ;

16 16 16

 



 

 

Khi đó giá trị nhỏ nhất cần tìm chính là

27 3 3 5

16 2

EF r  

. Chọn đáp án B.

Câu 47. Cho số phức

thỏa mãn

3 4 5

z i  

. Gọi

và

lần lượt là giá trị lớn nhất và giá trị nhỏ

nhất của biểu thức

2 2

P z z i

   

. Tính modun của số phức

w M mi

 

2 314

w 

. B.

2 309

w 

. C.

1258

w 

. D.

3 137

w 

Lời giải

Vì





3 4 5z i

   

tập hợp các điểm biểu diễn số phức

là đường tròn





có tâm





3;4

và bán kính



. Ta có

       

2 2

2 1 2 1 4 2 3

P x yi x y i x y x y x y

 

              

 

 

4 2 3 0.

x y P

    

Ta tìm

sao cho đường thẳng

: 4 2 3 0

x y P

    

và đường tròn





có điểm chung

 

12 8 3

, 5 23 10 13 33.

d I R P P

  

          

Suy ra:

13 33

w M mi i

   

tức

1258

w 

. Chọn đáp án C.

Câu 48. Cho hàm số





f x

có đạo hàm là

   





2 ,f x x x x x



   



. Gọi

là tập hợp tất cả các giá trị

nguyên dương của tham số

để hàm số

f x x m

 

 

 

 

có 5 điểm cực trị. Tính tổng tất cả các phần tử

của

154

. B.

. C.

213

. D.

153

Lời giải

Đặt

     

2 2

1 1

6 6 6

2 2

g x f x x m g x x f x x m

   

 

       

   

   

(chỉ tính nghiệm bội lẻ)

Cho

     

   

0 6 0 1

6 1 2

g x x x m g x

x x m g x











     



   



. Như vậy để hàm số





g x

có 5 điểm cực trị thì cả phương

trình (2) và (3) đều phải có 2 nghiệm và khác

, tức ta suy ra điều kiện cần có là:

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

 

 

18; 19

9 0;9 0

1;17

2 2

6 0

18 0; 19 0

6 0

m m







 











 

 

   







   

  







 

   











là

153





.Chọn đáp án D.

Câu 49. Có bao nhiêu số nguyên dương

sao cho ứng với mỗi

, có đúng ba giá trị nguyên dương

thỏa

mãn

 

log 2 1

a b



  

. B.

. C.

. D.

Lời giải

Bất phương trình tương đương với:

 

   

2 2 2

log 2 1 log 2 2 log

a a a

a b a a ab ab



        

Hàm số





log

y g t t t

  

luôn đồng biến trên







nên suy ra

a ab

 

. Do

nguyên dương nên

bất phương trình tương đương với:





. Xét hàm số

 

y f a



 

trên







có

 





2 ln 2 1

1 1

0 ; 0

ln 2 ln 2

f a a f



 

 

    

 

 

suy ra

1, 44

ln 2

a  

là điểm cực tiểu của





f a

Do đề bài yêu cầu có đúng ba giá trị nguyên dương

tức giá trị

lấy từ 1 đến 3

Như vậy điều kiện cần và đủ là









2 4 3 5 4

f b f b b



      



. Chọn đáp án A.

Câu 50. Trên parabol





P y x



lấy hai điểm









1;1 , 2;4

A B

. Gọi

là điểm trên cung

của





sao cho diện tích của tam giác

AMB

lớn nhất. Biết chu vi của tam giác

MAB

là

2 5 29

a b c  , khi đó

giá trị

a b c

 

bằng

. B.

. C.

. D.

Lời giải

Trên





lấy điểm





;

M a a

với





1;2

a 

Ta có đường thẳng

có phương trình là

2 0

x y

  

, phương trình đường thẳng

có dạng là





y a x a

  

, phương trình đường thẳng

có dạng là





2 2

y a x a

  

Suy ra ta có:

   

 

   

 

2 1 2 2 2

AMB

S x a x a dx x a x a dx



         

 

     

















  

      

   

2 2

2 2 1 1 4 4

2 1 1 2

2 2

1 2

2 1

3 3 27

1 2 2 1

2 2 2 4 8

a a a a a a

a x dx a x dx

a a

a a a a



     

       

   

 

 

        

 

 

 

Vậy

max

AMB

S 

khi và chỉ khi

1 1 1

2 1 ;

2 2 4

a a a M

 

     

 

 

Suy ra:

3 3

3 2 5 29

4 4

MA MB AB    

tức

3 3 9

4 4 2

a b c

     

. Chọn đáp án C.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

THPT KIM LIÊN – HÀ NỘI LẦN 2

Câu 46. Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 1 3 2 25

S x y z

     

và hai đường thẳng









1 2

d d

lần lượt có phương trình

: 1

x mt

d y

z t

 





 





 



và

: 1

x t

d y

z mt

 





 





 



. Có bao nhiêu giá trị của

để









cắt mặt cầu





tại 4 điểm phân biệt sao cho bốn điểm đó tạo thành tứ giác có diện tích lớn nhất

. B.

. C.

. D.

Lời giải

Cách 1:

Ta nhận thấy hai đường thẳng









1 2

d d

chung điểm





1; 1;1

A 

và

3 5

IA R

  

với





1; 3;2

I  

Tiếp đến hai vector chỉ phương của









1 2

d d

lần lượt là









1 2

;0;1 , 1;0;

u m u m

  

 

, nhận thấy

1 2

. 0

u u



 

nên suy ra









1 2

d d







1 2

; 0;1 ;0

u u m

 

 

 

 

nên 2 đường thẵng trên luôn thuộc mặt phẳng





: 1

P y

 

với





0;1;0

n 



là

vector pháp tuyến của mặt phẳng tương ứng.

Gọi

, , ,

M N P Q

lần lượt là các giao điểm giữa hai đường thẳng









1 2

d d

và mặt cầu, từ đó suy ra bốn

điểm trên đều nằm trên đường tròn





giao tuyến giữa mặt phẳng





và mặt cầu đó.

Gọi

, , ,

E F G H

lần lượt là trung điểm

, , ,

MN NP PQ QM

khi đó ta luôn có

EFGH

là hình chữ nhật.

Khi diện tích tứ giác

MNPQ

lớn nhất thì diện tích tứ giác

EFGH

lớn nhất tức

EFGH

là hình vuông.

Dựa vào hình vẽ trên, ta suy ra diện tích tứ giác

MNPQ

lớn nhất khi vector



chính là vector phân giác

giữa hai vector chỉ phương của









1 2

d d

tức

1 2

u u

 

 



 

với

; ;

u IA n n

 



 

   

Ta có:

 

1 2

2 2

1 2

1 1

;0;

1 1

; ; 2;0;1

u u m m

u u

m m

u IA n n



 

 

  



 



 

 





 

  



 



 





 

   

. Suy ra ta có hệ thức sau:

2 1

1 1

2 1

1 1

m m











  









 









 



NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Vậy chỉ có 2 giá trị

thỏa mãn yêu cầu đề bài. Chọn đáp án C.

Cách 2: Ta có đánh giá khác như sau: (Gọi

là bán kính của đường tròn thiết diện





)

   









2 2 2

2 2 2 2

2 ; ;

1 1

. .2 ; .2 ; 2

2 2 2

MNPQ C C

R d O MP d O NQ

S MP NQ R d O MP R d O NQ

 

 

 

 

    

 

 

2 2

R O A const



  

với





1; 1;2



 

là tâm đường tròn





Dấu bằng xảy ra khi và chỉ khi

       

1 2 1 2

; ; ; ; ; ;

d O MP d O NQ d O d d O d O A u O A u

   

     

    

   

   

2 2 1

m m







     



 



, Vậy chỉ có 2 giá trị

thỏa mãn yêu cầu đề bài. Chọn đáp án C.

THPT PHỤ DỰC THÁI BÌNH LẦN 2

Câu 42. Cho hình chóp đều

S ABCD

có đáy

ABCD

là hình vuông cạnh

vuông góc với đáy

ABCD

biết cosin góc giữa hai mặt phẳng





SBD

và





SBC

bằng

. Tính thể tích khối chóp

S ABCD

V 

. B.

V a

 . C.

V 

. D.

V 

Lời giải

Ta chuẩn hóa



và đặt

SA x



Ta có:

 

2 2

1 1

; 1;

; ; ;

2 2 1

d C SB BC AO AC

SA AO x

d C SBD d A SBD d A SO

SA AO



   





   











Suy ra:

   

 



 

;

5 2

sin ; 1 2

; 3 3

2 2 1

d C SBD

SBD SBC x SA

d C SB

 

       

 



 

Vậy

1 2

3 3

ABCD

V SA S

 

tức

V 

. Chọn đáp án C.

Câu 43. Trên tập hợp các số phức, xét phương trình

2 2

2 2 0

z az b b

   

(

a b

là các tham số thực). Gọi

là tập hợp các cặp





;

a b

sao cho phương trình đó có hai nghiệm

1 2

z z

thỏa mãn

1 2

3 2 3 6

z iz i

  

. Số

phần tử thuộc

bằng

. B.

. C.

. D.

Lời giải

Ta có phương trình

2 2

2 2 0

z az b b

   

có hai nghiệm

1 2

z z

nên ta luôn có:

1 2

z z a

z z b b

  





 



Trường hợp 1:

1 2

z z

là số thực.

Khi đó phương trình

1 2

3 2 3 6

z iz i

  

tồn tại nghiệm duy nhất với

2 4

2 3

b b











 

 



  



 















Suy ra có 2 cặp





;

a b

tồn tại.

Trường hợp 2:

1 2

z z

không phải là số thực.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

1 2

z z



nên ta suy ra

     

1 1

3 2 3 6

3 2 3 6 5 3 6

z iz i

x yi i x yi i x y i i

z x yi



  



         



 





Suy ra

; 6

x y

 

tức

 

1 2

3 3

6 ; 6

5 5

2 36 *

z i z i

b b







    





  





. Do pt (*) có 2 nghiệm nên ta suy ra

có 2 cặp





;

a b

tồn tại. Chọn đáp án D.

Câu 44. Cho hai hàm đa thức bậc 4 và bậc 3 là









y f x y g x

 

(hình vẽ dưới đây chỉ mang tính chất

minh họa). Biết rằng hai đồ thị









y f x y g x

 

tiếp xúc nhau tại điểm có hoành độ bằng 1 và cắt nhau

tại 2 điểm khác có hoành độ lần lượt là

2;0



. Gọi

1 2

S S

lần lượt là diện tích hình phẳng giới hạn bởi hai

đồ thị trên ở nửa mặt phẳng bên trái và nửa bên phải của trục tung. Khi



thì

S 

. B.

S 

. C.



. D.

S 

Lời giải

Ta có hai đồ thị









y f x y g x

 

tiếp xúc nhau tại điểm có hoành độ bằng 1 và cắt nhau tại 2 điểm khác

có hoành độ lần lượt là

2;0



nên suy ra

         

1 2

h x f x g x ax x x

    

       

1 1

0 0

2 2

1 2

15 3

S f x g x dx ax x x dx a

        

 

Suy ra:

       

0 0

2 2

2 56

1 2

3 15

S f x g x dx x x x dx

 

      

 

. Chọn đáp án B.

Câu 46. Có bao nhiêu số nguyên





2022; 2022

y  

sao cho bất phương trình sau có nghiệm ?





2 2

2 2 4 2022

x x

e y e yx y     

4016

. B.

1993

. C.

4015

. D.

1994

Lời giải

Ta có bất phương trình:





2 2

2 2 4 2022 0

x x

e y e yx y

     

(1)

Xét hàm số









2 2

2 2 4 2022

x x

f x e y e yx y     

(hàm theo biến

, và

là tham số) có

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

   

2 2 2 4 0

2 2 0 *

4 2 2

x x

f x e y e y

e y

e y e y

f x e y e





    







     





 



   





(nghiệm đẹp).

Trường hợp 1:

 

0 1

x y

e y







 









. Do









lim 0; lim

y y

x x

f x f x

 

  

nên

x y



là điểm cực tiểu với

       

2ln ln 2 2

ln 4 2 2 4 2 2 2 4 0 2

y y

f y e y e y y y y y







         



 



Từ (1) và (2) ta rút ra điều kiện cần cho

là



Cùng với điều kiện đủ là









2 2

ln 2 2 4 ln 2022 0

f y y y y y y y

      

nên ta có

29.5



Trường hợp 2: phương trình (*) vô nghiệm tức ta luôn tồn tại tập bù của



tức



để bất phương

trình

   

2 2 2 4 0

x x

f x e y e y



    

có nghĩa

 

2 0 2

y y



      

Xét



ta thấy không thỏa bất phương trình đề bài. Suy ra trường hợp 2 ta thu được



Vậy tổng hai trường hợp ta thu được

 

   

2022;2022

2022; 1 30; 2022

29.5

 





    







tức có tất cả 4015

giá trị nguyên

thỏa mãn bài toán. Chọn đáp án C.

Câu 47. Cho





f x

là hàm số bậc ba có đồ thị hàm số





f x



như hình vẽ sau

Có bao nhiêu số nguyên





2022;2022

m 

để hàm số

 





2023 2

2022

g x f x x m m

   

có số

điểm cực trị nhiều nhất ?

2022

. B.

2021

. C.

2023

. D.

2020

Lời giải

Để





g x

có số điểm cực trị max thì số nghiệm bội lẻ của phương trình





2023 2

2022 0

f x x m m

   

cũng

phải đạt max. Kéo theo số điểm cực trị của hàm số

 





2023 2

2022

h x f x x m m

   

cũng phải đạt max.

Suy ra tiếp số nghiệm bội lẻ nguyên dương của









2023 2

2022

u x f x x m

  

cũng phải đạt max và



Giải thích: vì khi càng tịnh tiến về bên phải theo trục hoành của hàm số





u x

thì số nghiệm và điểm cực

trị của





h x

càng lớn và đạt max.

Khi đó ta có:

 

   

2023 2

2022 2023 2

2023 2

2022 1

2023 2022 2022 0

2022 1

x x m

u x x f x x m

x x m



   

 

     



  



2023 2

2022 1

x x m



  





  



. Như vậy để có nhiều nghiệm nhất thì

1 0

 



  







Suy ra









2022;2022

1 2; 2021

m m

 

  

tức có 2020 giá trị nguyên

thỏa mãn. Chọn đáp án D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 48. Gọi

là tập hợp các số phức

thỏa mãn phần thực của

z z



bằng

. Biết các số phức

1 2 3

, ,

z z z

thuộc

thỏa mãn

1 2 3 2

18, 9 2

z z z z   

. Giá trị lớn nhất của biểu thức

2 2

1 2 3

1 1 4 1

F z i z i z i

        

gần nhất với số nguyên nào trong các số sau đây ?

268



. B.



. C.

. D.



Lời giải

Gọi





,z x yi x y  



. Do

z z





nên

z z

 





2 2

2 2 2

x y x yi

x y x y

  

  

  

  

Từ đó theo giả thiết ta có:





2 2 2 2

2 2 2 2 2 2

2 2 2

1 1

18 18

x y x x y x

x y x x y x y

x y x y

   

  

    

  

 

2 2

2 2 2 2

1 1 1

18 18

x y x

x y

x y x y x

 

      



  





2 2

x y x

  

Từ đó ta suy ra ba điểm













1 2 3

, ,

A z B z C z

luôn thuộc đường tròn tâm

, bán kính



1 2 3 2

18, 9 2

z z z z   

nên ta suy ra

2 18

AB R

 

và

2 9 2

BC R 

Từ đó ta có hình vẽ được biểu diễn như trên: (với





1;1

)

Suy ra:

2 2 2 2 2

2 2 2

1 2 3 1 2 3

1 1 4 1 1 1 4 1 4

F z i z i z i z i z i z i AE BE CE

                    

là trung điểm

nên





2 2 2

2 2 2 2

2 166

4 2

AE BE AB

EI AE BE EI

 

      .

Khi đó ta suy ra

max khi

min

Vậy





min max

2 9 9 2 166 4 9 2 64,176 64

CE EI R F

             

. Chọn đáp án B.

Câu 49. Trong hệ tọa độ

Oxyz

cho mặt cầu

   

2 2

: 1 7

S x y z

   

. Hỏi có bao nhiêu điểm

trên mặt

phẳng





Oxy

với

có tọa độ nguyên sao cho qua

kẻ được ít nhất hai tiếp tuyến vuông góc với nhau

đến mặt cầu





. B.

. C.

. D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Lời giải

Ta có mặt cầu





có tâm





0;0;1

, bán kính

R  .





M Oxy



nên ta suy ra





; ;0

M a b

Nhận xét: Nếu từ

kẻ được ít nhất 2 tiếp tuyến vuông góc đến mặt cầu khi và chỉ khi

2 2 2 2 2 2 2

2 2 7 1 14 6 13

R IM R R IM R a b a b

             

Tập các điểm thỏa đề là các điểm nguyên nằm trong hình vành khăn (kể cả biên), nằm trong mặt phẳng





Oxy

, tạo bởi 2 đường tròn đồng tâm





0;0;0

bán kính lần lượt là

và

Từ hình vẽ trên ta kết luận có 24 điểm

thỏa mãn. Chọn đáp án D.

Câu 50. Cho hình trụ có đường kính đáy bằng

. Hình vuông

ABCD

nội tiếp hình trụ với hai điểm

A B

thuộc đường tròn là đáy trên và

C D

thuộc đường tròn đáy dưới của hình trụ và



. Biết diện tích

hình chiếu của hình vuông

ABCD

trên mặt đáy bằng 2 (đơn vị diện tích). Tính thể tích của khối trụ đó.

5 3



. B.

5 6



. C.

5 6



. D.

5 3



Lời giải

Ta có hình vẽ như sau:

Ta kẻ lần lượt các đường sinh



và



với

, ;

C D O

 

 



 

 

sao cho

ABC D

 



Khi đó với

ABC D

 

là hình chữ nhật ta có:

. 2

ABC D

S AB BC

 



 

Mà

 

2 2

2 5

AB BC R



  

nên ta có hệ phương trình sau:

2 2

. 2

AB BC











 



NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

3AB 

nên hệ phương trình có nghiệm:

AB BC

 











hoặc

AB BC

 











Trường hợp 1:

2 2

AB BC

CC h BC BC

 



 

   









không tồn tại nên loại.

Trường hợp 2:

2 2

AB BC

CC h BC BC

 



 

    









Vậy ta suy ra thể tích khối trụ là:

5 5 3

2 4

V R h



 

 

  

 

 

. Chọn đáp án D.

THPT CHUYÊN VINH LẦN 2

Câu 38. Có bao nhiêu số tự nhiên

sao cho phương trình

2 1

4 2 1 2 2

x x x

 

    

có đúng

nghiệm

thực phân biệt?

. B.

. C.

. D.

Lời giải

Đặt

 

2 0

t t 

. Phương trình đã cho trở thành

 

4 1 2 2 *t t m t    

 

2 2

6 3

4 1 2 2

4 1 2 2 2 1

m t t P

t t m t

t t m t m t t P



   



    

 



         





Vẽ hai parabol

   

1 2

,P P

trên khoảng

 

0; 

Yêu cầu bài toán

 

*

có hai nghiệm dương phân biệt

1 2

,t t

12 3 3 12

0 0

1 1

m m

      

 

 

    

 

   

 

. Vì

m  

nên





0;4;5;...;11

m 

tức có 9 giá trị nguyên

thỏa mãn. Chọn đáp án A.

Câu 39. Cho phương trình

2 6 8 0z mz m    (

là tham số thực). Có bao nhiêu giá trị nguyên của

tham số

để phương trình có hai nghiệm phức phân biệt

1 2

,z z thỏa

1 1 2 2

. .z z z z

. B.

. C.

. D.

Lời giải

Phương trình

 

2 6 8 0 *z mz m   

có biệt số

6 8m m



    .

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Giả thiết

 

2 2

1 1 2 2 1 2 1 2

. . . 1

z z z z z z z z    

Xét







  







. Khi đó





1 2 1 2

1 0 0

z z z z m

       

(nhận).

Xét

0 2 4



    

Khi đó phương trình





có hai nghiệm phức liên hợp với nhau nên





luôn đúng.

Mà

nguyên nên



(nhận). Vậy có hai giá trị nguyên của tham số

thỏa mãn. Chọn đáp án D.

Câu 41. Biết đồ thị





của hàm số





4 2

f x x bx c

  





,b c 



có điểm cực trị là





1; 0

. Gọi





là

parabol có đỉnh





0; 1



và đi qua điểm





2;3

. Diện tích hình phẳng giới hạn bởi





và





thuộc khoảng

nào sau đây?





0;1

. B.





2;3

. C.





3; 4

. D.





1; 2

Lời giải

Ta có:





là parabol có đỉnh





0; 1



   

: 0 1

P y a x

   

Mà









2;3

B P



nên

 

3 2 0 1 1

a a

    





: 1

P y x

  

Ta có:





có điểm cực trị là





1;0





 

1 0

1 0 2

4 2 0 1

1 0

b c b

b c



    

 



  

  

  





 













4 2

: 2 1

C f x x x

   

Phương trình hoành độ giao điểm của





và





là:

4 2 2

2 1 1

x x x

   

4 2

3 2 0

x x

   

 







 



4 2

3 2 d

S x x x



   



1 1 2

4 2 4 2 4 2

1 1

3 2 d 3 2 d 3 2 d

x x x x x x x x x



        

  

     

1 1 2

4 2 4 2 4 2

1 1

3 2 d 3 2 d 3 2 d

x x x x x x x x x



        

  

2,54



. Chọn đáp án B.

Câu 43. Cho hàm số





f x x x

  

và









2 sin

g x f x m

  

(

là tham số thực). Có bao nhiêu giá

trị của

để









max min 50

g x g x

 



A. 0. B. 1. C. 2. D. 3.

Lời giải

Xét hàm số









2 sin

h x f x m

  

. Khi đó









g x h x



Ta có : 1 2 sin 3,x x

    



. Đặt





1 2 sin , 1;3

x t t  

Hàm số trở thành









h t f t m

 

trên đoạn





1;3













3 3 0, 1;3

h t f t t t

 

      

, hàm số





h t

nghịch biến trên





1;3

Suy ra

 









1;3

max 1 2

h t h m

  

và

 









1;3

min 3 18

h t h m

  

. Vậy





max 2

h x m

 



và





min 18

h x m

 



Trường hợp 1:









2 18 0

m m

  





2;18

m  

Khi đó





min 0

g x





;

 

















2 18 2 18

max 8 10

m m m m

g x m

      

   



Do đó:









max min 50

g x g x

 



8 40 ( )

m l

 



   







Trường hợp 2:









2 18 0

m m

  









; 2 18;m

      

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Khi đó ta suy ra:

 

       

 

       

2 18 2 18

min 8 10

2 18 2 18

max 8 10

m m m m

g x m

m m m m

g x m



      

   





      



   







Do đó:

   

max min 50g x g x 



8 25m  

( )









 



Vậy có 2 giá trị của

thỏa mãn. Chọn đáp án C.

Câu 44. Cho hàm số bậc bốn

 

y f x

. Biết hàm số

 

1y f x



 

có đồ thị như trong hình bên. Có bao

nhiêu số nguyên dương

sao cho hàm số

 

2 2022g x f x x m    

đồng biến trên khoảng

 

0;1

2021

. B.

2023

. C.

2022

. D.

2024

Lời giải

Tịnh tiến đồ thị hàm số

 

1y f x



 

sang phải

đơn vị ta được đồ thị hàm số

 

y f x





   

 

2 2 2 2022g x x f x x m

 

      

Hàm số

 

g x

đồng biến trên khoảng

 

0;1

   

0, 0;1g x x



   

 

2 2022 0, 0;1f x x m x



       

(vì

 

2 2 0, 0;1x x    

)

 

1 2 2022, 0;1

2 2022 1, 0;1

2 2 2022, 0;1

2 2 2022 3, 0;1

3 2 2022, 0;1

m x x x

x x m x

m x x x

x x m x

m x x x



     





      



 

     





       







     









Xét hàm số

 

2 2022h x x x  

trên khoảng

 

0;1









2 2 0, 0;1

h x x x



    

nên hàm số





h x

nghịch biến trên khoảng





0;1

Do đó

 

1 1

1 2021

2022

* 2 0

2 2022

2024

3 2021

3 1

m h

 

 











    

 



















 













Vì

nguyên dương nên





1; 2;...; 2022;2024

m 

. Chọn đáp án B.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 45. Cho khối chóp

S ABCD

có đáy

ABCD

là hình bình hành và

vuông góc với mặt phẳng đáy.

Biết



2 , 2 , 45

AB a AD a ABC  



và góc giữa hai mặt phẳng









SBC SCD

bằng



. Thể tích khối chóp

đã cho bằng

. B.

. C.

. D.

Lời giải

Cách 1:



2 , 2 , 45

AB a AD a ABC  



nên suy ra



2 2

135 ; 2 . cos135 10

BAD BD AB AD AB AD    

 

Suy ra





2 2 2

AC AO AB AD BD AB

     

nên

ABC



cân tại

tức

SBC



cân tại

Đặt

SA x

 

. Kẻ

, ,

AI BC AH CD AE SH

  

khi đó ta có

AI a



, suy ra

2 2 2 2

; 2

SI x a SC x a

   

Ta có

1 1

. .

2 2

SBC

S SI BC SC BF

 

với

BF SC



nên suy ra

 

2 2

; 2

SI BC x a

d B SC BF

SC x a



  



Ta lại có:

   

 

2 2 2 2

. . 2

; 2 ; ;

AI BC SA AH xa

AH d C AB a d B SCD d A SCD AE

SA AH x a

       

 

Từ đó ta suy ra

   

 











 

2 2

;

2 1

sin ,

; 2

d B SCD

BX xa

SBC SCD x SA a

BF d B SC

x a

      



Vậy

 

1 1 2

. 2 . . sin135

3 3 3

S ABCD ABD

V SA S SA AB AD a



  



. Chọn đáp án C.

Cách 2: Ta có hình vẽ như sau:

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Ta có:









SC SBC SCD

 

. Kẻ

AE SC



tại

(1) và đường thẳng qua

song song với

cắt

tại



2 , 2 , 45

AB a AD a ABC  



nên suy ra



2 2

135 ; 2 . cos135 10

BAD BD AB AD AB AD    

 

Suy ra





2 2 2

AC AO AB AD BD AB

     

, từ đó ta thu được mặt đáy như hình trên, suy ra

AC CD



tức





CD SAC AE CD

   (2). Từ (1) và (2) suy ra





AE SCD AE EF

   tức



AEF 



Từ đó ta có được:





SC ABEF

 và

   

 



 







, , 180 180

SBC SCD BE EF BEF BEA AEF

     

 



90 BEA



  



. Tiếp đến lại có:



tan cot cot 30

AB a

BEA AE



    



Lại có:

2 2 2 2 2 2

1 1 1 3 1 1

2 2

SA a

AE AS AC a AS a

      

Vậy

 

1 1 2

. 2 . . sin135

3 3 3

S ABCD ABD

V SA S SA AB AD a



  



. Chọn đáp án C.

Câu 46. Cho hàm số





y f x

 có đạo hàm trên



và













1 ,

f x f x x e



   với mọi x





. Biết

 



, giá trị





bằng

e e



. B.

e e



. C.

e e



. D.

e e



Lời giải

Ta có:

             

 

3 2 2

1 1 1

x x x x x x

f x f x x e e f x e f x x e e f x x e

  



 

         

Khi đó:

     

2 2 2

1 1

2 4

x x x x

e f x x e dx x e e C



     



 



nên:

   

3 3

1 5 1 1

1 1

4 4 2 4

x x x

C C f x x e e e

        

. Vậy

 

f e e

 

Chọn đáp án C.

Câu 47. Có bao nhiêu số nguyên

sao cho ứng với mỗi

, tồn tại số thực

b a



thỏa mãn 4 2

a b

 

và

đoạn





;

a b

chứa không quá 5 số nguyên ?

. B.

. C.

. D.

Lời giải

Ta có

4 2 2 4 0

a b b a

b b

     

Xét hàm số









2 4 2 ln 1 0

b a b

f b b f b b



      

nên hàm số





f b

luôn đồng biến trên





;

 

Ta có





4 2 2 2 4 0 0

a b a a a

b a a f a

         

Nên để tồn tại số thực

và đoạn





;

a b

không chứ quá 5 số nguyên:





 

 

2 4 0

5; 4;..; 4;5

5 0

2 5 4 0

a a

f a







  



     

 

 

   





tức có 11 giá trị nguyên

sao cho thỏa

mãn yêu cầu đề bài. Chọn đáp án D.

Câu 48. Cho hàm số





y f x



có đạo hàm là













2 2

9 9

f x x x x



  

với mọi





. Có bao nhiêu giá trị

nguyên của tham số

để hàm số

 





3 2

y g x f x x m m

     có không quá 6 điểm cực trị ?

. B.

. C.

. D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Lời giải

 









 

3 2 3 2

g x f x x m m f x x m m g x

           nên hàm số này là hàm số chẵn tức để

hàm số





g x

có không quá 6 điểm cực trị (cụ thể là tối đa 5 cực trị) thì hàm









3 2

h x f x x m m

   

có tối đa 2 điểm cực trị dương.

Kéo theo phương trình













2 3 2

3 3 3 2 0

h x x f x x m m

 

     

có tối đa 2 nghiệm bội lẻ dương.

3 2

3 2 3 2

3 2

3 2 0

3 2 9

3 2 3 3 2 3

3 2 3

x x m m y

x x m m

x x m m y

x x m m

x x m m y

x x m m

x x m m y



   

   



     

    



 



         



   

    



(*)

Như vậy để thỏa mãn đề bài thì bốn đường thẳng lần lượt là

1 2 3 4

, , ,

y y y y

phải cắt đồ thị

y x x

 

tại tối

đa hai nghiệm dương. Xét hàm số

y x x

 

có

3 3 0,y x x



    



và





0 0



Nhận thấy

 

2 3 1 2 0

m m m

     

luôn đúng nên hệ (*) có tối thiểu 1 nghiệm, từ đó ta có:

Trường hợp 1:





2 0 0;2

m m m   

thì hệ (*) có 1 nghiệm tức hàm số luôn có 3 điểm cực trị

Trường hợp 2:

2 0

m m





  







thì hệ (*) đang có 2 nghiệm dương. Do hàm số có tối đa 5 điểm cực

trị nên chỉ có tối đa 2 nghiệm dương tức ta có điều kiện đủ là:

 

2 9 0

1;3

2 3 0

m m



  



  



  





So với điều kiện ta suy ra





1;3

m 

Từ hai trường hợp ta suy ra





1;0;1;2;3

m 

tức có 5 giá trị nguyên

thỏa. Chọn đáp án B.

Câu 49. Trong không gian

Oxyz

, cho mặt phẳng





: 2 2 16 0

P x y z

   

và mặt cầu

       

2 2 2

: 2 1 3 21

S x y z

     

. Một khối hộp chữ nhật





có bốn đỉnh nằm trên mặt phẳng





và

bốn đỉnh còn lại nằm trên mặt cầu





. Khi





có thể tích lớn nhất, thì mặt phẳng chứa bốn đỉnh của





nằm trên mặt cầu





là





: 2 0

Q x by cz d

   

. Giá trị

b c d

 

bằng



. B.



. C.



. D.



Lời giải

Đầu tiên, ta có mặt cầu





tâm





2; 1;3

I 

, bán kính

R 

Tiếp đến ta nhận thấy:









; 9 21

d I P  

nên suy ra mặt phẳng





không cắt mặt cầu





Gọi

a b

là các kích thước mặt đáy hình hộp chữ nhật và









;

d d I Q



. Khi đó ta có:

Ta có:

 

     

 

2 2

; ; 9 9 2 9 21

a b

V d I P d I Q ab d ab d d d f d

 



         

 

 

Xét hàm số













9 21

y f d d d

    trên







có





0 1

f d d



  









max 1

f d f



 



Suy ra thể tích khối hộp đạt max khi và chỉ khi

















; 1,

d d I Q P Q

 



Suy ra:

   

 





 

: 2 2 8 0

: 2 2 0; ; 1

: 2 2 14 0

Q x y z

Q x y z d d I Q

Q x y z

   

 





       



 

   







NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Xét điểm





0;0; 8



bất kì thuộc mặt phẳng





ta nhận ra để thể tích max thì chiều cao hộp phải max

tức hai điểm

và

phải nằm cùng phía với mặt phẳng





Như vậy ta nhận mặt phẳng





: 2 2 14 0

Q x y z

   









2 2 14 2 2 14 0

I I I N N N

x y z x y z

      

Với





: 2 0

Q x by cz d

   

, ta đồng nhất hệ số ra

b c d

   

. Chọn đáp án B.

Câu 50. Xét các số phức

và

thỏa mãn

z w

 

và

z w 

. Giá trị nhỏ nhất của biểu thức





2 4

P zw i z w

   

bằng

3 2

. B.

1 5 2



. C.

5 2 2



. D.

Lời giải

Cách 1: Gọi

A B

lần lượt là các điểm biểu diễn số phức

z w

, khi đó với

z w 

ta luôn có

OAB



là

tam giác vuông tại

với

. 0

OA OB



 

, khi đó ta luôn có

z w

là số thuần ảo tức





.z w ki k 



Khi đó

   

 

2 2

2 4 2 4 2 4 2 2 4

1 1 2 1

w ki

P zw i z w ki i w kiw i kiw w kiw kw iw

w w

z w w w ki w k k



 

               



 

  





         





Đặt





,w a bi a b  



khi đó ta có:

     

2 2

2 2 4 2 2 4 1 2

P iw i w w i w i w i i

           

Đặt

1 1 1 1

u w i w u i w u i

           

, khi đó ta suy ra (đặt trước

z i

  

) (*)

















2 2

4 4 2 4 2

2 2 2 2 2 2

0 0 0 0

2 . . 2 . 4 4 . .

o o o o o

P u i u z u z u z u z u z z u u z u u u z z u

                

Mà

 





 

2 2 2 2 2

1 1 * . . 1 1

o o o o o

u z u z u z u i u z z u u z u

               

Suy ra

 

4 2 2 4 2 2

9 1 9 9 3 2

4 4 1 2 2 5 2

2 2 2 2 2

u u u u u u P

 

             

 

 

. Chọn đáp án A.

Cách 2: Ta biến đổi biểu thức

như sau:













2 4 2 2 2 . 2

P zw i z w w i z i z i w i

         

Gọi

A B

lần lượt là các điểm biểu diễn số phức

z w

, cùng với điểm





0; 2



Khi đó hai điểm

A B

cùng thuộc đường tròn tâm

, bán kính



z w 

nên ta suy ra

z w z w AB    

và

P MA MB



NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Ta có:

sin

cos













, do

OA OB



nên ta suy ra

sin cos

cos sin



 



 



 

  

 



  



 



   

 



 



. Suy ra ta có tọa độ hai điểm

A B

mới lần lượt là









sin ;cos , cos ; sin

A B

   



Suy ra:

    

. 5 4cos 5 4 sin 25 20 sin cos 16 sin cos

P MA MB

     

       

Đặt

sin cos 2 sin 2; 2

t x t



 

 

 

      

 

 

 

 

sin cos 1 2sin cos sin cos

     



      

Khi đó ta có:





 

2 2

25 20 8 1 8 20 17

P t t t t f t

       

Xét hàm số





f t

ta thấy

 

2; 2

5 3 2

min min

4 2

P f t f

 



 

 

  

 

 

. Chọn đáp án A.

ĐỀ THPT QUẢNG XƯƠNG LẦN 2

Câu 43. Cho hình chóp .

S ABCD

có đáy là hình thoi tâm





SH ABCD

 . Hai đường chéo

AC a



BD a

 . Gọi

M N

lần lượt là trung điểm các cạnh

SA SB

và điểm

thuộc cạnh

. Biết rằng khoảng

cách từ

đến mặt phẳng





MNP

bằng

, thể tích khối đa diện

AMNP

bằng

. B.

. C.

. D.

Lời giải

Đầu tiên ta chuẩn hóa



. Gọi

O CM DN

 

khi đó

là trọng tâm

SAC



. (*)

Ta nhận thấy do mặt phẳng





MNP

luôn trùng với mặt phẳng





MNCD

nên ta đặc biệt hóa điểm

nằm

tại chân đường vuông góc hạ từ

xuống

. Khi đó ta có:





CD OHP



tức ta suy ra:

 

   

; 2 ; 2 ; 1 ;

d A MNP d H MNP d H OP d H OP

    

. Đặt

SH x



, khi đó

3 3

OH SO

 

(*)

HP CD



nên xét trong tam giác vuông

CHD

ta có:

2 2

. 1

HC HD

 



NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Suy ra:

 

2 2

. 1

; 3

3 3

OH HP x

d H OP x SH

OH HP

     



Ta giả sử tiếp

di động đến trùng điểm

, khi đó ta có:

1 1

4 8

AMNP AMND SMND SABD S ABCD

V V V V V   

Vậy

1 1 1 1 2

. .3. . .

8 24 24 2 8

AMNP S ABCD ABCD

V V SH S AC BD   

. Chọn đáp án A.

Câu 44. Tại một cửa hàng kinh doanh quần áo

có doanh thu





R t

với tốc độ





7250 18

R t t



 

(triệu/

năm) sau thời gian

năm. Chi phí kinh doanh





C t

của cửa hàng tăng với tốc độ





3620 12

C t t



 

(triệu/ năm). Hỏi sau bao nhiêu năm lợi nhuận













L t R t C t

 

, của cửa hàng bắt đầu giảm và lợi

nhuận

sinh ra trong khoảng thời gian đó là bao nhiêu ?



năm,

26620



triệu đồng. B.



năm,

26620



triệu đồng.



năm,

26620



triệu đồng. D.



năm,

26620



triệu đồng.

Lời giải

Ta có tốc độ lợi nhuận sau thời gian

năm là:

















2 2 2

7250 18 3620 12 3630 30

L t R t C t t t t

  

       

Giải phương trình:

 

0 11

L t t







   



 



, như vậy sau 11 năm thì việc sinh lời không còn nữa

Khi đó giá trị tiền lãi thực trên khoảng thời gian

0 11

 

là

     

 

11 11

0 0

11 0 3630 30 26620

L L L t dt t dt



    

 

(triệu đồng). Chọn đáp án C.

Câu 45. Hai bạn

và

, mỗi bạn viết ngẫu nhiên một số tự nhiên gồm ba chữ số đôi một khác nhau. Xác

suất để các chữ số có mặt ở hai số bạn

và

viết giống nhau bằng

2916

. B.

2916

. C.

648

. D.

108

Lời giải

Đầu tiên mỗi bạn có

cách viết nên không gian mẫu là

 





n A

  cách.

Ta tìm cách viết mà các chữ số có mặt trong hai số mà bạn

và

viết giống nhau. Bạn

có tất cả

cách viết mà số không bao gồm chữ số 0 và có





2 3

9 9

A A



cách viết mà số có bao gồm chữ số 0.

Trường hợp 1: Nếu

viết số không gồm chữ số 0 có

cách, lúc này

có

cách viết.

Trường hợp 2: Nếu

viết số có bao gồm chữ số 0 có





2 3

9 9

A A



cách, lúc này

có 4 cách viết.

Vậy xác suất cần tìm là:





 

3 2 3

9 9 9

.3! 9. 4

2916

A A A

 

 

. Chọn đáp án A.

Câu 46. Cho số phức

có phần thực không âm, phần ảo không dương, đồng thời thỏa mãn

2 3

z i z i

   

và





2 4 1

z z i i

   

là số phức có phần ảo không dương. Khi số phức

w z zi

  có

phần ảo nhỏ nhất thì modun của

bằng

2 5

. B.

. C.

2 10

. D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Lời giải

Đầu tiên ta đặt





0, 0

z a bi a b

   

. Khi đó ta có:

2 3 2 3

z i z i z i z i

        

     

2 2 2

2 1 3 1 0 1 0

a b a b a b a b

              

Lại có:





         

2 4 1 2 1 4 1 .... 2 4

z z i i a bi a b i i a b i

               

 

là số phức có phần ảo

không dương nên ta suy ra

2 4 0

a b

  

. Từ đó ta có hình vẽ dưới đây với miền





là phần chứa các số

phức

thỏa. Tiếp đến ta có









3 3 3

w z zi a b b a i

     

có phần ảo nhỏ nhất tức

b a



nhỏ nhất.

Suy ra

b a



nhỏ nhất khi









; 0; 2

a b

 

tức

6 2

w i

  

. Vậy

2 10

w 

. Chọn đáp án C.

Câu 47. Có bao nhiêu cặp số nguyên





;

a b

thỏa mãn

0 , 20

a b

 

sao cho đồ thị của hai hàm số

1 1

a b

 

và

1 1

b a

 

cắt nhau tại đúng hai điểm phân biệt ?

340

. B.

342

. C.

361

. D.

324

Lời giải

Đầu tiên ta nhận thấy

1, 1

a b

 

. Dễ dàng nhận ra nếu

a b



thì hai đồ thị lúc này trùng nhau nên có vô số

điểm chung, suy ra loại. Do đó

a b



, tiếp đến, vì vai trò của

và

như nhau nên ta chỉ cần tìm cặp số

nguyên





;

a b

 

sao cho phương trình

1 1 1 1 1 1 1 1

x x x x

a b b a a b b a

       

có 2 nghiệm phân biệt.

Xét hàm số

 

1 1 1 1

x x

y f x

a b b a

    

có

 

ln ln

x x

a b

f x

a b



  

và





1 0



Giải phương trình

   

ln ln ln

0 log , 0

x x

a b b

f x x x f x

a b a

 

 

       

 

 

Cùng với





f x





khi

x x



và





f x





khi

x x



. Nên ta xét 2 trường hợp sau:

Trường hợp 1:

   

ln ln ln

log 1 ; 4; 2

b a b

x a b

a a b

 

     

 

 

Xét hàm số

 

y g t

 

ta có:

ln3 ln 2 2ln 2 ln 4 ln 5 ln 20

....

3 2 4 4 5 20

     

Khi đó













1 0

f x f x f

  

tức





f x

có đúng 1 nghiệm



Trường hợp 2:

log 1

 

 

 

 

. Khi đó vẽ bảng biến thiên ta thấy





f x



luôn có hai nghiệm phân

biệt. Với mỗi





2;3;...;19

b k 

thì





1;....;20

a k 

tức có



cách chọn giá trị

Suy ra có

 

100 171



 



cặp





;

a b

với

a b

 

và loại đi cặp





4;2

ta có 170 cặp.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Xét tương tự với

b a

 

ta cũng có 170 cặp. Vậy có tất cà 340 cặp số thỏa mãn. Chọn đáp án A.

Câu 48. Cho hàm số





y f x



có đạo hàm liên tục trên







6 0

 

và bảng xét dấu đạo hàm.

Hàm số





4 2 6 4 2

3 4 6 2 3 12

y f x x x x x

       có tất cả bao nhiêu điểm cực tiểu ?

. B.

. C.

. D.

Lời giải

Xét hàm số









4 2 6 4 2

3 4 6 2 3 12

y h x f x x x x x

       

ta có:





























3 4 2 5 3 2 4 2 2 2

12 24 4 6 12 12 24 12 2 4 6 12 2 1

h x x x f x x x x x x x f x x x x x

  

                 

Giải

 

   

 

4 2 2

0; 2

4 6 1 0 *

x x

h x

f x x x



  





 



     





Ta đánh giá (*) như sau: do













 

4 2 2 2

4 6 2 2 2 0; 1 1,f x x f x f x x

  

             



Nên phương trình (*) vô nghiệm, tức hàm số





h x

có ba điểm cực trị, từ đó ta có bảng xét dấu như sau:





6 0

 

nên kéo theo





6 0

 

, suy ra ta có hai trường hợp xảy ra, đó là





0 0



và





0 0



Căn cứ vào đó ta có hai trường hợp xảy ra với đồ thị





h x

, tức đồ thị đề cần tìm.

Vậy





h x

chỉ có 2 trường hợp là 3 điểm cực tiểu hoặc 4 điểm cực tiểu. Chọn đáp án C.

Câu 49. Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu





có phương trình

 

2 2

1 4

x y z

   

và

điểm





3;0;3

. Gọi



là đường thẳng đi qua điểm

và cắt mặt cầu theo dây cung

4 3

BC 

không đổi.

Khi khoảng cách từ

đến



lớn nhất thì



đi qua điểm





20; ;

N m n



. Tính

m n

 

m n

 

. B.

m n

 

. C.

m n

 

. D.

m n

  

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Lời giải

Ta có mặt cầu





có tâm





0;1;0

và bán kính



. Khi đó ta có:

 

2 6

;

2 3

d I IE R

 

    

 

 

Dễ dàng đánh giá được khoảng cách từ

đến



lớn nhất khi



và hai điểm

I O

đồng phẳng.

Ta có:

2 2 2

3 2; 1; 19

OH OI IH

IH IO OH



  





 





nên

IOH



vuông tại

và

 

1 3 2

sin ;cos

19 19

IO HO

IHO IHO

IH IH

    .

Mặt khác ta có:

 

2 2

2 6 7

sin ;cos

3 19 57

IE HE IH IE

IHE IHE

IH IH IH



    

Nên với OF

 

ta suy ra:

 













; sin 3 2 sin 3 2 sin cos cos sin

1 7 3 2 2 6 1

3 2 . . 3 2. 6

19 57 19 3 19 3

max

d O OF OH OHE IHO IHE IHO IHE IHO IHE

      

 

   

 

 

Gọi M OI

  

, khi đó ta suy ra

2 2

3 2 0

3 3

MI EI

MI MO MI MO

MO OF

      

   

Giải hệ tâm ti cự trên ta ra được





0;3;0

M , suy ra

 

1; 1;1 :

1 1 1

x y z

u HM





      



 

Mà



đi qua





20;23; 20

N   nên đồng nhất suy ra

m n

 

. Chọn đáp án A.

Câu 50. Cho hàm số





f x

là hàm số bậc hai có đồ thị là một parabol có trục đối xứng là trục

và thỏa

mãn điều kiện













2 2 3

1 1,x x f x f x x x

      



. Biết giá trị của tích phân





 

ln 1

f x









(với ,a b

 





, 1

UCLN a b



). Tính giá trị của biểu thức

3 3

S a b a b

   

. B.

. C.

122

. D.

Lời giải

Do hàm số





f x

là một parabol có trục đối xứng là trục

nên ta có :









, , 0

f x ax c a b a

   



Thế vào phương trình:













2 2 3

1 1,x x f x f x x x

      



, từ đó ta có:





 









 

   

2 2 3

2 4 3 2 2 3

1 1,

2 1,

x x a x c ax c x x

a a x ax c ac a x a c x c x x

         

            



NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Đồng nhất hệ số ta suy ra hệ phương trình sau:

 

1; 0 1

a a

a a c f x x



 







      

 

 





  



Suy ra





 





3 3

2 2

ln 1 ln 1

x x

dx dx

f x x

 





 

(từng phần)

 

3 3

2 2

ln 1 ln 1

1 1

x x

dx x

x x x x x

 

   

 

     

   

 

 

 

   



5 32 4

ln 2 ln 3 ln ln 92

3 3

3 2

 





 

      

 



 



 



 

. Chọn đáp án A.

ĐỀ THPT LÊ QUÝ ĐÔN ĐÀ NẴNG LẦN 2

Câu 46. Trong không gian

Oxyz

, cho hai mặt cầu

       

2 2 2

: 6 7 8 9

S x y z

     

và

       

2 2 2

: 6 7 8 1

S x y z

     

. Có bao nhiêu điểm

thuộc mặt phẳng





Oxy

, với tọa độ là số

nguyên, mà từ

kẻ được đến





ba tiếp tuyến , ,

MX MY MZ

(với

, ,

X Y Z

là các tiếp điểm và đôi một

khác nhau) sao cho mặt phẳng





XYZ

tiếp xúc với





. B.

. C.

. D.

Lời giải

Đầu tiên ta có hai mặt cầu





và





chung tâm





6;7;8

I và bán kính lần lượt là

1 2

3, 1

R R

 

Ta đặc biệt hóa hai điểm

X Y

và có hình vẽ sau đây:

Đặt









; ;0 , ,M a b a b



khi đó ta có: (áp dụng hệ thức lượng trong tam giác vuông).

       

2 2 2 2

9 6 7 64 81 6 7 17

RIX

MI MI a b a b

IE R

              

Từ đó ta suy ra điểm

thuộc đường tròn

     

2 2

: 6 7 17

C x y

   

. Bài toán chuyển về tìm số nghiệm

nguyên





;

a b

thỏa phương trình

   

2 2

6 7 17

a b

   

. Khi ấy ta suy ra:

6, 7

a b

 

là các căn bậc hai củ

số chính phương. Từ đó ta chia thành hai trường hợp như sau:

Trường hợp 1:

 

         

6 1

1 6 1

; 5;3 ; 5

;11 ; 7;3 ; 7;11

4 7 4 3 11

7 1

a b



 

   

 



   

  

     

 







 



Trường hợp 2:

 

         

6 16

4 6 4 2 10

; 2;6 ; 10;6 ; 2;8 ; 10;8

6 81 7 1

7 1



 

     

 



   

 



 



   



 





Như vậy tổng lại ta có 8 tọa độ nguyên

thỏa mãn. Chọn đáp án D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 47. Gọi

là tập hợp tất cả các số phức

sao cho

1 3 4 5

z i z i

     

. Xét các số phức

1 2

z z

thuộc

thỏa mãn

1 2

z z

 

, giá trị lớn nhất của

2 2

1 2

5 5

P z i z i

    bằng

4 10

. B.

. C.

. D.

4 17

Lời giải

Gọi





M z

là điểm biểu diễn số phức

, cùng với









1;1 , 3; 4

A B và phương trình 5

MA MB AB

  

Ta suy ra

di động trên đoạn

. Tiếp đến gọi









1 2

N z P z

sao cho

1 2

z z NP

  

Cùng với điểm





0;5

Q , ta có:

2 2

1 2

5 5

P z i z i NQ PQ

     













1 2

, : 3 4 7 0

N z P z AB x y

    

nên ta đặt

3 7 3 7

; , ;

4 4

a b

N a P b

 

   

   

   

Quỹ tích của đoạn

là 1 đoạn thẳng trượt qua lại trên đoạn

nên ta suy ra





1;3

a  

Khi đó ta có:

   

2 2

3 7 3 7 25 8

4 4

4 4 16 5

a b

NP a b a b b a

a b



  

 



 

           



 

 







 

2 2

2 2 2

3 7

3 7 8 19 19 44

5 5 ... 5 5 1

4 5 4 5 5 5

P NQ PQ a a a

 

 

 



   

 

 

                 

   

 

   

 

 

với

mọi





1;3

a   . Vậy

max

P 

. Chọn đáp án B.

Câu 49. Có bao nhiêu số nguyên





12;12

a 

sao cho ứng với mỗi

, tồn tại ít nhất 4 số nguyên

thỏa

mãn

4 2022 2

b a a b

 

  ?

. B.

. C.

. D.

Lời giải

Ta có bất phương trình tương đương với:

4 2 2022 0

b a a b 

  

Xét hàm số

 

4 2 2022

b a a b

y f b

 

    có

 

2 2

2 2 1

ln 2 1

4 ln 4 2 ln 2 0 2 2

ln 4 2

b a a b b a a b

f b

     



      

2 2

2 1 0 2 1

b a a b b a a

         

. Mặt khác

     

2 2

1 2 2 2 1 2

4 ln 4 2 ln 2 0

a a a a

f b

   



  

nên ta suy

b b



là điểm cực tiểu hàm số





f b

Suy ra điều kiện cần để tồn tại nghiệm bất phương trình





f b



là





2 1 0

f a a

  

2 2

1 2 2 1

4 2 2022 0

a a a a   

   

(CALC)

 

   

12;12

11; 4 3;11

 

 



     







. (1)

Tiếp đến ta đánh giá như sau:

2 2 2 2

1 1

2 4 2022 2 2022.4 2 . 2022 2 2 2022

a b b a b a b a a a      

     

Suy ra:

 

log 2022 1

a a





   



 



(*) Khi đó ta luôn có

a a

 

Từ đó ta thấy ngay với mọi giá trị của





2 2

1; ; 1;...

b a a a   thì bất phương trình ban đầu luôn đúng với

mọi

thuộc tập (*) (2).

Vậy ta suy ra





11; 10;...; 4;3; 4;...;11

a     tức có 17 giá trị nguyên

thỏa mãn. Chọn đáp án B.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 50. Cho hàm số

 

    

2 3

2 2 2

1 2 3f x x x x    . Có bao nhiêu giá trị nguyên của tham số

để hàm

số

 

4 2

8y f x x m   có đúng 7 điểm cực trị ?

. B.

. C.

. D.

Lời giải

Xét hàm

 

    

2 3

2 2 2

1 2 3f x x x x    có

   

f x f x 

nên

 

f x

là hàm số chẵn.

Như vậy chắc chắn hàm số

 

f x

có một điểm cực trị là

0x 

Mà

 

0f x





với mọi

0x 

nên suy ra hàm số luôn đồng biến trên

 

0;

Từ đó suy ra hàm số có duy nhất 1 cực trị

0x 

Xét hàm số

 

4 2

8y g x f x x m   

có

 

   

3 4 2

4 2

0; 2

4 16 8 0

8 0

x x

g x x x f x x m

x x m

  



 

     



  



Như vậy để

 

g x

có 7 điểm cực trị thì phương trình

4 2

8 0x x m   phải có 4 nghiệm bội lẻ phân biệt và

khác

 

2;0;2

. PT tương đương với:

 

4 2

8m x x u x   

Khi đó ta có bảng biến thiên hàm

 

u x

như sau:

Từ đó ta suy ra

   

0;16 1;2;...;15

ycbt m m



   



tức có tất cả 15 giá trị nguyên m thỏa mãn.

Chọn đáp án A.

ĐỀ CHUYÊN KHTN HÀ NỘI LẦN 2

Câu 48. Xét số phức

thỏa mãn

2z 

, giá trị lớn nhất của biểu thức 2 3 3z i z i z i       bằng

4 2 3

. B.

2 2 3

. C.

. D.

Lời giải

Gọi

là điểm biểu diễn số phức z sao cho thuộc đường tròn

 

2 2

: 4C x y 

. Cùng với ba điểm lần lượt

là

 

   

0; 2 , 3; 1 , 3; 1A B C   , suy ra

ABC

đều. Gọi

E AM

sao cho

MB ME

. Ta có như sau:

Tứ giác

ABMC

nội tiếp nên



60ACB AMB 



, khi đó ta suy ra

BME

đều.

Lại có tiếp



 



60ABE CBE CBE CBM ABE CBM     



Xét

ABE

và

CBM

có:



 



; ;AB BC ABE CBM BAM BCM  

, suy ra

 

ABE CBM c g c    

Khi đó ta suy ra

AE CM

(hai cạnh tương ứng bằng nhau).

–

∞

+ ∞

–

∞

–

∞

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Suy ra:

 

2 3 3 2

P z i z i z i MA MB MC MA ME CE AM AM AM

                

Như vậy khi biểu thức

max thì đoạn

đạt max. Suy ra:

max

2 2 4

P AM R

  

. Chọn đáp án C.

SỞ NINH BÌNH LẦN 2

Câu 47. Cho khối hộp

ABCD A B C D

   

có



 . Biết rằng các khoảng cách từ các điểm

, ,

A B D



đến

đường thẳng



là độ dài ba cạnh của một tam giác có diện tích

S 

, thể tích của khối hộp đã cho là

. B.

. C.

. D.

3 2

Lời giải

Gọi





G AC A BD

 

 

, khi đó dễ thấy

là trọng tâm

A BD





và





nên

AG 

Lấy điểm

đối xứng với

qua

và dựng hình lăng trụ

GDK APN

Nhận thấy rằng khoảng cách giữa các mặt bên của lăng trụ

GDK APN

bằng với khoảng cách từ đỉnh

, ,

A B D



đến

Từ đó, qua cách dựng các mặt phẳng đi qua

A G

và vuông góc với các cạnh bên của lăng trụ

GDK APN

đồng thời cắt các mặt phẳng chứa các mặt bên của lăng trụ này, ta lại thu được một lăng trụ mới (như

hình vẽ) là một lăng trụ đứng có chiều cao là

, tam giác đáy có kích thước lần lượt bằng độ dài khoảng

cách từ các đỉnh

, ,

A B D



đến đường thẳng



NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Khối lăng trụ mới và lăng trụ

GDK APN

có cùng thể tích nên

m GDK APN m

V V S AG  

với

S 

Suy ra:

. . .

2 2

6 6 6.

12 2

ABCD A B C D A ABD GDK APN

V V V

    

   

. Chọn đáp án C.

Câu 48. Cho hàm số

 

3 2

y f x x ax bx c

    

có đồ thị cắt trục hoành tại 3 điểm phân biệt. Biết hàm

số

         

2 2

g x f x f x f x f x

  

  

   

   

có 3 điểm cực trị

1 2 3

x x x

 

và













1 2 3

2, 5, 1

g x g x g x

  

Diện tích hình phẳng giới hạn bởi đồ thị

 





 

f x

h x

g x





và trục

bằng

1 3

2 2

. B.

ln6

. C.

ln 6

. D.

2ln 6

Lời giải

Ta có:





f x





nên

                   

2 2 2 2

g x f x f x f x f x f x f x f x f x g x

      

       

Tiếp đến ta có:

 





 

0 0

f x

h x f x

g x

   



nên phương trình cũng có 3 nghiệm

1 2 3

x x x

 

, và cũng là

các điểm cực trị của hàm số





g x

nên diện tích hình phẳng cần tìm là:

 

3 3 32 2

1 1 2 1 2

1 1 1 2 1 1

x x xx x

x x x x x

f x f x f x g x g x

S dx dx dx dx dx

g x g x g x g x g x

 

 

 

    

 

    

 

    

 





 





 

1 2

2 1 1

g x

g x g x

d g x d g x

g x g x

 

 

 

 

 

 

 

















1 2 3

2, 5, 1

g x g x g x

  

 

5 1

2 5

1 1 ln 6

ln 6 ln 3 ln 2 ln 6

2 1 1 2 2

dx dx

x x

 

      

 

 

 

 

. Vậy

ln 6

S 

. Chọn đáp án B.

Câu 49. Biết nửa khoảng







; , ,

m n

S p p p m n



  



là tập hợp tất cả các số thực

sao cho ứng với mỗi

tồn tại đúng 6 số nguyên

thỏa mãn









2 2

3 27 5 0

x x x



  

. Tổng

m n p

 

bằng

m n p

  

. B.

m n p

  

. C.

m n p

  

. D.

m n p

  

Lời giải

Trường hợp 1:



, khi đó ta suy ra

5 0

 

Do đó bất phương trình ban đầu trở thành:

2 2

3 27 0 2 3 1 3

x x

x x x



         

tức có 5 giá trị nguyên

(loại)

Trường hợp 2:



, khi đó ta suy ra

2 2

5 5 1 0

x x

   

Do đó bất phương trình ban đầu trở thành:

3 27 0

2 3

1 3

5 1

x x





 



 

     











tức có 5 giá trị nguyên

(loại)

Trường hợp 3:



, khi đó ta xét:

3 27 0

x x



 



  







và

5 0 log

y x y

    

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

-Nếu

log 3



hay

log 3

  

thì tập nghiệm cần tìm chính là

5 5

log ; 1 log ;3

1; log log ;3

y y



   

  

   



   

  



   



, tuy

nhiên các cặp nghiệm này không chứa đủ 6 số nguyên nên ta loại.

-Nếu

log 3



hay

log 3

  

thì tập nghiệm cần tìm chính là

5 5

log ; 1 3; log

y y

   

  

   

, và tập

này chỉ chứa đúng 6 số nguyên khi và chỉ khi

16 25

4 log 5 5 5

y y

    

Từ đó ta suy ra:



16 25

5 ;5







chính là tập nghiệm cần tìm, tức

m n p

  

. Chọn đáp án A.

Câu 50. Xét số phức

có phần thực âm và thỏa mãn

1 2

 

. Giá trị nhỏ nhất của biểu thức

3 3 3

P z i z i z i

       bằng

. B.

. C.

4 17



. D.

3 17



Lời giải

Gọi

là điểm biểu diễn số phức

. Xét các điểm

 









3; 1 , 0; 3 , 0; 3

A B C 

. Cùng với điểm





M z

thỏa mãn

1 2

 

, ta có hình vẽ như sau:

Gọi

thuộc đường tròn

   

: 1 4

C x y

  

sao cho

BCD



đều và

E MD



sao cho

MB ME



Khi đó ta suy ra





3;0

D và nhận định như sau:

Tứ giác

DBMC

nội tiếp nên



DCB DMB 



, khi đó ta suy ra

BME



đều.

Lại có tiếp



DBE CBE CBE CBM DBE CBM

     



Xét

ABE



và

CBM



có:



; ;

DB BC DBE CBM BDM BCM

  

, suy ra





DBE CBM c g c

    

Khi đó ta suy ra

DE CM



(hai cạnh tương ứng bằng nhau).

Suy ra:

3 3 3 37

P z i z i z i MA MB MC MA ME DE MA MD AD                

Dấu bằng xảy ra khi





M AD C

 

. Chọn đáp án B.

THỊ XÃ QUẢNG TRỊ LẦN 1

Câu 46. Gọi

là tập hợp tất cả các số phức

2 5

w z i

  

sao cho số phức

thỏa mãn

 





3 3 36

z i z i

    

. Xét các số phức

1 2

w w S



thỏa mãn

1 2

w w

 

. Giá trị lớn nhất của

2 2

1 2

5 5

P w i w i

   

bằng

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

7 13

. B.

4 37

. C.

5 17

. D.

Lời giải

Ta có:

 





  

36 3 3 3 3 3 3 6 2 6 2 12

z i z i z i z i z i z i z i

                    

Mà số phức

2 5

w z i

  

nên suy ra





2 6 2 2 5 1 1 12

z i z i i w i

          

Suy ra điểm





M w

luôn thuộc đường tròn





tâm





1; 1



, bán kính



Tiếp đến xét các điểm









1 2

A w B w

thuộc đường tròn





sao cho

1 2

w w AB

  

, cùng với tọa độ

điểm





0;5

, và gọi

là trung điểm

, khi đó ta có:













2 2

1 2

5 5 2 2 .

P w i w i CA CB CI IA CI IB IA IB CI IA IB CI AB

              

          

Ta có:







2 . 2 . cos ,

CI AB CI AB CI AB



   

nên

max khi hai vector



và



cùng phương.

Suy ra:







2 . cos , 2 . 4 37

P CI AB CI AB CI AB  

 

. Chọn đáp án B.

Câu 47. Trong không gian

Oxyz

cho mặt phẳng





: 3 2 5 0

x y z



   

và hai điểm





8; 3;3 ,

A 





11; 2;13 .

B 

Gọi

M N

là hai điểm thuộc mặt phẳng







sao cho

MN  Giá trị nhỏ nhất của

AM BN



là

2 13

. B.

. C.

4 33

. D.

2 33

Lời giải

Đầu tiên ta có hình vẽ như sau:

Đầu tiên ta cần vẽ một mặt phẳng





chứa

và song song với mặt phẳng





: 3 2 5 0

x y z



   

Xét mặt phẳng





: 3 2 33 0

P x y z

   

. Dựng đường tròn





tâm

, bán kính

AA MN



  với





A C





sao cho

AA NM



là hình bình hành. Đến đây ta nhận thấy

A B



đều cùng phía với mặt phẳng







nên ta suy ra:

AM BN A N BN A N B N A B

    

     

với





13; 6; 3



 

là điểm đối xứng với

qua







Gọi





5; 0;9

là hình chiếu của



lên





khi đó ta suy ra



đạt giá trị nhỏ nhất khi ba điểm

, ,

A H A



thẳng hàng với

nằm giữa

và



. Ta có:

3 6

AH  nên suy ra

min

2 6

HA AA AH MN AH

 

    

Vậy với

6 14

B H



 ta suy ra

 

   

2 2

min

6 14 2 6 4 33

AM BN A B B H A H

   

       .

Chọn đáp án C.

Câu 49. Cho hàm số





y f x



xác định trên



và có đồ thị hàm số





y f x



như hình bên.

Số giá trị nguyên của tham số





10; 10

m  

để hàm số

y f x x

 

  

 

 

có 9 điểm cực trị là

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

A. 11. B.

. C.

. D. 12.

Lời giải

Nhìn vào đồ thị trên ta suy ra:

      

' 1 1 2f x x x x x   

(trong đó

1x  

là nghiệm bội chẵn).

Khi đó ta xét:

 

y g x f x x

 

   

 

 

có

   

g x g x 

nên suy ra

 

g x

là hàm chẵn.

Suy ra hàm số

 

h x f x x

 

  

 

 

phải có 4 điểm cực trị dương tức phương trình

 

0h x





có 4

nghiệm bội lẻ dương phân biệt.

   

2 2

1; 2 0

2 2 2 0

2 1; 2 2

2 2

x x x

h x x f x x

m m

x x x x



   



 

 

     



 

 



     





Khi đó ta cần hệ:

2 4 2

2 4 4

2 4

m x x



   



    



  



có 3 nghiệm dương phân biệt khác 1. Từ đó ta có hình vẽ sau:

Từ hình vẽ trên ta suy ra:

 

 

10; 10

9; 8;.. 1; 0;3

ycbt m

 





     







tức có 11 giá trị nguyên m thỏa

mãn. Chọn đáp án A.

Câu 50. Có bao nhiêu số nguyên

11a 

sao cho ứng với mỗi a tồn tại ít nhất

số nguyên

 

0;8b

thỏa

mãn

 

    

4 3 5

log 12 log 7 3 log 19 7?b b a a      

 

 

. B.

. C. 7 . D. 4 .

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Lời giải

Ta có bất phương trình tương đương với:

















4 3 5

log 12 log 7 3 log 19 7 0

b b a a

       

 

 

Xét hàm số





















4 3 5

log 12 log 7 3 log 19 7

y f b b b a a

        

 

 

có

 

2 1

0, 0;8

7 ln 3

12 ln 4

f b b



    



nên hàm số





f b

luôn đồng biến trên





0;8

Do ứng với mỗi

tồn tại ít nhất

số nguyên





0; 8

b tức

: 7 2



nên suy ra





2 0















       

4 3 5

3 5 3 5

log 16 log 9 3 log 19 7 0, 3;11

log 3 log 19 3 0 log 3 log 19 3

a a a

a a a a

         

 

          

Xét hàm số













3 5

log 3 log 19

y g a a a     có









0, 3;11

g a a



   và





6 3



, suy ra



Vậy ta suy ra:





6;7;8;9;10

a  tức có 5 giá trị nguyên

thỏa mãn. Chọn đáp án B.

SỞ PHÚ THỌ LẦN 2

Câu 45. Có bao nhiêu giá trị nguyên của tham số

để bất phương trình













2 2 2

8 8 8

log 4 12 log 4 12 log 8 24

x mx m x x x x       nghiệm đúng với mọi





. B.

. C.

. D.

Lời giải

Ta có:

   

2 2

4 12 2 8 0; 8 24 4 8 0

x x x x x x

           

nên bất phương trình tương đương với:





 





 





2 2

8 8 8

log 4 12 log 2 8 log 4 8

x mx m x x

       

. (*)

Xét











thì bất phương trình lần lượt trở thành:

 

4 4 2 0

8 16 4 0

x x x



    

 







 

 



    





(loại)

Suy ra điều kiện cần chính là:





2 2

( )

4 12 0 4 12 0 0 3

g x

g x x mx m m m m



           

Khi đó ta suy ra





1; 2

m 

và (*) trở thành:

 





 





2 2

8 8

log 2 8 log 4 8

4 12 8

x x

x mx m

   

  

   

 





log 4 8

4 12 2 8

x m x x

 

     

(1).

Xét

 

thì (1) thành:

8 8 8

log 9 log 9 log 9

9 3 3x x     (loại).

Xét

 

thì (1) thành:

 





log 4 8

2 8

4 12

x x

 

  

 



Xét hàm số

 





log 4 8

2 8

4 12

x x

y g x

 

  

 



có

 

g x

 





 



 



. Cùng với





2 0



 

nên ta suy

ra điều kiện đủ là:









min 2 2

m g x g m

    

Kết hợp điều kiện cần và đủ ta suy ra





0 2 1;2

m m   

. Do ta đã loại 2 giá trị này ban đầu nên suy ra

không có giá trị

nào thỏa. Chọn đáp án C.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 46. Cho hàm số

4 2

y ax bx c

  

có đồ thị như hình vẽ. Biết miền tô đậm có diện tích bằng

và điểm

có hoành độ bằng



. Số giá trị nguyên của tham số

thuộc đoạn





3;3

 để hàm số





y f m  có

đúng một điểm cực trị là

. B.

. C.

. D.

Lời giải

Đường thẳng









d y g x



song song với trục hoành cắt đồ thị





4 2

C y ax bx c

  

tại hai điểm

và

Mà điểm

có hoành độ bằng



nên điểm

có hoành độ bằng

. Khi đó ta có:

   

 

1 1

2 2

1 1

S f x g x dx ax x dx a

 

    

 

, mà



nên suy ra



, tức

4 2

y x bx c

  

Mà mặt khác

















4 2 3

1 1 0 1 4 2

f b c f c b y f x x x c f x x x



                

Giải phương trình

 

3 2

0 4 2 2 2 1 0 0;

f x x x x x x x



         

Xét hàm số









y h x f m  

có

 

3 0

3 ln 3 3 0

1 1

3 ; 3

2 2

x x

h x f m

m m



 



 

    



    





 

1 1

3 ; 3

2 2

x x

m m











   





. Mà

lim 3 0

1 1 1 1

lim 3 ; lim 3

2 2 2 2

x x



 









    





nên ta suy ra để





g x

có

đúng 1 điểm cực trị (tức (*) có 1 nghiệm duy nhất) thì



. Chọn đáp án A.

Câu 47. Cho phương trình









2 2

log 4 log 2 4 log 5 0

a a

x ax x ax

      

. Gọi

là tập các giá trị

nguyên của tham số

để phương trình có nghiệm duy nhất. Tổng các phần tử của

bằng

. B.

. C.

. D.

Lời giải

Điều kiện:

0 1

 

. Ta có phương trình:









2 2

log 4 log 2 4 log 5 0

a a

x ax x ax

      

(1)









2 2

log 2 4 log 5 log 4

a a

x ax x ax       .

Đặt

2 0

t x ax

   

khi đó phương trình trở thành









log 4 log 3 log 4

a a

t t    (2). Khi đó ta chia

hai trường hợp như sau:

Trường hợp 1:

0 1 0

log

   

thì (2) thành









5 4

log 4 log 3 log 4 0

t t

    

Hàm vế trái













5 4

log 4 log 3

y f t t t

   

có









0, 0;f t t



   

tức





f t

đồng biến trên







NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Để ý





1 1



nên ta suy ra

 

log 4 1

1 0 *

x ax













  





Phương trình có nghiệm duy nhất nên ta suy ra

 

. Đối chiếu với điều kiện, ta loại.

Trường hợp 2:



thì (2) ta đánh giá tương tự









5 4

log 4 log 3 log 4 0

t t

    

, đánh giá tương tự

trường hợp ta cũng suy ra

 

, đối chiếu điều kiện ta thu được





a  . Chọn đáp án D.

Câu 48. Cho hàm số





y f x



có đạo hàm cấp hai liên tục trên



. Hình vẽ bên dưới là đồ thị hàm số





y f x





trên





; 2

 

, đồ thị hàm số





y f x



trên đoạn





2;3



và đồ thị hàm số





y f x





trên







. Số điểm cực trị tối đa của hàm số





y f x



là

. B.

. C.

. D.

Lời giải

Đầu tiên từ hình vẽ, ta dễ dàng nhận thấy





f x

có 2 điểm cực trị trên đoạn





2;3



Tiếp đến xét trên





; 2

 

, ta thấy phương trình





f x





có 1 nghiệm nên





f x

có 1 điểm cực trị.

Cuối cùng, xét trên







, ta nhận thấy phương trình





f x





có 1 nghiệm nên suy ra





f x





có tối

đa 2 nghiệm trên







, tức





f x

có tối đa 2 điểm cực trị trên







Vậy tổng cộng số điểm cực trị tối đa của hàm số





y f x



là 5 điểm cực trị. Chọn đáp án B.

Câu 49. Cho hai số phức

1 2

z z

thỏa mãn

2 2

z i

  

và

2 2

1 1 2 5

z z   

. Số phức

thỏa mãn

2 2 5 2 3 6

z i z i

    

. Giá trị nhỏ nhất của biểu thức

1 2

z z z z

  

bằng

. B.

. C.

. D.

Lời giải

Thông qua biến đổi đại số ta suy ra được quỹ tích của các số phức

1 2

2 ,

z z

và

như sau:

       

2 2

1 2

2 : 4 4

: 1; : 4

A z C x y

P z z z z MA MB

B z E x M z d y x



    



      





     





Ta gọi







là đường tròn đối xứng với





qua





, suy ra ta có:

   

: 8

C x y



  

với





A C

 



Từ hình vẽ trên ta kết luận.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

1 2 0 0

P z z z z MA MB MA MB A B



          . Chọn đáp án A.

Câu 50. Trong không gian

Oxyz

, cho hai điểm









2; 2;6 , 3;3; 9

A B

 

và mặt phẳng





: 2 2 12 0

P x y z

   

. Điểm

di động trên





sao cho ,

MA MB

luôn tạo với





các góc bằng nhau.

Biết rằng điểm

luôn thuộc một đường tròn cố định. Tung độ của tâm đường tròn đó bằng

. B.



. C.



. D.

Lời giải

Đặt





; ;

M a b c

, khi đó ta gọi

E F

là các chân đường vuông góc từ

A B

hạ xuống





Ycbt



 

















2 2

; ;

6 3

sin sin 4

d A P d B P

AE BF

AME BMF MA MB

AM BM AM BM AM BM

        

           





2 2 2 2 2 2

2 2 2

20 28 352

2 2 6 4 3 3 9 28 0

3 3 3

a b c a b c a b c a b c

                   

Suy ra





M S



tâm

10 14

; ; 14

3 3

 



 

 

và bán kính

...



. Mặt khác





M P



nên suy ra quỹ tích điểm

là

một đường tròn





thiết diện tạo bởi mặt cắt giữa mặt phẳng





và mặt cầu với tâm đường tròn

là

hình chiếu của

lên mặt phẳng





Ta có phương trình đường thẳng





, qua

, vuông góc





là:

2 ,

x t

y t t

z t



 



  





  







. Mà









E d P

 

nên

ta suy ra:

   

10 14 14 2

2 2 2 2 14 12 0 2 2 2

3 3 3 3

t t t t y

   

               

   

   

. Chọn đáp án D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

SỞ LAI CHÂU LẦN 1

Câu 40. Tìm số giá trị nguyên của tham số thực

để tồn tại các số thực

x y

thỏa mãn

2 2

x y m x y xy m

e e x y x y xy m

    

       

. B.

. C.

. D.

Lời giải

Xét hàm số





f t e t

  

 







f t e



 

và





0 0

f t t



  

Ta thấy





f t



đổi dấu từ “- ” sang “+” khi qua



nên









0 0,f t f t

   



Do đó:





 

2 2

1 0, ,

x y m

x y xy m

e x y m x y

e x y xy m x y

 

  



      





       







. Dấu “=” xảy ra khi và chỉ khi

2 2

x y m

x y xy m



 



  



Hay





 

2 2

x y m x y xy m

x y m

e e x y x y xy m

x y xy m

    



 



        



  





Đặt

, .

S x y P x y

  

, ta có:

3 0

S P m

S S P

S P m



 

   



 



. Vì





4 0;4

S P S  

Lấy









1 2. 2



vế theo vế ta được:





2 3 3

S S m 

Xét hàm số









2 , 0;4

f S S S S  

, có









2 2 0, 0;4

f S S S



    

Yêu cầu bài toán







có nghiệm









0 3 4 0 8

f m f m

     

. Vậy, có

giá trị nguyên của tham số

thỏa mãn. Chọn đáp án B.

Câu 41. Cho hai số phức

1 2

z z

thỏa mãn

1 2

3 2 1 , 2 2

z i z z z      và số phức

thỏa mãn

2 4 1

w i

  

. Giá trị nhỏ nhất của biểu thức

2 1

2 3

P z i z w

    

bằng

. B.

17 1



. C.

. D.

Lời giải

Cách 1:

Đặt





,z x yi x y  



, sử dụng phép biến đổi đại số, suy ra

3 2 1 3 0

z i z x y

       

Suy ra:













       

1 2

2 2

, : 3 0

: 2 4 1

A z B z d x y

C w C x y

   







    





với





có tâm





2;4 , 1

I R



Đặt





 

A a a

b a

B b b















, khi đó ta suy ra:

 





 

1 2

2 2 8 2 8

2 ;1

A a a

b a

z z AB AB b a

b a

B a a



 





         

 

 

 







Cùng với





2;3

, ta suy ra:

     

2 2 2

2 1

2 3 2 1 2 1

P z i z w BE AC BE AI R a a a a

                 

Xét hàm số

       

2 2 2

2 1 2

y f a a a a a       

có

 

min 17

f a f

 

  

 

 

nên từ đó ta suy ra

17 1

 

. Chọn đáp án B.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 42. Cho hàm số

 

y f x

liên tục trên  và có bảng biến thiên

Gọi

là tập hợp các giá trị nguyên của

để phương trình

 

1 2f f x m   có

nghiệm phân biệt

thuộc đoạn

 

3;3

. Số phần tử của tập hợp

là

. B. 1. C. 2 . D.

Lời giải

Đặt

 

1 2t f x  

. Khi

1 x

, ta có

 

1 2 1    y f x f x

Tịnh tiến đồ thị hàm số

 

y f x

sang phải 1 đơn vị ta được đồ thị hàm số

 

1 y f x

và vì đồ thị hàm số

 

1 2  y f x

nhận đường thẳng

1 x

làm trục đối xứng nên ta có bảng biến thiên của hàm số

 

1 2  y f x

Với

 

3;3 x

, ta có

 

4;0 t

+) Nhận xét:

Mỗi

 

4; 2t   

cho 4 nghiệm

 

3;3x 

; Mỗi





2;0t  

cho

nghiệm

 

3;3x 

Với

4t  

, ta có 2 nghiệm

 

3;3x 

; Với

0t 

, ta có

nghiệm

 

3;3x 

+) Ta có phương trình

 

1 2  f f x m trở thành phương trình

 

 f t m

+) Phương trình

 

1 2f f x m   có

nghiệm phân biệt thuộc đoạn

 

3;3

 Phương trình

 

f t m

có 2 nghiệm phân biệt





2;0t  

2 0m   

Vậy có 1 giá trị nguyên của

thỏa mãn yêu cầu bài toán là

1m  

. Chọn đáp án B.

Câu 43. Trong không gian với hệ tọa độ

Oxyz

, cho hai mặt phẳng

 

: 3 0P x y z   

 

: 2 2 5 0Q x y z   

, và mặt cầu

 

2 2 2

: 2 4 6 11 0S x y z x y z      

. Gọi M là điểm di động trên

 

và

là điểm di động trên

 

sao cho

luôn vuông góc với

 

. Giá trị lớn nhất của độ dài đoạn

thẳng

là

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

3 5 3



. B.

. C.

9 5 3



. D.

Lời giải

Đầu tiên ta có: mặt cầu





tâm





1; 2;3

I 

, bán kính











; 3 3 5

d I P

 

tức ta suy ra mặt phẳng





không cắt mặt cầu





luôn vuông góc với





nên vector chỉ phương của

là





1;2; 2

 



, cùng với vector pháp

tuyến mặt phẳng





có dạng





1; 1;1

n  



ta suy ra sin góc giữa

và





là:

 







. 1

sin ;

u n

MN P

u n

 

 

từ đó suy ra









 







 

;

3 ; 3 ; 9 5 3

sin ;

d M P

MN d M P d I P R

MN P

 

     

 

Vậy giá trị lớn nhất của độ dài đoạn thẳng

là

9 5 3



. Chọn đáp án C.

Câu 44. Trên tập hợp các số phức, xét phương trình

6 0

z z m

  

(

là tham số thực). Gọi

là một

giá trị nguyên của

để phương trình đó có hai nghiệm phân biệt

1 2

z z

thỏa mãn

1 1 2 2

. .

z z z z



. Hỏi trong

khoảng





0;20

có bao nhiêu giá trị





. B.

. C.

. D.

Lời giải

Ta có



  

. Nếu

0 9 0 9

m m



      

thì phương trình có hai nghiệm thực phân biệt

1 2

z z

và

1 1 2 2

;

z z z z

 

nên

2 2

1 1 2 2 1 2 1 2 1 2

. .z z z z z z z z z z     

 

. Điều này không xảy ra.

Nếu

0 9 0 9

m m



      

, thì phương trình có hai nghiệm phức là hai số phức liên hợp .

Khi đó

1 2 1 2

;

z z z z

 

nên ta luôn có

1 1 2 2

. .

z z z z



, hay



luôn thỏa mãn.

Vì

 

và





0; 20

m 

nên có

giá trị

thỏa mãn. Chọn đáp án D.

Câu 45. Cho lăng trụ

ABC A B C

  

có đáy

ABC

là tam giác vuông tại

, cạnh

BC a



và



ABC 



. Biết

tứ giác

BCC B

 

là hình thoi có



B BC



nhọn, mặt phẳng





BCC B

 

vuông góc với





ABC

, góc giữa hai mặt

phẳng





ABB A

 

và





ABC

bằng



. Thể tích khối lăng trụ

ABC A B C

  

bằng

. B.

. C.

. D.

3 7

Lời giải

Đầu tiên ta có:

, 3

AB a AC a

 

. Gọi

là hình chiếu của



lên

Suy ra

H BC



(do



B BC



nhọn). Kéo theo





B H ABC





(do









BCC B ABC

 



Kẻ

HK AC



với

K AB



, suy ra

HK AB



Từ đó ta có:

   

 



; 45

ABB A ABC B KH

  

 



, suy ra

B KH





vuông cân tại

tức

B H KH





. (1)

Mặt khác ta có:

HK AC



nên ta có tỉ số sau:

BH HK HK a

BC AC

   (2)

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Tiếp đến ta lại có:

2 2

BH a B H



  (3)

Từ (1), (2) và (3) suy ra phương trình sau:

2 2

.2 12

B H a

BH a B H B H a



 

     .

Vậy

1 3

. . .

ABC A B C ABC

V B H S AB AC B H

  



 

  

. Chọn đáp án C.

Câu 46. Cho hàm số





f x

có đạo hàm liên tục trên



. Biết





5 1



và

 

5 1

xf x dx





, khi đó tích phân

 

x f x dx





bằng



. B.

123

. C.

. D.

Lời giải

Đầu tiên ta có:

         

1 1 5 5

0 0 0 0

1 1

5 5 5 1 25

5 5 5

xf x dx xf x d x f x dx xf x dx

    

   

Ta có tiếp:









u f x du f x dx

dv xdx v



   





  





       

5 5 5

0 0 0

2 2 2

x x

xf x dx f x x f x dx f x dx

 

 

     

 

 

  

Vậy

   

5 5

0 0

25 25

2 2 2

f x dx x f x dx

 

      

 

. Chọn đáp án A.

Câu 47. Cho hàm số bậc ba





y f x



có đồ thị như hình vẽ bên.

Số nghiệm thực của phương trình





4 2

2 2

f x x

 

là

. B.

. C.

. D.

Lời giải

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Phương trình

 





 

4 2

2 2

f x x



 



  



  



* Phương trình

 





   

4 2

4 2 4 2

2 , 1 0

2 2

2 , 0 1 ; 2 , 2 3

x x b b

f x x

x x c c x x d d



    

  



       





* Phương trình









4 2 4 2

2 2 2 , 2 1

f x x x x a a

         

Đồ thị hàm số

4 2

y x x

  như hình vẽ sau:

Dựa vào đồ thị trên ta có:

- Phương trình





4 2

2 , 2 1

x x a a

     

không có nghiệm thực.

- Phương trình





4 2

2 , 1 0

x x b b

    

có 4 nghiệm thực phân biệt.

- Phương trình





4 2

2 , 0 1

x x c c

   

có 2 nghiệm thực phân biệt.

- Phương trình





4 2

2 , 2 3

x x d d

   

có 2 nghiệm thực phân biệt.

Vậy phương trình





4 2

2 2

f x x

 

có 8 nghiệm thực phân biệt. Chọn đáp án A.

Câu 48. Trong không gian với hệ tọa độ

Oxyz

, từ điểm





1;1;0

ta kẻ các tiếp tuyến đến mặt cầu





có

tâm





1;1;1

I 

, bán kính



. Gọi





; ;

M a b c

là một trong các tiếp điểm ứng với các tiếp tuyến trên. Tìm

giá trị lớn nhất của biểu thức

2 2

T a b c

  

3 41



. B.

3 2 41



. C.

3 41



. D.

3 2 41



NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Lời giải

Ta có

IA  nên ta suy ra

2 2

AM IA R

  

, từ đó ta suy ra

sẽ luôn thuộc mặt phẳng





với mặt

phẳng





là phương trình từ phép tính









; ;1

A AM I



, tức ta suy ra phương trình có dạng là:





: 2 2 0

P x z

  

, mà





M S



nên suy ra

thuộc đường tròn thiết diện













C S P

 

có tâm

Xét

MAI



vuông tại

có đường cao

, ta có:

3 4

4 4 0 ;1;

5 5

HA HI HA HI H

 

     

 

 

 

Suy ra đường tròn





có tâm

3 4

;1;

5 5

 



 

 

và bán kính

r  tức ta có hình vẽ như sau:

Xét mặt phẳng





: 2 2 0

Q x y z

  

, ta có:

   

 



2 41

cos cos ; sin 1 cos

3 5 3 5

P Q

  

      .

Mà ta có:

 

;

d H Q



nên ta suy ra









;

3 3 2

sin

205 205 5

d H Q

HK KM KH HM



       .

Nhận thấy

 

2 2

;

3 3

a b c

d M Q

 

 

nên ta suy ra:









3 ;

T d M Q



, kéo theo đó ta có được:

 

3 2 41 3 2 41

3 ; 3 sin 3

205 5 3 5

T d M Q KM





 

    

 

 

. Chọn đáp án B.

Câu 49. Cho hàm số bậc ba





y f x



có đồ thị là đường cong ở hình bên dưới. Gọi

1 2

x x

lần lượt là hai

điểm cực trị thỏa mãn

2 1

x x

 

và









1 2

3 0

f x f x

 

, và đồ thị luôn đi qua









0 0

;

M x f x

trong đó

0 1

x x

 





g x

là hàm số bậc hai có đồ thị qua 2 điểm cực trị và

. Tính tỉ số

(

và

lần lượt là

diện tích hai hình phẳng được tạo bởi đồ thị hai hàm









f x g x

như hình vẽ ).

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

. B.

. C.

. D.

Lời giải:

Nhận thấy hình phẳng trên có diện tích không đổi khi ta tịnh tiến đồ thị sang trái sao cho



. Khi đó ta

có

1 2

1, 3

x x

 

. Xét hàm

3 2

( )

f x ax bx cx d

   

và

g( )

x mx nx p

  

Vì

1 2

1, 3

x x

 

là các điểm cực trị nên ta có:





 

1 0

3 2 0

(1)

27 6 0

3 0

a b c





  







 

  











Hơn nữa, ta có









1 3 3 81 27 9 3 (2)

f f a b c d a b c d        

. Từ (1) và (2) suy ra

b a

c a

d a

 















Mặt khác dựa vào đồ thị ta thấy:









   

0 0

2 2

1 3 3 6 6

9 3 2 2

0 3

g f

p a m a

g g m n p a n a

m n p a p a

g g





  

 



 

      

  

  

   



 



Suy ra:









3 2

6 9 2

f x a x x x

   









g 2 6 2

x a x x

   

Khi đó ta có:

3 2

. 4 3 d

S a x x x x a

   



3 2

4 3 d

S a x x x x a

   



. Do đó,



Câu 50. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm









2;1;3 , 6;5;5

A B

. Xét khối nón





ngoại

tiếp mặt cầu đường kính

có

là tâm đường tròn đáy khối nón. Gọi

là đỉnh khối nón





. Khi thể

tích của khối nón





nhỏ nhất thì mặt phẳng qud đỉnh

và song song với mặt phẳng chứa đường tròn

đáy của





có phương trình

2 0

x by cz d

   

. Tính

T b c d

  



. B.



. C.



. D.



Lời giải

Thể tích của khối nón





nhỏ nhất khi chiều cao của khối nón gấp đôi đường kính mặt cầu.

( Chứng minh: Gọi tâm mặt cầu là

, khi đó có

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG





2 2 2

1 1 1

. . . .

2 2 2 2

SBH SIH BIH

r y

S S S SB BH IK SH IB BH y x r y x x x

y r

          



Với chiều cao khối nón là

, bán kính đáy là

; bán kính mặt cầu là r

 

0; 2x y r 

Thể tích khối nón là

 

2 2 2 2

2 2 2 2 2 3

1 1 1 1 4 1 4 8

. . . 2 4 . 2 2 . 4 .

3 3 2 3 2 3 2 3 2 3

y y r r

V x y r r r y r r r y r r r

y r y r y r y r

     

 

 

          

 

   

 

Thể tích khối nón nhỏ nhất khi

2 4 .

y r y r dpcm

y r

    



)

Tiếp đến ta có đường kính mặt cầu:

2 2 2

4 4 2 6AB     .

Mặt phẳng

 



chứa đường tròn đáy của

 

đi qua B và nhận

 

4;4;2AB 



làm vectơ pháp tuyến. Suy

ra phương trình mặt phẳng







là:













4 6 4 5 2 5 0 2 2 z 27 0

x y z x y

          

Do mặt phẳng

 



qua đỉnh S và song song với mặt phẳng chứa đường tròn đáy của

 

có phương trình

2 z 0x by c d   

nên ta có:

 

2 2

2, 1

2.6 .5 .5

27 36

d ; 2

2 2 1

b c

b c d

B AB



 



 



 



 

 

 

  

  





   



 









 



 

  





Vậy

2, 1, 19b c d   

( do

 

d ; d ;B A

 



). Khi đó 12.b c d   Chọn đáp án B.

CHUYÊN HÀ TĨNH LẦN 1

Câu 44. Cho hai hàm số

 

3 2

3 1 2f x ax x bx d    

và

 

2g x cx x d  

có bảng biến thiên như hình

vẽ. Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ

1 2 3

, ,x x x thỏa mãn

2 2 2

1 2 3

30x x x   . Diện tích hình phẳng giới hạn bởi các đường

   

, , 3, 6y f x y g x x x    

bằng

2113

. B.

1123

. C.

1231

. D.

1321

Lời giải

Ta có





3 6

f x ax x b



  

Từ BBT suy ra

 

f x



và có chung hai nghiệm là



và



2 6

a c

c a

d b b d

c a

 



  









 

 







 





Từ BBT suy ra đồ thị hàm số

 

g x

có đỉnh

; 4I

 



 

 

và

0c 





g x

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

1 2 1 3 12

. 4 4

c d d b

c c c c



         

Xét





















3 2

0 3 2 1 3 0 *

f x g x ax c x b x d         

Từ giả thiết suy ra phương trình (*) có 3 nghiệm phân biệt

1 2 3

, ,x x x thỏa mãn

   

 

2 2 2

1 2 3 1 2 3 1 2 2 3 3 1

2 2

30 2 30

3 12

3 2 3

2. 30 2. 30 3 2 3 10 30 0

29 26 3 0

x x x x x x x x x x x x

c b c

c c c

a a c c

c tm

c c

c loai

         





  

   

           

   

   







     



 





1; 1; 9; 3c a b d      









3 2

4 7 10

f x g x x x x

     

   

6 6

3 2

3 3

1321

d 4 7 10d

S f x g x x x x x x

 

       

 

. Chọn đáp án D.

Câu 46. Có bao nhiêu cặp số nguyên dương

 

;x y

thỏa mãn:

 

3 2

2 3 1

log 14 3 7 1

6 1 2 3

x x

x y x

xy x y

 

   

  

đồng thời 1 2022x  ?

1347

. B.

1348

. C.

674

. D.

673

Lời giải

Ta có

 

3 2

2 3 1

log 14 3 7 1

6 1 2 3

x x

x y x

xy x y

 

   

  

   

  

 

1 2 1

log 14 3 7 1

3 1 2 1

x x

x y x

y x

 

    

 

     

2 2

7 7

log 1 log 3 1 3 7 1x y y x      

     

2 2

7 7

log 1 7 1 log 3 1 3x x y y      

     

2 2

7 7

log 7 1 7 1 log 3 1 3 1x x y y       

(*).

Xét hàm số

 

logf t t t 

. Ta có

 

1 0

ln 7

f t



   , 0t  nên

 

f t

đồng biến trên khoảng

 

0;

Do đó, (*)

 

7 1 3 1x y   

 

7 1 1

 

  .

nguyên dương khi

 

7 1 1 3x   

x chia hết cho 3

hoặc

chia 3 dư 2. Do đó

   

2;3;...; 2021 \ 4;7;10;....; 2020x 

. Vậy có 2020 673 1347 cặp

 

;x y

thỏa

mãn. Chọn đáp án A

Câu 50. Cho hàm số bậc ba có bảng biến thiên của hàm số

( ) ( 1) 2g x f x  

như sau

Giá trị lớn nhất của hàm số

 

3 sin cos 2 2 cos 2 4sin 1y f x x x x      

là:

9

. B. 2 . C. 2 . D. 4 .

Lời giải

( )

y f x



–

∞

+ ∞

–

+ ∞

–

∞

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG









 

3 sin cos 2 2 cos 2 4sin 1 3 sin cos 2 2 2

sin 1

y f x x x x x xf x          



 





3 sin cos 2 2

f x x

    

. Dấu bằng xảy ra khi và chỉ khi

sin 1 0

x k





 



  



 





Đặt

1 3 sin cos 2 3 sin cos 3

t x x x x t

        

. Mà

0 3 sin cos 2

x x

  

nên

0 3 2 1 3

t t

     

. Cho









1 2 4

g t f t

   

. Với

 

4 3 3 sin cos 0

g t t x x x k



        

Vậy

max

4 2

y x k



   

. Chọn đáp án D.

SỞ QUẢNG BÌNH LẦN 1

Câu 41. Có bao nhiêu số nguyên dương

sao cho ứng với mỗi

, có không quá 22 số nguyên

thỏa

mãn

2 4.6 2 3

a b a b b

 

  

. B.

. C.

. D.

Lời giải

Ta có





2 2

2 4.6 2 3 2 4.6 2 3 0 2 3 4.2 2 3 0

a b a b b a b a b b a b b a b   

            

















1 4.2 2 3 0 4.2 1 3 2 0

b a b b b a

       

Trường hợp 1:

4.2 1 0 2 3

b b



       



Xét phương trình

 

log 4,75...

3 2 0 log 2 3 2

b a a a

b a





 

  



 

          

 











Trường hợp 2:

4.2 1 0 2 1

b b



       



Xét phương trình

 

log 1,5

3 2 0 log 2 1 2 0

b a a a

b a





 

  



 

          

 











Mà theo đề ứng với mỗi

, có không quá 22 số nguyên

thỏa mãn nên cùng với

 

ta suy ra

   

 

21 21

3 2

33, 284

: 1 20 1 log 2 21 2 3 log 3 1; 2;...;33

a a

b a a







            









tức có 33 giá

trị nguyên

thỏa mãn bài toán. Chọn đáp án C.

Câu 45. Cho số phức

thỏa mãn

 





1 1 5

z i z i

    

và

2 2

2 1

P z i z

   

. Tích giá trị lớn nhất và giá

trị nhỏ nhất của biểu thức

bằng



. B.

. C.



. D.

Lời giải

Ta có:

 





  

1 1 1 1 1 5 1 5

z i z i z i z i z i z i                 . Đặt

z x yi

 

, ta có:

   

1 5 cos

2 4 3 2 1 5 cos 4 1 5 sin 3

2 4 3

1 5 sin

M z C

x t

P x y t t

P x y

y t





 

 

            

 

  



 





NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

1 2 5 cos 4 5 sin

P t t

    . Mà













 

2 2 2

2 2

2 5 cos 4 5 sin 2 5 4 5 cos sin 100

t t t t

 

      

 

 

nên ta

suy ra

10 1 1 2 5 cos 4 5 sin 1 10 9 11

t t P

           

Tích bằng -99. Chọn đáp án C.

Câu 46. Cho hàm số





3 2

y f x x ax bx c

     

có đồ thị cắt trục hoành tại 3 điểm có hoành độ lần

lượt là

1;1; 3







F x

là một nguyên hàm của





f x

và





y g x



là hàm số bậc hai đi qua ba điểm cực trị

của đồ thị hàm số





y f x



. Diện tích hình phẳng giới hạn bởi hai đường





y F x



và





y g x



bằng

128

. B.

. C.

. D.

6 4

Lời giải

Ta có:





















2 4 3 2

4 1 3 4 2 12

f x x x F x f x dx x x x x d

           



. Với





1 9 ,

F d

  









1 7 , 3 9

F d F d

    

ta suy ra ba điểm cục trị của hàm số





y F x



có tọa độ lần lượt là





1; 9

 





1; 7

 

và





3; 9



. Xét hàm số bậc hai





, ,y mx nx p m n p   



đi qua ba điểm





1; 9







1; 7



và





3; 9

. Từ đó ta có hệ phương trình sau:

9 4

7 8 4 8 3

9 3 9 3

m n p m

m n p n y x x

m n p p

   

 

 

          

 

 

    

 

. Suy ra





4 8 3 .

g x x x d

   

Ta có













4 3 2 2 4 3 2

4 2 12 4 8 3 4 2 4 3

F x g x x x x x x x x x x x

              

Giải phương trình









0 1; 1; 3

F x g x x x x

      

Vậy diện tích giới hạn bởi hai đường





y F x



và





y g x



là

   

3 3

4 3 2

1 1

128

4 2 4 3 .

S F x g x dx x x x x dx

 

        

 

Chọn đáp án A.

Câu 50. Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

       

2 2 2

: 1 1 1 12

S x y z

     

và mặt

phẳng





: 2 2 2 0

P x y z

   

. Xét điểm

di động trên





, các điểm

, ,

A B C

phân biệt di động trên





sao cho

, ,

MA MB MC

là các tiếp tuyến của





. Mặt phẳng





ABC

luôn đi qua điểm cố định nào dưới đây ?





12; 23; 25

. B.

1 1 1

; ;

4 2 2

 

 

 

 

. C.





12; 23; 25

G  

. D.

;0; 2

 

 

 

Lời giải

Ta đặt





; ;

M a b c

với

2 2 2 0

a b c

   

và









; ;

A x y z S



có tâm





1; 1; 1

  

và bán kính

2 3

R  .

, ,

MA MB MC

là các tiếp tuyến của





nên ta luôn có:

2 2 2 2 2 2

MI MA AI MA R MA

     

           

2 2 2 2 2 2

1 1 1 12

a b c x a y b z c

            

(*)

Mà

       

2 2 2

1 1 1 12 9 2

x y z x y z x y z

            

nên thế vào (*) ta suy ra:





















               

2 2 2

2 3 2 12 2 3 9 2 2 12

1 1 1 9 0 1 1 1 9 0

a b c x y z ax by cz a b c x y z ax by cz

a x b y c z a b c x a y b z c x y z

                      

                     

Mà ta có phương trình:

2 2 2 0

a b c

   

nên ta lập dãy tỉ số bằng nhau như sau:





















   

9 1 1 1 9

1 1 1 12

1 2 2 2 1 2 2 2 2 1

x y z x y z x y z

x y z

            

   

      

       

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Từ đó ta suy ra:

   

1 1 1

12; 12; 12 ; ; 13; 23; 25

1 2 2

x y z

  

         



tức mặt phẳng





ABC

luôn

đi qua điểm cố định





12; 23; 25

G  

. Chọn đáp án C.

THPT TRẦN NHÂN TÔNG - QUẢNG NINH LẦN 1

Câu 44. Gọi

là tập hợp tất cả các số phức

sao cho số phức

z i z





có phần ảo bằng

. Xét các

số phức

1 2 3

, ,

z z z S



, giá trị lớn nhất của

     

1 3 2 2 3 1 3 1 2

P z z z z z z z z z

     

bằng

. B.

. C.

. D.

Lời giải

Gọi





,z x yi x y  



i z z



 

nên





2 2

. 0 0 0

z i z x y x y i x

x y y







         



 





Ta có:









 

2 2

2 2 2

1 1

x y x y i

z i z

x y x y i

x y x y

  

  



  

, với số phức

z i z





có phần ảo bằng

nên theo giả thiết ta có:





2 2

2 2 2 2 2 2

2 2 2

2 2

x y y

x y y x y y x y

x y x y

 

       

  

 

2 2 2 2

2 2 0

x y y x y y

      

(*). Quy về phương trình bậc hai theo

2 2

x y



, ta có:

   









   

2 2

(*) 2 4.2 2 0

2 2

y y

x y y

z x y

y y y

y y

x y

  



  





  





        



  









  





Từ đó ta suy ra:













1 2 3

, ,

A z B z C z

thuộc đường tròn tâm

, bán kính



Ta có:

     

1 3 2 2 3 1 3 1 2 1 3 1 2 2 3 2 1 3 1 3 2

P z z z z z z z z z z z z z z z z z z z z z

           













1 3 3 1 2 3 3 2 1 2 1 2

z z z z z z z z z z z z

     

Sử dụng tính chất sau:

2 2 2

1 2 1 2 1 2 1 2

z z z z z z z z

    

, từ đó ta biến đổi tiếp biểu thức trên:













     

2 2 2 2 2 2 2 2 2

1 3 3 1 2 3 3 2 1 2 1 2 1 3 1 3 2 3 2 3 1 2 1 2

2 2 2 2

2 2 2

2 2 2 2

3 1 3 2 3 1 2

2 2 2 2

2 2 8 2 sin 2 sin 2 sin

1 1 1 cos 2 1 co

16 sin sin sin 8 1 cos

2 2 2

P z z z z z z z z z z z z z z z z z z z z z z z z

z z z z z z z OC AC BC AB R B R A R C

C A B C

                 

              

 

 

        

 

 

         

 

2 2

s 2

1 1 1

16 cos cos 2 cos 2 16 cos cos cos

2 2 2

16 cos cos cos

A B A B A B A B A B

C C A B

 

 

 

   

          

   

   

 

   

 

 

Với





1 cos 1

A B

    

ta suy ra

1 1 1 1 3

16 cos cos 16 cos 16. 12

2 2 2 4 4

P C C C

 

   

        

 

   

 

   

 

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Vậy giá trị lớn nhất của biểu thức

bằng 12. Chọn đáp án D.

Câu 45. Cho hàm số bậc ba

 

3 2

f x x bx cx d



   

có đồ thị là





cắt trục hoành tại 3 điểm phân

biệt trong đó có 2 điểm có hoành độ lần lượt là

1, 2

x x

 

. Đường thẳng





tiếp tuyến của đồ thị





tại điểm có hoành độ





cắt đồ thị





có hòanh độ



. Gọi

1 2

S S

lần lượt là các diện tích hình

phẳng giới hạn bởi đồ thị





, trục hoành và trục tung (như hình vẽ bên ). Khi tỉ số

S b



(với

là

phân số tối giản) thì

a b



bằng

4 5 9

. B.

4 3 5

. C.

7 0 5

. D.

7 7 5

Lời giải

Từ hình vẽ ban đầu ta suy ra:

     

1 2

f x x a x x

    

(1)

Gọi phương trình tiếp tuyến cần tìm là:





d y mx n

 

, từ đó ta suy ra:

     

2 2

1 5 5 1 5 5

2 4 3 2 4 3

f x mx n x x f x x x mx n

       

            

       

       

(2), so sánh hệ số chứa

trong hai cách biểu diễn hàm





f x

giữa (1) và (2) ta suy ra

 

tức

    

1 11

1 2

2 6

f x x x x

 

    

 

 

Khi đó ta suy ra:

     

5 59

4 96

59 5 91 59 204

: :

96 4 384 96 384

5 91

4 384

d y x d y g x x



 



 

 



  

 

       



 

 

 



  

 



 



Suy ra:

  

    

1 1

11 11

6 6

5 5

3 3

5 5

4 4

1 11 5125

( ) 1 2

2 6 31104

656

12005

1 11 59 204 1500625

( ) 1 2

2 6 96 384 497664

S f x dx x x x dx

S f x g x dx x x x x dx

 



 

      



 

 



 





   

         



   

   





 

Vậy

656, 12005

a b

 

tức

19 459

a b

 

. Chọn đáp án A.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 46. Cho hình chóp

S A BC D

có

ABC D

là hình bình hành biết rằng



SAD BAC 



, cạnh

2 2 , 2 , 6

SA a BC a SB a

  

. Gọi

là hình chiếu vuông góc của

trên

biết khoảng cách giữa

C H

và

bằng

. Thể tích khối chóp

S A BC D

bằng

. B.

. C.

. D.

Lời giải

Ta gọi

là trung điểm

A D

và

là trọng tâm

ACD



, kẻ

HG SB



, khi đó ta có:

DG DH

DB DS

 

Kẻ

BK IC



với

K AD



ta suy ra









HCI SBK



và

























, ; ;

d CH SB d HCI SBK d I SBK

 

Tiếp đến ta dễ thấy

IKBC

là hình bình hành nên suy ra

là trung điểm

, từ đó ta có

SK a



và

CI BK a

  

. Mà

SB a

 nên ta suy ra: (Công thức He-rông)

SBK

S a





Mặt khác ta có:

   

 

6 6

, ; 2 ; 2

SABK SABK

SBK

V V

d CH SB d I SBK d A SBK a



     nên ta suy ra

2 3

1 5 10

. 2

6 2 12

S ABK

V a a a

 

, mà

4 4

ABCD S ABCD

ABK ABI SABK

S V

S S V

 

   

nên ta suy ra

3 3

. .

10 10

4 4

12 3

S ABCD S ABK

V V a a

  

. Chọn đáp án D.

Câu 48. Có bao nhiêu số nguyên





10;10

x  

sao cho ứng với mỗi

có ít nhất

số nguyên

thỏa

mãn

 

2 2

70 6

2 4 .log 10 65.4

y x y x y

x y

  

   

. B.

. C.

. D.

Lời giải

Ta có bất phương trình sau:

 

2 2

70 6

2 4 .log 10 65.4

y x y x y

x y

  

   

(*), điều kiện:

y x

 

   

2 2 2

70 6 70 8 2

2 2

2 4 .log 10 65.4 0 2 log 10 65 0

y x y x y y x

x y x y

    

          

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Xét hàm số

   

70 8 2

2 log 10 65

y x

f y x y

 

    

trên





;10

 

ta có

 

70 8 2

8.2 ln 2 0, ;10

10 ln 2

y x

f y y x

x y

 



      

 

Từ đó ta suy ra hàm số





f y

luôn nghịch biến trên





;10

 

Ta có bất phương trình









0 0 10

f y f y x



    

. Do theo đề bài ứng với mỗi

có ít nhất

số

nguyên

thỏa mãn nên ta suy ra

sẽ chạy từ



tới



Từ đó ta suy ra

   

 

70 8 1 2

0 1 1 0 2 log 9 65 0

x x

f x f x

  



        









 

   

2 2

2 2 2 2

10;10

2 8 62 log 65 log 9 2 8 62 log 65 log 9 0

7.659

10; 3.65 7.659;10

3.65

x x x x

 

            





     



 



Mà





nên ta suy ra





9; 8;...; 4;8; 9

x    

tức có 8 giá trị nguyên

thỏa mãn. Chọn đáp án B.

Câu 49. Trong không gian

Oxyz

, cho mặt phẳng





: 2 2 7 0

P x y z

   

, điểm





2; 1;1

M 

và mặt cầu





2 2 2

: 4 2 4 7 0

S x y z x y z

      

. Đường thẳng





đi qua

cắt









P S

lần lượt tại các điểm

và

sao cho

là trung điểm

. Biết độ dài ngắn nhất của đoạn

là

2 2

a b



, giá trị

a b



bằng

2 3 2

. B.

2 2 3

. C.

212

. D.

192

Lời giải

Ta có mặt cầu





tâm





2; 1; 2

I  

, bán kính



và









; 5 4

d I P R

  

nên suy ra mặt phẳng





không cắt mặt cầu





. Tiếp đến ta tìm mặt phẳng





đối xứng với





qua

Ta có





: 2 2 0

Q x y z D

   

và

 

; ; 3 3 11

d M P d M Q D



     

Suy ra:





: 2 2 11 0

Q x y z

   

. Tới đây ta tìm quỹ tích điểm

như sau:

Theo giả thiết, ta có





MA M B B Q

  

, do đó

luôn nằm trong hình tròn





được tạo từ mặt phẳng





cắt mặt cầu





. Gọi

là hình chiếu của

lên trên





, giải hình chiếu trên ra

7 5 8

; ;

3 3 3

 

 

 

 

Từ đó ta suy ra bán kính của





bằng

2 2

r R IJ  

Suy ra điểm

luôn thuộc đường tròn





tâm

7 5 8

; ;

3 3 3

 

 

 

 

, bán kính

r  .

AB MB



nên

lớn nhất chỉ khi

M B

lớn nhất, khi đó ta có hình vẽ như sau:

Từ hình vẽ trên ta suy ra

 

2 2 2

0 0

2 2 2 2 2 9 15 13

AB MB MB ME EB ME EJ r         

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

2 37 2 195

 

. Đồng nhất hệ số ra

37, 195

a b

 

tức

23 2

a b

 

. Chọn đáp án A.

Câu 50. Cho hàm số





y f x



là hàm đa thức có









2 36, 2 32

f f

   

. Hàm số





f x



có bảng biến

thiên như sau:

Có bao nhiêu giá trị nguyên của tham số





50;50

m  

để hàm số

 

2 1 6

1 2 1

g x f m

x x



 

  

 

 

 

có 5 điểm

cực trị ?

6 3

. B.

3 4

. C.

3 6

. D.

Lời giải

Xét

 

2 1 6

1 2 1



 

 

 

 

 

h x f

x x

\ ; 1

 

 

 

 



. Ta có

 

   

2 2

2 1 3 12

1 2 1



 

 

 

 



 

 

h x f

x x

 

4 1

2 1

 



 

 

  

 



 



h x f

đặt

2 1







ta được phương trình

 





f t

Đặt

 



u t

dễ dàng suy ra được bảng sau

Do đó

 









 



 



f t

thay lại ta được









h x

có nghiệm duy nhất



x

. Ta có bảng biến thiên

của







h x





h x

có 1 điểm cực trị nên để hàm số





h x

có 5 điểm cực trị khi chỉ khi





h x

cắt trục hoành tại 4 điểm

phân biệt do đó ta suy ra

36 0

36 28

28 0

 



   



  



. Vậy có 63 giá trị của m. Chọn đáp án A.



 



NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

SỞ NGHỆ AN LẦN 2

Câu 45. Cho số phức

thỏa mãn điều kiện

3 6 2 5

z i z i

    

và số phức

có phần thực bằng phần

ảo. Giá trị nhỏ nhất của biểu thức

1 1

z z z

 

là

. B.

2 6

. C.

3 2 6

1 3

. D.

Lời giải

Đặt





,z x yi x y  



khi đó ta có:

3 6 2 5 5 8 0

z i z i x y

        

tức









: 5 8 0

M z d x y

   

Gọi





1 1

A z z



với số phức

phần thực bằng phần ảo, ta suy ra

z a ai

 

Suy ra

 

2 2

1 1

x a

z z a a a i

y a a





    



 



tức









2 2

1 1

: 2

A z z P y x x

   

Gọi







là tiếp tuyến tiếp xúc với





và song song với





với





: 5 0

d x y C



  

Khi đó gọi





0 0 0

;

A x y

là điểm tiếp xúc đó, ta suy ra

 

2 5 1

x x

x x x



    

tức





: 5 2 0

d x y



  

Vậy

 

   

2 2

1 1 1 1 0 0

3 26

; ;

z z z z z z MA MA d d d d A d



         

. Chọn đáp án C.

Câu 48. Cho hàm số









3 2

,y f x x ax bx a b    



. Biết hàm số

       

1 2 1

3 3 2

g x f x f x f x

 

  

có hai điểm cực trị là

1, 3

x x

 

. Với mỗi

là hằng số tùy ý thuộc đoạn





0;1

, gọi

là diện tích hình

phẳng giới hạn bởi các đường









0, ,

x y f t y f x

  

và

là diện tích hình phẳng giới hạn bởi các

đường









1, ,

x y f t y f x

  

. Biểu thức

1 2

12 4

Q S S

  có thể nhận được bao nhiêu giá trị là số nguyên ?

. B.

1 0

. C.

. D.

Lời giải

Ta có:

















3 2 2

3 2 6 2 6

f x x ax bx f x x ax b f x x a f x

  

           

Từ đó ta suy ra:

       





2 6 2

1 2 1 3 2

3 3 2 3 3

x a

x ax b

g x f x f x f x



 

   

     

Do hàm số





g x

có hai điểm cực trị là

1, 3

x x

 

nên suy ra





 

1 0

3 0













 













tức





y f x x

 

Xét phương trình hoành độ giao điểm của









y f t y f x

 

có

3 3

x t x t

  

Từ đó ta suy ra:

 

3 3

4 3

1 2

3 3 3

12 4 12 4 1

3 1

4 4

S t x dt

Q S S t t f t

S x t dt t



  



      





    







Xét hàm số





f t

ta có

 

0 0;

f t t t



   

với



là điểm cực tiểu và

1 63

4 64

 



 

 





0;1

t 

nên ta suy ra

 



 

 

tức

có thể nhận 9 giá trị nguyên. Chọn đáp án C.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 49. Cho các số thực

, , 1

a b c



thỏa mãn

2 2

6 log 1 log .log

ab b a

c c c

  và biết phương trình

x x

c a





có nghiệm. Giá trị lớn nhất của biểu thức





log 2

P bc



bằng

m n



trong đó

, ,

m n p

là các số nguyên

dương và

là phân số tối giản. Giá trị của

m n p

 

bằng

4 8

. B.

6 0

. C.

5 6

. D.

Lời giải

Ta có:

1 2

1 1 1 1 1 5

1 log log 2 . 2 log

log 2 log 2

x x

c c c

c c

c a x x a a x x a

x x a a



             

(1)

Tiếp đến ta có:

2 2

6 1 1

6log 1 log .log 1 .

log 2 log log 2 log

ab b a

c c c c

c c c

b a b a

    



   

1 1 1 1

6 1 . log 2 log 6 log 2 log 1

log 2 log log 2 log

c c c c

b a b a

 

        

 

 

5 1 7 33 7 33

log 2 6 log 2 ;

2 log 2 4 4

c c

b b

 

 

     

 

 

. Từ đó ta suy ra:

 

   

7 33

log 2 log 2 4

4 23 33

log 2 log 2 4 log

log log log 2 8

c c

a a a

c c c

b b

P bc b c

a a a



       

Đồng nhất hệ số suy ra

23; 33

m n

 









tức

m n p

  

. Chọn đáp án D.

Cách 2: Đặt









;2 ;

u v

a b c c



, khi đó ta luôn có:

2 2

6 log 1 log .log

ab b a

c c c

  tương ứng với bất phương

trình:

  

6 1

6log 1 log log 1 6 1

u v u v

c c c

c c c uv u v uv

u v uv



        







2 2 2 2

6 6 1 0

uv u v uv u v uv v u u u

          

. (*)

Tiếp đến ta lại có phương trình

2 2

1 1 2

1 0

x x x ux

c a c c x ux

 

      

, xét phương trình bậc hai trên theo

ta có:

4 0

   

(điều kiện có nghiệm)

 

Với

min



ta thế vào (*) khi đó ta có:

7 33 7 33

2 7 2 0

4 4

v v v

 

     

Từ đó ta suy ra:

   

4 4

7 33

4 4 23 33

log 2 log , 2

2 2 8

v v

P bc c u



  

       

Đồng nhất hệ số suy ra

23; 33

m n

 









tức

m n p

  

Câu 50. Trong không gian

Oxyz

cho các điểm

















4; 0; 0 , 0;8; 0 , 0; 0; 12 , 1; 1; 1

A B C D

   

và

là

điểm nằm ngoài mặt cầu





ngoại tiếp tứ diện

O ABC

. Các đường thẳng

, , ,

MA MB MC MO

lần lượt cắt

mặt cầu





tại các điểm

, , ,

A B C O

   

(khác

, , ,

A B C O

) sao cho

MA MB MC MO

   

   

. Tìm giá trị

nhỏ nhất của

M D M O



NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

229

. B.

227

. C.

226

. D.

228

Lời giải

Ta gọi

là tâm mặt cầu





, nhận ra ba điểm

, ,

A B C

nhận thành mặt chắn nên ta suy ra tọa độ của

có

dạng là:

 

; ; 2;4; 6

2 2 2

A B

zx y

I I

 

  

 

 

và bán kính mặt cầu





là

2 14

R IA 

Tiếp đến ta có:

2 2

MA MA MA

MA MA MA MI R

 

 



, tương tự với các tỉ số còn lại là:

, ,

MB MC MO

  

ta suy ra:

 

2 2 2 2

2 2 2 2 2 2

2 2

4 4

MA MB MC MO MA MB MC MO

MA MB MC MO MI R

  

          

   



(*)

Gọi





; ;

M x y z

khi đó thế vào (*) ta suy ra phương trình trở thành:

     





     





2 2 2 2 2 2

2 2 2

4 8 12 3 4 2 4 6 224

x y z x y z x y z              

2 3 28 0

x y z

    

tức





: 2 3 28 0

M P x y z

    

. Bài toán trở thành tìm giá trị nhỏ nhất của

M D M O



với





: 2 3 28 0

M P x y z

    

. Do

D O

cùng phía với





nên ta gọi



là điểm đối xứng

với

qua





với





4; 8;12





. Suy ra giá trị nhỏ nhất là

227

MD MO DO



   . Chọn đáp án B.

Bấm Tải xuống để xem toàn bộ.

| 1/98

| | Tải xuống

Preview text:

ĐỀ LIÊN TRƯỜNG NGHỆ AN LẦN 1
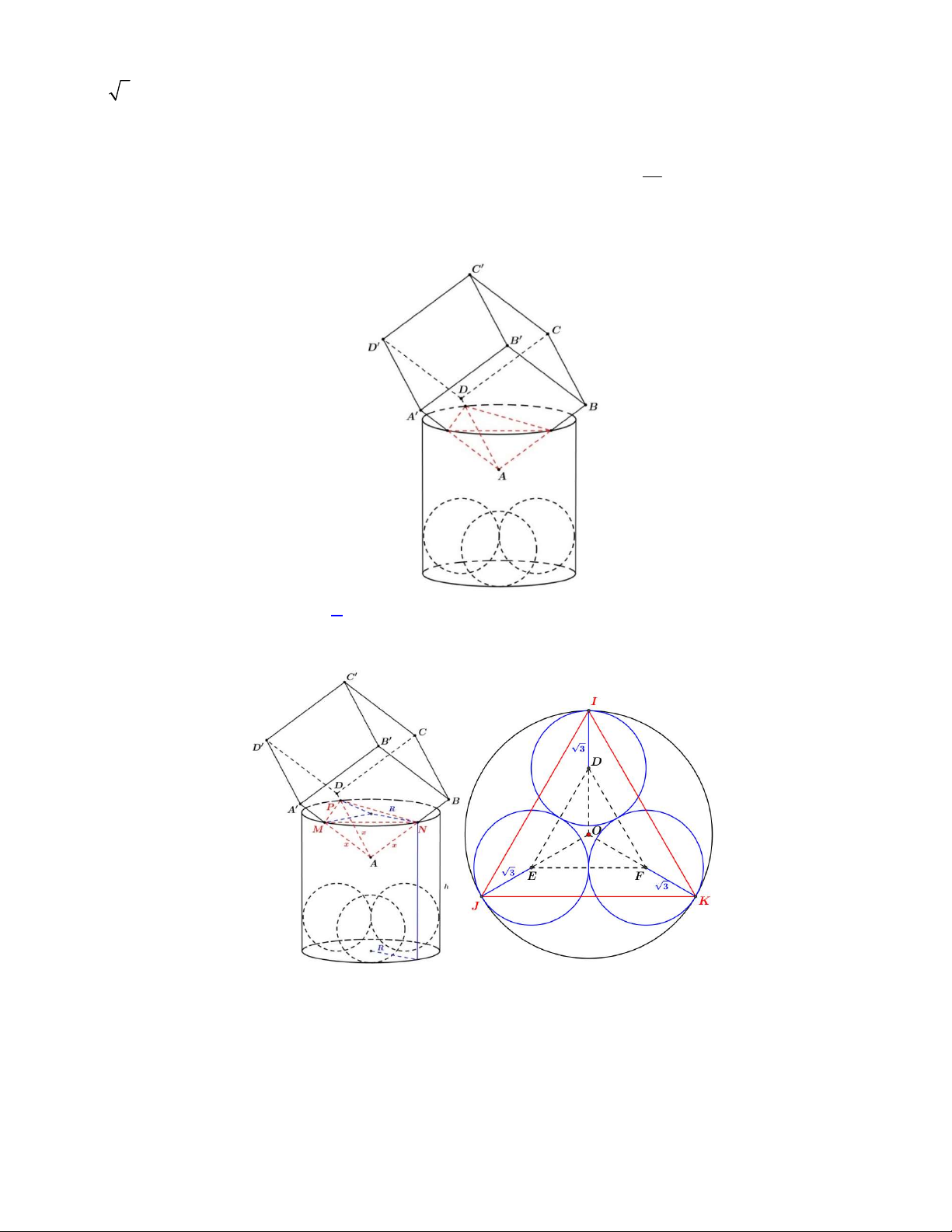
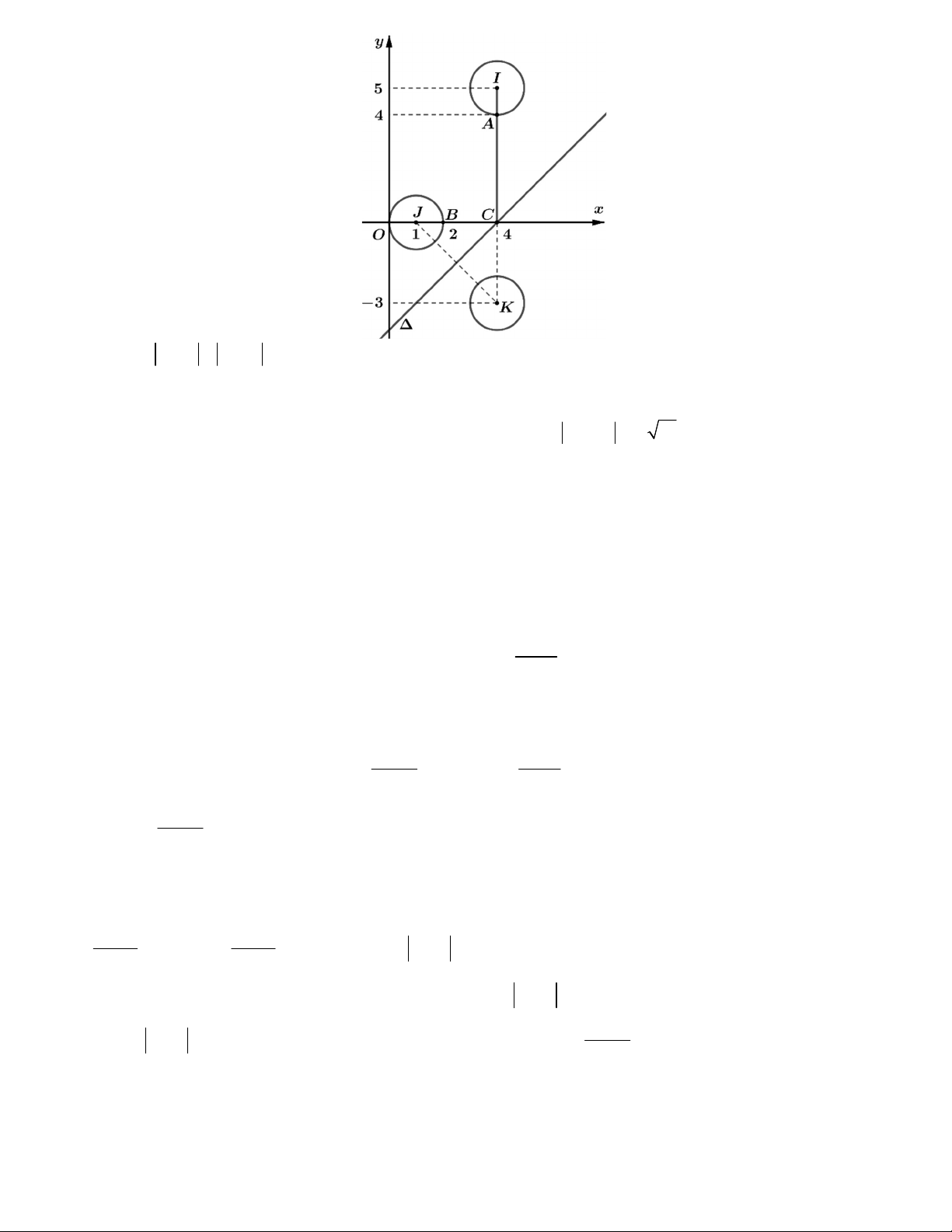
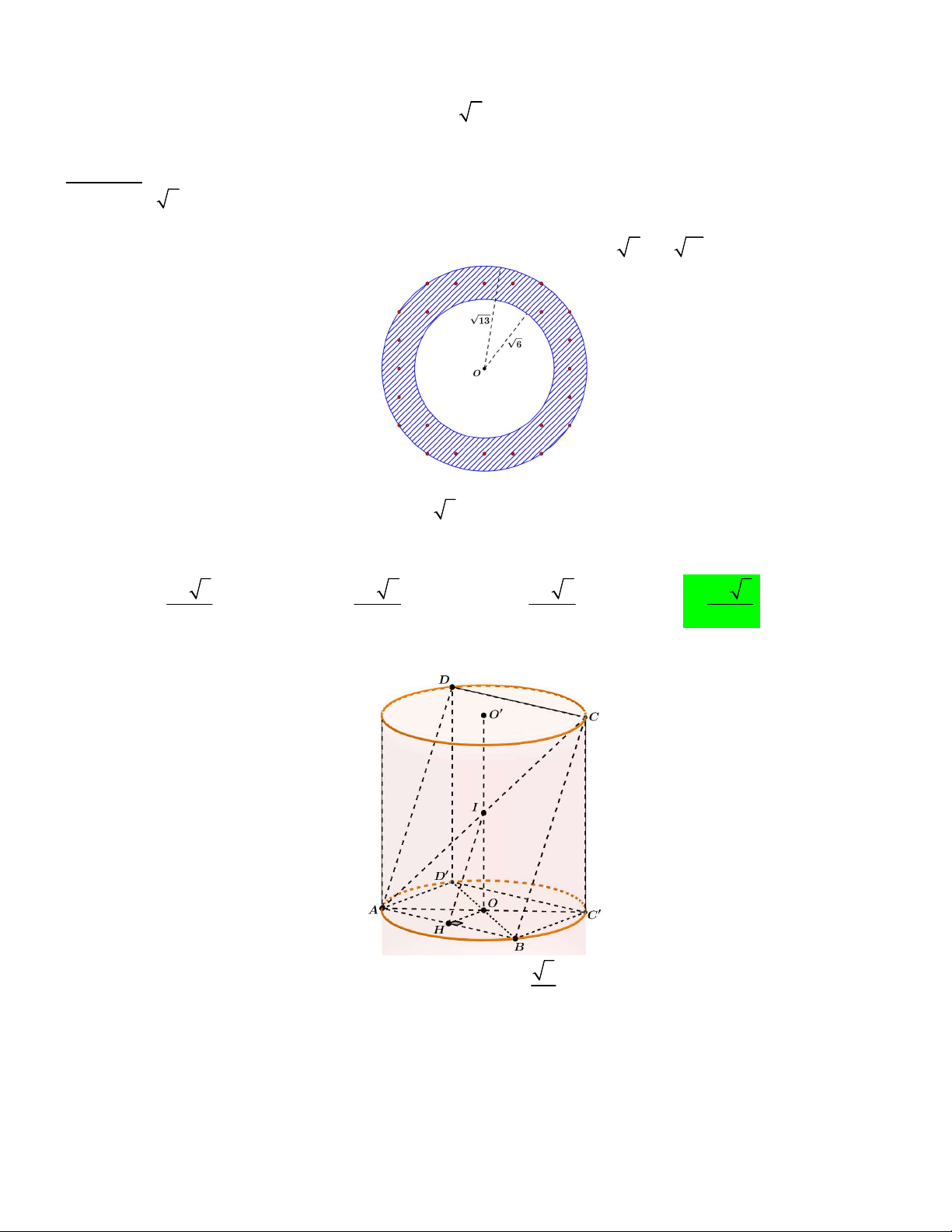
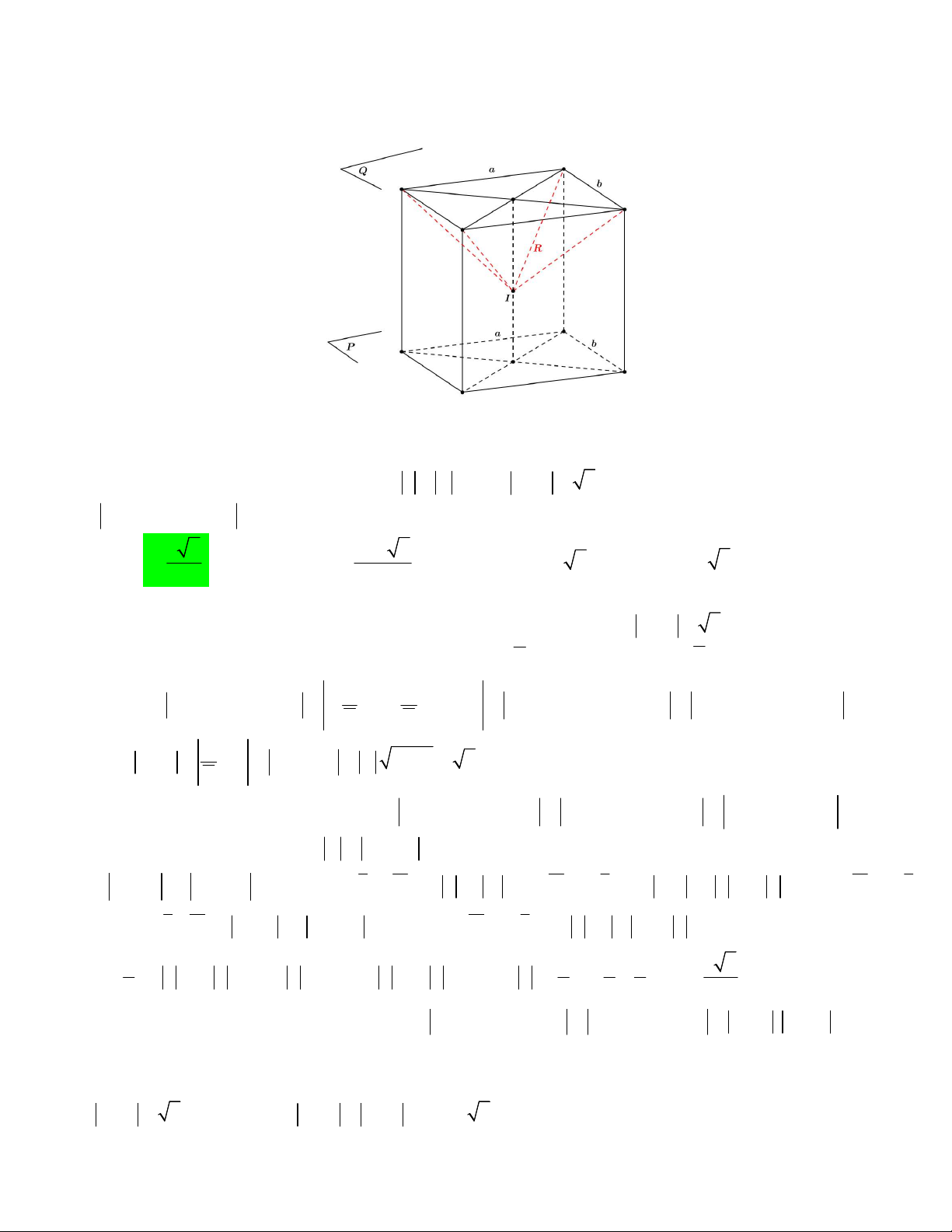
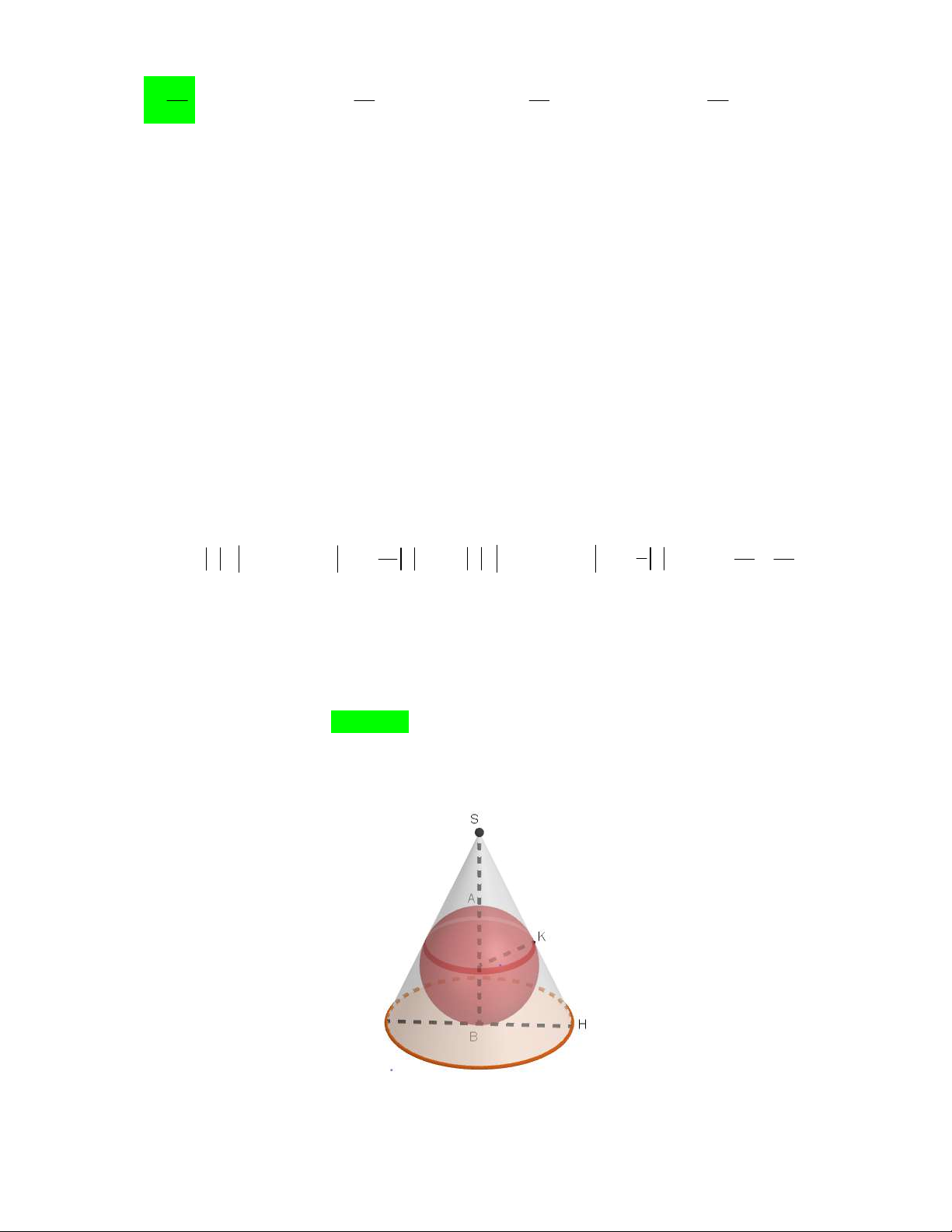
Câu 46. Một bình thủy tinh hình trụ không có nắp, trong bình được xếp vào ba viên bi bằng nhau có bán
kính 3dm sao cho các viên bi đều tiếp xúc với đáy, đôi một tiếp xúc nhau và tiếp xúc với đường sinh của
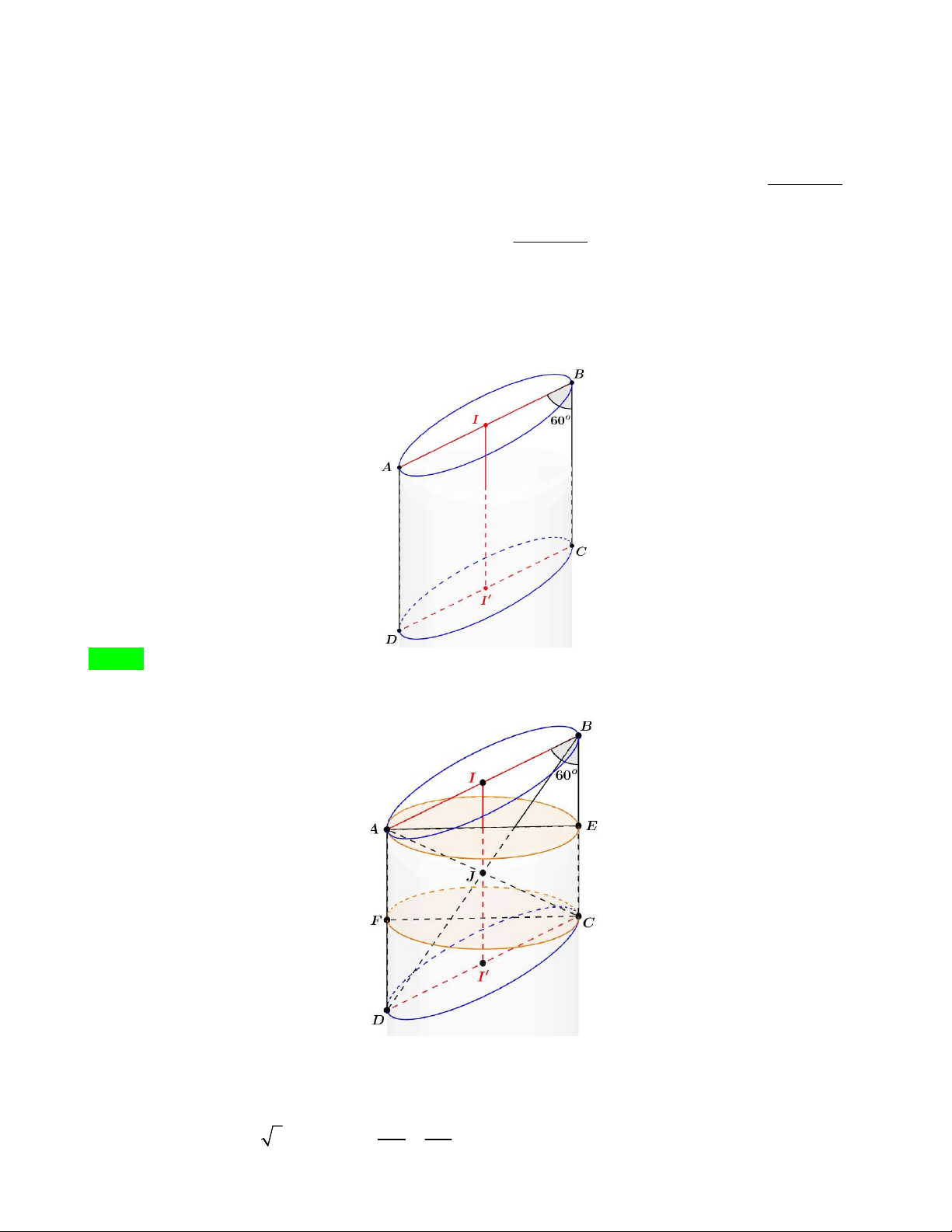
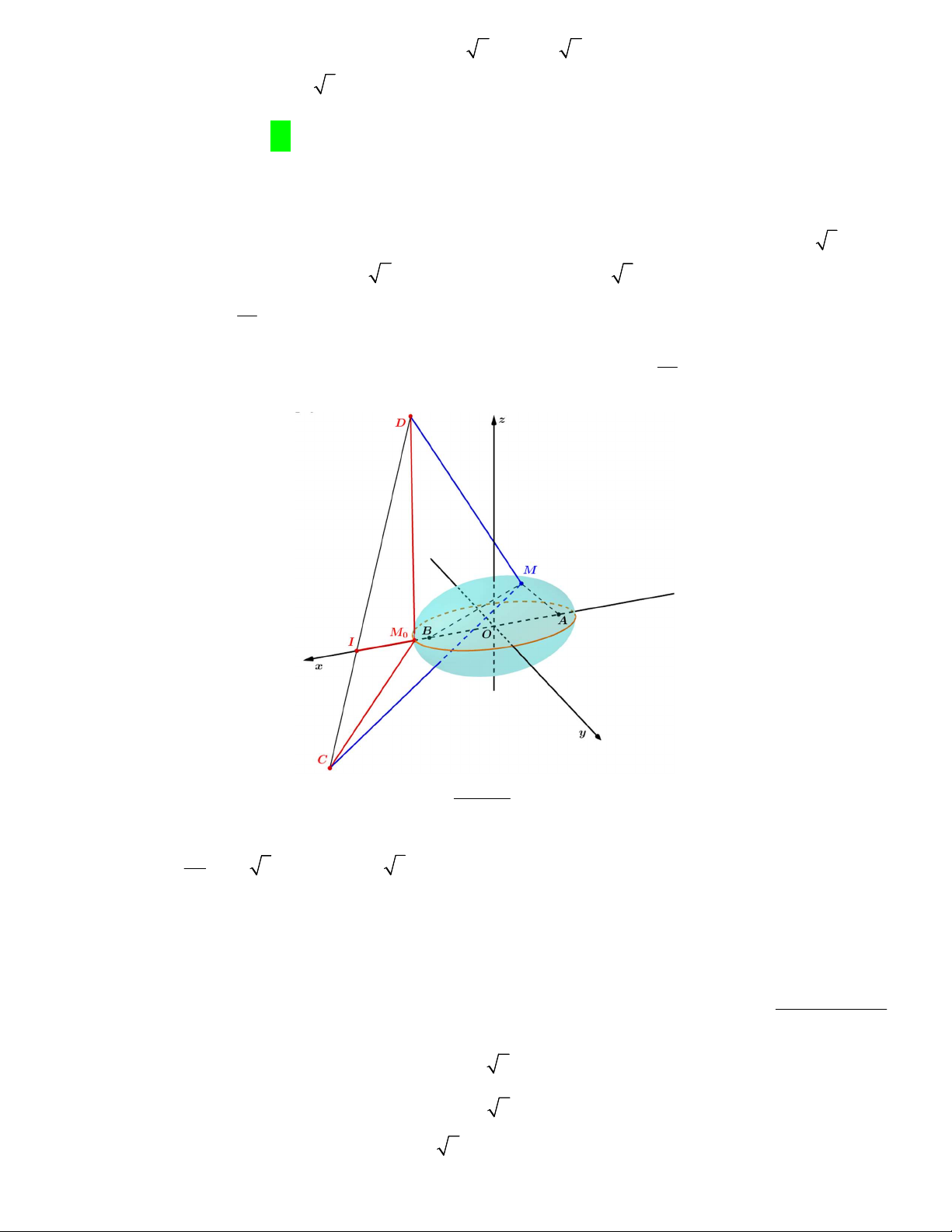
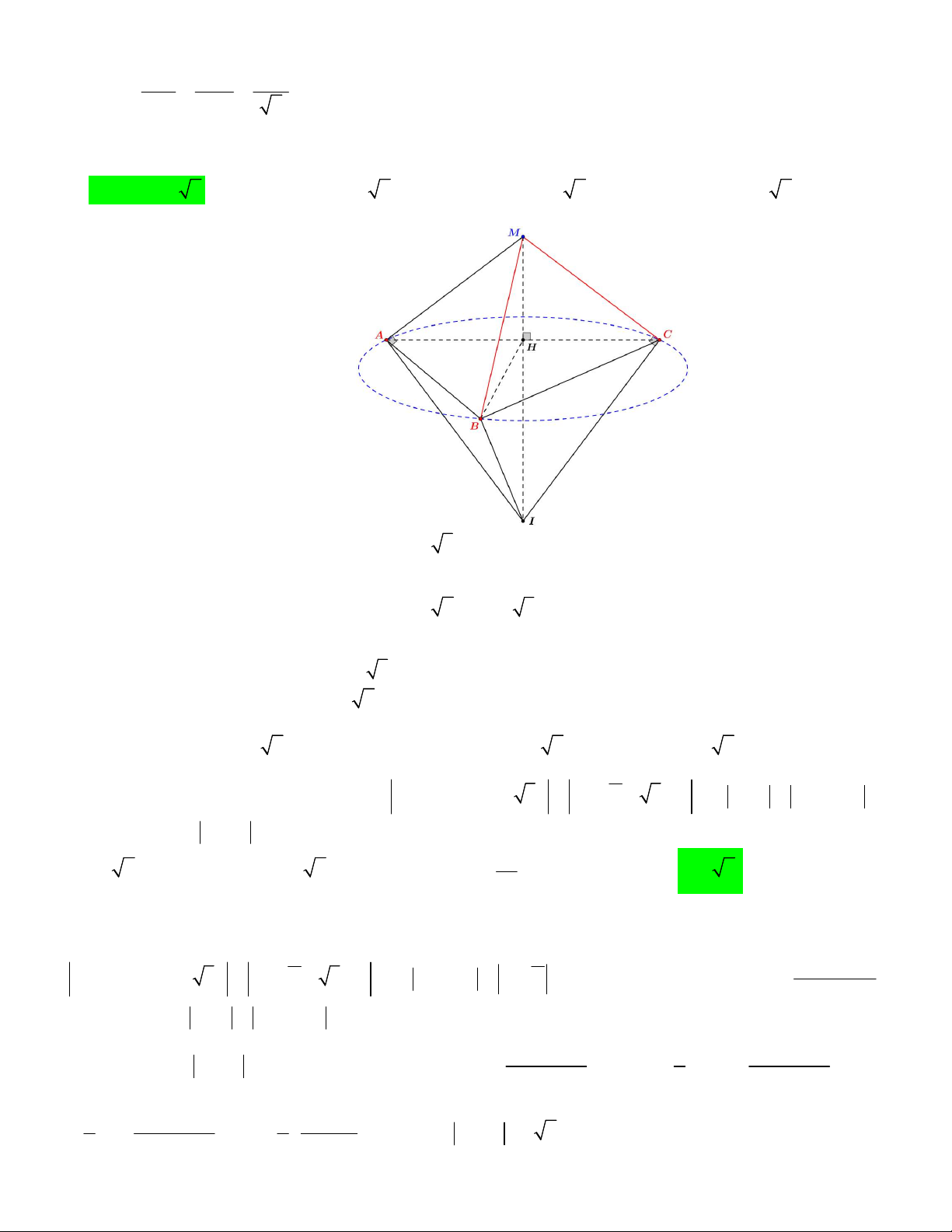
bình. Người ta đổ đầy nước vào rồi đặt lên miệng bình một khối lập phương ABC . D AB C  D   đặc, sao cho
đường chéo AC có phương vuông góc với mặt đáy của bình và các cạnh AA , AB, AD tiếp xúc với miệng
bình (xem hình vẽ). Sau đó quan sát thấy lượng nước tràn ra ngoài bằng 1 lượng nước ban đầu có trong 16
bình. Giả sử chiều dày của vỏ bình không đáng kể, hỏi thể tích của bình thủy tinh gần nhất với số nào sau đây ? A.  3 276, 41 dm  . B.  3 319,94 dm . C.  3 350,31 dm . D.  3 275, 44 dm  . Lời giải
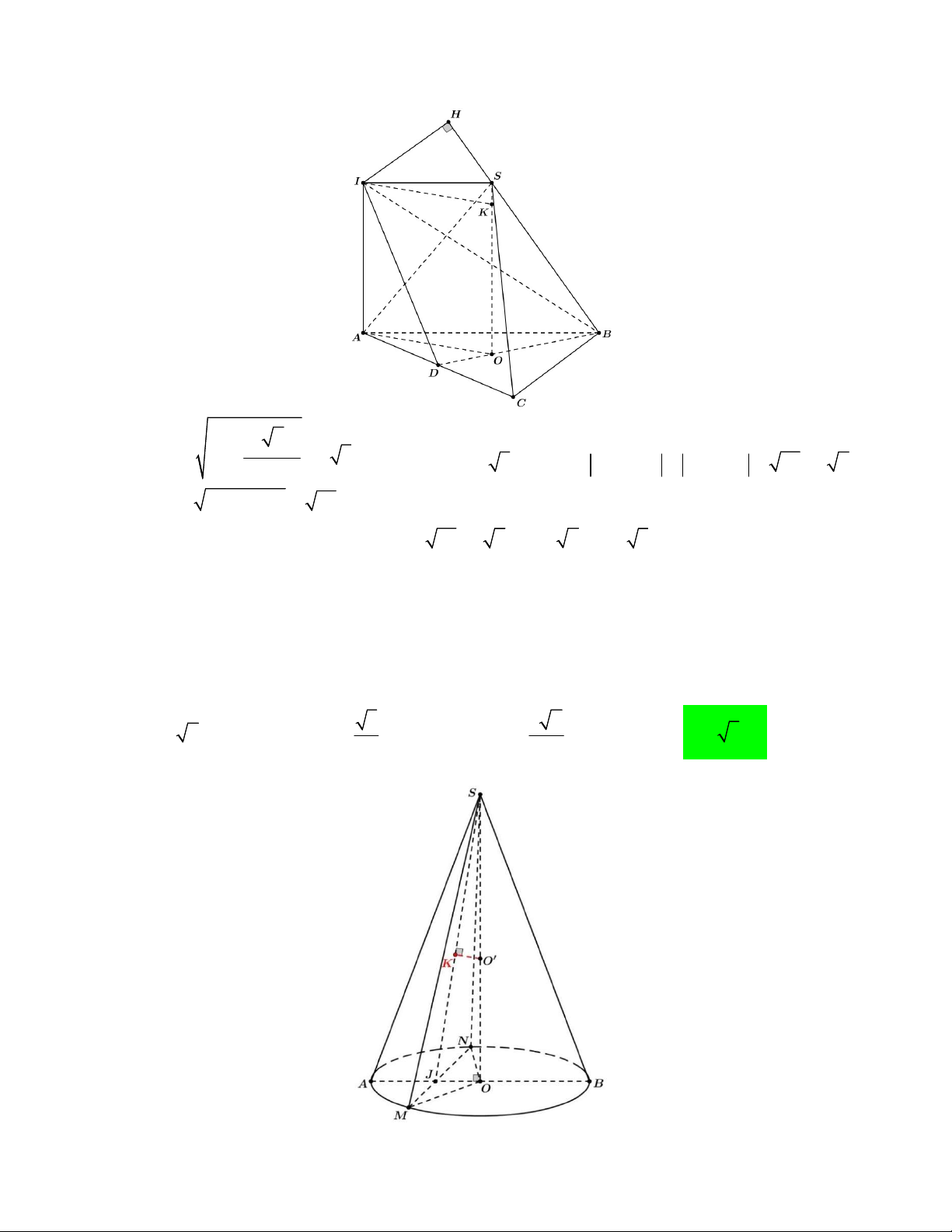
Đầu tiên ta có hình vẽ sau đây. Hình 1 Hình 2
Chú thích: hình 2 là hình mặt cắt khối hình 1 qua khối trụ và ba khối cầu trong khối trụ đó.
Gọi các cạnh AA , AB, AD tiếp xúc với miệng bình lần lượt là các điểm M , N, P . Theo hình 1, ta có:
Nhận xét: do đường chéo AC có phương vuông góc với mặt đáy của bình nên ta suy ra khối tứ diện
AMNP là một khối tam diện vuông có ba cạnh AA , AB, AD bằng nhau và bằng x dm , thể tích bằng 1 3 x  3
dm  . Khi đó M, N, P đều nằm trên đường tròn đáy của khối trụ tức bán kính đường tròn đáy của 6
trụ R cũng chính bằng bán kính đường tròn ngoại tiếp tam giác đều M  NP , suy ra MN AM 2 x 2 R  R    dm . (1) MNP     3 3 3
Do đổ nước đầy bình sau khi bỏ ba quả cầu nên ta có thể tích nước ban đầu bằng: 4
V   R h  3.   33 2 2   R h 12 3  3
dm với h là chiều cao của khối trụ. 0  3 Theo hình 2, ta có:
Gọi D, E, F lần lượt là tâm đường tròn mặt cắt tử ba quả cầu và O là tâm đường tròn ngoại tiếp DEF .
Tiếp đến ta gọi I, J , K là các điểm tiếp xúc của đường tròn mặt cắt với đường tròn ngoài có bán kính 2 3
bằng R . Ta có DEF đều có cạnh bằng 2 3 dm nên suy ra OF   2dm 3
Suy ra: R  OK  OF  FK  2  3 dm (2) x 2 3
Từ (1) và (2) ta có được:  2  3  x  6  dm 3 2
Theo giả thiết thì thể tích phần nước tràn (tức thể tích khối tứ diện AMNP bằng 1 lượng nước ban đầu 16 3  
có trong bình nên ta có phương trình sau: 1 1 1 3 1 3 x   2  R h 12 3  6      2  R h 12 3 6 16 6  2  16
Giải phương trình ta thu được h  7,312dm. 2
Vậy thể tích khối trụ cần tìm là: 2
V   R h        3 2 3 7,312 319,94 dm . Chọn B tru  1  
Câu 50. Xét các số thực dương x, y, z thỏa mãn    x y2 2 3  27 z y z   xy  2xz  3  
. Tìm giá trị nhỏ nhất   1  3y  6z 
của biểu thức P  log  2 2 y  z  2 2 2  log  3y  3z 5 5   4  x  A. 1. B. 2 . C. 4  log 3 . D. 2 3  log 5 . 5 3 Lời giải 1 1     x y z x y z 3
Giả thiết ban đầu suy ra:  y  2z 2 3  27   x  y  2z 2  3  3  27   x      y  2z     3 x y z 3 2  3  x  3 
. Xét hàm số     3t y f t
 t trên 0;có    3t f t
ln 3 1  0,t 0; y  2z 3
Suy ra f t  đồng biến trên 0; tức x  y  2z 3y  6z 3 y  2z Ta có:  3y 3z 
 3y  3z   y  2z2  3y 3z  4y  z  4yz  2y  z2 2 2 2 2 2 2 2 2 x x 2 y z 2 y  z 2y  z2 1 2 2  2  2 2 Cùng với: y  z    (Svac-xo) nên P  log  log 2y  z . 5 5  2 2 4 1 5 5 4
Đặt t  2y  z  0 ta suy ra:  t  1  
P  log    log t  2 2 2 1 2 2 
log t 1  2  2 . Vậy P  2 khi 1
t  2 y  z  . Chọn B 5 5  5   5  4  2  min 5
ĐỀ THCS – THPT NGUYỄN KHUYẾN TPHCM
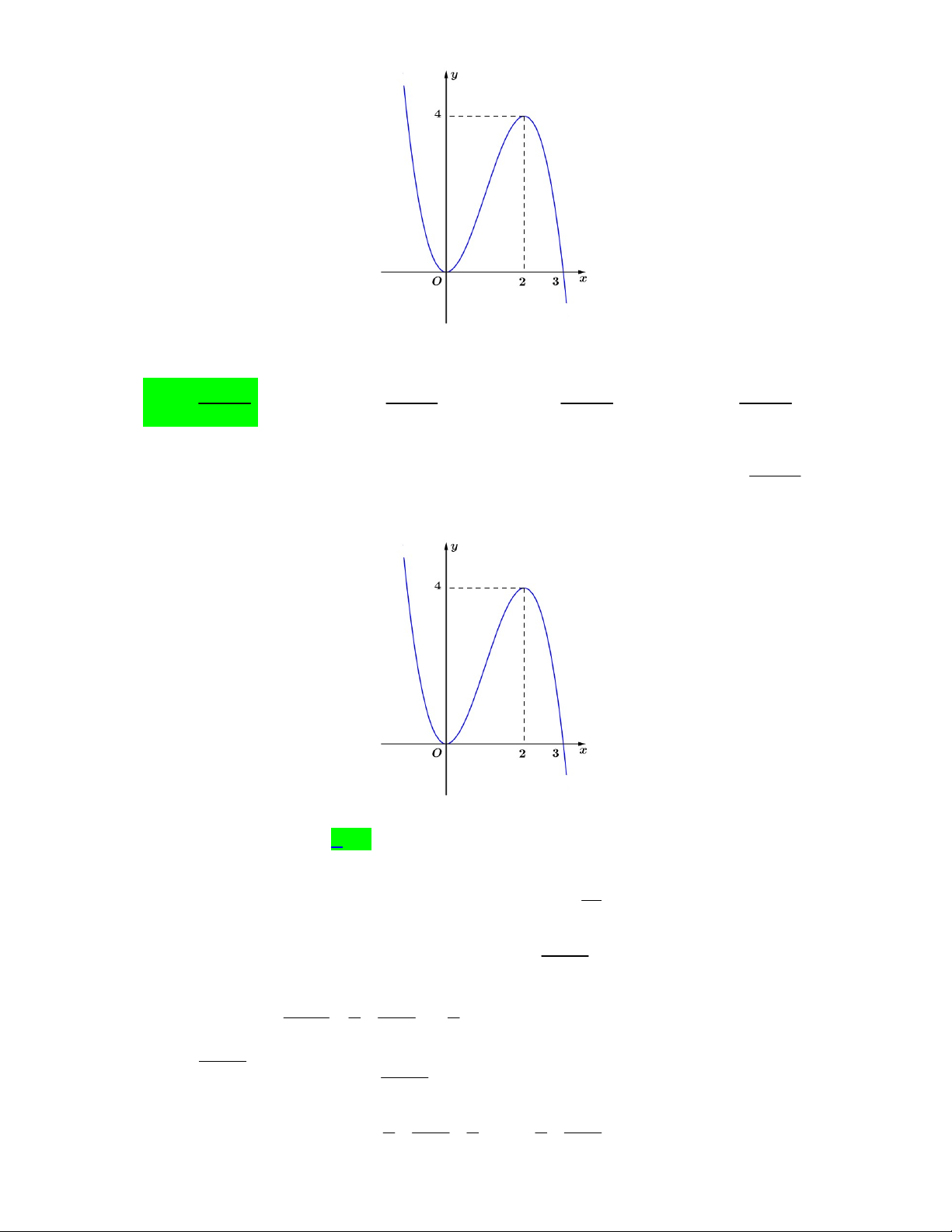
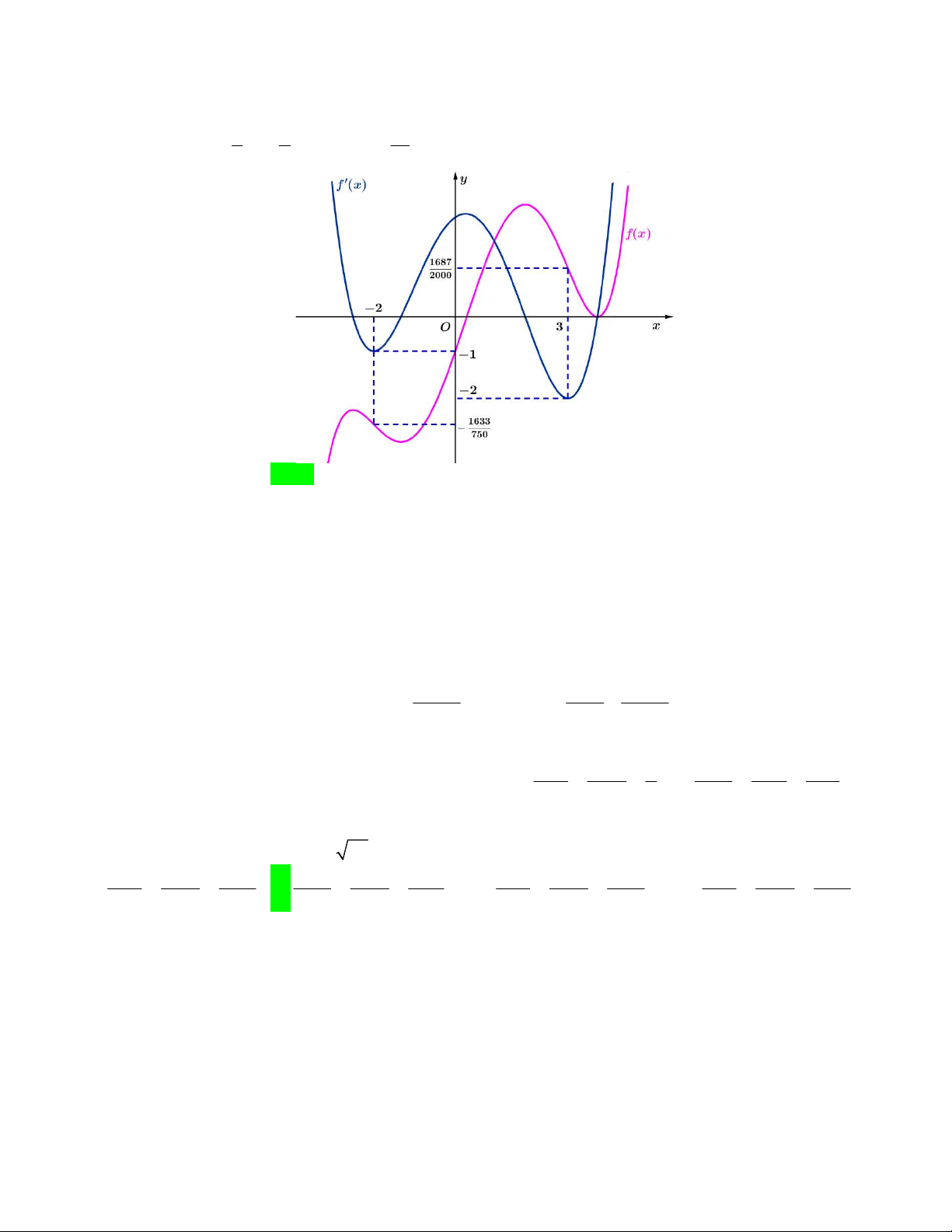
Câu 43. Cho hàm số y  f x có f  3   1  1 và f  x 2
 ax  bx  c a,b,c  R . Đồ thị hàm số y  f  x như sau: 2  f x  6 f x 
Số điểm cực trị của g  x  f  f x  2 8 3 f x         là 8    A. 5 . B. 2 . C. 7 . D. 6 . Lời giải 3 x
Đầu tiên, dễ dàng giải hệ a, , b c ra được f  x 2
 x  x   f x 2 2 2    x  2x  C 3 3 x 11 Với f  3   1  1 ta suy ra 11 C   2 3 , tức f x 2    x  2x   2 3 3 3 3 2  f x 6 f x 9 1   
Ta có: g x  f  f x  2 8 3 f x        1  8        f   f x 32 f  x  f  x 1 3 5 8 3         1  8      4 3 u 9 u Đặt u 
f  x  3  0 khi đó g u  f  2 u  5 8u 
  gu  2uf  2 u  5 8  0 8 8 2   u u u f u  5 2 2 2 4 2 2 2 2 2       3 . .  3  f  2 3
u  5  3 (đánh giá Cauchy 3 số không âm). 4 u 4 u u 4 u u  u  u  5 2 2 2  2 2 u  5  2  3  Khi đó: 
 u  2 u  2   u  2 2 2 0    f  x  3  2   f x 2  x  2x  2   u  f  x 3  3  x 11 2   x  2x   2 3  1 
Suy ra: f  x    f  x 3 3 3 4  1    (1) 3  x 11 2   x  2x   2 3  1   3 3
Thử bằng máy tính casio ta thấy (1) có 5 nghiệm bội lẻ nên ta suy ra g  x có tất cả 5 điểm cực trị.
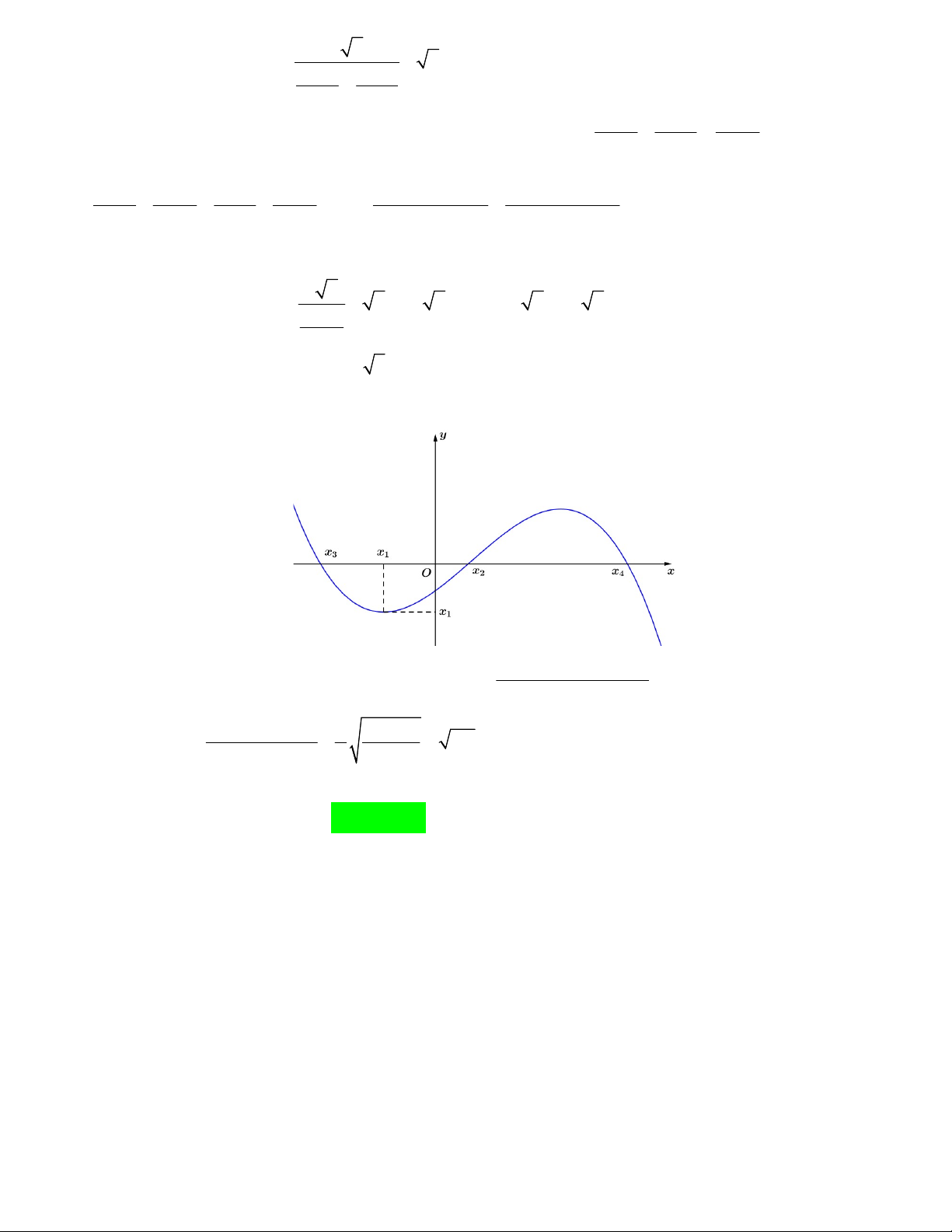
Câu 45. Cho hàm số    3 2 y
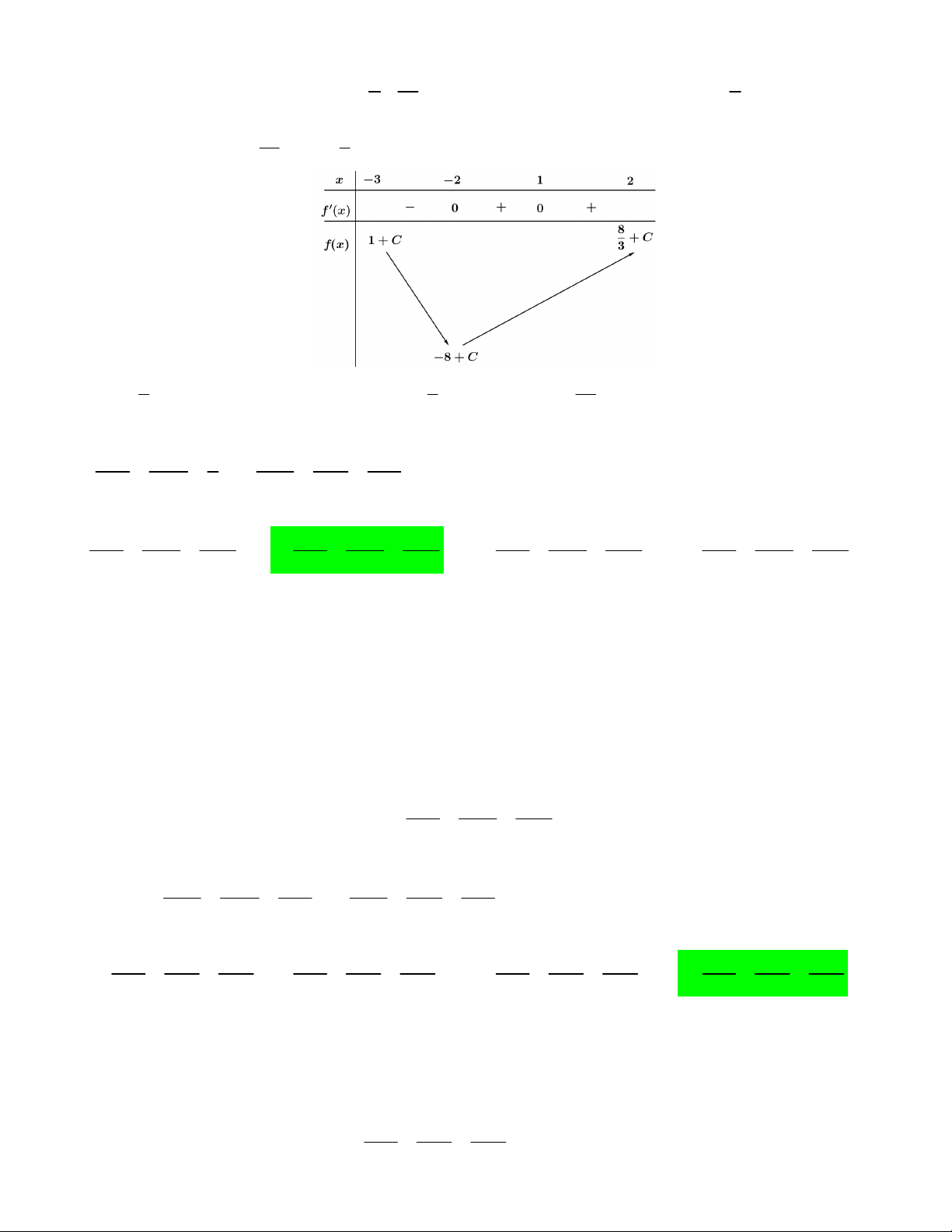
f x  x  bx  cx có đồ thị như hình sau:
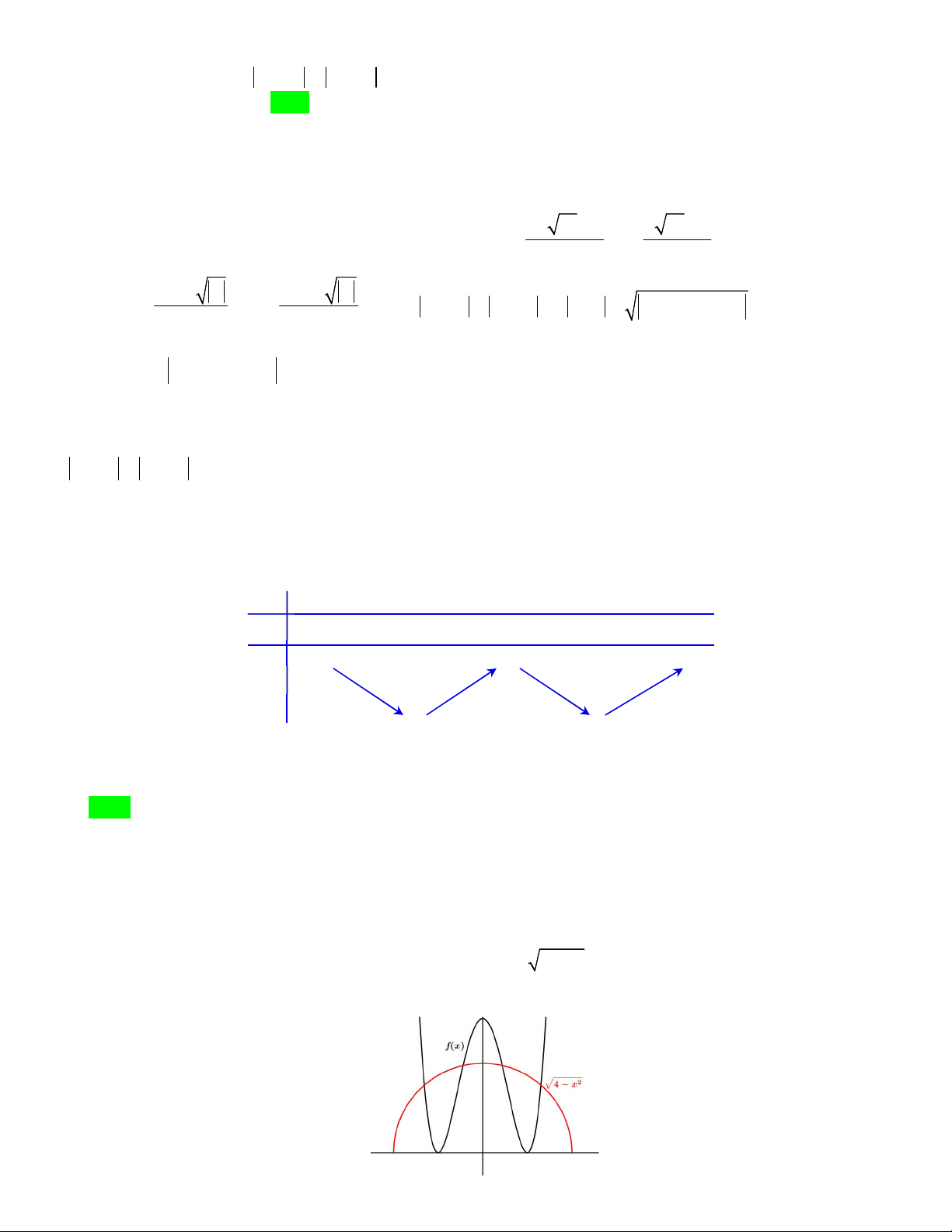
Hình phẳng H  giới hạn bởi y  f x, y  0, x  0, x  4 quay quanh Ox sinh ra một khối tròn
xoay có thể tích bằng V . Khẳng định đúng là 3072 3073 3074 3076 A. V  . B. V  . C. V  . D. V  . 35 35 35 35 Lời giải 4 4 
Giả thiết ban đầu suy ra: 2 3072 f  x 3 2  x  3x . Suy ra 2
V   f  x dx    3 2 x  3x  dx    35 0 0
Câu 48. Cho hàm số    3 2 y
f x  ax  bx  cx có đồ thị hàm số y  f  x như sau
Và f 0  0 . Số điểm cực trị của hàm g x  f xf x  ln xf x bằng A. 9 . B. 7 . C. 8 . D. 10 . Lời giải 4 x
Giả thiết ban đầu suy ra: f  x 3 2 2
 x  x  x   x  f x 3 3 3    x với f 0  0. 4   1 
Ta có: g  x  f xf x  lnxf x  xf x  f xf x 
  . Cho g x  0 . xf  x 0   f x
 f  x  xf x 3 1 1  0      f    x (1) x x  4 x    . f xf x 1    xf  x  f xf x 1    xf  x (2)
Tại (1) phương trình tương đương với: 3 1 1 4 1    0    0 . x x  4 x x x  4 Xét hàm số 4 1 h  x 4 1   có h x   
 0 tức h x nghịch biến trên từng khoảng xác x x  4 2 x x  42 định.
Vậy phương trình (1) có nghiệm duy nhất 16 x  (nhận). 5 1 1 t  0.764
Tại (2) phương trình tương đương với: (đặt t  xf x )  f t 3 2   t  3t   . t t  t  2.961   f  x 0.764  f  x 0.764    Suy ra: x x   
. Khảo sát sự tương giao của đồ thị y  f x và hai đường cong  f x 2.961   f  x 2.961   x  x lần lượt là 0.764 y  và 2.961 y 
ta thấy có 6 nghiệm bội lẻ (2). x x
Từ (1) và (2) ta kết luận hàm số g  x có tổng cộng 7 điểm cực trị.  3 
Câu 49. Cho C  y  g  x 2 :
 ;C  : y  f  x 2
 4x  bx  c , C tiếp xúc Ox tại A ;0 và C qua 2  2  1 2   x  2 
 4  x  2 f x  a B 2; 
1 . Giá trị nhỏ nhất của 2.g 
trên đoạn 0;2 bằng và       f x  x x 2x 3 1 2   b 2 2 a  b M  2 2 a  b Khẳng định đúng là A. M 2;0 . B. M 0;  1 . C. M 1;2 . D. M  2;4 . Lời giải  3   3 
Ta có: f  x  8x  b . Do C tiếp xúc Ox tại A ;0 nên A ;0 là điểm cực trị của đồ thị C 2  2       2   2    3  f   0    1  2  b  0 b  1  2    2     
 y  f x  4x 12x  9  2x  32 2  0        f    16 2b c 1 c 9 2  1 4  x  2 f  x
21 f x  2  x 2 1 1 1 Tiếp đến, ta có:      
1 f  x2  x
1 f x2 x x  2
f  x 1 x  2x 32 1 1 2
 4  x  2 f x  Khi đó, suy ra: 2 x P  2.g      x x    x 
1 f  x2  x 2 3 2. 2 2 3  1 1 2   2 2   2x  3 1 x   1 2     Đặt   x a b   x     x y     2 2 ; ; 2 3 ;
2a ; 4a  3 . Do x0;2nên a0;  1 ,b0;3 2   a 2 4a  3  1 a   1 2a  2 1  0 -Nếu ab  1 thì 2 a 4a  3  1     (vô lí do a 0;  1 ) a   2 4a  3  1
a  12a  2 1  0
-Nếu 0  ab 1 thì ta có: 2 2 P   2ab 1 1  2 2 a 1 b 1
Đến đây ta có bất đẳng thức (*) sau: 1 1 2 a
 ,b thỏa 0  ab 1 thì ta có:   2 2 a 1 b 1 1 ab
Thật vậy, bất đẳng thức (*) tương đương với: 2 2 1 1 1 1 ab  a ab  b      0    0 2 2 a 1 1 ab b 1 1 ab
 2a  1ab 1  2b  1ab 1
 ab  ab   bb  aa     b  a2 2 2 1 1 0
ab  1  0 luôn đúng với 0  ab 1 Như vậy (*) đúng, suy ra 2 2 P   2ab  2 ab   1  2ab  2 2 1 ab
Như vậy giá trị nhỏ nhất của P bằng 2 khi x  2 . Chọn đáp án B.
Câu 50. Cho hàm số y  f x liên tục trên R , có f   x  0, x
 x ; x và có đồ thị y  f x như hình 3 2  dưới đây 2 1 f  f x f x  0   0  2
Gọi  f  x  xf  
 f x  f f x 1  m ;
  n ; x  x ;0 . Khi giá trị 0    0   0  3   2   2 1 m  4n nhỏ nhất của S  
trên x x ; x bằng k và 3 2      mn m 1 4n   1 2 4mn 1
T  k  f  x k  f x  2
 x . Khẳng định đúng là 0 0 A. T 0;  1 . B. T  2;3 . C. T 4;5 . D. T  5;6 . Lời giải
Từ đồ thị ta có: f x  x ; f x  0 1  1  3  f   x  0, x  x ;0 0  0  3 
-Trên x ;0 thì f  x  0 (dựa vào đồ thị)    f  x  x ;0 0   1  3   f   x  f x  x  x 0   1 1 3 -Vì f   x  0, x
 x ; x nên theo bất đẳng thức tiếp tuyến, với mọi f x  x ;0 thì 0   3  3 2 
f  x  f  f  x x  f x  f f x 0    0    0
 f x  xf  f x  f f x 1 f  f x x  f x  f f x  xf  f x  f f x 1 0    0   0  0   0
  0   0
 f x  xf  f x  f f x 11 f  f x f x 1 0    0
  0  0  
-Lại có f   x  0, x
 x ; x nên suy ra f  x đồng biến và liên tục trên x ; x 3 2  3 2 
Do x  x ;0 nên x  f x  0 (suy ra từ nhìn nhận đồ thị) 1  0  0  3 
 f  f x  f  x  0 (do x  x là điểm cực trị của đồ thị hàm số). 0   1 1 1 f  f x f x  0   0  2 Mà mặt khác 1
f  x  0 nên suy ra f  f x f x  0     n  0   0    0  2 4  
Kéo theo  f x  xf  
 f x  f  f x  2 1  m  1 0 0  Đặt  ;
m 4n  a;b thì khi đó a,b 1 và a  b 2 1 m  4n 2 1 a  b 1 Ta có: S       mn    ab m 1 4n   1 2 4mn 1 a  1b   1 2 ab 1 2
Do a,b 1 nên ta có: a   1 b  
1  0  ab 1  a  b  a   1 b   1  ab  
1  a  b  2ab   1 1 1 a  b 1
2  a  bab   1  ab ab   1 Suy ra: S    ab  ab 1 2 ab 1 2 2 ab 12
2  a  bab   1  ab ab   1 3
Đến đây ta cần chứng minh   (**) ab  2 2 2 1
 2  a bab   1  ab ab   1  3ab  
1  a  bab   1  ab ab   1  3ab 1
Ta nhận thấy: do ab 1  a  b nên
a bab 1  ab ab 1  a b ab ab 1  2 ab  ab ab 1
Đến đây ta cần chứng minh 2 ab  ab ab  
1  3ab 1 (*). Thật vậy, ta có: t  ab 1 
(*) tương đương với:    t 
 và luôn đúng với mọi t  1 2t  t  t    3 1 0 2 2 1  3t 1
Như vậy bất đẳng thức (*) đúng, tức kéo theo (**) đúng, từ đó suy ra 3 min S  k  2
Dấu bằng xảy ra khi và chỉ khi x  x  x và f x  x 0  0 1 0 9 9
Suy ra: T  k  f x k  f  x  2 2 2  x  k  f x  2 2 2
 x   x  x   2;3 0 0 0 0 0 0   4 4
ĐỀ THPT ĐÔ LƯƠNG 1 NGHỆ AN
Câu 46. Cho hai số thực x và y thỏa mãn x  2y  log log 5 . Biết giá trị nhỏ nhất của biểu thức 3  3  x 1 P  3 
là a  log c trong đó a, ,
b c là các số tự nhiên, ,
b c là số nguyên tố. Tính giá trị của biểu thức 25y b T  a  2b  3c . A. T  22 B. T  23 . C. T  17 D. T  8 . Lời giải
Ta thực hiện biến đổi biểu thức P như sau: log log 5 1 1 5 log 5 log 5  3x  x x x x x  log 5 3 log35  3 log35 log3 5 3 3  3 P  3   3   3   3   3   log 5   2 y xlog log 5 x log 3 log 5 3  x  3  3  5 5 5 5x 3 3x 3 log 5    3  3 log 5   1  Đặt log 5 3 t 
 0 , xét hàm số y  f t log log 5 1 3 5 3  t  có f t 3  log 5 t   0  t 1   3x t 3 2  t  Mà f   
1  0 nên ta suy ra min P  min f  x  f   1  1 log 5 . 3
Đồng nhất hệ số ta suy ra a 1,b  3,c  5. Vậy T  a  2b  3c  22 . Chọn đáp án A.
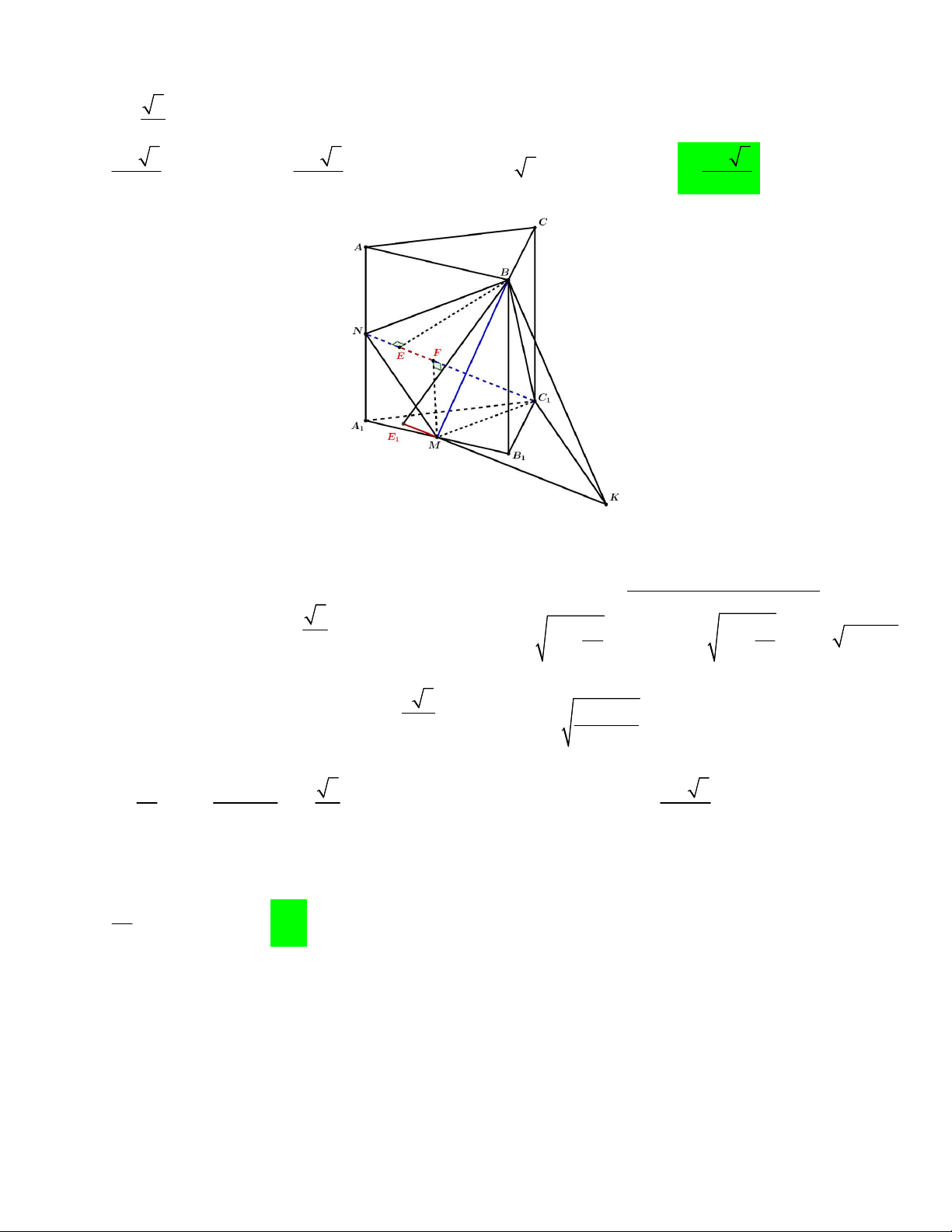
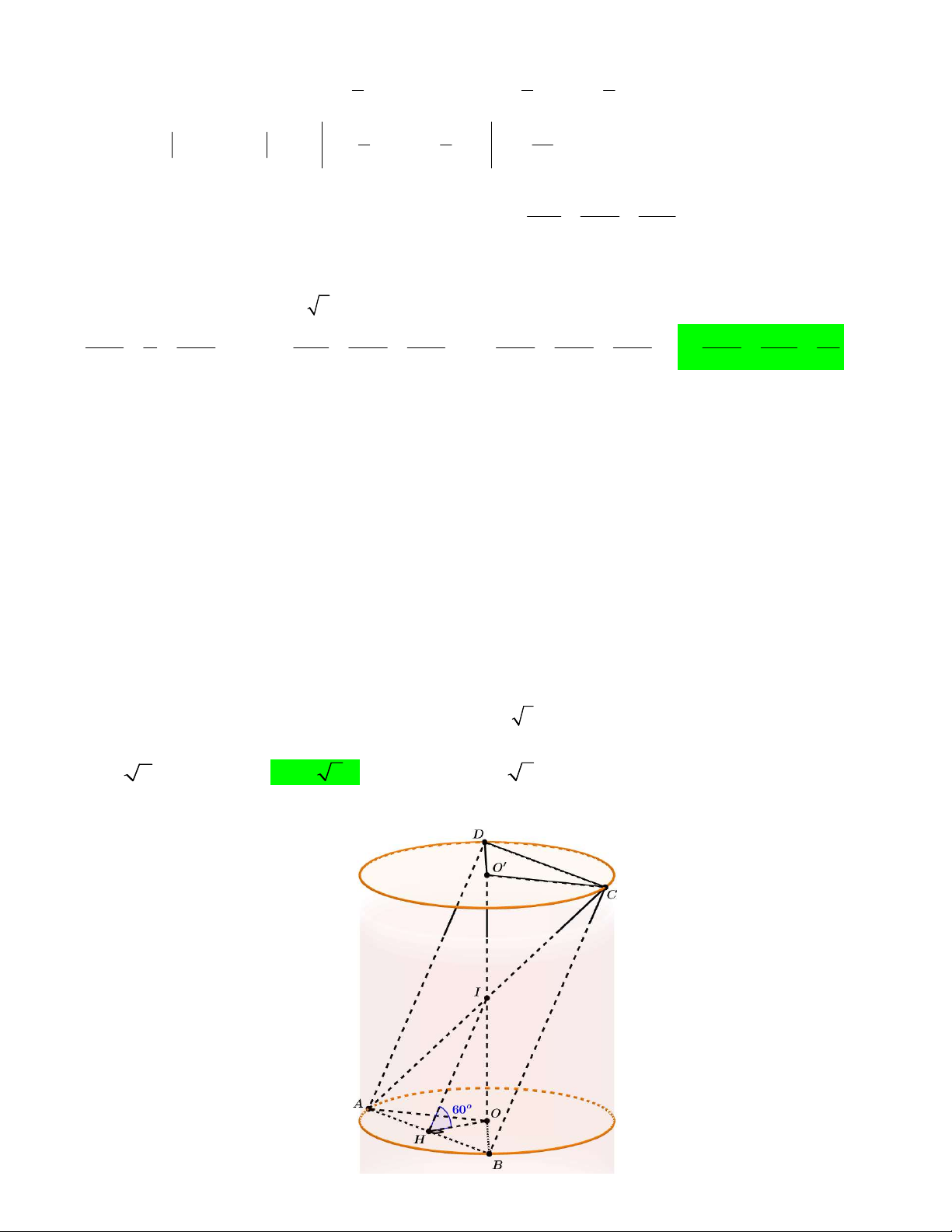
Câu 47. Cho hình lăng trụ tam giác đều ABC.A B C có cạnh đáy AB  5 . Gọi M , N thứ tự là trung 1 1 1
điểm của A B và AA . Biết rằng hình chiếu của BM lên đường thẳng C N là đoạn thẳng có độ 1 1 1 1
dài bằng 5 và chiều AA  3. Tính thể tích của khối lăng trụ ABC.A B C . 2 1 1 1 1 A. 125 3 . B. 125 3 . C. 25 3 . D. 125 3 . 8 2 4 Lời giải
Ta kẻ BE  C N; MF  C N thì khi đó ta thu được hình chiếu của BM lên đường thẳng C N chính là đoạn 1 1 1
EF . Mặt khác, khi ta dựng hình bình hành NC KM và kẻ BE  KM tại E thì hình chiếu lúc này chính là 1 1 1
ME , ta nhận thấy cả hai trường hợp này đều cho ra 2 đoạn hình chiếu song song và bằng nhau. 1  5    2 25 x Khi đó ta suy ra EF ME1  2 . Đặt AA  x  3 2 2  BM  x  ;C N  BN  25  ; BC  x  25 1 1 1  4 4 BE  BE  1  d  5 3 N; BC  d A ; B C  3x  75 1   1 1 1 2 Tiếp đến ta có: 2 2 2  2  BE  BE  5  ME  MB  BE 1 2 1 1  d   4x 25 N; BC .BC  BE.C N 1  1 1 2 2  25   3x  75   5  125 3 2  x   25         x  AA  5  V  AA S  . Chọn đáp án D. 2 1 ABC.   1 A 1 B 1 C 1  4   4x  25  2 ABC 4  
Câu 48. Cho hàm số   10x f x  x và g x 3 2  x  mx   2 m  
1 x  2 . Gọi M là giá trị lớn nhất của hàm số
y  g x  f x trên đoạn 0; 
1 . Khi M đạt giá trị nhỏ nhất thì giá trị của m bằng? A. 21 B. 6 C. 21 D. 5 2 Lời giải
Ta có:     10x  2      10x ln10 2 10x y h x g x h x g  2x 2
  m  m    m   g x  2  2 3 1 2 3 0 Xét g x 2  x  mx   2 3 2 m   1 có   
nên suy ra hàm số g x luôn đồng 3   0 biến trên đoạn 0; 
1 tức giá trị lớn nhất của hàm số h  x tại x  1
Khi đó ta có: h   g     m  m     m  m   m  2 3 2 2 2 1 12 12 12 12 1 2 12 144 1738 12 6 1306 1306
Như vậy dấu bằng xảy ra khi m  6  0  m  6 . Chọn đáp án B. 1
Câu 49. Cho hàm số y  f x liên tục trên  1  ; 
1 và thỏa mãn f x  2  3 x  t f tdt. với x   1  ;  1 2 1 1 Khi đó I  f  xdx bằng 1  A. I  3 B. I  4 C. I  2 D. I 1 Lời giải
Chú ý trong tích phân lấy theo biến t do đó x trong tích phân lúc này là tham số các em nhé, nên không đặt 1 3 1 3 1 1   3 1 3 1
m  x t f tdt được: f x2 x t f tdt   xf  tdt  tf  tdt x f  tdt  tf  tdt 2 2 2 2 1 1 1 1  1 1  3 1 3 1 
Do đó  f x2 ax b;a f  tdt;b tf  tdt.  2 2 1 1 
Thay ngược lại đẳng thức đã cho 3 1 3 1 3 3 2
ax  b  x at b2dt  t
 at b2dt  x ´2b2 ´ a3b2x a 2 2 2 2 3 1 1 a 3b2 1 1  
 a  b  3 f x 3x 1 f
 xdx  3x1dx 2. Chọn đáp án C. b  a 1 1
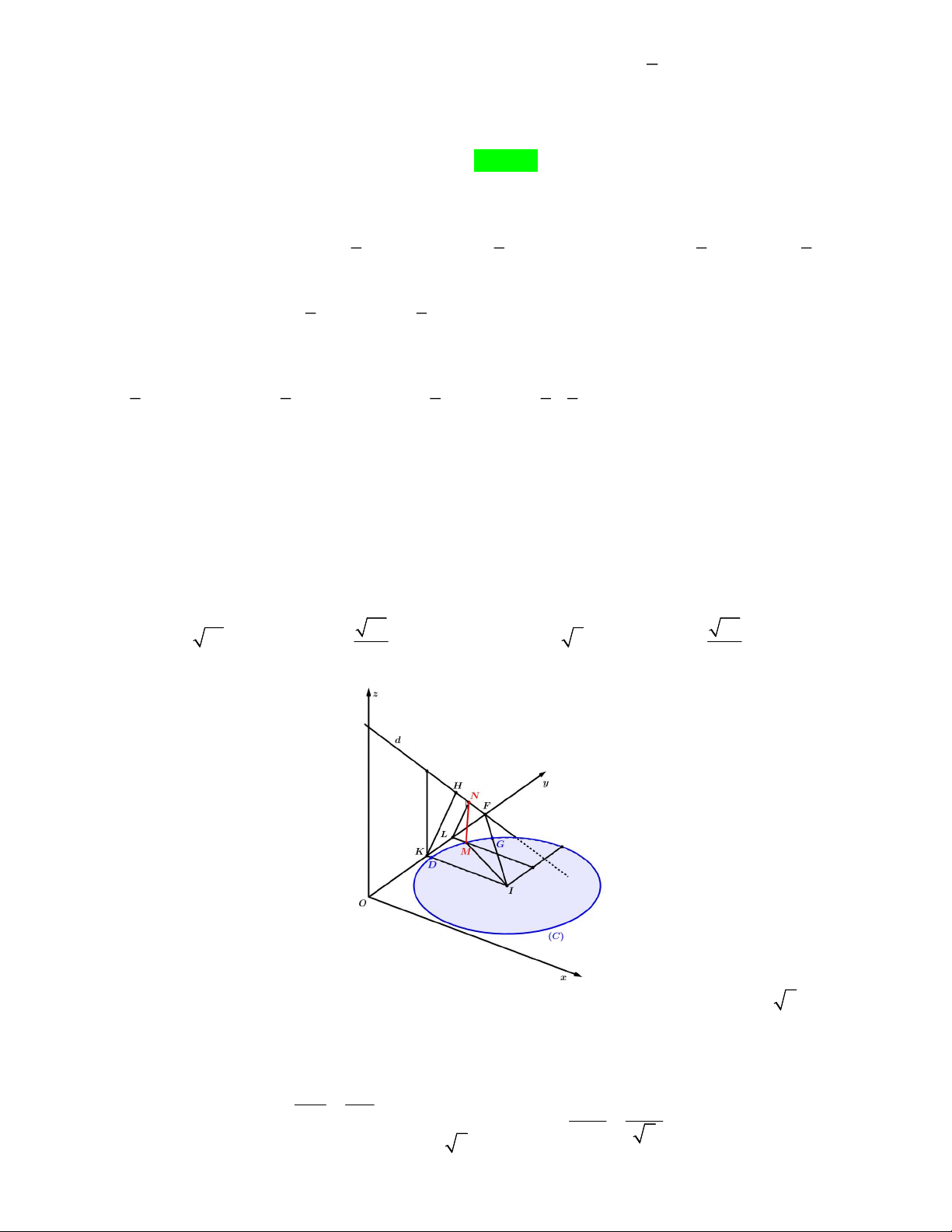
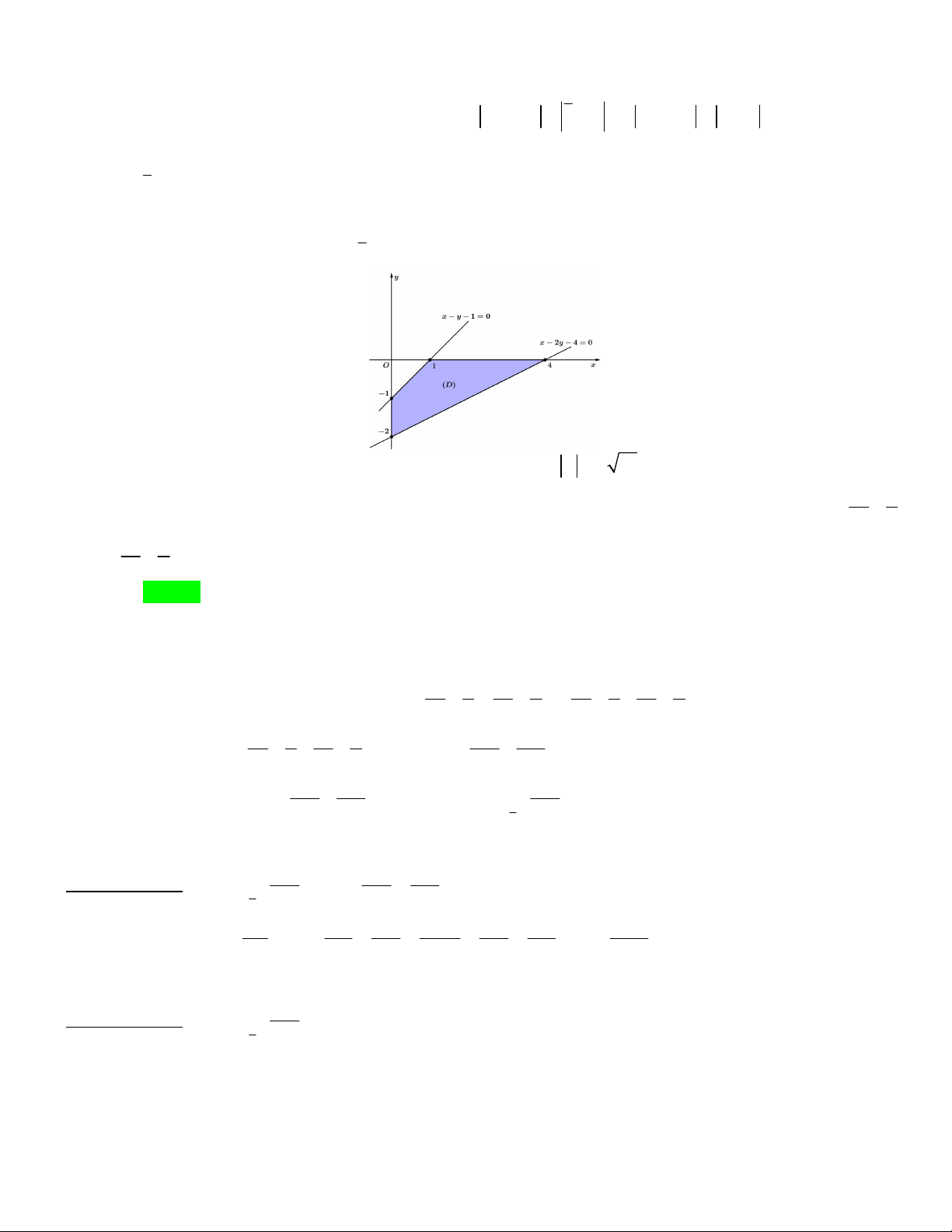
Câu 50. Trong không gian với hệ trục tọa độ Oxyz cho đường tròn C  là giao tuyến của mặt phẳng tọa
độ  xOy với mặt cầu S x  2   y  2   z  2 : 6 6
3  41. Gọi d là đường thẳng đi qua các điểm
A0;0;12 và B 0;4;8 . Với M , N là các điểm thay đổi thứ tự trên C  và d . Giá trị nhỏ nhất của độ dài đoạn thẳng MN là A. 2  17 . B. 34 . C. 1 2 5 . D. 34 . 3 2 Lời giải
Đầu tiên ta có phương trình C  x  2   y  2 : 6
6  32 với tâm I 6;6 và bán kính R  4 2
Gọi F  d  Oy , IK  Oy , D  IK  C  ,G  IF  C  , ML  Oy . Như vậy để MN đạt giá trị nhỏ nhất
thì M phải thuộc cung nhỏ  DG .      NL FL KH d ; NL  d      Kẻ 6 x 6 x   KH FK   NL  KH  LK  x KH  d  K d 6 2 ;  3 2 Cùng với 2 2
LM   R  d I ML 2 2 6 ;
 6  32  KL  6  32  x 2 2 2 2  6  x  6  x Suy ra 2 2 MN  ML  LN      2 6  32  x       2
6  32  x   f x  2  2 2 2 6  x Xét hàm số y  f x      2 6  32  x  , x    4  2;4 2 2   . Có
f  x  0  12x   x  6 2
32  x  0  x  x  3,5145  4 2; 4 2   min f x  f 3,5145  2.35488 0      
Như vậy giá trị nhỏ nhất của MN bằng xấp xỉ 2.35488 . Chọn đáp án E.
ĐỀ THI THỬ LẦN 2 SỞ HẢI DƯƠNG
Câu 46. Cho hàm số y  f x có đạo hàm trên R . Biết hàm số y  f  x là hàm bậc 3 có đồ thị như hình vẽ bên dưới
Có bao nhiêu giá trị nguyên của tham số m để hàm số g  x  f  3 2x  3x  m   1 có đúng 5 điểm cực trị. A. 4 . B. 7 . C. 5 . D. 6 . Lời giải
Đầu tiên ta thấy f  x  0 có ba nghiệm lần lượt là 2;2;6 .
Tiếp đến, ta có: g x  f  3
 x  x  m    f   3 2 3 1 2x  3x  m  
1  g  x nên suy ra g  x là hàm chẵn
tức đồ thị hàm số g  x đối xứng qua Oy . Suy ra để hàm số g  x có đúng 5 điểm cực trị thì hàm số h x  f  3 2x  3x  m  
1 phải có 2 điểm cực trị dương. Tức h x   2 x   f  3 6 3 2x  3x  m  
1  0 phải có nghiệm dương bội lẻ. Phương trình tương đương với: 3 3 2x  3x  m 1  2 
m  2x  3x  3  u x 1     f  3 2x  3x  m   3 3
1  0  2x  3x  m 1  2  
m  2x  3x 1  u x . Khi đó ta có bảng biến thiên 2    3  3 2x  3x  m 1  8 
m  2x  3x  7  u x  3  
gộp từ ba hàm u x ,u x ,u x như sau: 1   2   3  
Vậy để thỏa yêu cầu đề bài thì 1  m  3 tức có 4 giá trị nguyên m thỏa. Chọn đáp án A.
Câu 47. Có bao nhiêu số nguyên y thuộc đoạn 2022;2022 sao cho tồn tại x R thỏa mãn 3 x 3 12 3 12.2  2 x y 3y A. 2028 B. 2027 C. 2021 D. 2022 Lời giải Ta có: 3 x 3 12 3 12.2  2 x y 3y . Đặt 3  3 12.2x u y
khi đó phương trình ban đầu trở thành: 3 1  2u  2 x 3y 
. Lấy hai phương trình cộng vế theo vế ta có được phương trình mới như sau: 3 u   3y 12.2x 3 3  12  2 x 12.2x u u
. Xét hàm số y  f t 3  t 12t có f t 2
 3u 12  0, u  R . Như vậy ta suy ra 3  x x x 2 x 12.2x
hàm số f t đồng biến trên R. Khi đó: 3
u  2  3y 12.2  2  y  3 3 2 x 12.2x
Xét hàm số y  g  x 
có    8x ln 2  4.2x g x ln 2  0  x  1 3 16 y  16
Như vậy để tồn tại x  R thì tham số y phải thỏa: y  g    2022;2022 1     y  2022 3 3
Như vậy có tất cả 2022  (5) 1  2028 giá trị y nguyên thỏa mãn. Chọn đáp án A.
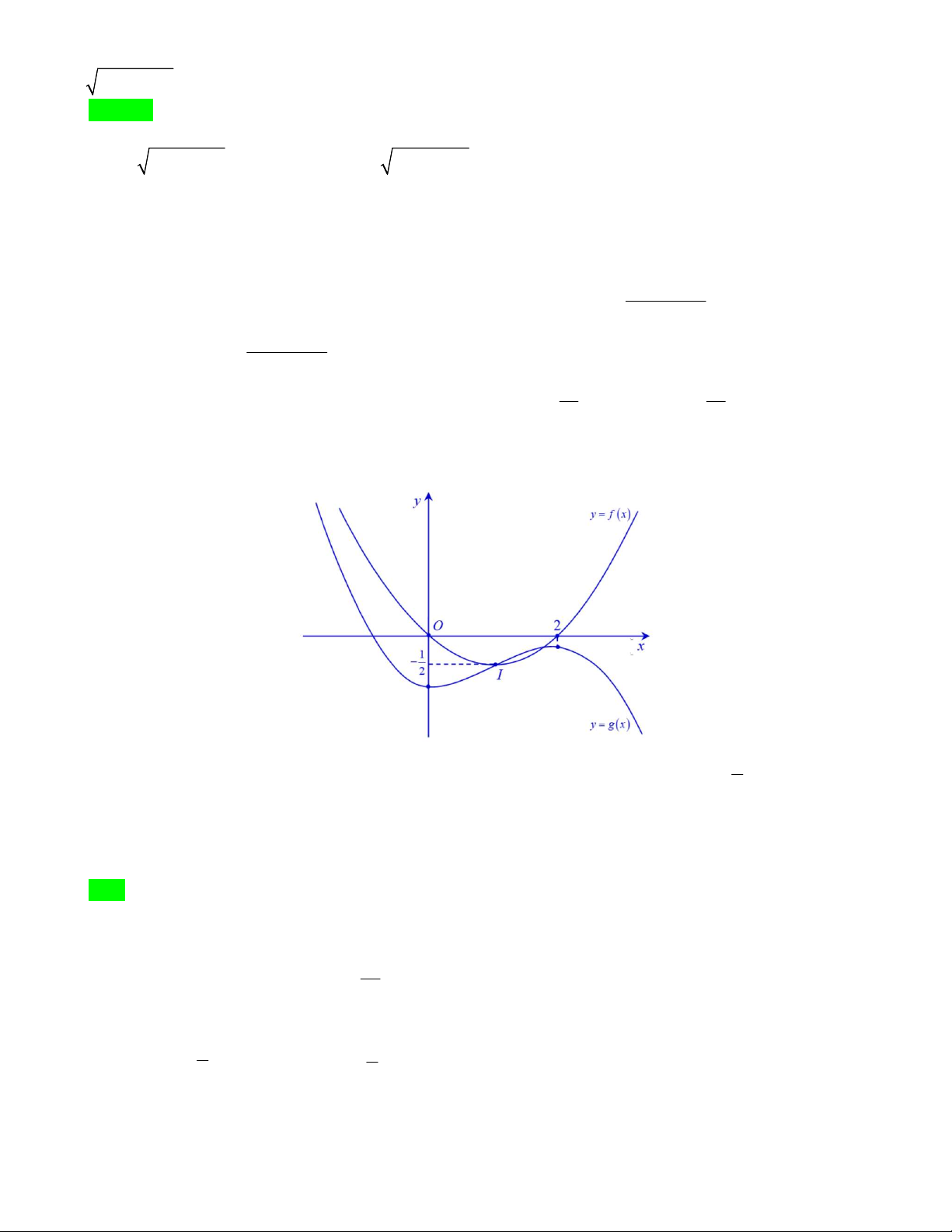
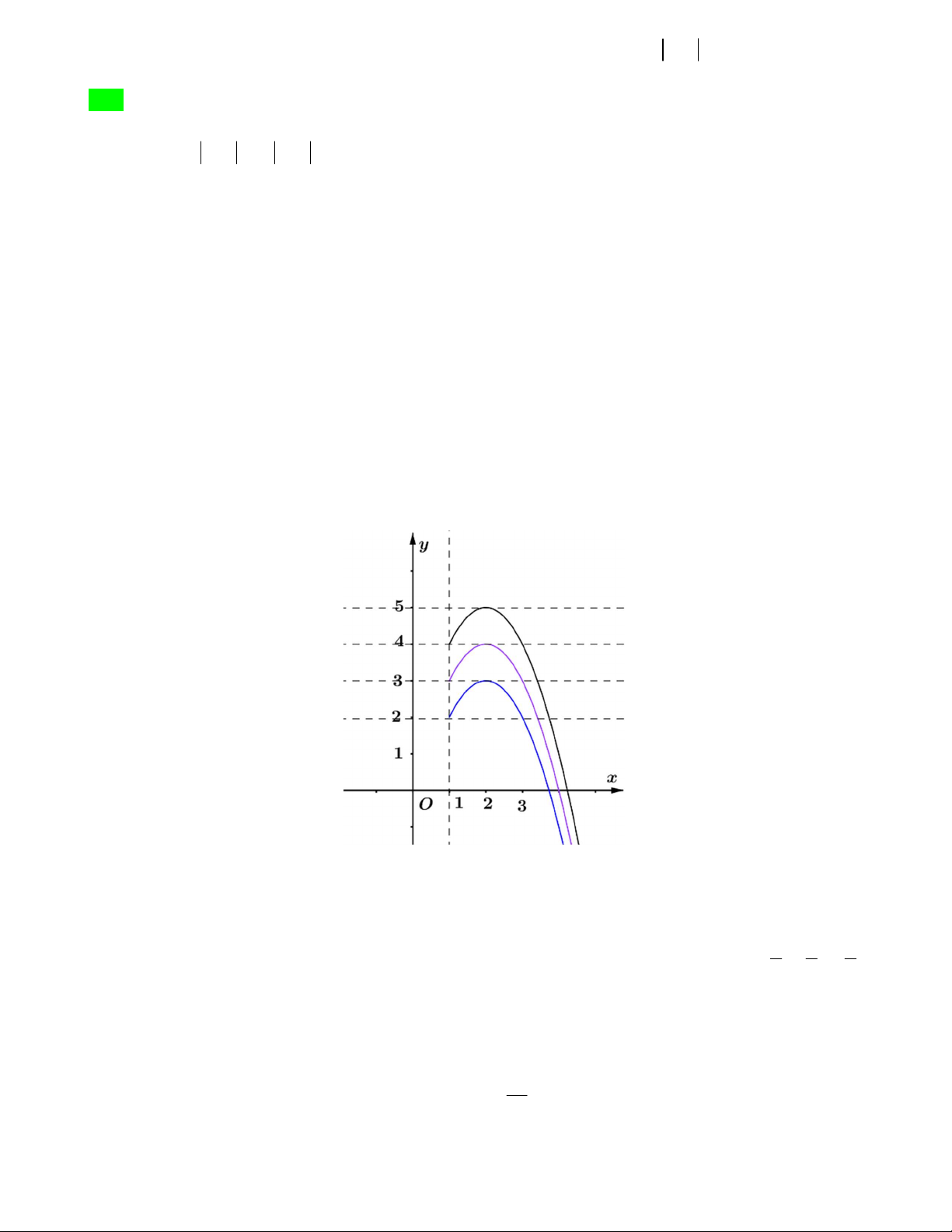
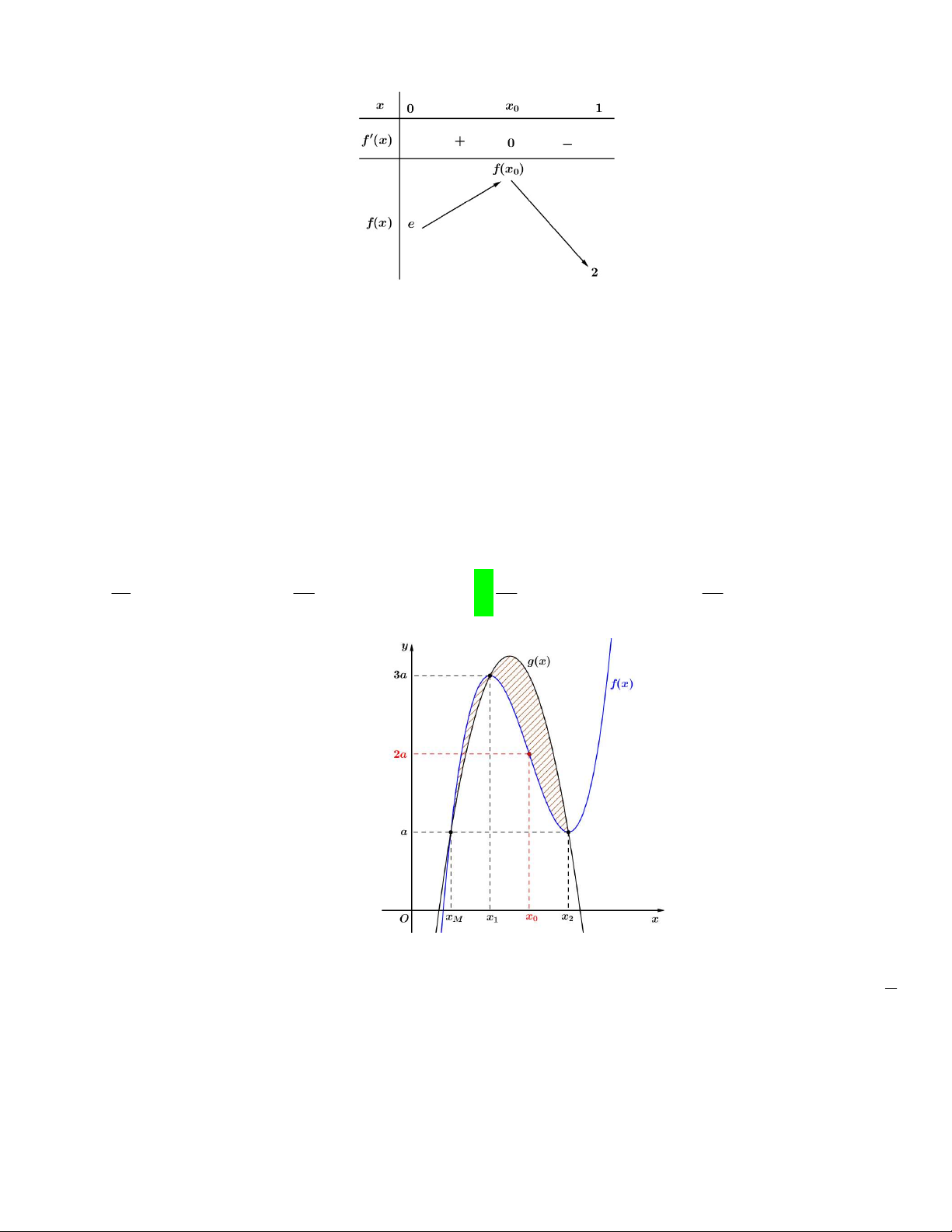
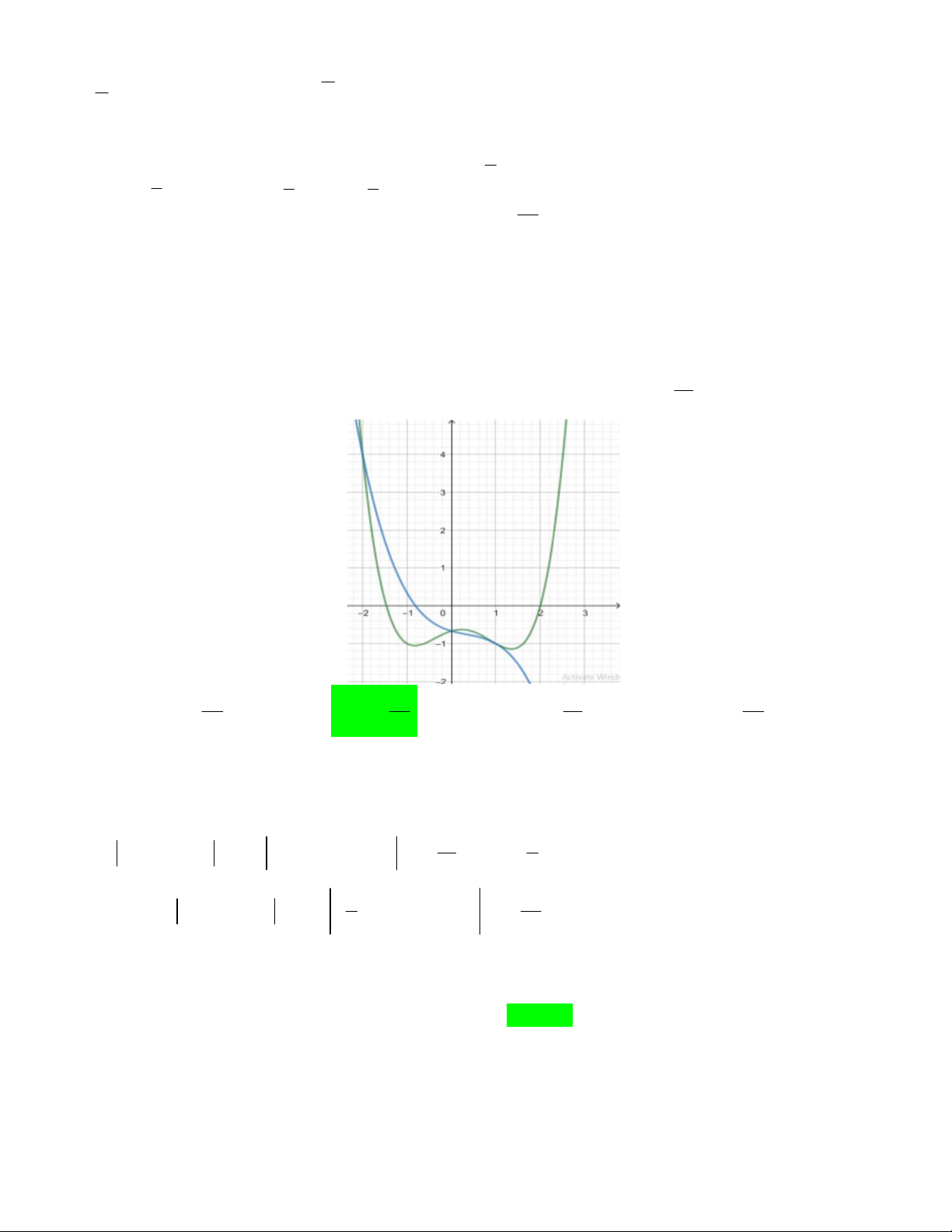
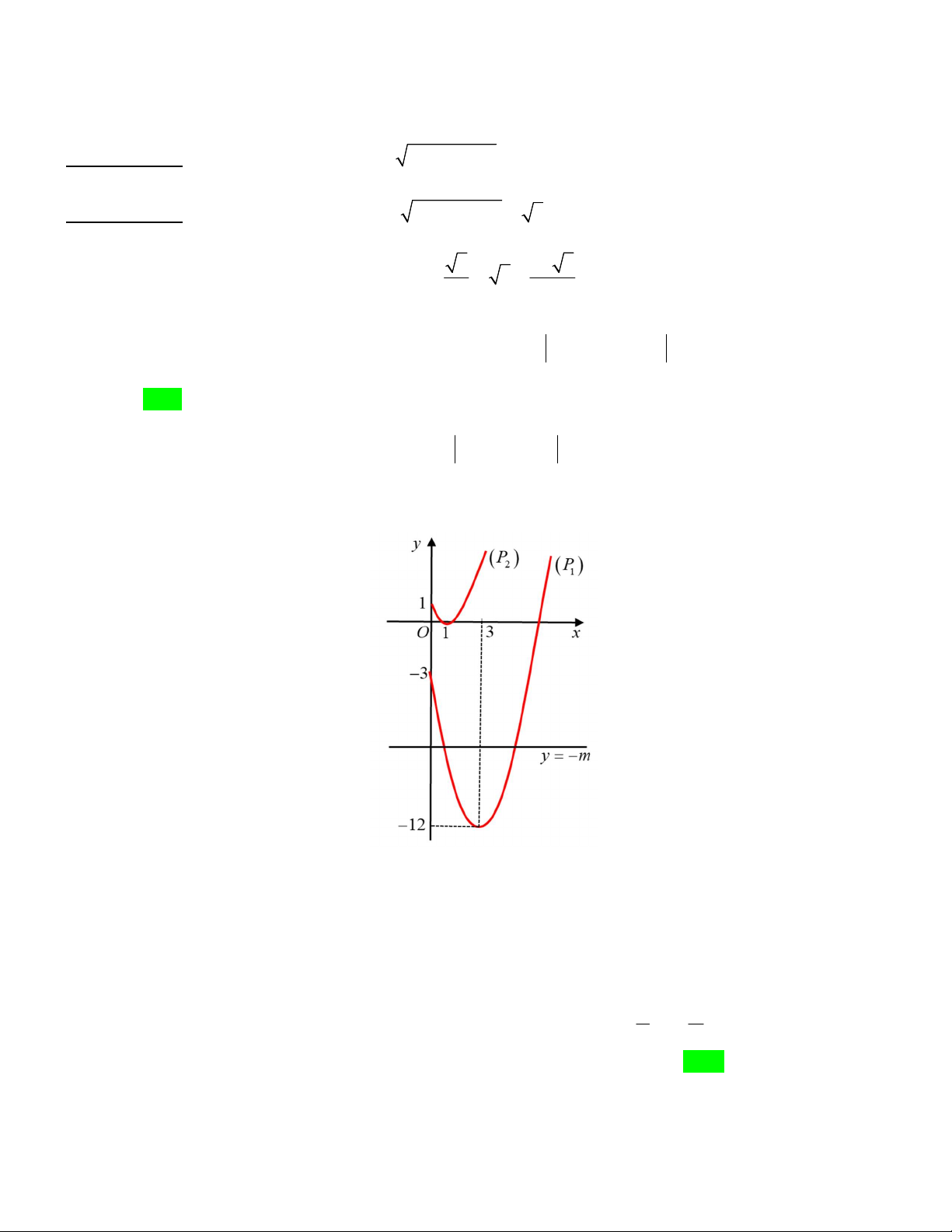
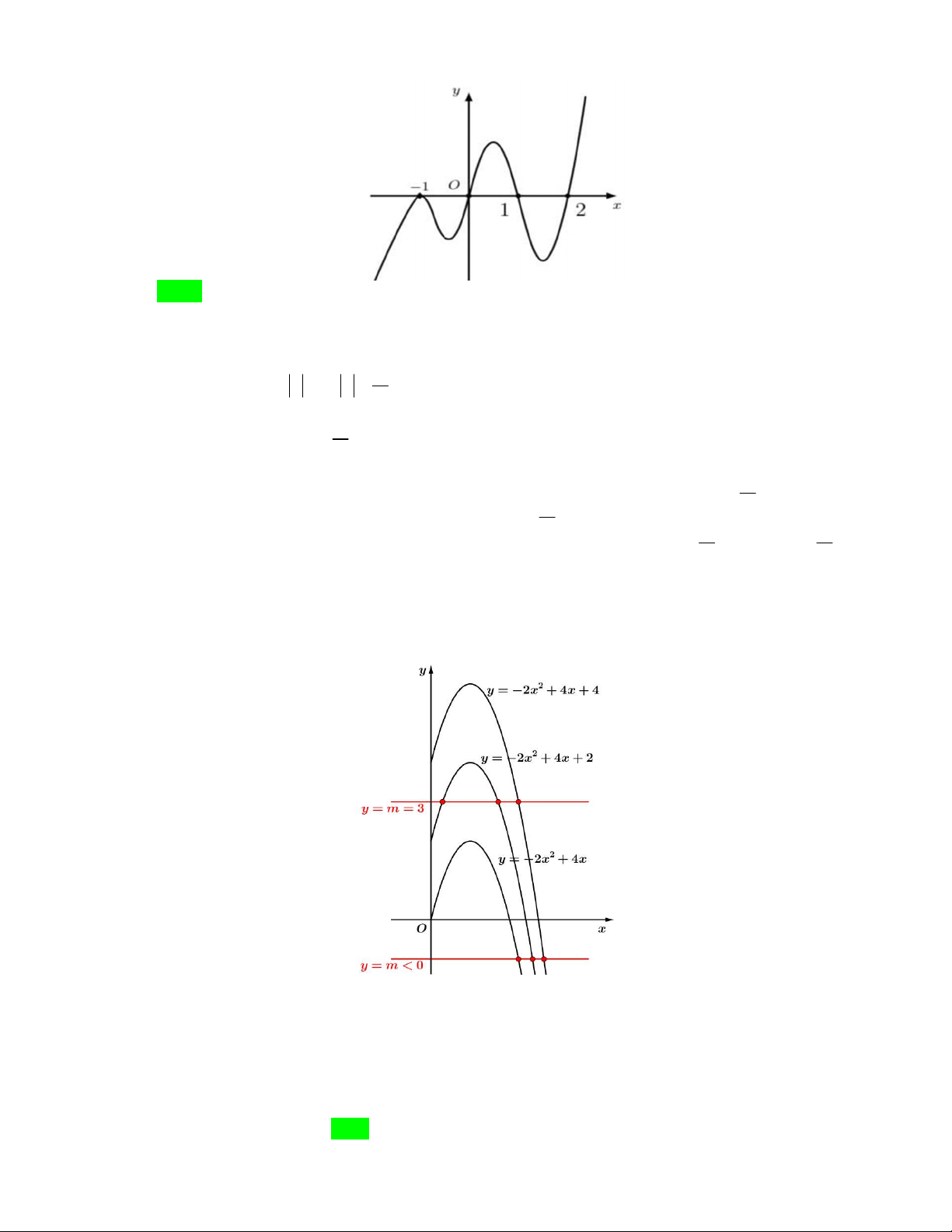
Câu 48. Cho đồ thị hai hàm số y  f x và y  g x như hình vẽ bên dưới 1
Biết đồ thị của hàm số y  f x là một Parabol đỉnh I có tung độ bằng  và y  g x là một 2
hàm số bậc ba. Hoành độ giao điểm của hai đồ thị là x , x , x thỏa mãn x x x  6 . Diện tích hình phẳng 1 2 3 1 2 3
giới hạn bởi hai đồ thị hàm số y  f x và y  g x gần nhất với giá trị nào dưới đây ? A. 6 B. 7 C. 5 D. 8 Lời giải
Từ hình trên ta quy ước hoành độ giao điểm giữa hai hàm số từ trái qua phải là x , x , x . 1 2 3 2 x
Đầu tiên ta dễ dàng tìm được f x 
 x với x 1, khi đó ta suy ra x x  6  2 I 1 3 Gọi   3 2
g x  ax  bx  cx  d a  0 . Nhận ra điểm I cũng chính là điểm uốn của hàm số y  g  x nên ta  g   1  1 1   a  b  c  d   suy ra  2   2 . g    1  0 6a  2b  0
Tiếp theo, xét phương trình hoành độ giao điểm của y  f x và y  g x , ta có: 2 x  1 3 2 3  2 ax  bx  cx  d   x  ax  b  x    c   1 x  d  0 (1) 2  2 
Biết rằng phương trình (1) có ba nghiệm phân biệt x , x , x nên theo định lí Viét ta có được: 1 2 3 d 1 3 3 x x x  6  
 d  6a . Từ đó ta giải hệ 4 ẩn ra được: a   ,b  ,c  0, d   1 2 3 a 8 8 4 1 3 3    Suy ra: x f  x  g  x 3 2
  x  x  x  kéo theo phương trình f x  g x có nghiệm là 1 7  8 8 4 x   1 1 7 Vậy S  f
 x gx dx 6,22 gần với 6. Chọn đáp án A. 1 7
Câu 49. Xét các số phức z, w thỏa mãn z  2  2i  1 và w  2  i  w  3i . Khi z  w  w  3  3i đạt giá
trị nhỏ nhất. Tính z  2w A. 61 B. 7 C. 2 5 D. 2 13 Lời giải
Gọi M , N lần lượt là các điểm biểu diễn số phức z, w
M zC x  2   y  2 : 2 2  1
Qua biến đổi đại số, ta suy ra: 
. Gọi A3;3 , khi đó ta có: N
 wd  : x  y 1  0
P  z  w  w  3  3i  MN  NA  MN  NB  MB trong đó B 4;2 là điểm đối xứng với A qua d  . Như vậy P  MB
 MI  R  6 1  5 với I  2  ; 2
  là tâm đường tròn C . min min C  
Dấu bằng xảy ra khi M 1; 2 và N 3;2. Vậy z  2w  OM  2ON  61 Chọn đáp án A.
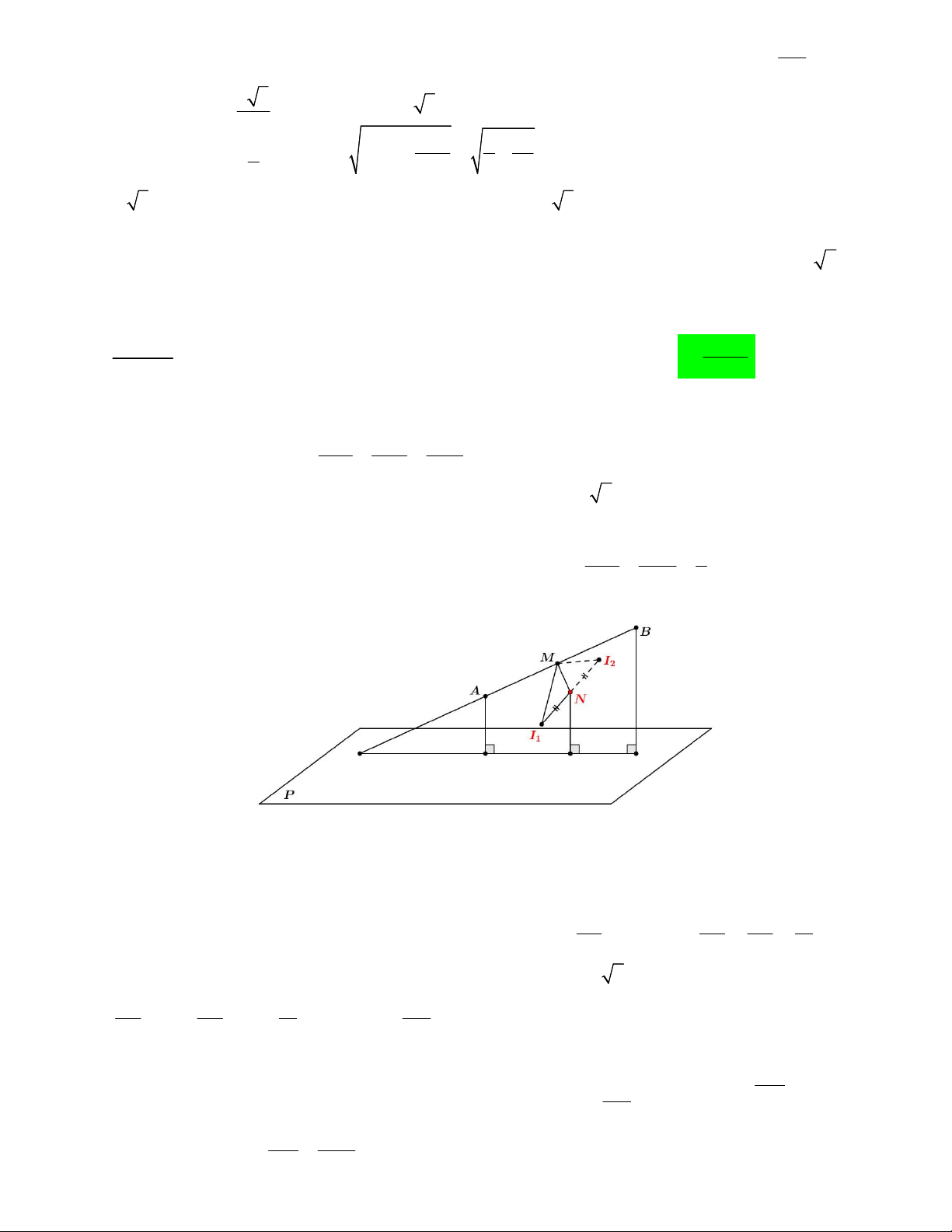
Câu 50. Trong không gian Oxyz , cho hai điểm A1;1;3 và B 2  ;3; 
1 . Xét hai điểm M , N thay đổi thuộc
mặt phẳng Oxz sao cho MN  2 . Giá trị nhỏ nhất của AM  BN bằng A. 5 B. 4 C. 6 D. 7 Lời giải
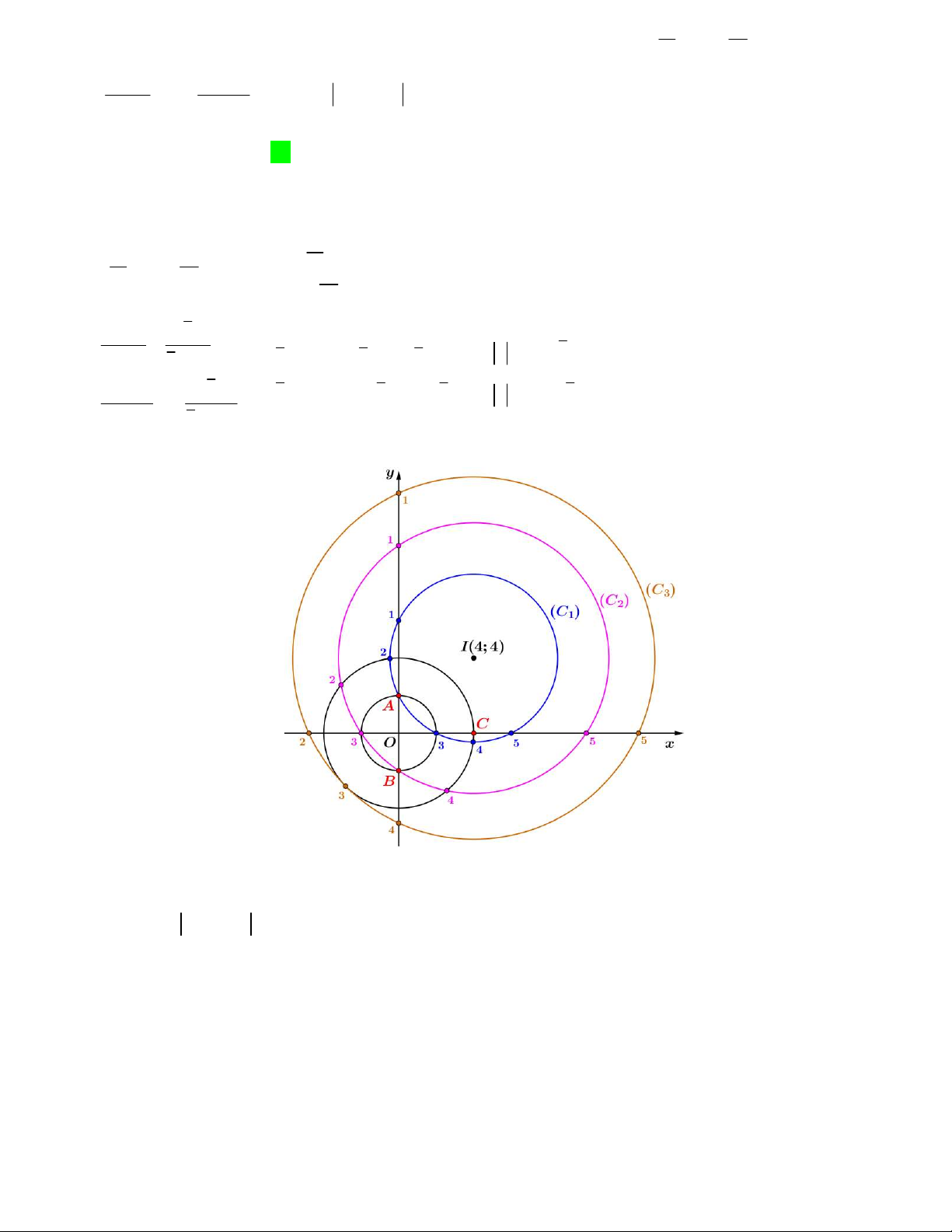
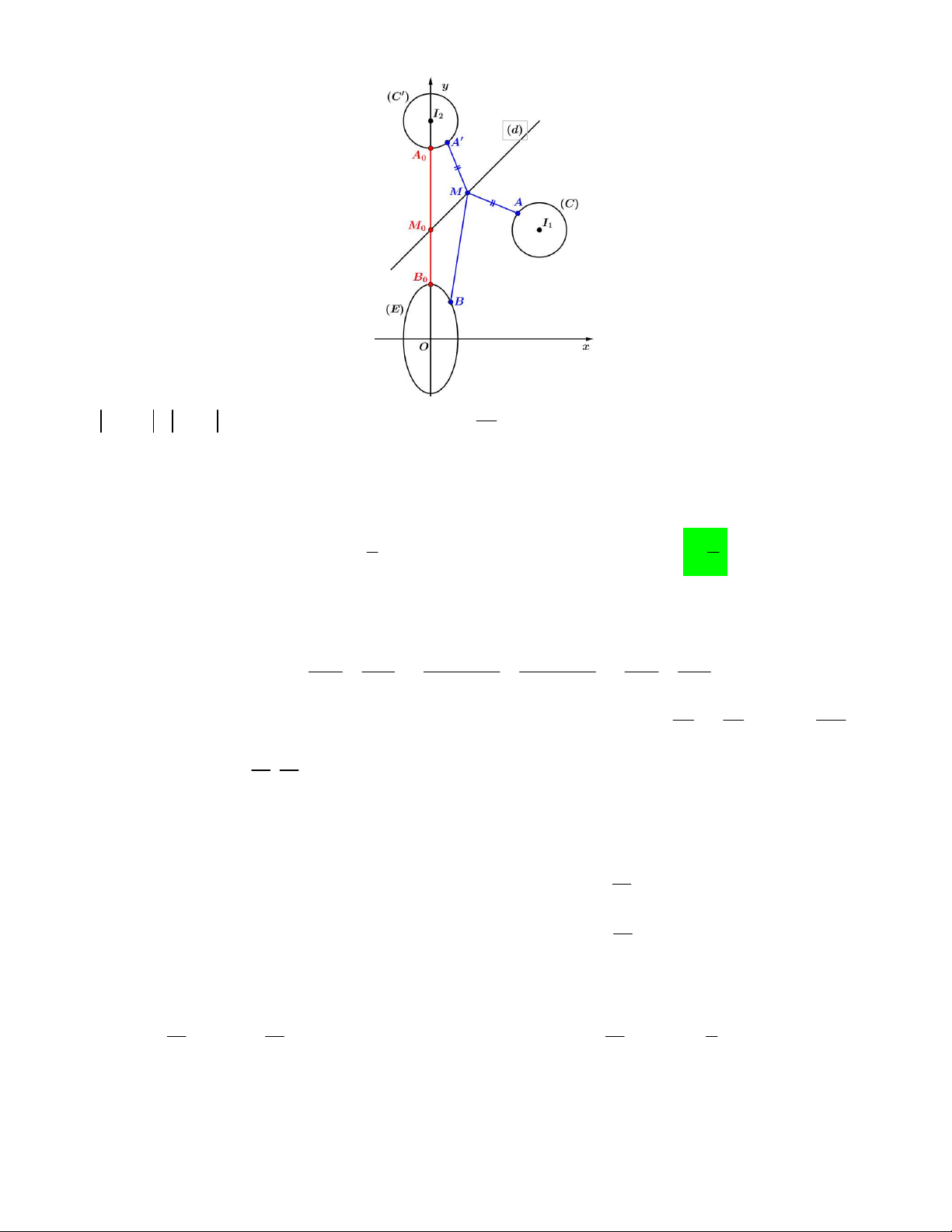
Đầu tiên ta có hình vẽ như sau:
Xét mặt phẳng P : y 1. Dựng đường tròn C  tâm A , bán kính AA  MN  2 với AC  sao cho
AANM là hình bình hành. Đến đây ta nhận thấy A , B đều cùng phía với mặt phẳng Oxz nên ta suy ra:
AM  BN  AN  BN  AN  B N
  AB với B2; 3  ; 
1 là điểm đối xứng với B qua Oxz Gọi H 2;1; 
1 là hình chiếu của B lên P khi đó ta suy ra HA đạt giá trị nhỏ nhất khi ba điểm , A H , A
thẳng hàng với H nằm giữa A và A. Ta có: AH  5 nên suy ra HA  AA  AH  MN  AH  3 min Vậy  AM  BN  2 2 2 2  AB  B H 
 AH  3  4  5 . Chọn đáp án A. min min
ĐỀ THI THỬ LẦN 1 SỞ HÀ NỘI
Câu 42. Cho bất phương trình: x x    2   x x x   3 m   3 8 3 .4 3 2 2 1 x  2m  
1 x . Số các giá trị nguyên của
tham số m để bất phương trình trên có đúng năm nghiệm nguyên dương phân biệt là A. 6 B. 4 C. 3 D. 5 Lời giải
Đầu tiên ta có bất phương trình tương đương với: x   x2 x  
  x     3      x  3   x x x x x mx mx x  x  mx3 2 3 8 3 . 2 3 .2 2 2 2 2 2 2  2mx
Xét hàm đặc trưng y  f t 3  t  2t có f t 2
 3t  2  0 với mọi t  R nên f t luôn đồng biến trên R .
Từ đó ta suy ra 2x       2x f x f mx  x  mx (*) 2x 2x
Với x  0 thì bất phương trình (1) tương đương với m 
1. Xét hàm số y  g x  1, x  0; x x
thì ta có: g x  0  x  x 1,44, cùng với g  x  0 nên suy ra x  x là điểm cực tiểu. 0  0 0 Do g  
1  g 2  3 nên để có 5 nghiệm nguyên dương phân biệt thì
Suy ra để thỏa yêu cầu đề bài thì 4 6 7,4 11,6 m g m g m        m8;9;10;1  1 tức có 4 giá trị
nguyên m thỏa mãn yêu cầu đề bài. Chọn đáp án B.
Câu 43. Trong không gian Oxyz cho điểm M 1;2;3 . Đường thẳng d  đi qua điểm M , d  cắt tia Ox tại
A và cắt mặt phẳng Oyz tại B sao cho MA  2MB . Độ dài đoạn thẳng AB bằng A. 3 17 B. 5 17 C. 17 D. 17 2 2 2 Lời giải
   Ta có: A ; a 0;0 và B0; ;
b c cùng với M là điểm thỏa MA 2MB  O . 3   a
 x  2x y  2y z  2z    9  3 17 Suy ra A B M ; A B ; A B    6  2b   ; a ; b c  3;3;  AB    Chọn đáp án A.  2 2 2    2  2 9  2c 
Câu 44. Có bao nhiêu số phức z z thỏa mãn
là số thực và  z  2z  2i là số thuần ảo ? 2 z  2z A. 1 B. 0 C. 2 D. 3 Lời giải Cách 1:
Đầu tiên ta đặt z  a  bi a,b R 2 2 a  b  2a  0 Điều kiện: 2 z  2z  0   2 2
a  b  2a  2ab  2bi  0  0i    a;b   2  ;0 2ab  2b  0 a bi 2 2
a  b  2a 2ab  2bi z  Do   là số thực nên suy ra 2 z  2z
a b 2a2 2ab2b2 2 2   b  a 2ab  2b  b 0 2 2 a  b  2a 2 3
 0  4ab  a b b  0   (1) 2 2 b  4a  a
Tiếp theo ta có:  z  z  i 2 2
2  z  2i a  bi  2a  bi  4i , do  z  2z  2i là số thuần ảo nên suy ra 2 2
a  b  2b  2a  0 (2). Từ (1) và (2) ta xét hai trường hợp như sau: TH1: b  0 loại TH2: 2 2
b  4a  a thì thế vào (2) suy ra b  3a . Đưa về hình học Oxy thì số nghiệm  ; a b chính là số giao
điểm giữa đường tròn C x  2   y  2 : 1 1  2 có tâm I  1  ; 
1 , R  2 và đường thẳng d  : y  3x
Nhận thấy d I;d   R nên suy ra d  cắt C tại 2 điểm tức có 2 số phức tồn tại là 0;0 (L) và  2 6  ;   .  5 5 
Tổng hợp ta kết luận có tất cả 1 số phức thỏa mãn yêu cầu đề bài. Chọn đáp án A. Cách 2:
Điều kiện: b  0 . Nhận xét: số phức w là một số thực thì khi đó ta luôn có: w  w . Từ đó, ta có: z  z 1) z z 2 2 2 
 z z  2z  z z  2z  z  z z  2z  2z  0   2 2   2 2  2 z  2z z  2z  z  2  z  z b  0
Đặt z  a  bi a,b R thì khi đó phương trình tương đương với:  . 2 2 a  b  2a
2)  z  2z  2i là số thuần ảo, khi đó ta có: 2 2 a  b  2a  2b  0 C : x 1  y 1 1   2 2
Chuyển về xét tương giao trên hệ trục tọa độ Oxy , ta có:  ; y  0 C :x  2 1   y  2 1  2 2
Từ đó ta có hình vẽ như sau:
Đối chiếu với điều kiện b  0 nên ta suy ra chỉ có 1 số phức thỏa mãn, tức điểm N . Chọn đáp án A.
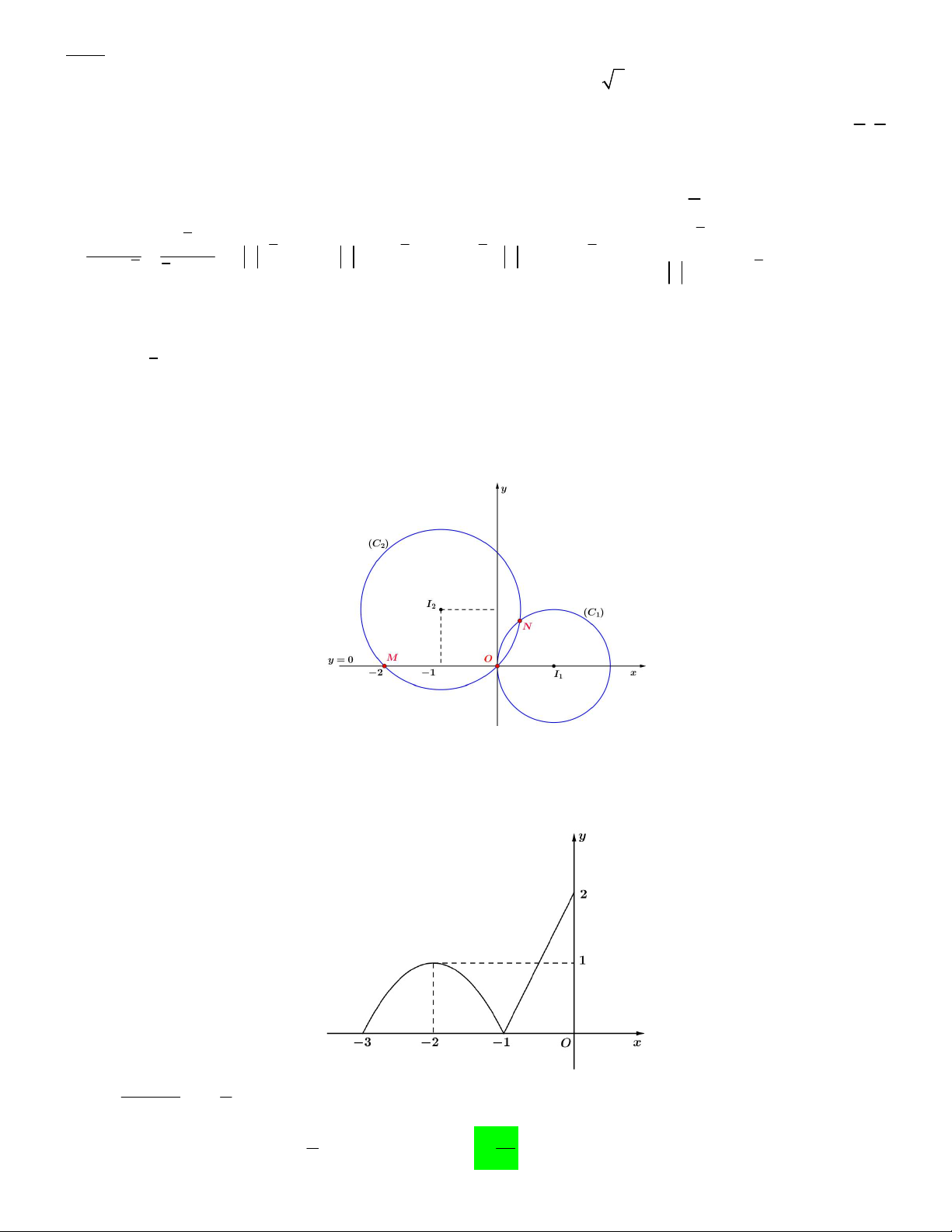
Câu 45. Cho hàm số y  f  x . Đồ thị y  f x trên  3  ; 
0 có hình vẽ như sau (phần đường cong của đồ
thị là một phần của parabol 2 y  ax  bx  c ) 1 f ln x Cho 2 dx   , giá trị f 0 bằng  x 3 3 e A. 2 B. 7  C. 14 D. 1 9 9 Lời giải 2
x  4x  3, 3  x  1
Đầu tiên từ đồ thị trên ta dễ dàng có được: y  f  x   2x  2 , 1  x  0 1 2 f ln x 1 0 Khi đó ta có:  dx  f 
 ln xd ln x  f  xdx 3  x 3 3 e e 3 u  f x du  f xdx Đặt    . dv  dx v  x  3 0 0 1 0 Suy ra 2  f
 xdx  3 f 0  x 3 f xdx  3f 0  x 3 f xdx   x 3 f xdx 3 3  3 3 1 1  0
 3 f 0   x  3 2
x  4x  3dx   x 32x  2dx  3 f 0 4. Suy ra f   14 0  . Chọn đáp án C. 9 3  1
Câu 46. Trong không gian Oxyz , cho ba điểm A1;1; 
1 , B1;2;2, I 0;0;4. Mặt cầu S  đi qua hai điểm , A B
và tiếp xúc với mặt phẳng Oxy tại điểm C . Giá trị lớn nhất của độ dài đoạn IC là A. 5 B. 2 3 C. 4 D. 3 2 Lời giải
Cách 1: Nhận xét: để tồn tại mặt cầu S  đi qua hai điểm , A B thì tâm K  ; a ;
b c của mặt cầu đó phải nằm
trên mặt phẳng trung trực của đoạn thẳng AB , tức mặt phẳng P . 
Mặt phẳng P đi qua trung điểm AB nhận AB là pháp tuyến có phương trình là: P : y  z 3  0
Ta có C là hình chiếu của K lên mặt phẳng Oxy với C  ; a ;
b 0. Từ đó ta có phương trình sau:
KA  KC  a  2  b  2  c  2 2 2 2 2 2 1 1
1  c  a  b  3  2a  b  c (1)
Mặt khác ta lại có K thuộc mặt phẳng P nên b  c  3  0 (2)
Từ (1) và (2) ta suy ra a  b   a    a  2 2 2 2 3 2 3
1  b  4 tức điểm C thuộc đường tròn tâm I 1;0 1  
và bán kính R  2 . Tiếp theo ta có: 2 2 2
IC  IO  OC  16  OC tức khi IC max thì OC cũng max Mà OC
 OI  R  2  2  4 nên suy ra 2 IC
 16  3  5 . Chọn đáp án A. max 1 max
Cách 2: Sử dụng phương tích x 1 
Ta có phương trình đường thẳng AB có dạng:  AB : y 1 t . Gọi M  AB Oxy nên suy ra M 1;0;0 z 1t 
Từ đó ta có được MC  MA MB    x  2 2 2 . 4 1  y  4 với x  1  ;  3 Suy ra: 2 2 2
IC  x  y 16  2x 19  2.3 19  25  IC  5 . Chọn đáp án A. max
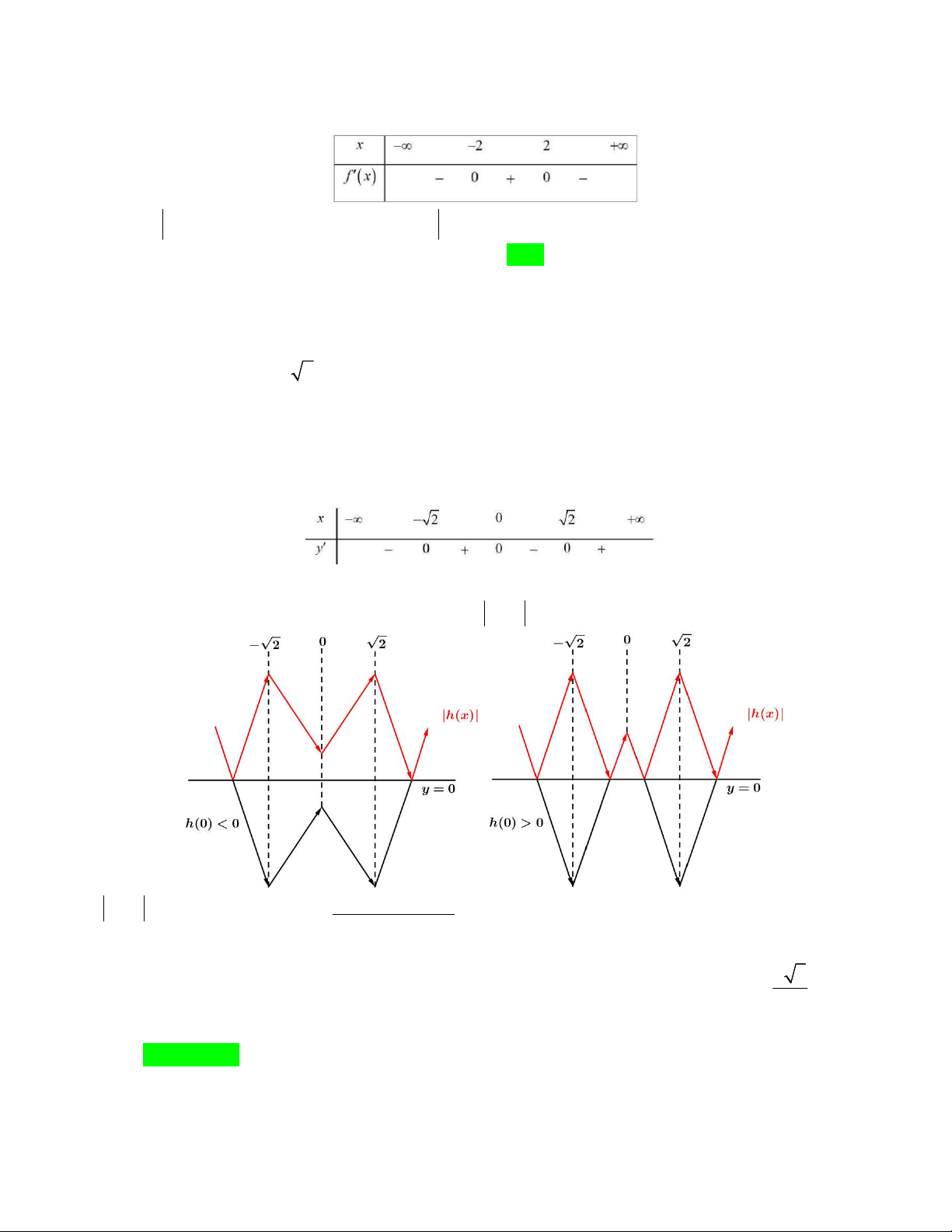
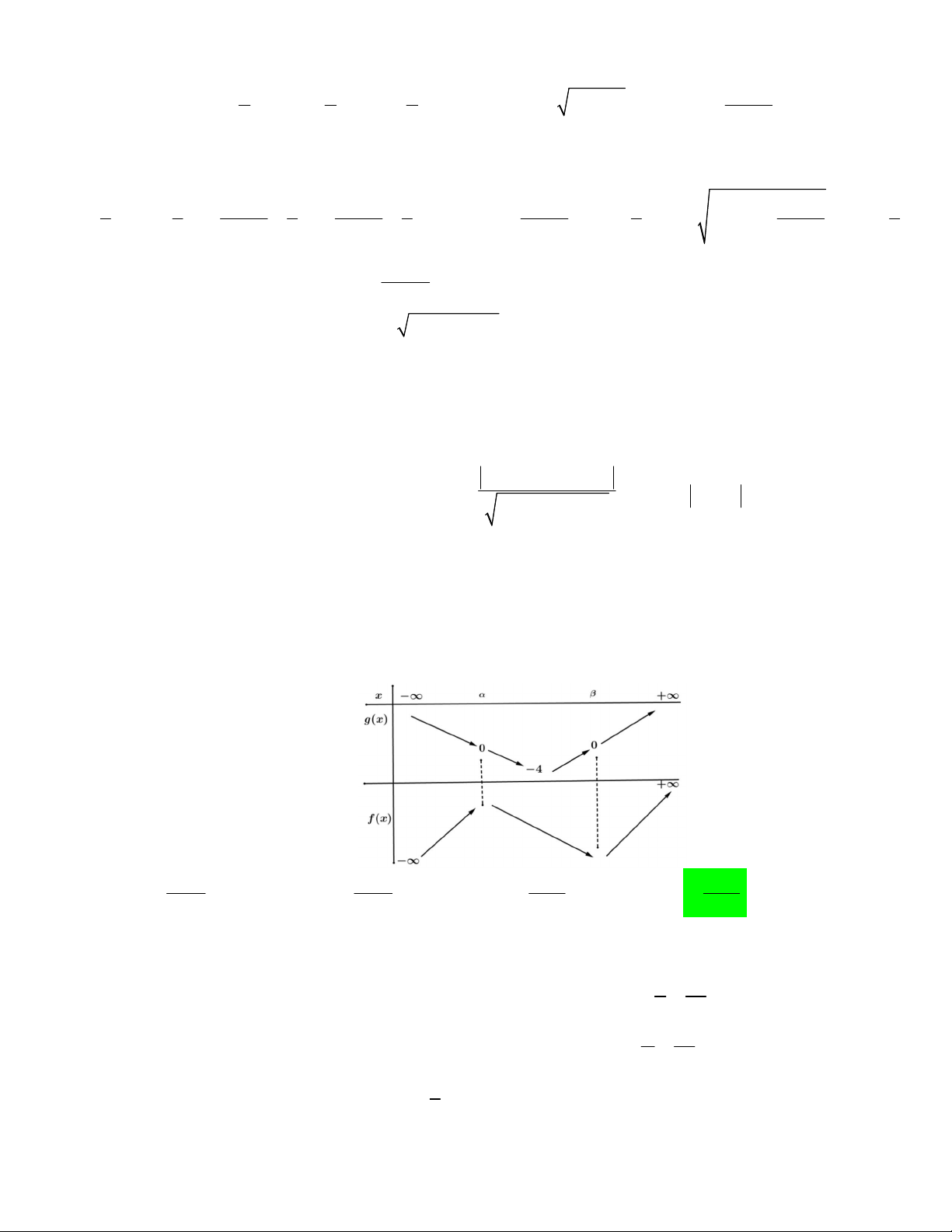
Câu 47. Cho hàm số y  f  x có bảng biến thiên như sau: x – ∞ 1 3 + ∞ y' + 0 – 0 + 1 + ∞ y – ∞ 0
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  1
 0;10 để hàm số hx  f x  m có đúng 3 điểm cực trị ? A. 19 B. 20 C. 18 D. 21 Lời giải
Để hàm số hx có đúng 3 điểm cực trị thì phương trình f x  m phải có 1 nghiệm bội lẻ.
Dễ dàng thấy rõ với m 0; 
1 thì hx có đúng 5 điểm cực trị nên suy ra để thỏa yêu cầu đề bài thì m  0 
. Mà m  nên suy ra m 1
 0;10 tức có 21 giá trị nguyên thỏa mãn. Chọn đáp án D. m  1
Câu 48. Cho hai số phức z, w phân biệt thỏa mãn z  w  4 và  z  iw  i là số thực. Giá trị nhỏ nhất của z  w bằng A. 8 B. 2 3 C. 2 15 D. 2 14 Lời giải z  4cosu  4i sin u
Cách 1: Đầu tiên ta đặt ẩn dạng lượng giác như sau:  w  4cos v  4i sin v
Suy ra ta có:  z  iw  i  4cosu  4isinu  i4cosv  4isin v  i mà do là số thực nên ta có được     phương trình sau: u v u v u v 
cos u  cos v  4sin u  v  0  2sin sin  4cos  0   2  2 2       Cùng với u v u v 
z, w là hai số phức phân biệt nên ta suy ra sin  4cos      2   2             Ta có: u v u v u v    sin    1;  1 1 1 2 1  cos  ;  cos  0;       2 2 4 4 2  16           2 z  w Suy ra: 2 z  w  
 u  v2  u  v2 16 16. sin sin cos cos  16.2  2   
sinusin v  cosucosv 16     u  v     u  v   
 32.1 cosu  v 1 2 2  321 2cos 1      32 2  2cos  32 2  2  60         2     2   16 
Vậy z  w  60  2 15 . Chọn đáp án C. a  z  i
Cách 2: Đầu tiên ta đặt ẩn như sau: 
thì khi đó ta có: a  i  b  i  4 b  w  i
z iwi  a bi icdi i  acbd b d  1a c ad bci  Mà do  a b
z  iw  i là số thực nên suy ra 1
a  c  ad  bc  0   . Gọi ,
A B lần lượt là điểm biểu c d 1
diễn số phức z, w và điểm C 0;  1
Từ đó ta suy ra với hệ thức trên ta có được ,
A C, B thẳng hàng. Khi đó ta có hình vẽ như sau: Ta suy ra 2 2 z  w  AB
 2 4 1  2 15 . Chọn đáp án C. max max
Cách 3: Sử dụng cách thuần đại số
Ta có:  z  iw i  z iw i  z iwiR  z i  k wi  k   1 i  kw  z k   1 Suy ra: 2 2
k 1  kw  z   kw  z 2 16 k  2
1 . Mà vì k  1 nên suy ra k  0 Do đó k  2 2 2 2 2
 kw  z  k w  z  k zw  zw  k zw zw    2 1 15 k   1  2k
Tiếp theo, ta nhận thấy:  k  2 2
  k  k      2 15 1 15 30 15 0 15 k   1  2k  28k nên suy ra
k zw zw  28k  zw zw  28 k  0 . Từ đó ta có được: 2
z  w  32  zw  zw  32  28  60  z  w  2 15 . Chọn đáp án C.
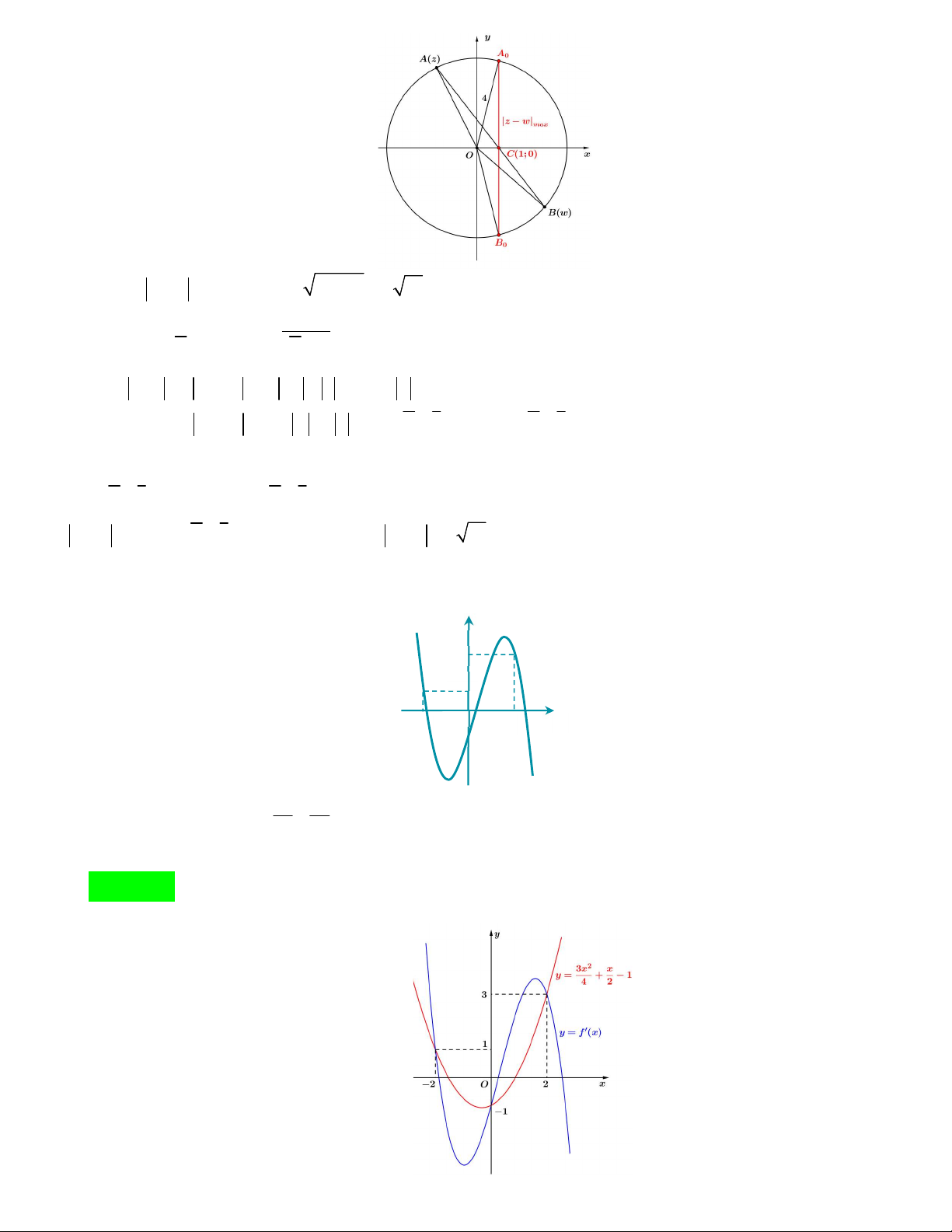
Câu 50. Cho hàm số y  f  x là hàm đa thức bậc bốn. Đồ thị hàm số y  f x được cho trong hình vẽ dưới đây y 3 1 O - 2 x 2 - 1 3 2 x x
Đặt hàm số g x  f  x  
 x . Tập hợp tất cả các giá trị thực của tham số m để hàm số y  g x  m 4 4
nghịch biến trên khoảng 3; là A.  1  ; B. 5; 1 C. ; 5 D. 1;  Lời giải 2 2 3x x 3x x
Ta có: gx  f x 
 1 0  f  x   1 4 2 4 2 2 3x x
Xét tương giáo giữa hai đồ thị y  f  x và y 
 1 thì khoảng x làm cho gx  0 là các khoảng 4 2 2  x  0 sau:  . x  2 2  x  m  0
Tiếp đến, ta có: y  g x  m  0  , x   3  m  2  x, x
  3  m  max 2  x  m  1   . x  m  2
Giải thích: trường hợp 2
  x  m  0 bị loại vì x   bị sai. Chọn đáp án A.
ĐỀ THI THỬ CHUYÊN SƠN LA LẦN 1
Câu 39. Cho hàm số xác định trên R \ 2  ;  1 thỏa mãn f  x 1 1 
, f 3  f 3  0, f 0  . Giá trị 2       x  x  2 3 của biểu thức f  4    f   1  f 4 bằng A. 1 1 ln 2  B. 1 1 ln 20  C. ln 80 1 D. 1 8 ln 1 3 3 3 3 3 5 Lời giải 1 x 1 ln  C , x    ;  2   1   3 x  2    Ta có: f  x  f   x dx dx 1 x 1 dx       ln  C ,x  2;1 2 x  x  2 x  1x  2 2   3 x  2  1 x 1  ln  C , x   1; 3   3 x  2  Trên  ;  2   ta có: l 1 1 1 ln 2 f   ln 4 3   C . Trên  2  ; 
1 , ta có f 0  ln  C   C  1 3 2 2 3 2 3 3  Từ đó suy ra: 1 2 f   2ln 2 1 1 
. Trên 1; ta có: f 3  ln  C . Mà f  3
   f 3  0 nên 3 3 3 5  ln10 1 5 ln 2 ln 2 1 5 2 ln 2 C  C 
 f 4  f  
1  f 4  ln  C   C   C  ln   C  C  C 1 2 3 2  1 3  1 3 3 3 2 3 3 3 2 3 1 5 2 ln 2 1 ln 2 ln10 1 1  ln   
 ln 2  . Chọn đáp án A. 3 2 3 3 3 3 3    Câu 40. Trong không gian x y z Oxyz , cho đường thẳng 1 2 2 d :   và mặt phẳng 3 2 2
P: x 3y  2z  2  0. Đường thẳng  song song với P , đi qua M 2;2;4 và cắt đường thẳng d có phương trình là             A. x 2 y 2 z 4   B. x 2 y 2 z 4   C. x 2 y 2 z 4   D. x 2 y 2 z 4   9 7 6 9 7 6 9 7 6 9 7 6 Lời giải
Đầu tiên ta loại đáp án C,D đi vì vector chỉ phương nhân vô hướng với vector pháp tuyến mặt phẳng P
khác 0. Tiếp đến do đường thẳng  qua M 2;2;4 nên ta khoanh B. Chọn đáp án B.
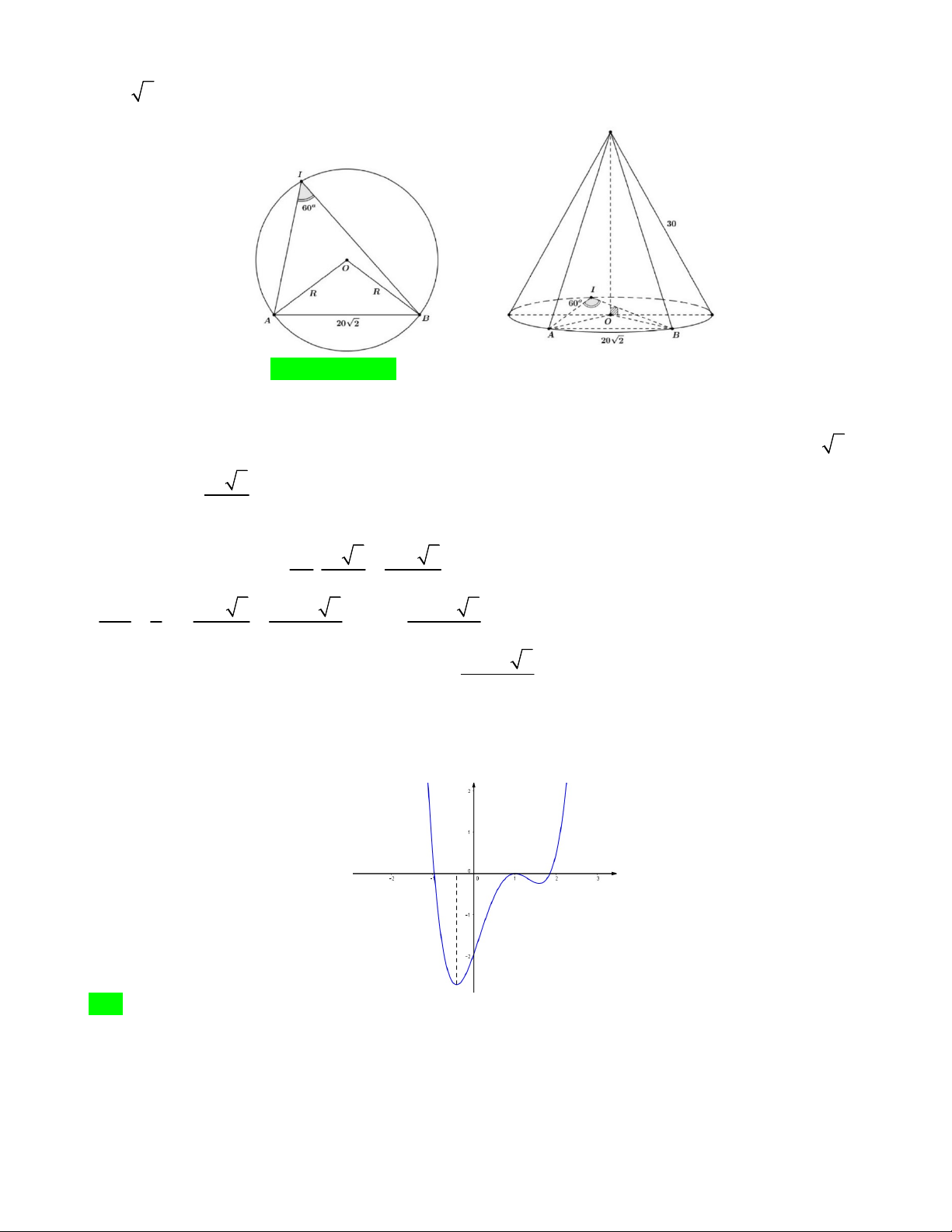
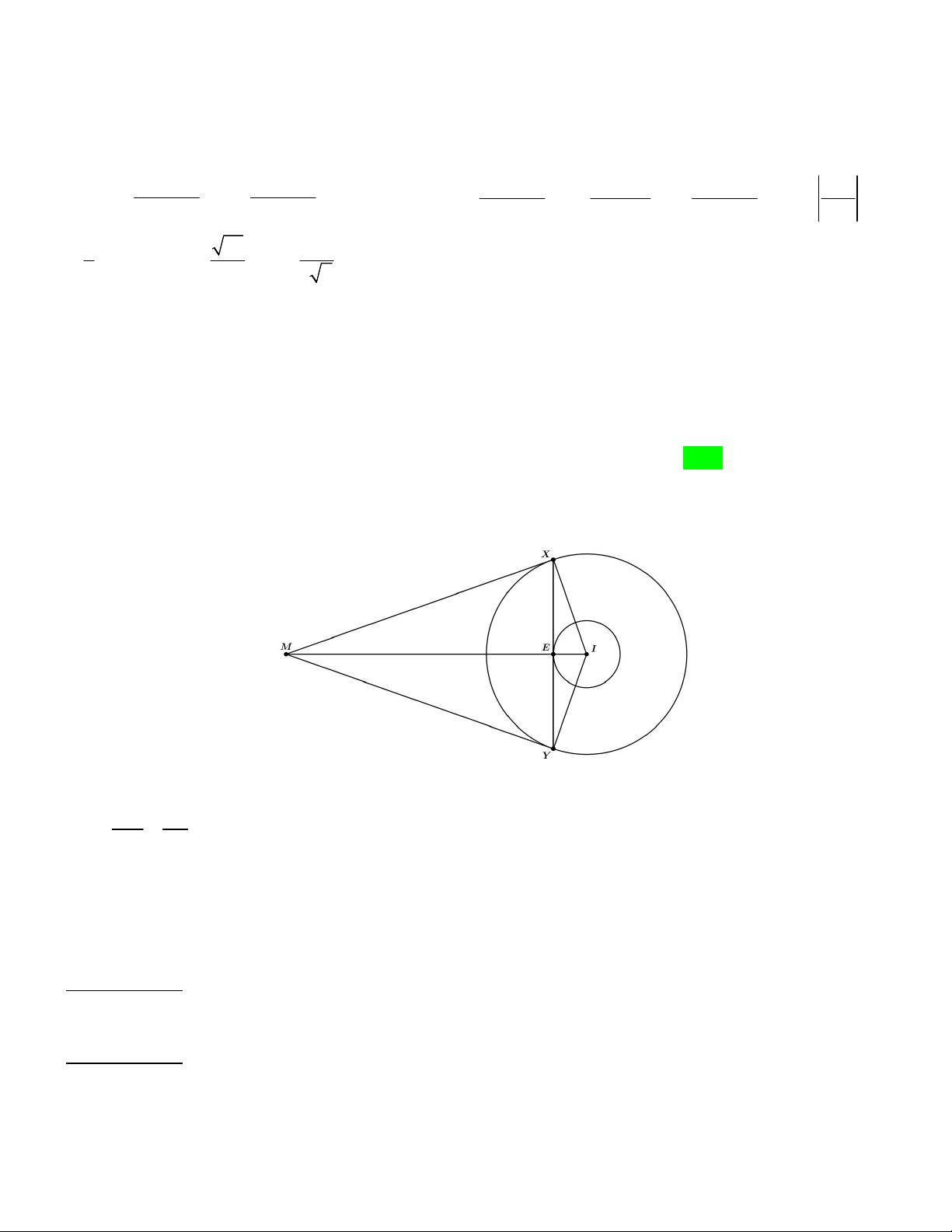
Câu 42. Bà Hương nhận làm 100 chiếc nón lá giống nhau có độ dài đường sinh là 30cm . Ở phần mặt trước
của mỗi chiếc nón (từ A đến B như hình vẽ) bà Hương thuê người sơn và vẽ hình trang trí. Biết
AB  20 2cm và giá tiền công để sơn trang trí 2
1m là 50000 đồng. Tính số tiền (làm tròn đến hàng nghìn)
mà bà Hương phải thuê sơn trang trí cho cả đợt làm nón A. 128.000 đồng B. 257.000 đồng C. 384.000 đồng D. 209.000 đồng Lời giải
Đầu tiên theo tính chất góc ở tâm bằng hai lần góc nội tiếp chắn cung tương ứng nên ta suy ra:  AOB  2
AIB  120 . Sử dụng đính li Cosin ta có: AB  OA  OB  OA OB   R   2 2 2 2 2 2 . cos120 3 20 2 Từ đó suy ra 20 6 R 
cm. Tiếp theo, ta gọi đỉnh của hình nón là S , sau đó ta trải phẳng mặt xung 3
quanh của nón ra, khi ấy diện tích mặt cần sơn và trang trí chính là phần hình quạt SAB .   Ta có độ dài cung  2 20 6 40 6 AB là l  . 
cm. Từ đó ta tính được diện tích hình quạt SAB là: 3 3 9 l.SA 1 40 6 1200 6  S   .30.   1200 6 2 cm  4  .10  2
m  . Mà giá tiền công để sơn trang trí 2 1m là 2 2 9 18 18 
50000 đồng nên giá tiền công sơn 100 cái nón là: 1200 6 4
.10 .50.000.100  256.509 (đồng). 18
Như vậy tổng tiền này gần với đáp án B nhất. Chọn đáp án B.
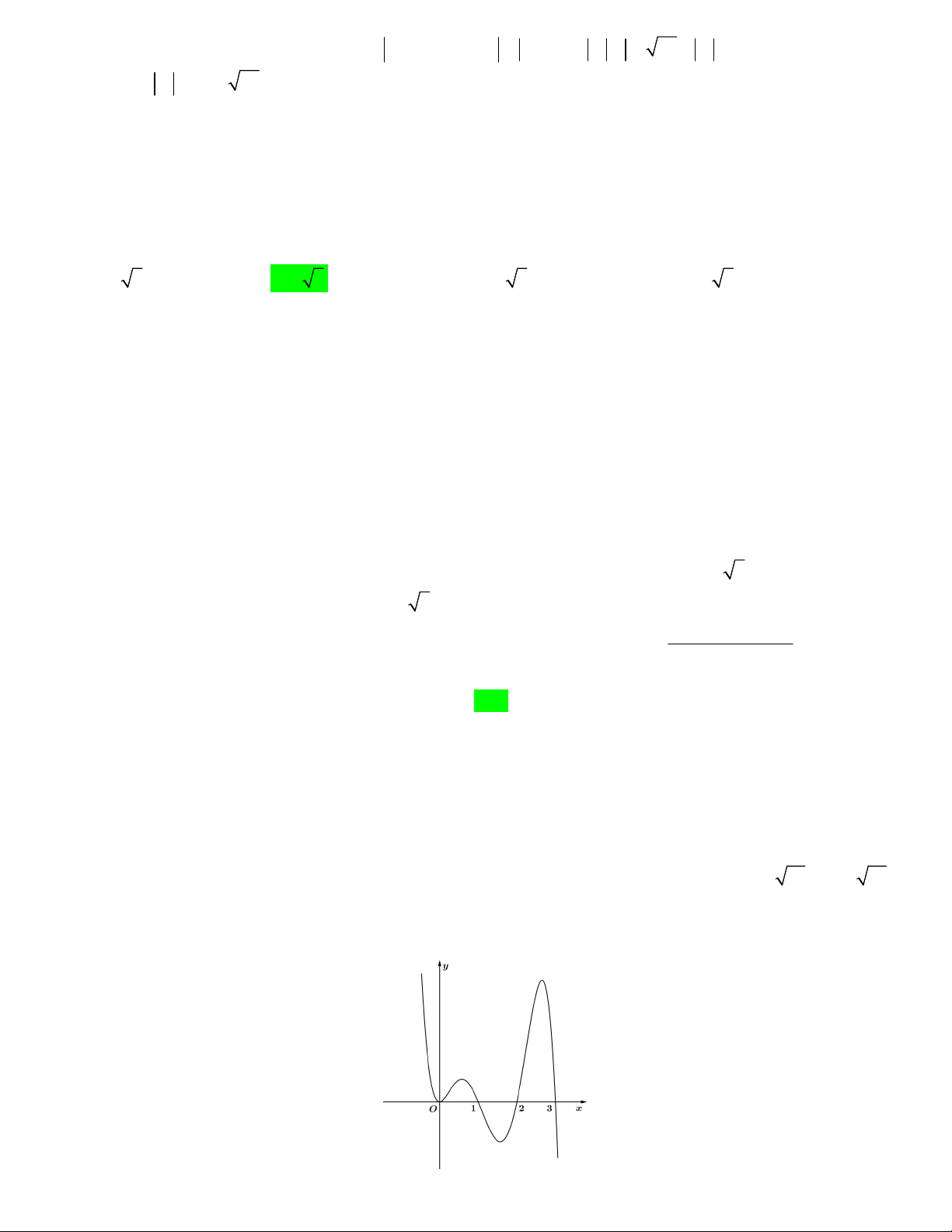
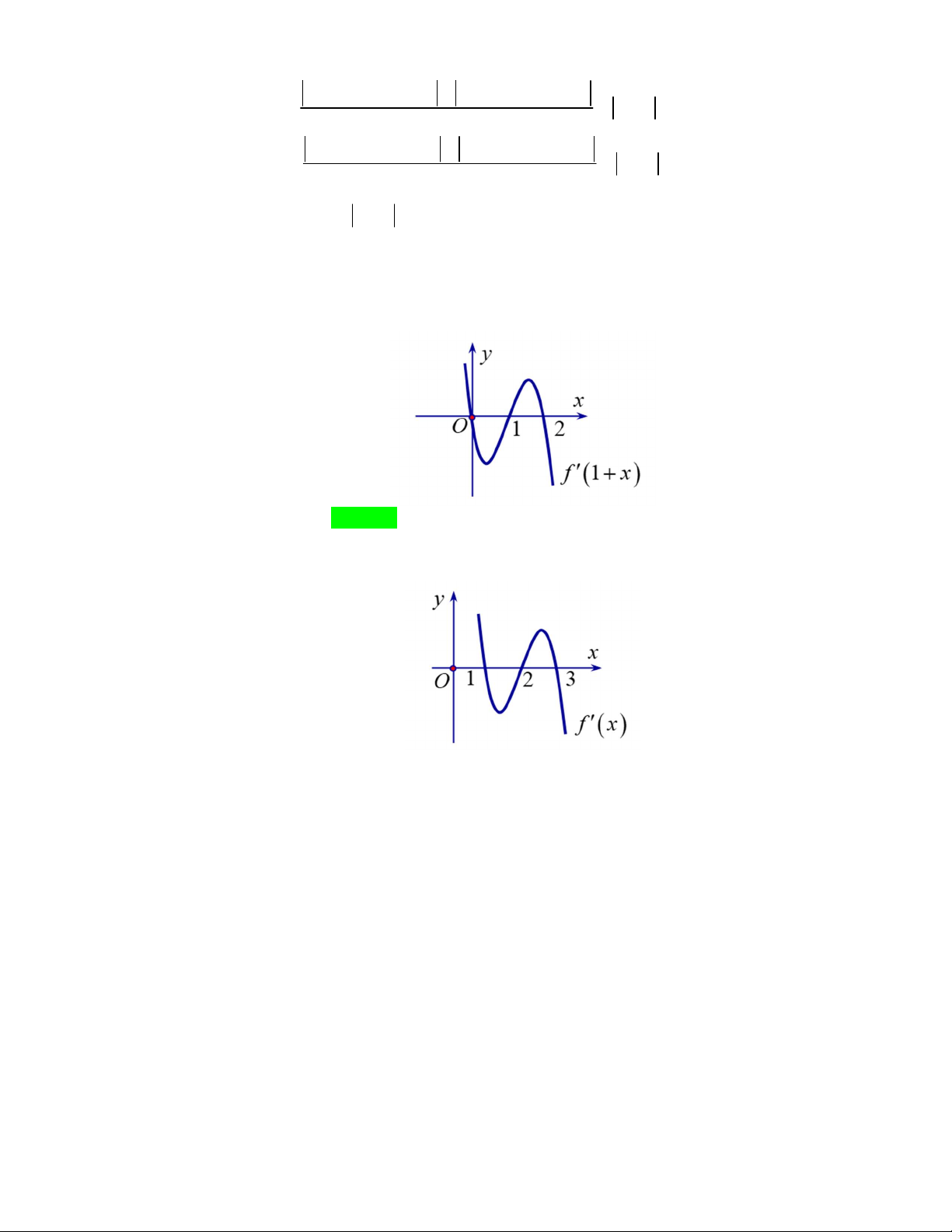
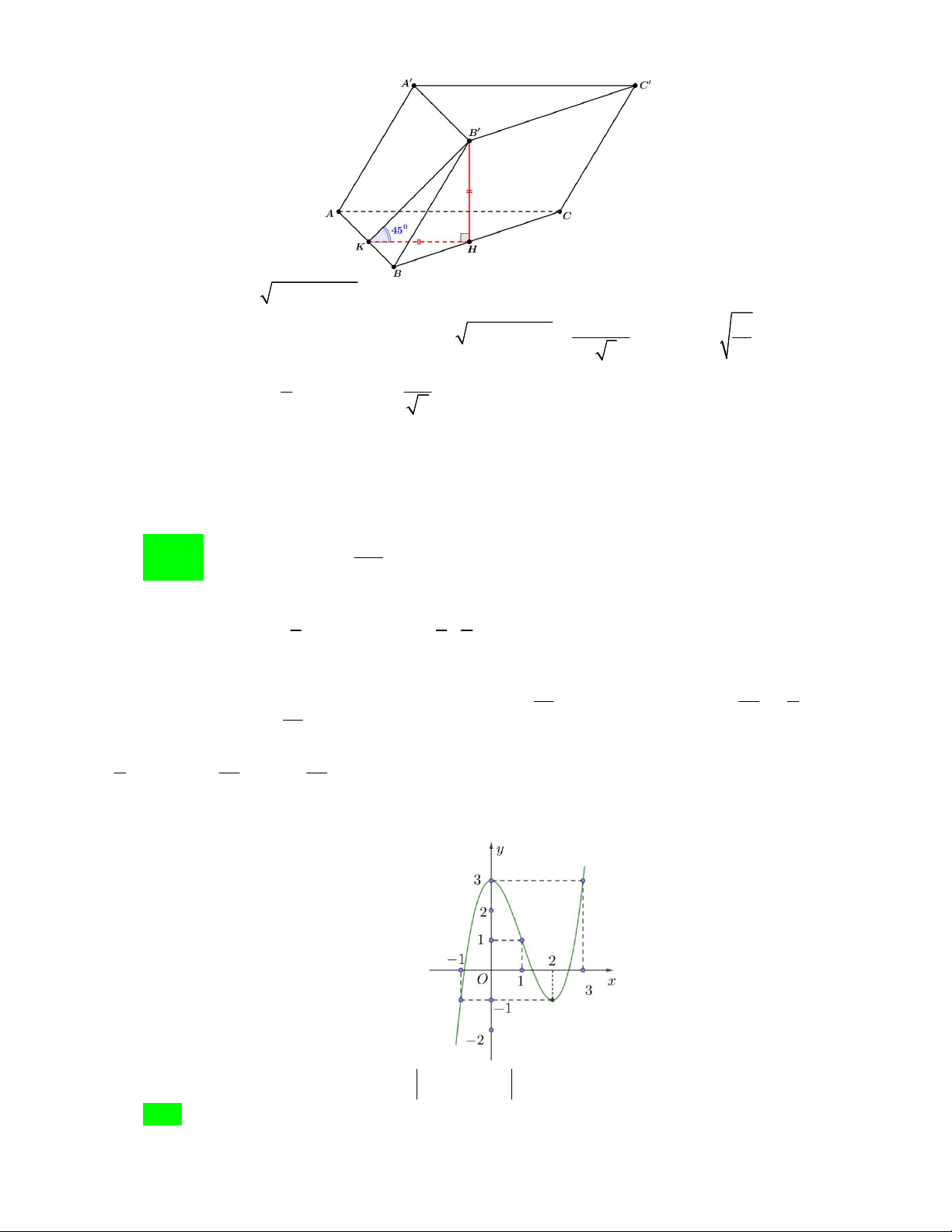
Câu 43. Cho hàm số f x có đồ thị như hình vẽ . Đặt g x  f  f x  
1 . Tìm số nghiệm của phương trình g x  0 A. 9 B. 6 C. 10 D. 8 Lời giải  f  x  0 1
Ta có: g x  f  x. f  f x       1  0    f    f  x   1  0 2
Nhìn vào đồ thị, dễ thấy (1) có 3 nghiệm.
 f  x 1 a  1  ;0
 f x  a 10;  1  2n0  
(2) tương đương với:  f  x 11   f x  2  2n . Tổng là 6 nghiệm. 0  f   x 1 b 1;2     f
  x  b 12;3  2n0
Như vậy hàm số cần tìm có tất cả 9 nghiệm. Chọn đáp án A.
Câu 44. Có bao nhiêu giá trị nguyên của m thuộc đoạn 0;2022 để bất phương trình   m   x 2 1 4   2m 1 1 x  4 x  
nghiệm đúng với mọi x thuộc 0;  1 ? x  0  4  A. 2021 B. 1011 C. 2022 D. 1 Lời giải  x4x  x 4 Đầu tiên ta xét 1 x  4   0, x   , do 4x x  4, x  0; 
1 nên bất phương trình tương đương x 0; 1 4 với: m   x 2 1 4   2m 1  0 . Đặt 4x t 
1;4 , khi bất phương trình trở thành: 4x 2    2 t  t 
m 1 t   2m 1  0  m   2 2 1 t  2m   1 t  2  0, t  1;4  m  , t   1;4 2   t t  2t 2 t  t  2 2 3t  4t  4
Xét hàm số y  f t  , t
  1;4 có f t   0  t  2 2   t  2t t 2t2 2 Mà f t  2  f t 7  f   1 lim ; lim ;
2  nên ta suy ra được f t  1  tức f t  1 min  t 1 t 4 3    12 2 2 2
Suy ra để bất phương trình có nghiệm đúng trên tập cho trước thì m  f t  1 min  m  2
Với m0;2022 ta thu được  1  m  0; 
tức có 1 giá trị nguyên m thỏa mãn. Chọn đáp án D. 2   
Câu 45. Có bao nhiêu số phức z thỏa mãn z  2  i  2 và w  z  3  iz 1 3i là số thực ? A. 0 B. 2 C. 3 D. 1 Lời giải
Đầu tiên ta đặt z  a  bi a,b R
w   z   iz   i 2 3
1 3  z  1 3ia  bi  3  ia  bi  6  8i . Do w là số thực nên ta suy ra
Imw  b  3a  3b  a 8  2a  2b  8  0. Cùng với z  2  i  2 ta quy về hình học Oxy nên số các số
phức z thỏa chính là số giao điểm giữa đường tròn C  x  2   y  2 : 2 1  4 với tâm I  2  ;  1 , R  2 và
đường thẳng x  y  4  0 .
Ta nhận thấy d I,d   R nên d  cắt C tại 2 điểm tức có 2 số phức thỏa mãn. Chọn đáp án B.
Câu 46. Cho ba số phức z , z , z thỏa mãn z 1, z  7, z  z  2 và giá trị lớn nhất của biểu thức 1 2 3 1 2 1 2
3z  2z  z bằng 78. Giá trị z bằng 1 2 3 3 A. 78  53 B. 25 C. 78  73 D. 5 Lời giải Ta có: 2 2 2 z  z
 z  z  2 z z  2  z z  3, khi đó ta suy ra: 1 2 1 2 1 2 1 2 2 2 3z  2z  9 z  4 z
12 z z  9  4.7 12.3  73 . 1 2 1 2 1 2
Mà theo bất đẳng thức Mincopski ta có: 3z  2z  z  3z  2z  z  73  z  78 nên ta suy ra: 1 2  3 1 2 3 3
Giá trị của z  78  73 . Thử lại dấu bằng xảy ra tại bất đẳng thức trên ta thấy z , z không tồn tại dấu 3 1 2
bằng thỏa mãn nên ta kết luận không có đáp án nào đúng. x 1 3a  at 
Câu 47. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  : y  2  t . Biết rằng khi a z  2  3a   1 at
thay đổi thì luôn tồn tại một mặt cầu cố định đi qua điểm M 1;1; 
1 và tiếp xúc với đường thẳng  . Tìm bán kính của mặt cầu đó. A. 6 3 B. 5 3 C. 7 3 D. 4 3 Lời giải x 1 3a  at x  1  
Ta có:  : y  2  t
 x  y  z  3 . Thế t  3
 vào ta thu được: y  5  z  23a    1 at z  1 
Khi đó ta suy ra rằng  luôn qua điểm A1;5; 
1 cố định, và nằm trong mặt phẳng P : x  y  z  3  0 .
Mặt cầu tiếp xúc với đường thẳng  với mọi a nên mặt cầu tiếp xúc với mặt phẳng P tại A . x 1 t 
Đường thẳng IA vuông góc với P có phương trình là: y  5   t  I 1 t; 5   t; 1   t . z  1   t 
Mà IA  IM nên t  t  t  t  t  2  t  2 2 2 2 2 6
2  t  5  I 6;0;6  R  IM  5 3
Vậy bán kính của mặt cầu cần tìm là bằng 5 3 . Chọn đáp án B. 2 2    x  x  m  m x x 2 11
Câu 48. Có bao nhiêu giá trị nguyên m để bất phương trình 2 2 14 2 3 2  2  nghiệm đúng x3 2
với mọi giá trị thực của x A. 6 B. 9 C. 7 D. 8 Lời giải
Bất phương trình tương đương với: 2 2 m 1  4 x3 x 2x3 x3 2 2 2 .2  2 .2  x  2x  m 11 2 2 m x x x    x  x  m   2 m x   m  x   2 17 6 2 2 17 2 x x6    2 2 2 2 11 2 17 2 x  x  6
Xét hàm đặc trưng     2t y f t  t có    2t f t
ln 2 1  0 với mọi t  R
Suy ra hàm số f t đồng biến trên R. Từ đó kéo theo: 2 2 2 2 m  x 
 x  x   x  x  m        2 17 6 2 11 0 1 m 1 
1  0   10  m  10 Do m  nên m 3  ; 
3 tức có 7 giá trị nguyên m thỏa mãn đề bài. Chọn đáp án C.
Câu 49. Cho hàm đa thức y  f  x . Hàm số y  f x có đồ thị như hình vẽ sau:
Có bao nhiêu giá trị của m để m0;6,2m để hàm số g  x  f  2
x  2 x 1  2x  m có đúng 9 điểm cực trị. A. 6 B. 5 C. 7 D. 3 Lời giải Ta có: g  x  f  2
x 1  2 x 1  m   1 .
Đồ thị hàm số y  g x nhận đường thẳng x 1 làm trục đối xứng và hàm số y  g x luôn có một điểm cực trị là x 1.
Xét trường hợp x 1, ta có: g x  f  2
x  4x  2  m . g x   x   f  2 2 4 . x  4x  2  m . x  2 x  2 
x 4x 2m  0 x 4x 2m  0 *   g x  0 
 x  4x  2  m 1  x  4x 1  m    1 .  x 4x 2 m 2      x  4x  m 2 
x 4x 2m  3   x  4x 1  m  3
Phương trình * nếu có nghiệm thì các nghiệm này sẽ là nghiệm bội chẵn của g x  0 nên hàm số g  x
không đạt cực trị tại các nghiệm này. Đồ thị các hàm số y x    4x 1, y x    4x , y x
   4x 1 trên khoảng 1;  được cho bởi hình dưới đây:
Hàm số y  g x có 9 cực trị  Hàm số y  g x có 4 cực trị x 1 3  m  4 6  2m  8
 Phương trình g x  0 có 4 nghiệm phân biệt x 1    . m 2   2m  4
Kết hợp với điều kiện 2m  và 0  2m 12 ta được: 2m0;1;2;3;4;  7 , tức là  1 3 7  m  0; ;1; ;2;  .  2 2 2 
Vậy có 6 giá trị của m thỏa mãn yêu cầu bài toán. Chọn đáp án A.
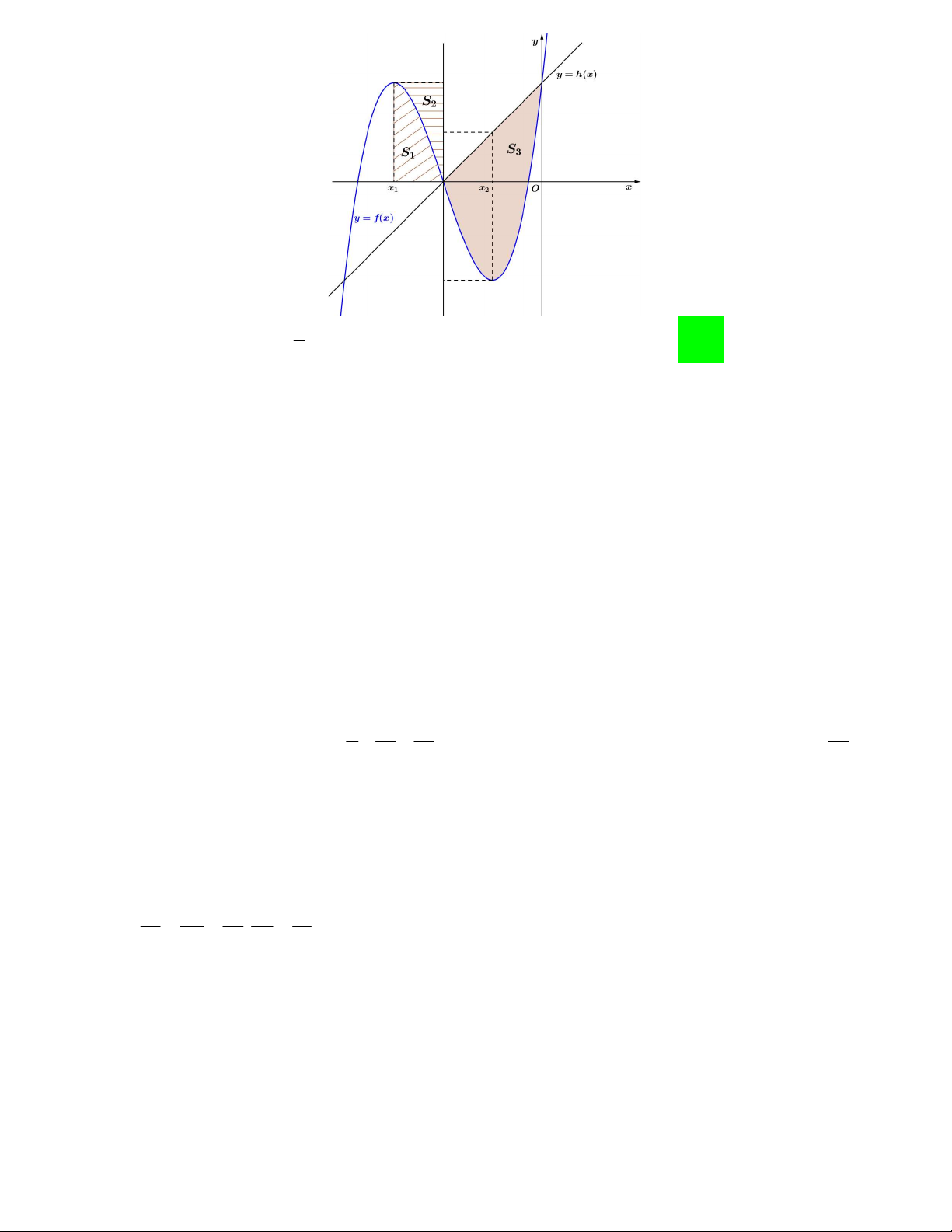
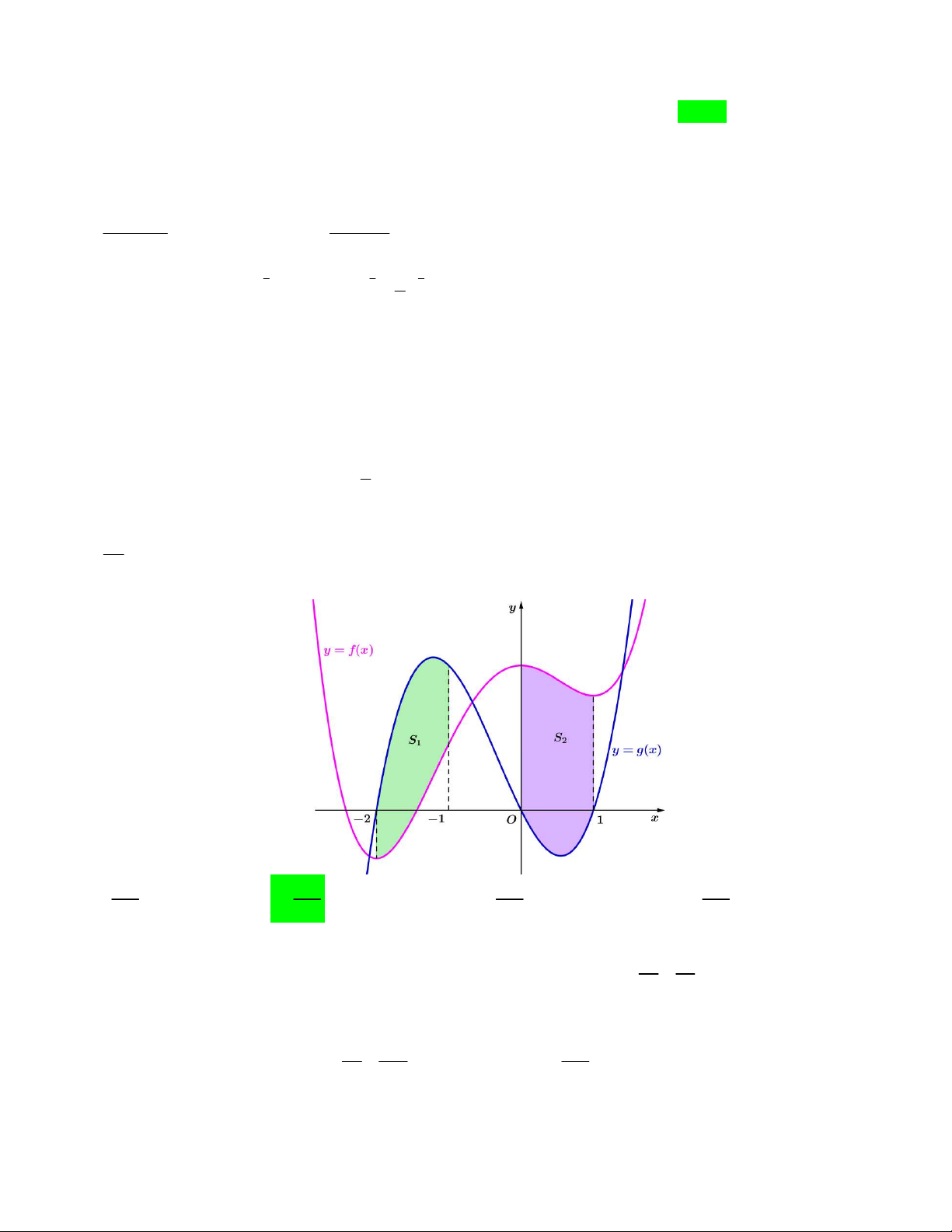
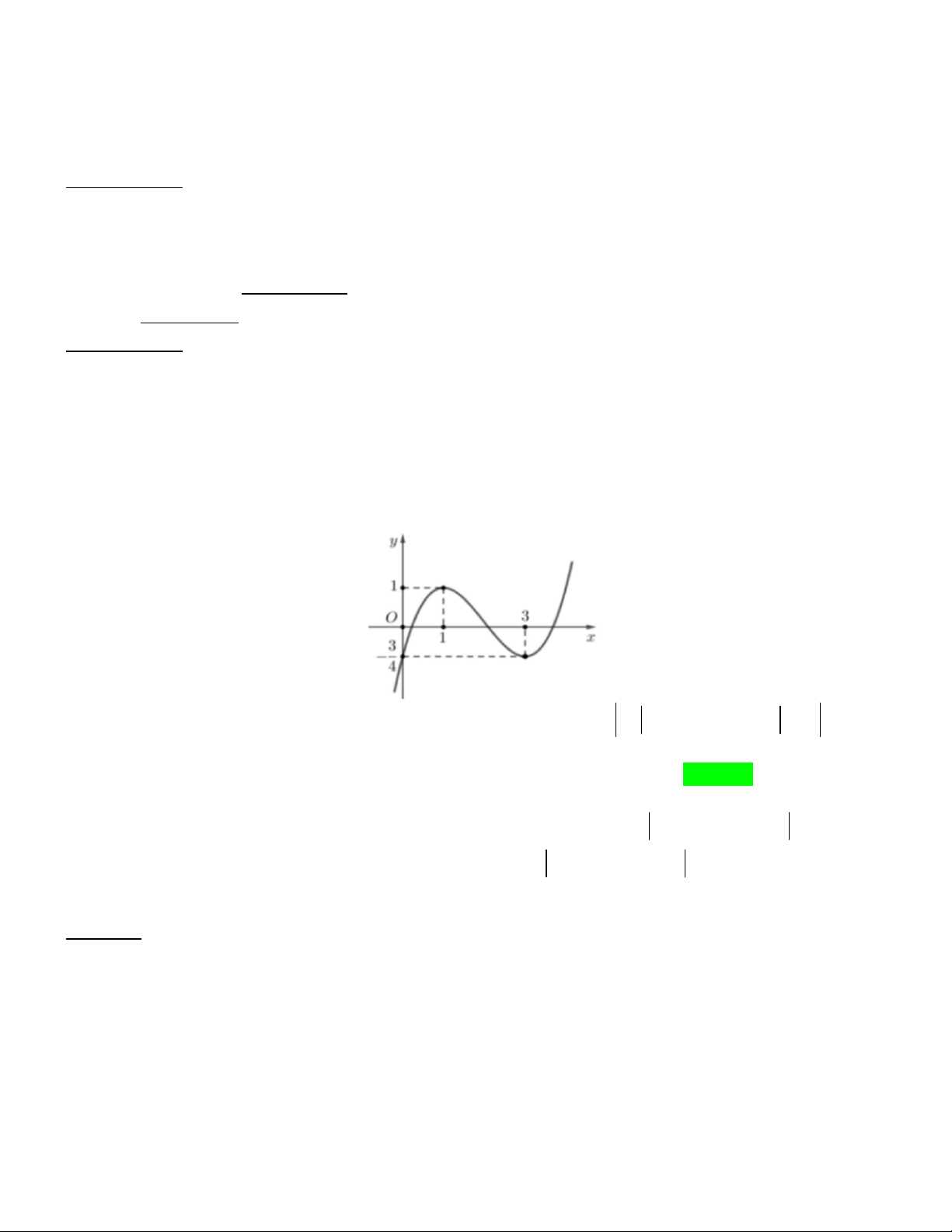
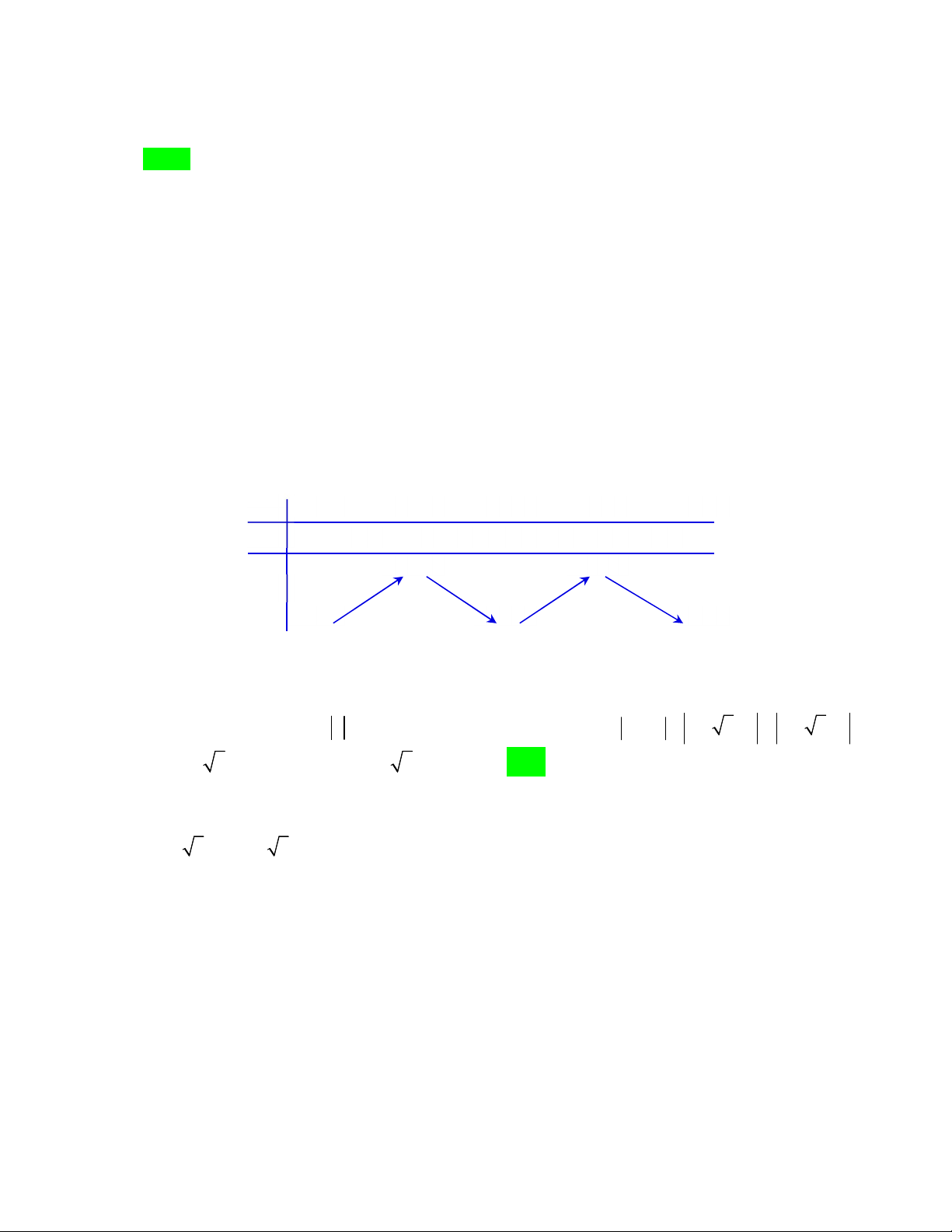
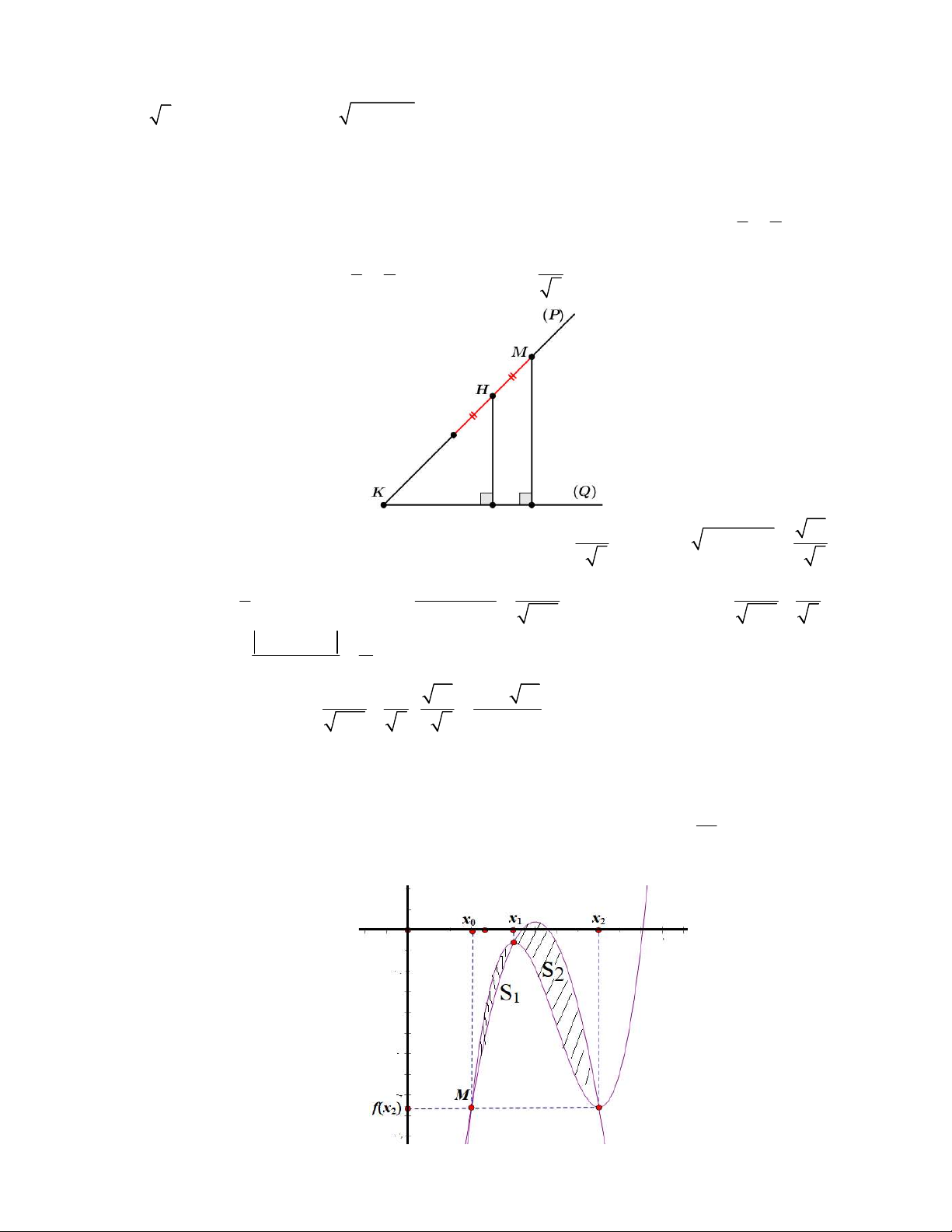
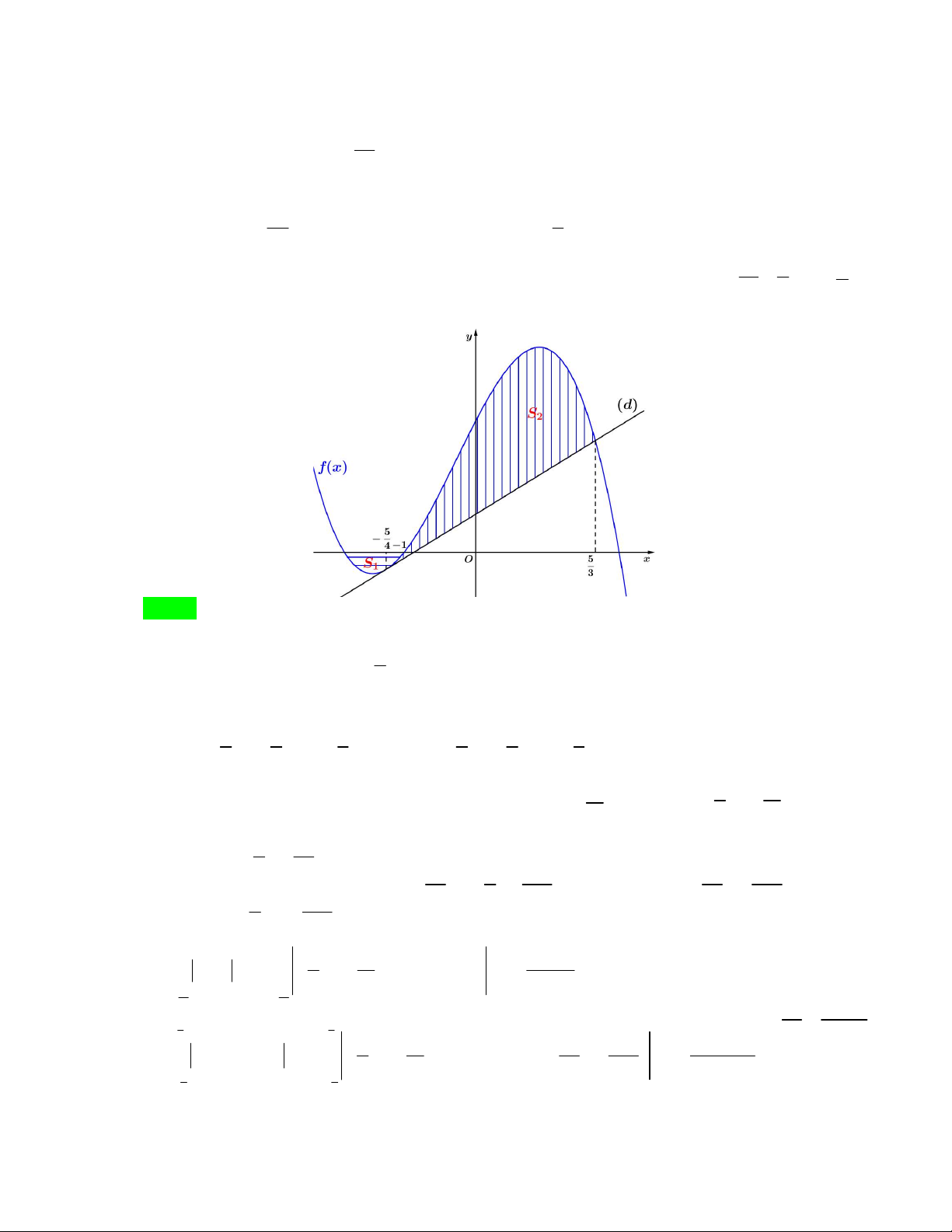
Câu 50. Cho hàm số bậc ba y  f  x có đồ thị là đường cong như hình bên. Biết hàm số f  x đạt cực trị
tại hai điểm x , x thỏa mãn x  x  2 và f x  f x  0. Gọi S , S là diện tích hình phẳng được gạch 1   2 1 2 2 1 1 2 như hình bên và S
S là diện tích phần tô đậm. Tính tỉ số 2 ? 3 S3 A. 1 B. 3 C. 2 D. 3 4 8 16 16 Lời giải Cách 1:
Ta thực hiện tịnh tiến điểm gốc tọa độ vào trùng với tọa độ trung điểm hai hoành độ x , x . Khi đó diện 1 2  y  f x  y    gx
tích của các phần cần tính không thay đổi và hàm số   y hx     y   h x 1  
 Ta thấy S và S trở thành S ' và S ' tương ứng không thay đổi giá trị. 1 2 1 2
 Ta thấy y  gx là hàm lẻ  y  gx  3
ax  bx a  0 có hai điểm cực trị x ' và x ' thỏa mãn 1 2 x '  x ' . 2 1 x '  1 Mặt khác x '  x  ' 2   1 . 2 1 x '   1 2  Ta có g x  2 '
3ax  b có nghiệm x '  1 và x ' 1 . 1 2
 g'1  0 b  3a. gx  3
ax 3ax  Tại x '  1 thì g1  2a. 1 0 0 0 0   a 3a 5a 3a S ' g x ax 3ax dx  S '  2a   3 g x dx 2a ax 3ax dx 2              1
    3         4 2 2  4 1 1 1 1
Do đường thẳng h x cắt g x tại ba điểm trong đó có điểm uốn nên suy ra hai hoành độ còn lại lần lượt 1  
là 2x '  2 và 2x '  2 với g1  g2 2a , suy ra h x  ax a  0 1  1 2 2 2 2 Suy ra:  S '  h x g x dx ax ax 3ax dx ax 4ax dx 4a 3
 1       3     3       0 0 0 S S  3a 1 3 Vậy tỉ số 2 2   .  . Chọn đáp án D. S S  4 4a 16 3 3
Cách 2: Chọn y  g  x 3
 x 3x, y  h x  x để tính toán cho gọn 1  
ĐỀ THI THỬ CHUYÊN KHTN – HÀ NỘI LẦN 1
Câu 42. Cho số phức z thỏa mãn z  1. Tìm giá trị lớn nhất của biểu thức P  z 1  z  i A. 8  4 2 B. 2 C. 2 2  2 D. 2 2 Lời giải
Đặt z  a  bi,a,b  Rvà gọi M là điểm biểu diễn của số phức z thỏa mãn z 1.
Khi đó điểm M chạy trên đường tròn tâm O , bán kính R  1 . Đặt A1;0, B0;  1 , ta suy ra  1 1 
P  z 1  z  i  MA  MB . Gọi C  ; 
 là trung điểm của AB . Theo công thức đường trung tuyến ta  2 2  2 MA  MB  AB 2  2 2  2 có: MC   2 2 2 MA  MB  2 2 2  4MC  AB  4MC  2 4 Suy ra: P   2 2 MA  MB  2 2
 4MC  2 . Mà theo hình dưới thì MC max khi M  M với 0 2 2  2  M C  CO  R  1 nên suy ra P  41
  2  2 2  2 . Chọn đáp án C. 0 2  2   
Câu 45. Cho hàm số y  f x là hàm đa thức bậc bốn. Biết hàm số y  f  x có đồ thị C  như hình vẽ và
diện tích hình phẳng giới hạn bởi đồ thị C  và trục hoành bằng 9. Gọi M và m lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số y  f x trên đoạn 3;2 . Khi đó, giá trị M  m bằng A. 16 B. 32 C. 27 D. 5 3 3 3 3 Lời giải
Đầu tiên, từ đồ thị trên ta dễ dàng suy ra: f  x  a x  2 x   3 1
2  ax  3ax  2a với a  0 ax 3ax
Khi đó, ta có: f x  f 
 xdx  ax 3ax 2a 4 2 3 dx    2ax  C 4 2
Mà diện tích hình phẳng giới hạn bởi đồ thị C  và trục hoành bằng 9 nên ta suy ra: 1 
          a 3a  f x dx f f   
 a  C   a  a  a  C 4 9 1 2 9 2 4 6 4  9  a    .  4 2  3 2  4 x 8 Khi đó ta suy ra: f x 2 
 2x  x  C , ta có bảng biến thiên trên đoạn 3;2như sau: 3 3 8  8  32 Với M   C, m  8
  C ta suy ra M  m   C   8   C    . Chọn đáp án B. 3  3  3
Câu 46. Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng lần lượt có phương trình là: x 1 y  2 z x  2 y 1 z 1 d :   , d :  
và mặt phẳng P : x  y  2z  5  0 . Lập phương trình đường 1 2 1 2 1 2 1 1
thẳng song song với mặt phẳng P và cắt d , d lần lượt tại ,
A B sao cho độ dài AB đạt giá trị nhỏ nhất ? 1 2             A. x 1 y 2 z 2   B. x 1 y 2 z 2   C. x 1 y 2 z 2   D. x 1 y 2 z 2   1  1 1 1 1 1 1 1 1  1 1 1 Lời giải A  d  d A 1   ; a 2   2a;a  1    Đầu tiên ta có:   
 AB  3 2b  a;3 b  2 ; a 1 b  a (1) B  d  d  B 2  2 ; b 1 ; b 1 b 2    
Mặt phẳng P : x  y  2z  5  0 có vector pháp tuyến n  1;1; 2
  cùng với AB  Pnên ta có:   A .
B n  0  3 2b  a  3 b  2a  21 b  a  0  a  b  4 (2)
Từ (1) và (2) ta suy ra: AB    b  a2    b  a2    b  a2  b  b   b  2 2 2 3 2 3 2 1 2 8 35 2 2  27  27 
Khi đó dấu bằng xảy ra khi và chỉ khi b  2
  a  2  AB   3  ; 3  ; 3    k 1;1;  1   
Như vậy phương trình đường thẳng x 1 y 2 z 2 AB là   . Chọn đáp án B. 1 1 1
Câu 47. Trong không gian với hệ tọa độ Oxyz , cho điểm A1;1;3 và hai đường thẳng lần lượt có phương x  4 y  2 z 1 x  2 y 1 z 1 trình là: d :   , d :  
. Viết phương trình đường thẳng d đi qua điểm A , 1 2 1 4 2  1 1  1
vuông góc với đường thẳng d và cắt đường thẳng d 1 2             A. x 1 y 1 z 3   B. x 1 y 1 z 3   C. x 1 y 1 z 3   D. x 1 y 1 z 3   2 1 1 2 1 1 2 1 1 2 1 1 Lời giải  
Đầu tiên, ta gọi B  d  d tức B  d , khi đó ta có: B 2  t; 1
  t;1 t   AB  1 t; t  ;t  2 khi đó AB 2 2 
chính là vector chỉ phương của đường thẳng d . Mà d  d với vector chỉ phương d là u  1;4; 2   nên 1 1 
suy ra: 1.1 t  4t  2t  2  0  t 1 AB  2; 1  ;  1 .   
Vậy phương trình đường thẳng x y z d là: 1 1 3   . Chọn đáp án D. 2 1 1 z  i
Câu 48. Biết rằng có đúng một số phức z thỏa mãn z  2i  z  2  4i và
là số thuần ảo. Tính tổng z  i
phần thực và phần ảo của z A. 4 B. 4 C. 1 D. 1 Lời giải
Đặt z  a  bi,a,b  R. Khi đó ta có:
z  i  z   i  a  b  2  a  2  b  2 2 2 2 4 2 2 4  b  a  4 (1) z  i
a b 1ia b 1i a b 2 2 1  2a b   1 i  
là số thuần ảo, khi đó a  b  2 2 1  1 (2) z  i a  b  2 1 a  b  2 2 2 1 3
Thế (1) vào (2) ta có: a  a  32 2
 a   . Vậy tổng cần tìm là a  b  2a  4  1. Chọn đáp án D. 2
Câu 49. Cho hàm số f  x có đạo hàm trên R và thỏa mãn f  3 x  x 2
3  x  2 với mọi số thực x . Từ đó hãy 4 tính 2 x f   xdx 0 A. 27 B. 219 C. 357 D. 27 4 18 4 8 Lời giải
Đầu tiên, ta thế x  1 vào phương trình f  3 x  x 2
3  x  2 thu được f 4  3 4 2 u   x du  2xdx 
Ta gọi tích phân cần tìm là 2 I  x f   xdx . Đặt    dv  f   xdx v  f  x 0 4 4 4 Suy ra: 2 I  x f  
xdx 16 f 4 2xf  xdx  48 2xf  xdx 0 0 0 3
x  t  3t  dx   2 3t  3 4 1 dt Đặt   2xf  xdx  2   2
3t  3 3t  3t f  3t  3tdt t  : 0 1 0 0 1  165 27 2 165 2
3t  3 3t  3t 2t  2dt   . Vậy I  48   . Chọn đáp án A. 4 4 4 0
Câu 50. Có bao nhiêu số nguyên dương a để phương trình sau đây có ít nhất một nghiệm thực.   log log a x log 1 x a  a  2x  2 A. 8 B. 1 C. 0 D. 9 Lời giải Điều kiện ban đầu: a
x  0 của phương trình  x  log log log 1 x a  a  2x  2 (1)
Đầu tiên ta xét hai trường hợp cơ bản nhất như sau:
-Trường hợp 1: Nếu a  1 thì (1) trở thành: 2  2x  2  x  2 (thỏa mãn)
-Trường hợp 2: Nếu a  1 thì ta luôn có: log a  0 . Khi đó ta đặt  log  0   10t t a a t
Phương trình (1) trở thành:  t logx    t logx t 10 1 10  2  2   t   1 t x x  x  2x  2 (2) t x  y 1  0 Đặt t y  x 1  
. Khi ấy phương trình (2) trở thành: t  y  y 1  2x  2 y  1 t x  y 1 Từ đó ta có hệ sau: 
. Trừ hai phương trình theo vế ta thu được phương trình mới tương t y  2x  y 1 ứng là: t t   2  2 t   2 t x y y x x x  y  2 y (3)
-Nếu x  y  0 thì ta luôn có VT 3  VP 3 . Tương tự nếu y  x  0 thì ta luôn có VP 3  VT 3 x  y log x  t   1
Như vậy, để dấu bằng phương trình (3) xảy ra thì ta phải có:   x  x 1 t  t  y  x 1 log  x log x   1 Do 
x  2  0  log  x  
1  log x nên ta suy ra: log a a  t    a    a log x 1 10 2;9
Vậy có tất cả 9 giá trị nguyên dương a thỏa mãn. Chọn đáp án D.
ĐỀ THI THỬ CÂU LẠC BỘ TOÁN LIM ++
Câu 42. Tính thể tích của hình trụ bị cắt bởi hai mặt phẳng song song (hình vẽ) dưới đây. Biết rằng ABCD
là hình thoi cạnh bằng 4 và  ABC  60 A. 12 B. 16 C. 8 D. 6 Lời giải
Đầu tiên ta có hình vẽ như sau:
Ta kẻ AE  BC,CF  AD . Khi đó ta gọi V là thể tích giới hạn bởi đường tròn đường kính AE , elip trục 1
lớn AB và đường cao BE , V là thể tích giới hạn bởi đường tròn đường kính CF , elip trục lớn CD và 2
đường cao , và V là thể tích khối trụ có đường tròn đáy đường kính AE và đường sinh AF . BC AB
AE  CF  ABsin 60  2 3; AF  CE    2 (do ABC đều). 2 2 V  V  V V Nhận thấy rằng 1 2  nên suy ra V  V 
, lúc này thể tích của khối tròn xoay cần tìm là: V  V  1 2 2 1 2 2  CF 
V  V V V  2V  2 AF.
 2.2.3 12 . Chọn đáp án A ct 1 2    2 
Câu 43. Xét trên tập số phức phương trình: 2 2
z  2mz  m  2m  4  0 (với m là tham số thực). Có bao
nhiêu giá trị thực của m để phương trình trên có hai nghiệm phân biệt z ; z sao cho 2 2 z  z 10 ? 1 2 1 2 A. 1 B. 2 C. 3 D. 4 Lời giải Ta có 2
  2m  2m  4 . Phương trình có hai nghiệm phân biệt    0  m  1;  2 . Nên để phương
trình đó có hai nghiệm phân biệt z , z thỏa mãn 2 2 z  z 10 Khi đó ta có: 1 2 1 2 
 z  z 2  z  z 2  4z z  8 2 m  m  2 1 2 1 2 1 2    . Từ đó ta suy ra: 20  2   2 2 z  z  2 2 2 2 2 2
 z  z  z  z  4m  8 m  m  2  m  2 m  m  2  5 1 2 1 2 1 2 2 m  m  2  0  2  1 2 7  3  m  2m  4  5 m  1   2 7 1 2 7     3  S   ;1;  2 m m 2 0       3 3     m 1   2
m  2m  4  5
Vậy có duy nhất 3 giá trị thực m thỏa mãn yêu cầu đề bài. Chọn đáp án C.
Câu 44. Có 6 vị khách tham gia bữa tiệc trong đó có Phượng và Hòa, cần phải sắp xếp họ ngồi quanh một
bàn tròn có 6 ghế phân biệt. Có bao nhiêu cách xếp để Phượng và Hòa không ngồi cạnh nhau ? A. 600 B. 280 C. 576 D. 432 Lời giải
Số cách để xếp 6 người (trong đó có Phượng và Hòa) vào 1 bàn tròn ghế bất kì là: 6! (cách) (do 6 ghế đã
phân biệt nên cách xếp xem như tương tự với xếp 1 hàng ngang).
Ta sẽ giải phần bù tức tìm số cách xếp để Phượng và Hòa ngồi cạnh nhau
Coi Phượng và Hòa là một phần tử ngồi cạnh nhau, 2 bạn tự hoán đổi nhau trong lúc xếp nên có 2! cách,
như vậy có tất cả 6 cách để xếp phần tử này vào 6 ghế cố định.
Còn 4 vị trí còn lại cho 4 người, có tất cả 4! cách.
Suy ra số cách xếp để Phượng và Hòa ngồi cạnh nhau là 2.6.4! cách
Suy ra số cách xếp cần tìm là 6! 2.6.4!  432 cách. Chọn đáp án D.
Câu 45. Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a tồn tại ít nhất 6 số nguyên b 1  2;12 để bất phương trình x 1 a  xe    x xb 1 1 1 ln  be     0   có nghiệm A. 1210 B. 890 C. 1211 D. 891 Lời giải
Ta có bất phương trình tương đương với: x 1  xb 1 1 xe 1 ln x     be  x 1 a 1   xe 1 ln x x b 1   1   be  0  a       0 x  a e  x 1 ln b x   be  0 (1) x 1  x 1    e e     x x 1 1 1
Tiếp theo ta xét hàm số:    1 x y f x  e
 x 1 ln x có f x 1
 e  ln x ; f  x 1  e    x 1 x e  x 1 1 x 1 Ta nhận thấy với x   0 thì x 1 e   x nên suy ra  tức f  x 1  e   0, x   0 x 1 e  x x
Khi đó suy ra f  x là hàm lõm và f  x  0 có nhiều nhất một cực trị trên 0;  1
Khi đó ta suy ra x  x  0.08 với f  x  2,79. Với lim           1 x e x 1 ln x ; e lim  1 x e x 1 ln x 2 0  0 x0 x 1 
Từ đó ta có bảng biến thiên như sau:
Từ bảng biến thiên trên, với min f  x  f   1  2 ta suy ra (1)  2 b   0  2 b a be a  b  e 0; 1
Như vậy với b  0 thì hàm số   b y g b be   
luôn đồng biến, tức 2a có nghĩa, mà theo đề bài ứng với
mỗi a tồn tại ít nhất 6 số nguyên b 1
 2;12 nên suy ra b12; 6
  kéo theo h6  0 với   2 b h x a be   , tương đương 6 6 2 6 0 3 a a e a e        1 a 1210
Vậy có tất cả 1210 số nguyên dương a thỏa mãn yêu cầu bài toán. Chọn đáp án A.
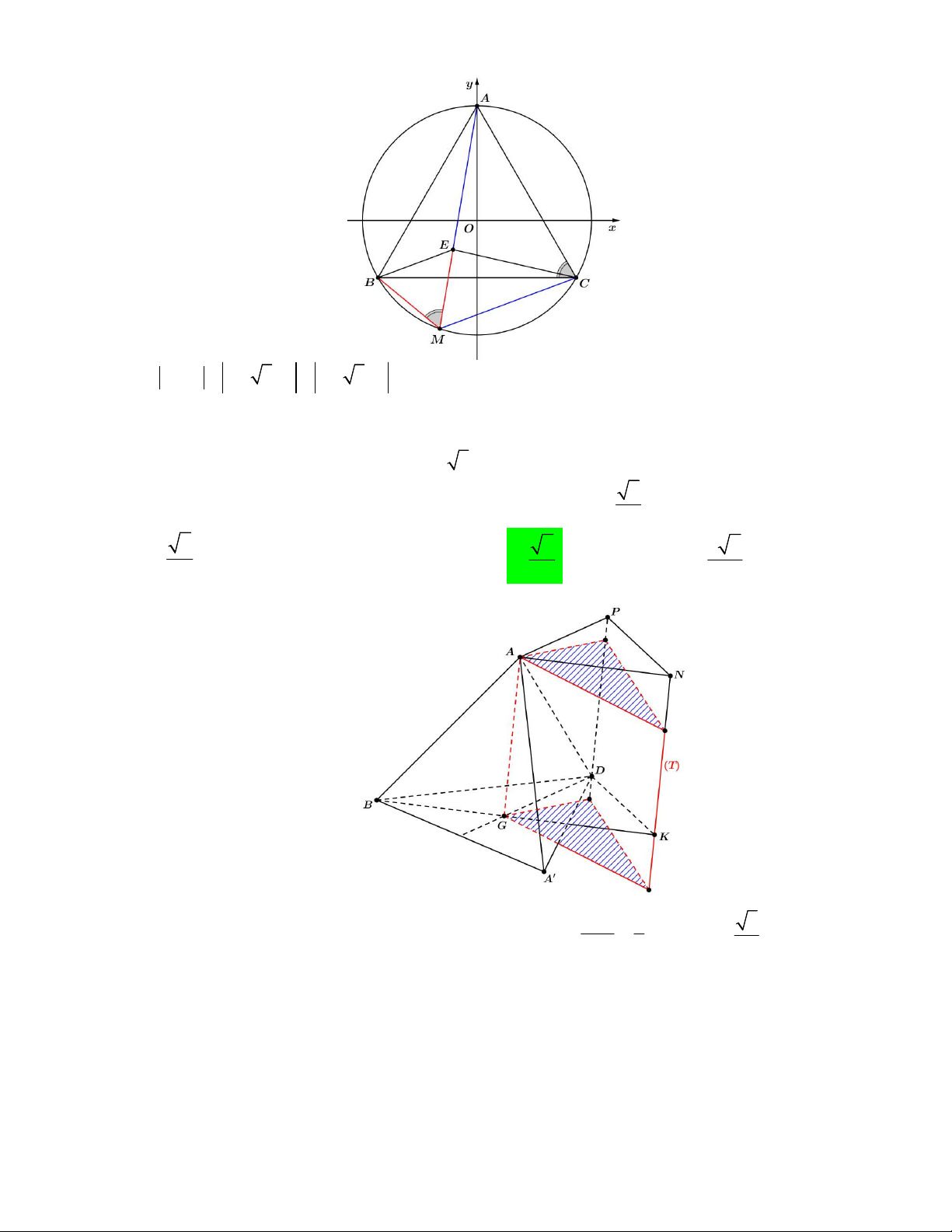
Câu 46. Cho hàm số    3 2 y
f x  x  bx  cx  d có hai điểm cực trị x , x thỏa mãn x  x  2 1 2 2 1
f x 3 f x  0 và đồ thị y  f  x luôn đi qua điểm M x 1; f x . Gọi y  g  x là hàm bậc 2 có đồ 1  2 1   2
thị đi qua 2 điểm cực trị của f x và đi qua M . Tính diện tích hình phẳng giới hạn bởi hai đồ thị f  x, g  x 19 25 37 23 A. B. C. D. 4 6 12 4 Lời giải
Gọi x là hoành độ trung điểm giữa hai hoành độ x , x tức hoành độ điểm uốn của đồ thị . y  f x . 0 1 2 1
Đầu tiên, ta dễ dàng nhận ra x , x , x và x , x , x lần lượt là các cấp số cộng có công sai lần lượt là 1 và M 1 2 1 0 2 2
Khi đó ta xem như x  x 1 1 x  2, x  3, x  4 và diện tích hình phẳng giới hạn bởi hai đồ thị M 1 1 0 2  f   3 18  2b  0
f  x, g  x không thay đổi. Từ đó ta có hệ sau:   f x 3 2 (1)      x  9x  24x  d f 2  12  4b  c  0
Ta lại có: f 2  3 f  
1  0  20  d  3d 16  d  1  4 . Như vậy ta suy ra f  x 3 2
 x  9x  24x 14 . Tiếp theo, ta đặt: g x 2
 ax  dx  e a  0 , khi đó ta có hệ phương trình sau: g   1  a  d  e  3 a  2   
g 2  4a  2d  e  9  b   10  g  x 2  2  x 10x  6 . (2)  
g 4 16a  4d  e  3 c  6    4 37
Từ (1) và (2), ta suy ra diện tích cần tìm là: S  f  x  g  x dx   . Chọn đáp án C. 12 1
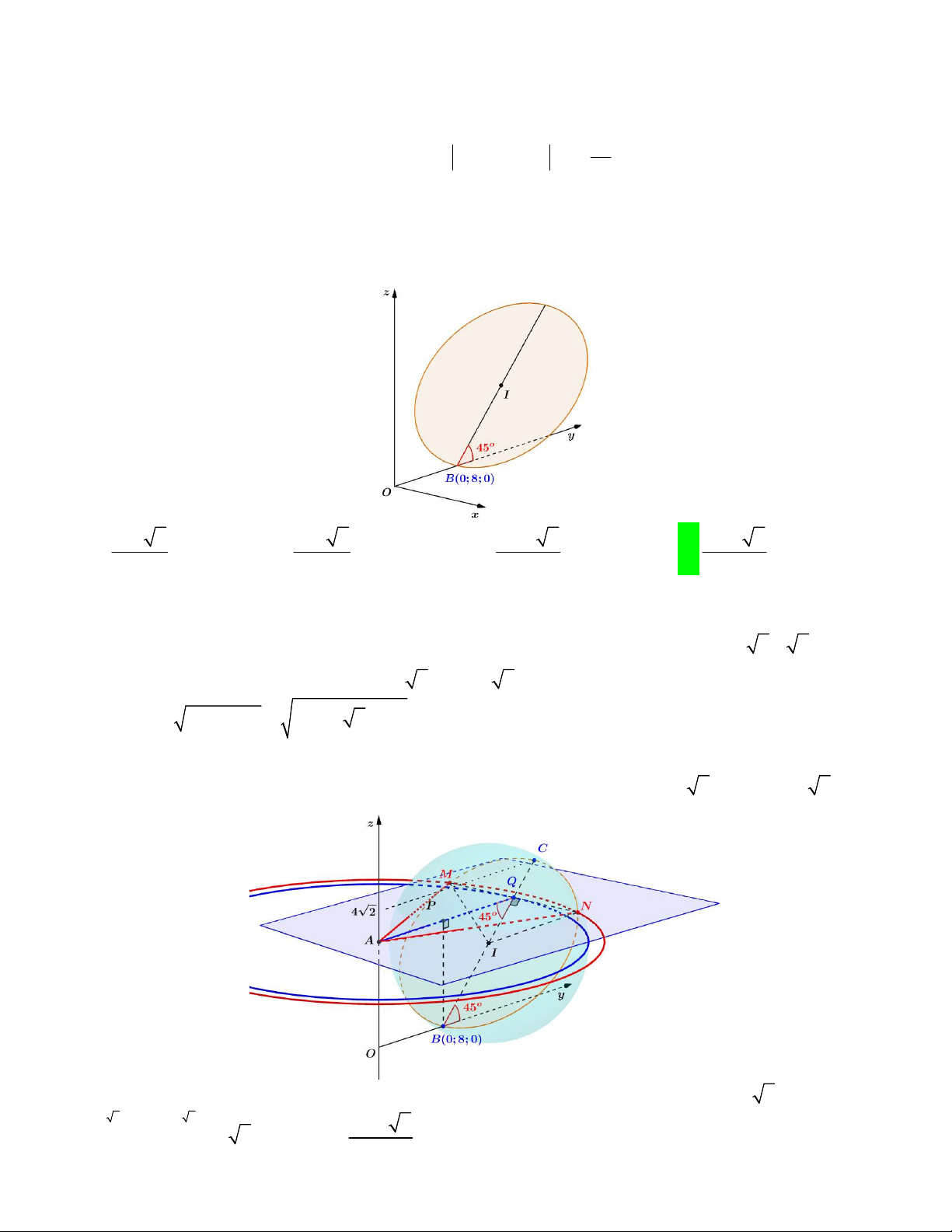
Câu 47. Tính thể tích vật thể khi quay hình tròn I  , đường kính AB  2R  8 quanh trục Oz . Biết hình
tròn tiếp xúc với Oy tại B 0;8;0 , mặt Oyz chứa tâm I vuông góc với mặt phẳng chứa hình tròn. Hình
tròn nghiêng 1 góc 45 so với đáy Oxy (xem hình vẽ). 32 2 64 2 160 2 128 2 A. B. C. D. 3 3 3 3 Lời giải
Đầu tiên ta có hình vẽ như sau: (Xét mặt phẳng cắt hình tròn I  và vuông góc với trục Oz )
Do hình tròn nghiêng 1 góc 45 so với đáy Oxy nên dễ dàng tính được tâm I 0;8  2 2;2 2
Đặt OA  PB  z , khi đó IQ  BQ  IB  PB 2  IB  z 2  4 . Suy ra: QN  IN  IQ   z  2 2 2 16
2 4 . Do dùng mặt cắt vuông góc với Oz và hình tròn ta thu được
chính là đoạn MN ta suy ra thiết diện mặt cắt của khối tròn xoay chính là hình vành khăn tâm A . 2
Tức ta có diện tích thiết diện cần tìm là: S   2 2 AN AQ  2 QN   z           .    2 16 2 4 8 2z  2z  
Từ đó ta suy ra thể tích khối tròn xoay cần tìm với thiết diện S chạy từ cao độ 0 đến 4 2 là: 4 2 4 2  V  S dx     128 2 2 8 2z  2z dx   . Chọn đáp án D. 0  3 0 0
Câu 48. Trong không gian Oxyz cho các điểm A 2;0;0, B 2;0;0,C 4;1;2 và D1; 2  ;4 . Điểm M
thay đổi thỏa mãn MA  MB  2 3 . Giá trị nhỏ nhất của biểu thức 2 2
T  2MC  MD thuộc khoảng nào dưới đây ? A.  ;  40 B. 40;4  1 C. 41;42 D. 42; Lời giải
Cách 1: Phương pháp hình học
Gọi tọa độ điểm M là M  ; x y; z , khi đó ta có:
Xét riêng trên mặt phẳng Oxy ta nhận thấy quỹ tích điểm M để thỏa đẳng thức MA  MB  2 3 là một
elip chính tắc có tiêu cự là AB  2c  2 2 và độ dài trục lớn là 2a  2 3 , từ đó suy ra hệ số b 1, tức 2 x phương trình elip là: 2  y 1 (1). 3 2 x
Tương tự xét riêng trên mặt phẳng Oxz ta cũng thu được phương trình: 2  z 1 (2). 3
Từ (1) và (2) ta sẽ thu được quỹ tích chính thức của điểm M như hình dưới đây.    2C  D
Gọi I là điểm thỏa 2IC  ID  0 từ đó suy ra I 
 3;0;0 (tâm tỉ cự) 3
Như vậy biểu thức T min khi MI min, mà I Ox nên ta suy ra giá trị nhỏ nhất của MI là: 2a MI  OM   3  3 với M  M 3;0;0 . 0   min 0 2 Vậy ta suy ra T   2 2 2MC  MD
 40.7 40;41 . Chọn đáp án B. min    min
Cách 2: Phương pháp đại số Ta có: 2 2 2 MA  MB
12  MA  MB2  MA  2M .
A MB  MB  2MA  MB   MA  MB2 2 2 2 2  2 2 2 MA  MB     MA MB2 MA   x 22 2 2 2  y  z Tiếp theo ta đặt M  ;
x y; z , khi đó ta có:  . Từ đó ta suy ra: MB   x 22 2 2 2  y  z 2 2 MA  MB   2 2 2 x  y  z   2 2 2
2 ; MB  MA  4 2x . Thế vào phương trình trên ta suy ra được: x
12  4x  y  z  2 2 32 2 2 2 2 2 2 2 2 2 2 2 
 3  x  y  z  2  x  x  3y  3z  3 . 12 3 2 x Như vậy điểm M  ;
x y; z dao động trên đường cong khép kín T  2 2 2 2 2
: x  3y  3z  3  y  z  1 3
T  2MC  MD  2 x  42   y  2
1   z  22  x  2
1   y  22   z  42 2 2  x   3x  y  z  2 2 2 2 2 2
18x  63  3 x 1  18x  63  2x 18x  66  3  Mà 2 2 2
x  3y  3z  3 nên suy ra x   3; 3   
 . Xét hàm số y  f  x 2  2x 18x  66 trên 3; 3  
Do f x  4x 18  0, x    3; 3 
 nên T  f  3  72 18 3  40,8240;4  1 . Chọn đáp án B.
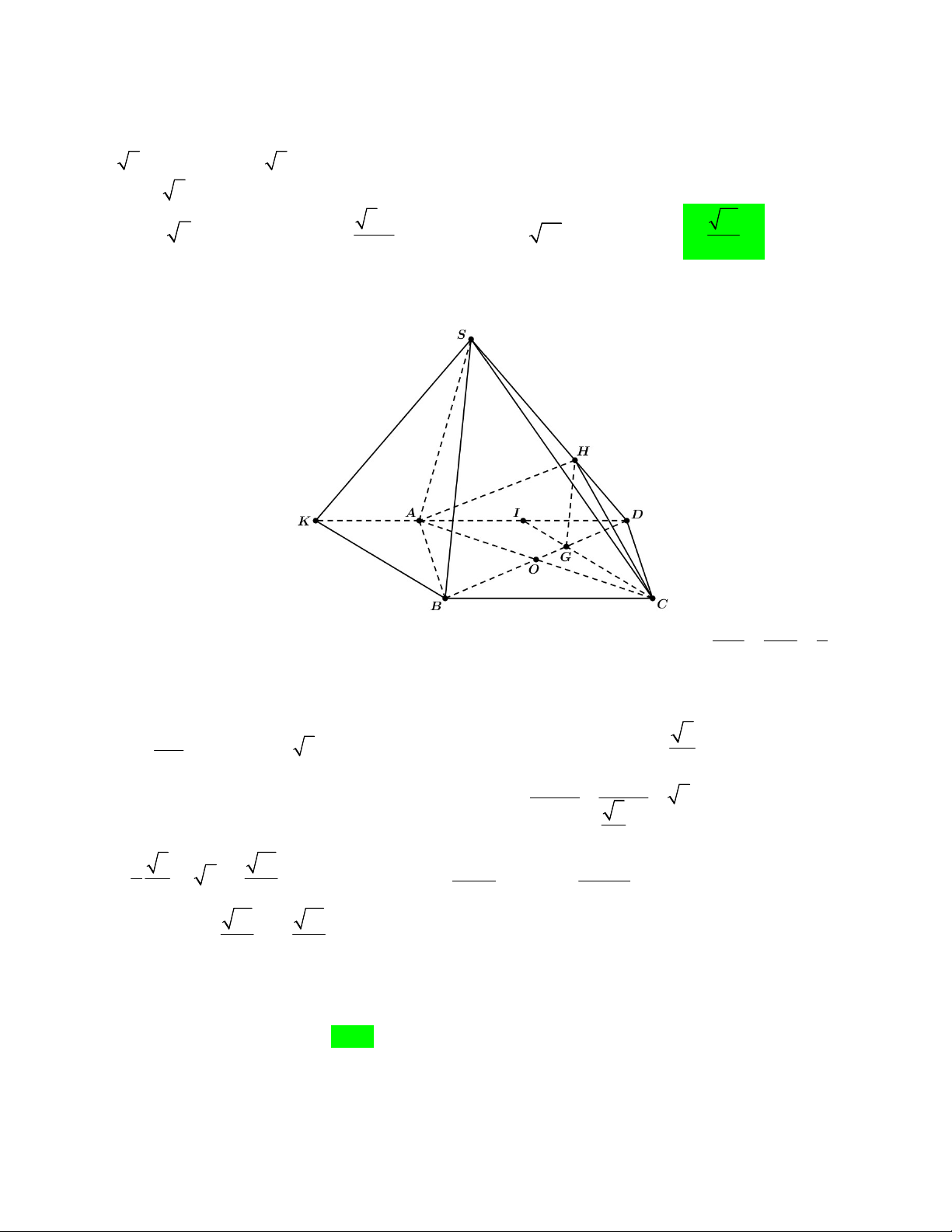
Câu 49. Cho hình chóp S.ABC có SA vuông góc với đáy, các cạnh AB  a, AC  2a và góc  BAC  120 . Gọi
M , N lần lượt là hình chiếu của A lên các cạnh SB, SC . Gọi  là góc giữa hai mặt phẳng  AMN  và  ABC 3 sao cho cos 
. Tính cosin góc giữa hai mặt phẳng SAB và SBC  ? 7 7 3 10 6 A. B. C. D. 13 13 13 13 Lời giải
Đầu tiên ta có hình vẽ như sau: (chuẩn hóa a 1).
Dựng đường kính AD của đường tròn ngoại tiếp tam giác ABC , khi đó ta có:  ABD   ACD  90 . BD   SAB AM  BD AM  SB AM   SBD
Mà SA   ABC nên suy ra    mà  nên  . C  D   SAC AN  CD AN  SC AN   SCD SD   AMN  2 AD Suy ra 
tức  AMN ; ABC   SD;SA   
ASD   , suy ra: tan   (1). SA   ABC 3 SA BC 2 7 3 Mà : 2 2 BC  AB  AC  2A .
B AC cos120  7; AD  2R   nên SA  AD  7 . sin120 3 2 1 21 1 7 Khi đó ta có: V  S . A A . B AC.sin120  ; S  S . A AB  ; SB  2 2; SC  11 . S.ABC 6 6 SAB 2 2 S    SAB SBC S  BC      13; ;  6 7 Suy ra:   sin   cos  . Chọn đáp án A. 2sinS .S 21 S  AB S  BC 13 13 V    SABC  3SB 6
Câu 50. Cho số phức z thỏa mãn tồn tại các số phức w , w sao cho w  w w  w  0 trong đó ta có 1 1   2 2  1 2 z z w  ; w 
. Ngoài ra z  4  4i  m (với m là tham số thực). Có bao nhiêu giá trị thực của tham 1 2 2 2 z  4 z 16
số m sao cho tồn tại đúng 5 số phức z như vậy ? A. 2 B. 3 C. 4 D. Vô số. Lời giải 2 z  4  0 z  4
Đầu tiên ta có điều kiện ban đầu là:    . Tiếp theo ta có: 2 z 16  0 z  2i    w  w w  w  w w 1 1  0  
như vậy ta suy ra: với z  a  bi, a
 ,b  R ta có hệ sau: 1 1 2 2 w  w  2 2  b  0 z z     2 2  2  z  4  z .z  4z  z.z  4 z  z  z  4 z z  2 2 4    2 2 0 a  b  4         2  z z   
z .z 16z  z.z 16z  2 2  z  
z z a 0 16 0 2 2   2 2 z 16  z 16 a  b  16
Chuyển về hệ trục tọa độ Oxy ta có được hình vẽ như sau: z  4 Do  nên ta loại các điểm , A B,C đi (như hình vẽ). z  2i
Phương trình z  4  4i  m biểu diễn số phức z thuộc đường tròn C tâm I 4;4 có bán kính R  m
Với đúng 5 số phức z thỏa mãn ta nhận thấy qua hình vẽ đường tròn C qua tiếp xúc ngoài với đường tròn 2 2
x  y  16 , đi qua 0;2 và đi qua 0; 2   .
Với ba đường tròn thỏa mãn ta suy ra có 3 giá trị nguyên m thỏa mãn. Chọn đáp án B.
ĐỀ THI THỬ CHUYÊN BIÊN HÒA – HÀ NAM
Câu 39. Cho hàm số y  f x là hàm đa thức và có đồ thị f x, f  x như hình vẽ bên dưới. Có bao nhiêu
giá trị nguyên của tham số m để giá trị lớn nhất của hàm số dưới đây trên đoạn  2  ;  3 không vượt quá 3 1 1 x 4044: g x  f  x 5 4  x  x   2 3  m  m   2 1 x  4x  2022 . 5 2 3 A. 32 B. 30 C. 31 D. 29 . Lời giải
Ta có: gx  f x 4 3  x  x   2  m  2 2 3 x  2m   1 x  4   f    x   
  x  x2  mx  2  x   x  2 2 2 2 1
1 . Nhận thấy khi tịnh tiến thêm 2 đơn vị theo chiều dương
Oy của đồ thị f  x thì đồ thị f  x  2 luôn dương trên đoạn  2  ;  3
Mà x  x2  mx  2  x  x  2 2 2 1 1  0, x   2  ; 
3 nên suy ra g x  0, x   2  ;  3 tức hàm số g x
luôn đồng biến trên đoạn  2  ;  3 20601 1687 20601
Khi đó ta có được max g x  g 3  f 3 2 2   9m  9m    9m  9m  4044  2  ;  3 10 200 10 Suy ra: 14.32 15.32 m m      m 1  4;1 
5 tức có 30 giá trị nguyên m thỏa. Chọn đáp án B. x 1 y  2 z x  2 y 1 z 1
Câu 41. Trong không gian Oxyz cho hai đường thẳng d :   , d :   và mặt 1 2 1 2 1 2 1 1
phẳng P : x  y  2z  5  0 . Tìm phương trình đường thẳng d song song với mặt phẳng P và cắt . d ,d 1 2
. lần lượt tại A và B sao cho AB  29 và điểm A có hoành độ dương. x 1 y  2 z  2 x  2 y  4 z  3 x 1 y  2 z  2 x 1 y  2 z  2 A.   B.   C.   D.   . 2  4 3 2 4 3 2 4 3  2 4 3 Lời giải A  1 ; a 2  2 ; a a Đầu tiên ta có ,
A B lần lượt là các điểm thuộc d , d nên ta suy ra: 1 2  B  2  2 ; b 1 ; b 1 b    
 AB  a  2b  3; 2
 a  b  3;1 a  bmà d  P nên ta suy ra AB  n với n  1;1; 2   là vector pháp
tuyến của P . Khi đó: a  2b  3   2
 a  b  3  21 a  b  0  a  b  4   b  a  4 (1).
Ta có: AB  a  b  2   a  b  2    a  b2  a  2  a  2 2 2 3 2 3 1 5
1  9  29 thế từ (1). a  1 A0;0;  1 A  2;4;3 Giải phương trình suy ra x 0 A       R . Chọn đáp án B. a  3 A  2;4;3 B  0;0;0
Câu 42. Tính tổng các nghiệm nguyên thuộc  5
 ;10 của bất phương trình sau đây: 2 x  x  2 x  x   2 2 3 6 6  7x  29x  34 A. 54 B. 40 C. 55 D. 41 . Lời giải
Bất phương trình tương đương với: 2xx2  2 x  x     2 2 12 24 24 7x  29x  34 (1) Ta nhận thấy:  2 x  x   2x  x  2  x  x    2 12 24 24 7 29 34 5 5
10 5 x  x  2 nên (1) trở thành: 2 2 12 x 24x24     x  x   7x 29x 34 2   2 5 5 2 12 24 24 2 7x  29x  34 t t t t Xét hàm số y  f t 5  t.2 có f t 5 5
 2  2 ln 2  0 với mọi số thực t nên suy ra hàm số f t luôn 5 x  1 đồng biến trên tức 2 2 2
12x  24x  24  7x  29x  34  x  x  2  0   x  2 Mà x  5  ;10 nên x5; 2
 1;10 . Suy ra tổng nghiệm nguyên của bất phương trình (1) là: 2  10
S   X   X  41. Chọn đáp án D. k 5 k 1  1
Câu 44. Cho hàm số y  f  x 4 3 2
 ax  x  x  bx  2 và hàm số y  g  x 3 2
 cx  dx  2x (với a, , b c, d  R ) 3
là các hàm số có đồ thị như hình vẽ bên dưới. Gọi S , S là diện tích hình phẳng tô màu trong hình vẽ, biết 1 2 97 S  . Tính S 1 60 2 143 133 153 163 A. B. C. D. . 60 60 60 60 Lời giải 4 3   x x g  2  g   1  0  f  x 2    x  2 Ta nhận thấy 
, Giải 2 hệ ta lần lượt ra được:  4 3  f 
 2  f   1  0 g   x 3 2  x  x  2x 1 1 4 3  x 2x  133
Suy ra: S   f x gx 2 dx     2x  2x  2dx  . Chọn đáp án B. 2  4 3  60 0 0
Câu 45. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  x  2   y  2  z  2 ( ) : 1 2 3  48 và đường x 1 y  2 z  3 thẳng d :   . Điểm M ( ; a ;
b c),(a  0) nằm trên đường thẳng d sao cho từ M kẻ được ba 1 1 2 tiếp tuyến M ,
A MB, MC đến mặt cầu (S),( ,
A B,C là các tiếp điểm) và  0 AMB   0 BMC   0 60 , 90 ,CMA  120 . Tính Q  a  b  c . A. Q  6  4 2 B. Q  10  4 2 C. Q  9  4 2 D. Q  9  4 2 . Lời giải
Mặt cầu S  có tâm I  1
 ;2;3 , bán kính R  4 3 .
Gọi C là đường tròn giao tuyến của mặt phẳng  ABC và mặt cầu S  .
Đặt MA  MB  MC  x khi đó AB  x, BC  x 2,CA  x 3 do đó A
 BC vuông tại B nên trung điểm H
của AC là tâm đường tròn C và H , I, M thẳng hàng. Vì  0 AMC  120 nên A
 IC đều do đó x 3  R  x  AM  4 suy ra IM  2AM  2x  8 . Lại có M  d nên M  1
  t;2  t;3 2t,(t 1) . 2 t  4 Mà IM  8 nên 2 2
t  t   2t  64   M 
3;6;34 2 abc 64 2 . Chọn đáp án A. t  4
Câu 47. Xét hai số phức z , z thỏa mãn  z  2  i 2  2 3i  z  z
3  i và z  i  z 1 2i . Giá 1    1 1  1 2 2 2
trị nhỏ nhất của z  z bằng 1 2 A. 7 B. 2 6 C. 34 D. 2 2 . 5 Lời giải
Đặt z  a  bi ; z  c  di, a,b,c, d  R . Khi đó ta có: 1 2     a 
z  2  i2  2 3i  z  z  3 i  2 z  2 i  z  z  a  2  b   1  22 2 2 2 1  b  b  1 1 1 1 1 1 2
Tiếp đến ta có: z  i  z 1 2i  c  d  2  0 2 2 2 2 2 2  a  4a  5  1  a  4a  5  Từ đó ta suy ra: 2 z  z
 a  c2  b  d 2  a  c2  
 c  2  a  c   c  2 1 2   2  2  2  1  a  4a  5  1  a   2 2 2 2 1   a   2    
 4  8  z  z  2 2 . Chọn đáp án D. 1 2 2 2 2  2     
Câu 49. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 255 giá trị nguyên y thỏa mãn log  2 x  y  log x  y ? 5  4   A. 3 7 B. 3 8 C. 4 0 D. 3 6 . Lời giải Cách 1: Ta có 2 x
  x  x nên điều kiện: y  x mà x   nên y  x  1
 tức  x  1 là nghiệm đầu tiên của tham số y (tức y ) 1
Tiếp theo ta có bất phương trình tương đương với: log  x  y log  2 x  y  0 4 5 
Xét hàm số f  y  log x  y log x  y có: f  y  
 . Từ đó ta suy ra hàm x   1 1 x  2 4 5  x  yln 4  0 2 x  yln 5
số f y luôn đồng biến trên tập xác định. Ta có bảng biến thiên như sau: x  
Ta có bất phương trình là: f  y  0 . x
Do đề bài cần không qua 255 giá trị nguyên y nên ta chỉ nhận đúng 255 giá trị, tức từ y đến y để 1 255
f  y   0 , suy ra tại giá trị y
phải làm cho f y  tức ta có điều kiện cần và đủ để tồn tại nghiệm thỏa x   0 x 256
là: f  y   f x     x  x   x  256 0 log 256 log  2 256 0 x 256 4 5   log  2x  x256 2
 log 256  x  x  2565  0  1  8.72  x 19.72. 5 4  log4 256 
Mà x   nên ta suy ra 18  x  19 tức có 19  18  1  38 giá trị nguyên x thỏa mãn. Chọn đáp án B. Cách 2: Đầu tiên, với , x y ta luôn có: log   log
    5 xy    5 xy x y x y x y x x  x  y (*) 5  2  4   2 log4  2 log4    Đặt 1
t  x  y . Xét hàm số    log log t t    4  5 t y f t  t có f t  4  5 1  0 với mọi t  1 t ln 5
Từ đó ta suy ra bất phương trình (*) tương đương với: 1      2 1 x y f x  x
Ta có nhận xét sau: khi giá trị nguyên của y không quá 255 thì giá trị nguyên của t  x  y cũng không quá 255 giá trị, tức 1 x y f   2 x x 1 f         2x x 2 1 256
 256  x  x  f 256 2 lo 4 g 256 2 lo 4 g 256  x  x  5 256  x  x5 256  0  1  8.72  x 19.72
Mà x   nên ta suy ra 18  x  19 tức có 19  18  1  38 giá trị nguyên x thỏa mãn. Chọn đáp án B.
Câu 50. Có bao nhiêu số nguyên dương a để phương trình 2 z  a   2
3 z  a  a  0 có hai nghiệm phức z , z sao cho thỏa mãn    ? 1 2 z z z z 1 2 1 2 A. 3 B. 4 C. 2 D. 1. Lời giải
Ta chia hai trường hợp như sau:
Trường hợp 1: Hai nghiệm là hai số phức z và z có phần ảo khác không 1 2
Để phương trình bậc hai với hệ số thực có hai nghiệm phức có phần ảo khác không khi       
  a  2   2 a  a 2 3 4  0  3  a 10a  9  2 13 5 2 13 5 0  a   ;    ;  . 3   3      b  i  b  i  Giả sử z  ; z  . Ta có 2
z  z  z  z  a  3  3a 10a  9 1 2 2 2 1 2 1 2 a  9 a 32 2 3a 10a 9         a  1 
so với điều kiện ta nhận được a  9 ; a  1 . a  0 
Trường hợp 2: Hai nghiệm là hai số thực z và z . 1 2 a  0 2 2
z  z  z  z  S  S  4P  P  0  . Thử lại thỏa mãn. 1 2 1 2  a  1 
Vậy ta suy ra S  9; 1;0; 
1 tức có 4 giá trị nguyên a thỏa mãn. Chọn đáp án B. a
ĐỀ THI THỬ SỞ THANH HÓA LẦN 2
Câu 40. Cho hàm số bậc bốn y  f x có bảng biến thiên như hình sau: x – ∞ -1 0 1 + ∞ y' – 0 + 0 – 0 + + ∞ 3 + ∞ y 0 0
Có bao nhiêu giá trị nguyên của tham số m2022;2022 để phương trình sau có đúng 5 nghiệm phân
biệt:  f x  x 2 m  m   f x  x   m  2 2 2 2 2 2 2 14 4 1  36  0 A. 0 B. 4 0 4 3 C. 4 0 4 4 D. 1. Lời giải
Đầu tiên, từ bảng biến thiên đã cho ta dễ dàng tìm được f x 4 2  3x  6x  3
Ta có phương trình tương đương với:  f x  x 2 m  m   f x  x   m  2 2 2 2 2 2 2 14 4 1  36  0 Đặt 2    2 t f
x  x thì khi đó phương trình trở thành:  t t    m  2 2 4
1 4  t  9t  4  0 t  4  f x  4  x 2   2
 t  4t 9 m  1   0     f x  0 2     t  9   m   2 1  f x 2  x    2
m  2m 10  0   * Ta để ý rằng hàm số 2
y  4  x là phương trình nửa trên đường tròn có tâm là gốc tọa độ nên từ đó ta nhận thấy f  x 2
 4  x có 4 nghiệm phân biệt. Do hàm số 2 y  f  x 2  x   2
m  2m 10 là hàm số chẵn nên có 2 nghiệm, suy ra m  1  , thử lại ta thấy
phương trình (*) có 3 nghiệm. Mặt khác ta nhận thấy (1) có 4 nghiệm phân biệt nên suy ra (2) phải có duy
nhất 1 nghiệm nên ta kết luận không có giá trị m nào thỏa mãn. Chọn đáp án A.
Câu 41. Cho hàm số y  f x có đạo hàm   x
f x  e  2x 1, x  R và f 0 1. Biết F  x là một nguyên
hàm của hàm số f x thỏa mãn F   1  e . Tính F 0 A. 1 B. 5 C. 1  D. 5  . 6 6 6 6 Lời giải Ta có: f  x  f 
 xdx   xe  x   x 2 2
1 dx  e  x  x  C mà f 0 1 nên C  0 . Suy ra: 3 2 5 f  x x x x 2
 e  x  x  F  x  f  x x dx  e    C mà F  
1  e nên C   nên ta suy ra: 3 2 6 3 2 F  x x x x 5  e     F   1 0  . Chọn đáp án A. 3 2 6 6 Câu 42. Cho hàm số   y  f  x 4 3 2
 x  ax  bx  cx  d a, , b c, d  R thỏa mãn f   x 1 min  f    và hàm R  4  f x số g x   
. Biết đồ thị hàm số y  g  x có 3 điểm cực trị là A ;
m g m, B0; g 0,C 1; g   1  . Gọi 2 x 1
y  h x là hàm số bậc hai có đồ thị đi qua 3 điểm ,
A C và D 2;b  5 . Diện tích hình phẳng giới hạn bởi
hai đồ thị hàm số y  f x và y   2 x   1 h x  x   1 bằng A. 4 6 B. 6 4 C. 5 6 D. 4 4 . 1 5 1 5 1 5 1 5 Lời giải
 f  x 12x  6ax  2b 3 2   2 Ta có:  
y  f  x  4x  3ax  2bx  c   . Mà f   x 1 min
 f    nên ta suy ra:  f   x  24x  6a R  4   1  f    x 4 3 2
 x  x  bx  cx  d f 
 0  6  6a  0  a  1     4   f    x 3 2  4x  3x  2bx  c
 2x  1 f x2xf x g  0  0
Tiếp đến ta có: g x  
 . Từ giả thiết đề bài ta suy ra:  x   0 2 2 1 g    1  0  f   0  0 c  0      f x 4 3 2
 x  x  bx  b 1   4 3 x  x   1  b 2 x    f     1  f   1 1 b   d  2b 1  4 3 x  x   1  b  2 x   4 3 1 x  x 1 Khi đó: g x    b . 2 2 x 1 x 1 f  x 3 2 4x  3x  2bx 3 Ta nhận thấy ba điểm ,
A B,C cùng nằm trên đồ thị 2 y  
 2x  x  b . Mặt khác  2x   2x 2 1
điểm D 2;b  5 cũng thuộc đồ thị tương ứng nên ta suy ra: đồ thị của hàm số y  hx cũng có dạng là:  3  h  x 3 2
 2x  x  b . Suy ra: y   2 x   1 h x  x   1   2 x   2
1 2x  x  b  x 1  u   x 2  2 
Xét phương trình hoành độ giao điểm của u x và f x , ta có:  3  1 1 4 3 x  x  b  2 x   1 1   2 x   2 4 3 2
1 2x  x  b  x 1  x  x  x  x  2  0  x  1     2  2 2 1 1 1 1 44
Suy ra: S  u  x  f x 4 3 2 dx 
x  x  x  x  2 dx    . Chọn đáp án D. 2 2 15 1  1  x  2  t x 1 y  2 z  2 
Câu 43. Trong không gian Oxyz cho hai đường thẳng d :  
, d : y  3 t (t là tham số) 1 2 2 1 2  z  4t 
và mặt phẳng P : x  y  z  6  0 . Đường thẳng d  song song với mặt phẳng P và cắt d , d lần 1   2 
lượt tại A và B sao cho AB  3 6 . Phương trình của d  là A. x  5 y z  2           B. x 1 y 3 z 4   C. x 2 y 3 z 4   D. x 4 y 1 z   . 1 1 2 2 1 1 1 1 2 1 1 2 Lời giải
Ta chia hai trường hợp như sau: A  1 2 ; a 2  a; 2  2a Đầu tiên ta có ,
A B lần lượt là các điểm thuộc d , d nên ta suy ra: 1 2  B  2  ; b 3  ; b 4  b      AB  1 2a  ;
b b  a  5; 2a  b  2 mà d  P nên ta suy ra AB  n với n  1;1;  1 là vector pháp
tuyến của P . Khi đó: 1 2a  b  b  a  5  2a  b  2  0  a  b  2  b  a  2 (1).
Ta có: AB    a  b2  b  a  2   a  b  2    a2 2 2 1 2 5 2 2 3 3
 9  9a  54 thế từ (1).  a  1  ;b  3   A1;3;4 AB  6;3; 3    k 2;1;  1 Giải phương trình suy ra      . a  2;b  0  A  0;5;6 AB    3
 ;3;6  k 1;1;2
Mà đường thẳng tại phương án B nằm trong P nên ta chọn đáp án D.
Câu 44. Cho hình trụ O và O là tâm của hai đáy. Xét hình chữ nhật ABCD có ,
A B cùng thuộc đường tròn
O và C,D cùng thuộc đường tròn O sao cho AB  3 3,BC  6 , đồng thời mặt phẳng  ABCD tạo với
mặt phẳng đáy hình trụ góc 60 . Thể tích khối trụ bằng A. 3 3  B. 2 7 3 C. 9 3 D. 8 1 . Lời giải
Đầu tiên ta có hình vẽ như sau: BC
Gọi I là trung điểm OO và kẻ OH  AB tại H khi đó ta suy ra 
IHO  60 . Cùng với IH   3 , ta suy 2  3 3  O  O  2IO  3 3 IO  IH sin 60    ra: 2   2  AB 9 27
. Như vậy, khối trụ có đường sinh 2 3   OA  OH     3 OH  IH cos 60    4 4 4  2
OO  3 3 và bán kính đáy R  3 có thể tích là: 2
V   R h  27 3 . Chọn đáp án B.
Câu 45. Trong không gian Oxyz cho mặt phẳng P : x  y  2z 10  0 và hai điểm A1; 1  ; 2, B2;0; 4   . Gọi M a; ;
b c là điểm thuộc đoạn thẳng AB sao cho luôn tồn tại hai mặt cầu có bán kính R  6 tiếp xúc
với mặt phẳng P , đồng thời tiếp xúc với đoạn thẳng AB tại M . Gọi T   ;
m n là tập giá trị của biểu thức 2 2 2
25a  b  2c . Tổng m  n bằng A. 1 2 3 7 1 B. 8 6 C. 1 4 0 D. 1 3 4 0 . 7 6 1 9 Lời giải
Đầu tiên, ta nhận thấy: ,
A B đều nằm cùng phía với mặt phẳng P . x 1 y 1 z  2
Phương trình  AB có dạng là:   1 1 6
Gọi I , I lần lượt là tâm của hai mặt cầu cố định đó. Suy ra I I  2 6 và MI I là tam giác cân tại M 1 2 1 2 1 2
Gọi Q là mặt phẳng chứa AB và vuông góc với P , suy ra: Q : x  y  2  0 x  y  z
Gọi d  là giao tuyến của hai mặt phẳng Q và R , suy ra: d  1 3 :   1 1 1
Gọi mặt phẳng R : x  y  2z  4  0 và N là trung điểm của I I . Ta có hình vẽ như sau: 1 2
Vì N thuộc giao tuyến Q và R nên tọa độ là: N  1   ; a 3   ; a a .
Ta có: M  AB  M 1 t; 1
  t;2  6t. Mà M là điểm thuộc đoạn thẳng AB nên t 0;  1 . 
Suy ra: MN  a  t  2;a  t  2;a  6t  2 . Mà MN vuông góc với AB nên ta có:   t   t t t  MN u   a  t   a  t   a  t    a     MN     AB       19 21 21 7 . 0 2 2 6 6 2 0 2 ; ;   2  2 2 2 
Suy ra điều kiện để tồn tại hai mặt cầu cố định thỏa đề bài là: 2 MN  6  MN  6 2 2 2  21t   21t   7t  24 2        6  t         2   2   2  931 2 T   98t  34  34   694 Lại có: 2 2 2 2 
T  25a  b  2c  98t  34 nên suy ra:   T  34; 24   2 T  98t  34  98.  34   19   931 694 1340
Vậy ta suy ra m  n  34   . Chọn đáp án D. 19 19
Câu 46. Có bao nhiêu số nguyên x thỏa mãn  2
 log x  5log x  6 3  log x  0 2 2  5 A. 6 4 B. 9 C. 6 5 D. 8 . Lời giải x  0
Đầu tiên ta có điều kiện:   0  x 125 . 3  log x  0  5 x  125 x  125 Trường hợp 1:  2 log x 5log x 6 3 log x 0          . 2 2  5  2 1
 log x  5log x  6  0 x  ; x  64 2 2   2 Trường hợp 2:  2
 log x  5log x  6 3  log x  0 . 2 2  5 2 1
 log x  5log x  6  0    x  64 ++Trường hợp 2a: 2 2   2
. So với điều kiện, ta nhận.  3 log x  0  5 x 125 2
log x  5log x  6  0  ++Trường hợp 2b: 2 2 
 x  .So với điều kiện, ta loại.  3 log x  0  5 1
Vậy, tổng 2 trường hợp ta suy ra:  x  ;64 12  5 
tức có 65 giá trị nguyên x thỏa mãn. Chọn đáp án C. 2   
Câu 47. Cho hàm số y  f x có đạo hàm f x 3  x  3x  2, x
  R . Có bao nhiêu giá trị nguyên của tham
số m 30;30 để hàm số y  f  4 2
x  8x  m có đúng 7 điểm cực trị ? A. 2 B. 1 6 C. 1 7 D. 1 . Lời giải
Ta có f  x  x  x    x  2 3 3 2
1  x  2  0  x  1
 (nghiệm kép) hoặc x  2 (nghiệm đơn).
Đặt y  g  x  f  4 2 x  8x  m . Ta có:  4 2 x  8x  3 4x 16x x  2 g x 
f  x  8x  m  0   4 2  4 2  x  8x  f    4 2 x  8x  m  0
Vì hàm số g x không xác định tại x  0, x   2 và đổi dấu khi x qua điểm x  0, x   2 nên ta suy ra
g x đạt cực trị tại x  0, x   2 . Suy ra hàm số g x có 5 điểm cực trị là x  0, x   2, x  2 4 2  x 8x  m  1 1
Tiếp đến ta có: f  4 2 x  8x  m    0  
, các nghiệm của (1) (nếu có) là nghiệm bội 4 2  x 8x  m  2 2 
chẵn nên không phải là cực trị của hàm số. x  Từ (2) ta suy ra: 4 2
x  8x  2  m . Xét hàm số y  h x 4 2  x 8x có hx 0  0   x  2
Từ đó ta có bảng biến thiên như sau:
Như vậy để g x có 7 điểm cực trị thì (2) phải có 2 nghiệm phân biệt x  2  ; 2;  0 tức ta có được m   30;30 m 16  2  m  1  4  3
 0  m  14. Như vậy có tất cả 17 giá trị nguyên m thỏa mãn đề bài. Chọn đáp án C.
Câu 48. Trên tập hợp các số phức, xét phương trình 2
z  2z  m  2  0 ( m là tham số thực). Gọi T là tập
hợp các giá trị của m để phương trình trên có hai nghiệm phân biệt được biểu diễn hình học bởi hai điểm ,
A B trên mặt phẳng tọa độ sao cho diện tích tam giác ABC bằng 2 2 , với C  1  ; 
1 . Tổng các phần tử trong T bằng A. 4 B. 9 C. 8 D.  1 . Lời giải
Gọi z , z là 2 nghiệm của phương trình đề cho. Khi đó ta có:   m 1  0 . Sau đó ta xét 2 trường hợp sau: 1 2
Trường hợp 1: m 1  0 , tức z , z là 2 số thực. Khi đó ta có: z 1 m 1 tức , A B Ox 1 2 1,2 1
Suy ra: AB  z  z  2 m 1  S  .A .
B d C;Ox  m 1  2 2  m  9 (1) 1 2 ABC   2
Trường hợp 2: m 1  0 , tức z , z là 2 số phức. Khi đó ta có: z  1 i 1 m mà ,
A B d  : x  1 nên suy 1 2 1,2 1
ra: AB  z  z  2 1 m  S  .A .
B d C;Ox  2 1 m  2 2  m  1  (2) 1 2 ABC   2
Từ (1) và (2) ta suy ra tổng các phần tử T bằng 9    1  8 . Chọn đáp án C.
Câu 49. Có tất cả bao nhiêu cặp số nguyên dương với y  20 thỏa mãn những x 1 4 3 2 2 2 log  y  2y  x y  2y x 2022 y 1 A. 3 8 0 B. 2 0 0 C. 4 2 0 D. 2 1 0 . Lời giải x 1
Ta có bất phương trình tương đương với: 2  log  y  2 2 y  x  2  2y y  x 2022   y 1 x 1  log  y  y   1   x   1  y   1   x   1   log
x  1 log  y   1  y  y  2 1   x  2 2 2 1 (*) 2022 2022 2022  y 1
Xét hai trường hợp sau: ( 2 y  0 luôn đúng)
- x 1  y 1  x  y thì VT  
*  VP * nên ta loại trường hợp này. x  y 20 - x 1  y 1    x 1;2;...;  y . Suy ra số cặp  ;
x y thỏa mãn yêu cầu đề bài là  y  210 (cặp). y  20 y 1 
Vậy có tất 210 cặp số nguyên dương  ;
x y thỏa mãn đề bài. Chọn đáp án D.
Câu 50. Xét các số phức z, z , z thỏa mãn z  4  5i  z 1  1 và z  4i  z  8  4i . Tính M  z  z khi 1 2 1 2 1 2
biểu thức P  z  z  z  z đạt giá trị nhỏ nhất. 1 2 A. M  4 1 B. M  6 C. M  2 5 D. M  2 1 3 . Lời giải Ta có như sau:
z  4  5i  1 tập hợp điểm A biểu diễn số phức z là đường tròn C có tâm I 4;5, bán kính R 1. 1  1 1 1
z 1  1 tập hợp điểm B biểu diễn số phức z là đường tròn C có tâm J 1;0, bán kính R  1. 2  2 2 2
Đặt z  a  bi a, b. Ta có z  i  z   i 
 a  b  2  a  2  b  2 2 4 8 4 4 8 4  a  b  4 . Suy
ra tập hợp điểm C biểu diễn số phức z nằm trên đường thẳng  : x  y  4.
Khi đó P  z  z  z  z  CA  C .
B Gọi K là điểm đối xứng của J qua đường thẳng , khi đó ta tìm được 1 2 K 4; 3   
 phương trình đường thẳng IK : x  4. Do đó P khi và chỉ khi C  IK   và min A  CI   C A o giua CI 1     
 A4;4,B2;0 M  z  z  2 13. Chọn đáp án D. 1 2 B  CJ   C B o giua CJ 2   
ĐỀ THI THỬ THPT QUỐC HỌC HUẾ LẦN 1
Câu 2. Cho số nguyên dương n và số phức z thỏa mãn 101 n  6 8   n iz
i z i . Chứng minh rằng z là một số thực. Lời giải
Đặt z  cos  i sin , khi đó phương trình trở thành: 101 cos  sinn  6 8 cos  sin  n i i i i i
Câu 3. Cho hàm số f nhận giá trị dương, có đạo hàm trên R và thỏa mãn x    f t  f x  2022 2 x  4   1 dt  , x   R 2 t  4  0 
Tính giá trị của f   1 Lời giải   x f x  f t 
Ta có phương trình tương đương với:  20221 dt  , x   R (1) 2 2 x  4 t  4  0  f x x   Đặt g x   
thì (1) trở thành: g  x  20221 g  tdt, x   R (2) 2 x  4  0 
Thay x  0 vào (2) ta dễ dàng có được g 0  2022
Tiếp theo, ta đạo hàm hai vế cho phương trình (2) thu được: gx  2022g  x g x g x
    2022    dx  2022x  ln gx  2022xC g x g x
Thay x  0 vào, cùng với g 0  2022 ta thu được C  ln f 0  ln 2022 f x Suy ra:        2022 ln 2022 ln 2022  2022 x g x x g x e . Với g x    ta suy ra: 2 x  4     2   2022 2022 4 x f x x e . Vậy f   2022 1  10110e
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
ĐỀ CHUYÊN QUỐC HỌC HUẾ LẦN 1 z  z
Câu 36. Cho hai số phức phân biệt z , z thỏa mãn 1
2 là số ảo và z 1 1. Giá trị lớn nhất của 1 2 z  z 1 1 2 z  z bằng 1 2 A. 1. B. 2 2 . C. 4 . D. 2 . Lời giải   Gọi ,
A B lần lượt là điểm biểu diễn số phức z , z , khi đó OC  z  z và BA  z  z 1 2 1 2 1 2 z  z z  z Do 1
2 là số ảo nên OC  BA . Ta cũng có: 1
2  ki k    1 ki z   1 ki z 1   z  z 2 z  z 1 2 1 2
 1 ki z  1 ki z  z  z . Suy ra OACB là hình thoi và z  z  AB 1 2 1 2 1 2
Trường hợp 1: A và B đối xứng nhau qua trục tung, khi đó C Oy , suy ra AB đạt max khi A và B nằm z  z
trên trục hoành, nhưng loại vì khi đó 1 2 là số thực. z  z 1 2
Trường hợp 2: A và B đối xứng nhau qua trục hoành, khi đó C  Ox , suy ra AB đạt max khi tâm đường
tròn số phức z là trung điểm AB tức max z  z  AB
 2R  2 . Chọn đáp án D. 1 1 2 max
Câu 42. Cho tứ diện ABCD có AB  AC  BC  CD  BD  a . Gọi M , N lần lượt là trung điểm B , D CD .
Góc giữa hai đường thẳng MN và AD là A. 30 . B. 60 . C. 90 . D. 45 . Lời giải Dễ nhận thấy A  BC, B
 CD đều. Gọi E là trung điểm BC thì khi đó AI  BC 
 BC   AID  AD  BC . Mà MN  BC (tính chất đường trung bình) DI  BC
Nên MN  AD tức góc giữa hai đường thẳng MN và AD là 90 . Chọn đáp án C.
Câu 48. Trong không gian Oxyz , cho hình chóp tam giác đều S.ABC có tọa độ đỉnh S 6; 2  ;3 , thể tích x 1 y 1 z
V  18 và AB  a a  7 . Đường thẳng BC có phương trình là 
 . Gọi S  là mặt cầu tiếp 1 2 1
xúc với mặt phẳng  ABC tại A và tiếp xúc với cạnh SB . Khi đó bán kính của mặt cầu S  thuộc khoảng nào sau đây ? A. 2;  3 . B. 4;5 . C. 3;4. D. 5;6. Lời giải
Gọi E là trung điểm BC khi đó ta dễ dàng có E 1 t; 1
  2t;t t  SO  BC   Ta có: 
 BC  SOE  SE  BC tức S . E u  0  t 1 E  SE  . BC 2;1; 1 29 O  E  BC
AB  BC  a a  7 2 2  1 1 a a 3    Ta có: a AB 2 6 2   V  S . O S  . 29  .  18  . ABC a  2 2 3 3 12 4 SO  SE  OE  29  a  7  12
Gọi R là bán kính mặt cầu với I là tâm.
Ta có IA   ABC, BS  IH, IA  IH  R và O là tâm đường tròn ngoại tiếp tam giác ABC
Tiếp đến gọi K là hình chiếu của I lên SO , khi đó, IKOA là hình chữ nhật
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Do IA  IH  R nên B  HI  B
 AI ch cgv  BH  BA   2 62  Ta lại có: SO  29   3 3 
; SK  SO  IA  3 3  R; HS  BH  BS  BA  BS  35  2 6 12  2 2 SB  SE  EB  35 2 2 2 Vì 2 2 2 2
IH  HS  IK  SK nên ta suy ra 2
R   35  2 6  2 2 3 3  R . Giải phương trình trên ta
suy ra được R  3,26....3;4 . Chọn đáp án C.
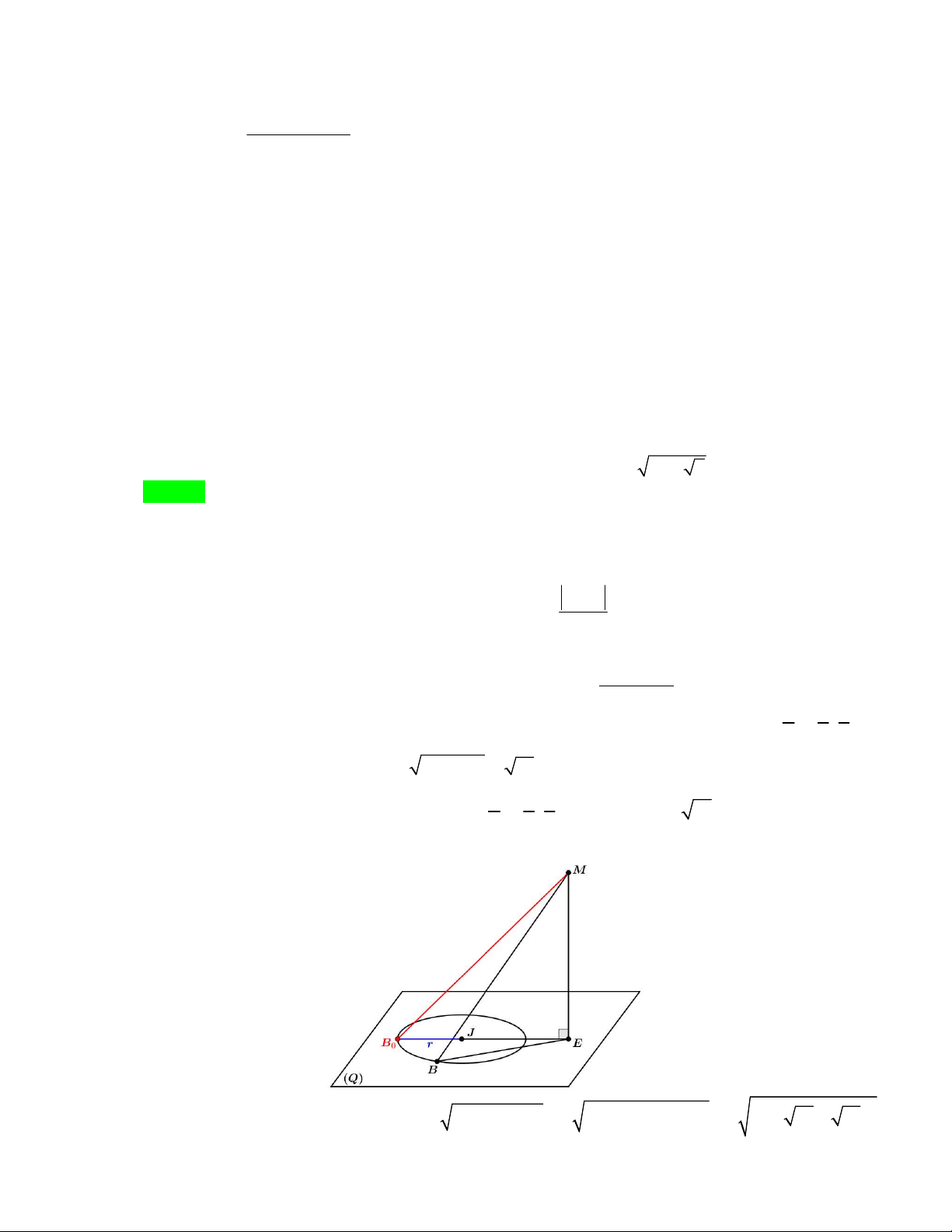
Câu 49. Cho hình nón đỉnh S có góc ở đỉnh bằng 60 và có độ dài đường sinh l  12cm . Gọi AB là một
đường kính cố định của đáy hình nón, MN là một dây cung thay đổi của đường tròn đáy và luôn vuông
góc với AB . Biết rằng tâm đường tròn ngoại tiếp của tam giác SMN luôn thuộc một đường tròn C cố
định. Tính bán kính của đường tròn C . 3 3 2 A. 6 2cm . B. cm . C. cm . D. 2 3cm. 2 2 Lời giải
Gọi J là giao điểm của AB và MN . Theo đề bài ta có được MN  AB tại J .
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Gọi O là tâm đường tròn ngoại tiếp của SAB và O là điểm cố định. Lúc này ta có được O E   O F   O A   O S
 , (do O nằm trên mặt phẳng trung trực của MN ). Vẽ tiếp O K
  SMN  khi đó ta giả sử E là trung điểm SN (1), thì khi đó O E   SN Mà O K
  SN,SN  SMN nên SN  KO E
  , suy ra KE  SN (2)
Từ (1) và (2) ta suy ra K là tâm đường tròn ngoại tiếp tam giác SMN với K  SJ .
Do K SAB và nhìn O S
 dưới một góc vuông nên điểm K sẽ di động trên đường tròn đường kính O S  . Tới đây ta có:  ASB  2 ASO  60  
ASO  30  SO  SAcos  ASO 12cos30  6 3 . 2 2 Khi đó ta suy ra SA 12 R  S O     4 3 SAB 2SO 2.6 3 O S 
Vậy điểm K sẽ di động trên đường tròn C bán kính là R   2 3 . Chọn đáp án D. 2
Câu 50. Số các giá trị nguyên của m 2  021;2022 để log b log 5 a a  3 b a b
 m log b  2 với mọi a , a b1; là A. 4044 . B. 2020 . C. 2021. D. 2022 . Lời giải
Ta đặt log b  x  0 . Khi đó bất phương trình ban đầu trở thành: a x  log b log a a b a x  a  b  m b   a  a
 mx   a  a  mx   m  (1) a  12 x x x x 2 2 5 3 log 2 5 3 2 5 3 2 x x a  2 x a x ln a  2
Xét hàm số y  f  x 2 2 
với mọi x  0 , ta có f  x     0, x   0; 2   x x
Suy ra hàm số f x luôn đồng biến trên 0; .
Từ đó ta nhận thấy để (1) có nghĩa thì m  min f x  2ln a 0; Mà do ln a  0, a  1 nên suy ra m   2  021;2022
m  0  m 2
 021;0 tức có tất cà 2021 giá trị nguyên m
thỏa mãn yêu cầu đề bài. Chọn đáp án C. SỞ BÌNH PHƯỚC LẦN 1
Câu 46. Trong không gian Oxyz , cho mặt cầu S  x   y  2  z  2 2 : 1 2  9 và điểm A2; 1  ;2 . Từ A kẻ
ba tiếp tuyến bất kì AM , AN , AP đến S  . Gọi T là điểm thay đổi trên mặt phẳng MNP sao cho từ T
kẻ được hai tiếp tuyến vuông góc với nhau đến S  và cả hai tiếp tuyến này đều nằm trong mặt phẳng x  1   t  
MNP Khoảng cách từ điểm T đến giao điểm của đường thẳng  : y  2  t với mặt phẳng MNP có z 13t 
giá trị nhỏ nhất bằng 27 3 3 5 27 3 3 5 27 3 3 5 27 3 A.  . B.  . C.  . D. . 16 2 16 2 8 2 16 Lời giải
Đầu tiên ta có mặt cầu S  tâm I 0;1; 2   , bán kính R  3. IA
Ta có tiếp phương trình mặt cầu S với tâm là trung điểm IA và bán kính là 1  2
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG S :x  2 2 2
1  y  z  12 thì khi đó phương trình mặt phẳng MNP chính là kết quả của phép trừ vế 1
theo vế của phương trình mặt cầu S  và S tức MNP : 2x  2y  4z 1 0 . 1 
Tiếp đến gọi C là đường tròn thiết diện của mặt cầu S  và mặt phẳng MNP và tâm là E .   Khi đó ta có 9 IE 3  3 1 1 2 2  R  MI  IE.IA  IE  
  5EI  3EA  0  E ; ;    . 2 6 EA 5  4 4 2 
Khi đó đường tròn C sẽ có tâm  3 1 1  E ; ;    và bán kính 2 2 3 10 r  R  IE  .  4 4 2  4
Tiếp theo, do hai tiếp tuyến qua T và vuông góc với nhau nên đoạn ET luôn bằng 2 lần r tức ta có quỹ
tích điểm T là đường tròn C có tâm  3 1 1   là bán kính 3 10 3 5    . 1  E ; ;   r r 2 2  4 4 2  1 4 2
Mặt khác, ta dễ dàng tìm được giao điểm của  và MNP là  17 33 13  F  ; ;   .  16 16 16 
Khi đó giá trị nhỏ nhất cần tìm chính là 27 3 3 5 EF  r   . Chọn đáp án B. 1 16 2
Câu 47. Cho số phức z thỏa mãn z  3  4i  5 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
P  z  2  z  i . Tính modun của số phức w  M  mi . A. w  2 314 . B. w  2 309 . C. w  1258 . D. w  3 137 . Lời giải
Vì z  3  4i  5 
 tập hợp các điểm biểu diễn số phức z là đường tròn C có tâm I 3;4 và bán kính R  5 . Ta có P x  2 yi x y  2i x 2 y x y 2 2 2 2 1 2 1               4x  2y  3   
 4x  2y  3 P  0. Ta tìm P sao cho đường thẳng  : 4x 2y 3P  0 và đường tròn C có điểm chung    12 8 3P d I ,  R 
 5  23P 10  13  P  33. 20
Suy ra: w  M  mi 13 33i tức w  1258 . Chọn đáp án C.
Câu 48. Cho hàm số f x có đạo hàm là f  x   x  2  2 2
x  x, x   . Gọi S là tập hợp tất cả các giá trị
nguyên dương của tham số  1  m để hàm số 2 f x  6x  m 
 có 5 điểm cực trị. Tính tổng tất cả các phần tử  2  của S . A. 154 . B. 17 . C. 213. D. 153 . Lời giải Đặt     g  x 1 1 2  f x  6x  m  g   x  x  6 2 f  x  6x  m 
 (chỉ tính nghiệm bội lẻ)  2   2   x  6 1 Cho gx 2
 0   x  6x  m  g x  0 1 . Như vậy để hàm số gx có 5 điểm cực trị thì cả phương 1      2 1 2
 x  6x  m  g x  1 2 2      2
trình (2) và (3) đều phải có 2 nghiệm và khác 6, tức ta suy ra điều kiện cần có là:
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG    0 1   m m 1   0 17 2 9    0;9   0 m  18; m  19     2 2 m   
  m1;17 S là  X 153 .Chọn đáp án D. g 6  0  m  18 1   m 18  0;m 19  0 k 1  g 6  0  2  
Câu 49. Có bao nhiêu số nguyên dương b sao cho ứng với mỗi b , có đúng ba giá trị nguyên dương a thỏa 2a  a mãn log  2a  a b 1 ? 2   ab A. 1. B. 2 . C. 3 . D. 0 . Lời giải 2a  a
Bất phương trình tương đương với: log
 2a  a b 1  log 2a  a  2a  a  log ab  ab 2   2     2     ab
Hàm số y  g t  log t  t luôn đồng biến trên 0; nên suy ra   . Do 2 2a a ab a nguyên dương nên 2a  a 
bất phương trình tương đương với: b 
. Xét hàm số    2a a y f a  trên 0; có a a a    1 f a 2 a ln 2  1 1 1   0  a  ; f   0 suy ra a 
1,44 là điểm cực tiểu của f a 2   a ln 2  ln 2  ln 2
Do đề bài yêu cầu có đúng ba giá trị nguyên dương a tức giá trị a lấy từ 1 đến 3
Như vậy điều kiện cần và đủ là 2 4 3 5 b f b f b       
b  4. Chọn đáp án A. Câu 50. Trên parabol P 2
: y  x lấy hai điểm A 1  ; 
1 , B2;4 . Gọi M là điểm trên cung AB của P
sao cho diện tích của tam giác AMB lớn nhất. Biết chu vi của tam giác MAB là a 2  b 5  c 29 , khi đó
giá trị a  b  c bằng 29 41 9 13 A. . B. . C. . D. . 6 9 2 3 Lời giải
Trên P lấy điểm M  2 a; a  với a 1  ;2
Ta có đường thẳng AB có phương trình là x  y  2  0 , phương trình đường thẳng AM có dạng là y  a  
1 x  a , phương trình đường thẳng BM có dạng là y  a  2 x 2a a 2 Suy ra ta có: S  x   a  x  a dx  x   a  x  a dx AMB  2  1   2  2 2  1  a a
2  a 2a  2a  1 a  1 2 2 a  4a  4
  2 ax  1dx  a  12 xdx   2 2 1 a 2 aa   2 1        a      a 3   
  aa   3 a  1 2 a 27 1 2 2 1   2 2 2 4 8 27 Vậy S max  khi và chỉ khi 1  1 1  2  a  a 1  a   M ; AMB 8   2  2 4  3 3 3 3 9
Suy ra: MA  MB  AB  3 2  5 
29 tức a  b  c  3    . Chọn đáp án C. 4 4 4 4 2
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
THPT KIM LIÊN – HÀ NỘI LẦN 2
Câu 46. Trong không gian Oxyz , cho mặt cầu S   x  2   y  2  z  2 : 1 3
2  25 và hai đường thẳng x  1 mt x  1 t   
d , d lần lượt có phương trình d : y  1  và d : y  1 
. Có bao nhiêu giá trị của m để d , 1  1   2  1 2 z 1t   z  1 mt 
d cắt mặt cầu S tại 4 điểm phân biệt sao cho bốn điểm đó tạo thành tứ giác có diện tích lớn nhất 2  A. 0 . B. 3 . C. 2 . D. 1. Lời giải Cách 1:
Ta nhận thấy hai đường thẳng d , d chung điểm A1; 1  ; 
1 và IA  3  5  R với I  1  ; 3  ;2 . 1   2     
Tiếp đến hai vector chỉ phương của d , d lần lượt là u  ;
m 0;1 ,u  1;0;m , nhận thấy u .u  0 1   2   1   2  1 2 nên suy ra d  d . 1   2    Do u ;u      2
0;1 m ;0 nên 2 đường thẵng trên luôn thuộc mặt phẳng P : y  1
 với n  0;1;0 là 1 2 
vector pháp tuyến của mặt phẳng tương ứng.
Gọi M , N, P,Q lần lượt là các giao điểm giữa hai đường thẳng d , d và mặt cầu, từ đó suy ra bốn 1   2 
điểm trên đều nằm trên đường tròn C giao tuyến giữa mặt phẳng P và mặt cầu đó.
Gọi E, F,G, H lần lượt là trung điểm MN, NP, PQ,QM khi đó ta luôn có EFGH là hình chữ nhật.
Khi diện tích tứ giác MNPQ lớn nhất thì diện tích tứ giác EFGH lớn nhất tức EFGH là hình vuông. 
Dựa vào hình vẽ trên, ta suy ra diện tích tứ giác MNPQ lớn nhất khi vector u chính là vector phân giác    u u    
giữa hai vector chỉ phương của d , d tức 1 2
u     với u  I ; A n;n . 1   2  u u    1 2    u u  m 1 m 1   2  1 1 2 u
       ;0;   m  3      Ta có: 2 2 u u  m 1 m 1 m 1 m 1  1 2  
. Suy ra ta có hệ thức sau:   1     2  1   m   u  I ; A n ; n    2;0; 1  3     m 1 m 1
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Vậy chỉ có 2 giá trị m thỏa mãn yêu cầu đề bài. Chọn đáp án C.
Cách 2: Ta có đánh giá khác như sau: (Gọi R là bán kính của đường tròn thiết diện C ) C 2 2 2 1 1
 2R  d O ;MP  d O ; NQ  2 2 S  M . P NQ  .2 R  d O MP R  d O NQ  MNPQ C  ;  2 2 .2 C  ;  C     2  2 2 2   2 2  2R  O A   const với O 1  ; 1
 ;2 là tâm đường tròn C. C    
Dấu bằng xảy ra khi và chỉ khi d O ; MP  d O ; NQ  d O ;d  d O ;d  O ; A u   O ; A u  1   2  1 2     m  3 2 m 2m 1       
1 , Vậy chỉ có 2 giá trị m thỏa mãn yêu cầu đề bài. Chọn đáp án C. m    3
THPT PHỤ DỰC THÁI BÌNH LẦN 2
Câu 42. Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy ABCD,
biết cosin góc giữa hai mặt phẳng SBD và SBC bằng 5 . Tính thể tích khối chóp S.ABCD ? 3 3 a 3 3 2a 3 a 3 A. V  . B. 3 V  2a . C. V  . D. V  . 6 3 2 Lời giải
Ta chuẩn hóa a 1 và đặt SA  x d C SB 1 1 ;  BC  1; AO  AC   2 2 Ta có: 
  SBD  d  A SBD  d  A SO S . A AO x d C; ; ;   2 2  SA  AO 2  2 2x   1  d C; SBD  2 x  5  2
Suy ra: sin SBD;SBC             x  SA  d C; SB  1 2   2 x   3 3 2 2 1   1 2 3 2a Vậy V  S . A S  tức V  . Chọn đáp án C. 3 ABCD 3 3
Câu 43. Trên tập hợp các số phức, xét phương trình 2 2
z  2az  b  2b  0 ( a, b là các tham số thực). Gọi S
là tập hợp các cặp  ;
a b sao cho phương trình đó có hai nghiệm z , z thỏa mãn 3z  2iz  3  6i . Số 1 2 1 2 phần tử thuộc S bằng A. 1. B. 3 . C. 2 . D. 4 . Lời giải z  z  2a Ta có phương trình 2 2
z  2az  b  2b  0 có hai nghiệm z , z nên ta luôn có: 1 2 1 2  2 z z  b  2b  1 2
Trường hợp 1: z , z là số thực. 1 2 a  2 z 1 2a  4 
Khi đó phương trình 3z  2iz  3  6i tồn tại nghiệm duy nhất với 1     b  1  1 2 2 z  3  b   2b  3 2  b  3 Suy ra có 2 cặp  ; a b tồn tại.
Trường hợp 2: z , z không phải là số thực. 1 2
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG 3  z  2iz  3 6i Do z  z nên ta suy ra 1 1 
 3x  yi  2ix  yi  3 6i  5x  yi  3 6i 1 2 z  x  yi  1  6 2a  3 3 3  Suy ra x  ; y  6 tức 5
z   6 ;i z   6i  
. Do pt (*) có 2 nghiệm nên ta suy ra 5 1 2 5 5 9 2 b  2b   36 *  25 có 2 cặp  ;
a b tồn tại. Chọn đáp án D.
Câu 44. Cho hai hàm đa thức bậc 4 và bậc 3 là y  f  x, y  g x (hình vẽ dưới đây chỉ mang tính chất
minh họa). Biết rằng hai đồ thị y  f  x, y  g x tiếp xúc nhau tại điểm có hoành độ bằng 1 và cắt nhau
tại 2 điểm khác có hoành độ lần lượt là 2;0 . Gọi S , S lần lượt là diện tích hình phẳng giới hạn bởi hai 1 2 2
đồ thị trên ở nửa mặt phẳng bên trái và nửa bên phải của trục tung. Khi S  thì 2 15 28 56 51 28 A. S  . B. S  . C. S  . D. S  . 1 5 1 15 1 15 1 15 Lời giải
Ta có hai đồ thị y  f  x, y  g x tiếp xúc nhau tại điểm có hoành độ bằng 1 và cắt nhau tại 2 điểm khác
có hoành độ lần lượt là 2;0 nên suy ra h x  f  x  g  x  ax x  2 1  x  2 1 1 S  f
 x gx dx  ax  x 2 2 2 1 x  2 dx   a   2   15 3 0 0 0 0 2 56 Suy ra: S  f
 x g x dx   x  x  2 1 x  2 dx  . Chọn đáp án B. 1   3 15 2 2 
Câu 46. Có bao nhiêu số nguyên y  2  022;202 
2 sao cho bất phương trình sau có nghiệm ? 2x e    y x 2 2 2 e  4yx  y  2  022 A. 4016 . B. 1993 . C. 4015 . D. 1994 . Lời giải
Ta có bất phương trình: 2x e    y x 2 2 2
e  4yx  y  2022  0 (1) Xét hàm số f x  e   y e  yx  y 
(hàm theo biến x , và y là tham số) có y   2x   x 2 2 2 4 2022
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG  f   x 2  2 x e  22  y x e  4 y  0 x  y e  y 2 x   e  2  y x e  2y  0 *   (nghiệm đẹp).      e f x e y e    y   2   x x x 2 4 2 2 x  ln y  Trường hợp 1: x e  y  
. Do lim f  x  0; lim f x   nên x  ln y là điểm cực tiểu với y y   y  0   1 x x y  0 f  y  e 
 y e  y  y  y  y  y   y  ln  2ln 4 y 22  lny 2 4 2 2  2 2 4 0  2 y  2 
Từ (1) và (2) ta rút ra điều kiện cần cho y là y  0 .
Cùng với điều kiện đủ là f  y 2  y  y  y 2 ln 2 2
 4y ln y  y  2022  0 nên ta có y  29.5 y
Trường hợp 2: phương trình (*) vô nghiệm tức ta luôn tồn tại tập bù của y  0 tức y  0 để bất phương trình f  x  e 
 y e  y  có nghĩa         y y f  2 2 0 2 y   2 2 x 22  x 4 0
Xét y  0 ta thấy không thỏa bất phương trình đề bài. Suy ra trường hợp 2 ta thu được y  0 y  0
Vậy tổng hai trường hợp ta thu được y   2  022;2022 
 y 2022; 
1 30;2022 tức có tất cả 4015 y  29.5
giá trị nguyên y thỏa mãn bài toán. Chọn đáp án C.
Câu 47. Cho f  x là hàm số bậc ba có đồ thị hàm số f 2  x như hình vẽ sau
Có bao nhiêu số nguyên m 2
 022;2022 để hàm số g x  f  2023 2 x
 2022x  m  m có số
điểm cực trị nhiều nhất ? A. 2022 . B. 2021. C. 2023. D. 2020 . Lời giải
Để g x có số điểm cực trị max thì số nghiệm bội lẻ của phương trình f  2023 2 x
 2022x  m  m  0 cũng
phải đạt max. Kéo theo số điểm cực trị của hàm số hx  f  2023 2 x
 2022x  m  m cũng phải đạt max.
Suy ra tiếp số nghiệm bội lẻ nguyên dương của u  x  f  2023 2 x
 2022x  m  cũng phải đạt max và m  0
Giải thích: vì khi càng tịnh tiến về bên phải theo trục hoành của hàm số u x thì số nghiệm và điểm cực
trị của hx càng lớn và đạt max. x  2022x  m  1 
Khi đó ta có: u x  2023x
 2022 f x  2022x  m  2023 2 2022 2023 2  0   2023 2 x  2022x  m  1 2023 2 x  2022x  m 1 m  1   
. Như vậy để có nhiều nghiệm nhất thì 2 m 1  0   2023 2 x  2022x  m 1 m  1 Suy ra m   2  022;2022
m  1 m 2;202 
1 tức có 2020 giá trị nguyên m thỏa mãn. Chọn đáp án D.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG 1 1
Câu 48. Gọi S là tập hợp các số phức z thỏa mãn phần thực của bằng . Biết các số phức z  z 18
z , z , z thuộc S thỏa mãn z  z  18, z  z  9 2 . Giá trị lớn nhất của biểu thức 1 2 3 1 2 3 2 2 2 2
F  z 1 i  z 1 i  4 z 1 i gần nhất với số nguyên nào trong các số sau đây ? 1 2 3 A. 2  68. B. 6  4. C. 55 . D. 5  5. Lời giải 1 2 2 1 x  y  x  yi Gọi z  x  yi  , x y  . Do w  nên z  z  0  w   z  z x  y  x  yi  x  y x2 2 2 2 2 2  y 2 2 2 2 x  y  x 1 x  y  x 1
Từ đó theo giả thiết ta có:     x  y  x2 2 2 2 2 2 2 2 2 2 18
x  y  2x x  y  x  y 18  y 2 2 x  y  x 1 1 1      x  y  9 .  2 2 x  y  x  0 2 2 2 x  y  2 2 x  y  x 2 2 2 2 18 2 x  y 18
Từ đó ta suy ra ba điểm A z , B z ,C z luôn thuộc đường tròn tâm O, bán kính R  9. 1   2  3
Do z  z  18, z  z  9 2 nên ta suy ra AB  2R 18 và BC  R 2  9 2 1 2 3 2
Từ đó ta có hình vẽ được biểu diễn như trên: (với E 1;  1 ) 2 Suy ra: 2 2 2 2 2 2 2 2
F  z 1 i  z 1 i  4 z 1 i  z 1 i  z 1 i  4 z 1 i  AE  BE  4CE . 1 2 3 1 2 3 2 AE  BE  AB AB 2  2 2  2 2
Do I là trung điểm AB nên 2 2 2 EI   AE  BE  2EI   166 . 4 2
Khi đó ta suy ra F max khi CE min Vậy CE
 EI  R  2  9  9  2  F
 166  49  22  6  4,176  6  4 . Chọn đáp án B. min max
Câu 49. Trong hệ tọa độ Oxyz cho mặt cầu S  x  y   z  2 2 2 :
1  7 . Hỏi có bao nhiêu điểm M trên mặt
phẳng Oxy với M có tọa độ nguyên sao cho qua M kẻ được ít nhất hai tiếp tuyến vuông góc với nhau đến mặt cầu S  . A. 8 . B. 45 . C. 36 . D. 24 .
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Lời giải
Ta có mặt cầu S  có tâm I 0;0;  1 , bán kính R  7 .
Do M Oxy nên ta suy ra M  ; a ; b 0
Nhận xét: Nếu từ M kẻ được ít nhất 2 tiếp tuyến vuông góc đến mặt cầu khi và chỉ khi 2 2 2 2 2 2 2
R  IM  R 2  R  IM  2R  7  a  b 1  14  6  a  b  13 .
Tập các điểm thỏa đề là các điểm nguyên nằm trong hình vành khăn (kể cả biên), nằm trong mặt phẳng
Oxy, tạo bởi 2 đường tròn đồng tâm O0;0;0 bán kính lần lượt là 6 và 13 .
Từ hình vẽ trên ta kết luận có 24 điểm M thỏa mãn. Chọn đáp án D.
Câu 50. Cho hình trụ có đường kính đáy bằng 5 . Hình vuông ABCD nội tiếp hình trụ với hai điểm , A B
thuộc đường tròn là đáy trên và C, D thuộc đường tròn đáy dưới của hình trụ và AB  3 . Biết diện tích
hình chiếu của hình vuông ABCD trên mặt đáy bằng 2 (đơn vị diện tích). Tính thể tích của khối trụ đó. 5 3 5 6 5 6 5 3 A. . B. . C. . D. . 12 6 2 4 Lời giải Ta có hình vẽ như sau:  5 
Ta kẻ lần lượt các đường sinh CC và DD với C , DO;   sao cho S    2 2  ABC D   Khi đó với ABC D
  là hình chữ nhật ta có: S      A . B BC 2 ABC D A . B BC  2 Mà AB  BC   R2 2 2 2
 5 nên ta có hệ phương trình sau:  2 2 AB  BC  5
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG AB  BC  1 AB  BC  2
Do AB  3 nên hệ phương trình có nghiệm:  hoặc  BC  2 BC  1 AB  BC  1 Trường hợp 1: 2 2 
 CC  h  BC  BC không tồn tại nên loại. BC  2 AB  BC  2 Trường hợp 2: 2 2 
 CC  h  BC  BC  3 BC  1 2  5  5 3
Vậy ta suy ra thể tích khối trụ là: 2 V   R h     3   . Chọn đáp án D. 2  4   THPT CHUYÊN VINH LẦN 2
Câu 38. Có bao nhiêu số tự nhiên m sao cho phương trình x x2 x 1 4 2 m 1 2       2 có đúng 2 nghiệm thực phân biệt? A. 9 . B. 10 . C. 11. D. 8 . Lời giải Đặt  2x t
t  0 . Phương trình đã cho trở thành 2t  4t  m 1  2t  2 * 2 2
t  4t  m 1  2t  2
m  t  6t  3 P1     . 2 2 t  4t  m 1  2  t  2 m  t  2t 1  P2
Vẽ hai parabol P , P trên khoảng 0; . 1   2  12  m  3 3  m  12
Yêu cầu bài toán  * có hai nghiệm dương phân biệt t ,t  m 0      m  0 . Vì m   1 2   m  1 m  1    nên m 0;4;5;...;1 
1 tức có 9 giá trị nguyên m thỏa mãn. Chọn đáp án A. Câu 39. Cho phương trình 2
z  2mz  6m  8  0 ( m là tham số thực). Có bao nhiêu giá trị nguyên của
tham số m để phương trình có hai nghiệm phức phân biệt z , z thỏa z .z  z .z ? 1 2 1 1 2 2 A. 4 . B. 1. C. 3. D. 2 . Lời giải Phương trình 2
z  2mz  6m  8  0 * có biệt số 2    m  6m 8.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Giả thiết 2 2 z .z  z .z  z  z  z  z . 1 1 1 2 2 1 2 1 2   m  4 Xét   0   . Khi đó  
1  z  z  z  z  0  m  0 (nhận). m  2. 1 2 1 2
Xét   0  2  m  4 .
Khi đó phương trình * có hai nghiệm phức liên hợp với nhau nên   1 luôn đúng.
Mà m nguyên nên m  3 (nhận). Vậy có hai giá trị nguyên của tham số m thỏa mãn. Chọn đáp án D.
Câu 41. Biết đồ thị C  của hàm số   4 2
f x  x  bx  c b,c   có điểm cực trị là A1;0 . Gọi P là
parabol có đỉnh I 0; 
1 và đi qua điểm B 2;3 . Diện tích hình phẳng giới hạn bởi C  và P thuộc khoảng nào sau đây? A. 0;  1 . B. 2;3. C. 3;4. D. 1;2 . Lời giải
Ta có: P là parabol có đỉnh I 0; 
1  P y  a  x  2 : 0 1
Mà B2;3P nên  a   2 3
2 0 1  a  1   P 2 : y  x 1  f    1  0 1   b  c  0 b   2
Ta có: C có điểm cực trị là A1;0        C f x 4 2 :  x  2x 1  f     1  0 4  2b  0 c 1 x  1 
Phương trình hoành độ giao điểm của P và C là: 4 2 2 x  2x 1  x 1 4 2
 x  3x  2  0   x   2 2 1  1 2 4 2  S  x  3x  2 dx  4 2 4 2 4 2  x  3x  2 dx  x  3x  2 dx  x  3x  2 dx     2  2 1  1 1   x 3x  2 1 dx   x 3x  2 2 4 2 4 2 dx    4 2
x  3x  2dx  2,54 . Chọn đáp án B.  2 1 1
Câu 43. Cho hàm số f  x 3
 x  3x và g x  f 2  sin x  m ( m là tham số thực). Có bao nhiêu giá
trị của m để max g x  min g  x  50 ?   A. 0. B. 1. C. 2. D. 3. Lời giải
Xét hàm số h  x  f 2  sin x  m . Khi đó g  x  h x .
Ta có : 1 2  sin x  3, x
 . Đặt 1 2sin x  t,t 1;  3
Hàm số trở thành h t  f t  m trên đoạn 1;3 . ht   f t 2  3t  3  0, t
 1;3, hàm số ht nghịch biến trên 1;3 .
Suy ra max ht  h 
1  m  2 và min ht  h3  m 18 . Vậy max h x  m  2 và min h x  m 18. 1; 3 1; 3  
Trường hợp 1: m  2m 18  0  m 2  ;18
m  2  m 18  m  2  m 18
Khi đó min g x  0 ; max g  x           m 8 10   2 m  32
Do đó: max g  x  min g x  50  m 8  40  (l)  .   m  48
Trường hợp 2: m  2m 18  0  m; 2 18; 
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG  m   m   m   m  min g  x  2  18  2  18   m 8 10  Khi đó ta suy ra:  2   m   m   m   m  max g  x  2  18  2  18   m 8 10   2 m  33
Do đó: max g  x  min g  x  50  m 8  25  (t)  .   m  1  7
Vậy có 2 giá trị của m thỏa mãn. Chọn đáp án C.
Câu 44. Cho hàm số bậc bốn y  f  x . Biết hàm số y  f 1 x có đồ thị như trong hình bên. Có bao
nhiêu số nguyên dương m sao cho hàm số g  x  f  2
x  2x  2022  m đồng biến trên khoảng 0;  1 ? A. 2021. B. 2023. C. 2022 . D. 2024 . Lời giải
Tịnh tiến đồ thị hàm số y  f 1 x sang phải 1 đơn vị ta được đồ thị hàm số y  f x .
g x   x   f  2 2 2
x  2x  2022  m.
Hàm số g  x đồng biến trên khoảng 0; 
1  g x  0,x 0;  1  f  2
x  2x  2022  m  0, x  0;  1 (vì 2x  2  0, x   0;  1 ) 2
m 1  x  2x  2022, x  0;  1 2
x  2x  2022  m 1, x  0;  1  2  
 m  2  x  2x  2022, x    0;  1   * . 2
2  x  2x  2022  m  3,x   0;  1  2
m  3  x  2x  2022, x    0; 1 Xét hàm số h  x 2
 x  2x  2022 trên khoảng 0;  1 .
h x  2x  2  0,x 0; 
1 nên hàm số h  x nghịch biến trên khoảng 0;  1 . m 1 h  1 m 1 2021   m  2022
Do đó *  m  2  h 
0  m 2  2022    .   m  2024 m 3  h   1 m3  2021
Vì m nguyên dương nên m 1;2;...;2022;202  4 . Chọn đáp án B.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 45. Cho khối chóp S.ABCD có đáy ABCD là hình bình hành và SAvuông góc với mặt phẳng đáy. Biết AB  2 , a AD  2 , a 
ABC  45 và góc giữa hai mặt phẳng SBC,SCD bằng 30 . Thể tích khối chóp đã cho bằng 2 3 A. 3 3a . B. 3 a . C. 3 a . D. 3 a . 3 4 Lời giải Cách 1: Do AB  2 , a AD  2 , a  ABC  45 nên suy ra   2 2
BAD  135 ; BD  AB  AD  2A . B AD cos135  10 Suy ra AC  AO   2 2 AB  AD  2 2 2  BD  2  AB nên A  BC cân tại A tức S  BC cân tại S .
Đặt SA  x  0 . Kẻ AI  BC, AH  CD, AE  SH khi đó ta có AI  a , suy ra 2 2 2 2
SI  x  a ; SC  x  2a 1 1 2 2 SI.BC x  a Ta có S
 SI.BC  SC.BF với BF  SC nên suy ra d B;SC  BF   2 SBC 2 2 2 2 SC x  2a AI.BC S . A AH xa 2
Ta lại có: AH  d C; AB   a 2  d  ; B SCD  d  ; A SCD  AE   2 2 2 2 AB SA  AH x  2a BX d  ; B SCD  xa 2 1
Từ đó ta suy ra sin SBC,SCD          x  SA  a BF d ; B SC 2 2 2 x  a 2 1 1 2 Vậy V  S . A S  SA AB AD
  a . Chọn đáp án C. S ABCD 2 ABD  . . sin135  3 . 3 3 3
Cách 2: Ta có hình vẽ như sau:
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Ta có: SC  SBC  SCD . Kẻ AE  SC tại E (1) và đường thẳng qua E song song với CD cắt SD tại F . Do AB  2a, AD  2a,  ABC  45 nên suy ra   2 2
BAD  135 ; BD  AB  AD  2A . B AD cos135  10 Suy ra AC  AO   2 2 AB  AD  2 2 2
 BD  2  AB , từ đó ta thu được mặt đáy như hình trên, suy ra
AC  CD tức CD  SAC  AE  CD (2). Từ (1) và (2) suy ra AE  SCD  AE  EF tức  AEF  90 .
Từ đó ta có được: SC   ABEF  và SBC,SCD   BE,EF  180   BEF  180   BEA    AEF   AB a 90  
BEA   . Tiếp đến lại có:  6 tan BEA 
 cot  cot 30  AE  AE 3 1 1 1 3 1 1 Lại có:       SA  a . 2 2 2 2 2 2 AE AS AC 2a AS 2a 1 1 2 Vậy V  S . A S  SA AB AD
  a . Chọn đáp án C. S ABCD 2 ABD  . . sin135  3 . 3 3 3
Câu 46. Cho hàm số y  f  x có đạo hàm trên  và          3 1 x f x f x x
e , với mọi x   . Biết f   5 0  , giá trị f   1 bằng 4 5 3 3 5 A. 3 e  e . B. 3 e  e . C. 3 e  e . D. 3 e  e . 4 4 4 4 Lời giải
Ta có:          3x x    x 
      2x   x         2 1 1 1 x f x f x x e e f x e f x x e e f x x e x x 1 x 1 Khi đó:       2 1     2 2 1 x e f x x e dx x e  e  C 2 4 1 5 1 3 x 1 Do f   5
0  nên:     1       3 3 1 x x C C f x x
e  e  e . Vậy f   3 1  e  e . 4 4 4 2 4 4 Chọn đáp án C.
Câu 47. Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại số thực b  a thỏa mãn 4a  2b  b và đoạn  ;
a b chứa không quá 5 số nguyên ? A. 5 . B. 10 . C. 6 . D. 11. Lời giải
Ta có 4a  2b   2b   4a b b  0
Xét hàm số    2b   4a     2b f b b f b
ln b 1  0 nên hàm số f b luôn đồng biến trên  ;  
Ta có 4a  2b   2a   2a   4a b a a  0  f a  0
Nên để tồn tại số thực b và đoạn  ;
a b không chứ quá 5 số nguyên:  f a  0  2a  a  4a  0  
tức có 11 giá trị nguyên a sao cho thỏa      a    f a  5  5; 4;..;4;  5 a5  0 2  a  5  4a  0
mãn yêu cầu đề bài. Chọn đáp án D.
Câu 48. Cho hàm số y  f  x có đạo hàm là f x   2 x  x 2 9
x  9 với mọi x. Có bao nhiêu giá trị
nguyên của tham số m để hàm số y  g  x  f  3 2
x  3x  2m  m  có không quá 6 điểm cực trị ? A. 2 . B. 5 . C. 4 . D. 7 .
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Lời giải Do g x  f  3 2
x  x  m  m   f  3 2 3 2
x  3x  2m  m   g x nên hàm số này là hàm số chẵn tức để
hàm số g  x có không quá 6 điểm cực trị (cụ thể là tối đa 5 cực trị) thì hàm hx  f  3 2 x  3x  2m  m 
có tối đa 2 điểm cực trị dương.
Kéo theo phương trình hx   2 x   f  3 2 3 3
x  3x  2m  m   0 có tối đa 2 nghiệm bội lẻ dương. 3 2 3 2 x  3x  2m  m  0
x  3x  m  2m  y3   3 2 3 2 x  3x  2m  m  9  
x  3x  m  2m  9  y1    (*) 3 2  3 2 x  3x  2m  m  3 
x  3x  m  2m  3  y2   3 2 3 2
x 3x  2m  m  3
x  3x  m  2m  3  y  4
Như vậy để thỏa mãn đề bài thì bốn đường thẳng lần lượt là y , y , y , y phải cắt đồ thị 3 y  x  3x tại tối 1 2 3 4
đa hai nghiệm dương. Xét hàm số 3 y  x  3x có 2 y  3x  3  0, x
   và y0  0 .
Nhận thấy m  m   m  2 2 2 3
1  2  0 luôn đúng nên hệ (*) có tối thiểu 1 nghiệm, từ đó ta có: Trường hợp 1: 2
m  2m  0  m0;2 thì hệ (*) có 1 nghiệm tức hàm số luôn có 3 điểm cực trị m  0 Trường hợp 2: 2 m  2m  0  
thì hệ (*) đang có 2 nghiệm dương. Do hàm số có tối đa 5 điểm cực m  2 2 m  2m  9  0
trị nên chỉ có tối đa 2 nghiệm dương tức ta có điều kiện đủ là:   m 1;  3 2 m  2m  3  0
So với điều kiện ta suy ra m 1  ;  3 .
Từ hai trường hợp ta suy ra m 1  ;0;1;2; 
3 tức có 5 giá trị nguyên m thỏa. Chọn đáp án B.
Câu 49. Trong không gian Oxyz , cho mặt phẳng P : 2x  y  2z 16  0 và mặt cầu
S x  2  y  2  z  2 : 2 1
3  21. Một khối hộp chữ nhật H  có bốn đỉnh nằm trên mặt phẳng  P và
bốn đỉnh còn lại nằm trên mặt cầu S  . Khi H  có thể tích lớn nhất, thì mặt phẳng chứa bốn đỉnh của
H  nằm trên mặt cầu S là Q:2x by cz  d  0. Giá trị bc  d bằng A. 1  5. B. 1  3. C. 1  4. D. 7  . Lời giải
Đầu tiên, ta có mặt cầu S  tâm I 2; 1  ;  3 , bán kính R  21
Tiếp đến ta nhận thấy: d I;P  9  21 nên suy ra mặt phẳng P không cắt mặt cầu S  .
Gọi a,b là các kích thước mặt đáy hình hộp chữ nhật và d  d I;Q . Khi đó ta có: 2 2  a  b 
Ta có: V  d I P  d I Qab    d ab    d      d  2 ; ; 9 9 2 9 21 d   f d   2 
Xét hàm số y  f d     d  2 9
21 d  trên 0; có f d   0  d 1  max f d   f   1  
Suy ra thể tích khối hộp đạt max khi và chỉ khi d  d I;Q 1, P  Q 11 d d  8
 Q : 2x  y  2z 8  0
Suy ra: Q : 2x  y  2z  d  0; d I;Q  1   1     3 d  14
Q : 2x  y  2z 14  0 2 
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Xét điểm N 0;0; 8
  bất kì thuộc mặt phẳng P ta nhận ra để thể tích max thì chiều cao hộp phải max
tức hai điểm I và N phải nằm cùng phía với mặt phẳng Q
Như vậy ta nhận mặt phẳng Q : 2x  y  2z 14  0 do 2x  y  2z 14 x  y  z   I I I 2 2 14 N N N  0 2 
Với Q : 2x  by  cz  d  0 , ta đồng nhất hệ số ra b  c  d  1  3. Chọn đáp án B.
Câu 50. Xét các số phức z và w thỏa mãn z  w 1 và z  w  2 . Giá trị nhỏ nhất của biểu thức
P  zw  2i  z  w  4 bằng 3 2 1 5 2 A. . B. . C. 5  2 2 . D. 5 . 2 4 Lời giải Cách 1: Gọi ,
A B lần lượt là các điểm biểu diễn số phức z, w, khi đó với z  w  2 ta luôn có O  AB là  
tam giác vuông tại O với O .
A OB  0 , khi đó ta luôn có z.w là số thuần ảo tức . z w  ki k   w  ki  P  zw  2i  z  w 2  4  ki  2i  w  4  kiw  2i   kiw w 2
 4  kiw  2kw  2iw  4  w  w  Khi đó   ki z  w   w  wki   2
1  w k 1  2  k  1  w
Đặt w  a  bi a,b khi đó ta có: P  iw   i   w  w    i w i  w  i2 2 2 2 2 4 2 2 4 1  2i
Đặt u  w 1 i  w  u 1 i  w  u 1 i 1, khi đó ta suy ra (đặt trước z  1 i ) (*) 0 2 2 P  u  2i  u  z  u  z  2 2 u  z  4 4
 u  z  u.z  z .u  u z  u  u   u z  z u o o 2 2 4 2 2 2 2 2 2 2 2 . 4 4 . . 0 0 0 0 o  o o 2
Mà u  z u  z  2 2
 u  z  u 1 i  1 * 2 2 2
 u.z  z .u  1 u  z   u 1 o o 0 o o o 2 2 9  1  9 9 3 2 Suy ra 4 2  u  4 u  4   2 u   2 4 2 2
1  2 u  2 u  5  2 u     P    . Chọn đáp án A. 2  2  2 2 2
Cách 2: Ta biến đổi biểu thức P như sau: P  zw  2i  z  w  4  w  2iz  2i  z  2i . w  2i Gọi ,
A B lần lượt là các điểm biểu diễn số phức z, w, cùng với điểm M 0; 2   Khi đó hai điểm ,
A B cùng thuộc đường tròn tâm O , bán kính R 1.
Do z  w  2 nên ta suy ra z  w  z  w  AB  2 và P  M . A MB
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG     x  sin    cos x  sin  B     2  Ta có: A 
, do OA  OB nên ta suy ra 
. Suy ra ta có tọa độ hai điểm , A B y  cos     A  y  cos    sin B     2 
mới lần lượt là Asin;cos , Bcos;sin  Suy ra: P  M .
A MB  5  4cos 5  4sin   25  20sin  cos  16sin cos  Đặt t  sin  cos    2 sin x   t   2; 2    4     2  t t sin cos 2 1 2 1 2sin cos sin cos         2 Khi đó ta có: P   t   2t   2 25 20 8
1  8t  20t 17  f t  5  3 2
Xét hàm số f t ta thấy min P  min f t  f    . Chọn đáp án A.  2; 2    4  2
ĐỀ THPT QUẢNG XƯƠNG LẦN 2
Câu 43. Cho hình chóp S.ABCD có đáy là hình thoi tâm H , SH   ABCD. Hai đường chéo AC  2a
BD  a 2 . Gọi M , N lần lượt là trung điểm các cạnh S ,
A SB và điểm P thuộc cạnh CD . Biết rằng khoảng
cách từ A đến mặt phẳng MNP bằng a , thể tích khối đa diện AMNP bằng 3 a 2 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 8 4 4 8 Lời giải
Đầu tiên ta chuẩn hóa a  1. Gọi O  CM  DN khi đó O là trọng tâm S  AC . (*)
Ta nhận thấy do mặt phẳng MNP luôn trùng với mặt phẳng MNCD nên ta đặc biệt hóa điểm P nằm
tại chân đường vuông góc hạ từ H xuống CD . Khi đó ta có: CD  OHP tức ta suy ra: 1 x
d  A MNP  d H MNP  d H OP   d H OP 1 ; 2 ; 2 ; 1 ;
 . Đặt SH  x , khi đó OH  SO  (*) 2 3 3
Do HP  CD nên xét trong tam giác vuông CHD ta có: HC.HD 1 HP   2 2 HC  HD 3
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG OH.HP x 1 Suy ra: d H;OP     x  SH  3. 2 2 OH  HP  2x   2 3 3 1 1
Ta giả sử tiếp P di động đến trùng điểm D , khi đó ta có: V V V  V  V AMNP AMND SMND SABD S. 4 8 ABCD 3 Vậy 1 1 1 1 a 2 V  V  SH.S  .3. .AC.BD  . Chọn đáp án A. AMNP S. 8 ABCD 24 ABCD 24 2 8
Câu 44. Tại một cửa hàng kinh doanh quần áo X có doanh thu R t với tốc độ Rt 2  7250 18t (triệu/
năm) sau thời gian t năm. Chi phí kinh doanh C t của cửa hàng tăng với tốc độ Ct 2  3620 12t
(triệu/ năm). Hỏi sau bao nhiêu năm lợi nhuận Lt  Rt C t , của cửa hàng bắt đầu giảm và lợi
nhuận L sinh ra trong khoảng thời gian đó là bao nhiêu ?
A. t 12 năm, L  26620 triệu đồng.
B. t 12 năm, L  26620 triệu đồng.
C. t 12 năm, L  26620 triệu đồng.
D. t 12 năm, L  26620 triệu đồng. Lời giải
Ta có tốc độ lợi nhuận sau thời gian t năm là:
Lt  Rt   Ct  2   t   2  t  2 7250 18 3620 12  3630  30t t 
Giải phương trình: Lt 11  0   t 11 
, như vậy sau 11 năm thì việc sinh lời không còn nữa t  11
Khi đó giá trị tiền lãi thực trên khoảng thời gian 0  t 11 là 11 11 L 1  1  L 0  L  tdt   2
3630  30t dt  26620 (triệu đồng). Chọn đáp án C. 0 0
Câu 45. Hai bạn A và B , mỗi bạn viết ngẫu nhiên một số tự nhiên gồm ba chữ số đôi một khác nhau. Xác
suất để các chữ số có mặt ở hai số bạn A và B viết giống nhau bằng 25 31 1 1 A. . B. . C. . D. . 2916 2916 648 108 Lời giải Đầu tiên mỗi bạn có 2
9.A cách viết nên không gian mẫu là n  9.A cách. 9 2 2 9
Ta tìm cách viết mà các chữ số có mặt trong hai số mà bạn A và B viết giống nhau. Bạn A có tất cả 2 9.A9
cách viết mà số không bao gồm chữ số 0 và có  2 3
9.A  A cách viết mà số có bao gồm chữ số 0. 9 9 
Trường hợp 1: Nếu A viết số không gồm chữ số 0 có 3
A cách, lúc này B có 3! cách viết. 9
Trường hợp 2: Nếu A viết số có bao gồm chữ số 0 có  2 3
9.A  A cách, lúc này B có 4 cách viết. 9 9  3 A .3!  2 3 9.A  A 4 9 9 9  25
Vậy xác suất cần tìm là: P    . Chọn đáp án A. A 2 2 2916 9. 9
Câu 46. Cho số phức z có phần thực không âm, phần ảo không dương, đồng thời thỏa mãn
z  2  i  z  3i và z z  2  i  4i 1 là số phức có phần ảo không dương. Khi số phức w  z  3zi có
phần ảo nhỏ nhất thì modun của w bằng A. 2 5 . B. 13 . C. 2 10 . D. 5 .
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Lời giải
Đầu tiên ta đặt z  a  bi a  0,b  0 . Khi đó ta có: z  2  i  z  3i  z  2  i  z  3i
a  2  b  2  a  b  2 2 2 1
3  a  b 1  0  a  b 1  0 .
Lại có: z z  2 i  4i 1 a  bia  2  1bi  4i 1 
... . a  2b  4i là số phức có phần ảo
không dương nên ta suy ra a  2b  4  0 . Từ đó ta có hình vẽ dưới đây với miền D là phần chứa các số
phức z thỏa. Tiếp đến ta có w  z  3zi  a  3b  b  3ai có phần ảo nhỏ nhất tức b  3a nhỏ nhất.
Suy ra b  3a nhỏ nhất khi  ; a b  0; 2   tức w  6
  2i . Vậy w  2 10 . Chọn đáp án C. 1 1
Câu 47. Có bao nhiêu cặp số nguyên  ;
a b thỏa mãn 0  a,b  20 sao cho đồ thị của hai hàm số y   x a b 1 1 và y 
 cắt nhau tại đúng hai điểm phân biệt ? x b a A. 340. B. 342. C. 361. D. 324. Lời giải
Đầu tiên ta nhận thấy a  1,b  1. Dễ dàng nhận ra nếu a  b thì hai đồ thị lúc này trùng nhau nên có vô số
điểm chung, suy ra loại. Do đó a  b , tiếp đến, vì vai trò của a và b như nhau nên ta chỉ cần tìm cặp số 1 1 1 1 1 1 1 1 nguyên  ;
a b, a  b 1sao cho phương trình      
  0 có 2 nghiệm phân biệt. x x x x a b b a a b b a a b
Xét hàm số y  f  x 1 1 1 1     có f x ln ln    và f   1  0 x x a b b a x x a b ln a ln b  ln b Giải phương trình  f  x     0  x  x  log , f  x  0 x x 0 b     a b  ln a  a
Cùng với f  x  0 khi x  x và f  x  0 khi x  x . Nên ta xét 2 trường hợp sau: 0 0  ln b  ln a ln b Trường hợp 1: x  log  1    a;b  4;2 0 b        ln a  a b a ln 3 ln 2 2ln 2 ln 4 ln 5 ln 20
Xét hàm số    ln t y g t  ta có:      ....  t 3 2 4 4 5 20
Khi đó f x  f x  f 1  0 tức f  x có đúng 1 nghiệm x 1 0    0  ln b Trường hợp 2:  x  log
 1. Khi đó vẽ bảng biến thiên ta thấy f x  0 luôn có hai nghiệm phân 0 b    ln a  a
biệt. Với mỗi b  k 2;3;...;1 
9 thì a k 1;....;2 
0 tức có 20  k cách chọn giá trị a . 19
Suy ra có 100  k 171 cặp  ;
a b với a  b 1 và loại đi cặp 4;2 ta có 170 cặp. k 2
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Xét tương tự với b  a 1 ta cũng có 170 cặp. Vậy có tất cà 340 cặp số thỏa mãn. Chọn đáp án A.
Câu 48. Cho hàm số y  f x có đạo hàm liên tục trên  , f  6
   0 và bảng xét dấu đạo hàm. Hàm số y  f  4 2 x  x   6 4 2 3 4
6  2x  3x 12x có tất cả bao nhiêu điểm cực tiểu ? A. 5 . B. 7 . C. 3 . D. 8 . Lời giải
Xét hàm số y  h x  f  4 2 x  x   6 4 2 3 4
6  2x  3x 12x ta có: h x   3  x  x f  4 2 x  x   5 3  x  x  x   x  2 x   f  4 2 x  x    x 2 x   2 12 24 4 6 12 12 24 12 2 4 6 12 2 x   1 x  0; x   2
Giải h x  0    f    4 2 x  4x  6  2 x   1  0 *
Ta đánh giá (*) như sau: do f x  x    f x  2 4 2 2    f   2 4 6 2 2 2  0; x 1  1, x   
Nên phương trình (*) vô nghiệm, tức hàm số hx có ba điểm cực trị, từ đó ta có bảng xét dấu như sau: Do f  6
   0 nên kéo theo h 6
   0 , suy ra ta có hai trường hợp xảy ra, đó là h0  0 và h0  0
Căn cứ vào đó ta có hai trường hợp xảy ra với đồ thị h  x , tức đồ thị đề cần tìm.
Vậy h  x chỉ có 2 trường hợp là 3 điểm cực tiểu hoặc 4 điểm cực tiểu. Chọn đáp án C.
Câu 49. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  có phương trình x   y  2 2 2 1  z  4 và
điểm H 3;0;3 . Gọi  là đường thẳng đi qua điểm H và cắt mặt cầu theo dây cung 4 3 BC  không đổi. 3
Khi khoảng cách từ O đến  lớn nhất thì  đi qua điểm N  2  0; ; m n . Tính m  n  ? A. m  n  3 . B. m  n  5 . C. m  n  20. D. m  n  20 .
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Lời giải 2  BC  2 6
Ta có mặt cầu S  có tâm I 0;1;0 và bán kính R  2 . Khi đó ta có: d I; 2  IE  R     .  2  3
Dễ dàng đánh giá được khoảng cách từ O đến  lớn nhất khi  và hai điểm I,O đồng phẳng. O
 H  3 2;OI 1;IH  19 IO 1 HO 3 2 Ta có:  nên I
 OH vuông tại O và sin  IHO   ;cos  IHO   . 2 2 2 IH  IO  OH IH 19 IH 19 IE HE IH  IE Mặt khác ta có:  IHE    2 2 2 6 7 sin ;cos IHE    IH 3 19 IH IH 57
Nên với OF   ta suy ra: d O;  OF  OH sin  OHE  3 2 sin  IHO   IHE  IHO IHE  IHO IHE max 
 3 2 sin cos cossin     1 7 3 2 2 6  1  3 2  .  .   3 2.  6  19 57 19 3 19  3   MI EI 2  2   
Gọi M  OI   , khi đó ta suy ra 
  MI  MO  3MI  2MO  0 MO OF 3 3   x y  z
Giải hệ tâm ti cự trên ta ra được M 0;3;0 , suy ra u  HM          3 1; 1;1 : 1 1  1 Mà  đi qua N  2
 0;23;20 nên đồng nhất suy ra m  n  3 . Chọn đáp án A.
Câu 50. Cho hàm số f x là hàm số bậc hai có đồ thị là một parabol có trục đối xứng là trục Oy và thỏa 3 ln x   1 a mãn điều kiện  2 x  x f  x   2  f  x 3 1  x 1, x
   . Biết giá trị của tích phân   , f  x dx ln 3 1 b 2 2
(với a,b   , UCLN a,b 1). Tính giá trị của biểu thức 3 3 S  a  b  a  b A. 92 . B. 8 . C. 122. D. 62 . Lời giải
Do hàm số f x là một parabol có trục đối xứng là trục Oy nên ta có : f  x 2  ax  c  , a b ,a  0 .
Thế vào phương trình:  2 x  x f x   2  f  x 3 1  x 1, x
   , từ đó ta có:
 x  xax  1  cax  c2 2 2 2 3  x 1, x      2 a  a  4 3
x  ax  c  2ac  a 2 x  a  c 2 3 x  c  x 1, x   
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG 2 a  a  0  a  1
Đồng nhất hệ số ta suy ra hệ phương trình sau: a 1;a  c  0    f x 2  x 1.  c  1 2 c  1   3 ln x   3 1 ln  x   1  ln x   3 1  dx  ln x   3 3 3 1    Suy ra    (từng phần) x           ln f  x dx dx 2 1 x x x x 1 x       x 1     2 2   2 2 2 2 3 5  32   4  a  4  ln 2  ln 3  ln    ln      
 S  92 . Chọn đáp án A. 3 3 3    3 2  b   3
ĐỀ THPT LÊ QUÝ ĐÔN ĐÀ NẴNG LẦN 2
Câu 46. Trong không gian Oxyz , cho hai mặt cầu S  : x  62   y  72   z 82  9 và 1
S :x 62   y 72 z 82 1. Có bao nhiêu điểm M thuộc mặt phẳng Oxy, với tọa độ là số 2
nguyên, mà từ M kẻ được đến S ba tiếp tuyến MX , MY, MZ (với X ,Y, Z là các tiếp điểm và đôi một 1 
khác nhau) sao cho mặt phẳng  XYZ  tiếp xúc với S ? 2  A. 6 . B. 12. C. 10 . D. 8 . Lời giải
Đầu tiên ta có hai mặt cầu S và S chung tâm I 6;7;8 và bán kính lần lượt là R  3, R 1 2  1  1 2
Ta đặc biệt hóa hai điểm X ,Y và có hình vẽ sau đây: Đặt M  ; a ;
b 0,a,b  khi đó ta có: (áp dụng hệ thức lượng trong tam giác vuông). 2 2 IX R1 MI  
 9  MI  a  62  b  72  64  81  a  62  b  72 2  17 IE R2
Từ đó ta suy ra điểm M thuộc đường tròn C  x  2   y  2 : 6
7  17 . Bài toán chuyển về tìm số nghiệm nguyên  ;
a b thỏa phương trình a  2  b  2 6
7  17 . Khi ấy ta suy ra: a  6,b  7 là các căn bậc hai củ
số chính phương. Từ đó ta chia thành hai trường hợp như sau:   a  6  2 1  1   a  6 1 5   a  7 Trường hợp 1:        ;
a b  5;3;5;1  1 ;7;3;7;1  1   b  7  2   4   b  7  4 3   b 11 6 1   a  6  2 16  4   a  6  4 2  a 10 Trường hợp 2:        ;
a b  2;6;10;6;2;8;10;8   b  7  2   1   b  7  1 6  b  8 1
Như vậy tổng lại ta có 8 tọa độ nguyên M thỏa mãn. Chọn đáp án D.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 47. Gọi S là tập hợp tất cả các số phức z sao cho z 1 i  z  3 4i  5. Xét các số phức z , z thuộc 1 2
S thỏa mãn z  z  2 , giá trị lớn nhất của 2 2
P  z  5i  z  5i bằng 1 2 1 2 44 16 A. 4 10 . B. . C. . D. 4 17 . 5 5 Lời giải
Gọi M  z là điểm biểu diễn số phức z , cùng với A1; 
1 , B 3;4 và phương trình MA  MB  5  AB
Ta suy ra M di động trên đoạn AB . Tiếp đến gọi N  z , P z sao cho z  z  NP  2 . 1   2  1 2
Cùng với điểm Q 0;5 , ta có: 2 2 2 2
P  z  5i  z  5i  NQ  PQ 1 2  3a  7   3b  7 Do 
N  z , P z  AB : 3x  4y  7  0 nên ta đặt N a; , P ; b 1   2        4   4 
Quỹ tích của đoạn NP là 1 đoạn thẳng trượt qua lại trên đoạn AB nên ta suy ra a  1  ;  3 2  8  3a  7 3b  7  25 a  b   8
Khi đó ta có: NP  a  b2    4    a b2 2  4   5  b  a  .  4 4  16 5 a  b 2   8   2 2 3 a   7  3a 7   8      5    19 19 44 2 2 2 P  NQ  PQ  a   5  a     5  ...  5a   5    1       với  4   5   4  5 5 5     44 mọi a  1  ;  3 . Vậy P  . Chọn đáp án B. max 5
Câu 49. Có bao nhiêu số nguyên a  1
 2;12 sao cho ứng với mỗi a , tồn tại ít nhất 4 số nguyên b thỏa mãn 2 4ba  2022  2ab ? A. 19 . B. 17 . C. 16 . D. 18 . Lời giải
Ta có bất phương trình tương đương với: 2
4ba  2ab  2022  0 . ba ab b a a b  ln 2 1 Xét hàm số   2 4b a 2a b y f b       2022 có f b 2 2 2 2 1 4 ln 4 2 ln 2 0 2 2         ln 4 2 2 2
 b  2a  a 1  0  b  b  2a  a 1. Mặt khác f  b  2  4a a ln 4 2 1 2 2a 2a 1  2  2 ln 2  0 nên ta suy 0   0
ra b  b là điểm cực tiểu hàm số f b . 0
Suy ra điều kiện cần để tồn tại nghiệm bất phương trình f b  0 là f  2 2a  a   1  0    2 2 a 4 a a 1  2a 2a 1 4 2     2022  0 (CALC) a   1  2;12 
a 11;4  3;1 1. (1) a  3
Tiếp đến ta đánh giá như sau: 2 2 2 2 ab ba ba ba 1  a a 1 2 4 2022 2 2022.4 2 . 2022 2        2 2022 a  3 Suy ra: 2 a  a  log 2022 1  (*) Khi đó ta luôn có 2 a  a  12 . 2    a  4
Từ đó ta thấy ngay với mọi giá trị của b  2 2 a 1; ;
a a 1;.. . thì bất phương trình ban đầu luôn đúng với
mọi a thuộc tập (*) (2).
Vậy ta suy ra a 11;10;...;4;3;4;...;1 
1 tức có 17 giá trị nguyên a thỏa mãn. Chọn đáp án B.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 50. Cho hàm số f x  x  x  2 x  3 2 2 2 1 2
3 . Có bao nhiêu giá trị nguyên của tham số m để hàm số y  f  4 2
x  8x  m có đúng 7 điểm cực trị ? A. 15 . B. 13 . C. 14 . D. 16 . Lời giải
Xét hàm f x  x  x  2 x  3 2 2 2 1 2
3 có f x  f  x nên f  x là hàm số chẵn.
Như vậy chắc chắn hàm số f  x có một điểm cực trị là x  0
Mà f x  0 với mọi x  0 nên suy ra hàm số luôn đồng biến trên 0;
Từ đó suy ra hàm số có duy nhất 1 cực trị x  0 x  0; x  2
Xét hàm số y  g x  f  4 2
x  8x  m có gx   3 4x 16x f  4 2
x  8x  m  0   4 2 x  8x  m  0
Như vậy để g  x có 7 điểm cực trị thì phương trình 4 2
x  8x  m  0 phải có 4 nghiệm bội lẻ phân biệt và khác 2;0; 
2 . PT tương đương với: 4 2
m  x  8x  u  x .
Khi đó ta có bảng biến thiên hàm u x như sau: x – ∞ -2 0 2 + ∞ y' + 0 – 0 + 0 – 16 16 y – ∞ 0 – ∞ Từ đó ta suy ra 0;16 m ycbt m      m 1;2;...;1 
5 tức có tất cả 15 giá trị nguyên m thỏa mãn. Chọn đáp án A.
ĐỀ CHUYÊN KHTN HÀ NỘI LẦN 2
Câu 48. Xét số phức z thỏa mãn z  2 , giá trị lớn nhất của biểu thức z  2i  z  3  i  z  3  i bằng A. 4  2 3 . B. 2  2 3 . C. 4 . D. 8 . Lời giải
Gọi M là điểm biểu diễn số phức z sao cho thuộc đường tròn C 2 2
: x  y  4 . Cùng với ba điểm lần lượt
là A0;2, B 3;  1 ,C  3;  1 , suy ra A
 BC đều. Gọi E  AM sao cho MB  ME . Ta có như sau:
Tứ giác ABMC nội tiếp nên  ACB  
AMB  60 , khi đó ta suy ra B  ME đều. Lại có tiếp  ABE   CBE  60   CBE   CBM   ABE   CBM Xét A  BE và C  BM có: AB  BC;  ABE   CBM ;  BAM   BCM , suy ra A  BE  C  BM c  g c
Khi đó ta suy ra AE  CM (hai cạnh tương ứng bằng nhau).
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Suy ra: P  z  2i  z  3  i  z  3  i  MA  MB  MC  MA  ME  CE  AM  AM  2AM
Như vậy khi biểu thức P max thì đoạn AM đạt max. Suy ra: P
 2AM  2R  4 . Chọn đáp án C. max C SỞ NINH BÌNH LẦN 2
Câu 47. Cho khối hộp ABC . D A B  C  D
  có AC  3 . Biết rằng các khoảng cách từ các điểm A , B, D đến
đường thẳng AC là độ dài ba cạnh của một tam giác có diện tích 6 S 
, thể tích của khối hộp đã cho là 12 2 2 3 2 A. . B. 1. C. . D. . 12 2 4 Lời giải AG 1 Gọi G  AC  A B
 D, khi đó dễ thấy G là trọng tâm A  B  D và  nên 3 AG  . AC 3 3
Lấy điểm K đối xứng với B qua G và dựng hình lăng trụ GDK.APN .
Nhận thấy rằng khoảng cách giữa các mặt bên của lăng trụ GDK.APN bằng với khoảng cách từ đỉnh A , B, D đến AG .
Từ đó, qua cách dựng các mặt phẳng đi qua ,
A G và vuông góc với các cạnh bên của lăng trụ GDK.APN ,
đồng thời cắt các mặt phẳng chứa các mặt bên của lăng trụ này, ta lại thu được một lăng trụ mới (như
hình vẽ) là một lăng trụ đứng có chiều cao là AG , tam giác đáy có kích thước lần lượt bằng độ dài khoảng
cách từ các đỉnh A , B, D đến đường thẳng AC.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Khối lăng trụ mới và lăng trụ GDK.APN có cùng thể tích nên 2 V  V  S .AG  với 6 S  . m GDK .APN m 12 m 12 Suy ra: 2 2 V     . Chọn đáp án C.     6V  6V 6. ABCD.A B C D A .ABD GDK .APN 12 2 1
Câu 48. Cho hàm số y  f  x 3 2
 x  ax  bx  c có đồ thị cắt trục hoành tại 3 điểm phân biệt. Biết hàm 6
số g x   f x 2
  f  x f x   f x 2 2    
 có 3 điểm cực trị x  x  x và g  x  2, g x  5, g x 1. 1   2  3 1 2 3 f x
Diện tích hình phẳng giới hạn bởi đồ thị h x    và trục Ox bằng g  x 1 1 3 ln6 A. ln . B. . C. ln 6 . D. 2ln 6 . 2 2 2 Lời giải 1
Ta có: f  x 1 nên g x  2 f  x f   x  2 f  x f x  2 f  x f   x  2
 f x  f x   gx 2 f x Tiếp đến ta có: hx     
 nên phương trình cũng có 3 nghiệm x  x  x , và cũng là g  x 0 f  x 0 1 1 2 3
các điểm cực trị của hàm số g  x nên diện tích hình phẳng cần tìm là: 3 x f  x 2 x f  x 3 x f  x  2 1 x g x 3 x g x  S  dx  dx  dx   dx  dx       g x  g x  g x   g x  g x   x   1 x   1 x   1 2 x   1 x   1 1 1 2  1 2  g  2x 1 d g x g 3 x  d g x       
g x  2, g x  5, g x 1 1   2   3  2  g x 1 g x 1  g 1 x g 2 x          5 1 1  dx dx  1 ln 6             ln6 ln 6 ln 3 ln 2 ln 6  . Vậy S  . Chọn đáp án B. 2  x 1 x 1    2 2  2 2 5 
Câu 49. Biết nửa khoảng m n S   p p   * ; p, , m n   
 là tập hợp tất cả các số thực ysao cho ứng với mỗi
y tồn tại đúng 6 số nguyên x thỏa mãn  2x x   2 2 3
27 5x  y  0. Tổng m  n  p bằng A. m  n  p  46 . B. m  n  p  66 . C. m  n  p  14 . D. m  n  p  30 . Lời giải
Trường hợp 1: y  1, khi đó ta suy ra 2 5x  y  0 .
Do đó bất phương trình ban đầu trở thành: 2 x 2x 2  3
 27  0  x  2x  3  1
  x  3 tức có 5 giá trị nguyên x (loại)
Trường hợp 2: y  1, khi đó ta suy ra 2 2 5x   5x y 1 0 .
Do đó bất phương trình ban đầu trở thành: 2 x 2 x 2 3  27  0 x  2x  3      1
  x  3tức có 5 giá trị nguyên x (loại) 2 5x 1 x  0 x  1 
Trường hợp 3: y  1, khi đó ta xét: 2x2 3 x  27  0   và 2
5x  y  0  x   log y x  3 5
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG  log y; 1     log y;3 5 5    
-Nếu log y  3 hay  log y  3
 thì tập nghiệm cần tìm chính là  , tuy 5 5  1
 ; log y    log y;3  5 5    
nhiên các cặp nghiệm này không chứa đủ 6 số nguyên nên ta loại.
-Nếu log y  3 hay  log y  3
 thì tập nghiệm cần tìm chính là  log y;1  3; log y  5 5 5 5     , và tập
này chỉ chứa đúng 6 số nguyên khi và chỉ khi 16 25
4  log y  5  5  y  5 5 Từ đó ta suy ra: 16 25 S  5 ;5 
 chính là tập nghiệm cần tìm, tức m n p  46. Chọn đáp án A.
Câu 50. Xét số phức z có phần thực âm và thỏa mãn z 1  2 . Giá trị nhỏ nhất của biểu thức
P  z  3  i  z  3i  z  3i bằng A. 6 . B. 37 . C. 4  17 . D. 3 17 . Lời giải A3; 
1 , B 0; 3,C 0; 3 M  z
Gọi M là điểm biểu diễn số phức z . Xét các điểm . Cùng với điểm
thỏa mãn z 1  2 , ta có hình vẽ như sau:
Gọi D thuộc đường tròn C  x  2 2 : 1  y  4 sao cho B
 CD đều và E MD sao cho MB  ME
Khi đó ta suy ra D 3;0 và nhận định như sau:
Tứ giác DBMC nội tiếp nên  DCB  
DMB  60 , khi đó ta suy ra B  ME đều. Lại có tiếp  DBE   CBE  60   CBE   CBM   DBE   CBM Xét A  BE và C  BM có: DB  BC;  DBE   CBM;  BDM   BCM , suy ra D  BE  C  BM c  g c
Khi đó ta suy ra DE  CM (hai cạnh tương ứng bằng nhau).
Suy ra: P  z  3  i  z  3i  z  3i  MA  MB  MC  MA  ME  DE  MA  MD  AD  37
Dấu bằng xảy ra khi M  AD  C  . Chọn đáp án B.
THỊ XÃ QUẢNG TRỊ LẦN 1
Câu 46. Gọi S là tập hợp tất cả các số phức w  2z  5  i sao cho số phức z thỏa mãn
z 3 iz 3i  36. Xét các số phức w ,w S thỏa mãn w  w  2 . Giá trị lớn nhất của 1 2 1 2 2 2
P  w  5i  w  5i bằng 1 2
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG A. 7 13 . B. 4 37 . C. 5 17 . D. 20 . Lời giải Ta có:
 z   iz  i  z  iz  i 2 36 3 3 3 3
 z  3 i  z  3 i  6  2z  6  2i  12
Mà số phức w  2z  5  i nên suy ra 2z  6  2i  2z 5  i 1 i  w 1 i 12
Suy ra điểm M w luôn thuộc đường tròn C  tâm I 1;  1 , bán kính R  12 .
Tiếp đến xét các điểm Aw , B w thuộc đường tròn C  sao cho w  w  AB  2 , cùng với tọa độ 1   2  1 2
điểm C 0;5, và gọi E là trung điểm AB , khi đó ta có: 2 2          2 2
P  w  5i  w  5i  CA  CB  CI  IA2  CI  IB2 2 2
 IA  IB  2CI IA  IB  2CI.AB 1 2         Ta có: 
2CI.AB  2CI.AB cos CI, AB nên P max khi hai vector CI và AB cùng phương.   Suy ra: 
P  2CI.AB cos CI, AB  2CI.AB  4 37 . Chọn đáp án B.
Câu 47. Trong không gian Oxyz, cho mặt phẳng   :3x  y  2z  5  0 và hai điểm A8;3;3, B 11; 2
 ;13. Gọi M, N là hai điểm thuộc mặt phẳng   sao cho MN  6. Giá trị nhỏ nhất của AM  BN là A. 2 13 . B. 53 . C. 4 33 . D. 2 33 . Lời giải
Đầu tiên ta có hình vẽ như sau:
Đầu tiên ta cần vẽ một mặt phẳng P chứa A và song song với mặt phẳng   :3x  y  2z  5  0.
Xét mặt phẳng P : 3x  y  2z  33  0. Dựng đường tròn C  tâm A , bán kính AA  MN  6 với
A C  sao cho AANM là hình bình hành. Đến đây ta nhận thấy A , B đều cùng phía với mặt phẳng  
nên ta suy ra: AM  BN  AN  BN  AN  B N
  AB với B13;6;3 là điểm đối xứng với B qua  
Gọi H 5;0;9 là hình chiếu của B lên P khi đó ta suy ra HA đạt giá trị nhỏ nhất khi ba điểm , A H , A
thẳng hàng với H nằm giữa A và A. Ta có: AH  3 6 nên suy ra HA  AA  AH  MN  AH  2 6 min 2 2 Vậy với B H
  6 14 ta suy ra  AM  BN  2 2  AB  B H   AH  6 14  2 6  4 33 . min min     Chọn đáp án C.
Câu 49. Cho hàm số y  f  x xác định trên  và có đồ thị hàm số y  f 'x như hình bên.  m 
Số giá trị nguyên của tham số m 10; 10 để hàm số 2 y  f x  2 x  
 có 9 điểm cực trị là  2 
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG A. 11. B. 13 . C. 10 . D. 12. Lời giải
Nhìn vào đồ thị trên ta suy ra: f x   x  2 ' 1 x x  
1  x  2 (trong đó x  1 là nghiệm bội chẵn).  m 
Khi đó ta xét: y  g  x 2  f x  2 x  
 có g x  g  x nên suy ra g  x là hàm chẵn.  2   m  Suy ra hàm số h x 2  f x  2x  
 phải có 4 điểm cực trị dương tức phương trình h x  0 có 4  2   m 2 x  1; x  2x   0  m 
nghiệm bội lẻ dương phân biệt.  h x   x   2 2 2 2 f  x  2x   0      2  m m  2 2 x  2x   1; x  2x   2  2 2 2 m  2x  4x  2  Khi đó ta cần hệ: 2  m  2x  4x  4 
có 3 nghiệm dương phân biệt khác 1. Từ đó ta có hình vẽ sau:  2 m  2x  4x  m  0
Từ hình vẽ trên ta suy ra: m   10; 10 ycbt  
 m 9;8;..1;0; 
3 tức có 11 giá trị nguyên m thỏa m  3 mãn. Chọn đáp án A.
Câu 50. Có bao nhiêu số nguyên a  11 sao cho ứng với mỗi a tồn tại ít nhất 6 số nguyên b  0;8 thỏa mãn log  2
b 12  log  b  7 a  3   log a 19  7? 4  3    5   A. 6 . B. 5 . C. 7 . D. 4 .
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Lời giải
Ta có bất phương trình tương đương với: log  2
b 12  log  b  7 a  3   log a 19  7  0 4  3    5  
Xét hàm số y  f b  log  2
b 12  log  b  7 a  3   log a 19  7 a 4  3    có 5   b f  b    b  
nên hàm số f b luôn đồng biến trên 0;8 . a   a   2 1 b 12ln4 b7 0, 0;8 2 ln 3
Do ứng với mỗi a tồn tại ít nhất 6 số nguyên b 0; 8 tức b : 7  2nên suy ra f 2  0 a
 log 16  log 9 a  3   log a 19  7  0, a   3;11 4 3    5    
 log a  3  log a 19  3  0  log a  3  log a 19  3 3   5   3   5  
Xét hàm số y  g a  log a  3  log a 19 có ga  0, a  3;1 
1 và g 6  3 , suy ra a  6 3   5  
Vậy ta suy ra: a 6;7;8;9;1 
0 tức có 5 giá trị nguyên a thỏa mãn. Chọn đáp án B. SỞ PHÚ THỌ LẦN 2
Câu 45. Có bao nhiêu giá trị nguyên của tham số m để bất phương trình log  2
x  4mx 12m  log  2 x  4x 12log  2
x  8x  24 nghiệm đúng với mọi x  8 8 8  A. 1. B. 3 . C. 0 . D. 2 . Lời giải
x  4x 12   x  22  8  0; x  8x  24   x  42 2 2   Ta có:
8 0 nên bất phương trình tương đương với:
 log x  4mx 12m  log  x  22 8log  x  42 2  8 . (*) 8 8 8   2 m  1 2 x  4x  4   x  2  0 x  2  Xét 
thì bất phương trình lần lượt trở thành:    (loại) m  2 x  x    x  2 2  x  4 8 16 4 0 
Suy ra điều kiện cần chính là: g  x 2 2
 x  4mx 12m  0   
 4m 12m  0  0  m  3. g( x)
log x228log x42  8 8 8 2 
Khi đó ta suy ra m  1; 
2 và (*) trở thành: x  4mx 12m  8 2 x  2
 x  m4x 12   x  2 8log8 4 8 2  (1). Xét m  3  thì (1) thành: 2 log8 9 log8 9 log8 9 x  9  3   x  3 (loại).  2   
x    log8x 4 8 2  2 2 8  x Xét m  3  thì (1) thành:  m  . 4x 12  2   
x    log8x 4 8 2  2 2 8  x x  
Xét hàm số y  g x  có gx 4  0  . Cùng với g  2    0 nên ta suy 4x 12  x  2
ra điều kiện đủ là: m  min g  x  g 2  m  2 R
Kết hợp điều kiện cần và đủ ta suy ra 0  m  2  m1; 
2 . Do ta đã loại 2 giá trị này ban đầu nên suy ra
không có giá trị m nào thỏa. Chọn đáp án C.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG 4 Câu 46. Cho hàm số 4 2
y  ax  bx  c có đồ thị như hình vẽ. Biết miền tô đậm có diện tích bằng và điểm 15 B có hoành độ bằng 1
 . Số giá trị nguyên của tham số m thuộc đoạn 3; 
3 để hàm số    3x y f m  có
đúng một điểm cực trị là A. 1. B. 6 . C. 2 . D. 0 . Lời giải d: y  g x C 4 2    Đường thẳng
song song với trục hoành cắt đồ thị : y ax bx c tại hai điểm B và C
Mà điểm B có hoành độ bằng 1
 nên điểm C có hoành độ bằng 1. Khi đó ta có: 1 1 4 4 2 S  f  x gx 4 2 dx  ax 
 2x  1 dx  a , mà S  nên suy ra a 1, tức y  x bx c. 15 15 1 1 f  
1  1 b  c  f 0  c  b  1 y  f  x 4 2
 x  x  c  f x 3   Mà mặt khác 4x 2x . f  x 1 3
 0  4x  2x  2x 2 2x   1  0  x  0; x   Giải phương trình 2 . m  3x  0 h  x  3x
 ln 3 f m 3x   0     x 1 x 1             3x y h x f m  m 3 ;m 3 Xét hàm số có  2 2  x m  3x  lim 3  0  x    x 1 x 1   *  x 1 1 x 1 1 m  3  ;m  3   lim 3    ; lim 3    2 2 g  x . Mà x  2 2 x 2 2 nên ta suy ra để có
đúng 1 điểm cực trị (tức (*) có 1 nghiệm duy nhất) thì m  0 . Chọn đáp án A.
Câu 47. Cho phương trình log 4  log  2x  ax  2  4log x  ax   . Gọi S là tập các giá trị a  2 5 0 a 1  5
nguyên của tham số a để phương trình có nghiệm duy nhất. Tổng các phần tử của S bằng A. 4 . B. 3 . C. 0 . D. 2 . Lời giải
Điều kiện: 0  a  1. Ta có phương trình: log 4  log  2x  ax  2  4log x  ax   (1) a  2 5 0 a 1  5
(1)  log  2x  ax  2  4log x  ax   . a  2 5 log 4 5  a Đặt 2
t  x  ax  2  0 khi đó phương trình trở thành  log t  4log t   (2). Khi đó ta chia a  2 3 log 4 5  a hai trường hợp như sau: 1
Trường hợp 1: 0  a  1
 0 thì (2) thành  log t  4log  2t  3  log 4  0 5 4  log a a 4
Hàm vế trái y  f t  log t  4log  2t  3 có f t  0, t
 0; tức f t đồng biến trên 0; . 5 4 
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG log 4  1 a  4 Để ý f   1  1 nên ta suy ra a    . 2 t  1 x  ax 1  0    *
Phương trình có nghiệm duy nhất nên ta suy ra a  2
 . Đối chiếu với điều kiện, ta loại.
Trường hợp 2: a  1 thì (2) ta đánh giá tương tự  log t  4log  2t  3  log 4  0 , đánh giá tương tự 5 4  a
trường hợp ta cũng suy ra a  2
 , đối chiếu điều kiện ta thu được a   2 . Chọn đáp án D.
Câu 48. Cho hàm số y  f  x có đạo hàm cấp hai liên tục trên  . Hình vẽ bên dưới là đồ thị hàm số
y  f  x trên ;2, đồ thị hàm số y  f  x trên đoạn 2;3 và đồ thị hàm số y  f   x trên
3;. Số điểm cực trị tối đa của hàm số y  f x là A. 7 . B. 5 . C. 3 . D. 6 . Lời giải f  x 2;3
Đầu tiên từ hình vẽ, ta dễ dàng nhận thấy
có 2 điểm cực trị trên đoạn f  x
Tiếp đến xét trên ;2, ta thấy phương trình f x  0 có 1 nghiệm nên có 1 điểm cực trị.
Cuối cùng, xét trên 3; , ta nhận thấy phương trình f   x  0 có 1 nghiệm nên suy ra f x  0 có tối f  x
đa 2 nghiệm trên 3; , tức
có tối đa 2 điểm cực trị trên 3; .
Vậy tổng cộng số điểm cực trị tối đa của hàm số y  f  x là 5 điểm cực trị. Chọn đáp án B. 1
Câu 49. Cho hai số phức z , z thỏa mãn z  2  2i  và z 1  z 1  2 5 . Số phức z thỏa mãn 1 2 1 8 2 2
2z  2  5i  2z  3  6i . Giá trị nhỏ nhất của biểu thức z  2z  z  z bằng 1 2 23 13 11 A. . B. . C. . D. 5 . 4 2 2 Lời giải
Thông qua biến đổi đại số ta suy ra được quỹ tích của các số phức 2z , z và z như sau: 1 2
A z C x 2 y  2 1 2 : 4 4   1  16 
 P  z  2z  z  z  MA  MB . 1 2 2 Bz E y 2 : x 
 1; M z  d : y  x  4 2      4 1
Ta gọi C là đường tròn đối xứng với C  qua d  , suy ra ta có: C : x   y 82 2  với A C . 16
Từ hình vẽ trên ta kết luận.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG 23
P  z  2z  z  z  MA  MB  MA  MB  A B  . Chọn đáp án A. 1 2 0 0 4
Câu 50. Trong không gian Oxyz , cho hai điểm A2;2;6, B3;3;9 và mặt phẳng
P: 2x  2y  z 12  0. Điểm M di động trên P sao cho M ,
A MB luôn tạo với P các góc bằng nhau.
Biết rằng điểm M luôn thuộc một đường tròn cố định. Tung độ của tâm đường tròn đó bằng 2 2 A. 0 . B.  . C. 12 . D. . 3 3 Lời giải M  ; a ; b c Đặt
, khi đó ta gọi E, F là các chân đường vuông góc từ , A B hạ xuống P . AE BF d  ; A P  d  ; B P 6 3 Ycbt  sin  AME  sin    2 2 BMF        MA  4MB AM BM AM BM AM BM
 a  22  b  22  c  62  4 a 32 b 32 c 92 20 28 352 2 2 2  a  b  c  a  b  28c   0 3 3 3 10 14  Suy ra M  S  tâm I ; ; 1  4 
 và bán kính R  .... Mặt khác M P nên suy ra quỹ tích điểm M là  3 3 
một đường tròn C  thiết diện tạo bởi mặt cắt giữa mặt phẳng P và mặt cầu với tâm đường tròn E là
hình chiếu của I lên mặt phẳng P .  10 x   2t  3  
Ta có phương trình đường thẳng  14
d  , qua I , vuông góc P là: y 
 2t ,t   . Mà E d  P nên 3  z  1  4  t  10  14  14 2 ta suy ra: 2  2t  2  2t   1
 4  t  12  0  t  2   y   2       . Chọn đáp án D. E  2  3   3  3 3
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG SỞ LAI CHÂU LẦN 1
Câu 40. Tìm số giá trị nguyên của tham số thực m để tồn tại các số thực x, y thỏa mãn 2 2 x  y m x yxym 2 2 e e
 x  y  x  y  xy 2m  2 . A. 6 . B. 9 . C. 8 . D. 7. Lời giải Xét hàm số   t f t  e  t 1, t  .   t
f t  e 1 và f t  0 t  0 .
Ta thấy f t đổi dấu từ “- ” sang “+” khi qua t  0 nên f t  f 0  0, t   . 2 2 x  y m e    2 2 x  y  m 1 0, x  , y   2 2 x  y  m Do đó: 
. Dấu “=” xảy ra khi và chỉ khi  . x y xym e  
x  y  xy  m10,x, y  x  y  xy  m 2 2 x  y  m 1 2 2        Hay x y m x y xy m 2 2 e e
 x  y  x  y  xy  2m  2   x  y  xy  m  2 2 S  2P  m
Đặt S  x  y, P  x.y , ta có: 2 
 S  S 3P  0 . Vì 2 S 4P  S 0;  4 S  P  m Lấy  
1  2.2 vế theo vế ta được: 2 S  2S  3m   3 . Xét hàm số f S 2
 S  2S, S 0;4 , có f S  2S  2  0, S  0;4 .
Yêu cầu bài toán 3 có nghiệm
 f 0 3m  f 4 0  m  8 . Vậy, có 9 giá trị nguyên của tham số m thỏa mãn. Chọn đáp án B.
Câu 41. Cho hai số phức z , z thỏa mãn z  3  2i  z 1 , z  z  2 2 và số phức w thỏa mãn 1 2 1 2
w  2  4i 1. Giá trị nhỏ nhất của biểu thức P  z  2  3i  z  w bằng 2 1 A. 10 . B. 17 1. C. 4 . D. 26 . Lời giải Cách 1:
z  x  yi  x, y   Đặt
, sử dụng phép biến đổi đại số, suy ra z  3  2i  z 1  x  y  3  0 A
  z , B z  d : x  y  3  0 1   2   Suy ra: 
với C có tâm I 2;4, R 1. C
 wC :x  22   y  42 1 A  a;3  a Đặt 
b  a, khi đó ta suy ra: B   ; b 3  b b   a  2 A a;3 a 2    2
z  z  AB  2 2  AB  8  2 b  a  8    . 1 2    b   a  0 B  2  a;1 a
Cùng với E 2;3 , ta suy ra:
P  z  2  3i  z  w  BE  AC  BE  AI  R  a  22  a  2 1  a  a  22 2 1. 2 1
Xét hàm số y  f a  a  2  a  2  a  a  2 2 2 1 2 có   f a 2 min  f   17   nên từ đó ta suy ra R  5 
P  17 1. Chọn đáp án B.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 42. Cho hàm số y  f x liên tục trên  và có bảng biến thiên
Gọi S là tập hợp các giá trị nguyên của m để phương trình f  f  x 1  2  m có 10 nghiệm phân biệt thuộc đoạn  3  ; 
3 . Số phần tử của tập hợp S là A. 0 . B. 1. C. 2 . D. 3 . Lời giải
Đặt t  f  x 1  2 . Khi x  1
 , ta có y  f  x 1 2  f x   1 .
Tịnh tiến đồ thị hàm số y  f x sang phải 1 đơn vị ta được đồ thị hàm số y  f  x  
1 và vì đồ thị hàm số
y  f  x 1  2 nhận đường thẳng x  1
 làm trục đối xứng nên ta có bảng biến thiên của hàm số y  f  x 1  2 : Với x  3  ;  3 , ta có t 4;0. +) Nhận xét: Mỗi t  4  ; 2
  cho 4 nghiệm x 3  ;  3 ; Mỗi t  2
 ;0 cho 5 nghiệm x 3  ;  3 .
Với t  4 , ta có 2 nghiệm x  3  ; 
3 ; Với t  0 , ta có 3 nghiệm x  3  ;  3 .
+) Ta có phương trình f  f  x 1  2  m trở thành phương trình  f t  m .
+) Phương trình f  f  x 1  2  m có 10 nghiệm phân biệt thuộc đoạn  3  ;  3
 Phương trình f t  m có 2 nghiệm phân biệt t  2
 ;0  2  m  0 .
Vậy có 1 giá trị nguyên của m thỏa mãn yêu cầu bài toán là m  1. Chọn đáp án B.
Câu 43. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng P : x  y  z  3  0 ,
Q: x 2y 2z 5  0, và mặt cầu S 2 2 2
: x  y  z  2x  4 y  6z 11  0 . Gọi M là điểm di động trên
S và N là điểm di động trên P sao cho MN luôn vuông góc với Q . Giá trị lớn nhất của độ dài đoạn thẳng MN là
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG A. 3  5 3 . B. 28 . C. 9  5 3 . D. 14. Lời giải
Đầu tiên ta có: mặt cầu S  tâm I 1;2;3, bán kính R  5 , d I;P  3 3  5tức ta suy ra mặt phẳng
P không cắt mặt cầu S 
Do MN luôn vuông góc với Q nên vector chỉ phương của MN là u  1;2;2 , cùng với vector pháp 
tuyến mặt phẳng P có dạng n  1; 1  ; 
1 ta suy ra sin góc giữa MN và P là:   d M ;P MN P    u.n 1 sin ;     từ đó suy ra MN   3d M; P   3 d
 I; P  R  9  5 3  . u . n 3 sin MN;P     
Vậy giá trị lớn nhất của độ dài đoạn thẳng MN là 9  5 3 . Chọn đáp án C.
Câu 44. Trên tập hợp các số phức, xét phương trình 2
z  6z  m  0 ( m là tham số thực). Gọi m là một 0
giá trị nguyên của m để phương trình đó có hai nghiệm phân biệt z , z thỏa mãn z .z  z .z . Hỏi trong 1 2 1 1 2 2
khoảng 0;20 có bao nhiêu giá trị m  . 0 A. 13 . B. 11. C. 12 . D. 10 . Lời giải Ta có    9  m . Nếu 
  0  9  m  0  m  9 thì phương trình có hai nghiệm thực phân biệt z , z và 1 2 z  z ; z  z nên 2 2
z .z  z .z  z  z  z  z  z  z  0 . Điều này không xảy ra. 1 1 2 2 1 1 2 2 1 2 1 2 1 2 Nếu 
  0  9  m  0  m  9 , thì phương trình có hai nghiệm phức là hai số phức liên hợp .
Khi đó z  z ; z  z nên ta luôn có z .z  z .z , hay m  9 luôn thỏa mãn. 1 2 1 2 1 1 2 2
Vì m   và m  0;20 nên có 10 giá trị m thỏa mãn. Chọn đáp án D. 0   0 0
Câu 45. Cho lăng trụ ABC.AB C
  có đáy ABC là tam giác vuông tại A , cạnh BC  2a và  ABC  60 . Biết tứ giác BCC B  là hình thoi có  B B
 C nhọn, mặt phẳng BCC B
  vuông góc với  ABC , góc giữa hai mặt phẳng  ABB A
  và  ABC bằng 45 . Thể tích khối lăng trụ ABC.AB C   bằng 3 3 3 3 a A. 6a . B. a . C. 3a . D. . 7 7 7 3 7 Lời giải
Đầu tiên ta có: AB  a, AC  a 3 . Gọi H là hình chiếu của B lên BC Suy ra H  BC (do  B B  C nhọn). Kéo theo B H
   ABC (do BCC B     ABC ).
Kẻ HK  AC với K  AB , suy ra HK  AB . Từ đó ta có:  ABB A  ; ABC    B K
 H  45 , suy ra B K
 H vuông cân tại H tức B H   KH . (1) BH HK HK.2a
Mặt khác ta có: HK  AC nên ta có tỉ số sau:   BH  (2) BC AC a 3
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Tiếp đến ta lại có: 2 2 BH  4a  B H  (3) B H  .2a 12
Từ (1), (2) và (3) suy ra phương trình sau: 2 2 BH  4a  B H    B H   a . a 3 7 3 1 3a Vậy V      . Chọn đáp án C.    B H.S A . B AC.B H ABC.A B C ABC 2 7 1
Câu 46. Cho hàm số f  x có đạo hàm liên tục trên  . Biết f 5  1 và xf
 5xdx 1, khi đó tích phân 0 5 2 x f   xdx bằng 0 A. 25 . B. 123 . C. 23 . D. 15 . 5 Lời giải 1 1 5 5 1 1 x Đầu tiên ta có: xf  5xdx  xf  5xd 5x  f  xdx 1 xf  xdx  25 5 5 5 0 0 0 0 u
  f  x  du  f  xdx  5 5 2 5 5 2  x  25 x Ta có tiếp: 2 2  x , 25  xf  xdx  f  x  x f    xdx   f   xdx dv  xdx  v   2  2 2  2 0 0 0 0 5 2 5 x 25 25 Vậy f   x 2 dx   25    x f  
xdx  25. Chọn đáp án A. 2 2 2 0 0
Câu 47. Cho hàm số bậc ba y  f x có đồ thị như hình vẽ bên.
Số nghiệm thực của phương trình f  4 2 x  2x   2 là A. 8 . B. 9 . C. 7 . D. 10 . Lời giải
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG  f  4 2 x  2x   2 Phương trình f  4 2 x  2x   2   .  f   4 2 x  2x   2 4 2
x  2x  b, 1 b  0 * Phương trình f  4 2 x  2x     2   . 4 2 x  2x  c,  0  c   4 2
1 ; x  2x  d, 2  d  3 * Phương trình f  4 2 x  x  4 2 2
 2  x  2x  a,  2   a    1 . Đồ thị hàm số 4 2
y  x  2x như hình vẽ sau:
Dựa vào đồ thị trên ta có: - Phương trình 4 2 x  2x  , a  2   a    1 không có nghiệm thực. - Phương trình 4 2 x  2x  , b  1
  b  0 có 4 nghiệm thực phân biệt. - Phương trình 4 2 x  2x  , c 0  c  
1 có 2 nghiệm thực phân biệt. - Phương trình 4 2
x  2x  d, 2  d  
3 có 2 nghiệm thực phân biệt. Vậy phương trình f  4 2
x  2x   2 có 8 nghiệm thực phân biệt. Chọn đáp án A.
Câu 48. Trong không gian với hệ tọa độ Oxyz , từ điểm A1;1;0 ta kẻ các tiếp tuyến đến mặt cầu S  có tâm I 1;1; 
1 , bán kính R  1 . Gọi M a; ;
b c là một trong các tiếp điểm ứng với các tiếp tuyến trên. Tìm
giá trị lớn nhất của biểu thức T  2a  b  2c 3  41 3  2 41 3  41 3  2 41 A. . B. . C. . D. . 15 5 5 15
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Lời giải
Ta có IA  5 nên ta suy ra 2 2
AM  IA  R  2 , từ đó ta suy ra M sẽ luôn thuộc mặt phẳng P với mặt
phẳng P là phương trình từ phép tính  ; A AM    I; 
1 , tức ta suy ra phương trình có dạng là:
P: 2x  z  2  0 , mà M S  nên suy ra M thuộc đường tròn thiết diện C  SP có tâm H .    3 4 
Xét MAI vuông tại M có đường cao MH , ta có: HA  4HI  HA  4HI  0  H  ;1;   .  5 5   3 4  2
Suy ra đường tròn C  có tâm H  ;1;   và bán kính r 
tức ta có hình vẽ như sau:  5 5  5 2 41
Xét mặt phẳng Q : 2x  y  2z  0 , ta có: cos  cosP;Q  2 
 sin  1 cos   . 3 5 3 5 d H;Q 3 3 2
Mà ta có: d H Q 1 ;  nên ta suy ra HK    KM  KH  HM   . 5 sin 205 205 5 a  b  c T
Nhận thấy d M Q 2 2 ; 
 nên ta suy ra: T  3d M ;Q , kéo theo đó ta có được: 3 3   T  d M Q 3 2 41 3 2 41 3 ;  3KM sin   3     . Chọn đáp án B.  205 5  3 5 5
Câu 49. Cho hàm số bậc ba y  f x có đồ thị là đường cong ở hình bên dưới. Gọi x , x lần lượt là hai 1 2
điểm cực trị thỏa mãn x  x  2 và f x 3 f x  0 , và đồ thị luôn đi qua M x ; f x trong đó 0  0 1   2 2 1 S
x  x 1. g x là hàm số bậc hai có đồ thị qua 2 điểm cực trị và M . Tính tỉ số 1 ( S và S lần lượt là 0 1 S 1 2 2
diện tích hai hình phẳng được tạo bởi đồ thị hai hàm f  x, g  x như hình vẽ ).
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG A. 5 . B. 6 . C. 7 . D. 4 . 32 35 33 29 Lời giải:
Nhận thấy hình phẳng trên có diện tích không đổi khi ta tịnh tiến đồ thị sang trái sao cho x  0 . Khi đó ta 0
có x  1, x  3. Xét hàm 3 2
f (x)  ax  bx  cx  d và 2 g(x)  mx  nx  p . 1 2  f     1  0 3  a  2b  c  0
Vì x  1, x  3 là các điểm cực trị nên ta có:    (1) . 1 2  f   3  0 27a  6b  c  0 b  6  a  Hơn nữa, ta có f  
1  3 f 3  a  b  c  d  81a  27b  9c  3d (2) . Từ (1) và (2) suy ra c  9a . d  2a  g 0  f 0  p  2a m  2a   
Mặt khác dựa vào đồ thị ta thấy: g  
1  3g 3  m  n  p  6a  n  6a .    g 0  g 3 9m  3n  p  2a p  2a    Suy ra: f  x  a 3 2
x  6x  9x  2 ,  x  a 2 g 2x  6x  2. 1 3 8 Khi đó ta có: 5 3 2 S 5
S  a . x  4x  3x dx  a 3 2 S  a x  4x  3x dx  a  . 1  ,  . Do đó, 1 12 2 3 S 32 0 1 2
Câu 50. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2;1;3, B 6;5;5 . Xét khối nón  N  ngoại
tiếp mặt cầu đường kính AB có B là tâm đường tròn đáy khối nón. Gọi S là đỉnh khối nón  N  . Khi thể
tích của khối nón  N  nhỏ nhất thì mặt phẳng qud đỉnh S và song song với mặt phẳng chứa đường tròn
đáy của  N  có phương trình 2x  by  cz  d  0 . Tính T  b  c  d ? A. T  24 . B. T 12 . C. T  36 . D. T 18 . Lời giải
Thể tích của khối nón N  nhỏ nhất khi chiều cao của khối nón gấp đôi đường kính mặt cầu.
( Chứng minh: Gọi tâm mặt cầu là I , khi đó có
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG 1 1 1 r y S  S  S  S . B BH  IK.SH  I . B BH  y.      SBH SIH BIH x r y x x x 2 2 2   2 2 2 2 y  2r
Với chiều cao khối nón là y , bán kính đáy là x ; bán kính mặt cầu là r x  0; y  2r . Thể tích khối nón là 2 2 2    2 1  2 1 2 y 1 2 y 1 2 4r 1 2 r V   x y   r .  r .   r . y  2r 
 4r    r . 2  y  2r 4 8 3 .  4r    r . 3 3 y  2r 3 y  2r 3  y  2r  3  y  2r  3     2 4r
Thể tích khối nón nhỏ nhất khi y  2r   y  4r  dpc . m ) y  2r
Tiếp đến ta có đường kính mặt cầu: 2 2 2 AB  4  4  2  6 . 
Mặt phẳng   chứa đường tròn đáy của N  đi qua B và nhận AB  4;4;2 làm vectơ pháp tuyến. Suy
ra phương trình mặt phẳng   là: 4x  6  4 y  5  2z  5  0  2x  2 y  z  27  0
Do mặt phẳng   qua đỉnh S và song song với mặt phẳng chứa đường tròn đáy của N  có phương trình b  2,c  1 b  2,c  1 b  2,c  1   b  2,c  1 
2x  by  cz  d  0 nên ta có:    b  c  d     d  d   2.6 .5 .5 B;  9 .  12  2AB 27  d  36  2   2  22 2 1  d  63 Vậy b  2,c  1
 ,d  19 ( do d B;   d ;
A   ). Khi đó b  c  d  12. Chọn đáp án B. CHUYÊN HÀ TĨNH LẦN 1
Câu 44. Cho hai hàm số f  x 3 2
 ax  3x  bx 1 2d và g x 2
 cx  2x  d có bảng biến thiên như hình
vẽ. Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ x , x , x thỏa mãn 1 2 3 2 2 2
x  x  x  30 . Diện tích hình phẳng giới hạn bởi các đường y  f  x, y  g  x, x  3, x  6 bằng 1 2 3 2113 1123 1231 1321 A. . B. . C. . D. . 12 12 12 12 Lời giải Ta có f x 2  3ax  6x  b  2 6       c a a  c
Từ BBT suy ra f x và g  x có chung hai nghiệm là  và  3     d b b    3d .    c 3a  1 
Từ BBT suy ra đồ thị hàm số g x có đỉnh I ; 4   và c  0  c 
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG 1 2 1 3 12c  . c
  d  4  d   4  b  2 c c c c Xét f  x  g x 3   ax    c 2 0 3
x  b  2 x 1 3d  0 *
Từ giả thiết suy ra phương trình (*) có 3 nghiệm phân biệt x , x , x thỏa mãn 1 2 3
x  x  x  30   x  x  x 2 2 2 2
 2 x x  x x  x x  30 1 2 3 1 2 3  1 2 2 3 3 1 3 12c 2 2  2  c  3  b  2  c  3    2.  30   2. c  30     
c 32  2310c 2  30c  0  a  a  c  c c  1 tm 2 29c 26c 3 0        3 c   loai  29  c 1;a 1;b  9  ;d  3
  f x  g x 3 2  x  4x  7x 10 6 6  S  f  x  g  x 3 2 1321 dx  x  4x  7x 10dx    . Chọn đáp án D. 12 3  3  3 2 2x  3x 1
Câu 46. Có bao nhiêu cặp số nguyên dương  ; x y thỏa mãn: log 14x  3y  7 2 x 1 7  6xy 1 2x  3y
đồng thời 1 x  2022 ? A. 1347 . B. 1348 . C. 674 . D. 673 . Lời giải 3 2 2 2x  3x 1 x  1 2x  1 Ta có log 14x  3y  7 2 x 1  log 14x  3y  7 2 x 1 7  7  6xy 1 2x  3y 3y  12x  1  log  x  2 1  log 3y   1  3y  7  x  2 1  log  x  2 1  7  x  2 1  log 3y 1  3y 7 7   7 7  log 7 x  2
1  7  x 12  log 3y 1  3y 1 (*). 7 7  
Xét hàm số f t  log t  t . Ta có f t 1  1  0 , t
  0 nên f t đồng biến trên khoảng 0;. 7 t ln 7 x  2 7 1 1 Do đó, (*)  x  2 7 1  3y 1  y 
. y nguyên dương khi  x  2 7
1 13  x chia hết cho 3 3
hoặc x chia 3 dư 2. Do đó x 2;3;...;202  1 \4;7;10;....;202 
0 . Vậy có 2020  673  1347 cặp  ; x y thỏa mãn. Chọn đáp án A
Câu 50. Cho hàm số bậc ba y  f (x) có bảng biến thiên của hàm số g(x)  f (x 1)  2 như sau x – ∞ 1 3 + ∞ y' – 0 + 0 – + ∞ 4 y 0 – ∞
Giá trị lớn nhất của hàm số y  f  3sin x cos x  2  2cos2x  4sin x 1 là: A. 9 . B. 2  . C. 2 . D. 4 . Lời giải
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG y  f  x  x    x  x   f  x  x     x  2 3 sin cos 2 2cos 2 4sin 1 3 sin cos 2 2 2sin 1   x   k2 
 f  3sin x  cos x  2 2. Dấu bằng xảy ra khi và chỉ khi 2 6 sin x 1  0   5 x   k2  6
Đặt t 1   3sin x  cos x  2  3sin x  cos x  3 t . Mà 0  3sin x  cos x  2 nên 
0  3  t  2  1  t  3 . Cho g t   f t 1  2  4 . Với g t   4  t  3  3 sin x  cos x  0  x   k 6  Vậy y  4  x 
 k2 . Chọn đáp án D. max 6 SỞ QUẢNG BÌNH LẦN 1
Câu 41. Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a , có không quá 22 số nguyên b thỏa mãn a b ab2 2  4.6  2  3b ? A. 31. B. 32 . C. 33 . D. 34 . Lời giải Ta có a b ab2 b a b ab2 2  4.6  2  3  2  4.6  2
 3b  0  2a  3b  4.2b 2a 3b   0
1 4.2b2a 3b 0 4.2b 13b 2a          0 Trường hợp 1: 4.2b 1 0 b 2 b       b  3  .   1  a    b a a a 1 log 4,75...  
Xét phương trình 3  2  0  b  log 2  2  3   2     27   a  . 3 27  a   Trường hợp 2: 4.2b 1 0 b 2 b       b  1.   1  a    b a a a 1 log 1,5  
Xét phương trình 3  2  0  b  log 2  2  1   2     3   a  0 . 3 3  a  
Mà theo đề ứng với mỗi a , có không quá 22 số nguyên b thỏa mãn nên cùng với b  1  ta suy ra a  b : 1
  20  1 log 2a  33, 284 a 21
 21 2  3  a  log  21 3  
 a  1;2;...;33 tức có 33 giá 3 2    a  
trị nguyên a thỏa mãn bài toán. Chọn đáp án C.
Câu 45. Cho số phức z thỏa mãn  z 1 iz 1 i  5 và 2 2
P  z  2i  z 1 . Tích giá trị lớn nhất và giá
trị nhỏ nhất của biểu thức P bằng A. 9  . B. 11. C. 9  9. D. 99 . Lời giải
Ta có:  z   iz   i  z  iz  i 2 1 1 1 1
 z 1 i  5  z 1 i  5 . Đặt z  x  yi , ta có: M zC x 1 5 cost     P  2
 x  4y  3  21 5 cost 41 5 sint3 P  2x  4y  3 y 1  5 sin t
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG 2 2 2
 P  1 2 5 cost  4 5 sin t . Mà  t t             2 2 2 5 cos 4 5 sin 2 5 4 5
cos t  sin t  100 nên ta  
suy ra 10 1  1 2 5 cost  4 5 sin t  110  9
  P 11  Tích bằng -99. Chọn đáp án C.
Câu 46. Cho hàm số y  f x 3 2  4
 x  ax  bx  c có đồ thị cắt trục hoành tại 3 điểm có hoành độ lần
lượt là 1;1;3 . F  x là một nguyên hàm của f  x và y  g  x là hàm số bậc hai đi qua ba điểm cực trị
của đồ thị hàm số y  f x . Diện tích hình phẳng giới hạn bởi hai đường y  F x và y  g  x bằng 128 64 A. . B. . C. 16. D. 6 4 . 15 15 Lời giải
Ta có: f  x    2
x  x   Fx  f  x 4 3 2 4 1 3
dx  x  4x  2x 12x  d . Với F 1  9  d ,
F 1  7  d , F 3  9  d ta suy ra ba điểm cục trị của hàm số y  F  x có tọa độ lần lượt là 1; 9  d  ,
1; 7  d  và 3;9  d  . Xét hàm số bậc hai 2
y  mx  nx  p m, n, p    đi qua ba điểm 1; 9  ,1;  7  và m  n  p  9 m  4   
3; 9  . Từ đó ta có hệ phương trình sau: 2
m  n  p  7  n  8  y  4x  8x  3 . Suy ra 9m 3n p 9     p  3   4 3 2 2 4 3 2 g  x  2
 4 x  8x  3  d . Ta có F  x  g  x  x  4x  2x 12x 4x 8x  
3  x  4x 2x 4x 3.
Giải phương trình F x  g  x  0  x  1; x  1; x  3
Vậy diện tích giới hạn bởi hai đường y  F x và y  g  x là 3 3 S  F  x gx 128 4 3 2 dx 
x  4x  2x  4x  3 dx  .  Chọn đáp án A. 15 1 1 
Câu 50. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  x 2  y  2  z  2 : 1 1 1 12 và mặt
phẳng P  : x  2 y  2z  2  0 . Xét điểm M di động trên  P  , các điểm , A ,
B C phân biệt di động trên S sao cho M , A M ,
B MClà các tiếp tuyến của S. Mặt phẳng  ABC  luôn đi qua điểm cố định nào dưới đây ?  1 1 1   3  A. E 12; 23; 25 . B. F ; ;  .
C. G 12; 23; 25 . D. H ;0; 2   .  4 2 2   2  Lời giải
Ta đặt M a;b;c  với a  2b  2c  2  0 và A x; y; z  S  có tâm I 1; 1; 1 và bán kính R  2 3 . Do M , A M ,
B MClà các tiếp tuyến của S nên ta luôn có: 2 2 2 2 2 2
MI  MA  AI  MA R  MA 1  2.
a 2 b 2 c 2 xa2  yb2 zc2 1 1 1 12 (*)
Mà  x 2  y 2 z  2 2 2 2 1 1
1 12  x  y  z 92x y z nên thế vào (*) ta suy ra:  abc 2 2 2 2
3  x  y  z 2axbycz 12  2abc 3 92x y  z 2axby cz12  a  1 x b  1 y c  
1 z a bc 9  0 x   1 a  y   1 b  z  
1 c x  y  z 9  0
Mà ta có phương trình: a  2b  2c  2  0 nên ta lập dãy tỉ số bằng nhau như sau: x 1 y 1 z 1
 x  y  z  9 x   1   y   1   z  
1   x  y  z  9 12      
          12 1 2 2 2 1 2 2 2 2 1
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG    Từ đó ta suy ra: x 1 y 1 z 1  12;  12;
 12  x; y; z  13;23;25 tức mặt phẳng  ABC  luôn 1 2 2
đi qua điểm cố định G 12; 23; 25 . Chọn đáp án C.
THPT TRẦN NHÂN TÔNG - QUẢNG NINH LẦN 1 1
Câu 44. Gọi S là tập hợp tất cả các số phức z sao cho số phức w 
có phần ảo bằng 1 . Xét các z  .i z 4
số phức z , z , z  S , giá trị lớn nhất của P  z z  z  z z  z  z z  z bằng 1 3 2  2  3 1  3 1 2  1 2 3 A. 6 . B. 8 . C. 10. D. 12. Lời giải 1 x  0 
Gọi z  x  yi  x, y    . w 
nên z  .i z  0  x   2 2
y  x  y i  0    x  0 . i  z  z 2 2  x  y  y  1 1 x   2 2 y  x  y i 1 Ta có: w    , với số phức w  có phần ảo bằng z  .i z x   y  x  y i  x   y  x  y 2 2 2 2 2 2 z .i z 1 2 2
nên theo giả thiết ta có: x  y  y 1 2 2 2 2 2 2
  2 x  y  2 y  x  y  y x  y 4 x   y  x  y 2 2 2 2 4 2 2  x  y  y   2 2 2
x  y  2y  0 (*). Quy về phương trình bậc hai theo 2 2 x  y , ta có:  y  2  y  2 2 2     x  y   y  2 2  z  x  y 
(*)   y  22  4.2y   y  22 2 2  0     .  y  2  y  2 2 2     x  0 x  y   2  2
Từ đó ta suy ra: A z , B z ,C z thuộc đường tròn tâm O , bán kính R  2 . 1   2   3 
Ta có: P  z z  z  z z  z  z z  z  z z  z z  z z  z z  z z  z z 1 3 2  2 3 1  3 1 2  1 3 1 2 2 3 2 1 3 1 3 2
 z z  z z  z z  z z  z z  z z 1 3 3 1   2 3 3 2  1 2 1 2 Sử dụng tính chất sau: 2 2 2
z z  z z  z  z  z  z , từ đó ta biến đổi tiếp biểu thức trên: 1 2 1 2 1 2 1 2
P  z z  z z  z z  z z  z z  z z  2 2 2 2 2 2 2 2 2
 z  z  z  z  z  z  z  z  z  z  z  z 1 3 3 1 2 3 3 2 1 2 1 2 1 3 1 3 2 3 2 3 1 2 1 2 2 2 2 2
 2 z  z  z  z  z  z  z  2OC  AC  BC  AB  8  2Rsin B2 2Rsin A2  2RsinC2 2 2 2 2 3 1 3 2 3 1 2  1   1 1 cos 2A 1 cos 2B 2 2 2 2   16
 sin C  sin A sin B  8 1 cos C        2   2 2 2   1 2    16  cos  A B 1  cos2A cos2B 1 2 16  cos  
A Bcos A BcosA B  2 2   2   1 2  16  cos C  cosC cos  A B  2  2 1  1 1 1      3 Với  2
1   cos  A  B   1 ta suy ra P 16 cos C cosC 16     cosC      16. 12. 2  2 2 4      4  
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Vậy giá trị lớn nhất của biểu thức P bằng 12. Chọn đáp án D. 
Câu 45. Cho hàm số bậc ba f  x 1 3 2 
x  bx  cx  d có đồ thị là C  cắt trục hoành tại 3 điểm phân 2
biệt trong đó có 2 điểm có hoành độ lần lượt là x  1
 ,x 2. Đường thẳng d tiếp tuyến của đồ thị C  
tại điểm có hoành độ 5 x 
cắt đồ thị C  có hòanh độ 5
x  . Gọi S , S lần lượt là các diện tích hình 4 3 1 2 S a
phẳng giới hạn bởi đồ thị C  , trục hoành và trục tung (như hình vẽ bên ). Khi tỉ số 1  (với a là S b b 2
phân số tối giản) thì 19a  b bằng A. 45 9 . B. 43 5 . C. 7 0 5 . D. 7 7 5 . Lời giải
Từ hình vẽ ban đầu ta suy ra: f  x 1
  x  a x 1 x  2 (1) 2
Gọi phương trình tiếp tuyến cần tìm là: d  : y  mx  n , từ đó ta suy ra: 2 2         f  x  mx  n 1 5 5   x  x   f     x 1 5 5   x  x   mx  n    
(2), so sánh hệ số chứa 2 x 2  4   3  2  4   3  1  11
trong hai cách biểu diễn hàm f  x  giữa (1) và (2) ta suy ra 11 a   tức f x   x   x   1 x  2 . 6 2  6    5  59 f         4  96 59  5  91 59 204 Khi đó ta suy ra:   d  : y  x     
d : y  g x  x    5  91 96  4  384 96 384 f        4  384 1  1   1  11 5125 S  f (x) dx   x  x 1 x  2 dx  1       2  6  31104 11 11    6 6 Suy ra:  S 656 1  5 5   3 3 S 12005      S  f x  g  x 1 11 dx   x     x   x   2 59 204 1500625 ( ) 1 2  x  dx  2   2   6   96 384  497664 5 5    4 4
Vậy a  656,b 12005 tức 19a  b  459 . Chọn đáp án A.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 46. Cho hình chóp S .A BC D có ABCD là hình bình hành biết rằng  SAD   BAC  90 , cạnh
SA  2 2a, BC  2a, SB  6a . Gọi H là hình chiếu vuông góc của A trên SD biết khoảng cách giữa C H
và SB bằng 2a . Thể tích khối chóp S .A BC D bằng 3 2a 10 A. 3 2a . B. . C. 3 10a . D. 3 a . 3 3 Lời giải Ta gọi DG DH
I là trung điểm A D và G là trọng tâm A C D , kẻ HG  SB , khi đó ta có: 1   . DB DS 3
Kẻ BK  IC với K  AD ta suy ra HCI   SBK  và d CH , SB   d HCI ;SBK   d I;SBK .
Tiếp đến ta dễ thấy IKBC là hình bình hành nên suy ra A là trung điểm IK , từ đó ta có SK  3a và AD 5 CI  BK 
 a . Mà SB  6a nên ta suy ra: (Công thức He-rông) 2 S  a . 2 S  BK 2 6V 6V
Mặt khác ta có: d CH, SB  d I;SBK   2d  ; A SBK  SABK SABK    2a nên ta suy ra S S  BK 5 2 a 2 1 5 10 2 3 V  a . 2a  a , mà S V ABCD S .ABCD     nên ta suy ra S.ABK S S V 6 2 12 ABK ABI 4 SABK 4 10 10 3 3 V  4V  4 a  a . Chọn đáp án D. S.ABCD S.ABK 12 3
Câu 48. Có bao nhiêu số nguyên x  10;10 sao cho ứng với mỗi x có ít nhất 8 số nguyên y thỏa 2 2 mãn 706 2 y  4x  .ylog 10   65.4x y x y ? 2   A. 7 . B. 8 . C. 10. D. 15. Lời giải 2 2
Ta có bất phương trình sau: 70 6
2  y 4x  .ylog 10  65.4x y x y
(*), điều kiện: y 10 x. 2   2
2  y 4x  .ylog 10   2 2 70 6 x y 70 8  y 2 65.4 0 2  x x y log 10 x y 650 2 2  
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG 2 Xét hàm số   70 8  y 2 2  x f y
log 10x y 65 trên ;10  x ta có 2   f  y 2 708 y2 x 1  8.2 ln 2    y   x 10  x  y  0,  ;10  ln 2
Từ đó ta suy ra hàm số f  y luôn nghịch biến trên ;10  x .
Ta có bất phương trình f  y 1
 0  f 0  y  10  x . Do theo đề bài ứng với mỗi x có ít nhất 8 số
nguyên y thỏa mãn nên ta suy ra y sẽ chạy từ 2  x tới 9  x . 2 Từ đó ta suy ra 1    0 1  1  70  8 1 x 2  0  2 x f x f x    log 9 65 0 2   2
 2x  8x  62  log 65  log 9 2
 2x  8x  62  log 65  log 9  0 2 2 2  2  x  7.659 x   10;10 
 x  10;3.65   7.659;10 x  3.65
Mà x   nên ta suy ra x 9; 8;...; 4;8; 
9 tức có 8 giá trị nguyên x thỏa mãn. Chọn đáp án B.
Câu 49. Trong không gian Oxyz, cho mặt phẳng P  : x  2 y  2z  7  0 , điểm M 2; 1;1 và mặt cầu S  2 2 2
: x  y  z  4 x  2 y  4 z  7  0 . Đường thẳng d  đi qua M cắt P , S  lần lượt tại các điểm A và
B sao cho M là trung điểm AB . Biết độ dài ngắn nhất của đoạn AB là 2 a  2 b , giá trị a  b bằng A. 23 2 . B. 2 2 3 . C. 212 . D. 192 . Lời giải
Ta có mặt cầu S  tâm I 2; 1; 2 , bán kính R  4 và d I ;P   5  R  4 nên suy ra mặt phẳng P 
không cắt mặt cầu S . Tiếp đến ta tìm mặt phẳng Q  đối xứng với  P  qua M . D
Ta có Q  : x  2 y  2z  D  0 và d M P  d M Q 2 ; ;  3   3  D 11 3
Suy ra: Q  : x  2 y  2z  11  0 . Tới đây ta tìm quỹ tích điểm B như sau:
Theo giả thiết, ta có MA  MB  B  Q  , do đó B luôn nằm trong hình tròn C  được tạo từ mặt phẳng  7 5 8 
Q  cắt mặt cầu S. Gọi J là hình chiếu của I lên trên Q  , giải hình chiếu trên ra J  ; ;    3 3 3 
Từ đó ta suy ra bán kính của C  bằng 2 2 r  R  IJ  15 .  7 5 8 
Suy ra điểm B luôn thuộc đường tròn C  tâm J  ; ;   , bán kính r  15 .  3 3 3 
Do AB  2MB nên AB lớn nhất chỉ khi M B lớn nhất, khi đó ta có hình vẽ như sau:
Từ hình vẽ trên ta suy ra AB  2MB  2MB  2 ME  EB  2 ME  EJ  r  2 9   15  132 2 2 2 2 0 0
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
 2 37  2 195 . Đồng nhất hệ số ra a 37,b 195 tức a  b  232 . Chọn đáp án A.
Câu 50. Cho hàm số y  f x là hàm đa thức có f 2  36, f 2  32 . Hàm số f  x có bảng biến thiên như sau:  x 
Có bao nhiêu giá trị nguyên của tham số 
m  50;50 để hàm số g  x 2 1 6  f   m   có 5 điểm  x 1  2x 1 cực trị ? A. 6 3 . B. 3 4 . C. 3 6 . D. 62. Lời giải  x   Xét h x 2 1 6  f  ,  x     1  2 1  3 12
    . Ta có h x  f  .   x 1  2x 1 D \ ; 1    2   x 1   x  2 1 2x  2 1 2 x  4 h x
 2x 1 4 x   1  0  f     đặt 2 1 t 
ta được phương trình f t    x 1  2x  2 1 x 1 2 t Đặt u t 4  
dễ dàng suy ra được bảng sau 2 t 4 t  2  Do đó f t  
thay lại ta được h x  0 có nghiệm duy nhất 1 x  . Ta có bảng biến thiên 2  t t  2 4 của h  x   0 . 36  m 36  m 28  m
Do h  x  có 1 điểm cực trị nên để hàm số h x có 5 điểm cực trị khi chỉ khi h  x  cắt trục hoành tại 4 điểm 3  6  m  0
phân biệt do đó ta suy ra   3
 6  m  28. Vậy có 63 giá trị của m. Chọn đáp án A.  2  8  m  0
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG SỞ NGHỆ AN LẦN 2
Câu 45. Cho số phức z thỏa mãn điều kiện z  3  6i  z  2  5i và số phức z có phần thực bằng phần 1
ảo. Giá trị nhỏ nhất của biểu thức 2 z  z  z là 1 1 A. 9 . B. 26 . C. 3 26 . D. 1 . 8 2 6 1 3 5 Lời giải
Đặt z  x  yi x, y    khi đó ta có: z  3 6i  z  2 5i  5x  y 8  0 tức M  z  d  : 5x  y  8  0 . Gọi A 2 z  z với số phức   1 1 
z phần thực bằng phần ảo, ta suy ra z a ai 1 1 x  a Suy ra 2 z  z  a   2 a  2 A a i  tức A 2
z  z  P : y  x  2x . 1 1    2 1 1   2 y  a  2a  A
Gọi d  là tiếp tuyến tiếp xúc với  P  và song song với d  với d  : 5x  y  C  0 . Khi đó gọi d A x ; y
là điểm tiếp xúc đó, ta suy ra  2 x  2x 
 5  x  1 tức d  : 5x  y  2  0 0  0 0  0 x 0 x dx  3 26 Vậy 2 z  z  z  z  2 z  z
 MA  MA  d d;d  d A ;d  . Chọn đáp án C. 1 1 1 1  0    0  13 Câu 48. Cho hàm số 1 2 1 y  f  x  3 2
 x  ax  bx a, b    . Biết hàm số g  x  f  x  f  x  f   x 3 3 2
có hai điểm cực trị là x 1, x  3. Với mỗi t là hằng số tùy ý thuộc đoạn 0; 
1 , gọi S là diện tích hình 1
phẳng giới hạn bởi các đường x  0, y  f t , y  f  x và S là diện tích hình phẳng giới hạn bởi các 2
đường x  1, y  f t , y  f  x . Biểu thức Q 12S  4S có thể nhận được bao nhiêu giá trị là số nguyên ? 1 2 A. 7 . B. 1 0 . C. 9 . D. 8. Lời giải Ta có: f x 3 2
 x  ax  bx  f  x  2
 3x  2ax  b  f   x   6x  2a  f  x  6 2 1 2 1 3x  2ax b 2 6x  2a
Từ đó ta suy ra: g x  f  x  f   x  f   x     3 3 3 2 3 3 g    1  0 a  0
Do hàm số g  x  có hai điểm cực trị là x 1, x  3 nên suy ra    tức    3 y f x  x . g  3  0 b   0
Xét phương trình hoành độ giao điểm của y  f t , y  f  x có 3 3 x  t  x  t 1  S  t  x  4 3t 3 3 dt  1  4 Từ đó ta suy ra: 0 4 3 
 Q 12S  4S 12t  4t 1  f t 1 2   1 S  x t  4 3 3 3t 3 1 dt  t  2  4 4  t  1  63
Xét hàm số f t  ta có f t 1  0  t  0;t  với 1 t  là điểm cực tiểu và f    . 4 4  4  64 63 
Do t  0;1 nên ta suy ra Q ;9 
tức Q có thể nhận 9 giá trị nguyên. Chọn đáp án C. 64   
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 49. Cho các số thực , a ,
b c 1 thỏa mãn 6log c  1 log .
c log c và biết phương trình 2x 1  x c  a 2ab 2b a m  n
có nghiệm. Giá trị lớn nhất của biểu thức P   4 log 2bc bằng trong đó a  m, n, p là các số nguyên p m
dương và là phân số tối giản. Giá trị của m  n  p bằng p A. 4 8 . B. 6 0 . C. 5 6 . D. 64. Lời giải Ta có: 2x x 1 1 1 1 1 5 1 2 c
 a  x 1  x log a  log a  x   2 . x  2    log a   (1) c c x x log a 2 c log a 2 c c 6 1 1
Tiếp đến ta có: 6log c 1 log . c log c  1 . 2ab 2b a log 2b  log a log 2b log a c c c c  1 1        b  a   b  a   c c  1 1 6 1 . log 2 log 6 log 2 log c c 1 log 2b log a log 2b log a  c c  c c 5 1 7  33 7  33  log 2b    6  log 2b ; . Từ đó ta suy ra: c  2 log 2 c b 4 4 c   7  33  4 b b   P  bc  b  c      a  log 2 c 4 log 2 4 4  a     c   23 33 4 log 2 log 2 4 loga log a log a log a 2 8 c c c m  23; n  33
Đồng nhất hệ số suy ra 
tức m n p  64. Chọn đáp án D.  p  8
Cách 2: Đặt  ;2    u; v a b
c c  , khi đó ta luôn có: 6log c  1 log .
c log c tương ứng với bất phương 2ab 2b a 6 1 trình: 6log           c c c uv u v uv u v 1 log u log v 1 6    1 c c c u  v uv 2 2 2
 uv  u v  uv  u  v  uv  v  2 6 u  6u   1  u  0 . (*)
Tiếp đến ta lại có phương trình 2 2 x 1  x x 1  ux 2 c  a  c
 c  x  ux 1  0 , xét phương trình bậc hai trên theo x ta có: 2
  u  4  0 (điều kiện có nghiệm)  u  2 . 7  33 7  33 Với u
 2 ta thế vào (*) khi đó ta có: 2 2v  7v  2  0   v  min 4 4 7  33  4  v  v   v 4 4 23 33 Từ đó ta suy ra: P  bc  c     u   a  4  u c  4  4 log 2 log , 2 u 2 2 8 m  23; n  33
Đồng nhất hệ số suy ra  tức m n p  64  p  8
Câu 50. Trong không gian Oxyz cho các điểm A 4;0;0, B 0;8;0,C 0;0;12, D 1; 1;1 và M là
điểm nằm ngoài mặt cầu S  ngoại tiếp tứ diện OABC . Các đường thẳng M , A M , B M , C MO lần lượt cắt mặt cầu  MA MB MC MO
S  tại các điểm A , B ,C ,O (khác , A , B , C O) sao cho     4 . Tìm giá trị MA MB MC MO
nhỏ nhất của M D  M O
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG A. 229 . B. 227 . C. 226 . D. 228 . Lời giải
Ta gọi I là tâm mặt cầu S , nhận ra ba điểm , A ,
B C nhận thành mặt chắn nên ta suy ra tọa độ của I có  x y z  dạng là: A I ; B ; C  I  2  ;4; 6   
 và bán kính mặt cầu S là R  IA 2 14 .  2 2 2  2 2 MA MA MA Tiếp đến ta có:  
, tương tự với các tỉ số còn lại là: MB MC MO , , ta suy ra: 2 2 MA MA.MA MI  R MB MC MO 2 2 2 2 MA MB MC MO MA  MB  MC  MO 2 2 2 2 4     
 MA  MB  MC  MO  4  2 2 MI  R (*) 2 2  MA MB MC  MO MI  R
Gọi M  x; y; z  khi đó thế vào (*) ta suy ra phương trình trở thành:
x  2   y  2  z  2  x  y  z    x  2  y  2 z  2 2 2 2 4 8 12 3 4 2 4 6   224
 x 2y 3z 28  0 tức M  P: x  2 y  3z  28  0 . Bài toán trở thành tìm giá trị nhỏ nhất của
M D  M O với M   P  : x  2 y  3z  28  0 . Do ,
D O cùng phía với P  nên ta gọi O  là điểm đối xứng
với O qua  P  với O4; 8;12  . Suy ra giá trị nhỏ nhất là MD  MO  DO  227 . Chọn đáp án B.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Document Outline

TỔNG HỢP VẬN DỤNG CAO ĐỀ THI THỬ
TỔNG HỢP VẬN DỤNG CAO ĐỀ THI THỬ (PHẦN 2)

Hướng dẫn giải toán VDC trong các đề thi thử TN THPT 2022 môn Toán

Thông tin :

Tài liệu liên quan:

TOP 20 câu trắc nghiệm phát triển câu 39 từ đề minh họa THPTQG môn Toán năm 2024 (có đáp án)

TOP 20 câu trắc nghiệm phát triển câu 40 từ đề minh họa THPTQG môn Toán năm 2024 (có đáp án)

Phát triển các bài toán VD – VDC trong đề tham khảo TN THPT 2024 môn Toán

Tài liệu ôn tập lý thuyết thi tốt nghiệp Trung học Phổ thông môn Toán

Chuyên đề khảo sát hàm số: Tính đơn điệu của hàm số | Tài liệu ôn thi THPTQG môn Toán