96 trang 5 lượt tải

Hướng dẫn giải toán VDC trong các đề thi thử TN THPT 2024 môn Toán

Tài liệu gồm 75 trang, được biên soạn bởi tác giả Trần Minh Quang, hướng dẫn giải một số bài toán mức độ vận dụng cao (khó / nâng cao) trong các đề thi thử tốt nghiệp THPT năm 2024 môn Toán. Mời bạn đọc đón xem!

Chủ đề: Đề thi Toán 12 519 tài liệu

Môn: Toán 12 4.5 K tài liệu

Tác giả:

VietJack

1 năm trước

Tải xuống Báo cáo

Danh sách Quiz

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

ĐỀ THI THỬ THPT CHUYÊN KHTN – HÀ NỘI

Câu 47: Có bao nhiêu số nguyên

sao cho ứng với mỗi

tồn tại số thực

 

1; 2

y 

thỏa mãn

2 1

x y 

. B.

. C.

. D.

Lời giải

Cách 1: Trước hết ta xét



thì khi ấy phương trình luôn đúng với mọi số thực

 

1; 2

y 

nên nhận.

Tiếp đến với



ta xét hàm số

 

2 1

f y x y  

trên khoảng

 

1; 2

khi đó ta có:

 

2 ln 2

f y x x



 

Điều kiện cần: để tồn tại

 

1; 2

y 

thỏa mãn thì

   

1 2 0

x x

f f



Trường hợp 1:



thì ta giải

 

2 0

0 log 1

ln 2

2 ln 2

f y y y







     







Khảo sát nhanh hàm số

 

log

ln 2

g x



dễ thấy

     

ln 2 , 0;

ln 2

g x g e x

    

tức

 

1;2

y 

Cùng với

   

0, 1;2

f y y



  

, khi ấy để

 

1; 2

y 

thì:

 

 

2 2

1 0

2 1 0

2;3;4

2 0

2 2 1 0







  

 

  

 



  







Trường hợp 2:



thì khi ấy

   

0, 1;2

f y y



  

. Suy ra để

 

1; 2

y 

thỏa mãn thì

 

2 2

1 0

2 1 0

2 0

2 2 1 0







  

 

  

 



  







. (loại)

Vậy tóm lại

 

0;2;3; 4

x 

tức có 4 giá trị nguyên

thỏa mãn. Chọn đáp án D.

Cách 2: Dễ thấy xét



thì hàm số

 

2 1

f x x y  

có

 

2 2

2 ln 2

2 ln 2 0

f y x x

f y x





 







 





Suy ra hàm

 

f y

là hàm lồi nghiêm ngặt và có tối đa 1 cực tiểu, khi ấy cùng với thì ta suy ra điều kiện cần và đủ

để

 

f y



có nghiệm với mọi

 

1; 2

y 

là

   

1 2 0

x x

f f



Câu 48: Trong không gian

Oxyz

, cho đường thẳng

: 3

d y z



  

. Xét mặt phẳng

 

thay đổi và luôn chứa

đường thẳng

 

. Gọi

là hình chiếu vuông góc của điểm

 

2; 1; 2

A 

lên mặt phẳng

 

. Khi

 

thay

đổi thì

luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng

. B.

. C.

. D.

Lời giải

Đầu tiên ta gọi

là hình chiếu của

lên

 

, từ đó dễ dàng tính được tọa độ điểm

 

1;0;3

Khi ấy ta suy ra

thuộc mặt cầu

 

đường kính

có tâm là trung điểm

và bán kính

R 

Tiếp đến ta có

         

   

 

, 2;1;1

AHC d

AH d P AC d d AHC n u       

 

tức suy ra

 

H AHC



Mà

 

AHC

qua đường kính mặt cầu

 

nên đường tròn cố định có bán kính

r R 

. Chọn đáp án D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 50: Xét các số phức

1 2

,z z

thỏa mãn

1 2 2

1 2, 1z i z z i     

và

1 2

z z





là số thực. Khi ấy giá trị nhỏ

nhất của biểu thức

1 2

z z

bằng

3 5

. B.

2 5

. C.

5 5

. D.

Lời giải

Đầu tiên ta đặt:

   

2 1

, ,

1 2, 1

w z A z B w

z i w w i

 





     





, bằng biến đổi đại số thông thường ta dễ dàng lần lượt suy ra

được:

 

A C



tâm

 

1; 1

 

, bán kính

R 

và

 

: 1 0

B d x y

   

Tiếp đến ta có:

 

1 2

1 2 1

1 2 1 2 1 2

z z

z z z w

i i i

 

 

 

  

là số thực tức

 

1 2 ,z w k i k

     

, suy ra được

BA ku

 

với

 

1; 2

 



tức đường thẳng

có vector pháp tuyến là

 

2;1

n 



. Từ đây ta có hình vẽ như sau:

Ta có:

 

cos ; cos

u d



 



và

 

1 2 1 2 1

z z z z z w     

min khi

 

min min

min

;

sin sin

d A d

 

 

Khi ấy ta suy ra:

 

min

3 1

; ; 2

2 2

d A d d I d R    

tức

min

AB  

Vậy ta kết luận giá trị nhỏ nhất của biểu thức

1 2

z z

bằng

. Chọn đáp án D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

ĐỀ THI THỬ LIÊN TRƯỜNG NGHỆ AN

Câu 33: Trong một đề thi trắc nghiệm môn Toán có loại câu trả lời dạng đúng sai. Một câu hỏi có 4 ý hỏi, mỗi ý hỏi

học sinh chỉ cần trả lời đúng hoặc chỉ trả lời sai. Nếu 1 ý trả lời đúng đáp án thì được 0,1 điểm, đúng đáp

án 2 ý được 0,25 điểm, đúng đáp án 3 ý được 0,5 điểm và đúng đáp án cả 4 ý được 1 điểm. Giả sử một thí

sinh làm bài bằng cách chọn phương án ngẫu nhiên để trả lời cho 2 câu hỏi loại đúng sai này. Tính xác suất

để học sinh đó được 1 điểm ở phần trả lời 2 câu hỏi này

128

. B.

128

. C.

256

. D.

Lời giải

Trước hết ta chia thành hai công việc:

- Công việc (1): Tính xác suất để mỗi ý trong 4 ý của 1 trong 2 câu hỏi là đúng/sai.

+ Dễ tính được xác suất để học sinh trả lời ý hỏi đúng là

và ý hỏi sai là

- Công việc (2): Tính xác suất để có số ý đúng cần thỏa mãn mỗI câu trong mỗi trường hợp (sẽ nêu dưới đây).

 Nhận xét: do hai công việc có tính chất liên kết nhau nên ta sử dụng quy tắc nhân. (*)

Ta có 2 trường hợp như sau:

Trường hợp 1: Cả 2 câu đều đúng được 3 trong 4 ý, tức mỗi câu đạt 0,5 điểm.

Câu hỏi 1 trả lời đúng 3 câu: Chọn 3 trong 4 câu đúng có

(cách) và xác suất mỗi ý trả lời đúng là

, với 3 ý

đúng là

 

 

 

, ý còn lại sai có xác suất là

nên theo (*), suy ra xác suất câu hỏi 1 đúng 3 câu là:

1 1

2 2

 

 

 

(1)

Câu hỏi 2 trả lời đúng 3 câu, thực hiện tương tự như (1) ta có:

1 1

2 2

 

 

 

Suy ra tại trường hợp 1 ta có xác suất cần tìm là

3 3

4 4

1 1 1 1 1

. . . . .

2 2 2 2 16

C C

   



   

   

Trường hợp 2: 1 trong 2 câu đạt điểm tối đa (1 điểm), câu còn lại 0 điểm.

Giải thích: tức 1 trong 2 câu (

cách) có 4 ý đều đúng (với xác suất mỗi ý đúng là

) và câu còn lại không đúng cả

4 ý (với xác suất mỗi ý sai là

) nên theo quy tắc (*), ta suy ra trường hợp này xác suất là

1 1 2

2 2 16

   



   

   

Vậy, cộng hai trường hợp ta có xác suất cần tìm là

1 2 9

16 16 128

 

. Chọn đáp án B.

Câu 39: Có bao nhiêu số nguyên

 

2024;7000

x 

là nghiệm của bất phương trình sau:

3 3

0,3 6

log 9log 80

log log 0

log 4

x x

 

 



 



 

600

. B.

603

. C.

601

. D.

602

Lời giải

Bất phương trình tương đương với:

3 3

log 9 log 80

log 1

log 4

x x

 

 



 



 

(*) (do

0,3 1

nên dấu đổi chiều).

Đặt

logt x



, thì khi ấy (*)

  

8 7

log

9 80

6 8 7 0 3 3 0

t x

t t

t t x x



 

         



Kết hợp với

 

2024;7000

















ta có:

2024 3

3 7000



 



 



. Dễ dàng đếm được có

163 439 602 

(số). Chọn đáp án D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 41: Cho số phức

thỏa mãn

2 2 2 6

w i w i    

và hai số phức

1 2

,z z

cùng thỏa mãn

 

z z

 

có phần thực, phần ảo là các số âm,

có phần thực, phần ảo là các số dương và

2 1

z z

bé nhất. Giá trị

nhỏ nhất của

1 2

w z w z  

thuộc khoảng nào dưới đây ?

 





 

. B.

 





 

. C.

 





 

. D.

 





 

Lời giải

Ta đặt

   

: ,S z x yi x y  



, khi ấy

    

  

4 2 2 1

z z z z z z yi x xy

       

Với

   

1 1 1

1 2 12 12

2 2 2

, : ,

z x y i

z z S x y

z x y i

 



 



 





. Do phần thực, ảo của

1 2

,z z

cùng dấu nên

  

1 1 2 2

x y x y

   

, mà

2 1

z z

bé nhất nên suy ra:

 

2 2

2 1 1 2 1 2

1 2 1 2

1 1

i i

z z x x x x

x x x x

     

         

     



     

2 2

1 2 1 2

2 2

1 2 1 2

2 2

1 1 1

2 8

x x x x

 



 

      

 

 

 



với dấu bằng xảy ra khi

1 2

x x

 

tức ta suy ra

z i

 





  



Tiếp đến xét điểm:

   

, ,M w w a bi a b  



, bằng phương pháp đại số ta suy ra

 

: 2 4

M d y x

  

Cách 1: Phương pháp đại số (Sử dụng bất đẳng thức Mincopski)

Ta có:

       

2 2 2 2

2 2

1 2

1 2 5 1 2 3 5 22 26 5 10 10

T w z w z a a a a a a a a

                 

   

2 2

3 3

11 1

5 5 5 5

5 5

a a a a

   

    

   

   

   



   

  





   

Cách 2: Phương pháp hình học.

Không cần vẽ hình, xét

 

: 2 4 0

M d x y

   

nhận thấy

   

1;1 , 1; 1

A B

 

cùng phía với

 

nên gọi



là điểm

đối xứng với

qua

 

, khi ấy dễ dàng tìm được tọa độ

17 1

;

5 5

 





 

 

, khi ấy ta kết luận:

1 2

2 5

T w z w z MA MB MA MB A B

 

         

. Chọn đáp án D.

Câu 42: Có bao nhiêu cặp số thực

 

;x y

thỏa mãn điều kiện sau:

     

4 2 2 2 2 2

2 2 6

6 9 log 2 4 16 2 log 3log 5 3 2 1

x y

x x y y x y x x y x           

. B.

. C.

. D.

Lời giải.

Trước hết ta dự đoán như sau:

   

4 2 2 2 2

2 2

log 2 4 16 2 log 0

x x y y x y

     

   

2 2 2

2 2

1 log 8 log 0

x y x y

 

      

 

 

(*) , đặt

 

log

t x y 

thì khi ấy

(*)

 

2 2

2 1 1

1 log 4 8 0 4 8 2 2 8 4

t t t t t

 

          

(1). Mà (1) đúng với bất đẳng thức Cauchy:

2 2

1 1 3 2

2 8 2 2 .2 2 2 2 4

t t t t



 

     

với dấu bằng xảy ra khi

2 8









 









nên kết hợp điều kiện

căn thức có nghĩa, suy ra

     

4 2 2 2 2 2 2

2 2 2

log 2 4 16 2 log 0 log 2 4

x x y y x y t x y x y

            

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Khi ấy phương trình ban đầu trở thành:

 

log 5 1

6 3log 5 1 2 1 6 3 l g3 o6 5

x x

x x x x



      



Xét hàm đặc trưng

 

6 3

f t t 

có

 

6 ln 6 3 0, 0

f t t



    

tức

 

f t

luôn đồng biến trên

 



 

log 5 1 6 5 1 0

x x x

      

Xét hàm số

 

6 5 1

g x x  

có

   

6 ln 6 5 0 log 0;1

ln 6

g x x



     

(điểm cực tiểu), do hàm

 

g x

có

1 điểm cực trị nên suy ra

 

g x



có 2 nghiệm, dễ dàng nhẩm nhanh ra 2 nghiệm

0, 1x x 

Lại có:

2 2

4 4

x y y x    

(ứng với 1 giá trị

cho ra 1 giá trị

) nên có 2 cặp

 

,x y

. Chọn đáp án A.

Câu 43: Trong không gian

Oxyz

cho các điểm

   

5;8;3 , 2; 1; 4

M Q

  

và hai đường thẳng lần lượt có phương

trình là

1 2

: 3; : 3 ,

x t x

y y t t

z z t

  

 

 



     

 

 



  

 



. Biết điểm

di động trên đường thẳng



và điểm

di động

trên đường thẳng



. Giá trị nhỏ nhất của

T MN NP PQ  

là

289

. B.

459

. C.

179

. D.

369

Lời giải

Trước hết từ giả thiết ta gọi

   

;3;3 , 5;3;M a P b



với

,a b

 

Khi ấy:

       

2 2 2 2

5 25 5 3 4 25

T MN NP PQ a a b b

            

Ta xử lí biểu thức trên bằng bất đẳng thức Mincopski như sau:

       

   

2 2

369

5 3 4

5 3

5 5 5

5 5 5 15 24 1

aT P a

a a

b bMN N

P     

 



   

  

  

 

 

Dấu bằng xảy ra khi và chỉ khi

 

5 5

15 5

; ;0

5 4

12 4 4

a b



 

    

 



 

. Chọn đáp án D.

Câu 45: Cho hàm số

 

y f x



liên tục và có đạo hàm trên

 



thỏa mãn các điều kiện:

 

1 0



và

 

2 2

2 1 , 0;

x f x

x xf x e x e x





     

. Biết

   

4 ln 2, ,f a b a b  



. Giá trị

a b

bằng

. B.

. C.

. D.

Lời giải

Ta có:

 

2 2 2

2 1 2 1

x f x x f x

x x

x xf x e x e x x f x e x e

 

 

      

(1)

Đặt

 

   

 

2 2

x f x x f x

g x e g x x f x e

 

 

   

, (1) thành:

   

 

1 1

x x

g x

g x g x e e

x x x



 



    

 

 

Suy ra:

 

1 0

ln 2

0 ln

x f x

x x x x

g x

e C C e xe e f x x x x

x x









           

Khi ấy ta suy ra:

 

4 12 2 ln 2

f  

tức

12, 2 14

a b a b

     

. Chọn đáp án B.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 46: Trên tập hợp số phức, xét phương trình

10 0

z mz

  

, (với

là tham số). Biết phương trình đã cho có

hai nghiệm phân biệt

1 2

,z z

. Các điểm biểu diễn số phức

1 2

1 1

, , ,

z z

tạo thành một đa giác lồi có diện

tích lớn nhất bằng

. B.

. C.

. D.

Lời giải

Trước hết từ giả thiết, ta đặt:

 

z a bi

a b

z a bi

 







 





với

2 2

1 2

10 10

z z a b

   

(do

1 2

,z z

liên hợp nhau).

Tiếp đến ta gọi

   

; , ; , ; , ;

10 10 10 10

a b a b

A a b B a b C D

   

 

   

   

ứng với

   

1 2

1 1

, , ,A z B z C D

z z

   

   

   

. Nhận thấy

cặp điểm

,A B

và

,C D

cùng phần thực nên dễ dàng thấy được

ABCD

là hình thang cân.

Khi ấy dễ dàng suy ra

   

 

2 2

1 99 99

. , 2 .

2 2 5 10 200 2

ABCD

AB CD b a

S bd AB CD b a ab a



   

     

   

 

   

Chọn đáp án A.

Câu 47: Cho hàm số bậc ba

 

y f x



và hàm số bậc hai

 

y g x



có đồ thị như hình vẽ.

Biết rằng đồ thị hàm số

 

y f x



cắt đồ thị hàm số

 

y g x



tại 3 điểm phân biệt

1 2 3

, ,x x x

thỏa mãn

1 2 3

x x x

 

. Diện tích miền tô đậm nằm trong khoảng nào sau đây ?

 

 

 

. B.

 

 

 

. C.

 

 

 

. D.

 

 

 

Lời giải

Trước hết từ đồ thị ta dễ dàng có:

 

2 3 2

3 3

f x a x x f x a x x C

 



     

 

 

Nhận ra

hoành độ đỉnh parabol đồ thị

 

y g x



nên

3 3 29 27 29

2 2 12 4 12

x f C a

 

     

 

 

. (1)

Từ đây ta cũng suy ra:

 

g x k x b

 

  

 

 

, mà

   

0 3 3

3 29

2 12

f f

 







 



 



 



nên giải được

 

7 3 29

27 2 12

g x x

 

  

 

 

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Xét hàm số

       

     

   

1 2 3

0 0 5

3 5

0 0 3

f g a x x x a

f x g x a x x x x x x C a

f g C

   



        



  





(2)

Từ (1) và (2) ta có hệ phương trình sau:

   

3 2

27 29

14 1 95 7 5

;

4 12

3 3 3 54 9 3

3 5

C a

x x

C a f x g x x

C a



 



        





 



Thêm nữa,

1 2 3

, ,x x x

chính là nghiệm của phương trình hoành độ giao điểm của

   

f x g x

tức ta suy ra:

   

 

3 2

Chia Hookne

17 559

95 7 5 1 3

0 9 34 30 0

3 54 9 3 54 2

17 559

x x

f x g x x x x x











 



           

 



 











Vậy diện tích cần tìm là

   

17 559

3 2

95 7 5

5,709

3 54 9 3

x x

S f x g x dx x dx



      

 

. Chọn đáp án C.

ĐỀ THI THỬ SỞ NGHỆ AN

Câu 36: Cho hàm số

3 2

5 3y x x x  

. Xét các số thực

a b

, giá trị nhỏ nhất của

   

f b f a



bằng

256



. B.

256

. C.

500

. D.

500



Lời giải

Trước hết ta giải phương trình

3 10 3 0 3

y x x x x



       

Đến đây dễ thấy

3 10 3 0 3

y x x x



      

và

     

f b f a f x dx



 



Từ đây ta có:

 

 

 

2 2

;3 ;

256

3 10 3 3 10 3

a b

f x dx x x dx x x dx

 



 

 



       

  

Khi ấy suy ra:

3 2 3 2

256

5 3 5 3

x x x y y y     

, đặt

m y x

  

, từ đây ta có được:

     

 

3 2 3 2 3 3 2 2

256 256

5 3 5 3 5 3

27 27

y y y x x x y x y x y x            

   

2 2

10 16 256 10 1

3 3 3 8 3 16 0

3 4 3 27 3 108

m x m m m x m m m

   

            

   

   

(luôn đúng)

Vậy ta kết luận giá trị nhỏ nhất của

   

f b f a



bằng

256



. Chọn đáp án A.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 39: Có bao nhiêu giá trị nguyên của tham số

để phương trình

2 2

4 0

z z m

  

có nghiệm

z z

sao cho

1 2 3

z i

  

. B.

. C.

. D.

Lời giải

Ta có:

16 4m

  

, tiếp đến theo bất đẳng thức Mincopski ta có:

 

0 0 0

1 2 1 2 1 2z i z i z i        

Mà

 

1 2 3

z i

   

nên suy ra:

3 5 3 5

z   

(*)

Trường hợp 1:

0 16 4 0 2 2

m m

        

khi ấy phương trình có 2 nghiệm thực

2 4

z m



  



  



Kết hợp với (*), suy ra:

3 5 2 4 3 5



     



     



(luôn đúng với mọi

 

2; 2

m  

) (1)

Trường hợp 2:

0 2 2

m m

      

khi ấy phương trình có 2 nghiệm phức với

1 2

z z m 

Kết hợp với (*), suy ra:

3 5 3 5 3 5

m m

 

      



(2)

Từ (1) và (2) ta suy ra:

 

5; 4; 3; 2; 1; 0

m      

tức có 11 giá trị nguyên

thỏa mãn. Chọn đáp án A.

Câu 40: Cho hàm số

 

2 log 8 17

f x x x



   

. Có bao nhiêu cặp số nguyên

 

;x y

thỏa mãn

 

2 1

2 4 4 log 2

x y

f f x y

 

  

và

0 2024

 

2025

. B.

1012

. C.

2023

. D.

2024

Lời giải

Trước hết ta xét

 

4 4

2 2

2 log 8 17 2 log 4 1

x x

f x x x x

 

       

Xét tiếp:

   

 

2 2

8 4 4

2 2

8 2 log 8 4 1 2 log 4 1

x x

f x x x f x

  

          

tức

   

f x f x 

, khi ấy

phương trình đề cho có 2 trường hợp sau:

 

2 1

2 4 4 log 2

2 8 4 4log 2

2 4 4 log 2

x y

 



  



  





   

 

  



 



(*)

Tiếp đến đặt

2 0 1

t x y t



    



thì khi ấy (*) thành

2 4log 4 0

2 1

2 2

2 4 log 4 0

t x y





  

  



 



  

  





   

2 2

11 2024 1

0 1011

2 2 2

1011 0 1 1010 0 1 2023

2 0 1010

2024 2

2 2

x y

 



   



 



        



  







   





cặp

 

;x y

Chọn đáp án C.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 41: Cho hàm số

 

y f x



có đạo hàm

   

3 2

5 14 2 ,f x x x m x m x



       

và hàm số

 

   

3 3

1 4

3 1 3

3 3

g x f x x x x m

    

, với

là tham số. Hỏi có bao nhiêu giá trị nguyên

để đồ thị

hàm số

 

y g x





cắt trục hoành tại 9 điểm phân biệt ?

. B.

. C.

. D.

Lời giải

Ta có:

 

     

 

2 3 2

1 3 1 4 1 0

3 1 4

g x x f x x m x

f x x m

 



 

       





   





, khi ấy để thỏa mãn bài toán thì

phương trình

 

3 1 4f x x m



   

cần có 7 nghiệm phân biệt. Đặt

3 1t x x  

thì

 

4f t m



 

Mặt khác, xét

        

3 2

5 14 2 2 7 2f t t t t t m t t t t m



         

Giải phương trình

      

 

   

2 3 1 0 1

4 2 7 2 0

7 2

t x x

f t m t t t t m

t t m



    



        



 





Do (1) có 3 nghiệm phân biệt khác

1

nên để thỏa mãn bài toán thì (2) phải có 4 nghiệm phân biệt khác

1

và 3

nghiệm của phương trình (1). Ta có:

   

m t t h t

  

. (*). Trước hết (*) cần điều kiện

 

2 18

m h m

  

(3)

Tiếp đến ta khảo sát hàm số

   

7 , 3 1h t t t t x x    

bằng phương pháp ghép trục như sau:

     

3 3 0 1 1 1 1

3 ,

2 7 0

t x x t t h t t t

 

                

Khi đó ta có bảng biến thiên như sau:

Như vậy để thỏa mãn yêu cầu bài toán thì

 

6 30 5; 4;...; 28;29

m m



      



(4)

Từ (3) và (4) ta suy ra

 

5; 4;...;17;19; 20;...; 28; 29

m   

tức có 34 giá trị nguyên

thỏa mãn. Chọn đáp án B.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 42: Cho hai số phức

,z w

thỏa mãn

3 4 1w i  

4 4z z

 

. Gọi

,M m

lần lượt là giá trị lớn nhất và giá

trị nhỏ nhất của

 

2 2

z i w

 

. Giá trị

2M m

thuộc khoảng

 

4,5;5

. B.

 

3;3,5

. C.

 

4; 4,5

. D.

 

3,5; 4

Lời giải

Trước hết ta đặt

 

, ,z x yi x y  



thì khi ấy ta có:

 

2 2 2 2 2 2 2 2 2 2 2

4 4 2 4 4 4 4 4

z z x y xyi x y x y x y x y

             

   

 

2 2

4 4 2 2 2 2 2 2 2

2 2

2 2 2

4 4

16 8 8 2 16 4 4

4 4

2 2 2

z i

x y y

x y x y x y y x y y

x y y

z i



 



  



            



   



 



Từ đó ta suy ra

   

A z C



tâm

 

0; 2 , 2 2

I R 

và

 

tâm

 

0; 2 , 2 2

I R 

. Đặt

 

2 2

u i w

 

thì khi đó

    

2 2 2 2 3 4 14 2 2 2 2 2

i w i i u i i         

tức

   

B u C



tâm

 

14; 2 , 2 2

J R 

Dùng hình vẽ trên

Oxy

ta có:

 

 

1 2

2 2 2 ; 2 14 4 2; 2 53 4 2

z i w z u JI R JI R z u

 

           

 

Khi ấy ta thu được:

14 4 2; 2 53 4 2

m M   

tức

 

2 3,533 3,5; 4

M m  

. Chọn đáp án D.

Câu 44: Trong không gian

Oxyz

, cho các điểm

   

0;3; 3 , 6; 3;3

A B 

, mặt cầu

 

2 2 2

: 1

S x y z

  

và đường

thẳng

2 2



  

. Mặt phẳng

 

song song với



và luôn tiếp xúc với mặt cầu

 

. Một điểm

thay đổi và thỏa mãn

2MA MB

. Khoảng cách lớn nhất từ

đến

 

thuộc khoảng nào sau đây ?

 

18;18,5

. B.

 

18,5;19

. C.

 

19;19,5

. D.

 

17, 5;18

Lời giải

Gọi

 

; ;M m n p

để:

         

2 2 2 2 2

2 2 2

2 4 3 3 4 6 3 3

MA MB MA MB m n p m n p

 

             

 

     

2 2 2

8 5 5 48

m n p

      

, từ đó suy ra

 

M S





tâm

 

8; 5;5

J 

và bán kính

4 3





Với

   

0;0;0 , 8; 5;5 ,

I J IJ R R



  

nên ta suy ra hai mặt cầu

 

và

 



nằm ngoài nhau.

Tiếp đến ta xét mặt phẳng

 

: 1 0

P ax by cz

   

, do

 

luôn tiếp xúc với mặt cầu

 

Khi ấy gọi

 

   

 

; ; , 2; 2;1 ,

P P

n a b c u n u

 

  

   

, khi ấy suy ra:

2 2 0

a b c

  

Tiếp đến ta lại có:

 

2 2 2

; 1 1

d I P R R a b c

a b c

       

 

Suy ra

 

2 2 2

8 5 5 1

; ; 4 3 4 3 1 8 5 5 2 2

a b c

d M P d J P R a b c p a b c

a b c

  



           

 

           

2 2 2

4 3 1 8 2 2 5 5 4 3 1 8 2 2 5 5

p a p b p c p p p               



Nhận xét:

 

max

;d M P

khi và chỉ khi

 

max

;d J P

và kéo theo đó biểu thức

đạt min

Dễ dàng đánh giá được:

     

2 2 2

11 905 905

8 2 2 5 5 3

9 9 3

A p p p p

 

         

 

 

Nên suy ra

 

max

905

; 4 3 1 17,955 17,5;18

d M P     

. Chọn đáp án D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Cách 2:

Gọi

 

; ;M m n p

để:

         

2 2 2 2 2

2 2 2

2 4 3 3 4 6 3 3

MA MB MA MB m n p m n p

 

             

 

     

2 2 2

8 5 5 48

m n p

      

, từ đó suy ra

 

M S





tâm

 

8; 5;5

J 

và bán kính

4 3





Với

   

0;0;0 , 8; 5;5 ,

I J IJ R R



  

nên ta suy ra hai mặt cầu

 

và

 



nằm ngoài nhau.

Gọi

đường thẳng song song với



và luôn tiếp xúc với

 

tức

 

 

và

đi qua tiếp điểm của mặt phẳng

 

với mặt cầu

 

. Khi ấy suy ra quỹ tích của

là một mặt trụ có trục là đường thẳng qua

song song với

đường thẳng



và bán kính đúng bằng

1R 

Gọi

,A B

lần lượt là hình chiếu của

,M M

lên mặt phẳng

 

với

là giao điểm giữa đường thẳng qua

vuông góc với

 

và

 

sao cho

 

nhất. Dựng mặt phẳng

 

qua tâm

song song với hai đường

hình chiếu vừa vẽ cắt

 

tạo thiết diện là đường tròn

   

C M C

 

Khi ấy:

 

1 1

; ; ;

d M P d M P JM JB d J P R



    

Vẽ 1 đường tròn

   

C Q





có tâm

, bán kính

1R 

thuộc mặt trụ. Tiếp tục gọi

là hình chiếu của

lên

thì

khi ấy

 

C C JB JC



 

tức

 

; ; ;

d M P d J P R d J l R

 

   

Từ đó ta suy ra:

 

; ; sin 1 4 3 sin

d M P R d J l M D R JK KD R JI R JI

 

  

           

Với

 



 



 



sin sin ; sin ; 1 cos ;IK IJ u IJ u IJ



 

   

     

và

114

IJ 

thì khi đó ta suy ra:

 

max

905

; 1 4 3 sin 1 4 3 17,955 17,5;18

d M P JI



       

. Chọn đáp án D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 46: Cho hàm số

 

y f x



có đạo hàm liên tục trên



và thỏa mãn điều kiện

   

 

2 2 1

2 2 1 ,

x x

f x f x x e dx x

 



    





và

 

f e

. Biết

 

2 5

f ae be

 

với

,a b



. Khi

ấy tính giá trị của

T a b 



. B.

1T 

. C.

2T 

. D.

4T 

Lời giải

Ta có:

   

 

2 2 1

2 2 1 ,

x x

f x f x x e dx x

 



    





, thì khi ấy ta suy ra:

   

 

2 2

2 2 1 2 2 2 1

2 2 1 2 2 1

x x x x x

f x f x x e e f x e f x x e

    

 

        

 

   

2 2 1

2 1

x x

e f x dx x e dx A

 



   

 

. Tới đây ta có thể giải nguyên hàm thành phần

như sau:

Đặt:

2 2

2 2 22 22

1 1

2 1 1 1 1

2 1 2 1

2 2 2

x x

x x x x

e x e

dx x e d

e du xe dx

A x e dx dx xe xe

d dx x



  



 

 

 

 

      

 

 

 



 



 



 

 

Suy ra:

   

2 2

2 1 2 1 2x x x x x

e f x xe C f x xe Ce

   

    

. Mà

 

f e

nên

C e 

tức suy ra:

 

2 1 2 3x x x

f x xe e

  

 

, khi ấy:

 

2 5

f e e 

tức

1, 1 2

a b T a b

      

. Chọn đáp án C.

Câu 47: Một vật trang trí có dạng khối tròn xoay được tạo thành khi quay miền

 

(phần gạch sọc như hình vẽ

bên dưới) quanh trục

. Biết rằng

5 , 3AC cm BC cm 

, miền

 

được giới hạn bởi đoạn thẳng

, cung tròn

có tâm

, đường cong elip

có trục

và

Thể tích của vật trang trí bằng

 

. B.

 



. C.

 



. D.

 



Lời giải

Trước hết ta chọn hệ quy chiếu

Oxy

như hình vẽ dưới đây.

Chọn đáp án C.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 50: Có tất cả bao nhiêu giá trị nguyên của tham số

 

20; 20

m  

để phương trình sau có đúng 2 nghiệm phân

biệt:

 

6 3 6

log 1 log 1.log 6

x x x x m

    

. B.

. C.

. D.

Lời giải

Trước hết ta có:

 

6 3 6

1 0, 6 0

log 1 log 1.log 6

x x x m

x x x x m



    





    





. Khi ấy phương trình tương đương với:

   

 

6 3 3 6

6 6 6

log 1 0

log 3log 1 log 1 .log 6

2log 3 log 9 lo 6

x x x x m

x x



  



      











   













Xét nhanh trường hợp

0 0 0

2, 6 0 8

x x x x m m

      

, tức từ phương trình đã cho ta có:

 

9 6

m x x u x









   







phải có 2 nghiệm phân biệt lớn hơn 1. Khảo sát hàm số

 

9 6

u x x x  

trên

 



với điểm cực trị tại



, ta suy ra:

14 18

 

, đối chiếu điều kiện



, ta loại tức PTVN.

Trở lại bài toán, từ (1):

9 6

2, 8x m

m x x





  

 





. Khi ấy từ yêu cầu bài toán ta suy ra phương trình

9 6

m x x  

(*)

phải có đúng 2 nghiệm phân biệt

1 2

,x x

sao cho

1 2

, 2

x x



và

1 2

, 1

x x



. Khảo sát hàm số

 

9 6

u x x x  

trên

   

1; \ 2



với điểm cực trị tại



, ta suy ra:





 

;14 17;18

m   

, đối chiếu với điều kiện



ta suy ra

 

 

9;14 17;18



  



có 8 giá trị nguyên

thỏa mãn. Chọn đáp án D.

ĐỀ THI THỬ CHUYÊN HÙNG VƯƠNG – GIA LAI

Câu 46: Xét các số thực âm

,x y

mà

xy y

là số nguyên sao cho thỏa mãn hệ thức sau:

 

3 3 3

log 2 1 2 log 2 2 2 log 2 1 3 0

xy y xy y xy y

         

Khi biểu thức

P x y 

đạt giá trị lớn nhất thì giá trị của biểu thức

4 3Q x y 

bằng

2

. B.

. C.

. D.

9

Lời giải

Điều kiện:

2 0 2 1

xy y

xy y xy y

 

    



Ta đặt

 

log 2

xy y t 

thì khi ấy phương trình ban đầu trở thành:

 

     

3 3

3 3 3

1 2 1 1 3 2 1 0 1 1 2 1 2 1t t t t t t t               

(1)

Xét hàm đặc trưng

 

y f t t t  

dễ dàng đánh giá được

 

f t

luôn đồng biến trên



Khi ấy từ (1) suy ra:

2 3 3 2

2 2 2

1 2 1 2 2 1 2 1 0

1 5

2 1

t a

t t a a a a a

t a







 





             







 











Suy ra:

5 2 5

t a





  



 



, mà

 

log 2

xy y t 

nên:

 

5 2 5

log 2 0

2 1

2 3

log 2 5 2 5

xy y



  

 







  

  







2 1

xy y y

    



(thỏa mãn)

8 8

2 1

P x y x

    



, xét hàm số

   

8 , ; 0

2 1

f x x x

    



dễ thấy

max 8

P f

 

   

 

 

nên

 

; ; 2

x y

 

  

 

 

tức

4 3 9

Q x y

   

. Chọn đáp án D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 47: Trong không gian

Oxyz

, cho hình nón

 

có đỉnh

 

6;0; 4 3

đáy là hình tròn tâm

 

0;0; 2 3

E 

và

bán kính

4 3

R 

. Mặt phẳng

 

Oxy

cắt mặt nón theo giao tuyến là đường elip tâm

và có tiêu điểm

1 2

,F F

trên trục

, đường thẳng



đi qua

(

có hoành độ dương) và song song với trục

cắt

mặt nón tại hai điểm

,M N

. Độ dài

bằng

. B.

9 3

. C.

6 3

. D.

Lời giải

Cách 1: Ta có:

   

 

6;0;6 3 1;0; 3

12, 0;0;1

Oxy

ES m

SE k n



 





  







 

và

 







 



 



; 60

sin ; sin ;

ES Oxy

ES Oxy ES k









  









 

Đầu tiên ta viết được phương trình mặt phẳng

 

qua

và vuông góc với

và gọi

 

A SO P

 

Suy ra:

 

: 3 6 0

P x z

  

và giải ra tọa độ

4 3

2;0;

 

 

 

 

, suy ra

8 21 4 3

3 3

SA AE 

, mà

4 3

BE R 

nên khi ấy suy ra:

2 2

8 6

AB R AE  

, theo định lí Thales ta có:

SO OD

SA AB



và gọi

,a b

lần lượt là các độ

dài bán trục lớn, trục bé của elip thiết diện trên, khi ấy ta suy ra:

2 6

SO AB

b OD

  

, cùng với



Khi đó ta lập được phương trình elip

 

2 2

: 1

36 24

x y

 

, gọi

   

1 2

;0 , ;0 , 0

F c F c c

 

lần lượt là tọa độ hai tiêu

điểm của

 

, ta luôn có:

2 2

2 3

c a b  

tức

 

2 3; 0

kéo theo đó

2 3

M N

x x c  

Từ giả thiết ta suy ra tung độ của hai điểm

,M N

lần lượt là:

2 6. 1 4

M N

    

Vậy độ dài của đoạn thẳng

M N

MN y y

  

. Chọn đáp án A.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Cách 2:

Từ hình vẽ trên, ta có:

   

 

     

2 2 2

: ; ;

cos

; ;

x y z

SE u l m n

l x m y n z

l m n

l m n x y z

SM x y z

  



  

  



   

    



  





      

   





Vậy, phương trình tổng quát mặt nón là:

     

2 2 2

cos

l x m y n z

x y z

l m n

  

   

    

 

 

 

     

 

 

Áp dụng tính chất trên, ta giải bài toán này như sau: hình nón

 

có

 

1;0; 3

ES k



là vector chỉ phương chứa

trục của

 

, đỉnh có tọa độ

 

6;0;4 3

và góc giữa đường sinh và trục bằng

30 cos

 

  



, suy ra:

Phương trình của mặt nón

   

 

: 3 6 4 3 6 3 4 3

N x y z x z

 

       

 

Gọi

 

là mặt elip thiết diện của mặt phẳng

 

: 0

Oxy z



khi cắt mặt nón

 

, khi ấy ta suy ra:

 

2 2

3 6 4 3 6 3 4 3

: 3 6 48 18

x y z x z

E x y x



 

       



 

     









 

2 2

2 2 2 2 2 2

3 36 108 3 48 36 18 2 3 72 1

36 24

x y

x x y x x x y

             

Khi ấy suy ra phương trình:

 

2 2

: 1

36 24

x y

 

, kéo theo đó ta cũng có:

   

2 2

1 2

6, 3, 2 3

2 3;0 , 2 3;0

a b c a b

F F



    











với

, ,a b c

lần lượt là các độ dài bán trục lớn, bán trục bé và bán tiêu cự của

 

Từ đó theo giả thiết ta suy ra:

2 3

M N

x x



 





 





tức ta kết luận được

M N

MN y y

  

. Chọn đáp án A.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 48: Cho hai hàm đa thức bậc bốn

 

4 3 2

y f x ax bx cx dx e     

 

4 3 2

y g x a x b x c x d x e

    

     

và có

a a



  

. Biết rằng đồ thị của hai hàm số này cắt nhau tại đúng 3 điểm có hoành độ lần lượt là

2;1; 2

và diện tích hình phẳng

 

giới hạn bởi đồ thị của hai hàm số (phần gạcn sọc như hình vẽ) là

. Khi hình

 

quay xung quanh trục

, khối tròn xoay tạo thành có thể tích gần nhất với số nào ?

21, 26

. B.

1748,58

. C.

177,17

. D.

66, 79

Lời giải

Trước hết từ giả thiết ta suy ra:

 

     

 

     

 

...

1 4

...

f x x

f x g x x x

g x x

f x g x



 

   



 



 

 

 

    





 



 

 







 









Suy ra:

 

96 1

3 3

2 21 4

5 55 2

S xa ax dx





 



      



 











   

0 0 1

f g

 

nên

 

Từ đó ta suy ra:

     

 

1f x g x x x 

  

Vậy

       

 

   

 

2 2 2

1 4 66,791

V f x g x dx f x g x f x g x dx x x dx



 

  

        

  

Chọn đáp án D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

ĐỀ THI THỬ SỞ HẢI DƯƠNG

Câu 41: Cho hai số phức

,z w

thỏa mãn

2 3, 2 3 5

z w z w

   

và

3 4

z w

 

. Khi đó tính giá trị của biểu thức

P zw zw

 

. B.

. C.

. D.

Lời giải

Từ giả thiết ta suy ra:

 

2 2

4 9 6 25

9 3 16

4 2 9

z w zw zw



   



   





   



, giải hệ thu được:

zw zw













 





. Chọn đáp án D.

Câu 42: Cho hai hàm số

 

f x

và

 

g x

liên tục trên



và hàm số

 

3 2

f x ax bx cx d



   

và

 

g x mx nx p



  

có đồ thị như hình vẽ. Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số

 

y f x





và

 

y g x





bằng 10 và

   

2 2

f g

. Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm

số

 

y f x



và

 

y g x



bằng

(với

,a b



và

,a b

nguyên tố cùng nhau). Tính

a b

. B.

. C.

. D.

Lời giải

Từ hình vẽ, ta suy ra:

      

1 2

f x g x ax x x

 

   

Do diện tích hình phẳng giới hạn bởi hai đồ thị hàm số

 

y f x





và

 

y g x





bằng 10 nên khi đó ta suy ra:

      

2 2

0 0

10 1 2 10 20

S f x g x dx a x x x dx a

 

        

 

tức

      

20 1 2

f x g x x x x

 

   

Đặt

     

h x f x g x

 

thì khi đó ta suy ra:

     

        

2 2 2 0

20 1 2

h f g

h x f x g x x x x

  





  

    





Suy ra:

    

4 3 2

20 1 2 5 20 20

h x x x x dx x x x C      



mà

 

2 0



nên



Suy ra diện tích cần tìm bằng:

 

2 2

4 3 2

0 0

5 20 20

S h x dx x x x dx

    

 

tức

a b

 

. Chọn đáp án D.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Câu 49: Giả sử

1 2

,z z

là hai trong các số phức

thỏa mãn

1 2

z i

  

và

1 2 1 2

z z z z  

. Khi biểu thức

1 2

2P z z

 

đạt giá trị nhỏ nhất thì số phức

có tích phần thực và phần ảo bằng

. B.



. C.



. D.

Lời giải

Từ giả thiết ta gọi

   

1 2

A z B z

với hai điểm

,A B

thuộc đường tròn

 

tâm

 

1; 1

 

, bán kính

2R 

Tiếp đến ta có

1 2 1 2

z z z z  

tức

OA OB AB 

nên suy ra

, ,O A B

thẳng hàng tức

nằm giữa

Suy ra:

2 2

1 2

2 4 2 .P z z OA OB OAOB

    

 

, do

nằm giữa

nên áp dụng bất đẳng thức Cauchy, ta suy ra:

 

2 2

1 2

2 2 4 . 4 . 4 . 8 .P z z OA OB OAOB OAOB OAOB OAOB

       

Cát tuyến qua

cắt đường tròn tại hai điểm

,A B

, khi ấy sử dụng phương tích đường tròn, ta luôn có:

2 2

. . 2

OAOB OAOB OI R

     

 

tức

8 . 4

P OA OB

 

(luôn đúng với

nằm trong và ngoài đoạn

Khi ấy dấu bằng xảy ra khi và chỉ khi

2OA OB

mà

. 2

OAOB



nên

2, 1

OA OB

 

tức



Gọi

z a bi 

thì khi đó:

   

 

2 2

2 2 2

2 4

1 1 1 4

z a b

a b ab

a b

z i a b



  

  

 

   

 

  

       





. Chọn đáp án C.

Câu 50: Trong không gian với hệ tọa độ

Oxyz

, cho hình nón

 

có đỉnh

 

0;0;0

, có độ dài đường sinh là

4 2

và đường tròn đáy nằm trên mặt phẳng

 

: 2 2 12 0

P x y z

   

. Gọi

 

là giao tuyến của mặt xung

quanh

 

với mặt phẳng

 

: 4 0

Q x z

  

và

là một điểm di động trên đường cong

 

. Giá trị

nhỏ nhất của độ dài đoạn thẳng

thuộc khoảng nào dưới đây ?

 

 

 

. B.

 

 

 

. C.

; 2

 

 

 

. D.

 

 

 

Lời giải

Cách 1: Từ giả thiết, ta gọi

 

là đường thẳng qua

chứa đường cao

của hình nón

 

và



là góc giữa

đường cao và đường sinh của

 

, khi ấy suy ra

 

; 4, 1; 2;2

h d O P u   



và







, ta có hình vẽ sau:

Từ hình vẽ, ta suy ra quỹ tích của điểm

là một đường conic (một parabol) gọi là đường cong

 

Khi ấy ta đánh giá được

nhỏ nhất khi và chỉ khi

M M



Dễ thấy

OHC

và thiết diện của mặt phẳng qua trục đều là các tam giác vuông cân lần lượt tại

và

nên suy ra

HM OC



, khi ấy ta dễ dàng suy ra

2 2

OM  

tức

min

2 2 2,83 ;3

 

  

 

 

. Chọn đáp án A.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Cách 2: (Sử dụng cho mặt phẳng bất kì cắt mặt nón và không có yếu tố đặc biệt)

Từ hình vẽ trên, ta có:

   

 

     

2 2 2

: ; ;

cos

; ;

x y z

SE u l m n

l x m y n z

l m n

l m n x y z

SM x y z

  



  

  



   

    



  





      

   





Phương trình tổng quát mặt nón là:

     

2 2 2

cos

l x m y n z

x y z

l m n

  

   

    

 

 

 

     

 

 

Áp dụng tính chất trên, ta giải bài toán này như sau: gọi

 

là đường thẳng qua

chứa đường cao

của hình

nón

 

và



là góc giữa đường cao và đường sinh của

 

, khi ấy suy ra

 

; 4, 1; 2;2

h d O P u   



và







Suy ra tập hợp điểm

   

 

2 2 2

2 2

; ; :

2 9

x y z

M x y z N

 

 

 

, mặt khác

 

: 4 0

M Q x z

   

nên suy ra

       

   

2 2

4 2 8

: 16 40 8 64 16 0

2 9

x y x x y

M C N Q M C x x xy y y

    

            

Suy ra:

2 2

16 40 64 1

x x yx yy     

, kéo theo đó ta phân tích được:

   

 

2 2

2 2 2 2 2 2

2 2 1

2 2 2 8 2 8 32 64 128

9 9

OM x y z x y z x y yx y y xx              

 

2 2 22 2 22

1 8

6 4

2 8 32 64 28 2 8 16 2 20 64 16 8

x x y yx y x y x y x x y            

 

Vậy giá trị nhỏ nhất của

bằng

2 2 2,83 ;3

 

 

 

 

với dấu bằng xảy ra khi và chỉ khi

2, 0

x y

  

, thế vào

phương trình

 

ta thu được

2z  

, tức min xảy ra khi

 

2;0; 2

M M

  

trùng với đỉnh của parabol

 

Chọn đáp án A.

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

ĐỀ THI THỬ THPT CHUYÊN HÙNG VƯƠNG – PHÚ THỌ

Câu 42: Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 50

S x y z

  

và hai mặt phẳng

 

: 2 15 0

P x y z

   

 

: 4 3 25 0

Q x y z

   

. Hai điểm

,M N

thay đổi lần lượt thuộc các đường tròn là giao tuyến của

   

,P Q

với

 

, giá trị nhỏ nhất của

bằng bao nhiêu ?

. B.

2 10

. C.

2 5

. D.

Lời giải

Dễ thấy khi đọc 4 đáp án A,B,C,D các kết quả đều là số dương, chứng tỏ rằng hai đường tròn giao tuyến mà đề bài

nêu trên không cắt nhau (vì nếu cắt nhau thì giá trị nhỏ nhất của

bằng không).

Trước hết ta có mặt cầu

 

có tâm trùng với gốc tọa độ, bán kính

5 2

R 

Giả sử hai đường tròn thiết diện của khi hai mặt phẳng

   

,P Q

cắt

 

là

   

1 2

C C

có tâm lần lượt là

,I J

và

bán kính lần lượt là

,a b

. Khi đó ta suy ra:

 

2 2

5 6

;

5 6

;

a MI R d O P

d O P OI

d O Q OJ

b NJ R d O Q

 

   

 

 



 

 

 

   

 

 

Lại có:

 

: 2 15 0

2 15 0

4 3 25 0

: 4 3 25 0

O O

P x y z

z x y

Q x y z

    

   



 



 

   

   





nên

bị kẹp giữa hai mặt phẳng

   

,P Q

Khi đó ta dễ dàng đánh giá được

đạt giá trị nhỏ nhất (

0 0

MN M N



) khi và chỉ khi đoạn thẳng

đồng

phẳng với mặt phẳng

 

OIJ

như hình vẽ dưới đây:

Tới đây ta có:



0 0 0

0 0 0 0

0 0

OI JN IOM IN J

IOM JON IOM OM I

OJ IM

JON OM I



 





     

 



 







Khi ấy ta lần lượt suy ra:



  

2 2 2

0 0

cos

2 . 5

cos cos

sin 1 cos

OI OJ IJ

IOJ

OI OJ

M ON IOJ IOJ IOJ





 

  





 



     

 



 



Vậy ta suy ra:



2 2

min 0 0 0 0

2 . .cos 2 2. 2 10

MN M N R R R R M ON R

 

       

 

 

. Chọn đáp án B.

Bấm Tải xuống để xem toàn bộ.

Preview text:

NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
ĐỀ THI THỬ THPT CHUYÊN KHTN – HÀ NỘI
Câu 47: Có bao nhiêu số nguyên x sao cho ứng với mỗi x tồn tại số thực y  1; 2 thỏa mãn xy 2 2  x y 1 ? A. 3 . B. 6 . C. 5 . D. 4 . Lời giải
Cách 1: Trước hết ta xét x  0 thì khi ấy phương trình luôn đúng với mọi số thực y  1; 2 nên nhận.
Tiếp đến với x  0 ta xét hàm số f y 
 x y  trên khoảng 1; 2 khi đó ta có: f  y  x  x x   xy 2 2 ln 2 x   xy 2 2 1
Điều kiện cần: để tồn tại y  1; 2 thỏa mãn thì f   1 f 2  0 . x x  x  0 1 x
Trường hợp 1: x  0 thì ta giải f  y    y   y  . x   0 log 1  2 0 2xy ln 2  x x ln 2  1 x 1
Khảo sát nhanh hàm số g  x  log
dễ thấy g  x  g e ln 2 
, x  0;  tức y  1; 2 0   2   2 x ln 2 e ln 2  f    x 2 1  0  2  x 1  0
Cùng với f   y  0, y
 1; 2 , khi ấy để 
y  1; 2 thì: x      x 2;3;  4 x  f  2 2 x 2  0 2  2x 1  0  
Trường hợp 2: x  0 thì khi ấy f   y  0, y
 1;2 . Suy ra để y  1; 2 thỏa mãn thì x   f    x 2 1  0  2  x 1  0 x    
 x   . (loại) f  2 2 x 2  0 2  2x 1  0  
Vậy tóm lại x 0; 2;3; 
4 tức có 4 giá trị nguyên x thỏa mãn. Chọn đáp án D.
 f  y  x  x  x   xy 2 2 ln 2
Cách 2: Dễ thấy xét x  0 thì hàm số f x   x y  có y   xy 2 2 1 
 f  y  x   x   2 xy 2 2 ln 2 0 Suy ra hàm f
y là hàm lồi nghiêm ngặt và có tối đa 1 cực tiểu, khi ấy cùng với thì ta suy ra điều kiện cần và đủ x  
để f  y  0 có nghiệm với mọi y  1; 2 là f f  x   1 x  2  0 x x 1
Câu 48: Trong không gian Oxyz , cho đường thẳng d :
 y  z  3 . Xét mặt phẳng  P  thay đổi và luôn chứa 2
đường thẳng d  . Gọi H là hình chiếu vuông góc của điểm A2;1;2 lên mặt phẳng  P  . Khi  P  thay
đổi thì H luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng 2 3 A. . B. 2 . C. 3 . D. . 2 2 Lời giải
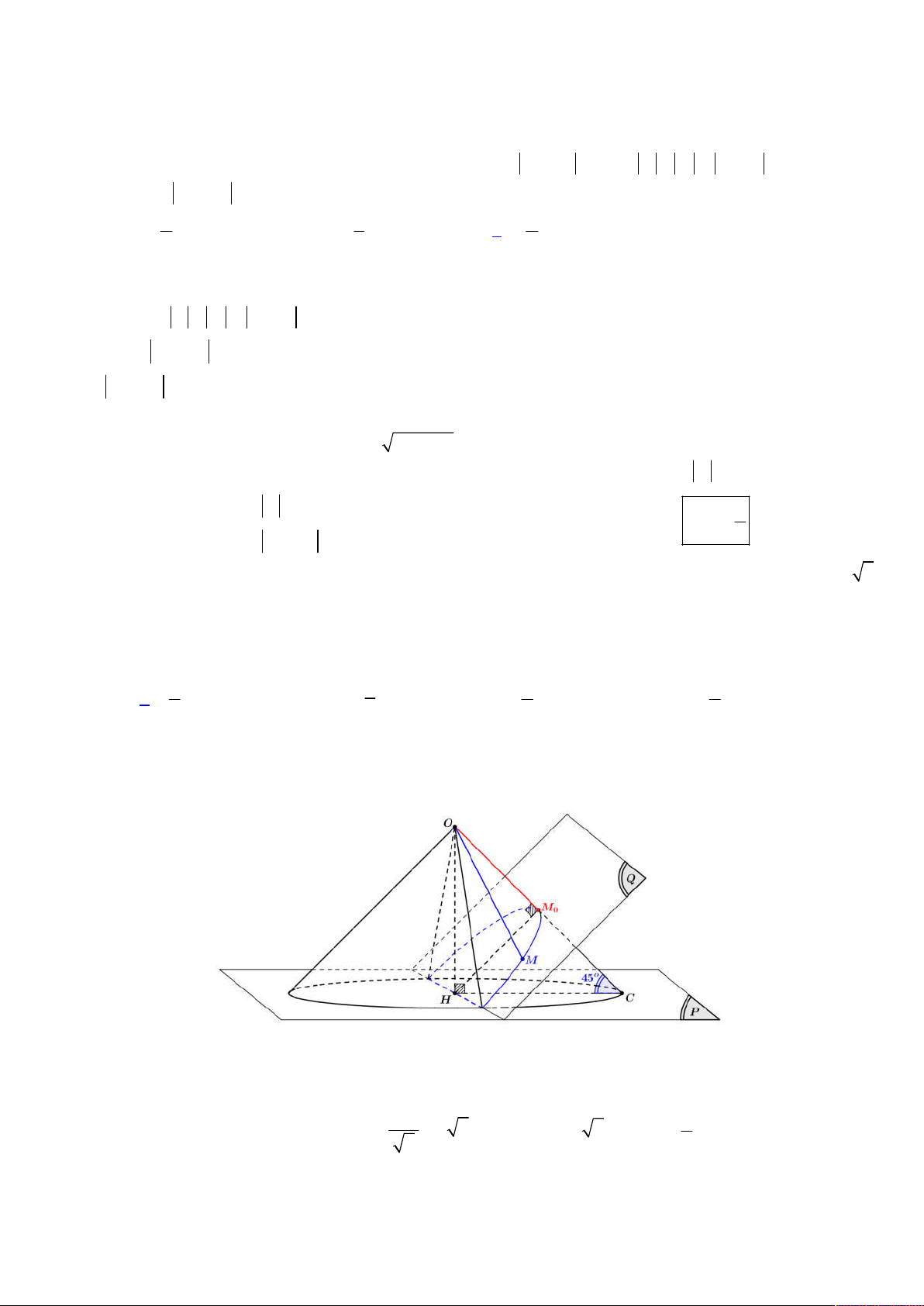
Đầu tiên ta gọi C là hình chiếu của A lên d  , từ đó dễ dàng tính được tọa độ điểm C 1;0;3 3
Khi ấy ta suy ra H thuộc mặt cầu S  đường kính AC có tâm là trung điểm AC và bán kính R  . 2
 
Tiếp đến ta có AH  d    P, AC  d   d    AHC   n  u 
tức suy ra H   AHC  . AHC d 2;1  ;1     3
Mà  AHC  qua đường kính mặt cầu S  nên đường tròn cố định có bán kính r  R  . Chọn đáp án D. 2
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG z  z
Câu 50: Xét các số phức z , z thỏa mãn z 1 i  2, z  z 1 i và 1
2 là số thực. Khi ấy giá trị nhỏ 1 2 1 2 2 1  2i
nhất của biểu thức z  z bằng 1 2 A. 3 5 . B. 2 5 . C. 5 5 . D. 5 . Lời giải
w  z , A z , B w  2  1    Đầu tiên ta đặt: 
, bằng biến đổi đại số thông thường ta dễ dàng lần lượt suy ra z 1 i 
2, w  w 1 i   1
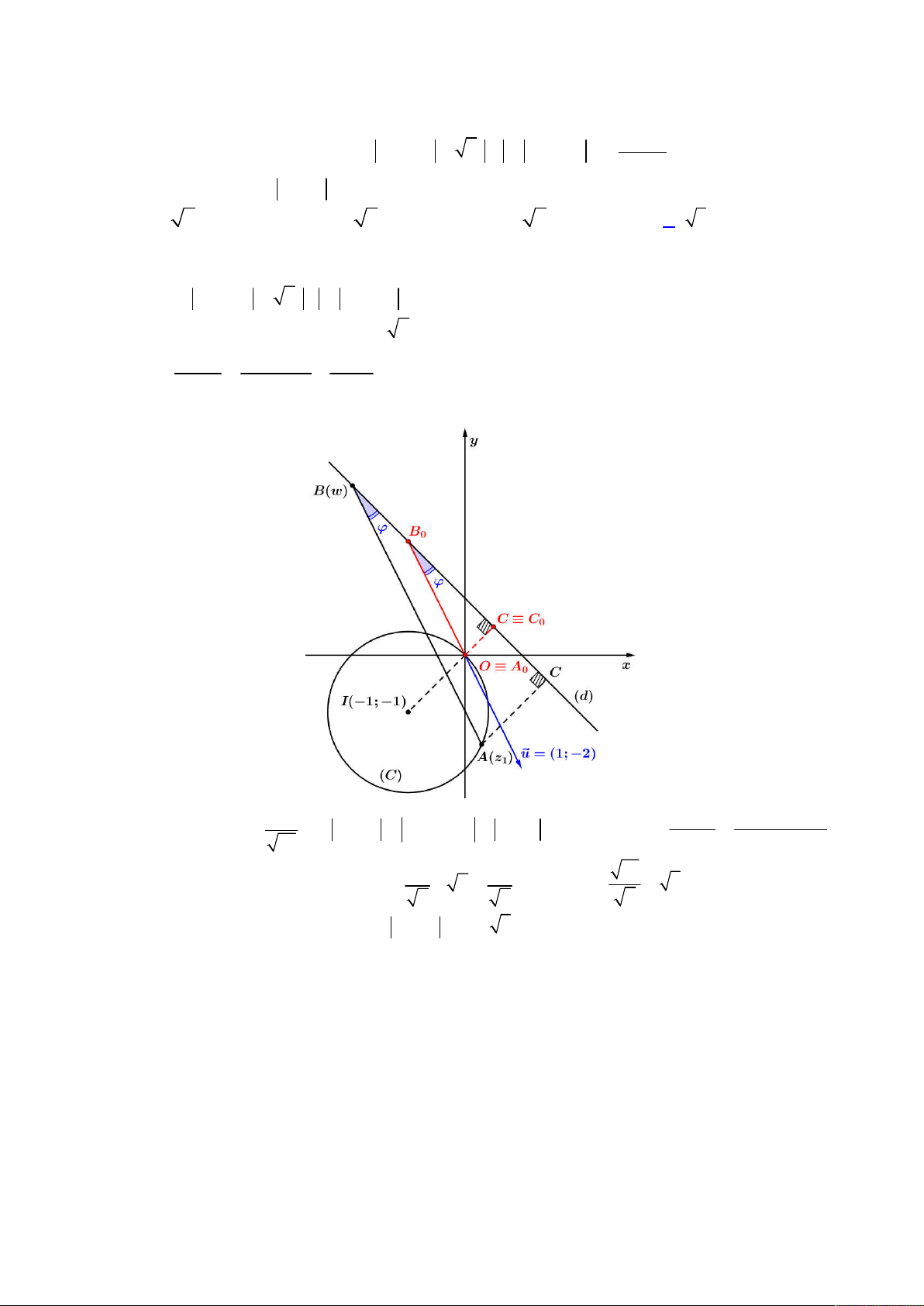
được: A  C  tâm I 1;   1 , bán kính R 
2 và B  d  : x  y 1  0 .   z  z z   z z  w 1 2 1  2  Tiếp đến ta có: 1  
là số thực tức z  w  k 1 2i , k   , suy ra được BA  ku với 1   1  2i 1  2i 1  2i   u  1; 2
  tức đường thẳng AB có vector pháp tuyến là n  2 
;1 . Từ đây ta có hình vẽ như sau:  d  ; A d AC  Ta có: u d  3 cos ;  cos  
và z  z  z  z
 z  w min khi min min AB   1 2 1  2  1 min 10 sin  sin  3 1 10
Khi ấy ta suy ra: d  ; A d 
 d  I;d   R   2  tức AB   5 . min min 2 2 2
Vậy ta kết luận giá trị nhỏ nhất của biểu thức z  z bằng 5 . Chọn đáp án D. 1 2
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
ĐỀ THI THỬ LIÊN TRƯỜNG NGHỆ AN
Câu 33: Trong một đề thi trắc nghiệm môn Toán có loại câu trả lời dạng đúng sai. Một câu hỏi có 4 ý hỏi, mỗi ý hỏi
học sinh chỉ cần trả lời đúng hoặc chỉ trả lời sai. Nếu 1 ý trả lời đúng đáp án thì được 0,1 điểm, đúng đáp
án 2 ý được 0,25 điểm, đúng đáp án 3 ý được 0,5 điểm và đúng đáp án cả 4 ý được 1 điểm. Giả sử một thí
sinh làm bài bằng cách chọn phương án ngẫu nhiên để trả lời cho 2 câu hỏi loại đúng sai này. Tính xác suất
để học sinh đó được 1 điểm ở phần trả lời 2 câu hỏi này 1 9 17 1 A. . B. . C. . D. . 128 128 256 16 Lời giải
Trước hết ta chia thành hai công việc: -
Công việc (1): Tính xác suất để mỗi ý trong 4 ý của 1 trong 2 câu hỏi là đúng/sai. 1 1
+ Dễ tính được xác suất để học sinh trả lời ý hỏi đúng là và ý hỏi sai là . 2 2 -
Công việc (2): Tính xác suất để có số ý đúng cần thỏa mãn mỗI câu trong mỗi trường hợp (sẽ nêu dưới đây).
 Nhận xét: do hai công việc có tính chất liên kết nhau nên ta sử dụng quy tắc nhân. (*)
Ta có 2 trường hợp như sau:
Trường hợp 1: Cả 2 câu đều đúng được 3 trong 4 ý, tức mỗi câu đạt 0,5 điểm. 1
Câu hỏi 1 trả lời đúng 3 câu: Chọn 3 trong 4 câu đúng có 3
C (cách) và xác suất mỗi ý trả lời đúng là , với 3 ý 4 2 3 3  1  1  1  1 đúng là 3 
 , ý còn lại sai có xác suất là
nên theo (*), suy ra xác suất câu hỏi 1 đúng 3 câu là: C (1) 4    2  2  2  2 3  1  1
Câu hỏi 2 trả lời đúng 3 câu, thực hiện tương tự như (1) ta có: 3 C 4    2  2 3 3  1  1  1  1 1
Suy ra tại trường hợp 1 ta có xác suất cần tìm là 3 3 C . . .C . .  4   4    2  2  2  2 16
Trường hợp 2: 1 trong 2 câu đạt điểm tối đa (1 điểm), câu còn lại 0 điểm. 1
Giải thích: tức 1 trong 2 câu ( 1
C cách) có 4 ý đều đúng (với xác suất mỗi ý đúng là
) và câu còn lại không đúng cả 2 2 4 4 1  1   1  2
4 ý (với xác suất mỗi ý sai là
) nên theo quy tắc (*), ta suy ra trường hợp này xác suất là 1 C      2 2 2  2   2  16 1 2 9
Vậy, cộng hai trường hợp ta có xác suất cần tìm là   . Chọn đáp án B. 2 16 16 128
Câu 39: Có bao nhiêu số nguyên x 2024;7000 là nghiệm của bất phương trình sau: 2 
 log x  9 log x  80  3 3 log  log     0 0,3 6  log x 4     3   A. 600 . B. 603 . C. 601 . D. 602 . Lời giải 2
 log x  9 log x  80 
Bất phương trình tương đương với: 3 3 log
 1 (*) (do 0, 3  1 nên dấu đổi chiều). 6   log x  4  3  2 t  9t  80
Đặt t  log x , thì khi ấy (*) 
 6  t  8t  7  0        8 x 3  7 x 3 0 log  3 3 t  4 t x  7
x 2024; 7000 2024  x  3 Kết hợp với  ta có: 
. Dễ dàng đếm được có 163  439  602 (số). Chọn đáp án D. x  8   3  x  7000 
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 41: Cho số phức w thỏa mãn 2w  2  i  2w  6  i và hai số phức z , z cùng thỏa mãn z   z2 2  4 , z 1 2 1
có phần thực, phần ảo là các số âm, z có phần thực, phần ảo là các số dương và z  z bé nhất. Giá trị 2 2 1
nhỏ nhất của w  z  w  z thuộc khoảng nào dưới đây ? 1 2  11  11   9   9  A. 5;   . B. ; 6   . C. ;5   . D. 4;   .  2   2   2   2  Lời giải 2
Ta đặt S  : z  x  yi  x, y   , khi ấy 2
4  z   z   z  z z  z  2yi2x  xy 1
z  x  y i
Với z , z  S  1 1 1 : 
x , y   . Do phần thực, ảo của z , z cùng dấu nên x y  x  y  1 , mà 1 1  2  2  1 2  12 12 
z  x  y i 1 2  2 2 2 2 2 2  i   i  2  1 1 
z  z bé nhất nên suy ra: z  z  x   x   x  x   2 1  1   2   1 2  2 1   x x x x  1   2   1 2  1 1  1  z  1 i 2 2  x   x   2 x x 
 8 với dấu bằng xảy ra khi x  x  1 tức ta suy ra 1 . 1 2 2 2  1 2   x x x x 1 2 z  1   i 1 2  1 2            2 2 2 2
Tiếp đến xét điểm: M  w, w  a  bi a,b   , bằng phương pháp đại số ta suy ra M  d  : y  2x  4 .
Cách 1: Phương pháp đại số (Sử dụng bất đẳng thức Mincopski) 2 2 2 2
Ta có: T  w  z  w  z  a  
1  2a  5  a   1  2a  3 2 2
 5a  22a  26  5a 10a 10 1 2 2 2 2 2  11   3       5a     
   5  5a2   2 11 3 5  5a   5  5a  5   2 5      5   5   5   5 
Cách 2: Phương pháp hình học.
Không cần vẽ hình, xét M  d  : 2x  y  4  0 nhận thấy A1;  1 , B 1;  
1 cùng phía với d  nên gọi A là điểm  17 1 
đối xứng với A qua d  , khi ấy dễ dàng tìm được tọa độ A ;  
 , khi ấy ta kết luận:  5 5 
T  w  z  w  z  MA  MB  MA  MB  AB  2 5 . Chọn đáp án D. 1 2
Câu 42: Có bao nhiêu cặp số thực  x; y thỏa mãn điều kiện sau:
6x  9y log  4 2 2
2x  4x y 16  2y  2  log  2
x  y  3log  2
x  5x  y  3  2x 1 2 2 6  A. 2 . B. 6 . C. 4 . D. 8 . Lời giải.
Trước hết ta dự đoán như sau: log  4 2 2
2x  4x y 16  2 y  2  log  2 x  y  0 2 2  1 log  x y 2 2 2 8      log  2
x  y  0 (*) , đặt t  log  2
x  y thì khi ấy 2  2 2    (*) 1 log 4t 8 2 2 2 t t 1 t 1 0 4 8 2 2 8 4t t             
(1). Mà (1) đúng với bất đẳng thức Cauchy: 2 2 t 1  2 2  t t 2  8 2 2 2 2 2 t 1  t 1  3  2 2 2 2  8  2 2 .2  2  2
 2 t  4t với dấu bằng xảy ra khi 2   t  2 t
nên kết hợp điều kiện   2  2
căn thức có nghĩa, suy ra log  4 2 2
2x  4x y 16  2 y  2  log  2
x  y   0  t  log  2 x  y 2
 2  x  y  4 2 2 2
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Khi ấy phương trình ban đầu trở thành: 6x 3log 5 1 2 1 6x x x  3x 6 x        3l g o 5x 1 6   log 5 1 6   6   Xét hàm đặc trưng    6t f t
 3t có    6t f t
ln 6  3  0, t  0 tức f t  luôn đồng biến trên 0;    log 5  1  6x x x  5x 1  0 . 6   x 5
Xét hàm số    6x g x
 5x 1 có g  x  6 ln 6  5  0  x  log
 0;1 (điểm cực tiểu), do hàm g  x có 6   ln 6
1 điểm cực trị nên suy ra g  x  0 có 2 nghiệm, dễ dàng nhẩm nhanh ra 2 nghiệm x  0, x  1 Lại có: 2 2
x  y  4  y  4  x (ứng với 1 giá trị x cho ra 1 giá trị y ) nên có 2 cặp  x, y . Chọn đáp án A.
Câu 43: Trong không gian Oxyz cho các điểm M 5;8;3,Q 2; 1; 4 và hai đường thẳng lần lượt có phương x  t x  5   
trình là  :  y  3;  :  y  3 t
 , t   . Biết điểm N di động trên đường thẳng  và điểm P di động 1 2 1 z  3 z  t    
trên đường thẳng  . Giá trị nhỏ nhất của T  MN  NP  PQ là 2 A. 289 . B. 459 . C. 179 . D. 369 . Lời giải
Trước hết từ giả thiết ta gọi M a;3;3, P 5;3;b với a,b   . 2 2 2 2
Khi ấy: T  MN  NP  PQ  5  a  25  a  5  3  b  b  4  25 .
Ta xử lí biểu thức trên bằng bất đẳng thức Mincopski như sau:
T  MN  P N  Q
P  5  a2  5  a  52  3b2 2 2
 5  b  42
 5  a  a  5  52  5  3 b  b  42 2 2  15  2 1  369 5  a 5 b  4 5  5  
Dấu bằng xảy ra khi và chỉ khi      ; a b  ; 0 
 . Chọn đáp án D. 15 12 4 5  4 
Câu 45: Cho hàm số y  f  x liên tục và có đạo hàm trên 0;  thỏa mãn các điều kiện: f   1  0 và
2x  xf x   2 2 x
2 x f  x 1 e  x e , x
 0; . Biết f 4  a  b ln 2,a,b   . Giá trị a  b bằng A. 12 . B. 14 . C. 11. D. 15 . Lời giải 2 2
Ta có:  2      x 2
x f  x    
     x  f x 2 2 1 2 1 x x xf x e x e x x f x e  x e (1)  2 2 1  1   g x  x  
Đặt g  x
x  f  x  e
 g x  2x  f  x x  f x e , (1) thành: g x x   g x  e   e  2      x  x  x   g  x 2
x  f  x 2 e Suy ra: x f   1 0
x  f  x x xln x 
 e  C C   e  xe  e  f  x 2 0
 x  x  ln x x x
Khi ấy ta suy ra: f 4  12  2 ln 2 tức a  12,b  2
  a  b  14 . Chọn đáp án B.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 46: Trên tập hợp số phức, xét phương trình 2
z  mz 10  0 , (với m là tham số). Biết phương trình đã cho có 1 1
hai nghiệm phân biệt z , z . Các điểm biểu diễn số phức z , z , ,
tạo thành một đa giác lồi có diện 1 2 1 2 z z 1 2 tích lớn nhất bằng 99 49 A. . B. 5 . C. . D. 4 . 20 10 Lời giải
z  a  bi
Trước hết từ giả thiết, ta đặt: 1 
a,b  với 2 2
z z  10  a  b  10 (do z , z liên hợp nhau).
z  a  bi 1 2 1 2  2  a b   a b   1   1 
Tiếp đến ta gọi A ;
a b, B a; b,C ;  , D ;   
 ứng với A z , B z , C , D . Nhận thấy 1   2       10 10   10 10  z z  1   2  cặp điểm ,
A B và C, D cùng phần thực nên dễ dàng thấy được ABCD là hình thang cân. AB  CD 1  b   a  99 99 99
Khi ấy dễ dàng suy ra S  .d AB CD  b  a   ab  a  b  ABCD  ,  2 .     2   2 2  2 2  5   10  200 200 0 2 Chọn đáp án A.
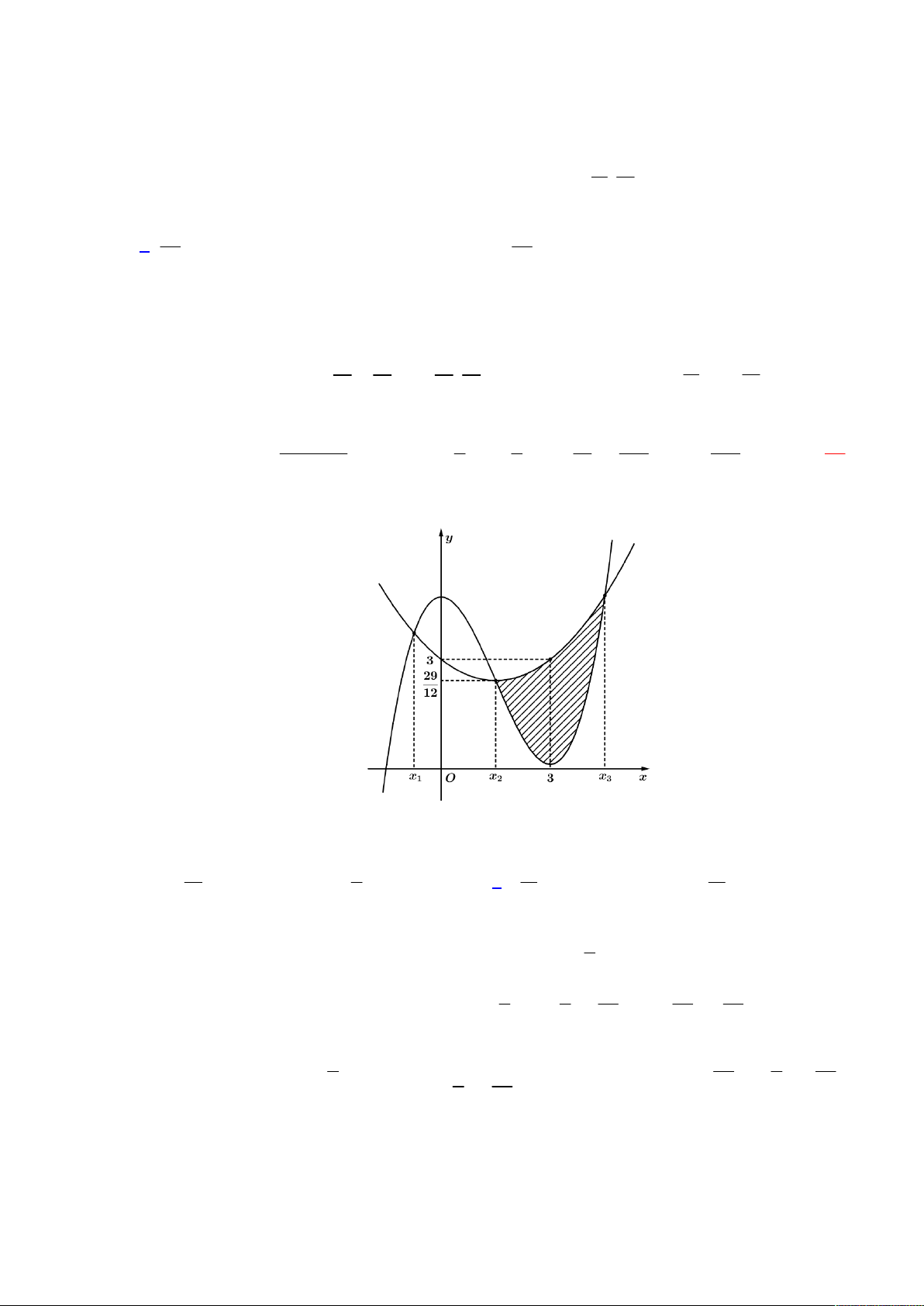
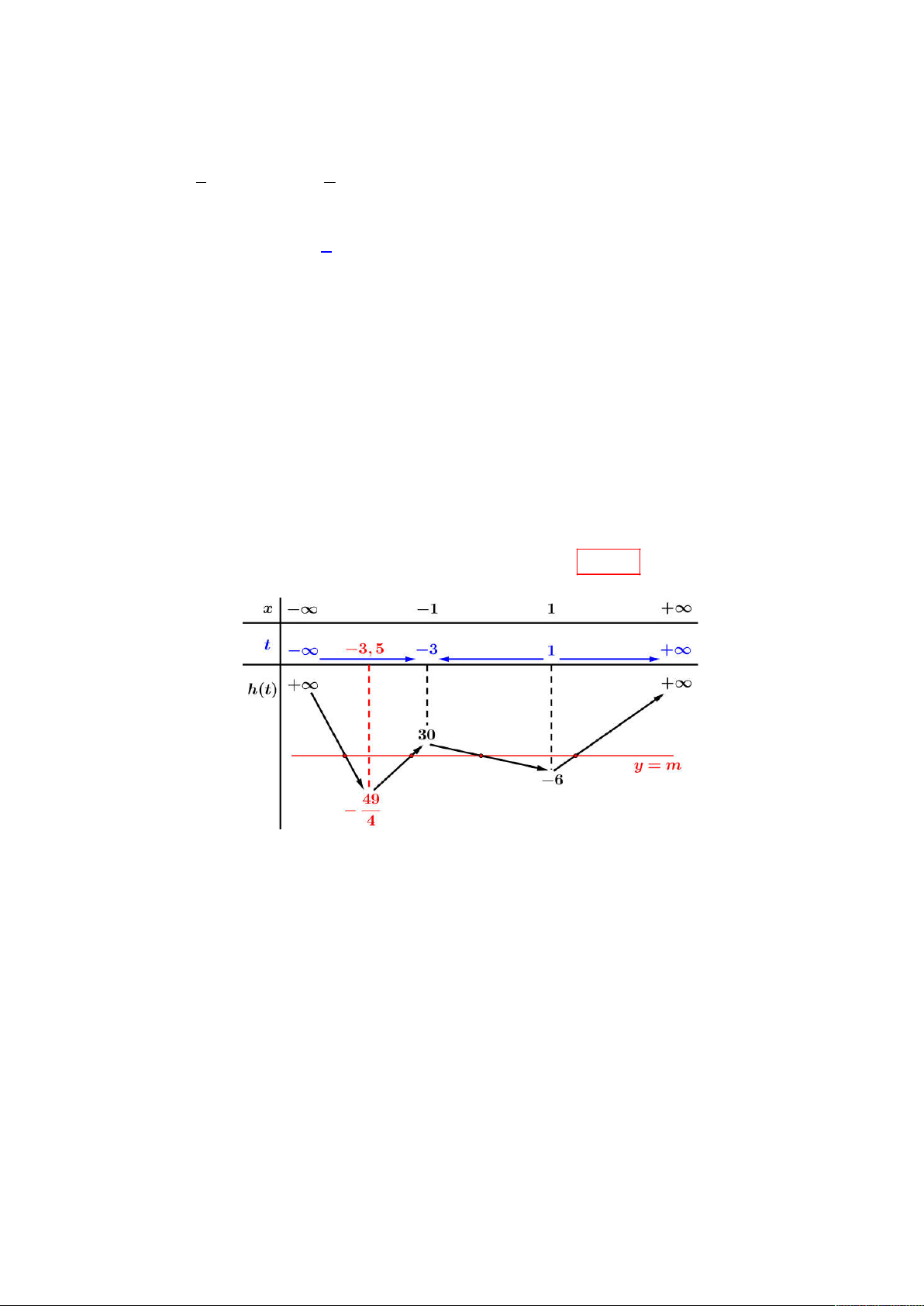
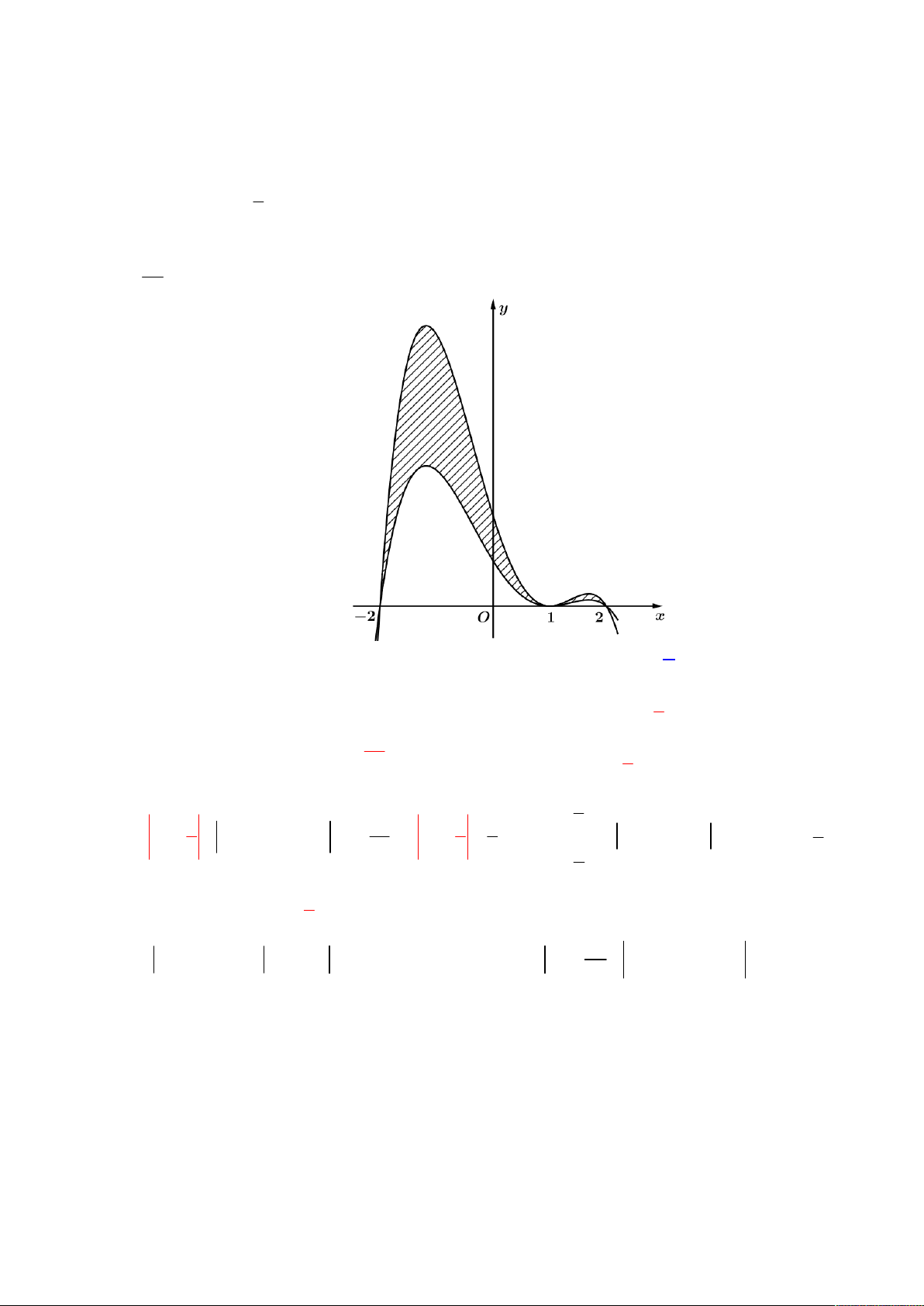
Câu 47: Cho hàm số bậc ba y  f  x và hàm số bậc hai y  g  x có đồ thị như hình vẽ.
Biết rằng đồ thị hàm số y  f  x cắt đồ thị hàm số y  g  x tại 3 điểm phân biệt x , x , x thỏa mãn 1 2 3 x x x  5
 . Diện tích miền tô đậm nằm trong khoảng nào sau đây ? 1 2 3  13   9   11   11  A. 6;   . B. ;5   . C. ; 6   . D. 5;   .  2   2   2   2  Lời giải  9 
Trước hết từ đồ thị ta dễ dàng có: f  x  3a  2
x  3x  f  x 3 2  a x  x  C    2  3  3  29 27 29
Nhận ra x hoành độ đỉnh parabol đồ thị y  g  x nên x   f   C  a  . (1) 2 2   2  2  12 4 12
 f 0  f 3  3 2 2  3   7  3  29
Từ đây ta cũng suy ra: g  x  k x   b   , mà   3  29
nên giải được g  x  x     .  2  f     27  2  12   2  12
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG  f
 0  g 0  a x x x  5a 1 2 3 
Xét hàm số f  x  g  x  a  x  x x  x x  x  
 C  3  5a (2) 1   2   3  f
 0  g 0  C  3   27 29 3 2 C   a  14 1 x 95x 7 5
Từ (1) và (2) ta có hệ phương trình sau:  4 12  C  ; a 
 f  x  g  x    x  3 3 3 54 9 3 C   3  5a 
Thêm nữa, x , x , x chính là nghiệm của phương trình hoành độ giao điểm của f  x, g  x tức ta suy ra: 1 2 3  17  559 x  3 2  1 x 95x 7 5 1  3 
f  x  g  x    x     x     2 9 0
9x  34x  30  0   Chia Hookne  3 54 9 3 54  2   17  559     x  3 x x2  9 17 559 x3 9 3 2 x 95x 7 5
Vậy diện tích cần tìm là S 
f  x  g  x dx    x  dx  5, 709   . Chọn đáp án C. 3 54 9 3 x 3 2 2
ĐỀ THI THỬ SỞ NGHỆ AN Câu 36: Cho hàm số 3 2
y  x  5x  3x . Xét các số thực a  b , giá trị nhỏ nhất của f b  f a bằng 256 256 500 500 A.  . B. . C. . D.  . 27 27 27 27 Lời giải 1
Trước hết ta giải phương trình 2
y  3x 10x  3  0  x   x  3 3 b 1 Đến đây dễ thấy 2
y  3x 10x  3  0 
 x  3 và f b  f a 
f  x dx  3 a b 3 256
Từ đây ta có: f  x dx   2
3x 10x  3 dx   2
3x 10x  3 dx      27 a 1  1 ;3   a;b 3    3 256 Khi ấy suy ra: 3 2 3 2
x  5x  3x  y  5 y  3 y 
, đặt m  y  x  0 , từ đây ta có được: 27 256 256 3 2
y  5 y  3 y    3 2
x  5x  3x   3 3
y  x   5 2 2
y  x   3 y  x  27 27 2 2 3  10  m 16 256  10  1
 3m x  m    m 
 3m x  m      
3m  82 3m 16  0 (luôn đúng)  3  4 3 27  3  108 256
Vậy ta kết luận giá trị nhỏ nhất của f b  f a bằng  . Chọn đáp án A. 27
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 39: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2
z  4z  m  0 có nghiệm z  z sao cho 0
z 1  2i  3 ? 0 A. 11. B. 12 . C. 10 . D. 9 . Lời giải Ta có: 2
  16  4m , tiếp đến theo bất đẳng thức Mincopski ta có: z  1 2i  z  1
  2i  z  1 2i 0 0   0 Mà z  1
  2i  3 nên suy ra: 3 5  z  3  5 (*) 0   0 2
z  2  4  m Trường hợp 1: 2
  0  16  4m  0  2  m  2 khi ấy phương trình có 2 nghiệm thực 1  . 2
z  2  4  m  2 2
3  5  2  4  m  3  5
Kết hợp với (*), suy ra: 
(luôn đúng với mọi m 2; 2 ) (1) 2
3  5  2  4  m  3  5 
Trường hợp 2:   0  m  2
  m  2 khi ấy phương trình có 2 nghiệm phức với z  z  m 1 2 
Kết hợp với (*), suy ra: m 3, 3 5 3 5  m m       3  m  5 (2)
Từ (1) và (2) ta suy ra: m 5; 4; 3; 2; 1; 
0 tức có 11 giá trị nguyên m thỏa mãn. Chọn đáp án A.
Câu 40: Cho hàm số f  x x4  2  log  2
x  8x 17 . Có bao nhiêu cặp số nguyên  x; y thỏa mãn 2 
f  x2y 1 2
   f 4  4log x  2y và 0  x  2024 ? 2   A. 2025 . B. 1012 . C. 2023 . D. 2024 . Lời giải x4 2 x4 2
Trước hết ta xét f  x  2  log
x  8x 17  2  log x  4 1 2   2    8x4 2 4x 2
Xét tiếp: f 8  x  2  log
8  x  4 1  2  log 4  x
1  f x tức f  x  f 8  x , khi ấy 2    2      x2 y 1 2 
 4  4 log  x  2 y x2 y 1 2   4  4 log x  2 y 2 2  
phương trình đề cho có 2 trường hợp sau:    (*) x2 y 1 2 
 8  4  4 log  x  2 y x2 y 1     2   4  4 log x  2 y 2  2   t 1
2   4 log t  4  0
t  x  2 y  1 Tiếp đến đặt 2 0 t t x y     
t  1 thì khi ấy (*) thành 2    t 1 
2   4 log t  4  0
t  x  2 y  2  2   1 x 1 2024 1 1   y   1  0  y  1011 2 2 2 1     
1011 0 1 1010  0 1  2023 cặp  ; x y  . x  2 2024  2 0  y  1010  2  2 1  y   2  2 2 Chọn đáp án C.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
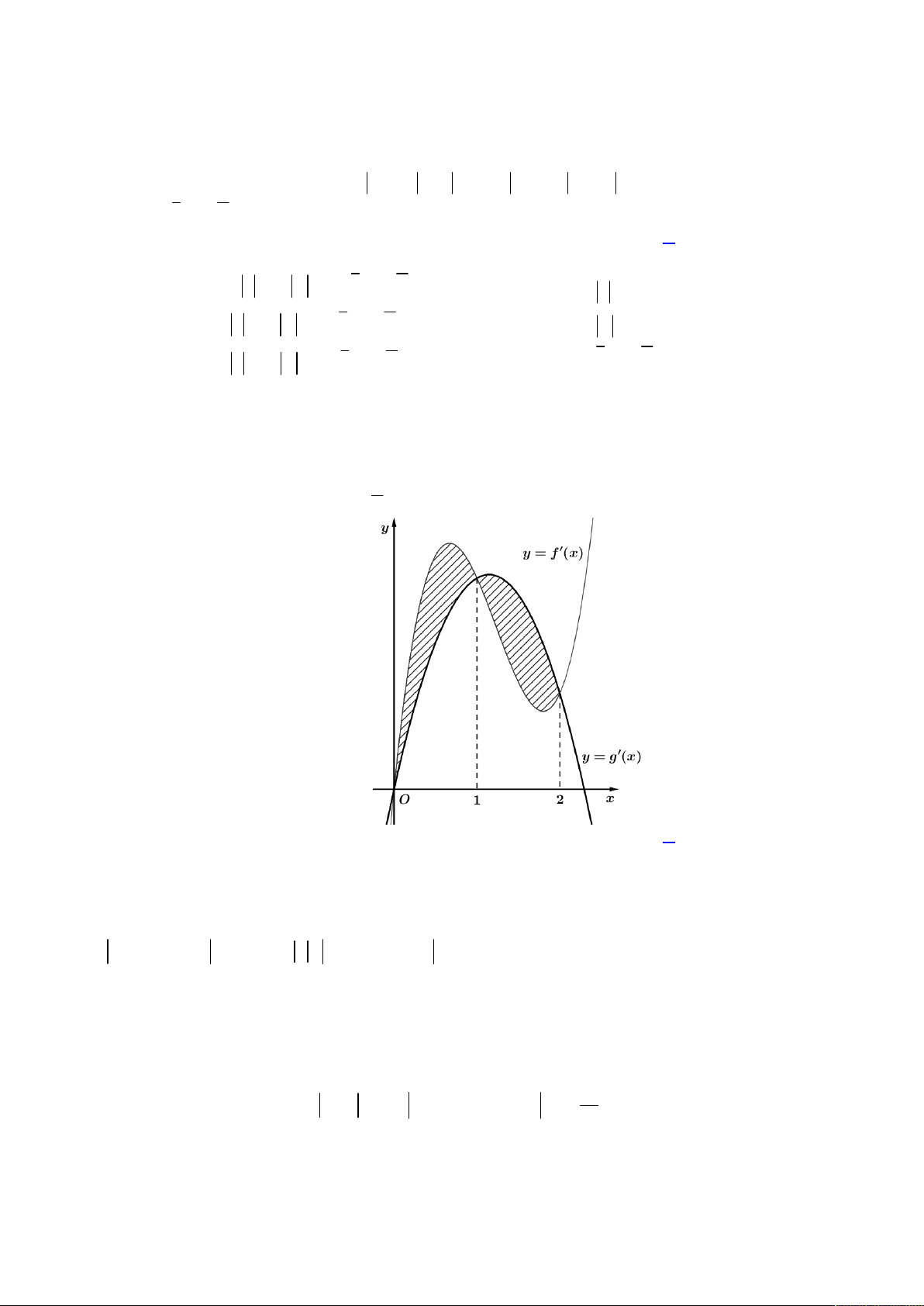
Câu 41: Cho hàm số y  f  x có đạo hàm f  x 3 2
 x  5x  m 14 x  2m, x    và hàm số 1 4 g  x  f  3 x  3x   1   3
x  3x m , với m là tham số. Hỏi có bao nhiêu giá trị nguyên m để đồ thị 3 3
hàm số y  g  x cắt trục hoành tại 9 điểm phân biệt ? A. 37 . B. 34 . C. 35 . D. 36 . Lời giải x  1
Ta có: g x   2 x   1 f  3 x  3x   1  4m  2 x   1  0  
, khi ấy để thỏa mãn bài toán thì f    3 x  3x   1  4  m 
phương trình f  3 x 3x   1  4
 m cần có 7 nghiệm phân biệt. Đặt 3
t  x  3x 1 thì f t   4m
Mặt khác, xét f t  3 2
 t  5t 14t  t  2 m  t t  2t  7  t  2 m 3
t  2  x  3x 1  0   1
Giải phương trình f t   4
 m  t t  2t  7  t  2 m  0  
t t  7  m  2 
Do (1) có 3 nghiệm phân biệt khác 1 nên để thỏa mãn bài toán thì (2) phải có 4 nghiệm phân biệt khác 1 và 3
nghiệm của phương trình (1). Ta có: m  t t  7  h t  . (*). Trước hết (*) cần điều kiện m  h 2  m  18 (3)
Tiếp đến ta khảo sát hàm số h t   t t   3
7 , t  x  3x 1 bằng phương pháp ghép trục như sau: 2
t  3x  3  0  x  1   t   1  1 t   1  3
 , ht  2t  7  0  t  3  ,5
Khi đó ta có bảng biến thiên như sau:
Như vậy để thỏa mãn yêu cầu bài toán thì 6 30 m m     
 m 5;4;...;28;2  9 (4)
Từ (3) và (4) ta suy ra m 5; 4;...;17;19; 20;...; 28; 2 
9 tức có 34 giá trị nguyên m thỏa mãn. Chọn đáp án B.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 42: Cho hai số phức z, w thỏa mãn w  3  4i  1, 2
z  4  4 z . Gọi M , m lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của z  2  2i w . Giá trị M  2m thuộc khoảng A. 4,5;5 . B. 3;3,5 . C. 4; 4,5 . D. 3,5; 4 . Lời giải
Trước hết ta đặt z  x  yi,  x, y   thì khi ấy ta có: z  
z  x  y  xyi  
x  y   x  y  2 2 2 2 2 2 2 2 2 2 2 2 4 4 2 4 4 4
 4x y  4 x  y 2 2
 x  y  4  4 y
 z  2i  2 2
 x  y 16  8x  8y   2x y  16y   x  y  42  4y2 4 4 2 2 2 2 2 2 2     2 2
x  y  4  4 y   z  2i  2 2 
Từ đó ta suy ra A z   C tâm I 0; 2 
, R  2 2 và C tâm I 0; 2 , R  2 2 . Đặt u  2  2i w thì khi đó 2   2  1   1 
2  2i w  2  2i3  4i  u 14  2i  2  2i  2 2 tức B u C tâm J 14; 2  , R  2 2 . 3 
Dùng hình vẽ trên Oxy ta có: z  2  2i w  z  u JI  2R; JI  2R  z  u  1
 4  4 2; 2 53  4 2  1 2   
Khi ấy ta thu được: m  14  4 2; M  2 53  4 2 tức M  2m  3,533 3,5; 4 . Chọn đáp án D.
Câu 44: Trong không gian Oxyz , cho các điểm A0;3; 3
 , B 6; 3;3 , mặt cầu S  2 2 2
: x  y  z  1 và đường 1 x  y thẳng 2  : 
 z . Mặt phẳng  P  song song với  và luôn tiếp xúc với mặt cầu S  . Một điểm M 2 2
thay đổi và thỏa mãn MA  2MB . Khoảng cách lớn nhất từ M đến  P  thuộc khoảng nào sau đây ? A. 18;18,5 . B. 18,5;19 . C. 19;19,5 . D. 17,5;18 . Lời giải 2 2 2 2 2 Gọi M  ; m ; n p để: 2 2 2 MA 2MB MA 4MB m n  3  p  3 4   m 6 n  3  p 3                 
 m  2  n  2   p  2 8 5 5
 48 , từ đó suy ra M  S tâm J 8; 5;5 và bán kính R  4 3 .
Với I 0;0;0, J 8; 5;5, IJ  R  R nên ta suy ra hai mặt cầu S  và S nằm ngoài nhau.
Tiếp đến ta xét mặt phẳng  P : ax  by  cz 1  0 , do  P  luôn tiếp xúc với mặt cầu S      Khi ấy gọi n  a b c u  n
 u , khi ấy suy ra: 2a  2b  c  0 P  ; ; ,  2;2  ;1 ,    P  1
Tiếp đến ta lại có: d I; P 2 2 2   R
 R  1  a  b  c  1 S  2 2 2
a  b  c
8a  5b  5c 1
Suy ra d M ; P  d  J; P  R  4 3 
 4 3 1 8a  5b  5c  p 2a  2b  c 2 2 2
a  b  c 
    p a   p  b   p   c 
    p2   p  2   p  2 4 3 1 8 2 2 5 5 4 3 1 8 2 2 5 5    A
Nhận xét: d M; P
khi và chỉ khi d  J; P
và kéo theo đó biểu thức A đạt min max max 2 2 2 2  11 905 905
Dễ dàng đánh giá được: A  8  2 p  2 p  5   p  5  3 p       9  9 3 905
Nên suy ra d M ; P  4 3 1
 17, 955  17,5;18 . Chọn đáp án D. max 3
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Cách 2: 2 2 2 2 2 Gọi M  ; m ; n p để: 2 2 2 MA 2MB MA 4MB m n  3  p  3 4   m 6 n  3  p 3                 
 m  2  n  2   p  2 8 5 5
 48 , từ đó suy ra M  S tâm J 8; 5;5 và bán kính R  4 3 .
Với I 0;0;0, J 8; 5;5, IJ  R  R nên ta suy ra hai mặt cầu S  và S nằm ngoài nhau.
Gọi l đường thẳng song song với  và luôn tiếp xúc với S  tức    P và l đi qua tiếp điểm của mặt phẳng
 P  với mặt cầu S  . Khi ấy suy ra quỹ tích của l là một mặt trụ có trục là đường thẳng qua I song song với
đường thẳng  và bán kính đúng bằng R  1 . Gọi ,
A B lần lượt là hình chiếu của M , M lên mặt phẳng  P  với M là giao điểm giữa đường thẳng qua J 1 1
vuông góc với  P  và S  sao cho M xa  P  nhất. Dựng mặt phẳng Q  qua tâm J song song với hai đường 1
hình chiếu vừa vẽ cắt S  tạo thiết diện là đường tròn C   M  C 1  
Khi ấy: d M ; P  d M ; P  JM  JB  d J ; P  R . 1   1   
Vẽ 1 đường tròn C Q có tâm K , bán kính R  1 thuộc mặt trụ. Tiếp tục gọi C là hình chiếu của B lên l thì
khi ấy C  C, JB  JC tức d M ; P  d  J; P  R  d  J ;l   R
Từ đó ta suy ra: d M;P  R  d  J;l  M D  R  JK  KD  R  JI sin  R 1 4 3  JI sin 0       Với   IK IJ    u IJ  
và IJ  114 thì khi đó ta suy ra:    u IJ    2 sin sin ; sin ; 1 cos ; d  905 M ; P
 1 4 3  JI sin   1 4 3 
 17, 955  17,5;18 . Chọn đáp án D. max 3
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Câu 46: Cho hàm số
y  f  x có đạo hàm liên tục trên  và thỏa mãn điều kiện 
f   x  
f  x   x   2 2 x  2 x 1 2 2 1 e
 dx ,x    và f   7
2  e . Biết f   2 5
1  ae  be với a, b   . Khi
ấy tính giá trị của T  a  b A. T  3. B. T  1 . C. T  2 . D. T  4 . Lời giải 2 
Ta có: f  x  
f  x   2
x   x 2x 1 2 2 1 e
 dx ,x  
 , thì khi ấy ta suy ra:
 f  x  f  x   x   2x x  x e  e
f  x    x  e
 f x   x   2 2 2 1 2 2 2 x 1 2 2 1 2 2 1 e      x   e
f  x dx   x   2 2 2 x 1 2
1 e  dx  A . Tới đây ta có thể giải nguyên hàm thành phần A như sau: 2 2 x 1  x 1      2 2 2 2 2 2 u e du  2xe dx Đặt: 2 x 1  x 1  2 x 1  x 1  2 x 1  x 1   A 2x e dx  e dx      2x e dx  xe 2x e dx   xe         v d dx  dv x      2 2 Suy ra: 2  x   x 1       x 2x 1  2x e f x xe C f x  xe
 Ce . Mà f   7 2  e nên 3
C  e tức suy ra: f  x 2 x 2x 1  2x3  xe  e , khi ấy: f   2 5
1  e  e tức a  1,b  1
  T  a  b  2 . Chọn đáp án C.
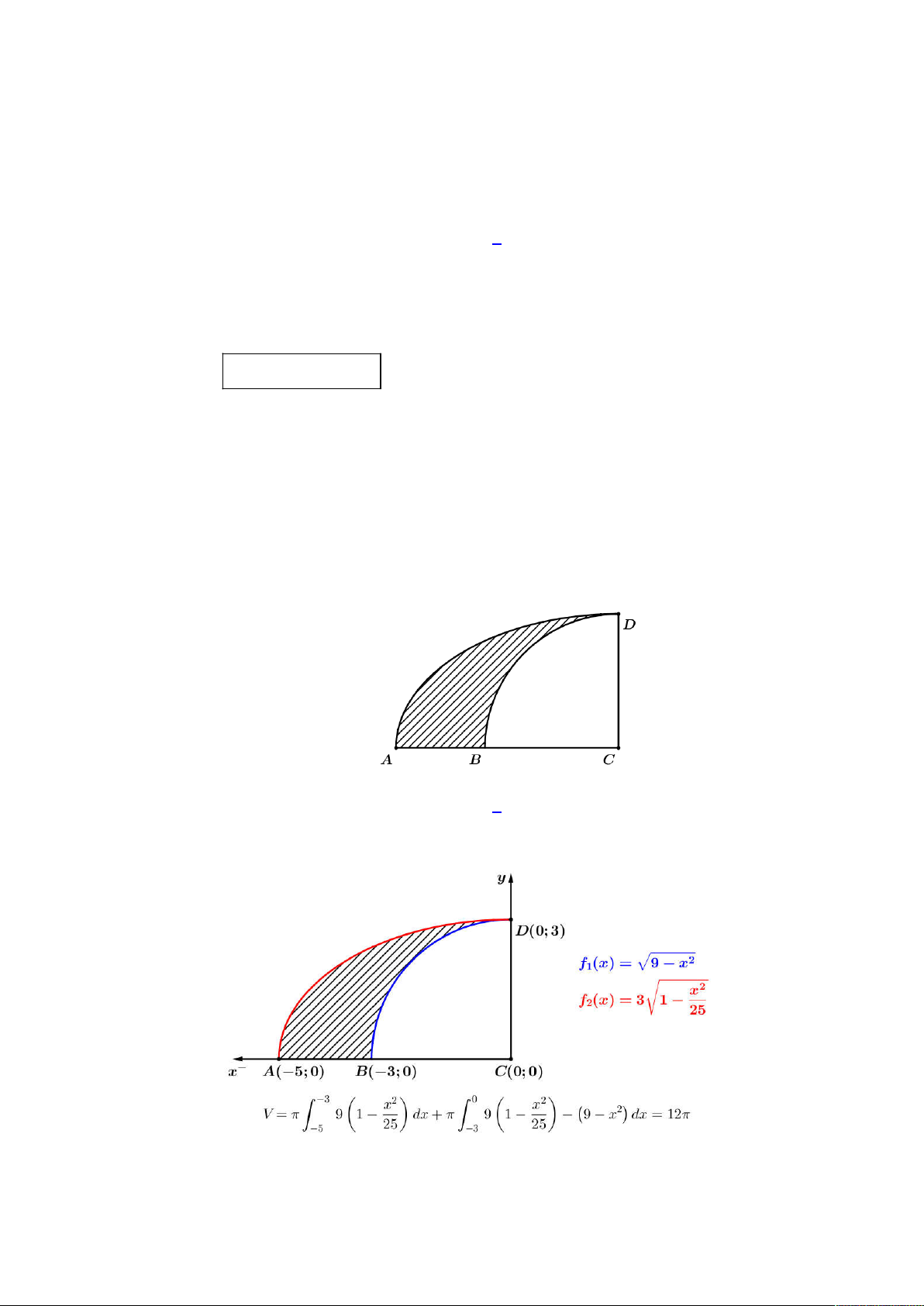
Câu 47: Một vật trang trí có dạng khối tròn xoay được tạo thành khi quay miền  H  (phần gạch sọc như hình vẽ
bên dưới) quanh trục AC . Biết rằng AC  5cm, BC  3cm , miền  H  được giới hạn bởi đoạn thẳng AB
, cung tròn BD có tâm C , đường cong elip AD có trục AC và CD .
Thể tích của vật trang trí bằng A.  3 12 cm  . B.   3 60 cm  . C.   3 12 cm . D.   3 30 cm  . Lời giải
Trước hết ta chọn hệ quy chiếu Oxy như hình vẽ dưới đây. Chọn đáp án C.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 50: Có tất cả bao nhiêu giá trị nguyên của tham số m 20; 20 để phương trình sau có đúng 2 nghiệm phân
biệt: log  x   1  log x 1.log  2
x  6x  m 6 3 6  A. 11. B. 9 . C. 10 . D. 8 . Lời giải 2
x 1  0, x  6x  m  0  Trước hết ta có: 
. Khi ấy phương trình tương đương với: log   x   1  log x 1.log  2
x  6x  m 6 3 6  
log x 1  0  x  2 3   1 
 log 3log  x   1  log  x   1 .log  2
x  6x  m  x  2 6 3 3 6  2   1 2   2 log 3  log 9  log
x  6x  m  6 6 6    Xét nhanh trường hợp 2
x  x  2, x
 6 x  m  0  m  8 , tức từ phương trình đã cho ta có: 0 0 0 m   8   
phải có 2 nghiệm phân biệt lớn hơn 1. Khảo sát hàm số u  x 2
 9  6x  x trên 2
m  9  6x  x  u   x 
1; với điểm cực trị tại x  3 , ta suy ra: 14  m 18, đối chiếu điều kiện m  8 , ta loại tức PTVN.
x  2, m  8
Trở lại bài toán, từ (1):  
. Khi ấy từ yêu cầu bài toán ta suy ra phương trình 2
m  9  6x  x (*) 2
m  9  6x  x 
phải có đúng 2 nghiệm phân biệt x , x sao cho x , x  2 và x , x  1 . Khảo sát hàm số u  x 2
 9  6x  x trên 1 2 1 2 1 2 1;  \  
2 với điểm cực trị tại x  3 , ta suy ra: m   ;14  17 
;18 , đối chiếu với điều kiện m  8 ta suy ra 9;14 17;  18 m m    
 có 8 giá trị nguyên m thỏa mãn. Chọn đáp án D.
ĐỀ THI THỬ CHUYÊN HÙNG VƯƠNG – GIA LAI
Câu 46: Xét các số thực âm x, y mà 2xy  y là số nguyên sao cho thỏa mãn hệ thức sau:
 log 2xy  y12log 2xy  y 2 3  2 log
2xy  y 1  3  0 3 3 3  
Khi biểu thức P  8x  y đạt giá trị lớn nhất thì giá trị của biểu thức Q  4x  3y bằng A. 2 . B. 2 . C. 5 . D. 9 . Lời giải Điều kiện: 2 2 0 xy y xy y    
2xy  y 1Ta đặt log 2xy  y  t thì khi ấy phương trình ban đầu trở thành: 3    t    3 3 t     3 
t      t    t    3 t   3 1 2 1 1 3 2 1 0 1 1 2 1  2t 1 (1) Xét hàm đặc trưng    3 y
f t  t  t dễ dàng đánh giá được f t  luôn đồng biến trên  a  1 2 
2t  2a  2 Khi ấy từ (1) suy ra: 3 2 3 3 2 t 1 2t 1 a  2a 2 a 1 a 2a 1 0                3 1 5 2t a 1    a    2 t   0 log 2xy  y  0
2xy  y  1 3   Suy ra: 2
t  a 1   , mà log
2xy  y  t nên:   3    t  5  2 5 52 5  log
2xy  y  5  2 5 2xy  y  3    3    1 1 1
 2xy  y  1  y 
(thỏa mãn)  P  8x  y  8x 
, xét hàm số f  x  8x 
, x  ; 0 2x  1 2x 1 2x  1  3   3 
dễ thấy max P  f   8    nên  ; x y    ; 2  
 tức Q  4x  3y  9
 . Chọn đáp án D.  4   4 
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
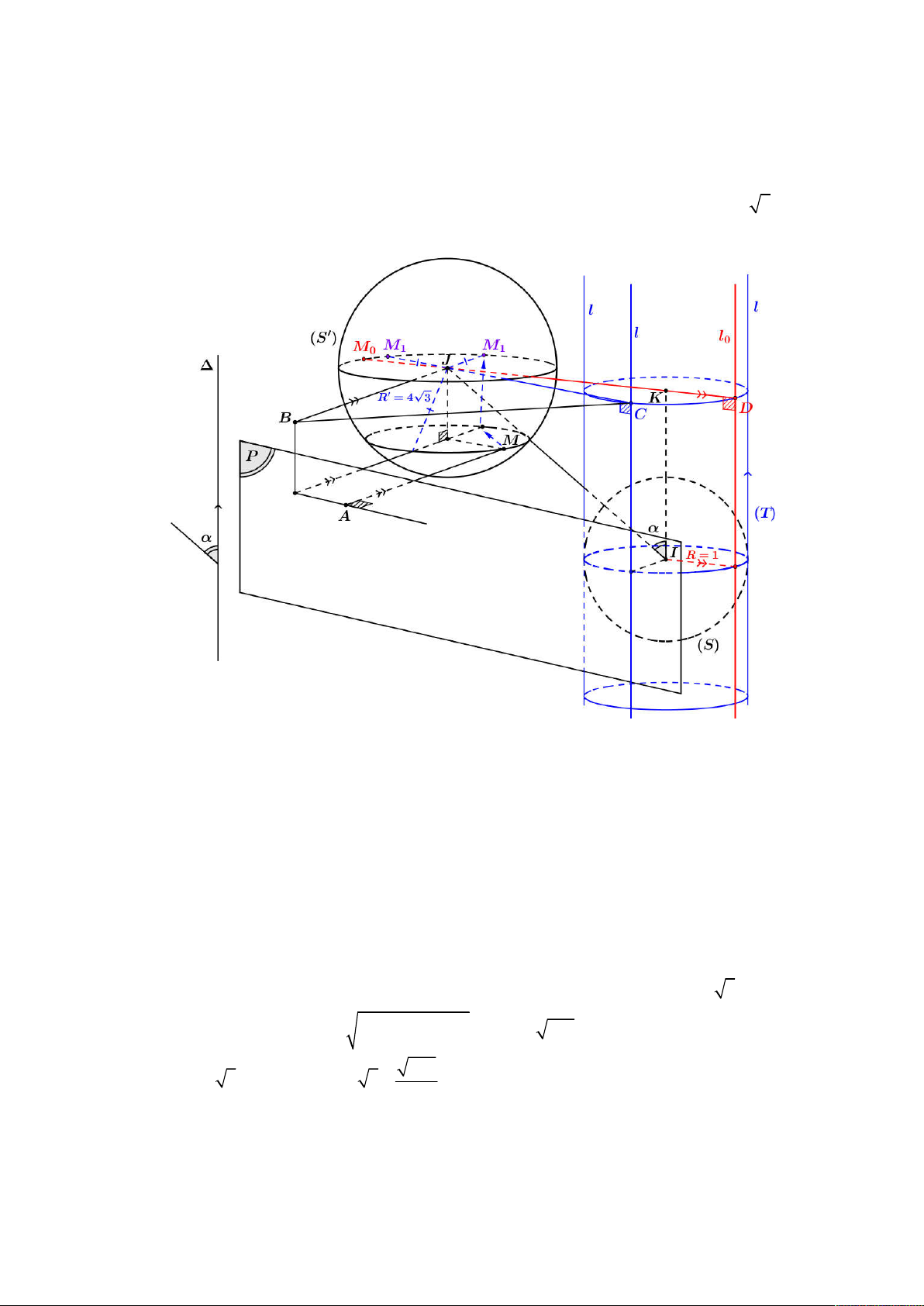
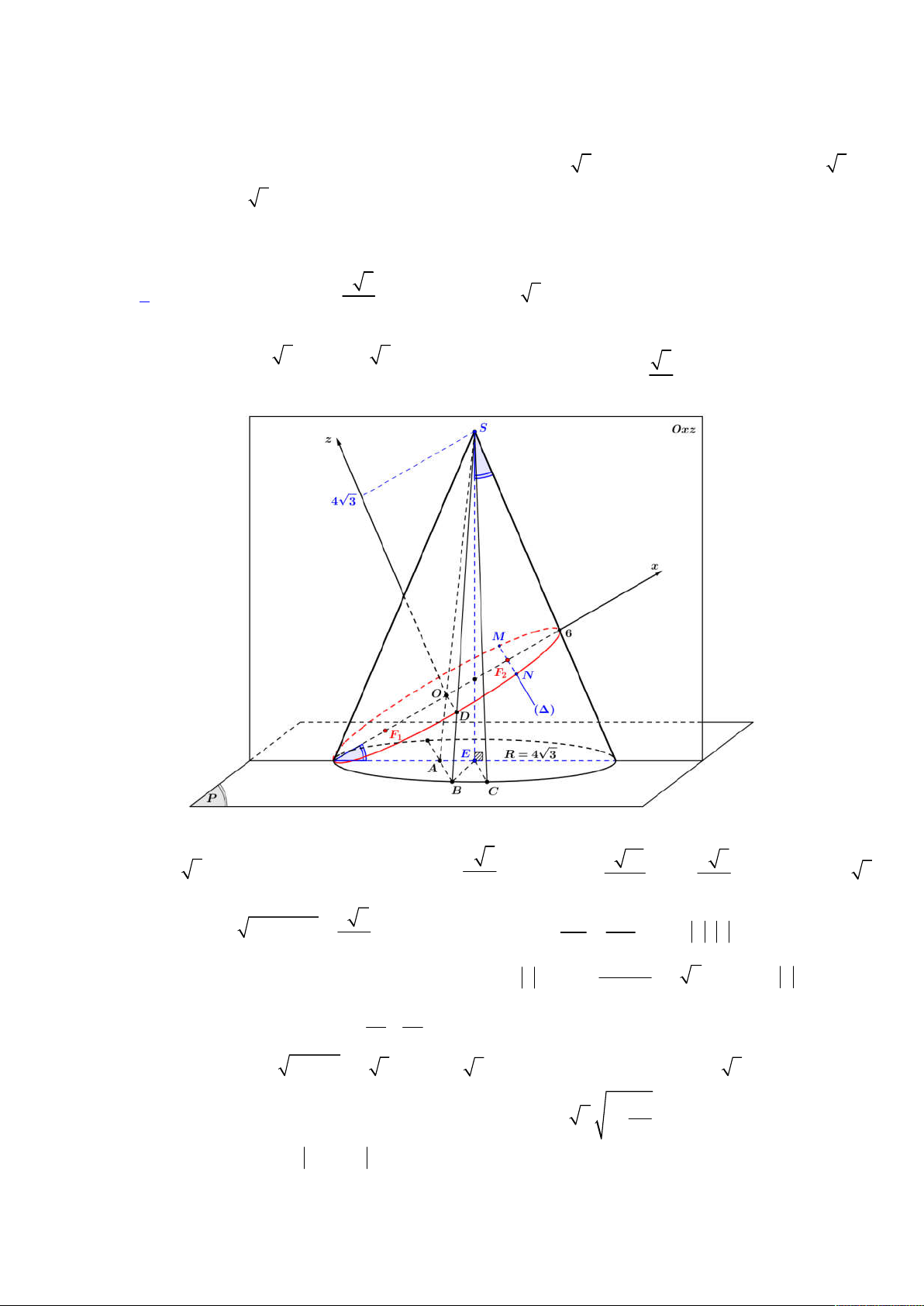
Câu 47: Trong không gian Oxyz , cho hình nón  N  có đỉnh S 6;0;4 3 đáy là hình tròn tâm E 0;0;2 3 và
bán kính R  4 3 . Mặt phẳng Oxy cắt mặt nón theo giao tuyến là đường elip tâm O và có tiêu điểm
F , F trên trục Ox , đường thẳng  đi qua F ( F có hoành độ dương) và song song với trục Oy cắt 1 2 2 2
mặt nón tại hai điểm M , N . Độ dài MN bằng 9 3 A. 8 . B. . C. 6 3 . D. 10 . 2 Lời giải  ES      
6;0;6 3  m1;0; 3 3   ES Oxy   ;  60 Cách 1: Ta có:   
và sin ES;Oxy  
 sinES;k      
SE  12, k  n  2    30 Oxy 0;0;  1    
Đầu tiên ta viết được phương trình mặt phẳng  P  qua E và vuông góc với SE và gọi A  SO   P  4 3  8 21 4 3
Suy ra:  P : x  3z  6  0 và giải ra tọa độ A 2  ;0;    , suy ra SA  , AE 
, mà BE  R  4 3 3    3 3 8 6 SO OD nên khi ấy suy ra: 2 2 AB  R  AE 
, theo định lí Thales ta có: 
và gọi a , b lần lượt là các độ 3 SA AB SO.AB
dài bán trục lớn, trục bé của elip thiết diện trên, khi ấy ta suy ra: b  OD 
 2 6 , cùng với a  6 SA 2 2 x y
Khi đó ta lập được phương trình elip  E : 
 1 , gọi F c; 0 , F c; 0 , c  0 lần lượt là tọa độ hai tiêu 1   2   36 24
điểm của  E  , ta luôn có: 2 2 c 
a  b  2 3 tức F 2 3; 0 kéo theo đó x  x  c  2 3 2   M N 0 2 c
Từ giả thiết ta suy ra tung độ của hai điểm M , N lần lượt là: 0 y  2  6. 1  4  M ,N 36
Vậy độ dài của đoạn thẳng MN  y  y
 8 . Chọn đáp án A. M N
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG Cách 2:
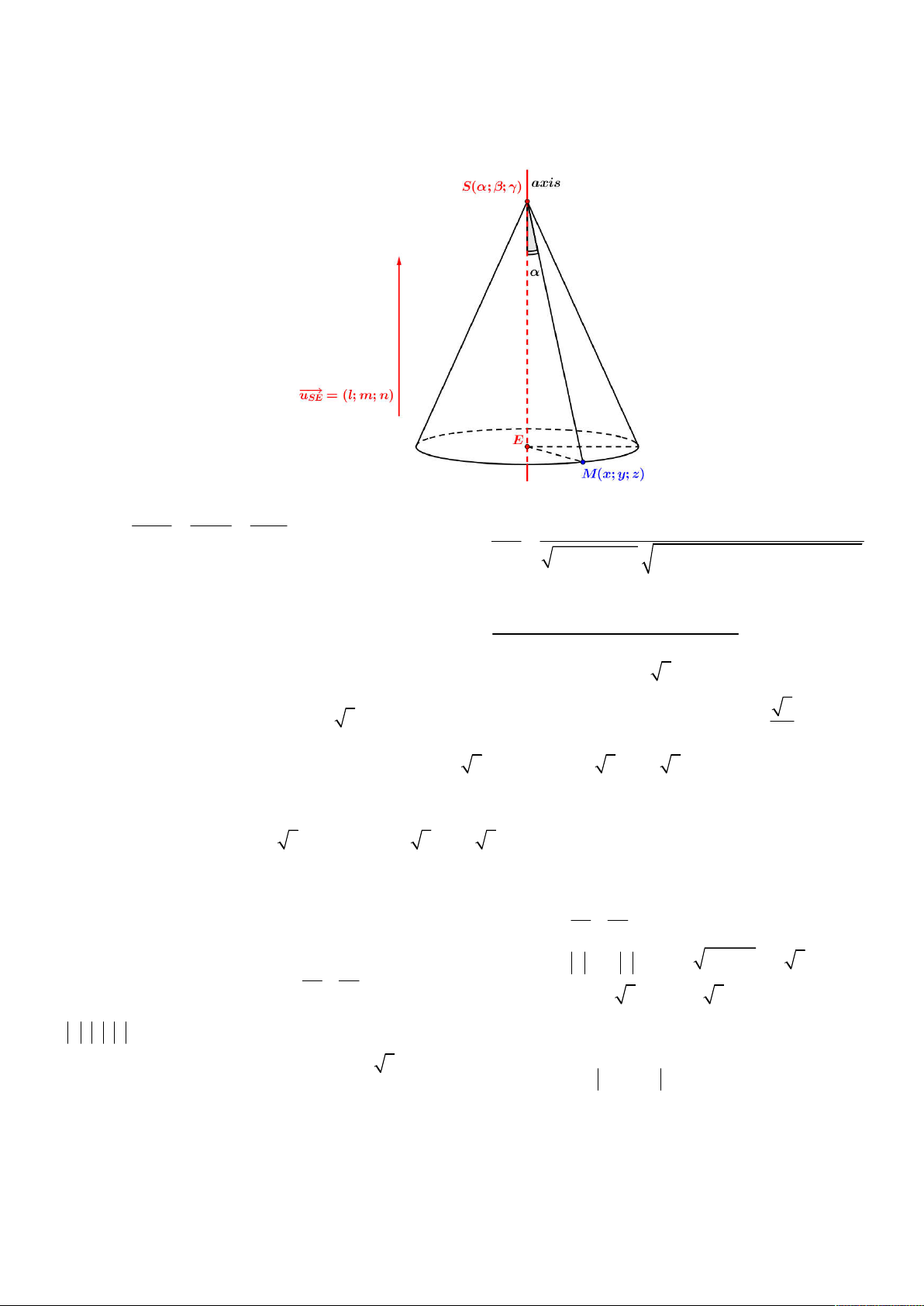
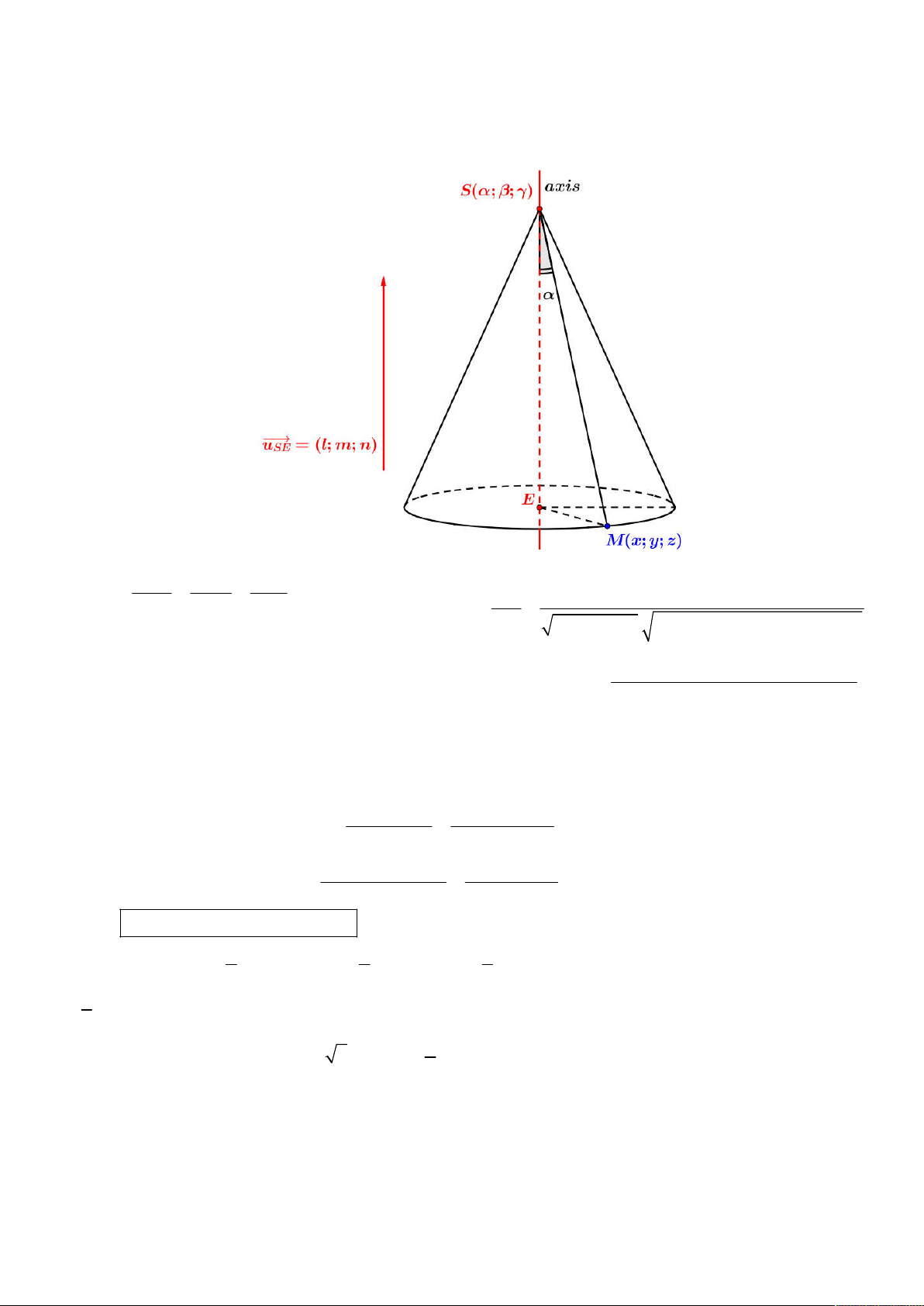
Từ hình vẽ trên, ta có:  x  y   z    SE   :    u  l m n SE  ; ;  SE
l  x    m y     n  z    l m n   cos    2 2 2 SM 2 2 2       
l  m  n . ; ;
 x     y      z SM x y z       
Vậy, phương trình tổng quát mặt nón là:
l x    m y    n z    2 2 2       2     x    y    z   2       cos   2 2 2  
l  m  n 
Áp dụng tính chất trên, ta giải bài toán này như sau: hình nón  N  có ES  k 1;0; 3 là vector chỉ phương chứa  3
trục của  N  , đỉnh có tọa độ S 6;0;4 3 và góc giữa đường sinh và trục bằng   30  cos  , suy ra: 2 2
Phương trình của mặt nón  N   x   2 2 : 3 6 y
z 4 3  x 6 3z 4 3 2          
Gọi  E  là mặt elip thiết diện của mặt phẳng Oxy  : z  0 khi cắt mặt nón  N  , khi ấy ta suy ra: 2 2 3   x 6 y z  x z          E :  2 2
 4 3   6 3 4 3     
 3 x  62  y  48   x 182 2 z  0  2 2 x y 2  x  x    2 y   2 2 2 2 3 36 108 3
48  x  36x  18  2x  3 y  72    1 36 24 2 2  2 2 x y
a  6, b  3, c  a  b  2 3 
Khi ấy suy ra phương trình:  E  : 
 1, kéo theo đó ta cũng có:  với 36 24 F 2  3;0 , F 2 3;0 1   2   
a , b , c lần lượt là các độ dài bán trục lớn, bán trục bé và bán tiêu cự của  E   x  x  2 3
Từ đó theo giả thiết ta suy ra: M N 
tức ta kết luận được MN  y  y
 8 . Chọn đáp án A. M N y  4  M ,N 
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 48: Cho hai hàm đa thức bậc bốn    4 3 2 y
f x  ax  bx  cx  dx  e ,    4 3 2 y g x  a x   b x   c x   d x   e 3
và có a  a   . Biết rằng đồ thị của hai hàm số này cắt nhau tại đúng 3 điểm có hoành độ lần lượt là 5 2
 ;1; 2 và diện tích hình phẳng  H  giới hạn bởi đồ thị của hai hàm số (phần gạcn sọc như hình vẽ) là
96 . Khi hình H  quay xung quanh trục Ox , khối tròn xoay tạo thành có thể tích gần nhất với số nào ? 25 A. 21, 26 . B. 1748, 58 . C. 177,17 . D. 66, 79 . Lời giải   f  x 4  3  x a  ... 
f  x  g  x  2a     x  2 1   2 x  4    5
Trước hết từ giả thiết ta suy ra:    3     g   x 4   a x  ... 3     5 f 
 x  g  x    x  2 1   2 x  4   5  1 2 a   3  2 96 3 1 5 3
Suy ra: S  2a   x   1   2
x  4 dx   2a    
do f 0  g 0 1 nên a   5 5 2 5 5 2 5 2 a    5 1
Từ đó ta suy ra: f  x  g  x    x  2 1  2 x  4 5 2 2 2 2 3 4 Vậy 2 V   f  x 2
 g  x dx   
  f x  g x f x  g x dx   x   1   2
x  4 dx  66,791 25 2  2  2  Chọn đáp án D.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
ĐỀ THI THỬ SỞ HẢI DƯƠNG
Câu 41: Cho hai số phức z, w thỏa mãn z  2w  3, 2z  3w  5 và z  3w  4 . Khi đó tính giá trị của biểu thức
P  zw  zw ? A. 4 . B. 3 . C. 1 . D. 2 . Lời giải 2 2
4 z  9 w  6zw zw  25 2   z  1   2 2  2
Từ giả thiết ta suy ra:  z  9 w  3 zw  zw 16 , giải hệ thu được:  w 1 . Chọn đáp án D.   2 2
 z  4 w  2 zw  zw  9 zw  zw  2   
Câu 42: Cho hai hàm số f  x và g  x liên tục trên  và hàm số   3 2 f
x  ax  bx  cx  d và   2
g x  mx  nx  p có đồ thị như hình vẽ. Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
y  f   x và y  g x bằng 10 và f 2  g 2 . Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm a
số y  f  x và y  g  x bằng (với a,b   và ,
a b nguyên tố cùng nhau). Tính a  b ? b A. 20 . B. 18 . C. 19 . D. 13 . Lời giải
Từ hình vẽ, ta suy ra: f  x  g x  ax  x   1  x  2
Do diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y  f   x và y  g x bằng 10 nên khi đó ta suy ra: 2 2 S 
f  x  g x dx  10  a x  x  
1  x  2 dx  10  a  20  
tức f  x  g x  20x  x   1  x  2 0 0 h
 2  f 2  g  2  0
Đặt h  x  f  x  g  x thì khi đó ta suy ra:  h
  x  f  x  g x  20x  x   1  x  2 
Suy ra: h x 
x x   x   4 3 2 20 1
2 dx  5x  20x  20x  C 
mà h 2  0 nên C  0 2 2 16
Suy ra diện tích cần tìm bằng: S  h  x 4 3 2 dx 
5x  20x  20x dx   
tức a  b  13 . Chọn đáp án D. 3 0 0
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Câu 49: Giả sử z , z là hai trong các số phức z thỏa mãn z 1  i  2 và z  z  z  z . Khi biểu thức 1 2 1 2 1 2
P  z  2z đạt giá trị nhỏ nhất thì số phức z có tích phần thực và phần ảo bằng 1 2 1 3 9 3 A. . B.  . C.  . D. 0 . 2 8 2 Lời giải
Từ giả thiết ta gọi A z , B z với hai điểm ,
A B thuộc đường tròn C  tâm I 1;   1 , bán kính R  2 1   2 
Tiếp đến ta có z  z  z  z tức OA  OB  AB nên suy ra , O ,
A B thẳng hàng tức O nằm giữa AB 1 2 1 2   2 Suy ra: 2 2
P  z  2z
 OA  4OB  2O .
AOB , do O nằm giữa AB nên áp dụng bất đẳng thức Cauchy, ta suy ra: 1 2 2
P  z  2z
 OA  2OB2 2 2  4O . AOB  4O . AOB  4O . AOB  8O . AOB 1 2
Cát tuyến qua O cắt đường tròn tại hai điểm ,
A B , khi ấy sử dụng phương tích đường tròn, ta luôn có:   2 2 O . AOB  O  .
AOB  OI  R  2
 tức P  8O .
A OB  4 (luôn đúng với O nằm trong và ngoài đoạn AB ).
Khi ấy dấu bằng xảy ra khi và chỉ khi OA  2OB mà O .
A OB  2 nên OA  2, OB  1 tức z  2 1 2 2 2
 z  a  b  4     a  b2 1  2ab  4 3
Gọi z  a  bi thì khi đó:     ab   . Chọn đáp án C. 1 2
 z 1 i  a  2 1  b  2 1  4 a  b  1  2  
Câu 50: Trong không gian với hệ tọa độ Oxyz , cho hình nón  N  có đỉnh O 0;0;0 , có độ dài đường sinh là 4 2
và đường tròn đáy nằm trên mặt phẳng  P : x  2 y  2z 12  0 . Gọi C là giao tuyến của mặt xung
quanh  N  với mặt phẳng Q : x  z  4  0 và M là một điểm di động trên đường cong C . Giá trị
nhỏ nhất của độ dài đoạn thẳng OM thuộc khoảng nào dưới đây ?  5   5   3   7  A. ;3   . B. 2;   . C. ; 2   . D. 3;   .  2   2   2   2  Lời giải
Cách 1: Từ giả thiết, ta gọi d  là đường thẳng qua O chứa đường cao h của hình nón  N  và  là góc giữa 
đường cao và đường sinh của  N  , khi ấy suy ra h  d  ;
O  P  4,u  1; 2
 ;2 và   45 , ta có hình vẽ sau: d   
Từ hình vẽ, ta suy ra quỹ tích của điểm M là một đường conic (một parabol) gọi là đường cong C 
Khi ấy ta đánh giá được OM nhỏ nhất khi và chỉ khi M  M 0 Dễ thấy O
 HC và thiết diện của mặt phẳng qua trục đều là các tam giác vuông cân lần lượt tại H và O nên suy ra OH  5 
HM  OC , khi ấy ta dễ dàng suy ra OM   2 2 tức OM  2 2  2,83
;3 . Chọn đáp án A. 0 0 min   2  2 
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
Cách 2: (Sử dụng cho mặt phẳng bất kì cắt mặt nón và không có yếu tố đặc biệt)
Từ hình vẽ trên, ta có:  x  y   z    SE   :    u  l m n SE  ; ;  SE
l  x    m y     n  z    l m n   cos    2 2 2 SM 2 2 2       
l  m  n . ; ;
 x     y      z SM x y z       
l x    m y    n z    2 2 2       2
Phương trình tổng quát mặt nón là:     x    y    z   2       cos   2 2 2  
l  m  n
Áp dụng tính chất trên, ta giải bài toán này như sau: gọi d  là đường thẳng qua O chứa đường cao h của hình 
nón  N  và  là góc giữa đường cao và đường sinh của  N  , khi ấy suy ra h  d  ;
O  P  4,u  1; 2  ;2 và d      45
x  y  z
 x  y  z2 2 2 2 2 2
Suy ra tập hợp điểm M  ;
x y; z   N  : 
, mặt khác M  Q : x  z  4  0 nên suy ra 2 9
x  y   x  42
 x  2y  82 2 2
M C   N   Q  M C  2 2 : 
 16x  40x  8xy  y  64 y 16  0 2 9 Suy ra: 2 2
8xy  16x  40x  y  64 y  6
1 , kéo theo đó ta phân tích được: 2 2 1
OM  x  y  z 
 x  2 y  2z2   x  2 y  82 2 2 2 2   2 2
2x  8 y  32x  64 y  8xy  128 9 9 9 1   2 2
2x  8 y  32x  64 y  16x  40x  y  64 y 16  128 2
 2x  y  8x  16  2  x  22 2 2 2 2  y  8  8 9  5 
Vậy giá trị nhỏ nhất của OM bằng 2 2  2,83 ;3 
 với dấu bằng xảy ra khi và chỉ khi x  2
 , y  0 , thế vào  2 
phương trình C ta thu được z  2 , tức min xảy ra khi M  M 2; 0; 2 trùng với đỉnh của parabol C 0   Chọn đáp án A.
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG
ĐỀ THI THỬ THPT CHUYÊN HÙNG VƯƠNG – PHÚ THỌ
Câu 42: Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z  50 và hai mặt phẳng  P : x  y  2z 15  0 ,
Q : x  y  4 3z  25  0. Hai điểm M , N thay đổi lần lượt thuộc các đường tròn là giao tuyến của
P,Q với S  , giá trị nhỏ nhất của MN bằng bao nhiêu ? A. 5 . B. 2 10 . C. 2 5 . D. 10 . Lời giải
Dễ thấy khi đọc 4 đáp án A,B,C,D các kết quả đều là số dương, chứng tỏ rằng hai đường tròn giao tuyến mà đề bài
nêu trên không cắt nhau (vì nếu cắt nhau thì giá trị nhỏ nhất của MN bằng không).
Trước hết ta có mặt cầu S  có tâm trùng với gốc tọa độ, bán kính R  5 2 .
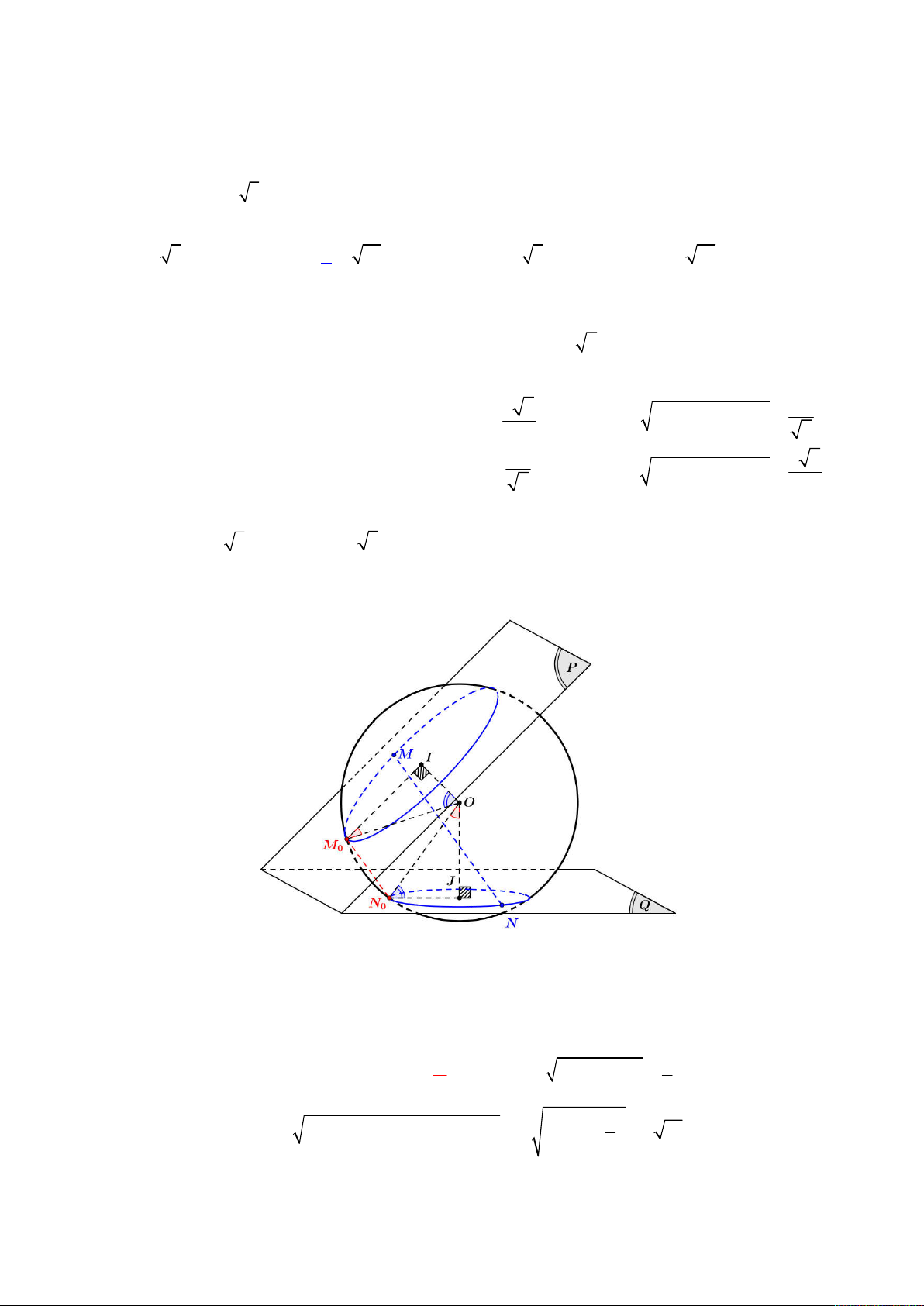
Giả sử hai đường tròn thiết diện của khi hai mặt phẳng  P,Q cắt S  là C , C có tâm lần lượt là I , J và 1   2    5  5 6   2 2 a  MI  R  d  ; ; O  P d O P OI        2  2 bán kính lần lượt là ,
a b . Khi đó ta suy ra:    d  5 ; O Q 5 6  2 2  OJ  b  NJ  R  d  ; O Q   2    2 
 P : x  y  2z 15  0
2z  15  x  y  0   O O Lại có:   
nên O bị kẹp giữa hai mặt phẳng  P,Q . Q 
 : x  y  4 3z  25  0
4 3z  x  y  25  0   O O
Khi đó ta dễ dàng đánh giá được MN đạt giá trị nhỏ nhất ( MN  M N ) khi và chỉ khi đoạn thẳng MN đồng 0 0
phẳng với mặt phẳng OIJ  như hình vẽ dưới đây:   OI  JN IOM  IN J  Tới đây ta có: 0 0 0        
 IOM  JON  IOM  OM I  90 OJ  IM   0 0 0 0  0 JON  OM I  0 0   2 2 2
OI  OJ  IJ 4 cos IOJ      2OI.OJ 5
Khi ấy ta lần lượt suy ra:         3 2 
cos M ON  cos IOJ 
 sin IOJ  1 cos IOJ  0 0      2  5  3  Vậy ta suy ra: 2 2  MN  M N  R  R  2 . R .
R cos M ON  R 2  2. 
 2 10 . Chọn đáp án B. min 0 0 0 0    5 
NGƯỜI BIÊN SOẠN: TRẦN MINH QUANG

Hướng dẫn giải toán VDC trong các đề thi thử TN THPT 2024 môn Toán

Tài liệu liên quan:

Đề thi học kì 1 Toán 12 Kết nối tri thức - Đề số 4

Đề thi học kì 1 Toán 12 Kết nối tri thức - Đề số 3

Đề thi thử TN THPT 2026 môn Toán đợt 1 liên trường THPT – Nghệ An

Đề thi thử TN THPT 2026 lần 1 môn Toán trường THPT Than Uyên – Lai Châu

Đề kiểm tra Toán 12 tháng 11 năm 2025 trường Nguyễn Khuyến & Lê Thánh Tông – TP HCM (3)